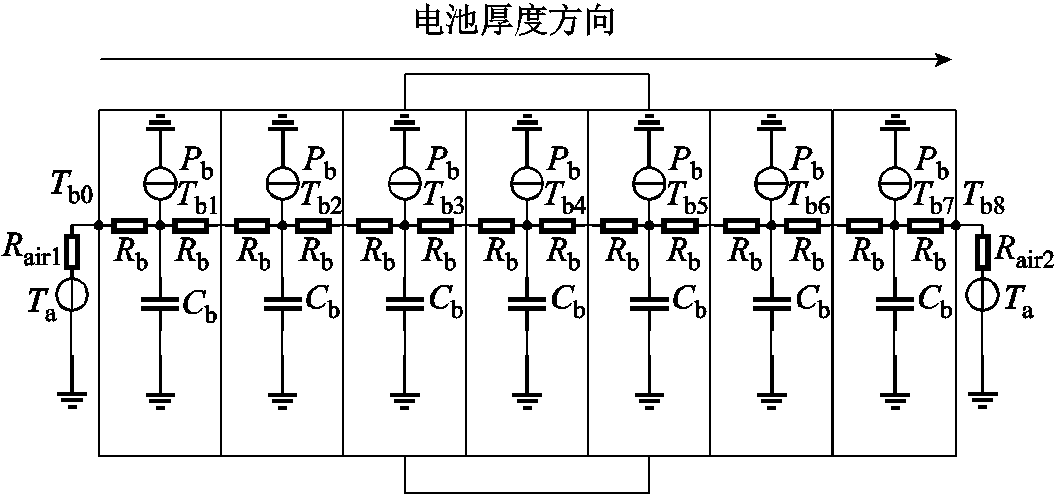
图1 锂离子电池等效热路模型
Fig.1 Equivalent thermal circuit model of lithium-ion battery
摘要 锂离子电池热学模型参数（热容和热阻）的准确辨识对电池热电耦合建模及状态参数估计至关重要。然而传统测量方法成本高且测试周期长，如何利用充放电工况结合产热和传热机理研究快速热参数辨识方法具有重要意义。以8 A×h软包锂离子电池为研究对象，建立分布式热路模型；设计双向脉冲工况实验，采用自适应粒子群算法（APSO）进行辨识；同时采用其他工况进行验证，实验和仿真温度误差小于0.1℃。另外，将热容和热阻转换为比热容和导热系数，并与其他文献中同类电池的参数进行比对，量级接近。研究结果表明，该方法可以有效解决层叠式软包锂离子电池热学模型参数辨识难的问题，且简便易行、成本低。
关键词：层叠式软包 锂离子电池 分布式热路模型 热容和热阻 自产热和外传热
随着我国电动汽车的快速发展，与电动汽车相关的新能源技术及设备也受到重视。锂离子电池因具有自放电率低、能量密度高、寿命长等优点而被广泛应用于电动汽车领域[1-4]。为了建立准确的锂离子电池外电压模型，进而对状态参数进行准确估计，通常要将热模型耦合到电模型中。常用的热模型有集总参数热模型[5-6]、有限元分析热模型[7-8]、偏微分方程热模型[9]等。电池的热学模型参数（热容和热阻）[10-11]的准确性，会直接影响到热模型的精度，不同数量级的热参数差异将会导致电池温度预测出现较大的差异[12]。锂离子电池的热模型参数与热物性参数（比热容和导热系数）[3]存在确定的换算公式[13]，因此这两组参数具有等价关系，对热模型参数的研究可参考热物性参数的研究方法。
针对锂离子电池准确的比热容测量方法，主要借助绝热加速量热仪（Accelerating Rate Calorimeter, ARC）等设备，J. Vertiz等[14]采用ARC测量14 A×h的磷酸铁锂软包锂离子电池在不同条件下的比热容，研究发现不同荷电状态（State of Charge, SOC）点、不同老化状态的电池比热容变化小于1%。对于电池导热系数的测量，S. J. Bazinski等[15]采用热流量仪法结合参数辨识方法获取磷酸铁锂软包锂离子电池的导热系数为0.35 W/(m·K)。这些方法能够准确地测量电池的比热容和导热系数，但是需要使用昂贵的测试设备。在不借助昂贵的测试设备时，J. Zhang等[16]采用耦合实验和计算的方法同时获得大尺寸层叠电池的比热容为1 243 J/(kg·℃)、导热系数为0.48 W/(m·K)，通过对比ARC测量的比热容与算法估算值，结果吻合较好。阮海军[13]将三元软包锂离子电池沿厚度方向进行等分处理，建立分布式热学等效电路模型，通过在两个电池中间贴加热膜，对加热膜施加电流，采用模型仿真法[17-18]辨识电池热学模型参数，实验验证最大仿真误差为3.3℃，但是需要借助加热膜，增加热模型建模复杂度。王帅林等[18]基于准稳态导热原理，将两个加热膜贴在两个电池两端进行加热，并做绝热处理，结果表明热量损失标定对测量方法极其重要，但是并未考虑大型软包锂离子电池不同位置的热量损失可能存在差异。
综上所述，准确的电池比热容和导热系数测量需要借助昂贵的测试设备，成本较高且测试时间较长。采用优化算法辨识热学模型参数不仅成本低，且计算周期短。本文在分布式热学等效电路模型[13]的基础上，综合考虑电池自产热和外传热机理，设计参数辨识实验，进行模型公式推导；采用自适应粒子群优化（Adaptive Particle Swarm Optimization, APSO）算法来辨识锂离子电池热学模型参数（热容和热阻），并将辨识的参数转化为比热容和导热系数与相关文献进行对比分析；最后将辨识的参数代入模型，并采用与参数辨识实验不同的策略进行仿真分析。
在热模型选取方面，针对层叠式软包锂离子电池，简单的一维模型无法体现电池厚度方向的温度梯度，且电池在传热过程中热面和冷面存在温度梯度，因此考虑使用分布式热学等效电路模型。可以将软包电池沿厚度方向进行等分处理，分层次数过多会使模型求解计算量增加，因此考虑等分为7份，则锂离子电池等效热路模型如图1所示，等分后的电池每一部分有相同的热阻和热容。为此，做出以下假设：①电池内部的产热是均匀分布的；②将电池等分后，在同一厚度上，电池温度均匀分布；③由于电池等分处理后，厚度变薄，电池与环境仅考虑最大表面与环境的热交换[16]；④电池内部仅考虑沿电池厚度方向上的热传导[5]。
图1 锂离子电池等效热路模型
Fig.1 Equivalent thermal circuit model of lithium-ion battery
对于电池等分的每一部分，都可以看作是集总热模型。其中，Rb为电池传热热阻、Cb为电池热容、Pb为产热功率、Tbi(i=1,…,7)为电池内部温度；Tb0、Tb8为电池表面温度；Rair1、Rair2为电池最大表面与环境的交换热阻；Ta为环境温度。
电池的热容为电池的质量与比热容的乘积，由于电池的比热容具有质量可加性[3]，对应电池的热容也应有质量可加性。
（1）
式中，m为电池的质量；c为电池的比热容。
电池的导热系数可以由各组件的参数计算得到[3]，本文仅考虑电池沿厚度方向的传热过程，对应导热系数计算公式为
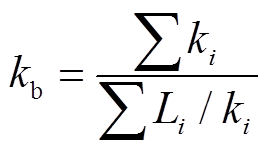（2）
式中，kb为电池的导热系数；ki为各组件的导热系数；Li为各组件的厚度。
则电池的传热热阻Rb与电池的导热系数的关系为
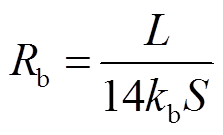（3）
式中，L为电池的厚度；S为电池最大表面面积。
当电池最大表面与空气接触时，就会与环境发生热交换，对应的散热热阻与空气对流有关。
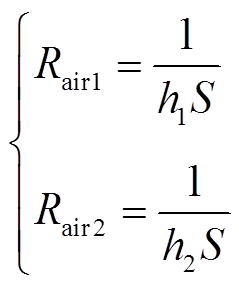（4）
其中，h1和h2为电池最大表面与空气的表面传热系数。
锂离子电池产热包括可逆热和不可逆热[13]。电池由于自身充电或放电，从而产生产热功率。电池产热使电池内部温度升高，电池最大表面与空气形成对流散热，使电池内部出现温差。
将电池热路模型中的参数等效为电路中的参数，热容和热阻等效为电容和电阻、电池温度等效为电压、环境温度等效为恒压源、产热功率等效为恒流源，由基尔霍夫电路定律，对电池各个温度点列写节点电压方程，则电池热学模型可表示为
（5）
式中，I为电池充放电电流；UOCV为电池开路电压。
式（5）中产热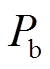
部分第一项为不可逆热；第二部分为可逆热，且可逆热占比较小。对于交流工况，一个周期内，可逆热几乎为0，因此仅考虑不可逆热[13]。则产热计算公式为
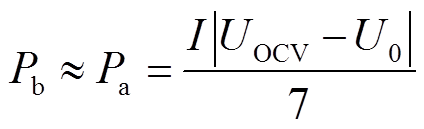（6）
式中，
为电池端电压。
以商用8 A×h软包三元锂离子电池为研究对象，其基本参数见表1。
表1 实验用电池基本参数
Tab.1 Basic parameters of experimental battery
项目性能指标 标称电压/V3.6 额定容量/(A·h)8 充放电截止电压/V2.75～4.2 电池重量/g300 电池尺寸/(mm´mm´mm)142´115´8.5
实验用到的具体设备主要有电池测试设备（Arbin）、温度采集系统（日置HIOKI）、高低温箱、热电偶、计算机主机等，其关系如图2所示。温箱控制电池环境温度，计算机控制电池测试设备（Arbin）给电池充放电，通过温度数据记录仪采集温度数据，并上传至计算机进行记录和保存。
图2 参数辨识实验设备示意图
Fig.2 Schematic diagram of the experimental equipment for parameter identification
具体实验时，用高温绝缘胶带将热电偶贴在每块电池的最大表面中心处，每个表面贴两个热电偶，将采集的温度平均值作为该表面的温度（T1b8、T1b0、T2b8、T2b0）。用导热硅脂均匀涂抹在高温绝缘胶带上，将涂抹导热硅脂的两块相同规格的电池最大表面贴在一起，如图3a所示。电池侧面和最大表面用保温材料进行包裹，以减小热量散失，仅考虑最大表面热量传递，则电池与外界空气可用等效热阻表示。当一块电池进行充放电时，电池温度就会升高，另一块电池仅考虑传热过程，可以通过产热功率和热电偶采集的电池表面温度来辨识热学模型参数，如图3b所示。
图3 参数辨识实验设计图
Fig.3 Parameter identification experiment design diagram
参考单体电池的热路模型建模方法，对热学模型参数辨识系统进行建模，参数辨识热路模型如图4所示。
图4 参数辨识热学等效电路模型
Fig.4 Parameter identification thermal equivalent circuit model
类比基尔霍夫电路定律，列写参数辨识系统的求解方程组为
（7）
式中，T1b0、T1b8和T2b0、T2b8分别为电池1和电池2两个表面的温度，T1bi、T2bi为电池1、电池2沿厚度方向各部分的温度分布；Ra为电池与环境等效传热热阻；Ta为环境温度；P1bi为电池1各部分产热功率；P2bi为电池2各部分产热功率。
在进行参数辨识时，以对电池1进行充放电为例，电池2仅考虑热传递，电池1各部分产热功率相等，即
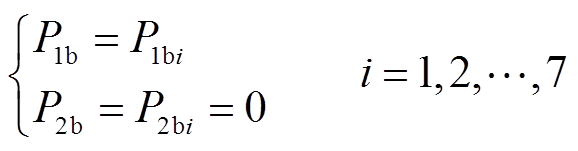（8）
以P1b和T1b0为已知量，通过式（7）采用离散时间处理方式推导T1b8和T2b0的温度。以温度T1b7为例，有
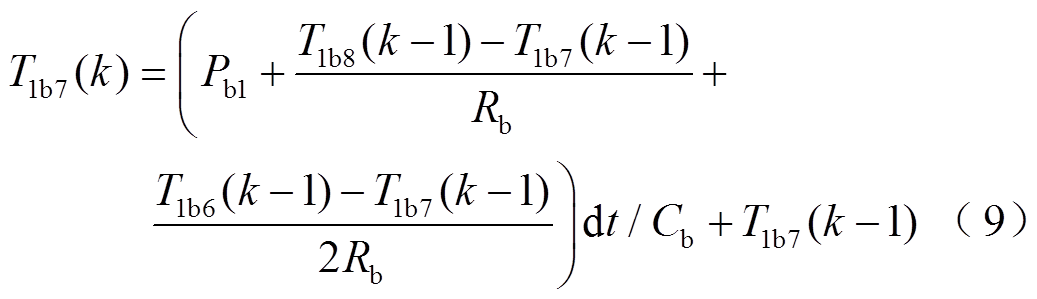
式中，k为离散时间步长，表示由前一时刻温度推导后一时刻温度的过程；dt为采样时间，本文设置采样时间为1s。
以实际测量的T1b8和T2b0和模型计算的
和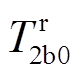
的差的二次方和最小为目标函数，并通过APSO算法来辨识热学模型参数，具体流程如图5所示，选取n个数据进行参数辨识，则目标函数为
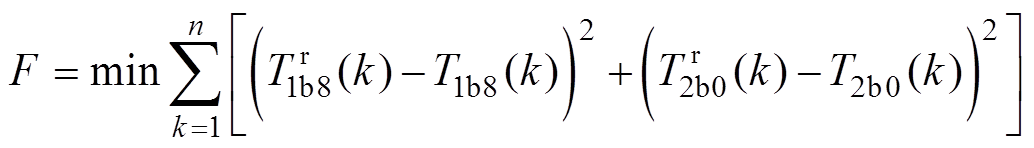（10）
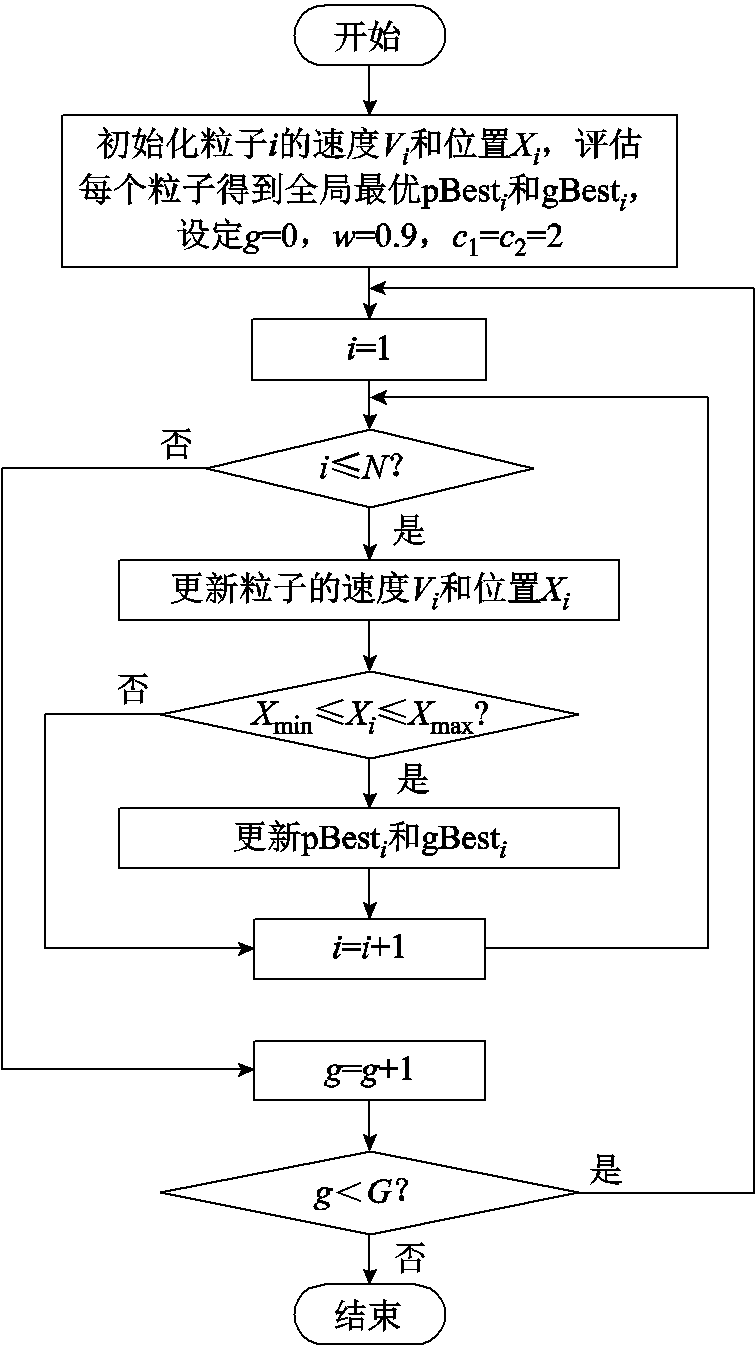
图5 APSO算法流程
Fig.5 APSO algorithm flow chart
为了排除电池SOC对实验的影响，首先将电池SOC调至50%左右，为了简化计算产热，保证SOC不发生太大变化，本文拟采用10 s脉冲充电和放电相结合的方法，使电池产热，且可以忽略电池可逆熵变热[13]。由于低温环境下，对锂离子电池充电容易发生析锂，且会带来不可逆的损伤[13,19]，因此考虑0℃以上温度点的选取；电池的阻抗随温度升高而减小，对于相同的加热功率，高温就需要更大的电流，因此温度选取不应太高，本文温度选择0℃、10℃、20℃进行参数辨识。由于电池的阻抗随温度变化呈非线性关系，即无法保证对应温度下产热功率的一致性，因此对于不同温度点选取，应适当改变电流激励的大小。本文以温箱设置温度0℃、10℃、20℃为例（实际电池温度存在2℃的偏差），对应电流设置为10 A、15 A、20 A，开展锂离子电池热学模型参数辨识研究。
当温箱设置温度为0℃时，对电池1施加10 A的脉冲充放电电流300 s，则电池1的电压、电流如图6a所示，温度、电池总产热功率如图6b所示。当温箱设置温度为10℃时，对电池1施加15A的脉冲充放电电流300 s，则电池1的电压、电流如图7a所示，温度、电池总产热功率数据如图7b所示。当温箱设置温度为20 ℃时，对电池1施加20A的脉冲充放电电流300 s，则电池1的电压、电流如图8a所示，温度、电池总产热功率数据如图8b所示。
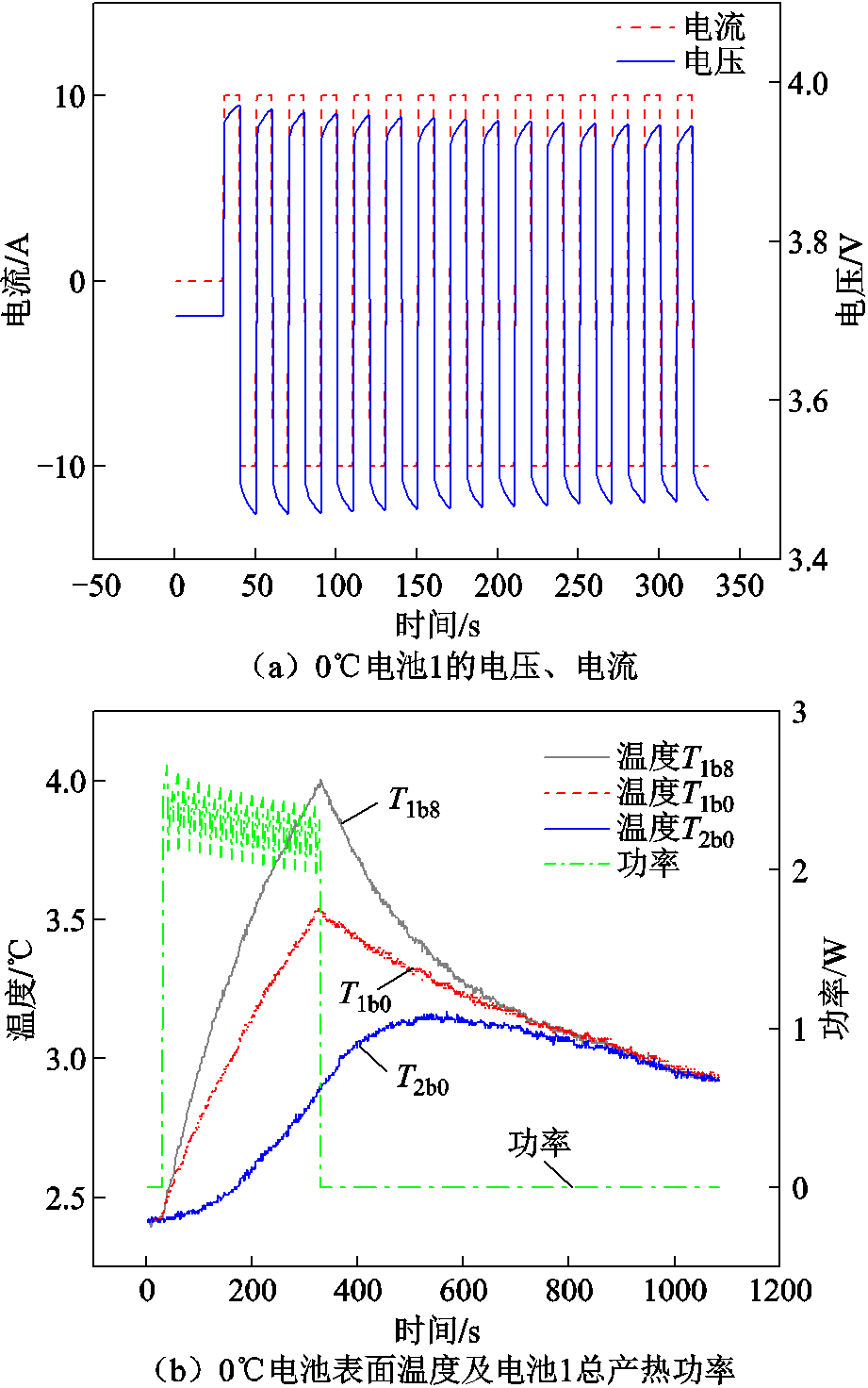
图6 0℃电池1电压、电流、总产热功率及电池表面温度
Fig.6 Voltage, current, total heat production and battery surface temperature of battery 1 at 0℃
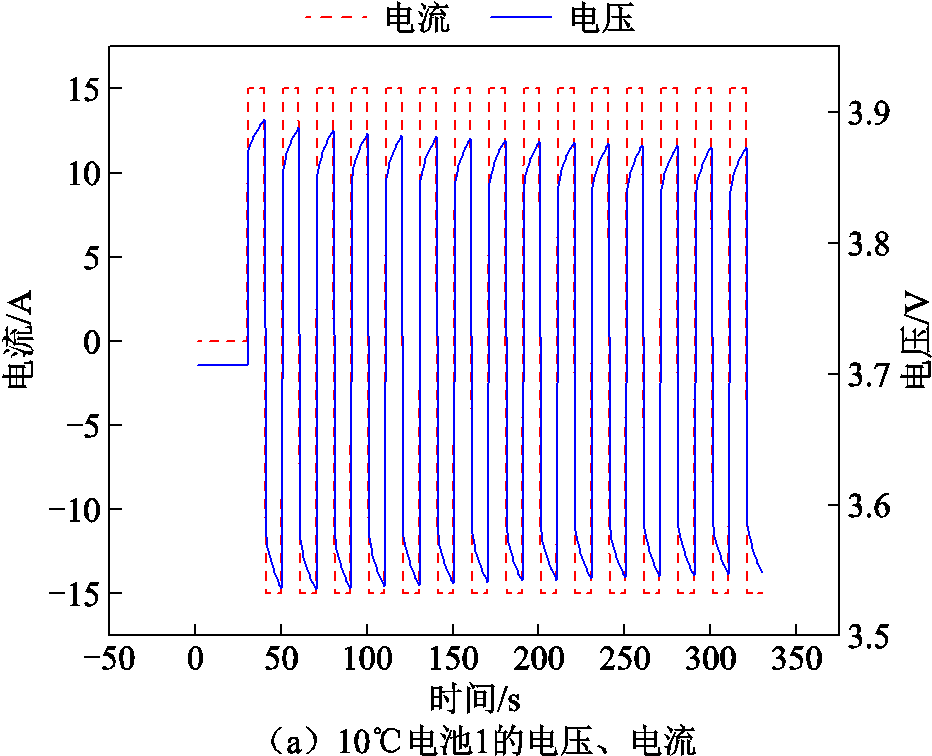
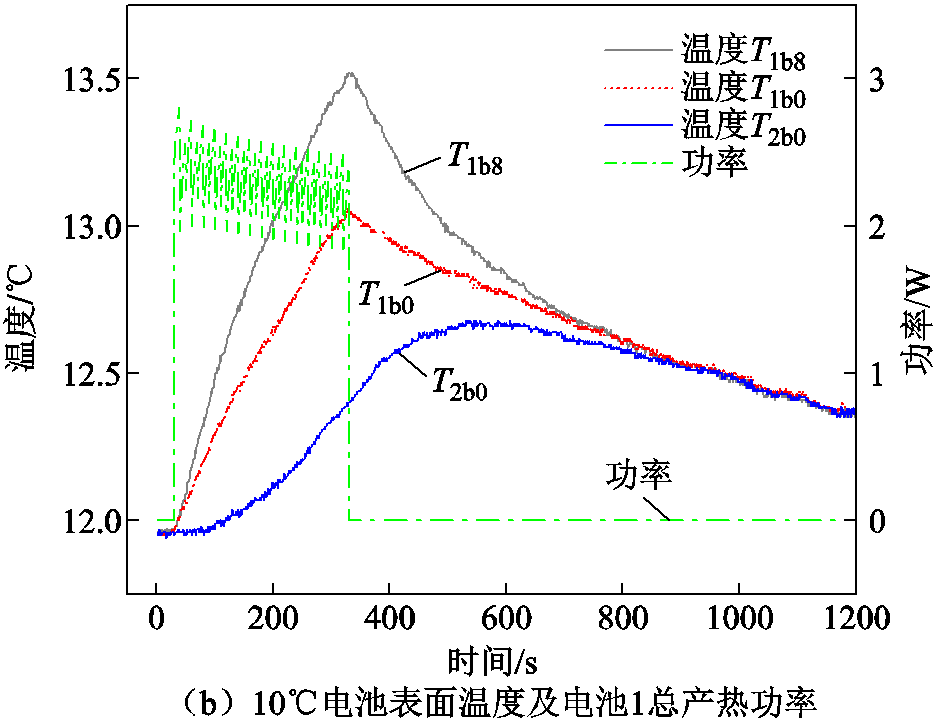
图7 10℃电池1电压、电流、总产热功率及电池表面温度
Fig.7 Voltage, current, total heat production and battery surface temperature of battery 1 at 10℃
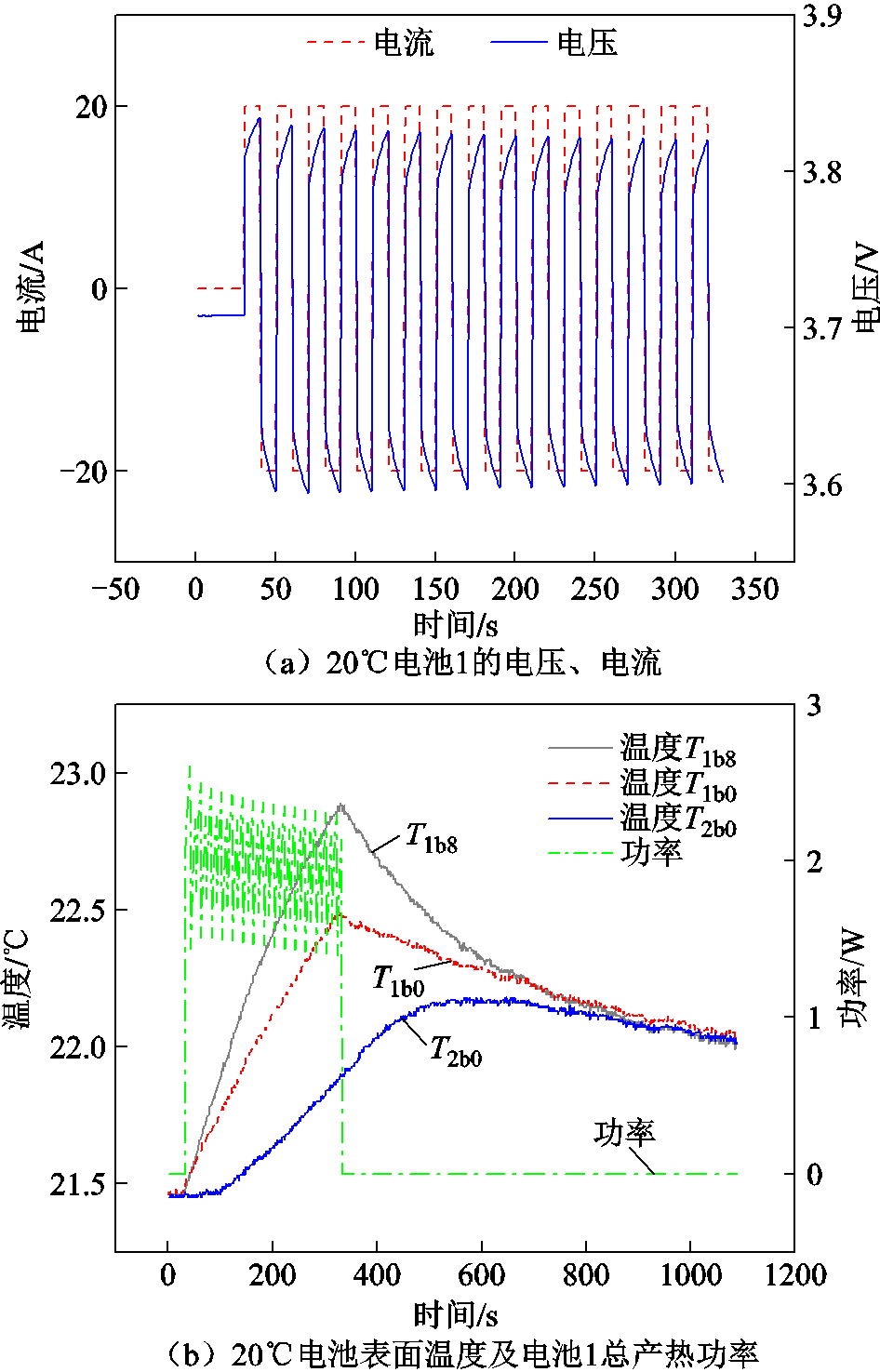
图8 20℃电池1电压、电流、总产热功率及电池表面温度
Fig.8 Voltage, current, total heat production and battery surface temperature of battery 1 at 20℃
从电池表面温度数据可以看出，给电池1通脉冲充放电电流时，电池1温度升高，由于温差，使电池2温度也逐渐升高。与电池2接触的表面温度T1b0低于与保温材料包裹的表面温度T1b8，这是由于保温材料的热阻大于电池传热热阻导致的；电池温度最高升高1.5℃，且在800 s之后电池1和电池2几乎没有温差，逐渐恢复至初始温度。
采用APSO算法进行热学模型参数辨识，将电池1总产热功率和电池1与电池2接触面温度T1b0作为已知量，式（10）为目标函数进行参数辨识，获取热容Cb、电池传热热阻Rb、电池和环境散热热阻Ra（主要为保温材料）。
表2 热学模型参数辨识结果
Tab.2 Thermal model parameter identification results
温度/℃热容Cb/(J/K)热阻Rb/(K/W)热阻Ra/(K/W) 041.660.0985.11 1043.510.099 55.63 2043.050.099 56.79
对于热学模型参数辨识的结果，电池表面与空气的等效散热热阻随温度的升高在逐渐增大，这是由于温度越低，温箱内的风速就越大，而热阻与表面传热系数成反比，则等效散热热阻就越小。
由于锂离子电池热学模型参数（热容和热阻）与电池热物性参数（比热容和导热系数）存在一定换算关系，且文献中大多是关于电池比热容和导热系数的测定，因此将热容和热阻变换为比热容和导热系数，见表3。
表3 电池比热容和导热系数
Tab.3 Specific heat capacity and thermal conductivity of batteries
温度/℃比热容c/[J/(g·K)]导热系数kb/[W/(m·K)] 00.9720.38 101.0150.374 201.0010.374
换算后可以看出，在0～20℃范围内，锂离子电池的导热系数与温度关系不大。比热容的平均值为0.996 J/(g·K)、导热系数平均值为0.377 W/(m·K)。
本文锂离子电池热物性参数与部分参考文献结果对比见表4。
表4 不同电池热物性参数
Tab.4 Thermal physical parameters of different batteries
文献材料比热容c/[J/(g·K)]导热系数kb/[W/(m·K)] 本文三元0.9960.377 文献[13]三元0.927 50.354 1
（续）
文献材料比热容c/[J/(g·K)]导热系数kb/[W/(m·K)] 文献[16]三元1.2430.48 文献[20]三元0.90.334 8 文献[14]磷酸铁锂1.1140.284 文献[15]磷酸铁锂1.390.35
对于锂离子电池的热物性参数，不同材料的电池表现出差异性，相同材料不同规格也表现出差异性，因此对于热学模型中的参数不能简单地从文献中获取。采用本文中提出的热学模型参数辨识方法，将辨识的热学模型参数换算为比热容和导热系数后，与文献中的进行对比，并未表现出较大的差异性。
为了验证热模型参数在0～20℃对温度的敏感性，将辨识的热模型参数的平均值波动±5%，对应输出结果见表5。
表5 热模型参数敏感性分析
Tab.5 Sensitivity analysis of thermal model parameters
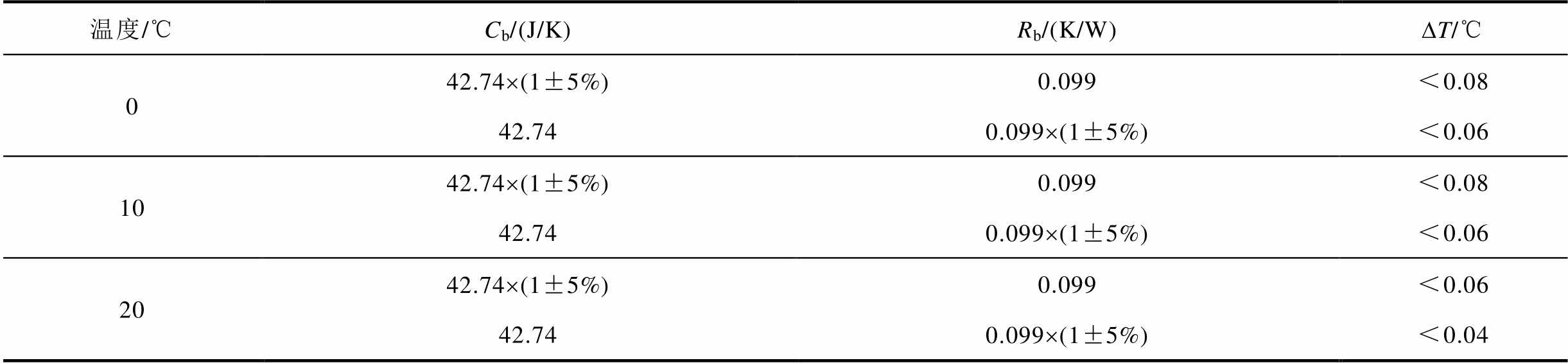
温度/℃Cb/(J/K)Rb/(K/W)DT/℃ 042.74´(1±5%)0.099＜0.08 42.740.099´(1±5%)＜0.06 1042.74´(1±5%)0.099＜0.08 42.740.099´(1±5%)＜0.06 2042.74´(1±5%)0.099＜0.06 42.740.099´(1±5%)＜0.04
由表5可以看出，当热模型参数改变±5%，模型仿真结果温度误差小于0.08℃。因此在0～20℃范围内，热模型参数对温度不敏感，所以下一节仿真验证部分的热模型参数均采用平均值。
为了验证该方法以及热学模型参数的准确性，本文考虑验证（20℃、15℃、10℃、5℃、0℃）多个温度点的仿真效果。针对不同温度点热阻Ra的选取，当温度为20℃、10℃、0℃时，热阻Ra采用表2参数辨识的结果；当温度为15℃和5℃时，热阻Ra采用插值的方法获取。实际温箱设置温度与电池实测温度存在一定偏差（2℃误差）。以20℃为例，设置温箱温度为20℃，实际测量为21.6℃。
将温箱温度调至20℃，改变脉冲充放电策略为以15A的电流脉冲充放570 s，电压和电流如图9a所示。将辨识的模型参数和电池产热功率代入模型进行计算，电池沿厚度方向的温度分布如图9b所示，则实测电池表面温度和仿真电池表面温度如图9c所示。
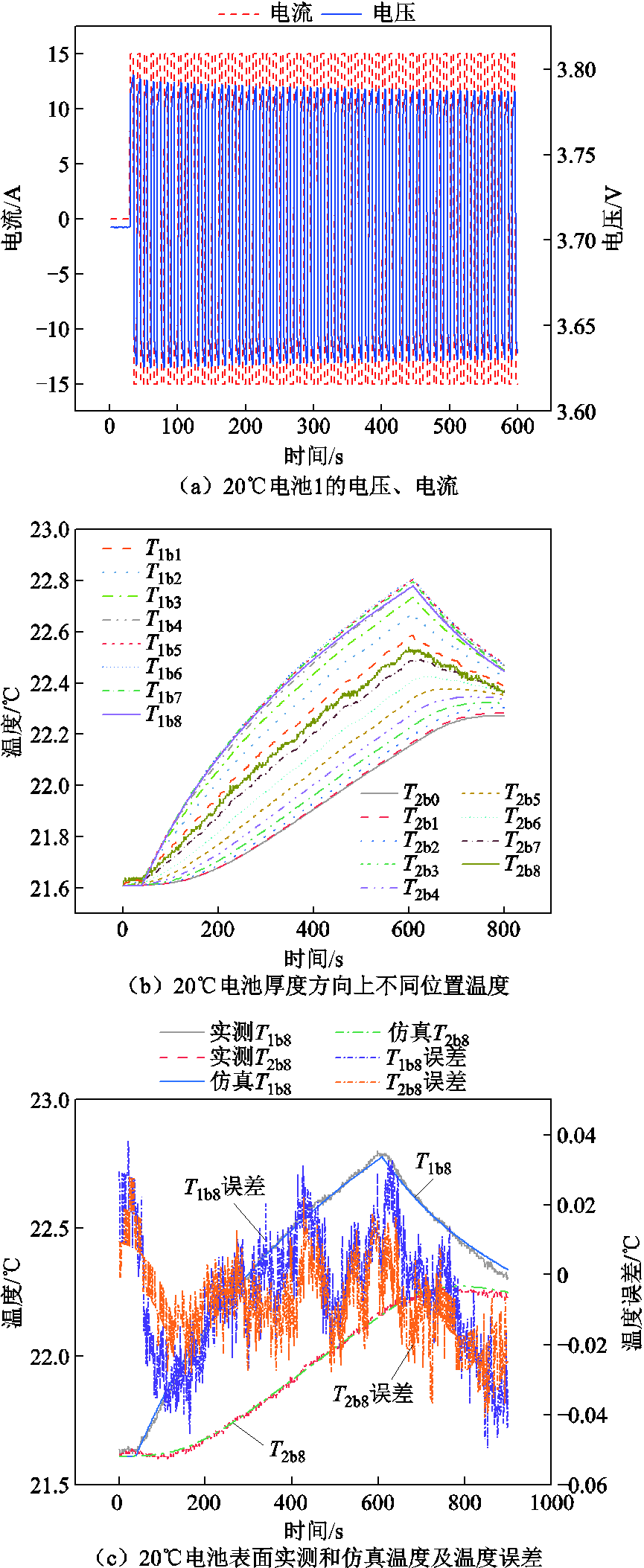
图9 20℃仿真结果
Fig.9 Simulation results at 20℃
将温箱温度调至15℃，改变脉冲充放电策略为以20 A的电流脉冲充放2 370 s，电压和电流如图10a所示。将辨识的模型参数和电池产热功率代入模型进行计算，电池沿厚度方向的温度分布如图10b所示，则实测电池表面温度和仿真电池表面温度如图10c所示。
将温箱温度调至10℃，改变脉冲充放电策略为以20A的电流脉冲充放870s，电压和电流如图11a所示。将辨识的模型参数和电池产热功率代入模型进行计算，电池沿厚度方向的温度分布如图11b所示，则实测电池表面温度和仿真电池表面温度如图11c所示。
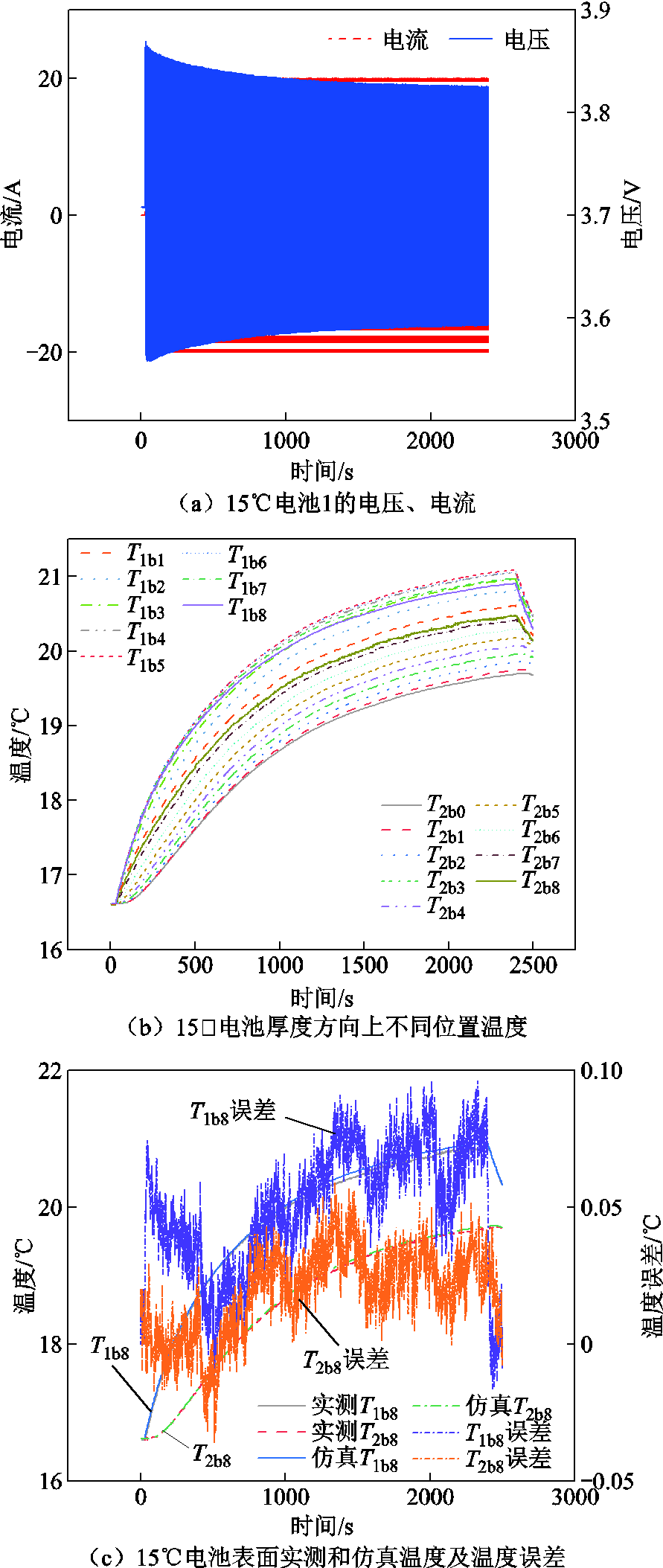
图10 15℃仿真结果
Fig.10 Simulation results at 15℃
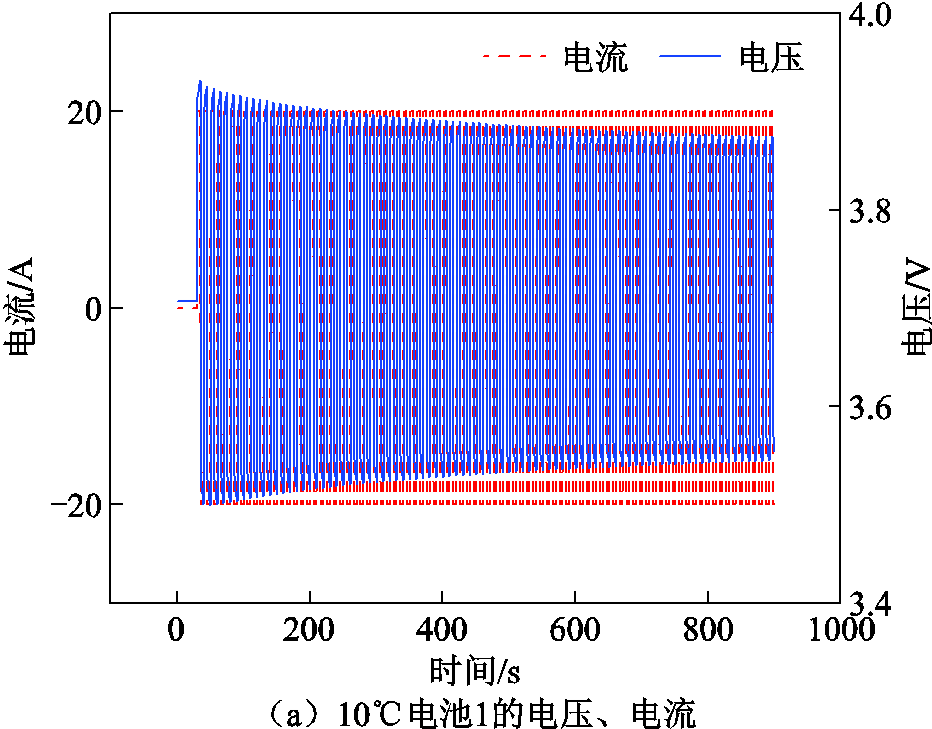
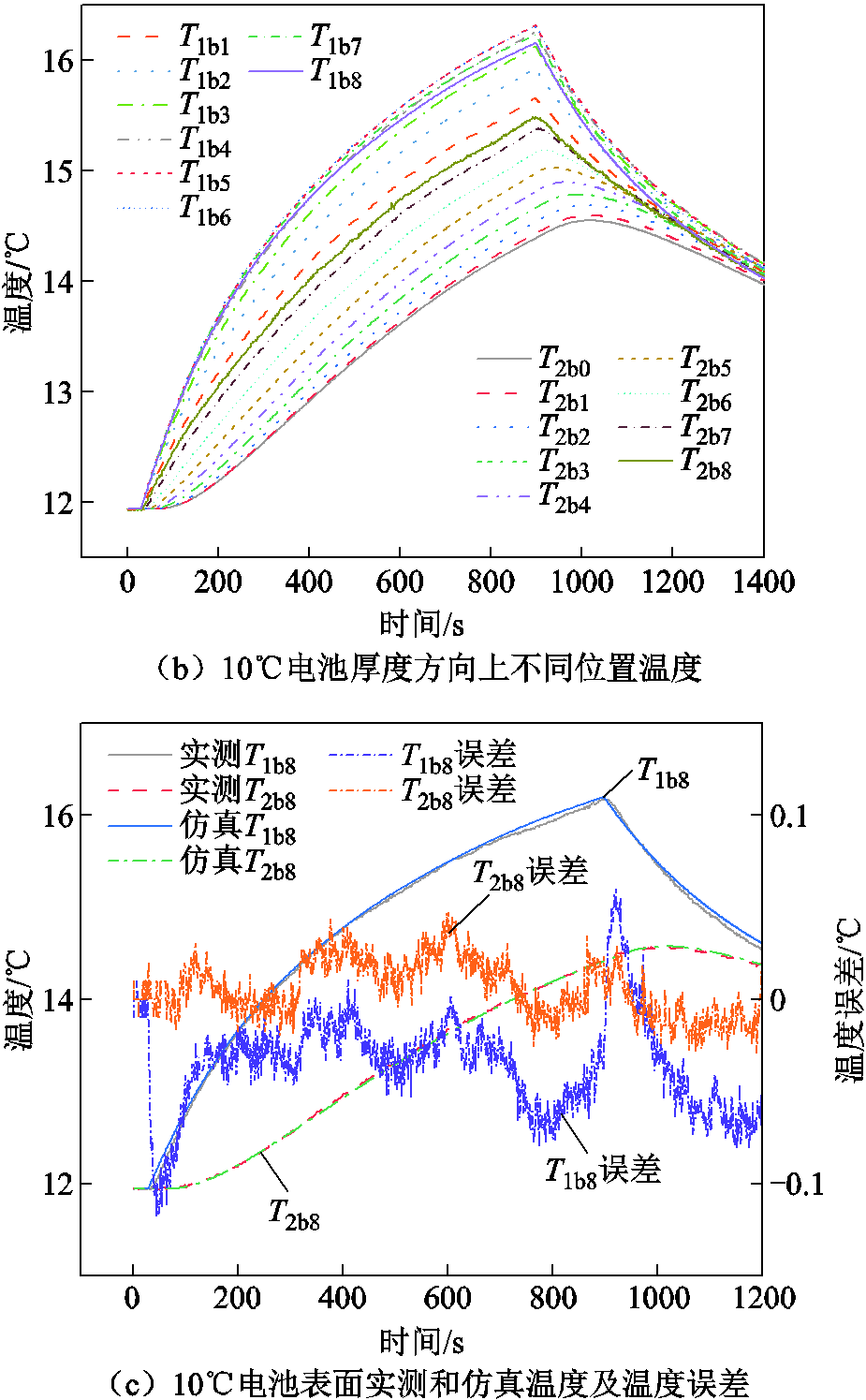
图11 10℃仿真结果
Fig.11 Simulation results at 10℃
将温箱温度调至5℃，改变脉冲充放电策略为以12A的电流脉冲充放2 370 s，电压和电流如图12a所示。将辨识的模型参数和电池产热功率代入模型进行计算，电池沿厚度方向的温度分布如图12b所示，则实测电池表面温度和仿真电池表面温度如图12c所示。
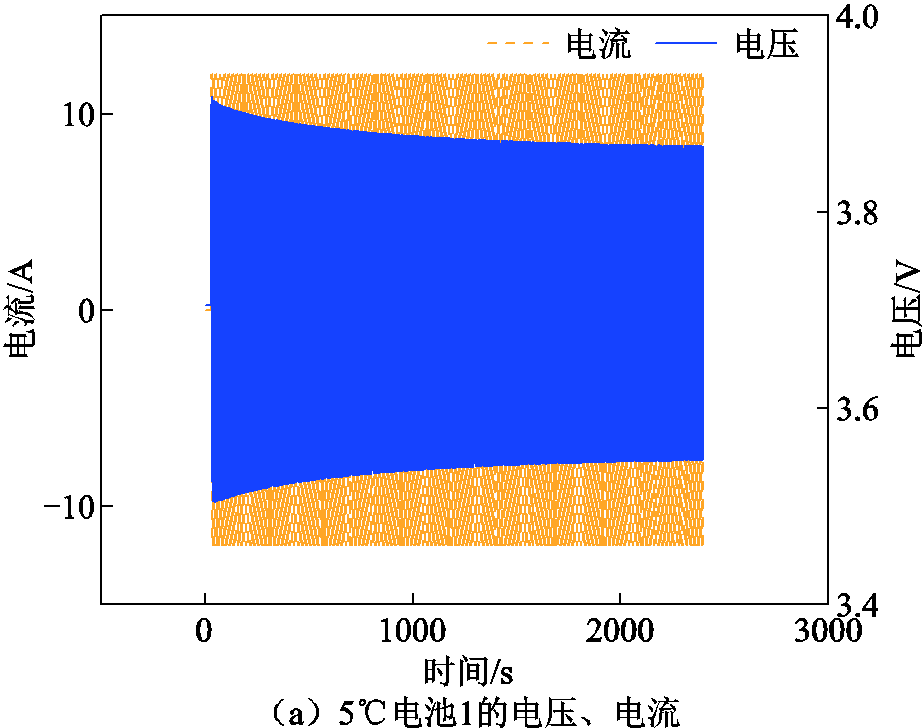
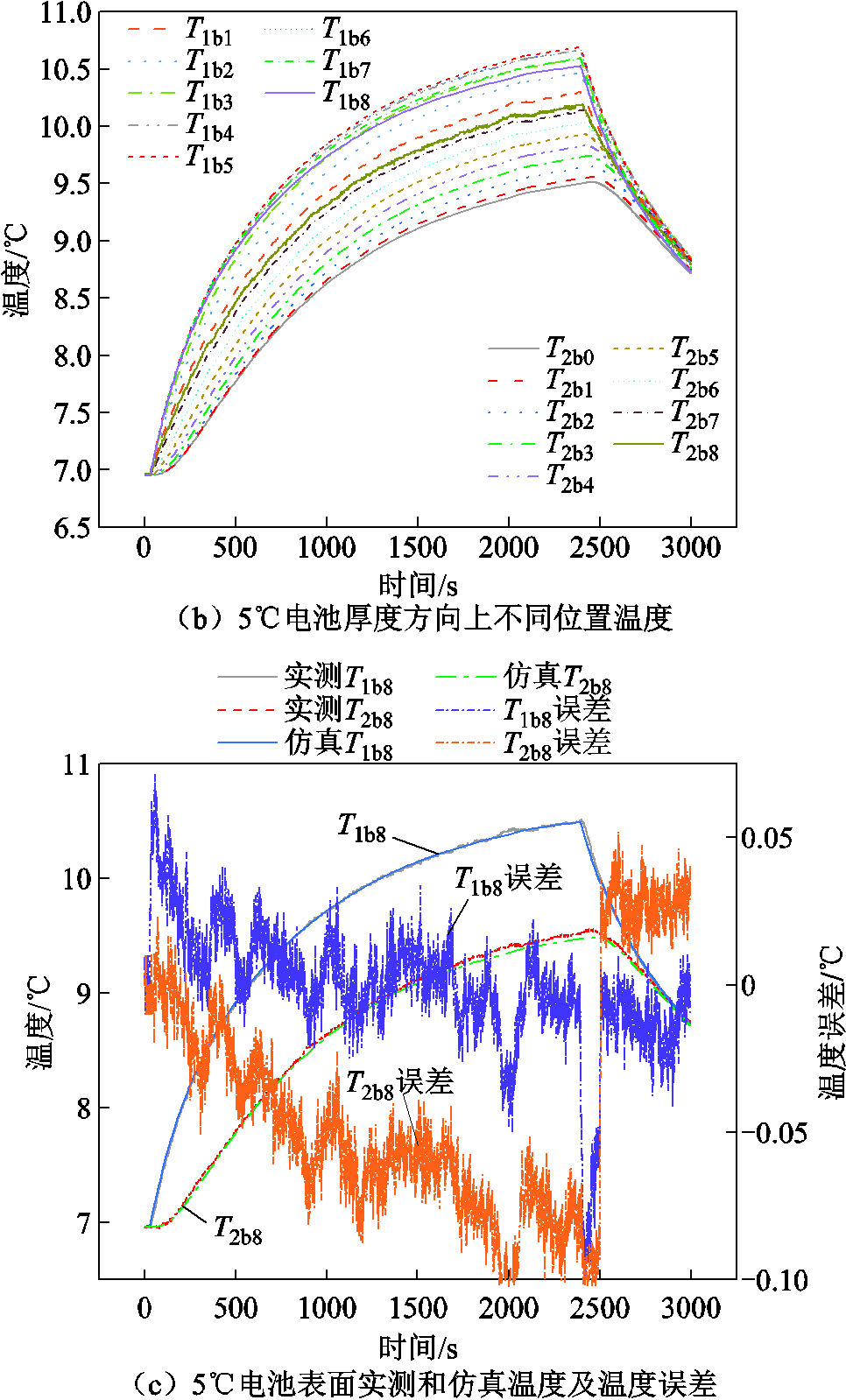
图12 5℃仿真结果
Fig.12 Simulation results at 5℃
将温箱温度调至0℃，改变脉冲充放电策略为以8A的电流脉冲充放1 170 s，电压和电流如图13a所示。将辨识的模型参数和电池产热功率代入模型进行计算，电池沿厚度方向的温度分布如图13b所示，则实测电池表面温度和仿真电池表面温度如图13c所示。
通过将温箱温度调至不同的温度，并对电池施加与参数辨识不一样的脉冲电流激励，对比实测和仿真的电池温度T1b8和T2b8。当温箱温度设置为20℃时，电池最高温升为1.14℃，实测和仿真温度误差小于0.04℃；当温箱温度设置为15℃时，电池最高温升为4.4℃，实测和仿真温度误差小于0.1℃；当温箱温度设置为10℃时，电池最高温升为4.19℃，实测和仿真温度误差小于0.1℃；当温箱温度设置为5℃时，电池最高温升为3.55℃，实测和仿真温度误差小于0.1℃。当温箱温度设置为0℃时，电池最高温升为2.02℃，实测和仿真温度误差小于0.05℃。可以看出在不同温度点，仿真计算的电池表面温度与实测的电池表面温度吻合度较高，证明所提方法能够较为准确辨识电池热学模型参数。
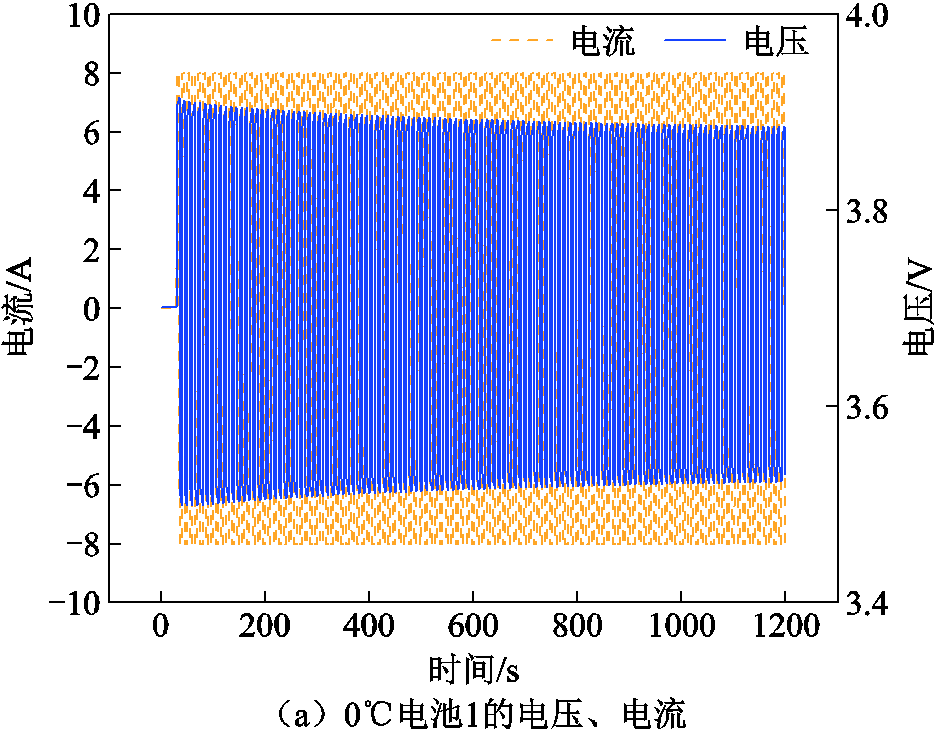
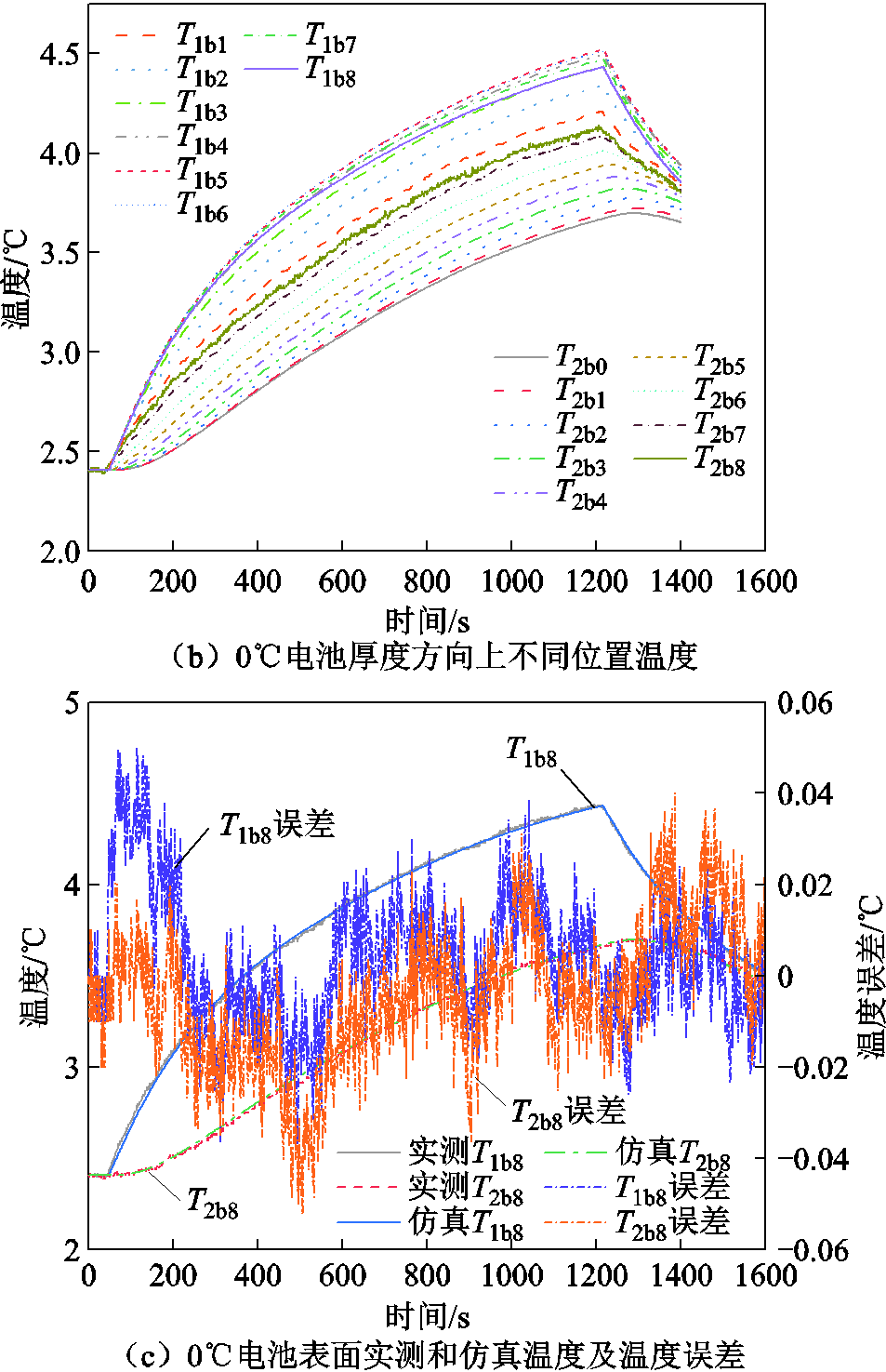
图13 0℃仿真结果
Fig.13 Simulation results at 0℃
为了准确快速地辨识锂离子电池热学模型参数（热容和热阻），本文提出了一种自产热和外传热相结合的方法。通过建立锂离子电池沿厚度方向的分布式热学等效电路模型，将温度离散化处理，采用APSO算法，辨识了0℃、10℃、20℃三个温度点的热学模型参数，并将辨识后的参数等效处理为比热容和导热系数，比热容的平均值为0.996 J/(g·K)、导热系数平均值为0.377 W/(m·K)，对比不同文献的电池比热容和导热系数，均在合理范围内，且差异不超过8%。将辨识后的模型参数代入热路模型，并采用不同的策略进行验证，实测和仿真计算的电池表面温度吻合度较高，温度误差小于0.1℃，证明所提热学模型参数辨识方法精度较高。而且所提方法具有简便易行的优点，只需要两块相同规格的电池，无需借助其他器件，测试周期短，可以为层叠式软包锂离子电池热学模型参数辨识提供技术支撑。
参考文献
[1] 孙丙香, 任鹏博, 陈育哲, 等. 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测[J]. 电工技术学报, 2021, 36(3): 666-674. Sun Bingxiang, Ren Pengbo, Chen Yuzhe, et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 666-674.
[2] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189. Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.
[3] 程夕明, 唐宇, 王寿群. 锂离子电池热物性参数测量方法综述[J]. 机械工程学报, 2019, 55(14): 140-150. Cheng Ximing, Tang Yu, Wang Shouqun. Thermophysical parameter measurements for lithium-ion batteries: a review[J]. Journal of Mechanical Engineering, 2019, 55(14): 140-150.
[4] 范文杰, 徐广昊, 于泊宁, 等. 基于电化学阻抗谱的锂离子电池内部温度在线估计方法研究[J]. 中国电机工程学报, 2021, 41(9): 3283-3292, 30. Fan Wenjie, Xu Guanghao, Yu Boning, et al. On-line estimation method for internal temperature of lithium-ion battery based on electrochemical impedance spectroscopy[J]. Proceedings of the CSEE, 2021, 41(9): 3283-3292, 30.
[5] 熊瑞, 李幸港. 基于双卡尔曼滤波算法的动力电池内部温度估计[J]. 机械工程学报, 2020, 56(14): 146-151. Xiong Rui, Li Xinggang. Battery internal temperature estimation method through double extended Kalman filtering algorithm[J]. Journal of Mechanical Engineering, 2020, 56(14): 146-151.
[6] 刘素贞, 陈晶晶, 张闯, 等. 基于区域电压的锂离子电池不均匀发热模型[J]. 电工技术学报, 2022, 37(21): 5627-5636. Liu Suzhen, Chen Jingjing, Zhang Chuang, et al. Regional voltage-based uneven heating model of lithium-ion battery[J]. Transactions of China Electro-technical Society, 2022, 37(21): 5627-5636.
[7] Wang Qian, Jiang Bin, Li Bo, et al. A critical review of thermal management models and solutions of lithium-ion batteries for the development of pure electric vehicles[J]. Renewable and Sustainable Energy Reviews, 2016, 64: 106-128.
[8] 潘国兵, 王杰, 欧阳静. 基于改进MRF-KFCM有效区域分割的储能系统三维温度场重构方法[J]. 电工技术学报, 2020, 35(19): 4019-4027. Pan Guobing, Wang Jie, Ouyang Jing. 3D temperature field reconstruction method for energy storage system based on improved MRF-KFCM effective region segmentation[J]. Transactions of China Electrote-chnical Society, 2020, 35(19): 4019-4027.
[9] Xu Meng, Zhang Zhuqian, Wang Xia, et al. Two-dimensional electrochemical-thermal coupled modeling of cylindrical LiFePO4 batteries[J]. Journal of Power Sources, 2014, 256: 233-243.
[10] Li M, Dong C, Mu Y, et al. Parameter estimation of lithium battery thermal model based on two-stage forgetting factor least square method[C]//2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 2021: 1718-1723.
[11] Yoshikawa G, Taguchi Y, Hatakeda K, et al. Development of a parameter identification method for the thermal circuit model of a lithium-ion battery installed on a battery-powered EMU[C]//2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 2017: 1-5.
[12] Zhang Jianbo, Wu Bin, Li Zhe, et al. Simultaneous estimation of thermal parameters for large-format laminated lithium-ion batteries[J]. Journal of Power Sources, 2014, 259: 106-116.
[13] 阮海军. 低温环境下锂离子电池优化加热及充电方法研究[D]. 北京: 北京交通大学, 2019. Ruan Haijun. Research on optimized heating and charging method of lithium-ion battery in low temperature environment[D]. Beijing: Beijing Jiaotong University, 2019.
[14] Vertiz G, Oyarbide M, Macicior H, et al. Thermal characterization of large size lithium-ion pouch cell based on 1d electro-thermal model[J]. Journal of Power Sources, 2014, 272: 476-484.
[15] Bazinski S J, Wang X, Sangeorzan B P, et al. Measuring and assessing the effective in-plane thermal conductivity of lithium iron phosphate pouch cells[J]. Energy, 2016, 114: 1085-1092.
[16] Zhang Jianbo, Wu Bin, Li Zhe, et al. Simultaneous estimation of multiple thermal parameters of large-format laminated lithium-ion batteries[C]//2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, 2013: 1-5.
[17] 林坚生, 宋文吉, 高日新, 等. LiFePO4动力电池热物性测定及温升特性研究[J]. 电源技术, 2015, 39(4): 739-742. Lin Jiansheng, Song Wenji, Gao Rixin, et al. Study on thermo-physical property measurement and temperature rise characteristic of LiFePO4 power battery[J]. Chinese Journal of Power Sources, 2015, 39(4): 739-742.
[18] 王帅林, 盛雷, 齐丽娜, 等. 大型软包锂离子电池的热物性实验研究[J]. 浙江大学学报(工学版), 2021, 55(10): 1986-1992.Wang Shuailin, Sheng Lei, Qi Lina, et al. Experimental investigation on thermophysical parameters of large-format pouch lithium-ion battery[J]. Journal of Zhejiang University: Engineering Science, 2021, 55(10): 1986-1992.
[19] Zhu Gaolong, Wen Kechun, Lü Weiqiang, et al. Materials insights into low-temperature performances of lithium-ion batteries[J]. Journal of Power Sources, 2015, 300: 29-40.
[20] 冯旭宁, 李建军, 王莉, 等. 锂离子电池各向异性导热的实验与建模[J]. 汽车安全与节能学报, 2012, 3(2): 158-164. Feng Xuning, Li Jianjun, Wang Li, et al. Experiments and modeling of anisotropic thermal conductivity of lithium-ion batteries[J]. Automotive Safety and Energy, 2012, 3(2):158-164.
Abstract Accurate identification of thermal model parameters (heat capacity and thermal resistance) of lithium ion batteries is crucial for thermoelectric coupling modeling and state parameter estimation of batteries. There is a certain conversion formula between the thermal model parameters and the thermophysical parameters (specific heat capacity and thermal conductivity) of lithium ion batteries, so the two sets of parameters have an equivalent relationship. The study of thermal model parameters can refer to the research methods of thermophysical parameters.
Accurate measurement of battery specific heat capacity and thermal conductivity requires the use of expensive testing equipment, which is costly and takes longer to test. Using optimization algorithms to identify thermal model parameters not only has low cost, but also has short calculation cycle. In this paper, a fast method for identifying the thermal model parameters of NCM laminated soft packaged lithium-ion batteries is proposed based on the charging and discharging conditions combined with the battery heat generation and heat transfer mechanisms.
By establishing a distributed thermal equivalent circuit model to simulate the temperature distribution along the thickness direction of the battery, the reversible heat can be ignored and the calculation of battery heat generation can be simplified by designing a bidirectional pulse operating condition; The temperature was discretized and the thermal model parameters of 0℃, 10℃, and 20℃ were identified using (adaptive particle swarm optimization (APSO) algorithm. The identified parameters are equivalently treated as specific heat capacity and thermal conductivity, with an average specific heat capacity of 0.996 J/(g·K) and an average thermal conductivity of 0.376 W/(m·K). Comparing the specific heat capacity and thermal conductivity of batteries from different literature, they are within a reasonable range, and the difference is not more than 8%. Temperature sensitivity analysis was conducted. When the thermal model parameters changed by ±5%, the temperature error of the model simulation results was less than 0.08℃. Therefore, in the range of 0 to 20℃, the thermal model parameters are not sensitive to temperature. Finally, the identified parameters are brought into the model and simulated using a different strategy than the parameter identification experiment. The measured and simulated battery surface temperatures agree well with a temperature error of less than 0.1℃, which proves that the proposed thermal model parameter identification method has a high accuracy. Moreover, the proposed method has the advantage of simplicity and simplicity, requiring only two batteries of the same specification, without the need for other devices, and having a short test cycle. It can provide technical support for the identification of thermal model parameters for stacked soft packaged lithium ion batteries.
keywords：Laminated flexible, lithium-ion battery, distributed thermal circuit model, heat capacity and thermal resistance, self-generated heat and external heat transfer
DOI:10.19595/j.cnki.1000-6753.tces.222104
中图分类号：TM911
收稿日期 2022-11-04
改稿日期 2023-02-10
孙丙香 女，1979年生，教授，博士生导师，研究方向为锂离子动力电池高效集成及智能管控技术。包括建模与仿真、热特性与低温加热策略、优化充电、储能电池性能评估与经济性分析等。E-mail：bxsun@bjtu.edu.cn（通信作者）
宋东林 男，1996年生，硕士研究生，研究方向为锂离子电池低温加热、电池热特性建模。E-mail：20121484@bjtu.edu.cn
（编辑 郭丽军）