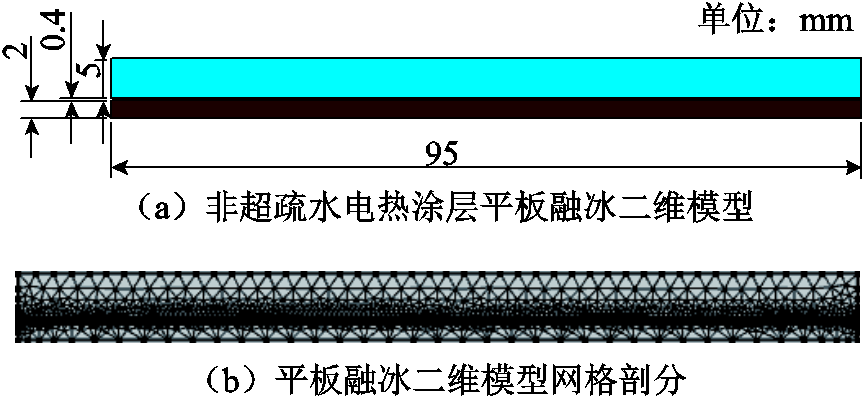
图1 融冰模型及其网格剖分
Fig.1 Melting ice model and its mesh division
摘要 针对电热超疏水涂层覆冰过程中表现出的三类不同冰层形貌,该文建立了电加热融冰数值计算模型,并对仿真计算结果进行了相应的试验验证,验证结果与仿真结果基本一致,该模型能有效模拟融冰过程和温度分布。临界融冰功率的计算结果表明,电热超疏水涂层融冰所需功率大于非超疏水电热涂层,尤其在乳突状冰层出现后,融冰功率将大幅增加。电热超疏水涂层防冰试验结果表明,在雨凇覆冰环境中,超疏水性能单独作用时,叶片在覆冰前期能延缓覆冰;电热性能与超疏水性能共同作用时,叶片无覆冰形成。电热超疏水涂层用于风力发电机防覆冰具有较好的效果,但用于覆冰后的融冰时将需要更多的能量。
关键词:风力发电机 超疏水电热涂层 防除冰 数值模型 人工试验
覆冰地区风力发电机(以下简称风力机)遭遇冰雪灾害概率极高,严重危害风电场安全运行[1-2],导致年电量损失达5%~25%[3-5]。超疏水等特性涂料防冰技术和电加热除冰技术是目前解决风力机叶片覆冰的主要技术,获得了国内外学者的广泛关注。
有学者制备了静态接触角大于150°,动态接触角小于10°的超疏水表面[6-9],使得超疏水表面与过冷却水滴之间的接触面积和粘附力显著减小,从而达到延缓或防止覆冰的效果[8-10]。M. Mohseni和A. Amirfazli[11]将康铜发热金属丝预埋在风力机叶片表面下方从而制成嵌入式发热元件,通过电热效应进行防冰和除冰;重庆大学[12]建立了架空地线的直流融冰模型,分析了风速、覆冰厚度对临界融冰电流的影响;文献[13]以T3001K碳纤维丝束作为发热元件对风力机叶片进行防冰和除冰,发现其具有优良的融冰性能;龚奕宇[14]在超疏水涂层的基础上加入炭黑,制备了一种具备电热性能的超疏水涂料,该半导体超疏水涂层具有出色的热效应、超疏水性能及防冰能力,但未对涂层的耐磨、耐候性能和临界防冰功率进行检测和计算;文献[15]开展风力机叶片电加热防冰试验,得出叶片防冰所需功率在1 000~3 500 W/m2之间;文献[16]将2 kW风力机置于自然覆冰环境中进行电加热防冰试验研究,得到在轻微雨凇覆冰环境中叶片临界防冰功率为2~3 kW/m2;文献[17]将风力机表面看成平板进行电热除冰功率数值计算,得到在不同温度的无风停机环境中电热功率为332~693 W/m2;文献[18]基于风力机叶片自然雨凇冰型建立临界融冰功率数值计算模型,得出临界除冰功率的数量级为1 kW/m2。
综上可知,国内外研究人员对超疏水涂料用于防覆冰和在风力机上使用电加热防除冰都已有大量研究,但关于电热性能的超疏水材料用于风力机防覆冰的研究非常少见。超疏水涂层覆冰后使用电热系统进行除冰时,所需的临界除冰功率是否会发生变化的问题尚未得到验证。本文将制备的电热超疏水涂层[19]用于风力机叶片进行防覆冰试验,通过试验统计观测,总结了风力机叶片正表面超疏水涂层覆冰出现的三种冰型。基于这三种冰型建立电加热融冰功率数值计算模型,对比非超疏水电热涂层的冰型,研究超疏水表面形成的冰型对电热涂层热过程的影响。计算了电热超疏水叶片的临界融冰功率,并对涂覆超疏水电热涂层的风力机叶片进行无电热防覆冰试验、电加热防覆冰试验和电加热临界融冰试验,对数值计算模型进行验证。
本文使用与风力机叶片材料成分相近的95 mm× 95 mm玻纤环氧树脂板代替100 W风力机叶尖部位,对涂覆电热超疏水涂层的环氧树脂板和涂覆非超疏水电热涂层的环氧树脂板进行温升计算。
环氧树脂板厚度为2 mm,电热涂层厚度均为0.4 mm,覆冰厚度分别为2 mm、5 mm和10 mm。非超疏水电热涂层的平板融冰二维模型如图1a所示。

图1 融冰模型及其网格剖分
Fig.1 Melting ice model and its mesh division
由电热超疏水叶片的防覆冰试验及表面观测研究可得,叶片表面可能出现三类冰型:第一类冰型,覆冰呈块状散落分布在涂层表面,多出现在覆冰初期;第二类冰型,涂层几乎被冰覆盖,形成乳突状冰层,多出现在覆冰中期;第三类冰型,全覆盖波纹状冰,与非超疏水涂层覆冰冰型类似,多出现在覆冰后期。故本文建立三类覆冰冰型如图2所示。
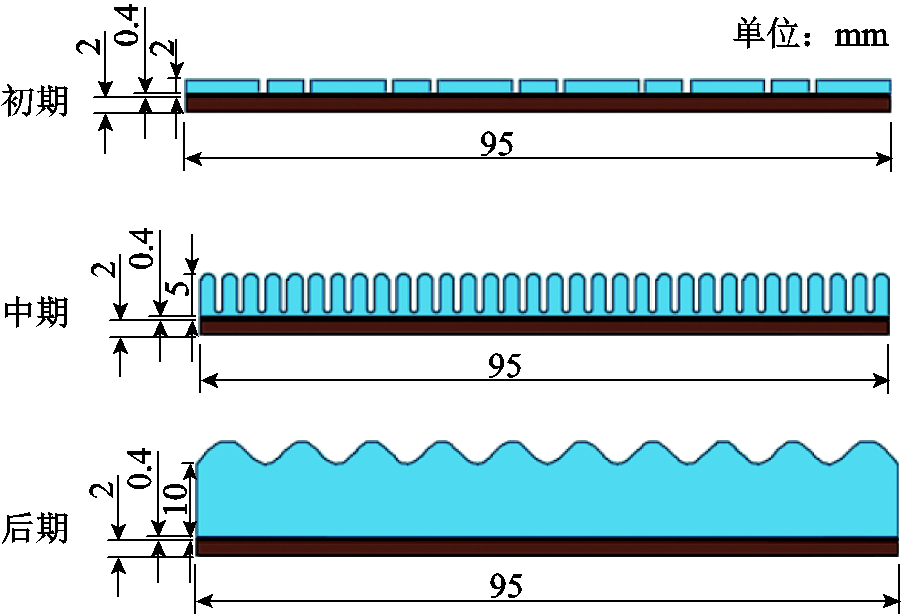
图2 超疏水涂层三类覆冰冰型
Fig.2 Three types of super-hydrophobic coating ice-coated ice type
由于涂层表面冰在温度达到0℃后,分子结构性质发生改变,吸收热量,逐渐融化成水,相变过程在0℃发生,会让数值模型计算更加非线性化[20]。为了避免计算过程繁杂且不易收敛,本文作如下假设:①相变发生在相变点附近的一个很小的区间,即ΔT=0.1 K;②水融化后不发生流失,即无气隙生成;③换流条件维持不变;④冰层纯净无杂质。
等效模型加热融冰过程主要有四个传热区域:环氧树脂板域、电热涂层域、冰层域和空气域。环氧树脂板、电热涂层域和冰层域等域内的热活动满足固体域传热微分方程。
在不考虑冰融化的情况下,其内部热活动主要为热传导,即平板模型的温度场可由固体域内的时变传热微分方程描述。
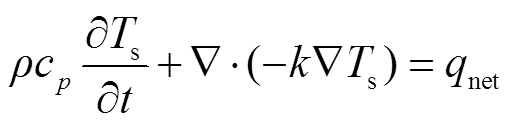 (1)
(1)
式中,Ts为固体域温度;ρ、cp和k分别为相应材料的密度、比定压热容和导热系数;qnet为发热涂层的电热功率。
固体域温度初始值Ts0应当与环境温度Ta一致,故初始条件为
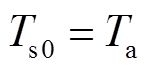 (2)
(2)
本文设置外部强制对流,风速设置为4 m/s。由于冰型已知,即可认为冰层与周围空气的表面传热系数已知,满足Robin边界条件,即
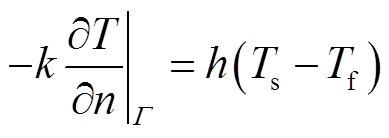 (3)
(3)
式中,Tf为空气域温度;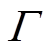 为边界;
为边界;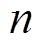 为边界面外法线方向;
为边界面外法线方向;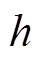 为表面传热系数。在电热融冰的计算中,通常认为冰层与周围空气的表面传热系数是已知的,根据覆冰的形状即可应用相应的经验公式对该系数进行计算。本文对平板模型利用相应的板平均传递系数的经验公式(4)代入强制表面传热系数进行计算;对圆柱模型利用气流外掠圆柱的经验公式(5)代入强制表面传热系数进行计算。
为表面传热系数。在电热融冰的计算中,通常认为冰层与周围空气的表面传热系数是已知的,根据覆冰的形状即可应用相应的经验公式对该系数进行计算。本文对平板模型利用相应的板平均传递系数的经验公式(4)代入强制表面传热系数进行计算;对圆柱模型利用气流外掠圆柱的经验公式(5)代入强制表面传热系数进行计算。
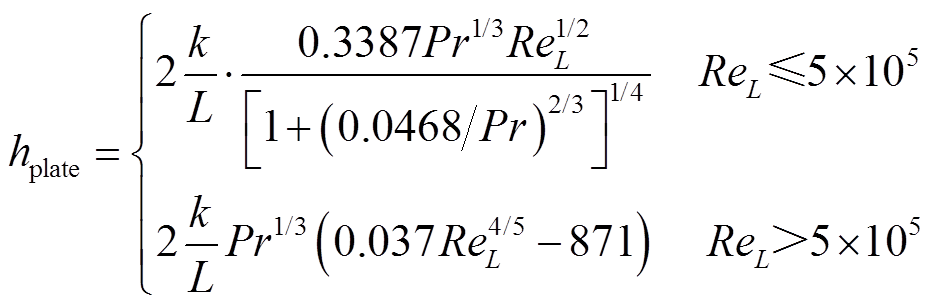 (4)
(4)
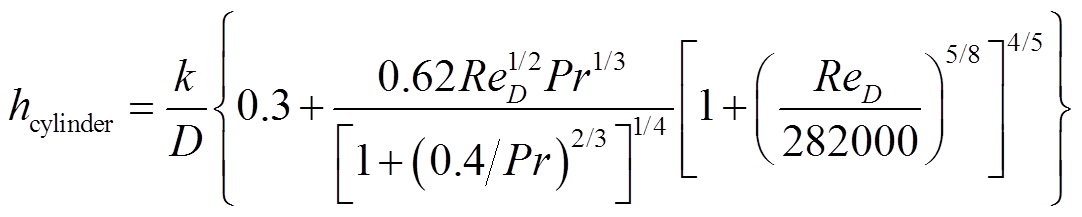 (5)
(5)
式中,hplate为平板表面传热系数;hcylinder为圆柱表面传热系数;L为板的长度;D为圆柱的直径;Pr为空气普朗特数;Re为对应模型的雷诺数。
融化模型中,根据V. R. Voller[21-22]提出的焓值-孔隙率法将融化过程中的固-液混合区域看作多孔介质。将冰层区域固态相所占体积与冰层区总体积的比值定义为固相分数,用θ1表示;将冰层区域液态相所占体积与冰层区总体积的比值定义为液相分数,用θ2表示。θ1=1(θ2=0)表示固态相;θ2=1(θ1=0)表示液态相;当θ处于0~1之间时,表示固液混合区域。在每次迭代计算过程中,都会基于焓值守恒原理对θ进行计算。
冰融化温度为Tpc,1→2=273.15 K,根据假设①,本文的固液过渡间隔设置为ΔT=0.1 K,则冰水转换的相变区间为Tpc,1→2-ΔT/2~Tpc,1→2+ΔT/2,如图3所示。
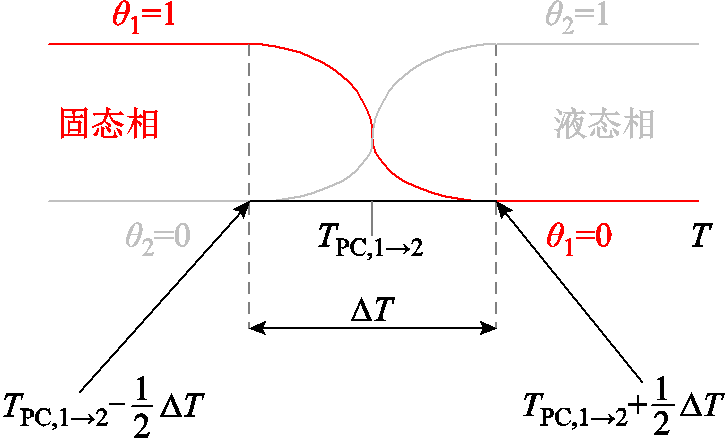
图3 冰融化相变过程
Fig.3 Phase transition diagram of ice melting
故该相变过程的等效物性参数计算式为
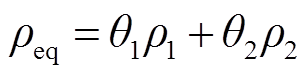 (6)
(6)
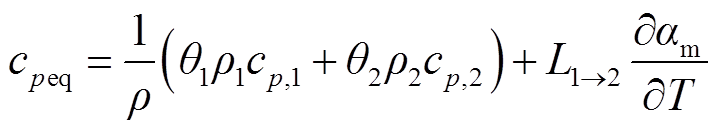 (7)
(7)
![]() (8)
(8)
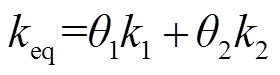 (9)
(9)
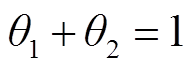 (10)
(10)
式中,ρeq、cpeq、keq分别为等效密度、等效比定压热容和等效导热系数;αm为融化相变过程中即将融化的冰的质量;L1→2为相变吸收的潜热;p1和p2、k1和k2、cp,1和cp,2分别为对应相的密度、导热系数和比定压热容。
因此,可以将相变吸热项加入固体域温度场计算过程,修正固体域温度控制方程为
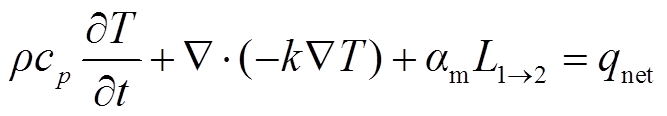 (11)
(11)
本文数值计算中,设置相变潜热L1→2=333.5 kJ/kg,环境温度为-7℃,电加热功率为1 413 W/m2,融化相变模型中材料各项参数见表1。
表1 数值计算所需材料参数
Tab.1 Material parameters required for numerical calculation

参数环氧树脂冰层电热层水 厚度/mm20.4 密度/(kg/m3)2 2039181 2041 000 导热系数/[W/(m·K)]115.082.311 1000.613 比定压热容/[J/(kg·K)]1 088.52 0521 0634 179
涂层热源中的一部分热量被叶片吸收,一部分用于冰融化,其余部分经过冰层热传导通过冰层表面对流和辐射散热损失在环境中。当除冰功率在满足这些热损失的同时使得冰层涂层表面温度为0℃,即可认为此时的除冰功率为满足该环境该冰厚的临界除冰功率。临界除冰功率随着环境条件及除冰时间的变化而变化,本文的相关条件如下:环境温度为-7℃,风速为4 m/s,外部强制对流,除冰时间为1 h。
临界融冰功率的计算在于找到一定时间内能使电热涂层表面温度T(q)刚好达到0℃的电热功率值q。由于不考虑融冰相变吸收潜热,故电热涂层表面温度与电热功率呈正相关关系,即可采用二分法寻找临界融冰功率。计算方法可以沿用1.2节的数值计算方法。
(1)确定临界融冰功率的下极限为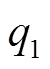 =0 W/m2;由1.5.1节和1.5.2节的仿真结果知电热功率为1 413 W/m2时可完成融冰,故上极限可设置为
=0 W/m2;由1.5.1节和1.5.2节的仿真结果知电热功率为1 413 W/m2时可完成融冰,故上极限可设置为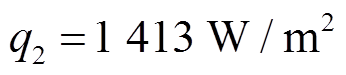 ;二分法的收敛精度为ξ=0.01。
;二分法的收敛精度为ξ=0.01。
(2)计算搜索区间的中点。
(3)调用1.1~1.3节中的涂层融冰数值计算模型,而后对温度场进行求解,输出电热涂层表面温度T(q1)和T(q),此处仿真计算不调用相变模块。
(4)计算判据是否大于0:若大于0,则将q值设为新的下极限;反之设为上极限。
(5)计算误差是否小于精度ξ,若满足收敛精度要求,则停止计算并输出临界融冰功率值q;否则,返回步骤(2)。
1.5.1 无超疏水性能的电热涂层冰型融化情况
冰层厚度分别设置为2 mm、5 mm和10 mm,步长设置为20 s,加热3 600 s,相对容差为0.001,取涂层中间与冰层交界处为标记点,得出计算结果如图4所示。
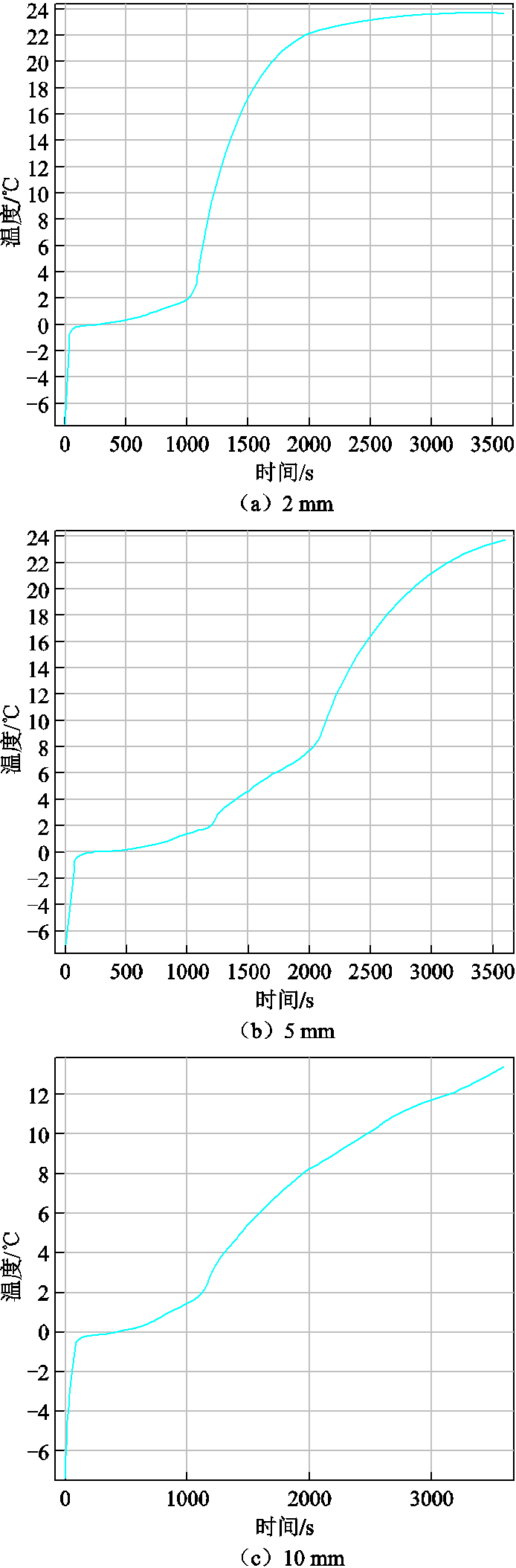
图4 标记点处冰层融化温度变化
Fig.4 Temperature of melting ice at the marked point
由图4可知,2 mm、5 mm和10 mm厚冰层在相同热源和外部对流条件下,冰融化开始时间分别为300 s、320 s和400 s。从涂层与冰交界处的温升情况可以看出,2 mm冰层40 min左右时温度平衡于23℃;5 mm冰层1 h后温度平衡于23℃;10 mm冰层交界处1 h后温度达到13℃仍有上升趋势,表明随着冰层厚度的增加,温升速率变缓。
1.5.2 电热超疏水涂层各冰型融化情况
步长设置为20 s,加热3 600 s,相对容差为0.001,取涂层中间与冰层交界处为标记点。按初期冰型,外部强制表面传热系数采用板平均传递系数的经验公式(4),超疏水表面第一类冰型融冰计算结果如图5所示。
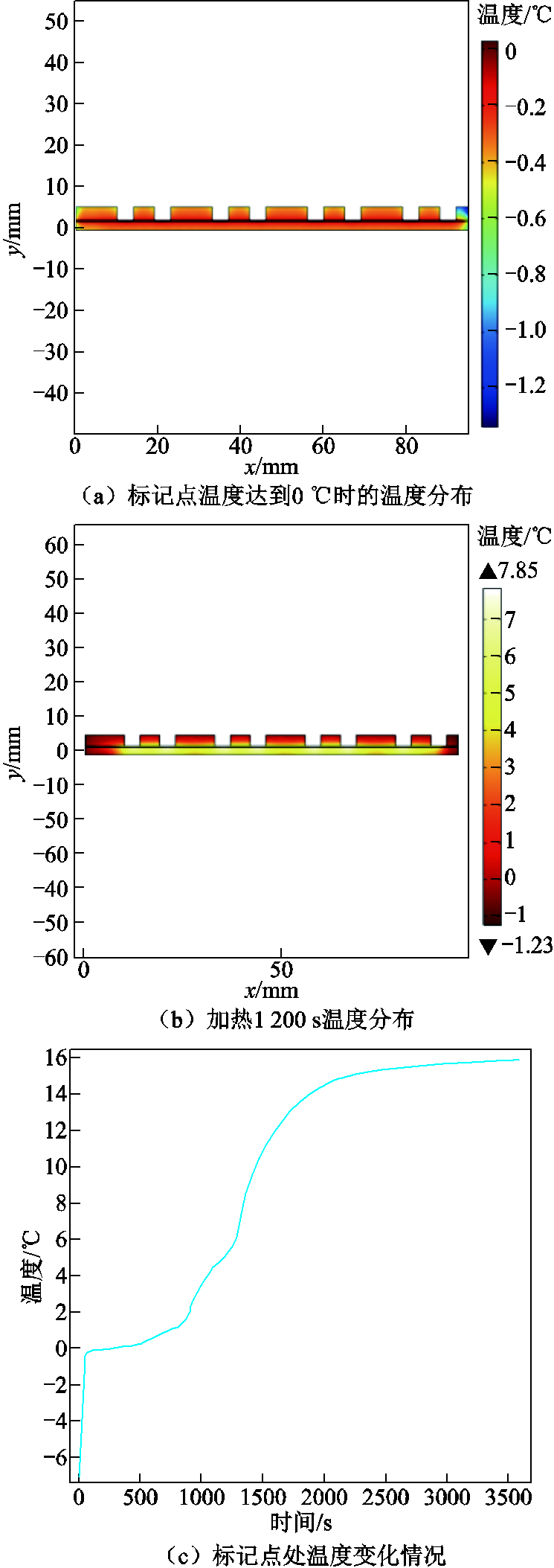
图5 第一类冰型融化温度变化
Fig.5 Type 1 ice melting temperature
按中期冰型,外部强制表面传热系数采用圆柱绕流系数的经验公式(5),其余设置不变,超疏水表面第二类冰型融冰计算结果如图6所示。
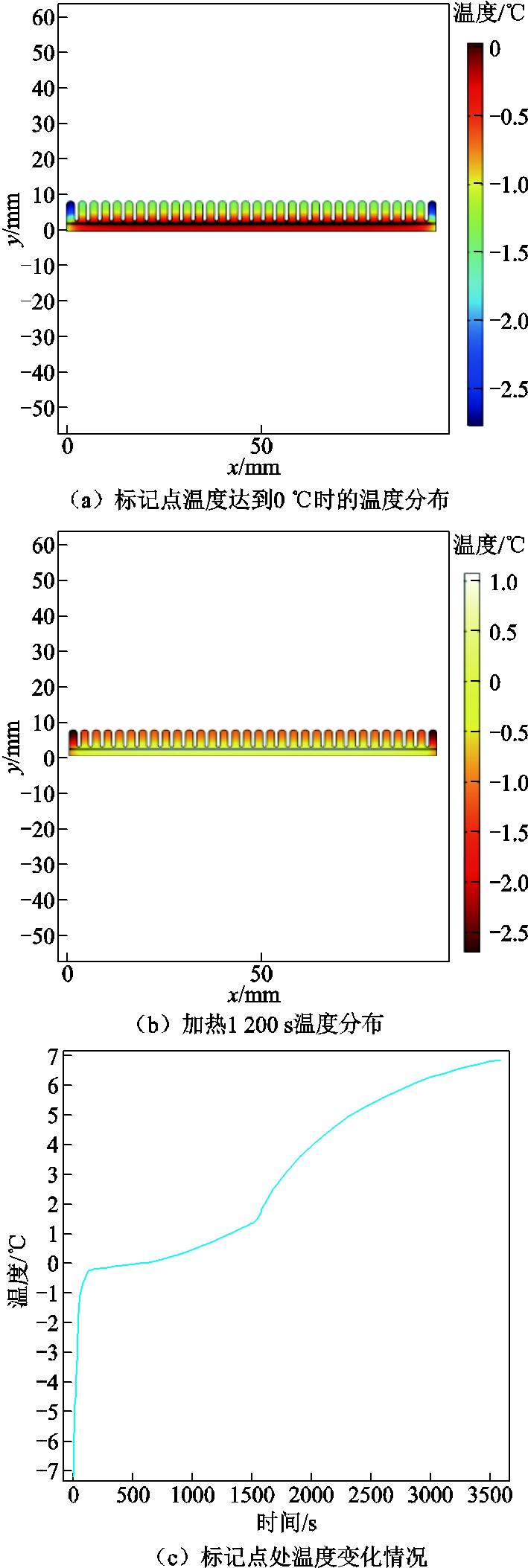
图6 第二类冰型融化温
Fig.6 Type 2 ice melting temperature
按后期冰型,外部强制表面传热系数采用板平均传递系数的经验公式(4),其余设置不变,超疏水表面第三类冰型融冰计算结果如图7所示。
由图5~图7可知,超疏水表面三类冰层在相同热源和外部对流条件下,冰融化开始时间分别为140 s、360 s和360 s。加热20 min后,第一类冰层表面温度大于0℃,冰基本融化;第二类和第三类冰层表面两端温度小于0℃,第二类薄弱处冰全部融化,第三类冰融化厚度约为1.5 mm。从涂层与冰交界处的温升情况可以看出,1 h后第一类冰层温度平衡于15℃,第二类冰层的温度平衡于6℃,第三类冰层交界处温度达到12℃仍有上升趋势。在相同功率情况下,超疏水涂层第一类冰型融化开始时间相对于无超疏水性能涂层快了将近3 min。
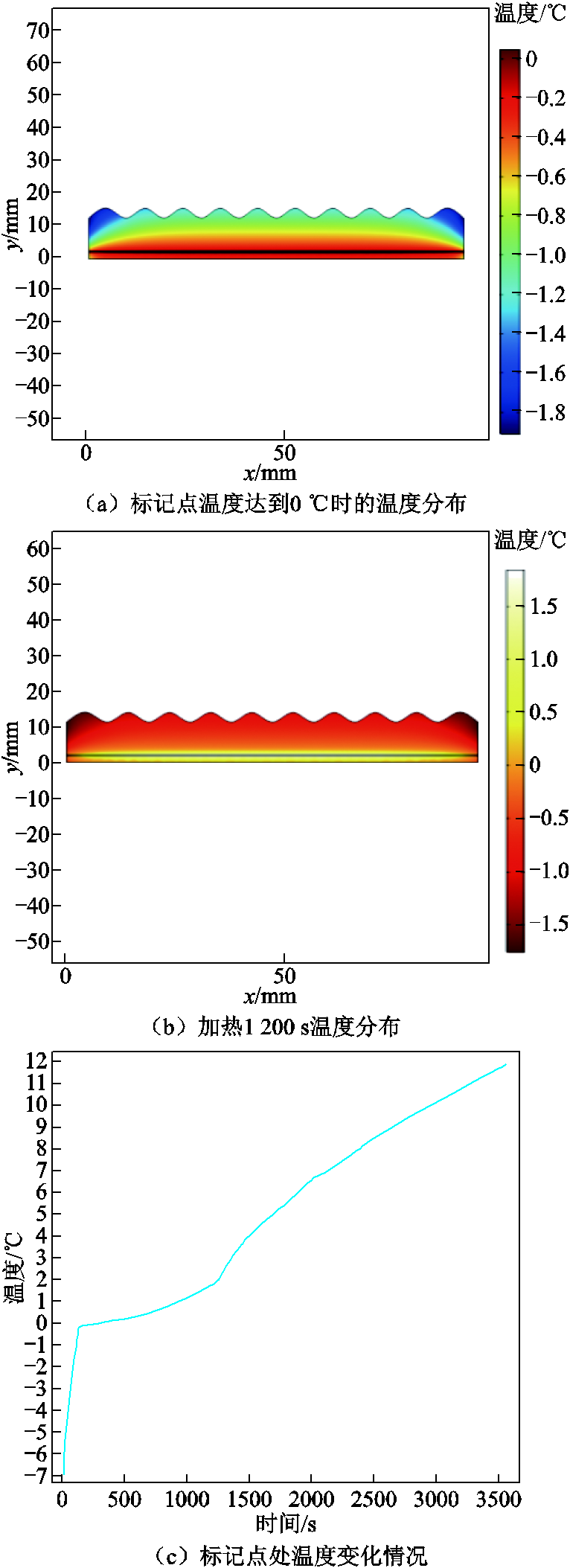
图7 第三类冰型融化温
Fig.7 Type 3 ice melting temperature rise
1.5.3 临界除冰功率
基于超疏水覆冰试验获得的冰型和前述计算模型,利用有限元法对防除冰涂层叶片临界除冰情形进行瞬态仿真,得到临界除冰功率如图8所示。其中,普通电热涂层冰层厚度的增加阻碍了涂层热量的流失,临界除冰功率降低。超疏水涂层第一类覆冰冰型,即覆冰初期接入电压加热所需的除冰功率较小;第二类由于柱状冰的形成,对流换热面积增加,热损失增多;第三类与普通涂层的覆冰冰型类似,冰厚阻碍了涂层的热量损失,所需除冰功率与普通电热涂层10 mm冰厚大致相当。
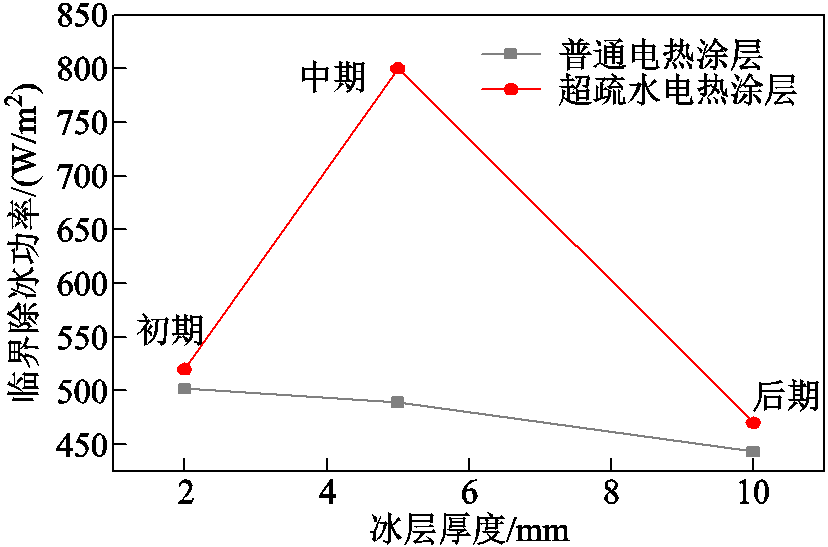
图8 临界除冰功率
Fig.8 Critical deicing power
运行状态下的风力机防除冰试验在大型多功能人工气候室进行[23],该气候室内径和高度均满足100 W风力机对运行空间的需求,风力机参数见表2。安装电热超疏水叶片的风力机示意图如图9所示。风力机装有一片电热超疏水涂层叶片及导电集电环,如图10所示,导电集电环内层为定子,外层为转子,定子与风机轴牢固连接,转子带着导线与叶片同步转动。电源信号通过导电集电环转子上的输入端输入,通过定子端的输出端输出。人工气候室风速设置为4 m/s,控制覆冰温度在-7℃左右,试验中采用国际电工委员会(International Electrotechnical Commission, IEC)推荐的喷头模拟雨凇覆冰降水,参考标准IEEE 1783TM—2009[24]控制水雾流量,进行雨凇覆冰试验。试验前对普通叶片和电热超疏水涂层叶片称重并记录。
表2 风力机参数
Tab.2 Wind turbine parameters

参数数值 型号NE-100S 额定功率/W100 起动风速/(m/s)2 额定风速/(m/s)10
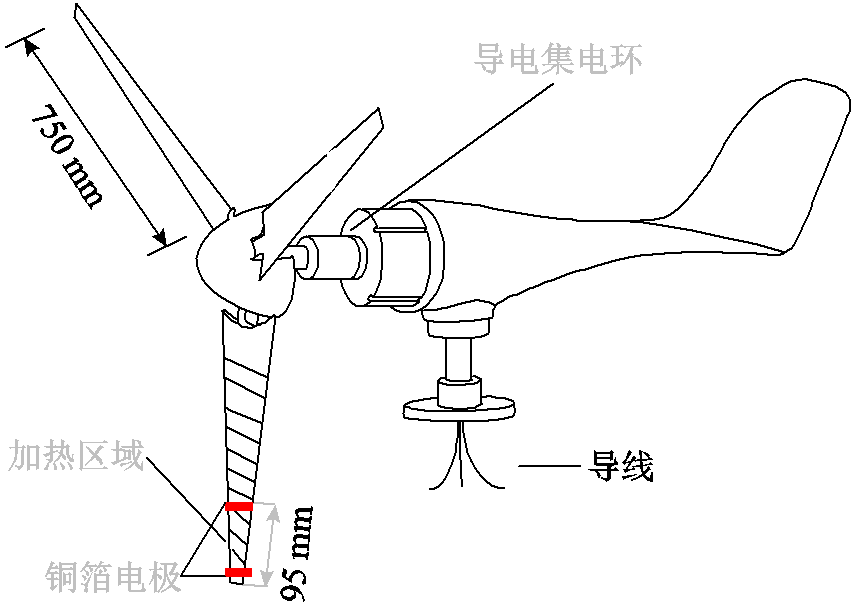
图9 安装电热超疏水叶片的风力机示意图
Fig.9 Schematic diagram of a wind turbine with electrically heated super-hydrophobic blades

图10 导电集电环安装实物图
Fig.10 Physical drawing of conductive slip ring installation
2.2.1 无电热防覆冰试验
无电热防覆冰试验步骤如下:
(1)先对覆冰水进行净化以免堵塞喷头,放置于人工气候室降温至5℃左右。
(2)设置气候室的雨凇覆冰环境参数,开启喷雾系统。
(3)将涂覆涂层的环氧树脂板和100 W风力机放置在气候室预定位置,开启鼓风机输送风力,待涂层上出现少量积冰后开始计时。
(4)达预定时间后关闭鼓风机,检查是否有冰层残缺,若无,拍照记录叶片冰型以及涂层冰型,同时进行称重;若有,放弃此组试验。
(5)清理叶片及涂层的积冰和水渍后,放置在70℃恒温箱确保叶片及涂层表面干燥,再重新开启下次试验。
2.2.2 电热防覆冰试验
电热防覆冰试验步骤与无电热防覆冰试验步骤一致,只是在覆冰过程中通过导电集电环元件连接旋转叶片上的电热涂层与交流电源,给涂层两端施加一定的电压,在叶片旋转的同时对涂层进行电加热。
1)涂覆涂层的环氧树脂板电加热融冰试验步骤如下:
(1)形成三类冰型。在人工气候室内按照2.2.1节人工覆冰的试验方法在涂覆涂层的环氧树脂板上生成所需的三类冰型。
(2)进行电加热融冰。关闭喷淋系统,保持4 m/s的风速,加适当电压使功率达到预定值(1 413 W/m2)。
(3)获取融冰功率为预定值时的融冰状况。加压一定时间后,关闭电源,观察融化冰层的表面形貌,使用游标卡尺测量冰层融化后出现的空气间隙。
(4)后续试验工作。一组试验完成后,关闭交流电源。仔细地去除涂覆涂层的环氧树脂板表面已有的积冰,利用纸巾吸取涂层表面液体,放置在70℃恒温箱中干燥5~10 min,并重新开始下一组试验。
2)涂覆涂层环氧树脂板临界融冰试验方法与步骤如下:
(1)形成三类冰型。在人工气候室内按照2.2.1节人工覆冰的试验方法在涂覆涂层的环氧树脂板上生成所需的三类冰型。
(2)获取临界融冰功率。关闭喷淋系统,保持4 m/s的风速,去除电极表面覆冰,并将热电偶放置在冰层、涂层和空气交界处,开始逐步加压,一边观察叶片的升温情况,一边缓慢调整电压,使得叶片温度趋近于0℃。
(3)试验结果获取。当冰层、涂层和空气交界处温度达到并维持0℃时,记录此时所施加的电压数值和覆冰冰型。
(4)后续试验工作。一组试验完成后,关闭电源。仔细地去除涂层表面已有的积冰,放置在70℃恒温箱中干燥,利用纸巾使涂层表面完全干燥,并重新开始下一组试验。
3)临界融冰功率获取方法为:将临界融冰试验中涂覆涂层的风力机叶片使用万用表测量涂层的电阻R,给涂层施加临界融冰电压,接入电流表测量得到临界融冰电流I,进而可由式(12)和式(13)计算得到临界融冰功率q。
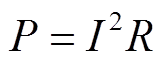 (12)
(12)
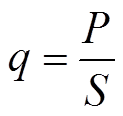 (13)
(13)
式中,P为融冰功率;S为涂层面积。
2.4.1 无电热防覆冰结果
风力机叶片的迎风面及叶尖前沿部分是覆冰的主要区域,因此本文针对迎风面进行分析。不同覆冰时间下,涂覆电热超疏水涂层风力机叶片迎风面与普通风力机叶片迎风面覆冰形貌如图11所示。

图11 风力机叶片覆冰后的迎风面覆冰形貌(左:涂覆涂层,右:无涂层)
Fig.11 The icing morphology of the windward side of the fan blades (left: coated, right: uncoated)
覆冰20~30 min后,电热超疏水叶片迎风面覆冰面积远小于普通叶片迎风面,只有叶尖部分由于叶片旋转水滴聚集以及过冷却水碰撞形成少许覆冰;普通叶片表面水滴在叶片表面形成水膜,冻结速度快,在迎风面表面形成连续覆冰,且从叶根到叶尖逐渐增厚。经分析,此阶段的电热超疏水叶片由于其超疏水性能,水滴冻结缓慢,与普通叶片相比有良好的防雨凇性能。
覆冰40~50 min后,电热超疏水叶片由于其超疏水性能迎风面不易留存水滴,水滴大量聚集在叶尖部分并冻结,使得其叶尖部分覆冰比普通叶片叶尖覆冰严重;试验期间发现一旦电热超疏水叶片迎风面出现如图12所示的乳突状覆冰,覆冰重量将会大幅增加,原因是雨凇覆冰喷雾中微小的水滴沉积在粗糙结构中(如图13所示),一方面提高了水滴的吸附能力,另一方面乳突状冰柱增大了冰层的表面积,增加了过冷液滴的碰撞概率。因此,一定覆冰时间过后,电热超疏水叶片的覆冰严重程度会大于普通叶片表面,表3中覆冰质量增长情况佐证了这一结论。

图12 乳突状特殊冰型
Fig.12 Papillary special ice type
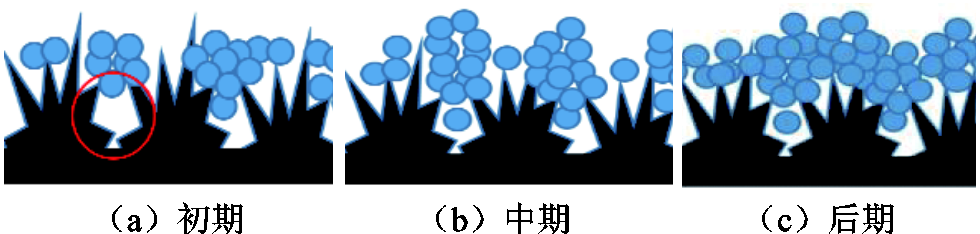
图13 过冷液滴撞击疏水表面冻结示意图
Fig.13 Schematic diagram of freezing of supercooled droplets impacting on a hydrophobic surface
表3 覆冰质量
Tab.3 Ice weight

叶片类型覆冰质量/g 20 min30 min40 min50 min 无涂层叶片90.8140.2168.1253.7 有涂层叶片77.9118.6198.2289
2.4.2 电加热防覆冰结果
电加热防覆冰试验结果如图14所示,可见在电热超疏水叶片迎风面的电加热区域,经60 min电热防覆冰试验后,无覆冰生成且表面干燥。

图14 电加热防覆冰试验结果
Fig.14 Electric heating anti-icing test results
这是因为加电压后,涂层表面温度升高,一方面微小的水滴无法侵入涂层的粗糙结构,可以一直保持超疏水状态;另一方面,电加热功率可以令涂层表面一直保持0℃以上,使得水滴无法冻结。
2.5.1 融冰试验验证结果
融冰试验结果如图15所示。初期覆冰5 min加压10 min,冰层已基本融化;中期覆冰10~15 min,加压14~16 min,冰层出现1~2 mm高的空腔;后期覆冰30 min加压18~20 min,冰层同样出现了1~2 mm的气隙。将数值计算中的0℃等温线作为冰层融化与未融化的分界线,对比图5b、图6b和图7b中20 min电加热温度分布可知,除了图5b两端顶点处温度未达0℃以上,其余各处均满足冰层融化要求。绘制融化20 min时的等温线如图16所示,图中红色虚线即为0℃等温线,冰层融化厚度约为1~2 mm,中间处冰融化最多,并向两边递减。融冰试验结果与仿真计算结果较为一致。

图15 融冰试验结果
Fig.15 Melting test results
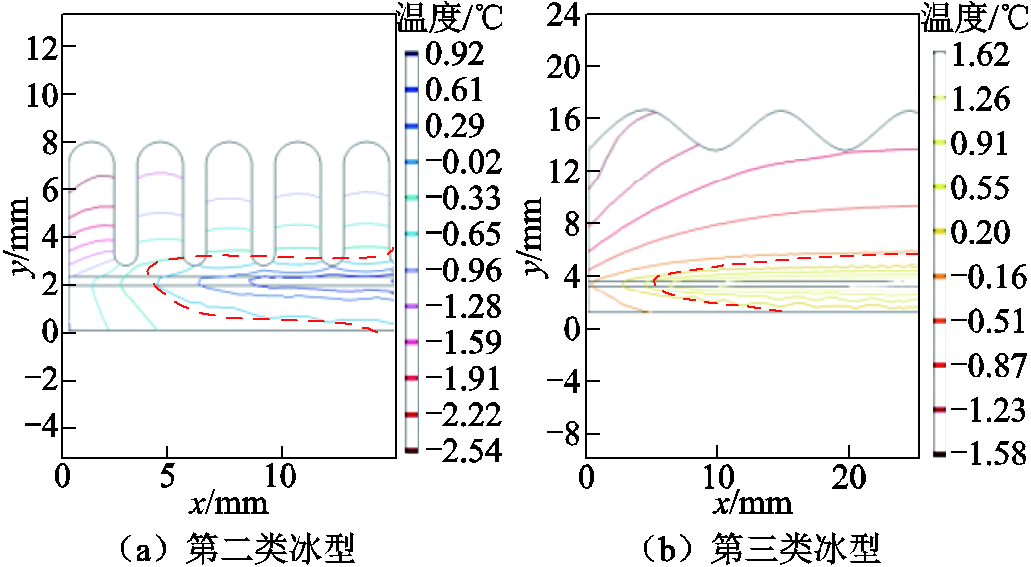
图16 融化20 min时0℃等温线
Fig.16 0℃ isotherm when melting for 20 min
2.5.2 临界融冰功率试验验证结果
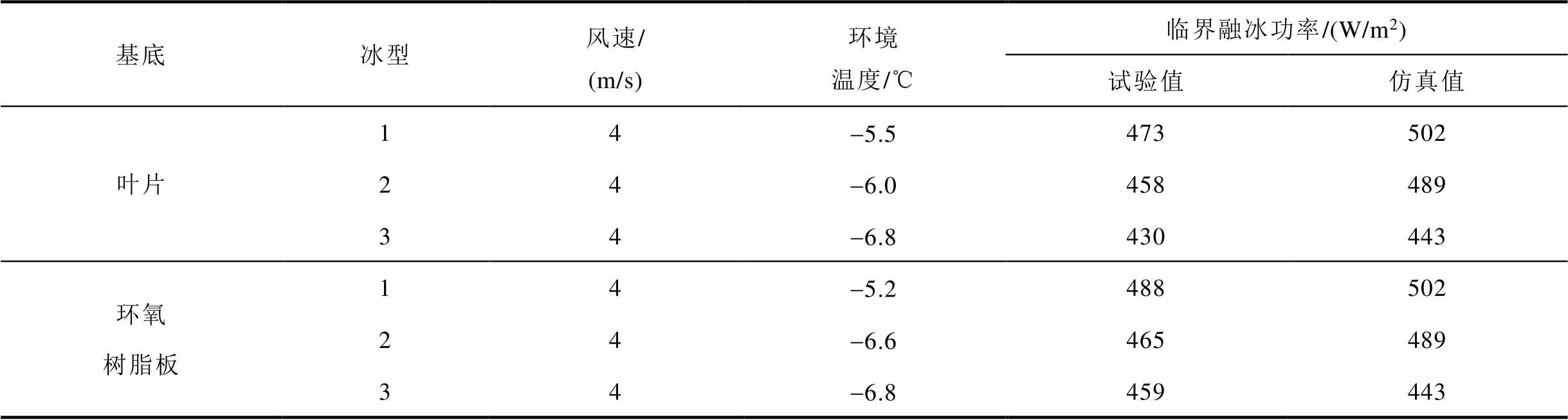
表4给出了临界融冰功率试验结果与仿真结果的对比情况。由表4可知,不同基底下的电热超疏水涂层临界融冰功率的试验结果与仿真结果较为接近。对试验值与仿真值的误差进行计算,可得最大误差为6.8%,平均误差为3.4%。验证试验结果表明,本文所建立的基于电热超疏水叶片正表面覆冰冰型的数值计算方法切实可行。
表4 不同基底临界融冰功率的试验与仿真结果
Tab.4 Experimental and simulation results of critical ice melting power for different substrates
基底冰型风速/(m/s)环境温度/℃临界融冰功率/(W/m2) 试验值仿真值 叶片14-5.5473502 24-6.0458489 34-6.8430443 环氧树脂板14-5.2488502 24-6.6465489 34-6.8459443
本文将文献[19]制备的电热超疏水涂层应用于风力机叶片进行防冰、融冰试验,从电热超疏水涂层覆冰试验中总结出三类冰型,建立了电热超疏水涂层电加热融冰数值计算模型,仿真计算了不同冰型电加热融冰的温度分布以及不同冰型下的临界融冰功率,并在人工气候室开展了电加热融冰试验进行验证。得出的主要结论有:
1)超疏水特性让叶片在覆冰前期具有一定的延缓覆冰能力,但一旦产生覆冰,覆冰增长速度将快于普通叶片;电热性能与超疏水性能共同作用时具有优良的防覆冰能力。
2)针对电热超疏水涂层覆冰的三类不同的冰层形貌,建立了电加热融冰数值计算模型,能有效地模拟融冰过程和温度分布,所得结果与试验结果具有较好的一致性。
3)从临界融冰功率计算结果可知,超疏水涂层融冰所需功率略大于非超疏水涂层电热融冰,尤其是在乳突状冰层出现后,故电热超疏水涂层用于风力机防覆冰具有较好的效果,但用于覆冰后融冰将需要更多的能量。
参考文献
[1] 胡琴, 杨大川, 蒋兴良, 等. 叶片模拟冰对风力发电机功率特性影响的试验研究[J]. 电工技术学报, 2020, 35(22): 4807-4815. Hu Qin, Yang Dachuan, Jiang Xingliang, et al. Experimental study on the effect of blade simulated icing on power characteristics of wind turbine[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4807-4815.
[2] 李程. 浅谈风电机组覆冰的影响及应对措施[J]. 科技创新导报, 2019, 16(15): 93-94.
[3] Barker A, Timco G, Gravesen H, et al. Ice loading on Danish wind turbines part 1: dynamic model tests[J]. Cold Regions Science and Technology, 2005, 41(1): 1-23.
[4] Gravesen H, Sørensen S L, Vølund P, et al. Ice loading on Danish wind turbines: part 2. Analyses of dynamic model test results[J]. Cold Regions Science and Technology, 2005, 41(1): 25-47.
[5] Lehtomäki V, Rissanen S, Wadham-Gagnon M, et al. Fatigue loads of iced turbines: two case studies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 158: 37-50.
[6] 李剑, 王湘雯, 黄正勇, 等. 超疏水绝缘涂层制备与防冰、防污研究现状[J]. 电工技术学报, 2017, 32(16): 61-75. Li Jian, Wang Xiangwen, Huang Zhengyong, et al. Research of preparation, anti-icing and anti-pollution of super hydrophobic insulation coatings[J]. Tran-sactions of China Electrotechnical Society, 2017, 32(16): 61-75.
[7] 徐兵兵, 黄月文, 王斌. 改性SiO2/聚硅氧烷无氟超疏水涂层的制备及性能[J]. 精细化工, 2019, 36(10): 2009-2015. Xu Bingbing, Huang Yuewen, Wang Bin. Preparaion and performance of fluorine-free superhydrophobic coatings based on modified silica and polysiloxane[J]. Fine Chemicals, 2019, 36(10): 2009-2015.
[8] Zhang Fan, Qian Hongchang, Wang Luntao, et al. Superhydrophobic carbon nanotubes/epoxy nanocomposite coating by facile one-step spraying[J]. Surface and Coatings Technology, 2018, 341: 15-23.
[9] 张迅, 曾华荣, 田承越, 等. 大气压等离子体制备超疏水表面及其防冰抑霜研究[J]. 电工技术学报, 2019, 34(24): 5289-5296. Zhang Xun, Zeng Huarong, Tian Chengyue, et al. Super-hydrophobic surface prepared by atmospheric-pressure plasma and its anti-icing, anti-frosting performance[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5289-5296.
[10] Zhao Yushun, Li Jian, Hu Jianlin, et al. Icing performances of super-hydrophobic PDMS/Nano-silica hybrid coating on insulators[C]//2010 International Conference on High Voltage Engineering and Application, New Orleans, LA, USA, 2010: 489-492.
[11] Mohseni M, Amirfazli A. A novel electro-thermal anti-icing system for fiber-reinforced polymer composite airfoils[J]. Cold Regions Science and Technology, 2013, 87: 47-58.
[12] 蒋兴良, 孟志高, 张志劲, 等. OPGW临界融冰电流及其影响因素[J]. 电工技术学报, 2016, 31(9): 174-180. Jiang Xingliang, Meng Zhigao, Zhang Zhijin, et al. Critical ice-melting current of ice-covered OPGW and its impacting factors[J]. Transactions of China Electrotechnical Society, 2016, 31(9): 174-180.
[13] 舒立春, 谭进峰, 胡琴, 等. 网格尺寸对碳纤维丝束风力发电机叶片融冰效果的影响研究[J]. 中国电机工程学报, 2019, 39(13): 4008-4015. Shu Lichun, Tan Jinfeng, Hu Qin, et al. Study on the effect of mesh size on carbon fiber tow wind turbine blade ice melting[J]. Proceedings of the CSEE, 2019, 39(13): 4008-4015.
[14] 龚奕宇. 绝缘子半导体超疏水复合涂层的制备方法与防雾冰性能[D]. 重庆: 重庆大学, 2012.
[15] Mayer C, Ilinca A, Fortin G, et al. Wind tunnel study of electro-thermal de-icing of wind turbine blades[J]. International Journal of Offshore and Polar Engineering, 2007, 17(3): 182-188.
[16] 邱刚, 舒立春, 胡琴, 等. 风力发电机叶片防冰的数值计算模型及现场试验研究[J]. 中国电机工程学报, 2018, 38(7): 2198-2204, 2235. Qiu Gang, Shu Lichun, Hu Qin, et al. Numerical anti-icing model and field experimental investigation of wind turbine blade[J]. Proceedings of the CSEE, 2018, 38(7): 2198-2204, 2235.
[17] 倪爱清, 王延明, 王继辉, 等. 基于高分子电热膜的风电叶片电热除冰功率密度计算模型[J]. 玻璃钢/复合材料, 2015(9): 17-23. Ni Aiqing, Wang Yanming, Wang Jihui, et al. Computational model of wind turbine blades de-icing power density based on polymer electric heating film[J]. Fiber Reinforced Plastics/Composites, 2015(9): 17-23.
[18] 黄亚飞, 蒋兴良, 任晓东, 等. 采用涡流自热环防止输电线路冰雪灾害的方法研究[J]. 电工技术学报, 2021, 36(10): 2169-2177. Huang Yafei, Jiang Xingliang, Ren Xiaodong, et al. Study on preventing icing disasters of transmission lines by use of eddy self-heating ring[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2169-2177.
[19] 胡琴, 朱茂林, 舒立春, 等. 风力发电机叶片防除冰涂层(一):制备及性能测试[J]. 电工技术学报, 2023, 38(24): 6839-6849. Hu Qin, Zhu Maolin, Shu Lichun, et al. Anti-icing coatings for wind turbine blades part 1: preparation and performance testing[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6839-6849.
[20] 王经. 传热学与流体力学基础[M]. 上海: 上海交通大学出版社, 2007.
[21] Voller V R, Prakash C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems[J]. International Journal of Heat and Mass Transfer, 1987, 30(8): 1709-1719.
[22] Voller V R, Swaminathan C R, Thomas B G. Fixed grid techniques for phase change problems: a review[J]. International Journal for Numerical Methods in Engineering, 1990, 30(4): 875-898.
[23] 舒立春, 任晓凯, 胡琴, 等. 环境参数对小型风力发电机叶片覆冰特性及输出功率的影响[J]. 中国电机工程学报, 2016, 36(21): 5873-5878, 6031. Shu Lichun, Ren Xiaokai, Hu Qin, et al. Influences of environmental parameters on icing characteristics and output power of small wind turbine[J]. Proceedings of the CSEE, 2016, 36(21): 5873-5878, 6031.
[24] IEEE Dielectrics and Electrical Insulation Society. IEEE guide for test methods and procedures to evaluate the electrical performance of insulators in freezing conditions: IEEE 1783—2009[S]. IEEE, 2009.
Abstract According to the observation and statistics of the ice morphology on the surface of the electrothermal superhydrophobic coating, the coating shows three different types of ice morphology in the process of ice coating. The first ice type, the ice coating is scattered on the surface of the coating in blocks, mostly in the early stage of ice coating; The second ice type, the coating is almost covered by ice, forming a papillary ice layer, mostly in the middle of the ice coating; The third ice type, which is fully covered with corrugated ice, is similar to the non superhydrophobic coating ice type, and mostly occurs in the late stage of ice coating. Based on these three types of icing, a numerical calculation model of electric heating ice melting is established, including the calculation model of coating temperature rise and critical deicing power. The results of the simulation model are verified by experiments. The experimental results are basically consistent with the simulation results. The model can effectively simulate the ice melting process and temperature distribution of the electrothermal superhydrophobic coating. The anti icing and deicing tests of fan blades coated with electrothermal superhydrophobic coatings are carried out in this paper. The results of relevant simulation calculations and icing tests are as follows:
The calculation results of the critical deicing power show that: The increase of the ice thickness of the common electrothermal coating hinders the loss of the coating heat, and the critical deicing power decreases; For the first ice type of electrothermal superhydrophobic coating, the deicing power required for power supply heating is small; For ice type 2, due to the formation of its columnar ice type, the convective heat transfer area increases, the heat loss increases, and the critical ice melting power is large; The ice type 3 is similar to the ice coated type of ordinary coating, the ice thickness hinders the heat loss of the coating, and the required deicing power is roughly equivalent to that of ordinary electrothermal coating. The calculation results indicate that the power required for ice melting of electrothermal superhydrophobic coatings is greater than that of non superhydrophobic electrothermal coatings, especially after the emergence of papillary ice, the ice melting power will increase significantly.
The results of the anti-icing and deicing test of the electrothermal superhydrophobic coating show that: In the glaze icing environment, when the superhydrophobic performance acts alone, the blade can delay the ice coating in the early stage of the ice coating. Once the papillary ice coating appears on the windward side of the electrothermal superhydrophobic blade, the ice coating weight will increase significantly, and with the increase of the ice coating time, the ice coating severity will be greater than that of the ordinary blade surface; When electrothermal performance and superhydrophobic performance are combined, no ice coating is formed on the blade coating surface. The synergistic effect of electrothermal superhydrophobic coating has a good effect on anti-icing of wind turbine, but it will require more energy when used for ice melting after icing.
keywords:Wind turbine, super-hydrophobic electric heating coating, anti-icing, numerical model, manual test
DOI:10.19595/j.cnki.1000-6753.tces.221778
中图分类号:TM242
国家自然科学基金(51977016)和重庆市科技局(cstc2021jscx-dxwtB0002)资助项目。
收稿日期 2022-09-19
改稿日期 2022-11-03
胡 琴 男,1981年生,教授,博士生导师,研究方向为电网防冰减灾。E-mail:huqin@cqu.edu.cn(通信作者)
朱茂林 男,1994年生,硕士研究生,研究方向为风力发电机电热超疏水涂层制备及性能。E-mail:1584118777@qq.com
(编辑 李 冰)