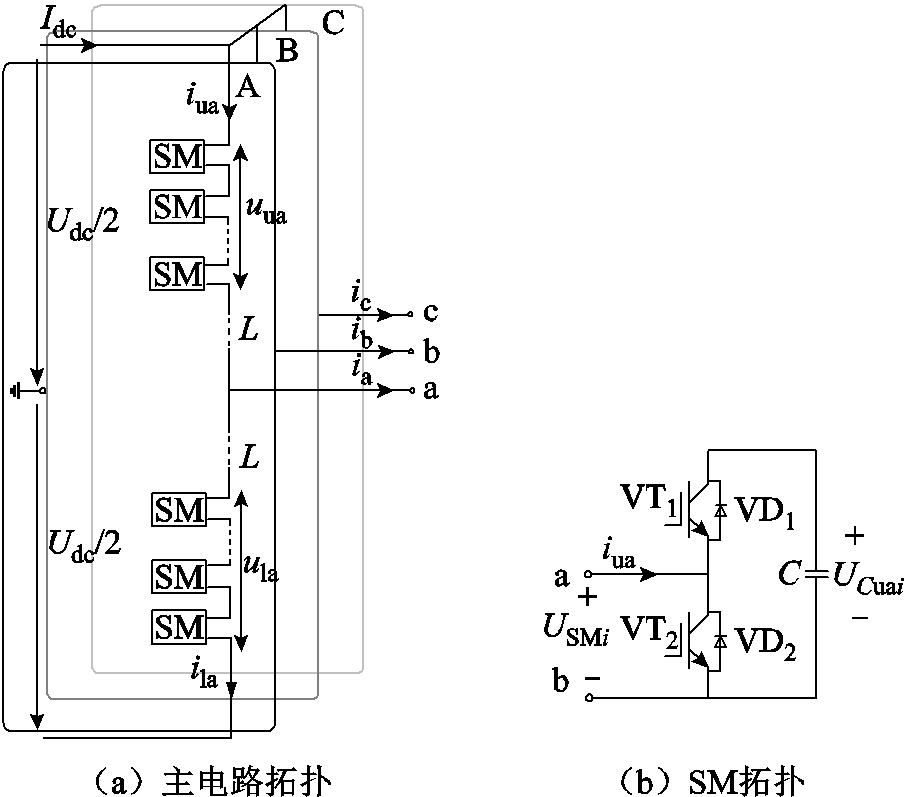
图1 MMC拓扑结构
Fig.1 MMC topology
摘要 模块化多电平换流器（MMC）子模块（SM）发生故障时，快速检测到故障并定位故障SM是提升MMC可靠性的关键。现有研究基于经验的阈值设置在不同运行功率间难以推广。针对于此，提出一种适用于不同运行功率的最近电平调制（NLM）策略下MMC子模块开路故障诊断策略。所提策略通过判断SM电容电压预测值与实际值间的绝对误差是否超出阈值来检测并定位故障。通过数学推导给出了设置阈值的可靠依据，并验证了当运行功率发生改变时无需重新手动设置阈值，与现有研究相比降低了阈值设置难度。此外，所提策略整合了现有策略的优点，包括无需额外硬件，计算负担小，诊断速度快（＜20ms），适用于多个SM发生故障的情形等。同时，通过理论分析验证了所提策略不仅适用于NLM策略的情形，在调整SM开关函数的预测方法后可推广至其他MMC调制策略。在硬件在环平台中的实验结果验证了该策略可以在不同功率点准确、快速地诊断出两种MMC子模块开路故障。
关键词：模块化多电平换流器 运行功率 故障诊断 绝对误差
模块化多电平换流器（Modular Multilevel Converter, MMC）具有模块化结构、冗余配置及功率可拓展等特点[1-3]。这些优势使MMC在高压大功率场景中得到了广泛应用，例如高压直流（High Voltage Direct Current, HVDC）输电系统、海上风电等[4-7]。
随着MMC的电压等级和功率不断提升，其子模块（Sub-Module, SM）数量也随着增加，可靠性问题凸显，任何一个SM中绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）发生故障均会影响MMC的正常运行，甚至会进一步导致其他元件损坏，最终导致整个系统崩溃[8]。IGBT故障可分为短路故障和开路故障两种。其中，短路故障通常会导致过电流现象，危害较大，但目前工程中已有成熟的解决方案，即在栅极驱动器集成了短路保护，在短路故障时，会迅速闭合开关，切除短路SM[9]。而与短路故障相比，由键合线脱落或栅极驱动电路故障引起的开路故障不会立即损坏SM，可能会在很长一段时间内未被检测到[10-11]。同时，据估计，变流器故障中有超过38%的故障是由IGBT开路故障引起的[12]。而最近电平调制（Nearest Level Modulation, NLM）由于动态性能好、实现简便等优点，被广泛应用于高电平数的MMC中。因此，本文重点研究了NLM策略下MMC的子模块开路故障诊断策略。
目前，国内外研究学者已经提出一些MMC子模块开路故障诊断策略，主要可以分为两类：基于硬件的故障诊断策略和基于软件的故障诊断策略。
第一类是基于硬件的故障诊断策略[13-15]。文献[15]提出了一种基于改进泄放电阻电路（Rearranged Bleeding Resistor Circuit, RBRC）的故障检测方法，通过RBRC和SM开关函数的逻辑输出来识别故障，能够适用于不同运行功率的情形。这些策略简单可靠，但由于其诊断过程需要引入额外的硬件电路，因此会导致整个系统成本的增加。
第二类是基于软件的故障诊断策略。文献[16-18]利用观测器对故障进行诊断。文献[16-17]应用滑模观测器检测并定位SM故障，文献[18]采用卡尔曼滤波器检测SM故障，并通过比较SM电容电压来定位故障SM。这些诊断策略无需额外的传感器，但它们普遍存在计算复杂度高、诊断时间长等缺点。文献[19-21]引入人工智能（Artificial Intelligence, AI）算法对故障进行诊断。文献[19]中提出基于SM电压相似性的故障诊断策略，通过计算同一桥臂中两两SM的电容电压相关系数对故障SM进行定位。文献[20]提出基于一维卷积神经网络（Convolutional Neural Network, CNN）的故障诊断策略，通过将大量原始电流及电压数据发送至CNN实现故障诊断。文献[21]根据相邻滑动时间窗间的特征关系提取MMC的特征，并使用二维神经网络对MMC中的开路故障进行检测和定位，能够适用于不同运行功率的情形。这些引入AI算法的诊断策略同样无需额外硬件，但算法计算量较大，会加重控制器计算负担，这一点随着SM数量上升将越发显著。文献[22-25]则利用模型对故障进行诊断。文献[22]中提出基于单环定理的故障诊断策略，利用单环定理提供的平均光谱半径检测故障，利用箱线图的异常点识别定位故障SM。文献[23]中通过判断子模块序列队首（First in the SM Number, FSN）检测故障，并针对同一桥臂中多SM同时发生故障的情形提出辅助定位策略。文献[24]通过计算SM电容累计放电电压对故障SM进行定位。文献[25]依据SM组电压的估计值和计算值间的差异是否超出阈值判断故障。这些基于模型的诊断策略具有无需额外硬件、计算负担小、诊断时间短等优势，具有良好的应用前景。但其诊断过程通常需要手动设置经验阈值，该阈值设定的准确性直接决定了诊断方法的准确性，由于这些文献中并未给出所设阈值与运行功率间的具体关系，因而当MMC运行于不同功率时，现有策略阈值的设置及推广较为困难[9,21]，阻碍了基于模型的故障诊断策略的进一步发展。
对此，本文提出了一种适用于不同运行功率的NLM策略下MMC子模块开路故障诊断策略。所提策略根据SM投入个数及SM电容电压排列位置预测SM开关函数，进而预测对应SM电容电压，之后通过判断SM电容电压预测值与实际值间的绝对误差是否超出阈值来检测并定位故障。与现有研究中受运行功率影响的依据相比，所提方法在MMC运行功率发生改变时，无需重新手动设置诊断阈值，极大地降低了阈值设定的难度。此外，所提策略还整合了现有策略的优点，如无需额外硬件，计算负担小，诊断速度快（＜20 ms），适用于多个SM发生故障的情形等。同时，通过理论分析验证了所提策略不仅适用于NLM策略的情形，在调整SM开关函数的预测方法后可推广至其他MMC调制策略。最后在搭建的硬件在环（Hardware-in-the-Loop, HIL）实验平台上验证了本文所提的诊断策略可以在不同功率点准确、快速地诊断出两种MMC子模块开路故障。
三相MMC拓扑结构如图1a所示。MMC拓扑结构采用三相六桥臂结构，每相包含上、下两个桥臂，每个桥臂由N个SM，桥臂电抗器L及桥臂等效电阻R组成。图中，uuj和ulj分别为j相上、下桥臂中SM的总电压；Udc为直流母线电压；uoj为相对于中性点的输出电压；iuj和ilj分别为j相上、下桥臂电流；j=a, b, c。
图1 MMC拓扑结构
Fig.1 MMC topology
a相上桥臂第i个SM如图1b所示，SM采用半桥型结构，由2个IGBT、2个反并联二极管和1个直流电容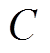
组成。正常运行时，SM的输出电压USMi可以表示为
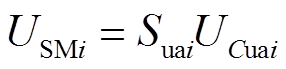（1）
式中，UCuai为SM电容电压；Suai为a相上桥臂第i个SM对应开关函数。当上管VT1导通，下管VT2截止时，Suai=1，该SM被投入；当VT1截止，VT2导通时，Suai=0，该SM被切除。
不同状态下SM行为见表1。对于一个正常子模块，其有四种运行模式。在模式1中，iua≥0且Suai=1，SM被投入，SM电容处于充电状态；在模式2中，iua≥0，且Suai=0，SM被切除，SM电容处于旁路状态；在模式3中，iua＜0且Suai=1，SM被投入，SM电容处于放电状态；在模式4中，iua＜0且Suai=0，SM被切除，SM电容处于旁路状态。
表1 不同状态下SM行为
Tab.1 SM behavior in different states
状态iuaSuai流经器件USMi电容状态 正常SM≥01VD1UCuai充电 0VT20旁路 ＜01VT1UCuai放电 0VD20旁路 类型Ⅰ： S1开路≥01VD1UCuai充电 0VT20旁路 ＜01VD20放电→旁路 0VD20旁路 类型Ⅱ： S2开路≥01VD1UCuai充电 0VD1UCuai旁路→充电 ＜01VT1UCuai放电 0VD20旁路
MMC a相上臂的电容电压平衡控制如图2所示。首先接收来自换流器控制器的桥臂SM投入数目指令Non，并根据电容电压降序排列臂中的N个SM。当桥臂电流iua≥0时，投入电压较低的Non个子模块；当iua＜0时，投入电压较高的Non个子模块，以此保证子模块电容电压的动态平衡。
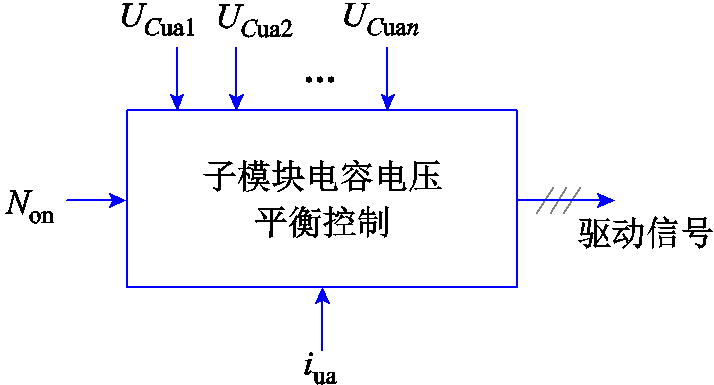
图2 MMC电容电压平衡控制
Fig.2 MMC capacitor voltage balance control
SM开路故障的两种类型如图3所示。VT1开路故障，本文称为Ⅰ型故障；VT2开路故障，本文称为Ⅱ型故障。
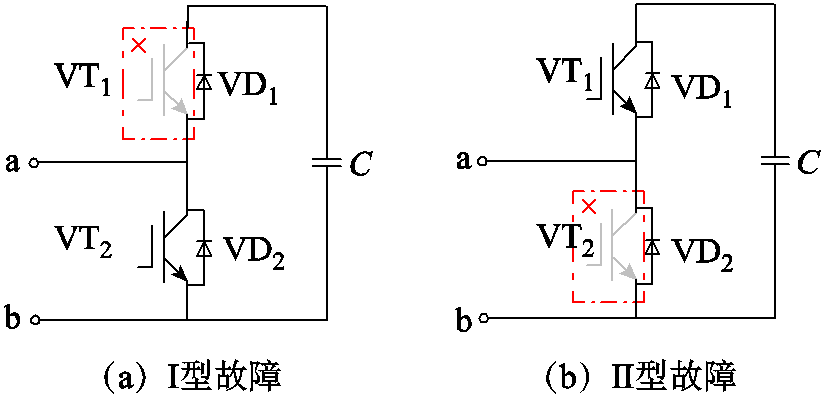
图3 SM开路故障的两种类型
Fig.3 Two types of SM open circuit faults
如式（1）所示，对于正常SM，其输出电压由开关函数和电容电压共同决定。而当SM发生开路故障时，存在两种异常状态，如表1中标记所示。当发生Ⅰ型故障时，故障SM在iua＜0时不受开关函数控制，SM电容始终被旁路；当发生Ⅱ型故障时，故障SM在iua≥0时不受开关函数控制，SM电容始终被充电。
当iua＜0且发生Ⅰ型故障时，根据表1，故障SM电容将始终被旁路，其电容电压将保持不变。而正常SM会受均压控制依次被投入放电，电容电压会降低，因此在iua＜0时，故障SM电容电压将超出正常SM电容电压。
当iua≥0且发生Ⅱ型故障时，根据表1，故障SM电容始终被充电，其电容电压将不断升高。而正常SM会受均压控制依次被投入充电，电容电压的增幅小于故障SM。因此在iua≥0时，故障SM电容电压将超出正常SM电容电压。
综上所述，无论发生何种类型开路故障，故障SM电容电压在其产生故障特征时间段内均会超出正常SM电容电压。
对于电容电压最大SM，若当前iua≥0且Non＜N，由于均压控制，该SM应被旁路以防止其电容电压进一步增大；若当前iua＜0且Non＞0，由于均压控制，该SM应被投入以使其电容电压下降。若该SM为正常SM，则其行为与上述分析一致，但若其为故障SM，由于如表1中所示的异常行为，会与上述分析不一致，由此可提出故障诊断策略。
以a相上桥臂为例进行说明，令第k个控制周期桥臂电流采样值为iua(k)，电容电压最大SM的电容电压采样值为UC_max(k)。
若iua(k)≥0，按照2.2节中分析，若此时刻桥臂SM投入指令Non(k)＜N，则电容电压最大SM应被旁路，即对应开关函数Suai(k)=0，据此可预测该SM在k+1个周期电容电压UC_est(k+1)表达式为
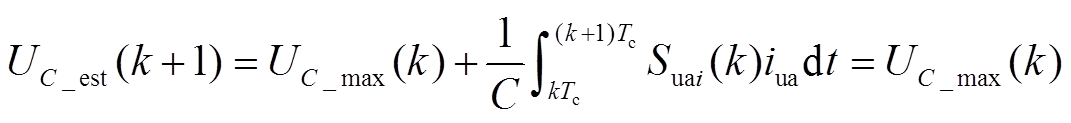（2）
式中，Tc为控制周期。由该SM第k+1个周期的实际值UC_rea(k+1)和预测值UC_est(k+1)，可计算二者之间绝对误差为
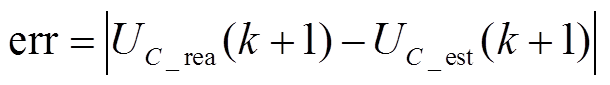（3）
当该SM正常时，通过式（3）计算所得err是一较小值。而若该SM发生了Ⅱ型故障，由于其故障特性，本应被旁路的SM被投入充电，电容电压升高，则UC_rea(k+1)可表示为
（4）
由于Tc足够小，因此可以进行平均近似，用iua(k)和iua(k+1)的平均值来近似iua在第k个周期到第k+1个周期之间的取值，因此有
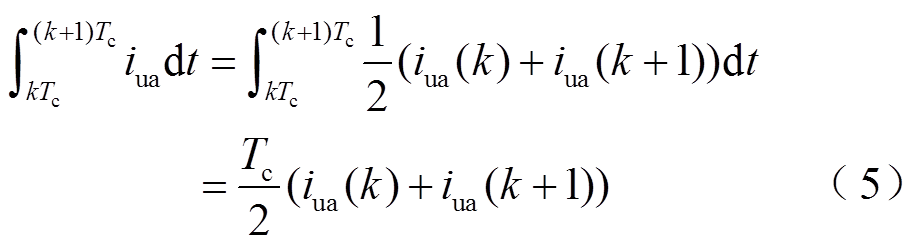
则由式（3）～式（5），此时err可表示为
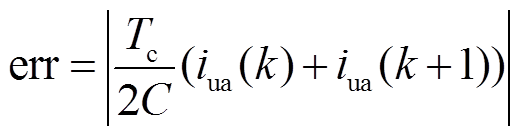（6）
而若iua(k)＜0，按照2.2节中分析，若Non(k)＞0，则电容电压最大，SM应被投入，即对应开关函数Suai(k)=1，据此可预测UC_est(k+1)表达式为
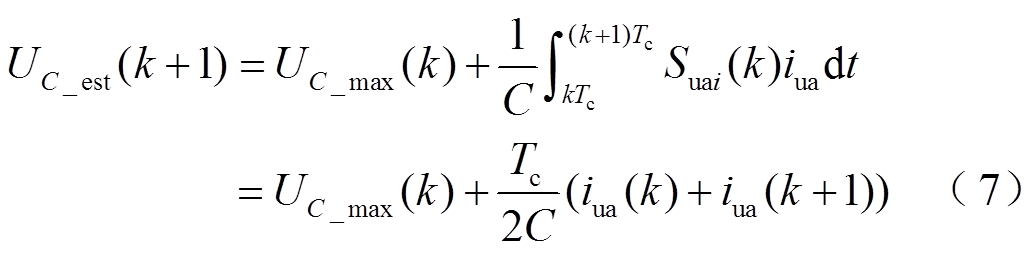
式中，UC_max(k)为第k个控制周期电容电压最大SM的电容电压采样值。
当该子模块为正常SM时，通过式（3）计算所得err是一较小值。而若该SM发生了Ⅰ型故障，由于其故障特性，本应被投入放电的SM被旁路，电容电压不变，则UC_rea(k+1）可表示为
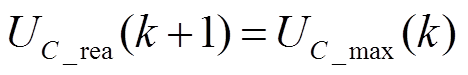（8）
由式（7）和式（8），此时err同样可以用式（6）来表示。从上述分析可以看出，SM正常运行时对应绝对误差errnormal是一较小值，而SM发生故障对应绝对误差errfault较大，据此可提出故障检测流程如图4所示。
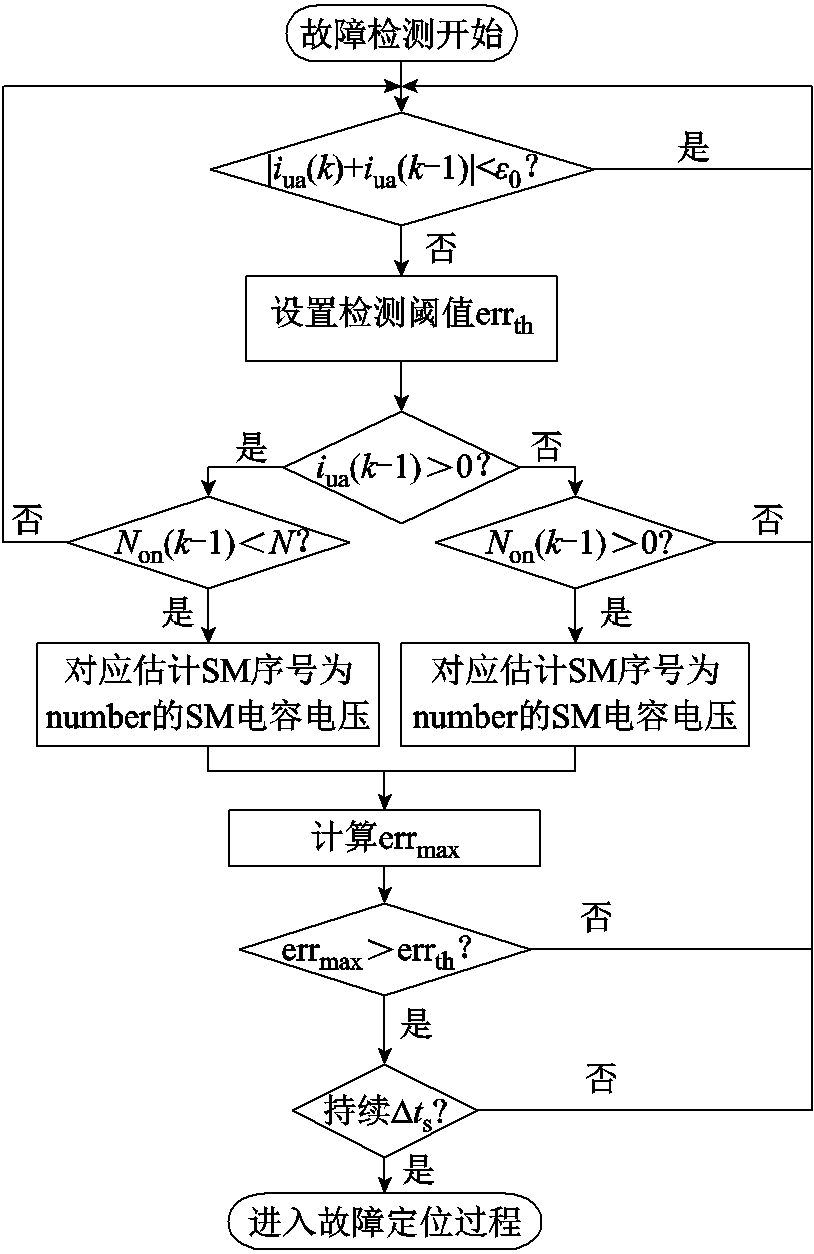
图4 检测流程
Fig.4 Detection flow chart
故障检测具体实现过程如下：
1）判断|iua(k)+iua(k-1)|是否小于电流过零滤除环节所设阈值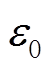
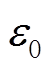，若其小于，说明此时桥臂电流大小不满足电流过零滤除环节，更新疑似故障SM_1序号number为本时刻电容电压最大SM序号，并记录其电容电压UC_max(k)，本控制周期故障检测结束；若其大于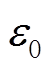，则对检测阈值errth进行设置。
2）判断iua(k-1)的正负，若其为正且Non(k-1)＜N，则按照式（2）估计SM序号为number的SM电容电压，若其为正但Non(k-1)=N，则更新number为本时刻电容电压最大SM，并记录其电容电压UC_max(k)，结束本周期故障检测；若iua(k-1)为负且Non(k-1)＞0，则按照式（7）估计SM序号为number的电容电压，若iua(k-1)为负且Non(k-1)=0，则同样更新疑似故障SM_1序号number为本时刻电容电压最大SM序号，并记录其电容电压UC_max(k)，结束本周期故障检测。
3） 按照式（3)计算errmax，并将其与设定阈值errth进行比较，若其小于errth，则说明此时不存在故障，更新疑似故障SM_1序号number为本时刻电容电压最大SM序号，并记录其电容电压UC_max(k)，结束本周期故障检测；若其大于errth但无法持续一段时间Dts，说明是误诊断现象，不存在故障，同样记录本时刻电容电压最大SM序号number及其电容电压UC_max(k)，结束本周期故障检测；而如果其大于errth且能够持续一段时间Dts，说明有故障发生，进入故障定位过程。
电流过零滤除环节是为了避免桥臂电流过零点附近造成的误诊断影响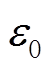，是电流过零滤除环节设置的阈值。当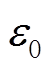取值较大时，对于err信号过零点附近发生SM开路故障的情况，可能由于电流过零滤除环节的存在导致无法诊断到故障，后续由于电流正负的改变故障特征暂时消失，但在电流正负再次变化时，故障特征会再次显现而被所提故障诊断策略识别；而当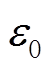取值较小时，依然有可能因为传感器误差、计算偏差等导致误诊断现象的发生。对此，本文选取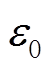为桥臂电流从负半轴穿过零点到正半轴时离电流过零点三个控制周期电流值的两倍，在实际工程中需根据现场调试情况进一步调整确定。
考虑到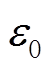和|iua(k)+iua(k-1)|的大小关系在一个工频周期内不易通过波形展示，因此将二者的大小关系转换为逻辑信号进行表示。当|iua(k)+iua(k-1)|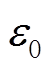＜，电流过零滤除环节输出逻辑0；反之则输出逻辑1。
Dts的存在是为了进一步消除传感器误差、通信丢包等影响，防止故障误报情况的存在，可取Dts=3～5Tc。
根据故障SM数量及发生故障类型可将其分为以下四类分别进行说明：
（1）桥臂中单个SM发生Ⅰ型故障或Ⅱ型故障。根据2.2节中分析，当只有一个故障SM，该SM在其故障特征时间段内为电容电压最大SM。
（2）桥臂中多个SM发生同种类型故障。根据2.2节中分析，当有多个故障SM时，这些SM电容电压在对应故障特征时间段内会超出正常SM电容电压。
（3）桥臂中两个SM分别发生Ⅰ型故障和Ⅱ型故障。在这种情况下，由于Ⅰ型故障和Ⅱ型故障产生故障特征时间段不同，任意时刻实际上仅有一个故障SM产生故障特征。根据2.2节中分析，当任意时刻实际上仅有一个故障SM产生故障特征，该SM在其故障特征时间段内为电容电压最大SM。
（4）桥臂中mI个SM发生Ⅰ型故障，mII个SM发生Ⅱ型故障。在这种情况下，由于Ⅰ型故障和Ⅱ型故障产生故障特征时间段不同，任意时刻实际上仅有mI或mII个故障SM产生故障特征。根据2.2节中分析，当有多个故障SM时，这些SM电容电压在对应故障特征时间段内会超出正常SM电容电压。
对于电容电压超出正常SM电容电压的故障SM，其会位于均压控制给出的排序队列前位。对于这些故障SM，只需对应Non的限制条件后，同样可以按照3.1节中的方式预测其开关函数，进而预测其电容电压，之后便可通过判断其err是否超过阈值来判断该SM是否为故障SM，据此提出的故障定位流程如图5所示。
图5 定位流程
Fig.5 Location flow chart
故障定位具体过程如下：
（1）判断|iua(k)+iua(k-1)|是否小于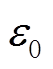
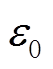，若其小于，说明此时桥臂电流大小不满足电流过零滤除环节，更新疑似故障SM_m序号number_m为本时刻电容电压最大SM序号，并记录其电容电压UC_max(k)，其中m的初值为2，本控制周期故障定位结束；若其大于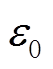，则对检测阈值errth进行设置。
（2）判断iua(k-1)的正负，若其为正且Non(k-1)＜N-m+1，则按照式（2）估计SM序号为number_m的SM电容电压，否则结束本周期故障检测；若iua(k-1)为负且Non(k-1)＞m-1，则按照式（7）估计SM序号为number_m的电容电压，否则结束本周期故障检测。
（3）按照式（3）计算errm，并将其与设定阈值errth进行比较，若其大于errth，说明该SM为故障SM，令故障数量标志m=m+1，之后返回到步骤（1）中，继续判断下一个位置的SM是否存在故障；若小于errth，说明该SM为正常SM，说明桥臂中只存在m-1个故障，输出故障SM数量及对应序号，故障诊断过程结束。
由于所提的故障检测和故障定位策略能够在单个故障时间段内完成一轮诊断过程，因此对于第一类情形和第二类情形，只需一轮诊断过程便能够定位所有故障SM。而对于第三类情形，其可以看作是两个第一类情形的叠加，第四类情形则可以看作是两个第二类情形的叠加，因此第三类情形和第四类情形需要两轮诊断过程定位所有故障SM。根据以上分析，所提故障可以适用于多个SM发生故障的情形。同时，无论发生何种情形，所提出的故障诊断策略均能在两轮诊断过程中，即一个工频周期内检测出故障并定位所有故障SM。
由3.1节中分析可知，正常SM的绝对误差errnormal是一较小值，而故障SM的绝对误差errfault较大，因此阈值errth需满足
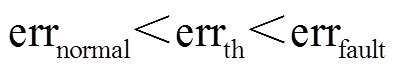（9）
当iua＜0且SM正常工作时，计算所得绝对误差errnormal_neg(k+1)可以表示为
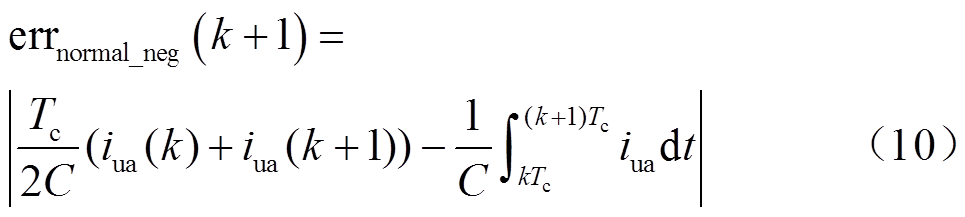
当iua＜0且SM发生Ⅰ型故障时，计算所得绝对误差errfault_I(k+1)可以表示为
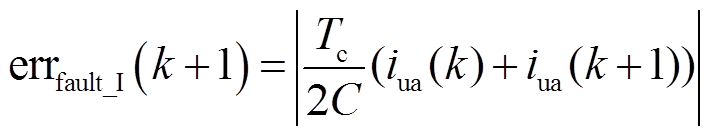（11）
当iua≥0且SM正常工作时，计算所得绝对误差errnormal_pos(k+1)为0。
当iua≥0且SM发生Ⅱ型故障时，计算所得绝对误差errfault_II(k+1)可以表示为
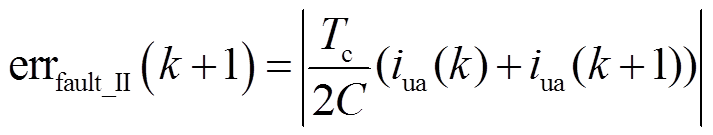（12）
根据式（9），为使得所提策略在SM正常时不发生误检测现象，同时能够在Ⅰ型故障和Ⅱ型故障发生时准确诊断，errnormal和errfault可以进一步表示为
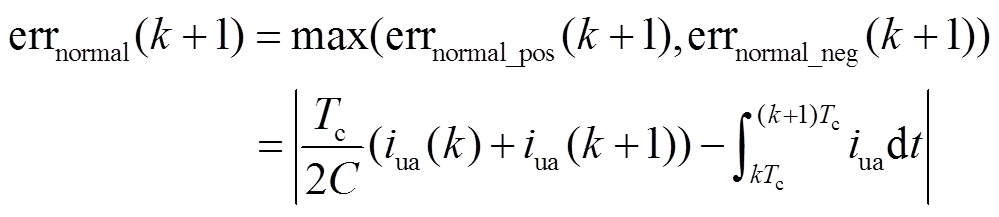（13）
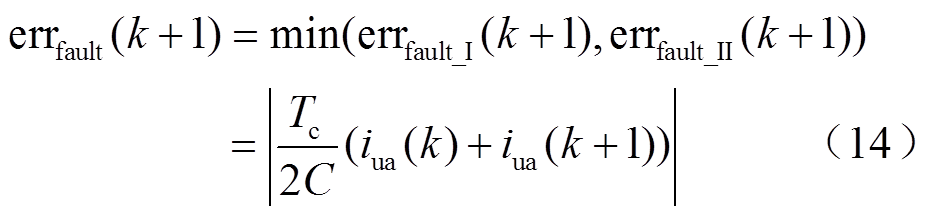
将式（13）和式（14）代入式（9）可得
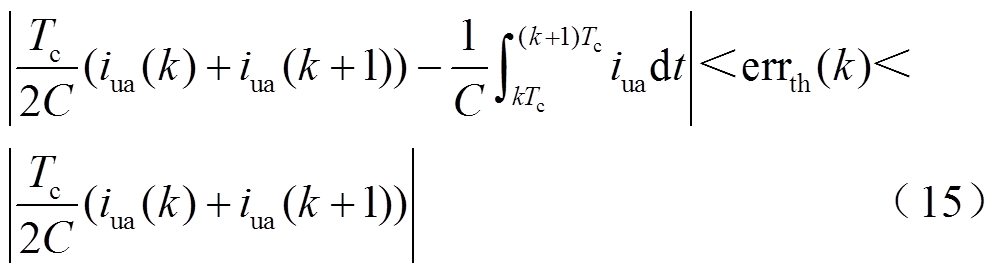
从式（15）可以看出，errth的取值只与两个控制周期的桥臂电流采样值有关。与现有研究相比，所提方法在MMC运行功率发生改变时，无需重新手动设置诊断阈值，极大地降低了阈值设定的难度。同时，式（15）中不等式的左边本质上是采用平均近似所带来的计算误差，由于Tc足够小，因此不等式左边限制是一个极小量，趋近于零。因而本文在进行阈值设置时，主要考虑对不等式右边进行限制。
所提故障诊断策略不仅适用于NLM策略，在经过简单调整后能够推广到其他MMC调制策略中。NLM策略由于动态性能好、实现简便等优点，被广泛应用于高电平数的MMC中，因此本文以NLM策略为例进行了展开。而在低、中电平数的MMC中，应用最为广泛的是载波移相调制（Carrier Phase Shifter Pulse Width Modulation, CPSPWM）策略，因此以CPSPWM为例说明本方法在不同MMC调制策略中的推广方法。
本文所提故障诊断策略中，首先根据SM投入个数及SM电容电压排列位置预测对应SM电容电压，之后通过判断SM电容电压预测值与实际值间的绝对误差是否超过阈值来检测并定位故障。实际上，无论MMC采用何种调制策略，发生开路故障SM的基本故障特征都是一致的[26]，即在发生Ⅰ型故障时，故障SM在桥臂电流为负时不受开关函数控制，SM电容始终被旁路，而当发生Ⅱ型故障时，故障SM电容电压始终被充电。当采用CPSPWM调制策略时，无论是Ⅰ型故障还是Ⅱ型故障，故障SM电容电压均会不断升高，超出正常SM电容电压[27]。在均压控制中，电容电压较高的SM由于超出设定的理想值，需要降低该SM的充电时间，增大其放电时间，故障SM电容电压由于不断升高，其充电时间会不断降低，放电时间会不断升高[28]。由此，只需对应调整开关函数的预测过程，不根据SM投入个数及SM电容电压排列位置预测SM开关函数，而是借由调制波与载波相比所得触发脉冲信号得到SM开关函数，之后便可通过相同的过程预测对应SM电容电压，最后通过判断SM电容电压预测值与实际值间的绝对误差是否超过阈值来检测并定位故障。
综上分析，由于不同的调制策略并不会影响故障SM的基本故障特征，因而本文所提策略在不同调制策略中，只需对开关函数的预测方法稍作调整，便可推广应用到其他MMC调制策略中。
电容作为MMC中较脆弱的部件之一，由于化学过程、老化等原因，电容会逐渐劣化[29]。因此，在MMC运行时，需要对MMC的SM中电容进行状态检测，以此避免电容老化可能引发的故障[28]。利用MMC中运行的电容状态监测算法便可以在真实系统中获取各个SM电容的容值[30-32]。
通常，利用电容状态监测算法获得的各个SM电容的容值，误差小于2%[30-32]。而由式（15）可知，不等式左边为趋近于零的较小值，右边为较大值。因此，在进行阈值设置时，主要考虑的是不等式的右边。显然，电容监测算法所带来的容值误差会影响其计算精度，结合式（15）可知阈值设置时不可过于接近不等式的右边限制，本文取经验系数0.8以保证诊断阈值与不等式右边限制间留有一定裕量，对应设定errth为
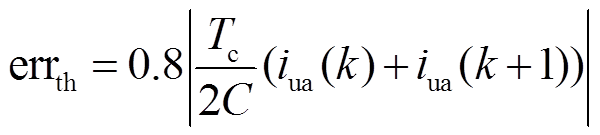（16）
本文所提诊断策略与现有诊断策略的对比见表2。
表2 与现有诊断策略的对比
Tab.2 Comparison with existing diagnostic strategies
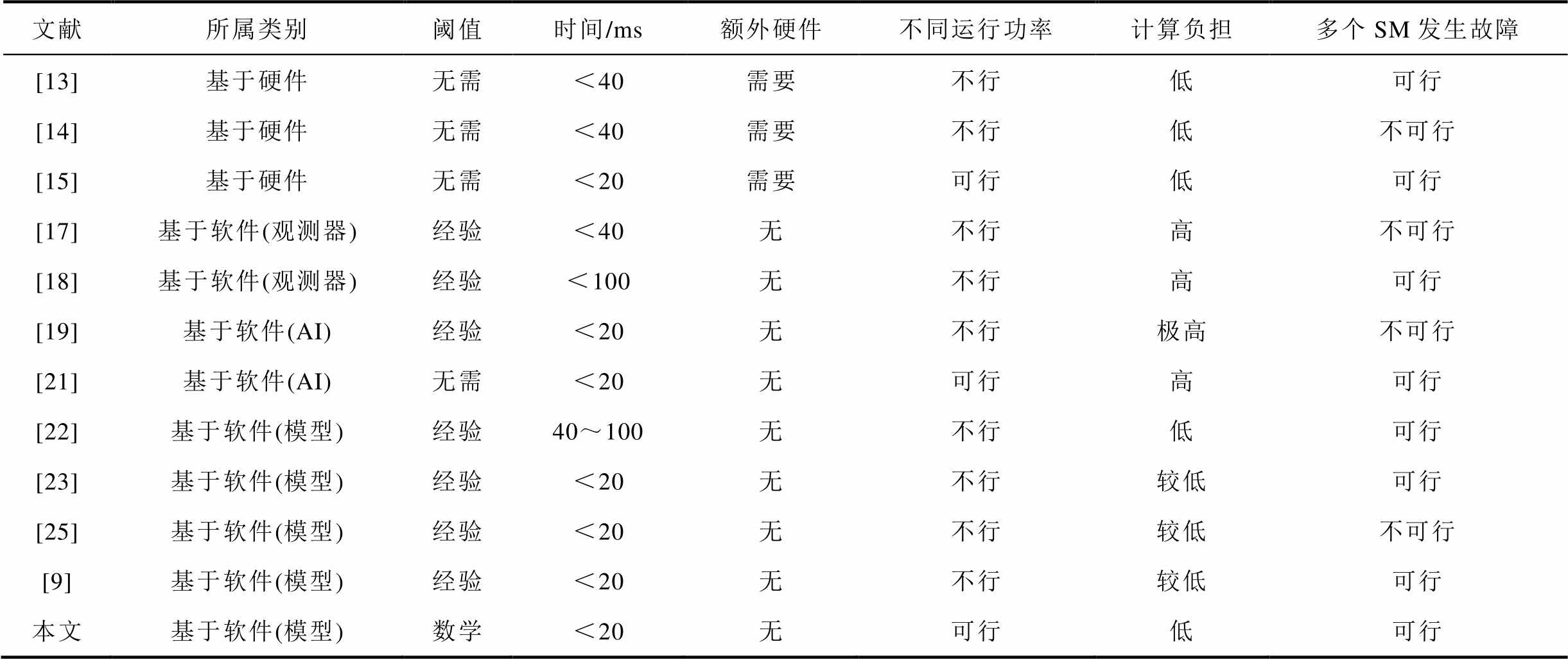
文献所属类别阈值时间/ms额外硬件不同运行功率计算负担多个SM发生故障 [13]基于硬件无需＜40需要不行低可行 [14]基于硬件无需＜40 需要不行低不可行 [15]基于硬件无需＜20需要可行低可行 [17]基于软件(观测器)经验＜40 无不行高不可行 [18]基于软件(观测器)经验＜100 无不行高可行 [19]基于软件(AI)经验＜20 无不行极高不可行 [21]基于软件(AI)无需＜20 无可行高可行 [22]基于软件(模型)经验40～100 无不行低可行 [23]基于软件(模型)经验＜20 无不行较低可行 [25]基于软件(模型)经验＜20 无不行较低不可行 [9]基于软件(模型)经验＜20 无不行较低可行 本文基于软件(模型)数学＜20 无可行低可行
文献[13-14]的方法简单可靠，但需要在已有系统基础上引入额外硬件，因此会使成本增加。而文献[15]针对轻载下的SM故障诊断问题，提出了一种基于RBRC的故障检测方法，通过RBRC和SM开关函数的逻辑输出识别故障，能够适用于不同运行功率的情形。该方法在每个SM中需额外引入改进RBRC电路，会导致系统成本增加。
文献[9,17-19, 21-23, 25]中的方法无需引入额外硬件，而依靠软件的方法进行故障诊断。文献[17-19]依靠观测器检测并定位故障，但无论是文献[17]中的滑模观测器还是文献[18]中的卡尔曼滤波器均会对控制器造成较大的控制负担，同时所需诊断时间较长（＞20 ms）。文献[19,21]中引入AI算法来对故障进行诊断。其中，文献[19]通过计算同一桥臂中两两SM的电容电压相关系数来对故障SM进行定位，而文献[21]则提出了基于滑动时间窗的故障诊断策略，并利用二维神经网络对MMC中的开路故障进行检测和定位，但引入的AI算法会带来较大的计算量，进而增加控制器的计算负担。文献[22]通过引入单环定理，减小了控制器的计算负担。文献[23]中则更进一步，缩短了所需诊断时间。文献[25]中利用组电压检测，节省了电压传感器数量，进而降低了系统成本，但无法适用于多个SM发生故障的情形。文献[8]则引入虚拟电压的概念，使所提策略能够适用于多个SM发生故障的情形。相较于基于硬件的策略，基于观测器的策略、基于AI的策略和基于模型的策略具有无需额外硬件，诊断时间短，计算负担小等优势。但上述基于模型的故障诊断策略在进行故障诊断时，均依赖相应的阈值设定，即通过判断某一指标是否超出设定阈值来判断是否存在故障，并定位故障SM，因而阈值的设定准确与否直接决定了诊断策略的可行性。在进行阈值设定时，现有方法多是依赖经验手动进行设置，因而当MMC运行于不同功率时，现有策略阈值的设置及推广较为困难，阻碍了基于模型策略的进一步发展。
与现有策略相比，当MMC运行功率改变时本文所提策略涉及诊断阈值无需重新手动设置，并通过数学推导给出了阈值设置的可靠依据，使之能够在不同运行功率下准确诊断出两种MMC子模块开路故障。此外，所提策略还整合了现有基于模型诊断策略的优点，如无需额外硬件，计算负担小，诊断时间短（＜20 ms），可适用于多个SM故障的情形。
为了验证所提MMC子模块开路故障诊断策略的有效性，本文利用HIL平台进行实验验证，实验平台如图6所示。HVDC系统的功率级模型经由上位机编译后，由目标机实时仿真，控制系统通过DSP TMS320F28335控制板实现。仿真模型结构如图1所示，调制方式采用NLM，控制周期设定为30 ms，仿真系统具体参数见表3。同时为验证所提策略能够在不同运行功率下准确检测到故障并定位故障SM，分别考虑额定负载（P=1.0(pu)）和轻载（P=0.3(pu), 负载率为30%）下发生Ⅰ型故障或Ⅱ型故障的情形，其中P为MMC传输有功功率。
图6 硬件在环实验平台示意图
Fig.6 Diagram of hardware-in-loop experimental system
表3 仿真参数
Tab.3 Experimental parameters
参数数值 交流侧额定电压/kV290 交流侧电压频率/Hz50 直流侧额定电压/kV500 额定有功功率/MW750 单桥臂子模块数/个244 桥臂电抗器/H0.1 子模块电容值/mF8
5.1.1 额定负载下发生Ⅰ型故障
令额定负载下MMC a相上桥臂序号为1, 3的子模块发生Ⅰ型故障，实验波形如图7所示。可以看出，由于故障发生时桥臂电流为正，故障SM能正常动作，而当桥臂电流变为负后，故障SM电容被旁路，其电容电压保持不变，与理论分析一致。从图7中errmax及errth波形可以看出，在故障发生前，MMC正常运行时，电容电压最大子模块对应的绝对误差不会超出设定阈值，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，故障SM绝对误差超出设定阈值，同时此时电流过零滤除环节输出逻辑信号为1，说明此时已满足电流过零滤除环节，系统可以快速检测到故障，之后进入定位过程。在故障定位过程中，经过判断，电容电压排在第二位的SM为故障SM，而排在第三位的SM为正常SM，因此确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为12.14 ms，验证了所提策略在这种情况下的适用性。
5.1.2 轻载下发生Ⅰ型故障
令轻载下MMC a相上桥臂序号为1、3的子模块发生Ⅰ型故障，实验波形如图8所示。从图8中errmax及errth波形可以看出，在故障发生前，MMC正常运行时，电容电压最大子模块的绝对误差不会超出设定阈值，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，故障SM绝对误差超出设定阈值，同时此时电流过零滤除环节输出逻辑信号为1，说明此时已满足电流过零滤除环节，系统可以快速检测到故障，之后进入定位过程。在故障定位过程中，经过判断，电容电压排在第二位的SM为故障SM，而排在第三位的SM为正常SM，因此确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为12.20 ms，验证了所提策略在这种情况下的适用性。同时综合图7、图8可以看出，所提策略无需重新手动设置阈值即可准确检测并定位到不同功率下的故障。
图7 逆变模式MMC额定负载发生Ⅰ型故障实验波形
Fig.7 Experimental waveforms of TypeⅠfault with rated load of MMC in the inverter mode
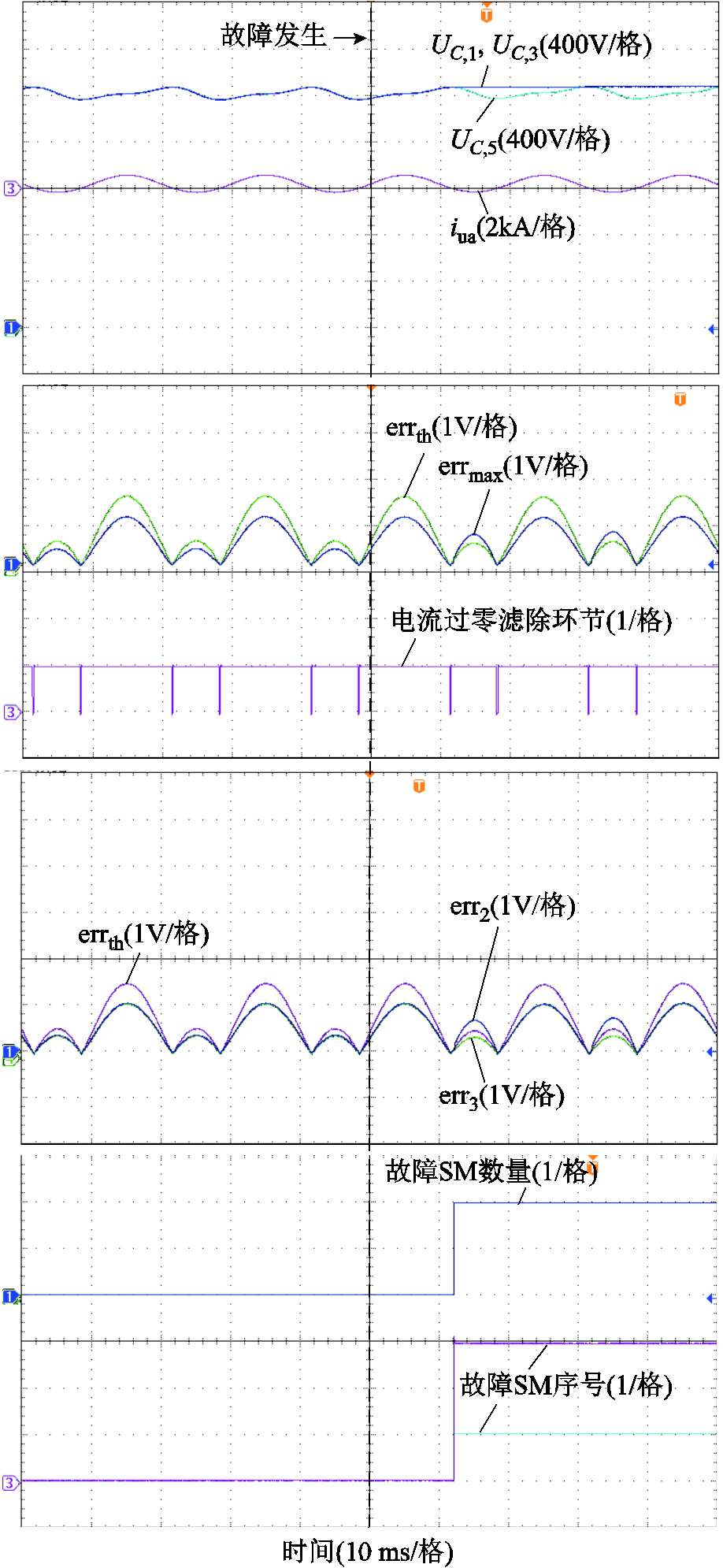
图8 逆变模式MMC轻载发生Ⅰ型故障实验波形
Fig.8 Experimental waveforms of TypeⅠfault with light load of MMC in the inverter mode
5.2.1 额定负载下发生Ⅱ型故障
令额定负载下MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图9所示。可以看出，由于故障时桥臂电流为正，故障SM电容始终被充电，故障SM电容电压迅速上升，与理论分析一致。从图9中errmax及errth波形可以看出，在故障发生前，MMC正常运行时，电容电压最大子模块的绝对误差不会超出设定阈值，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，故障SM绝对误差超出设定阈值，同时此时电流过零滤除环节输出逻辑信号为1，说明此时已满足电流过零滤除环节，系统可以快速检测到故障，之后进入定位过程。在故障定位过程中，经过判断，电容电压排在第二位的SM为故障SM，而排在第三位的SM为正常SM，因此确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为0.46 ms，验证了所提策略在这种情况下的适用性。
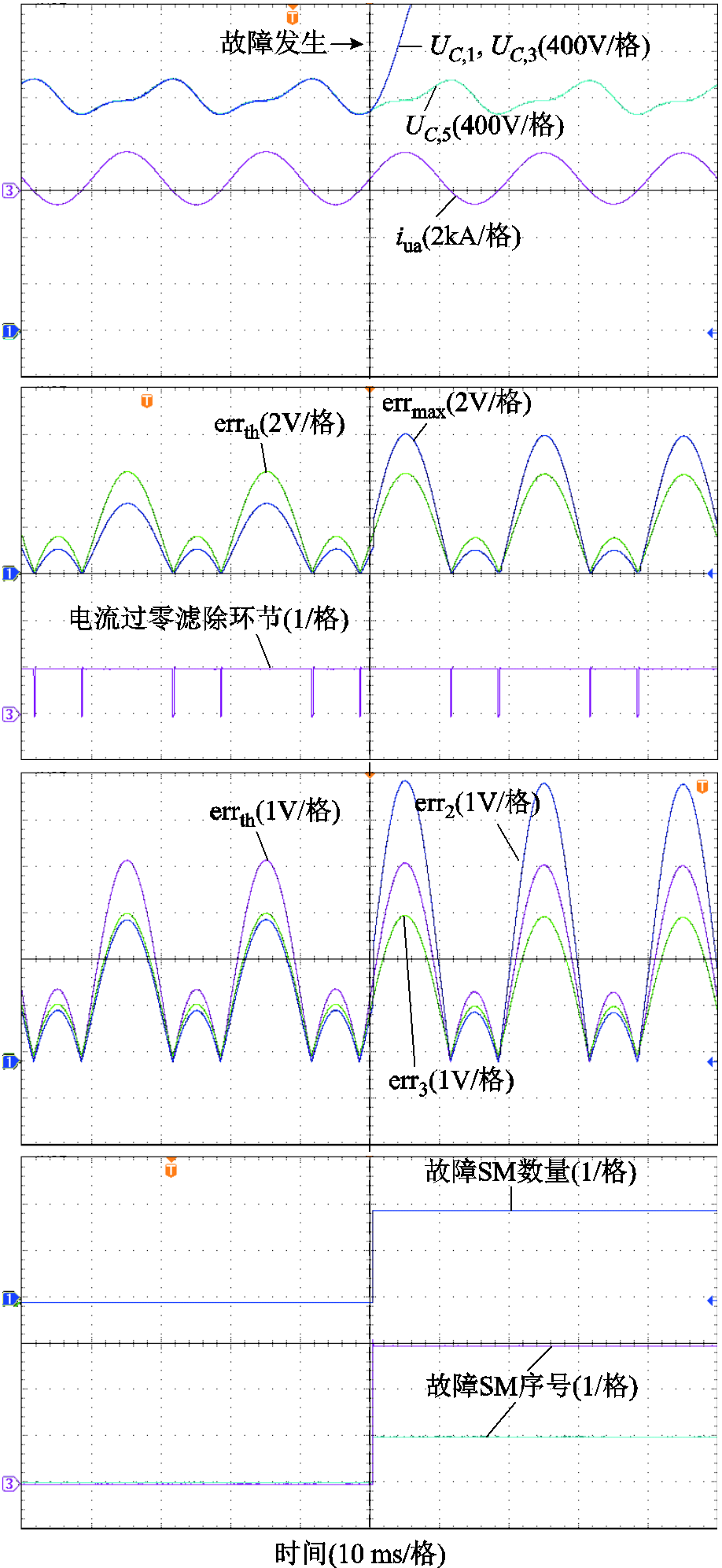
图9 逆变模式MMC额定负载发生Ⅱ型故障实验波形
Fig.9 Experimental waveform of TypeⅡfault with rated load of MMC in the inverter mode
5.2.2 轻载下发生Ⅱ型故障
令轻载下MMC a相上桥臂序号为1、3的子模块发生Ⅱ型故障，实验波形如图10所示。从图10中errmax及errth波形可以看出，在故障发生前，MMC正常运行时，电容电压最大子模块的绝对误差不会超出设定阈值，正常运行时不会发生误诊断，诊断显示故障SM数量始终为零。而在故障发生后，故障SM绝对误差超出设定阈值，此时电流过零滤除环节输出逻辑信号为1，说明此时已满足电流过零滤除环节，系统可以快速检测到故障，之后进入定位过程。在故障定位过程中，经过判断，电容电压排在第二位的SM为故障SM，而排在第三位的SM为正常SM，因此确定了当前桥臂中故障SM数量为2，序号分别为1和3，诊断用时为0.47ms，验证了所提策略在这种情况下的适用性。同时综合图9、图10可以看出，所提策略无需重新手动设置阈值即可准确诊断到不同功率下的故障。
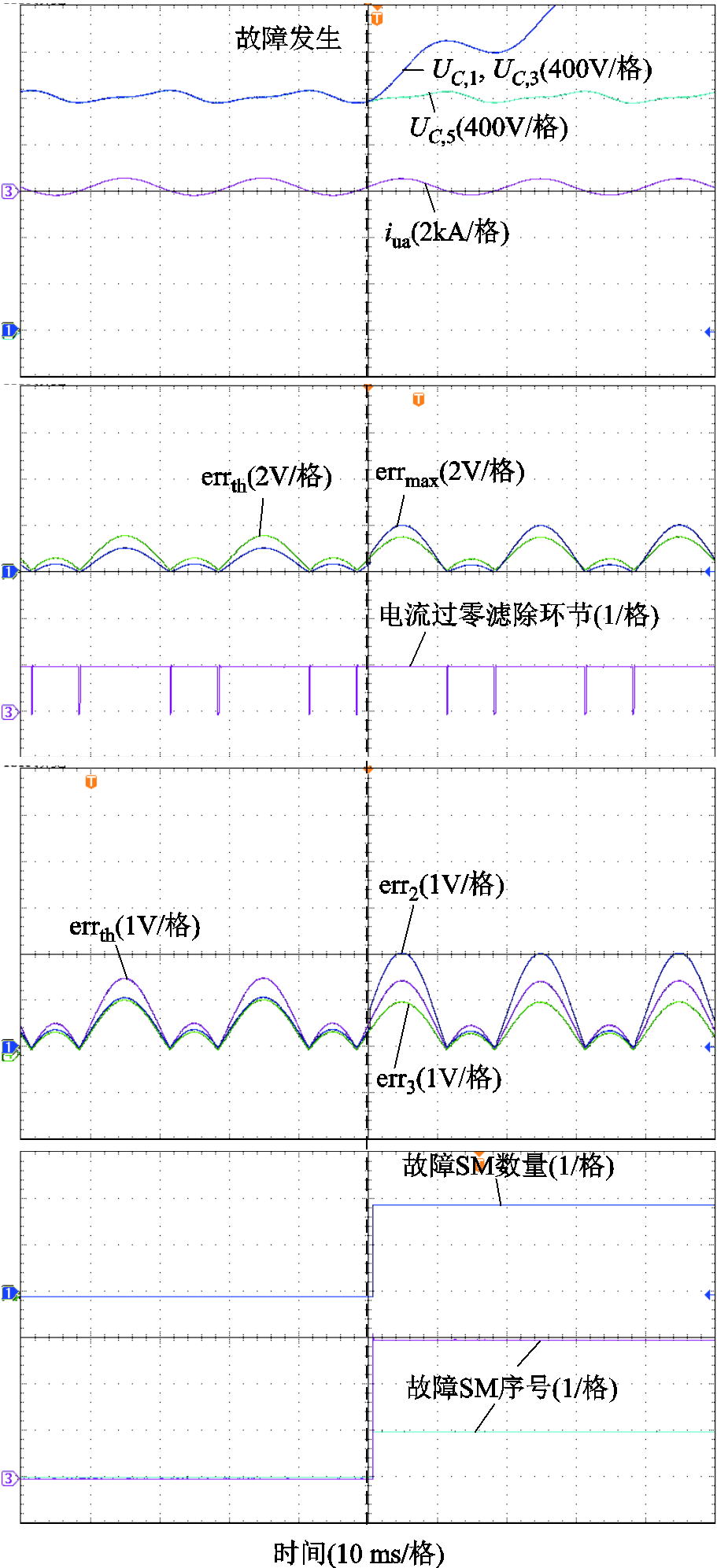
图10 逆变模式MMC轻载条件发生Ⅱ型故障实验波形
Fig.10 Experimental waveforms of TypeⅡfault with light load of MMC in the inverter mode
综合上述实验波形，可以验证所提策略能够在不同运行功率下准确诊断出两种类型的MMC子模块开路故障。此外，所提策略也可应对桥臂中多个SM发生故障的情况，并且可以在一个工频周期内完成诊断过程，同时与现有策略相比，降低了阈值设定的难度，便于推广。
为提升MMC的运行可靠性，需要在SM发生故障时，快速检测到故障并定位到故障子模块。本文提出了一种适用于不同运行功率的NLM策略下MMC子模块开路故障诊断策略，可解决现有研究中基于经验的阈值难以推广的问题。具体得到以下结论：
1）正常状态SM与故障状态SM电容电压预测值与实际值的绝对误差存在差异。分析表明，若SM正常工作，对应绝对误差较小，发生Ⅰ型故障的SM在桥臂电流为负时对应绝对误差较大，发生Ⅱ型故障的SM则在桥臂电流为正时对应绝对误差较大。
2）解决了基于模型策略在不同运行功率下阈值难以设置的问题。通过数学推导给出了所提策略中诊断阈值的设置依据，并验证了诊断阈值当MMC运行功率改变时无需重新手动设置，与现有策略相比，降低了阈值设定的难度，同时增加了其可靠性，便于推广。
3）所提故障诊断策略具备较好的普适性。通过理论分析验证了所提策略不仅适用于NLM策略的情形，在调整SM开关函数的预测方法后可推广至其他MMC调制策略。
4）HIL平台的实验结果可以验证所提策略能够在不同运行功率下准确诊断出两种类型的MMC子模块开路故障。此外，所提策略还整合了现有策略的优点，如无需额外硬件，计算负担小，诊断时间短（＜20 ms），适用于多个SM发生故障的情形等。
参考文献
[1] 罗丹, 陈民铀, 赖伟, 等. 基于Harr小波变换重构开关序列的MMC子模块电容值在线监测方法[J]. 电工技术学报, 2022, 37(20): 5278-5289. Luo Dan, Chen Minyou, Lai Wei, et al. Online monitoring method for sub-module capacitance in modular multilevel converter based on Haar wavelet transform reconstruction switch sequence[J]. Transa-ctions of China Electrotechnical Society, 2022, 37(20): 5278-5289.
[2] 束洪春, 代月, 安娜, 等. 基于交叉重叠差分变换的MMC-HVDC线路故障识别方法[J]. 电工技术学报, 2021, 36(1): 203-214, 226. Shu Hongchun, Dai Yue, An Na, et al. Fault identification method of MMC-HVDC line based on sequential overlapping derivative transform[J]. Trans-actions of China Electrotechnical Society, 2021, 36(1): 203-214, 226.
[3] 束洪春, 代月, 安娜, 等. 基于线性回归的柔性直流电网纵联保护方法[J]. 电工技术学报, 2022, 37(13): 3213-3226, 3288. Shu Hongchun, Dai Yue, An Na, et al. Pilot protection method of flexible DC grid based on linear regression[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3213-3226, 3288.
[4] 付华, 陈浩轩, 李秀菊, 等. 含边界元件的MMC-MTDC直流侧单端量故障辨识方法[J]. 电工技术学报, 2021, 36(1): 215-226. Fu Hua, Chen Haoxuan, Li Xiuju, et al. MMC-MTDC DC side single-ended quantity fault identification method with boundary elements[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 215-226.
[5] 蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22. Cai Xu, Yang Renxin, Zhou Jianqiao, et al. Review on offshore wind power integration via DC transmission[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.
[6] 徐海亮, 高铭琨, 吴瀚, 等. 海上风电场-MMC互联系统频率耦合建模及稳定性分析[J]. 电力系统自动化, 2021, 45(21): 92-102. Xu Hailiang, Gao Mingkun, Wu Han, et al. Frequency-coupling modeling and stability analysis of offshore wind farm-modular multilevel converter interconnection system[J]. Automation of Electric Power Systems, 2021, 45(21): 92-102.
[7] 徐政. 海上风电送出主要方案及其关键技术问题[J]. 电力系统自动化, 2022, 46(21): 1-10. Xu Zheng. Main schemes and key technical problems for grid integration of offshore wind farm[J]. Automation of Electric Power Systems, 2022, 46(21): 1-10.
[8] 徐政, 肖晃庆, 张哲任. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[9] Chen Xingxing, Liu Jinjun, Deng Zhifeng, et al. A diagnosis strategy for multiple IGBT open-circuit faults of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 191-203.
[10] 武鸿, 王跃, 刘熠, 等. 基于广义电容电压不平衡度的MMC子模块开路故障诊断策略[J]. 电工技术学报, 2023, 38(14): 3909-3922. Wu Hong, Wang Yue, Liu Yi, et al. Open circuit fault diagnosis strategy of MMC sub-module based on generalized capacitor voltage unbalance[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3909-3922.
[11] Choi U M, Blaabjerg F, Lee K B. Study and handling methods of power IGBT module failures in power electronic converter systems[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2517-2533.
[12] Wang Jinyu, Liu Xiong, Xiao Qian, et al. Modulated model predictive control for modular multilevel converters with easy implementation and enhanced steady-state performance[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9107-9118.
[13] Picas R, Zaragoza J, Pou J, et al. Reliable modular multilevel converter fault detection with redundant voltage sensor[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 39-51.
[14] An Quntao, Sun Lizhi, Zhao Ke, et al. Switching function model-based fast-diagnostic method of open-switch faults in inverters without sensors[J]. IEEE Transactions on Power Electronics, 2011, 26(1): 119-126.
[15] Liu Chengkai, Deng Fujin, Cai Xu, et al. Submodule open-circuit fault detection for modular multilevel converters under light load condition with rearranged bleeding resistor circuit[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4600-4613.
[16] Shao Shuai, Wheeler P W, Clare J C, et al. Fault detection for modular multilevel converters based on sliding mode observer[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 4867-4872.
[17] Shao Shuai, Watson A J, Clare J C, et al. Robustness analysis and experimental validation of a fault detection and isolation method for the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3794-3805.
[18] Deng Fujin, Chen Zhe, Khan M R, et al. Fault detection and localization method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2721-2732.
[19] Zhou Dehong, Qiu Huan, Yang Shunfeng, et al. Submodule voltage similarity-based open-circuit fault diagnosis for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 8008-8016.
[20] Kiranyaz S, Gastli A, Ben-Brahim L, et al. Real-time fault detection and identification for MMC using 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8760-8771.
[21] Deng Fujin, Jin Ming, Liu Chengkai, et al. Switch open-circuit fault localization strategy for MMCs using sliding-time window based features extraction algorithm[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 10193-10206.
[22] Zhou Weihao, Sheng Jing, Luo Haoze, et al. Detection and localization of submodule open-circuit failures for modular multilevel converters with single ring theorem[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3729-3739.
[23] Geng Zhi, Han Minxiao, Khan Z W, et al. Detection and localization strategy for switch open-circuit fault in modular multilevel converters[J]. IEEE Transa-ctions on Power Delivery, 2020, 35(6): 2630-2640.
[24] Liu Chengkai, Deng Fujin, Heng Qian, et al. Fault localization strategy for modular multilevel converters under submodule lower switch open-circuit fault[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5190-5204.
[25] Wang Zhen, Peng Li. Grouping capacitor voltage estimation and fault diagnosis with capacitance self-updating in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1532-1543.
[26] Wang Jun, Ma Hao, Bai Zhihong. A submodule fault ride-through strategy for modular multilevel converters with nearest level modulation[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1597-1608.
[27] Hagiwara M, Akagi H. Control and experiment of pulsewidth-modulated modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2009, 24(7): 1737-1746.
[28] Lewis P T, Grainger B M, Al Hassan H A, et al. Fault section identification protection algorithm for modular multilevel converter-based high voltage DC with a hybrid transmission corridor[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5652-5662.
[29] Soliman H, Wang Huai, Blaabjerg F. A review of the condition monitoring of capacitors in power electronic converters[J]. IEEE Transactions on Industry Applications, 2016, 52(6): 4976-4989.
[30] Wang Zhongxu, Zhang Yi, Wang Huai, et al. A reference submodule based capacitor condition monitoring method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6691-6696.
[31] Deng Fujin, Heng Qian, Liu Chengkai, et al. Capacitor ESR and C monitoring in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4063-4075.
[32] Wang Kun, Jin Lin, Li Guangdi, et al. Online capacitance estimation of submodule capacitors for modular multilevel converter with nearest level modulation[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6678-6681.
Abstract With the increasing voltage and power level of modular multilevel converters (MMC), the number of its submodules (SMs) also increases, and the issue of its reliability is highlighted. The failure of IGBT in any SM can affect the normal operation of MMC and even further lead to the damage of other components, which eventually lead to the collapse of the whole system. Thus, it is necessary to detect the fault and locate the malfunctioning SMs accurately to improve its reliability. MMC’s SM open-circuit diagnosis strategy can be divided into two categories: hardware-based and software-based. Compared with the hardware-based strategy, the software-based strategies need no extra hardware, have low computational burden. However, it is difficult to set the empirical threshold of existing software-based strategies between different operating powers, which hinders its further development.
To solve this issue, a diagnosis strategy for open-circuit SM faults in MMCs suitable for different operating powers is proposed. The SM switching function is predicted based on the number of SM inputs and the position of SM capacitor voltage sorting arrangement and then the corresponding SM capacitor voltage is predicted. On the basis, the fault is detected and located by judging whether the absolute error between the predicted value and the actual value of the SM capacitor voltage exceeds a threshold. Moreover, to further eliminate the effects of errors and prevent the existence of fault misdiagnosis situations, a time flag is used in both the detection process and location process.
In the proposed strategy, to avoid the effects of misdiagnosis near the arm current-over-zero point, a current-over-zero filtering part is proposed. Based on the mathematical deduction, the principle of setting threshold is given. It is indicated that the proposed strategy eliminates the need to manually set the threshold when the MMC operating power changes, which greatly reduce the difficulty of setting the threshold compared with the existing strategies. At the same time, theoretical analysis verifies that the proposed strategy is not only suitable for NLM modulation strategy, but also can be extended to other MMC modulation strategies after adjusting the prediction method of SM switching function.
A detailed real-time digital simulation model of the MMC-HVDC system is built in a hardware-in-the-loop platform. The power-stage model is emulated by the target machine and the control system is realized by the DSP TMS320F28335 control board. The experimental result verify that the proposed strategy can accurately diagnose two types of MMC SM open-circuit faults at different operating powers. It is observed that the absolute error of a Type I malfunctioning SM is high when the arm current is negative and the absolute error of a Type II malfunctioning SM is high when the arm current is positive, which verifies the correctness of the theoretical analysis. Before the fault occurs, the absolute error will not exceed the threshold so that misdiagnosis will not occur during normal operation. After the fault occurs, the absolute error exceeds the threshold, the system can quickly detect the fault and then locate the remaining malfunctioning SMs. Moreover, the proposed strategy integrates the advantages of existing strategies, including no extra hardware, low computational burden, fast diagnosis (＜20 ms), and can cope with the cases of multiple SM failures in the arm.
keywords：Modular multilevel converter, operating power, fault diagnosis, absolute error
DOI:10.19595/j.cnki.1000-6753.tces.221897
中图分类号：TM46
国家电网公司科技项目资助（5100-202156434A-0-0-00）。
收稿日期 2022-10-08
改稿日期 2022-11-21
武 鸿 男，1999年生，博士研究生，研究方向为模块化多电平换流器。E-mail：wuhong30@stu.xjtu.edu.cn
王 跃 男，1972年生，教授，博士生导师，研究方向为模块化多电平换流器、虚拟同步发电机、无线电能传输技术等。E-mail：davidwangyue@mail.xjtu.edu.cn（通信作者）
（编辑 赫 蕾）