图1 稳态工作点与小信号扰动的多频效应
Fig.1 Multi-freqeuncy characteristic of steady-state point and small-signal perturbation
摘要 峰值电流控制Buck变换器广泛应用于电源管理芯片。小信号建模是设计其控制器的关键。现有模型忽略电压外环引入的稳态控制信号纹波与小信号扰动延拓频谱对系统的影响，在高控制带宽场景下失效，从而无法指导控制器的设计。该文首先指出控制器设计决定了控制信号纹波类型，进而研究了可导型纹波对系统建模的影响；然后综合考虑电压、电流环导致的频谱耦合，得到精确的高频模型；最后基于高频模型，提出一种结合遗传算法的高带宽控制器优化设计方法。仿真与实验证明了该模型的精确性与设计方法的优越性。
关键词：Buck变换器 峰值电流控制 高带宽 高频建模 遗传算法
峰值电流控制Buck变换器广泛应用于电源管理芯片[1-3]。与传统电压控制相比，其具备如下优点[4-5]：电流内环能够在负载变动时直接调整电感电流，以提高系统的动态响应；峰值电流参考限定了电感电流的最大值，起到过电流保护；在多机并联时，可直接通过设定每一单机的电流参考值实现均流。但峰值电流控制的电流内环具备独特的采样保持效应：当系统稳态占空比D＞0.5时，初始小扰动会随着开关周期不断增大，导致系统发生次谐波振荡[6]。
随着微处理器集成度的不断提高[7-8]，高带宽设计已成为其前端Buck变换器的需求。高集成度增加了微处理器的工作电流，为了降低系统功耗，其内核供电电压不断下降，已从5 V降低到1 V左右[9]。大电流、低电压的发展趋势给前端电源管理带来了如下挑战：负载切换工作模式时，电流变化率提高，容易造成过电压；随着内核供电电压的不断下降，电压变化容限收窄。通过提高电感电流调整速率能够快速跟随负载电流的变化，减小输出电压的波动，从而减小输出电容所需容值。研究表明，在系统占空比未饱和时，环路带宽与电感电流调整速率成正相关，决定了系统的动态响应能力[10-11]。综上所述，增加Buck变换器的环路带宽，能够在保障微处理器供电需求的同时，助益电源的体积与成本控制。
精确的小信号建模是分析系统稳定性与设计高性能控制器的关键。平均小信号模型[12-13]简明易用，通过对开关过程的滑动平均处理，消除了系统的时变性。该模型能够较好地描述系统的低频特性，但不能用于对次谐波振荡的预测与分析。R. B. Ridley模型[6]借助频域拟合方法在电流反馈回路上增加了表征采样保持效应的环节，成功地解决了该问题。但其采用的频域拟合方法是一种数学等价手段，并不具备物理意义。此外，该模型未能精确分析输入与输出电压扰动对电流内环的影响，并非完备的电流内环模型。为了探求电流控制的本质，Li Jian模型[14]利用描述函数法刻画了电流内环，将主电路与反馈回路组建为整体进行建模，充分考虑了电流环导致的频谱耦合。该模型具备清晰的物理意义，是精度很高的电流内环模型，除了能够准确预测次谐波振荡的发生，也能够推导较为精确的音频敏感度等频域特性。文献[15]同样分析了电流内环存在的频谱耦合问题，并将主电路与反馈回路独立分析，借助采样数据建模方法将所有延拓频谱纳入建模，并通过无穷项级数恒等式简化模型，得出与Li Jian模型一致的结果。但是该模型没有考虑输入电压扰动对反馈电流上升下降斜率的影响，本身为不完备的电流内环模型。
以上提及的三种模型均属于仅考虑电流内环的高频模型。实际应用中，电压外环是保证输出电压质量的关键，电压外环引入的稳态控制信号纹波与小信号扰动延拓频谱会大幅增加系统的复杂度与建模的挑战性。
图1展示了系统存在的稳态工作点与小信号扰动这两个维度的多频效应。
图1 稳态工作点与小信号扰动的多频效应
Fig.1 Multi-freqeuncy characteristic of steady-state point and small-signal perturbation
稳态工作点的多频效应是指稳态时，系统纹波除去直流分量，还包含开关频率fs整数倍次的纹波分量；小信号扰动的多频效应是指输入频率fp的小信号扰动时，系统输出扰动中除去频率fp的分量，还包含fp以fs整数倍次平移的延拓频谱。在低带宽设计下，电压环路能够大幅滤除fs附近及以上的频谱分量，三种电流内环的高频模型符合物理实际，能够精确描述系统主要频段的频率特性；但在高带宽设计下，电压环路滤波能力减弱，较多高频分量会在系统内流动，导致现有的电流环模型仅在低频段保留一定的准确性，且系统带宽越高，频域有效范围越窄。
为了描述系统的高频特性，进而指导高带宽控制器的设计，必须对高频建模展开研究。
电压控制Buck变换器的高频建模已经得到深入研究。文献[16]在不考虑控制信号纹波的情况下，利用描述函数分析了电压反馈引入的主要延拓频谱分量fp-fs，但模型精度不足。文献[17]在其基础上增加了延拓频谱分量fp+fs与fp-2fs，然而对控制信号纹波的忽略同样制约了模型精度。文献[17]的主要贡献在于利用矩阵运算来推导系统频域解析表达式，这比利用梅森增益公式处理高频模型复杂的信号流图更为高效简洁，该方法也被借鉴推广到本文的建模工作之中。文献[18-19]在文献[16]基础上增加必要延拓频谱，并考虑了可导型纹波，实现了该工况的高频建模。在文献[19]的基础上，文献[20]探究了不可导型纹波工况，将纹波的影响等效为其在相交点左右导数的平均值，实现了该工况的高频建模。
峰值电流控制包含电压、电流环，其高频建模面临更高挑战。文献[21]在不考虑控制信号纹波的情况下，借鉴文献[16]将电压外环引入的主要延拓频谱分量fp-fs纳入建模，但该建模过程缺乏足够的理论支撑和物理意义，且没有考虑控制信号纹波及fp-fs之外的必要频谱分量，精度有限。迄今为止，峰值电流控制Buck变换器的完整高频模型研究仍十分匮乏。
考虑到可导型纹波工况较为普遍，本文旨在提出该工况下的高频模型，用以指导高带宽控制器的优化设计。同时，高频建模由于考虑了控制信号纹波和延拓频谱的影响，模型较为复杂，难以直接通过系统传递函数的零极点分析进行控制器的设计，因此，本文提出一种结合遗传算法的高带宽控制器优化设计方法。首先指出控制器设计决定了控制信号纹波类型，并给出稳态建模方法，进而研究了可导型纹波对系统的影响；然后分析电压、电流环引入的频谱耦合得到高频模型，结合提出的频谱定量选择法与矩阵运算，给出延拓四个频域分析通用的解析表达式；最后结合遗传算法进行高带宽控制器的优化设计，仿真和实验证明了模型的精确性和优化设计的优越性。
下文中，大写字母表示稳态变量；小写字母表示扰动变量；带有波浪号的字母表示小信号扰动量。
峰值电流控制Buck变换器如图2所示。L、C分别为输出滤波电感和电容，RC为电容寄生电阻（Equivalent Serial Resistor, ESR），RL为负载电阻，Hv为控制器，Vref为基准电压，Add为加法器，COMP为比较器，Se为斜坡补偿Vs的斜率，Ri为电流采样增益，CLK为开关频率fs的时钟发生器，iL和iC分别为电感电流和电容电流，vin和vo分别为输入电压和输出电压，vC为电容电压，vct为控制信号，is为采样电流信号（iLRi），d为开关信号。
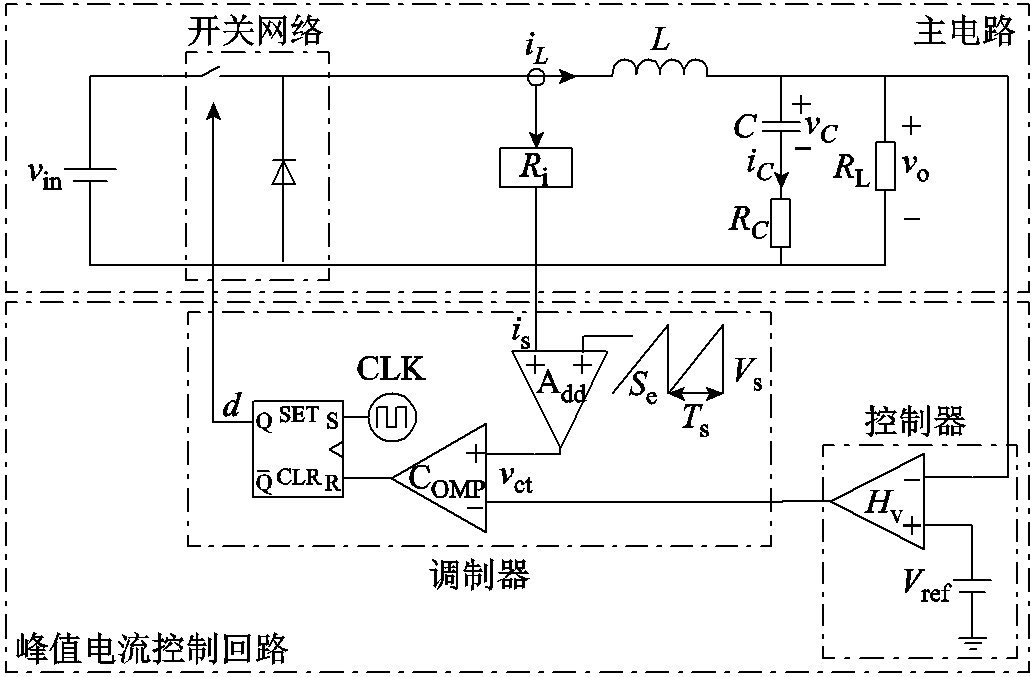
图2 峰值电流控制Buck变换器
Fig.2 Buck converter under peak current-mode control
vo与Vref的差值经控制器处理后生成vct，vct与is+Vs比较后，进一步触发RS触发器生成d。具体调制逻辑为：当时钟上沿到来时，RS触发器接收到置位信号，d为高电平，开关导通，iL逐步增大；当is+Vs＞vct时，RS触发器接收到复位信号，d翻转为低电平，开关关断，iL逐步减小。系统就是如此周而复始地运行。
稳态情况下，IL随开关通断上升下降，其纹波可近似为三角波。在输出滤波电容作用下，负载电流Io可近似为IL的平均值，根据基尔霍夫电流定律，IC可近似为IL的纹波。电容电压纹波
为C对IC的积分，ESR电压纹波
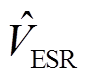为RC与IC的乘积。如图3所示，输出电压纹波
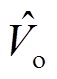为与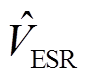的叠加。该纹波含有开关频率整数倍次的频谱。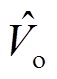经控制器进一步生成控制信号纹波
，控制器的性质决定了的类型。
图3 输出电压纹波的构成
Fig.3 Composition of output voltage ripple
控制器的作用是通过合理的零极点配置来补偿开环系统自身动态响应速度和稳定裕度的不足。物理可实现的控制器中，传递函数的分母阶次一般不低于分子阶次。典型控制器的幅频特性示意图如图4所示，比例（Proportional, P）控制器与比例积分（Proportional-Integral, PI）控制器传递函数的分子分母阶次相同，在开关频率以上的频段等效为全通滤波器；Ⅱ型、Ⅲ型控制器传递函数的分母阶次高于分子阶次，在开关频率以上的频段等效为低通滤波器。
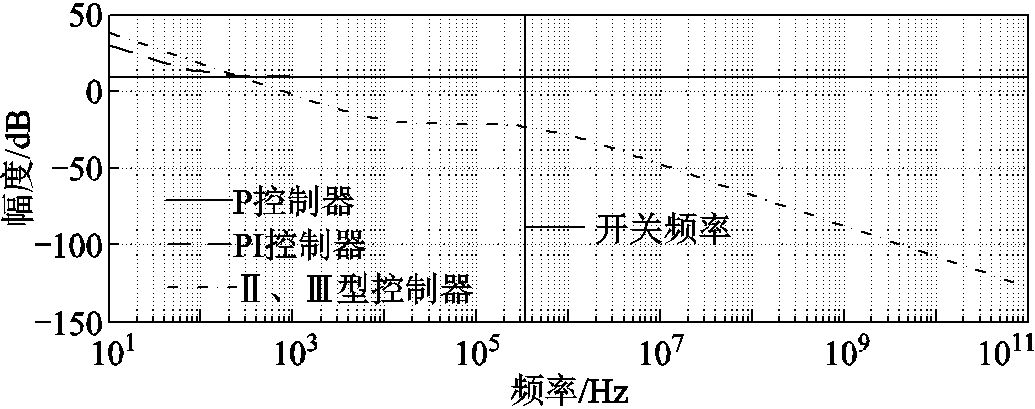
图4 典型控制器的幅频特性示意图
Fig.4 Amplitude-frequency curve of typical controllers
不同类型的控制信号纹波如图5所示。当采用Ⅱ型、Ⅲ型控制器时，主要保留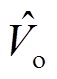中开关频率的频谱分量，时域为准正弦波，在与is相交点处能够求导，为可导型纹波；当采用P、PI控制器时，为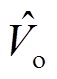的等比例值，保留了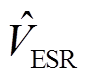引入的三角波几何特性，在与is相交点处的左右导数不相等，为不可导型纹波。
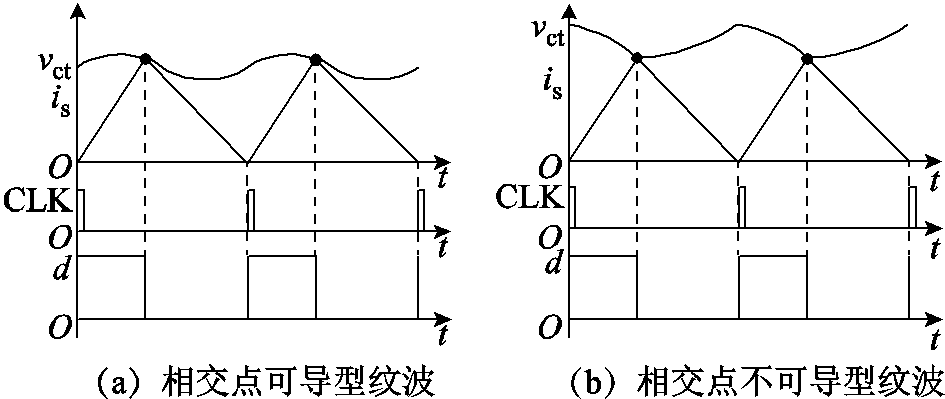
图5 不同类型的控制信号纹波
Fig.5 Different types of control signal ripples
理想情况下，峰值电流控制Buck变换器的滤波电感将被电流环控制为电流源，主电路从二阶系统降阶为由电容主导的一阶系统，含一个零点的Ⅱ型控制器就足以补偿环路相位，广泛应用于实际电路设计，其表达式为
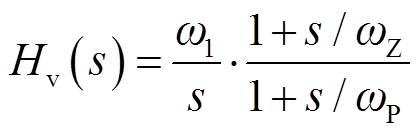（1）
式中，ω1为增益系数；ωZ与ωP为零极点系数。
不可导型纹波的稳态建模适合从时域分析入手，控制器作用等价为负比例系数，具体推导参考文献[20]。可导型纹波的稳态建模适合从频域分析入手。考虑到可导型纹波为本文研究对象的主流工况，以下对其稳态建模开展详细介绍。
稳态开关信号为周期函数，其傅里叶级数为
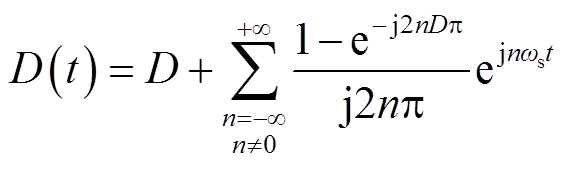（2）
式中，ωs=2πfs。主电路输出滤波环节的传递函数为
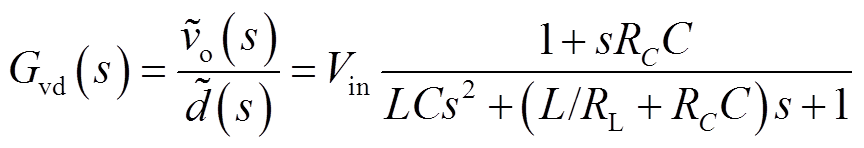（3）
将Gvd(s)与Hv(s)作用于D(t)的主要谐波即可求得为
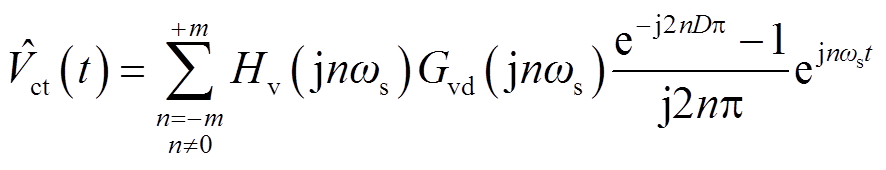（4）
式中，m为需要选取的谐波次数，一般令m=1，考虑开关频率谐波即可满足建模需求。
线性控制下的直流开关变换器存在主电路与调制器两大非线性时变环节。Buck变换器主电路的非线性时变集中于开关对输入电压的斩波，不影响系统的环路特性，因此调制器的分析成为判断环路稳定性的重点。
图6展示了调制器受小信号扰动时的工作过程，其中ti表示第i个开关周期的起始，Ton表示稳态导通时间，Ton(i)与ΔTon(i)分别表示扰动下第i个开关周期的导通时间与对应扰动量，Ts表示开关周期。
图6 小信号扰动下调制器工作过程
Fig.6 Working mechanism of modulator under small-signal perturbation
波浪实线表示稳态控制信号，Sn与Sf分别表示is的上升与下降斜率，此处先不考虑输入、输出电压扰动对Sn与Sf的影响，表达式为
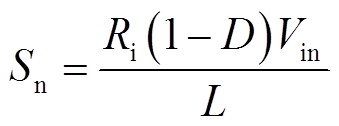（5）
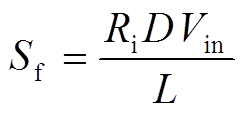（6）
波浪虚线表示叠加了正弦小信号扰动
的受扰控制信号，表达式为
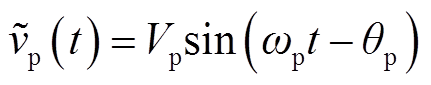（7）
式中，Vp、ωp与θp分别为扰动幅值、角频率与相位。
虚折线表示叠加斜坡补偿的受扰电流反馈信号，其在ti时刻的幅值可以从相邻两个周期分别求得，由此得到
式（8）可化简为
小信号扰动下，Ton(i)与Ton非常接近，基于泰勒公式可将Vct(ti+Ton(i))近似为
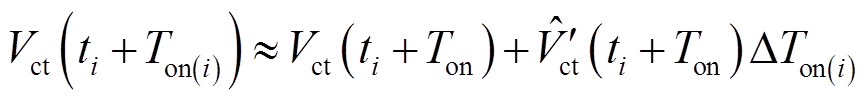（10）
将式（10）代入式（9）可求得相邻开关周期的导通时间扰动量关系为
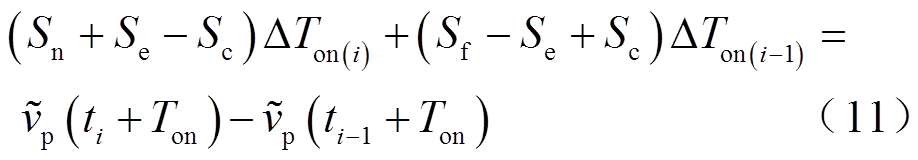
式中，Sc为控制信号纹波在相交点的斜率，有
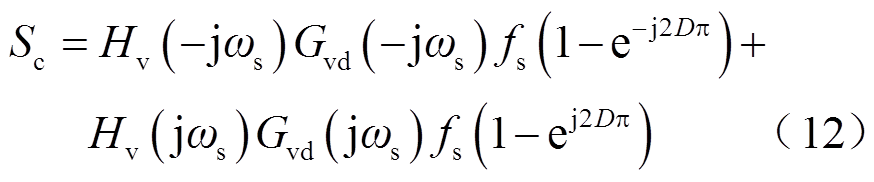
如图6所示，
可近似为由高度为ΔTon(i)的冲击信号构成，有
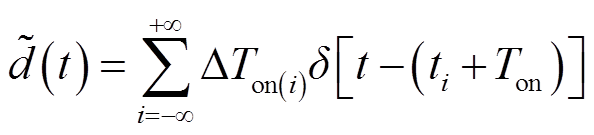（13）
定义
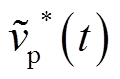为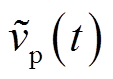
的理想采样信号，有
（14）
将式（13）与式（14）代入式（11）可得
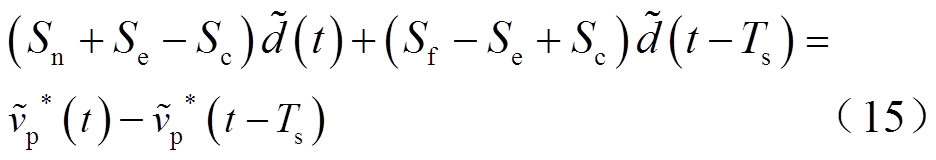
基于采样定理与傅里叶变换的移位性质可将式（15）转换到频域，有
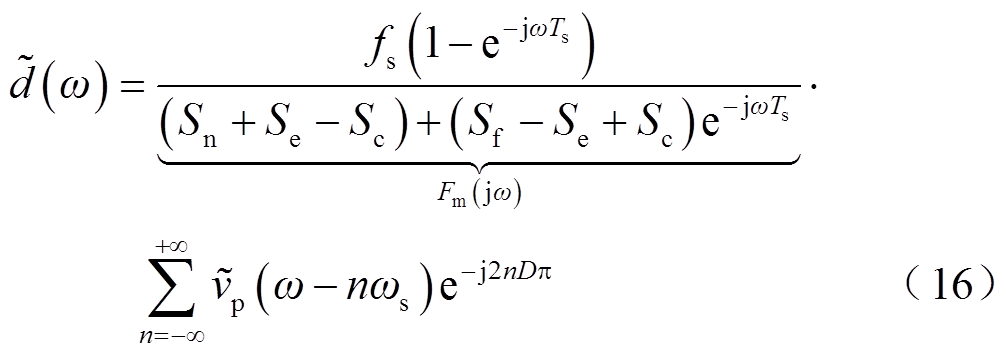
由此可见，本质为受包含滞后环节的函数Fm(jω)调制的开关频率采样信号，控制信号纹波能够影响Fm(jω)的分母，从数值上等效为其在相交点处的导数值Sc。
(t)为单频小信号扰动，仅在ωp处存在频谱分量
。结合式（16）可知的频谱分量分布于ωp+nωs处，即
、
、
等，并求得延拓频谱与小信号扰动之间的定量关系为
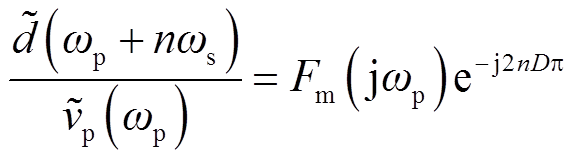（17）
上述分析表明，对调制器输入单频扰动，将输出多频成分，且这些延拓频谱的幅值均相等，仅存在相位上的变化。
输入电压扰动
(t)与输出电压扰动
(t)将改变iL的上升与下降斜率，进而产生。与第2节类似，结合几何关系与冲击等效可求得它们的关系如式（18）与式（19）所示，推导过程详见附录。
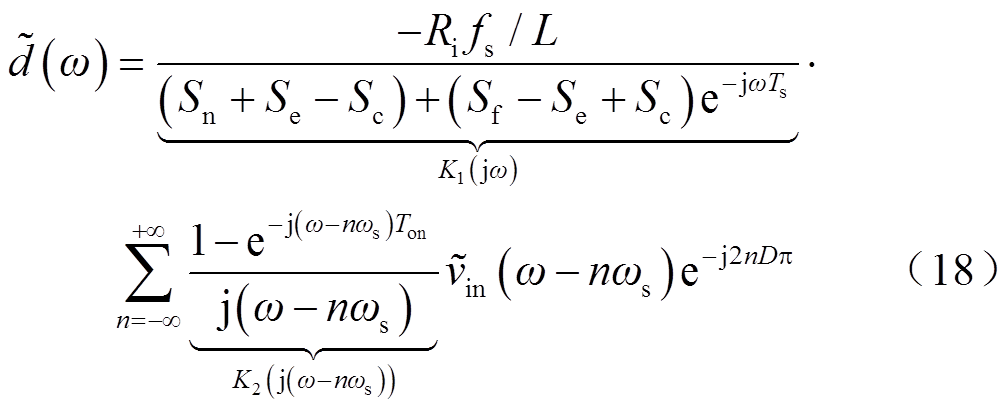
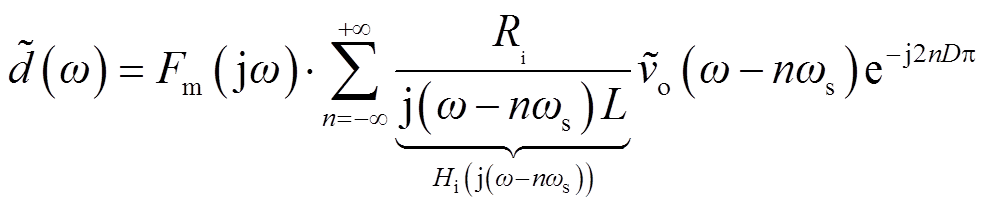（19）
(t)除了通过电流控制回路，也会通过主电路影响系统，分析扰动下的开环系统易得其等效表达式为[16]
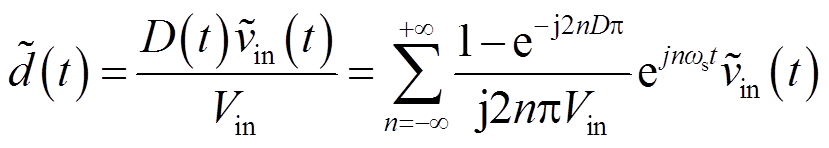（20）
将其转换到频域可得
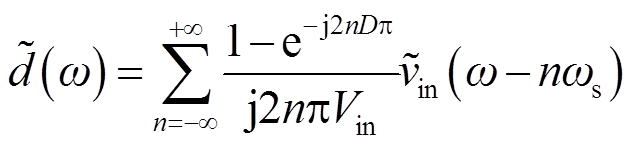（21）
为了推导输出阻抗，还需考虑负载电流扰动。易知开环输出阻抗为电感、电容、负载电阻三者并联的线性时不变环节[10]，表达式为
（22）
将主电路输出滤波器Gvd(jω)、控制器Hv(jω)、开环输出阻抗Zo(jω)这三个线性时不变环节与调制器、输入电压扰动、输出电压扰动这三个频谱延拓环节结合，并考虑双环控制引入的频谱耦合，即可得到如图7所示的系统高频模型，其中Hi(jω)为等效的电流反馈环节。注入系统的控制信号扰动在经过开关采样后生成初代延拓频谱
，(
)也通过主电路开关采样和电流反馈叠加到，继而通过Gvd(jω)传递到
，通过电流反馈Hi(jω)与电压反馈Hv(jω)传递到调制器输入端，成为新的控制信号扰动频谱
，这些频谱再次经过调制器的采样生成二代延拓频谱，并与初代发生频谱耦合。该过程循环往复，直到系统达到谐波平衡。模型中，调制器频谱耦合环节定量关系可由式（16）进一步推出，有
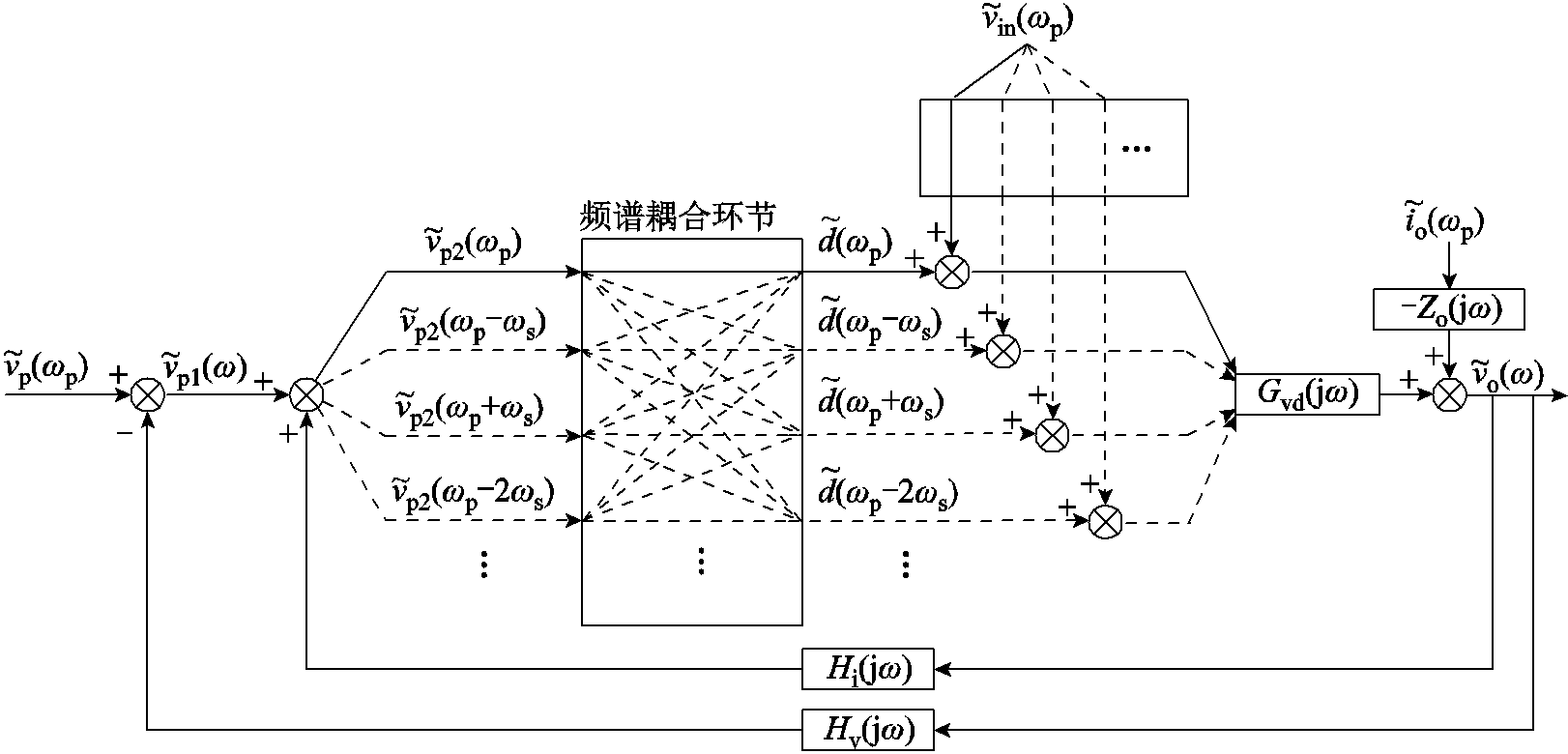
图7 恒频峰值电流控制Buck变换器的高频模型
Fig.7 High-frequency model of PCM Buck converter
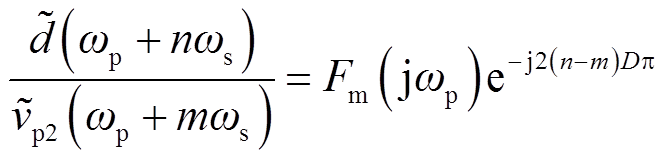（23）
输入电压扰动频谱延拓环节的定量关系可结合式（18）与式（21）给出，有
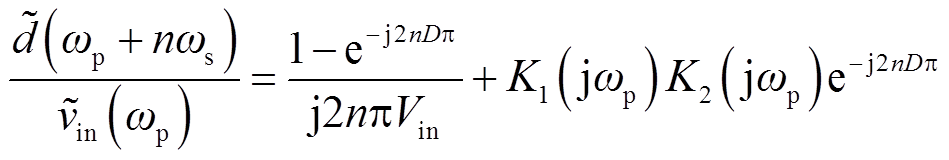（24）
恒频峰值电流控制Buck变换器的高频模型如图7所示。双环频谱混叠使得系统的信号流图复杂交错，频谱延拓使得图7中每个信号都可等效为多维向量，举例如下。
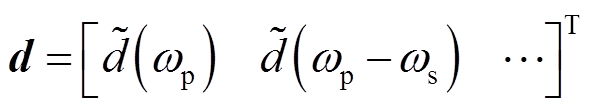（25）
进而每个传递环节都等效为传递函数矩阵，得到如图8所示的向量化模型。其中Gvd为主电路滤波器矩阵；Zo为开环输出阻抗矩阵；Hi为等效电流反馈矩阵；Hv为电压反馈矩阵；S1为频谱耦合矩阵；S2为频谱延拓矩阵。Gvd、Zo、Hi与Hv均为对角矩阵，对角元素均为Gvd(jω)、Zo(jω)、Hi(jω)与Hv(jω)在对应频率处的取值，举例说明如下。
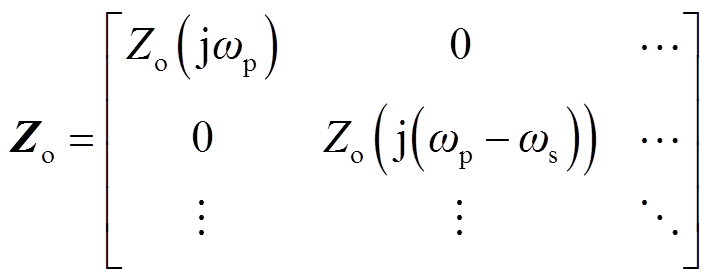（26）
S1与S2的矩阵元素可分别由式（23）与式（24）求得。
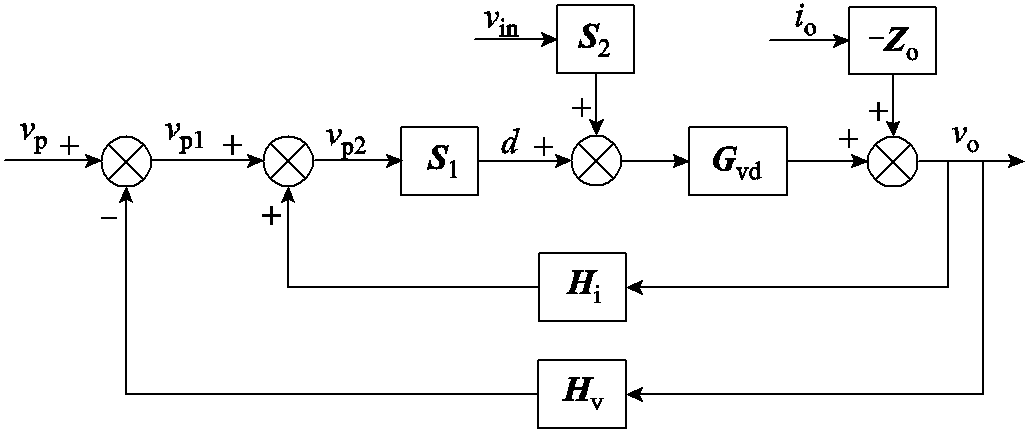
图8 向量化模型
Fig.8 Simplified model by vectors
利用矩阵运算[17]可求得电压外环的环路增益为
（27）
式中，T_sf(jω)为图7中仅考虑实信号线时的单频环路增益，表达式为
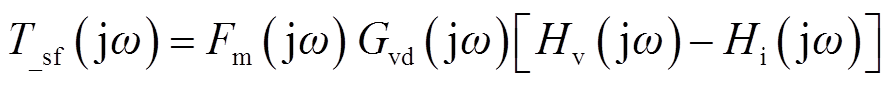（28）
音频敏感度为
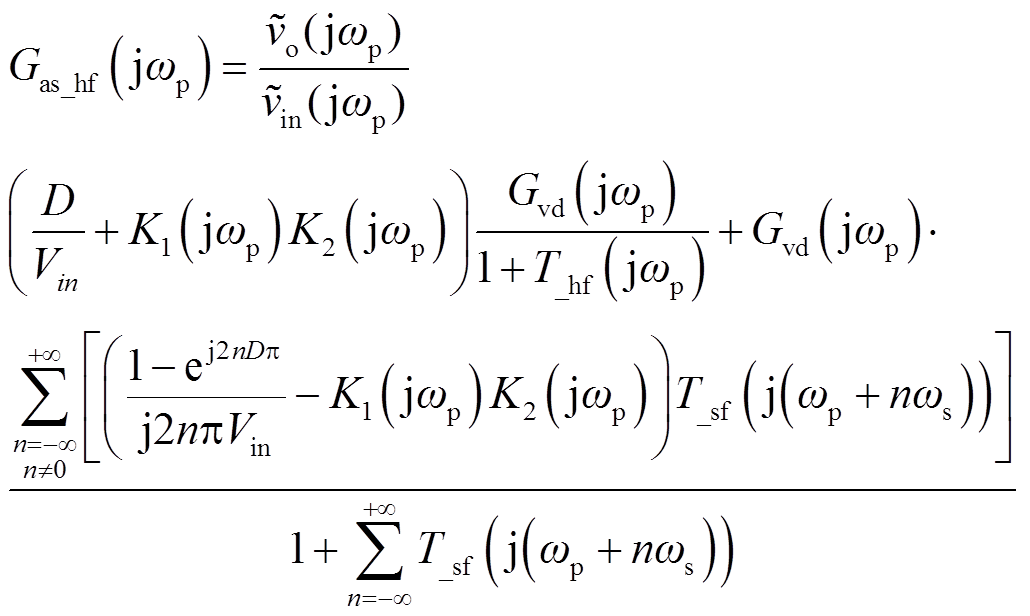（29）
输出阻抗为
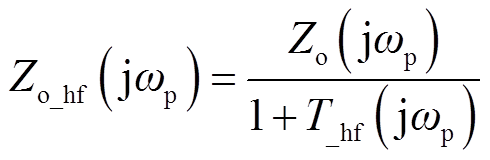（30）
输入阻抗为
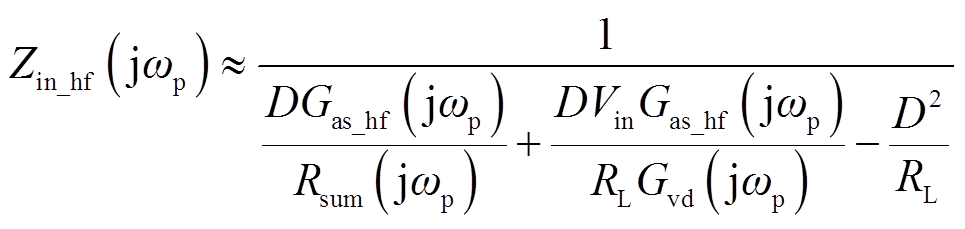（31）
推导输入阻抗时，为了简化表达式，利用平均小信号模型中输入电流与电感电流的近似关系，即
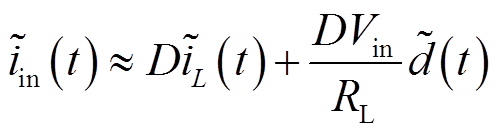（32）
式（27）与式（29）包含T_sf(j(ωp+nωs))的无穷求和项，式（30）与式（31）分别包含式（27）与式（29），实际也隐含该无穷求和项。无穷求和项可以确保传递函数在整个频域的准确性，然而却不适用于实际分析。实际上，T_sf(j(ωp+nωs))与纳入建模考虑的延拓频谱一一对应。对于单台变换器而言，考虑开关频率以下的传递函数就足以支撑系统的稳定性分析与控制器设计，所以注入的小信号扰动频率一般也限制在ωs以下。由式（28）可知，T_sf(jω)为主电路滤波器、控制器及调制器直流增益的乘积，在频域上呈现低通特性。当ωp∈(0, ωs)时，T_sf(j(ωp+nωs))随着n绝对值的增大逐步衰减，这意味着考虑频率最低的有限项延拓频谱即可确保开关频率内的模型精确性。在该定性认识的基础上，本文提出一种定量选取判据来辅助实际应用。
由于n的取值存在正负两个序列，需要将两个序列边界的关系确定。定义整数k为边界系数，当ωp∈(0,0.5ωs)时，|ωp-(k+1)ωs|＞|ωp+kωs|，此时T_sf(j(ωp+kωs))的幅值高于T_sf[j(ωp-(k+1)ωs)]，更值得纳入系统建模；当ωp∈(0.5ωs, ωs)时，|ωp-(k+1)ωs|＜|ωp+kωs|，此时T_sf[j(ωp-(k+1)ωs)]的幅值高于T_sf(j(ωp+kωs))，更值得纳入系统建模。所以在ωp∈(0, ωs)区间内，n=k和n=-(k+1)分别作为正、负边界系数以确保选择策略的严谨性。
继而引入一个经验判据来定量选取k。k值选择判据示意图如图9所示，记|T_sf (jω)|＝-20 dB的最大解为ωmax，则求得k为
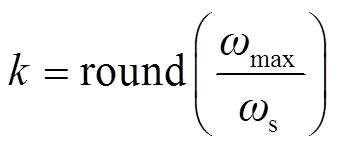（33）
式中，round为四舍五入取整函数。这意味着模型仅考虑幅值在-20dB附近及以上的T_sf(j(ωp+nωs))，忽略其余延拓频谱对系统的影响。
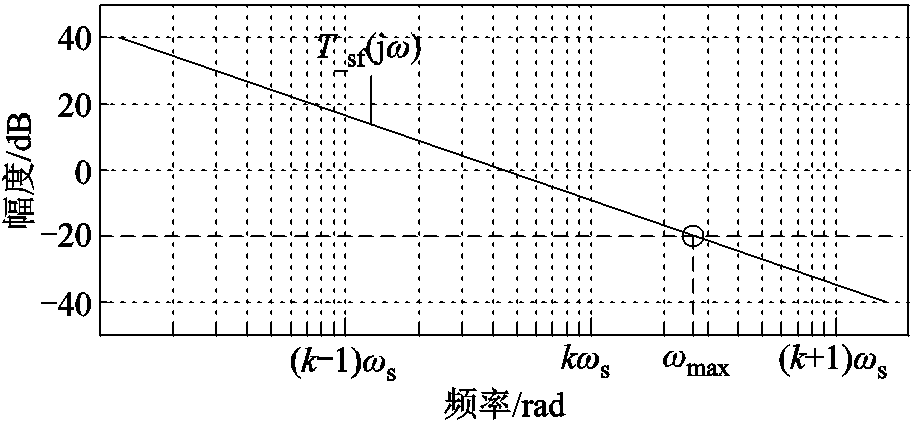
图9 k值选择判据示意图
Fig.9 Quantitative choice of k
Buck变换器是非线性时变系统，这给控制器设计带来了挑战。目前常用的设计方法主要包含：
1）试错法。根据经验进行控制器参数设计，通过仿真或者实验不断调整，从而使系统达到所需性能要求。该方法依赖人工经验，主观性较强，便于简单控制器的设计。但对于高阶非线性系统，尤其是在控制器参数较多情况下，难以寻得较优方案，且耗时较长。
2）基于解析模型的控制器参数设计。解析模型具有明晰的物理意义，诸如平均小信号模型等低频模型将开关电源转换为线性时不变系统，从而基于零极点分析配置控制器参数[12]。但是低频模型忽略了开关导致的稳态系统纹波和小信号扰动延拓频谱的影响，无法应用于高带宽变换器设计[19]。
3）结合智能算法和仿真的控制器参数设计。近年来，智能算法常被用于控制器的设计当中，模拟退火算法、粒子群算法、遗传算法等为控制器设计提供了有力工具[22-25]。其中遗传算法具有强大的随机搜索能力，不需要系统的结构信息和梯度信息，全局寻优能力强，常结合电路仿真进行控制器参数的智能寻优[26-28]。该寻优方法的核心步骤之一是求取遗传算法获得的候选设计的适应度，适应度越高，意味着该设计越符合要求。电路仿真能够保障参数设计的有效性，然而寻优过程中的每一次迭代均需运行若干次时域仿真，设计效率较低。
高频模型为提高遗传算法的效率提供了可能。高频模型尽管表达式相对复杂，无法直接通过提取传递函数的零极点来设计控制器，但其仍然是解析模型，利用它计算候选设计适应度的效率远远高于时域仿真。另一方面，高频模型在开关频率以内的频域特性预测能够达到仿真测量精度，能够确保适应度计算的准确性。将高频模型与遗传算法相结合，能够优势互补，实现精确且快速的参数寻优设计。
控制器参数寻优设计流程如图10所示，以下逐步介绍。
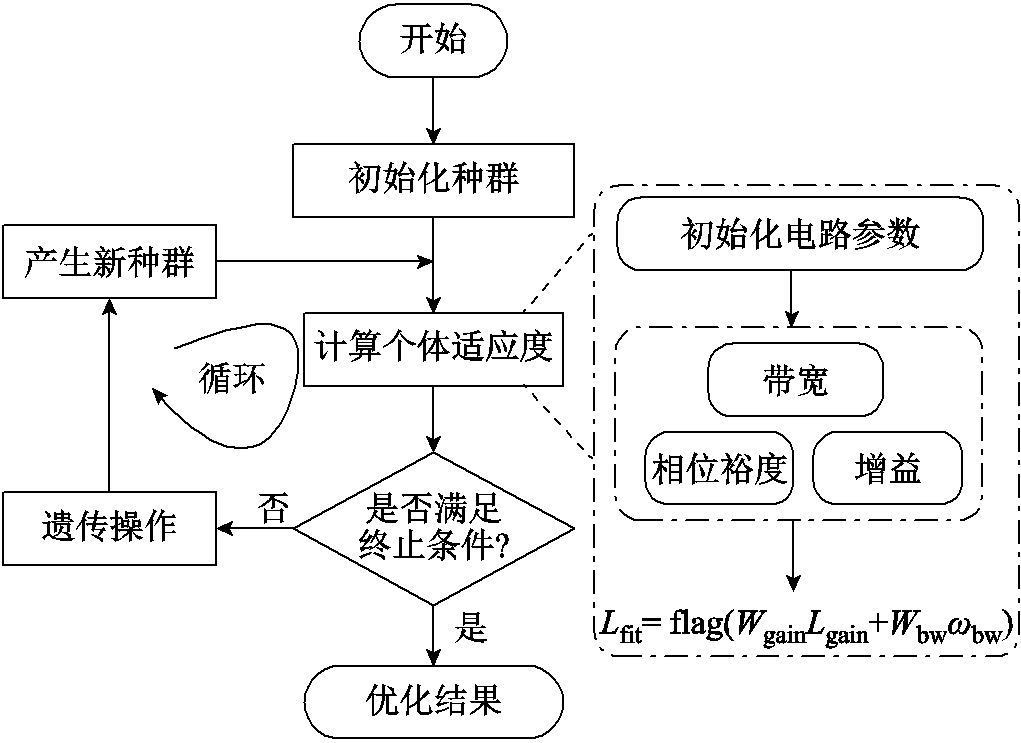
图10 控制器参数优化设计流程
Fig.10 Optimization process of controller parameters
1）初始化种群
式（1）中的ω1、ωZ与ωP为设计过程中所需优化的参数，也称为遗传算法中个体的基因。将基因组合起来，就能形成包含参数设计方案的个体A为
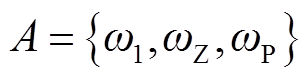（34）
A中的每个参数都具备特定的选取范围，通过随机函数rand选取随机值即可产生一个特定的候选个体，操作N次即可得到N个候选个体。
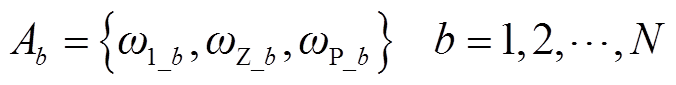（35）
将N个个体汇总，即可获得第一代的初始化种群P为
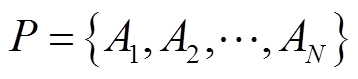（36）
2）构造适应度函数并计算个体适应度
为了计算个体的适应度，必须先构造适应度函数。适应度函数一般由关键的设计指标构成，从而能够反映个体与设计目标的契合度。控制器设计的三大指标为“稳”“准”“好”，因此本文选取以下三个指标进行高带宽设计：
（1）环路带宽ωbw越高，系统的动态响应速度越快。
（2）相位裕度Lpm越大，系统的稳定性越好，Lpm为
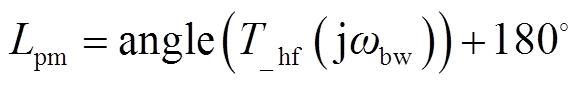（37）
式中，angle为相位求取函数。
（3）环路增益的低频幅值越大，系统的稳态精度越高。将环路增益在0 Hz处的幅值作为低频增益的代表，并记为Lgain，有
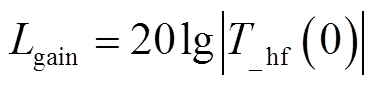（38）
综合考虑Lgain、Lpm与ωbw三个指标即可设计如式（39）所示的适应度函数。
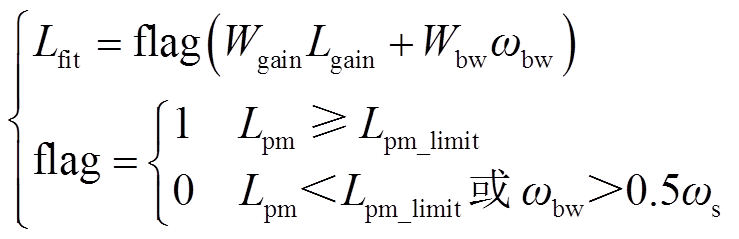（39）
式中，Wgain与Wbw分别为Lgain与ωbw的权重系数，需根据Lgain与ωbw的数量级合理选择；标志函数flag确保寻优得到的Lpm大于或等于相位裕度限制Lpm_limit，同时确保带宽符合采样定理的限制，不高于二分之一开关频率；Lfit为适应度值，该值越大，对应的控制器参数设计越优。
由于本文采用的Ⅱ型控制器包含积分环节，使得环路增益在0 Hz的幅值为无穷大，能够实现无差控制，无需考虑稳态精度指标，因此将Wgain取为0，此时Lfit仅取决于ωbw，可将Wbw取为1。实际寻优目标为：在确保系统稳定裕度大于Lpm_limit的情况下，追求尽可能快的动态响应。
3）判断是否满足终止条件
计算种群P所有个体适应度的平均值Lfit_av。初始种群的Lfit_av一般较小，随着迭代次数的增加，Lfit_av会逐渐提高直到达到饱和值，即可认为种群P已经进化到寻优目标，可以终止循环。在Lfit_av没有达到饱和值之前，需要对种群P进行步骤4）的遗传操作以提高Lfit_av。由于不同的适应度函数对应的饱和值不同，下文将迭代次数M直接设置为15次，能够保障Lfit_av达到饱和值。
4）遗传操作
为增加进化和寻优速度，对每一代种群的个体适应度进行比较，选取其中最高的若干个，将基因保留到下一代。接着对种群中其他个体进行选择、交叉、变异操作[29-30]。
（1）选择：从前一代中选取若干高适应度个体作为父代、母代，将其基因传递到下一代。对前一代种群的N个个体进行选择概率计算，选择概率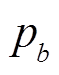
计算方法为
（40）
式中，Lfit_b为第b个个体的适应度。按照概率将0～1划分为N个区间，与N个个体一一对应，区域大小取决于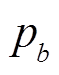，通过产生若干个0～1之间的随机数选取若干个个体。高适应度个体将大概率获选。
（2）交叉：如式（41）所示，根据所设定的交叉概率pcross随机选取两个个体Ai和Aj，将两者的某一基因片段交叉互换，从而产生下一代，此处以基因片段ωZ为例。
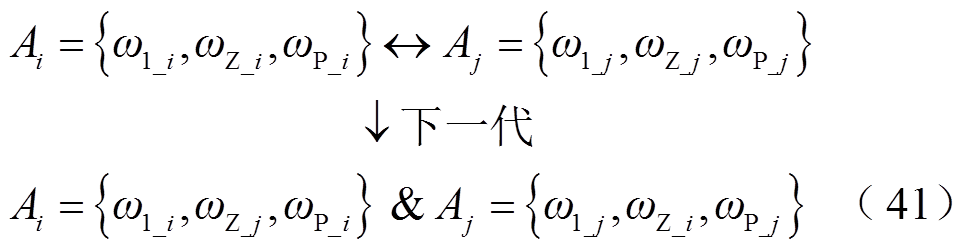
（3）变异：为跳出局部最优解陷阱，更好地在全局进行寻优，通过设定变异概率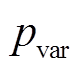
，对个体上的基因进行变异替换，变异值借助随机函数rand在各基因型的取值范围内随机产生，举例如下。
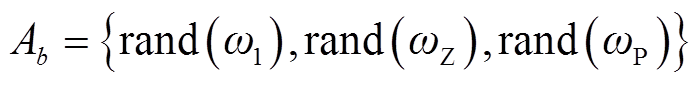（42）
通过选择、交叉、变异的综合作用，即可进化出适应度更高的下一代种群，获得更优的控制器参数设计方案。
该寻优设计流程具备应用普适性，只需将其与不同控制策略下的高频模型相结合，并根据实际需求选择合适的Wgain、Wbw、Lpm_limit，即可广泛应用于多种控制策略下DC-DC变换器的P或PI控制器、Ⅱ型控制器、Ⅲ型控制器等线性补偿网络的参数寻优。
为充分证明模型精确性与参数寻优设计有效性，以下采用两个案例展开证明。
案例Ⅰ系统参数见表1，选取Lpm_limit=30°，对其展开控制器的优化设计。
表1 案例Ⅰ系统参数
Tab.1 Parameters of CaseⅠ
参数数值 输入电压Vin/V12 输出电压Vo/V6 开关频率fs/kHz600 滤波电感L/mH4.7 滤波电容C/mF44 滤波电容ESR RC/mΩ10 负载电阻RL/Ω2 斜坡补偿斜率Se6.0×104 电流采样增益Ri0.05
首先需要确定参数ω1、ωZ与ωP的寻优范围：选取ωbw=ωs/3=1.26×106 rad/s，此为典型的高带宽设计；将零点ωZ放置在主电路谐振频率
前用以提高系统的相位裕度，由此限定ωZ∈(0, 7.0×104 rad/s)，可预设为ωZ=7.0×104 rad/s；将ωP放置在高频处用以衰减系统的高频噪声，将最高范围设为10ωbw，由此限定ωP∈(0, 1.26×107 rad/s)，可预设为ωP=1.26×107 rad/s；将以上预设值代入Li Jian模型即可求得ω1=3.2×105 rad/s，将其扩大一个数量级即可得到ω1∈(0, 3.2×106 rad/s)。给定遗传算法参数见表2。
表2 遗传算法参数
Tab.2 Parameters of genetic algorithm
参数数值 种群规模N/个100 最大迭代次数M/次15 ω1寻优范围/(rad/s)0～3.2×105 ωZ寻优范围/(rad/s)0～7×104 ωP寻优范围/(rad/s)0～1.26×107 变异概率0.1 交叉概率0.9
在Matlab中按照图10的流程实现参数寻优，利用式（27）所示的高频模型环路增益实现个体适应度的计算。为简化算法，将延拓频谱的选取边界统一为k=10。确保模型的绝对准确。优化过程中每一代种群的平均适应度Lfit_av的变化曲线如图11所示。当迭代次数达到13次时，Lfit_av就已经达到饱和值，15次的迭代次数是非常保守的选择，此时种群中个体的最佳适应度为2.23×105，该个体的具体基因型为：ω1=1.04×105 rad/s、ωZ=2.89×104 rad/s、ωP=5.02×106 rad/s，此即最优的控制器参数设计，整个寻优过程仅耗时55 s，体现了该方案的高效性。
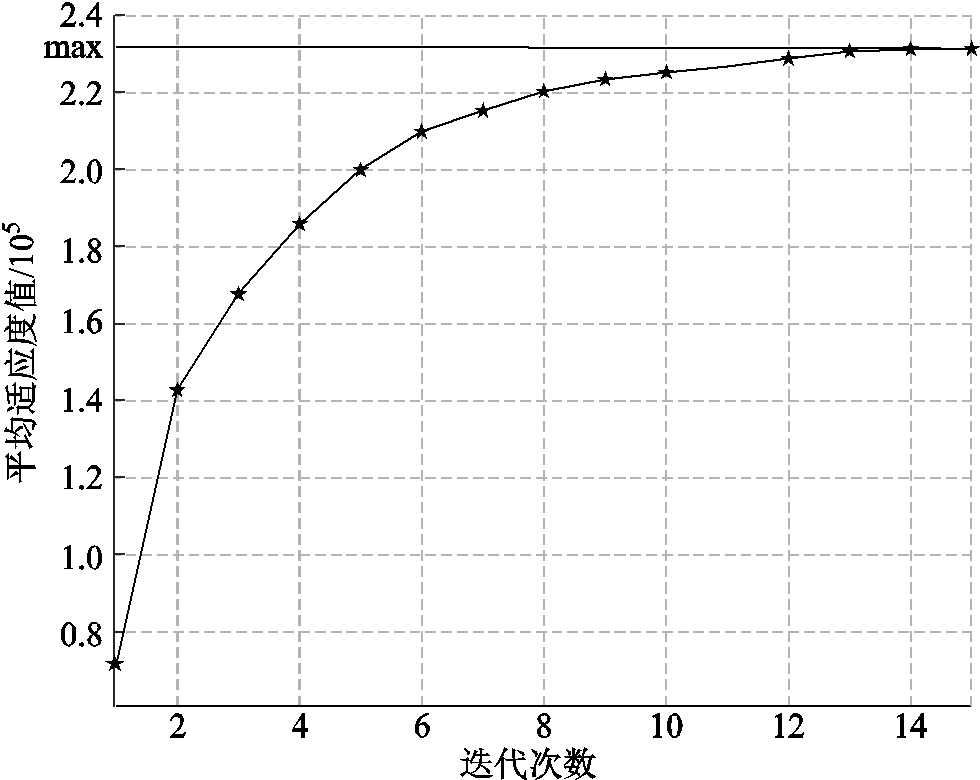
图11 Lfit_av随迭代次数的变化
Fig.11 Variation of Lfit_av during optimization process
案例Ⅱ系统参数见表3，选取Lpm_limit=13°，对其展开控制器的优化设计。设计流程与案例Ⅰ一致，当迭代次数达到8次时，Lfit_av就已达到饱和值，15次迭代后，种群中个体的最佳适应度为1.62×105，该个体的具体基因型为：ω1=3.65×104 rad/s、ωZ=1.47×104 rad/s、ωP=2.22×106 rad/s，此即最优的控制器参数设计，整个寻优过程仅耗时53 s。
表3 案例Ⅱ系统参数
Tab.3 Parameters of Case Ⅱ
参数数值 输入电压Vin/V12 输出电压Vo/V3.3 开关频率fs/kHz620 电感L/mH4.7 滤波电容C/mF15 滤波电容ESR RC/mΩ1.5 负载电阻RL/Ω2 斜坡补偿斜率Se1.49×105 电流采样增益Ri0.1
本文利用Simplis仿真软件搭建了如图2所示的仿真电路。该软件扫频模块原理与实际扫频仪器一致，其测量结果可作为频域分析理论结果的比较基准。利用4.2节中案例Ⅰ的控制器优化参数得到仿真波形如图12所示，系统能够稳定运行，且控制信号纹波主要包含一阶频谱分量，利用式（12）可求得相交点处的斜率Sc=-5.05×104，其绝对值与Se几乎相等。由式（16）可知，若不考虑系统纹波的影响，将严重误判调制器传递函数中的Fm(jω)，进而影响系统模型的准确性。
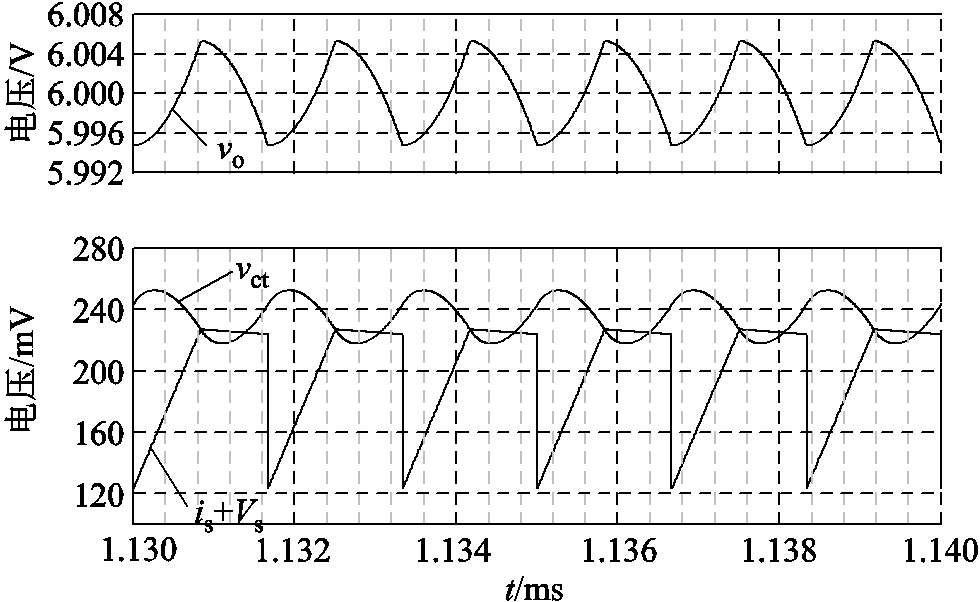
图12 稳定系统的仿真波形
Fig.12 Simulated waveforms in stable condition
由式（28）可求得T_sf(jω)的幅频特性如图13所示，幅值为-20 dB的频率最大值为fmax=466.9 kHz，k取为round(fmax/fs)=1。确定了k的取值，即可根据式（27）与式（29）～式（31）求得系统关键的频域特性。
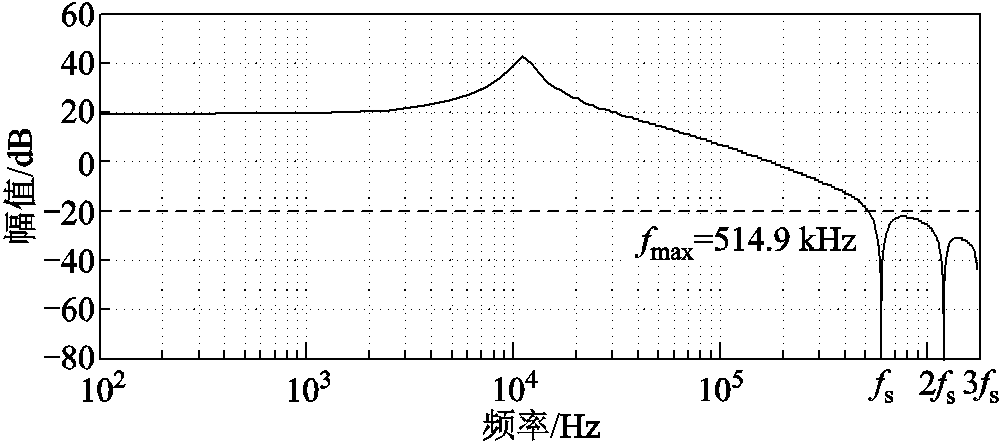
图13 T_sf( jω)的幅频特性
Fig.13 Amplitude-frequency curve of T_sf(jω)
图14～图17将多种理论模型推导的频域特性同仿真测量结果进行对比，现有模型的预测结果均用其提出者的姓氏首字母作为下标，其中文献[14]为L，文献[21]为X。文献[6]与文献[15]的模型结果和文献[14]等价，因此用文献[14]统一代表；文献[21]仅给出模型对应的环路增益推导，并未推导其余关键扰动对系统的影响，因此本文也仅将其纳入环路增益的对比；为了凸显系统纹波的重要影响，对比中还给出了不考虑纹波影响（Sc=0）的高频模型预测结果作为对照。仿真测得的环路带宽为224.3 kHz，接近开关频率的二分之一，为高带宽设计；测得的相位裕度为29.8°，判断系统工作稳定，与图12的仿真波形互为印证。Li Jian模型忽略控制信号纹波对调制器的影响，且不考虑电压外环、电流内环引入的频谱耦合，仅能较好地描述系统的低频特性，其预测的环路带宽与相位裕度分别为239.3 kHz与35.6°，对系统的稳定裕度过于乐观。文献[21]在忽略控制信号纹波的情况下，将电压外环引入的位于ωp-ωs的延拓频谱分量纳入建模，求得的环路增益在高频段的精确性有所提高，然而中低频段的误差反而高于Li Jian模型，其预测的环路带宽与相位裕度分别为347.7 kHz与-62.6°，误判系统处于不稳定状态。不考虑系统纹波（Sc=0）的高频模型虽然充分考虑了电压外环、电流内环引入的频谱耦合，但模型精度大打折扣，其预测的环路带宽与相位裕度分别为345.7 kHz与-83.4°，同样误判了系统的稳定性。由此可见，系统纹波与延拓频谱这两个影响模型精度的因素必须综合考虑。本文提出的高频模型正是将两种因素一同纳入建模，从而实现高精度预测，四种频域特性推导结果均与仿真测量高度一致，其预测的环路带宽与相位裕度分别为222.5 kHz与29.9°。
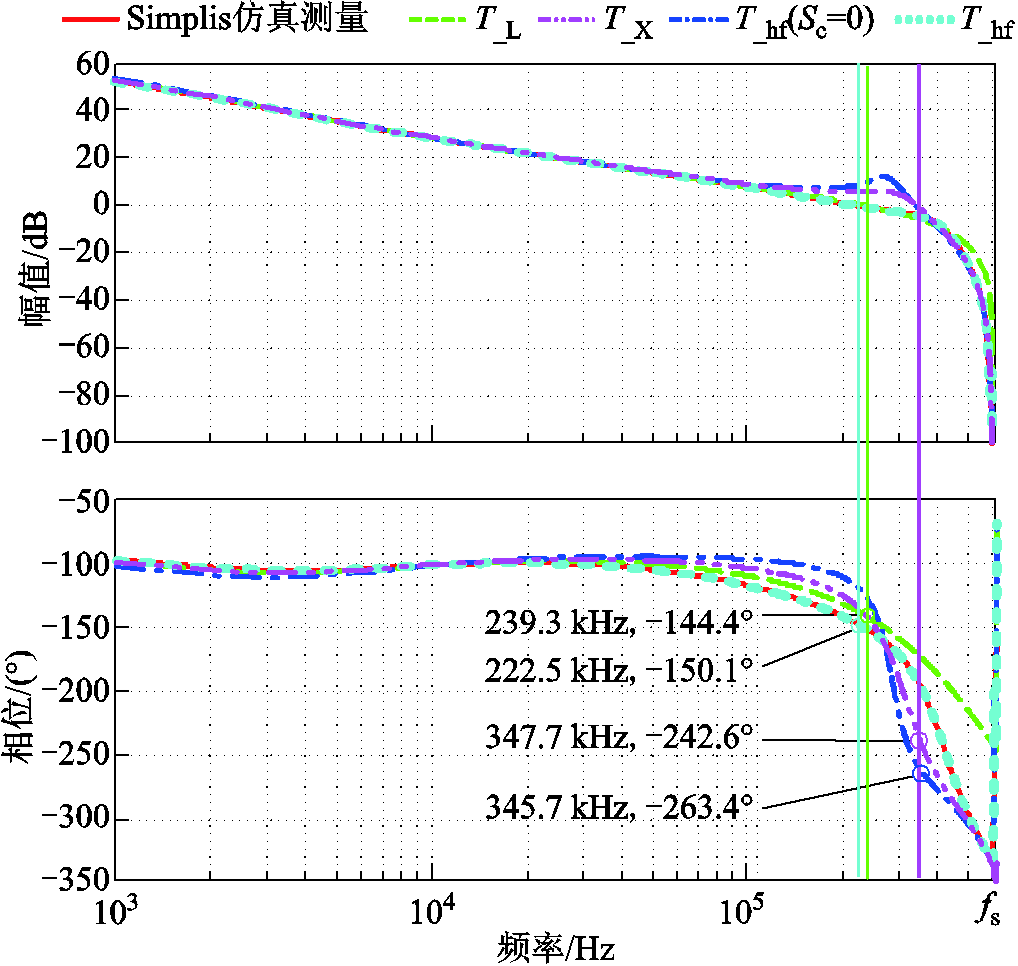
图14 四种模型理论预测环路增益与仿真比较
Fig.14 Loop gain obtained by simulation and four small-signal models
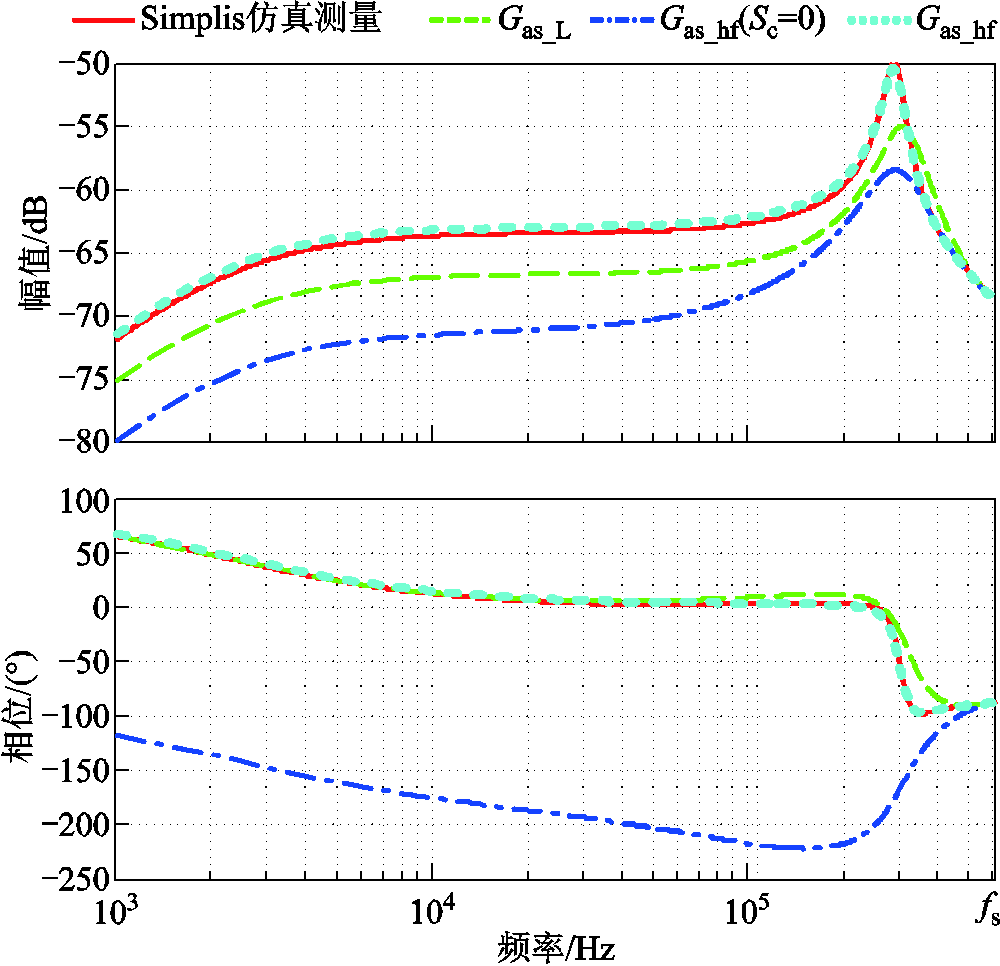
图15 三种模型理论预测音频敏感度与仿真
Fig.15 Audio susceptibility obtained by simulation and three small-signal models
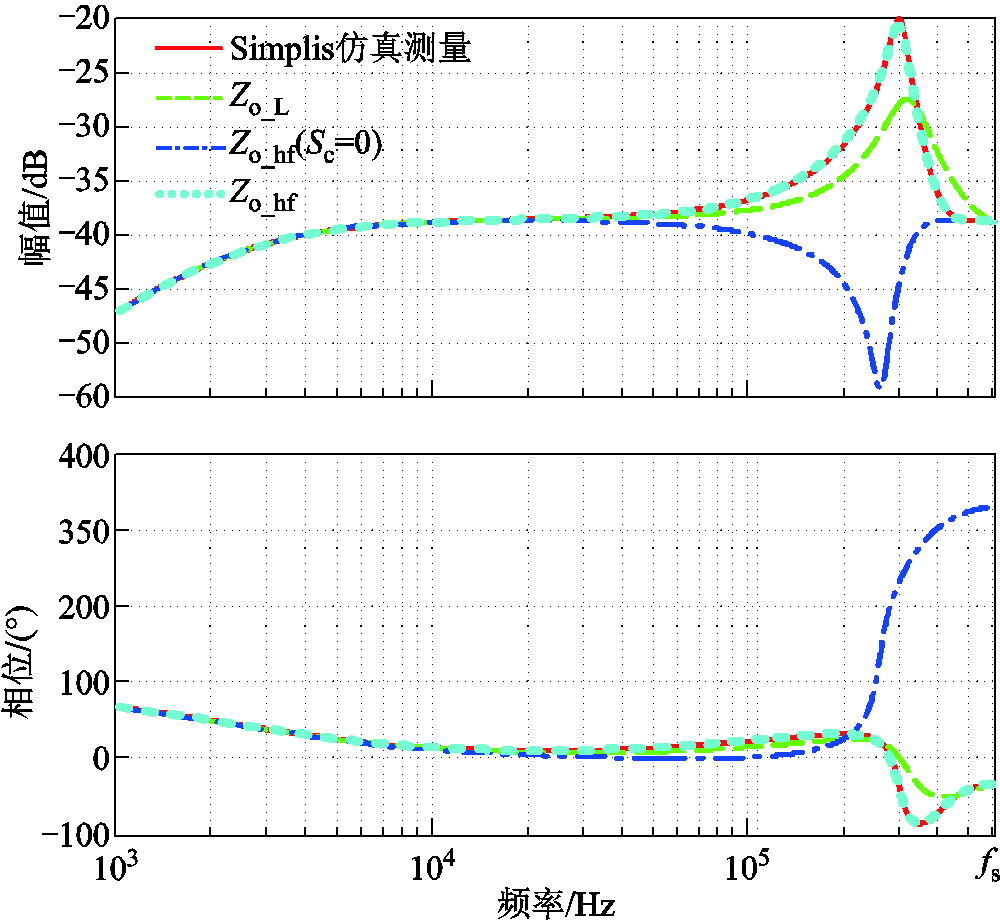
图16 三种模型理论预测输出阻抗与仿真比较
Fig.16 Output impedance obtained by simulation and three small-signal models
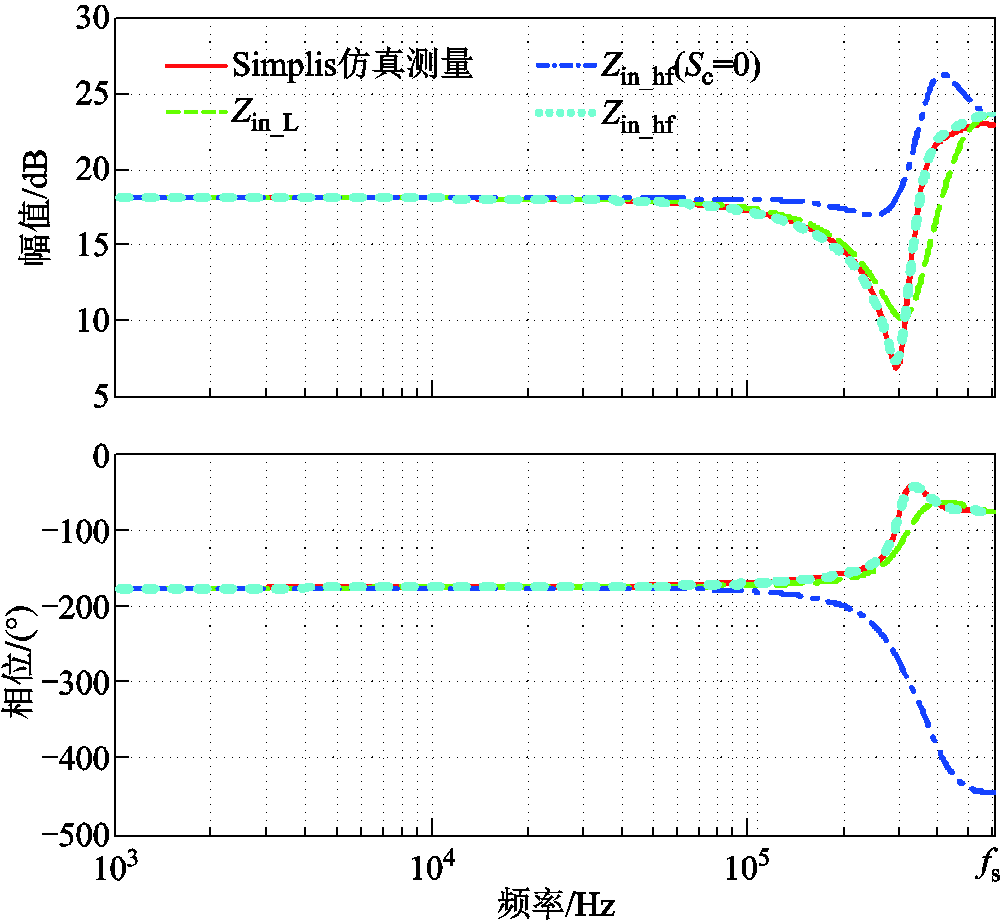
图17 三种模型理论预测输入阻抗与仿真比较
Fig.17 Input impedance obtained by simulation and three small-signal models
观察图17可以发现，本文预测的输入阻抗Zin_hf(jω)在高频段存在微小误差，根源在于其推导采用了如式（32）所示的假设。该假设在牺牲细微精度的同时，大幅精简了表达式，值得采用。
案例Ⅱ中，利用式（12）可求得相交点处的斜率Sc=2.47×104，其绝对值远小于Se，控制信号纹波对系统环路的影响有限。仿真测得的环路带宽为162.0 kHz，相位裕度为12.8°。图18将案例Ⅱ的多种理论模型推导的环路增益与仿真测量结果进行对比，除了Li Jian模型误差较大外，其余模型的预测结果均较为精确，较小的Sc使得不考虑控制信号纹波模型的模型误差得以缩小。本文提出的高频模型预测的环路带宽与相位裕度分别为161.9 kHz与13.1°，与仿真测量结果高度一致。
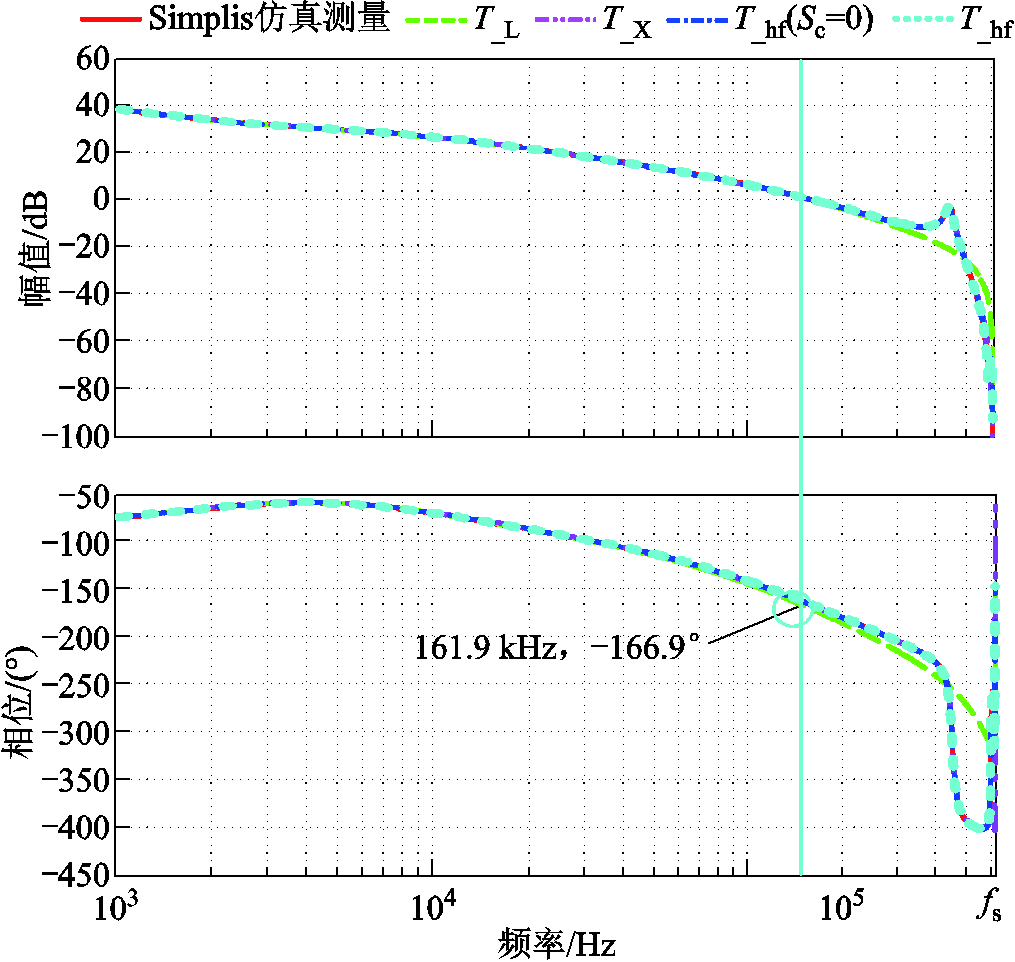
图18 案例Ⅱ模型理论预测环路增益与仿真比较
Fig.18 Loop gain obtained by simulation and small-signal models under Case II
将案例Ⅱ的滤波电容改为C=15 mF，系统将进入不稳定状态。不稳定系统的仿真波形如图19所示，此时输出电压发生了次谐波振荡，导致纹波幅值增大，进而使得控制信号也发生振荡。图20给出了高频模型推导的环路增益T_hf(jω)的伯德图，其求得的相位裕度为负数，能够准确预测系统的不稳定。案例Ⅱ进一步佐证了本文提出的模型的有效性。
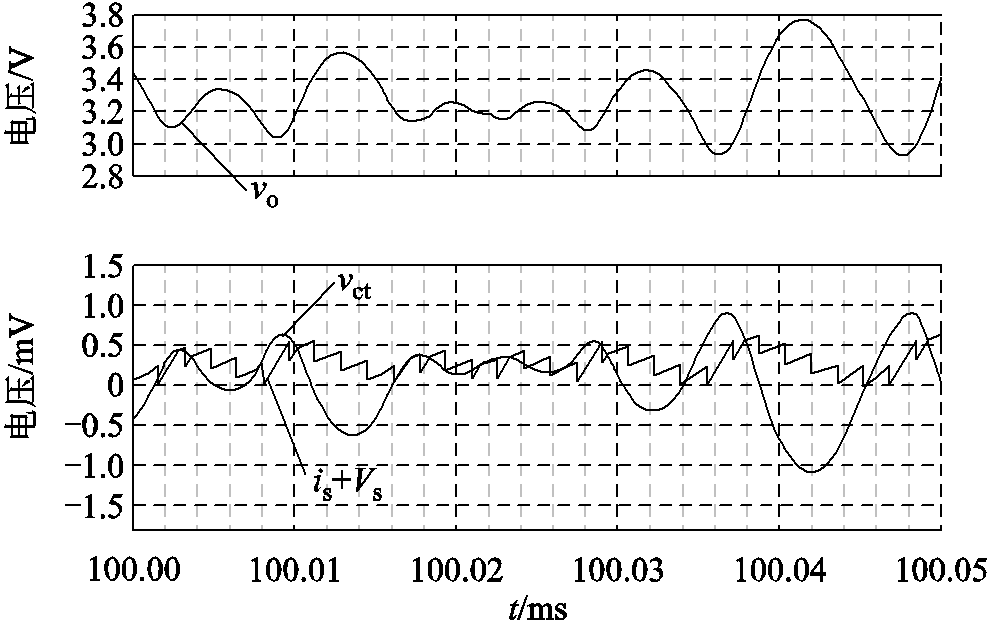
图19 不稳定系统的仿真波形
Fig.19 Simulated waveforms in unstable condition
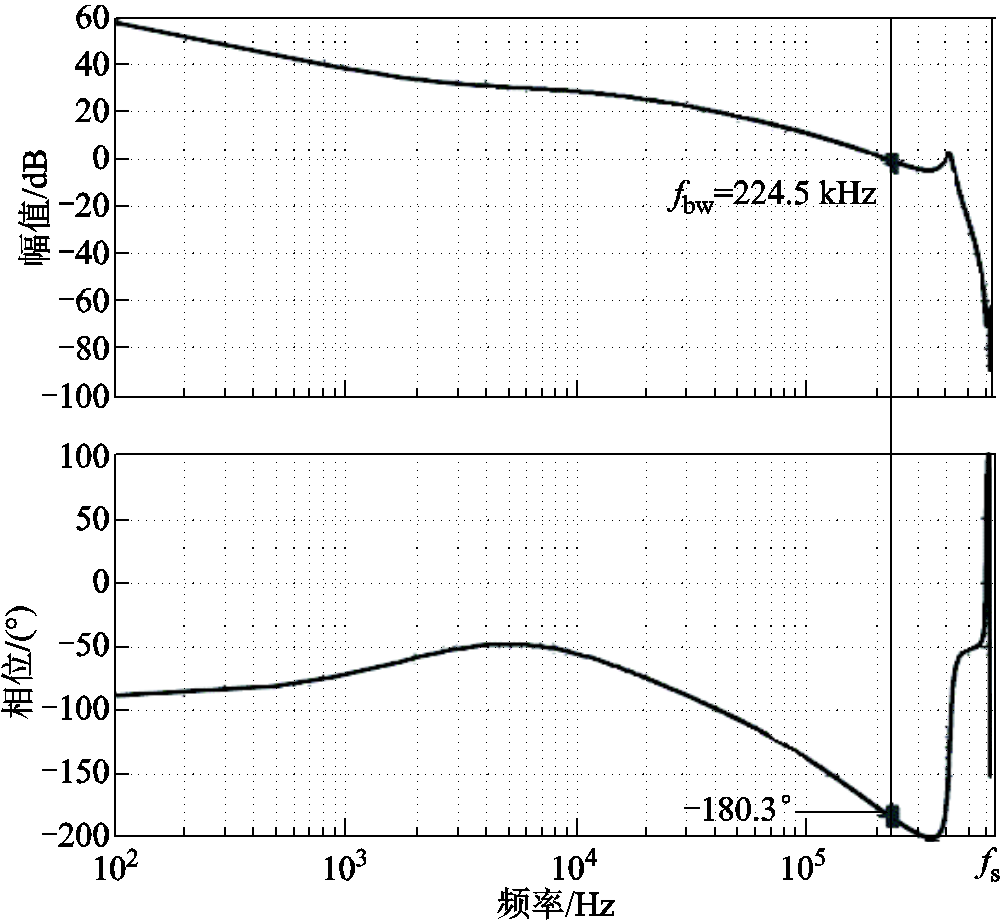
图20 系统不稳定时高频模型预测的环路增益
Fig.20 Loop gain predicted by high-frequency model in unstable condition
为了体现所提出设计方案的高效性，本文复现了文献[26]中基于Simulink时域仿真的遗传算法寻优方案。该方案的时域仿真步长设置为50 ms；适应度函数设计为系统输出电压、电感电流等关键控制对象的绝对误差时间积分；为了实现公平对比，同样在Matlab中展开遗传算法寻优计算，且采用的遗传算法参数与表2保持一致。最终获得案例Ⅰ的优化结果为ω1=1.75×105 rad/s、ωZ=6.17×104 rad/s、ωP=4.32×106 rad/s；案例Ⅱ的优化结果为ω1=1.16× 105 rad/s、ωZ=3.31×104 rad/s、ωP=1.12×106 rad/s。利用Simplis仿真检测得案例Ⅰ参数设计对应的环路带宽与相位裕度分别为183.1 kHz与39.6°，案例Ⅱ参数设计对应的环路带宽与相位裕度分别为215.4 kHz与16.6°，同样实现了稳定的高带宽设计。然而在同样的计算机配置下，案例Ⅰ花费的时间高达4.8 h；案例Ⅱ花费的时间高达3.8 h。本文所提出的寻优方案仅分别耗时55 s与53 s，效率提升数百倍，体现了其高效性。相较于基于时域仿真的参数寻优，基于精确解析模型的另一个优势在于能够通过设置Lpm_limit获取定量的稳定裕度设计。
为进一步验证高频模型准确性，本文选用案例Ⅱ的系统参数，搭建了如图21所示的实验平台。用示波器测得实验波形如图22所示，系统稳定，控制信号纹波为准正弦波，开关频率谐波的近似合理有效；用Venable频率响应分析仪测得系统环路增益如图23所示，与所提出模型的预测结果高度拟合。
图21 实验测量平台
Fig.21 Experimental measurement platform
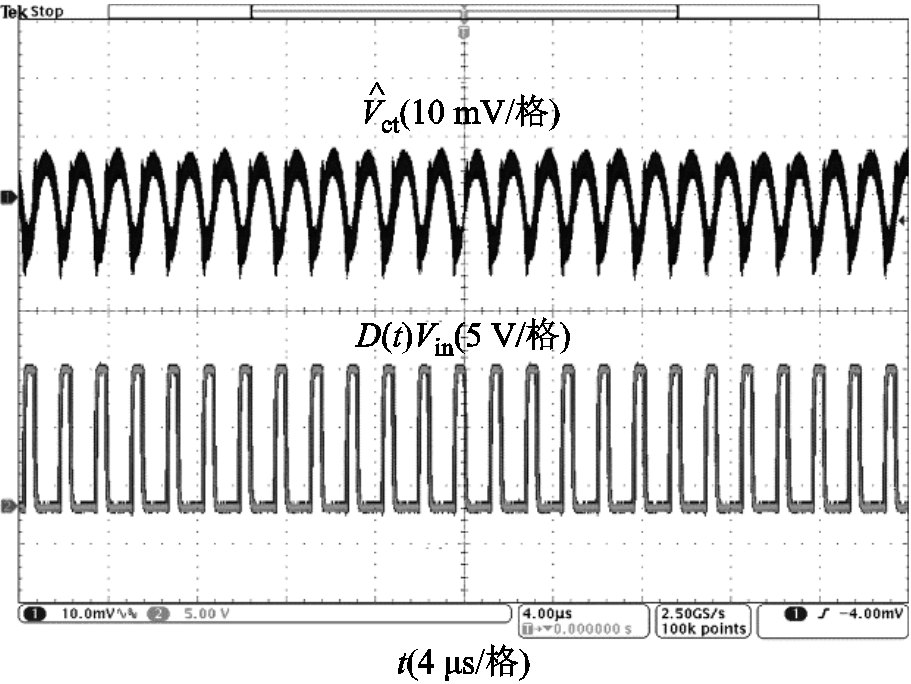
图22 实验波形
Fig.22 Experimental waveforms
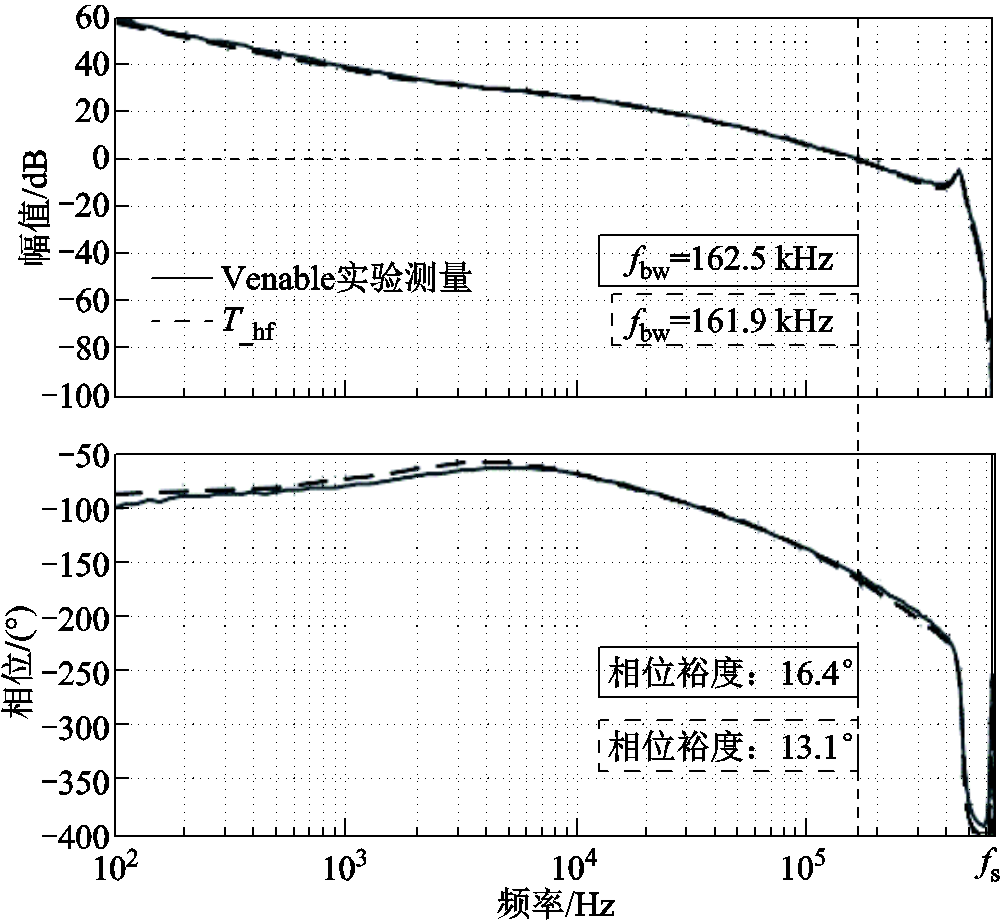
图23 高频模型理论预测环路增益与实验比较
Fig.23 Loop gain obtained by experiment and proposed small-signal model
本文提出了适用于峰值电流控制Buck变换器的高频模型。电压外环引入的控制信号纹波类型由控制器的高频滤波特性决定，可导型纹波对调制器传递函数的影响可等效为与载波相交点处的导数；开关导致的频谱延拓叠加电压、电流环的反馈作用共同导致了小信号扰动下的频谱混叠效应；衰减幅度高于-20 dB的频谱分量对模型精度的影响可以忽略不计以简化模型，矩阵运算能够进一步降低多频谱分量导致的模型复杂度；获得的系统环路增益、音频敏感度、输入阻抗与输出阻抗四个频域分析通用的解析表达式无法转换为零极点形式直接指导控制器设计，通过结合遗传算法的全局寻优能力，能够精确且快速地判断迭代过程中个体的适应度，大幅降低设计耗时，开发出具有工程实用价值的控制器参数优化设计方法。与现有该领域建模工作相比，本文将系统纹波、双闭环引入的频谱混叠综合纳入建模，提高了模型精度；提出了定量的模型简化依据，并探索了基于高频模型的实用化控制器设计方法。下一步拟将该建模思路扩展至其余类型的直流变换器，得出统一的建模框架，并改进智能寻优算法，进一步提高控制器设计的效率。
附 录
详细推导输入电压扰动
与输出电压扰动
(t)对电流内环的影响。
定义(t)的表达式为
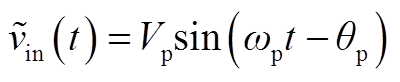（A1）
并定义
(t)的表达式为
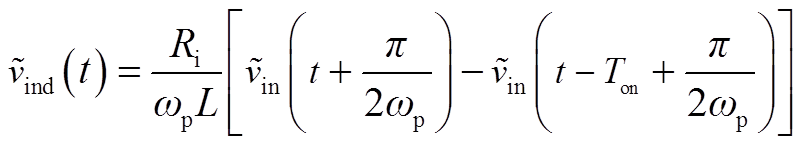（A2）
根据扰动下相邻两个开关周期的几何关系求得
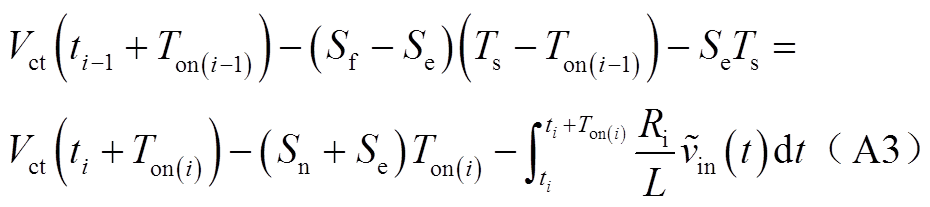
基于泰勒公式可将式（A3）化简为
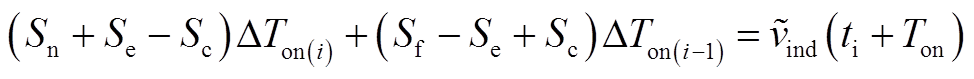（A4）
将(t)的开关频率采样信号记为
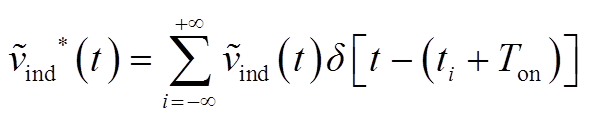（A5）
可近似为由高度为ΔTon(i)的冲击信号构成，有
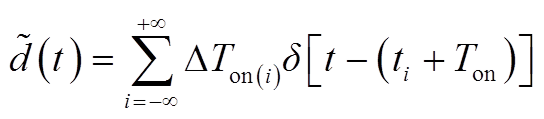（A6）
结合式（A4）～式（A6）可得
（A7）
基于采样定理与傅里叶变换移位性质将式（A7）转换到频域为
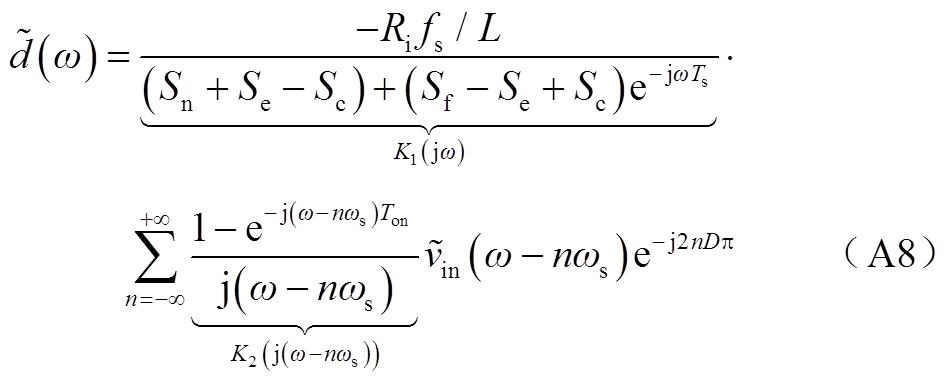
定义(t)的表达式为
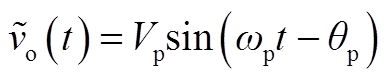（A9）
并定义
(t)的表达式为
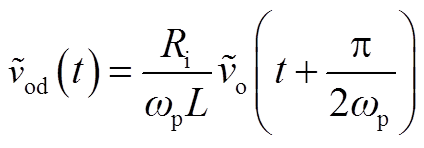（A10）
根据扰动下相邻两个开关周期的几何关系求得
基于泰勒公式可将式（A11）化简为
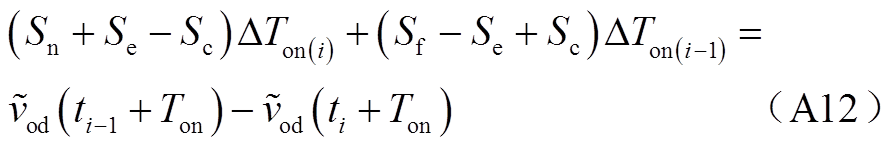
将(t)的开关频率采样信号记为
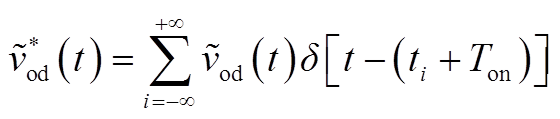（A13）
结合式（A6）与式（A12）、式（A13）可得
（A14）
基于采样定理与傅里叶变换移位性质将式（A14）转换到频域为
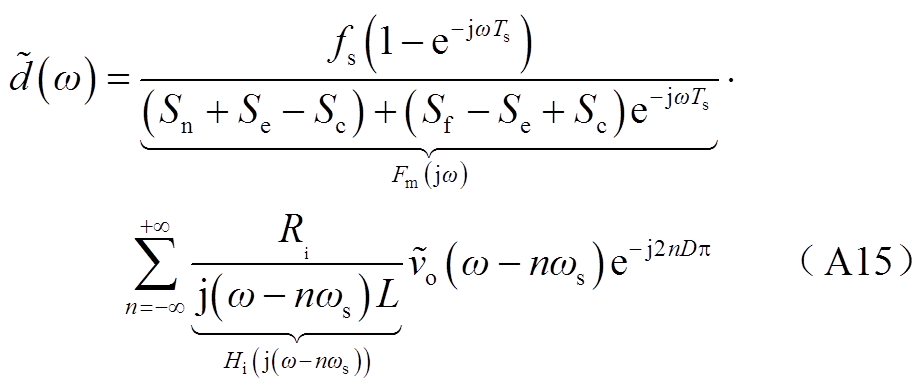
参考文献
[1] Texas Instruments, LM25149 datasheet (2020) [R/OL]. https://www.ti.com.cn/cn/lit/ds/symlink/lm25149. pdf.
[2] Texas Instruments. TPS2585x datasheet (2021) [R/OL]. https://www.ti.com.cn/cn/lit/ds/symlink/tps25850-q1. pdf.
[3] Texas Instruments. LM5143Q1 datasheet (2021) [R/OL]. https://www.ti.com.cn/cn/lit/ds/ symlink/lm5143-q1.pdf.
[4] 何亮, 方宇, 李吉, 等. 峰值电流控制DC/DC变换器的恒值限流方法[J]. 电工技术学报, 2006, 21(10): 86-89, 105. He Liang, Fang Yu, Li Ji, et al. Over Current protection for peak current controlled DC-DC converter[J]. Transactions of China Electrotechnical Society, 2006, 21(10): 86-89, 105.
[5] Suntio T. On dynamic modeling of PCM-controlled converters—Buck converter as an example[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5502-5518.
[6] Ridley R B. A new, continuous-time model for current-mode control (power convertors)[J]. IEEE Transactions on Power Electronics, 1991, 6(2): 271-280.
[7] James D. Moore’s law continues into the 1x-nm era[C]//2016 21st International Conference on Ion Implantation Technology (IIT), Tainan, Taiwan, China, 2017: 1-10.
[8] Borkar S, Dubey P, Kahn K C, et al. Platform 2015: intel ® processor and platform evolution for the next decade[N]. Technology, 2005: 1-10
[9] Stanford E. New processors will require new powering technologies[J]. Power Electronics Technology, 2002, 28(2): 32-42.
[10] Wong P L, Lee F C, Xu Peng, et al. Critical inductance in voltage regulator modules[J]. IEEE Transactions on Power Electronics, 2002, 17(4): 485-492.
[11] Qiu Yang, Yao Kaiwei, Meng Yu, et al. Control-loop bandwidth limitations for multiphase interleaving Buck converters[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2004. APEC '04, Anaheim, CA, USA, 2004: 1322-1328.
[12] Middlebrook R D. Topics in multiple-loop regulators and current-mode programming[J]. IEEE Transactions on Power Electronics, 1987, PE-2(2): 109-124.
[13] 高国庆, 雷万钧, 袁晓杰, 等. 双有源全桥变换器全状态离散迭代建模与输出电压纹波分析[J]. 电工技术学报, 2021, 36(2): 330-340. Gao Guoqing, Lei Wanjun, Yuan Xiaojie, et al. Full-state discrete-time model and the output-voltage-ripple analysis of the dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 330-340.
[14] Li Jian. Current-mode control: modeling and its digital application[D]. Virginia: Virginia Tech Dissertation, 2009.
[15] Yan Na, Ruan Xinbo, Li Xin. A general approach to sampled-data modeling for ripple-based control—part I: peak/valley current mode and peak/valley voltage mode[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6371-6384.
[16] Qiu Yang, Xu Ming, Sun Juanjuan, et al. A generic high-frequency model for the nonlinearities in Buck converters[J]. IEEE Transactions on Power Electronics, 2007, 22(5): 1970-1977.
[17] 岳小龙, 卓放, 杨书豪, 等. Buck变换器的多频率矩阵模型及其在分布式供电系统中的应用[J]. 电工技术学报, 2017, 32(4): 250-259. Yue Xiaolong, Zhuo Fang, Yang Shuhao, et al. A multifrequency matrix model for Buck converters and its application in distributed power system[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 250-259.
[18] Hsiao S F, Chen Dan, Chen C J, et al. A new multiple-frequency small-signal model for high-bandwidth computer V-core regulator applications[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 733-742.
[19] Cheng Xiangpeng, Liu Jinjun, Liu Zeng. A generalized multifrequency small-signal model for high-bandwidth Buck converters under constant-frequency voltage-mode control[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8186-8199.
[20] Cheng Xiangpeng, Liu Jinjun, Liu Zeng. Accurate small-signal modeling and stability analysis of wide-input Buck converter considering modulation waveform ripples[J]. IEEE Transactions on Power Electronics, 2022, 37(6): 6962-6971.
[21] Xu Shen, Li Fei, Yao Yunpeng, et al. A high-frequency model for a PCM Buck converter[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 2304-2312.
[22] Hung M H, Shu Lisun, Ho S J, et al. A novel intelligent multiobjective simulated annealing algorithm for designing robust PID controllers[J]. IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 2008, 38(2): 319-330.
[23] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76. Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76.
[24] 江凌峰, 龚邻骁, 金新宇, 等. 基于遗传算法的多模块IPOP双有源全桥DC-DC变换器总电流有效值优化策略[J]. 电工技术学报, 2023, 38(24): 6782-6797. Jiang Lingfeng, Gong Lingxiao, Jin Xinyu, et al. Total root mean square current optimization of IPOP dual active bridge DC-DC converter based on genetic algorithm[J/OL]. Transactions of China Electrotechnical Society, 2023, 38(24): 6782-6797.
[25] 袁立强, 陆子贤, 孙建宁, 等. 电能路由器设计自动化综述—设计流程架构和遗传算法[J]. 电工技术学报, 2020, 35(18): 3878-3893. Yuan Liqiang, Lu Zixian, Sun Jianning, et al. Design automation for electrical energy router-design workflow framework and genetic algorithm: a review[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3878-3893.
[26] Divakar A, Jacob J. Genetic algorithm based tuning of nonfragile and robust PI controller for PSFB DC-DC converter[C]//2019 International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 2020: 1846-1851.
[27] Peng C C, Lee C L. Performance demands based servo motor speed control: a genetic algorithm proportional-integral control parameters design[C]//2020 International Symposium on Computer, Consumer and Control (IS3C), Taichung City, Taiwan, China, 2021: 469-472.
[28] Wang Chang, Zsurzsan T G, Zhang Zhe. Genetic algorithm assisted parametric design of splitting inductance in high frequency GaN-based dual active bridge converter[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 522-531.
[29] Kostov K S, Kyyra J J. Genetic algorithm optimization of peak current mode controlled Buck converter[C]// Proceedings of the 2005 IEEE Midnight-Summer Workshop on Soft Computing in Industrial Applications, 2005, SMCia/05, Espoo, Finland, 2005: 111-116.
[30] 蔡子龙, 束洪春, 单节杉. 考虑运营成本的电动公交车集群换电优化调度策略[J]. 电力系统自动化, 2022, 46(17): 205-217. Cai Zilong, Shu Hongchun, Shan Jieshan. Optimal dispatching strategy for battery swapping of electric bus cluster considering operation cost[J]. Automation of Electric Power Systems, 2022, 46(17): 205-217.
Abstract Peak current-model (PCM) Buck converters are widely employed in power management ICs. As microprocessors integrate continuously, high-bandwidth design has become a requisite for the front-end Buck converters. Accurate small-signal modeling is crucial for analyzing system stability and designing high-performance controllers. Existing models neglect control signal ripples (CSRs) in steady-state and extended-spectrum under small-signal perturbation transferred by voltage-loop, which makes significant errors under high control bandwidth and fails to guide controller design. To portray the high-frequency characteristics of the system and direct the design of high-bandwidth controllers, this paper proposed a high-frequency model for PCM Buck converters. An optimal controller design method was conducted based on the proposed model and genetic algorithm.
Firstly, this paper emphasized that different types of CSRs are initiated by different types of controllers. Subsequently, influences caused by differentiable CSRs were analyzed, wherein the impact of differentiable ripples on the system can be equivalent to the derivative values at crossing points. The spectrum coupling from the voltage-loop and current-loop was incorporated, and the maximum frequency point corresponding to -20 dB amplitude of the single-frequency loop gain was taken as the selection boundary of the extended spectrum to simplify the model. Thereby an accurate small-signal model was obtained. Analytical expressions for loop gain, audio susceptibility, input impedance, and output impedance were derived based on matrix operations. Lastly, based on the proposed high-frequency model, an efficient optimization design of high-bandwidth controllers was conducted by combining genetic algorithm.
To assert the accuracy of the proposed model and the effectiveness of the optimal controller design method, this paper devised two cases and conducted simulations and experimental verifications. For case Ⅰ, the loop gain predicted by the proposed model (Bandwidth: 222.5 kHz, Phase margin: 29.9°) matches well with the simulated results (Bandwidth: 224.3 kHz, Phase margin: 29.8°). For case Ⅱ, the loop gain predicted by the proposed model (Bandwidth: 161.9 kHz, Phase margin: 13.1°) also matches well with the simulated results (Bandwidth: 162.0 kHz, Phase margin: 12.8°). The parameters of case Ⅱ were leveraged to construct an experimental platform. The loop gain of the system is measured using a Venable Frequency Analyzer. The experimental results (Bandwidth: 162.5 kHz, Phase margin: 16.4°) further confirm the accuracy of the proposed model. Deviations between them are mainly due to parameter variations and measurement errors in the real system. The simulation-based genetic algorithm optimization method in Simulink was redone to illustrate the efficiency of the proposed optimal controller design method. To achieve a fair comparison, the genetic algorithm optimization calculation was also carried out in Matlab, and even with the same computer settings, case Ⅰ takes up to 4.8 h and case Ⅱ takes up to 3.8h. The proposed optimal controller design method takes only 55 s and 53 s respectively, which are hundreds of times more efficient, showcasing its effectiveness. Compared with the time-domain simulation-based parameter search method, the ability to attain a quantitative stability margin design by setting Lpm_limit is another advantage by utilizing the precise analytical model.
Simulation and experimental results demonstrate that the proposed high-frequency model is accurate enough to portray frequency domain characteristics and forecast system stability precisely, compared with existing models. Additionally, the proposed optimal controller design method enables fast and efficient implementation of high-bandwidth controller designs. The proposed high-frequency model belongs to an analytical model and significantly reduces the computational burden on computers. Combining it with a genetic algorithm results in complementary benefits. This combination facilitates quick and precise appraisal of individual fitness during the iteration process, thereby reducing design time considerably and offering practical value in engineering applications.
keywords：Buck converter, peak current-mode, high-bandwidth, high-frequency modeling, genetic algorithm
DOI:10.19595/j.cnki.1000-6753.tces.221916
中图分类号：TM46
国家自然科学基金资助项目（51437007）。
收稿日期 2022-10-07
改稿日期 2023-06-26
程翔鹏 男，1994年生，博士，研究方向为DC-DC变换器精确小信号建模、基于智能算法的控制器设计与多电力电子变换器系统稳定性分析。E-mail：alexcheng1994@163.com
刘进军 男，1970年生，教授，博士生导师，研究方向为电力电子技术在电能质量控制、输配电系统以及分布式发电系统中的应用、电力电子电路和系统的建模、仿真、分析和控制等。E-mail：jjliu@mail.xjtu.edu.cn（通信作者）
（编辑 赫 蕾）