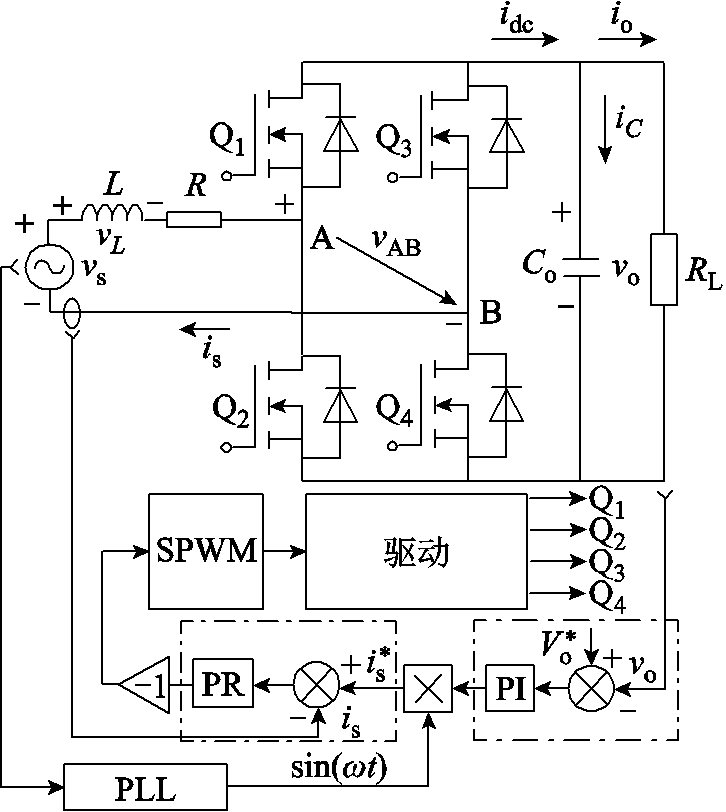
图1 单相PWM整流器
Fig.1 Single-phase PWM rectifier
摘要 单相PWM整流器一般采用电压外环比例积分、电流内环比例谐振的双闭环控制方法，在实现交流侧高功率因数的同时稳定直流侧输出电压，因此受到国内外学者的广泛研究。然而，在内外环控制参数设计阶段，传统设计方法一般根据经验选取控制参数，参数选取范围较大，且无法量化评估控制参数的时域控制效果，导致参数优化整定困难。为此，该文提出一种基于离散时域模型的内外环控制参数多目标优化设计方法。首先，采用传统设计方法确定电压外环比例、积分控制参数以及电流内环比例、谐振控制参数的安全设计空间；然后，基于离散时域模型将安全设计空间正映射至控制参数的时域性能空间，实现电流内环控制参数对交流侧功率因数以及电压外环控制参数对直流侧电压超调量的量化评估。在此基础上，通过进一步约束性能目标得到性能优化设计空间，考虑内外环控制参数的耦合效应，对内外环性能优化设计空间进行重新组合，再将其映射至性能空间，得到内外环控制目标帕累托最优前沿下的最优设计空间，从中选取内外环控制参数的优化设计点，在典型工况下实验测得的交流侧功率因数为0.981 26，直流输出电压超调量绝对值为1.37%，证明了所提优化设计方法的正确性。
关键词：PWM整流器 离散时域模型 控制器参数 多目标优化 动态性能优化
单相PWM整流器相比于传统的整流器，具有交流侧功率因数高、可实现能量双向流动、电流谐波含量低等优点[1-2]，广泛应用于铁路机车牵引[3]、车载充电机[4]等领域。
单相PWM整流器一般采用电压外环、电流内环的双闭环控制策略。其中电流内环控制交流侧电流与电压同相，实现功率因数校正功能，电压外环控制直流侧输出电压稳定；电压外环常采用比例积分（Proportional Integral, PI）控制器，而电流内环常采用PI控制或比例谐振（Proportional Resonant, PR）控制器[5]。比较而言，PR控制器能够有效地抑制工频交流稳态误差，但其控制参数难于整定，整定不当会引起系统稳定性问题。常用的参数整定方法如文献[6]应用频率响应法对PR控制器的参数进行整定，文献[7]针对三相系统的交叉耦合提出矢量PI整定方法；文献[8]对PR控制器进行离散化，并通过Bode图分析控制参数的取值；文献[9]采用根轨迹法在离散域中对PR控制器的参数进行设计。然而，现有对控制参数的设计方法大都需要观察频率响应并根据经验选取，很难形成一套通用、定量的优化设计方案。
传统控制参数设计方法基于系统频域下的控制模型，根据相位裕量及控制带宽的要求，采用“先内后外”的方法完成控制参数的设计。然而，单相PWM整流器为非线性时变系统，其频域控制模型并不能完全描述其时域动态行为，无法在设计阶段确保系统的时域动稳态性能指标达到设计要求。此外，由于内外环控制参数存在较强的耦合作用，也会对系统的动稳态性能产生较大的影响，而传统方法并没有考虑它们的耦合效应。可以看出，由于缺乏内外环控制参数大小与时域动稳态性能指标的准确映射关系，还需要通过实验调试来确定实际控制参数，导致大量的人力耗费。
为此，本文提出了一种新的多目标控制参数优化设计方法，通过时域的性能指标而不是频率响应进行分析，更直观地展示控制参数的定量控制效果。该方法中，传统的频域控制模型用来确定控制参数的安全设计空间，将变换器的离散时域模型作为映射工具，获取内外环被控变量的时域波形，对控制参数的效果进行量化评估，得到性能空间，再根据设计要求得到性能优化设计空间。随后考虑内外环控制的耦合效应，获取性能优化设计空间下，内外环控制目标的帕累托前沿，从中选取最优设计空间，得到控制参数的最优取值范围。上述优化设计方法目前鲜有相关研究报道，有必要做进一步的研究。
本文首先介绍单相PWM整流器的电压外环与电流内环控制模型；然后分析离散时域模型和控制参数的自动迭代求解方法；随后分析并选取内外环时域性能指标；最后在双闭环控制参数的多目标性能空间中，分析最优控制参数的取值范围，并通过PLECS、Matlab软件的理论分析及PWM整流器实验样机证明本文所提出方法的正确性。
单相PWM整流器系统如图1所示，主电路主要由输入电感、全桥电路、输出电容、负载电阻等部分组成。其中，vs、is分别为电网电压和电流，L和R分别为网侧电感和等效电阻，Q1～Q4为全桥电路的开关管，vAB为交流侧电压，Co为直流侧电容，vo为输出电压，idc为直流侧输出电流，iC为电容Co的电流，io为负载的电流。
图1 单相PWM整流器
Fig.1 Single-phase PWM rectifier
单相PWM整流器的双闭环控制结构在图1中由电压外环与电流内环组成，电压外环将电压参考信号与实际电压的误差输入至比例积分控制器，得到电流内环参考信号的幅值。内环参考信号的相位与频率通过采样输入电压，再进入锁相环计算得到。内环参考信号与实际电流的误差通过比例谐振控制器后进行反向，得到的调制信号再经过SPWM调制和驱动电路后得到各个开关管的占空比信号。因此，系统主电路参数确定后，双闭环控制系统中外环比例、积分控制参数，内环比例、谐振控制参数的优化设计是提升系统动稳态性能的关键所在。
由于单相PWM整流器主电路参数也会对系统动稳态性能产生影响，为验证本文所提出的控制器参数多目标优化设计方法对不同的主电路参数系统具备普适性，本文按照实际需求中的设计指标，以电感电流纹波系数5%，直流母线电压纹波ΔVo=10 V设计主电路参数，进而验证本文的控制器参数多目标优化设计方法的可行性。所搭建的PWM整流器主电路参数见表1。
表1 PWM整流器主电路参数
Tab.1 PWM rectifier main circuit parameters
参数数值 输入电压有效值Vs/V220 额定输出电压Vo/V400 额定负载RL/Ω225 电网频率fL/Hz50 开关频率fs/kHz75 网侧电感L/mH网侧等效电阻R/Ω10.1 直流侧电容Co/μF470
通过传统设计方法得到单相PWM整流器电流内环和电压外环的控制框图，如图2所示[10-11]。
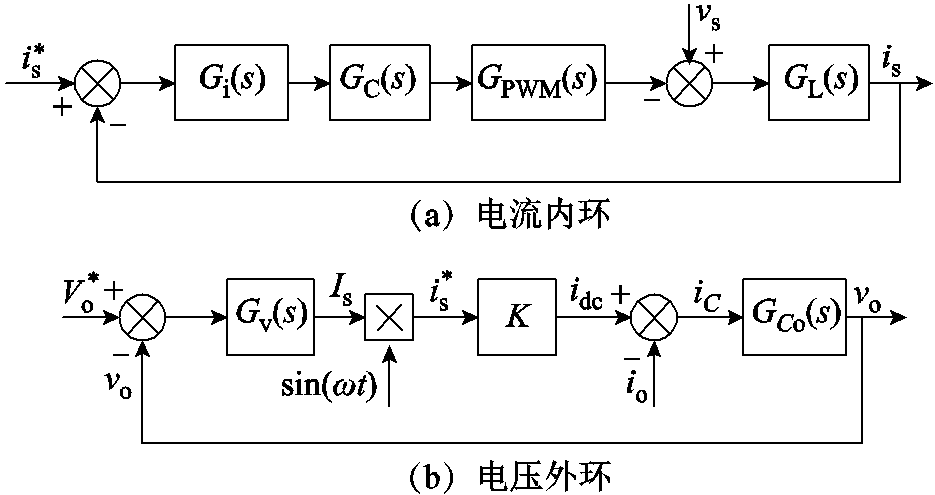
图2 双闭环控制框图
Fig.2 Block diagram of double control loop
图2a电流内环控制框图中，交流侧滤波器是被控对象，其传递函数为
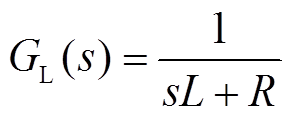（1）
Gi(s)采用PR控制器，理想的传递函数为
（2）
式中，Kp,i为比例系数；Kr为谐振系数；wo为电网电压角频率，wo=2πfL。理想PR控制器可以在wo处获得无穷大增益，从而实现网侧电流基波分量的无静差调节。由于实际电网的频率存在波动，当电网频率偏离所设置的基波角频率时，PR控制器提供的增益将迅速下降，使得网侧电流的稳态误差迅速增大。为保证PR控制器在电网的基波频率处始终具有很高的增益，实际采用在较宽频带内获得高增益的PR控制器[12]，其表达式为
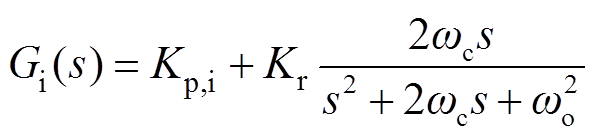（3）
考虑实验过程中交流电源输出频率存在一定的波动范围，式（3）中截止频率ωc取3.14 rad/s。
PWM延时等效为零阶保持器，同时考虑连续域到离散域的采样，PWM延时的传递函数为
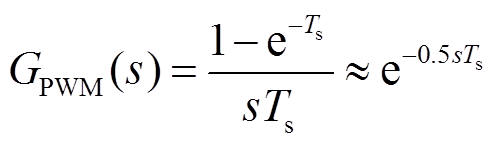（4）
式中，Ts为控制周期。计算延时为一拍时延，传递函数为
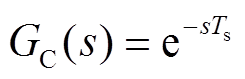（5）
由以上分析及图2a可知，电流内环的开环传递函数Go1为
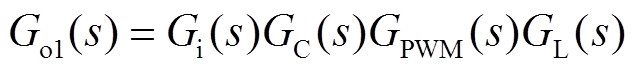（6）
图2b电压外环控制框图中，输出电容是被控对象，传递函数为
（7）
电压外环Gv(s)采用PI控制器，传递函数为
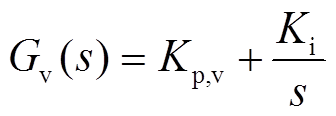（8）
式中，Kp,v为比例系数；Ki为积分系数。
当电流内环能够实现无静差跟踪时，可将其近似为1，则在图2b中内环给定值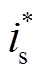
近似为输入电流实际值is。其中，输入电流is至直流侧输出电流idc的增益为
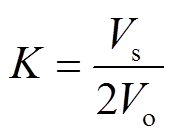（9）
由以上分析及图2b可知，电压外环的开环传递函数Go2为
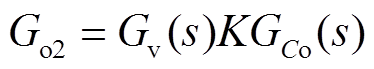（10）
为使系统具有良好的动态响应性能，在内环控制器参数设计时，设置电流内环控制系统的约束条件为相位裕度15°～60°，带宽为500 Hz～1 kHz；外环控制系统的约束条件为相位裕度30°～80°，同时为了抑制输出电压的二倍工频纹波，带宽小于100 Hz。在式（6）与式（10）中，改变控制参数的取值，分别计算内外环传递函数的相位裕度与带宽，判断是否满足各自的约束条件，即可得到满足要求的控制参数安全设计空间，其结果如图3所示，其中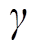
表示相位裕度。
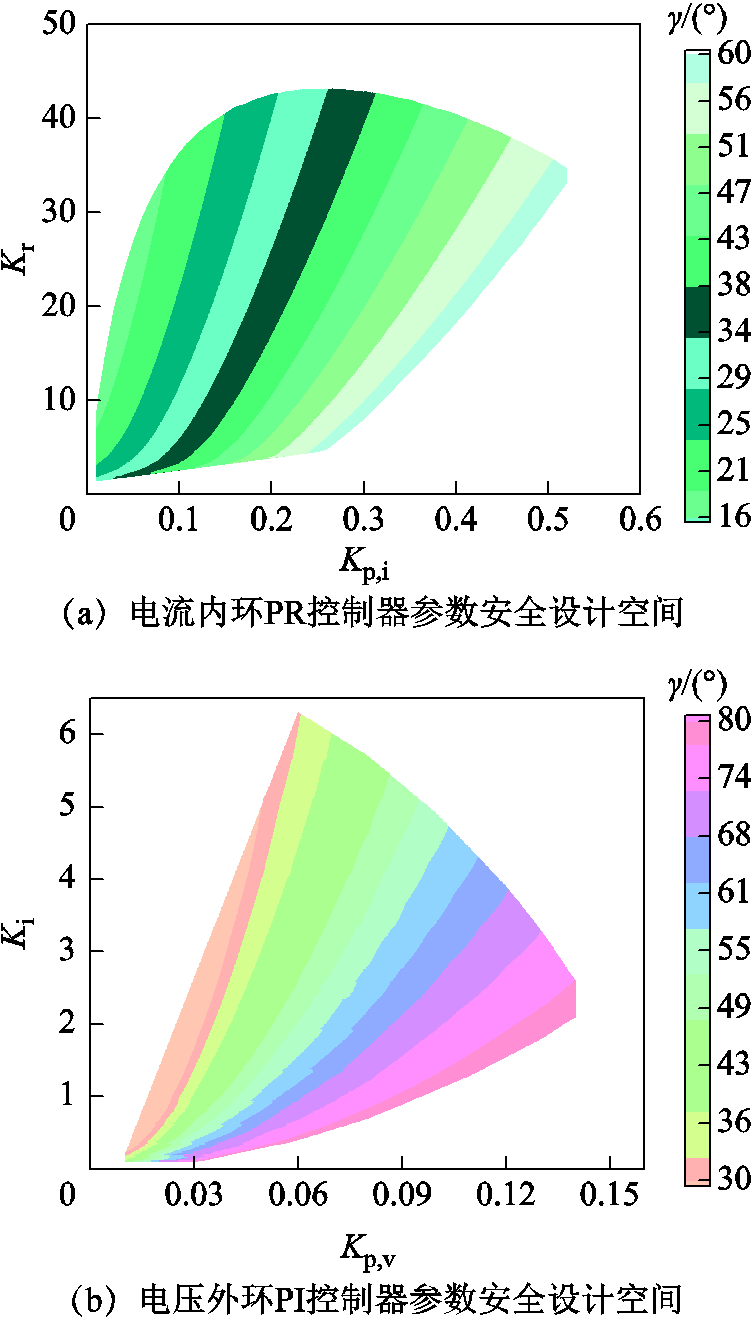
图3 内外环控制器参数安全设计空间
Fig.3 Inner and outer loop controller parameter safe design space
通过频域下对电压外环、电流内环传递函数相位裕度与带宽范围的约束，得到图3所示电流内环PR控制参数与电压外环PI控制参数的安全设计空间。从内环控制参数的设计空间可知，相同Kp,i参数下，随着Kr参数的增大，相位裕度逐渐减小，内环控制系统的带宽逐渐增加；相同Kr参数下，随着Kp,i参数的增大，相位裕度逐渐增加，带宽逐渐减小。从式（3）可知，随着Kp,i参数的增加，整个频率范围内环控制系统的开环增益均有所提高；Kr参数的增加，对频率wo处的开环增益增加得更为明显，使系统能够更快地响应该特定频率，带宽也有所增加。可见，带宽越高，内环控制系统响应速度越快，但抗干扰能力越差，相位裕度有所下降，同理，可对外环控制参数进行分析。
从图3所示的范围取值得到的控制参数，能够控制系统的稳定运行。然而从图中不难发现，各控制参数的取值范围非常宽泛，难以在系统的响应速度与稳定程度之间进行直观的权衡，从中获取最优控制目标下的设计空间较为困难，需要经过反复不断的参数调试才能得到。因此，如能将参数的控制效果进行量化评估，那么根据量化结果，可将安全设计空间中的取值范围更加精确。安全设计空间提供有效控制参数的取值范围，后续将在此基础上，对其逐步约束，获取最优设计空间。为量化评估安全设计空间，最直接的方式是分析被控变量受到扰动后的动态响应波形，得到控制参数的控制效果，因此，实现控制参数的自动迭代并能求解得到电压外环与电流内环被控变量的时域波形，是将图3的安全设计空间进行优化的关键。
在电力电子设计自动化中，“设计空间”到“性能空间”的映射称为“正映射”[13]，如图4所示。传统频域模型中，内、外环传递函数中的控制参数组成设计空间，为保障系统的安全稳定运行，约束相位裕度和带宽范围，得到的控制参数范围即为安全设计空间。由于安全设计空间范围较大，不同控制参数的效果差异也较大。为了量化评估控制效果，本文采用的正映射方法是PLECS软件仿真离散时域模型，得到被控变量的时域波形用于分析控制参数对应的功率因数与超调量性能参数，形成性能空间，从而建立控制器参数与控制性能指标的联系。
图4 电力电子设计自动化的设计流程架构
Fig.4 Design framework of design automation for power electronics
在传统的频域模型下，相位裕度表征系统的稳定裕量，而高阶非线性时变系统无法建立频域指标与时域响应性能的定量关系。为此，可建立系统的离散时域模型求解被控变量的时域波形，分析不同控制参数的效果。离散时域模型以系统状态变量的变化为时间节点[14]，对于图1所示的单相 PWM 整流器，常用的调制方式主要有单极性和双极性调制。下面以双极性调制为例，建立其离散时域模型。按照输入电流不同的状态将其分为图5所示的四个工作模态，在t=(k+1)T的状态变量x[k+1]利用x[k]进行求解得
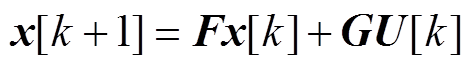（11）
其中，x=[isvo]T, U=[vs]，根据各个工作模式的开关状态可求解得到矩阵F和G。在离散时域模型中，所有的开关器件均被建模为理想的开关器件，同时要完成大量控制参数设计空间的正映射，要求仿真软件能够实现控制参数的自动迭代仿真运行，保证较快的仿真运行速度，以免优化时间过长。因此，本文选用PLECS高性能电力电子求解工具，建立单相PWM整流器的主电路及双闭环控制离散时域模型，其将电力电子器件建模为理想的开关器件，使用强大的Simulation Script自动迭代仿真功能，能够求解在不同双闭环控制器参数下，被控变量的时域波形，并且该仿真软件对于求解算法的优化使得仿真运行速度较快。通过该工具将前述所得到的控制器参数安全设计空间进行正映射，实现对控制器参数控制效果的定量评估，在此基础上，合理选取内外环控制系统的性能指标，得到性能空间也非常重要。
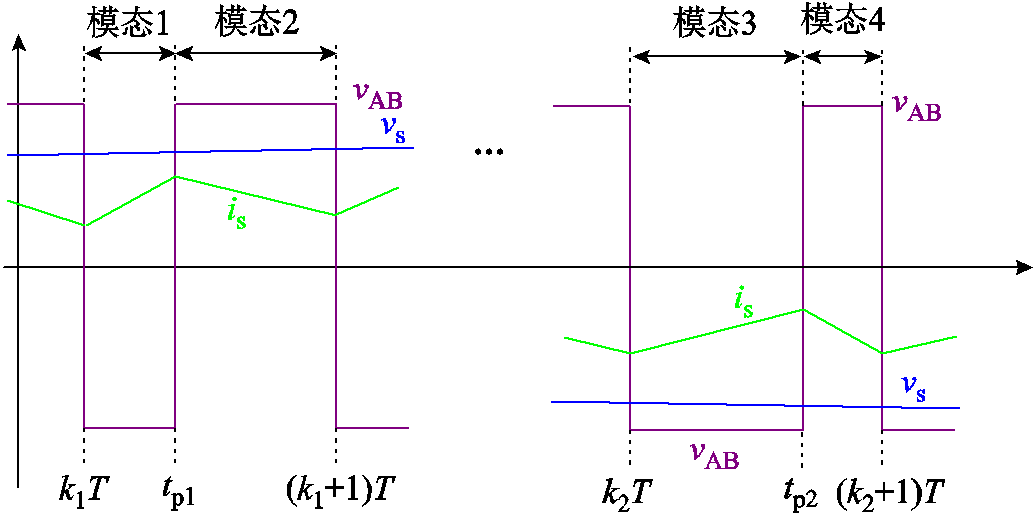
图5 PWM整流器离散时域模型的建立过程
Fig.5 Discrete-time modeling for PWM rectifier
通过PLECS工具求解各电流内环控制参数下的离散时域模型，能够得到不同控制参数对应的输入电流时域波形。单相PWM整流器的电流内环最终控制目标是使输入电流跟随输入电压的相位，尽可能做到同相位，实现功率因数校正功能，所以电流内环控制参数的性能空间可定义为功率因数。在PLECS中建立单电流内环控制的离散时域仿真模型，使用双极性调制方式，并且在电流控制环中将电流给定值由3/4的额定给定值跳变至额定值，仿真得到输入电流的稳态波形，通过快速傅里叶变换（Fast Fourier Transformation, FFT）分析图6所示重新稳定后的工频周期红色波形，计算输入电流有效值Irms及其基波有效值I1，则基波因数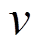
为
（12）
通过比较输入电流的基波相位与输入电压的相位值可得到相位差φ，计算位移因数为
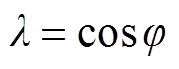（13）
功率因数[15]为
（14）
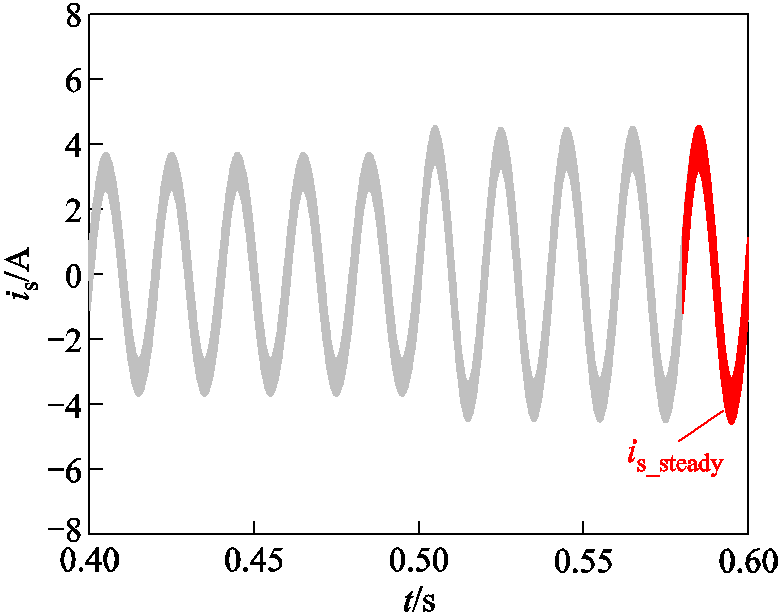
图6 输入电流工频周期稳态时域波形
Fig.6 Input current steady domain waveform in AC cycle
将图3a中内环参数设计空间中所有不同的控制参数按照上述过程，代入电流内环控制的离散时域模型，仿真运行得到不同控制参数对应的稳态电流时域波形，并计算功率因数值，完成正映射，得到内环控制参数设计空间所对应的性能空间，其结果如图7a所示。
图7a的性能空间能够可视化地展示控制参数的控制效果，采用功率因数量化评估控制参数可知，在控制参数的安全设计空间内，各个参数的控制效果具有较大的差异，基于表1的主电路参数，改变控制参数所能达到的最高功率因数值为0.981 6。由于内环控制目标是实现高功率因数，因此，可对内环控制参数的性能空间进行约束。图7a中的水平截面所对应的功率因数值为0.980，在该截面之上的值均能够满足约束要求。将此约束之上的范围投影至水平面，可得到满足要求的性能优化设计空间，如图7b红色部分所示，灰色区域表示不满足性能要求。结合图3a分析可知，在安全设计空间中，控制参数取值较小的区域，其稳态功率因数值越高。因此，基于上述分析，建立了频域相位裕度与时域功率因数之间的联系，并且通过约束得到的性能优化设计空间相比较于安全设计空间更加精确。可见，传统设计方法得到的安全设计空间较最优设计空间仍有较大差距，导致在设计初期阶段就产生偏差，增加实际参数整定的困难。
图7 电流内环PR控制器参数性能空间
Fig.7 Performance space of current PR controller parameters
电压外环以稳定输出电压为控制目标，可将输出电压受到扰动后的超调量和调节时间作为其性能空间。传统设计方法中，由于内环带宽远大于外环带宽，为此，当在PLECS软件中建立双闭环控制的离散时域模型时，可认为不同的内环控制器参数不影响外环性能空间，电流内环控制参数可在其性能优化设计空间中进行取值，设定Kp,i=0.05，Kr=5.0，同时设定负载由3/4满载切换至满载，求解得到暂态响应过程中输出电压的时域波形，对其进行分析，计算得到超调量与调节时间。相比较于调节时间，超调量更能反映暂态过程中电压的波动程度，因此采用超调量作为外环控制参数的性能空间，其计算过程如图8所示。
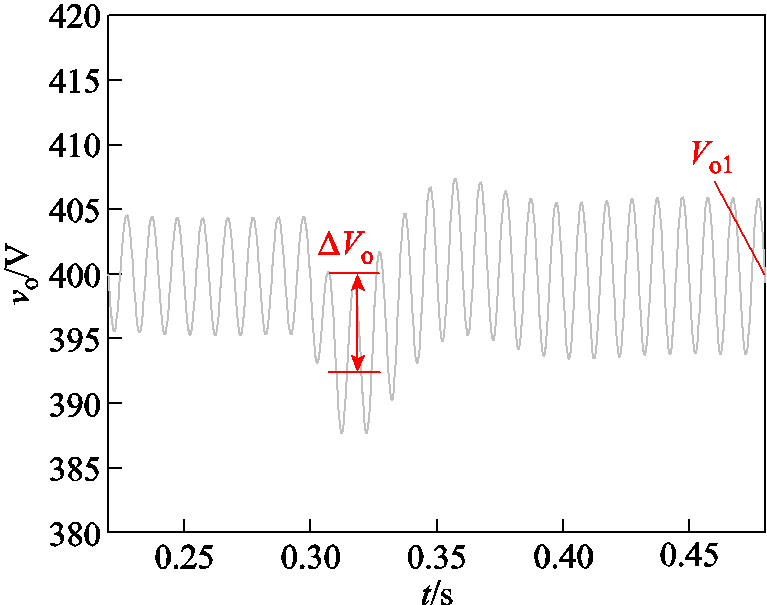
图8 负载发生扰动后，输出电压的动态响应波形
Fig.8 Dynamic response waveform of output voltage after load disturbance
由于输出电压具有纹波，为保证计算结果的准确性，本文将输出电压的纹波中间值作为计算超调量的依据，定义响应过程中出现的输出电压纹波中间值的最小值与稳态值差为ΔVo，稳态值为Vo1，则超调量σv为
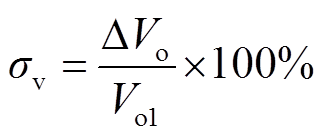（15）
将图3b外环安全设计空间中所有不同的控制参数依次代入双闭环控制的离散时域模型，仿真得到不同控制参数对应的输出电压暂态响应时域波形，并按照式（15）计算超调量，从而得到不同外环控制参数与之对应的超调量值，完成正映射，其性能空间结果图9所示。
在外环控制器参数的安全设计空间内，各参数的控制效果也有较大差异，基于现有的主电路参数，从图9a可知，通过改变控制参数，能够达到的最小超调量绝对值为1.18%，最大为6.44%。由于外环控制目标是稳定输出电压，超调量的绝对值越小，可以表征控制效果越好，因此，可对外环控制参数的性能空间进行约束。图9a的水平截面所对应的超调量值为-3%，在该截面之上的超调量值均能够满足约束要求。将其投影至水平面，可得到约束后的外环性能优化设计空间，如图9b红色部分（深色部分）区域所示，灰色部分表示不满足约束要求。结合图3b分析可知，在外环控制参数的安全设计中，控制参数取值越大的区域，其超调量绝对值越小，控制参数取值越大，外环的带宽越高，所以负载发生扰动时，响应越快，出现的超调也越小。
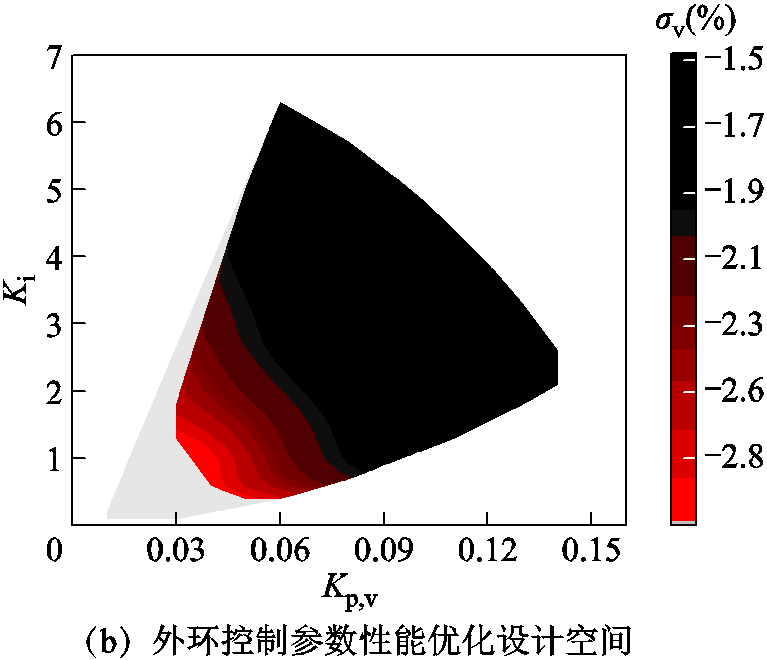
图9 电压外环PI控制器性能空间
Fig.9 Performance space of voltage PI controller parameters
因此，基于上述分析，得到的外环性能优化设计空间相比于传统设计方法得到的安全设计空间更加精确。可见，由于传统控制器参数设计方法的设计空间重点在于保证系统的稳定正常工作，无法对设计空间的性能空间进行定量评估，使其最优设计空间仍需要进行大量的参数调试才能得到，延长了设计研发周期。
在传统设计方法得到的控制器参数安全设计空间的基础上，本文提出了单相PWM整流器双闭环控制器参数的多目标优化设计方法，如图10所示。在经过相位裕度和带宽约束后的安全设计空间范围内，采用PLECS软件进行正映射，分别求解内外环控制参数安全设计空间对应的性能空间，对其做定量评估，在此基础上约束性能空间，获得内外环控制参数的性能优化设计空间。再考虑内外环控制参数耦合效应，将内外环性能优化设计空间进行组合，通过正映射得到两个控制目标的性能空间，从中选取多目标帕累托最优性能空间对应的最优设计空间，完成控制参数的多目标优化设计。
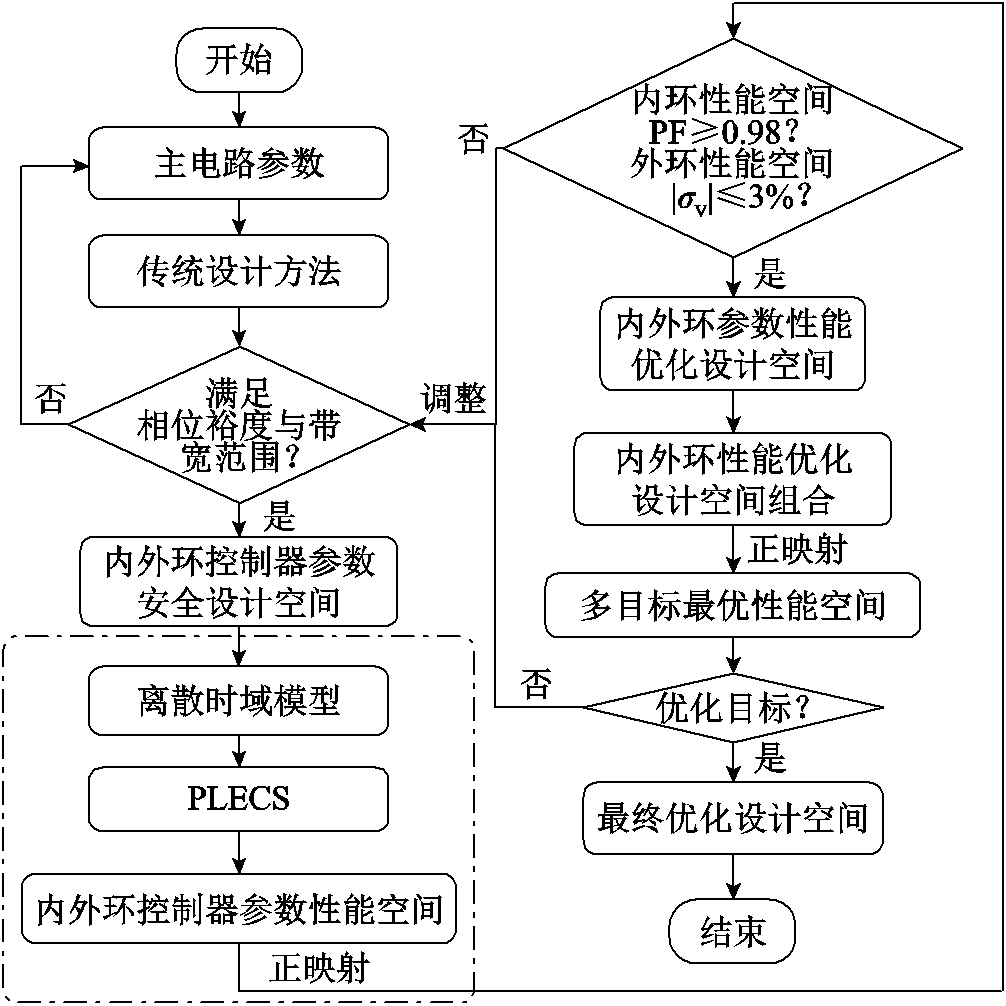
图10 一种基于离散时域模型的控制器参数多目标优化设计方法
Fig.10 A multi-objective controller parameters design optimization methods based on discrete-time domain model
采用本文所提出的控制器参数多目标优化设计方法对单相PWM整流器内外环控制参数进行优化设计，首先基于传统的设计方法，建立电压外环与电流内环的控制模型，通过约束内环与外环传递函数的相位裕度与带宽范围，获得图3所示的内外环控制参数安全设计空间；再通过PLECS软件求解离散时域模型将其分别正映射至图7a内环功率因数与图9a外环超调量性能空间，建立控制参数与性能指标的映射关系。通过对性能空间进行约束，选取内环控制参数所对应的功率因数值不小于0.98与外环控制参数所对应的超调量绝对值不大于3%的设计空间取值范围，得到性能优化设计空间，即图7b、图9b红色部分（深色）所示的区域。之后考虑内外环控制参数的耦合效应，在两个性能优化设计空间中重新组合，将组合得到的每一组内外环控制参数依次代入双闭环控制的离散时域模型，再次利用PLECS软件正映射至内环功率因数与外环控制目标超调量的性能空间，从而获得每一组控制参数对应的功率因数值与超调量值，得到如图11所示的多目标性能空间，图中所有的点便是通过遍历组合内外环性能优化设计空间得到的，红色（A）点是性能空间的帕累托前沿。
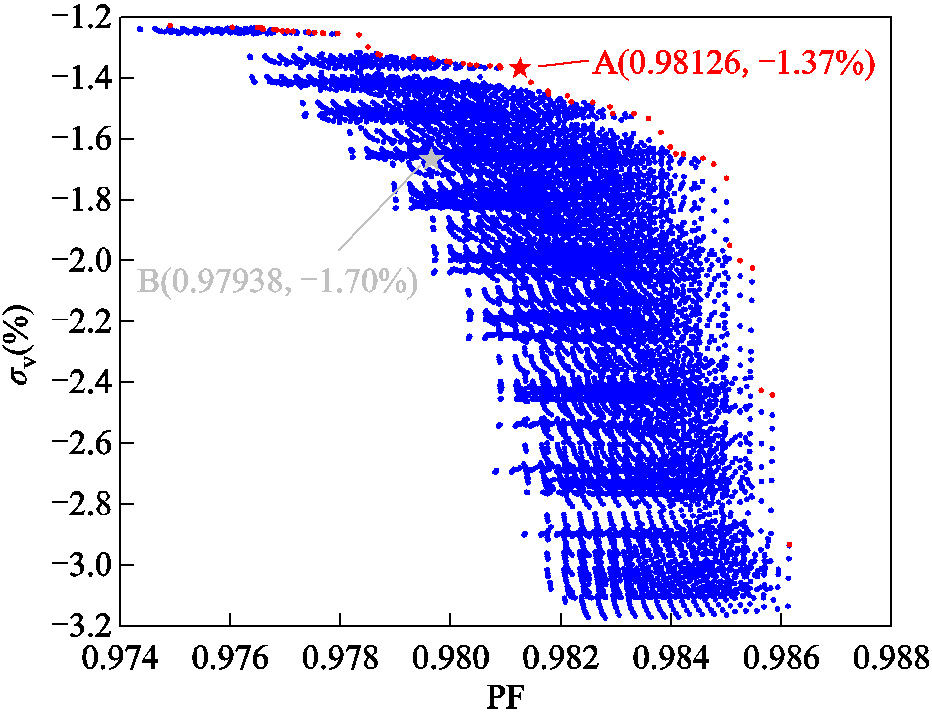
图11 “功率因数-超调量”帕累托前沿
Fig.11 “Power factor-overshoot” Pareto front
由于采用遍历方法对内外环性能优化设计空间进行重新组合，因此图11得到的性能空间能够覆盖所有性能优化设计空间的控制参数范围，可作为最终的性能空间，进而选取最优设计空间。从图11中红色点所示的“功率因数-超调量”帕累托最优前沿可知，该前沿下能够得到最小超调量绝对值为1.23%，能够得到最大的功率因数为0.986 14，两个性能目标无法同时实现最优，追求更高的功率因数，则必然使得超调量增大，反之亦然。
为了验证本文所提方法得到多目标帕累托前沿最优设计空间的可行性，选取了帕累托前沿上的点A(0.981 26, -1.37)设计结果对应的控制参数Kp,i=0.03、Kr=16、Kp,v=0.11、Ki=4.4进行实验验证。由于采用传统设计方法得到的设计结果只能通过实验调试验证其控制效果，因此，本文通过传统设计方法得到典型控制参数Kp,i=0.02、Kr=2.5、Kp,v=0.1、Ki=1.1，并通过离散时域模型对控制效果进行定量评估，得到了如图11所示的点B(0.979 38, -1.70%)，对其进行实验验证，验证基于离散时域模型所得到的理论控制效果的量化评估值与实际效果的准确性。
采用TMS320F28335控制器搭建实验硬件平台，主要包括H桥主电路、信号调理电路和驱动电路等部分，实验平台系统如图12所示。
本文首先对图11中B点控制参数进行实验验证，测量对应的功率因数与超调量值，并与理论性能目标数值进行比较，以验证基于离散时域模型的控制效果量化评估的准确性；然后测量A点控制参数对应的功率因数与超调量值，通过A点、B点控制参数理论性能目标数值与对应实验性能目标数值比较，证明了所得帕累托最优设计空间的正确性；最后对不同输出功率下A点、B点控制参数对应的功率因数进行了测量，以验证优化设计点A的控制参数对不同负载工况具有良好的适应性。
图12 实验平台系统
Fig.12 Platform system
将单相PWM整流器实验平台中DSP控制器的控制参数设置为图11中B点的控制参数（Kp,i=0.02, Kr=2.5, Kp,v=0.1, Ki=1.1），在运行过程中，设置单相PWM整流器的负载由3/4满载切换至满载，测量响应过程中输出电压的超调量与稳态之后系统的功率因数值，实验结果如图13所示。
从实验结果图中可分析得到，对于B点的控制参数，负载发生突变后，输出电压的超调量值约为-3.25%，稳态之后，输入电流的稳态功率因数约为0.982 31。实验过程中，采用Fluke NORMA 5000高精度功率分析仪测量功率因数，该仪器对信号的FFT分析最高为40次谐波，而理论计算功率因数时，对于输入电流的FFT分析最高为开关频率，因此，实际测量的电流有效值会偏低，使实际功率因数高于计算值。超调量则由示波器的测量数据计算得到。在测量误差允许的范围内，通过离散时域模型理论计算得到的功率因数值、超调量与实际的测量结果具有良好的一致性，可以证明基于离散时域模型对控制效果量化评估的准确性。
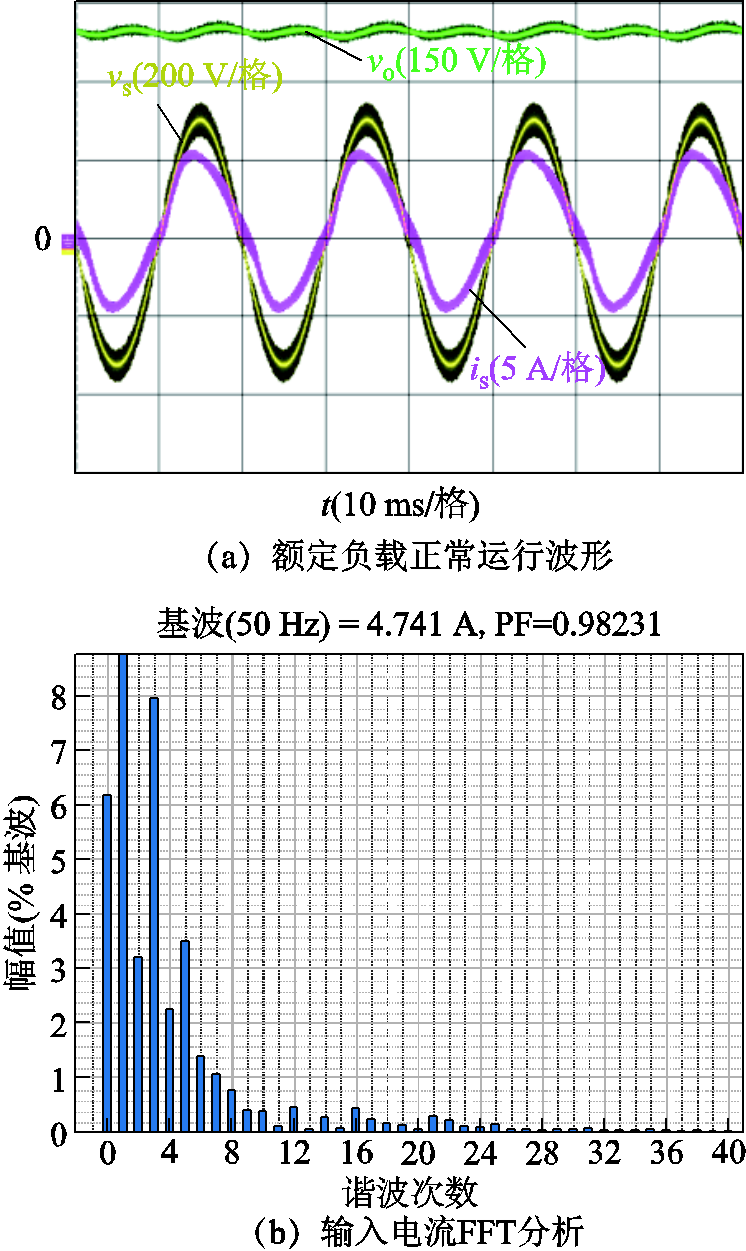
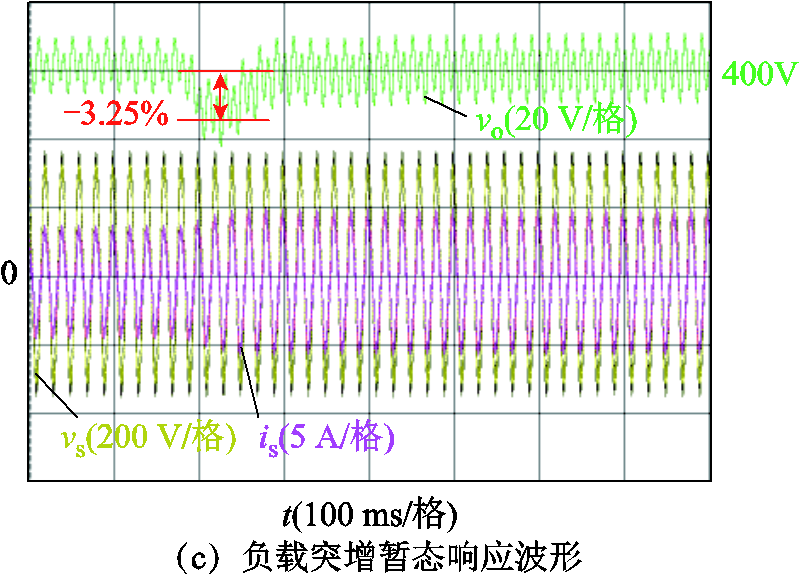
图13 传统设计方法典型设计点的测试波形
Fig.13 Test waveforms of design point by traditional controller parameter design method
将单相PWM整流器实验平台中DSP控制器的控制参数设置为图11中A点的控制参数（Kp,i=0.03, Kr=16, Kp,v=0.11, Ki=4.4），并且设置单相PWM整流器的负载由3/4的满载切换至满载，实验结果如图14所示。在A点的控制参数下，负载发生突变后，输出电压的超调量值约为-2.65%，稳态后系统的功率因数为0.983 51，控制参数优化设计点的实验结果与理论结果较为一致。由图11可知，在理论分析中，B点控制参数对应的超调量绝对值大于A点，功率因数值小于A点。通过5.1节B点所对应控制参数的实验验证与本节A点所对应控制参数的实验验证可知，B点控制参数在实验结果中的超调量绝对值大于A点，功率因数值小于A点，与理论分析的比较结果具有一致的趋势。因此通过A点与B点控制参数所对应的理论分析结果和实验结果的验证，可以证明优化设计方法所得到帕累托前沿最优设计空间的正确性。
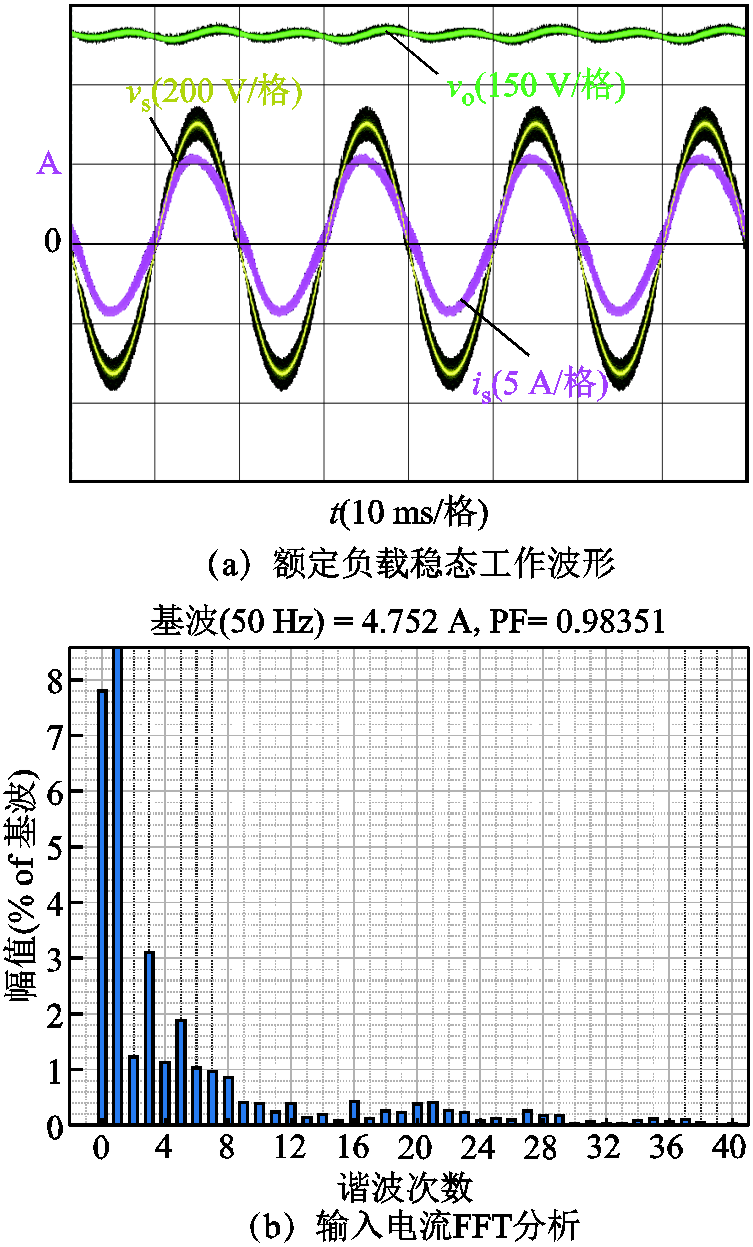
图14 帕累托前沿上的优化设计点测试波形
Fig.14 Test waveforms from the Pareto front optimized design point
在实验中测量不同输出功率下，A点与B点控制参数对应的功率因数，结果如图15所示。
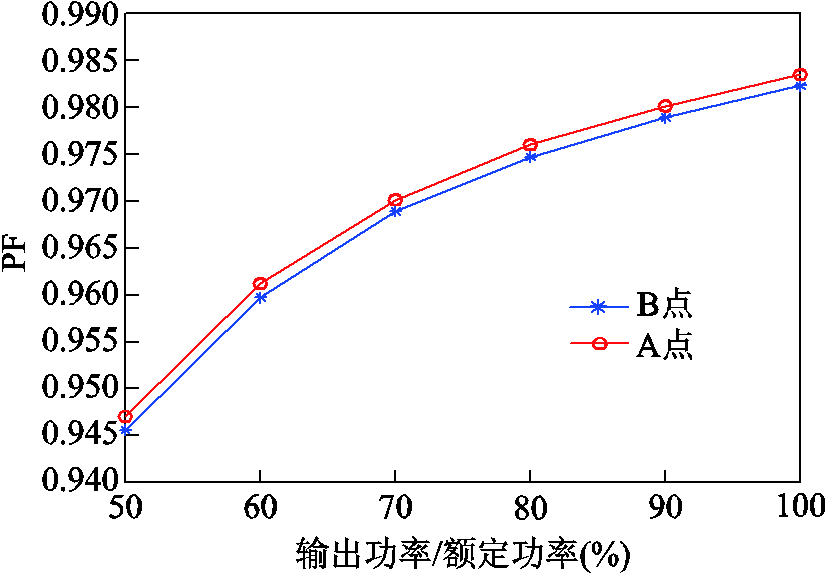
图15 不同控制参数对应的功率因数随输出功率的变化曲线
Fig.15 Curves of PF values withdifferent control parameters under different output powers
由图15可知，在不同输出功率下，优化设计点A的控制参数对应的功率因数均高于B点，结合图13b与图14b中对电流的FFT分析可知，优化设计点A的输入电流波形中，3次谐波的含量明显低于B点。因此，可以证明优化设计点A的控制参数对于不同负载工况具有良好的适应性。
本文提出一种基于离散时域模型的控制器参数多目标优化设计方法，对单相PWM整流器的电压外环比例、积分控制参数及电流内环比例、谐振控制参数进行优化设计。该优化设计方法对传统设计方法得到的宽范围控制参数安全设计空间进行逐步优化，通过正映射将内外环控制参数的控制效果进行可视化的定量评估比较，得到多目标的性能空间，并且通过帕累托前沿最优性能空间获得优化设计空间。通过仿真和实验验证帕累托最优设计空间的可行性，最终实现了功率因数值0.981 26与超调量绝对值1.37%的权衡设计。本文优化设计方法获得的帕累托最优设计空间较大程度精确了控制器参数的取值范围，减少了实际控制参数的整定范围。该方法为控制器参数设计提供了新的设计思路，避免了繁琐的参数整定过程。
参考文献
[1] 邓知先, 宋文胜, 曹梦华. 单相PWM整流器模型预测电流控制算法[J]. 中国电机工程学报, 2016, 36(11): 2996-3004. Deng Zhixian, Song Wensheng, Cao Menghua. A model predictive current control scheme for single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2016, 36(11): 2996-3004.
[2] 赵方平, 杨勇, 阮毅, 等. 三相并网逆变器直接功率控制和直接功率预测控制的对比[J]. 电工技术学报, 2012, 27(7): 212-220. Zhao Fangping, Yang Yong, Ruan Yi, et al. Comparative study for direct power control and direct power predictive control in three-phase grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 212-220.
[3] 张立伟, 黄先进, 游小杰, 等. 欧洲主力交流传动机车主牵引系统介绍[J]. 电工技术学报, 2007, 22(7): 186-190 Zhang Liwei, Huang Xianjin, You Xiaojie, et al. Introduction of electrical traction system for European main AC locomotives[J]. Transactions of China Electrotechnical Society, 2007, 22(7): 186-190.
[4] Subotic I, Bodo N, Levi E. Single-phase on-board integrated battery chargers for EVs based on multiphase machines[J]. IEEE Transactions on Power Electronics, 2015, 31(9): 6511-6523.
[5] Zmood D N, Holmes D G. Stationary frame current regulation of PWM inverters with zero steady-state error[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 814-822.
[6] Holmes D G, Lipo T A, McGrath B P, et al. Optimized design of stationary frame three phase AC current regulators[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2417-2426.
[7] Lascu C, Asiminoaei L, Boldea I, et al. Frequency response analysis of current controllers for selective harmonic compensation in active power filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2): 337-347.
[8] Yepes A G, Freijedo F D, Doval-Gandoy J, et al. Effects of discretization methods on the performance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.
[9] 王剑, 郑琼林, 高吉磊. 基于根轨迹法的单相PWM整流器比例-谐振电流调节器设计[J]. 电工技术学报, 2012, 27(9): 251-256. Wang Jian, Zheng Qionglin, Gao Jilei. Design of current proportional-resonant regulator for single-phase PWM rectifier based on root-locus method[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 251-256.
[10] 游小杰, 杨才伟, 王剑, 等. 一种适用于机车PWM整流器的比例积分-谐振电流控制器设计[J]. 电工技术学报, 2021, 36(23): 4926-4936. You Xiaojie, Yang Caiwei, Wang Jian, et al. A tuning method for proportional integral-resonant current controller in locomotive PWM rectifiers[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4926-4936.
[11] 袁义生, 毛凯翔. 单相PWM整流器控制器设计与动态特性的改善[J]. 电机与控制学报, 2020, 24(5): 34-42. Yuan Yisheng, Mao Kaixiang. Design of the controller and improvement of the dynamic performance for single-phase PWM rectifiers[J]. Electric Machines and Control, 2020, 24(5): 34-42.
[12] Callegaro L, Rojas C A, Ciobotaru M, et al. A controller improving photovoltaic voltage regulation in the single-stage single-phase inverter[J]. IEEE Transactions on Power Electronics, 2022, 37(1): 354-363.
[13] 袁立强, 陆子贤, 戴宇轩, 等. 高性能电力电子设计自动化求解器关键因素与解决方法[J]. 中国电机工程学报, 2021, 41(20): 7055-7067. Yuan Liqiang, Lu Zixian, Dai Yuxuan, et al. Key factors and methodology of high-performance design automation solver for power electronics[J]. Proceedings of the CSEE, 2021, 41(20): 7055-7067.
[14] Shao Shuai, Chen Linglin, Shan Zhenyu, et al. Modeling and advanced control of dual-active-bridge DC–DC converters: a review[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1524-1547.
[15] 王兆安, 刘进军. 电力电子技术[M]. 5版. 北京: 机械工业出版社, 2009.
Abstract The double closed-loop control of single-phase PWM rectifier can achieve high power factor and stable output DC voltage, which has been widely studied by scholars. The double closed-loop control strategy of voltage outer loop and current inner loop is generally used in single-phase PWM rectifier. In current inner loop, PR controller is used to control AC current in phase with voltage to achieve power factor correction, while PI controller is usually applied to control stability of DC output voltage in voltage outer loop. However, in the design stage of the innerand outerloop controller parameters, traditional design method generally selects controller parameters by experience, which causes a wide range of parameter selection and cannot quantitatively evaluate the time-domain control effect of the controller parameters, leading to difficulties in parameter optimization and adjustment. Accordingly, this paper proposed a multi-objectiveoptimization design method for controller parameters based on discrete-time domain model.
Firstly, traditional design method in frequency domain was used to determine safe design space of voltage outer loop and current inner loop controller parameters by constraint phase margin and bandwidth. Secondly, the PLECS software was applied to simulate discrete time domain model and automatic iterative controller parameters to obtain the time domain waveforms of controlled variables for analyzing the control performance parameters, thus establishing positive mapping relationship between the controller parameters and controller performance. Thirdly, power factor was selected for current inner loop PR controller performance parameter and the overshoot value was set for voltage outer loop PI controller performance parameter according to the control requirements. then, positively mapped the safe design space to the performance space by PLECS software, in which constrain the value of the performance space to get the performance optimized design space. Finally, the coupling effect of inner and outer loop controller parameters was considered by recombing them in the two performance optimized design spaces and positively mapping to the performance space, in which the multi-objective performance space of current inner loop power factor and voltage outer loop overshoot is obtained.
Simulation results show that the minimum overshoot absolute value of 1.23% and the maximum power factor of 0.986 14 can be obtained by Pareto front optimal design space respectively. However, these two objectives cannot be optimized at the same time, and the pursuit of higher power factor will certainly increase the overshoot. The Pareto Front shows an intuitive quantitative relationship between different optimization objectives and effectively makes the range of controller parameters values precise.
An experimental platform was established and typical design points were selected from the multi-objective Pareto Front optimal design space. Experiments with control parameters by conventional design method demonstrated the accuracy of quantitative assessment of control effects based on discrete-time domain models. And optimized design control parameters proved the correctness of the Pareto front optimal design space, in which verified to achieve power factor value of 0.981 26 and absolute overshoot value of 1.37%. Finally, power factors at different output powers were measured to verify that the optimized design control parameters showed good adaptability to different load conditions, thus proving the correctness of the optimizationdesign method in this paper.
keywords：Single-phase PWM rectifier, discrete-time domain model, multi-objective optimization controller parameters, dynamic performance optimization
DOI:10.19595/j.cnki.1000-6753.tces.221728
中图分类号：TM46
国家自然科学基金资助项目（52177170）。
收稿日期 2022-09-13
改稿日期 2023-03-21
晏益朋 男，1997年生，硕士研究生，研究方向为双向功率变换系统数字化建模及设计。E-mail：Yanyipeng1217@163.com
罗全明 男，1976年生，博士，教授，博士生导师，研究方向为电力电子拓扑及控制、电力电子数字设计、宽禁带器件特性及应用等。E-mail：lqm394@126.com（通信作者）
（编辑 郭丽军）