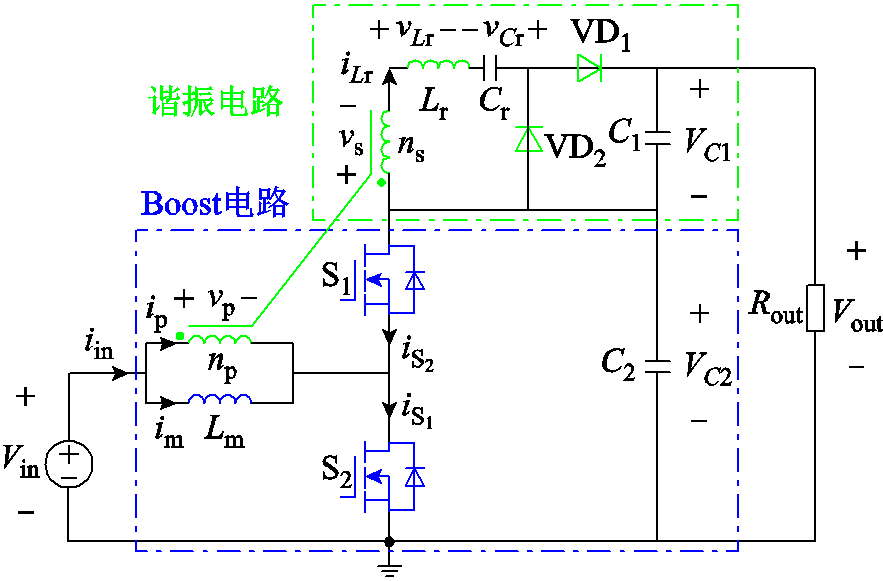
图1 提出的基于耦合电感的高增益谐振型变换器拓扑
Fig.1 Proposed high step-up resonant converter based with coupled inductor
摘要 该文提出了一种具有高增益、软开关的新型谐振变换器。该谐振变换器使用耦合电感来提高电压增益,升压比不仅取决于占空比,还取决于耦合电感的变比,具有高增益的优点。此外,由于采用了有源钳位技术,漏感中的能量可以被回收利用,用来对开关管的结电容充放电提供能量,从而实现软开关。由于采用了耦合电感,所提出的变换器可以在较低的开关管电压应力的情况下实现较高的输出电压,因此可以使用低导通电阻的低压器件,从而提升系统的效率。该文分析了该谐振变换器的工作原理,并推导了输出电压、关断电流应力等参数的解析表达式。在此基础上,从理论上分析了该变换器取得软开关的条件,并对该变换器的各个器件的电压电流应力进行分析,为器件选型提供了理论依据。最后,搭建1 kW实验样机,针对该文提出的基于耦合电感的谐振变换器的高增益、软开关、低电压应力、高效率等性能进行了实验验证。通过实验得出所提出的拓扑可以在10倍增益的情况下达到最高97.5%的效率,表明所提拓扑的优越性。
关键词:耦合电感 谐振变换器 高增益 软开关
燃料电池是一种高效、高功率密度的清洁能源,在汽车、航天等领域具有良好的应用前景。然而,在燃料电池的应用中主要有两个挑战[1]:①燃料电池不能独立工作,需要辅助设备,增加了系统体积,降低了系统功率密度,因此,功率密度是DC-DC变换器的一个重要因素;②燃料电池输出电压低,变化范围大,需要高电压转换比的DC-DC变换器将低压转换为恒高压。
传统Boost升压变换器在普通升压应用中简单有效,但在燃料电池汽车等高压升压应用中效率低下。为了满足燃料电池汽车对DC-DC变换器的要求,研究人员提出了多种技术。第一类是使用级联升压变换器[2-3],通过串联两个或多个基本升压变换器级联获得高电压增益。虽然该方法可以获得较高的电压增益,但由于其结构复杂、元器件数量多、运行不稳定等原因,不适用于需要高功率密度的应用。第二类是基于开关电容或/和开关电感[4-6],通过电容的并联充电和串联放电来实现高电压增益。然而,这种方法需要大量的元器件,增加了系统的复杂性,降低了功率密度。第三类是利用倍压电路实现高电压转换比[7-8]。这种方法简单但单独使用效果不是很好,通常与其他方法结合使用[9-11]。实现高电压增益最常用的技术是采用耦合电感的变换器[12-19]。在文献[12]中,研究人员首次将耦合电感的概念应用到升压变换器中,其中提出的拓扑结构可以通过调整占空比和一次、二次侧的匝数来获得高电压增益。然而,该电路的漏感会在开关断开时造成一个较大的电压尖峰。为了解决这一问题,文献[13-19]在此电路的基础上增加了无源或有源钳位电路来吸收泄漏电感中存储的能量。虽然钳位电路可以抑制开关的电压尖峰,但是耦合电感的加入使得开关管的电流应力变得很大。
为了减小开关管的电流应力,一系列的基于耦合电感的谐振变换器被提出。文献[20-24]引入谐振电容,并使其与耦合电感的漏感发生谐振,从而减小了电流应力。但是这些方法无法实现开关管的软开关运行。
为了实现基于耦合电感的谐振变换器的软开关运行,本文提出了一种具有高增益、软开关的新型谐振变换器。该谐振变换器使用耦合电感来提高电压增益,升压比不仅取决于占空比,还取决于耦合电感的变比,具有高增益的优点。此外,由于采用了有源钳位技术,漏感中的能量可以被回收利用,用来对开关管的结电容充放电提供能量,从而实现软开关。本文分析了该谐振变换器的工作原理,并推导得到了输出电压、关断电流应力等参数的解析表达式。在此基础上,理论分析了该变换器取得软开关的条件,并对该变换器的各个器件的电压电流应力进行分析,为器件选型提供了理论依据。最后,本文搭建了1 kW的实验样机,并对本文提出的基于耦合电感的谐振变换器的高增益、软开关、高效率等性能进行了实验验证,实验结果验证了本文提出拓扑的优越性。
图1为本文提出的基于耦合电感的高增益谐振型变换器,该拓扑主要由两部分组成:Boost电路和谐振电路。谐振电路叠加在Boost电路上,两者的输出电压相叠加,起到了增加电压增益的作用。

图1 提出的基于耦合电感的高增益谐振型变换器拓扑
Fig.1 Proposed high step-up resonant converter based with coupled inductor
Boost电路由耦合电感的励磁电感和两只开关管组成,辅助开关管 相当于普通Boost电路的二极管。该电路为单向高增益电路,辅助管
相当于普通Boost电路的二极管。该电路为单向高增益电路,辅助管 采用开关管的目的并非是为了能量双向流动,而是为了保证主管能够实现零电压开通,提高效率。电容
采用开关管的目的并非是为了能量双向流动,而是为了保证主管能够实现零电压开通,提高效率。电容 为Boost电路中的输出电容。采用有源钳位的目的是为了主管
为Boost电路中的输出电容。采用有源钳位的目的是为了主管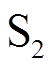 的软开关,同时同步整流减小导通损耗。
的软开关,同时同步整流减小导通损耗。
谐振电路由耦合电感的副边、耦合电感的漏感Lr(模型中耦合电感的漏感均折合到副边)、谐振电容Cr、两只二极管VD1和VD2、输出电容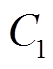 组成。其中,耦合电感的副边相当于一个电压源,其值随着开关管S2的状态而变化。当S2开通的时候,
组成。其中,耦合电感的副边相当于一个电压源,其值随着开关管S2的状态而变化。当S2开通的时候,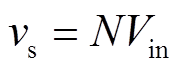 ;当S2关断的时候,
;当S2关断的时候,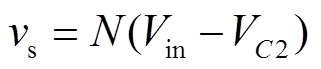 。其中,N是耦合电感的变比,定义为副边匝数ns与原边匝数np之比;
。其中,N是耦合电感的变比,定义为副边匝数ns与原边匝数np之比;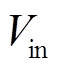 为输入电压。输出电容
为输入电压。输出电容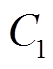 的值较大,其电压可以认为恒定直流。谐振电容
的值较大,其电压可以认为恒定直流。谐振电容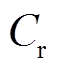 电容值较小,其电压是一个脉动的直流电压。耦合电感的漏感作为谐振电路的谐振电感
电容值较小,其电压是一个脉动的直流电压。耦合电感的漏感作为谐振电路的谐振电感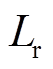 ,无需额外的电感,功率密度高。同时,漏感中的能量也被利用,提高效率。
,无需额外的电感,功率密度高。同时,漏感中的能量也被利用,提高效率。
按照谐振周期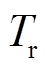 与二级管的导通时间的大小
与二级管的导通时间的大小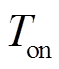 来划分,可以将谐振分为两种模式:欠谐振和过谐振。图2为两种不同谐振模式的波形,图2a为欠谐振,图2b为过谐振,介于两者之间的(红色)虚线波形为刚好完全谐振。其中,vgs1和vgs2分别为开关管S1和S2的驱动信号。
来划分,可以将谐振分为两种模式:欠谐振和过谐振。图2为两种不同谐振模式的波形,图2a为欠谐振,图2b为过谐振,介于两者之间的(红色)虚线波形为刚好完全谐振。其中,vgs1和vgs2分别为开关管S1和S2的驱动信号。 为过谐振时流过开关管S2的电流,
为过谐振时流过开关管S2的电流,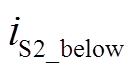 为欠谐振时流过开关管S2的电流,
为欠谐振时流过开关管S2的电流,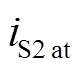 为刚好完全谐振时流过开关管S2的电流。
为刚好完全谐振时流过开关管S2的电流。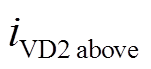 为过谐振时流过二极管VD2的电流,
为过谐振时流过二极管VD2的电流,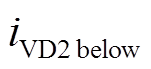 为欠谐振时流过二极管VD2的电流,
为欠谐振时流过二极管VD2的电流,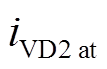 为刚好完全谐振时流过二极管VD2的电流,
为刚好完全谐振时流过二极管VD2的电流,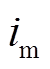 为励磁电感的电流。
为励磁电感的电流。
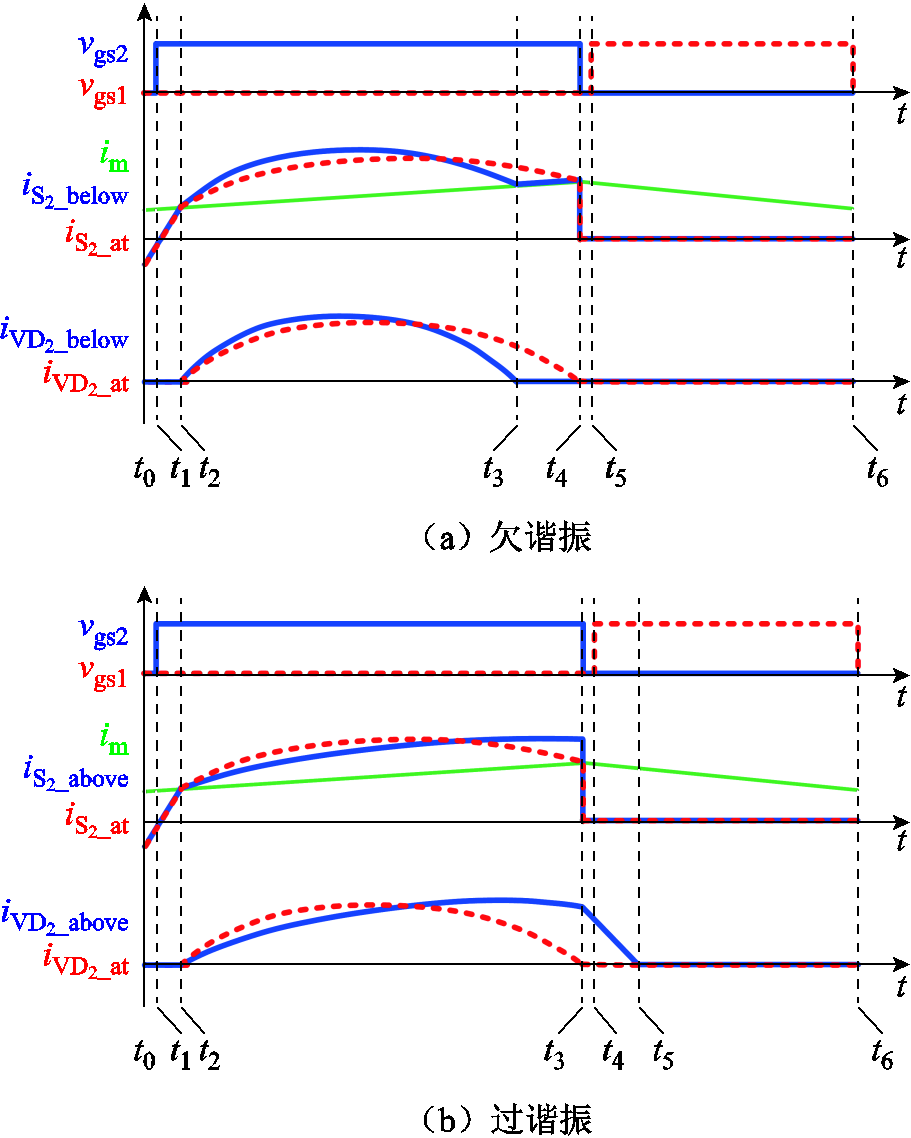
图2 两种不同谐振模式
Fig.2 The waveforms of two different resonant modes
记开关频率为f,开关周期为T=1/f,谐振频率为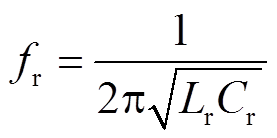 。随着占空比D的变化,主管导通时间DT和辅助管导通时间(1-D)T也随之变化。当谐振半周期大于主管导通时间时称为过谐振;反之则称为欠谐振。根据谐振半周期0.5/fr与二者的大小不同,可以分为三种工作模式,如图3所示。
。随着占空比D的变化,主管导通时间DT和辅助管导通时间(1-D)T也随之变化。当谐振半周期大于主管导通时间时称为过谐振;反之则称为欠谐振。根据谐振半周期0.5/fr与二者的大小不同,可以分为三种工作模式,如图3所示。
1)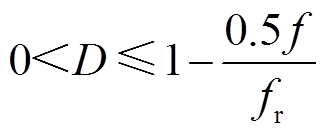 。这种情况下,VD2处于过谐振的状态(
。这种情况下,VD2处于过谐振的状态(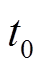 ~
~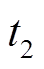 ),VD1处于欠谐振的状态(
),VD1处于欠谐振的状态(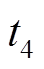 ~
~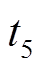 ),此时主管的关断电流应力大于励磁电感的最大电流,关断电流应力较大,不宜作为电路额定状态。
),此时主管的关断电流应力大于励磁电感的最大电流,关断电流应力较大,不宜作为电路额定状态。
2)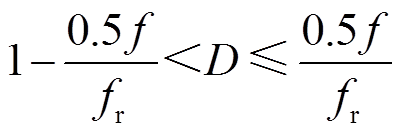 。这种情况下,VD2处于过谐振状态(
。这种情况下,VD2处于过谐振状态(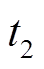 ~
~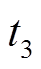 ),VD1也处在过谐振状态(
),VD1也处在过谐振状态(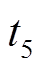 ~
~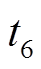 )。此时的主管关断电流应力大于励磁电感的最大电流,关断电流应力较大。
)。此时的主管关断电流应力大于励磁电感的最大电流,关断电流应力较大。
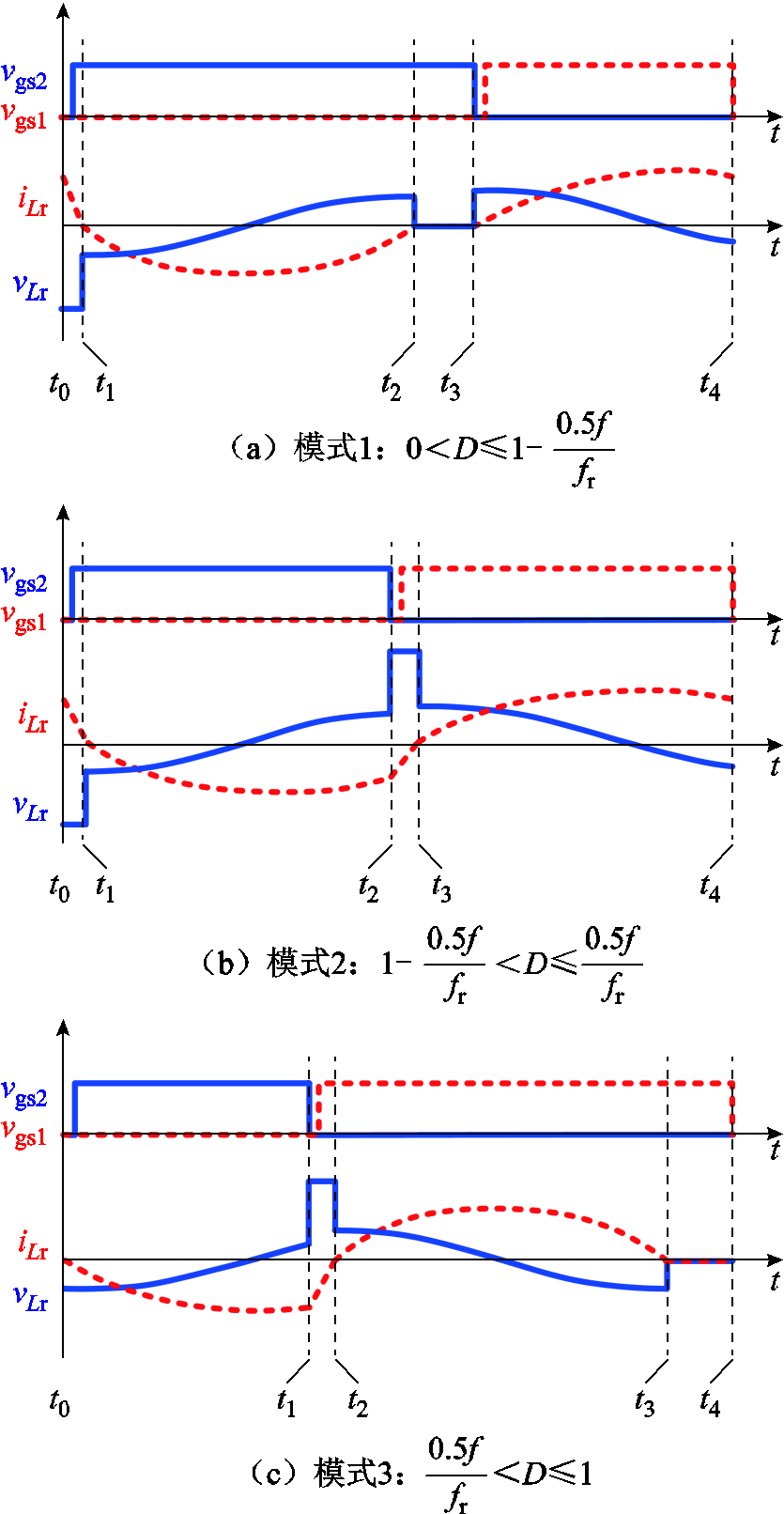
图3 随占空比D变化的三种工作模式
Fig.3 Three modes according to duty cycle
3)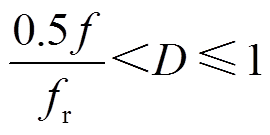 。这种情况下,VD2处于欠谐振状态(
。这种情况下,VD2处于欠谐振状态(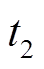 ~
~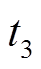 ), VD1处于过谐振状态(
), VD1处于过谐振状态(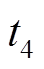 ~
~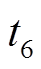 ),此时主管的关断电流应力为励磁电感中的最大电流,与前两种情况相比,开关管的关断电流应力较小。因此,将电路在额定负载下的运行工况设计在这一模式下。
),此时主管的关断电流应力为励磁电感中的最大电流,与前两种情况相比,开关管的关断电流应力较小。因此,将电路在额定负载下的运行工况设计在这一模式下。
下面以额定状态,即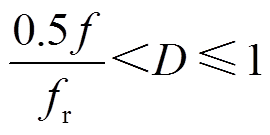 进行分析。图4为
进行分析。图4为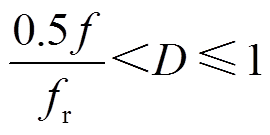 的模式下的波形。
的模式下的波形。
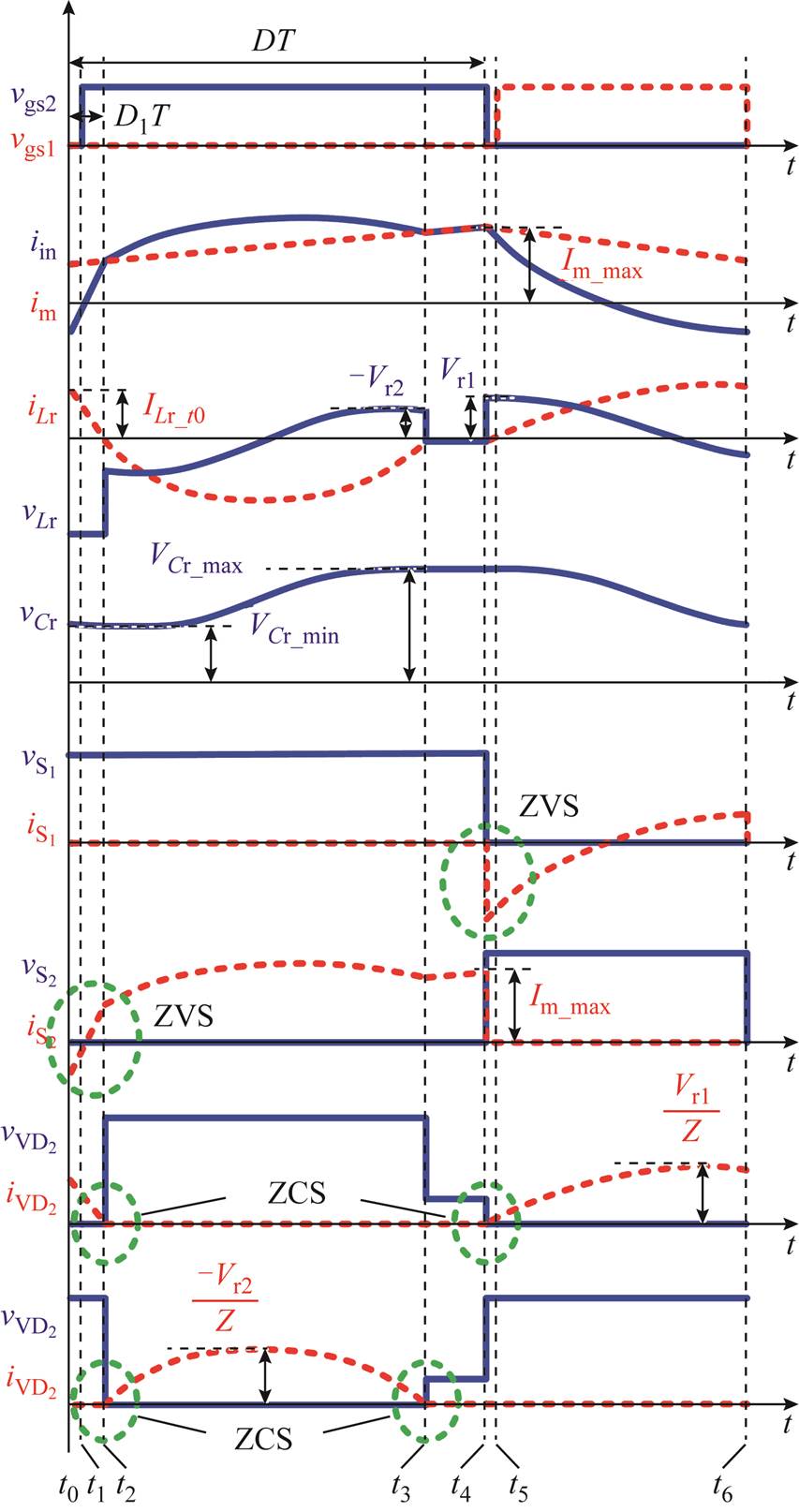
图4 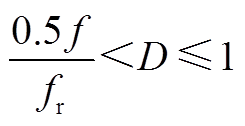 时的波形
时的波形
Fig.4 Waveforms when 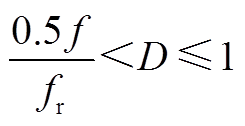
由图4可以看出,主开关管 和辅助开关管
和辅助开关管 均可以实现ZVS开通,二极管VD1和VD2均可以实现ZCS开通和关断。该模式一共分为6个阶段。如果忽略死区时间,则可以简化为4个阶段,分别如图5a~图5d所示。
均可以实现ZVS开通,二极管VD1和VD2均可以实现ZCS开通和关断。该模式一共分为6个阶段。如果忽略死区时间,则可以简化为4个阶段,分别如图5a~图5d所示。
1)阶段1[t0, t2):漏感通过二极管 放电阶段
放电阶段
主开关管S2的开通电流小于零,主开关管S2可以实现ZVS开通。此时的谐振回路如图6a所示。漏感通过二极管VD1线性放电,当漏感电流放电为零时,该阶段结束,此时二极管VD1实现ZCS关断。耦合电感的副边电压 为
为
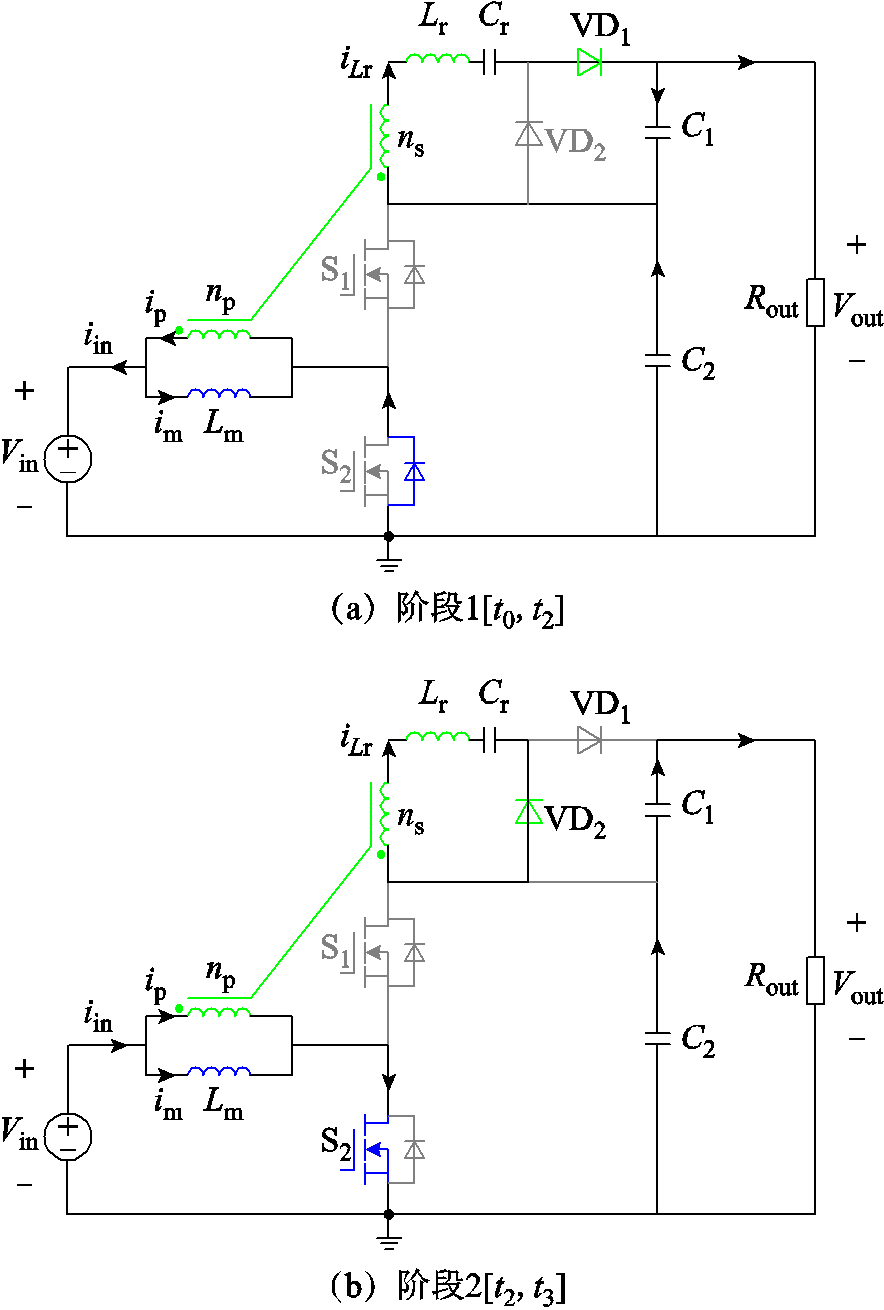
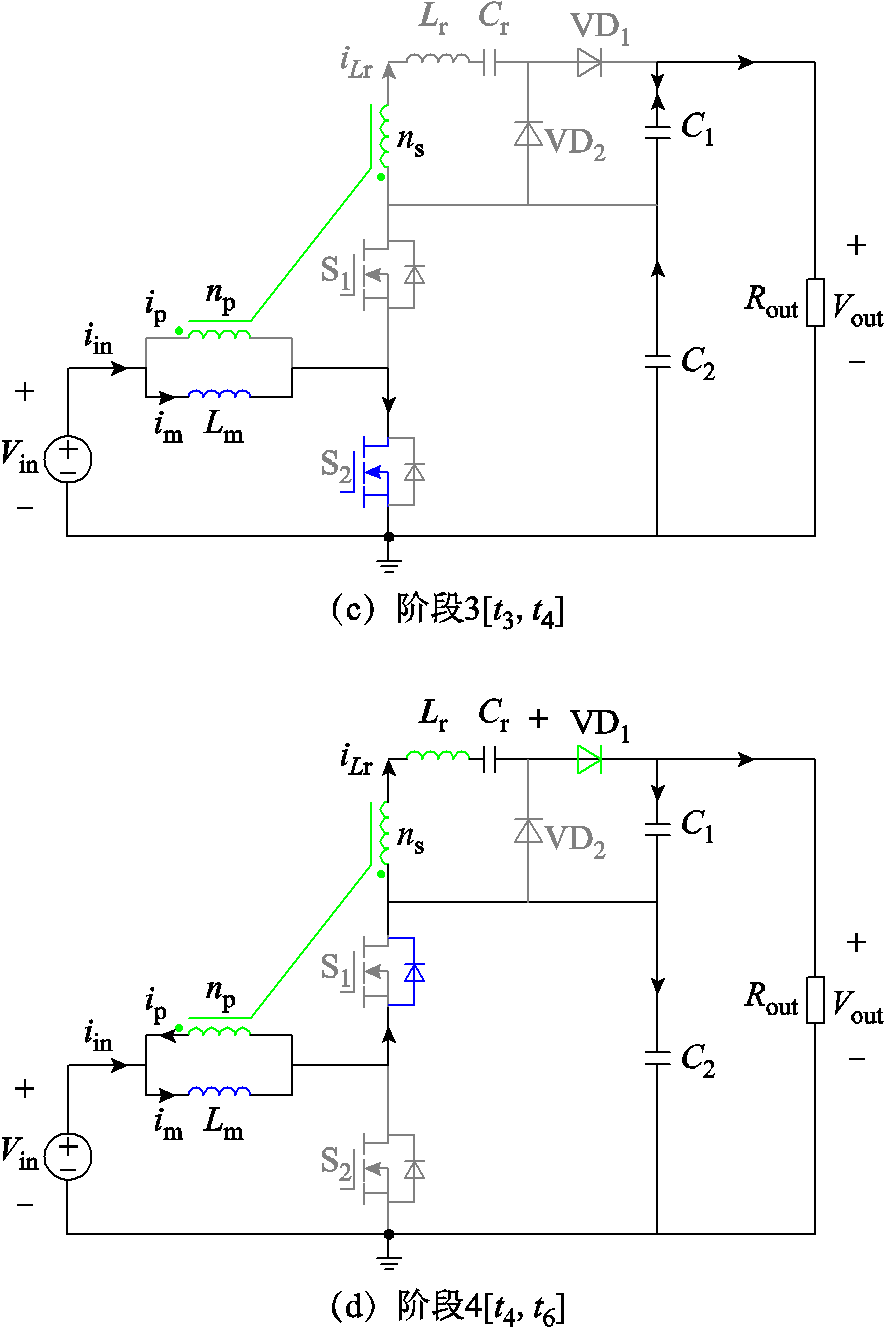
图5 四个阶段的电路
Fig.5 Four stages of circuit
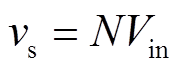 (1)
(1)
谐振电感两端的电压VLr为

图6 四个阶段的谐振回路
Fig.6 Four stages of resonant circuit
 (2)
(2)
式中,VCr_min为谐振电容的最小电压;VC1为输出电容C1上的电压。
此阶段的谐振电感两端的电压VLr较大,且持续时间短,所以此过程可视作谐振电感Lr线性放电。
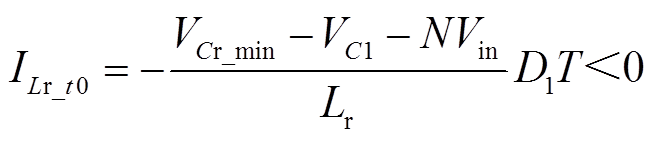 (3)
(3)
式中,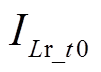 为t0时刻时的漏感电流,定义D1为漏感放电时间和整个开关周期的比值,则
为t0时刻时的漏感电流,定义D1为漏感放电时间和整个开关周期的比值,则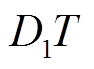 为漏感放电时段(图4中标注出了
为漏感放电时段(图4中标注出了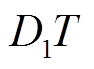 的大小)。
的大小)。
2)阶段2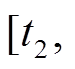
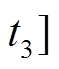 :二极管VD2谐振阶段
:二极管VD2谐振阶段
此时耦合电感的副边电压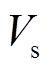 不变,依然为
不变,依然为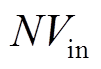 。但是由于漏感
。但是由于漏感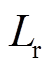 中的电流已经放电完毕,这时进入谐振状态,漏感
中的电流已经放电完毕,这时进入谐振状态,漏感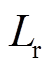 、谐振电容
、谐振电容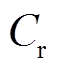 开始谐振。由于谐振电流从零开始增加,二极管VD2可以实现ZCS开通。由于该谐振过程为欠谐振,所以二极管VD2的电流谐振到零后,谐振过程结束,此时二极管VD2可实现ZCS关断。谐振回路如图6b所示。
开始谐振。由于谐振电流从零开始增加,二极管VD2可以实现ZCS开通。由于该谐振过程为欠谐振,所以二极管VD2的电流谐振到零后,谐振过程结束,此时二极管VD2可实现ZCS关断。谐振回路如图6b所示。
此时漏感电流ILr和谐振电容电压VCr分别为
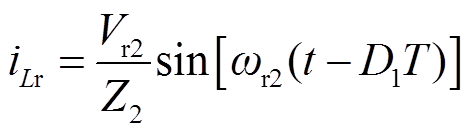 (4)
(4)
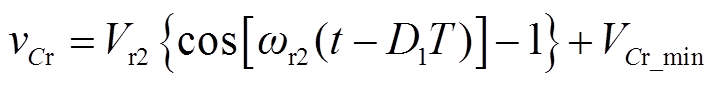 (5)
(5)
其中
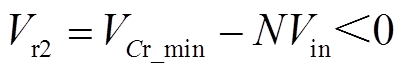 (6)
(6)
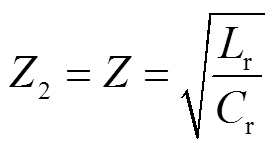 (7)
(7)
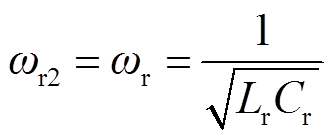 (8)
(8)
式中,VCr_min为谐振电容电压的最小值。
将式(6)代入式(3),可得
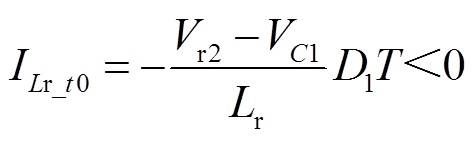 (9)
(9)
3)阶段3
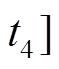 :二极管VD1和VD2均截止阶段
:二极管VD1和VD2均截止阶段
此时耦合电感的副边电压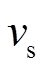 不变,依然为
不变,依然为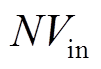 。如图6c所示,此时VD1和VD2均处于截止状态,两者共同承担VC1上的电压,即
。如图6c所示,此时VD1和VD2均处于截止状态,两者共同承担VC1上的电压,即
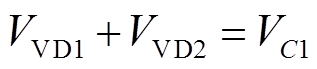 (10)
(10)
此时的谐振电路没有电流流过。
4)阶段4[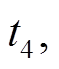
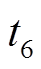 ]:二极管VD1谐振阶段
]:二极管VD1谐振阶段
如图6d所示,随着辅助开关管的开通,耦合电感的副边电压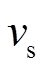 突变为
突变为
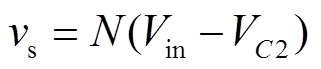 (11)
(11)
这时进入谐振状态,漏感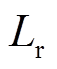 、谐振电容
、谐振电容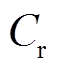 、输出电容
、输出电容 开始谐振。由于谐振电流从零开始增加,二极管VD1可以实现ZCS开通。谐振回路如图6d所示。此时,谐振电容
开始谐振。由于谐振电流从零开始增加,二极管VD1可以实现ZCS开通。谐振回路如图6d所示。此时,谐振电容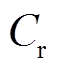 和输出电容
和输出电容 串联,由于谐振电容
串联,由于谐振电容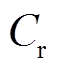 的值远小于输出电容
的值远小于输出电容 的值,所以此时谐振电路的等效电容
的值,所以此时谐振电路的等效电容 为
为
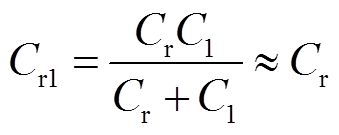 (12)
(12)
漏感电流ILr和谐振电容电压VCr分别为
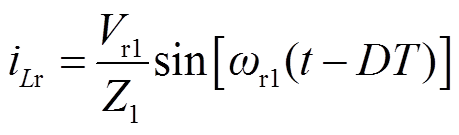 (13)
(13)
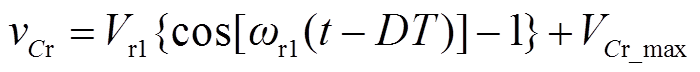 (14)
(14)
式中,DT指的是占空比D与开关周期T的乘积,即主管导通时间。
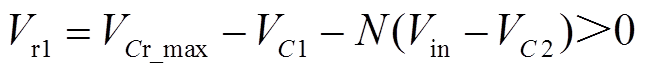 (15)
(15)
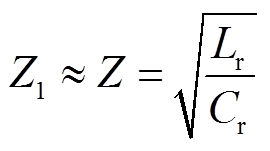 (16)
(16)
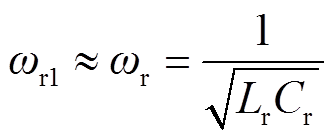 (17)
(17)
式中,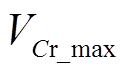 为谐振电容电压的最大值。
为谐振电容电压的最大值。
总之,阶段2和阶段4中的两个谐振过程的谐振电感值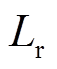 和电容值
和电容值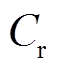 是几乎相同的,即谐振周期
是几乎相同的,即谐振周期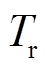 和谐振阻抗
和谐振阻抗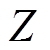 是相同的。不同的是两个谐振阶段的幅值:阶段2中的谐振幅值为
是相同的。不同的是两个谐振阶段的幅值:阶段2中的谐振幅值为 ,是一个负值;阶段4中的谐振幅值为
,是一个负值;阶段4中的谐振幅值为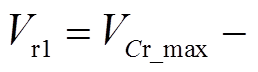
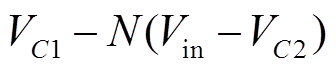 ,是一个正值。
,是一个正值。
下面将根据电压电流平衡关系,求输出电压的表达式。
1)二极管VD1的电流平衡关系
二极管VD1导通时存在漏感线性放电阶段和过谐振阶段。谐振时长为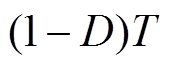 。由于漏感放电时间非常短,从而漏感电流的面积很小,因此在求流经二极管VD1电流的平均值时,可以忽略漏感放电阶段的电流,由流过VD1的电流平均值等于输出电流可得
。由于漏感放电时间非常短,从而漏感电流的面积很小,因此在求流经二极管VD1电流的平均值时,可以忽略漏感放电阶段的电流,由流过VD1的电流平均值等于输出电流可得
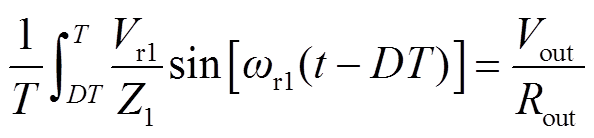 (18)
(18)
式中,Vout为输出电压;Rout为输出电阻。
化简得
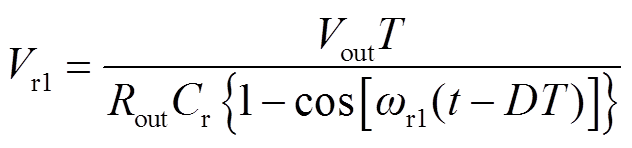 (19)
(19)
2)二极管VD2的电流平衡关系
二极管VD2导通时仅存在欠谐振阶段,谐振时长为半个周期值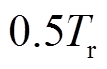 。由流过VD2的电流值等于输出电流可得
。由流过VD2的电流值等于输出电流可得
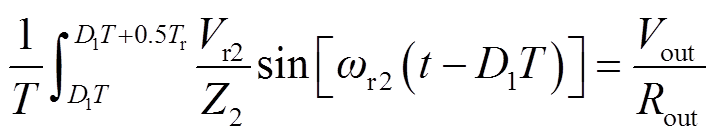 (20)
(20)
化简得
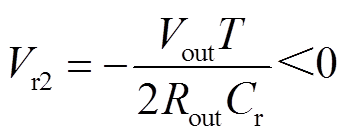 (21)
(21)
3)谐振电容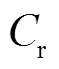 的电压平衡关系
的电压平衡关系
在漏感线性放电阶段,由于漏感放电时间很短,此时谐振电容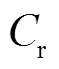 的电压VCr基本不变。在二极管VD1和VD2截止阶段,谐振电容
的电压VCr基本不变。在二极管VD1和VD2截止阶段,谐振电容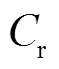 上没有电流流过,所以其谐振电容电压VCr维持不变。从而谐振电容电压VCr仅在二极管VD1和VD2发生谐振阶段的变化。在二极管VD2谐振阶段,由谐振电容上的电压平衡关系可得
上没有电流流过,所以其谐振电容电压VCr维持不变。从而谐振电容电压VCr仅在二极管VD1和VD2发生谐振阶段的变化。在二极管VD2谐振阶段,由谐振电容上的电压平衡关系可得
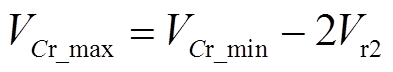 (22)
(22)
将式(6)和式(15)代入式(22),可得
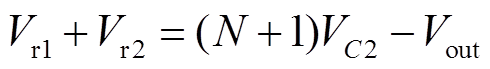 (23)
(23)
4)励磁电感Lm的电流平衡关系
耦合电感的励磁电感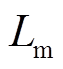 相当于Boost电路的输入电感,其工作原理与Boost电路相同,参考Boost电路的推导过程可得
相当于Boost电路的输入电感,其工作原理与Boost电路相同,参考Boost电路的推导过程可得
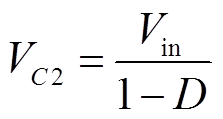 (24)
(24)
输出电压Vout等于两个输出电容的电压VC1和VC2叠加,即
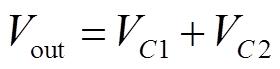 (25)
(25)
结合式(19)、式(21)、式(23)、式(24)和式(25),可以得到输出电压Vout、电压Vr1、Vr2的表达式分别为
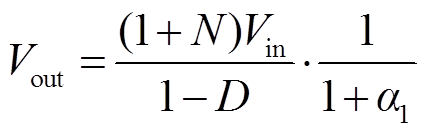 (26)
(26)
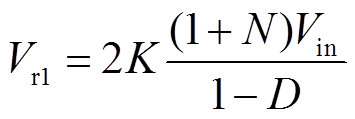 (27)
(27)
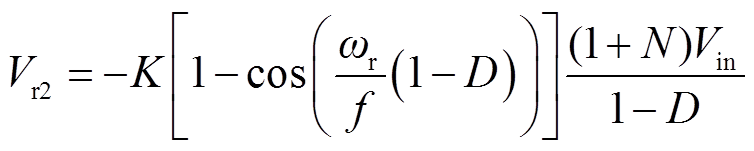 (28)
(28)
其中
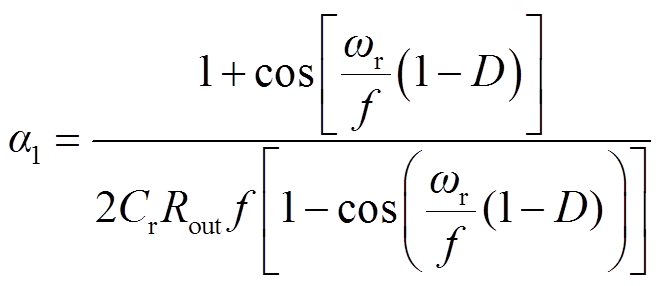 (29)
(29)
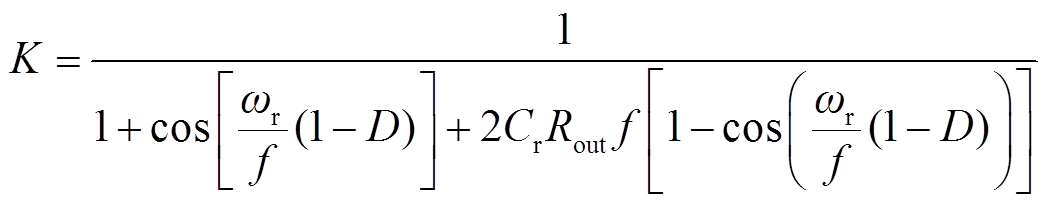 (30)
(30)
从而可以得出在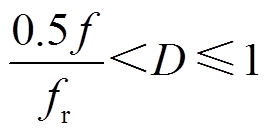 的情况时,升压比M的表达式为
的情况时,升压比M的表达式为
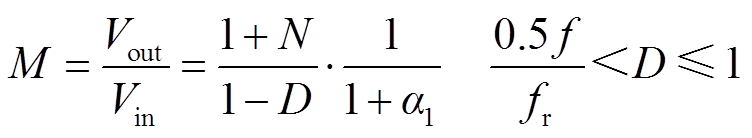 (31)
(31)
用同样的方法可以推导出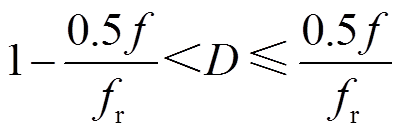 和
和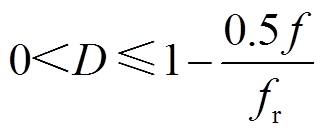 两种情况的升压比M的表达式为
两种情况的升压比M的表达式为
 (32)
(32)
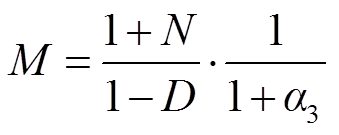
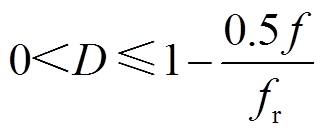 (33)
(33)
式中
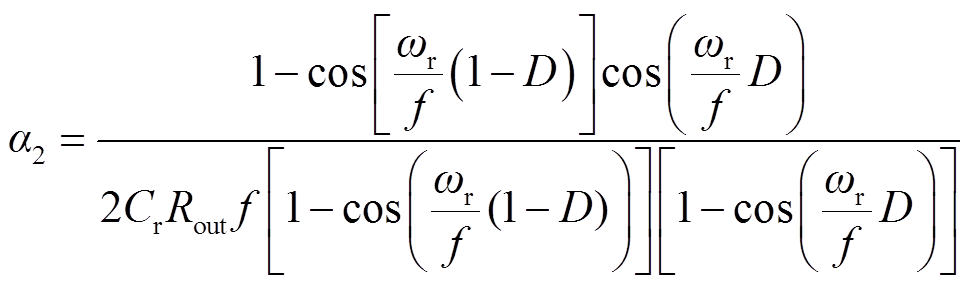 (34)
(34)
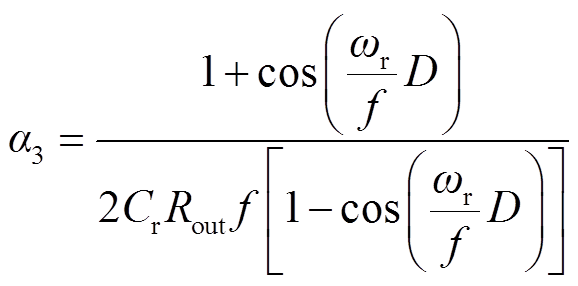 (35)
(35)
综合前文所述,可以得到升压比M的表达式为
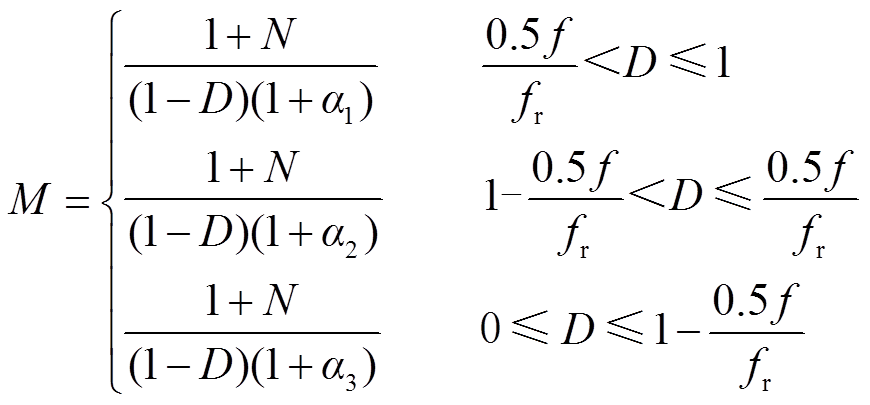 (36)
(36)
式中,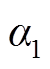 、
、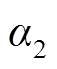 和
和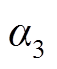 的定义分别如式(29)、式(34)和式(35)所示,均为关于占空比D的函数。从而在已知输入电压Vin和占空比D时,可以得到唯一确定的输出电压Vout为
的定义分别如式(29)、式(34)和式(35)所示,均为关于占空比D的函数。从而在已知输入电压Vin和占空比D时,可以得到唯一确定的输出电压Vout为
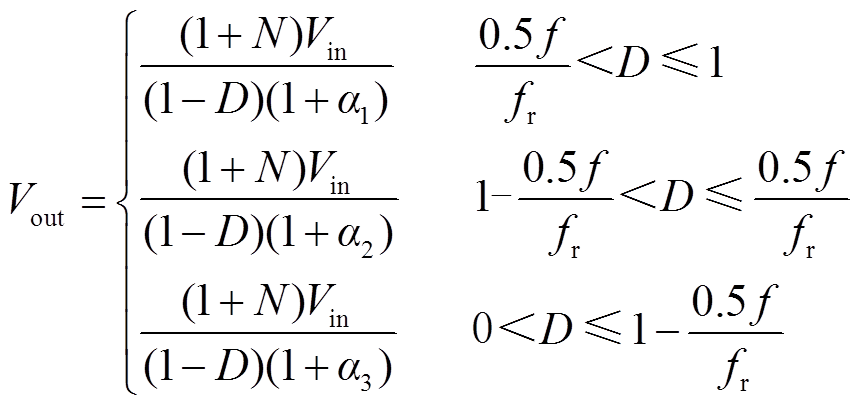 (37)
(37)
根据升压比的解析表达式,得到当耦合电感变比N=1,2,3时,该谐振变换器的电压增益如图7所示。可见本文所提出的变换器相比较传统Boost变换器在相同占空比的情况下具有更高的增益。
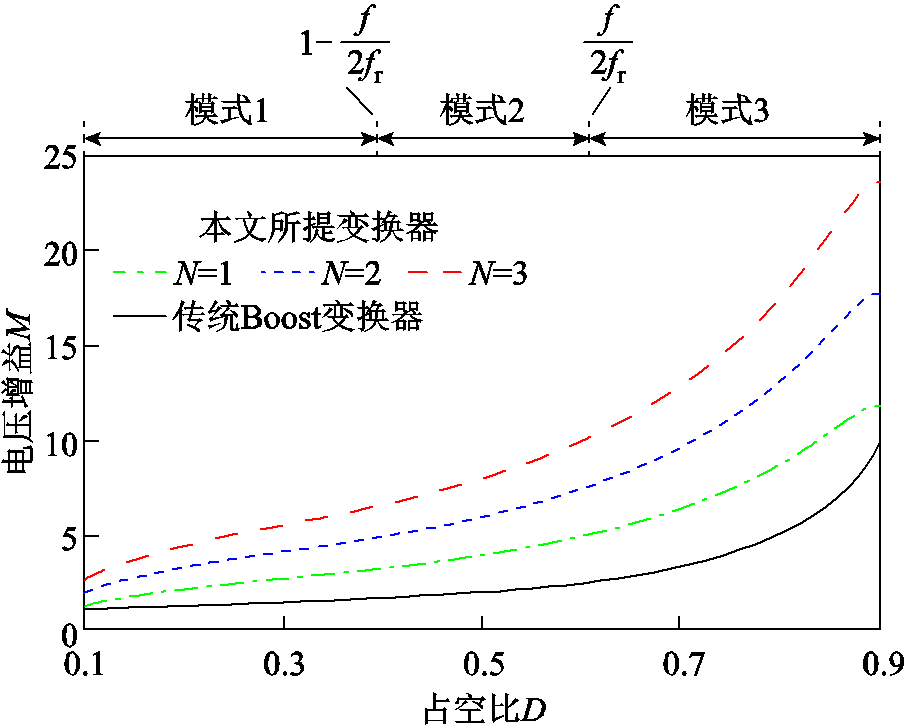
图7 本文提出的谐振变换器的电压增益
Fig.7 The voltage gain of the resonant converter proposed in this paper
由前文的电路时序分析可知,由于谐振的原因,二极管VD1和VD2在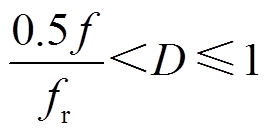 的模式下可以实现ZCS开通和关断。下面主要分析开关管S1和S2的软开关条件。
的模式下可以实现ZCS开通和关断。下面主要分析开关管S1和S2的软开关条件。
为了实现开关管的ZVS开通,一方面需要保证在开关管开通时刻流经开关管的电流的方向是从源极流向漏极,给开关管结电容放电,从而实现软开关;另一方面,在开关管开通时刻,储存在漏感中的能量要足够大,能够将开关管电容充分放电。也就是说,保证开关管实现软开关条件有两个:①导通时刻流经开关管的电流是负值(从源极流向漏极);②储存在漏感中的能量足以使上下两管的结电容完成充放电,即
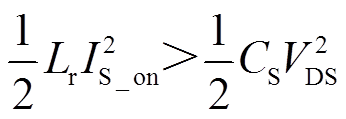 (38)
(38)
式中,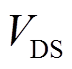 为开关管的漏源最大电压;
为开关管的漏源最大电压; 为主开关管和辅助开关管的结电容之和;
为主开关管和辅助开关管的结电容之和;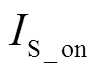 为开关管开通时的电流值,化简得
为开关管开通时的电流值,化简得
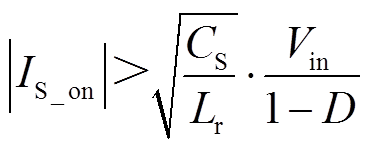 (39)
(39)
为了分析开关管的软开关条件,理论推导出了辅助开关管S1和主开关管S2在导通时刻的电流表达式。
辅助开关管S1的开通电流为
 (40)
(40)
主开关管S2的开通电流为
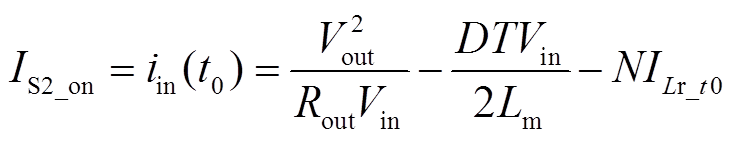 (41)
(41)
根据式(39)~式(41),可以作出主辅开关管的软开关范围,如图8所示。
从解析表达式可知,辅助开关管 的开通电流恒为负值且电流绝对值较大,很容易实现软开关。而主开关管S2实现软开关则需要一定条件。如图8b所示,主开关管S2的开通电流随着负载的增加或输入电压的降低而趋于减小,这意味着在负载较大或输入电压较低的情况下,主开关管S2的软开关条件更容易实现。
的开通电流恒为负值且电流绝对值较大,很容易实现软开关。而主开关管S2实现软开关则需要一定条件。如图8b所示,主开关管S2的开通电流随着负载的增加或输入电压的降低而趋于减小,这意味着在负载较大或输入电压较低的情况下,主开关管S2的软开关条件更容易实现。
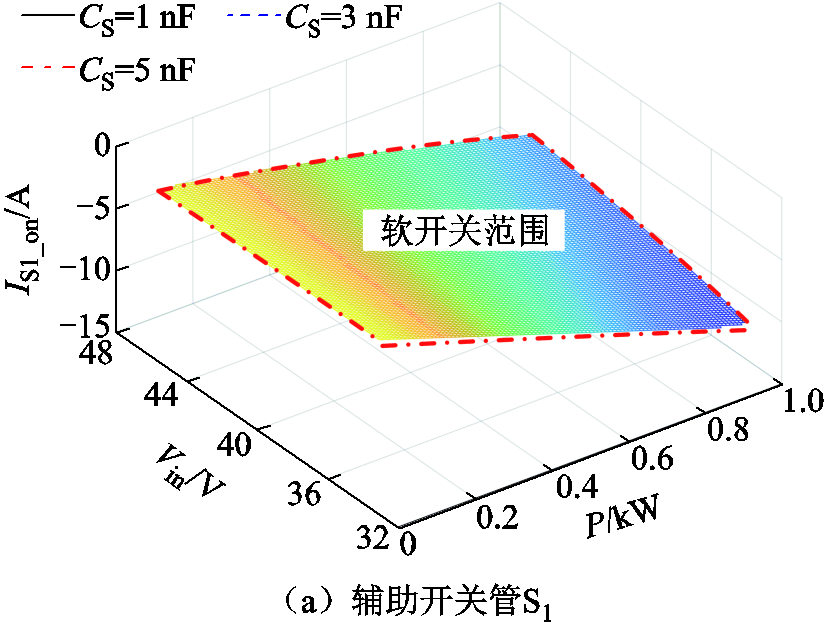

图8 软开关范围随输出功率和输入电压的变化
Fig.8 The ZVS ranges with respect to output power P and input voltage Vin
开关管上的电压应力等于输出电容C2的电压VC2。由式(24)可知,开关管的电压应力为
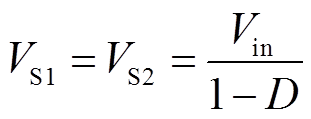 (42)
(42)
由谐振过程分析可知,二极管VD1和VD2的电压应力等于输出电容C1的电压VC1。从而可得二极管VD1和VD2的电压应力为
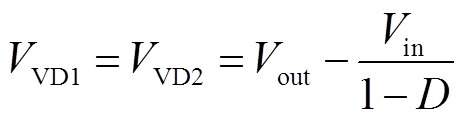 (43)
(43)
根据式(41)和式(42),可以绘制出以输出电压Vout为基准值的开关管和二极管的电压应力,如图9所示。由图9可见,无论是二极管还是开关管,电压应力均小于输出电压。尤其对于开关管来说,其电压应力远小于输出电压,因此可以采用更低导通电阻的开关管来实现较高的输出电压,从而提高系统的效率。
由式(6)、式(21)和式(22)可以求出,谐振电容的最大电压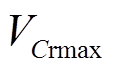 为
为
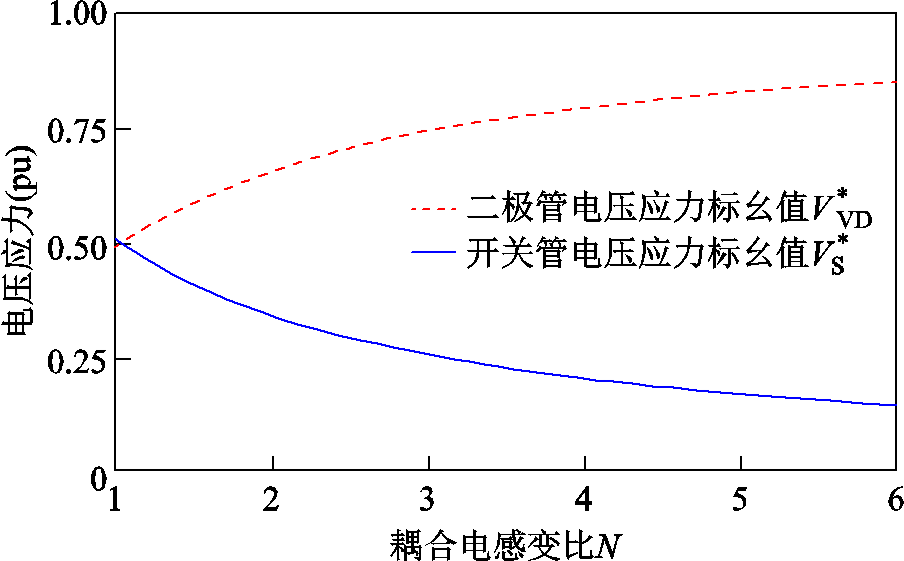
图9 二极管和开关管的电压应力
Fig.9 The voltage stress of diodes and switches
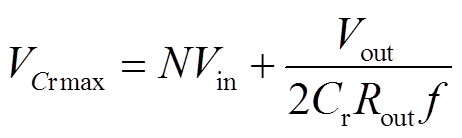 (44)
(44)
输出电容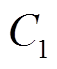 的电压应力等于输出电压
的电压应力等于输出电压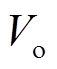 减去输出电容
减去输出电容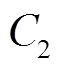 的电压,即
的电压,即
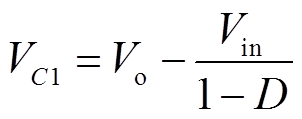 (45)
(45)
由式(24)可得,输出电容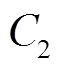 的电压为
的电压为
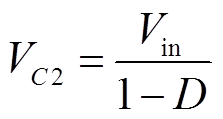 (46)
(46)
主开关管S2的关断电流应力等于辅助开关管S1开通电流的负值,即
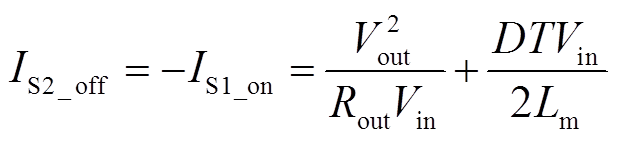 (47)
(47)
辅助开关管S1的关断电流应力等于主开关管S2开通电流的负值,即
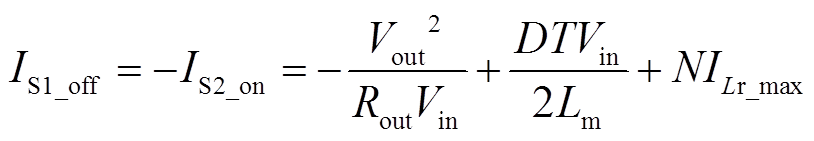 (48)
(48)
根据式(46)和式(47),可以绘制出以输入电流平均值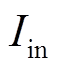 为基准值的主开关管和辅助开关管的电流应力,如图10所示。由图10可见,主开关管的电流应力略大于输入电流,因此在选择开关管时需要选取较大容量的开关管或采取多管并联的方式。辅助开关管的电流应力远小于输入电流,因此在选取辅助开关管时,可以选择容量较小的开关管,降低成本。
为基准值的主开关管和辅助开关管的电流应力,如图10所示。由图10可见,主开关管的电流应力略大于输入电流,因此在选择开关管时需要选取较大容量的开关管或采取多管并联的方式。辅助开关管的电流应力远小于输入电流,因此在选取辅助开关管时,可以选择容量较小的开关管,降低成本。
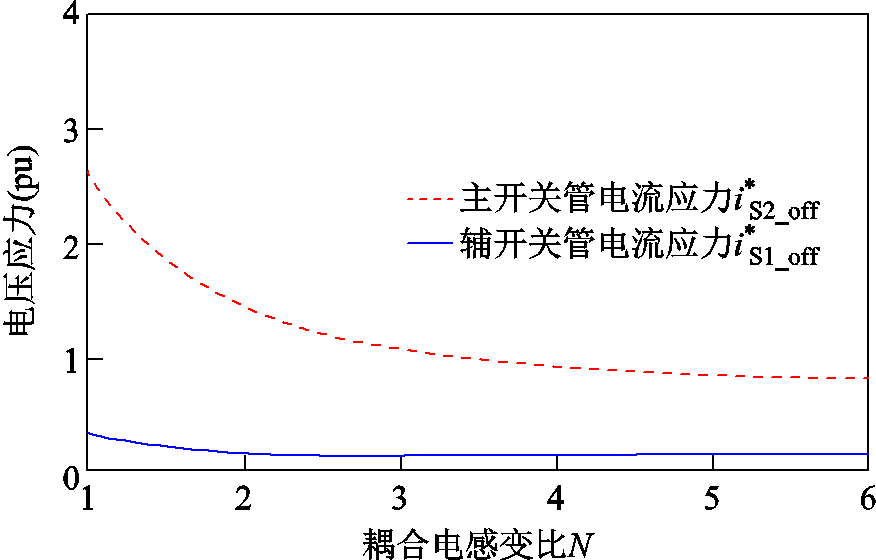
图10 主开关管和辅助开关管的电流应力
Fig.10 The current stress of main and auxiliy switches
二级管VD1电流应力为阶段4谐振电流最大值。
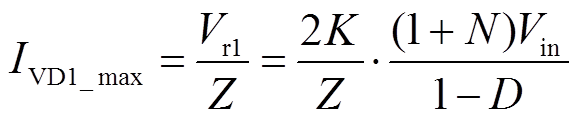 (49)
(49)
二级管VD2的电流应力为阶段2中谐振电流的最大值为
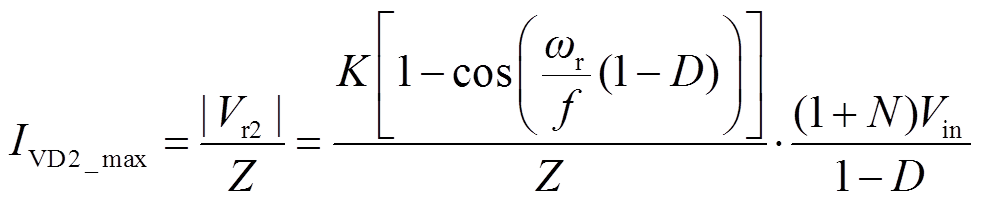 (50)
(50)
 和
和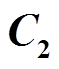 选型方法
选型方法输出电容的值取决于输出电压纹波的要求。输出电容C1和C2的充放电过程可以分为充电和放电两大类。以输出电容C1为例,在图5中,阶段1和阶段4属于给电容C1充电的过程,阶段2和阶段3属于电容C1放电给负载的过程。其中,在放电阶段[t2, t4],放电时长约为DT,输出电流为恒定值,输出电容C1上的电压线性下降可表示为
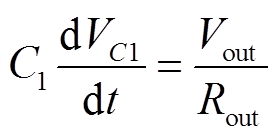 (51)
(51)
从而得到输出电容C1的选值公式为
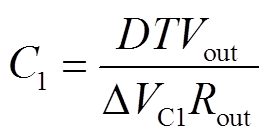 (52)
(52)
式中,DVC1为输出电容C1最大允许电压纹波。
同理,可得输出电容C2的选值公式为
 (53)
(53)
式中,DVC2为输出电容C2最大允许电压纹波。
为了验证前文的理论分析,证明本文提出的拓扑具有高增益、低电压应力、软开关、高效率等优点,搭建了1 kW的实验样机(两路交错并联,每路各500 W)。样机的实物如图11所示,具体的实验参数见表1。

图11 1 kW实验样机
Fig.11 The 1 kW prototype
表1 基于耦合电感的谐振变换器电路参数
Tab.1 The parameters of the resonant converter based on coupled converter

参数数值 输入电压/V32~48 输出电压/V380 额定功率P/W2路×500 开关频率f/kHz50 耦合电感变比N2.5 耦合电感漏感/mH12(折合到副边) 耦合电感励磁电感/mH50 谐振电容/mF1.5 输出电容/mF24 输出电容/mF24
图12是额定工况下为谐振电容电压VCr、输出电容电压VC1和VC2的波形。此时的输入电压Vin为40 V,输出电容C1和C2的电压分别为115 V和265 V,总的输出电压Vout为380 V,升压比高达9.5,验证了本文提出的谐振变换器的高增益特性。谐振电容的电压VCr随谐振的变化而变化,最大值和最小值分别为116 V和79 V,与根据式(6)和式(14)求出的理论值(119 V和82 V)相近。
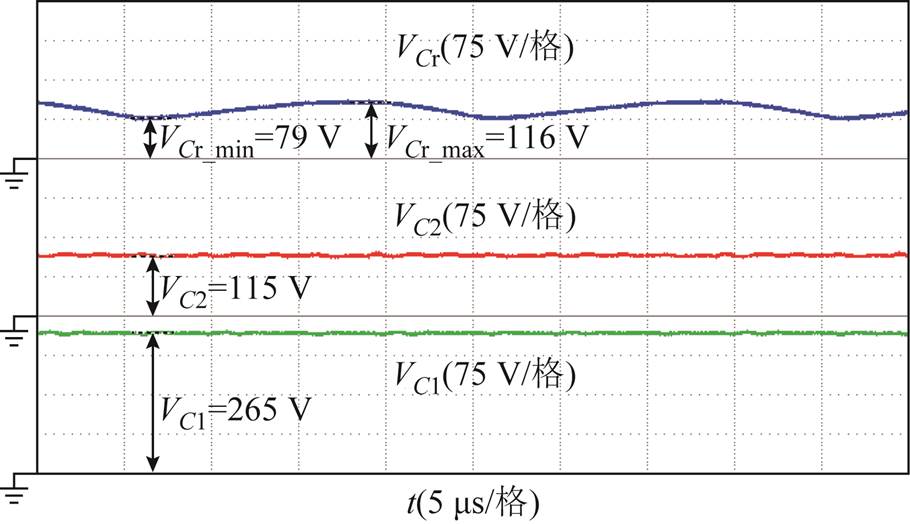
图12 谐振电容、输出电容电压波形
Fig.12 The waveforms of resonant capacitor voltage and output voltage
图13为耦合电感原边电流波形和副边电流(漏感电流)波形,由波形可见,和第2节中的理论分析波形一致。图14~图17分别为辅助开关管S1、主开关管S2、二极管VD1和二极管VD2的电压和电流波形。由图中波形可见,辅助开关管 和主开关管S2导通时刻的电流均为负值,可以实现ZVS导通。二极管VD1和二极管VD2可实现ZCS开通和关断。同时,辅助开关管S1和主开关管S2的电压应力均约为120 V,远低于输出电压380 V,因此可以采用低导通电阻的低压器件,从而可以提高系统的效率。
和主开关管S2导通时刻的电流均为负值,可以实现ZVS导通。二极管VD1和二极管VD2可实现ZCS开通和关断。同时,辅助开关管S1和主开关管S2的电压应力均约为120 V,远低于输出电压380 V,因此可以采用低导通电阻的低压器件,从而可以提高系统的效率。
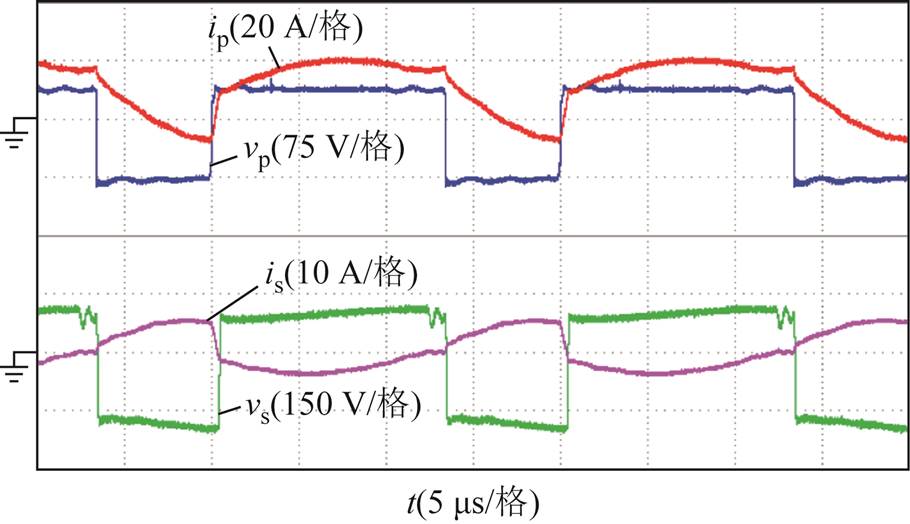
图13 耦合电感原、副边电压电流波形
Fig.13 The waveforms of coupled inductor primary and secondary side current and voltage
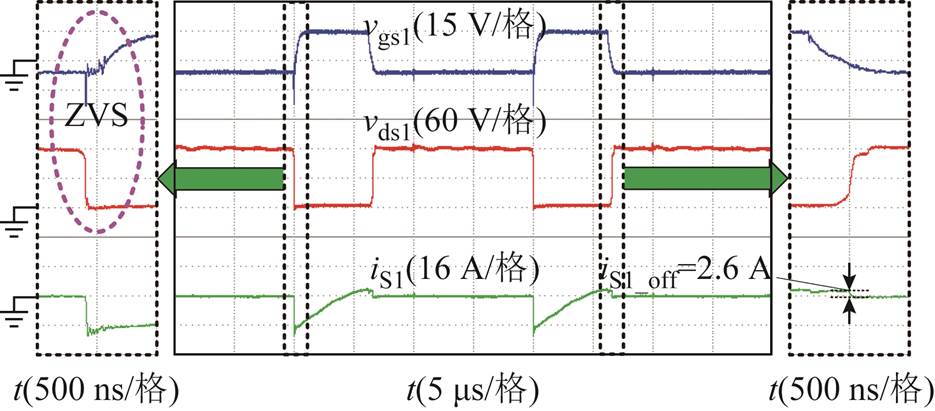
图14 开关管S1的软开关波形
Fig.14 The waveforms of switch S1
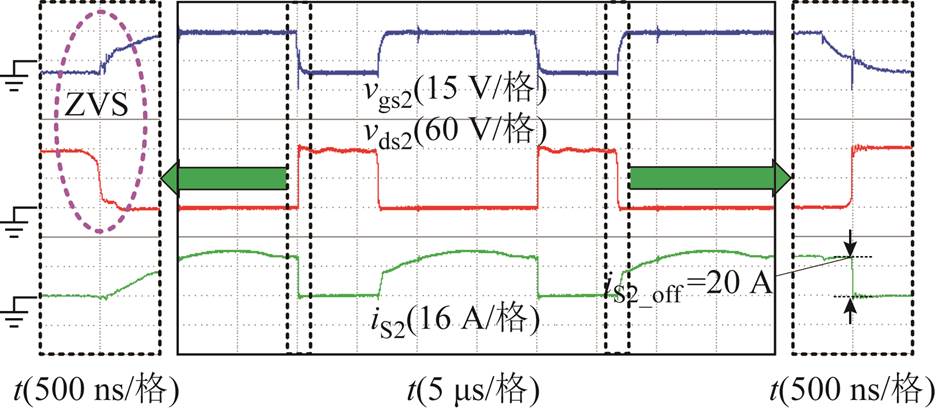
图15 开关管S2的波形
Fig.15 The waveforms of switch S2
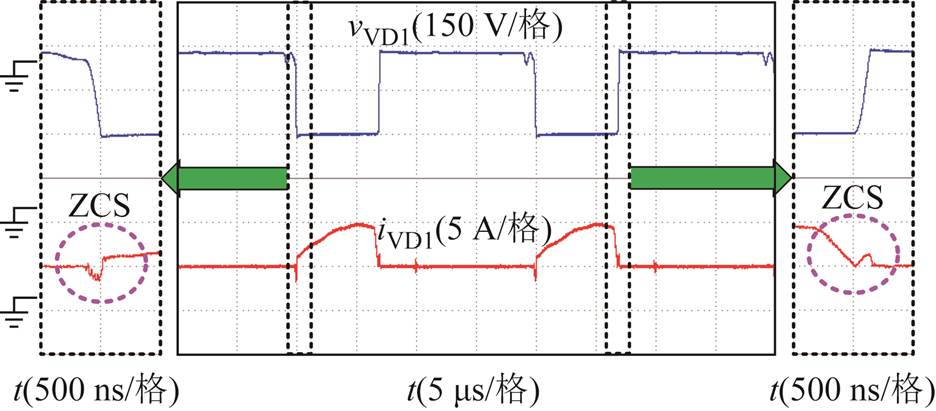
图16 二极管VD1的波形
Fig.16 The waveforms of diode VD1
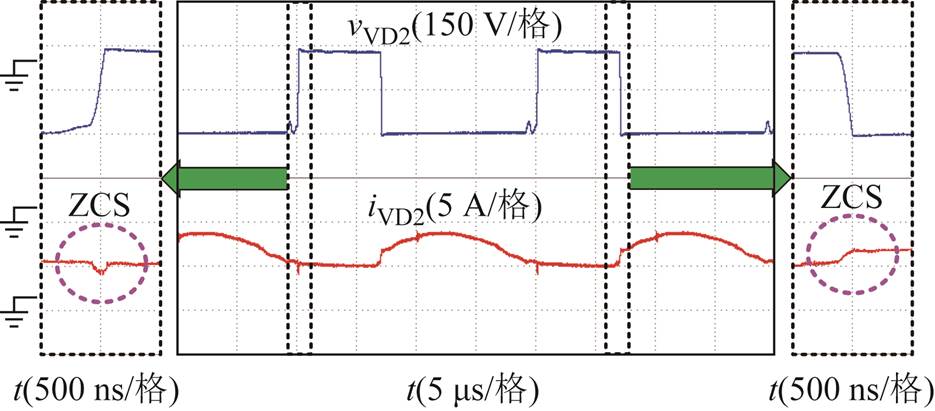
图17 二极管VD2的波形
Fig.17 The waveforms of diode VD2
图18给出了效率随着输出功率的变化曲线,由于本文所提出的变换器可以实现所有开关管的ZVS开通和所有二极管的ZCS开通和关断,因此具有较高的效率。所提出的高增益变换器的峰值效率约为97.5%,并可在大范围负载下实现96%以上的效率。
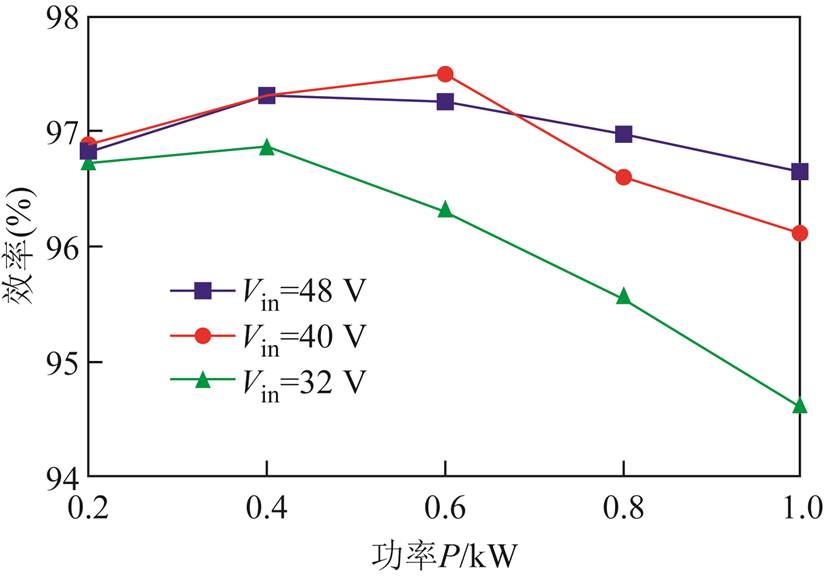
图18 效率曲线
Fig.18 The efficiency curves with coupled inductor
本文提出了一种具有高增益、软开关、低电压应力的新型谐振变换器。该谐振变换器使用耦合电感来提高电压增益,升压比不仅取决于占空比,还取决于耦合电感的变比,具有高增益的优点。此外,由于采用了有源钳位技术,漏感中的能量可以被回收利用,用来对开关管的结电容充放电提供能量,从而实现软开关。本文分析了该谐振变换器的工作原理,并推导得到了输出电压、关断电流应力等参数的解析表达式。在此基础上,从理论上分析了该变换器取得软开关的条件,并对该变换器的各个器件的电压电流应力进行分析,为器件选型提供了理论依据。最后,本文搭建了1 kW实验平台,针对本文提出的基于耦合电感的谐振变换器的高增益、软开关、低电压应力等性能进行了实验测试,验证了本文提出的拓扑的优越性。
参考文献
[1] Blaabjerg F, Chen Zhe, Kjaer S B. Power electronics as efficient interface in dispersed power generation systems[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1184-1194.
[2] Maksimovic D, Cuk S. Switching converters with wide DC conversion range[J]. IEEE Transactions on Power Electronics, 1991, 6(1): 151-157.
[3] Barreto L H S C, Coelho E A A, Farias V J, et al. A quasi-resonant quadratic boost converter using a single resonant network[J]. IEEE Transactions on Industrial Electronics, 2005, 52(2): 552-557.
[4] Zhao Jing, Han Yunlong, He Xiangning, et al. Multilevel circuit topologies based on the switched-capacitor converter and diode-clamped converter[J]. IEEE Transactions on Power Electronics, 2011, 26(8): 2127-2136.
[5] Gao Feng, Loh P C, Teodorescu R, et al. Diode-assisted buck–boost voltage-source inverters[J]. IEEE Transactions on Power Electronics, 2009, 24(9): 2057-2064.
[6] Qian Wei, Cao Dong, Cintron-Rivera J G, et al. A switched-capacitor DC-DC converter with high voltage gain and reduced component rating and count[J]. IEEE Transactions on Industry Applications, 2012, 48(4): 1397-1406.
[7] Kwon J M, Kwon B H. High step-up active-clamp converter with input-current doubler and output- voltage doubler for fuel cell power systems[J]. IEEE Transactions on Power Electronics, 2009, 24(1): 108-115.
[8] Zhang Zhe, Ouyang Ziwei, Thomsen O C, et al. Analysis and design of a bidirectional isolated DC-DC converter for fuel cells and supercapacitors hybrid system[J]. IEEE Transactions on Power Electronics, 2012, 27(2): 848-859.
[9] Wai R J, Duan R Y. High step-up converter with coupled-inductor[J]. IEEE Transactions on Power Electronics, 2005, 20(5): 1025-1035.
[10] Adib E, Farzanehfard H. Zero-voltage transition current-fed full-bridge PWM converter[J]. IEEE Transactions on Power Electronics, 2009, 24(4): 1041-1047.
[11] Liu Hongchen, Li Fei, Ai Jian. A novel high step-up dual switches converter with coupled inductor and voltage multiplier cell for a renewable energy system[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4974-4983.
[12] Middlebrook R D. A continuous model for the tapped-inductor boost converter[C]//1975 IEEE Power Electronics Specialists Conference, Culver City, CA, USA, 2015: 63-79.
[13] Vazquez N, Estrada L, Hernandez C, et al. The tapped-inductor boost converter[C]//2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 2007: 538-543.
[14] Packnezhad M, Farzanehfard H. Soft-switching high step-up/down converter using coupled inductors with minimum number of components[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7938-7945.
[15] Zhao Qun, Lee F C. High-efficiency, high step-up DC-DC converters[J]. IEEE Transactions on Power Electronics, 2003, 18(1): 65-73.
[16] Santra S B, Chatterjee D, Siwakoti Y P, et al. Generalized switch current stress reduction technique for coupled-inductor-based single-switch high step-up boost converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1863-1875.
[17] Zaoskoufis K, Tatakis E C. A thorough analysis for the impact of the coupling coefficient on the behavior of the coupled inductor high step-up converters[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8287-8302.
[18] Zheng Yifei, Brown B, Xie Wenhao, et al. High step- up DC-DC converter with zero voltage switching and low input current ripple[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9416-9429.
[19] Zheng Y, Smedley K M. analysis and design of a single-switch high step-up coupled-inductor boost converter[J]. IEEE Transactions on Power Electronics, 2020, 35(1): 535-545.
[20] Kwon J M, Kim E H, Kwon B H, et al. High-efficiency fuel cell power conditioning system with input current ripple reduction[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 826-834.
[21] Ye Yuanmao, Cheng K W E, Chen Sizhe. A high step-up PWM DC-DC converter with coupled-inductor and resonant switched-capacitor[J]. IEEE Transactions on Power Electronics, 2017, 32(10): 7739-7749.
[22] Deng Yan, Rong Qiang, Li Wuhua, et al. Single-switch high step-up converters with built-In transformer voltage multiplier cell[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3557-3567.
[23] 孙瑄, 荣德生, 王宁. 具有谐振软开关的高增益耦合电感组合Boost-Zeta变换器[J/OL].电工技术学报, 2023:1-13.
[24] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755. Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft-switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electrotech-nical Society, 2019, 34(4):747-755.
Abstract Fuel cell is a kind of clean energy with high efficiency and high power density, which has a good application prospect in automobile, aerospace and other fields. This paper presents a new type of resonant converter with high gain and soft switching for fuel cell. The resonant converter uses the coupling inductor to improve the voltage gain. The topology mainly consists of two parts: Boost circuit and resonant circuit. The resonant circuit is superimposed on the Boost circuit, and the output voltage of the two is superimposed to increase the voltage gain. The Boost circuit consists of the magnetic inductance of the coupled inductor and two switches, the auxiliary switches are equivalent to ordinary Boost diodes. The circuit is a unidirectional high-gain circuit. The purpose of using MOSFETs in the auxiliary switches is not to achieve bidirectional energy flow, but to ensure that the main switches can realize zero voltage opening and improve efficiency. The active clamping technique is used for the primary soft switch and synchronous rectification to reduce losses. The resonant circuit is composed of the auxiliary side of the coupled inductor, the leakage inductance of the coupled inductor, the resonant capacitor, two diodes and the output capacitance.
The voltage boost ratio depends not only on the duty ratio, but also on the variation ratio of the coupling inductor, which has the advantage of high gain. In addition, due to the active clamp technology, the energy in the leakage inductance can be recovered and utilized to provide energy for the charging and discharging of the junction capacitor of the switches, so as to realize the soft switching. Due to the coupled inductor, the proposed converter can achieve higher output voltage at lower voltage stress, so low voltage devices with low on-resistance can be used to improve the efficiency of the system. In this paper, the operation principle of the proposed converter is analyzed, and the expressions are derived theoretically. On this basis, the conditions of obtaining soft switch of the converter are analyzed theoretically. Besides, the voltage and current stress of each device of the converter are analyzed and the selection method of the output capacitor is given, which provides a theoretical basis for device selection.
In the experiment, a 1 kW rated prototype is made, and the experiment is carried out for the performance of the proposed converter, such as high step-up, soft switching, low voltage stress, high efficiency and etc. The input voltage is 40V and the output voltage is 380 V, which can realize the 9.5 voltage gain. All switching tubes can realize ZVS soft switching operation, and all diodes can realize ZCS operation. Because all switches have soft switching operation, and the switching current stress is small, the peak efficiency of the proposed converter is about 97.5% under 10 times Boost ratio which verifies the superiority of the proposed topology.
keywords:Coupled inductor, resonant converter, high step-up, soft switching
DOI:10.19595/j.cnki.1000-6753.tces.221942
中图分类号:TM131.3
广东省重点领域研发计划资助项目(2020B0909030003)。
收稿日期 2022-10-10
改稿日期 2023-03-22
王 哲 男,1997年生,博士,研究方向为燃料电池、DC-DC变换器。E-mail:wangzhe19@mails.tsinghua.edu.cn
郑泽东 男,1980年生,副教授,博士生导师,研究方向为高性能交流电机控制、高压大容量电力电子变换器及其应用、轨道交通电力牵引、船舶电力推进等。E-mail:zzd@mail.tsinghua.edu.cn(通信作者)
(编辑 郭丽军)