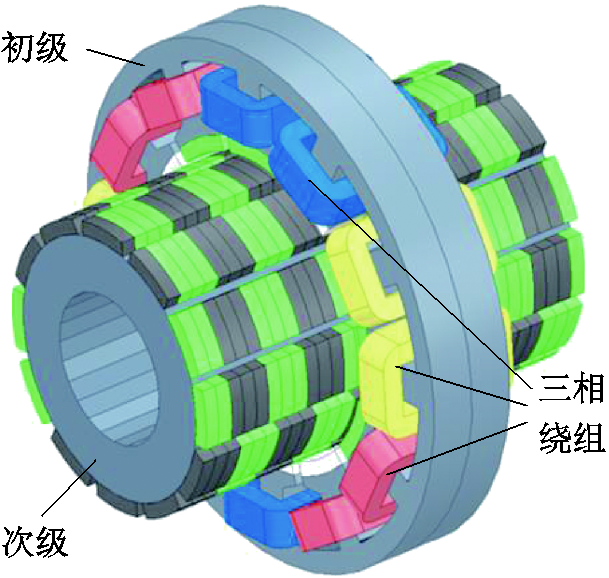
图1 TFPMLM三维有限元模型
Fig.1 TFPMLM 3D finite element model
摘要 横向磁通永磁直线电机的电负荷与磁负荷相互解耦，且各相之间相互解耦，易于实现模块化和多相化，因此在石油开采领域有着良好的应用前景。首先，该文基于磁场调制原理，对横向磁通永磁直线电机的径向电磁力波进行了推导计算，得出对径向电磁力波影响最大的因素为轴向气隙磁通密度分量与径向气隙磁通密度分量，在此基础上对径向电磁力波的时空特性与频谱特性进行仿真计算，得出电枢磁通密度对电机径向电磁力波的频谱特性的影响；然后，考虑到电机实际运行中可能出现的次级偏心问题，揭示偏心度的大小对径向电磁力波幅值的影响，并对比不同偏心度下的电机径向磁拉力与轴向磁拉力，定量分析偏心度对不平衡磁拉力的影响；最后，为避免共振，利用有限元软件对电机的初级进行了模态分析与谐响应分析，结果表明低速状态下横向磁通永磁直线电机的额定运行频率较低，不会引起初级的共振，适合用作往复式潜油电泵的驱动电机。
关键词：横向磁通永磁直线电机 径向电磁力波 电磁振动 偏心度
近年来，中国已经成为世界上第二大的石油消费国，同时也是世界上第一大的原油净进口国，石油能源的重要性不言而喻。井下往复式潜油电泵机组作为新型的石油开采设备，可以有效解决低渗透油田有杆泵举升方式存在管杆偏磨严重、系统效率低、能耗高的问题，也为低产直井、斜井的举升工艺提供了解决途径[1-2]。潜油直线电机是往复式潜油电泵系统的唯一动力源，其运行性能指标直接影响整个电泵系统的运行性能。因此，为满足井下各种恶劣工况的运行需求，潜油直线电机的选型、结构、材料、工艺及配套需满足特殊要求[3]：①具有良好的密封性、承压性和可靠性，以适应井下恶劣的运行环境；②结构受井下环境限制，潜油直线电机一般呈细长型，外径受井径限制，最大外径应小于118 mm，长度对外径之比可达20～50；③具备较大推力，油层埋藏深度大，泵也深，需要较大举升力。横向磁通永磁直线电机（Transverse Flux Permanent Magnet Linear Motor, TFPMLM）作为一种具有高推力密度的特种电机，得益于横向磁通结构，一方面电枢绕组和定子齿槽在空间上相互垂直，可实现电负荷和磁负荷的解耦，使电机的性能指标进一步提高，另一方面各相之间相互解耦便于独立控制，此外，TFPMLM易实现电机的模块化和多相化[4-9]。基于以上特点，横向磁通永磁直线电机比较适合应用于石油开采领域。
在实际的石油开采过程中，由于井下的恶劣环境，潜油直线电机容易遇到来自外部强烈的机械振动、冲击及高速流体的冲刷[10]，此外，电机本身振动所产生的行程误差累计也容易造成电机的撞击。电机振动会加速轴承的磨损从而降低轴承的寿命，而高强度的振动会加剧电机线圈、绝缘与机壳相互之间的摩擦，导致电机的绝缘性降低，大大降低电机的使用寿命[11]。电机振动还容易引起电机次级偏心，使得内部气隙磁通密度的分布发生改变，从而产生单边磁拉力，又因潜油直线电机往往功率较大，一旦产生单边磁拉力，摩擦损耗也会较大，影响电机的寿命与可靠性[12]。
电磁振动是电机本身产生振动的主要原因之一，且电磁振动是电机气隙磁场作用在电机初级产生的电磁力波与初级结构的各阶模态共同决定的，当电磁力波的频率与定子的固有频率接近时，将引发强烈的振动[13]，因此电磁力波和定子固有频率的研究与计算是电磁振动分析的关键。文献[14]对开关磁阻电机的减振降噪进行了研究分析，得出径向电磁力波是电机振动的主要来源。文献[15]提出一种基于表贴式永磁电机绕组电流的径向振动模型与一种可抑制电机各频次径向振动的模型，并在此基础上证明了基于多目标RMSProp（root mean square prop）算法的永磁电机径向振动抑制策略的有效性。文献[16]分析了高模数电磁力对开齿永磁电机低阶电磁振动的影响，得出高阶电磁力能引起低阶电磁振动，且在电机及减振结构设计过程中，可从永磁体的结构和定子齿开展优化工作。文献[17]对变频电机展开研究，探究了变频谐波对电机噪声特性的影响规律，得出变频器的输出谐波会使变频电机发出各种频率的噪声，使得电机更易发生共振，需要在设计阶段进行消除或削弱。
针对开关磁阻电机径向电磁力严重的非线性问题，文献[18]提出一种解析方法，该方法解析得到的径向电磁力可用于开关磁阻电机的振动噪声预测与优化研究。文献[19]研究了极槽配合对永磁同步电机振动和噪声影响，通过对径向力谐波的分析，得出可优选转子磁极谐波分量的整数倍槽数来避免低次径向力谐波。文献[20]推导了永磁同步电机径向电磁力的解析表达式并验证了其正确性。为了抑制永磁同步电机的振动噪声，文献[21]通过齿槽转矩和径向电磁力的仿真结果确定转子表面槽的最佳尺寸，分析了其电磁振动与噪声。另外，对于永磁同步电机的噪声抑制，文献[22-24]分别从定子齿削角、定子齿顶偏移结构、优化齿槽转矩方面进行了研究分析。综上所述，径向电磁力波是各类旋转电机发生电磁振动的主要振源，对径向电磁力波的分析与计算是电机电磁振动的研究重点。
在直线电机方面，韩国学者J. Y. Yoon等为了降低永磁直线电机的振动与噪声，先后提出一种具有细齿、窄槽与倾斜Halbach永磁体阵列的电机结构和一种利用对称结构直接抵消谐波的电机结构[25-26]。文献[27]对直线电机进行了模态分析计算，得出电机在空载工况的调速过程中所产生的电磁力易导致电机产生共振。综合国内外研究现状，现阶段国内外学者对电机的振动研究大量集中在旋转电机，于直线电机的振动研究相对较少。
本文以TFPMLM为研究对象，从径向电磁力波的分析与计算入手，推导出TFPMLM的径向电磁力的表达式，利用有限元软件对径向力波的时空特性与频谱特性进行分析。同时考虑电机运行过程中可能出现的偏心问题，对次级不同偏心度引起的电磁力波变化进行了计算与分析。最后，对TFPMLM初级模态及其电磁振动特性进行了分析总结。
本文所研究的TFPMLM三维有限元模型如图1所示。TFPMLM采用12 槽圆周三相结构与短初级长次级方案，电枢绕组为沿圆周三相对称分布的集中绕组。将电机次级沿圆周方向展开，得到电机次级铁心导磁齿的排列如图2所示，其中，TFPMLM的次级在切向方向上的凸极齿数与初级保持一致，在轴向方向上，相邻两相的导磁齿错开2τ/3（τ为极距）。永磁体分布于初级与次级两侧，为交替级结构，TFPMLM的主要尺寸参数见表1，尺寸参数示意图如图3所示。
图1 TFPMLM三维有限元模型
Fig.1 TFPMLM 3D finite element model
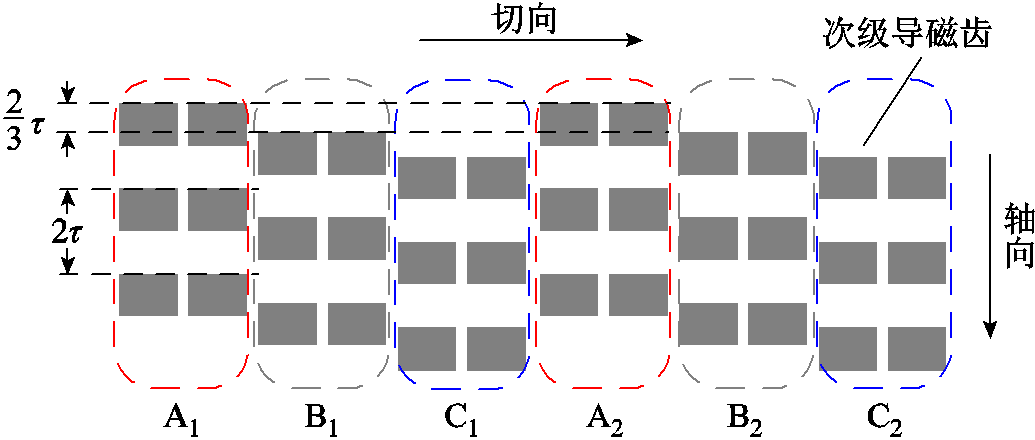
图2 圆周三相次级导磁齿排列示意图
Fig.2 Schematic diagram of the arrangement of the three-phase secondary magnetic conductive teeth on the circumference
表1 TFPMLM尺寸参数
Tab.1 The size parameters of TFPMLM
参数数值 初级铁心外半径Rpo/mm52 初级槽高度hpt/mm10.8 初级永磁体轴向长度lpm/mm8 初级轭高度hpy/mm5 初级齿宽wpt/mm7 气隙宽度g/mm1 次级铁心外半径Rso/mm27.4 极距τ/ mm9 次级铁心内半径Rsi/mm15 初级永磁体高hpm/mm3 次级永磁体高hst/mm3 次级极弧系数αst0.8 初级槽口宽度wpo/mm3.5
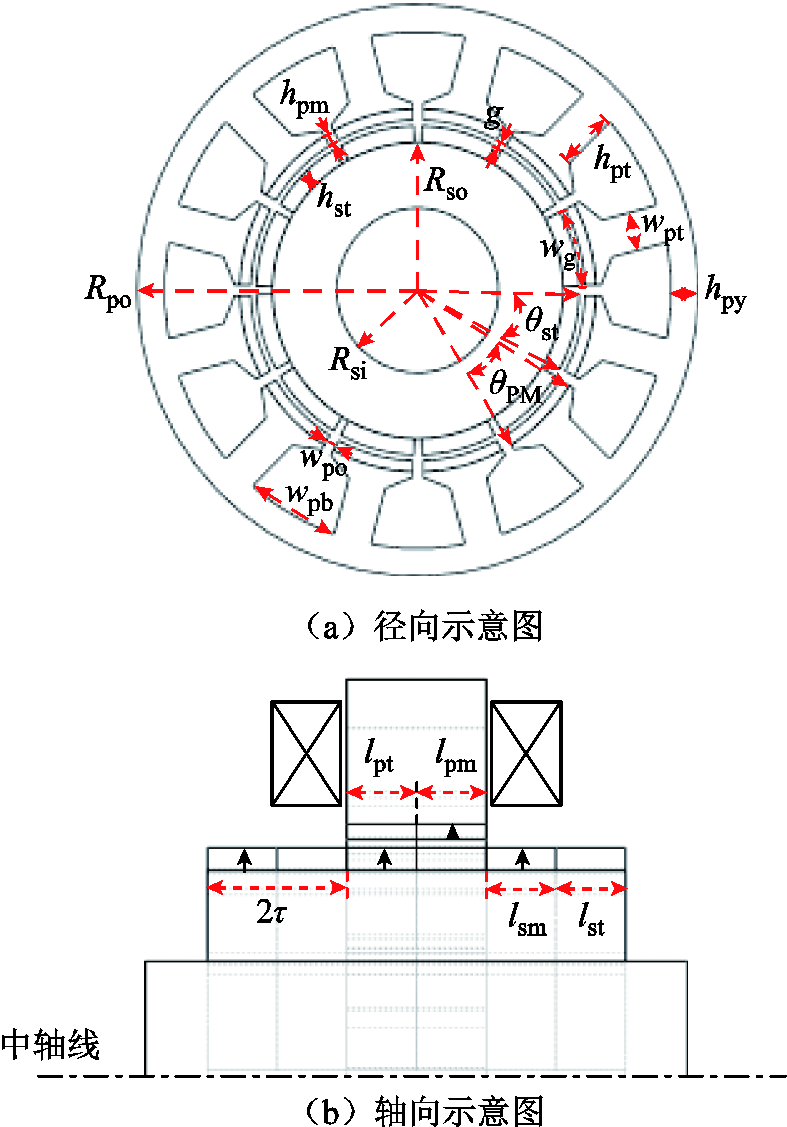
图3 电机尺寸参数示意图
Fig.3 Schematic diagram of motor size parameters
为便于分析需要作出如下假设：①忽略铁心饱和带来的影响；②不计涡流损耗及磁滞损耗；③磁场仅在径向发生变化。
由于TFPMLM的初级与次级两侧均安装有永磁体，且永磁体与导磁齿交替排列，因而在进行气隙磁通密度的解析计算时，可以分解成初级永磁体与次级铁心、次级永磁体与初级铁心两组磁动势-磁导模型进行计算。初、次级导磁齿磁导分布与磁动势分布如图4所示。其中，图4d、图4e分别对应图4a中的次级导磁齿与初级永磁体，图4c、图4f分别对应图4b中初级导磁齿与次级永磁体，分别计算两组磁动势-磁导模型气隙磁通密度，叠加后得到整体气隙磁通密度表达式。图4a和图4b中箭头表示充磁方向。
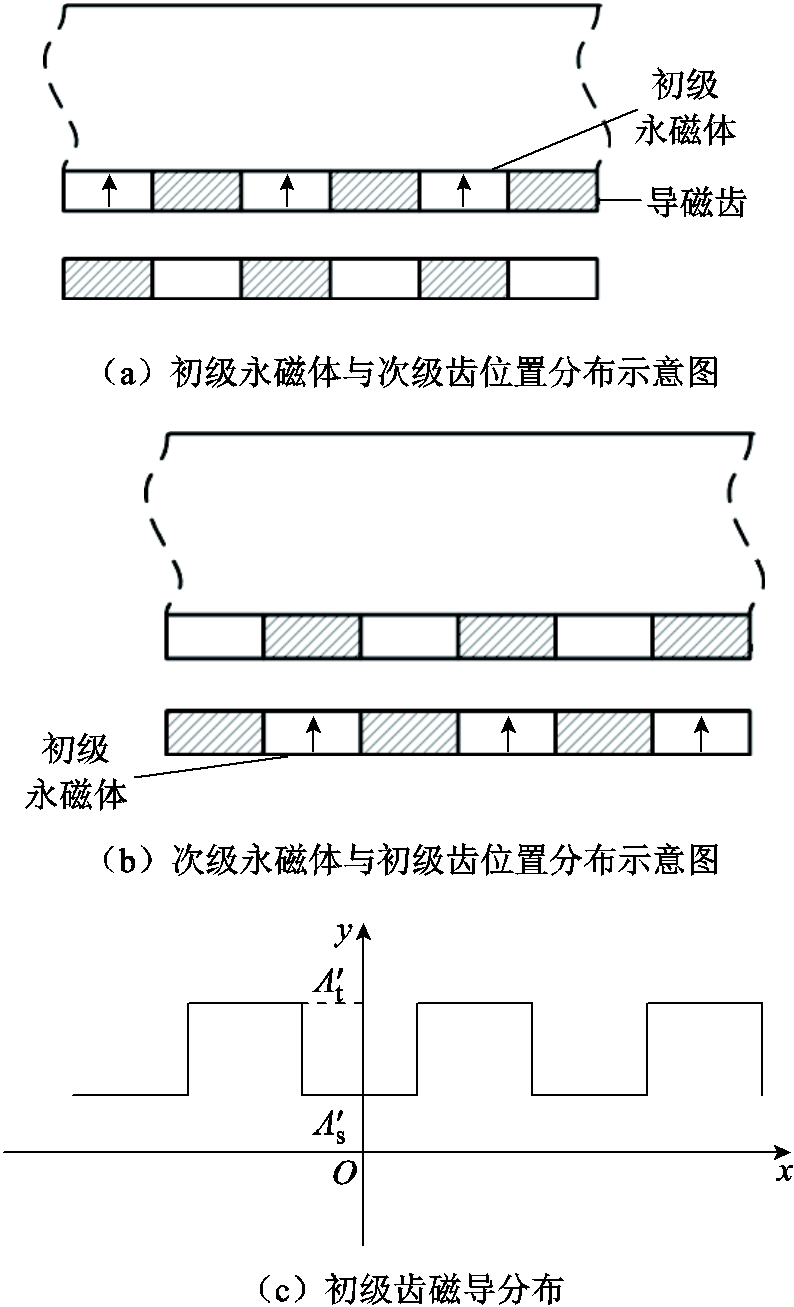
图4 初、次级导磁齿磁导分布与磁动势分布
Fig.4 Magnetic conductance distribution and magnetomotive force distribution of primary and secondary magnetic teeth
图4中
表示次级导磁齿单位面积下的磁导，有
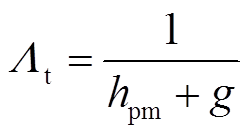（1）
次级无导磁齿处单位面积下的磁导可表示为
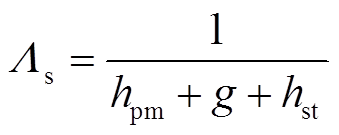（2）
图4d中所示次级导磁齿磁导分布波形分解为傅里叶级数形式得
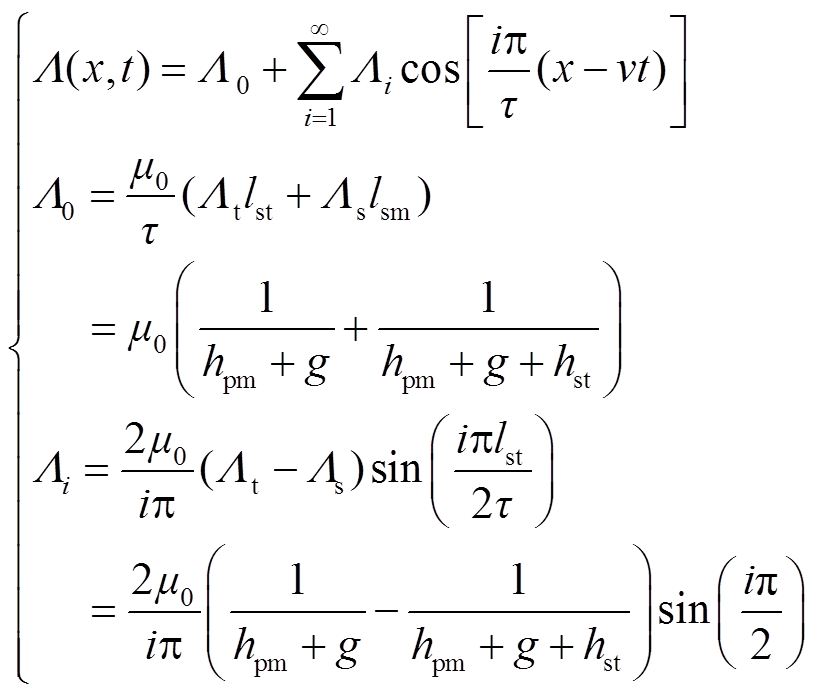（3）
式中，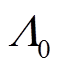
为次级磁导中的直流分量（H/m）；
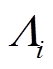为次级磁导i次谐波系数；v为次级的运动速度；m0为真空磁导率；lst与lsm分别为次级导磁齿对应的轴向长度与次级永磁体对应的轴向的长度。
同理，图4e中初级永磁体磁动势波形分解为傅里叶级数形式为
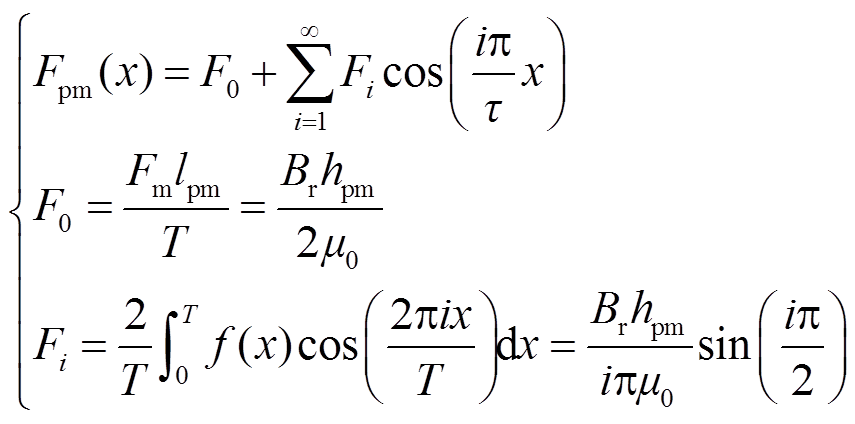（4）
式中，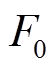
为初级磁动势中的直流分量；
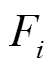为初级磁动势i次谐波系数；lpm为初级永磁体对应的轴向长度；T为电机运行周期；Br为永磁体剩磁。
因次级永磁体磁动势、初级磁导的波形分布与初级永磁体磁动势、次级磁导分布相差180°，所以次级永磁体磁动势可表示为
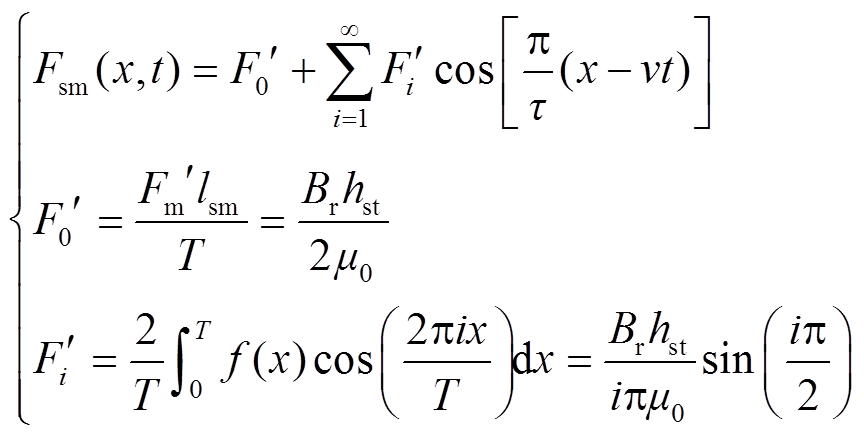（5）
式中，
为次级磁动势中的直流分量；
为次级磁动势各次谐波系数；lsm为次级永磁体对应的轴向长度。
同理初级磁导可表示为
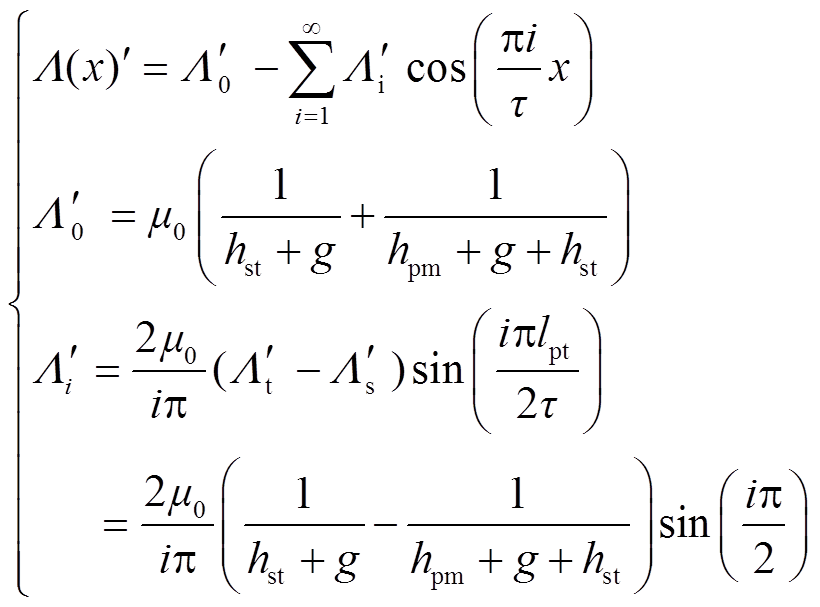（6）
式中，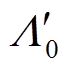
为初级磁导中的直流分量；
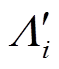为初级磁导i次谐波系数；lpt为初级导磁齿对应的轴向长度。
结合式（3）～式（6），忽略高次谐波的影响，仅考虑直流和基波分量时，求得气隙磁通密度的表达式为
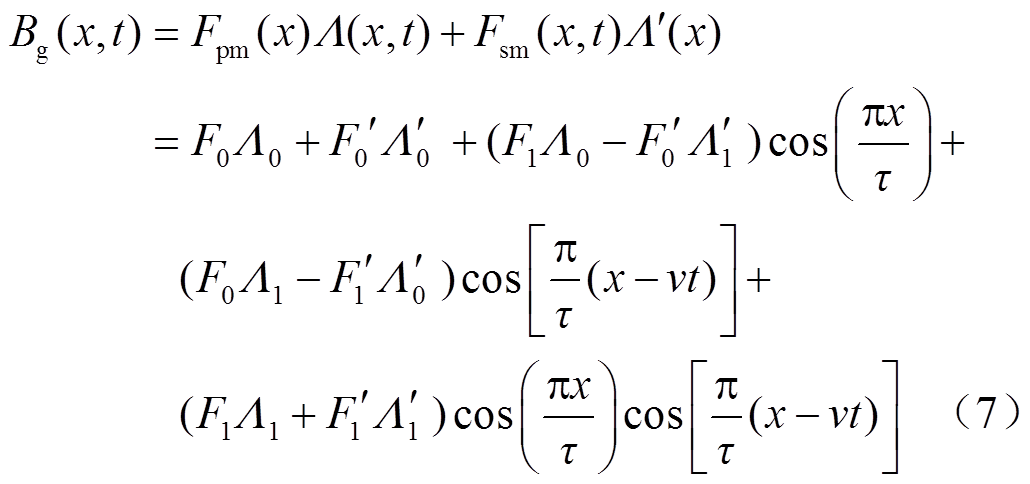
从式（7）可以看出，第一项与第二项分别为初级永磁体与次级永磁体所产生的直流分量，该分量不随时间与次级的运动而变化，其大小只与永磁体的性能有关；第三项由表贴于初级与次级的永磁体相互作用产生，该分量同样不随电机次级的运动而发生变化；第四项与第五项为谐波磁场分量，因初级与次级的凸极导磁齿对永磁体磁场的调制作用而产生，该分量与时间和初次级之间的相对运动均有关。
在式（7）的基础上再考虑电枢绕组的作用，可得到合成气隙磁通密度表达式为
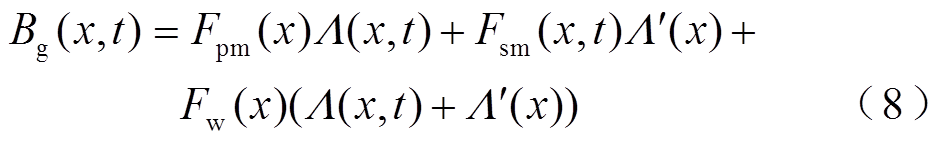
径向电磁力是气隙磁场作用于初级铁心的结果，而气隙磁场则是由永磁体磁动势、电枢反应磁动势与铁心磁导相互作用产生的。将初级视为固定部分，次级为运动部分，故次级相关数学表达式为位置与时间的函数。根据麦克斯韦张量法，作用于初级齿上的电磁力示意图如图5所示，各方向的电磁力波数学表达式如式（9）～式（11）所示。
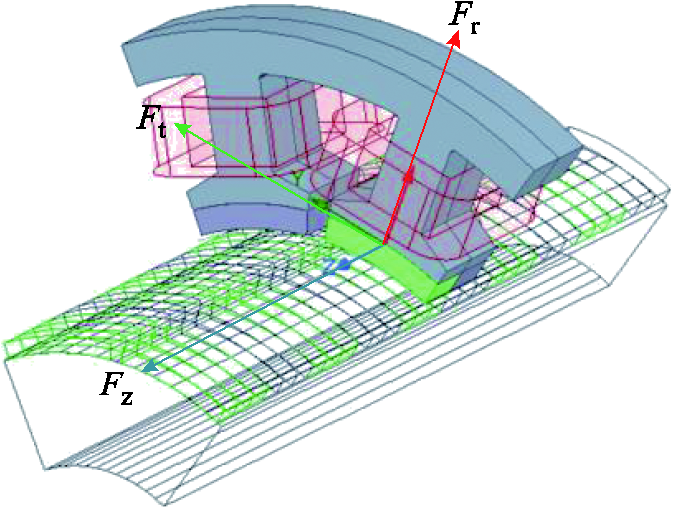
图5 电磁力波各方向示意图
Fig.5 Schematic diagram of electromagnetic force waves in various directions
径向电磁力波的表达式为
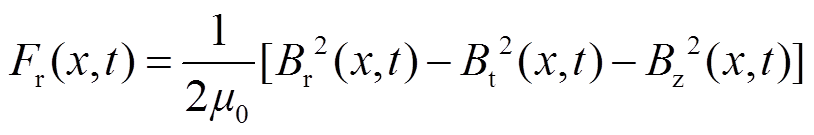（9）
切向电磁力波的表达式为
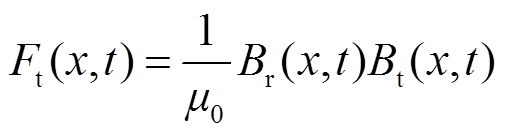（10）
轴向电磁力波的表达式为
（11）
式中，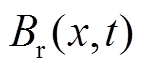
、
、
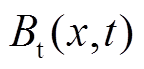分别为合成气隙磁通密度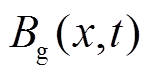
的径向、切向、轴向磁通密度分量。
传统纵向磁通永磁电机的次级运动方向与主磁通所在平面共面，次级并不存在轴向运动，轴向气隙磁通密度为0并忽略切向磁通密度，则径向电磁力波可以简化为
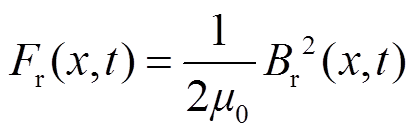（12）
可见传统纵向磁通电机的径向电磁力波仅与径向气隙磁通密度相关，但横向磁通永磁直线电机在次级运动方向上有不可忽略的轴向磁通密度分量。图6所示为初始时刻初级齿Ⅱ下，沿着轴向方向气隙磁通密度径向分量、轴向分量与切向分量分布。可以看出，沿轴向的气隙磁通密度径向分量是较规则的矩形波，切向分量很小基本可以忽略，而在磁通密度极性交替处出现了较大幅值的轴向磁通密度分量，这是因为在电机初级永磁体与导磁齿的交界处，部分次级永磁体产生的磁通，要先沿着轴向流通再进入初级导磁齿中，进而在交界处出现了磁通密度轴向分量的大幅波动。因此，对于TFPMLM来说，轴向磁通密度分量是电磁力波不可忽略的组成成分。
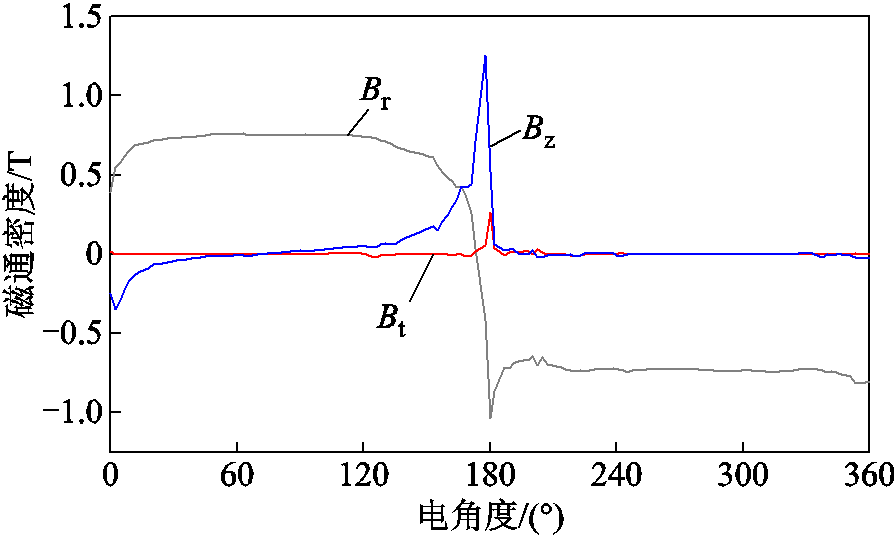
图6 初级齿Ⅱ下各向气隙磁通密度分布
Fig.6 The distribution of magnetic density in the air gap under primary tooth II
气隙磁通密度切向分量很小主要是因为TFPMLM永磁体均为径向充磁，主磁通与初级导磁齿表面垂直，此外，对于横向磁通永磁直线电机来说，切向磁通要远小于主磁通与纵向漏磁通，即气隙磁通密度的切向分量要远小于径向分量。因此，可以忽略切向气隙磁通密度分量，得到简化后的径向电磁力波数学表达式为
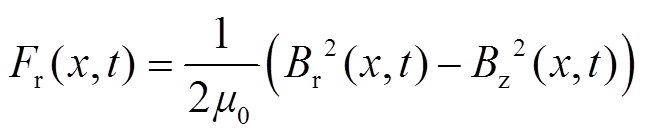（13）
根据磁通密度线性叠加原理，忽略电枢绕组输入电流谐波的影响，可将气隙磁通密度分为电枢磁通密度、初级永磁体磁通密度、次级永磁体磁通密度三类。
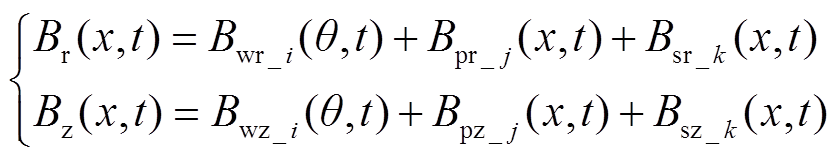（14）
式中，Bwr_i(θ,t)为电枢径向磁通密度；Bwz_i(θ,t)为电枢轴向磁通密度；Bpr_ j(x,t)为初级永磁体径向磁通密度；Bpz_ j(x,t)为初级永磁体轴向磁通密度；Bsr_k(x,t)次级永磁体径向磁通密度；Bsz_k(x,t)为次级永磁体轴向磁通密度。
1）由电枢绕组产生的电枢磁通密度，电枢径向磁通密度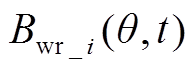
与电枢轴向磁通密度
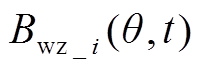可分别表示为
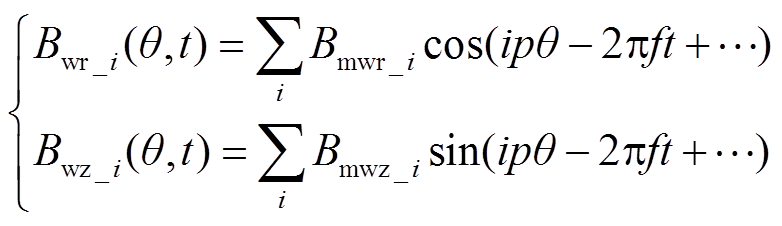（15）
式中，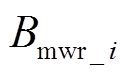
、
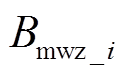分别为电枢径向与轴向气隙磁通密度的i次谐波幅值；p为极对数；f为电流基波频率（Hz）。
2）由初级永磁体与次级导磁齿相互作用产生的初级永磁体磁通密度，初级永磁体径向与轴向气隙磁通密度可分别表示为
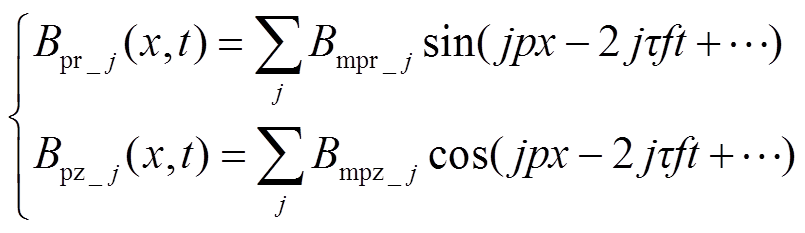（16）
式中，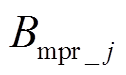
、
分别为初级永磁体径向与轴向气隙磁通密度的j次谐波幅值。
3）由次级永磁体与初级导磁齿相互作用产生的次级永磁体磁通密度可表示为
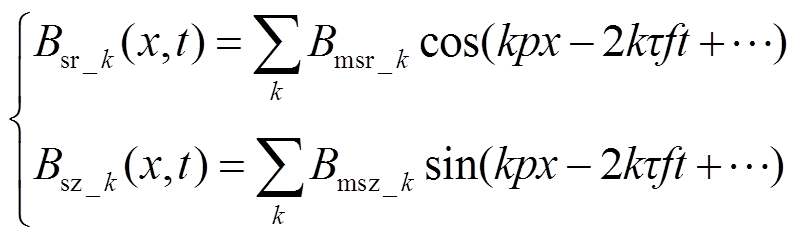（17）
式中，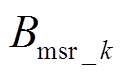
、
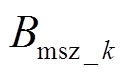分别为次级永磁体径向与轴向气隙磁通密度的k次谐波幅值。
电枢磁通密度是通电线圈在定子圆周方向上产生的磁通密度，由式（14）可知，电枢磁通密度是关于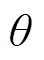
的函数，与次级在轴向运动方向无关。由式（15）、式（16）可知，初、次级永磁体产生的磁通密度均与次级运动方向有关，是关于轴向运动距离x的函数。为了简化计算过程，突出主要矛盾，上述磁通密度幅值均为简化表达式，正余弦函数中的省略号表示相位。
将各气隙磁通密度表达式代入式（13），通过三角函数积化和差，得到简化的径向电磁力数学表达式为
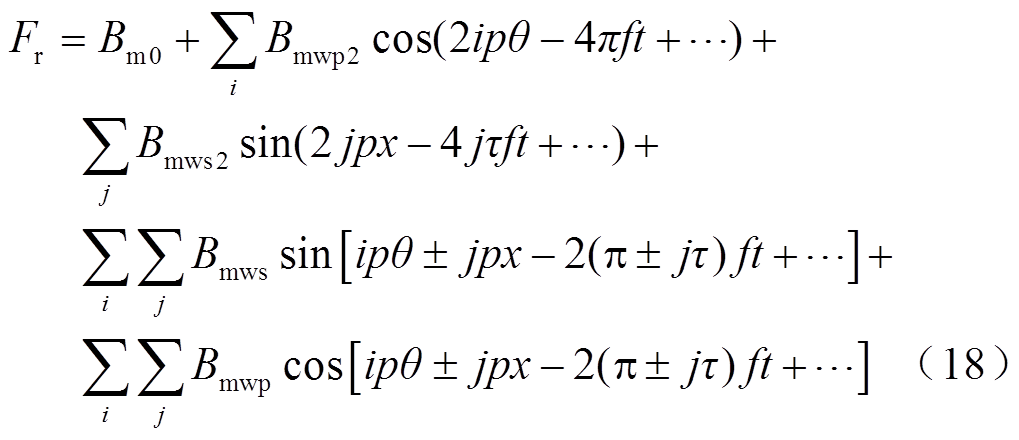
式中，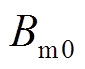
、
、
、
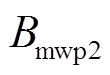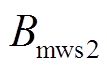和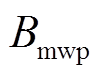
均表示幅值。
式（18）中第一项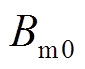为电枢磁通密度与初、次级永磁体磁通密度共同作用产生的直流分量之和；第二、第三项分别为电枢磁通密度与初级永磁体磁通密度、次级永磁体产生的磁通密度相互作用产生的二倍频谐波分量；第四项为电枢磁通密度与次级永磁体磁通密度相互作用产生的谐波分量；第五项为电枢磁通密度与初级永磁体磁通密度相互作用产生的谐波分量。
由于电机的交替极结构，初、次级的永磁体与导磁齿沿轴向交替排列具有三维特征，因此该电机的电磁力波沿圆周径向与沿轴向方向均为三维非对称分布，下面将电机初级沿轴向分为图7所示的Ⅰ、Ⅱ两段，第Ⅰ段为轴向4.5 mm处，第二段为轴向-4.5 mm处。
图7 电机轴向分段示意图
Fig.7 Schematic diagram of motor axial segment
不同轴向位置径向电磁力波的时空分布及其二维快速傅里叶变换（Fast Fourier Tvansformation, FFT）如图8所示。通过图8a与图8c、图8b与图8d的对比可以看出，虽然初级第Ⅰ段与初级第Ⅱ段下的永磁体安放位置不同，但在一个电周期内，Ⅰ、Ⅱ段下沿圆周径向方向的径向电磁力波时空分布波形及其二维傅里叶分解都是相同的，两者仅在相位上错开了一个极距。因此，分析电机初级齿下的径向电磁力波分布特性时，只需分析轴向上任意一段的电磁力波。
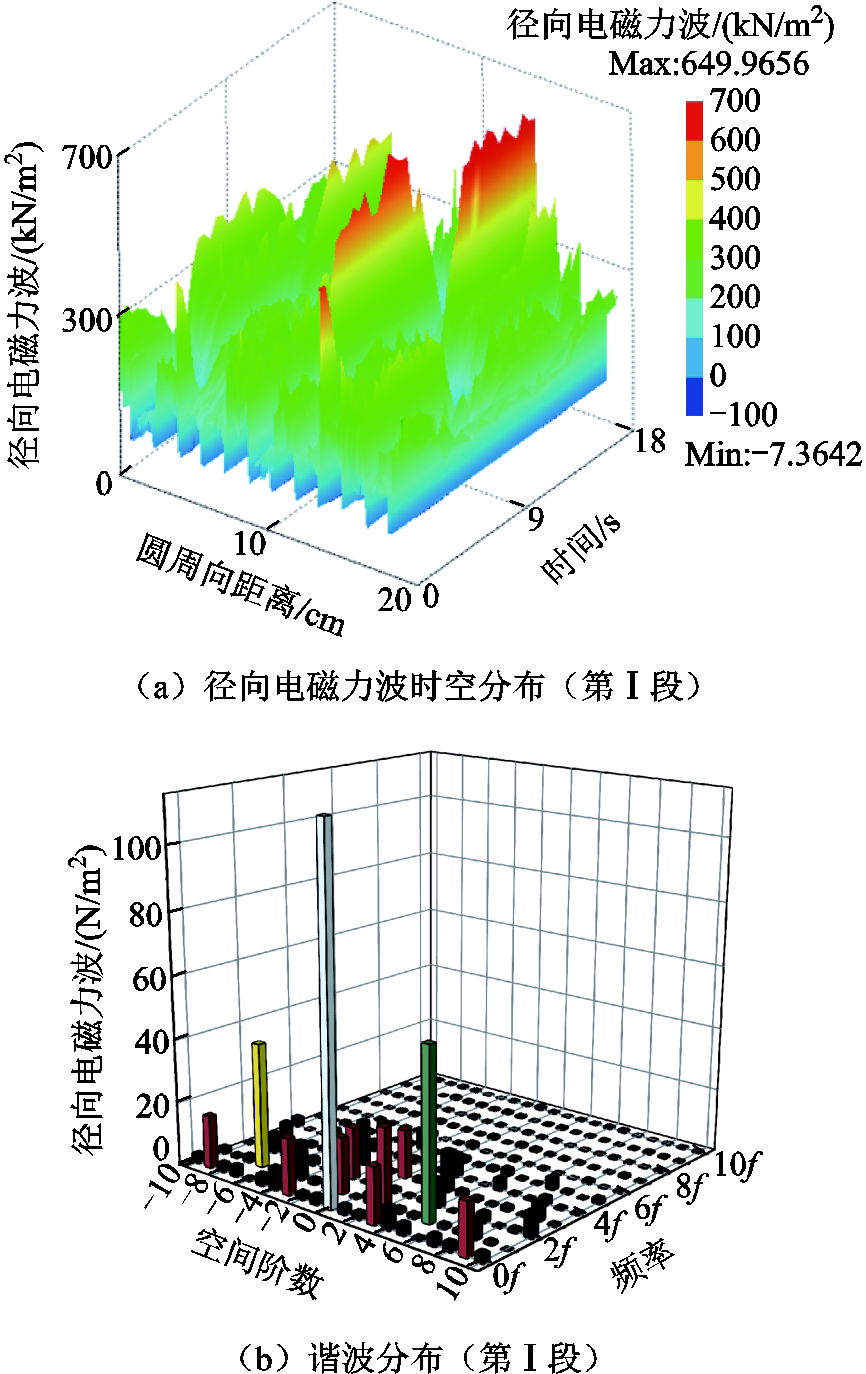
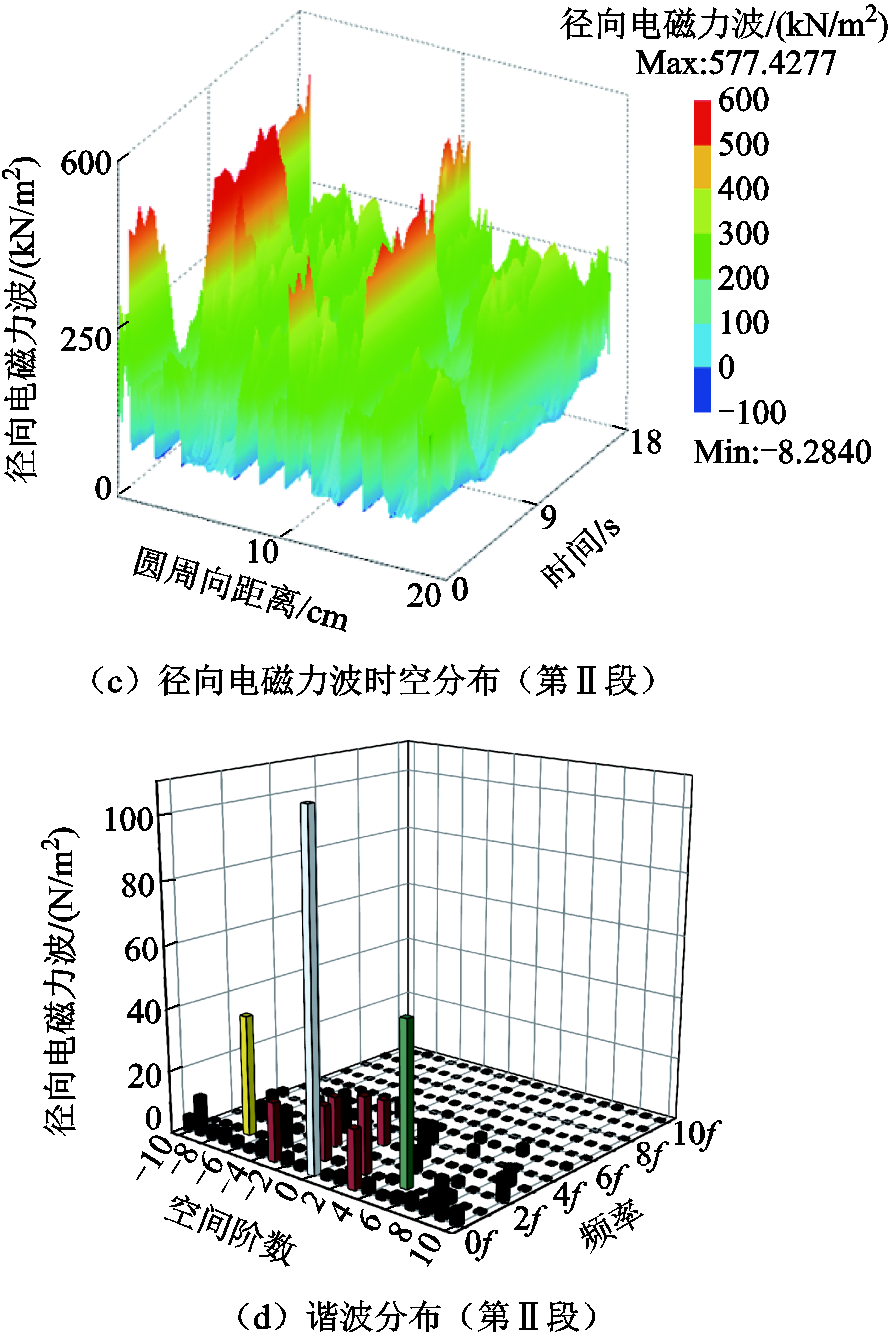
图8 不同轴向位置径向电磁力波的时空分布及其二维FFT
Fig.8 Spatio-temporal distribution of radial electromagnetic force waves at different axial positions and its two-dimensional FFT
为揭示电枢磁通密度对电机径向电磁力波频谱特性的影响，忽略电流谐波的影响，给三相电枢绕组通入10 A正弦交流电，得到负载状态下，第Ⅰ段沿圆周径向的电磁力波时空分布及其二维FFT如图9所示。相较于空载状态，电枢磁通密度使得径向电磁力波的（2，1f）、（-4，1f）有所增加，该部分由电枢磁通密度基波分量与初、次级永磁体磁通密度直流分量作用产生；（-5，2f）、（7，2f）的增加由电枢磁通密度基波分量与永磁体磁通密度的基波分量作用产生。
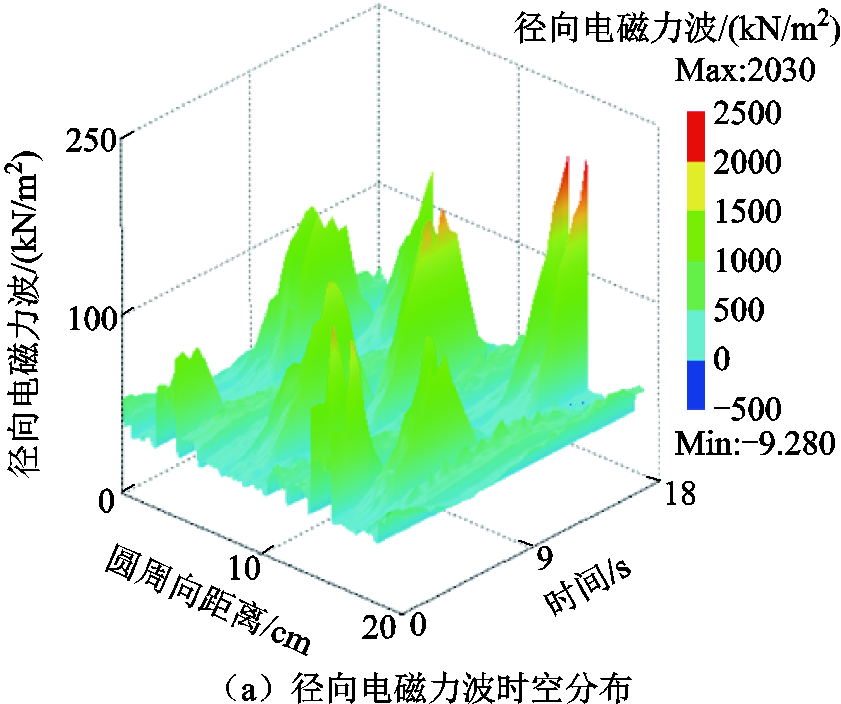
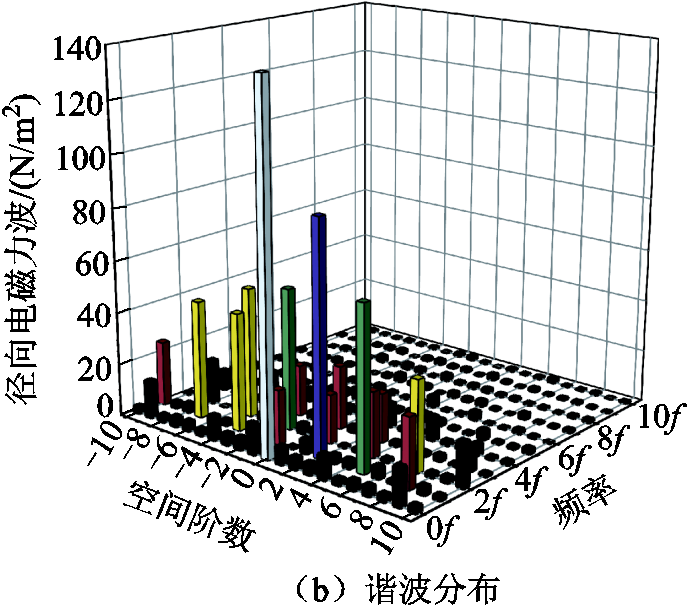
图9 负载状态下径向电磁力波的时空分布及其二维FFT
Fig.9 Spatio-temporal distribution of radial electromagnetic force wave under load and its two-dimensional FFT
潜油直线电机整体呈细长结构，当次级在运动过程中，扶正器发生故障或出现撞击时，会导致电机次级出现不同程度的偏心，进而影响电机的电磁性能与系统的稳定性。本节将对次级不同偏心度引起的电磁力波变化与不平衡磁拉力进行数值计算与分析。
TFPMLM的次级为轴向直线往复运动，在圆周径向方向并无旋转运动，因而电机的偏心故障主要为静态偏心，即初、次级的几何中心不重合。次级轴线与初级轴线产生偏移时，次级静偏心示意图如图10所示。
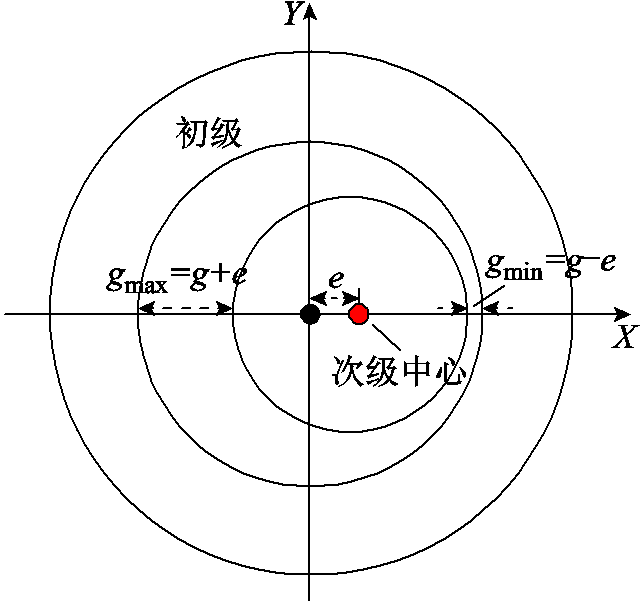
图10 次级静偏心示意图
Fig.10 Schematic diagram of secondary static eccentricity
假设电机次级中心沿X轴正方向产生偏心量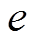
，电机气隙磁通密度分布发生改变，初级右侧气隙变小，左侧气隙变大，进而导致Y轴右半平面内初级受到的磁拉力变大，左半平面受到的磁拉力减少，从而产生较大的不平衡磁拉力。
将偏心度定义为偏心量与气隙的比值，利用有限元软件计算偏心度对电磁力波的影响。不同偏心度下，径向电磁力波沿圆周方向的空间分布及FFT分解如图11所示。从图11a中可以看出，在电机次级无偏心的情况下，在0～360°机械角度范围内的径向电磁力波是呈对称分布的，即此时沿圆周方向径向电磁合力为0，无单边磁拉力；当次级偏心20%、40%时，在气隙最小处径向电磁力波的幅值产生急剧变化，且偏心程度越高径向电磁力波变化的幅值越大，此时沿圆周方向径向电磁力合力不为0，产生较大的单边磁拉力。从图11b可以看出，次级偏心不仅会增加原各阶力波的幅值，还会产生新的阶次力波，这些力波主要由初、次级永磁体产生的各阶力波经偏心磁导调制产生。受次级偏心度影响较大的为1、3、6阶谐波，这些力波阶次低、幅值大，会对电机的振动噪声产生较大影响。
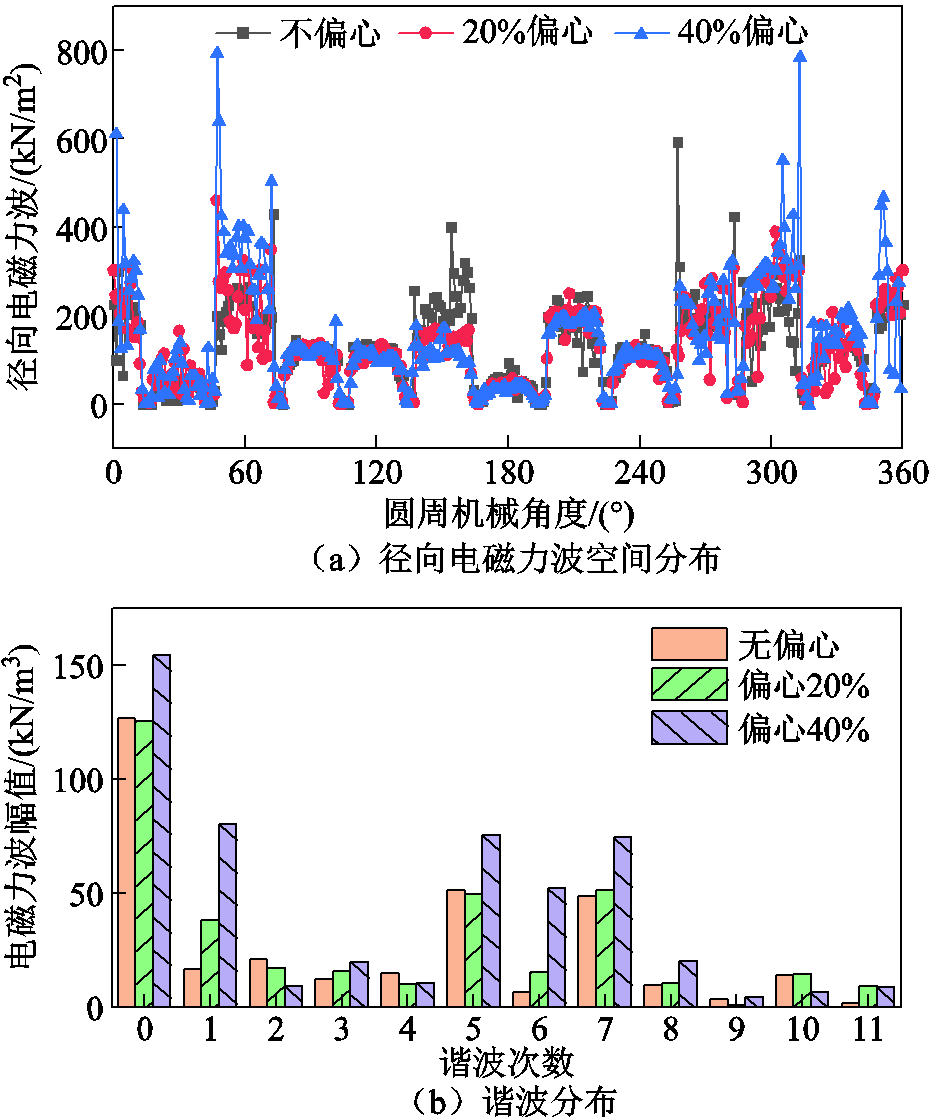
图11 不同偏心度下径向电磁力波空间分布及其谐波分布
Fig.11 Spatial distribution and harmonic distribution of radial electromagnetic force waves under different eccentricity
在初级导磁齿下取一点P（30.2,0,-4）得到该点受到的径向电磁力波随时间变化的分布及其FFT，如图12所示。由图12可知，静偏心并不影响电磁力波的频率分布规律，且偏心度只会影响该点径向电磁力波的幅值大小，偏心度越高径向电磁力波幅值越大。
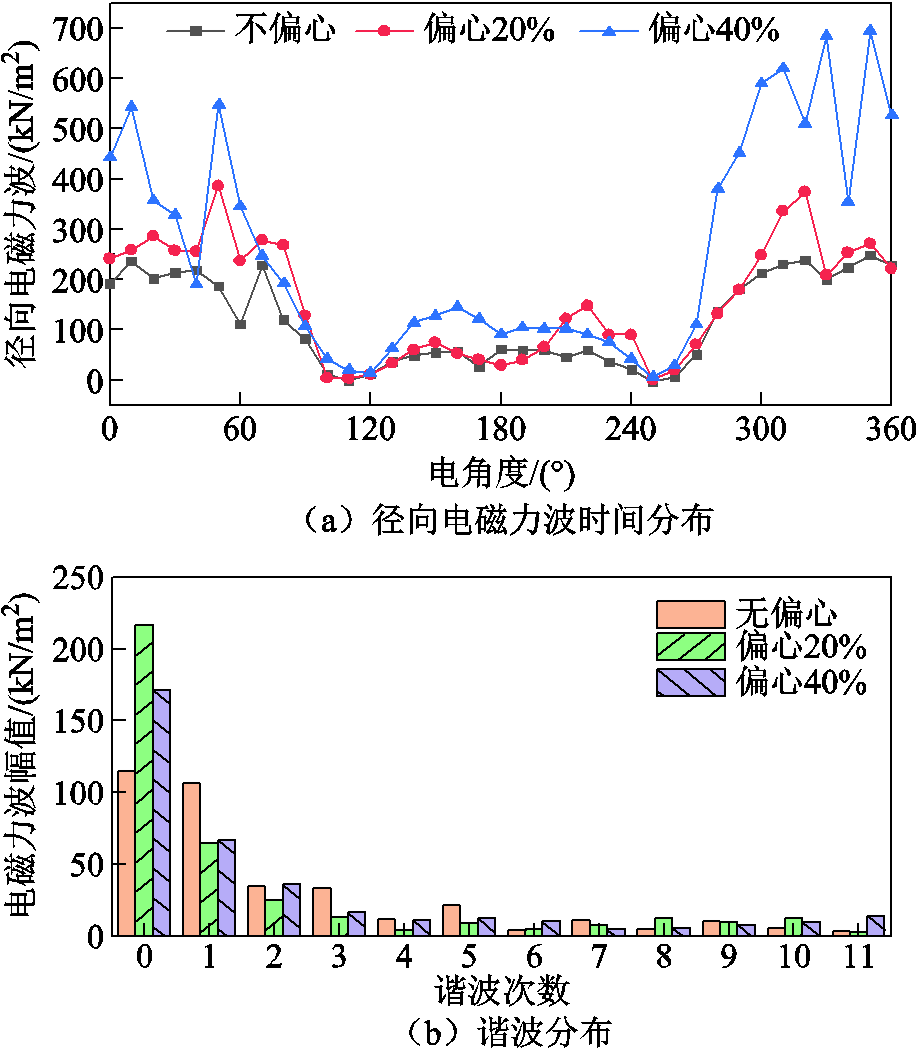
图12 不同偏心度下径向电磁力波时间分布及其谐波分布
Fig.12 Time distribution and harmonic distribution of radial electromagnetic force waves under different eccentricity
将圆周方向各齿面上的径向电磁力波进行积分与叠加即可得到初级整体的磁拉力数值。在空载状态下，将X轴正方向作为偏心方向，得到不同偏心度下径向电磁力随时间的分布，如图13a所示。可见随着次级沿轴向方向的直线运动，电机受到的径向电磁力随时间呈正弦分布，且偏心度并不影响径向电磁力的时间波形。随着偏心度的增加，磁拉力波形逐渐上移表现为沿X轴方向的磁拉力直流分量的增加。不同偏心度下径向电磁力直流分量变化趋势如图13b所示，可看出径向电磁力直流分量随偏心率的增加呈线性增大的趋势。当次级无偏心时，径向电磁力在一个电周期内的合力为0，即直流分量幅值为0；当次级发生偏心时，径向电磁力的直流分量幅值不为0，且偏心程度越大，径向电磁力直流分量幅值越大。这是因为在空载状态下，径向电磁力主要表现为初、次级永磁体与导磁齿之间的吸引力，而铁磁吸引力与气隙长度是呈线性相关的。
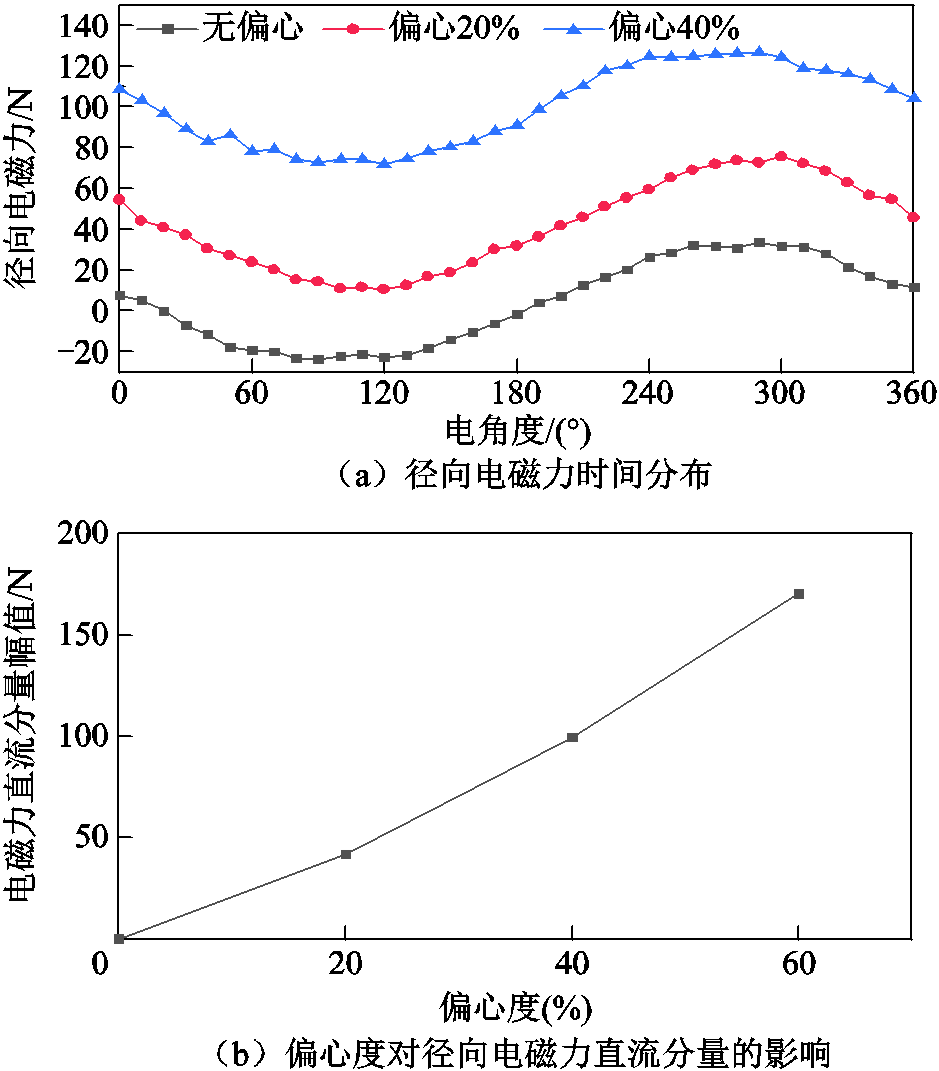
图13 不同偏心度下径向电磁力波形及其直流分量的变化趋势
Fig.13 Variation trend of radial electromagnetic force waveforms and its DC component under different eccentricity
图14所示为不同偏心度下轴向电磁力波形分布及其谐波分布。可以看出当次级不偏心时，电机的轴向电磁力在一个电周期内脉动6次，且脉动幅值较小，谐波以3、6次谐波为主；当次级发生偏心时，轴向电磁力的波形发生变化且波动幅值增大，这是因为次级偏心使得初、次级永磁体产生的磁通密度因偏心磁导的调制作用产生了新的轴向电磁力谐波分量，有2、4次等谐波分量。此外，基波分量增量最大，且偏心度越高，基波分量幅值越大，进而使得轴向电磁力整体的波动幅值增大，这会增加电机在运行过程中受到的阻力，降低电机的推力性能。
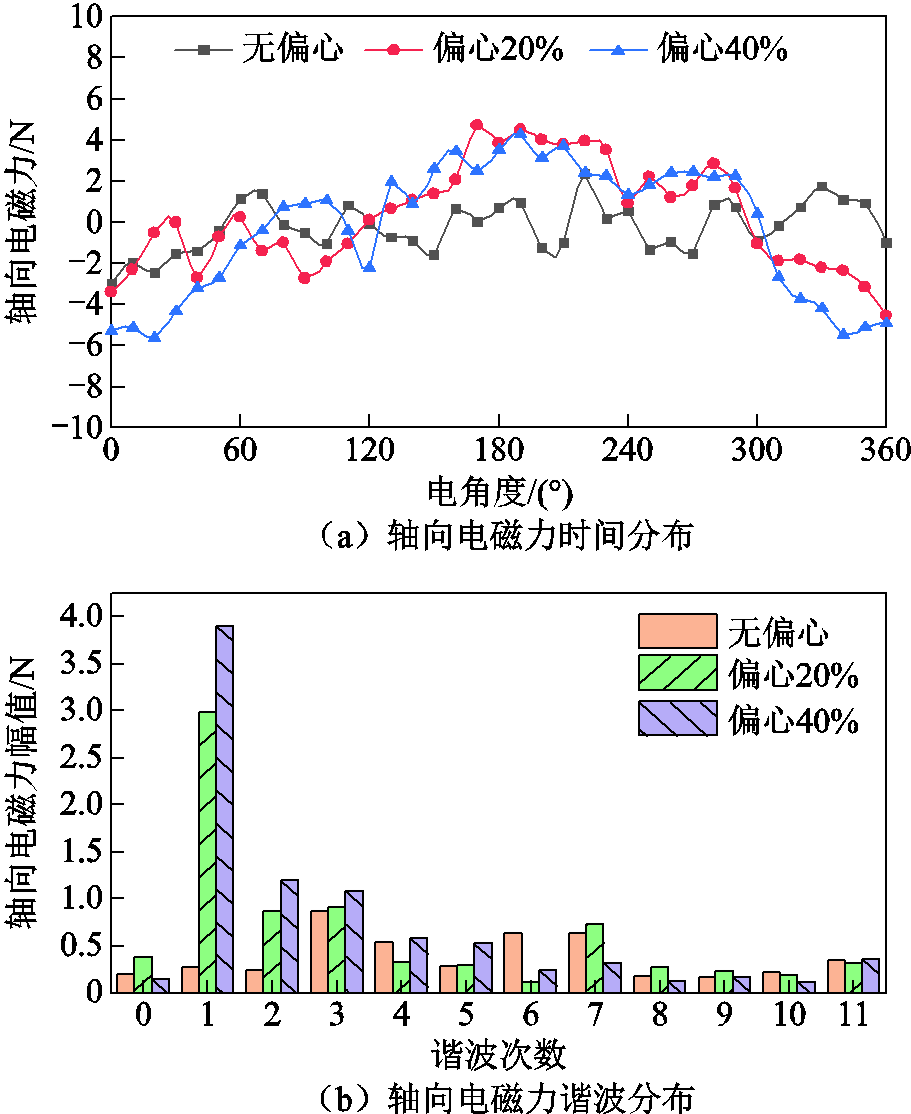
图14 不同偏心度下轴向电磁力波形及其谐波分布
Fig.14 Axial electromagnetic force waveforms and harmonic distribution under different eccentricity
通过对不同偏心度下电机径向磁拉力以及轴向电磁力的对比分析可知：次级发生静偏心故障时，不仅会在径向方向产生较大的单边磁拉力，还会增加电机次级在轴向直线运动过程中的推力波动幅值，从而影响电机的带载能力。
电机在稳定运行的过程中，电磁力波会作为激振力源作用在电机初级齿上，当电磁激振力的频率与电机系统的固有频率相接近且激振力波空间阶数与系统振型相匹配时，就会引起电机系统的共振，危害电机系统的安全。通过对电机进行模态分析，可以方便地求得系统的各阶振型与固有频率，从而在电机设计时就可以避免电机系统在运行过程中可能产生的共振。
TFPMLM的初级结构可以看成由多个单元电机的初级组合而成，其轴向长度对外径之比高达20～50，电磁力波对轴向振动的影响较小，因此本节主要分析径向模态及低阶轴向模态振型。单元电机的初级结构由铁心内嵌永磁体组合而成，铁心可以采用传统铁心叠片轴向叠压方式制成。为简化计算，忽略绕组等对电机初级振动特性影响较小的部件，仅考虑初级铁心与初级永磁体的结构特征，得到简化初级模型如图15所示，材料参数见表2。
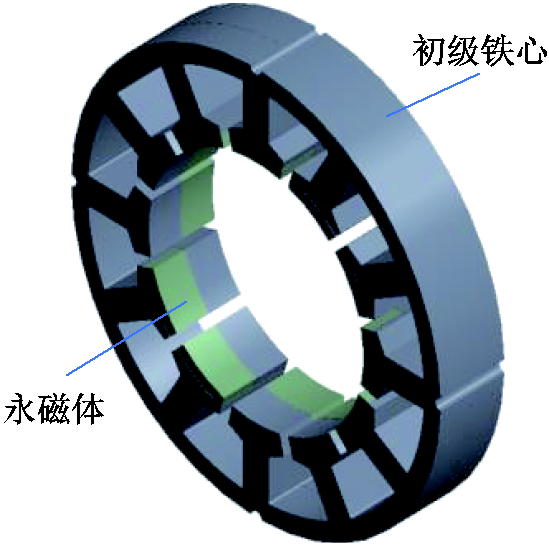
图15 模态分析初级模型
Fig.15 Modal analysis primary model
表2 TFPMLM初级材料属性
Tab.2 The primary material properties of TFPMLM
参数数值（型号） 硅钢片永磁体 型号DW465_50NdFe30 密度/(kg/m3)7 7007 550 杨氏模量/GPa170160 泊松比0.260.24
受油井工作环境的影响，在柱塞泵内的潜油直线电机额定运行频率较低，因此关于潜油直线电机的电磁振动问题，主要关注中低阶模态振型及其固有频率。利用Ansys Workbench平台的模态分析模块，采用模态叠加法计算电机在自由状态下前2～4阶模态振型及其固有频率如图16所示。由前文分析可知，电机初级受到的电磁力波中对电磁振动有影响的主要为低阶低频谐波，其中基频、二倍频谐波幅值最大，若电机次级以最高1 m/s的速度运行，其基频为55.56 Hz，二倍频为111.11 Hz，与各阶电机固有频率相差较大，因此不会产生共振。
图16 初级结构各阶模态
Fig.16 Modes of primary structure
在潜油电泵实际生产过程中，潜油电机往往需要在初级上开槽以固定在套管中，因此在初级开槽处分别设定无约束与固定约束。如图17所示，为电机初级在无约束及固定约束下模态阶数及其固有频率的关系。可见在具有固定约束的实际潜油电泵系统中，电机定子的各阶固有频率均相对较高，而电机次级的工作频率又相对较低，因此对该电机来说，因电磁力产生共振的概率较小。
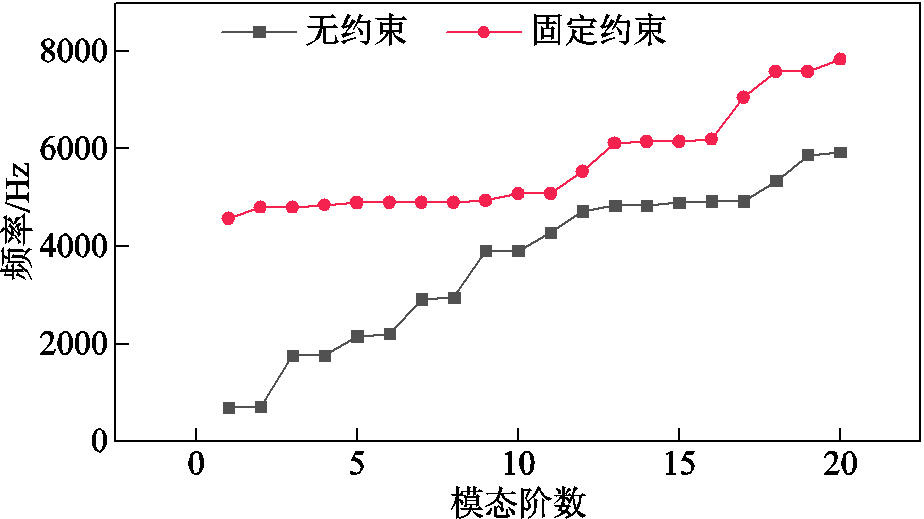
图17 无约束与固定约束状态下前20阶模态的固有频率
Fig.17 The natural frequency of the first 20th order modes under unconstrained and fixed constraints
为了进一步分析电机在运行过程中电磁力对电机振动特性的影响，利用Ansys Workbench平台，将有限元仿真计算得到的初级齿部电磁力作为激励导入谐波响应分析模块中进行磁固耦合分析。为了观测电机的振动特性，需要在初级表面布置振动测量点，本文选择初级齿部及圆周外表面两处作为振动测量面，如图18所示。
在电磁场中计算的电磁力为时域力，需要转换为频谱力作为谐波响应的激励力，在电磁场中有限元分析计算的步长为0.000 5 s，即计算频率为2 kHz，由香农采样定理可知，频率响应的最大分析频率为1 kHz，频率步长为55.56 Hz即为电磁力基频频率。通过全解法可以求解出在无约束状态下，初级齿部及圆周外表面上测量面的振动速度响应频谱图如图19所示。图19a为初级齿部的振动响应，振动速度幅值最大的频率为55.56 Hz，对应的是电磁力的基频频率。随着频率的增大，振动速度幅值逐渐趋于0，其中X轴与Z轴方向振动幅值最大，可见电磁力中的基频分量对初级齿部的振动影响最大，而电磁力的高频分量对振动的影响急剧下降，这一点与传统具有槽极配合的旋转电机差异较大。当电磁力的频率为666 Hz即12倍频时，与初级二阶径向固有模态频率接近，从而引起了较大的径向振动响应，在初级圆周外表面上的振动速度响应如图19b所示。可以看出电磁力对初级外表面的振动响应规律与初级齿面大致相同，区别是电磁力对初级圆周外表面轴向方向的振动响应更大。
图18 振动测量点位置
Fig.18 Vibration measurement point location
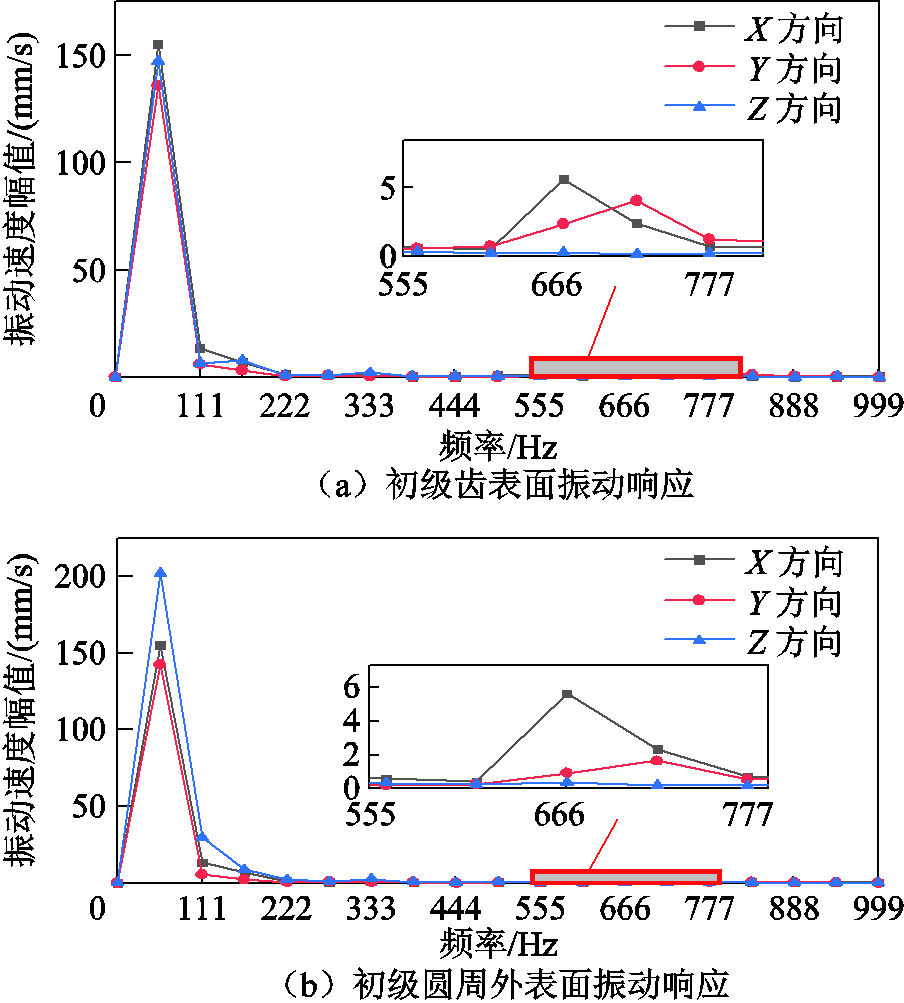
图19 初级齿表面与外表面的电磁振动响应
Fig.19 Electromagnetic vibration response of primary tooth surface and outer surface
考虑次级偏心对各测量面电磁振动的影响，使次级朝X轴负方向的偏心度为40%，在无约束状态下得到初级齿表面与圆周外表面的振动响应如图20所示。从图20a可看出次级偏心使得电磁力基频对应的初级齿部各方向电磁振动响应幅值均有所增加，其中Z方向上的振动响应幅值增加了一倍，而在12倍频电磁力作用下的振动响应幅值略有增加，这是因为次级偏心使得轴向电磁力的基波分量增加所导致的。图20b为初级圆周外表面的振动响应，次级偏心使得电磁力基频对应的初级外表面X、Y方向的电磁振动响应幅值增加，而Z方向的振动幅值基本不变。当频率达到666 Hz附近时，Z方向振动速度幅值增加，响应曲线与X方向响应曲线重合。
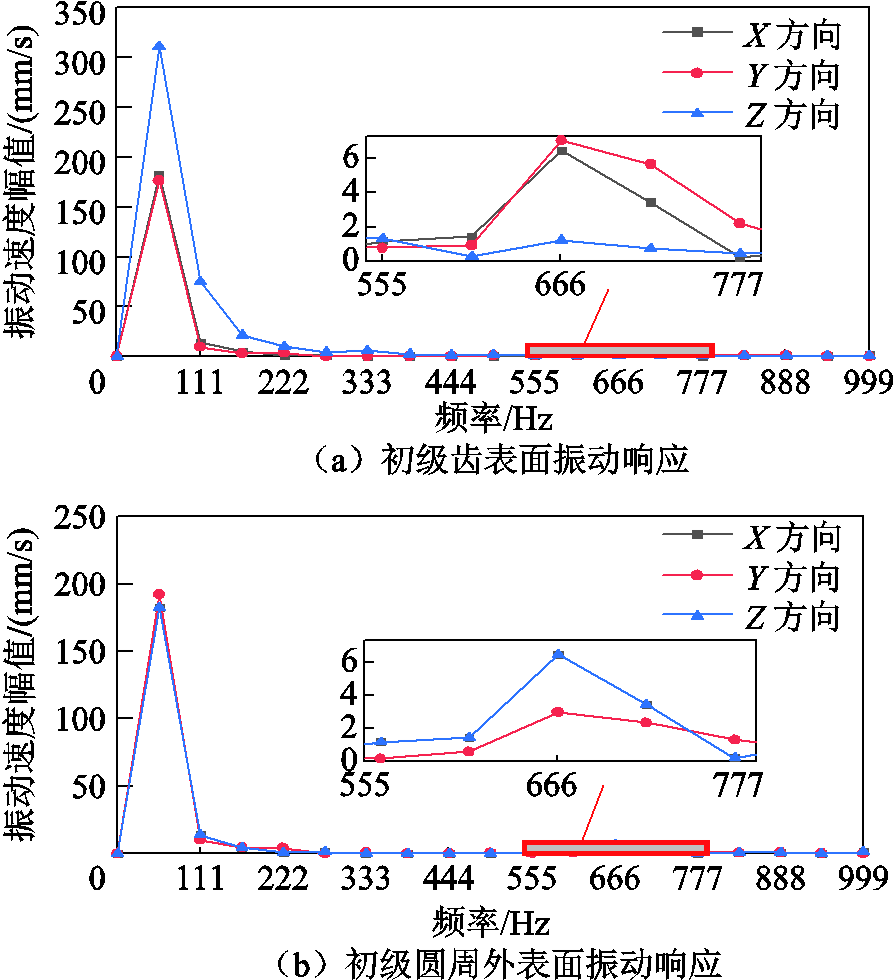
图20 次级偏心度40%时齿面与外表面电磁振动响应
Fig.20 Electromagnetic vibration response of tooth surface and outer surface when secondary eccentricity is 40%
本文对引起TFPMLM电磁振动的源头——径向电磁力波开展了研究。相比于旋转电机，考虑该电机的电磁振动时，必须考虑轴向磁通密度分量。本文运用磁场叠加原理推导了TFPMLM的各向电磁力波解析表达式，分析了径向力波的时空分布特性与频谱特性。考虑到次级偏心对电磁力波分布的影响，分析了偏心所致的不平衡磁拉力的分布特征。最后，使用有限元软件得到电机初级的模态特性，并对初级进行谐响应分析分别得到次级偏心与不偏心状态下测量面的电磁振动响应。研究结果表明，低速运动状态下TFPMLM的电磁力波不会引起初级的共振，且电磁力波的基频对初级齿面与外表面的振动影响最大。
参考文献
[1] 纪树立, 甄东芳, 李志鹏, 等. 海上直线潜油电泵的开发及在渤海油田的应用[J]. 海洋石油, 2019, 39(4): 19-22, 31. Ji Shuli, Zhen Dongfang, Li Zhipeng, et al. Development of offshore submersible electric pump and application in Bohai oilfield[J]. Offshore Oil, 2019, 39(4): 19-22, 31.
[2] 刘永新. 潜油柱塞泵机组优化设计与试验[J]. 石油机械, 2018, 46(6): 75-79. Liu Yongxin. Design optimization and test of submersible plunger pump power package[J]. China Petroleum Machinery, 2018, 46(6): 75-79.
[3] 周封, 杨力源, 刘志刚, 等. 井下直线举升装置中直线电机关键技术研究综述[J]. 微电机, 2015, 48(6): 100-108. Zhou Feng, Yang Liyuan, Liu Zhigang, et al. Overview of linear motor key technology research of underground linear lifting device[J]. Micromotors, 2015, 48(6): 100-108.
[4] 颜建虎, 冯奕. 聚磁式横向磁通永磁盘式风力发电机设计与分析[J]. 中国电机工程学报, 2017, 37(9): 2694-2701. Yan Jianhu, Feng Yi. Design and analysis of a flux-concentrated transverse flux permanent magnet disk wind generator[J]. Proceedings of the CSEE, 2017, 37(9): 2694-2701.
[5] Wang Qian, Zhao Bo, Zhao Hui, et al. Optimal design of tubular transverse flux motors with low cogging forces for direct drive applications[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-5.
[6] Luo Jun, Kou Baoquan, Yang Xiaobao, et al. Development, design, and analysis of a dual-consequent-pole transverse flux linear machine for direct-drive applications[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 6097-6108.
[7] Jia Zhou, Chen Weifeng, Yu Li, et al. A novel transverse-flux PM linear machine with double Ω-hoop stator[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-4.
[8] Hasanien H M, Abd-Rabou A S, Sakr S M. Design optimization of transverse flux linear motor for weight reduction and performance improvement using response surface methodology and genetic algorithms[J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 598-605.
[9] 罗俊, 寇宝泉, 杨小宝. 双交替极横向磁通直线电机的优化与设计[J]. 电工技术学报, 2020, 35(5): 991-1000.Luo Jun, Kou Baoquan, Yang Xiaobao. Optimization and design of dual-consequent-pole transverse flux linear machine[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 991-1000.
[10] 曹卉. 新型潜油式直线抽油机电机的设计及分析[D]. 哈尔滨: 哈尔滨理工大学, 2008.
[11] 时方敏, 张卫, 唐杨. 基于Ansys的永磁同步电机转子振动分析[J]. 电机与控制应用, 2017, 44(5): 116-120. Shi Fangmin, Zhang Wei, Tang Yang. Analysis of vibration for permanent magnet synchronous motor rotor based on ansys[J]. Electric Machines & Control Application, 2017, 44(5): 116-120.
[12] 李德儒. 潜油永磁直线电机单边磁拉力分析与计算[J]. 沈阳工业大学学报, 2017, 39(1): 1-5. Li Deru. Analysis and calculation of unilateral magnetic force in oil-submersible permanent magnet linear motor[J]. Journal of Shenyang University of Technology, 2017, 39(1): 1-5.
[13] 邢泽智, 王秀和, 赵文良, 等. 表贴式永磁同步电机电磁激振力波计算与定子振动特性分析[J]. 中国电机工程学报, 2021, 41(14): 5004-5013. Xing Zezhi, Wang Xiuhe, Zhao Wenliang, et al. Calculation of electromagnetic force waves and analysis of stator vibration characteristics of surface mount permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2021, 41(14): 5004-5013.
[14] Li Jian, Cho Y. Investigation into reduction of vibration and acoustic noise in switched reluctance motors in radial force excitation and frame transfer function aspects[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4664-4667.
[15] 康乐, 夏加宽, 苏航, 等. 表贴式永磁电机各次电流引起径向振动的机理分析及综合抑制策略[J]. 电工技术学报, 2022, 37(18): 4638-4650. Kang Le, Xia Jiakuan, Su Hang, et al. Mechanism analysis and comprehensive suppression strategy of radial vibration induced by each current of surface magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4638-4650.
[16] 洪剑锋, 王善铭, 孙宇光, 等. 高模数电磁力对永磁电机电磁振动影响[J]. 电工技术学报, 2022, 37(10): 2446-2458. Hong Jianfeng, Wang Shanming, Sun Yuguang, et al. The influence of high-order force on electromagnetic vibration of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2446-2458.
[17] 肖阳, 宋金元, 屈仁浩, 等. 变频谐波对电机振动噪声特性的影响规律[J]. 电工技术学报, 2021, 36(12): 2607-2615. Xiao Yang, Song Jinyuan, Qu Renhao, et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2607-2615.
[18] 胡胜龙, 左曙光, 刘明田. 开关磁阻电机非线性径向电磁力解析建模[J]. 电工技术学报, 2020, 35(6): 1189-1197. Hu Shenglong, Zuo Shuguang, Liu Mingtian. Analytical modeling of nonlinear radial electromagnetic force in switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1189-1197.
[19] Sun Tao, Kim J M, Lee G H, et al. Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1038-1041.
[20] 陈益广, 韩柏然, 沈勇环, 等. 永磁同步推进电机电磁振动分析[J]. 电工技术学报, 2017, 32(23): 16-22. Chen Yiguang, Han Boran, Shen Yonghuan, et al. Electromagnetic vibration analysis of permanent magnet synchronous propulsion motor[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 16-22.
[21] 陈明轩, 尹红彬, 高永超, 等. 采用转子开槽的内置永磁电机噪声抑制[J]. 重庆理工大学学报(自然科学), 2022, 36(8): 109-116. Chen Mingxuan, Yin Hongbin, Gao Yongchao, et al. Research on noise reduction for rotor slotting of internal permanent magnet motor[J]. Journal of Chongqing University of Technology (Natural Science), 2022, 36(8): 109-116.
[22] 李岩, 李双鹏, 周吉威, 等. 基于定子齿削角的近极槽永磁同步电机振动噪声削弱方法[J]. 电工技术学报, 2015, 30(6): 45-52. Li Yan, Li Shuangpeng, Zhou Jiwei, et al. Weakening approach of the vibration and noise based on the stator tooth chamfering in PMSM with similar number of poles and slots[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 45-52.
[23] 谢颖, 李飞, 黎志伟, 等. 内置永磁同步电机减振设计与研究[J]. 中国电机工程学报, 2017, 37(18): 5437-5445, 5543. Xie Ying, Li Fei, Li Zhiwei, et al. Optimized design and research of vibration reduction with an interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(18): 5437-5445, 5543.
[24] 王明星, 王爱元, 李轶华. 一种优化齿槽转矩抑制永磁同步电机振动和噪声的方法[J]. 电机与控制应用, 2017, 44(2): 110-114. Wang Mingxing, Wang Aiyuan, Li Yihua. A way of optimizing cogging torque to reduce vibration and noise for permanent magnet synchronous motor[J]. Electric Machines & Control Application, 2017, 44(2): 110-114.
[25] Yoon J Y, Lang J H, Trumper D L. Double-sided linear iron-core fine-tooth motor for low acoustic noise and high acceleration[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(5): 2161-2170.
[26] Yoon J Y, Lang J H, Trumper D L. Fine-tooth iron-core linear synchronous motor for low acoustic noise applications[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9895-9904.
[27] 岳非弘, 李争, 王群京. U型无铁芯直线电机的振动模态计算与分析[J]. 日用电器, 2018(11): 117-122. Yue Feihong, Li Zheng, Wang Qunjing. Vibration mode calculation and analysis of U-type ironless linear motor[J]. Electrical Appliances, 2018(11): 117-122.
Abstract As the only power source of the reciprocating submersible pump system, the operation performance of the submersible linear motor directly affects the operation performance of the whole pump system. Therefore, the selection of linear motor is particularly important. As a special motor with high thrust density, transverse flux permanent magnet linear motor (TFPMLM)benefits from the transverse flux structure, the electrical load and the magnetic load are mutually decouped and each phase is mutually decouped, and the motor is easy to achieve modularization and multiphase, based on the above characteristics, TFPMLM is more suitable for application in the field of oil exploitation.
In the actual process of oil exploitation, the disturbance from the outside of the motor and the vibration of the motor will lead to the reduction of the insulation of the motor and thus reduce the service life of the motor. In order to solve the vibration problem of TFPMLM, the radial electromagnetic force wave of TFPMLM is derived in this paper, and then the eccentricity problem which may occur in the operation of the motor is studied. Finally, the primary mode and electromagnetic vibration characteristics of TFPMLM are analyzed and summarized.
Firstly, the electromagnetic wave of TFPMLM is analyzed, and the expressions of the primary and secondary permeability and magnetomotive force of the motor are obtained by using the principle of magnetic field modulation, and the magnetic density of the air gap is obtained. On this basis, the magnetic density of the synthetic air gap is obtained by considering the role of the armature winding. Maxwell stress tensor method was used to obtain the expressions of electromagnetic force waves acting on the primary teeth in all directions. Then, according to the principle of linear superposition of magnetic density, the air gap magnetic density was decomposed into armature magnetic density, primary permanent magnet magnetic density and secondary permanent magnet magnetic density. By combining the above expressions, the simplified mathematical expression of radial electromagnetic force waves was finally obtained. Then the temporal and spatial characteristics and spectral characteristics of radial electromagnetic waves are simulated and the influence of armature magnetic density on the spectral characteristics of radial electromagnetic waves is obtained.
Secondly, in view of the secondary eccentricity which may be caused by motor vibration, the influence of eccentricity on electromagnetic wave spectrum characteristics is analyzed, and the results show that the secondary eccentricity has greater influence on the 3rd and 6th order harmonics. By comparing the radial magnetic pull and axial electromagnetic force wave of the motor under different eccentricity, it is concluded that when the secondary eccentricity fault occurs, a large unilateral magnetic pull will be generated in the radial direction of the secondary, and the amplitude of thrust fluctuation will increase.
Finally, in order to avoid resonance, the modal analysis and harmonic response analysis of the primary of TFPMLM are carried out. The results of modal analysis show that the motor will not resonate due to electromagnetic force. The results of harmonic response analysis show that compared with the primary teeth, the electromagnetic force wave has a greater impact on the outer surface of the primary circumference.
keywords：Transverse flux permanent magnet linear motor, radial electromagnetic force wave, electromagnetic vibration, eccentricity
DOI:10.19595/j.cnki.1000-6753.tces.221895
中图分类号：TM359.4
国家自然科学基金项目（52177032）、特种电机与高压电器教育部重点实验室项目（沈阳工业大学）（KFKT202107）资助。
收稿日期 2022-10-08
改稿日期 2022-11-28
赵 玫 女，1983年生，博士，副教授，硕士生导师，研究方向为直线电机系统及其控制。E-mail：zhaomei@hit.edu.cn（通信作者）
赵 君 男，1998年生，硕士研究生，研究方向为直线电机一体化设计。E-mail：21S130577@stu.hit.edu.cn
（编辑 赫 蕾）