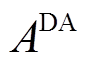 应大于最低限值
应大于最低限值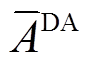 ,其值小于
,其值小于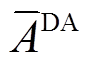 时按照式(1)计算日前考核电量
时按照式(1)计算日前考核电量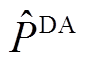 。
。摘要 针对两个细则考核风功率上报准确率的问题,提出一种可有效降低风-储场站风险考核电量的日前-日内两阶段功率优化上报策略。首先,提出面向两个细则的风-储场站日前-日内功率协同上报框架;然后,以期望考核电量最小化为目标,建立计及储能调节的日前-日内两阶段风-储功率优化上报模型,模型中,日前、日内风功率场景集通过基于预测误差分箱的Cornish-Fisher级数与Cholesky分解法生成;最后,针对模型的多重非线性特征与不同时间尺度的求解效率要求,制定基于小步长线性化迭代的求解算法。算例仿真结果表明,相较其余上报策略与求解算法,该文提出的日前-日内协同上报策略及相应算法有效地提升了上报准确率及求解性能。
关键词:两个细则 风功率上报 日前-日内协同优化 时间相关性 储能调节
在构建新型电力系统方针的驱动下,我国风电装机容量与发电量持续增长。2021年,我国风电装机量达3.28亿kW,风力发电量达6 526亿kW·h,较上年同比增长17%与40.5%[1]。大规模风电的间歇性增加了电网对灵活调节资源量的需求,导致电网运维费用提升。自2020年以来,各地能源监管局相继签署印发新的《发电厂并网运行管理实施细则》与《并网发电厂辅助服务管理实施细则》[2-4](下称两个细则),对风电场上报功率预测不准确的部分进行惩罚,将预测偏差引起的费用分摊给风电场。因此合理优化上报功率有助于提高风电场的运行效益。
早期,大多数风电场均直接将预测值上报给调度机构。由于风功率预测误差概率分布具有显著的“偏轴”特性[5],直接上报预测值难以取得期望最优效益。近十年来,计及不确定性的风功率上报策略研究逐渐开展起来。文献[6-7]分别利用场景抽样与分位数回归描述风功率不确定性,其仿真结果表明预测误差惩罚有助于提高上报的精度。文献[8]研究了预测误差服从不同分布时风电场面向自动发电控制补偿的功率上报策略。文献[9]基于贝塔分布构建了风电场参与备用辅助服务市场的随机功率上报模型。与文献[6-9]采用的随机优化策略不同,文献[10]利用鲁棒模型优化最坏预测情况的风功率申报策略。同时,部分研究已表明在新能源场站配置储能可以提升其不同时间尺度的整体运行效益[11-14];文献[15-17]则分别从风-储场站售电、市场竞价与辅助调频的角度优化了储能充放,论证了合理调节储能充放可以进一步优化风电出力计划。
现有风/风-储场站功率上报研究主要有以下局限性:
1)优化上报的时间尺度单一,缺乏对两个细则考核机制的针对性。一方面,绝大多数风功率上报策略局限于日前尺度[6-10,15-17],关于日内风功率优化上报的研究罕见报道。然而现行的两个细则在日前与日内两种尺度均对风功率提出考核要求。同时,部分研究在电网层面的风-储联合调度中论证了多时间尺度协同调度的可行性及其相较单时间尺度独立调度的优势[18-21],这也为本文日前-日内协同上报提供了依据。另一方面,现有功率上报模型主要以市场化电价[6-7]、辅助服务补偿[8-9,17]与售电收益[10,15-16]为优化目标,不同于两个细则中基于考核电量的形式,难以直接应用。
2)风功率随机性建模较为粗糙。一方面,大多数功率上报研究将所有样本作为一个整体参与随机建模[6-10,16],难以满足不同条件下误差特性的表征需求。另一方面,风功率与预测误差序列内在的时间相关性也尚未在上述功率上报研究中予以考虑。同时,已有研究从概率预测角度成功地探索了以气象序列为条件进行误差分箱的可行性[22-23],以及考虑误差时间相关性对风电场随机优化的积极作用[24],这也为本文研究提供了新思路。
针对已有风功率上报研究的不足,本文提出面向两个细则考核的日前-日内两阶段风-储功率优化上报策略。首先针对两个细则的电量考核形式,基于随机场景,以期望考核电量最小为优化目标,构建日前-日内两阶段风-储功率优化上报模型。其中,计及误差时间相关性的日前、日内风功率场景集通过基于预测误差分箱的Cornish-Fisher级数与Cholesky分解进行场景抽样与重排序后得到。进一步地,针对模型的多重非线性特征,设计了基于改进秃鹰搜索(Improved Bald Eagle Search, IBES)与小步长线性化迭代算法的求解方法。算例仿真首先从场景生成角度论证了考虑误差样本相关性的必要性;进而分析典型日与月度考核的结果,以体现本文所提功率上报策略相较预测值上报与单时间尺度优化上报的经济性;最后依据多个指标评析不同求解算法及储能优化方案,作为本文上报模型及算法优越性的补充。
我国大部分地区现行两个细则[2-4]中有关风功率上报的考核方法可总结如下:
1)日前考核。日前阶段,风电场需要上报次日共计T=96个时刻的功率。日前准确率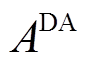 应大于最低限值
应大于最低限值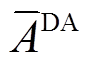 ,其值小于
,其值小于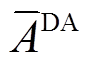 时按照式(1)计算日前考核电量
时按照式(1)计算日前考核电量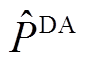 。
。
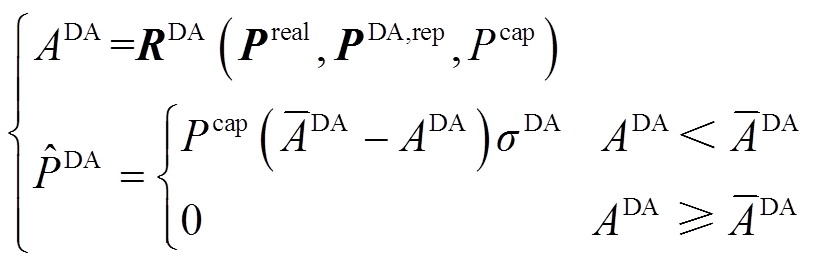 (1)
(1)
式中,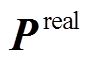 、
、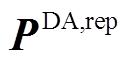 分别为实际与日前上报的风功率向量;
分别为实际与日前上报的风功率向量;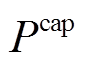 为风电场装机容量;
为风电场装机容量;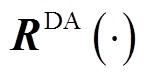 为日前准确率计算多项式;
为日前准确率计算多项式;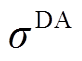 为日前考核电量系数。
为日前考核电量系数。
2)日内考核。日内阶段,风电场需要每15 min上报未来4 h共计S=16个时刻的功率,并依据每15 min上报的功率计算日内准确率。日内准确率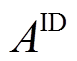 应大于最低限值
应大于最低限值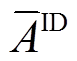 ,其值小于
,其值小于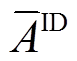 时按照式(2)计算日内考核电量
时按照式(2)计算日内考核电量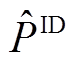 。
。
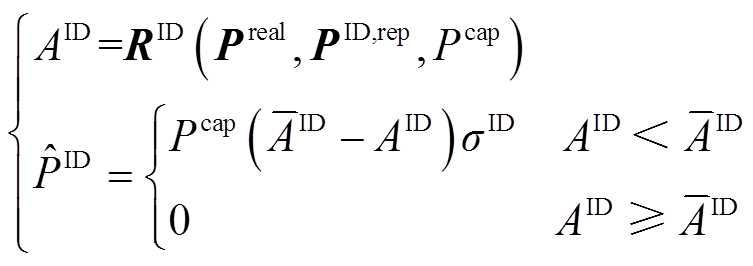 (2)
(2)
式中,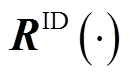 为日内准确率计算多项式;
为日内准确率计算多项式;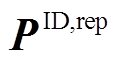 为日内上报风功率向量;
为日内上报风功率向量;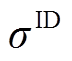 为日内考核电量系数。
为日内考核电量系数。
在以售电收益与辅助服务为驱动的传统风功率上报策略中[6-10,15-17],在满足风电场自身可用容量约束等前提下,风电场预测精度越高则收益越大。因此在上述研究中,将预测误差分布与预测功率叠加得到的“调度期望值”进行上报,即可实现良好的经济效益。然而,式(1)、式(2)所示的两个细则考核机制允许一定量的上报偏差,即考核时段的上报准确率低于限值时进行惩罚,达到或高于该限值时不惩罚。考核目标在限值处的非连续变化为风功率上报结果设置了独特的偏好,而上述上报调度期望值的策略中并未考虑,故难以照搬应用至现行两个细则的考核中。因此,在计及风电不确定性的基础上构建以式(1)、式(2)为优化目标的日前-日内优化上报模型具有现实意义。
另一方面,在风电场配置储能后,风-储场站的实际并网功率值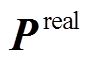 可调。因此在日内尺度下,如何依据日内滚动预测信息与既定的日前上报结果调节储能,以同时提升日前、日内上报准确率,将是日前-日内协同的关键。面向上述考核机制,本文提出的风-储场站两阶段功率上报策略框架如图1所示。
可调。因此在日内尺度下,如何依据日内滚动预测信息与既定的日前上报结果调节储能,以同时提升日前、日内上报准确率,将是日前-日内协同的关键。面向上述考核机制,本文提出的风-储场站两阶段功率上报策略框架如图1所示。
日前、日内上报功率分别通过求解日前与日内上报模型获取。其中,日前上报模型提前一天优化,以日前考核电量最小化为目标;日内上报模型每15 min滚动优化,以日前-日内总考核电量最小化为目标。同时,日前上报结果作为日内上报模型的输入参数参与日内优化以确定储能充放安排,实现日前-日内上报的协同。构造上报模型的日前、日内风功率场景通过第3节计及时间相关性的方法生成。
针对两个细则考核机制,该框架紧密结合了不同时间尺度的风功率上报。日前模型充分挖掘了误差的时间相关性,日内模型引入既定的日前上报结果,通过储能协调实际功率与上报功率,得到期望最优的日前-日内功率优化上报结果。值得说明的是,本文后续内容虽以华中地区两个细则为例构建模型并设置算例,但该框架适用于所有地区的考核机制,相应模型与算法经适当调整后可推广应用。
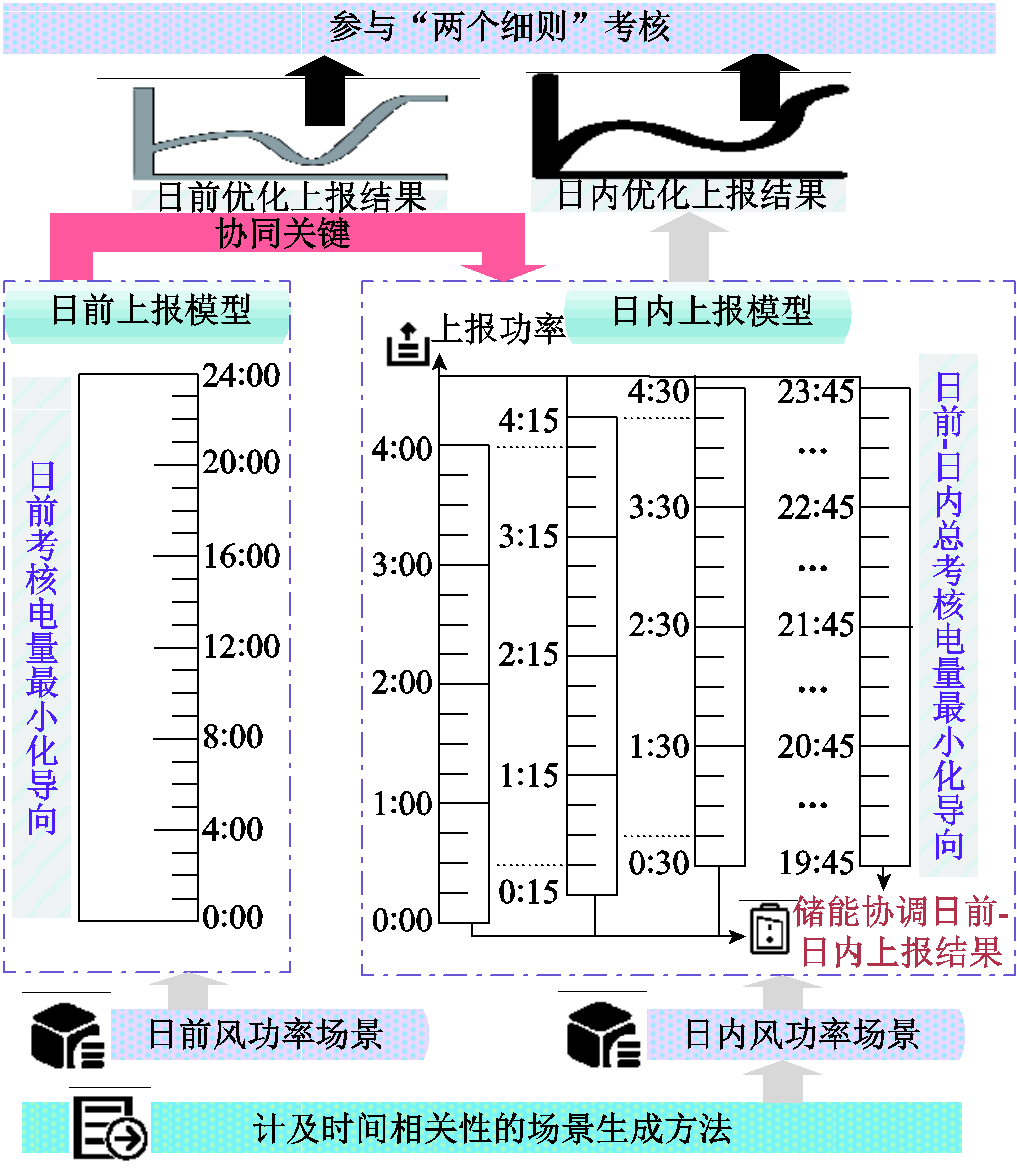
图1 风-储场站两阶段功率上报策略框架
Fig.1 Framework of the two-stage power reporting strategy for wind-storage stations
本节以华中地区两个细则[2]为例构建日前-日内两阶段风功率上报模型。其中,准确率限值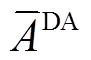 与
与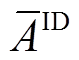 分别为80%与85%,考核电量系数
分别为80%与85%,考核电量系数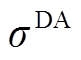 与
与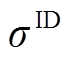 均为1 h。日内阶段仅考核各预测时段第4 h的上报功率(即参与日内准确率计算)。
均为1 h。日内阶段仅考核各预测时段第4 h的上报功率(即参与日内准确率计算)。
日前上报模型以各场景下考核电量期望值最小化为目标,即
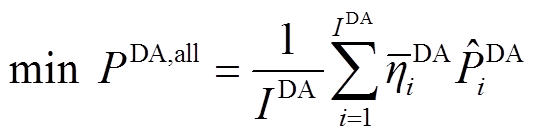 (3)
(3)
式中,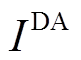 为日前风功率总场景数,i=1,2,…,
为日前风功率总场景数,i=1,2,…,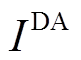 ;
; 为日前总期望考核电量;
为日前总期望考核电量; 为第i个场景的日前考核电量;
为第i个场景的日前考核电量;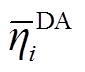 为日前第i个场景发生概率的权重系数。日前上报功率上、下限约束如式(4)所示,考核电量计算约束如式(5)、式(6)所示。
为日前第i个场景发生概率的权重系数。日前上报功率上、下限约束如式(4)所示,考核电量计算约束如式(5)、式(6)所示。
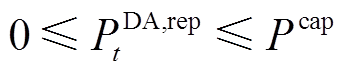 (4)
(4)
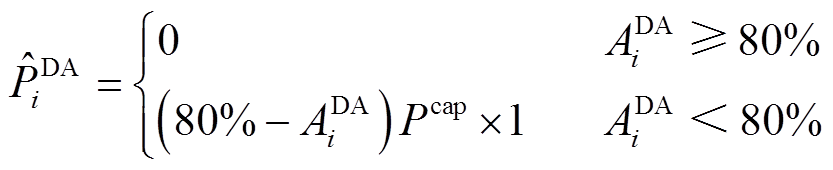 (5)
(5)
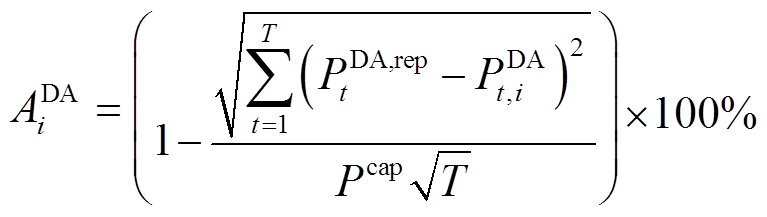 (6)
(6)
式中,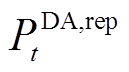 为t时刻风电场日前上报功率;
为t时刻风电场日前上报功率;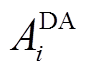 为第i个场景的日前准确率;
为第i个场景的日前准确率;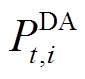 为日前t时刻第i个场景的风功率。该模型的待优化变量集
为日前t时刻第i个场景的风功率。该模型的待优化变量集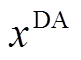 包括日前上报功率
包括日前上报功率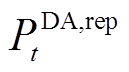 ,即
,即
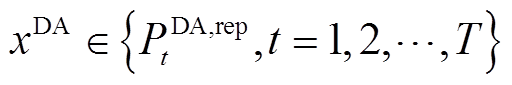 (7)
(7)
日内风功率优化上报示意图如图2所示。当处在日内t时刻上报未来4 h共S=16步的风功率时,日内准确率计算将采用第t+16时刻的上报功率,而亟待制定的实际功率调节量为第t+1时刻的储能充放功率,二者存在时间差。因此,当日内t时刻所在的时段不同,日内上报模型所包含的目标函数与决策变量将有所差别,具体如下。
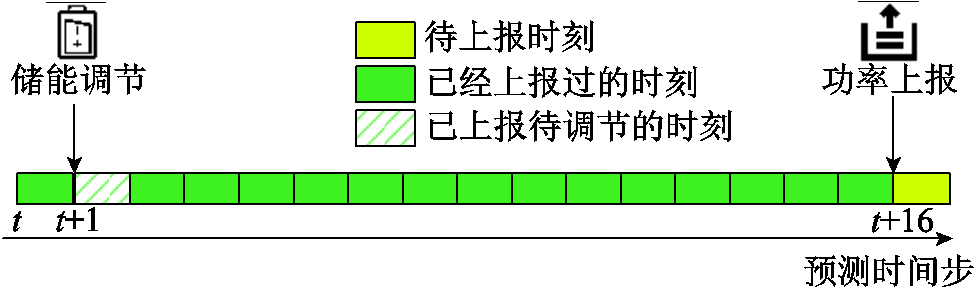
图2 日内风功率优化上报示意图
Fig.2 Schematic diagram of intra-day optimized wind power reporting
1)t+16≥1 & t+1<1时段。该时段为每日日内滚动上报的起始阶段,风功率上报已经开始,但当日该时段尚未引入储能(储能调节对应的t+1时刻位于上一日),故只需考虑第t+16时刻的风功率上报。其优化目标为日内期望考核电量的最小化,如式(8)所示;考核电量与准确率计算如式(9)、式(10)所示;日内上报功率上下限约束如式(11)所示;日内决策变量集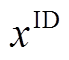 包括日内上报功率,如式(12)所示。
包括日内上报功率,如式(12)所示。
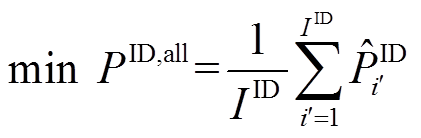 (8)
(8)
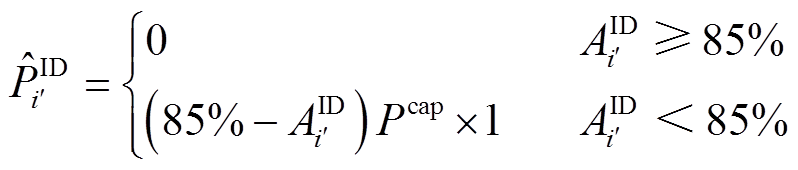 (9)
(9)
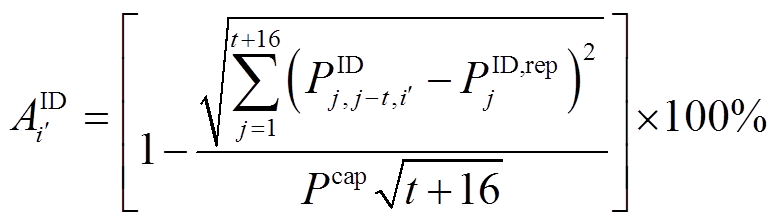 (10)
(10)
 (11)
(11)
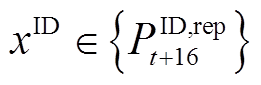 (12)
(12)
式中,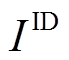 为日内风功率总场景数,
为日内风功率总场景数,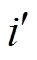 =1,2,…,
=1,2,…,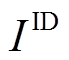 ;
;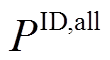 为日内总期望考核电量;
为日内总期望考核电量;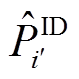 为第
为第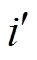 个场景的日内考核电量;
个场景的日内考核电量;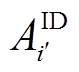 为第
为第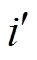 个场景的日内准确率;
个场景的日内准确率;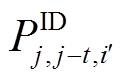 为日内j时刻第j-t步预测下第
为日内j时刻第j-t步预测下第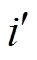 个场景的风功率;
个场景的风功率;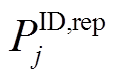 为日内第j时刻的上报功率。
为日内第j时刻的上报功率。
2)t+1≥1 & t+16<T时段。该时段功率上报与储能调节同时进行。此时,引入日前优化上报结果以优化储能充放量,实现式(13)所示的日前、日内总期望考核电量最小化。
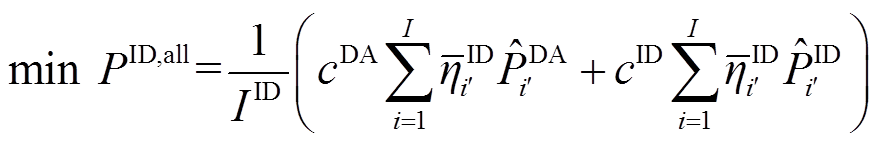 (13)
(13)
式中,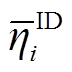 为日内第
为日内第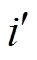 个场景发生概率的权重系数;
个场景发生概率的权重系数;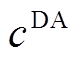 与
与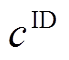 分别为日前、日内考核电量的惩罚系数。储能相关约束为
分别为日前、日内考核电量的惩罚系数。储能相关约束为
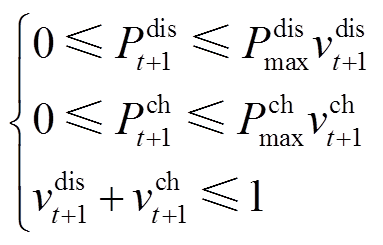 (14)
(14)
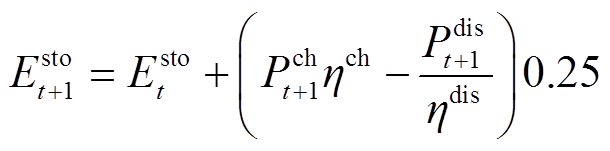 (15)
(15)
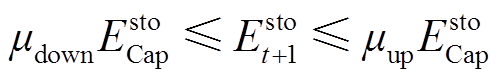 (16)
(16)
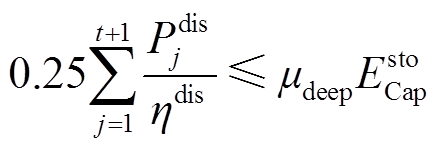 (17)
(17)
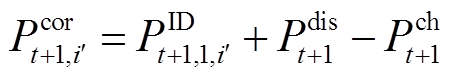 (18)
(18)
式中,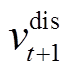 、
、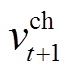 分别为t+1时刻储能放电、充电状态二进制变量;
分别为t+1时刻储能放电、充电状态二进制变量;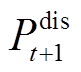 、
、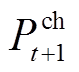 分别为t+1时刻储能放电、充电功率;
分别为t+1时刻储能放电、充电功率;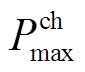 、
、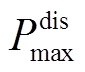 分别为储能最大充放功率;
分别为储能最大充放功率;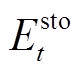 为t时刻的储能能量;
为t时刻的储能能量;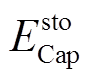 为储能总能量;
为储能总能量;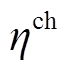 、
、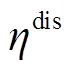 为充电、放电效率;
为充电、放电效率;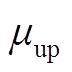 、
、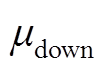 分别为储能能量的上、下限系数;
分别为储能能量的上、下限系数;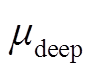 为放电深度系数;
为放电深度系数;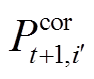 为t+1时刻第
为t+1时刻第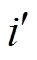 个风功率场景叠加储能充放量后的风-储功率。式(14)~式(16)为基本的储能充放约束。考虑到放电深度对储能寿命的影响,故安排所有时段总放电功率不超过一定的限值,如式(17)所示。
个风功率场景叠加储能充放量后的风-储功率。式(14)~式(16)为基本的储能充放约束。考虑到放电深度对储能寿命的影响,故安排所有时段总放电功率不超过一定的限值,如式(17)所示。
日前、日内准确率计算如式(19)、式(20)所示,其中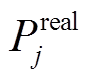 为第j时刻风-储功率实际值。日内各场景对应日前、日内考核电量的计算分别见式(21)与式(9)。由于式(18)将待优化的储能充放量与
为第j时刻风-储功率实际值。日内各场景对应日前、日内考核电量的计算分别见式(21)与式(9)。由于式(18)将待优化的储能充放量与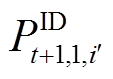 叠加,使得日内各场景风-储功率
叠加,使得日内各场景风-储功率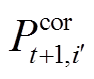 可调,故式(19)需要协调
可调,故式(19)需要协调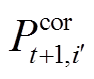 与相应时刻既定的日前上报功率
与相应时刻既定的日前上报功率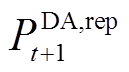 以计算各场景的日前准确率
以计算各场景的日前准确率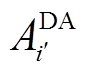 ,从而实现式(13)中日前期望考核电量的优化,并确定储能的功率调节量。
,从而实现式(13)中日前期望考核电量的优化,并确定储能的功率调节量。
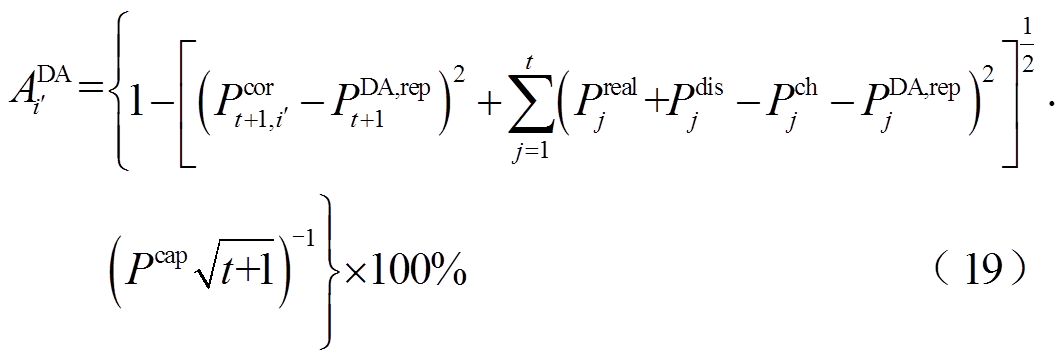
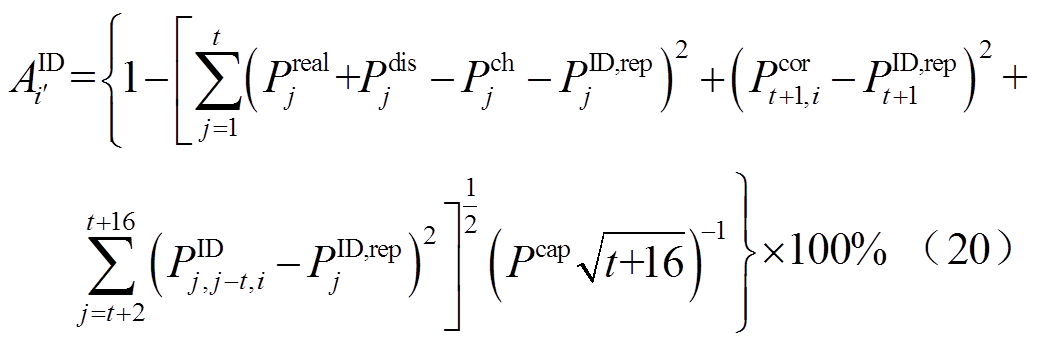
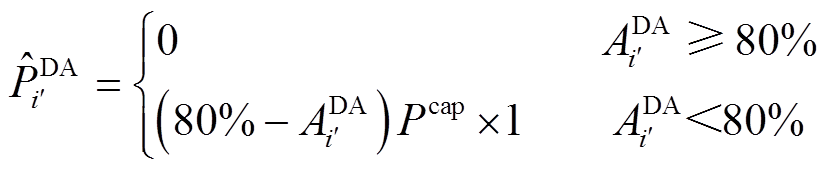 (21)
(21)
另外,考虑到日内0时起至第t+16时刻(待上报时刻)所有时段的误差信息,该时段准确率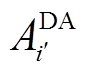 与
与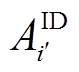 的计算分别与式(6)及式(10)有所不同。
的计算分别与式(6)及式(10)有所不同。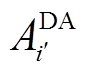 计算日内0:00起至t时刻实际功率与日前上报功率的误差,以及t+1时刻各场景叠加储能充放功率后风-储功率与既定日前上报功率的误差。
计算日内0:00起至t时刻实际功率与日前上报功率的误差,以及t+1时刻各场景叠加储能充放功率后风-储功率与既定日前上报功率的误差。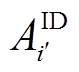 的计算分为三部分:①计算0:00起至t时刻实际功率与日内上报功率的误差;②计算t+1时刻各场景计及储能调节后的风-储功率与相应日内上报功率的误差;③计算t+2时刻至t+16时刻日内各场景预测功率与上报功率的误差。
的计算分为三部分:①计算0:00起至t时刻实际功率与日内上报功率的误差;②计算t+1时刻各场景计及储能调节后的风-储功率与相应日内上报功率的误差;③计算t+2时刻至t+16时刻日内各场景预测功率与上报功率的误差。
该时段的决策变量集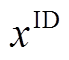 包括第t+16时刻的日内上报功率以及第t+1时刻储能调节量与荷电状态,有
包括第t+16时刻的日内上报功率以及第t+1时刻储能调节量与荷电状态,有
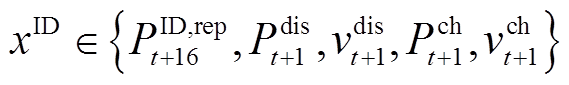 (22)
(22)
3)t+16>T & t+1≤T时段。该时段日内功率上报已经结束(第t+16时段位于次日),但储能调节仍在进行。因此,该时段优化目标与式(13)相同,储能约束与式(14)~式(18)保持一致,日前准确率计算见式(19),日前、日内考核电量计算见式(21)与式(9)。
该时段日内准确率计算与决策变量集如式(23)、式(24)所示。由于该时段不包含功率上报的决策变量,式(23)与式(21)的唯一区别在于最后一部分有关待预测时刻的准确率计算均为常数。
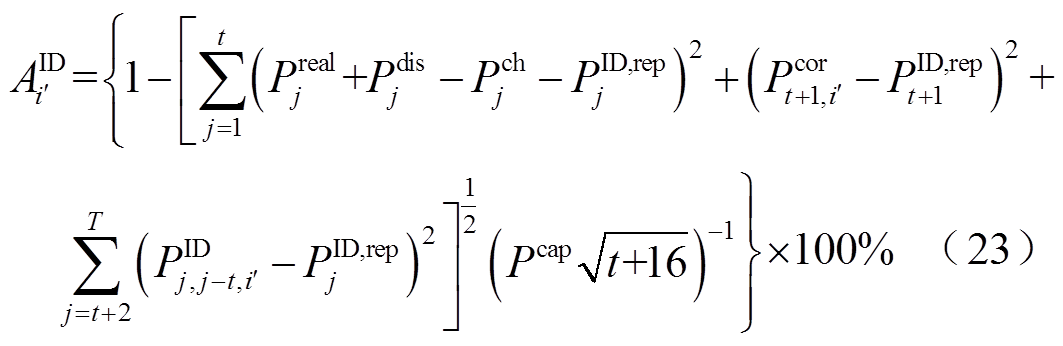
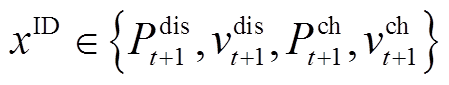 (24)
(24)
对于每个上报日,日内模型从第t+16时刻对应0:00开始每15 min滚动优化,直至第t+1时刻对应23:45时截止。每一时段日内模型求解结束后,记录优化上报功率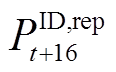 、储能功率
、储能功率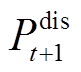 与
与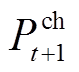 及储能剩余能量
及储能剩余能量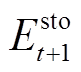 ,以供后续时刻的滚动计算使用。
,以供后续时刻的滚动计算使用。
统计日前、日内历史预测误差样本。考虑到气象动态过程与风功率不确定性的内在耦合,利用文献[22]中分布函数差异化导向的改进K-means算法进行以气象指标及其一阶变化量为条件的日前预测误差分箱,详见附录。对于日内预测误差,随着预测时间步的增加,预测时刻离当前时刻的跨度越大,预测误差越大。因此统计日内同一预测时间步的所有预测误差数据并划分为一个箱,共计16个箱。
误差分箱后,采用含五阶累积量的Cornish-Fisher级数[23]建立日前、日内各预测误差箱的累积概率函数(Cumulative Density Function, CDF),有
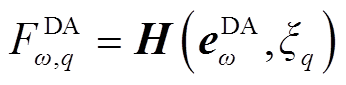 (25)
(25)
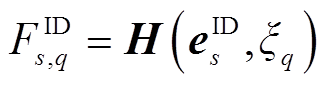 (26)
(26)
式中,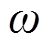 、s分别为日前、日内误差箱索引编号;
、s分别为日前、日内误差箱索引编号;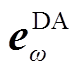 、
、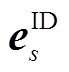 分别为日前第
分别为日前第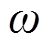 个误差箱、日内第s个误差箱的预测误差样本;
个误差箱、日内第s个误差箱的预测误差样本;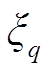 为标准正态分布对应概率q的分位点;
为标准正态分布对应概率q的分位点;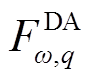 和
和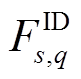 分别为日前第
分别为日前第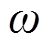 个误差箱、日内第
个误差箱、日内第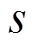 个误差箱中误差CDF对应概率q的分位点;
个误差箱中误差CDF对应概率q的分位点;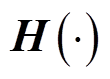 为Cornish-Fisher级数多项式,其以误差样本与标准正态分布的分位点作为输入,输出相应的误差CDF分位点。Cornish-Fisher级数能较为准确地拟合呈“偏轴”特征的概率分布,且直接对误差CDF进行计算,相较于核密度估计等方法省略了对CDF求逆从而间接获得分位点的步骤,因此相对更吻合本文研究,详见附录式(A3)~式(A8)。
为Cornish-Fisher级数多项式,其以误差样本与标准正态分布的分位点作为输入,输出相应的误差CDF分位点。Cornish-Fisher级数能较为准确地拟合呈“偏轴”特征的概率分布,且直接对误差CDF进行计算,相较于核密度估计等方法省略了对CDF求逆从而间接获得分位点的步骤,因此相对更吻合本文研究,详见附录式(A3)~式(A8)。
进一步地,利用拉丁超立方抽样(Latin Hypercube Sampling, LHS)[23]对各日前、日内预测误差箱的CDF分位点进行等概率间隔采样,分别得到包含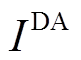 与
与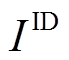 个分位点的误差向量,等价于令
个分位点的误差向量,等价于令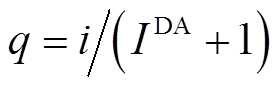 代入式(25)、
代入式(25)、 代入式(26)进行计算得到相应的
代入式(26)进行计算得到相应的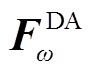 与
与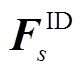 。进一步地,按以下步骤实现计及误差相关性的日前、日内风功率场景生成。
。进一步地,按以下步骤实现计及误差相关性的日前、日内风功率场景生成。
1)日前阶段。获取气象数据后,依据日前误差分箱结果及基于支持向量机的误差箱匹配方法[22]获取T=96个预测时段归属的误差箱,利用相应的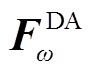 组成初步的日前预测误差场景集
组成初步的日前预测误差场景集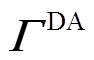 。
。
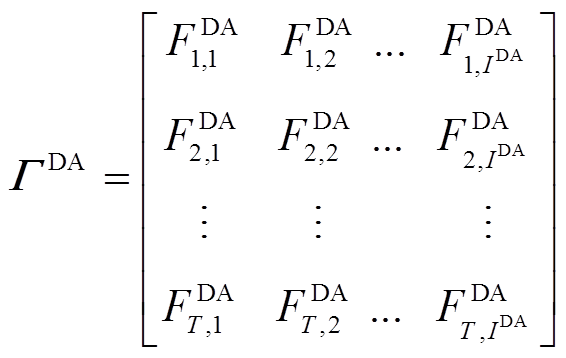 (27)
(27)
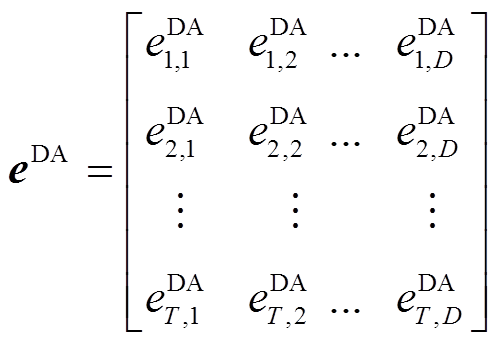 (28)
(28)
式(28)展示了原始日前预测误差样本的形式,其中D代表样本包括的历史天数。考虑到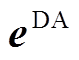 各行之间具有特定的时间相关性,而经过LHS得到的
各行之间具有特定的时间相关性,而经过LHS得到的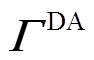 仅按照概率值大小进行排列,故利用Cholesky分解[24],以
仅按照概率值大小进行排列,故利用Cholesky分解[24],以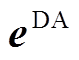 的时间相关性为基准进行
的时间相关性为基准进行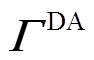 各行元素的重排序,得到近似
各行元素的重排序,得到近似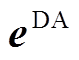 时间相关性的日前预测误差场景集
时间相关性的日前预测误差场景集 。
。
2)日内阶段。拼接各预测时间步下的场景集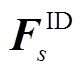 得到日内预测误差场景矩阵
得到日内预测误差场景矩阵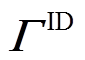 ,如式(29)所示。同时,按照式(30)整理日内预测误差样本。与日前阶段类似,以
,如式(29)所示。同时,按照式(30)整理日内预测误差样本。与日前阶段类似,以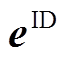 各行(预测时间步)之间的相关性为基准进行
各行(预测时间步)之间的相关性为基准进行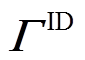 各行元素的重排序,得到最终的日内预测误差场景集
各行元素的重排序,得到最终的日内预测误差场景集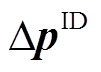 。
。
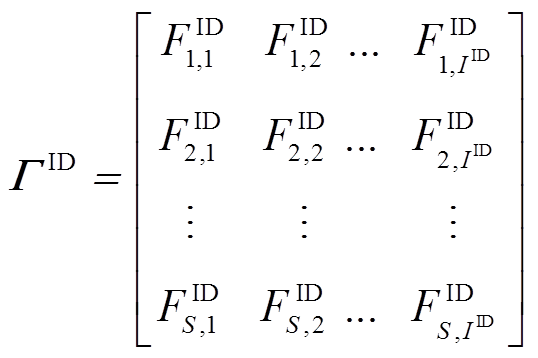 (29)
(29)
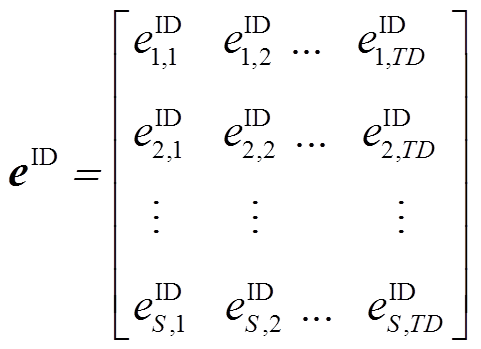 (30)
(30)
分别将 、
、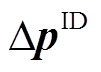 与已知的日前、日内风功率预测值叠加,得到对应的风功率场景集为
与已知的日前、日内风功率预测值叠加,得到对应的风功率场景集为
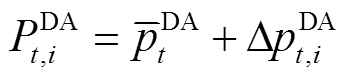 (31)
(31)
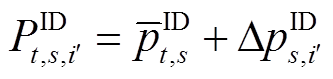 (32)
(32)
式中,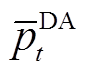 为日前t时刻的风功率预测值;
为日前t时刻的风功率预测值;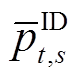 为日内t时刻第s步的风功率预测值。将
为日内t时刻第s步的风功率预测值。将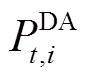 代入式(6),
代入式(6),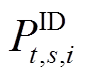 代入式(10)、式(20)、式(23)即可完善基于场景法的日前-日内两阶段功率优化上报模型。
代入式(10)、式(20)、式(23)即可完善基于场景法的日前-日内两阶段功率优化上报模型。
第2节中日前、日内上报模型均为包含逻辑约束与根式约束的非线性优化问题,难以直接采用商业求解器求解。因此,本节提出契合优化模型的两阶段求解方法。
1)日前阶段。考虑到式(3)~式(7)所示的日前上报模型问题规模较小,故采用具有较强全局搜索能力的IBES算法[23]进行求解,详见附录。
2)日内阶段。与日前阶段不同,日内每15 min须进行一次上报。一方面,考虑到日内包含储能决策变量及耦合性质更复杂的风功率场景约束,仿照日前模型采用IBES算法或其他智能算法进行求解无法同时兼顾求解速率与质量。另一方面,模型的非线性部分仅存在于考核电量与准确率的计算中。因此,可以通过恰当的重构方法将该非线性模型的求解转换为多个线性模型的求解。
首先,利用Big-M法[25]将式(21)与式(9)所示的逻辑约束分别转换为混合整数线性约束,有
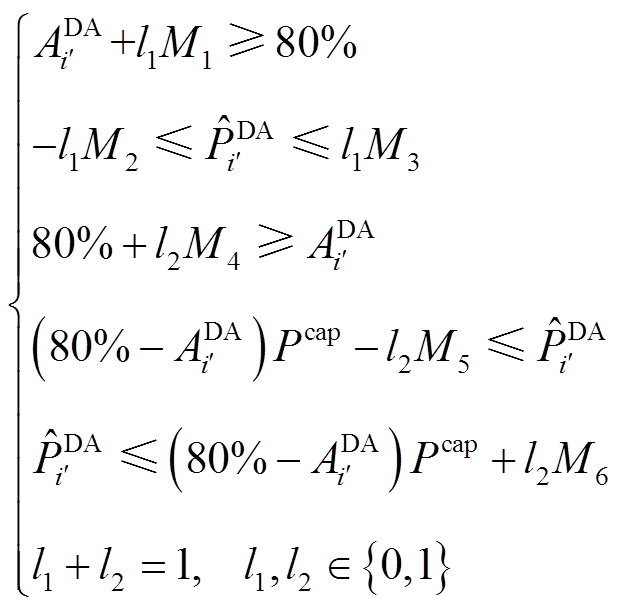 (33)
(33)
 (34)
(34)
式中,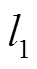 ~
~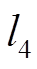 为0/1变量;
为0/1变量;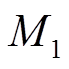 ~
~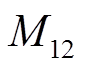 为较大的数。进一步地,提出小步长线性化迭代算法,详细如下。
为较大的数。进一步地,提出小步长线性化迭代算法,详细如下。
由于绝对值形式的准确率在很大程度上与方均根准确率呈正相关关系,且便于模型的线性化,故首先将式(10)、式(19)、式(20)、式(23)替换为绝对值形式(对应附录式(A9)~式(A12))代入日内模型进行求解。求解结束后,将与准确率计算相关的优化结果作为后续线性化迭代的初始点,记为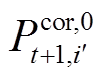 、
、 。另一方面,式(10)、式(19)、式(20)、式(23)所示的准确率计算可总结为以
。另一方面,式(10)、式(19)、式(20)、式(23)所示的准确率计算可总结为以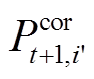 、
、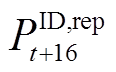 为变量的多项式,有
为变量的多项式,有
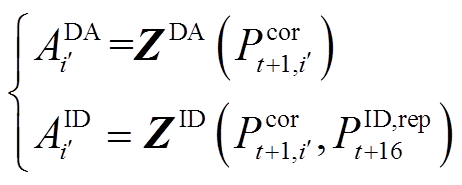 (35)
(35)
式中,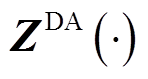 、
、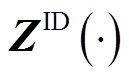 分别为日前、日内准确率计算的多项式。在每个时段的优化模型中增加小步长约束式(36),并以
分别为日前、日内准确率计算的多项式。在每个时段的优化模型中增加小步长约束式(36),并以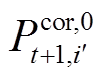 、
、 为中心对式(35)做一阶泰勒展开,得到线性化后的方均根准确率约束,如式(37)~式(38)所示。
为中心对式(35)做一阶泰勒展开,得到线性化后的方均根准确率约束,如式(37)~式(38)所示。
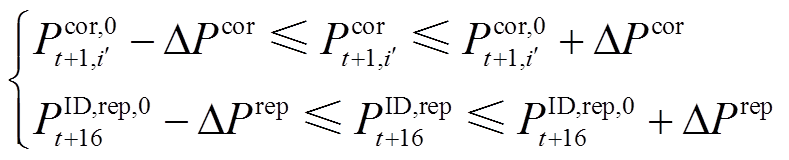 (36)
(36)
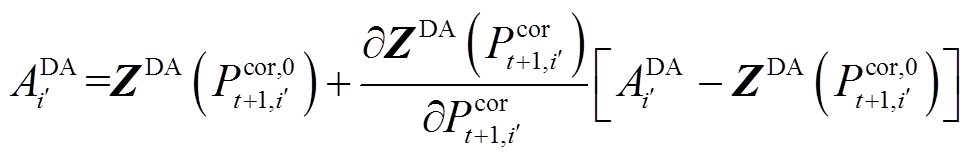 (37)
(37)
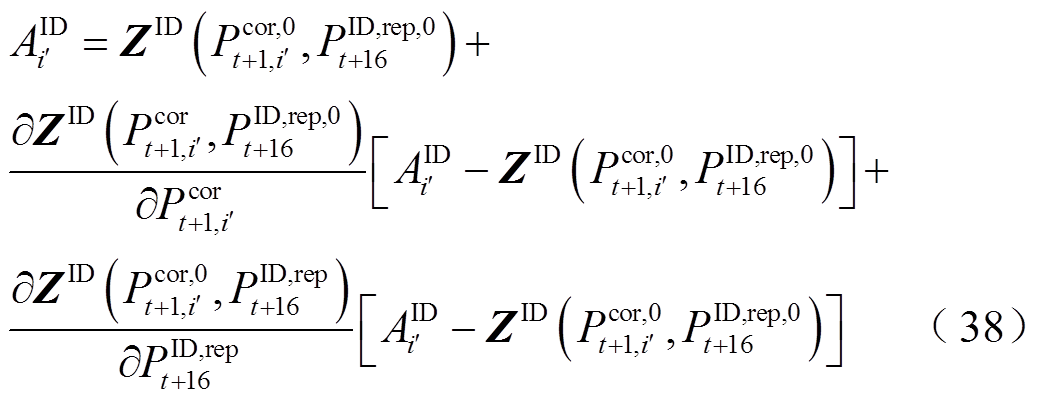
将式(37)替代式(19),式(38)替代式(10)、式(20)、式(23)构成线性化日内上报模型,并将优化结果作为新的初始点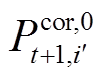 、
、 ,重复上述线性化迭代求解过程。迭代过程将在两种情况下终止:①达到迭代次数上限
,重复上述线性化迭代求解过程。迭代过程将在两种情况下终止:①达到迭代次数上限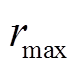 ;②前后两次迭代目标函数变化的绝对值小于阈值
;②前后两次迭代目标函数变化的绝对值小于阈值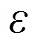 。
。
综上所述,本文提出的模型求解流程如图3所示。在进行两阶段上报之前,首先通过第3节的场景生成方法为上报模型提供支撑。到达日前阶段后进行日前上报模型的求解,得到日前上报结果以供日内上报模型构造准确率约束,实现日前-日内协同;到达日内阶段后,按照当前所在时段匹配并求解相应的日内上报模型,得到日内上报结果与储能充放安排。其中,基于IBES算法与小步长线性化迭代算法的两阶段模型求解方法大大降低了原上报模型的复杂度,同时兼顾了求解效率与优化效果。
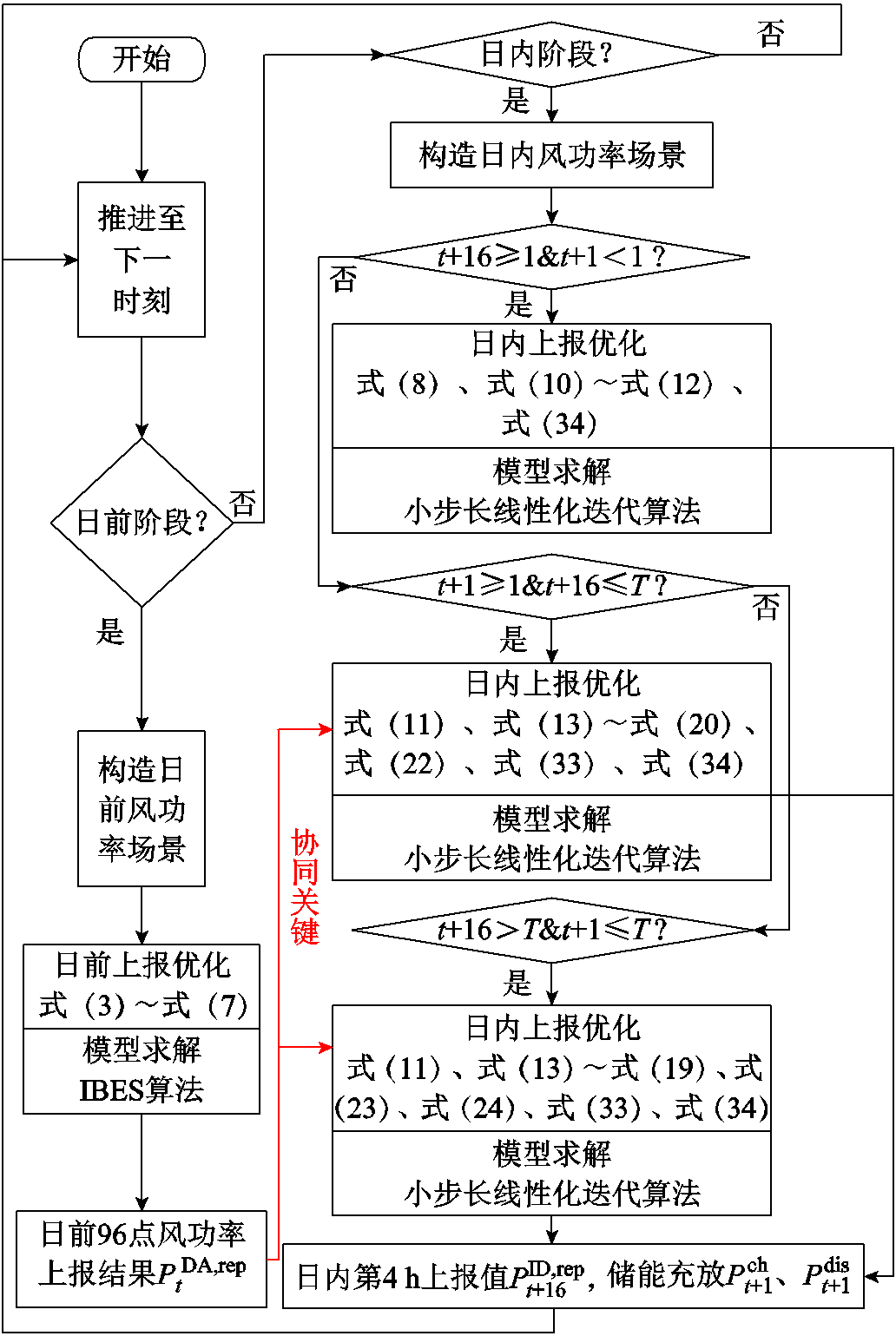
图3 两阶段优化上报策略求解流程
Fig.3 Flow chart of the solution for the two-stage optimized power reporting strategy
本节选取中国华中地区某风电场实际数据进行仿真,其装机容量为98.5 MW,时间跨度为2019年5月26日—2020年12月31日。数据的时间分辨率均为15 min,包括风功率实际值、日前预测值、配套的气象预报数据(包括风速、风向、气温、气压四要素)及日内未来4 h的超短期风功率预测值。所有样本按8:2的比例划分为训练集与测试集,并采用minmax归一化对所有功率与气象数据进行无量纲化处理[26]。配置储能总能量20 MW·h,能量系数 、
、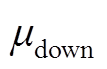 分别为85%、15%,充放电效率均为90%,最大充电功率为10 MW,最大放电功率为9 MW,最大放电深度为60%,初始能量设置为10 MW·h。模型与算法部分,用于有效气象指标检测的气象因素包括风速、风向、气温、气压及其一阶变化量,其过程详见附录;日前、日内风功率场景数
分别为85%、15%,充放电效率均为90%,最大充电功率为10 MW,最大放电功率为9 MW,最大放电深度为60%,初始能量设置为10 MW·h。模型与算法部分,用于有效气象指标检测的气象因素包括风速、风向、气温、气压及其一阶变化量,其过程详见附录;日前、日内风功率场景数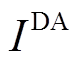 与
与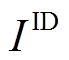 取100;由于LHS为等概率间隔采样,故日前、日内各场景发生概率相同,场景权重系数
取100;由于LHS为等概率间隔采样,故日前、日内各场景发生概率相同,场景权重系数 与
与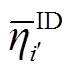 均为1。IBES算法的最大迭代次数为500次,其余参数设置参考文献[23];小步长线性化迭代次数上限
均为1。IBES算法的最大迭代次数为500次,其余参数设置参考文献[23];小步长线性化迭代次数上限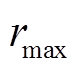 为8,
为8,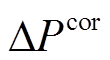 与
与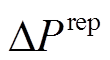 均为0.02,终止阈值
均为0.02,终止阈值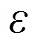 取0.001;Big-M参数
取0.001;Big-M参数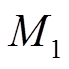 与
与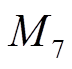 取0.9,
取0.9, 与
与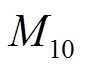 取0.25,
取0.25,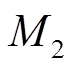 、
、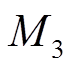 、
、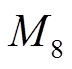 、
、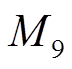 取98.5,
取98.5,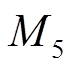 、
、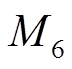 、
、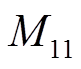 、
、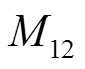 取20;
取20;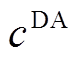 与
与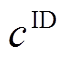 均为1。
均为1。
算例分析将分为以下小节展开。5.2节将针对日前、日内风功率场景进行比较与分析,以说明第3节中误差建模与场景重排序的必要性。一方面,由于现行两个细则大多以月为单位进行考核电量的结算[2-4],故5.3节与5.4节选用测试集中2020年11月的数据分别从典型日上报曲线与月度考核量统计的角度进行相关对比分析;另一方面,5.3节与5.4.1节将通过比较四种上报策略的考核情况来论证本文所提两阶段优化上报策略的优势。
策略1:日前、日内阶段均采用预测值上报;策略2:日前阶段采用日前上报模型进行优化上报,日内阶段采用预测值上报;策略3:日前阶段采用预测值上报,日内阶段采用日内上报模型进行优化上报;策略4:日前、日内阶段采用两阶段协同上报模型进行优化上报。
同时,5.4.2节将分别对比采用粒子群(Particle Swarm Optimization, PSO)算法、IBES算法与本文提出的小步长线性化迭代算法求解日内上报模型的考核结果与求解性能,以分析本文所提算法的优势。另外,5.4.3节引入一种基于储能调节与预测值上报相结合的理想化上报策略(下称策略5),以充分体现本文基于随机场景的两阶段上报模型有关考核电量与储能调节方式的优越性。
策略5:日前、日内阶段均采用预测值上报,假设优化各时段储能充放功率前实际风功率已知,并以之为基准直接优化储能。详细模型见附录。
由于每日各时段气象预报数据不同,依据第3节及附录的日前误差分箱方法得到的日前误差场景将有所差异,故本节以2020年11月28日的日前误差场景集为例作具体分析。
日前预测误差样本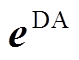 与该日按时间相关性排序前后的误差场景的相关系数矩阵对比如图4a、图4c、图4e所示。图中,
与该日按时间相关性排序前后的误差场景的相关系数矩阵对比如图4a、图4c、图4e所示。图中,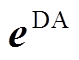 具有在相邻时刻(即图4a对角线附近)的相关系数大,而间隔较远的时段相关系数小的性质。图4c中,由于直接经过LHS得到的日前误差场景均按误差值从小到大排列(见附图3a),其相关系数矩阵值几乎均为1,与
具有在相邻时刻(即图4a对角线附近)的相关系数大,而间隔较远的时段相关系数小的性质。图4c中,由于直接经过LHS得到的日前误差场景均按误差值从小到大排列(见附图3a),其相关系数矩阵值几乎均为1,与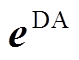 的性质相差甚远。而图4e中经过重排序后最终生成的场景,其时间相关性性质与样本几乎完全一致,二者相关系数矩阵的平均误差仅为0.022 8。
的性质相差甚远。而图4e中经过重排序后最终生成的场景,其时间相关性性质与样本几乎完全一致,二者相关系数矩阵的平均误差仅为0.022 8。

图4 误差样本与场景相关系数矩阵示意图
Fig.4 Schematic diagram of the correlation coefficient matrix of error samples and scenarios
由于日内预测时间步均为16步,故各时段日内预测误差场景相同。如图4b所示,由于相近时段的预测互相耦合,日内误差样本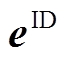 的相关系数在相邻预测步之间大,相距较远的预测步之间小。由图4d可知,由于按照误差值大小排列(见附图3b),直接由LHS生成的日内误差场景的相关系数同样均接近1。而图4f所示的经相关性排序后的日内误差场景,其相关系数与原始样本几乎一致,二者相关系数矩阵平均误差仅0.009 9。
的相关系数在相邻预测步之间大,相距较远的预测步之间小。由图4d可知,由于按照误差值大小排列(见附图3b),直接由LHS生成的日内误差场景的相关系数同样均接近1。而图4f所示的经相关性排序后的日内误差场景,其相关系数与原始样本几乎一致,二者相关系数矩阵平均误差仅0.009 9。
上述有关日前、日内误差场景相关性分析结果表明经Cholesky分解重排序后的误差场景基本符合样本的相关性特征,论证了场景重排序的必要性。
图5展示了2020年11月28日日前风功率场景与2020年11月4日第44个预测时段下日内风功率场景。结合附图3可知,通过统计历史预测误差样本生成的日前、日内预测误差场景整体为正误差居多,表明历史预测结果大多“低估”。因此,叠加相应预测值得到的日前、日内风功率场景整体位于预测曲线之上,并基本概括了图5a、图5b中相较预测曲线同样整体偏高实际值曲线。另一方面,图5中重排序后的风功率场景相较附图3所示的原始误差场景引入了更多风功率波动信息。因此,基于图5中的风功率场景进行日前、日内优化上报能够得到相较预测值更精确的优化上报结果(详见5.3节相关对比)。

图5 典型风功率场景示意图
Fig.5 Schematic diagram of typical wind power scenarios
本节将以2020年11月28日(下称典型日1)与11月4日(下称典型日2)的考核结果为例分析两阶段上报策略的具体优势。
图6展示了典型日1四种上报策略下上报功率及实际功率的对比。可以看出,由于该日实际功率具有较强的波动性,若采用策略1直接将平滑的预测值上报参与考核,难以取得较优的准确率。通过策略2、3与策略1的对比可知,日前、日内优化上报曲线相较预测曲线在大部分时段能够更好地匹配实际功率的波动,提升准确率。对比策略3与策略4,由于前15个时刻日内上报模型尚未引入储能调节,故二者前15个时刻的日内上报功率完全一致。然而,策略3与策略4日内模型中日前准确率的计算分别参考预测曲线与优化上报曲线,故从第16时刻开始,二者的日内上报功率有所差别,且策略4的日内上报曲线更贴合实际功率。这表明在日内上报模型中采用准确率更高的日前上报结果有助于提升日内准确率。
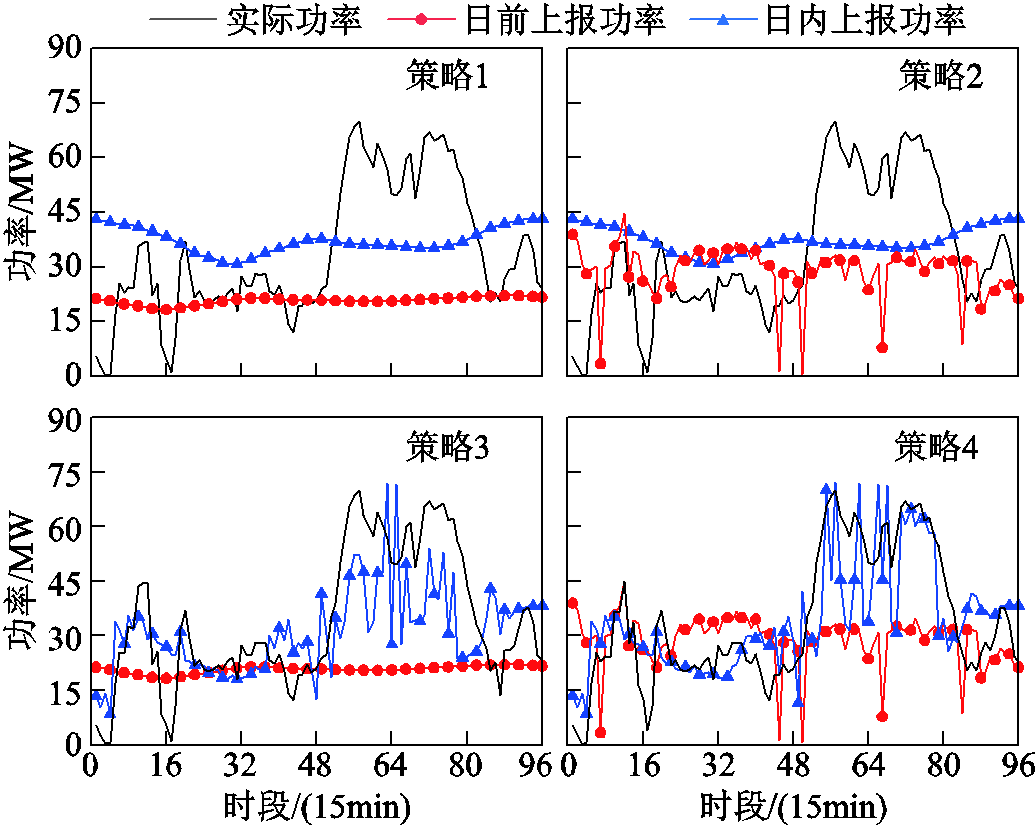
图6 典型日1上报功率对比
Fig.6 Comparison of reported power on 1st typical day
另一方面,对比策略4与策略2并结合图7可知,通过储能在第9~19时刻进行放电调节,策略4的实际功率曲线相较策略2向上平移,从而减小了与日前上报曲线之间的差距;而储能在第78~95时刻的充电调节使得相应时段的实际功率降低,整体减小了日前误差。

图7 典型日1策略4下储能能量变化曲线
Fig.7 Energy variation curve of energy storage under strategy 4 of 1st typical day
进一步对比该日的考核指标见表1。由表1可知,策略2相较策略1提升了约3%的日前准确率;策略3相较策略1提升了约5%的日内准确率。而策略4一方面在策略2的基础上通过储能调节进一步提升了日前准确率;另一方面,其相较策略1~3也提升了日内准确率,具有最佳的考核效果。
表1 典型日考核指标对比
Tab.1 Comparison of assessment indices on typical days
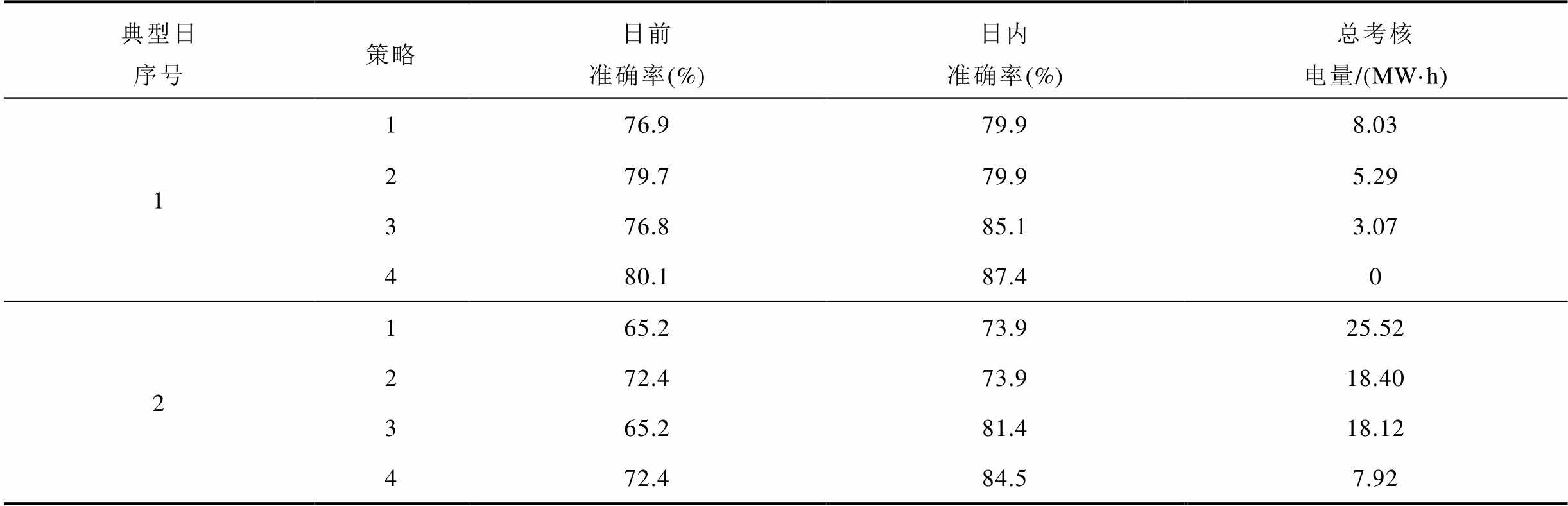
典型日序号策略日前准确率(%)日内准确率(%)总考核电量/(MW·h) 1176.979.98.03 279.779.95.29 376.885.13.07 480.187.40 2165.273.925.52 272.473.918.40 365.281.418.12 472.484.57.92
典型日2上报功率对比如图8所示。由图8可知,相较于典型日1,典型日2日前、日内预测功率与实际功率的误差更大,且大部分时刻的实际功率被严重低估。此外,典型日2储能能量变化曲线如图9所示,该典型日策略3与策略4的初始储能能量接近设定的能量上限,导致其难以通过充电降低过分低估的实际功率。在种种“不利因素”的叠加下,四种上报策略均难以避免考核电量的产生。
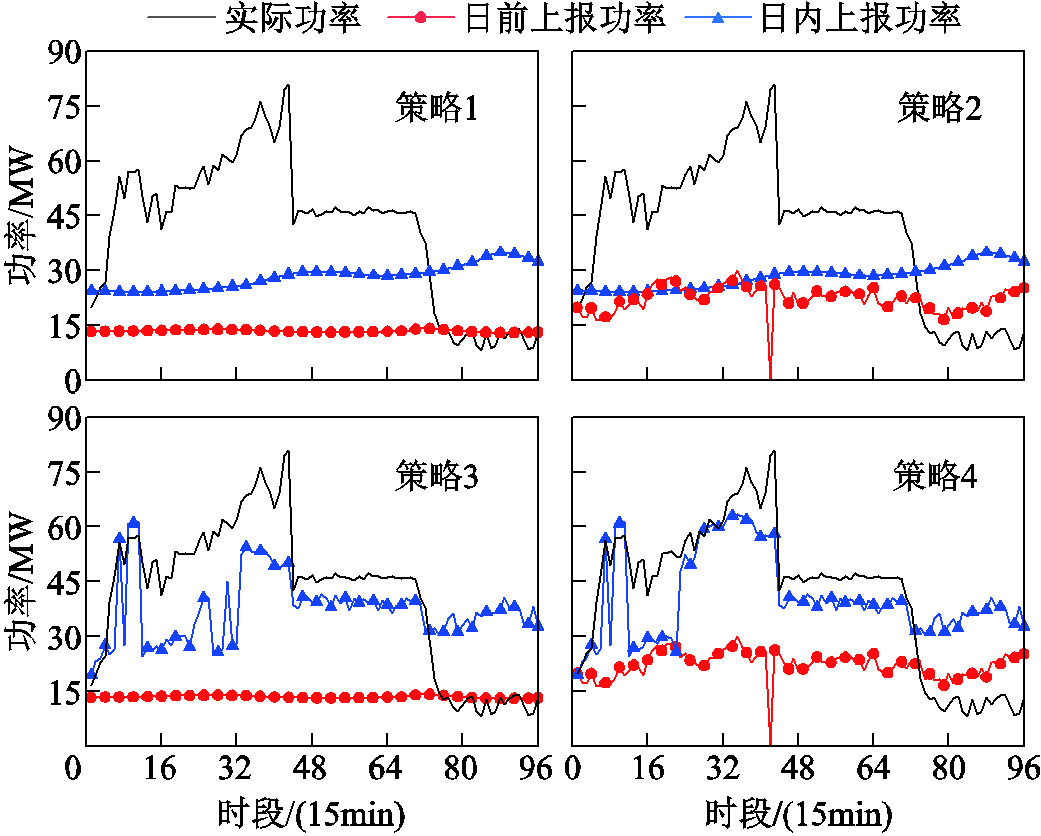
图8 典型日2上报功率对比
Fig.8 Comparison of reported power on 2nd typical day


图9 典型日2储能能量变化曲线
Fig.9 Energy variation curve of energy storage of 2nd typical day
在该预测不准确的情况下,策略2与策略4中日前优化上报曲线相较日前预测曲线整体上移;而策略3与策略4中日内优化上报曲线相较日内预测曲线在前70个时刻明显更为贴合实际功率的变化。如表1中,采用策略4的考核电量仅7.92 MW·h,相较其余策略减少了50%以上。这表明采用本文提出的日前-日内两阶段上报模型也能够在预测不准确的情况下提升上报曲线的质量。
5.4.1 不同上报策略对比
统计四种策略下每日的准确率均值、标准差及该月的考核电量,月度考核指标对比见表2,分别从三类指标的具体情况进行分析。
表2 月度考核指标对比
Tab.2 Comparison of assessment indices of the month

策略日前准确率(%)日内准确率(%)考核电量/(MW·h) 均值标准差均值标准差日前日内总计 182.817.5384.654.6964.7258.76123.48 285.155.1184.654.6915.9158.7674.67 382.907.4885.151.8063.4718.4382.00 485.515.0385.621.8214.6414.7329.37
1)日前准确率。策略2、4分别相较策略1、3整体提高了约2.5%的日前准确率,并降低了约2.4%的标准差,表明日前上报模型得到的日前优化上报功率更具准确性与鲁棒性。值得注意的是,策略3、4通过优化储能以调节实际功率,从而使其日前准确率分别相较策略1、2略有提升。
2)日内准确率。由于策略1、2均采用预测值进行上报,故二者日内准确率完全一致。相比之下,策略3、4的准确率分别提升了0.5%与1%,且标准差同样显著降低。此外,策略4相较策略3提升了约0.5%的日内准确率,这也表明提升日前上报结果的准确率同样有助于改善日内上报结果的准确率。
3)考核电量。整体而言,策略2、3相较策略1均有效降低了约1/3的总考核电量;而策略4相较其余策略均明显降低了日前、日内的考核电量,这也与准确率的对比结果相吻合。值得一提的是,虽然策略3、4相较策略1、2仅整体提升约0.5%与1%的日内准确率,但日内考核电量却均降低了70%以上。这源于日内上报模型对于考核细则的“高契合度”。如附图4所示,30天中,策略1、2共计15天日内考核不达标,而策略3、4分别仅11与8天日内考核不达标。进一步地,不同日内准确率下考核达标天数对比见表3,若考核达标的准确率由77.5%至85%变化,则策略3、4的考核达标天数均明显优于策略1、2;而当考核达标的准确率高于87.5%时,策略1、2反而占优。结合日内准确率的标准差对比结果可以认为,采用日内模型优化上报的策略3、4“牺牲”了部分高准确率的结果以换取低准确率情况下的提升,使得绝大多数日内准确率位于两个细则规定的考核达标准确率85%附近的区间,从而有效降低了考核电量。
表3 不同日内准确率下考核达标天数对比
Tab.3 Comparison of the number of days to meet the assessment standards under different intra-day accuracy(单位:d)

策略>77.5%>80%>82.5%>85%>87.5%>90% 1、22825221582 33029291910 43030292230
综上所述,策略4代表的日前-日内两阶段上报模型的考核效果与鲁棒性均得到了充分的验证。
5.4.2 不同日内模型求解算法对比
为论证本文提出的小步长线性化迭代算法(以下简称小步长算法)求解日内模型的优势,本节采用IBES、PSO算法进行对比。由于5.4.1节仿真结果表明策略4的考核效果最佳,故各算法均求解策略4的日内上报模型。其中,日内模型包含的二进制变量及储能等式约束分别采用sigmoid函数映射与罚函数法进行处理[27]。IBES算法最大迭代次数为300次,种群数为50,其余参数与日前求解保持一致。PSO算法种群数为200,所有学习因子均为1.2,惯性权重取0.5。为更好地展现对比效果,分别设置PSO算法最大迭代次数为500(下称PSO-1)与5 000(下称PSO-2)进行模型求解。
表4对比了不同算法下2020年11月的日内考核结果。可以发现,两种PSO算法的日内上报结果劣于小步长算法与IBES算法,其考核达标天数均不超过10天,平均准确率仅不到83%,并且承担了高额的考核电量惩罚。IBES算法对应的上报结果中考核达标天数达到18天,因此考核电量明显低于PSO算法。小步长算法的考核电量仅14.73 MW·h,其准确率与考核达标天数亦明显优于其余算法,具有最佳考核效果。
表4 不同算法下月度日内考核指标对比
Tab.4 Comparison of intra-day assessment indices of the month under different algorithms

算法考核达标天数日内准确率(%)日内考核电量/(MW·h) 均值标准差 小步长2285.651.7214.73 IBES1885.192.3324.56 PSO-1782.252.9190.80 PSO-21082.972.9271.37
进一步对比经不同算法优化的日内准确率结果,如图10所示。由于寻优策略相同,PSO-1与PSO-2算法的准确率趋势基本一致,仅在部分上报日有超过1%的差距。IBES算法独特的三阶段寻优增强了其全局搜索能力,故准确率整体高于两类PSO算法。小步长算法的准确率均值虽仅比IBES算法高0.46%,但其准确率的波动相比之下更小,故优化结果在四者中最好。
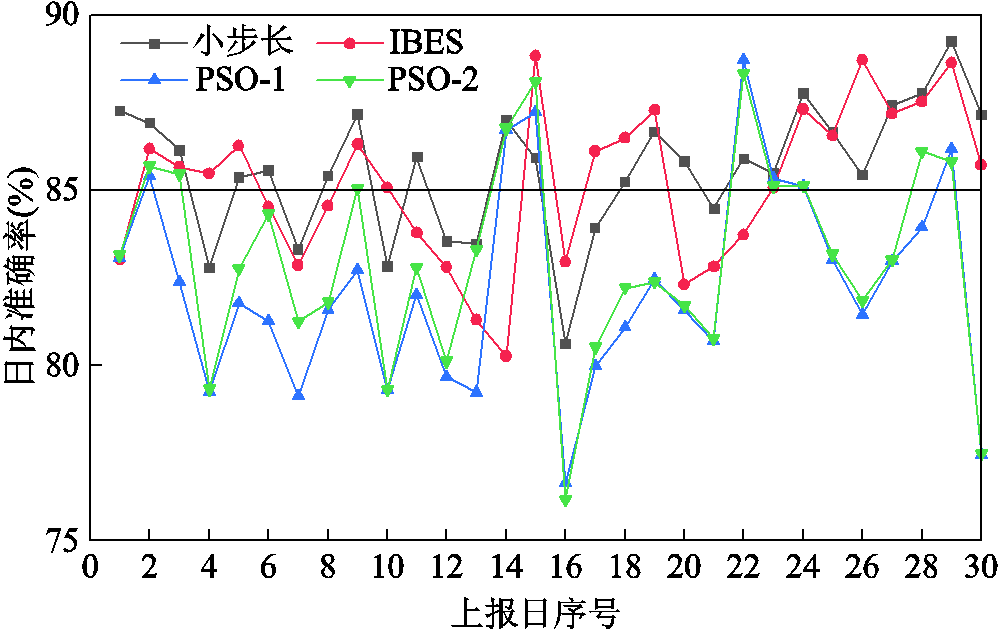
图10 不同算法下各上报日日内准确率
Fig.10 Intra-day accuracy comparison for each reporting day under different algorithms
另外,四种算法的求解效率对比见表5。如第2节所述,日内上报在三种时段下模型不同,故各算法在三种时段的求解用时不一。时段一的模型不包含储能,故求解速率最高;时段二、三引入了储能变量及约束,故求解用时更长。其中,PSO-2算法用时高达5 min以上,IBES算法用时也在2~3 min之间。考虑到实际应用中的通信耗时,二者在15 min滚动更新的日内上报中实用性较低。PSO-1虽求解效率高,然而如表4所示,其承担了高额的考核电量惩罚,故同样不具备较高的实用价值。相比之下,小步长算法兼顾了求解效率与优化效果,具有最佳的实用性。另外,有关算法具体收敛对比及小步长算法中的线性化误差分析详见附录。
表5 30日中不同算法求解日内上报模型平均用时
Tab.5 Average time consumption to solve the intra-day reporting model by different algorithms over 30 days(单位:s)

算法时段一平均用时时段二平均用时时段三平均用时 小步长4.3632.6439.51 IBES124.59155.34165.09 PSO-131.1237.6541.18 PSO-2314.21379.51414.78
5.4.3 不同储能优化方式对比
策略1、策略5及策略4在2020年11月的月度考核结果对比如表6与附图7所示。由于策略5假设风电实发功率已知,经储能优化后日前、日内准确率均较策略1有所提升,其平均提升量约为0.3%。同时,其总考核电量同比降低约6 MW,再次论证引入储能有助于提高风电场的考核效益。
表6 不同储能优化方式下月度考核结果对比
Tab.6 Comparison of assessment results of the month under different optimization methods of energy storage

策略日前准确率(%)日内准确率(%)考核电量/(MW·h) 均值标准差均值标准差日前日内总计 182.817.5384.654.6964.7258.76123.48 485.515.0385.621.8214.6414.7329.37 583.108.1984.994.7160.7956.71117.50
然而,策略5的考核电量仍远高于策略4,这表明对于考核效果的提升而言,合理优化上报功率的重要性高于优化储能。
策略4、5的储能调节情况对比见表7。其中,策略5储能的总充放电次数超过了策略4的3倍,其达到每日最大放电深度限制的天数也高达19天。同时,策略5储能的总放电功率接近策略4的两倍。进一步比较两种策略下储能每日的放电量,如图11所示。
表7 不同储能优化方式的调节量对比
Tab.7 Comparison of regulation amount under different energy storage optimization methods

策略总充放电次数达最大放电深度的天数总放电量/ (MW·h) 46218654.82 52094191191.76
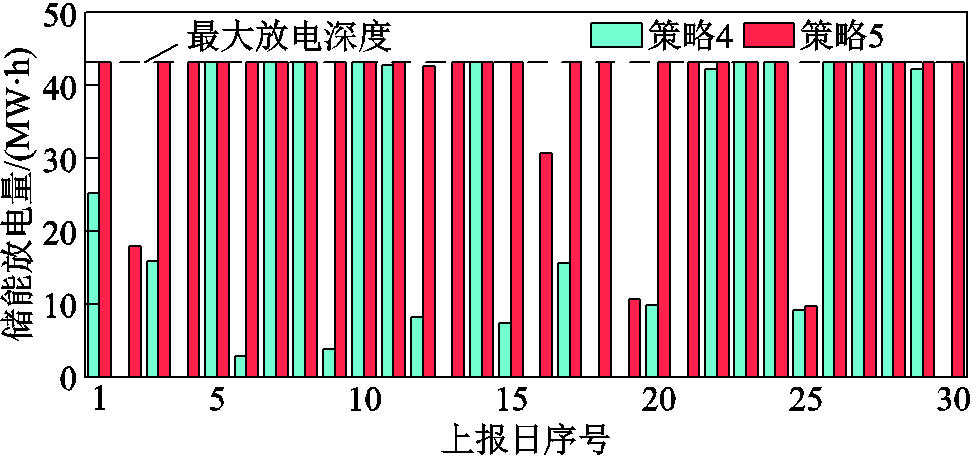
图11 不同储能优化方式下各上报日放电功率
Fig.11 The discharge power of each reporting day under different optimization methods of energy storage
可以看出,除去达到最大放电深度的8天外,策略4其余上报日的总放电量大多不超过10 MW·h。而策略5则在绝大多数上报日均具有较高的放电量。上述结果表明,策略5的储能调节方案具有频繁充放、倾向于过度放电的特征,长期执行该方案将有损于储能的使用寿命。而策略4的储能优化参考了准确率更高的日前优化上报功率,并利用随机场景刻画了日内风功率的变化,无需储能的过度调节便可实现优良的考核效果。
本文提出一种面向两个细则考核的风-储场站日前-日内两阶段功率优化上报策略。该策略计及了风功率不确定性,并在两个细则具体考核机制的基础上构建功率上报模型,实现了不同时间尺度下功率上报的协调配合,从而为两个细则考核机制下的风电场功率上报提供思路。通过算例仿真可以得出以下结论:
1)通过计及时间相关性重排序后生成的预测误差场景更贴合历史样本的相关性特征,并引入了多种风功率波动特征,为优化上报打下基础。
2)相较于预测值上报,单独采用日前或日内上报模型进行优化上报能更好地拟合实际风功率的变化趋势,而两阶段上报模型利用储能充放实现了日前-日内协同,进一步降低了考核电量。
3)本文提出的小步长线性化迭代算法能兼顾优化效果与求解速率,具有一定的实际应用价值。
4)本文提出的储能优化方案相比基于预测功率直接优化储能的方案更加节能,并有利于储能使用寿命的延长。
本研究后续工作将尝试引入爬坡约束,以平滑上报曲线中过于剧烈的功率波动。由于随机场景与预测功率的质量挂钩,因此后续研究还将构建以考核电量为导向的风功率预测模型,从预测的根源上提升准确率。此外,面向两个细则考核的光伏功率上报研究也亟待开展。
附 录
1. 模型与算法详述
1)风功率日前预测误差气象分型
首先基于气象预报数据及其一阶变化量,分析气象指标与日前风功率预测误差的相关性,提取有效气象指标作。相关性采用线性相关系数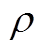 与互信息量M表征。
与互信息量M表征。
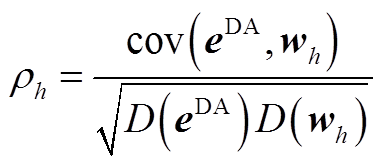 (A1)
(A1)
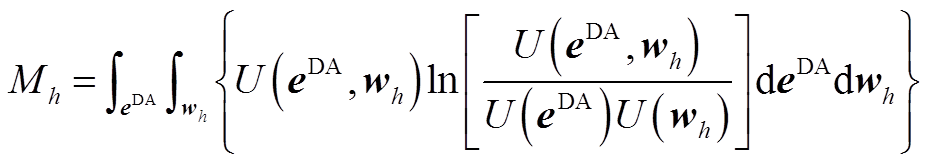 (A2)
(A2)
式中,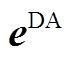 与
与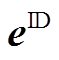 分别为日前、日内预测误差样本;
分别为日前、日内预测误差样本;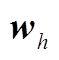 为第
为第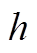 个气象指标序列;
个气象指标序列;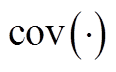 表示协方差;
表示协方差;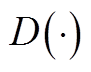 表示方差;
表示方差;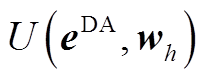 为
为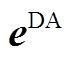 与
与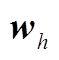 的联合概率密度;
的联合概率密度;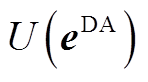 与
与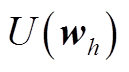 为边缘概率密度。
为边缘概率密度。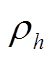 的绝对值越大,表明
的绝对值越大,表明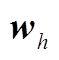 与
与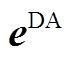 的线性相关性越强;
的线性相关性越强;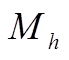 越大,表明
越大,表明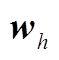 对
对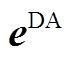 的非线性影响越大。
的非线性影响越大。
根据提取的有效气象指标,采用分布函数差异化导向的K-means算法进行误差分箱。
(1)基于有效气象指标数据集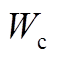 与风功率日前预测误差
与风功率日前预测误差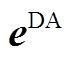 ,利用肘部法确定日前误差箱数(即聚类数)
,利用肘部法确定日前误差箱数(即聚类数)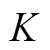 。
。
(2)计算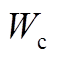 中各样本点数据密度,基于密度阈值确定初始聚类中心候选集
中各样本点数据密度,基于密度阈值确定初始聚类中心候选集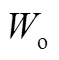 ,随机选取
,随机选取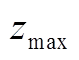 个点作为第1个初始聚类中心的候选集
个点作为第1个初始聚类中心的候选集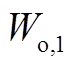 (迭代次数
(迭代次数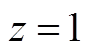 )。
)。
(3)取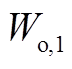 中的第
中的第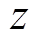 个点作为第1个初始聚类中心
个点作为第1个初始聚类中心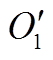 ,计算
,计算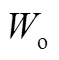 中各点与该初始聚类中心的距离,取距离最远的点作为第2个初始聚类中心
中各点与该初始聚类中心的距离,取距离最远的点作为第2个初始聚类中心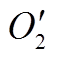 ,计算
,计算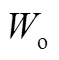 中其余各点与初始聚类中心
中其余各点与初始聚类中心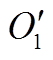 和
和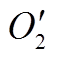 的最近距离,取距离最远的点作为第3个初始聚类中心
的最近距离,取距离最远的点作为第3个初始聚类中心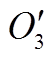 ,依此类推,直至求出
,依此类推,直至求出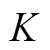 个初始聚类中心。
个初始聚类中心。
(4)基于步骤(1)与步骤(3)所得聚类数与初始聚类中心,进行经典K-means计算,得到相应聚类结果。
(5)基于聚类结果对相应风电功率预测误差数据进行分箱,并分别对各箱误差数据拟合其概率密度函数。
(6)校验聚类结果对应的指标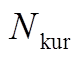 是否大于60%:若是,则转至下一步;否则,返回步骤(3),并取
是否大于60%:若是,则转至下一步;否则,返回步骤(3),并取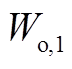 中下一个点进行计算(
中下一个点进行计算(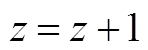 )。
)。
(7)计算聚类结果对应的目标函数SRMSE[22],比较相邻2次聚类SRMSE大小,保存其值较大者对应的聚类结果。
(8)重复步骤(3)~步骤(7),直到SRMSE大于阈值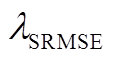 ,即各气象模式间风电功率预测误差概率分布的差异足够大或满足最大迭代次数(
,即各气象模式间风电功率预测误差概率分布的差异足够大或满足最大迭代次数(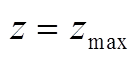 )。
)。
2)含五阶累积量的Cornish-Fisher级数计算多项式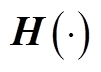 具体为(以日前预测误差为例)
具体为(以日前预测误差为例)
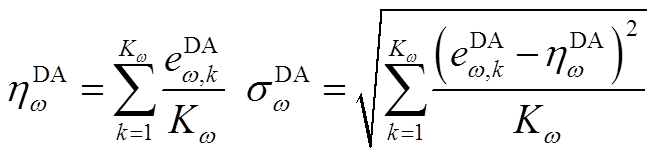 (A3)
(A3)
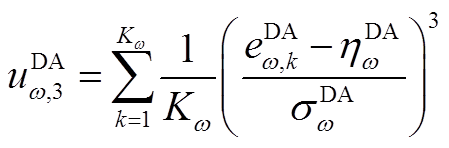 (A4)
(A4)
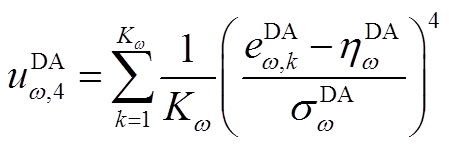 (A5)
(A5)
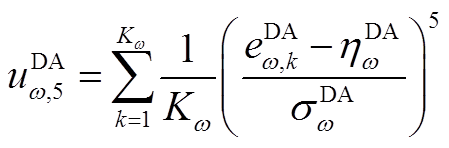 (A6)
(A6)
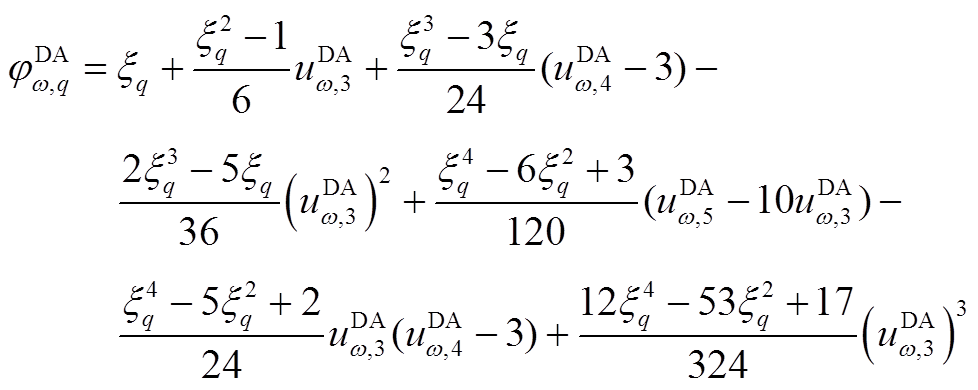 (A7)
(A7)
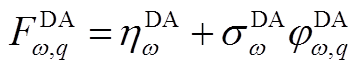 (A8)
(A8)
式中,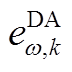 为日前第
为日前第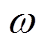 个误差箱中第k个误差样本的值;
个误差箱中第k个误差样本的值;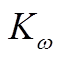 为日前第
为日前第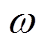 个误差箱包含的预测误差样本数;
个误差箱包含的预测误差样本数;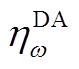 与
与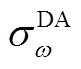 分别为日前第
分别为日前第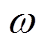 个误差箱下误差的均值与标准差;
个误差箱下误差的均值与标准差;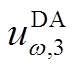 、
、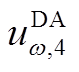 、
、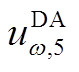 分别为日前第
分别为日前第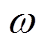 个误差箱预测误差的三、四、五阶原点矩;
个误差箱预测误差的三、四、五阶原点矩;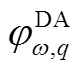 为日前第
为日前第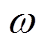 个误差箱下标准化的概率q分位点。
个误差箱下标准化的概率q分位点。
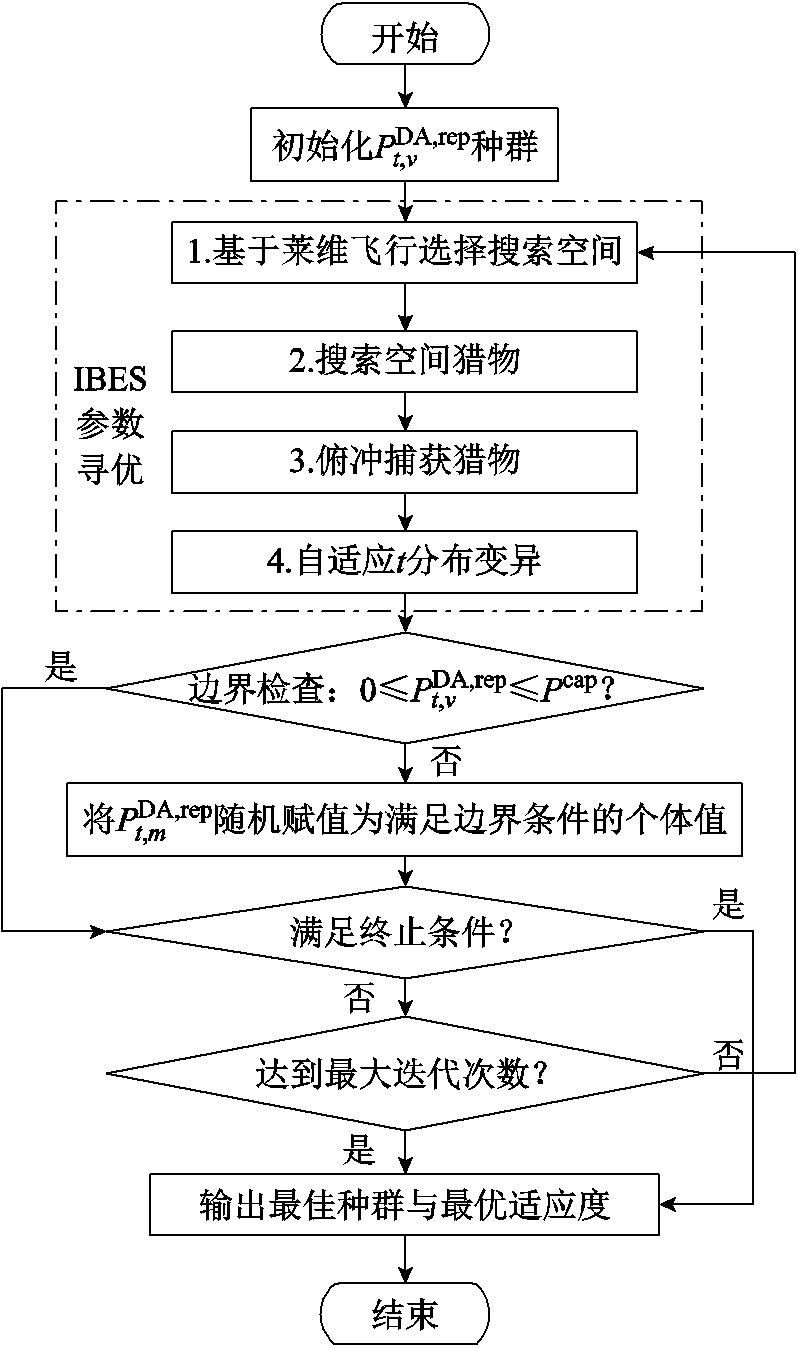
3)基于IBES算法的日前上报模型求解流程如附图1所示。首先,随机生成V个日前上报决策变量种群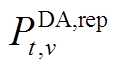 ,
,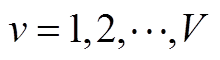 ,并通过IBES算法的四个参数寻优阶段更新种群。其次,对所有个体进行边界检查,将不满足式(4)的个体随机赋值为满足边界条件的种群对应的个体值。最后,依据更新后的种群计算适应度值,并判断其是否满足终止条件。若满足终止条件,则输出最佳种群与最佳适应度,作为日前上报模型的解;若不满足则重复上述迭代过程。其中,迭代终止条件及IBES参数寻优的详细过程参考文献[23]。
,并通过IBES算法的四个参数寻优阶段更新种群。其次,对所有个体进行边界检查,将不满足式(4)的个体随机赋值为满足边界条件的种群对应的个体值。最后,依据更新后的种群计算适应度值,并判断其是否满足终止条件。若满足终止条件,则输出最佳种群与最佳适应度,作为日前上报模型的解;若不满足则重复上述迭代过程。其中,迭代终止条件及IBES参数寻优的详细过程参考文献[23]。
4)式(10)、式(19)、式(20)、式(23)所示方均根准确率对应的绝对值准确率为
附图1 日前上报模型求解流程
App.Fig.1 Flowchart of the solving of day-ahead power reporting model
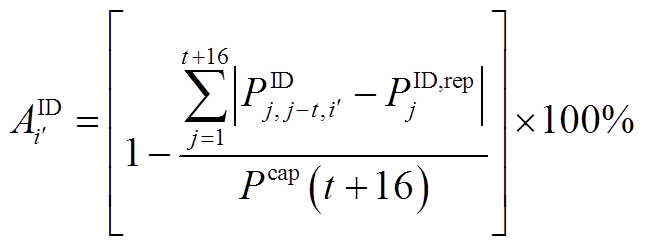 (A9)
(A9)
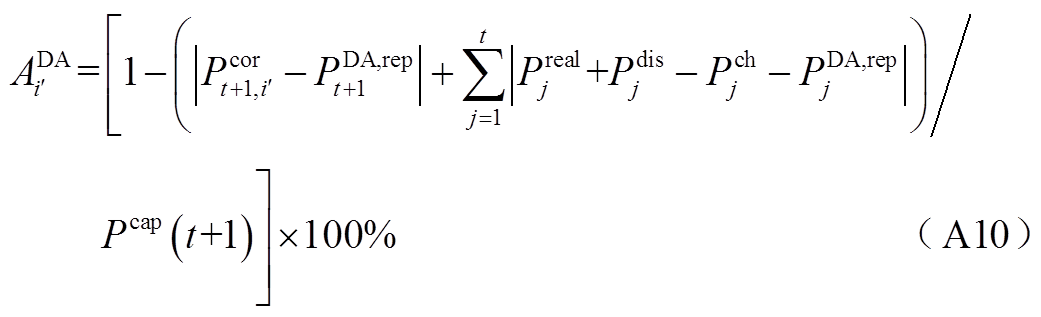

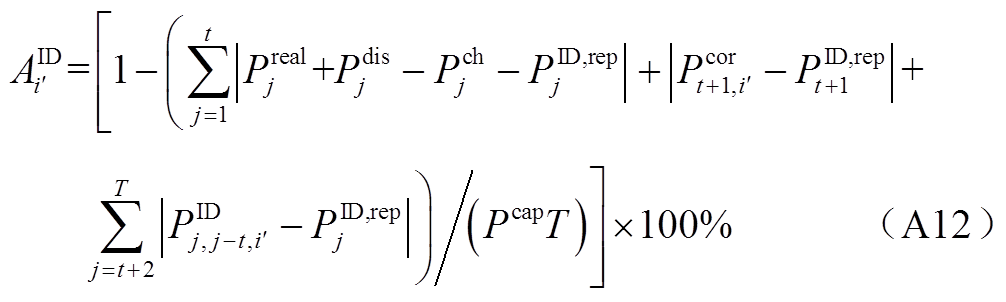
式(A9)~式(A12)中的绝对值部分同样可以利用Big-M法,按照类似式(A13)的形式进行混合整数线性化,从而得以利用商业求解器高效求解。
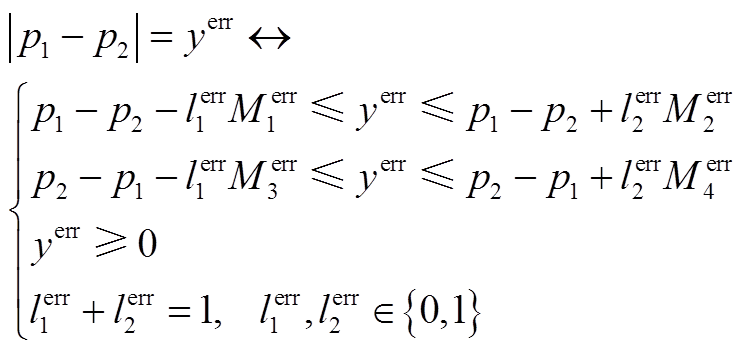 (A13)
(A13)
5)由于策略5日前阶段采用预测值上报,故日前阶段不包含优化上报模型。日内阶段通过优化储能充放,以减小日前、日内预测功率与实际功率的误差,降低考核电量。t时段日内模型目标函数为
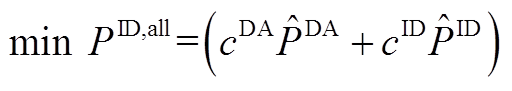 (A14)
(A14)
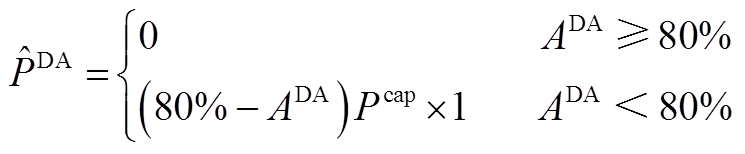 (A15)
(A15)
 (A16)
(A16)
储能约束如式(14)~式(17)所示。t时段经储能充放后的实际风-储功率为
 (A17)
(A17)
日前、日内准确率计算式为
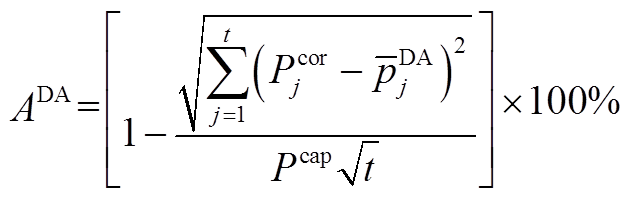 (A18)
(A18)
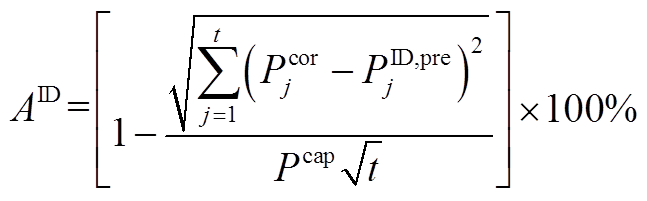 (A19)
(A19)
式中,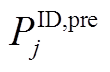 为j时段的风功率上报值,即4 h前的第16步风功率预测值。该模型决策变量集仅包含t时刻的储能调节量与荷电状态,即
为j时段的风功率上报值,即4 h前的第16步风功率预测值。该模型决策变量集仅包含t时刻的储能调节量与荷电状态,即
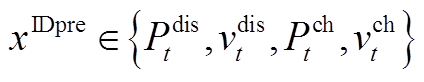 (A20)
(A20)
同样,式(A14)~式(A20)、式(14)~式(17)代表的策略5日内储能优化模型从0时起每15 min进行一次滚动优化,并利用小步长线性化迭代算法进行求解。
2. 仿真结果补充
1)气象指标筛选。遍历训练集,计算各气象指标序列与相应日前预测误差的相关系数与互信息量,其二维散点分布如附图2所示。由附图2可知,风速、风向、气温与风速一阶变化量到原点的距离均明显超过其余四项指标。因此在本文的评价指标体系下,该结果表明四者对训练集中的日前预测误差样本具有较强的相关性,故选择该四类气象指标序列参与日前预测误差分箱。
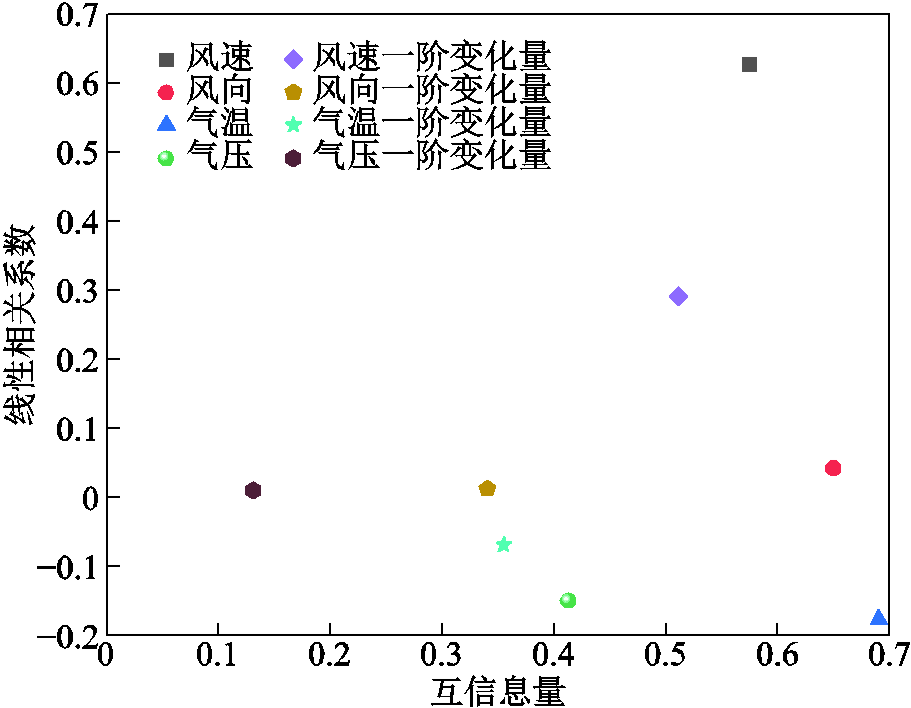
附图2 气象指标相关性分析散点图
App.Fig.2 Scatter plot for correlation analysis of meteorological indices
2)经LHS初步生成的日前、日内预测误差场景如附图3所示。
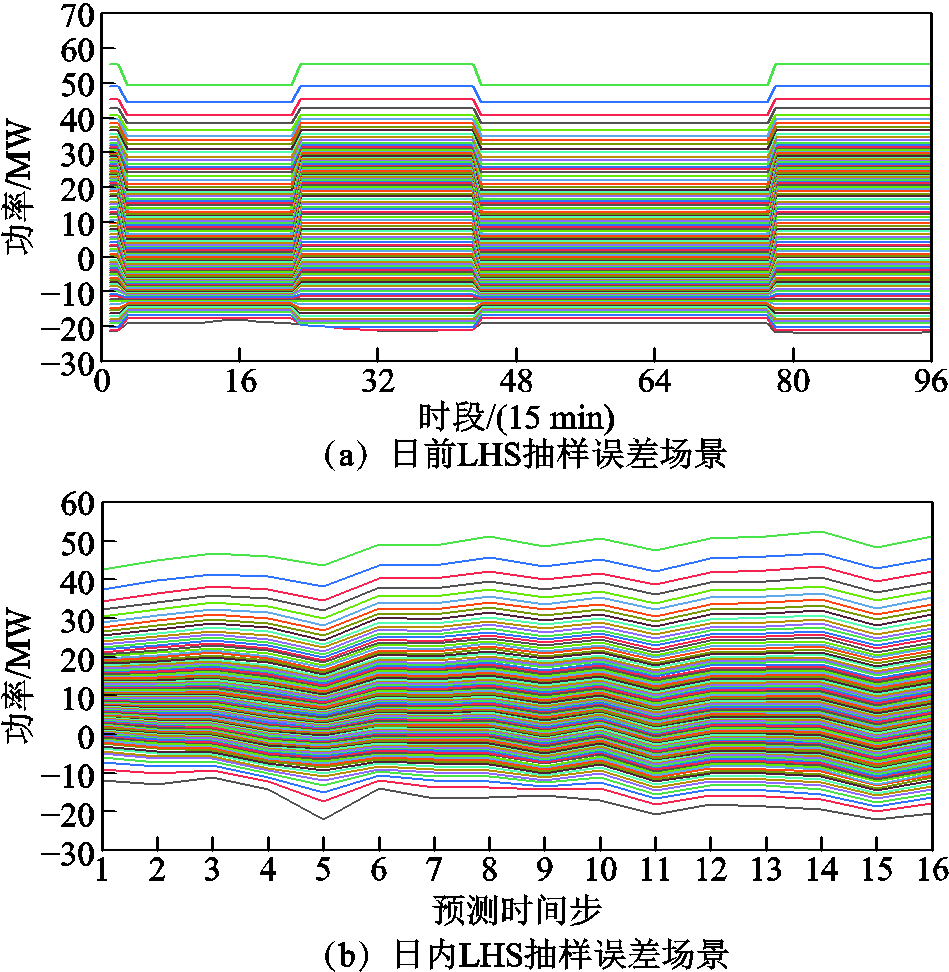
附图3 经LHS生成的预测误差场景
App.Fig.3 Forecast error scenarios generated by LHS
3)月度考核准确率详细结果。该月各上报日在四种策略下日前、日内考核准确率结果如附图4所示。
4)以算例中11月第四个上报日第76时段的日内上报模型优化结果为例,四种优化算法的收敛曲线如附图5所示。
由PSO-1与PSO-2算法的收敛对比可知,由于除迭代次数外的其余超参数设置相同,在相同的500次迭代下,二者均收敛至30左右。而PSO-2由于迭代次数的增加,其种群随机变异的次数亦增加,因而有更高的概率收敛至更低的目标函数值。而IBES算法在300次迭代过程中,其收敛曲线几乎处于持续走低的状态,而非PSO算法中“阶梯式”的下降。IBES算法的最终收敛值(20左右)也相较两种PSO算法更小,这表明其具有更好的全局搜索能力。相较三种智能算法随机给定初值的策略,小步长算法在迭代开始前首先以绝对值误差作为准确率计算的参考得到一组解,故线性化迭代一次后的目标函数(仅约为22)要远优于三种智能算法。另外,小步长算法在5次迭代后目标函数的变化就低于0.005,并在最后一次迭代达到收敛阈值,表明其收敛能力要远强于三种智能算法。
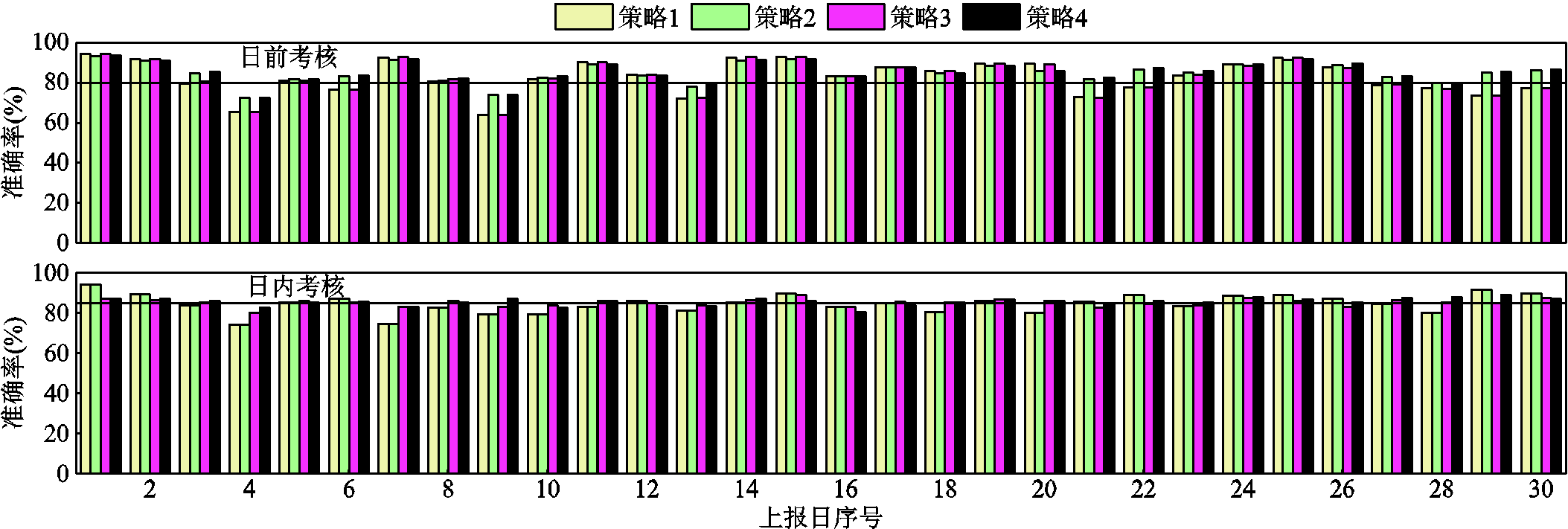
附图4 月度考核准确率对比
App.Fig.4 Comparison of assessment accuracy of the month
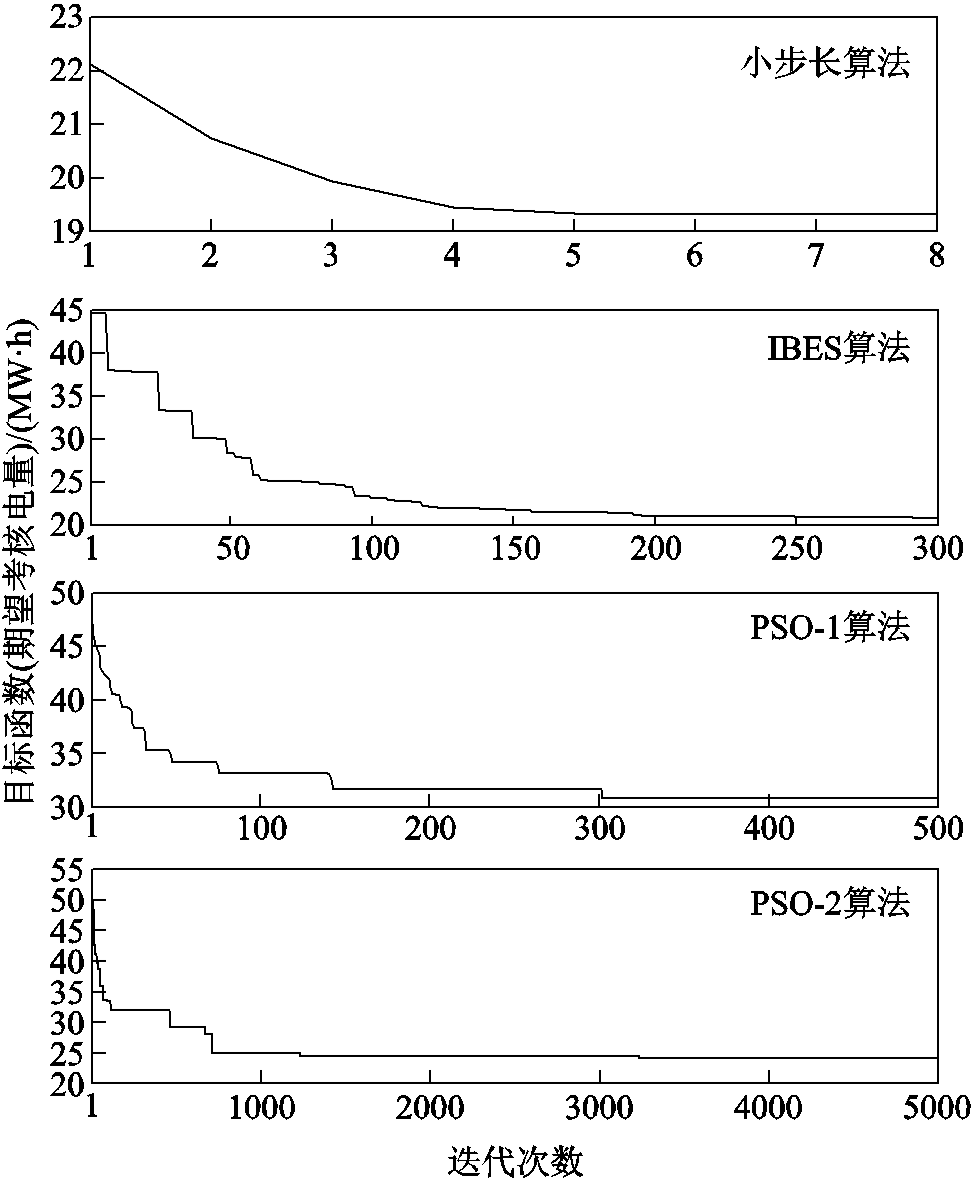
附图5 不同算法收敛曲线对比
App.Fig.5 Comparison of the convergence curves of different algorithms
5)式(10)、式(19)、式(20)、(23)所示的日前、日内准确率约束的线性化误差是衡量小步长算法求解精确程度的重要指标。统计30天所有时段各迭代次数的日前、日内准确率线性化误差(即按照式(10)、式(19)、式(20)、式(23)计算准确率与按照式(A9)~式(A12)计算的偏差),并绘制其概率分布如附图6所示。可以看出,约90%的情况下,日前、日内准确率计算误差分布在[-0.1%,0.1%]内。其中,最大日前误差约为0.6%,最大日内误差约为0.4%。因此,该线性化误差对于考核电量计算的影响几乎可以忽略不计,充分论证了小步长算法的精确性。
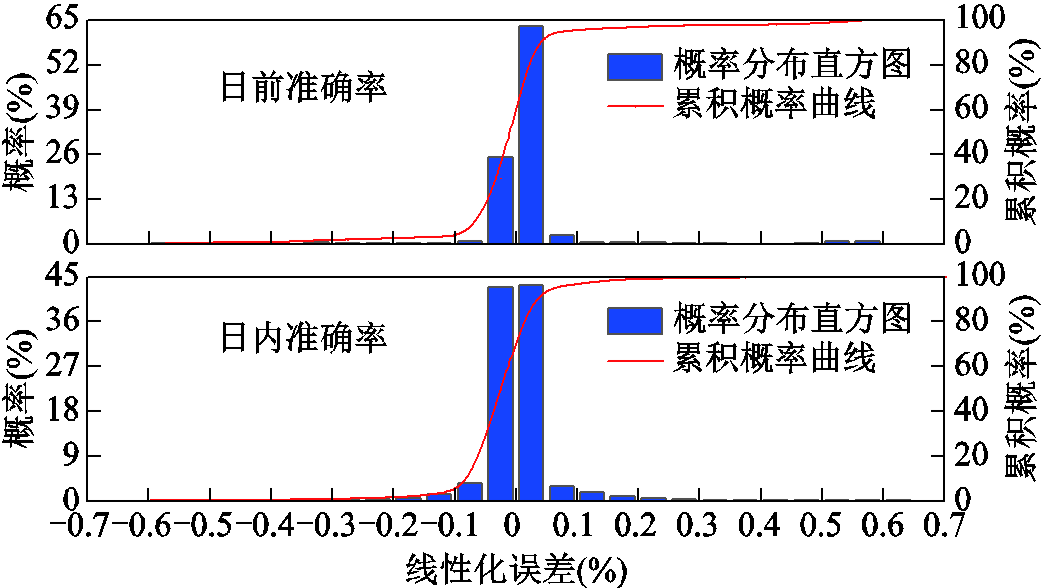
附图6 准确率约束线性化误差概率分布
App.Fig.6 The probability distribution graph of the linearization error for the accuracy constraints
6)不同储能优化方式下月度考核准确率详细结果。该月各上报日在策略1(无储能)、策略4(直接优化储能)、策略5(结合随机场景优化储能)下详细日前、日内考核准确率结果如附图7所示。
7)将算例中所有预测功率与真实值之间的误差均降低10%,再代入策略4模型进行仿真(该方案下称策略6),并计算相应的考核电量。三种策略的考核结果对比见附表1。
可以看出,策略6整体相较策略4提升了日前、日内考核电量。这说明,在相同的优化条件下,预测精度的提升(包括训练样本的精度)将促进优化上报准确率的提升。因此,寻求预测精度提升与优化上报结合的方法将是下一步的研究重点之一。
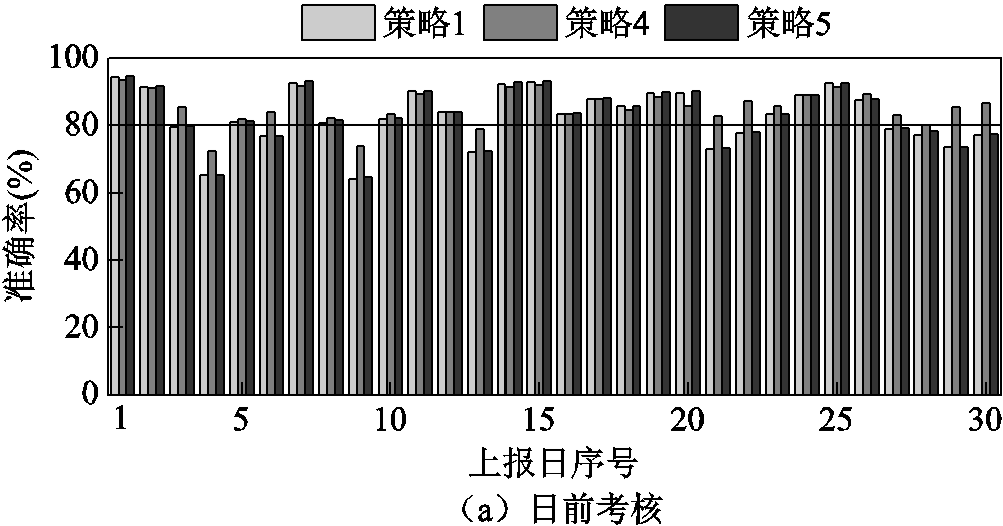
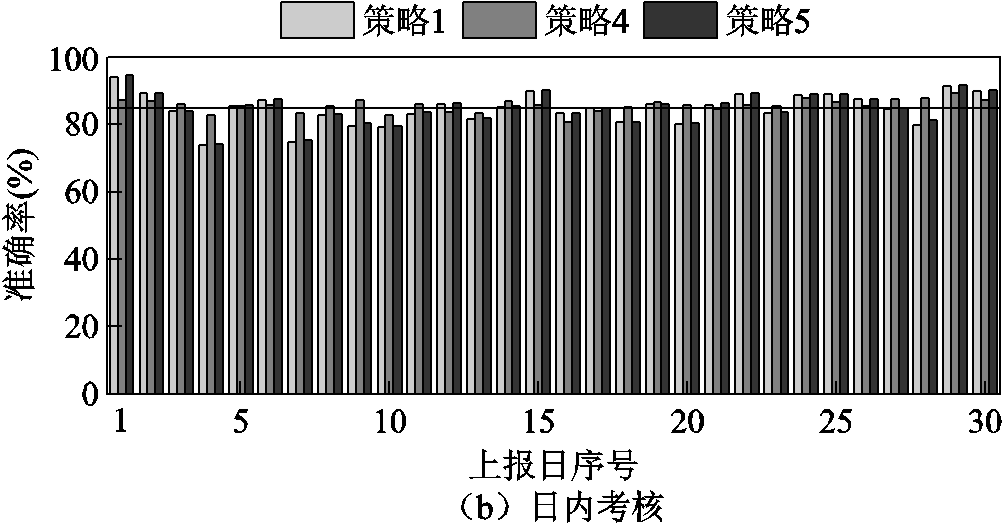
附图7 不同储能优化方式下准确率详细对比
App.Fig.7 Detailed comparison of accuracy indexes under different optimization methods of energy storage
附表1 提升预测精度后的月度考核结果对比
App.Tab.1 Comparison of assessment results of the month under different optimization methods of energy storage

策略日前准确率(%)日内准确率(%)考核电量/(MW·h) 均值标准差均值标准差日前日内总计 485.515.0385.621.8214.6414.7329.37 686.934.3587.151.784.433.337.76
参考文献
[1] 国家能源局. 国家能源局2022年一季度网上新闻发布会文字实录[EB/OL]. [2022-01-28]. http://www. nea.gov.cn/2022-01/28/c_1310445390.htm.
[2] 国家能源局华中监管局. 关于印发《华中区域并网发电厂辅助服务管理实施细则》和《华中区域发电厂并网运行管理实施细则》的通知[EB/OL]. [2020-09-07]. http://hzj.nea.gov.cn/adminContent/initViewContent.do?pk=AEB05CC013339FBDE050A8C0C1C8659B.
[3] 国家能源局南方监管局. 关于印发《南方区域发电厂并网运行管理实施细则》及《南方区域并网发电厂辅助服务管理实施细则》(2020年版)的通知[EB/ OL]. [2020-09-07]. http://nfj.nea.gov.cn/adminContent/ initViewContent.do?pk=4028811c752520120176b6b64cbf0147.
[4] 国家能源局华东监管局. 关于修订印发《华东区域并网发电厂辅助服务管理实施细则》和《华东区域发电厂并网运行管理实施细则》的通知[EB/OL]. [2020-11-30]. http://hdj.nea.gov.cn/load.loadPage.d?newsid= 1482854616&page=detail_index.xml&siteCode=hddjwucm&urlChannelId=1481001274&urlMenuId=1481001274.
[5] Tang Chenghui, Xu Jian, Sun Yuanzhang, et al. A versatile mixture distribution and its application in economic dispatch with multiple wind farms[J]. IEEE Transactions on Sustainable Energy, 2017, 8(4): 1747-1762.
[6] Botterud A, Wang J, Bessa R J, et al. Risk management and optimal bidding for a wind power producer[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-8.
[7] Bitar E Y, Rajagopal R, Khargonekar P P, et al. Bringing wind energy to market[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1225-1235.
[8] 吴政球, 王韬. 风电功率预测偏差管理与申报出力决策[J]. 电网技术, 2011, 35(12): 160-164. Wu Zhengqiu, Wang Tao. Deviation management of wind power prediction and decision-making of wind power bidding[J]. Power System Technology, 2011, 35(12): 160-164.
[9] 谢春雨. 风电场发电计划上报策略研究[D]. 北京: 华北电力大学, 2014.
[10] 赵会茹, 高婧瑶, 王玉玮, 等. 基于鲁棒优化的风电企业日前申报策略[J]. 电网技术, 2018, 42(4): 1177-1182. Zhao Huiru, Gao Jingyao, Wang Yuwei, et al. Day-ahead offering strategy for a wind power producer based on robust optimization[J]. Power System Technology, 2018, 42(4): 1177-1182.
[11] 周玮, 蓝嘉豪, 麦瑞坤, 等. 无线充电电动汽车V2G模式下光储直流微电网能量管理策略[J]. 电工技术学报, 2022, 37(1): 82-91. Zhou Wei, Lan Jiahao, Mai Ruikun, et al. Research on power management strategy of DC microgrid with photovoltaic, energy storage and EV-wireless power transfer in V2G mode[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 82-91.
[12] 曹明浩, 于继来. 面向风电场发电曲线偏差校正的电化学储能系统容量规划方法[J]. 电力系统自动化, 2022, 46(11): 27-36. Cao Minghao, Yu Jilai. Capacity planning method of electrochemical energy storage system for generation curve deviation correction of wind power farm[J]. Automation of Electric Power Systems, 2022, 46(11): 27-36.
[13] 郭立东, 雷鸣宇, 杨子龙, 等. 光储微网系统多目标协调控制策略[J]. 电工技术学报, 2021, 36(19): 4121-4131. Guo Lidong, Lei Mingyu, Yang Zilong, et al. Multi-objective coordinated control strategy for photovoltaic and energy-storage microgrid system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4121-4131.
[14] 张靖, 张志文, 胡斯佳, 等. 独立微电网风储协同调频的功率柔性分配策略[J]. 电工技术学报, 2022, 37(15): 3767-3780. Zhang Jing, Zhang Zhiwen, Hu Sijia, et al. A flexible power distribution strategy with wind turbine generator and energy storage for frequency regulation in isolated microgrid[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3767-3780.
[15] 张峰, 张鹏, 梁军. 考虑风电功率不确定性的风电场出力计划上报策略[J]. 电力自动化设备, 2019, 39(11): 34-40. Zhang Feng, Zhang Peng, Liang Jun. Wind farm generation schedule strategy considering wind power uncertainty[J]. Electric Power Automation Equipment, 2019, 39(11): 34-40.
[16] 德格吉日夫, 谭忠富, 李梦露, 等. 考虑不确定性的风储电站参与电力现货市场竞价策略[J]. 电网技术, 2019, 43(8): 2799-2807. De Gejirifu, Tan Zhongfu, Li Menglu, et al. Bidding strategy of wind-storage power plant participation in electricity spot market considering uncertainty[J]. Power System Technology, 2019, 43(8): 2799-2807.
[17] 李军徽, 侯涛, 穆钢, 等. 电力市场环境下考虑风电调度和调频极限的储能优化控制[J]. 电工技术学报, 2021, 36(9): 1791-1804. Li Junhui, Hou Tao, Mu Gang, et al. Optimal control strategy for energy storage considering wind farm scheduling plan and modulation frequency limitation under electricity market environment[J]. Transactions ofChina Electrotechnical Society, 2021, 36(9): 1791-1804.
[18] Bao Zhejing, Zhou Qin, Yang Zhihui, et al. A multi time-scale and multi energy-type coordinated microgrid scheduling solution—part I: model and methodology[J]. IEEE Transactions on Power Systems, 2014, 30(5): 2257-2266.
[19] 何翔路, 娄素华, 吴耀武, 等. 双结算模式下风储一体化电站两阶段市场投标调度策略[J]. 电力系统自动化, 2022, 46(4): 47-55. He Xianglu, Lou Suhua, Wu Yaowu, et al. Two-stage market bidding and scheduling strategy of integrated wind power and energy storage station in dual-settlement mode[J]. Automation of Electric Power Systems, 2022, 46(4): 47-55.
[20] 宋煜浩, 魏韡, 黄少伟, 等. 风储联合电站实时自调度的高效深度确定性策略梯度算法[J]. 电工技术学报, 2022, 37(23): 5987-5999. Song Yuhao, Wei Wei, Huang Shaowei, et al. Efficient deep deterministic policy gradient algorithm for real-time self-dispatch of wind-storage power plant[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5987-5999.
[21] 颜宁, 潘霄, 张明理, 等. 基于复合储能的多互联微电网日内调度研究[J]. 电工技术学报, 2018, 33(增刊2): 577-585. Yan Ning, Pan Xiao, Zhang Mingli, et al. Research on intra-day dispatch of multi-connected microgrids based on hybrid energy storage[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 577-585.
[22] 刘念璋, 杨健, 柳玉, 等. 分布函数差异化导向的风电功率预测误差气象条件概率建模方法[J]. 电力自动化设备, 2022, 42(12): 58-65. Liu Nianzhang, Yang Jian, Liu Yu, et al. Probabilistic modeling method of weather condition for wind power forecasting error based on differentiation orientation of distribution function[J]. Electric Power Automation Equipment, 2022, 42(12): 58-65.
[23] 吴浩天, 孙荣富, 廖思阳, 等. 基于改进气象聚类分型的短期风电功率概率预测方法[J]. 电力系统自动化, 2022, 46(15): 56-65. Wu Haotian, Sun Rongfu, Liao Siyang, et al. Short-term wind power probability forecasting method based on improved meteorological clustering and classification[J]. Automation of Electric Power Systems, 2022, 46(15): 56-65.
[24] Yu H, Chung C Y, Wong K P, et al. Probabilistic load flow evaluation with hybrid Latin hypercube sampling and cholesky decomposition[J]. IEEE Transactions on Power Systems, 2009, 24(2): 661-667.
[25] 方珂, 柯德平, 孙元章, 等. 考虑大规模直流馈入稳定约束的电网优化调度模型[J]. 南方电网技术, 2022, 16(7): 1-9. Fang Ke, Ke Deping, Sun Yuanzhang, et al. Grid optimal dispatching model considering stability constraints of large-scale HVDC infeed[J]. Southern Power System Technology, 2022, 16(7): 1-9.
[26] 赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测[J]. 电工技术学报, 2022, 37(5): 1242-1251. Zhao Yang, Wang Hanmo, Kang Li, et al. Temporal convolution network-based short-term electrical load forecasting[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1242-1251.
[27] 宫宇. 基于粒子群算法的配电网故障区段定位与恢复重构研究[D]. 重庆: 重庆理工大学, 2022.
Abstract The rational optimization of the power reported by wind farms to the grid is a critical routine to improve the benefits of wind farms under the assessment of the ‘two detailed rules’. However, most of the traditional wind power reporting studies report the predicted power directly, or report the expected wind power obtained by superimposing the forecast error distributions with the predicted power. In addition, the sales revenue, the compensation for ancillary services are employed as the main optimization goals in these studies. Hence, it is difficult to apply the traditional reporting strategies directly under the background of the ‘two detailed rules’ assessment. To address these issues, this paper proposes a two-stage day-ahead and intra-day optimized power reporting strategy of wind-storage stations that fits the mechanism of the ‘two detailed rules’ assessment.
Firstly, the framework of the proposed strategy is constructed, where the day-ahead reporting results are embedded in the intra-day reporting model as the key to synergy, in order to achieve the optimal power reporting on both two time scales for the ‘two detailed rules’ assessment. Secondly, the specific assessment mechanism of the ‘two detailed rules’ in central China is used as an example to formulate the day-ahead and intra-day optimized wind power reporting model respectively. Particularly, the expected assessment power of day-ahead wind power scenarios is regarded as the objective function of the day-ahead reporting model. Besides, the reported wind power series obtained by the day-ahead model is utilized in the intra-day reporting model. With the energy storage as the medium, the total assessment power of all intra-day wind power scenarios on the two time scales can be minimized in the intra-day model. As for the scenario generation, the day-ahead and intra-day historical errors are binned according to meteorological conditions and different forecast time steps respectively. The Cornish-Fisher series and Cholesky decomposition are applied to generate and reorder the error scenarios considering temporal correlations. By superimposing the reordered error scenarios with the predicted power, the day-ahead and intra-day wind power scenarios can be obtained to refine the wind power reporting model. Owing to the requirements of different time scales for the model solving, a two-stage algorithm is proposed. In the day-ahead stage, due to the small scale of the model, the improved bald eagle search (IBES) algorithm with strong global search ability is adopted. In the intra-day stage, in order to meet the requirements of 15-minutes rolling reporting for solving efficiency, a small step linearized iteration-based solving algorithm is developed to transform the intra-day model with multiple nonlinear constraints into linear models. Simulation results on an actual wind farm in central China show that, the difference between the correlation coefficients of reordered error scenarios and historical error samples are no more than 0.022 8 on average. Furthermore, compared with reporting the forecast power and reporting the optimized power based on independently solving the day-ahead and intra-day model, the two-stage collaborative power reporting strategy can reduce the assessment power by more than 50% in both two time scales. In addition, the small step linearized iteration-based solving algorithm can efficiently solve the intra-day model on average 30 s, which is less than other types of intelligent algorithms. Meanwhile, compared with the regulation of the energy storage based on the predicted power, the proposed reporting strategy saves about half of the discharge electricity.
The following conclusions can be drawn from the simulations: (1) The reordered wind power scenarios is more in line with the correlation characteristics of historical samples, which lays a foundation for the modeling of reporting. (2) Compared with other reporting strategies, the two-stage collaborative reporting strategy can better fit the trend of actual wind power and reduce the assessment power. (3) The small step linearized iteration-based solving algorithm balances the optimization effect and solution efficiency, which is worthy of practical application. (4) The proposed energy storage optimization scheme is more energy-efficient than the scheme based on the predicted power, and it helps to extend the life of energy storage.
keywords:Two detailed rules, wind power reporting, day-ahead and intra-day coordinative optimization, temporal correlation, regulation of energy storage
DOI:10.19595/j.cnki.1000-6753.tces.221837
中图分类号:TM76
国家电网公司总部科技项目资助(5100-202199286A-0-0-00)。
收稿日期 2022-09-30
改稿日期 2022-11-22
吴浩天 男,1998年生,博士研究生,研究方向为新能源概率预测与优化上报,随机经济调度等。E-mail: gswcurry30ww@qq.com
刘念璋 男,1997年生,硕士研究生,研究方向为新能源预测与误差建模等。E-mail: nianzhangliu@whu.edu.cn(通信作者)
(编辑 赫 蕾)