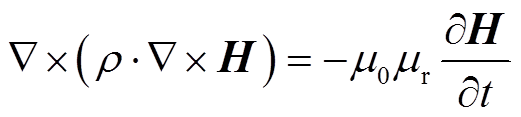（1）
摘要 高温超导带材失超会降低其通流能力，从而影响高温超导装置的运行稳定性。目前，高温超导带材失超仿真模型多为二维计算模型，无法准确模拟其失超过程中的电磁热行为。该文采用有限元方法对二代高温超导带材失超特性进行多物理场耦合分析。在三维直角坐标系下，以磁场强度矢量为求解变量，建立了二代高温超导带材失超演化电磁热仿真模型，研究了二代高温超导带材长度方向与宽度方向在不同热扰动工况下的电磁热特性及其演化过程，分析了高温超导带材过电流失超过程中的各层分流状况与超导层电阻率变化行为，区分了不同类型的过电流失超行为，并提出了高温超导带材过电流冲击失超的电阻率判据。
关键词：二代高温超导带材 失超特性 有限元 电磁热耦合
随着超导技术的进步，高温超导带材商业化应用发展迅速。目前二代高温超导带材已广泛应用于超导储能磁体、高场磁体、超导限流器、超导电缆等超导电工设备[1-4]。
稳定性对于超导电工装备的设计、制造和运行至关重要。超导带材失超会对其局部造成损害，使超导电工设备的运行失去稳定，进而导致超导电工设备损坏[5-6]。高温超导带材失超传播速度较低，缓慢的失超传播速度可能导致检测信号和失超保护动作滞后，从而引起局部热量积累[7]。另一方面，失超过程中的局部温升会产生巨大的热应力，失超传播通常伴随着高温超导带材应力应变的发生，进一步加剧超导电力设备失效。因此，对高温超导带材的失超特性研究尤为重要[8]。
在高温超导带材制作过程中，由于制作工艺问题，可能导致其各部分临界电流不均匀；在高温超导线圈绕制、浸渍过程中，其会受到拉力、应力等机械作用，容易造成局部超导层出现损伤。此外，高温超导磁体各个部位的磁场不同，也可能导致其局部高场区域先发生失超；在超导装置实际应用中，也可能由于短路故障或其他不可预见的意外导致超导带材承受过电流冲击。因此，有必要开展高温超导带材局部热点引起的失超传播持性[9-10]和超导带材整体过电流失超行为研究[11-13]。
目前，高温超导带材失超仿真模型多为二维计算模型[14]，且多只集中于研究带材长度方向由局部热点引发的失超问题。二维模型仅能用于计算超导带材失超传播速度及最小失超能，无法模拟超导带材失超过程中宽度方向的电磁热行为。此外，失超过程中电磁热多场耦合变化是非常复杂的非线性微分方程求解问题，无法直接通过求解微分方程得到准确解。因此，需要建立一种准确的多物理场耦合有限元模型，分析二代高温超导带材失超过程。
为解决上述问题，本文将借助COMSOL有限元多物理场仿真软件，以磁场强度矢量为求解变量，结合超导材料的E-J特性，建立二代高温超导带材失超传播三维仿真模型，对二代高温超导带材局部失超与过电流失超过程中的电磁热特性开展研究。
根据准静态近似，结合安培定律与电磁感应定律[15]，可以推导出
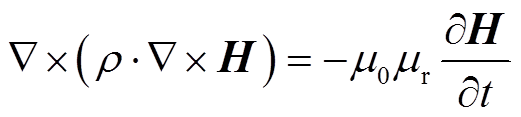（1）
式中，ρ为材料电阻率；H为磁场强度；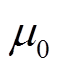
为真空磁导率；μr为相对磁导率。
以式（1）作为控制方程，在三维空间中定义磁场矢量为H=[Hx Hy Hz]，如图1所示。
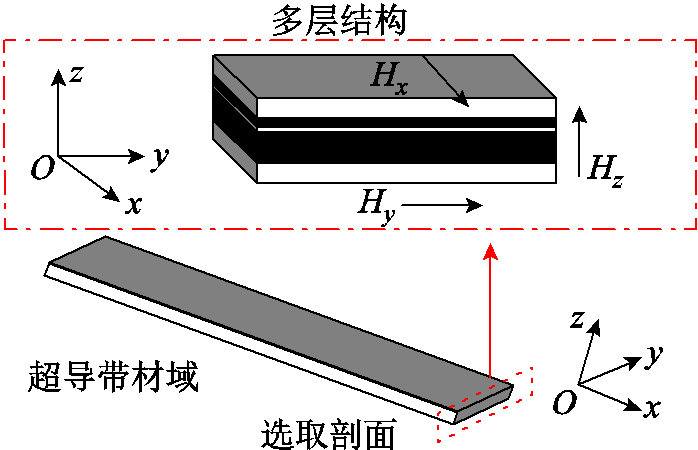
图1 三维空间中磁场强度矢量H定义
Fig.1 Definition of magnetic field intensity vector H in three-dimensional space
根据安培定律，可将电流密度矢量J求解为
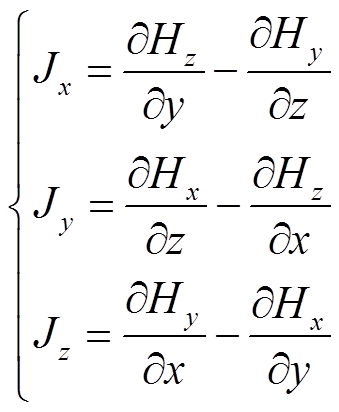（2）
进一步地，推导得到电磁计算的控制方程[16]
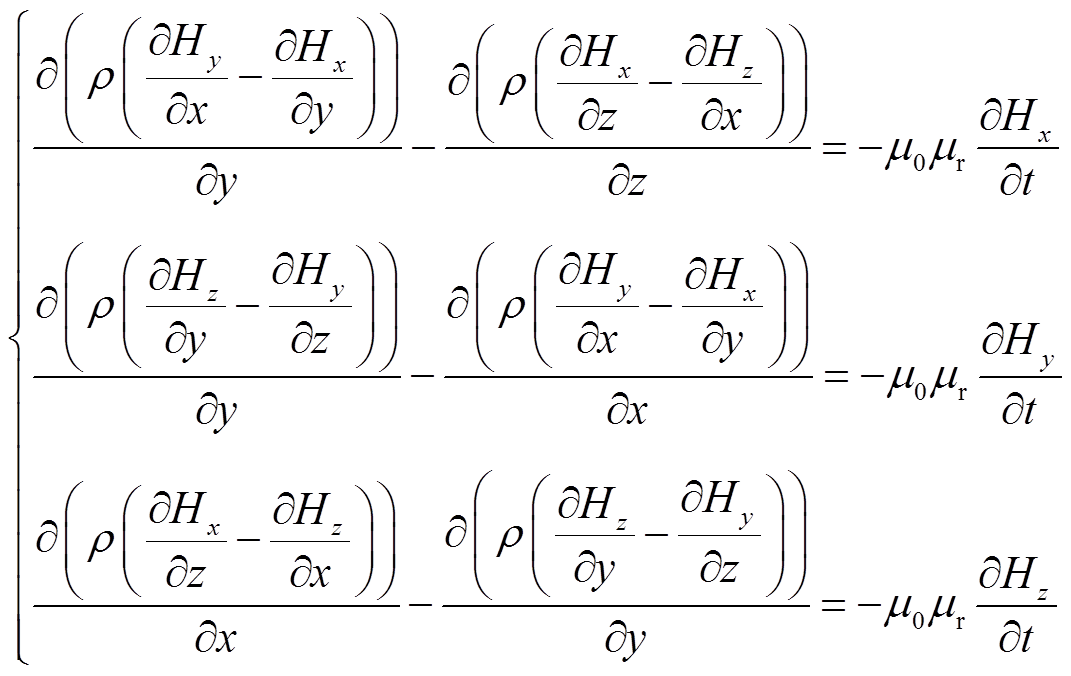（3）
结合超导E-J幂律，完成超导层电阻率rsc分段设置如式（4）所示。对超导层电阻率采用并联等效电路的方法以描述超导特性，将临界温度Tc作为状态转变的判据[17]。
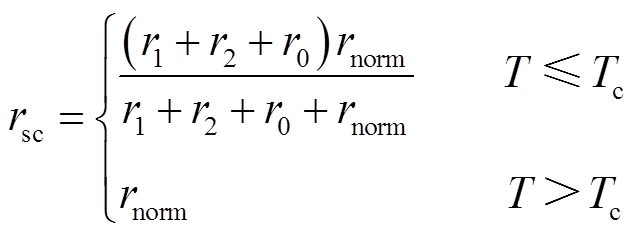（4）
式中，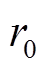
为残余电阻率；rnorm为失超后电阻态电阻。
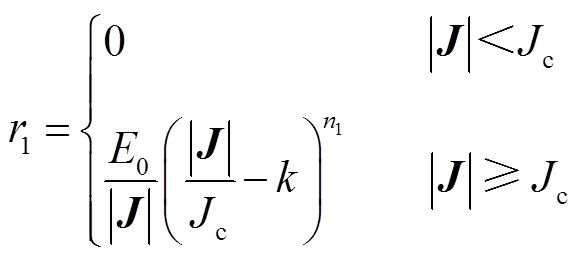（5）
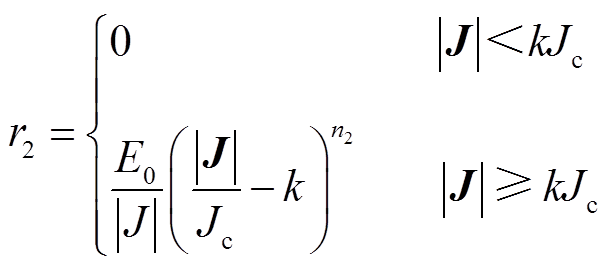（6）
式中，n1与n2为两个幂律关系的拟合参数，本文中，n1=2.8，n2=22；Jc为高温超导带材的临界电流密度；k为根据r1(3Jc)= r2(3Jc)计算出来的拟合参数[16]，k=1.92；E0为超导带材失超电压判据。
高温超导材料的临界电流密度Jc受到温度T的影响。根据文献[18]，其关系可表示为
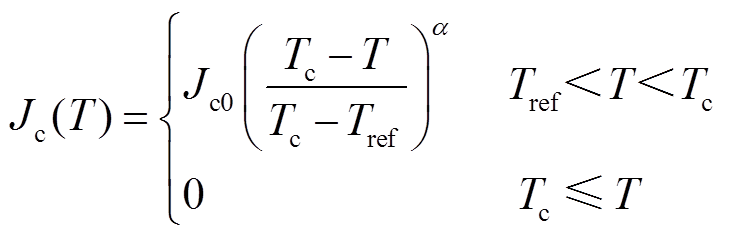（7）
式中，Jc0为参考温度时超导带材自场临界电流密度；Tref为超导带材参考温度；α为超导带材临界电流密度受到温度影响的函数拟合出的幂指数，本文中α =1.5。
结合热传导公式实现电磁热多场耦合，热传导方程为
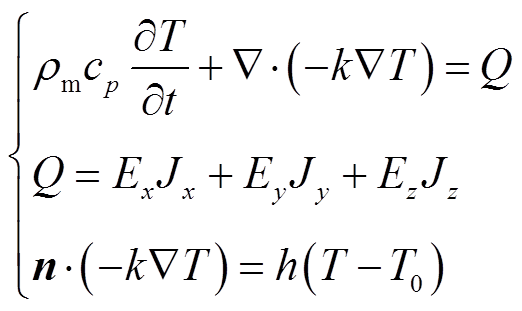（8）
式中，ρm为材料密度；cp(T)和k(T)分别为材料比热容和热导率；h(T)为表面传热系数，材料热学属性函数均与温度相关，在模型中通过拟合函数赋值。模型仿真物性参数见表1。在整个迭代求解过程中，超导带材产生的热量Q会被反复输入，实现热参数实时更新。
表1 模型仿真物性参数
Tab.1 The simulation physical parameters of modelling
参数数值 超导残余电阻率r0/(Ω·m)1×10-16 超导带材失超电压判据E0/(μV·cm-1)5 参考温度时超导带材自场临界电流密度Jc0/(A·m-2)2.5×1010 超导带材参考温度Tref/K超导带材临界温度Tc/K77 92 超导层材料密度/(kg/m3)5 900 铜层材料密度/(kg/m3)8 940 银层材料密度/(kg/m3)10 500 基底层材料密度/(kg/m3)8 910
在COMSOL有限元多物理场仿真软件中，以典型的二代高温超导带材SCS4050为例，建立超导带材三维模型，如图2所示。二代高温超导带材由超导层、哈氏合金基底层、镀银层、镀铜层、氧化物过渡层等组成，实际建模过程中忽略氧化物过渡层，超导各层材料热学属性通过函数拟合得到。超导带材仿真几何参数见表2。将超导线圈与冷却介质交界处设置为热通量边界，设置热通量类型为对流热通量，冷却介质换热系数为与温度相关的插值函数，用以模拟涂层超导带材在冷却介质中的实际冷却运行工况。
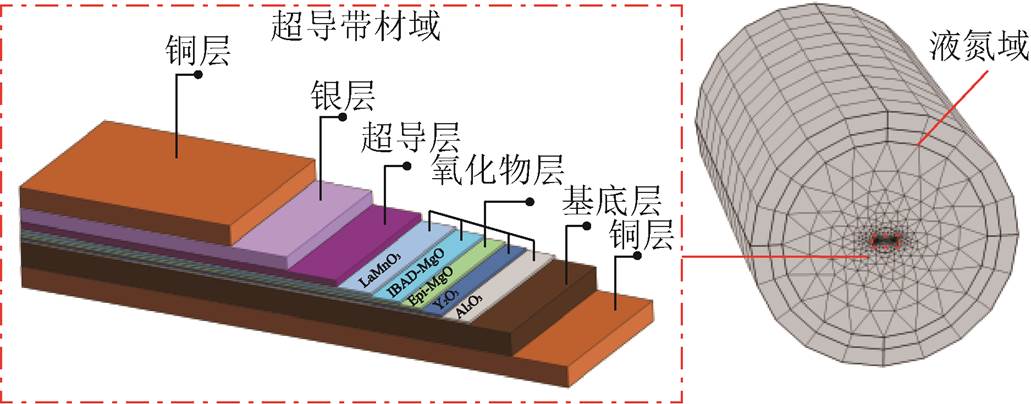
图2 仿真模型几何建模
Fig.2 The geometric of simulation model
表2 超导带材仿真几何参数
Tab.2 The geometric parameters of superconducting tape simulation
参数数值 带材长度lstape/mm260 带材宽度wstape/mm4 超导层厚度hsc/μm1 银层厚度hAg/μm2 铜层单层厚度hCu/μm20 基底层厚度hhast/μm50
鉴于高温超导带材的失超行为与其局部乃至整体热行为密切相关，且下文将对高温超导带材正常通流及不同热扰动下的温度分布进行分析，有必要对模型的有效性进行验证。本节拟使用上述三维模型对高温超导带材的交流损耗进行仿真，并将仿真结果与理论计算、实验测量值进行比较。
根据Norris经验法，单根高温超导带材不同电流幅值下的工频传输损耗解析计算式为
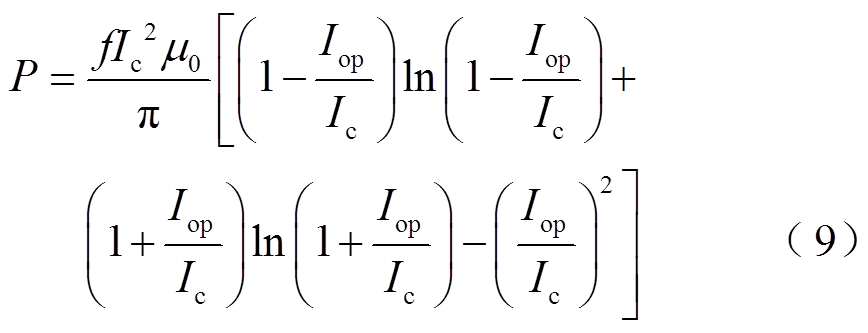
式中，f为传输电流的频率；Ic为超导带材的临界电流值；Iop为运行工作电流；μ0为真空磁导率，大小为4π×10-7。
交流损耗实验测量采用电测法。基于锁相放大器搭建了SCS4050单根带材交流损耗测量平台，交流损耗测量电路如图3所示。锁相放大器采用内参考模式，控制双极性电源输出正弦电压，采用环形变压器降压升流，采用高精度管式分流器作无感电阻，获取传输电流的相位，给锁相放大器提供参考信号，电流钳用来读取传输电流的有效值Irms。锁相放大器测得的带材电压引线间阻性电压分量Urmscosθ即为带材的等效损耗电压，则所测得超导带材交流损耗Q为
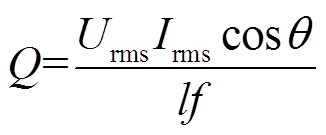（10）
式中，l为高温超导带材长度。
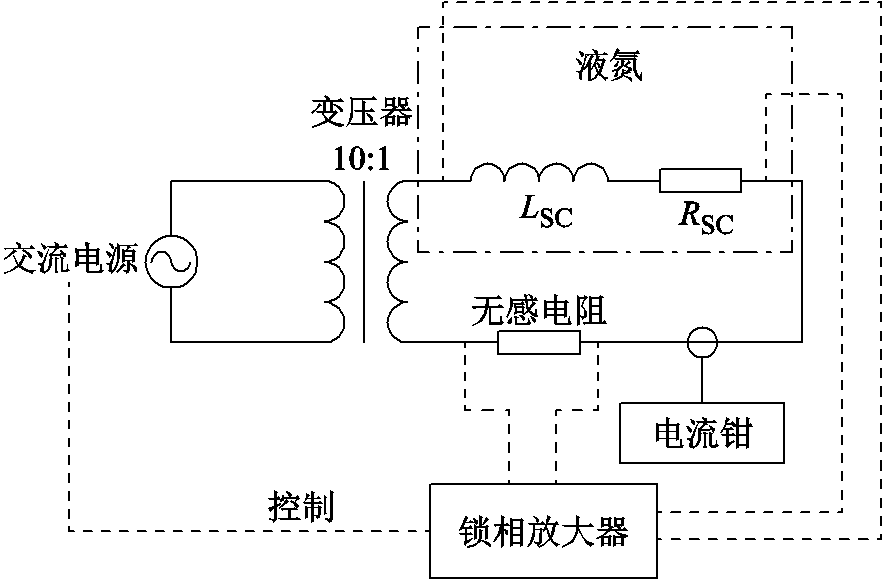
图3 超导带材交流损耗测量电路
Fig.3 AC loss measurement of superconducting tape
基于上述平台，测量了SCS4050单根带材的不同电流幅值下的交流损耗。将模型仿真计算结果与Norris经验公式计算结果、电测法实验测量结果进行比较如图4所示。
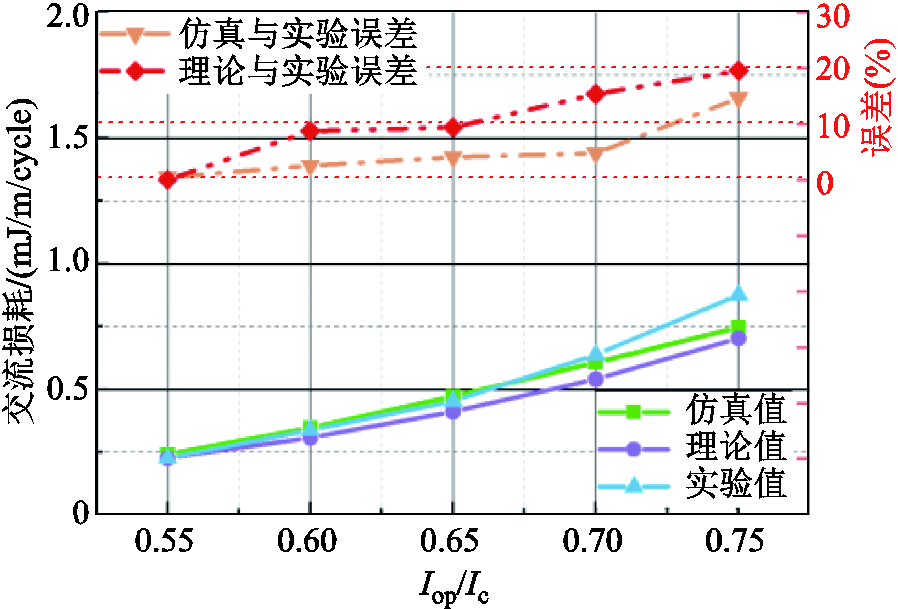
图4 交流损耗仿真、理论及实验结果对比
Fig.4 AC loss simulation, theoretical and experimental comparison
由图4可知，高温超导带材交流损耗仿真值随带材载流比的变化趋势与实验值、理论值的变化趋势一致，且仿真结果处于理论值与实验值之间，更贴近于实验结果。此外，由图中误差对比结果可知，该三维模型仿真计算误差更小，更接近实际值。
正常通流0.6Ic时，超导带材电磁热行为如图5所示。为了使多场分布更加直观清晰，图5中对带材长宽（带材宽度方向与长度方向）比重新进行了设置（下同）。正常通流过程中，超导带材的温度维持在冷却介质温度（77 K）；最大电流密度为2.32×1010 A/m2，达到0.928Jc，集中在图5中超导带材的上、下两端（即超导带材宽度方向两端）各约11%区域；最小电流密度为1.09×1010 A/m2，为0.436Jc，最大电流密度为最小电流密度的2.13倍。
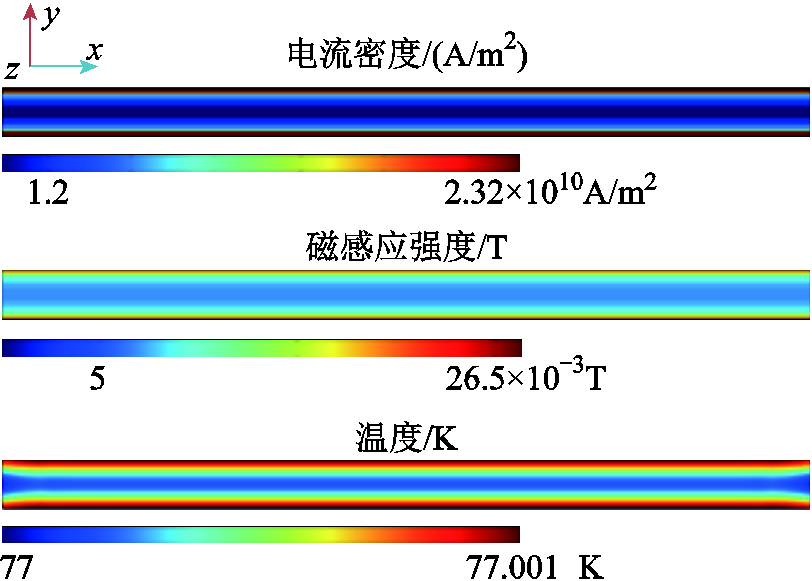
图5 超导带材正常通流时电磁热行为
Fig.5 Electromagnetic-thermal behavior of superconducting tape under normal current
电流集中在图5中超导带材的上、下两端，导致其产生的磁场也主要分布在带材宽度方向的两端边缘，最大磁感应强度为0.026 5 T。除此之外，带材中存在着未被磁通穿透的区域，即图5中磁场分布的深蓝色区域，模型体现出了超导体的抗磁性。
对于二代高温超导带材，最小失超能Qmq及失超传播速度Vnzp的研究是磁体稳定性分析及失超探测与保护方案选择的前提，是表征其失超传播特性的两个主要参数[19-20]。
在仿真软件中通过约束方式给超导带材通流，1 s后达到额定值，维持工作电流不变。在带材中间区域设置热源，热扰动在1.9 s时发生，3.2 s时结束，模拟带材在通流时由缺陷引发的局部热点。
2.2.1 最小失超能与失超传播速度
温度探针布置如图6所示，通过在带材上设置域点探针进行温升检测，可以方便、直观、有效地计算带材失超传播特性。在不同热扰动下，探针T1测得温度变化情况如图7所示。
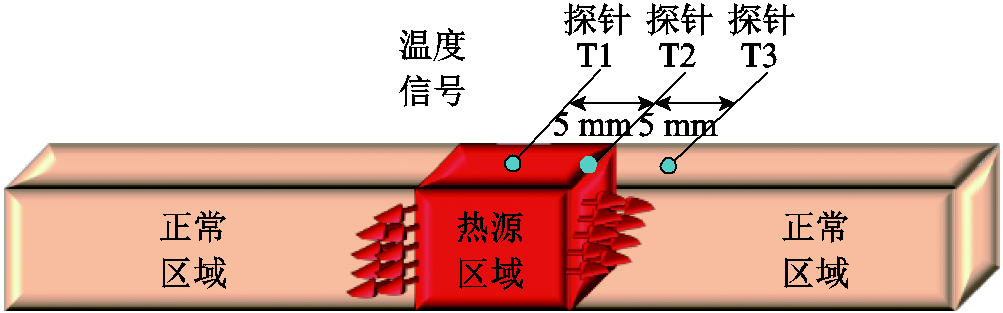
图6 温度探针布置
Fig.6 Temperature probe arrangement
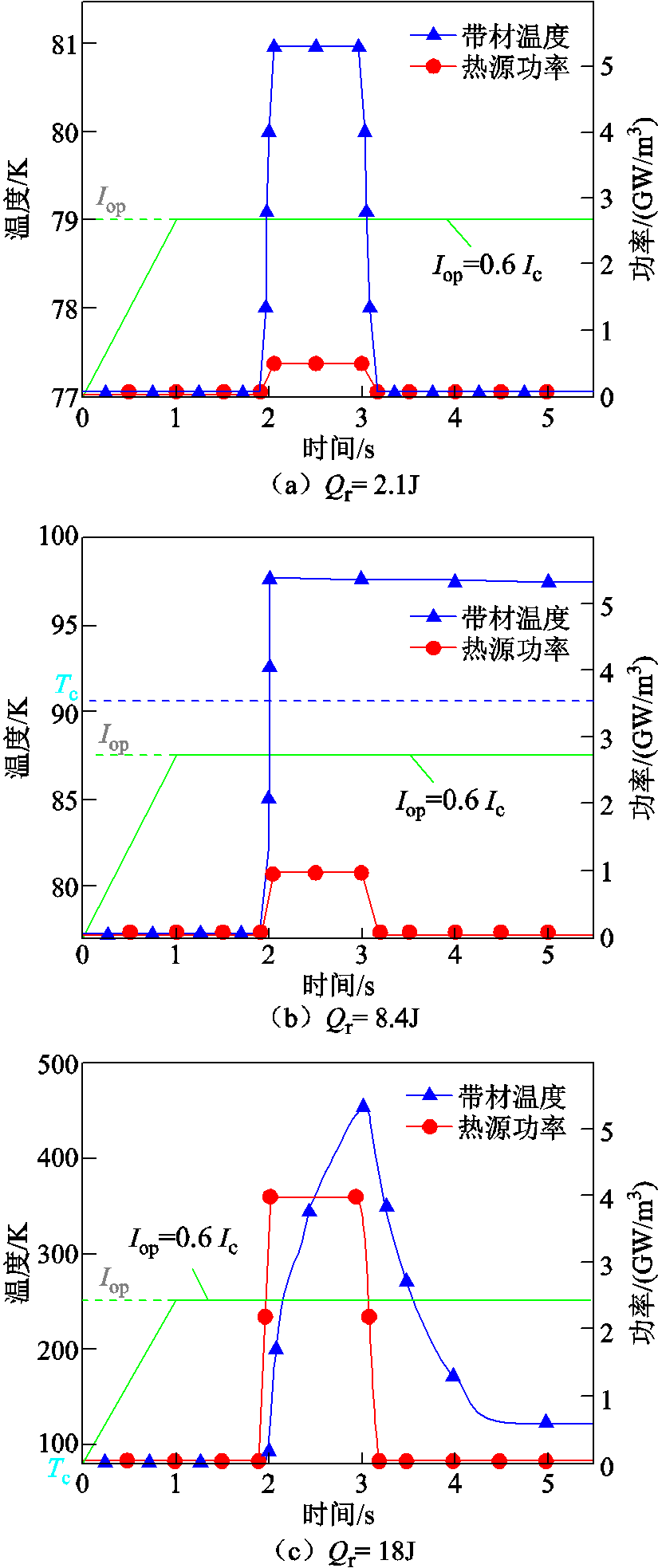
图7 不同热扰动下的温度变化情况
Fig.7 Temperature variation under different thermal disturbances
当热源能量Qr小于最小失超能Qmq时，热扰动结束后，热源区域探测点的温度将降至临界温度之下；当热源能量Qr大于最小失超能Qmq时，热扰动结束后，热源区域探测点的温度达到峰值。由于失超传播造成超导带材稳定性失衡，即使热扰动结束后温度回落，带材失超区域也一直维持在临界温度之上。
因此，对于最小失超能，可以采用二分法查找确定。可先用两组热扰动进行测试，若一组失超而另一组没有，则取中间值作为新的热扰动功率。如此重复，即可获得一个比较精确的最小失超能结果。
失超传播速度求解如图8所示。参考动力学速度公式求解二代高温超导带材失超传播速度，求解失超传播速度Vnzp公式为
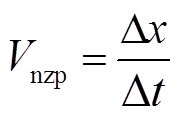（11）
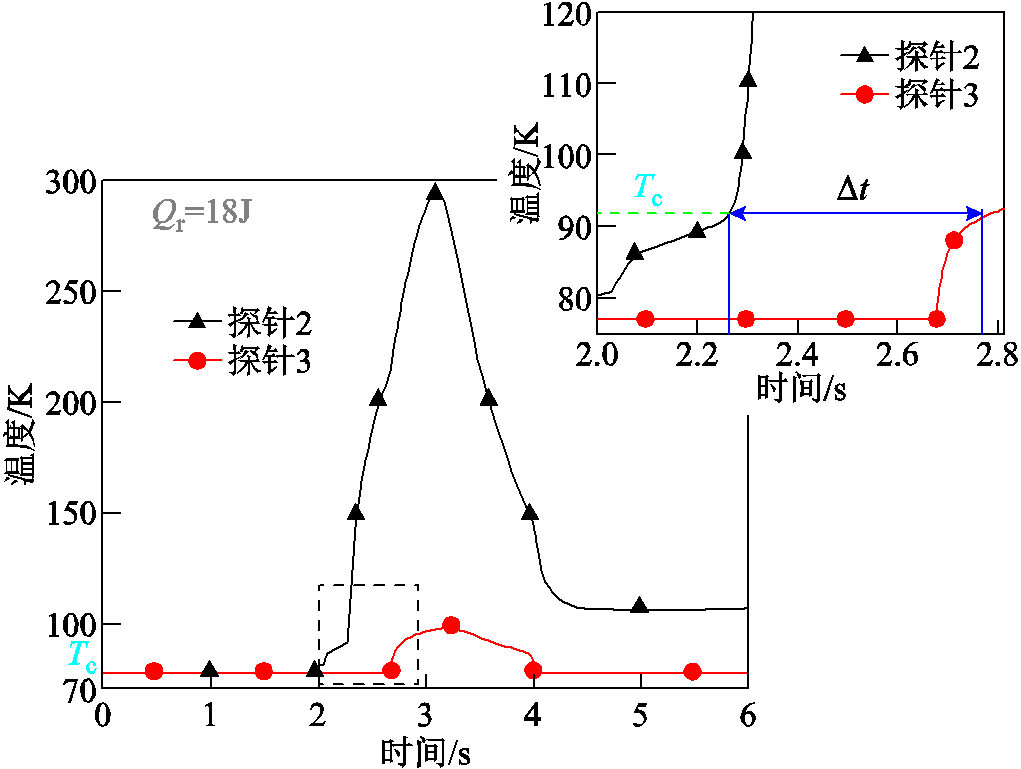
图8 失超传播速度求解
Fig.8 The solving process of quench propagation velocity
式中，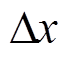
为两相邻温度信号采集点之间距离；
是两温度信号达到失超判据的时间差。
通过计算，在工作电流Iop=0.6Ic时，二代高温超导带材最小失超能为4.62J，失超传播速度为0.96 cm/s。
2.2.2 不同热扰动下电磁热行为
不同热扰动下，高温超导带材电磁热行为不同。当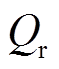
分别为2.1 J（0.45Qmq）、8.4 J（1.82Qmq）和18 J（3.90Qmq）时，其在2.1 s、2.5 s、3.1 s、4.0 s、4.5 s的电流密度、磁场和温度变化如图9所示。
由图9可知：
1）当局部热源能量Qr小于最小失超能Qmq时，热量积累将导致超导层最大电流密度从正常通流时的2.32×1010 A/m2降到2.03×1010 A/m2；在热扰动过程结束之后，由于热量尚未完全消散，最大电流密度将持续下降至1.88×1010 A/m2，整个过程中最大电流密度下降了19%。最小电流密度与之相反，从正常通流时1.09×1010 A/m2持续上升到1.25×1010 A/m2，达到正常通流时的115%。最大电流密度下降导致超导带材产生的磁场随之下降，4.0 s时，最大磁感应强度下降到0.022 1 T，为正常通流时最大磁场的83%。
结合图7a所示，热源区域超导带材的温度随着热扰动的施加开始上升，由77 K上升至81 K，但未达到临界温度，故超导带材未发生失超。随着热扰动结束，带材温度在4.0 s时恢复至初始温度77 K。4.0 s后虽然超导带材恢复至初始温度，但是其电流密度分布与磁场分布并未恢复至正常通流状态，这是由于热扰动过程在一定程度上影响了带材的热稳定性，使得热扰动结束后带材具有“疲劳特性”，无法恢复至正常通流状态。
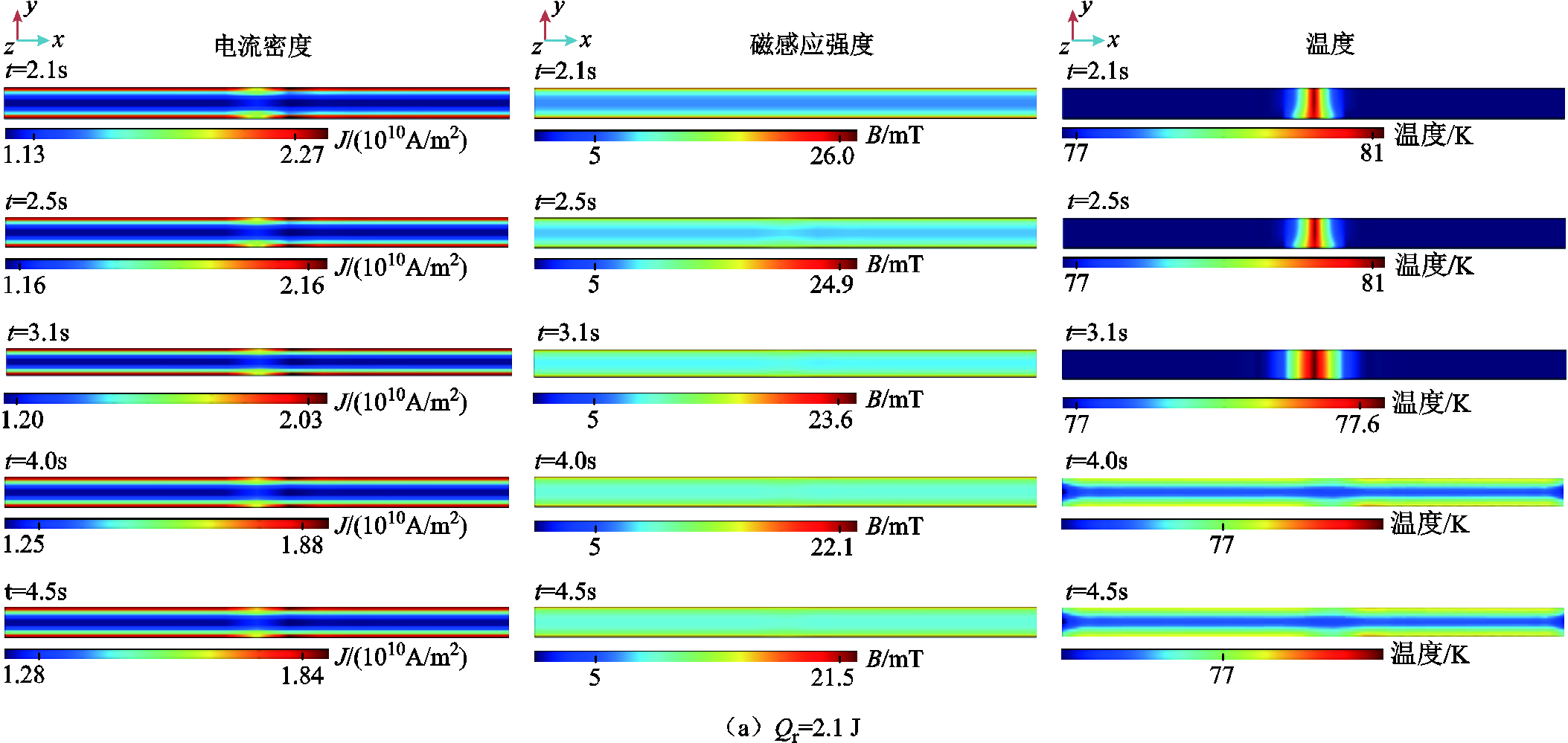
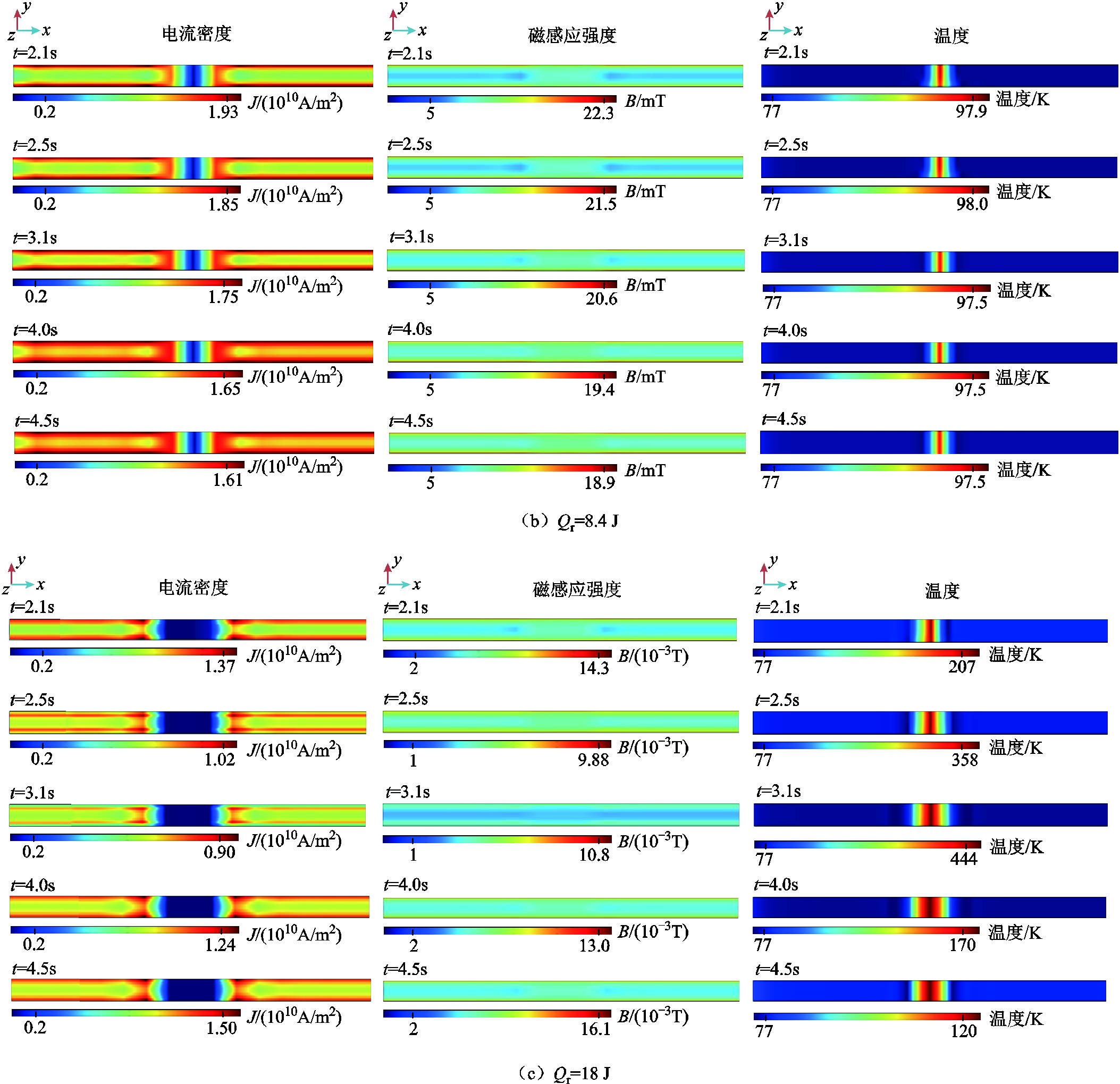
图9 不同工况下超导带材电磁热行为对比
Fig.9 Comparison of electromagnetic-thermal behavior of superconducting tape under different working condition
2）当局部热源能量Qr大于最小失超能Qmq时，带材发生失超。根据程度不同，分为两种情况：
（1）当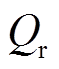=1.82Qmq时，整个过程中超导层最大电流密度持续下降。4.5 s时，下降至1.61×1010 A/m2，为正常通流时最大电流密度的69%。由于超导带材发生局部热点失超，故载流稳定性受到影响。热扰动结束后，超导带材上、下两端（即超导带材宽度方向两端）红色区域扩大，即超导带材最大电流密度区域扩大。同样，最大电流密度下降导致磁感应强度随之下降，4.5 s时最大磁场持续下降到0.018 9 T，为正常通流时最大磁场的71%。
结合图7b，热扰动发生时，超导带材热源区域温度随着热源扰动上升至97.9 K，高于超导带材临界温度，引发超导带材失超。由于热源功率较小，虽然对带材的热稳定性产生影响，但是超导带材的产热和散热能够达到平衡状态，超导带材内部并未完全转变为电阻态。故带材温度在达到峰值之后，在热源扰动期间维持在该温度，且产生的失超温度较低。但是，由于热源扰动能量大于最小失超能，产生超导带材阻性分量，引发超导带材失超，热扰动结束之后，带材温度有所恢复，但未恢复至正常温度，仍保持在临界温度之上，使得带材局部区域一直处于失超状态。
（2）当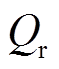=3.90Qmq时，在热扰动阶段，超导层载流能力显著性下降。3.1 s时，最大电流密度下降到0.90×1010 A/m2，仅为正常通流时的39%，且最大电流密度区域（图9c中红色区域）向带材内部偏移。热扰动结束之后，最大电流密度回升，但受到失超传播影响，4.5 s时仍仅为正常通流时最大电流密度的65%，最大电流密度区域偏移回到带材两端边缘。对比图9b与图9c可知，失超程度的加深使得电流密度分布区域（图中深蓝色区域）扩大，由占整根带材的6%上升到19%。磁场分布变化与电流密度变化趋势相同，在此不再赘述。
结合图7c可知，在整个热扰动期间，超导带材温度持续上升，且上升速率逐渐变缓。热扰动结束时，超导带材温度达到最高温度444 K，4.5 s时温度回降到120 K，并一直维持在该温度。此过程中，带材内部热量高于散热，热量不断积累，带材温度远高于临界温度，热源区域由超导态转变为电阻态，失超产生并沿带材左右对称传播，使得失超区域进一步扩展至扰动初始阶段失超区域2倍。
2.2.3 超导层局部热点失超电磁热行为
超导层局部热点失超热源设置如图10所示，更改热源设置，使热扰动仅在超导层发生，模拟二代高温超导带材超导层缺陷形成局部热点所产生的失超传播过程。当热扰动能量为18 J时，探针1测得温度变化情况如图11所示。
图10 超导层局部热点失超热源设置
Fig.10 Setting of hot spot in superconducting layer
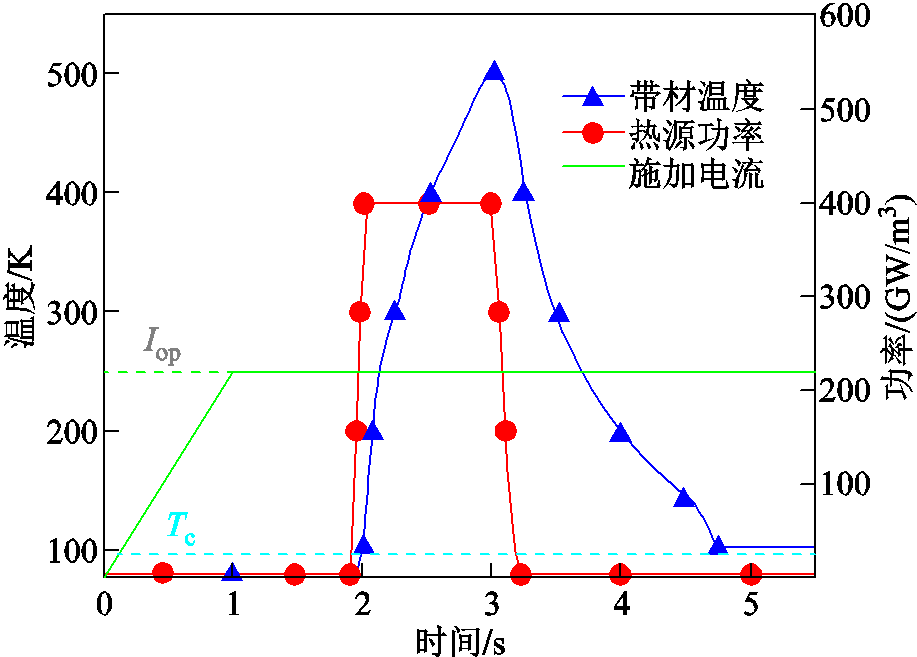
图11 超导层局部热点失超过程中温度变化情况
Fig.11 Temperature variation during hot spot quench of superconducting layer
随着热源扰动，带材温度持续上升，热源扰动结束时，温度达到最高温度500 K。与图7c相比，由于热源区域较小，热扰动消除之后，带材温度下降至96 K，超导带材热稳定性受到影响，仍为部分电阻态，即为局部失超状态。
当仅在超导层产生缺陷造成局部热点失超时，三个方向的电流密度变化行为如图12所示。此时电流不再只在超导层沿带材方向流动，而是通过超导带材非超导层向其他方向流动，绕过热点区域，从而实现超导带材通流。
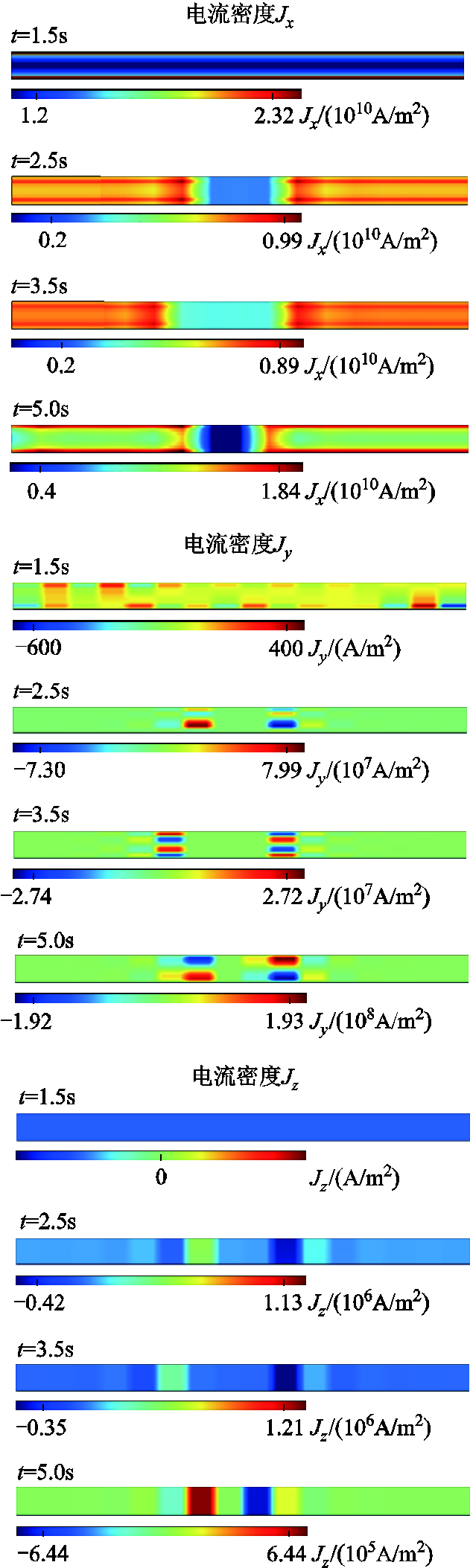
图12 失超过程中电流密度矢量变化情况
Fig.12 The variation of different current density vectors during quench
2.3.1 过电流冲击过程中电流分层行为
为了解过电流冲击下高温超导带材的失超行为，对构建的超导带材模型施加过电流冲击，整个过程持续0.8 ms，电流最大值约为1.5Ic，通过电流波形与冲击时间模拟实际故障情况。过电流冲击下，超导带材各层电流分流情况如图13所示。
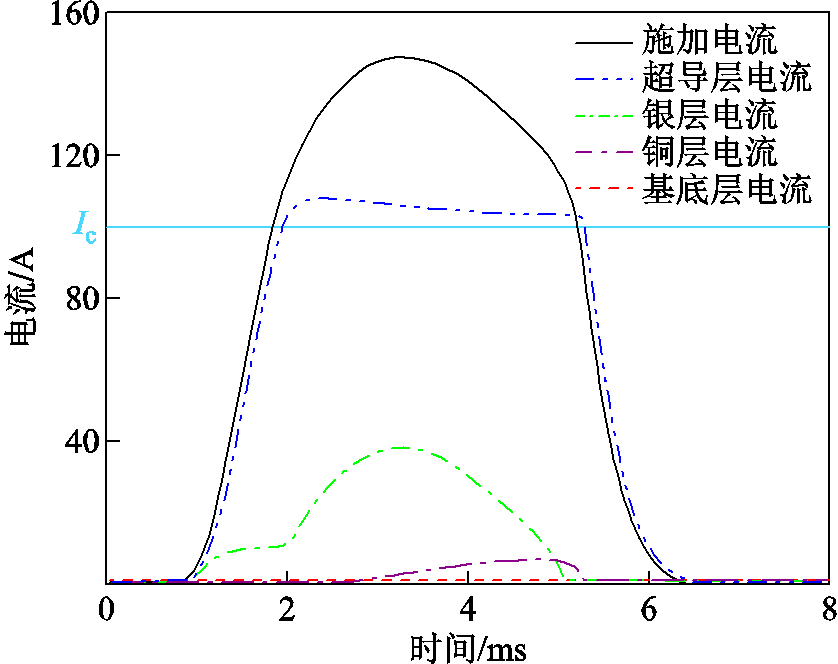
图13 过电流冲击下超导带材各层分流情况
Fig.13 The shunt situation of superconducting tape layers in the process of overcurrent
当冲击电流低于超导带材临界电流时，传输电流基本上由超导层承载。2 ms后，当冲击电流高于临界电流后，电流在超导带材各层中具有明显的分流行为：由于基底层电阻率远高于其他层，基底层在整个过程中基本上无电流流过；铜层与银层电流逐渐上升，5 ms后，随着冲击电流降为低于带材临界电流，铜层、银层电流降为0；2～5 ms过程中，冲击电流超过临界电流，超导层承载电流基本维持在临界电流。
通过该模型，可计算整个过程中超导带材各层载流情况。在4 ms时，分流现象较为明显，此时除去超导层所承载电流，银层与铜层各分得剩余电流的16%与84%。当施加电流超过临界电流时，银层承载电流随着冲击电流先升高后减小，而铜层承载电流逐渐增加，这是由于银层贴近超导层，当冲击电流超过临界电流，超导层先向银层分流，银层载流持续增加产生热量积累，电阻率逐渐上升至与铜电阻率相近，铜层此时逐渐承载电流，且铜层厚度高于银层，故铜层承载电流逐渐上升。
图14展示了过电流冲击下超导层电阻率变化情况。2 ms时施加电流超过临界电流，超导层电阻率开始上升，4.3 ms时超导层电阻率上升至峰值1.2×10-11 Ω·m。5 ms时，施加电流降至低于临界电流，超导层电阻率恢复至超导态1×10-17 Ω·m，此时超导层承载全部的施加电流。因此，结合图13可知，在过电流冲击过程中，由于施加电流导致的热量积累，超导层电阻率的上升使得超导带材各层呈现分流。
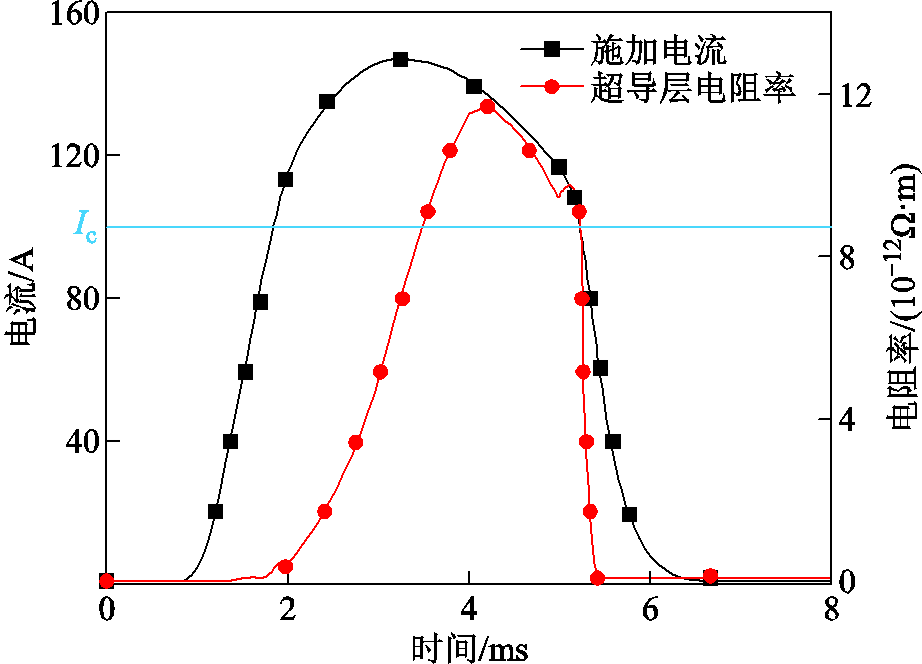
图14 过电流冲击过程中超导层电阻率变化情况
Fig.14 Resistivity change during overcurrent
2.3.2 不同程度过电流冲击下的超导层电阻率变化
对超导带材分别施加峰值为1.5Ic和2Ic的连续工频正弦波电流，得到带材各层承载电流能力如图15所示。
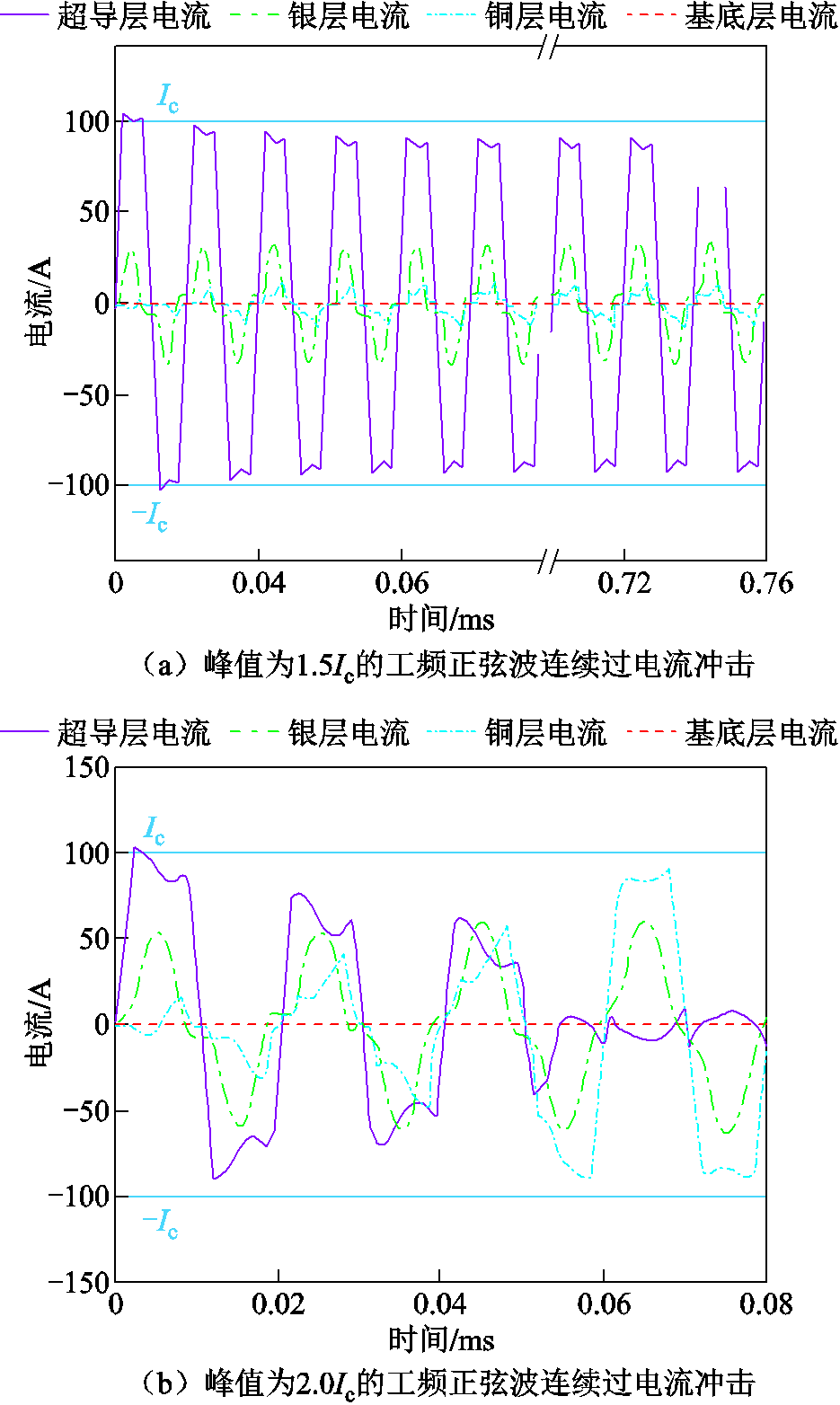
图15 连续过电流冲击中超导带材各层分流情况
Fig.15 Change of current and resistivity of superconducting layer under continuous overcurrent
由图15可知，过电流冲击电流峰值和持续时间不同，高温超导带材各层的分流情况有差异。整个电流冲击过程中，根据过电流程度与持续时间、以及超导带材各层载流情况，可将二代高温超导带材各层分流情况分为四个阶段：①当工频电流峰值低于Ic时，超导层承载全部电流，超导带材未失超；②当工频电流峰值低于1.5Ic时，且持续时间高于38个周波时，超导层电流开始向其他层穿透，但超导层仍具备稳定承载约0.8Ic的能力；③当工频电流峰值高于2Ic时，超导层电流向其他层高度穿透，3个工频周期后，超导层承载电流能力下降至0.5Ic，仍可具备一定载流能力；④当2Ic峰值电流持续4个工频周期后，超导层几乎不再承载电流。
第②、③阶段中，超导层在过电流冲击下仍具有承载电流的能力，可称此类型为可恢复型过电流失超；而第④阶段时，超导层不再承载电流，其他层承担绝大部分施加电流，此时，超导带材完全失超。因非超导层不具备大电流载流能力，热量在超导带材内部大量积累，最终可能导致超导带材烧毁，称此类型为不可恢复型过电流失超。
在以上四个阶段中，伴随着超导层载流情况的变化，其电阻率也相应发生改变。连续过电流冲击中超导层电阻率变化行为如图16所示，在第②、③阶段中，超导层电阻率峰值随着热量积累不断上升，达到整个过程中最高值5×10-8 Ω·m，高于银层、铜层电阻率5×10-9 Ω·m，本文将此电阻率峰值称为临界电阻率。因第②、③阶段中内部热量并未超过带材散热能力，因此，仍可在电流下降后逐渐恢复超导态，本文将此时的电阻率称为可恢复过电流失超导层电阻率。在第④个阶段，超导电阻率达到临界电阻率并持续过渡时间0.01 s后，内部积累热量远大于带材散热能力，在电流下降后，超导层无法恢复至超导态，将此电阻率称为不可恢复过电流失超电阻率。
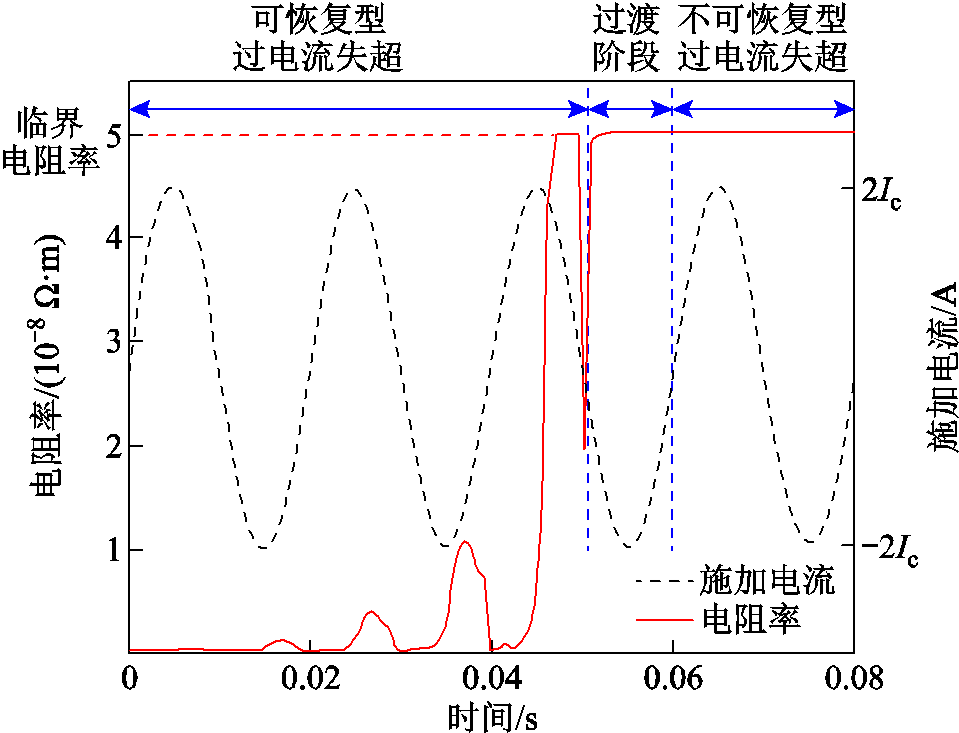
图16 连续过电流冲击中超导层电阻率变化行为
Fig.16 Resistivity change behavior of superconducting layer under continuous overcurrent
本文建立了二代高温超导带材电磁热耦合分析模型，对高温超导带材局部热点与整体过电流两种情况下带材失超过程中的电磁热特性进行了研究。结论如下：
1）与二维高温超导带材失超模型相比，该三维模型解决了二维模型无法模拟超导带材失超过程中超导带材宽度方向电磁热行为的不足，可对二代高温超导带材长度与宽度方向在不同热扰动下的电磁热特性及其演化过程进行准确模拟。
2）针对本文所研究的超导带材，在工作电流Iop=0.6Ic时，其最小失超能为4.62 J，失超传播速度为0.96 cm/s。当局部热源能量为1.82Qmq时，热扰动结束后，带材温度在短时保持在临界温度之上，且带材局部区域处于失超态；当局部热源能量为3.90Qmq时，在热扰动期间，超导层最大电流密度区域向其他区域扩散，热源区域由超导态转变为电阻态，并沿带材左右对称传播，2 s后失超区域扩展至热扰动初始阶段失超区域的2倍。
3）根据高温超导带材过电流程度与持续时间、带材各层分流状况以及对应的超导层电阻率变化情况，提出了过电流冲击失超电阻率判据：当过电流冲击造成超导层电阻率低于银层、铜层电阻率时，过电流冲击导致带材发生可恢复型过电流失超；当过电流冲击造成超导层热量积累使得超导层电阻率持续高于银层、铜层电阻率，达到临界电阻率一定过渡时间后，过电流冲击会导致带材发生不可恢复型过电流失超。
参考文献
[1] 肖立业, 林良真. 超导输电技术发展现状与趋势[J]. 电工技术学报, 2015, 30(7)1-9. Xiao Liye, Lin Liangzhen. Status quo and trends of superconducting power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(7)1-9.
[2] 丘明, 饶双全, 诸嘉慧, 等. 基于磁-路耦合分析法的高温超导环形储能磁体电磁优化设计[J]. 电工技术学报, 2016, 31(增刊2): 176-182. Qiu Ming, Rao Shuangquan, Zhu Jiahui, et al. Electromagnetic optimization design of a toroidal HTS-SMES magnet using magneto-circuit coupling analysis method[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 176-182.
[3] 蒲东昇, 任丽, 胡子珩, 等. 超导带材并联结构的失超传播特性研究[J]. 低温与超导, 2020, 48(6): 36-42. Pu Dongsheng, Ren Li, Hu Ziheng, et al. Experimental study on the quench characteristic of YBCO tapes with different arranggements[J]. Cryogenics & Supercon-ductivity, 2020, 48(6): 36-42.
[4] 龚珺, 诸嘉慧, 方进, 等. 电阻型高温超导限流器暂态电阻特性分析[J]. 电工技术学报, 2018, 33(9): 2130-2138. Gong Jun, Zhu Jiahui, Fang Jin, et al. Analysis of transient resistance characteristics for resistive type high temperature superconducting fault current limiter[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2130-2138.
[5] 方进, 丘明, 范瑜, 等. 超导磁体失超检测电路的设计[J]. 电工技术学报, 2012, 27(8): 239-247. Fang Jin, Qiu Ming, Fan Yu, et al. Design of the circuit in superconducting magnet quench detection[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 239-247.
[6] 龙嘉杰, 李敬东, 任丽, 等. 一种高温超导电缆优化软件的设计与实现[J]. 低温与超导, 2021, 49(10): 1-6, 33. Long Jiajie, Li Jingdong, Ren Li, et al. Design and implementation of a HTS cable optimization software[J]. Cryogenics & Superconductivity, 2021, 49(10): 1-6, 33.
[7] 郭大鹏, 胡燕兰, 陈斌, 等. 液氮浸泡式高性能ReBCO超导带材失超传播特性研究[J]. 低温与超导, 2020, 48(4): 29-34, 78. Guo Dapeng, Hu Yanlan, Chen Bin, et al. Study on the quench propagation characteristics of liquid nitrogen soaked high performance ReBCO superconducting tape[J]. Cryogenics & Superconductivity, 2020, 48(4): 29-34, 78.
[8] Huang Chenguang, Song Zengyu, Zhang Tianyu, et al. Electro-thermal-mechanical modeling of quench and stress evolution triggered by various factors in high-temperature superconducting coils[J]. Journal of Applied Physics, 2021, 129(21): 213902.
[9] 杨平, 盛杰, 王禹程, 等. YBa2Cu3O7-δ超导带材非均匀性对失超传播特性的影响[J]. 上海交通大学学报, 2017, 51(9): 1090-1096. Yang Ping, Sheng Jie, Wang Yucheng, et al. Quench propagation characteristics influenced by non-uniform properties of YBa2Ou3O7-δ high temperature super-conducting tape[J]. Journal of Shanghai Jiao Tong University, 2017, 51(9): 1090-1096.
[10] 邓能. 超导失超传播行为及失超判定准则的数值研究[D]. 兰州: 兰州大学,2015. Deng Neng. Numerical study of quench behavior and quench detection criterion of HTS[D]. Lanzhou: Lanzhou University, 2015.
[11] 柯其琛, 徐国顺, 庄劲武, 等. YBCO带材过电流特性与抗过电流能力研究[J]. 低温与超导, 2019, 47(12): 25-31. Ke Qichen, Xu Guoshun, Zhuang Jinwu, et al. Study on overcurrent characteristics and overcurrent resistance of YBCO strip[J]. Cryogenics & Supercon-ductivity, 2019, 47(12): 25-31.
[12] 王浩男, 张志丰, 邱清泉, 等. YBCO带材在直流冲击下的电阻变化规律研究[J]. 稀有金属, 2018, 42(10): 1040-1045. Wang Haonan, Zhang Zhifeng, Qiu Qingquan, et al. Resistance characteristics of YBCO tape under direct current impact[J]. Chinese Journal of Rare Metals, 2018, 42(10): 1040-1045.
[13] 祝乘风, 厉彦忠, 谭宏博, 等. 热扰动冲击下的高温超导电缆失超恢复特性[J]. 电工技术学报, 2021, 36(18): 3884-3890. Zhu Chengfeng, Li Yanzhong, Tan Hongbo, et al. Numerical analysis on the quench and recovery of the high temperature superconducting cable subjected to thermal disturbance[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3884-3890.
[14] Ma Jun, Geng Jianzhao, Chan Wankan, et al. A temperature-dependent multilayer model for direct current carrying HTS coated-conductors under perpendicular AC magnetic fields[J]. Superconductor Science and Technology, 2020, 33(4): 045007.
[15] Shen B, Grilli F, Coombs T. Overview of H-formulation: a versatile tool for modeling electromagnetics in high-temperature superconductor applications[J]. IEEE Access, 2020, 8: 100403-100414.
[16] 陈海宇, 方进, 华俊威. 基于COMSOL的超导带材交流损耗仿真分析[J]. 低温与超导, 2021, 49(12): 15-21. Chen Haiyu, Fang Jin, Hua Junwei. Simulation and analysis of AC loss in HTS strip based on COMSOL[J]. Cryogenics & Superconductivity, 2021, 49(12): 15-21.
[17] Liang Siyuan, Ren Li, Ma Tao, et al. Study on quenching characteristics and resistance equivalent estimation method of second-generation high temperature superconducting tape under different overcurrent[J]. Materials, 2019, 12(15): 2374.
[18] Duron J, Grilli F, Antognazza L, et al. Finite-element modelling of YBCO fault current limiter with temperature dependent parameters[J]. Superconductor Science and Technology, 2007, 20(4): 338-344.
[19] 瞿青云, 马媛媛, 刘华军, 等. YBCO高温超导带材失超传播特性研究[J]. 低温与超导, 2014, 42(9): 38-43. Qu Qingyun, Ma Yuanyuan, Liu Huajun, et al. Study on the quench propagation properties of YBCO HTS tapes[J]. Cryogenics & Superconductivity, 2014, 42(9): 38-43.
[20] 许君. 高温超导体的失超传播特性研究[D]. 武汉: 华中科技大学, 2017.
Abstract The quench of high temperature superconducting (HTS) tapes will reduce their flow capacity and thus affect the operation stability of high temperature superconducting devices. At present, most simulation models of superconducting tapes are two-dimensional models, which cannot accurately simulate the electromagnetic-thermal behavior in the process of quench. A finite element method with multiple physical field coupling is used to study the quench characteristics of the second-generation high temperature superconducting tapes. In the three-dimensional coordinate system, the magnetic field intensity vector is taken as the solution variable to establish the second-generation HTS tape quench evolution electromagnetic-thermal simulation model. The electromagnetic-thermal characteristics and evolution under different thermal disturbance conditions of the second-generation HTS tapes along the length direction as well as the width direction are studied. The shunt state of each layer and the resistivity change behavior of the superconducting layer in the process of superconducting tapes overcurrent are analyzed, different types of overcurrent and overcurrent behaviors are distinguished, and the resistivity criterion of overcurrent quench is proposed.
For the superconducting tapes studied in this paper, the minimum quench energy is 4.62 J and the propagation velocity is 0.96 cm/s when Iop = 0.6Ic. When the local heat energy is 1.82Qmq, the temperature of tape stays above critical temperature for a short time after the thermal disturbance ends, and the tape stays quenching. When the local heat energy is 3.9Qmq, during the thermal disturbance the maximum current density region of the superconducting layer diffusing to other regions, the hot region changes from superconducting state to resistive state, and propagates symmetrically along the tapes. After 2 s, the quench region expands to twice the quenching region than the initial stage of the thermal disturbance.
According to the overcurrent degree, duration and the shunt condition of high temperature superconducting tapes, and corresponding resistivity change of the superconducting layer, the criterion of overcurrent quench resistivity is put forward as follows. When the overcurrent causes the resistivity of the superconducting layer to be lower than that of the silver layer and the copper layer, the overcurrent causes the recoverable quench of the tapes. When the overcurrent causes heat accumulates in the superconducting layer, the resistivity of the superconducting layer continues to be higher than that of the silver layer and the copper layer, and when the critical resistivity reaches a certain transition time, the overcurrent impact leads to unrecoverable quench.
Compared with the two-dimensional model, the three-dimensional model solves the problem that the two-dimensional model cannot simulate the electromagnetic-thermal behavior of the superconducting tapesin width direction during the quench process. It can accurately simulate the electromagnetic-thermal characteristics and evolution process of the second-generation superconducting tapes in length and width direction under different thermal disturbances.
keywords：Second-generation high temperature superconducting tape, quench characteristic, finite element method, electromagnetic-thermal coupling
DOI:10.19595/j.cnki.1000-6753.tces.221793
中图分类号：TM26
国家重点研发计划资助项目（2018YFA0704300）。
收稿日期 2022-09-12
改稿日期 2022-11-10
杨志星 男，1998年生，硕士研究生，研究方向为超导电力技术。E-mail：yangzhixingasc@163.com
任 丽 女，1968年生，教授，博士生导师，研究方向为超导电力技术。E-mail：renli@mail.hust.edu.cn（通信作者）
（编辑 郭丽军）