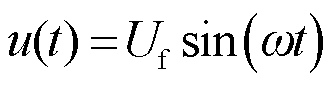（1）
摘要 感应同步器作为一种电磁式位置传感器，具有精度高、安装简单等优点，广泛应用于各类高性能伺服系统。传统的感应同步器采用定子分段式结构，绕组制作工艺的严苛要求制约了感应同步器向小型化高精度的发展。该文提出一种新型的定子双排绕组结构感应同步器，可以有效地抑制加工不善带来的导体偏差。对双排绕组感应同步器的测角原理进行分析，计算了其输出的偏差电动势，并通过建立有效导体的电流密度模型来提出抑制3、5次谐波的优化策略，进一步提高感应同步器的测角精度，最终根据比电动势一致原理提出双排绕组感应同步器的设计方法并建立3D仿真模型，采用有限元分析与快速傅里叶分解的方法验证了策略的正确性与可行性，并制作样机进行实验。
关键词：小尺寸双排绕组导体偏差有限元法
作为一种多极的、高精度的角位置传感器[1-3]，感应同步器在航空飞船或者卫星对地观测设备中，发挥着不可或缺的作用。目前，常用的角位置传感器主要有光栅[4-6]、旋转编码器[7-9]、感应同步器等，但是光栅和旋转编码器的码盘都属于光学原理位置传感器，无法工作于具有强宇宙射线以及温度急剧变化的场合，且维护难度与成本较高，但感应同步器通过电磁感应原理传递位置信号，抗干扰性较强且便于清洁维护，于是感应同步器成为上述场合的最优选择，同时随着航天设备的小型化，小尺寸的感应同步器的研究与发展具有重要意义，其中小尺寸主要是指外径或者长度小于150 mm的感应同步器。
目前，针对感应同步器的研究主要集中在误差补偿算法、角度测量系统及外电路的设计等方面[10-13]，文献[10]在建立了引入扇区刻划误差项的误差模型之后，对误差源的正交性与耦合性进行分析，并对误差项进行了分离与测算；文献[11]提出了一种稀疏误差采样及补偿方法，首先对零位误差进行测补，再处理剩余的细分误差，基于稀疏的数据将测角系统精度最大误差峰峰值从11.7角秒（1°=3 600角秒）提升至2.9角秒；文献[12]设计了一种带外电枢的感应同步器，并且使用二维有限差分方法对其进行分析，该方法主要适用于感应同步器的快速分析与测补；文献[13]设计了一种利用720极与718极旋转感应同步器配合来获得高精度的绝对角度的方法，具有绝对测角、精度高、可靠性高等优点；近年来，对于感应同步器本体以及绕组耦合形式的研究相对较少，而感应同步器一般工作在连续绕组励磁、分段绕组输出的鉴幅工作模式下，通过解算两相绕组输出的电动势幅值，得到唯一的角位置信息，但是分段绕组的每一相绕组仅与一半的连续绕组有效导体耦合，极大地限制了平均效应，同时，由于导体偏差是传统感应同步器误差的重要来源[14-18]，尺寸越小的感应同步器对加工工艺和刻线精度的要求越苛刻，使其成本难以降低[19-20]，而双排绕组感应同步器被设计来解决这一问题，双排绕组的形式并不是第一次被提出，但是相关文献较少，所总结出的模型与理论并不完善，也无学者对其测角偏差进行探讨。
本文主要研究用于补偿导体偏差的小尺寸双排绕组的感应同步器，将分段绕组同步器的定子绕组按照比电动势一致的原理分为内外排并相互错开一个组节距，内外排导体之间通过有效导体直接相连并且近似为连续绕组的形式，使有效导体耦合数量变为传统绕组两倍的同时没有增加多余的引出线，并且抑制了导体偏差带来的影响，有效地提高了测角精度，对降低感应同步器的加工难度和成本具有重要意义。
本文首先对双排绕组的感应同步器测角原理进行分析，将角度偏差量化为偏差电动势，通过对偏差电动势的求解证明了双排绕组对导体偏差的补偿作用。接着给出了双排绕组感应同步器的设计方法并建立了对应的电流密度模型，通过对电流密度进行傅里叶分解得到谐波抑制的关键，即宽度系数，并且基于该系数提出对3、5次谐波的抑制策略，后续建立3D模型，通过有限元法和快速傅里叶分解法对比分析优化前后的3、5次谐波含量，验证了设计方法的正确性。
在连续绕组励磁、分段绕组输出的鉴幅工作模式下[21]，通过解算双排绕组感应同步器两相输出电动势的幅值来得到相对应的角位置信息，每经过两个极距，其磁通变化一个周期，对应的输出电动势也变化一个周期。
基于鉴幅的工作模式，向连续绕组通入正弦激励信号u(t)，假设
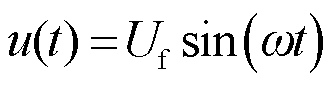（1）
式中，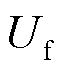
为励磁电压幅值；
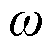为励磁信号的角频率；
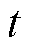为时间。
则两相输出绕组的正弦、余弦输出信号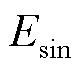
、
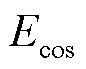可以分别表示为
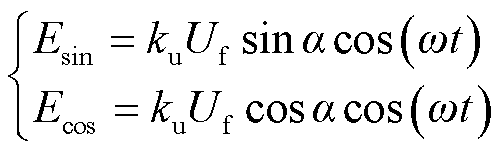（2）
式中，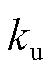
为感应电动势系数；
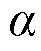为转子转过的机械角度。
将两相输出信号经过高精度的正余弦乘法器分别与测角系统的输出角度相乘，则可以得到输出端的一组新的信号为
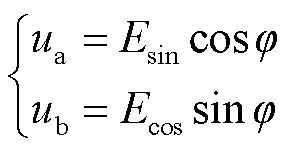（3）
式中，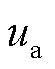
、
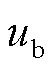分别为解算后a、b相输出信号；
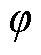为测角系统的输出角度。
再将经过乘法器的信号送入误差放大器中，得到输入角度与输出角度之间的误差函数ue为
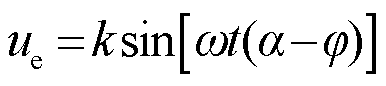（4）
式中，k为电动势系数与放大倍数的乘积。
将误差函数信号送入高通滤波器，并且始终使得误差函数的输出为零，则测角系统的输出角度就等于实际的感应同步器转子角度[22]，鉴幅工作的基本流程如图1所示。
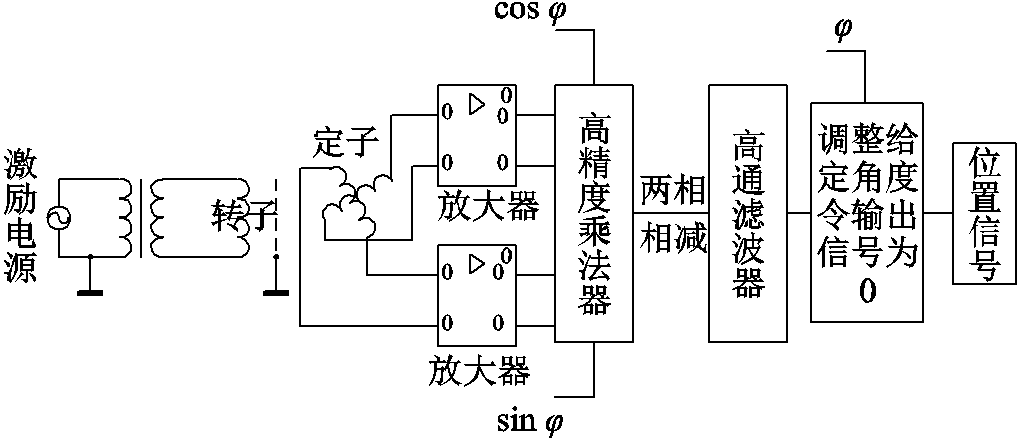
图1 感应同步器测角系统工作流程
Fig.1 Flow chart of angle measuring system of inductosyn
零位误差是衡量感应同步器测角精度的重要指标，在讨论零位误差时，首先将由导体偏差带来的感应同步器测角误差分为高次成分和低次成分，其中低次成分主要是指零位误差中的系统成分，主要由基板变形、安装不善等外在因素导致，只能通过调整安装工序、提高加工精度予以改善；而高次成分则主要是随机成分，在传统的感应同步器中，输出绕组的分段式结构是产生上述误差的根本原因，这是双排绕组感应同步器需要解决的主要问题。就零位误差中的高次成分来说，当转子为连续绕组、定子为分段绕组时，任意一根导体的输出电动势为
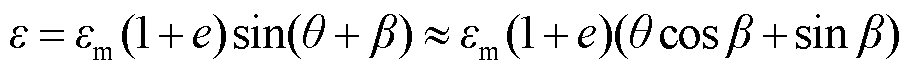（5）
式中，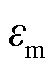
为单根导体输出电动势幅值的增益；
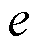为该导体的输出电动势幅值偏差；
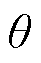为导体中心线偏离磁场中心线的电角度；
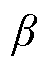为偏离角。
于是以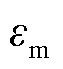
为基值将单根导体的输出电动势用标幺值表示为
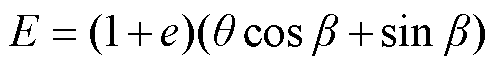（6）
从式（6）可以看出，电动势幅值偏差是由定、转子共同来决定的，并且是由定、转子有效导体的偏离角度和输出电动势表示，于是一般形式可以书写为
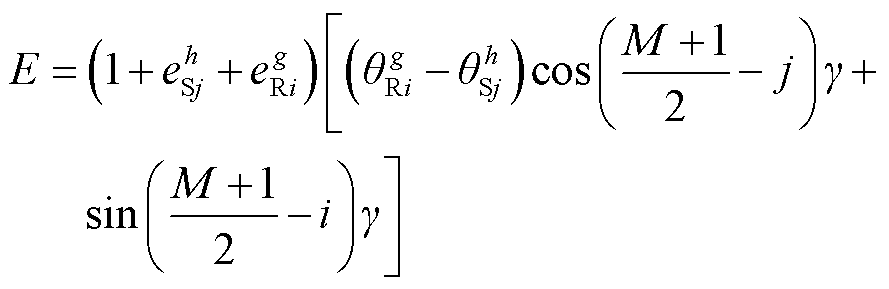(7)
式中，R为连续绕组；S为分段绕组；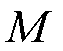
为每一组导体的导体数；
、
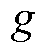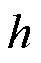为扇形组的序号；
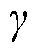为分段绕组节距与连续绕组极距之差；
、
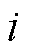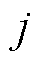为导体的序号。
考虑电动势幅值偏差以及分段绕组的影响，可以将第n个零位偏差电动势写为
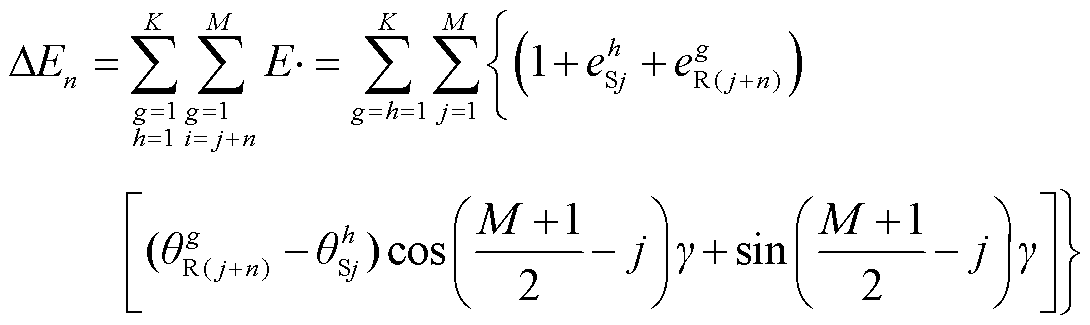（8）
第n个零位偏差与第一个零位之间的偏移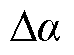
可以表示为
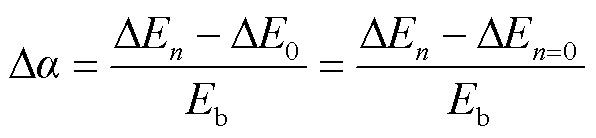（9）
其中
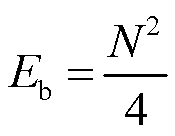
式中，N为总导体数。
于是偏差电动势可以进一步地写为
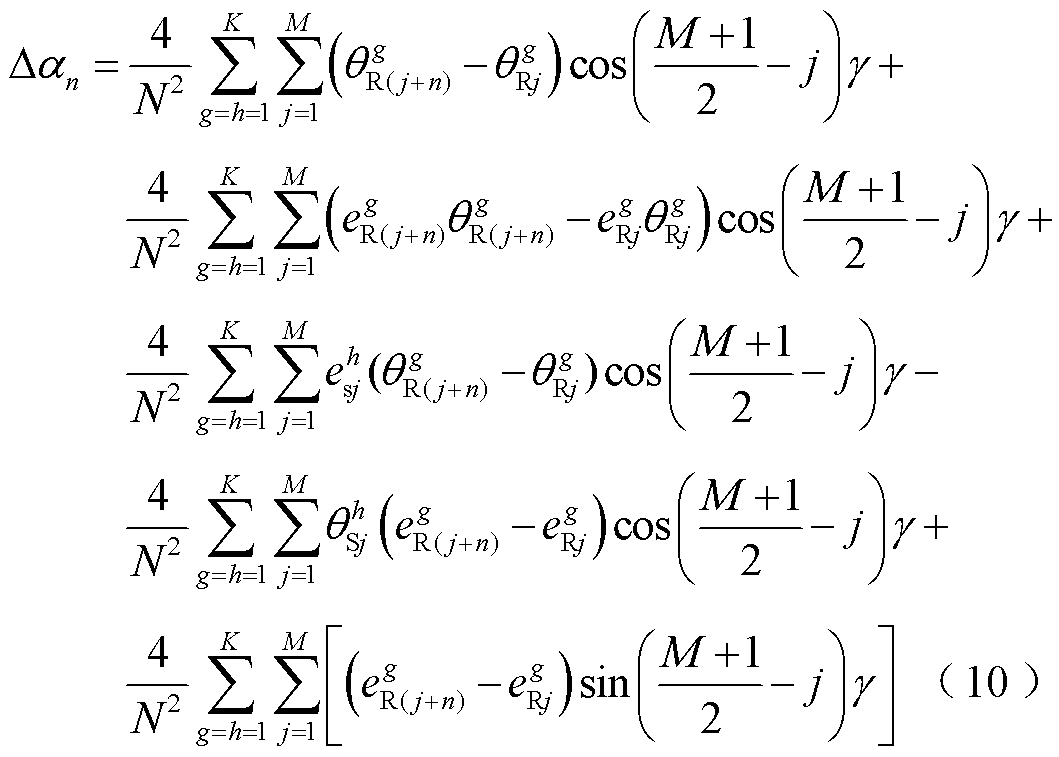
可以看出，对于传统的感应同步器，偏差电动势是多项随机量的和，式中的第一项主要是导体偏差导致的偏差电动势，其余各项的数值一般远小于第一项，并且属于随机误差难以预测，因此抑制导体偏差是提高感应同步器误差精度的主要方法。
当定、转子绕组都为连续绕组时，导体偏差所带来的零点漂移可以得到很好的抑制，双排绕组即是为了满足这种需要而设计的。首先将单根有效导体的输出电动势简化为
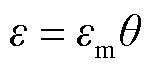（11）
同样，也可以将它表示为标幺值的形式，有
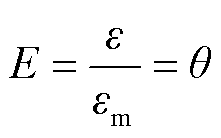（12）
后续建立简化的感应同步器截面模型如图2所示，图中，矩形为简化的导体截面，依据该模型对零位之间的偏差进行分析，首先零位偏差电动势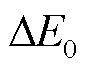
为
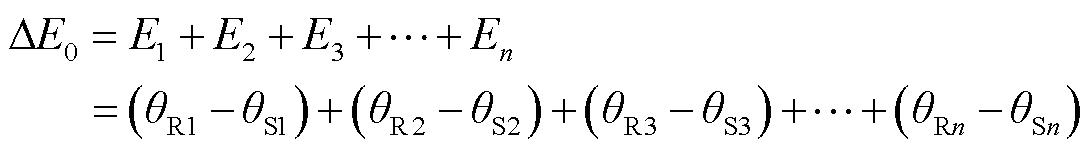（13）
式中，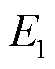
、
、…、
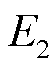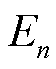分别为1、2…n个导体的偏差电动势。
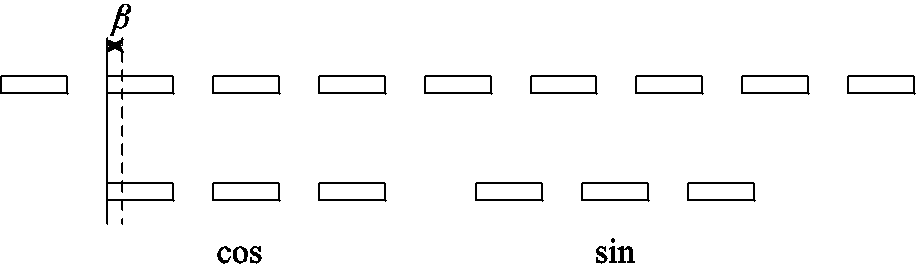
图2 零位误差示意图
Fig. 2 Zero error diagram
将零位偏差电动势与比电动势相除即可得到对应的偏移机械角度为
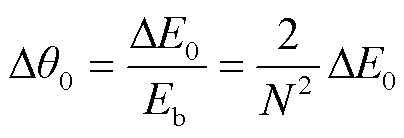（14）
接着将转子精确地转过一个极距，就可以得到新的偏差电动势为
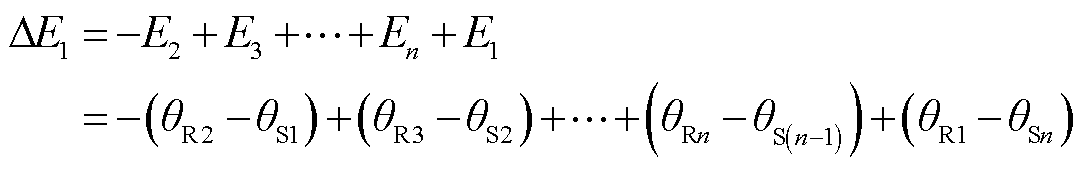（15）
新的零位误差与第n个零点处的偏差电动势和角度偏差可以分别表示为
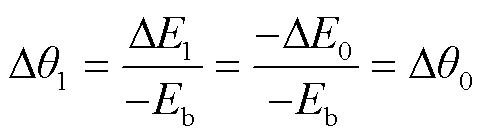（16）
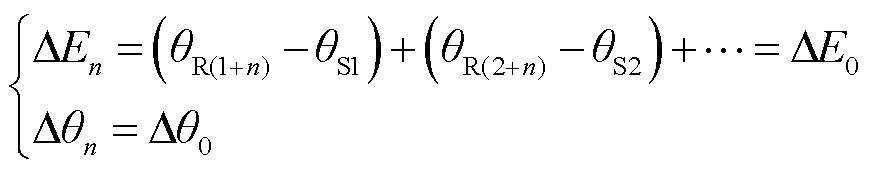（17）
于是可以得到，对于定、转子都是连续绕组的感应同步器，即双排绕组感应同步器来说，不同零位之间的零位偏差电动势以及偏离角恒定，因此可以通过电动势注入进一步提高感应同步器的测角精度。由于双排绕组实现了励磁绕组和输出绕组都为连续绕组的形式，可以有效地抑制其高次的零位误差，补偿了导体偏差带来的影响，在加工过程中并不要求较高的加工工艺和刻线精度，从而有利于感应同步器的小型化，提高测角精度的同时也降低了生产的难度和成本。
双排绕组可以看作是组导体数为奇数的分段绕组的特例，而偏差电动势是感应同步器测角误差产生的最直接原因，于是需要对偏差电动势进行分析与求解，双排绕组在结构上形成了定、转子都为连续绕组的耦合形式，由于感应同步器的导体厚度大于磁场透入深度，同步器阻抗远大于容抗与感抗，且恒定不变，可近似看作电阻性元件，有
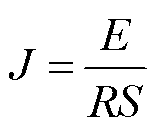（18）
式中，J为电流密度，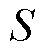
为导体的横截面积；
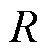为同步器一相电阻。
感应同步器的输出电动势可以通过对电流密度进行分析得出相同谐波分布，在此基础上对电流密度进行分析与建模，当定子做成双排绕组时，电流密度分布呈奇函数，双排绕组感应同步器电流密度分布如图3所示。
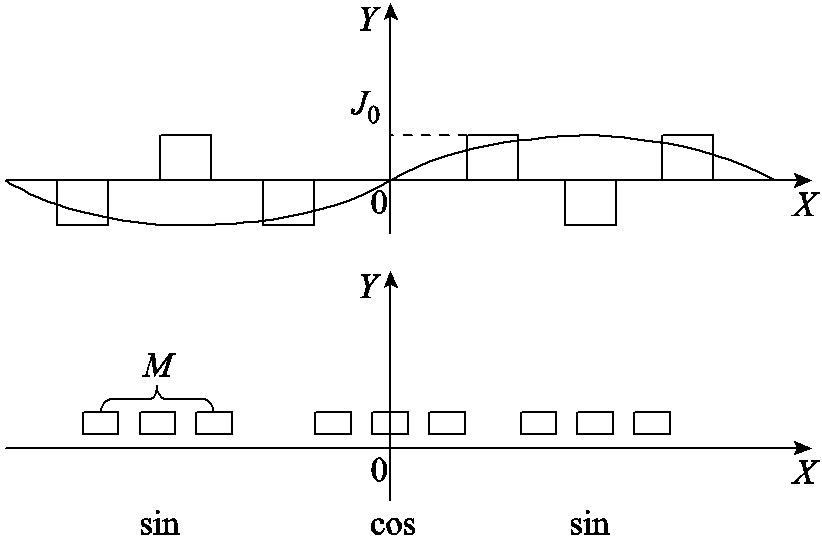
图3 双排绕组感应同步器电流密度分布
Fig.3 Current density distribution of double - row winding inductosyn
将电流密度傅里叶展开只得到奇次项，有
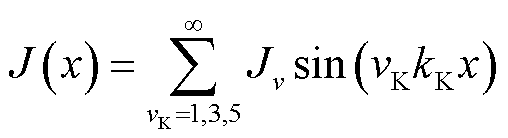（19）
式中，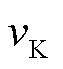
为以组节距为基波节距的谐波次数；
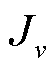为电流密度第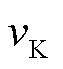次的谐波幅值；
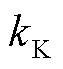为组节距弧度转换系数；x为在横轴方向的距离。其中，弧度转换系数可以表示为
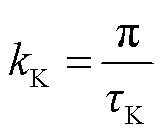（20）
式中，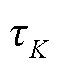
为组节距，进一步可以用极距表示为
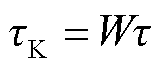（21）
式中，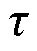
为同步器的极距，也为连续绕组的节距；
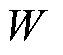为对应一个组节距的连续绕组导体数。
进一步来求取傅里叶级数中的谐波幅值为
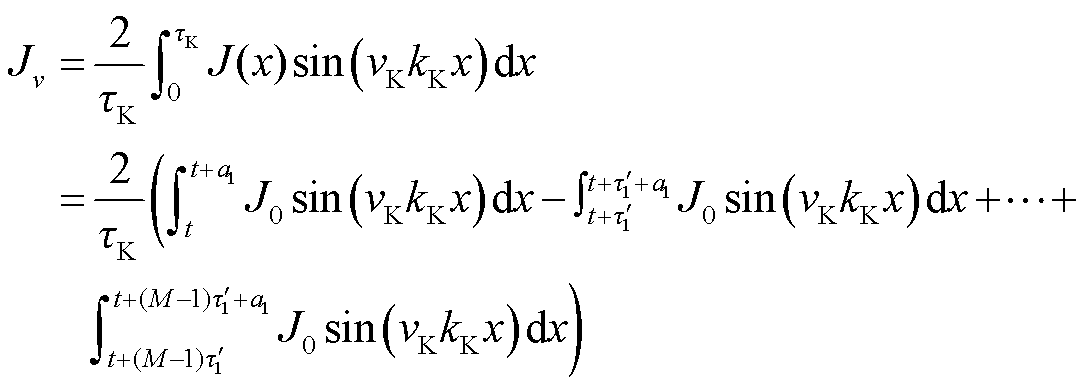(22)
式中，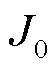
为同步器的电流密度；
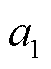为导体宽度；
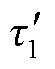为绕组的节距；
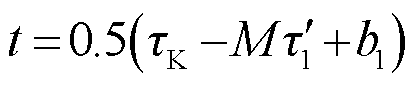为第一根导体左边缘对应的横坐标；
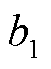为绕组的导体间隔。
电流谐波作为后续仿真以及优化的重点对象，需要进一步地分解与整理，将其幅值进一步写成有限项之和的形式并进行积分，然后利用三角函数进行运算可得
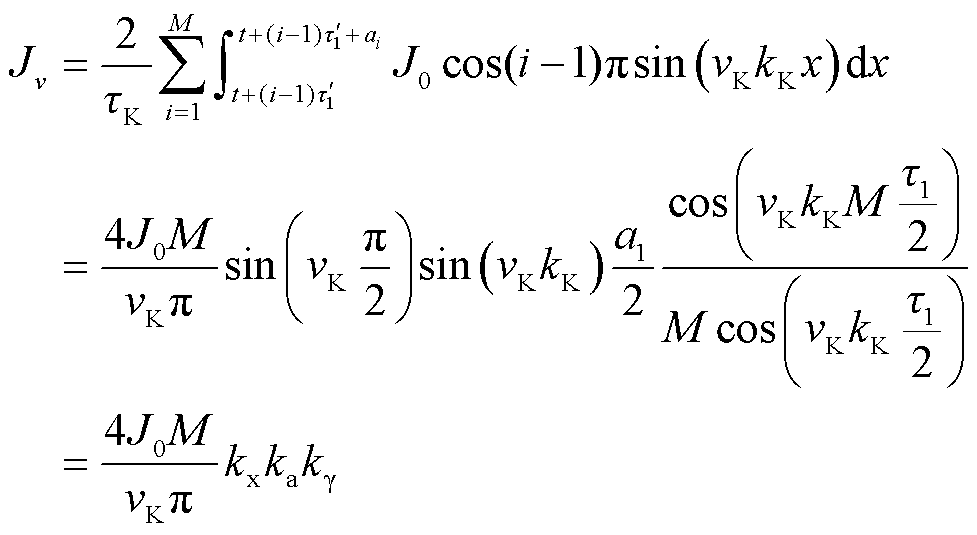(23)
其中
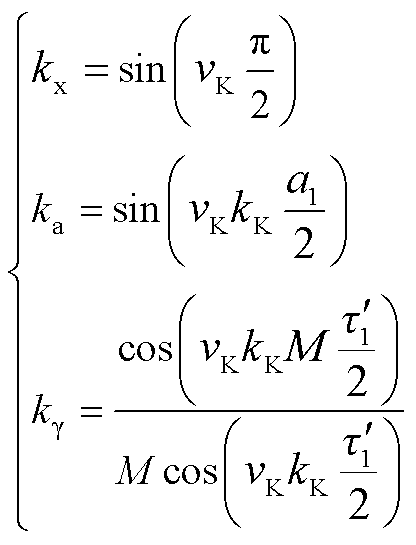（24）
式中，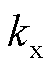
、
、
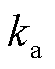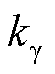分别为绕组的符号系数、宽度系数和分布系数，其中，宽度系数为重点讨论的对象，通过设计感应同步器导体的宽度使得对应某次谐波的宽度系数为0，即谐波幅值为0，从而达到抑制谐波的目的。
对于连续绕组励磁的双排定子感应同步器而言，电流密度只有基波及其奇数倍次数的谐波，则其中符号系数为1或者-1，分布系数为0、1或者-1，而宽度系数的绝对值总小于1。同时也可以看出，对于某次谐波，合理地选择宽度系数或者分布系数可以使得其幅值为0，但分布系数仍然对有效导体的刻线精度有较高的要求，提高了生产成本，因此针对宽度系数的设计是后续的主要优化策略，为了消除某次谐波，只需要使得对应的宽度系数为零即可，也即取
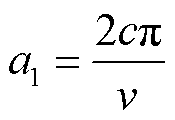（25）
式中，c为大于零的整数，通常取1或者2；v为欲消除的谐波次数。
由于过高的谐波电动势限制了感应同步器测角精度的进一步提升，而其幅值又随着次数的上升而迅速衰减，可以分别对定转子进行宽度优化设计来消除影响最为严重的3、5次谐波。
本文采用360极的感应同步器转子，为了使双排绕组具有与连续绕组相同的作用，其内外排导体需要满足比电动势一致原则，本文提出了一套系统的设计方法，当确定了定转子绕组间有效的耦合长度后，需要将其分为内排和外排两部分，但由于比电动势一致的需要，内外排的长度比不能为1，于是引入一个比例系数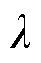
为
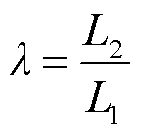（26）
式中，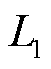
为内排绕组有效长度；
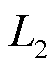为外排绕组有效长度。
如果求出了比例系数，那么内外排的有效长度也就分别得到了确定，为了比电动势相等，需要满足
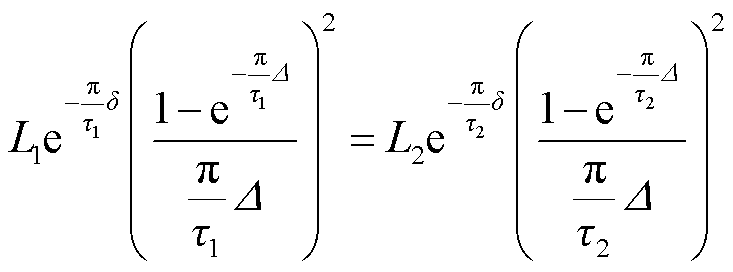（27）
式中，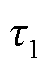
为内排绕组的平均几何节距；
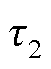为外排绕组的平均几何节距；
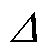为导体的厚度；
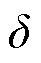为气隙的长度。
将满足比电动势相等的表达式经过进一步整理可得
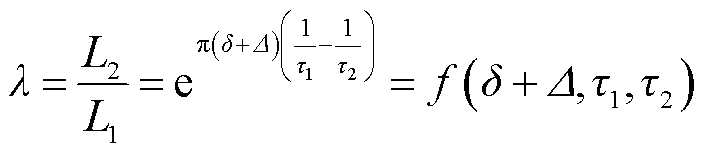（28）
为了设计的方便，可以进一步地引入内外半径的比值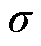
，有
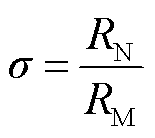（29）
式中，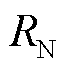
为绕组内侧半径；
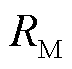为绕组外侧半径。
同时内外圆周处的平均节距也可以确定下来，有
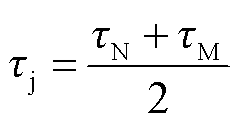（30）
式中，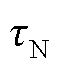
为内圆周半径处几何节距；
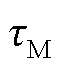为外圆周半径处几何节距。
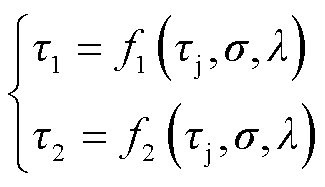（31）
可以将内外平均节距根据新设系数重新表示出来。
用解析法联立比电动势方程组进行求解可以得到比例系数与内外节距比在不同的平均节距、气隙、导体厚度下的唯一解，从而为双排绕组的设计提供参考。
本文给出双排绕组感应同步器设计的具体流程，依照此流程设计感应同步器定子与匹配的转子并进行仿真，首先给定小尺寸双排绕组感应同步器主要尺寸以及极对数，并确定定、转子耦合的有效长度，从而确定平均节距和内外节距比，感应同步器正常工作所需气隙为0.1 mm，而常规工艺生产的感应同步器绕组厚度通常为0.033 mm，后续通过计算得出对应的双排绕组感应同步器尺寸参数见表1，而为了避免端部非有效电动势的影响，与其对应的转子需要在内、外径处与定子错开，主要采取定子大于转子的形式，间隔为3～4 mm，这也使得转子有效导体可以得到充分的利用，从而有利于输出电动势的提高。
表1 双排绕组感应同步器尺寸参数
Tab.1 Dimension parameters of double – row winding inductosyn
参数数值 绕组内径/mm37 绕组外径/mm60.5 比例系数0.82 内排绕组平均几何节距/mm0.646 外排绕组平均几何节距/mm1.056 比半径0.61 气隙/mm0.1 导体厚度/mm0.033 内排绕组有效长度/mm13 外排绕组有效长度/mm10.4 平均节距/mm0.85
为了进一步提升感应同步器测角精度，分别对连续、分段绕组感应同步器和双排定子绕组感应同步器进行3D建模，并对输出电动势进行快速傅里叶分解，通过分析其3、5次谐波含量来得到感应同步器的误差优化效果。同时，由于同步器本身具有重复性和高度对称性，因此为了减少计算量，提高仿真效率，采用部分等效建模。对于连续绕组励磁、分段绕组输出的感应同步器，简化的模型建立如图4所示。
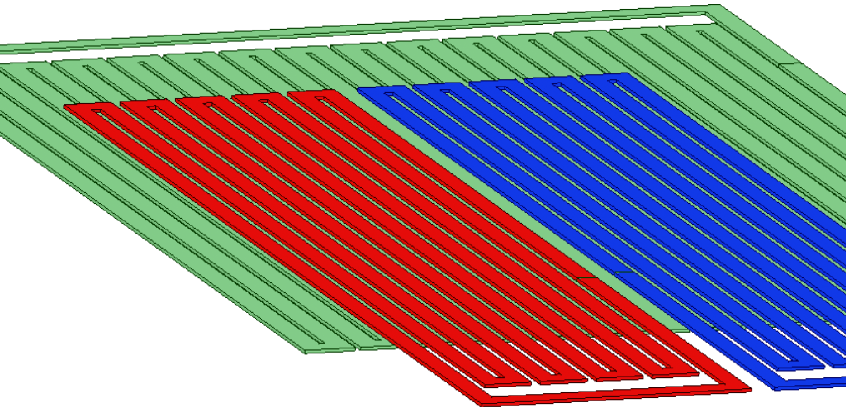
图4 连续、分段绕组感应同步器简化仿真模型
Fig.4 Simplified simulation model of continuous and segmented winding inductosyn
由于感应同步器高度的对称性以及重复性，对于正弦、余弦两相绕组的输出电动势，其3、5次谐波含量基本相同，因此本文统一选择余弦相进行分析对比，传统感应同步器的余弦绕组输出电动势波形如图5所示，通过提取其包络线并进行快速傅里叶分解可得对应的3、5次谐波含量如图6所示，可以看出，谐波占比随着谐波次数的升高而迅速减小，印证了第3节的分析，同时谐波含量占比最大的为3、5次谐波分量，其含量过大造成输出电动势波形的畸变是影响感应同步器测角精度的最直接原因，输出电动势的畸变不仅引起了零点的偏移，也造成偏差电动势的增加，因此通过设计有效导体的宽度抑制3、5次谐波有着重要的意义。
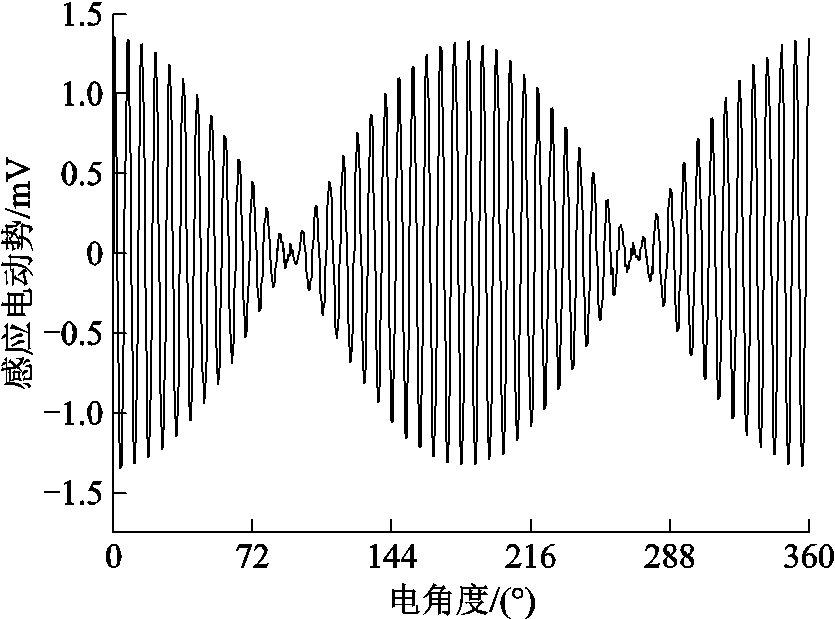
图5 余弦绕组输出波形
Fig.5 Output waveform of cosine winding
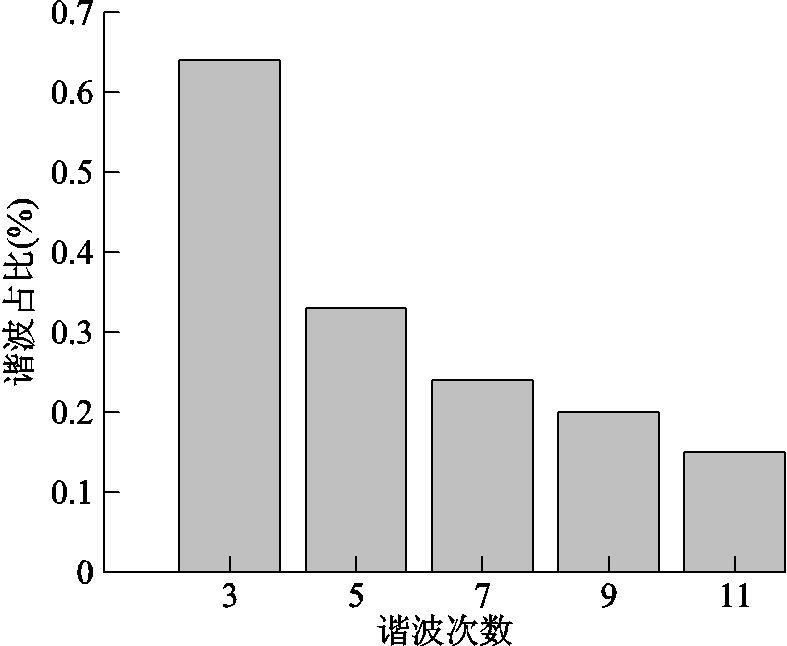
图6 优化前谐波占比
Fig.6 Harmonic ratio diagram before optimization
接下来根据表1的相关数据建立双排定子绕组的感应同步器3D仿真模型，同样根据其高度对称性建立部分等效模型如图7所示。
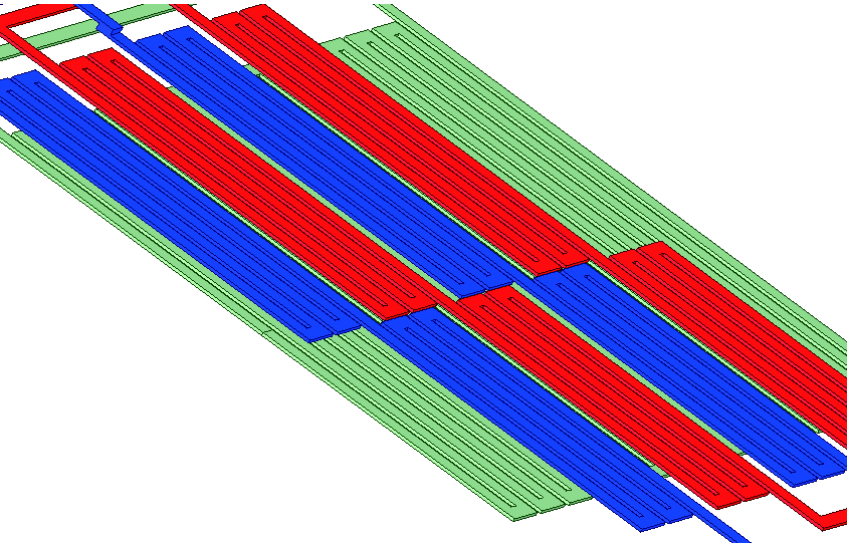
图7 双排定子绕组感应同步器简化仿真模型
Fig.7 Simplified simulation model of dual-arranged subwinding inductosyn
其余弦绕组仿真输出波形如图8所示，谐波占比和谐波含量对比分别如图8和图9所示。从图9以及图10中数据可以得知，谐波占比相比分段绕组已经得到了一定的抑制，表现为3、5次谐波占比的减小，其中3次谐波误差含量仅为分段绕组感应同步器的29.69%，而5次谐波含量更是只有其18.75%，因此双排绕组自身结构的优势得到验证。
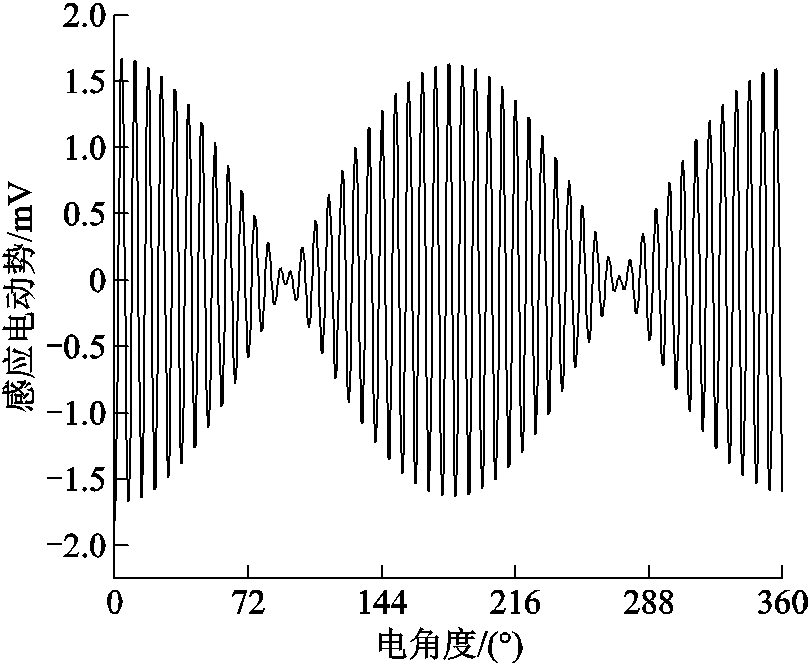
图8 输出波形
Fig.8 Output waveform
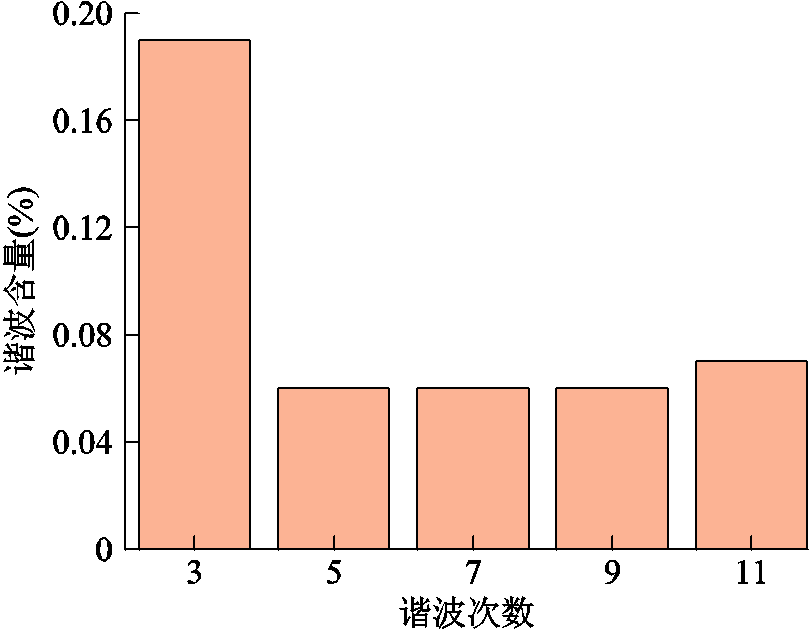
图9 谐波占比
Fig.9 Harmonic ratio diagram
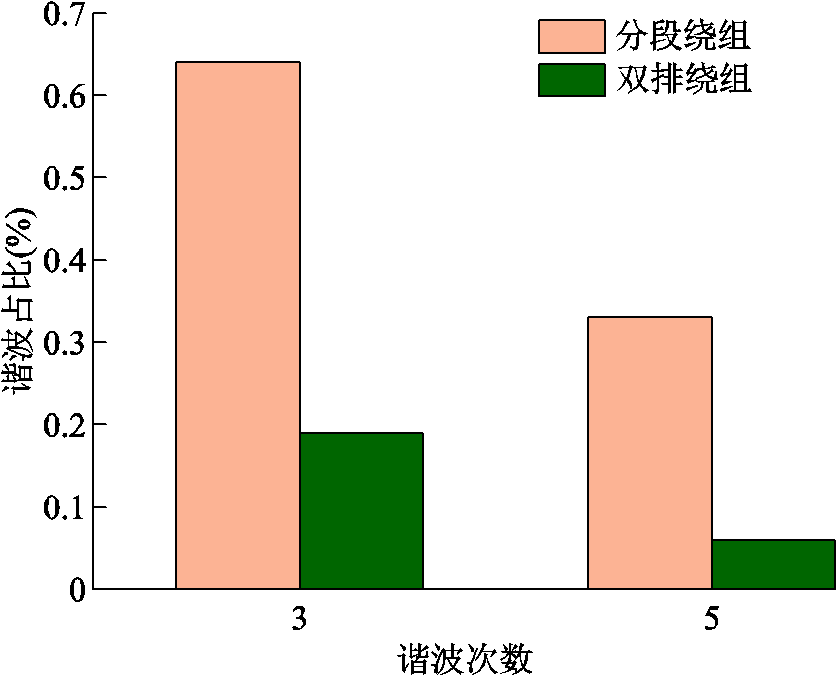
图10 3次和5次谐波含量对比
Fig.10 Comparison of third and fifth harmonic content
在此基础上，通过双排绕组有效导体宽度设计，使得对应的谐波电流宽度系数为0，从而达到抑制谐波、提高测角精度的目的，按照式（25）重新设计同步器绕组宽度，仿真所得余弦绕组输出波形如图11所示。
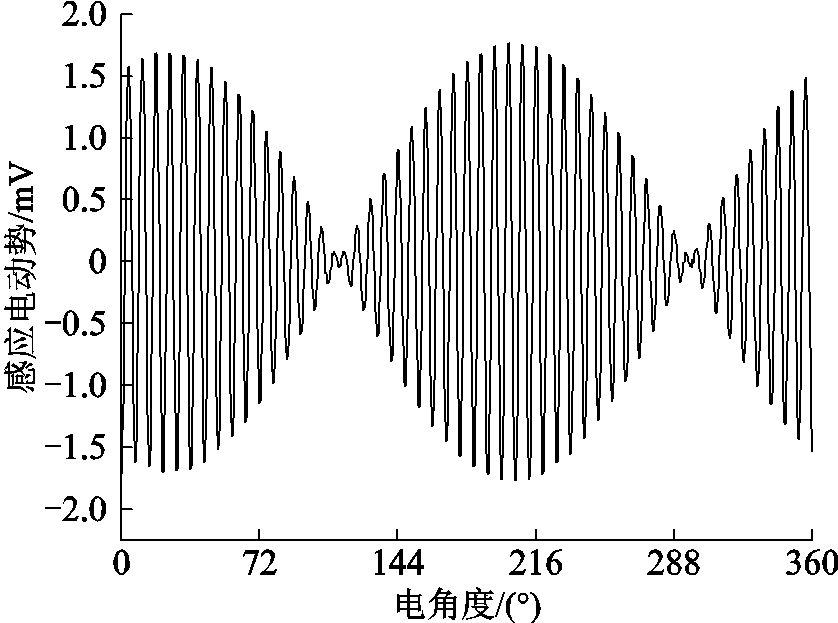
图11 优化后输出波形
Fig.11 Output waveform after optimization
优化后谐波占比如图12所示。从图12中谐波占比数据可以看出，经过宽度设计优化后的双排定子绕组感应同步器的各次谐波次数占比已经小于0.07%，对比于单排绕组同步器以及初步设计的双排定子绕组感应同步器已经明显减少，其主要的3次谐波占比仅为单排绕组感应同步器的9.375%，可见由谐波带来的误差得到了有效的抑制，有限元分析结果证明了该设计方法的正确性。优化前后谐波含量对比如图13所示。
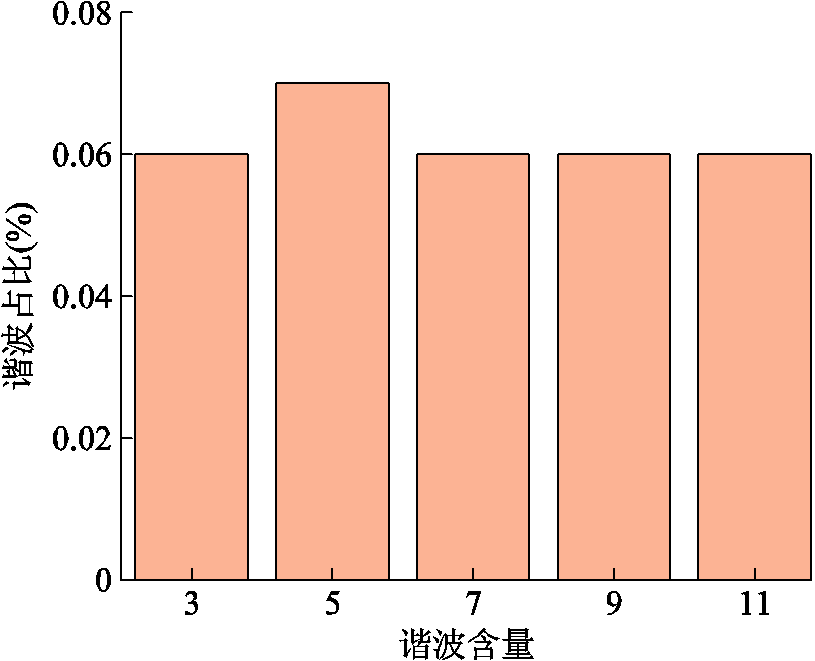
图12 优化后谐波占比
Fig.12 Harmonic ratio after optimization
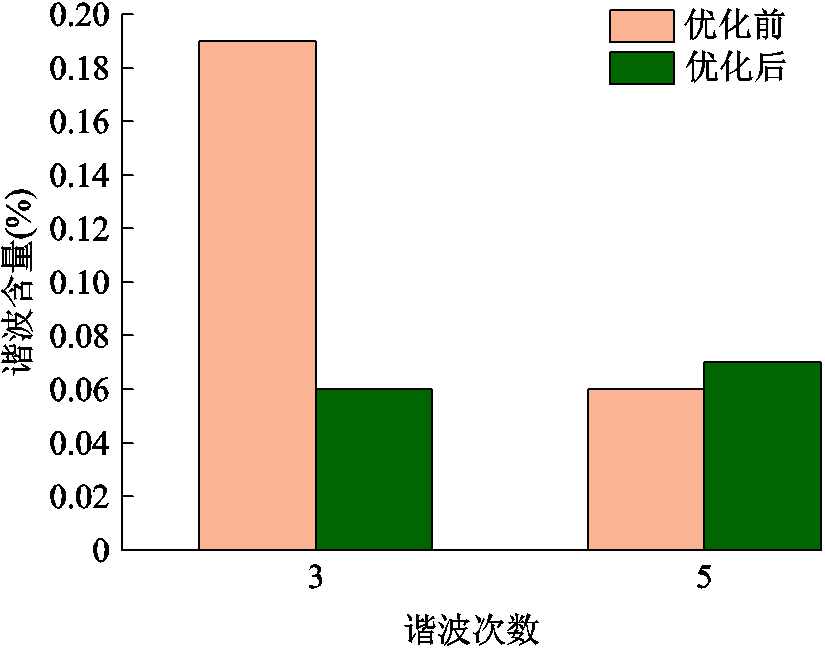
图13 优化前后谐波含量对比
Fig.13 Comparison of harmonic content before and after optimization
在此基础上，制作双排绕组感应同步器样机并进行实验测试其精度，其中同步器绕组采用超薄印制电路板（Printed Circuit Board, PCB）刻蚀，从而满足绕组厚度的要求，并且制造相同工艺的传统单排绕组感应同步器进行对比，实物如图14所示，测得误差对比如图15所示。
图14 双排绕组感应同步器实物
Fig.14 Double row winding induction synchronizer
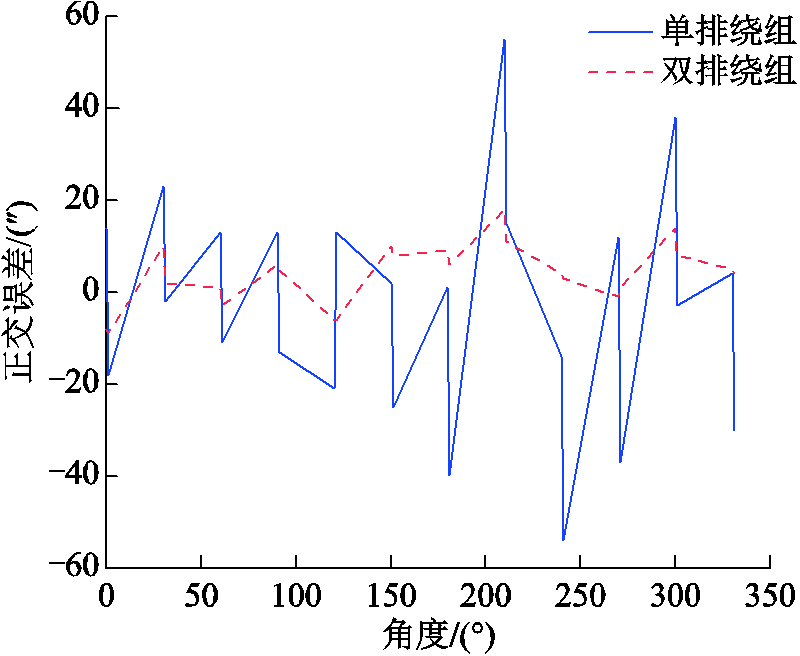
图15 误差对比
Fig.15 Comparison of errors
基于高精度光学分度头每隔10°测试感应同步器的角度偏差，通过正交误差分布可以看出，优化后的双排绕组感应同步器的正交误差角度变化范围约为单排感应同步器的30%，即在相同工艺下可以达到±10 s的误差范围，从而极大地抑制了感应同步器的谐波误差，并且降低了刻线精度要求，利用超薄PCB即可生产，使得感应同步器的小型化、集成化成为可能，但对于大型感应同步器来说，过度调整绕组宽度，如在极数较多的情况下不断增大绕组宽度可能会造成容性电动势增加，从而影响测角精度，因此该方法对于小尺寸的感应同步器以及同步器的小型化更为有效。
本文分析了双排绕组同步器对导体偏差的补偿作用，建立了其电流密度模型并对电流谐波进行傅里叶分解，提出了谐波抑制的关键，即宽度系数，后续基于该系数以及比电动势一致原理提出了抑制3、5次谐波的优化策略，将各次谐波次数含量降低为优化前的0.07%以下，同时建立双排绕组感应同步器的3D仿真模型加以分析和验证，证明了该方法的正确性以及可行性。
参考文献
[1] 刘莎莎, 王博文, 黄文美, 等. 仿生磁致伸缩触觉传感阵列设计与输出特性[J]. 电工技术学报, 2021, 36(12): 2576-2584. Liu Shasha, Wang Bowen, Huang Wenmei, et al. Design and output characteristics of bionic magnetostrictive tactile sensor array[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2576-2584.
[2] 郭强, 李山, 谢诗云, 等. 多相交错并联DC-DC变换器单电流传感器控制策略[J]. 电工技术学报, 2022, 37(4): 964-975. Guo Qiang, Li Shan, Xie Shiyun, et al. Single-sensor sampling current control strategy of multiphase interleaved DC-DC converters[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 964-975.
[3] 陈起超, 张伟超, 白仕光, 等. 非本征光纤法-珀传感器局部放电检测研究进展[J]. 电工技术学报, 2022, 37(5): 1305-1320. Chen Qichao, Zhang Weichao, Bai Shiguang, et al. Research progress of extrinsic fiber fabry-perot interferometer sensor in partial discharge detection[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1305-1320.
[4] 李姗姗, 王力农, 方雅琪, 等. 基于布拉格光纤光栅传感技术的复合材料杆塔老化寿命预测[J]. 电工技术学报, 2018, 33(1): 217-224. Li Shanshan, Wang Linong, Fang Yaqi, et al. Aging prediction of composite tower based on FBG sensing technology[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 217-224.
[5] 江军, 马国明, 宋宏图, 等. 基于侧边抛磨光纤布拉格光栅的变压器油中溶解氢气传感器[J]. 电工技术学报, 2017, 32(13): 264-270. Jiang Jun, Ma Guoming, Song Hongtu, et al. Dissolved hydrogen sensor in power transformer oil based on side polishing fiber Bragg grating[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 264-270.
[6] Ou Qibiao, Zhao Jianchuan, He Wei, et al. Effect of grating period on transmission spectrum of long-period fiber grating coupled at turning point[C]//2020 4th Annual International Conference on Data Science and Business Analytics (ICDSBA), Changsha, China, 2021: 199-204.
[7] Lee K, Hwang H Y, Kim Y. Efficient PWM waveform generation using rotary encoder on spartan-6E starter kit[C]//2020 International Conference on Electronics, Information, and Communication (ICEIC), Barcelona, Spain, 2020: 1-2.
[8] Mata-Contreras J, Herrojo C, Martín F. Electromagnetic rotary encoders based on split ring resonators (SRR) loaded microstrip lines[C]//2018 IEEE/MTT-S International Microwave Symposium - IMS, Philadelphia, PA, USA, 2018: 43-46.
[9] Wang Jinxiang, Cui Xu. Rotary encoder based self-positioning method for mobile robot[C]//2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 2019: 500-504.
[10] 霍炎, 任顺清, 李巍. 圆感应同步器扇区刻划误差的测试方法[J]. 电机与控制学报, 2019, 23(7): 19-26, 37. Huo Yan, Ren Shunqing, Li Wei. Measurement method for sector etching error of round inductosyn[J]. Electric Machines and Control, 2019, 23(7): 19-26, 37.
[11] 李海霞, 张嵘, 韩丰田. 感应同步器测角系统误差测试及补偿[J]. 清华大学学报(自然科学版), 2016, 56(6): 611-616. Li Haixia, Zhang Rong, Han Fengtian. Error testing and compensation of an inductosyn-based angular measurement system[J]. Journal of Tsinghua University (Science and Technology), 2016, 56(6): 611-616.
[12] Mirzaei M, Machac J, Ripka P, et al. Design of a flat-type magnetic position sensor using a finite-difference method[J]. IET Science, Measurement & Technology, 2020, 14(5): 514-524.
[13] Liu Chengjun, Xu Fanrong. A novel absolute angle-measuring method with rotary inductosyn[C]//2018 Eighth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 2020: 1753-1757.
[14] 肖飞, 许观达, 连传强, 等. 永磁同步电机单电流传感器系统的三相电流重构策略[J]. 电工技术学报, 2022, 37(7): 1609-1617. Xiao Fei, Xu Guanda, Lian Chuanqiang, et al. Three-phase current reconstruction strategy of permanent magnet synchronous machine drives using a single current sensor[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1609-1617.
[15] 李帆, 罗海云, 杜娟, 等. 基于直流辉光放电等离子体的气体压力传感器[J]. 电工技术学报, 2021, 36(15): 3163-3171. Li Fan, Luo Haiyun, Du Juan, et al. Pressure sensor based on direct current discharge plasma[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3163-3171.
[16] Yan Jiaxuan, Feng Renjian, Wu Yinfeng, et al. A calibration scheme with combination of the optical shaft encoder and laser triangulation sensor for low-frequency angular acceleration rotary table[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-13.
[17] Böller S, Alić B, Hennig A, et al. Noninvasive current measurement in multi-conductor cables[C]//2021 IEEE Sensors, Sydney, Australia, 2021: 1-4.
[18] Brandão G L F, Silva E J, Soares Í V, et al. Analysis of angular stability of fractal artificial magnetic conductor metasurface using generalized boundary conditions[C]//2021 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Fortaleza, Brazil, 2021: 1-3.
[19] Kwon O I, Sajib S Z K, Sersa I, et al. Current density imaging during transcranial direct current stimulation using DT-MRI and MREIT: algorithm development and numerical simulations[J]. IEEE Transactions on Biomedical Engineering, 2016, 63(1): 168-175.
[20] Chen Hao, Wang Yinshun, Wang Jiuke, et al. Experimental study on quasi-isotropic critical current of an HTS conductor with high engineering current density[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(5): 1-4.
[21] Jiu Yuanwei, Chen Ziyin, Cui Chenpeng, et al. A round inductosyn measuring system based on quadrant comparison and adjustment fusion algorithm[C]//2021 China Automation Congress (CAC), Beijing, China, 2022: 8068-8071.
[22] Song Li, Kang Jianbing, Li Jing. A design of inductosyn angle measurement system based on AD2S80A and FPGA[C] //2017 36th Chinese Control Conference (CCC)，Dalian, China，2017: 5350-5353.
Abstract With the continuous development of aerospace, military, industrial production and other related fields, the requirements for machining accuracy and Angle measurement in related industries are also gradually increased. However, the code disk of grating and rotary encoder belong to the position sensor of optical principle, which cannot work in the occasions with strong cosmic rays and rapid temperature changes, and the maintenance difficulty and cost are high, but the induction synchronizer through electromagnetic Induction principle transmits position signal, strong anti-interference and easy to clean and maintain, has relatively stable performance and long service life, Therefore, this kind of non-contact position sensor is widely used in high-speed and high-precision occasions such as Angle measurement and platform Angle position measurement of spacecraft. At the same time, with the miniaturization of space equipment, the research and development of small-size induction synchronizer is of great significance. However, the traditional induction synchronizer uses segmentalized stator structure, which has very strict requirements on the precision of line cutting. Thus, the further miniaturization and integration of induction synchronizer are limited.
The form of double-row winding induction synchronizer is constructed to compensate the influence caused by the wire cutting deviation. The stator windings of the segmented winding synchronizer are divided into inner and outer rows and staggered by a group of pitch according to the principle of consistent specific potential. The inner and outer row conductors are directly connected through effective conductors and are approximately in the form of continuous windings. The number of effective conductor coupling becomes twice as much as that of the traditional winding, and no extra lead wire is added, and the influence of conductor deviation is suppressed. In the actual design process, the inner and outer conductors are staggered so as to inhibit the influence of the non-effective potential generated at the end on the output potential, and a 3D model is established for simulation. The output potential is decomposed by fast Fourier and compared with the traditional induction synchronizer, which effectively improves the accuracy of Angle measurement and has important significance for reducing the difficulty and cost of the induction synchronizer.
By establishing the effective conductor current density model, the optimization strategy of suppressing the third and fifth harmonics is proposed, which further improves the Angle measurement accuracy of the induction synchronizer. On this basis, the 3D simulation model of the induction synchronizer is established. The correctness and feasibility of this method are verified by finite element analysis and fast Fourier decomposition of the output potential. Through the winding width design, the third and fifth harmonics of output potential can be effectively suppressed and the sinusoidal property of output potential can be guaranteed. Finally, the ultra-thin PCB prototype is used for verification. Compared with the traditional induction synchronizer with the same processing technology and size, the orthogonal error Angle of the optimized double-row winding induction synchronizer is about 30% of that of the single-row induction synchronizer. In other words, the error range of plus or minus 10 seconds can be reached under the same process, which greatly inhibits the harmonic error of the induction synchronizer and reduces the requirement of line precision.
Keywords：Small size, double-row winding, conductor deviation, finite element method
DOI:10.19595/j.cnki.1000-6753.tces.L10070
中图分类号：TM 383.2
收稿日期 2023-01-13
改稿日期 2023-03-10
刘承军 男，1976年生，副教授，研究方向为测角电机、特种电机系统。E-mail：liucj@hit.edu.cn（通信作者）
张逸飞 男，1999年生，硕士，研究方向为测角电机、特种电机系统。E-mail：21S006105@stu.hit.edu.cn
（编辑 崔文静）