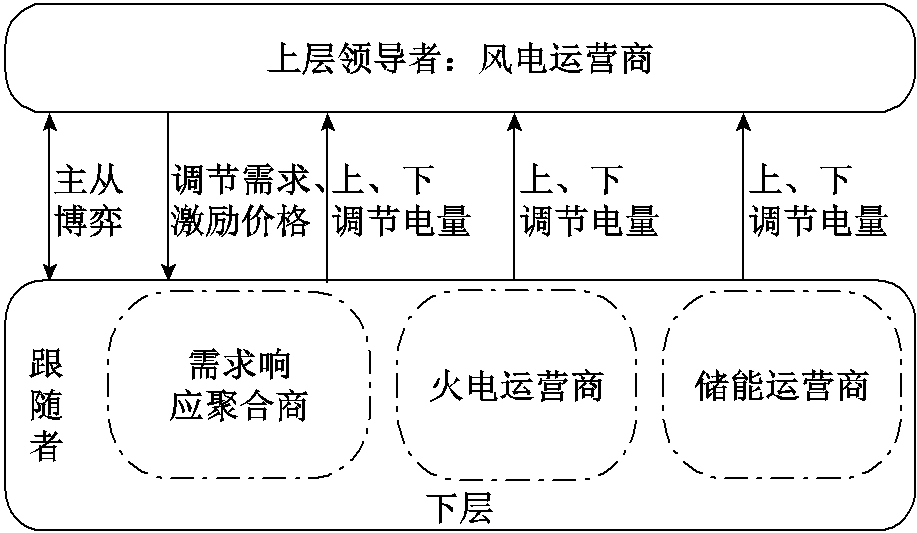
图1 灵活性资源供需多主体双层博弈互动框架
Fig.1 Flexible resource supply and demand multi-agent bi-level game interaction framework
摘要 在含高比例风电的新型电力系统中,针对由于缺乏灵活性调节激励机制造成的灵活性资源调节积极性不高、风电波动性平衡困难的问题,该文提出一种考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度方法。首先,计及风电波动性与负荷波动性的时空耦合特性,定义了风电波动性评价指标,并以此为基础提出了风电灵活性调节需求量化方法;然后,考虑各灵活性资源主体决策的差异性和趋利性,提出了基于主从博弈的灵活性供需均衡分析方法,以各主体利益最大化为目标建立灵活性资源供需博弈优化模型;最后,通过仿真案例验证了所提方法可以有效提高源-荷-储多方灵活性资源参与调节的积极性,并促进高比例风电的上网消纳。
关键词:高比例风电 灵活性补偿 主从博弈 风电波动性
在“双碳”目标的驱动下,电力行业低碳化发展的重要性日益突出,建设以新能源为主体的新型电力系统,既是能源转型的必然趋势,也是实现碳达峰、碳中和目标的重要途经[1]。随着以风电为主的新能源大规模并网,电力系统面临的不确定性与反调峰特性不断增强,系统的电力电量平衡面临着巨大挑战,充足的灵活性调节能力成为新型电力系统安全、经济运行的必要条件[2]。因此,如何保证系统有充足的灵活性调节能力应对持续增长的新能源与原有负荷的双重冲击成为人们关注的焦点。
充足的灵活性调节能力意味着电力系统能够以合理的经济成本应对源-荷的波动性和不确定性,经济高效地消纳大规模新能源[3]。然而,高速发展的新能源使系统的灵活性调节能力匮乏的问题日益突出,在迫切的灵活性需求下,探索新的灵活性来源和深度挖掘系统灵活性潜力成为诸多学者研究的热点。文献[4]建立火电机组深度调峰模型,通过降低火电机组最小技术出力提高源侧运行灵活性;文献[5]通过为火电厂配置储能装置实现源侧灵活性改造,并提出一种储能辅助火电机组深度调峰的优化调度方案;文献[6]提出一种储能参与调峰的日前优化调度策略,以此来减小电网的负荷峰谷差,提高风电接纳量;文献[7]将储能系统与空调负荷纳入可调度资源,以运行成本及负荷方差最小为目标建立优化调度模型;文献[8]通过综合需求响应实现源荷协同互动,提出工业园区需求响应优化调度模型;文献[9]以聚合商的形式整合负荷侧柔性资源,建立资源聚合商模式下的柔性资源联合调度模型。上述文献从“源-荷-储”多个层面挖掘系统灵活性调节潜力,在一定程度上提高了系统运行的灵活性,但并未考虑到由于缺乏合理的激励机制,导致灵活性资源参与调节的积极性不高的问题。
电力系统运行灵活性一方面取决于上述“源-荷-储”各类资源的技术特性;另一方面各类技术手段所对应的系统灵活性潜力需要依靠合理的激励手段激活。文献[10]研究了火-储深度调峰的定价策略,有效地提高了火-储深度调峰的积极性,改善了系统运行的灵活性;文献[11]通过混合博弈协调风火网间的利益,避免了因风电、火电、电网独立运行造成的弃风及经济效益下降;文献[12]基于合作博弈理论对风储联合参与现货市场的收益进行分配,有效地解决了风储各主体间的利益分配问题,提高了风储联合参与市场的积极性;文献[13]提出一种考虑可再生能源保障性消纳的电力市场出清机制,现货市场在发生弃能时触发该机制,实现可再生能源的保障性消纳;文献[14]建立了含灵活性资源交易的电力市场实时出清模型,实现了合理补偿机组机会成本,有效地提高了新能源消纳能力;文献[15]分析了国内外辅助服务市场中灵活性资源的应用现状与前景,提出面向灵活性提升的我国辅助服务市场发展思路;文献[16]设计了高比例可再生能源渗透下的电力市场价值分配机制,实现对可再生能源并网消纳的波动成本的合理分摊。目前对灵活性调节补偿机制的研究中,主要采用向下调峰的电价补偿,且一般考虑的调峰主体为电网,而非风电集团,不能有效调动多元灵活性资源的调节潜能,灵活性资源的价值没有得到充分体现。缺乏对于高比例风电如何参与到灵活性调节服务交易,并与灵活性调节资源协调优化的研究。
为此,本文在合理量化风电波动性及风电灵活性调节需求的基础上,考虑风电及各灵活性资源主体的个体趋利属性,运用主从博弈的思想,建立灵活性调节服务供需多主体博弈优化调度模型,实现灵活性资源的供需优化和灵活性价值的合理补偿。具体而言,风电运营商实施灵活性调节补偿政策,根据自身的调节需求确定灵活性调节电价,激励灵活性资源为其提供调节服务。灵活性资源运营商响应风电运营商的激励策略,充分考虑提供灵活性调节的成本价值关系,提供向上或向下的灵活性调节服务。通过博弈优化,实现灵活性的供需平衡,促进高比例风电的消纳,实现源-荷-储的协同运行。
相较于传统电力系统,含高比例新能源的新型电力系统的电力电量平衡模式和各主体价值关系均发生改变。以风电为代表的新能源发电逐渐向供电主体地位转变,系统电力电量平衡模式由以“确定性”为主导的机组组合模型转变为以“波动性”为主导的灵活性资源调节模式。风电运营商作为灵活性调节服务的需求者,需要对源-荷-储三方面各主体提供的灵活性价值进行辨识与量化,并制定合理的激励策略激励各灵活性资源主体参与到灵活性调节中,确保充足的灵活性调节能力应对风电出力的波动性,实现高比例风电的经济、高效消纳。灵活性资源的供给和需求与系统在不同时空的运行状态呈现高度的相关性。为此,本文通过构建风电运营商与灵活性资源主体间的博弈关系,揭示不同时段、不同运行状态下系统灵活性资源的真实供需关系,基于博弈均衡原理得到灵活性供需均衡状态,使个体的灵活性价值实现与系统灵活运行目标相趋同,促进不同主体的深度协同。图1为灵活性资源供需多主体双层博弈互动框架。上层风电运营商作为领导者,根据自身的灵活性调节需求,以合理有效的激励价格信号引导跟随者的行为,激励有能力的灵活性资源主体提供灵活性调节服务;下层火电运营商、储能运营商、需求响应聚合商作为跟随者,根据激励价格传递的灵活性价值,确定最优的灵活性调节电量,提高灵活性资源的跨时空配置效率。

图1 灵活性资源供需多主体双层博弈互动框架
Fig.1 Flexible resource supply and demand multi-agent bi-level game interaction framework
上层领导者风电运营商需要根据风电出力的波动性量化自身灵活性需求,并制定有效的激励策略引导灵活性资源为其提供调节服务。本节首先定义了风电的波动性评价指标;然后,基于理想模型法合理量化风电的灵活性调节需求;最后,以利益最大化为目标建立风电运营商优化模型。
风电波动性与负荷波动性具有时空耦合特性,风电出力变化趋势与负荷曲线变化趋势的相似度越高,则风电出力对跟踪负荷波动的贡献程度越大,对系统而言风电的波动性越小。给定两条风电、负荷出力时间序列Pw=(Pw 1, Pw 1, …, Pw t)和Pd=(Pd 1, Pd 1,…, Pd t),若直接采用欧式距离度量,其距离值只能反映点对点的数值相似程度,而无法反映两条时间序列波形上的相似程度。为此,本文对风电、负荷的出力时间序列做出改进,利用风电、负荷的变化率时间序列代替风电、负荷的出力时间序列,通过计算变化率时间序列的欧式距离实现对风电、负荷波形相似程度的度量。改进后的欧式距离表达式为
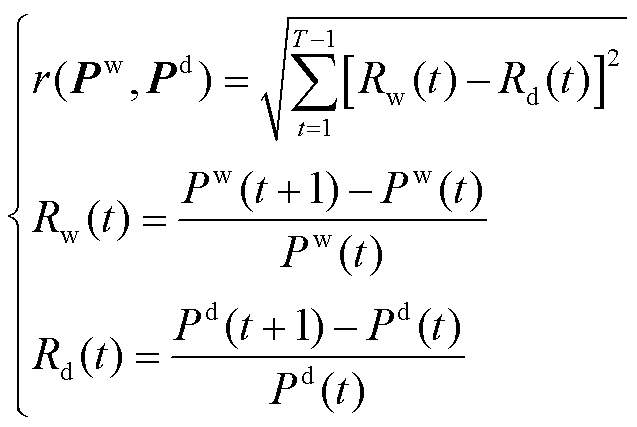 (1)
(1)
式中,Rw(t)为t时段风电出力的变化率;Rd(t)为t时段负荷出力的变化率;r(Pw,Pd)为风电出力变化率序列与负荷出力变化率序列的欧式距离。欧式距离r可以反映风电出力变化趋势与负荷曲线变化趋势的相似程度,欧式距离越小,风电出力与负荷曲线的波形相似度越高,对系统而言风电出力的波动性越小。欧式距离为0表示风电出力与负荷变化趋势完全相同,即“顺负荷”[17]。电网运营商通过设置合理的欧式距离指标实现对风电出力波动性的考核。
风电运营商灵活性调节的目的在于以最小的调节电量平抑风电出力的波动性,同时实现风电的最大消纳。本文基于理想模型法量化风电运营商的灵活性调节需求,核心思路在于:风电运营商根据预测出力Pw,pre t制定日前风电计划出力Pw t后,通过对风电日前出力计划曲线进行电量等效,以灵活性调节电量最小为目标,构造满足波动性指标的风电理想出力场景;通过计算风电理想出力曲线与日前风电出力计划曲线之差,实现对风电运营商灵活性调节需求的量化。其中,满足波动性指标的风电理想出力场景的构造模型为
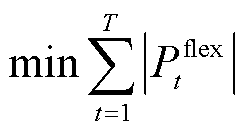 (2)
(2)
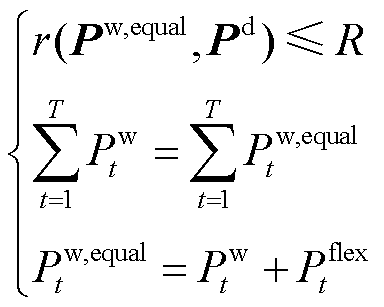 (3)
(3)
式中,Pw,equal为满足波动性指标的风电理想出力序列;Pw t为t时段风电运营商制定的日前风电计划出力;Pw,equal t为t时段的满足波动性指标的风电理想出力;Pflex t为t时段风电运营商所需的灵活性调节电量;R为电网运营商设置的风电波动性考核指标。式(3)中,第一个公式保证了Pw,equal出力序列满足波动性指标,第二个公式保证了Pw,equal与Pw t的电量等效。
满足波动性指标的风电理想出力曲线示意图如图2所示。当Pw t>Pw,equal t时,Pflex t为负,风电运营商需要向下的灵活性调节电量;当Pw t<Pw,equal t时,Pflex t为正,风电运营商需要向上的灵活性调节电量。风电运营商的灵活性调节需求可表示为
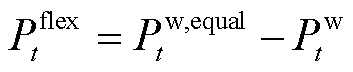 (4)
(4)
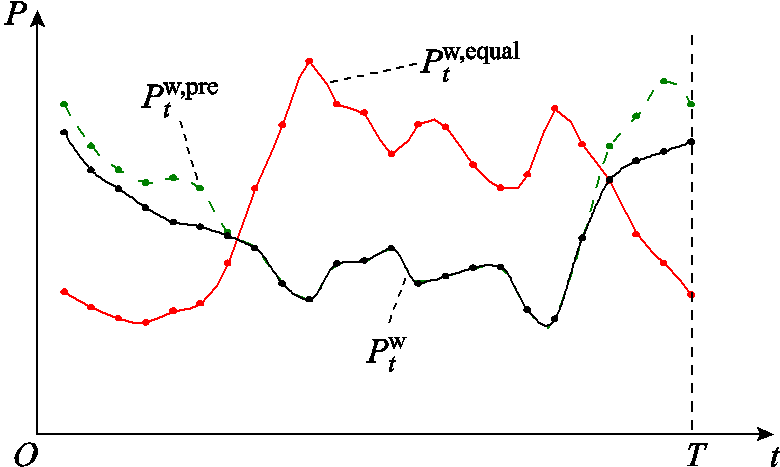
图2 满足波动性指标的风电理想出力曲线示意图
Fig.2 Diagram of ideal wind power output curve satisfying fluctuation index
以风电收益最大化为目标构建优化模型,有
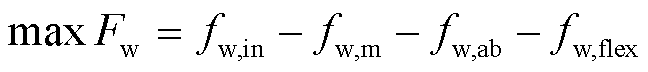 (5)
(5)
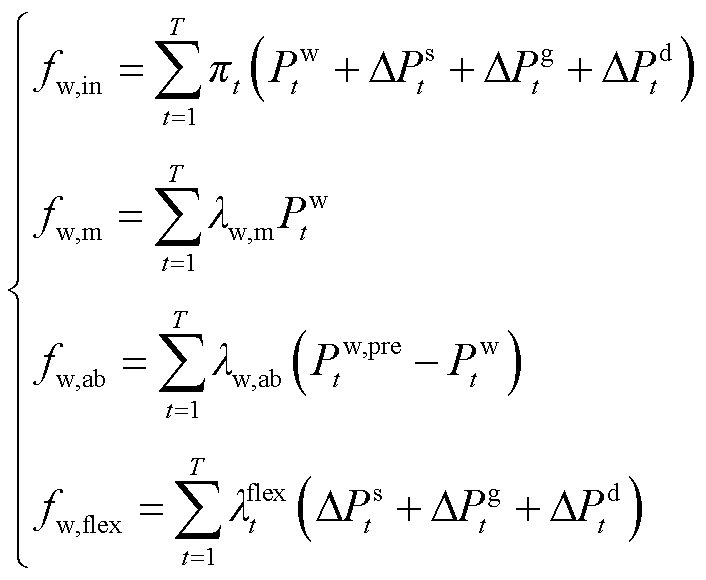 (6)
(6)
式中,Fw为风电运营商的净收益;fw,in为电量上网的收益;fw,m为运维成本;fw,ab为弃风成本;fw,flex为风电的灵活性调节成本;pt为t时段的市场电价;lw,m为风电的运维成本系数;lw,ab为风电的弃风成本系数;Pw,pre t为t时段风电的预测出力;lflex t为t时段风电运营商制定的灵活性调节电价;ΔPs t、ΔPg t、ΔPd t分别为t时段储能运营商、火电运营商、需求响应聚合商为风电运营商提供的灵活性调节电量,其大小由下层各灵活性资源主体确定。
模型的约束条件包括:
1)日前风电计划出力约束
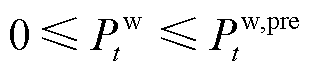 (7)
(7)
2)灵活性供需平衡约束
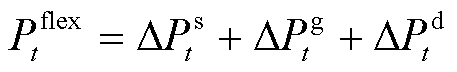 (8)
(8)
3)灵活性调节方向状态变量约束


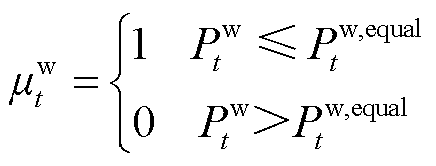 (9)
(9)
4)灵活性调节激励价格约束
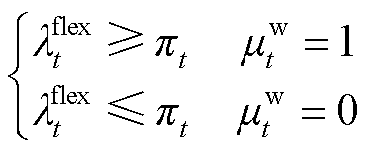 (10)
(10)
式中, mw t为t时段风电的灵活性调节需求方向的状态变量。mw t=1时表示风电需要向上的灵活性调节电量;mw t=0时表示风电需要向下的灵活性调节电量。
下层跟随者火电运营商、储能运营商、需求响应聚合商响应上层风电运营商的灵活性调节激励策略,考虑自身提供灵活性调节服务的成本、价值关系,以净收益最大化为目标建立灵活性调节电量出清模型。
储能运营商利用储能的时空平移能力,为风电运营商提供灵活调节服务,其收益可表示为
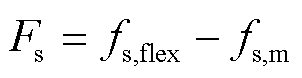 (11)
(11)
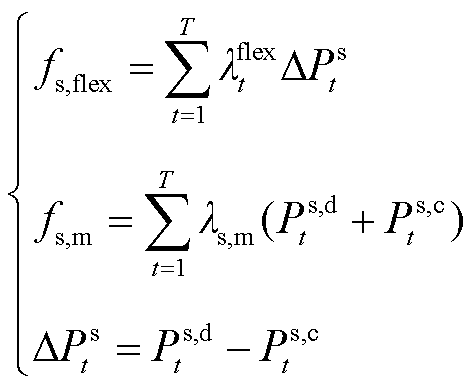 (12)
(12)
式中,Fs为储能运营商的净收益;fs,flex为储能提供灵活性调节服务所获得的收益;fs,m为储能的运维成本;Ps,c t、Ps,d t分别为t时段储能的充、放电功率;ls,m为储能的运维成本系数;ΔPs t为t时段储能提供的灵活性调节电量,当其为正时,储能放电,提供向上的灵活性调节电量,为负时,储能充电,提供向下的灵活性调节电量。
火电运营商的收益包含为负荷供电获得的收益以及为风电运营商提供灵活性调节服务获得的收益,其总收益可表示为
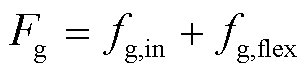 (13)
(13)
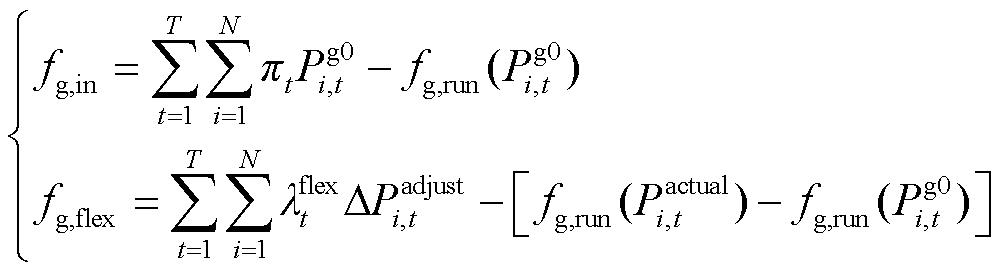 (14)
(14)
式中,Fg为火电运营商的净收益;fg,in为火电机组为负荷提供电能获得的净收益;fg,flex为火电提供灵活性调节服务获得的净收益;N为火电机组数量;ΔPadjust i,t为t时段第i台火电机组提供的灵活性调节电量,当其为正时,增加火电机组出力,提供向上的灵活性调节电量,为负时,减少火电机组出力,提供向下的灵活性调节电量;Pactual i,t为t时段第i台火电机组的计划出力;fg,run为火电机组的运行成本;Pg0 i,t为t时段第i台火电机组提供灵活性调节电量前的出力。火电机组计划出力与火电机组提供灵活性调节电量前出力关系可表示为
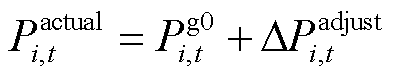 (15)
(15)
深度调峰机组的运行成本根据运行状态不同有所改变,可表示为
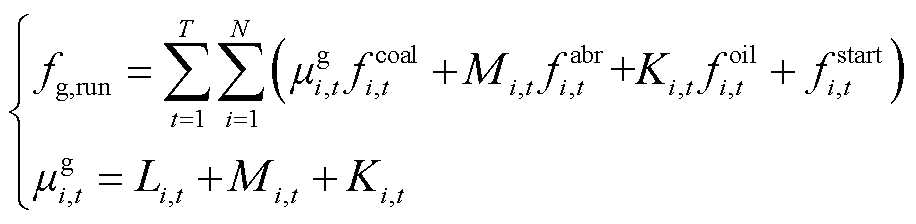 (16)
(16)
式中,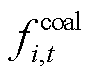 、
、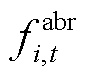 、
、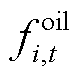 分别为t时段第i台火电机组的煤耗成本、寿命损耗成本、投油成本,详细的计算方法见文献[18];Li,t、Mi,t、Ki,t分别为火电机组处于基本调峰阶段、不投油深度调峰阶段、投油深度调峰阶段的0-1状态变量;
分别为t时段第i台火电机组的煤耗成本、寿命损耗成本、投油成本,详细的计算方法见文献[18];Li,t、Mi,t、Ki,t分别为火电机组处于基本调峰阶段、不投油深度调峰阶段、投油深度调峰阶段的0-1状态变量;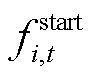 为机组的起停成本。
为机组的起停成本。
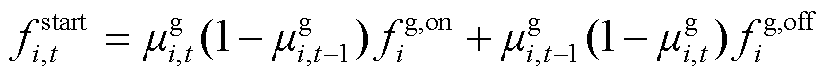 (17)
(17)
式中,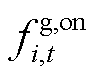 、
、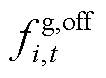 分别为火电机组的开机和停机成本;mg i,t为火电机组的起停状态变量。
分别为火电机组的开机和停机成本;mg i,t为火电机组的起停状态变量。
火电运营商为t时段风电运营商提供的灵活性调节总电量为
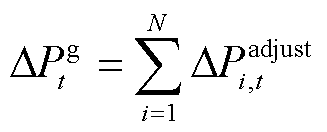 (18)
(18)
基于激励型的可转移负荷调节方式灵活、调节潜力较大,同时具备时空平移特性,能够有效应对高比例风电的波动性、反调峰特性。本节考虑可转移负荷的功率特性与时间特性对用户用能体验的影响,建立需求响应的成本及收益模型。
3.3.1 考虑时间特性的可转移负荷建模
针对可转移负荷的响应特性,现有研究从可转移负荷的功率特性对用户的舒适度损失进行建模,但缺乏考虑可转移负荷的时间特性对用户用能体验的影响。为此,本文对可转移负荷的转移时间进行区分和细化,在可转移负荷允许转移的时间段内划分出用户指定的理想转移时间段。将可转移负荷的实际转移时间偏离理想转移时间的程度定义为转移偏离度,用户的用能体验与可转移负荷的转移偏离度之间具有负相关性。通过构建如下可转移负荷转移偏离度矩阵对可转移负荷的时间特性进行建模。
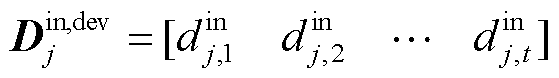 (19)
(19)
式中,Din,dev j为可转移负荷j转入时的转移偏离度矩阵;din j,t为可转移负荷j在t时段转入的转移偏离度系数,其大小可由式(20)计算得到。
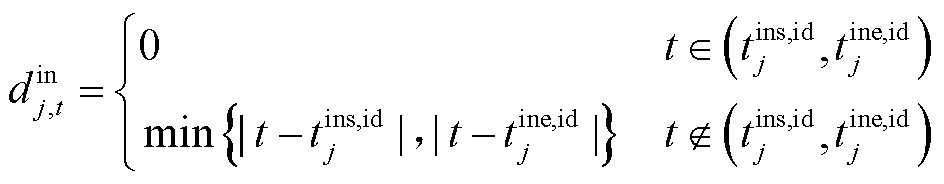 (20)
(20)
式中,tins,id j、tine,id j分别为可转移负荷j理想转入时间段的起始时间与结束时间。可转移负荷j转出时的转移偏离度矩阵Dout,dev j计算方法与Din,dev j类似。
综合考虑可转移负荷的功率特性、时间特性对用户舒适度的影响,可转移负荷用户参与需求响应的响应成本可表示为
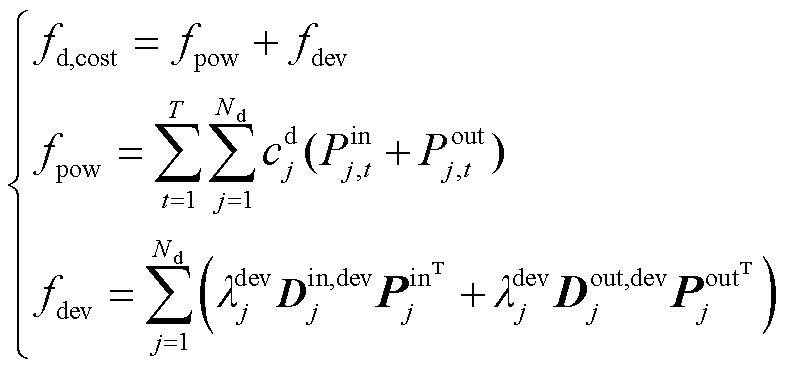 (21)
(21)
式中,fd,cost为可转移负荷参与需求响应的响应成本;fpow、fdev分别为可转移负荷转移功率、转移偏离度对用户舒适度造成的损失;cd j为可转移负荷j的单位电量转移成本系数;ldev j为可转移负荷j单位电量的偏离度成本系数;Pin j为可转移负荷j各时段的转入功率,Pin j=[Pin j,1 Pin j,2…Pin j,T];Pout j为可转移负荷j各时段的转出功率,Pout j=[Pout j,1Pout j,2…Pout j,T]。
3.3.2 考虑时间特性的可转移负荷建模
需求响应聚合商通过对可转移负荷进行激励调度,为风电运营商提供灵活性调节服务,其净收益可表示为
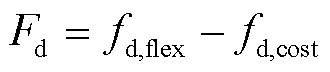 (22)
(22)
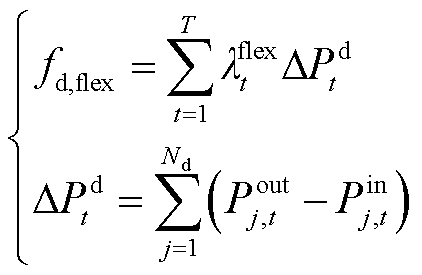 (23)
(23)
式中,Fd为需求响应聚合商净收益;fd,flex为需求响应聚合商提供灵活性调节服务获得的收益;fd,cost为需求响应聚合商激励成本;ΔPd t为t时段需求响应聚合商为风电提供的灵活性调节电量,当其为正时转出负荷,提供向上的灵活性调节电量,为负时转入负荷,提供向下的灵活性调节电量。
3.4.1 目标函数
在灵活性调节电价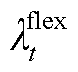 下,储能运营商、火电运营商、需求响应聚合商提供单位调节电量获得的收益是相同的,但其提供灵活性调节电量的成本不尽相同,灵活性调节电量应依据成本由小到大顺序出清。因此,以多元灵活性资源净收益最大为目标函数,即成本最小,建立下层多主体灵活性调节电量出清模型为
下,储能运营商、火电运营商、需求响应聚合商提供单位调节电量获得的收益是相同的,但其提供灵活性调节电量的成本不尽相同,灵活性调节电量应依据成本由小到大顺序出清。因此,以多元灵活性资源净收益最大为目标函数,即成本最小,建立下层多主体灵活性调节电量出清模型为
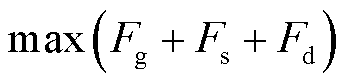 (24)
(24)
3.4.2 储能运营商约束条件
1)储能充放电约束
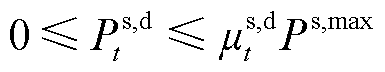 (25)
(25)
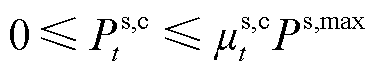 (26)
(26)
2)储能容量约束
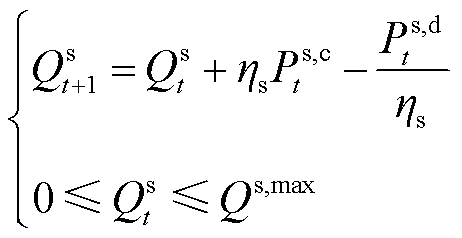 (27)
(27)
3)状态变量约束
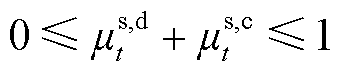 (28)
(28)
式中,Ps,max为储能的最大充放电功率;ms,c t、ms,d t分别为t时段储能充、放电的状态变量;Qs t为t时刻储能的储能容量;Qs,max为储能的最大储存容量;hs为储能的充放电效率。
3.4.3 火电运营商约束条件
1)火电机组出力约束
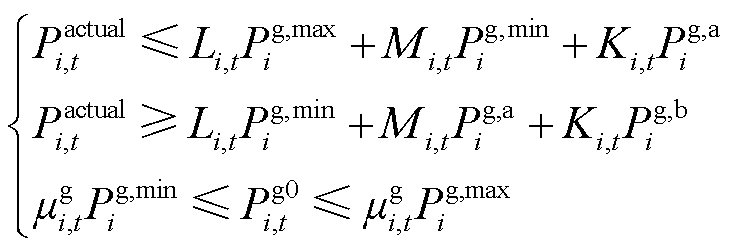 (29)
(29)
2)火电机组爬坡约束
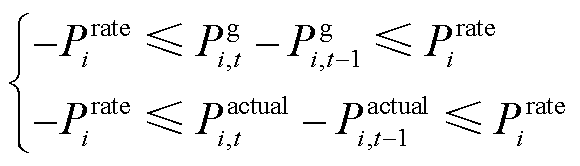 (30)
(30)
3)最小起停时间约束
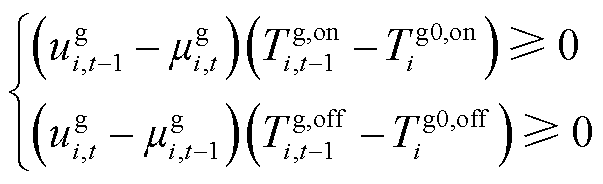 (31)
(31)
4)状态变量约束
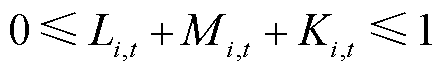 (32)
(32)
式中,Pg,max i、Pg,min i分别为第i台火电机组常规调峰出力上、下限;Pg,a i为第i台火电机组不投油深度调峰出力下限;Pg,b i为第i台火电机组投油深度调峰出力下限;Prate i为第i台火电机组的爬坡率;Tg,on i,t-1、Tg,offi,t-1分别为t-1时刻第i台火电机组的连续运行时长和连续停机时长;Tg0,on i、Tg0,off i分别为第i火电台机组允许的最小连续运行时长和连续停机时长。
3.4.4 需求响应聚合商约束条件
1)转移功率约束
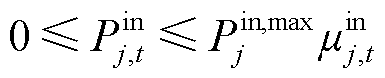 (33)
(33)
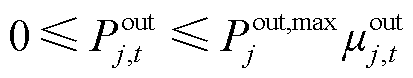 (34)
(34)
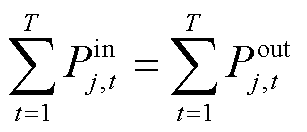 (35)
(35)
2)转移时间约束
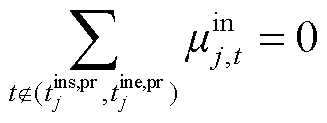 (36)
(36)
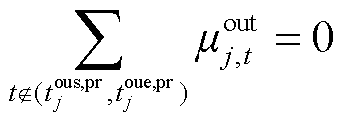 (37)
(37)
3)状态变量约束
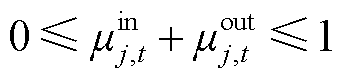 (38)
(38)
式中,Pin,max j、Pout,max j分别为可转移负荷j最大的转入、转出功率;µin j,t、µout j,t分别为可转移负荷转入、转出状态变量;tins,pr j、tine,pr j分别为可转移负荷j允许转入时间段的起始时间、结束时间;tous,pr j、toue,pr j分别为可转移负荷j允许转出时间段的起始时间、结束时间。
3.4.5 其他约束条件
1)功率平衡约束
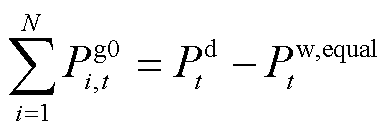 (39)
(39)
2)灵活性调节电量约束
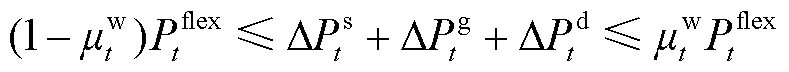 (40)
(40)
3)灵活性调节方向约束
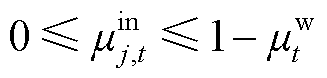 (41)
(41)
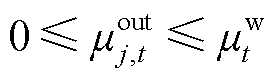 (42)
(42)
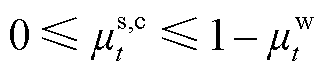 (43)
(43)
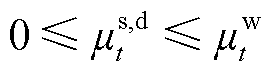 (44)
(44)
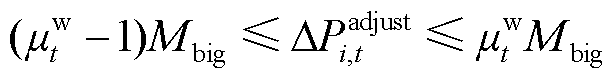 (45)
(45)
式中,Mbig为一个大正数。
4)激励相容约束
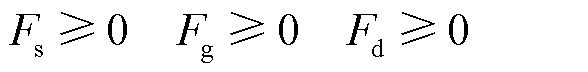 (46)
(46)
本文采用双层嵌套的方法求解主从博弈模型的均衡解。利用融合多种策略的改进粒子群算法[19]更新上层风电运营商的风电出力计划及灵活性补偿价格,下层问题通过分段线性化的方法,将二次方项转换为混合整合规划模型,采用Gurobi求解器进行求解,具体求解步骤如下:
1)输入原始数据及参数,包括风电预测数据、负荷预测数据、实时电价数据、风电运行参数、火电运行参数、储能运行参数、需求响应运行参数,设置风电上网波动性指标参数R=0。
2)设置粒子群算法参数,初始化迭代次数k=0,初始化风电运营商策略粒子群{Pw k,t, λflex k,t}。
3)根据式(1)~式(4)量化风电运营商灵活性调节需求{Pflex k,t, µw k,t},并将参数{λflex k,t, µw k,t, Pflex k,t}传递给下层多元灵活性资源主体。
4)下层接收到参数{λflex k,t, µw k,t, Pflex k,t},根据模型式(24)进行灵活性调节电量的出清{ΔPs k+1,t, ΔPg k+1,t, ΔPd k+1,t},并将出清结果传递回上层风电运营商。
5)风电运营商接受到跟随者的决策信息{ΔPs k+1,t, ΔPg k+1,t, ΔPd k+1,t},根据模型式(5)计算各粒子的适应度,并根据粒子适应度更新粒子群{λflex k+1,t, Pw k,t},迭代次数k=k+1。
6)判断主从博弈模型是否达到博弈均衡点,即判断第k+1轮主体和寻优结果是否与k轮一致,如果有
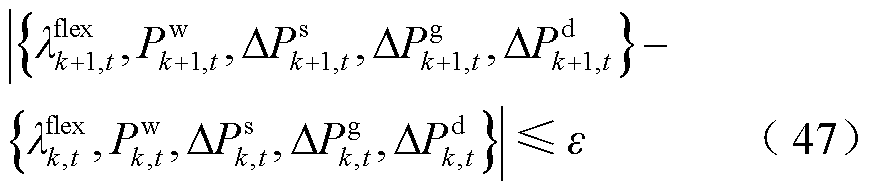
则表示找到主从博弈均衡解{Pw*t, λflex*t, ΔPs*t, ΔPg*t, ΔPd* t};否则转入步骤3)继续迭代求解,直至找到博弈均衡解或达到最大迭代次数。
本文以含高比例风电的新型电力系统为对象开展仿真研究,其中参与灵活性调节交易的灵活性资源包含4台火电机组、1个储能电站、5类可转移负荷。源侧4台火电机组中2台具有深度调峰能力,机组详细参数见附表1;储能的额定容量为80 MW·h,具体参数见附表2;荷侧包含5类可转移负荷,详细参数见附表3;风电装机容量为840 MW,风电弃风惩罚系数为250元/(MW·h),风电上网波动性考核指标取R=0。系统负荷预测曲线、风电预测曲线、实时电价曲线如附图1所示。
为验证本文所提策略的有效性,本文设置了四个场景进行对比分析,场景具体设置如下。
场景1:系统中包含源-荷-储三个方面的灵活性资源,以系统运行成本最小为目标对源-荷-储进行集中优化调度。
场景2:系统中包含源-储两个方面的灵活性资源,采用本文所提的灵活性资源供需博弈策略对源-储进行协同优化。
场景3:系统中包含源-荷两个方面的灵活性资源,采用本文所提的灵活性资源供需博弈策略对源-荷进行协同优化。
场景4:系统中包含源-荷-储三个方面的灵活性资源,采用本文所提的灵活性资源供需博弈策略对源-荷-储进行协同优化。
5.2.1 电力电量平衡结果
图3、图4分别为场景1、场景4的电力电量平衡结果。
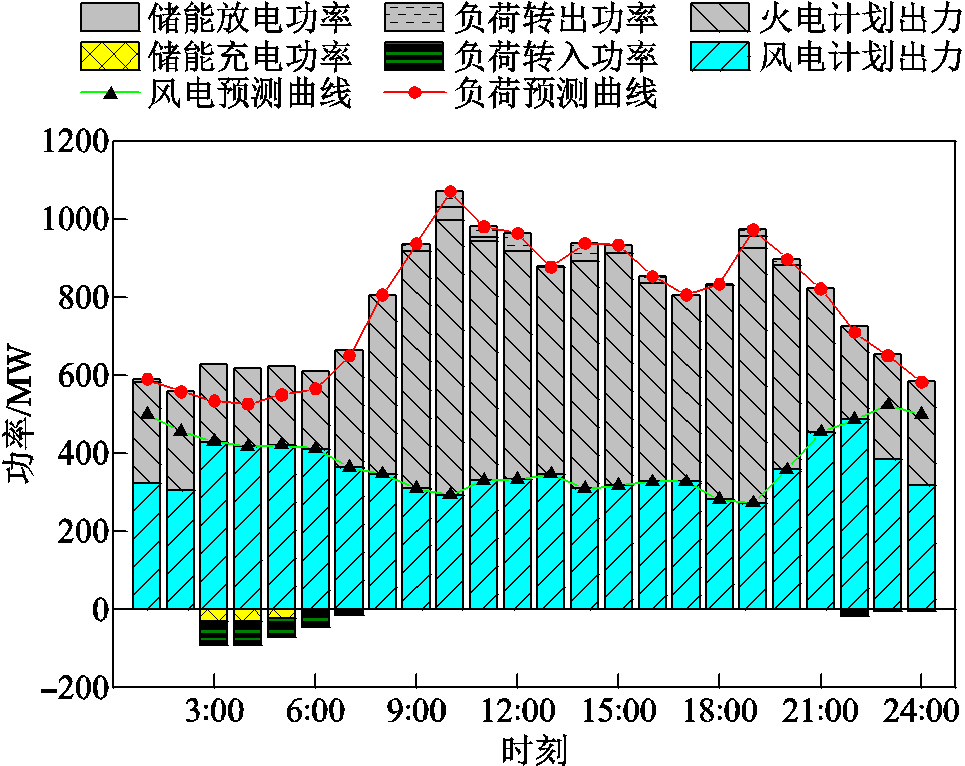
图3 场景1电力电量平衡结果
Fig.3 Power balance results in scenario 1
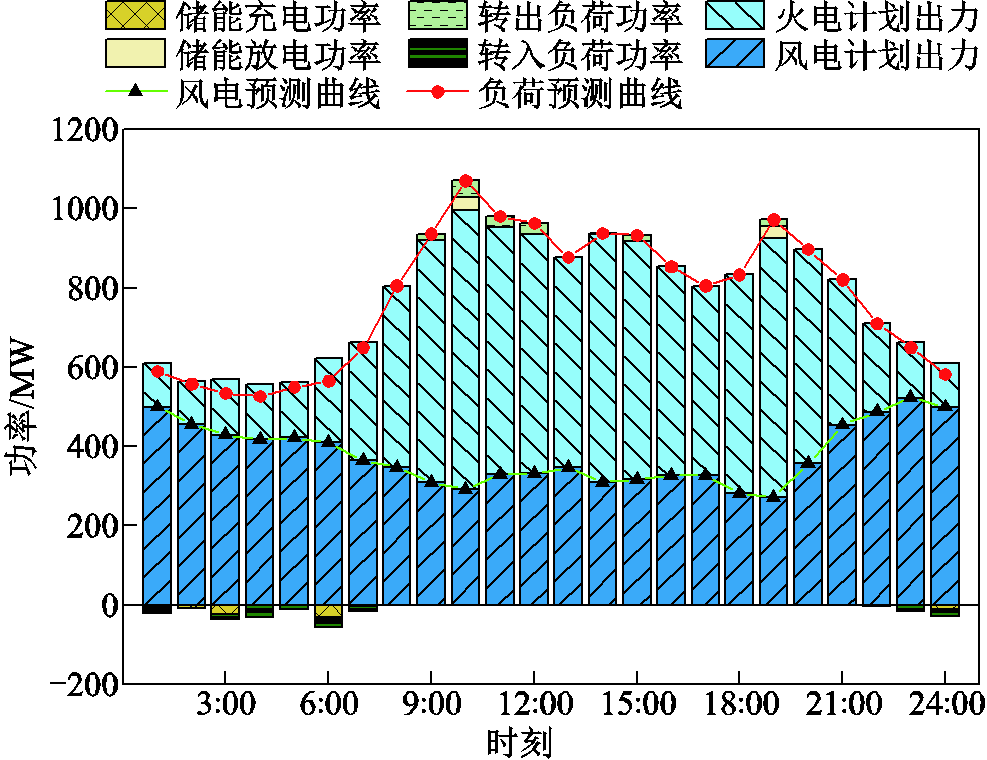
图4 场景4电力电量平衡结果
Fig.4 Power balance results in scenario 4
如图3所示,场景1中,在3:00—7:00、22:00,储能及需求响应利用自身的时空平移能力,将338.290 MW·h成本较低的风电转移至负荷高峰时段,减少系统风电高发时段的弃风量。但是,由于缺乏激励机制,1:00—2:00、23:00—24:00火电机组只运行于不投油深度调峰状态,产生了647.840 MW·h的弃风。分析图4可知,相较于场景1,场景4中1:00—2:00、23:00—24:00火电机组运行于投油深度调峰状态,调峰深度更深,基本实现了高比例风电的高效消纳。这表明本文所提策略能够提高灵活性资源主体参与调节的积极性,充分挖掘系统的调节能力,有效地促进高比例风电的消纳。
5.2.2 灵活性资源供需博弈结果
图5为场景4中风电运营商与灵活性资源运营商的博弈结果,场景4中灵活性调节电价博弈结果如附图2所示,博弈迭代收敛过程如附图3所示。
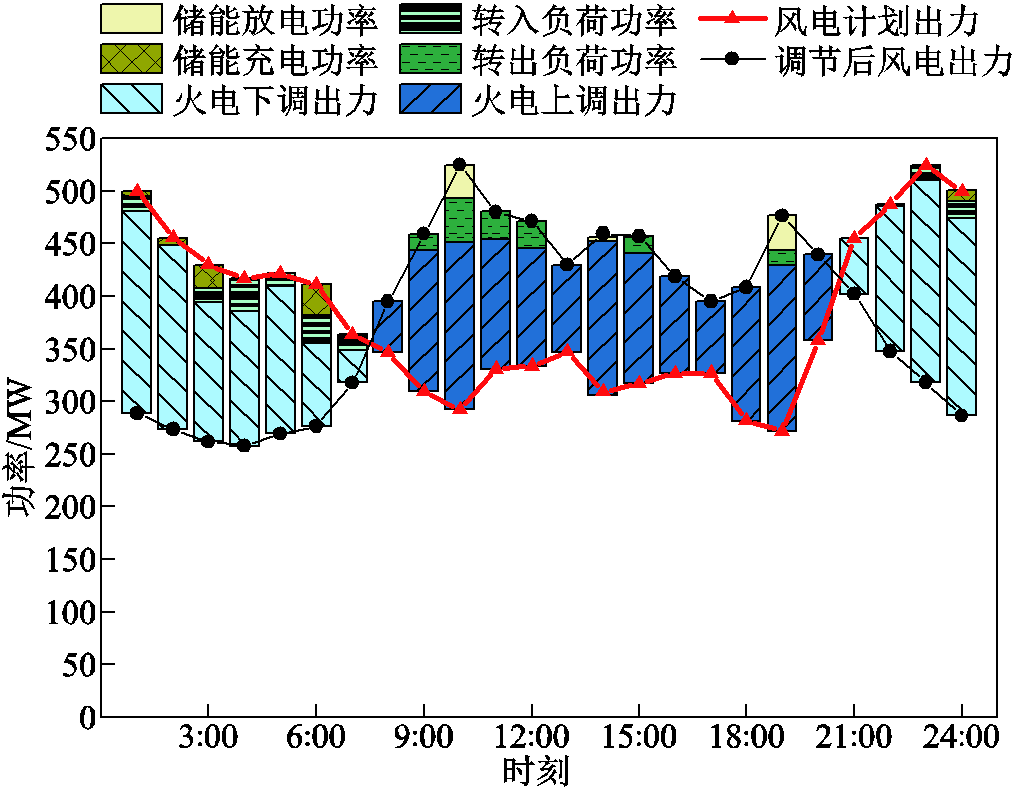
图5 场景4灵活性电量供需博弈结果
Fig.5 Flexible power supply and demand game results in scenario 4
分析图5及附图2可知,在1:00—7:00、21:00—24:00,风电运营商制定的灵活性调节电价低于实时电价。对于储能运营商而言,以较低的价格购入风电而后在电价较高时卖出能够获得更多的利润;对于需求响应聚合商而言,将电价较高时段的负荷转移到价格较低时段能够节约供电成本,获得收益;对于火电运营商而言,通过降低自身出力而购入相同电量价格较低的风电能够有效地减少煤耗成本,增加收益。因此,在1:00—7:00、21:00—24:00,储能、需求响应、火电等灵活性资源主体倾向于为风电提供向下的灵活性调节服务,且风电运营商的灵活性调节电价越低,灵活性资源主体参与调节的积极性越强。在8:00—20:00时段,实时电价较高,火电机组、储能及需求响应提供上调电量的成本小于实时电价,因此,风电运营商制定的灵活性调节电价即为实时电价。通过上述分析可知,本文所构建的灵活性资源供需博弈能够有效反映出系统中灵活性资源的供需关系,合理量化灵活性调节电量的价值。
5.2.3 经济性分析
表1为场景1、场景4中各主体的成本及收益情况。分析表1可知,在场景1中,风电运营商获得的净收益远远高于其他各主体获得的净收益,需求响应聚合商的净收益为负值。其原因在于,以系统运行成本最小对源-荷-储进行集中优化调度过程中,火电运营商、储能运营商、需求响应聚合商承担了风电波动性、反调峰特性带来的额外平衡成本,由于缺乏合理的平衡成本分摊机制与灵活性价值补偿机制,导致系统最大消纳风电降低系统运行成本的目标与响应聚合商个体价值的实现相背离,造成了需求响应聚合商的负收益。场景4中,风电承担了平衡自身波动性的责任,在灵活性调节电价的激励作用下,火电运营商、储能运营商、需求响应聚合商的灵活性价值得到合理的补偿,净收益分别提高了8.710万元、0.800万元、4.003万元。相较于场景1,场景4中各主体的收益更加均衡,同时各灵活性资源主体的个体价值实现与系统灵活运行目标相趋同。
表1 各主体的成本及收益情况
Tab.1 The costs and benefits of each subject (单位:万元)

场景项目风电运营商火电运营商储能运营商需求响应聚合商 1售电收益270.041351.1231.0541.129 运行成本16.880183.1830.5872.292 净收益253.161167.9400.467-1.163 4售电收益305.711318.110—— 灵活性收益-40.87735.1521.7743.951 运行成本18.237176.6120.5071.111 净收益246.597176.6501.2672.840
相较于场景4,场景2、场景3中系统的灵活性资源有所减少,而灵活性资源的充裕程度将会对风电与多元灵活性资源的博弈结果产生影响,场景2、场景3的优化结果如附图2、附图4~附图7所示。分析附图2可知,灵活性资源充裕度越小,风电运营商的下调灵活性电价越低,意味着风电运营在灵活性交易中下调电量获得的收益减少而上调电量付出的成本不变,最终导致风电运营商的灵活性调节成本上升。不同场景下风电运营商运行情况见表2,相较于场景4,场景2、场景3中风电运营商的灵活性调节成本分别提高了1.850万元、0.671万元,净收益也出现了相应的下降。由此可见,系统的灵活性资源越充裕,风电的灵活性调节成本就越低,因此,保证系统充裕的灵活性调节资源是实现高比例风电经济高效消纳的必要条件。
表2 不同场景下风电运营商运行情况
Tab.2 Operation of wind power operators in different scenarios (单位:万元)

项目场景2场景3场景4 售电收益305.711305.711305.711 灵活性调节成本42.72741.54840.877 运维成本18.23718.23718.237 净收益244.747245.932246.597
本文对波动性考核指标R分别为0、0.3rbase、0.5rbase进行仿真,分析不同波动性考核指标对电力电量平衡结果的影响,其中rbase为风电预测出力曲线的波动性参数,其大小可由式(1)计算得到。仿真结果如图6所示,其他优化结果如附图8~附图12所示。
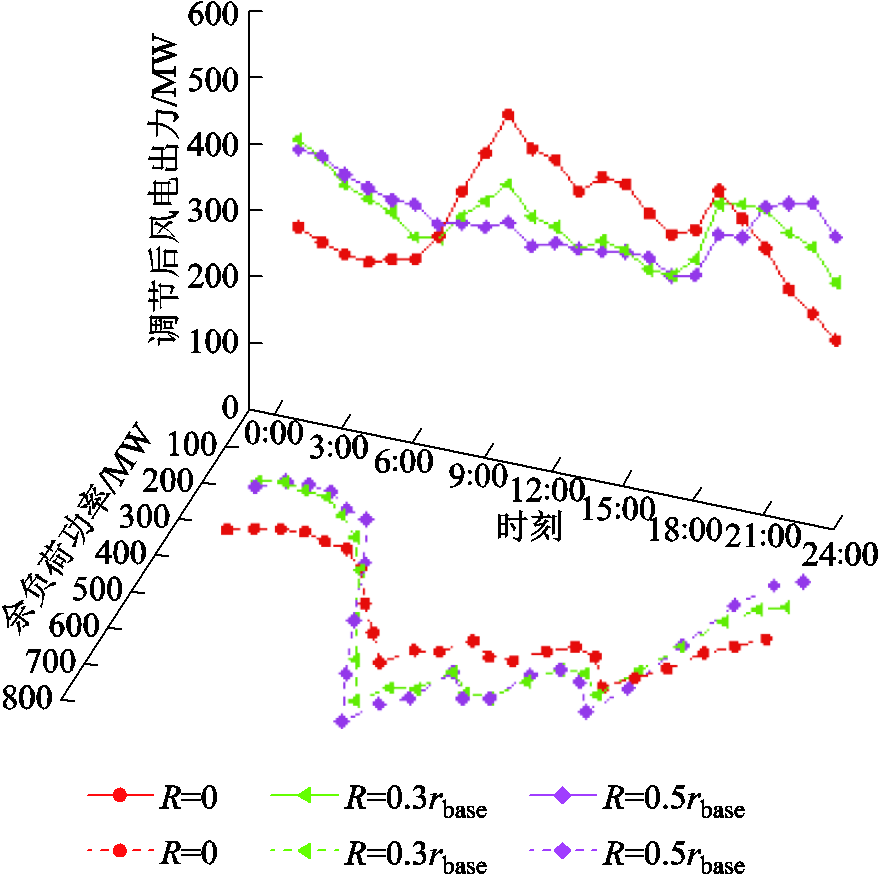
图6 不同R下的余负荷曲线以及调节后风电出力
Fig.6 The residual load curve and the wind power output after adjustment under different R
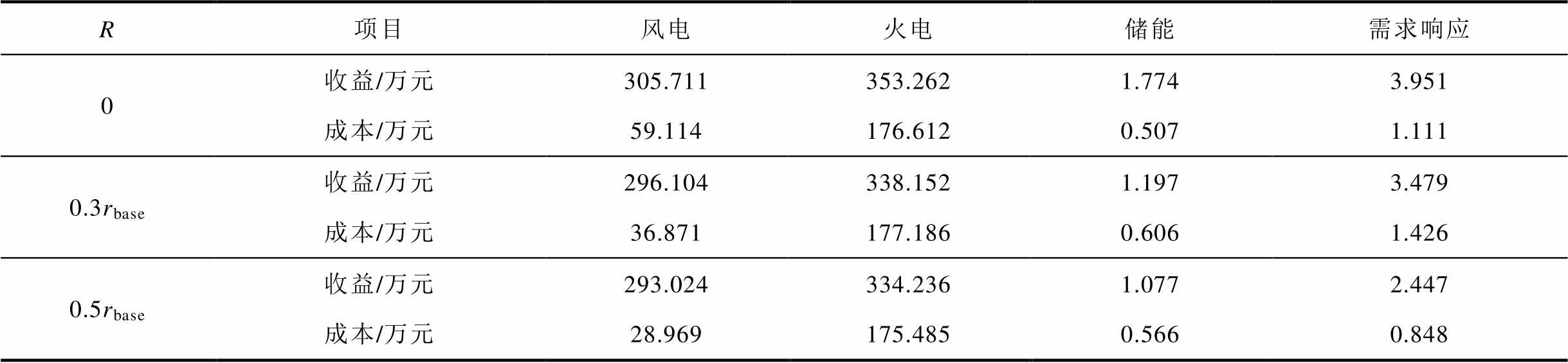
分析图6可知,当R由0增加到0.5rbase时,风电运营商所需承担的波动性平衡责任逐渐减少,余负荷的波动性逐渐上升,余负荷的峰谷差由278.07 MW上升到了568.69 MW。表3为不同R下各主体的成本及收益情况,当R由0增加到0.5rbase,风电运营商波动性平衡责任逐渐减少使其灵活性调节需求下降,风电运营商的净收益上升了17.458万元,同时,余负荷的波动性逐渐增加,火电运营商需要付出更多的波动性平衡成本,收益下降了17.899万元,储能运营商、需求响应聚合商获得的灵活性调节收益分别下降了0.756万元、1.241万元。因此,设置合理的R值能够实现对波动性平衡责任的合理划分,有效地保障各主体的利益。
表3 不同波动性指标下各主体成本及收益情况
Tab.3 Costs and benefits of each subject under different volatility indicators
R项目风电火电储能需求响应 0收益/万元305.711353.2621.7743.951 成本/万元59.114176.6120.5071.111 0.3rbase收益/万元296.104338.1521.1973.479 成本/万元36.871177.1860.6061.426 0.5rbase收益/万元293.024334.2361.0772.447 成本/万元28.969175.4850.5660.848
本文针含高比例风电的新型电力系统电力电量平衡问题,提出一种考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度策略,通过建立风电运营商与火电运营商、储能运营商、需求响应聚合商的博弈关系,实现对灵活性资源的供需博弈优化。通过仿真算例验证,得出如下结论:
1)灵活性补偿机制能够有效提高灵活性资源参与调节的积极性,充分挖掘源-荷-储各方面的灵活性调节潜力,促进高比例风电的上网消纳。
2)采用本文所提主从博弈策略对灵活性资源进行供需优化后,有效地反映了灵活性资源的供需关系,火电运营商、储能运营商、需求响应聚合商的灵活性价值得到了合理的补偿。
3)波动性考核指标可以实现对风电上网波动性的管理,有效地降低了高比例风电波动性对电力电量平衡造成的困难。
附 录
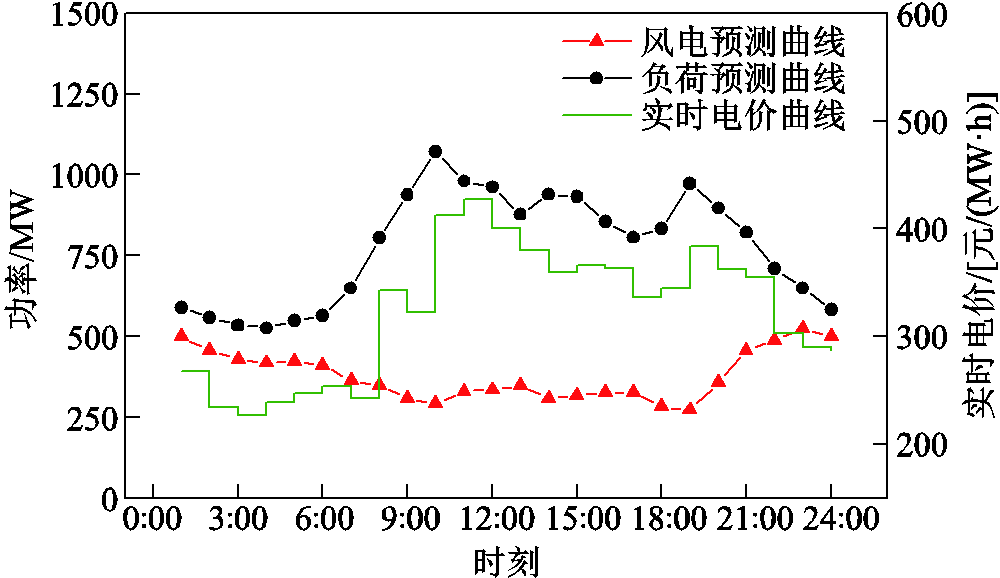
附图1 原始数据
App.Fig.1 Raw data
附表1 火电机组参数
App.Tab.1 Parameters of thermal power units

参数数值G1G2G3G4 Pg,max i/MW300302180148 Pg,min i/MW1401289080 Pg,a i/MW110100—— Pg,b i /MW6062——
(续)
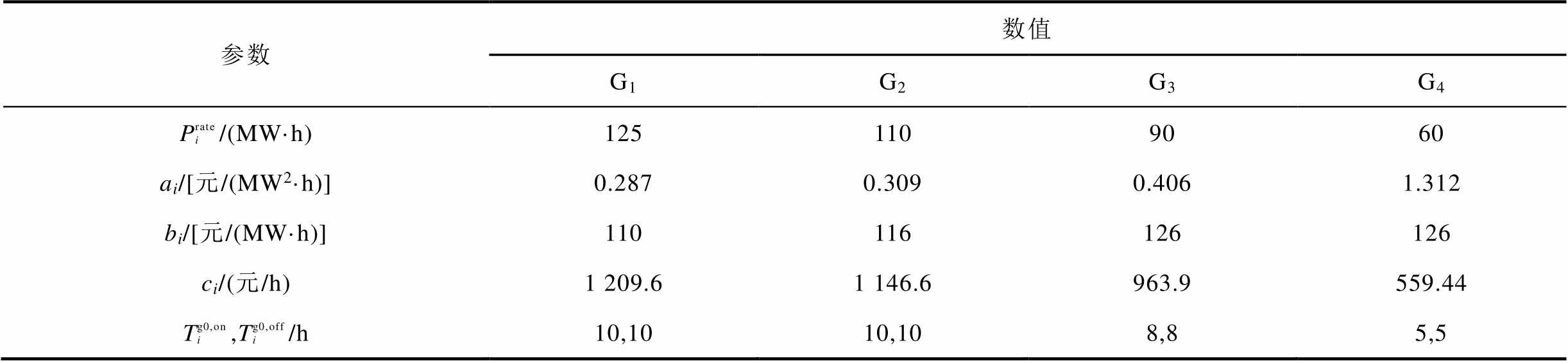
参数数值G1G2G3G4 Prate i/(MW·h)1251109060 ai/[元/(MW2·h)]0.2870.3090.4061.312 bi/[元/(MW·h)]110116126126 ci/(元/h)1209.61146.6963.9559.44 Tg0,on i,Tg0,off i/h10,1010,108,85,5
附表2 储能设备参数表
App.Tab.2 Parameters table of energy storage equipment

参数数值 储能设备容量/(MW·h)80 储能充、放电效率0.95 初始荷电状态/(MW·h)8 储能最大充电功率/MW32 储能最大放电功率/MW32 储能充放电运维成本系数/[元/(MW·h)]35
附表3 可转移负荷参数
App.Tab.3 Transferable load parameters

参数数值 D1D2D3D4D5 tous,pr j~toue,pr j/h7~129~1418~2112~1610~15 tous,id j~toue,id j/h8~911~1219~2015~1611~12 tins,pr j~tine,pr j/h21~243~71~53~71~6 tins,id j~tine,id j/h21~225~614~54~6 cd j/[元/(MW·h)]3532384035 ldev j/[元/(MW·h)]1010101010 最大转入/转出功率/MW16/1613/1315/1520/2013/13
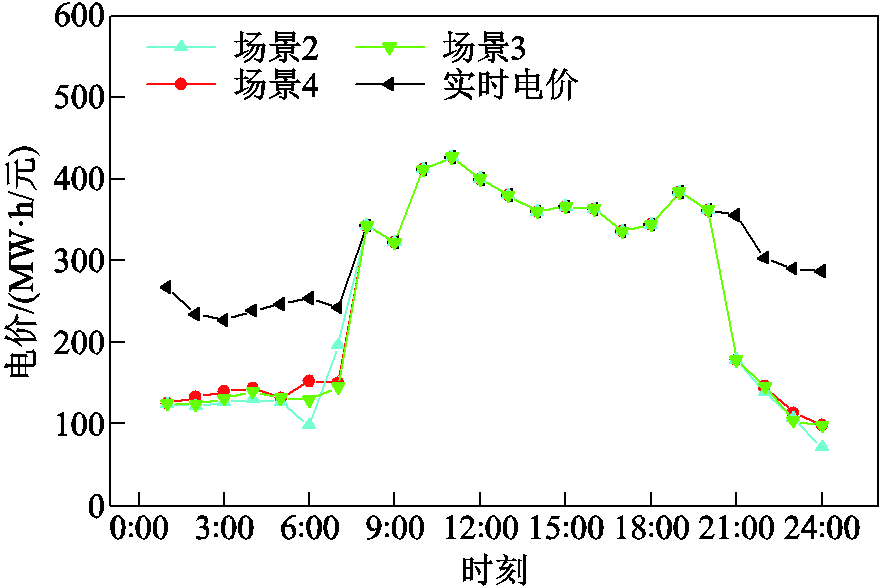
附图2 灵活性调节电价博弈结果
App.Fig.2 Flexibility adjustment price game results
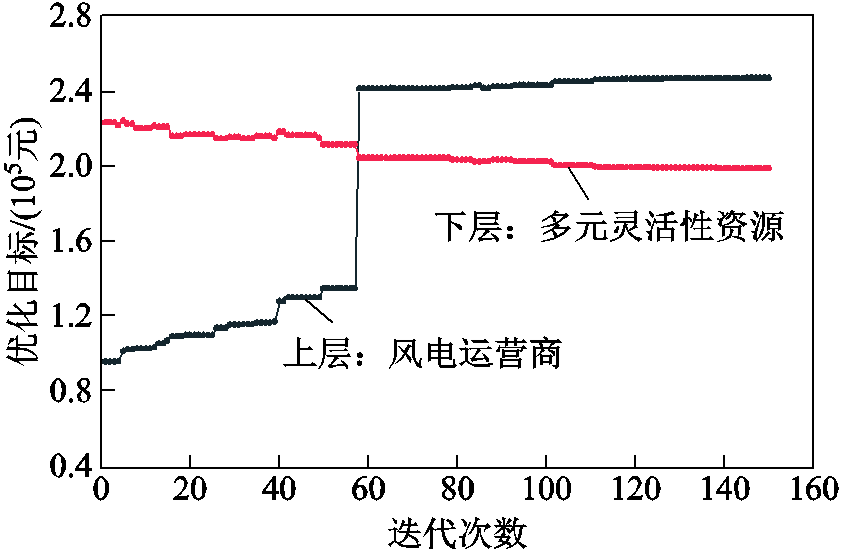
附图3 主从博弈迭代收敛结果
App.Fig.3 Iterative convergence result of Stackelberg game
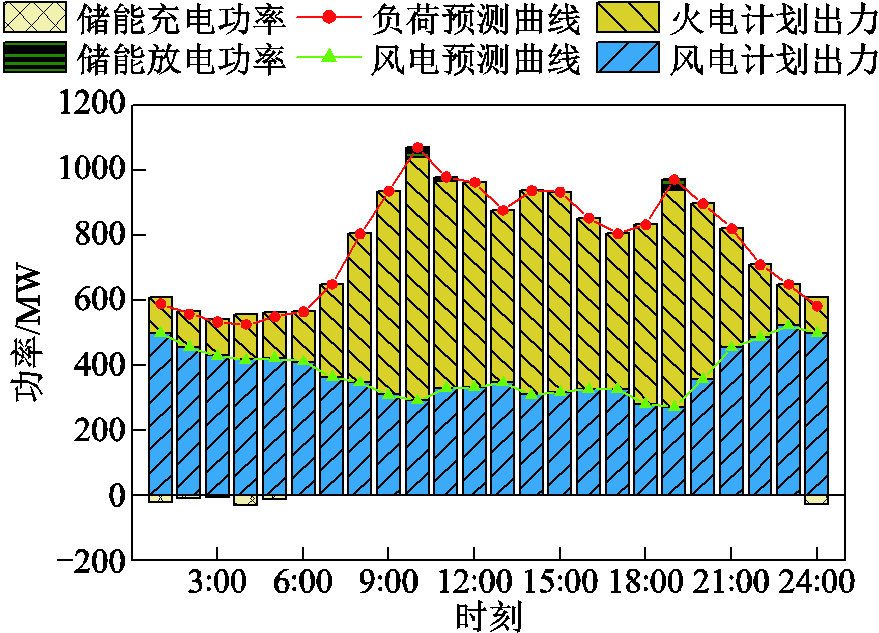
附图4 场景2电力电量平衡结果
App.Fig.4 Power balance results in scenario 2
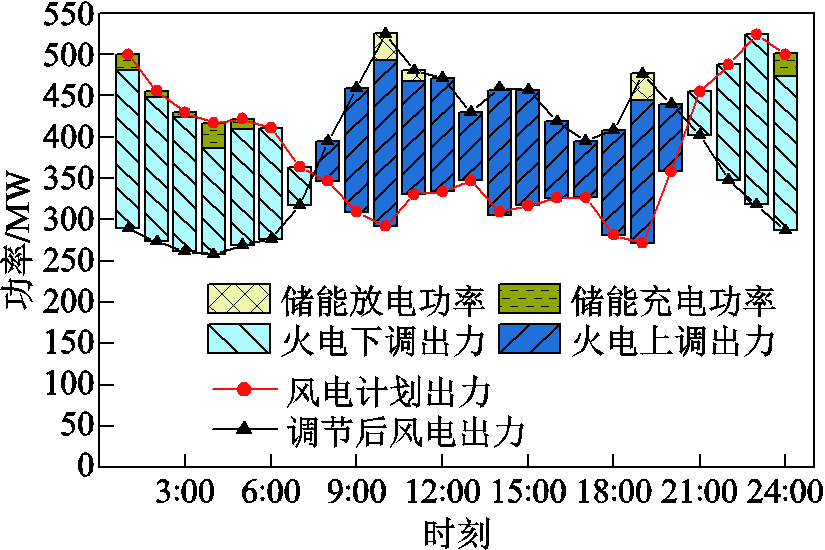
附图5 场景2灵活性电量供需博弈结果
App.Fig.5 Flexible power supply and demand game results in scenario 2

附图6 场景3电力电量平衡结果
App.Fig.6 Power balance results in scenario 3
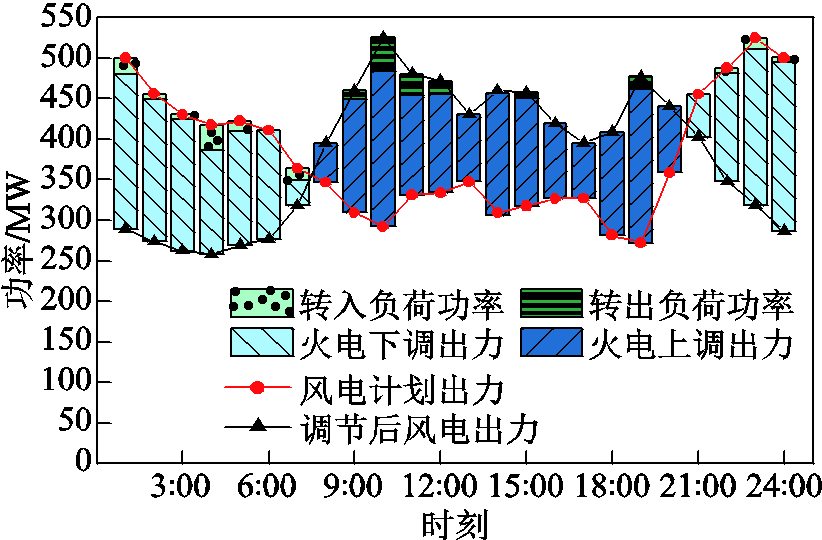
附图7 场景3灵活性电量供需博弈结果
App.Fig.7 Flexible power supply and demand game results in scenario 3
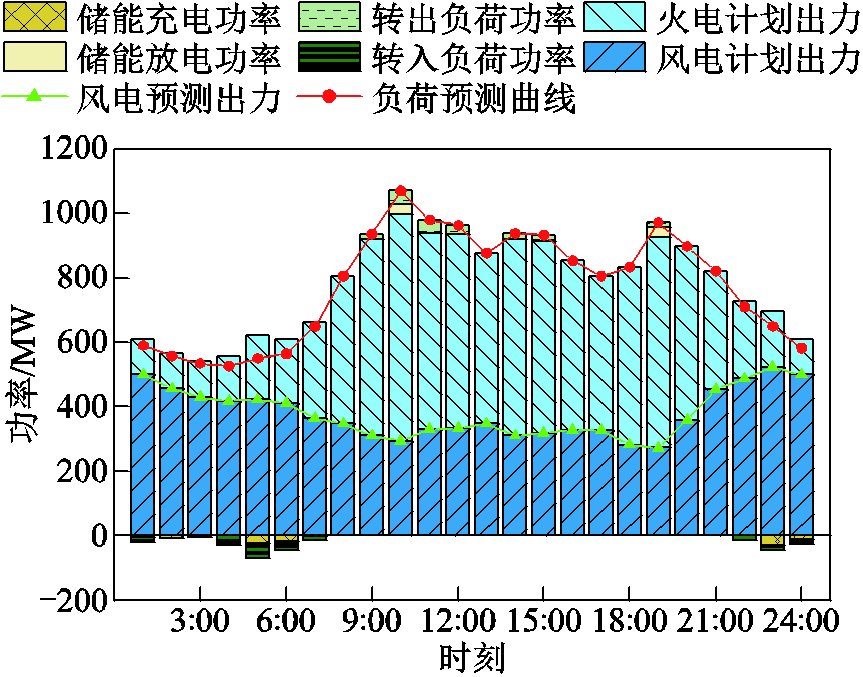
附图8 R=0.3rbase时电力电量平衡结果
App.Fig.8 Results of power balance at R=0.3rbase
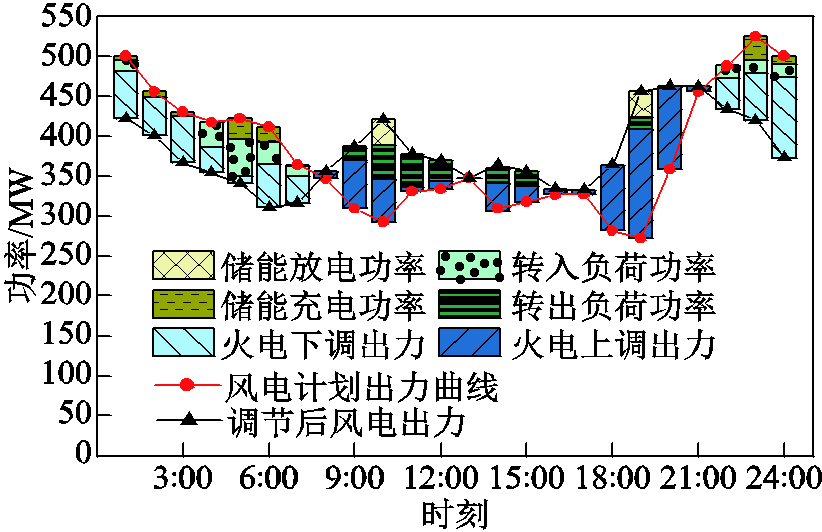
附图9 R=0.3rbase时灵活性资源供需博弈结果
App.Fig.9 Flexibility resource supply and demand game results at R=0.3rbase

附图10 R=0.5rbase时电力电量平衡结果
App.Fig.10 Results of power balance at R=0.5rbase
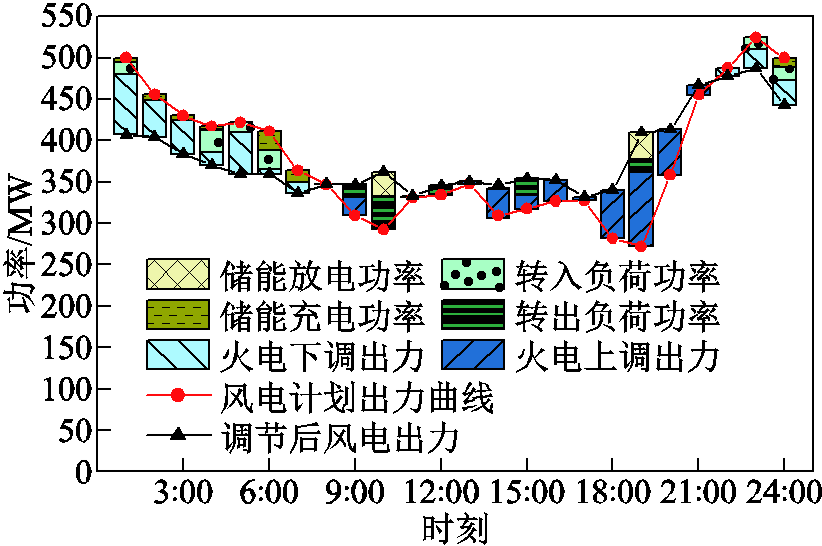
附图11 R=0.5rbase时灵活性资源供需博弈结果
App.Fig.11 Flexibility resource supply and demand game results at R=0.5rbase
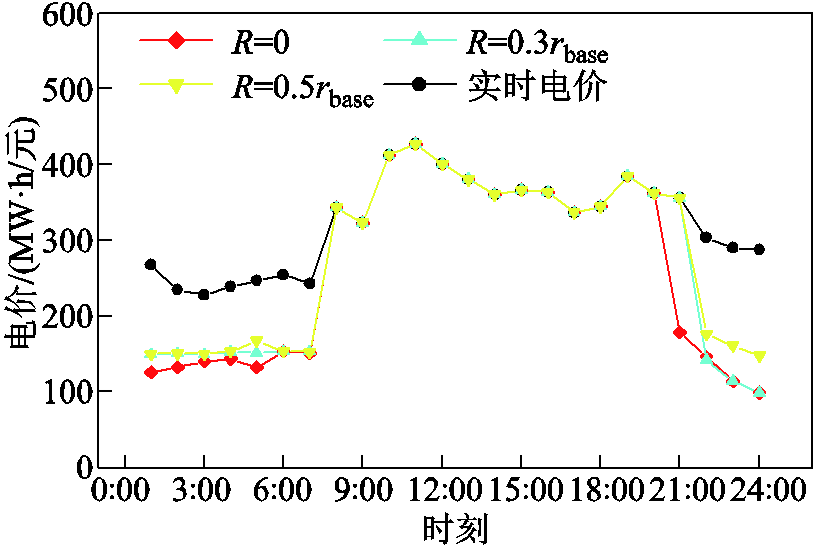
附图12 不同R下灵活性调节电价博弈结果
App.Fig.12 Game results of flexible adjustment price under different R
参考文献
[1] 亢丽君, 王蓓蓓, 薛必克, 等. 计及爬坡场景覆盖的高比例新能源电网平衡策略研究[J]. 电工技术学报, 2022, 37(13): 3275-3288. Kang Lijun, Wang Beibei, Xue Bike, et al. Research on the balance strategy for power grid with high proportion renewable energy considering the ramping scenario coverage[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3275-3288.
[2] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219. Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[3] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[4] 菅学辉, 张利, 杨立滨, 等. 高比例风电并网下基于卡尔多改进的深度调峰机制[J]. 电力系统自动化, 2018, 42(8): 110-118. Jian Xuehui, Zhang Li, Yang Libin, et al. Deep-peak regulation mechanism based on kaldor improvement under high-penetration wind power[J]. Automation of Electric Power Systems, 2018, 42(8): 110-118.
[5] 李军徽, 张嘉辉, 穆钢, 等. 储能辅助火电机组深度调峰的分层优化调度[J]. 电网技术, 2019, 43(11): 3961-3970. Li Junhui, Zhang Jiahui, Mu Gang, et al. Hierarchical optimization scheduling of deep peak shaving for energy-storage auxiliary thermal power generating units[J]. Power System Technology, 2019, 43(11): 3961-3970.
[6] 李军徽, 张嘉辉, 穆钢, 等. 计及负荷峰谷特性的储能调峰日前优化调度策略[J]. 电力自动化设备, 2020, 40(7): 128-133, 140, 134. Li Junhui, Zhang Jiahui, Mu Gang, et al. Day-ahead optimal scheduling strategy of peak regulation for energy storage considering peak and valley characteristics of load[J]. Electric Power Automation Equipment, 2020, 40(7): 128-133, 140, 134.
[7] 韩笑, 周明, 李庚银. 计及储能和空调负荷的主动配电网多目标优化调度[J]. 电力系统保护与控制, 2018, 46(7): 14-23. Han Xiao, Zhou Ming, Li Gengyin. Multi-objective optimal dispatching of active distribution networks considering energy storage systems and air-conditioning loads[J]. Power System Protection and Control, 2018, 46(7): 14-23.
[8] 徐成司, 董树锋, 华一波, 等. 基于改进一致性算法的工业园区分布式综合需求响应[J]. 电工技术学报, 2022, 37(20): 5175-5187. Xu Chengsi, Dong Shufeng, Hua Yibo, et al. Distributed comprehensive demand response of industrial parks based on improved consistency algorithm[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5175-5187.
[9] 袁晓冬, 费骏韬, 胡波, 等. 资源聚合商模式下的分布式电源、储能与柔性负荷联合调度模型[J]. 电力系统保护与控制, 2019, 47(22): 17-26. Yuan Xiaodong, Fei Juntao, Hu Bo, et al. Joint scheduling model of distributed generation, energy storage and flexible load under resource aggregator mode[J]. Power System Protection and Control, 2019, 47(22): 17-26.
[10] 崔杨, 修志坚, 刘闯, 等. 计及需求响应与火–储深度调峰定价策略的电力系统双层优化调度[J]. 中国电机工程学报, 2021, 41(13): 4403-4415. Cui Yang, Xiu Zhijian, Liu Chuang, et al. Dual level optimal dispatch of power system considering demand response and pricing strategy on deep peak regulation[J]. Proceedings of the CSEE, 2021, 41(13): 4403-4415.
[11] 常源, 刘宗歧, 黄珊, 等. 风火网混合博弈协调规划及利益分配方法[J]. 电网技术, 2019, 43(11): 3899-3907. Chang Yuan, Liu Zongqi, Huang Shan, et al. Coordinated planning and profit distribution of wind power, thermal power and grid based on mixed game theory[J]. Power System Technology, 2019, 43(11): 3899-3907.
[12] 武昭原, 周明, 姚尚润, 等. 基于合作博弈论的风储联合参与现货市场优化运行策略[J]. 电网技术, 2019, 43(8): 2815-2824. Wu Zhaoyuan, Zhou Ming, Yao Shangrun, et al. Optimization operation strategy of wind-storage coalition in spot market based on cooperative game theory[J]. Power System Technology, 2019, 43(8): 2815-2824.
[13] 陈启鑫, 刘学, 房曦晨, 等. 考虑可再生能源保障性消纳的电力市场出清机制[J]. 电力系统自动化, 2021, 45(6): 26-33. Chen Qixin, Liu Xue, Fang Xichen, et al. Electricity market clearing mechanism considering guaranteed accommodation of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(6): 26-33.
[14] 钟佳宇, 陈皓勇, 陈武涛, 等. 含灵活性资源交易的电力市场实时出清[J]. 电网技术, 2021, 45(3): 1032-1041. Zhong Jiayu, Chen Haoyong, Chen Wutao, et al. Real-time clearing of electricity markets with flexible resource transactions[J]. Power System Technology, 2021, 45(3): 1032-1041.
[15] 吴珊, 边晓燕, 张菁娴, 等. 面向新型电力系统灵活性提升的国内外辅助服务市场研究综述[J]. 电工技术学报, 2023, 38(6): 1662-1677. Wu Shan, Bian Xiaoyan, Zhang Jingxian, et al. A review of domestic and foreign ancillary services market for improving flexibility of new power system[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1662-1677.
[16] 安麒, 王剑晓, 武昭原, 等. 高比例可再生能源渗透下的电力市场价值分配机制设计[J]. 电力系统自动化, 2022, 46(7): 13-22. An Qi, Wang Jianxiao, Wu Zhaoyuan, et al. Benefit allocation mechanism design of electricity markets with penetration of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(7): 13-22.
[17] 李璐, 郑亚先, 陈长升, 等. 风电的波动成本计算及应用研究[J]. 中国电机工程学报, 2016, 36(19): 5155-5163, 5396. Li Lu, Zheng Yaxian, Chen Changsheng, et al. Calculation of wind power variation costs and its application research[J]. Proceedings of the CSEE, 2016, 36(19): 5155-5163, 5396.
[18] 赵书强, 吴杨, 李志伟, 等. 考虑风光出力不确定性的电力系统调峰能力及经济性分析[J]. 电网技术, 2022, 46(5): 1752-1761. Zhao Shuqiang, Wu Yang, Li Zhiwei, et al. Analysis of power system peaking capacity and economy considering uncertainty of wind and solar output[J]. Power System Technology, 2022, 46(5): 1752-1761.
[19] 胡佳. 融合多种策略的改进粒子群算法[J]. 计算机系统应用, 2021, 30(7): 172-177. Hu Jia. Improved particle swarm optimization algorithm combining multiple strategies[J]. Computer Systems & Applications, 2021, 30(7): 172-177.
Abstract The large scale grid connection of new energy sources, mainly wind power, has led to increasing uncertainty and anti-peak characteristics of the system, and the system is facing a huge challenge in terms of power balance. At present, scholars have explored the flexibility regulation potential of the system from multiple levels of "source-load-storage", which has improved the flexibility of system operation to a certain extent, but there are problems such as the lack of incentive mechanisms for flexibility regulation, the lack of reasonable compensation for the flexibility value of flexibility resources, and the lack of enthusiasm of flexibility resources to participate in regulation. This paper proposed an optimal dispatching method taking into account the game between a high proportion of wind power and multiple flexibility resources. On the basis of the individual profit-seeking properties of wind power and each flexibility resource subject, it used the idea of Stackelberg game to establish a multi-object game optimal dispatching model for supply and demand of flexibility regulation services, so as to achieve the optimization of supply and demand of flexibility resources and reasonable compensation of flexibility value.
Firstly, considering the spatial and temporal coupling characteristics of wind power volatility and load volatility, the evaluation index of wind power volatility was defined, and based on this, a method for quantifying the demand for wind power flexibility regulation was proposed. Secondly, considering the differences and tendency of each flexibility resource’s decisions, a method of equilibrium analysis of flexibility supply and demand based on Stackelberg game was proposed, and an optimization model of flexibility resource supply and demand game was established with the objective of maximizing the interests of each subject. Finally, the proposed method was verified through simulation cases that the proposed method can effectively improve the enthusiasm of multiple flexibility resources to participate in regulation and promote the online consumption of a high proportion of wind power.
The simulation results of the new power system with high percentage of wind power show that the proposed model effectively improves the depth of thermal power peaking and the enthusiasm of energy storage and demand response to participate in flexibility regulation during the high time of wind power at night. And it achieves the full consumption of wind power. Meanwhile, in terms of economics, the proposed model improves the net benefits of thermal power, energy storage, and demand response, so that the individual value of each flexibility resource subject converges with the system's flexible operation goal. The experimental results under different flexibility resource adequacy show that the higher the flexibility resource adequacy of the system, the lower the flexibility regulation cost of wind power, and the more economical and efficient the consumption of wind power. The sensitivity analysis results of the volatility assessment index parameters show that the larger the R is, the gradually less volatility balancing responsibility the wind power operator needs to bear, and the volatility of the residual load gradually rises, and setting a reasonable R value can realize a reasonable division of the volatility balancing responsibility and effectively protect the interests of each subject.
The following conclusions can be drawn from the simulation analysis: (1) The flexibility compensation mechanism can effectively increase the enthusiasm of flexibility resources to participate in regulation, fully exploit the flexibility regulation potential of source-load-storage, and promote the online consumption of a high proportion of wind power. (2) After adopting the Stackelberg game strategy proposed in this paper to optimize the supply and demand of flexibility resources, it effectively reflects the supply and demand of flexibility resources, and the flexibility values of thermal power operators, energy storage operators and demand response aggregators are reasonably compensated. (3) The volatility assessment index can realize the management of wind power feed-in volatility and effectively reduce the difficulties caused by high percentage of wind power volatility on power balance.
keywords:High proportion of wind power, flexibility compensation, Stackelberg game, wind power fluctuation
DOI:10.19595/j.cnki.1000-6753.tces.L10037
中图分类号:TM73
国家自然科学基金项目(52167010)、国家重点研发计划项目(2017YFB0903705)、云南省基础研究计划项目(202101AU070015)和国家电网有限公司科技项目(SGGSJY00DYJS2200098)资助。
收稿日期 2023-01-09
改稿日期 2023-02-19
潘郑楠 男,1997年生,硕士研究生,研究方向为电力系统优化调度。E-mail:1562103979@qq.com
梁 宁 男,1985年生,博士,副教授,硕士生导师,研究方向为电力系统优化调度。E-mail:liangning@whu.edu.cn(通信作者)
(编辑 赫蕾)