基于电磁式旋转潮流控制器的有源配电网多场景控制
颜湘武1 邵 晨1 吴 鸣2 彭维锋1 贾焦心1 张宸宇3
(1. 河北省分布式储能与微网重点实验室(华北电力大学) 保定 071003 2. 国网上海能源互联网研究院有限公司 上海 201210 3. 国网江苏省电力有限公司电力科学研究院 南京 211100)
摘要 分布式电源的高比例接入及两端电源供电系统的发展推进,给配电网带来了电压越限、相位差线路合环、潮流调控困难等问题,为此该文提出采用电磁式旋转潮流控制器(RPFC)的解决方案,具有适用性强、成本低、可靠性高的优点。首先,分析了RPFC的拓扑结构和工作原理,建立了RPFC稳态电压源模型;然后,分别构建了基于RPFC的电压越限模型及变转速控制策略,基于相量合成原理的RPFC相位差线路柔性合环模型及其控制策略,基于瞬时无功理论的RPFC功率解耦控制模型及对应转速协调控制策略;最后,搭建了RPFC的380 V/40 kV·A样机,实验结果表明,仅改变RPFC控制策略即可实现其在多种场景下有效稳定的调节,验证了所提控制策略的有效性和正确性。
关键词:电磁式旋转潮流控制器 有源配电网 潮流控制 柔性合环 电压调节
0 引言
绿色低碳转型和应对气候变化,已经成为世界潮流和人心所向,风电、光伏、电动汽车等清洁能源和负荷将会广泛接入城市配电网[1-2]。由于传统配电网的网架结构简单、控制手段比较单一,在面对多样化的源荷时,暴露了它自身存在的一些问题,如难以满足区域平衡的发展需求,加剧了配电网电压和潮流的复杂性与调控难度[3-4]。
针对有源配电网安全运行面临的主要难题,包括电压越限[5]、双电源相位差线路合环及潮流失控现象[6],现有解决方法均具有其局限性。在电压调节方面,由于配电网线路特性表现出了R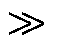 X,电压-有功灵敏度远大于电压-无功灵敏度,此时采用静止同步补偿器[7]的方案难以满足调压要求;而动态电压调节器[8]及电力弹簧调压[9]的方式具有成本高、可靠性低的缺陷,同时电力电子器件的使用会带来谐波问题[10]。在相位差线路柔性合环方面,文献[11]提出一种双心对称移相变压器的方案,通过改变励磁变压器二次绕组抽头位置,即可在电压幅值不变的前提下实现电压移相的功能,但其属于一种有载分接开关式移相器,因此表现出了调节速度慢、调节离散、使用寿命短的缺陷。在潮流控制方面,智能软开关具有较好的调节功能,其基本结构由大功率全控型电力电子元件组成[11],通过对两侧换流器施加控制策略,满足接入点输出电压幅值与相位的独立控制,实现互联线路流过有功和无功功率的双向解耦控制,但背靠背型智能软开关的设计容量由线路需转供的最大功率决定,因此其表现出了容量大、成本高、体积大的缺点。
X,电压-有功灵敏度远大于电压-无功灵敏度,此时采用静止同步补偿器[7]的方案难以满足调压要求;而动态电压调节器[8]及电力弹簧调压[9]的方式具有成本高、可靠性低的缺陷,同时电力电子器件的使用会带来谐波问题[10]。在相位差线路柔性合环方面,文献[11]提出一种双心对称移相变压器的方案,通过改变励磁变压器二次绕组抽头位置,即可在电压幅值不变的前提下实现电压移相的功能,但其属于一种有载分接开关式移相器,因此表现出了调节速度慢、调节离散、使用寿命短的缺陷。在潮流控制方面,智能软开关具有较好的调节功能,其基本结构由大功率全控型电力电子元件组成[11],通过对两侧换流器施加控制策略,满足接入点输出电压幅值与相位的独立控制,实现互联线路流过有功和无功功率的双向解耦控制,但背靠背型智能软开关的设计容量由线路需转供的最大功率决定,因此其表现出了容量大、成本高、体积大的缺点。
20世纪90年代,美国通用电气公司提出一种基于传统变压器和旋转移相变压器(Rotary Phase Shifting Transformer, RPST)的柔性交流输电装置——旋转潮流控制器(Rotary Power Flow Controller, RPFC)。它可以灵活控制线路补偿电压,而不受线路电流的影响,从而为电力系统的经济、灵活、频繁控制提供了新的方法[12]。目前国内外研究多集中在RPFC稳态建模[13]及输电线路的潮流控制[14],文献[15]对比了RPFC与统一潮流控制器在输电网潮流控制中的工作特性,指出RPFC在运行维护、抗冲击性和成本等方面均有较大优势。但针对RPFC在低压配电网中的应用研究较少,这是因为传统配电网是基于电网与用户之间的单向电力分配网络,其运行和控制模式较为被动,对于潮流控制的需求较小[16],而随着大规模分布式电源的接入及电机智能化生产和数字化控制技术的不断发展[17],RPFC重新走入了人们的视野,但仍需对其控制策略进行进一步研究,以充分发挥RPFC在电压调节、相位差线路柔性合环、潮流控制方面调控性能。RPFC通过伺服电动机来控制双旋转移相变压器转子相位,难点在于如何协调控制双伺服电动机。现有双电机驱动方式分为两类[18]:一类是双电机具备独立速度环(双环)的结构;另一类是双电机共用一个速度环(单环)的结构。由双RPST独立旋转从而实现串入补偿电压的结构可知,采用双环控制结构能够表现出更为灵活的功率控制效果。在双环结构的具体控制器设计中,现有同步联动控制方法包括差电流负反馈[19]和差转速负反馈[20]。由于两电机参数不可能完全一致,即使电流一致也未必能达到相同控制速度,因此差速负反馈控制更适用于RPFC控制系统。然而现有电机差速负反馈控制多为定转速控制,通过实验发现,双环定转速的RPFC控制方案在柔性合环及复杂功率控制工况下表现出了稳定性差的缺点,需对其作出进一步改进。文献[21]提出一种电机变转速负反馈单闭环调速方法,通过采集当前转速作为反馈量与给定动态转速进行比较,并控制输出脉冲宽度调制(Pulse Width Modulation, PWM)的占空比来调节输出电压,达到控制转速的要求,在恒转矩变转速仿真中表现出了较好的响应速度。
本文基于现有文献研究成果,针对有源配电网建设面临的电压越限控制、相位差线路柔性合环以及功率控制难题,提出了采用RPFC的解决方案。分别构建了基于RPFC的电压越限模型、基于相量合成原理的相位差线路柔性合环模型以及基于瞬时无功理论功率解耦控制模型,并针对RPFC调控特性设计了两RPST转速协调控制策略;最后,在实验室中搭建了一套380 V/40 kV·A电磁式旋转潮流控制器样机进行验证,实验结果表明,在复杂有源配电网多运行场景中,仅通过改变RPFC控制策略,即可完成调控目标,具有较好的适用性和推广价值。
1 RPFC拓扑结构及工作原理
1.1 RPFC拓扑结构
RPFC原理如图1a所示,其中RPST1和RPST2为两旋转移相变压器,基于电磁感应原理,利用两组RPST的转子角转动,分别合成一个幅值不变,相位360°可调的定子电压相量,两组定子电压相量经过叠加,从而在线路中注入一个幅值、相位可调的串联电压。RPST在静止时类似于一台变压器,其定子侧电压和转子侧电压存在一定的变比关系,而相位差则与定转子之间的角度α1和α2有关,对于多极RPST,转子角只需移动很小的机械角度,就可改变串入线路的电压相量[13-16]。
1.2 工作原理分析
RPFC单相等效电路如图1b所示,其中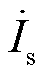 为接入RPST前系统线路电流;
为接入RPST前系统线路电流;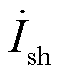 为转子总电流;
为转子总电流;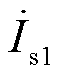 为定子侧电流;
为定子侧电流;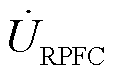 为RPFC串入线路的电压;Zsh为归算到转子侧的阻抗;ZRPST为归算到定子侧的阻抗,k为RPST电压比;a1和a2分别为两台RPST定、转子电压移相角。此时可得到RPFC产生的注入电压为
为RPFC串入线路的电压;Zsh为归算到转子侧的阻抗;ZRPST为归算到定子侧的阻抗,k为RPST电压比;a1和a2分别为两台RPST定、转子电压移相角。此时可得到RPFC产生的注入电压为
其中
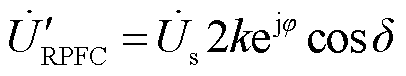 (2)
(2)
式中, 为RPFC串入线路电压相量;
为RPFC串入线路电压相量;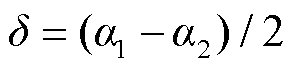 ,
,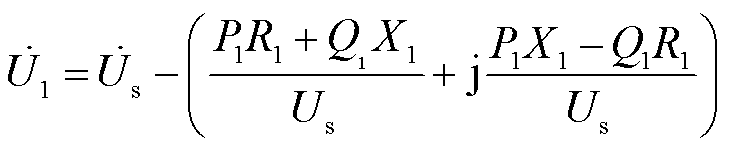 。从而可以得到RPFC简化电路模型如图1c所示,详细推导过程见附录,其串联部分由一个受控理想电压源和一个等效内阻抗组成,并联支路为受控电流源。通过改变a1和a2的大小,完成对注入线路电压的连续调节。由图1a可以看到,RPFC由伺服电动机驱动,其响应调节速度一般在百毫秒级,因此仅对其稳态调节模型及特性进行了分析,今后考虑装置在线路故障和保护工况下的特性时,将进一步分析其暂态特性。
。从而可以得到RPFC简化电路模型如图1c所示,详细推导过程见附录,其串联部分由一个受控理想电压源和一个等效内阻抗组成,并联支路为受控电流源。通过改变a1和a2的大小,完成对注入线路电压的连续调节。由图1a可以看到,RPFC由伺服电动机驱动,其响应调节速度一般在百毫秒级,因此仅对其稳态调节模型及特性进行了分析,今后考虑装置在线路故障和保护工况下的特性时,将进一步分析其暂态特性。
2 有源配电网模型构建及RPFC控制策略
有源配电网典型运行场景如图2所示,S1为馈线1母线开关;S2为馈线1和馈线2的联络开关;S3为馈线2和馈线3的联络开关;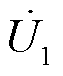 为馈线1并网点电压;
为馈线1并网点电压; 为电网侧电压;Rm+jXm为110 kV变电站至35 kV母线线路阻抗;Rn+jXn为35 kV变电站至10 kV母线2线路阻抗;Rc+jXc为35 kV变电站至10 kV母线3线路阻抗;PL1+jQL1为各馈线本地负荷;PDG+jQDG为馈线1分布式光伏电源发出功率。
为电网侧电压;Rm+jXm为110 kV变电站至35 kV母线线路阻抗;Rn+jXn为35 kV变电站至10 kV母线2线路阻抗;Rc+jXc为35 kV变电站至10 kV母线3线路阻抗;PL1+jQL1为各馈线本地负荷;PDG+jQDG为馈线1分布式光伏电源发出功率。
此时在配电网建设运行中的主要场景包括:
电压越限场景一:由于分布式光伏高比例接入导致的馈线1并网点电压越限。
柔性合环场景二:由于电网布局设计等因素,造成两座35 kV变电站进线端分别来自110 kV变电站中压侧(三角形联结)和220 kV变电站高压侧(星形联结),此时由于线路阻抗及负荷的影响,馈线1和馈线2之间存在一种配电线路30°左右相位差的现象,直接合环会导致在线路中产生较大环流,对电网安全运行造成一定威胁。
潮流控制场景三:由于线路建设和负荷发展的不同步,造成部分线路长期处于过载状态(馈线2),而其他线路处于轻载状态(馈线3)。采取双电源合环运行的方式可以有效解决此类问题,但直接合环运行会导致线路潮流失控,影响供电可靠性。
2.1 电压越限模型及控制策略
2.1.1 电压越限控制模型
在配电网中由于电阻分量占比较重,节点电压同时受线路有功功率和无功功率影响。因此,当分布式电源发出功率较大无法就地消纳时,功率方向将发生改变,令P1=PDG+PL1、Q1=QDG+QL1,此时光伏并网点电压与线路首段电压的关系可表达为
根据《电能质量供电电压偏差》(GB/T 12325—2008)[22]规定,不同电压等级的线路允许通过的电压偏差限值不同。将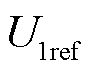 作为节点电压的基准电压幅值,通常为1.0(pu),将S1作为RPFC接入位置后存在
作为节点电压的基准电压幅值,通常为1.0(pu),将S1作为RPFC接入位置后存在
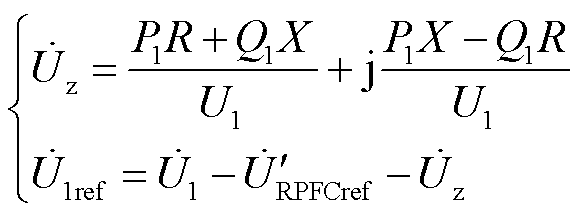 (5)
(5)
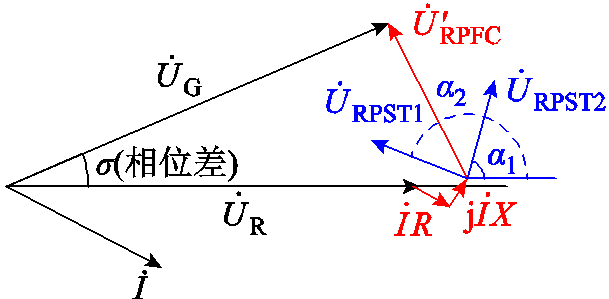
式中,R、X分别为RPFC电阻、电抗;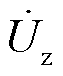 为RPFC内电阻压降。两旋转移相变压器采用对称调节的方式可有效避免线路相位的变化,且对线路功率因数不产生影响,如图3所示,此时存在
为RPFC内电阻压降。两旋转移相变压器采用对称调节的方式可有效避免线路相位的变化,且对线路功率因数不产生影响,如图3所示,此时存在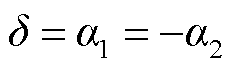 、φ=0。
、φ=0。
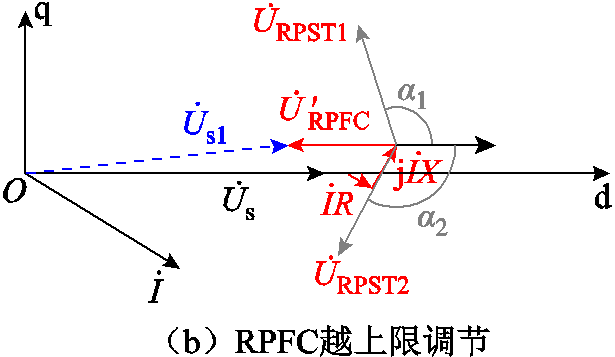
2.1.2 电压越限变转速控制策略
下面结合RPFC的电压输出特性进行分析。在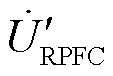 已知的情况下,可以根据式(2)计算此时d 的目标角度dref,进一步计算得到两旋转移相变压器转子角aref(在电压调节模型中存在d=a1=-a2),将RPFC实际转子位置角d与设定值作差后经PI调节得到Dd,通过调节伺服电动机的转速实现转子角的改变,控制输出电压满足设定要求。
已知的情况下,可以根据式(2)计算此时d 的目标角度dref,进一步计算得到两旋转移相变压器转子角aref(在电压调节模型中存在d=a1=-a2),将RPFC实际转子位置角d与设定值作差后经PI调节得到Dd,通过调节伺服电动机的转速实现转子角的改变,控制输出电压满足设定要求。
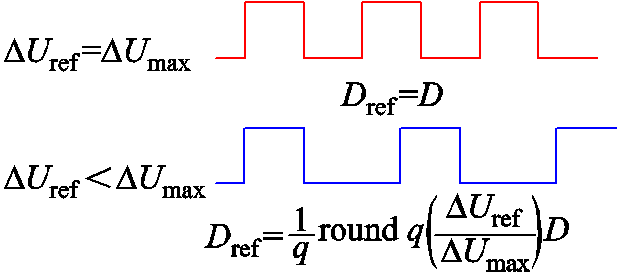
伺服电动机采用PWM方式控制两台RPST动作,通过调节占空比的大小来改变RPST的转速。在RPFC伺服电动机单元采用固定转速调节时,在特殊工况下趋近设定位置角位置时可能出现周期性振荡现象,具体原因在于达到设定角后伺服电动机会停止驱动,但由于RPST存在一定机械惯性,如图4所示,将导致实际位置角与设定位置角出现一定超调现象,在进一步调节中可能再次出现反向超调问题。
在此基础上对伺服电动机进行转速自适应控制,使a满足在接近设定值时降低伺服电动机转速并在达到设定值时准确停止。首先对PWM波占空比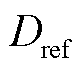 进行量化计算,令其满足
进行量化计算,令其满足
2.2 相位差线路柔性合环转供电模型及控制策略
2.2.1 相位差线路柔性合环模型
如图7所示为含RPFC的相位差线路等效电路,R0+jX0为合环线路外端口等值阻抗;R1+jX1、R2+jX2分别为母线1和母线2的线路阻抗;P1+jQ1、P2+jQ2分别为两线路传输功率;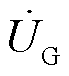 和
和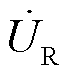 分别为RPFC两端电压;Ssc和Sbp分别为RPFC闭合开关和旁路开关。
分别为RPFC两端电压;Ssc和Sbp分别为RPFC闭合开关和旁路开关。
在已知合环路径内线路参数、合环前馈线负荷
和合环开关两侧电压的前提下,计算包含RPFC的稳态合环电流(循环电流),对系统环路分析,由基尔霍夫电流定律可得到
2.2.2 相位差线路柔性合环控制策略
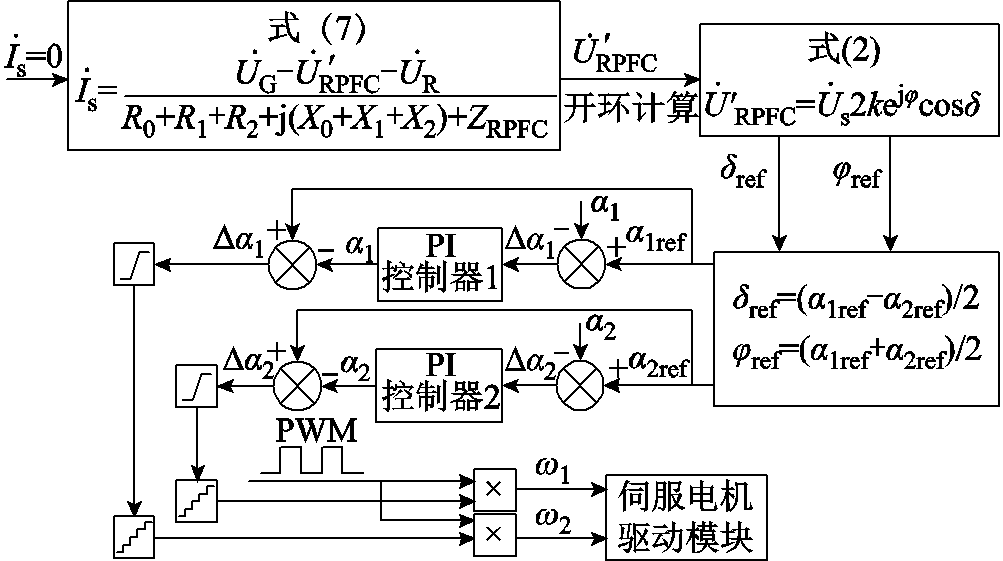
在相位差线路柔性合环控制中,将以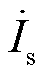 最小作为内环控制目标,基于式(7)求解此时
最小作为内环控制目标,基于式(7)求解此时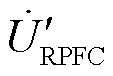 的值,并根据式(2)求解两旋转移相变压器角度α1ref、α2ref。将RPFC实际旋转角a1和a2与设定值a1ref和a2ref作差后经PI调节得到Da1和Da2,并根据Da1和Da2实现伺服电动机的正反旋转,满足移相变压器调节需求。与电压调节略有不同之处在于,相位差线路柔性合环转供电操作的外部控制环节并非闭环控制系统,因此无法实现整体系统的无差控制,但仍能大大减少合环电流,使其接近为零,如图9所示为相位差线路柔性合环转供电控制策略。
的值,并根据式(2)求解两旋转移相变压器角度α1ref、α2ref。将RPFC实际旋转角a1和a2与设定值a1ref和a2ref作差后经PI调节得到Da1和Da2,并根据Da1和Da2实现伺服电动机的正反旋转,满足移相变压器调节需求。与电压调节略有不同之处在于,相位差线路柔性合环转供电操作的外部控制环节并非闭环控制系统,因此无法实现整体系统的无差控制,但仍能大大减少合环电流,使其接近为零,如图9所示为相位差线路柔性合环转供电控制策略。
2.3 潮流控制模型及控制策略
2.3.1 功率解耦控制模型
双电源供电潮流控制等效电路与相位差线路柔性合环等效电路基本相同,如图7所示,基于瞬时无功理论,在dq坐标系下可以得到RPFC接入点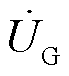 处功率计算公式为
处功率计算公式为
且在单相坐标系下合环点两侧电路方程存在如下关系
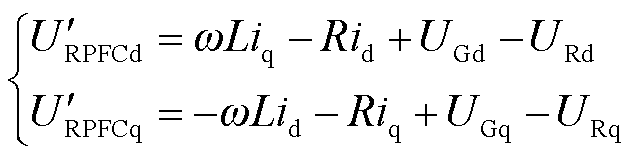 (9)
(9)
令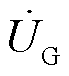 作为参考电压固定在d轴上,则有UGd=UG,UGq=0。在RPFC内部存在ωL>>R,此时由式(8)、式(9)经过化简计算可得到
作为参考电压固定在d轴上,则有UGd=UG,UGq=0。在RPFC内部存在ωL>>R,此时由式(8)、式(9)经过化简计算可得到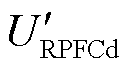 、
、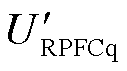 与线路传输功率P、Q的关系为
与线路传输功率P、Q的关系为
2.3.2 功率解耦控制及转速协调策略
通过2.3.1节功率解耦控制模型分析,在给定线路传输功率前提下,可计算此时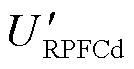 、
、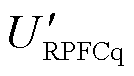 的值,在式(9)基础上即可计算得到δref和φref。进一步地,分别计算出RPST旋转角度设定值a1ref和a2ref。
的值,在式(9)基础上即可计算得到δref和φref。进一步地,分别计算出RPST旋转角度设定值a1ref和a2ref。
由于功率解耦控制模型相对复杂,当两组RPST电机模块采用定转速方式时,其输出电压的变化情况如图10所示。两台RPST转速w1和w2维持不变,运行过程中两个旋转角与设定值的偏差Da1和Da2通常并不相同,因此存在一台RPST达到设定值停止转动而另一台RPST继续运行的情况,从而导致RPFC输出功率存在周期性振荡的问题。
设t=t0时刻,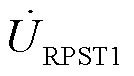 达到设定值
达到设定值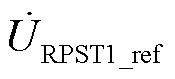 而
而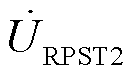 未达到设定值
未达到设定值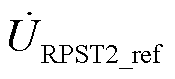 ,此时Da1=0而Da2≠0,则a1停止转动而伺服电动机控制a2继续往设定值方向运行。
,此时Da1=0而Da2≠0,则a1停止转动而伺服电动机控制a2继续往设定值方向运行。
当t=t1时刻,由于a2的动作改变了此时RPFC的输出电压,引起线路功率发生变动,此时将由式(10)计算得到新的定子电压设定值 与
与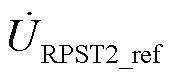 ,使原本停转的a1重新运行,而a2继续往新的设定值方向转动,最终导致输出功率在设定值范围附近反复振荡。
,使原本停转的a1重新运行,而a2继续往新的设定值方向转动,最终导致输出功率在设定值范围附近反复振荡。
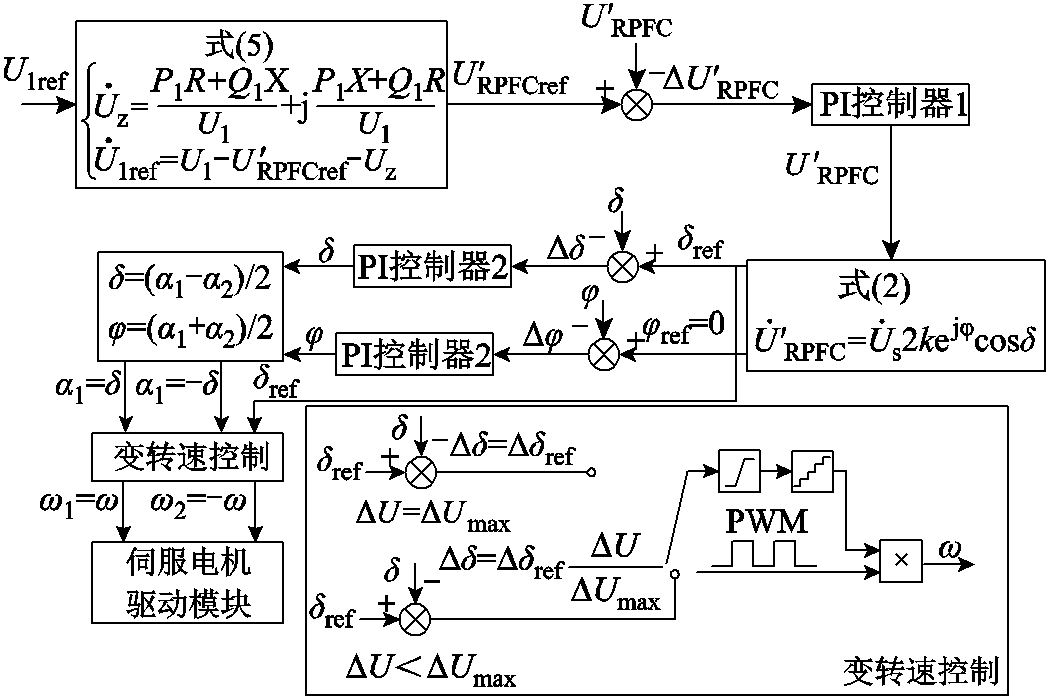
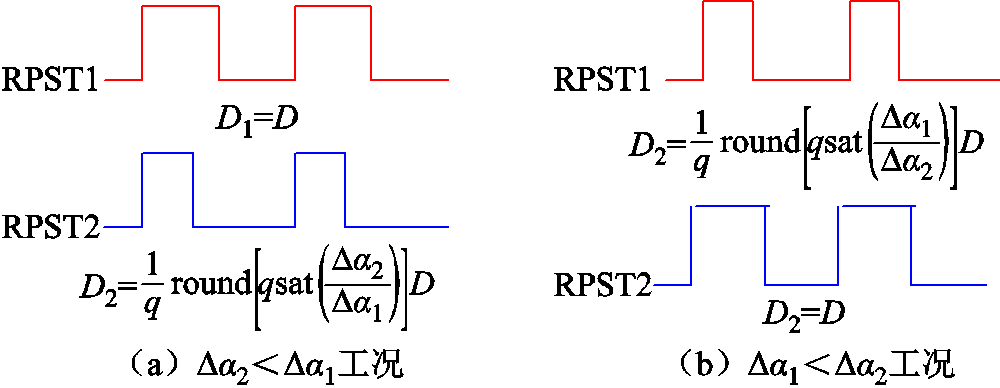
在此基础上对两组伺服电动机进行转速协调控制设计,使a1和a2满足在设定值范围内同时停止运动,具体设计方案如图11所示。当两组旋转移相变压器的设定值与实际值的角度差Da1和Da2存在差异且均不为0时,则对两台伺服电动机的PWM波占空比进行量化计算,当Daj<Dai时存在
当Da2<Da1时如图11a所示,PWM波占空比D1=D,w1保持最大转速;对PWM波占空比D2进行量化计算,减小占空比的大小,降低w2转速,使a1和a2同时达到设定值。同理,当Da1<Da2时如图11b所示,RPST2的伺服电动机转速w2保持最大转速;对RPST1的PWM波进行量化计算,减小占空比的大小,降低w1转速,实现转速的协调控制。功率控制转速协调控制框图如图12所示。
2.4 多场景下RPFC控制策略
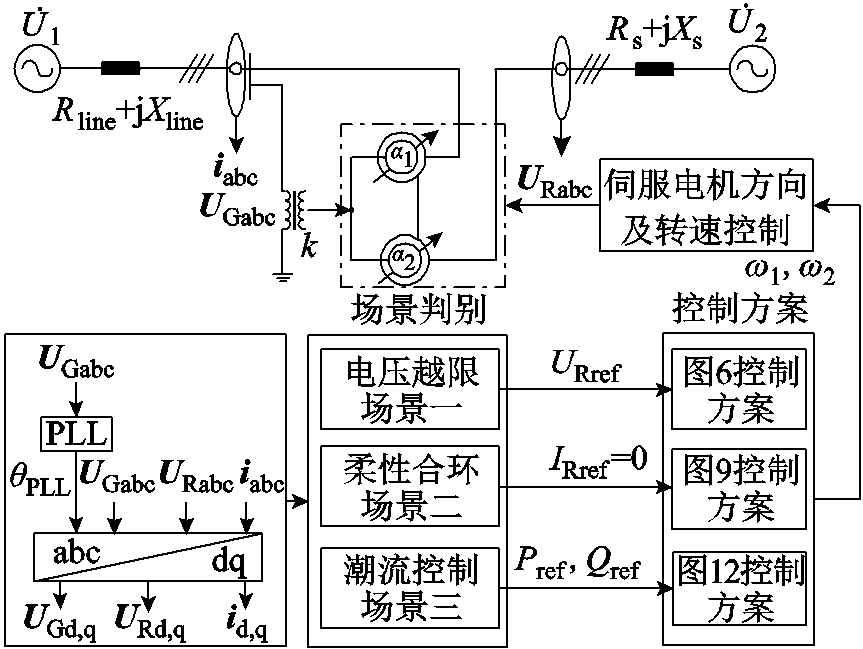
多场景下RPFC整体控制策略框图如图13所示,其中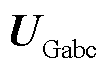 、
、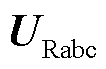 、
、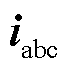 分别为三相输电系统的瞬时电压和电流。在完成自动或手动场景判别后,根据不同控制方案输出实际w1、w2,随后对执行电机方向及转速进行控制,从而实现RPFC串入线路电压的连续调节,达成多场景控制目标。
分别为三相输电系统的瞬时电压和电流。在完成自动或手动场景判别后,根据不同控制方案输出实际w1、w2,随后对执行电机方向及转速进行控制,从而实现RPFC串入线路电压的连续调节,达成多场景控制目标。
3 实验验证
3.1 硬件实验平台
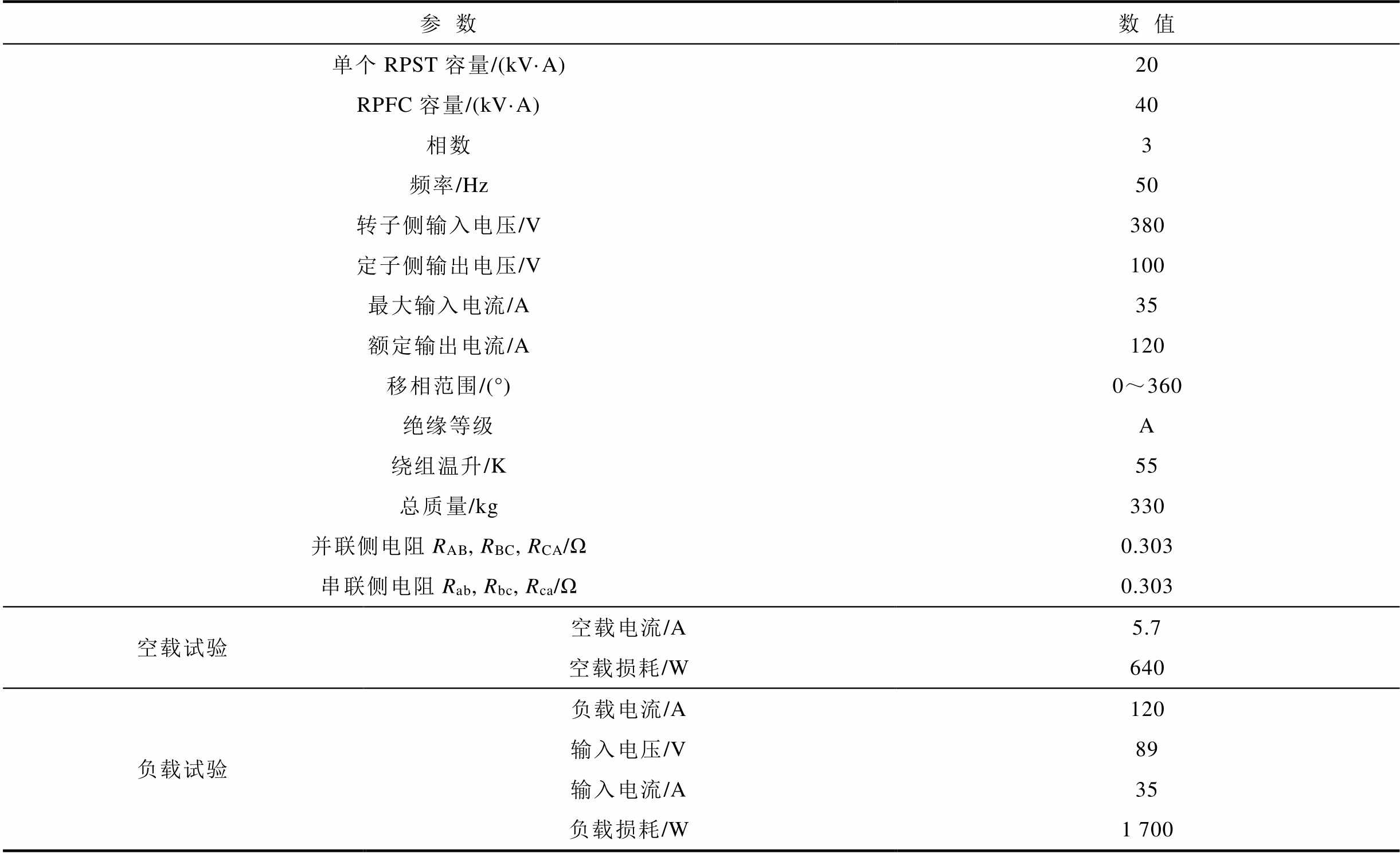
为验证所提电磁式旋转潮流控制器控制策略的有效性与正确性,在实验室中搭建了RPFC的380 V/ 40 kV·A实验样机,并通过多种实验工况进行验证,实验硬件装置如图14所示。实验平台中RPFC主体部分由两组电压比为380 kV:100 kV,容量为20 kV·A的旋转移相变压器组成,控制模块采用DSP控制器,伺服电动机转速归算到RPST转子转速为1°/s,RPFC装置参数见附表1,控制器参数见附表2。
图14中,1为DSP处理器;2和3为两台RPST;4为电流采集器,5为RPST取能侧输入开关,电源对转子绕组产生励磁时自动闭合,取消励磁时自动断开;6为等效电路中串联开关Sss;7为等效电路中旁路开关Sbp;8为RS485接口;9和10为负载箱;11为示波器;12为伺服电动机、蜗轮蜗杆与转子齿轮关联方式;13和14为两组RPST对应的伺服电动机;15为一种手动控制的蜗轮蜗杆;16为位置继电器。
3.2 电压调节实验
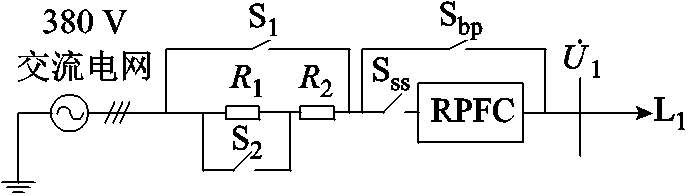
RPFC电压调节实验等效电路如图15所示。设计负载扰动及线路阻抗扰动实验对RPFC调压性能进行验证,实验参数见附表3,调节效果如图16所示。
1)工况一:负载扰动
t=0 s,S1断开,S2闭合,R2为线路阻抗,L1作为线路负载,此时线路末端相电压有效值为220 V。
t=23 s,线路负载L1由1.1+j0.5 kV·A突变为1.7+j0.5 kV·A。此时并网点电压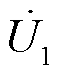 越下限,Sbp断开,Sss闭合,经过5 s左右调节,系统线路末端电压在28 s达到设定值。
越下限,Sbp断开,Sss闭合,经过5 s左右调节,系统线路末端电压在28 s达到设定值。
t=47 s,线路负载L1由1.7+j0.5 kV·A突变为3.3+j0.5 kV·A。经过10 s左右调节,系统末端电压在第57 s时刻达到系统设定值。
t=74 s,线路负载L1由3.3+j0.5 kV·A突变为1.1+j0.3 kV·A。经过11 s左右调节,系统末端电压在第85 s时刻达到系统设定值。
2)工况二:线路阻抗扰动
t=0 s,S1断开,S2闭合,R2为线路阻抗,L1为线路负载,此时线路末端相电压有效值为220 V。
t=32 s,S2断开,线路阻抗由R2突变为R1+R2,此时检测到并网点电压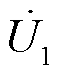 越下限,Sbp断开,Sss闭合,经过6 s左右调节,系统线路末端电压在38 s达到设定值。
越下限,Sbp断开,Sss闭合,经过6 s左右调节,系统线路末端电压在38 s达到设定值。
t=63 s,S1闭合,经过14 s左右调节,系统末端电压在77 s时达到系统设定值。
3.3 相位差线路柔性合环转供电实验
相位差线路柔性合环转供电实验等效电路如图17所示,实验参数见附表3。可以看到,在R1=ωL的情况下,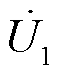 、
、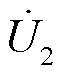 表现为一定相位差的情况,对应柔性合环实验时序设定如下。
表现为一定相位差的情况,对应柔性合环实验时序设定如下。
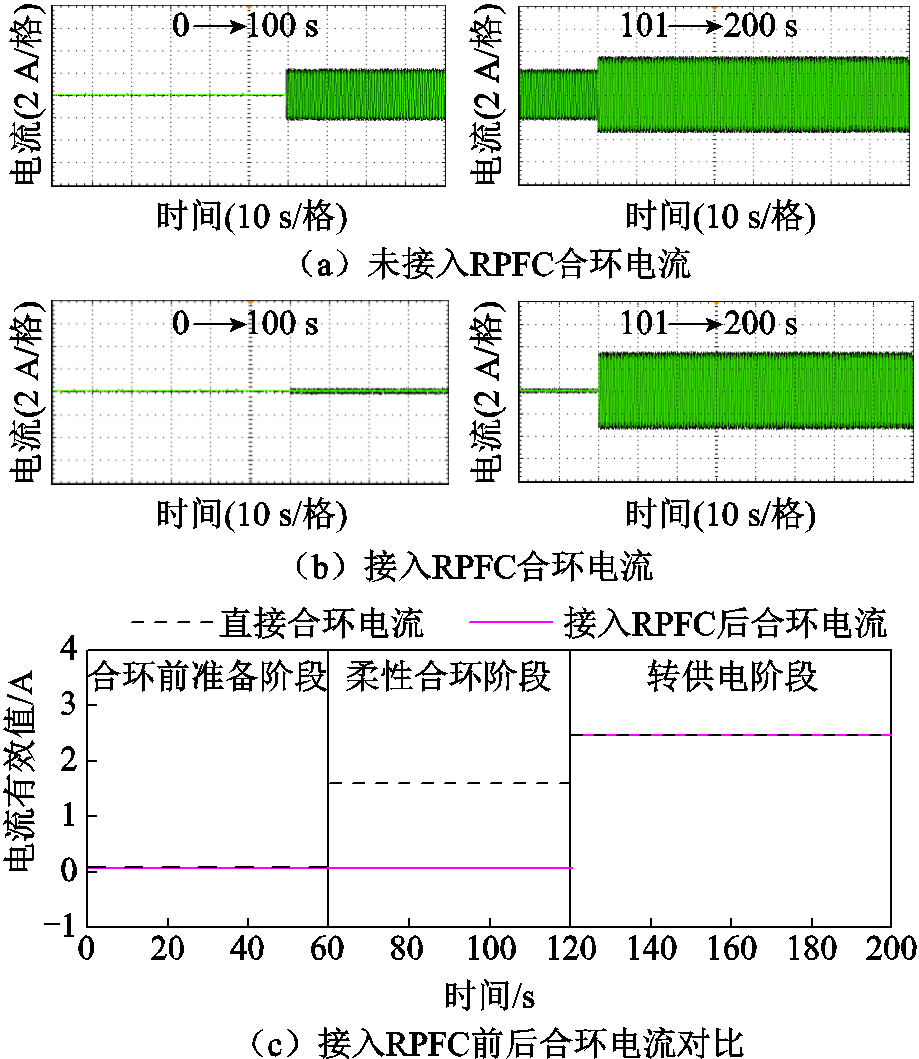
t=0 s:S1、S2闭合,Sss断开,系统提出合环需求后,RPFC采集Sss两端电压,并输出柔性合环所需电压矢量。
t=60 s:Sss闭合,柔性合环实验结果如图18所示,可以看到直接合环电流约为1.9 A,加入RPFC后合环电流控制在0.1 A以内,有效地实现了相位差线路柔性合环。
t=120 s:S2断开,此时系统进行转供电操作。
3.4 潮流控制实验
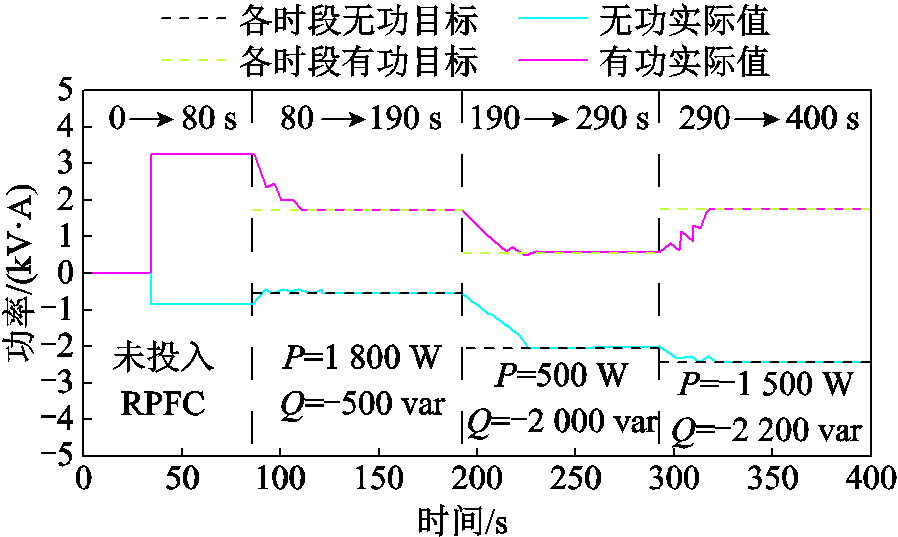
潮流控制实验等效电路如图17所示,实验参数见附表3,实验结果如图19所示,其控制过程包含如下阶段:
t=0 s:S1、S2闭合,Sss断开,此时两支路开环运行,合环点潮流为0。
t=30 s:Sss、Sbp闭合,观察无RPFC投入下合环点潮流情况,此时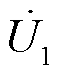 侧向
侧向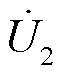 侧流动3 kW有功和-800 var无功。
侧流动3 kW有功和-800 var无功。
t=80 s:Sbp断开,RPFC投入运行,令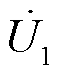 侧向
侧向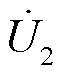 侧流动1 800 W有功和-500 var无功。
侧流动1 800 W有功和-500 var无功。
t=190 s:令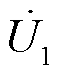 侧向
侧向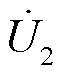 侧流动500 W有功和-2 kvar无功。
侧流动500 W有功和-2 kvar无功。
t=290 s:令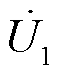 侧向
侧向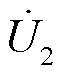 侧流动1 500 W有功和-2 200 var无功。
侧流动1 500 W有功和-2 200 var无功。
可以看到,多种调控目标下,RPFC均能完成精准潮流调控。
可见,在三种实验场景下RPFC均表现出了较好的调节性能,验证了本文所提RPFC拓扑及控制策略的可行性与有效性。
在RPFC各工况控制过程中,均存在一定系统误差,是由于转子角旋转时属于一种机械调节,存在惯性等其他因素的偏差,通过提高移相变压器制造精度,能够有效避免此类问题。
4 结论
本文提出了一种面向有源配电网多场景调控的电磁式旋转潮流控制器控制策略,并研制实验样机进行了验证,得到以下结论:
1)RPFC主体结构为两组移相变压器,通过改变定转子相对角度完成对注入线路电压的连续调节,属于一种电磁式潮流控制器,因此具有成本低、无谐波、可靠性高的优势。
2)针对不同运行场景,分别构建了基于RPFC的电压越限模型及变转速控制策略、基于相量合成原理的RPFC相位差线路柔性合环模型及其控制策略、基于瞬时无功理论的RPFC功率解耦控制模型及对应转速协调控制策略,实验结果验证了所提控制策略的有效性。
3)面对复杂有源配电网多运行场景,仅通过改变RPFC控制策略即可达成调控目标,表现出了较好的适用性及可推广性,对于未来有源配电网建设具有一定参考价值。
附 录
忽略变压器励磁电流,根据传统变压器分析方法可得到
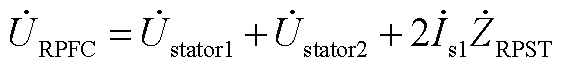 (A2)
(A2)
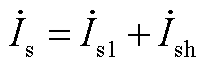 (A3)
(A3)
参照图1b,两台RPST的定子和转子电压满足
令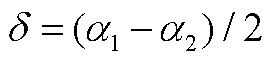 ,
,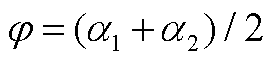 ,根据式(A2)、式(A4),可以得到
,根据式(A2)、式(A4),可以得到
由图1b可得到
由式(A3)、式(A4)、式(A6)可以计算得到转子总电流和系统线路电流分别为
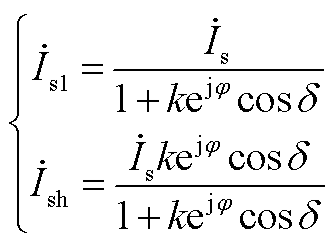 (A7)
(A7)
由式(A5)、式(A7)可以计算得到
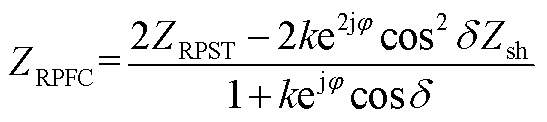 (A9)
(A9)
附表1 40 kV·A-RPFC系统参数
App.Tab.1 40 kV·A-RPFC system parameters
附表2 各运行场景控制器参数
App.Tab.2 Controller parameters in each running scenario
附表3 实验系统参数
App.Tab.3 Experimental system parameters
参考文献
[1] 郭立东, 雷鸣宇, 杨子龙, 等. 光储微网系统多目标协调控制策略[J]. 电工技术学报, 2021, 36(19): 4121-4131. Guo Lidong, Lei Mingyu, Yang Zilong, et al. Multi-objective coordinated control strategy for photovoltaic and energy-storage microgrid system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4121-4131.
[2] 赵毅, 吴志, 钱仲豪, 等. 计及源-荷时空相关性的主动配电网分布式优化调度[J]. 电力系统自动化, 2019, 43(19): 68-76. Zhao Yi, Wu Zhi, Qian Zhonghao, et al. Distributed optimal dispatch of active distribution network considering source-load temporal and spatial correlations[J]. Automation of Electric Power Systems, 2019, 43(19): 68-76.
[3] 郑重, 苗世洪, 李超, 等. 面向微型能源互联网接入的交直流配电网协同优化调度策略[J]. 电工技术学报, 2022, 37(1): 192-207. Zheng Zhong, Miao Shihong, Li Chao, et al. Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy internet[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 192-207.
[4] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685. Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[5] 赵玉林, 李海凤, 牛泽晗, 等. 配电变压器无触点有载自动调压的一种新方案[J]. 电网技术, 2016, 40(12): 3888-3893. Zhao Yulin, Li Haifeng, Niu Zehan, et al. A new scheme of contactless on-load automatic voltage regulation for distribution transformers[J]. Power System Technology, 2016, 40(12): 3888-3893.
[6] 孙惠, 翟海保, 吴鑫. 源网荷储多元协调控制系统的研究及应用[J]. 电工技术学报, 2021, 36(15): 3264-3271. Sun Hui, Zhai Haibao, Wu Xin. Research and application of multi-energy coordinated control of generation, network, load and storage[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3264-3271.
[7] 吴晓蓉, 莫骏, 魏金萧. 基于分区协调控制的主动配电网电压支撑运行策略[J/OL]. 现代电力, 2023, DOI:/10.19725/j.cnki.1007-2322.2022.0138. Wu Xiaorong, Mo Jun, Wei Jinxiao. Voltage support operation strategy of active distribution network based on zone coordination control [J/OL]. Modern Power, 2023, DOI:/10.19725/j.cnki.1007-2322.2022.0138.
[8] 刘广艳, 何春. 简述动态电压恢复器(DVR)在配电网中的应用[J]. 电气时代, 2022(5): 51-55. Liu Guangyan, He Chun. The application of dynamic voltage restorer (DVR) in distribution network is briefly described[J]. Electric Age, 2022(5): 51-55.
[9] 颜湘武, 贾焦心, 王德胜, 等. 基于电力弹簧的低压台区用户侧电压调节方法[J]. 电工技术学报, 2020, 35(12): 2623-2631. Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. User-side voltage regulation method for transformer areas based on electric spring[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2623-2631.
[10] 刘欣, 梁贵书, 王利桐, 等. 双芯移相变压器中有载分接开关技术参数确定方法[J]. 高电压技术, 2017, 43(3): 838-844. Liu Xin, Liang Guishu, Wang Litong, et al. Calculation method for technical parameters of on-load tap changer in phase shifting transformer[J]. High Voltage Engineering, 2017, 43(3): 838-844.
[11] 高聪哲, 黄文焘, 余墨多, 等. 基于智能软开关的主动配电网电压模型预测控制优化方法[J]. 电工技术学报, 2022, 37(13): 3263-3274. Gao Congzhe, Huang Wentao, Yu Moduo, et al. A model predictive control method to optimize voltages for active distribution networks with soft open point[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3263-3274.
[12] Fujita H,Baker D H, Ihara S, et al. Power flow controller using rotary phase shifting transformers, CIGRE Session.2000:37-102.
[13] Ba A O, Peng Tao, Lefebvre S. Rotary power flow controller modeling for dynamic performance evaluation[C]//2008 IEEE Power and Energy Society General Meeting - Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 2008: 1-10.
[14] Ba A O, Peng Tao, Lefebvre S. Rotary power-flow controller for dynamic performance evaluation—part I: RPFC modeling[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1406-1416.
[15] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器与统一潮流控制器和Sen Transformer的对比[J]. 电网技术, 2016, 40(3): 868-874. Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Comparative research on rotary power flow controller, unified power flow controller and Sen Transformer[J]. Power System Technology, 2016, 40(3): 868-874.
[16] 颜湘武,邵晨,彭维锋,等.基于旋转式潮流控制器的有源配电网柔性合环及紧急功率控制方法[J].中国电机工程学报, 2023, 43(16): 6192-6205. Yan Xiangwu, Shao Chen, Peng Weifeng, et al. Flexible loop and emergency power control method of active distribution network based on rotary power flow controller[J]. Proceedings of the CSEE, 2023, 43(16): 6192-6205.
[17] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器稳态特性研究[J]. 电网技术, 2015, 39(7): 1921-1926. Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Study on steady state characteristics of rotary power flow controller[J]. Power System Technology, 2015, 39(7): 1921-1926.
[18] 姚远, 李叶松, 雷力, 等. 基于电机驱动系统自传感的机械故障诊断研究综述[J]. 电工技术学报, 2022, 37(12): 2936-2948. Yao Yuan, Li Yesong, Lei Li, et al. A research review on application of motor drive system self-sensing in mechanical fault diagnosis[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2936-2948.
[19] 王治国, 郑泽东, 李永东, 等. 三相异步电机电流多步预测控制方法[J]. 电工技术学报, 2018, 33(9): 1975-1984. Wang Zhiguo, Zheng Zedong, Li Yongdong, et al. Predictive current control for three phase induction machine using multi-steps prediction horizon[J]. Transactions of china Electrotechnical Society, 2018, 33(9): 1975-1984.
[20] 夏长亮, 李莉, 谷鑫, 等. 双永磁电机系统转速同步控制[J]. 电工技术学报, 2017, 32(23): 1-8. Xia Changliang, Li Li, Gu Xin, et al. Speed synchronization control of dual-PMSM system[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 1-8.
[21] 杨影, 张杰鸣, 徐国卿, 等. 转速负反馈在伺服系统机械谐振抑制中的应用研究[J]. 电工技术学报, 2018, 33(23): 5459-5469. Yang Ying, Zhang Jieming, Xu Guoqing, et al. Application research on speed negative feedback in mechanical resonance suppression in servo system[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5459-5469.
[22] 虞宋楠, 刘念, 赵波. 面向光伏用户群的多主体分级电压调控方法[J]. 电力系统自动化, 2022, 46(5): 20-41. Yu Songnan, Liu Nian, Zhao Bo. Multi-agent classified voltage regulation method for photovoltaic user group[J]. Automation of Electric Power Systems, 2022, 46(5): 20-41.
Multi-Scene Control Method of Active Distribution Network Based on Electromagnetic Rotating Power Flow Controller
Yan Xiangwu1 Shao Chen1 Wu Ming2 Peng Weifeng1 Jia Jiaoxin1 Zhang Chenyu3
(1. Hebei Provincial Key Laboratory of Distributed Energy Storage and Microgrid North China Electric Power University Baoding 071003 China 2. State Grid Shanghai Energy Internet Research Institute Co. Shanghai 201210 China 3. Electric Power Scientific Research Institute of State Grid Jiangsu Electric Power Co. Nanjing 211100 China)
Abstract The high proportion of distributed power supply access and the advancement of the development of two-end power supply system bring the problems of voltage crossing limit, phase angle difference line closing loop, and tidal current regulation and control difficulties to the distribution network, etc. The solution of using electromagnetic rotary tidal current controller (RPFC) is proposed, which has the advantages of high applicability, low cost and high reliability.
Firstly, the RPFC topology and working principle are analyzed, and the RPFC steady-state voltage source model is established. RPFC consists of two rotor transfer phase transformers RPST1 and RPST2, and based on the electromagnetic induction principle, the rotor angle rotation of the two RPSTs is used to synthesize a stator voltage phase volume with constant amplitude and adjustable phase angle of 360°, respectively, and the two stator voltage phase volumes are superimposed so as to inject a series voltage with adjustable amplitude and phase angle in the line The RPST is similar to a transformer at rest, with a certain ratio between the stator side voltage and the rotor side voltage, and the phase difference is related to the angle α1 and α2 between the stator and the rotor, for the multi-pole RPST, the rotor angle only needs to be moved by a small mechanical angle to change the voltage phase in the line.
On this basis, the voltage crossing limit model and variable speed control strategy based on RPFC are constructed respectively, and the specific principle is to make the servo motor perform complete speed adaptive control, so thatαsatisfies to reduce the servo motor speed when it is close to the set value and stop exactly when it reaches the set value. The RPFC phase-angle difference line flexible loop-closing model and its control strategy based on the principle of phase synthesis are constructed. For the phase-angle difference line loop-closing problem, the voltage vector difference on both sides of the loop-closing point is compensated by RPFC, which can effectively suppress the loop current and meet the demand of non-stop loop-closing of the system. The RPFC power decoupling control model based on instantaneous reactive power theory and the corresponding speed coordination control strategy are constructed, and the speed coordination control design is carried out for two sets of servo motors, so that α1 and α2 can meet the requirement of high precision regulation by stopping the motion at the same time within the set value range.
Finally, a 380 V/40 kV·A test prototype of RPFC is built and verified by various experimental conditions. The experimental results show that only changing the RPFC control strategy can achieve its effective and stable regulation under various scenarios, which verifies the effectiveness and correctness of the proposed control strategy.
keywords:Electromagnetic rotating power flow controller, active distribution network, power flow control, flexible closing loop, voltage regulation
DOI:10.19595/j.cnki.1000-6753.tces.L10096
中图分类号:TM761
国家电网有限公司总部科技资助项目(5108-202218280A-2-227-XG)。
收稿日期 2023-01-09
改稿日期 2023-03-30
作者简介
颜湘武 男,1965年生,博士,研究方向为新能源电力系分析与控制、现代电力与变换、新型储能与节能等。E-mail:xiangwuy@ncepu.edu.cn
邵 晨 男,1995年生,博士研究生,研究方向为潮流控制器理论及控制。E-mail:shaochen@ncepu.edu.cn(通信作者)
(编辑 赫蕾)
 X,电压-有功灵敏度远大于电压-无功灵敏度,此时采用静止同步补偿器[7]的方案难以满足调压要求;而动态电压调节器[8]及电力弹簧调压[9]的方式具有成本高、可靠性低的缺陷,同时电力电子器件的使用会带来谐波问题[10]。在相位差线路柔性合环方面,文献[11]提出一种双心对称移相变压器的方案,通过改变励磁变压器二次绕组抽头位置,即可在电压幅值不变的前提下实现电压移相的功能,但其属于一种有载分接开关式移相器,因此表现出了调节速度慢、调节离散、使用寿命短的缺陷。在潮流控制方面,智能软开关具有较好的调节功能,其基本结构由大功率全控型电力电子元件组成[11],通过对两侧换流器施加控制策略,满足接入点输出电压幅值与相位的独立控制,实现互联线路流过有功和无功功率的双向解耦控制,但背靠背型智能软开关的设计容量由线路需转供的最大功率决定,因此其表现出了容量大、成本高、体积大的缺点。
X,电压-有功灵敏度远大于电压-无功灵敏度,此时采用静止同步补偿器[7]的方案难以满足调压要求;而动态电压调节器[8]及电力弹簧调压[9]的方式具有成本高、可靠性低的缺陷,同时电力电子器件的使用会带来谐波问题[10]。在相位差线路柔性合环方面,文献[11]提出一种双心对称移相变压器的方案,通过改变励磁变压器二次绕组抽头位置,即可在电压幅值不变的前提下实现电压移相的功能,但其属于一种有载分接开关式移相器,因此表现出了调节速度慢、调节离散、使用寿命短的缺陷。在潮流控制方面,智能软开关具有较好的调节功能,其基本结构由大功率全控型电力电子元件组成[11],通过对两侧换流器施加控制策略,满足接入点输出电压幅值与相位的独立控制,实现互联线路流过有功和无功功率的双向解耦控制,但背靠背型智能软开关的设计容量由线路需转供的最大功率决定,因此其表现出了容量大、成本高、体积大的缺点。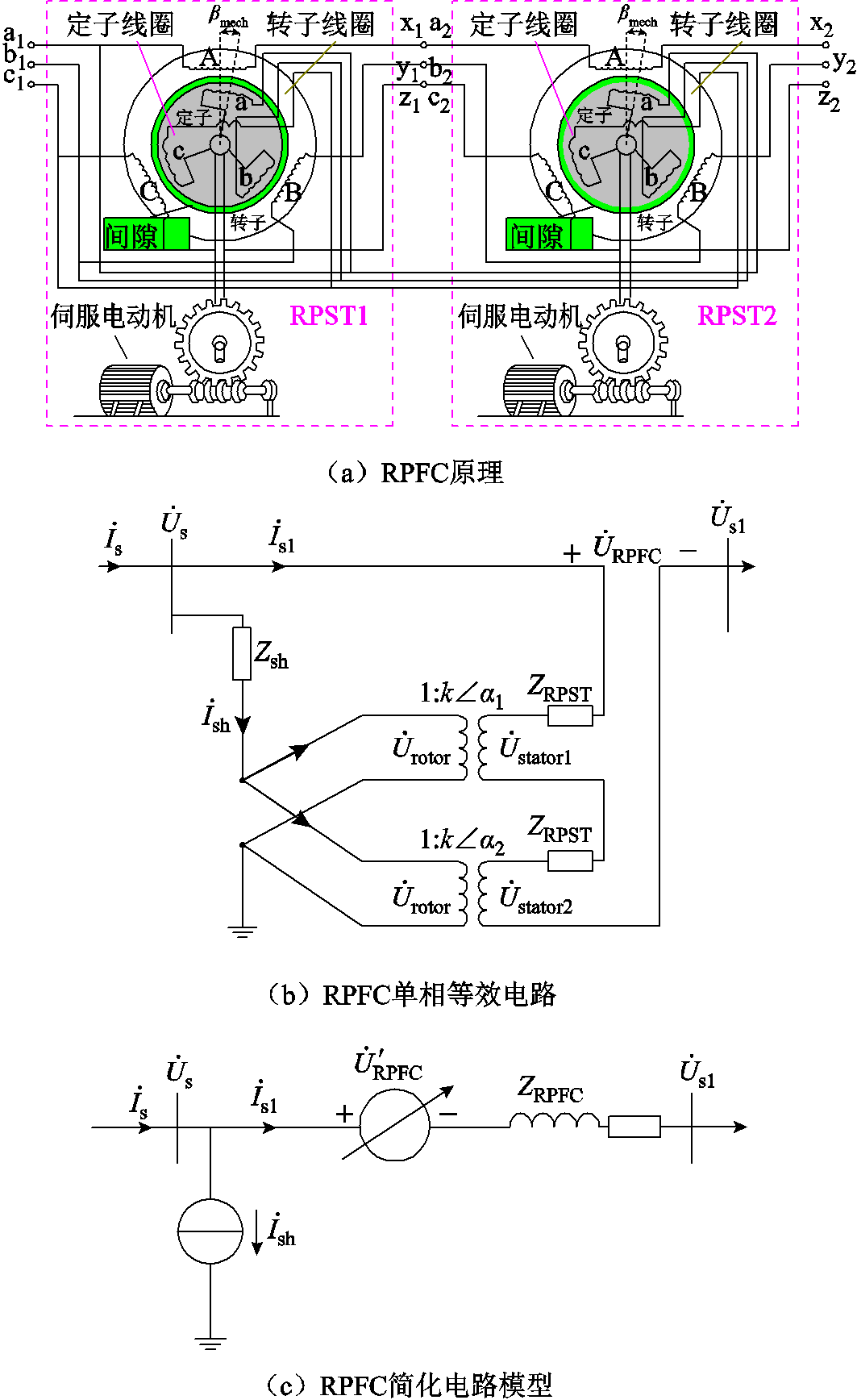
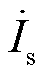 为接入RPST前系统线路电流;
为接入RPST前系统线路电流;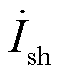 为转子总电流;
为转子总电流;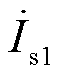 为定子侧电流;
为定子侧电流;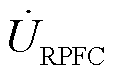 为RPFC串入线路的电压;Z
为RPFC串入线路的电压;Z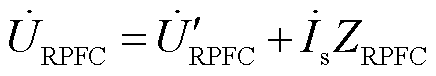 (1)
(1)
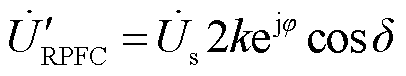 (2)
(2)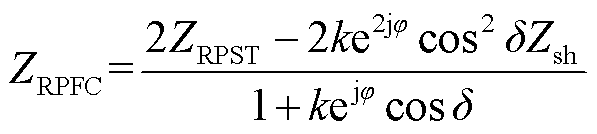 (3)
(3)
 为RPFC串入线路电压相量;
为RPFC串入线路电压相量;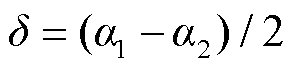 ,
,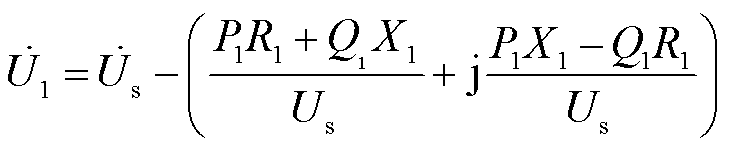 。从而可以得到RPFC简化电路模型如图1c所示,详细推导过程见附录,其串联部分由一个受控理想电压源和一个等效内阻抗组成,并联支路为受控电流源。通过改变
。从而可以得到RPFC简化电路模型如图1c所示,详细推导过程见附录,其串联部分由一个受控理想电压源和一个等效内阻抗组成,并联支路为受控电流源。通过改变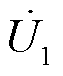 为馈线1并网点电压;
为馈线1并网点电压;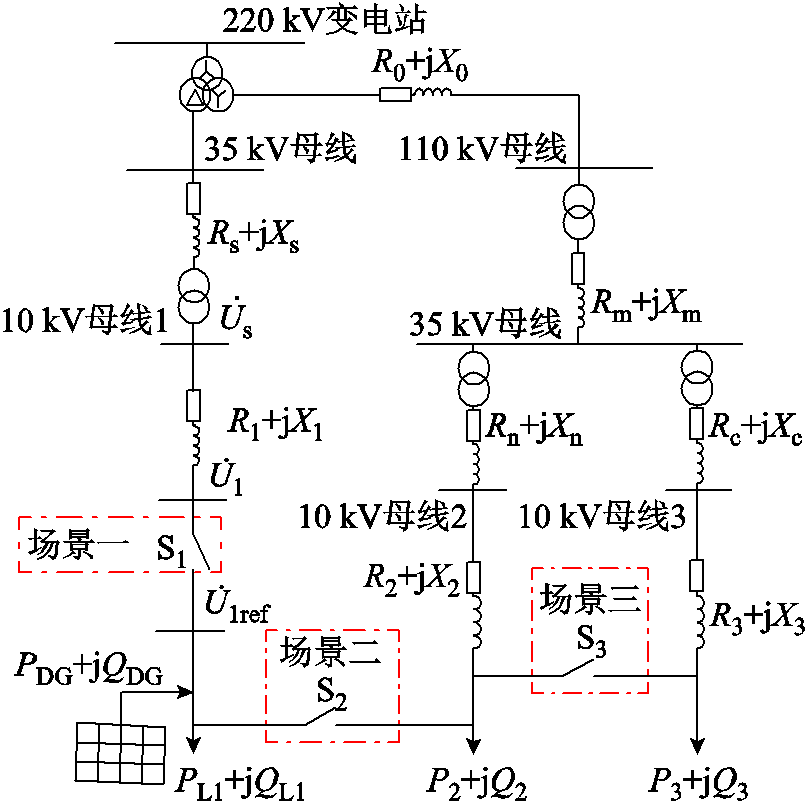
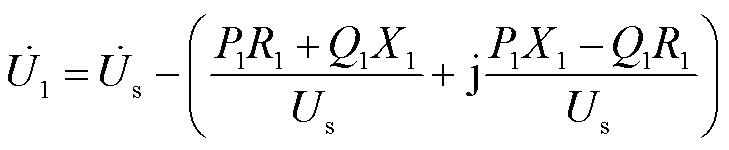 (4)
(4)
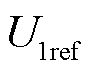 作为节点电压的基准电压幅值,通常为1.0(pu),将S
作为节点电压的基准电压幅值,通常为1.0(pu),将S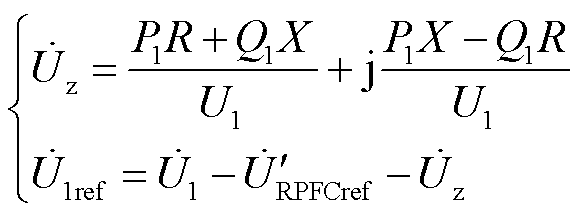 (5)
(5)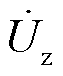 为RPFC内电阻压降。两旋转移相变压器采用对称调节的方式可有效避免线路相位的变化,且对线路功率因数不产生影响,如图3所示,此时存在
为RPFC内电阻压降。两旋转移相变压器采用对称调节的方式可有效避免线路相位的变化,且对线路功率因数不产生影响,如图3所示,此时存在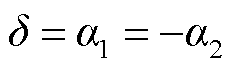 、φ=0。
、φ=0。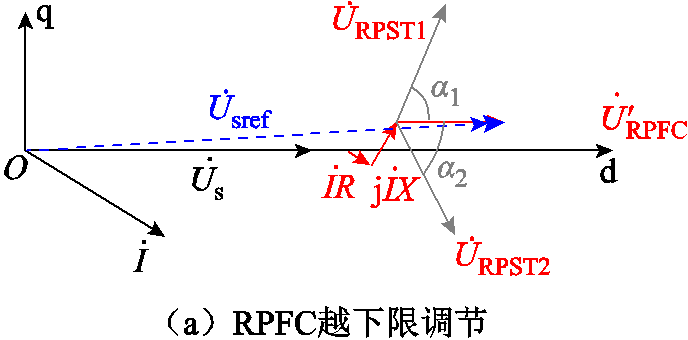
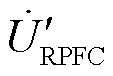 已知的情况下,可以根据式(2)计算此时
已知的情况下,可以根据式(2)计算此时
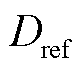 进行量化计算,令其满足
进行量化计算,令其满足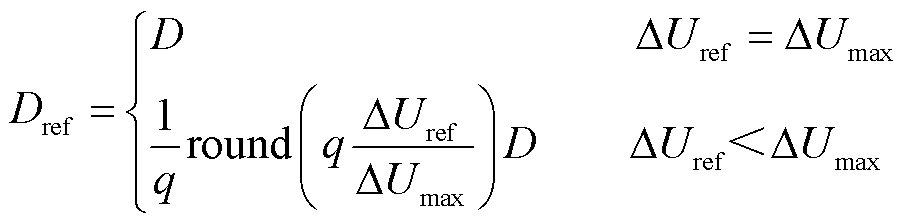 (6)
(6)
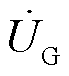 和
和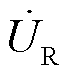 分别为RPFC两端电压;S
分别为RPFC两端电压;S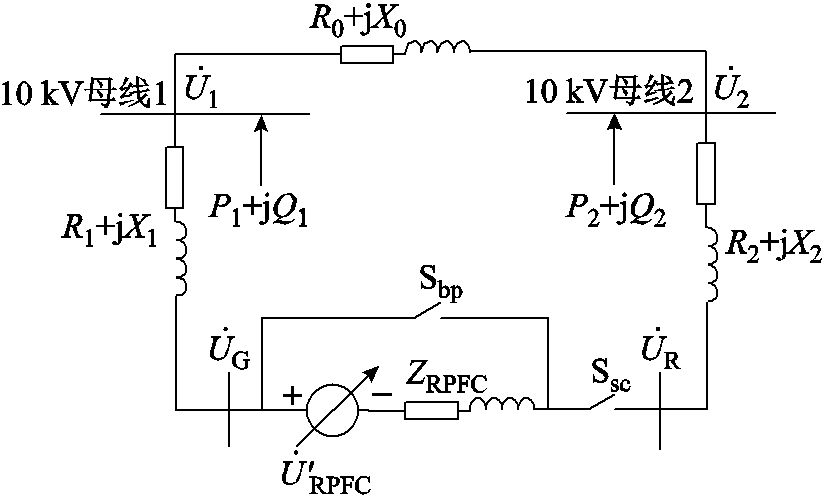
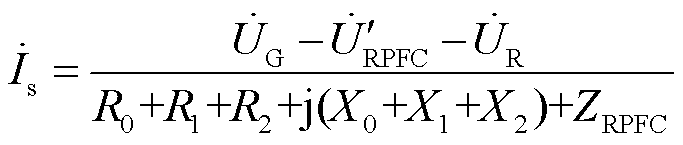 (7)
(7)
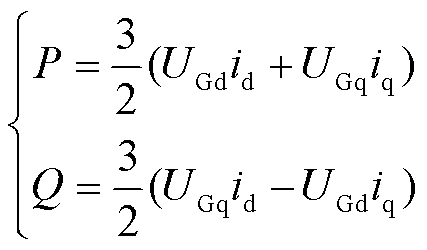 (8)
(8)
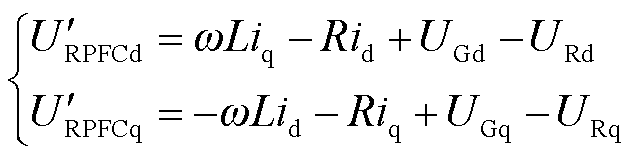 (9)
(9)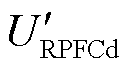 、
、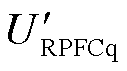 与线路传输功率P、Q的关系为
与线路传输功率P、Q的关系为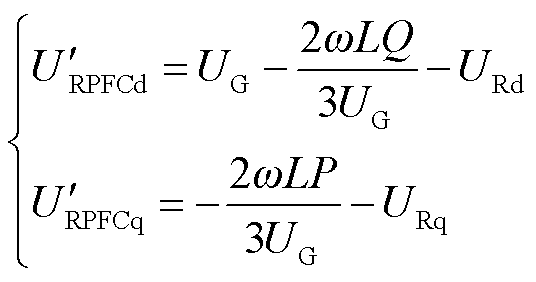 (10)
(10)
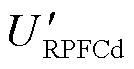 、
、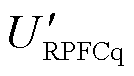 的值,在式(9)基础上即可计算得到δ
的值,在式(9)基础上即可计算得到δ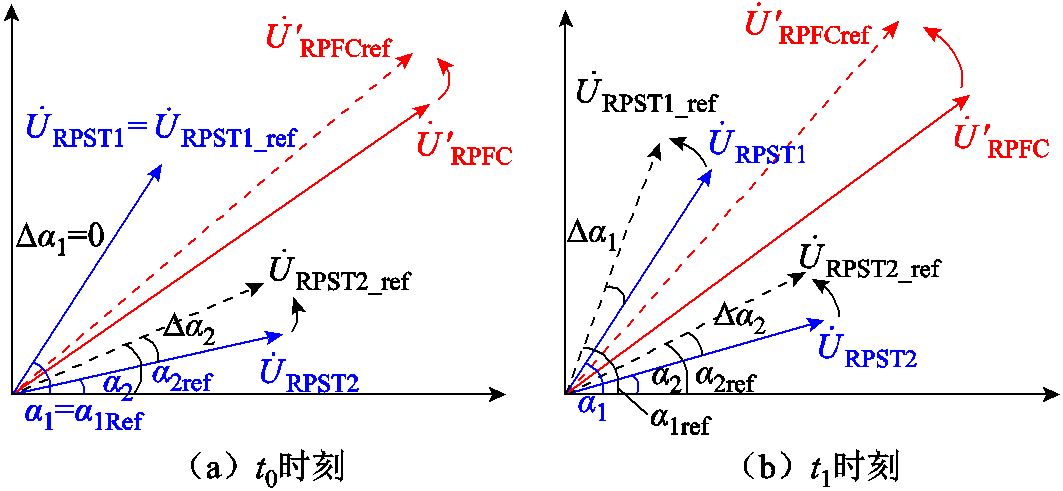
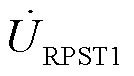 达到设定值
达到设定值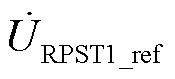 而
而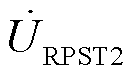 未达到设定值
未达到设定值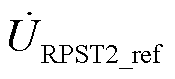 ,此时
,此时 与
与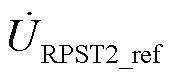 ,使原本停转的
,使原本停转的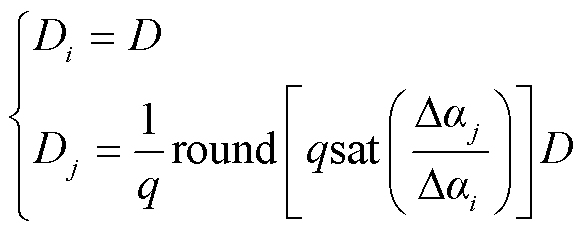 (11)
(11)
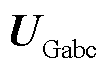 、
、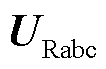 、
、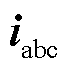 分别为三相输电系统的瞬时电压和电流。在完成自动或手动场景判别后,根据不同控制方案输出实际
分别为三相输电系统的瞬时电压和电流。在完成自动或手动场景判别后,根据不同控制方案输出实际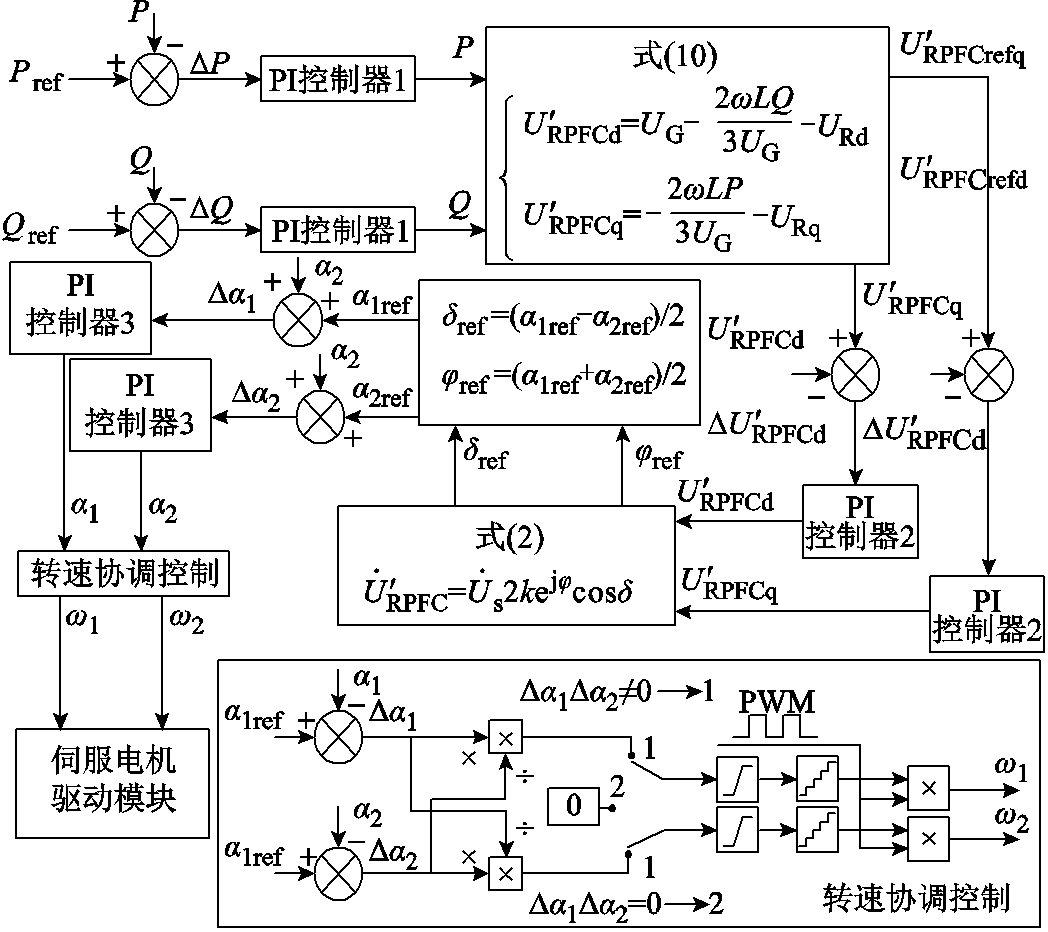

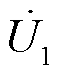 越下限,S
越下限,S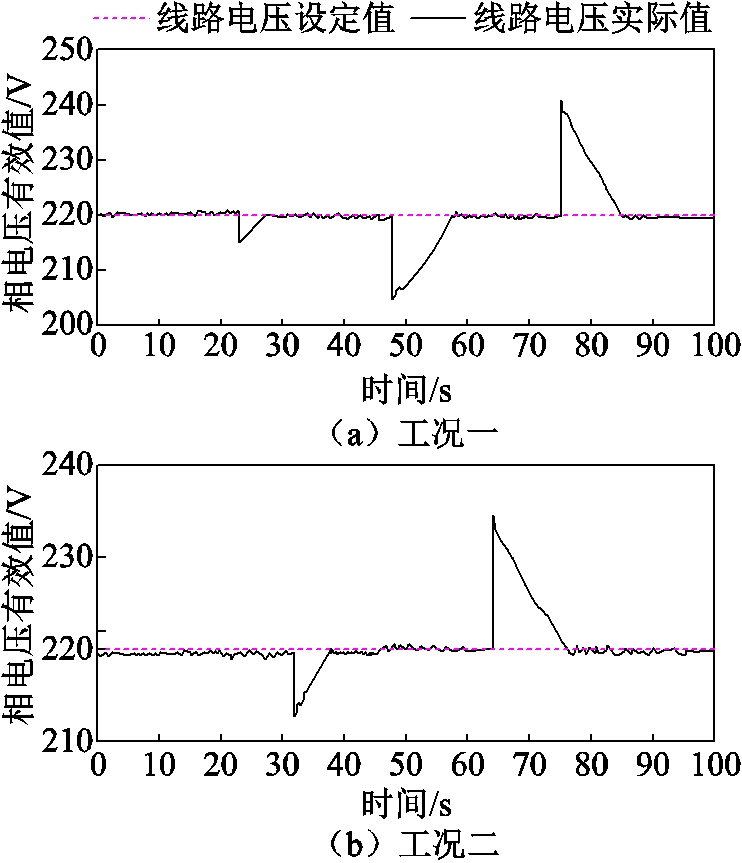
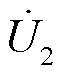 表现为一定相位差的情况,对应柔性合环实验时序设定如下。
表现为一定相位差的情况,对应柔性合环实验时序设定如下。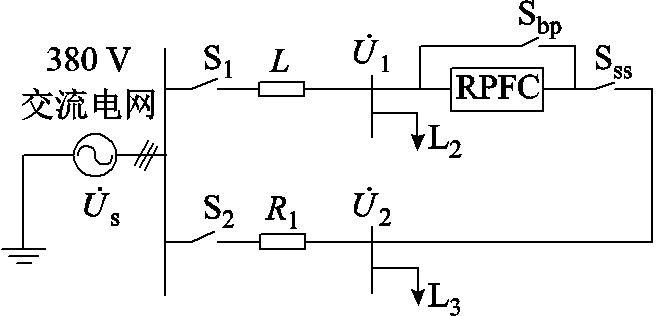
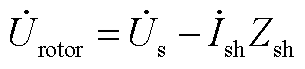 (A1)
(A1)
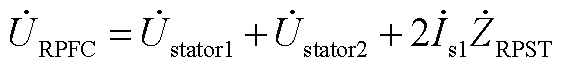 (A2)
(A2)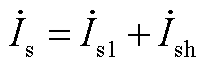 (A3)
(A3)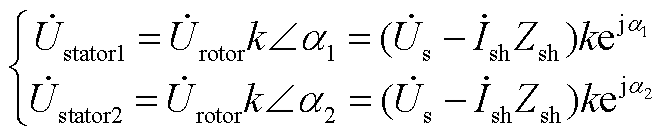 (A4)
(A4)
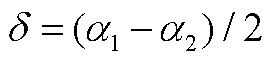 ,
,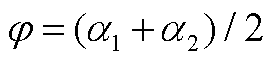 ,根据式(A2)、式(A4),可以得到
,根据式(A2)、式(A4),可以得到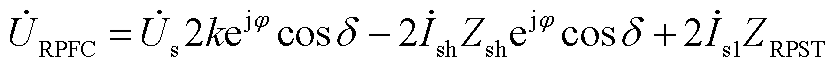 (A5)
(A5)
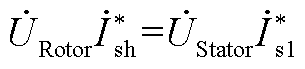 (A6)
(A6)
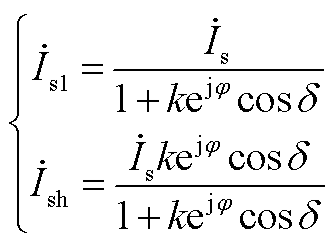 (A7)
(A7)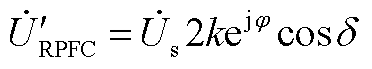 (A8)
(A8)
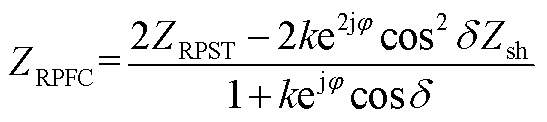 (A9)
(A9)