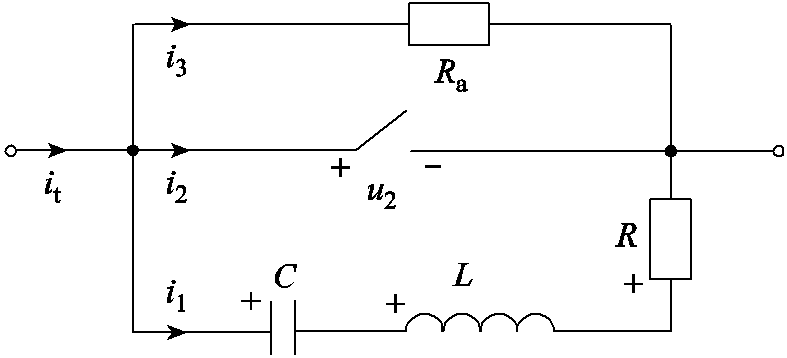
图1 无源式直流转换开关结构
Fig.1 Structure diagram of passive DC transfer switch
摘要 振荡回路在直流开关开断过程中通过提供振荡电流来创造“过零点”，振荡过程对成功开断与否具有决定性作用，因此亟须研究振荡回路参数对开断的影响。现有研究尚未在结合开断回路电弧特性的基础上考虑振荡回路寄生参数，存在参数不匹配、准确性低等局限性。该文首先根据实际工程参数，建立了含寄生参数的等效多电容组合的振荡回路改进模型。然后，基于Simulink仿真平台对振荡回路改进模型开展仿真研究；同时开展了振荡回路本体特性实验，验证了仿真的正确性。最后，在考虑电弧特征的基础上，深入研究振荡回路参数对开断过程的影响机理，得出了RLC参数与开断特性间的映射关系。
关键词：电弧模型 直流开关 振荡回路 电容
直流转换开关是特高压直流输电工程中极为重要的一次主设备，可按需求改变直流系统运行方式，隔离故障设备，保证系统非故障部分的正常运行。当前国内各大换流站装设的主要有中性母线开关、金属回路转换开关、大地回路转换开关等，主要用于增加输电运行方式的灵活性和保护切除故障。
特高压直流开关由开断回路、吸能回路、振荡回路三部分构成，分为有源式和无源式两种，后者结构如图1所示。图中，it为直流开关总电流，i2为开断支路电流，u2为断路器电压，i1为振荡支路电流，i3为吸能支路电流，Ra为避雷器等效电阻。振荡回路由电容器组构成，旨在产生可叠加在直流电上的振荡交流电[1-2]，强制在某一时刻实现电流过零，使开断回路中的断路器动作。
图1 无源式直流转换开关结构
Fig.1 Structure diagram of passive DC transfer switch
振荡回路中电容器参数会受到制造、运输、使用等过程的影响，可能出现初期型故障、偶发性故障、过载运行故障和老化运行故障[3]。故障会导致电容值发生改变，可能造成直流开关开断失败。文献[4-8]将振荡回路的电容组等效为一个电容，降低了模型的复杂性，但无法反映实际的寄生参数。文献[9-10]讨论了寄生参数，但未考虑电容器局部故障对系统的影响，现有的模型存在参数不匹配、考虑因素不全面等问题，振荡回路参数对开断过程的影响机理尚不明确。
此外，直流转换开关在开断过程中会产生电弧，电弧模型参数与振荡回路参数间存在强耦合非线性关系，因此电弧模型的建立是准确研究直流转换开关的核心步骤。现阶段已有多位研究学者在实验的基础上提出了电弧的动态物理模型[11-19]，采用多个非线性方程式描述电弧过程，最常用的为Mayr电弧模型。此外，Cassie电弧模型[20]、Schwarz电弧模型[21]也被应用在接地开关、隔离开关等研究中。然而，适用于直流转换开关的电弧模型研究较少。
综上所述，现有研究总结见表1。针对上述问题，本文首先详细分析各个电弧模型的原理及特性；其次依照某特高压直流输电系统参数，构建含寄生参数的等效多电容组合改进模型，提高振荡回路模型的准确性；接着基于Simulink仿真平台对振荡回路改进模型开展仿真研究，同时开展了现场振荡回路本体特性实验，对比分析理论计算结果、仿真与实验结果，验证模型的正确性；然后理论研究了开断回路的电弧等效模型，对比直流开关在不同电弧模型下的仿真结果；最后为了模拟现场可能出现的状况，进一步在正常状态和故障状态下，深入研究振荡回路参数对开断过程的影响机理。
表1 研究现状对比
Tab.1 Comparison of research status
文献电弧模型振荡回路模型应用场景 [13,18,23-24]Mayr电弧模型无断路器拉弧 [11-12, 14-17,19-22]多种电弧模型无接地故障电弧 [4-7]无单一电容模型变流器振荡回路 [8-9]无多个电容模型超级电容储能技术 [10]无考虑多电容寄生参数电容器状态评估 本文Mayr、Schwarz、Cassie电弧模型含寄生参数的组合电容模型直流开关振荡回路
针对现有含集中式电容振荡回路模型存在的建模精度不足的问题，建立详细的含寄生参数的电容模型振荡回路拓扑。
开断过程主要分为电流强迫过零、断口介质恢复、避雷器动作吸能三个阶段。其中，电流强迫过零阶段为整个开断过程中最为关键的环节。
直流转换开关接到开断指令后，振荡回路并联在开断回路两端，然后开断回路的断路器先对直流电进行拉弧，电弧电压迅速对振荡回路中的电容充电，由于电弧不稳定，具有跳跃性，电弧电压无法保持为一个固定值，且由于振荡回路中等效电感L、等效电容C以及等效电阻R的谐振，在电弧与电容之间会有一个往返的充放电过程，产生振荡交流电并叠加在直流电上，强迫电流过零，熄灭电弧。
无源式直流开关产生振荡电流拓扑如图2所示。以图2中的无源式直流开关为例，开关一旦开断，振荡回路便并联在开断回路两端，电弧电压对电容充电，构成充放电回路[22-24]。振荡回路的衰减系数δ、振荡角频率ω和振荡电流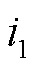
的表达式分别为
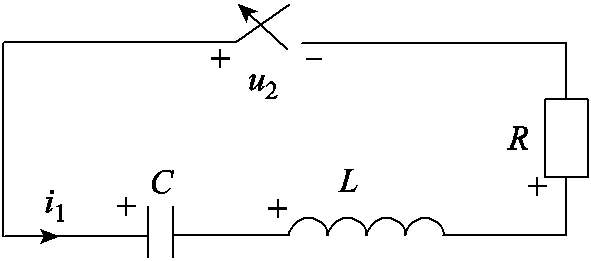
图2 无源式直流开关产生振荡电流拓扑
Fig.2 Topology of oscillating loop of passive DC switch
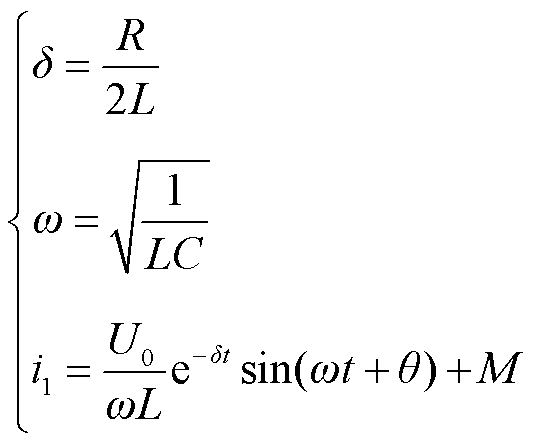（1）
式中，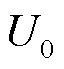
为电弧充电初始电压；θ为考虑到非线性电感和电容对角度的影响而引入的调整角度量；M为与电压U一次导数有关的变量，即方程的特解。
工程实际中，振荡回路电容并不是由一个电容器组成，而是通过多组小电容器串并联构成电容器组，而电容器组内部存在寄生参数，Ls和Rs分别为在电容器外部连接线以及外加空心电抗器所等效的电感和电阻，分别为μH级别、mΩ级别。为了更好地反映实际接线，本文将传统的单一电容模型改进为一种含寄生参数的多电容组合等效模型，采用常见的“两串四并”结构，振荡回路等效模型如图3所示。
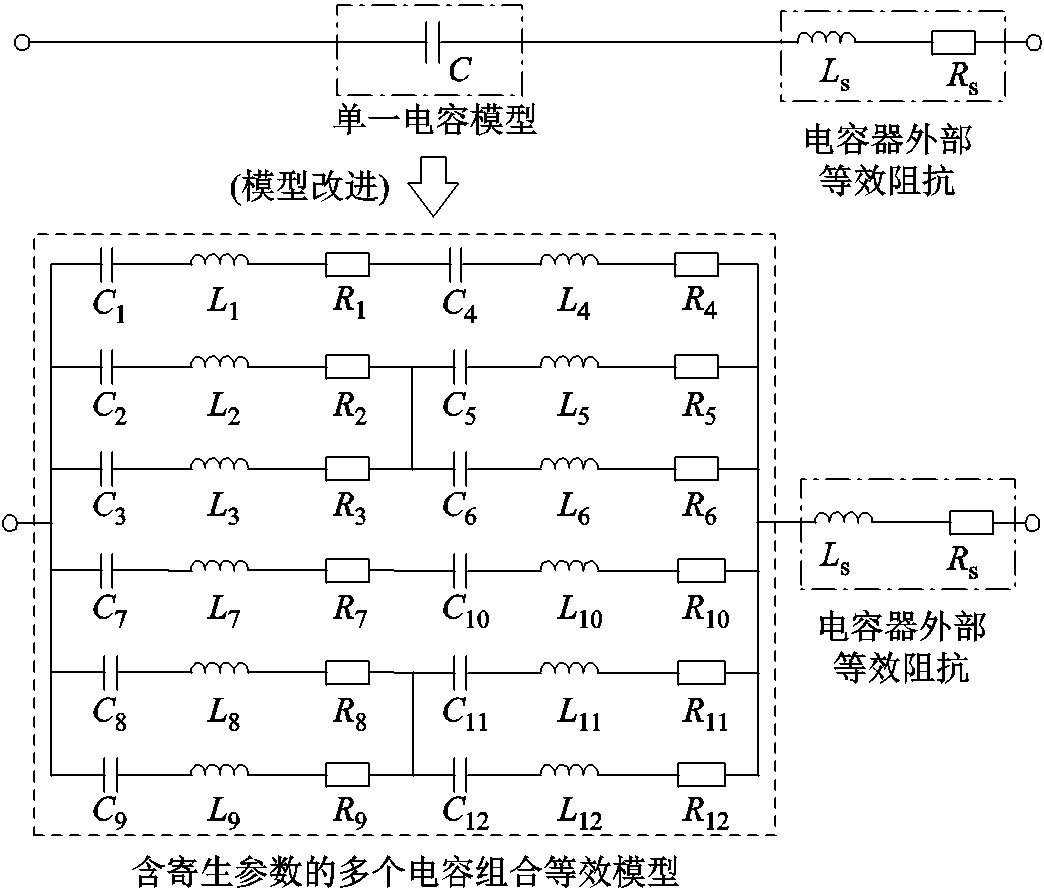
图3 振荡回路等效模型
Fig.3 Equivalent model of oscillation circuit
图3中，C1～C12共同组成了振荡回路中的电容；而L1～L12分别为电容C1～C12连接线的寄生电感；R1～R12分别为电容C1～C12连接线的寄生电阻。而C1～C12组合关系满足
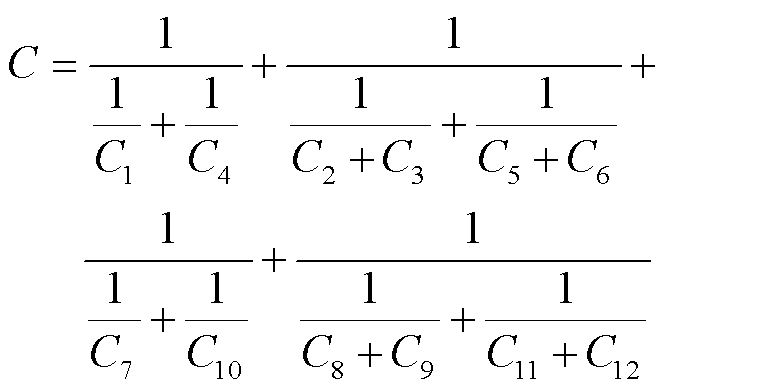(2)
与各个小电容串联的寄生电感Lp的数值一般为nH级别，寄生电阻Rp的数值一般为mΩ级别，表达式分别为
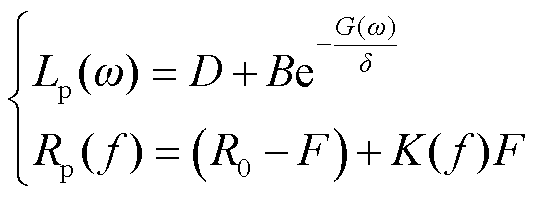（3）
式中，R0为薄膜电容中的一种基本电阻；f、F、K(f)分别为电容的工作频率、电容器出厂时给定的一个与电容器本身大小有关的系数、与频率有关的函数式，K(f)在实际计算中表示为一个二次或者三次函数，与实际计算方法有关；D和B为与电容器本身有关的参数；G(ω)为与角频率有关的函数。
本文依照某特高压系统换流站直流转换开关技术指标开展实验研究，实验电气接线如图4所示，直流开关振荡回路中的电容器组外观如图5a所示，等效电容的设计参数为22 μF，电容器组按照图3将多个电容器通过连接线进行串并联组合，在电容器组外部串联一个设计参数为60 μH的空心电抗器来构成振荡回路。
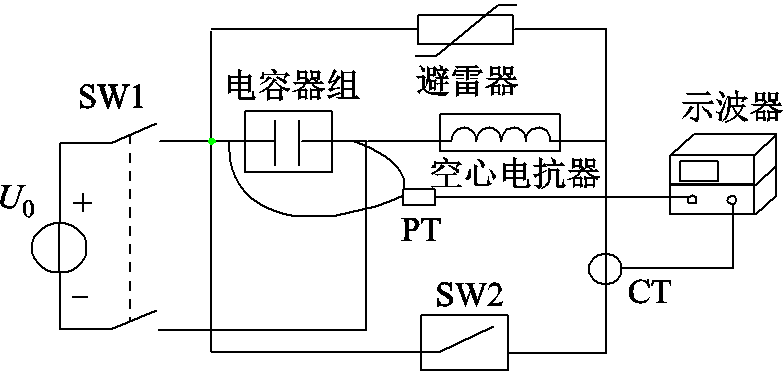
图4 实验电气接线
Fig. 4 Experimental wiring diagram
图5 振荡特性实验接线
Fig. 5 Oscillation characteristic experimental wiring diagram
为了探究实际的振荡回路参数，本文图5按照图4所示的实验接线，在室内搭建了如图5b所示的现场接线，然后开展振荡特性实验。首先闭合SW1对电容器组充电，当电压达到U0 (U0=1 100V)后，先断开SW1再闭合SW2，形成RLC振荡回路，通过电流探头CT测得振荡电流波形，电压探头PT测得振荡电压波形。
按照2.1节接线开展振荡特性实验，对测得的实验波形按照式（1）拟合得到整个振荡回路的等效参数分别为：C=22.8 μF、L=64.2 μH、R=41.6 mΩ。将上述等效参数代入到振荡回路参数计算。求得振荡频率理论计算值为4.160 kHz，衰减系数为32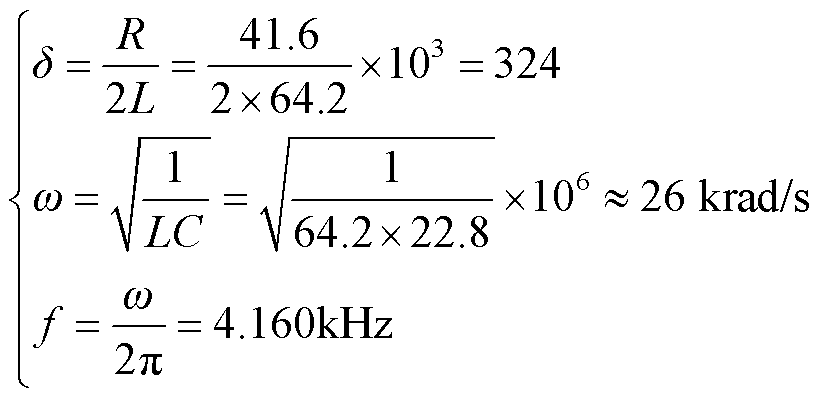4。
（4）
基于Matlab/Simulink平台，为了充分模拟实验中的电容器组，本文按照图3中的改进模型来建立振荡回路仿真模块，建立模拟实验过程的仿真模型，电容C1～C12的取值均为7.6 μF，寄生电感、寄生电阻参数由式（3）计算可得，具体取值见表2。然后按照振荡特性实验的外电路接线和操作步骤进行仿真。
此外，本文按照该振荡回路的设计参数，搭建传统单一电容模型并开展相同的仿真研究。现场实验与两种模型下的仿真结果如图6所示。其中，实验和仿真得到的波形趋势一致，均发生了欠阻尼衰减振动，但基于工程设计参数搭建的传统模型仿真波形在第二个波谷后出现明显的偏移，这是因为工程设计时为理想情况，但受到实际器件搬运安装、本体老化、寄生参数等影响，设计值与实际值存在一定误差，因此振荡回路参数的确定应以实验结果为准。现场实验、理论计算、两组仿真得到的结果见表3，其中，改进模型仿真与现场实验之间的电流波形误差率、电压波形误差率分别为6.93%、7.03%，其他指标误差均小于2%，满足工程应用。
表2 寄生电感、寄生电阻参数
Tab.2 Parasitic inductance and parasitic resistance
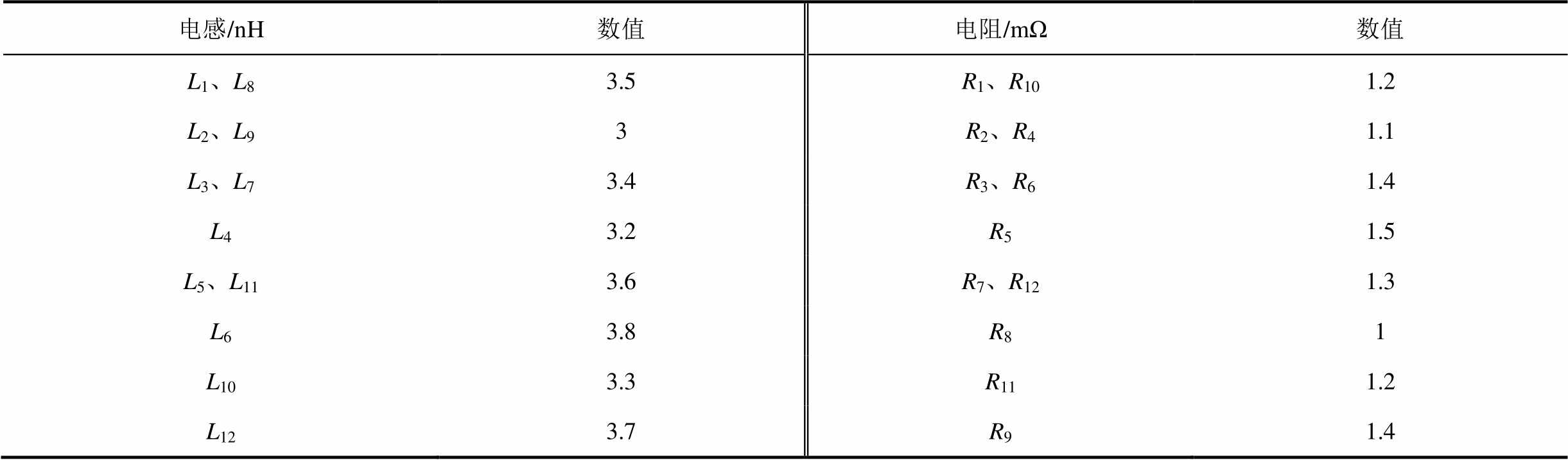
电感/nH数值电阻/mΩ数值 L1、L83.5R1、R101.2 L2、L93R2、R41.1 L3、L73.4R3、R61.4 L43.2R51.5 L5、L113.6R7、R121.3 L63.8R81 L103.3R111.2 L123.7R91.4
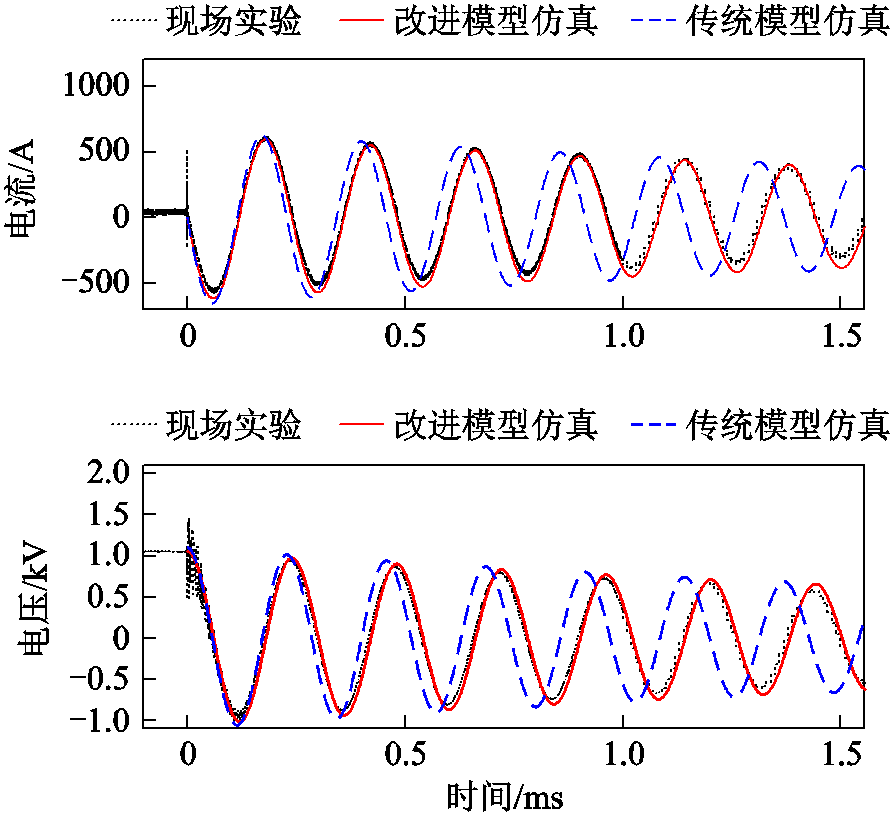
图6 振荡回路仿真与实验结果
Fig.6 Simulation and test results of oscillation circuit
表3 实验、理论计算、仿真值
Tab.3 Experimental, theoretical, simulation values
项目衰减系数δ振荡频率ω/kHz 数值与实验误差（%）数值与实验误差（%） 现场实验360—4.170 8— 理论计算324104.1600.26 改进模型仿真353.31.864.1520.45 传统模型仿真315.612.34.4085.69
由此可以认为，改进模型更加适用于振荡回路的特性分析，后续可应用于实际系统中各类运行情况下的直流开关开断仿真中。
在断路器实际断开过程中，不可避免地会产生暂态电弧，振荡回路的振荡电压由电弧电压提供，若无电弧模型，振荡回路会因缺乏电源导致无法形成振荡电流，这显然不符合实际开断过程。
此外，电弧的存在会使断路器开断电压不发生理想突变，即图1中的u2和i2存在一段过渡变化过程，需建立能够准确模拟电弧电导变化的电弧模型。
现阶段有不少电弧模型来模拟电弧燃烧过程，本文将依次分析Mayr电弧模型、Cassie电弧模型、Schwarz电弧模型这三种经典电弧模型。
（1）Mayr电弧模型。主要基于热惯性、热平衡和热游离三个基本理论推导得到[18]，模型方程式为
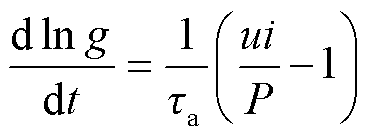（5）
式中，u、i分别为电弧电压、电弧电流；g为电弧电导，g=i/u；τa、P分别为电弧时间常数、电弧散热功率常数；u与i乘积为电弧的燃烧功率。
熄灭电弧的条件为电流过零，且熄灭后不再发生电击穿或者热击穿。当ui＞P时，由于热量积累，电弧气温会增高，且由于电弧的热惯性，电弧升温和电导加强过程都十分缓慢。只有当ui＜P时，电弧才能成功被断开。
根据出厂试验报告的波形，可计算出τa和P[18]。u、i为随着时间t变化的变量，参照实测经验，u、i相乘后的波形可近似表示为
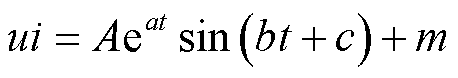（6）
式中，A、a、b、c、m均为与波形相关的系数。由此可以推导电弧电导g的表达式为
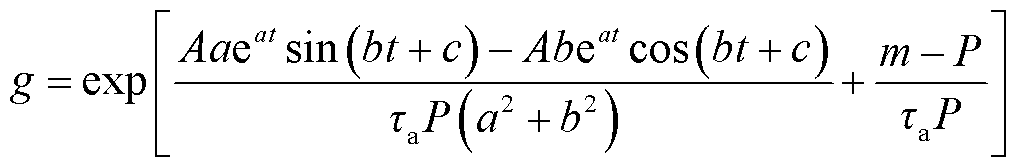（7）
（2）Cassie电弧模型。假设电弧气体通道形状为圆柱形，可忽略弧柱以外的电导，且气体通道截面温度沿截面径向均匀分布。模型方程式为
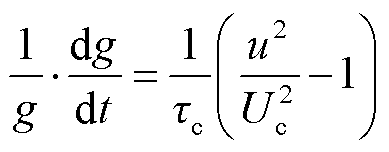（8）
式中，Uc为电弧电压梯度；τc为Cassie电弧模型时间常数。
（3）Schwarz电弧模型为
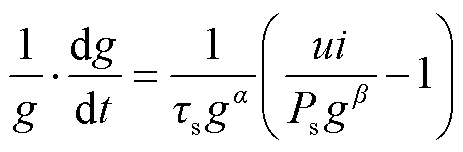（9）
式中，Ps和τs分别为Schwarz模型的耗散功率常数和时间常数；α（取值范围[0.1,0.5]）、β（取值范围[0.1,0.9]）均为常数，二者的取值受系统电压以及回路电流和环境等方面的影响。
上述模型的数学表达形式相似，模型变量均为瞬时电弧电导g(t)，需要结合外电路的条件对微分方程进行求解。
本文依据某换流站资料，基于Simulink搭建了额定电流为1 700 A的特高压直流开关仿真模型，如图7所示。图中，振荡回路模块、电弧模块、吸能回路模块三个模块分别为振荡回路、电弧模型、由避雷器组构成的吸能回路。
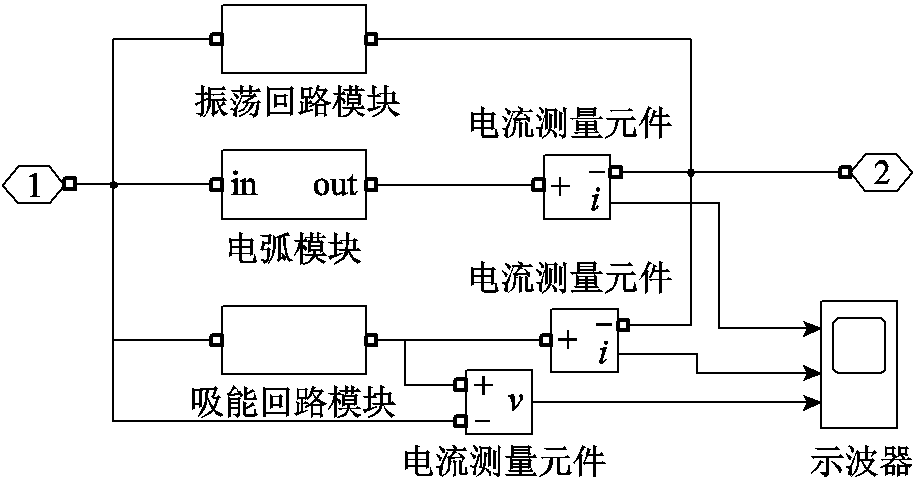
图7 换流站直流开关仿真模型
Fig.7 Simulation model of DC switch in converter station
（1）振荡回路采用如图3所示的含寄生参数的多电容组合改进模型，参数设置与2.2节保持一致。
（2）实际的吸能回路采用12支大避雷器并联组成，所用避雷器型号为MXE-T 1.59/58/8.77，即该单支避雷器最大吸收能量为 8.77×106 J，最大电压为58 kV，单支避雷器流过最大电流为1.59 kA。因此，仿真中采用12支并联的避雷器。
（3）对于电弧模块，以如图8a所示的Mayr电弧模型为例，以电弧电流i为控制量，输出电弧电压u，两者关系如式（5）所示。其中，τa=4.1×10-7 s、P=2.5×105 W。同理，根据Cassie电弧模型、Schwarz电弧模型基本原理，搭建相应的仿真模型分别如图8b和图8c所示。
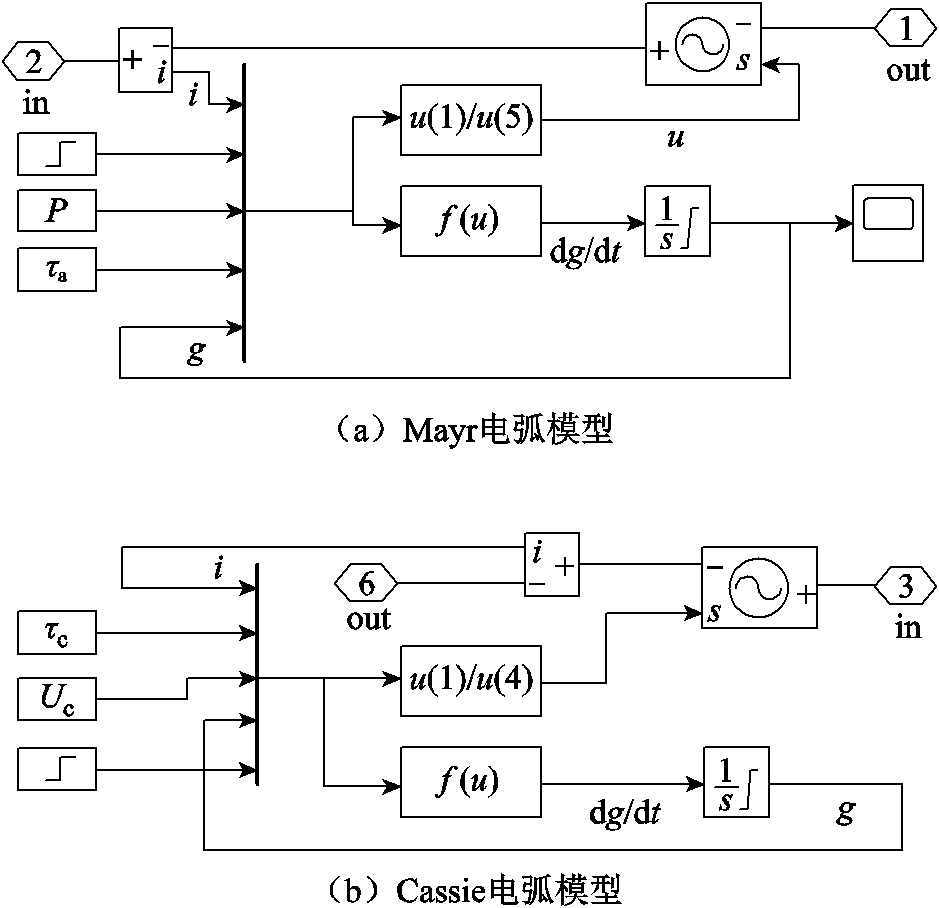
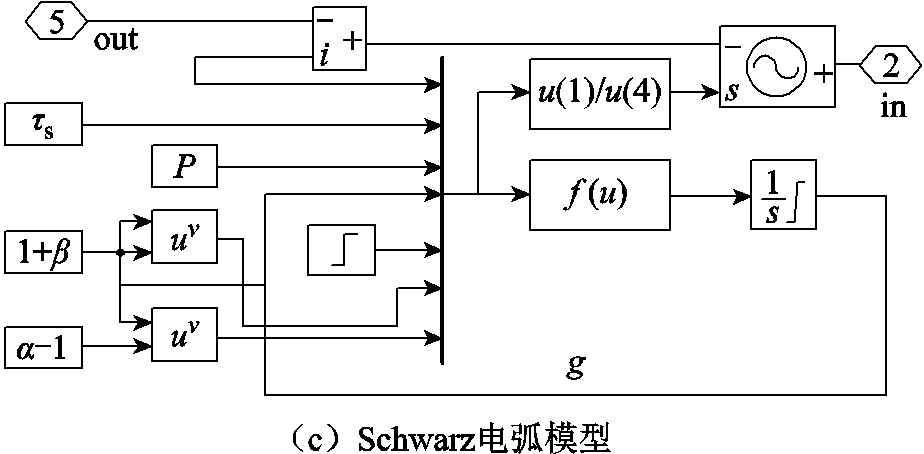
图8 电弧模型仿真接线
Fig.8 Arc model simulation wiring
保持振荡回路和吸能回路参数不变，依次使用三种电弧模型进行仿真，仿真结果如图9所示。
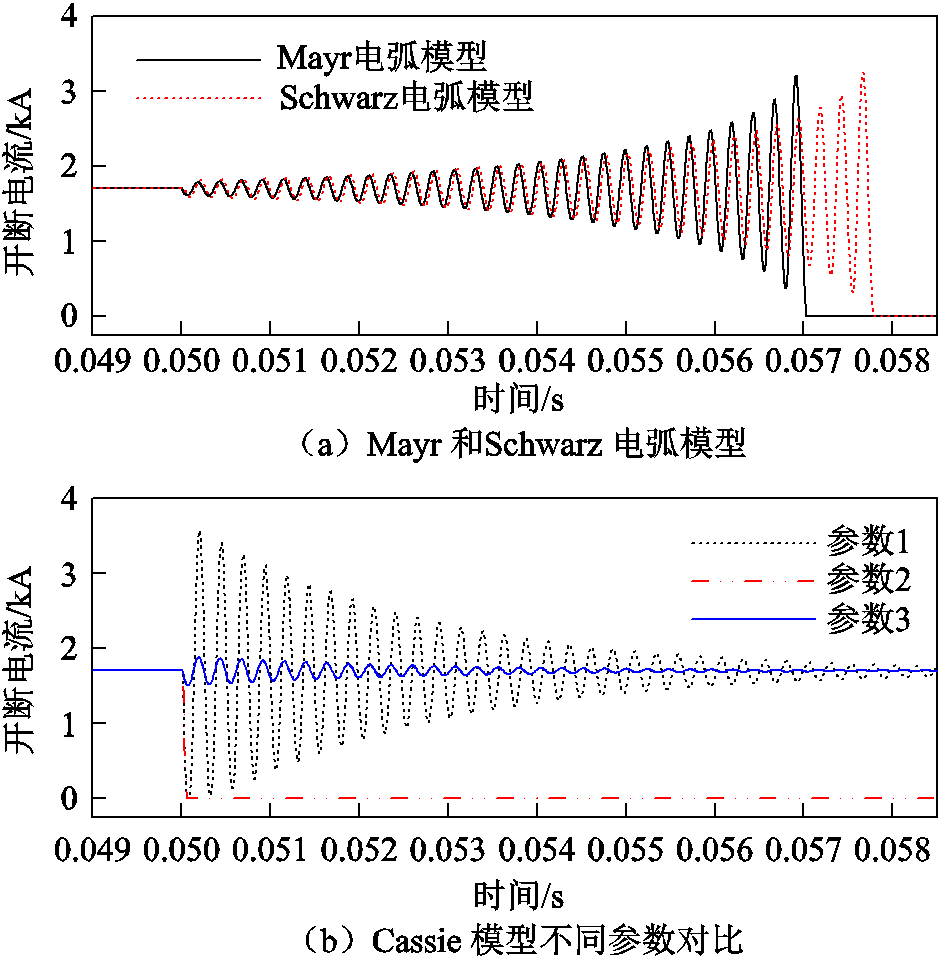
图9 不同电弧模型下电流开断仿真结果
Fig.9 Simulation results of current interruption under different arc models
Mayr模型适用于模拟高阻抗和低电流电弧，其在描述电流零区的电弧伏安特性方面比其他模型更准确，但它在描述大电流电弧方面有所欠缺。
Schwarz电弧模型是在Mayr模型的基础上改进的，其认为时间常数和耗散功率是电弧电导的函数，电弧电导和其他参数相互作用使电弧电气特性动态变化，能很好地反映本文所研究的关断电弧的动态特性，但所需参数更多。
而Cassie电弧模型适用于高电流和低电弧阻抗条件下的电弧特性，其在描述连续电弧阶段有很高的精度，然而对电流过零特性描述不足[12,21]。如图9所示，将Cassie模型用于直流开关关断仿真时无法出现电流零区。从数学模型层面分析，仿真电流波形趋势受到电弧模型的数学结构影响，其中化简后的Cassie模型为一个带有一次分式的微分方程，仿真得到电导g振荡幅值从大到小变化，不符合实际开断过程。
综上所述，Mayr电弧模型、Schwarz电弧模型比Cassie模型更适用于描述特高压直流开关开断时拉弧的过程，而Cassie模型更多用于电力系统故障时的电弧过程。本文采用准确性高、模型较为简单的Mayr电弧模型来模拟开断电弧，仿真结果如图10所示。
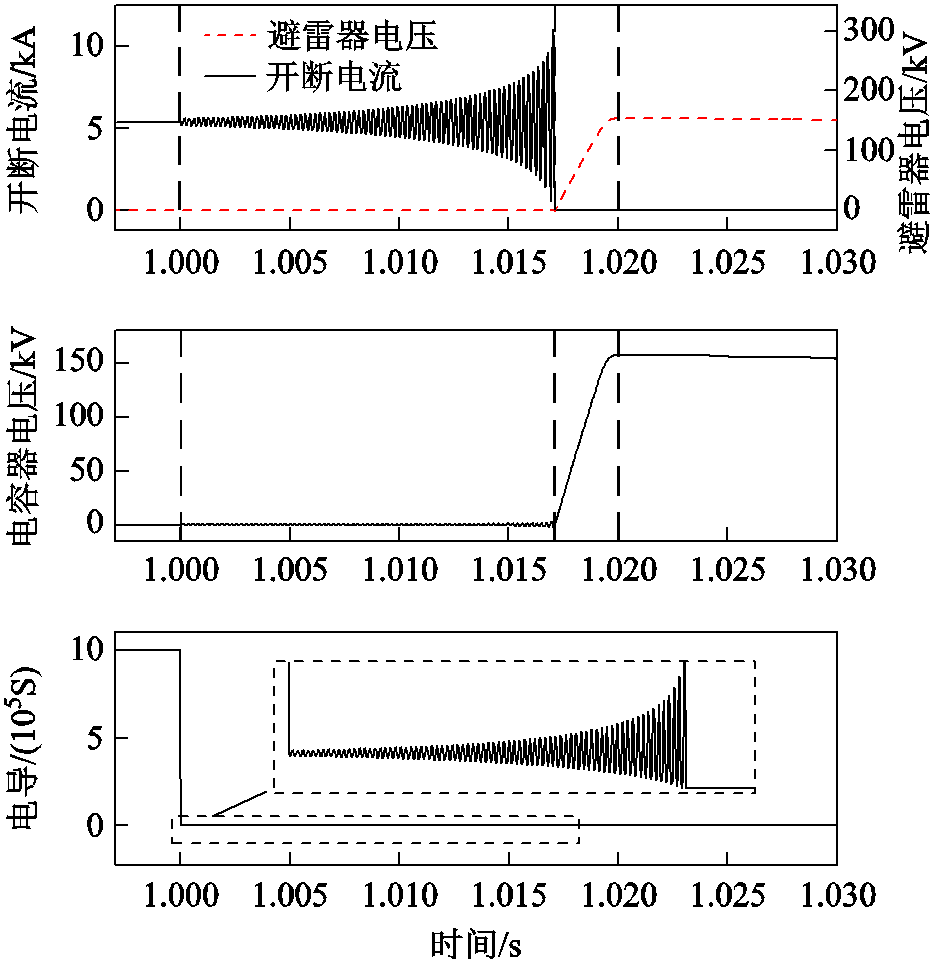
图10 特高压直流开关开断过程仿真结果
Fig.10 Simulation results of the breaking process
断路器从1 s时刻开始关断，关断过程包括电流强迫过零、断口介质恢复、避雷器工作吸能三个阶段。1～1.017 1 s为第一阶段，电弧与电容C之间产生一个往返的充放电过程，振荡交流电叠加在直流电上创造出电流过零点，电弧熄灭。
1.017 1～1.02 s为第二阶段，燃弧过程的能量转化为恢复电压加在电容C两端，当断路器触头间隙的介质恢复电压速度大于电弧的恢复电压速度，电弧才不会重燃。
1.02 s后为第三阶段，避雷器动作，吸收以及泄放回路中的巨大能量。
为了分析振荡回路参数变化对直流开关开断过程的影响，本节基于Mayr电弧模型，研究振荡回路参数处于临界条件这一极端情况下，参数发生变化产生的影响。其中，Rs、Ls 临界值分别为50 mΩ、80 μH，单个电容器的电容值为7.6 μF，随着电路状态变化，寄生参数的值会变化，本文改变部分寄生参数，依据仿真结果来观察寄生参数值的变化对直流转换开关的影响。
寄生参数改变前后开断回路电流波形如图11所示。使R3=R4=10 mΩ，结果如图11a所示，原参数开断时间为24.7 ms，改变后的开断时间变为25.2 ms。电阻R3和R4增大，振荡电流幅值减小，衰减更大，开断时间增加。由式（1）可知、振荡周期的值与电阻的值无关，电阻增大，阻碍电流增加，交流电幅值达到直流电幅值所需时间增大，开断时间变长。
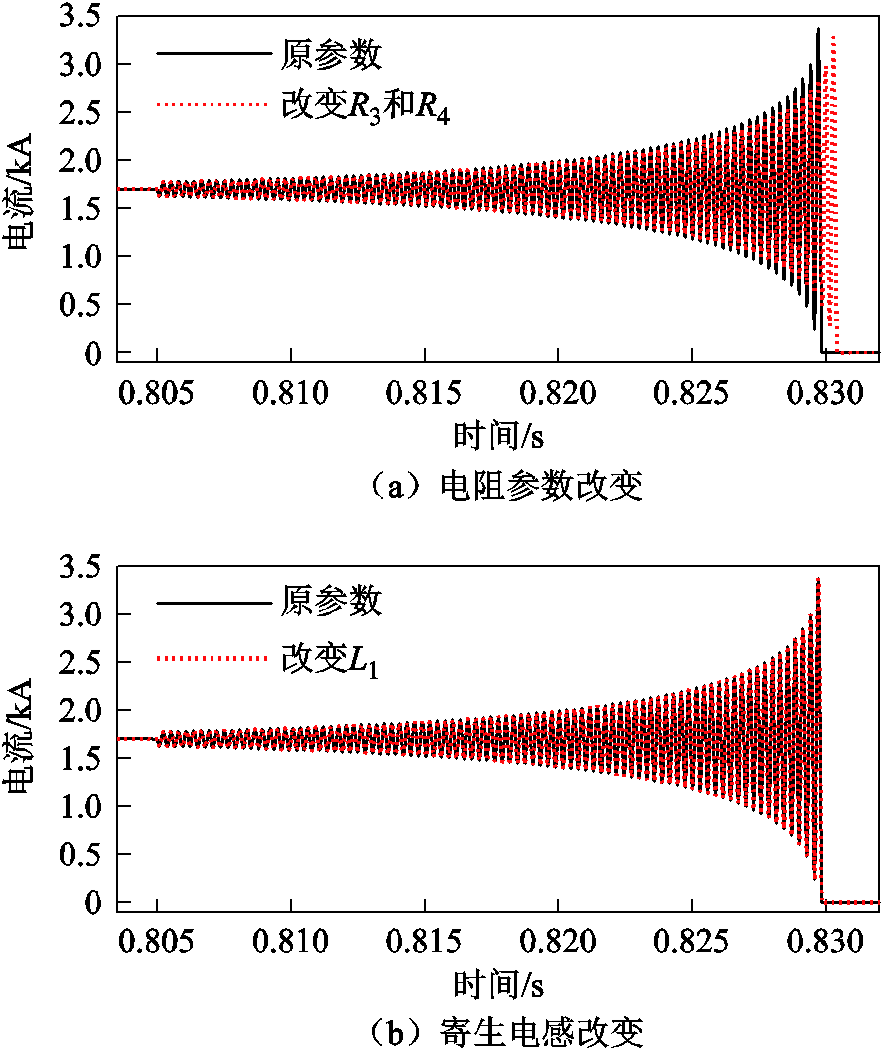
图11 寄生参数改变前后对比
Fig.11 Comparison before and after parameters change
此外，保证其他参数不变，仅将L1改为0.1 μH，开断波形如图11b所示。寄生电感值的改变相对于外部电感来说很小，所以开断波形的变化很小。在电容不变的情况下，电感增大时衰减系数变小，振荡周期变长，振荡频率变小，即电流变化速度变慢，因此振荡电流幅值增加到直流电幅值相同时需要更长的时间，灭弧所需时间就会增大。
采用短接部分电容的方式来模拟电容器的部分故障，以此来展示电容器在发生部分小电容故障时整个电容器发生的变化。分别短接C4、短接C4和C10、短接C4和C6，仿真得到如图12所示的电流波形。
短接电容C4所在支路后，开断时间变为23.8 ms，振荡电流的周期略微减小，衰减系数变小，振荡电流的幅值也变小。此时电容的值增大一倍，电感和电阻都大约减小1/2。
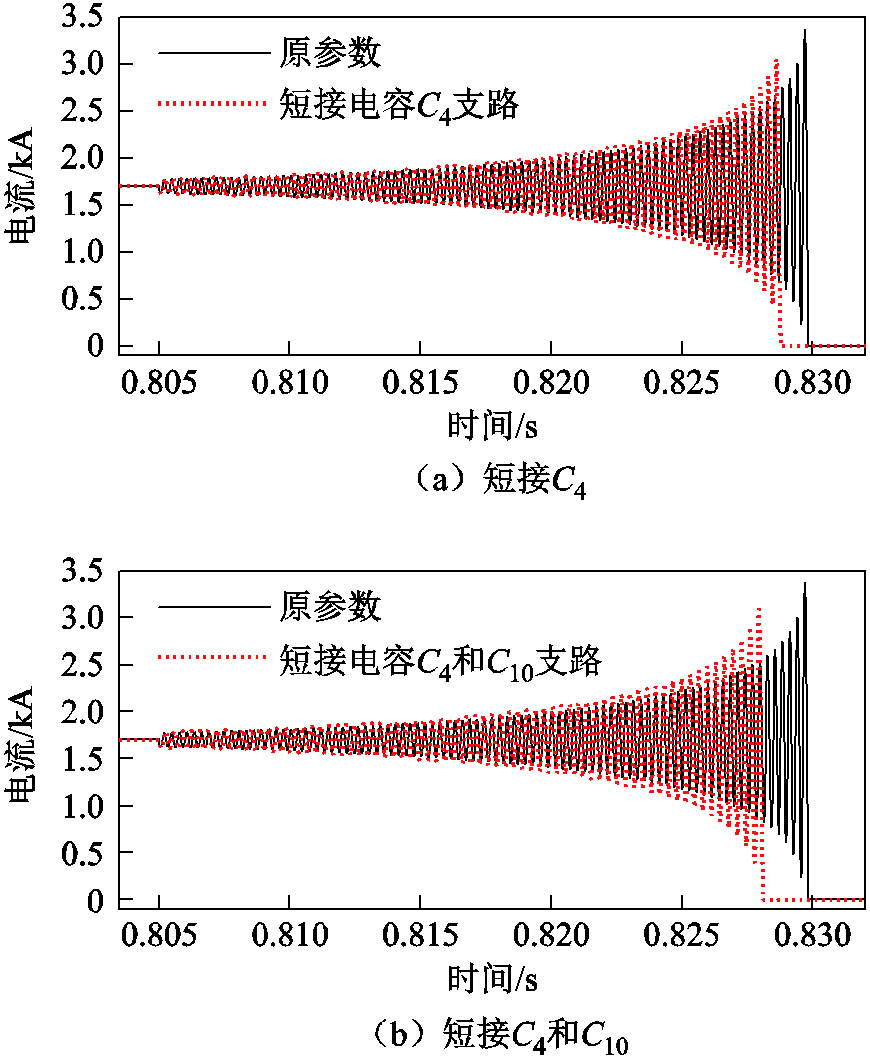
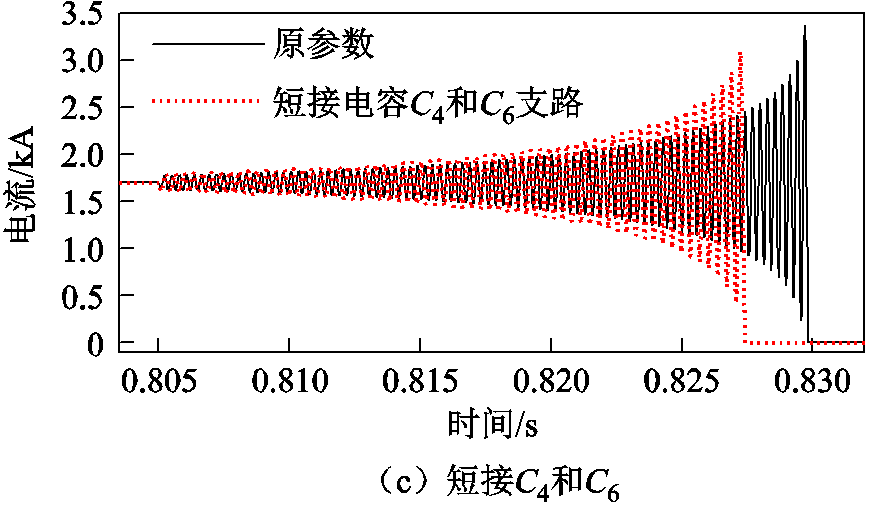
图12 短接前后开断回路电流波形
Fig.12 Circuit current waveforms before and after shorting
短路电容C4和C10后，阻抗值变小，灭弧时间为23.1 ms，振荡回路中电阻值变小、电容值变大、电感值变小，导致最后振荡幅值、衰减系数增大。
短接C4和C6两条电容支路，短路C6相当于将C5与C6一起短路，开断时间变为22.4 ms，相邻两个周期间的振荡周期差值明显。
短路不同的电容支路得到的开断时间及相对于原始开断时间的变化率见表4。对于单个电容支路来说，短路部分小电容，相当于使得组合电容的值变大，燃弧时间变短。另一方面，当被短路的电容支路旁有其他串联支路时，则通过该串联支路的电流幅值会增大到原来的数倍，电流增加的速率也会变快。
表4 短路情况下的开断时间
Tab.4 Breaking time in case of short circuit
短路对象开断时间/ms变化率(%) C423.8-3.643 7
（续）
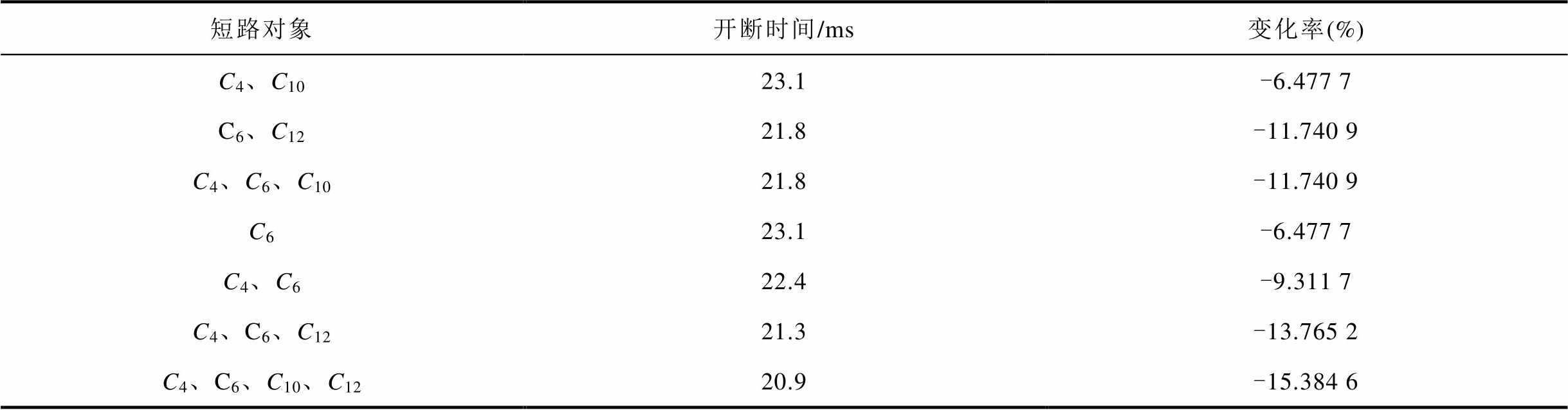
短路对象开断时间/ms变化率(%) C4、C1023.1-6.477 7 C6、C1221.8-11.740 9 C4、C6、C1021.8-11.740 9 C623.1-6.477 7 C4、C622.4-9.311 7 C4、C6、C1221.3-13.765 2 C4、C6、C10、C1220.9-15.384 6
本文依托实际直流输电工程，建立了含寄生参数的等效多电容组合的振荡回路改进模型，在考虑电弧特征的基础上，深入研究振荡回路参数对开断过程的影响机理，得到如下结论：
1）理论计算值、暂态仿真结果和振荡特性实验结果的误差较小，验证了含寄生参数的等效多电容组合改进模型的有效性。
2）直流开关的建模不能忽略电弧模型，应用Mayr电弧模型能真实、高效地模拟直流开关开断过程的电弧特性变化。
3）振荡回路参数对开断过程影响重大，过大的振荡回路电阻会延长燃弧时间，不利于开断；部分小电容故障虽然能缩短燃弧时间，但会加速电流变化率并增大数倍电流幅值，建议定期检修振荡回路，保证振荡参数处于合理值。
参考文献
[1] 李斌, 李鹏宇, 温伟杰, 等. 机械式直流断路器性能分析及谐振换流方法[J]. 电工技术学报, 2022, 37(9): 2139-2149. Li Bin, Li Pengyu, Wen Weijie, et al. Performance analysis and resonant commutation method of mechanical DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2139-2149.
[2] 陈龙龙, 魏晓光, 焦重庆, 等. 混合式高压直流断路器分断过程电磁瞬态建模和测试[J]. 电工技术学报, 2021, 36(24): 5261-5271. Chen Longlong, Wei Xiaoguang, Jiao Chongqing, et al. Electromagnetic transient modeling and test of hybrid DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5261-5271.
[3] Wen Weijie, Huang Yulong, Sun Yinshan, et al. Research on current commutation measures for hybrid DC circuit breakers[J]. IEEE Transactions on Power Delivery, 2016, 31(4): 1456-1463.
[4] 彭畅, 温家良, 马国华, 等. 特高压直流输电系统中直流转换开关的电流转换分析与仿真[J]. 中国电机工程学报, 2011, 31(36): 1-7, 236. Peng Chang, Wen Jialiang, Ma Guohua, et al. Analysis and simulation on current commutation of the DC transfer switches in UHVDC transmission systems[J]. Proceedings of the CSEE, 2011, 31(36): 1-7, 236.
[5] 李兴文, 郭泽, 傅明利, 等. 高压直流转换开关电流转换特性及其影响因素[J]. 高电压技术, 2018, 44(9): 2856-2864. Li Xingwen, Guo Ze, Fu Mingli, et al. Current commutation characteristics and its influential factors for high-voltage direct current transfer switches[J]. High Voltage Engineering, 2018, 44(9): 2856-2864.
[6] 吴宇. 三相变流器中直流母线电容的状态监测技术研究[D]. 重庆: 重庆大学, 2016.
[7] 李劲彬, 童歆, 张致, 等. 基于改进电容模型的直流开关振荡回路参数计算方法[J]. 智慧电力, 2019, 47(4): 87-92, 117. Li Jinbin, Tong Xin, Zhang Zhi, et al. Calculation method of DC switch oscillation loop parameters based on improved capacitance model[J]. Smart Power, 2019, 47(4): 87-92, 117.
[8] 刘俊峰, 高鹏举, 廖武兵, 等. 基于储能电容复用的超级电容阵列自均衡拓扑结构的分析[J]. 电工技术学报, 2021, 36(增刊1): 372-380. Liu Junfeng, Gao Pengju, Liao Wubing, et al. Analysis of voltage self-balancing topology of super-capacitor array based on reutilization of super-capacitors[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 372-380.
[9] 苑长富. 超级电容器串并联变换技术研究[D]. 大连: 大连理工大学, 2016.
[10] Amaral A M R, Marques C A J. A simple offline technique for evaluating the condition of aluminum–electrolytic–capacitors[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8): 3230-3237.
[11] 刘艳丽, 郭凤仪, 李磊, 等. 一种串联型故障电弧数学模型[J]. 电工技术学报, 2019, 34(14): 2901-2912. Liu Yanli, Guo Fengyi, Li Lei, et al. A kind of series fault arc mathematical model[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2901-2912.
[12] 钟逸涵, 邓丰, 史鸿飞, 等. 基于动态电阻串联的高阻接地故障精确建模[J/OL].电工技术学报, 2023，DOI:10.19595/j.cnki.1000-6753.tces.230065. Zhong Yihan, Feng Deng, Shi Hongfei, et al. Accurate modeling of high impedance fault based on dynamic impedance series connection[J/OL]. Transactions of China Electrotechnical Society, 2023, DOI:10.19595/ j.cnki.1000-6753.tces.230065.
[13] 贾博文, 武建文, 夏尚文, 等. 直流自然换流式接触器设计与均压开断研究[J]. 电工技术学报, 2021, 36(20): 4371-4378. Jia Bowen, Wu Jianwen, Xia Shangwen, et al. Design and uniform voltage breaking research of a DC natural current commutation contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(20): 4371-4378.
[14] Andrea J, Bournat M, Landfried R，et al. Model of an electric arc for circuit analysis[C]//28th International Conference on Electric Contacts (ICEC), Edinburgh, 2016: 361-366.
[15] 许晔, 郭谋发, 陈彬, 等. 配电网单相接地电弧建模及仿真分析研究[J]. 电力系统保护与控制, 2015, 43(7): 57-64. Xu Ye, Guo Moufa, Chen Bin, et al. Modeling and simulation analysis of arc in distribution network[J]. Power System Protection and Control, 2015, 43(7): 57-64.
[16] 姜斌峰, 王莉. 低压交流电线故障电弧模型研究[J]. 电力系统及其自动化学报, 2009, 21(4): 20-24. Jiang Binfeng, Wang Li. Research on arc model in AC low-voltage electrical wire fault[J]. Proceedings of the Chinese Society of Universities for Electric Power System and Its Automation, 2009, 21(4): 20-24.
[17] Li Shurong, Xue Yongduan, Feng Guang, et al. Simulation analysis of intermittent arc grounding fault applying with improved cybernetic arc model[J]. The Journal of Engineering, 2019(16): 3196-3201.
[18] 尚振球. 麦也尔电弧数学模型的表达形式及其参数的确定方法[J]. 高压电器, 1985, 21(6): 40-45. Shang Zhenqiu. Expressions of O.Mayr’s mathematical model of electrical arc and the determination of their parameters[J]. High Voltage Apparatus, 1985, 21(6): 40-45.
[19] Li Tian, Li Huawei. Simulation of electric arc characteristics based on MATLAB/simulink[J]. IOP Conference Series: Materials Science and Engineering, 2018, 452: 042080.
[20] 杨明波, 龙毅, 樊三军, 等. 基于组合Mayr和Cassie电弧模型的弧光接地故障仿真及分析[J]. 电测与仪表, 2019, 56(10): 8-13. Yang Mingbo, Long Yi, Fan Sanjun, et al. Simulation and analysis of arc grounding fault based on combined Mayr and Cassie arc models[J]. Electrical Measurement & Instrumentation, 2019, 56(10): 8-13.
[21] 李景丽, 袁豪, 徐铭铭, 等. 小电阻接地系统高阻接地故障检测技术综述[J]. 电测与仪表, 2023, 60(6): 10-18, 51. Li Jingli, Yuan Hao, Xu Mingming, et al. Overview of high impedance fault detection technology in small resistance grounding system[J]. Electrical Measurement & Instrumentation, 2023, 60(6): 10-18, 51.
[22] Khan U A, Lee J G, Amir F, et al. A novel model of HVDC hybrid-type superconducting circuit breaker and its performance analysis for limiting and breaking DC fault currents[J]. IEEE Transactions on Applied Superconductivity, 2015, 25(6): 1-9.
[23] 刘守豹, 侯玉成, 盛明珺, 等. 特高压直流换流站金属回线转换开关电磁暂态特性分析[J]. 电力自动化设备, 2021, 41(6): 220-226. Liu Shoubao, Hou Yucheng, Sheng Mingjun, et al. Analysis of electromagnetic transient characteristics of metallic return transfer breaker in UHVDC converter station[J]. Electric Power Automation Equipment, 2021, 41(6): 220-226.
[24] 孙舒捷, 邰能灵, 薄志谦. 高压直流输电工程中的直流断路器设计及应用仿真[J]. 华东电力, 2009, 37(3): 412-417. Sun Shujie, Tai Nengling, Bo Zhiqian. Design and simulation of DC breakers for HVDC projects[J]. East China Electric Power, 2009, 37(3): 412-417.
Abstract The DC transfer switch is an essential piece of equipment in ultra-high voltage DC transmission projects. It is mainly used to increase the flexibility of transmission operations and to protect and remove faults. The DC transfer switch is composed of three parts: the breaking circuit, energy absorption circuit, and oscillation circuit. The oscillation circuit creates a “zero-crossing point” by providing oscillation current during the DC switch breaking process. The oscillation process plays a decisive role in the successful breaking or not. Therefore, it is urgent to study the influence of oscillation circuit parameters on the breaking. The parameters of capacitors in the oscillation circuit are affected by manufacturing, transportation, use, and other processes, which may result in initial type faults, occasional faults, overload operation faults, and aging operation faults. A fault can cause a change in the capacitance value, which may cause the DC switch to fail to open. The existing research has not yet considered the parasitic parameters of the oscillation circuit based on the arc characteristics of the breaking circuit, which has limitations such as parameter mismatch and low accuracy. Moreover, there is limited research on various arc models applicable to DC conversion switches.
This article first analyzes in detail the principles and characteristics of various arc models. Then, based on the parameters of a certain ultra-high voltage DC transmission system, an improved model with equivalent multi-capacitor combination and parasitic parameters is constructed to improve the accuracy of the oscillating circuit model. Next, simulation research on the improved oscillating circuit model is carried out based on the Simulink simulation platform, and the characteristics of the oscillating circuit itself are also experimentally studied on site. The theoretical calculation results, simulation results and experimental results are compared and analyzed to verify the correctness of the model. Subsequently, the equivalent arc model of the breaking circuit is theoretically studied, and the working results of the DC switch under different arc models are compared by simulation. Finally, in order to simulate possible situations on site, the influence mechanism of oscillating circuit parameters on the breaking process is further studied in depth under normal and fault conditions. and the following conclusions were drawn:
(1) The error between theoretical calculation values, transient simulation results, and oscillation characteristics experimental results is relatively small, which verifies the effectiveness of the improved model of equivalent multi capacitor combination with parasitic parameters.
(2) The modeling of DC switches cannot ignore the arc model, and the application of the Mayr arc model can accurately and efficiently simulate the changes in arc characteristics during the breaking process of DC switches.
(3) The parameters of the oscillation circuit have a significant impact on the breaking process, and excessive oscillation circuit resistance will prolong the arcing time, which is not conducive to breaking; Although some small capacitor faults can shorten the arcing time, they will accelerate the current change rate and increase the current amplitude several times. It is recommended to regularly inspect the oscillation circuit to ensure that the oscillation parameters are at a reasonable value.
keywords：Arc model, DC switch, oscillation circuit, capacitance
DOI:10.19595/j.cnki.1000-6753.tces.L10058
中图分类号：TM561.6
湖北省自然科学基金杰出青年基金（2020CFA098）和国家自然科学基金（52207182）资助项目。
收稿日期 2023-01-13
改稿日期 2023-03-31
于 雷 男，1976年生，高级工程师，研究方向为直流一次设备运检技术。E-mail：yul2@hb.sgcc.com.cn
王伊帆 女，2001年生，硕士研究生，研究方向为高压直流输电。E-mail：supingfang@whu.edu.cn（通信作者）
（编辑 崔文静）