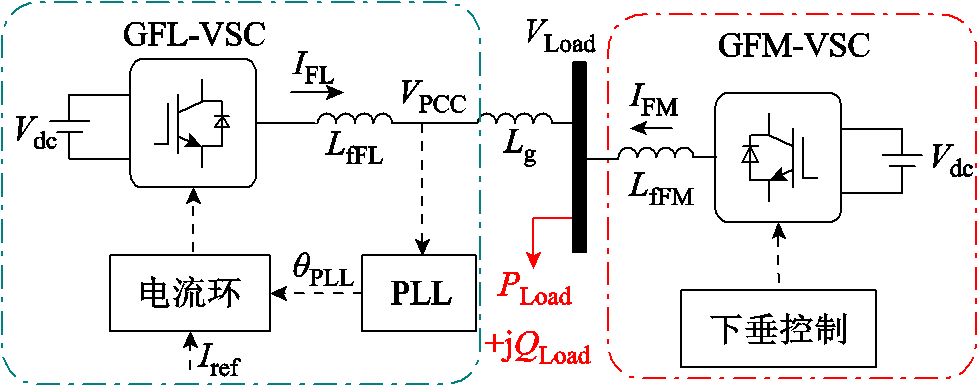
图1 孤岛微电网系统结构示意图
Fig.1 Schematic diagram of islanded microgrid system
摘要 以电力电子变流器为主导的微电网作为一种灵活、可靠的分布式能源消纳和集成方式,近年来越来越受到关注。由于缺少电网稳定的电压和频率支撑,孤岛微电网在故障扰动下易出现暂态失稳现象。考虑锁相环受扰瞬间的被动频率突变和下垂控制器无功环影响,该文建立了由构网型和跟网型逆变器共同组成的孤岛微电网的改进暂态模型,改善了暂态模型精度。在此基础上,构建了一种二次型Lyapunov函数,用于孤岛微电网的暂态稳定性分析。通过待定系数,减小了非耗散区的影响,从而改善了传统Lyapunov方法的保守性。利用Lyapunov稳定判据,对不同形式扰动下的功角稳定边界进行了估计,分析了孤岛微电网对不同形式扰动的敏感度,揭示了系统参数对暂态稳定性的影响。最后,利用Matlab/Simulink仿真和基于RT-Lab的硬件在环实验对该文所提方法进行了验证。
关键词:并网逆变器 孤岛微电网 同步稳定性 频率突变 Lyapunov稳定判据
随着分布式可再生能源发电的快速发展,大型电力电子设备集成到现代电力系统中,构建了电力电子化电力系统[1-3]。与基于同步发电机的常规电力系统相比,高渗透率的电力电子设备具有高效率、灵活运行和快速响应等优势,但其低惯量非线性的特性也使得新型电力系统的稳定运行面临较大的挑战。变流器主导的微电网作为一种有效可靠的分布式能源集成和消耗模式,其稳定性研究近年来得到了较为广泛的关注。交流微电网可以在并网模式或孤岛模式两种模式下运行,两者都可实现功率平衡和稳定运行。孤岛模式下,交流微电网失去来自强电网的频率支撑和电压支撑,成为一个容易在大扰动干扰下失去稳定性的自治系统[4]。
常见的并网变流器,根据控制策略不同,可大致分为两类:①动态类似电压源的构网型变流器(Grid-Forming-Voltage Source Converter, GFM-VSC)。常见的构网控制策略如虚拟振荡器控制、下垂控制和虚拟同步电机等[3-5],其输出电压幅值与频率由控制器直接控制,输出电流则受系统中其他变流器的钳位。构网控制策略通过模拟传统电网中的同步电机外特性,为系统提供频率和电压支撑,在稳定性支持和频率响应方面表现出卓越的性能优势。②动态类似电流源的跟网型变流器(Grid-Following-Voltage Source Converter, GFL-VSC)。输出电流相位和幅值由锁相环(Phase-Locked-Loop, PLL)和电流控制器级联控制。与GFM-VSC相比,GFL-VSC的响应快,但因为没有惯量与电压支撑能力,其面对大扰动时易失稳。综上所述,GFL-VSC和GFM-VSC各有优缺点,二者在孤岛微电网系统中互相配合,互相补足。
变流器主导电力系统的稳定性得到了广泛的研究。文献[6]基于阻抗法研究了并网逆变器与电网阻抗交互失稳机理及阻尼策略。然而小信号分析方法只能分析系统受小扰动时的稳定性,无法分析大扰动暂态过程中的系统稳定性。文献[7]使用一种改进等面积法则分析了变流器系统的暂态稳定性,有效地定量分析了负阻尼对系统稳定性的不利影响。文献[8]创新性地使用端口Hamilton原理,分析了逆变器并网系统的暂态稳定性。并网逆变器系统暂态稳定性的分析难点主要在于如何处理摆动方程中的可变阻尼项对系统稳定性的不利影响。不同于同步发电机(Synchronous Generator, SG)的常数阻尼项,逆变器主导系统的功角摆动方程中,阻尼项是随着系统功角变化而变化的,且在功角较大时(如大于90°)将会表现出负阻尼特性。此时如果再忽略阻尼项对系统稳定性的影响,则会发生稳定性误判[2]。考虑阻尼的常规Lyapunov法面临着保守性过大的问题需要解决[9]。文献[10]提出了一种迭代等面积法,通过对频率分布函数和阻尼做功的迭代计算,得到了一个保守性极佳的单机并网系统稳定判据,但文献[10]的高精确性是以较大的计算量为代价的。文献[11]通过一种参量化Lyapunov方法,实现了对考虑无功环影响的VSG并网系统的暂态稳定估计。文献[12]基于虚拟功角对下垂控制逆变器进行稳定性分析,并指出不考虑电压环动态的虚拟功角比真实功角更具有稳定性分析意义。文献[13]分析了GFL-VSC并联低惯量网络系统的稳定性,独创性地提出加速失稳和减速失稳两种不同的失稳机理,深入阐述了GFL-VSC与低惯量网络交互机理,但其所建模型的精度(采用恒阻抗模型且忽略阻尼)有待提高。文献[14-15]采用等面积法分析了GFL-VSC并联系统暂态失稳机理,却因为无法处理不可积分交互项而不能给出暂态稳定域的精确量化估计。
现有的稳定性分析大多是对单一控制类型变流器系统展开的,有关多类型并网逆变器交互的稳定性研究仍较少。针对考虑GFL-VSC与GFM-VSC交互影响的孤岛微电网系统,文献[16]推导了其线性化数学模型,并运用特征值分析方法分析了二者功率渗透率对孤岛微电网系统稳定性的影响规律。虽然孤岛微电网线路电感值较低,但因为其电压等级低,同样容易发生暂态失稳。同时,GFM-VSC中广泛采用的基于虚拟阻抗[17-18]的暂态限流策略也会进一步恶化孤岛微电网系统的稳定性,因此孤岛微电网暂态稳定性研究具有较强的工程应用意义。文献[19]推导了上述系统的非线性模型,但只做了一定的定性分析。文献[20]进一步将直流电压环和无功环影响纳入考虑,但同样未给出稳定性量化判据,只依据时域数值积分法进行了一定的定性分析。文献[2]针对上述孤岛微电网系统,采用等面积法给出了其正阻尼区域内的稳定域子集,保守性较大,且未考虑无功环和无功负载对系统稳定性的影响。现有的含锁相环的变流器并网系统暂态稳定性研究大多数是基于类似文献[21]中提出的二阶摆动数学模型。但仿真结果表明,该模型与实际电路模型相比仍有较大的误差,主要表现在时延和超调量上。这是因为该模型忽略了受扰后瞬间,公共连接点(Point of Common Coupling, PCC)处电压突变所带来的频率突变,其产生是锁相环PI控制器中的比例控制环节所致。频率突变量相当于增加了系统受扰后瞬间的初始能量,如果忽略这部分增加的初始能量无疑会造成稳定性的误判。本文的主要创新点如下:
1)指出了一种广泛存在于锁相环中的频率突变效应,推导了一个考虑频率突变效应的统一公式。
2)提出一种基于Lyapunov第二法的孤岛微电网暂态稳定域估计方法,通过待定系数,极大地改善了现有方法在保守性和无法分析无功环等方面的不足[2,9]。
3)指出由于频率突变效应,孤岛微电网系统面对不同扰动形式时的敏感度不同。
4)基于所提出的稳定性分析方法,研究了不同参数对孤岛微电网系统暂态稳定性的影响。
变流器主导的孤岛微电网如图1所示,由一个GFM-VSC和GFL-VSC通过线路电感Lg和各自的滤波电感LfFM和LfFL并联,同时对恒功率负载PLoad+jQLoad供能。该模型是实际孤岛微电网中多台GFM-VSC和GFL-VSC经过同调等值后的等值模型[22-23]。本文主要探究GFM-VSC和GFL-VSC间的交互作用对系统暂态稳定性的影响,故而分析如图1所示的简化系统。图中,Vdc为直流电压。GFM-VSC和GFL-VSC的输出电压电流分别定义为VFM、IFM、VFL和IFL。GFM-VSC采用下垂控制策略,控制示意图如图2a所示。功率计算器由输入的电压电流量计算得到GFM-VSC的输出有功功率PFM和无功功率QFM,并作为下垂控制器的输入量。有功无功下垂系数分别为mp和nq;Vn和ωn分别为额定电压和额定角频率;θFM、ωFM和VFM分别为下垂控制器输出电压的相位、频率和幅值。GFL-VSC的控制部分主要包括PLL和电流环。PLL通过追踪公共端点PCC处三相电压VPCC的相位,实现与系统的同步。PLL结构如图2b所示,包含Park坐标变换/反变换器和一个比例积分(Proportional Integra, PI)控制器。VPCCq表示VPCC的q轴分量,Kp和Ki分别为锁相环PI控制器的比例系数和积分系数,θPLL和ωPLL分别为锁相环输出相位和相应的角频率,其也是GFL-VSC的d轴输出电流的相位和频率。电流环控制策略如图2b所示,dq轴电流参考值分别为Irefd和Irefq。

图1 孤岛微电网系统结构示意图
Fig.1 Schematic diagram of islanded microgrid system
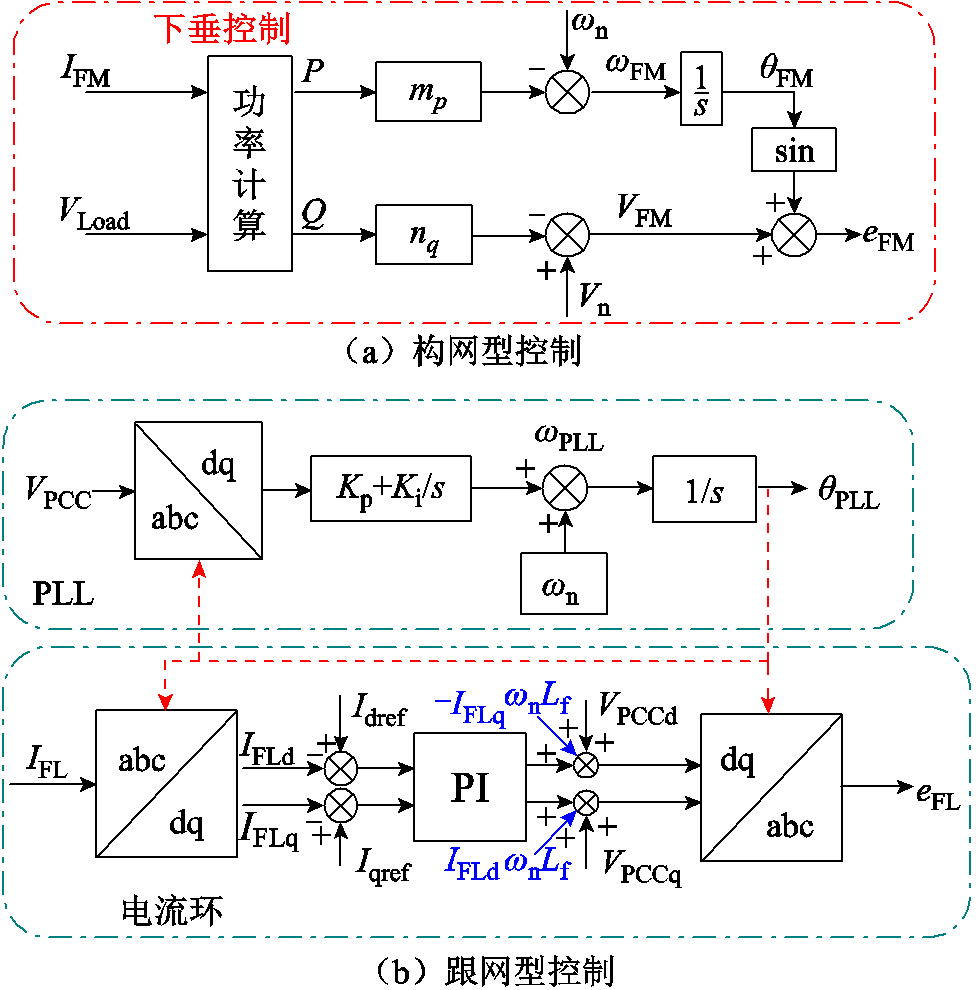
图2 控制示意图
Fig.2 Controller block diagram
由于电流环动态远快于锁相环动态。较快的电流环动态对系统稳定性分析的影响较小,故而可以认为GFL-VSC输出的dq轴电流IFLd和IFLq 恒等于电流环的参考值Irefd 和Irefq,即
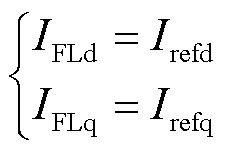 (1)
(1)
由基尔霍夫电压定律可知VPCC表达式为
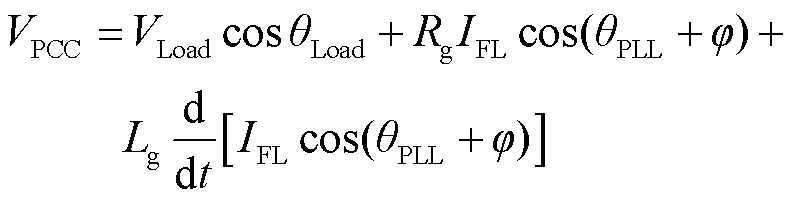 (2)
(2)
式中,VLoad和θLoad分别为负载处电压幅值与相位;φ为GFL-VSC的功率因数角,表示为
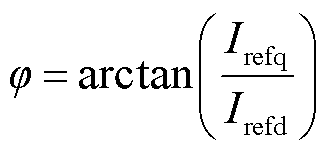 (3)
(3)
当GFL-VSC运行在单位功率因数下时,φ=0。对式(2)两端进行Park变换并取q轴分量,忽略交流网络快动态可得
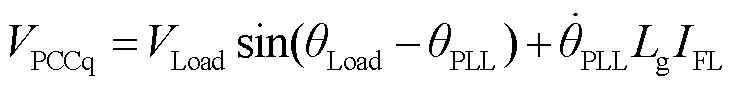 (4)
(4)
由图2b可知,锁相环动态可表示为
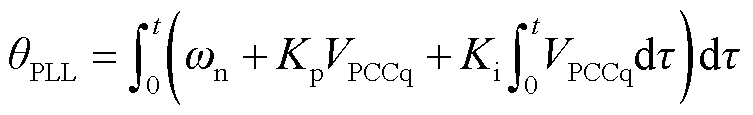 (5)
(5)
定义锁相环输出相位与负载处的相位差δ=θPLL-θLoad为孤岛微电网系统的虚拟功角,联立式(4)和式(5)可得
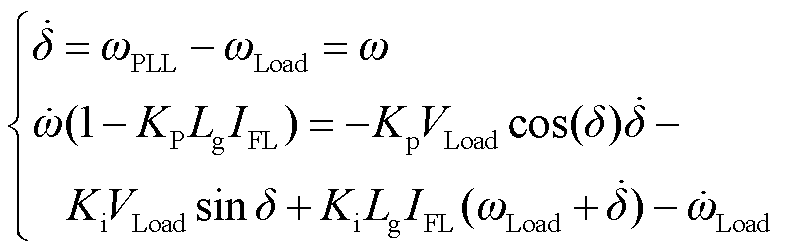 (6)
(6)
式中,ω为δ对时间t的导数。定义GFL-VSC输出的有功功率和无功功率分别为PFL和QFL,线路电感上消耗的有功功率和无功功率分别为PLg和QLg,有
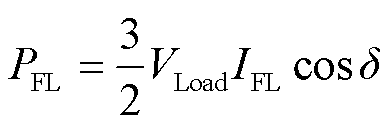 (7)
(7)
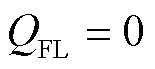 (8)
(8)
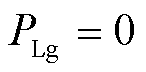 (9)
(9)
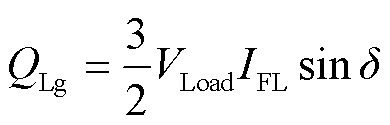 (10)
(10)
GFM-VSC处有功功率PFM和无功功率QFM可分别表示为
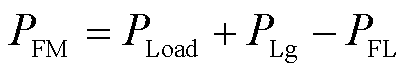 (11)
(11)
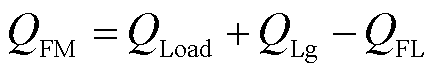 (12)
(12)
则下垂控制的输出频率ωFM为
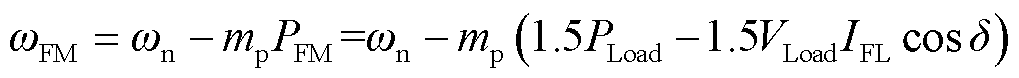 (13)
(13)
考虑到LfFM较小,因此可以近似认为
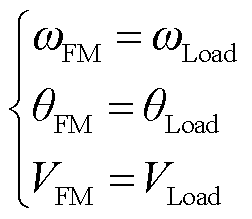 (14)
(14)
由图2a所示的GFM-VSC的无功下垂环的控制示意图,可推导出GFM-VSC的输出电压VFM为
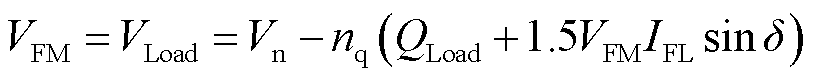 (15)
(15)
进一步推导可得VFM关于功角δ的代数分布函数为
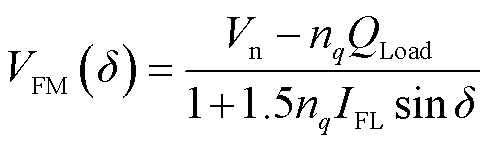 (16)
(16)
联立式(6)、式(13)~式(16)可得图1所示的孤岛微电网系统的传统二阶简化数学模型为
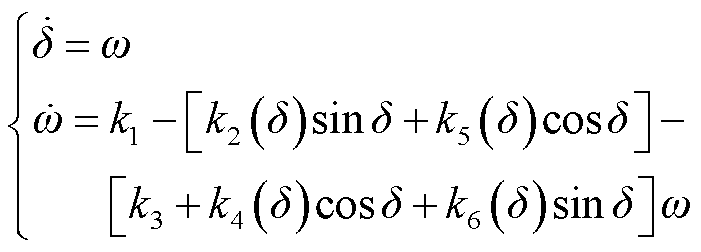 (17)
(17)
式中,ki为与系统参数相关的变量。
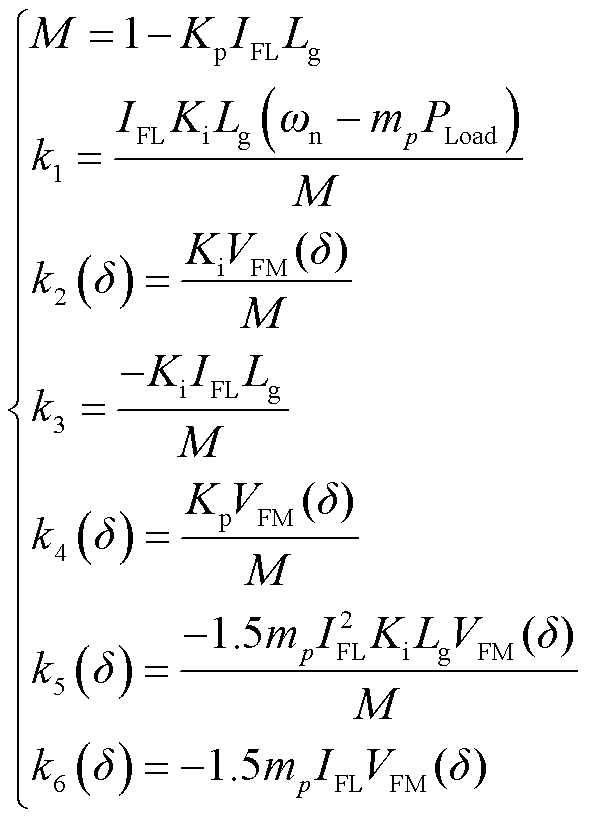 (18)
(18)
式(17)即为考虑无功环影响下的孤岛微电网系统二阶传统模型,式(18)中含VFM的系数是功角δ的函数。然而图3所示的大扰动下的仿真结果表明,式(17)与实际电路模型相比误差较大:①式(17)的时域响应相比电路模型超调量偏小;②相比电路模型,数学模型式(17)的响应波形有明显的时间上的延迟。
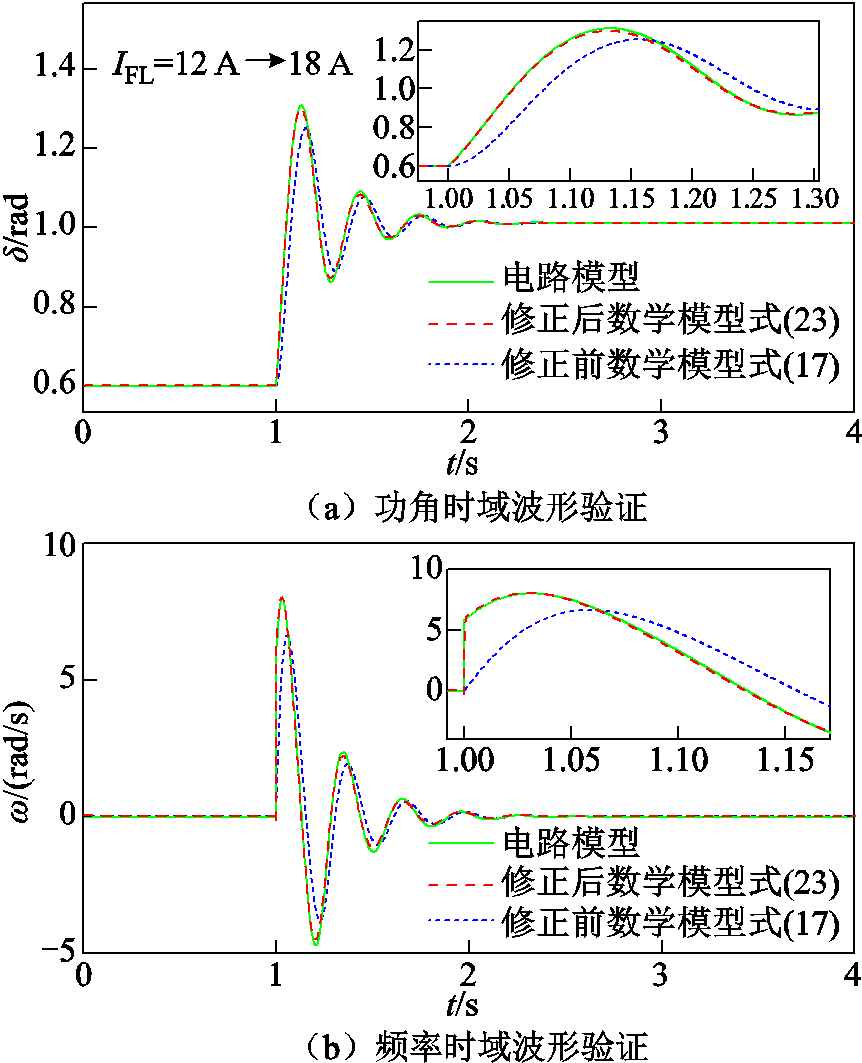
图3 大信号扰动下模型比较
Fig.3 Models comparison under large-signal disturbance
传统建模过程中,认为锁相环频率与同步发电机一样是连续变化的,故而直接对式(5)求二阶导数,从而得到式(6)。式(17)中ω的导数是有界函数,即认为频率是连续变化的。同步发电机中,由于其转子的惯性效应,转子角速度的确不能突变。然而对于基于PLL的跟网型变流器,由于PLL中的比例控制器的存在,PLL输出频率ωPLL的变化始终与VPCCq的变化成正比。在系统受大扰动瞬间,譬如线路三相短路接地、电压暂降等情况时,PCC处电压会产生突变。当VPCCq发生突变时,锁相环输出频率突变量ΔωPLL为
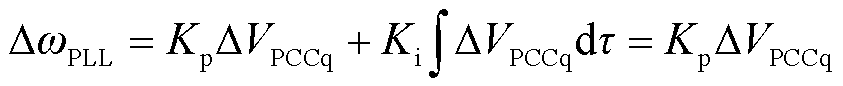 (19)
(19)
本文中所有出现的Δ(•)均表示大扰动情况下的系统参数和状态变量的突变量,而非小信号分析中线性化过程的微增量,这里需要区分。
PLL没有物理意义上的惯量存在,其加减速运动并不像同步电机转子一样受牛顿第二定律制约。大扰动瞬间的频率突变量ΔωPLL相当于增加了一部分初始动能。如果忽略频率突变量ΔωPLL,认为系统受扰后瞬间初始动能为零,无疑会导致稳定性误判。
综上所述,考虑受扰后瞬间的频率突变量ΔωPLL不仅可以提高模型精度,更重要的是防止出现稳定性误判。下面推导系统角频率Δω的表达式为
 (20)
(20)
其中
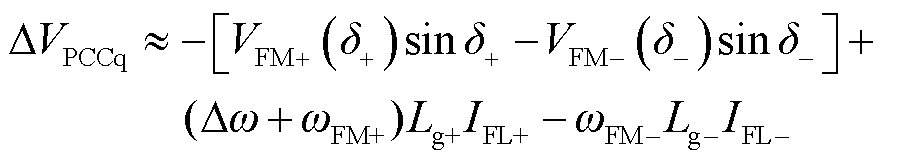 (21)
(21)
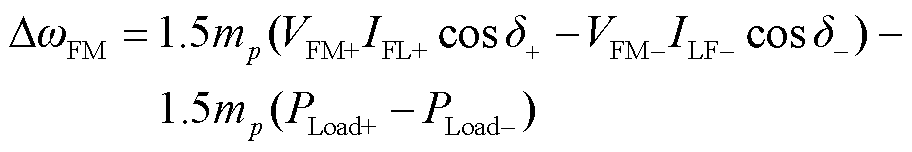 (22)
(22)
下角标“+”和“-”分别代表系统扰动后和扰动前的参数。将式(20)~式(22)代入式(17),即可得到修正后的孤岛微电网系统的二阶简化数学模型为
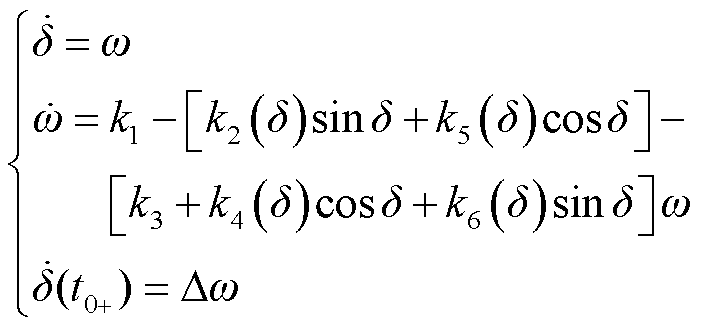 (23)
(23)
式中,t0+为系统受扰时刻。如图3给出了修正后模型式(23)受大扰动下的暂态时域波形与电路模型的对比,功角峰值误差率由8.23%降至1.41%,频率误差则由25%降至0.625%。
因为系统频率ω在受大扰动后瞬间会产生突变,再使用ω作为系统动能构造Lyapunov函数会导致受扰瞬间的能量函数突变。因此考虑基于二次型原理[24],重新构造如式(24)所示的Lyapunov备选函数。
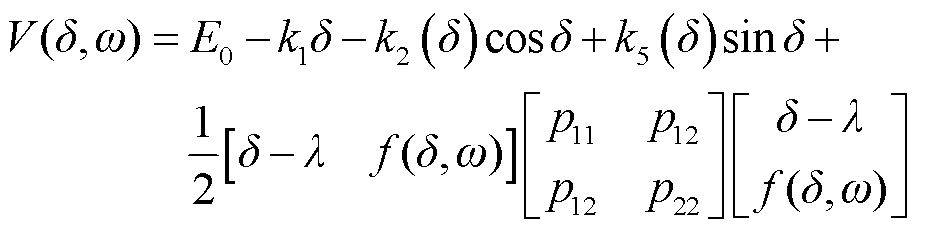 (24)
(24)
式中,E0为系统能量基准值;f(δ, ω)为PLL中积分控制器的输出,其在受扰瞬间不会突变,表达式为
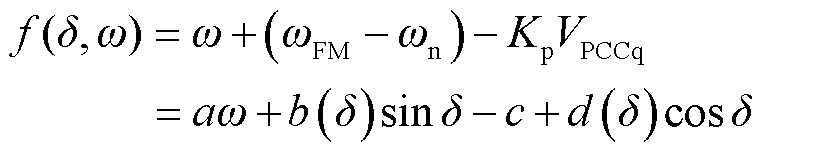 (25)
(25)
其中
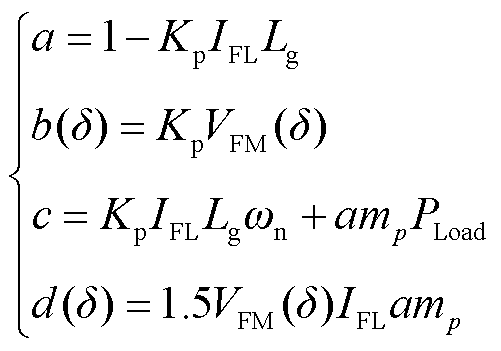 (26)
(26)
式(24)中,λ、p11、p12和p22为待定的系数。为保证V(x)的正定性,应满足p11>0, p11p22≥p12p12。如果直接视电压VFM为状态变量,则式(24)的耗散性难以保证[11]。文献[11]创新性地提出了基于电压参量化的Lyapunov分析方法,并给出了详细的证明过程。针对式(24),在每个不同的功角δi处,计算其电压VFM(δi)。基于式(34)~式(36)计算该点对应的临界点δimax以及相对应的临界能量Vicr。在每个不同δi处,只要系统能量V(δi,ω)不超过该处对应的临界能量Vicr,则可判定系统暂态稳定[11]。因为视电压VFM为参数,所以所有因VFM而与δ间接相关的系数均不参与V(δ,ω)求导。结合运用式(27)所示的恒等式消去恒零项,可得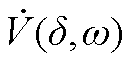 的表达式如式(28)所示。
的表达式如式(28)所示。
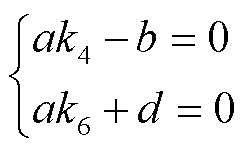 (27)
(27)
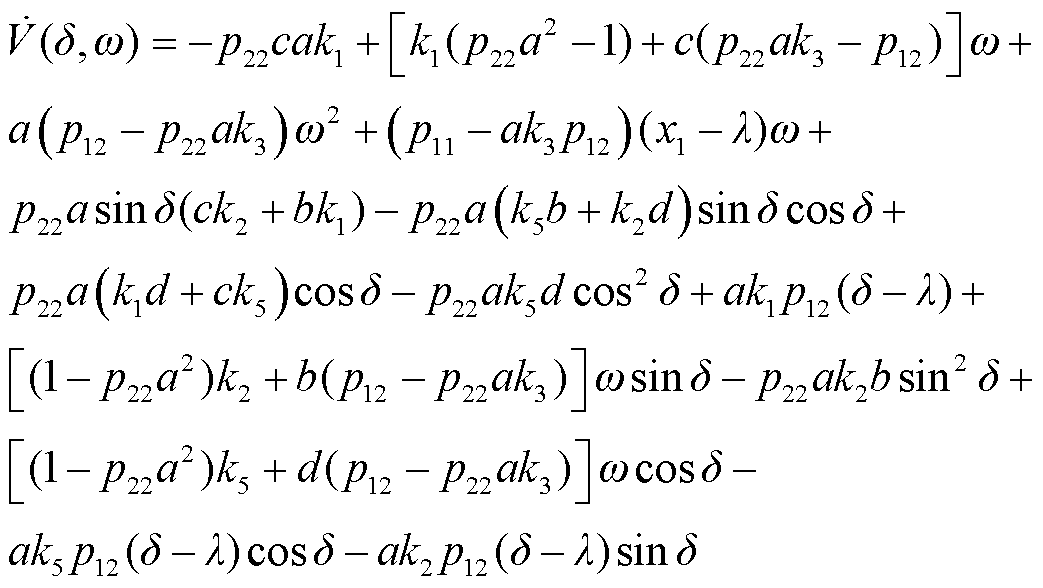 (28)
(28)
为消去频率相关项,可令
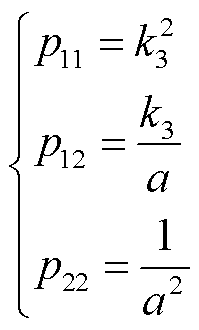 (29)
(29)
将式(29)代入式(28),可进一步化简得
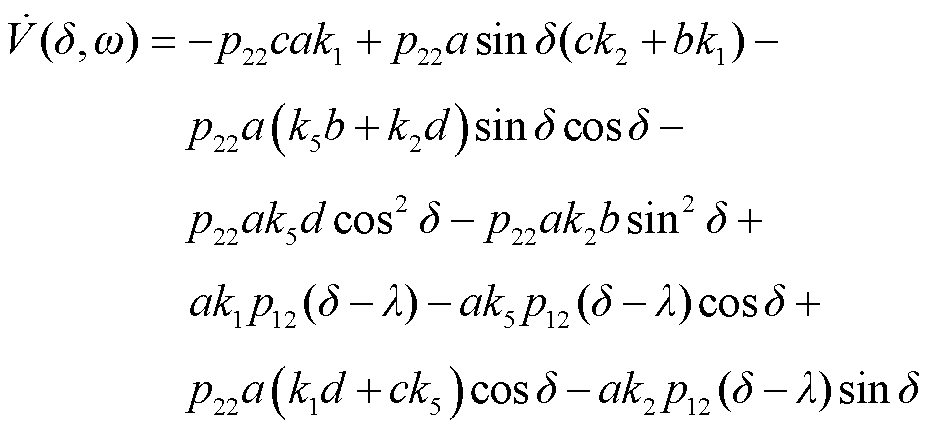 (30)
(30)
则
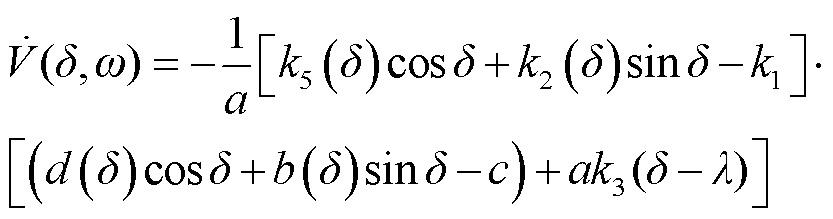 (31)
(31)
取λ为
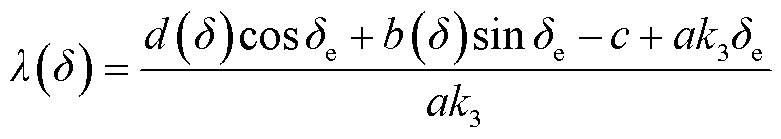 (32)
(32)
分别定义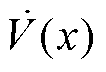 中的两个多项式为f1(δ)和f2(δ),有
中的两个多项式为f1(δ)和f2(δ),有
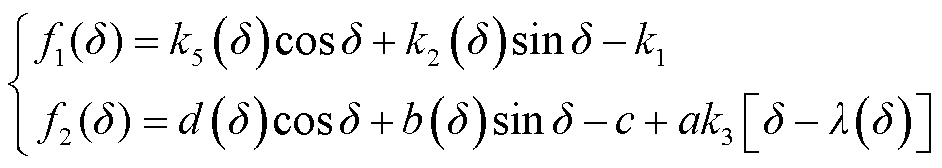 (33)
(33)
f1(δ)和f2(δ)的正负直接决定了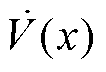 的正负性。当且仅当二者同号时,系统满足
的正负性。当且仅当二者同号时,系统满足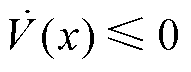 (即系统耗散)。λ按式(32)取值的目的就是为了保证f2(δe)=0,从而保证平衡点δe周边的耗散区域存在。
(即系统耗散)。λ按式(32)取值的目的就是为了保证f2(δe)=0,从而保证平衡点δe周边的耗散区域存在。
针对δi,其对应的临界点δimax满足
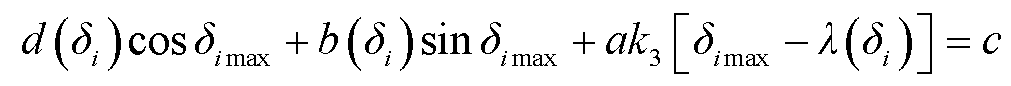 (34)
(34)
则此时δimax相对应的临界能量Vicr为
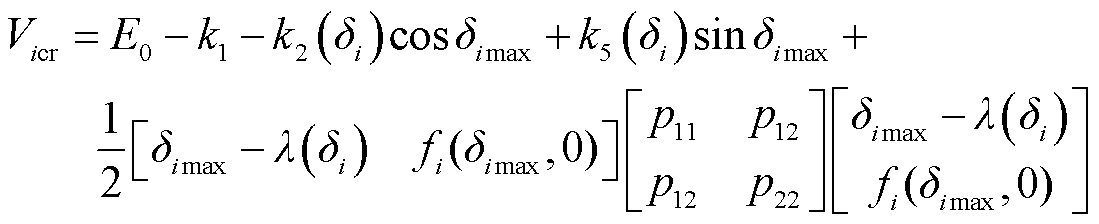 (35)
(35)
其中
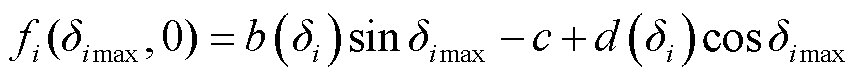 (36)
(36)
由局部LaSalle不变定理可知,系统式(23)在受扰后如果能渐近稳定,则需满足
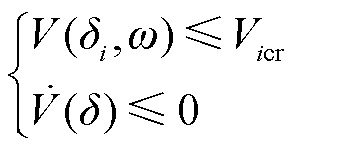 (37)
(37)
非耗散区示意图如图4所示。由图4可见,式(32)使得本文提出的Lyapunov函数V(x)的非耗散区(红色阴影部分),相比于传统Lyapunov函数的非耗散区(负阻尼区,即蓝色阴影部分)[9],减小了许多。其中δmax是系统式(23)整体的功角稳定最大边界,其满足δmax=δimax=δi。
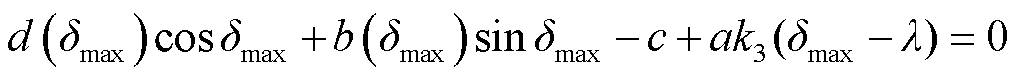 (38)
(38)
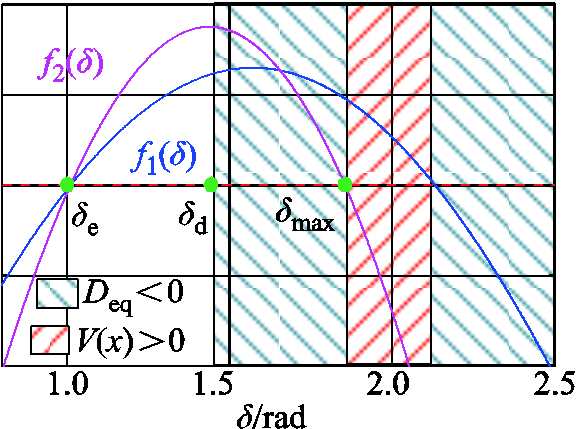
图4 非耗散区示意图
Fig.4 Schematic diagram of the non-dissipative area
传统Lyapunov法的稳定域功角右边界被认为在阻尼过零点(即δd=1.436 1 rad),而本文提出的Lyapunov法的稳定域功角右边界则在δmax=1.827 3 rad。下面给出δmax和阻尼过零点δd的大小关系的数学证明。
阻尼过零点δd满足
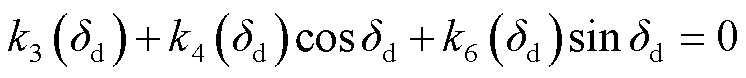 (39)
(39)
定义f2d(δ)中与功角有关的系数ki(δ)取ki(δd),而δ、cosδ和sinδ项则保持为自变量δ的函数。
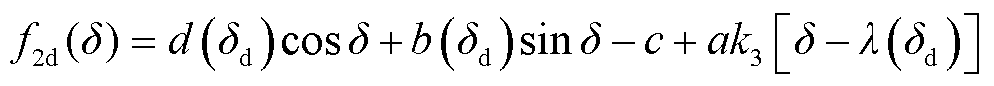 (40)
(40)
f2d(δ)的单调性可由其相对于δ的导数确定,即
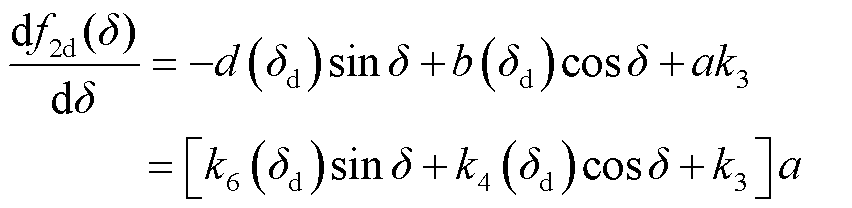 (41)
(41)
由式(41)可知: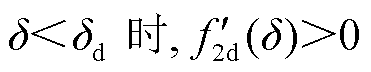 ;
;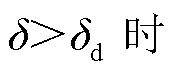 ,
,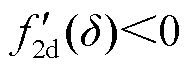 。即f2d(δ)在δ<δd时递增,δ>δd时递减。考虑到有f2d(δdmax)=0(即将δd代入式(34)中的δi),所以有f2d(δd)≥0,这也与图4中一致。综上所述,此时必有δd≤δdmax≤δmax。因此所提方法的保守性优于传统Lyapunov法。图5给出了传统Lyapunov法和本文所提的Lyapunov法的稳定域估计对比,可见本文所提方法较大地改进了传统Lyapunov法的保守性。
。即f2d(δ)在δ<δd时递增,δ>δd时递减。考虑到有f2d(δdmax)=0(即将δd代入式(34)中的δi),所以有f2d(δd)≥0,这也与图4中一致。综上所述,此时必有δd≤δdmax≤δmax。因此所提方法的保守性优于传统Lyapunov法。图5给出了传统Lyapunov法和本文所提的Lyapunov法的稳定域估计对比,可见本文所提方法较大地改进了传统Lyapunov法的保守性。
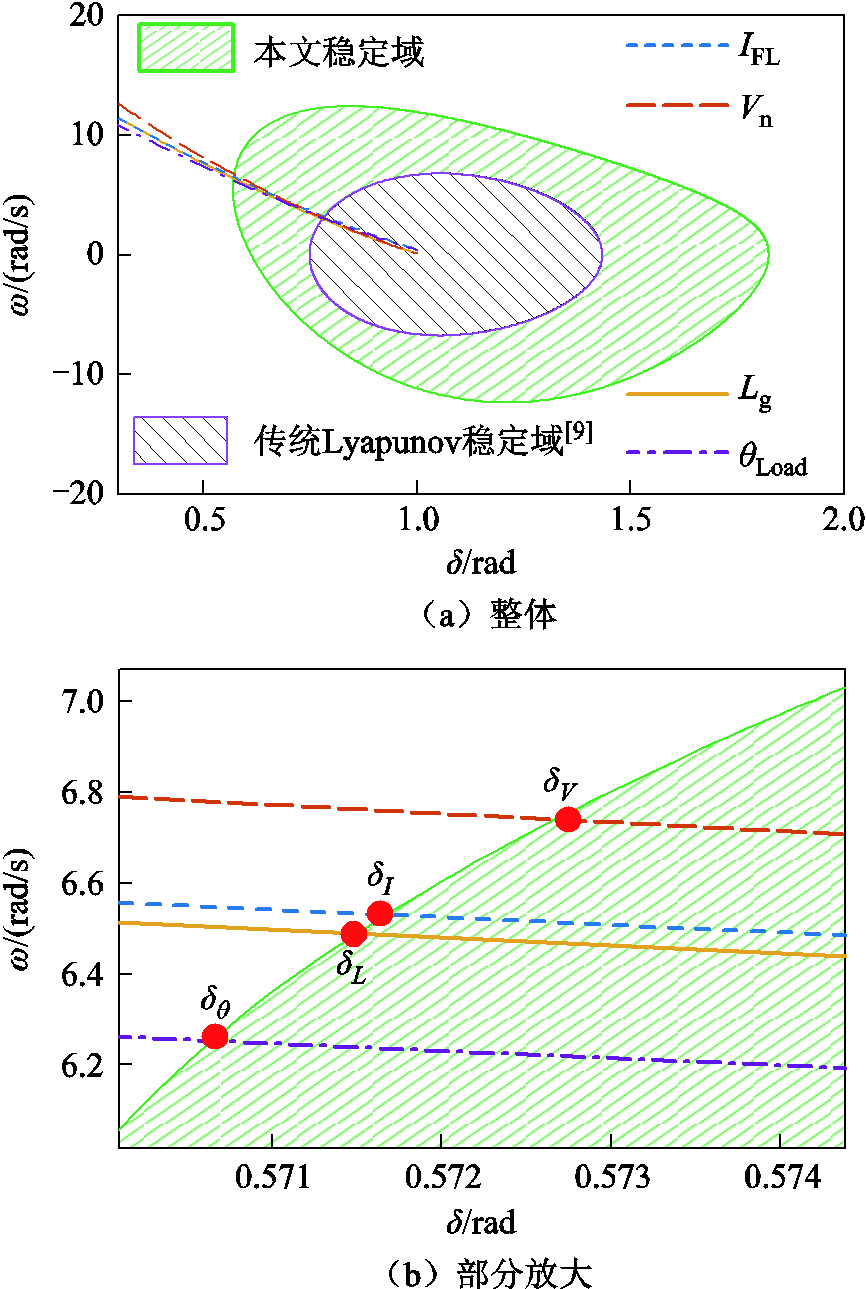
图5 考虑频率突变的功角稳定范围示意图
Fig.5 Schematic diagram of the power angle stability range considering frequency mutation
考虑受扰瞬间的频率突变,以电流扰动为例,假设扰动前后的GFL-VSC的电流参考值分别为IFL_和IFL+,系统扰动前功角δP即扰动前系统平衡点满足
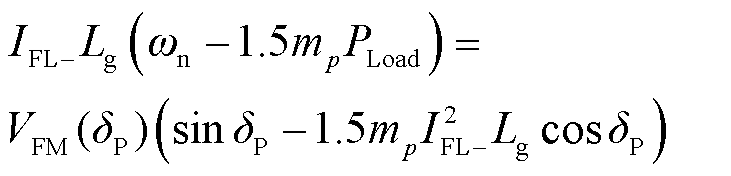 (42)
(42)
相应的频率突变量ΔωI为
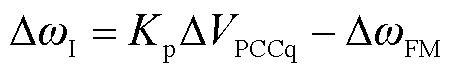 (43)
(43)
其中
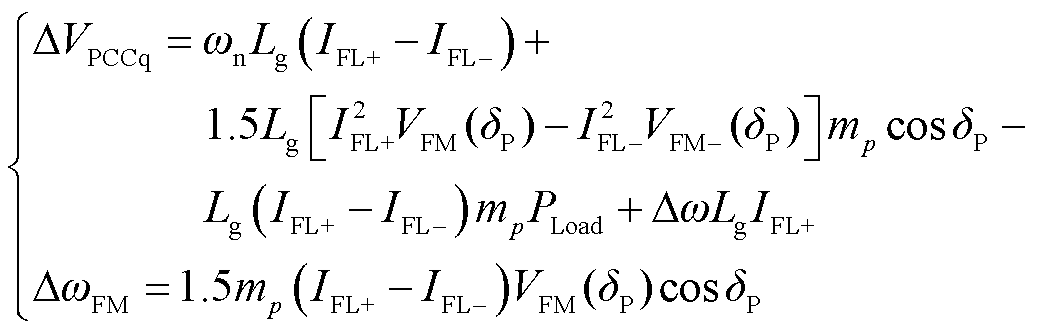 (44)
(44)
联立式(42)~式(44),将IFL-视作一个中间变量,即可得到一个自δP至ΔωI的函数ΔωI(δP)。其物理意义是当电流扰动后系统结构已知的情况下,扰动前系统平衡点为δP时,其受扰瞬间产生的频率突变量为ΔωI(δP)。图5中分别给出了ΔωI(δP)和式(37)所得的吸引域的范围。ΔωI(δP)和吸引域的边界交于δI,表示如果系统在电流扰动前的平衡点在δI,那么系统受扰后的能量V(δI, ΔωI(δP))=VIcr,即对于IFL的扰动,系统式(23)的功角稳定范围为(δI, δmax)。类似地,对于下垂控制参考电压Vn、线路电感Lg及负载相位θLoad突变[25-26]扰动情况下的突变频率函数ΔωV(δP)、ΔωL(δP)和Δωθ(δP)分别如式(45)~式(47)所示。
 (45)
(45)
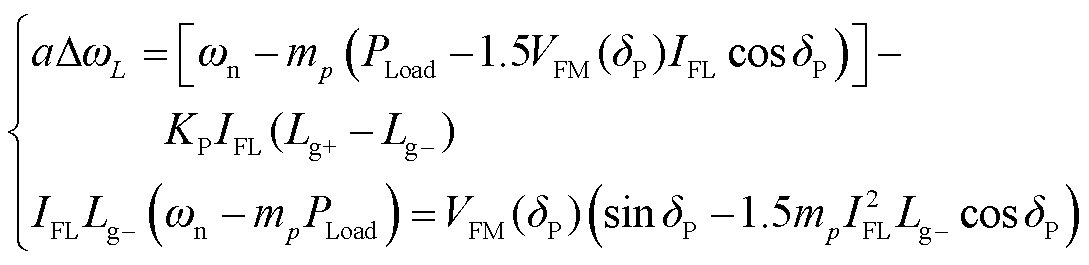 (46)
(46)
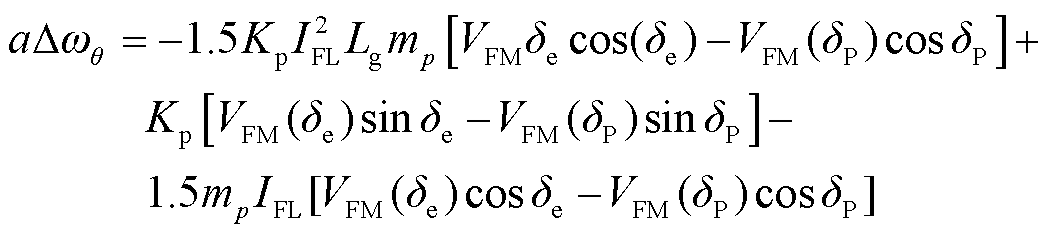 (47)
(47)
如图5所示,ΔωV(δP)、ΔωL(δP)和Δωθ(δP)分别与吸引域的边界交于δV、δL和δθ,即系统式(23)面对Vn、Lg和θLoad突变扰动时的暂态稳定功角范围分别为:(δV, δmax)、(δL, δmax)和(δθ, δmax)。
不同形式的扰动产生频率突变的机理不同,对应的频率突变值也不同,从而造成了不同形式扰动对应的功角稳定范围不一的现象。频率突变值越大,频率突变效应对暂态稳定性的不利影响也就越大,相应扰动形式的功角稳定范围也就越小,即系统面对该型扰动的敏感度也就越大。在表1所给的参数下,系统面对暂态扰动的敏感度顺序排列是:电压扰动>电流扰动>电感绕道>相位扰动。
表1 孤岛微电网系统参数
Tab.1 System parameters of islanded microgrid

参数数值 线路电感Lg/mH3 锁相环PI比例系数Kp1 锁相环PI积分系数KiGFM额定电压幅值Vn/V40 20 d轴电流参考值Irefd/A18 下垂控制有功系数mp下垂控制无功系数nq有功负载PLoad/W无功负载QLoad/var0.0010.001600100
本节从物理机理角度出发,探究孤岛微电网系统中GFL-VSC和GFM-VSC间的动态交互作用对稳定性的影响,并将其与状态空间方程中的各项对应。
1)无功下垂使得GFM-VSC输出电压幅值VFM下降,从而导致GFL-VSC输出有功能力降低,进而加剧交直流侧的功率不平衡风险。当GFL-VSC输出最高有功能力低于直流侧功率时,系统会发生失稳。该交互特性对应式(18)中电压下垂导致系统等效电磁功率k2sinδ下降。
2)由于GFM-VSC的有功下垂使得负载处频率变化,导致GFL-VSC并网处d轴电压变化,有
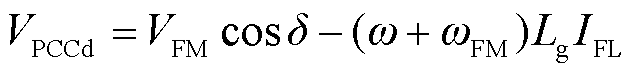 (48)
(48)
继而导致GFL-VSC输出有功变化ΔPFL,即
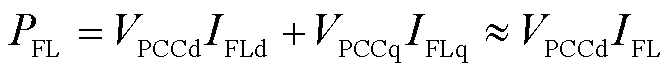 (49)
(49)
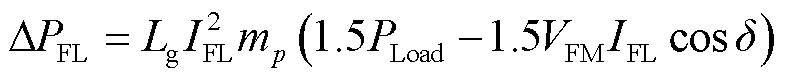 (50)
(50)
式(50)中第一项使得GFL-VSC的输出有功功率增加了1.5LgIFL2mpPLoad 有利于平衡交直流侧功率差额,利于系统稳定性,与式(18)中有功下垂导致等效机械功率减小相对应。第二项使得GFL-VSC输出有功功率降低了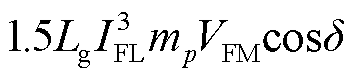 。当系统等效功角δ<π/2时,其弱化了GFL-VSC的有功输出能力,不利于稳定性。当系统等效功角δ>π/2时,其强化了GFL-VSC的有功输出能力,有利于稳定性。因为在稳定域内有π-δe>δmax>δe>δmin。如式(51)所示,该交互整体导致系统在稳定范围内的等效电磁功率做功下降,不利于系统稳定。其与式(18)中有功下垂导致k5cosδ相对应。
。当系统等效功角δ<π/2时,其弱化了GFL-VSC的有功输出能力,不利于稳定性。当系统等效功角δ>π/2时,其强化了GFL-VSC的有功输出能力,有利于稳定性。因为在稳定域内有π-δe>δmax>δe>δmin。如式(51)所示,该交互整体导致系统在稳定范围内的等效电磁功率做功下降,不利于系统稳定。其与式(18)中有功下垂导致k5cosδ相对应。
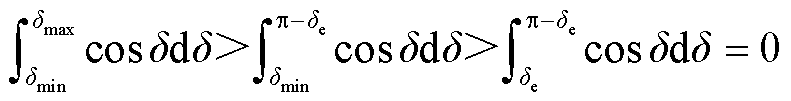 (51)
(51)
3)以Iref突增为例,随着首摆进行,二者之间的相位差δ持续变大,进而使得PFL=1.5VFMIrefcosδ下降,因此PFM会上升,从而导致ωFM减小,使二者相对速度进一步变大,从而进恶化稳定性。即无功下垂使得系统相对频率ω=ωPLL-ωFM以1.5mpVFMIrefcosδ变化, 其等效于系统相对加速度以-1.5mpVFMIrefωsinδ变化,对应式(18)中的阻尼正弦项k6ωsinδ。
4)以Iref突增为例,扰动瞬间系统功角因为积分器的存在不会发生突变。此时GFL-VSC输出功率PFL=1.5VFMIrefcosδ骤增,则PFM=PLoad-PFL骤减,则ωFM因为有功下垂作用而骤增,GFL-VSC和GFM-VSC间转速差骤减(此时ωPLL>ωFM),有利于系统稳定性。这与式(20)~式(22)中GFM-VSC使得系统频率突变量降低相对应。
本节利用第3节中基于Lyapunov第二法推导的孤岛微电网系统暂态稳定吸引域大小,结合理论分析不同网络参数和控制器参数对孤岛微电网系统稳定性的影响。
1)GFM额定电压Vn和GFL参考电流Iref
Vn和GFL-VSC的交流侧最大传输有功能力正相关,而Iref则与GFL-VSC的直流侧功率相关。前者越大,后者越小,则GFL-VSC因交直流侧功率不平衡而失稳的风险越小,系统越稳定。从式(18)中也可看出,Vn越大则k2越大,Iref越小则k1越小且k5越大。二者均可使式(24)中系统势能变小,从而利好暂态稳定。Iref越小还可使系统阻尼系数k3和k6变大。如图6a、图6b所示,Iref越小,Vn越大,系统稳定域越大,与理论分析一致。需要指出的是,Vn变大的同时会导致k5和k6变小,均不利于稳定。但因为常有1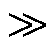 1.5mpIFL2Lg和Kp
1.5mpIFL2Lg和Kp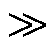 1.5mpIFL, Vn对稳定性的有利影响远大于不利影响。
1.5mpIFL, Vn对稳定性的有利影响远大于不利影响。
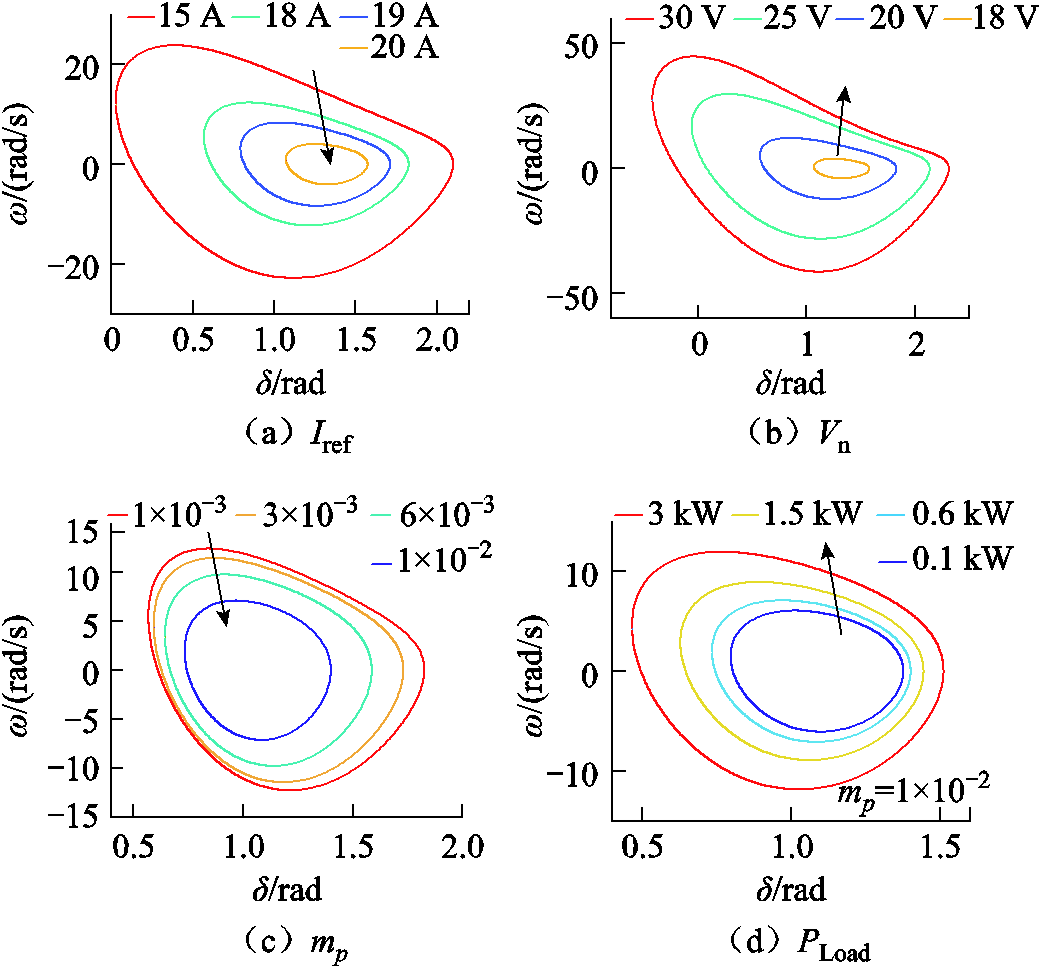
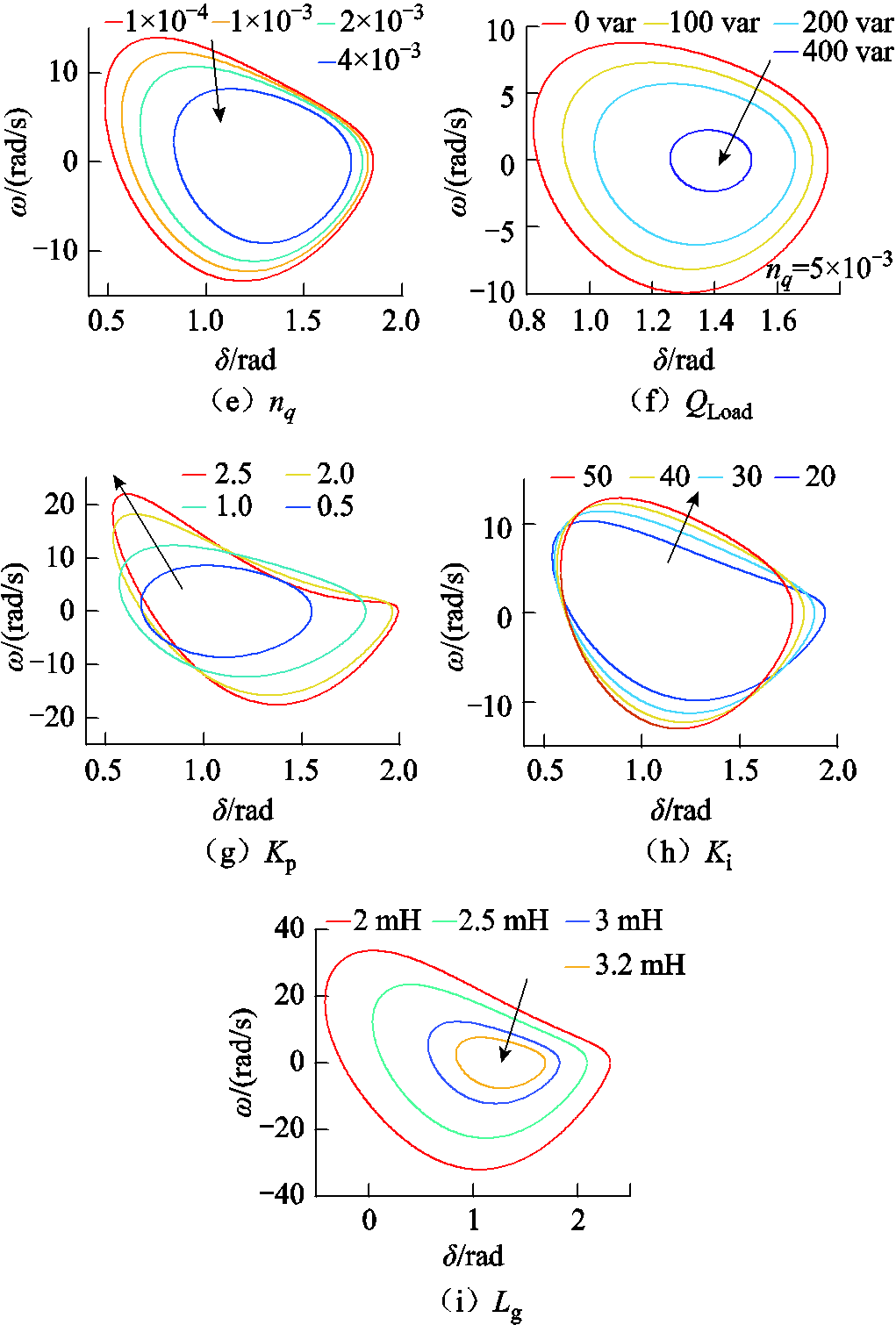
图6 参数对孤岛微电网系统暂态稳定性影响
Fig.6 Impact of parameters on the transient stability of island microgrid system
2)有功下垂系数mp和有功负载PLoad
4.1节中列举了有功下垂两个不利稳定性的交互特性和两个有利稳定性的交互特性,这里不再赘述。分析有功下垂系数和有功负载时需综合考虑多项因素影响。例如,当ωn mpPLoad时,k1的下降值相对较小,因此较大的mp对系统的总影响是不利的。如图6c所示,mp越大、系统稳定域越小,与理论分析一致。由于增大PLoad对系统稳定性的影响只体现于k1的下降,因此较大的PLoad有利于稳定性。如图6d所示,PLoad越大、系统稳定域越大,与理论分析一致。要指出的是,图6d提高了相应的下垂系数,以使得稳定域变化趋势对比更加明显。
mpPLoad时,k1的下降值相对较小,因此较大的mp对系统的总影响是不利的。如图6c所示,mp越大、系统稳定域越小,与理论分析一致。由于增大PLoad对系统稳定性的影响只体现于k1的下降,因此较大的PLoad有利于稳定性。如图6d所示,PLoad越大、系统稳定域越大,与理论分析一致。要指出的是,图6d提高了相应的下垂系数,以使得稳定域变化趋势对比更加明显。
3)无功下垂系数nq和无功负载QLoad
由式(16)可知,无功下垂系数nq和无功负载QLoad越大均会导致系统电压降低,从而使得GFL-VSC的交直流侧功率不平衡风险增大,从而导致系统稳定性变差。如图6e和图6f所示,二者的增大均不利于稳定性,与理论分析一致。
4)PLL积分系数Ki和比例系数Kp
PLL的PI控制器对系统稳定性的影响较为复杂,同时影响了电磁/机械功率和阻尼项,难以给出其和稳定性间明确的单调关系,且Kp和Ki的整定也和时域响应指标密切相关。图6g和图6h分别给出了不同Kp和Ki下系统暂态稳定域估计结果。
5)线路电感Lg
由式(18)可知,Lg越大则系统等效机械功率k1增大,系统电磁功率系数k5下降,阻尼系数k3减小,均不利于系统稳定性。需要指出的是,虽然孤岛微电网因为其地理距离较小,可能线路电感并不大。但是考虑到GFM-VSC中广泛使用的虚拟阻抗暂态限流控制,系统在暂态故障下的等效电感对稳定性的不利影响不能忽视。图6i给出了不同Lg下系统暂态稳定域估计结果。与理论分析一致,Lg越大,系统稳定性越差。
本节利用Matlab/Simulink仿真验证本文提出的基于Lyapunov直接法的孤岛微电网暂态稳定性分析方法的有效性和准确性。仿真参数见表1。5.1节和5.2节分别给出了电流Iref和相位θFM扰动的验证。
在t=0.5 s时刻分别给Iref施加ΔIcri=6.722 7 A,ΔIlar=10.42 A和ΔIsma=6 A的扰动,仿真结果如图7所示。如图7a所示,系统受临界扰动ΔIcri时,系统相轨迹未越过吸引域边界,系统保持稳定。如图7b所示,系统受扰动ΔIlar时,系统相轨迹越过稳定域边界,系统失稳。如图7c所示,系统受扰动ΔIsma时,系统相轨迹一直在稳定域内,系统保持稳定。仿真结果与理论分析一致,验证了本文提出的Lyapunov方法的有效性。
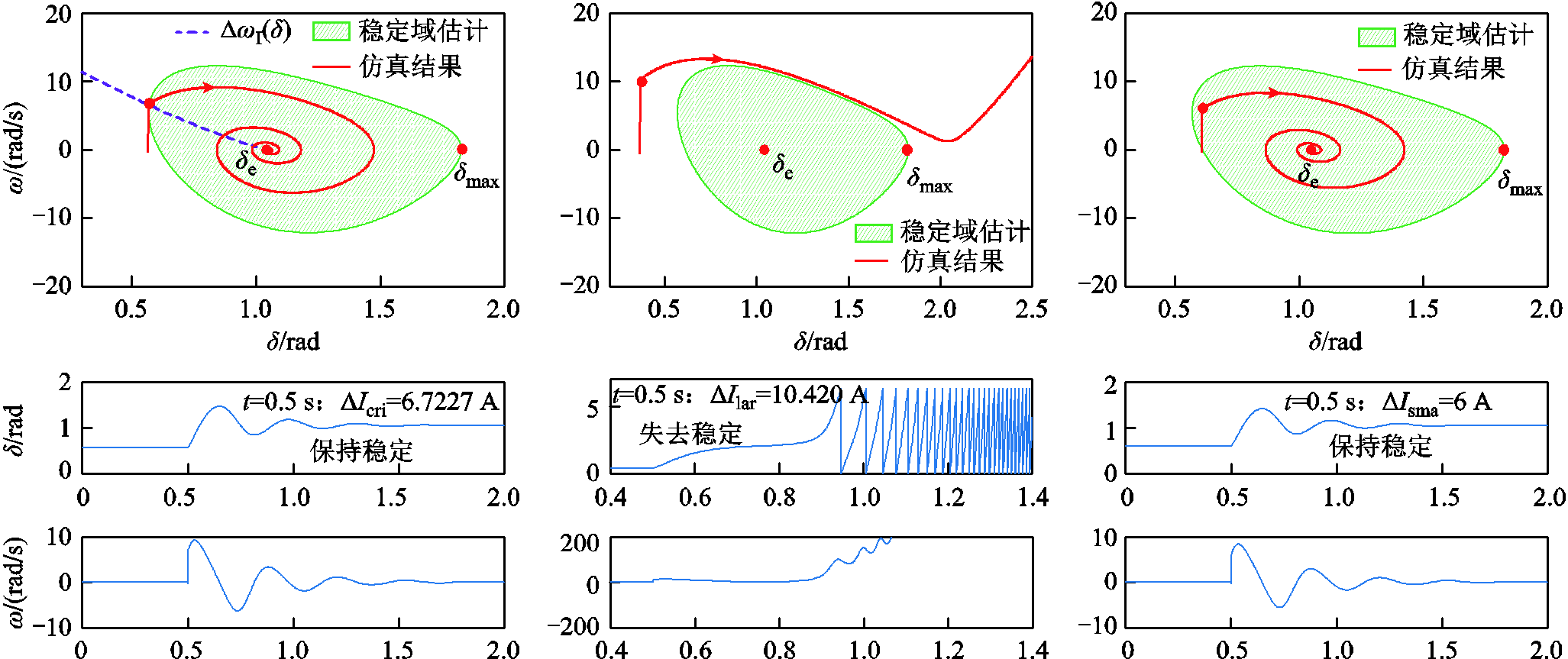
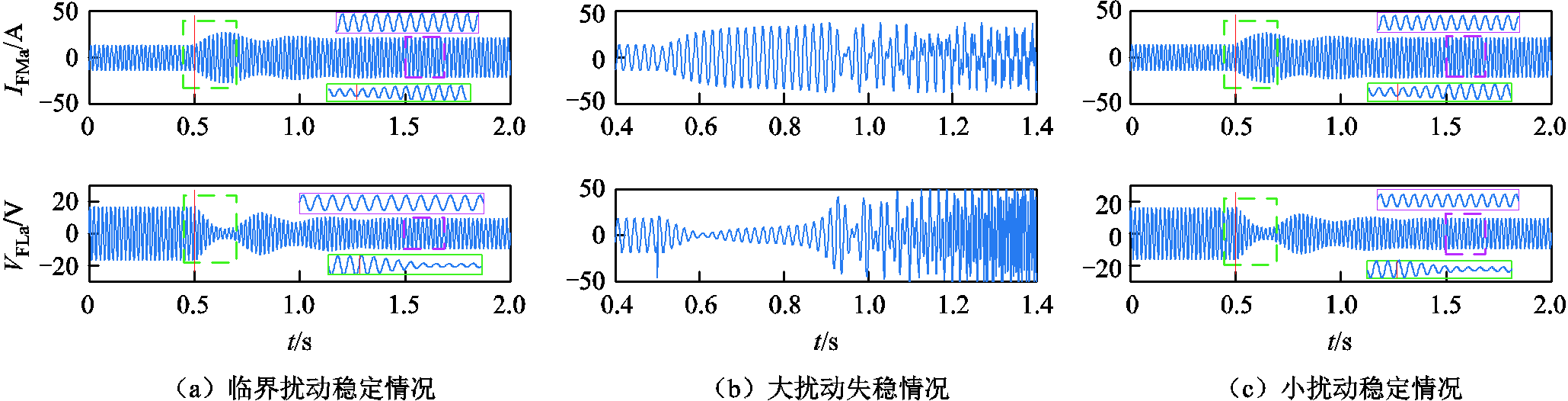
图7 孤岛微电网系统受不同电流扰动仿真结果
Fig.7 Simulation results of the islanded-mircogrid system under different current reference disturbances
t=0.5 s时分别给θFM施加Δθcri=0.471 1 rad,Δθlar=0.681 6 rad和Δθsma=0.441 2 rad的扰动,仿真结果如图8所示。如图8a所示,系统受临界扰动Δθcri时,系统相轨迹未越过吸引域边界,系统保持稳定。如图8b所示,系统受扰动Δθlar时,系统相轨迹越过稳定域边界,系统失稳。如图8c所示,系统受扰动Δθsma时,系统相轨迹一直在稳定域内,系统保持稳定。仿真结果与理论分析一致,验证了本文提出的Lyapunov方法的有效性。需要指出的是,ΔIlar和Δθlar都是经过仿真尝试验证出的系统实际临界失稳情况。由式(14)可算出ΔIlar扰动时,对应的系统功角稳定下边界是0.370 8 rad>δe+Δθlar=0.360 0 rad,表明孤岛微电网系统面对电流形式扰动比相位形式扰动更加敏感,功角稳定范围更小,这也与图5所示的理论分析一致。
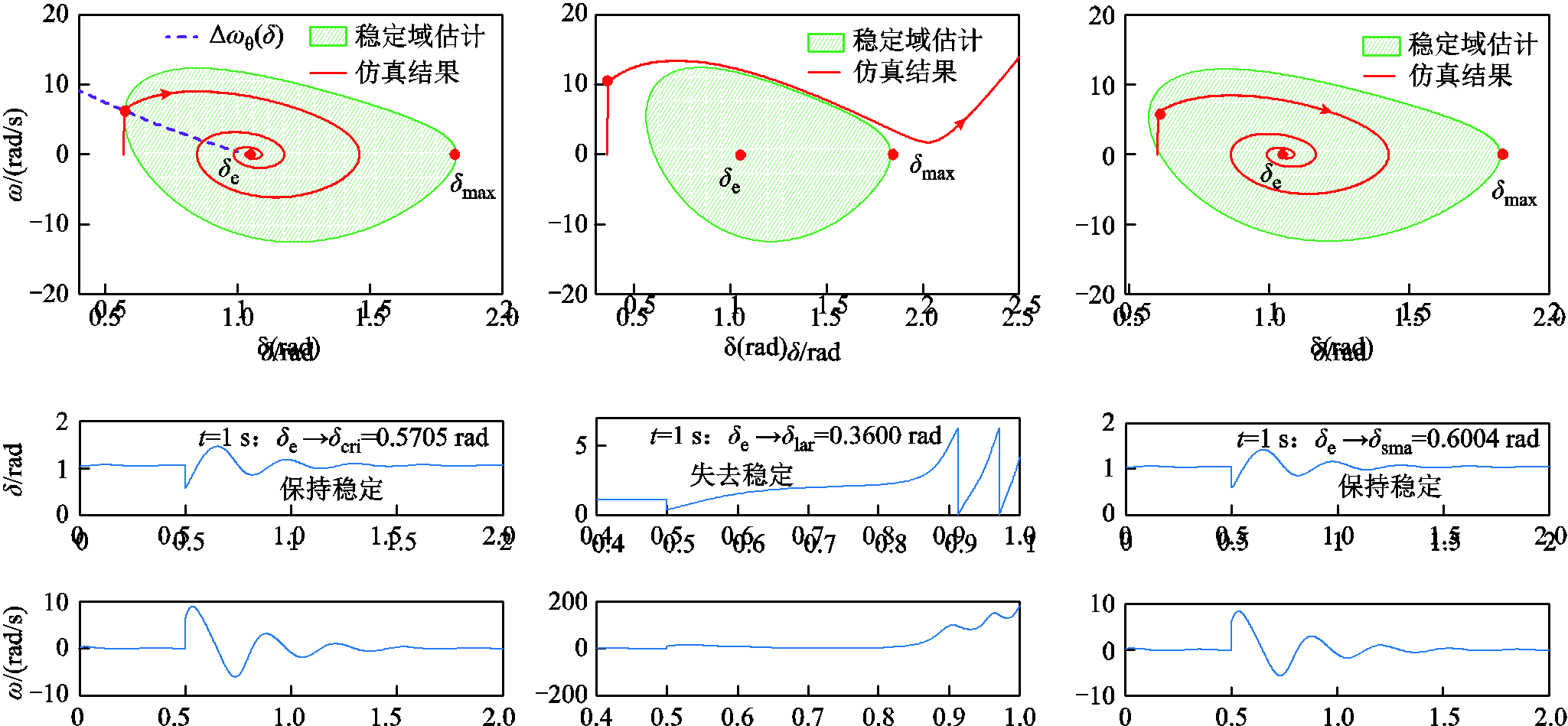
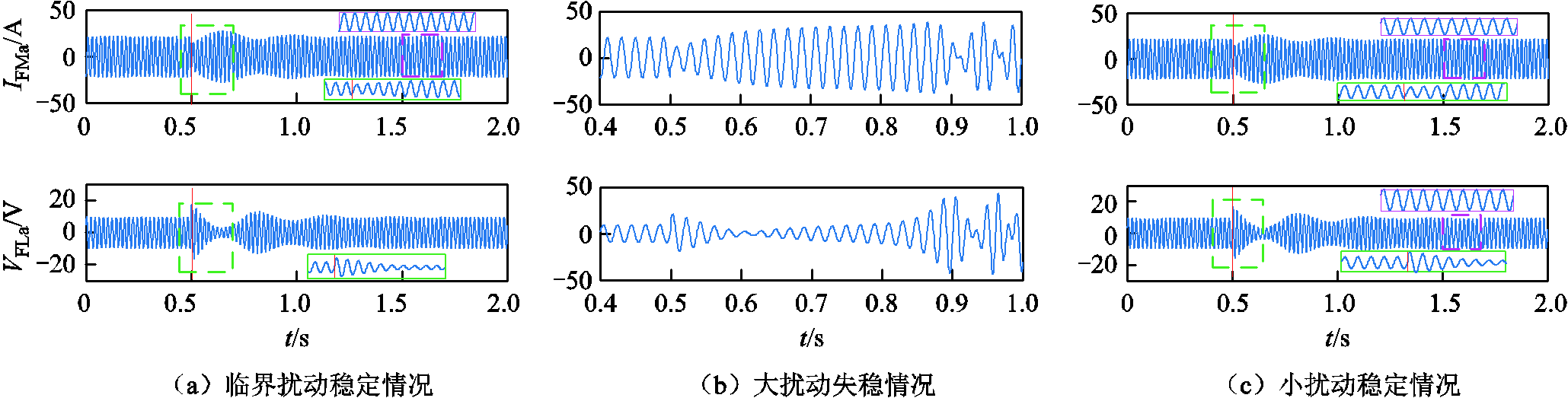
图8 孤岛微电网系统受不同相位扰动仿真结果
Fig.8 Simulation results of the islanded-mircogrid system under different phase disturbances
为进一步验证所提Lyapunov法的准确性,建立如图9所示的基于RT-Lab的硬件在环实验验证平台。硬件在环实验所采用的参数与第5节的仿真验证一致。
分别给Iref分别施加在稳定域边界上的临界扰动ΔIcri=6.722 7 A,在稳定域外的大扰动ΔIlar=10.42 A和在稳定域内的小扰动ΔIsma=6 A。硬件在环实验结果如图10a~图10c所示。当系统处于稳定域内时,系统能最终回到平衡点并保持稳定。当扰动过大,导致系统越过稳定域边界后,系统的稳定性无法得到保证,图10b中系统受大扰动ΔIlar后失稳。

图9 基于RT-Lab的硬件在环实验平台
Fig.9 Hardware-in-the-loop experiment platform based on RT-Lab

图10 不同电流扰动实验结果
Fig.10 Experimental results under different current reference disturbances
给θFM施加位于其稳定域边界上的临界扰动Δθcri=0.4711rad,位于其稳定域外的大扰动Δθlar= 0.6816rad和位于其稳定域内的小扰动Δθsma=0.4412rad。硬件在环实验结果分别如图11a~图11c所示。当系统处于稳定域内时,系统在暂态过程后最终能回到平衡点并保持稳定。当扰动过大导致系统越过稳定域边界后,系统的暂态稳定性无法保证。如图11b中所示,系统受大扰动ΔIlar后最终失稳。
本文研究了由构网型和跟网型变流器组成的孤岛微电网的暂态稳定性。首先,考虑锁相环的频率突变现象,给出了不同扰动形式下的频率突变计算公式,建立了孤岛微电网的暂态修正模型,提高了模型准确度,避免了稳定性误判的产生。其次,基于二次型原理构造了一个考虑频率突变的Lyapunov暂态稳定判据,极大地改善了传统Lyapunov方法的保守性,给出了一个较为精确的孤岛微电网系统暂态稳定吸引域的估计。从物理机理角度出发,深入揭示了构网型和跟网型逆变器的动态交互作用及其对系统稳定性的影响。基于所提出的Lyapunov分析方法,研究了不同参数对系统稳定性的影响。本文的主要发现总结如下:

图11 不同相位扰动实验结果
Fig.11 Experimental results under different phase disturbances
1)在跟网型逆变器受扰动的瞬间,锁相环的输出频率会由于PCC处电压的突然变化而发生突变。传统建模方法忽略了该现象,这将导致暂态模型误差和对系统稳定性的潜在误判。
2)基于不同扰动的频率突变产生机理不同,指出孤岛微电网系统面对不同形式扰动的敏感度不同。通过理论推导得到了:电压扰动>电流扰动>电感绕道>相位扰动的敏感度排序,敏感度越高,功角稳定范围越小,系统越容易发生失稳。
3)构网型变流器的电压参考值Vn越大,系统稳定性越强。跟网型变流器的电流参考值Iref,GFM-VSC的有功下垂系数mp和线路电感Lg越小,系统稳定性越强。但需要指出的是,上述针对Vn和mp的结论是在常见参数条件下,综合考虑其对稳定性的有利影响和不利影响所得到的。锁相环的控制器参数对系统稳定性的影响较为复杂,不是一种单调的关系。无功负载和无功下垂系数越大,系统稳定性越差。
后续研究重点是基于互联系统理论[24],将本文所提出的Lyapunov方法扩展到直流电压环影响的孤岛微电网系统中,以及推广至多变流器并联系统。
参考文献
[1] 胡家兵, 袁小明, 程时杰. 电力电子并网装备多尺度切换控制与电力电子化电力系统多尺度暂态问题[J]. 中国电机工程学报, 2019, 39(18): 5457-5467, 5594. Hu Jiabing, Yuan Xiaoming, Cheng Shijie. Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus[J]. Proceedings of the CSEE, 2019, 39(18): 5457-5467, 5594.
[2] 唐英杰, 查晓明, 田震, 等. 考虑非线性阻尼效应的孤岛微电网暂态稳定性分析及提升策略研究[J/OL].电源学报, 2022, 1-11.http:kns.cnki.net/kcms/ detail/12.1420.tm.20220411.1145.002.html. Tang Yinjie, Zha Xiaoming, Tian Zhen, et al. Transient stability analysis and enhanced control strategy for islanded microgrid considering nonlinear damping effect[J/OL].Journal of Power Supply, 2022: 1-11. http:kns.cnki.net/kcms/detail/12.1420.tm.20220411. 1145.002.html.
[3] 周晖, 王跃, 李明烜, 等. 孤岛并联虚拟同步发电机暂态功率分配机理分析与优化控制[J]. 电工技术学报, 2019, 34(增刊2): 654-663. Zhou Hui, Wang Yue, Li Mingxuan, et al. Analysis and optimal control of transient active power sharing between islanded parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 654-663.
[4] 涂春鸣, 邹凯星, 高家元, 等. 基于不对称正负反馈效应的PQ功率控制并网逆变器稳定性分析[J]. 电工技术学报, 2023, 38(2): 496-509. Tu Chunming, Zou Kaixing, Gao Jiayuan, et al. Stability analysis of grid-connected inverter under PQ power control based on asymmetric positive-negative-feedback effects[J]. Transactions of China Electro-technical Society, 2023, 38(2): 496-509.
[5] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595. Xu Jieyi, Liu Wei, Liu Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.
[6] 汪春江, 孙建军, 宫金武, 等. 并网逆变器与电网阻抗交互失稳机理及阻尼策略[J]. 电工技术学报, 2020, 35(增刊2): 503-511. Wang Chunjiang, Sun Jianjun, Gong Jinwu, et al. Mechanism and damping strategy of interactive instability between grid-connected inverter and grid impedance[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 503-511.
[7] 李锡林, 唐英杰, 田震, 等. 基于改进等面积法则的并网逆变器同步稳定性分析[J]. 电力系统自动化, 2022, 46(18): 208-215. Li Xilin, Tang Yingjie, Tian Zhen, et al. Synchronization stability analysis of grid-connected inverter based on improved equal area criterion[J]. Automation of Electric Power Systems, 2022, 46(18): 208-215.
[8] Tian Zhen, Tang Yingjie, Zha Xiaoming, et al. Hamilton-based stability criterion and attraction region estimation for grid-tied inverters under large-signal disturbances[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 413-423.
[9] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large-signal stability of grid-forming and grid-following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.
[10] Li Xilin, Tian Zhen, Zha Xiaoming, et al. An iterative equal area criterion for transient stability analysis of grid-tied converter systems with varying damping[J/OL]. IEEE Transactions on Power Systems, 2023: 1-13. doi: 10.1109/TPWRS.2023.3241079.
[11] Shuai Zhikang, Shen Chao, Liu Xuan, et al. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4648-4661.
[12] 黄林彬, 章雷其, 辛焕海, 等. 下垂控制逆变器的虚拟功角稳定机理分析[J]. 电力系统自动化, 2016, 40(12): 117-123, 150. Huang Linbin, Zhang Leiqi, Xin Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123, 150.
[13] He Changjun, He Xiuqiang, Geng Hua, et al. Transient stability of low-inertia power systems with inverter-based generation[J]. IEEE Transactions on Energy Conversion, 2022, 37(4): 2903-2912.
[14] He Xiuqiang, Geng Hua. PLL synchronization stability of grid-connected multiconverter systems[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 830-842.
[15] Yi Xiangtong, Peng Yelun, Zhou Quan, et al. Transient synchronization stability analysis and enhancement of paralleled converters considering different current injection strategies[J]. IEEE Transactions on Sustainable Energy, 2022, 13(4): 1957-1968.
[16] 李翼翔, 田震, 唐英杰, 等. 考虑构网型与跟网型逆变器交互的孤岛微电网小信号稳定性分析[J]. 电力自动化设备, 2022, 42(8): 11-18. Li Yixiang, Tian Zhen, Tang Yingjie, et al. Small-signal stability analysis of island microgrid considering interaction between grid-forming converter and grid-following converter[J]. Electric Power Automation Equipment, 2022, 42(8): 11-18.
[17] 王雪梅, 王艺博, 刘雨桐, 等. 基于虚拟电抗的主动支撑型新能源机组低电压穿越控制方法[J]. 电网技术, 2022, 46(11): 4435-4444. Wang Xuemei, Wang Yibo, Liu Yutong, et al. Low voltage ride-through control of actively-supported new energy unit based on virtual reactance[J]. Power System Technology, 2022, 46(11): 4435-4444.
[18] 刘航, 王跃, 刘永慧, 等. 基于定量设计虚拟阻抗的VSG低电压穿越策略[J]. 高电压技术, 2022, 48(1): 245-256. Liu Hang, Wang Yue, Liu Yonghui, et al. The LVRT strategy for VSG based on the quantitatively designed virtual impedance[J]. High Voltage Engineering, 2022, 48(1): 245-256.
[19] Li Mingfei, Quan Xiangjun, Wu Zaijun, et al. Modeling and transient stability analysis of mixed-GFM-GFL-based power system[C]//2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 2022: 2755-2759.
[20] Sun Huiqiang, Lin Xinchun, Chen Songbai, et al. Transient stability analysis of the standalone solar-storage AC supply system based on grid-forming and grid-following converters during sudden load variation[J]. IET Renewable Power Generation, 2022, 66: 1.
[21] Hu Qi, Fu Lijun, Ma Fan, et al. Large signal synchronizing instability of PLL-based VSC connected to weak AC grid[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3220-3229.
[22] 廖书寒, 查晓明, 黄萌, 等. 适用于电力电子化电力系统的同调等值判据[J]. 中国电机工程学报, 2018, 38(9): 2589-2598, 2827. Liao Shuhan, Zha Xiaoming, Huang Meng, et al. Coherency criterion applicable to power electronics dominated large power systems[J]. Proceedings of the CSEE, 2018, 38(9): 2589-2598, 2827.
[23] 查晓明, 张扬, 成燕, 等. 用于简化微电网结构的微分几何广义同调方法[J]. 电工技术学报, 2012, 27(1): 24-31. Zha Xiaoming, Zhang Yang, Cheng Yan, et al. New method of extended coherency for micro-grid based on homology in differential geometry[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 24-31.
[24] Khalil H K. Nonlinear systems[M]. 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2002.
[25] Liu Yushuang, Huang Meng, Tse C K, et al. Stability and multiconstraint operating region of grid-connected modular multilevel converter under grid phase disturbance[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12551-12564.
[26] Tian Xinshou, Wang Weisheng, Li Xiang, et al. Fault ride through strategy of DFIG using rotor voltage direct compensation control under voltage phase angle jump[J]. CSEE Journal of Power and Energy Systems, 2019, 5(4): 515-523.
Abstract As an effective and reliable distributed energy integration and consumption mode, converter-based microgrids can operate in grid-connected mode and islanded mode Due to the lack of stable voltage and frequency support, the islanded microgrid is prone to lose stability under fault disturbance. Besides, various converters with different control types interact with each other in the microgrid, making the system easier to lose stability. The interactions of GFL-VSC and GFM-VSC in the islanded microgrid system and their effects on system stability are rarely analyzed in the former studies. In addition, due to the negative damping characteristics of GFL-VSC, the analysis methods of the previous studies are quite conservative. A new Lyapunov analysis method based on quadratic form principle considering PLL frequency mutation effect is proposed in this paper, which provides a conservatively improved stability region estimation.
Firstly, a conventional second order nonlinear mathematical model of GFL-VSC parallel GFM-VSC system considering the effect of reactive power loop is established. Simulation comparison shows that the conventional model has some transient errors. Secondly, a passive frequency mutation effect widely exists in GFL-VSCs is revealed, which is caused by the proportional controller of PLL.By deducing a unified frequency mutation formula for different types of large disturbances, a modified model considering frequency mutation effect is obtained, which greatly improves the transient-state error of the existing conventional model. Third, considering the influence of reactive power loop on the output voltage of GFM-VSC, a new parametric Lyapunov function based on quadratic form theory is proposed. By undetermined coefficient, the obtained dissipation interval is larger than that of conventional Lyapunov function. Therefore, a less conservative estimation of the transient stable domain of islanded microgrid system can be obtained. The less-conservatism of the proposed method is mathematical proved.Fourthly, considering the frequency mutation effect and combining with the obtained stable domain, the power angle stability range corresponding to different disturbance forms is derived, and the conclusion is drawn that the sensitivity of the system to different disturbance forms is different. Fifth, from the point of view of physical mechanism, the influence of dynamic interaction between GFL-VSC and GFM-VSC on the stability of the islanded microgrid system is explored, and corresponding to the terms in the state space equation.Sixth, based on the proposed Lyapunov's method, the size of transient stable domain of the islanded microgrid system is derived and compared to analyze the influence of different network parameters and controller parameters on the stability of the islanded microgrid system. Finally, the proposed method is verified by MATLAB/Simulink simulation and the RT-Lab based hardware-in-loop experiments.
The following conclusions can be drawn from this paper: (1) The output frequency of the PLL will mutate due to the sudden change of voltage at the PCC when the converter is disturbed under large disturbance. Conventional modeling method ignore this phenomenon, which leads to transient model errors and potential misjudgment of stability. (2) Based on the different frequency mutation mechanism of different disturbances, the sensitivity of the islanded microgrid system to different forms of disturbances is different. The sensitivity order is voltage disturbance>current disturbance>inductance disturbance>phase disturbance. The higher the sensitivity, the more likely the system instability occurs. (3) The larger the voltage reference value, the stronger the system stability. The smaller the current reference value, droop coefficient andline inductance, the stronger the system stability will be. The influence of PLL’s parameters on the stability is more complex and not a monotonous relationship. The larger the reactive load and reactive droop coefficient, the worse the system stability.
keywords:Grid-connected inverter, islanded microgrid, synchronization stability, frequency mutation, Lyapunov stability criterion
DOI:10.19595/j.cnki.1000-6753.tces.L10069
中图分类号:TM464
国家重点研发计划项目(2022YFB2402701)和国家自然科学基金青年项目(52007134)资助。
收稿日期 2023-01-09
改稿日期 2023-03-15
李锡林 男,1999年生,博士研究生,研究方向为电力电子化电力系统暂态稳定性分析E-mail:snplee@whu.edu.cn
查晓明 男,1967年生,博士,教授,博士生导师,研究方向为大功率电力电子装置等。E-mail:xmzha@whu.edu.cn(通信作者)
(编辑 赫蕾)