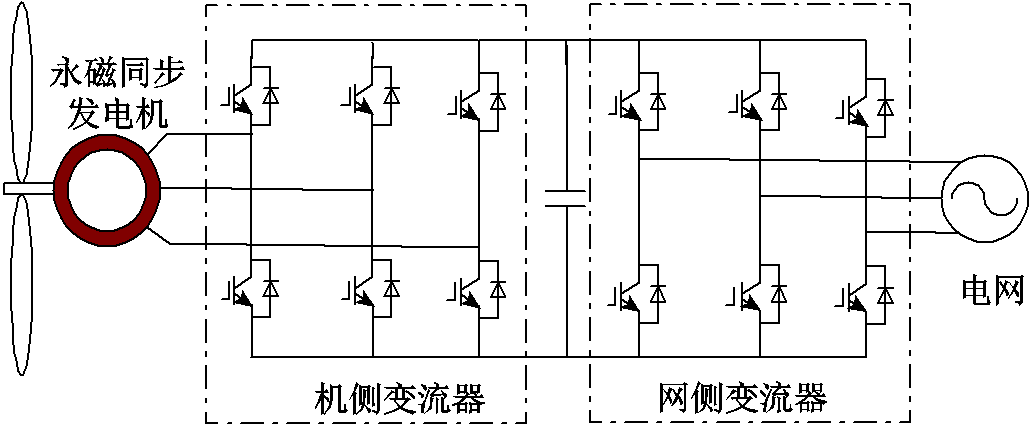
图1 永磁同步风力发电系统结构
Fig.1 Structure diagram of permanent magnet wind power generation system
摘要 永磁同步发电机由于能量密度大、结构简单、运行效率高等优点，成为风力发电系统广泛使用的机型之一。永磁同步发电机在通过变流器向电网供电时，变流器产生的高频共模电流会带来严重的电磁干扰和轴承电腐蚀问题。定量研究共模电流频谱分布以及幅值的影响因素，就可以根据需要人为地改变共模电流的谐波分布，将共模电流的幅值控制在合理的范围内，从而降低共模电流对系统的负面效应。该文从一台MW级风力永磁同步发电机的共模电流测试实验出发，提出一种变流器-电缆-电机的建模及实验提取参数的方法，从时域和频域两个方面验证了模型的准确性。在此模型基础上，针对谐振和上升时间两个因素，对共模电流的谐波分布和幅值的影响进行定量分析和仿真研究，结果表明，共模回路阻抗决定共模电流的谐波分布，共模电流上升时间与共模电流的幅值成反比。
关键词：永磁同步发电机（PMSG） 共模电流 谐波分布 幅值
随着国家大力倡导碳中和与碳达峰的方针，绿色能源未来成为主流能源是必然趋势。其中风力发电占据重要的地位。目前，MW级以上的风力发电机组主要为双馈异步型和永磁同步型。与双馈异步型发电机相比，永磁同步发电机组无需励磁绕组，无需集电环和电刷，具有能量密度高、运行效率高、可靠性高、结构简单和维护成本低等优点。随着海上风电技术的快速发展，永磁同步发电机（Permanent Magnet Synchronous Generators, PMSG）在大功率风能转换系统中得到了广泛的应用[1]。永磁同步风力发电系统中发电机经过变流器向电网供电。永磁同步风力发电系统结构如图1所示。近些年来，随着风力发电技术的快速发展，系统中变流器开关频率越来越高，带来了不容忽视的负面影响。
系统采用永磁同步风力发电机，定子绕组通过变流器连接到电网，变流器通常为电压型脉冲宽度调制变换器结构，按照其位置可分为机侧变流器和网侧变流器。对于由变流器、电缆和电机组成的电气传动系统，变流器作为一个干扰源，会将干扰通过传输电缆以共模电流的形式传送给电机，这意味着电机是一个噪声接收器，电机对这种干扰的反应就表现为轴电压，当轴电压大于轴承油膜阈值电压时，油膜被击穿，产生高频放电击穿轴电流，导致轴承滚道产生熔化性凹点，最终产生凹槽，增大轴承的摩擦，使得轴承的寿命缩减，危害电机的安全运行[2-4]。文献[5]通过测量250 kW电机轴承在不同频率下的阻抗与容值曲线，发现频率越高，对应阻抗越低，高频时轴承更易发生腐蚀，绝缘轴承在高频下也会发生电腐蚀。文献[6]通过测量发现，较高频次的共模电流是某MW级双馈风电机组在并网时出现主柜断路器频繁跳闸的原因，然后通过中性点接地和加装磁环的方式降低了共模电流的幅值，并发现共模电流幅值降低的程度与故障下降率有高度的一致性。除了上述负面效应外，共模电流可能会引起桥臂电流振荡，并网系统失稳[7]；带来电磁干扰，影响无线电子设备的正常工作[8]；增加损耗，降低系统效率等问题[9]。
图1 永磁同步风力发电系统结构
Fig.1 Structure diagram of permanent magnet wind power generation system
面对共模电流的这些负面效应，许多学者对此展开了研究。文献[10]以共模系统为研究对象分析共模电流的时、频域特性和共模回路阻抗特性，指出共模回路中的分布电感和分布电容之间的谐振是造成共模电流和辐射超标的主要原因。文献[11]通过对共模电流时、频域的研究，证明了共模电流的衰减时间和谐振频率主要受系统参数的影响，电机的转速和负载情况对衰减时间和谐振频率没有影响，同时文献将系统简化为RLC串联电路进行研究。文献[12]分析了共模电流流经电机的路径，并给出了电缆-电机系统的简化模型，但是该电机模型过于简单，无法准确表征电机的特征。文献[13-14]指出永磁同步发电机内部存在的所有杂散电容，并给出了共模回路下的电路模型，但是这种模型不适用于永磁体与转子金属连接的永磁同步发电机，并且该模型缺乏实验验证。文献[15]通过仿真进一步指出，当开关管上升和下降时间相等，都为tr时，则tr只影响共模电压高频段（高于转折频率1/(πtr)）的波形，并且开关管上升时间越长，电机侧共模电压对应频率的幅值越小，但是没有定量说明这种关系，也没有给出上升时间对共模电流幅值的影响。在抑制共模电流上，共模磁环由于安装方便，应用比较广泛，但是由于缺乏对共模电流时、频域的了解，在选用磁环上比较盲目[5-6,16]，文献[17-18]给出了一种磁环等效电感的计算方法，但是并没有给出共模电流频谱分布的计算方法。确定共模电流的时域和频域特征，了解共模电流的谐波分布、幅值大小是共模电流抑制方案制定、选型的基础。而对共模电流时域和频域的分析需要建立变频器-电缆-电机系统的共模回路模型，并确定电路模型的参数，在此基础上研究电路参数对共模电流谐波分布和幅值大小的影响。
本文以一台中速永磁同步风力发电机系统的共模电流实验测试案例为基础，给出了永磁同步发电机和电缆的建模及参数的实验提取方法，将仿真和实验测试结果进行对比，验证模型的准确性。解析研究共模电流谐波分布及幅值的影响因素，并进行仿真验证。
以一台5.5 MW永磁同步风力发电机为研究对象，在地面上搭建测试平台，测试共模电压、轴电压和共模电流。变频器的开关频率为2 kHz，开关管的上升时间为2 μs，通过70 m的三相线缆驱动电机，将发电机作为电动机使用。电机空载运行。共模电流实验测试平台如图2所示，测试示意图如图3所示。
图2 实验测试平台
Fig.2 Test platform
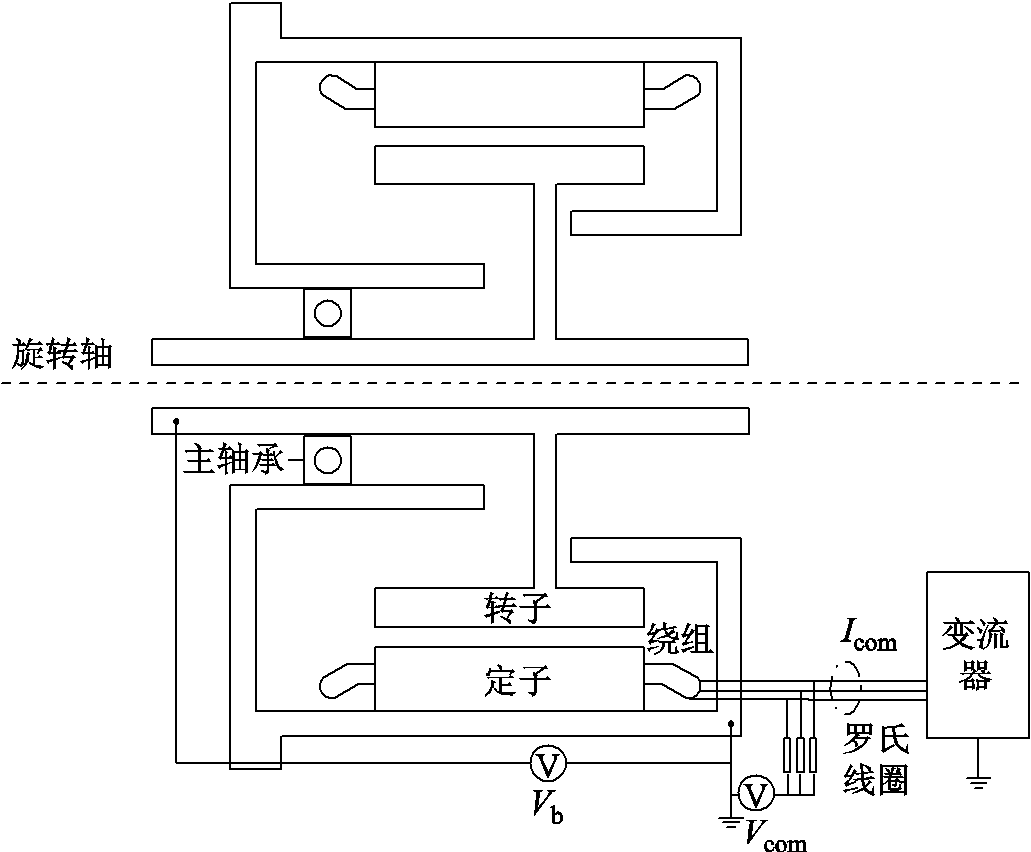
图3 实验测试示意图
Fig.3 Test diagram
电机采用星形联结。测量电机绕组中性点对机壳电压，即共模电压Vcom；罗氏线圈[19]套在三相电缆外，采用高频电流探头测量共模电流Icom。在转轴上安装毛刷，引出测量点，采用差分电压探头测量毛刷与机壳之间的电压，作为轴电压Vb。实验所采用的设备及参数见表1。
表1 测试设备信息
Tab.1 Test equipment information
设备名称型号参数 横河示波器DLM4058最高采样频率：500 MHz阻抗：1 MΩ精度：1% 电压探头VPS410最高采样频率：300 MHz精度：2%量程：1 000 Vpk DP6280最高采样频率：100 MHz精度：2%量程：2 800 Vpk 电流探头PEM 301fb量程：6 kA HCP8150带宽：DC12 MHz 阻抗分析仪WK6500B量程：10 MHz
测试时变频器母线电压为718 V、开关频率为2 kHz、电机转速为300 r/min、示波器采样频率为 125 MHz、电机为空载。测试波形如图4所示。
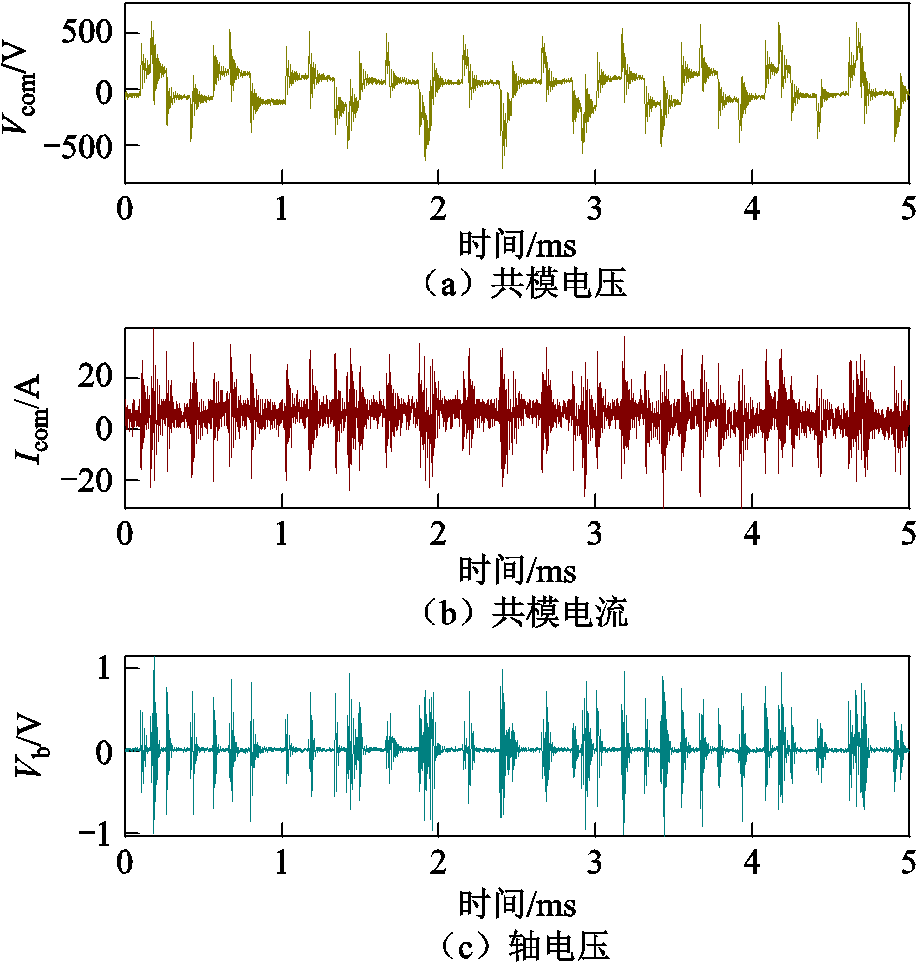
图4 测试波形
Fig.4 Test waveforms
从图4测试波形可知，共模电压振荡峰值为487 V，稳态峰值为345 V，约为母线电压（718 V）的一半。共模电流主要出现在开关动作时刻，峰峰值为74 A，轴电压与共模电流波形相似，峰峰值为2.06 V，对共模电流和轴电压进行频谱分析，如图5所示。由图5可知，共模电流和轴电压具有相同的谐波分布特性，主要谐波都集中在80 kHz附近。研究共模电流谐波分布的原因，对于抑制共模电流、改善轴电压都有一定的工程意义。
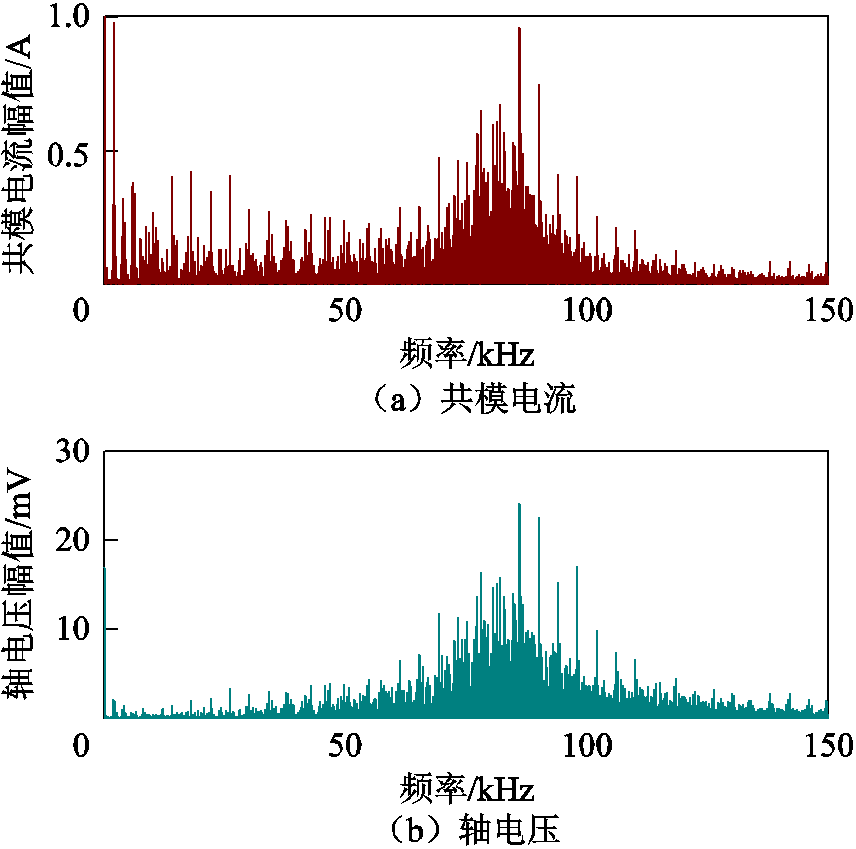
图5 共模电流和轴电压实测波形频谱图
Fig.5 Spectrum of measured waveforms of common-mode current and bearing voltage
变流器、线缆和永磁同步发电机组成的风力发电系统中，变流器输出的共模电压是共模电流产生的根源，线缆的分布参数和电机内杂散参数构成了共模回路阻抗。永磁同步发电机的杂散电容是回路的重要参数之一。本文以表贴式永磁同步发电机为研究对象，表贴式永磁同步发电机内部主要构成部件为定子绕组、定子铁心、磁极和转子铁心。磁极盒通过金属螺栓固定在转子铁心表面上，从电场角度，可以认为是由定子绕组、定子铁心、转子铁心和磁极盒构成的整体组成的三导体系统。定子绕组与定子铁心之间存在匝间绝缘、线圈绝缘、层压板、槽绝缘等介质，转子铁心及磁极盒构成的导体与定子绕组通过槽楔、垫条、槽绝缘、气隙等介质隔开，与定子铁心通过气隙隔开，因此内部主要存在三种杂散电容，分别为定子绕组与定子铁心之间的电容Cwf、定子绕组与转子铁心及磁极盒整体之间的电容Cwr、定子铁心与转子及磁极盒整体之间的电容Crf。表贴式永磁同步发电机内部杂散电容示意图如图6所示。
当发电机向变流器传输能量时，变流器产生的共模电压Vcom会施加在定子绕组中性点与地之间，共模电压通过共模电感Lcom和涡流电阻Re作用于电机内部杂散电容网络。将永磁体与转子当作一个导体时，可以参照笼型感应电机三导体系统的建模方法[20]，永磁同步发电机共模模型如图7所示。图7中，Ib为流过轴承的电流。假设电机定子接地良好，忽略定子机壳到地的接地阻抗，电机轴承润滑良好，轴承内外圈与滚道之间形成均匀油膜，本文研究的永磁同步发电机主轴承采用一个双列圆锥滚子轴承，其油膜电容用Cb表示。
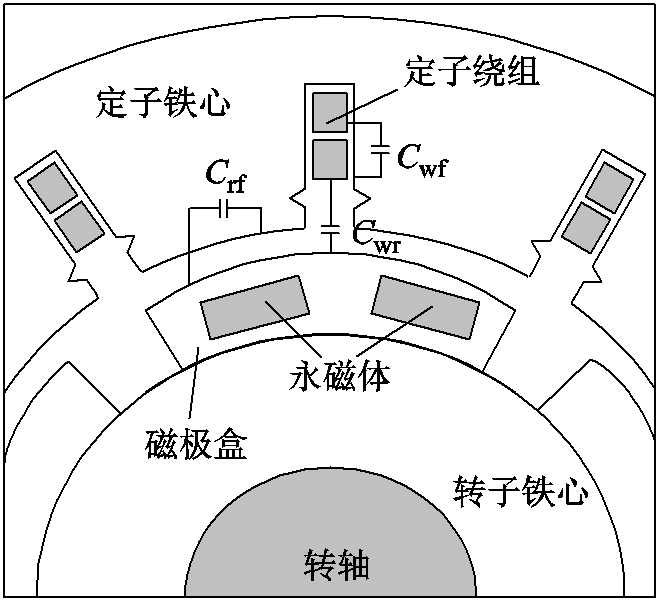
图6 表贴式永磁同步发电机内部杂散电容示意图
Fig.6 Schematic diagram of stray capacitances of surface mounted permanent magnet synchronous generator
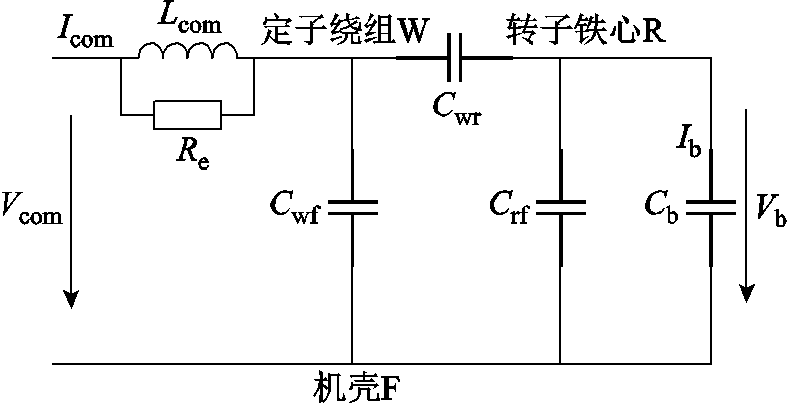
图7 永磁同步发电机共模模型
Fig.7 Common-mode model of permanent magnet generator
当轴电压Vb小于轴承润滑油膜的击穿阈值电压时，轴承上只流过较小的dv/dt容性电流；当Vb超过油膜的阈值电压时，润滑油膜将会被击穿，产生幅值较高的轴电流，润滑脂性能变差，轴承表面产生坑蚀，影响电机正常运行[21-22]。
共模模型参数获取的方法有很多，包括解析计算、有限元仿真和实验测试提取等。解析计算和有限元计算会存在一定的误差，下面主要介绍通过实验测试来提取共模电感、涡流损耗电阻和杂散电容的方法。
2.3.1 共模电感和涡流电阻的提取
根据文献[23]，为了提取共模电感和涡流损耗电阻，采用阻抗分析仪进行共模阻抗测试和差模阻抗测试。在电机静止时，将电机底部用绝缘隔离，测试定子绕组三相短接点与机壳之间的阻抗，即为共模阻抗测试，如图8a所示。测试定子绕组任意两相短接后与第三相绕组间的阻抗，即为差模阻抗测试，如图8b所示。
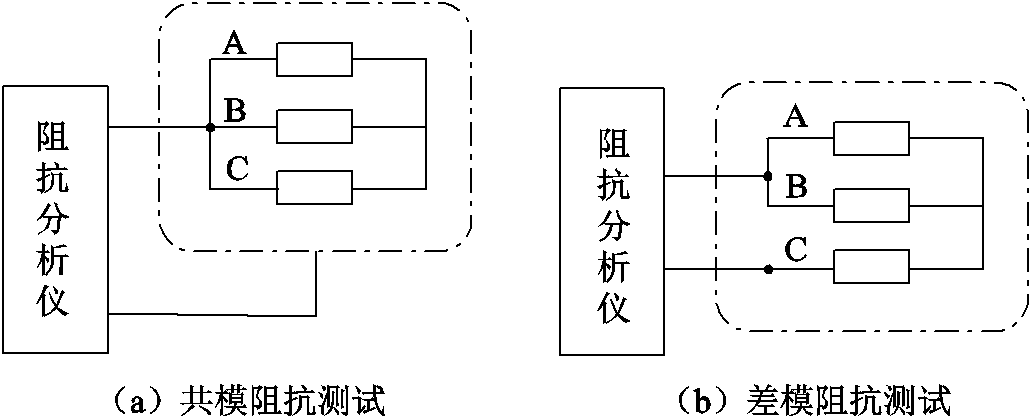
图8 发电机阻抗特性测试接线示意图
Fig.8 Wiring diagram of impedance characteristic test of the PMSG
本文实验电机的共模阻抗特性曲线和差模阻抗特性曲线如图9所示。
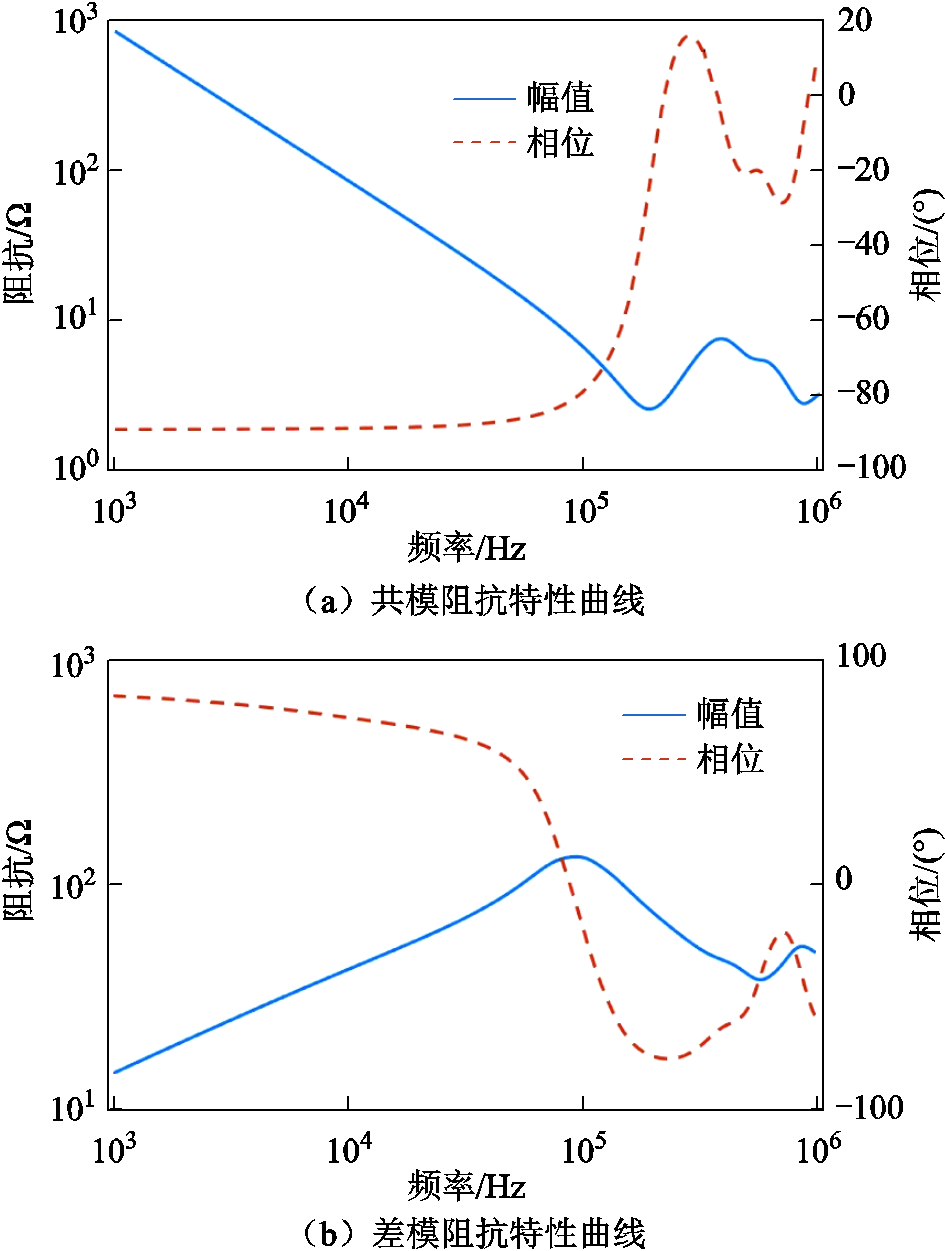
图9 永磁同步发电机的共模和差模阻抗特性曲线
Fig.9 Common-mode and differential-mode impedance characteristic curves of the PMSG
图8a中A点为低频段最接近-90°的频率点，绕组与机壳端口电容为Cwfp，可以由该点的频率fA和在A点的阻抗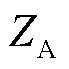
确定，即
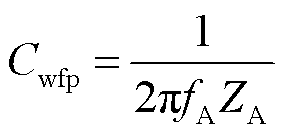（1）
在B点处，电机共模电感Lcom与低频段端口电容Cwfp发生串联谐振，利用B点处谐振频率fB可以推算出共模电感Lcom，即
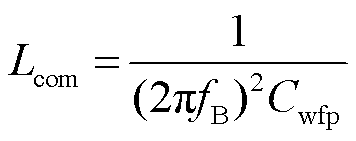（2）
在图8b中C点呈现纯阻性，电阻为Re，是共模回路的涡流电阻，可以认为是3个单相涡流电阻Re1的并联，即Re=Re1/3，而差模阻抗特性等效为两相并联后与第三相的串联，则谐振点的阻抗ZC=3Re1/2，因此涡流损耗电阻Re为
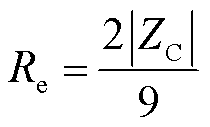（3）
通过上述测试和分析，就可以将电机共模等效电路当中的共模电感Lcom和涡流损耗电阻Re提取出来。A、B和C三点的数据见表2。
表2 A、B和C三点数据
Tab.2 Data of A, B and C
频率/kHz幅值/Ω相位/（°） A3.79253.15-89.58 B221.752.820 C95.309154.460
根据表2中数据，计算得到的绕组与机壳之间的端口电容Cwfp＝197.28 nF，共模电感Lcom＝2.77 μH。涡流损耗电阻Re＝34.32 Ω。
2.3.2 电机杂散电容的提取
在电机静止时，转子与机壳通过轴承短路，这样是无法测量电机轴承的，参考笼型电机电容测试的方法[20]，在电机静止时，通过采用绝缘端盖的方法将转子与机壳分离，达到测试电容的目的，采用LCR表测量三相绕组短接点“W”、转子“R”和机壳“F”两两之间的端口电容Cwrp、Crfp和Cwfp。此时，电机端口等效电路如图10所示。
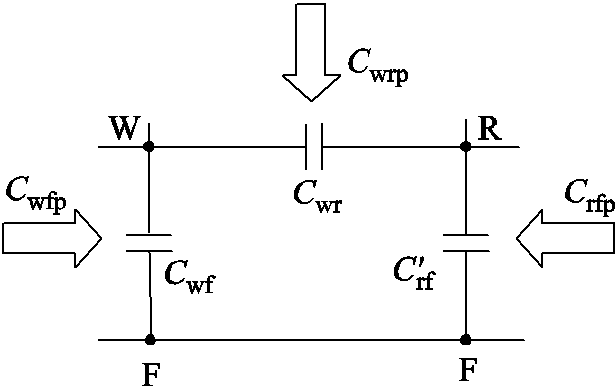
图10 端口电容等效电路
Fig.10 Equivalent circuit of port capacitance
图10中，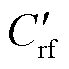
为转子与机壳之间的电容Crf与绝缘端盖的电容Ciso并联后的等效电容。根据端口等效电路，可得永磁同步发电机的内部杂散电容与端口电容的关系为
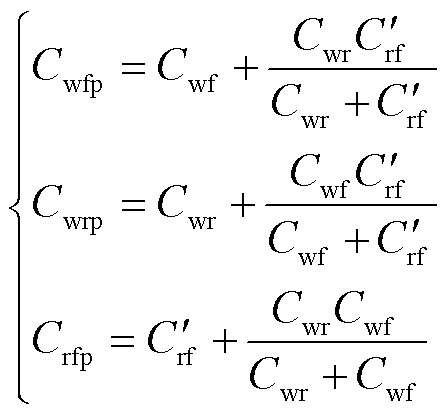（4）
联立求解式（4）中的3个公式，可以得到电机内部的杂散电容。
通过上述测试和提取参数的方法，可以获得电机共模回路当中的所有主要的分布电容和分布电感的参数值。
不论是海上风电还是陆上风电，风机安装在高高的塔架上，线缆长度越来越长。对电缆的建模也非常重要，建立如图11所示的电缆共模等效模型[24]。图11中，Lcab1、Lcab2为电缆串联电感，Rd1、Rd2为电缆串联电阻，Ccab1、Ccab2为电缆对地电容。
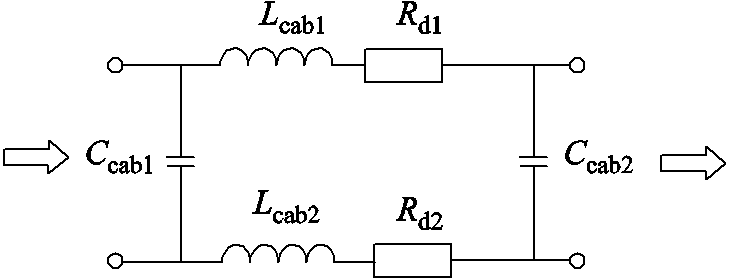
图11 电缆共模等效模型
Fig.11 Common-mode equivalent model of cable
考虑到电流在电缆中传输的特点，电流总是从一根线缆流出，从另外两根电缆流回，即两相并联后再与另一相串联，可以采用测量电缆开路阻抗和短路阻抗的方式获得电缆的阻抗特性。电缆模型的参数可以通过测量到的开路阻抗特性和短路阻抗特性计算得到。采用阻抗分析仪对电缆进行测试，测试方式如图12所示。
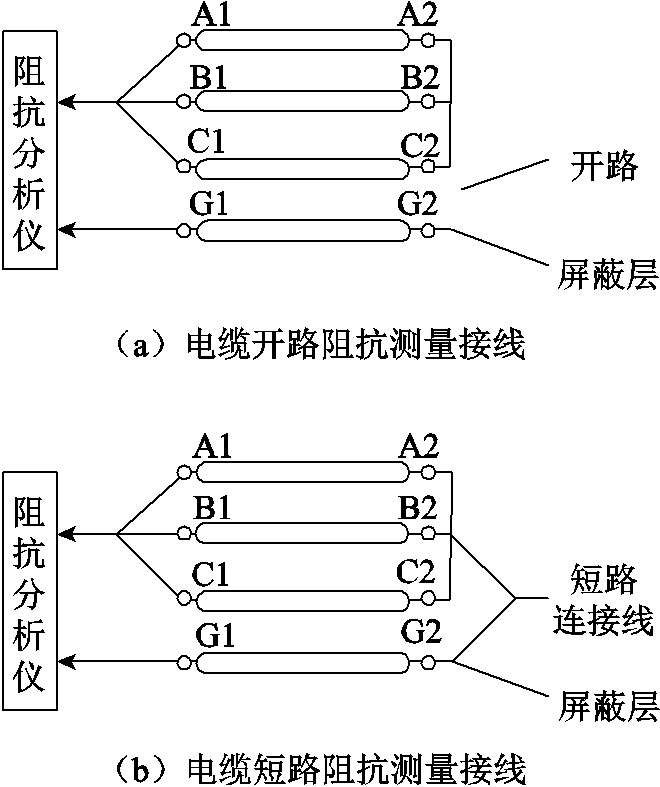
图12 电缆开路阻抗和短路阻抗测量接线
Fig.12 Wiring diagram of characteristic test
分别测量电缆的开路阻抗特性和短路阻抗特性，如图13所示。
在D点，相位接近-90°，近似呈现纯容性，频率为fD，阻抗为ZD，可得电缆对地电容为
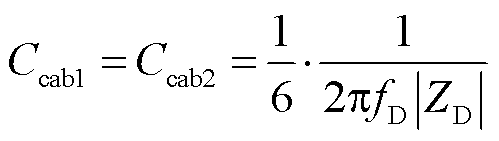（5）
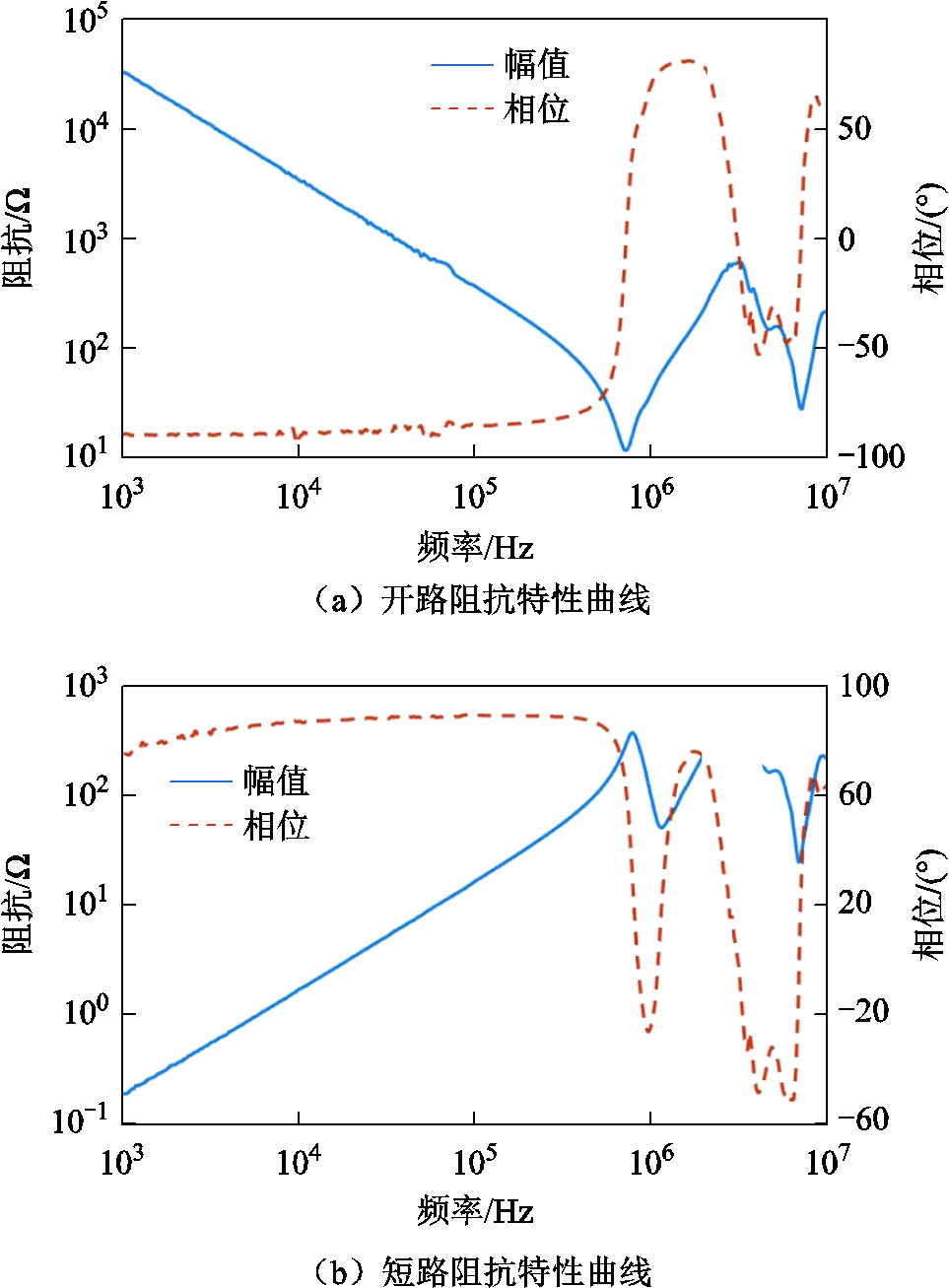
图13 电缆的开路和短路阻抗特性曲线
Fig.13 Open-circuit and short-circuit impedance characteristic curves of cable
在E点，相位接近0°，近似呈现纯阻性，阻抗为ZE，则线缆串联电阻为
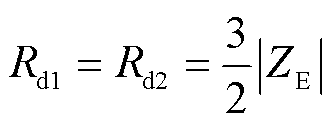（6）
在F点，相位接近90°，近似呈现纯感性，阻抗为ZF，频率为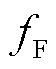
，线缆的串联电感为
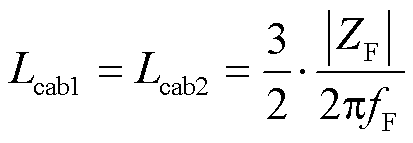（7）
为了方便分析，将Ccab1和Ccab2、Rd1和Rd2、Lcab1和Lcab2分别合并，得到电缆共模等效简化模型如图14所示。图14中，Lcab=2Lcab1、Rd=2Rd1、Ccab=2Ccab1。
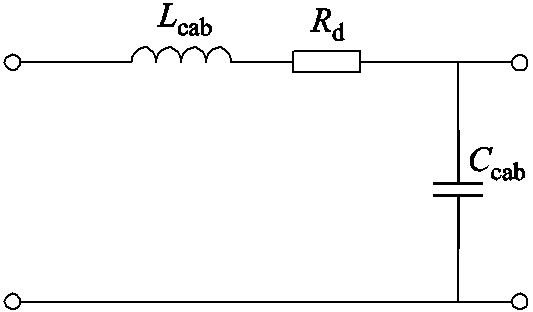
图14 电缆共模等效简化模型
Fig.14 Common-mode equivalent simplified model of cable
第2节介绍了共模系统模型的建立以及参数提取方法，为了进一步验证模型的准确性，在Matlab/ Simulink中搭建了如图15所示的共模通路仿真模型。在电机转速为300 r/min时，测试发现，油膜未完全形成，轴承电阻近似呈现阻态，电阻大约为50 Ω，推测是本实验没有安装齿轮传动系统，破坏了油路，所以没有形成润滑油膜。采用伏安法测量轴承阻抗，阻值大约为50 Ω，所以用阻值为50 Ω的电阻取代图7模型中的轴承电容Cb进行仿真。
图15 共模通路仿真模型
Fig.15 Common-mode simulation model
仿真模型由变频器模块、电缆模块及电机模块组成，系统的共模激励由线缆三相短接点输出的机侧共模电压提供。
根据实验测试，按照第2节方法处理，得到系统电路的参数见表3。
表3 系统电路参数
Tab.3 Parameter of the circuit
参数数值 电缆串联电感Lcab/μH16.05 电缆串联电阻Rd/Ω0.26 电缆对地电容Ccab/nF15.75 电机共模电感Lcom/μH2.77 电机涡流电阻Re/Ω34.32 定子绕组与定子铁心之间的电容Cwf/nF196.94 定子绕组与转子铁心及磁极盒整体之间的电容Cwr/nF0.35 定子铁心与转子及磁极盒整体之间的电容Crf/nF6.17 轴承油膜等效电容Cb/nF2.60
仿真得到共模电压、共模电流、轴电压，与实测波形进行对比，结果如图16所示。
从图16可以看出，仿真波形与测试波形能够较好地吻合，共模电压、共模电流、轴电压在IGBT器件开关动作处的波形振荡幅度基本一致。
共模电流和轴电压仿真波形频谱图如图17所示。对比图17和图5，由仿真和实测的共模电流和轴电压的频谱图可知，二者谐波分布基本一致，主要谐波都集中分布在80 kHz附近。综合时域和频域波形，验证了所建立模型的准确性。
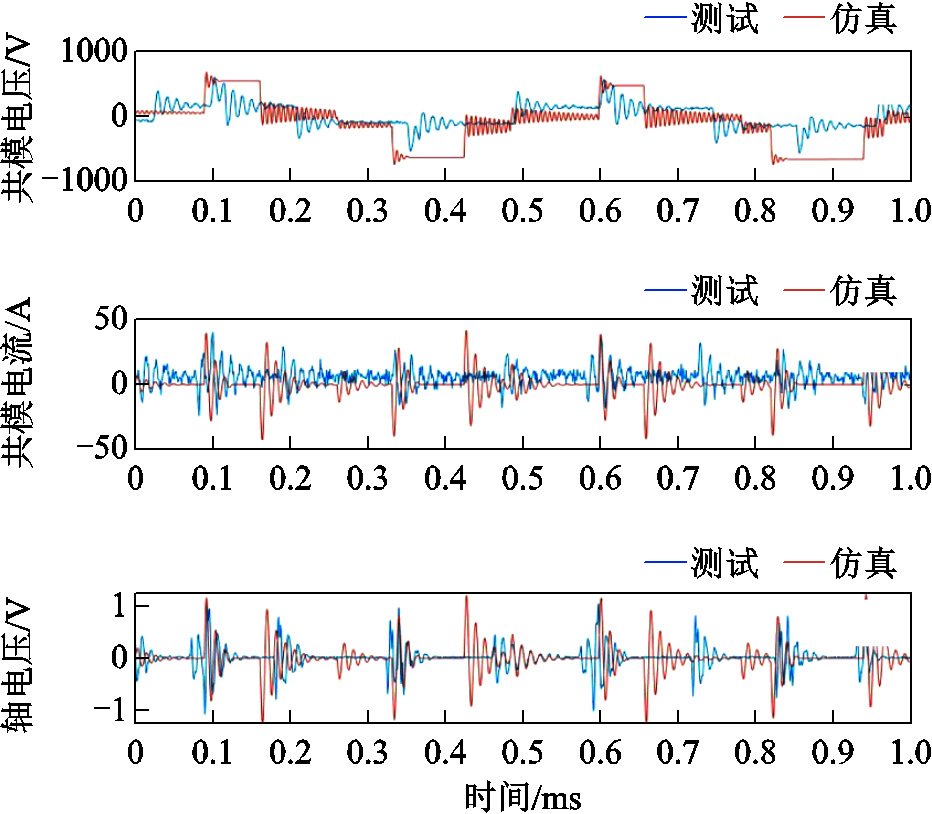
图16 仿真和实测波形对比
Fig.16 Comparison between simulated waveform and measured waveform
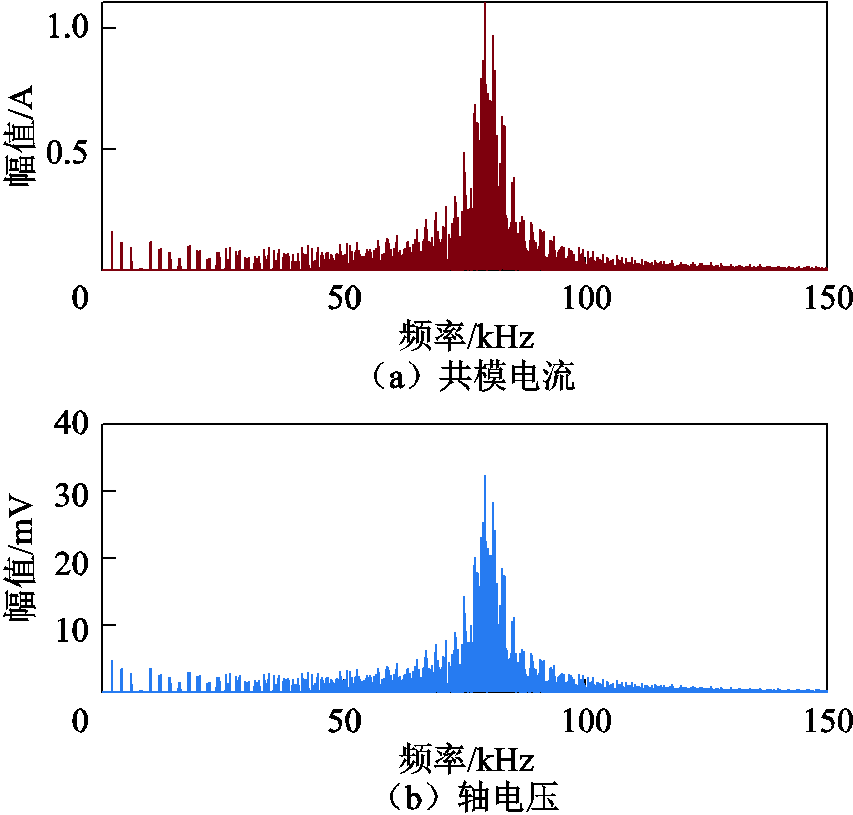
图17 共模电流和轴电压仿真波形频谱图
Fig.17 Spectrum diagram of common-mode current and shaft voltage simulation waveform
根据文献[10-11,15]，共模回路参数和开关管上升时间对共模电流有着重要影响，下面以二者作为研究对象，定量研究其对共模电流的影响。
从实测的共模电流和轴电压的频谱图中可以看出，共模电流和轴电压的谐波主要分布在60～100 kHz范围内，结合文献[10]提到的共模回路中的分布电感和分布电容之间的谐振是造成共模电流和辐射超标的主要原因，因此这种谐波分布特点有可能是电路谐振造成的，为了验证这个猜想，进行下面的分析。
根据2.3.1节可知，在频率范围第一个谐振点前的电机共模端口特性主要是由绕组与机壳的端口电容Cwfp和共模电感Lcom决定的，因此在该带宽下，可以近似用这两个元器件来代替电机共模模型。则电缆电机简化模型如图18所示。
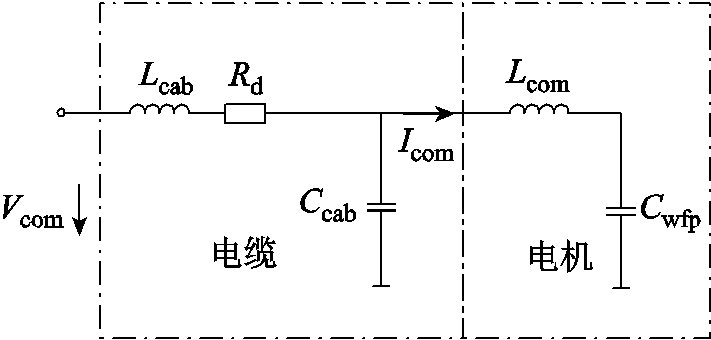
图18 共模回路简化模型
Fig.18 Common-mode simplified model
实际中，电缆对地电容Ccab远小于定子绕组与定子机壳之间的杂散电容Cwfp。为了方便计算，可以忽略，则电缆与电机的谐振频率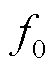
为
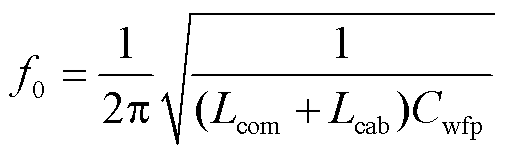（8）
将表3数据代入式（8），可以求得电路系统的谐振频率为82.60 kHz。仿真得到的其电缆-电机端口的阻抗特性曲线如图19所示。
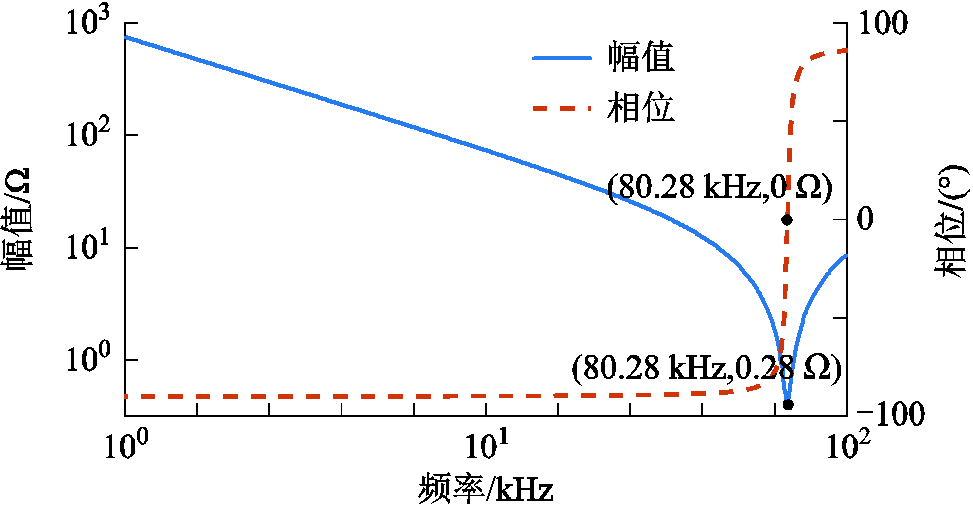
图19 电缆-电机共模端口阻抗特性曲线
Fig.19 Cable-motor common-mode port impedance characteristic curves
从共模等效电路的阻抗特性曲线中可知电路端口的谐振频率为80.28 kHz，以此为参考，根据式（8）计算的谐振频率的相对误差为2.90%。
进一步检查式（8）的可行性，分别改变Lcab、Cwfp和Lcom的参数，绘制通过式（8）计算以及通过模型扫频两种方法得到的谐振频率随参数变化的曲线，如图20所示。
在误差允许范围内，可以认为通过公式计算和模型扫频两种方法获得的谐振频率随参数变化在数值和趋势上基本一致，因此证明可以通过式（8）近似估算电缆-电机等效电路的谐振频率。
同时，当改变不同参数，共模电流的波形谐波分布集中频率与模型谐振频率基本一致，因此证明谐振是影响电缆-电机系统共模回路高频谐波分布的关键因素。根据式（8），可以得到影响系统共模回路高频谐振点的主要因素是：线缆等效电感Lcab、电机共模电感Lcom和电机绕组与机壳的端口电容Cwfp。
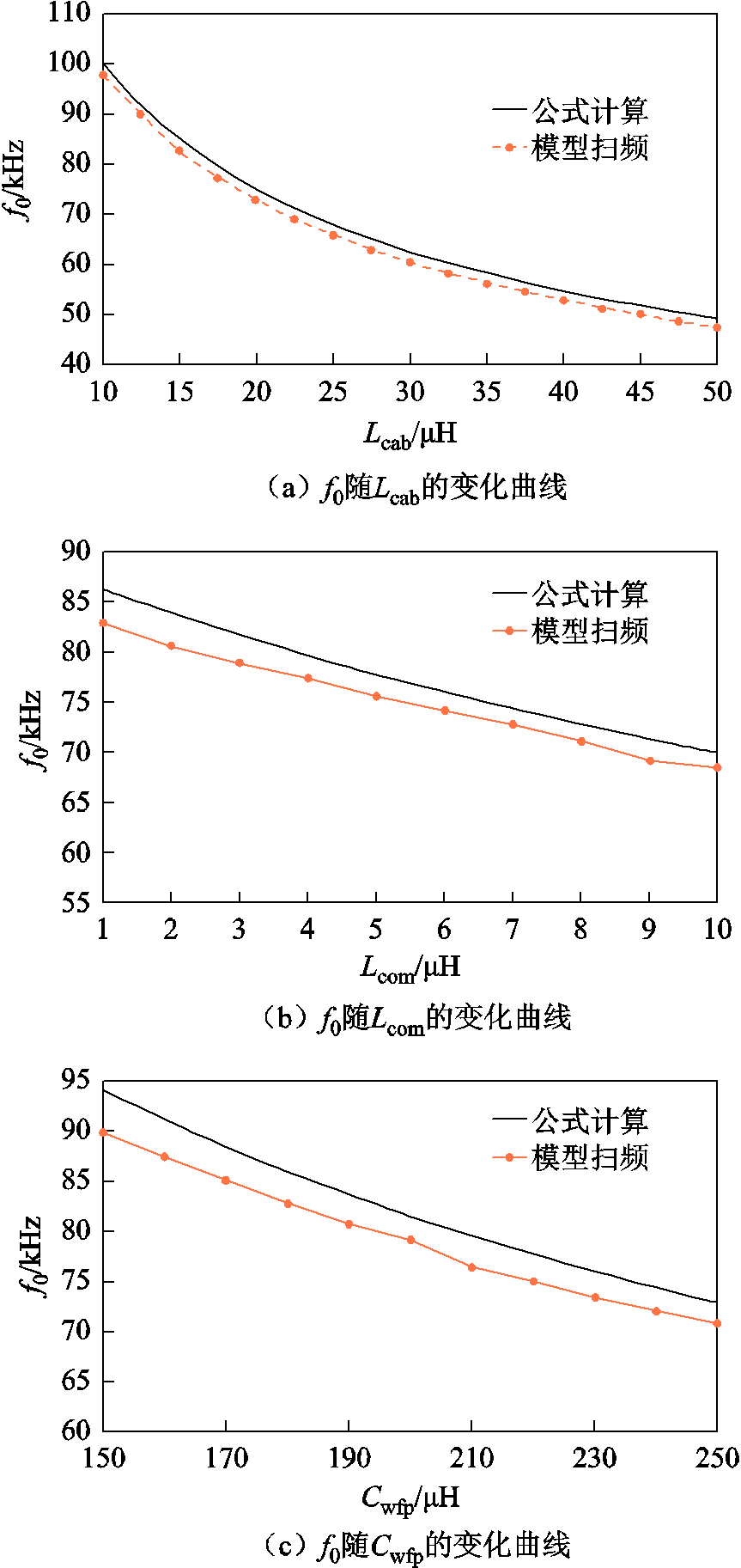
图20 两种方式下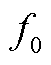
随不同参数变化的曲线
Fig.20 Curves of 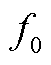changing with different parameters in two ways
按照文献[15]，开关管上升时间对于共模电压有着重要影响，共模电压作用于共模回路，产生共模电流，上升时间也应该与共模电流有关，下面研究开关管上升时间对共模电流的影响。
为了研究变流器开关管不同上升时间对共模电流的影响，对系统做了如下简化，将电缆与电机简化为RLC串联电路，共模电压上升时间与下降时间相同，简化为梯形波，电路模型如图21所示。图21中，Vcom为将共模电压等效后的梯形波源，L为等效串联电感，R为等效串联电阻，C为等效串联电容。
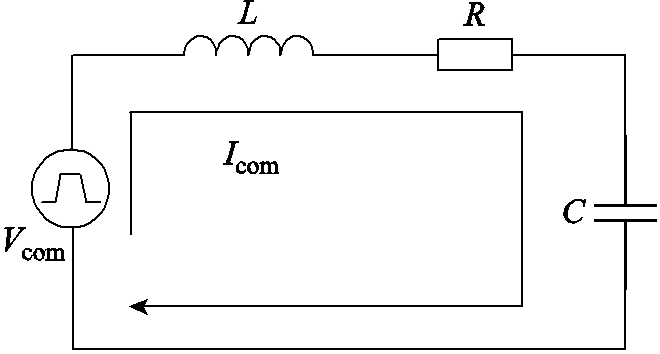
图21 共模电路简化模型
Fig.21 Simplified model of common-mode circuit
对于周期为T，幅值为A，上升时间为tr的梯形波，波形如图22所示。
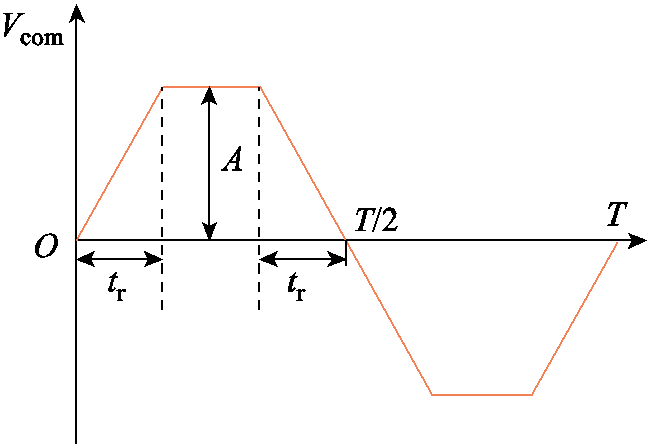
图22 梯形波波形
Fig.22 Trapezoidal waveform
在区间[0,T/2]的函数表达式为
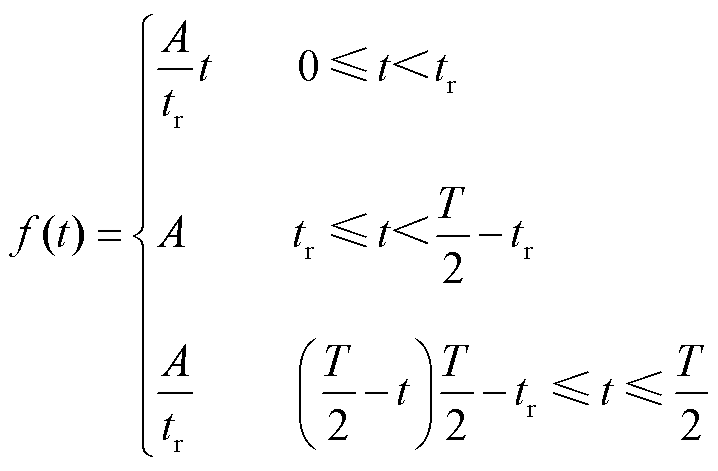（9）
根据奇偶性，该波形在区间[-T/2,T/2]的傅里叶级数展开式为
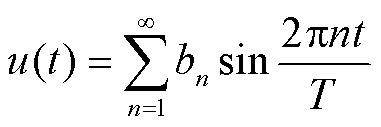（10）
其中，傅里叶级数系数bn为
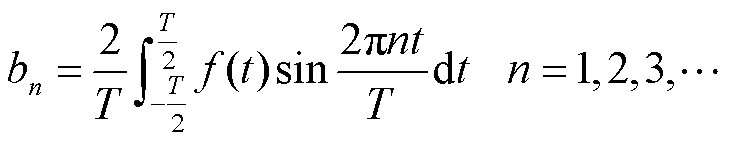（11）
代入式（9）化简得
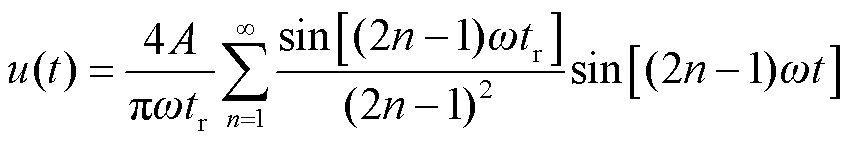（12）
当角频率为(2n-1)ω时，其中，ω=2π/T，该频率分量的电压相量形式为
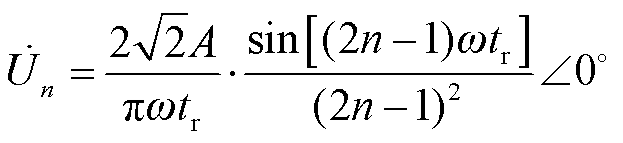（13）
该频率下电路阻抗为
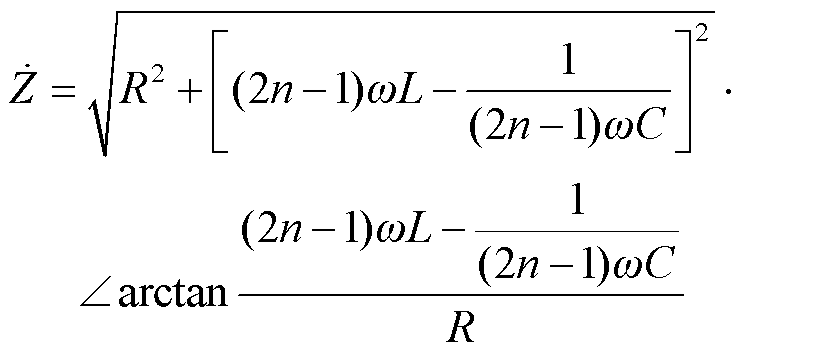(14)
该频率分量下的电流为
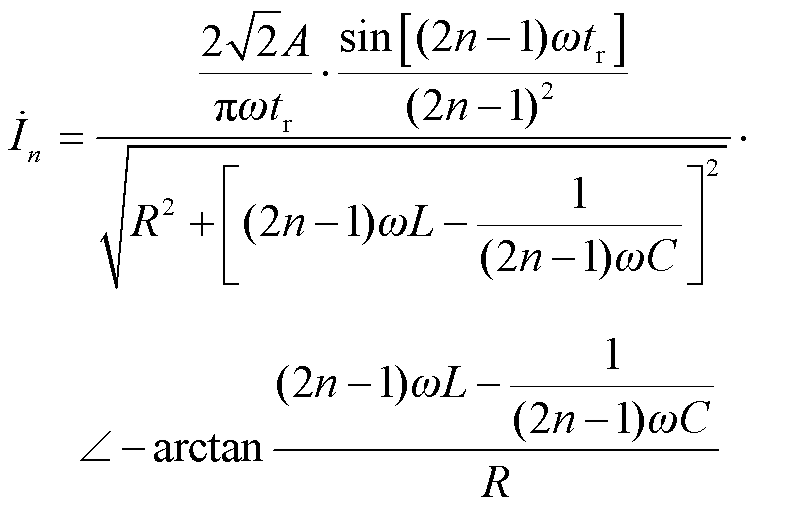(15)
n次谐波频率下电流的模值In与频率的关系为
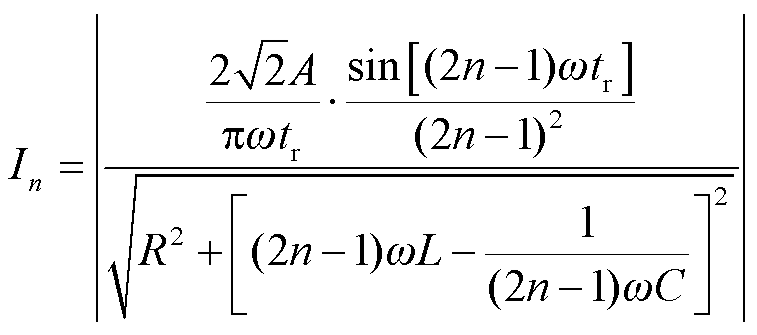（16）
仅以上升时间作为变量，tr通常特别小（对于本实验用到的开关频率为2 kHz的变流器，上升时间仅有2 μs），当谐波次数n较低时，(2n-1)ωtr趋向于0，根据极限的定义，式（17）的值为1。
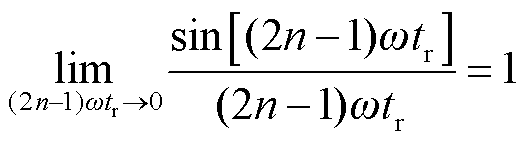（17）
此时，有
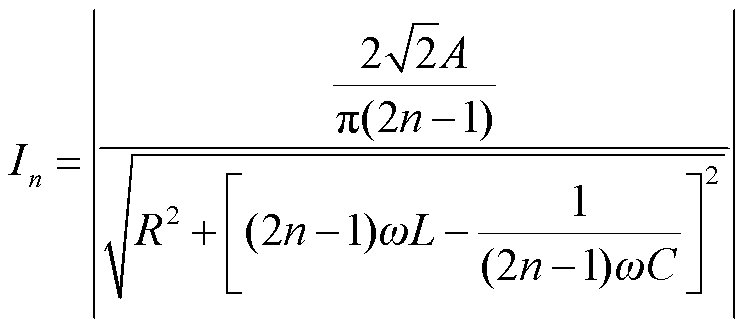（18）
根据式（17）和式（18）可知，在较低频域范围内，电流分量与上升时间无关。
当频率较高时，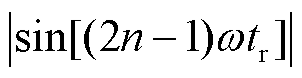
在区间[0,1]内变动，当tr在比较小的范围内变化时，可认为sin[(2n-1)ωtr]不变，则有
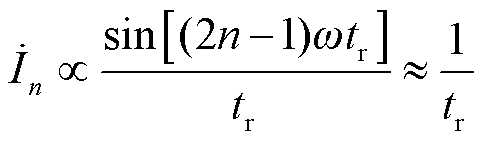（19）
从式（19）可得，在较高频率时，电流与上升时间近似成反比，又因为共模电流主要是由高频谐波构成的，电流在各个频域内属于叠加关系，因此共模电流与上升时间也近似成反比关系。
为了验证推导的支路电流与上升时间的关系的准确性，以峰峰值为10 V，不同上升时间的梯形波作为激励，代入图15中的模型，仿真共模电流的频谱图如图23所示。限于篇幅，仅展示了部分上升时间共模电流的频谱图。
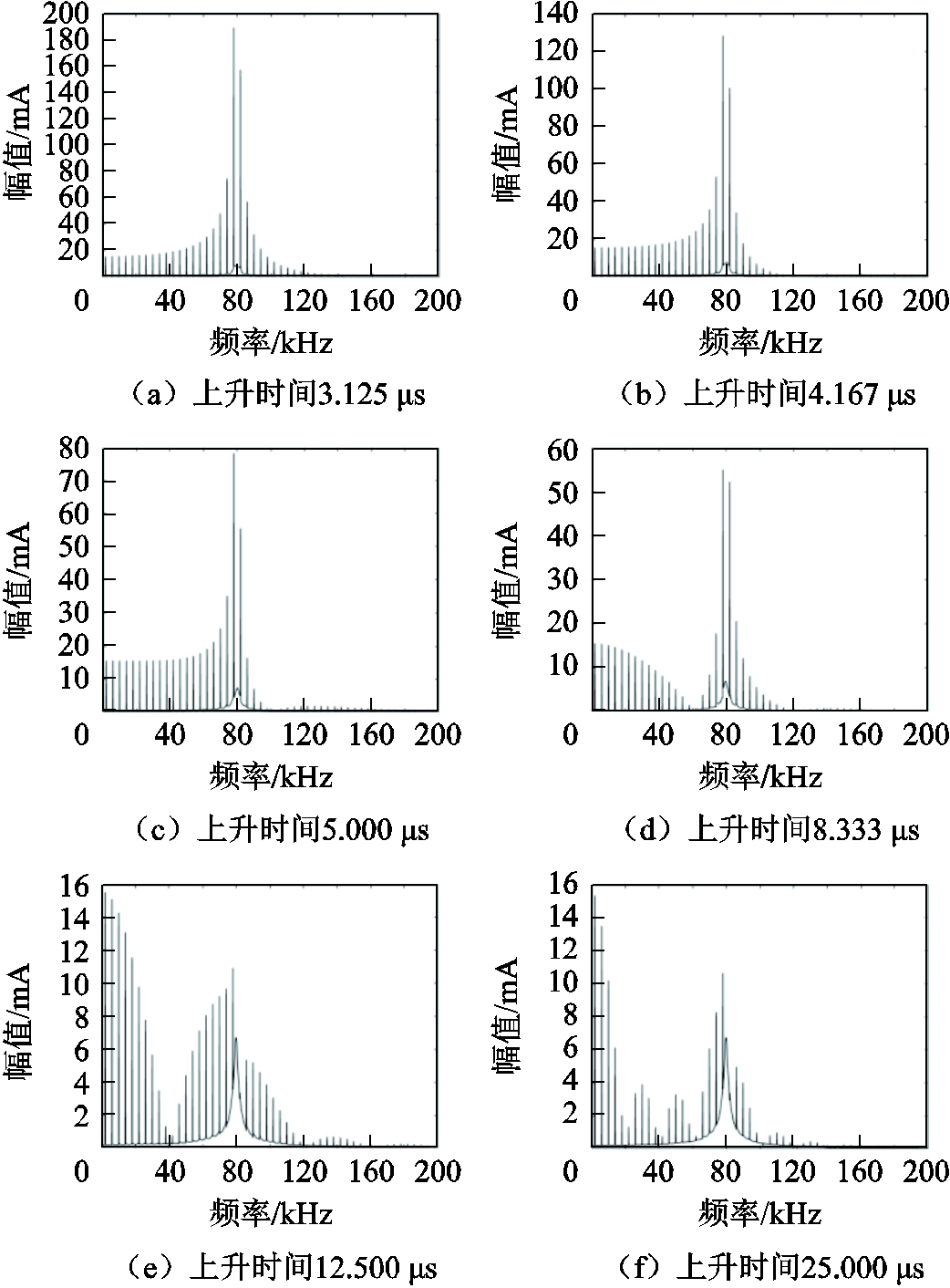
图23 不同上升时间共模电流的频谱图
Fig.23 Spectrum of common-mode current at different rising times
观察图23不同上升时间的共模电流的频域波形可知，在低频段，不同上升时间对应的共模电流的分量都在16 mA附近，因此可以说明上升时间对共模电流的低频分量影响不大。
同时，随着上升时间由3.125 μs增加到25 μs，在谐振频率附近的共模电流分量幅值大约由0.2 A减小到0.01 A，且当上升时间比较小时，变化十分明显。
记录不同上升时间下的共模电流峰峰值，同时采用反比例函数进行拟合，将二者放在一起，结果如图24所示。
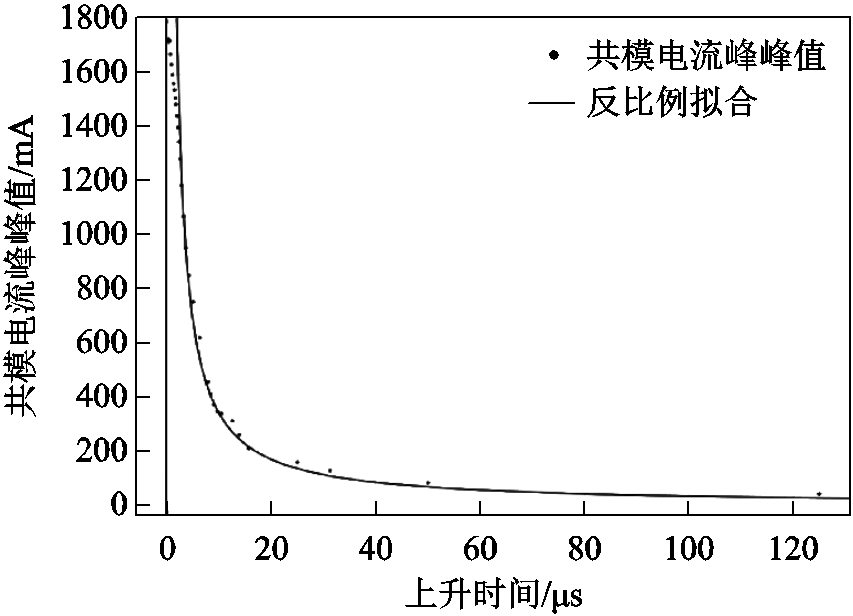
图24 共模电流峰峰值随上升时间的变化曲线
Fig.24 Variation curve of peak-to-peak value of common-mode current with rising time
由图24可知，不同上升时间对应的共模电流峰峰值与反比例函数高度拟合，因此可以说明共模电流峰值与开关管上升时间成反比例变化。
通过上述仿真也可以说明，随着开关管上升时间的减小，共模电流高频谐波分量的幅值上升，对整个系统有着很大的负面影响。
针对风力永磁发电系统共模电流带来的负面问题，本文给出了一种永磁同步发电机系统共模回路的建模及参数提取方法，为了验证模型的准确性，搭建了永磁同步发电机共模电流测试平台，根据测试结果与仿真结果的对比，证明了仿真模型的有效性。在仿真模型基础上，进一步开展了共模电流的谐波分布以及幅值的影响因素研究。通过解析推导和仿真验证相结合的形式，得到以下结论：
1）确定了共模电流的谐波集中处频率的计算方法，指出该频率是由系统分布参数的谐振点决定的，由电机和电缆的共模阻抗共同决定。
2）将电缆及电机系统简化为RLC串联电路，证明了共模电流在低频分量与开关管上升时间无关，在高频率分量幅值与上升时间成反比。
3）由于共模电流主要是由高频谐波构成的，忽略低频谐波，共模电流的峰峰值近似与上升时间成反比。
因此，通过合理调整线缆的参数，或者加装滤波器装置等，原理上可以使得系统的谐振点向低频迁移，从而有效降低共模电流的高频分量。同时，上升时间与共模电流的峰峰值成反比，在满足开关频率等性能的基础上，合理选用采用较大上升时间的开关管的变流器可以有效降低共模电流的幅值。
参考文献
[1] 崔鹤松, 李雪萍, 黄晟, 等. 模块化多相永磁风力发电机串并联直流海上风电场电压协调控制[J]. 电工技术学报, 2023, 38(4): 925-935. Cui Hesong, Li Xueping, Huang Sheng, et al. Voltage coordination control of modular multiphase permanent magnet wind turbine series-parallel DC offshore wind farm[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 925-935.
[2] Svimonishvili T, Fan Fei, See K Y, et al. High-frequency model and simulation for the investigation of bearing current in inverter-driven induction machines[C]//2016 IEEE Region 10 Conference (TENCON), Singapore, 2017: 55-59.
[3] 贾磊, 刘瑞芳, 王芹芹. 变频驱动感应电机轴电流问题中端部杂散电容的解析计算[J]. 电机与控制学报, 2022, 26(8): 30-39. Jia Lei, Liu Ruifang, Wang Qinqin. Analytical calculation of stray capacitance of motor end in bearing current problem of induction motor driven by frequency convertor[J]. Electric Machines and Control, 2022, 26(8): 30-39.
[4] 王芹芹, 刘瑞芳, 任雪娇. 基于多物理场分析的电机轴承放电击穿[J]. 电工技术学报, 2020, 35(20): 4251-4257. Wang Qinqin, Liu Ruifang, Ren Xuejiao. Discharge breakdown of motor bearings based on multi-physical field analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4251-4257.
[5] 季学平, 白洁. 磁环滤波器在双馈风电机发电机轴承电磁干扰处理中的应用[C]//第八届中国风电后市场交流合作大会论文集, 包头, 2021: 160-167.
[6] 牟金善. 一种海上风电机组变流器共模电流干扰的抑制方法[J]. 电气应用, 2021, 40(5): 76-81, 106. Mou Jinshan. Suppression method of common-mode current interference of offshore wind turbine converter[J]. Electrotechnical Application, 2021, 40(5): 76-81, 106.
[7] 张洪亮, 张子成, 陈杰, 等. 自适应三次谐波注入的回接型LCL光伏逆变器共模谐振电流抑制方法[J]. 电工技术学报, 2023, 38(1): 220-233. Zhang Hongliang, Zhang Zicheng, Chen Jie, et al. Common-mode resonance current suppression method of self-adaptive third harmonic injection for tieback LCL photovoltaic inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 220-233.
[8] 胡烽, 孙宏博, 蒋栋, 等. 基于四相全桥的磁悬浮轴承开关器件开路故障容错控制策略[J]. 电工技术学报, 2022, 37(9): 2295-2305, 2340. Hu Feng, Sun Hongbo, Jiang Dong, et al. Fault-tolerant control strategy for open circuit fault of switching devices of magnetic bearing based on four-phase full bridge[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2295-2305, 2340.
[9] 张开颜, 王世山, 李孟子, 等. 基于容性参数等效的功率变换器系统电磁辐射预估方法及抑制措施[J]. 电工技术学报, 2021, 36(2): 235-247. Zhang Kaiyan, Wang Shishan, Li Mengzi, et al. Method of electromagnetic radiation prediction and suppression based on capacitance parameter equivalence in power converter system[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 235-247.
[10] 黄勇, 陈全世, 陈伏虎. 电动汽车共模电流抑制方法的研究[J]. 高技术通讯, 2008, 18(11): 1206-1210. Huang Yong, Chen Quanshi, Chen Fuhu. A method for attenuation of common-mode current in electric vehicles[J]. Chinese High Technology Letters, 2008, 18(11): 1206-1210.
[11] Cao Shiran, Niu Feng, Huang Xiaoyan, et al. Time–frequency characteristics research of common mode current in PWM motor system[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1450-1458.
[12] 薛利晨. 变频驱动电机轴承电腐蚀的预防和测试方法研究[J]. 大电机技术, 2020(4): 45-51. Xue Lichen. The research and analysis on the prevention and test method of electric corrosion of converter driven motor bearing[J]. Large Electric Machine and Hydraulic Turbine, 2020(4): 45-51.
[13] 刘瑞芳, 孟延停. 表贴式与内置式永磁同步风力发电机的轴电流模型对比分析[J]. 北京交通大学学报, 2017, 41(2): 106-111. Liu Ruifang, Meng Yanting. Comparison analysis of bearing currents model in surface mounted and built-in permanent magnet synchronous wind generators[J]. Journal of Beijing Jiaotong University, 2017, 41(2): 106-111.
[14] 刘瑞芳, 孟延停, 任雪娇, 等. 直驱式永磁同步风力发电机轴电流问题分析[J]. 电机与控制学报, 2019, 23(8): 43-49. Liu Ruifang, Meng Yanting, Ren Xuejiao, et al. Analysis of bearing currents of the direct-drive permanent magnet synchronous wind generators[J]. Electric Machines and Control, 2019, 23(8): 43-49.
[15] 严云帆. 变频传动系统电机侧共模干扰研究及其对通讯系统的影响分析[D]. 杭州: 浙江大学, 2016.
[16] 刘从来, 张善刚, 陈晨. 共轭磁环用于双馈风力发电机组共模电流抑制的研究[J]. 山东电力技术, 2020, 47(4): 63-67. Liu Conglai, Zhang Shangang, Chen Chen. Application of conjugate magnetic rings in common mode current suppression of doubly fed wind turbines[J]. Shandong Electric Power, 2020, 47(4): 63-67.
[17] 孟延停. 永磁同步风力发电机轴电流与共模电流的分析与抑制[D]. 北京: 北京交通大学, 2017.
[18] 王晨. 双馈风力发电系统电磁兼容设计[D]. 上海: 上海电机学院, 2016.
[19] Jin Hui, Yang Libin, Gan Jiatian, et al. Risk assessment of grid frequency deviation related to correlation considering wind speed and wind direction in a wind farm[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 2018: 1-5.
[20] 刘瑞芳, 陈嘉垚, 马喜平, 等. 基于PWM逆变器供电轴电流问题的交流电机耦合电容的计算与测量[J]. 电工技术学报, 2014, 29(1): 60-67. Liu Ruifang, Chen Jiayao, Ma Xiping, et al. Calculation and measurement of coupling capacitances in AC motors based on bearing currents problem induced by PWM inverters[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 60-67.
[21] 赵方伟, 王秀和, 赵文良, 等. 内置式永磁同步发电机动态偏心故障下的轴电压解析分析和削弱[J]. 电工技术学报, 2022, 37(4): 837-848. Zhao Fangwei, Wang Xiuhe, Zhao Wenliang, et al. Analysis and reduction of shaft voltage in interior permanent magnet synchronous motors under dynamic eccentricity fault[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 837-848.
[22] Muetze A, Binder A. Calculation of motor capacitances for prediction of the voltage across the bearings in machines of inverter-based drive systems[J]. IEEE Transactions on Industry Applications, 2007, 43(3): 665-672.
[23] 赵秦聪, 杨二乐, 刘瑞芳, 等. 一种变频供电感应电机高频轴电流建模方法[J]. 中国电机工程学报, 2021, 41(23): 8139-8148. Zhao Qincong, Yang Erle, Liu Ruifang, et al. Modeling of high frequency bearing currents of induction motors powered by frequency converters[J]. Proceedings of the CSEE, 2021, 41(23): 8139-8148.
[24] Ran L, Gokani S, Clare J, et al. Conducted electromagnetic emissions in induction motor drive systems. II. frequency domain models[J]. IEEE Transactions on Power Electronics, 1998, 13(4): 768-776.
Abstract When the permanent magnet synchronous wind turbine supplies power to the power grid through the converter, the high-frequency common-mode current generated by the converter will bring serious electromagnetic interference and bearing electrical corrosion problems. By studying the spectrum distribution of common-mode current and the influencing factors of its amplitude, the harmonic distribution of common-mode current can be artificially changed according to the needs, and the amplitude of common-mode current can be controlled within a reasonable range, thus reducing the negative effects of common-mode current on the system. In this paper, the 5.5 MW permanent magnet synchronous wind turbine system is taken as the object to carry out measurement and simulation analysis, and a common-mode loop model modeling method and parameter determination method of converter-cable-motor are put forward, and the decisive factors of common-mode current resonance frequency and influencing factors of amplitude are quantitatively analyzed and simulated.
Firstly, the common-mode test platform of wind-driven permanent magnet synchronous motor is built to collect common-mode voltage, common-mode current and bearing voltage waveforms. Through the port impedance test method, the stray capacitances, common-mode inductance, eddy current resistance and cable parameters in the motor are extracted. The common-mode equivalent circuit model of permanent magnet synchronous wind turbine system is established. The model is simulated and analyzed, and compared with the measured results in time domain and frequency domain, which proves the effectiveness of the simulation circuit and parameter extraction method. Then, based on the above circuit model, the determinants of common-mode current amplitude and harmonic distribution are studied, and the frequency determinants of common-mode current harmonic concentration are deduced and verified by simulation. The common-mode voltage is simplified as a trapezoidal wave with rise time of tr, and the common-mode circuit is simplified as a RLC series circuit. The relationship between the rise time of inverter switch and the amplitude of common-mode current is deduced analytically and verified in the original cable-motor simulation model.
The results show that the three key parameters that affect the harmonic distribution of common-mode current are equivalent inductance of cable, common-mode inductance of motor and capacitance between motor winding and casing, which determine the distribution of resonance frequency of common-mode current. The simulation results of common-mode current amplitude and switching rise time show that the low-frequency component of common-mode current has nothing to do with the rise time, and the high-frequency component of common-mode current is approximately inversely proportional to the rise time. Because the common-mode current is mainly composed of high-frequency components, the simulation results show that the curve of the amplitude and rise time of common-mode current has a good fitting relationship with the inverse proportional function, which verifies the above inference.
Through the above analysis, we can draw the following conclusions: the frequency of harmonic concentration of common-mode current in permanent magnet synchronous wind turbine system is determined by the common-mode impedance of motor and cable; The peak-to-peak value of common-mode current is approximately inversely proportional to the switching rise time. By adjusting the parameters of the cable or installing a filter device, the resonance point of the system can be shifted to low frequency, thus effectively reducing the high frequency component of the common-mode current. At the same time, on the basis of satisfying the switching frequency and other properties, the amplitude of common-mode current can be effectively reduced by choosing a switching tube with a long rise time.
keywords：Permanent magnet synchronous generators (PMSG), common-mode current, harmonic distribution, amplitude
DOI:10.19595/j.cnki.1000-6753.tces.L10097
中图分类号：TM32
中央高校基本科研业务费专项资金（2021YJS149）和北京市自然科学基金（3222055）资助项目。
收稿日期 2023-01-09
改稿日期 2023-02-22
贾 磊 男，1997年生，硕士，研究方向为电磁场理论及数值计算。E-mail：20121446@bjtu.edu.cn
刘瑞芳 女，1971年生，教授，博士生导师，研究方向为电磁场理论及数值计算。E-mail：rfliu@bjtu.edu.cn（通信作者）
（编辑 崔文静）