0 引言
雷击是输电线路发生跳闸的主要原因且危害较大[1-4]。云南电网统计资料显示,2013—2017 年的跳闸原因占比如图1 所示,其中雷击跳闸占比均达到50%以上,部分年份甚至接近70%。2009 年,巴西里约热内卢和圣保罗等地区的“11·10”大停电发生之前显示附近存在强降雨及密集雷电[5];2019 年,英国英格兰与威尔士地区的“8·9”大停电调查报告显示,该事故的直接原因是雷击跳闸引起线路停运后引发的一系列故障[6]。因此,如果能准确地实现输电线路雷击跳闸预警,便有助于电网相关部门提前做出针对性的预防措施,尽可能降低雷击跳闸的风险与损失,对电网的安全运行具有重要意义。
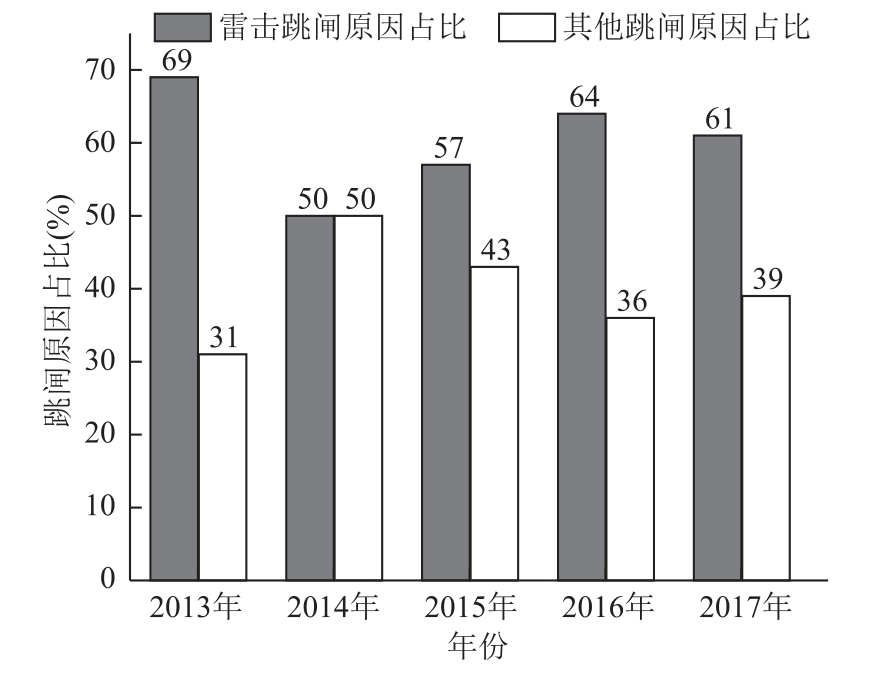
图1 云南电网2013—2017 年的跳闸原因占比
Fig.1 Proportion of tripping causes of Yunnan Power Grid from 2013 to 2017
目前国内外学者已开展大量关于电网输电线路雷害风险的相关研究,其中就包括输电线路耐雷性能评估及线路雷击跳闸预警的研究。对于输电线路耐雷性能的评估方法包括规程法、电气几何模型及其相关改进方法[7-9]、雷电先导发展模型(Leader Progression Model, LPM)及其相关改进方法[10-11]等。其中雷电先导发展模型与规程法、电气几何模型相比,更细致地模拟了雷击输电线路的物理过程,并且雷电先导分形模型可以更好地模拟雷电先导发展路径随机性和确定性相统一的特征,与实际雷击输电线路过程更加相符[10,12-13]。因此,本文选用雷电先导分形模型判断线路雷击位置,结合耐雷水平判断是否发生跳闸。
现有对输电线路雷击跳闸预警的研究可以分为雷电活动区域预测法与大数据分析方法。雷电活动区域预测法主要是采用雷击跳闸预报概率代替传统固定不变的年平均雷击故障率,通过预测未来时间段内可能遭受雷击的范围,开展电网雷击故障的在线预警[14-16]。鲍捷等通过预测得到雷暴云运动轨迹,综合考虑是否为高风险雷暴云、预测区域内是否有低防雷性能线路来判断是否发出线路的雷击跳闸预警[17]。赵芝等利用相邻3 个时次的雷区预测下一时次的落雷区域,与经验公式相结合实现雷击跳闸预警[18]。在此基础上,重庆大学王伟以输电线路的引雷宽度和落雷面积计算线路的雷击跳闸概率[19]。然而,上述雷击跳闸预警方法主要关注大气分布情况与雷电活动轨迹的预测,未充分考虑线路周围的微地形条件、线路自身参数及雷击线路物理过程,无法确定雷击输电线路的具体位置(导线或避雷线),并且以经验公式计算雷击跳闸概率,对是否发出雷击跳闸预警的判断比较粗糙,存在预警准确率低、虚报率高的问题。
大数据分析方法则是在电网累积的雷击跳闸数据的基础上,引入遗传算法(Genetic Algorithm, GA)优化的BP(back propagation)神经网络技术[20-21],将落雷位置、雷电流大小、输电线路杆塔参数等影响输电线路雷击跳闸的因素作为算法输入层,提出的一种雷击跳闸预警新方法。有学者进一步提出采用模拟退火遗传算法优化的BP 算法模型[22],具有良好的预警效果。而神经网络算法受限于输入特征量的数量,特征量越多、网络越复杂、效率越低,所能考虑的影响因素受限,且无法考虑雷击线路的物理过程,受限于训练样本,样本容量的大小及所选样本是否全面将直接影响预警效果。
鉴于上述分析,为充分考虑影响输电线路雷击跳闸的因素以及雷击输电线路物理过程,使得预警结果更加准确,本文提出一种考虑微地形的山区输电线路雷击跳闸预警融合算法。一方面考虑到雷电活动预警系统精度较低,云南电网现有系统的预测精度只能达到经纬度为0.01°×0.01°(约1 km×1 km)的区域,本文通过对云南省雷电活动监测数据进行统计分析,得到云南省的雷电流幅值累积概率分布函数与落雷频次随海拔高度的变化规律,以此构建蒙特卡罗法所需的目标分布样本,模拟雷电流幅值与落雷位置在一定区域内的分布情况;另一方面采用雷电先导分形模型,实现了对雷电先导发展路径随机性与确定性相统一的物理过程的模拟。同时,在本文算法的基础上构建输电线路雷击跳闸概率数据库,形成输电线路雷击跳闸预警系统,实际应用于云南电网,进行算例验证及预警性能的评估。
1 输电线路雷击跳闸概率预警算法构成及数据预处理
1.1 输电线路雷击跳闸概率预警算法构成
输电线路雷击跳闸概率预警算法构成如图2 所示。计算中输入雷电活动短时预警系统的数据包括:杆塔附近未来2 h 内1 km×1 km 区域中的最大雷电流幅值Imax、落雷频次n 以及预警区域杆塔所处的微地形条件。
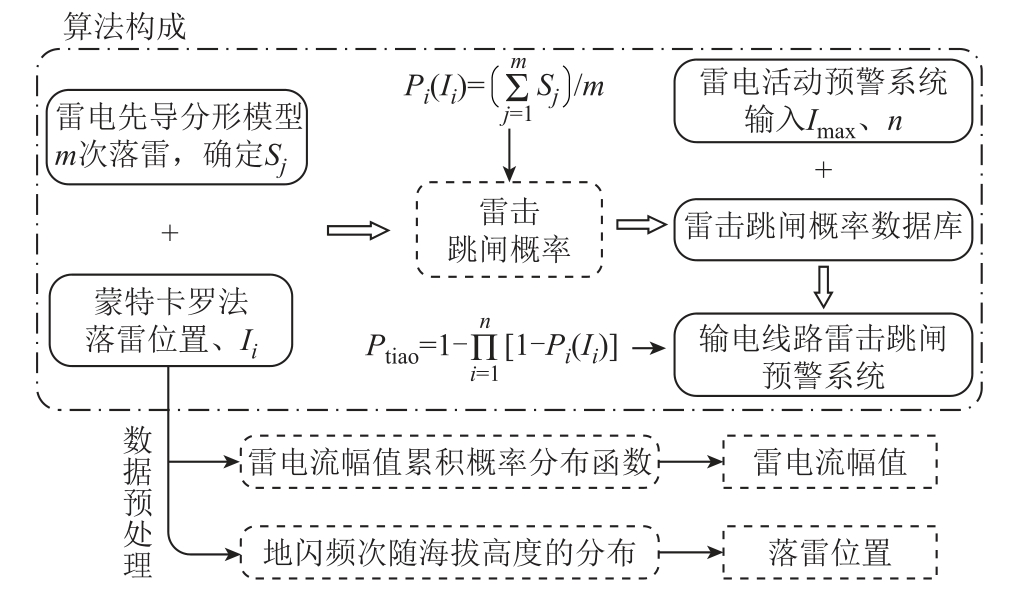
图2 输电线路雷击跳闸概率预警算法构成
Fig.2 Lightning strike trip probability prediction algorithm for transmission lines
蒙特卡罗法计算步骤如图3 所示。采用蒙特卡罗法计算雷击跳闸概率时,首先根据输入数据随机生成符合云南省雷电活动特征的雷电流幅值Ii(小于Imax,i=1, 2,…, n)。然后对每次落雷(雷电流幅值Ii)采用雷电先导分形模型开展大量的雷击仿真计算,落雷位置同样根据雷电活动特征随机生成。
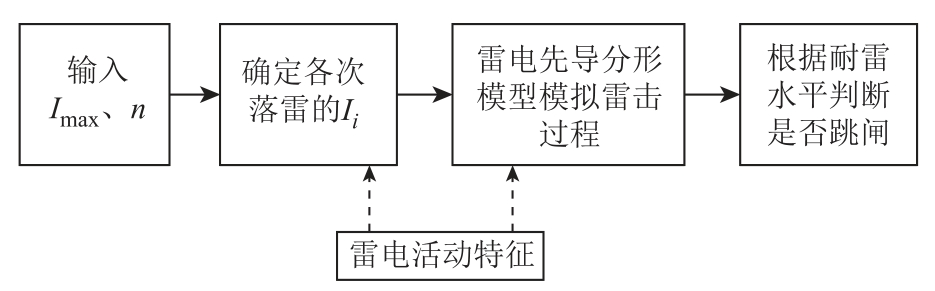
图3 蒙特卡罗法计算步骤
Fig.3 Calculation steps of Monte-Carlo method
对每次落雷模拟m 次,根据耐雷水平判断是否发生跳闸,并记第j 次发生跳闸为Sj=1,反之Sj=0,当模拟次数m 足够大时,第i 次落雷的雷击跳闸概率可表示为
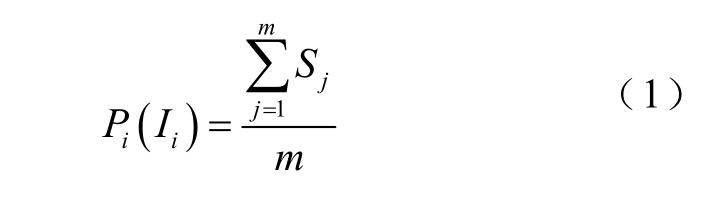
式中,Pi(Ii)为第i 次落雷的雷击跳闸概率;Ii 为第i次落雷的雷电流幅值,kA;m 为每次落雷计算机模拟的总次数。
最终由式(2)计算得到未来2 h 内n 次落雷中该线路至少发生一次跳闸的概率。
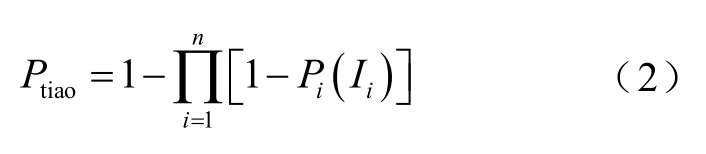
式中,Ptiao 为未来2 h 内预警区域的雷击跳闸概率;n 为未来2 h 内预警区域的落雷总频次。
进一步考虑不同的电压等级(110 kV、220 kV、500 kV)、不同的雷电流(5~300 kA)和不同的微地形条件(地面倾角0°~50°),开展大量的雷击仿真计算,构建雷击跳闸概率数据库,形成输电线路雷击跳闸预警系统。
1.2 考虑雷电活动特征与微地形条件的雷电流与落雷位置的随机生成方法
雷电预警示意图如图4 所示。现有雷电预警系统的预测精度为0.01°×0.01°,即大约1 km×1 km范围。考虑落雷区域的对称性,本文在算法中设置计算区域为输电线路侧面500 m 的范围。
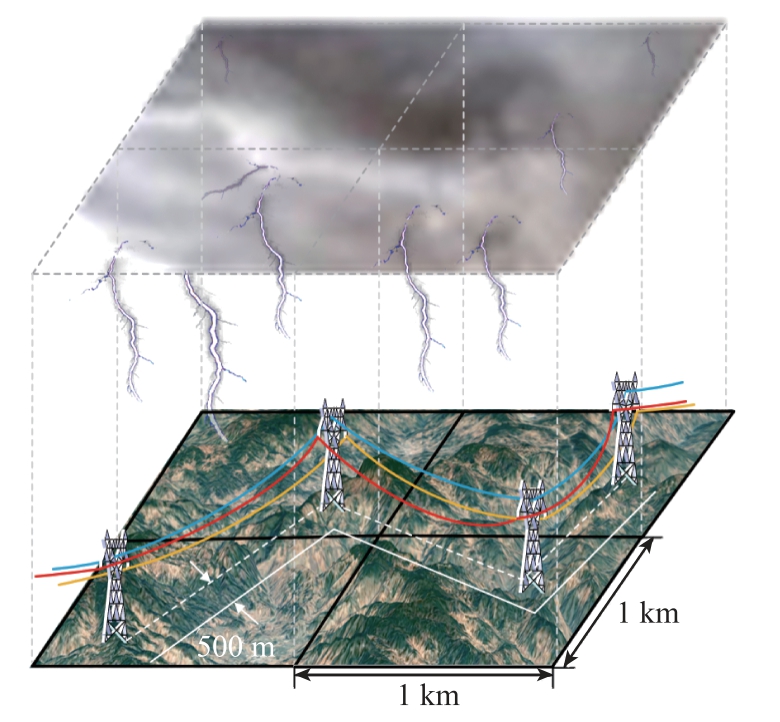
图4 雷电预警示意图
Fig.4 Schematic diagram of lightning warning
雷电活动短时系统只能给出区域内(1 km×1 km方格)未来2 h 内的落雷频次及最大落雷强度,各次落雷的雷电流幅值及落雷位置未知。因此,需要根据当地的雷电活动特征随机生成符合其雷电流幅值概率分布函数的雷电流,以及符合当地落雷规律的落雷位置。
1.2.1 云南省雷电流幅值累积概率分布函数与随机变量雷电流幅值的生成方法
雷电流幅值累积概率分布函数是输电线路雷击跳闸概率计算的重要参数之一,然而目前国内外使用的雷电流幅值累积概率分布函数各异,国内相关标准(GB/T 50064—2014《交流电气装置的过电压保护和绝缘配合设计规范》)推荐采用对数表达式;国际上不同组织和研究者则分别总结出不同的雷电流幅值概率公式,见表1[23-25]。
表1 不同文献总结的雷电流幅值累积概率分布公式
Tab.1 The cumulative probability distribution formula of lightning current amplitude summarized in literature

来 源 雷电流幅值累积概率分布公式GB/T 50064—2014 I lg ( ) 44 P I =- ,I lg ( ) 88 P I =-Pobolansky P I= +I 1( ) 1 ( 25)2.0 IEEE 标准P I= +I 1( ) 1 ( 31)2.6国际大电网会议P I= +I 1( ) 1 ( 12)2.7韩国电力研究院P I= +I 1( ) 1 ( 15.9)2.8
可以看出表1 中公式具有相似的形式,可写成标准形式为
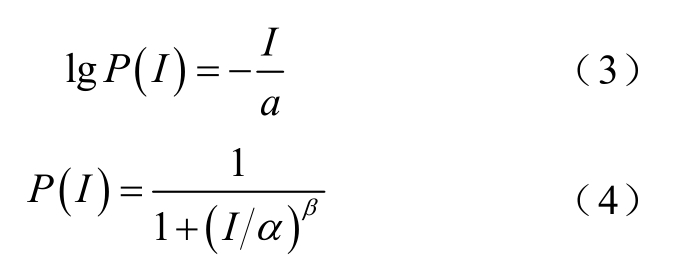
式中,I 为雷电流幅值,kA;P(I)为雷电流幅值大于I 的概率。
云南省雷电流幅值的累积概率分布如图5所示,分别以式(3)、式(4)对图中数据进行参数拟合,拟合结果及国内外学者总结的雷电流幅值累积概率曲线均标于图5 中。
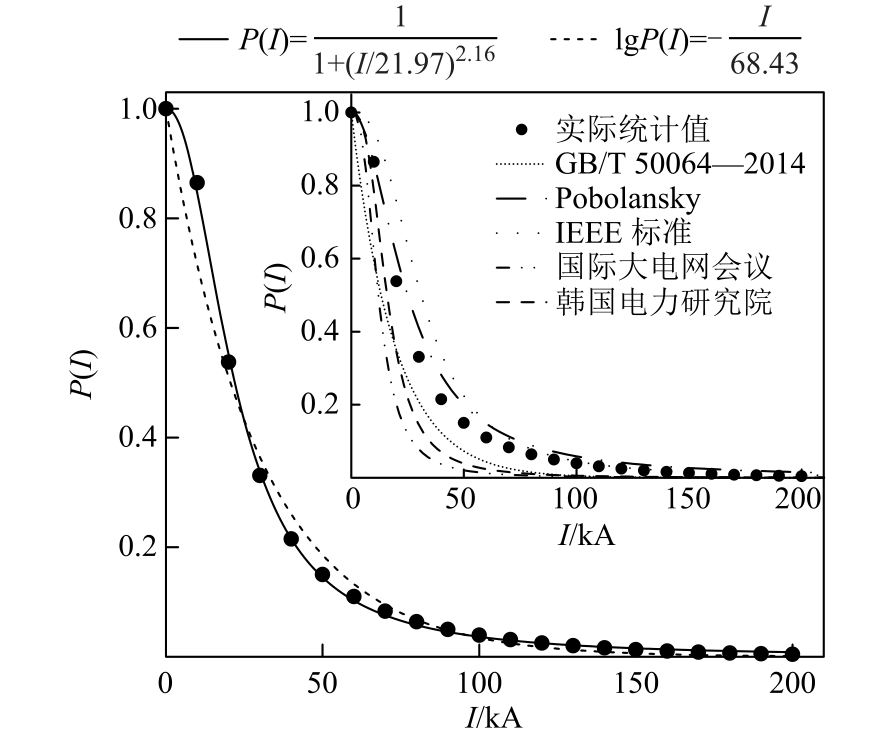
图5 雷电流幅值累积概率分布曲线
Fig.5 The lightning current amplitude cumulative probability distribution
可以看出,现有的雷电流幅值累积概率分布函数与云南省的实际雷电活动特征差异较大,若采用其作为计算依据将会造成较大的误差。
以决定系数R2 来检验拟合效果,R2 越接近于1拟合效果越佳,其表达式为

式中,SSR 为回归平方和(regression sum of squares),即拟合结果与原样本均值之差的平方和;SST 为总离差平方和(sum of squares for total),即各样本与样本均值的平方和。
各参数的最终拟合结果及决定系数R2 见表2,以式(3)拟合的决定系数为0.982 25,以式(4)拟合的决定系数为0.999 44,后者的拟合效果更佳,因此本文采用式(6)开展后续计算。
表2 拟合结果及决定系数
Tab.2 Fitting results and the determination coefficient

拟合公式lg ( ) I P I=-a 1 P I I β α( ) 1 ( )= +拟合结果 a = 68.43 α = 21.97, β = 2.16决定系数R2 0.982 25 0.999 44
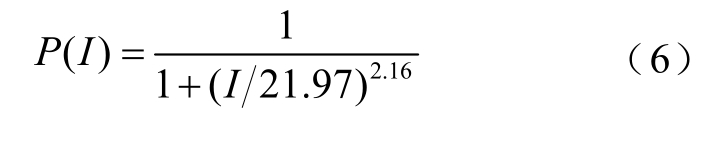
对于随机变量雷电流幅值I 的生成,则根据雷电流幅值概率分布的拟合结果,采用直接抽样法,对式(6)求反,可得到
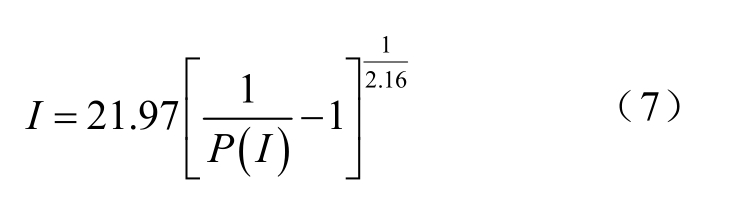
随机抽取P(I),代入式(7)即可得到雷电流幅值I,其中P(I)在[0, 1]上均匀分布。
1.2.2 云南省雷电地闪频次随海拔高度的分布与随机变量落雷位置的生成方法
研究发现,海拔高度是雷电地闪分布的影响因素之一,云南省2007—2016 年的地闪概率随海拔高度的分布如图6 所示[26]。可以看到地闪分布随海拔高度的变化近似呈正态分布,以海拔高度2 000 m为中心向两侧逐渐减弱,采用高斯多峰拟合法[27],对统计数据分为2 个高斯峰进行拟合,决定系数R2为0.991 77。地闪概率与海拔高度的关系可近似表示为
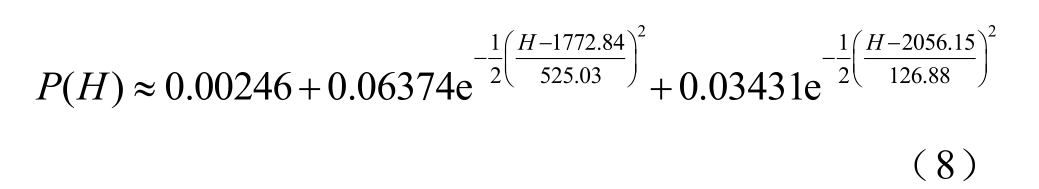
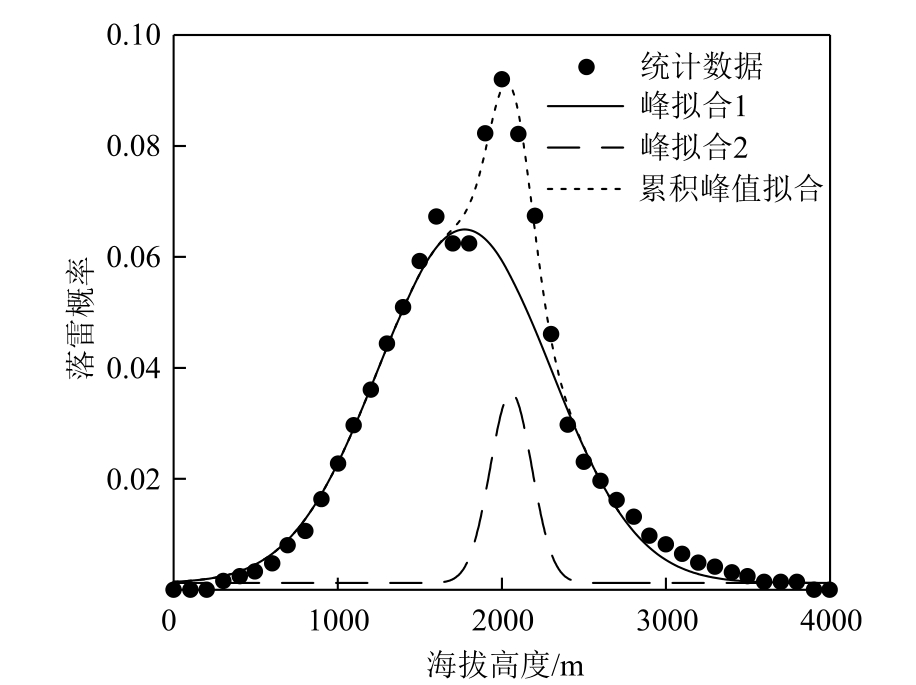
图6 云南省2007—2016 年地闪概率随海拔高度的分布
Fig.6 Distribution of ground lightning frequency with altitude in Yunnan Province from 2007 to 2016
式中,H 为海拔高度,m;P(H)为海拔高度为H 时的地闪概率。
对于随机变量海拔高度H 的生成,则采用舍选抽样法,即在P(H)较大的位置保留较多的随机数,在P(H)较小的位置保留较少的随机数。
侧面距离计算示意图如图7 所示,由于计算中采用雷电先导分形模型模拟雷击输电线路过程,因此需将海拔高度H 转换为输电线路侧面落雷距离D。
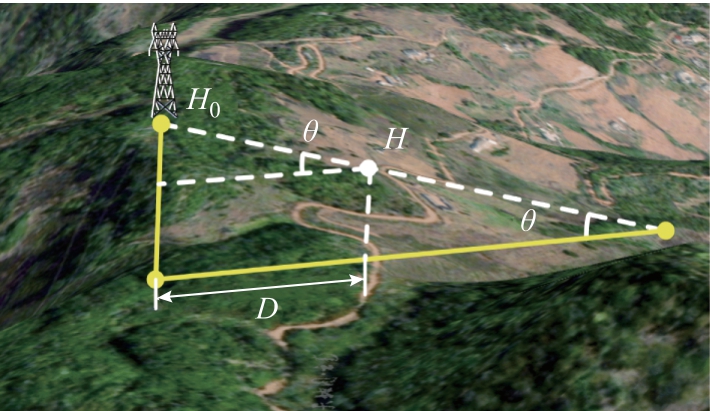
图7 侧面距离计算示意图
Fig.7 Diagram of side distance calculation
根据随机生成的海拔高度、杆塔所处位置的海拔高度与地面倾角,计算输电线路侧面落雷距离D,即

式中,H0 为杆塔位置海拔高度,m;H 为根据式(8)生成的随机量,m;θ 为地面倾角。
2 输电线路雷击跳闸概率计算方法
本文第1 节根据云南省雷电活动短时预警系统输入数据和雷电活动特征以及微地形条件,确定了各次落雷的雷电流幅值及落雷位置,为雷击跳闸概率的计算奠定基础。进一步地,将雷电先导分形模型和蒙特卡罗法相结合,开展大量的雷击输电线路仿真计算,记录雷击位置及雷电流幅值,根据输电线路的耐雷水平建立雷击跳闸概率数据库。
2.1 输电线路耐雷水平的计算
在电磁暂态计算软件中分别建立雷电流模型、杆塔模型、绝缘子串闪络模型、杆塔冲击接地电阻模型、架空线路模型,计算中采用典型输电线路参数开展110 kV、220 kV、500 kV 输电线路耐雷水平的计算。以Heilder 模型模拟2.6/50 μs 的负极性雷电流波形。架空线路采用考虑频率特性的Jmarti 模型,为防止波的多次折反射对计算结果造成影响,在线路末端连接一条相对较长的线路以消除折反射带来的误差。各电压等级架空线路参数见表3。
表3 各电压等级架空线路参数
Tab.3 Parameters of overhead lines at each voltage level
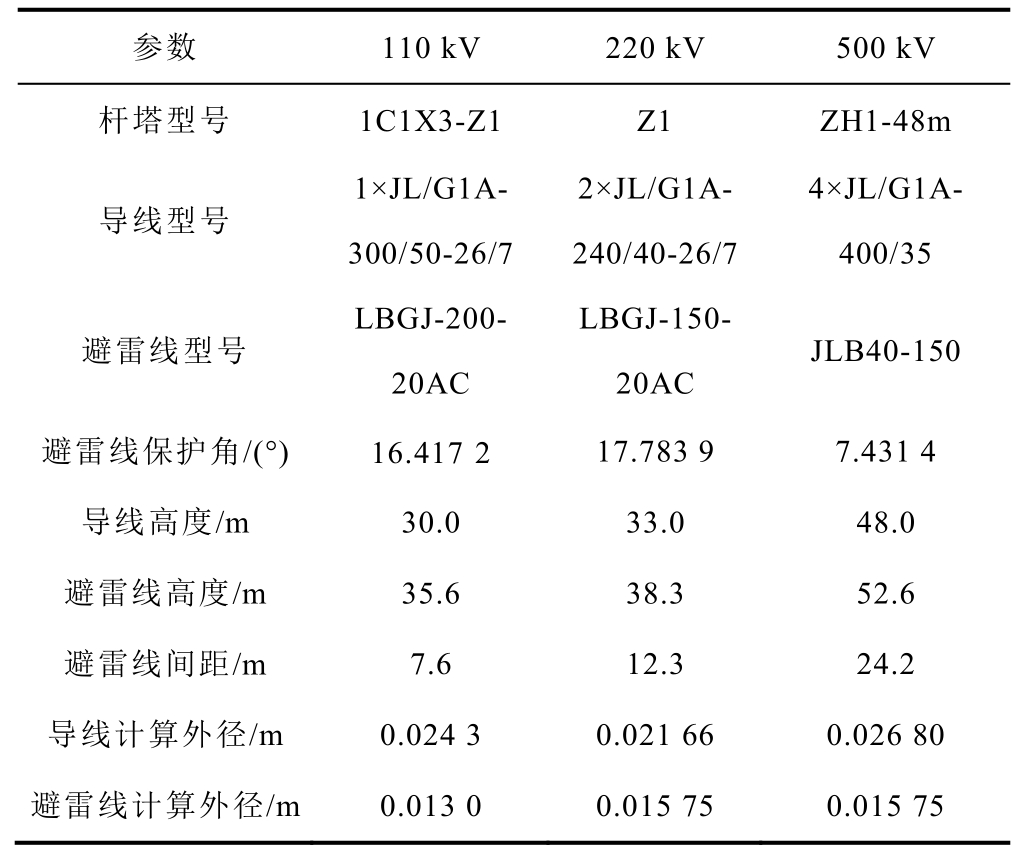
参数 110 kV 220 kV 500 kV杆塔型号 1C1X3-Z1 Z1 ZH1-48m导线型号1×JL/G1A-300/50-26/7 2×JL/G1A-240/40-26/7 4×JL/G1A-400/35避雷线型号LBGJ-200-20AC LBGJ-150-20AC JLB40-150 16.417 2 17.783 9 7.431 4导线高度/m 30.0 33.0 48.0避雷线高度/m 35.6 38.3 52.6避雷线间距/m 7.6 12.3 24.2导线计算外径/m 0.024 3 0.021 66 0.026 80避雷线计算外径/m 0.013 0 0.015 75 0.015 75避雷线保护角/(°)
绝缘子串闪络模型采用伏秒特性相交法,采用EMTP 程序中的TACS(数值仿真)功能,充分考虑绝缘子串雷电冲击伏秒特性,当绝缘子串两端电压与其伏秒特性相交时,绝缘子串发生闪络。
考虑波在杆塔上的传播过程以及在杆塔传播过程中的衰减现象,建立多层传输杆塔模型[28],其波阻抗模型如图8 所示。行波在杆塔中的传播速度约为光速c,ZT1=ZT2=220Ω,ZT3=150Ω,阻尼电阻Ri和阻尼电感Li 分别为
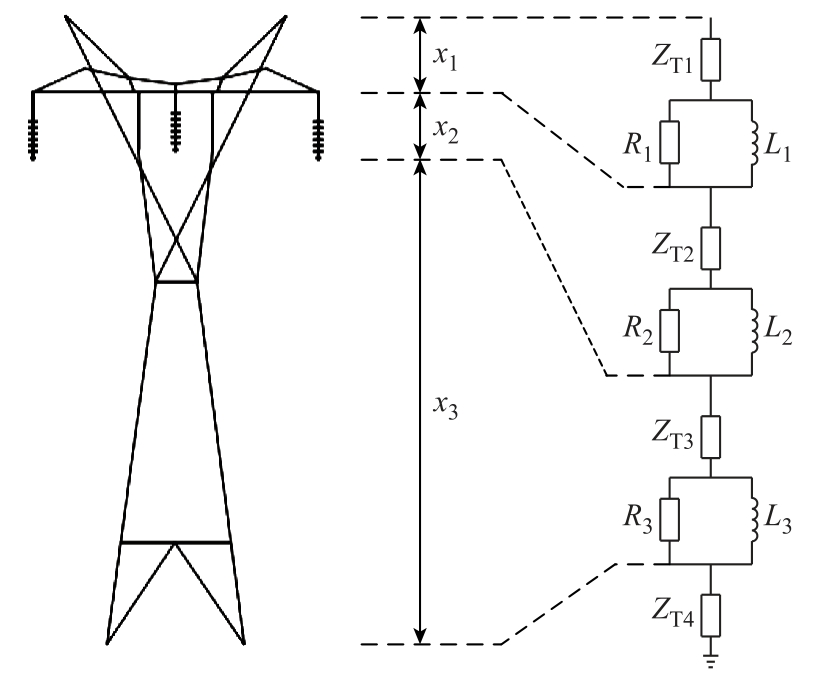
图8 多层传输杆塔模型
Fig.8 Model of multilayer transmission tower
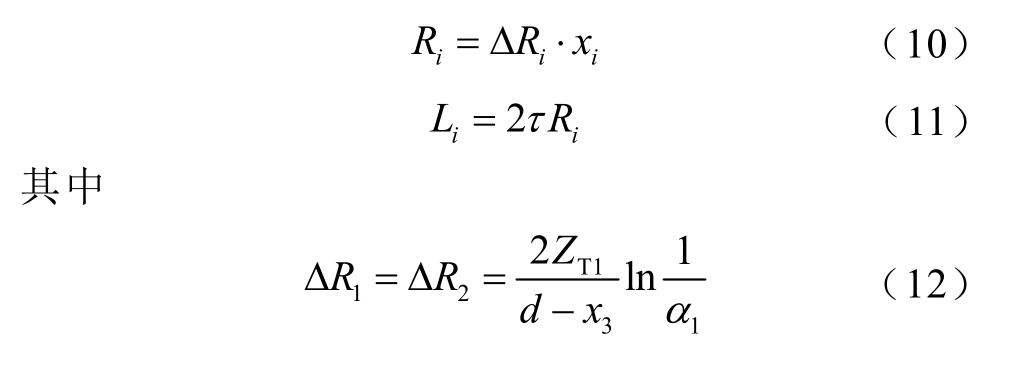
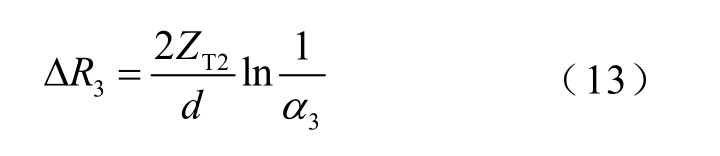
式中,i=1, 2, 3,表示杆塔分层;xi 为杆塔不同的层高,m;d 为杆塔高度,m;τ 为波在杆塔上的传播时间,m/s,τ=d/c;α1 和α2 为行波在杆塔上的衰减系数,α1=α2=0.89。
研究发现,杆塔冲击接地电阻受流过其的电流幅值的影响,具有明显的非线性,本文采用国际电工委员会(International Electrotechnical Commission, IEC)推荐式来计算杆塔的冲击接地电阻[29-31],即
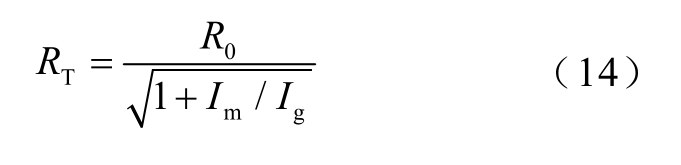
式中,R0 为低频低电流幅值下的电阻值,Ω;Im 为流过接地体的冲击电流幅值,kA;Ig 为使土壤发生电离的最小电流,可表示为

式中,ρ 为土壤电阻率,Ω·m;E0 为土壤电离时的电场强度,kV/m。
最终计算得到云南省各电压等级典型输电线路的耐雷水平见表4。
表4 各电压等级输电线路耐雷水平
Tab.4 Lightning withstand level of each voltage level transmission line

电压等级/kV 110 220 500绕击电流/kA 8.3 12.2 24.8反击电流/kA 65.6 99.2 165.4
2.2 雷电先导分形模型
不同于传统的雷电先导发展模型(LPM),雷电先导分形模型可以充分考虑雷电通道发展的随机性与分支特性,与实际情况更加吻合。雷击输电线路过程可以分为以下四个阶段[10,13]:
1)下行先导的发展。雷云底部电荷积累到一定量时,形成向下发展的流注及先导放电通道。
2)上行先导的起始。随着下行先导的发展,地面物体感应电荷逐渐增多,当达到上行先导起始条件时,上行先导起始并向上发展形成放电通道。
3)上下行先导相互发展。在地面物体上行先导起始后,雷电下行先导和地面物体上行先导相向发展。
4)最终击穿。随着上下行先导的不断发展,当上下行先导之间(或雷电先导与大地之间)达到击穿条件时,两者相连,形成主放电通道。
2.2.1 雷电下行先导发展模型
研究表明,自然雷云放电具有明显的分支曲折发展特征[32],在局部和整体上具有明显的自相似性,可以采用分形几何学来描述雷电通道发展的随机性。电介质击穿模型(Dielectric Breakdown Model, DBM)是一种电介质路径发展分形模型,本节以DBM 模型为基础[10,32],在软件Matlab 中编写数值计算程序来实现雷电先导的分形发展。先导发展路径示意图如图9 所示,具体计算流程如下:
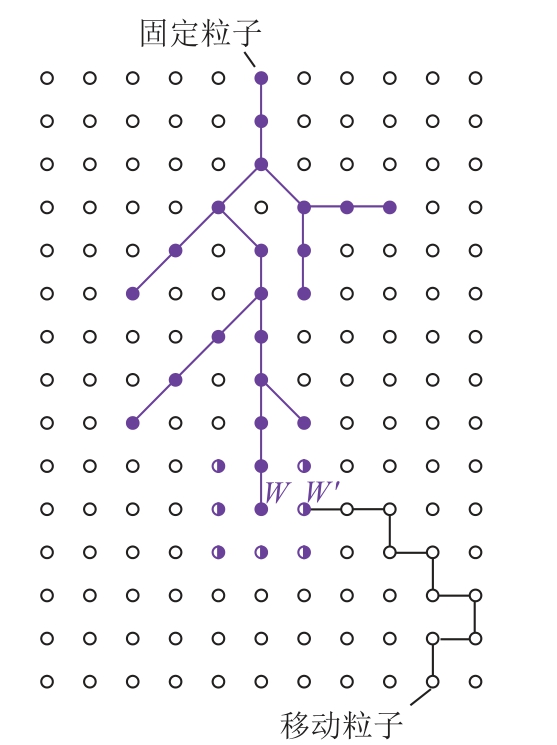
图9 先导发展路径示意图
Fig.9 Schematic diagram of leader branch growth
1)确定计算空间,在先导可能发展的初始位置(输电线路导线、避雷线、雷电下行先导处)设置固定粒子。
2)在上下行先导头部附近位置设置移动粒子,并做无规则布朗运动,当移动粒子运动到先导头部的吸引范围内后,移动粒子停止运动,计算该移动粒子所处位置的击穿概率为
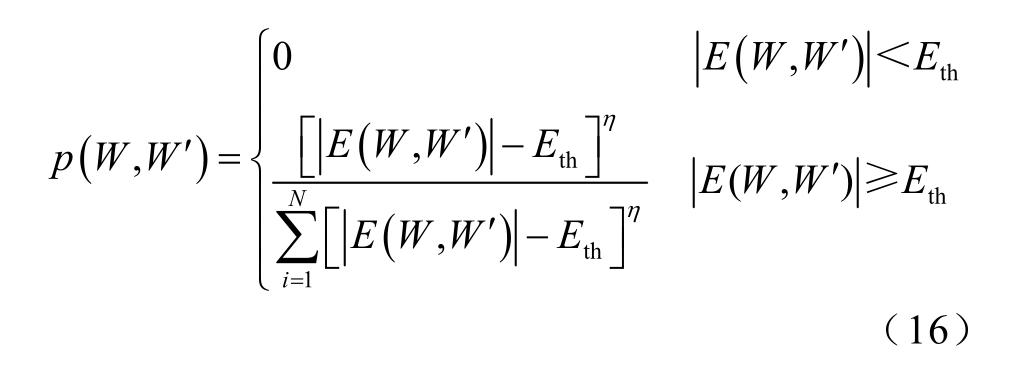
式中,W 为固定粒子位置;W′为移动粒子位置;E(W,W′)为固定粒子与移动粒子之间的电场强度;Eth 为临界击穿场强,Eth=500 kV/m;η 为分形参数,取1[10]。
3)在步骤2)中计算出p(W, W′)后,生成随机数O,O 在区间[0, 1]内均匀分布,当O<p(W, W′)时,判定击穿;当O≥p(W, W′)时,判定不击穿。
如此往复,在先导头部附近(固定粒子)放置移动粒子,随着固定粒子的生长,最终得到雷电先导的分形发展路径。
在计算固定粒子与移动粒子之间的击穿概率时,需确定通道附近的电场分布,雷电通道周围电场主要由通道内的电荷产生,在上行先导起始前,假设雷电通道竖直向下发展,通道内电荷沿先导通道线性分布;在上行先导起始之后,雷电先导分形发展,分支通道内的电荷密度采用均匀分布形式,如图10所示[10,32-33]。图中,δ 为竖直向下发展通道的电荷密度;δf 为分支部分通道的电荷密度;Hc 为雷云高度,m;h0 为雷电头部先导高度,m;h 为雷电先导通道高度,m;C0 为先导头部对地高度,m;CT 为先导分支起始点对地高度,m;Lf 为分支部分先导总长度,m;QT 为雷电通道总电荷量,C;Q0 为先导头部半球内电荷量[32],C。
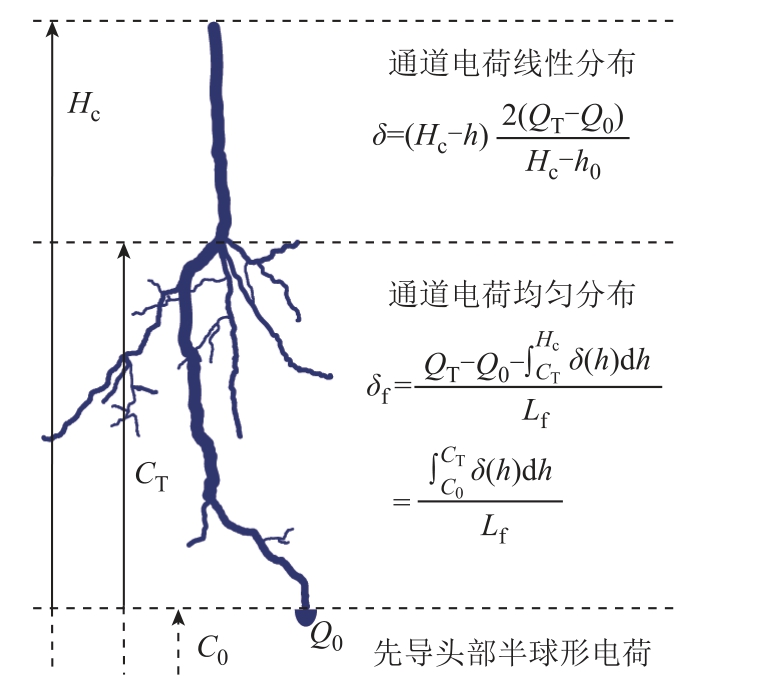
图10 雷电先导分形模型电荷分布形式
Fig.10 Charge distribution form of lightning leader fractal model
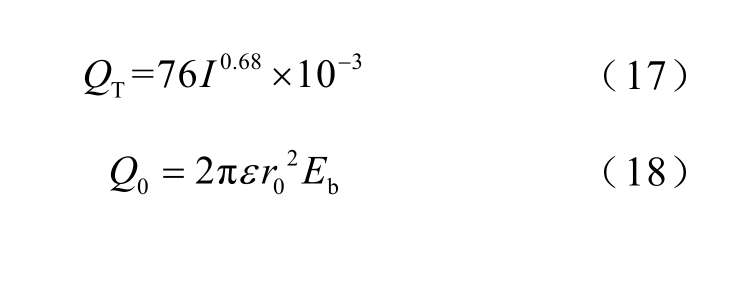
式中,I 为雷电流幅值,kA;ε 为空气介电常数,取8.8551×10-12 F/m;Eb 为空气临界击穿场强,kV/m;r0 为先导头部半径,取6 m。
2.2.2 上行先导发展模型
当导线(或避雷线)表面电场强度超过其临界起始场强时,上行先导起始,临界起始场强计算式[34-35]为
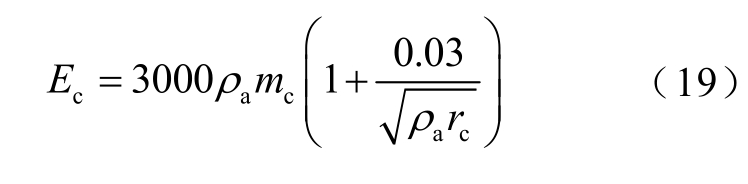
式中,Ec 为导线(避雷线)上行先导临界起始场强,kV/m;mc 为导线表面粗糙系数; aρ 为相对空气密度;rc 为导线(避雷线)的临界电晕半径,m。
采用线电荷等效输电线路导线和避雷线,随着雷电下行先导的发展,输电线路导线、避雷线上的电位可以表示为[34]
式中,A 为电位系数矩阵;Vs 为雷电先导产生的感应电位矩阵;Q 为电荷密度矩阵。
可以计算得到输电线路导线、避雷线的等效线电荷密度为
导线、避雷线表面的电场强度可表示为

式中,r 为导线、避雷线半径矩阵。
2.2.3 雷击过程基本判据
雷电先导分形模型发展流程如图11 所示。
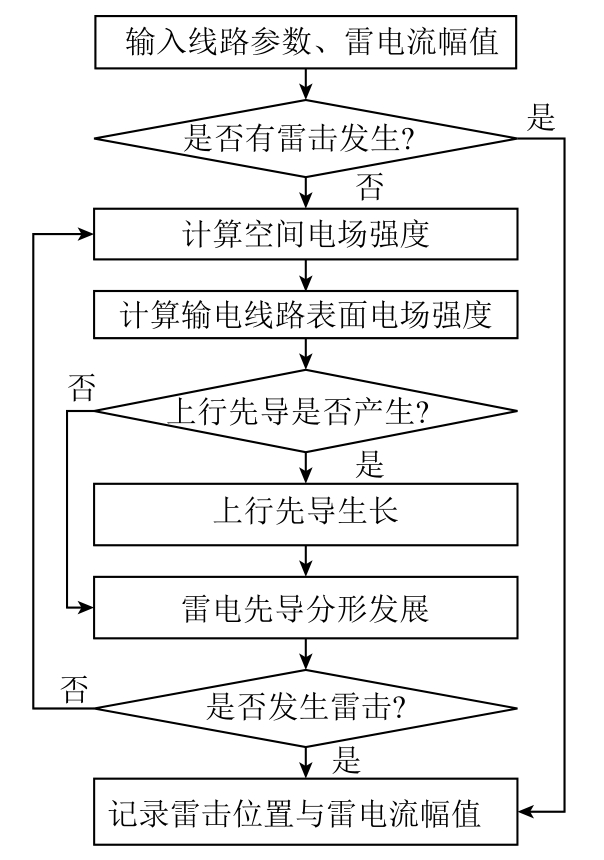
图11 雷电先导分形模型发展流程
Fig.11 Calculation process of the fractal leader progression
上行先导起始后,沿电场强度最大的方向发展,上下行先导相互发展,其发展速度之比设置为4∶1,当先导之间或者下行先导与未产生上行先导的某目的物(如大地)间的平均场强超过平均击穿临界场强500 kV/m 或当上下行先导相遇时,发生雷击放电[32]。
2.3 输电线路雷击跳闸概率计算与跳闸预警的实现
1.2 节已得到雷电流幅值的累积概率分布函数与落雷频次随海拔高度的变化规律,使得在生成随机变量雷电流幅值与落雷位置时可以充分考虑当地的雷电活动特征以及微地形条件,并且建立雷电先导分形模型模拟雷击输电线路过程。在以上研究的基础上,本文提出一种融合蒙特卡罗法与雷电先导分形模型的输电线路雷击跳闸预警算法,其流程如图12 所示,具体算法流程如下:
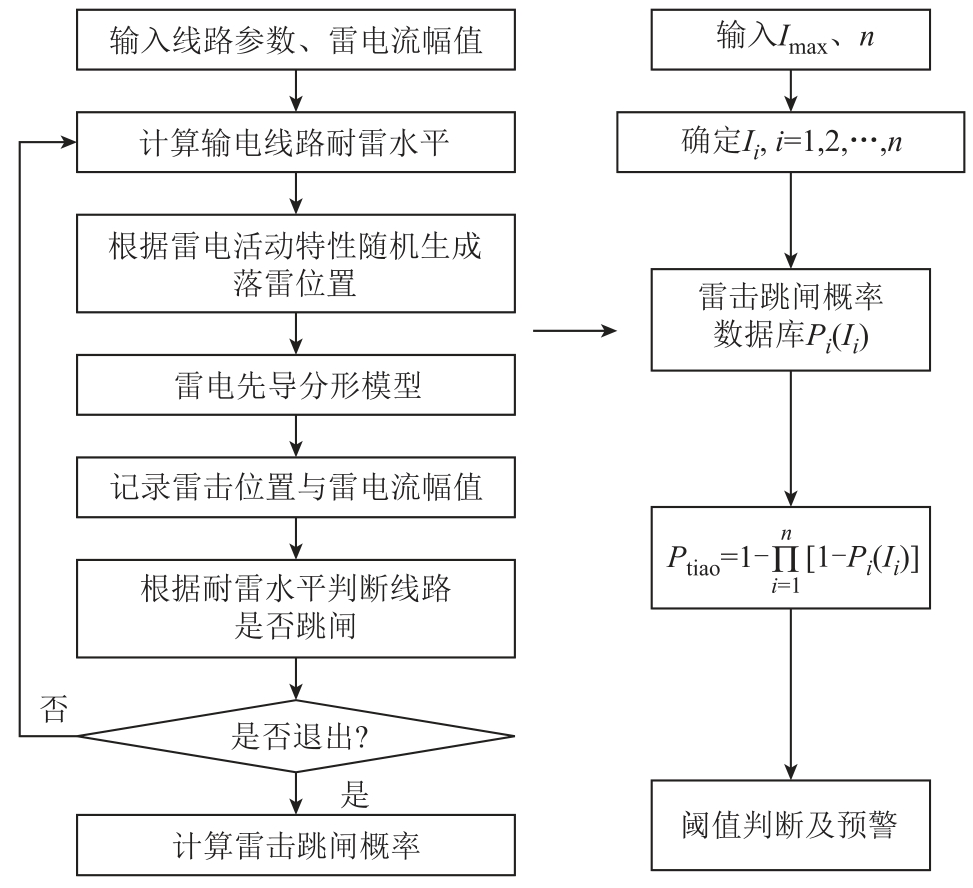
图12 输电线路雷击跳闸预警融合算法流程
Fig.12 Flow chart of lightning strike trip warning algorithm for transmission line
1)首先采用蒙特卡罗法与雷电先导分形模型相结合的方法,结合式(8)进行大量的仿真计算,分别得到不同雷电流幅值、不同微地形条件下各电压等级(110 kV、220 kV、500 kV)输电线路的雷击跳闸概率,形成雷击跳闸概率数据库。
2)输入雷电活动短时预警系统数据:未来2 h内的最大雷电流幅值Imax、落雷频次n、预警区域杆塔所处的微地形条件。
3)根据式(7)随机生成各次落雷的雷电流幅值Ii(小于输入的最大雷电流幅值)。
4)根据步骤2)、步骤3)确定的输入条件与步骤1)建立的雷击跳闸概率数据库,确定各次落雷的雷击跳闸概率Pi(Ii)。
5)将落雷频次、各次落雷的雷击跳闸概率Pi(Ii)代入式(2),计算得到预警区域未来2 h 内可能影响线路的雷击跳闸概率Ptiao,根据设定的雷击跳闸概率阈值,判断是否发出雷击跳闸预警。
3 输电线路雷击跳闸预警示范系统应用
3.1 云南电网雷电活动短时预警与输电线路雷击跳闸预警示范系统
根据计算得到的各电压等级输电线路的雷击跳闸概率数据库与云南电网现有的雷电活动短时预警系统相结合,形成输电线路雷击跳闸概率预警示范系统。将雷电活动短时预警系统输出的区域最大雷电流幅值与落雷频次输入雷击跳闸预警算法,可实现未来2 h 内可能受影响线路的雷击跳闸预警。雷击跳闸预警系统界面、闪电频次以及闪电强度预警图分别如图13a、图13b 和图13c 所示。

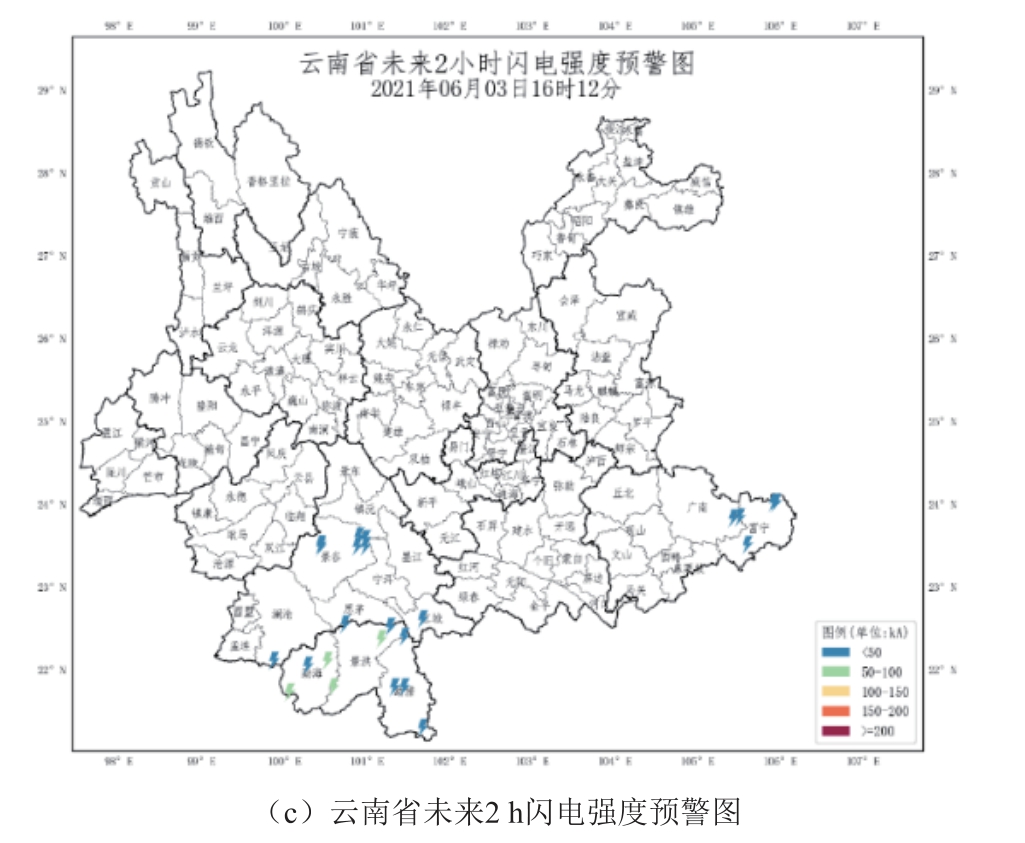
图13 云南电网雷电活动短时预警与输电线路雷击跳闸预警系统
Fig.13 Yunnan Power Grid Lightning Early Warning and Transmission Line Lightning Trip Warning System
3.2 输电线路雷击跳闸概率计算示例
云南电网雷电活动短时预警系统显示,2021 年7月18 日18∶54 未来2 h 内500 kV 观永甲线47 号杆塔区域附近的落雷频次将达到20 次,最大落雷强度为122 kA,杆塔处海拔高度为1 707.4 m,地面倾角为31.4°。根据第2 节所述的雷击跳闸概率计算方法,在计算中,设置最大雷电流幅值为122 kA,其余(19 次)落雷根据云南省雷电流幅值概率分布函数(见式(6))随机生成不同的雷电流幅值,得到对应的雷击跳闸概率Pi(Ii),见表5。
表5 各次落雷的雷击跳闸概率
Tab.5 Lightning trip probability of each lightning stroke
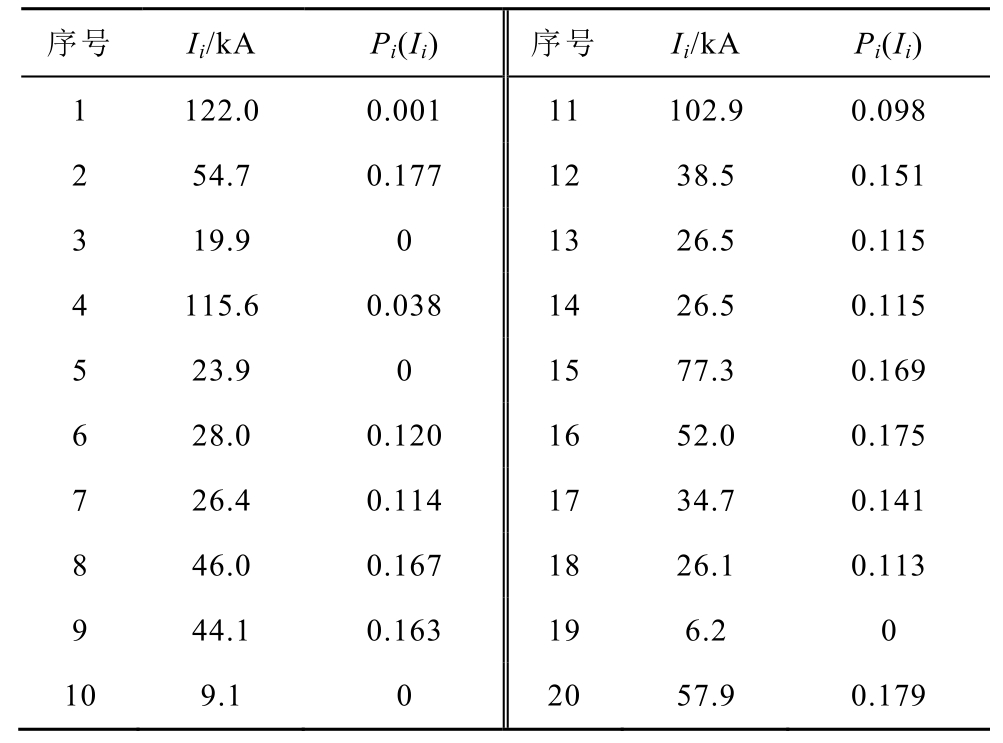
序号 Ii/kA Pi(Ii) 序号 Ii/kA Pi(Ii)1 122.0 0.001 11 102.9 0.098 2 54.7 0.177 12 38.5 0.151 3 19.9 0 13 26.5 0.115 4 115.6 0.038 14 26.5 0.115 5 23.9 0 15 77.3 0.169 6 28.0 0.120 16 52.0 0.175 7 26.4 0.114 17 34.7 0.141 8 46.0 0.167 18 26.1 0.113 9 44.1 0.163 19 6.2 0 10 9.1 0 20 57.9 0.179
确定各次落雷的雷击跳闸概率 Pi(Ii)后,将n=20、Pi(Ii)分别代入到式(2)中,可以计算得到500 kV 观永甲线47 号杆塔2021 年7 月18 日19∶00未来2 h 内的雷击跳闸概率为
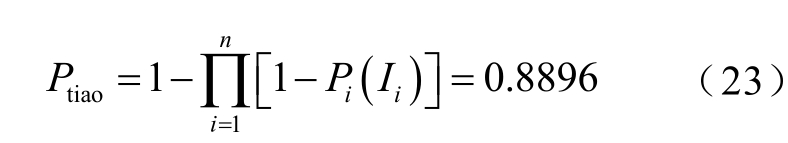
因此得到500 kV 观永甲线2021 年7 月18 日19∶00 未来2 h 内的雷击跳闸概率达88.96%,风险较高,可对该线路做出雷击跳闸预警。实际上,该线路47 号杆塔于2021 年7 月18 日19∶06 发生跳闸。
3.3 雷击跳闸预警准确性的验证
将所形成的雷击跳闸预警系统实际应用于云南电网,开展输电线路雷击跳闸预警,各次预警的线路名称、雷击跳闸概率、预警结果见表6。其中,预警准确指预测跳闸且实际发生跳闸;漏警指预测不跳闸但实际发生跳闸或预测区域位置错误(雷电活动短时预警系统误差);虚警指预测跳闸但实际不发生跳闸。雷击跳闸概率的计算结果如图14 所示。
表6 各次预警的线路名称、雷击跳闸概率、预警结果
Tab.6 Line name, predicted lightning trip-out probability, warning results

序号 线路名称 雷击跳闸概率(%) 预警结果 序号 线路名称 雷击跳闸概率(%) 预警结果1 110 kV 双鄂大线 84.60 准确 27 220 kV 大文Ⅱ回线 88.76 准确2 110 kV 清永线 61.08 准确 28 220 kV 罗丹Ⅱ回线 61.20 虚警3 110 kV 里瓦T 线 71.38 准确 29 110 kV 锦小线 83.88 准确4 220 kV 建岗Ⅱ回线 95.30 漏警 30 110 kV 芦八线’ 86.57 准确5 110 kV 瓦尼线 87.53 准确 31 110 kV 坪洒线 66.74 准确6 110 kV 香尼线 45.67 漏警 32 110 kV 听洒星线’ 68.55 准确7 110 kV 洱西线 89.98 准确 33 110 kV 格乐线 87.11 准确8 110 kV 听洒星线 76.37 准确 34 110 kV 马清线 77.93 准确9 110 kV 香居Ⅱ回线 78.64 准确 35 220 kV 勐蔓Ⅰ回线 65.09 准确10 110 kV 香居Ⅰ回线 78.01 准确 36 500 kV 苗新乙线 71.74 准确11 220 kV 贡福线 73.37 准确 37 110 kV 路西羊线 66.85 准确12 110 kV 称兔Ⅱ回线 44.48 漏警 38 220 kV 鲁草Ⅱ回线 66.87 准确13 500 kV 观永甲线 88.96 准确 39 110 kV 清八线 62.86 准确14 110 kV 八小达线 36.61 漏警 40 110 kV 腰洪指线 67.70 准确15 500 kV 大理和平Ⅰ回线 61.10 虚警 41 110 kV 腰挥线 70.03 准确16 500 kV 大苗甲线 86.60 准确 42 220 kV 南草Ⅰ回线 0 漏警17 220 kV 宝乔线 68.13 准确 43 220 kV 小泉Ⅰ回线 66.32 准确18 110 kV 红绿线 90.40 准确 44 110 kV 普谷Ⅰ回线 85.94 准确19 220 kV 玉元Ⅰ回线 77.34 准确 45 220 kV 勐蔓Ⅱ回线 97.73 准确20 220 kV 玉元Ⅱ回线 87.23 准确 46 220 kV 金者线 83.96 准确21 220 kV 草水Ⅱ回线 81.80 准确 47 110 kV 永万的线 90.75 准确22 220 kV 草水Ⅰ回线 80.40 准确 48 110 kV 徐马Ⅰ回线 80.07 准确23 500 kV 观永乙线 80.50 漏警 49 110 kV 大邓T 线 79.50 准确24 110 kV 称金Ⅰ、Ⅱ回线 78.60 准确 50 220 kV 马昆牵线 71.50 准确25 110 kV 芦八线 98.01 准确 51 110 kV 竹冒线 64.50 虚警26 220 kV 新谷Ⅱ回线 67.79 准确
由于雷电先导发展路径的随机性和分散性,以及现有的雷电活动短时预警系统存在的误差,使得雷击跳闸预警结果也存在一定的误差。在实际应用中,报警阈值的高低直接影响预警性能,阈值偏低则导致虚警率偏高,阈值偏高则导致漏警率偏高。在云南电网的实际应用中推荐设置雷击跳闸报警阈值为60%,与实际情况(表6)对比(见图14),可以看出:预测跳闸且实际发生跳闸的次数为42 次(预警准确);预测不跳闸实际发生跳闸的次数为3 次(漏警);预测跳闸杆塔位置错误2次(漏警),分别为第4 组的220 kV 建岗Ⅱ回线(预测跳闸杆塔为129 号,实际跳闸杆塔为98 号)与第23 组的500 kV 观永乙线(预测跳闸杆塔为27 号,实际跳闸杆塔为32 号);雷电活动短时预警系统漏报1 次(漏警);预测跳闸实际不跳闸的次数为3 次(虚警)。为有效评估雷击跳闸预警性能,提出预警准确率、漏警率、虚警率三项预警性能指标,表达式[17,20,36]分别为
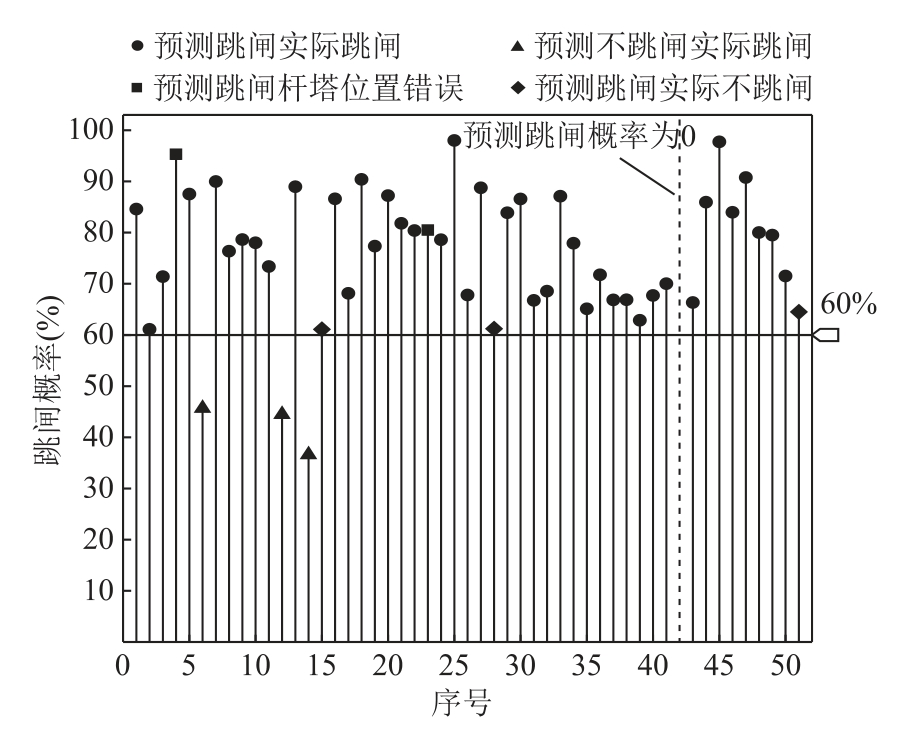
图14 雷击跳闸概率计算结果
Fig.14 Calculation results of lightning strike trip probability
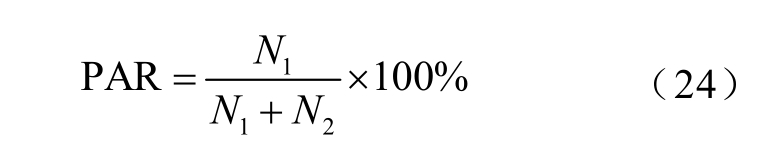
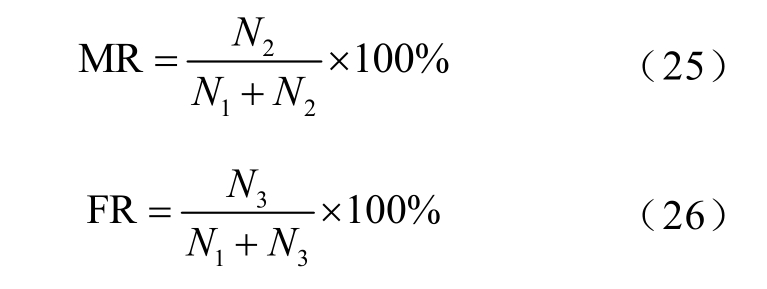
式中,N1 为预测跳闸实际发生跳闸的次数;N2 为预测不跳闸实际发生跳闸的次数;N3 为预测跳闸实际不发生跳闸的次数。
由式(24)~式(26)计算得到预警性能指标,并与文献[17, 21]的雷击跳闸预警方法作对比,结果见表7。可以看出本文模型的三项预警性能指标优于文献[17, 21],预警性能较为理想,其中预警准确率为87%,漏警率为12%,虚警率为7%。由此可见,本文所提出算法在实际应用中具有良好的预警效果。
表7 预警性能指标对比
Tab.7 Comparison of early warning performance indicators
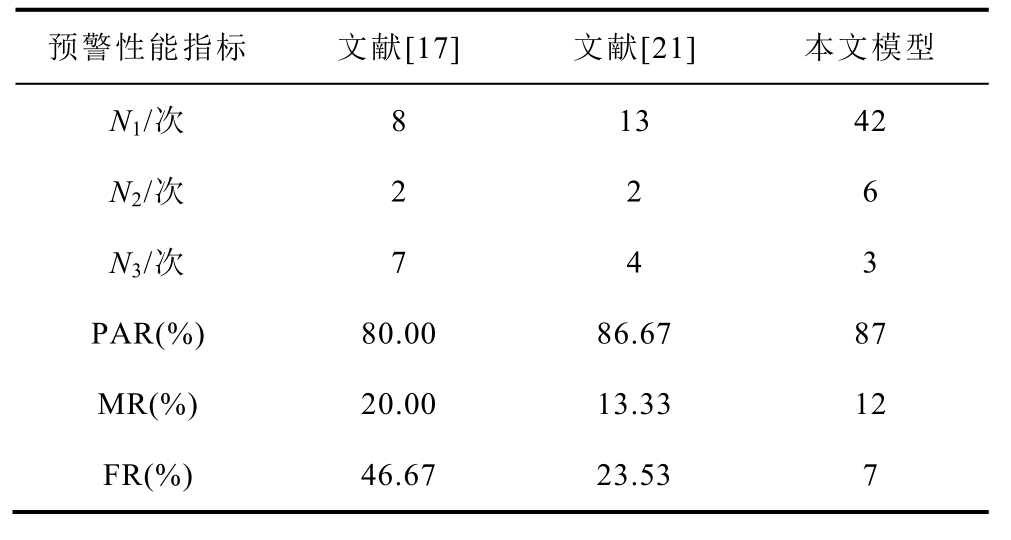
预警性能指标 文献[17] 文献[21] 本文模型N1/次 8 13 42 N2/次 2 2 6 N3/次 7 4 3 PAR(%) 80.00 86.67 87 MR(%) 20.00 13.33 12 FR(%) 46.67 23.53 7
4 结论
本文提出一种山区输电线路雷击跳闸预警融合算法,将蒙特卡罗法与雷电先导分形模型相结合,可以充分考虑区域雷电活动特征与微地形条件;在本文算法的基础上,构建了不同雷电流幅值、不同电压等级(110 kV、220 kV、500 kV)、不同微地形条件的输电线路雷击跳闸概率数据库,形成了输电线路雷击跳闸预警示范系统;在云南电网的实际应用中显示预警准确率为87%,漏警率为12%,虚警率为7%,各项性能指标优于已有的雷击跳闸预警算法,并且虚警率得到显著降低,具有良好的预警效果,可以辅助电网相关部门提前采取针对性的预防措施。
[1] 张刘春. ±1100 kV 特高压直流输电线路防雷保护[J]. 电工技术学报, 2018, 33(19): 4611-4617.Zhang Liuchun. Lightning protection of ±1 100 kV UHVDC transmission line[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4611-4617.
[2] 曾辉, 孙峰, 李铁, 等. 澳大利亚“9·28”大停电事故分析及对中国启示[J]. 电力系统自动化, 2017,41(13): 1-6.Zeng Hui, Sun Feng, Li Tie, et al. Analysis of “9·28”blackout in South Australia and its enlightenment to China[J]. Automation of Electric Power Systems,2017, 41(13): 1-6.
[3] 黎鹏, 肖盼, 屈莹莹, 等. 带长连续电流多重回击作用下500 kV 避雷器温升特性分析[J]. 电工技术学报, 2020, 35(增刊2): 603-611.Li Peng, Xiao Pan, Qu Yingying, et al. Temperature rise characteristics of 500 kV arrester under the action of multiple return-strokes with long continuous current[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 603-611.
[4] 高艳丰, 朱永利, 闫红艳, 等. 基于VMD 和TEO的高压输电线路雷击故障测距研究[J]. 电工技术学报, 2016, 31(1): 24-33.Gao Yanfeng, Zhu Yongli, Yan Hongyan, et al. Study on lighting fault locating of high-voltage transmission lines based on VMD and TEO[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 24-33.
[5] 林伟芳, 孙华东, 汤涌, 等. 巴西“11·10”大停电事故分析及启示[J]. 电力系统自动化, 2010, 34(7):1-5.Lin Weifang, Sun Huadong, Tang Yong, et al.Analysis and lessons of the blackout in Brazil power grid on November 10, 2009[J]. Automation of Electric Power Systems, 2010, 34(7): 1-5.
[6] 孙华东, 许涛, 郭强, 等. 英国“8·9”大停电事故分析及对中国电网的启示[J]. 中国电机工程学报,2019, 39(21): 6183-6192.Sun Huadong, Xu Tao, Guo Qiang, et al. Analysis on blackout in Great Britain power grid on August 9th,2019 and its enlightenment to power grid in China[J].Proceedings of the CSEE, 2019, 39(21): 6183-6192.
[7] 李雍, 李舜, 戴玉松, 等. 超特高压输电线路绕击屏蔽模型及计算方法[J]. 电气技术, 2016, 17(1): 1-5.Li Yong, Li Shun, Dai Yusong, et al. Review on shielding lightning model and calculation method of extra-high voltage and ultra-high voltage transmission lines[J]. Electrical Engineering, 2016, 17(1): 1-5.
[8] 李瑞芳, 吴广宁, 曹晓斌, 等. 输电线路雷电绕击率的三维计算方法[J]. 电工技术学报, 2009, 24(10):134-138.Li Ruifang, Wu Guangning, Cao Xiaobin, et al. Threedimensional calculation method on shielding failure rate of transmission lines[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 134-138.
[9] 袁海燕, 傅正财, 魏本刚, 等. 综合考虑风偏、地形和工作电压的特高压交流线路雷电绕击性能[J].电工技术学报, 2009, 24(5): 148-153.Yuan Haiyan, Fu Zhengcai, Wei Bengang, et al.Lightning shielding failure analysis of UHVAC transmission lines based on improved EGM[J].Transactions of China Electrotechnical Society, 2009,24(5): 148-153.
[10] 李建标. 雷电先导分形模型及线路耐雷性能评估方法的研究[D]. 重庆: 重庆大学, 2012.
[11] 司马文霞, 杨庆, 李永福, 等. 输电线路雷电绕击评估方法分析及展望[J]. 高电压技术, 2015, 41(8):2500-2513.Sima Wenxia, Yang Qing, Li Yongfu, et al. Analysis and prospect of lightning shielding failure evaluation methods of transmission lines[J]. High Voltage Engineering, 2015, 41(8): 2500-2513.
[12] Shi Wei, Li Qingmin, Zhang Li. A stepped leader model for lightning including charge distribution in branched channels[J]. Journal of Applied Physics,2014, 116(10): 103303.
[13] 师伟. 雷击特高压输电线路先导连接过程数值模拟研究[D]. 济南: 山东大学, 2015.
[14] 谢云云, 薛禹胜, 王昊昊, 等. 电网雷击故障概率的时空在线预警[J]. 电力系统自动化, 2013, 37(17):44-51.Xie Yunyun, Xue Yusheng, Wang Haohao, et al.Space-time early-warning of power grid fault probability by lightning[J]. Automation of Electric Power Systems, 2013, 37(17): 44-51.
[15] 王红斌, 程思, 范伟男, 等. 雷暴活动全闪电定位及空间演变过程分析[J]. 电工技术学报, 2021,36(2): 373-379.Wang Hongbin, Cheng Si, Fan Weinan, et al. Total lightning location of thunderstorm activities and spatial evolution process analysis[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 373-379.
[16] 张博文. 基于雷电定位系统的输电线路实时雷击跳闸概率预测[D]. 成都: 西南交通大学, 2014.
[17] 鲍捷, 王昕, 张峰, 等. 基于雷电定位数据驱动的紧密输电通道连续雷击跳闸预警方法[J]. 电网技术, 2022, 46(3): 1194-1205.Bao Jie, Wang Xin, Zhang Feng, et al. Data-driven early warning for continuous lightning trip-out of compact power corridors based on lightning location data[J]. Power System Technology, 2022, 46(3):1194-1205.
[18] 赵芝, 石季英, 袁启海, 等. 输电线路的雷击跳闸概率预测计算新方法[J]. 电力系统自动化, 2015,39(3): 51-58, 139.Zhao Zhi, Shi Jiying, Yuan Qihai, et al. A new prediction calculation method of transmission lines lightning trip probability[J]. Automation of Electric Power Systems, 2015, 39(3): 51-58, 139.
[19] 王伟. 强对流天气下输电线路风偏放电与雷击跳闸风险预警方法研究[D]. 重庆: 重庆大学, 2017.
[20] 夏桥. 输电线路雷击实时风险评估及跳闸预警模型研究[D]. 广州: 华南理工大学, 2019.
[21] Gu Su, Tang Chongwang, Deng Zhiyong, et al.Lightning trip warning based on GA-BP neural network technology[C]//2020 4th International Conference on HVDC (HVDC), Xi'an, China, 2020:833-840.
[22] 唐古玥. 架空输电线路档距段雷击跳闸预测[J]. 电力大数据, 2021, 24(5): 65-71.Tang Guyue. Lightning trip predictionin span section of overhead transmission line[J]. Power Systems and Big Data, 2021, 24(5): 65-71.
[23] 中华人民共和国住房和城乡建设部. 交流电气装置的过电压保护和绝缘配合设计规范: GB/T 50064—2014[S]. 北京: 中国计划出版社, 2014.
[24] 晏威, 肖纯, 吴细秀, 等. 基于雷电活动特征的10 kV 配电线路雷击跳闸率计算[J]. 高电压技术, 2021,47(3): 1118-1127.Yan Wei, Xiao Chun, Wu Xixiu, et al. Calculation of lightning trip out rate of 10 kV distribution lines based on lightning activity characteristics[J]. High Voltage Engineering, 2021, 47(3): 1118-1127.
[25] 李瑞芳, 吴广宁, 曹晓斌, 等. 雷电流幅值概率计算公式[J]. 电工技术学报, 2011, 26(4): 161-167.Li Ruifang, Wu Guangning, Cao Xiaobin, et al.Formula for probability of lightning current amplitude[J]. Transactions of China Electrotechnical Society, 2011, 26(4): 161-167.
[26] 尹丽云, 王灏樾, 金文杰, 等. 低纬高原复杂地形对闪电的影响分析[C]//第35 届中国气象学会年会S19 雷电物理和防雷新技术——第十六届防雷减灾论坛, 合肥, 2018: 543-554.
[27] 王擎, 贾春霞, 刘洪鹏. 汪清油页岩燃烧动力学模型[J]. 中国电机工程学报, 2012, 32(23): 27-31, 146.Wang Qing, Jia Chunxia, Liu Hongpeng. Combustion kinetic model of Wangqing oil shale[J]. Proceedings of the CSEE, 2012, 32(23): 27-31, 146.
[28] Ametani A, Kawamura T. A method of a lightning surge analysis recommended in Japan using EMTP[J].IEEE Transactions on Power Delivery, 2005, 20(2):867-875.
[29] International Electrotechnical Commission. Insulation co-ordination-part 2: application guide: IEC 60071—2: 2018[S]. 2018.
[30] 冯杰. 云广±800 kV 特高压直流输电线路耐雷性能研究[D]. 重庆: 重庆大学, 2007.
[31] Martinez J A, Castro-Aranda F. Lightning performance analysis of overhead transmission lines using the EMTP[J]. IEEE Transactions on Power Delivery, 2005, 20(3): 2200-2210.
[32] Li Jianbiao, Yang Qing, Sima Wenxia, et al. A new estimation model of the lightning shielding performance of transmission lines using a fractal approach[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(5): 1712-1723.
[33] 伏进. 特高压直流输电线路耐雷性能分析方法研究[D]. 重庆: 重庆大学, 2009.
[34] He Jinliang, Tu Youping, Zeng Rong, et al. Numeral analysis model for shielding failure of transmission line under lightning stroke[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 815-822.
[35] Peek F W. The law of corona and the dielectric strength of air-IV the mechanism of corona formation and loss[J]. Transactions of the American Institute of Electrical Engineers, 1927, XLVI: 1009-1024.
[36] 王建. 输电线路气象灾害风险分析与预警方法研究[D]. 重庆: 重庆大学, 2016.