0 引言
大型电力变压器绝缘系统为油纸绝缘，绝缘油理论上为纯净绝缘油，不含杂质颗粒[1]。但现实中，基本上不存在绝对纯净的绝缘油，电力变压器在生产、运输、安装、绝缘油加注、运行和维修等过程中，都会掺杂不同属性且尺寸不一的杂质颗粒[2]。通过对现场绝缘油进行分析，发现绝缘油中的杂质颗粒主要是纤维、碳化合物、金属颗粒，在这些不同属性的杂质颗粒当中，超过90%的杂质为纤维固体颗粒[3]。绝缘油中的杂质颗粒在强梯度电场环境中，会发生积聚现象并可能形成杂质颗粒小桥，诱发放电现象，使变压器绝缘性能劣化。
近年来，国内外学者陆续开展含纤维杂质颗粒绝缘油耐受能力研究。在绝缘油静止条件下，英国南安普顿大学S. Mahmud、G. Chen 等[4-8]研究了在不同的直流电场、交流电场及交直流混合电场模式下纤维颗粒的运动轨迹及其特性，并描述了纤维杂质颗粒在不同电压强度下积聚成桥的过程和影响因素。英国曼彻斯特大学刘强等[9]探究了在不同形状电极下纤维杂质颗粒对绝缘油击穿特性的影响，发现纤维颗粒的存在降低了绝缘油的击穿电压。马来西亚M. H. S. Zainuddin 等[10]对直流电场作用下的纤维杂质颗粒在植物油中形成杂质小桥的现象进行了探究。I. L. Hosier 等学者[11]探究了不同含量的纤维杂质颗粒、碳颗粒对矿物油的击穿特性的影响，并对介电光谱和电导率进行了测量。华北电力大学赵涛[12]通过锥-板电极模型分析了纤维杂质颗粒对矿物油冲击击穿特性的影响，通过低、中、高三种纤维颗粒含量水平下油间隙在四种冲击波形下的击穿实验，获得了不同纤维颗粒含量下油间隙击穿电压的分布规律。重庆大学李原龙[13]研究了固体颗粒在绝缘油中的运动特性及其对绝缘油击穿强度的影响，通过模拟固体杂质颗粒在油中的运动轨迹，分析了不同颗粒尺寸大小、电场强度、电压类型与颗粒运动的关系。西安交通大学张乔根教授课题组[14-15]研究了直流电压下纤维杂质颗粒成桥的形成过程，并发现杂质小桥是由绝缘纸表面的纤维丝束构成。重庆大学郝建等[16]研究了颗粒属性对矿物绝缘油直流击穿特性的影响差异，发现纤维颗粒粒径的增加进一步降低了油品的击穿特性。但大型电力变压器内部绝缘油一般采用强迫油循环风冷（Forced-Oil and Forced-Air cooled, OFAF）或强迫油循环导向风冷（Forced-Directed-Oil and Forced-Air cooled, ODAF），其内部绝缘油基本处于流动状态（油流速度一般小于1 m/s）[17]，导致悬浮在流动绝缘油中的纤维杂质颗粒的运动特性将发生改变，但关于绝缘油流动对纤维杂质颗粒运动特性的影响还未有相关研究。
基于此，本文提出了流动绝缘油中纤维杂质颗粒运动特性仿真研究，通过对流动绝缘油中纤维杂质颗粒进行受力分析，利用动力学分析法构建单颗粒纤维杂质在流动绝缘中运动的固-液两相流多物理场模型，研究分析在不同颗粒尺寸、电场强度幅值、油流速度、油温、初始速度及位置条件下单颗粒纤维杂质在高压直流电场下的运动特性和影响因素。
1 流动绝缘油中纤维杂质颗粒动力学分析和运动固-液两相流建模
1.1 纤维杂质颗粒的动力学分析
悬浮在流动绝缘油中的纤维杂质颗粒主要受到电场力、重力、浮力、油体粘滞阻力、曳力、介电泳力等作用力。其中重力和浮力是一对方向相反的作用力，与纤维杂质颗粒尺寸、材料属性及油体密度有关[18]。
1.1.1 电场力
带电极板会在其周围形成一定的电场梯度，电场会对其中的带电粒子产生作用力，这种力被称为电场力。纤维杂质颗粒本身不带电或带少量电荷，而悬浮在绝缘油中的纤维杂质颗粒经过运动触碰到电极后，颗粒与极板之间发生电荷转移，这期间会出现短暂的脉冲电流[19]。纤维颗粒充满电荷后，会朝着与电荷极性相反的极板运动。在这过程中，纤维杂质颗粒充当电荷载体，在电极之间反复传递电流[20]。纤维杂质颗粒受到的电场力Fe 为
式中，E 为纤维杂质颗粒所处环境的电场强度；q 为纤维颗粒本身所带电荷。q 与颗粒尺寸、颗粒所处液体介质的相对介电常数及外加电场强度相关。对于半径为r 的球形颗粒，颗粒所带电荷量为
式中，εm 和ε0 分别为液体介质的相对介电常数和真空介电常数。
1.1.2 重力与浮力
悬浮在绝缘油中的纤维杂质颗粒受到的压力来自各个方向，该压力总和被称为油体对颗粒产生的浮力[21]。颗粒所受的浮力与重力是一对方向相反的力，都与其材料密度、尺寸大小相关。当绝缘油的密度、颗粒尺寸、颗粒材料密度一定时，颗粒所受的浮力和自身重力便可确定。为了简化重力和浮力，故只考虑它们的合力。以Fm 表示颗粒所受其合力，其公式为
式中，ρ1 为绝缘油密度；ρ2 为纤维杂质颗粒密度；m0 为纤维杂质颗粒质量；g 为重力加速度。
1.1.3 油体粘滞阻力
绝缘油都具有一定的粘性，当沉浸其中的纤维杂质颗粒运动时，其表面会附着一些粘滞性油体。这些油体会跟随颗粒一起运动，两者间便出现一定的内摩擦力，该作用力被称为油体粘滞阻力[22]。仿真过程中，通过固-液两相流物理场来解决纤维杂质颗粒与绝缘油之间相互作用力的问题。根据斯托克斯模型来计算颗粒在油体中受到的粘滞阻力F0 为
式中，ηoil 为油体的粘度；v 为颗粒的运动速度。
1.1.4 曳力
在物体和流体之间发生相对运动的情况下，流体施加给物体的作用力，被称为流体曳力[23]。油流施加给纤维杂质颗粒的曳力，其作用方向与颗粒相对运动方向一致。曳力FD 的计算公式为
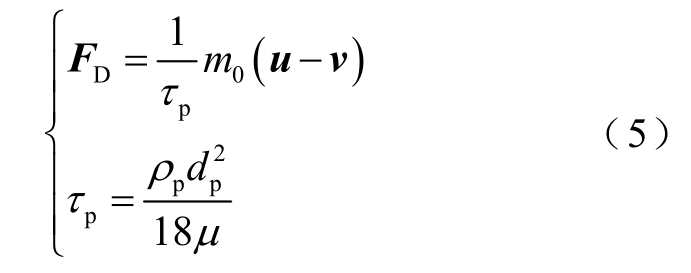
式中，u 为流体流速；ρp 为颗粒数密度；dp 为颗粒直径；μ为流体粘度。
1.2 运动固-液两相流建模
在流体力学领域对流体运动常用的研究方法有以下两种。
1）拉格朗日分析法。以流体中的每一个质点为研究对象，探究各参数在流动过程中的变化规律，再对所有质点进行一定的分析，最终得到整体流场的分布特性[24]。质点的运动参数是具体位置和时间的函数，确定某一质点的空间位置矢量h(t),便能给出速度和加速度分别为
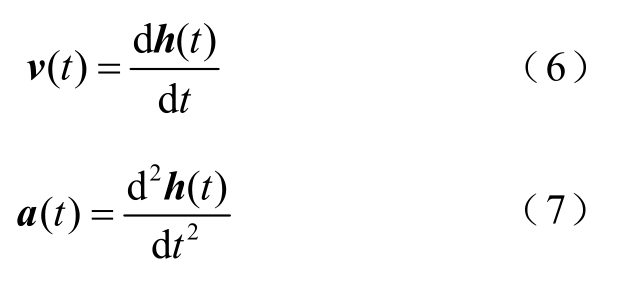
在拉格朗日方法中，流体质点规律也是靠位置矢量h(t)来体现[25]。通常取t=t0 时刻，以空间位置坐标 ( xt0 , y t0 , z t0)来标识某一质点。则直角坐标系中t0时刻，该流体质点位置坐标为
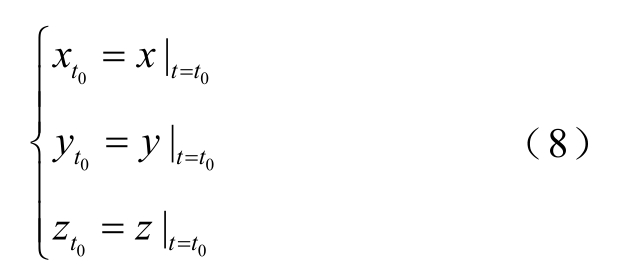
显然，不同流体质点将有不同的 ( xt0 , y t 0 , z t0)值。
2）欧拉方法。以整个空间点为研究基础，在某时刻对流体所有质点的运动进行分析，综合考虑质点对场域的分布情况。欧拉方法中，也是以位置矢量h(t)来探究质点的运动规律，但流动参量是流体速度。在t 时刻，空间某一点速度可表示为
式中，h 为空间坐标，在直角坐标系中有h=xi+yj+zk，则可得到
表示为分量的形式为
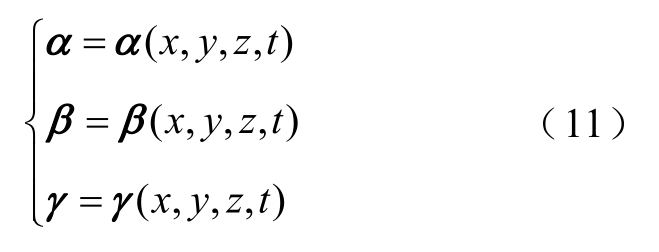
式中，α、β、γ 为v 在空间上的速度分量；x、y、z为欧拉变数，是自变量；速度v 为待求解的因变量；(x, y, z)为空间点的坐标值，因此，这里的v(x, y, z, t)是速度场[26]。
本文利用颗粒轨道模型来研究纤维杂质颗粒运动的过程中，采用拉格朗日方法计算固相，用欧拉方法计算流体相，将颗粒运动方程和流体N-S 方程进行耦合求解，得到颗粒运动速度，再与运动时间积分，最终得到颗粒运动轨迹[27-28]。该方法计算简单，可以对轨迹复杂的颗粒进行求解，但颗粒数要求不宜过多，符合本文仿真内容。
2 纤维杂质颗粒仿真模型
2.1 仿真模型的建立
对于大型变压器内油体流动的问题，通常会采用强迫油循环冷却的方式来对变压器内部结构进行降温。油流从底部流入、顶部流出，起到循环散热及绝缘的作用。油流速度主要集中在高、低压绕组两侧纵向油道；而在绕组中间的大部分区域，由于两侧的油流压力差别较小，导致水平油道中的绝缘油几乎没有流动[29]。故采用纵向板-板均匀场的电极模型来模拟变压器内两侧纵向油道，电极直径为25 mm、厚度为3 mm，电极板间距为5 mm。剖分后的板-板电极二维模型结构如图1 所示，模型所采用的材料属性见表1。
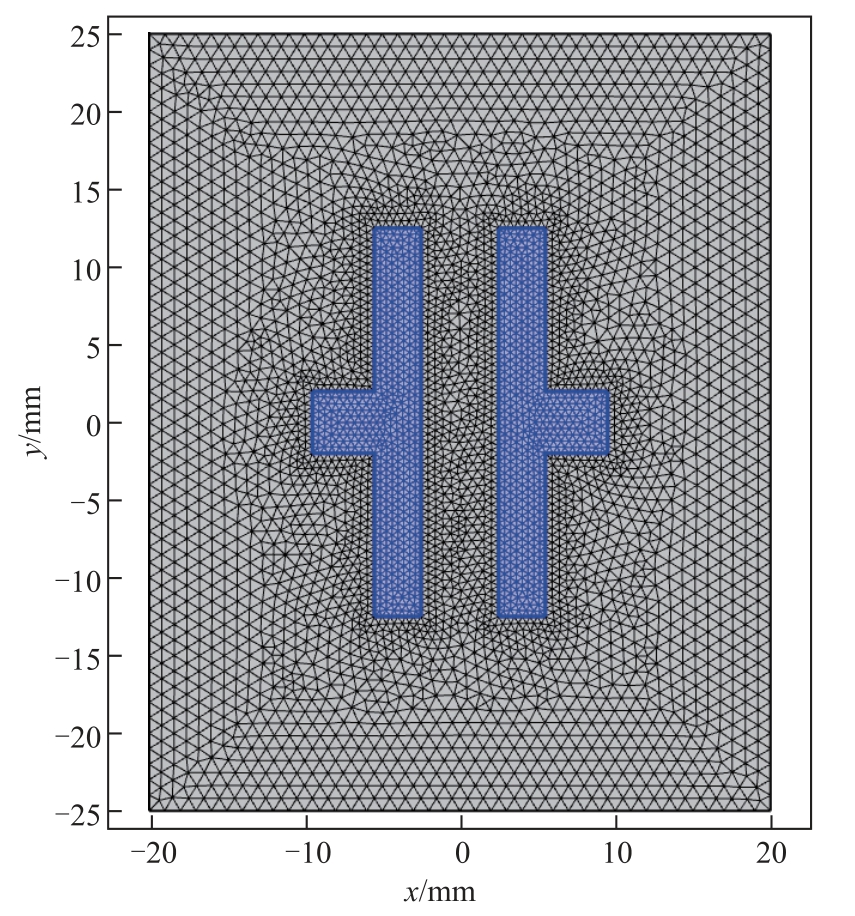
图1 二维模型结构
Fig.1 Structure diagram of two-dimensional model
表1 材料属性
Tab.1 Material properties
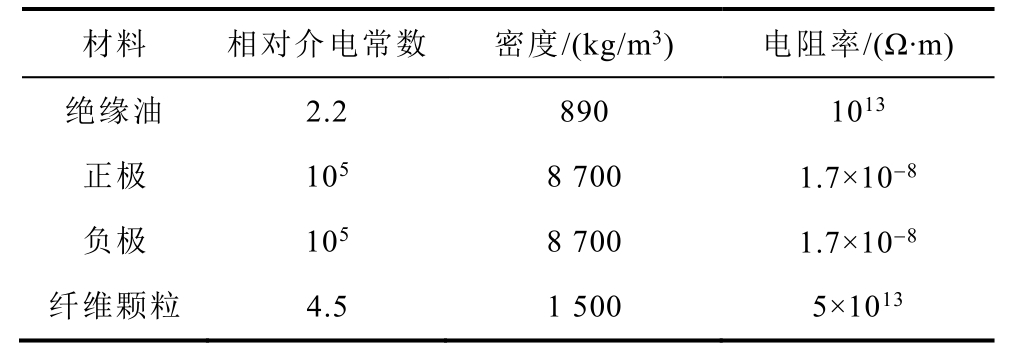
材料 相对介电常数 密度/(kg/m3) 电阻率/(Ω·m)绝缘油 2.2 890 1013正极 105 8 700 1.7×10-8负极 105 8 700 1.7×10-8纤维颗粒 4.5 1 500 5×1013
2.2 物理场环境
2.2.1 电流场
根据麦克斯韦方程组，电场中的有限元方程为
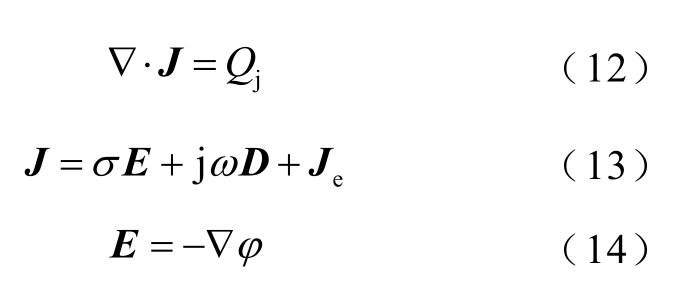
式中，J 为电流密度；Qj 为改变的电荷量；E 为电场强度，σ为电导率，则σE 为传导电流；ω为角频率，D 为电位移矢量，则jωD 为位移电流；Je 为外施电流密度；φ 为电位。
2.2.2 流体场
大型油浸式变压器内部油道结构复杂，绝缘油在其中的流动一般为湍流。流体力学理论研究表明，任何流体流动和传热都遵循质量、动量和能量三大守恒定律。如果为湍流流动，通过在时间域上对流场中的各个物理量进行雷诺平均化处理，得到时均化Reynolds 平均可压缩的N-S 方程组[30]为
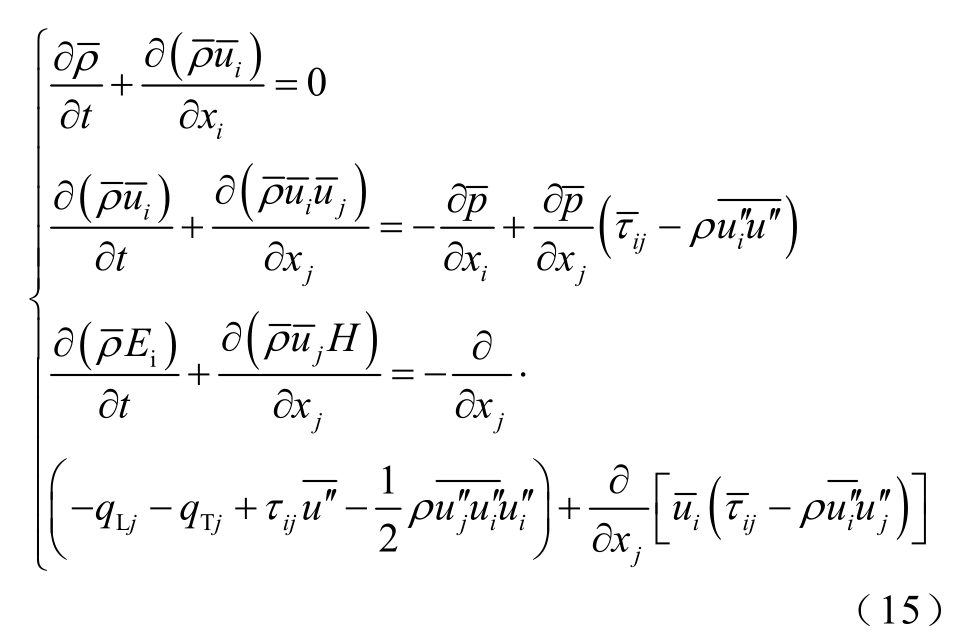
式中，ρ 为流体密度；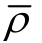
为雷诺平均流体密度；
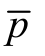为雷诺平均压力；Ei 为内能；H 为无量纲参数；
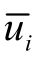和
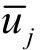为雷诺平均速度分量；
、
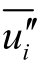和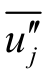
分别为雷诺脉动平均速度及其分量；τ ij和
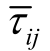分别为应力张量分量和雷诺平均应力张量分量；q Lj为层流热流；q T j为湍流热流。
2.2.3 流体粒子追踪
流体粒子追踪通过拉格朗日方式来描述问题，以牛顿运动定律进行力学计算，最后得到粒子运动轨迹。在描绘粒子每时刻的运动位置时，需要进行常微分方程求解。由于粒子在不同时刻运动位置也不同，导致粒子受到的作用力也随时间变化。流体颗粒追踪通过对颗粒运动进行实时监测，并计算出各个时刻运动粒子所受作用力Ft 及其矢量速度，以此得到纤维杂质颗粒的运动轨迹。根据牛顿第二定律可得到
3 纤维杂质颗粒在流动绝缘油中的运动特性分析
大型电力变压器的电压等级不同，其内部形成的电场梯度也有所差别，而悬浮于油流中的纤维杂质颗粒数量众多、尺寸不一，其初始速度和初始位置也不尽相同。此外，在运变压器会发生介质损耗产生局部过热现象，造成油体温度升高[31]，不同带载状态变压器内油温也不相同，这些因素都会影响到纤维杂质颗粒的运动特性，因此，有必要对不同电场强度、颗粒尺寸、油流速度、油体温度、初始速度及位置条件下纤维杂质颗粒在绝缘油流动中的运动特性展开分析。
3.1 电场强度对纤维颗粒运动的影响
在研究电场强度对纤维杂质颗粒运动特性影响的过程中，设定纤维杂质颗粒半径为25 μm，板间距为5 mm，由于变压器内油流速度分布非常不均匀，呈抛物线状分布,最高速度为1.5 m/s,而最低速度达到了0.01 m/s[32]，这里设置绝缘油流速为恒定值0.01 m/s。
施加2 kV 电压时，纤维杂质颗粒运动轨迹如图2 所示。不同电压下纤维杂质颗粒运动参量的统计结果见表2。
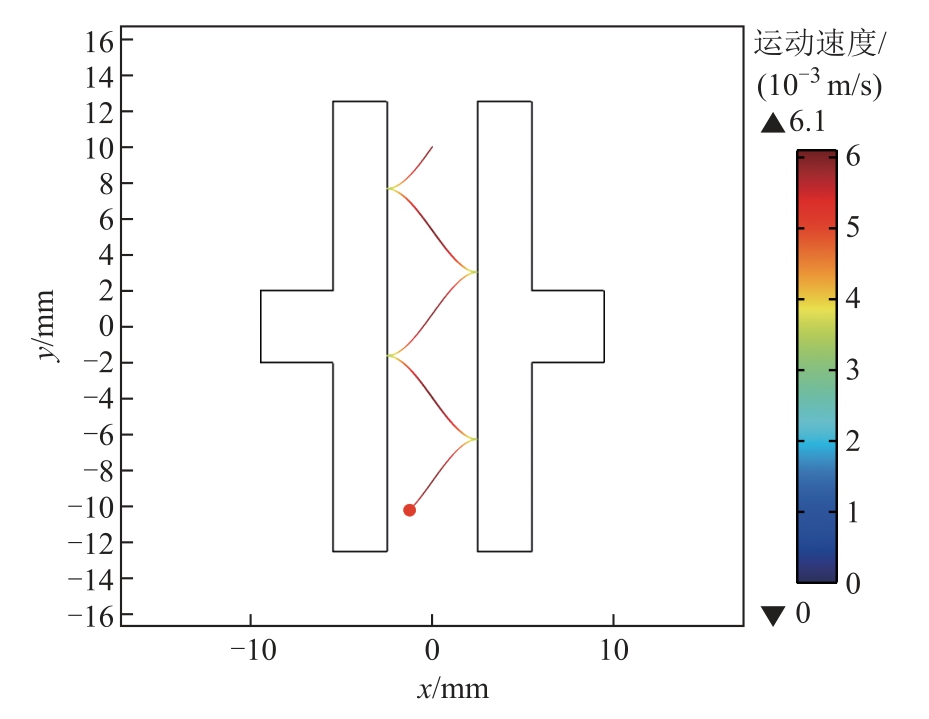
图2 不同电压下纤维杂质颗粒运动轨迹
Fig.2 Movement track of fiber impurity particles under different voltages
表2 不同电压下纤维杂质颗粒运动参量
Tab.2 Movement parameters of fiber impurity particles under different voltages
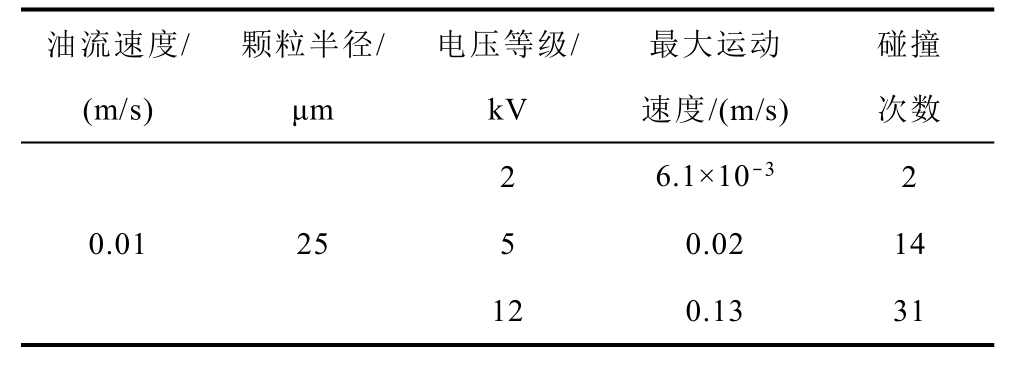
油流速度/(m/s)颗粒半径/μm电压等级/kV最大运动速度/(m/s)碰撞次数2 6.1×10-3 2 0.01 25 5 0.02 14 12 0.13 31
由表2 可以明显看出，随着电压等级的提高，在相同时间内，纤维杂质颗粒在电极间的最大运动速度以及颗粒与电极的碰撞次数明显增加。这是因为由式（1）、式（2）可知，电场力Fe 的大小与电场强度E 的二次方成正比，纤维杂质颗粒所受电场力随着电场强度的增强而增大，颗粒横向运动速度加快，在极板间的往返运动轨迹越密集，导致纤维杂质颗粒与电极的碰撞次数逐渐增加。
3.2 尺寸大小对纤维颗粒运动的影响
DL/T 1096—2018《变压器油中颗粒度限值》中规定了400、500、800 kV 换流变压器注油前，100 mL油中大于5 μm 的颗粒数分别不超过2 000、1 000、1 000 个；要求500 kV 和800 kV 换流变压器运行时100 mL 油中大于5 μm 的颗粒数不超过3 000 个，其中500 kV 变压器颗粒数要求为推荐值。
实际在运变压器油道中绝缘油所含纤维杂质颗粒大小不一，颗粒尺寸在几微米到几百微米之间，不同尺寸纤维杂质颗粒在绝缘油中的运动特性可能也不相同。
为了探究纤维杂质颗粒尺寸大小对其运动特性的影响，在仿真过程中分别设置了五种不同半径尺寸的纤维杂质颗粒，电极板施加5 kV 电压，极板间距为5 mm，油流速度为0.01 m/s。颗粒半径为2.5 μm时纤维杂质颗粒运动轨迹如图3 所示，表3 为不同颗粒尺寸下纤维杂质颗粒运动参量的统计结果。
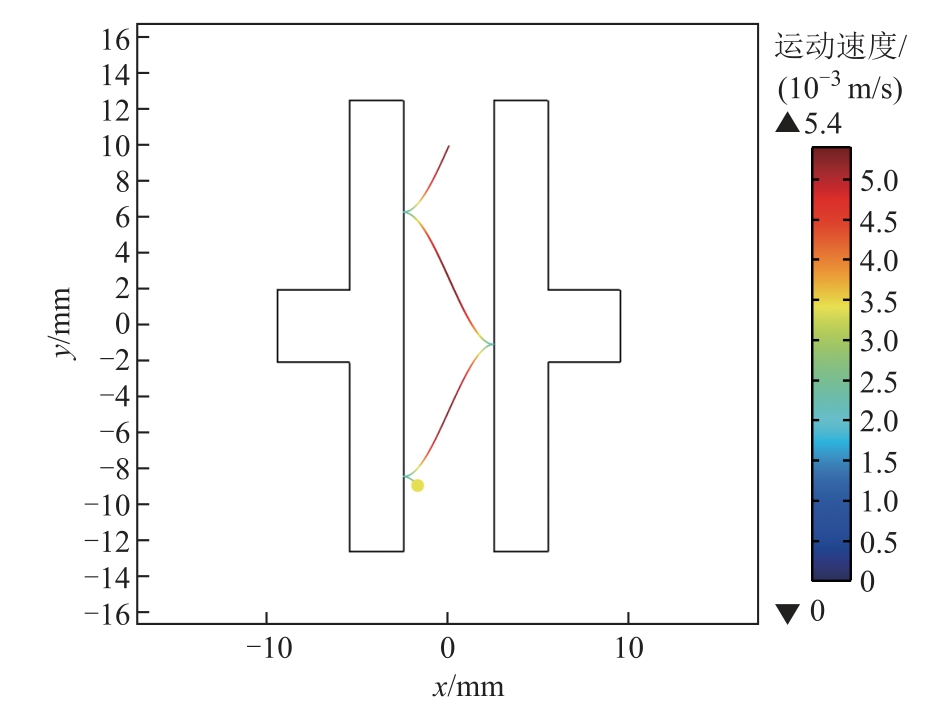
图3 不同颗粒尺寸纤维杂质颗粒运动轨迹
Fig.3 Motion trajectory of fiber impurity particles under different sizes
由表3 可知，随着纤维杂质颗粒尺寸的增大，纤维颗粒在极板间的最大运动速度及颗粒与电极的碰撞次数将会增大，且由不同颗粒尺寸下的碰撞次数增量可以看出，纤维杂质颗粒与电极的碰撞次数和颗粒尺寸几乎呈线性关系。不同尺寸下纤维颗粒与极板的碰撞次数关系如图4 所示。
表3 不同颗粒尺寸下纤维杂质颗粒运动参量
Tab.3 Movement parameters of fiber impurity particles under different particle sizes
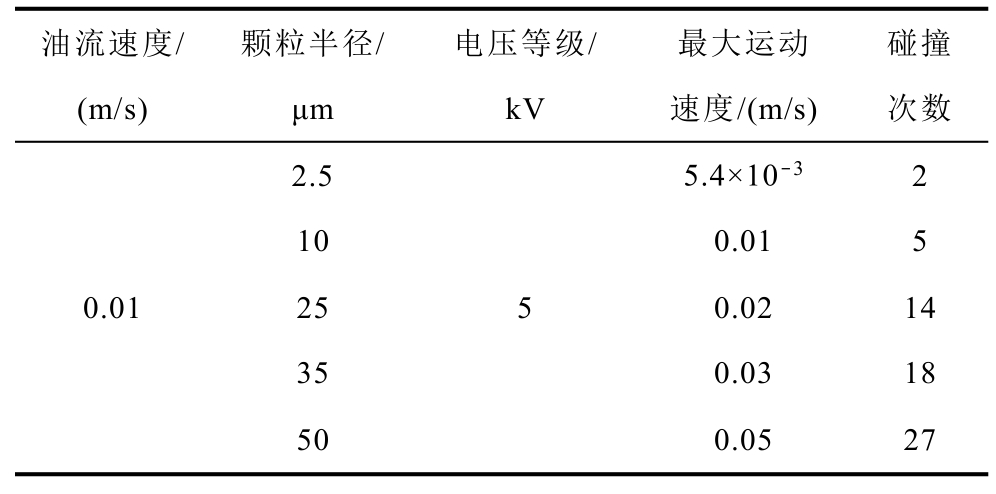
油流速度/(m/s)颗粒半径/μm电压等级/kV最大运动速度/(m/s)碰撞次数2.5 5.4×10-3 2 0.01 10 0.01 5 25 0.02 14 35 0.03 18 50 0.05 27 5
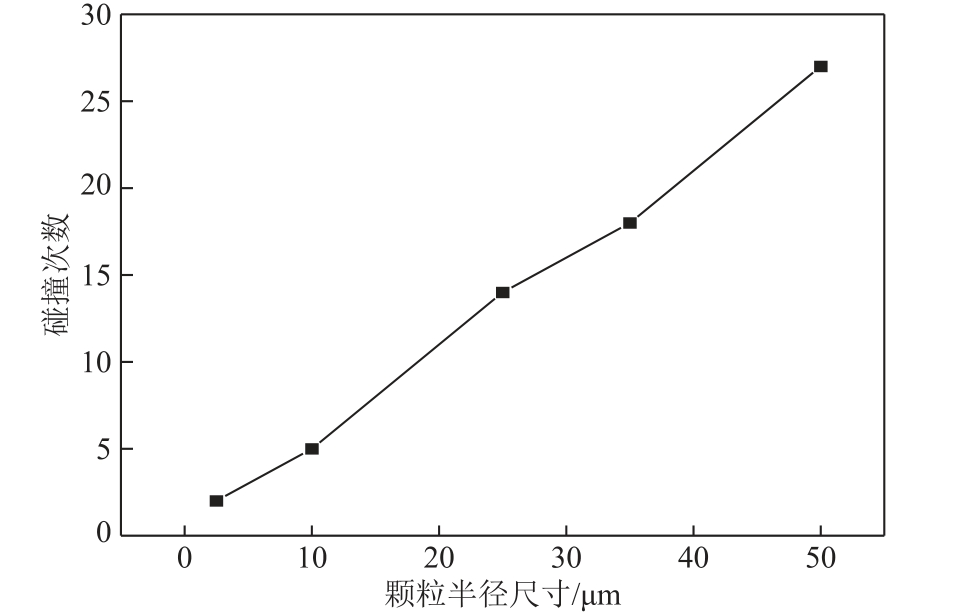
图4 不同尺寸下纤维颗粒与极板的碰撞次数关系Fig.4 The relationship between the number of collisions between fiber particles and the polar plate under different sizes
这是因为在较低油体流速条件下，电场力和油体粘滞阻力为颗粒运动主要作用力，由式（1）、式（2）、式（4）分析可知，电场力Fe 与颗粒半径r 的二次方成正比，粘滞阻力F0 与颗粒半径r 成正比，故颗粒半径r 对电场力Fe 的影响大于粘滞阻力F0。因此，颗粒半径尺寸的增加间接性增大了纤维杂质颗粒所受的电场力，导致颗粒横向运动速度变快，在极板间往返频率增加，与电极碰撞次数增多。
3.3 油流流速对纤维颗粒运动的影响
对于不同容量、电压等级的换流变压器，其内部油道构造也不同，配备的油泵型号也不一样。变压器内油体流速一般小于1 m/s，对于容量较大、电压等级较高的变压器平均油体流速可达到0.2 m/s[33]，变压器内绝缘油流速基本上不高于0.5 m/s，但在油泵周围的流动速度可能会更高[34]。为了探究油流速对纤维杂质颗粒运动特性的影响，设置流速为唯一变量，在极板施加5 kV 电压，颗粒直径为50 μm，分别选取0.02、0.1、0.4 m/s 三种油流速度。流速0.02 m/s时纤维杂质颗粒运动轨迹如图5 所示，不同油流速度下纤维杂质颗粒运动参量的统计结果见表4。
表4 不同油流速度下纤维杂质颗粒运动参量
Tab.4 Movement parameters of fiber impurity particles under different oil flow speeds
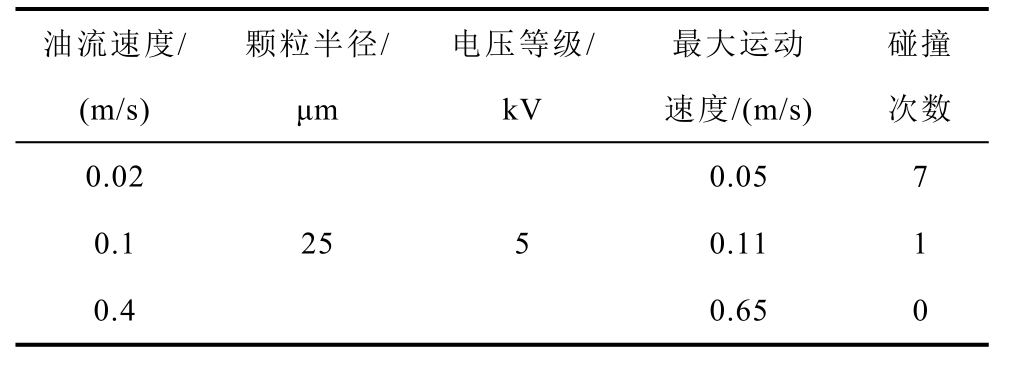
油流速度/(m/s)颗粒半径/μm电压等级/kV最大运动速度/(m/s)碰撞次数0.02 0.05 7 0.1 0.11 1 0.4 0.65 0 25 5
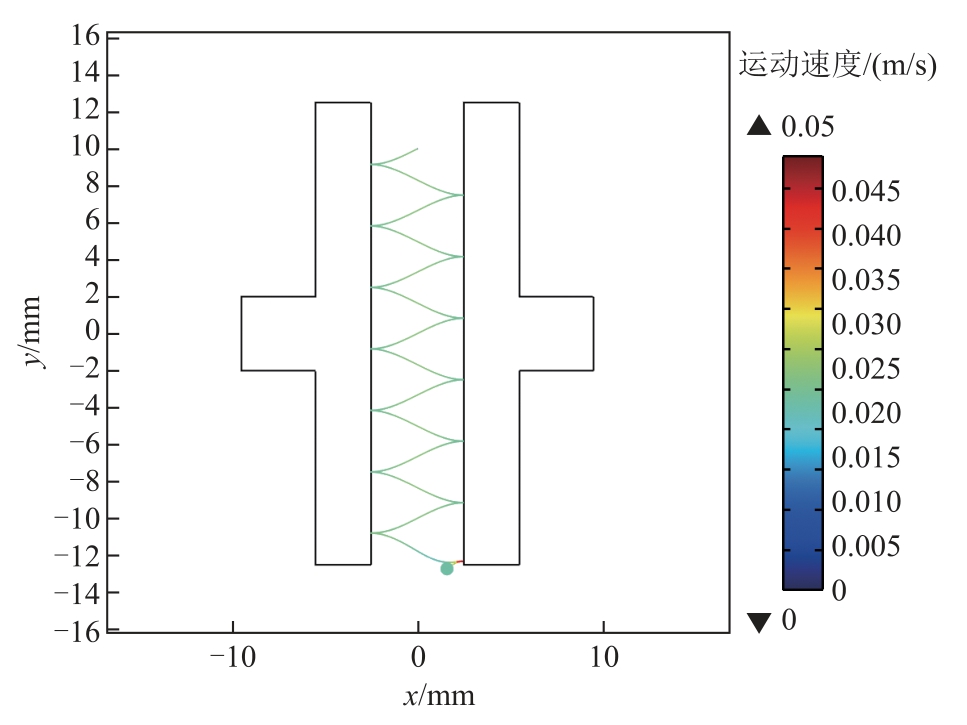
图5 流速0.02 m/s 时纤维杂质颗粒运动轨迹
Fig.5 Movement track of fiber impurity particles at flow rate of 0.02 m/s
由图5 和表4 可知，纤维杂质颗粒从同一个地方释放，随着油流速的增加，到达电极边缘的时间越短，最大运动速度越大，与电极的碰撞次数也越少。经过分析，纤维颗粒的横向运动并没有发生改变，油流速度对纤维杂质颗粒的纵向运动影响较大，由于油流速度的影响，纤维颗粒的运动轨迹发生了纵向位移。随着油流速度的增加，位移程度加大，绝缘油流速达到0.4 m/s 时，颗粒与极板几乎不会碰撞。可以得出，绝缘油流动速度是在研究大型电力变压器绝缘油内纤维杂质颗粒集聚特性中需要重点考虑的因素。
3.4 油体温度对纤维颗粒运动的影响
对于强迫导油循环风冷变压器，冷却风最高温度不大于40℃，最高顶层油温不得超过85℃，温升不超过45℃。对于变压器油运行的最低温度，我国以凝固点高低来划分标准，10 号、25 号和45 号变压器油的凝固点分别不高于-10℃、-25℃及-45℃。受外界环境和运行状况的影响，变压器油温存在一定的波动，可能会对纤维杂质颗粒的运动特性产生影响。
为了探究绝缘油温度变化对纤维杂质颗粒运动轨迹的影响，在仿真过程中，分别设置油温为-5℃、20℃、40℃、60℃和80℃，电极端施加5 kV 电压，板间距为5 mm，流速恒定为0.01 m/s。不同温度下纤维杂质颗粒运动参量如图6 所示。
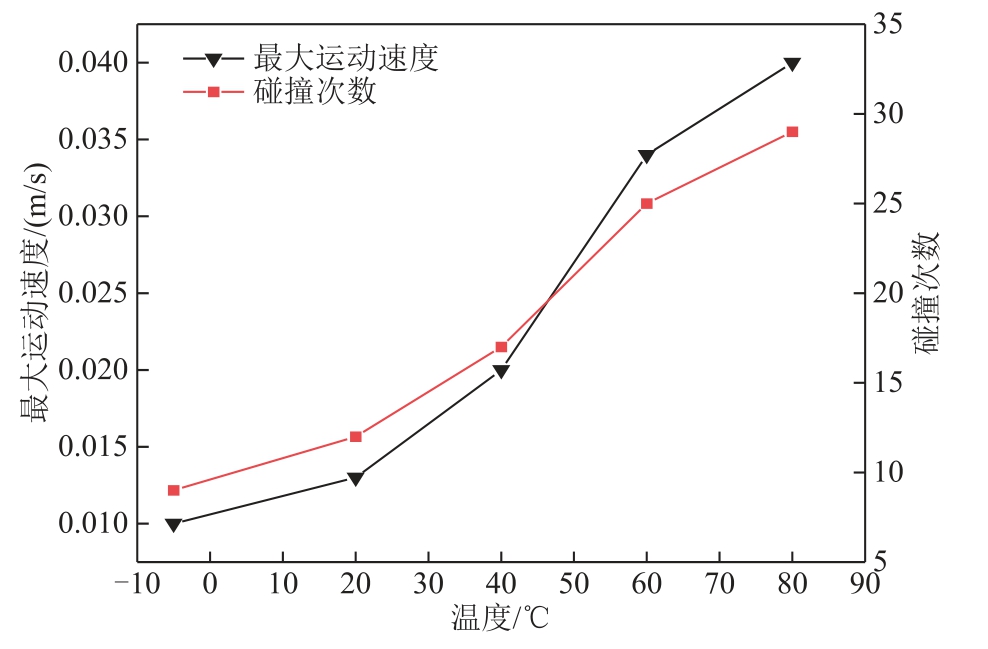
图6 不同温度下纤维杂质颗粒运动参量
Fig.6 Movement parameters of fiber trash particles at
different temperatures
从图6 可以看出，随着温度的升高，纤维杂质颗粒在电极间的运动速度增大，与极板的碰撞次数增多。经过分析，在较低油体流速条件下，电场力和粘滞阻力为颗粒运动主要作用力，随着油温升高，绝缘油分子间的内聚力减小，油体粘度不断减小。由式（4）可知，油体粘滞阻力F0 随着粘度ηoil 降低而减小，间接增大了颗粒所受的电场力Fe，颗粒横向运动速度增加，纤维杂质颗粒与电极的碰撞更加频繁。
3.5 初始速度对纤维颗粒运动的影响
为了研究均匀电场中初始速度对纤维杂质颗粒运动特性的影响，仿真过程中，设置极板电压为5 kV，颗粒半径为25 μm，油流速为0.01 m/s，以纤维颗粒在x、y 轴的速度分量α、β 为变量。x、y 轴正方向为纤维颗粒速度的正方向。初始速度为零时纤维杂质颗粒运动轨迹如图7 所示，不同初始速度分量下纤维杂质颗粒运动参量统计结果见表5。
表5 不同初始速度分量下纤维杂质颗粒运动参量
Tab.5 Movement parameters of fiber impurity particles under different initial velocity components
α/(m/s) β/(m/s) 最大运动速度/(m/s) 碰撞次数0 0 0.02 14-0.05 0 0.05 14 0.05 0 0.05 14 0 -0.05 0.05 14 0 0.05 0.05 14
图7 初始速度为零时纤维杂质颗粒运动轨迹
Fig.7 Motion trajectory of fiber impurity particles when the initial velocity is zero
由表5 可知，纤维杂质颗粒初始速度的变化只引起了最大运动速度的改变，并没有对碰撞次数产生影响。由式（4）、式（5）分析可知，纤维颗粒所受阻力F0 和曳力FD 受到颗粒运动速度v 的影响，初始速度方向的改变引起了阻力和曳力的相对变化，并未对颗粒造成影响。具有一定初始速度的纤维杂质颗粒在开始时速度变化最大，随着阻力F0 和曳力FD 的持续作用，纤维杂质颗粒速度最终趋于稳定，由于这一过程比较短暂，因此该过程仅对纤维颗粒最大运动速度产生了影响，没有改变纤维杂质颗粒与电极间的碰撞次数。
3.6 初始位置对纤维颗粒运动的影响
为了研究均匀电场中初始位置对纤维杂质颗粒运动特性的影响，仿真过程中，设置电极电压为5 kV，颗粒直径为50 μm，板间距为5 mm，油流速为0.01 m/s，以纤维颗粒初始位置x0、y0 为变量。以(0, 10)为基准坐标的纤维杂质颗粒运动轨迹如图7 所示，不同初始位置下纤维杂质颗粒运动参量统计结果见表6。
表6 不同初始位置下纤维杂质颗粒运动参量
Tab.6 Movement parameters of fiber trash particles under different initial positions
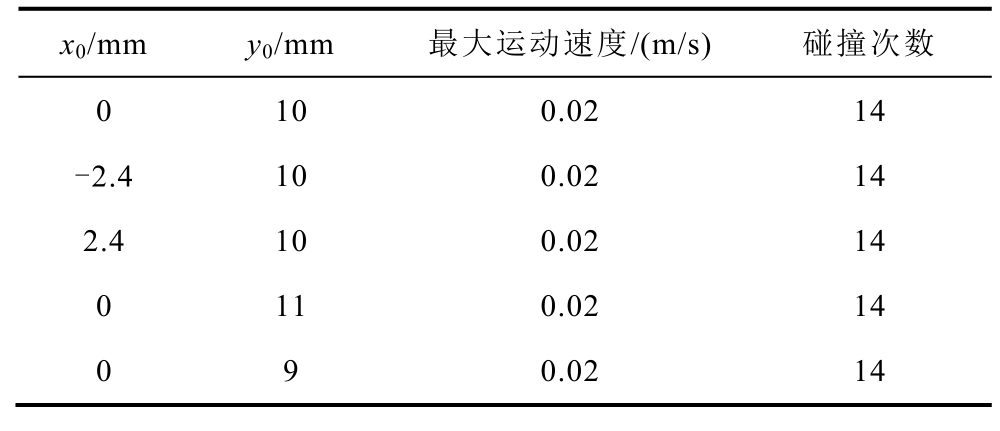
x0/mm y0/mm 最大运动速度/(m/s) 碰撞次数0 10 0.02 14-2.4 10 0.02 14 2.4 10 0.02 14 0 11 0.02 14 0 9 0.02 14
由表6 可知，在均匀电场中，纤维杂质颗粒的初始位置变化并没有对最大运动速度和碰撞次数产生影响。经分析可知，纤维杂质颗粒在均匀电场各个位置下所受的电场强度梯度均相同，受到的电场力也一致，从而导致均匀电场下纤维杂质颗粒的初始位置对其运动特性不造成影响。
4 结论
本文对绝缘油中非金属固体颗粒在油流状态下的运动特性及影响因素做了理论探究。通过仿真取得的主要结论如下：
纤维颗粒的横向运动只与电场力有关，电场强度的增加、颗粒尺寸的增大、油体温度的升高将直接或间接性地导致电场力增大，使纤维颗粒横向运动速度加快，在极板间的往返运动轨迹越密集，与电极表面碰撞次数增多；而随着绝缘油流速的增大，纤维杂质颗粒的运动轨迹纵向位移增加，与电极表面的碰撞次数越来越少；纤维颗粒的初始速度仅对最大运动速度有影响，对颗粒与电极的碰撞次数无影响；在均匀电场中，纤维颗粒初始位置的改变对其运动特性无影响。同时发现绝缘油流速对纤维杂质颗粒运动的影响较大，直径为50 μm 的纤维杂质颗粒在电场强度10 kV/cm、油流速度0.4 m/s 条件下几乎不会和电极发生碰撞，表明在该条件下很难形成杂质颗粒小桥，绝缘油流速是在研究大型电力变压器绝缘油内纤维杂质颗粒集聚特性中需要重点考虑的因素。
[1] 杜伯学, 朱闻博, 李进, 等. 换流变压器阀侧套管油纸绝缘研究现状[J]. 电工技术学报, 2019, 34(6):1300-1309.Du Boxue, Zhu Wenbo, Li Jin, et al. Research status of oil-paper insulation for valve side bushing of converter transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1300-1309.
[2] 高思航. 绝缘油中DBDS 对变压器绕组的腐蚀作用及绝缘性能影响研究[D]. 重庆: 重庆大学, 2017.
[3] 但敏. 杂质颗粒对矿物油和植物油绝缘性能的影响规律及差异研究[D]. 重庆: 重庆大学, 2019.
[4] Mahmud S, Golosnoy I O, Chen G, et al. Numerical simulations of bridging phenomena in contaminated transformer oil[C]//2012 Annual Report Conference on Electrical Insulation and Dielectric Phenomena,Montreal, QC, Canada, 2012: 383-386.
[5] Mahmud S, Chen G, Golosnoy I O, et al. Experimental studies of influence of DC and AC electric fields on bridging in contaminated transformer oil[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2015, 22(1): 152-160.
[6] Mahmud S, Chen G, Golosnoy I O, et al. Bridging in contaminated transformer oil under DC and AC electric field[J]. Journal of Physics: Conference Series,2013, 472: 012007.
[7] Mahmud S, Chen G, Golosnoy I O, et al. Experimental studies of influence of different electrodes on bridging in contaminated transformer oil[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(5):2433-2441.
[8] Mahmud S, Chen G, Golosnoy I O, et al. Bridging in contaminated transformer oil under AC, DC and DC biased AC electric field[C]//2013 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Shenzhen, China, 2013: 943-946.
[9] Lu W, Liu Q. Effect of cellulose particles on impulse breakdown in ester transformer liquids in uniform electric fields[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(5): 2554-2564.
[10] Zainuddin M H S, Zainoddin H, Aman A.Investigation of bridging phenomena in ester oils contaminated with cellulose particles[C]//International Conference on Power, Energy and Communication Systems (IPECS), Perlis, Malaysia,2015: 408-413.
[11] Hosier I L, Vaughan A S. Effect of particulates on the dielectric properties and breakdown strength of insulation oil[C]//2017 IEEE Electrical Insulation Conference, Baltimore, MD, USA, 2017: 376-379.
[12] 赵涛. 气泡和纤维素颗粒对变压器油冲击击穿特性影响研究[D]. 北京: 华北电力大学, 2017.
[13] 李原龙. 固体颗粒在绝缘油中的运动特性及对绝缘油击穿强度的影响[D]. 重庆: 重庆大学, 2017.
[14] 李金忠, 张乔根, 李原, 等. 油纸绝缘局部放电脉冲参数统计分析与老化状态诊断技术[J]. 高电压技术, 2015, 41(11): 3821-3829.Li Jinzhong, Zhang Qiaogen, Li Yuan, et al. Statistical analysis of pulse parameters and diagnose of aging state based on partial discharge in paper-oil insulation[J]. High Voltage Engineering, 2015, 41(11):3821-3829.
[15] 李金忠, 张乔根, 李原, 等. 直流电压下油纸绝缘杂质小桥的形成过程[J]. 高电压技术, 2016, 42(12):3901-3908.Li Jinzhong, Zhang Qiaogen, Li Yuan, et al.Generation process of impurity bridges in oil-paper insulation under DC voltage[J]. High Voltage Engineering, 2016, 42(12): 3901-3908.
[16] 郝建, 但敏, 廖瑞金, 等. 颗粒属性对矿物绝缘油直流击穿特性的影响差异及原因分析[J]. 电工技术学报, 2019, 34(24): 5270-5281.Hao Jian, Dan Min, Liao Ruijin, et al. Influence of particle properties on DC breakdown characteristics of mineral oil and its difference reason analysis[J].Transactions of China Electrotechnical Society, 2019,34(24): 5270-5281.
[17] Zhang Guozhi, Yan Weiyang, Zhang Xiaoxing.Influence of fiber particles on DC breakdown characteristics of transformer oil[C]//2022 IEEE 5th International Electrical and Energy Conference,Nangjing, China, 2022: 1671-1676.
[18] 贺博, 王鹏, 吴锴, 等. 多物理场中染污绝缘油内杂质相动力学行为研究综述[J]. 电工技术学报,2022, 37(1): 266-282.He Bo, Wang Peng, Wu Kai, et al. Reviews on impurity phase dynamics in contaminated insulating oil under multi-physical field conditions[J].Transactions of China Electrotechnical Society, 2022,37(1): 266-282.
[19] 李国倡, 梁箫剑, 魏艳慧, 等. 配电电缆附件复合绝缘界面缺陷类型和位置对电场分布的影响研究[J]. 电工技术学报, 2022, 37(11): 2707-2715.Li Guochang, Liang Xiaojian, Wei Yanhui, et al.Influence of composite insulation interface defect types and position on electric field distribution of distribution cable accessories[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2707-2715.
[20] 潘祖欣, 胡晓. 考虑直流电压谐波和绝缘温度的局部放电仿真[J]. 电力系统及其自动化学报, 2021,33(8): 49-55.Pan Zuxin, Hu Xiao. Simulation of partial discharge considering DC voltage harmonics and insulation temperature[J]. Proceedings of the CSU-EPSA, 2021,33(8): 49-55.
[21] 化世榜. 含流体孔缝介质地震岩石物理模型研究[D].东营: 中国石油大学(华东), 2016.
[22] 胡洋, 胡婷, 曾夯夫, 等. 酯交换工艺对植物绝缘油运动黏度的影响[J]. 绝缘材料, 2022, 55(6): 40-44.Hu Yang, Hu Ting, Zeng Hangfu, et al. Effect of transesterification process on kinematic viscosity of vegetable insulating oil[J]. Insulating Materials, 2022,55(6): 40-44.
[23] 蔡圃. 水力旋流器内多相流动分离机制的计算研究[D]. 兰州: 兰州大学, 2014.
[24] 张福龙. 流体力学经典实验雷诺实验FLASH 模拟[J]. 科技风, 2013(11): 60.
[25] 周大庆, 米紫昊, 茅媛婷. 基于欧拉固液两相流模型的泵站进水侧流场三维模拟[J]. 农业机械学报,2013, 44(1): 48-52.Zhou Daqing, Mi Zihao, Mao Yuanting. 3-D numerical simulation of inlet structure flow in pumping station based on eulerian solid-liquid twophase flow model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1): 48-52.
[26] 刘向军, 石磊, 徐旭常. 稠密气固两相流欧拉-拉格朗日法的研究现状[J]. 计算力学学报, 2007, 24(2):166-172.Liu Xiangjun, Shi Lei, Xu Xuchang. Activities of dense particle-gas two-phase flow modeling in Eulerian-Lagrangian approach[J]. Chinese Journal of Computational Mechanics, 2007, 24(2): 166-172.
[27] 唐学林, 余欣, 任松长. 固-液两相流体动力学及其在水力机械中的应用[M]. 郑州: 黄河水利出版社,2006.
[28] 张国强, 吴家鸣. 流体力学[M]. 北京: 机械工业出版社, 2006.
[29] 李大建. 油浸式变压器温度场分析与油流对内部温升影响因素研究[D]. 成都: 西南交通大学, 2013.
[30] 吴玉林, 刘树红. 粘性流体力学[M]. 北京: 中国水利水电出版社, 2007.
[31] 张国治, 王堃, 闫伟阳. 换流变压器液体绝缘中纤维杂质颗粒研究[J]. 高电压技术, 2022, 48(11):4297-4305.Zhang Guozhi, Wang Kun, Yan Weiyang. Study on fiber impurity particles in liquid insulation of converter transformer[J]. High Voltage Engineering,2022, 48(11): 4297-4305.
[32] 杨海晶, 晏东日, 石光, 等. 油浸式变压器油流速与温度场关联性建模[J]. 电力科学与技术学报,2017, 32(2): 140-144.Yang Haijing, Yan Dongri, Shi Guang, et al.Correlation modeling of oil flow rate and temperature field in oil-immersed transformer[J]. Journal of Electric Power Science and Technology, 2017, 32(2):140-144.
[33] 王娜. 具有竖直油道的变压器阻力特性研究及结构改进[D]. 大连: 大连理工大学, 2018.
[34] 粟茂, 李春茂, 夏国强, 等. 不同油流速度下油纸绝缘的局部放电特性研究[J]. 电工电能新技术,2019, 38(7): 47-55.Su Mao, Li Chunmao, Xia Guoqiang, et al. Study on partial discharge characteristics of oil-paper insulation under different oil flow rates[J]. Advanced Technology of Electrical Engineering and Energy,2019, 38(7): 47-55.