0 引言
我国能源资源与负荷中心分布不均,一次能源资源主要分布在用能需求小的西部和北部地区,而人口密度高、用能需求大的东中部地区能源资源相对紧缺。高压直流输电(High Voltage Direct Current,HVDC)技术具有输送容量大、输电距离远、线路走廊窄且损耗小的优点,因此在我国远距离输电、异步电网互联和大规模可再生能源接入电网中得到大规模应用[1-6]。但是,实际直流输电工程输电距离长、工作环境复杂、架空线路故障概率较高[7-8]。
现阶段,高压直流输电线路的保护方案大多采用ABB 和SIEMENS 公司的技术路线,以行波保护为主保护,以微分欠电压保护和电流差动保护为后备保护[9-10]。与交流系统不同,直流线路结构相对较为简单,且故障行波波头不受故障初相位影响,因此行波保护在全世界范围内得到普遍应用。然而,行波保护易受干扰且需要准确识别行波波头,高阻接地故障下行波信号较为微弱,近端故障时行波波头不易识别,因此动作可靠性不高[11]。作为行波保护的快速后备保护,微分欠电压保护通过电压微分和欠电压水平两个动作判据相结合来实现保护功能,然而高阻接地故障容易导致电压变化率不足,进而可能引起保护拒动。电流差动保护是检测高阻接地故障的慢速后备保护,然而任何电压变化的过程都会引起线路分布电容产生暂态充放电电流,为躲避此暂态过程,保护需要较长的延时,难以起到后备保护的作用[12]。
直流输电线路两端均安装平波电抗器及直流滤波器,它们共同构成了直流输电线路的物理边界。根据故障后线路边界处暂态能量的特征,国内外专家学者做了诸多有价值的研究。主要可分为单端边界能量保护和纵联边界能量保护。
1)单端边界能量保护:利用物理边界对故障信号中高频分量的衰减作用,文献[13]提出一种直流线路单端暂态能量保护方案;文献[14]利用12.5 kHz、25 kHz 和37.5 kHz 谱线能量的平均能量和构造了单端暂态量保护判据;文献[15]利用单端暂态电压高、低频小波能量的比值来识别区内外故障。但是实际架空线路直流输工程可达上千千米,2019 年准东—皖南±1 100 kV 特高压直流输电工程正式投入运行,其线路长度长达3 324 km,长距离线路对高频信号的衰减作用有可能超过直流输电线路边界的衰减作用,因此保护难以区分整流侧区外故障和直流线路末端故障[16-17]。文献[18-20]将高频暂态能量判据和行波保护判据相结合,构成单端复合式边界能量保护判据。文献[21]利用 5 ~7 kHz 暂态高频带Hilbert 能量幅值和波形形状差异,构造了区内外故障识别判据,故障后高频带内的能量相对较小[22],对装置采样频率要求较高。
2)纵联边界能量保护:忽略线路对地电容的分流,文献[23]根据线路两端低频段突变量能量的差值构造纵联保护判据;考虑故障暂态过程中线路等效并联电容的影响,文献[24]提出一种基于线路两端暂态能量增量之差的保护方案。上述两种保护方案需要线路两端进行数据同步。文献[25]提出一种基于线路两侧暂态能量的纵联方向保护方案;文献[22]扩大了边界的范围,并利用全频带故障电压电流信息构建暂态能量信号,提出一种基于边界暂态能量的多端柔性直流线路的保护方案。上述两种保护方法不需要数据同步,但仍需要双端电气量进行故障判别,速动性相对不足。
现有单端边界能量保护,难以区分整流侧区外故障和直流线路末端故障,单端复合式边界能量保护解决了此问题,但方法相对复杂。此外,利用物理边界对高频分量衰减作用的单端边界能量保护对装置采样频率要求较高。纵联边界能量保护速动性又相对不足。为克服以上问题,本文根据直流输电工程线路边界的结构特点,提出一种高压直流输电线路单端边界能量全线速动保护方案。逆变侧区外故障时,由于故障暂态信号经过逆变侧线路边界和直流输电线路的双重衰减作用,整流侧保护安装处边界能量值明显小于区内故障时的值;整流侧区外故障时,整流侧保护安装处边界能量值小于整流侧平波电抗器阀侧的值;区内故障时,整流侧保护安装处边界能量值大于整流侧平波电抗器阀侧的值,且大于逆变侧区外故障时保护安装处检测到的值。根据整流侧保护安装处、平波电抗器阀侧边界能量值的大小特征可以实现区内外故障判别。为提高本保护在极端情况下的可靠性和抗过渡电阻能力,本文通过分析直流滤波器、线路边界传递函数的幅频特性,优化了故障信号的频带选取范围。在此基础上,利用正负极整流侧保护安装处边界能量的大小关系,实现快速选极。最后,通过大量仿真对保护方案进行了验证。
1 区内外故障特征分析
两端高压直流输电系统主要由整流站、逆变站和直流输电线路三部分构成,如图1 所示。
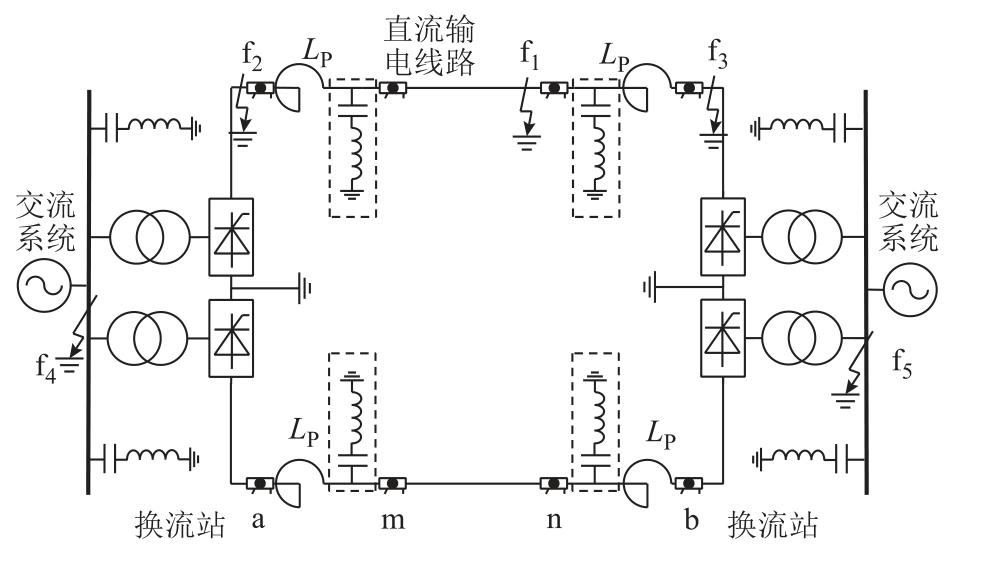
图1 双极直流输电系统
Fig.1 HVDC transmission system with two electrodes
线路两端均配置有平波电抗器和直流滤波器组,它们共同构成了直流输电线路的物理边界。物理边界两侧均安装有分压器和分流器,可以测量该处电压电流量(即图1 中a、m、n 和b 点)。图1 中,虚线框是直流滤波器组;LP 表示平波电抗器;f1~f5 表示不同位置的故障:f1 是直流线路内部的故障,即区内故障;f2 是整流侧平波电抗器阀侧故障,f3 是逆变侧平波电抗器阀侧故障,f4 是整流侧交流系统故障,f5 是逆变侧交流系统故障,即f2~f5 为区外故障。
1.1 区内故障分析
高压直流输电系统故障发生后,根据叠加原理,系统的故障状态可以等效为非故障状态和故障附加状态的叠加。故障附加状态中包含故障分量和系统故障信息。
区内故障(即图1 中故障点f1)发生后,系统的故障附加状态的交流网络如图2 所示。图2 中,F 为故障点的位置;-UF 为故障点叠加的电压源;RF为故障点的过渡电阻;ZP 为平波电抗器等效阻抗;Zlb 为直流滤波器组的等效阻抗;Zsm 为从整流侧a点看进去的换流器戴维南等值阻抗;Zsn 为从逆变侧b 点看进去的换流器戴维南等值阻抗;( c Z , )γ 表示分布参数输电线路;Zx、Zy、Zline 为分布参数输电线路的等效阻抗。
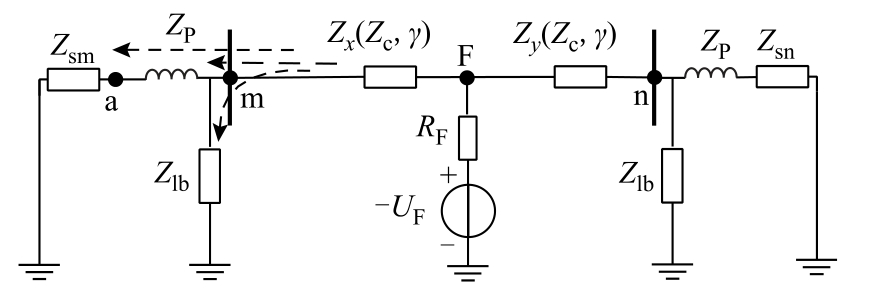
图2 区内故障时故障附加状态的交流网络
Fig.2 Equivalent circuit for fault AC superimposed network during DC line faults
区内故障后的暂态过程中,a 点、m 点的故障电压分量、故障电流分量的关系为
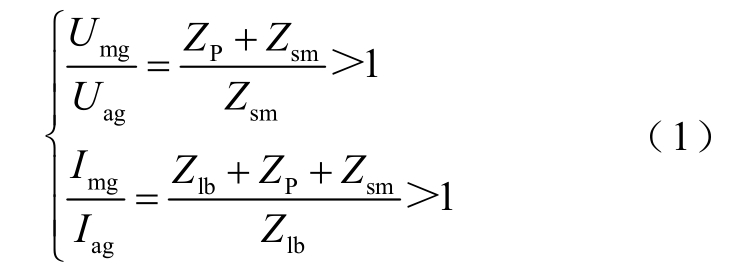
式中,Uag 和Umg 分别为a 点、m 点的故障电压分量;Iag 和Img 分别为a 点、m 点的故障电流分量。
定义直流输电系统整流侧保护安装处(m 点)暂态能量、平波电抗器阀侧(a 点)暂态能量为
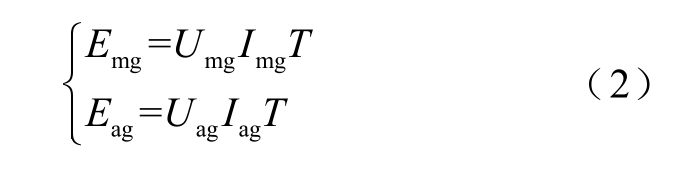
式中,T 为暂态能量的时间窗。根据式(1)与式(2),有
1.2 整流侧区外故障分析
整流侧区外故障(即图1 中故障点f2、f4)发生后,系统的故障附加状态的交流网络如图3a 所示。整流侧区外故障发生后,线路电压波动将导致分布参数线路的分布电容产生暂态充放电电流。由文献[24]可知,线路暂态充放电电流的值小于故障电流的值,图3a 中故障电流由a 点流向m 点,a 点的故障电流等于m 点的故障电流和直流滤波器支路的故障电流之和。
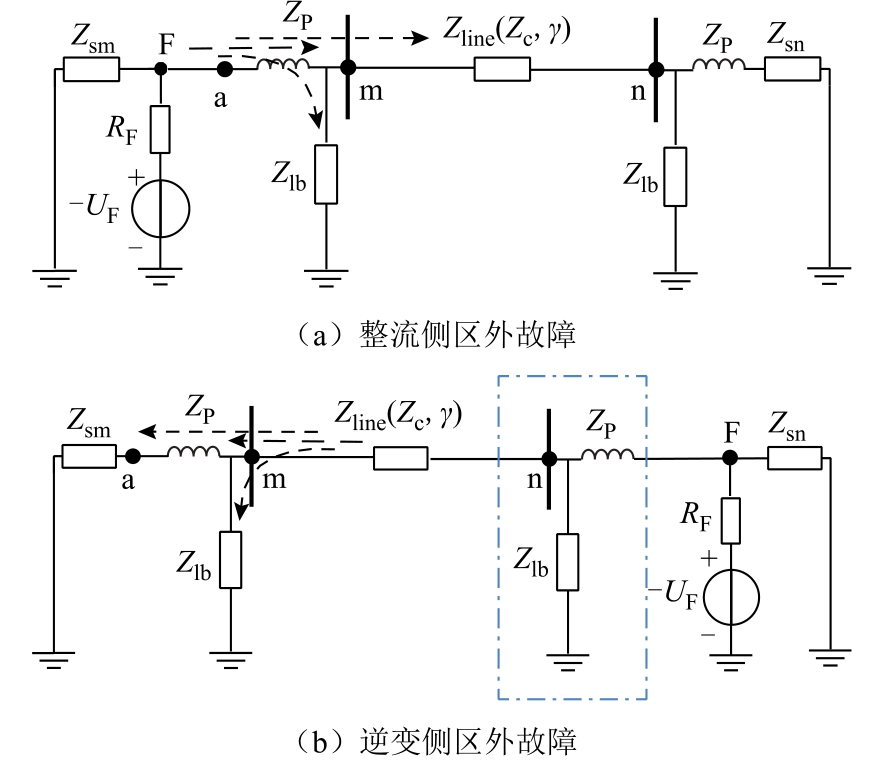
图3 区外故障时故障附加状态的交流网络
Fig.3 Equivalent circuit for fault AC superimposed network during external faults
由于线路边界处平波电抗器的串联分压作用和直流滤波支路的分流作用,a 点、m 点的故障电压分量、故障电流分量的关系为
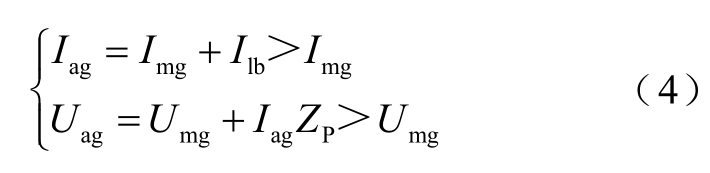
根据式(2)与式(4),有
1.3 逆变侧区外故障分析
逆变侧区外故障(即图1 中故障点f3、f5)发生后,系统的故障附加状态的交流网络如图3b 所示。F 点的故障电压、电流先后经过逆变侧物理边界、直流输电线路的双重衰减才会到达整流侧保护安装处。与区内故障相比,此时整流侧保护安装处检测到的故障信号数值更小,即
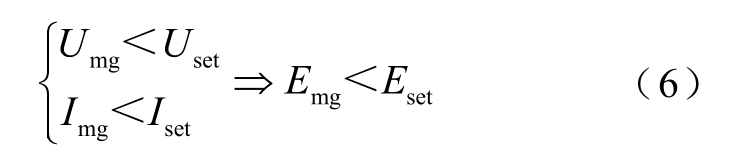
式中,Uset 和Iset 分别为m 点故障电压、故障电流交流分量的阈值;Eset 为整流侧保护安装处(m 点)暂态能量的阈值。相应地,区内故障时m 点暂态能量满足
因此,根据整流侧保护安装处、平波电抗器阀侧暂态能量的大小关系可以区分区内故障和整流侧区外故障;根据整流侧保护安装处暂态能量和Eset的大小关系可以区分区内故障和逆变侧区外故障。
2 边界能量的计算方法
2.1 线路边界特性分析
直流输电线路两端均安装有平波电抗器及直流滤波器,它们共同构成了直流输电线路的物理边界。目前,直流滤波器主要采用双调谐直流滤波器或者三调谐直流滤波器。
2.1.1 边界两侧电压分析
直流线路边界特征如图4a 所示,UA 和UB 分别是直流线路边界两侧测量点的对地电压[14]。线路边界两侧对地电压的传递函数为
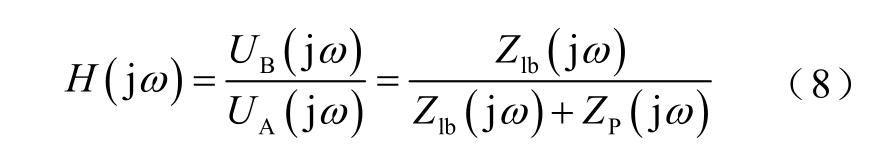
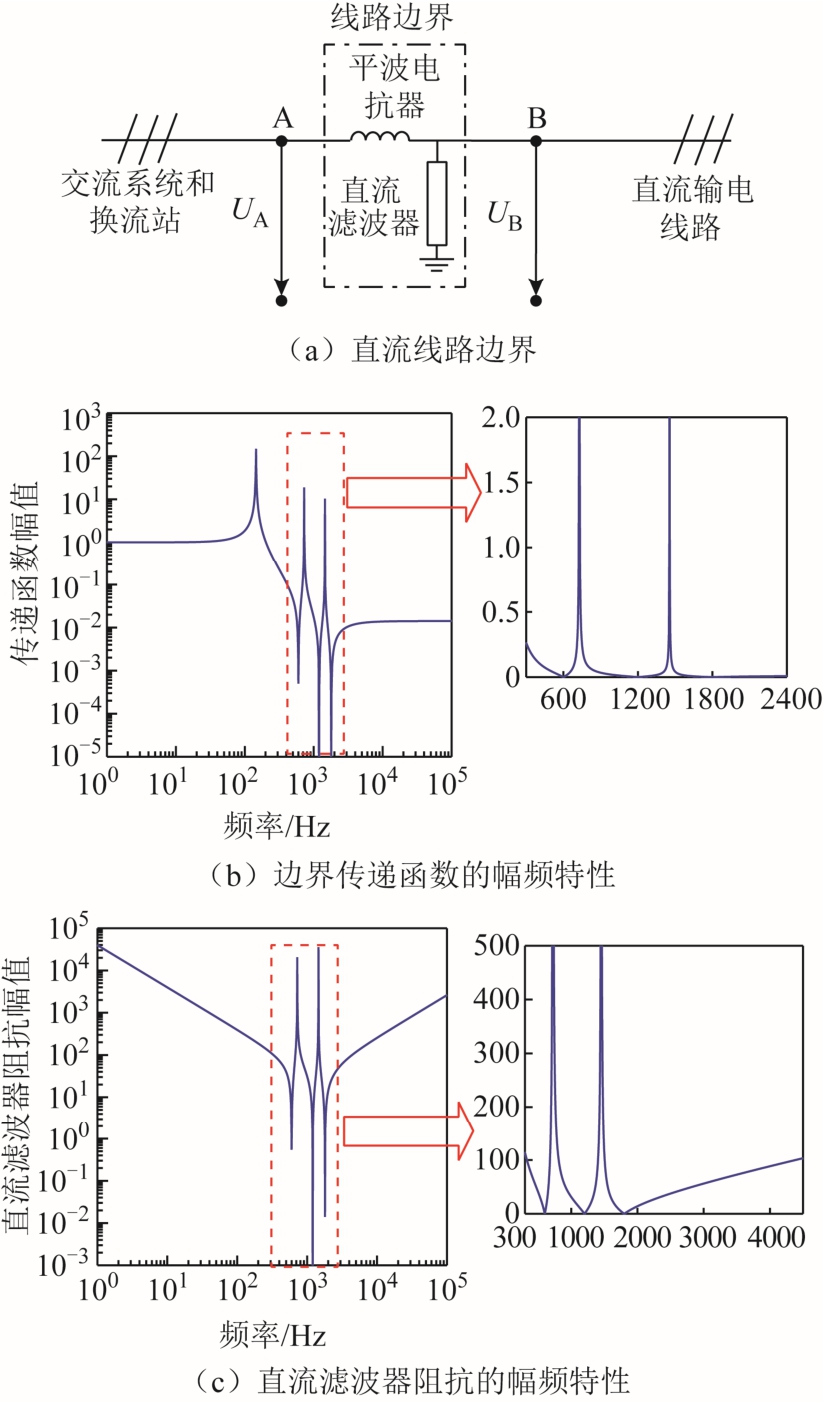
图4 线路边界的特征
Fig.4 Characteristic of line boundary
以国内某实际直流工程为例,为抑制12 脉动换流器产生的12k(k 为自然数)次谐波,其直流侧配置了12/24 和12/36 两组双调谐直流滤波器,其线路边界的传递函数的幅频特性如图4b 所示,可以看出,线路边界在调谐频率附近频段和高频段对故障电压信号的衰减作用最为明显。
2.1.2 边界两侧电流分析
对于直流线路边界两侧的电流IA 和IB,两者之差即直流滤波器上流过的电流。图4c 给出了此直流输电工程直流滤波器阻抗的幅频特性。可以看出,直流滤波器在调谐频率附近频段的阻抗很小,但在低频段和高频段阻抗很大。因此,直流滤波器对调谐频率附近频段故障电流的分流作用强,对低频段和高频段故障电流的分流作用弱,直流滤波器(线路边界)在调谐频率附近频段对故障电流信号的分流作用最为明显。
由第1 节的分析可知:根据m 点暂态能量和Eset的大小关系可以区分区内故障和逆变侧区外故障。考虑最极端的情况,区内线路末端经过渡电阻接地故障和逆变侧平波电抗器阀侧故障相比,两者仅相差一个线路物理边界。为提高本保护在最极端情况下的可靠性和抗过渡电阻能力,可选择300 Hz 以上的电压信号、300~4 500 Hz 的电流信号计算暂态能量。
2.2 换流器的谐波电压源特性
对于12 脉动换流器,理想情况下,其在直流侧会产生12k(k 为自然数)次谐波电压。通过傅里叶变换,各次谐波电压的有效值为[26]
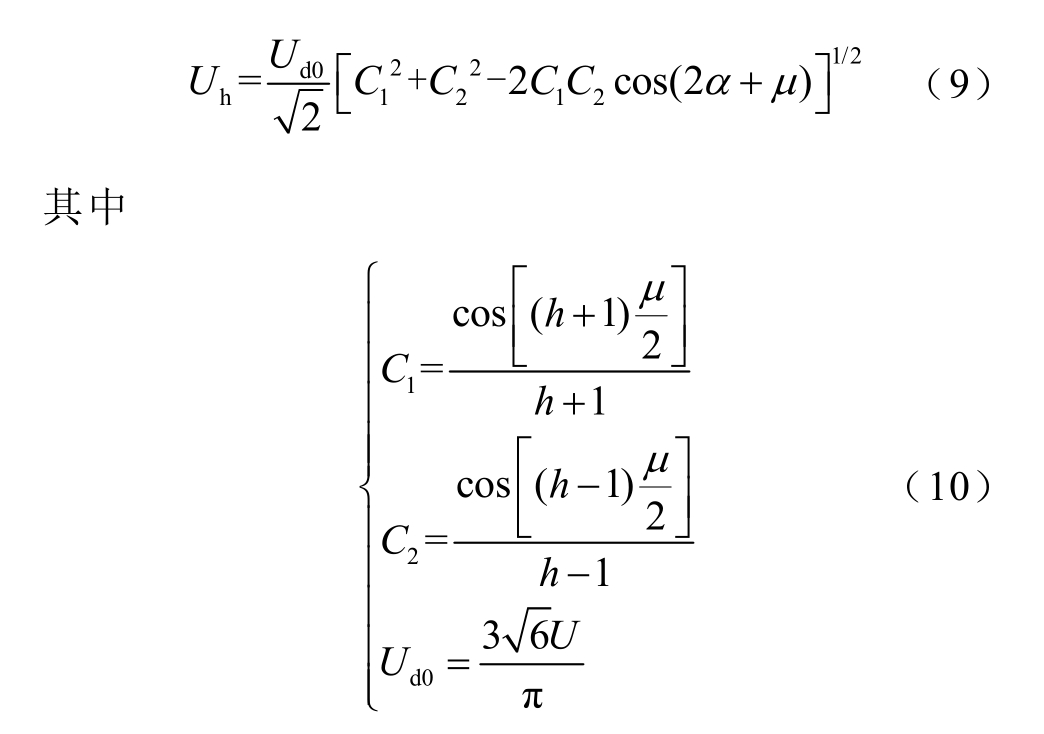
式中,h 为谐波次数,h=12k;α为触发角;μ为换相角,整流侧的换相角为[27]
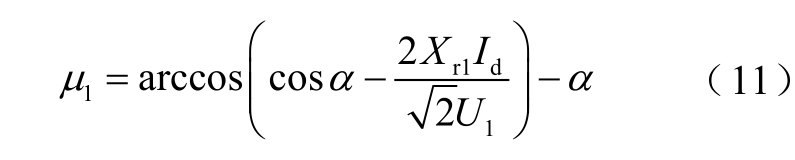
逆变侧的换相角为
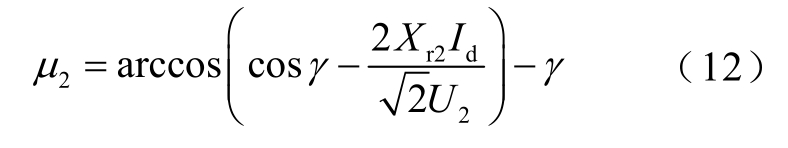
式中,Xr1 和Xr2 分别为整流站的等值换相电抗和逆变站的等值换相电抗。
直流系统故障发生后,控制系统将开始动作,整流侧的触发角α和逆变侧的关断角γ 将发生变化,换流器的换相角μ 也随之变化。因此,换流器的等效谐波电压源在故障后也发生了变化。根据叠加原理和故障附加网络,区内外故障发生后,换流器会向a 点注入12k 次谐波。
为避免换流器谐波电压源效应对保护方案的影响,需要在故障信号中剔除12k 次谐波分量。
2.3 边界能量的计算方法
实际工程中,为保证计算精度和数字滤波的性能要求,数字式继电保护的采样频率一般按照保护原理所用信号的4~10 倍选择[28]。目前,国内直流输电工程的最大采样频率为10 kHz。同时,故障信号中高频分量含量低,更容易受到噪声干扰[29]。综合考虑,本文选取剔除12k 次谐波后的300~1 500 Hz故障电压、电流信号计算边界能量。
根据式(2)与2.1 节、2.2 节的分析,定义m点、a 点边界能量分别为
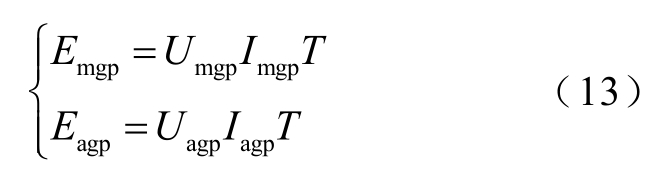
考虑到300 Hz 信号的一个周波为3.3 ms,本文边界能量和保护算法时间窗选为1 个周波,即T=3.3 ms。直流输电工程控制保护系统对于故障的响应速度约为5 ms,大于3.3 ms 的时间窗,理想情况下,在控制系统动作前即可完成故障识别,其中
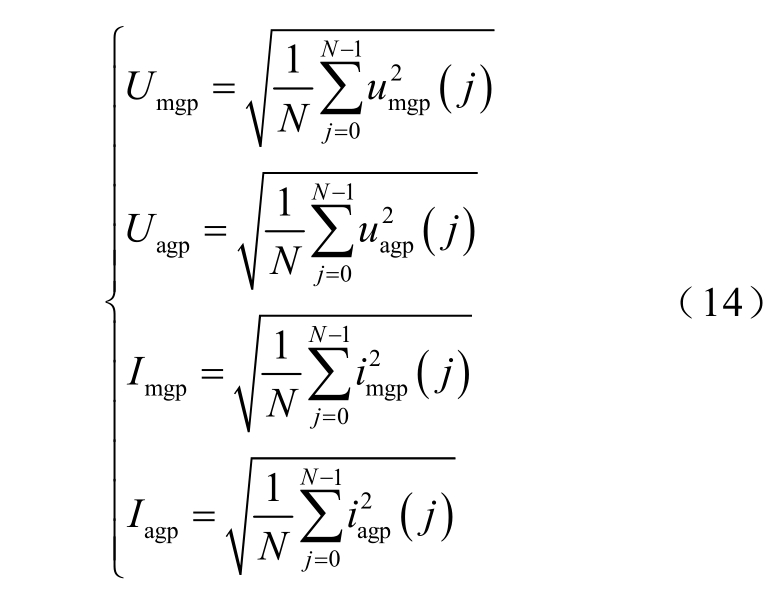
式中,N 为时间窗内的采样点个数;j 为时间窗内采样点的序号,j= 1,2,···, N;uagp 和umgp 分别为a 点、m 点剔除12 次、24 次谐波后300~1 500 Hz 故障电压分量;iagp 和imgp 分别为a 点、m 点剔除12 次、24 次谐波后300~1 500 Hz 故障电流分量。
边界能量计算方法如图5 所示。
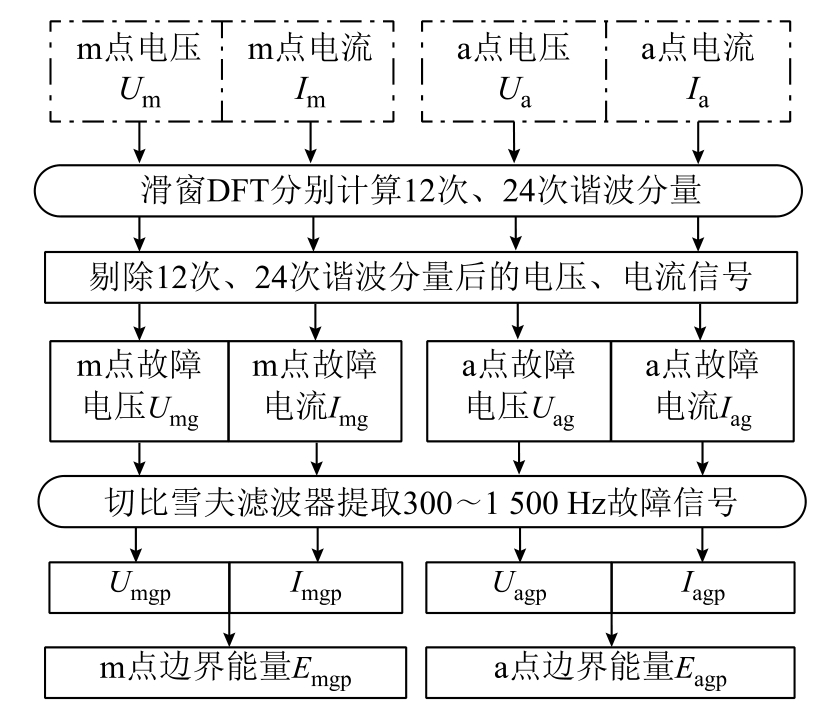
图5 边界能量计算方法
Fig.5 Method of calculating boundary energy
(1)(在m 点)利用离散傅里叶变换算法提取m 点电压信号、电流信号的12 次谐波信号;利用离散傅里叶变换算法提取整流侧m 点的电压信号、电流信号的24 次谐波信号。
(2)(在m 点)用m 点电压减去其600 Hz、1 200 Hz谐波电压,得到剔除12 次、24 次谐波后的电压信号;用m 点电流减去其600 Hz、1 200 Hz 谐波电流,得到剔除12 次、24 次谐波后的电流信号。
(3)(在m 点)根据叠加原理,计算m 点的故障电压、故障电流。m 点故障电压等于故障状态下剔除12 次、24 次谐波后的电压减去非故障状态下剔除12 次、24 次谐波后的电压;m 点故障电流等于故障状态下剔除12 次、24 次谐波后的电流减去非故障状态下剔除12 次、24 次谐波后的电流。
(4)(在m 点)利用切比雪夫带通滤波器对上一步输出的电压、电流信号进行滤波,提取其300~1 500 Hz 频段分量。
(5)计算m 点的边界能量;与m 点计算方式相同,重复步骤(1)~(4),计算a 点的边界能量。
3 保护方案
3.1 区内外故障识别判据
根据m 点边界能量、a 点边界能量、Eset 的大小关系可以实现区内外故障判别,构造保护判据为
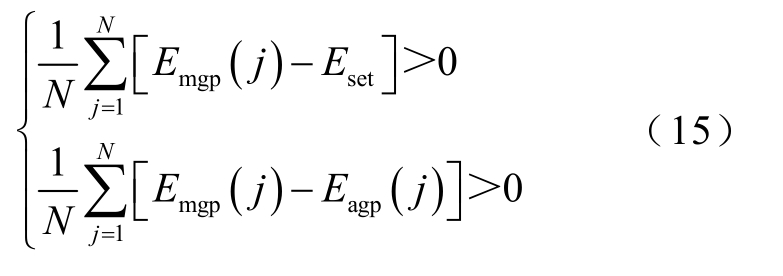
高压直流输电线路除正常运行方式,还包括降功率运行方式。假设降功率运行时,直流线路电压为KUUd,直流线路电流为KIId,则线路实际传输功率为KUKIPd。其中,Ud 为直流线路额定电压;KU 为电压降低系数,0 < K U ≤ 1;Id 为直流线路额定电流;KI 为电流降低系数, 0< K I≤ 1;Pd 为直流线路额定功率。
根据式(15),考虑高压直流输电线路的多种运行方式,利用边界能量构造保护判据为
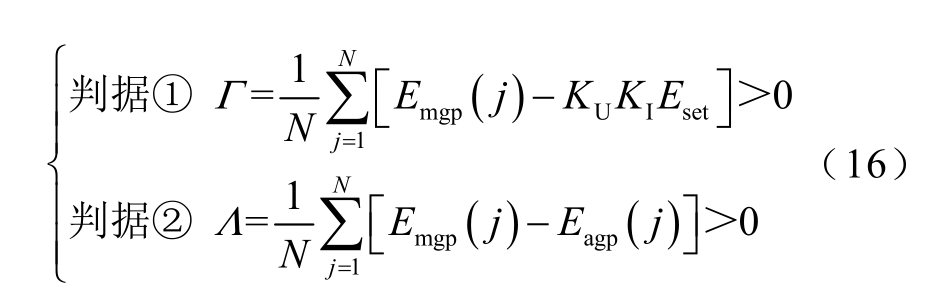
式中,判据①和判据②同时满足时,判定为区内故障;否则,为区外故障。其中,Eset 是额定功率运行方式下,各种逆变侧区外故障时,由整流侧保护安装处(m 点)检测到的最大边界能量和各种典型区内故障时整流侧保护安装处检测到的最小边界能量共同确定的。
目前,工程应用中,边界保护的整定值主要依靠大量仿真。一般情况下,线路末端故障经过渡电阻接地故障是电压、电流能量最小的区内故障类型;逆变侧平波电抗器阀侧(即图1 中f3 处)金属性接地故障是电压、电流能量最大的逆变侧区外故障类型[30-33]。因此,可以根据以上原则,额定功率运行方式下,仿真确定区内故障时检测到的最小边界能量和逆变侧区外故障时检测到的最大边界能量。在此基础上,考虑一定裕度确定Eset 的大小。本文取
Eset=2 kV·A·s。
3.2 故障启动判据
正常运行时,高压直流输电系统整流侧保护安装处的故障电压、故障电流分量几乎为零,m 点边界能量也接近于零。故障后整流侧保护安装处边界能量明显增大,利用此特征可以构造保护启动判据。
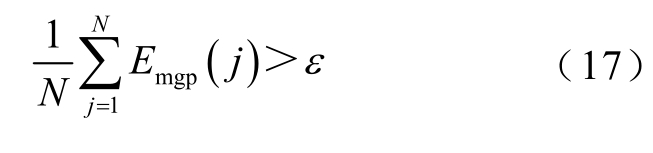
式中,ε 为保护启动判据阈值,ε 略大于零并接近于零,本文取ε=0.1 kV·A·s。考虑到0<ε<KUKIEset,可以看出,区内外故障识别判据①也可以区分区内故障状态和无故障状态。因此,本保护方案中,区内外故障识别判据①可兼作故障启动判据。
3.3 选极判据
目前,国内新建的两端直流输电工程均为双极系统。单极故障发生后,由于电磁耦合效应,同杆并架的健全极上也会产生暂态故障信号,健全极上的保护可能会误动作。
注意到,单极故障时,健全极上产生的暂态故障信号幅值小于故障极上的值[19];双极故障时,健全极上产生的暂态故障信号与故障极上的暂态故障信号较为接近。因此,利用正负极整流侧保护安装处的边界能量的大小关系可以实现故障选极。选极判据为

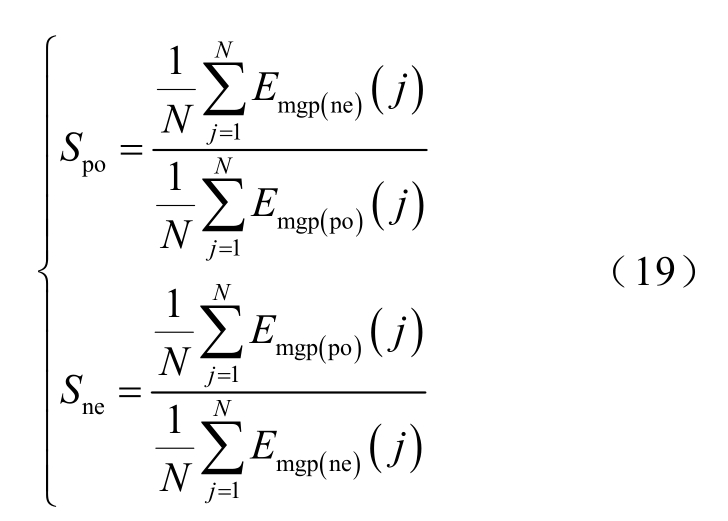
式中,Spo 为负极整流侧保护安装处边界能量与正极整流侧保护安装处边界能量的比值,定义Spo 为正极选极因子;Sne 为正极整流侧保护安装处边界能量与负极整流侧保护安装处边界能量的比值,定义Sne为负极选极因子;Sset 为故障选极判据的阈值。
直流输电系统包括双极对称运行方式和双极不对称运行方式,双极不对称运行时,降功率运行的极上,电流或电压额定值最小为0.7(pu)[34],此时两极的电流或电压额定值之比为0.7。故障选极判据的阈值按照避开此值进行整定,因此
式(20)为故障选极判据阈值的取值范围。在本文中,取Sset=0.65。根据实际直流工程的具体运行方式和对保护可靠性的具体要求,其数值是可以改变的,但其表现为Sset<0.7 的特征不变。
3.4 保护方案及其逻辑
保护方案流程如图6 所示。整流侧采集m 点、a 点的电压信号和电流信号,并计算m 点的边界能量值。如果m 点边界能量小于KUKIEset,判定为系统无故障或逆变侧区外故障;否则计算a 点边界能量。如果m 点边界能量小于a 点边界能量,判定为整流侧区外故障;否则判定为区内故障并进行故障选极。如果正极选极因子小于阈值Sset,判定为正极故障;如果负极选极因子小于阈值Sset,判定为负极故障;如果正、负极选极因子均不满足式(18),判定为双极故障。

图6 保护方案流程
Fig.6 Flowchart of proposed protection scheme
4 仿真验证
利用PSCAD/EMTDC 电磁暂态仿真软件,建立图1 所示的±500 kV 高压直流输电系统模型。系统额定电流2 kA, 送电距离1 000 km,双极直流线路同杆并架,均为六分裂导线,输电线路采用频变参数模型。直流滤波器采用典型的12/24/36 三调谐滤波器。参考实际工程,数据采样频率设为10 kHz。故障发生时刻为t=1 000 ms,故障持续时间250 ms。
4.1 区内故障时保护动作特性
正极直流输电线路在线路中点发生金属性接地故障时,保护方案的动作特性如图7 所示。由图7可以看出,故障发生后,整流侧保护安装处边界能量Emgp 显著大于阈值Eset,保护启动并判定为区内故障或者整流侧区外故障。进一步地,在故障发生后的几十ms 内,保护安装处边界能量均大于平波电抗器阀侧的值Eagp。因此,判据①和②同时满足,保护判定为区内故障。
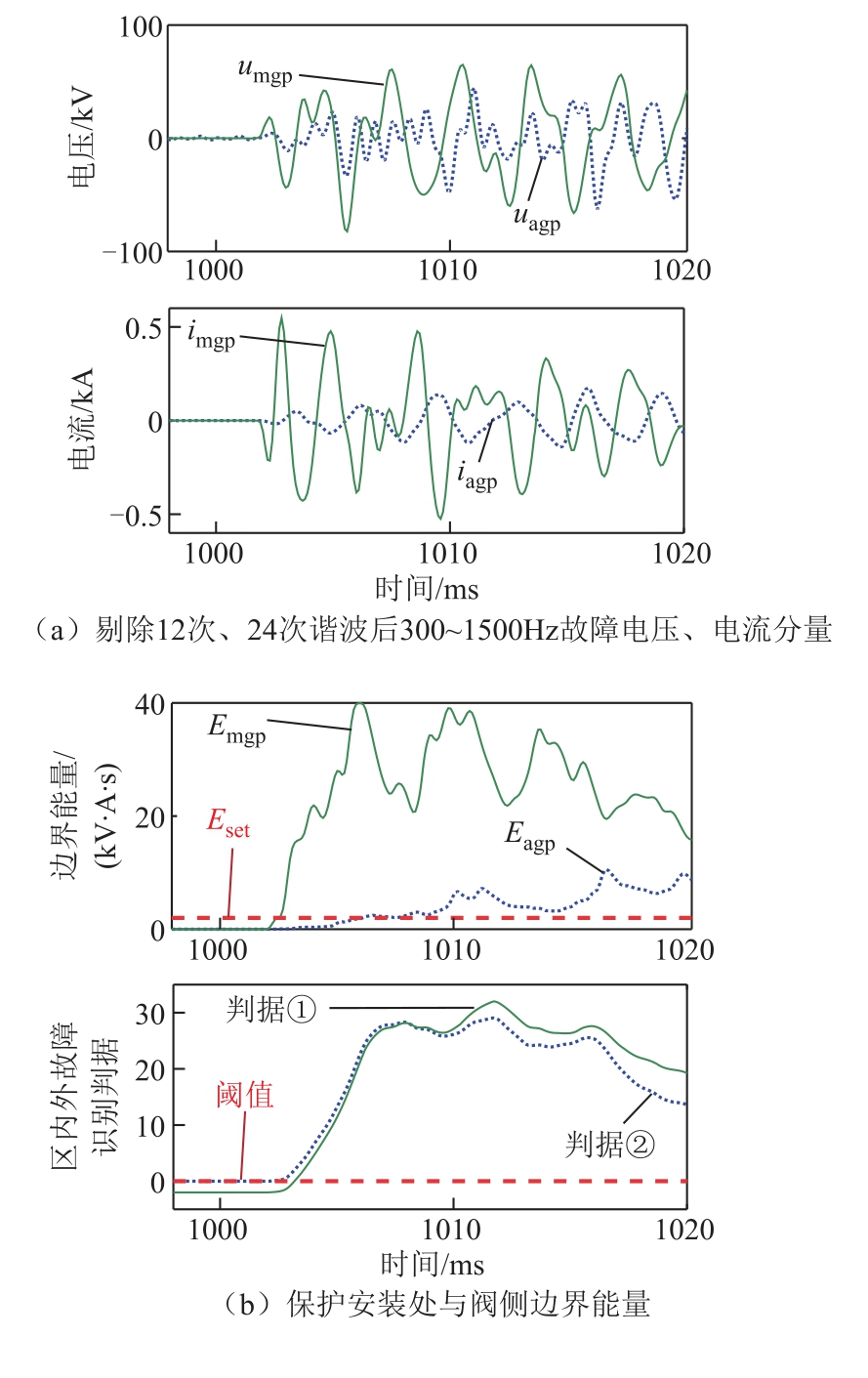
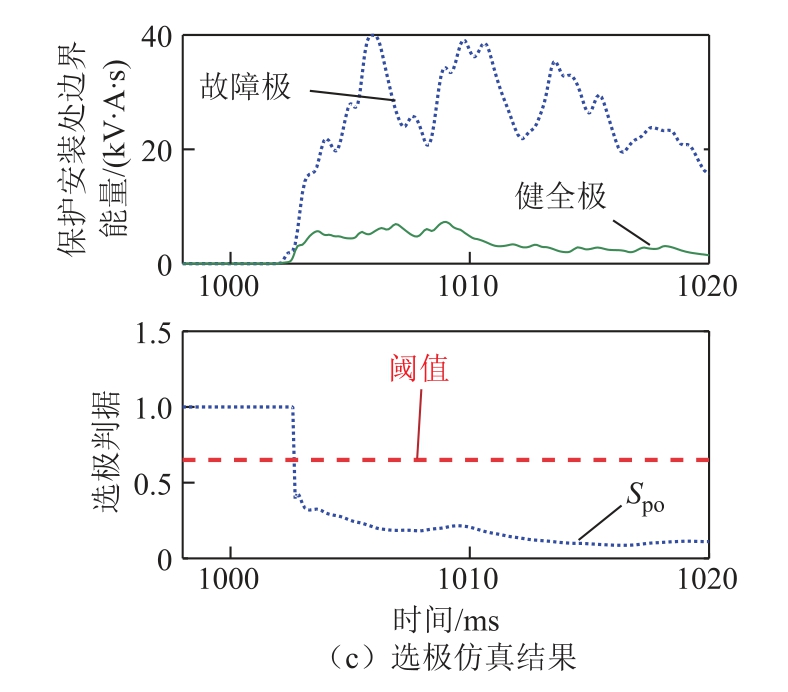
图7 区内故障时保护仿真结果
Fig.7 Protection response during a DC line fault
如图7c 所示,正极保护安装处边界能量明显大于负极(健全极)的值,Spo 小于故障选极判据的阈值,保护判定为正极故障。
由图7 仿真结果可以看出,从故障发生到实现区内外故障判别、故障选极,本保护方案用时不到5 ms,保护速动性好。
4.2 不同区内故障条件下保护的动作特性
正极输电线路在不同位置故障下经不同过渡电阻的仿真结果见表1。
表1 不同过渡电阻和故障位置下的仿真结果
Tab.1 Simulation results for different fault resistances and fault locations
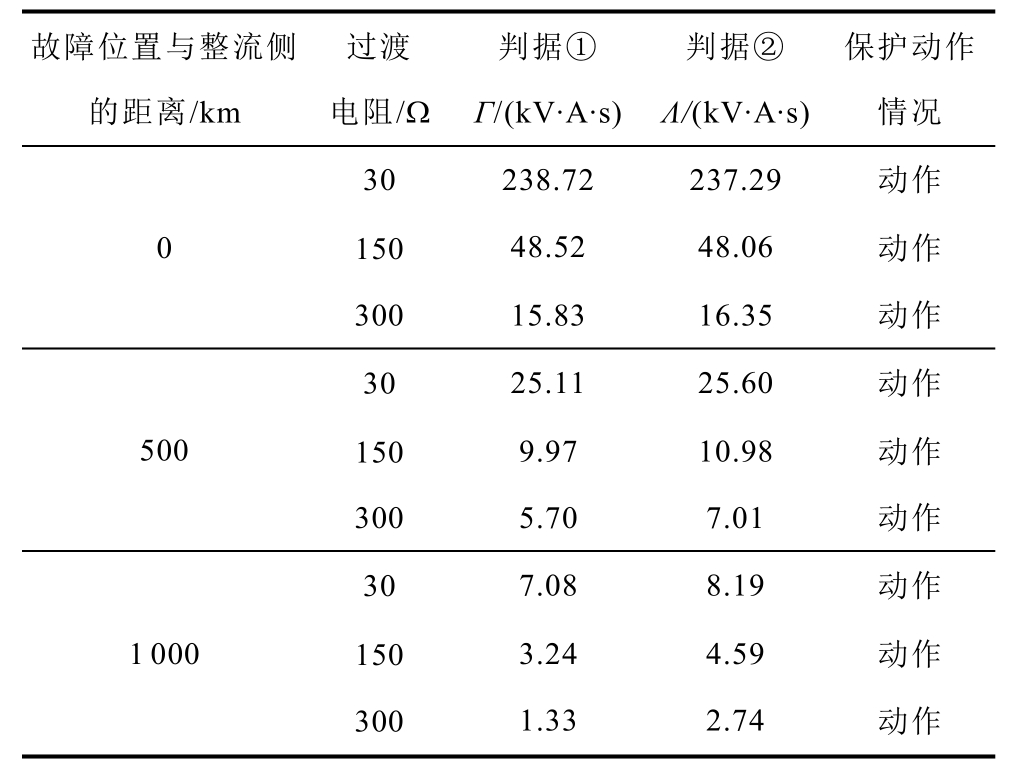
故障位置与整流侧的距离/km过渡电阻/Ω判据①Γ/(kV·A·s)判据②Λ/(kV·A·s)保护动作情况30 238.72 237.29 动作0 150 48.52 48.06 动作300 15.83 16.35 动作30 25.11 25.60 动作500150 9.97 10.98 动作300 5.70 7.01 动作30 7.08 8.19 动作1 000150 3.24 4.59 动作300 1.33 2.74 动作
从表1 可以看出:
(1)故障位置距离整流侧越远,保护安装处边界能量值越小。但即使线路末端故障时,保护仍可以准确动作。
(2)过渡电阻阻值越大,保护安装处边界能量值越小。最恶劣的情况下,线路末端经300 Ω 过渡电阻接地时,Emgp 和Eagp 分别为3.33 kV·A·s、0.59 kV·A·s,经计算,判据①和判据②同时满足,保护可靠动作。
(3)本保护方案在不同故障位置经不同过渡电阻接地故障时,都可以准确动作,可靠性好。
直流输电线路不同位置正极故障、负极故障、双极故障时的仿真结果见表2。
表2 不同区内故障类型下的仿真结果
Tab.2 Simulation results for various internal fault types
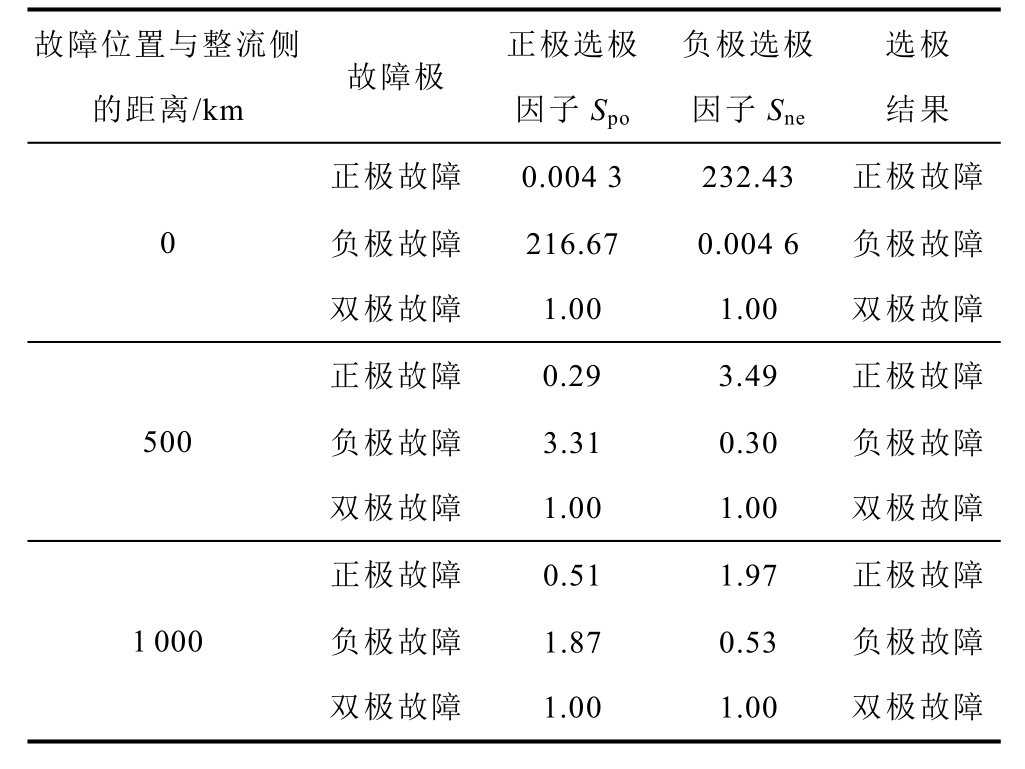
故障位置与整流侧的距离/km故障极正极选极因子Spo负极选极因子Sne选极结果正极故障 0.004 3 232.43 正极故障0负极故障 216.67 0.004 6 负极故障双极故障 1.00 1.00 双极故障正极故障 0.29 3.49 正极故障500负极故障 3.31 0.30 负极故障双极故障 1.00 1.00 双极故障正极故障 0.51 1.97 正极故障1 000负极故障 1.87 0.53 负极故障双极故障 1.00 1.00 双极故障
从表2 可以看出:正极故障时,正极选极因子Spo 均小于阈值;负极故障时,负极选极因子Sne 均小于阈值;双极故障时,正、负极整流侧保护安装处的边界能量接近,Spo 和Sne 均为1。不同故障下,保护均可以实现准确选极。
4.3 区外故障时保护动作特性
正极直流输电线路整流侧平波电抗器阀侧(即图1 中f2 处)发生金属性接地故障时,保护方案的动作特性如图8 所示。
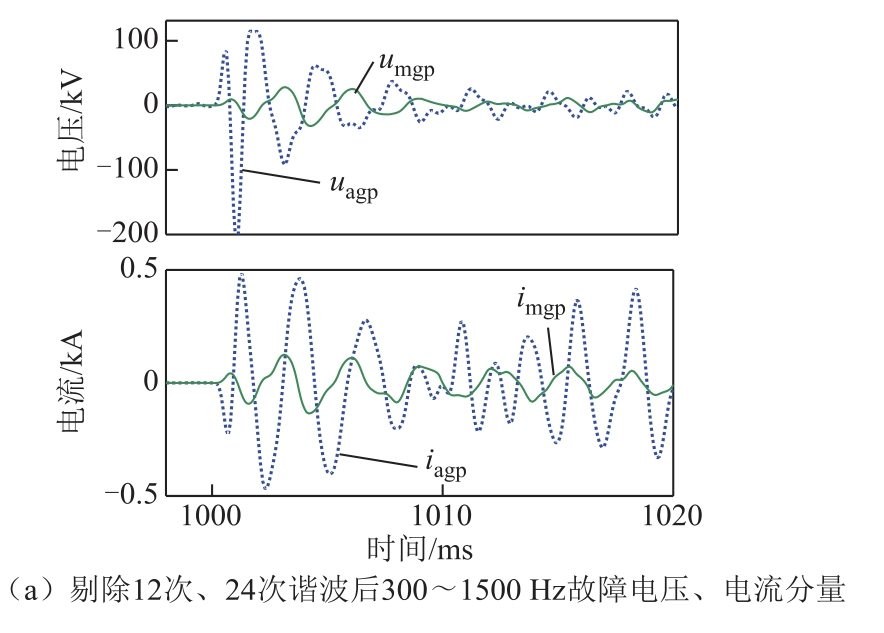
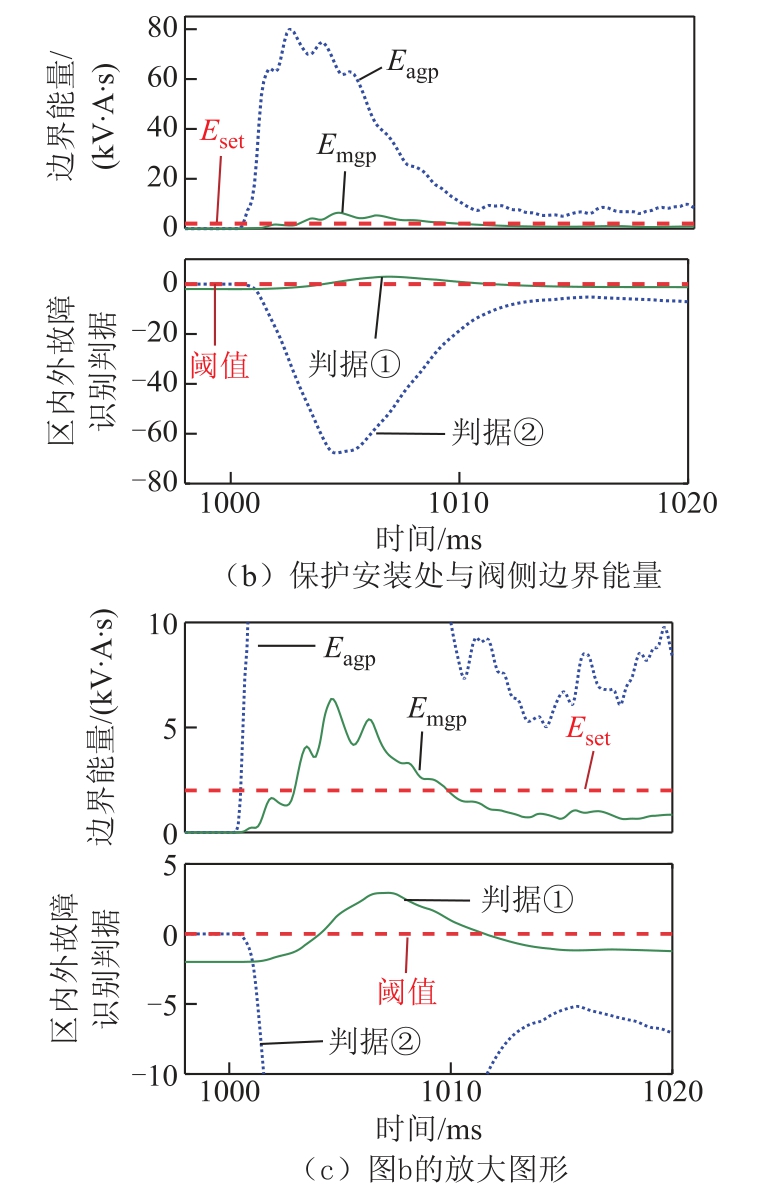
图8 整流侧区外故障时保护仿真结果
Fig.8 Protection response during an rectifier-sideexternal fault
故障发生后整流侧保护安装处边界能量Emgp增大,并大于阈值Eset,根据判据①,保护启动并计算a 点边界能量。如图8b 所示,由于线路边界处平波电抗器的串联分压作用和直流滤波支路的分流作用,保护安装处边界能量小于平波电抗器阀侧的值,判据②不满足,因此保护判定为整流侧区外故障。
正极直流输电线路逆变侧平波电抗器阀侧(即图1 中f3 处)发生金属性接地故障时,保护方案的动作特性如图9 所示。
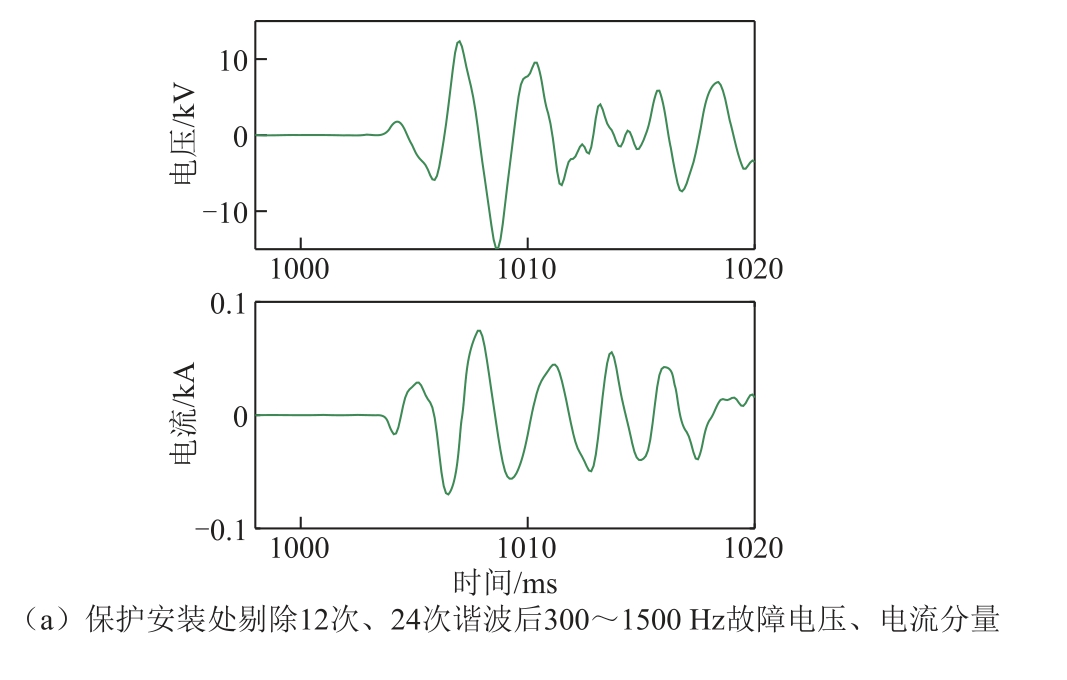
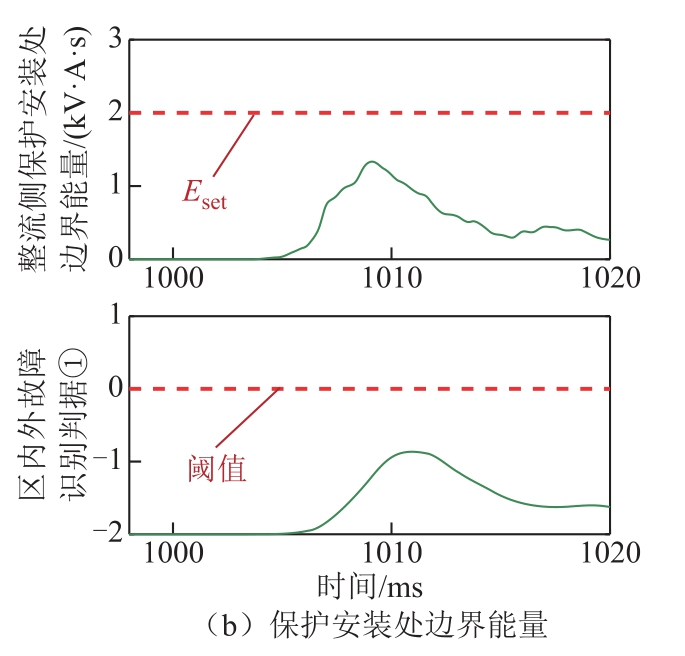
图9 逆变区外故障时保护仿真结果
Fig.9 Protection response during an inverter-sideexternal fault
故障发生后,整流侧保护安装处剔除12 次、24次谐波后300~1 500 Hz 故障电压、电流分量均增大。虽然保护安装处边界能量Emgp 增大,但仍小于阈值Eset,因此不满足判据①,保护不动作。无需计算a 点边界能量,即实现区内外故障判别。
4.4 不同交流系统故障下保护的动作特性
不同交流系统故障类型下保护的动作情况见表3。
表3 各种区外故障条件下的仿真结果
Tab.3 Simulation results for various external faults
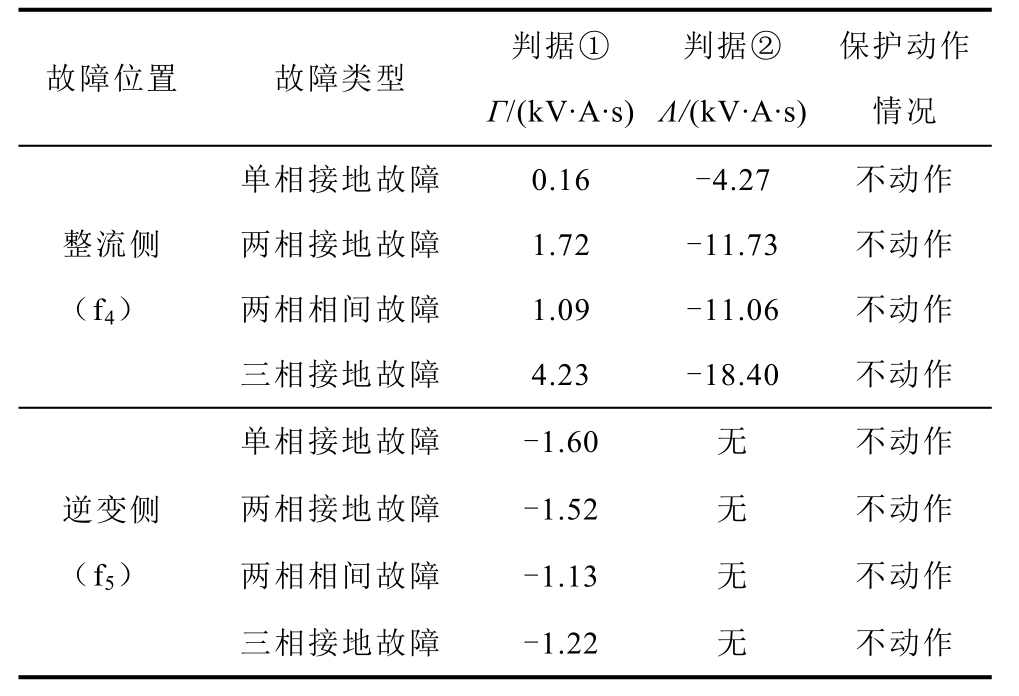
故障位置 故障类型判据①Γ/(kV·A·s)判据②Λ/(kV·A·s)保护动作情况单相接地故障 0.16 -4.27 不动作整流侧(f4)两相接地故障 1.72 -11.73 不动作两相相间故障 1.09 -11.06 不动作三相接地故障 4.23 -18.40 不动作单相接地故障 -1.60 无 不动作逆变侧(f5)两相接地故障 -1.52 无 不动作两相相间故障 -1.13 无 不动作三相接地故障 -1.22 无 不动作
整流侧交流系统(f4)发生不同类型故障时,整流侧保护安装处边界能量Emgp 小于Eagp,Λ 小于阈值,因此保护均未动作。逆变侧交流系统(f5)发生不同类型故障时,故障信号经过线路边界和直流输电线路的双重衰减,整流侧保护安装处的边界能量很小,且均远小于Eset,保护均未动作。
从仿真结果可以看出:在4.3 节、4.4 节的典型区外故障下,保护均没有误动作,保护可靠性较好。
5 影响因素分析与讨论
5.1 改变故障信号频段对保护的影响
根据第2 节的分析,为更加准确地区分区内线路末端故障和逆变侧区外故障,本保护方案选择剔除12k 次谐波后的300~1 500 Hz 故障电压、电流信号计算边界能量。为验证理论分析的正确性,本节在三种典型故障情况下分别提取全频段交流故障信号、300 Hz 以下低频故障信号、剔除12k 次谐波后的300~1 500 Hz 故障信号,计算整流侧保护安装处(m 点)边界能量。
仿真结果如图10 所示,其中,Case①:逆变侧平波电抗器阀侧(f3 处)金属性接地故障;Case②:正极直流输电线路在线路末端金属性接地故障;Case③:正极直流输电线路在线路末端经200 Ω 过渡电阻接地故障。

图10 不同故障情况下不同边界能量的仿真结果
Fig.10 Simulation results for different boundary energies during different fault cases
从图10 可以看出:
(1)Case①和Case②两种故障情况下,提取全频段交流故障信号计算的m 点边界能量十分接近,保护难以利用判据①区分这两种故障。线路末端经200 Ω 过渡电阻接地故障时,m 点边界能量明显低于Case①时的值,保护将拒动。
(2)同理,提取300 Hz 以下低频故障信号计算的m 点边界能量也难以区分Case①和Case②。在Case③故障发生后,保护将拒动。
(3)即使线路末端经200 Ω 过渡电阻接地故障时,本保护方案的边界能量值也明显大于逆变侧平波电抗器阀侧故障时的值,保护将正常动作。本保护具有较好的抗过渡电阻能力。
(4)仿真结果进一步验证了2.1 节理论分析的正确性。
5.2 线路边界参数对保护的影响
本文所提出的保护原理与线路边界参数密切相关。
首先,直流输电系统运行过程中,由于环境温度的变化、自身的发热和老化等因素的影响,直流滤波器的电容和电感等元件的值可能会变化。实际工程中,运行部门一方面会定期检修,对退出运行的滤波器的参数进行检测;另一方面当滤波器元件参数偏离到一定程度时,直流滤波器失谐保护将发出警告。因此,定期参数检测和直流滤波器失谐保护在一定程度上可以保证本保护方案的可靠性[35]。
其次,以国内某实际直流工程为例,其边界参数改变时,线路边界的传递函数的变化特性如图11所示。可以看出,在极端情况下,当直流滤波器、平波电抗器参数变化±30%时,线路边界在调谐频率附近频段和高频段对故障电压信号衰减作用最为明显的特征保持不变。当直流滤波器参数变化时,直流滤波器(线路边界)在调谐频率附近频段对故障电流信号分流作用最为明显的特征也保持不变。因此,边界参数改变对本保护方案影响不大。
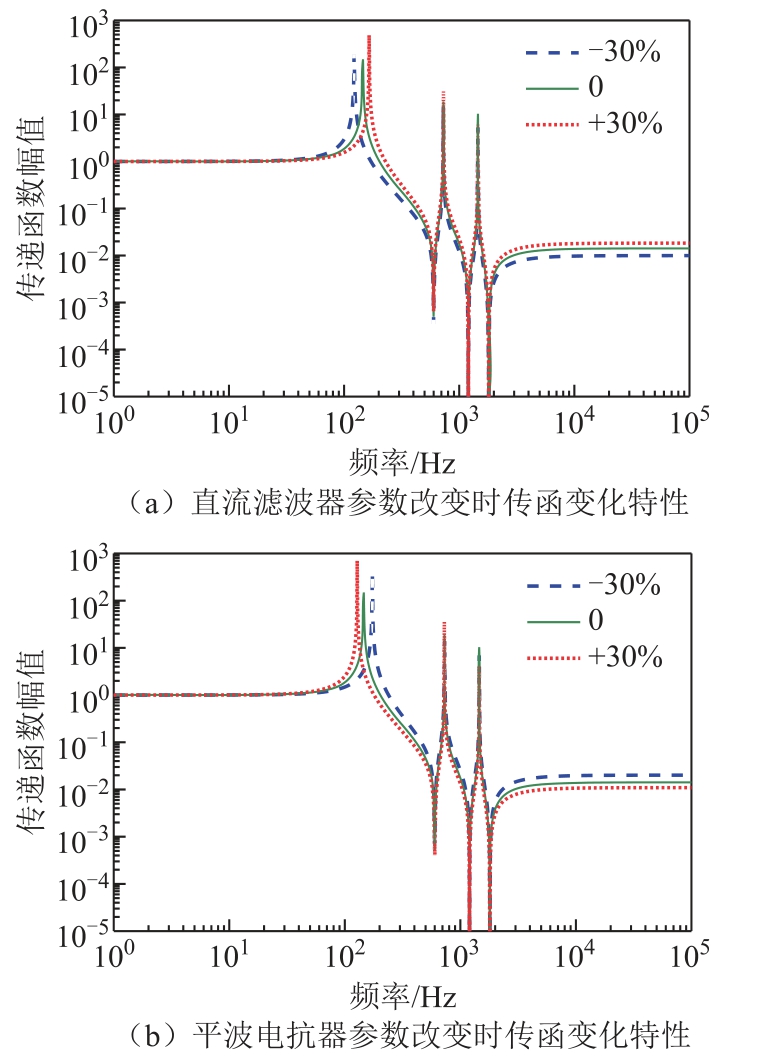
图11 边界参数改变时传函变化特性
Fig.11 Characteristics of transfer function when boundary parameters are changed
5.3 采样率对保护的影响
本保护方案选取频段为剔除12、24 次谐波后的300~1 500 Hz 故障信号,因此对实际装置采样率要求不高。不同采样频率下,距整流侧500 km 处经30 Ω过渡电阻接地故障和整流侧三相接地故障时保护的仿真结果见表4。可以看出,当采样频率从3 kHz 逐步变化到20 kHz,区内故障(距整流侧500 km 处经30 Ω 过渡电阻接地故障)时,判据①和判据②同时满足,且数值差别不大,保护准确动作;区外故障(整流侧三相接地故障)时,Λ 均小于阈值,保护不会误动。不同采样频率下,本方案可以可靠识别区内外故障。
表4 不同采样频率下的仿真结果
Tab.4 Simulation results for different faults with different sampling frequencies
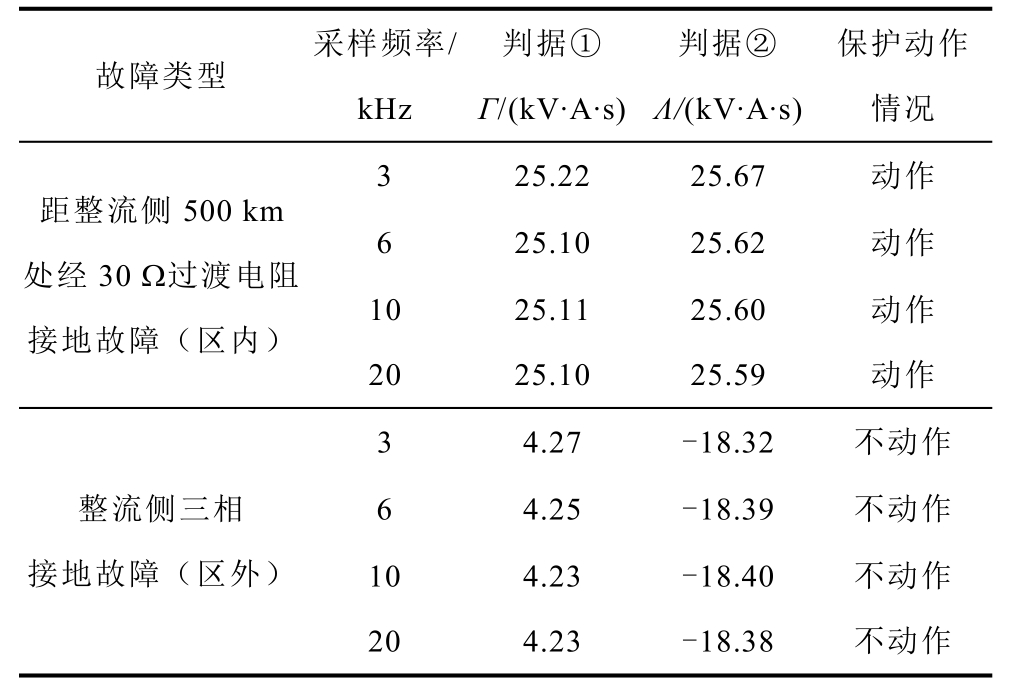
故障类型采样频率/kHz判据①Γ/(kV·A·s)判据②Λ/(kV·A·s)保护动作情况3 25.22 25.67 动作距整流侧500 km处经30 Ω过渡电阻接地故障(区内)6 25.10 25.62 动作10 25.11 25.60 动作20 25.10 25.59 动作3 4.27 -18.32 不动作整流侧三相接地故障(区外)6 4.25 -18.39 不动作10 4.23 -18.40 不动作20 4.23 -18.38 不动作
6 对比与分析
本文所提出的保护为单端边界能量保护,实际工程中线路主保护为行波保护。以下针对不同保护方案进行对比和分析。
6.1 与已有行波保护方案对比
目前,国内高压直流输电线路的保护方案大多采用ABB 和SIEMENS 公司的技术路线,主保护为行波保护。SIEMENS 的行波保护方案已广泛应用于天广、贵广及云广等直流输电工程中,主要采用电压微分、电压突变量和电流突变量来识别故障。动作判据为[36]
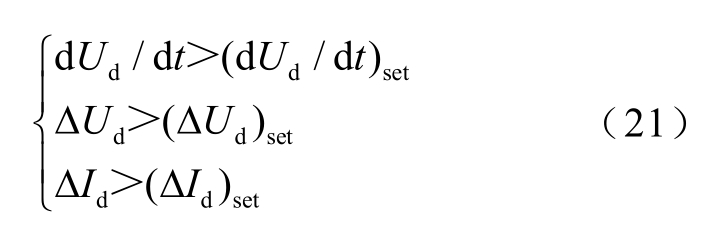
式中,dUd/dt 为线路直流电压的变化率;ΔUd 为直流电压变化量;ΔId 为直流电流变化量;下标set 表示对应的整定值。三种典型故障情况下行波保护方案的仿真结果如图12 所示。
从图12 可以看出,线路末端金属性接地故障时,线路直流电压变化率、直流电压变化量和直流电流变化量均大于逆变侧平波电抗器阀侧(f3 处)金属性接地故障时的值。因此,根据式(21),行波保护可以准确区分Case①与Case②。但线路末端经200 Ω 过渡电阻接地故障时,线路直流电压变化量、直流电流变化量却远小于逆变侧平波电抗器阀侧金属性接地故障时的值。Case①与Case③条件下,两者直流电压变化率较为接近,区分度不大。因此,Case③情况下,行波保护将拒动。如图10c 所示,本文所述保护方案可以准确区分Case①与Case③,可靠性更高。
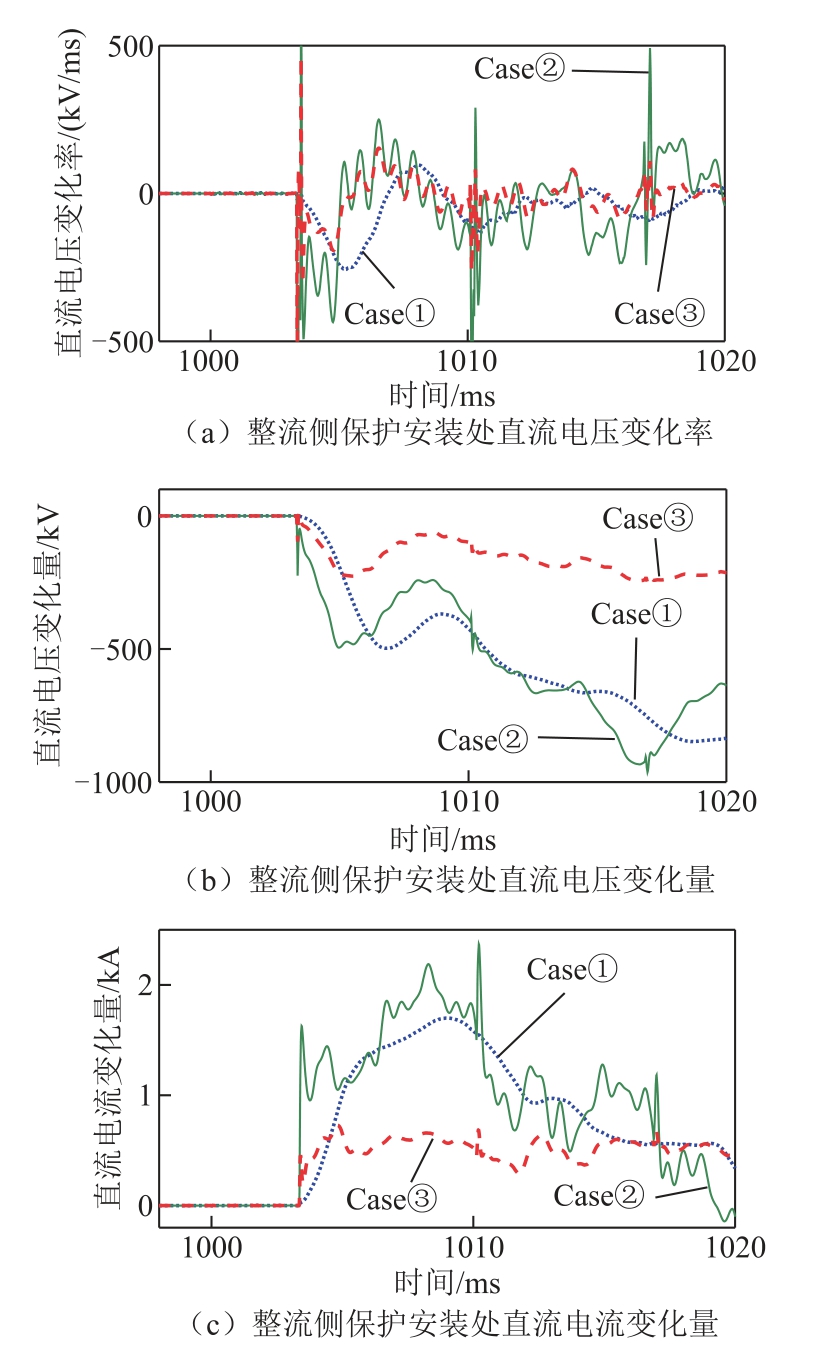
图12 行波保护方案的仿真结果
Fig.12 Simulation results for traveling wave based protection
目前常用无限冲激响应(Infinite Impulse Response, IIR)带通滤波器延时在1 μs 以内,本文保护算法时间窗仅3.3 ms。考虑最极端情况,1 000 km的直流输电线路末端故障时,整流侧检测到故障信号约3~4 ms,也可以在10 ms 内完成故障判别。考虑到实际工程中行波保护的动作时间约10~20 ms,本保护方案速动性好,可以作为目前国内直流输电工程线路主保护的重要补充。
6.2 与已有单端边界能量保护对比
本文针对已有单端边界能量保护的不足,展开了相关研究,为更好地说明本文的贡献与创新性,本文与已有单端边界能量保护对比如下:
(1)文献[13-15]利用物理边界对故障信号中高频分量的衰减作用实现保护功能,但长距离线路对高频信号的衰减作用有可能超过直流输电线路边界的衰减作用,因此保护难以区分整流侧区外故障和直流线路末端故障。为解决此问题,文献[16-20]通过增加故障方向元件,或与行波保护判据相结合等方式,提出了单端复合式保护判据。同时,复合式主保护判据也增加了保护复杂度。
与复合式保护不同,本文所述单端边界能量保护方法利用m 点边界能量、a 点边界能量、Eset 的大小关系实现区内外故障判别,解决了保护难以区分整流侧区外故障和直流线路末端故障的问题,同时降低了保护复杂度。
(2)文献[13]利用10~50 kHz 的高频能量信号实现保护功能;文献[14]利用12.5 kHz、25 kHz 和37.5 kHz 谱线能量的平均能量和构造保护判据,文献[15]利用5~10 kHz 和156.25~312.5 Hz 信号识别区内外故障;文献[21]利用5~7 kHz 暂态高频信号构造单端边界能量保护。利用物理边界对故障信号中高频分量的衰减作用的单端边界能量保护对装置采样频率要求较高。本保护方案重点在于结合理论研究成果解决实际工程问题。所用信号为剔除12次、24 次谐波后的300~1 500Hz 故障信号,因此对实际装置采样率要求不高,更易于工程实现。
(3)文献[37]提出一种基于限流电感功率(Current Limiting Reactor Power, CLRP)的单端主保护方法。该原理属于边界能量保护范围。该主保护方法原理简单、对装置采样率要求低,既适用于VSC-HVDC 系统,也适用于LCC-HVDC 系统。为对比本文所述保护和文献[37]的主保护的可靠性,三种典型故障情况下的仿真结果如图13 所示。
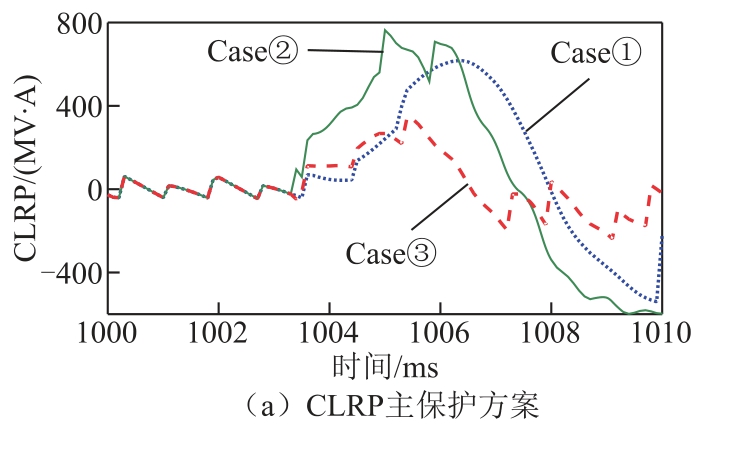
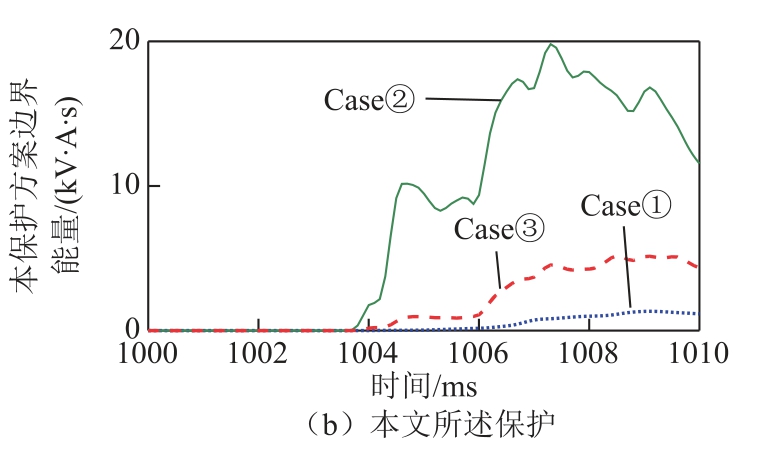
图13 本文所述保护与CLRP 保护的对比
Fig.13 Simulation results for proposed method and CLRP-based protection
从图13a 看出,逆变侧平波电抗器阀侧金属性接地故障时,CLRP 的最大值为616.47 MV·A,线路末端金属性接地故障时,CLRP 的最大值为763.35 MV·A。保护可以区分 Case①与 Case②。但线路末端经200 Ω 过渡电阻接地故障时,CLRP 的最大值仅为346.32 MV·A,判据失效。如图13b 所示,本文所述保护方案可以准确区分线路末端经200 Ω 过渡电阻接地故障和区外故障。作为主保护方案,本文所述方案具备更好的抗过渡电阻能力,可靠性高。
7 结论
针对已有单端边界能量保护的不足,本文以高压直流输电系统线路边界特性和故障特征为基础,提出一种新型直流线路单端边界能量全线速动保护方案。该保护方案利用整流侧保护安装处边界能量、整流侧平波电抗器阀侧边界能量的数值大小实现保护功能。考虑到利用双端故障信号选极速动性不足,提出了一种单端故障选极新方法。本文所提出的新型单端边界能量保护方案贡献在于:
1)解决了单端边界能量保护难以区分整流侧区外故障和直流线路末端故障的问题,同时所提方法简单,降低了保护复杂度。
2)其次,该保护对实际装置采样率要求不高,更易于实际工程实现,且满足数字式继电保护的要求。
3)线路末端经300 Ω 过渡电阻接地时,保护仍可以准确动作。该方案具备更好的抗过渡电阻能力,可靠性更高。
仿真验证表明:该保护方案速动性好,可靠性优于已有行波保护方案,可作为国内外高压直流输电工程直流线路主保护的重要参考。
[1] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J].电工技术学报, 2020, 35(8): 1776-1786.Xu Hanping, Yang Weichen, Zhang Dongyin, et al.Commutation failure judgment method for multiinfeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1776-1786.
[2] He Jiangbiao, Yang Qichen, Wang Zheng. On-line fault diagnosis and fault-tolerant operation of modular multilevel converters—a comprehensive review[J].CES Transactions on Electrical Machines and Systems,2020, 4(4): 360-372.
[3] 贺永杰, 向往, 周家培, 等. LCC-MMC 串联型混合直流输电系统小信号建模[J]. 电工技术学报, 2021,36(7): 1492-1506.He Yongjie, Xiang Wang, Zhou Jiapei, et al. Smallsignal modelling of LCC-MMC series hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1492-1506.
[4] 王增平, 刘席洋, 郑博文, 等. 基于电压波形拟合的换相失败快速预测与抑制措施[J]. 电工技术学报, 2020, 35(7): 1454-1463.Wang Zengping, Liu Xiyang, Zheng Bowen, et al. The research on fast prediction and suppression measures of commutation failure based on voltage waveform fitting[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1454-1463.
[5] Chen Yongyang, Pan Shangzhi, Huang Meng, et al.MMC-MTDC transmission system with partially hybrid branches[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 124-132.
[6] 高本锋, 王刚, 刘毅, 等. LCC-HVDC 送端电网等值方案研究[J]. 电工技术学报, 2021, 36(15): 3250-3263, 3271.Gao Benfeng, Wang Gang, Liu Yi, et al. Study on equivalence method of AC system in sending-end of LCC-HVDC[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3250-3263, 3271.
[7] 甄永赞, 苏宁赛, 杨荆宜. 直流输电线路极波变化率保护的拓展方法研究[J]. 中国电机工程学报,2021, 41(15): 5212-5220.Zhen Yongzan, Su Ningsai, Yang Jingyi. Research on extension method of polar wave change rate protection for HVDC transmission line[J]. Proceedings of the CSEE, 2021, 41(15): 5212-5220.
[8] 陈鑫全, 李海锋, 顾广坤, 等. 基于时域电压比的高压直流输电线路暂态保护方案[J]. 电力系统自动化, 2020, 44(22): 62-69.Chen Xinquan, Li Haifeng, Gu Guangkun, et al.Transient protection scheme of HVDC transmission line based on time-domain voltage ratio[J]. Automation of Electric Power Systems, 2020, 44(22): 62-69.
[9] 李海锋, 祝新驰, 梁远升, 等. 基于电流控制补偿的高压直流线路快速差动保护[J]. 电力系统自动化, 2021, 45(11): 111-119.Li Haifeng, Zhu Xinchi, Liang Yuansheng, et al. Fast differential protection for HVDC transmission line based on current control compensation[J]. Automation of Electric Power Systems, 2021, 45(11): 111-119.
[10] 童晓阳, 杨明杰, 张广骁. 基于改进 DTW 的行波波形相似性的高压直流输电线路保护方案[J]. 中国电机工程学报, 2020, 40(12): 3878-3887.Tong Xiaoyang, Yang Mingjie, Zhang Guangxiao. A protection scheme for HVDC transmission line based on traveling waveform similarity using improved DTW algorithm[J]. Proceedings of the CSEE, 2020,40(12): 3878-3887.
[11] Ma Jing, Wu Yuchong, Liu Chen, et al. Pilot directional protection scheme for LCC-HVDC transmission lines based on the voltage difference between positive and negative poles[J]. IEEE Transactions on Power Delivery, 2022, 37(2): 696-709.
[12] 束洪春, 田鑫萃, 董俊, 等. 利用电压相关性的±800kV 直流输电线路区内外故障判断方法[J]. 中国电机工程学报, 2012, 32(4): 151-160.Shu Hongchun, Tian Xincui, Dong Jun, et al.Identification between internal and external faults of±800 kV HVDC transmission lines based on voltage correlation[J]. Proceedings of the CSEE, 2012, 32(4):151-160.
[13] 王钢, 李志铿, 李海锋. ±800kV 特高压直流线路暂态保护[J]. 电力系统自动化, 2007, 31(21): 40-43, 48.Wang Gang, Li Zhikeng, Li Haifeng. Transient based protection for ±800kV UHVDC transmission lines[J].Automation of Electric Power Systems, 2007, 31(21):40-43, 48.
[14] 张保会, 张嵩, 尤敏, 等. 高压直流线路单端暂态量保护研究[J]. 电力系统保护与控制, 2010, 38(15): 18-23.Zhang Baohui, Zhang Song, You Min, et al. Research on transient-based protection for HVDC lines[J]. Power System Protection and Control, 2010, 38(15): 18-23.
[15] 束洪春, 刘可真, 朱盛强, 等. ±800kV 特高压直流输电线路单端电气量暂态保护[J]. 中国电机工程学报, 2010, 30(31): 108-117.Shu Hongchun, Liu Kezhen, Zhu Shengqiang, et al.±800kV UHVDC transmission line protection based on single end electrical transient signal[J].Proceedings of the CSEE, 2010, 30(31): 108-117.
[16] 陈仕龙, 张杰, 刘红锐, 等. 特高压直流输电线路单端电流方向暂态保护[J]. 电工技术学报, 2016,31(2): 171-177.Chen Shilong, Zhang Jie, Liu Hongrui, et al. A singleended current direction transient protection of UHVDC transmission line[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 171-177.
[17] 侯俊杰, 宋国兵, 常仲学, 等. 基于暂态功率的高压直流线路单端量保护[J]. 电力系统自动化, 2019,43(21): 203-212.Hou Junjie, Song Guobing, Chang Zhongxue, et al.Transient power based single-end protection for HVDC transmission line[J]. Automation of Electric Power Systems, 2019, 43(21): 203-212.
[18] 张保会, 孔飞, 张嵩, 等. 高压直流输电线路单端暂态量保护装置的技术开发[J]. 中国电机工程学报, 2013, 33(4): 179-185.Zhang Baohui, Kong Fei, Zhang Song, et al. Technical development of non-unit protection devices based on transient signals for HVDC transmission lines[J].Proceedings of the CSEE, 2013, 33(4): 179-185.
[19] Kong Fei, Hao Zhiguo, Zhang Song, et al.Development of a novel protection device for bipolar HVDC transmission lines[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2270-2278.
[20] Liu Xiaolei, Osman A H, Malik O P. Real-time implementation of a hybrid protection scheme for bipolar HVDC line using FPGA[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 101-108.
[21] 樊艳芳, 王永进. 基于Hilbert 能量幅值信息和波形信息的特高压直流输电线路单端保护方法[J]. 电工技术学报, 2021, 36(9): 1818-1830.Fan Yanfang, Wang Yongjin. Single-ended protection method for UHVDC transmission line based on Hilbert energy amplitude information and waveform information[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1818-1830.
[22] 高飘, 郑晓冬, 晁晨栩, 等. 基于边界暂态能量的多端柔性直流输电线路保护[J]. 电力系统自动化,2021, 45(17): 171-179.Gao Piao, Zheng Xiaodong, Chao Chenxu, et al.Protection for multi-terminal flexible DC transmission lines based on boundary transient energy[J]. Automation of Electric Power Systems, 2021, 45(17): 171-179.
[23] 王钢, 罗健斌, 李海锋, 等. 特高压直流输电线路暂态能量保护[J]. 电力系统自动化, 2010, 34(1): 28-31.Wang Gang, Luo Jianbin, Li Haifeng, et al. Transient energy protection for ±800 kV UHVDC transmission lines[J]. Automation of Electric Power Systems, 2010,34(1): 28-31.
[24] Zheng Xiaodong, Tai Nengling, Yang Guangliang, et al.A transient protection scheme for HVDC transmission line[J]. IEEE Transactions on Power Delivery, 2012,27(2): 718-724.
[25] 杨亚宇, 邰能灵, 刘剑, 等. 利用边界能量的高压直流线路纵联保护方案[J]. 中国电机工程学报,2015, 35(22): 5757-5767.Yang Yayu, Tai Nengling, Liu Jian, et al. A pilot protection scheme for HVDC transmission lines based on boundary energy[J]. Proceedings of the CSEE,2015, 35(22): 5757-5767.
[26] 韩民晓, 文俊, 徐永海. 高压直流输电原理与运行[M]. 3 版. 北京: 机械工业出版社, 2020.
[27] 赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2004.
[28] 张保会,尹项根, 索南加乐, 等. 电力系统继电保护[M]. 北京: 中国电力出版社, 2010.
[29] Suonan Jiale, Zhang Jiankang, Jiao Zaibin, et al.Distance protection for HVDC transmission lines considering frequency-dependent parameters[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 723-732.
[30] 罗澍忻, 董新洲. 基于LCC 的高压直流输电线路保护分析及展望[J]. 广东电力, 2019, 32(12): 121-129.Luo Shuxin, Dong Xinzhou. Analysis and prospects of HVDC transmission line protection based on LCC[J].Guangdong Electric Power, 2019, 32(12): 121-129.
[31] 李斌, 何佳伟, 李晔, 等. 基于边界特性的多端柔性直流配电系统单端量保护方案[J]. 中国电机工程学报, 2016, 36(21): 5741-5749, 6016.Li Bin, He Jiawei, Li Ye, et al. Single-ended protection scheme based on boundary characteristic for the multi-terminal VSC-based DC distribution system[J]. Proceedings of the CSEE, 2016, 36(21):5741-5749, 6016.
[32] de Kerf K, Srivastava K, Reza M, et al. Wavelet-based protection strategy for DC faults in multi-terminal VSC HVDC systems[J]. IET Generation, Transmission& Distribution, 2011, 5(4): 496.
[33] 高本锋, 董沛毅, 刘辛晔, 等. 高压直流输电线路微分欠压保护特性与定值整定[J]. 电网技术, 2015,39(8): 2303-2311.Gao Benfeng, Dong Peiyi, Liu Xinye, et al. Research of HVDC transmission line differential under-voltage protection characteristics and value setting[J]. Power System Technology, 2015, 39(8): 2303-2311.
[34] 刘剑, 范春菊, 邰能灵. 用于高压直流输电线路的新型横差保护方法[J]. 高电压技术, 2016, 42(7):2266-2274.Liu Jian, Fan Chunju, Tai Nengling. Novel transverse differential protection method for HVDC transmission line[J]. High Voltage Engineering, 2016, 42(7): 2266-2274.
[35] 黄银龙, 乐健, 毛涛, 等. 基于谐波电流变化率的高压直流输电系统直流侧滤波器参数的在线辨识[J]. 电工技术学报, 2016, 31(6): 162-170.Huang Yinlong, Le Jian, Mao Tao, et al. The online parameters identification of the DC-side filter of highvoltage direct current system based on harmonic current change ratio[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 162-170.
[36] 任师铎, 肖浩, 李银红. 高压直流输电线路行波保护实用整定原则[J]. 电力自动化设备, 2019, 39(9):54-60.Ren Shiduo, Xiao Hao, Li Yinhong. Practical setting principle of traveling wave protection for HVDC power transmission line[J]. Electric Power Automation Equipment, 2019, 39(9): 54-60.
[37] Li Shilong, Chen Wei, Yin Xianggen, et al. A novel integrated protection for VSC-HVDC transmission line based on current limiting reactor power[J]. IEEE Transactions on Power Delivery, 2020, 35(1): 226-233.