0 引言
近年来，随着分布式发电与电力电子设备高密度接入电网，使电网中谐波源数目激增，运行状态多变，谐波污染日益严重。谐波源定位对于明确谐波污染源头具有重要的作用，是谐波责任划分和解决经济纠纷的前提[1-3]。
现有的研究主要围绕基于谐波状态估计（Harmonic State Estimation, HSE）的多点式谐波源定位方法。谐波状态估计是谐波潮流计算的逆问题，在建立谐波量测矩阵后，根据谐波监测数据来求解谐波状态模型，再根据谐波状态量估计值来确定谐波源位置[4]。
目前由于量测装置的成本问题，无法对全部节点进行直接监测。虽然可以通过优化配置测点[5]，对部分节点进行间接监测，但是在有限的量测数目下，系统仍可能存在谐波信息不可观区域。文献[6]针对谐波源随机分布以及非谐波源节点存在干扰电流的问题，提出基于改进稀疏表示法的谐波源定位方法，通过二次稀疏表示法调整量测节点，提高谐波电流估计值的准确性。文献[7-8]考虑量测量的不确定性问题，提出了具有二次约束的l1 极小化谐波状态估计方法。此外，还有借助谐波源稀疏特性，通过压缩感知算法[9-11]来求解欠定方程从而重构源信号。上述方法虽然能够在局部不可观系统中定位谐波源，但其结果的准确性容易受到测点位置等因素影响，致使最终定位失败。
另一方面，以卡尔曼滤波为主的动态谐波状态估计考虑谐波电流的波动特征，在系统完全可观的前提下，求解出电网的谐波动态信息。文献[12]以谐波功率、谐波电压为量测量，引入卡尔曼滤波器对三相不平衡电网中的谐波源进行实时跟踪。文献[13]基于历史谐波波动特性，将慢波动分量用于计算状态转移矩阵，恢复其一定的预测能力，同时引入协方差匹配判据和时变噪声估值器得到自适应卡尔曼滤波算法。然而，当前的动态谐波状态估计均属于确定性的范畴。实际上，由于现场环境变化、运行状态以及设备老化等原因，线路参数可能发生偏差，致使确定性动态状态估计难以计算出准确的谐波状态量，无法为后续定位、评估以及治理提供有效的帮助。
针对以上问题，本文将局部不可观系统转化为等效可观系统，在此基础上进行区间动态谐波状态估计，并基于状态量的估计结果，定位局部不可观系统中的谐波源。首先在已有量测装置数目不满足完全可观要求的前提下，对电力系统网络进行多端口等效，将局部不可观系统转化为等效完全可观系统；然后利用区间数描述线路参数的不确定性，采用基于误差最优上界的区间卡尔曼滤波（Minimum Upper Bound of Variance Interval Kalman Filter,UBIKF）算法求解谐波电流区间估计值，从而确定谐波源的位置信息；接着对于不可观区域中存在谐波源的情况，通过指标筛选出区域边界节点之间高度线性相关的状态量，再利用区间中点线性回归辨识状态量之间的回归系数，将回归系数与区域内节点所对应的等效系数进行匹配度计算，将匹配度最高的节点视为谐波源节点，实现对不可观区域内谐波源的定位；最后通过算例验证本文方法的可行性，算例结果表明本文方法能够对局部不可观系统中的谐波源进行准确定位。
1 区间动态谐波状态估计
1.1 传统动态谐波状态估计问题分析
目前，谐波状态估计的一般化方程为
式中，下标“h”为谐波次数；zh 为谐波量测量；Hh为谐波量测矩阵；Ih 为谐波注入电流；δh、εh 分别为谐波参数偏差和谐波量测噪声的随机变量。本文与谐波有关的参数均为复数。
采用连续多个时刻的量测量对式（1）进行估计，能够追踪谐波状态变化，属于动态谐波状态估计[14-15]。但如果假定式（1）中的参数矩阵保持恒定，即在忽略参数偏差δh 的前提下进行状态估计，会导致状态量的估计精度下降。虽然参数偏差δh 在数值上具有不确定性，但可掌握其偏差边界[16-18]。因此，可将传统确定性动态谐波状态估计问题转换为计及线路参数不确定性影响的区间动态谐波状态估计问题。
区间动态谐波状态估计在式（1）的基础上，将谐波量测矩阵Hh 与参数偏差δh 合并成区间矩阵，结合谐波量测量zh 共同估计出谐波状态量的区间值。针对传统标准卡尔曼滤波无法处理不确定性的动态状态估计问题，Chen Guanrong 最早提出区间卡尔曼滤波（Interval Kalman Filter, IKF）算法[19]，以区间数刻画系统参数的不确定性，从而估计状态量的区间值，解决参数不确定下的估计问题，这为后续研究了提供新的求解思路。
1.2 采用改进区间卡尔曼滤波的状态估计
在迭代过程中，采用区间卡尔曼滤波计算的区间结果保守性较大且易发散，致使计算结果失去应用价值[20]。基于误差最优上界的区间卡尔曼滤波算法通过求解误差矩阵最优上界，进而将部分区间参数矩阵化为确定性矩阵，最后降低区间动态状态估计保守性的同时实现收敛。该算法公式说明如下：
预测阶段：
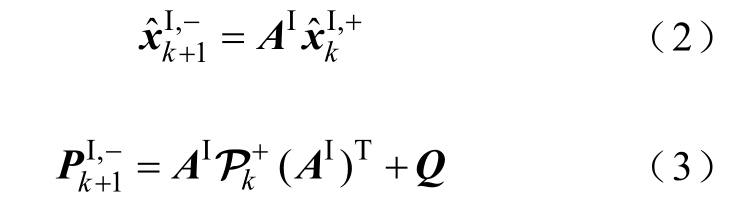
校正阶段：
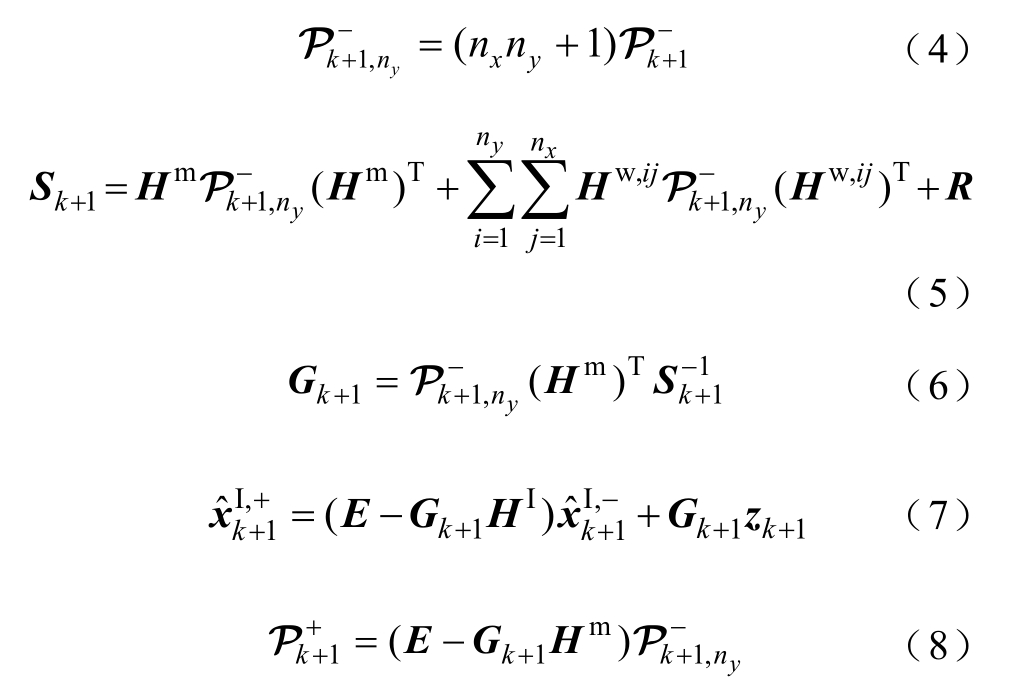
式中，上标“－”表示先验估计；上标“＋”表示后验估计；上标“I”表示矩阵元素均为区间数；上标“m”表示矩阵由区间中心值构成；上标“w”表示其元素均为区间半径；下标“k”表示时间；G 为增益矩阵；P 为误差矩阵；H 为量测矩阵；A 为状态转移矩阵，谐波估计时可取为单位矩阵；R 为噪声误差矩阵；Q 为系统误差矩阵；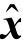
为状态量；z 为量测量；E 为单位矩阵；P为最优上界，即P≥PI；Hw,ij 为除（i, j）之外的元素均为零的矩阵；nx、ny分别为区间矩阵中的列数与行数。式（4）、式（5）为简写表达，避免公式表达繁琐，公式详细推导见文献[21]。
基于UBIKF 的动态状态估计，围绕式（2）～式（8）进行迭代更新。式（2）预测k+1 时刻状态量；式（3）则表示真实值与预测状态量之间的误差；式（6）通过计算增益矩阵来校正更新式（7）中k+1时刻最优的状态量；式（8）更新最优状态量与真实值之间的误差，以便执行下一次迭代。
1.3 评估指标
为验证区间动态状态估计结果的准确性，本文定义区间估计上界方均根误差
为
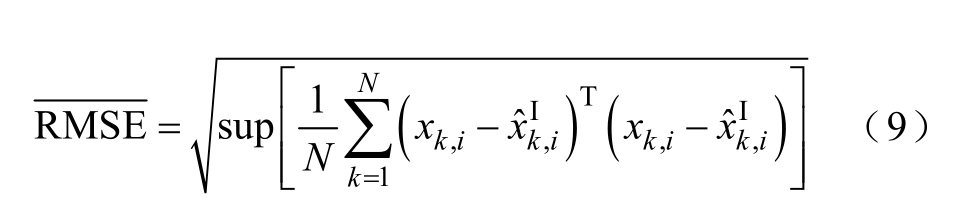
式中，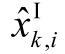
为节点i 区间状态估计结果；xk,i 为节点i状态量实际值；N 为采样周期数；sup 表示上界。
越小表示参数不确定性对区间状态估计影响越小，结果越接近实际状态量。
完备性表明区间估计结果是否能囊括实际节点状态量xk,i 的取值，若完备性能够满足囊括要求，则表明估计结果能够包含实际值。定义区间动态估计平均完备性指标μ为
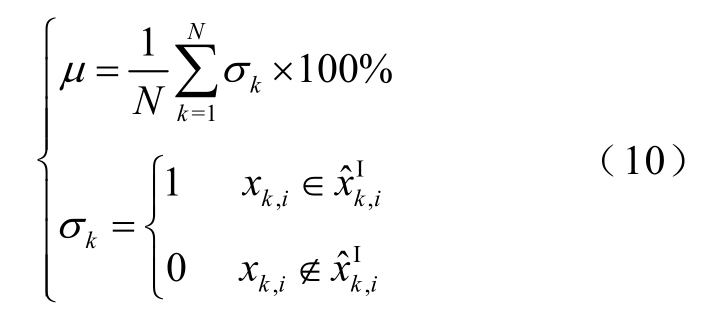
保守性是衡量区间状态估计值优劣的指标，保守性越小，状态估计的参考价值越高。本文以基于蒙特卡罗的标准卡尔曼滤波（Standard Kalman Filter Based on Monte Carlo, MCSKF）算法作为参照值，定义区间动态估计平均保守性指标η为
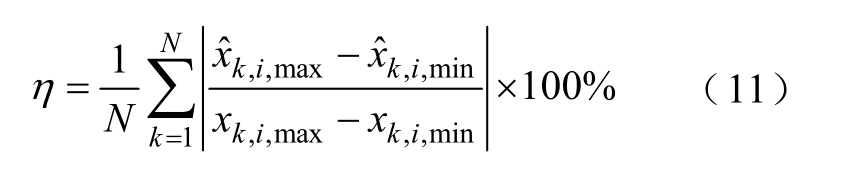
式中，
分别为采用UBIKF 计算得到的节点i 区间估计值上、下限；xk,i,max 和xk,i,min 分别为采用MCSKF 计算得到的相应状态量区间上、下限。
2 不可观区域处理方法及状态估计模型
2.1 不可观区域多端口等效原理及方法
谐波状态估计中的可观性定义[22]：
（1）若节点存在量测装置，则该节点的状态可观。
（2）若某节点电压可观，通过支路电流量测可使对端节点间接可观。
（3）若某支路两端的节点电压均可观，则该支路的电流可观。
目前电网中配置的谐波监测装置难以做到电网节点完全可观。不可观节点构成电力系统中的信息盲区，表现为量测数小于状态数，导致状态方程为欠定形式，难以求解出正确的结果。具体情况如图1 所示，节点19、30、45、51 为直接观测节点，其相邻节点为间接可观节点，其中节点18、29、44、50 是不可观区域的边界节点，其余不可观节点形成三处不可观区域。
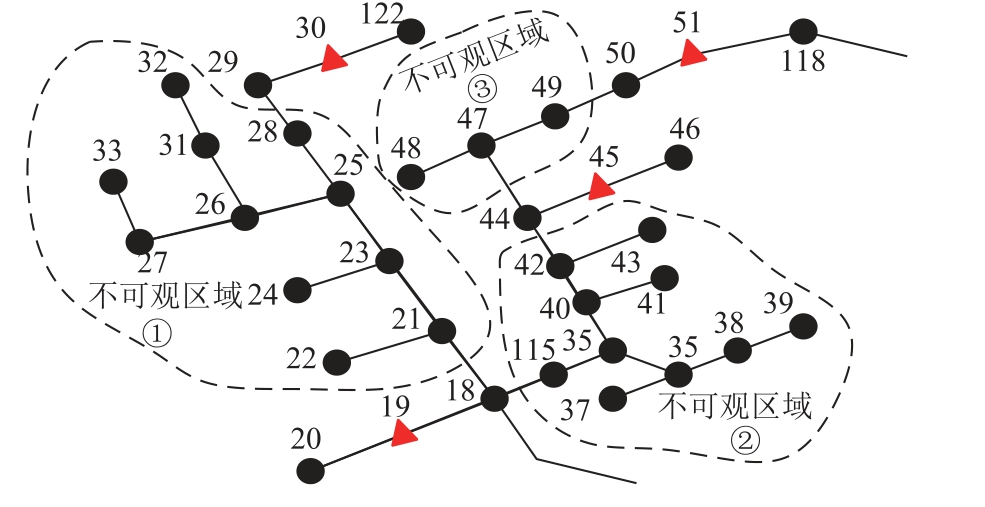
图1 IEEE 123 节点系统部分拓扑
Fig.1 Partial network topology of IEEE 123 node model
采用多端口网络等效对网络进行化简，消去不可观区域内的节点，可以将状态方程转化为超定或正定形式。此时区域内部的谐波电流源等效为外部端口节点上的谐波电流源，如图2 所示。多端口等效采用谐波电流移置矩阵表示法[23]，具体过程见附录。
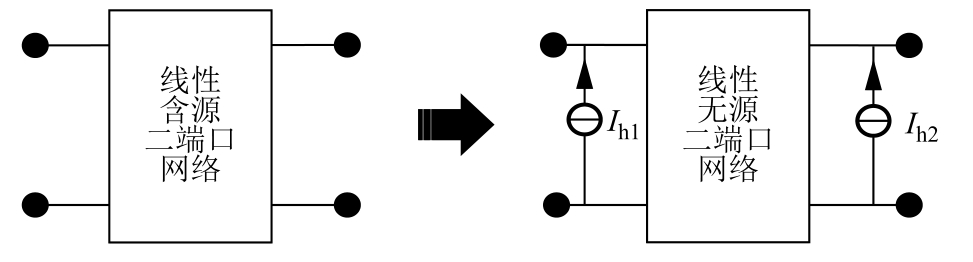
图2 端口等效示意图
Fig.2 Diagram of port equivalence
反之，在求解等效后的谐波状态估计方程以后，如果端口节点的谐波电流近似为零，则可以判断等值区域不含谐波源。
2.2 网络等效后的谐波状态估计方程
量测数据包含节点谐波电压以及支路谐波电流，两种电气量对应的量测方程如下。
节点谐波电压量测方程为
支路谐波电流量测方程为
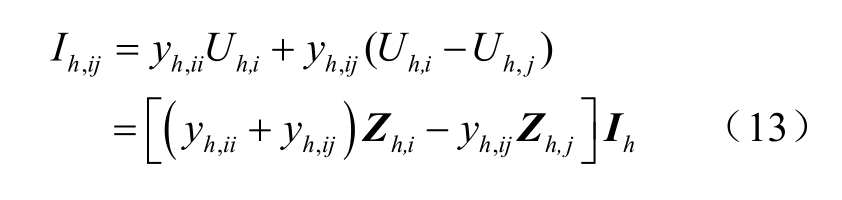
式中，Uh 为节点谐波电压；Uh,i 为节点i 的谐波电压；Zh 为谐波阻抗矩阵；Zh,i 为谐波阻抗矩阵中节点i 对应的行；yh,ii 为节点i 对地谐波导纳；yh,ij 为节点i 和j 之间的谐波导纳；Ih,ij 为节点i 和j 之间的支路谐波电流。
当对不可观区域等效后，将原系统对应的式（1）进行变化，构成谐波状态估计等效模型为
式中，zh 为谐波量测量，含节点谐波电压与支路谐波电流；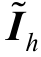
为等效后的谐波注入电流；
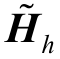为系统等效后的谐波量测矩阵；
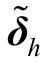为等效后的谐波量测矩阵偏差，量测矩阵偏差区间采用Monte Carlo 生成。
3 不可观区域内谐波源定位策略
3.1 边界节点等效谐波电流的相关性
谐波源定位应优先定位出污染威胁相对严重的谐波源，即谐波电流注入量相对较大的谐波源。在一段相对较长的监测时段中，因为工况的不断变化，谐波源电流会呈现特定的波动特征。对不可观区域等效后，该区域中谐波源的波动特征也包含在边界节点等效谐波电流的波动特征中。本文将注入量相对较大且具有主导波动特征的谐波源称为主谐波源。其中，谐波源具有主导波动特征是指相对于其余谐波源，该谐波源波动成分更显著，占主导地位。
易证以下两个命题的正确性，详见附录。
命题1 当不可观区域内存在主谐波源时，边界节点等效谐波电流的波动特征在一定程度上与主谐波源相关。
命题2 对于不同的边界节点，其等效谐波电流都包含等效区域内同一个主谐波源的主导特征。
由命题可知，在完成状态估计确定有谐波源存在的不可观区域以后，对不可观区域边界节点的谐波电流进行相关性分析，寻找主谐波作用的时间段，此后可进一步基于主导特征定位不可观区域内的主谐波源。
3.2 不可观区域内谐波源节点匹配度计算
假设不可观区域中存在主谐波源HS1，而谐波源HS2 的谐波电流基本保持稳定。边界节点r 和l的等效谐波电流Ih,r 与Ih,l 为
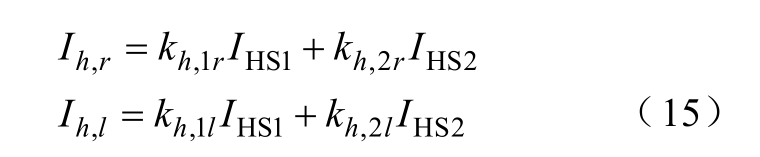
式中，kh 为内部节点相对边界节点的状态转移系数，具体计算过程见附录。由式（15）可见，边界节点等效谐波电流Ih,r 与Ih,l 都包含主谐波源的主导特征。
消去主谐波源变量IHS1，形成关于边界节点谐波电流的线性关系式为
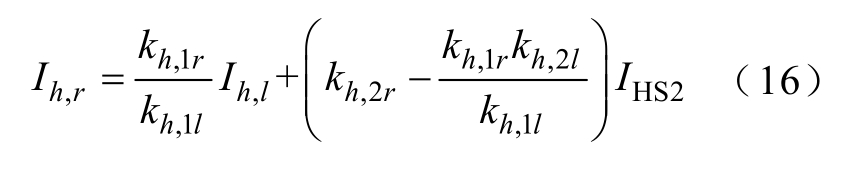
式中，Ih,r 为边界节点r 的等效谐波电流；Ih,l 为边界节点l 的等效谐波电流；IHS2 变化较小，可看作常量；定义Kh=kh,1r/kh,1l 为主谐波源节点对应的等效系数，由内部节点相对于边界节点的状态转移系数计算得到。由式（16）可见，Kh 一方面代表Ih,r 与Ih,l中主导特征的数量关系；另一方面也与主谐波源的位置有关。值得注意的是，无论内部节点是否存在谐波源，都可以定义一个等效系数Kh，并且在状态估计之前即可计算得到，称之为内部节点等效系数的计算值。
将式（16）改写为边界节点谐波电流之间的一般关系式为
式中，Kh 为等效系数；Bh 为常量。
在状态估计完成以后，对式（17）进行线性回归可辨识得到等效系数Kh 的估计值Kˆh ，其包含主谐波源的位置信息。此后将Kˆh 与该区域内各个节点的等效系数计算值进行匹配对比，寻找与其最接近的数值，即可确定主谐波源所处位置。鉴于本文所涉及的谐波电流估计值为区间数，而区间中点表示区间位置，在一定程度上能够表征谐波电流整体波动趋势，因此本文采用区间中点回归辨识回归系数，并定义匹配度g 为
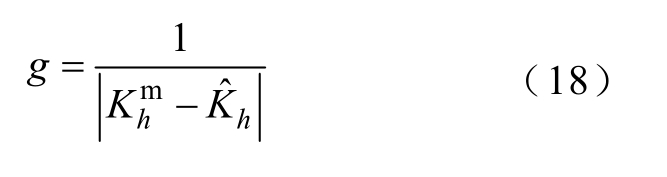
式中，K hm为区域内节点对应的等效系数中点值；Kˆh为等效系数估计值。当回归系数越接近该节点对应的等效系数时，相应的g 越大，表明不可观区域内谐波源处于该节点的可能性越大。
为筛选主谐波源作用时间段，提高线性回归的准确性，采用决定系数R2 进行数据的筛选，设定窗宽为b，将边界节点等效谐波电流划分为多个子序列。
式中，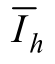
为谐波电流平均值；
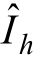为由线性回归得到谐波电流估计值。R2 的值越接近于1，该子序列线性关系越明显，表明主谐波源主导作用越强，越有利于上述匹配度计算。
3.3 定位流程
综上所述，谐波源定位流程如图3 所示，具体如下：
图3 谐波源定位流程
Fig.3 Flow chart of harmonic source location
（1）根据测点布置情况，将局部不可观系统进行多端口等效，生成全局等效可观系统。
（2）在全局等效可观系统下，采用UBIKF 算法进行区间动态谐波状态估计，并获取谐波电流区间估计值。
（3）根据结果辨识谐波源存在于可观区域还是不可观区域，若谐波源存在于可观区域内，准确定位；若谐波源存在于不可观区域内，执行步骤（4）。
（4）筛选边界节点谐波电流序列中主谐波源作用时间段，对满足指标阈值要求的子序列执行步骤（5）；若子序列均不满足要求，确定谐波源存在区域，完成区域定位。
（5）对筛选出的谐波电流进行区间中点线性回归辨识等效系数估计值，再与区域内节点对应的等效系数进行匹配度计算。
（6）匹配度最高所对应的节点视为不可观区域内谐波源位置。
4 算例分析
本文以IEEE 33 节点系统为例验证方法的可行性与准确性，该系统基准容量为100 MV·A，基准电压为12.66 kV。仿真软件为Matlab 2018b，工具箱为Matpower 以及INTLAB V10.2。测点布置于节点2、6、17、21、24、32，如图4a 所示，等效后的系统如图4b 所示。线路参数不确定性程度为标称值c的±γ %[16]；量测噪声为正态分布，均值为零，标准差取量测值的α %[24]。
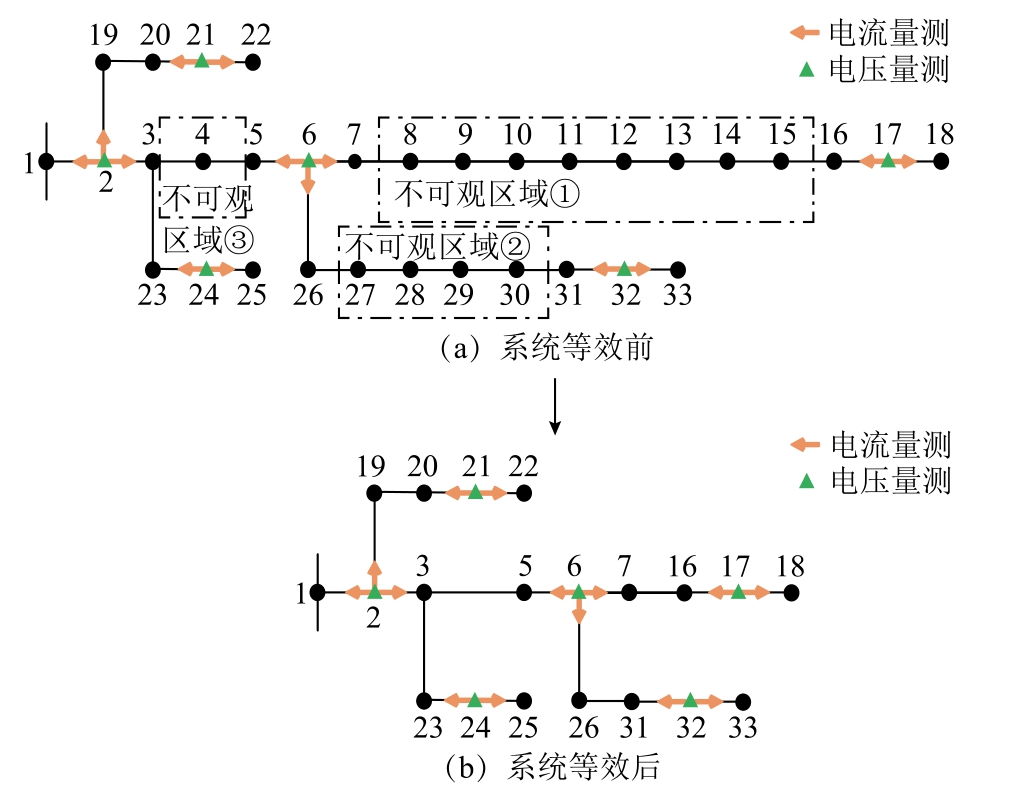
图4 IEEE 33 节点系统
Fig.4 IEEE 33-bus system
采用某地区实际负荷一天内的变化曲线，以Matpower 计算基波潮流，结合基波电流与谐波典型频谱[25]，见表1，建立相应的谐波电流模型，从而获取谐波注入电流；再通过谐波潮流计算，将对应量测方案的节点谐波电压和支路谐波电流作为量测量，通过添加噪声得到含噪测量数据，以3 min 为数据间隔，仿真1 天得到480 组数据。本文以第5次谐波电流为例。
表1 谐波负荷频谱表
Tab.1 Spectrum table of harmonic loads
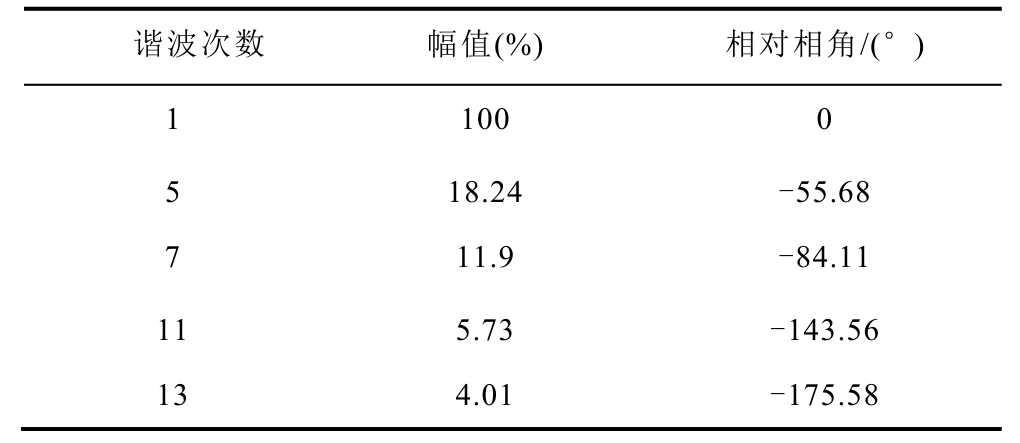
谐波次数 幅值(%) 相对相角/(°)1 100 0 5 18.24 -55.68 7 11.9 -84.11 11 5.73 -143.56 13 4.01 -175.58
4.1 不可观区域等效效果验证
设置两个谐波源分别接入不可观区域中的节点9 与节点15，其中节点9 和节点15 处的谐波源分别设定主导波动的时间段，在两个谐波源各自主导的时段内将另一个谐波源的谐波注入电流添加±3%的随机波动，保持相对稳定状态。线路参数不确定性程度为±5%，量测噪声为±0.3%。此外，由于非谐波源节点的谐波电流实际注入量为零，其估计结果区间值包含零值且无波动特征。为了区别谐波源节点与非谐波源节点，定义谐波电流状态量的平均幅值αavg 为
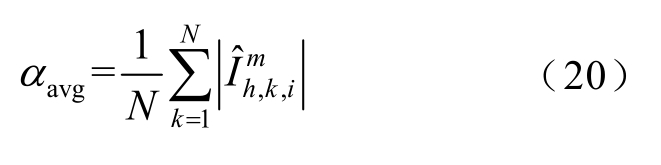
式中，
为节点i 谐波电流区间中点估计值。当αavg 小于阈值λ，认为该节点为非谐波源节点；反之，则为谐波源相关节点，本文的λ取为10-3。
本文分别采用两种方法处理局部不可观系统下的谐波状态估计问题，即方法一为基于正交匹配追踪的卡尔曼滤波方法[26]，方法二为本文采用的多端口等效方法，以此对比验证采用本文方法处理局部不可观系统的效果。两种方法计算得到的谐波电流平均幅值如图5 所示，其中图5a 为系统未等效时，采用方法一计算得到的节点谐波电流平均幅值；图5b 为采用本文等效可观方法计算得到的谐波电流平均幅值。
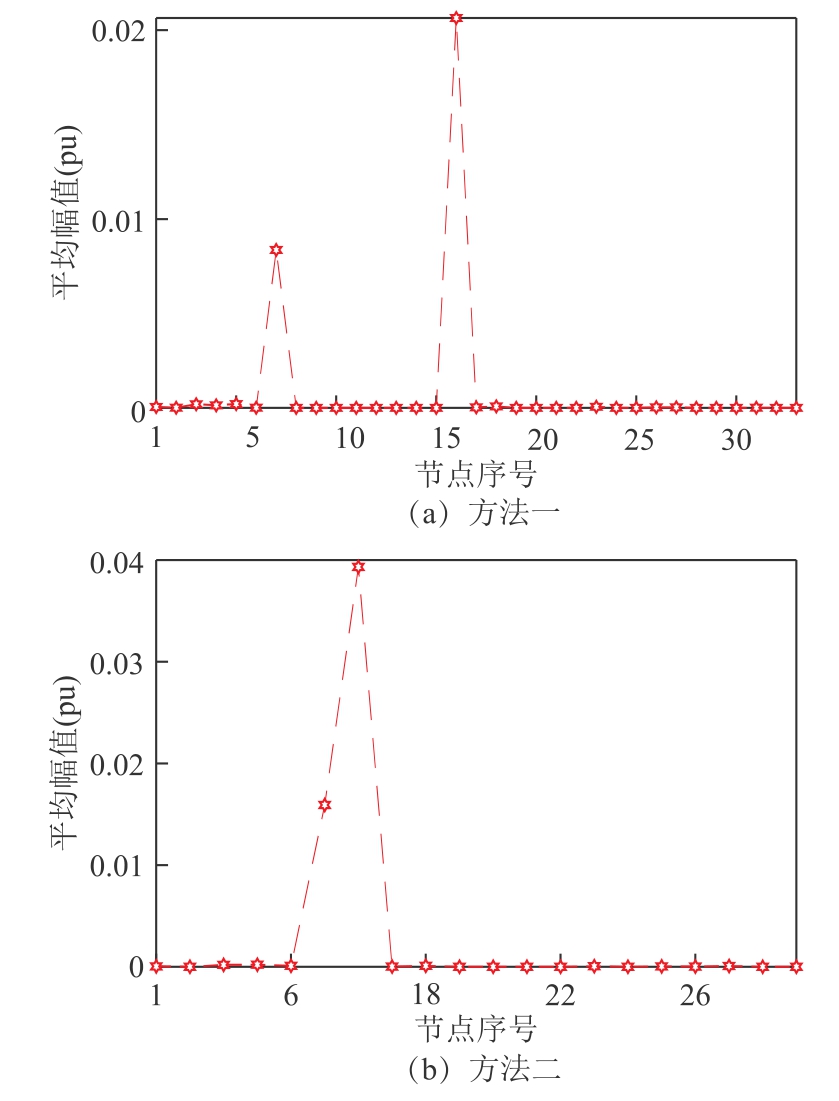
图5 平均幅值计算结果
Fig.5 Calculation results of average amplitude
采用方法一时，对局部不可观IEEE 33 系统不作等效，此时无边界节点，节点总数为33 个，根据图5a 结果推断出谐波源是处于节点7 与节点16，但谐波源实际位于节点9 和节点15，因此定位错误。原因在于该方法求解欠定模型的重构结果在一定程度上受量测配置情况的影响，不同的量测矩阵会使算法在求解过程中选择错误的相关列，导致重构失败，最终无法准确判断出谐波源位置。而采用本文的方法二将系统等效可观后，得到以节点7 和节点16 等为边界节点的等效系统，根据图5b 中的计算结果判断谐波源处于节点7 与节点16 之间的区域。因此，相较于基于稀疏特征的求解方法，本文采用等效方法求解局部不可观系统，其准确性与稳定性更好。同时，从附图2、附图3 可以看出，将系统中不可观区域进行等效后，等效谐波电流区间估计值不仅涵盖实际值，还能够跟踪其动态变化，进一步表明本文方法能够有效解决量测数目不足时谐波状态估计中的欠定问题，为谐波源定位提供有效的帮助。
4.2 区间动态谐波状态估计性能验证
4.2.1 算法性能对比
在本算例中，分别采用UBIKF、IKF、MCSKF三种算法进行区间动态谐波状态估计。区间卡尔曼滤波估计结果如图6 所示。从图6 可知，采用IKF算法进行区间动态谐波状态估计，其区间结果随着估计次数的增加，区间上、下界向外扩张发散。原因在于区间运算法则存在解集扩张问题，而IKF 算法又涉及多个区间矩阵之间的运算，其扩张问题容易在动态估计过程中逐渐放大，以致结果出现发散现象，失去参考价值。
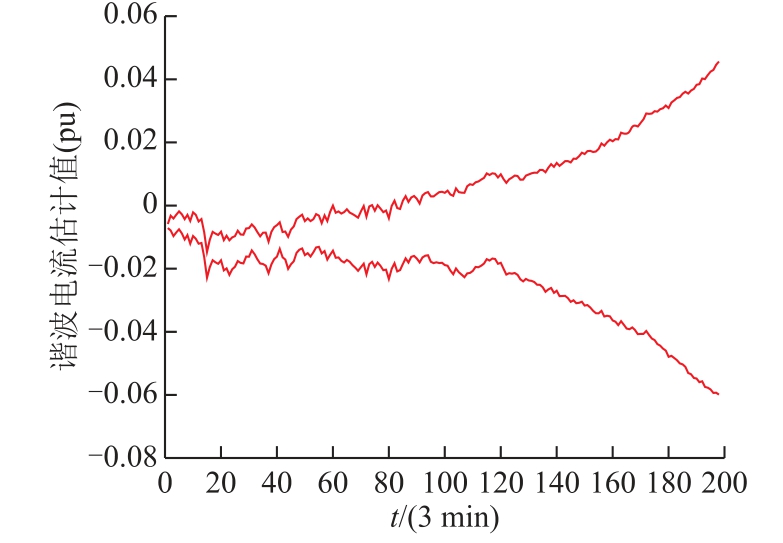
图6 区间卡尔曼滤波估计结果
Fig.6 The results of interval Kalman filtering
误差最优上界矩阵迹趋势如图7 所示。由图7 可知，在进行区间动态状态估计时，其误差最优上界矩阵的迹基本在迭代 5 次后趋于稳定，即表明UBIKF 算法能够在区间动态估计中实现收敛。
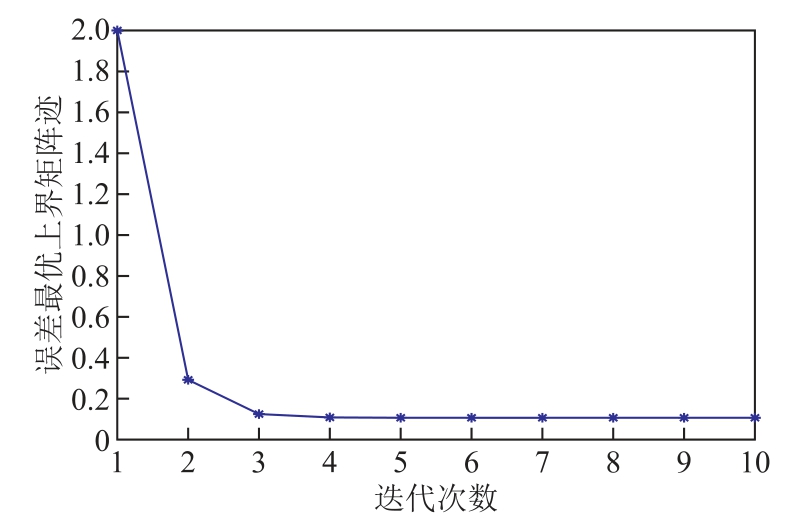
图7 误差最优上界矩阵迹趋势
Fig.7 Trend of the trace of a minimal upper bound of error covariance
进一步从图8 和图9 所示的区间谐波电流估计结果可知，采用UBIKF 算法的谐波电流区间结果能够囊括采用MCSKF 算法的谐波电流区间结果。同时由表2 可知，虽然MCSKF 的上界方均根误差比UBIKF 与IKF 更小，但MCSKF 执行50 000 次标准卡尔曼滤波估计的耗时达到11 919.44 s，而UBIKF耗时仅为27.844 7 s，效率更高；在完备性上，基于UBIKF 的谐波电流区间结果能够包含实际值，如附图2、附图3 所示，完备性达到100%；在保守性上，根据计算可知，UBIKF 平均保守性较小，而IKF 算法结果发散严重，其保守性过大。
附图2 边界节点7 谐波电流估计结果
App.Fig.2 Estimation results of harmonic current at boundary node 7
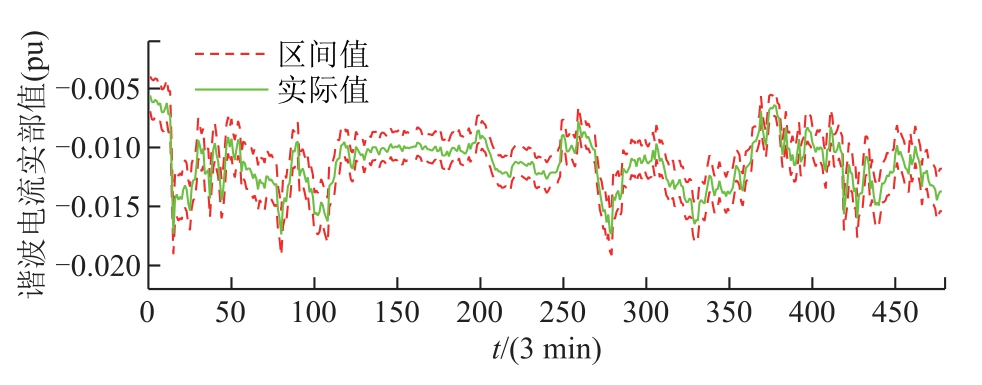
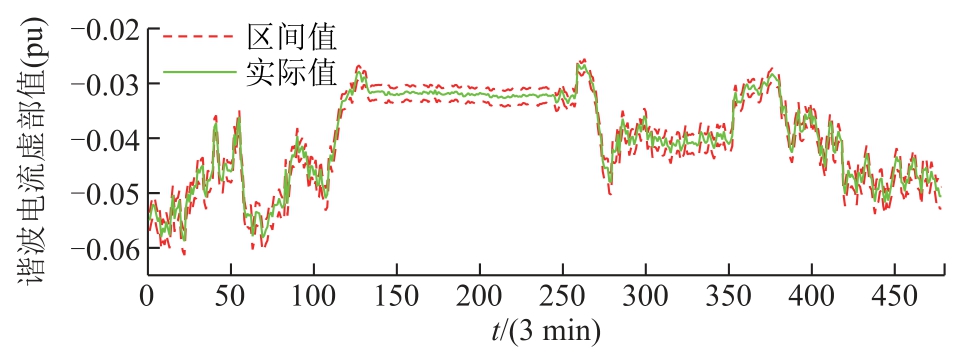
附图3 边界节点16 谐波电流估计结果
App.Fig.3 Estimation results of harmonic current at boundary node 16
图8 边界节点7 不同算法估计结果
Fig.8 Estimation results of harmonic current at boundary node 7 by different methods
图9 边界节点16 不同算法估计结果
Fig.9 Estimation results of harmonic current at boundary node 16 by different methods
表2 计算结果对比
Tab.2 Comparison of calculation results
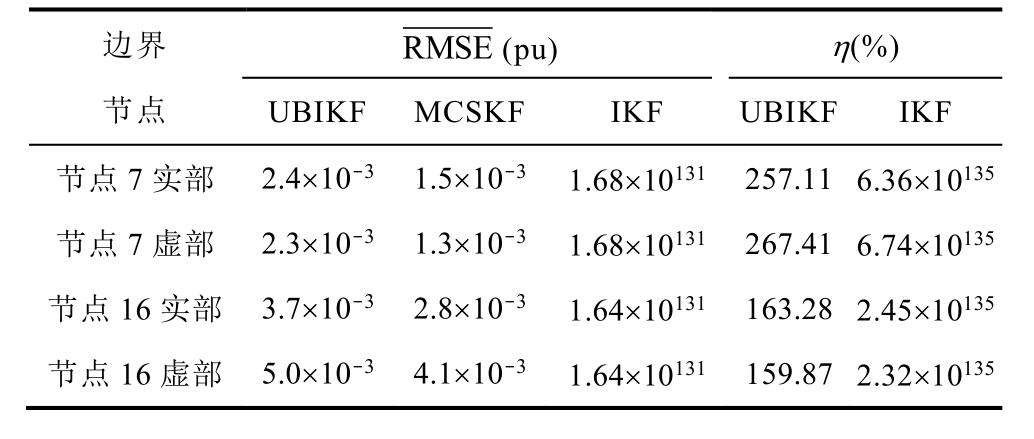
边界节点RMSE(pu) η(%)UBIKF MCSKF IKF UBIKF IKF节点7 实部 2.4×10-3 1.5×10-3 1.68×10131 257.11 6.36×10135节点7 虚部 2.3×10-3 1.3×10-3 1.68×10131 267.41 6.74×10135节点16 实部 3.7×10-3 2.8×10-3 1.64×10131 163.28 2.45×10135节点16 虚部 5.0×10-3 4.1×10-3 1.64×10131 159.87 2.32×10135
综上所述，采用蒙特卡洛法估计状态量区间时，需要在区间数范围里对参数进行多次采样并进行确定性状态估计，此后才能从解的分布范围得到状态量区间，因而计算时间较长，效率低下；而IKF 算法和UBIKF 算法均直接采用区间数进行计算，因此不需要进行多次采样，执行一次就能得到状态量区间，计算效率较高。IKF 算法最先引入区间数来刻画系统的不确定性，并提出了区间动态状态估计的求解思路与步骤，但IKF 算法中参与运算的参数均为区间数形式，因此采用区间运算法则，导致其解有所扩张。而UBIKF 是在IKF 整体基础框架上对其中部分运算过程进行改进，即通过求解区间误差矩阵的最优上界，进而使IKF 中的部分区间数型参数矩阵转化为确定数型参数矩阵，即将运算转换为确定数与区间数之间的运算，因此在一定程度上降低区间结果保守性。
4.2.2 参数不确定程度对状态估计影响
分别设置线路参数不确定性程度为±1%、±3%、±5%、±7%、±9%，上界方均根误差如图10 和图11所示。
图10 谐波电流实部上界方均根误差
Fig.10 Root mean square error of upper bound of real part of harmonic current
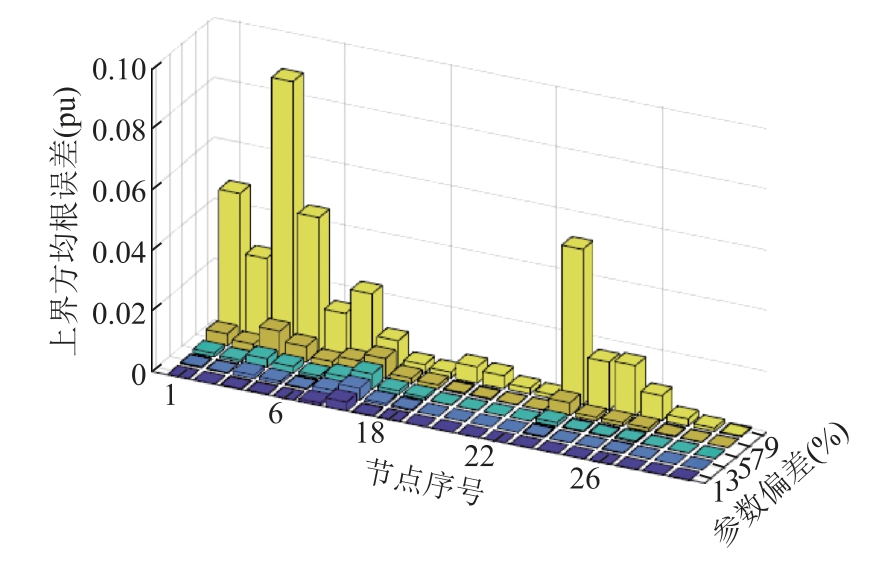
图11 谐波电流虚部上界方均根误差
Fig.11 Root mean square error of upper bound of imaginary part of harmonic current
当参数不确定性程度增大时，区间估计上界方均根误差逐渐增加，表明参数不确定性对区间动态估计结果的影响也相应提升；当参数不确定性程度达到±9%，尽管区间动态估计仍能够收敛，但对于部分节点，上界方均根误差增长率相对较大，则表明在该参数不确定程度下，部分节点的结果在区间运算过程中遇到区间解集扩张的问题较为严重，若继续增加参数不确定性程度，误差增长率较高的节点区间量会影响整体区间状态结果，再加之区间动态估计是对连续多个时刻进行迭代求解，其中存在的保守性可能会逐步放大。
4.3 谐波源定位准确性分析
4.3.1 可观区域内谐波源定位结果分析
仍采用4.1 节的谐波源参数设置，在可观区域中节点18 和节点33 分别接入谐波源，计算各节点谐波电流的平均幅值如图12 所示。
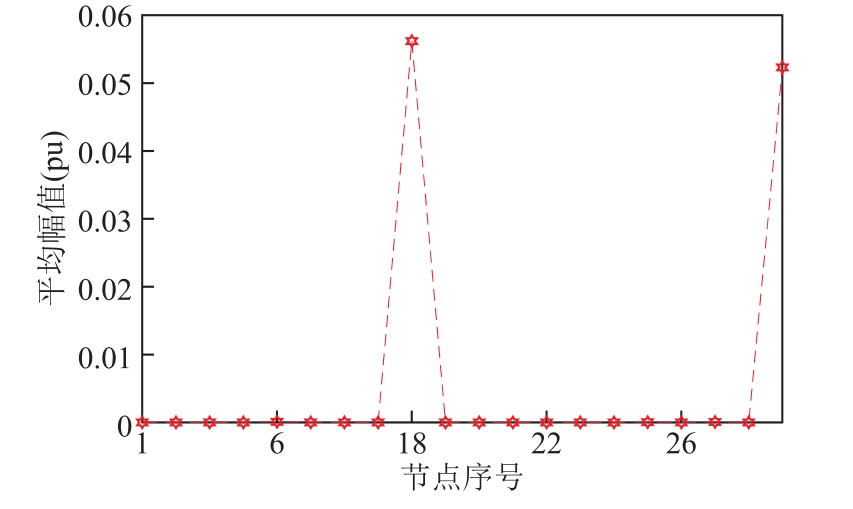
图12 各节点对应的平均幅值
Fig.12 Average amplitude of each node
从图12 可知，节点18 与节点33 的平均幅值大于阈值λ，且两节点为可观区域内部的节点，因此无需执行下一步骤，可直接判断谐波源处于可观节点18 和节点33，与设定一致，表明利用本文方法处理欠定模型，可以得到准确解，并准确识别出可观区域内的谐波源位置。
4.3.2 不可观区域内谐波定位结果分析
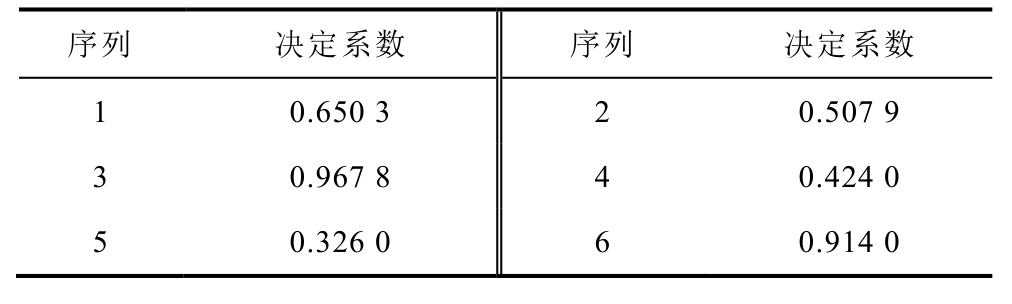
根据4.1 节计算结果，首先由αavg 确定4.1 节中的谐波源处于不可观区域中，此后根据第3 节不可观区域内谐波源定位策略，推测区域内部谐波源。设置窗宽为80，总共6 个序列，寻找主谐波源主导作用时间序列，得到的结果见表3。设置阈值为0.8。
表3 子序列计算结果
Tab.3 Results of subsequence calculation
序列 决定系数 序列 决定系数1 0.650 3 2 0.507 9 3 0.967 8 4 0.424 0 5 0.326 0 6 0.914 0
从表3 中可知，当序列为3 和6 时，其决定系数均大于0.8，此时判断序列3 和6 内的谐波电流子序列隐含谐波源的主导波动特征，其匹配结果的可信度高。在此基础上，进一步进行匹配度计算，具体结果如图13 所示。
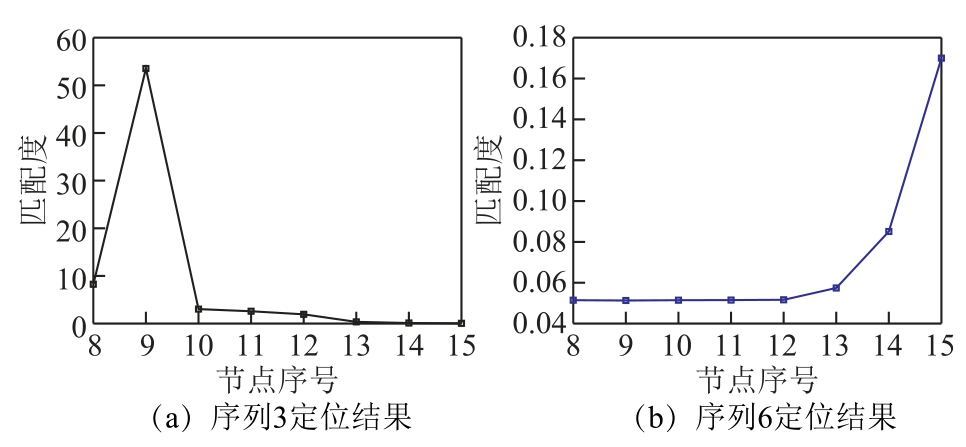
图13 谐波源匹配计算结果
Fig.13 Calculation results of harmonic source matching
从图13a 的节点匹配度曲线可知，序列3 中，节点9 的匹配度比其他节点更大，说明谐波源位于节点9 的可能性最大，因此判断谐波污染位于节点9，与设置一致。从图13b 的节点匹配度曲线可知，序列6 中，节点15 的匹配度最大，说明该时段内主谐波源位于节点15 的可能性最大，因此判断谐波污染位于节点15，也与设置一致。
如果节点9 和节点15 处的谐波源波动不明显或波动程度接近，则无法筛选出具有主导波动特征的时间段并进行定位，此时本文将该不可观区域判断为存在谐波源的区域。
为进一步验证在不可观区域内线路参数不确定时，本文方法定位不可观区域内谐波源的准确性。本文对不同的参数不确定性程度，分别采用蒙特卡洛模拟5 000 次，谐波源定位成功率如图14所示。
从图14 可知，在参数不确定性程度为1%，成功率为100%；当参数不确定性程度为7%，本文方法的成功率仍然能达到90%以上。
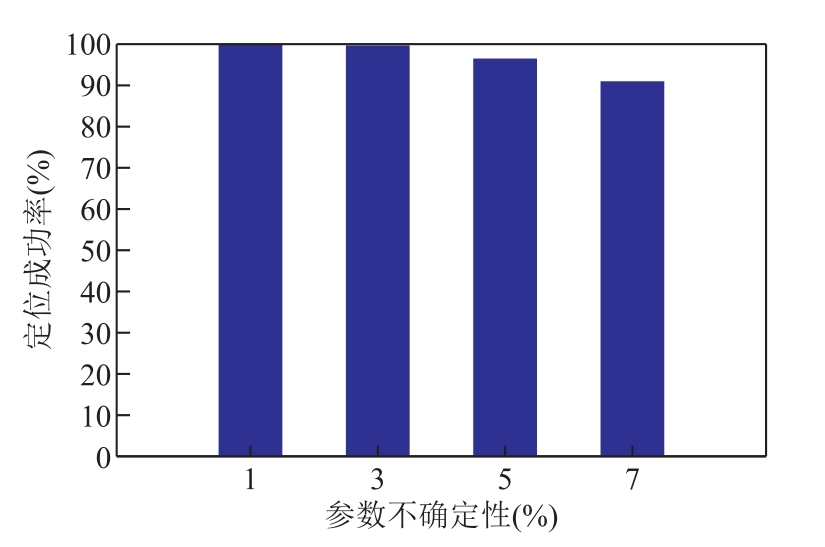
图14 谐波源定位成功率
Fig.14 Success rate of harmonic source localization
5 结论
针对谐波源定位研究中存在的局部不可观与参数不确定问题，本文提出了基于区间动态状态估计的局部不可观系统谐波源定位方法，得到的主要结论如下：
1）在有限量测装置的前提下，难以对局部不可观系统进行谐波状态估计。通过系统多端口等效，将局部不可观系统转化为等效可观系统，可以提高谐波状态估计结果的准确性，从而辨识可观节点处的谐波源或含谐波源的不可观区域。
2）本文采用UBIKF 算法进行区间动态谐波状态估计，不仅能够表征谐波电流估计结果的不确定性，同时可以反映出谐波的波动特征。且从结果上可知，在完备性和保守性上，较之IKF 更具有适用性，在运行时间上，较之MCSKF 所耗时间更小，效率更高。
3）本文针对不可观区域内存在谐波源的情况，通过数据筛选再计算匹配度，能够准确判断不可观区域内的谐波源位置。
附 录
1. 谐波电流移置法具体过程
不可观节点等效示意如附图1 所示。
附图1 不可观节点等效示意图
App.Fig.1 Diagram of unobservable node equivalence
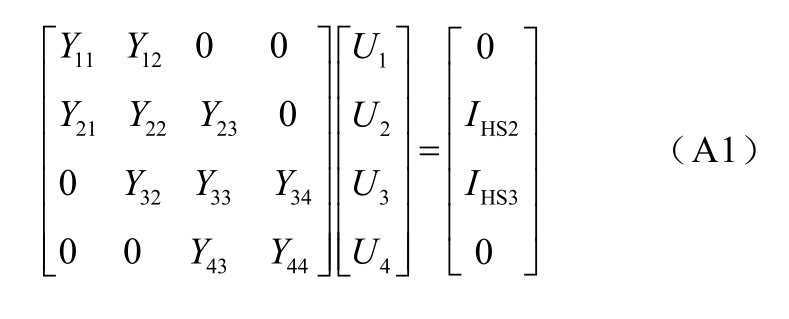
经过高斯消元，消去不可观节点2 和节点3 得到
此时边界节点1、4 的等效电流分别为
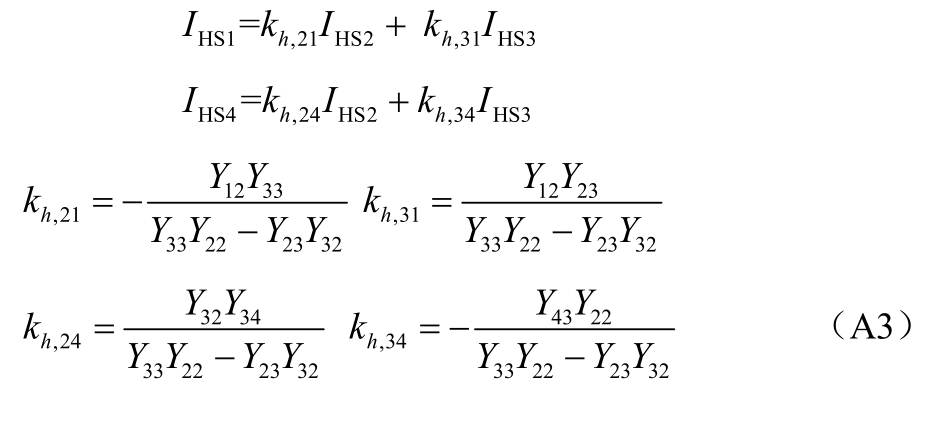
式中，状态转移系数kh 由导纳构成，表示网络等效后该节点处谐波电流与边界节点等效谐波电流之间的数量关系。假设HS2 为主谐波源，从式（A3）可知，边界节点等效谐波电流与主谐波源存在一定的等式关系，同时边界节点1、4 的等效谐波电流均含有同一主谐波源IHS2。
2. 实际值与区间估计值结果
[1] 严静, 邵振国. 电能质量谐波监测与评估综述[J].电气技术, 2020, 21(7): 1-7.Yan Jing, Shao Zhenguo. Summary of harmonic monitoring and evaluation[J]. Electrical Engineering,2020, 21(7): 1-7.
[2] 熊敏, 杨洪耕. 基于改进协方差特性的永磁直驱风电场谐波发射水平评估[J]. 电工技术学报, 2020,35(3): 603-611.Xiong Min, Yang Honggeng. Assessment method of D-PMSG wind farm harmonic emission level based on the improved covariance characteristic[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 603-611.
[3] 丁同, 陈红坤, 吴斌, 等. 多谐波源定位及谐波责任量化区分方法综述[J]. 电力自动化设备, 2020,40(1): 19-30.Ding Tong, Chen Hongkun, Wu Bin, et al. Overview on location and harmonic responsibility quantitative determination methods of multiple harmonic sources[J]. Electric Power Automation Equipment,2020, 40(1): 19-30.
[4] 吴笃贵, 徐政. 基于相量量测的电力系统谐波状态估计(I): 理论、模型与求解算法[J]. 电工技术学报,2004, 19(2): 64-68, 88.Wu Dugui, Xu Zheng. Power system harmonic state estimation based on phasor measurements(I)—theory,model and solution algorithm[J]. Transactions of China Electrotechnical Society, 2004, 19(2): 64-68, 88.
[5] 罗深增, 李银红, 石东源. 广域测量系统可观性概率评估及其在PMU 优化配置中的应用[J]. 电工技术学报, 2018, 33(8): 1844-1853.Luo Shenzeng, Li Yinhong, Shi Dongyuan. Wide area monitoring system observability probabilistic evaluation and it's application in optimal PMU placement[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1844-1853.
[6] 杨源, 林圣, 臧天磊, 等. 基于改进稀疏表示法的谐波源定位[J]. 电网技术, 2013, 37(5): 1279-1284.Yang Yuan, Lin Sheng, Zang Tianlei, et al. Improved sparse representation-based location of harmonic sources in power system[J]. Power System Technology, 2013, 37(5): 1279-1284.
[7] Carta D, Muscas C, Pegoraro P A, et al. Identification and estimation of harmonic sources based on compressive sensing[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(1): 95-104.
[8] Carta D, Muscas C, Pegoraro P A, et al. Compressive sensing-based harmonic sources identification in smart grids[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-10.
[9] 于华楠, 李永鑫, 王鹤. 基于过完备字典设计的电力系统扰动定位方法[J]. 电工技术学报, 2020,35(7): 1444-1453.Yu Huanan, Li Yongxin, Wang He. Disturbance location method of power system based on overcomplete reconstruction dictionary design[J].Transactions of China Electrotechnical Society, 2020,35(7): 1444-1453.
[10] 王鹤, 李石强, 于华楠, 等. 基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法[J]. 电工技术学报, 2020, 35(21): 4553-4564.Wang He, Li Shiqiang, Yu Huanan, et al. Compression acquisition method for power quality data of distribution network based on distributed compressed sensing and edge computing[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4553-4564.
[11] 辛国庆, 董唯光, 高锋阳, 等. 感应电能供电技术下含间谐波的谐波信号重构[J]. 电工技术学报,2020, 35(21): 4544-4552.Xin Guoqing, Dong Weiguang, Gao Fengyang, et al.Reconstruction of harmonic signal with interharmonics under inductive power supply technology[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4544-4552.
[12] Ma Haili, Girgis A A. Identification and tracking of harmonic sources in a power system using a Kalman filter[J]. IEEE Transactions on Power Delivery, 1996,11(3): 1659-1665.
[13] 王艳, 臧天磊, 符玲, 等. 基于谐波源特征提取的电力系统动态谐波状态估计自适应方法[J]. 电网技术, 2018, 42(8): 2612-2619.Wang Yan, Zang Tianlei, Fu Ling, et al. Adaptive method for dynamic harmonic state estimation in power system based on feature extraction of harmonic source[J]. Power System Technology, 2018, 42(8):2612-2619.
[14] Molina-Moreno I, Medina A, Cisneros-Magaña R, et al. Enhanced harmonic state estimation in unbalanced three-phase electrical grids based on the Kalman filter and physical scale-down implementation[J].International Journal of Electrical Power & Energy Systems, 2020, 123: 106243.
[15] Xi Yanhui, Tang Xin, Li Zewen, et al. Harmonic estimation in power systems using an optimised adaptive Kalman filter based on PSO-GA[J]. IET Generation, Transmission & Distribution, 2019,13(17): 3968-3979.
[16] Rakpenthai C, Uatrongjit S, Premrudeepreechacharn S.State estimation of power system considering network parameter uncertainty based on parametric interval linear systems[J]. IEEE Transactions on Power Systems, 2012, 27(1): 305-313..
[17] Rakpenthai C, Uatrongjit S, Watson N R, et al. On harmonic state estimation of power system with uncertain network parameters[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4829-4838.
[18] 卫志农, 颜全椿, 孙国强, 等. 考虑参数不确定性的电力系统区间线性状态估计[J]. 电网技术, 2015,39(10): 2862-2868.Wei Zhinong, Yan Quanchun, Sun Guoqiang, et al.Power system interval linear state estimation considering network parameter uncertainty[J]. Power System Technology, 2015, 39(10): 2862-2868.
[19] Chen Guanrong, Wang Jianrong, Shieh L S. Interval Kalman filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 250-259.
[20] Ahn H S, Kim Y S, Chen Yangquan. An interval Kalman filtering with minimal conservatism[J].Applied Mathematics and Computation, 2012, 218(18):9563-9570.
[21] Tran T A, Jauberthie C, Gall F L, et al. Interval Kalman filter enhanced by positive definite upper bounds[J]. IFAC-PapersOnLine, 2017, 50(1): 1595-1600.
[22] 吴笃贵, 徐政. 基于相量量测的电力系统谐波状态估计(Ⅱ): 可观性、质量评估与算例研究[J]. 电工技术学报, 2004, 19(3): 76-81.Wu Dugui, Xu Zheng. Power system harmonic state estimation based on phasor measurements(II)—observability analysis, quality evaluation algorithm and example studies[J]. Transactions of China Electrotechnical Society, 2004, 19(3): 76-81.
[23] 陈珩. 电力系统稳态分析[M]. 3 版. 北京: 中国电力出版社, 2007.
[24] 徐俊俊, 吴在军, 胡秦然, 等. 考虑多类型分布式电源和负荷不确定性的主动配电网区间状态估计[J]. 中国电机工程学报, 2018, 38(11): 3255-3266.Xu Junjun, Wu Zaijun, Hu Qinran, et al. Interval state estimation for active distribution networks considering uncertainties of multiple types of DGs and loads[J]. Proceedings of the CSEE, 2018, 38(11):3255-3266.
[25] 肖先勇, 胡誉蓉, 王杨, 等. 基于非同步电能质量监测系统的谐波状态估计[J]. 中国电机工程学报,2021, 41(12): 4121-4131.Xiao Xianyong, Hu Yurong, Wang Yang, et al.Harmonic state estimation based on asynchronous power quality monitoring system[J]. Proceedings of the CSEE, 2021, 41(12): 4121-4131.
[26] 汪玲, 朱栋强, 马凯莉, 等. 空间目标卡尔曼滤波稀疏成像方法[J]. 电子与信息学报, 2018, 40(4):846-852.Wang Ling, Zhu Dongqiang, Ma Kaili, et al. Sparse imaging of space targets using Kalman filter[J].Journal of Electronics & Information Technology,2018, 40(4): 846-852.