0 引言
为应对全球变暖，实施节能减排，我国于2020年提出未来碳排放目标，即二氧化碳排放力争于2030 年前达峰，努力争取2060 年前实现碳中和[1-2]。近年来，以风能、太阳能、水能为代表的清洁可再生能源在全球范围得到快速发展[3-4]，且由于其环保、可再生等优点，被认为是未来能源系统的主力军。利用丰富的水、风、光资源，构建绿色、低碳的新型电力系统，提升清洁能源利用水平和电力系统运行效率，是实现“双碳”目标的必由之路。
然而，风、光出力具有强随机性、间歇性和波动性，直接并网会加剧电网调度运行的难度，不利于电网的经济运行[5-7]。将风电、光电与水电整合打捆，利用水轮机组的快速调节能力对冲风、光出力的波动，形成优质、稳定的互补发电系统，能够有效促进新能源并网消纳[5,8]；此外，随着储能技术的进步与成本的降低，大型储能电站也逐渐成为促进风、光消纳的方式之一[9-10]。因此，水-风-光-储多能互补一体化是促进新能源并网消纳、提升新能源电网渗透率的有效方式[11-14]。
我国清洁能源储量丰富，但大都集中于西部地区。“十四五”期间，我国规划建设九大清洁能源基地，其中包括四个流域级大型水-风-光互补基地，均位于我国西部。由于西部灵活性电源装机不足，并且本地消纳能力有限，需借助特高压直流工程将西部丰沛的清洁电能输送至东部负荷中心，以实现清洁能源的跨区域消纳。考虑到高压直流联络线稳定运行、设备运行寿命等因素，高压直流换流设备不宜频繁调节，输电功率不宜频繁波动，输电曲线应滤除毛刺、锯齿、往复波动等因素[15-16]。因此，目前特高压直流外送主要采用“直线式”定功率的输电方式，日输电功率曲线呈现出平稳的阶梯状[17-18]。
首先风、光出力易受地形、气象等因素影响，其次日出力过程难以准确预测。在多能互补短期调度中，如何应对风、光出力预测的不确定性，为互补系统制订合理、可靠的日前发电计划，是目前多能互补研究的核心与难点[19]。针对此问题，国内外学者进行了诸多探索。文献[20]考虑了光伏出力预测的不确定性，建立了水光互补日前优化调度模型，并采用三层嵌套递阶求解算法优化系统功率、水电机组状态以及机组负荷分配策略；文献[21]考虑了风功率预测的不确定性，设计了一种双层规划模型以获取水-风互补系统的日前发电计划；文献[22]采用核密度估计方法分析风电和光电的预测误差，建立了以剩余负荷峰谷差最小为目标的水-风-光互补日前调峰随机优化模型，并将其应用于中国南方某省级电网的日前调度；文献[23]采用集合预测和情景树的形式模拟了水-风-光互补系统中的多维不确定性，并以剩余负荷峰谷差最小为目标建立随机优化模型。
随机优化是处理多能互补调度不确定性问题的一种经典方法。然而，随机优化需事先确定不确定性变量的概率分布函数，其求解过程复杂，且参数估计可能存在偏差。鲁棒优化采用场景集合表征变量的不确定性，使约束条件能够在所有不确定性场景下均能满足[24]，已广泛应用于电力系统调度领域。例如：文献[25]考虑光伏电站接入电网引发的不确定性，建立了可调节鲁棒优化模型，以协调系统的可靠性与经济性；文献[26]考虑风、光极端出力场景，构建主动配电网鲁棒优化经济调度模型，保证了系统鲁棒性和经济性的协调关系；文献[27]分析了广义储能特性，以成本最低为目标构建了多能源系统可调节鲁棒调度模型；文献[28]应用信息间隙决策理论准确描述综合能源系统的不确定性，并基于此建立了综合能源系统多目标鲁棒优化调度模型。
然而，传统的互补优化调度模型通常以可调节电源出力为决策变量，难以保证系统总输电功率的平稳性。对于承担特高压直流打捆外送任务，尤其是包含具有复杂水力联系的梯级水电站的大型水-风-光-储互补发电系统，如何在风、光出力预测不确定性条件下保证输电功率的平稳性是目前多能互补系统短期调度运行面临的挑战。此外，大规模储能电站的应用为互补系统带来了更强的灵活性。但相比于发电装机，储能装机规模仍有限，如何充分发挥储能电站和梯级水电的灵活性对风、光出力进行补偿，制订能够对冲由预测不确定性诱发的运行风险的日发电计划，是目前亟待解决的难题。
为此，本文考虑风、光出力预测不确定性及特高压输电的平稳性需求，建立了水-风-光-储互补日前多目标鲁棒优化调度模型；为实现模型的高效降维求解，研制了一种双层嵌套优化框架，制订互补系统日前发电计划，有效地保证了输电功率的平稳性以及梯级水电站间负荷的高效分配；并基于多情景调度结果，提出了梯级水电与储能电站的日内联合运行策略。将该方法应用于黄河上游清洁能源基地“青-豫”直流输电工程，验证了该方法的有效性和实用性。
1 水-风-光-储短期互补运行管理过程
水-风-光-储互补系统短期运行管理过程如图1所示。
图1 水-风-光-储互补系统短期运行管理过程
Fig.1 Short-term management process of the hydro-wind-PV-storage complementary system
对于包含梯级水电站的大型水-风-光-储互补发电系统，短期运行过程包括两部分：日前发电计划编制与实时经济运行。具体过程如下：
（1）预测次日的径流过程、风电和光伏出力过程，并将其上报给互补发电系统的集控中心。
（2）集控中心根据预测的大电网负荷、径流、风电和光伏出力曲线，制订水-风-光-储互补系统日前发电计划，并于次日前4～6 h 将发电计划提交给大电网调度中心[29]。
（3）调度中心协调其他电源，修改申报的发电计划，并将其反馈给集控中心。经双方商议，最终确定次日互补系统的发电计划。
（4）在次日的实时运行期间，互补系统需要在集控中心的指令下，尽可能按照发电计划发电。考虑到储能电站在充放电过程中存在耗电；且互补系统中水电装机容量远高于储能，需要水电提供较大电力支撑以满足发电计划，若储能电站在调度期初放空，在负荷早高峰或晚高峰时段易发生失负荷风险，降低互补运行效能；另外，储能电站频繁充放电会影响其使用寿命。基于以上考虑，本着经济性和可靠性原则，由梯级水电优先补偿风、光电。如果通过梯级水电的调节仍然不能满足负荷需求，则通过储能电站放电或充电进行二次补偿。
需要说明的是，在日前发电计划编制过程中，由于风、光电的预测不确定性，计划输电功率较高可能会导致次日失负荷。相反，计划输电功率较低可能会导致弃电[30-31]。因此，制定的互补系统日前发电计划不宜太高或太低，应充分发挥水电和储能电站的灵活性以规避系统的失负荷风险和弃电风险。同时，水-风-光-储互补系统弃电和失负荷示意图如图2 所示，对于承担特高压直流输电任务的互补系统，制订的日前发电计划应为平滑的阶梯型。
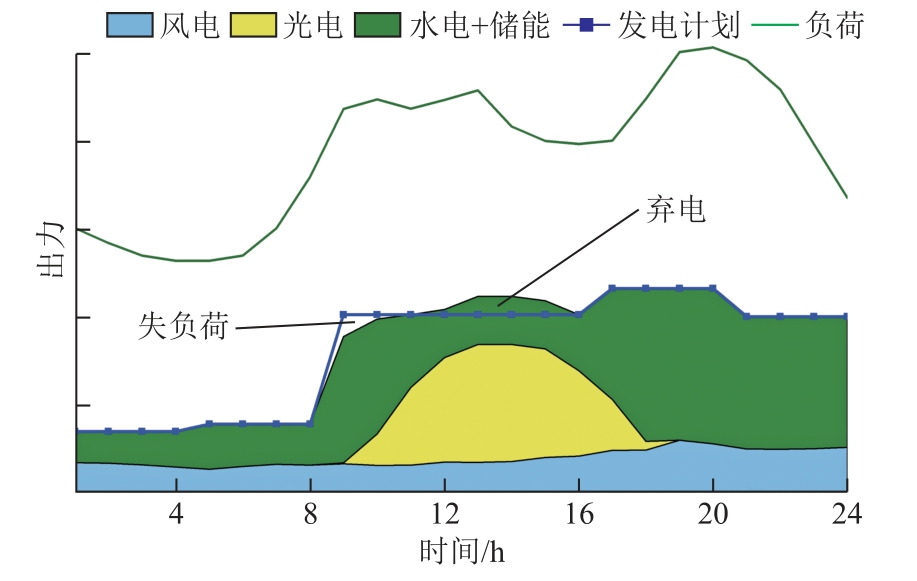
图2 水-风-光-储互补系统弃电和失负荷示意图
Fig.2 Schematic diagram of electricity curtailment and power shortage of the hydro-wind-PV-storage complementary system
2 风、光出力预测不确定性表征
经文献调研，风、光出力预测误差通常服从正态分布[29,32]，且目前的风、光出力预测技术能够将预测误差控制在10%以内[33-35]。基于此，本文基于预测的风、光出力过程及给定±10%的预测误差，确定了各个时段95%置信水平下的正态分布参数。进而通过场景模拟与场景缩减技术得到能够表征风、光出力预测不确定性的代表性场景集。
相比于蒙特卡洛模拟，拉丁超立方体抽样（Latin Hypercube Sampling, LHS）具有更强的遍历特性，并被广泛应用于不确定性研究中[15]。因此，本文采用拉丁超立方体抽样分别对风、光出力误差进行模拟，将误差与预测出力相加得到模拟的出力场景集 N w 和 N p为
式中， N fw和 N fp分别为预测的风、光出力过程； e w和 e p分别为模拟的风、光出力预测误差。随后，将模拟的风、光出力过程两两随机组合，得到风、光组合出力场景。为了减小模型的计算负担，采用同步回代缩减法（Simultaneous Backward Reduction,SBR）[36]得到代表性风、光组合出力场景及其概率。
3 水-风-光-储互补日前多目标鲁棒优化调度模型
3.1 目标函数
对于承担特高压直流输电任务的水-风-光-储互补系统，系统的总输电量和调峰性能是评估互补运行效能的重要指标。因此，本文以互补系统日均输电功率最大和受端电网剩余负荷标准差最小为目标建立模型。
目标1：互补系统日均出力最大。
式中，T 为调度时段数； N tplan 为制定的日前发电计划在t 时段的出力值。
目标2：受端电网剩余负荷标准差最小。
式中，std(x)为变量x 的标准差； re
L 和L 分别为电网剩余负荷和电网负荷；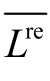
为剩余负荷平均值。
由于风、光出力预测的不确定性，互补系统次日在执行发电计划时可能存在失负荷或弃电风险。因此，互补系统日前发电计划编制需考虑风、光出力预测不确定性的影响，有效规避次日互补系统运行风险。即在所有代表性风、光出力场景下，水-风-光-储互补系统均能严格按照发电计划执行，以保证电力输送的经济性与可靠性。因此，上述调度问题可采用鲁棒优化描述为
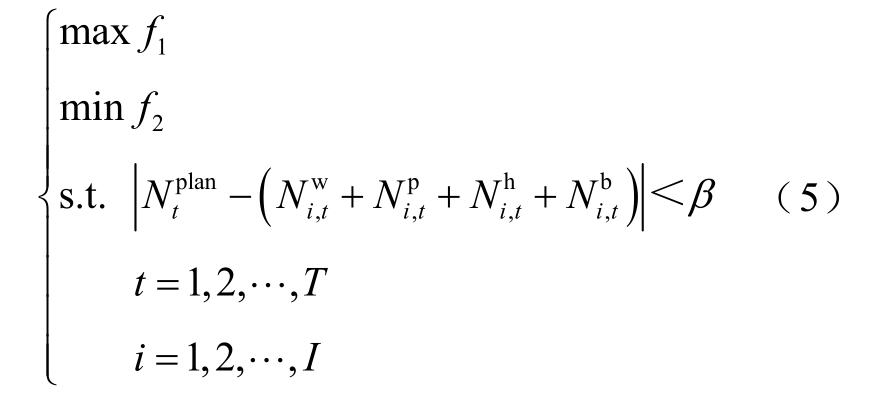
式中，
分别为风电、光电、水电和储能电站在场景i 下t 时段的出力或充、放电功率；β 为系统出力精度控制指标，即某时段互补系统的实际出力与发电计划的功率之差的绝对值小于β，即认为该时段的发电计划被有效地执行，β=1 MW。
3.2 约束条件
1）输电平稳性约束
特高压直流输电要求输电功率曲线为平滑的阶梯状。
式中，sP 为互补系统第s 个稳定运行时段的输电功率；tc 为阶梯状输电曲线出力改变的时间点。此时，互补系统日前发电计划可表达为
式中，S 为输电曲线的阶梯数。
2）输送容量限制
式中， Tc max为输电通道的最大传输容量。
3）水量平衡约束
式中，m 为梯级水库编号；Vt ,m和Vt+1 ,m分别为m 水库t 时段初、末的库容；QI t,m和 QOt ,m 分别为m 水库t 时段的入库流量和下泄流量；Q Itt , m:m +1 为m 水库与m+1 水库之间的区间来水。
4）水库特征约束
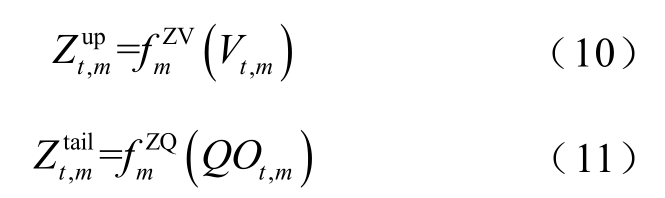
式中，
分别为m 水库在t 时段的坝前水位和坝后水位；
分别为m 水库的水位-库容关系和泄流量-尾水位关系。
5）水位约束
式中，
分别为m 水库在t 时段的水库水位上、下限。
6）水电站出力约束
式中
分别为m 电站在t 时段的出力上、下限；
为m 水电站在t 时段的出力。
计算式为
式中，km 为m 水电站的出力系数； QE t,m 为m 水库在t 时段的发电引用流量；ΔH t,m 为m 水库在t 时段的水头， ΔH t,m 计算式为
式中，
为m 水库在t 时段的平均水位。
7）下泄流量约束
式中，
分别为m 水库在t 时段的下泄流量上、下限。
8）梯级水库蓄能变化约束
式中，SE1 和SET 分别为梯级水库在调度期初、末的蓄能；α 为最大可接受的蓄能变化率；
为m水库死水位对应的库容；ρ 为水的密度
为m 水库与位于m 水库下游的所有水库的平均水头之和。
9）储能电站充、放电深度约束
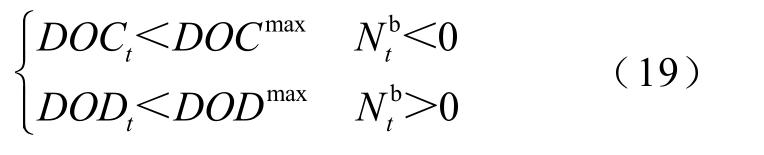
式中， DOC t 和 DODt 分别为储能电站在t 时段末充电深度和放电深度； DOC max 和 DOD max分别为储能电站最大充、放电深度。储能电站最大充电、放电深度均为95%。
10）储能电站最大充、放电功率约束
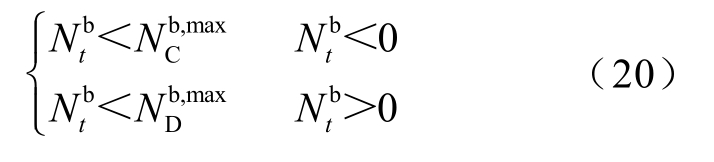
式中，
分别为储能电站最大充电、放电功率。
4 双层嵌套优化框架
传统的包含梯级水电站的多能互补优化调度模型的决策变量通常是水位或流量。然而，当梯级水电站规模增大时，模型的决策变量数量也成倍增加，容易造成“维数灾”问题，模型优化效率低；此外，互补系统总出力难以在多个连续时段内保持稳定。因此，本文研制了一个双层嵌套优化框架来解决水-风-光-储互补系统日前发电计划编制问题，双层嵌套优化框架如图3 所示。其中，外层优化互补系统的输电功率，内层确定梯级水电站的负荷分配及储能电站的荷电状态（State of Charge, SOC）。
图3 双层嵌套优化框架
Fig.3 Flow chart of the two-layer nested optimization framework
4.1 外层优化互补系统的输电功率
为满足特高压直流输电平稳性需求，外层采用二维编码策略直接推求互补系统的总出力过程[32]。二维编码策略示意图如图4 所示，模型的决策变量为互补系统输电功率SP 和输电功率改变的时间点tc。二维编码策略的应用保证了互补系统出力的平稳性，模型的解可表达为
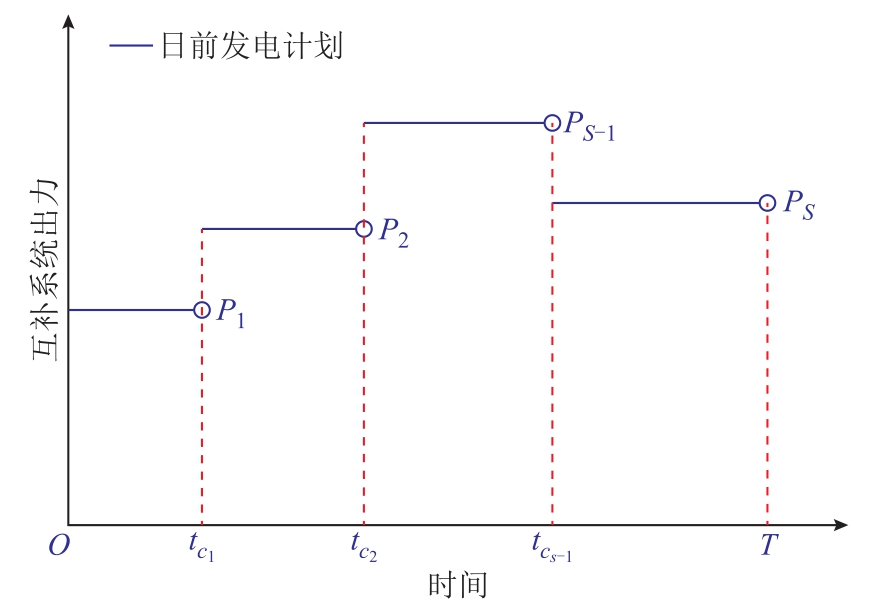
图4 二维编码策略示意图
Fig.4 Schematic diagram of the two-dimensional encoding strategy
从式（21）中可看出，采用二维编码策略的决策变量数量为2S-1。以由三座水电站组成的梯级水电站为例，调度时段为1 h，当输电曲线为五段线时，该模型的决策变量数量为9。而传统模型的决策变量数量为24×3=72。因此，二维编码策略显著降低了模型决策变量数量。
4.2 内层确定梯级水电站间负荷分配策略及储能电站的荷电状态
本文采用判别系数和相对蓄水率相结合的方法[37]确定梯级水电站的负荷分配策略。
将外层得到的系统输电功率做为内层的输入，按照式（22）计算场景i 下梯级水电和储能需承担的负荷过程
为
以及在天然径流过程下梯级水电出力
并做以下判断：①如果
梯级水库需蓄水以降低系统出力；②如果
梯级水库需放水以增大系统出力；③如果
梯级水库按照天然来水下泄，不蓄不放。
梯级水库运行需依据科学的蓄放水次序以保证梯级水库的蓄能及水库的可持续运行。采用判别系数和相对蓄水率相结合的方法确定梯级水库的蓄放水次序，进而确定梯级水电站的负荷分配。其中，判别系数能够保证梯级水库的蓄能，相对蓄水率则能够避免某一水库蓄满或放空，保证了梯级水库运行调度的灵活性[37]，计算式分别为
式中，K i, t,m 为场景i 下m 水库在t 时段的判别系数；Wi , t,m 为m 水库在t 时段的水库入库水量；
为场景i 下t 时段初位于m 水库上游的水库的可用水量之和；Fi, t,m 为场景i 下t 时段初m 水库的水面面积；sri, t,m 为场景i 下t 时段初m 水库的蓄水率；
分别为场景i 下t 时段初m 水库的库容、m 水库死水位对应库容和m 水库正常蓄水位对应库容； rsri ,t ( m ,n )为在场景i 下t 时段初m 水库和n 水库之间的相对蓄水率；δ 为相对蓄水率的控制值。
梯级水电站负荷分配过程如下：
1）确定梯级水库的蓄放水次序
当梯级水库蓄水，按照式（23）计算各水库的判别系数K，将K 值最大的水库标记为x，并按照式（24）、式（25）计算水库x 和其他水库之间的相对蓄水率。当 ∀rsri ,t ( m ,x )≤ δ，梯级水库按照K值从大到小的次序蓄水；当 ∃ r sri ,t ( m ,x )＞δ ，将其记为X，并按照 rsri ,t ( m,n )值从大到小的次序蓄水，剩余水库排序位于X 之后，仍按照K 值从大到小次序蓄水。
当梯级水库放水，按照式（23）计算各水库的判别系数K，将K 值最小的水库标记为x，并按照式（24）、式（25）计算水库x 和其他水库之间的相对蓄水率。当 ∀rsri ,t ( m ,x )≤ δ，梯级水库按照K 值从小到大的次序放水；当 ∃ r sri ,t ( m ,x )＞δ ，将其记为X，并按照 rsri ,t ( m ,n )值从大到小的次序放水，剩余水库排序位于X 之后，仍按照K 值从小到大次序放水。
2）梯级水库按照确定的次序蓄水或放水，直到梯级水电出力等于
或梯级各个水库达到其约束边界。
3）当梯级水电站出力大于或小于
时，储能电站充电或放电以维持系统总出力等于
重复上述步骤，得到所有代表性场景下日内所有时段的梯级水电站负荷分配策略及储能电站荷电状态。当互补系统不能保证发电计划在所有不确定性场景下均可被有效执行，则该发电计划被视为无效解。
4.3 求解算法
非支配排序差分进化算法（Non-Dominated Sorting Differential Evolution algorithm, NSDE）是一种成熟的多目标进化算法。相比传统的NSGA-Ⅱ算法，NSDE 在算法鲁棒性和搜索能力等方面具有更强的竞争力[38-39]。因此，本文采用NSDE 算法求解水-风-光-储互补日前多目标鲁棒优化调度模型。
5 实例分析
5.1 工程概况
黄河上游水能资源丰富，且具有良好的风、光资源开发条件。黄河上游清洁能源基地是目前世界上已建规模最大的多能互补集成工程。本文以黄河上游清洁能源基地“青—豫”直流输电工程为例，验证所提出的水-风-光-储互补系统日前鲁棒调度方法。
“青—豫”特高压直流输电工程连接了位于青海省海南州的水-风-光-储清洁能源基地与河南省驻马店市，能够将西北地区的清洁电能源源不断地输送至中原负荷中心，其最大输送容量为8 000 MW，是世界上第一条专为清洁能源建设的特高压直流输送通道。根据“青—豫”直流输电规划，承担输电任务的电站包括由三座水电站组成的梯级水电站（茨哈峡，2 600 MW；班多，360 MW；羊曲，1 200 MW）、两座风电站（切吉，1 500 MW；二塔拉，500 MW）及两座光伏电站（一塔拉，1 000MW；三塔拉，3 000 MW），总发电装机高达10 160 MW。储能容量按照新能源装机的10%配置（600 MW·h），储能时长为2 h。梯级水电站的参数见表1。
表1 茨哈峡—班多—羊曲梯级水电站的参数
Tab.1 Parameters of the Cihaxia-Banduo-Yangqu cascade hydropower plants
数 值参 数茨哈峡 班多 羊曲调节性能 季 日 日调节库容/(108m3) 18.54 0.02 2.39装机容量/MW 2 600 360 1 200正常蓄水位/m 2 990 2 760 2 715平均水头/m 219.1 35.8 117.8下泄流量上/下限/(m³/s) 6 000/200 6 000/200 6 000/200
5.2 数据与参数设置
收集了黄河上游清洁能源基地2019 年逐小时风、光出力数据；豫南地区各季节典型日负荷过程及黄河上游唐乃亥水文站2019 年逐小时径流数据，后根据流域控制面积同倍比放大得到茨哈峡水库入库径流及区间入流过程。
为了验证本文所提方法在不同季节的适用性，在2019 年各季节各选取一个典型日，其茨哈峡日均入库流量分别为669、1 507、980 和332m³/s。采用LHS 方法生成的风、光出力场景数为500；采用SBR方法得到代表性风、光组合出力场景数I=10。各典型日代表性出力场景及典型日负荷过程如图5 所示。
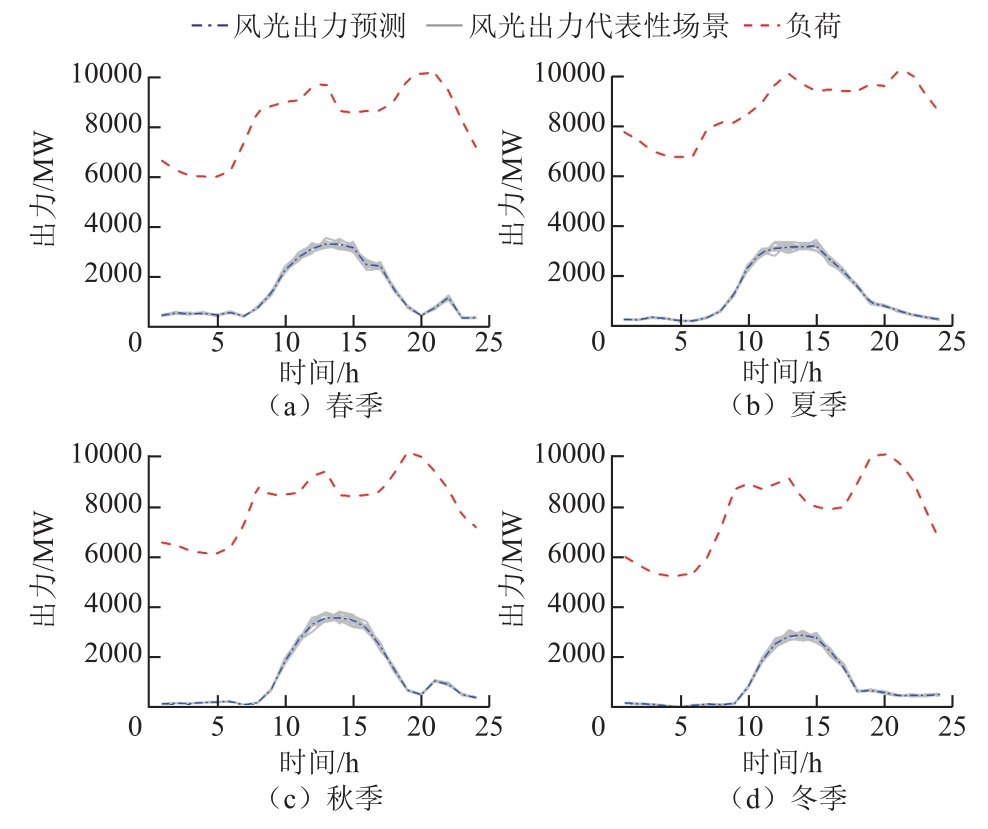
图5 各典型日代表性出力场景及各典型日负荷过程
Fig.5 Representative scenario sets of wind and PV power output and daily load processes for each typical day
针对日前优化调度问题，调度时段长为1 h，模型参数设置如下：输电曲线为五段线；每个稳定输电时段最小为4 h；茨哈峡、班多、羊曲水库起调水位分别为2 970 m、2 758 m 和2 712 m；储能电站初始荷电状态为 50%；春夏秋冬季的α 值分别为0.03、0.15、0.03 和0.03；δ =0.4。以上参数可根据决策者的需求或实际运行情况进行设定。储能电站充放电效率为0.9；NSDE 算法中种群数量为50，迭代次数Iter 为800。
模型和算法程序均采用Matlab 平台编写。模型运行环境：CPU 为 Intel(R) Core(TM) i7-9750H@2.60GHz；内存为16 G；操作系统为Windows10；软件环境为Matlab 2018a 版本。
5.3 结果分析与讨论
5.3.1 日前发电计划的有效性
求解水-风-光-储互补日前多目标鲁棒优化调度模型得到的Pareto 解集如图6 所示。可以看出，互补系统日均出力与调峰性能之间存在明显的竞争关系。其中，冬季典型日径流较小，加之最小下泄流量等约束，水电站灵活性受到较大限制。因此，冬季典型日的多目标竞争关系更为复杂。模型求解耗时见表2，可以看出：在5.2 节介绍的环境下，模型求解时间在3.5 h 之内，能够满足次日前4～6 h 上报发电计划的时效性。
表2 各典型日模型求解耗时
Tab.2 Model solving times of each typical days
典型日 春季 夏季 秋季 冬季模型求解耗时/min 183.8 194.6 182.9 203.3
图6 各典型日Pareto 解集
Fig.6 Pareto solution sets of each typical days
从各典型日的Pareto 解集中选取一个均衡解。首先，依据Pareto 解集，找到各目标函数最佳值，并标记其坐标；其次，计算各个解与该点之间的欧氏距离D；最后选取D 值最小的解为模型的均衡解（图 6）。进一步观察发现：选取的均衡解往往是Pareto 前沿曲线的转折点（春）、局部转折点（秋、冬）或是目标效益较为折中的解（夏），表明了均衡解选取的合理性。
以选取的均衡解为例，绘制了水-风-光-储互补系统日前发电计划及各电站在不确定性场景下的出力期望，如图7 所示。可以看出：①互补系统的输电曲线呈现平滑的阶梯状，各阶梯输电功率稳定，满足特高压输电的平稳性需求[17-18]；②在“五段线”输电曲线的限制下，通过对日前发电计划的多目标优化，互补系统出力能够尽可能地跟踪负荷变化，发挥其调峰能力；③得到的日前发电计划能够保证在所有风光出力不确定性场景下均能够被水-风-光-储互补系统有效执行，从而规避次日运行的弃电风险和失负荷风险，证明了水-风-光-储互补系统日前发电计划鲁棒优化方法的有效性。
图7 各典型日均衡解互补出力过程
Fig.7 Output process of the balanced solution in each
typical day
各均衡解的发电计划互补运行指标见表3。相比于风、光电直接并网，水-风-光-储互补系统在满足输电平稳性需求的同时，系统的调峰性能在各季节典型日中分别提高了44%、13.3%、25%和46.0%。此外，梯级水库蓄能变化率均在约束范围内，决策者亦可依据梯级水库蓄、放水需求选取发电计划。
表3 各均衡解的发电计划互补运行指标
Tab.3 Complementary operational indexes of each of balanced solution
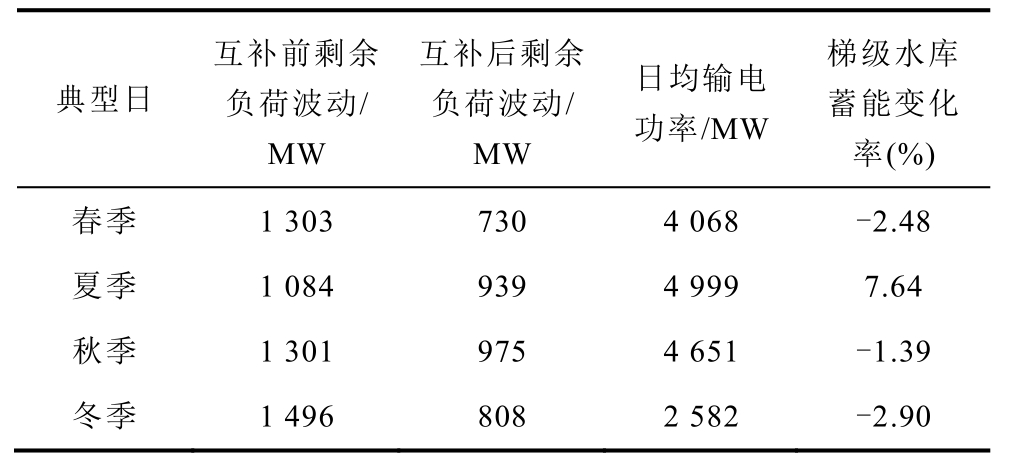
典型日互补前剩余负荷波动/MW互补后剩余负荷波动/MW日均输电功率/MW梯级水库蓄能变化率(%)春季 1 303 730 4 068 -2.48夏季 1 084 939 4 999 7.64秋季 1 301 975 4 651 -1.39冬季 1 496 808 2 582 -2.90
以春季典型日均衡解为例，梯级各水库在所有不确定性场景下的运行过程如图8 所示。各水电站运行均在约束范围内。水电站通过加大或者减小下泄流量，尽可能地平滑风、光出力的波动性，能够有效应对大部分风、光出力预测不确定性的影响，满足互补系统出力需求。其中，茨哈峡水电站作为“龙头”电站，库容较大，风、光出力不确定性对其水位运行过程影响不大；而对于班多和羊曲水电站，仅具有日调节性能，加之不同场景下梯级水库蓄、放水次序不同，造成水库的水位运行过程差异较大。
图8 春季典型日均衡解的梯级水电站运行过程
Fig.8 Operation process of cascade hydropower plants of the balance solution in typical spring day
5.3.2 鲁棒优化与确定性优化模型对比
为进一步验证提出的水-风-光-储互补日前多目标鲁棒优化调度模型（模型1）的有效性，构建确定性多目标日前优化调度模型（模型2）作为对比实验，采用同样的优化框架和算法进行求解，统计各均衡解的优化结果，并计算该发电计划在不确定性影响下的弃电概率和失负荷概率，结果见表4。
表4 模型1 与模型2 的均衡解对比
Tab.4 Comparsion of balanced solutions of Model 1 and Model 2
典型日 模型日均输电功率/MW剩余负荷波动/MW弃电概率失负荷概率模型1 4 068 730 0 0春季模型2 4 106 727 0 0.57模型1 4 999 939 0 0夏季模型2 4 999 923 0 0.77模型1 4 651 975 0 0秋季模型2 4 661 972 0 0.39模型1 2 582 808 0 0冬季模型2 2 581 791 0.34 0
从表4 可以看出，确定性优化模型的发电和调峰性能略优于鲁棒优化模型，但难以应对风、光出力预测不确定性，弃电或失负荷风险较高。而鲁棒优化模型能够充分发挥水电和储能电站的灵活性，有效应对风、光出力预测不确定性，降低了系统弃电和失负荷风险。
5.3.3 不同储能配比对互补调度结果的影响
进一步探究不同储能配比对互补系统调度运行的影响，本文设置对比实验如下：以春季典型日为例，设置系统储能配比分别为0%、5%、15%和20%，采用同样的模型、参数及求解算法求解，得到Pareto解集，并选取均衡解。以10%储能配比的调度结果作为基准进行对比，结果见表5。可以发现，随着储能配比的增大，互补系统的运行性能随之增加，特别是系统的调峰性能。以上结果进一步验证了模型的可靠性和准确性。
表5 不同储能配比下春季典型日均衡解对比
Tab.5 Comparison of the balanced solution in spring typical day under different of battery storage ratio
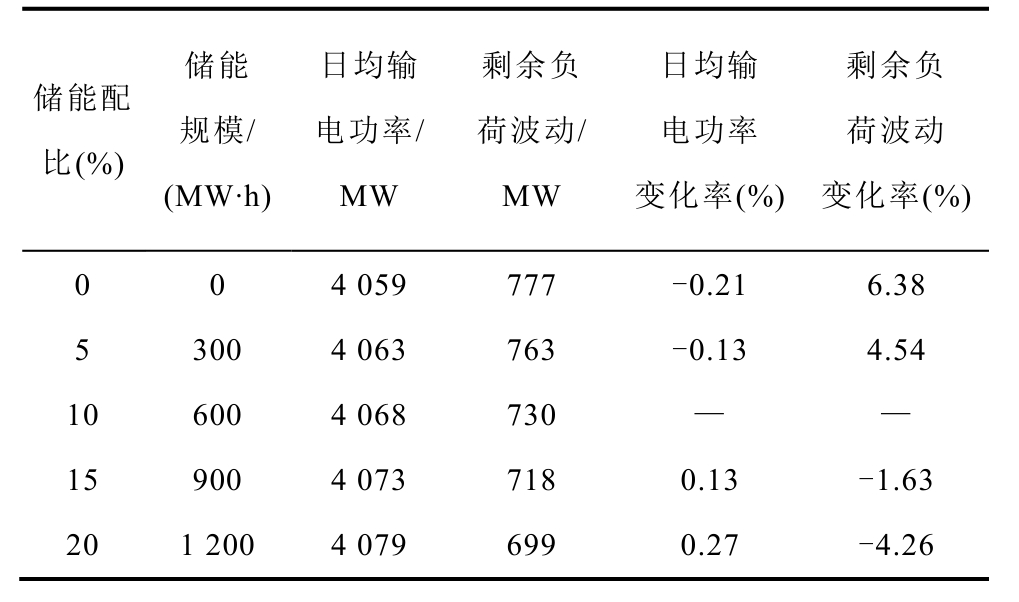
储能配比(%)储能规模/(MW·h)日均输电功率/MW剩余负荷波动/MW日均输电功率变化率(%)剩余负荷波动变化率(%)0 0 4 059 777 -0.21 6.38 5 300 4 063 763 -0.13 4.54 10 600 4 068 730 — —15 900 4 073 718 0.13 -1.63 20 1 200 4 079 699 0.27 -4.26
5.3.4 梯级水电站与储能电站联合运行策略
各均衡解的储能电站运行过程如图9 所示。在风、光出力不确定性影响下，春、夏、秋季发电计划执行时出现了水风光不能满足发电计划的情况。此时，储能电站发挥调节作用，且均为放电，有效地规避了互补系统的失负荷风险。在冬季则出现了水风光出力高于发电计划的情况。此时，由储能电站充电以规避系统弃电风险。
图9 各典型日均衡解储能电站运行过程
Fig.9 Operation process of battery storage of the balanced solution in each typical day
在第1 节介绍的水-风-光-储互补运行模式下，当互补系统需减小/增大出力时，首先由梯级水电站蓄水/放水。而在仅当各水电站均运行至水位或下泄流量约束边界，即水库不可继续蓄水/放水或下泄流量不可继续降低/升高时，由储能电站充电/放电以减小/增大互补系统出力。
因此，当春、夏、秋季径流较充足，水电承担的负荷较高时，若风、光出力预测偏低，梯级水电有足够的下调空间以满足互补出力需求；若风、光出力预测偏高，梯级水电出力达到最大约束，则由储能电站放电，从而避免系统出现失负荷现象（图9）。进一步分析储能电站运行过程可以发现：在0:00—6:00 时段，一方面，该时段光电出力为零，风电出力波动与预测不确定性相对较小；另一方面，该时段为负荷低谷时段，制定的发电计划相对较低，梯级水电站需蓄水减小出力（图8）。因此，在春、夏、秋季节，通过梯级水电的调节即可满足该时段的输电需求。而在白天，光伏出力通常先增大后减小，风、光出力波动与预测不确定性相对较高。此时，若存在某个风、光出力过小的极端场景，会导致梯级水电不能满足系统出力需求，需储能电站放电补偿。同理，在负荷晚高峰时段，制定的发电计划较高，若此时风电出力偏小，同样需要储能电站进行补偿。综上所述，在春、夏、秋季节，储能电站在7:00—24:00 放电，以应对风、光出力波动及预测不确定性对互补系统运行的影响。但储能电站持续放电会导致其丧失调节能力，影响互补系统的稳定运行。因此，维持储能电站的灵活性对互补系统十分重要。在0:00—6:00 负荷低谷时段，梯级水电可在满足计划出力的基础上适当多发，以维持储能荷电状态，进而有效发挥储能电站的灵活性，保证互补系统持续高效、稳定运行。
在冬季，水库来水量小，水电主要在负荷早高峰和晚高峰时段增大出力，发挥系统的调峰性能。而在0:00—6:00 负荷低谷时段及11:00—16:00 风、光出力较高时段，梯级水电站所承担的负荷较小。此时，若风、光出力预测偏小，梯级水电站即使在流量约束边界运行，系统出力仍高于计划出力，则由储能电站充电以避免弃电。为维持储能电站的灵活性，储能电站可在负荷晚高峰时段放电，将调度时段末的SOC 控制在较低水平，能够在缓解水电压力的同时，保证互补系统持续高效、稳定运行。
6 结论
针对承担特高压输电任务的水-风-光-储互补发电系统日前发电计划编制问题，在保证输电平稳性的基础上考虑风、光出力预测的不确定性，建立了水-风-光-储互补日前多目标鲁棒优化调度模型，并研制了一个双层嵌套优化框架推求互补系统日前发电计划、梯级水电站的负荷分配及储能电站的荷电状态。以黄河上游清洁能源基地“青—豫”直流输电工程为实例研究，得到以下结论：
1）提出的水-风-光-储互补系统日前发电计划鲁棒优化方法能够满足特高压直流输电平稳性需求：“五段线”输电曲线呈现平滑的阶梯状，各阶梯满足“直线式”定功率的输电方式。
2）鲁棒优化能够充分发挥梯级水电站和储能电站的灵活性，提高互补系统的调峰能力，有效地应对风、光出力预测不确定性，降低互补系统的弃电和失负荷风险，保证互补系统的稳定运行。
3）在径流相对充足的春、夏、秋季：风、光出力波动较大和负荷晚高峰时段，往往需要储能电站放电以应对风、光出力预测的不确定性，规避失负荷风险；而在0:00—6:00 负荷低谷时段，梯级水电则可在满足计划出力需求的基础上适当多发，以维持储能灵活性。而在径流相对匮乏的冬季：储能电站往往在梯级水电站承担负荷较小的0:00—6:00 和11:00—16:00 时段充电，规避弃电风险；储能电站可在负荷晚高峰时段放电，能够在缓解水电压力的同时，保证储能的灵活性。
本文所提方法不仅适用于实施特高压打捆电力外送的水-风-光-储互补发电系统，也适用于水-光、水-风、水-风-光等其他由水电作为主要调节电源的全清洁能源多能互补发电系统。在未来研究中，可进一步在模型中扩展火电模块，从而提升模型的通用性；同时，可采用解空间降维、GPU 并行计算等技术进一步提高模型求解效率。
[1] 习近平. 在第七十五届联合国大会一般性辩论上的讲话[EB/OL]. [2020-09-22]. http://www.gov.cn/xinwen/2020-09/22/content_5546168.htm.
[2] Mallapaty S. How China could be carbon neutral by mid-century[J]. Nature, 2020, 586(7830): 482-483.
[3] 武平, 郭巍, 晋春杰, 等. 浅谈我国电力与能源现状及解决途径[J]. 电气技术, 2018, 19(5): 1-4, 14.Wu Ping, Guo Wei, Jin Chunjie, et al. Analysis on the current situation of electricity and energy in China and its solution[J]. Electrical Engineering, 2018, 19(5): 1-4, 14.
[4] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835.Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[5] 畅建霞, 王义民, 黄强, 等. 水电与风电联合补偿调度机理研究与应用[J]. 水力发电学报, 2014,33(3): 68-73, 80.Chang Jianxia, Wang Yimin, Huang Qiang, et al.Compensation operation mechanism of hydropower plant and wind power plant[J]. Journal of Hydroelectric Engineering, 2014, 33(3): 68-73, 80.
[6] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J].电工技术学报, 2018, 33(23): 5541-5554.Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[7] Guo Yi, Ming Bo, Huang Qiang, et al. Risk-averse day-ahead generation scheduling of hydro-windphotovoltaic complementary systems considering the steady requirement of power delivery[J]. Applied Energy, 2022, 309: 118467.
[8] 程春田. 碳中和下的水电角色重塑及其关键问题[J]. 电力系统自动化, 2021, 45(16): 29-36.Cheng Chuntian. Function remolding of hydropower systems for carbon neutral and its key problems[J].Automation of Electric Power Systems, 2021, 45(16):29-36.
[9] 叶晨, 王蓓蓓, 薛必克, 等. 考虑超售的共享分布式光储混合运营模式协同策略研究[J]. 电工技术学报, 2022, 37(7): 1836-1846.Ye Chen, Wang Beibei, Xue Bike, et al. Study on the coordination strategy of sharing distributed photovoltaic energy storage hybrid operation mode considering overselling[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1836-1846.
[10] Braff W A, Mueller J M, Trancik J E. Value of storage technologies for wind and solar energy[J]. Nature Climate Change, 2016, 6(10): 964-969.
[11] Siddaiah R, Saini R P. A review on planning,configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications[J]. Renewable and Sustainable Energy Reviews, 2016, 58: 376-396.
[12] 国家发展改革委，国家能源局. 关于推进电力源网荷储一体化和多能互补发展的指导意见[Z]. 2021.
[13] 罗仕华, 胡维昊, 黄琦, 等. 市场机制下光伏/小水电/抽水蓄能电站系统容量优化配置[J]. 电工技术学报, 2020, 35(13): 2792-2804.Luo Shihua, Hu Weihao, Huang Qi, et al. Optimization of photovoltaic/small hydropower/pumped storage power station system sizing under the market mechanism[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2792-2804.
[14] 朱燕梅, 陈仕军, 马光文, 等. 计及发电量和出力波动的水光互补短期调度[J]. 电工技术学报, 2020,35(13): 2769-2779.Zhu Yanmei, Chen Shijun, Ma Guangwen, et al. Shortterm complementary operation of hydro-photovoltaic integrated system considering power generation and output fluctuation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2769-2779.
[15] 苏承国. 大规模清洁能源接入下电网调峰问题研究[D].大连: 大连理工大学, 2019.
[16] Su Chengguo, Cheng Chuntian, Wang Peilin, et al.Optimization model for the short-term operation of hydropower plants transmitting power to multiple power grids via HVDC transmission lines[J]. IEEE Access, 2019, 7: 139236-139248.
[17] 崔杨, 程广岩, 仲悟之, 等. 计及受端电网调峰趋势的风-光-火特高压直流外送调度方法[J]. 太阳能学报, 2021, 42(8): 32-40.Cui Yang, Cheng Guangyan, Zhong Wuzhi, et al.Wind-photovoltaic-fire UHV DC external dispatching method considering peaking trend of power grid[J].Acta Energiae Solaris Sinica, 2021, 42(8): 32-40.
[18] 贺元康, 刘瑞丰, 陈天恩, 等. 全清洁能源特高压青豫直流初期打捆外送模式[J]. 中国电力, 2021,54(7): 83-92.He Yuankang, Liu Ruifeng, Chen Tianen, et al.Exploration of bundled transaction model for all clean energy transmission of Qing-Yu UHV DC project[J].Electric Power, 2021, 54(7): 83-92.
[19] 闻昕, 孙圆亮, 谭乔凤, 等. 考虑预测不确定性的风-光-水多能互补系统调度风险和效益分析[J]. 工程科学与技术, 2020, 52(3): 32-41.Wen Xin, Sun Yuanliang, Tan Qiaofeng, et al. Risk and benefit analysis of hydro-wind-solar multi-energy system considering the one-day ahead output forecast uncertainty[J]. Advanced Engineering Sciences, 2020,52(3): 32-41.
[20] 明波. 大规模水光互补系统全生命周期协同运行研究[D]. 武汉: 武汉大学, 2019.
[21] Yang Yuqi, Zhou Jianzhong, Liu Guangbiao, et al.Multi-plan formulation of hydropower generation considering uncertainty of wind power[J]. Applied Energy, 2020, 260: 114239.
[22] Liu Benxi, Lund J R, Liao Shengli, et al. Optimal power peak shaving using hydropower to complement wind and solar power uncertainty[J]. Energy Conversion and Management, 2020, 209: 112628.
[23] Zhu Feilin, Zhong Pingan, Xu Bin, et al. Short-term stochastic optimization of a hydro-wind-photovoltaic hybrid system under multiple uncertainties[J]. Energy Conversion and Management, 2020, 214: 112902.
[24] Ben-Tal A, Nemirovski A. Robust optimization -methodology and applications[J]. Mathematical Programming, 2002, 92(3): 453-480.
[25] 彭春华, 谢鹏, 陈臣. 大规模光伏电站接入电网可调节鲁棒优化调度[J]. 中国电机工程学报, 2014,34(25): 4324-4332.Peng Chunhua, Xie Peng, Chen Chen. Adjustable robust optimal dispatch of power system with largescale photovoltaic power stations[J]. Proceedings of the CSEE, 2014, 34(25): 4324-4332.
[26] 叶畅, 苗世洪, 李姚旺, 等. 基于改进不确定边界的主动配电网鲁棒优化调度[J]. 电工技术学报,2019, 34(19): 4084-4095.Ye Chang, Miao Shihong, Li Yaowang, et al. Robust optimal scheduling for active distribution network based on improved uncertain boundary[J]. Transactions of China Electrotechnical Society, 2019, 34(19):4084-4095.
[27] 叶畅, 曹侃, 丁凯, 等. 基于广义储能的多能源系统不确定优化调度策略[J]. 电工技术学报, 2021,36(17): 3753-3764.Ye Chang, Cao Kan, Ding Kai, et al. Uncertain optimal dispatch strategy based on generalized energy storage for multi-energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3753-3764.
[28] 彭春华, 郑聪, 陈婧, 等. 基于置信间隙决策的综合能源系统鲁棒优化调度[J]. 中国电机工程学报,2021, 41(16): 5593-5603.Peng Chunhua, Zheng Cong, Chen Jing, et al. Robust optimal dispatching of integrated energy system based on confidence gap decision[J]. Proceedings of the CSEE, 2021, 41(16): 5593-5603.
[29] Lu Lu, Yuan Wenlin, Su Chengguo, et al.Optimization model for the short-term joint operation of a grid-connected wind-photovoltaic-hydro hybrid energy system with cascade hydropower plants[J].Energy Conversion and Management, 2021, 236:114055.
[30] Tan Qiaofeng, Wen Xin, Sun Yuanliang, et al.Evaluation of the risk and benefit of the complementary operation of the large windphotovoltaic-hydropower system considering forecast uncertainty[J]. Applied Energy, 2021, 285: 116442.
[31] 明波, 李研, 刘攀, 等. 嵌套短期弃电风险的水光互补中长期优化调度研究[J]. 水利学报, 2021,52(6): 712-722.Ming Bo, Li Yan, Liu Pan, et al. Long-term optimal operation of hydro-solar hybrid energy systems nested with short-term energy curtailment risk[J]. Journal of Hydraulic Engineering, 2021, 52(6): 712-722.
[32] Ming Bo, Liu Pan, Guo Shenglian, et al. Robust hydroelectric unit commitment considering integration of large-scale photovoltaic power: a case study in China[J]. Applied Energy, 2018, 228: 1341-1352.
[33] Zhang Yu, Li Yanting, Zhang Guangyao. Short-term wind power forecasting approach based on Seq2Seq model using NWP data[J]. Energy, 2020, 213: 118371.
[34] 刘嘉诚, 刘俊, 赵宏炎, 等. 基于 DKDE 与改进mRMR 特征选择的短期光伏出力预测[J]. 电力系统自动化, 2021, 45(14): 13-21.Liu Jiacheng, Liu Jun, Zhao Hongyan, et al. Shortterm photovoltaic output forecasting based on diffusion kernel density estimation and improved max-relevance and Min-redundancy feature selection[J]. Automation of Electric Power Systems,2021, 45(14): 13-21.
[35] 潘超, 李润宇, 蔡国伟, 等. 基于时空关联分解重构的风速超短期预测[J]. 电工技术学报, 2021,36(22): 4739-4748.Pan Chao, Li Runyu, Cai Guowei, et al. Multi-step ultra-short-term wind speed prediction based on decomposition and reconstruction of time-spatial correlation[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4739-4748.
[36] 钟华昱, 黄强, 明波, 等. 耦合集合预报信息的水库高效调度方法研究[J]. 水力发电学报, 2021,40(5): 44-55.Zhong Huayu, Huang Qiang, Ming Bo, et al. An efficient method for deriving reservoir operating rules by coupling ensemble forecasting information[J].Journal of Hydroelectric Engineering, 2021, 40(5):44-55.
[37] 胡学东. 梯级水电站群负荷分配方法及蓄能调度图的研究[D]. 武汉: 华中科技大学, 2017.
[38] Peng Chunhua, Sun Huijuan, Guo Jianfeng. Multiobjective optimal PMU placement using a nondominated sorting differential evolution algorithm[J].International Journal of Electrical Power & Energy Systems, 2010, 32(8): 886-892.
[39] Qasem S N, Shamsuddin S M. Memetic elitist Pareto differential Evolution algorithm based radial basis function networks for classification problems[J].Applied Soft Computing, 2011, 11(8): 5565-5581.