0 引言
潮流计算是电力系统分析的基础,保证潮流的收敛性对电网的规划运行具有不可忽视的作用[1-7]。从数学层面而言,潮流计算的本质是对非线性方程组的求解,其收敛性受诸多因素影响。当初值选取不当、方式安排不合理等情况发生时,潮流计算无法收敛。潮流不收敛表明潮流方程无解或者方程有解但囿于潮流算法的局限性而无法得到潮流解。若潮流有解,应采用鲁棒的病态潮流算法求取潮流解;若潮流无解,应改变潮流方程边界条件,调整潮流运行方式,使潮流恢复可解性并求取潮流解。目前,潮流调整的主要方法是专家经验法,不仅需要消耗大量人力资源,而且计算量大,效率较低。因此,亟须一种高效、稳定的潮流调整策略来保证潮流的可靠收敛。
潮流调整的研究方法可分为非线性规划类方法、手动调整方法与人工智能类算法。作为非线性规划类方法的代表,文献[8]将潮流无解的程度定义为功率空间上运行点至稳定边界的欧式距离,将潮流调整问题转换为最优调整方向的求解问题,并提出以最优乘子法为基础的一种迭代算法来求解该模型。基于文献[8]提出的模型,文献[9-10]将潮流调整问题视为一类特殊的最优潮流(Optimal Power Flow,OPF)问题,并采用内点法对模型进行求解。文献[11]将潮流调整问题转换为最优负荷减载方向的计算问题,提出以灵敏度计算为核心的解决思路。文献[12]在文献[9-10]的基础上,优化目标函数,提出了新的潮流调整模型。随着网络规模扩大,运行方式多样化后,模型变量数目增多,非线性规划类方法的复杂度与计算量将大幅增加,进而影响算法的计算效率及鲁棒性。
与以求解非线性优化模型为核心的思路相比,以调度员经验为基础的手动调整方法侧重于对特定场景下潮流调整问题的分析。文献[13]提出采用PQ-PV 节点转换策略应对潮流无解时调整方式难以确定的问题。文献[14]通过求取薄弱输电通道并辅以灵敏度计算调整潮流运行方式,使潮流收敛。文献[15]提出一种基于薄弱点识别的潮流调整方法,但该方法只适用于过负荷类无解场景,对于发电机出力不合理的情形考虑不足。文献[16]提出基于虚拟中点功率的潮流估算模型,实现了潮流在无解时的可靠收敛,但并未给出自动调整措施。上述方法以因过负荷而无解的潮流作为样本,对于计算量更大,无解原因更复杂的潮流问题没有进一步说明。
随着人工智能技术的兴起,学者们也尝试将相关理论应用于潮流调整问题的研究中。文献[17]提出了基于改进直流法的潮流调整策略;文献[18-19]提出了采用深度强化学习模型解决潮流调整问题的思路,将强化学习理论应用于潮流调整领域。但人工智能类方法的性能较依赖参数设置及训练机制;另一方面,此类方法的黑箱特性使得调整结果缺乏可解释性。
为解决潮流调整方式难以确定的问题,本文提出基于功率下垂节点与两步式分析的扩展潮流计算模型。首先定义新的节点类型,构建引入功率下垂节点的扩展潮流模型,恢复了潮流的可解性。为确定功率下垂节点的转换规则,提出以PQ/PV 网络拆解为核心的两步式分析方法,从电压与功角两个角度定位需要进行类型转换的节点。以此为基础,定义并计算节点功率缺额,给出发电机出力调整与无功补偿量的计算方法。最后,基于IEEE 118 节点系统与TEXAS-2000 节点系统对模型进行测试,与基于内点法的最优潮流方法等多种方法进行对比。仿真结果表明,扩展模型收敛性能优越,与牛顿法潮流计算程序兼容性强,能适应多种潮流无解的场景。
1 基于功率下垂节点与两步式分析的扩展潮流计算模型
1.1 潮流调整问题的数学模型
考虑电力系统的潮流方程,有
式中,g 为潮流方程的映射;x 为状态变量,极坐标系下为PQ 节点电压模与相角、PV 节点相角;H 为注入参数变量,包括PQ 节点的有功负荷、无功负荷及PV 节点的有功出力。
潮流计算的本质就是对潮流方程(1)的求解,当系统运行方式不合理,功率参数超出稳定极限时,数学表现为方程组(1)无解。潮流无解的实际原因为网架功率传输能力与当前的功率需求不匹配,具体可分为负荷过重或出力分配不合理两类情形。潮流调整的目标就是通过采取调整发电机出力,增设无功补偿装置等措施使系统运行点回到可解域内,令潮流收敛。
本节思路如下:首先,给出功率下垂节点的定义,并分别从物理和数学的角度论证功率下垂节点对恢复潮流可解性的作用;然后,构造引入新型节点的扩展潮流模型,在三节点算例上验证模型处理无解潮流的效果;接着,提出基于PQ/PV 子网拆解的两步式分析方法,采用最优乘子法与不动点迭代法确定功率下垂节点的转换规则;最后定义并讨论状态回溯过程,确定具体的潮流调整方式。本节将以此思路为逻辑,详细阐述各部分内容。
1.2 功率下垂节点的定义
常规的潮流计算,包括PQ 节点、PV 节点与平衡节点。从数学的角度看,方程与未知量数目相等是方程组可解的必要条件。保证可解性的前提下考虑新节点类型的潮流计算可满足多元化的计算需求[20-21]。文献[21]提出考虑新节点类型的扩展潮流计算系统,并对新系统潮流的可解性做了详尽的讨论。在此基础上,本文通过定义功率下垂节点(KV节点)来恢复潮流的可解性。
设节点d 为KV 节点,其极坐标下的定义式为

式中,U 为节点电压模;θ 为节点电压相角;fPd 与fQd 分别为节点d 有功功率与无功功率;Uset 为电压设定值;K 为功率比例系数,当该KV 节点是由PQ转换而来时该系数记为KPQ,当该节点由PV 节点转换而来时记为KPV;PC 与QC 分别为有功修正系数与无功修正系数。
采用节点类型转换恢复潮流可解性的原理,在于使得转换后节点的特性曲线与原可解域流形相交。因此,有必要讨论节点转换前可行域的拓扑结构。对于PQ 节点,其可行域边界由鞍结分岔点(Saddle Node Bifurcation, SNB)组成(SNB 点处系统特征方程在后文给出),通常情况下该流形在PoQ 平面上的投影为包含原点的闭合曲线[22],此时修正系数可都设为零;对于PV 节点,可通过在潮流计算中将其转换为平衡节点,并用平衡节点吸收的功率作为修正系数。仿真经验表明,将PV 节点的修正系数取为零也可取得不错的效果。
从形式上看,KV 节点与传统的PV 节点定义相似,不同之处在于KV 节点通过引入功率比例系数K 将节点的无功功率与有功功率相关联。以PQ 节点为例,潮流无解时,PQ-KV 节点转换比PQ-PV 节点转换具备更好的收敛性。下面分别从潮流收敛域与物理意义两方面论证。
以修正系数取零为前提进行讨论,图1 中某PQ节点的潮流解可行域边界为S,AB 曲线为S 在其功率注入平面的投影,曲线上的点为SNB 点。潮流无解时,系统运行点在该平面的投影点位于边界外部,C0、C1、C2 为三个无解时的投影点,分别表示无解的三类典型情形。
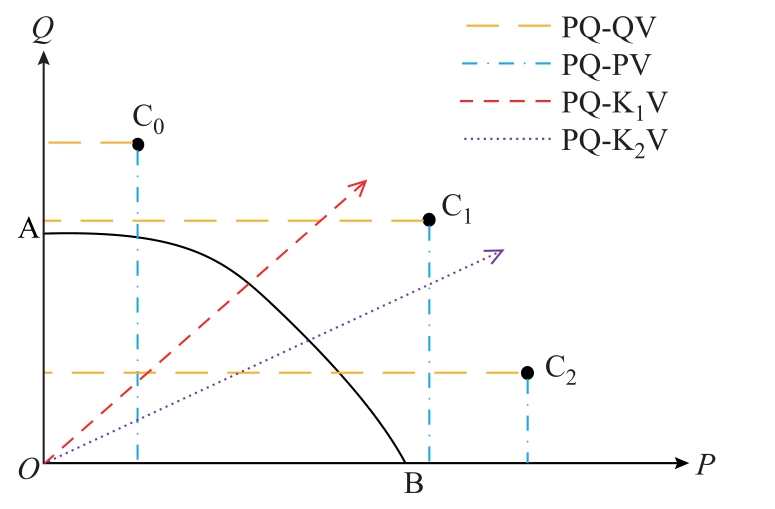
图1 PQ 节点潮流可行域示意图
Fig.1 Schematic diagram of power flow feasible region of PQ bus
对于C0 与C2,分别只有无功与有功负荷超过极限值,因此分别转换为QV 与PV 节点后,节点的特性曲线与潮流可行域相交,潮流可解性重新恢复。对于C1,此时转换为PV 或QV 节点皆无法令潮流收敛。但经PQ-KV 转换后,即使K 值不同,由于新流形会穿过坐标系原点,新流形仍会穿过原可行域,方程此时存在潮流解,C0 与C2 同理。
潮流无解时,由于可用信息过少,一般难以区分无解情形,故对恢复潮流可解性而言,将节点转为PV 或QV 节点的方式会受到限制。但KV 节点不存在这方面的约束,不同的潮流边界条件并不会影响KV 节点特性曲线与可行域的相交。综上所述,与PV、QV 节点相比,将PQ 节点转换为KV 节点可以在潮流无解时提升潮流的收敛性。
另一方面,每个因重负荷而无解的系统都可视为良态系统负荷逐步增加演化而来,因此通过负荷减载的方式能让系统回归良态,令潮流收敛。将PQ节点转换为KV 节点,等同于为该节点提供了充足的功率支撑,其物理意义相当于负荷减载。因此对无潮流解的系统,将PQ 节点转换为KV 节点有助于提升潮流的收敛性。同理,对于PV 节点而言,转换为KV 节点松弛有功约束,等同于平衡了该节点的有功出力,同样可恢复PV 节点有功出力安排不合理场景下的潮流可解性。
经过PQ-KV 节点转换后潮流收敛,可计算节点d 需要补偿的功率缺额为
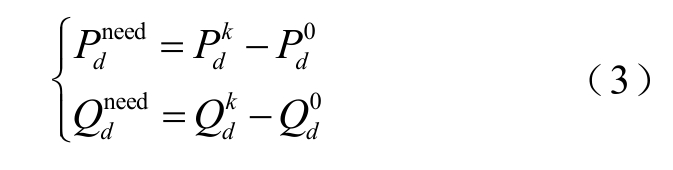
式中, Pd k、 Qd k分别为经PQ-KV 节点转换潮流收敛后节点d 的有功与无功功率; P d 0、Q d 0分别为节点d原始的有功与无功功率。
1.3 引入功率下垂节点的扩展潮流模型
考虑包含n 节点的电力系统,其中有m 个PV节点。为表述方便,设1 号节点为平衡节点,将PQ节点的无功功率平衡方程置于最后。忽略平衡节点功率方程,则该系统极坐标下的潮流方程为
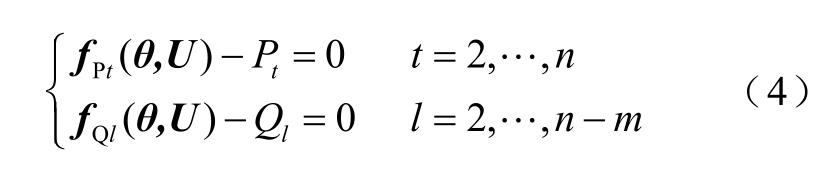
式中,Pt 与Ql 分别为给定有功功率与无功功率。
引入功率下垂节点,将a 个PQ 节点与b 个PV节点转换为功率下垂节点,有
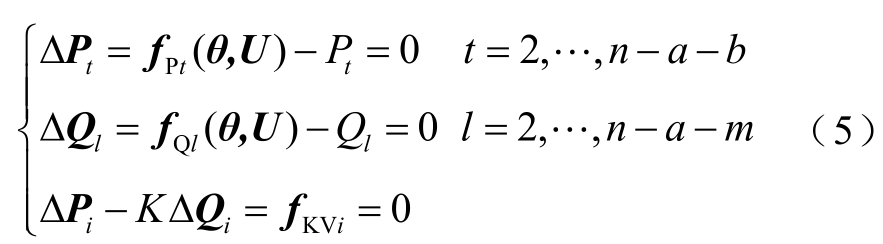
式中,i=1,…, a+b;fKVi=fPi(θ,U)-PC-K( fQi(θ,U)- QC)。
式(5)即为引入功率下垂节点的扩展潮流模型。采用式(5)对无解潮流系统进行求解。考虑用牛顿法求解式(5),有
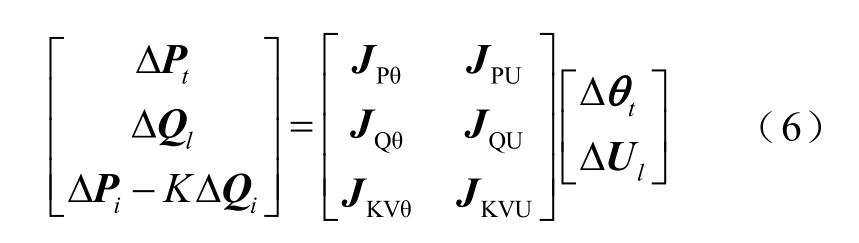
式中,J 为雅克比矩阵,下标为对应元素,则有JKVθ=JPθ-KJQθ, JKVU=JPU-KJQU, JPθ=∂ΔPt /∂ΔθT, JPU= ∂ΔPt/∂ΔUT, JQθ=∂ΔQl/∂ΔθT, JQU=∂ΔQl/∂ΔUT。
以三节点系统为例,对扩展潮流模型恢复潮流可解性的有效性进行测试。
三节点测试系统如图2 所示,相关参数设置如下:E=1∠0o,X1=X2=0.1(pu),P2=6.0(pu),Q2=2.5(pu),P3=1.0(pu),U3=1.0(pu),基准容量为100 MV·A,其余参数均为标幺值,比例系数K 取2,功率下垂节点电压设为1(pu)。
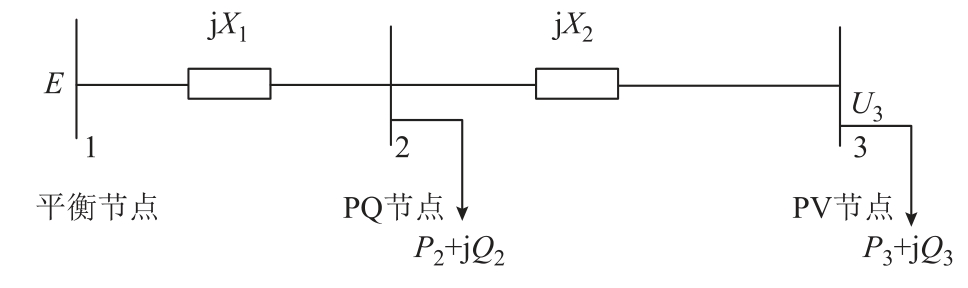
图2 三节点测试系统
Fig.2 Three bus test system
扩展模型求解潮流如图3 所示。图3 中静态电压稳定边界曲线均由SNB 点组成,当2 号PQ 节点的功率参数位于边界外部时,潮流方程无解。图3表明,初始潮流点A 位于稳定边界外潮流无解,采用扩展潮流模型将2 号PQ 节点转换为KV 节点,潮流运行点来到B 点,位于边界内部,潮流解存在。将2 号PQ 节点转换为KV 节点的详细过程见附录。
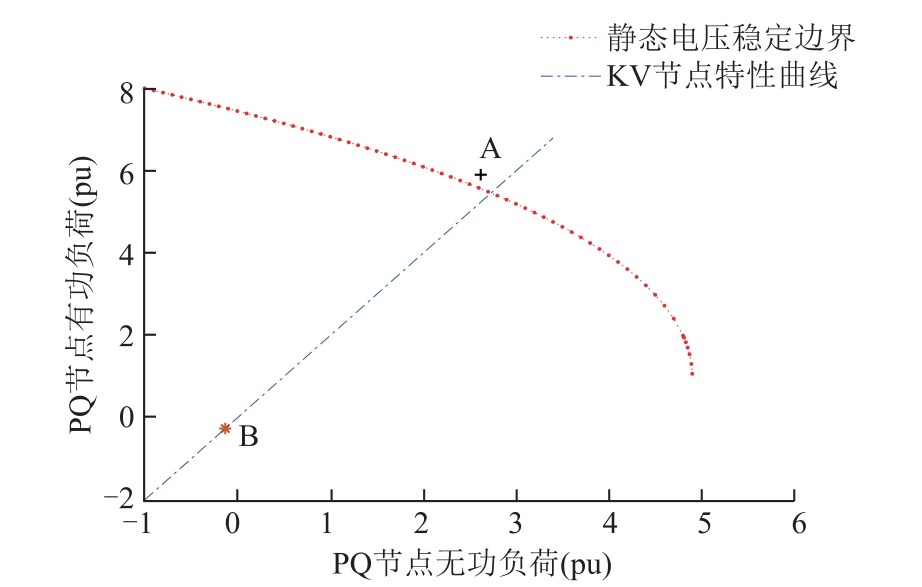
图3 扩展模型求解潮流
Fig.3 Extended model solving power flow
采用扩展模型求解得到的潮流解见表1,PQ 节点功率为负代表发出功率。功率下垂节点的出力由潮流解直接计算。根据式(3)计算功率缺额,有功缺额为6.259 5(pu),无功缺额为2.629 8(pu)。该缺额具有如下意义:若想令该无解潮流恢复可解性且2 号节点的电压模为1(pu),则需要为2 号节点补充该功率缺额。三节点系统的仿真结果表明,考虑功率下垂节点的扩展潮流模型,可以使无潮流解的系统恢复潮流可解性,并给出需要的功率缺额。
表1 三节点系统潮流解
Tab.1 Power flow solution of three bus system

节点 A 点电压(pu) B 点电压(pu) SB(pu)1 无解 1∠0° 1.259 5+j0.079 6 2 无解 1∠12.978° -0.259 5-j0.129 8 3 无解 1∠7.237° 1.0+j0.050 1
1.4 基于两步式分析方法的KV 节点转换规则
考虑KV 节点的扩展潮流模型可恢复潮流的可解性,但无规则地将PQ/PV 节点转换成KV 节点会增加计算量,甚至导致不收敛。对此,本节研究了一种基于两步式分析方法的KV 节点转换逻辑,根据合理的节点转换规则引入KV 节点,在降低计算量的同时保证扩展潮流模型的可靠收敛。
潮流无解时,必然存在功率超越稳定极限的节点。在功率严重越限的薄弱节点处增加功率源,提供功率支撑是恢复潮流可解性的有效思路[13]。KV节点的物理意义等同于功率源。因此,确定以下KV节点的转换逻辑:提出两步式分析方法,将网络拆分为PQ 子网与PV 子网,从电压与功角的角度分析潮流薄弱点。根据各节点薄弱程度依序将薄弱节点转换为KV 节点,直至潮流收敛为止。
两步式分析的核心内容,是以节点电压方程为基础,将原网络分解为PQ 子网与PV 子网进行讨论。
考虑电力系统的节点电压方程,有
式中,Y 为节点导纳矩阵;U 为节点电压向量;I 为节点注入电流向量,I=S*/U,*表示共轭。保留原有节点,将系统原节点电压方程(7)按节点类型重新排序为

式中,下标PQ、PV、Vθ 分别为对应的节点类型。
将PQ 节点等值为导纳,移至方程左侧,有

式中,Y P ′Q为PQ 节点等值导纳,Y P′Q=IPQ/UPQ。对该网络做WARD 等值,使原网络分离为只包含PQ 节点与平衡节点的PQ 子网与只包含PV 节点与平衡节点的PV 子网,有

式中,![]() 为对应的节点类型下标。PQ 子网与PV 子网的节点电压方程为
为对应的节点类型下标。PQ 子网与PV 子网的节点电压方程为
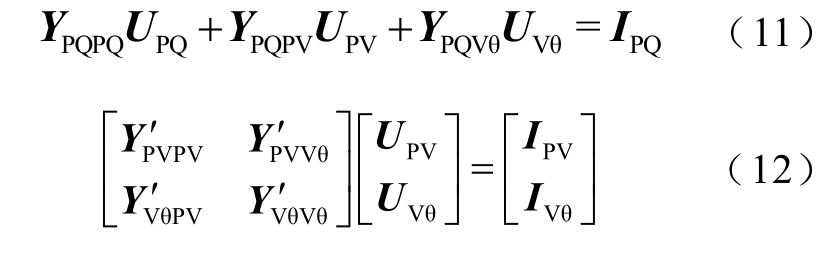
至此,原网络被分解为PQ 子网与PV 子网。PQ 子网等价于将原网络的所有PV 节点视作相角已知的平衡节点后得到的网络,而PV 子网则是将原网络的PQ 节点等值为导纳后得到的网络。两个子网间通过PQ 节点电压和PV 节点相角参数互相耦合,原始网络即为耦合作用的结果。
1.4.1 PV 子网功角薄弱点的识别方法
首先采用最优乘子法求解PV 子网潮流,最优乘子法模型及求解迭代步骤为

式中,μ为最优乘子;k 为迭代次数;J 为雅克比矩阵。若PV 子网有潮流解,则潮流无解的主要原因在PQ 子网,无需分析PV 子网薄弱节点;若PV 子网无潮流解,则最优乘子法会收敛至局部的最小二乘解。利用该解的电压模值、不平衡量与灵敏度信息,可定位网络薄弱点[23]。为适应PV 节点出力过剩的场景,本文采用如下改进措施以辨识PV 子网的薄弱点:将最小二乘解中与原PV 节点电压模值相差最大的节点视为薄弱节点,设薄弱节点为节点P,则
式中,i=1,2,…,m,m 为PV 网络节点数;ei、fi 分别为直角坐标下节点i 最小二乘解的横坐标与纵坐标。
1.4.2 PQ 子网电压薄弱点的识别方法
PQ 子网不包含PV 节点,仅包含PQ 节点与平衡节点。研究采用不动点迭代法求解式(11)的迭代过程,通过分析两次迭代前后解的变化来确定电压薄弱点。
将式(11)整理为
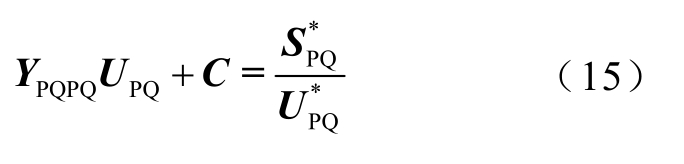
式中,C 为平衡节点注入量,C= YPQPVUPV + YPQVθUVθ,在PQ 子网中为常量。设Usolve 为式(15)的解,为表达简洁,省略PQ 下标,则有
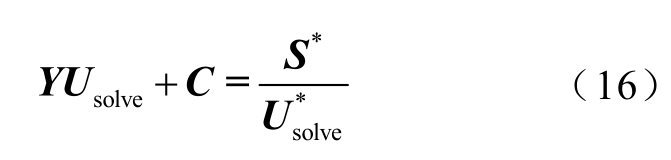
设k≥1,分析第k 次和第k+1 次迭代电压的关系,有
式中,Uk 与Uk+1 分别为第k 次与第k+1 次的电压向量。考虑到式(15)存在解Usolve,则Uk 与Uk+1 可表达为
式中,ΔUk 与ΔUk+1 分别为第k 次与第k+1 次迭代电压向量与潮流解Usolve 的差。将式(16)与式(18)代入式(17)可得
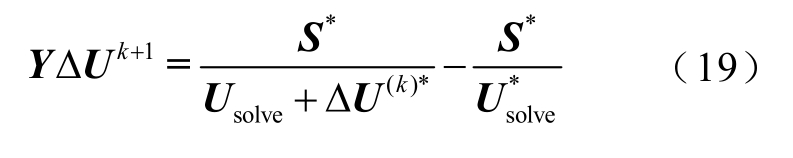
将式(19)右侧通分,并在等式两端取模,考虑到|ΔUk|<<|Usolve|,有
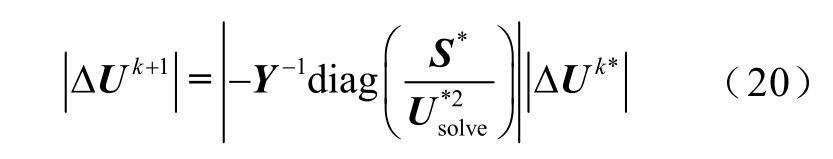
记![]() 为对角矩阵,则有
为对角矩阵,则有
式(21)表达了在第k 次迭代中,电压与最终解的误差模|ΔUk*|,经WPQ 作用的变化过程。在已知Usolve 的前提下,WPQ 为常系数矩阵。将该矩阵对角化,则有
式中,Λ 为WPQ 对角化后的特征向量矩阵;λW 为WPQ 的特征值,且WPQ=Λ-1diag(λW) Λ。
式(22)表明,两次迭代前后误差放大的程度,将由WPQ 的最大特征值决定。最大特征值越大,则误差在迭代前后被放大的倍数越大,潮流也越难收敛。此时最大特征值对应的节点即为导致潮流收敛困难的节点,为PQ 子网的电压薄弱点。定义WPQ特征值为PQ 子网的电压薄弱点识别指标。
实际计算中,WPQ 的维数较高,精确求解大型矩阵的特征值会耗费相当可观的计算资源。对此,在计算前先进行PQ 网络解耦的处理:在计算某一PQ 节点对应的特征值时,把其他PQ 节点等值成阻抗,把所有平衡节点接地。处理后系统变为n- m- 1个分别由1 个PQ 节点与1 个平衡节点组成的两节点解耦系统,WPQ 此时为严格对角矩阵。这样的处理方式在保留一定准确性的同时,提升计算速度,有助于程序的后续应用。
上述分析是在PQ 子网存在潮流解Usolve 的前提下进行的。当式(8)对应的原网络无潮流解时,对PQ 网络而言,存在的大量平衡节点会扩大原网络的可解域,大部分情况下Usolve 仍然存在。当Usolve 不存在时,可考虑采用最优乘子法求解该子网潮流,用电压模的最小二乘解替代Usolve 进行分析。为提升计算速度,在仿真中本文用常量替代Usolve 模值进行计算,也可取得理想的效果。
1.5 状态回溯
在功率注入空间内,潮流无解时系统运行点位于可行域边界之外。可行域边界是由SNB 点组成的集合,SNB 点处系统特征方程为

式中,gx 为潮流雅可比矩阵;w 为gx 的左零特征向量。在SNB 点处,潮流方程的雅可比矩阵奇异,其对应的左特征向量w 是该SNB 处切平面的法向量,蕴藏了系统稳定状态的关键信息,其物理意义是状态变量对系统静态电压稳定裕度的灵敏度[24]。计算w 并沿其反方向控制系统可令运行点以最快的速度远离边界,实现最优调整。
潮流调整的最终目标是要在维持负荷不变前提下,通过改变发电机出力,设置无功补偿等方式实现潮流收敛。经过之前的潮流调整初步处理后,已得到需要令潮流收敛的功率缺额,实质上等同于通过减负荷的方式实现了潮流收敛,负荷边界条件已被改变。因此,本节通过引入雅可比矩阵左零特征向量w 的计算进行状态回溯,还原边界条件,根据功率缺额确定发电机出力调整方案。对于无功功率缺额,采用无功补偿装置就地补偿,对于有功功率缺额,由发电机改变出力来弥补。
要计算左特征向量,首先要计算SNB 点,考虑到计算速度及收敛性,本文拟采用边界全导数直接法BDDM(boundary-derivative direct method)[25]计算SNB 点。
如果该向量发电机出力部分分向量为零向量,说明改变发电机出力难以回溯潮流使其收敛。此时,当前系统存在因负荷过重导致联络线达到功率传输极限的问题,需要根据功率缺额增加无功补偿。若该向量非零,则将有功缺额按灵敏度分配至对应发电机,即
式中,wi 为单位化后左特征向量对应发电机i 的分量,也是发电机i 关于系统静态电压稳定裕度的灵敏度;ΔPgi 为发电机i 出力改变量;D 为动作发电机集合,由w 中所有非零分量对应发电机组成。
系统运行点变化示意图如图4 所示。以图4 中A、B、C 三个运行点来表示本方法的物理过程。A点为系统原始运行点,位于可行域之外,潮流无解。确定潮流薄弱点,转换节点类型得到功率缺额,补充该功率缺额使系统运行点来到B 点,B 点位于可行域内潮流收敛。然后以B 点为起点,沿着功率缺额的反方向增加功率至SNB 点C,计算C 点雅可比矩阵的左特征向量,确定发电机动作集合,以及发电机出力和无功补偿调整方案。最后将负荷恢复至A 点的负荷,调整相应发电机出力并增设无功补偿,潮流可行域将由S0 增扩至S1,重新计算潮流,潮流收敛。
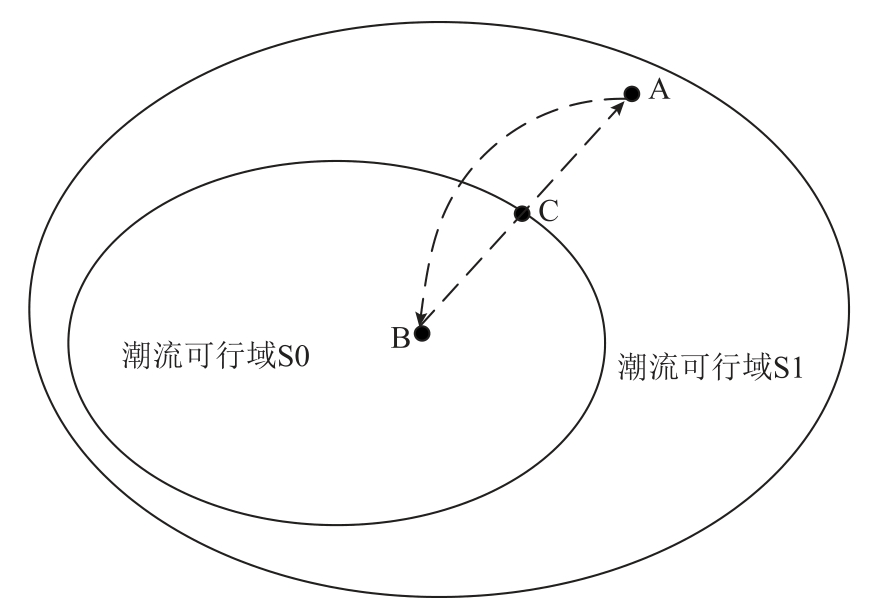
图4 系统运行点变化示意图
Fig.4 Schematic diagram of system operating point changes
1.6 算法步骤
本算法详细步骤如下:
(1)数据初始化,读入不收敛潮流数据。
(2)按节点类型将网络节点重新编号排序,对不收敛数据进行两步式分析,得到PV 与PQ 子网的网络方程。
(3)设定PQ 节点电压模为1(pu),首先采用最优乘子法计算PV 子网潮流能否收敛,如能收敛则转步骤(5),否则依潮流最小二乘解确定PV 网络薄弱点,然后转步骤(4)。
(4)将最薄弱PV 节点转为KV 节点,转至步骤(3)。
(5)若PV子网潮流未引入KV节点就直接收敛,转至步骤(6);否则计算PV 节点有功缺额,修正PV 节点出力,然后转至步骤(6)。
(6)判断原网潮流是否收敛,如未在PQ 网络引入KV 节点潮流收敛则程序结束,否则转至步骤(7)。
(7)确定PQ 网络薄弱点,将最薄弱PQ 节点转为KV 节点,转至步骤(8)。
(8)判断潮流是否收敛,收敛则转至步骤(9),否则转至步骤(7)。
(9)状态回溯,计算回溯SNB 点及对应左特征向量,转步骤(10)。
(10)判断特征向量发电机出力分向量是否为零向量,是则根据功率缺额计算无功补偿量,程序结束;否则根据功率缺额计算发电机出力调整量,程序结束。
图5 为本文方法流程,核心迭代过程仍属于牛顿法潮流计算的范畴,这意味着在处理大型网络潮流调整问题时,本方法具备与牛顿法潮流计算相近的计算性能,且不会出现维数灾难问题,具备处理大型网络潮流调整问题的能力。

图5 方法流程
Fig.5 The flow chart of the wholesale methodology
2 算例分析
基于IEEE 118 节点系统与TEXAS 2000 节点系统,分别构建潮流无解不收敛的场景。在118 节点系统构建了两种特殊场景以验证模型有效性,在2 000 节点系统构建了更契合工程实际的多个无解算例以验证模型在大电网的适应性。采用本文策略进行调整,并与多种潮流调整方法进行对比,讨论参数设置对算法收敛性的影响。
采取以下方式验证调整结果:将调整措施应用于不收敛潮流,修改发电机出力和无功补偿,然后用牛顿法以平启动的方式计算调整后潮流,观察潮流是否收敛,若收敛则认为调整成功。各算法收敛精度统一取10-6,程序采用Matlab 编写,计算机内存16.0 GB,CPU 型号为i7-10875,最优潮流算法调用matpower[26]软件包。算法参数取值由大量仿真经验确定,本节所有算例参数均取同样数值。参数相关参数设置为
2.1 IEEE 118 节点系统潮流调整算例
为验证模型的有效性,本部分基于IEEE 118 节点系统,构建了重负荷与出力过剩两种典型的潮流无解场景,采用扩展模型调整潮流,均成功收敛。
2.1.1 场景1:部分节点重负荷
部分节点重负荷考虑部分PQ 节点有功功率过重时潮流无解的情形,将节点2、3、7 的有功负荷增加至20 倍,此时潮流无解。采用扩展模型进行调整,最终潮流收敛。
首先进行两步式分析,PV 子网潮流可收敛,这与此场景PV 节点出力正常的前提相吻合。分析PQ子网薄弱节点,结果如图6 所示。图6 表明,节点1、2、4(排序前原网络的2、3、7 节点)为PQ 网络的电压薄弱点。分析结果同样与场景前提一致,验证了两步式分析方法的准确性。

图6 薄弱指标Wpq 柱状图
Fig.6 Histogram of Wpq index
根据薄弱点辨识结果,计算功率缺额。仿真结果表明,将3 号节点转换为KV 节点后潮流收敛,有功缺额为9.173 0(pu),无功缺额为0.786 5(pu)。在此场景中,有三个节点负荷过重,但只将其中一个节点转换为KV 节点即可恢复潮流的可解性。这是因为根据网络结构,这三个节点处于同一区域之中,将节点3 转换为KV 节点相当于给该区域提供了电压支撑。
根据功率缺额结果,进行状态回溯至SNB 点,得到左特征向量,确定发电机动作集合。最后,根据发电机灵敏度及功率缺额,确定各发电机有功出力调整量,潮流收敛,收敛后潮流解列于附录中。
动作发电机及灵敏度见表2,发电机1、12、6、4、8 的灵敏度较高,这说明调整这些发电机的出力对于恢复潮流可解性效果最为显著。
表2 动作发电机及灵敏度
Tab.2 Operating generators and sensitivity

发电机 灵敏度 发电机 灵敏度 发电机 灵敏度1 0.341 1 15 0.236 7 27 0.199 3 12 0.305 0 18 0.230 9 26 0.187 7 6 0.299 7 19 0.228 7 36 0.183 4 4 0.273 7 113 0.225 8 34 0.182 7 8 0.265 7 31 0.211 4 25 0.180 8 10 0.254 9 32 0.199 5 40 0.136 3
2.1.2 场景2:部分发电机出力过剩
考虑部分PV 节点有功出力过剩时潮流无解的情形,将排序后PV 节点89、90 的有功出力增至20倍,此时潮流无解。采用扩展模型进行调整,最终潮流收敛,收敛后潮流解列于附录中。
PV 子网潮流不收敛,采用最优乘子法求解,结果如图7 所示。根据最小二乘解,定位此时功角薄弱点为发电机25、26(排序后的89、90 节点)。将薄弱节点转换为KV 节点后算得两节点有功缺额为-23.767 9(pu)与-30.704 9(pu),修改两节点有功出力后潮流收敛。根据前置条件,此场景中不收敛原因为部分发电机出力过多导致的远距离功率传输,结果表明所提方法可以有效地定位薄弱点并恢复潮流的收敛性。
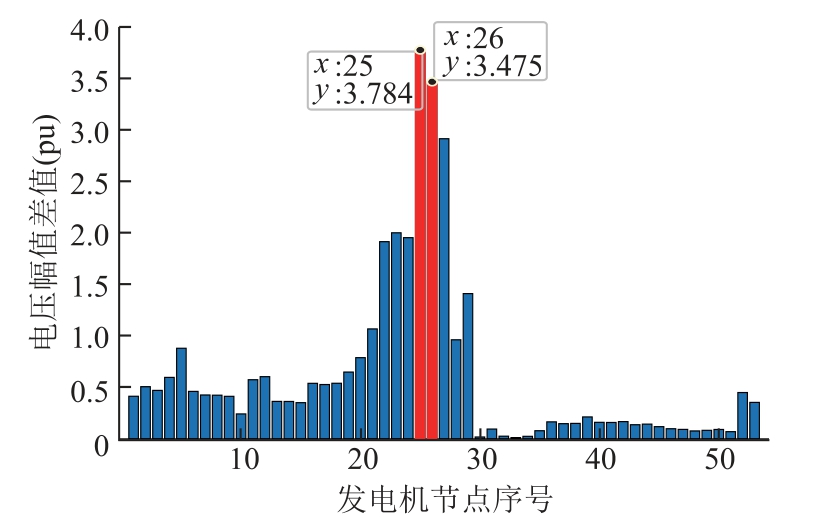
图7 PV 网络薄弱点示意图
Fig.7 Schematic diagram of weak nodes of PV network
2.2 TEXAS-2000 节点系统潮流调整算例
为验证模型在大型系统中的适用性,采用TEXAS-2000 节点系统数据进行测试。为验证模型的鲁棒性,构建多种潮流无解场景,包括单节点、区域和全网的负荷及出力过重等情形。最后,将所提模型与其他方法对比。其中对比所用最优潮流数学模型为
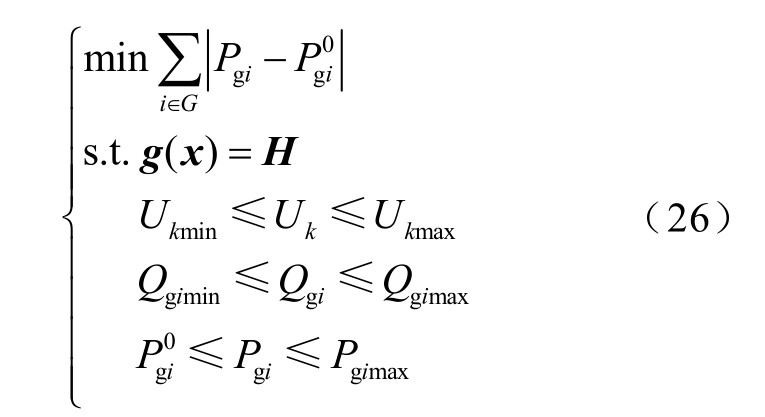
式中,k=1,2,…,n,i=1,2,…,m,n 和m 分别为节点总数与PV 节点总数;Pgi 为发电机调整后的出力; 为发电机原始出力;Ukmin、Ukmax 分别为节点电压的下限与上限;Qgimin、Qgimax 分别为发电机无功出力下限与上限;Pgimax 为发电机有功出力上限,等式约束为潮流方程,优化目标是发电机有功出力调整量最小,模型采用内点法求解。
为发电机原始出力;Ukmin、Ukmax 分别为节点电压的下限与上限;Qgimin、Qgimax 分别为发电机无功出力下限与上限;Pgimax 为发电机有功出力上限,等式约束为潮流方程,优化目标是发电机有功出力调整量最小,模型采用内点法求解。
各方法对比结果见表3。表3 中A 类场景为重负荷无解场景,B 类场景为出力过剩无解场景,标号1、2、3 为无解类型,分别表示单节点、多节点与全网,每一子类选择5 个无解算例作为测试场景,以各方法收敛算例数作为评价指标[18]。表3 中结果表明,在大型电网中,本文所提方法与最优潮流法效果更好,最短距离法[8]与灵敏度法[11]在A-3 与B 类场景中效果一般。这是因为最短距离法与灵敏度法都是以灵敏度计算与最优乘子潮流的迭代方法,对初值的要求较高。当潮流无解程度严重时,平启动的初值往往无法满足求解的需要,此时上述两种方法效果不佳。扩展潮流模型引入了功率下垂节点与薄弱点识别环节,准确地将薄弱点转变为KV 节点,改变了潮流方程的结构,可有效淡化不合理边界条件对初值的影响,平启动即可取得良好的效果。
表3 各方法对比结果
Tab.3 Comparison results of each algorithm
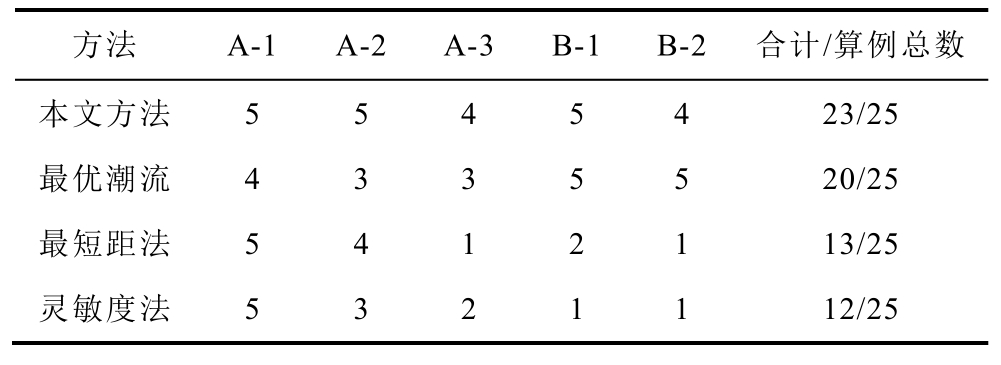
方法 A-1 A-2 A-3 B-1 B-2 合计/算例总数本文方法 5 5 4 5 4 23/25最优潮流 4 3 3 5 5 20/25最短距法 5 4 1 2 1 13/25灵敏度法 5 3 2 1 1 12/25
为细化本文所提方法与最优潮流法之间的差别,另构造多例无解场景,研究不同参数配置下最优潮流方法的有效性。工程中,一般不会出现出力与负荷差异显著的情形。这里采用以下方式构建无解算例:将2 000 节点系统中所有节点负荷随机增加15%~25%,PV 节点出力随机增加5%~15%,采用普通牛顿法求解潮流,潮流不收敛则视为无解[19],选取50 个不收敛潮流作为测试样本。分别采用所提方法与最优潮流法对不收敛潮流进行调整,其中将最优潮流法中发电机出力上限改为原出力的 105%、110%、115%与 120%,分别记为OPF-1、OPF-2、OPF-3 与OPF-4。
OPF 参数测试结果见表4。结果表明,扩大变量动作区间可以改善最优潮流的收敛性,但潮流无解时,可用信息较少,为各发电机确定合适的动作区间难度很大。另一方面,在某些场景中需要补偿无功使潮流收敛,OPF 法动作变量只有发电机出力,无法应对此类问题,此时扩大区间并不能改善OPF 的调整效果。与OPF 相比,本文所提方法在多个场景设置同一K 值即可,无需刻意改变参数;对于无功补偿类问题,模型中加入了特征向量分析模块,给出了相应的应对方案,可以处理类似问题。与OPF 相比,扩展潮流模型具备更强的鲁棒性。
表4 OPF 参数测试结果
Tab.4 Parameter test results of OPF

本文方法 OPF-1 OPF-2 OPF-3 OPF-4 48/50 17/50 19/50 22/50 22/50
2.3 参数设置讨论
2.3.1 KV 节点K 与U 参数设置的讨论
选取2.1 节中的两个算例进行讨论,研究不同K 与U 取值对模型收敛性的影响。
基于2.1.1 节和2.1.2 节算例采用不同参数时的收敛性见表5 与表6。结果表明,与K 相比,扩展模型的收敛性主要取决于电压U 的设置,U 越靠近1 收敛效果越好,这是因为大多数情况下PQ 节点的潮流可行域都存在电压模在1 附近的解。电压一定时,K 值越大收敛性越差。大量仿真经验表明,对PQ-KV 类问题,将电压U 设为1(pu),K 值设为2;对于PV-KV 类问题,K 值设为-2 时模型收敛性良好,可处理多种潮流无解问题。
表5 基于2.1.1 节算例采用不同参数时的收敛性
Tab.5 Convergence with different parameters based on 2.1.1 example
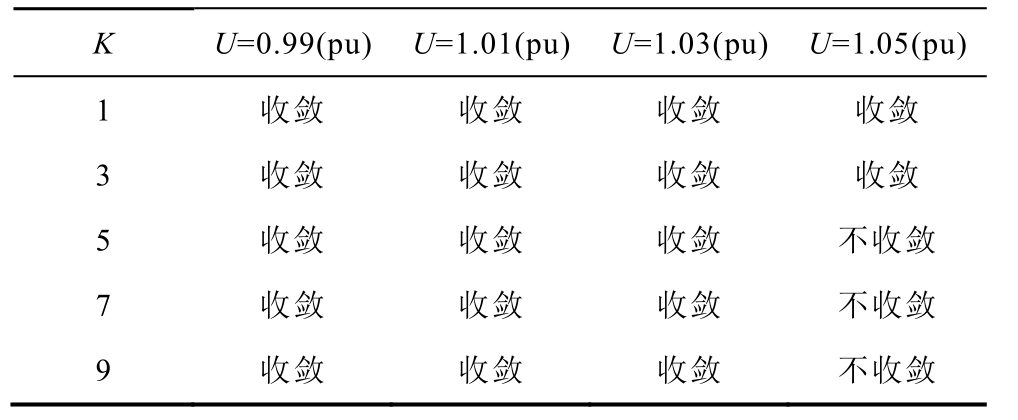
K U=0.99(pu) U=1.01(pu) U=1.03(pu) U=1.05(pu)1 收敛 收敛 收敛 收敛3 收敛 收敛 收敛 收敛5 收敛 收敛 收敛 不收敛7 收敛 收敛 收敛 不收敛9 收敛 收敛 收敛 不收敛
表6 基于2.1.2 节算例采用不同参数时的收敛性
Tab.6 Convergence with different parameters based on 2.1.2 example

转换类型 K=-2 K=0 K=2 K=4 K=6 PV-KV 收敛 收敛 收敛 收敛 收敛
2.3.2 KV、PV 和QV 三类节点的讨论
潮流计算中,PV 与QV 节点是两种较为通用的节点类型,其中PQ-PV 节点转换已被应用于潮流调整领域中,在某些情形下可以取得良好的效果[10]。与KV 节点相比,这两种节点类型同样将节点电压模设为定值,具有很高的相似性。下面考虑五种潮流无解的情形,并将本文中的PQ-KV 转换分别改为PQ-PV 与PQ-QV,以对比不同节点类型对潮流收敛性的影响。在 118 节点系统中,当 KPtotal=2 或KQtotal=11 时潮流均无解,故以此为基准构造了五种潮流无解的情形,得到不同节点类型对潮流收敛性的影响见表7。计算结果不收敛表明将全网PQ 节点全部转换为对应类型后潮流仍不收敛。由表7 结果可知,PV 与QV 节点在特定场景中可改善潮流收敛性,KV 节点比另外两种节点具备更良好的收敛性。结合图1 可知,PV 与QV 节点的物理意义分别是无功电源与有功电源,当潮流无解是无功/有功负荷过重引起时,将PQ 节点转换为PV/QV 节点往往能取得收敛的潮流解。但当潮流无解是有功/无功负荷过重引起时,PV/QV 节点转换后节点的运行曲线与其可行域并无交集,潮流仍然发散。
表7 不同节点类型对潮流收敛性的影响
Tab.7 The influence of different node types on the convergence of power flow
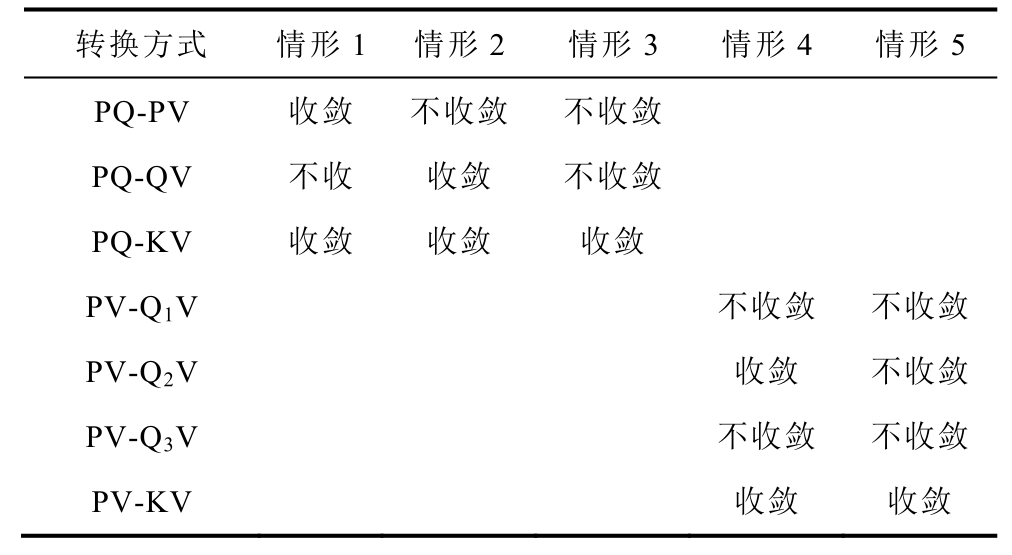
转换方式 情形1 情形2 情形3 情形4 情形5 PQ-PV 收敛 不收敛 不收敛PQ-QV 不收 收敛 不收敛PQ-KV 收敛 收敛 收敛PV-Q1V 不收敛 不收敛PV-Q2V 收敛 不收敛PV-Q3V 不收敛 不收敛PV-KV 收敛 收敛
参数设置见表8,KPtotal、KQtotal 分别为全网有功负荷系数与全网无功负荷系数,KQPgtotal 为全网发电机有功出力系数,情形4 为2.1.2 部分算例,比例系数K 沿用2.3.1 节的讨论结果。
表8 参数设置
Tab.8 Parameter setting
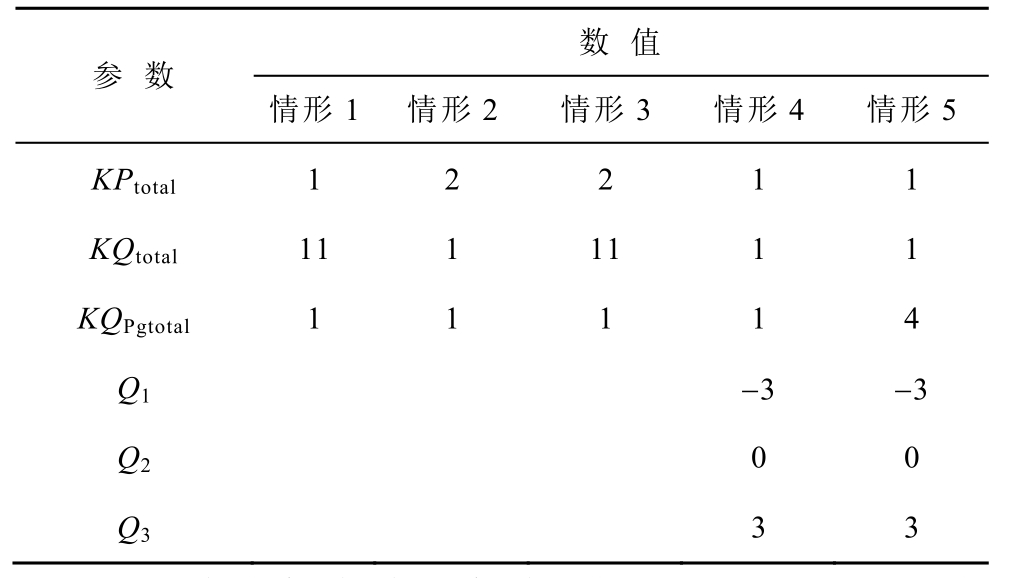
数 值参 数情形1 情形2 情形3 情形4 情形5 KPtotal 1 2 2 1 1 KQtotal 11 1 11 1 1 KQPgtotal 1 1 1 1 4 Q1 -3 -3 Q2 0 0 Q3 3 3
对于发电机有功出力过剩的场景,PV-QV 节点转换虽然可松弛无功约束,恢复潮流可解性,但不同Q 值会极大影响节点转换的有效性,且在无解的前提下合理地估算发电机无功出力较为困难;对KV 节点而言,一方面,比例系数K 的设定不依赖潮流边界条件;另一方面,相比于QV 节点,KV 节点的有功、无功功率都可松弛。因此,KV 节点比QV 节点具备更强恢复潮流可解性的能力。
综上所述,本文提出的KV 节点能够适应多种潮流无解的情形,与PV/QV 节点相比,具有更良好、更稳定的改善潮流收敛性的能力。
3 结论
本文提出了一种基于功率下垂节点与两步式分析的扩展潮流计算模型。该方法通过两步式分析,引入功率下垂节点计算功率缺额与状态回溯计算,实现了潮流调整方式的确定。仿真结果表明,方法适用于大型系统中的潮流无解问题,收敛性能稳定,具备一定的理论与工程价值。
附 录
对该三节点系统,极坐标下采用牛顿法求解扩展潮流模型的迭代步骤如下,首先考虑原潮流的牛顿迭代过程,即
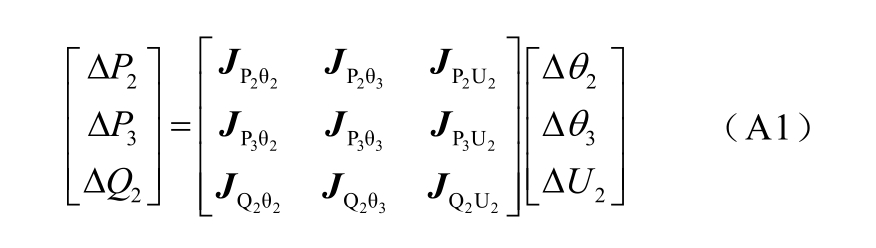
将2 号节点转换为KV 节点,只需改变2 号节点对应的两行不平衡量与雅可比矩阵元素即可。根据KV 节点定义,新雅可比矩阵元素及可由原雅可比矩阵第一行减去K 乘以第三行得到,不平衡量同理。
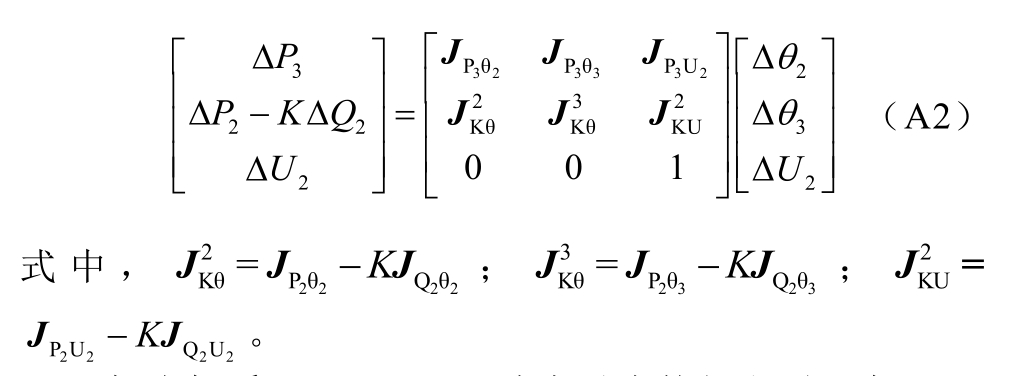
极坐标系下,ΔU2=0,消去对应的行和列,有

求解式(A3)获得本次迭代修正量,对状态变量进行修正,之后按上述步骤,反复迭代直至收敛。分析此迭代过程,与常规潮流计算的牛顿迭代过程相比,扩展潮流模型多余的计算量仅在于多做有限次初等行变换,计算量增加较小。
2.1.1 节与2.1.2 节部分采用本算法调整后收敛的潮流解见附表1 和附表2。
附表1 例2.1.1 节潮流解
App.Tab.1 Power flow solution of example in 2.1.1

节点 电压(pu) 节点 电压(pu) 节点 电压(pu)1 0.955∠-171.424o 41 0.963∠-73.018o 81 0.996∠-12.464o 2 0.884∠-166.051o 42 0.985∠-63.872o 82 0.989∠-10.852o 3 0.861∠-173.011o 43 0.914∠-70.705o 83 0.985∠-9.709o 4 0.998∠-134.805o 44 0.908∠-50.529o 84 0.980∠-7.252o 5 0.987∠-134.019o 45 0.937∠-42.938o 85 0.985∠-5.734o 6 0.990∠-143.799o 46 1.005∠-35.407o 86 0.985∠-7.078o 7 0.977∠-147.700o 47 1.000∠-29.198o 87 1.015∠-6.832o 8 1.015∠-116.578o 48 1.020∠-32.655o 88 0.988∠-2.667o 9 1.040∠-108.326o 49 1.025∠-31.306o 89 1.005∠-1.345o 10 1.050∠-99.726o 50 1.002∠-33.000o 90 0.985∠-5.608o 11 0.972∠-141.463o 51 0.968∠-35.183o 91 0.980∠-5.060o
附表2 例2.1.2 节潮流解
App.Tab.2 Power flow solution of example in 2.1.2

节点 电压(pu) 节点 电压(pu) 节点 电压(pu)1 0.955∠-10.859o 41 0.967∠-13.171o 81 0.995∠3.391o 2 0.971∠-10.321o 42 0.985∠-11.079o 82 0.989∠0.703o 3 0.968∠-9.975o 43 0.976∠-9.041o 83 0.984∠1.929o 4 0.998∠-6.253o 44 0.983∠-5.774o 84 0.980∠4.519o 5 1.002∠-5.807o 45 0.985∠-3.657o 85 0.985∠6.100o 6 0.990∠-8.539o 46 1.005∠-1.053o 86 0.985∠4.731o 7 0.989∠-8.985o 47 1.019∠0.421o 87 1.015∠4.990o 8 1.015∠-0.779o 48 1.020∠1.232o 88 0.987∠9.281o 9 1.043∠6.475o 49 1.025∠2.458o 89 1.005∠13.370o
(续)

节点 电压(pu) 节点 电压(pu) 节点 电压(pu)12 0.990∠-146.437o 52 0.958∠-36.022o 92 0.993∠-4.590o 13 0.926∠-134.764o 53 0.946∠-36.685o 93 0.987∠-7.612o 14 0.938∠-136.782o 54 0.955∠-35.544o 94 0.991∠-9.777o 15 0.970∠-106.540o 55 0.952∠-35.725o 95 0.981∠-10.730o 16 0.911∠-133.820o 56 0.954∠-35.600o 96 0.993∠-10.872o 17 0.964∠-101.711o 57 0.971∠-34.885o 97 1.011∠-10.692o 18 0.973∠-102.042o 58 0.960∠-35.657o 98 1.024∠-11.263o 19 0.963∠-101.750 o 59 0.985∠-30.177o 99 1.010∠-11.533o 20 0.935∠-96.461 o 60 0.993∠-25.967o 100 1.017∠-10.460o 21 0.926∠-91.465 o 61 0.995∠-25.016o 101 0.993∠-8.845o 22 0.934∠-84.928 o 62 0.998∠-25.774o 102 0.992∠-6.111o 23 0.984∠-73.858o 63 0.968∠-26.293o 103 1.001∠-14.060o 24 0.992∠-65.346o 64 0.983∠-24.252o 104 0.971∠-16.799o 25 1.050∠-72.959o 65 1.005∠-20.390o 105 0.965∠-17.907o 26 1.015∠-74.257o 66 1.050∠-22.267o 106 0.961∠-18.161o 27 0.968∠-85.990o 67 1.020∠-24.659o 107 0.952∠-20.965o 28 0.961∠-89.093o 68 1.001∠-14.108o 108 0.966∠-19.106o 29 0.963∠-91.622o 69 1.035∠0.000o 109 0.967∠-19.559o 30 0.906∠-96.025o 70 0.984∠-23.551o 110 0.973∠-20.405o 31 0.967∠-92.053o 71 0.980∠-27.609o 111 0.980∠-18.760o 32 0.964∠-87.063o 72 0.980∠-47.232o 112 0.975∠-23.505o 33 0.936∠-95.315o 73 0.991∠-27.899o 113 0.993∠-99.720o 34 0.986∠-81.370o 74 0.958∠-19.388o 114 0.961∠-87.174o 35 0.976∠-81.423o 75 0.960∠-16.340o 115 0.961∠-87.144o 36 0.980∠-81.413o 76 0.943∠-16.842o 116 1.005∠-14.555o 37 0.967∠-80.527o 77 1.006∠-10.793o 117 0.974∠-147.978o 38 0.835∠-75.715o 78 1.003∠-11.249o 118 0.945∠-17.042o 39 0.961∠-77.780o 79 1.009∠-11.243o 40 0.970∠-75.315o 80 1.040∠-9.812o
(续)

节点 电压(pu) 节点 电压(pu) 节点 电压(pu)10 1.050∠14.056o 50 1.002∠1.976o 90 0.985∠6.967o 11 0.985∠-8.826o 51 0.969∠1.322o 91 0.980∠6.988o 12 0.990∠-9.346o 52 0.960∠0.881o 92 0.990∠7.532o 13 0.969∠-10.201o 53 0.947∠1.312o 93 0.986∠4.514o 14 0.984∠-10.061o 54 0.955∠3.268o 94 0.990∠2.358o 15 0.970∠-10.351o 55 0.952∠3.480o 95 0.980∠1.372o 16 0.984∠-9.676o 56 0.954∠3.381o 96 0.992∠1.188o 17 0.995∠-7.929o 57 0.971∠2.370o 97 1.011∠1.702o 18 0.973∠-10.108o 58 0.960∠1.895o 98 1.024∠1.289o 19 0.962∠-10.541o 59 0.985∠13.278o 99 1.010∠0.855o 20 0.958∠-10.072o 60 0.993∠9.819o 100 1.017∠1.790o 21 0.959∠-8.784o 61 0.995∠10.325o 101 0.992∠3.345o 22 0.970∠-6.571o 62 0.998∠8.932o 102 0.989∠6.032o 23 1.000∠-2.188o 63 0.974∠11.052o 103 1.010∠-1.951o 24 0.992∠-3.227o 64 0.987∠9.782o 104 0.971∠-4.521o 25 1.050∠5.408o 65 1.005∠7.308o 105 0.965∠-5.625o 26 1.015∠7.462o 66 1.050∠8.682o 106 0.961∠-5.885o 27 0.968∠-7.073o 67 1.020∠7.988o 107 0.952∠-8.686o 28 0.962∠-8.710o 68 1.002∠3.647o 108 0.966∠-6.825o 29 0.963∠-9.605o 69 1.035∠0.000o 109 0.967∠-7.278o 30 0.986∠-2.774o 70 0.984∠-5.415o 110 0.973∠-8.124o 31 0.967∠-9.454o 71 0.987∠-5.508o 111 0.980∠-6.479o 32 0.963∠-7.639o 72 0.980∠-4.989o 112 0.975∠-11.224o 33 0.971∠-10.595o 73 0.991∠-5.719o 113 0.993∠-8.026o 34 0.984∠-9.520o 74 0.958∠-6.535o 114 0.960∠-7.964o 35 0.980∠-9.975o 75 0.968∠-5.337o 115 0.960∠-7.971o 36 0.980∠-9.975o 76 0.943∠-5.934o 116 1.005∠3.205o 37 0.991∠-9.062o 77 1.006∠-0.238o 117 0.974∠-10.887o 38 0.961∠-4.064o 78 1.002∠-0.432o 118 0.950∠-6.078o 39 0.971∠-12.056o 79 1.009∠0.080o 40 0.970∠-12.906o 80 1.040∠2.918o
[1] 姜涛, 李雪, 李国庆, 等. 含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J]. 电工技术学报, 2022, 37(7): 1746-1759.Jiang Tao, Li Xue, Li Guoqing, et al. A predictorcorrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1746-1759.
[2] 刘明凯, 王占山, 邢彦丽. 基于强化多目标差分进化算法的电-气互联系统最优潮流计算[J]. 电工技术学报, 2021, 36(11): 2220-2232.Liu Mingkai, Wang Zhanshan, Xing Yanli. Enhanced multi-objective differential evolutionary algorithm based optimal power flow calculation for integrated electricity and gas systems[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2220-2232.
[3] 王晨旭, 唐飞, 刘涤尘, 等. 基于双层代理模型的概率-区间潮流计算及灵敏度分析[J]. 电工技术学报, 2022, 37(5): 1181-1193.Wang Chenxu, Tang Fei, Liu Dichen, et al.Probabilistic-interval power flow and sensitivity analysis using double layer surrogate method[J].Transactions of China Electrotechnical Society, 2022,37(5): 1181-1193.
[4] 胡健, 付立军, 马凡, 等. 基于仿射算术优化的不确定系统区间潮流快速分解法[J]. 电工技术学报,2016, 31(23): 125-131.Hu Jian, Fu Lijun, Ma Fan, et al. Fast decoupled power flow calculation of uncertainty system based on interval affine arithmetic optimization[J].Transactions of China Electrotechnical Society, 2016,31(23): 125-131.
[5] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429-4443, 4481.Jiang Tao, Zhang Yong, Li Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4429-4443,4481.
[6] 卢志刚, 程慧琳, 冯磊. 基于支路功率选取的功率扩展潮流计算[J]. 电工技术学报, 2013, 28(6): 208-215.Lu Zhigang, Cheng Huilin, Feng Lei. Extended-power load flow calculation based on selection of branch power[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 208-215.
[7] 王家融, 艾欣, 王坤宇, 等. 基于增广雅可比矩阵的交直流解耦潮流新算法[J]. 电工技术学报, 2018,33(6): 1382-1389.Wang Jiarong, Ai Xin, Wang Kunyu, et al. A novel AC-DC decoupled power flow calculation method based on the augmented Jacobian matrix[J].Transactions of China Electrotechnical Society, 2018,33(6): 1382-1389.
[8] Overbye T J. A power flow measure for unsolvable cases[J]. IEEE Transactions on Power Systems, 1994,9(3): 1359-1365.
[9] Granville S, Mello J C O, Melo A C G. Application of interior point methods to power flow unsolvability[J].IEEE Transactions on Power Systems, 1996, 11(2):1096-1103.
[10] Barboza L V, Salgado R. Unsolvable power flow analysis-an approach based on interior point nonlinear optimization methods[C]//2001 IEEE Porto Power Tech Proceedings (Cat. No.01EX502), Porto, Portugal,2002, 2: 6.
[11] Van Cutsem T. An approach to corrective control of voltage instability using simulation and sensitivity[J].IEEE Transactions on Power Systems, 1995, 10(2):616-622.
[12] 陶向红, 卜广全, 王虹富, 等. 基于加权最小绝对值的大电力系统潮流可行解优化恢复方法[J]. 电力系统自动化, 2014, 38(23): 60-64, 76.Tao Xianghong, Bu Guangquan, Wang Hongfu, et al.An optimization method based on weighted least absolute value to restore power flow solvability of bulk power system[J]. Automation of Electric Power Systems, 2014, 38(23): 60-64, 76.
[13] 李智欢, 韩云飞, 苏寅生, 等. 基于节点类型转换的潮流收敛性调整方法[J]. 电力系统自动化, 2015,39(7): 188-193.Li Zhihuan, Han Yunfei, Su Yinsheng, et al. A convergence adjustment method of power flow based on node type switching[J]. Automation of Electric Power Systems, 2015, 39(7): 188-193.
[14] 李敏, 陈金富, 陈海焱, 等. 一类潮流计算无解的实用性调整研究[J]. 电力系统自动化, 2006, 30(8):11-15.Li Min, Chen Jinfu, Chen Haiyan, et al. Load flow regulation for unsolvable cases in a power system[J].Automation of Electric Power Systems, 2006, 30(8):11-15.
[15] Jiang Tong, Feng Zhuocheng, Wan Kaiyao, et al. A power flow adjustment strategy based on weak bus identification and new bus type conversion[J].International Journal of Electrical Power & Energy Systems, 2022, 137: 107705.
[16] 王虹富, 陶向红, 李柏青, 等. 基于虚拟中点功率的潮流估算模型[J]. 中国电机工程学报, 2018,38(21): 6305-6313, 6492.Wang Hongfu, Tao Xianghong, Li Baiqing, et al. An approximate power flow model based on virtual midpoint power[J]. Proceedings of the CSEE, 2018,38(21): 6305-6313, 6492.
[17] 张松涛, 张东霞, 黄彦浩, 等. 基于改进直流潮流算法的潮流计算收敛自动调整方法研究[J]. 电网技术, 2021, 45(1): 86-97.Zhang Songtao, Zhang Dongxia, Huang Yanhao, et al.Research on automatic power flow convergence adjustment method based on modified DC power flow algorithm[J]. Power System Technology, 2021, 45(1):86-97.
[18] 王甜婧, 汤涌, 郭强, 等. 基于知识经验和深度强化学习的大电网潮流计算收敛自动调整方法[J].中国电机工程学报, 2020, 40(8): 2396-2406.Wang Tianjing, Tang Yong, Guo Qiang, et al.Automatic adjustment method of power flow calculation convergence for large-scale power grid based on knowledge experience and deep reinforcement learning[J]. Proceedings of the CSEE, 2020, 40(8):2396-2406.
[19] Wu Shuang, Hu Wei, Lu Zongxiang, et al. Power system flow adjustment and sample generation based on deep reinforcement learning[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(6): 1115-1127.
[20] 郭烨, 吴文传, 张伯明, 等. 节点类型扩展潮流计算的应用研究[J]. 中国电机工程学报, 2011, 31(16):81-87.Guo Ye, Wu Wenchuan, Zhang Boming, et al.Application research on bus-type extended load flow[J]. Proceedings of the CSEE, 2011, 31(16): 81-87.
[21] 郭烨, 张伯明, 吴文传. 节点类型扩展潮流计算及其可解性研究[J]. 中国电机工程学报, 2011, 31(13):79-85.Guo Ye, Zhang Boming, Wu Wenchuan. Study on bustype extended load flow and its solvability[J].Proceedings of the CSEE, 2011, 31(13): 79-85.
[22] 姜涛, 张明宇, 李雪, 等. 静态电压稳定域局部边界的快速搜索新方法[J]. 中国电机工程学报, 2018,38(14): 4126-4137, 4318.Jiang Tao, Zhang Mingyu, Li Xue, et al. A novel algorithm to explore static voltage stability region boundary in power systems[J]. Proceedings of the CSEE, 2018, 38(14): 4126-4137, 4318.
[23] Barboza L V, Francisco J B, Zambaldi M C. Restoring solution of electric network equations: an approach using the augmented lagrangean algorithm[J]. IEEE Latin America Transactions, 2010, 8(6): 670-677.
[24] Wan Kaiyao, Jiang Tong. Augmented system for detecting the steady-state voltage stability margin[J].IET Generation, Transmission & Distribution, 2020,14(21): 4788-4795.
[25] Jiang Tong, Wan Kaiyao, Feng Zhuocheng. Boundaryderivative direct method for com pu ting saddle node bifurcation points in voltage stability analysis[J].International Journal of Electrical Power & Energy Systems, 2019, 112: 199-208.
[26] Daniel Zimmerman R, Murillo-Sánchez C E, Thomas R J. MATPOWER: steady-state operations, planning,and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems,2011, 26(1): 12-19.