0 引言
为适应电气化铁路安全高效、经济环保的发展理念,助力实现“双碳”目标,当前铁路牵引供电系统正朝着柔性化、智能化的方向发展,越来越多的新型电气化铁路牵引供电系统方案被提出[1-2],如:基于电力电子变压器的贯通柔性牵引供电系统[3-4],基于模块化多电平换流器(Modular Multilevel Converter, MMC)的24 kV 柔性直流牵引供电系统[5]。其中,24 kV 柔性直流牵引供电系统因不存在机车过分相问题,牵引变电所(Traction Substation, TSS)供电距离长,可高效接纳利用光伏、风电等新能源和储能等优势,受到了国内外学者的广泛关注。自2014 年西班牙学者首次提出该系统以来,相关文献仅对该新型牵引供电系统的供电结构[5]、运行控制方案[6-8]、稳定性[9-10]问题做过报道,关于该系统的诸多研究仍处于探索阶段,诸多相关理论与技术难点亟待突破。为充分认识系统运行原理及规律,亟须全面探讨该系统的供电特性。
牵引网稳态潮流计算是模拟供电系统运行的一种基本方法,可以作为分析系统供电特性的工具。然而据作者所知,当前鲜有关于该系统潮流计算方法的报道。对于24 kV 柔性直流牵引供电系统而言,牵引网全线贯通,各个变电所以及牵引负荷互相连通,牵引变电所之间的电压和功率存在强耦合关系,而传统 25 kV 交流牵引供电系统采用单边供电模式,已有的分析方法显然无法直接用来求解该系统的潮流问题。同样作为交直流混合电力网络,地铁直流牵引供电系统、高压直流输电以及柔性直流输电系统的交直流混合潮流计算已有较多研究。目前,相关研究主要聚焦于两方面:一方面侧重于计算方法,针对交直流混合网络中交替迭代法与统一迭代法存在的不足进行改进,重点分析潮流计算效率、收敛性,以及交直流耦合变量的转换关系等[11-14];另一方面为求解交直流系统最优潮流问题[15-17]。以上两方面的研究中,较少系统地考虑换流站间复杂的协调控制对潮流的影响。
24 kV 柔性直流牵引供电系统采用MMC 作为电能变换的核心设备,可实现牵引网潮流的灵活控制,潮流迭代计算的核心在于考虑多层级控制对潮流分布的影响。此外,为了保证供电可靠性,通常情况下系统中各个牵引变电所交流侧接入不同的外部源,不同变电所交流侧之间无直接耦合关系,该系统重点关注直流牵引网的潮流求解。文献[18]详细分析了定电压、定有功、下垂制策略下直流电网潮流求解模型与计算方法,但未探讨多层级系统控制对电网潮流分布的调节作用。文献[19]基于牵引网最优潮流提出了考虑逆变回馈装置的地铁牵引供电系统能量管理方案,侧重点在于交直流潮流迭代计算的转换与最优潮流算法。文献[20]研究了电压源换流器型地铁柔性直流牵引供电系统中改进下垂控制的潮流计算方法,在潮流迭代过程中通过动态修改下垂系数和初始电压体现系统级控制对牵引网潮流的影响,然而在24 kV 柔性直流牵引供电系统中,为了实现多层级控制目标,系统级控制通常包含多个比例积分(Proportional-Integral, PI)控制器,上述方法没有体现系统级PI 控制器对牵引网潮流调节的过程。
由于研究对象的拓扑结构、控制方案的差异,现有文献中所提出的计算方法不能完全适用于求解24kV 柔性直流牵引供电系统潮流问题,因此本文提出一种将系统级PI 控制方程的迭代嵌入潮流计算方法,可在不同控制策略下求解该系统直流牵引网潮流。首先建立“控制器-源-网-车”一体化潮流计算模型;然后推导牵引变电所、机车、牵引网首末端切面在潮流计算中的等效处理方法,并分析潮流迭代过程与控制器迭代的交互关系。在连续线性潮流法(Sequential Linear Power Flow Method,SLPFM)和PI 控制器交替迭代过程中,PI 控制器的输出动态修正潮流计算初始电压值,体现系统级控制对牵引网潮流的调节作用,结果表明潮流计算可以稳定收敛。进一步地,基于潮流计算,以机车运行电压、接触网载流量为限制条件,给出24 kV柔性直流牵引供电系统供电距离的分析方法。最后研究了不同控制方案下接触网电压水平、钢轨电位与杂散电流、系统效率、牵引变电所容量等供电特性的差异。
1 24 kV 柔性直流牵引供电系统
1.1 系统结构
24 kV 柔性直流牵引供电系统结构示意图如图1 所示,牵引变电所从220 kV/110 kV 区域电网引入三相交流电,经过牵引变压器降压至与MMC 交流侧匹配的电压等级,通过三相MMC 整流后馈送至接触网。为满足电气化铁路高电压、大功率的应用场合的需求,该系统选择MMC 作为交直流变换设备。此外,牵引变压器低压侧母线通过电力变压器再次降压后供给变电所内设备用电。根据接触网分段检修的要求,同时为了缩小事故发生时的停电范围,直流接触网应设置若干分段。图1 中在牵引变电所出口处及分区所处均设置了电分段,系统正常运行时,电分段处开关连通不同供电区间的接触网,牵引网实现全线贯通供电,牵引网某处发生故障后,根据系统继电保护配置方案,各分段处开关动作以隔离故障区段,保障系统安全稳定运行。
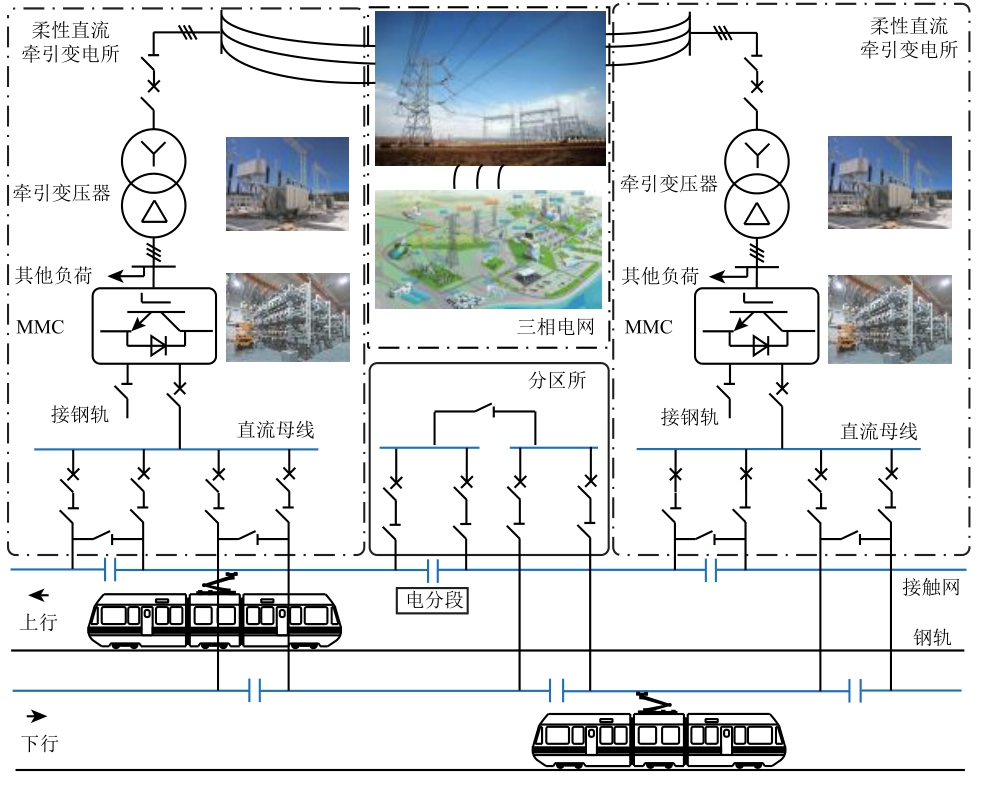
图1 柔性直流牵引供电系统
Fig.1 Flexible DC traction power system
1.2 柔性直流牵引供电系统运行方式与控制方法
贯通供电方式下,多个并联运行牵引变电所之间电压、功率的协调控制是系统稳定运行的关键,文献[6-8]提出了多种适用于24 kV 柔性直流牵引供电系统的控制策略,其主要可分为三类,见表1。
表1 柔性直流牵引供电系统控制方案
Tab.1 Control schemes of flexible DC TPS

方案 控制方法 电压控制方程1下垂控制 Ud=UN-Pdkd下垂控制+电压平均值调节 Ud=UN-Pdkd+δu 3 下垂控制+电压平均值调节+输出功率调节 Ud=UN-Pdkd+δu+δp 2
方案1 中每个牵引变电所均采用传统功率-电压下垂控制,实现机车功率就近分配,其中Ud 为牵引变电所期望输出电压值,UN 为系统额定电压值,Pd 为牵引变电所实际输出功率值,kd 为牵引变电所的下垂系数。
方案2 在功率-电压下垂控制的基础上增加电压调节器,牵引变电所采用分布式协调控制。每个牵引变电所的电压调节器利用通信获取其他牵引变电所的输出电压后,通过PI 控制器计算该牵引变电所输出电压修正量δu,控制全线牵引变电所输出电压平均值达到系统额定电压UN,补偿下垂控制带来的电压跌落,维持牵引变电所输出直流电压的稳定。控制方程中δu 为牵引变电所电压调节器的输出,由式(1)计算得到。
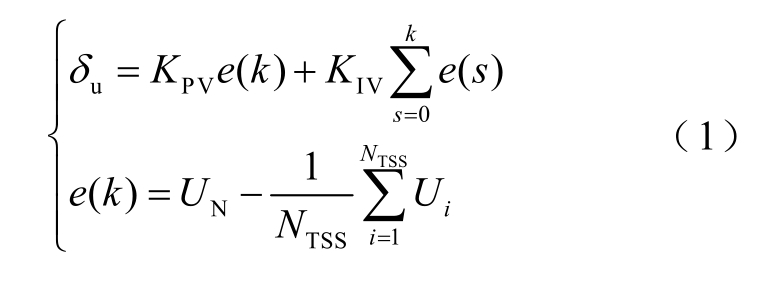
式中,KPV 和KIV 分别为电压调节器的比例系数和积分系数;e(k)、e(s)为偏差信号;NTSS 为牵引变电所的数量;Ui 为第i 个牵引变电所的输出电压值。
方案3 在方案2 的基础上进一步增加输出功率调节器,牵引变电所同样采用分布式协调控制。每个牵引变电所功率调节器利用通信获取其他牵引变电所的输出功率后,通过PI 控制器计算该牵引变电所输出电压修正量δp,控制牵引变电所按照各自容量的比例来分担全线所有机车的功率。为简化分析,后文中设置所有牵引变电所等容量,即采用均分功率控制策略。控制方程中δp 为牵引变电所功率调节器的输出,由式(2)计算得到。
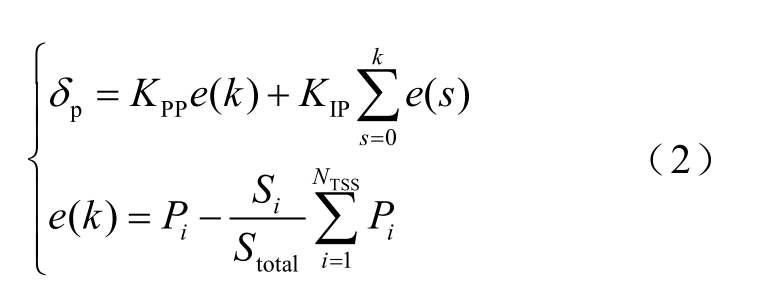
式中,Pi 为第i 个牵引变电所的实际输出功率;Si 和Stotal 分别为第i 个牵引变电所的额定容量和全线所有牵引变电所的额定容量的总和;KPP 和KIP 分别为功率调节器的比例系数和积分系数。
2 系统建模
2.1 “源-网-车”等效建模
柔性直流牵引供电系统的“源”模型如图2 所示。图2 中,点画线框中为MMC 的等效电路,由于潮流计算主要关注系统稳态时的电压与功率分布,所以只需建立其简化等效电路,这里省略了详细的电磁暂态模型的构建。其中,MMC 交流侧等效为一交流源,同时串联有滤波电抗器Zc,牵引变压器与电抗器连接点处电压相量为Uc∠δc,Pc+jQc 为注入MMC 的功率,连接在牵引变压器低压侧母线的站内其他负荷为Pf+jQf。根据牵引供电系统不同的系统级控制策略,直流侧等效为实际直流电压源或者功率源,两种模式可根据系统运行状态的不同而进行切换。此外,柔性直流牵引供电系统的特点在于可通过对牵引变电所的控制实现电压与潮流分布的灵活控制,因此,电压源的直流电压和内阻、功率源的功率将根据不同的控制策略在潮流计算的迭代过程中不断更新,实现系统级控制对牵引变电所潮流的调节,Ud、Id 和Pd 分别为牵引变电所出口处的电压、电流和功率。Zt 表示换流变压器的等效阻抗,牵引变压器高压侧为牵引供电系统与三相电网的公共连接点,该点的电压为Us∠δs,Ps+jQs 为三相电网注入牵引变电所的功率,Es 和Zs 分别代表三相交流电网电压和输电线路阻抗。
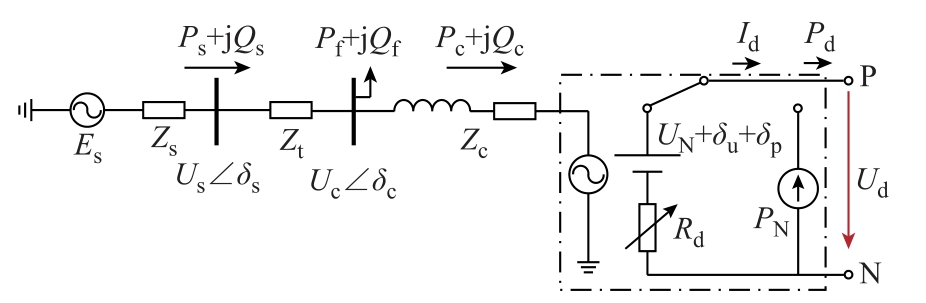
图2 柔性直流牵引供电系统“源”模型
Fig.2 “Source” model of flexible DC TPS
柔性直流牵引网结构示意图如图3 所示,其中接触网由接触线和承力索构成,构成牵引网的正极,钢轨为负极。直流供电系统中,钢轨与道床之间放置绝缘垫,减小牵引电流泄漏进入大地。此外,每400~600 m 会设置均流线,将上、下行共4 根钢轨进行并联,以此减小钢轨电位,保证供电安全,同时进一步减小杂散电流。潮流计算中直流牵引网导体等效为电阻网络。
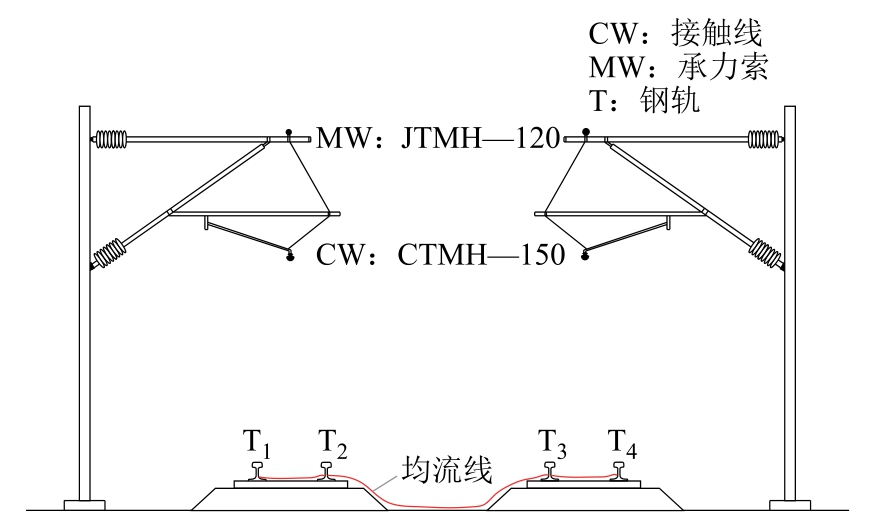
图3 柔性直流牵引网结构示意图
Fig.3 Structure diagram of traction network
柔性直流牵引供电系统中机车结构示意图如图4 所示。机车牵引传动系统完成直-直-交两级电能变换,其中输入串联输出并联(Input Series Output Parallel, ISOP)的双有源全桥变换器(Dual Active Bridge, DAB)降低接触网直流电压,同时,可以在列车制动时将再生制动能量返送回接触网,牵引逆变器将降压后的直流电逆变为三相交流电,驱动异步牵引电机。在潮流计算的某一时刻,认为机车功率大小是确定的,机车功率可结合线路信息与行车运行图进行机车牵引计算得到,本文潮流计算中机车采用功率源模型。
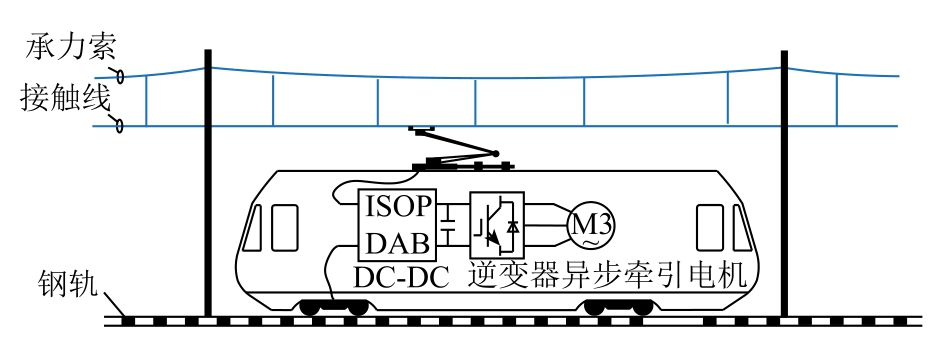
图4 机车结构示意图
Fig.4 Structure diagram of locomotives
2.2 柔性直流牵引供电系统统一建模
24 kV 柔性直流牵引供电系统的“源-网-车”潮流计算模型如图5 所示。潮流计算中为了减小迭代计算规模,将并联的导体进行了合并简化。其中,接触线与承力索通过吊弦并联构成牵引网的正极,故将上行接触线与承力索合并为同一根导体,二者的并联电阻为Rc,下行线路相同。均流线使上、下行四条钢轨并联为同一根导体。牵引网地回流模型较为复杂,包括地回流和结构钢筋回流,但这一部分对系统潮流影响较小,故省略此部分的精确建模,将回流轨等效为π 模型,Rr 为钢轨和回流线的并联电阻,Rg 为钢轨与大地之间的泄漏电阻。简化后,源-网-车潮流计算模型从8 导体平行传输线路简化为3 导体平行传输线路,减小了迭代计算中矩阵的阶数,可在满足计算精度的前提下,提高潮流计算速度。
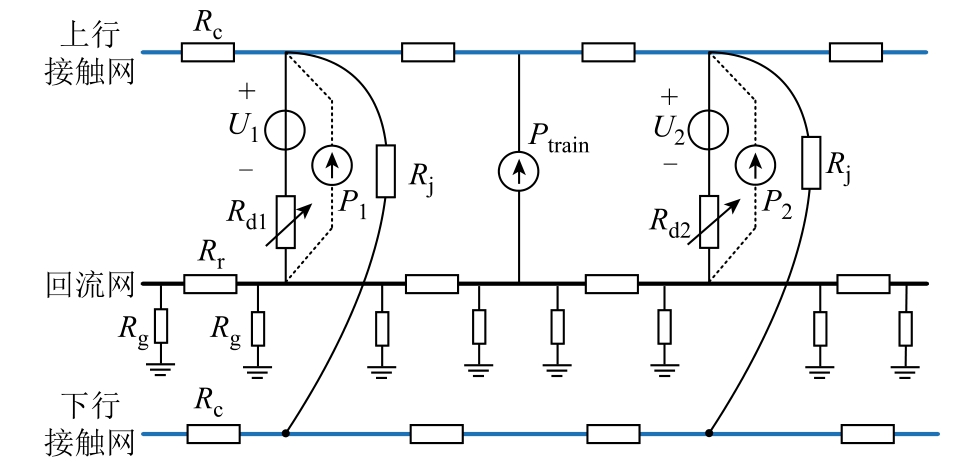
图5 柔性直流牵引供电系统“源-网-车”潮流计算模型
Fig.5 “Source-network-train” power flow calculation model of flexible DC TPS
将图5 中柔性直流牵引供电系统多导体平行传输线路根据不同切面的划分等效为如图6 所示的“源-网-车”统一链式电路模型。本文在潮流计算中划分了三类切面,分别为牵引变电所切面,机车切面,以及牵引网首、末端切面。图6 中Zi-1 为两个切面之间串联元件的阻抗矩阵,Yi 为切面i 处纵向元件不同节点之间的导纳矩阵,Ii 为切面i 处的电流矩阵,以注入为正,Ui 为切面i 处的电压矩阵。由于系统等效为3 导体平行传输线路,Yi 和Zi-1 为3×3 的子矩阵,Ui 和Ii 为3 维列向量,根据图6 链式电路模型可以列写出系统节点导纳矩阵 G,为3N×3N 方阵。
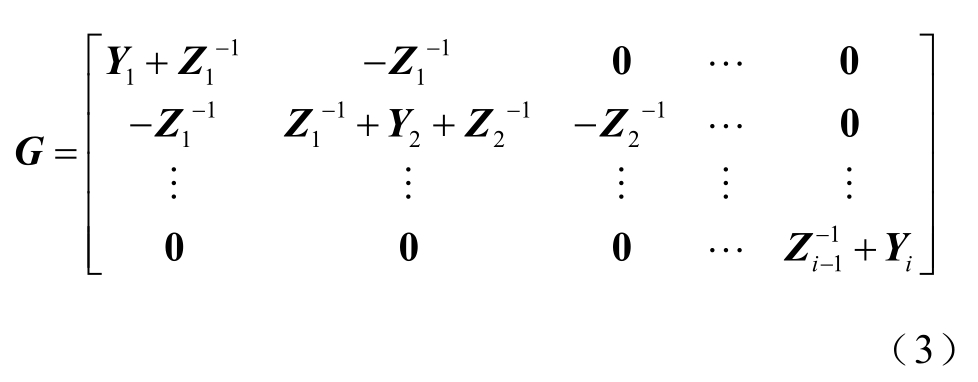
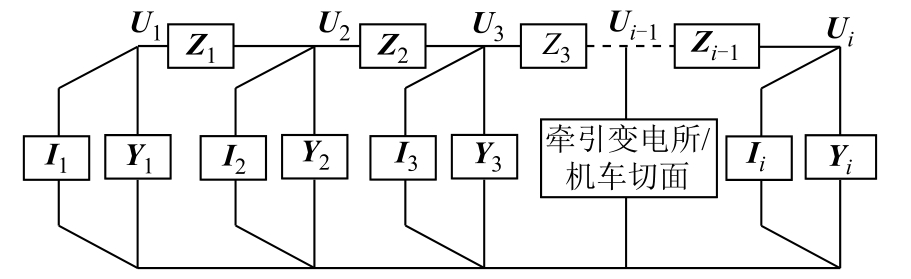
图6 柔性直流牵引供电系统“源-网-车”链式电路模型
Fig.6 “Source-network-train” chain circuit model of flexible DC TPS
同样根据图6,可得系统节点电压方程如式(4),利用连续线性潮流法,即通过式(4)迭代求解牵引网潮流。
3 计及控制的潮流计算方法
3.1 计及站级下垂控制的柔性直流牵引网潮流计算方法
根据图2 所示建模方法,牵引变电所在正常运行工况时,变流器直流侧等效为直流电压源,牵引变电所输出电压为
式中,Rd 等于电压源内阻,同时也可将Rd 看作电流-电压下垂曲线中的虚拟下垂电阻。利用图2 所建电压源模型进行潮流迭代计算得到的牵引变电所输出电压自然满足电流-电压下垂特性。
而表1 所述控制方案中,牵引变电所采用了功率-电压下垂控制,在利用电压源模型进行潮流计算前需要对牵引变电所电压控制方程进行转换,即
将功率Pd 转换为电压与电流的乘积,将Ud 与kd 的乘积等效为电流-电压下垂控制中的虚拟电阻Rd。通过等效变换后,即可利用图2 所示模型进行潮流迭代计算,在每次迭代前需要根据牵引变电所输出电压与下垂系数kd 更新电压源阻抗Rd,然后进行潮流迭代计算,即可求解符合功率-电压下垂特性的牵引变电所潮流。
在潮流计算的每一时刻,潮流迭代程序均要完成一次完整的潮流迭代计算,求解出每一时刻下系统的潮流分布。在某一时刻,由行车运行图确定各个机车的位置和功率后,由式(4)进行潮流迭代计算。初始状态下,设定各个切面初始电压子矩阵U (0) =[UN 0 UN],求取切面注入电流子矩阵I (0)和系统初始导纳矩阵 G (0),根据迭代式 U(1)=(G (0))-1I (0)计算,得到节点电压新值U (1)后,更新系统节点导纳矩阵G (1)与电流矩阵I (1)。以此规律迭代至每一个节点电压误差均小于收敛精度时迭代结束。
对于牵引变电所切面,获得切面电压矩阵后,首先计算等效电压源内阻Rd=Udkd,再将电压源模型等效变化为电流源模型,以此求得牵引变电所切面的电流矩阵I=[UN/Rd -UN/Rd 0],同时牵引变电所切面上行接触网节点与钢轨节点之间通过电源内阻Rd 连接,节点导纳矩阵G 中相应位置元素在每一次迭代时需进行更新。
机车切面在每次迭代时只需根据前一步迭代电压值求取切面电流矩阵,上行机车所在切面I=[-Ptrain/(UT1-UR) Ptrain/(UT1-UR) 0],其中Ptrain、UT1、UR 分别为机车功率、上行接触网节点电压以及钢轨节点电位。下行机车所在切面 I=[0 Ptrain/(UT2-UR) -Ptrain/(UT2-UR)],其中UT2 为下行接触网节点电压。
牵引网首端与末端切面6 个节点作为无源节点,切面电流矩阵I 为零矩阵。
3.2 计及系统级控制的柔性直流牵引网潮流计算方法
本文在1.2 节中介绍了两种系统级控制方案以实现牵引网电压和功率的协调控制,系统级控制器通过控制方程进行多次迭代,修正牵引变电所输出电压,最终达到控制目标。本文提出采用潮流计算与系统级PI 控制器交替迭代的方法计算考虑多层控制的24 kV 柔性直流牵引网潮流,计及下垂控制的潮流计算与系统级PI 控制的交替迭代过程如图7所示。首先SLPFM 进行一次计算,更新系统节点电压U 和节点功率P,各个牵引变电所的输出电压Ud和输出功率Pd 作为系统级PI 控制器的输入参数,根据式(1)、式(2)完成一次PI 迭代计算,得到控制参数δu、δp,该参数修正牵引变电所初始电压值UN,作为下一次SLPFM 计算的边界条件,如此交替迭代至系统电压收敛。需要说明的是,潮流计算前需根据系统控制方案选择不同的修正方程,此外,需要为电压调节器与功率调节器选取适当的PI控制参数,否则潮流迭代会出现不收敛或者收敛时无法达到控制目标的情况。
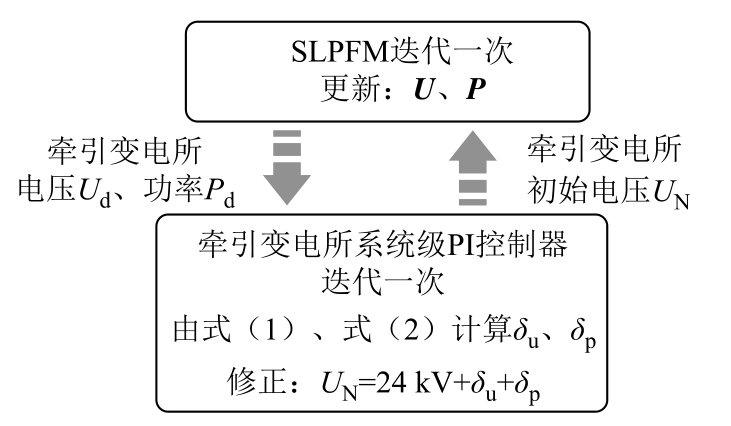
图7 SLPFM-PI 交替迭代过程
Fig.7 SLPFM-PI alternating iteration
当潮流计算中引入电压调节器修正量δu或功率调节器修正量δp 后,在迭代计算的初始阶段,UN 会出现较大的波动,使得单次SLPFM 计算后系统节点电压U 更新较快,导致迭代无法收敛。此时可以引入收敛因子α,利用式(7)减小单次SLPFM 法更新电压新值的速度,保证迭代准确收敛[20]。
式中,U (k)为第k 次迭代时的系统节点电压矩阵;α为大于0 小于1 的数。
计及系统级控制的 24 kV 柔性直流牵引供电系统潮流计算流程如图8 所示。图8 中,Δt 为潮流计算步长,通常选为1 s,SLPFM 与系统级PI 控制器交替迭代一次,记为潮流计算完成一次迭代,当电压矩阵所有元素的迭代误差均小于收敛精度时迭代结束。此外,如果潮流收敛时,某个牵引变电所输出功率越限,那么设定该牵引变电所切面连接电源的两个节点由下垂节点转为功率节点,牵引变电所以额定功率输出,重新计算此时刻牵引网潮流。
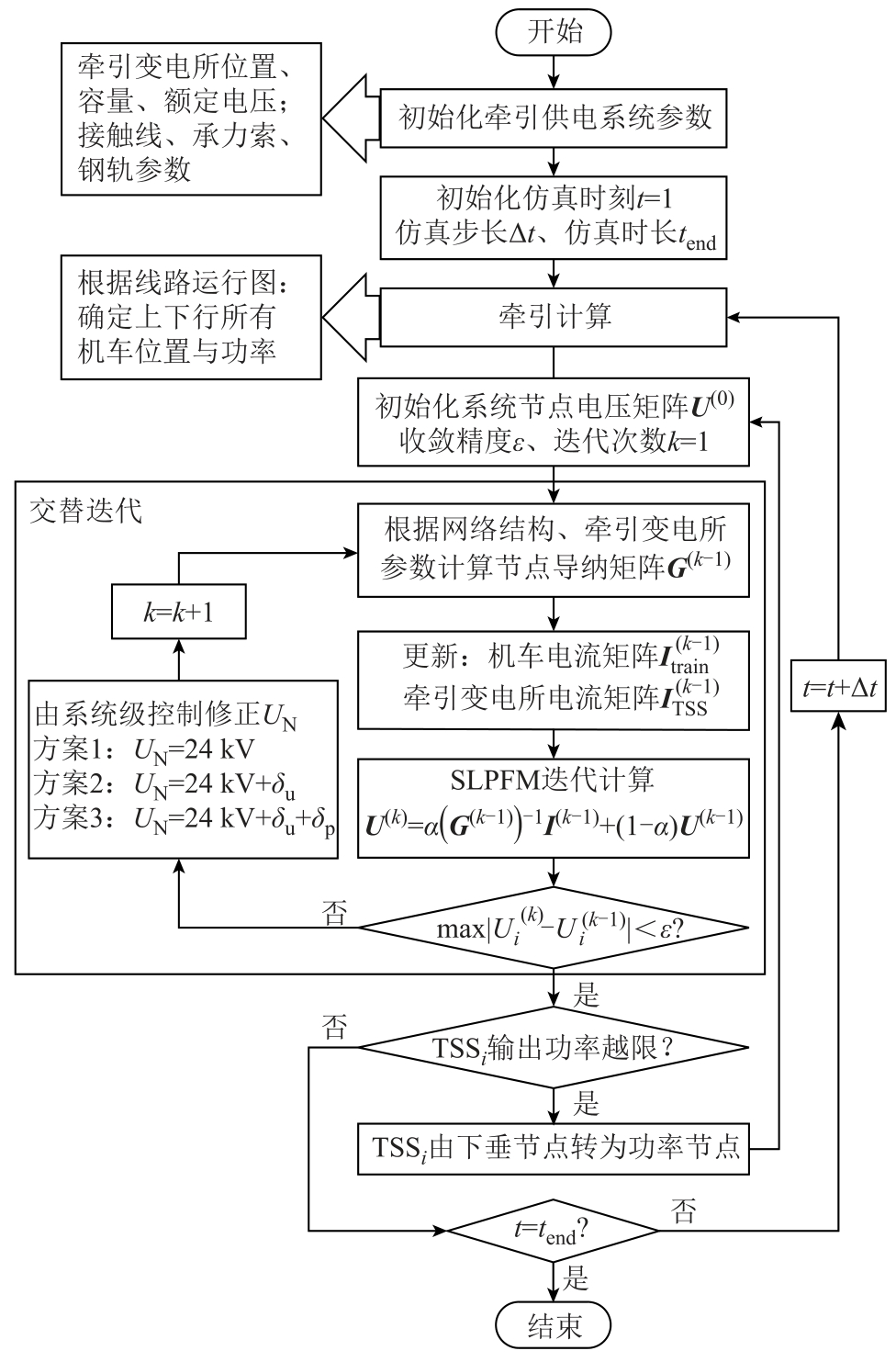
图8 24 kV 柔性直流牵引供电系统潮流计算流程
Fig.8 The calculation flow chart of 24 kV flexible DC TPS power flow algorithm
3.3 潮流计算模型验证
为验证本文所提潮流计算方法的正确性,本文在Matlab/Simulink 仿真软件中搭建如图9 所示的24 kV 柔性直流牵引供电系统仿真模型。仿真系统由4 个牵引变电所和若干机车组成,每两个牵引变电所之间距离设置为L,首末端牵引变电所左、右侧单边供电区间距离设置为L/4。由于本节仅验证潮流计算的正确性,故暂将供电距离L 设置为80 km,同时在上行线路40 km、130 km 以及下行线路220 km处分别设置一辆机车,功率均为10 MW。此外,仿真中牵引网直流电阻参数见表2,牵引变电所功率-电压下垂系数kd 取1×10-5,潮流计算迭代精度取10-3,牵引变电所MMC 以及机车DAB 的控制方法见文献[6-8],本文不做详细介绍,Simulink 仿真中系统参数见附录。三种控制方案下,使用Simulink仿真与本文提出的潮流计算方法得到的牵引变电所输出电压、机车受电电压,牵引变电所输出功率、牵引网功率损失的计算结果见表3 和表4。可以看出:使用所提潮流计算方法计算的结果与Simulink仿真获得的结果基本相等,以Simulink 仿真值为基准,电压最大误差仅为 0.09%,功率最大误差为0.96%,说明本文所提潮流计算方法可以正确计算24 kV 柔性直流牵引供电系统在三种不同控制方案下的稳态潮流。
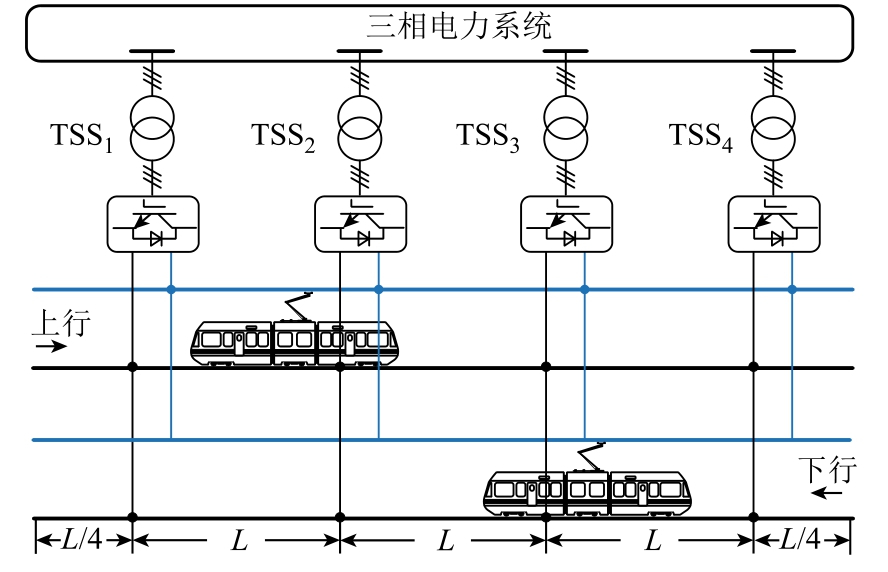
图9 潮流计算系统结构
Fig.9 TPS structure of power flow calculation
表2 牵引网直流电阻参数
Tab.2 TPS parameters of traction network DC resistance

参 数 数 值接触线(CTMH150)/(Ω/km) 0.184承力索(JTMH120)/(Ω/km) 0.242钢轨(P60)/(Ω/km/条) 0.04钢轨对地过渡电阻/(Ω·km) 15
表3 节点电压计算结果对比
Tab.3 Node voltage calculation comparison

方案 UTSS1 UTSS2 UTSS3 UTSS4 Utrain1 Utrain2 Utrain3潮流计算/kV 23.92 23.91 23.91 23.95 23.23 23.04 23.00 1Simulink/kV 23.92 23.91 23.91 23.95 23.21 23.02 22.98误差(%) 0.00 0.00 0.00 0.00 0.09 0.09 0.09潮流计算/kV 24.00 23.99 23.99 24.02 23.31 23.13 23.09 2Simulink/kV 24.00 23.99 23.99 24.02 23.30 23.11 23.08误差(%) 0.00 0.00 0.00 0.00 0.04 0.09 0.04潮流计算/kV 23.80 23.79 23.99 24.42 23.10 22.99 23.29 3Simulink/kV 23.80 23.78 23.99 24.42 23.09 22.97 23.28误差(%) 0.00 0.04 0.00 0.00 0.04 0.09 0.04
表4 功率计算结果对比
Tab.4 Power calculation comparison
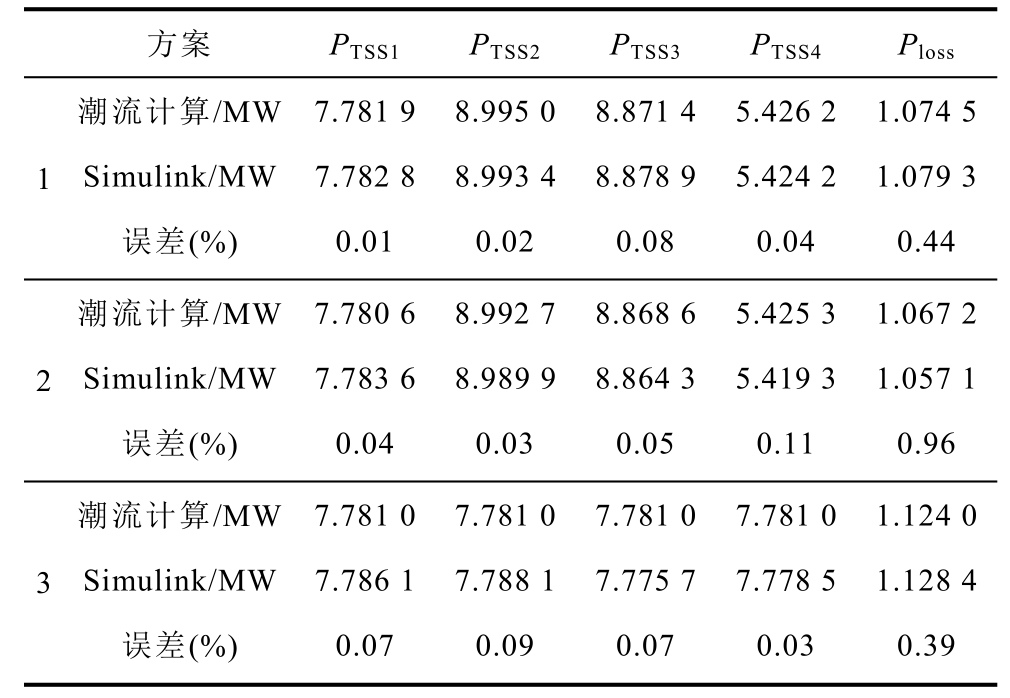
方案 PTSS1 PTSS2 PTSS3 PTSS4 Ploss潮流计算/MW 7.781 9 8.995 0 8.871 4 5.426 2 1.074 5 1 Simulink/MW 7.782 8 8.993 4 8.878 9 5.424 2 1.079 3误差(%) 0.01 0.02 0.08 0.04 0.44潮流计算/MW 7.780 6 8.992 7 8.868 6 5.425 3 1.067 2 2 Simulink/MW 7.783 6 8.989 9 8.864 3 5.419 3 1.057 1误差(%) 0.04 0.03 0.05 0.11 0.96潮流计算/MW 7.781 0 7.781 0 7.781 0 7.781 0 1.124 0 3 Simulink/MW 7.786 1 7.788 1 7.775 7 7.778 5 1.128 4误差(%) 0.07 0.09 0.07 0.03 0.39
4 供电距离分析
本节将利用第3 节中提出的潮流计算方法,定量分析24 kV 柔性直流牵引供电系统的供电距离。对于机车而言,其从接触网取流会在接触网纵向电阻上产生压降导致机车受电电压低于额定网压。合理的供电距离应使机车紧密运行时,全线接触网电压大于机车正常运行最低电压限值,同时接触网电流不能超过导体的载流量。
同样以图9 所示的24 kV 柔性直流牵引供电系统潮流计算模型为例,潮流计算参数设置同3.3 节案例。在本节案例中,设定上、下行机车运行速度均为350 km/h,功率为8 MW,发车间隔6 min,记录第一辆机车从牵引网首端发车至行驶到牵引网末端为止,机车运行全过程中牵引网各个节点电压、电流的动态变化情况。计算过程中,供电距离L 以5 km 的步长从80 km 增大到180 km,在每一个供电距离下,均使机车按照前述设定的运行图及工况运行。图10 分别给出了三种控制方案下,当L 取不同的值时,机车运行全过程中接触网电压的最小值、接触网电流的最大值,综合以上两个约束条件即可确定出系统采用不同控制方案时符合要求的牵引变电所最长供电距离。图中①~③分别代表控制方案1~方案3。
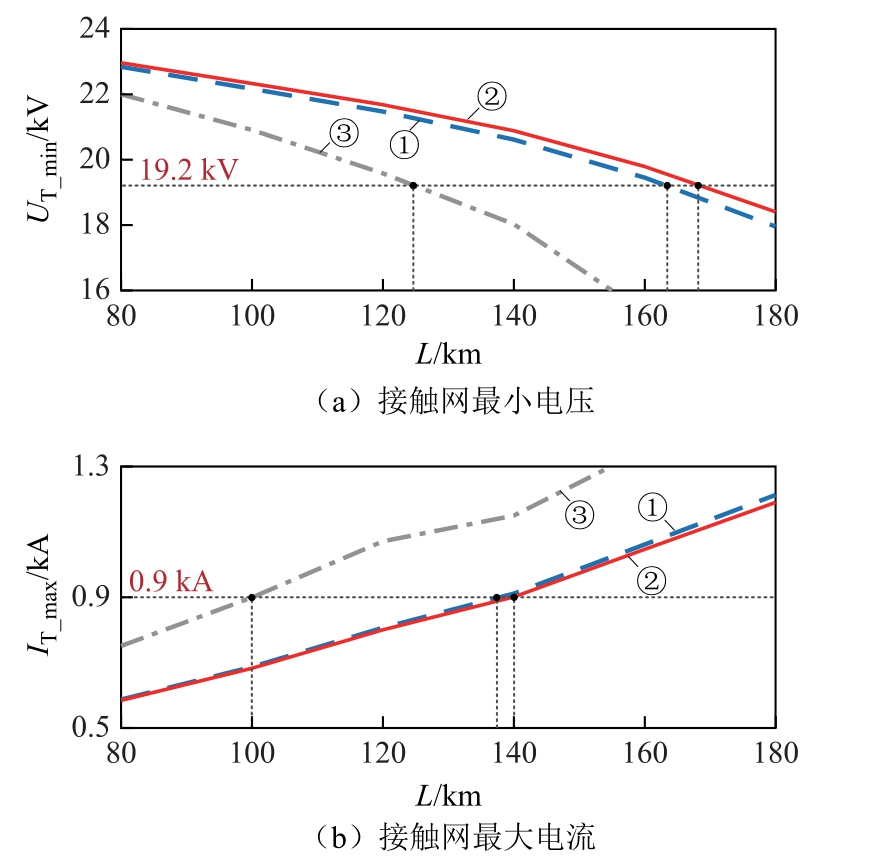
图10 供电距离计算结果
Fig.10 Results of power distance calculation
图10a 中将机车最小工作电压取为0.8 倍额定电压,即19.2 kV,根据这一限值,可以确定出三种控制方案下可以取得的最大供电距离分别为165 km、170 km、125 km。图10b 中取最高允许工作温度为95℃,JTMH120+CTMH150 接触网线索组合的持续工作载流量为900A,根据这一限值,可以最终确定最大供电距离取为135 km、140 km、100 km。方案2 相比于方案1 增加了输出电压平均值调节,补偿了下垂控制带来的电压跌落,故使用方案2 时最大供电距离略长于方案1。方案3 中跨区间功率传输使得部分牵引变电所电压被降低,导致该方案下供电距离小于前两种方案。综合上述分析,可以确定出三种控制策略下的最长供电距离,即方案1 为135 km,方案2 为140 km,方案3 为100 km。
从分析结果来看,相较于传统25 kV 交流牵引供电系统50 km 左右的供电距离,24 kV 柔性直流牵引变电所的供电距离大幅增加。这是由于:①直流供电系统中导体无趋肤效应,在同等工况下,牵引网阻抗更低;②直流供电系统中不存在电抗压降;③采用贯通供电,这些使得该系统中电压损失更小,系统供电能力得到了显著提升。
5 不同控制方案的运行特性对比
在第4 节供电距离计算的基础上,进一步在多车牵引、多车牵引-多车制动工况下对比分析使用三种控制方案时系统的运行特性。以图9 所示24 kV柔性直流牵引供电系统为例,潮流计算参数设置同3.3 节案例,结合第4 节供电距离计算结果,将L选定为100 km,在相同供电距离下对三种方案进行比较。
5.1 多车牵引
在本节案例中,设定上、下行机车运行速度均为350 km/h,单车功率8 MW,发车间隔6 min,记录第一辆机车从牵引网首端发车至行驶到牵引网末端为止,机车运行全过程中牵引网各个节点电压、功率的动态变化情况。
三种控制方案下机车运行过程中每一时刻牵引网最小电压如图11a 所示,从图中可以看出,在机车运行全过程中,牵引网最低电压均在21 kV 以上,电压水平较好。由于控制方案3 存在跨区间功率调配,部分牵引变电所电压会产生较大波动,所以该控制方案下牵引网最低电压普遍低于前两种方案。方案2 在方案1 下垂控制的基础上增加输出电压平均值调节,整体提升牵引网电压水平,所以方案2相比方案1 电压水平整体有所提升。
机车运行过程中每一时刻钢轨电位最大值以及杂散电流最大值如图11b、图11c 所示。本文分析中,杂散电流为经由轨-地过渡电阻流入大地的电流。从计算结果来看,方案1 与方案2 计算结果基本相同,方案3 的钢轨电位略大于方案1 与方案2,但三种方案下,钢轨电位最大值均小于150 V。在机车运行的初始阶段,由于机车密度小且位于牵引网的首末端,为使牵引变电所同等功率输出,方案3 存在跨区间大功率传输,使得杂散电流数值较大,最大值接近400 A,对于以功率就近分配为原则的方案1 与方案2,杂散电流最大值分布在200 A左右。
图11d 给出了三种方案下,机车运行过程中系统效率的变化趋势,在该系统中,系统损耗主要产生在牵引网导体的电能传输过程中,故本文未考虑牵引变电所换流器损耗,系统效率等于机车总功率除以牵引变电所输出总功率。从结果可以看到,在行车密度较小的前半程以及行车密度较大的后半程,方案1、2 下系统效率均高于方案3,表明机车功率就近分配可以有效减小供电损耗,方案2 提升了输出电压,整体效率略高于方案1,此外。三种方案下系统效率均在92%以上。
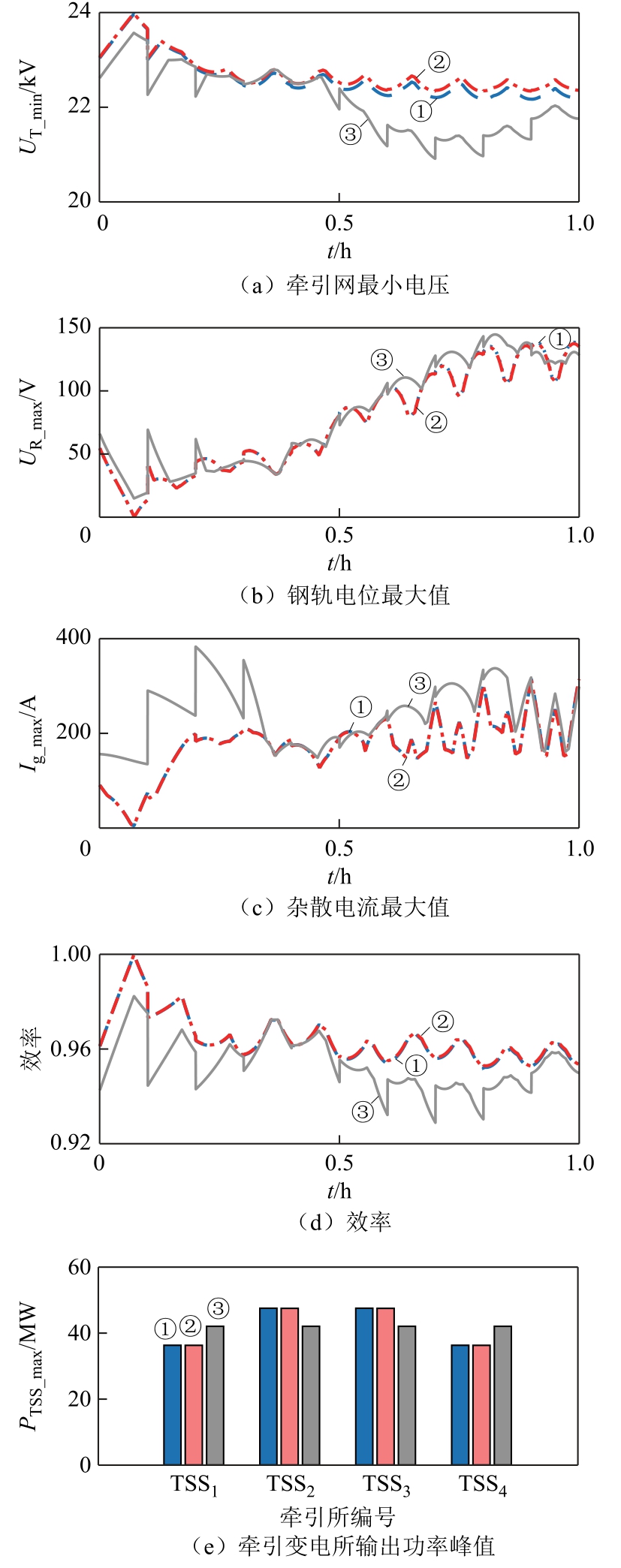
图11 不同控制方案下多车牵引工况计算结果
Fig.11 Calculation results of multi-locomotives traction condition under different control schemes
三种方案下,机车运行过程中四个牵引变电所的峰值功率如图11e 所示,方案1、2 采用机车功率就近分配策略,故中间牵引变电所需要配置更高的容量满足牵引负载的需要,在均分功率的控制策略下,方案3 中各个牵引变电所输出功率始终相同。
5.2 多车牵引-多车制动
在本节案例中,设定牵引网存在多车牵引、多车制动,上、下行机车位置及功率随机设定,机车位置功率信息见表5。
表5 机车位置功率信息
Tab.5 Position and power of trains
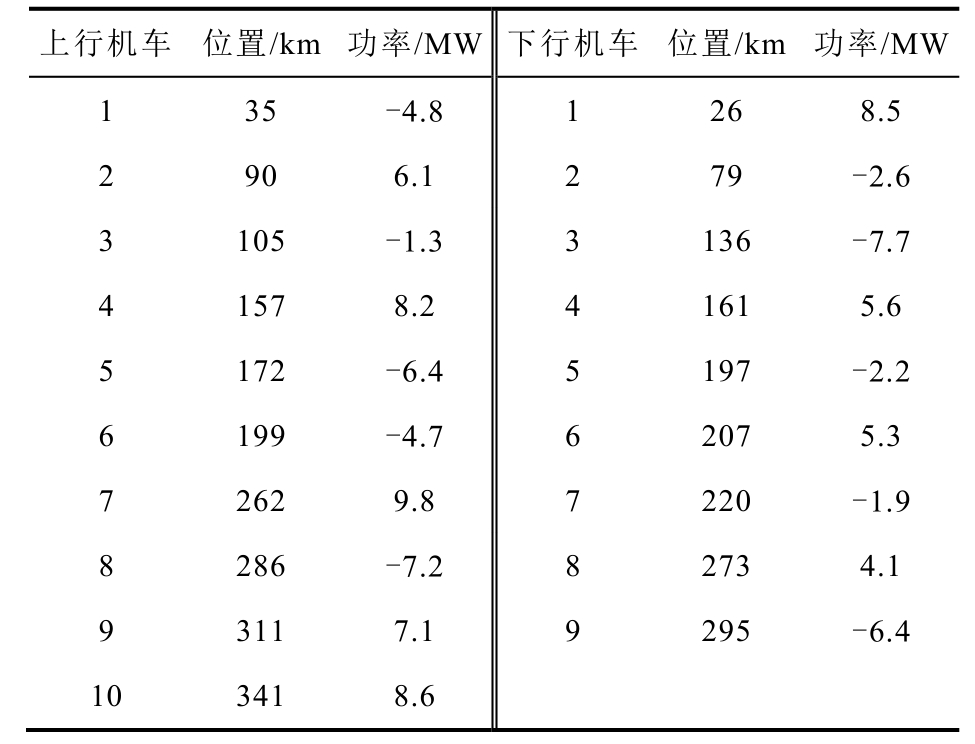
上行机车 位置/km 功率/MW 下行机车 位置/km 功率/MW 1 35 -4.8 1 26 8.5 2 90 6.1 2 79 -2.6 3 105 -1.3 3 136 -7.7 4 157 8.2 4 161 5.6 5 172 -6.4 5 197 -2.2 6 199 -4.7 6 207 5.3 7 262 9.8 7 220 -1.9 8 286 -7.2 8 273 4.1 9 311 7.1 9 295 -6.4 10 341 8.6
某一时刻三种控制方案下,上、下行线路的接触网-钢轨电压、钢轨电位及杂散电流的计算结果如图12 所示。牵引变电所的输出电压和功率见表6。从潮流计算结果可以看出,系统采用控制方案1、2 时,各个牵引变电所输出电压相差较小,且均稳定在额定值附近,使用方案2 时四个牵引所输出电压平均值被控制在24 kV,机车功率绝大部分由距其最近的两个牵引变电所承担,全线牵引网电压在牵引工况机车处出现极小值,再生制动机车出为极大值。当机车再生制动功率无法被同区间机车完全消耗时,满足就近消纳原则,由最近的牵引变电所返送回电网。采用控制方案3 时,为达到牵引变电所均分机车功率的控制目标,会出现较大功率的跨区间传输情况,导致各个牵引变电所电压出现较大偏差。
表6 牵引变电所的输出电压和功率
Tab.6 Voltage and power of traction power substations
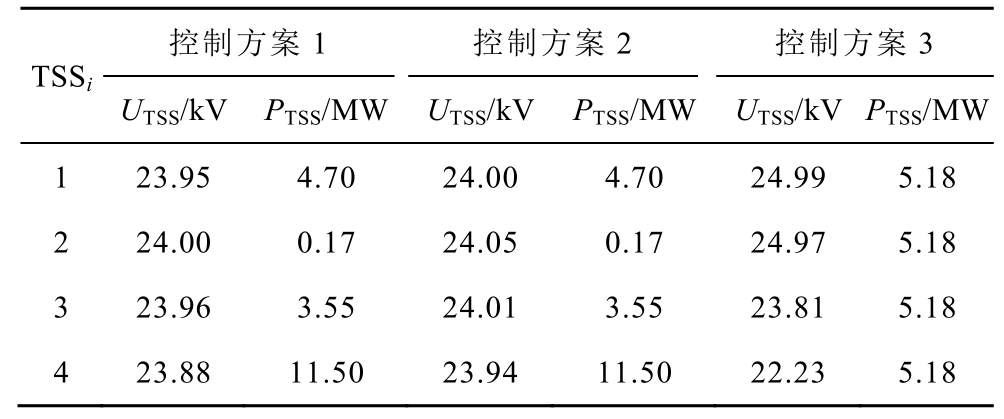
控制方案1 控制方案2 控制方案3 TSSi UTSS/kV PTSS/MW UTSS/kV PTSS/MW UTSS/kV PTSS/MW 1 23.95 4.70 24.00 4.70 24.99 5.18 2 24.00 0.17 24.05 0.17 24.97 5.18 3 23.96 3.55 24.01 3.55 23.81 5.18 4 23.88 11.50 23.94 11.50 22.23 5.18
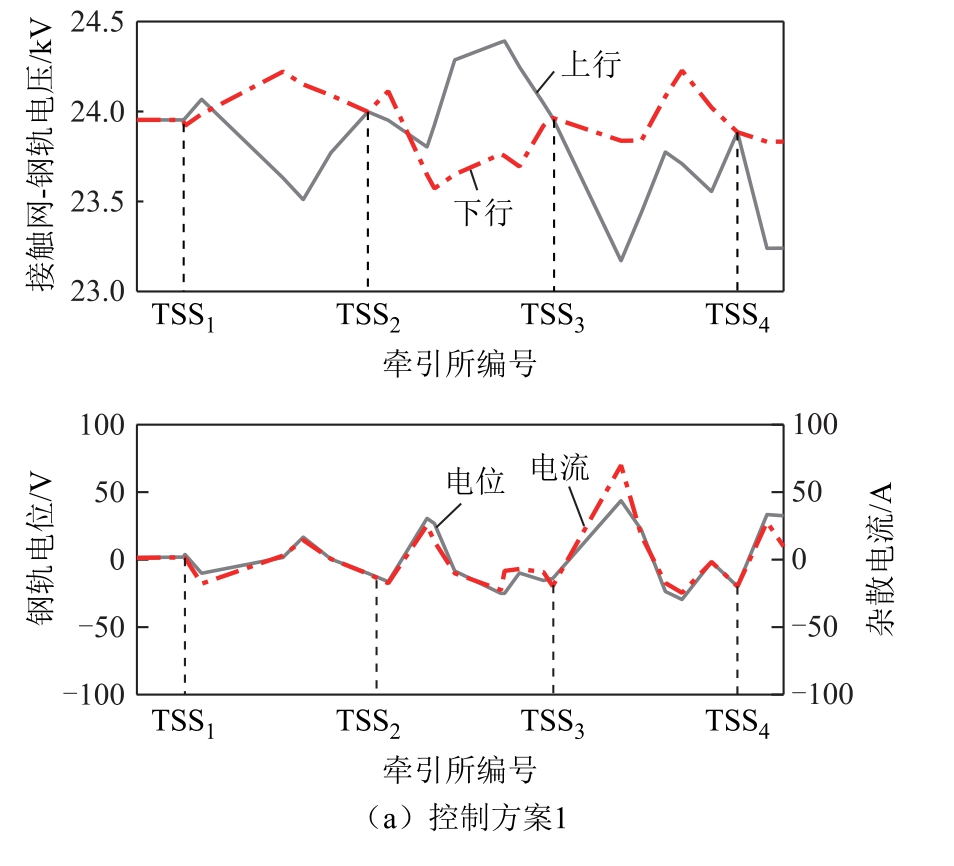
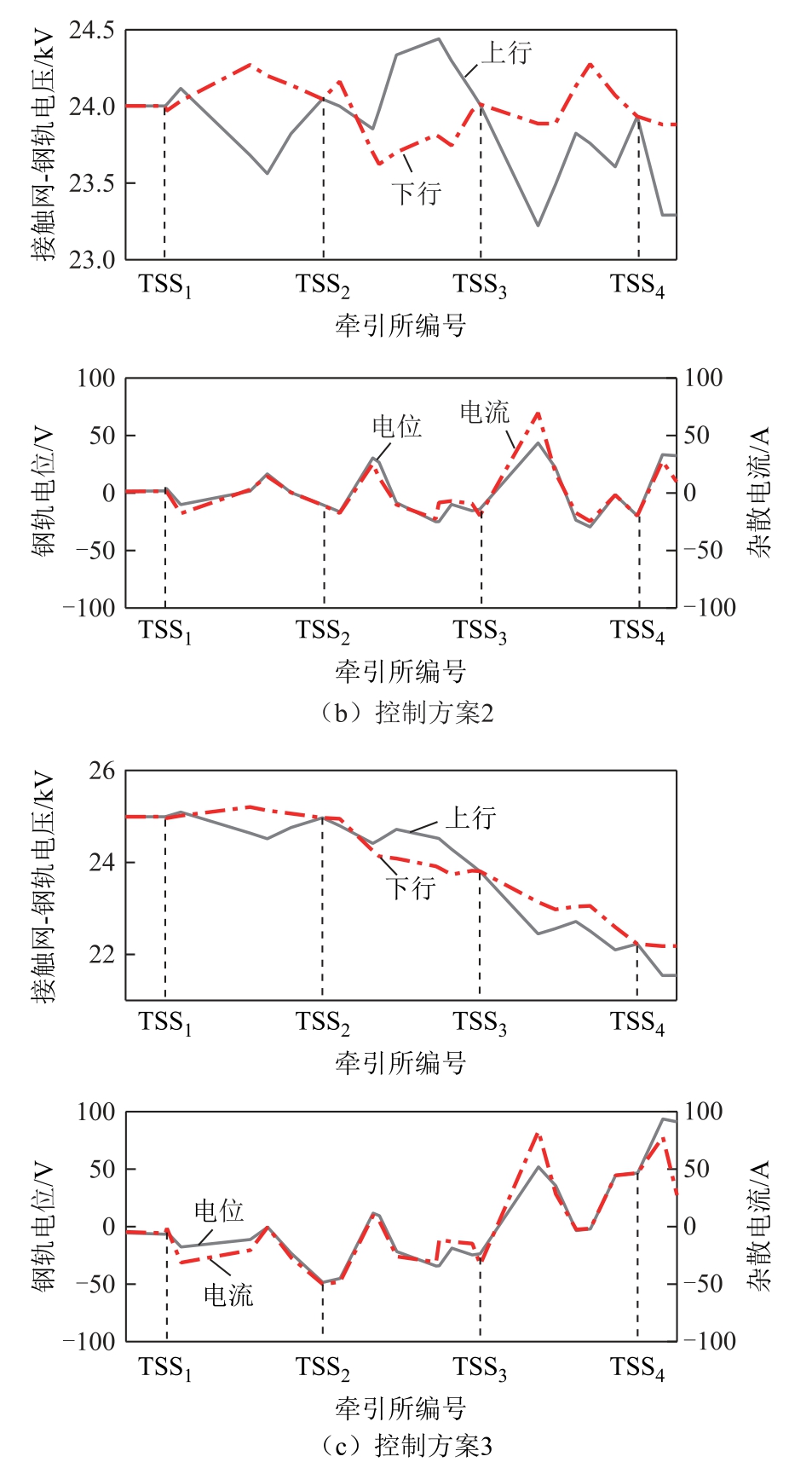
图12 不同控制方案下多车牵引-多车制动工况计算结果
Fig.12 Calculation results of multi-locomotives traction and multi-locomotives braking condition under different control schemes
钢轨电位与杂散电流的大小有着相同的变化趋势,减小钢轨电位可以在一定程度上降低杂散电流。三种控制方案相比,由于方案3 存在跨区间大功率传输,钢轨电位与杂散电流最大值分别为93.60 V、83.11 A,高于方案1 中的43.71 V、69.94 A 以及方案2 中的43.61 V、69.78 A。
类似地,用机车输出功率的代数和除以牵引变电所输出功率的代数和求取系统效率,以此评估三种控制方案下,存在再生制动机车时牵引网的损耗情况。计算可得三种控制方案下系统效率分别为:93.52%、93.55%、89.96%,方案3 中未被同区间牵引机车消耗的再生制动能量会远距离传输给其他区间牵引机车利用,造成了较大的损耗。综合以上分析,说明柔性直流牵引供电系统中,控制方案的设计应尽量减小跨区间功率传输以稳定牵引网电压,减小供电损耗、钢轨电位和杂散电流。
6 结论
本文建立了24 kV 柔性直流牵引供电的“控制器-源-网-车”潮流计算模型,提出了一种SLPFMPI 交替迭代的方法,以计算考虑系统级控制的柔性直流牵引网潮流,通过理论分析和潮流计算结果可以得到以下结论:
1)所提出的潮流计算方法能够准确计算不同系统级控制方案下的牵引网潮流,引入迭代因子,使潮流迭代可以准确收敛。
2)根据机车正常工作电压、接触网载流量限制,确定出三种控制方案下,24 kV 柔性直流牵引供电系统最大供电距离分别为135 km、140 km、100 km。
3)跨区间功率传输会带来额外的供电损耗、增大网压波动、钢轨电位及杂散电流,该系统控制方案的设计应考虑尽量减小系统中功率的跨区间流动。对于一条实际的运行线路,如果线路长度短,行车密度高,采用控制方案3 则不会造成机车功率长距离的跨区间传输,此时可以充分发挥该方案提高牵引变电所容量利用率的优势,而对于一条长距离线路,方案1 或方案2 是一种更优的选择。
4)所提潮流计算方法以及供电特性分析思路对于柔性直流牵引供电系统的理论分析与工程设计具有一定借鉴意义。
附 录
附表1 牵引供电系统参数
App.Tab.1 Parameters of TPS simulation system
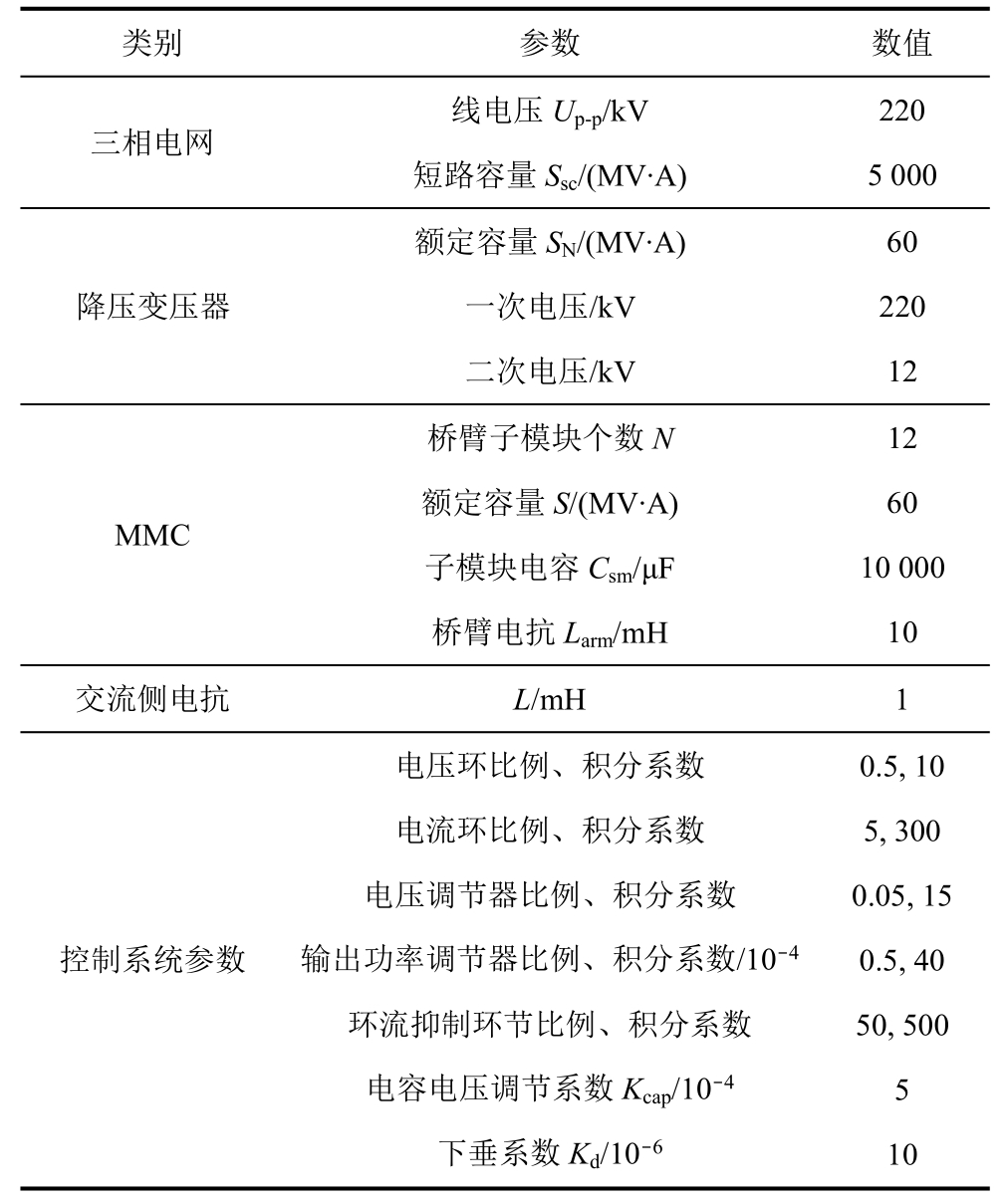
类别 参数 数值线电压Up-p/kV 220三相电网短路容量Ssc/(MV·A) 5 000额定容量SN/(MV·A) 60降压变压器一次电压/kV 220二次电压/kV 12桥臂子模块个数N 12额定容量S/(MV·A) 60子模块电容Csm/μF 10 000桥臂电抗Larm/mH 10交流侧电抗 L/mH 1 MMC电压环比例、积分系数 0.5, 10控制系统参数电流环比例、积分系数 5, 300电压调节器比例、积分系数 0.05, 15输出功率调节器比例、积分系数/10-4 0.5, 40环流抑制环节比例、积分系数 50, 500电容电压调节系数Kcap/10-4 5下垂系数Kd/10-6 10
附表2 DAB 仿真参数
App.Tab.2 Simulation parameters of DAB
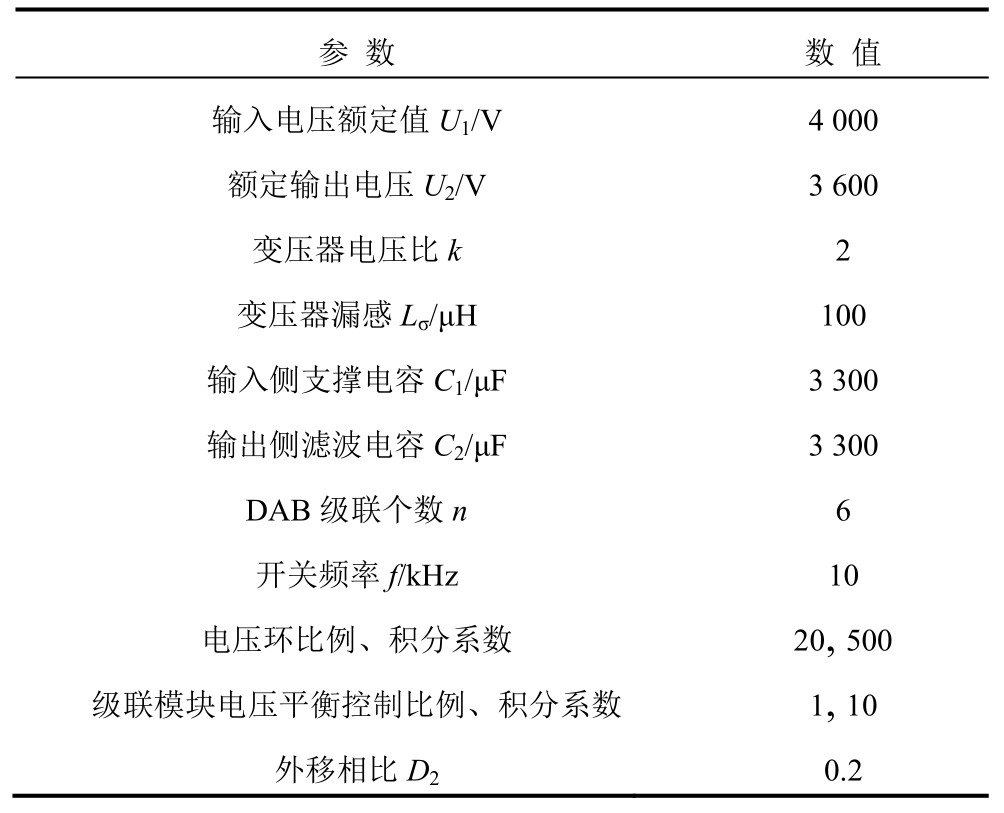
参 数 数 值输入电压额定值U1/V 4 000额定输出电压U2/V 3 600变压器电压比k 2变压器漏感Lσ/μH 100输入侧支撑电容C1/μF 3 300输出侧滤波电容C2/μF 3 300 DAB 级联个数n 6开关频率f/kHz 10电压环比例、积分系数 20, 500级联模块电压平衡控制比例、积分系数 1, 10外移相比D2 0.2
[1] Cheng Peng, Kong Huiwen, Ma Jing, et al. Overview of resilient traction power supply systems in railways with interconnected microgrid[J]. CSEE Journal of Power and Energy Systems, 2021, 7(5): 1122-1132.
[2] Verdicchio A, Ladoux P, Caron H, et al. New mediumvoltage DC railway electrification system[J]. IEEE Transactions on Transportation Electrification, 2018,4(2): 591-604.
[3] 李群湛, 王辉, 黄文勋, 等. 电气化铁路牵引变电所群贯通供电系统及其关键技术[J]. 电工技术学报, 2021, 36(5): 1064-1074.Li Qunzhan, Wang Hui, Huang Wenxun, et al.Interconnected power supply system of traction substation group and its key technologies for the electrified railway[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1064-1074.
[4] 王辉, 李群湛, 解绍锋, 等. 基于一种新型牵引补偿变压器的牵引变电群贯通供电系统负序补偿[J].电工技术学报, 2021, 36(10): 2140-2152.Wang Hui, Li Qunzhan, Xie Shaofeng, et al.Compensation of interconnected power supply system of traction substation group based on a new type of traction compensation transformer[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2140-2152.
[5] Gómez-Expósito A, Mauricio J M, Maza-Ortega J M.VSC-based MVDC railway electrification system[J].IEEE Transactions on Power Delivery, 2014, 29(1):422-431.
[6] 胡海涛, 孟玺, 杨孝伟, 等. 新型24kV 柔性直流铁路牵引供电系统分层控制策略研究[J]. 中国电机工程学报, 2021, 41(10): 3373-3382.Hu Haitao, Meng Xi, Yang Xiaowei, et al. A hierarchical control strategy for the novel 24kV flexible direct current railway traction power system[J]. Proceedings of the CSEE, 2021, 41(10):3373-3382.
[7] 刘芸江, 胡海涛, 杨孝伟, 等. 柔性中压直流铁路牵引供电系统分布式协调控制策略[J]. 电力自动化设备,2022, 42(12): 184-190.Liu Yunjiang, Hu Haitao, Yang Xiaowei, et al.Distributed coordinated control strategy for flexible medium voltage direct current railway traction power system[J]. Electric Power Automation Equipment,2022, 42(12): 184-190
[8] Yang Xiaowei, Hu Haitao, Ge Yinbo, et al. An improved droop control strategy for VSC-based MVDC traction power supply system[J]. IEEE Transactions on Industry Applications, 2018, 54(5):5173-5186.
[9] Zhu Xiaojuan, Hu Haitao, Tao Haidong, et al. Stability prediction and damping enhancement for MVDC railway electrification system[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 7683-7698.
[10] Zhu Xiaojuan, Hu Haitao, Tao Haidong, et al. Stability analysis of PV plant-tied MVDC railway electrification system[J]. IEEE Transactions on Transportation Electrification, 2019, 5(1): 311-323.
[11] 刘炜, 娄颖, 张戬, 等. 计及城市轨道逆变回馈装置的交直流统一供电计算[J]. 电工技术学报, 2019,34(20): 4381-4391.Liu Wei, Lou Ying, Zhang Jian, et al. Unified AC/DC power supply calculation taking into account urban rail inverter feedback devices[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4381-4391.
[12] 张戬, 刘炜, 潘卫国, 等. 基于改进暴力搜索算法的全双向变流供电系统参数设计[J]. 电工技术学报, 2021, 36(23): 4896-4904.Zhang Jian, Liu Wei, Pan Weiguo, et al. Parameter designing in power supply system with bidirectional converter devices as only converters based on enhanced brute force algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4896-4904.
[13] 周涛, 陈中, 戴中坚, 等. 含VSC-MTDC 的交直流系统潮流算法[J]. 中国电机工程学报, 2019, 39(11):3140-3149.Zhou Tao, Chen Zhong, Dai Zhongjian, et al. An AC/DC system power flow algorithm with VSCMTDC[J]. Proceedings of the CSEE, 2019, 39(11):3140-3149.
[14] 姜涛, 张勇, 李雪, 等. 电力系统交直流潮流的全纯嵌入计算[J]. 电工技术学报, 2021, 36(21): 4429-4443, 4481.Jiang Tao, Zhang Yong, Li Xue, et al. A holomorphic embedded method for solving power flow in hybrid AC-DC power system[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4429-4443,4481.
[15] Zhang Yuanshi, Meng Xuekun, Shotorbani A M, et al.Minimization of AC-DC grid transmission loss and DC voltage deviation using adaptive droop control and improved AC-DC power flow algorithm[J]. IEEE Transactions on Power Systems, 2021, 36(1): 744-756.
[16] 巨云涛, 黄炎, 张若思. 基于二阶锥规划凸松弛的三相交直流混合主动配电网最优潮流[J]. 电工技术学报, 2021, 36(9): 1866-1875.Ju Yuntao, Huang Yan, Zhang Ruosi. Optimal power flow of three-phase hybrid AC-DC in active distribution network based on second order cone programming[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1866-1875.
[17] 王浩翔, 赵冬梅, 陶然, 等. 基于分解的多目标进化算法的含MMC-HVDC 交直流混合系统最优潮流研究[J]. 电工技术学报, 2020, 35(17): 3691-3702.Wang Haoxiang, Zhao Dongmei, Tao Ran, et al. Study on optimal power flow for AC/DC hybrid system incorporating MMC-HVDC based on MOEA/D[J].Transactions of China Electrotechnical Society, 2020,35(17): 3691-3702.
[18] 和敬涵, 李智诚, 王小君, 等. 计及多种控制方式的直流电网潮流计算方法[J]. 电网技术, 2016,40(3): 712-718.He Jinghan, Li Zhicheng, Wang Xiaojun, et al. Power flow algorithm for DC grid considering various control modes[J]. Power System Technology, 2016,40(3): 712-718.
[19] Hao Fengjie, Zhang Gang, Chen Jie, et al. Optimal voltage regulation and power sharing in traction power systems with reversible converters[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2726-2735.
[20] 席嫣娜, 王方敏, 李占赫, 等. 计及系统级控制的柔性直流牵引供电系统潮流计算方法[J]. 电工电能新技术, 2021, 40(2): 9-14.Xi Yanna, Wang Fangmin, Li Zhanhe, et al. Power flow of voltage source converter based DC traction power supply system with system-level control[J].Advanced Technology of Electrical Engineering and Energy, 2021, 40(2): 9-14.