0 引言
磁耦合谐振式无线电能传输作为一种安全、高效的近场能量传输技术,近年来在电动汽车无线充电领域得到了广泛研究和应用。根据无线充电过程中车辆是处于泊车状态或行驶状态,可分为静态无线充电和动态无线充电[1]。其中,动态无线充电由于具有安全性高、节省充电时间和场地、能够在汽车行驶过程中充电进而缓解里程焦虑等优点,成为无线充电领域的一个研究热点,具有广阔的应用前景[2-4]。分段导轨式电动汽车动态无线充电系统的示意图如图1 所示,在电动汽车行驶过程中,路面下的供电导轨(线圈)实时为其提供电能。由于车辆行驶过程中不可避免地发生随机性横向偏移以及分段导轨切换区域的耦合关系改变,线圈之间的互感系数和系统等效负载都将发生变化,导致系统长期处于不健康的工作状态以及输出功率无法稳定在额定范围内[5-6]。因此需要采取有效措施,使系统能够对上述情况做出快速响应且具有较强的鲁棒性。

图1 分段导轨式电动汽车动态无线充电系统示意图
Fig.1 Schematic diagram of an electric vehicle dynamic wireless charging system with segmented coils
针对上述问题,国内外已经从系统参数优化[7]、谐振拓扑改进[8]、多接收线圈/供电导轨协同[9-11]等方面展开了广泛研究,以提升动态无线充电功率的稳定性。然而,一方面系统参数优化和谐振拓扑改进方法只能在一定范围内保持系统输出功率的相对稳定,并且无法解决导轨切换过程中的功率波动问题;另一方面多接收线圈/供电导轨协同方法虽然可以有效降低线圈偏移和导轨切换条件下的功率波动,但往往需要依赖于额外的车辆位置检测和导轨切换策略,从而增加了系统的成本和复杂程度,并且需要解决多线圈之间的交叉耦合问题[12]。相比于上述方法,采用控制器对系统输出功率进行调节的方式,对系统设计没有过多的约束,所需硬件成本更低且适应性更强。在相关控制策略研究方面,文献[13]基于LCL-T 型无线电能传输系统,分析其基本特性并建立相应的小信号模型,使用PI 数字控制器减少车辆进入充电区域时输出电流的调节时间;但该方法仅考虑了单边谐振补偿,抗偏移性能较差,接收端电气参数容易漂移。文献[14]基于SS 型补偿结构,以一次侧逆变电路以及双边DC-DC 调压电路为控制对象,通过控制三者的开关频率最终确保系统的传输效率最大化;但是该方法控制对象较多,控制算法实现难度大。文献[15]利用μ 控制器鲁棒性强的优势,通过闭环控制策略,实时采集输出电压并控制供电电源端的降压电路,针对性地解决因线圈横向偏移所带来的传输功率波动问题;但是该方法响应时间较长,且需要实时地进行双边通信,难以满足快速响应要求。文献[16]基于LCL-S 型谐振拓扑动态无线电能传输(Dynamic Wireless Power Transfer, DWPT)系统,建立广义状态空间模型并分析其动态响应特性,采用PI 控制器对输出电压进行调节;但该方法对整个系统进行建模,较为繁琐复杂。文献[17]通过测量一次线圈电流的幅值和相位,推算出互感系数和二次侧负载电阻,并使用模型预测控制算法实现供能端输出功率恒定控制,但该方法仅用传递函数描述系统输入输出关系,涉及参数众多且不能很好地描述系统动态特性,控制器性能易受参数漂移影响。文献[18]基于双边LCC 型谐振拓扑结构的恒流特性,采用模型预测控制(Model Predictive Control, MPC)实现了DWPT 系统负载电压的快速调节。为了实现MPC 控制,该论文对二次侧Buck 电路进行了状态平均建模,并针对传感器采样时间延迟设计了多步补偿式MPC 控制策略,搭建2 kW 级DWPT 系统验证了该方法的可行性。但是该方法需要实时采集Buck 电路电感电流和电容电压,存储和计算过去若干个采集周期内的目标数据,使得控制算法计算量较大,硬件实现成本和空间占用较高。
基于上述分析,本文为满足DWPT 系统的快速响应和强鲁棒性需求,提出一种针对互感和负载动态变化条件下的负载电流快速调节方法。首先采用状态空间平均建模方法得到系统二次侧Buck 降压电路的近似模型,基于此模型设计MPC 控制器;然后,引入卡尔曼滤波算法在线估计Buck 电路电感电流和电容电压,以减少物理传感器数量、节省硬件成本,在仅检测负载电流的条件下,即可实现对系统负载电流的快速调节。仿真和实验结果表明,相比于传统的PI 控制器,本文所提出的控制策略具有更快的响应速度,并且对互感和负载的变化具有较强的鲁棒性,能够满足DWPT 系统的应用需求。
1 动态无线电能传输系统及其控制原理
在磁耦合谐振式无线电能传输系统中,线圈可通过谐振补偿拓扑结构实现阻抗匹配,以提高系统的能效特性。其中,LCC-S 型补偿网络能够在一次侧输入电压和线圈互感不变的条件下,实现二次侧恒压输出,且二次侧结构简单,因而在电动汽车动态无线电能传输领域得到广泛应用[19]。因此,本文以LCC-S 型无线电能传输系统为研究对象,如图2所示,电能由若干基于LCC 型谐振拓扑的分段式供电导轨通过开关切换轮流传输到二次侧,并经整流滤波转换成直流电。由于不同类型、不同状态的负载对功率需求也不尽相同,因此需要通过DC-DC 变换器进行电压转换。鉴于同等硬件条件下,Buck 电路比Boost 电路具有更高的功率控制范围[18],故本文采用Buck 电路。

图2 LCC-S 型动态无线充电系统恒流控制原理框图
Fig.2 Block diagram of constant current control for the LCC-S dynamic wireless charging system
LCC-S 拓扑结构的输出电压UF 与负载接收功率Pout 可表示为[19]

式中,ω 为系统工作角频率;L1 为一次补偿电感;Uin 为一次侧输入电压;M 为线圈互感;Req 为包含整流滤波器的二次等效电阻,Req=8RL/π2,RL 为负载电阻;Uinv 为逆变器输出电压,![]()
由式(1)可知,Buck 电路的输入电压UF 与互感M 正相关,互感和负载波动将使系统输出电压和功率发生变化。因此,为了在车辆行驶过程中始终保持充电电流恒定或者适时调节输出功率,需要对负载电流 IL 进行及时有效的控制。本文采用的控制策略是对二次侧Buck 电路的占空比进行调节,以实时调控负载电流。控制原理如图2 右侧的点划线框所示:电流采集模块实时采集目标参数 IL 并同时传输给卡尔曼滤波器和模型预测控制器;卡尔曼滤波器根据Buck 电路状态空间模型以及IL 测量值即可计算出系统的状态估计值,即Buck 电路电感电流IB 和电容电压UB,省去测量状态量所需的硬件成本和时间成本;状态估计值将实时传输给模型预测控制器,经过控制器计算后得到当前采样时刻的最优控制信号,最终由PWM 发生器和驱动模块作用到开关管上,控制负载电流 IL 快速稳定至参考值。
2 控制器设计
在电动汽车高速行驶状态下,二次线圈与一次导轨线圈之间的互感系数将以毫秒量级的速度发生动态变化,因此要求输出电流控制器具有很快的响应速度。模型预测控制是一类约束优化反馈控制策略,其原理是在每一个采样时刻,在线求解有限时域的二次规划问题,将局部最优解的第一个元素作用于被控对象,实现滚动优化,以此逼近优化目标的全局最优解[20]。其优势是在已知系统模型和优化目标的前提下,控制流程简单有效,且能够达到采样周期量级的响应速度,对参数漂移和外部干扰等具有较强的鲁棒性[21],因此本文采用模型预测控制作为核心控制算法。
2.1 Buck 电路建模
要实现模型预测控制,首先需要建立控制对象的数学模型。根据LCC-S 型谐振拓扑的恒压特性,可以在每个采样时刻将Buck 电路的输入电压UF 视为恒压源,这样可以降低建模难度。然后采用经典的状态空间平均建模法即可描述其动态特性[22]。本文仅考虑连续电流模式(Continuous Current Mode,CCM),该模式下只有开关管导通和关断两种状态,如图3 所示,其中IB 和UB 分别为Buck 电路中流过电感的电流和电容两端的电压,并且在建模过程中忽略状态转换时间。
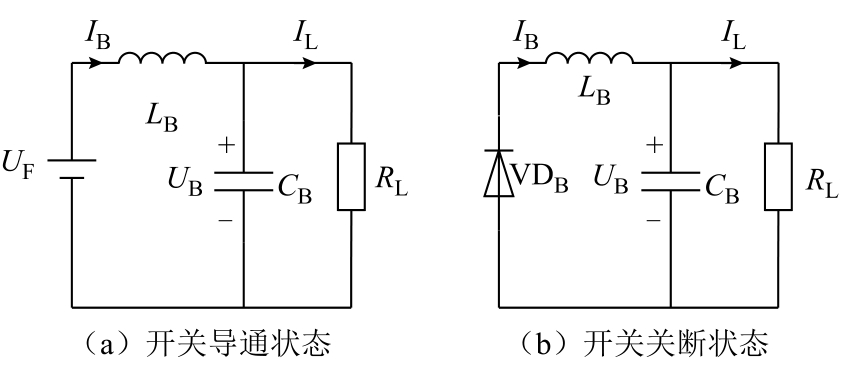
图3 连续电流工作模式下的Buck 等效电路
Fig.3 Equivalent circuit of the Buck converter at CCM
分别对Buck 电路的上述两种工作状态进行建模,选择Buck 电路中电容电压和电感电流作为系统状态变量,则有X=[UB, IB]T。根据基尔霍夫电压、电流定律,可将图3 电路用数学模型描述为

式中,CB 为Buck 电路的电容值;LB 为电感值。
由式(2)和式(3)可得到连续状态空间方程为
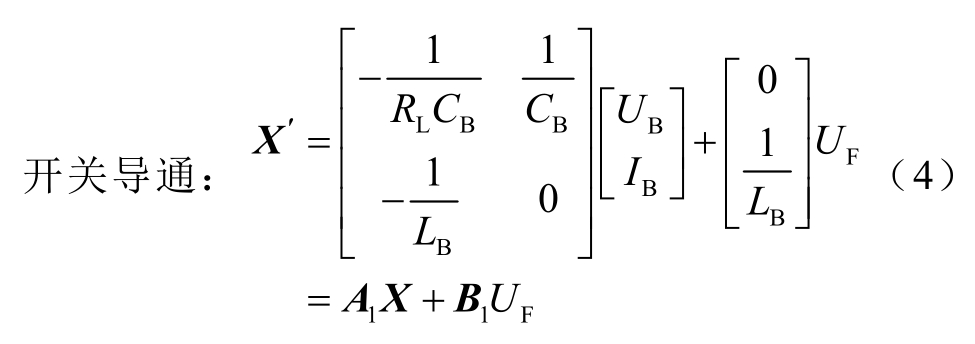

将式(4)和式(5)离散化,可得
式中,A=I+A1dT+A1(1-d)T=I+A1T,B=B1dT,I 为单位矩阵;d 为开关管占空比,其取值范围为0~1;T 为开关管驱动信号周期。
结合LCC-S 型拓扑结构的恒压特性,可以认为UF 是常数,并将占空比d 作为模型输入u、负载电流IL 作为模型输出y,则Buck 电路的离散模型为
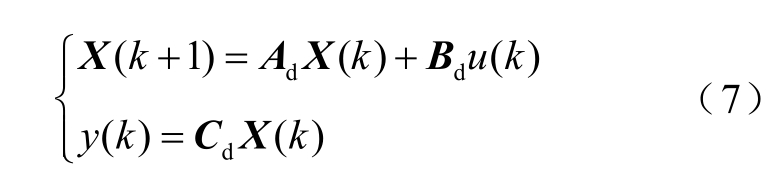
式中,Ad=(I+A1T),Bd=B1TUF,Cd=[1/RL 0]。下文将基于该模型进行预测控制器设计和状态估计。
2.2 模型预测控制器
根据模型预测控制算法原理[23],对Buck 电路的状态空间模型(7)建立增广矩阵,有

式中,On 为零矩阵。
建立增广矩阵的目的在于弱化模型参数漂移带来的动态估计误差,使控制器更聚焦在状态变化趋势和目标物理量上,从而增强对互感系数和负载值变化的鲁棒性。通过增广矩阵,可将模型在未来NP个采样时刻内的状态用预测方程表示为


式中,NP 为预测时域步长;NC 为控制序列长度。
一般地,增大预测时域步长NP 有利于增强控制系统的稳定性和鲁棒性,但是系统的动态响应速度将会变慢[24];反之,减小NP 有利于增加系统的动态响应速度,但会降低系统的稳定性和鲁棒性。在动态响应速度基本满足的条件下,NP 应适当选取大一些。控制序列长度NC 应小于等于NP,一般取NC<NP。NC 的取值对系统性能的影响与NP 近似相反,减小NC 有利于改善系统的稳定性和鲁棒性,但动态响应速度变慢;反之,增大NC 有利于提高系统的动态响应速度,但是系统的稳定性和鲁棒性随之降低。
然后,根据追踪精度和控制需求建立代价函数J 为
式(15)可化简为二次规划问题,即

式中,Rr(k)=[0, …, 0, ref(k)]T,是与X(k)相同维度的矩阵,ref(k)为k 时刻的目标参考值;Qˉ和Rˉ为权重矩阵,分别由权重常数qw 和rw 乘以单位矩阵I 得到。qw 和rw 共同决定了代价函数的求解过程是更注重控制精度还是控制信号变化幅度,增加qw,则系统动态响应速度增加,稳定性减弱[24],反之亦然;rw 对系统的影响与qw 相反,即增加rw,则系统稳定性增强,但动态响应速度变慢。
通过求解二次规划问题,即可得到当前时刻的最优占空比控制信号ΔU 为
上述过程会在每个采样周期执行一次,以实现滚动优化,进而应对各种参数漂移和外部干扰所带来的影响。控制系统的稳定性对于实际应用至关重要,对于模型预测控制的稳定性已有文献进行了充分证明,具体可参见文献[25-27]。
2.3 卡尔曼滤波状态估计器
2.2 节介绍的模型预测控制器要求在每个控制周期获得三个实时测量值,即电容电压UB、电感电流IB 和负载电流IL,而采用直接测量方式会增加额外的硬件成本和空间。通过式(7)可以看出,两个状态变量[UB IB]与负载电流IL 之间能够通过该离散模型进行关联,因此可以在仅测量负载电流IL 的条件下,使用状态估计算法对两个状态变量进行最优估计。卡尔曼滤波适用于估计一个动态系统的最优状态,即使观测到的系统状态参数含有噪声或者观测值不准确,卡尔曼滤波也能够完成对状态值的最优估计[28],因此本文采取卡尔曼滤波算法来实现对Buck 电路状态量[UB IB]的在线估计。
根据式(7)和卡尔曼滤波算法原理,可在k-1时刻得到k 时刻的状态预测值X(k|k-1)及其协方差预测值P(k|k-1)为
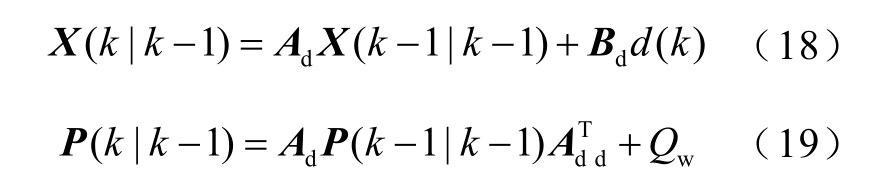
式中,Qw 为系统过程噪声协方差;d(k)为控制器输出的控制信号。
进一步地,结合系统输出测量值和上述状态预测值,可以得到k时刻的最优状态估计值为
式中,K(k)为卡尔曼增益权重矩阵,其表达式为

式中,Rv 为系统测量噪声协方差。
至此,已经得到了当前时刻的状态估计值,并且为了在下一时刻能够再次进行状态估计,需要更新估计值X(k|k)的协方差为
上述状态估计过程可概括为:将当前时刻的控制信号d(k)和电流测量值y(k)输入到卡尔曼滤波器中,经式(18)~式(22)计算后,得到当前时刻的状态变量最优估计值,此后该估计值又将作用于下一时刻的状态估计过程,如此循环,即可实时估计状态量。
3 结果与分析
3.1 仿真验证与分析
为验证卡尔曼滤波-模型预测融合控制的有效性,根据图2 所示电路,在Matlab/Simulink 环境中搭建仿真模型,相关参数见表1。其中,预测时域步长NP 和控制序列维度NC 直接决定了MPC 控制器的综合性能,权重系数rw 和qw 决定MPC 的控制精度,系统过程噪声协方差Qw 和测量噪声协方差Rv决定卡尔曼滤波器状态估计的精度。表1 中给出的参数值是经过多次试验后得到的最优结果。将MPC与两组不同参数的PI 控制器进行比较分析,PI_1 控制器的参数设置为P=3.5×10-5,I=2×10-6,PI_2 控制器的参数设置为P=5×10-4,I=1×10-4。上述两组PI 控制参数是通过Matlab/Simulink 的PID tuner 模块,根据预设的响应波形进行反复调节后得到的值。仿真模型的离散采样周期和控制器的输出信号周期均为0.1 μs。仿真中将参考电流、互感和负载值设置为周期性跳变,以模拟实际应用中充电导轨切换和线圈偏移等对系统输出造成的影响。
表1 仿真模型参数
Tab.1 Parameters of the simulation model

参 数 数 值 参 数 数 值输入电压Uin/V 45 二次侧电感Ls/μH 45工作频率f/kHz 85 补偿电容Cs/nF 80线圈互感M/μH 7.25 滤波电感LB/μH 22耦合系数k 0.15 滤波电容CB/nF 5.2滤波电容CF/μF 50 噪声协方差Qw 10额定负载RL/Ω 20 噪声协方差Rv 5补偿电感L1/μH 7.8 预测时域步长NP 10补偿电容C1/nF 452 控制序列长度NC 5一次侧电感Lp/μH 48 权重常数qw 1补偿电容Cp/nF 91 权重常数rw 10-5
卡尔曼滤波器得到的 Buck 电路状态变量[UB IB]估计值和实际值的比较结果如图4 所示。可以看出,无论系统是处于稳态或者阶跃响应过程,卡尔曼滤波器估计得到的电容电压UB 和电感电流IB 的变化规律与实际结果都比较吻合。虽然估计出的IL在幅值上与实际值存在一定的偏差,但是正如在2.2节所讨论的那样,本文所采用的MPC 控制策略主要关注状态量的变化趋势,而对于状态量的幅值大小具有较强的容错能力。这一点将在后面的电流控制仿真和实验部分得到进一步验证。
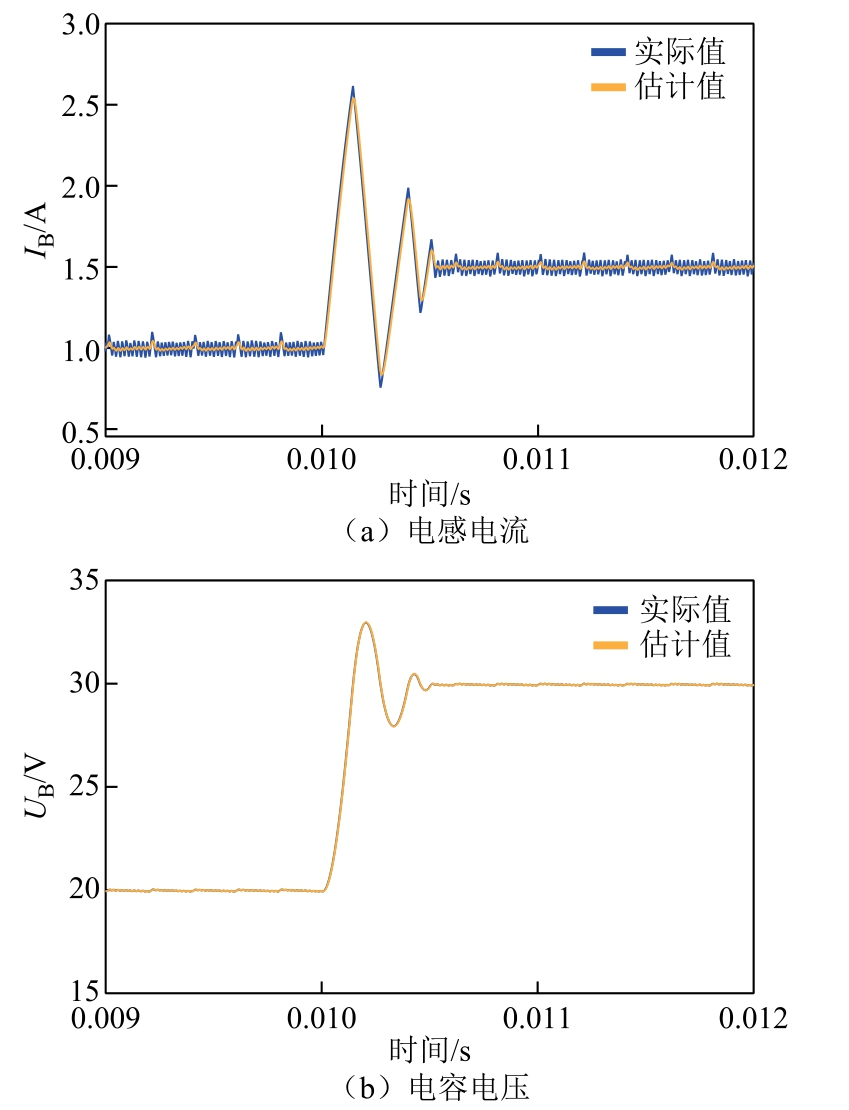
图4 Buck 电路状态变量实际值与估计值比较
Fig.4 Comparison between the actual and estimated state values of the Buck circuit
模型预测控制器和两组PI 控制器对阶跃参考信号的响应结果如图5 所示,其中负载电流IL 的初始参考值设为1 A,并在0.01 s 和0.02 s 时刻发生阶跃变化。可以看出,三组控制器均能准确跟踪参考值的阶跃变化,跟踪精度没有明显不同,但在跟踪速度和超调量方面存在显著差异。MPC 控制器在参考电流由1 A 跳变为1.5 A 时,超调量仅为0.07 A,且只用了0.6 ms 即完成了参考值追踪;当参考电流在0.02 s 时刻恢复为1 A 时,MPC 控制器在没有明显超调的情况下仅用约1.1 ms 即可达到稳定状态。PI_1 控制器在具有显著超调的情况下,响应速度仍然比MPC 慢,调节时间约为4.8 ms,并且过大的超调量存在影响系统器件安全的潜在风险;PI_2 控制器虽然没有超调,但响应时间长达6.8 ms,难以满足DWPT 系统对于功率快速调节的要求。由此可见,MPC 控制在追踪参考值的速度方面比PI 控制具有明显优势,更加符合DWPT 系统对快速响应的需求。

图5 参考电流突变时的MPC 与PI 控制器仿真波形
Fig.5 Simulation waveforms of MPC and PI controllers with suddenly changed reference current
除了快速响应外,控制器还需要应对DWPT 系统中互感系数和负载值动态扰动所带来的影响。当互感在0.01 s 处从7 μH 跳变至5 μH 时,输入电压幅值会由40 V 降至27.8 V,而互感在0.02 s 恢复至7 μH 时,输入电压也恢复为40 V。此过程模拟了DWPT 系统中充电区域切换以及线圈横向偏移时的互感变化情况,而控制器需要在该条件下尽可能地保持负载电流稳定。互感跳变时MPC 和PI 控制器的响应波形如图6 所示。由图6 可知,两组PI 控制器均需要一定的调整时间以稳定负载电流,PI_1 控制器虽然能够更快达到稳定,但振荡较为剧烈;PI_2控制器虽然振荡次数更少,但超调更加明显。因此,在多段充电区域切换过程中,两组PI 控制器作用下的IR 均会出现明显波动。而在MPC 控制下的IR 波动始终小于0.5%。由此可知,相比于PI 控制器,MPC 控制器对于互感的变化具有很好的鲁棒性。
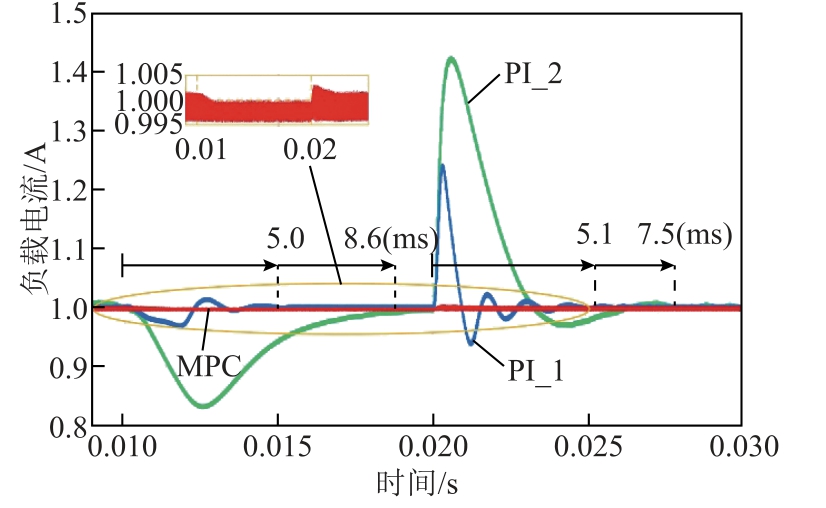
图6 互感突变时的MPC 与PI 控制器仿真波形
Fig.6 Simulation waveforms of MPC and PI controllers with suddenly changed mutual inductance
MPC 与PI 控制器在负载跳变时的响应波形如图7 所示,其中,负载电阻值在0.01 s 时刻由20 Ω跳变至10 Ω,在0.02 s 时刻再恢复为20 Ω。可以看出,在负载电阻值跳变瞬间三种控制器均产生了明显的电流尖峰,这是由于跳变前参考电流值设置为1 A,使得第一次跳变时,负载两端电压仍为20 V,故电流会瞬间变为2 A,同理可以解释另一个电流尖峰的产生。在两次负载切换过程中,MPC 控制器的调节时间分别为1.0 ms 和0.9 ms,而两组PI 控制器的调节时间分别为3.9 ms 和4.8 ms,以及4.8 ms和5.0 ms。因此,当负载电阻发生变化时,MPC 控制相较于PI 控制在响应速度方面具有明显优势。综合图6 和图7 可知,MPC 对于互感和负载的动态变化具有很强的鲁棒性,能够较好地满足DWPT 系统对于鲁棒性的需求。

图7 负载电阻突变时的MPC 与PI 控制器仿真波形
Fig.7 Simulation waveforms of MPC and PI controllers with suddenly changed load resistance
3.2 实验验证与分析
为进一步验证本文方法的有效性,搭建了一套LCC-S 型动态无线充电实验系统,如图8 所示。系统主要由可编程直流电源、可编程电子负载、高频逆变器、充电线圈(含一次侧供电导轨和二次侧接收线圈)、线圈谐振补偿网络、Buck 电路及其控制器、自动巡航小车(Automated Guided Vehicle, AGV)和示波器等部分组成。其中,Buck 电路输入电压10~60 V、输出电压5~48 V、最大功率150 W,主控芯片采用STM32F334(时钟频率为64 MHz)。为了减少超调量对于系统器件的冲击,实验中仅选择PI_2 控制器进行比较验证。由于实验系统和仿真模型参数存在一定差异,并且信号采样周期也不同,实验中模型预测控制器的参数实际配置为:预测时域步长NP=5,控制序列长度NC=3,权重系数qw=1、rw=0.01。

图8 动态无线充电实验系统
Fig.8 Prototype of a dynamic wireless charging system
通过测试,STM32F334 芯片运行一次PI 算法并执行控制指令的平均耗时约为22 μs,而MPC 算法的耗时约为153 μs,即MPC 算法的计算复杂度约为 PI 算法的 7 倍。但考虑到在普通性能的STM32F334 芯片上得到的153 μs 耗时本身并不长,因此可以认为本文所提出的MPC 控制算法对于硬件实现并没有困难,能够满足DWPT 系统功率实时控制要求。另外,从后面的实验结果可知,MPC 控制的总体耗时明显少于PI 控制,说明MPC 控制需要的控制周期数远远少于PI 控制。
3.2.1 与PI 控制器的比较分析
MPC 控制器与PI 控制器对参考值的跟踪结果如图9 所示。图9 中波形由上往下分别为逆变器输出电压、逆变器输出电流、Buck 电路输入电压以及负载电流。可以看出,MPC 和PI 控制器均能够在无超调的条件下准确跟踪参考值,控制误差均小于0.02 A,二者的控制精度并没有显著差异,但MPC所需的调节时间明显更短,因此本文着重比较两种算法在响应速度方面的差异。具体地,当参考值由1 A 跳变至1.5 A 时,PI 控制器需要约2.2 s 才能完成追踪,当参考值恢复至1 A 时,PI 控制器的调节时间约2 s。而MPC 控制器在上述两次跳变过程中,平均仅需约15 ms 即可完成参考值跟踪,耗时远小于PI 控制器。

图9 参考电流突变时MPC 与PI 控制器的实验波形
Fig.9 Experimental waveforms of MPC and PI controllers with suddenly changed reference current
互感突变时MPC 与PI 控制器的实验波形如图10 所示。需要指出的是,为了在多次实验中能够更准确地重复实现相同量的互感变化,实验中采用定量横向移动一次侧充电线圈的方式来实现互感的变化。实验中一次线圈宽14.5 cm,线圈完全对准时的互感约为7.25 μH,线圈横向偏移量为5 cm,对应的互感约为4 μH,即线圈偏移量和对应的互感变化量分别达到了35%和45%。从实验结果可以看出,当线圈完全对准时,Buck 电路的输入电压约为36 V,横向移动一次侧导轨线圈后,输入电压降至23 V,下降约37%。在两次切换过程中,MPC 和PI 控制器的稳态控制精度不变。但是,PI 控制器的平均调节时间约为3 s,而MPC 控制器几乎能在整个过程中始终保持负载电流不变。说明MPC 控制器对于互感变化具有很强的鲁棒性,这与图6 中的仿真结论相一致。

图10 互感突变时MPC 与PI 控制器的实验波形
Fig.10 Experimental waveforms of MPC and PI controllers with suddenly changed mutual inductance
负载电阻突变时的MPC 与PI 控制器实验波形如图11 所示。实验中,将负载先由20 Ω 减小为15 Ω,随后再增大至25 Ω。可以看出,当负载发生变化时,MPC 控制器对负载电流的调节速度依然明显快于PI 控制器。具体地,PI 控制器平均调节时间约为1.4 s,而MPC 控制器平均调节时间仅为10 ms,耗时明显小于PI 控制器。

图11 负载电阻突变时的MPC 与PI 控制器实验波形
Fig.11 Experimental waveforms of MPC and PI controllers with suddenly changed load resistance
综合图9~图11 的实验结果可知,在参考值改变、互感波动和负载变化时,本文提出的卡尔曼滤波-模型预测融合控制在仅测量负载电流的条件下,均能快速、准确地实现负载电流稳定控制,响应速度相较于PI 控制器有了较大提升(详细数据统计见表2),尤其对于互感变化具有很强的鲁棒性。
表2 MPC 与PI 控制器响应速度比较
Tab.2 Response comparison of MPC and PI controllers

测试条件 PID 响应时间/s MPC 响应时间/ms参考值1 A→1.5 A 2.2 15参考值1.5 A→1 A 2.0 15互感7.25 μH→4 μH 4 输出保持恒定互感4 μH→7.25 μH 2 输出保持恒定负载20 Ω→15 Ω 1.2 10负载15 Ω→25 Ω 1.6 10
3.2.2 系统传输效率分析
为了验证不同控制器是否对系统传输效率产生影响,本文测试了输入电压60 V,不同输出功率时,在无控制器、MPC 控制器和PI 控制器作用下的系统传输效率,结果如图12 和表3 所示。可以看出:①在无控制器、MPC 控制器和PI 控制器的作用下,当输出功率相同时,系统传输效率基本相同,说明控制器的引入并不会给系统传输效率带来显著影响;②在功率较低时,系统传输效率较低,但随着输出功率的增大,系统传输效率也随之增大,当输出功率超过250 W 时,系统传输效率可达80%以上,且受输出功率的影响不明显。上述规律与文献[29]的结果一致,分析其原因,主要有以下两点:①系统存在相对固定的静态损耗(如线圈损耗、磁心损耗、AGV 车体涡流损耗等),以一次线圈损耗为例,本文采用的LCC-S 拓扑结构具有一次线圈恒流特性,这部分损耗并不会随负载的改变而改变,随着输出功率的增加,静态损耗所占总功率的比重将逐渐减小,传输效率相应地就会提高;②随着输出功率的增加,Buck 电路的占空比也将增大,其输出电压和输入电压的差值减小,效率增加,因此也将使系统整体传输效率增加。
在此需要说明的是,导致表3 整体效率(尤其是在低功率时)不高的原因主要有两点:①如前所述,受所采用的Buck 电路模块功率的限制,本文仅在小功率条件下对控制器的性能进行了验证,此时系统静态损耗的大小与输出功率相当,如图12a 所示,静态损耗约为40 W,静态损耗在传输功率中的占比较大,根据系统传输效率计算公式(23)可知,低功率输出时传输效率较低;②本文实验系统的一次线圈长度(150 cm)是二次线圈长度(40 cm)的近4 倍,线圈耦合系数较小,仅为0.15,即便如此,当输出功率达到1 kW 时,在线圈对齐条件下系统整体传输效率依然可以达到85%左右[30]。


图12 系统静态损耗及传输效率
Fig.12 Static loss and transfer efficiency of the system
表3 系统传输效率测试结果
Tab.3 Power transfer efficiency of the system
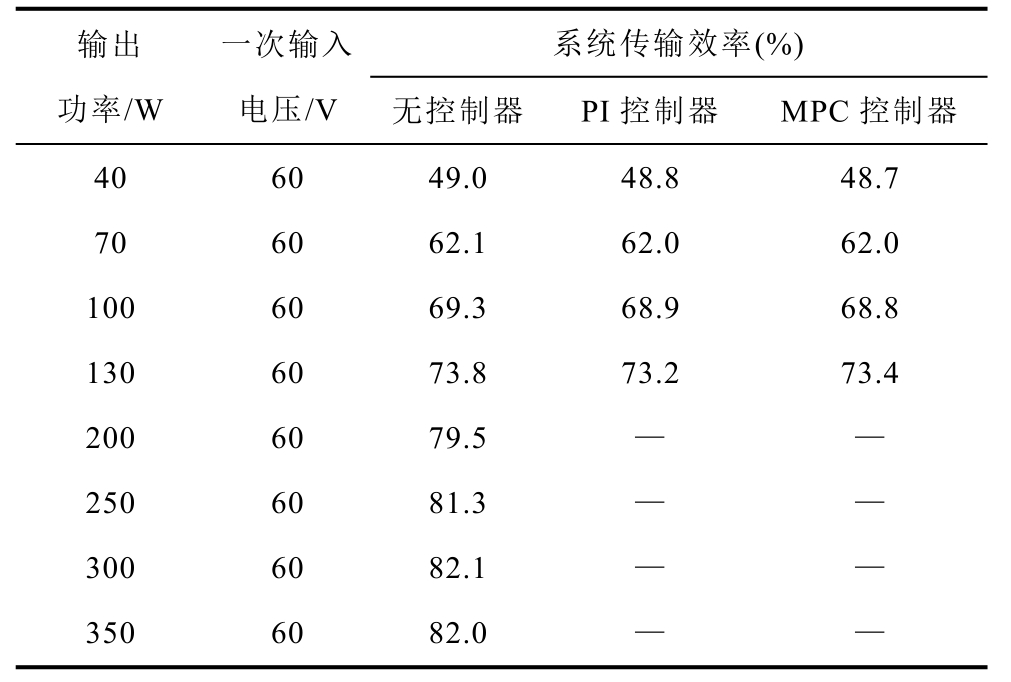
输出功率/W一次输入电压/V系统传输效率(%)无控制器 PI 控制器 MPC 控制器40 60 49.0 48.8 48.7 70 60 62.1 62.0 62.0 100 60 69.3 68.9 68.8 130 60 73.8 73.2 73.4 200 60 79.5 — —250 60 81.3 — —300 60 82.1 — —350 60 82.0 — —
式中,η 为系统传输效率;Pout 为系统有效输出功率;Ploss_static 为系统静态损耗,在输入电压不变的情况下,其值相对比较固定;Ploss_dynamic 为系统动态损耗,与输出功率有关。
3.2.3 MPC 控制器稳定性分析
综合图5~图7 的仿真结果和图9~图11 的实验结果可知,在系统参考电流、互感和负载突变时,本文所设计的模型预测控制器均能够快速准确地追踪到参考值,说明模型预测控制器在上述条件下始终是稳定的。为了进一步分析MPC 控制器参数配置对其性能尤其是稳定性的影响,采用不同参数配置进行恒流控制实验,部分实验结果如图13 所示。由于NP 和NC,rw 和qw 对于控制系统性能分别具有相反规律的影响,故保持NC=3 和qw=1 不变,仅以NP 和rw 为例进行分析。
图13 的结果表明,rw 在0.001~1 范围内变化时,控制性能并不会有明显差异;当rw<10-4 时,负载电流会随着rw 的持续减小出现越来越明显的振荡,即系统将逐渐失去稳定性,当rw=10-6 时,振荡范围已经超过30%,如图13a 所示;而当rw>1时,负载电流稳定性不变,但响应速度越来越慢,当rw=10 时,响应速度约为100 ms,如图13b 所示;NP 增大至100 时,系统性能仍然不会出现明显差异,仅仅是响应时间从15 ms 增加至20 ms,如图13c 所示。上述结果与2.2 节中的理论分析相符,并且进一步验证了本文所设计的MPC 控制器在很宽的参数范围内均能保持系统稳定,即参数选择自由度较大,这也是MPC 控制的一个突出优势。

图13 不同参数配置下的MPC 控制器实验波形
Fig.13 Experimental waveforms of MPC with different parameter configurations
3.3 与现有技术对比分析
为了进一步说明本文所提出的卡尔曼滤波-模型预测融合控制方法的优势,从所采用的谐振补偿拓扑结构、功率控制电路、是否需要一次侧和二次侧双边通信、模型依赖度、控制效果测试条件和需要测量的参数数量等方面,将其与现有文献中的方法进行比较,结果见表4,其中,模型依赖度包含所采用的系统建模方法的复杂程度以及控制策略对模型精度的要求两个方面。比如,文献[15]需要对整个S-P(一次侧串联-二次侧并联)型无线电能传输系统进行广义状态空间平均(Generalized State-Space Averaging, GSSA)建模,建模过程复杂;文献[17]根据系统模型来推算负载电阻和互感系数,进而估计系统输出功率,这对模型的精度要求较高。从表4 的比较结果可以看出,本文采用LCC-S 型拓扑结构,一次侧具有线圈恒流特性,二次侧具有输出恒压特性且结构简单,比较适合于动态无线充电的应用;采用二次侧Buck 电路对输出功率进行调节,无需系统一次侧和二次侧通信,并且通过引入卡尔曼滤波器在线估计Buck 电路的电感电流和电容电压,减少了所需传感器数量,有利于节省硬件成本、提升系统可靠性;采用增量式MPC 控制算法,使控制器更加关注系统状态的变化趋势,从而增强了对互感和负载变化的鲁棒性,这一点从图10 和图11 中的结果得到了很好的验证,尤其是互感连续变化过程中,本文方法始终能够维持负载电流不变。
表4 本文方法与其他文献比较
Tab.4 Comparison of the proposed method with other methods

参考文献 控制策略 拓扑结构 控制电路 双边通信 模型依赖度 测试条件 所需参数量[15]@2018 μ S-P 一次侧Buck 是 高 参考值/互感变化 1[16]@2018 PI LCC-S 一次侧逆变器 是 低 负载变化 1[18]@2020 MPC LCC-LCC 二次侧Buck 否 低 负载/参考值/互感变化 3[17]@2021 MPC S-P 一次侧逆变器 否 高 互感变化 2本文 增量MPC LCC-S 二次侧Buck 否 低 负载/参考值/互感变化 1
4 结论
为满足电动汽车动态无线充电系统对于功率调节的快速响应和高鲁棒性需求,本文基于LCC-S 补偿拓扑结构,提出一种结合卡尔曼滤波和模型预测控制的负载电流控制策略。建立了二次侧Buck 电路的状态空间模型,基于该模型设计了模型预测控制器,并结合卡尔曼滤波算法,实现了单参数测量条件下对负载电流的稳定控制。通过搭建仿真模型和硬件实验系统,将本文的模型预测控制器与传统的PI 控制器进行比较。结果表明,在具有相近超调量的条件下,模型预测控制器的响应速度明显优于PI 控制器,并且对于互感变化具有很强的鲁棒性。与其他现有技术相比,本文方法无需一次侧和二次侧通信,对系统模型的依赖度低。
[1] Zhang Zhen, Pang Hongliang, Georgiadis A, et al.Wireless power transfer—an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2):1044-1058.
[2] 朱春波, 姜金海, 宋凯, 等. 电动汽车动态无线充电关键技术研究进展[J]. 电力系统自动化, 2017,41(2): 60-65, 72.Zhu Chunbo, Jiang Jinhai, Song Kai, et al. Research progress of key technologies for dynamic wireless charging of electric vehicle[J]. Automation of Electric Power Systems, 2017, 41(2): 60-65, 72.
[3] Patil D, McDonough M K, Miller J M, et al. Wireless power transfer for vehicular applications: overview and challenges[J]. IEEE Transactions on Transportation Electrification, 2018, 4(1): 3-37.
[4] 孙跃, 蒋成, 王智慧, 等. 基于PSGA 的电动汽车动态无线供电系统优化布局[J]. 电力系统自动化,2019, 43(9): 125-131.Sun Yue, Jiang Cheng, Wang Zhihui, et al. Optimal planning of dynamic wireless supply system for electric vehicles based on particle swarm genetic algorithm[J]. Automation of Electric Power Systems,2019, 43(9): 125-131.
[5] Dai Xin, Jiang Jincheng, Wu Jianqing. Charging area determining and power enhancement method for multiexcitation unit configuration of wirelessly dynamic charging EV system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 4086-4096.
[6] 薛明, 王嘉浩, 杨庆新, 等. 电动汽车动态无线供电系统发射单元切换模式分析[J]. 电工技术学报,2020, 35(12): 2517-2525.Xue Ming, Wang Jiahao, Yang Qingxin, et al.Analysis of transmitter unit switching mode in dynamic wireless charging for electric vehicles[J].Transactions of China Electrotechnical Society, 2020,35(12): 2517-2525.
[7] Wang Chao, Zhu Chunbo, Wei Guo, et al. Design of compact three-phase receiver for meander-type dynamic wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 6854-6866.
[8] Li Yong, Hu Jiefeng, Lin Tianren, et al. A new coil structure and its optimization design with constant output voltage and constant output current for electric vehicle dynamic wireless charging[J]. IEEE Transactions on Industrial Informatics, 2019, 15(9):5244-5256.
[9] Li Shufan, Wang Lifang, Guo Yanjie, et al. Power stabilization with double transmitting coils and T-type compensation network for dynamic wireless charging of EV[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1801-1812.
[10] Zhou Shijie, Mi C C. Multi-paralleled LCC reactive power compensation networks and their tuning method for electric vehicle dynamic wireless charging[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6546-6556.
[11] Farajizadeh F, Vilathgamuwa D M, Jovanovic D, et al.Expandable N-legged converter to drive closely spaced multitransmitter wireless power transfer systems for dynamic charging[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3794-3806.
[12] 崔淑梅, 宋贝贝, 王志远. 电动汽车动态无线供电磁耦合机构研究综述[J]. 电工技术学报, 2022,37(3): 537-554.Cui Shumei, Song Beibei, Wang Zhiyuan. Overview of magnetic coupler for electric vehicles dynamic wireless charging[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 537-554.
[13] Hao Hao, Covic G A, Boys J T. An approximate dynamic model of LCL-T-based inductive power transfer power supplies[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5554-5567.
[14] Dai Xin, Li Xiaofei, Li Yanling, et al. Maximum efficiency tracking for wireless power transfer systems with dynamic coupling coefficient estimation[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5005-5015.
[15] Xia Chenyang, Wang Wei, Ren Siyuan, et al. Robust control for inductively coupled power transfer systems with coil misalignment[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8110-8122.
[16] 林天仁, 李勇, 麦瑞坤. 基于LCL-S 拓扑的感应电能传输系统的建模与控制方法[J]. 电工技术学报,2018, 33(1): 104-111.Lin Tianren, Li Yong, Mai Ruikun. Modeling and control method of inductive power transfer system based on LCL-S topology[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 104-111.
[17] 欧术培, 张海燕, 路燈杰. 电动汽车动态无线电能恒功率充电[J]. 电源技术, 2021, 45(4): 528-531.Ou Shupei, Zhang Haiyan, Lu Dengjie. Dynamic wireless power constant power charging of electric vehicle[J]. Chinese Journal of Power Sources, 2021,45(4): 528-531.
[18] Zhou Ze, Zhang Liyan, Liu Zhitao, et al. Model predictive control for the receiving-side DC-DC converter of dynamic wireless power transfer[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 8985-8997.
[19] 国玉刚, 崔纳新. LCC-S 型无线电能传输系统优化配置及特性研究[J]. 电工技术学报, 2019, 34(18):3723-3731.Guo Yugang, Cui Naxin. Research on optimal configuration and characteristics based on LCC-S type wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3723-3731.
[20] 乐健, 廖小兵, 章琰天, 等. 电力系统分布式模型预测控制方法综述与展望[J]. 电力系统自动化,2020, 44(23): 179-191.Le Jian, Liao Xiaobing, Zhang Yantian, et al. Review and prospect on distributed model predictive control method for power system[J]. Automation of Electric Power Systems, 2020, 44(23): 179-191.
[21] Beccuti A G, Mariethoz S, Cliquennois S, et al.Explicit model predictive control of DC-DC switchedmode power supplies with extended Kalman filtering[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1864-1874.
[22] Priewasser R, Agostinelli M, Unterrieder C, et al.Modeling, control, and implementation of DC-DC converters for variable frequency operation[J]. IEEE Transactions on Power Electronics, 2014, 29(1): 287-301.
[23] Gu D W, Petkov P H, Konstantinov M M. Robust control design with MATLAB®[M]. 2nd ed. London:Springer, 2013.
[24] 丛爽, 邓娟. MATLAB 环境下的模型预测控制理论的应用[J]. 计算机工程与应用, 2005, 41(16): 196-198, 212.Cong Shuang, Deng Juan. Model predictive control theory and application under MATLAB environment[J].Computer Engineering and Applications, 2005, 41(16):196-198, 212.
[25] 郝平, 张聚. 模型预测控制系统的低保守稳定性分析[J]. 清华大学学报(自然科学版), 2008, 48(增刊2):1718-1722.Hao Ping, Zhang Ju. Stability analysis of a less conservative model predictive control system[J].Journal of Tsinghua University (Science and Technology), 2008, 48(S2): 1718-1722.
[26] 郑凯华, 何德峰, 鲍荣. 增量预测控制策略的稳定性分析[J]. 化工自动化及仪表, 2012, 39(11): 1414-1417, 1441.Zheng Kaihua, He Defeng, Bao Rong. Stability analysis of incremental predictive control scheme[J].Control and Instruments in Chemical Industry, 2012,39(11): 1414-1417, 1441.
[27] Mayne D Q. Model predictive control: recent developments and future promise[J]. Automatica,2014, 50(12): 2967-2986.
[28] Han Xiaojuan, Liu Xingyu, Wang Hui. Dualregulating feedback optimization control of distributed energy storage system in power smoothing scenariox based on KF-MPC[J]. IEEE Access, 2020,8: 172601-172609.
[29] Ramezani A, Farhangi S, Iman-Eini H, et al.Optimized LCC-series compensated resonant network for stationary wireless EV chargers[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4):2756-2765.
[30] 田勇, 朱泽, 田劲东, 等. 基于LCC-S 补偿的电动汽车动态无线充电系统拓扑参数优化[J]. 机械工程学报, 2021, 57(14): 150-159.Tian Yong, Zhu Ze, Tian Jindong, et al. Parameters optimization of electric vehicles dynamic wireless power transfer system based on LCC-S compensation topology[J]. Journal of Mechanical Engineering, 2021,57(14): 150-159.