0 引言
微位移制动器(Giant Magnetostrictive Actuator,GMA)广泛应用于超精密加工、振动控制等领域。与其他类型的制动器相比,超磁致伸缩制动器因其磁-机耦合系数高、能量密度大、推进力强、响应速度快、驱动方式简单[1-2]等优点有着更为广阔的应用前景。为了避免倍频效应并获得更大的输出位移往往需要给超磁致伸缩制动器提供一个偏置磁场,目前提供偏置磁场的方式有永磁体或者直流线圈两种。永磁体因其功耗低、可靠性好、结构简单等优势成为更为普遍应用的偏置磁场提供方式[3-4]。因此,为了更好地提供均匀的偏置磁场,超磁致伸缩材料(Giant Magnetostrictive Material, GMM)棒和永磁体交替结构的堆栈式制动器(Stacked Giant Magnetostrictive Actuator, SGMA)成为了目前微位移制动器的常用结构[5-6],这种结构也是低频大功率水声换能器所常用的[7]。
为了设计、优化并充分利用该类制动器,必须建立有效的超磁致伸缩制动器多场耦合模型,分析其动态特性并准确预测其输出性能。但超磁致伸缩制动器的输入和输出间由于材料本身的饱和及磁滞现象以及复杂的电磁、机械场耦合作用表现出显著的非线性多物理场耦合特性[8-11]。因此,对制动器多场耦合特性的准确建模是预测其输出特性的关键。
现有研究主要聚焦于材料层次,针对超磁致伸缩材料自身的非线性磁-机耦合特性进行探讨,G. P.Carman 等[12]提出了能够反映应力对磁化强度和应变影响的标准平方模型,但该模型无法模拟强磁场下磁致伸缩应变的饱和现象;为了解决这个问题,万永平等[13]接连提出了双曲正切模型和磁畴翻转密度模型,这两个模型在高场区对应变的预测能力相较于标准平方模型显著提升;T. A. Duenas 等[14]基于自由能函数提出了一种D-H 改进模型,该模型虽然可以准确地预测各预应力下中低磁场区域的磁致伸缩应变值,但无法体现最大磁致伸缩应变与预应力的关系。因此,本文使用在中低磁场及高磁场下均有良好预测能力的D-H 改进模型[15],更加有效且全面地描述磁致伸缩材料的非线性磁-机耦合特性。
仅限于材料层次的研究方法并未考虑到制动器的整体结构以及负载影响,无法描述制动器的系统特性。为了追求更加完善的制动器系统层次模型,Wang Tianzhong 等[16]提出了考虑涡流影响的超磁致伸缩制动器多场耦合非线性动力学模型,研究了在无偏置条件下涡流效应和结构动态特性对超磁致伸缩制动器系统滞回特性的影响;黄文美等[17]建立了超磁致伸缩换能器的磁-机-热多场耦合动态模型,准确模拟了换能器在不同温度和动态损耗影响下的输出特性;ZhuYuchuan 等[18]考虑预应力及功率放大器电输入动力学的影响,搭建了完整的超磁致伸缩制动器多场耦合模型,以磁滞回线为工具从电输入动力学、磁化动力学和机械结构动力学三个方面分析了制动器的静态和动态输出特性。
虽然以上模型均能准确地反映制动器某些工况下的工作特性,但它们都缺少详细的漏磁建模,这意味着以上模型无法精准描述SGMA 这类特殊结构制动器的动态输出特性。因为永磁体与GMM 棒的串联磁阻相当大,SGMA 内部会出现明显的磁场不均匀现象[19-20],这导致磁路中各棒材的应变和输出力会因为磁-机耦合作用呈现出不均匀的分布特性,所以SGMA 动态特性与传统的制动器相比有很大的差异。因此,想要准确预测SGMA 的动态输出特性,必须对其磁回路的漏磁行为进行详细精准的建模。现有的研究通常使用漏磁系数来描述漏磁行为对输出位移的影响[21-22],但这种方法极其粗略且普适性低。更重要的是,漏磁系数只修正了激励线圈由于气隙等因素产生的磁场计算误差,并不能考虑永磁体的漏磁,即无法准确描述偏置磁场,更无法表征漏磁所带来的磁场不均匀现象,因此这种方法并不适用于SGMA。除此之外,目前常用的制动器动力学模型主要为线性磁致伸缩模型、单自由度模型[23]和连续振动模型[24]。但线性磁致伸缩模型未考虑负载影响,其计算结果往往与实际相差较大;而传统的单自由度模型是基于磁场均匀分布的前提;连续振动模型虽然能较好地反映制动器实际的振动情况,但其求解方式较为复杂,常常难以获得有效的数值解。
本文将堆栈式制动器(SGMA)作为研究对象,针对其磁场不均匀现象以及耦合漏磁效应的力学分布特性等问题,基于有限元仿真搭建了计及漏磁的等效磁路,并结合Jiles-Atherton 模型、非线性本构模型及考虑应变分布特性的优化结构动力学模型搭建了完整的材料层次与系统层次耦合的超磁致伸缩制动器动态模型。该模型能反映SGMA 磁路中磁场不均匀和应变分布现象,并准确地预测该制动器的输出位移,分析其输入输出特性。最后,搭建了制动器位移测量实验平台,验证了本文所提出模型的准确性和有效性,并对模型结果进行了误差分析和对比讨论。
1 SGMA 的结构及工作原理
堆栈式超磁致伸缩制动器结构剖面图如图1 所示。主要部件包括超磁致伸缩棒、永磁体、驱动线圈、上盖板和底座、套筒、输出杆、压板和碟簧。其中,振子部分由3 根超磁致伸缩棒与4 个钐钴永磁体以交替结构组成,棒材经径向切缝处理以削弱涡流影响。同时,为了尽可能地提高磁路内部磁场均匀性,棒材采用了“两长一短”的组合方式,使用了两种不同尺寸的超磁致伸缩棒;驱动线圈为超磁致伸缩棒提供交变磁场促使其振动;永磁体为制动器提供合适的偏置磁场以避免“倍频”现象;上盖板和底座选用高磁导率的电工软铁DT4,为了减小涡流效应带来的影响,套筒使用厚度为0.35 mm的硅钢片卷叠形成,三者与GMM 棒、永磁体共同组成闭合磁路;输出杆和压板使用不导磁的304 不锈钢,与碟簧一起为棒材施加适当大小的轴向稳定预应力。制动器工作时,在驱动线圈中通入交流电流,GMM 棒在交变磁场和偏置磁场的共同作用下产生轴向伸缩变化,以周期性的振动推动输出杆运动,实现力和位移的输出。
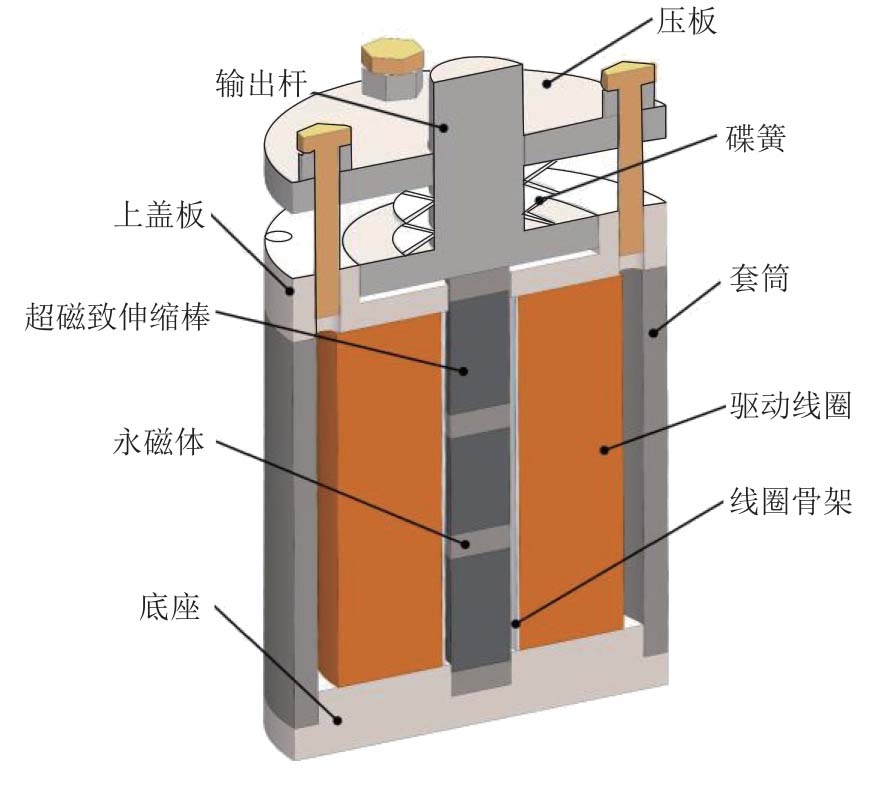
图1 SGMA 结构剖面图
Fig.1 SGMA structure section view
2 SGMA 多物理场耦合动态模型
2.1 计及漏磁的等效磁路模型
为了表征激励电流与磁场强度的关系,许多模型使用Hl = Ni来近似,其中,H 为激励磁场强度,l 为磁路长度,N 为驱动线圈匝数,i 为激励电流。但这种近似关系的成立条件是基于磁路内磁场均匀且漏磁可以忽略的假设。由于GMM 棒和永磁体的磁导率都比较低,漏磁会导致磁场出现明显的不均匀现象,尤其是对于SGMA 这类特殊结构的制动器而言,这种近似的计算方式显得尤为粗略。由于制动器内振子所使用的超磁致伸缩材料相对磁导率较低且棒材经过径向切缝处理,磁路中很难产生磁饱和及明显的涡流效应,因此,本文使用能够描述磁场分布的线性等效磁路模型[25-27]对制动器的漏磁行为进行详细的建模,快速有效地计算磁路内不同部位的磁场。
利用有限元仿真软件Ansoft 建立制动器二维静磁场模型,得到不同激励电流下SGMA 内部磁路磁力线的分布情况,如图2 所示。由图2 中仿真结果可知,改变激励电流幅值并不会对磁路内部磁力线的分布特性产生明显影响,磁力线总体呈现上下近似、中间对称分布的特点,漏磁主要集中在永磁体和棒材附近,少量漏磁由经过线圈气隙的磁通与两侧磁轭共同形成。处于磁路中部的两个永磁体漏磁分布与棒材相似,而两端永磁体嵌入磁轭,相较于前者略有区别。

图2 SGMA 在不同激励电流下磁路磁力线分布图
Fig.2 Flux path distribution of the SGMA under different excitation currents
为了和后文实验条件保持一致,基于图2b 仿真结果,使用磁场分割法[28-29]针对磁场分布情况进行分区计算。漏磁通可被大致划分为如图3 所示的四种类型的磁通管:拱形磁通管、类圆环磁通管、半月形磁通管和半圆环形磁通管。
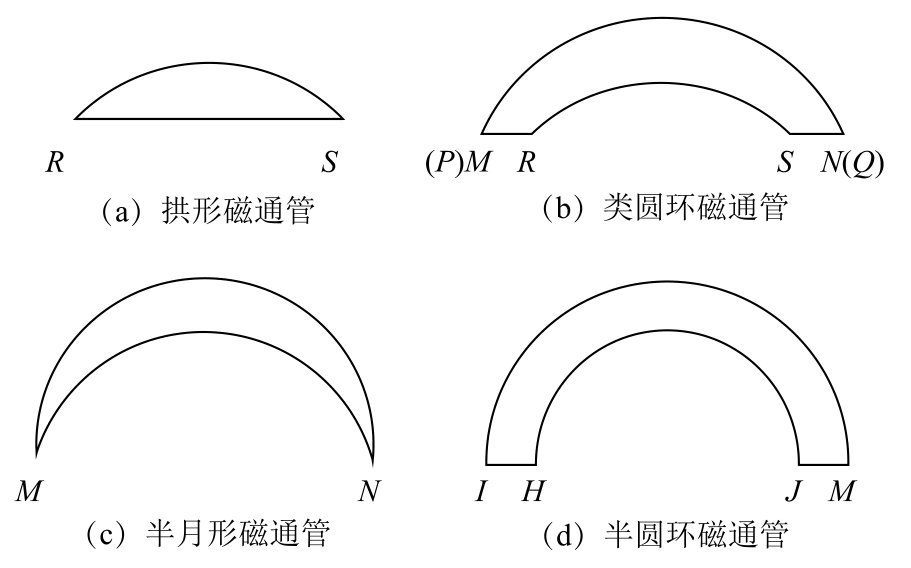
图3 四种不同类型的磁通管
Fig.3 Four different types of flux tubes
结合SGMA 内部结构和有限元仿真结果,将制动器内部漏磁通按照磁通管类型划分为如图4 和图5 所示的5 个截面形状不同的磁通管A1、A2、A3、A4、A5。所有的磁通管都是沿轴向旋转的结构,旋转轴是GMM 棒的中心轴。
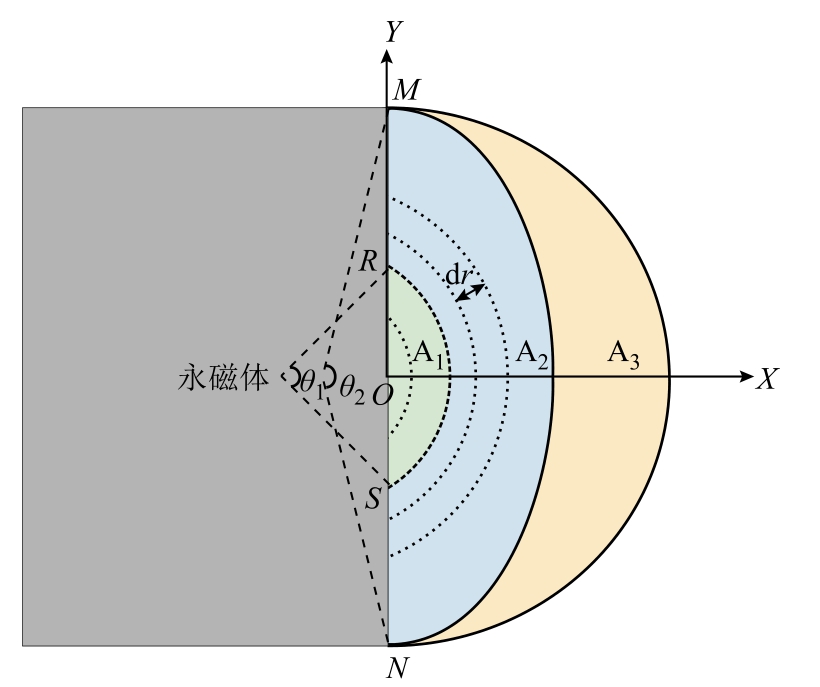
图4 永磁体附近三种不同类型磁通管
Fig.4 Three different types of flux tubes near permanent magnets and GMM rods
位于磁路中部的永磁体和棒材漏磁通有着相似的分布,他们附近存在三种不同截面形状的磁通管,如图4 所示。部分漏磁通由导磁体外围发射并返回,形成了拱形磁通管A1;类圆环形磁通管A2 表示从导磁体边线MR 发射出来,并返回到其外侧边线SN的漏磁通量;剩余的漏磁通从导磁体边缘发射并返回,即半月形磁通管A3。

图5 磁回路中的磁通管分布
Fig.5 Distribution of flux tubes in the magnetic circuit
位于磁路两侧的永磁体和棒材附近的漏磁分布与中部的略有区别,如图5 所示。两侧的棒材附近也存在三种类型的磁通管,除了前文提到的拱形磁通管A1、类圆环磁通管A2 以外,从边缘发射的磁通并未像半月形磁通管A3 一样按原路返回,而是与磁轭中的磁通汇合形成1/2 个半圆环形磁通管A4。端部的两个永磁体由于其嵌入磁轭,部分磁通未经过主磁路,而是直接于磁轭中闭合。因此,其漏磁磁通管主要为3/2 个半圆环形磁通管A5。
根据前文分析的漏磁分布,结合制动器内部磁路结构,构建如图6 所示的SGMA 等效磁路。其中,激励等效磁动势FE=NIE,IE 为交变激励电流;使用永磁体磁阻RM(ii=1,2,3,4)及磁动势FM(ii=1,2,3,4)串联结构来表示永磁体在磁回路中的作用;GMM棒磁阻 RGi(i=1,2,3)相继串联在主磁路中;Rδi(i=1,2,3,…,9)表示磁路中的漏磁阻;套筒、上盖板和底座共同组成的磁轭磁阻由RYi(i=1,2,3,4,5)表示。值得一提的是,在磁路结构大致不变的情况下,若磁路中部件尺寸变化,虽然会影响等效磁路的磁阻阻值,但是并不会改变图4、图5 中漏磁通管类型和图6 所示的等效磁路的网络结构。

图6 SGMA 等效磁路示意图
Fig.6 Diagram for the equivalent magnetic circuit of the SGMA
2.1.1 部件磁阻计算
制动器各部件磁阻计算所需部件尺寸、材料相关参数都汇总于表1 中。
表1 SGMA 相关尺寸及材料参数
Tab.1 SGMA related dimensions and material parameters

参 数数 值永磁体长度lpm/mm 7.5永磁体直径dpm/mm 20两端GMM 棒长度lG1/mm 35中部GMM 棒长度lG2/mm 30 GMM 棒直径dG/mm 20线圈匝数N 2 037真空磁导率μ0/(H/m)4π×10-7 GMM 棒相对磁导率 r1μ 4永磁体相对磁导率 r2μ 1.05底座及上盖板相对磁导率 r3μ 4 000套筒相对磁导率 r4μ 8 000底座高度h1 /mm 20底座开槽深度l1 /mm 10套筒长度l2/mm 120套筒内直径d1/mm 110套筒外直径d2/mm 126上盖板高度h2 /mm 20上盖板内直径d3 /mm 81
类似永磁体、GMM 棒等磁通沿恒定横截面穿过的柱形部件磁阻可表示为[30]

式中,l 为材料中的通量所穿过的距离;A 为横截面积;µ为材料的磁导率。
而对于上盖板、底座等磁通沿圆环径向穿过的环状柱形部件磁阻可表示为

式中,h 为穿过该部件的磁通宽度;r1 为圆环内径;r2 为圆环外径。
根据表1 中尺寸及材料参数,结合式(1)、式(2)可计算图6 等效磁路模型中各磁阻大小。
2.1.2 漏磁阻计算
为了获得图6 中各漏磁阻阻值,本文简化分析,将等效磁路模型视作二维模型,即假设各磁通管在垂直于棒材径向的每个横截面上的磁场分布均相同。因此,各磁通管的宽度D 可简化为导磁体的截面周长,即 D = πd pm = 6.283 × 1 0-2m。
振子中部永磁体附近的三种漏磁磁通管A1、A2、A3 的磁导由文献[28]可分别表示为
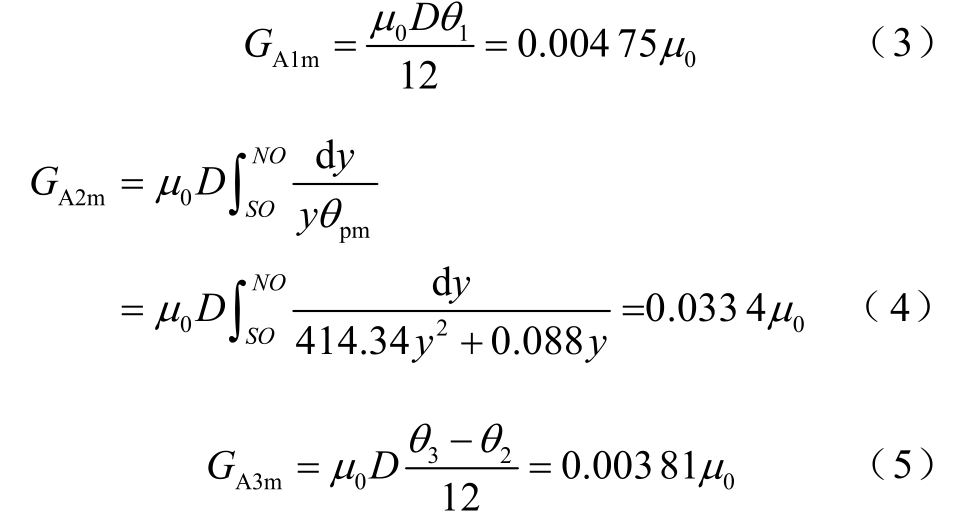
式中,θ1、θ2、θ3 根据图2b 可分别估计为0.908 rad、1.642 rad、2.369 rad;NO 为0.003 75 m;SO 为0.001 979 m。式(4)中y 和dy 分别为半径r 及其微元dr 的Y 轴分量,由于θpm和y 近似为线性关系[29],因此根据图 2b 磁力线分布情况经拟合后可写为θpm =414.34y+0.088。
根据式(3)~式(5),同理可得位于振子中央长度为30 mm GMM 棒附近的漏磁磁通管磁导分别为

式中,如图5 所示的角度θ4、θ5、θ6 分别估计为0.433 rad、1.942 rad、2.677 rad;式(7)中S ′O ′= 0.004 5 2m, M ′O ′= 0.015 m,角度 拟合 式为θr1 =144y-0.22。
位于磁路两侧长度为35 mm 的GMM 棒漏磁分布和中部的棒材相比稍有区别:除了拱形磁通管A1、类圆环磁通管A2 以外,还存在1/2 个半圆环形磁通管A4。各磁通管磁导可分别表示为

式中,θ 7 = 0.589 rad,θ 8 =1.274 rad; S ′′O ′= 0.006 m,QO′= 0.009 8 m,KV=0.018 22 m,KU=0.026 74 m;式(10)中θr2=179.32y-0.49。
两端的永磁体漏磁磁通管主要为如图5 所示的3/2 个半圆环形磁通管A5,其磁导为

式中,M ′N ′为永磁体的厚度, M ′N ′= 0.007 5m。
由以上计算结果,可得到图6 中各漏磁阻阻值为

综上所述,建立了考虑漏磁的制动器等效磁路模型,根据制动器实际工况确定激励等效磁动势FE的幅值和频率,即可通过模型计算得到磁路中不同部位的瞬态磁场。在没有出现严重的非线性现象时,如图6 所示的等效磁路模型这一线性模型完全可以描述制动器磁路的磁场分布特性及漏磁行为,且有较强的适用性。
2.2 磁化模型
为了表征GMM 材料的不可逆磁化过程,使用具有物理意义且所需参数较少的Jiles-Atherton 模型来描述磁场强度与磁化强度的磁滞关系,具体关系式为

式中,H 为外磁场强度;M 为磁化强度;Man 为无磁滞磁化强度;Mrev 和Mirr 分别为可逆磁化强度和不可逆磁化强度;α、Ms、a、c、k 分别为畴壁相互作用系数、饱和磁化强度、无磁滞磁化强度形状系数、可逆系数、畴壁钉扎系数;Hσ为碟簧所施加的预应力 σ 0引发的磁场;参数 被定义为
被定义为  ≡ α+ 9λ sσ 0/
≡ α+ 9λ sσ 0/![]() ;当H 增大时,δ =+1,当H 减小时,δ =-1。
;当H 增大时,δ =+1,当H 减小时,δ =-1。
将前文中经计及漏磁的等效磁路模型得到的各部位磁场作为输入量H,通过Jiles-Atherton 模型反映磁致伸缩材料的磁滞特性,计算出不同部位的磁化强度M。该磁化模型能够从本征意义上描述铁磁材料的不可逆磁化过程,其适用于表征各种材料中存在的非线性静态磁滞损耗特性。
2.3 非线性本构模型
GMM 材料的应变量与施加的预应力密切相关。在大多数研究中,通常使用二次畴转模型近似计算材料的磁致伸缩应变[31],而忽略了预应力的影响。本文在传统二次畴转模型中引入双曲正切函数[18]以表征预应力对磁致伸缩应变λ的影响,表达式为

式中,λs 为饱和磁致伸缩应变;σ 为施加的预应力;Ms为饱和磁化强度;σmax为棒材的最大磁致伸缩力;σs 为最佳预应力,由文献[18]的推导,σs 可写为σ s =λs E G AG /2。
该模型在各个磁场范围内都能良好预测材料应变与磁化强度的非线性关系,且能够准确描述磁饱和现象,更加有效且全面地体现磁致伸缩材料的非线性磁-机耦合特性,对于磁场和预应力的变化都有良好的适应性。
2.4 考虑分布特性的结构动力学模型
为了描述制动器的动态特性,本文建立动力学模型求解制动器的输出位移。相比于GMM 棒材,永磁体的刚度较大,假设其在振动过程中不发生形变,则SGMA 的动态行为可以由一个单自由度振动系统表征,制动器动力学模型如图7 所示。
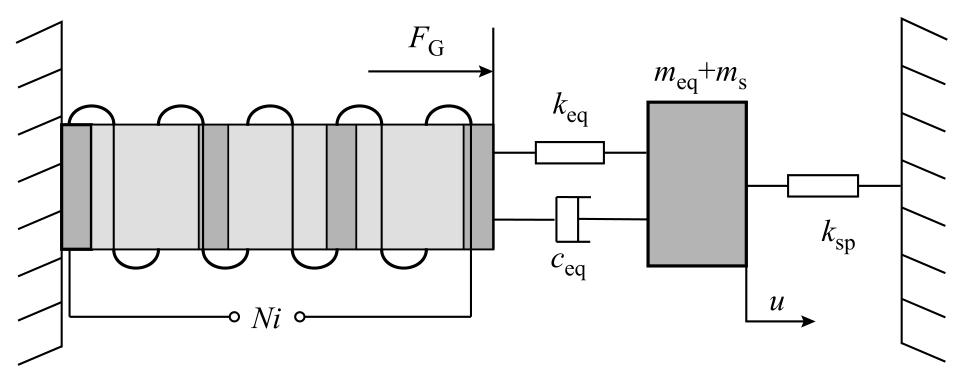
图7 制动器动力学模型
Fig.7 Dynamics model of the actuator
图7 中磁致伸缩输出力FG 可表示为
式中,AG、EG 分别为棒材的横截面积和杨氏模量。对于如图7 所示的单自由度振动系统进行受力分析,根据牛顿第二定律,制动器输出位移u 可表示为
式中,meq、ceq、keq 分别为永磁体、棒材组合结构的等效质量、等效阻尼系数、等效刚度;ms 为输出杆的质量;ksp 为碟簧的刚度;σ 0为碟簧施加的预应力。
由于SGMA 堆栈结构的特殊性,各棒材的平均磁场并不相等,其应变量及输出力和速度也会不同,磁-机耦合会导致其动力学特性相较于传统结构的制动器更为复杂,不同棒材分布特性示意图如图8所示。图中,FGi、vGi、λi(i=1,2,3)分别为各棒材的输出力、输出速度、应变量,vG1j、vG2j、vG3j(j=1,2,···,n)分别为三根棒材各微元的速度,假设各棒材内部应变分布均匀,则存在vGij=jvGi/n,各微元的位移差可表示为λjlj/n。

图8 不同棒材分布特性示意图
Fig.8 Schematic diagram of distribution characteristics of different bars
因此,为了充分考虑不同棒材的应变分布特性,对该单自由度系统进行优化计算,提出一种改进的单自由度模型,即借助动能定理重新推导等效质量以此来反映不同棒材的力与应变分布。根据前文模型结果可得制动器中由下至上三根棒材应变量比λ1∶λ2∶λ3=1.05∶1.37∶1。当输出杆轴向速度为v 时,根据各棒材长度折算,各棒材输出速度分别为0.33v、0.69v、v。由动能定理可得
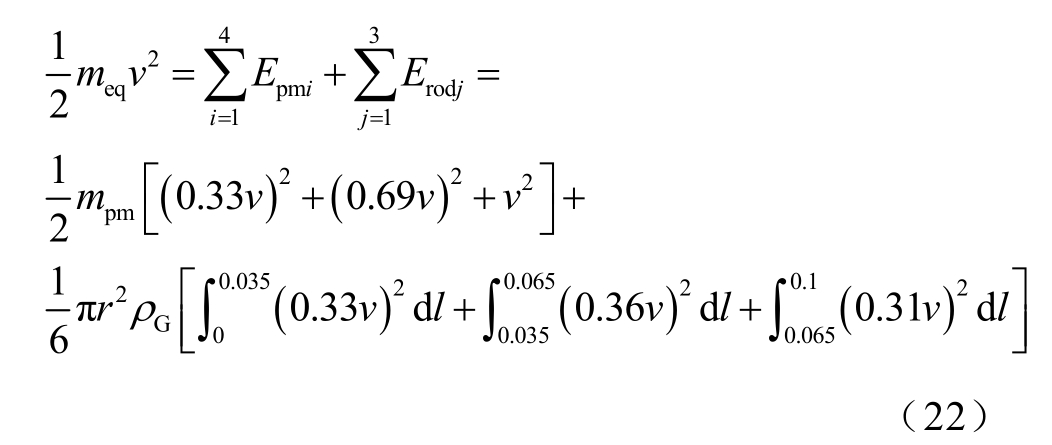
式中,mpm 为永磁体的质量;ρ G为GMM 棒的密度。
一般情况下,GMM 棒受碟簧施加的预应力作用而被压缩,且由于SGMA 结构中永磁体的特殊性,偏置磁场带来的伸缩应变量不便测量。因此,本文将经偏置磁场磁化且施加预应力后的输出杆位置作为位移零点,实验中使用激光位移传感器所测得的制动器位移u2 为相对于棒材在偏置磁场下伸长且被预应力压缩时的位移,式(21)可改写为
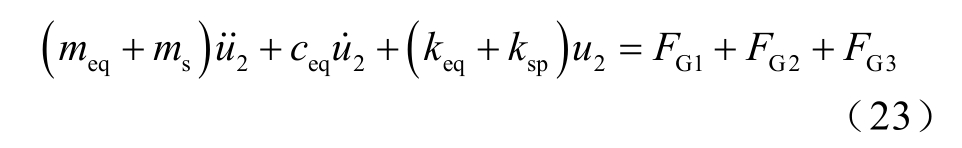
这种考虑分布特性的结构动力学模型能够描述并表征由磁场不均匀引起的力学分布特性,更加准确地预测制动器的输出位移,且求解方式简单,收敛速度快。
3 模型计算结果与实验验证
3.1 参数辨识
上文所需参数中,磁化模型中的Jiles-Atherton模型参数α、Ms、a、c、k 无法通过测量或计算获得,因此由10 Hz 下的B-H 实验曲线经粒子群算法[32]辨识得到,其余模型参数根据现有文献经验值及理论计算确定,所有参数汇总于表2 中。模型通过Pspice 电路仿真软件搭建并求解,得到制动器瞬态输出位移。
表2 SGMA 模型相关主要参数
Tab.2 Main parameters related to SGMA model

参 数 数 值饱和磁致伸缩系数λs 1.005×10-3饱和磁化强度Ms/(kA/m)800无磁滞磁化强度形状系数a/(kA/m)38.5畴壁相互作用系数α-0.001可逆系数c 0.18畴壁钉扎系数k/(kA/m)0.628 GMM 棒杨氏模量EG/GPa 30 GMM 棒密度ρG/(kg/m3)9 250单个永磁体质量mpm/kg 0.017 9等效质量meq/kg 0.039等效刚度keq/(N/m)1.6× 108等效阻尼ceq/(N·s/m)78 000输出杆质量m/kg 0.781 s碟簧刚度ksp/(N/m)2× 106
3.2 超磁致伸缩制动器实验平台
为验证本文多物理场耦合动态模型的准确性,搭建了超磁致伸缩制动器位移测量实验平台,如图9所示。平台主要分为驱动模块、负载模块、测量及数据采集模块三个部分。驱动模块由信号发生器、功率放大器、直流电源组成:信号发生器产生正弦激励信号,经功率放大器输出合适的激励电流,电流通过交流线圈产生磁场驱动棒材振动,直流电源为霍尔芯片供电测量棒材中部表面磁场;负载模块即超磁致伸缩制动器,制动器输出位移由激光位移传感器测量得到;测量及数据采集模块包含激光位移传感器、泰克MDO34 混合域示波器、环形压力传感器、数据分析仪、PC 上位机,它们共同完成数据的显示、采集、处理和后期分析。制动器固定在减振台上,减振台的作用是为制动器后端配置一个无穷大的后质量块,提供一个固定边界并防止外部的振动干扰[33],确保其产生单方向的位移输出[17],便于测量位移和建立模型。为了抑制涡流效应,提高制动器输出稳定性,本文选用径向切缝的GMM棒作为驱动振子。

图9 超磁致伸缩制动器实验平台
Fig.9 Giant magnetostrictive actuator experiment platform
3.3 实验对比及误差分析
SGMA 在环境温度20℃、预应力5 MPa 且激励电流幅值为0.85 A 的工作情况下,不同频率下(10 Hz、50 Hz、60 Hz、100 Hz)制动器输入-输出特性的实验与模型结果对比如图10 所示。从两者对比曲线可以看出,模型和实验结果有较好的吻合度,在最大激励电流处的输出位移的最大绝对误差为0.54 μm,其相对误差约为9.3%,说明本文所搭建的多物理场耦合模型能够有效地描述SGMA 的动态输出特性,并充分表征制动器输出位移衰减和滞后的变化趋势。随着频率的增加,制动器由于磁滞和阻尼等原因在最大激励电流处的输出位移逐渐衰减,其滞后现象也越发明显,且频率增大使模型对滞后值的预测精度略微降低,驱动频率为100 Hz 时模型与实验的输出位移滞后值相对误差约为20.4%,这可能是本文模型未考虑涡流效应及材料参数会随着工作频率变化所导致的。


图10 SGMA 不同频率下的输出特性
Fig.10 Output characteristics of SGMA at different frequencies
为验证本文漏磁建模及考虑力学分布特性的动力学模型的必要性和准确性,比较分析了漏磁和应变分布对制动器输出位移的影响,如图11 所示。图11 中方式一为本文搭建的模型结果,即完整地考虑了漏磁及分布特性;方式二曲线表示忽略应变分布的模型计算结果;方式三为忽略漏磁所得到的计算结果;方式四为既不考虑漏磁也不考虑分布特性的计算结果。通过与实验结果对比可以发现,在不同频率下忽略漏磁均会导致所预测的输出位移和滞后值明显偏小,原因是不考虑漏磁影响致使磁路内的偏置磁场相较实际值偏大,进而棒材在正弦激励下的交变应变量偏小[34],引起输出位移的偏差。除此之外,由于磁路中磁场不均匀,各棒材的实际应变必定会产生差异,因此忽略不同棒材的应变分布也会影响模型的准确性。
以上结果说明详细的漏磁建模并考虑其分布特性对于准确预测SGMA 输出位移至关重要。对图11中的对比结果进行量化分析,忽略这两个关键因素会导致模型预测出现明显的误差,相对误差在10 Hz时最大,约为38.79%,如图12 所示。由图中误差分析可知,本文所搭建的计及漏磁并考虑应变分布的堆栈式超磁致伸缩制动器多场耦合模型相较于忽略漏磁和不考虑分布特性的传统制动器模型预测准确率分别至多提高了20.77%和12.93%,能够更精准地表征制动器的动态输出特性。
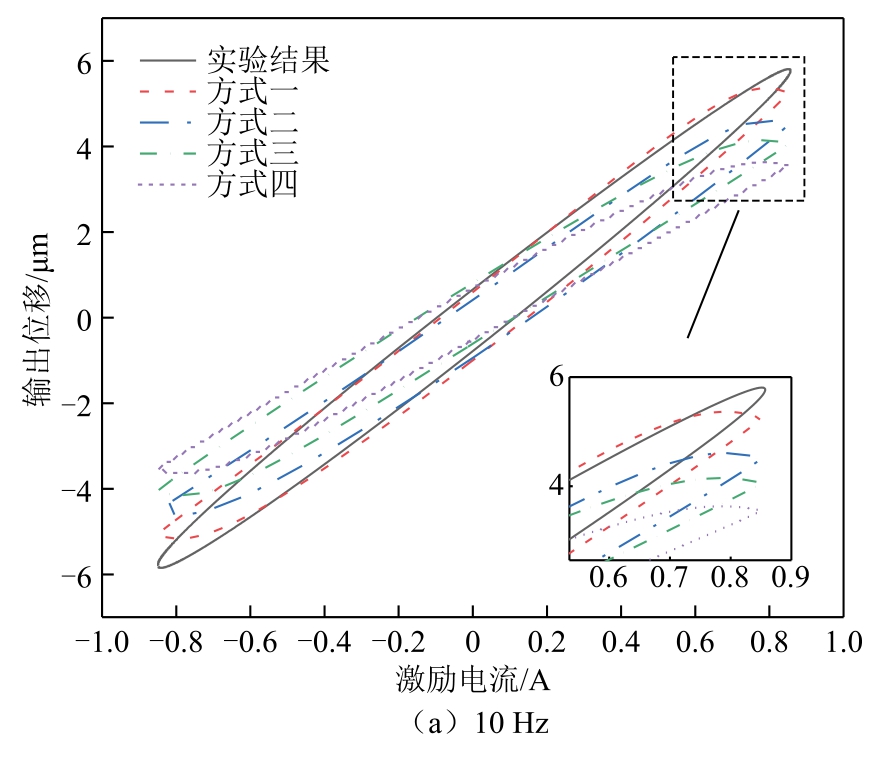
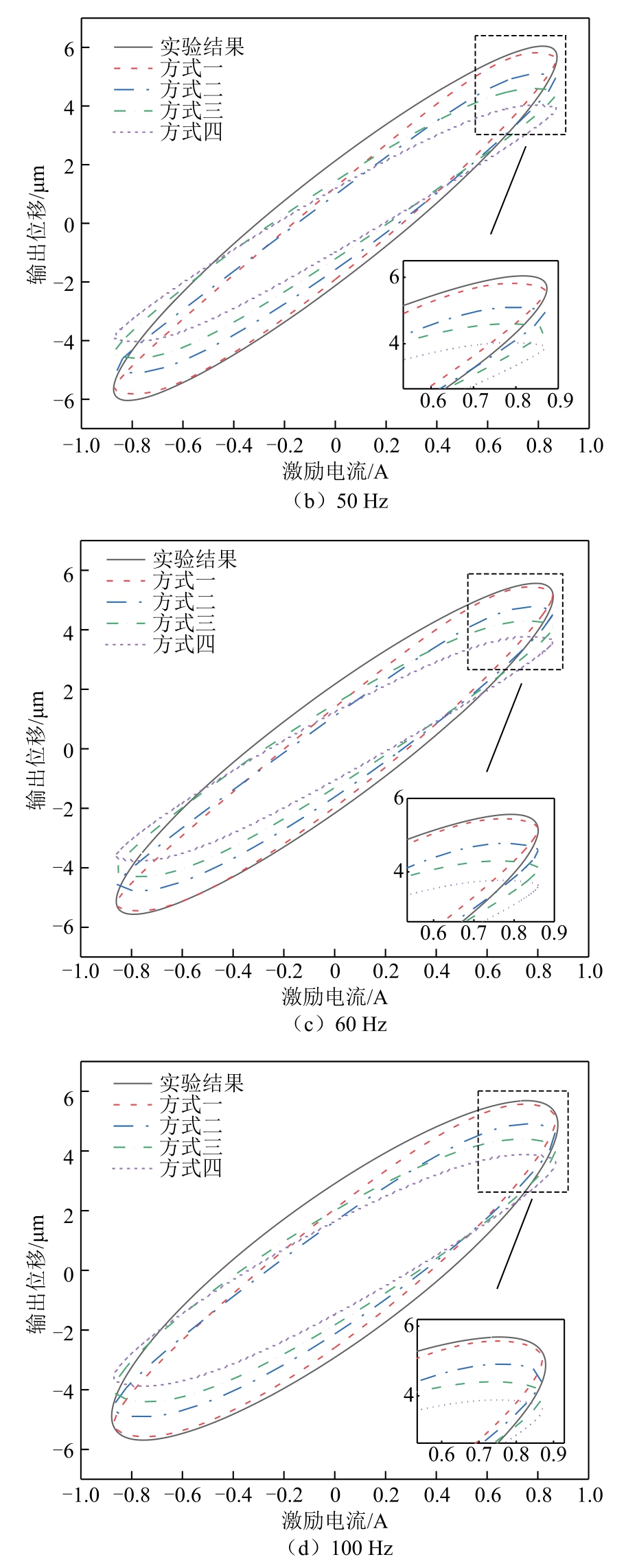
图11 SGMA 不同情况下的输出特性对比
Fig.11 Comparison of output characteristics of SGMA under different situations

图12 不同情况下输出位移误差对比
Fig.12 Error comparison of output displacement under different situations
4 结论
本文以堆栈式超磁致伸缩制动器为研究对象,充分考虑了SGMA 磁路复杂的漏磁行为所引起的磁场不均匀现象,基于有限元仿真及磁场分割法建立了详细的等效磁路模型,并借助Jiles-Atherton 模型、非线性本构模型和考虑力学分布特性的优化动力学模型搭建了计及漏磁的超磁致伸缩制动器多物理场耦合动态模型,通过Pspice 电路仿真软件搭建仿真平台快速模拟了制动器激励电流与输出位移的关系。为了验证本文模型的准确性和有效性,搭建制动器位移测量平台,对比模型与实验结果得到以下结论:
1)本文构建的多物理场耦合的动态模型能够考虑漏磁、磁场不均匀、输出力及应变存在分布等因素的影响,准确有效地表征制动器的输入-输出特性,较好地预测SGMA 的输出位移。
2)本文利用等效磁路及磁场分割法对制动器内复杂的漏磁行为建模,方法简便且具有普适性。同时,使用Pspice 电路仿真软件搭建模型求解,速度快、收敛性好、可操作性高。
3)本文使用径向切缝式的棒材削弱涡流效应,使其对在低频条件下工作的制动器影响较小,因此本文未考虑涡流损耗。对于更高频率下的制动器应用,今后将以此为目标进行下一步的研究和优化。
[1] 杜杲娴, 杨鑫, 韦艳飞, 等. 稀土超磁致伸缩棒材特性测试平台优化与实验研究[J]. 电工技术学报,2021, 36(18): 3867-3875.Du Gaoxian, Yang Xin, Wei Yanfei, et al.Optimization and experimental research on the test platform of rare-earth gaint magnetostrictive rod characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3867-3875.
[2] 翁玲, 常振, 孙英, 等. 不同磁致伸缩材料的高频磁能损耗分析与实验研究[J]. 电工技术学报, 2020,35(10): 2079-2087.Weng Ling, Chang Zhen, Sun Ying, et al. Analysis and experimental study on high frequency magnetostrictive energy loss of different magnetostrictive materials[J].Transactions of China Electrotechnical Society, 2020,35(10): 2079-2087.
[3] Yang Bintang, Yang Dehua, Xu Pengyou, et al. Large stroke and nanometer-resolution giant magnetostrictive assembled actuator for driving segmented mirrors in very large astronomical telescopes[J]. Sensors and Actuators A: Physical, 2012, 179: 193-203.
[4] Liu X H, Zhang H, Gao X L, et al. Design and simulation analysis of giant magnetostrictive actuator[J].Materials Technology, 2015, 30(3): 155-158.
[5] Yang Zhaoshu, He Zhongbo, Li Dongwei, et al. Bias magnetic field of stack giant magnetostrictive actuator:design, analysis, and optimization[J]. Advances in Materials Science and Engineering, 2016, 2016: 1-13.
[6] Rong Ce, He Zhongbo, Li Dongwei, et al. Dynamic modeling and analysis of stack giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2018,276: 205-218.
[7] Teng Duo, Li Yatian. Finite element solutions for magnetic field problems in terfenol-D transducers[J].Sensors, 2020, 20(10): 2808.
[8] 张纳, 王博文, 王莉, 等. 磁致伸缩、压电层状复合磁电传感器非线性动态有限元模型[J]. 电工技术学报, 2012, 27(7): 146-152.Zhang Na, Wang Bowen, Wang Li, et al. Nonlinear dynamic finite element model for magnetostrictive/piezoelectric laminated composite magnetoelectric sensors[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 146-152.
[9] Kim S, Kim K, Choe K, et al. A nonlinear magnetomechanical coupling model for magnetization and magnetostriction of ferromagnetic materials[J]. AIP Advances, 2020, 10(8): 085304.
[10] 刘慧芳, 王汉玉, 王洁, 等. 精密磁致伸缩致动器的动态非线性多场耦合建模[J]. 光学精密工程,2016, 24(5): 1128-1137.Liu Huifang, Wang Hanyu, Wang Jie, et al. Modeling of dynamic nonlinear multi-field coupling for precision magnetostrictive actuator[J]. Optics and Precision Engineering, 2016, 24(5): 1128-1137.
[11] 薛胤龙. 超磁致伸缩换能器多场耦合非线性模型及其数值分析[D]. 天津: 河北工业大学, 2015.
[12] Carman G P, Mitrovic M. Nonlinear constitutive relations for magnetostrictive materials with applications to 1-D problems[J]. Journal of Intelligent Material Systems and Structures, 1995, 6(5): 673-683.
[13] Wan Yongping, Fang Daining, Hwang K C. Nonlinear constitutive relations for magnetostrictive materials[J]. International Journal of Non-Linear Mechanics, 2003, 38(7): 1053-1065.
[14] Duenas T A, Hsu L, Cakman G P. Magnetostrictive composite material systems analytical/experimental[J].MRS Online Proceedings Library, 1996, 459(1): 527-543.
[15] Zheng X J, Liu X E. A nonlinear constitutive model for Terfenol-D rods[J]. Journal of Applied Physics,2005, 97(5): 053901.
[16] Wang Tianzhong, Zhou Youhe. Nonlinear dynamic model with multi-fields coupling effects for giant magnetostrictive actuators[J]. International Journal of Solids and Structures, 2013, 50(19): 2970-2979.
[17] 黄文美, 薛胤龙, 王莉, 等. 考虑动态损耗的超磁致伸缩换能器的多场耦合模型[J]. 电工技术学报,2016, 31(7): 173-178.Huang Wenmei, Xue Yinlong, Wang Li, et al. Multifield coupling model considering dynamic losses for giant magnetostrictive transducers[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 173-178.
[18] Zhu Yuchuan, Yang Xulei, Wereley N M. Research on hysteresis loop considering the prestress effect and electrical input dynamics for a giant magnetostrictive actuator[J]. Smart Materials and Structures, 2016,25(8): 085030.
[19] Zhang Heng, Zhang Tianli, Jiang Chengbao. Design of a uniform bias magnetic field for giant magnetostrictive actuators applying triple-ring magnets[J]. Smart Materials and Structures, 2013, 22(11): 115009.
[20] 晋宏炎, 鞠晓君, 辛涛, 等. 偏置磁场对超磁致伸缩致动器输出特性的影响分析[J]. 传感技术学报,2017, 30(12): 1862-1868.Jin Hongyan, Ju Xiaojun, Xin Tao, et al. Effect of bias magnetic field on output characteristics of giant magnetostrictive actuator[J]. Chinese Journal of Sensors and Actuators, 2017, 30(12): 1862-1868.
[21] Zhu Yuchuan, Li Yuesong. A hysteresis nonlinear model of giant magnetostrictive transducer[J]. Journal of Intelligent Material Systems and Structures, 2015,26(16): 2242-2255.
[22] Li Renqiang, Zhu Yuchuan, Wang Rui, et al. Design and analysis of a nested structure micro-displacement amplification mechanism for a galfenol-based actuator[J]. Smart Materials and Structures, 2019,28(9): 095026.
[23] Xu Aiqun. Study on the dynamic characteristics of a high frequency brake based on giant magnetostrictive material[J]. Smart Materials and Structures, 2016,25(6): 065001.
[24] Chen Long, Zhu Yuchuan, Ling Jie, et al.Development and test of a two-dimensional stacked terfenol-D actuator with high bandwidth and large stroke[J]. IEEE/ASME Transactions on Mechatronics,2021, 26(4): 1951-1959.
[25] Chen Hao, Yan Wenju. Flux characteristics analysis of a double-sided switched reluctance linear machine under the asymmetric air gap[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9843-9852.
[26] Yeo H K, Lim D K, Jung H K. Magnetic equivalent circuit model considering the overhang structure of an interior permanent-magnet machine[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4.
[27] 叶品州, 李红伟, 于文涛, 等. 考虑材料非线性及涡流影响的径向电磁轴承等效磁路建模[J]. 电工技术学报, 2020, 35(9): 1858-1867.Ye Pinzhou, Li Hongwei, Yu Wentao, et al. Equivalent magnetic circuit modeling of radial active magnetic bearing considering material nonlinearity and eddy current effects[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1858-1867.
[28] Li Q, Xu J, Zou L, et al. Modelling methodology and experimental verification of the permanent-magnetbiased saturation-based fault current limiter[J]. IET Electric Power Applications, 2012, 6(8): 504.
[29] 邹亮, 李庆民, 许家响, 等. 考虑漏磁效应的永磁饱和型故障限流器磁路建模与实验研究[J]. 中国电机工程学报, 2012, 32(21): 137-145.Zou Liang, Li Qingmin, Xu Jiaxiang, et al. Magnetic topology modeling and experimental study of permanentmagnet-biased saturation based fault current limiter with leakage flux effect[J]. Proceedings of the CSEE,2012, 32(21): 137-145.
[30] Porter S P. A design approach for a configurable highpower magnetostrictive drive made from iron-gallium alloy (Galfenol)[D]. Pennsylvania: The Pennsylvania State University, 2011.
[31] 翁玲, 梁淑智, 王博文, 等. 考虑预应力的双励磁线圈铁镓换能器输出特性[J]. 电工技术学报, 2019,34(23): 4859-4869.Weng Ling, Liang Shuzhi, Wang Bowen, et al. Output characteristics of double-excited coil Fe-Ga transducer considering pre-stress[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4859-4869.
[32] Chen Yukai, Yang Xin, Yang Mingzhi, et al.Characterization of giant magnetostrictive materials using three complex material parameters by particle swarm optimization[J]. Micromachines, 2021, 12(11): 1416.
[33] Dapino M J, Flatau A B, Calkins F T. Statistical analysis of terfenol-D material properties[J]. Journal of Intelligent Material Systems and Structures, 2006,17(7): 587-599.
[34] Zheng Xiaojing, Sun Le, Jin Ke. A dynamic hysteresis constitutive relation for giant magnetostrictive materials[J]. Mechanics of Advanced Materials and Structures, 2009, 16(7): 516-521.