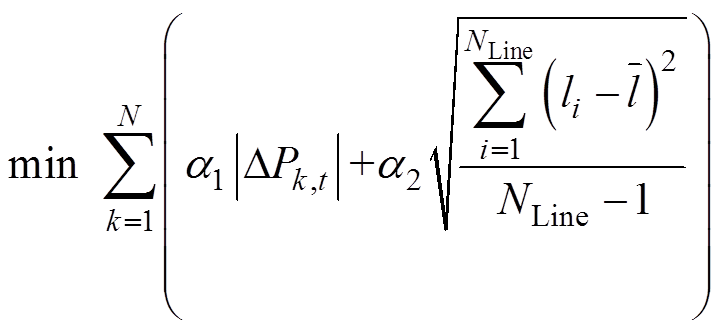 (1)
(1)
摘要 新型电力系统中,由于源荷不确定性的影响,发生线路过载事故的风险增大,传统的有功安全校正方法无法有效兼顾计算速度及效果等。基于此,该文提出一种基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制方法。首先,在满足系统静态安全约束条件下,以可调元件出力调整量最小且保证系统整体运行安全性最高为目标,建立有功安全校正控制模型。其次,构建有功安全校正的深度强化学习框架,定义计及目标与约束的奖励函数、反映电力系统运行的观测状态、可改变系统状态的调节动作以及基于改进双延迟深度确定性策略梯度算法的智能体。最后,构造考虑源荷不确定性的历史系统过载场景,借助深度强化学习模型对智能体进行持续交互训练以获得良好的决策效果;并且进行在线应用,计及源荷未来可能的取值,快速得到最优的元件调整方案,消除过载线路。IEEE 39节点系统和IEEE 118节点系统算例结果表明,所提方法能够有效消除电力系统中的线路过载且避免短时间内再次越限,在计算速度、校正效果等方面,与传统方法相比具有明显的优势。
关键词:新型电力系统 有功安全校正 深度强化学习 改进双延迟深度确定性策略 最优调整方案
随着新型电力系统的建设与发展,输电线路的传输功率持续增多,源荷等不确定性因素大幅增加,由元件故障、源荷波动等引发线路过载的概率显著提高[1-3]。由于电网在元件故障情况下较脆弱、受源荷波动性影响较大等,若线路出现过载且无法得到及时、有效的校正处理,则可能加剧联锁故障的传播速度与范围,继而引发大停电事故。因此,研究系统正常运行状态或事故发生后,安全校正措施的及时、有效实施以消除潮流越限,对保障系统安全运行具有重要意义。
传统有功安全校正方法分为优化法和灵敏度法两大类。优化法虽能全面考虑各类约束条件,但可能导致参与调整设备过多,收敛速度较慢、计算耗时较长,计算结果难以适应电力系统实际运行场 景[4-8]。灵敏度法计算速度较快,但调整过程中易出现反复过载现象,导致调整效率较低[9-10]。有研究提出安全域视角下的基于有功灵敏度的安全校正控制方法[10-11],但该类方法对调节措施的调整方向、优先级以及调节措施组合的自由度有所限定,可能遗漏最优解甚至造成无解[7]。近年来,已有部分研究将人工智能技术应用于系统的安全校正控制,如文献[12]对比分析了基于灵敏度法和粒子群优化法的有功安全校正控制效果,并给出各自适用场景,但粒子群优化法需要在线迭代求解,计算速度较慢。文献[13]利用深度神经网络快速确定参与调整的机组,之后通过规划法求解各调整机组出力,提高了规划方法的求解速度,但没有从本质上克服规划法的不足。
此外,当前新型电力系统运行工况复杂多变,新能源出力的波动幅度大,已有基于传统方法和智能算法的校正方案除无法很好地兼顾计算速度与计算效果外,亦未考虑校正过程中源荷等不确定性因素的影响以及校正后系统的安全性,极易导致校正结果无效或校正后短时间内再次出现潮流越限问题。因此,校正过程中,在保证以较快的速度和最小调整量(或发电成本最低)消除过载线路的前提下,亦应计及源荷波动性影响使计算结果更符合实际运行场景,同时尽可能地提高系统运行安全性,保证较好的校正效果。
强化学习[14]是一种通过环境与智能体不断交互学习达成回报最大化,寻找最优目标的人工智能技术,具备全局决策能力,且受系统规模和复杂度影响较小,能够较好地计及源荷波动性。同时,强化学习依据离线学习、在线应用的方式,可实现快速、有效的在线决策,减小不确定性因素的影响。深度强化学习将深度学习的感知能力与强化学习的决策能力相结合,具备连续状态特征提取能力和较大动作空间,改善了传统强化学习仅能在离散状态和动作空间中学习的不足,在电力领域得到广泛应用,如风速预测、自动发电控制等[15-20]。目前使用较多的一种深度强化学习算法为深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)。文献[17]提出基于多智能体DDPG算法有功-无功协调调度模型,并证明该算法比深度Q网络、双深度Q网络深度强化学习算法在训练效率、应用效果等方面好,亦比传统的基于二阶锥规划的优化法在线计算耗时少、综合效果好。然而,DDPG算法通常学习到的Q函数会高估真实的Q值,从而使得学到的策略失效。双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic Policy Gradient, TD3)算法为在DDPG基础上的扩展,有效改善了原有的不足[20-21]。
本文提出一种基于TD3算法的电网有功安全校正控制方法。首先,依据实际系统有功安全校正控制的特点,同时兼顾系统运行安全性,建立有功安全校正模型。之后,搭建有功安全校正深度强化学习框架,定义奖励函数、动作空间、系统观测状态等。为进一步地提高最优解质量,采用多经验池概率回放的TD3算法进行环境与动作之间交互学习,得到全局最优决策方案。通过预学习、在线应用方式,快速获得任意场景下线路过载的有效消除方案。IEEE 39节点系统和IEEE 118节点系统算例验证了本文方法的可行性和有效性。
当电网运行过程中出现单条或多条线路潮流越限时,需要采取校正控制措施使系统满足静态安全约束。常规可调元件主要包括机组、直流系统、负荷。由于调整负荷将造成用户供电中断,在实际调度运行中通常不会采用,一般可采用调整可调机组出力和直流系统功率两种控制措施[7]。为提高新能源发电利用率,文中选取常规机组和直流系统作为可调元件。
考虑到机组出力调整将导致机组磨损、辅机启停,直流系统的功率调整将影响其他区域电网的功率平衡等,为最大化降低不利影响,本文定义各可调元件调整量绝对值之和最小为目标之一。同时,兼顾系统运行安全性,即保证在调整量最小的情况下,系统安全性最高。安全性大小可由系统载荷均匀度来表示,载荷均匀度则由线路负载率标准差表征,标准差越小,系统均匀度越高,安全性越高[22]。目标函数为
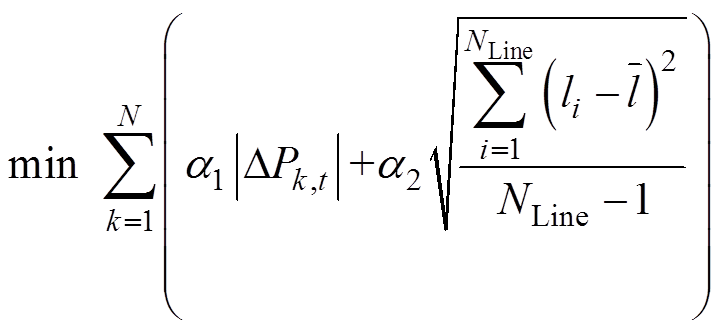 (1)
(1)
式中,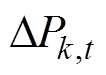 为可调元件k在t时刻的调整量,
为可调元件k在t时刻的调整量,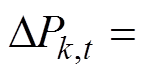
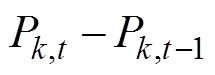 ;N为可调元件数量;li为线路i负载率,li=Pi/Pimax,Pi为线路i的传输功率,Pimax为线路i的最大传输功率;
;N为可调元件数量;li为线路i负载率,li=Pi/Pimax,Pi为线路i的传输功率,Pimax为线路i的最大传输功率;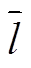 为线路负载率的平均值;
为线路负载率的平均值;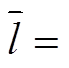
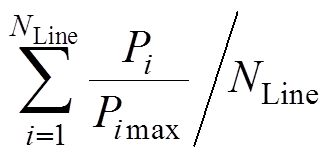 ,
, 为线路数;a1、a2为将调整量、系统均匀度两种指标约束到一定范围内的常系数。
为线路数;a1、a2为将调整量、系统均匀度两种指标约束到一定范围内的常系数。
(1)功率平衡约束
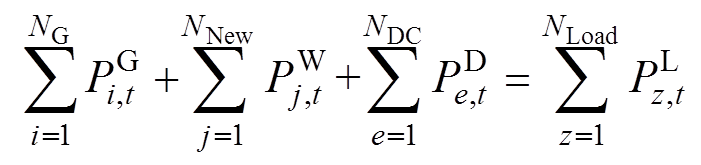 (2)
(2)
式中,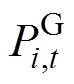 、
、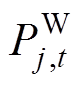 、
、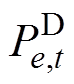 分别为常规机组、新能源机组、直流系统在t时刻注入的有功功率;
分别为常规机组、新能源机组、直流系统在t时刻注入的有功功率;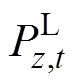 为负荷量;NG、NNew、NDC、NLoad分别为常规机组、新能源机组、直流系统、负荷的数量。
为负荷量;NG、NNew、NDC、NLoad分别为常规机组、新能源机组、直流系统、负荷的数量。
(2)出力约束
常规机组出力的约束上、下限为
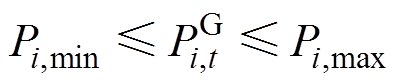 (3)
(3)
式中,Pi,min、Pi,max为常规机组i有功出力上、下限。
新能源机组出力约束上、下限为
 (4)
(4)
式中,Pj,max、Pj,min为新能源机组j有功出力上、下限。
直流系统传输功率的上、下限约束
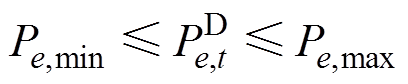 (5)
(5)
式中,Pe,max、Pe,min为直流系统e有功出力上、下限。
(3)在计及系统载荷均匀度目标的基础上,文中将校正后线路负载率不超过90 %作为校正后线路的传输约束,以保证必要的安全裕度,如式(6)所示[7]。
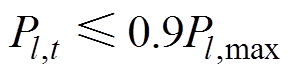 (6)
(6)
式中,Pl,max为线路l最大允许传输功率。
(4)可调元件爬坡速率约束
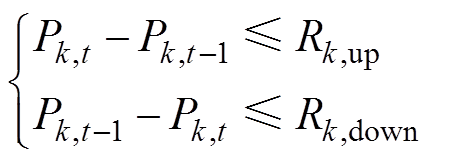 (7)
(7)
式中,Rk,up和Rk,down分别为机组k在一个调度时段内的最大向上、向下爬坡功率。
强化学习是智能体与环境不断交互,寻找一个最优策略来最大化期望回报值的过程,组成部分包括环境、智能体、表征环境的状态集合S、表征智能体动作的集合A及对智能体的奖励r。某时刻t交互过程如图1所示。

图1 智能体与环境交互过程
Fig.1 Interaction process between agent and environment
由图1可知,在t时刻,环境向智能体提供观测到的系统状态st∈S,智能体基于深度强化学习算法和系统状态st生成动作at,环境根据动作更新下一时刻状态,并返回一个奖励值rt给智能体。
本文中,电力系统为环境,设可调元件数量为N、节点数量为NNode、线路数量为NLine、负荷节点数量为NLoad、新能源机组数量为NNew,有功安全校正问题的深度强化学习框架内各组成部分表征 如下。
1)状态空间s
状态空间应尽可能表达系统的特征,因此,选择系统拓扑、线路潮流、节点负荷、新能源出力作为观测状态,对于任意时刻t,状态st表示为
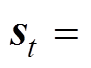
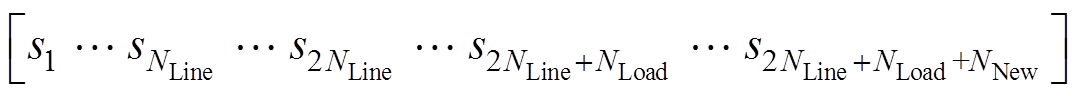 (8)
(8)
式中,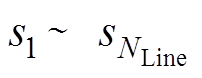 为线路开断状况,为1表示线路未断开,为0表示线路断开;
为线路开断状况,为1表示线路未断开,为0表示线路断开;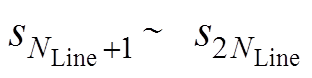 为线路 传输功率;
为线路 传输功率;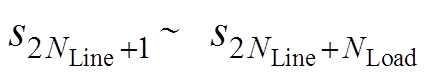 为节点负荷值,
为节点负荷值,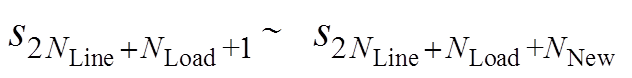 表示新能源出力值。
表示新能源出力值。
2)动作空间a
动作空间为优化模型中的相关决策量。文中将可调元件出力的调整作为动作,考虑到爬坡约束,将调度出力的调整用增量形式表示。以任意可调元件k为例,其在t时刻的动作表示为
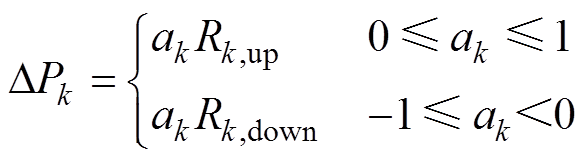 (9)
(9)
式中,DPk为可调元件当前时刻t较上一时刻t-1的出力变化量;ak为强化学习输出的可调元件k出力动作值,ak∈[-1, 1]。
系统中共包含N个元件动作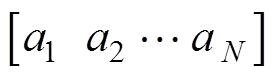 。为减少无效机组出力调整,提高调整效率,设置每步动作只选择两个元件分别进行增出力与减出力。t时刻,动作空间at表示为
。为减少无效机组出力调整,提高调整效率,设置每步动作只选择两个元件分别进行增出力与减出力。t时刻,动作空间at表示为
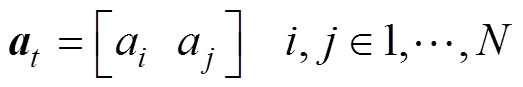 (10)
(10)
3)奖励r
有功安全校正的目标是以最小的调整量同时保证较高的系统运行安全性消除线路过载。此外,环境在反馈给智能体奖励时,应当根据式(2)~式(7),计及系统功率平衡、线路负载率是否小于等于0.9等。因此,在时刻t获得的奖励表示为
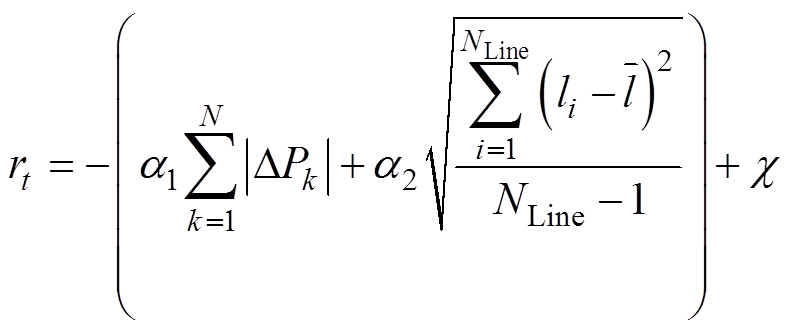 (11)
(11)
式中,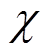 为惩罚项,当任一约束不满足时,惩罚项取值为-30,否则为0。
为惩罚项,当任一约束不满足时,惩罚项取值为-30,否则为0。
4)智能体
智能体由深度强化学习算法及其得到的调整策略组成,深度强化学习分为策略学习、价值学习、Actor-Critic三大类。Actor-Critic结合了策略学习与价值学习的优势,可以很好地解决连续动作空间问题,实现单步更新,提高学习效率。文中采用基于Actor-Critic架构的TD3深度强化学习算法,进行可调元件最优出力调整决策。
TD3算法由6个深度神经网络组成,分别为主策略网络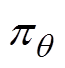 、目标策略网络
、目标策略网络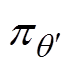 、主值网络
、主值网络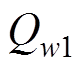 、目标值网络
、目标值网络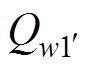 、主值网络
、主值网络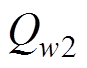 、目标值网络
、目标值网络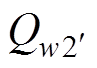 。其中,主策略网络
。其中,主策略网络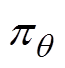 负责读取电力系统当前空间状态st,给出当前时刻机组出力调整at,并和电力系统交互生成下一时刻电网空间状态st+1和当前时刻奖励值r;目标策略网络
负责读取电力系统当前空间状态st,给出当前时刻机组出力调整at,并和电力系统交互生成下一时刻电网空间状态st+1和当前时刻奖励值r;目标策略网络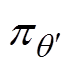 负责读取下一时刻状态st+1生成下一时刻动作at+1;主值网络Qw1、Qw2负责对st、at进行评价;目标值网络
负责读取下一时刻状态st+1生成下一时刻动作at+1;主值网络Qw1、Qw2负责对st、at进行评价;目标值网络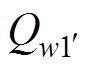 、
、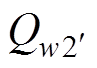 负责对st+1、at+1进行评价。结构见表1。
负责对st+1、at+1进行评价。结构见表1。
表1 TD3算法网络结构
Tab.1 Network structure of TD3 algorithm

方法输入输出 主策略网络st 目标策略网络st+1 主值网络Qw1st,at 目标值网络st+1,at+1 主值网络Qw2st,at 目标值网络st+1, at+1
表1中,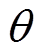 、
、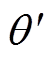 、w1、
、w1、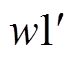 、w2、
、w2、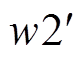 分别为6个深度神经网络的参数;
分别为6个深度神经网络的参数;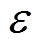 、
、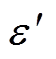 为环境噪声。
为环境噪声。
TD3算法通过与电力系统环境不断交互,获得6个神经网络参数的最优取值,进而实现最优机组出力动作调整,这一过程也称为离线训练。网络参数优化方式如下。
(1)主值网络
主值网络Qw通过最小化损失函数L(w)来优化参数w,L(w)表示为
 (12)
(12)
式中,m为经验池中抽取的训练样本数量,包括电力系统不同运行场景下校正过程中不同时刻的空间状态s、机组动作a、奖励值r等;i代表第i个历史样本;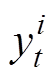 为目标Q值。
为目标Q值。
TD3算法同时学习2个目标值网络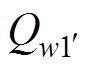 、
、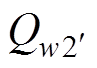 ,取最小值进行策略更新,故目标Q值
,取最小值进行策略更新,故目标Q值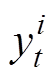 为
为
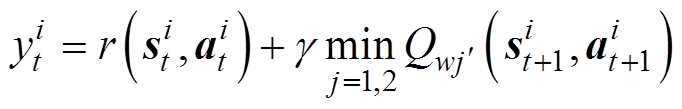 (13)
(13)
式中,r为奖励函数;g∈[0, 1]为奖励折扣系数; 由目标策略网络
由目标策略网络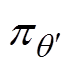 计算所得
计算所得
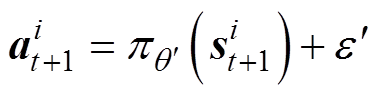 (14)
(14)
式中,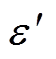 ~clip[N(0,
~clip[N(0,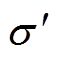 )-c, c]为添加的基于正态分布的噪声;c、-c分别为噪声的上、下边界。
)-c, c]为添加的基于正态分布的噪声;c、-c分别为噪声的上、下边界。
根据梯度规则更新Qw参数w,公式为
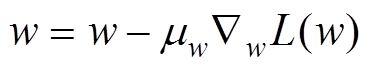 (15)
(15)
式中,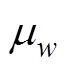 为主值网络学习率。
为主值网络学习率。
(2)策略网络
策略网络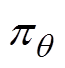 采用梯度下降策略对参数
采用梯度下降策略对参数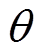 进行优化,即
进行优化,即
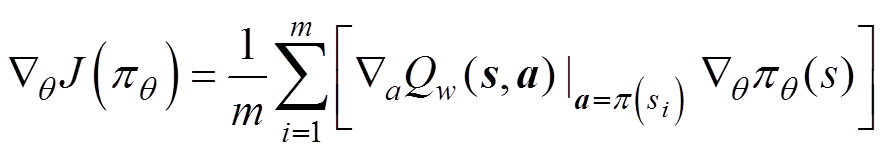 (16)
(16)
根据确定性策略梯度,更新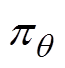 参数
参数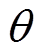 为
为
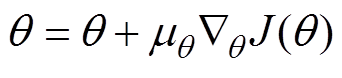 (17)
(17)
式中,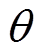 为策略网络学习率。
为策略网络学习率。
相对于主值网络部分参数的每一步更新一次,策略网络参数的更新频率较低,通常更新频率大于2,即策略网络隔几步更新一次。
之后,采用软更新方式,对目标网络参数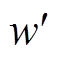 、
、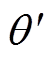 进行更新,即
进行更新,即
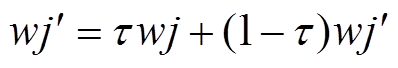 (18)
(18)
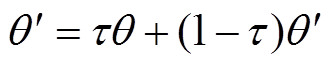 (19)
(19)
式中,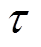 为软更新系数;j为1或2。
为软更新系数;j为1或2。
经验回放(Experience Replay, ER)方法为将探索得到的经验数据存储在经验池中,通过随机抽取样本的方式更新神经网络的参数。然而,通过随机采样的方式抽取的样本数据质量参差不齐,可能会出现大量无用样本的情况,影响训练效果、收敛速度、计算时间等。因此,本文将经验池分为成功经验池Msuccess和失败经验池Mfailure,分别存储成功和失败两种调整经验。当经验池中存满时,最早存入的经验将被最新存入的经验代替。
在Msuccess中,希望抽取到价值更高的经验,因此采用优先经验回放法;在Mfailure中无需考虑。成功经验池和失败经验池的采样比例如下
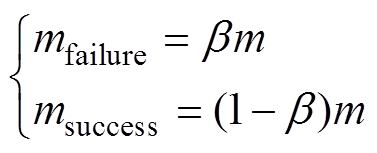 (20)
(20)
式中,m为经验池中抽取的总训练样本数量;mfailure、msuccess分别为失败经验和成功经验样本的采样数量;b 为失败经验池样本抽取率。
优先经验回放法为在经验池中优先抽取价值较高的经验数据,数据优先级p通过TD误差衡量,如第k个样本的优先级为
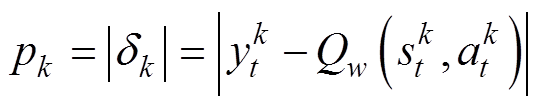 (21)
(21)
第k个样本被采样的概率为
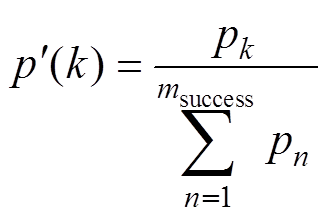 (22)
(22)
基于改进TD3算法的有功安全校正控制模型分为预学习和在线测试两部分。不同于深度学习将固定的历史样本集作为模型训练样本,深度强化学习使历史样本集每一步决策结果均有机会作为训练样本,增大了训练样本数量,使模型在线应用时适应能力更佳;此外,区别于深度学习在训练好的模型上根据特征直接进行分类的方式,深度强化学习借助训练好的模型逐步得到最优决策,使得在线应用效果更好。
3.3.1 预学习阶段
预学习即为离线训练,TD3算法通过与不同潮流越限运行工况下的电网进行交互,产生大量训练样本,将这些训练样本按照回放经验标准存入经验池组,同时使用多经验池概率回放的方式抽取样本对智能体进行离线训练。通过离线训练,得到一种可以满足随机环境下的控制性能最优的策略。
考虑到校正过程中源荷波动性对校正结果的影响,在构造不同潮流越限运行工况时,针对每个运行工况下源荷出力计及了可能的波动值,即根据每个工况衍生多种可能的波动的运行工况进行交互训练。首先,根据历史源荷实际与预测的误差值构造数据集;之后,对预测误差值数据集拟合概率密度分布,再拟合累积分布;最后通过拉丁超立方采样方法抽取风电预测误差值和负荷预测误差值,与系统预测的源荷值相加得到未来取值。已知当前系统可预测5 min、15 min、24 h的风电出力值、负荷值,而有功安全校正一般情况下可以用较短时间完成,因此,文中选取预测5 min后的源荷值。
训练步骤如下:
1)随机初始化两个主值网络和主策略网络的参数w1、w2、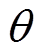 。
。
2)初始化目标网络参数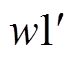 =w1、
=w1、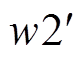 =w2、
=w2、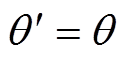 。
。
3)初始化成功经验池和失败经验池。
4)对每次迭代,循环执行以下步骤:
(1)随机选一个历史样本,获取初始状态s0。
(2)若调整步数小于最大限定步数(t<Tmax ,则对其每一步循环执行以下步骤:
,则对其每一步循环执行以下步骤:
①根据状态st,选择动作并加入噪声,at= 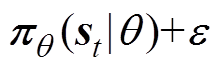 ,
,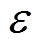 ~N(0,1)。
~N(0,1)。
②执行动作at,得到奖励rt和下一状态st+1。
③将四元组(st, at, rt, st+1)根据奖励值大小,存入成功经验池Msuccess或失败经验池Mfailure中。
④经验池是否存满,若没存满,则转至步骤①将st+1代替st进行循环;否则,进行下一步。
⑤计算从Msuccess中抽取的样本的TD误差dk,更新样本优先级pk=|dk|。
⑥从Msuccess和Mfailure中共采样m个样本(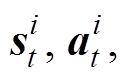
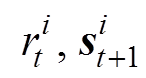 ),i=1, 2,∙∙∙, m。
),i=1, 2,∙∙∙, m。
⑦通过目标策略网络计算下一时刻动作at+1。
⑧计算小批量经验样本中每个样本的目标值yt。
⑨根据式(15)更新w。
⑩每隔d步,根据式(17)更新策略网络参数θ。
⑪更新目标网络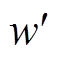 、
、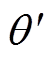 。
。
(3)结束步数循环,输出当前回合平均累积奖励值。
5)结束迭代循环。
训练结束后,基于改进TD3算法的有功安全校正控制模型的参数将被保存。训练过程中某一时间步示意图如图2所示。
3.3.2 计及源荷不确定性的在线应用阶段
在线应用时,将系统未来5 min的源荷预测值加上随机抽取的预测误差值作为当前时刻新能源出力值和负荷值,与系统其他元件状态共同输入Actor网络,经过充分预学习的改进TD3算法便可依据系统状态快速做出最优决策,即电力系统运行中,若出现线路过载情况,将新能源与负荷预测值代入系统运行状态,然后映射到训练好的模型,便可快速得出各可调元件调整量。
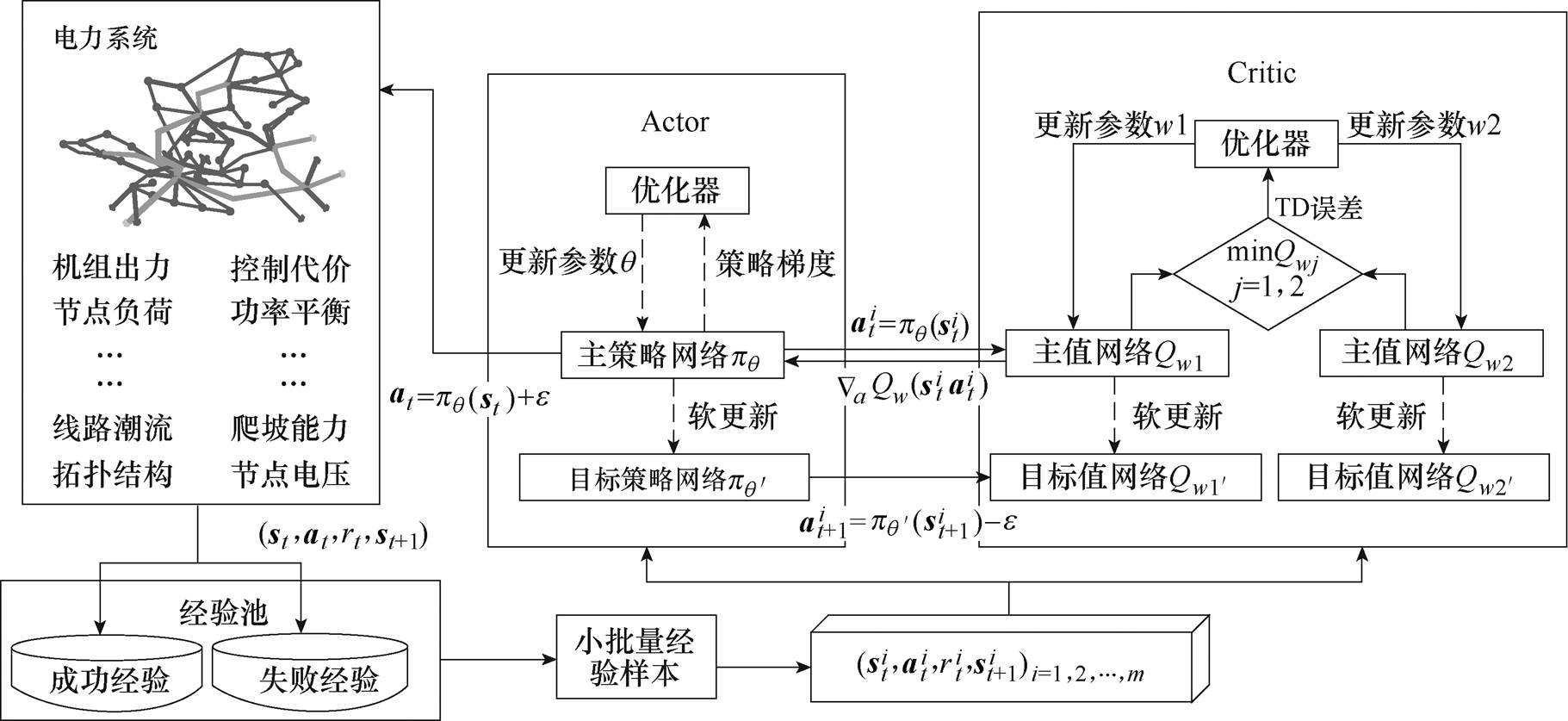
图2 基于改进TD3算法的有功安全校正控制模型训练过程中某一时间步示意图
Fig.2 Schematic diagram of a time step in the training process of active power security correction control model based on improved TD3 algorithm
在线决策过程中,每步决策的结果将被分类存入经验池。之后,可以在已有模型的基础上,利用在线决策得到的经验对模型参数进行完善优化,提高模型泛化能力。
文中利用IEEE 39节点系统和IEEE 118节点系统作为算例,对基于深度强化学习的有功安全校正控制方法进行验证与评估。采用Matpower软件平台计算潮流;利用Pycharm平台构造用于有功安全校正控制的深度强化学习模型。
首先利用IEEE 39节点系统作为算例,对基于深度强化学习的有功安全校正控制方法进行验证与评估。将算例系统的第34号节点机组用风电机组代替,第38号节点机组用常规高压直流代替,节点系统拓扑如图3所示。
4.1.1 参数设置
TD3深度强化学习算法包含六个神经网络,每个神经网络包括两个隐藏层,维数为512。预学习中改进的TD3算法超参数取值和奖励函数中常数系数取值见表2。
在以上参数基础上,采用Python语言,基于TensorFlow框架实现模型构建,计算机硬件条件为Core i5-7300CPU,2.5 GHz。
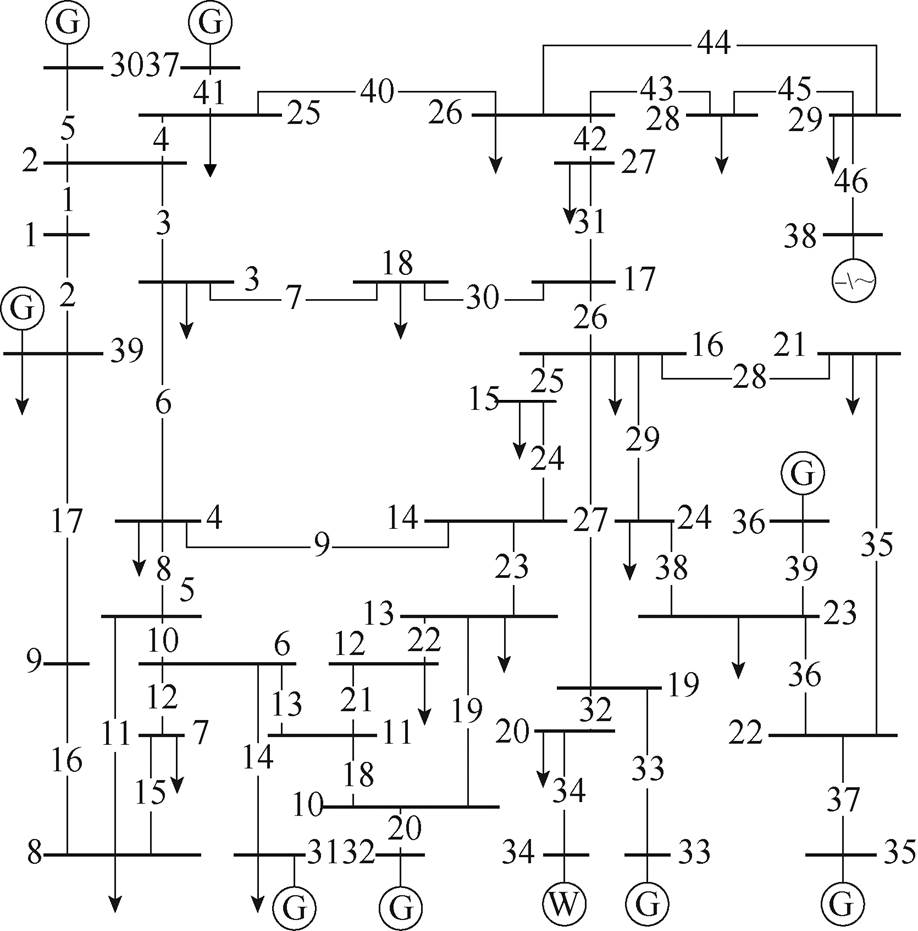
图3 修改的IEEE 39节点系统
Fig.3 Modified IEEE 39-bus system
表2 参数取值
Tab.2 Parameter settings

参 数数 值 折扣率g0.9 软更新系数t0.01 策略网络学习率mw0.000 1 价值网络学习率mq0.000 1 成功经验池容量Msuccess100 000 失败经验池容量Mfailure100 000 单次训练步数Tmax3 000 策略网络参数更新周期d5 最大迭代次数4 250 失败样本抽取率b0.8 策略噪声标准差0.3 奖励指标系数1 a10.01 奖励指标系数2 a210
4.1.2 模型预测学习
在预学习阶段,通过改变负荷、机组出力、开断线路等,仿真模拟得到不同的运行工况;对每个运行工况进行N-1、N-2安全校核,得到不同运行工况下的线路过载状态,共5 000个过载场景。利用历史中一年的风电、负荷的实际与预测的误差值集合拟合概率密度与累积分布,之后通过拉丁超立方采样方法抽取风电预测误差值和负荷预测误差值,每个新能源机组、负荷抽取量均为20个,之后随机组合为20组系统新能源出力与负荷误差值,使系统5 min后预测值加上误差值作为风电出力和负荷值,训练场景共计100 000个。历史中风电与负荷预测误差的拟合结果如图4所示(文中暂且考虑系统中风电出力服从一种分布,所有负荷服从一种分布)。

图4 系统中新能源与负荷的有功预测误差值
Fig.4 Active power prediction error value of new energy and load in the system
模型与不同越限状态下的电网场景进行不断交互,产生数量为20万个(经验池总容量)的训练样本集进行离线训练,从而得到一个经过充分训练的智能体,在线测试时可以及时做出最优决策。
参考已有深度强化学习模型训练效果评估方法,文中采用每次迭代的平均奖励值判断模型训练的效果。模型训练过程中,每次迭代产生奖励总值,除以步数便得到平均奖励总值,为更好地观测平均奖励总值的趋势,采用移动平均方式对曲线进行平滑处理。前1 500次迭代结果如图5所示。
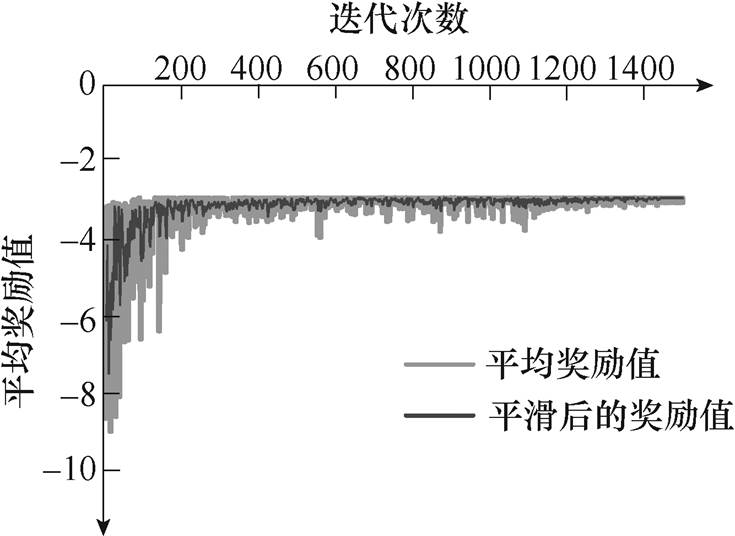
图5 训练过程中的平均累积奖励值
Fig.5 The average accumulated reward profile during the training process
由图5可知,随着训练的进行,平均奖励值逐步升高,模型的表现效果越来越好。由于不同运行状态的差异和在动作上叠加了随机探索,因此,平均奖励值存在一定程度的振荡,这一现象是合理的。训练用时约1 071.73 min。
4.1.3 模型在线应用
以系统某一运行状态作为初始状态,该状态下无线路停运,元件出力、节点负荷等状态参数见表3。可调元件出力上下限、机组爬坡速率上下限、线路传输上下限见附表1~附表3。
表3 系统初始状态参数
Tab.3 System initial state parameters
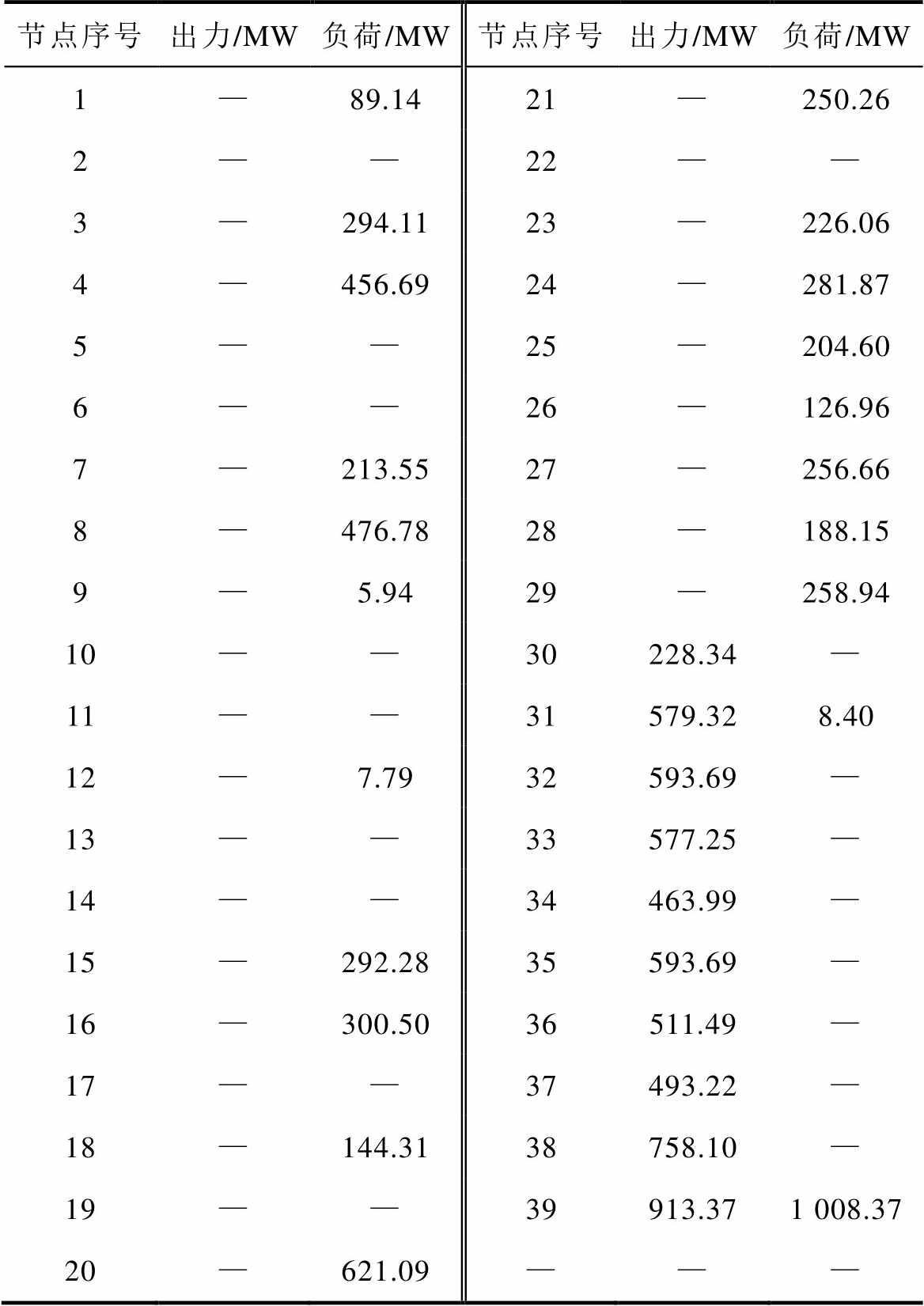
节点序号出力/MW负荷/MW节点序号出力/MW负荷/MW 1—89.1421—250.26 2——22—— 3—294.1123—226.06 4—456.6924—281.87 5——25—204.60 6——26—126.96 7—213.5527—256.66 8—476.7828—188.15 9—5.9429—258.94 10——30228.34— 11——31579.328.40 12—7.7932593.69— 13——33577.25— 14——34463.99— 15—292.2835593.69— 16—300.5036511.49— 17——37493.22— 18—144.3138758.10— 19——39913.371 008.37 20—621.09———
假设该状态下线路23因故断开,线路13出现过载,负载率为122.06 %。将5 min后系统风电出力和负荷值(预测值加预测误差值)代入系统环境并输入4.1.2节已训练完成的模型中,得到可消除线路过载的最优决策方案。调整元件分别为节点31、32号机组和38号直流系统,对应调整量为+21.72 MW、-152.37 MW、+114.00 MW,计算所用时间为0.028 s。其中,5 min后风电机组增加出力20.50 MW,系统整体负荷增加3.85 MW。校正后系统均匀度由0.717提高到0.746,校正前后各线路负载率如图6所示。
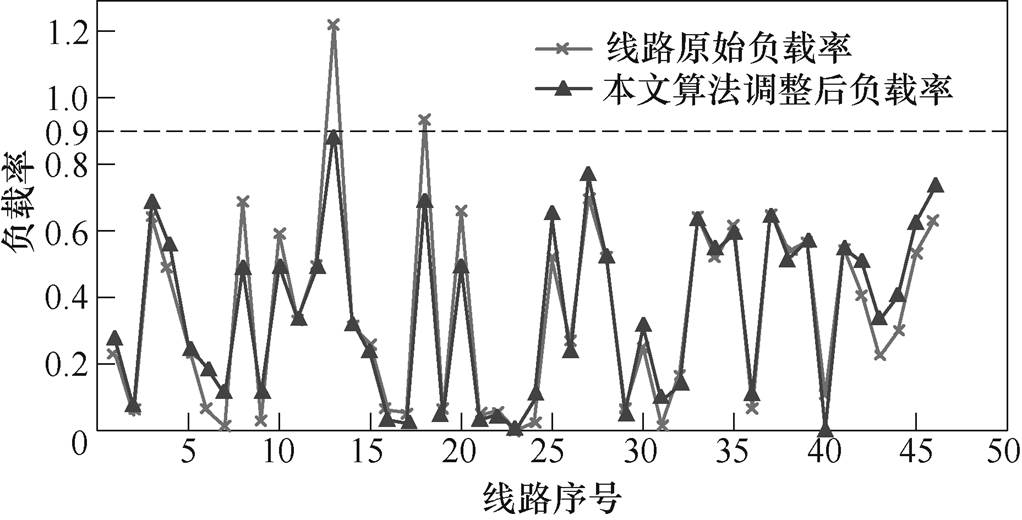
图6 校正前后各线路负载率
Fig.6 Load rate of each line before and after correction
由图6可知,各线路负载率均被调整到0.9以下,为减轻未来的不确定性因素的影响提供了一定的安全裕度。
若校正过程中不计及新能源出力和负荷变化,则机组调整量分别为31号机组增加出力40 MW、32号机组减少出力154 MW、38号直流系统增加出力114 MW。假设校正过程中或校正完成后短时间内系统中新能源出力值与负荷值发生变化,依据4.1.2节方法抽取100组源荷预测误差值,加上预测值对本文方法校正后的系统安全性进行评估,同时将不考虑新能源出力和负荷变化的校正结果用于对比,结果见表4。
由表4可知,在100组测试结果中,基于本文方法的综合考虑源荷波动性、系统均匀度和线路最高负载率的校正效果最好,能够承受相对较多的不确定性影响保证系统短时间内不再出现过载,适用于当前新型电力系统。
4.1.4 不同深度强化学习算法的对比分析
已知本文所用TD3算法为DDPG算法的拓展,且在原有TD3算法基础上增添双经验池进行了改进,为证明本文方法的优势,将DDPG、TD3和改进TD3算法设置相同的参数,对其训练与测试效果进行对比。
表4 校正后系统受源荷不确定性因素影响的结果
Tab.4 Results of the system affected by source-load uncertainty after correction
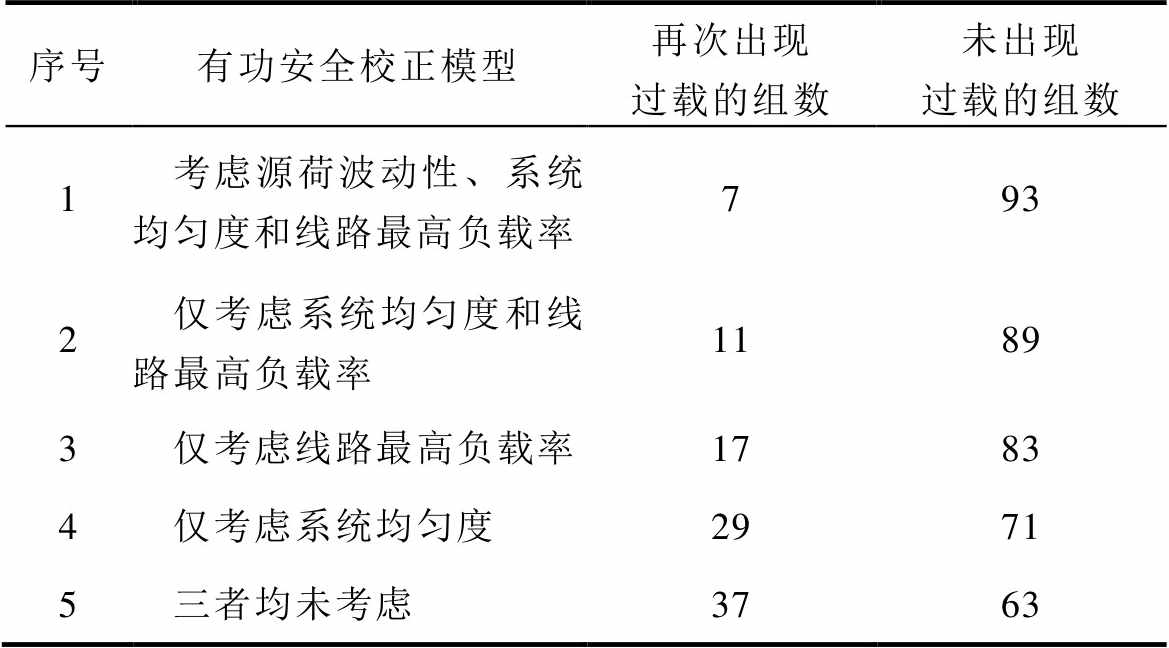
序号有功安全校正模型再次出现过载的组数未出现过载的组数 1考虑源荷波动性、系统均匀度和线路最高负载率793 2仅考虑系统均匀度和线路最高负载率1189 3仅考虑线路最高负载率1783 4仅考虑系统均匀度2971 5三者均未考虑3763
首先利用4.1.3节构造的历史过载场景,对三种方法的训练效果进行对比。为便于直观分析,仅呈现平滑处理后的三种方法训练过程中的平均奖励值,如图7所示。
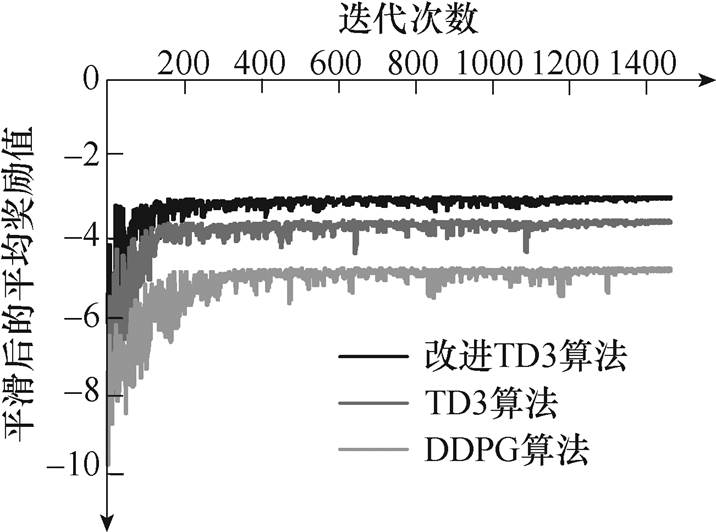
图7 不同深度强化学习算法训练中的平均奖励值
Fig.7 Average reward value in different deep reinforcement learning algorithm training
由图7可知,本文所提改进TD3算法相对较快地达到收敛,波动较小,且最高平均奖励值大于其余两种算法。
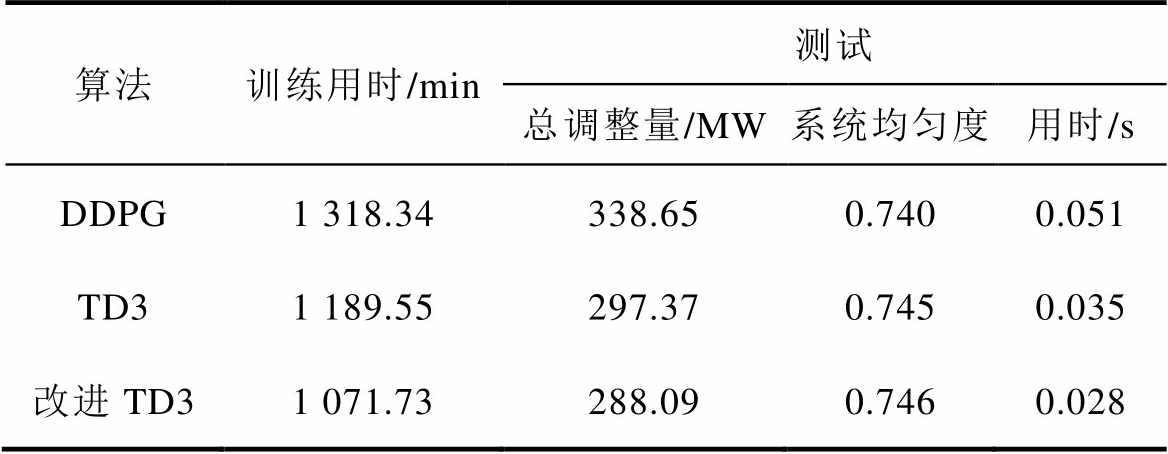
进一步地,在计及系统源荷波动性、均匀度和线路最高负载率训练完成的情况下,以4.1.3节运行状态为例进行测试。各算法应用效果见表5。
表5 相同背景下不同深度强化学习算法的应用效果
Tab.5 Application effects of different deep reinforcement learning algorithms under the same background
算法训练用时/min测试 总调整量/MW系统均匀度用时/s DDPG1 318.34338.650.7400.051 TD31 189.55297.370.7450.035 改进TD31 071.73288.090.7460.028
由表5可知,在相同背景下,本文所提改进TD3算法训练、测试用时以及计算结果方面相比其他两种算法好。
综上分析,由于本文所提改进TD3算法具备成功和失败两种经验池,在训练过程中便更易得到有重要参考价值的样本,因此,训练效果、收敛速度较其他两种算法好,计算时间相对较短。相较于DDPG算法,TD3算法因使用双Q网络改善Q值高估计问题,同时给策略网络加入噪声以及延迟策略网络更新,增加了算法的稳定性。因具备良好的训练效果,所以在线应用时优于其他算法。
4.1.5 与传统校正方法的对比分析
将本文方法与传统灵敏度法和优化法的计算结果进行对比,其中传统灵敏度法参见文献[10];优化法目标函数仅考虑最小调整量,采用CPLEX优化求解器,设置三种方法校正后线路负载率均在0.9以下且计及源荷波动性影响。系统初始运行状态见附表4,可调元件出力上下限、机组爬坡速率上下限、线路传输上下限见附表1~附表3。假设该状态下系统发生N-2严重故障,线路16、42因故断开,线路3、4出现过载,负载率分别为118.63 %和106.29 %。分别采用灵敏度法、优化法、本文方法对系统进行有功安全校正,消除潮流越限。对应的调整元件、调整量、计算时间以及校正后系统均匀度见表6。其中,5 min后风电机组增出力24.22 MW,系统整体负荷增加4.69 MW。
表6 不同方法下可调元件出力调整结果
Tab.6 The output adjustment results of adjustable components under different methods
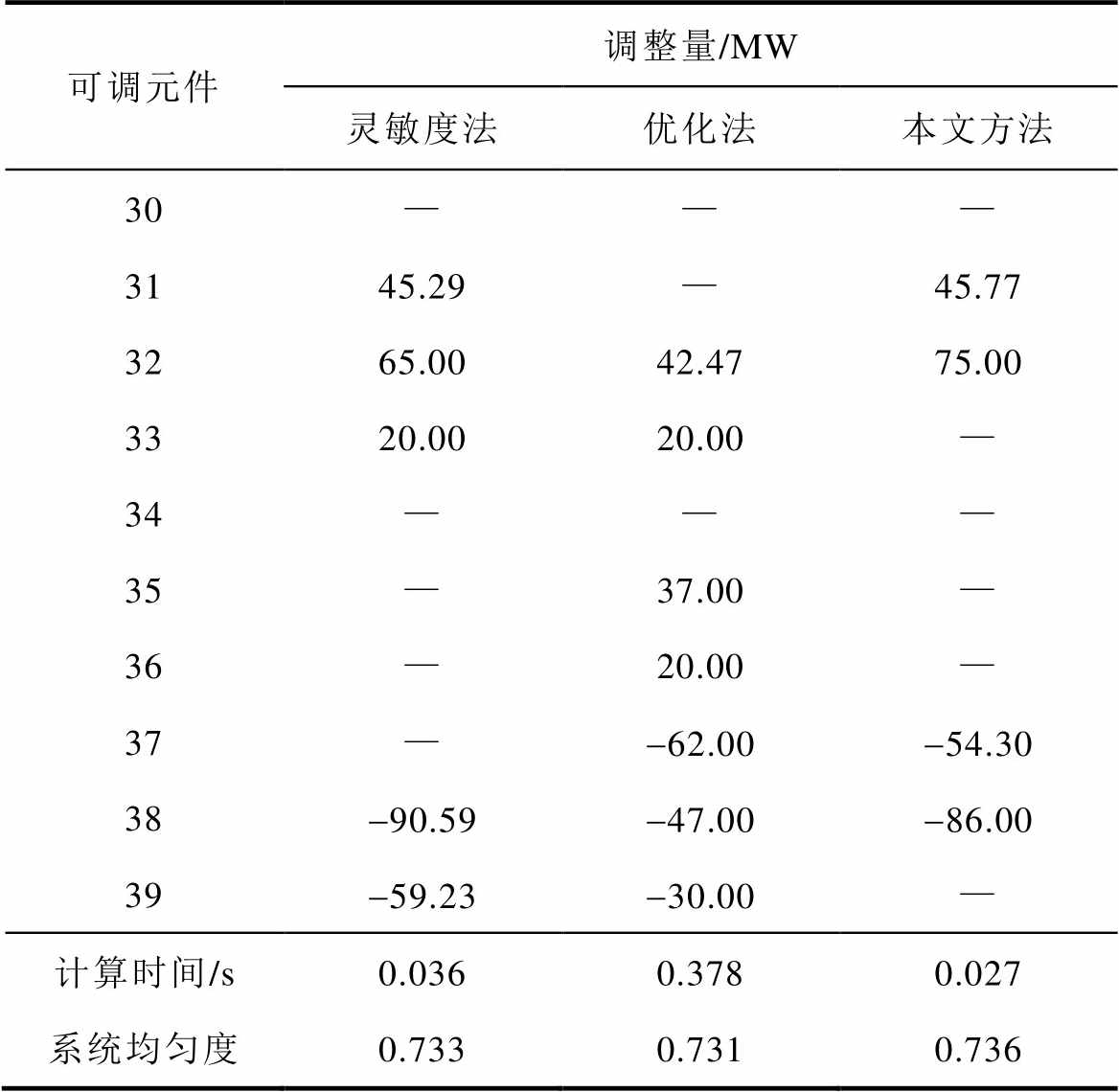
可调元件调整量/MW 灵敏度法优化法本文方法 30——— 3145.29—45.77 3265.0042.4775.00 3320.0020.00— 34——— 35—37.00— 36—20.00— 37—-62.00-54.30 38-90.59-47.00-86.00 39-59.23-30.00— 计算时间/s0.0360.3780.027 系统均匀度0.7330.7310.736
由表6可知,灵敏度法总调整量为280.11 MW,调整元件个数为5个,计算时间为0.036 s,校正后系统均匀度为0.733;优化法总调整量为258.47 MW,调整元件个数为7个,计算时间为0.378 s,校正后系统均匀度为0.731;本文所提方法总调整量为261.07 MW,调整元件个数为4个,计算时间为0.027 s,校正后系统均匀度为0.736。
可见,灵敏度法计算时间较短,但总调整量较多;优化法总调整量最少,但计算时间较长,约为灵敏法的10倍。本文方法通过调整动作与系统环境逐步交互,得到最优方案,模型设置单次调整元件数量为2,分别进行增出力和减出力,可以保证相同调整效果下参与调整的机组较少,且模型为经过离线训练后进行在线应用,因此,计算结果中调整元件数量以及所用时间均较小;校正后系统均匀度最高,但由于计及了系统运行安全性,导致总调整量略大于优化法。
综上所述,从模型计算结果、计算速度以及校正效果等多方面综合考量,本文所提方法具备一定的应用优势。
将本文所提基于深度强化学习的计及系统运行安全性的有功安全校正方法在IEEE 118节点系统中进行验证与评估。IEEE 118节点系统拓扑如图8所示。系统中仅部分机组投入运行并参与调整,序号分别为10、12、25、26、31、46、49、54、59、61、65、66、69、80、87、89、100、103、111。系统可调元件出力上下限、机组爬坡速率上下限、线路序号及传输上下限见附表5~附表7。设置机组66、80为新能源机组,参考4.1.2节新能源与负荷预测误差值概率密度与累积分布。
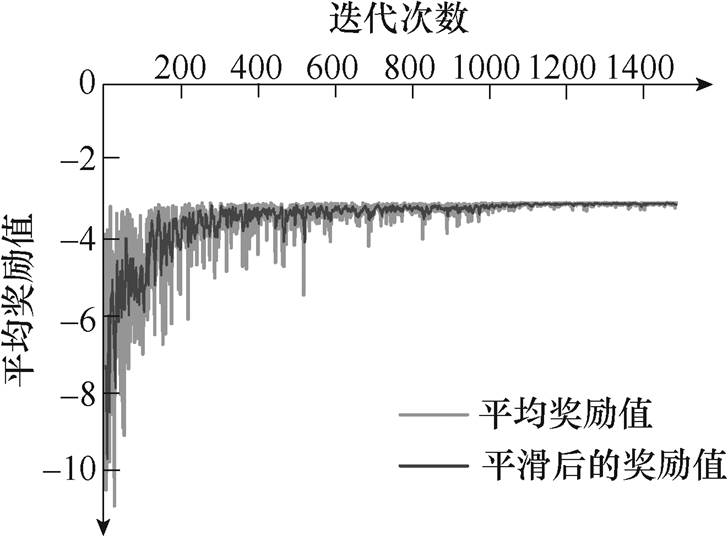
通过改变系统负荷、开断线路等获得不同运行工况,然后进行N-1、N-2安全校核,得到不同的越限状态,共计5 000个。考虑源荷波动性影响,抽取20组预测误差值加上预测值代入系统状态进行训练,共产生25万条经验(经验池总容量),得到良好的智能体。训练过程用时1 489.96 min,训练效果见附表5。
然后,利用新的越限场景对训练完成的模型进行测试。同时,在同一越限场景下,利用优化法和灵敏度法分别进行有功安全校正控制测试(优化法和灵敏度法仅考虑源荷波动性和线路最高负载率限制,不计及系统均匀度)。假设系统某一运行状态下,线路11断开,引发线路5、6、10出现过载,过载率分别为106.43 %、108.85 %、101.34 %。三种方法校正控制结果见表7。其中,5 min后风电机组总出力增加10.28 MW,系统整体负荷减少5.44 MW。
图8 IEEE 118节点系统
Fig.8 IEEE 118-bus system
表7 三种方法的计算结果
Tab.7 Calculation results of the three methods
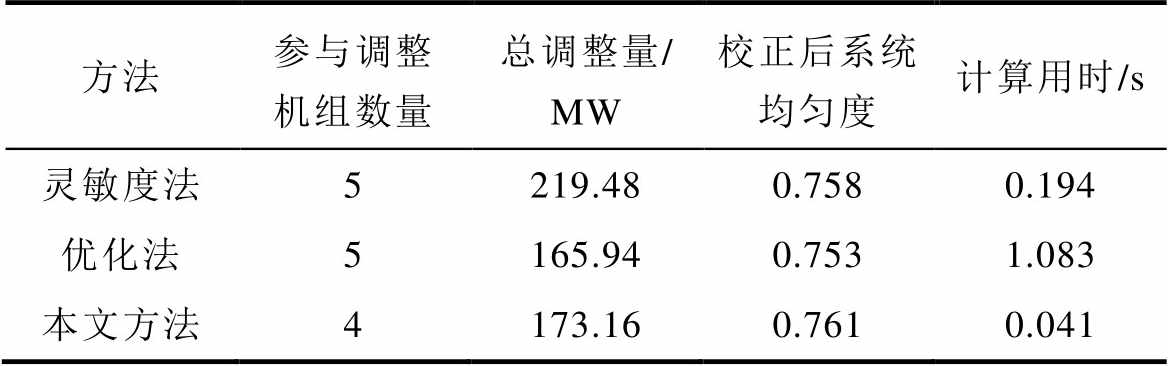
方法参与调整机组数量总调整量/ MW校正后系统均匀度计算用时/s 灵敏度法5219.480.7580.194 优化法5165.940.7531.083 本文方法4173.160.7610.041
由表7可知,灵敏度法涉及5个调整机组,该方法两两配对依次实施调整,调整过程为:第一轮机组10减出力78.54 MW、机组12增出力78.54 MW,第二轮机组10增出力19.11 MW、机组89减出力19.11 MW,第三轮机组61增出力12.09 MW、机组111减出力12.09 MW,总调整量为219.48 MW,校正后系统均匀度为0.758,用时0.194s。优化法涉及5个调整机组,分别为机组10、12、31、61,对应调整量为-74.47 MW、+41.80 MW、+18.13 MW、+20.62 MW、-10.92 MW,总调整量为165.94 MW,校正后系统均匀度为0.753,用时1.083s。本文所提方法涉及4个调整机组,分别为机组10、12、61、89,对应调整量为-60.21 MW、+60.21 MW、+26.37 MW、-26.37 MW,总调整量为173.16 MW,校正后系统均匀度为0.761,用时0.041 s。
由上述分析可知,从参与调整机组数量、总调整量、计算用时、校正后系统运行安全性等方面对比三种有功安全校正控制方法,证实本文所提方法应用效果较好。此外,当系统规模扩大后,本文方法在计算速度方面的优势得到进一步体现,能够实现在预想事故或实时运行中及时阻断因线路过载引发的连锁故障的传播,避免由源荷不确定性等因素加剧故障传播速度与范围。
本文以机组调整量最小为目标,同时计及系统运行安全性,在满足静态安全约束前提下提出一种基于双延迟深度确定性策略梯度深度强化学习算法的有功安全校正方法。通过IEEE 39节点系统和IEEE 118节点系统算例验证了本文方法的有效性和可行性。本文方法的主要优势如下:
1)本文方法在有功安全校正计算过程中计及了源荷波动性影响,计算结果更符合电网实际运行场景,适用于当前新型电力系统。
2)本文方法建立的有功安全校正模型不仅考虑了机组总调整量,亦考虑了系统载荷均匀度,同时约束了校正后系统线路最高负载率,在消除线路过载的同时尽可能提高系统运行安全性,避免短时间内再次出现潮流越限。
3)与优化类方法相比,本文方法通过离线训练、在线测试方式能够以较快的速度得出调整方案,实现过载线路的及时、有效消除;与灵敏度类方法相比,本文方法基于深度强化学习算法进行系统整体运行状态与调整动作的持续性交互、反馈,可学习得到计及全局的最优调整策略;与其他深度强化学习算法相比,本文采用的改进TD3算法的训练与应用效果更好。
附表1 可调元件出力上、下限
App.Tab.1 Upper and lower limits of adjustable element output (单位: MW)
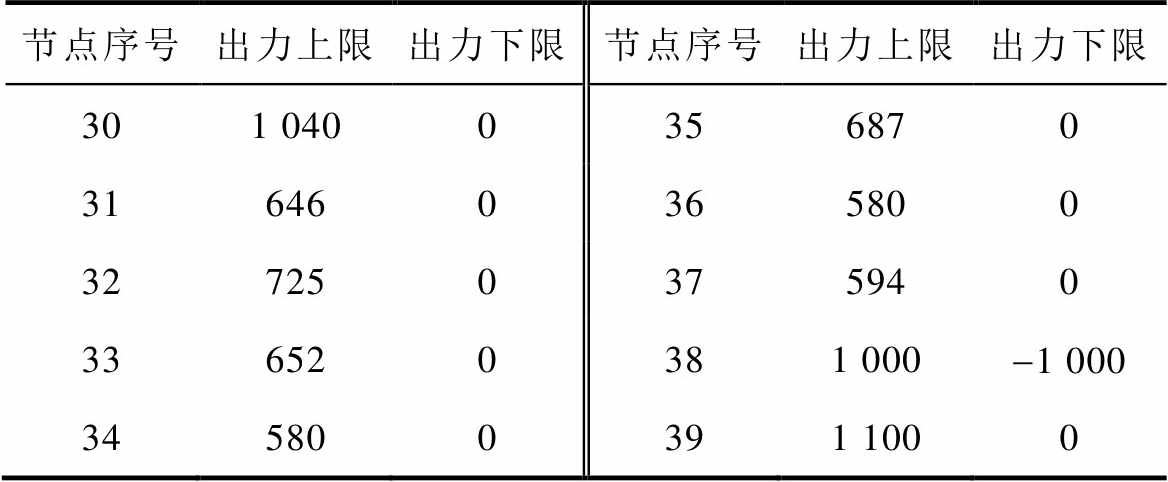
节点序号出力上限出力下限节点序号出力上限出力下限 301 0400356870 316460365800 327250375940 336520381 000-1 000 345800391 1000
附表2 机组爬坡速率
App.Tab.2 Unit ramp rate(单位: MW/min)
节点序号向上爬坡速率向下爬坡速率节点序号向上爬坡速率向下爬坡速率 30312-31235206-206 31194-19436174-174 32217-21737178-178 33196-19639330-330 34174-174———
附表3 线路传输上下限
App.Tab.3 Upper and lower limits of line transmission(单位: MW)
线路序号传输上限传输下限线路序号传输上限传输下限 1600-6005900-900 21 000-1 0006500-500 3500-5007500-500 4500-5008600-600
(续)
线路序号传输上限传输下限线路序号传输上限传输下限 9500-50028600-600 101 200-1 20029600-600 11900-90030600-600 12900-90031600-600 13480-48032900-900 141 800-1 80033900-900 15900-90034900-900 16900-90035900-900 17900-90036600-600 18600-60037900-900 19600-60038600-600 20900-90039900-900 21500-50040600-600 22500-50041900-900 23600-60042600-600 24600-60043600-600 25600-60044600-600 26600-60045600-600 27600-600461 200-1 200
附表4 系统运行状态参数
App.Tab.4 System initial state parameters(单位: MW)

节点序号出力负荷节点序号出力负荷 1—96.0021—269.51 2——22—— 3—316.7223—243.44 4—491.8124—303.54 5——25—220.33 6——26—136.72 7—229.9727—276.40 8—513.4428—202.62 9—6.3929—278.85 10——30250— 11——31531.79.05 12—8.3932650— 13——33632— 14——34508— 15—314.7635650— 16—323.6136560— 17——37540— 18—155.4138830— 19——391 0001 085.91 20—668.86———
附表5 可调元件出力上、下限
App.Tab.5 Upper and lower limits of adjustable element output(单位: MW)
节点序号出力上限出力下限节点序号出力上限出力下限 105500654910 121850664920 25320069805.20 264140805770 311070871040 461190897070 4930401003520 5414801031400 5925501111360 612600———
附表6 机组爬坡速率
App.Tab.6 Unit ramp rate(单位: MW/min)

节点序号向上爬坡速率向下爬坡速率节点序号向上爬坡速率向下爬坡速率 10165-16565147.3-147.3 1255.5-55.566147.6-147.6 2596-9669241.56-241.56 26124.2-124.280173.1-173.1 3132.1-32.18731.2-31.2 4635.7-35.789212.1-212.1 4991.2-91.2100105.6-105.6 5444.4-44.410342-42 5976.5-76.511140.8-40.8 6178-78———
附表7 线路序号及传输上、下限
App.Tab.7 Line number and transmission upper and lower limits(单位: MW)
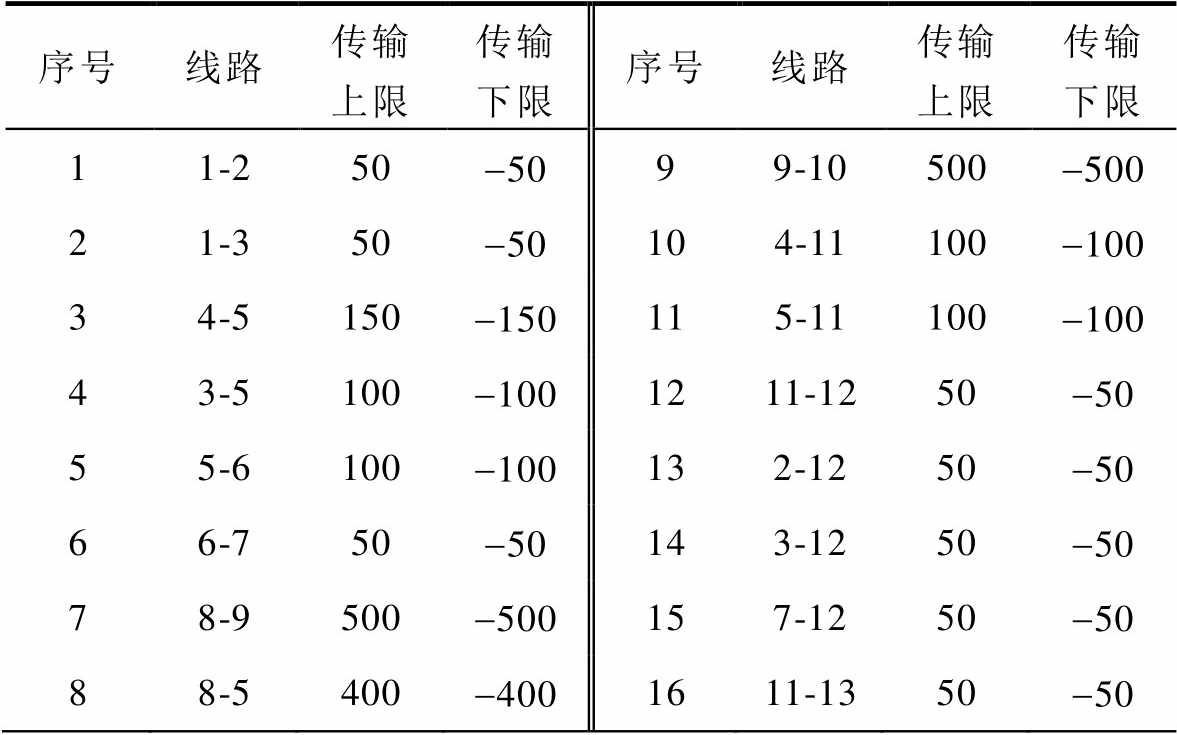
序号线路传输上限传输下限序号线路传输上限传输下限 11-250-5099-10500-500 21-350-50104-11100-100 34-5150-150115-11100-100 43-5100-1001211-1250-50 55-6100-100132-1250-50 66-750-50143-1250-50 78-9500-500157-1250-50 88-5400-4001611-1350-50
(续)
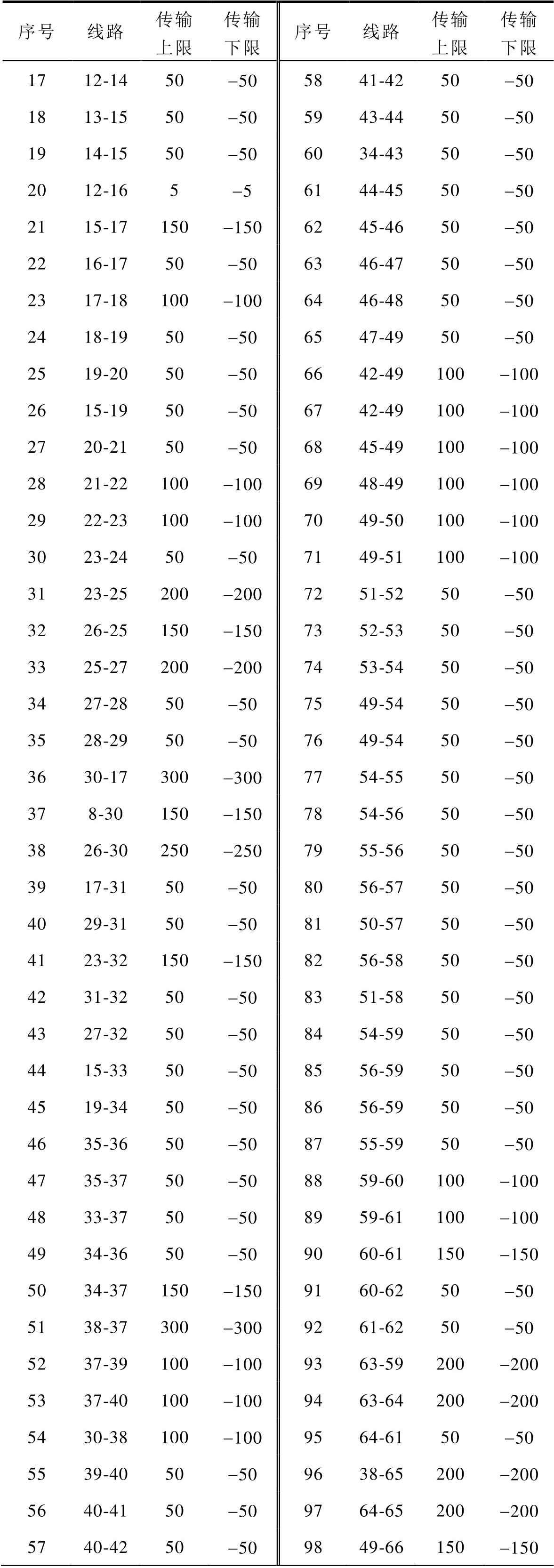
序号线路传输上限传输下限序号线路传输上限传输下限 1712-1450-505841-4250-50 1813-1550-505943-4450-50 1914-1550-506034-4350-50 2012-165-56144-4550-50 2115-17150-1506245-4650-50 2216-1750-506346-4750-50 2317-18100-1006446-4850-50 2418-1950-506547-4950-50 2519-2050-506642-49100-100 2615-1950-506742-49100-100 2720-2150-506845-49100-100 2821-22100-1006948-49100-100 2922-23100-1007049-50100-100 3023-2450-507149-51100-100 3123-25200-2007251-5250-50 3226-25150-1507352-5350-50 3325-27200-2007453-5450-50 3427-2850-507549-5450-50 3528-2950-507649-5450-50 3630-17300-3007754-5550-50 378-30150-1507854-5650-50 3826-30250-2507955-5650-50 3917-3150-508056-5750-50 4029-3150-508150-5750-50 4123-32150-1508256-5850-50 4231-3250-508351-5850-50 4327-3250-508454-5950-50 4415-3350-508556-5950-50 4519-3450-508656-5950-50 4635-3650-508755-5950-50 4735-3750-508859-60100-100 4833-3750-508959-61100-100 4934-3650-509060-61150-150 5034-37150-1509160-6250-50 5138-37300-3009261-6250-50 5237-39100-1009363-59200-200 5337-40100-1009463-64200-200 5430-38100-1009564-6150-50 5539-4050-509638-65200-200 5640-4150-509764-65200-200 5740-4250-509849-66150-150
(续)
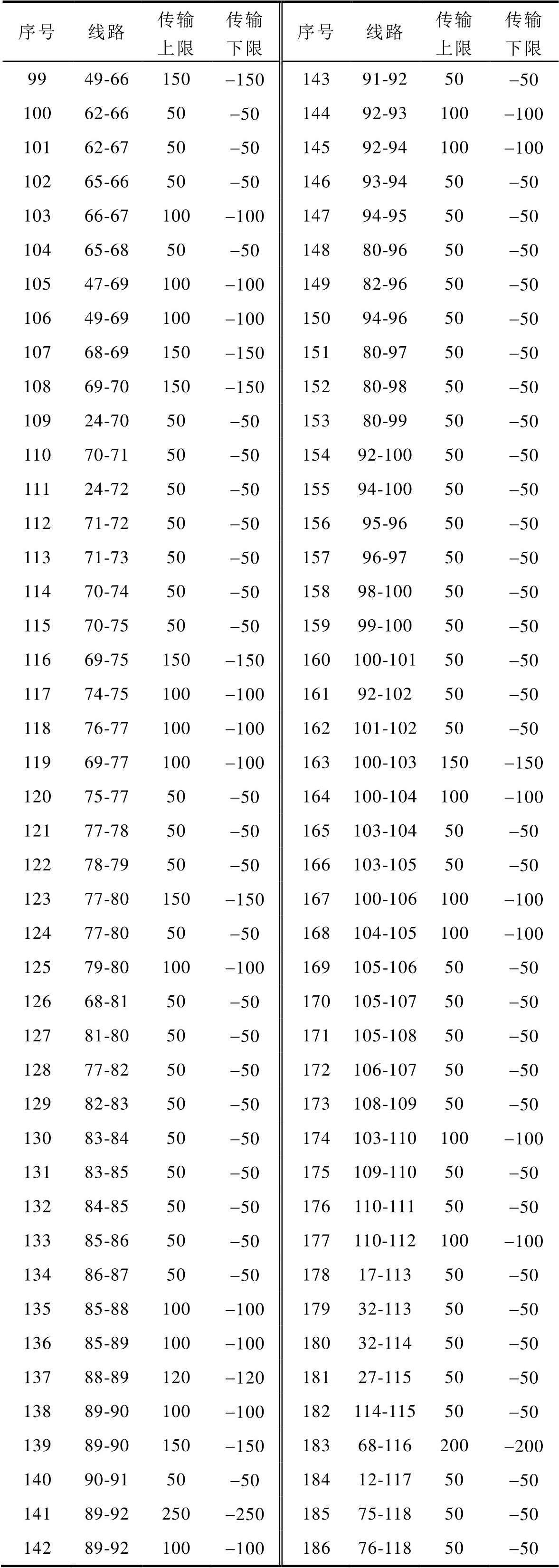
序号线路传输上限传输下限序号线路传输上限传输下限 9949-66150-15014391-9250-50 10062-6650-5014492-93100-100 10162-6750-5014592-94100-100 10265-6650-5014693-9450-50 10366-67100-10014794-9550-50 10465-6850-5014880-9650-50 10547-69100-10014982-9650-50 10649-69100-10015094-9650-50 10768-69150-15015180-9750-50 10869-70150-15015280-9850-50 10924-7050-5015380-9950-50 11070-7150-5015492-10050-50 11124-7250-5015594-10050-50 11271-7250-5015695-9650-50 11371-7350-5015796-9750-50 11470-7450-5015898-10050-50 11570-7550-5015999-10050-50 11669-75150-150160100-10150-50 11774-75100-10016192-10250-50 11876-77100-100162101-10250-50 11969-77100-100163100-103150-150 12075-7750-50164100-104100-100 12177-7850-50165103-10450-50 12278-7950-50166103-10550-50 12377-80150-150167100-106100-100 12477-8050-50168104-105100-100 12579-80100-100169105-10650-50 12668-8150-50170105-10750-50 12781-8050-50171105-10850-50 12877-8250-50172106-10750-50 12982-8350-50173108-10950-50 13083-8450-50174103-110100-100 13183-8550-50175109-11050-50 13284-8550-50176110-11150-50 13385-8650-50177110-112100-100 13486-8750-5017817-11350-50 13585-88100-10017932-11350-50 13685-89100-10018032-11450-50 13788-89120-12018127-11550-50 13889-90100-100182114-11550-50 13989-90150-15018368-116200-200 14090-9150-5018412-11750-50 14189-92250-25018575-11850-50 14289-92100-10018676-11850-50
附图1 模型在IEEE 118节点系统中的训练效果
App.Fig.1 Training effect of the model in IEEE 118-bus system
参考文献
[1] 林涛, 毕如玉, 陈汝斯, 等. 基于二阶锥规划的计及多种快速控制手段的综合安全校正策略[J]. 电工技术学报, 2020, 35(1): 167-178.
Lin Tao, Bi Ruyu, Chen Rusi, et al. Comprehensive security correction strategy based on second-order cone programming considering multiple fast control measures[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 167-178.
[2] 刘瑶, 彭书涛, 张志华, 等. 基于抽样盲数的线路N-1静态安全评估[J]. 电力系统保护与控制, 2019, 47(7): 106-112.
Liu Yao, Peng Shutao, Zhang Zhihua, et al. Static security assessment according to N-1 criterion for transmission lines based on sampled-blind-number[J]. Power System Protection and Control, 2019, 47(7): 106-112.
[3] 陈中, 朱政光, 严俊, 等. 基于交直流混联系统静态安全域安全校正控制后的优化调度[J]. 电力自动化设备, 2021, 41(4): 139-147, 169.
Chen Zhong, Zhu Zhengguang, Yan Jun, et al. Optimal dispatch after security correction control based on steady-state security region of AC/DC hybrid system[J]. Electric Power Automation Equip- ment, 2021, 41(4): 139-147, 169.
[4] 孙淑琴, 颜文丽, 吴晨悦, 等. 基于原-对偶内点法的输电断面有功安全校正控制方法[J]. 电力系统保护与控制, 2021, 49(7): 75-85.
Sun Shuqin, Yan Wenli, Wu Chenyue, et al. Active power flow safety correction control method of transmission sections based on a primal-dual interior point method[J]. Power System Protection and Control, 2021, 49(7): 75-85.
[5] 王艳松, 卢志强, 李强, 等. 基于源-荷协同的电网静态安全校正最优控制算法[J]. 电力系统保护与控制, 2019, 47(20): 73-80.
Wang Yansong, Lu Zhiqiang, Li Qiang, et al. Optimal control algorithm for static safety correction of power grid based on source-load coordination[J]. Power System Protection and Control, 2019, 47(20): 73-80.
[6] Wang Qin, McCalley J D, Zheng Tongxin, et al. Solving corrective risk-based security-constrained optimal power flow with Lagrangian relaxation and Benders decomposition[J]. International Journal of Electrical Power & Energy Systems, 2016, 75: 255-264.
[7] 刘阳, 夏添, 汪旸. 区域电网内多输电断面有功协同控制策略在线生成方法[J]. 电力自动化设备, 2020, 40(7): 204-210.
Liu Yang, Xia Tian, Wang Yang. On-line generation method of active power coordinated control strategy for multiple transmission sections in regional power grid[J]. Electric Power Automation Equipment, 2020, 40(7): 204-210.
[8] Wang Chenlu, Feng Changyou, Zeng Yuan, et al. Improved correction strategy for power flow control based on multi-machine sensitivity analysis[J]. IEEE Access, 8: 82391-82403.
[9] 邓佑满, 黎辉, 张伯明, 等. 电力系统有功安全校正策略的反向等量配对调整法[J]. 电力系统自动化, 1999, 23(18): 5-8.
Deng Youman, Li Hui, Zhang Boming, et al. Adjust- ment of equal and opposite quantities in pair s for strategy of active power security correction of power systems[J]. Automation of Electric Power Systems, 1999, 23(18): 5-8.
[10] 顾雪平, 张尚, 王涛, 等. 安全域视角下的有功安全校正优化控制方法[J]. 电力系统自动化, 2017, 41(18): 17-24.
Gu Xueping, Zhang Shang, Wang Tao, et al. Opti- mization control strategy for active power correction from perspective of security region[J]. Automation of Electric Power Systems, 2017, 41(18): 17-24.
[11] 陈中, 朱政光, 严俊. 基于安全距离灵敏度的交直流混联系统安全校正策略[J]. 电力自动化设备, 2019, 39(9): 144-150, 165.
Chen Zhong, Zhu Zhengguang, Yan Jun. Security correction strategy of AC/DC hybrid system based on security distance sensitivity[J]. Electric Power Auto- mation Equipment, 2019, 39(9): 144-150, 165.
[12] 徐正清, 肖艳炜, 李群山, 等. 基于灵敏度及粒子群算法的输电断面功率越限控制方法对比研究[J]. 电力系统保护与控制, 2020, 48(15): 177-186.
Xu Zhengqing, Xiao Yanwei, Li Qunshan, et al. Comparative study based on sensitivity and particle swarm optimization algorithm for power flow over- limit control method of transmission section[J]. Power System Protection and Control, 2020, 48(15): 177-186.
[13] 孙国强, 张恪, 卫志农, 等. 基于深度学习的含统一潮流控制器的电力系统快速安全校正[J]. 电力系统自动化, 2020, 44(19): 119-127.
Sun Guoqiang, Zhang Ke, Wei Zhinong, et al. Deep learning based fast security correction of power system with unified power flow controller[J]. Auto- mation of Electric Power Systems, 2020, 44(19): 119-127.
[14] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533.
[15] 李永刚, 王月, 吴滨源. 基于双重Q学习的动态风速预测模型[J]. 电工技术学报, 2022, 37(7): 1810-1819.
Li Yonggang, Wang Yue, Wu Binyuan. Dynamic wind speed prediction model based on double Q learning[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1810-1819.
[16] 梁煜东, 陈峦, 张国洲, 等. 基于深度强化学习的多能互补发电系统负荷频率控制策略[J]. 电工技术学报, 2022, 37(7): 1768-1779.
Liang Yudong, Chen Luan, Zhang Guozhou, et al. Load frequency control strategy of hybrid power generation system: a deep reinforcement learning— based approach[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1768-1779.
[17] 赵冬梅, 陶然, 马泰屹, 等. 基于多智能体深度确定策略梯度算法的有功-无功协调调度模型[J]. 电工技术学报, 2021, 36(9): 1914-1925.
Zhao Dongmei, Tao Ran, Ma Taiyi, et al. Active and reactive power coordinated dispatching based on multi-agent deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1914-1925.
[19] Mocanu E, Mocanu D C, Nguyen P H, et al. On-line building energy optimization using deep reinforce- ment learning[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 3698-3708.
[20] 李嘉文, 余涛, 张孝顺, 等. 基于改进深度确定性梯度算法的AGC发电功率指令分配方法[J]. 中国电机工程学报, 2021, 41(21): 7198-7211.
Li Jiawen, Yu Tao, Zhang Xiaoshun, et al. AGC power generation command allocation method based on improved deep deterministic policy gradient algorithm[J]. Proceedings of the CSEE, 2021, 41(21): 7198-7211.
[21] 叶宇剑, 袁泉, 汤奕, 等. 抑制柔性负荷过响应的微网分散式调控参数优化[J]. 中国电机工程学报, 2022, 42(5): 1748-1759.
Ye Yujian, Yuan Quan, Tang Yi, et al. Decentralized coordination parameters optimization in microgrids mitigating demand response synchronization effect of flexible loads[J]. Proceedings of the CSEE, 2022, 42(5): 1748-1759.
[22] 孙伟卿, 王承民, 张焰, 等. 电力系统运行均匀性分析与评估[J]. 电工技术学报, 2014, 29(4): 173-180.
Sun Weiqing, Wang Chengmin, Zhang Yan, et al. Analysis and evaluation on power system operation homogeneity[J]. Transactions of China Electro- technical Society, 2014, 29(4): 173-180.
Abstract With the construction and development of the novel power system, the probability of line overload caused by component faults or source-load fluctuations has been significantly increased. If the system cannot be corrected timely and effectively, the propagation speed and range of cascading faults may be aggravated and lead to a blackout accident. Therefore, the timely and effective implementation of safety correction measuresto eliminate power flow over the limit is of great significance to ensure the safe operation of the system.
An active power safety correction control method is proposed based on the twin delayed deep deterministic policy gradient algorithm (TD3) algorithm. Firstly, an active power safety correction model is established. One of the objectives is to minimize the sum of the absolute values of the adjustments of the adjustable components, and the other is to ensure the maximum safety of the system.
Secondly, a deep reinforcement learning framework for active power safety correction is established, as shown in Fig.A1. State expresses the characteristics of the power system. Action is the output of adjustable components. The reward function comprises the objective function and constraint conditions of the active power safety correction model. The agent selects the TD3 algorithm.
Finally, the active power safety correction control is carried out based on the improved TD3 algorithm. The historical overload scenario is constructed to pre-train the active power safety correction model based on the improved TD3 algorithm. Considering the influence of source-load fluctuation on the correction results during the correction process, the possible fluctuation value of the source-load output is calculated for each operating condition. During the online application, the predicted value of source and load in the next 5 minutes plus the prediction error value are used as the output value of new energy and the load value at the current time, which are input into the actor network together with the states of other system components. The improved TD3 algorithm with sufficient pre-learning can make the optimal decision quickly according to the system state.
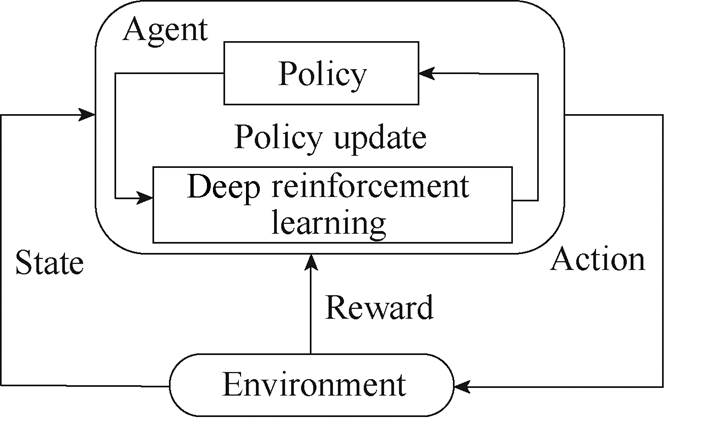
Fig.A1 Interaction process between agent and environment
An operation state of the IEEE39-bus system is used to verify the effectiveness and feasibility of the proposed method. In this state, line 23 is suddenly disconnected, then leads to line 13 overload. The correction result is shown in Fig.A2.
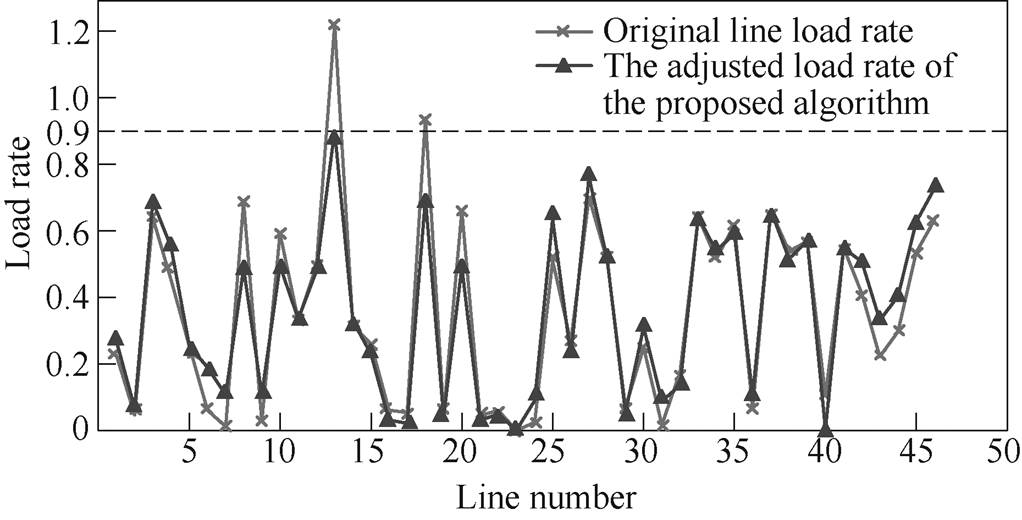
Fig.A2 Load rate of each line before and after correction
100 groups of source and load prediction error values are selected, and the predicted values are added to evaluate the system’s security after correcting the proposed method. At the same time, the correction results without considering the change of new energy output and load are used for comparison. The results show that the correction effect based on the proposed method considering the fluctuation of source load, system uniformity, and the line’s highest load rate is the best. It can withstand relatively more uncertainties to ensure that the system will not appear overloaded in a short time.
The same historical overload scenario trains and tests Deep Deterministic Policy Gradient (DDPG), TD3, and improved TD3 deep reinforcement learning algorithms. The results show that the proposed improved TD3 method is better than the other two algorithms regarding training time, testing time, and calculation results.
Compared with the traditional sensitivity method and optimization method, the calculation time of the proposed method is shorter, but the total adjustment amount is more. The optimization method has the slightest adjustment, but the calculation time is about 10 times the sensitive method. Regarding the proposed method, the number of adjustment components is small, and the time is short. The system uniformity after correction is the highest, but the total adjustment amount is slightly greater than the optimization method.
In conclusion, the calculation results of the active power safety correction model established by the proposed method are more consistent with the actual operation scenario of the power grid. In addition, compared with the traditional methods, the proposed method has certain advantages and is more suitable for the current novel power system.
keywords:Novel power systems, active power security correction, deep reinforcement learning, improved twin delayed deep deterministic policy gradient, optimal adjustment scheme
DOI: 10.19595/j.cnki.1000-6753.tces.221073
中图分类号:TM732
国家电网公司科技资助项目(SGTYHT/17-JS-199)。
收稿日期 2022-06-08
改稿日期 2022-07-12
顾雪平 男,1964年生,教授,博士生导师,研究方向为电力系统安全稳定评估与控制、电力系统安全防御与恢复控制、人工智能技术及其在电力系统中的应用等。E-mail: xpgu@ncepu.edu.cn
李少岩 男,1989年生,副教授,研究方向为电力系统安全防御与恢复控制、人工智能技术及其在电力系统中的应用等。E-mail: shaoyan.li@ncepu.edu.cn(通信作者)
(编辑 郭丽军)