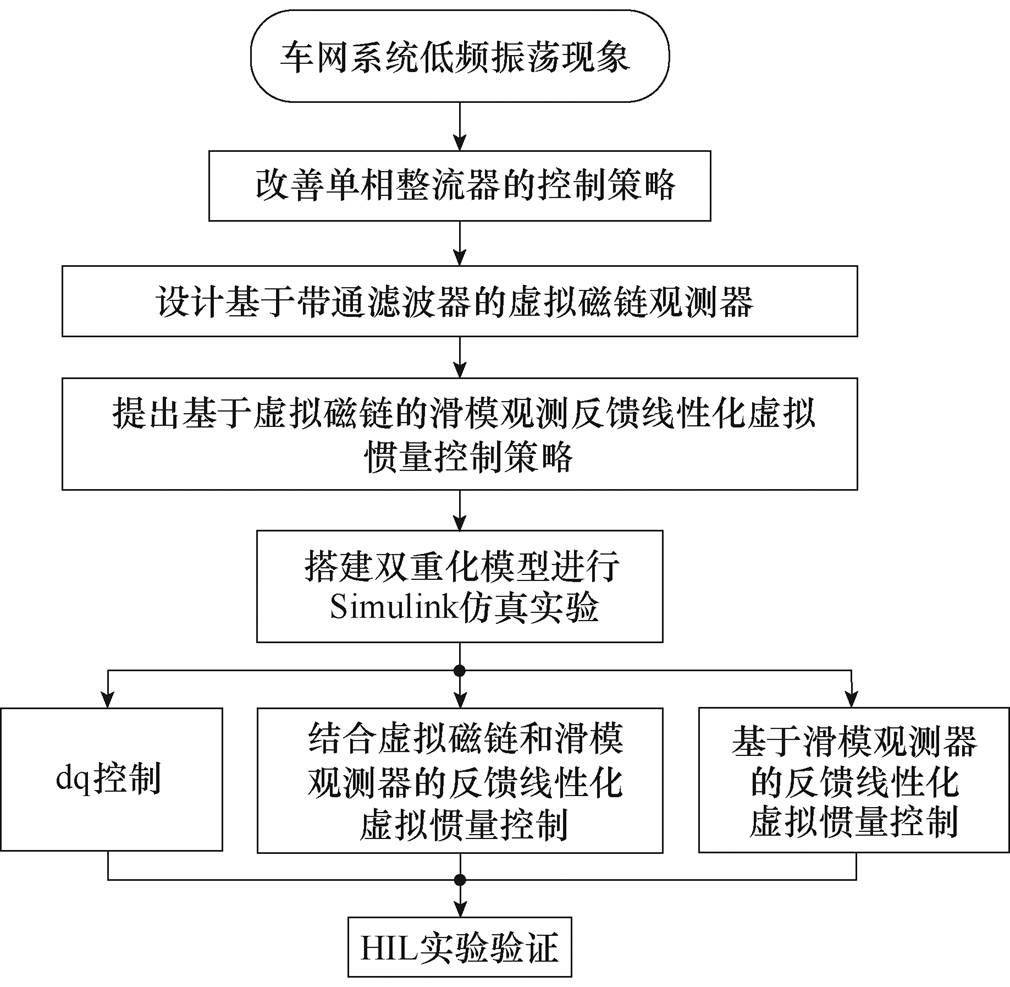
图1 本文框架结构
Fig.1 Article frame structure
摘要 针对车网系统存在的低频振荡现象，提出一种结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略，在减少传感器数量的同时，提高系统的鲁棒性。首先，该文分析现有积分器的缺点，提出改进的虚拟磁链观测器，在消除直流偏置影响的同时可以进行滤波；然后，阐述所提控制策略的推导过程，包括反馈线性化控制、滑模观测器、虚拟惯量控制以及虚拟磁链观测器的设计；最后，在Simulink和硬件在环仿真平台中建立车网系统仿真模型，将该文所提控制方式与传统dq控制以及基于滑模观测器的反馈线性化虚拟惯量控制方式进行对比。仿真和实验结果表明，所提控制策略具有更好的静态和动态特性，能有效地抑制低频振荡的发生。
关键词：虚拟磁链观测器 低频振荡 反馈线性化控制 虚拟惯量 高速铁路
随着大量交-直-交型高速列车接入运营，牵引供电系统的非线性负荷不断增多。而动车组作为移动的时变非线性负载，与牵引网之间存在非线性强耦合关系，增加了车网系统出现低频振荡现象的概率。当场站中多辆机车同时处于升弓准备状态时，容易出现低频振荡现象，造成牵引封锁，导致机车不能正常运行。
由于车网系统的低频振荡与传统电力系统中的低频振荡是不一样的，因此，研究车网系统的低频振荡产生机理、对低频振荡现象进行抑制，是十分必要的。目前针对机理的研究还没有明确的定论，主流观点认为，低频振荡现象是由车网系统的参数不匹配造成的[1]。为了揭示低频振荡产生的原因，现有的文献对其进行了大量的分析。文献[2]提出了车网系统的dq阻抗模型，基于禁区判据，对车网系统的电路和控制参数进行了分析，表明电路和控制参数是影响车网系统稳定性的重要因素。文献[3]分析了车网系统主导极点的阻尼比，提出使用欠阻尼原理来解释牵引网电压电流出现持续振荡的原因。针对多车接入后，牵引供电系统出现的电压电流波动情况，文献[4]展示了间谐波在牵引传动系统的传播机理。在低频振荡的抑制措施方面，可以从牵引网侧和电力机车侧两方面进行考虑。牵引网侧主要是通过改变牵引网的结构或者架设补偿装置[5]对低频振荡现象进行抑制。但是该方法操作复杂、实施比较困难、成本也比较高。因此，基于现有文献的研究，对电力机车侧的控制策略进行改进是更加经济的做法。文献[6]提出了模糊控制方法对低频振荡现象进行抑制，该方法鲁棒性较强，但是模糊规则的设计过程复杂，响应时间较长。针对车网系统的基于扩张状态观测器的模型预测控制方式和无源控制方式在文献[7-8]中被提出，虽然成功地抑制了低频振荡现象的发生，但是仍存在控制器设计过程复杂、计算量大的缺点。
反馈线性化控制是一种设计简单、响应速度快的控制方式[9-11]，但是需要对直流侧的电流进行测量，因此文献[12]采用了滑模观测器（Sliding Mode Observer, SMO）对直流侧电流进行在线估计，实现了三相整流器在未知负载情况下的控制。而文献[13]考虑SMO本身鲁棒性差的缺点，进一步提出了虚拟惯量控制策略，设计基于滑模观测器的反馈线性化虚拟惯量控制策略（Feedback linearization Virtual Inertia Control strategy based on Sliding Mode Observer, Feedback+SMO+VIC）对车网系统的低频振荡现象进行抑制，并且具有没有超调量、稳态时间短、响应速度快的特点。
上述的控制方式都需要对交流侧电压的幅值和相位进行测量，不仅增加了传感器的数量，提高了成本，还存在传感器故障的安全隐患，于是逐渐采用无网侧电压传感器的控制方式[14]。无网侧电压传感器控制的关键在于获取坐标变换时所需要的角度，以替代控制中对网侧电压信息的需求。目前常见的做法是通过参考交流电机中磁链的概念，构造虚拟磁链观测器，进而可通过电压重构得到所需电气量。
传统虚拟磁链观测器中采用的纯积分环节存在直流偏置和积分初值的问题[15]，会严重影响磁链的观测结果。为了解决积分初始值问题，采用一阶低通滤波器（Low-Pass Filter, LPF）替代纯积分器，虽然可以减小直流偏置，但是会出现相位偏移，造成观测结果出现误差[16]。后续也有采用两个LPF串联[17]、并联[18]或三个一阶LPF串联[19]的方式对磁链进行观测。
本文针对上述问题，提出了结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略。首先通过分析现有积分器的缺点，设计了基于带通滤波的新型磁链观测器，实现无压传感器的控制，解决积分初值问题的同时，避免了相位偏移带来的影响，同时还可以对低频和高频的杂波起到一定的抑制效果，提高了磁链观测器的观测精度。然后通过仿真，对所提观测器的有效性和正确性进行验证。接着将提出的控制策略应用于车网系统低频振荡的抑制，通过仿真和硬件在环（Hardware-In-the-Loop, HIL）实验对所提控制器的性能进行验证，通过与传统dq解耦控制、基于滑模观测器的反馈线性化虚拟惯量控制相对比，说明本文提出的控制器不仅能实现磁链的准确跟踪，还能提高系统的鲁棒性。本文的整体框架结构如图1所示。
图1 本文框架结构
Fig.1 Article frame structure
车网系统中，线路侧整流器（Line-Side Conver- ter, LSC）是单相两电平整流器，此时，考虑电机和逆变器处于静止的状态，将其等效为电阻Rd。等效后的拓扑结构，如图2所示。
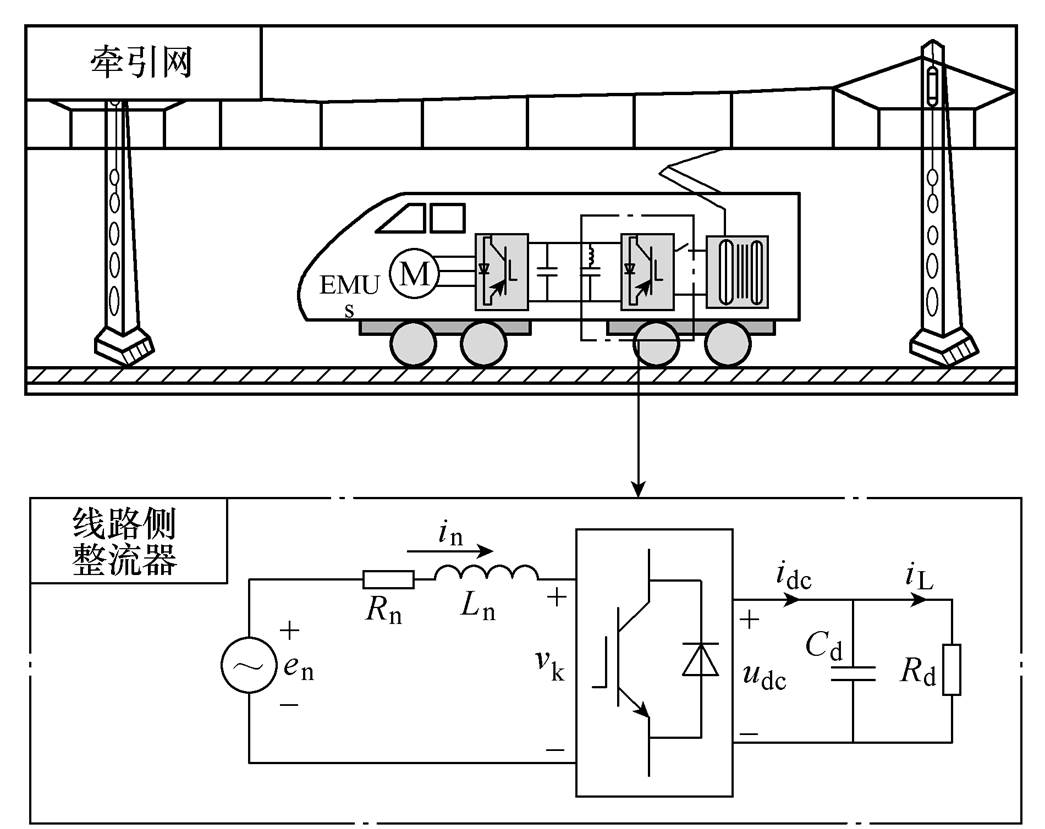
图2 LSC等效拓扑结构
Fig.2 Circuit topology of the equivalent LSC
图2中，en为等效电源，in为网侧电流，Rn为等效电阻，Ln为等效电感，vk为整流器的输入电压，idc为直流侧的总电流，iL为直流侧负载支路的负载电流，udc为输出的直流母线电压。连接到理想四臂开关转换器的直流侧等效电容用Cd表示。
交流侧的动态方程为
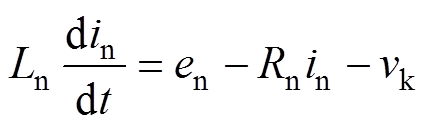（1）
将其在静止坐标系下进行分解，并忽略交流侧电阻Rn的影响，得到ab 坐标系下的方程组为
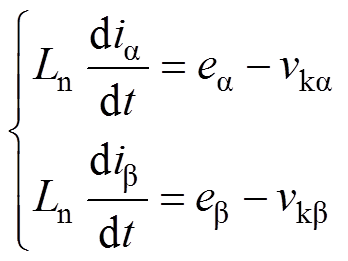（2）
式中，ea 和eb 为等效电源在a、b 坐标系中的分量；ia 和ib 为网侧电流在a、b 坐标系中的分量；vka 和vkb为整流器的输入电压在a、b 坐标系中的分量。为了构造虚拟磁链，对式（2）两边进行积分，再将表达式转换到频域中，可得
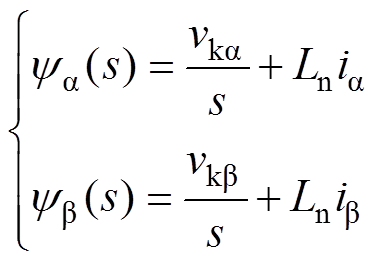（3）
经过进一步推导可得，电压源电压en与虚拟磁链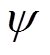
之间的转换关系为
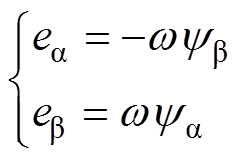（4）
传统的虚拟磁链观测器采用的是纯积分器对整流器输入电压进行积分计算，但是当输入信号存在零点偏移时，采用纯积分器会使得偏移量随着时间的增长而叠加[14]。并且纯积分对积分的初始值有要求，初始值的设置会影响最终的输出。
通常的改进措施是使用一阶LPF对纯积分器进行替代的做法，一阶LPF的传递函数为
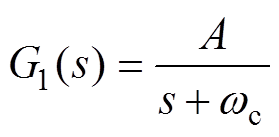（5）
式中，A为滤波器增益；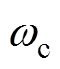
为截止频率。
一般设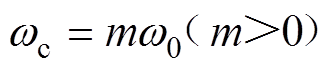
，则此时
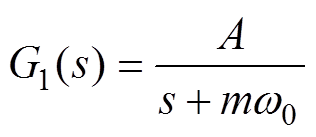（6）
通过计算其幅值和相位，并且与纯积分器进行对比可得，若想对纯积分器进行替代，需要令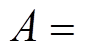
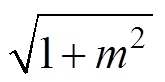，同时要求m为极小的正数。文献[16]指出，一阶LPF可以解决积分初始值的问题，并且m越大，输出直流偏置越小[17]，但同时也会使得输出信号的相位偏移增大。
文献[20]提出采用两个一阶LPF串联，对纯积分器进行替代，表达式为
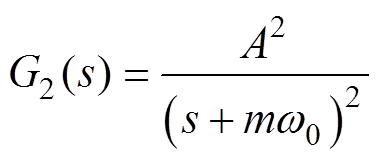（7）
若想实现纯积分器的功能，需要令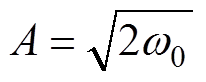
，m=1。因此，两个一阶LPF串联的传递函数变为
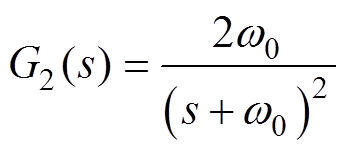（8）
由文献[19]可知，当输入信号为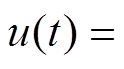
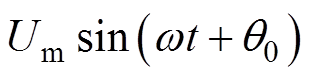时，在经过该传递函数后的输出信号为
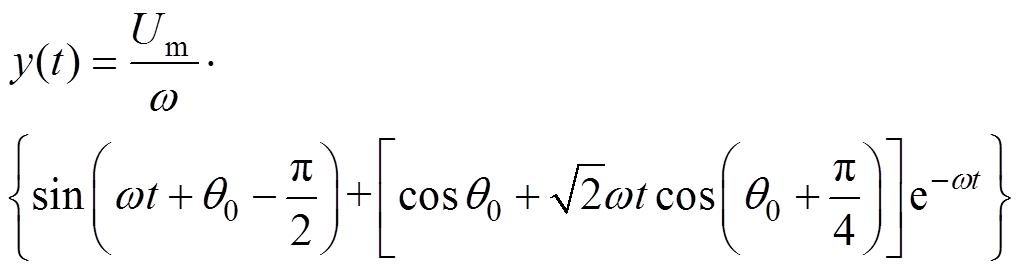（9）
由此可以看出，串联的一阶LPF可以消除稳态误差[21]，但是输出信号含有较大的暂态分量。
为了消除串联一阶LPF暂态分量的影响，考虑在其后面接入一个带通滤波器进行滤波。改进的虚拟磁链观测器如图3所示。
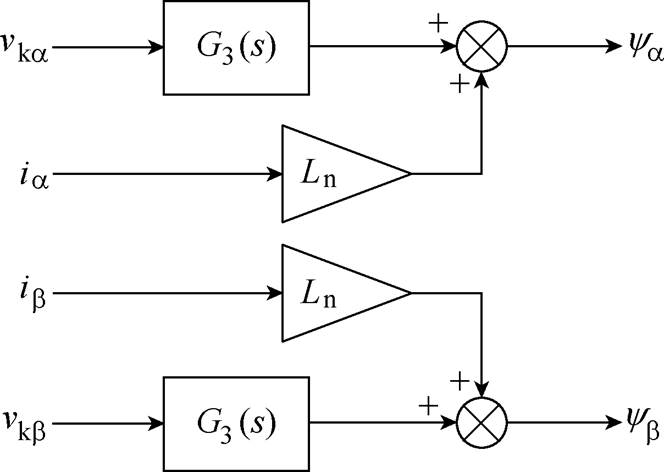
图3 改进的虚拟磁链观测器
Fig.3 Improved virtual flux observer
图3中的G3(s)是对积分器进行改进后的表达式，即
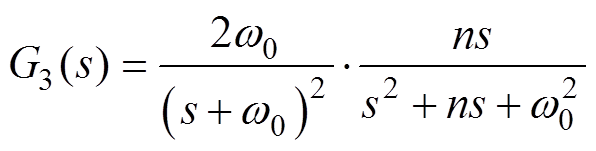（10）
关于带通滤波器中系数n的选择，可以通过绘制Bode图和单位阶跃响应曲线进行观察，如图4所示。通过Bode图可以看出，n越小，对其他频率的抑制效果越好；而单位阶跃响应则说明n越小，需要的稳定时间就越长，但是n过大，超调会变大。所以n的选择应该适中。
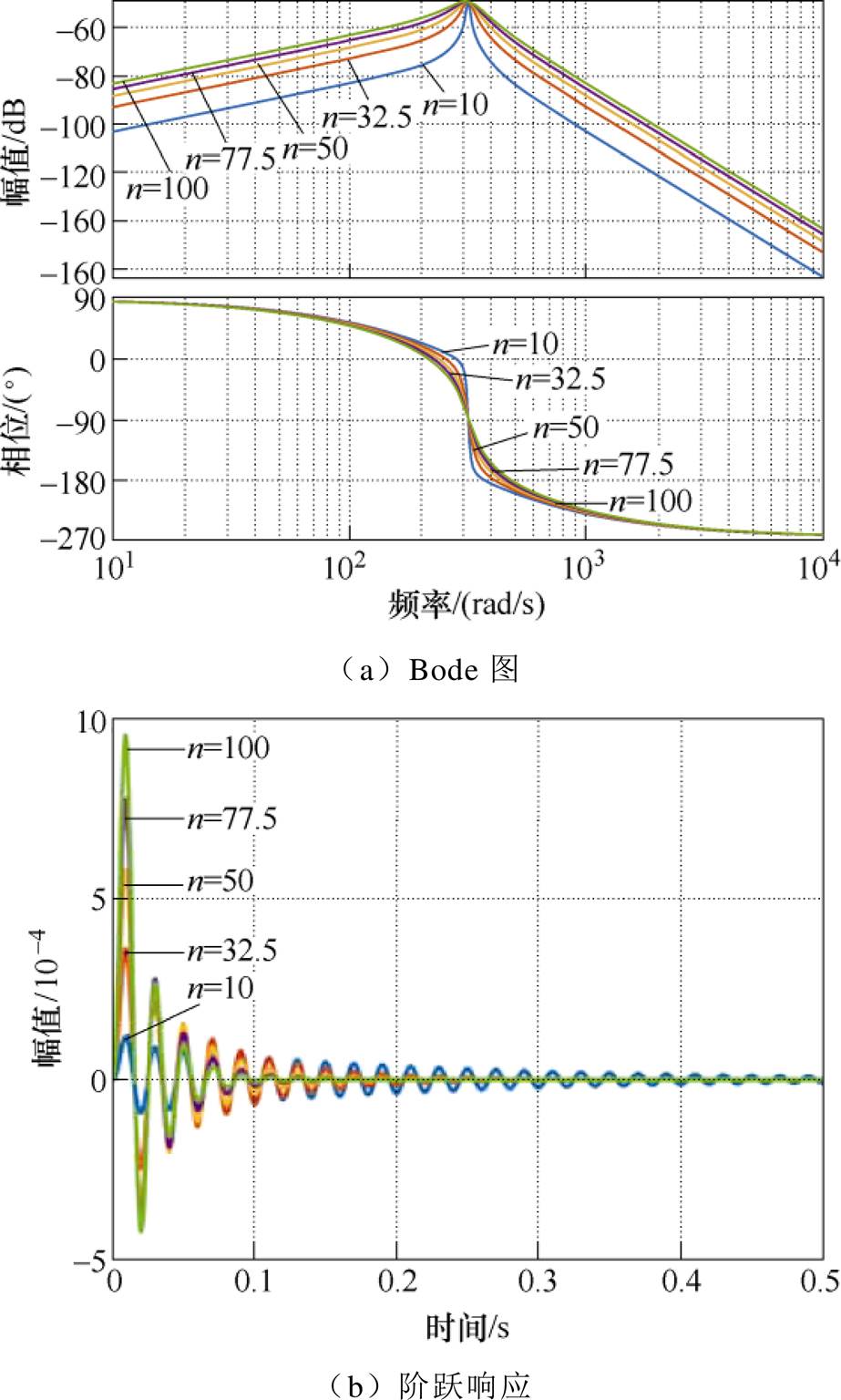
图4 G3的Bode图和单位阶跃响应
Fig.4 Bode diagram and step response of G3
在车网系统中，存在负载突变、网侧电压波动等干扰，为了进一步减小外界扰动对系统的影响，结合1.3节提出的如图3所示的改进虚拟磁链观测器，本文提出了结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略，在提高系统动态响应的同时，进一步提高系统的鲁棒性。
反馈线性化电流内环控制表达式为
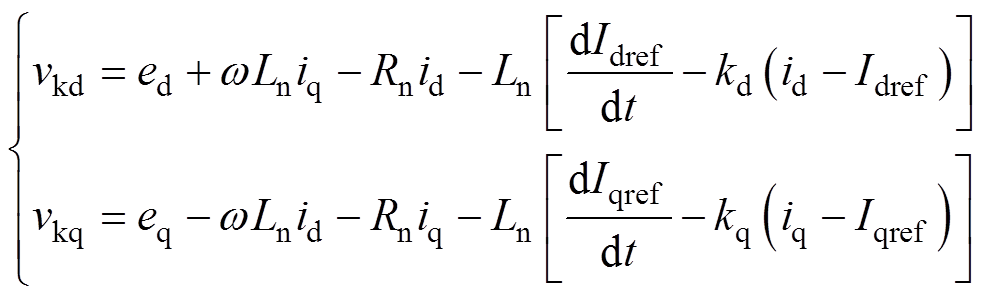（11）
式中，ed和eq为等效电源在dq坐标系中的分量，本文中，该分量由虚拟磁链观测器的输出经过电压重构和坐标转换后获得；id和iq为网侧电流在dq坐标系中的分量；vkd和vkq分别为整流器的输入电压在dq坐标系中的分量，w 为系统的基频；Idref和Iqref为电流在dq坐标系中的参考值；kd和kq为电流内环的比例系数。
反馈线性化电压外环控制表达式为
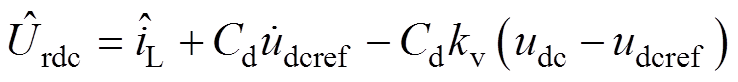（12）
式中，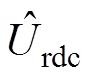
为电压外环控制量的估计值；
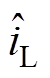为直流侧电流的估计值，由SMO输出得到；udcref为直流电压参考值；kv为电压外环比例增益。
电压外环输出表达式为
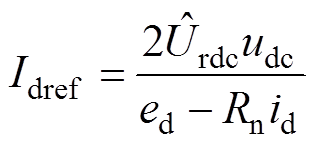（13）
滑模观测器可以描述为
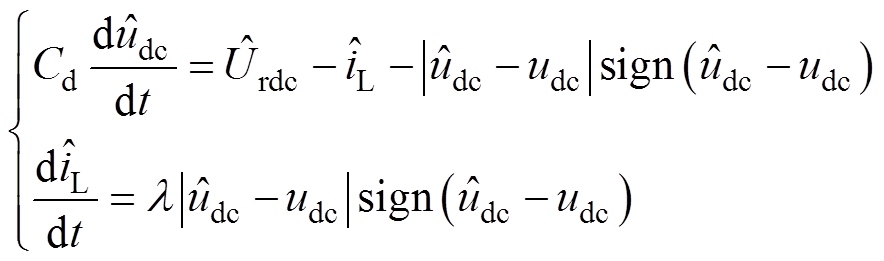（14）
式中，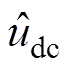
为直流侧电压估计值；
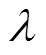为滑模观测器增益；sign(·) 为符号函数。
虚拟惯量控制策略的方程[13]可写为
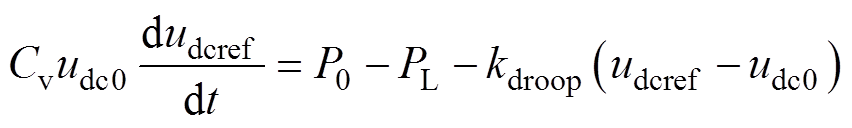（15）
式中，P0为额定输出功率；Cv为虚拟电容；PL为负载消耗的功率；kdroop为虚拟惯性系数；udc0为直流电压额定值。
结合虚拟磁链观测器，本文提出的控制器框图如图5所示。控制器主要由电压外环和电流内环两部分组成，滑模观测器是为了向反馈线性化电压外环控制提供直流侧的电流估计值，虚拟惯量控制则是为了提高系统整体的惯性，减小外界波动对系统的影响。本文设计的虚拟磁链观测器则是为了对网侧电压进行估计，并且提供坐标转换所需的相位信息，进一步提高系统的鲁棒性。
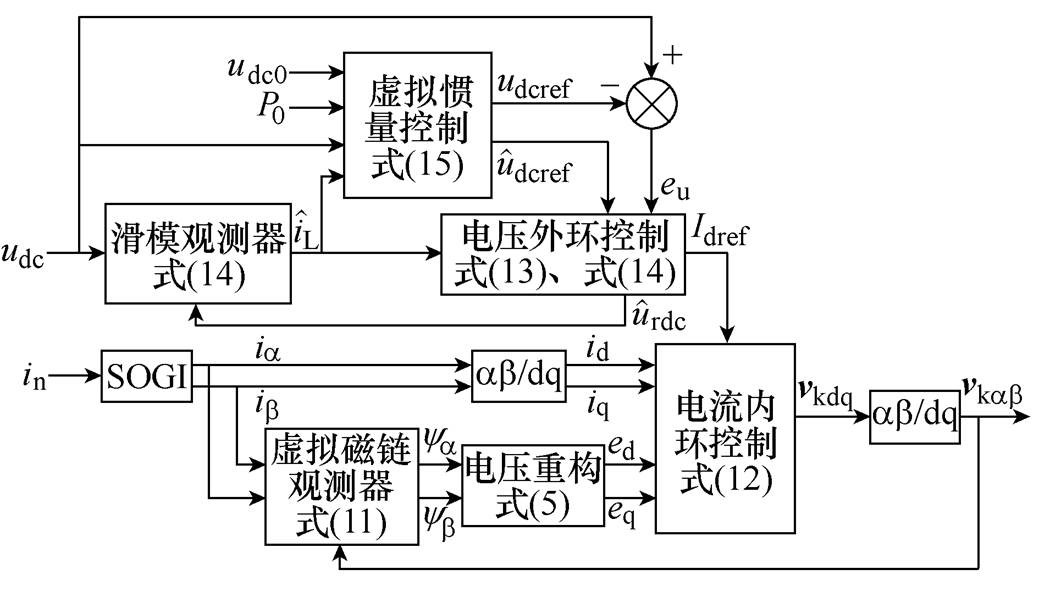
图5 控制器框图
Fig.5 Controller block diagram
假设原始输入信号为含有低频、高频以及直流偏置时，表达式可以写为
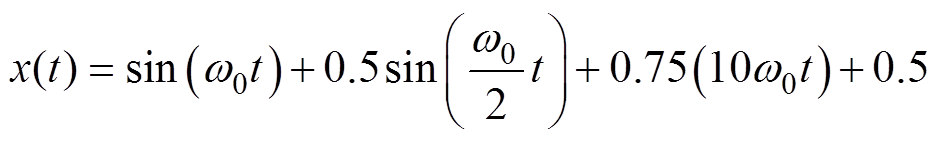（16）
原始信号波形，采用纯积分器、一阶LPF、一阶LPF串联和带有带通滤波器的一阶LPF串联滤波器进行滤波后的波形，以及总谐波畸变率（Total Harmonic Distortion, THD）分析结果如图6所示。
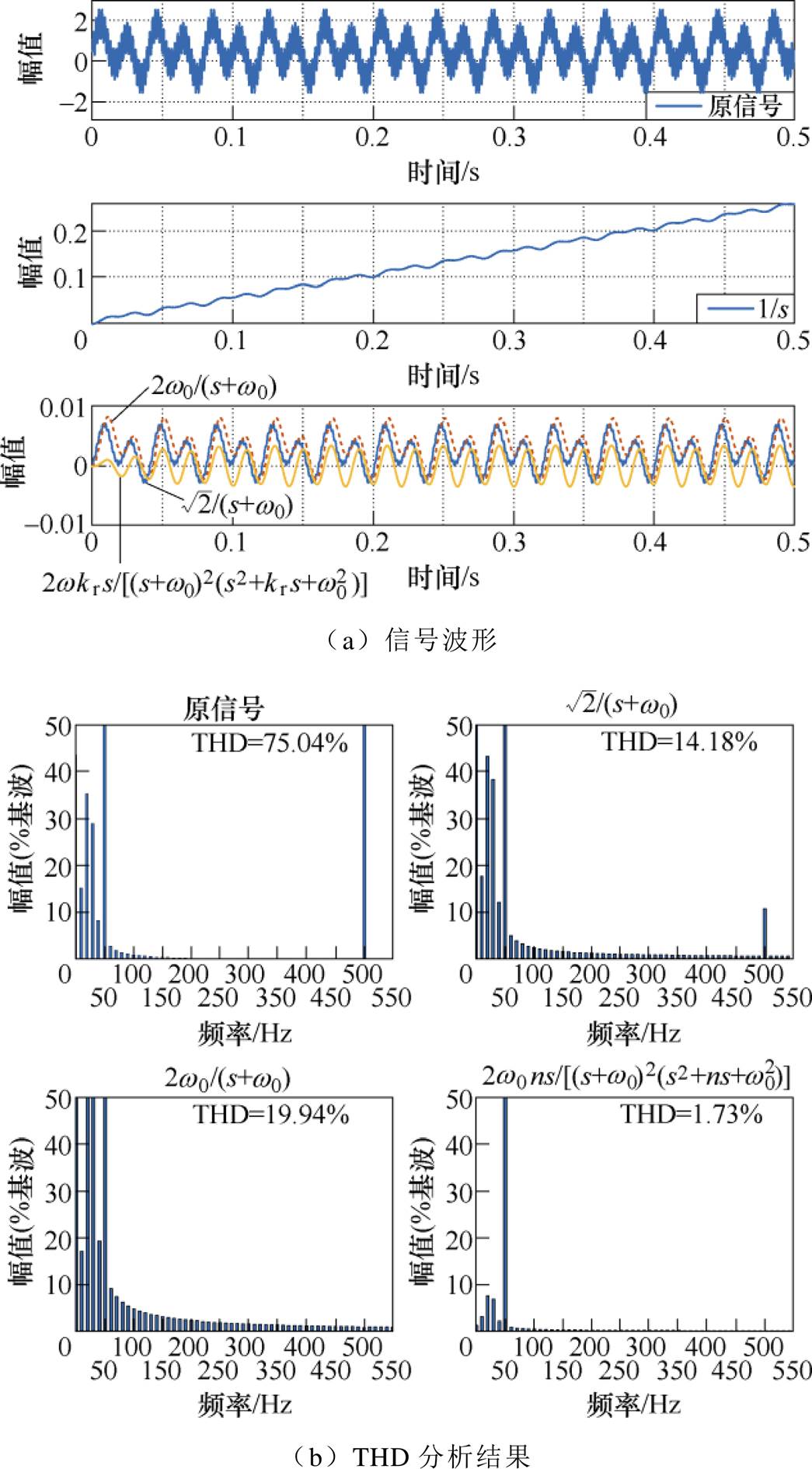
图6 信号波形与THD分析
Fig.6 Signal waveforms and THD analysis
由图6a可以看出，纯积分器因为有直流偏置的存在，输出值会随时间的推移进行叠加，导致结果的发散。一阶LPF和一阶LPF串联，可以实现一定的滤波效果，但是还是存在直流偏置的问题。观察图6b的结果可以发现，本文提出的基于带通滤波器的磁链观测器在完全消除直流偏置和初始值问题影响的同时，又可以对低频和高频信号进行滤波，证明了本文所提观测器的有效性。
为了验证所提控制器的有效性，在Simulink中搭建双重化LSC车网系统模型对控制器性能进行验证，双重化LSC仿真模型如图7所示，系统参数见表1。
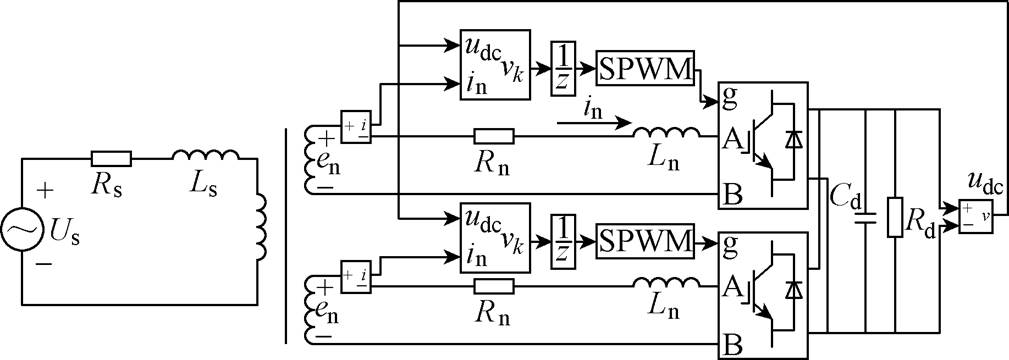
图7 双重化LSC仿真模型
Fig.7 Dual LSC simulation model
表1 双重化LSC仿真模型参数
Tab.1 Dual LSC simulation model parameters
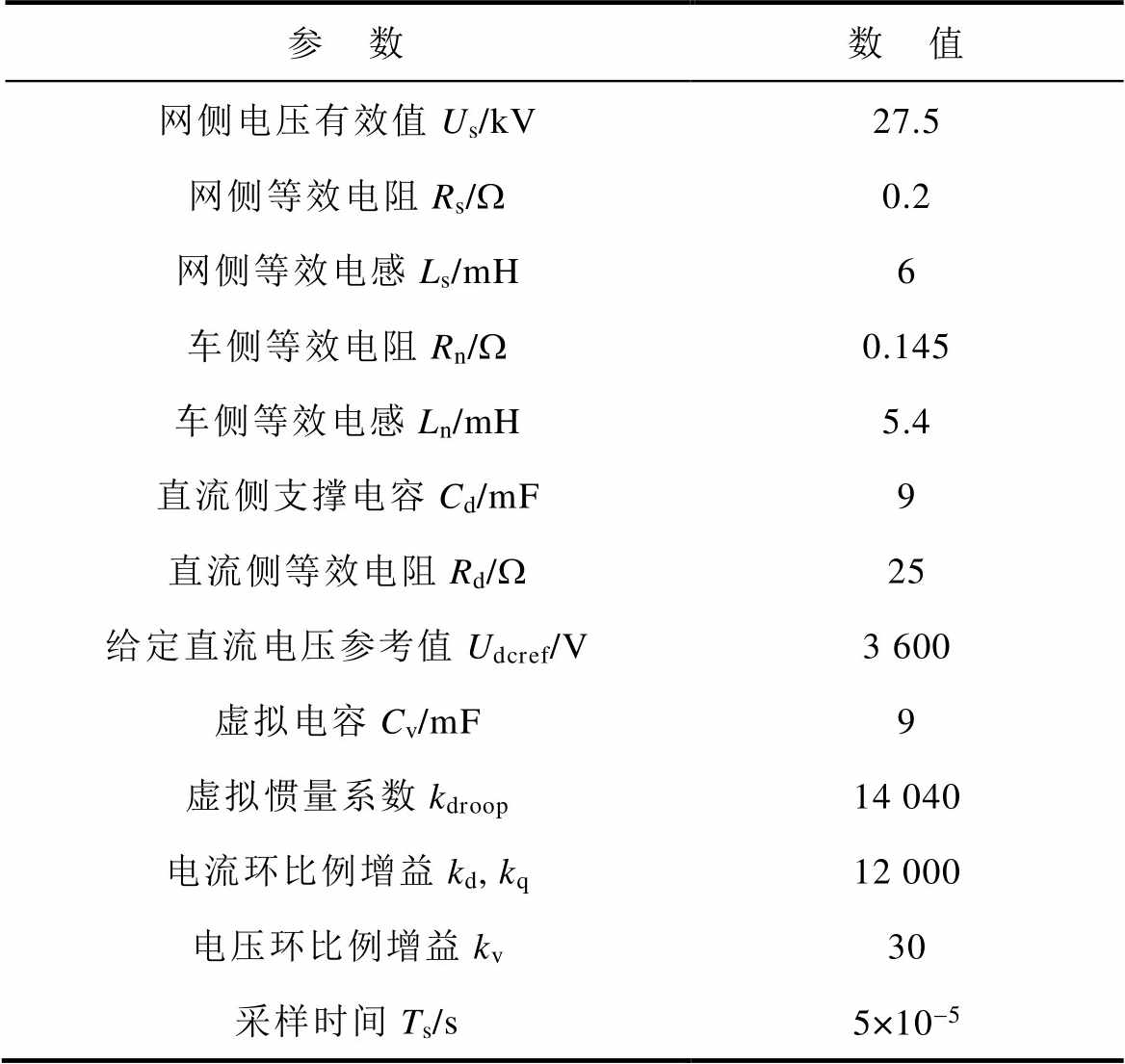
参 数数 值 网侧电压有效值Us/kV27.5 网侧等效电阻Rs/W0.2 网侧等效电感Ls/mH6 车侧等效电阻Rn/W0.145 车侧等效电感Ln/mH5.4 直流侧支撑电容Cd/mF9 直流侧等效电阻Rd/W25 给定直流电压参考值Udcref/V3 600 虚拟电容Cv/mF9 虚拟惯量系数kdroop14 040 电流环比例增益kd, kq12 000 电压环比例增益kv30 采样时间Ts/s5×10-5
控制中虚拟磁链观测器的输出结果如图8所示，可以看出，本文采用的观测器不仅解决了积分初值问题，还消除了直流偏置，得到准确的观测结果。将无网侧电压传感器，经过电压重构后的估计交流侧电压值与含有网压传感器实际测量得到电压结果进行对比，可以看出，采用本文提出的虚拟磁链观测器可以在0.1 s内得到精确的交流侧电压。并且在1.50 s和3.00 s，负载发生突变时，也能保持电压的稳定，得到的a 轴和b 轴的电压测量值和估计值波形比较如图9所示。
将本文所提控制方式与Feedback+SMO+VIC以及传统dq解耦控制方式进行了对比，并且在1.50 s和3.00 s时设置负载的突变，1.50 s时直流侧电阻从25 W 变成60 W，3.00 s时直流侧负载从60 W 减小到20 W。在图7所示的双重化LSC模型中，各种控制方式采用的传感器数量见表2。传统的dq解耦控制需要对交流侧电压en、交流侧电流in及直流侧电压udc进行测量，本文提出的控制方式，可以取消交流侧电压传感器的使用，仅需对交流侧电流和直流侧电压进行测量，即可完成对系统的控制。
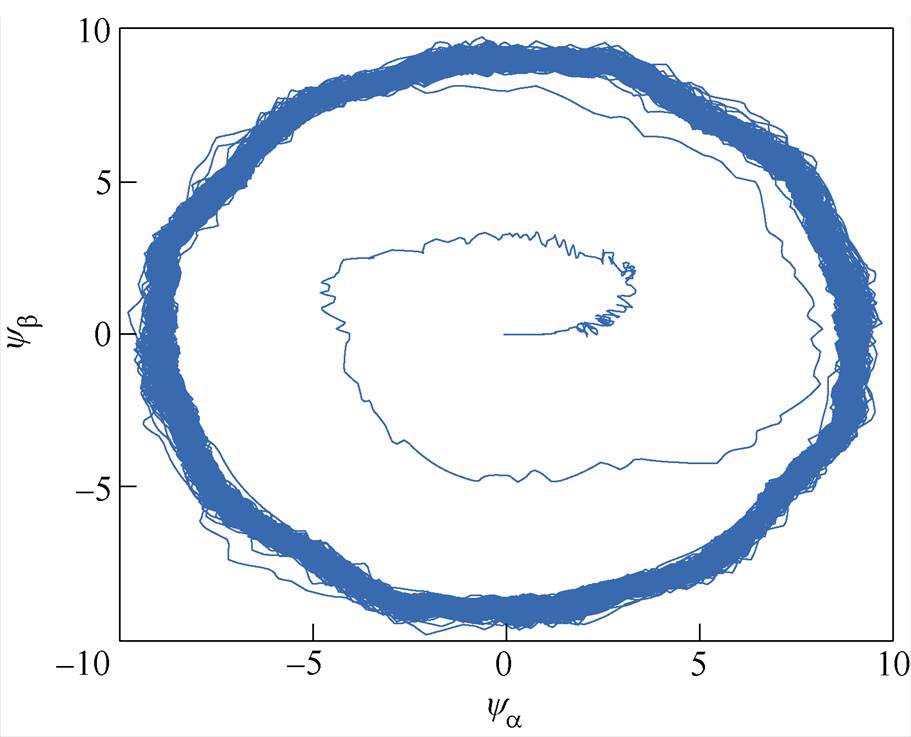
图8 车网系统虚拟磁连
Fig.8 Vehicle-grid system virtual flux linkage
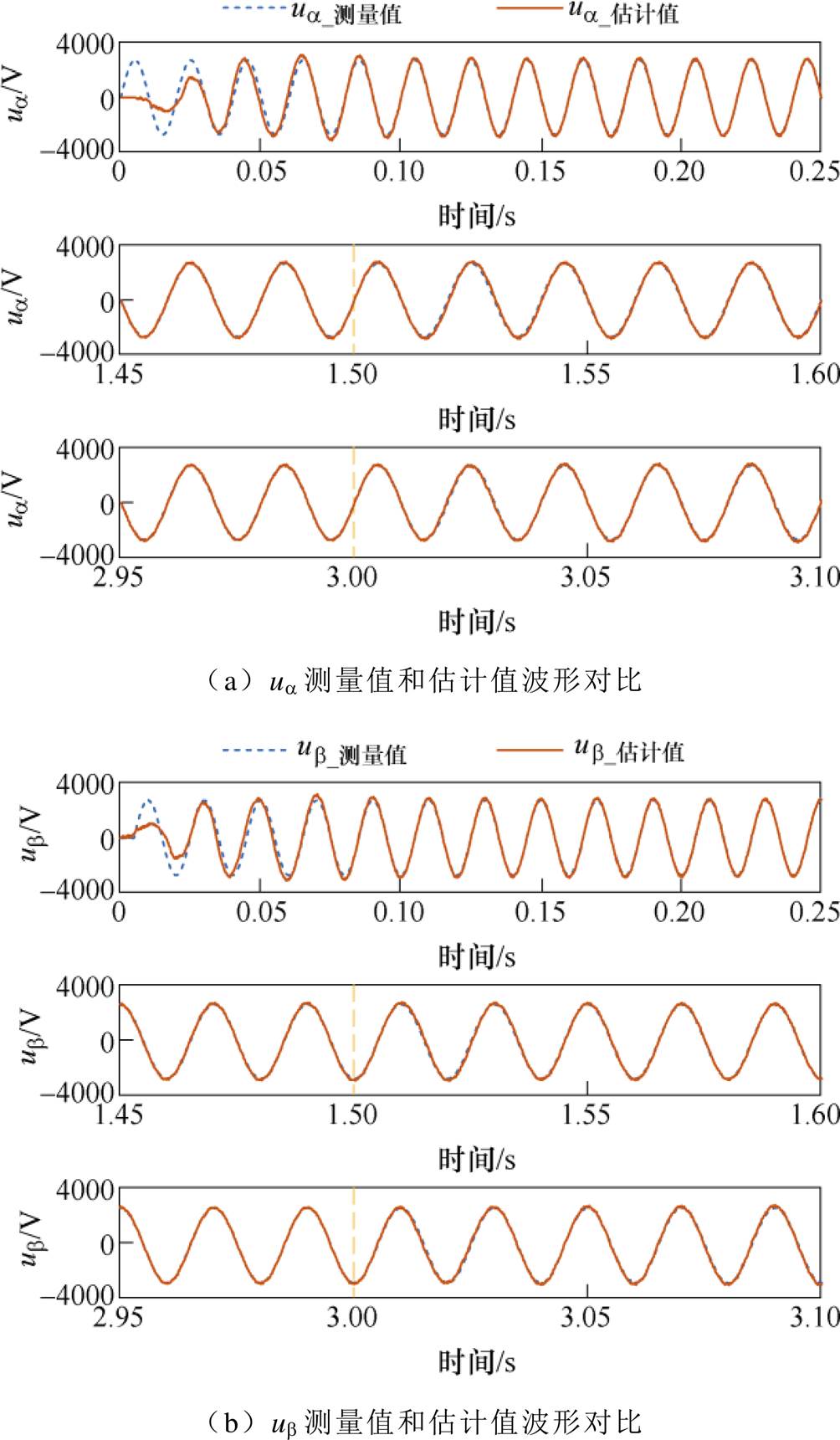
图9 网侧电压测量值和估计值波形比较
Fig.9 Grid-side voltage measurement and estimated value waveforms comparison
表2 所需传感器数量的比较
Tab.2 Comparison of the number of sensors required
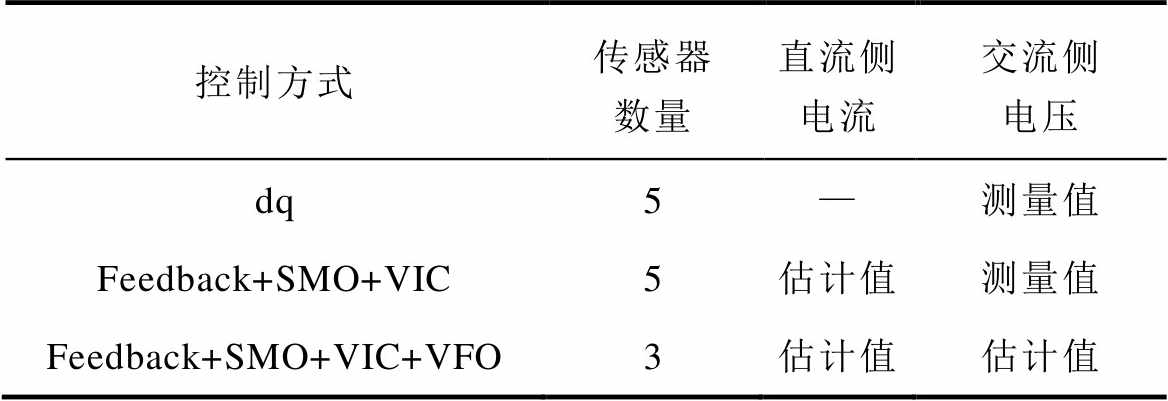
控制方式传感器数量直流侧电流交流侧电压 dq5—测量值 Feedback+SMO+VIC5估计值测量值 Feedback+SMO+VIC+VFO3估计值估计值
各双重化LSC仿真结果比较见表3。双重化仿真模型直流输出电压udc对比结果如图10所示。
表3 双重化LSC仿真结果比较
Tab.3 Comparison of dual LSC simulation results
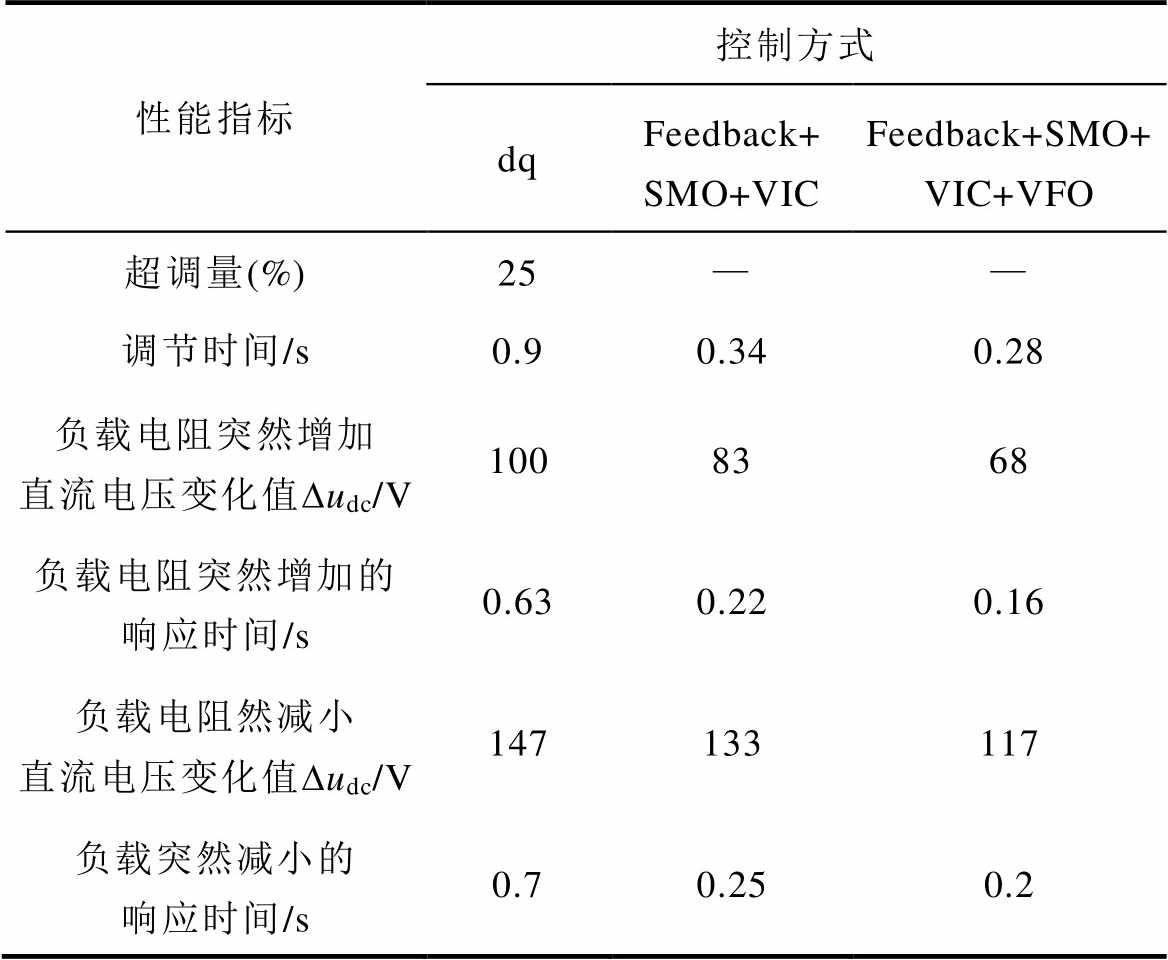
性能指标控制方式 dqFeedback+ SMO+VICFeedback+SMO+VIC+VFO 超调量(%)25—— 调节时间/s0.90.340.28 负载电阻突然增加直流电压变化值Dudc/V1008368 负载电阻突然增加的响应时间/s0.630.220.16 负载电阻然减小直流电压变化值Dudc/V147133117 负载突然减小的响应时间/s0.70.250.2
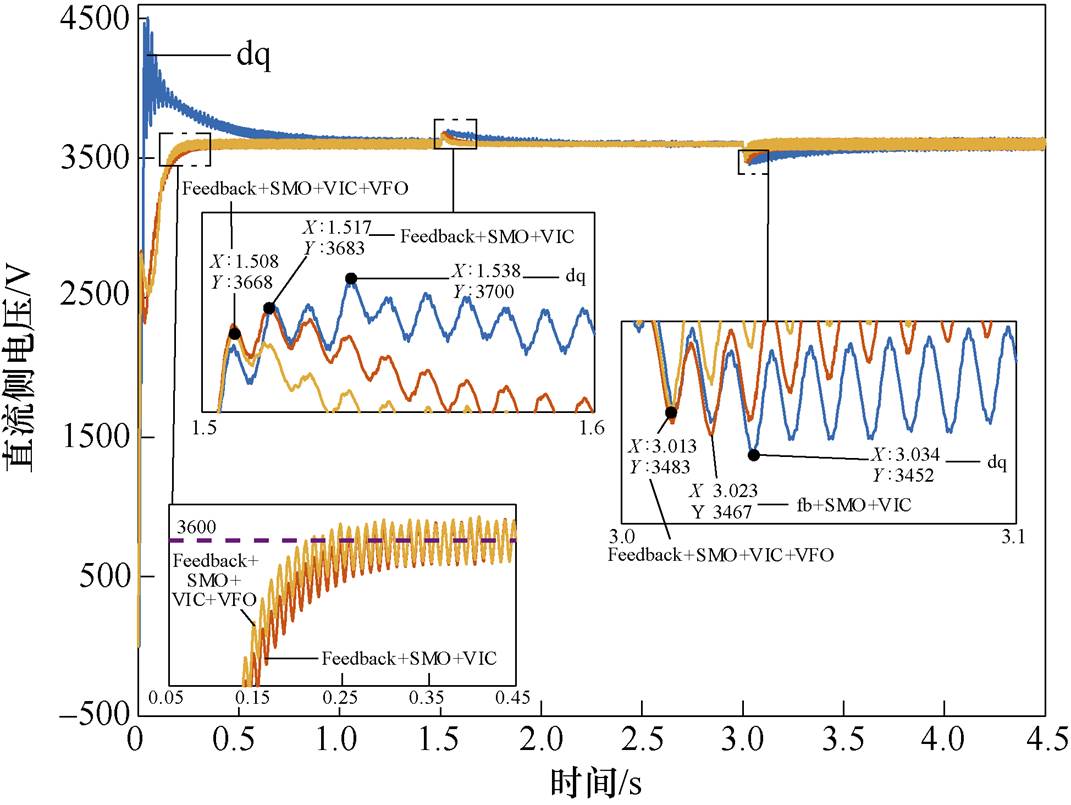
图10 负载突然变化时的直流电压波形比较
Fig.10 Comparison of DC voltage waveforms during sudden load changes
从图10可以看出，本文所提出的控制方式，与没有虚拟磁链观测器的控制方式相比，可以更快地达到稳定，并且在负载突变时，电压波动更小，并且可以更快地恢复到稳定的状态。与传统的dq解耦控制相比，性能有了大幅度的提升。虚拟磁链观测器的增加，不仅可以减少传感器的数量，节约控制器成本，减小因传感器失灵、故障而导致系统不稳定的风险，还可以提高系统的稳定性和响应速度。
将本文所提控制策略与Feedback+SMO+VIC方式进行对比，控制器中滑模观测器输出直流侧电压结果如图11a所示，为了更清晰地观察预测结果，对输出结果进行了快速傅里叶变换（Fast Fourier Transform, FFT）分析，结果如图11b所示。
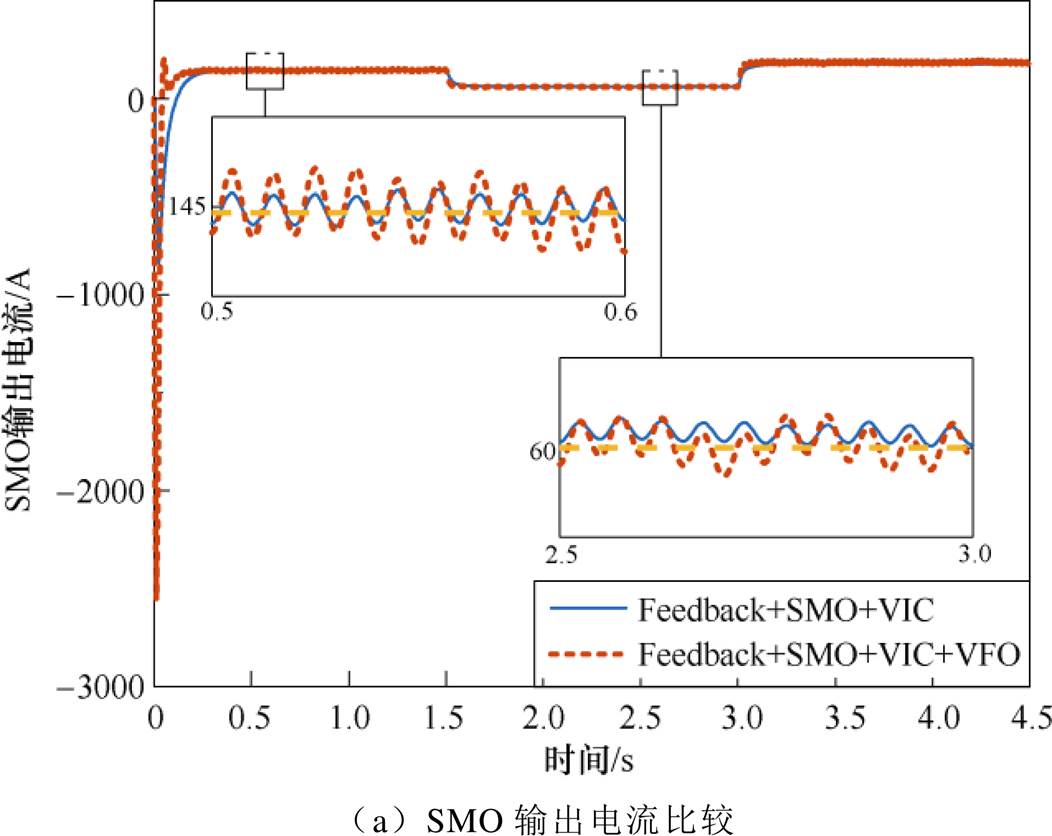
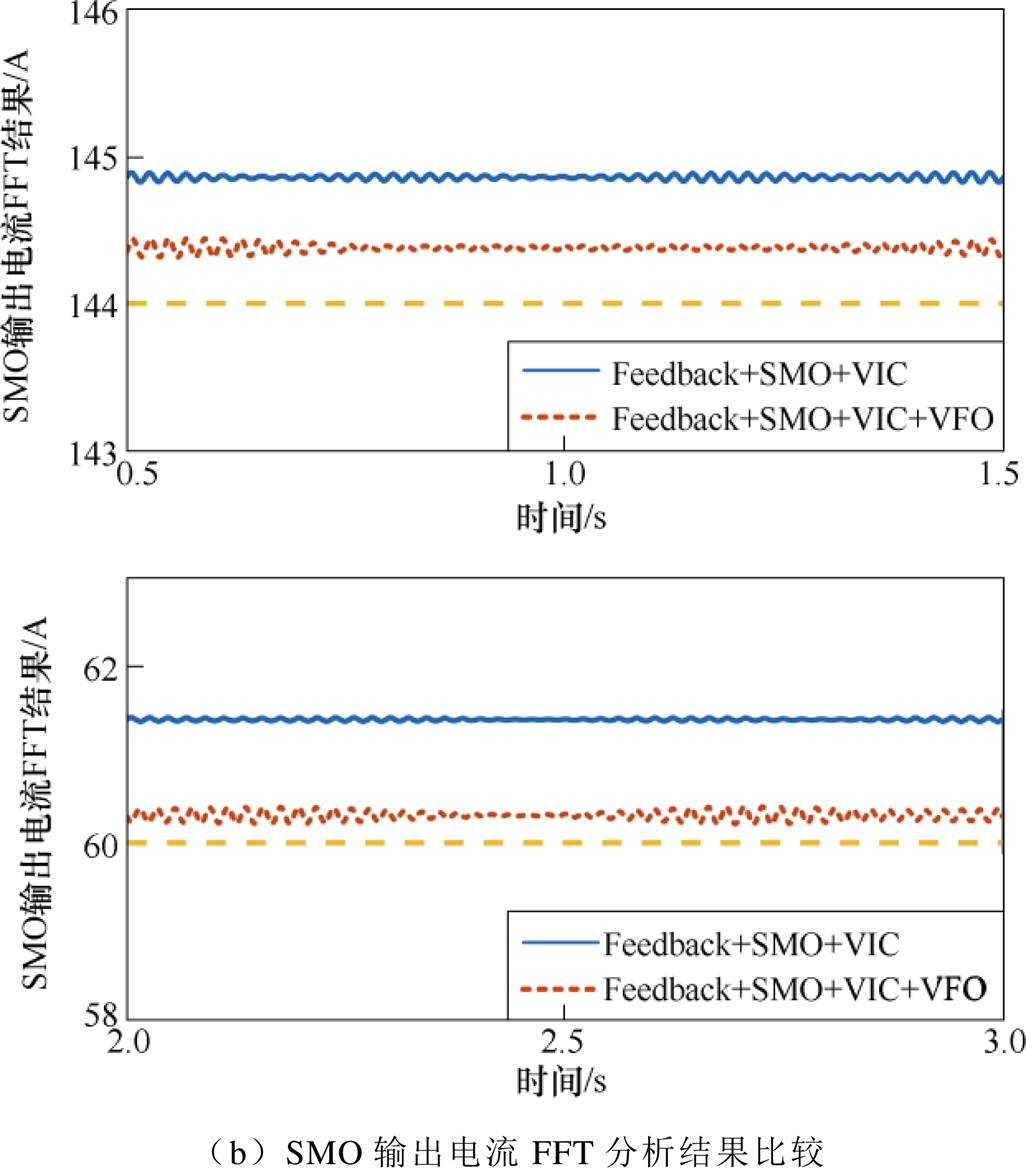
图11 SMO输出电流比较
Fig.11 SMO output current comparison
从图11可以看出，在加入本文提出的虚拟磁链观测器后，滑模观测器输出的直流侧电流估计值更加贴近理论的直流电流数值。
综上所述，可以看出，加上虚拟磁链观测器后系统性能指标得到了优化，控制中的各环节都能输出准确的结果；并且在负载发生扰动时，也能输出准确的电压，保持系统稳定；减少了外界干扰对系统影响的同时，增加了系统的鲁棒性。
为了进一步验证本文所提控制策略的鲁棒性，通过改变网侧电感Ls的参数，首先观察相同电路条件下，不同控制器的控制效果，比较结果如图12所示。然后继续增大网侧电感参数，观察不同控制器下参数的临界值，不同控制器网侧电感临界值比较结果如图13所示。
从图12可知，当网侧电感Ls增大到4.5 mH时，采用dq解耦控制方式的系统会出现振荡频率约为2.2 Hz的低频振荡，而相同电路情况下，采用Feedback+SMO+VIC以及本文提出的控制方式，则可以使系统保持稳定运行，并且含有虚拟磁链观测器的控制可以更快的使系统达到稳定的状态。图13中，Feedback+SMO+VIC方式在网侧电感增加到17 mH时，就会出现振荡的现象。而增加了虚拟磁链观测器，网侧电感在23 mH时可以保持稳定，增大到24 mH才出现振荡，说明本文采用的控制策略可以提高系统的鲁棒性，使系统参数拥有更大的稳定区域。
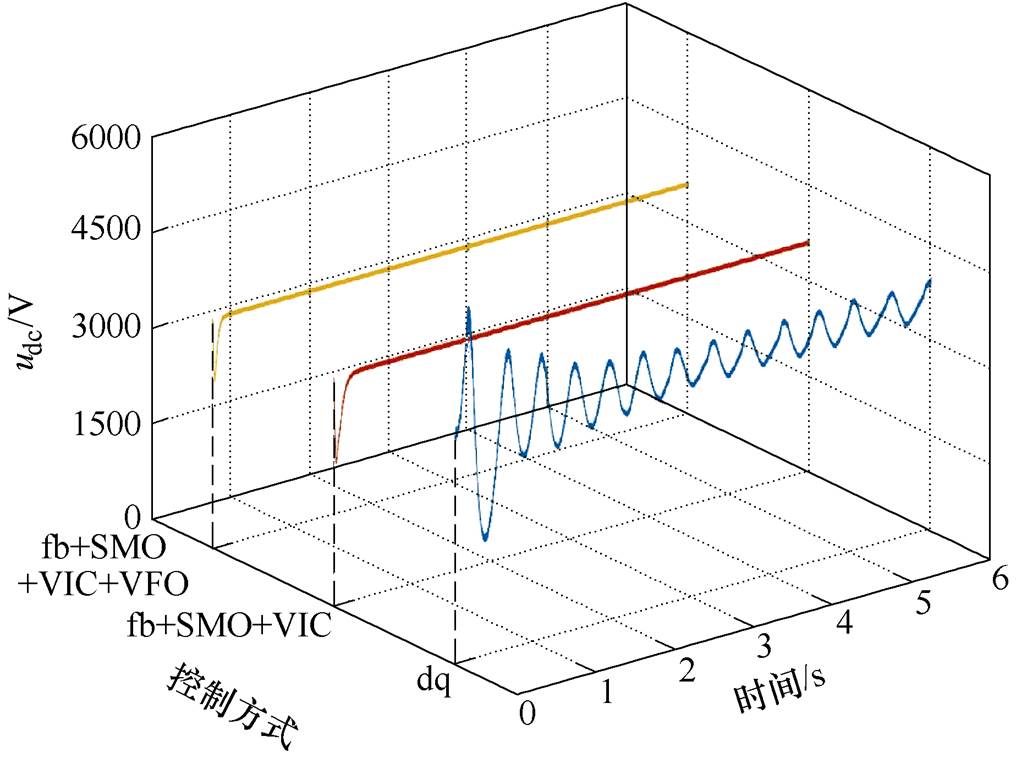
图12 相同电路参数下不同控制器比较结果
Fig.12 Comparison results of different controllers under the same circuit parameters
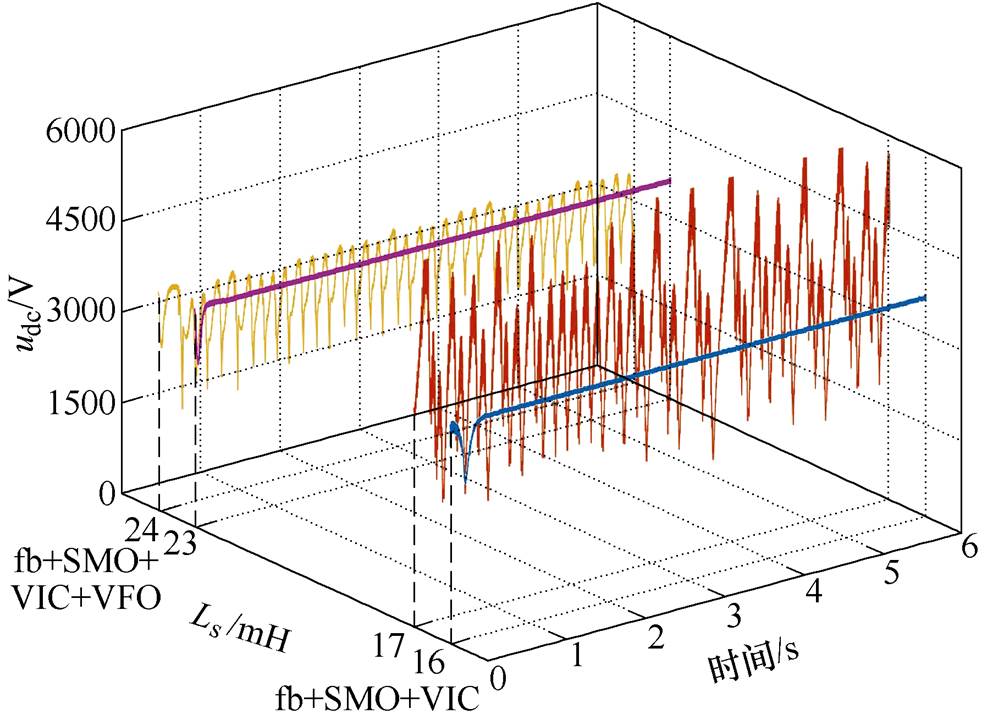
图13 不同控制器网侧电感临界值比较结果
Fig.13 Comparison results of critical value of grid-side inductance of different controllers
为了验证本文所提的结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略对车网系统低频振荡的抑制效果，首先将多个两重化LSC模型进行并联，然后与牵引网仿真模型级联，搭建车网耦合系统多车仿真模型，进行仿真[22]。多车仿真结果如图14所示。
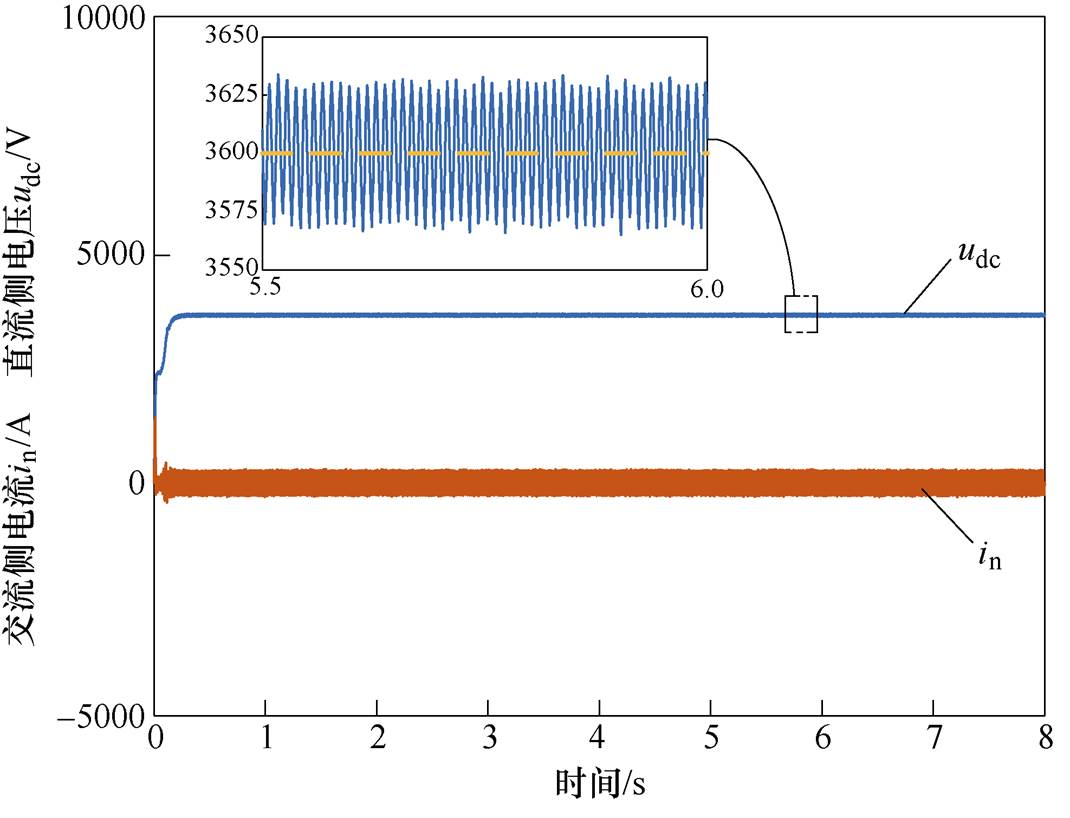
图14 Feedback+SMO+VIC+VFO多车仿真结果
Fig.14 Multi-vehicle simulation results of Feedback+SMO+VIC+VFO
将本文所提控制方式，与传统dq解耦控制以及Feedback+SMO+VIC方式的多车仿真结果进行对比，直流侧电压对比结果如图15所示。采用Feedback+ SMO+VIC以及本文所提控制策略的多车仿真性能对比结果见表4。
从图15以及表4的数据可以看出，采用传统dq解耦控制方式，多车并联之后会出现振荡频率为2.5 Hz的低频振荡现象，采用Feedback+SMO+VIC以及本文所提控制策略都可以保持系统稳定运行。并且，本文所提控制方式达到稳定的时间更短，稳定后的电压波动更小，牵引网侧电流THD更低。
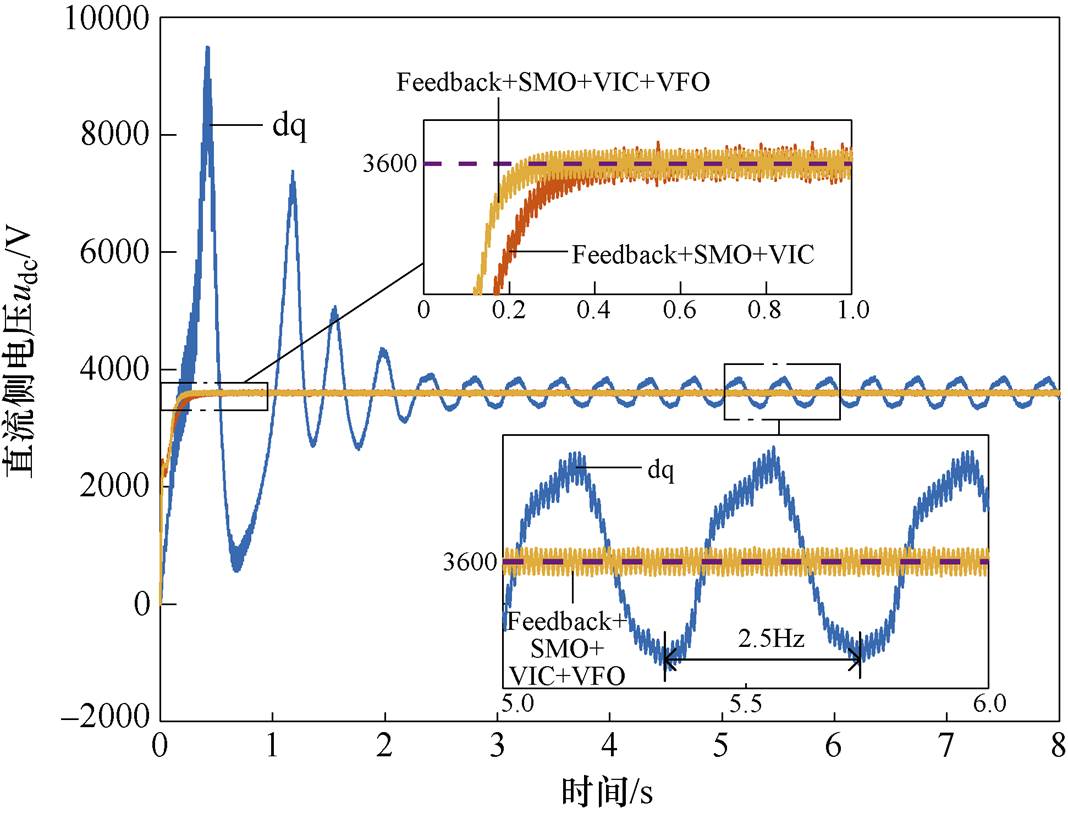
图15 不同控制器多车仿真结果对比
Fig.15 Comparison of multi-vehicle simulation results with different controllers
表4 多车仿真结果比较
Tab.4 Comparison of multi-vehicle simulation results
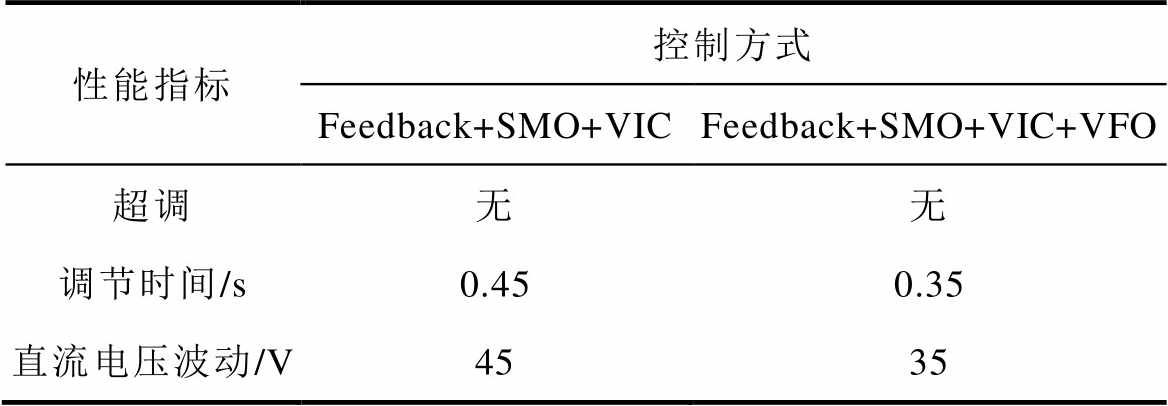
性能指标控制方式 Feedback+SMO+VICFeedback+SMO+VIC+VFO 超调无无 调节时间/s0.450.35 直流电压波动/V4535
为了进一步验证所提控制方式的有效性，采用硬件在环仿真（Hardware in Loop, HIL）半实物实验平台进行实验。首先将车网系统拆分成电路和控制两个部分，利用StarSim软件，分别下载到硬件在环（HIL）实时仿真系统和快速控制原型（Rapid Control Prototype, RCP）系统中，再通过实际的物理输入输出（Input/Output, I/O）模块进行连接，形成闭环回路，仿真平台如图16所示。实验参数与仿真参数一致，见表1。
图16 HIL仿真平台
Fig.16 HIL simulation platform
与仿真模型相对应，针对双重化LSC模型，分别采用dq解耦控制、Feedback+SMO+VIC以及本文所提控制策略进行半实物验证。在负载连续变化的情况下，观察直流侧电压的变化情况，波形比较结果如图17所示。
图17 双重化模型HIL实验结果
Fig.17 Dualization model HIL experimental results
从图17a中可以看出，dq解耦控制的HIL实验结果与仿真波形一致，存在超调，并且在受到外界扰动时，电压波动较大，恢复到稳态的时间较长。在相同的电路条件下，本文所提出的控制策略与Feedback+ SMO+VIC相比，同样没有超调，但是在受到扰动（直流侧负载突变）后的电压波动更小，恢复时间更短，如图17b和图17c所示。
Feedback+SMO+VIC，负载扰动后的局部放大波形如图18a所示，本文所提控制策略局部放大如图18b所示。可以看出，在其余控制部分相同的情况下，取消网压传感器，在相同的外界干扰下，增设虚拟磁链观测器后的直流电压波动更小，恢复时间更快。
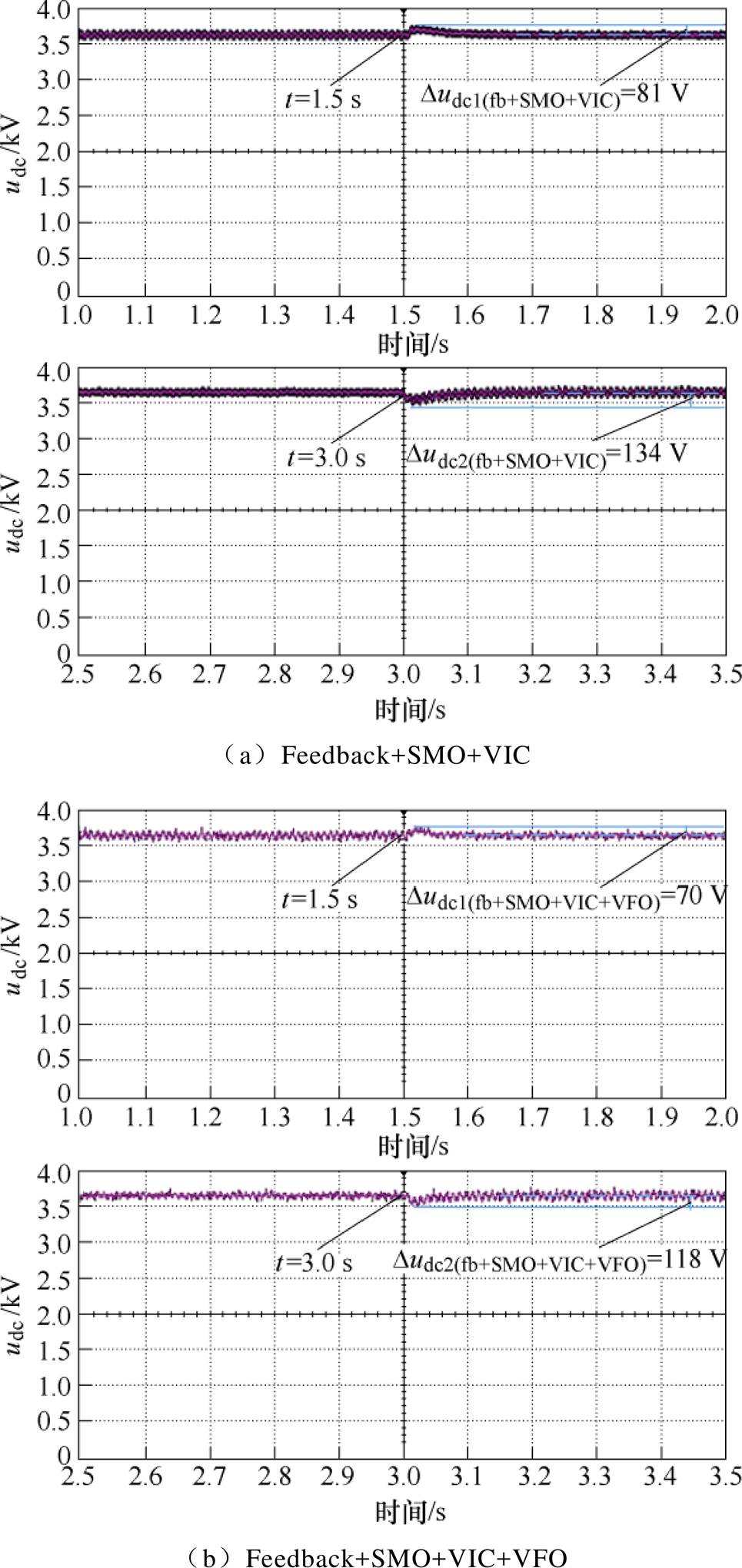
图18 负载突变时的电压峰值放大
Fig.18 Magnified view of the voltage peak when the load suddenly changes
在HIL实验平台上，观察在相同电路条件下，不同控制器的控制效果，结果如图19所示。
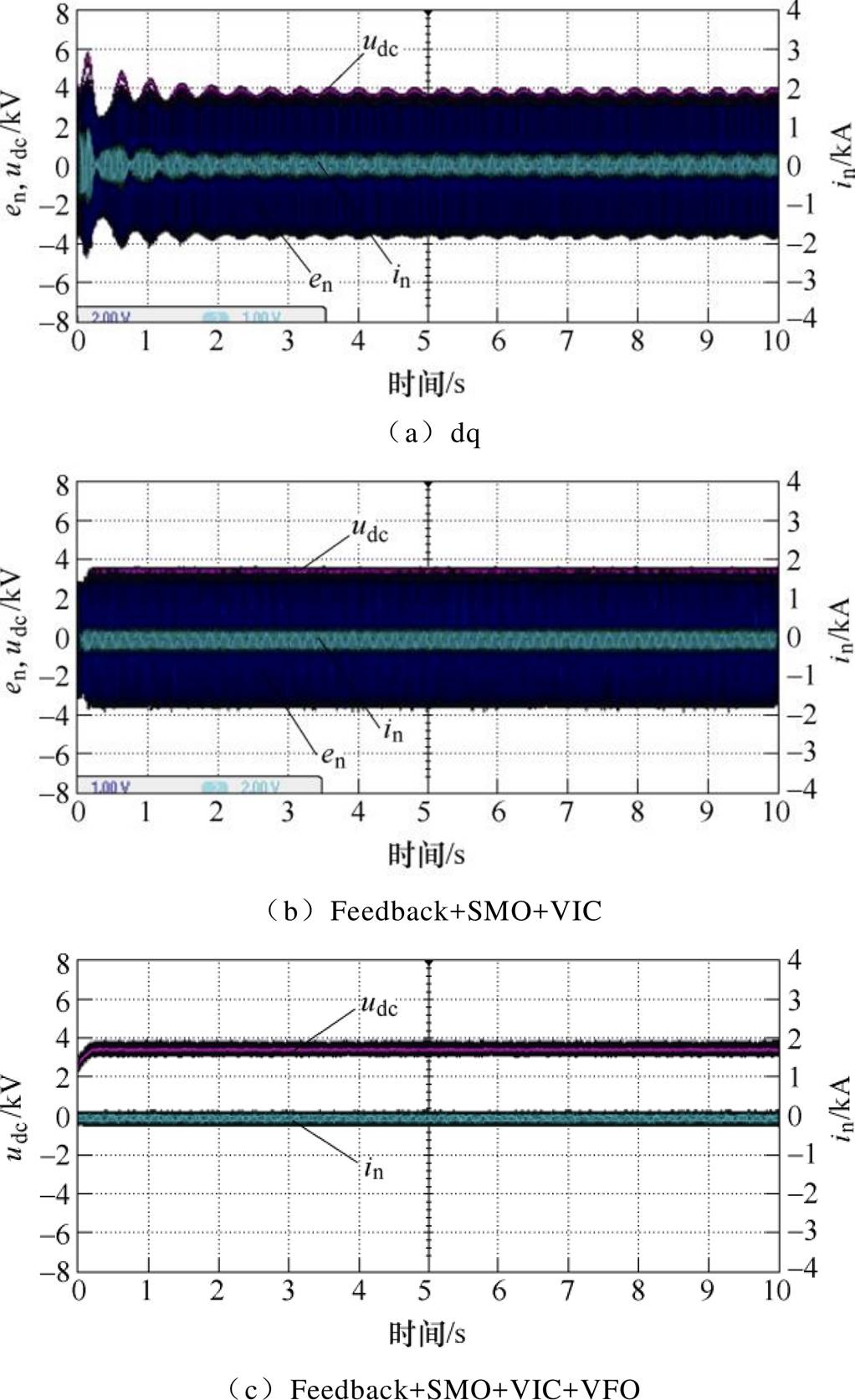
图19 相同电路参数下不同控制器HIL实验结果
Fig.19 HIL experimental results of different controllers under the same circuit parameters
从图19a可以看出，当网侧电感Ls增加到4.5 mH时，采用传统dq解耦控制，会出现振荡频率为2 Hz的低频振荡现象。而采用Feedback+SMO+ VIC以及本文提出的控制策略，在相同的电路参数下可以使系统保持稳定，并且本文所提控制方式达到稳态的时间更短，如图19b和图19c所示。
本文针对车网系统中存在的低频振荡现象，设计了新的虚拟磁链观测器，提出了结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略。基于新提出的控制器，搭建了双重化LSC仿真模型，与传统dq控制和Feedback+SMO+VIC进行控制性能对比，并进行了多车仿真实验，验证其对低频振荡的抑制作用。最后通过HIL仿真平台对所提控制器的性能进行进一步验证。综合以上的比较，可以得出下面的结论：
1）本文新设计的虚拟磁链观测器不仅消除了对积分初始值的依赖，还可以消除直流偏置现象，正确地对牵引网侧电压进行估计。
2）本文提出的结合虚拟磁链和滑模观测器的反馈线性化虚拟惯量控制策略，与传统dq控制相比，抑制了低频振荡现象的发生；与有网压传感器的控制相比，在减少了传感器数量的同时，降低了外界干扰对系统的影响。并且在相同的电路参数下，表现出了更好的动态性能。
3）本文提出的控制策略能增大系统参数的稳定范围，增强系统抗干扰能力，提高系统的鲁棒性。
参考文献
[1] Liu Zhigang, Zhang Guinan, Liao Yicheng. Stability research of high-speed railway EMUs and traction network cascade system considering impedance matching[J]. IEEE Transactions on Industry Appli- cations, 2016, 52(5): 4315-4326.
[2] Liao Yicheng, Liu Zhigang, Zhang Guinan, et al. Vehicle-grid system stability analysis considering impedance specification based on norm criterion[C]// 2016 IEEE Transportation Electrification Conference and Expo, Asia-Pacific, South Korea, Busan, 2016: 118-123.
[3] 王晖. 电气化铁路车网电气低频振荡研究[D]. 北京: 北京交通大学, 2015.
[4] 张桂南, 张波, 黄金, 等. 计及网压波动的牵引传动系统间谐波传播机理研究[J]. 电力自动化设备, 2021, 41(2): 186-192.
Zhang Guinan, Zhang Bo, Huang Jin, et al. Study on the mechanism of harmonic propagation between traction drive systems considering network voltage fluctuations[J]. Electric Power Automation Equipment, 2021, 41(2): 186-192.
[5] Wu Siqi, Liu Zhigang. Low-frequency stability analysis of vehicle-grid system with active power filter based on dq-frame impedance[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(8): 9027-9040.
[6] Yan Qixiang, Tasiu I A, Chen Hong, et al. Design and hardware-in-the-loop implementation of fuzzy-based proportional-integral control for the traction line-side converter of a high-speed train[J]. Energies, 2019, 12(21): 4094.
[7] Liu Zhigang, Wang Yaqi, Liu Shuang, et al. An approach to suppress low-frequency oscillation by combining extended state observer with model predictive control of EMUs rectifier[J]. IEEE Transactions on Power Electronics, 2019, 34(10): 10282-10297.
[8] Liu Zhigang, Geng Zhaozhao, Wu Siqi, et al. A passivity-based control of Euler-Lagrange model for suppressing voltage low-frequency oscillation in high-speed railway[J]. IEEE Transactions on Indu- strial Informatics, 2019, 15(10): 5551-5560.
[9] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[10] 夏超英, 张耀华, 郭海宇. 无刷双馈电机反馈线性化控制方法[J]. 电工技术学报, 2020, 35(7): 1387- 1397.
Xia Chaoying, Zhang Yaohua, Guo Haiyu. Feedback linearization control approach of brushless doubly fed machine[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1387-1397.
[11] Guo Xin, Ren Haipeng. Nonlinear feedback control of compound active-clamp soft-switching three-phase PFC converter base on load observer[C]//2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 2014: 1153-1158.
[12] 张国荣, 侯立凯, 彭勃, 等. 柔性多状态开关反馈线性化滑模控制[J]. 电力系统自动化, 2020, 44(1): 126-133.
Zhang Guorong, Hou Likai, Peng Bo, et al. Feedback linearization sliding mode control strategy for soft open point[J]. Automation of Electric Power Systems, 2020, 44(1): 126-133.
[13] Yu Wenqian, Liu Zhigang, Tasiu I A. Virtual inertia control strategy of traction converter in high-speed railways based on feedback linearization of sliding mode observer[J]. IEEE Transactions on Vehicular Technology, 2021, 70(11): 11390-11403.
[14] Choi J, Nam K, Bobtsov A A, et al. Robust adaptive sensorless control for permanent-magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2016, 32(5): 3989-3997.
[15] 王震宇, 孙伟, 蒋栋. 基于虚拟电压注入的闭环磁链观测器的感应电机无速度传感器矢量控制系统[J]. 电工技术学报, 2022, 37(2): 332-343.
Wang Zhenyu, Sun Wei, Jiang Dong. Speed sensor- less vector control system for induction motor based on virtual voltage injection and closed-loop flux observer[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 332-343.
[16] 操张鹏, 廖勇, 李福. 双低通滤波器法改进电压型定子磁链观测器研究[J]. 电工电能新技术, 2015, 34(3): 35-40.
Cao Zhangpeng, Liao Yong, Li Fu. Research on the improvement of voltage-type stator flux linkage observer by double low-pass filter method[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(3): 35-40.
[17] 肖蕙蕙, 苏新柱, 郭强, 等. 三相Vienna整流器无网压传感器预测电流控制策略[J]. 电工技术学报, 2021, 36(6): 1304-1312.
Xiao Huihui, Su Xinzhu, Guo Qiang, et al. Predictive current control strategy for three-phase Vienna rectifier without grid voltage sensor[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1304-1312.
[18] 熊成林, 宋智威, 黄路, 等. 基于谐波补偿的单相PWM整流器虚拟磁链模型预测算法[J]. 电机与控制学报, 2020, 24(11): 93-101.
Xiong Chenglin, Song Zhiwei, Huang Lu, et al. Prediction algorithm of virtual flux linkage model for single-phase PWM rectifier based on harmonic compensation[J]. Electric Machines and Control, 2020, 24(11): 93-101.
[19] Bu Wenshao, Xu Leilei. Improved virtual-flux- linkage observation method of PWM rectifier[J]. Applied Mechanics and Materials, 2014, 678: 528- 532.
[20] Tan Guojun, Wu Xuanqin, Zhao Yanping, et al. Study on sensorless control strategy of multi-level PWM rectifier based on a novel virtual flux observer[C]// 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, Sichuan, 2010: 1-4.
[21] 史经丛. 无网侧电压传感器PWM整流器控制技术的研究[D]. 江苏: 中国矿业大学, 2016.
[22] 姚书龙, 刘志刚, 张桂南, 等. 基于自抗扰控制的牵引网网压低频振荡抑制方法[J]. 电网技术, 2016, 40(1): 207-213.
Yao Shulong, Liu Zhigang, Zhang Guinan, et al. Suppression method of low frequency oscillation of traction network voltage based on active disturbance rejection control[J]. Power System Technology, 2016, 40(1): 207-213.
Abstract In the traditional control mode adopted in the vehicle-grid system, the AC side voltage sensor is used to measure the AC side voltage to obtain the phase information for coordinate transformation and the voltage amplitude of the AC side. In order to reduce the risk of instability caused by sensor faults and reduce the influence of AC side voltage fluctuation on the system, a feedback linearized virtual inertia control (VIC) strategy based on virtual flux and sliding mode observer (SMO) is proposed.
Referring to the concept of flux in AC motor, the integrator of traditional virtual flux observer (VFO) used in rectifier is analyzed. It is pointed out that the existing integrator is easily affected by the initial value of integration and the amount of DC bias, and the integrated signal contains a large harmonic component. An improved integrator is proposed by concatenating a second-order low-pass filter followed by a band-pass filter. The gain selection in the proposed integrator is theoretically analyzed using the Bode diagram and unit step response curve, the value of the gain is determined, and the new VFO is obtained. Using the virtual flux estimate obtained by VFO and voltage reconstruction calculation, the amplitude and phase information of AC side voltage needed for coordinate change can be obtained. Then, the control mode without a voltage sensor is realized by combining with the current inner loop control part of feedback linearized VIC based on SMO.
The results of Matlab/Simulink simulation and hardware in-loop experiments show that the improved integrator can eliminate the uncertainty of the initial value of integration and the adverse effects caused by DC voltage bias. Because of the addition of a band-pass filter, it can filter the low-frequency and high-frequency clutter except for the fundamental signal. Compared with the traditional dq decoupling control and the feedback linearized VIC based on SMO control, the proposed control strategy has the largest critical value of the grid side inductance. Under the same circuit conditions, the low-frequency oscillation (LFO) phenomenon will not occur, and the DC voltage offset phenomenon will not occur before reaching the critical value. The response time of the grid side inductance mutation is the shortest, and the voltage fluctuation is the least. In the dual simulation experiment, the proposed improved control mode has the slightest fluctuation of output voltage and the shortest response time when the load suddenly increases or decreases. It can be further found that the estimated DC-side current of SMO output is closer to the theoretical value than that of the control method with a grid voltage sensor. In the multi-vehicle simulation, the LFO phenomenon can be suppressed compared with dq decoupling control, and the response time and DC voltage fluctuation can be reduced. In addition, the number of sensors can be greatly reduced compared with the control mode of network pressure sensors.
The proposed control method enhances the robustness of the vehicle-grid system, reduces the influence of external interference on the vehicle-grid system, and saves the hardware cost of the controller.
keywords：Virtual flux observer, low frequency oscillation, feedback linearization control, virtual inertia, high-speed railway
DOI: 10.19595/j.cnki.1000-6753.tces.220557
中图分类号：TM712
国家自然科学基金高铁联合基金重点项目（1434203）、四川省青年科技创新研究团队项目（2016TD0012）、四川省科技计划科技创新人才项目（2021JDRC0008）和国家电网公司科技项目（SGSCJY00GHJS2100041）资助。
收稿日期 2022-04-11
改稿日期 2022-05-23
喻文倩 女，1994年生，博士研究生，研究方向为高速铁路车网系统稳定性分析与控制。E-mail: wenqianyu@my.swjtu.edu.cn
刘志刚 男，1975年生，教授，博士生导师，研究方向为高速铁路动车组-牵引网电气关系与弓网状态检测评估。E-mail: liuzg_cd@126.com（通信作者）
（编辑 陈 诚）