
图1 基于分立器件并联型SiC逆变器
Fig.1 The SiC inverter based on the discrete devices in parallel
摘要 并联应用SiC MOSFET是一种适应大功率变流场景的有效方案,但是容易出现器件电流不均衡现象。该文根据一款分立器件并联型逆变器出现的静态不均流问题,在建立的寄生参数模型基础上分析寄生参数差异性对于并联均流的影响,指出影响静态均流的关键因素。同时分析交流母排汇流点位置对于静态寄生参数的影响,提出一种定位真实汇流点的方法,从而可以准确提取静态寄生参数。最后探究路径间的耦合效应对于等效寄生电感的影响,通过调整交流母排汇流点匹配路径的自感和互感,实现等效寄生参数的均衡性。基于此,对该叠层母排进行优化设计,最终的实验结果表明,优化后的叠层母排极大地改善了静态均流,验证了该优化设计方案的有 效性。
关键词:分立器件 并联型 叠层母排 寄生参数
由于碳化硅(Silicon Carbide, SiC)晶元技术尚未很成熟,单个SiC 金属-氧化物-半导体场效应晶体管(Metal-Oxide-Semiconductor Field Effect Transi- stor, MOSFET)的载流能力较弱,为了适应大功率电能变换的应用场景,需要并联使用多个SiC MOSFET[1]。多芯片并联大功率模块[2-3]、并联使用小功率模块[4-5]以及并联使用分立器件[6-7]是从器件类型角度来讲的三种常规方案。目前,相比于SiC功率模块,TO247封装形式的分立器件大多基于标准封装、工艺成熟、优良品率高且产量大。因此,在器件价格上,分立器件每安培的成本比模块小很多[8-9]。另外,分立器件并联型方案可通过增减并联器件数目实现功率的灵活扩展[7]。综上所述,围绕成本、器件资源以及功率灵活扩展性等角度,采用SiC分立器件并联型方案搭建主电路具备一定优势。
然而,器件在并联应用中会出现电流分配不均的现象[10],包括开关瞬态中的动态电流不均衡,以及导通后的静态电流不均衡[11]。除了器件自身参数如通态电阻以及阈值电压存在的分散性[12-13],外电路寄生参数的非对称设计也是影响器件均流的重要原因[14-15]。由于SiC功率器件具有更快的开关速度,其对外电路寄生参数将更为敏感[16-17]。随着器件封装技术的成熟,加之厂商的严格把控,同一批次器件的分散性不会很大。因此,聚焦于外电路的对称性设计,实现并联支路寄生参数的均衡,是确保分立器件并联均流的关键。
在中大功率电力电子变流装置中,通常采用叠层母排作为母线电容和功率器件的互连载体,从而使主功率回路具备高电流承载能力、低回路寄生电感等优点[18-20]。目前已有大量文献对叠层母排的低电感结构进行了研究,主要聚焦在通过合理的结构设计[21]、器件布局[22-23]来实现较低的换流回路电感,从而降低器件关断时的电压应力。此外,也有文献针对电路拓扑在不同开关序列下的各换流回路寄生电感一致性问题,对母排结构进行设计,以提高各功率器件电压应力的均衡性[24-25]。对于器件并联应用中的叠层母排,其不合理的结构设计也会导致并联支路寄生参数的不对称,影响电流在并联器件中的均衡分配。文献[26]针对多芯片并联压接型绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT),从磁场耦合角度研究了外部汇流母排对芯片并联均流的影响。文献[27]以两个IGBT并联模块为研究对象,从电路模型角度分析母排寄生电感对器件动态均流的影响,设计了一种能改善均流的交流母排结构。类似地,文献[28-29]分析了叠层母排寄生电感对并联IGBT模块均流影响,但母排结构以及整个分析过程相对简单。上述文献中的叠层母排结构均针对的是功率模块并联应用场景,而对于分立器件并联型叠层母排的研究却鲜有文献报道。
另外,在变流装置实际运行过程中,主电路存在不同组合的开关状态,使得叠层母排表面存在着不同的电流路径,而母排的电感建模与电流路径有关。因此,叠层母排的寄生电感模型会随着不同开关状态而改变[30]。文献[31]针对一款分立器件并联型叠层母排,根据动静态过程的电流路径,建立了寄生参数模型,并测得该系统存在着较大的静态不均流情况。虽然该文献解决了分立器件并联型叠层母排寄生参数的精准建模问题,但没有进一步给出相关优化设计方法。实际上,由于并联器件各端子间存在多条电流路径,且路径间相互耦合,使得模型中存在着复杂的互感网络,进而会综合影响叠层母排的等效寄生参数。文献[29]指出了母排路径间的互感会影响等效电感,进而对于动态均流有着影响,但没有给出较为详细的分析以及优化设计方法。
本文从优化分立器件并联型叠层母排结构入手,以提升并联器件的静态均流为目标。首先,分析叠层母排等效寄生参数在不同开关速度以及负载电感下对动静态均流的影响,指出影响静态均流的关键因素。接着,分析了交流母排汇流点位置对于静态寄生参数均衡性的影响,提出一种可以定位交流母排真实汇流点的方法,提高静态寄生参数的提取精度。最后,分析了路径间耦合效应对于等效寄生参数的影响,通过调整交流母排汇流点位置合理匹配路径的自感和互感,从而实现并联支路寄生参数的对称性。实验结果表明,优化后的叠层母排静态均流得到极大改善,验证了优化设计方案的准确性,为器件并联型叠层母排的设计提供有益支撑。
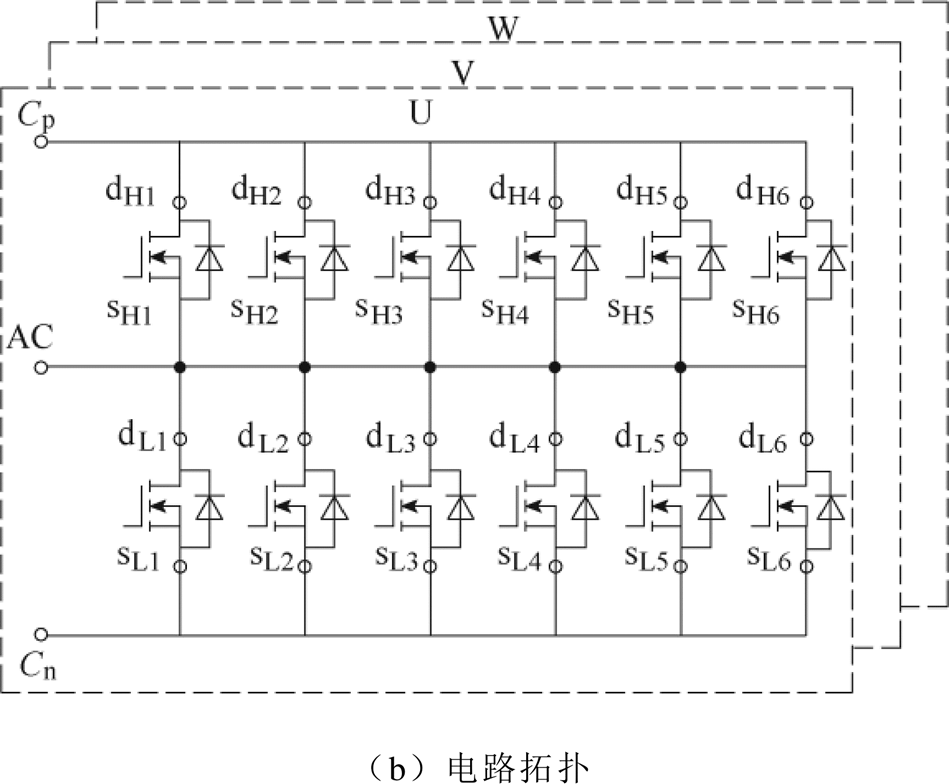
该分立器件并联型逆变器以及内部叠层母排结构如图1a所示,图1b为对应的电路拓扑,每个桥臂由6个SiC单管并联构成,图中,dHj、sHj分别为上桥臂器件的漏极和源极,dLj、sLj分别为下桥臂器件的漏极和源极,j为并联支路编号。由于三相对称,以W相为例进行分析,图2给出了W相母排的详细结构以及电气连接形式。该母排有三层导电层,分别为正母排、交流母排以及负母排。正母排伸出端子与上桥臂MOSFET的漏极相连,交流母排两侧伸出端子与上桥臂的源极以及下桥臂的漏极相连,负母排伸出端子与下桥臂的源极相连。此外,正负母排在边侧伸出端子与电容模组相连,以此构成主功率单元的电气连接。


图1 基于分立器件并联型SiC逆变器
Fig.1 The SiC inverter based on the discrete devices in parallel
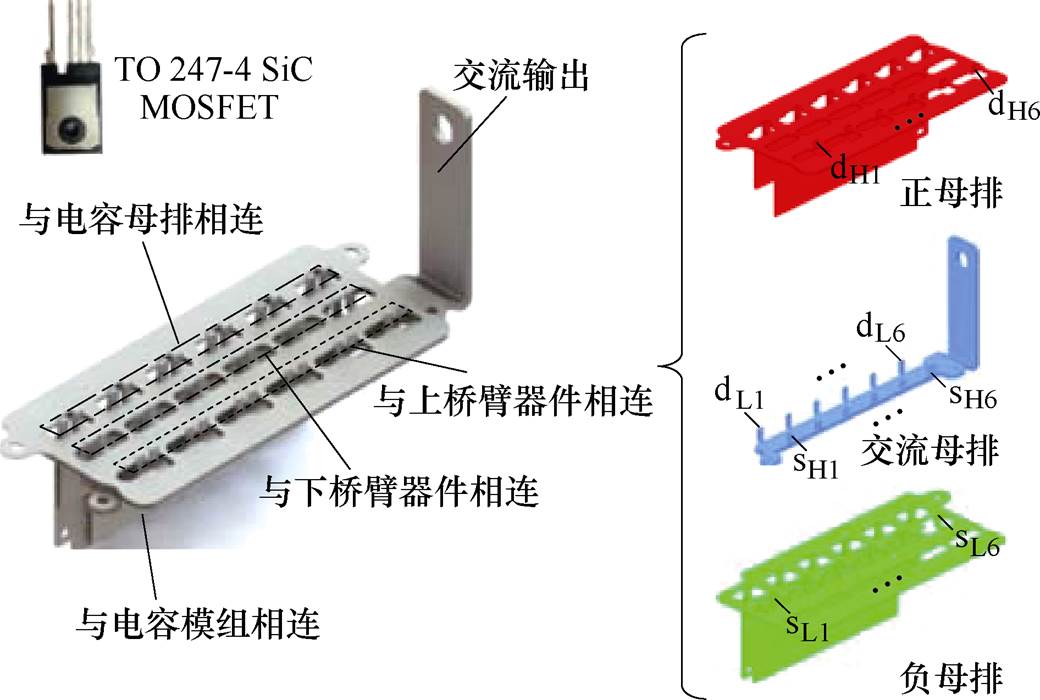
图2 单相母排电气连接结构
Fig.2 The electric connection of the single-phase busbar
根据动静态过程中叠层母排各并联支路端子间的电流路径,文献[31]建立了该分立器件并联型叠层母排的寄生参数模型,如图3所示。在动态过程中,换流电流在正母排、交流母排以及负母排中形成回路,因此母排中的电流路径都对应着寄生参数。而在静态过程中,电流通过正母排(或负母排)以及交流母排流向负载侧,因此只对某桥臂进行寄生参数建模。所建立的动态过程中的寄生参数模型如图3a所示,静态过程中上桥臂的寄生参数模型如图3b所示。图中,Lajaj、Lbjbj、Lcjcj、Ldjdj为支路在叠层母排各端子间的电流路径所对应的自感,Ma1b1、Ma1c1、Ma1d1等为路径间的耦合互感。为了清晰展现该电路模型,图中只标识出了路径a1与其他支路间的互感。寄生电阻标号方式与电感一致,不再赘述。

图3 叠层母排寄生参数建模
Fig.3 The modeling of the parasitic parameter model for the laminated busbar
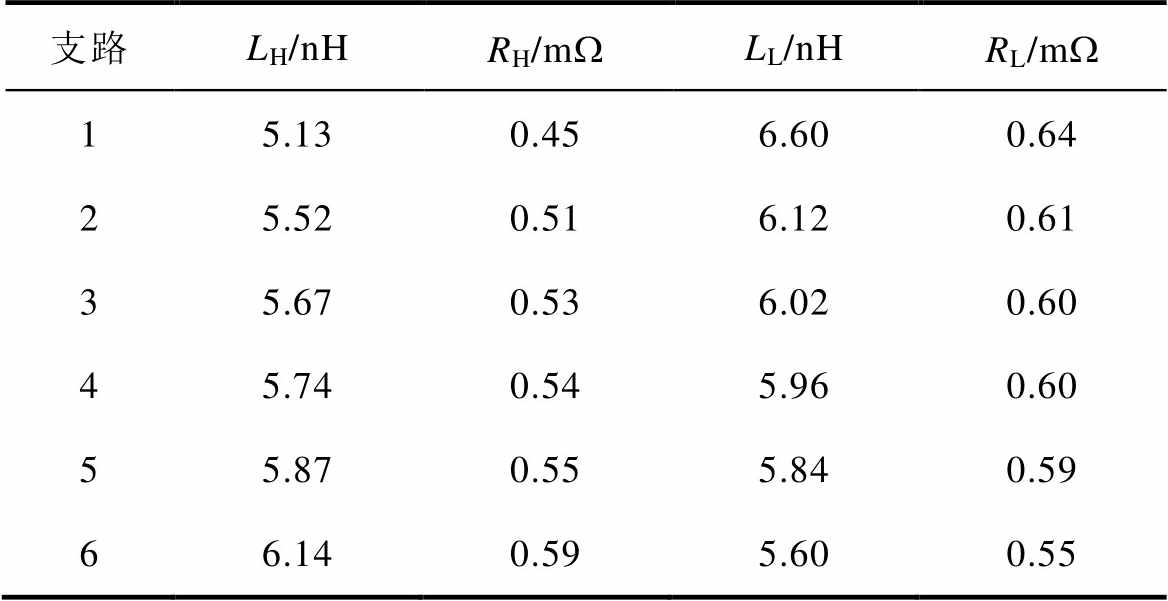
文献[31]提出一种场路联合仿真方法可以从复杂寄生参数网络中提取出叠层母排各并联支路的等效寄生参数,从而用以评估并联均流。依据该方法,提取出的动、静过程中的寄生参数分别见表1和表2。
表1 动态过程中的寄生参数
Tab.1 The parasitic parameters in the dynamic process
支路LH/nHRH/mWLL/nHRL/mW 15.130.456.600.64 25.520.516.120.61 35.670.536.020.60 45.740.545.960.60 55.870.555.840.59 66.140.595.600.55
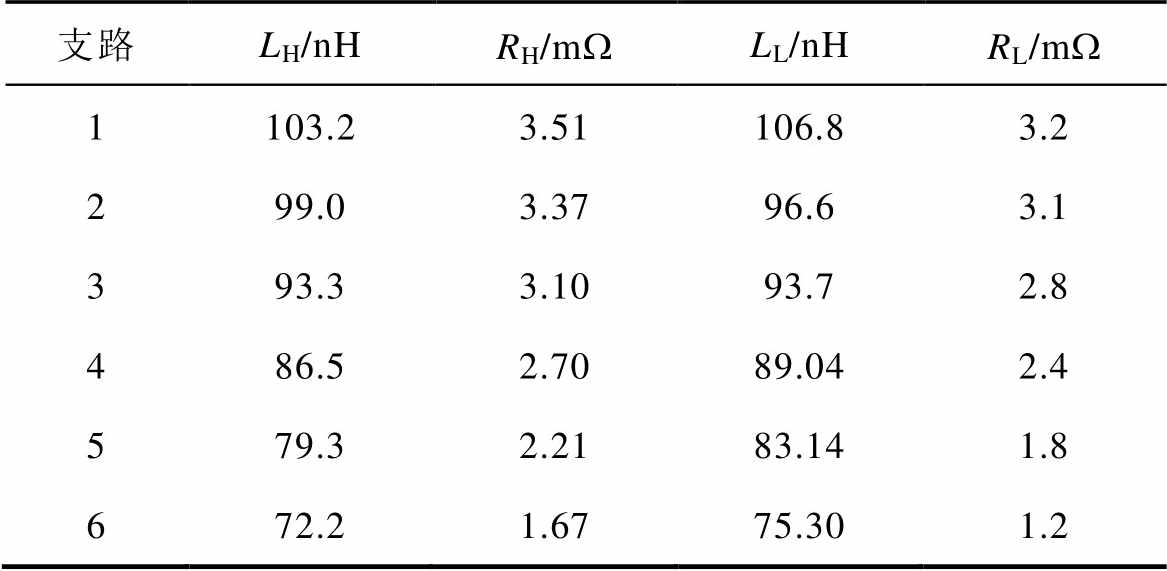
表2 静态过程中的寄生参数
Tab.2 The parasitic parameters in the static process
支路LH/nHRH/mWLL/nHRL/mW 1103.23.51106.83.2 299.03.3796.63.1 393.33.1093.72.8 486.52.7089.042.4 579.32.2183.141.8 672.21.6775.301.2
表中,LH、LL分别为上、下桥臂总的等效寄生电感,RH、RL分别为上、下桥臂总的等效寄生电阻。可以看到,动态过程中上、下桥臂各支路寄生参数差异性非常小,而在静态过程中,则有较大差异。
在实际的电路运行中,由于动静态过程对应在叠层母排电流路径不相同,导致路径间的耦合关系不一样,最终反映在两个过程中的等效寄生参数不相同。但是对于电路仿真软件,很难实现基于同一仿真电路对动静态均流同时进行分析。因此,只能分别建立电路仿真模型进行评估。
首先以2管并联为例,分析动态过程中的寄生参数差异性对均流的影响。在LTspice中搭建双脉冲仿真电路如图4所示,Vdc为直流侧电压,Cdc为支撑电容,Vdrive为驱动电压,QHj为功率器件,其仿真模型可从Wolfspeed官网获得。VDj为续流二极管,Cfj为对应的结电容,Lload为负载电感,Ldynj、Rdynj为动态过程上桥臂各支路的等效寄生电感和电阻,LLj、RLj为下桥臂各支路的等效寄生电感和电阻。在分析上桥臂并联器件电流时,下桥臂节点AC和n之间的两条支路可等效并联成单个支路,LL和RL即为对应单个支路的寄生参数,VD和Cf即为等效后的续流二极管和结电容。
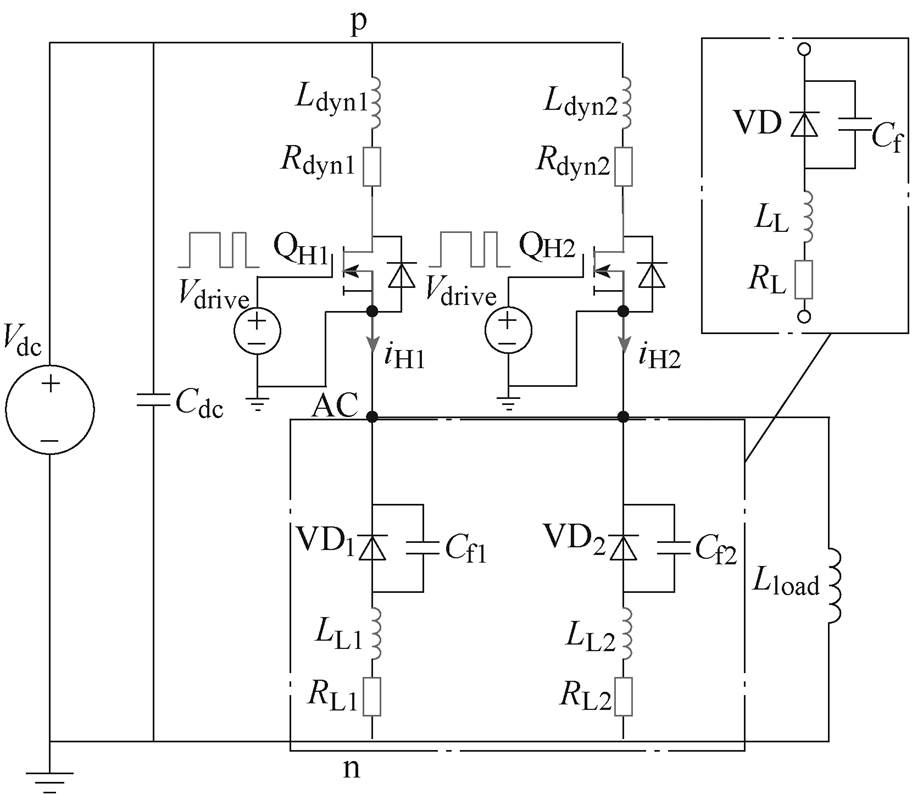
图4 评估动态电流的仿真电路
Fig.4 The simulation circuit for evaluating the dynamic current
开关波形示意图如图5所示。结合图5所示的开关过程,在t0时刻之前上桥臂器件未开启,t0~t1阶段为上桥臂漏极电流上升阶段,此时漏源极电压vdsj和电流iHj可由式(1)表示,由于只分析外电路寄生参数,器件内部寄生参数不写入公式中。
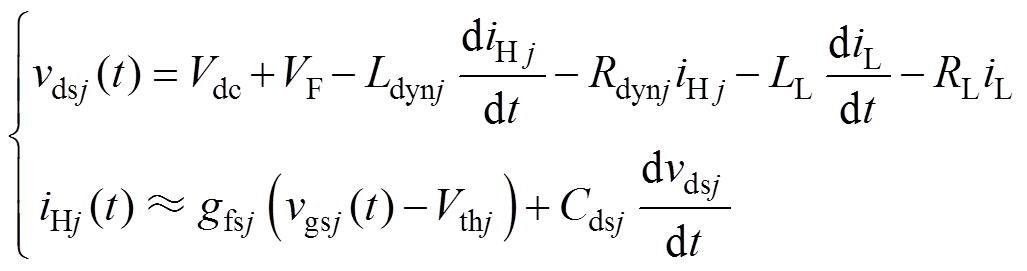 (1)
(1)
式中,VF为续流二极管的导通压降;gfsj为各器件跨导;vgsj为门极和源极间电压;Vthj为阈值电压;Cdsj为漏源极结电容。在该阶段,由于电流急剧变化,会在寄生电感两端感应电压,致使vdsj下降,使得Cdsj通过器件沟通释放电荷。因此,并联支路寄生参数的不一致会使得vdsj存在差异,带来Cdsj上位移电流的差异性,最终使得iHj在该阶段存在一定差异。
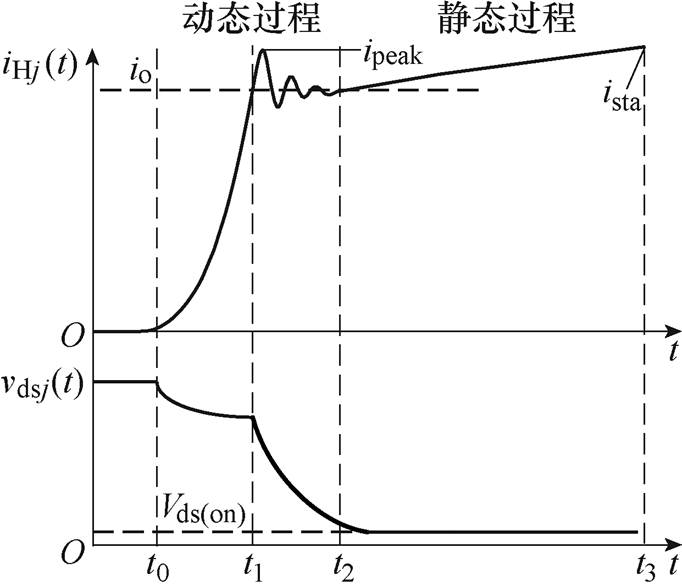
图5 开关波形示意图
Fig.5 Schematic diagram of switching waveform
在t1~t2阶段,上、下桥臂完成换流,iHj维持负载电流并且给二极管结电容充电。由于寄生电感和结电容的共同作用,电流发生振荡。该过程的漏源极电压vdsj、电流iHj可分别表示为
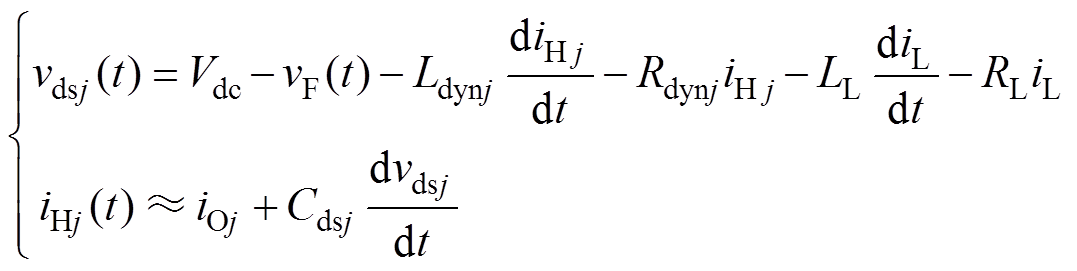 (2)
(2)
式中,vF(t)为二极管两端电压;iOj为各支路在开关过程前分配得到负载电流。同样地,在该阶段若寄生参数不一致,会造成vdsj的差异,致使iHj存在差异性。
动态过程中各器件漏极电流iHj到达峰值点处的电流差值Didyn一般用来评估动态均流程度。通过对式(1)和式(2)的分析可知,电流变化率会影响漏源极两端电压,进而影响漏极电流,因此动态均流也与开关速度相关。图6给出寄生参数差异性在不同开关速度下对动态均流的影响。首先可以看到,电阻差异性对动态均流没有影响,这是因为寄生电阻为mW 级别,其端电压相比于寄生电感两端因电流急剧变化而带来的感应压降要小很多。另外,开关速度的降低会弱化寄生电感差异性对于动态均流的影响,并且2 nH以内的差异性对于动态均流的影响非常小。
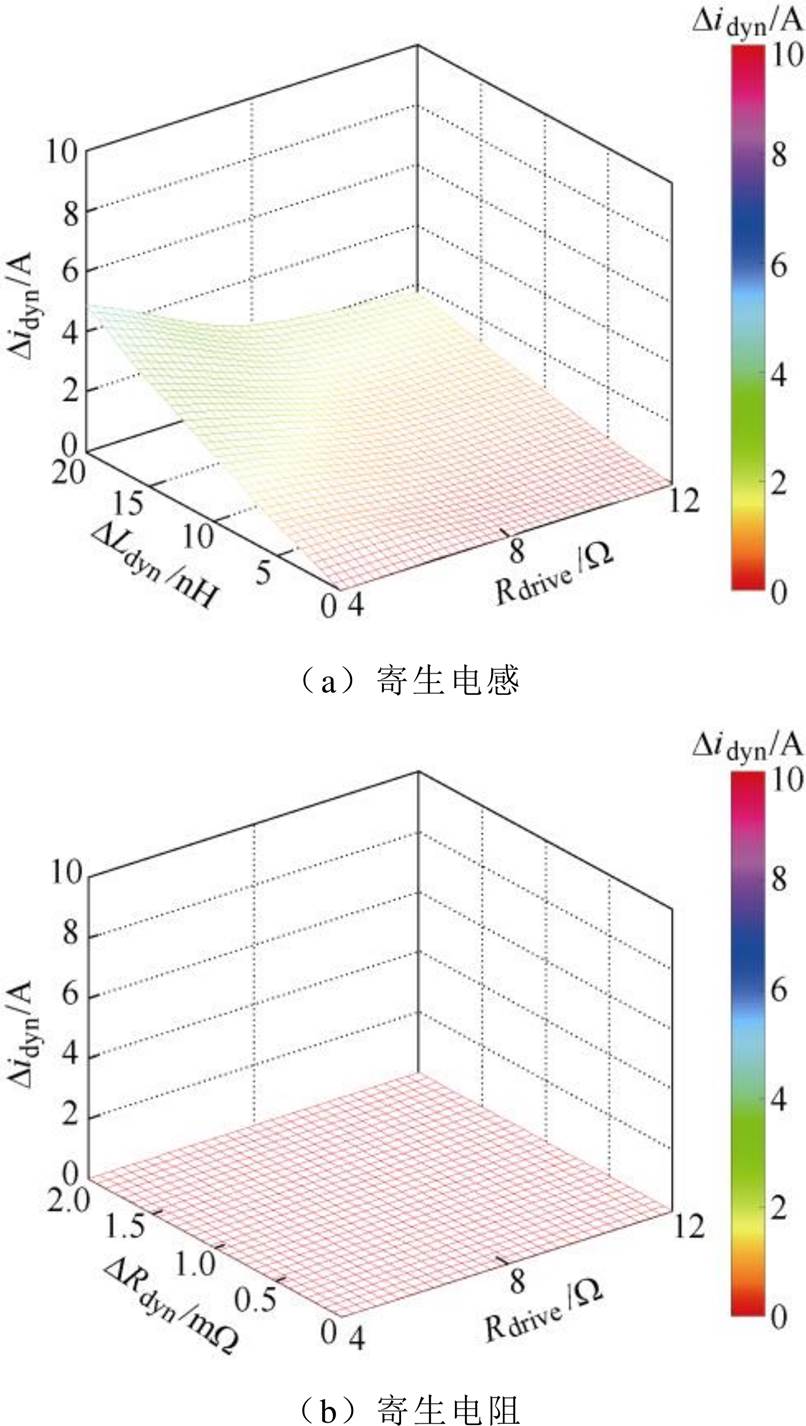
图6 不同开关速度下电路寄生参数对动态均流的影响
Fig.6 The effect of the parasitic parameters on the dynamic current balance at different switching speed
t2时刻,上桥臂器件完全关断,等效为电阻,评估静态均流的仿真电路如图7所示。图中,Lstaj、Rstaj分别为静态过程各支路的等效寄生电感和电阻,Rds(on)为器件的通态电阻。该阶段电源给负载电感充电,iHj以一定的斜率上升,电路关系满足
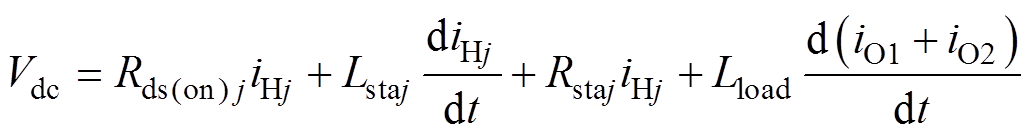 (3)
(3)
从式(3)可以直接看到,静态电流与功率回路寄生参数、通态电阻以及负载电感均相关。在静态均流分析中,一般用第一个脉冲结束前各器件漏极电流的差值Dista来评估不均流程度。图8a和图8b分别给出寄生电感和寄生电阻的差异性在不同负载电感下对静态均流的影响,可以看到寄生电阻差异性对静态均流的影响程度不低于寄生电感。然而目前对于并联均流的研究大多关注外电路的寄生电感。另外,从图8中还可以看到,负载电感的增大会弱化寄生电感差异性对于静态均流的影响,这是因为负载电感大、电流上升斜率低、寄生电感感应电压占的比重相对降低。因此,在大负载应用背景下,更应关注电路寄生电阻差异性对于静态均流的影响。
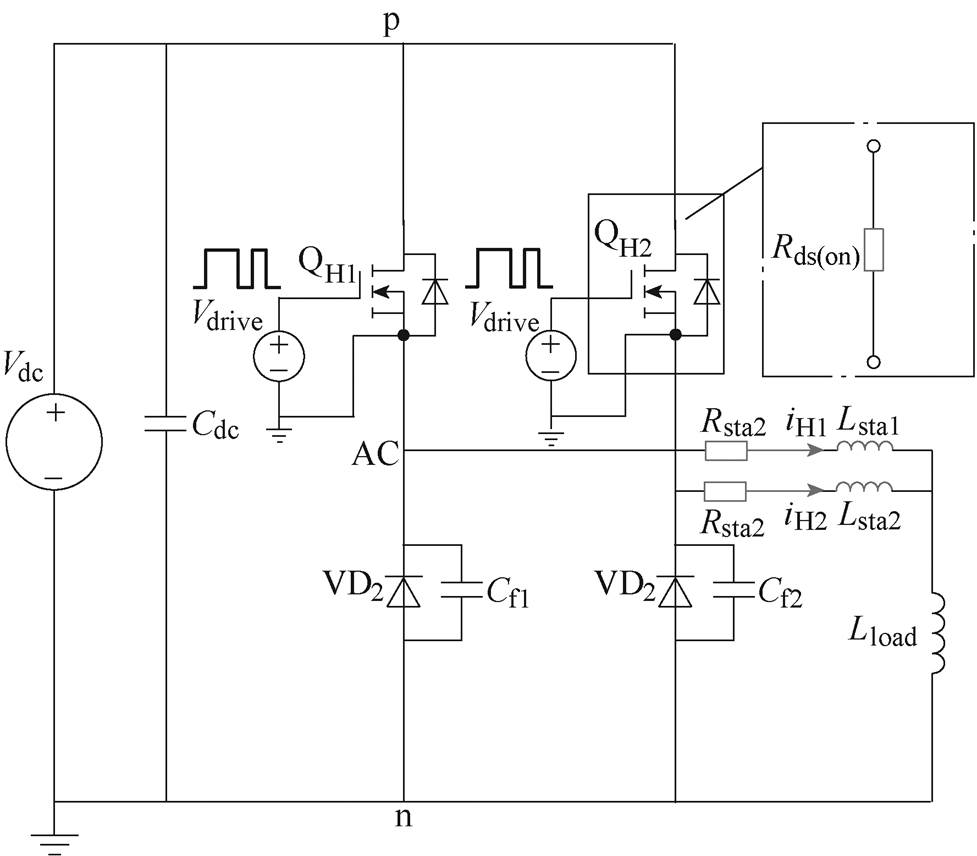
图7 评估静态均流的仿真电路
Fig.7 The simulated circuit for evaluating the static current
动态过程寄生参数与静态过程寄生参数对均流也存在着耦合影响,如器件关断前各管电流因静态寄生参数的差异性会分配到不同的负载电流iOj,而器件再次开通后,除了受寄生参数的影响,因iOj的不同,动态电流的分配也会受到影响,如式(2)所示。另外,动态过程中的电流分配状态也会在一定程度上影响静态电流。从提取的该叠层母排各支路动态寄生参数可以看到,最大差值小于1.5 nH。从图6a的仿真结果看到,1 nH左右的寄生参数影响对于动态均流影响程度并不是很大,因此在该应用中其对于静态均流的分析影响也不会很大。将图7中的2管并联仿真电路扩展为6管并联,并输入表2中提取的等效寄生参数,仿真得到双脉冲波形如图9所示。第一个脉冲开始时,各支路电流为零,不受前一时刻开关状态的影响,适合用来分析静态均流[31]。电流上升与电路寄生参数、通态电阻以及负载电感相关,电路寄生参数的差异性能直接反映在静态电流的分配上,可以较为准确地评估静态寄生参数差异性对于均流的影响。从图9中可以看到,在该负载电感下,由于各支路寄生参数的不均衡性,使得静态电流存在较大的差异。
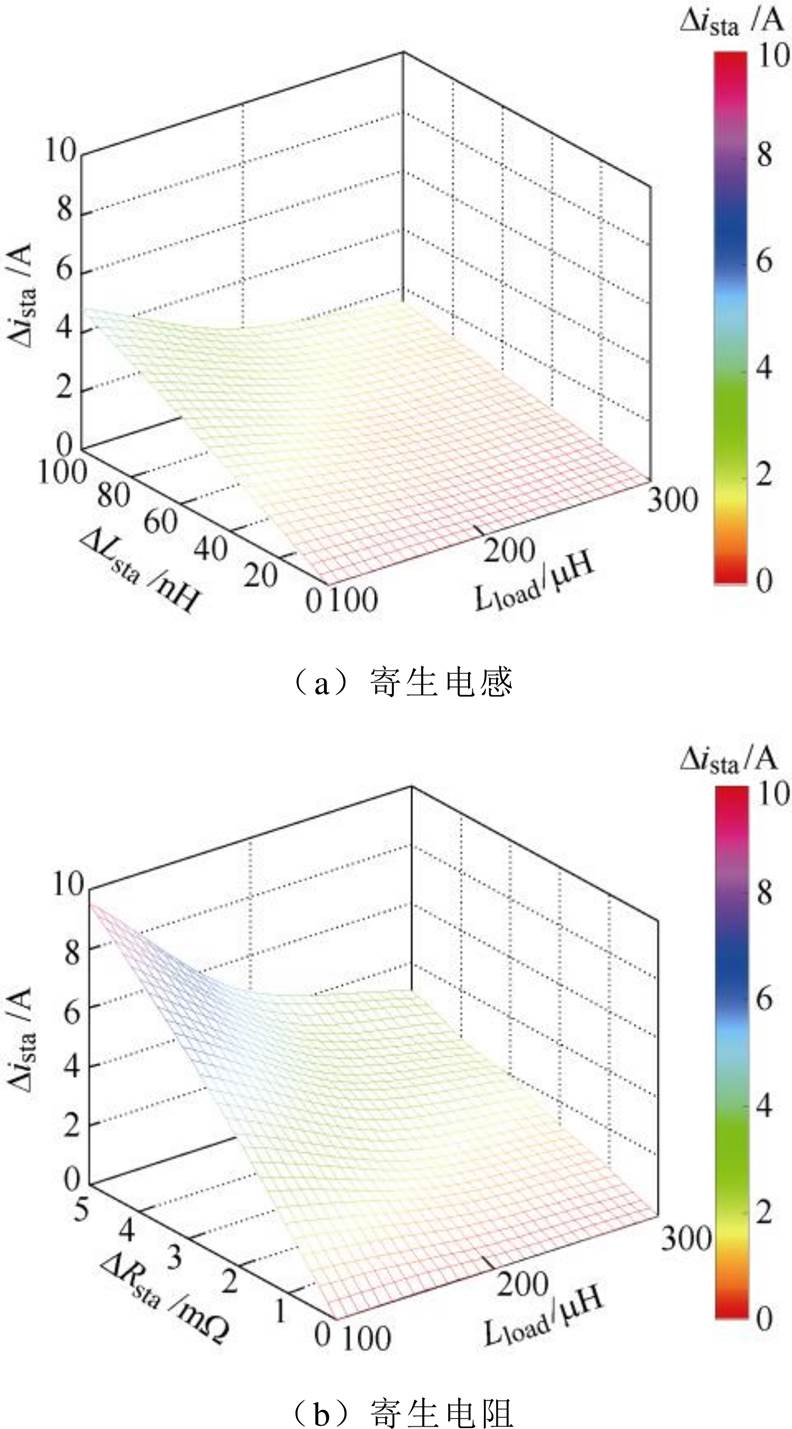
图8 不同负载电感下电路寄生参数对静态均流的影响
Fig.8 The effect of the parasitic parameters on the static current balance at different load inductance
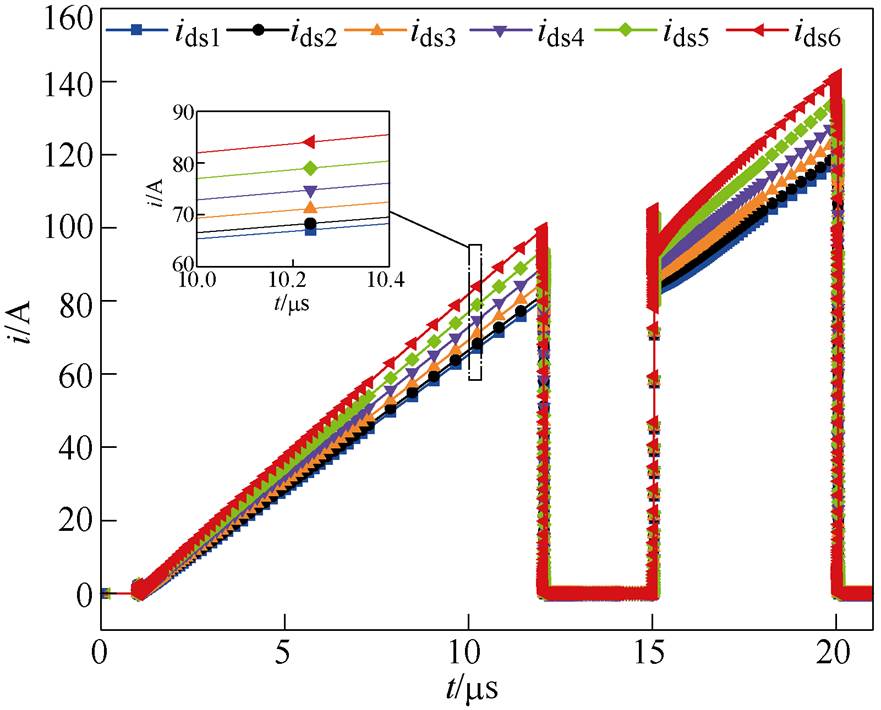
图9 叠层母排静态均流仿真分析
Fig.9 The simulation analysis of the static current sharing performance of the laminated busbar
该叠层母排静态寄生参数存在较大差异,因此需对其进行优化设计,以实现各并联支路静态寄生参数的均衡性。
以上桥臂为例,在静态过程中,电流从正母排流向交流母排进而流向负载侧。文献[31]对于叠层母排寄生参数的建模是基于端子间的电流路径,从静态寄生参数建模过程中可以看到,交流母排中的汇流点位置影响各支路电流路径的长短,因此寄生参数的提取与交流母排汇流点的位置选取相关。在文献[27]中,将交流母排与负载连接点作为汇流点来提取母排寄生电感,但没有给出详细解释。图10为本文所分析的交流母排结构,从图中路径l的起点o开始每隔20 mm取一点模拟为交流母排的汇流点,通过文献[31]的场-路联合仿真方法提取出不同汇流点处的各并联支路等效寄生电感。求得6个并联支路寄生电感的标准方差s,以此衡量均衡性,同时给出支路间电感的最大差值,结果如图11所示。可以看到不同汇流点下,各并联支路寄生参数均不相同,导致其之间的均衡性和差值均不一样。因此,定位出交流母排真实汇流点的位置对静态寄生参数的准确提取非常重要。实际上,从电路层面,汇流点处的电流应为各支路电流之和,且汇流点之后任意电位处的电流是恒定不变的。因此,对应于实际物理结构,汇流点应为交流母排中电流达到最大值且开始稳定的截点处。
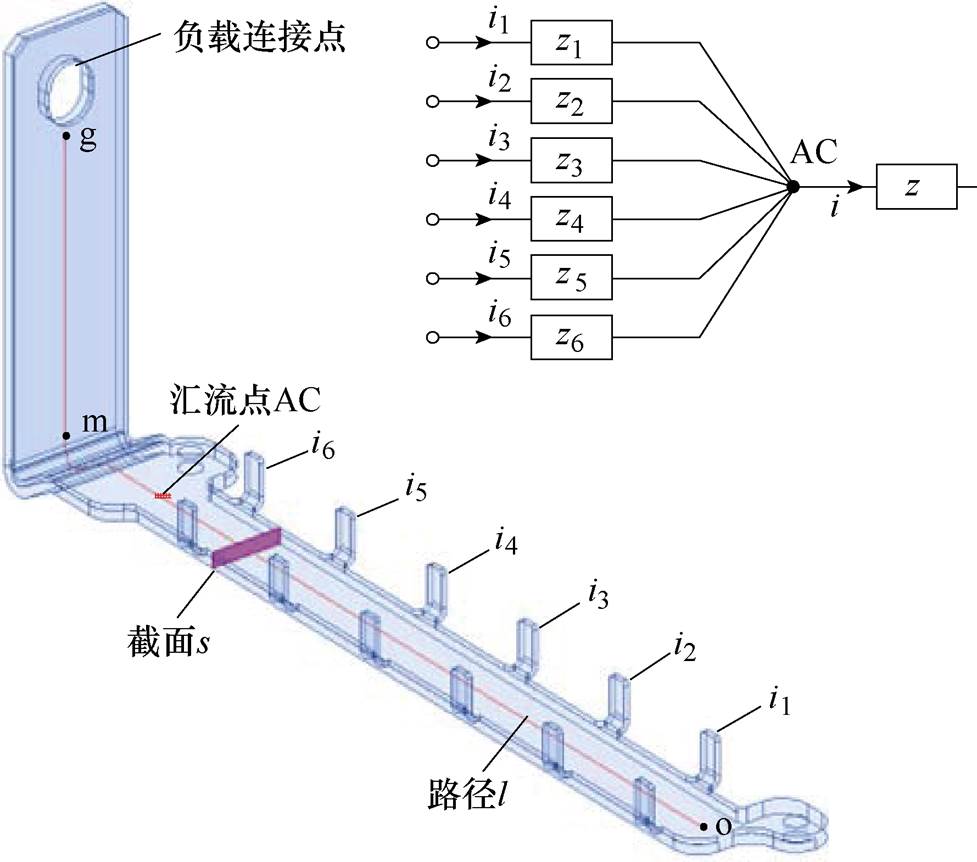
图10 交流母排汇流点
Fig.10 The current sink of AC busbar
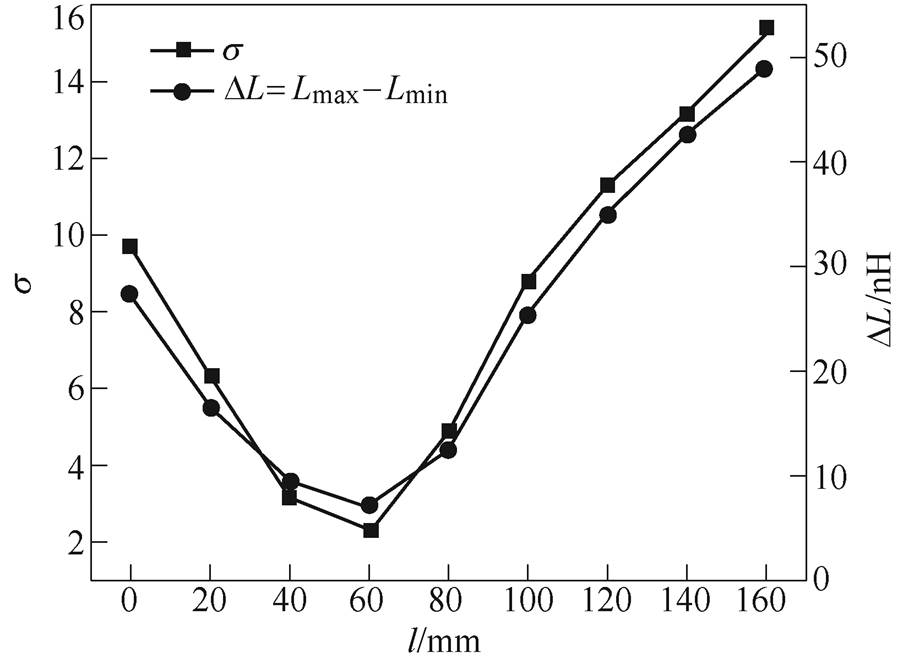
图11 不同汇流点对并联支路寄生电感均衡性的影响
Fig.11 The effect of different current sink on parasitic inductance balance among the paralleled branches
基于该思路,交流母排中汇流点的定位方法如图10所示,在上桥臂对应每个器件端口赋值1 A的电流激励(source),电流汇(sink)赋在负载连接点上。然后沿着路径l的方向从o点开始垂直切若干个截面s,仿真后通过Q3D处理运算器,结合式(4)求得通过该截面的电流大小。
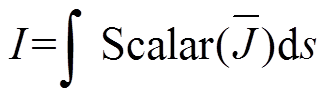 (4)
(4)
式中,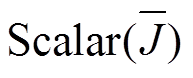 为垂直穿过所截截面电流密度J的幅值,其与对应截面s的面积分即为穿过该截面的电流I,汇流点定位原则如图12所示。结合图10,从起始点o到AC点之前,截面对应的总电流随着各并联端子电流的注入而不断的增大,在AC点处达到最大值,而在AC点之后电流不变。因此,AC点即为该交流母排的汇流点。另外,图12中也给了母排电流密度J沿着路径l的分布,在AC点之前,电流不断叠加,但截面积恒定,因此电流密度J的分布呈阶梯式上升。在AC点之后以及m点之前,虽然电流总量I不变,但母排截面积发生变化,因此电流密度J波动。在m点与g点之间,电流恒定且截面积恒定,因此电流密度J也恒定。
为垂直穿过所截截面电流密度J的幅值,其与对应截面s的面积分即为穿过该截面的电流I,汇流点定位原则如图12所示。结合图10,从起始点o到AC点之前,截面对应的总电流随着各并联端子电流的注入而不断的增大,在AC点处达到最大值,而在AC点之后电流不变。因此,AC点即为该交流母排的汇流点。另外,图12中也给了母排电流密度J沿着路径l的分布,在AC点之前,电流不断叠加,但截面积恒定,因此电流密度J的分布呈阶梯式上升。在AC点之后以及m点之前,虽然电流总量I不变,但母排截面积发生变化,因此电流密度J波动。在m点与g点之间,电流恒定且截面积恒定,因此电流密度J也恒定。
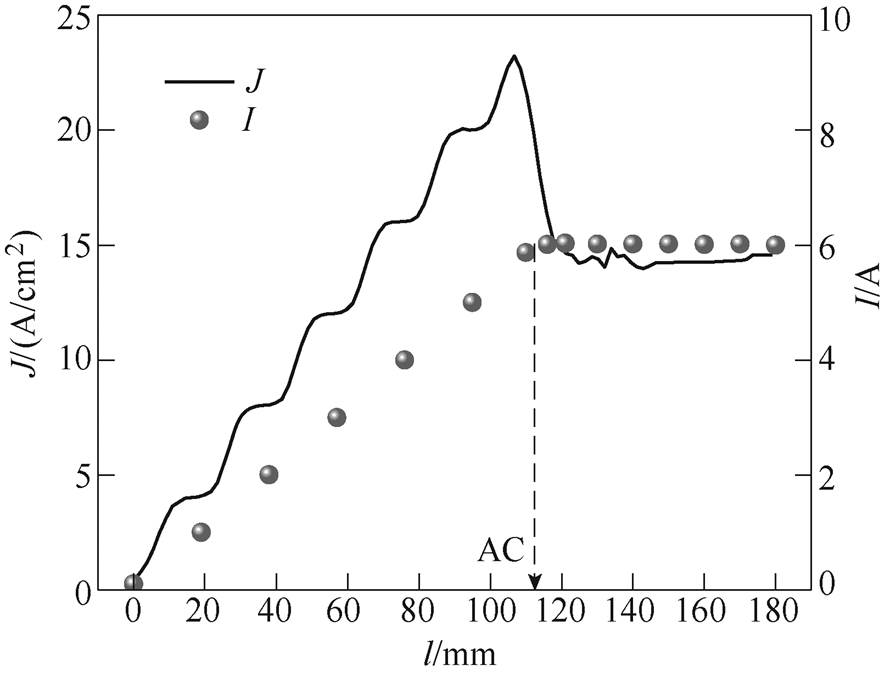
图12 汇流点定位原则
Fig.12 The principle of current sink positioning
综上所述,通过分析可知,用来提取寄生参数的汇流点并不一定是负载连接点。在实际工程应用中可根据所提的方法确定汇流点,从而更为准确地提取叠层母排寄生参数。
在文献[31]示意出的母排电流路径中可以看到,各并联端子与汇流点AC之间的路径长短有差异,其规律与提取的各支路静态寄生参数的变化趋势看起来一致。但实际上,叠层母排寄生参数的大小并不是简单取决于母排各端子间的距离,路径间的相互耦合关系也会综合影响等效寄生参数,进而影响并联均流[29]。由于电路模型中同时存在寄生电感和电阻,很难通过时域方程直接推导等效寄生参数,因此无法探究路径间的耦合关系对于等效寄生参数的影响。为了清晰说明,暂忽略电路中的电阻元素,并以2并联支路为例。图13a中简化示意出正母排和交流母排中的连接端子,其对应的原始寄生电感模型和等效寄生电感模型如图13b所示。
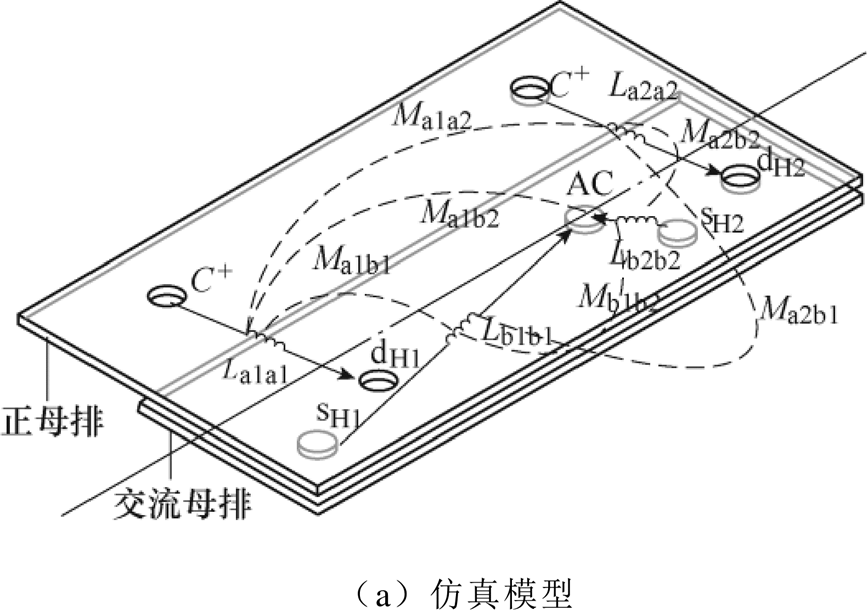
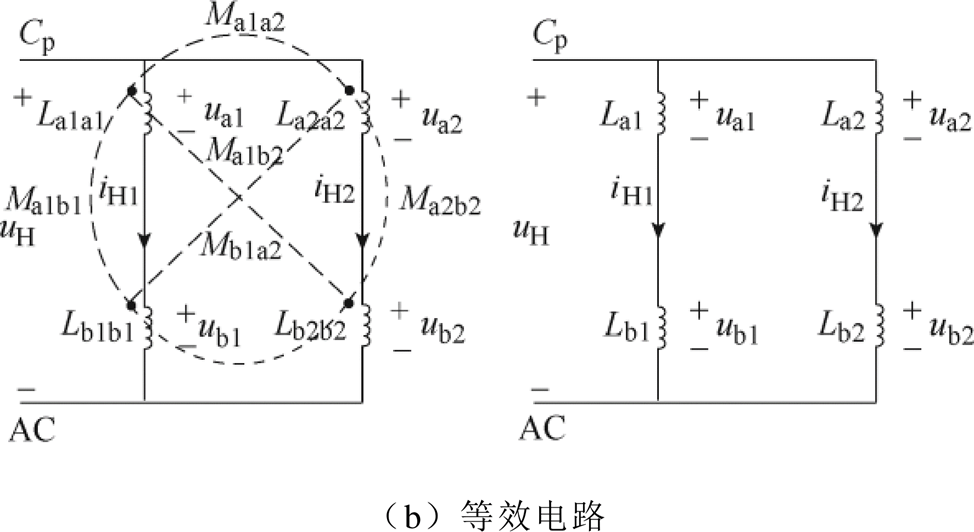
图13 不同汇流点对寄生电感网络的影响
Fig.13 The effect of different current sink on the parasitic inductance network
原始寄生电感模型包含了路径自感和互感,因此是一个多维电感网络,可由矩阵Lmatrix表示。解耦等效后,各路径的等效寄生电感可由矩阵LEmatrix表示。由于具有等效关系,两个矩阵具备相同的V-I特性,因此其电路关系满足
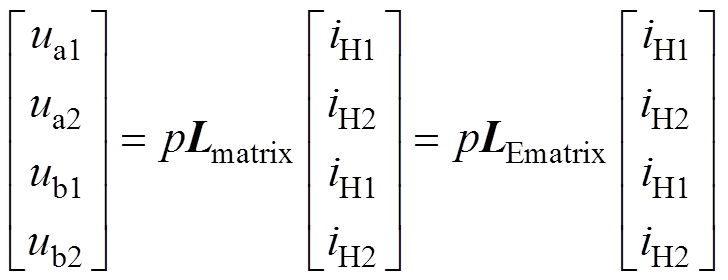 (5)
(5)
式中,p为微分算子,p=di/dt;矩阵Lmatrix和LEmatrix分别表示为
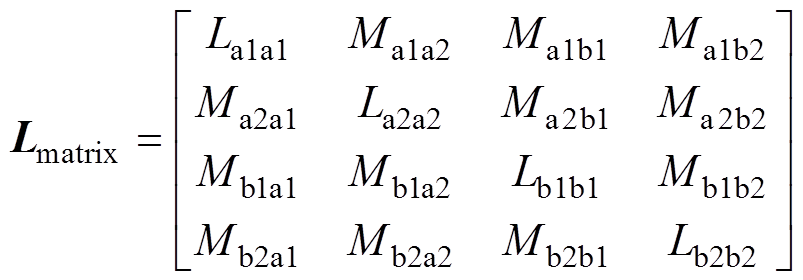
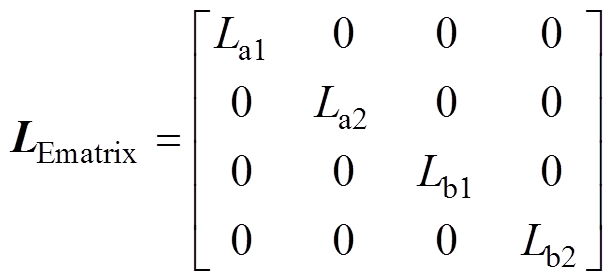
式(5)进一步化简后,支路1和支路2的等效寄生电感可由式(6)表示,化简过程在附录中给出。桥臂电压uH和对应支路中各电感电压关系满足式(8),桥臂电流和电感电流满足式(9)。
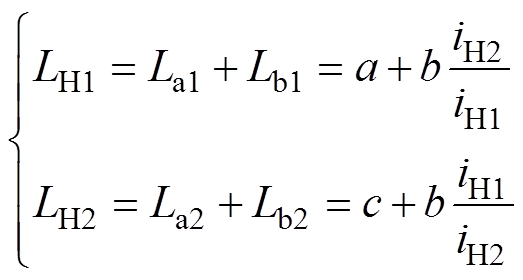 (6)
(6)
其中
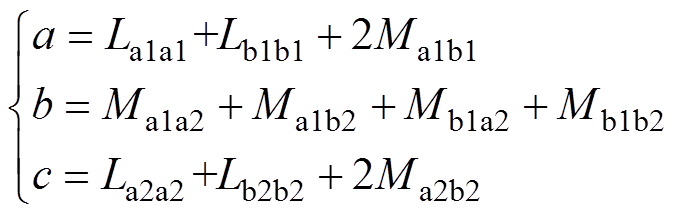 (7)
(7)
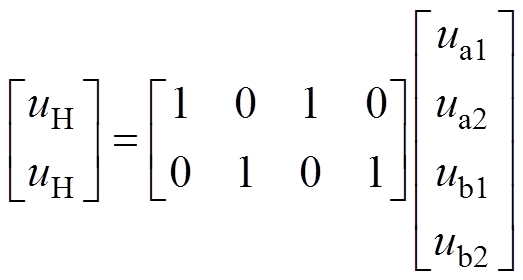 (8)
(8)
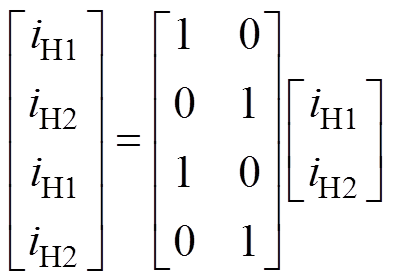 (9)
(9)
联立式(5)、式(8)和式(9)即可得式(10),进一步化简可得式(11)。
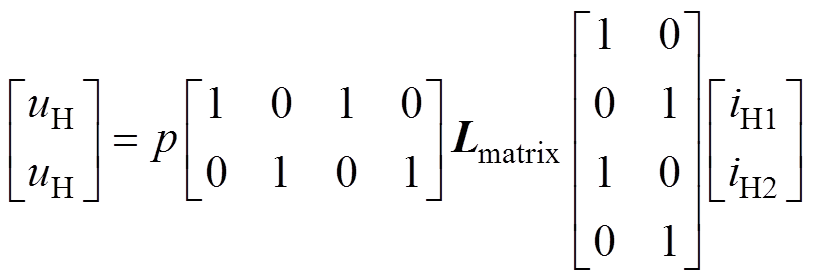 (10)
(10)
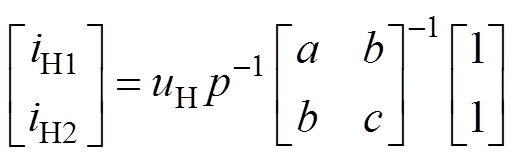 (11)
(11)
最终可化简得到支路1和支路2的电流比值,如式(12)所示。式(10)~式(12)的推导过程见附录。
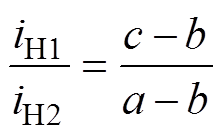 (12)
(12)
结合式(6),各支路等效寄生电感为
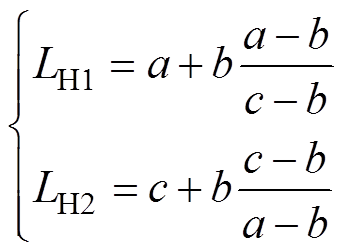 (13)
(13)
通过式(13)可以看到,各支路等效寄生电感LHj(j=1或2)是由对应路径的自感以及与其他所有路径之间的耦合互感共同决定。而LHj之间的差异性是由a和c决定的,若a=c,则LH1=LH2。对应于式(7),可以看到Lajaj、Lbjbj和Majbj为影响等效寄生电感一致性的关键元素。其中,Lajaj、Lbjbj为 第j条支路在正母排、交流母排中电流路径所对应的自感,Majbj为其在上下母排间对应的互感。一般情况下,若两条支路对应的电流路径总长度不相等,那么各支路的自感之和也会不一致,这是因为自感的大小与路径的长短相关。然而,由于路径间耦合互感Majbj的作用,使得两条支路等效寄生电感可能相等,这是因为耦合互感不仅与路径长度相关也与路径间的角度相关[32]。因此,由于耦合互感的作用,会使得非对称支路的等效寄生参数存在一致的 可能。
在3.1节分析了汇流点AC的位置对于静态寄生参数的影响,实际上汇流点的改变不仅影响各支路的路径长短,也会影响路径间的角度,进而影响耦合互感。通过调整汇流点位置,可以合理匹配自感和互感,实现并联支路等效寄生参数的一致性。由于很难定性地去分析多支路间的自感和互感变化情况,因此需要借助参数化仿真去定位出可以平衡各并联支路寄生参数的关键汇流点位置。以图13a中简化示意的2并联支路为例,使汇流点AC沿着路径l移动,进行参数化仿真,计算得到的每点处的a、c值以及等效电感差异值如图14所示。可以看到,在路径l上存在一点使得a、c值非常接近,即调整汇流点的位置可使得各支路路径对应的自感和两倍互感的代数和相等,此时支路间的寄生电感差异性非常小。这也解释了图11中,在路径l上存在一定区域可以使得各并联支路等效寄生电感相对比较均衡以及差值比较小的原因。
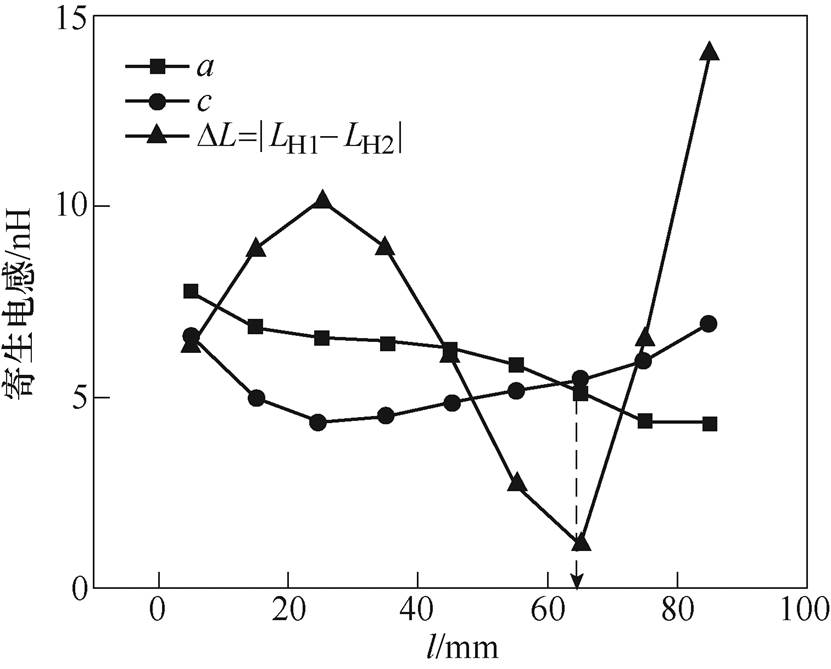
图14 不同汇流点对于等效寄生电感的影响
Fig.14 The effect of different current sink on the equivalent parasitic inductance
原6管并联型叠层母在排除了各并联支路静态等效寄生参数存在较大差异性外,实际工程应用中还存在如下问题:电容模组被设计在母排底部,对器件散热性能存在一定影响。另外单相母排独立装配,虽然可实现一定的模块化应用,但装配效率低。因此,综合以上问题,对该叠层母排进行优化设计。最终所优化后的叠层母排结构如图15a所示,基于其搭建的分立器件并联型SiC逆变器如图15b所示。

图15 优化后的叠层母排结构及分立器件并联型SiC样机
Fig.15 The optimized laminated busbar and the inverter prototype with discrete device in parallel SiC
该叠层母排的具体优化设计过程如下,将电容模组从底部移至前端,与叠层母排前侧伸出的端子相连。针对各相母排单独安装带来的装配效率较低的问题,将三相母排设计为整体,便于统一装配。接着对寄生参数进行优化,图16为优化后的叠层母排在静态过程中的电流路径,可以看到各支路在正母排和交流母排中的电流路径并不均匀。基于3.1节的分析可知,汇流点的位置会影响各并联路径的长短以及路径间夹角,进而影响路径的自感和互感,而并联支路的等效寄生电感是由自感和互感共同影响的。因此通过调整汇流点位置,从而合理匹配路径自感和路径间的互感,一定程度上可实现并联支路寄生电感的均衡性。基于该结论,可通过在交流母排中设计出合适汇流点的位置实现非对称路径的寄生参数对称布局。图17为优化后的交流母排结构,由于底部是散热器,接线端可从侧面引出。首先根据3.1节中提出的汇流点定位方法,图17给出的截面s处算得电流达到了并联电流的总和,因此汇流点可定位在该位置。然后使得输出侧端子沿着路径l从o点向n点移动,对其进行参数化仿真分析,提取出不同汇流点位置下的各并支路等效寄生参数。参照图11,图18给出不同汇流点位置对优化设计后各并联支路寄生电感均衡性的影响,可以看到存在一定区域使的各并联支路寄生电感相对比较均衡,最终输出侧端子在该区域内伸出即可。
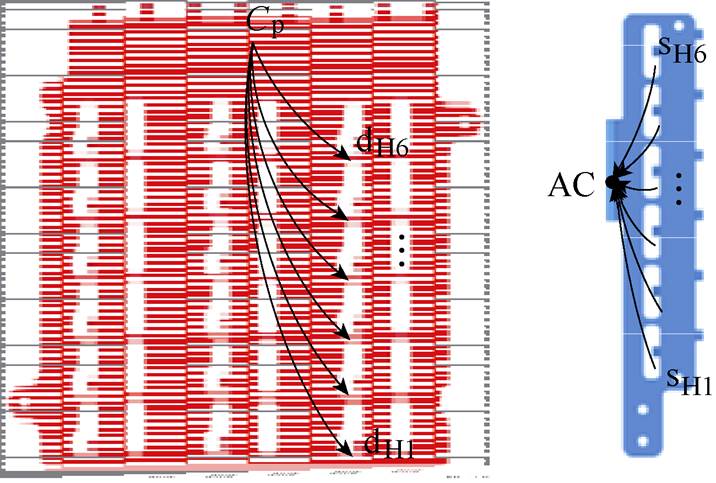
图16 优化后叠层母排电流路径分析
Fig.16 Analysis of the current paths on the optimized busbar
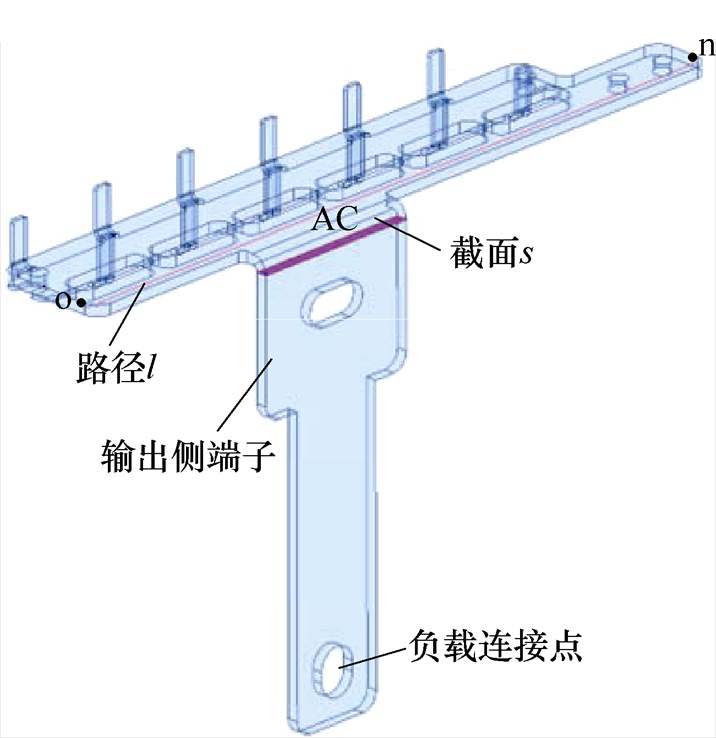
图17 优化后交流母排汇流点AC
Fig.17 The current sink point AC of the optimized busbar
提取到的该叠层母排在动、静态过程中的等效寄生参数分别见表3和表4。可以看到,动态过程中的寄生参数仍相差不大,而优化后的静态过程中各支路寄生参数比原先要均衡很多。
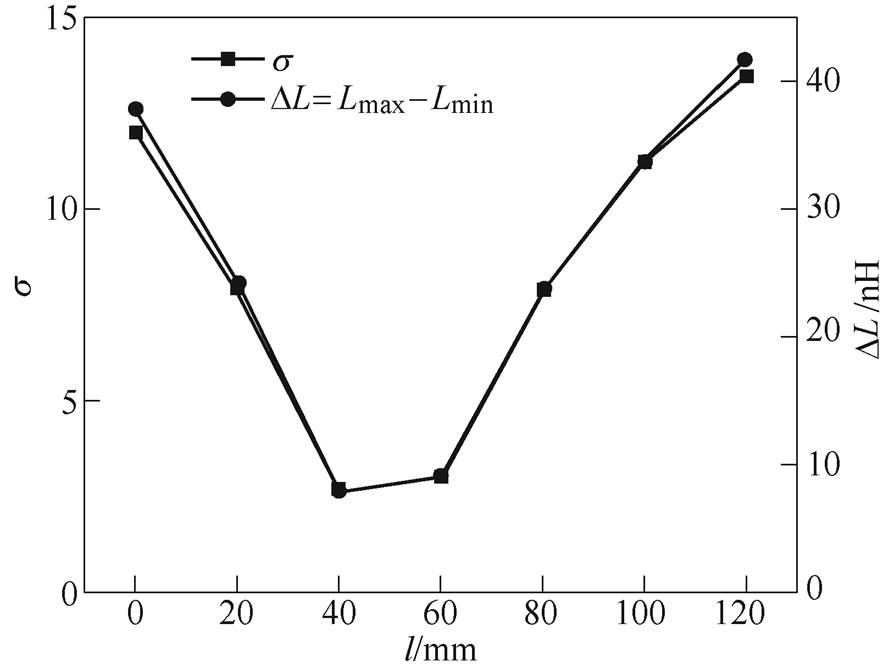
图18 不同汇流点对优化后并联支路寄生电感均衡性的影响
Fig.18 The effect of different current sink on parasitic inductance balance among the optimized branches
表3 优化后动态过程中的寄生参数
Tab.3 The optimized parasitic parameters in the dynamic process
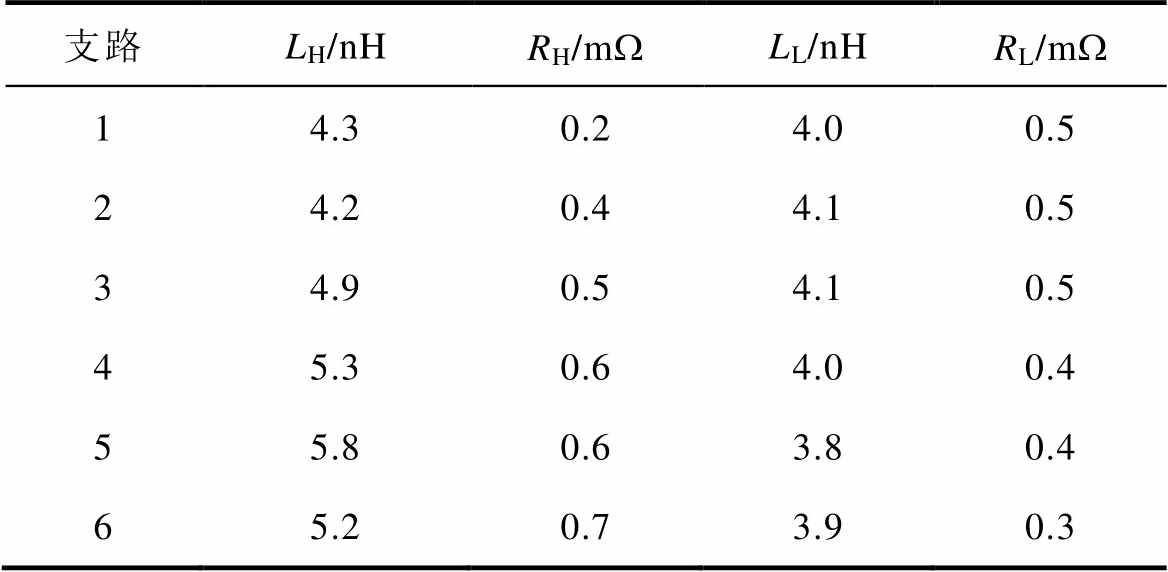
支路LH/nHRH/mWLL/nHRL/mW 14.30.24.00.5 24.20.44.10.5 34.90.54.10.5 45.30.64.00.4 55.80.63.80.4 65.20.73.90.3
表4 优化后静态过程中的寄生参数
Tab.4 The optimized parasitic parameters in the static process
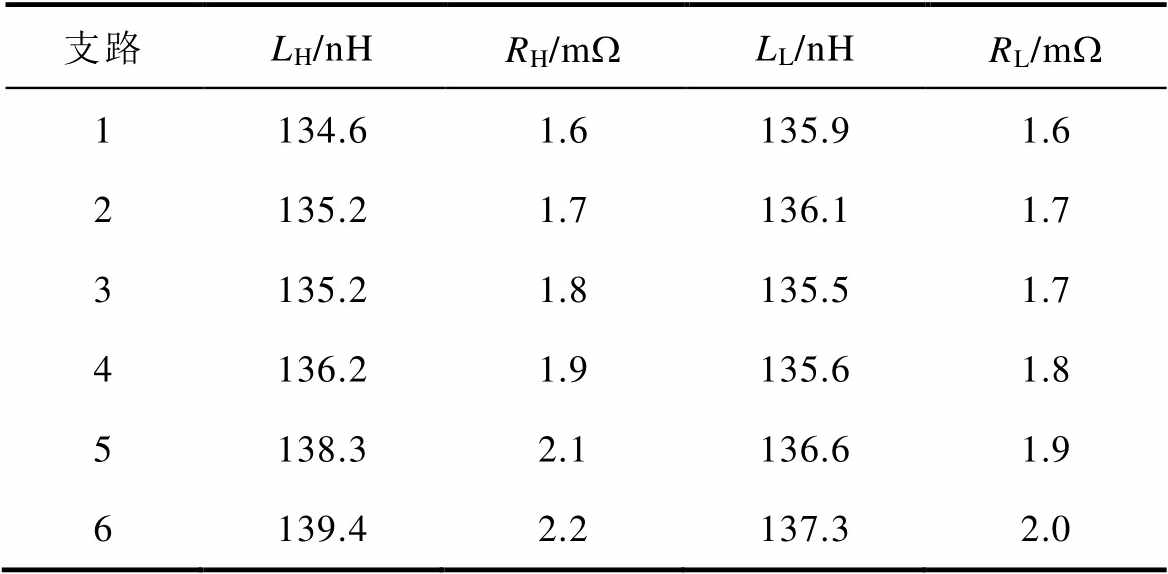
支路LH/nHRH/mWLL/nHRL/mW 1134.61.6135.91.6 2135.21.7136.11.7 3135.21.8135.51.7 4136.21.9135.61.8 5138.32.1136.61.9 6139.42.2137.32.0
对于器件并联型叠层母排设计,器件的布局位置对应并联支路寄生参数的均衡性设计至关重要。虽然器件在空间域中的绝对对称布局能够实现外电路的对称设计,但增加了设计难度,并有可能牺牲其他的一些性能。本文所提的优化设计方法针对并联型叠层母排具备多电流路径这一特征,通过调整汇流点的位置合理匹配路径自感以及路径间的互感,从而实现非对称路径等效寄生参数的均衡性。该优化设计方法对于器件并联型母排均可适用。
为了验证叠层母排优化设计的有效性,本文搭建多管并联逆变器的双脉冲测试,测试得到第一个脉冲期间各管电流,与文献[31]中的测试结果进行对比,从而验证静态均流的改善程度。
文献[31]搭建的原分立器件并联型逆变器的双脉冲测试平台如图19a所示。为了避免器件通态电阻的分散性对于静态均流的影响,利用静态参数测试仪筛选出了通态电阻较为接近的单管。在测试中,测试条件如脉冲时间、直流电压与负载电感均与图9中的仿真条件保持一致。由于电流探头数量有限,每次测两个单管电流,如图19b所示。将测得的上桥臂6个并联管子在第一个脉冲期间的电流进行对比,如图19c所示。从趋势上看,测试得到的各管电流变化趋势与图9中的仿真值一致,证明了提取到的上桥臂6个支路等效寄生参数的变化趋势是准确的。
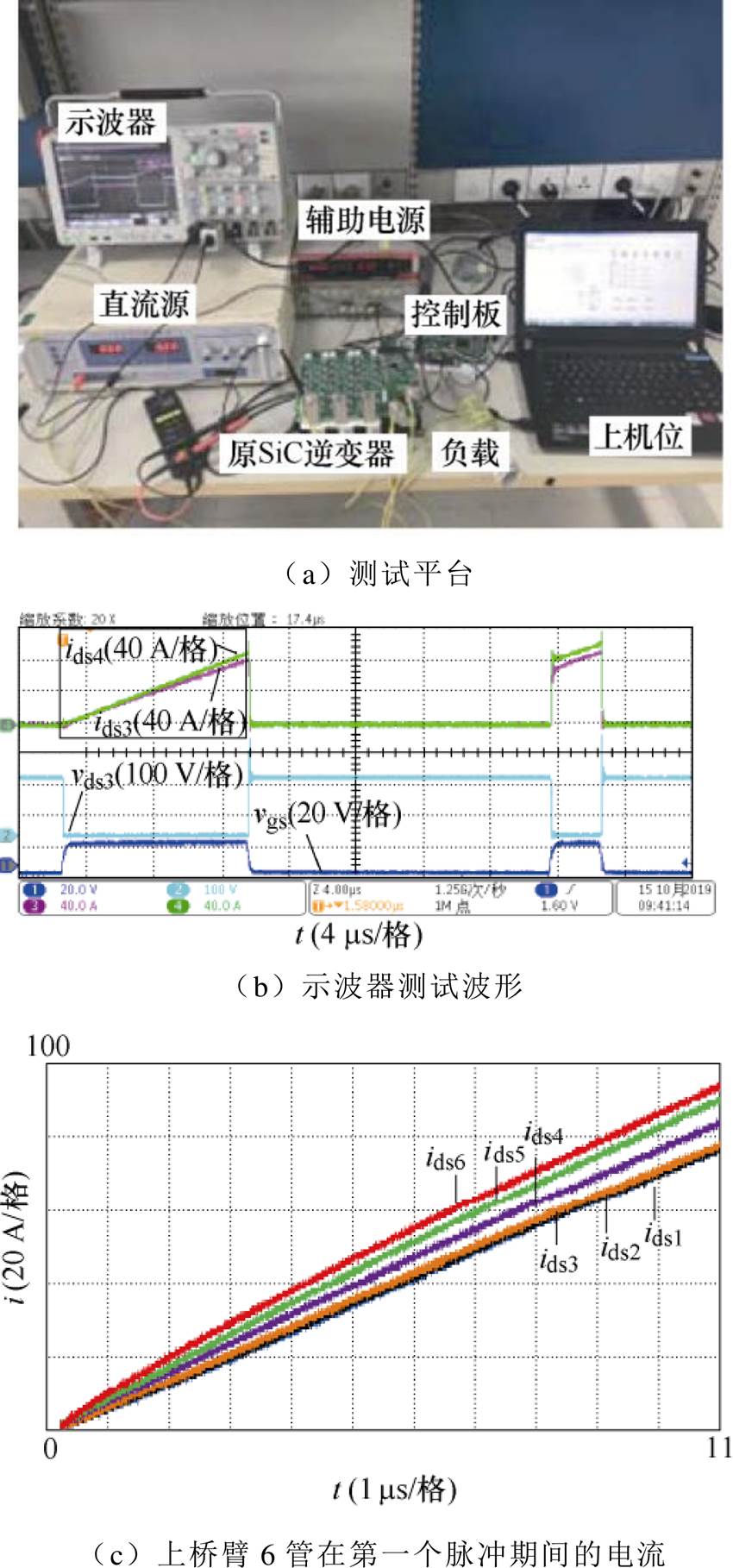
图19 原SiC逆变器双脉冲测试
Fig.19 The double pulse tests of the original SiC inverter in paper
同样地,首先通过图20所示的功率器件静态测试仪对器件进行筛选,选出通态电阻较为一致的分立器件。接着对优化后的分立器件并联型SiC逆变器平台进行双脉冲测试,如图21a所示,测试条件与原测试平台一致。同样测得第3管、4管电流波形如图21b所示,将6管第一个脉冲期间的电流进行对比,如图21c所示。与图19c中优化前的测试结果进行对比,可以看到优化设计后的6管并联平台在第一个脉冲期间的各管电流明显均衡,静态均流得到极大的改善。该测试结果证明了所提叠层母排优化设计方案的有效性。

图20 器件筛选
Fig.20 The screening of the discrete devices
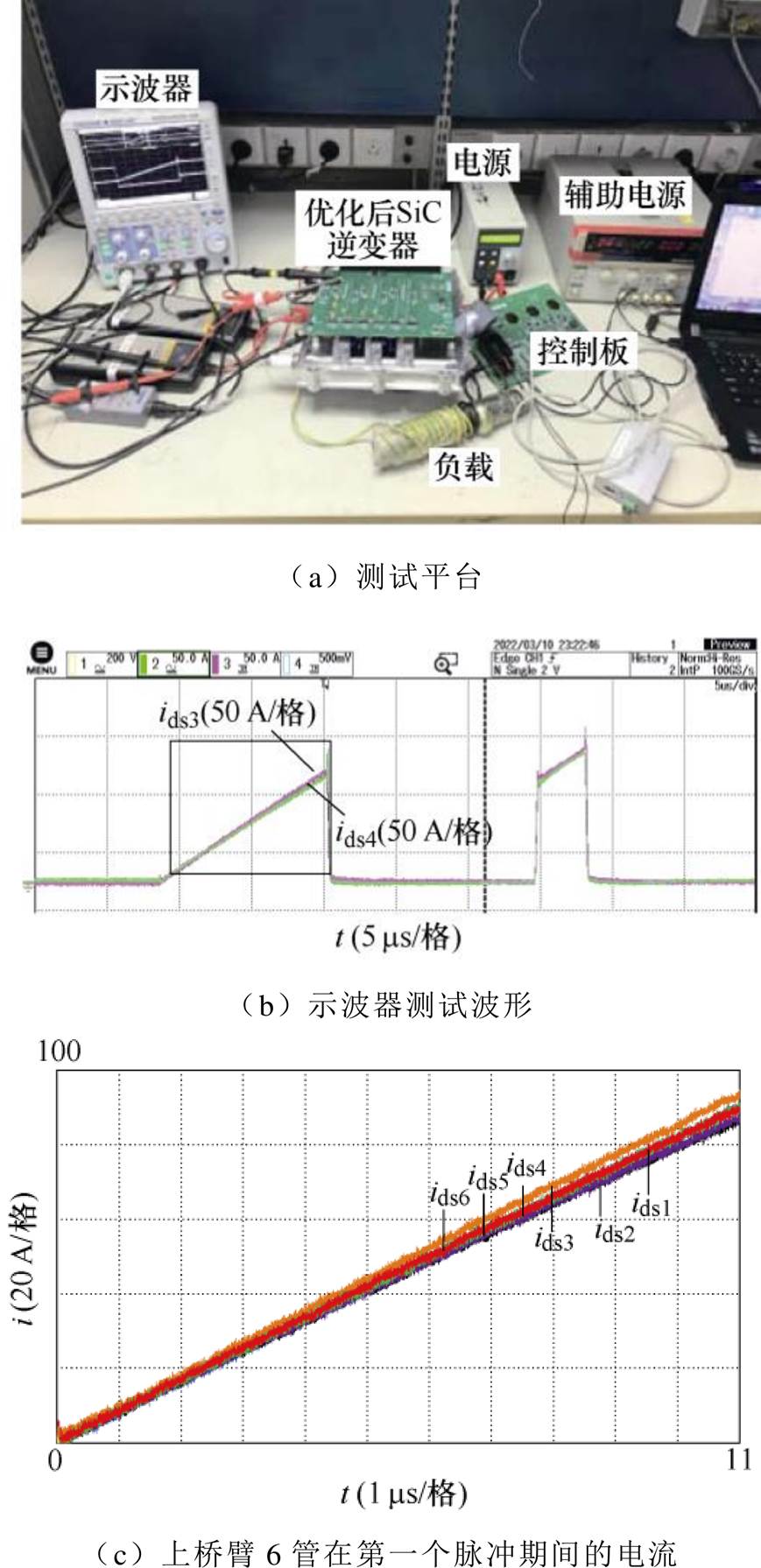
图21 优化后的SiC逆变器双脉冲测试
Fig.21 The double pulse tests of the optimized SiC inverter
本文针对一款分立器件并联型SiC逆变器出现的静态不均流问题,分析了寄生参数的不对称性对并联均流的影响,并最终对其进行优化设计,主要包括以下内容:
1)基于双脉冲仿真电路,仿真分析了叠层母排寄生参数对于并联均流的影响,结果表明开关速度的降低会弱化寄生电感差异性对于动态均流影响。另外在大负载电感应用背景下,更应关注寄生电阻差异性对于静态均流的影响。
2)分析了交流母排汇流点位置对应静态寄生参数的影响,指出了实际汇流点位置应为电流达到最大值且开始稳定的截点,提出了一种交流母排汇流点的定位方法,从而可以精准提取静态寄生参数。
3)探究了路径间耦合效应对于等效寄生参数的影响。提出通过改变汇流点位置合理匹配自感和互感,从而实现非对称路径等效寄生参数的一致性。
基于以上研究,对该叠层母排进行了优化设计,最终的实验结果表明,静态不均流得到了极大的改善。本文的理论分析在实际工程问题中得到应用,对于器件并联型叠层母排的设计具有一定的技术支撑。
公式推导过程:
1. 式(5)、式(6)的推导过程。
将式(5)展开得
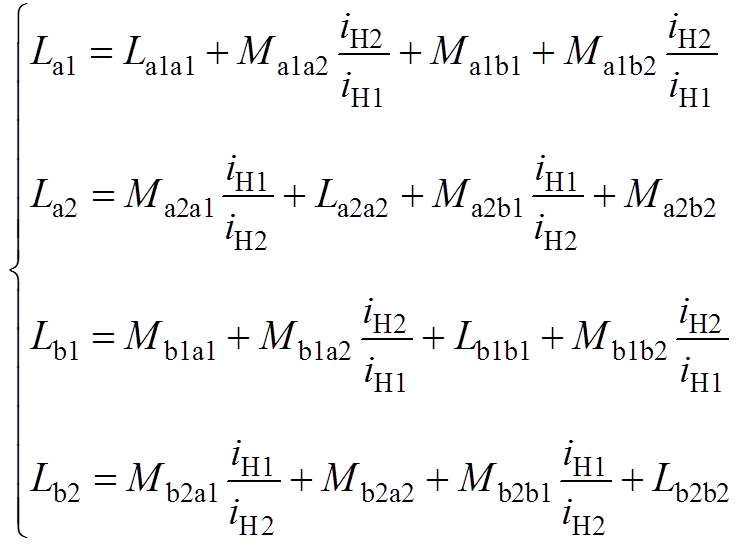 (A1)
(A1)
各支路等效寄生电感为
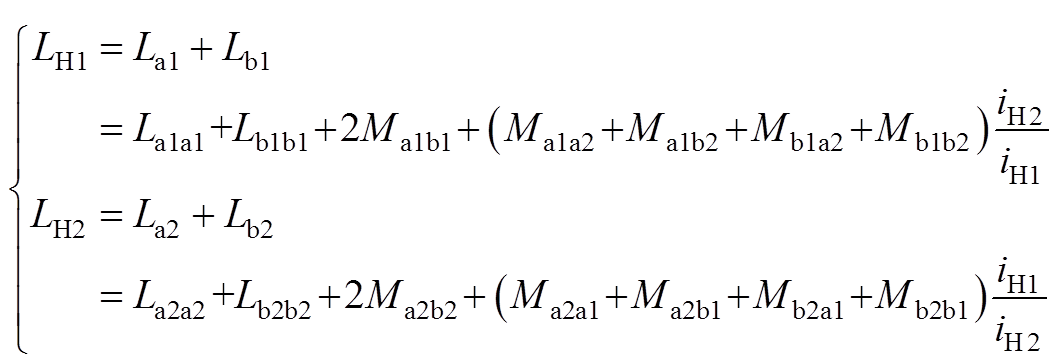 (A2)
(A2)
2. 式(10)~式(12)的推导过程。
式(10)中矩阵计算结果为
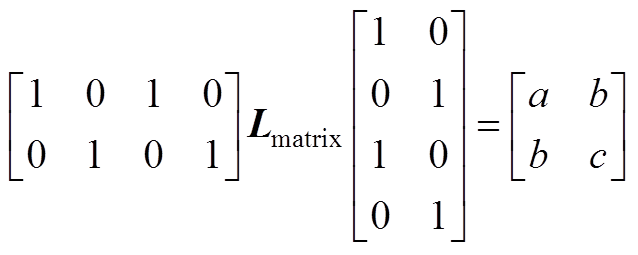 (A3)
(A3)
式(11)中的矩阵计算结果为
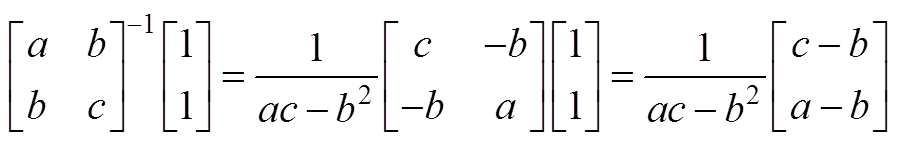 (A4)
(A4)
参考文献
[1] 邵伟华, 冉立, 曾正, 等. 基于优化对称布局的多芯片SiC模块动态均流[J]. 中国电机工程学报, 2018, 38(6): 1826-1836, 1920.
Shao Weihua, Ran Li, Zeng Zheng, et al. Dynamic current sharing of multichip SiC module with optimal symmetric layout[J]. Proceedings of the CSEE, 2018, 38(6): 1826-1836, 1920.
[2] Li Helong, Munk-Nielsen S, Bczkowski S, et al. A novel DBC layout for current imbalance mitigation in SiC MOSFET multichip power modules[J]. IEEE Transactions on Power Electronics, 2016, 31(12): 8042-8045.
[3] Zeng Zheng, Zhang Xin, Li Xiaoling. Layout- dominated dynamic current imbalance in multichip power module: mechanism modeling and comparative evaluation[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(11): 11199-11214.
[4] 惠城武. SiC MOSFET并联模块均流技术研究[D]. 西安: 西安理工大学, 2018.
[5] Fabre J, Ladoux P. Parallel connection of 1200-V/ 100-A SiC MOSFET half-bridge modules[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1669-1676.
[6] Rabkowski J, Peftitsis D, Nee H P. Parallel-operation of discrete SiC BJTs in a 6-kW/250-kHz DC/DC boost converter[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2482-2491.
[7] 钟华, 刘志强, 宋佳茵, 等. 分立器件电机控制器功率单元设计与实现[J]. 汽车文摘, 2021(1): 42-47.
Zhong Hua, Liu Zhiqiang, Song Jiayin, et al. Design and implementation of intelligent power unit for discrete device motor controller[J]. Automotive Digest, 2021(1): 42-47.
[8] Chen C, Su Ming, Xu Zhuxian, et al. SiC-based automotive traction drives, opportunities and challen- ges[C]//IEEE 5th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Albuquerque, NM, 2017: 25-30.
[9] Yu Shaolin, Wang Jianing, Zhang Xing, et al. The potential impact of using traction inverters with SiC MOSFETs for electric buses[J]. IEEE Access, 2021, 9: 51561-51572.
[10] Hu Ji, Alatise O, Ortiz Gonzalez J A, et al. Robu- stness and balancing of parallel-connected power devices: SiC versus CoolMOS[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2092-2102.
[11] 曾正, 邵伟华, 胡博容, 等. 基于耦合电感的SiC MOSFET并联主动均流[J]. 中国电机工程学报, 2017, 37(7): 2068-2081.
Zeng Zheng, Shao Weihua, Hu Borong, et al. Active current sharing of paralleled SiC MOSFETs by coupling inductors[J]. Proceedings of the CSEE, 2017, 37(7): 2068-2081.
[12] Ke Junji, Zhao Zhibin, Sun Peng, et al. New screening method for improving transient current sharing of paralleled SiC MOSFETs[C]//International Power Electronics Conference, Niigata, Japan, 2018: 1125- 1130.
[13] Tiwari S, Rabiei A, Shrestha P, et al. Design considerations and laboratory testing of power circuits for parallel operation of silicon carbide MOSFETs[C]//European Conference on Power Electronics and Applications, Geneva, Switzerland, 2015: 1-10.
[14] Qin Haihong, Zhang Ying, Zhu Ziyue, et al. Influences of circuit mismatch on paralleling silicon carbide MOSFETs[C]//IEEE Conference on Industrial Electronics and Applications, Siem Reap, Cambodia, 2018: 556-561.
[15] 黄华震, 柯俊吉, 孙鹏, 等. 寄生电感不匹配对SiC MOSFET并联电流分配的影响[J]. 半导体技术, 2018, 43(11): 833-840.
Huang Huazhen, Ke Junji, Sun Peng, et al. Influence of parasitic inductance mismatch on the parallel SiC MOSFETs current distribution[J]. Semiconductor Technology, 2018, 43(11): 833-840.
[16] 成林, 欧宏, 毕闯, 等. 基于SiC MOSFET的同步Buck变换器电磁干扰噪声分析及预测[J]. 电工技术学报, 2021, 36(增刊2): 627-634, 643.
Cheng Lin, Ou Hong, Bi Chuang, et al. Analysis and prediction of electromagnetic interference noise in synchronous Buck converter with SiC MOSFET[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 627-634, 643.
[17] 段卓琳, 张栋, 范涛. SiC电机驱动系统传导电磁干扰建模及预测[J]. 电工技术学报, 2020, 35(22): 4726-4738.
Duan Zhuolin, Zhang Dong, Fan Tao. Modeling and prediction of electromagnetic interference in SiC motor drive systems[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4726-4738.
[18] 刘妍, 杨晓峰, 闫成章, 等. 考虑寄生电感的谐振开关电容变换器电压尖峰抑制[J]. 电工技术学报, 2021, 36(12): 2627-2639.
Liu Yan, Yang Xiaofeng, Yan Chengzhang, et al. Suppression of voltage spike in resonant switched capacitor converter considering parasitic indu- ctance[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2627-2639.
[19] 刘博, 刘伟志, 董侃, 等. 基于全碳化硅功率组件的变流器母排杂散电感解析计算方法[J]. 电工技术学报, 2021, 36(10): 2105-2114.
Liu Bo, Liu Weizhi, Dong Kan, et al. Analytical calculation method for stray inductance of converter busbar based on full silicon carbide power module[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2105-2114.
[20] 金祝锋, 李威辰, 胡斯登, 等. 大容量电力电子装置中母排杂散电感提取方法的优化研究[J]. 电工技术学报, 2017, 32(14): 1-7.
Jin Zhufeng, Li Weichen, Hu Sideng, et al. Opti- mization inductance extraction of bus bar in large- capacity power electronic equipment[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 1-7.
[21] Mehrabadi N R, Cvetkovic I, Wang Jun, et al. Busbar design for SiC-based H-bridge PEBB using 1.7kV, 400 a SiC MOSFETs operating at 100kHz[C]//IEEE Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 2017: 1-7.
[22] 董玉斐, 罗皓泽, 杨贺雅, 等. 1.2MV·A混合钳位五电平变流模块的结构布局优化和叠层母排设计[J]. 电工技术学报, 2016, 31(8): 11-18.
Dong Yufei, Luo Haoze, Yang Heya, et al. Engineering design for structure and bus bar of 1.2MV·A hybrid clamped five-level converter module[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 11-18.
[23] 朱俊杰, 原景鑫, 聂子玲, 等. 基于全碳化硅功率组件的叠层母排优化设计研究[J]. 中国电机工程学报, 2019, 39(21): 6383-6394.
Zhu Junjie, Yuan Jingxin, Nie Ziling, et al. Optimum design of planer busbar based on all-silicon carbide power module[J]. Proceedings of the CSEE, 2019, 39(21): 6383-6394.
[24] 阮杰, 刘畅, 李广卓, 等. 适用于器件并联型ANPC拓扑的低感叠层母排设计方法[J]. 高电压技术, 2019, 45(7): 2093-2100.
Ruan Jie, Liu Chang, Li Guangzhuo, et al. Design method of low-inductance laminated busbar for device-parallel ANPC circuit[J]. High Voltage Engin- eering, 2019, 45(7): 2093-2100.
[25] Chen Cai, Pei Xuejun, Chen Yu, et al. Investigation, evaluation, and optimization of stray inductance in laminated busbar[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3679-3693.
[26] 顾妙松, 崔翔, 彭程, 等. 外部汇流母排对压接型IGBT器件内部多芯片并联均流特性的影响[J]. 中国电机工程学报, 2020, 40(1): 234-245, 390.
Gu Miaosong, Cui Xiang, Peng Cheng, et al. Influence of the external busbar on current sharing performance inside a multi-chip press-pack IGBT device[J]. Proceedings of the CSEE, 2020, 40(1): 234-245, 390.
[27] 薛燕鹏, 刘钧, 苏伟, 等. 一种IGBT并联模块用交流母排的设计方法[J]. 电力电子技术, 2019, 53(2): 16-18.
Xue Yanpeng, Liu Jun, Su Wei, et al. A design method of AC busbar for paralleled-IGBT module[J]. Power Electronics, 2019, 53(2): 16-18.
[28] 王磊, 罗毅飞, 马天兆, 等. 功率回路杂散电感对IGBT并联均流的影响[J]. 电力电子技术, 2020, 54(4): 33-35.
Wang Lei, Luo Yifei, Ma Tianzhao, et al. Effect of stray inductance in power circuit on parallel current sharing of high-power IGBT modules[J]. Power Electronics, 2020, 54(4): 33-35.
[29] 房雷, 刘钧, 苏伟. 母排互感对IGBT模块并联动态均流的影响[J]. 电力电子技术, 2017, 51(10): 60- 62.
Fang Lei, Liu Jun, Su Wei. The influence of busbar mutual inductance on current balancing of parallel IGBT[J]. Power Electronics, 2017, 51(10): 60-62.
[30] Zhang Ning, Wang Shuo, Zhao Hui. Develop parasitic inductance model for the planar busbar of an IGBT H bridge in a power inverter[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6924-6933.
[31] Wang Jianing, Yu Shaolin, Zhang Xing, et al. Accurate modeling of the effective parasitic para- meters for the laminated busbar connected with paralleled SiC MOSFETs[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2021, 68(5): 2107-2120.
[32] Zhang Boyi, Wang Shuo. Parasitic inductance modeling and reduction for wire-bonded half-bridge SiC multichip power modules[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5892-5903.
Abstract To accommodate high-power power conversion application scenarios, the SiC MOSFETs must be used in parallel. In medium and high-power inverters, the laminated busbar with low parasitic inductance characteristics is usually used as an interconnection structure for DC-link capacitors and power devices. An asymmetrical laminated busbar structure can lead to asymmetrical parasitic parameters, which in turn causes unbalanced current distribution among the parallel devices. Therefore, in addition to the low parasitic inductance, the symmetry of the parasitic parameter for each parallel branch is a critical design factor for the laminated busbar with discrete devices in parallel. This paper analyzed the current sharing performance of the laminated busbar with six discrete devices in parallel and further optimized the busbar structure.
Firstly, the equivalent parasitic parameters of each parallel branch of the original laminated busbar are extracted by the established parasitic parameter model. The results show that the equivalent parasitic inductance and parasitic resistance of each parallel branch are unbalanced in the static process. The effect of the unbalanced parasitic parameters on the current distribution among the paralleled devices is analyzed by the established double-pulse simulation circuit. It is shown that reducing the switching speed can weaken the effect of the parasitic inductance variability on the dynamic current imbalance. In the context of large-load applications, it is necessary to pay more attention to the effect of parasitic resistance differences on the static current imbalance.
Then, aiming at the extraction accuracy of the static parasitic parameters for the laminated busbar with discrete devices in parallel, this paper proposes a sink location method. It points out that the current sink should be the maximum point of the aggregated current, while the impedance after the point does not affect the current distribution. Based on this principle, the real sink point in the AC busbar is located in combination with the finite simulation software, which improves the extraction accuracy of static parasitic parameters. In addition, the mutual coupling effect on the parasitic parameters of the laminated busbar is explored. It is found that the presence of coupled mutual inductance will make it possible for the equivalent parasitic parameters of asymmetric parallel branches to be consistent. The original laminated busbar with six discrete devices in parallel is then optimized. By adjusting the position of the current sink point, thus matching the self-inductance and mutual inductance, the parasitic parameters of the parallel branch can be equalized. The parasitic parameters of the optimized laminated bus are extracted, and the results show that the parasitic parameters of each parallel branch are more balanced in the static process.
Finally, a double-pulse test platform was built to test the static currents of each parallel device of the optimized laminated busbar. Compared with the original laminated busbar, the experimental results show that the static unbalanced current has been greatly improved.
keywords:Discrete devices, parallel connection, the laminated busbar, parasitic parameters
DOI: 10.19595/j.cnki.1000-6753.tces.220871
中图分类号:TM46
国家自然科学基金面上项目(52077051)、合肥综合性国家科学中心能源研究院重点培育项目(21KZS203)和高等学校创新引智计划项目(BP0719039)资助。
收稿日期 2022-05-19
改稿日期 2022-06-23
於少林 男, 1992年生,博士研究生,研究方向为新型功率器件封装与应用、电力电子集成与电磁分析。E-mail: hajcysl@163.com
王佳宁 男,1985年生,博士,副教授,研究方向为新一代功率器件封装、测试、集成、运用等。E-mail: jianingwang@hfut.edu.cn(通信作者)
(编辑 陈 诚)