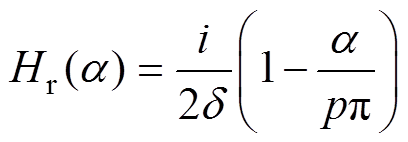（1）
摘要 电机稳态运行时的故障特征频率与基频接近，难以实现转子断条时的故障电流分量的有效提取。对此，该文根据起动过程中转子断条故障特征信号频率易与基频区分的特点，采用变模态分解（VMD）方法对起动过程中的定子电流进行分析并对故障进行诊断。首先，基于平均瞬时频率对VMD的模态个数进行优化，准确分解出能量集中的断条故障特征信号。在此基础上，利用维格纳准概率分布高时频分辨率的特点绘制断条故障特征信号的时频分布图，引入大津算法对图片进行抗噪处理，突出故障特征部分。然后，以故障特征信号能量值作为故障量化因子，以不同故障状态下多组实验数据的均值和标准差为依据设置阈值，实现系统自动故障预警的目的。最后，在一台5.5 kW异步电机上进行了实验，结果表明，所提诊断方法不仅能够实现包括不完全断条在内的故障诊断，还能够实现对断条故障严重程度的判断。
关键词：异步电机 转子断条 故障诊断 变模态分析（VMD） 本征模态函数（IMF） 大津算法（OTSU）
在发电领域，异步电机常作为送风机、引风机等电厂关键辅机的驱动设备，其故障的发生会直接影响主发电机的安全运行，引发严重的安全生产事故和重大经济损失。其中，转子断条故障是笼型异步电机的经典故障之一，对其开展研究工作，实现精准故障诊断和维护，能够减少经济损失，提高系统运行的稳定性[1]。
在故障诊断领域，诊断方法主要分为时域、频域和时频域三种分析方法。转子断条故障诊断的传统频域分析方法主要采用Fourier变换对电机电流的平稳信号进行分析，但是由于Fourier频谱分析固有局限，在低转差率情况下，故障特征频率fb与电源频率f在频谱上十分接近，因此进行Fourier变换分析必须要有足够长的信号以便获得高频率分辨 率[2]。同时，电机在运行过程中不可避免地会受到自身磁场谐波、供电电压波动和电磁噪声的影响，fb容易被基频f淹没，且Fourier变换分析受限于分辨率的原因还存在频谱泄露的缺点，这给故障特征的准确提取带来困难[3]。
为了克服传统的电机电流信号分析方法在低转差率时的缺陷，学者们提出了多种解决办法：①通过数学变换将故障特征频率转换为诸如2sf和(1±s)2 f等远离基频的频率。此类方法包括电机电流平方信号分析、电机电流模信号分析、Park矢量平方模量、Park矢量积方法等[4-6]。②通过信号处理的方法直接滤除基频分量或是将基频转化为直流再滤除，以便突出故障频率分量。此类方法包括扩展卡尔曼滤波法、希尔伯特变换法、Park矢量模分析法等[7-9]。这些方法较好地避免了故障特征频率被基频淹没的风险，但频谱泄露的问题仍旧无法解决。为了进一步解决频谱泄露的问题，一方面通过引入多重信号分类和旋转不变信号参数估计技术，来弥补高频率分辨力谱估计技术在计算效率、估计精度等方面不足的问题[10]；另一方面使用模拟退火算法等优化算法，进行幅值估计来提高故障特征精度[11]。
在电机稳定状态运行时，以Fourier变换为代表的平稳信号分析方法可以通过对定子电流进行频谱分析的方法提取出故障电流分量，从而实现转子断条故障的诊断。然而，在电机轻载时，转差率较低，故障特征频率在频谱上与基频十分接近，易被基频淹没，因此该类方法难以实现故障电流分量的有效提取。为了解决这个问题，本文根据起动过程中电机的转差率s从1到近似于0变化跨度大的特点，以起动过程电流为研究对象，研究转子断条故障特征电流频率fb=|1-2s|f在起动过程中随s的变化特点。对此类非平稳信号进行分析时，以Fourier变换为代表的平稳信号分析方法不再适用，因此时频域分析成为常用的分析方法。传统的时频域分析方法包括短时傅里叶变换、小波分析、维格纳准概率分布（Wigner-Ville Distribution, WVD）等[12-16]。为了改善非平稳信号的分析效果，有学者提出了具备信号自适应特点的经验模态分解和变分模态分解（Variational Mode Decomposition, VMD）方法[17-19]。VMD算法通过构造求解约束变分问题，将原始信号分解为指定个数的本征模态函数（Intrinsic Mode Function, IMF），每一个IMF都有一定的中心频率，同时相比于经验模态分解，VMD算法不仅有较好的自适应性和抗干扰性，还具有更坚实的理论基础，适用于起动过程的转子断条故障诊断。
本文对包含故障特征的起动电流进行分析，基于瞬时频率平均值对VMD算法进行参数优化，利用参数优化后的算法将故障特征信号剥离出来，对其使用WVD算法绘制时频分布图进行频谱分析，可在分布图上观察到故障特征频率的变化趋势为V形，对该图形使用大津算法（Otsu’s method, OTSU）进行图像处理去掉噪声干扰，突出故障特征，以处理后图像的区域积分值作为新的故障特征因子，可以准确判断出故障的严重程度。
当电机发生转子断条故障时，磁场的对称性遭到破坏，会在定子电流中感应出频率为(1±2s)f的故障特征频率，下文对故障特征频率产生的机理进行简要介绍[21]。
单根转子导条通入电流i产生的径向气隙磁场强度沿着气隙圆周方向分布，径向气隙磁场强度满足
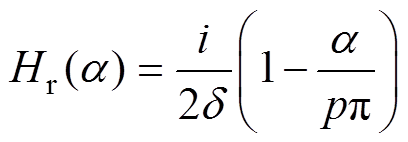（1）
式中，a 为转子坐标下的空间电角度；p为极对数；d 为气隙长度。
将式（1）用傅里叶级数表示为
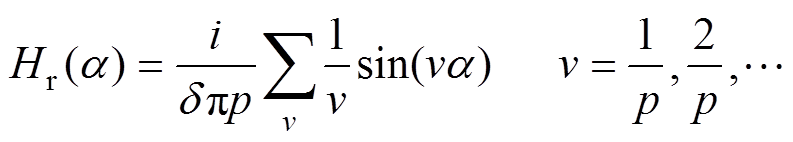（2）
当转子发生断条时，该导条中无电流流过，可认为有一相同电流反向叠加在原导条电流上，设该导条中叠加的反向电流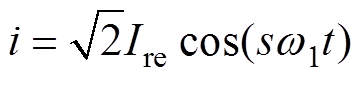
，其中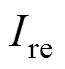
为反向电流有效值，s为异步电机转差率，则该电流产生的磁场强度为
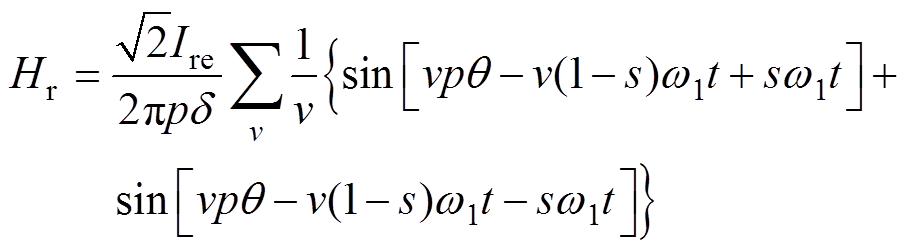（3）
式中，w1为电源角频率，w1=2p f，f为电源频率；q 为以定子坐标表示的转子机械角度。
由式（3）可知，转子反向电流产生多种谐波（包括分数次谐波、基波和高次谐波）磁场，由于定子绕组对称，可以只考虑基波磁场在其中产生的感应电动势和电流。转子反向电流产生的磁场强度在定子绕组中感应的电流频率分量为v(1-s)w1t±sw1t，当v=1时，定子电流中除了产生基频分量，还会产生频率为(1-2s) f的附加分量，即为左边频电流分量。
假设左边频电流分量和定子基频磁链分别为
（4）
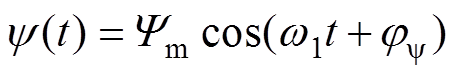（5）
式中，ImL和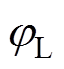
分别为左边频电流分量的幅值和初始相位；
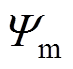和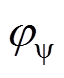
分别为定子基频磁链的幅值和初始相位。
左边频电流分量和基频磁链相互作用产生2倍基波频率的三相合成转矩脉动，转矩脉动产生转速波动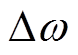
，转速的波动引起转子机械旋转角度的波动，导致转子位置偏差为
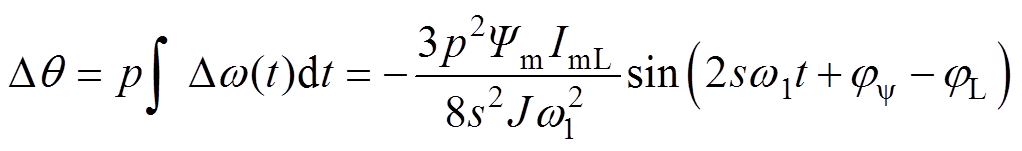（6）
式中，J为转动惯量。
考虑到转速的波动，基频磁链相位将受到Δθ的调制，则式（5）中定子基频磁链可近似表示为
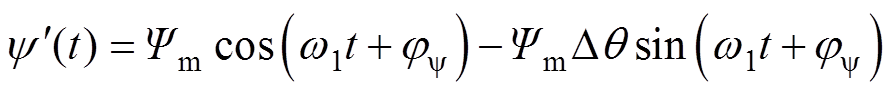（7）
将式（6）代入式（7），可得
（8）
可以看到，当电机发生转子断条时，会在基频磁链中引入如式（8）等号右边第二项所示的附加项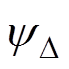
，对此附加项展开可得
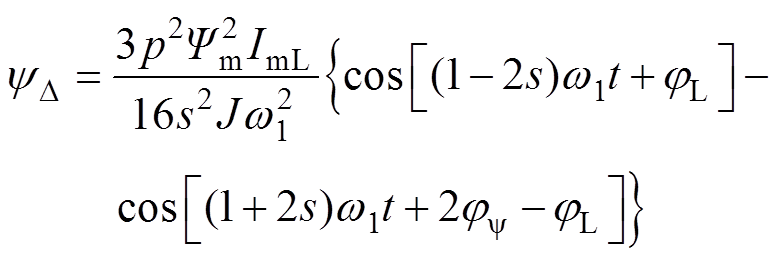（9）
该附加磁链在定子绕组中产生的感应电动势为
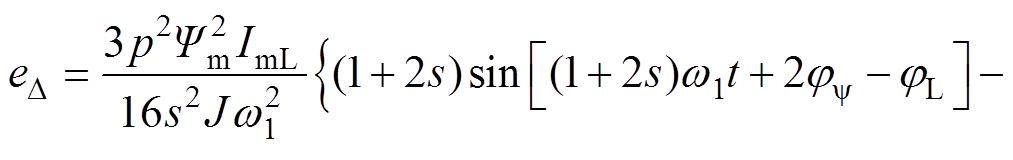
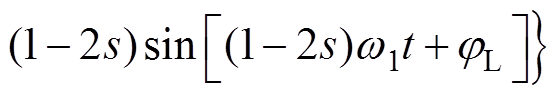（10）
由此，当电机发生转子断条时，将在定子电流中感应出频率为(1±2s) f的左、右边频电流分量。
左边频电流的出现是转子断条故障电机区别于健康电机的重要特征，并且随故障程度的增加，左边频电流分量的幅值也会增加。电机发生不完全断条故障时，即转子中有一根导条发生局部断裂，转子电阻和转子电流发生变化，电机磁场出现不对称，此时，电机处于轻度故障状态。当电机完全断条时，转子中至少有一根导条完全断裂，该断裂导条电阻为无穷大，电流为0，电机磁场畸变程度加重。图1为不完全断条时的起动电流时域波形和功率谱密度（au表示标幺值）。可见，发生转子断条故障时，转差率随起动时间从1递减至接近于0，左边频电流频率|1-2s| f呈现从50 Hz到0再到50 Hz的变化，且能量分散在基频以下的频带内，因此左边频电流为分布于基频以下的宽带信号。基频电流与左边频电流在起动过程表现出不同的特性，因此起动电流不仅能够用于电机额定负载时的断条故障诊断，还可以解决轻载甚至空载时故障特征易被基频淹没而难以提取的问题。
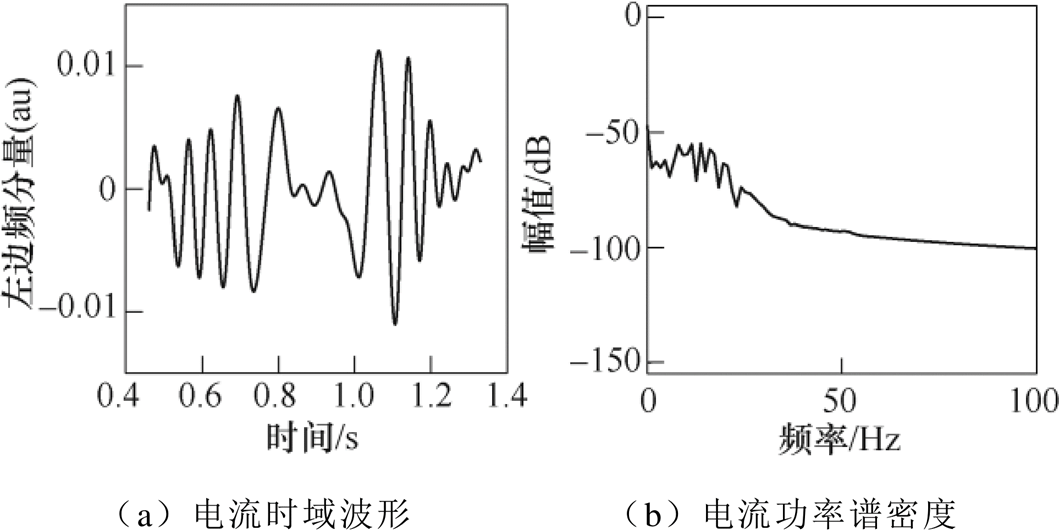
图1 左边频电流分量的时域波形和功率谱密度
Fig.1 Time-domain waveform and power spectral density diagram of left side harmonic current and components
基于上述分析，下文利用VMD算法强抗干扰性和自适应性的特点对起动电流进行分解，以左边频电流为故障特征电流进行故障诊断。
VMD算法认为信号是以不同频率为中心的子信号叠加而成，VMD算法可以自适应地确定各个子信号的中心频率和频率带宽，实现信号的分离，对于给定信号可以根据其含有的频率特性实现有效分离，适用于非平稳性信号[18]。
设采集到的电流信号为i(t)，通过VMD算法把该信号分解为不同频率的子信号，用ih(t)表示分解得到的第h个子信号，将原信号分解为K个子信号，ih(t)围绕其中心频率wh附近分布，构建如下变分问题
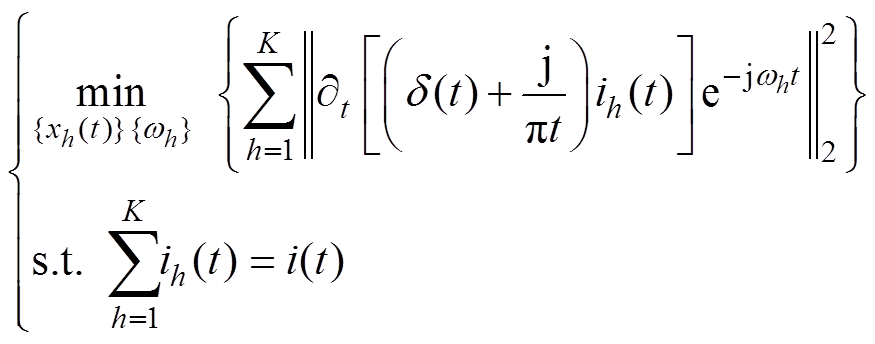（11）
式中，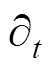
为关于时间的微分算子；
为狄拉克函数。
利用二次惩罚项和拉格朗日乘子将式（11）重构为一个无约束的最优化问题，对应的增广拉格朗日函数为
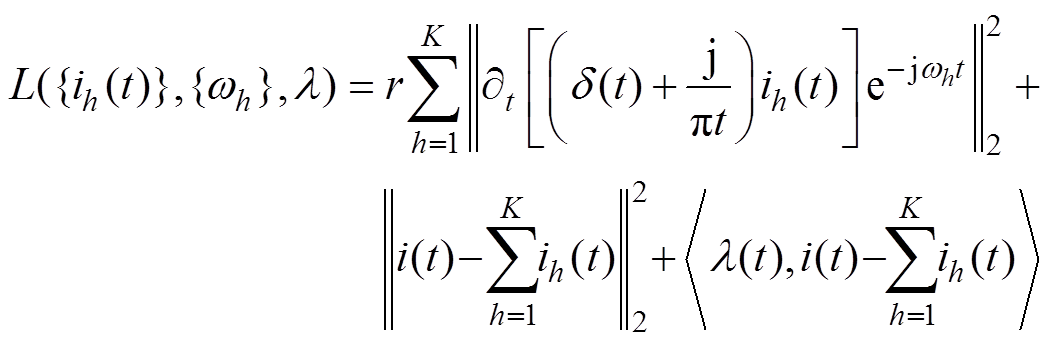（12）
其中
{ih(t)}={i1(t),…, iK(t)} {wh}={w1,…, w K}
式中，r为惩罚因子，与滤波器的带宽有关；l 为拉格朗日乘子。
每一个IMF序列的更新都基于其他的IMF，即每一个IMF序列都是原始信号剩余部分的低通滤波。利用Parseval原理对式（12）在频域上求解最小值，得到每一个IMF序列的更新公式为
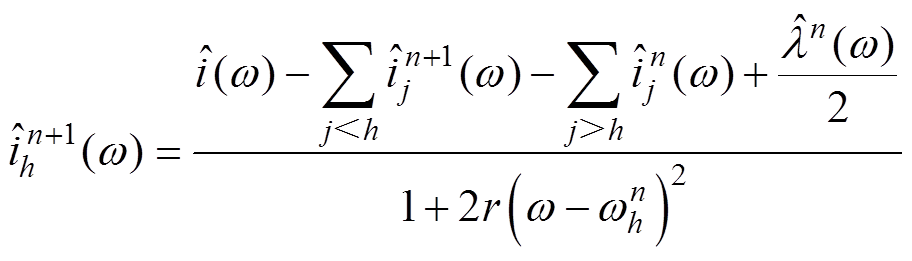（13）
同理求得中心频率wh和拉格朗日算子l 的更新公式为
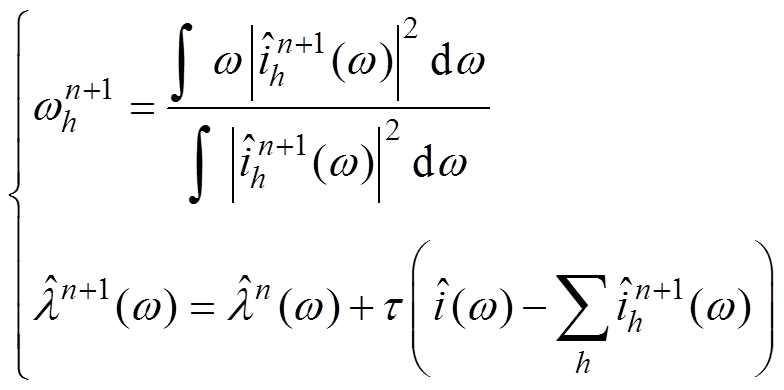（14）
式中，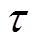
为拉格朗日乘子的梯度更新因子。
通过以上更新方法不断迭代找到最优解，实现对于信号的自适应分解，最终得到K个含有不同主频率的子信号。因此，根据信号特点合理设置VMD算法参数，就可以从原电流信号中分解出起动过程转子断条故障特征子信号。
断条故障诊断方案主要分为以下三个步骤：
（1）提取起动阶段定子电流，并对电流信号进行抗混叠滤波。
（2）VMD算法参数的优化和特征提取，待优化的参数包括惩罚因子和模态个数。
（3）故障特征电流时频分布图的绘制和优化，以及故障严重程度量化因子的确定。
下文以一台5.5 kW的笼型异步电机为例，进行诊断方案的说明，电机参数见表1。
表1 电机参数
Tab.1 The motor parameters
参 数数 值 额定电压/V380 额定功率/kW5.5 额定电流/A14 同步转速/(r/min)1 000 极对数3 定子槽数36 转子槽数28
异步电机的起动电流可达额定电流的数倍，因此可以通过电流幅值的变化来选取起动时间。下面借助Clarke变换求取电流空间矢量，空间矢量幅值满足的公式为
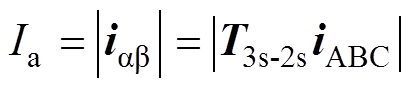（15）
式中，iab=[iaib]T，ia, ib 分别为定子在a、b 坐标系下的分量；iABC=[iAiBiC]T，iA, iB, iC为三相电流；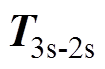
为Clarke变换矩阵，有
（16）
基于表1的电机参数，仿真得到健康状态下的定子电流和电流包络如图2a的ia和Ia所示，从图中可以观察到，当给电机加载电压瞬间，定子电流增大数倍达到最大值，随后电流幅值不断降低，显然借助Clarke变换求取的电流包络能够及时反映电流幅值变化情况。本文起动过程阈值设定为稳态时电流的2～3倍，所取起动时间片段T内的ia即为后续分析的起动过程定子电流片段，阈值可自适应地根据不同起动工况调整。相比较于Hilbert变换需截取整个电流片段后才能进行分析的方法，利用Clarke变换求取电流包络的方法可实时对电流数据点进行计算，因此可以减小计算量、缩短算法运行时间，从而提高诊断流程的在线实时性。此外，还可以根据电机不同工况情况，自适应确定起动时间。
实验设定的采样频率为5 kHz，采样得到的信号中能分析出的最高频率为2.5 kHz。为了避免高频混叠现象，提高系统的信噪比，减小后期故障特征信号分析时的误差，对健康状态下的定子起动电流进行抗混叠滤波，结果如图2b所示，其功率谱图如图2c所示，图中Fpass为截止频率，可以看出，抗混叠滤波后大部分高频噪声被滤除了。
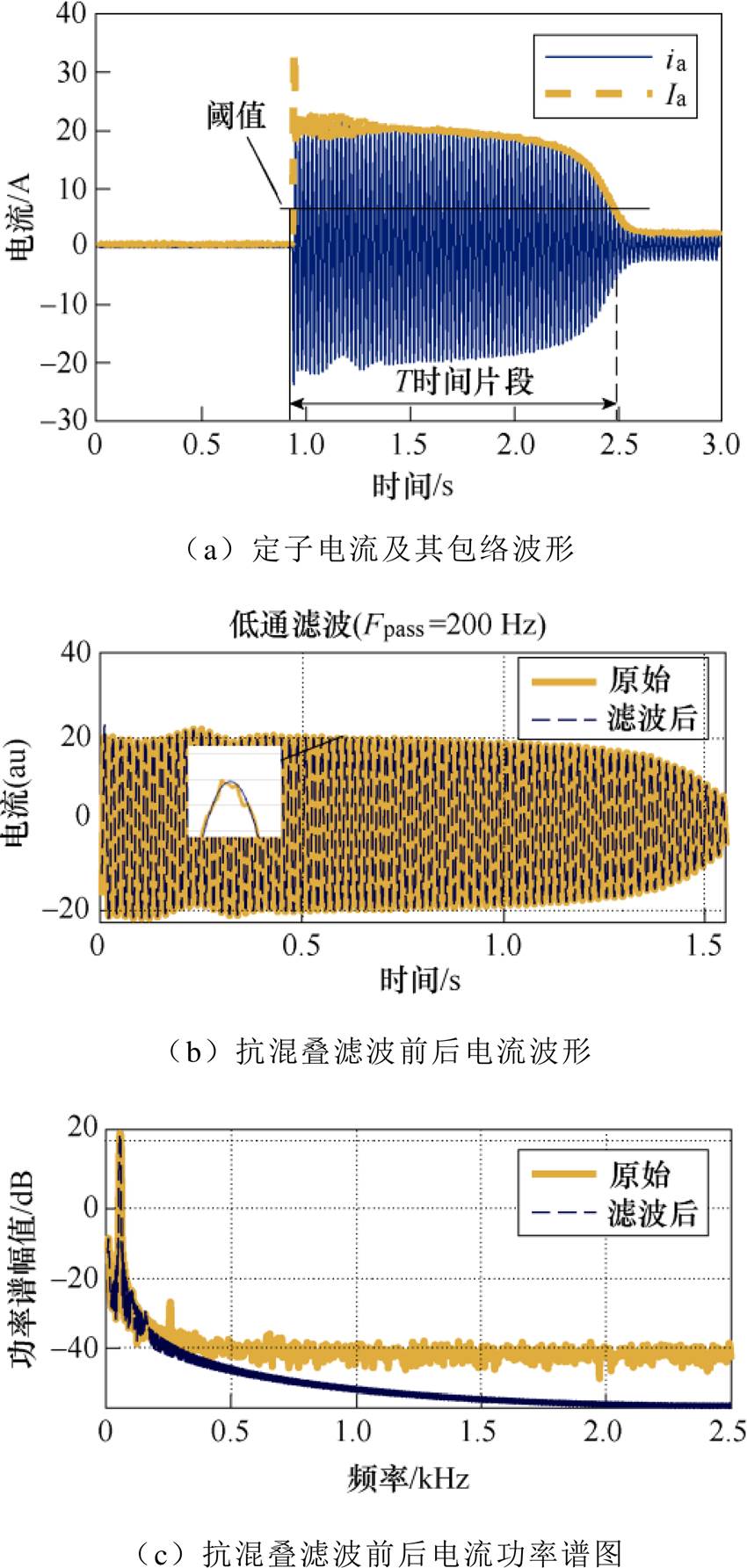
图2 正常情况下电机起动电流波形和功率谱图
Fig.2 Motor starting current and power spectrum under normal conditions
在使用VMD算法对信号进行剥离时，需要事先设定惩罚因子、模态个数等参数，选择合适的VMD参数有利于故障特征的提取。根据转子故障特征电流特点，设电机起动过程定子电流由基频电流分量、左边频电流分量和噪声三部分构成，对应表达式为
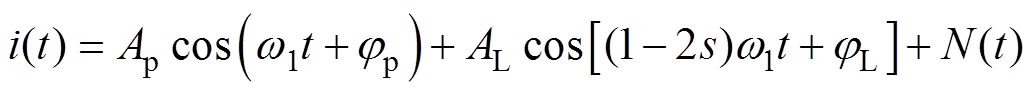（17）
式中，Ap、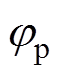
分别为基频电流分量幅值和初始相位；AL为左边频电流分量幅值；N(t)为噪声分量。
根据卡森带宽法则，由式（17）可知，在起动过程中，基频分量受电源影响为围绕基频的窄带信号，左边频电流分量为频率分布于基频以下的宽带信号。惩罚因子r用以保障信号的重构精度，模态个数K一定时，若r过大会使信号带宽过小，重构信号与原始信号之间的误差较大，但是如果r过小时会使信号带宽过大，相近的两个模态函数的频谱会有部分重叠。对本文样机的定子电流实验数据进行处理发现，在500～2 500范围内，惩罚因子大小对能量值变化的敏感度较低，同时随着惩罚因子增加，VMD分解信号的带宽变窄，抗干扰性提高。为使VMD更好地分解具有宽带特性的故障特征信号，同时兼顾基频的窄带和故障电流的宽带信号，本文设定惩罚因子r=2 500。
模态个数K的确定影响断条故障特征的提取，若模态选取个数较少，则会导致转子断条早期微弱的故障特征无法提取；若选取的模态个数过大，则故障特征信号的能量将分散于多个模态中，从而导致微弱故障信号无法提取。为使故障特征信号能量集中化，有必要对分解的模态个数K进行优化。
VMD分解的子信号围绕各自中心频率分布， 图3给出了VMD两个子信号的频域分布，图中，wh1、wh2分别为IMF1子信号和IMF2子信号的中心频率，
、
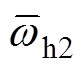分别为IMF1和IMF2的平均瞬时频率，平均瞬时频率反映该子信号的能量围绕中心频率的分布情况。当K设置合理时，VMD分解结果中子信号间的区分度高，如图3a所示，此时wh1＜wh2且
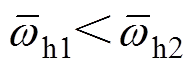；若K设置过大时，模态之间出现混叠，平均瞬时频率的变化规律不再服从该中心频率的变化规律，信号出现过分解，如图3b所示，此时wh1＜wh2但
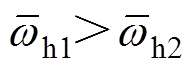。由此可以通过平均瞬时频率和中心频率的变化规律来确定最优的K值。
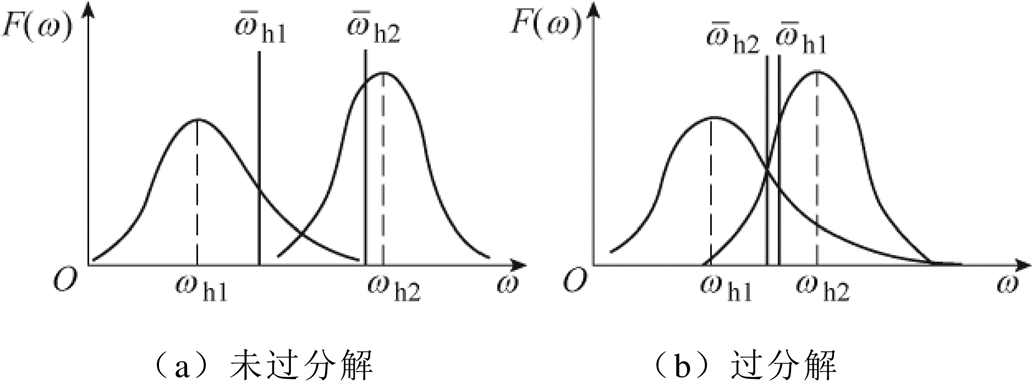
图3 VMD模态频域分布
Fig.3 Frequency domain distribution diagram of VMD mode
模态个数K从1增加至7，分别对一根断条的故障电机起动电流进行VMD分解，分解得到的子信号平均瞬时频率如图4所示。当K=5时，分解得到的5个子信号出现了图3b的情况，这表明VMD开始出现过分解，因此K=4时为最优模态个数。
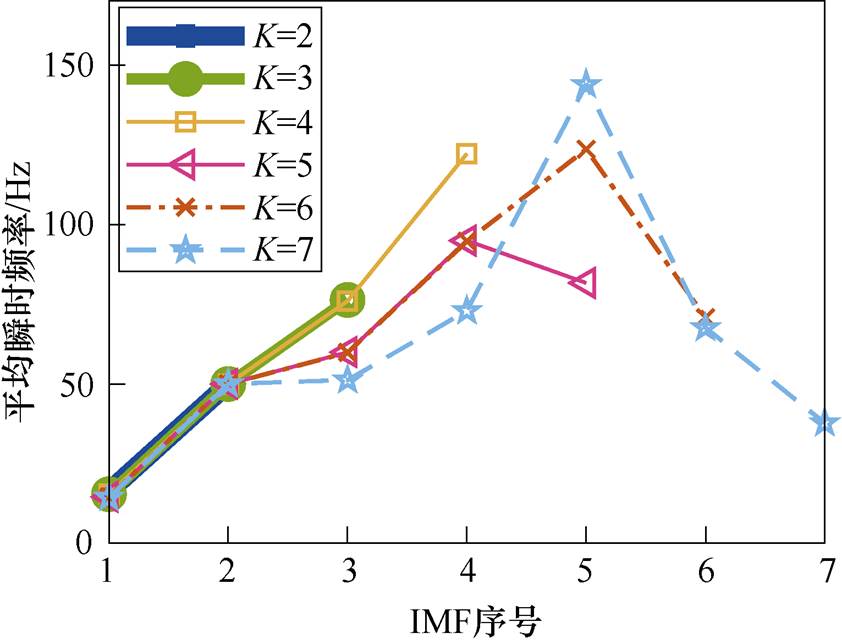
图4 不同模态个数下IMF序列平均瞬时频率
Fig.4 Average instantaneous frequency of IMF series under different number of modes
当模态个数为4时，该起动电流的VMD分解结果如图5所示，图5中的IMF0为起动电流信号，IMF1～IMF4为VMD分解起动电流得到的子信号，其中，IMF0和IMF3波形的幅值参考坐标系为右侧坐标轴，其他子信号幅值参考坐标系为左侧坐标轴。其中，IMF4符合图1所示的故障特征分量的时域变化特征，因此IMF4为左边频故障特征电流，由此可见，优化后的VMD算法可以较好地分离出故障特征电流信号。
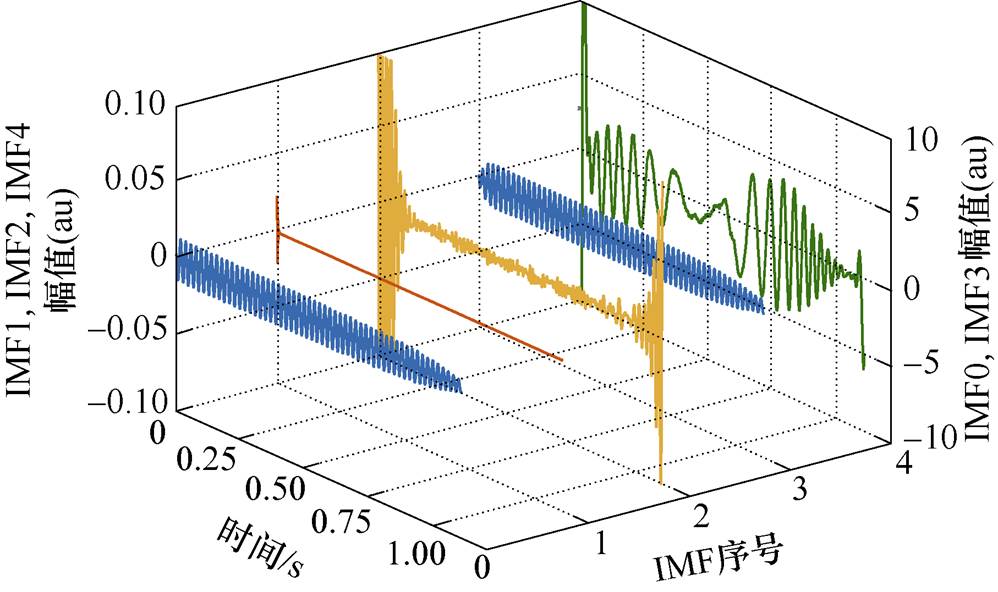
图5 一根断条时定子起动电流的VMD分解
Fig.5 Stator starting current VMD decomposition diagram of one broken bar
为了便于观察故障特征频率随时间的变化情况，对左边频电流使用WVD算法绘制时频分布图，由其在时频空间上积分值的大小。假设用VMD算法提取出的电流信号if(t)由故障特征频率电流i1(t)和干扰信号i2(t)组成，对if(t)使用WVD算法分析，则其Winger-Ville分布为
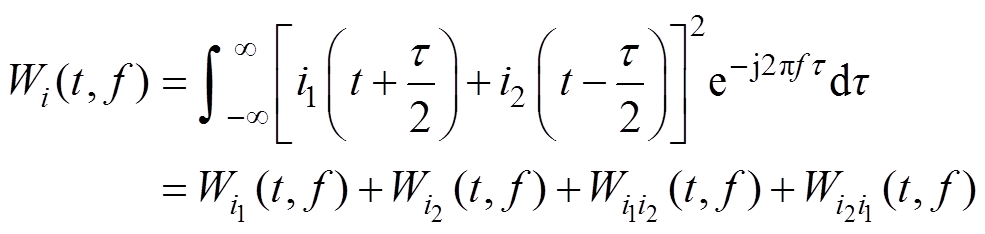（18）
式中，
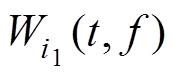和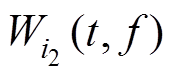
分别为i1(t)和i2(t)信号的自主项，而
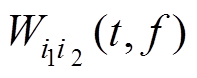和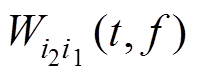
是由i1(t)和i2(t)之间的相互作用形成的交叉项。
当转子发生不完全断条时，故障信号微弱，交叉项的能量级与故障信号相近，会导致故障的误判。为解决使用WVD算法进行时频分析时交叉项的问题，同时避免WVD的信号能量分布出现负值情况，本文引入了大津算法[20]。
OTSU又称为最大类间方差法，由日本学者大津（Nobuyuki Otsu）提出的，是一种适用于双峰情况自动求取阈值的方法，该算法按图像的灰度特性将图像分成前景和背景两部分，对图像进行二值化分割，使得前景与背景图像的类间方差最大。将WVD时频分布图中所有像素点按照灰度分类[1, 2,…, L]，假设存在阈值k将所有像素按照灰度分为两类：小于k的k1（背景）和大于k的k2（前景），那么k1和k2在此幅图中出现的概率e1和e2分别为
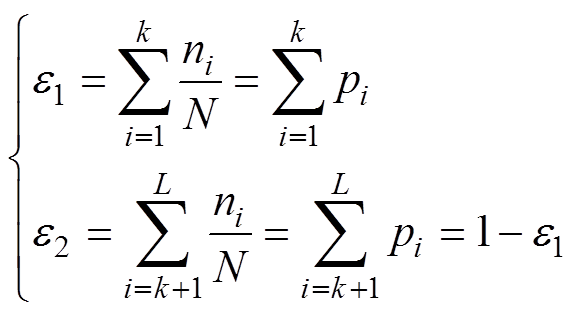（19）
式中，ni为灰度为i的像素点的个数；N为总的像素点个数；pi为灰度为i的像素点在图中出现的概率。
k1、k2两类像素以及整幅图像的灰度均值m1、m2、mL之间存在如下关系
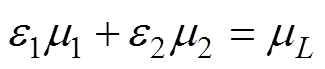（20）
类间方差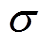
的表达式为
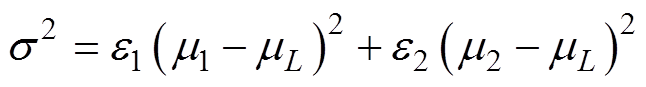（21）
将式（20）代入式（21）进行化简，构造最大类间方差的变分问题为
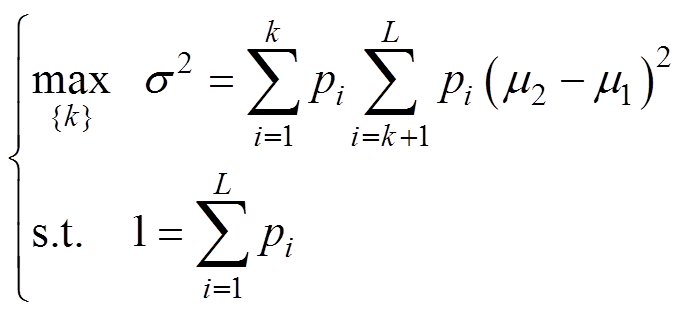（22）
根据阈值k对WVD时频分布图进行处理，将图中像素点低于k的点置为0，高于等于k的点保留。
使用WVD算法绘制图5中IMF4右半部分的能量时频分布图，结果如图6a所示。观察图6b，发现经过OTSU处理后，图中的能量更加集中，这是由于WVD图去除了大部分干扰项，突出了故障特征频率的部分，从而获得了较好的处理效果。
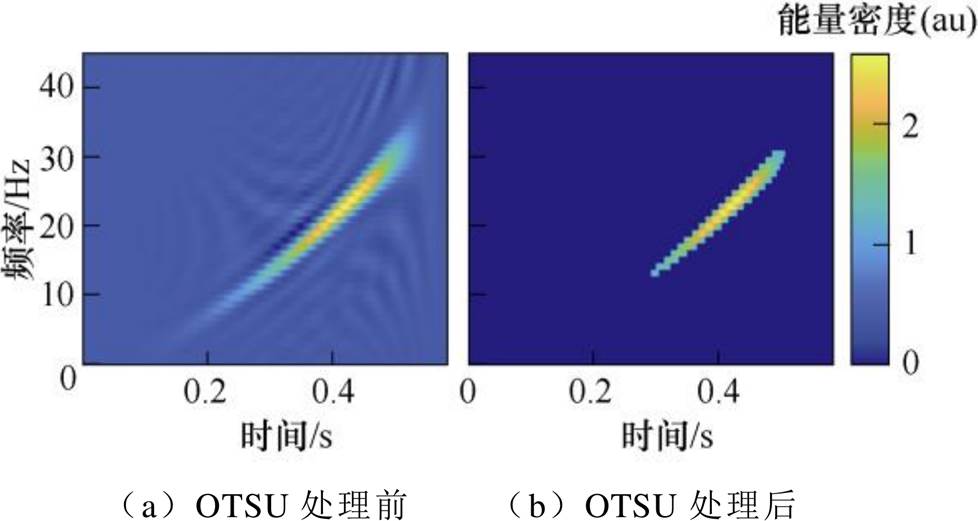
图6 一根断条时左边频电流WVD图
Fig.6 The right part of left-side harmonic current WVD diagram of one broken bar processed
为了对电机进行健康状态评估，实现系统自动故障预警的目的，需要对故障的严重程度进行量化。图7中给出了三根断条时左边频电流信号的变化曲线，其中图7a表示经过VMD分解得到的左边频故障特征电流信号，可见以0 Hz为界，该故障特征电流分为左、右两部分。故障特征电流的左半部分受起动初期电机暂态的影响较大会引入干扰，而右半部分能量更为集中，所以本文以右半部分曲线为分析对象，波形如图7b所示。计算右半部分曲线的频率在能量时频分布图上的积分值，获得能够量化故障严重程度的能量值为
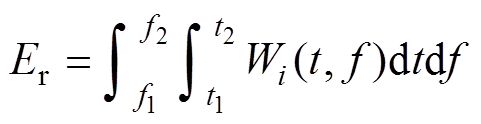（23）
式中，Wi(t, f )为左边频电流右半部分的Winger-Ville分布。将积分频率f的上、下限f1和f2设为2 Hz和45 Hz，以消除直流分量和基频分量的干扰。为了减少时频域的端部影响，将积分时间t的上限t2设为0.9T。
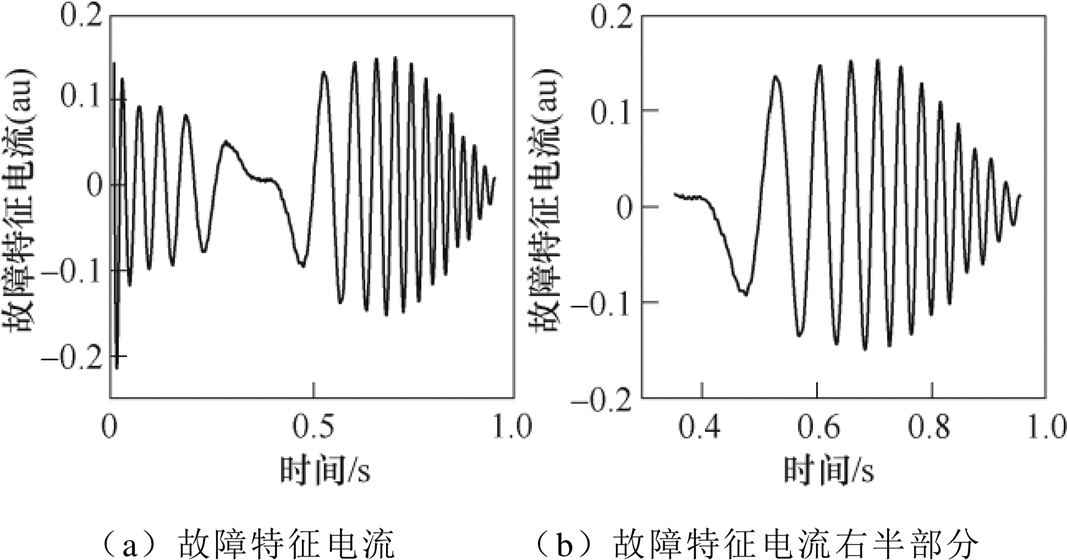
图7 左边频故障特征电流
Fig.7 Left-side harmonic current
将式（23）计算出的故障特征信号能量值作为故障量化因子与断条故障严重程度分类的预设阈值进行比较，从而达到故障预警的目的，具体阈值设置方法详见第4.4节。
实验测试平台如图8所示，该实验测试平台包括电源系统、数据采集系统和故障电机测试台。电源系统包括给电机供电的大功率可编程交流电源和给传感器供电的E36313A稳压直流电源；数据采集系统由IT200-S电流传感器、信号转接电路和DLM4000示波器组成；实验电机参数见表1。为了进一步验证方法的可行性，本文对健康、不完全断条、一根断条、两根断条和三根断条五种不同断条故障下的电机进行了实验。所有实验均为空载起动，起动电流的采样频率为5 kHz。
图8 实验平台及转子
Fig.8 The experiment platform
不同方法处理的不完全断条故障特征信号时频分布如图9所示。将本文提出的VMD算法用于不完全断条实验的起动电流处理，结果如图9a所示，其中No代表不对原信号添加噪声，35 dB和25 dB表示在原信号中加入额外噪声后的信噪比。为验证本文所提方法的有效性，使用经验小波变换（Empirical Wavelet Transform, EWT）和经验模态分解（Empirical Mode Decomposition, EMD）对同一信号进行处理，处理结果如图9b和图9c所示。将三种处理结果进行比较可以发现：EWT无法提取轨迹分明的故障特征分量；EMD的分析结果随着干扰加重变得模糊；相比之下，VMD在干扰加重的情况下也能获得清晰的故障特征信号。因此，本文提出的对VMD进行参数优化并提取故障特征信号的方法，在噪声较大的情况下，对转子断条故障的诊断具有明显优势。
对定子起动电流经过自适应片段选取和抗混叠滤波后，利用提出的VMD模态寻优方法进行参数寻优，根据优化结果得到不完全断条、一根断条、两根断条和三根断条的最优模态个数分别为5、4、3和2，其中不完全断条时VMD算法分解结果如图10所示。可见该寻优方法可以根据不同信号的特点自适应地选出模态个数的值，以实现故障特征信号完整的提取。
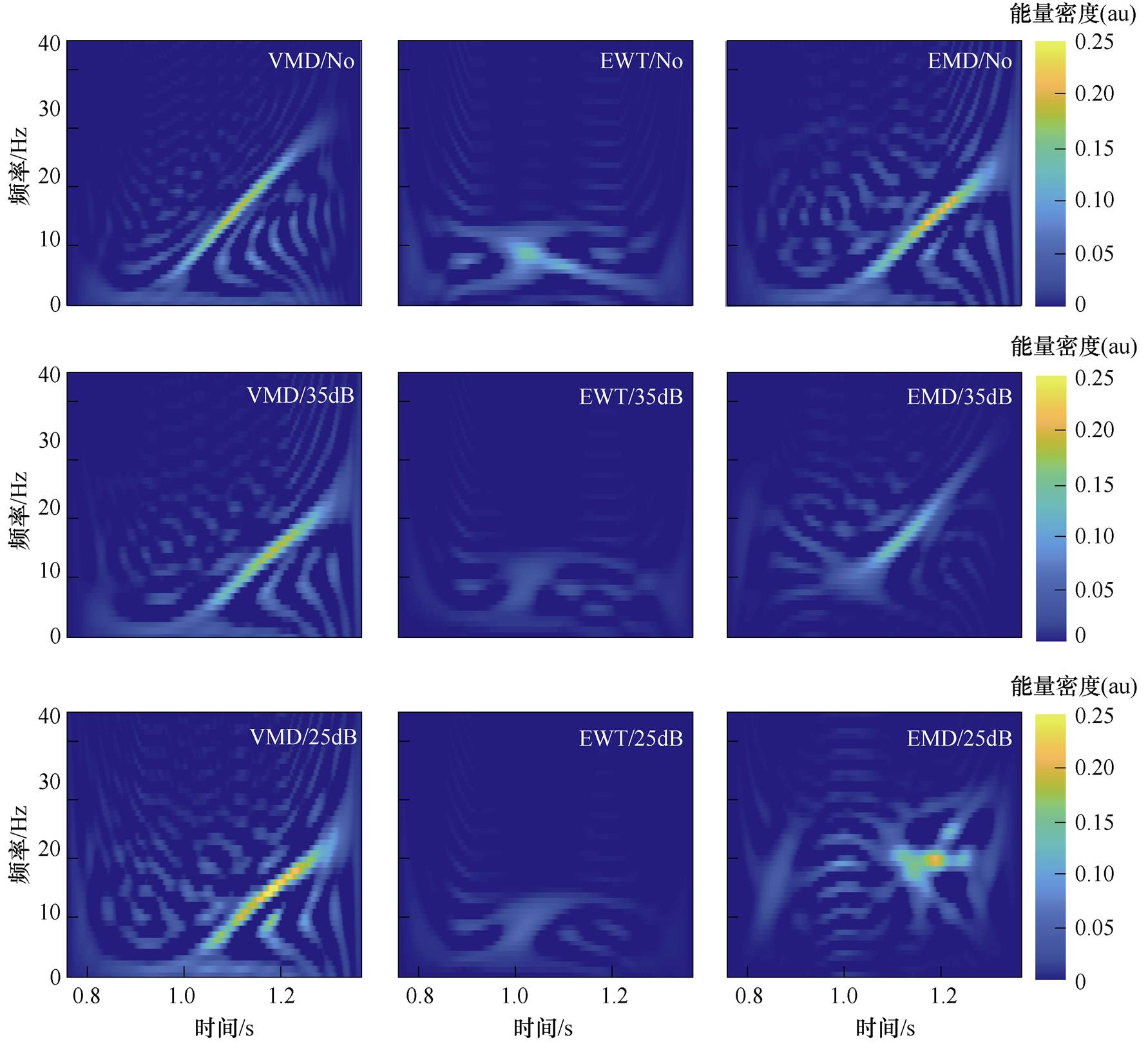
（a）VMD （b）EWT （c）EMD
图9 不同方法处理的不完全断条故障特征信号时频分布
Fig.9 Time-frequency distribution of fault characteristic signals of partical broken bars processed by different methods
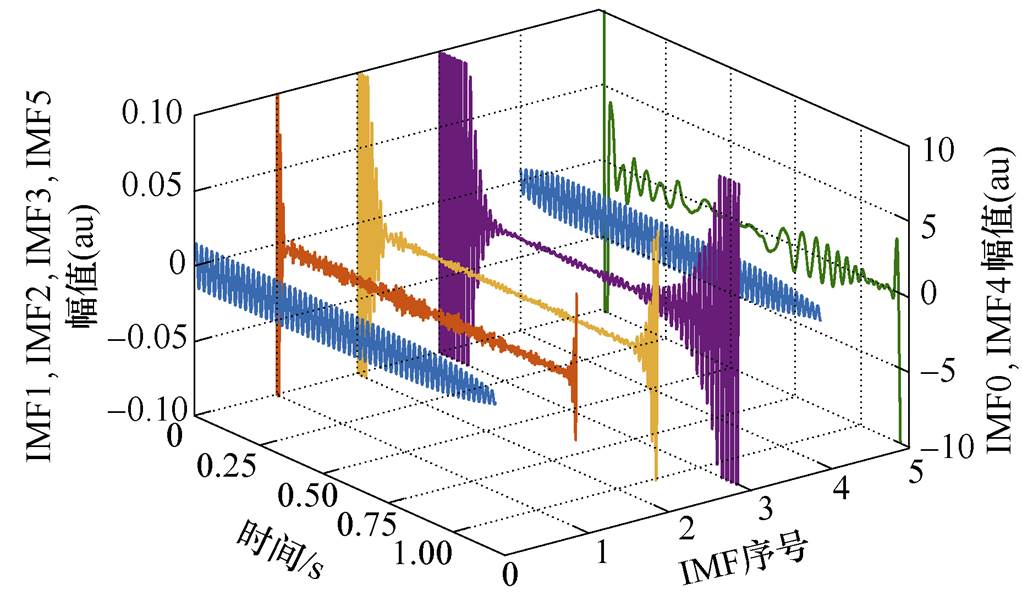
图10 不完全断条时定子起动电流的VMD分解图
Fig.10 Stator starting current VMD decomposition diagram of one broken bar
利用参数优化后的VMD算法对不完全断条的定子电流信号进行分解，结果如图10所示，图中IMF0为原信号，IMF1～IMF5为分解出的子信号。其中，IMF0和IMF4波形的幅值参考坐标系为右侧坐标轴，其他子信号幅值参考坐标系为左侧坐标轴。由图10可知，IMF5具备故障特征频率的特点，因此IMF5为左边频电流分量。
利用WVD算法绘制左边频电流分量右半部分时频分布，结果如图11所示，其中左图代表未作处理前的图像，右图代表使用OTSU算法对WVD图进行处理后的图像。通过观察图11可知，本文提出的诊断方法不仅可以区分出不完全断条故障和健康状态，还可以针对不同的断条故障进行很明显的故障严重程度区分。
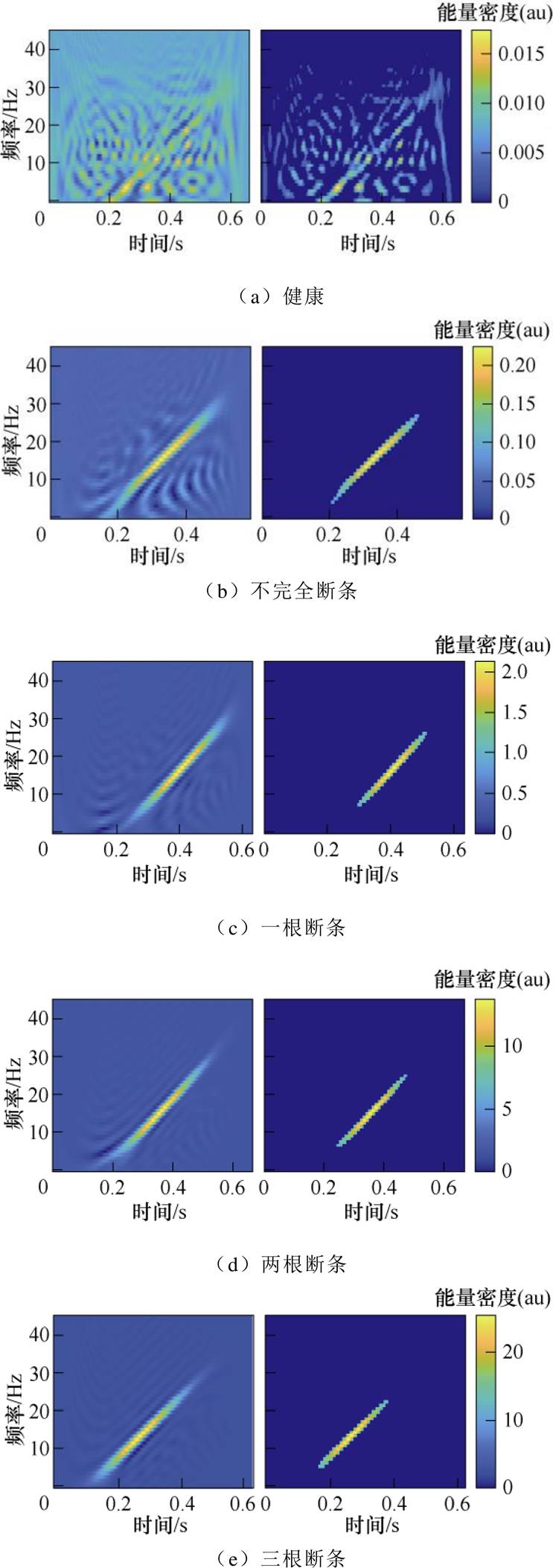
图11 左边频电流右半部分WVD图
Fig.11 The right part of left-side harmonic current WVD diagram
本文以故障特征电流的右半部分作为分析对象判断故障状态，对五种不同故障状态的电机各进行10组实验，根据式（23）对实验数据进行计算，得到故障特征电流信号的右半部分能量值。能量值的箱形图分布如图12所示。图中，箱型图的上边缘与下边缘为能量的最大值与最小值，箱体部分的上、下端为上、下四分位数，虚线代表中位数。对比不同状态故障特征能量的箱体，可见每种故障状态呈现的能量值区域均不重叠，即本文提出的方法可以准确地区分健康电机和不完全断条以及多根断条的故障状态。
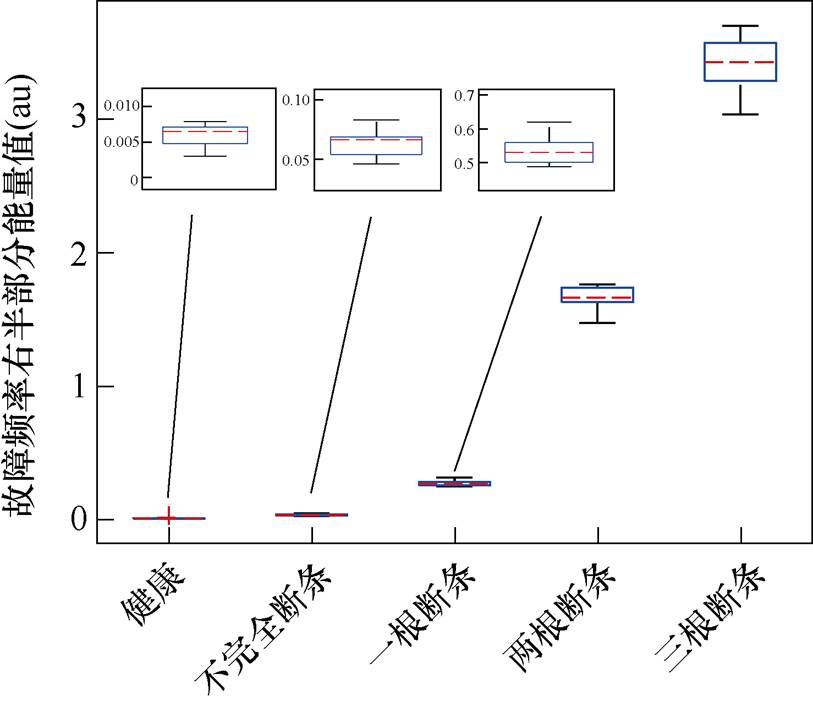
图12 故障特征电流右半部能量值箱形图
Fig.12 Box diagram of energy values in the right half ofthe fault characteristic current
由上述分析可知，故障特征电流右半部分的能量值可以用来构建断条故障严重程度的量化因子。为使故障判断更加准确，根据能量值的均值m 和标准差s 设定阈值范围[m-2s, m+2s]，即设置95 %的置信区间，保证被测量参数的可信度必定不小于95 %。五种不同状态能量值的均值m 和标准差s 见表2。同时为使故障严重程度量化指标能够拓展到其他规格的电机上，定子起动电流均经过标幺化处理，因此能量值的均值和标准差为标幺值。观察表2中的阈值区间，发现五种不同转子断条故障状态右半部能量值的区间均不重叠，因此本文提出的方法对于区分健康和故障状态有很好的效果。
表2 右半部能量值的均值和标准差
Tab.2 The mean and standard deviation of the right half of the energy value
电机状态均值m标准差s阈值区间 健康0.006 670.003 1[0.000 47，0.012 87] 不完全断条0.064 080.011 6[0.040 88，0.087 28] 一根断条0.538 230.041 0[0.456 23，0.620 23] 两根断条3.330 850.168 0[2.994 85，3.666 85] 三根断条6.808 050.426 0[5.956 05，7.660 05]
针对转子断条故障识别问题，本文利用起动过程定子电流故障特征频率随时间变化的特点，提出了使用VMD对起动电流进行分析并结合WVD和OTSU计算能量值对故障严重程度进行量化的转子断条故障诊断方法，该方法能够解决不同转子断条故障状态的诊断，主要特点如下：
1）使用Clarke变换方法自适应获取起动电流，提高了程序的在线实时性，同时避免了在转差率较低的情况下对平稳信号进行分析时，故障特征频率被基频淹没的问题。
2）利用VMD的自适应性和抗干扰性的特点剥离出起动过程的故障特征信号，同时使用瞬时频率平均值对VMD模态个数进行寻优，提高了VMD分解结果的准确性。
3）利用WVD算法高时频分辨率的特点绘制故障特征信号右半部分的时频分布图，使用OTSU算法对图片进行处理，弥补WVD存在交叉项以及其他噪声干扰的缺陷。
4）根据故障特征信号右半部分能量值大小设定阈值进行判断，最终实现了包含不完全断条的不同转子断条故障严重程度的区分。
5）当电机的平稳信号不足以准确判断转子断条故障时，结合本文非稳态信号的分析方法，可以提高转子断条故障诊断的准确性。
参考文献
[1] 谢颖, 单雪婷, 郭金鹏, 等. 笼型转子导条断裂引发电机各场量变化与故障程度关联性研究[J]. 中国电机工程学报, 2017, 37(14): 4222-4231, 4302.
Xie Ying, Shan Xueting, Guo Jinpeng, et al. The relationship study between field changes and faulty condition in squirrel-cage induction motor with broken bars fault[J]. Proceedings of the CSEE, 2017, 37(14): 4222-4231, 4302.
[2] Puche-Panadero R, Martinez-Roman J, Sapena-Bano A, et al. New method for spectral leakage reduction in the FFT of stator currents: application to the diagnosis of bar breakages in cage motors working at very low slip[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-11.
[3] 王保帅, 肖勇, 胡珊珊, 等. 适用于非整数次幂的高精度混合基FFT谐波测量算法[J]. 电工技术学报, 2021, 36(13): 2812-2820, 2843.
Wang Baoshuai, Xiao Yong, Hu Shanshan, et al. High precision mixed radix FFT algorithm for harmonic measurement under non-integer power sequence[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2812-2820, 2843.
[4] 王臻, 李承, 林志芳, 等. 定子电流二次方法的异步电机转子复合故障诊断[J]. 电工技术学报, 2016, 31(16): 50-56.
Wang Zhen, Li Cheng, Lin Zhifang, et al. Rotor composite fault diagnosis in asynchronous motor using the square calculation of stator current[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 50-56.
[5] Garcia-Calva T A, Morinigo-Sotelo D, Garcia-Perez A, et al. Demodulation technique for broken rotor bar detection in inverter-fed induction motor under non-stationary conditions[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1496-1503.
[6] Puche-Panadero R, Martinez-Roman J, Sapena-Bano A, et al. Diagnosis of rotor asymmetries faults in indu- ction machines using the rectified stator current[J]. IEEE Transactions on Energy Conversion, 2020, 35(1): 213-221.
[7] Naha A, Samanta A K, Routray A, et al. A method for detecting half-broken rotor bar in lightly loaded induction motors using current[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(7): 1614-1625.
[8] 程侃如, 万书亭, 绳晓玲, 等. 基于Hilbert变换的双馈风力发电机叶轮质量不平衡故障特性分析[J]. 电工技术学报, 2021, 36(24): 5225-5236.
Cheng Kanru, Wan Shuting, Sheng Xiaoling, et al. Characteristic analysis of blade mass imbalance fault of doubly-fed induction generator based on Hilbert transform[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5225-5236.
[9] Abd-El-Malek M, Abdelsalam A K, Hassan O E. Induction motor broken rotor bar fault location detection through envelope analysis of start-up current using Hilbert transform[J]. Mechanical Systems and Signal Processing, 2017, 93: 332-350.
[10] Trachi Y, Elbouchikhi E, Choqueuse V, et al. A novel induction machine fault detector based on hypothesis testing[J]. IEEE Transactions on Industry Appli- cations, 2017, 53(3): 3039-3048.
[11] 孙丽玲, 王续, 许伯强. 基于SVD滤波技术与快速四阶累积量ESPRIT算法的异步电动机转子断条故障检测新方法[J]. 电工技术学报, 2015, 30(10): 147-156.
Sun Liling, Wang Xu, Xu Boqiang. A detection method for broken rotor bar fault in induction motors based on SVD and SFOC-ESPRIT[J]. Transactions of China Electrotechnical Society, 2015, 30(10): 147-156.
[12] 贾朱植, 祝洪宇, 杨理践, 等. 鼠笼电机起动暂态转子断条Wigner-Ville分布诊断方法[J]. 电机与控制学报, 2018, 22(7): 69-77.
Jia Zhuzhi, Zhu Hongyu, Yang Lijian, et al. Diagnosis of broken rotor bars in squirrel cage induction motor during start-up transient based on Wigner-Ville distribution[J]. Electric Machines and Control, 2018, 22(7): 69-77.
[13] 郭凤仪, 高洪鑫, 唐爱霞, 等. 局部二值模式直方图匹配的串联故障电弧检测及选线[J]. 电工技术学报, 2020, 35(8): 1653-1661.
Guo Fengyi, Gao Hongxin, Tang Aixia, et al. Series arc fault detection and line selection based on local binary pattern histogram matching[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1653- 1661.
[14] 陈勇, 梁洪, 王成栋, 等. 基于改进小波包变换和信号融合的永磁同步电机匝间短路故障检测[J]. 电工技术学报, 2020, 35(增刊1): 228-234.
Chen Yong, Liang Hong, Wang Chengdong, et al. Detection of stator inter-turn short-circuit fault in PMSM based on improved wavelet packet transform and signal fusion[J]. Transactions of China Elec- trotechnical Society, 2020, 35(S1): 228-234.
[15] Ayon-Sicaeros R A, Cabal-Yepez E, Ledesma- Carrillo L M, et al. Broken-rotor-bar detection through STFT and windowing functions[C]//2019 IEEE Sensors Applications Symposium (SAS), Sophia Antipolis, France, 2019: 1-5.
[16] Hmida M A, Braham A. Fault detection of VFD-fed induction motor under transient conditions using harmonic wavelet transform[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(10): 8207-8215.
[17] Valtierra-Rodriguez M, Amezquita-Sanchez J, Garcia- Perez A, et al. Complete ensemble empirical mode decomposition on FPGA for condition monitoring of broken bars in induction motors[J]. Mathematics, 2019, 7(9): 783-802
[18] Dragomiretskiy K, Zosso D. Variational mode decom- position[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[19] 张民谣, 高云鹏, 吴聪, 等. 基于自适应变分模式分解的非稳态电压闪变包络参数检测[J]. 电工技术学报, 2021, 36(3): 599-608.
Zhang Minyao, Gao Yunpeng, Wu Cong, et al. Non- stationary voltage flicker envelope parameters detection based on adaptive variational mode decom- position[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 599-608.
[20] Lopez-Ramirez M, Ledesma-Carrillo L M, Garcia- Guevara F M, et al. Automatic early broken-rotor-bar detection and classification using Otsu segment- ation[J]. IEEE Access, 2020, 8: 112624-112632.
[21] 高景德, 王祥珩, 李发海. 交流电机及其系统的分析[M]. 北京: 清华大学出版社, 1993.
Abstract When the induction motor is operated under the steady-state operating condition with a light load, the fault characteristic frequency of the broken bar fault is close to the fundamental frequency, making it difficult to extract the fault current component from the stator current effectively. Moreover, the fault characteristic signal energy shares a fairly minor fraction of the total stator current energy in the early stages of incomplete broken bars, which increases the difficulty of fault current component extraction. In order to improve the diagnosis effect of the broken bar fault at the early stage when the motor is running at light load, according to the characteristics of distinguishing the characteristic signal of the broken bar fault from the fundamental signal during the starting period, this paper proposes the variational mode decomposition (VMD) method to process the stator start-up current, and the broken bar fault diagnosis is carried out by utilised the energy value of the fault characteristic current obtained by decomposition.
The proposed broken bar fault diagnosis scheme is mainly divided into three stages: stator current pre-processing, fault characteristic current extraction, fault characteristic current energy time-frequency distribution calculation and fault severity quantification. In the first stage, the Clarke transformation is applied to obtain the current space vector, and the amplitude variation of the current space vector during the starting process is utilised to adaptively extract the stator current for analysis, and the influence of high frequency interference on low frequency signal is removed by an anti-aliasing filter. In the second stage, a VMD algorithm based on the optimisation of the mean instantaneous frequency is proposed to extract the left frequency component of the fault characteristic current. In order to optimise the extraction effect, it is necessary to determine the appropriate parameters for the penalty factor and the number of modes in the VMD algorithm. The penalty factor should take into account the narrow-band nature of the fundamental signal and the broad-band nature of the fault characteristic current, and have low sensitivity to the change of the energy value of the fault characteristic current to accommodate to the diagnosis under different fault degree. Concerning the number of modes, in this paper we propose to determine the optimal number of modes to ensure the energy concentration of the fault characteristic current by exploiting the variation law of the centre frequency and the mean instantaneous frequency of the sub signals obtained from the VMD decomposition. In the third stage, Wigner-Ville Distribution (WVD) is utilised to extract the energy time-frequency distribution of the fault characteristic current, and Otsu’s method (OTSU) is applied to perform anti-noise processing on the time-frequency distribution to highlight the fault characteristic information. In order to further improve the disturbance rejection performance of the diagnosis scheme, we take the energy value of the characteristic curve of the right part of the left frequency component as the fault quantization factor, and set the threshold based on the mean and standard deviation of multiple groups of experimental data under different fault states, so as to realise the purpose of automatic fault warning.
In this paper, the experimental verification is carried out on a 5.5 kW induction motor. The results show the proposed fault diagnosis scheme performs well in terms of interference rejection and is able to extract the fault characteristic current component in the condition of incomplete broken bars fault at high noise level. Moreover, the energy value of the right part of the fault characteristic signal has a strong positive correlation with the fault severity, which can perform the rotor broken bar fault detection well and can realise the discrimination of different rotor broken bar fault severity including incomplete broken bars.
keywords：Induction motor, broken bars, fault diagnosis, variable mode decomposition (VMD), intrinsic mode function (IMF), Otsu’s method (OTSU)
DOI: 10.19595/j.cnki.1000-6753.tces.220124
中图分类号：TM307
浙能集团科技资助项目（208020210582）。
收稿日期 2022-01-24
改稿日期 2022-03-28
夏志凌 男，1980年生，高级工程师，研究方向为异步电机故障诊断。E-mail: xiazhiling@163.com
史婷娜 女，1969年生，博士，教授，研究方向为电机系统及其控制。E-mail: tnshi@zju.edu.cn（通信作者）
（编辑 崔文静）