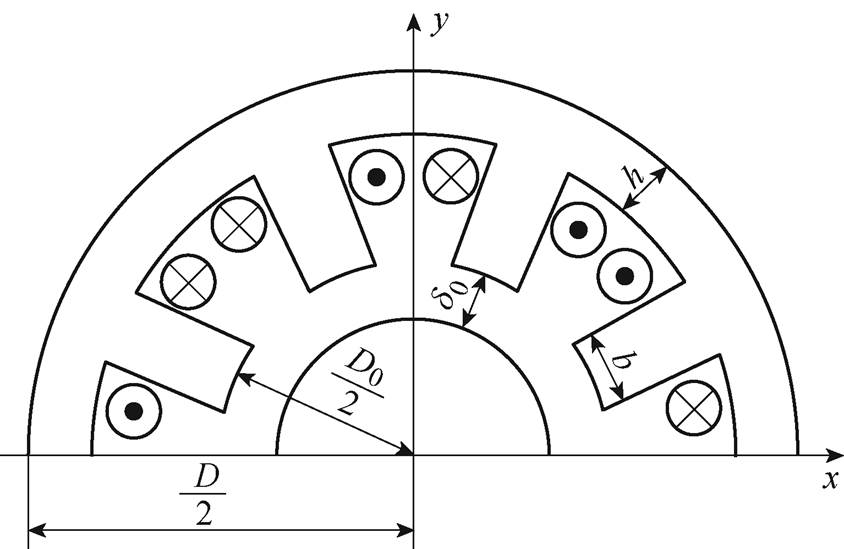
图1 NNSS磁极排布径向电磁轴承结构
Fig.1 Schematic diagram of NNSS magnetic pole discharge radial AMB
摘要 综合考虑磁路分布特性的电磁轴承解析模型是对电磁轴承优化设计的快速有效手段。该文通过计及铁心材料非线性磁导率、磁极边缘效应、磁场透入深度等影响因素,研究了磁极宽度对电磁轴承定子结构参数及其最大静态电磁力的影响,揭示了定子结构参数与磁路动态磁阻之间的规律,构建了计及磁路分布特性的电磁轴承解析模型。在此基础上,以异极径向电磁轴承结构参数为研究对象,分别以构建的解析模型和有限元法对其结构与最大电磁力及气隙磁通密度的影响规律进行计算对比,同时搭建了对应的实验平台进行验证分析,验证了解析模型的准确性和有效性。另一方面,基于构建的电磁轴承解析模型,揭示了定子极弧系数、励磁电流、气隙长度对于电磁轴承支撑性能的影响规律,为径向结构电磁轴承的设计及运行控制提供理论参考。
关键词:电磁轴承 解析模型 磁路分布 支撑性能
为实现高效机械传输与能量转换,电磁轴承(Active Magnetic Bearing, AMB)以其无摩擦、阻尼可控、寿命长等优势,在大功率高速电机、第四代核电主泵、飞轮储能、航空等领域中得到了广泛的应用。然而,随着科学技术的飞速发展,对于电磁轴承的优化设计与运行控制精度提出了更高的要求[1-3]。
目前,对于电磁轴承的电磁特性研究很多是基于有限元法结合温度场[4-5]或者电磁理论[6-7]分析其不同结构、转速时,运行性能的变化规律。事实上,通过有限元法设计和分析时存在参数设置复杂、计算时间长、可调节变量较少等问题,所以其理论解析模型的研究对于电磁轴承优化设计具有重要的意义。
由于电磁轴承运行过程中,其磁路分布会受到结构、非线性磁导率、气隙边缘效应等因素的影响。所以为了可以更加精准地揭示磁悬浮轴承磁路中各种变量之间的规律,国内外很多学者在等效磁路法、虚位移法、张量法[8-9]的基础上,对磁悬浮轴承的磁路分布及其影响因素进行了大量研究。
文献[10-11]针对磁悬浮轴承各部分铁心磁路分布不均匀的问题,通过分别计算不同区域铁心磁阻以建立解析模型,进而对磁悬浮轴承的静态特性与动态特性进行分析。文献[12]针对磁悬浮轴承转子高速旋转导致的柔性转子振动的问题,通过考虑涡流影响建立对应的理论模型进行相应的研究。文献[13-14]针对于气隙边缘效应所导致的气隙磁阻计算偏小的问题,采用磁场分割法对气隙磁阻进行计算分析,结果证明考虑了气隙边缘效应的解析模型计算结果的准确性有明显提高。文献[15]考虑到漏磁对于磁路的影响,结合磁路分布的规律,通过等效磁路法建立了考虑漏磁的精确磁路模型,通过实验验证了模型的可靠性。文献[16]针对铁心材料的非线性磁导率造成的磁饱和问题,在考虑了气隙边缘效应的基础之上,通过对铁磁材料的非线性磁导率进行拟合,进而建立了考虑材料非线性磁导率的径向电磁轴承理论模型,并与有限元法计算结果进行比对分析,结果表明其计算精度较高,与有限元计算结果相比误差小于3 %。
综上所述,尽管目前对于电磁轴承磁场分布及其影响因素方面较多学者已经做了大量有价值的研究,然而基于相关研究结果的基础上从动态运行性能需求以及结构参数改变对其的影响出发,为电磁轴承结构的优化与设计建立判据,更有利于高精度电磁轴承的设计与运行。同时,通过查阅相关文献了解到大部分电磁轴承的控制策略仍然采用线性控制策略。由于电流刚度系数和位移刚度系数是电磁轴承线性控制中最为关注的两个指标,因此,有必要研究分析励磁电流、气隙长度、结构参数对于电磁轴承支撑性能的影响。
本文首先研究不同结构参数时铁心材料非线性磁导率、磁极边缘效应、磁场透入深度等因素对电磁轴承磁场分布的影响规律,并在此基础上建立计及磁路分布特性的电磁轴承解析模型。然后,分别以构建的解析模型和有限元法对其结构与最大电磁力及气隙磁通密度的影响规律进行计算对比,同时通过搭建实验平台验证了解析模型的有效性和可靠性。最后,基于建立的解析模型,揭示不同定子极弧系数时,气隙长度、励磁电流等参数与电磁轴承支撑性能之间的规律。
由于NNSS磁极排布的异极励磁电磁轴承具有相邻磁极无磁场耦合的优势,更适合控制,应用范围更广泛[17]。故本文以8极NNSS磁极排布方式异极电磁轴承为例进行研究。由于电磁轴承的结构改变会对其磁路分布造成影响,所以首先需要分析其结构参数变化对磁路中各部分磁阻分布的影响。8极NNSS异极电磁轴承结构如图1所示。

图1 NNSS磁极排布径向电磁轴承结构
Fig.1 Schematic diagram of NNSS magnetic pole discharge radial AMB
图1中,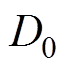 为定子内径,
为定子内径,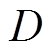 为定子外径,
为定子外径,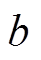 为磁极宽度,
为磁极宽度,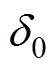 为气隙长度,
为气隙长度,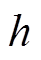 为磁轭厚度。由于在磁极排布为NNSS的定子铁心磁路中,磁通在磁极上流过的横截面积等于磁极面积。为了尽可能缩小尺寸,并且防止定子铁心发生局部磁饱和的情况,一般取磁轭厚度为
为磁轭厚度。由于在磁极排布为NNSS的定子铁心磁路中,磁通在磁极上流过的横截面积等于磁极面积。为了尽可能缩小尺寸,并且防止定子铁心发生局部磁饱和的情况,一般取磁轭厚度为
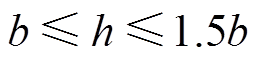 (1)
(1)
本文取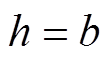 ,由于电磁轴承需要根据工况、使用场景等因素确定定子内、外径等基本参数。所以,直接使用磁极宽度这个变量不利于进行推广。本文定义定子磁极弧度之和与圆周弧度之比为电磁轴承的极弧系数。电磁轴承磁极宽度与定子内径关系如图2所示。
,由于电磁轴承需要根据工况、使用场景等因素确定定子内、外径等基本参数。所以,直接使用磁极宽度这个变量不利于进行推广。本文定义定子磁极弧度之和与圆周弧度之比为电磁轴承的极弧系数。电磁轴承磁极宽度与定子内径关系如图2所示。
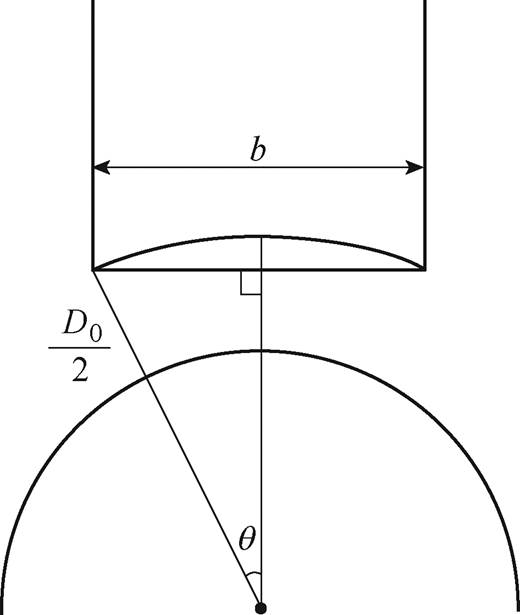
图2 电磁轴承磁极宽度与定子内径关系
Fig.2 Schematic diagram of relationship between magnetic pole width and stator inner diameter of electromagnetic bearing
图2中,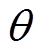 为定子磁极的弧度,结合图2的几何关系可知,单个磁极的弧度
为定子磁极的弧度,结合图2的几何关系可知,单个磁极的弧度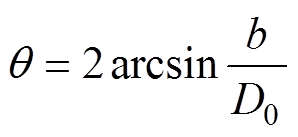 ,根据本文给出电磁轴承定子极弧系数的定义可得
,根据本文给出电磁轴承定子极弧系数的定义可得
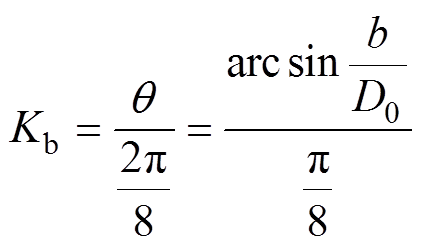 (2)
(2)
式中,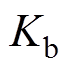 为定子极弧系数。
为定子极弧系数。
由于径向电磁轴承的轴向方向结构一致,故结合式(2)和图1的几何关系可以确定电磁轴承的磁极面积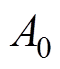 以及绕组腔面积
以及绕组腔面积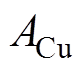 分别为
分别为
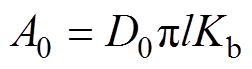 (3)
(3)
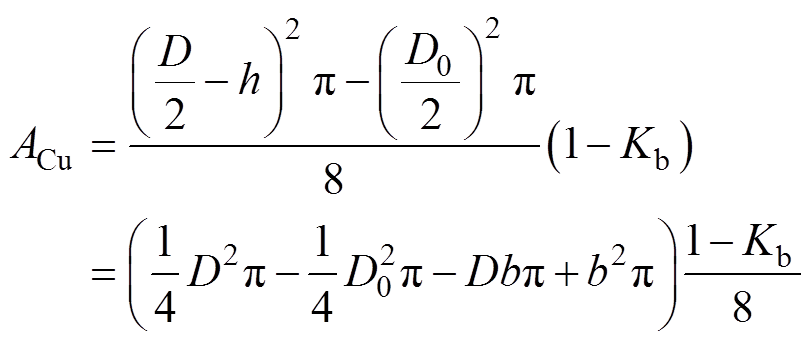 (4)
(4)
式中,l为轴向长度。
由电机设计理论[18]可知,绕组安匝数和绕组腔面积之间的关系为
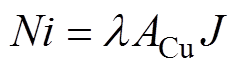 (5)
(5)
式中,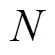 为定子绕组匝数;
为定子绕组匝数;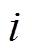 为定子绕组励磁电流;
为定子绕组励磁电流;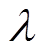 为槽满率;
为槽满率;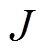 为电流密度。
为电流密度。
由于NNSS磁极排布的电磁轴承相邻的同极性磁极之间的轭部没有磁通流过,故其等效磁路如图3所示。
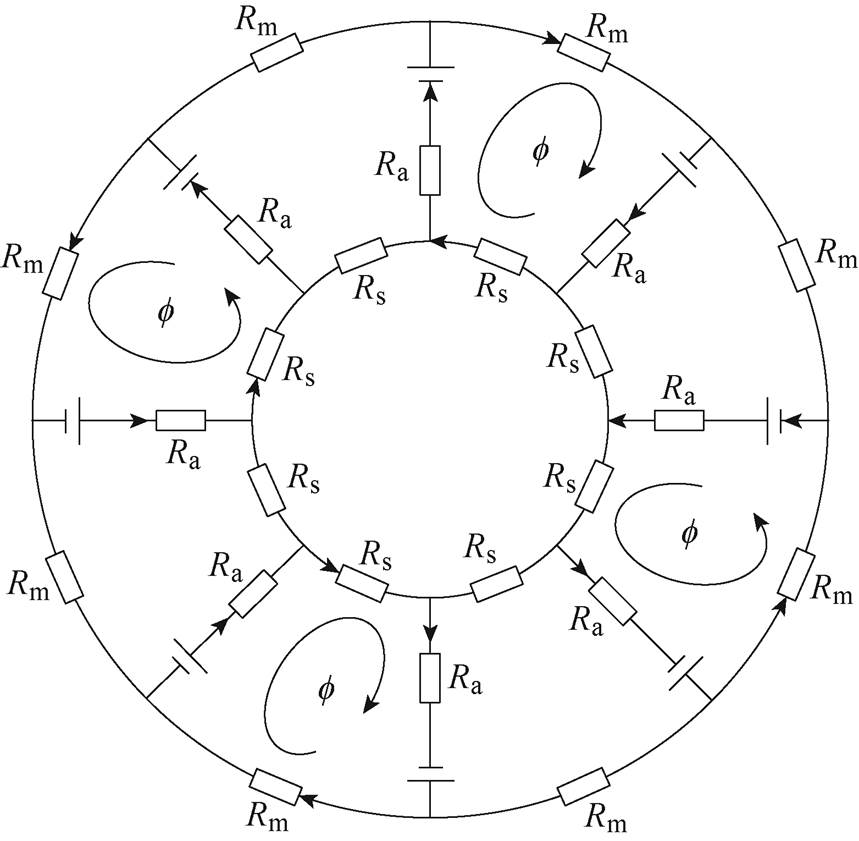
图3 NNSS磁极排布电磁轴承等效磁路
Fig.3 NNSS magnetic pole discharge of AMB equivalent magnetic circuit
以单一磁回路为研究对象,考虑到磁阻主要受到磁路中的磁导率、磁通流出面积以及磁路长度三个方面影响,本文按照磁路分布的特性,将主磁路分为三部分,即定子磁路段、气隙磁路段及转子磁路段。接下来将分别讨论结构参数变化对这三部分磁路分布的影响。
考虑到边缘效应对磁路分布的影响,文献[19]的磁场分割法,将气隙中磁通流过的体积分为7个部分,分别进行计算。气隙磁通分割模型如图4所示。
气隙中的磁导可以表示为
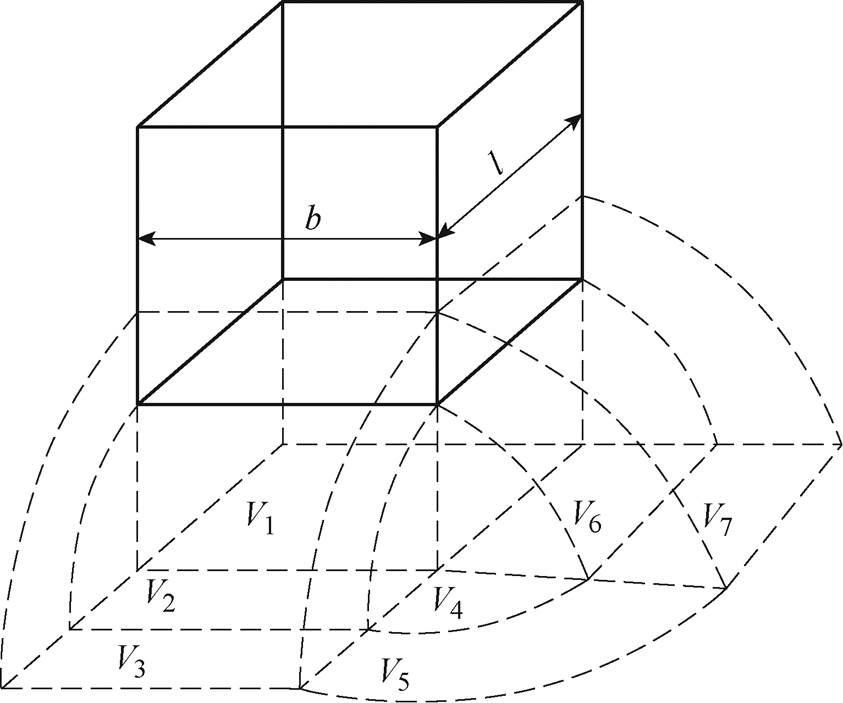
图4 气隙磁通分割模型
Fig.4 Air gap flux segmentation model
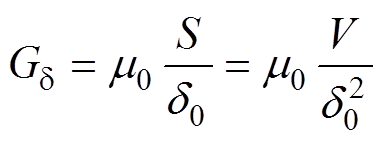 (6)
(6)
式中,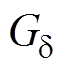 为气隙磁导;S为磁通流过的截面积;V为磁通流过立方体的体积;
为气隙磁导;S为磁通流过的截面积;V为磁通流过立方体的体积;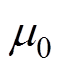 为空气的相对磁导率。
为空气的相对磁导率。
根据式(6)可以计算出图4中V1~V7各部分的磁导G1~G7分别为
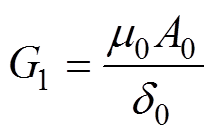 (7)
(7)
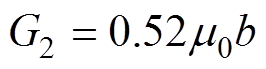 (8)
(8)
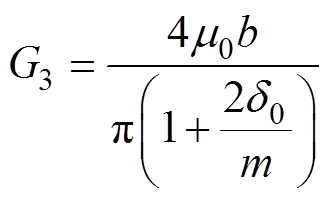 (9)
(9)
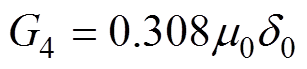 (10)
(10)
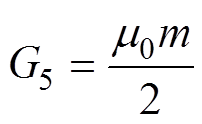 (11)
(11)
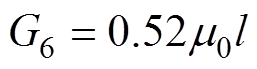 (12)
(12)
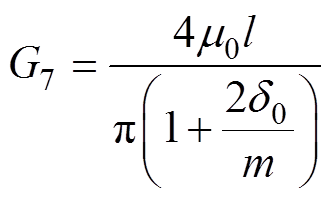 (13)
(13)
式中,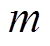 为边缘磁通沿磁极径向分布长度,一般取气隙长度的1~2倍,本文取2倍。
为边缘磁通沿磁极径向分布长度,一般取气隙长度的1~2倍,本文取2倍。
根据式(6)~式(13)可以得到单个磁极气隙总磁阻为
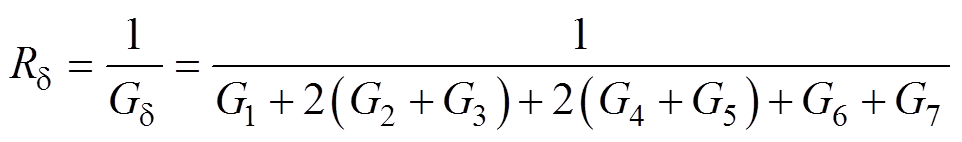 (14)
(14)
式中,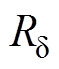 为单个磁极气隙磁阻。
为单个磁极气隙磁阻。
1.2.1 铁心材料B-H曲线拟合模型
考虑到铁心材料的非线性磁导率对磁路分布的影响,需要对铁心材料的B-H曲线进行拟合。
为了降低损耗,一般在加工时会通过热处理的方式在实心转子外侧套上一层硅钢片圆环。故为了简化计算,本文假设定子铁心以及转子磁路中铁心材料都为硅钢片。
本文选用的铁心材料为DW360_50硅钢片,数据通过Maxwell软件材料库提取,本文选用分段函数的形式作为拟合模型,得到的拟合模型为
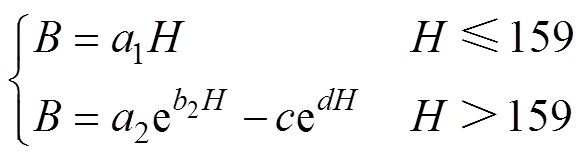 (15)
(15)
式中,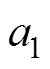 =0.006 9;
=0.006 9;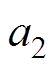 =1.405;
=1.405;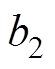 =4.374×10-5;
=4.374×10-5; = 0.779 8;d=0.005 77。
= 0.779 8;d=0.005 77。
DW360_50硅钢片磁化曲线及拟合曲线如图5所示。
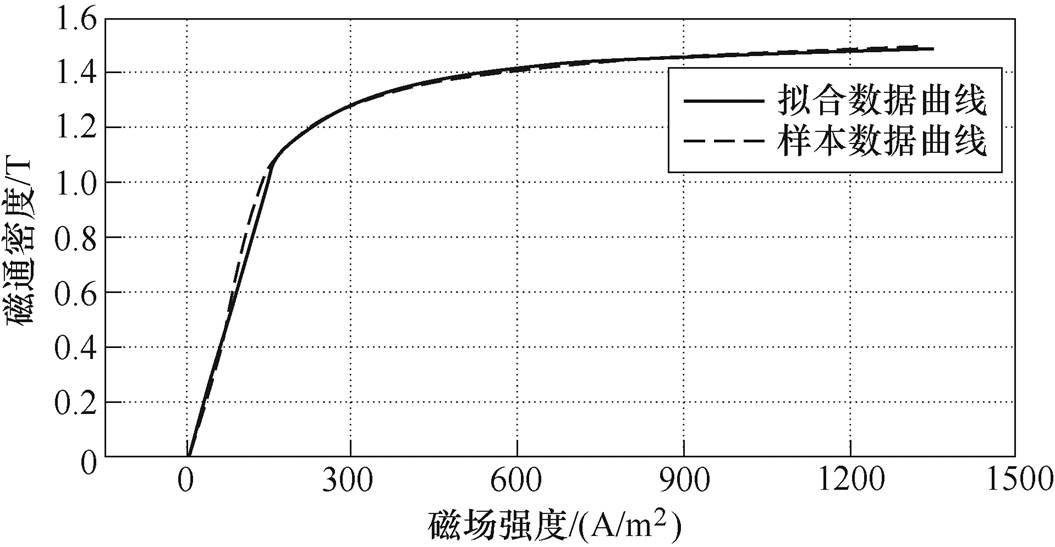
图5 DW360_50硅钢片磁化曲线及拟合曲线
Fig.5 DW360_50 magnetization curve and fit curves
1.2.2 铁心磁路磁阻计算
电磁轴承定、转子铁心结构示意图如图6所示。
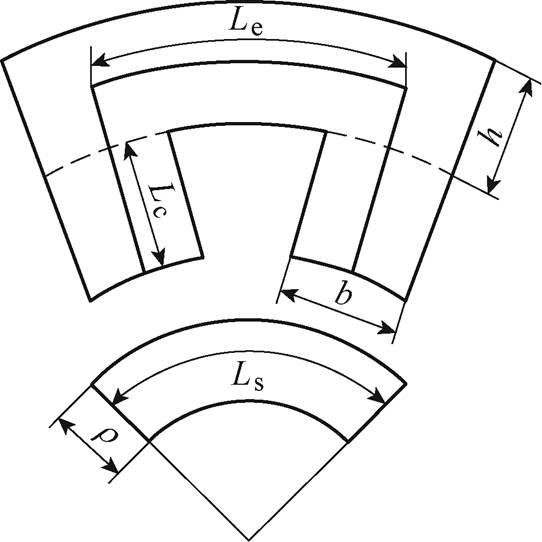
图6 定、转子铁心结构示意图
Fig.6 Schematic diagram of the structure of the rotor and the motor
假设铁心磁路中磁通分布处处均匀,铁心中磁路截面积都为磁极面积A,可得
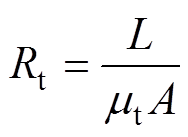 (16)
(16)
式中,Rt为磁路中铁心磁阻的总和;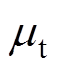 为铁心材料磁导率;L为磁路中铁心磁路的平均长度。
为铁心材料磁导率;L为磁路中铁心磁路的平均长度。
将整个铁心磁路分为定子齿、定子轭和转子三部分,如图6所示。可以分别计算出定子齿、轭部分的平均磁路长度分别为
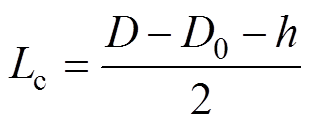 (17)
(17)
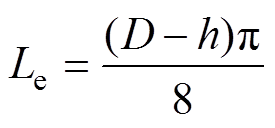 (18)
(18)
式中,Lc为定子齿部平均磁路长度;Le为定子轭部平均磁路长度。
定子齿、轭部分磁阻分别为
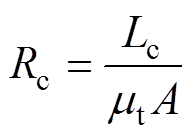 (19)
(19)
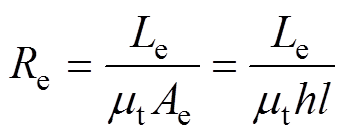 (20)
(20)
根据文献[20]的分析,可以知道,进入转子的磁场会受到其转速的影响,在时间上会产生交变,从而产生“涡流”,并且转子转速越高其磁场透入深度越低。超过透入深度的部分对于主磁路的影响会大大降低。故本文假设其透入深度等于磁路宽度 ,可得
,可得
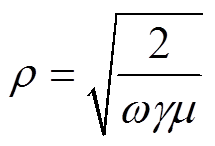 (21)
(21)
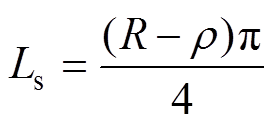 (22)
(22)
式中,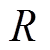 为转子外径;
为转子外径;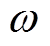 为旋转角速度;
为旋转角速度;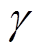 为铁心电导率;
为铁心电导率;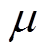 为铁心磁导率。
为铁心磁导率。
可以计算转子部分磁路铁心磁阻为
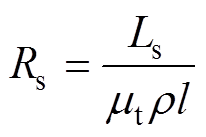 (23)
(23)
结合式(14)、式(19)、式(20)、式(23)可以计算出磁路中的磁通为
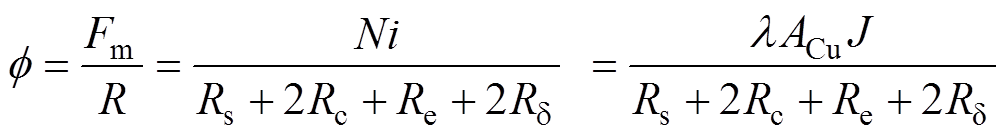 (24)
(24)
此时,磁极对应部分气隙磁通密度为
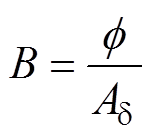 (25)
(25)
式中,Fm为磁回路中总磁压降;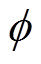 为磁路中的磁通;
为磁路中的磁通;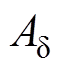 为单个磁极磁通流出面积。
为单个磁极磁通流出面积。
根据电磁张力计算的基本理论,可以得到单位周向长度的转子表面受到的径向电磁力Fr为
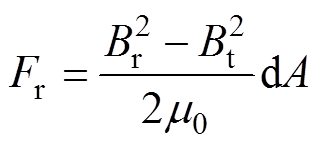 (26)
(26)
式中,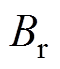 为转子受力表面接触的气隙中的径向磁通密度;
为转子受力表面接触的气隙中的径向磁通密度;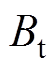 为转子受力表面接触的气隙中的切向磁通密度。
为转子受力表面接触的气隙中的切向磁通密度。
考虑到电磁轴承正常工作时切向磁通密度含量相比于径向磁通密度很小,设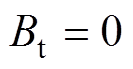 ,对式(26)在气隙中沿周向方向做积分计算可以得到单个磁极的电磁力计算公式为
,对式(26)在气隙中沿周向方向做积分计算可以得到单个磁极的电磁力计算公式为
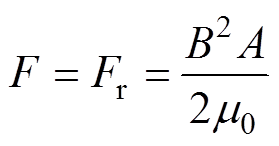 (27)
(27)
结合式(24)、式(25)可得转子受到的单个磁回路的电磁力为
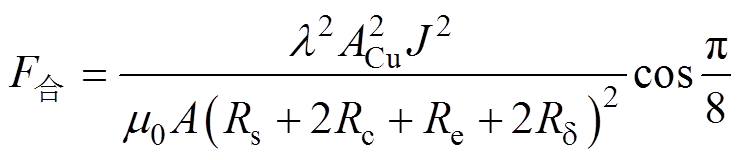 (28)
(28)
电磁力求解步骤如图7所示。
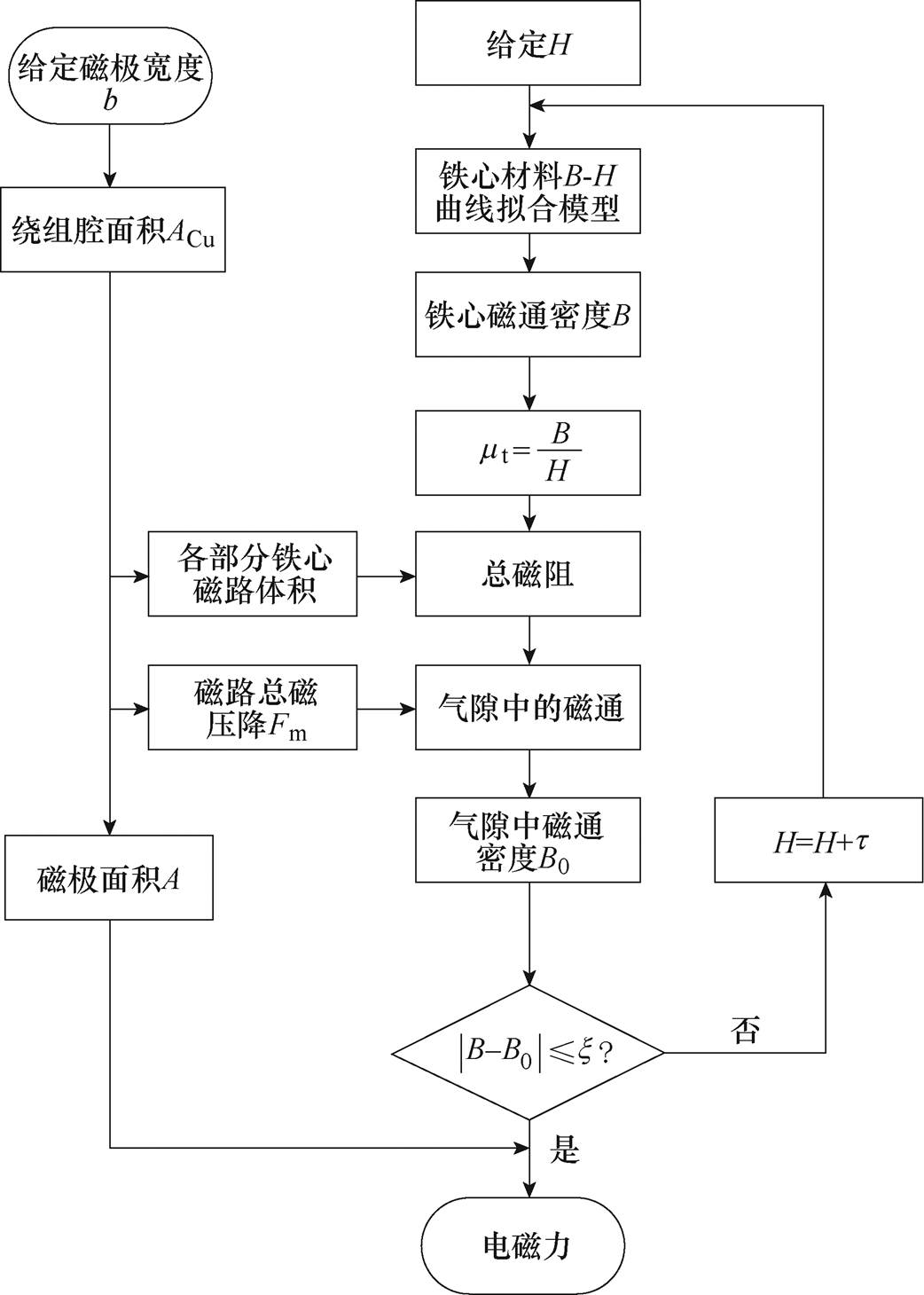
图7 电磁力求解步骤
Fig.7 Electromagnetic force to solve steps
图7中,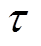 为迭代的磁动势,H为增加的步长,
为迭代的磁动势,H为增加的步长,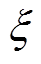 为磁通密度计算迭代的最大误差。由于定子不同结构时,影响其磁路分布的各个参数具有相互耦合的关系。为了准确计算不同结构时的磁通密度大小,本文通过结合最小二乘法参数辨识的思想进行求解。具体的求解步骤为给定初始磁极宽度b之后,可以确定电磁轴承的尺寸参数,从而可以确定该结构下磁路中的最大磁压降Fm。再给定一个较小的初始H代入铁心材料B-H曲线拟合模型,计算出B-H曲线上对应位置的铁心磁通密度B和铁心磁导率
为磁通密度计算迭代的最大误差。由于定子不同结构时,影响其磁路分布的各个参数具有相互耦合的关系。为了准确计算不同结构时的磁通密度大小,本文通过结合最小二乘法参数辨识的思想进行求解。具体的求解步骤为给定初始磁极宽度b之后,可以确定电磁轴承的尺寸参数,从而可以确定该结构下磁路中的最大磁压降Fm。再给定一个较小的初始H代入铁心材料B-H曲线拟合模型,计算出B-H曲线上对应位置的铁心磁通密度B和铁心磁导率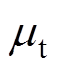 ,结合各部分铁心磁路的体积可以计算出磁路中的总磁阻情况。进而通过最大磁压降Fm便可以得到对应的气隙磁通密度B0。对于B和B0进行差值计算,如果其差值大于
,结合各部分铁心磁路的体积可以计算出磁路中的总磁阻情况。进而通过最大磁压降Fm便可以得到对应的气隙磁通密度B0。对于B和B0进行差值计算,如果其差值大于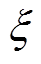 ,则将初始磁动势增加
,则将初始磁动势增加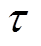 重新进行迭代计算;反之,结合计算出的此时磁极面积就可以求出此结构下的电磁力情况,结束迭代,然后计算下一个给定磁极宽度b。
重新进行迭代计算;反之,结合计算出的此时磁极面积就可以求出此结构下的电磁力情况,结束迭代,然后计算下一个给定磁极宽度b。
为了验证本文建立的等效磁路模型的准确性,通过有限元法,建立二维有限元模型如图8所示,径向电磁轴承具体参数见表1。
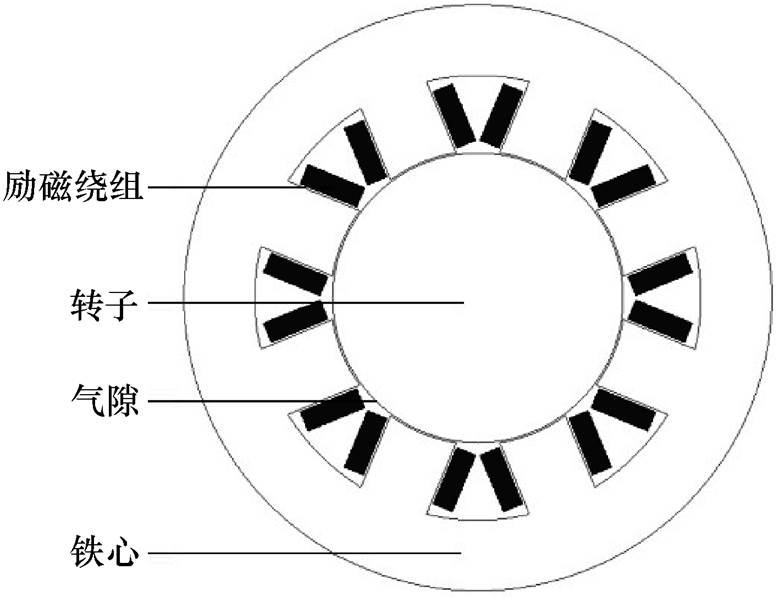
图8 径向电磁轴承有限元求解几何模型
Fig.8 Radial AMB finite element solving geometric model
表1 径向电磁轴承参数化模型参数
Tab.1 Radial AMB parameter modulation model parameters
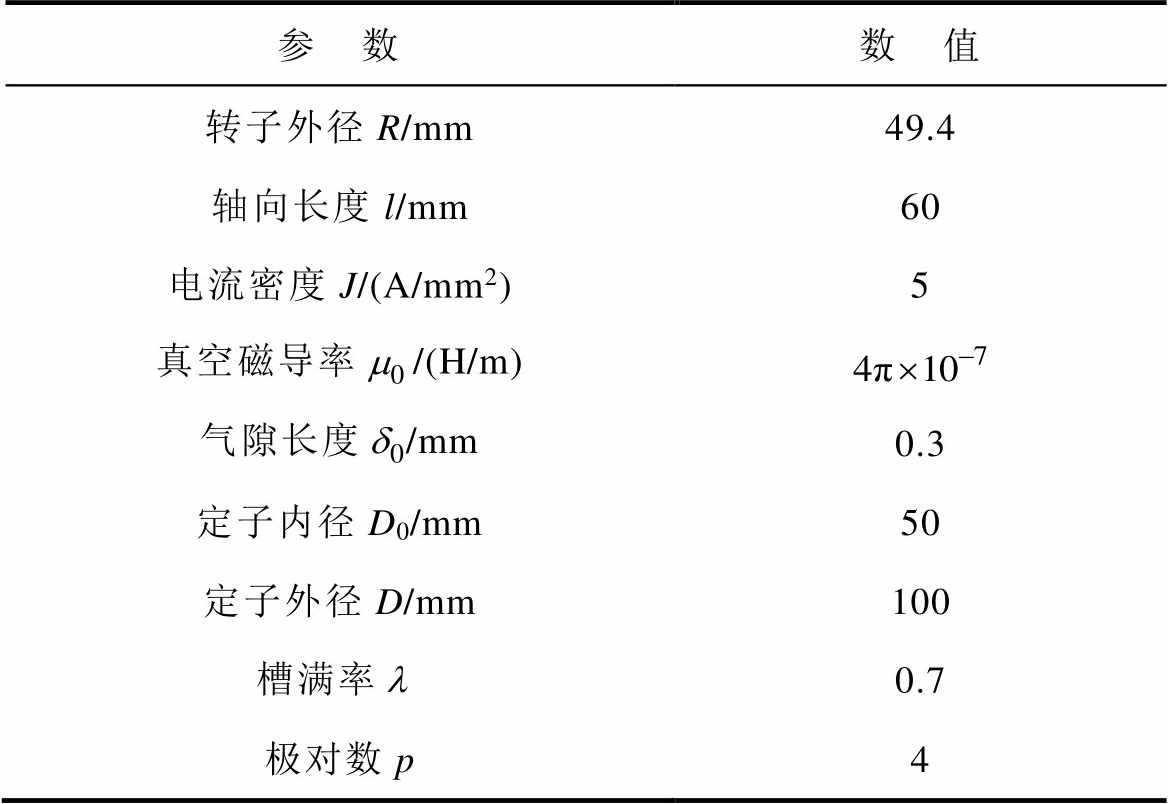
参 数数 值 转子外径R/mm49.4 轴向长度l/mm60 电流密度J/(A/mm2)5 真空磁导率/(H/m) 气隙长度/mm0.3 定子内径D0/mm50 定子外径D/mm100 槽满率0.7 极对数p4
本文提出的等效磁路模型的解析法与有限元法计算结果如图9所示。
分析图9可知,在极弧系数为0.2~0.8时,解析模型和有限元法计算结果吻合程度良好,规律完全一致,最大误差小于3.5 %,可以验证本文建立的解析模型的准确性。在极弧系数为0.1和0.9时,吻合程度相比于极弧系数0.2~0.8时有所下降。原因在于本文选用的是固定的磁通流出面积,导致在过大或过小极弧系数时,磁通流出面积会产生差距过大的问题。同时,由于槽间漏磁情况会随定子结构改变同样产生一定改变,对于气隙磁通密度的计算精度会造成一定的影响。
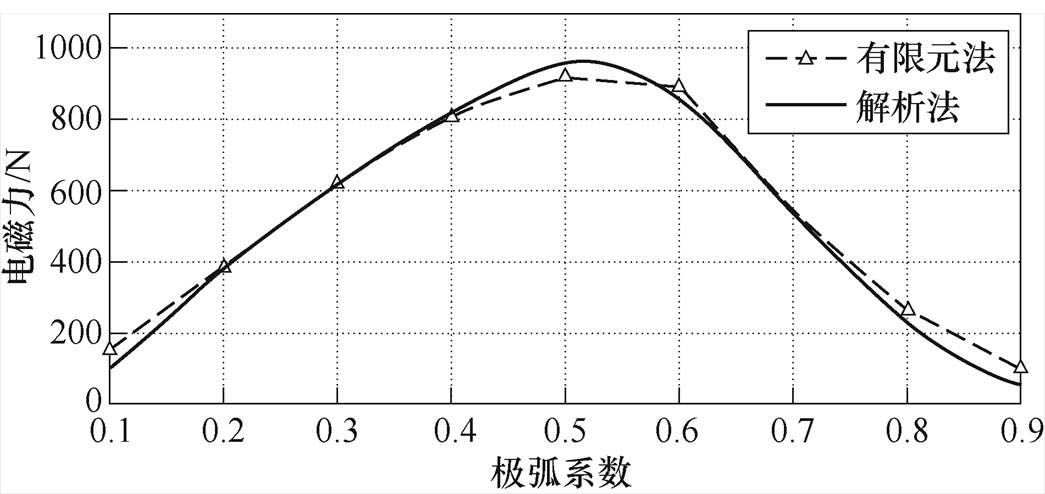
图9 不同极弧系数时最大电磁力对比
Fig.9 Maximum electromagnetic force comparison when different pole arc coefficients
通过有限元法计算的气隙径向磁通密度空间分布情况如图10所示。
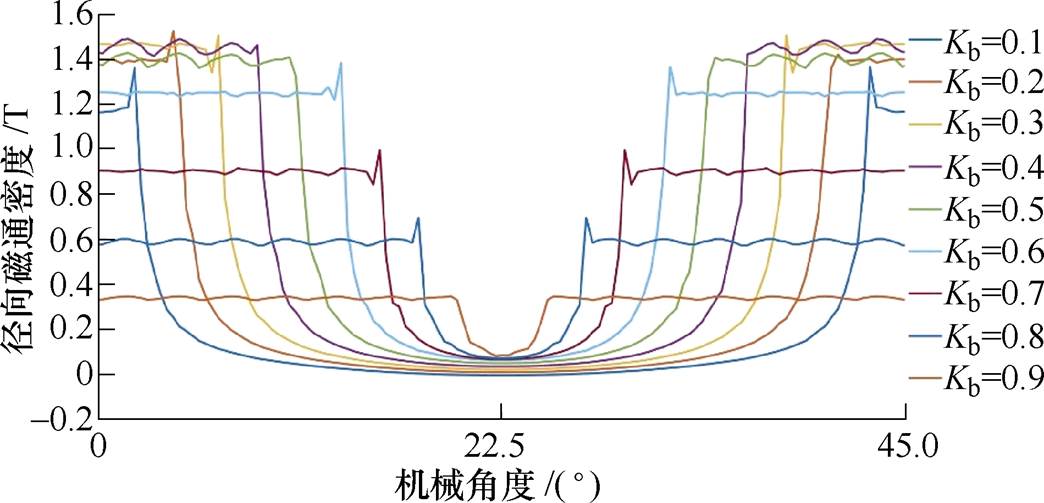
图10 气隙径向磁通密度空间分布情况
Fig.10 Air gap radial magnetic distribution of space
由图10可以看出,从磁极流出的磁通受到边缘效应影响很大,极弧系数越小其受到边缘效应影响越大,随着极弧系数变大其受到的边缘效应影响也随之变小。
不同极弧系数时气隙磁通密度幅值对比如图11所示。
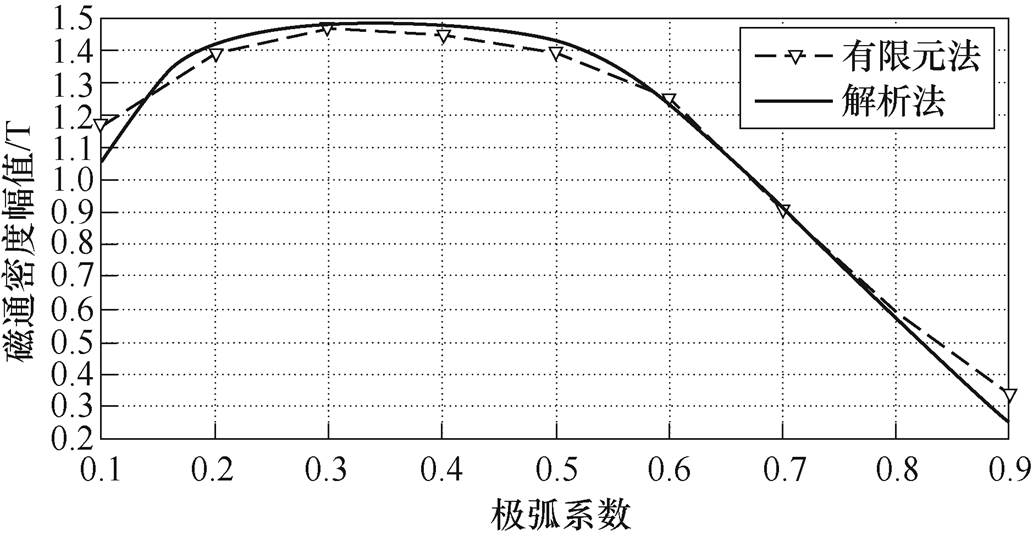
图11 不同极弧系数时气隙磁通密度幅值对比
Fig.11 Different polar arc coefficients of air gap magnetic amplitude value comparison
由图11可以看出,有限元法和解析法计算结果基本与图9分析一致,在极弧系数为0.2~0.8时,磁通密度解析模型计算准确度很高。虽然极弧系数为0.1和0.9时准确度有所下降,然而实际设计中很少选择如此极端的极弧系数。所以本文建立的解析模型的精度已经足够满足工程上初步的参数选择使用。
为了进一步对解析模型进行验证,本文选用定子外径150.5 mm,内径65.8 mm,轴向长度18.2 mm的8极NNSS异极电磁轴承搭建了实验平台进行实验验证,首先通过固定设备将高斯计探头部分固定于电磁轴承磁极表面的气隙中;然后通过可控电流源对一对NS磁极的励磁绕组抽头通入从0.5~3 A的电流进行励磁;最后观测不同励磁电流时的气隙磁通密度变化情况。电磁轴承样机实物结构以及搭建的实验平台分别如图12和图13所示。

图12 电磁轴承实物结构
Fig.12 Physical structure of electromagnetic bearing

图13 电磁轴承实验平台
Fig.13 Electromagnetic bearing experimental platform
图13中,实验使用的高斯计型号为YF80EXP,测量范围为0~2 000 mT;可控电流电源型号为HCP50-50,输出电压范围为0~50 V,输出电流范围为0~100 A。
通过上述实验平台测量不同励磁电流时其气隙磁通密度的变化情况,实验结果如图14所示。
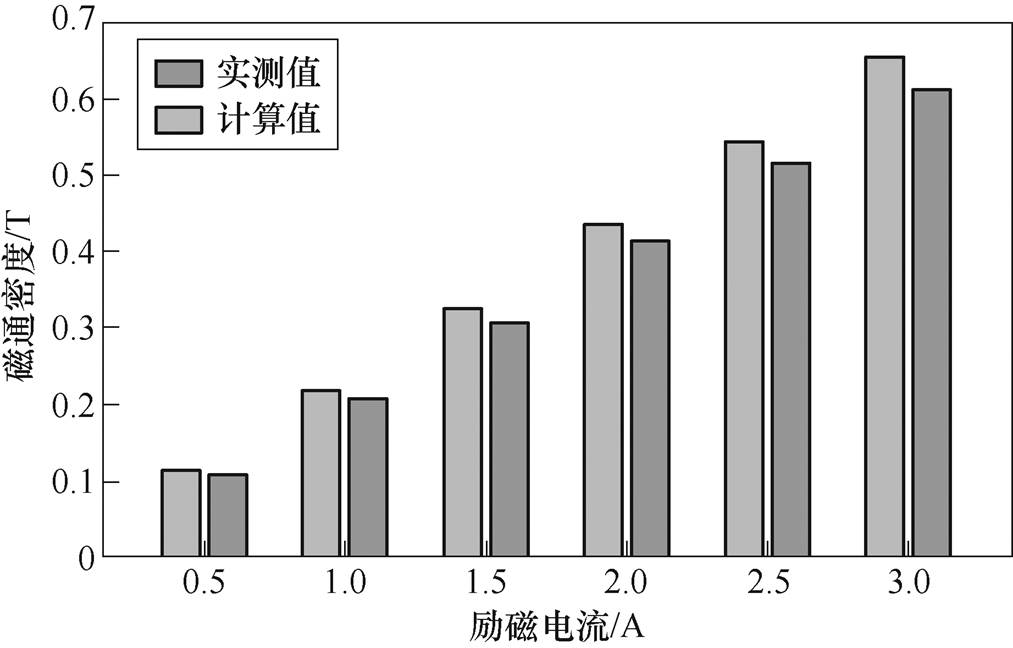
图14 不同励磁电流时解析计算结果与实验结果对比
Fig.14 Comparison between analytical calculation results and experimental results under different excitation currents
分析图14可以发现,实测值和解析计算结果基本一致,吻合度较高,可以验证本文提出的解析模型计算结果与实验测试结果的一致性,满足工程要求,足以验证该解析模型的有效性。由于测量设备精度、测量点、加工工艺、漏磁等因素都会对实验测量的结果造成一定的影响,所以导致实验结果与解析计算结果产生了一定误差。
由于目前PID控制这类线性控制器仍然广泛应用于电磁轴承控制,但是PID控制存在非线性段控制效果不佳,严重时会出现发散不收敛的情况[21];故为了提高PID控制这类线性控制器对电磁轴承控制时的灵敏性及可靠性,需要对于电磁轴承电流刚度系数与位移刚度系数非线性特性规律及其影响因素进行深入研究。故本文将基于构建的电磁轴承解析模型,讨论极弧系数、气隙长度、励磁电流等参数对电磁轴承电磁力非线性特性的影响规律。
本文通过建立的解析模型计算不同极弧系数时,不同励磁电流下的气隙、铁心磁阻与总磁阻的比值。计算结果如图15、图16所示。
分析图15、图16可知,在极弧系数不变时,由于受到铁心材料非线性磁导率的影响,随着励磁电流的增大,铁心磁阻占比开始变大,气隙磁阻占比逐渐减小。
另一方面,由于极弧系数改变会影响到磁路中铁心部分与气隙部分的体积,在励磁电流不变时,随着极弧系数变大,铁心磁阻占比以对数函数形式上升,气隙磁阻占比相应下降。
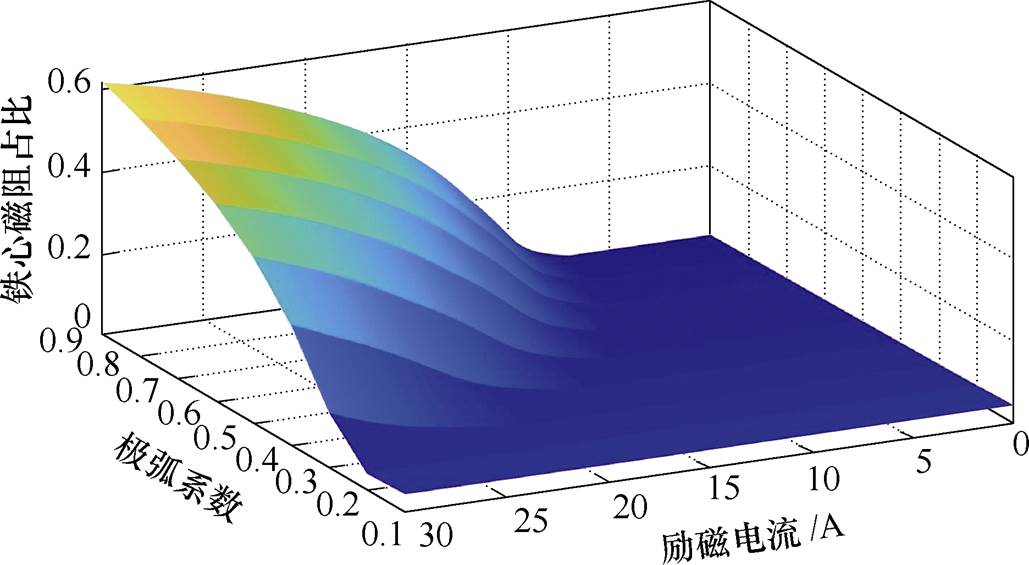
图15 励磁电流、极弧系数及铁心磁阻占比的三维关系
Fig.15 Three-dimensional relationship diagram of excitation current, pole arc coefficient, and iron magnetic implantation
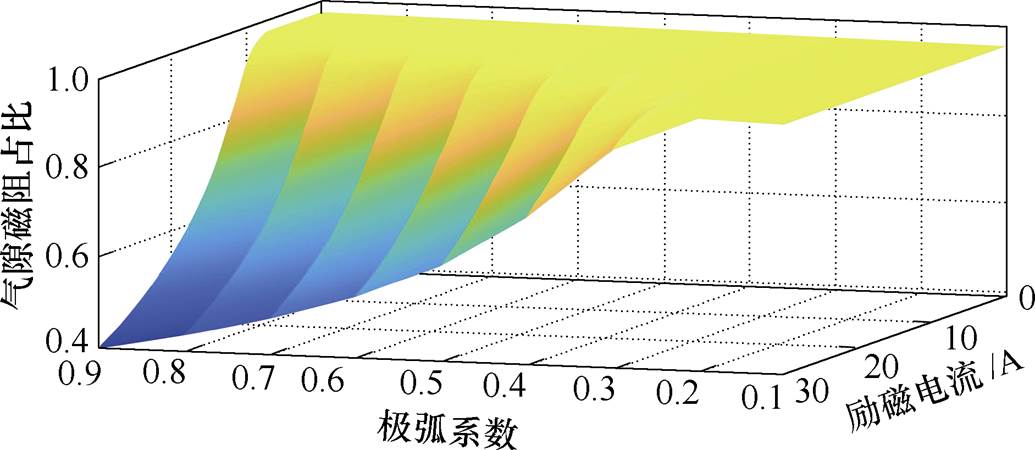
图16 励磁电流、极弧系数及气隙磁阻占比的三维关系
Fig.16 Three-dimensional relationship diagram of excitation current, pole arc coefficient, and air gap magnetic blocker
励磁电流、极弧系数以及气隙磁通密度的三维关系如图17所示。
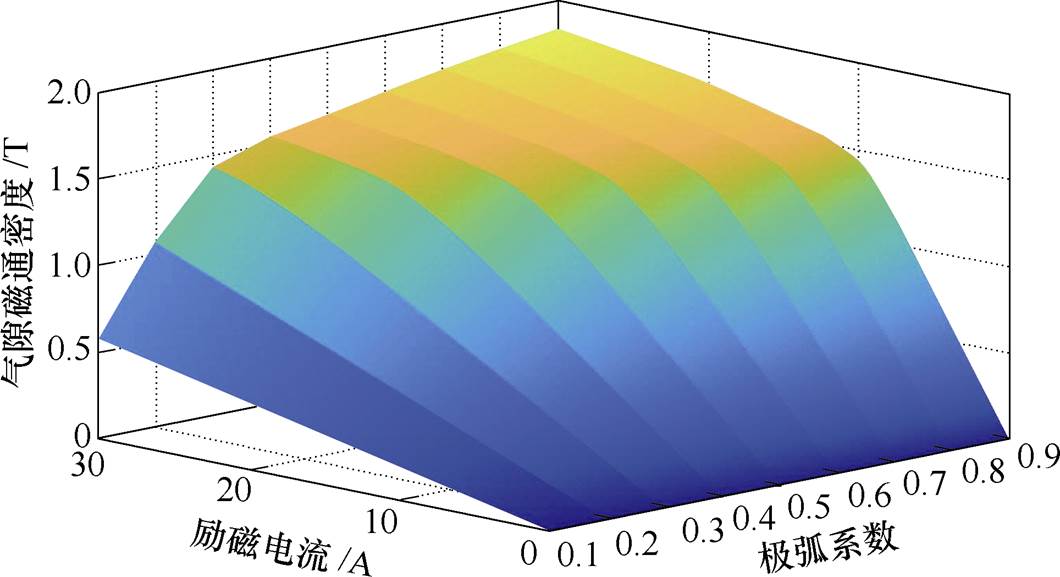
图17 励磁电流、极弧系数及气隙磁通密度的三维关系
Fig.17 Three-dimensional relationship diagram of excitation current, pole arc coefficient, and air gap magnetic tester
通过对图17进行分析,可以看到,在同一极弧系数时,电磁轴承的励磁电流与气隙磁通密度之间的变化规律仍然与铁心材料的磁化曲线保持一致。另外,由于极弧系数改变会导致磁路中的磁阻占比情况发生变化,随着极弧系数增大,达到“膝点”所需的励磁电流逐渐减小,“膝点”对应位置的磁通密度在以微小的趋势减小。
励磁电流、极弧系数及电磁力的三维关系如图18所示。
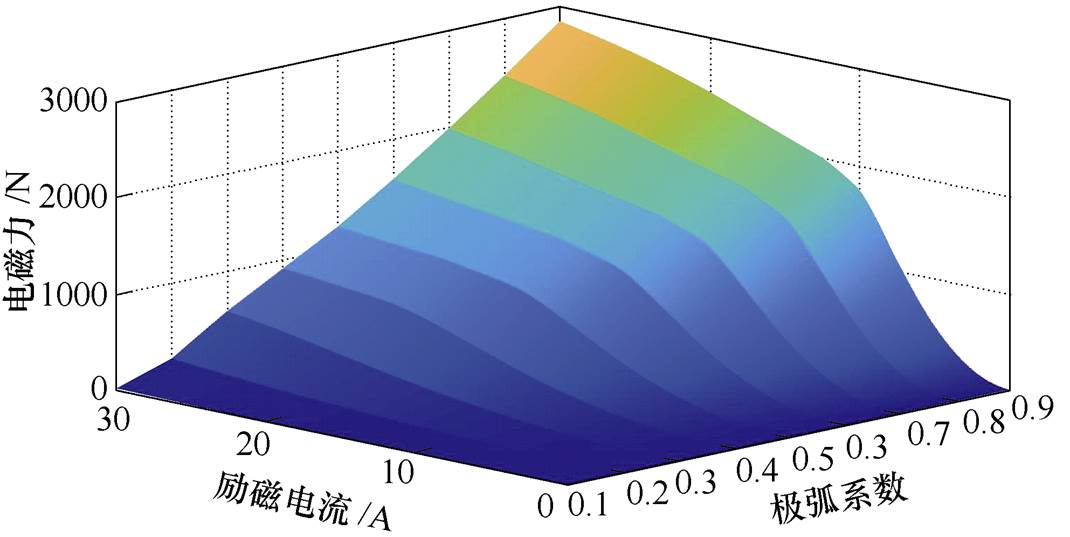
图18 励磁电流、极弧系数及电磁力的三维关系
Fig.18 Three-dimensional relationship diagram of excitation current, pole arc coefficient, and electromagnetic force
由于随着极弧系数的增大,导致磁极面积随之改变,分析图18可以发现,在极弧系数变大的同时,不仅达到“膝点”所需的励磁电流变小,而且“膝点”位置的电磁力在不断变大。
另一方面,由于磁通密度与电磁力为二次方关系,所以在非线性特征较强的“饱和段”气隙磁通密度则会令电磁力的非线性特征表现得更为突出。同时,随着极弧系数增大,磁路中铁心磁阻占比升高,该部分的非线性特征也会变得更为严重。由于电磁轴承运行时会受到外部干扰或者转子高速旋转产生的离心力的影响,令其产生偏心的情况[22]。此时需要增大励磁电流,可能导致其短时间触碰到“饱和段”,所以对于“饱和段”附近的影响也需要进行一定关注。
为了排除励磁电流对位移刚度系数影响,本文将基于3.1节分析极弧系数为0.9时的欠饱和部分的励磁电流进一步讨论,以保证不会由于过激励出现磁饱和的情况。另一方面,本文假设转子处于定子圆心处静态运行时气隙为0.3 mm,所以选择0.3~0.55 mm的气隙长度进行分析,模拟其偏心时的单个磁回路的各项参数的变化情况。不同气隙长度和极弧系数下的铁心、气隙磁阻与总磁阻的比值的计算结果如图19、图20所示。
分析图19、图20可得,在极弧系数不变时,随着气隙长度逐渐加大,其铁心磁阻占比随之减小,气隙磁阻占比逐渐增大。另一方面,在气隙长度不变时,随着极弧系数增大,气隙磁阻占比呈现先增大后减小的趋势。
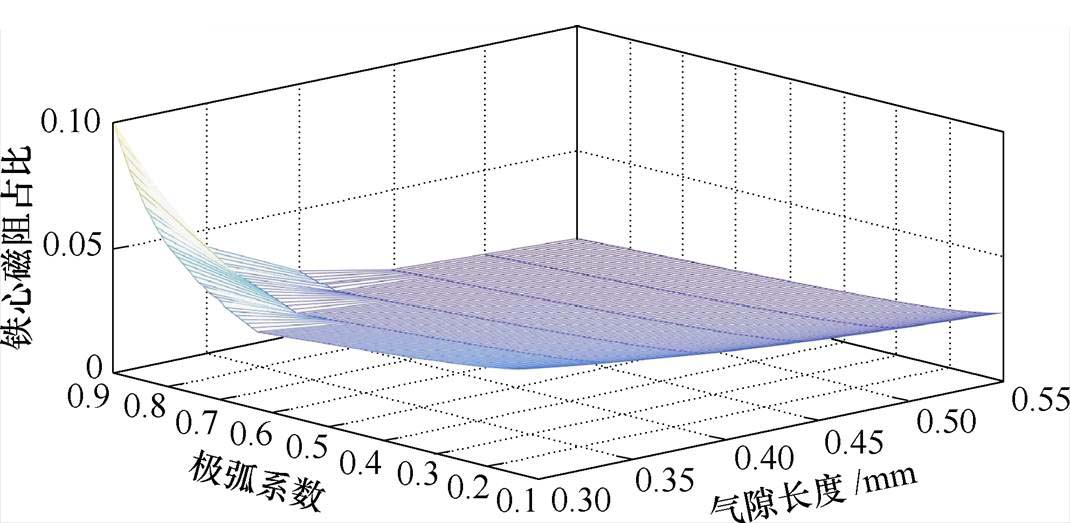
图19 气隙长度、极弧系数及铁心磁阻占比的三维关系
Fig.19 Three-dimensional relationship diagram of air gap length, pole arc coefficient, and iron magnetic implantation
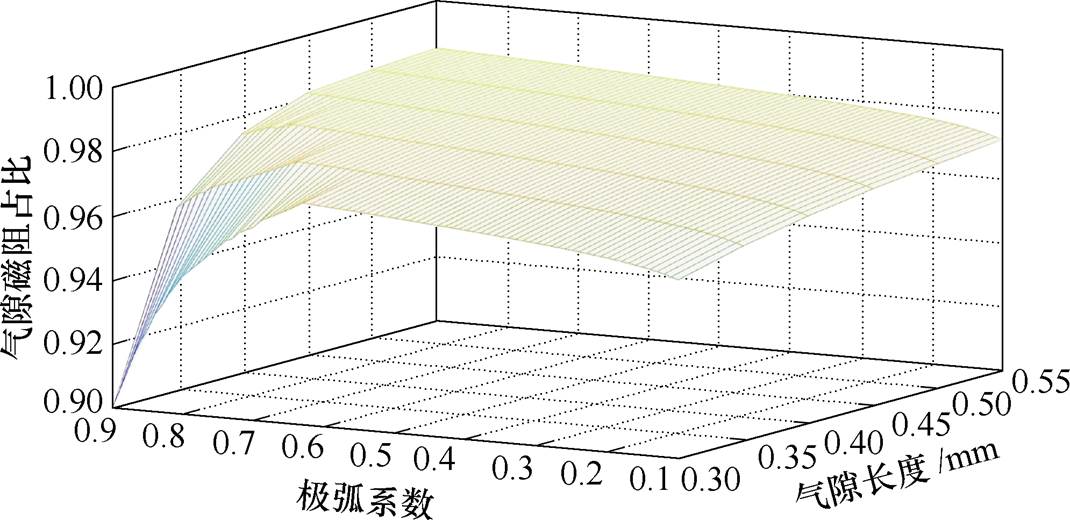
图20 气隙长度、极弧系数及气隙磁阻占比的三维关系
Fig.20 Three-dimensional relationship diagram of air gap length, pole arc coefficient, and air gap magnetic blocker
同时可以看出,在极弧系数减小到约为0.6时,气隙磁阻占比基本已经达到最大处。在极弧系数小于0.6以后,随着气隙长度改变,气隙和铁心磁阻占比情况与气隙长度之间的规律基本保持不变。气隙长度、极弧系数及气隙磁通密度的三维关系如图21所示。
从图21中可以看出,随着极弧系数变大,气隙长度与气隙磁通密度的线性度逐渐变差。同时结合图19、图20可以看出,气隙磁通密度和气隙长度线性度较差的部分都是铁心磁阻占比较高的部分。可以分析影响气隙长度和最大气隙磁通密度之间线性度的主要因素是铁心磁阻占比。铁心磁阻占比越高,气隙长度与气隙磁通密度之间的线性度越差。气隙磁阻占比越高,其气隙长度与气隙磁通密度之间的线性度越好。气隙长度、极弧系数及电磁力的三维关系如图22所示。
通过图22可以看出,在极弧系数为0.9时,气隙长度与电磁力之间非线性特征十分明显,在极弧系数逐渐变小的过程中气隙长度与电磁力之间线性度在逐渐变好。
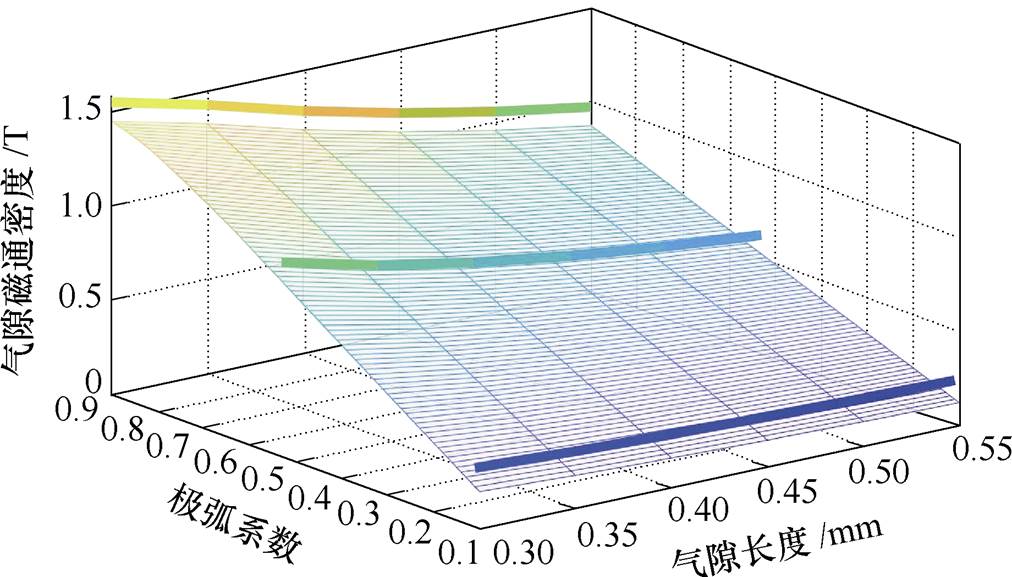
图21 气隙长度、极弧系数及气隙磁通密度的三维关系
Fig.21 Three-dimensional relationship diagram of air gap length, pole arc coefficient, and air gap magnetic flux density
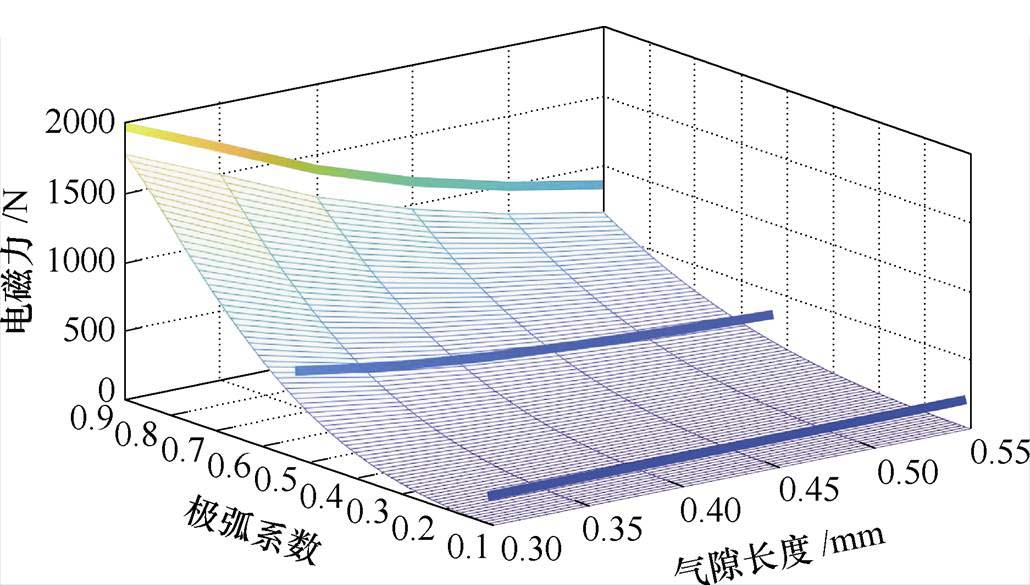
图22 气隙长度、极弧系数及电磁力的三维关系
Fig.22 Three-dimensional relationship diagram of air gap length, pole arc coefficient, and electromagnetic force
另外,虽然本文中计算的转子偏心0.25 mm时铁心磁阻占比仅为4 %左右,但是实际运行中需要考虑到励磁电流改变导致的磁路中磁阻占比情况。所以在偏心状态下,磁路中铁心磁阻占比相比于图中展示的更高,进而导致电磁力的非线性特征加剧。
通过将图18、图22与文献[23]进行的固定结构的电磁轴承实验结果进行对比,发现规律一致。可以验证本文对于不同结构下,电磁轴承位移刚度系数与电流刚度系数分析的有效性。
本文从研究径向电磁轴承结构变化对各部分磁阻的影响入手,建立了计及磁路分布特性的电磁轴承解析模型,通过有限元法进行计算对比,发现其最大误差小于3.5 %,吻合程度好,可以验证解析模型的准确性,相比于常规的线性解析模型,其计算准确度更高。同时通过与实验结果进行对比,可以发现,解析模型完全可以满足工程需要。通过构建的解析模型定子极弧系数、励磁电流、气隙长度对电磁轴承支撑性能进行分析得到了以下结论:
1)在保证径向电磁轴承定子内、外径以及轴向长度不变的情况下,随着极弧系数变大,其铁心磁阻的占比升高。由于磁通密度与电磁力是二次方关系,导致对电流刚度系数和位移刚度系数的非线性程度影响明显变大。
2)在设计电磁轴承时,在保证其最大承载能力的前提下,应该尽可能地选取气隙磁阻占比较高的磁路结构,以削弱电流刚度系数与位移刚度系数的非线性特征。
本文的研究成果可以为径向结构电磁轴承的设计及运行控制提供理论参考。
参考文献
[1] 周天豪, 陈磊, 祝长生, 等. 基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J]. 电工技术学报, 2020, 35(9): 1900-1911.
Zhou Tianhao, Chen Lei, Zhu Changsheng, et al. Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1900- 1911.
[2] 巩磊, 杨智, 祝长生, 等. 基于极性切换自适应陷波器的磁悬浮高速电机刚性转子自动平衡[J]. 电工技术学报, 2020, 35(7): 1410-1421.
Gong Lei, Yang Zhi, Zhu Changsheng, et al. Automatic balancing for rigid rotor of magnetically levitated high-speed motors based on adaptive Notch filter with polarity switching[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1410- 1421.
[3] 张维煜, 朱熀秋, 鞠金涛, 等. 磁悬浮轴承研究现状及其发展[J]. 轴承, 2016(12): 56-63.
Zhang Weiyu, Zhu Huangqiu, Ju Jintao, et al. Research status and development of magnetic bearings[J]. Bearing, 2016(12): 56-63.
[4] 李万杰, 张国民, 王新文, 等. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(增刊1): 10-18.
Li Wanjie, Zhang Guomin, Wang Xinwen, et al. Integration design of high-temperature supercondu- cting bearing and electromagnetic thrust bearing for flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 10-18.
[5] 孙玉坤, 郭帅坡, 杨帆. 飞轮储能用混合磁悬浮轴承温度场分析[J]. 电机与控制应用, 2019, 46(8): 76-81.
Sun Yukun, Guo Shuaipo, Yang Fan. Temperature field analysis of hybrid magnetic bearings for flywheel energy storage[J]. Electric Machines & Control Application, 2019, 46(8): 76-81.
[6] 周瑾, 高天宇, 董继勇, 等. 基于Isight的径向磁悬浮轴承结构优化设计[J]. 轴承, 2018(7): 6-11.
Zhou Jin, Gao Tianyu, Dong Jiyong, et al. Optimal design for structure of radial magnetic bearings based on Isight[J]. Bearing, 2018(7): 6-11.
[7] 白文鑫, 刘文韬. 基于遗传算法的零偏置磁轴承定子结构优化[J]. 机械工程与自动化, 2019(4): 31-34.
Bai Wenxin, Liu Wentao. Structure optimization of zero bias magnetic bearing stator based on genetic algorithm[J]. Mechanical Engineering & Automation, 2019(4): 31-34.
[8] 林子豪, 胡业发, 冉少林, 等. 3自由度混合磁轴承支承特性及仿真分析[J]. 机械设计与研究, 2019, 35(5): 32-35, 40.
Lin Zihao, Hu Yefa, Ran Shaolin, et al. Simulation study on supporting characteristics of three-DOF hybrid magnetic bearings[J]. Machine Design & Research, 2019, 35(5): 32-35, 40.
[9] Shakibapour F, Rahideh A, Mardaneh M. 2D analytical model for heteropolar active magnetic bearings considering eccentricity[J]. IET Electric Power Applications, 2018, 12(5): 614-626.
[10] 张云鹏, 刘淑琴, 李红伟, 等. 基于磁路分析的轴向混合磁轴承径向承载力解析计算[J]. 电工技术学报, 2012, 27(5): 137-142.
Zhang Yunpeng, Liu Shuqin, Li Hongwei, et al. Calculation of radial electromagnetic force of axial hybrid magnetic bearing based on magnetic circuit analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 137-142.
[11] Romanenko A, Smirnov A, Jastrzebski R P, et al. Losses estimation and modelling in active magnetic bearings[C]//2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 2014: 1-8.
[12] Le Yun, Fang Jiancheng, Wang Kun. Design and opti- mization of a radial magnetic bearing for high-speed motor with flexible rotor[J]. IEEE Transactions on Magnetics, 2015, 51(6): 1-13.
[13] 张云鹏, 薛博文, 刘淑琴, 等. 基于气隙磁通边缘效应的轴向混合磁轴承承载力解析计算[J]. 电机与控制学报, 2014, 18(9): 54-59, 67.
Zhang Yunpeng, Xue Bowen, Liu Shuqin, et al. Calculation of electromagnetic force of axial hybrid magnetic bearing based on fringe effect of magnetic flux[J]. Electric Machines and Control, 2014, 18(9): 54-59, 67.
[14] 朱熀秋, 丁书玲. 计及边缘效应的交流混合磁轴承建模[J]. 中国电机工程学报, 2016, 36(23): 6528- 6535, 6620.
Zhu Huangqiu, Ding Shuling. Modeling for AC hybrid magnetic bearings considering edge effect[J]. Proceedings of the CSEE, 2016, 36(23): 6528-6535, 6620.
[15] 禹春敏, 邓智泉, 梅磊, 等. 基于精确磁路的新型混合型轴向-径向磁悬浮轴承研究[J]. 电工技术学报, 2021, 36(6): 1219-1228.
Yu Chunmin, Deng Zhiquan, Mei Lei, et al. Research of new hybrid axial-radial magnetic bearing based on accurate magnetic circuit[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1219-1228.
[16] 叶品州, 李红伟, 于文涛, 等. 考虑材料非线性及涡流影响的径向电磁轴承等效磁路建模[J]. 电工技术学报, 2020, 35(9): 1858-1867.
Ye Pinzhou, Li Hongwei, Yu Wentao, et al. Equivalent magnetic circuit modeling of radial active magnetic bearing considering material nonlinearity and eddy current effects[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1858-1867.
[17] 丁国平, 胡业发, 周祖德. 径向磁力轴承磁极布置对磁场和磁力的影响[J]. 中国机械工程, 2008, 19(19): 2364-2367.
Ding Guoping, Hu Yefa, Zhou Zude. Efeects of magnetic pole arrangement on magnetic field and force in radial magnetic bearings[J]. China Mechani- cal Engineering, 2008, 19(19): 2364-2367.
[18] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 1982.
[19] 林其壬, 赵佑民. 磁路设计原理[M]. 北京: 机械工业出版社, 1987.
[20] 汪忠林. 主动磁悬浮轴承电磁场分析及涡流功耗研究[D]. 山东: 山东大学, 2009.
[21] 施佳余, 吴国庆, 茅靖峰, 等. 磁悬浮轴承系统控制方法研究[J]. 机械设计与制造, 2015(12): 265- 268.
Shi Jiayu, Wu Guoqing, Mao Jingfeng, et al. Research of magnetic bearing system control method[J]. Machinery Design & Manufacture, 2015(12): 265- 268.
[22] Sun Hongbo, Jiang Dong, Yang Jichang. Synchronous vibration suppression of magnetic bearing systems without angular sensors[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 70-77.
[23] 任正义, 杨立平, 聂发廷, 等. 大承载力径向电磁轴承的建模设计与分析[J]. 机床与液压, 2019, 47(13): 70-75.
Ren Zhengyi, Yang Liping, Nie Fating, et al. Modeling design and analysis of radial active magnetic bearings with large bearing capacity[J]. Machine Tool & Hydraulics, 2019, 47(13): 70-75.
Abstract Active magnetic bearing (AMB) has been widely used due to its advantages of no friction, controllable damping, and long service life. Currently, the research on the magnetic field distribution of AMB mainly focus on the performance characteristics of its fixed structure. It is necessary to establish an optimization and design judgment for the structure of the electromagnetic bearing based on the dynamic operation performance requirements and the influence of the structure according to relevant research results. Therefore, this paper proposes an accurate magnetic circuit analytical model of AMB considering the magnetic circuit distribution characteristics to analyze the influence of its structure on the AMB performance.
Firstly, the concept of “pole arc coefficient” of motor design is introduced to define the stator structure of AMB, and the formula for pole area, winding area, and ampere turns by pole arc coefficient is defined. Secondly, the magnetic resistance of the air gap, stator, and rotor is calculated by considering the nonlinear permeability of core material, pole edge effect, magnetic field penetration depth, and other factors. Finally, a method to establish the electromagnetic force calculation model of AMB with different structures is proposed based on Maxwell's tension method.
In order to verify the proposed analytical model, the corresponding two-dimensional finite element model is established to compare with the analytical model in terms of the air gap magnetic density and radial electromagnetic force. The calculation results of the two methods are entirely consistent, and the maximum error is less than 3.5 %. On the other hand, a corresponding experimental platform has been built to verify the accuracy of the model. It is verified that the analytical model can meet the engineering requirements.
The linear control strategy has a poor control effect on the current stiffness coefficient and displacement stiffness coefficient of AMB in the nonlinear section. Through the established analytical model, the influence of the pole arc coefficient, air gap length, excitation current and other parameters on the electromagnetic force of AMB are studied. Then, suggestions for the optimal design of the AMB are given.
The following conclusions can be drawn from this study: (1) Under the condition that the inner diameter, outer diameter, and axial length of the AMB stator remain unchanged, the proportion of the core magnetic resistance increases with the increase of the pole arc coefficient. Because the magnetic density is square with the electromagnetic force, the influence of the pole arc coefficient on the nonlinear degree of current stiffness coefficient and displacement stiffness coefficient becomes more apparent. (2) In designing AMB, ensuring its maximum load capacity, the magnetic circuit structure with high air gap magnetic resistance should be selected as far as possible to weaken the nonlinear characteristics of the current stiffness coefficient and displacement stiffness coefficient.
keywords:Active magnetic bearing (AMB), analytical model, magnetic circuit distribution, supply performance
DOI: 10.19595/j.cnki.1000-6753.tces.220203
中图分类号:TM14
国家自然科学基金资助项目(51777048)。
收稿日期 2022-02-15
改稿日期 2022-03-15
戈宝军 男,1960年生,博士,教授,博士生导师,研究方向为大电机与特种电机。E-mail: gebj@hrbust. edu. cn(通信作者)
杨子豪 男,1994年生,博士研究生,研究方向为电磁轴承电磁设计及控制。E-mail: 740206989@qq.com
(编辑 崔文静)