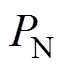可表示为摘要 换流变压器直流偏磁状态下油箱涡流损耗会大幅增加，导致变压器温度升高，威胁其安全稳定运行，因此快速评估直流偏磁下油箱涡流损耗的大小就显得十分必要。该文首先分析了换流变压器在额定和空载直流偏磁状态下油箱表面漏磁场的分布特点。再结合实际换流变压器非线性负载电流和励磁电流波形，得到了不同换流器触发角和直流电流下油箱涡流损耗的变化规律。并在IEC/IEEE 60076-57-129标准的基础上，给出了换流变压器直流偏磁状态下油箱涡流损耗的计算公式。针对一台800 kV单相四柱式换流变压器，利用场路耦合法进行油箱涡流损耗有限元计算。通过对损耗仿真数值以及油箱表面磁通密度和涡流损耗分布的分析，验证了理论分析的正确性，并获得了不同工况下，计算公式中的损耗占比值。利用不同属性的线性负载替代换流器触发角的变化，对两台单相四柱式380 V交流变压器进行了直流偏磁实验，进一步验证了理论分析的正确性。
关键词：直流偏磁 换流变压器 换流器触发角 油箱涡流损耗
变压器油箱由于表面积大和磁导率高等特点，其损耗很大，是结构件损耗的主要组成部分[1]。不同于交流变压器，换流变压器负载电流中含有大量谐波成分[2-3]，更容易引起热点温升，威胁其安全稳定运行[4-6]。在地磁暴等极端条件下，换流变压器绕组中会流过直流电流。由直流引起的铁心漏磁会大幅增加油箱内表面的磁场分量[7-8]，另外正常工作时负载电流在油箱内表面产生的磁场分量，两者相互作用，使得换流变压器直流偏磁状态下，油箱涡流损耗的分析与计算成为一个难点。
针对换流变压器负载电流的特殊性，目前对不同谐波含量与对应的结构件杂散损耗之间的关系已开展了大量的研究工作。文献[9]在假设结构件材料为线性磁化特性的基础上，推导了损耗与频率的关系，其认为结构件损耗与频率的1.5次方成正比。文献[10-11]将换流变压器负载损耗实验数据与不同参数下公式计算的损耗曲线进行拟合，得到了频率指数的最优解分别为0.9和1.4。为了更加精准地获取换流变压器不同结构件杂散损耗与频率的关系，文献[12-13]基于Problem 21系列基准模型，以实验的形式分别研究了换流变压器油箱、夹件和拉板的谐波损耗的频率特性。为了直接获得实际负载电流下，换流变压器不同结构件损耗的大小以及分布情况，文献[14-15]分别对换流变压器进行了有限元仿真计算，其中文献[14]同时还分析了油箱铜屏蔽的结构尺寸对损耗的影响。然而上述的研究与结论都没有考虑换流变压器施加直流偏磁时的情况。
目前关于变压器直流偏磁状态下油箱、拉板等结构件杂散损耗的研究大都是基于交流变压器进行的。文献[16]利用2D有限元法分析计算了交流变压器在地磁感应电流作用下，油箱涡流损耗与负载功率因数、变压器类型之间的关系。文献[17]采用新型的非线性三维计算方法分析了变压器直流偏磁状态下油箱的涡流损耗。文献[18-19]基于不同的数值模型，对变压器直流偏磁状态下铁磁类材料损耗进行了建模，并通过实验验证了模型的准确性。文献[20-21]分别针对一台500 kV单相自耦变压器和一台380 V实验变压器进行了直流偏磁状态下的有限元仿真计算和实验测试，得到了油箱表面不同位置的涡流损耗数值与直流大小之间的变化关系。
综上所述，本文考虑换流变压器非线性负载电流特点，分析了其直流偏磁状态下油箱涡流损耗的变化情况。通过油箱表面磁场分析，结合实际负载电流波形，得到了整流侧和逆变侧，不同换流器触发角和直流电流大小对油箱涡流损耗的影响规律。并给出了换流变压器直流偏磁状态下，油箱涡流损耗的计算公式。通过对一台800 kV换流变压器进行有限元仿真计算以及对一台380 V缩比变压器进行直流偏磁实验，验证了理论分析的正确性。本文研究可为快速估算不同工况下，换流变压器施加直流偏磁时的油箱涡流损耗大小提供理论支撑。
根据IEC/IEEE 60076-57-129标准，换流变压器正常工作状态下负载功率损耗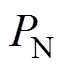可表示为
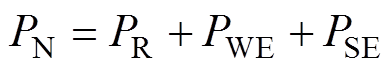（1）
式中，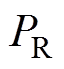
为绕组电阻损耗；
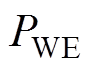为绕组涡流损耗；
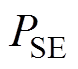为结构件杂散损耗。与交流变压器不同，换流变压器额定负载电流中含有大量谐波成分，不可能通过直接测量的方式获得任意电流频谱下的换流变压器负载损耗。因此该标准中假设：绕组涡流损耗与电流的二次方成正比，与频率
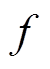的二次方成正比；结构件杂散损耗与电流的二次方成正比，与频率的0.8次方成正比。因此换流变压器的结构件损耗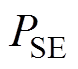计算式为
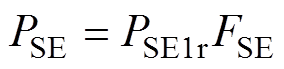（2）
式中，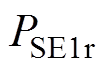
为结构件额定基波损耗；
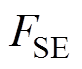为结构件损耗的谐波增值系数，其表达式为
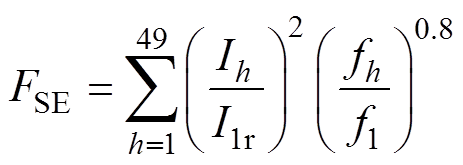（3）
式中，
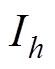和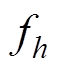
分别为不同谐波次数h下的电流有效值和频率；I1r为基波额定电流有效值；f1为基波频率；常系数2为损耗电流指数；常系数0.8为损耗频率指数。
换流变压器的结构件损耗主要由三部分组成：拉板损耗、夹件损耗、油箱损耗。其中拉板为不锈钢材料制成，其损耗所占比重很小，低于5 %[14]。夹件和油箱的材料都为Q235钢（低碳钢），杂散损耗的电流和频率特性相似，且油箱损耗占结构件损耗的绝大部分。所以式（3）可以看成是换流变压器油箱涡流损耗的谐波增值系数。此时油箱涡流损耗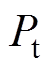
可按照式（2）的形式，表示为
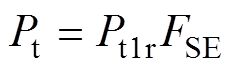（4）
式中，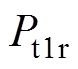
为油箱基波损耗。
换流变压器施加直流偏磁时，铁心迅速饱和，铁心中的部分漏磁通通过变压器绝缘油进入油箱壁，导致油箱涡流损耗变化。图1a和图1b分别为换流变压器处于额定状态和空载直流偏磁状态下油箱表面磁场分布。由于油箱侧壁距离阀侧绕组较近，阀侧绕组中的电流产生的磁场HL主要通过绕组间隙、空气、油箱侧壁形成闭合回路，因此正常工作状态下，油箱涡流损耗主要产生在油箱侧壁。换流变压器施加直流偏磁时，铁心漏磁HD从铁轭流出，通过顶面油箱壁、侧面油箱壁、空气返回。因此换流变压器处于负载直流偏磁状态下时，两种磁场将会在油箱侧壁表面相互作用，其数值是相加还是相减取决于阀侧绕组电流和励磁电流的流向。
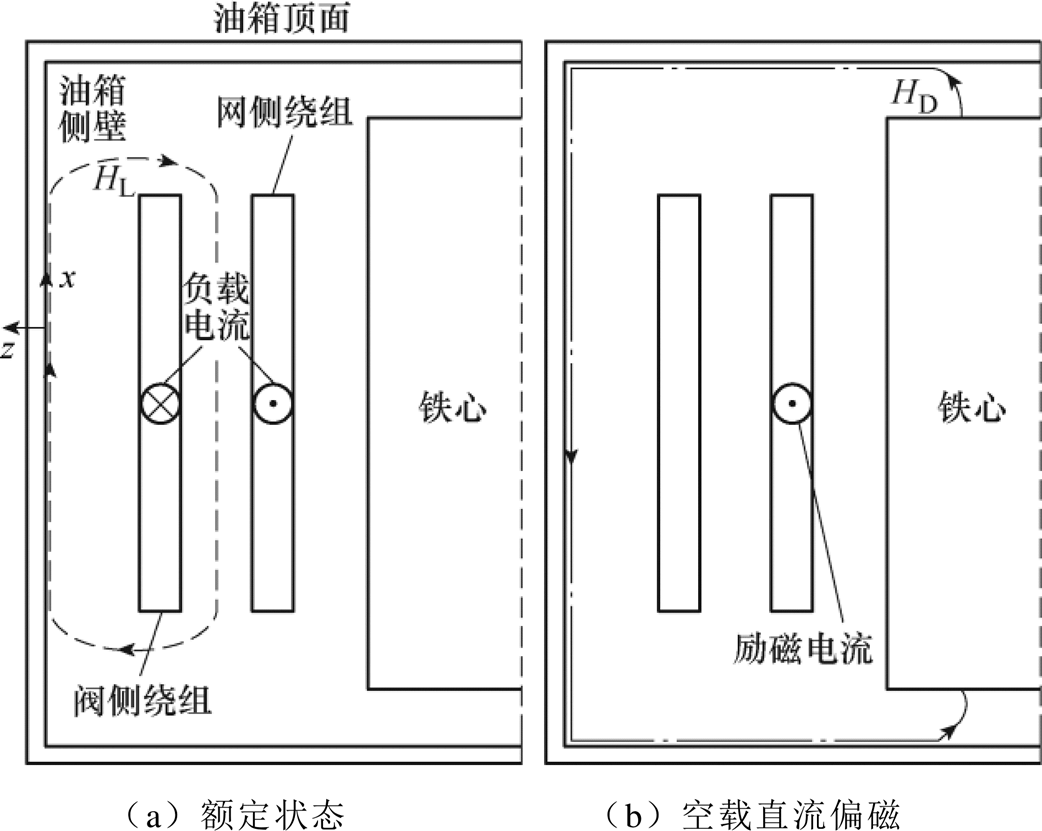
图1 油箱表面磁场分布
Fig.1 Magnetic field distribution on the surface of the tank
为了便于分析，假设油箱侧壁表面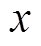
轴方向的磁场Hx为正弦变化量，且只是
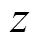轴方向的函数。磁场作用于油箱侧壁内表面，沿着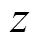轴正方向逐渐减弱，可认为无穷远处磁场为零。根据磁场的扩散方程，可以推导得到Hx的表达式为
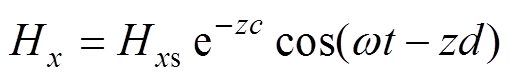（5）
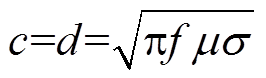（6）
式中，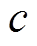
为衰减常数；
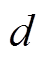为相量常数；
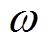为角频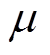率；
为磁导率；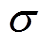
为电导率；Hxs为油箱内表面磁场强度数值最大值。根据安培环路定律，可以得到感应电场Ey为
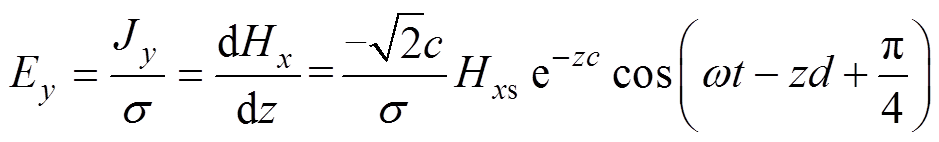（7）
式中，Jy为y方向电流密度。运用坡应廷定理，可得油箱侧壁上任意一点损耗的瞬时密度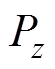
为
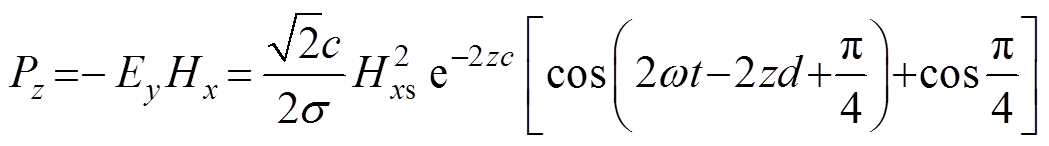（8）
由式（8）可知，换流变压器油箱涡流损耗与油箱表面磁场强度幅值的二次方成正比。因此换流变压器处于直流偏磁状态下，当网侧绕组中的励磁电流达到最大值时（即铁心饱和最严重时），若其流向与阀侧绕组中的负载电流流向相同，两者产生的磁场相互叠加，使得油箱涡流损耗数值大于额定损耗和空载直流偏磁损耗之和；若其流向与阀侧绕组中的负载电流流向相反（见图1），会导致油箱侧壁表面的合成磁场强度减小，造成油箱涡流损耗数值小于额定损耗和空载直流偏磁损耗之和。
换流变压器负载电流波形受到换流器触发角a的影响。换流变压器位于逆变侧，a又叫做触发超前角b；换流变压器位于整流侧，a又叫做触发延迟角a。以逆变侧为例，图2为换流变压器施加直流偏磁时，网侧额定电压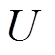
、网侧励磁电流Ii、触发超前角分别为32 °和40 °时的阀侧负载电流
、
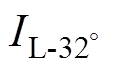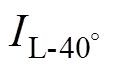之间的关系。
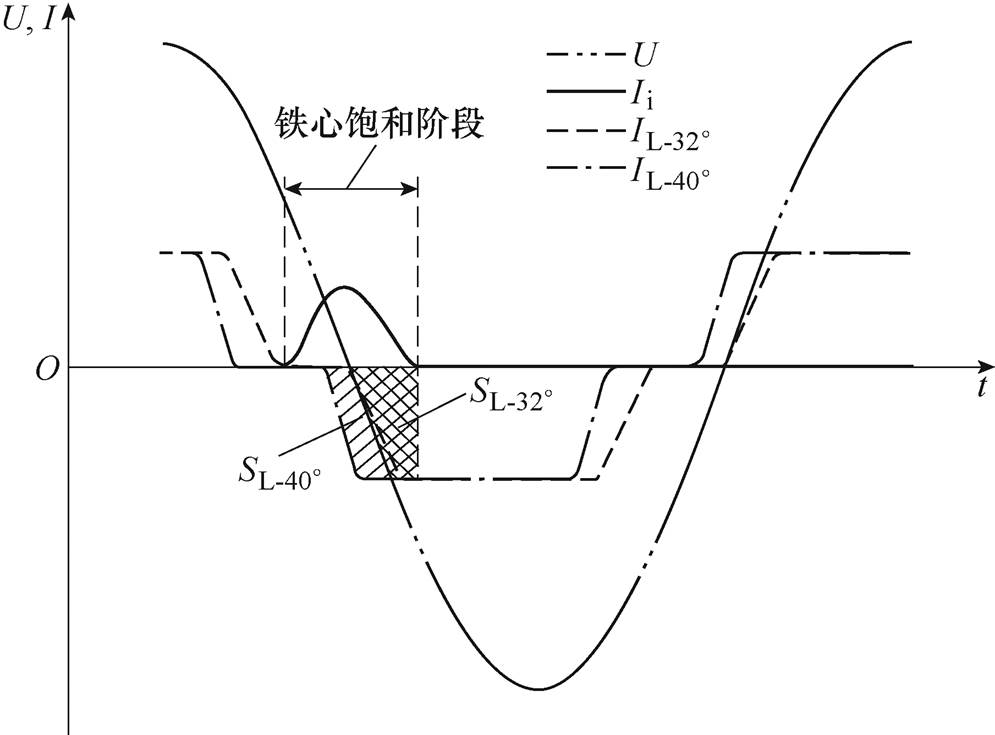
图2 换流变压器电压电流关系
Fig.2 The voltage and current waveforms of converter transformer
从图2中可以看出，励磁电流滞后额定电压 90°，在铁心饱和阶段负载电流数值为负，表明两者的流向相反，因此逆变侧换流变压器施加直流偏磁时，其油箱涡流损耗将会小于额定损耗加上空载直流偏磁损耗。又因为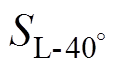
＞
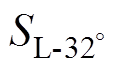，在铁心饱和阶段负载电流的平均值随着触发超前角的增大而增大。因此相同直流电流下，触发超前角越大，油箱侧壁表面的磁场强度越小，油箱涡流损耗数值也就越小。
因为换流变压器空载时，相同直流电流下铁心漏磁造成的油箱损耗（空载直流偏磁损耗）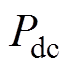
与换流器触发角无关。所以换流变压器施加直流偏磁时，其油箱涡流损耗
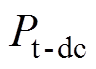可从式（4）变为
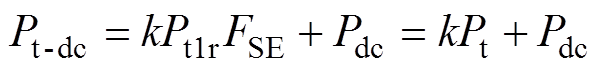（9）
式中，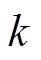
为换流变压器施加直流偏磁时油箱额定损耗占比系数，受直流电流大小和换流器触发角影响，直流电流和换流器触发角越大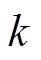，值越小。且由于励磁电流和负载电流在铁心饱和阶段方向相反，k在数值上小于1，其范围为0＜k＜1。而损耗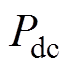可通过空载直流偏磁实验获取。因此只需计算出不同直流电流和换流器触发角下的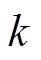值，即可快速计算出换流变压器施加直流偏磁时的油箱涡流损耗。
为了验证理论分析的正确性，并且计算出换流变压器施加直流偏磁时的损耗占比系数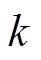。运用有限元仿真软件COMSOL，针对一台800 kV换流变压器的油箱涡流损耗进行了仿真计算。图3所示为换流变压器油箱损耗磁场模型。该换流变压器为单相四柱式结构，套在中间两主柱上的对应绕组之间并联连接，网侧绕组在内，阀侧绕组在外，两者的电流流向相反。油箱主侧壁和次侧壁的厚度为10 mm，油箱顶壁和铜屏蔽层的厚度分别为20 mm和4 mm。铁心主柱的横截面积为1.17 m2，其他尺寸如图3所示。换流变压器的额定参数和材料参数见表1和表2。B-H曲线如图4所示。
图5为换流变压器油箱涡流损耗八分之一有限元模型。在建模过程中进行了以下简化和考虑：①由于磁通在铁心截面均匀分布，因此对铁心进行整体建模，不考虑铁心叠片特性；②不考虑铁心和绕组的涡流损耗；③换流变压器负载电流中包含高频谐波，材料的趋肤效应尤其明显，350 Hz（7次谐 波）下油箱和铜屏蔽的趋肤深度分别为1.03 mm和3.58 mm，因此对其进行充分的网格剖分，保证在其厚度方向的一个趋肤深度内至少有五个单元；④由于换流变压器具有对称结构，为了减小计算量，只构建其八分之一模型，对应的边界条件为：XZ平面和XY平面设置为磁力线垂直边界条件，其余四个外边界设置为磁力线平行边界条件；⑤模型采用场路耦合的方法，网侧绕组施加电压源激励，阀侧绕组施加恒定负载电流源激励，换流变压器油箱损耗电路如图5所示。
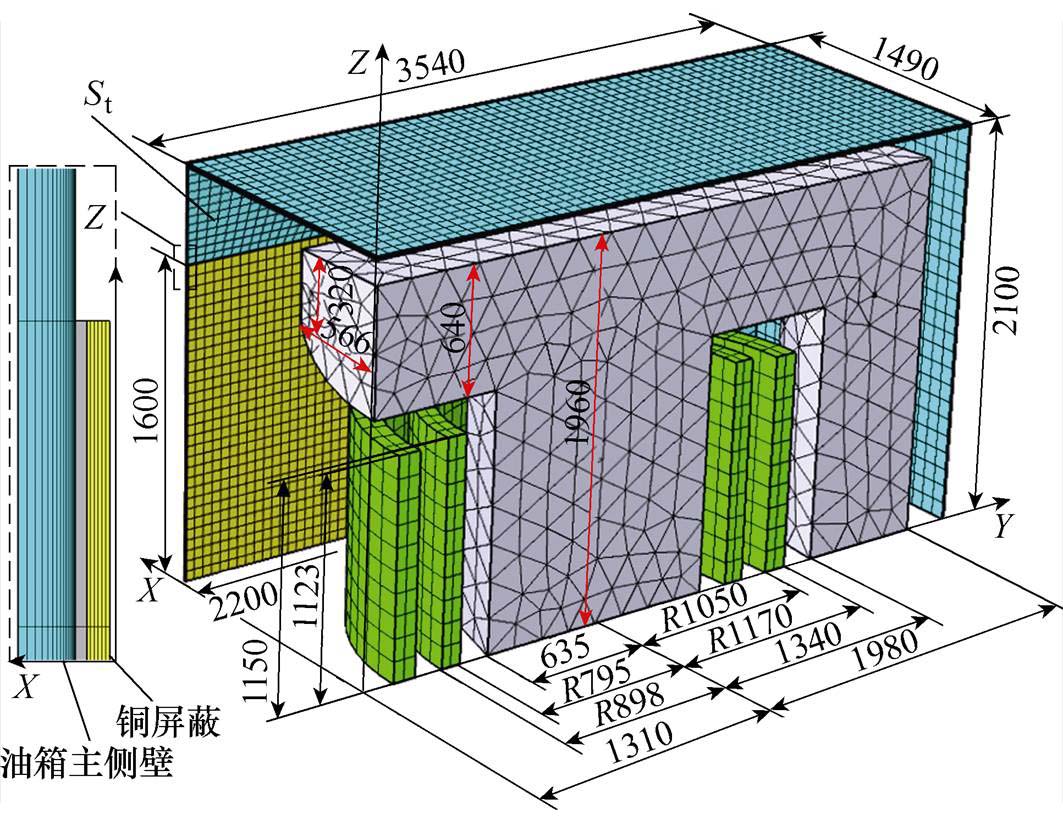
图3 换流变压器油箱损耗磁场模型
Fig.3 Magnetic field model of converter transformer tank loss
表1 换流变压器额定参数
Tab.1 Rated parameters of converter transformer
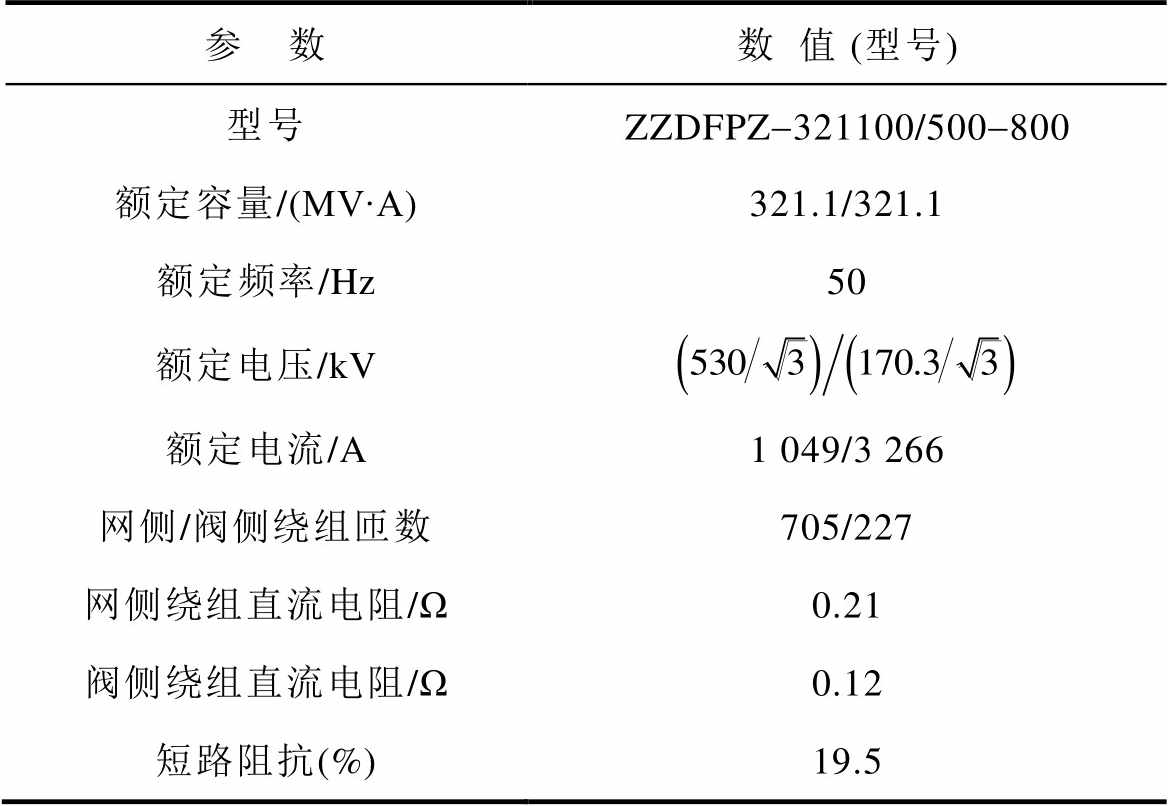
参 数数值 (型号) 型号ZZDFPZ-321100/500-800 额定容量/(MV∙A)321.1/321.1 额定频率/Hz50 额定电压/kV 额定电流/A1 049/3 266 网侧/阀侧绕组匝数705/227 网侧绕组直流电阻/Ω0.21 阀侧绕组直流电阻/Ω0.12 短路阻抗(%)19.5
表2 换流变压器材料参数
Tab.2 Material parameters of converter transformer
名称材料磁导率电导率/(S/m) 铁心27ZH095B-H曲线4 545 000 绕组Cu158 000 000 油箱Q235钢B-H曲线1 388 900 铜屏蔽Cu158 000 000
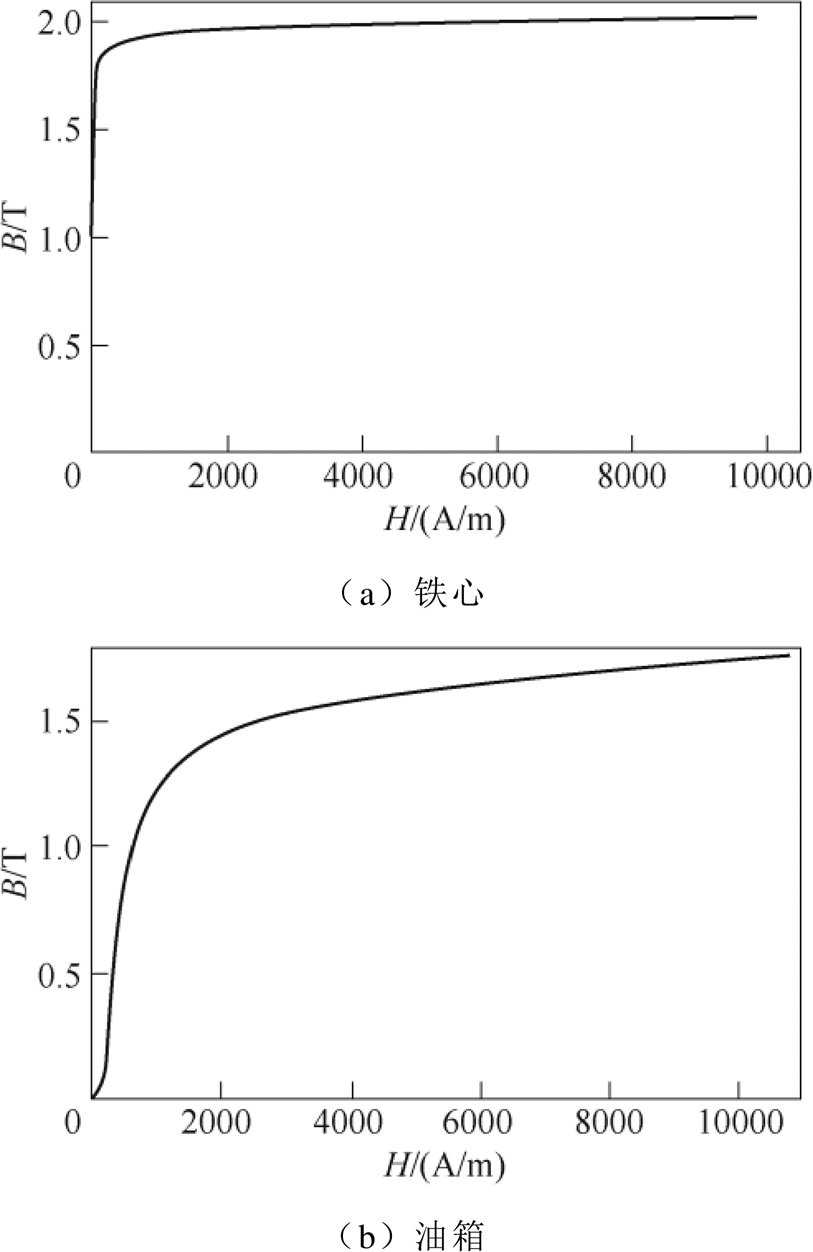
图4 B-H曲线
Fig.4 B-H curves
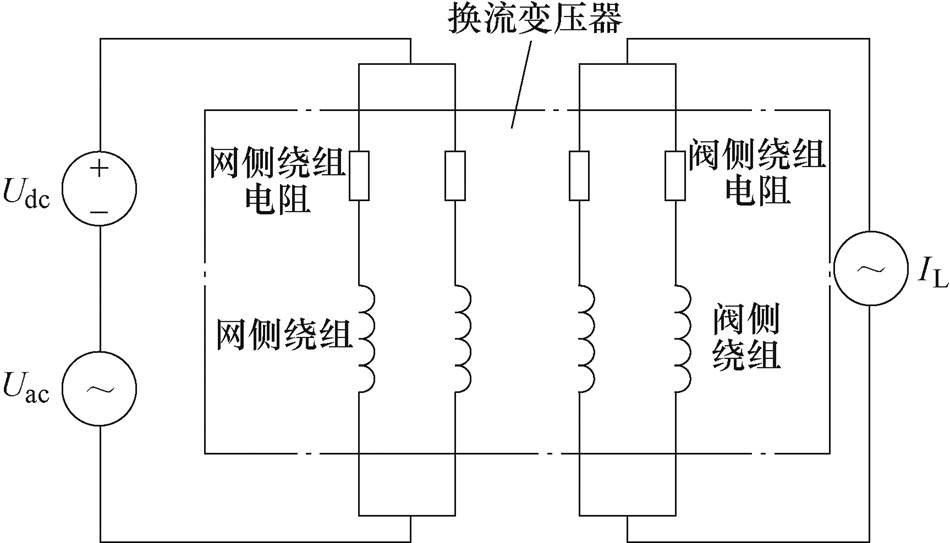
图5 换流变压器油箱损耗电路
Fig.5 Circuit model of converter transformer tank loss
基于调制波理论，计算获得任意触发角度下的负载电流波形。图6为逆变侧触发超前角为35 °时，换流变压器阀侧负载电流频谱图。
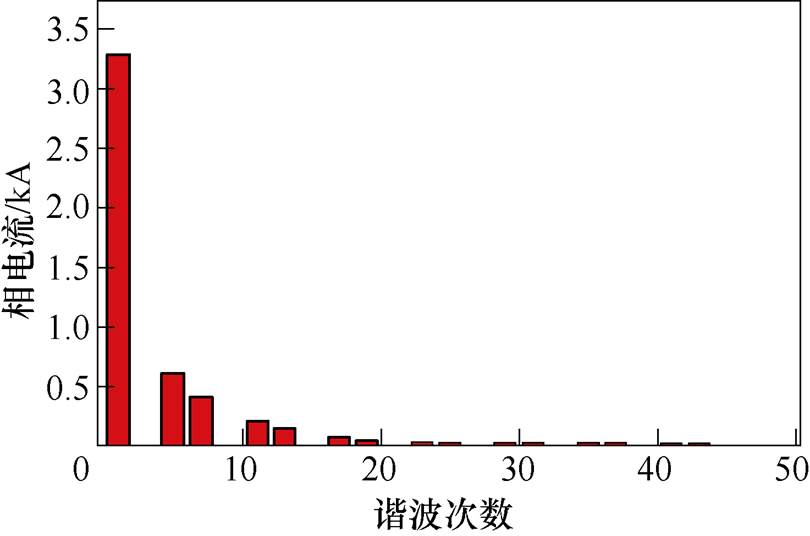
图6 换流变压器额定负载频谱
Fig.6 Rated load current spectrum of converter transformer
以图6中的负载电流频谱为例，仿真计算正弦波激励下不同电流幅值、频率时，换流变压器油箱涡流损耗。按照一个周期内取200个点的思路设置仿真时间步长，基波50 Hz下的时间步长为0.1 ms，其余谐波步长为基波步长的1/h。油箱涡流损耗计算结果见表3。
表3 不同谐波、不同电流有效值下油箱涡流损耗
Tab.3 Eddy current loss of tank under different harmonic and current amplitudes
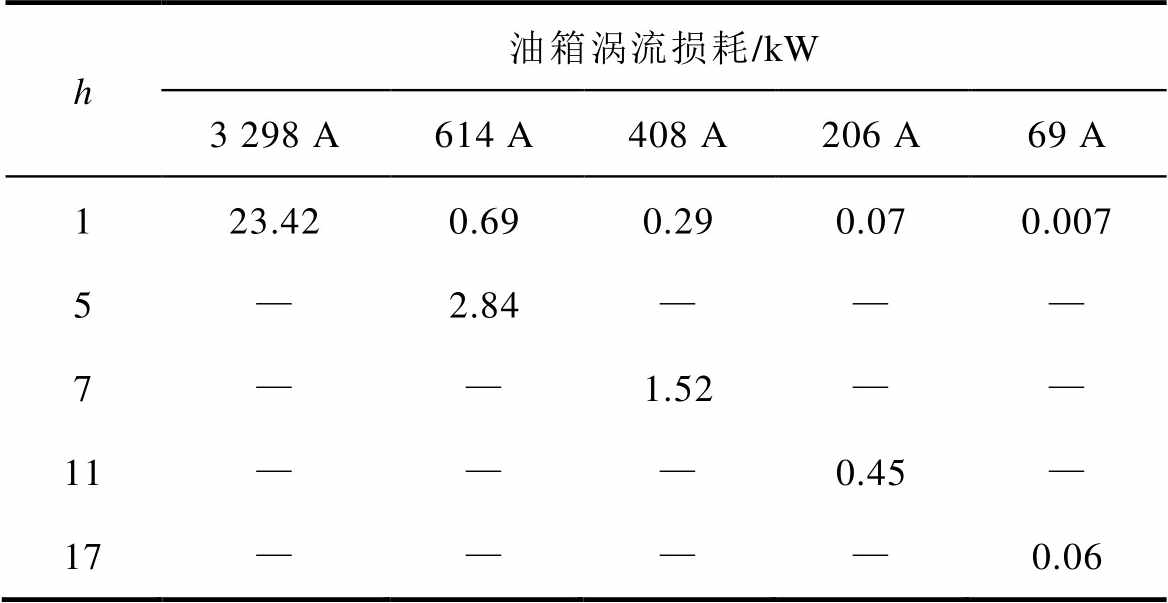
h油箱涡流损耗/kW 3 298 A614 A408 A206 A69 A 123.420.690.290.070.007 5—2.84——— 7——1.52—— 11———0.45— 17————0.06
以基波额定电流数值3 298 A对应的损耗为基准，计算可得基波电流614 A、408 A、206 A、69 A下的损耗电流指数分别为2.11、2.097、2.092、2.09，其数值略大于IEC标准中给出的数值2；以相同电流下的基波损耗为基准，计算可得谐波次数5、7、11、17下的损耗频率指数分别为0.88、0.85、0.78、0.75，该数值与IEC标准中给出的数值0.8相近。仿真数值与IEC标准公式中提供的数值之间的误差是由于没有考虑油箱的磁滞损耗以及不同换流变压器之间的结构尺寸差异造成的。
将仿真得到的损耗电流指数和频率指数分别取平均（数值分别为2.1和0.82），再利用式（4）进行计算，可得基波和5、7、11、17次谐波下的油箱涡流损耗之和为28 kW，该数值与表3中仿真得到的基波和各次谐波损耗之和28.29 kW相比，误差仅为1 %。根据图6的频谱图，结合式（4）计算得到的油箱总损耗为28.34 kW，直接使用非线性负载电流波形进行仿真得到的油箱涡流损耗见表4。式（4）得到的总损耗28.34 kW与表4的数值27.87 kW相比，误差仅为1.7 %，这也在一定程度上验证了4.2小节仿真结果的正确性。同时对比基波和不同谐波之间的损耗可以发现，谐波次数越大其损耗数值越小，对于17次谐波而言，其损耗仅为基波损耗的0.26 %。因此实际换流变压器油箱涡流损耗计算中，只需考虑到负载电流中的17次谐波分量即可。
表4 直流偏磁下油箱涡流损耗
Tab.4 Eddy current loss of tank under DC bias
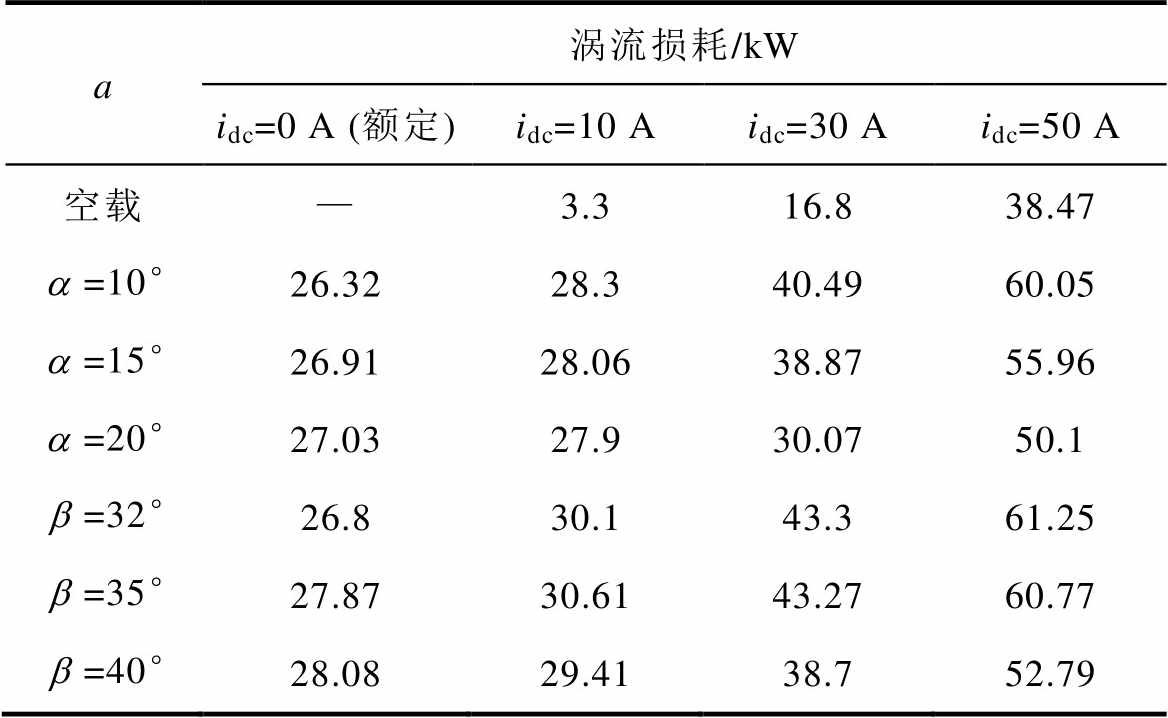
a涡流损耗/kW idc=0 A (额定)idc=10 Aidc=30 Aidc=50 A 空载—3.316.838.47 =10°26.3228.340.4960.05 =15°26.9128.0638.8755.96 =20°27.0327.930.0750.1 =32°26.830.143.361.25 =35°27.8730.6143.2760.77 =40°28.0829.4138.752.79
正常运行时直流输电系统整流侧触发延迟角的变化范围为10 °～20 °，逆变侧触发超前角的变化范围为32 °～40 °。因此仿真计算中分别取整流侧触发角10 °、15 °、20 °，逆变侧触发角32 °、35 °、40°对应的负载电流，直流电流取值为0 A、10 A、30 A、50 A。为了精确计算非线性负载电流中谐波含量造成的损耗，保证11次谐波在其一个周期（0.001 8 s）内取满200个点，即仿真计算的时间步长为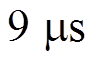
，计算时长为3个基波周期，即0.06 s。仿真硬件参数为：处理器为Intel(R) Core(TM) i7-7700@ 3.60 GHz，8核；内存为16 GB。仿真总用时约49 h。图7为仿真得到的换流变压器直流偏磁状态下的电压和电流波形（电压缩小了100倍）。在1/4个周期的时刻（0.05 s），励磁电流电流激增，使得网侧电流波形发生了较大的突变。
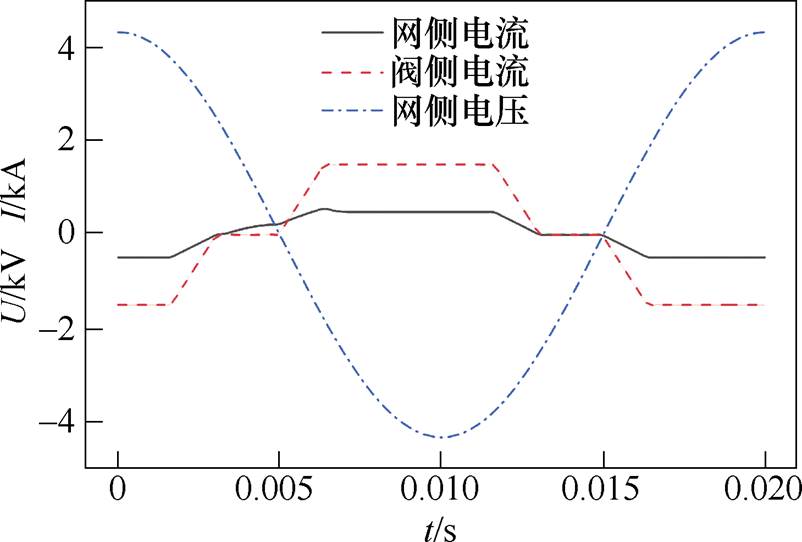
图7 电压电流仿真波形
Fig.7 Voltage and current simulation waveforms
4.2.1 涡流损耗数值分析
表4为整流侧（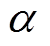
）和逆变侧（
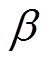）在不同触发角
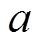和直流电流idc下的油箱涡流损耗数值。从表中可以看出，在额定状态下，无论整流侧还是逆变侧，箱涡流损耗都随着触发角的增大而增大，这是因为触发角越大，负载电流中的谐波含量相应更高，但当有直流电流流过时，损耗数值却随着触发角的增大而越小，且直流电流数值越大该现象越明显。整体上来看，逆变侧换流变压器油箱涡流损耗比整流侧要大，这表明逆变侧换流变压器更容易遭受直流偏磁的侵害。根据油箱损耗标准模型Problem21c-EM2的测量数据（数据来源于《TEAM Problem 21 Family（V.2009）》中的表3～表5），额定状态下油箱磁滞损耗占总损耗的21.7 %。而由表4可知，直流50 A的情况下，油箱空载直流偏磁损耗约为额定损耗（不同触发角下的平均值）的1.42倍，以此数值进行换算，在不考虑磁滞损耗变化的情况下，直流偏磁时油箱磁滞损耗约占总损耗的10.3 %。因此在对精度要求不高的场合，本文中的分析结论同样适用于换流变压器直流偏磁状态下油箱实际总损耗（涡流和磁滞损耗）的计算。
为了更加清晰地显示换流变压器油箱涡流损耗受直流电流和触发角的影响大小，按照2.2小节的定义，计算损耗占比系数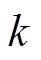，计算公式为
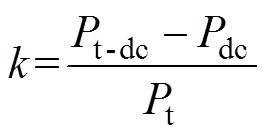（10）
表5为其计算结果。从表中可以看出，不论整流侧还是逆变侧，直流电流越大，额定油箱损耗占比系数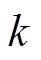越小；触发角越大，系数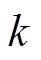越小，且其数值基本小于1。这表明换流变压器负载直流偏磁状态下，其油箱涡流损耗小于额定损耗与空载直流偏磁损耗之和。对于触发延迟角20 °，直流电流50 A的情况，油箱的额定负载损耗占比系数按照式（10）的定义，也为表5中相应k值为0.43，即仅为正常状态下数值的0.43，减小了57 %（(1-k)×100 %）。直流10 A、30 A、50 A时不同触发角下整流侧的平均损耗减小了7.3 %、17.7 %、36.7 %，逆变侧的平均损耗减小了3 %、9.3 %、28 %。上述仿真分析结果与2.2小节的理论分析是一致的。
表5 不同直流和触发角下损耗占比系数k
Tab.5 Loss ratio coefficient k under different DC and trigger angles
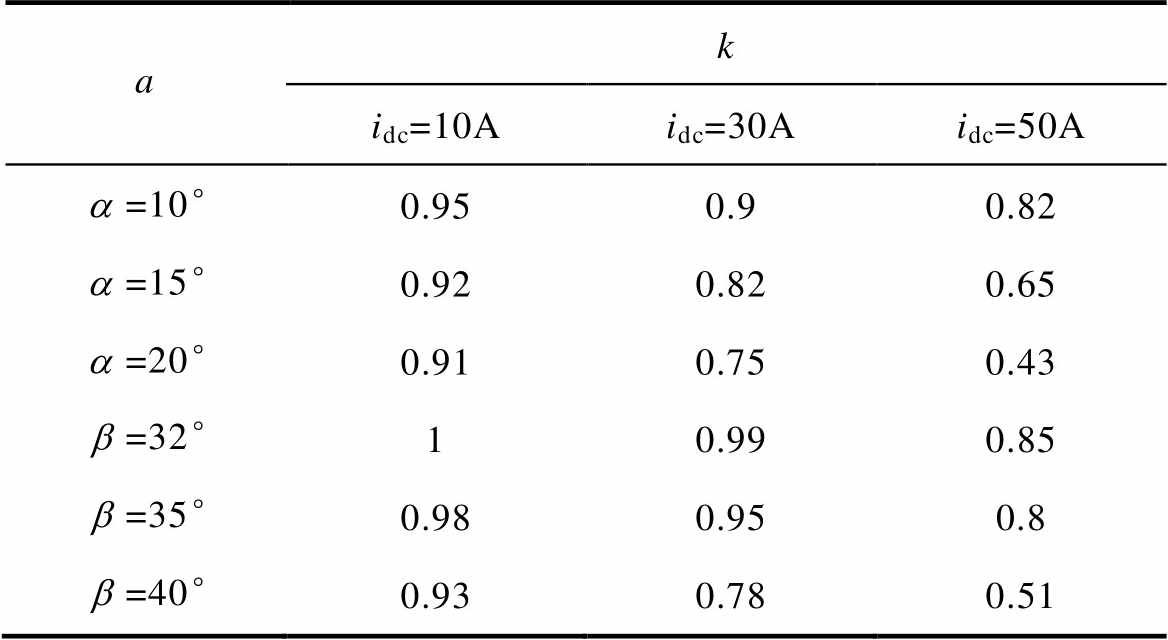
k idc=10Aidc=30Aidc=50A =10°0.950.90.82 =15°0.920.820.65 =20°0.910.750.43 =32°10.990.85 =35°0.980.950.8 =40°0.930.780.51
4.2.2 油箱内表面漏磁场和涡流损耗分析
因为额定负载状态下油箱涡流损耗主要集中在油箱主侧壁上，因此只需分析在励磁电流最大值时刻，油箱主侧壁内表面漏磁场和涡流损耗分布即可。由于对称性，图3中只展示了1/4油箱表面（St）。
图8为换流变压器不同状态下油箱表面磁通密度分布。如图8a所示，在额定状态下由于铜屏蔽的作用，在其所覆盖的油箱表面磁通密度与周围数值相比偏小，油箱表面的磁通密度流向为逆时针方向。然而，在图8b中，由于铁心饱和，大量漏磁从油箱右上角方位射入，其不受铜屏蔽的影响。因此，磁通密度均匀分布在油箱表面，方向为顺时针方向。由于图8a和图8b中磁通密度的方向相反，因此在直流电流为50 A的负载状态下（见图8c），两者的磁通密度相减，使得总的磁通密度数值减小。该结果与第2.2节中的理论分析结果一致。
图9为有无铜屏蔽时的油箱表面St上的涡流损耗密度分布。可以看出，涡流损耗在很大程度上受铜屏蔽的影响。在铜屏蔽区域，涡流损耗显著降低。最大损耗分布在油箱和铜屏蔽的接合处。油箱带铜屏蔽时的损耗数值为50.1 kW，不带铜屏蔽时为86.1 kW，铜屏蔽的存在使得损耗数值降低了42 %。铜屏蔽的损耗为6.5 kW。
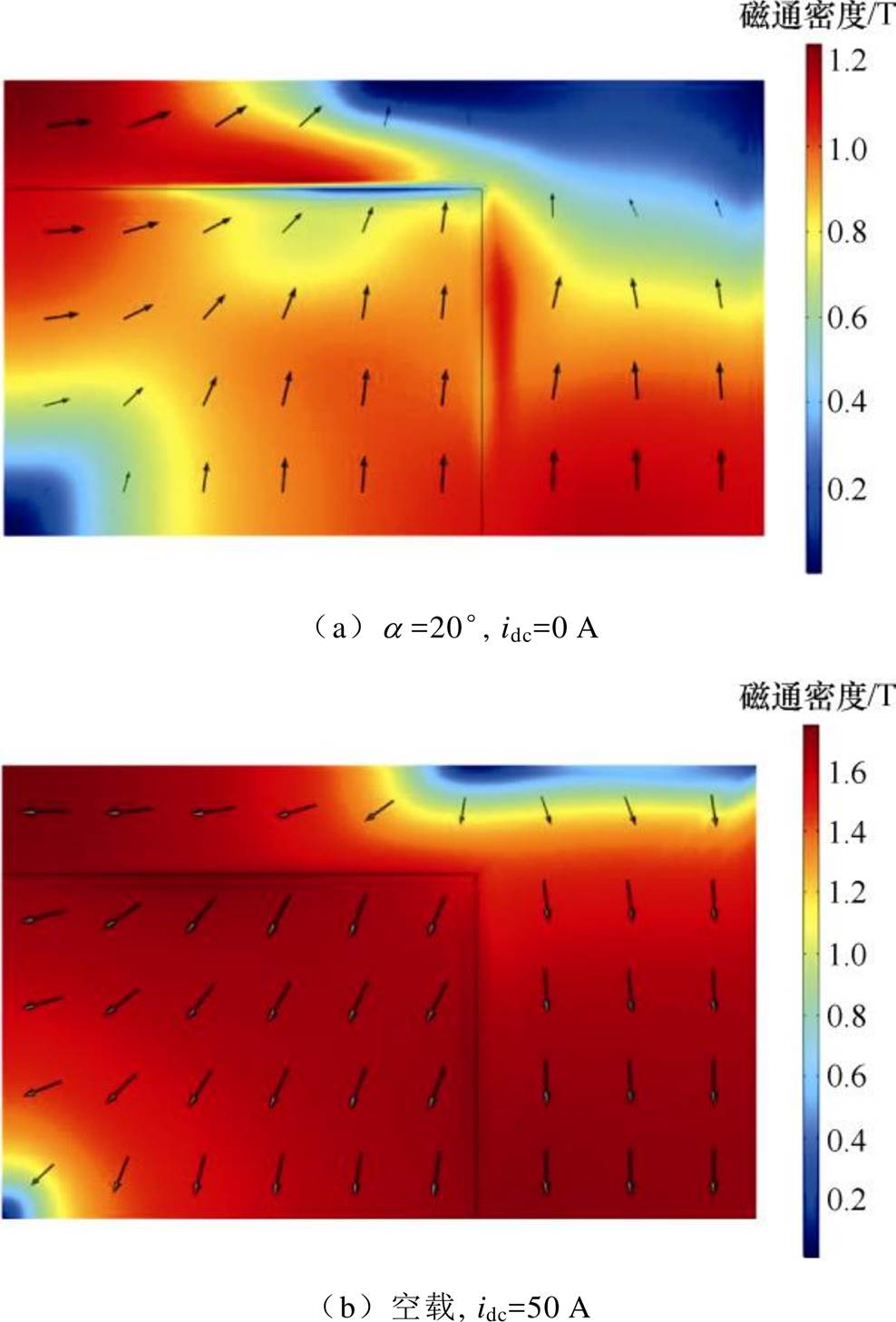
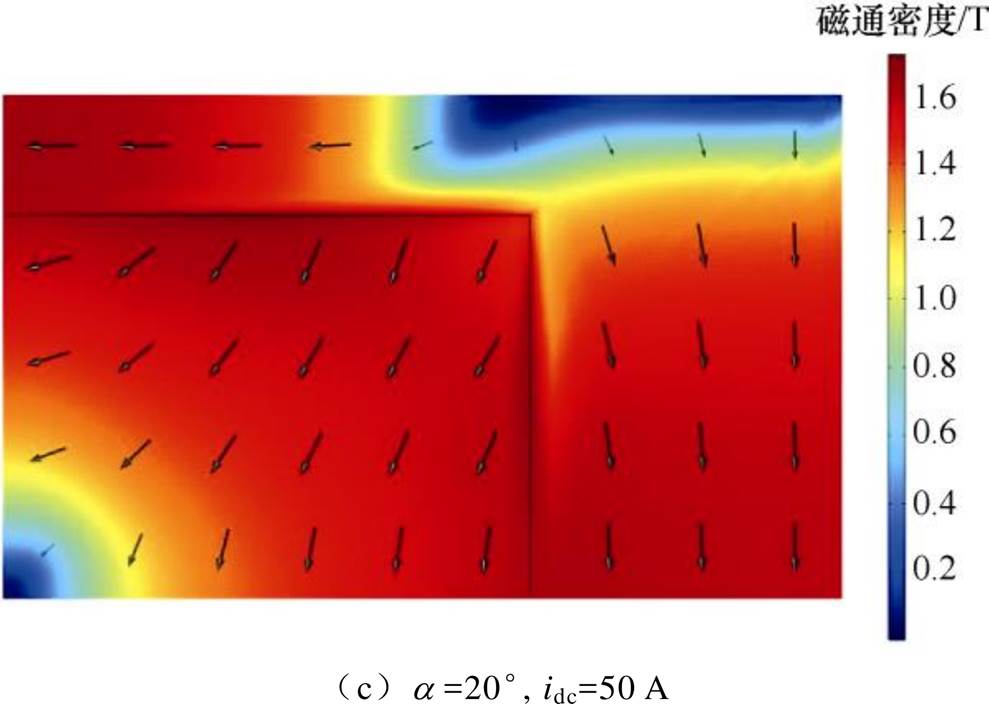
图8 油箱表面St的磁通密度
Fig.8 Magnetic flux density on the St of the tank
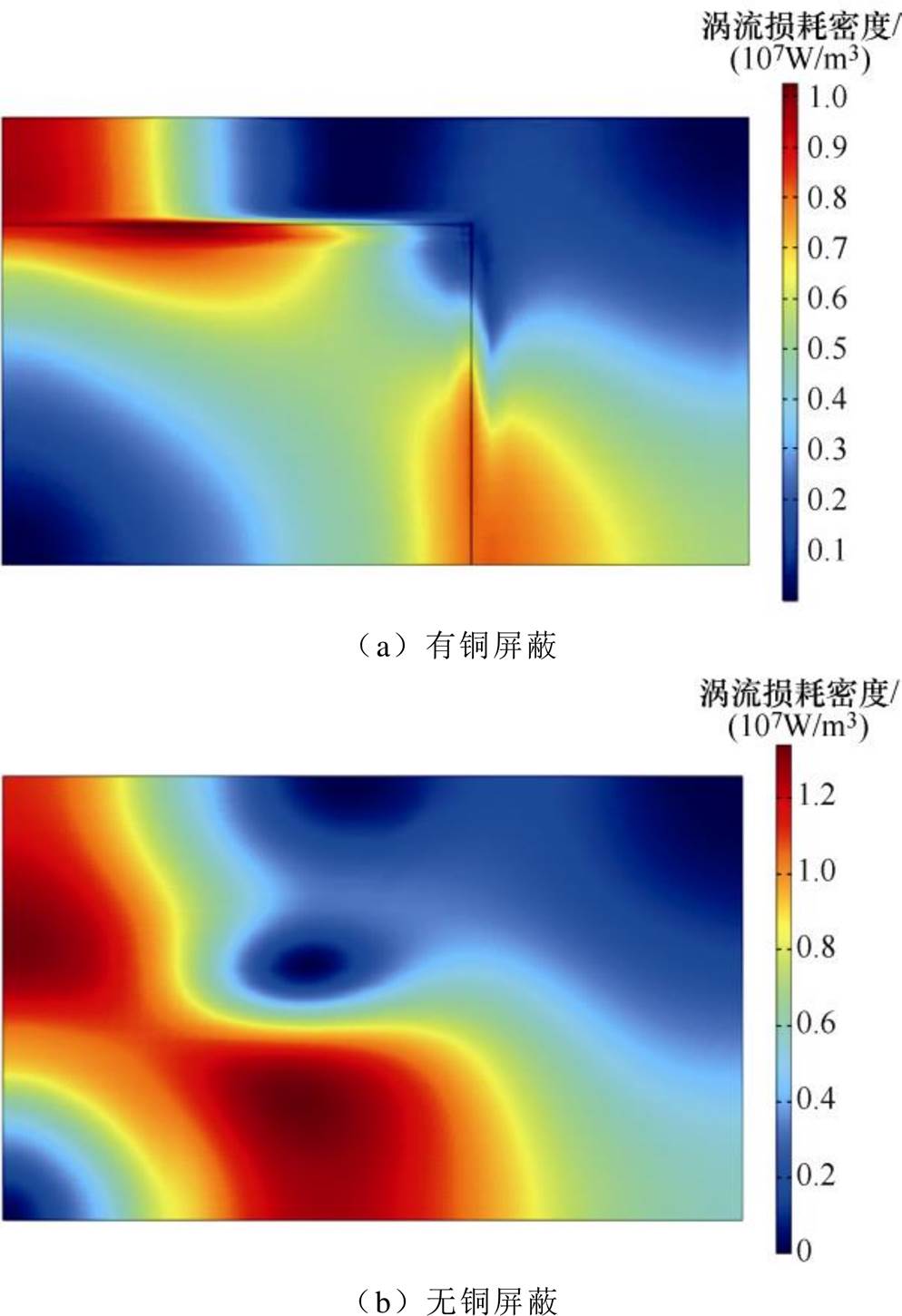
图9 油箱表面St的涡流损耗
Fig.9 Eddy current loss on the St of the tank
由于现有的实验条件无法产生实际换流变压器那样的非线性负载电流波形。因此通过在实验变压器二次侧施加不同性质的线性负载，以正弦负载电流与额定电压之间的相位差替代不同触发角下换流变压器负载电流波形差异，以此来验证2.1小节的理论分析，进而间接验证2.2小节对换流变压器油箱涡流损耗的分析结论。表6为实验变压器的基本参数。
表6 实验变压器参数
Tab.6 Experimental transformer parameters
参 数数 值 额定容量/(kV∙A)5/5 额定频率/Hz50 额定电压/V360/180 额定电流/A13.9/27.8 一次/二次绕组匝数126/63
实验变压器铁心结构与换流变压器相同，都为单相四柱式，结构尺寸近似1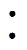
10的关系。一次绕组在外，二次绕组在内。图10a中两台实验变压器除了油箱外其余完全一致。图10b和图10c分别为实验设备和连接图。图中与直流电源并联的电容器是为了保护直流源免受交流电流的侵害。直流电流是以隔离变压器的二次侧和实验变压器的一次侧为回路产生的。
图10 实验平台
Fig.10 The experimental setup
实验中分别施加纯阻性R和阻感性RL两种额定负载，纯阻性负载中电阻值为6.5 W，阻感性负载为R=6.1 W 和L=7 mH串联，阻抗值也为6.5 W。实验变压器1和2的损耗Pm1和Pm2为一次侧输入功率减去二次侧输出功率，输入输出功率Pm-in/out为
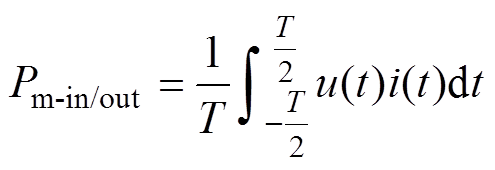（11）
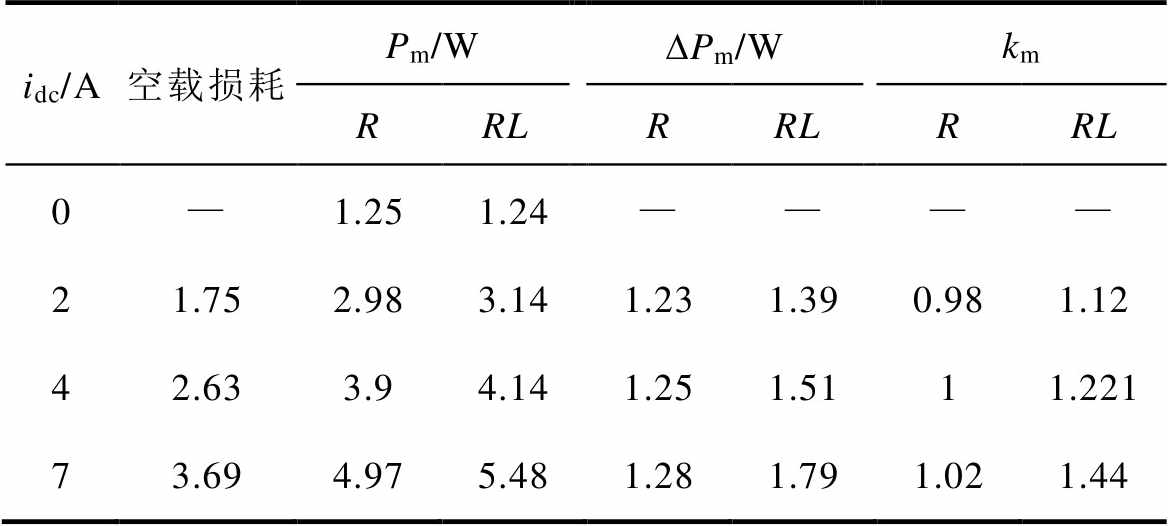
式中，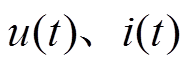
分别为一、二次侧测量的电压、电流点数据；
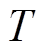为电压电流周期。实验变压器油箱损耗Pm为损耗Pm1减去损耗Pm2。负载直流偏磁、额定、空载直流偏磁状态下，油箱损耗分别用Pm-t-dc、Pm-t、Pm-dc表示。
表7为测量的实验变压器油箱损耗实测值。表中，DPm为相同直流电流下，实验变压器油箱负载损耗Pm-t-dc和空载直流偏磁损耗Pm-dc的差值。km为实验变压器油箱额定损耗占比系数。对于纯电阻性负载而言，km=DPm/1.25，DPm在数值上几乎等于额定状态下的油箱损耗Pm-t（1.25 W），因此损耗占比系数km约等于1。这表明实验变压器施加直流偏磁时，其油箱损耗Pm-t-dc等于额定损耗Pm-t和空载直流偏磁损耗Pm-dc之和，且这种关系不受直流电流大小的影响。然而对于阻感性负载，km=DPm/1.24，DPm却大于额定油箱损耗Pm-t（1.24 W），因此损耗占比系数km＞1，且随着所加直流电流的增大而增大。这表明负载为阻感性时，实验变压器施加直流偏磁时的油箱损耗Pm-t-dc大于额定损耗Pm-t和空载直流偏磁损耗Pm-dc之和，直流电流越大损耗偏差的数值越大。直流电流为7 A时，油箱的额定负载损耗为正常状态下的1.44倍（见表7），增加了44 %。
表7 实验变压器油箱损耗实测值
Tab.7 Measured value of tank loss of experimental transformer
idc/A空载损耗Pm/WDPm/Wkm RRLRRLRRL 0—1.251.24———— 21.752.983.141.231.390.981.12 42.633.94.141.251.5111.221 73.694.975.481.281.791.021.44
图11为直流为0和4 A时测量得到的不同负载下的一次电压、电流波形。图中电压数值为实际值的1/5。由图11可知，对于阻感性负载RL，由于电流滞后于电压，铁心饱和期间其额定电流的平均值大于零，且电流方向与励磁电流方向相同。再结合2.1小节的理论分析可知，实验变压器施加直流偏磁时，其油箱损耗将大于额定损耗和空载直流偏磁损耗之和，所以DPm大于额定值（1.24 W）。而对于纯阻性负载R，铁心饱和期间额定电流的平均值几乎等于零，所以油箱损耗等于额定损耗和空载直流偏磁损耗之和，因此DPm接近额定值（1.25 W）。由上述分析可知，2.1小节的理论分析同样适用于交流变压器，分析结果是正确的。同时也间接验证了基于2.1小节理论分析的2.2小节中的换流变压器油箱涡流损耗的结论正确性。
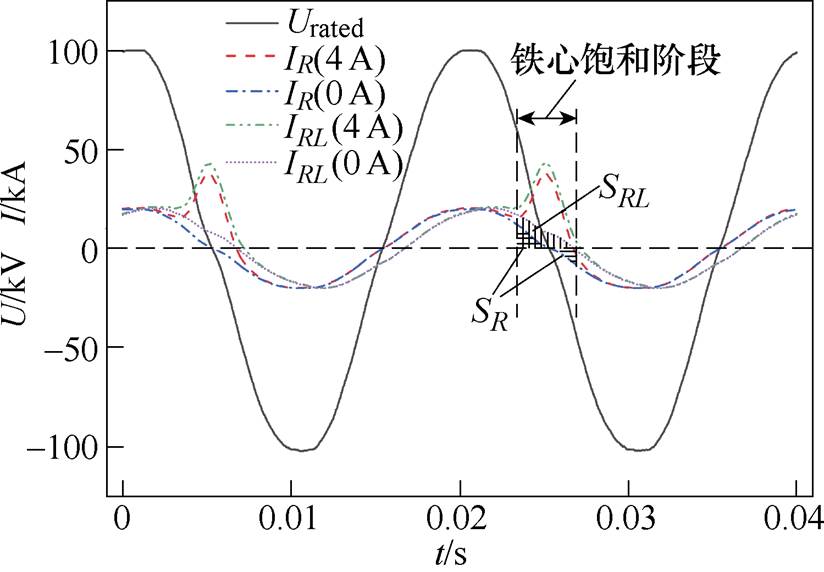
图11 一次电压、电流波形
Fig.11 Primary side voltage and current waveforms
本文研究了整流和逆变侧换流变压器直流偏磁状态下，油箱涡流损耗受到换流器触发角和直流电流影响的规律。通过引入一个损耗占比系数k，给出了换流变压器施加直流偏磁时，其油箱涡流损耗的简化计算公式。通过对一台800 kV换流变压器进行有限元仿真计算以及对一台380 V缩比变压器进行直流偏磁实验，验证了理论分析结论的正确性。主要结论如下：
1）换流变压器施加直流偏磁时，油箱涡流损耗可表示为额定损耗乘以占比系数k加上空载直流偏磁损耗。该系数小于1，且随着直流电流和换流器触发角的增大而减小。
2）相同直流电流下，换流器触发角越大，油箱涡流损耗数值越小。
3）逆变侧换流变压器直流偏磁状态下，其油箱涡流损耗数值整体上比整流侧更大，因此逆变侧的换流变压器更容易遭受直流偏磁的侵害。
参考文献
[1] Kulkarni S V, Khaparde S A. Transformer engineering:design, technology, and diagnostics[M]. 2nd Ed, Boca Raton: CRC Press, 2012.
[2] Smajic J, Hughes J, Steinmetz T, et al. Numerical computation of ohmic and eddy-current winding losses of converter transformers including higher harmonics of load current[J]. IEEE Transactions on Magnetics, 2012, 48(2): 827-830.
[3] Liu Yaqing, Zhang Dandan, Li Zhenbiao, et al. Calculation method of winding eddy-current losses for high-voltage direct current converter trans- formers[J]. IET Electric Power Applications, 2016, 10(6), 488-497.
[4] 潘超, 米俭, 王格万, 等. 基于场路耦合的变压器绕组匝间短路电磁谐响应分析方法[J]. 电工技术学报, 2019, 34(4): 673-682.
Pan Chao, Mi Jian, Wang Gewan, et al. Electro- magnetic harmonic response analysis method of inter-turn short circuit in transformer winding based on field circuit coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 673-682.
[5] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal- fluid model[J]. Transactions of China Electro- technical Society, 2020, 35(21): 4483-4491.
[6] Wang Qingpeng, Bai Baodong, Chen Dezhi, et al. Study of insulation material properties subjected to nonlinear AC-DC composite electric field for con- verter transformer[J]. IEEE Transactions on Mag- netics, 2019, 55(2): 1-4.
[7] 李冰, 王泽忠, 刘海波, 等. 直流偏磁下500 kV单相变压器振动噪声的试验研究[J]. 电工技术学报, 2021, 36(13): 2801-2811.
Li Bing, Wang Zezhong, Liu Haibo, et al. Experiment on vibro-acoustic characteristic of 500 kV single- phase transformer under DC-bias[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2801- 2811.
[8] Liu Chunming, Liu Lianguang, Pirjola R. Geomag- netically induced currents in the high-voltage power grid in China[J]. IEEE Transactions on Power Delivery, 2009, 24(4), 2368-2374.
[9] Emanuel A E, Wang X. Estimation of loss of life of power transformers supplying nonlinear loads[J]. IEEE Transactions on Power Apparatus and Systems, 1985 104(3): 628-636.
[10] Ram B S, Forrest J A C, Swift G W. Effects of harmonics on converter transformer load losses[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1059-1066.
[11] Forrest J A C. Harmonic load losses in HVDC converter transformers[J]. IEEE Transactions on Power Delivery, 1991, 6(1): 153-157.
[12] Liu Yaqing, Zhang Dandan, Li Zhenbiao, et al. Study of the stray losses calculation in structural parts for HVDC converter transformers based on the TEAM Problem 21 Family[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 605-612.
[13] 赵小军, 王佳雯, 刘洋, 等. 谐波激励下变压器结构件杂散损耗的模拟与验证[J]. 中国电机工程学报, 2020, 40(2): 652-663.
Zhao Xiaojun, Wang Jiawen, Liu Yang, et al. Simu- lation and verification of stray-field losses in structural components of transformers under multi- harmonic excitation[J]. Proceedings of the CSEE, 2020, 40(2): 652-663.
[14] 张良县, 陈模生, 于健, 等. 特高压换流变压器涡流损耗计算与屏蔽分析[J]. 变压器, 2013, 50(3): 15-21.
Zhang Liangxian, Chen Mosheng, Yu Jian, et al. Eddy current loss calculation and shield analysis of UHV converter transformer[J]. Transformer, 2013, 50(3): 15-21.
[15] 黄天超, 王泽忠. 特高压换流变压器拉板损耗的频率特性分析[J]. 电工技术学报, 2021, 36(19): 4132- 4139.
Huang Tianchao, Wang Zezhong. Frequency charac- eristic analysis of flitch plate losses in UHV converter transformer[J]. Transactions of China Electrotech- nical Society, 2021, 36(19): 4132-4139.
[16] Zhang B, Liu L, Liu Y, et al. Effect of geomag- netically induced current on the loss of transformer tank[J]. IET Electric Power Applications, 2010, 4(5), 373-379.
[17] Yao Yingying, Chang S K, Ni Guangzheng, et al. 3-D nonlinear transient eddy current calculation of online power transformer under DC bias[J]. IEEE Transa- ctions on Magnetics, 2005 ,41(5): 1840-1843.
[18] 澹台乐琰, 韩肖清, 王磊, 等. 一种用于变压器直流偏磁状态下的改进型Jiles-Atherton模型[J]. 电网技术, 2020, 44(1): 122-132.
TanTai Leyan, Han Xiaoqing, Wang Lei, et al. An improved Jiles-Atherton model for DC bias of transformer[J]. Power System Technology, 2020, 44(1): 122-132.
[19] 赵志刚, 马习纹, 姬俊安. 基于Energetic模型的直流偏磁条件下电工钢片磁特性模拟及实验验证[J]. 中国电机工程学报, 2020, 40(14): 4656-4665, 4743.
Zhao Zhigang, Ma Xiwen, Ji Junan. Simulation and experimental verification of magnetic characteristics of electrical steel sheet under DC bias based on energetic model[J]. Proceedings of the CSEE, 2020, 40(14): 4656-4665, 4743.
[20] 李明洋, 张俊双, 李海明, 等. 500 kV单相变压器直流偏磁下损耗及绕组热点温度的计算分析[J]. 电工电能新技术, 2021, 40(8): 51-59.
Li Mingyang, Zhang Junshuang, Li Haiming, et al. Calculation and analysis of loss and winding hot spot temperature under DC bias of 500 kV single-phase transformer[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(8): 51-59.
[21] 王泽忠, 李明洋, 宣梦真, 等. 单相四柱式变压器直流偏磁下的温升试验及仿真分析[J]. 电工技术学报, 2021, 36(5): 1006-1013.
Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al. Temperature rise test and simulation of single-phase four-column transformer under DC-bias[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
Abstract For the converter transformer, the eddy current loss of the tank under DC bias will increase significantly, which will lead to the temperature rise of the transformer and threaten its safe and stable operation. Therefore, it is necessary to quickly evaluate the eddy current loss of the tank under DC bias. At present, given the particularity of the load current of the converter transformer, much research work has been carried out to study the relationship between the stray losses of the structural components corresponding to different harmonic contents. However, the research conclusions do not consider the impact of DC bias applied to the converter transformer. The research on the stray loss of tanks, pull plates, and other structural parts under DC bias is mainly based on AC transformers. Therefore, considering the characteristics of the nonlinear load current of the converter transformer, this paper analyzes the change of eddy current loss of the tank under DC bias.
Firstly, the distribution of the magnetic circuit on the tank surface under different working conditions is analyzed. Combined with the actual nonlinear load current waveform and eddy current loss calculation formula, the influence of converter trigger angle and DC on the tank eddy current loss at the rectifier and inverter sides is obtained. According to the analysis conclusion, a loss ratio factor k is introduced, and a simplified formula for calculating the eddy current loss of the tank when the dc bias is applied is given. Then, the finite element simulation software COMSOL is used to build a finite element model of the eddy current loss of the tank of an 800 kV converter transformer. The field circuit coupling simulation is carried out with the external circuit of the primary and secondary sides of the converter transformer. The converter transformer tank current loss index under rated conditions has a small error compared with the value of the IEC standard, which also proves the correctness of the model to a certain extent. The simulation value variations of tank loss under DC bias, surface magnetic field, and eddy current distribution are also consistent with the theoretical analysis. Finally, two 380V transformers with a 1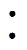10 structure scale are used to verify the theoretical analysis and simulation calculation.
The main conclusions of this paper are as follows: (1) When DC bias is applied to the converter transformer, the eddy current loss of the tank can be expressed as the rated loss multiplied by the ratio factor k and the no-load DC bias loss. The coefficient is less than 1 and decreases with the increase of DC and trigger angle of the converter. (2) Under the same DC, the larger the trigger angle of the converter is, the smaller the eddy current loss of the tank. (3) When the converter transformer on the inverter side is DC-biased, the eddy current loss of its tank is generally larger than that on the rectifier side, so the converter transformer on the inverter side is more vulnerable to the DC bias.
keywords：DC bias, converter transformer, converter trigger angle, eddy current loss of tank
DOI: 10.19595/j.cnki.1000-6753.tces.220140
中图分类号：TM41
国家重点研发计划专项（2016YFC0800103）和国家自然科学基金（52177081）资助项目。
收稿日期 2022-01-26
改稿日期 2022-02-27
黄天超 男，1993年生，博士，研究方向为换流变压器直流偏磁电、磁场数值计算。E-mail: 17717016682@163.com（通信作者）
王泽忠 男，1960年生，教授，博士生导师，研究方向为电磁场分析计算、电力系统电磁兼容和电磁测量。E-mail: wzzh@ncepu.edu.cn
（编辑 郭丽军）