Tab.1 Specifications of the racetrack HTS magnet
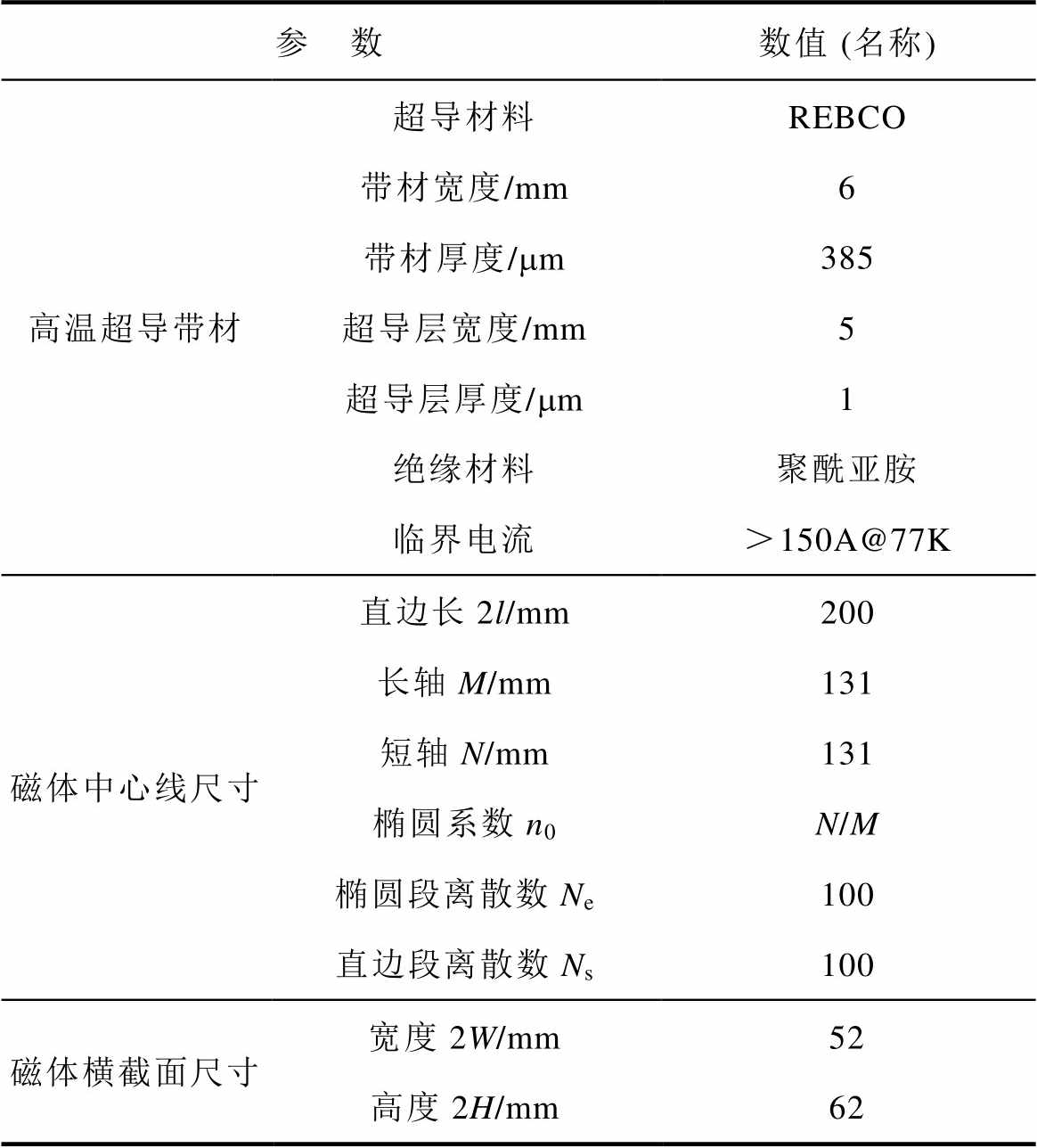
参 数数值 (名称) 高温超导带材超导材料REBCO 带材宽度/mm6 带材厚度/mm385 超导层宽度/mm5 超导层厚度/mm1 绝缘材料聚酰亚胺 临界电流>150A@77K 磁体中心线尺寸直边长2l/mm200 长轴M/mm131 短轴N/mm131 椭圆系数n0N/M 椭圆段离散数Ne100 直边段离散数Ns100 磁体横截面尺寸宽度2W/mm52 高度2H/mm62
摘要 基于均匀电流密度假设和毕奥-萨伐尔定律,该文建立了三种计算跑道型高温超导磁体磁场的解析模型。通过有限元仿真和实验测量验证了解析模型的有效性,对比分析了三种解析模型的计算精度和效率。基于解析模型,探究了椭圆段和电流密度穿透深度对跑道型超导磁体磁场分布的影响,揭示了自洽模型的磁场边界大小对超导磁体临界电流估计值的影响规律。该文建立的磁场解析模型能够准确快速地计算复杂形状超导磁体和常导磁体的磁场,可进一步应用于磁体电感、临界电流、交流损耗和电磁力等参数的计算,以提升磁体电磁设计效率。
关键词:跑道型磁体 高温超导磁体 磁场计算 电磁设计 电动磁悬浮
高温超导(High Temperature Superconducting, HTS)材料具有相对运行温度高、临界电流密度大和临界磁场高等优良特性[1-2],采用高温超导带材绕制而成的超导磁体在强磁场、医疗和轨道交通等领域有着极大应用优势和广阔应用前景。例如,以高温超导磁体为核心的超导储能系统可实现对电网功率波动的快速跟踪和实时补偿[3];高温超导内插磁体与水冷磁体的结合,创造了世界最强稳态磁场纪录45.5T[4];在飞轮储能系统中,将高温超导磁体作为混合磁悬浮轴承定子可降低储能系统损耗、提高电磁力密度[5];近几年,中日韩等国正在加快高温超导磁体在磁悬浮列车上的应用研究,以期推动超高速轨道交通技术的发展[6-12]。
为充分发挥超导材料性能和尽可能降低磁体制作成本,在实际应用前须对磁体进行优化设计,而磁场计算是磁体优化设计的关键环节。超导材料电阻率的非线性和临界电流密度的各向异性使超导磁体内电流密度呈非均匀分布。为准确计算这种非均匀电流密度分布及其产生的磁场,国内外学者建立了以磁场强度(H法[13])、矢量磁位(A法[14])、电流密度(J法[15])、矢量电位和矢量磁位(T-A法[16])等为控制变量的有限元模型。然而这些模型不仅建模复杂,而且计算相当耗时——尤其对于三维模型,不利于超导磁体的快速优化。
实际上,对磁体进行电磁设计时,更关心磁体在空间某一特定区域产生的磁场,而该区域的磁场对磁体电流密度的非均匀分布依赖较小,且距离磁体越远,这种依赖性越弱。鉴于此,在计算超导磁体磁场时,可将磁体电流密度近似为均匀分布。如此即可在保证一定计算精度条件下提高磁场计算效率,加速超导磁体的优化设计。这里需强调的一点是,这种均匀电流密度分布假设仅在超导磁体工作电流小于其临界电流时成立,因为当工作电流大于临界电流时,有绝缘超导磁体会发生失超,而无绝缘超导磁体会产生径向电流。
由二代高温超导带材绕制而成的超导磁体,其电流主要在超导层内流动,考虑到超导层厚度极薄(约1mm),可将其视为薄片,则超导层中实际的体电流密度可被近似为面电流密度[17]。在此基础上,考虑均匀电流密度假设,即可推导出面电流近似下超导磁体磁场的解析表达式。基于此,文献[18]建立了一种跑道型高温超导磁体的磁场解析模型,并将其与临界电流自洽模型结合,预测了磁体的临界电流。进一步地,将超导层电流均匀分布到整根带材,即可利用计算常导磁体磁场的方法[19-21]来计算超导磁体磁场,该方法已应用于计算圆形高温超导储能磁体磁场[22]和高温超导直线感应电机初级线圈磁场[23]。为进一步提高计算效率,文献[24]将磁体用其中心线等效,建立了一种大气隙无铁心高温超导直线同步电机气隙磁场解析模型,并通过实验验证了该解析模型的有效性。基于该模型,文献[25]优化设计了一种高温超导电动磁悬浮用驱动线圈。类似方法也应用了高温超导磁体的临界电流计算[26]和超导电动磁悬浮列车的电磁性能分析[27-29]。上述研究推导了线、面、体电流近似下磁体磁场的数值表达式,但表达式中仍含有积分符号,一定程度上限制了计算效率,不利用磁体的快速优化设计。
针对该问题,本文在前期研究基础上[18, 24, 30],利用离散求和的方法去除磁场表达式中的积分符号,提升计算效率;并通过对磁体横截面进行离散来提高模型计算精度。首先推导计算超导磁体磁场的线、面、体电流解析模型,基于仿真和实验手段验证模型有效性。然后对比分析三种解析计算模型的计算精度和效率,并基于线电流解析模型探究磁体几何参数对工作面磁场分布的影响规律,基于面电流解析模型探究超导层电流密度穿透深度(即非均匀电流密度分布)对磁体空间磁场分布的影响。最后结合体电流解析模型与自洽模型探究磁场边界大小对超导磁体临界电流估计值的影响规律。
该部分推导跑道型高温超导磁体磁场的解析表达式,主要推导步骤如下:
(1)对磁体横截面和中心线进行离散。
(2)将笛卡尔坐标系分别建立在椭圆段和直边段中心,根据毕奥-萨伐尔定律推导椭圆段和直边段磁场。
(3)将笛卡尔坐标系平移到跑道型磁体中心,利用坐标变换和叠加定理得到跑道型磁体磁场。
(4)利用旋转矩阵和平移矩阵修正磁体旋转和平移后的磁场表达式。
图1a为跑道型高温超导磁体的几何结构,包括两条直边段和两个半椭圆段。跑道型高温超导磁体的相关参数见表1。图1b~图1d分别对应线、面、体电流近似下磁体横截面的离散情况,三种情况的具体离散规则如下。
线电流模型:将磁体横截面等分为多个相同、接近正方形的小矩形,每个小矩形对应一个子磁体,每个子磁体由其中心线代替,将这些中心线产生的空间磁场叠加即为磁体磁场。
表1 跑道型高温超导磁体的相关参数
Tab.1 Specifications of the racetrack HTS magnet

参 数数值 (名称) 高温超导带材超导材料REBCO 带材宽度/mm6 带材厚度/mm385 超导层宽度/mm5 超导层厚度/mm1 绝缘材料聚酰亚胺 临界电流>150A@77K 磁体中心线尺寸直边长2l/mm200 长轴M/mm131 短轴N/mm131 椭圆系数n0N/M 椭圆段离散数Ne100 直边段离散数Ns100 磁体横截面尺寸宽度2W/mm52 高度2H/mm62
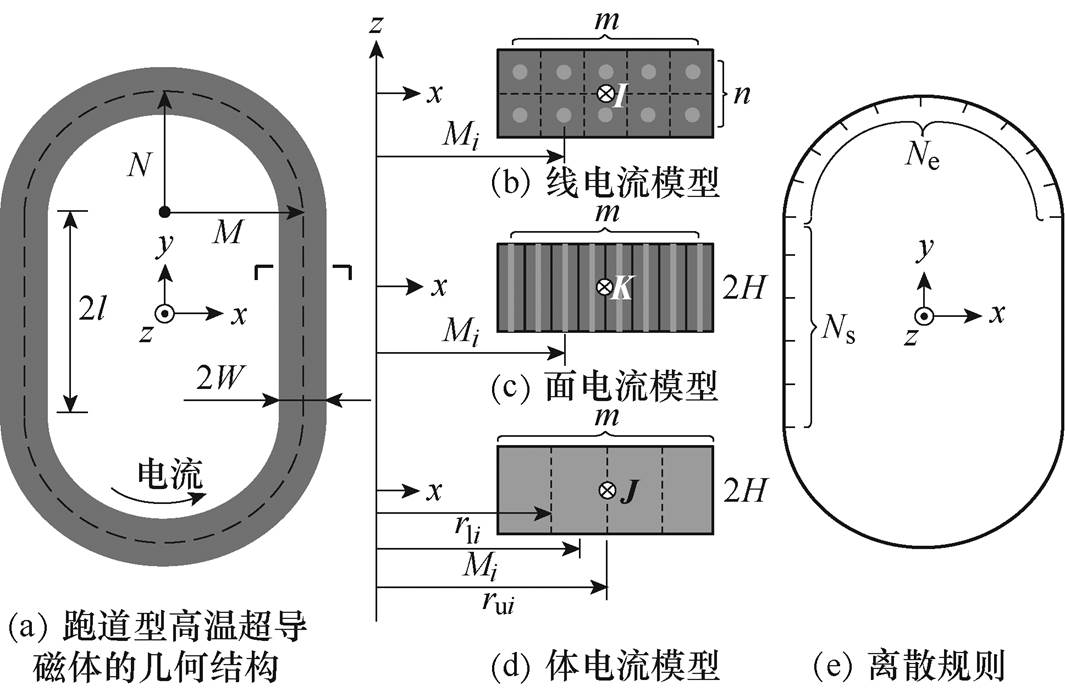
图1 跑道型高温超导磁体的几何结构及其离散规则
Fig.1 Geometric structure and discrete rule of a racetrack HTS magnet
面电流模型:在磁体横截面上等间距选取多条线段,每条线段对应一个单匝线圈,叠加所有单匝线圈的磁场即为磁体磁场。
体电流模型:将磁体横截面沿径向划分为多个面积相等的矩形,每个矩形对应一个子磁体,所有子磁体磁场的叠加即为磁体磁场。图1d中,rli、rui分别为第i个块的内半径和外半径。
在三种解析模型中,横截面离散前后磁体磁动势相等,且中心线离散规则相同,如图1e所示。
磁体横截面高度离散的数学表达式为
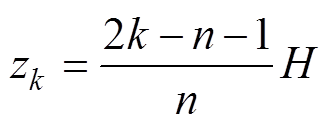 k=1, 2,…, n (1)
k=1, 2,…, n (1)
式中,n为横截面高度方向的分块数。设磁体横截面总的分块数为NZ,则
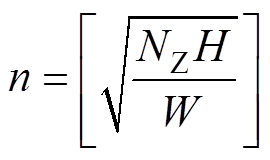 (2)
(2)
式中,[ · ]表示取整运算。
磁体横截面宽度离散的数学表达式为
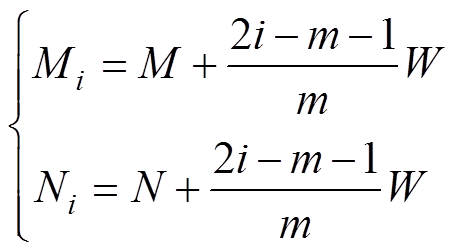 i=1, 2,…, m(3)
i=1, 2,…, m(3)
式中,m为磁体横截面水平分块数,定义为
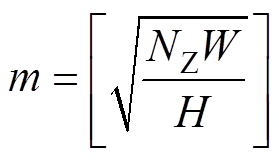 (4)
(4)
椭圆段中心线离散的数学表达式为
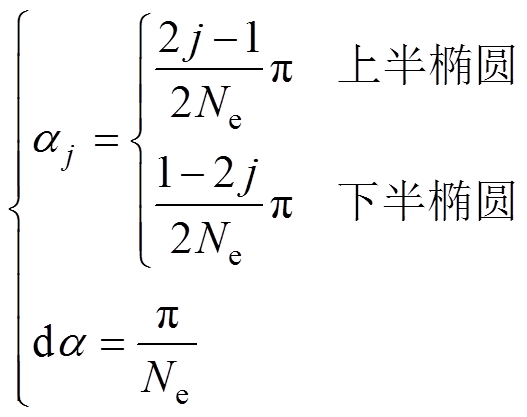 j=1, 2,…, Ne(5)
j=1, 2,…, Ne(5)
式中,Ne为椭圆段离散数;da 为每段的弧度。
磁体直边段离散的数学表达式为
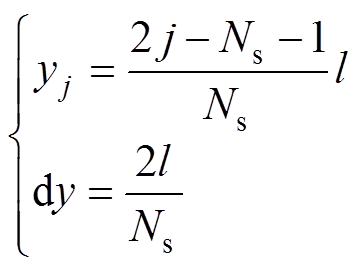 (6)
(6)
式中,Ns为直边段离散数;dy为每段长度。
下面对这三种解析模型进行详细介绍,但为节省篇幅,本文仅给出推导结果。需要统一说明的是:①在书写磁场表达式时,线、面、体模型分别用下标l、s、v区分,椭圆段和直边段分别用下标e和s区分;②在笛卡尔坐标系下,磁体磁场的三个分量分别用下标x、y、z区分;③为保证足够高的计算精度,磁体中心线椭圆段和直边段离散数量均取100;④磁感应强度矢量用B表示。本文基于仿真和实验手段验证解析模型的有效性,计算和测试的超导磁体均来自文献[10],相关参数见表1。为使对比更具说服力,解析模型和仿真模型均在COMSOL Multiphysics软件[31]中建立,仿真模型基于该软件的Magnetic Fields模块,而解析模型未添加任何物理场。
该解析模型的建立参考了文献[24],但本文作了两方面提升:①文献[24]直接将磁体简化为其中心线,而本文将磁体划分为多个子磁体,然后用所有子磁体的中心线等效磁体,提高了磁场计算精度;②文献[24]推导的磁场表达式含有积分符号,本文利用离散求和的方法去除了积分符号,提高了磁场计算效率。
椭圆段磁场表达式为
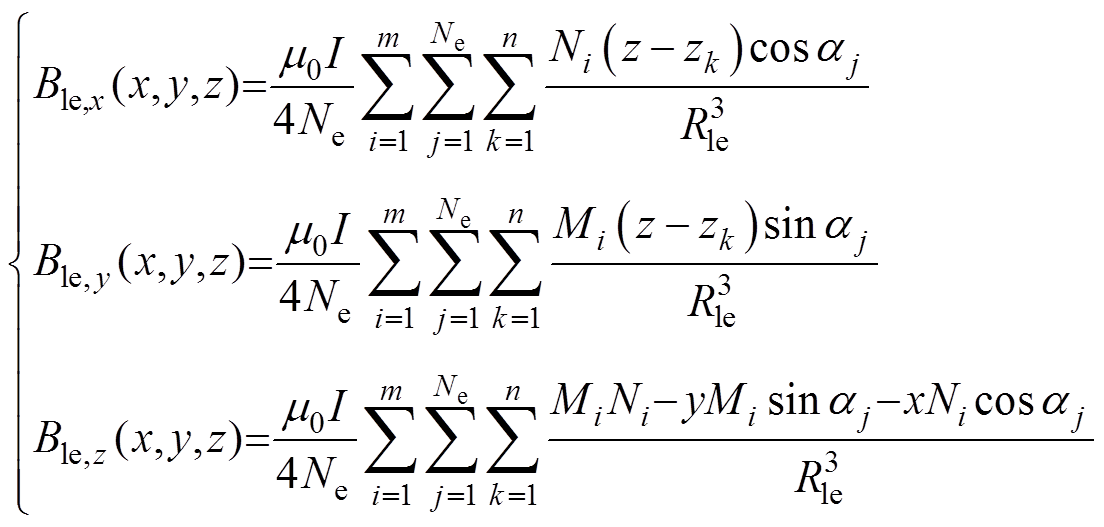 (7)
(7)
式中,m0为真空磁导率;变量Rle定义为
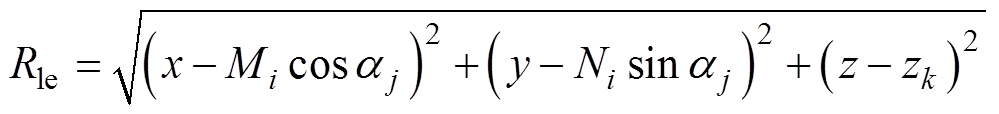 (8)
(8)
直边段磁场表达式为
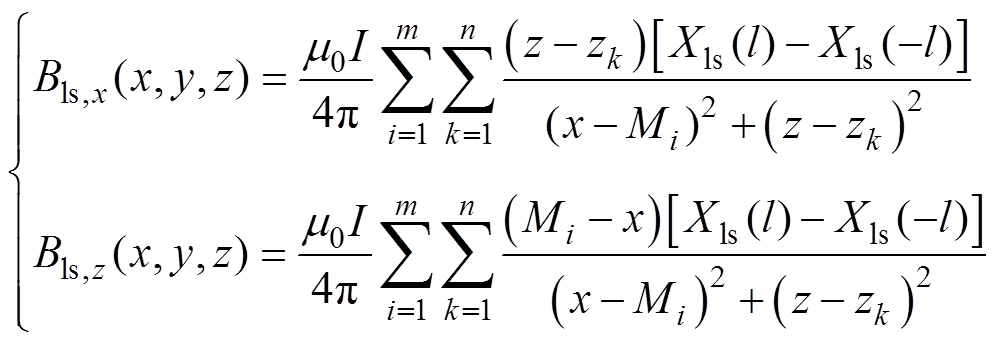 (9)
(9)
式中,函数Xls定义为
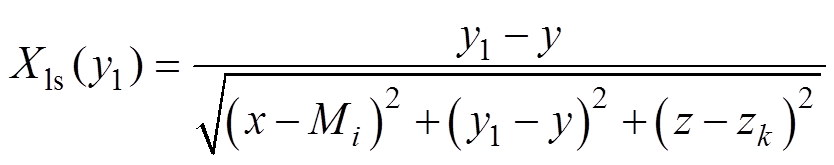 (10)
(10)
综上所述,线电流近似下跑道型磁体磁场表达式为
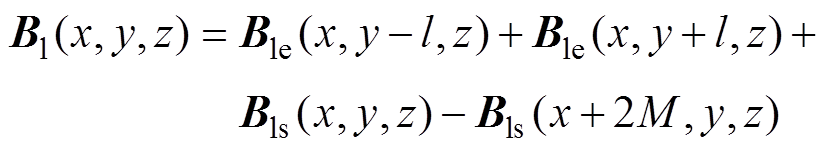 (11)
(11)
该解析模型的建立参考了文献[18],但这里作了如下两方面提升:①文献[18]需计算每匝带材产生的磁场,而本文仅通过计算典型位置带材的磁场即可得到整个磁体磁场,这在保证一定计算精度条件下可极大地提高磁场计算效率;②文献[18]推导的磁场表达式含有积分符号,本文利用离散求和的方法去除了积分符号,进一步提高了磁场计算效率。
椭圆段磁场表达式为
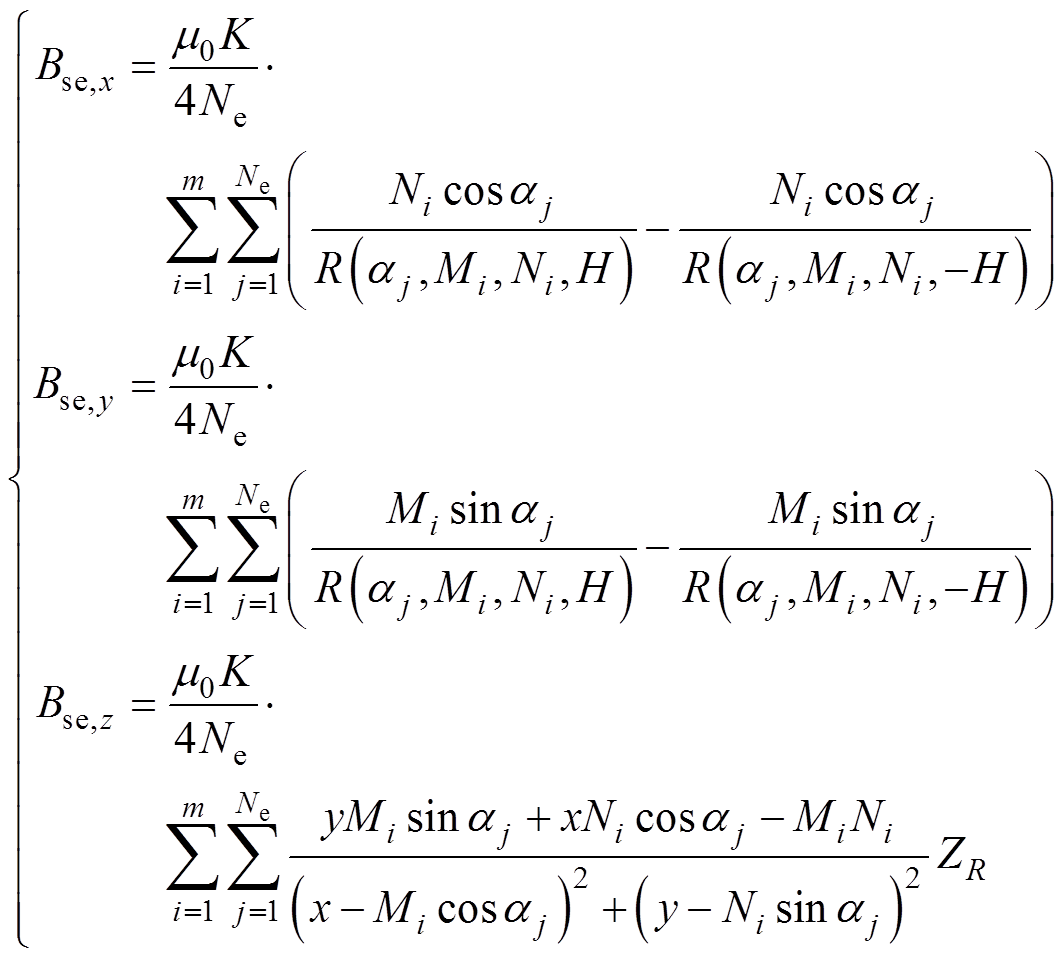 (12)
(12)
式中,函数R和ZR分别定义为
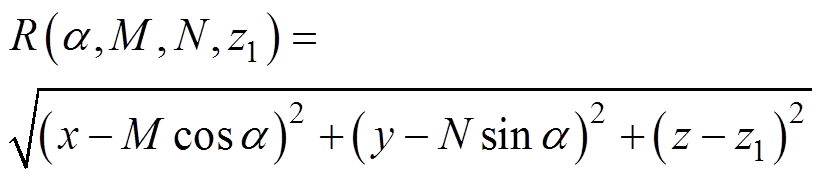 (13)
(13)
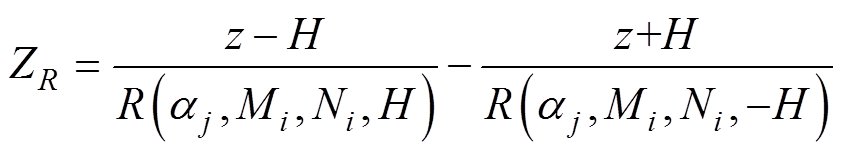 (14)
(14)
直边段的磁场计算表达式为
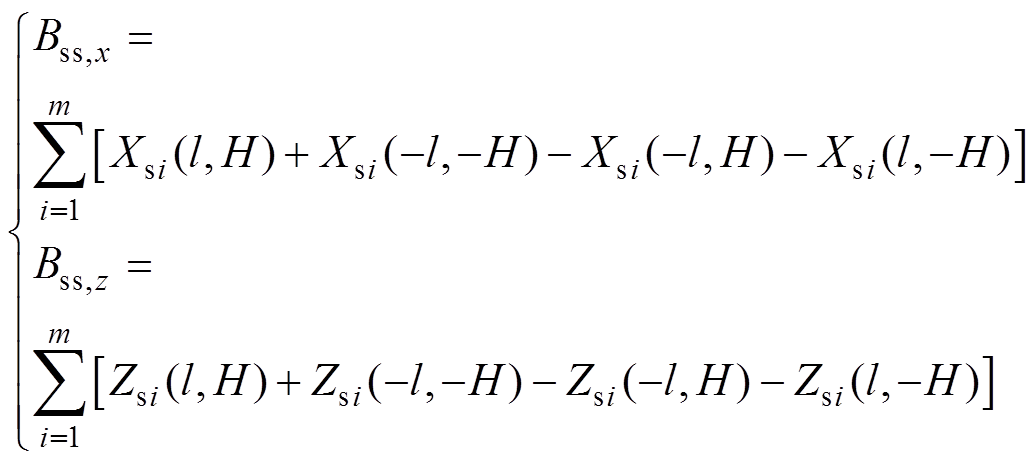 (15)
(15)
式中,函数Xsi和Zsi分别定义为
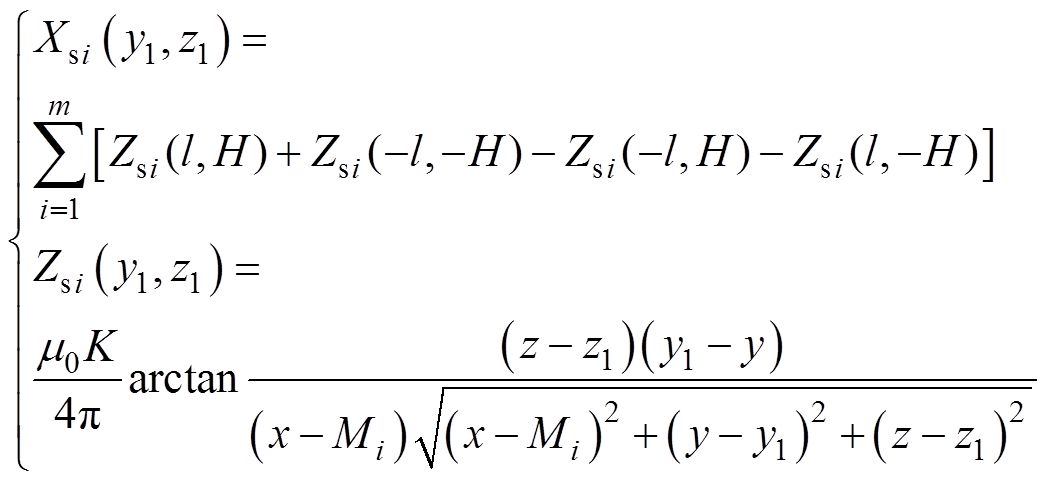 (16)
(16)
综上所述,面电流近似下跑道型磁体磁场表达式为
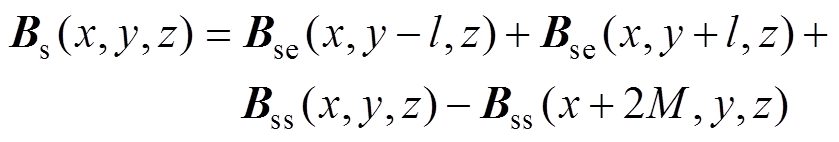 (17)
(17)
该解析模型的建立参考了文献[21, 30],且作了如下两方面提升:①上述文献在计算磁体椭圆段内体电流密度矢量时存在一定误差,而本文将磁体划分成多个子磁体,单独计算每个子磁体的体电流密度矢量及其磁场,然后叠加所有子磁体的磁场得到整个磁体磁场,提高了磁场计算精度;②上述文献推导的磁场表达式中含有积分符号,本文利用离散求和的方法去除积分符号,提高了计算效率。
椭圆段磁场表达式为
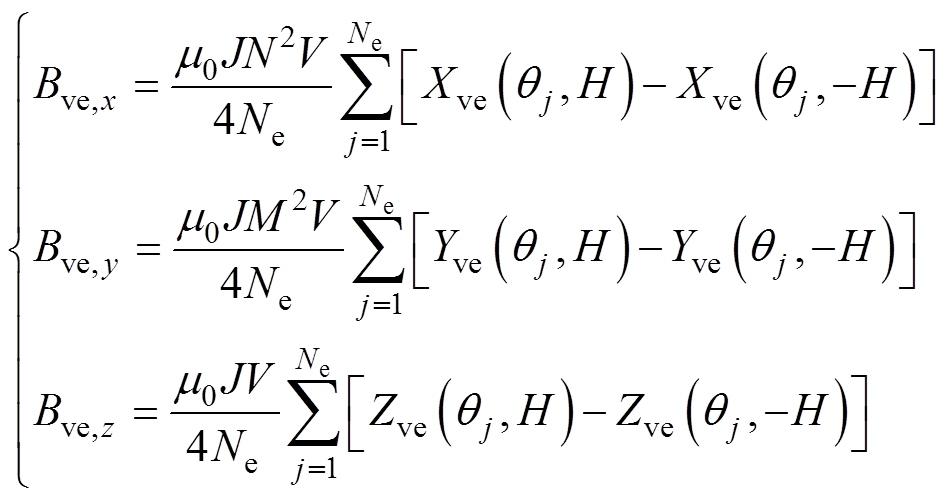 (18)
(18)
式中,J为体电流密度模值;函数Xve、Yve和Zve分别为
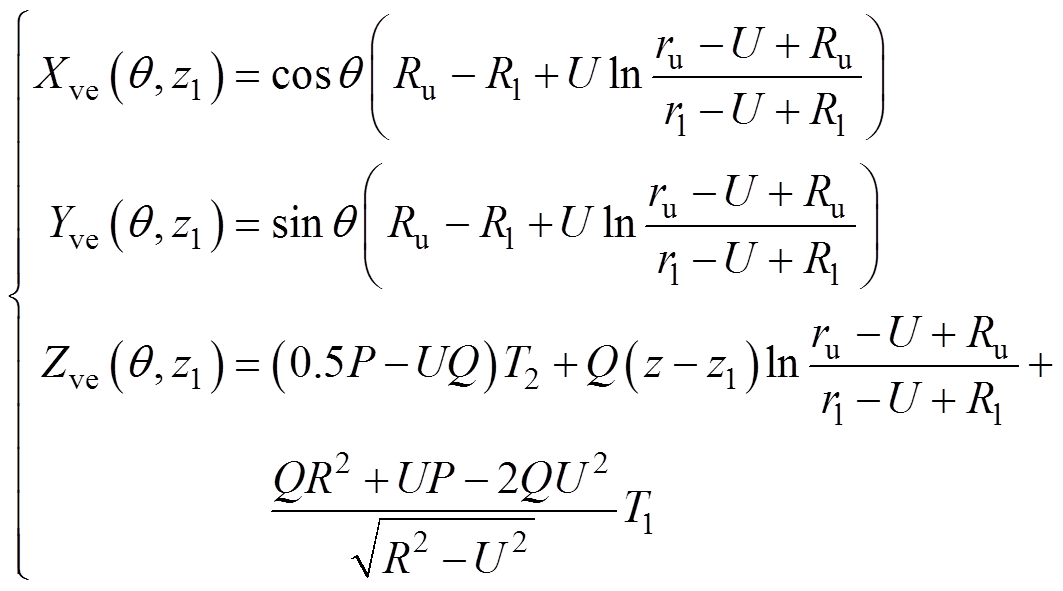 (19)
(19)
式中,变量U、V、P、Q、R分别定义为
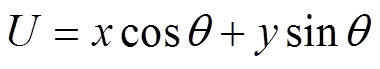 (20)
(20)
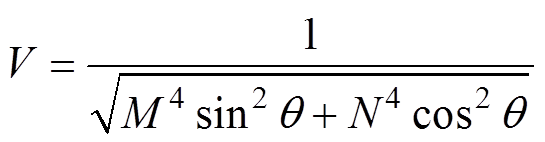 (21)
(21)
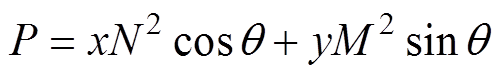 (22)
(22)
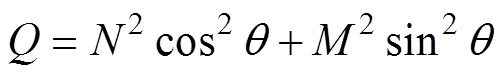 (23)
(23)
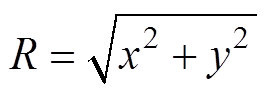 (24)
(24)
Ru和Rl定义为
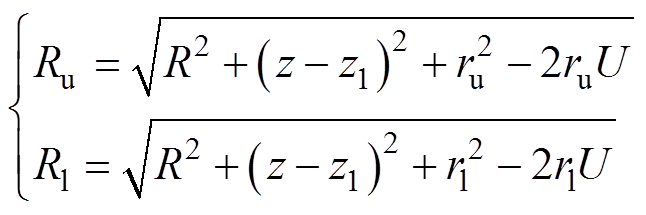 (25)
(25)
式中,ru和rl定义为
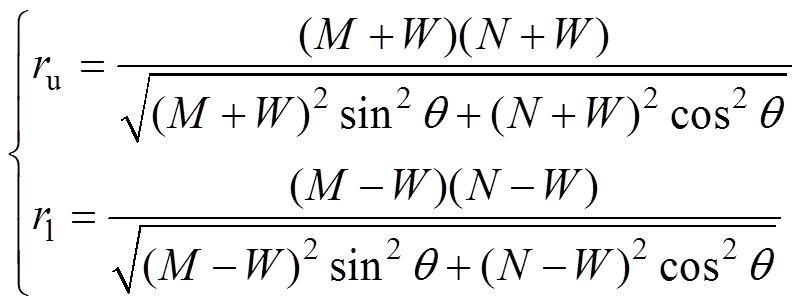 (26)
(26)
变量T1和T2分别定义为
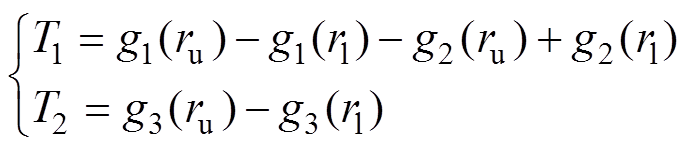 (27)
(27)
式中,函数g1、g2和g3分别定义为
 (28)
(28)
直边段的磁场表达式为
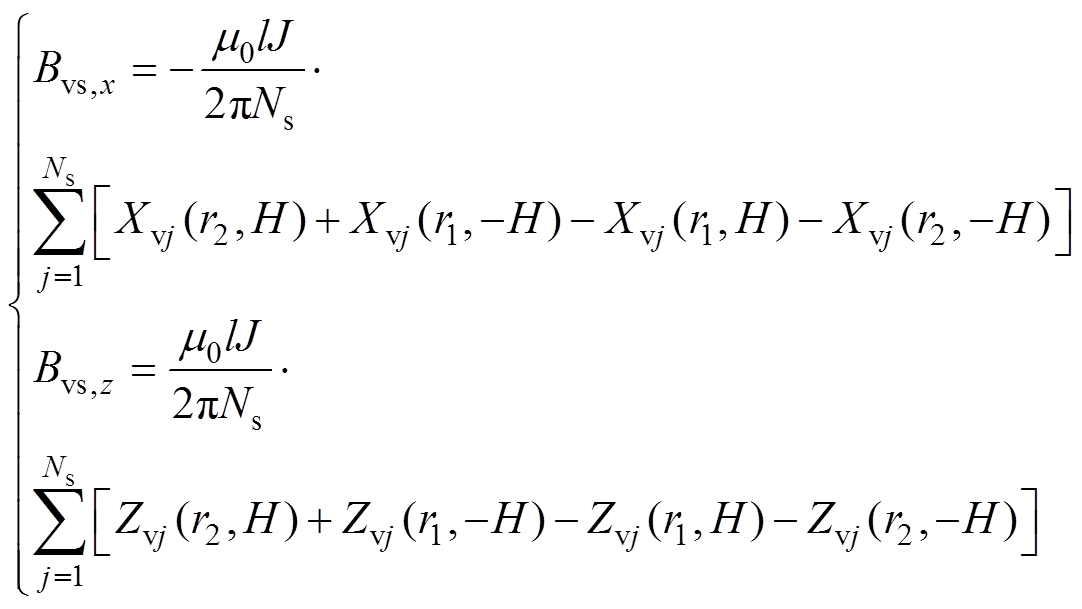 (29)
(29)
式中,函数Xvj和Zvj分别定义为
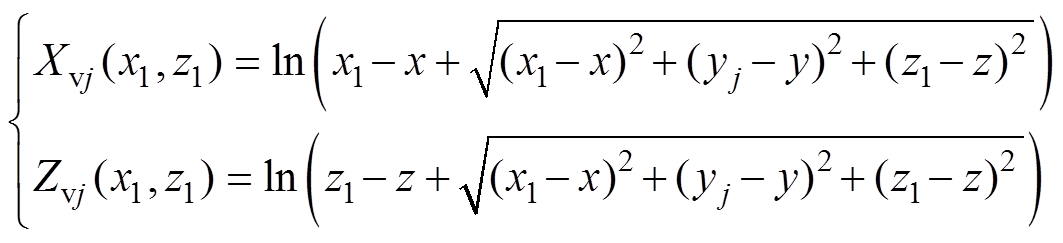 (30)
(30)
综上所述,体电流近似下跑道型磁体磁场表达式为
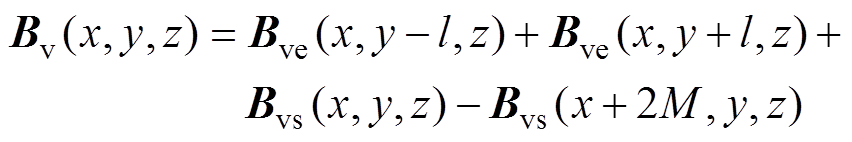 (31)
(31)
磁体旋转和平移后的磁场表达式可通过旋转矩阵和平移矩阵进行修正,如磁体先绕过点(Ox, Oy, Oz)的z轴旋转qz,再平移(Dx, Dy, Dz),则磁场修正为
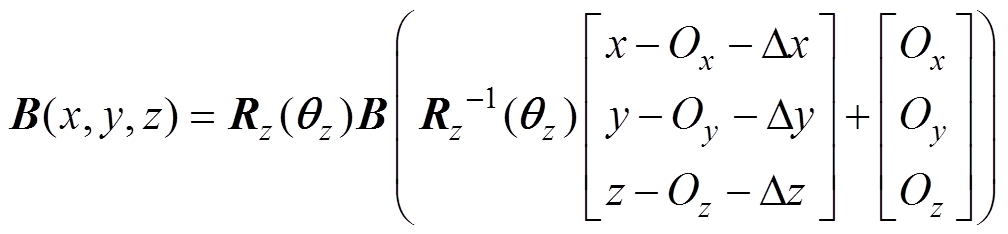 (32)
(32)
式中,Rz(qz)为关于z轴的旋转矩阵。
图2为线、面、体电流近似下跑道型磁体磁场的有限元仿真模型,磁体参数见表1。这里,磁体以点(30 mm, 40 mm, 50 mm)为旋转中心绕z轴顺时针方向旋转了50 °,旋转后沿x、y、z方向分别平移50 mm、30 mm、0 mm。在模型中,小空气域用于提高磁体周围空气域网格剖分质量;为可视化,包裹小空气域的大空气域被隐藏。为提高建模效率,三个模型中磁体划分如下,线电流模型:m=3, n=3;面电流模型:m=3;体电流模型:m=1。
图3和图4为线、面、体电流近似下跑道型磁体磁场的解析与仿真结果的比对,图3和图4中的结果分别提取于磁体表面上方5 mm处的一条直线段和一平面区域。对比发现,解析与仿真结果完全一致,验证了解析模型的准确性。另外,对于计算空间某一点处磁场而言,线、面、体电流仿真模型所需时间分别为15 s、71 s、191 s,而线、面、体电流解析模型所需时间分别为11 ms、14 ms、15 ms,其计算效率提升了至少3个数量级。尽管仿真模型可一次性计算出整个空间磁场分布,但就计算局部区域磁场而言,解析模型效率更高。
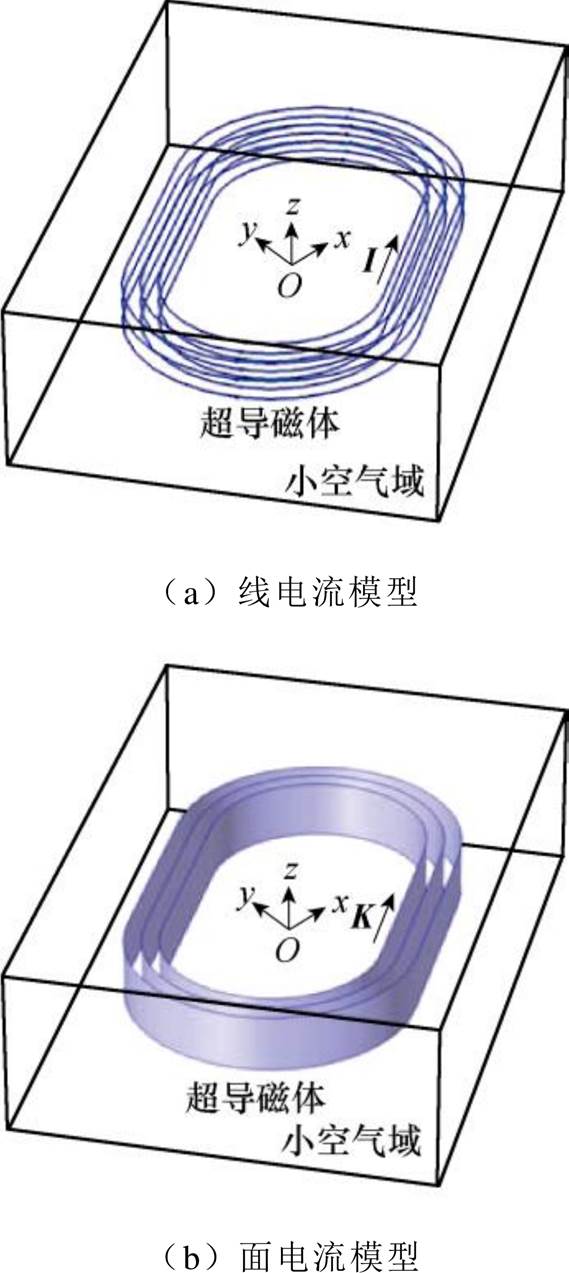
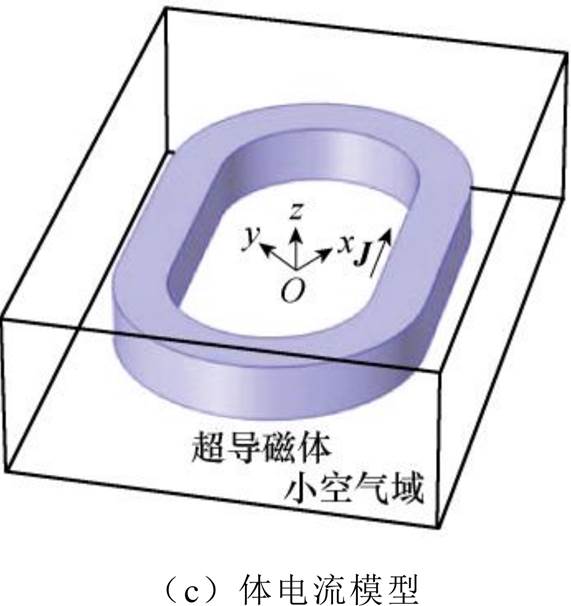
图2 跑道型磁体磁场的有限元仿真模型
Fig.2 Finite element models for the magnetic field calculation of racetrack magnet
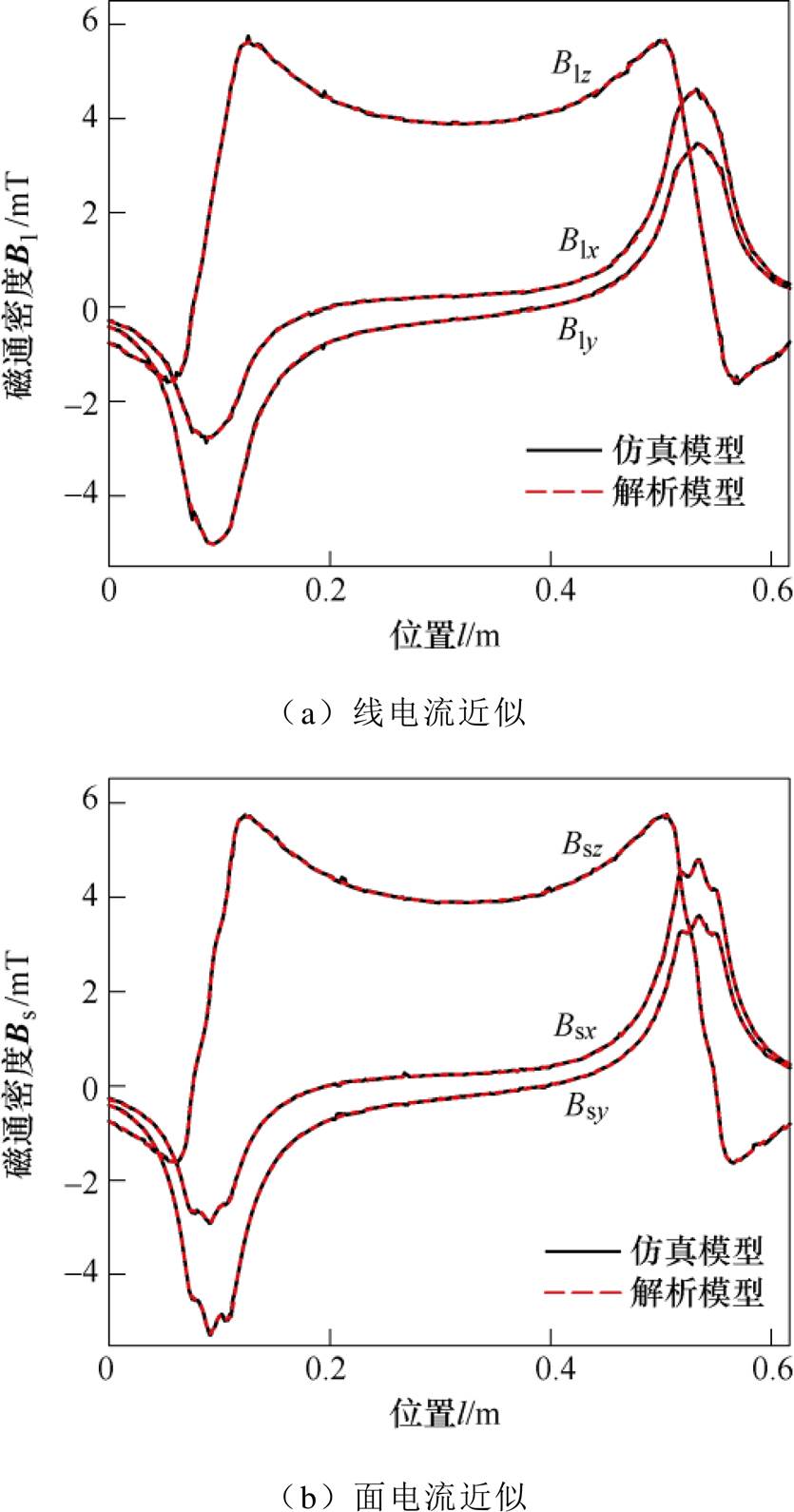
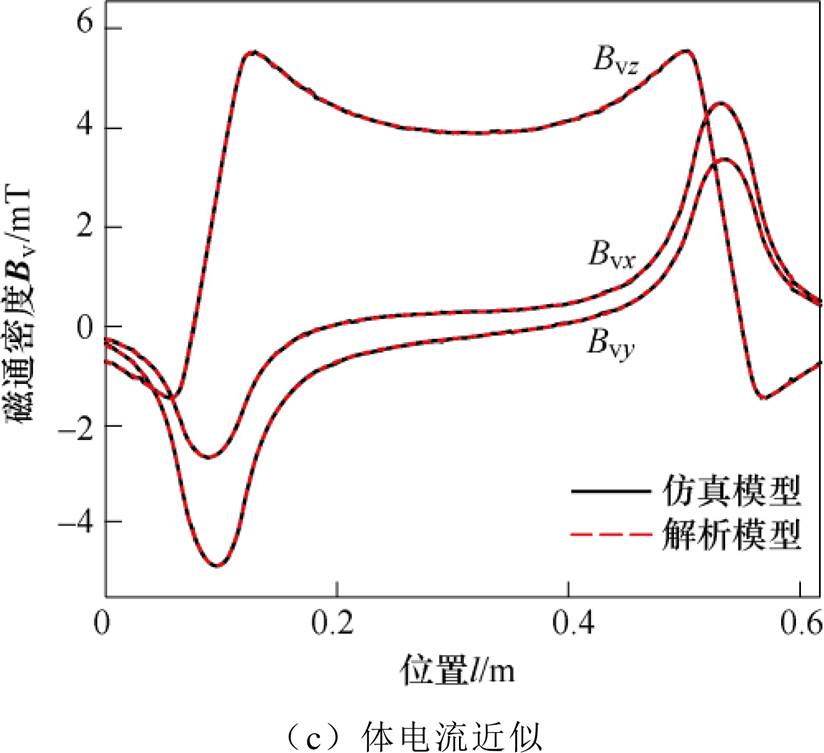
图3 跑道型磁体磁场的解析与仿真结果对比
Fig.3 Comparison on the magnetic fields of the racetrack magnet calculated by the analytical and FEM models
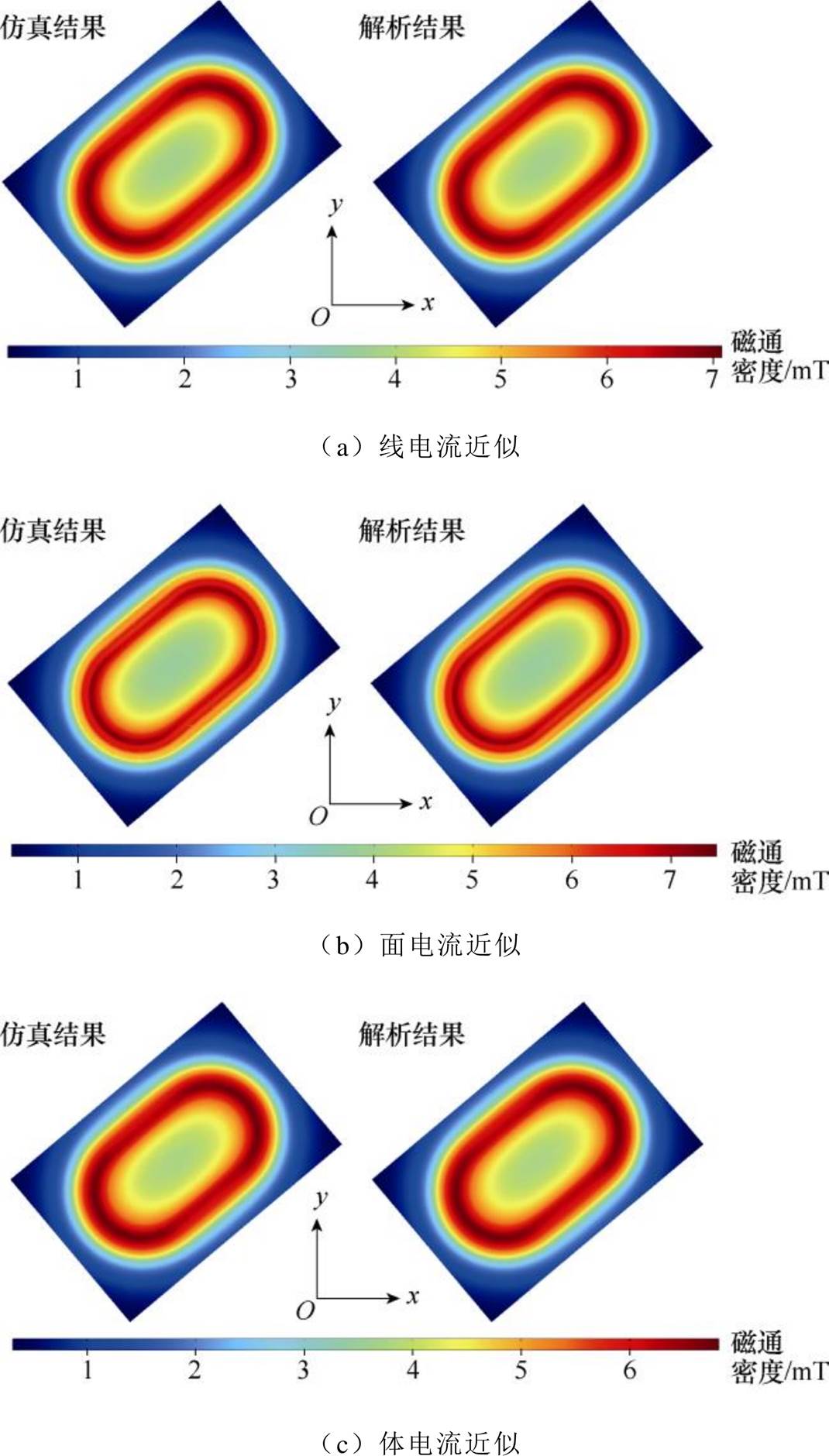
图4 跑道型磁体磁场的解析与仿真结果
Fig.4 Magnetic fields of the racetrack magnet calculated by the analytical and FEM models
基于前期研制的高温超导磁体,本文搭建了超导磁体的磁场测试平台,测试了不同气隙和高度下磁体的磁场分布,并与解析计算结果进行对比。在解析模型中,通过权衡计算精度和计算效率后确定磁体划分情况如下,线电流模型:m=3, n=3;面电流模型:m=30;体电流模型:m=1。
图5为传导冷却式高温超导磁体的三维示意图,关于该磁体的设计方法、制作工艺和性能测试结果见文献[10],磁体所用带材类型及其相关参数汇总在表1中。图6为磁体磁场测试平台,除了测试对象高温超导磁体外,该平台主要包括磁体性能监测系统、磁场测试工装、霍尔探头、高斯计、工控机。磁场测试工装上安装有滑块和刻度尺,霍尔探头固定在滑块上,高斯计实时显示霍尔探头数据并保存到工控机中。测试工装放置在磁体工作面侧,其滑块可沿刻度尺水平滑动实现对磁体水平位置磁场的测量;工装上设置有三个卡槽,可调整滑块与磁体之间的距离,实现不同气隙处磁场的测量;通过在滑块下方添加不同厚度的方块调节滑块高度,实现不同高度处磁场的测量。
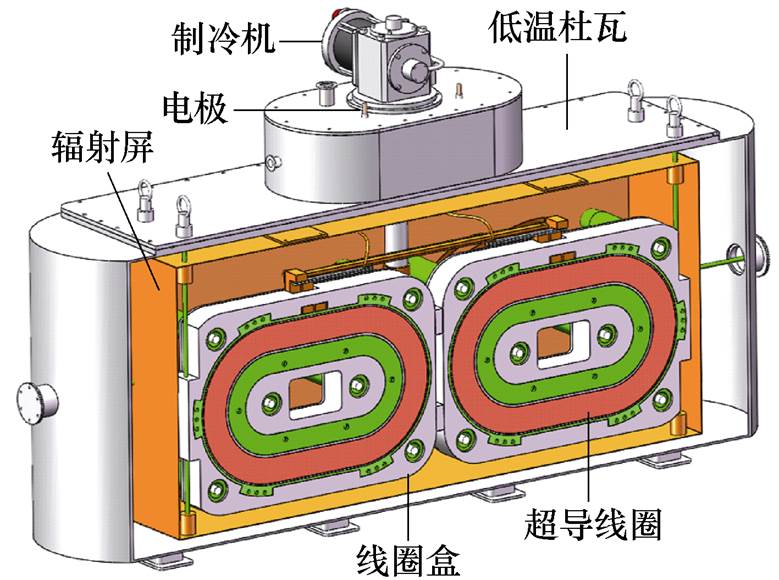
图5 高温超导磁体结构示意图
Fig.5 Geometric layout of the HTS magnet

图6 高温超导磁体的磁场测试平台
Fig.6 Test platform of the magnetic field of HTS magnet
由于两个线圈的几何对称性(见图5),对两个线圈输入方向相反的电流后,磁体磁场将关于两个线圈对称轴镜像对称,因此测量其一半空间的磁场即可,具体测量位置如图7所示,包括3个高度(h= 0、105、157 mm)和3个气隙(g=45、75、105 mm)的组合,共9个位置,其中h定义为测量位置与线圈水平对称轴的垂直距离,g定义为测量位置与超导线圈绕组表面的垂直距离,测试起点为两个线圈的竖直对称轴。磁体的励磁电流设定为25 A。考虑到z方向磁场分量最强,也是实际最关心的磁场分量,因此本文仅测量z方向分量。
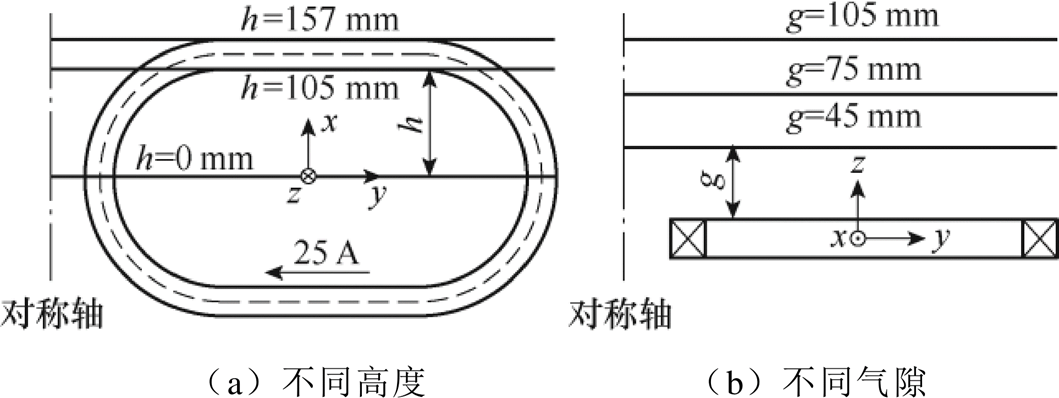
图7 高温超导磁体磁场的测量位置
Fig.7 Measurement location of the magnetic fields
图8为不同高度和不同气隙处z方向磁场分量的测试和解析结果的比对。对比发现,两者在趋势上保持较好的一致性,尤其在高度h=0 mm时,验证了解析模型的有效性。然而,解析与实验结果之间仍存在较明显的差异,如h=105 mm、g=45 mm时,导致误差的原因主要包括:①磁场测试工装的安装误差使实际测量位置偏离指定位置;②霍尔探头安装误差导致霍尔片不完全垂直于z方向磁场;③超导线圈在磁体中的安装误差。
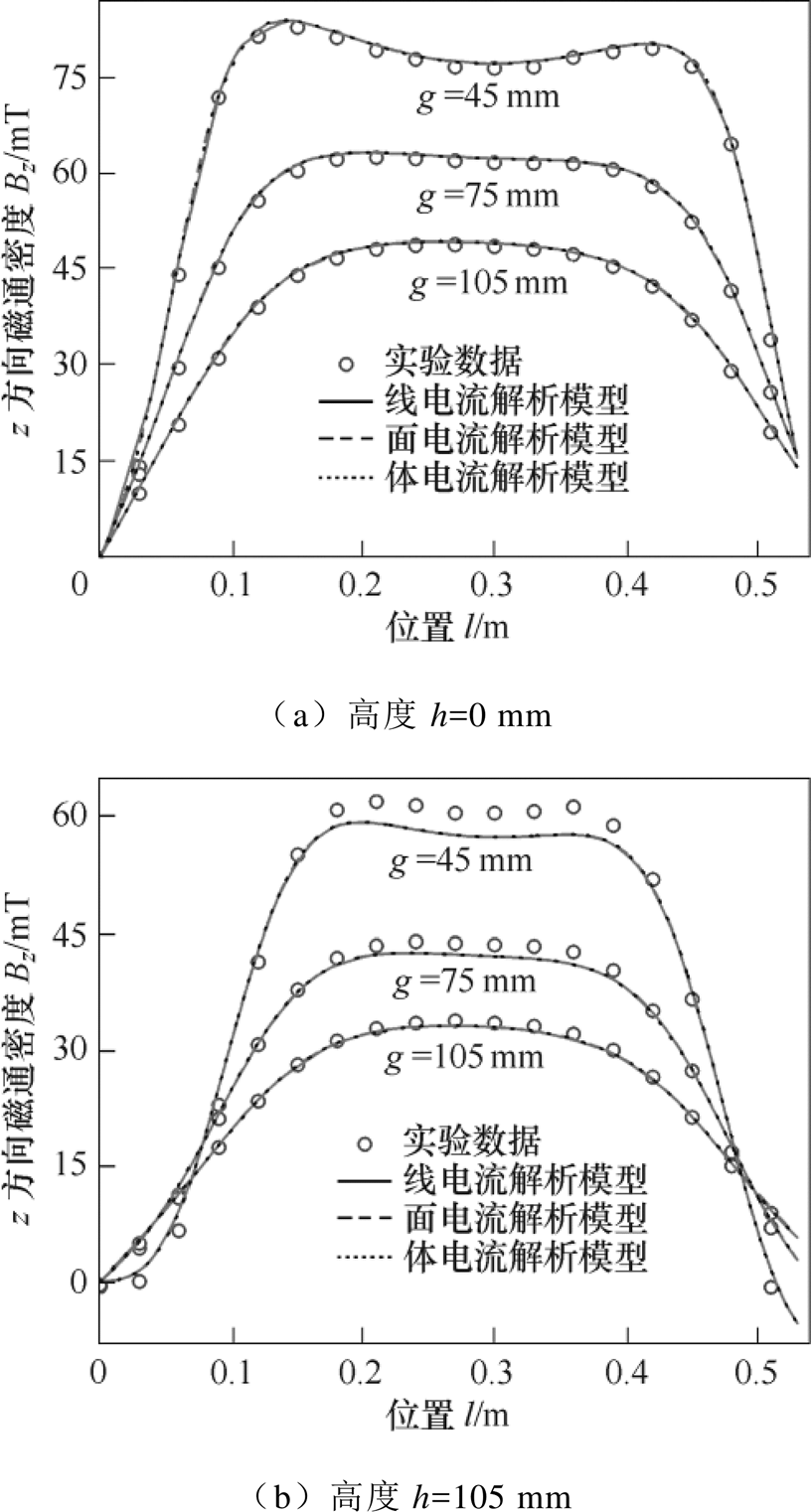
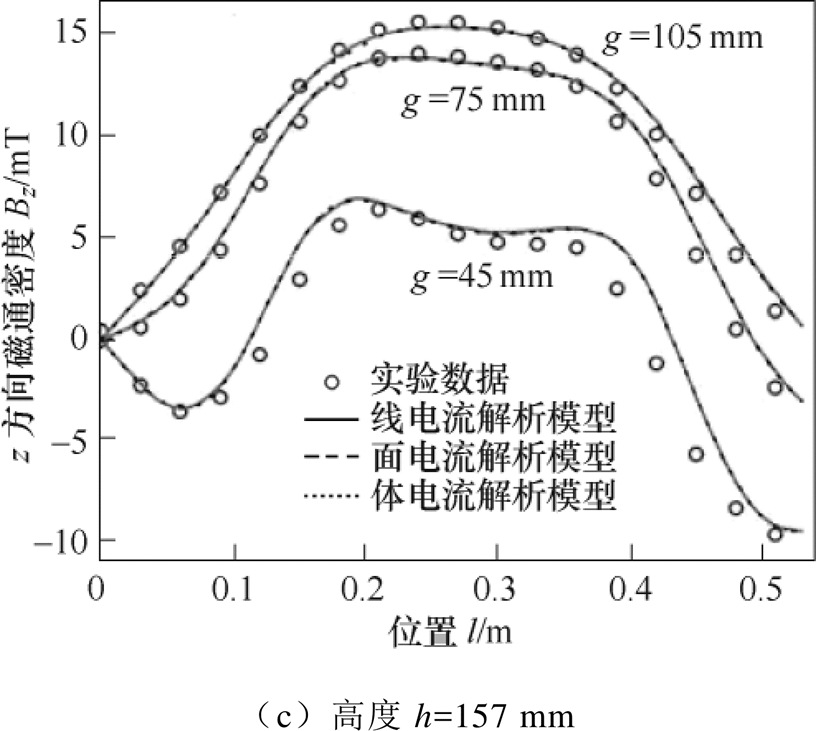
图8 高温超导磁体磁场的测量与解析结果对比
Fig.8 Measured and analytical magnetic fields produced by the HTS magnet
从图8还可以发现,当气隙较小时(如45 mm),磁体的最大磁场位置偏离线圈中心,且更靠近线圈圆边段。随着气隙增大,圆边段在线圈中心区域产生的磁场快速下降,此时磁体最大磁场向线圈中心移动。另外,当h=157 mm时,z方向磁场随着气隙的增大而增加,这区别于h=0 mm和105 mm时情况。原因在于,磁场的Bz分量与其模值Bm之间夹角b 随气隙增大而减小,即cosb 增加;又因为Bz=Bmcosb,虽然Bm随气隙增大而减小,但两者乘积最终导致了Bz分量增加。
本节将对比分析三种解析模型的计算精度和效率,然后对三种解析模型分别给出一个应用实例。默认情况下,磁场提取于磁体表面上方5 mm处某一点或某一直线段。
图9为三种解析模型计算跑道型磁体(n0=0.5)磁通密度模值和所需时间的对比。这里已通过调整三种解析模型中磁体横截面离散数量来统一每个模型计算时间,其中,线、面、体电流模型中磁体横截面最大离散数量分别为60、25、10。从离散数量的角度对比,线、面、体电流模型的计算效率依次降低。从磁场收敛情况来看,线、面、体电流模型收敛速度依次增加。由此可知,线电流模型适用于要求求解速度快的场合(如优化设计);面电流模型适用于计算精度要求高的场合(如预测实验值)。
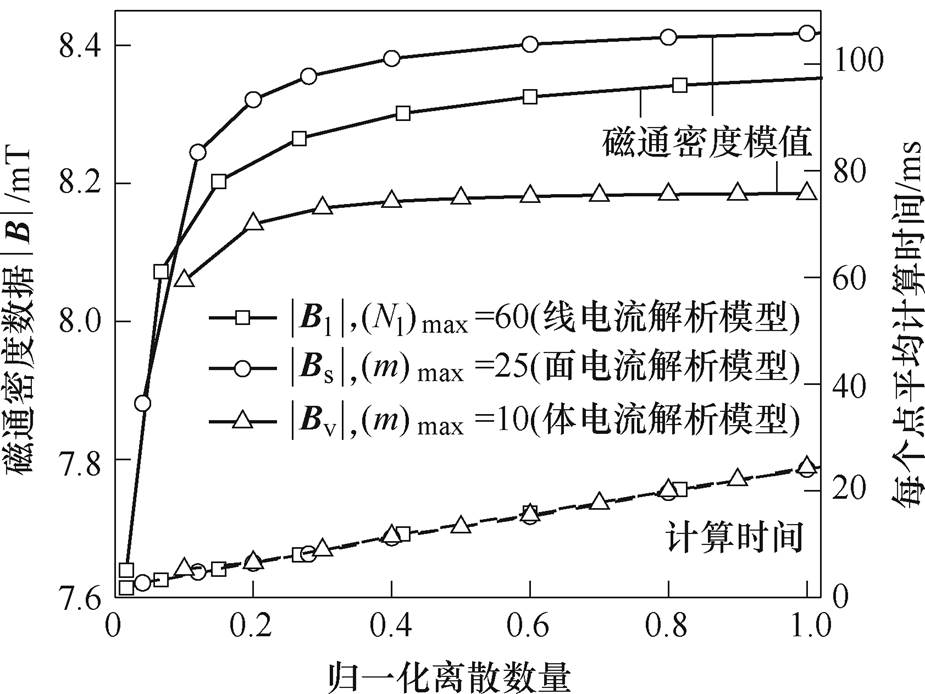
图9 三种解析模型计算的跑道型磁体磁通密度模值和所需时间随归一化离散数量的依赖关系
Fig.9 Dependences of the magnetic flux norm and requested computating time on the normalized descrete number of a racetrack magnet when resorting to these analytical models
关于体电流模型,这里需要说明的一点是:当n0≠1时,椭圆段内体电流密度的方向无法精确计 算[21],导致体电流模型计算结果偏小,如图9所示;当n0=1时,半圆段内体电流密度方向能够被准确表达,此时体电流模型中m可直接取为1,其计算效率将变得最高;另外,根据图8,当n0=1时,三种解析模型计算精度相当。因此,当n0=1时,体电流模型兼具计算效率高和精度高的优点,更适用于边端为半圆形的跑道型磁体的磁场计算。
图10为基于线电流解析模型计算的带有不同椭圆段(椭圆系数不同)的跑道型磁体在其工作面产生的磁通密度模值分布云图,磁场最大值放在对应云图下方,其位置用点标记在云图内。该图表明,随着椭圆系数的变小,磁体的最大磁通密度先减小后增加;且当n0≥1时,最大磁场点位于椭圆段中间;当n0<1时,最大磁场点向直边段靠近。以上现象表明,跑道型磁体的最大磁场在n0=1时达到最小值,其位置仅当n0<1时会发生偏移。
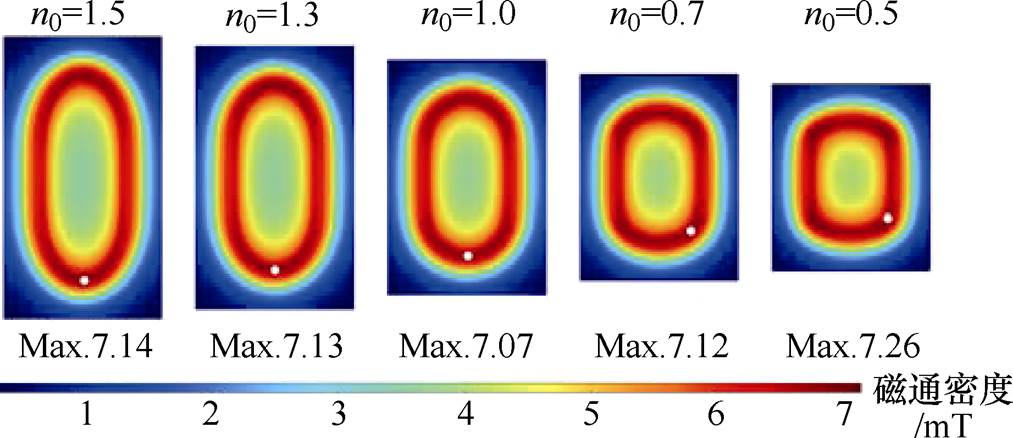
图10 带有不同椭圆段的跑道型磁体在其工作面上产生的磁通密度模值分布云图
Fig.10 Distribution of the magnetic flux density norm generated by the racetrack magnet with the different elleptical sections
图11为基于面电流解析模型计算的不同电流穿透系数d(d =1-w/W,w为未穿透区域的宽度)下跑道型超导磁体的空间磁场分布,这里考虑了面电流密度大小保持不变和单匝电流保持恒定两种情况,磁体内电流密度表达式如图11所示。图11a表明,磁体的磁通密度模值随穿透深度的增大而增加,因为穿透深度越大,单匝带材的总电流越大。图11b表明,磁通密度模值几乎不随穿透深度变化,即电流密度的非均匀分布不会明显改变空间磁场分布,验证了在推导解析模型时假设超导磁体中电流密度均匀分布的合理性。
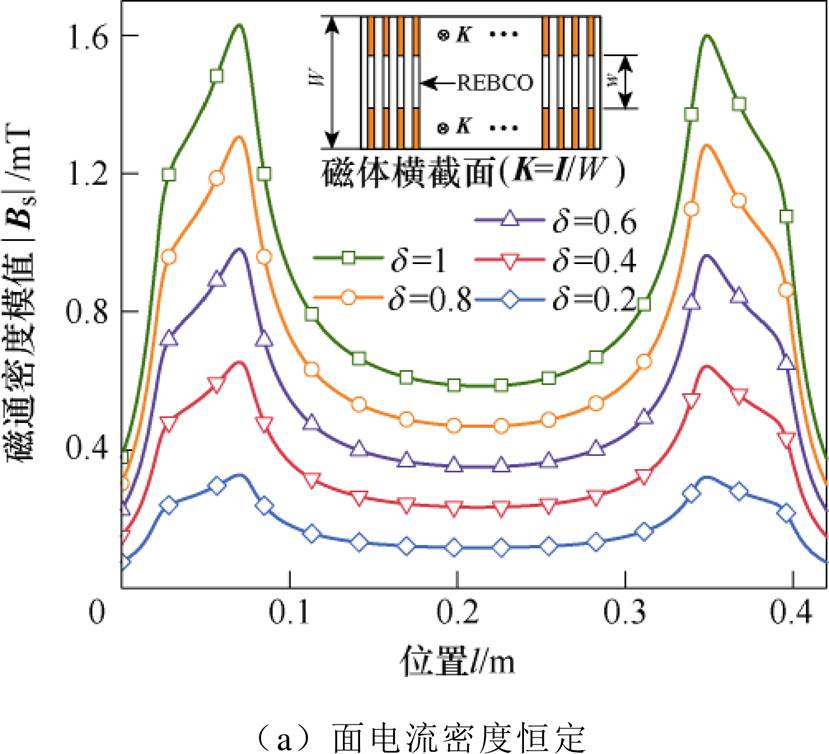
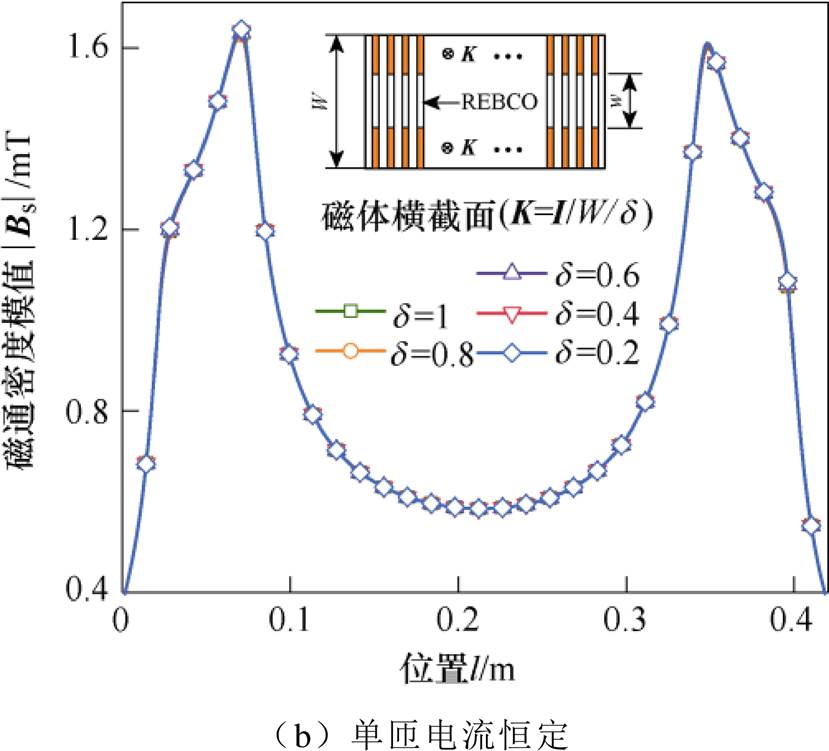
图11 不同电流穿透系数下磁体的磁场分布
Fig.11 Magnetic field distribution of the racetrack magnet with different current penetration depths
本节结合体电流解析模型与自洽模型计算跑道型高温超导磁体的临界电流,研究自洽模型磁场边界大小对临界电流计算精度的影响规律。
图12为高温超导磁体的临界电流自洽模型,该模型建立在磁场最强的横截面上(见图10),跑道型磁体的磁场采用体电流解析模型计算并施加于自洽模型的磁场边界上,详细建模过程见文献[18]。这里的磁场边界为2Wb×2Hb的矩形,与磁体横截面的宽、高分别相距dW、dH。
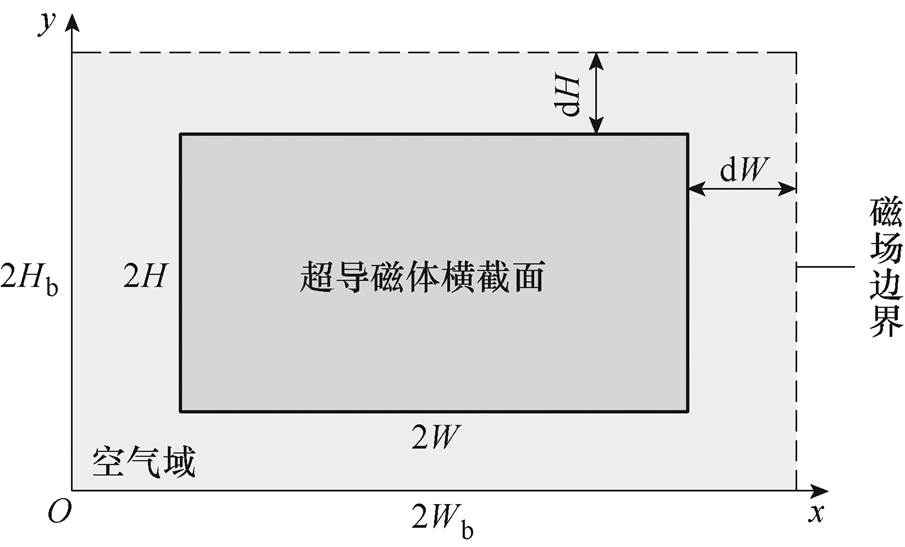
图12 高温超导磁体的临界电流自洽模型
Fig.12 Self-consistent model for estimating the critical current of HTS magnet
图13为不同磁场边界增量对应的磁体临界电流估计值,其中,实线表示临界电流等值线,虚线对应dH=dW。能够看到,临界电流估计值随着磁场边界的增大而增大,且对边界宽度和高度的依赖程度相当。在本文考虑的边界增量范围内,临界电流估计值误差小于5 %,证明磁场边界大小对临界电流估计值影响并不明显。另外,该磁体的临界电流实测值约64.7 A[10],与估计值接近,验证了计算模型的有效性。但随着磁场边界的增加,估计值与测试值差别增大。综上可得出结论:磁场边界大小对临界电流估计值影响较小,但建议选择更小的磁场边界。这里需要说明的一点是,超导磁体实际的临界电流取决于带材性能、磁体磁场和运行温度等参数,不依赖计算模型中磁场边界大小。
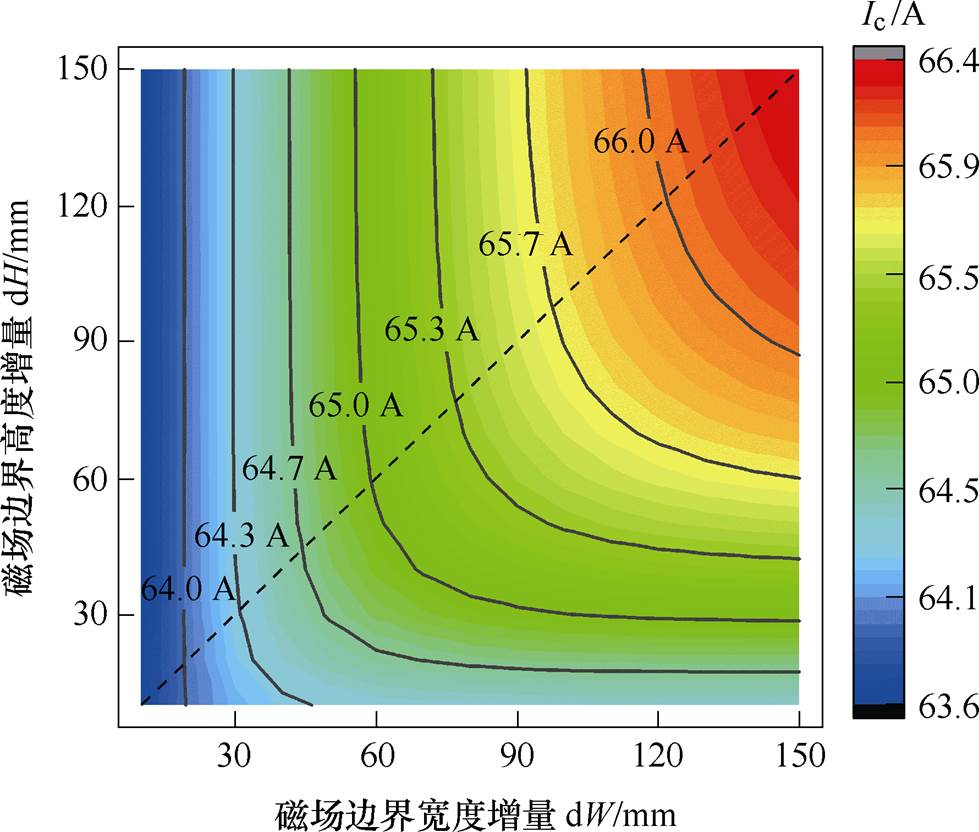
图13 不同边界增量下超导磁体的临界电流估计值
Fig.13 Estimated critical currents on the HTS magnet with respect to the boundary increament
图14为磁场边界宽度和高度增量均为20 mm时磁体横截面上的磁通密度分布,实线表示磁通密度流线,箭头表示磁通密度方向。可以看到,磁通密度主要集中于横截面左侧,即跑道型磁体内侧,而右侧区域磁场相对较弱,意味着磁体临界电流将取决于其内侧带材。
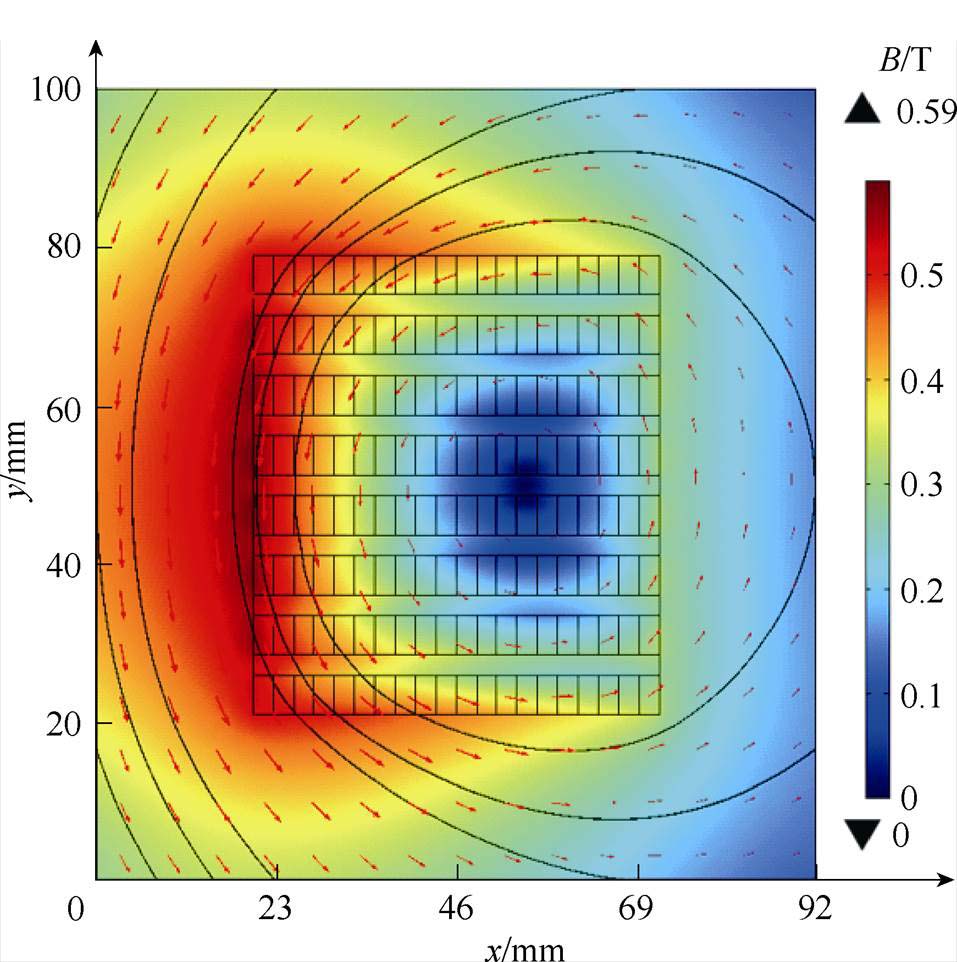
图14 磁场边界的宽度和高度增量均为20 mm时磁体横截面上的磁通密度分布
Fig.14 Magnetic flux density distribution on the cross-section of the magnet under dH=dW=20 mm
本文基于毕奥-萨伐尔定律建立了跑道型高温超导磁体的磁场解析计算模型,并采用仿真和实验手段验证了解析模型的有效性。对比分析了线、面、体电流解析模型的计算精度和效率,揭示了不同椭圆段和穿透深度下跑道型超导磁体磁场的空间分布特征,总结了自洽模型的磁场边界大小对超导磁体临界电流估计值的影响规律。
对于带有椭圆段的跑道型磁体,线电流解析模型计算效率最高,但精度一般;面电流解析模型计算精度最高,但效率一般;体电流模型计算精度和效率均较低。对带有圆边段的跑道型磁体,体电流模型计算精度和效率均最高。跑道型磁体的最大磁场在其边端为半圆形时达到最小值,且最大值位置可能会向其直边段偏移。利用自洽模型估计超导磁体临界电流时,其边界大小对临界电流估计值影响较小,但本文建议选择更小的磁场边界。
本文建立的磁场解析模型不仅适用于计算高温超导磁体磁场,还可用于计算低温超导磁体和常导磁体的磁场。
参考文献
[1] 蔡传兵, 池长鑫, 李敏娟, 等. 强磁场用第二代高温超导带材研究进展与挑战[J]. 科学通报, 2019, 64(8): 827-844.
Cai Chuanbing, Chi Changxin, Li Minjuan, et al. Advance and challenge of secondary-generation high-temperature superconducting tapes for high field applications[J]. Chinese Science Bulletin, 2019, 64(8): 827-844.
[2] Yao Chao, Ma Yanwei. Superconducting materials: challenges and opportunities for large-scale appli- cations[J]. iScience, 2021, 24(6): 102541.
[3] 诸嘉慧, 宝旭峥, 丘明, 等. 基于混合高温超导储能系统的电网动态功率补偿策略与试验[J]. 电工技术学报, 2012, 27(8): 14-20.
Zhu Jiahui, Bao Xuzheng, Qiu Ming, et al. Power fluctuation compensation research in power system using a high temperature hybrid SMES[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(8): 14-20.
[4] Hahn S, Kim K, Kim K, et al. 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet[J]. Nature, 2019, 570(7762): 496-499.
[5] 李万杰, 张国民, 王新文, 等. 飞轮储能系统用超导电磁混合磁悬浮轴承设计[J]. 电工技术学报, 2020, 35(增刊1): 10-18.
Li Wanjie, Zhang Guomin, Wang Xinwen, et al. Integration design of high-temperature supercon- ducting bearing and electromagnetic thrust bearing for flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 10-18.
[6] 王一宇, 蔡尧, 宋旭亮, 等. 零磁通式电动悬浮等效模拟系统的特性分析与实验[J]. 电工技术学报, 2021, 36(8): 1628-1635.
Wang Yiyu, Cai Yao, Song Xuliang, et al. Charac- teristic analysis and experiment of the equivalent simulation system for null-flux electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1628-1635.
[7] 卢力, 吴蔚, 金之俭, 等. 适用于高速电动磁浮的车载高温超导磁体综合设计[J]. 机车电传动, 2019(6): 66-70.
Lu Li, Wu Wei, Jin Zhijian, et al. Design of automotive HTS magnets for high-speed electric maglev[J]. Electric Drive for Locomotives, 2019(6): 66-70.
[8] Dong Fangliang. Improvement of magnetic and cryogenic energy preservation performances in a feeding-power-free superconducting magnet system for maglevs[J]. Energy, 2020, 190: 116403.
[9] Huang Zhen, Dong Fangliang, Xu Xiaoyong, et al. Evaluation of the structural dynamics of a 2G HTS magnet system considering electromagnetic and thermal stress[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(5): 1-5.
[10] Ma Guangtong, Gong Tianyong, Wang Ruichen, et al. Design, fabrication and testing of a coated conductor magnet for electrodynamic suspension[J]. Super- conductor Science and Technology, 2022, 35(2): 025013.
[11] Mizuno K, Tanaka M, Ogata M. Evaluation of eddy current heating in a REBCO magnet due to the magnetic field of ground coils for the maglev[J]. Superconductor Science and Technology, 2020, 33(7): 074009.
[12] Choi S Y, Lee C Y, Jo J M, et al. Sub-sonic linear synchronous motors using superconducting magnets for the hyperloop[J]. Energies, 2019, 12(24): 4611.
[13] Wang Lei, Zheng Jinxing, Li Quan, et al. Develop- ment of multiscale model in large-scale HTS coils with improved coupling[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(6): 1-7.
[14] Inanir F, Terzionlu R. AC loss evaluation of a super- conducting pancake coil with coated conductors using an extended A-V formulation[J]. Physica C: Super- conductivity and its Applications, 2021, 587: 1353910.
[15] Martins F R, Sass F, de Andrade R Jr. Simulations of REBCO tape jointless double crossed loop coils with an integral equations method[J]. Superconductor Science and Technology, 2019, 32(4): 044002.
[16] Zhang Huiming, Zhang Min, Yuan Weijia. An efficient 3D finite element method model based on the T-A formulation for superconducting coated con- ductors[J]. Superconductor Science and Technology, 2017, 30(2): 024005.
[17] Liang Fei, Venuturumilli S, Zhang Huiming, et al. A finite element model for simulating second generation high temperature superconducting coils/stacks with large number of turns[J]. Journal of Applied Physics, 2017, 122(4): 043903.
[18] Gong Tianyong, Ma Guangtong, Wang Ruichen, et al. An improved self-consistent model and its application to estimate the critical current of REBCO magnet[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-6.
[19] 雷银照. 关于电磁场解析方法的一些认识[J]. 电工技术学报, 2016, 31(19): 11-25.
Lei Yinzhao. Reviews of analytical methods for electromagnetic fields[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 11-25.
[20] 郑晓钦, 徐杰, 陈春涛, 等. 超高速磁浮涡流装置制动力的解析分析[J]. 电工技术学报, 2020, 35(9): 1891-1899.
Zheng Xiaoqin, Xu Jie, Chen Chuntao, et al. Analytical calculation of braking force of super high speed maglev eddy current device[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 1891- 1899.
[21] Crozier S, Forbes L K, Doddrell D M. A novel, open access, elliptical cross-section magnet for paediatric MRI[J]. Measurement Science and Technology, 1998, 9(1): 113-119.
[22] Chen Xiaoyuan, Pang Zhou, Gou Huayu, et al. Intelligent design of large-size HTS magnets for SMES and high-field applications: using a self- programmed GUI tool[J]. Superconductor Science and Technology, 2021, 34(9): 095008.
[23] 秦伟, 范瑜, 徐洪泽, 等. 高温超导运动磁场电磁Halbach初级结构直线感应磁悬浮电机[J]. 电工技术学报, 2018, 33(23): 5427-5434.
Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427- 5434.
[24] Gong Tianyong, Ma Guangtong, Wang Ruichen, et al. Three-dimensional analysis of the magnetic fields and forces in a coreless HTS linear synchronous motor[J]. Physica C: Super-Conductivity and its Applications, 2020, 568: 1353577.
[25] Gong Tianyong, Ma Guangtong, Cai Yao, et al. Calculation and optimization of propulsion force of a real-scale REBCO magnet for EDS train[J]. IEEE Transactions on Applied Superconductivity, 2019, 29(5): 1-6.
[26] Liu Donghui, Xia Jing, Yong Huadong, et al. Estimation of critical current distribution in Bi2Sr2CaCu2Ox cables and coils using a self- consistent model[J]. Superconductor Science and Technology, 2016, 29(6): 065020.
[27] Lim J, Lee C Y, Oh Y J, et al. Equivalent inductance model for the design analysis of electrodynamic suspension coils for hyperloop[J]. Scientific Reports, 2021, 11(1): 23499.
[28] Su Zhenhua, Luo Jun, Ma Guangtong, et al. Fast and precise calculation of mutual inductance for electro- dynamic suspension: methodology and validation[J]. IEEE Transactions on Industrial Electronics, 2022, 69(6): 6046-6057.
[29] Gong Tianyong, Ma Guangtong, Wang Ruichen. Eddy current losses in superconducting secondary of a linear synchronous motor: calculations and measure- ments[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 1895-1906.
[30] Gong Tianyong, Ma Guangtong, Li Jing, et al. Design optimization of high temperature superconducting magnets and null-flux coils for electrodynamic suspension train[J]. IEEE Transactions on Energy Conversion, 2022, 37(1): 526-536.
[31] COMSOL multiphysics software package[OL]. Available: http://www.comsol.com.
Abstract High-temperature superconducting (HTS) materials have excellent characteristics such as relatively high operating temperature, large critical current density, and strong critical magnetic field. Thus, the HTS magnets wound by HTS tapes have broad application prospects in high-field magnet, medicine, and rail transit. In order to reduce the production cost of HTS magnets, the magnet should be optimized in detail before the practical application, and the magnetic field calculation is significant to the optimization design. In the electromagnetic design of magnets, more attention is paid to the magnetic fields in a specific area of space, which is less dependent on the non-uniform current distribution inside the magnet. As a result, when calculating the magnetic fields of superconducting magnets, the current density inside the superconducting magnet can be fairly treated as a uniform distribution. In this way, the computational efficiency of magnetic fields can be improved, and the optimal superconducting magnet design can be accelerated without compromising the calculation accuracy.
In this paper, considering a racetrack structure of superconducting magnets, based on the assumption of uniform current density and Biot-Savart’s law, through discretization of both the cross-section and centerline of the magnet, three analytical models, line current model, surface current model, and volume current model, were established to calculate the magnetic fields of racetrack HTS magnets. These analytical models were validated against the finite element method (FEM) model and experiment. It was found that these models improve the computing efficiency at least three times that the FEM model in terms of calculating the magnetic field at any point in space. Afterward, a comprehensive comparison was conducted on the computational accuracy and efficiency of these analytical models. The conclusion is that in terms of the racetrack magnet with an elliptical segment, the linear current analytical model has the highest calculation efficiency, and the surface current analytical model has the highest calculation accuracy. The volume current analytical model has high computational efficiency and accuracy for the racetrack magnet with a circular segment.
Furthermore, the magnetic field distribution of racetrack HTS magnets was investigated with these analytical models. When the air gap is small (such as 45 mm), the maximum magnetic field position of the magnet, composed of two magnetic poles connected in series, deviates from the center of the magnet and is closer to the circular segment of one magnetic pole. As the air gap increases, the magnetic field generated by the circular segment in the center of the magnet decreases rapidly, and the maximum magnetic field moves toward the center of one magnetic pole. In addition, when the measuring location of magnetic fields is away from the center of the magnet in 157 mm, the magnetic field component named Bz increases with the increase of the air gap, which is different from the situation when the measuring location is equal to 0 mm or 105 mm. The reason is that the angle b between the Bz and its modulus Bm decreases with the increase of air gap, leading to an increase in cosb. Moreover, because Bz=Bmcosb, although Bm decreases with the increase of air gap, the product eventually leads to an increase in Bz. Besides, it was found that, for a racetrack magnet, when the elliptical coefficient is less than 1, the position of the maximum magnetic field will move, providing a valuable reference for the critical current estimate of racetrack HTS magnets.
Critical current is a core parameter to evaluate the application performance of the superconducting magnet. This paper established an improved self-consistent model with the help of the above analytical models for estimating the critical current of the racetrack HTS magnet. The modeling efficiency and computing accuracy are improved by the Dirichlet boundary condition that inputs the magnetic fields calculated with the analytical models. A smaller Dirichlet boundary corresponds to a higher computing accuracy, suggesting that a small boundary should be used in the improved self-consistent model.
keywords:Racetrack magnets, high-temperature superconducting (HTS) magnets, magnetic field calcula- tion, electromagnetic design, electrodynamic suspension
DOI: 10.19595/j.cnki.1000-6753.tces.220085
中图分类号:TM26; TM153
国家自然科学基金项目(52037008)和四川省科技厅项目(2020YFG0354)资助。
收稿日期 2022-01-16
改稿日期 2022-03-05
龚天勇 男,1991年生,博士研究生,研究方向为高温超导磁体技术。E-mail: gongtianyong178@163.com
马光同 男,1982年生,研究员,博士生导师,研究方向为磁悬浮理论及应用。E-mail: gtma@swjtu.edu.cn(通信作者)
(编辑 郭丽军)