0 引言
真空交流接触器作为一类重要的电力控制器件,被广泛地应用于各类输配电系统中[1-2],其机械寿命需远大于电气寿命才能确保产品能够可靠运行[3]。相较于其他机械失效形式,零件的断裂周期直接决定真空交流接触器的机械寿命。在材料等本质因素不变的前提下,根据制造参数对真空交流接触器内零件的断裂周期进行预测,能够有效地评估产品质量[4]。
一些学者通过寿命实验获得开关的性能退化过程,对产品的机械寿命和故障进行预测。M.Park等通过对产品开展高低温加速寿命试验,以温度作为加速应力获得开关运行可靠性与寿命间的退化关系[5]。Ye Xuerong 等引入退化不确定性和模糊信息熵方法对多源异构不确定性进行统一量化,对开关在运行过程中的可靠性退化问题进行研究[6]。游颖敏等通过音频采集器对运行中的开关音频信号进行采集,根据信号特征实现各类故障的判定目的[7]。以上方法对开关的本体进行模糊化处理,需要较大数量的研究样本才能保证故障识别和寿命预测的准确性[8]。为降低大规模实验带来的研究成本,一些学者使用虚拟样机技术对开关内的力学特性进行计算,实现对零件状态的精确评估。杨文英等以真空交流接触器作为研究对象,使用虚拟样机技术对影响弹跳特性的因素进行研究,并发现调整超程弹簧和返回弹簧的预压力值可以有效抑制弹跳现象[9]。在零件的疲劳寿命分析方面,S.H.Park 等使用有限元模型计算开关内零件的应力状态,再通过开展材料的拉伸寿命实验获取失效退化曲线,使用材料的失效退化曲线根据零件应力状态进行判断,对开关内关键零件的断裂周期进行预测[10]。陈允等通过有限元法对绝缘材料的机械应力进行计算,对绝缘子的老化寿命进行预测[11]。虚拟样机技术也适用于分析制造参数对开关动作特性的影响,但在进行大数量样本的评估时需要消耗大量的计算成本[12]。
现有的研究多关注制造参数对产品性能的影响,尚未实现对制造参数影响下的批量真空交流接触器进行机械寿命预测。为解决批量产品机械寿命预测中的计算耗时难题,需要使用具有良好非线性映射能力的神经网络降低机械寿命预测成本[13]。本文根据真空交流接触器的动作原理,结合多体动力学和电磁场理论建立考虑制造参数的虚拟样机。根据虚拟样机中零件的应力计算结果,使用Gerber 模型计算零件的断裂周期。对批量产品开展测量获得产品的制造参数作为输入,将虚拟样机计算的断裂周期作为输出训练神经网络。为改善传统BP 神经网络的预测精度,使用鲸鱼优化算法(Whale Optimization Algorithm,WOA)对神经网络中的权值和阈值进行优化。根据制造参数的分布特性使用蒙特卡洛法抽取虚拟真空交流接触器样本,通过WOA-BP 神经网络对样本中的零件断裂周期进行预测。选择真空交流接触器转臂与转臂套筒的间隙作为制造参数预测转臂的断裂周期分布,通过实际产品的寿命实验对预测结果准确性进行验证。
1 真空交流接触器零件断裂周期预测
为开展批量真空交流接触器的机械寿命预测,需要对生产线上的实物样本进行测量获取制造参数。根据接触器的动作原理,将实体模型和材料属性依次建立电磁场模型、多体动力学模型和断裂周期计算模型,使用考虑制造参数变化的虚拟样机计算各样本内零件断裂周期。将制造参数和断裂周期计算结果进行归一化处理,并划分训练样本和测试样本。确定BP 神经网络的隐含层节点个数后,使用WOA计算神经网络初始权值和阈值的个体适应度。在更新参数和随机算子后,对比预测结果与测试样本间的方均误差是否满足精度要求。在预测精度满足后,以优化后的权值和阈值代替BP 神经网络内的初始值。根据制造参数的分布特性,通过蒙特卡洛法抽取虚拟样本。使用优化后的WOA-BP 神经网络对虚拟样本进行预测,获取该批次真空交流接触器中关键零件的断裂周期。全部计算过程如图1 中所示。

图1 真空交流接触器零件断裂周期预测过程
Fig.1 Fracture life prediction of parts in switches
2 真空交流接触器零件断裂周期预测
2.1 研究对象
以某型号真空交流接触器作为研究的应用对象对计算过程进行说明。接触器通过线圈通电产生电磁场,吸合衔铁带动触点实现合闸过程。接触器内的主要结构如图2 所示,转臂与衔铁间通过紧固件连接构成转臂组件。在线圈未通入电流时,转臂受到弹簧力Fc、Fb 和Ff 的共同作用,让开关管内的触点保持在分断状态。当线圈通入电流后,静铁心产生磁场。当磁场经过静铁心与衔铁间的气隙时,使衔铁受到电磁吸力Fm。若Fm 对转臂组件的电磁吸力矩Mm 大于Fc、Fb 与Ff 对转臂组件的作用力矩Mf,转臂组件将沿图2a 中的箭头方向顺时针转动,直至衔铁与静铁心完全吸合。在接触器的合闸过程中,驱动开关管闭合的绝大多数能量通过转臂传递。因此,转臂是动作过程中最关键的零件,可将该零件的断裂周期视作接触器的机械寿命。
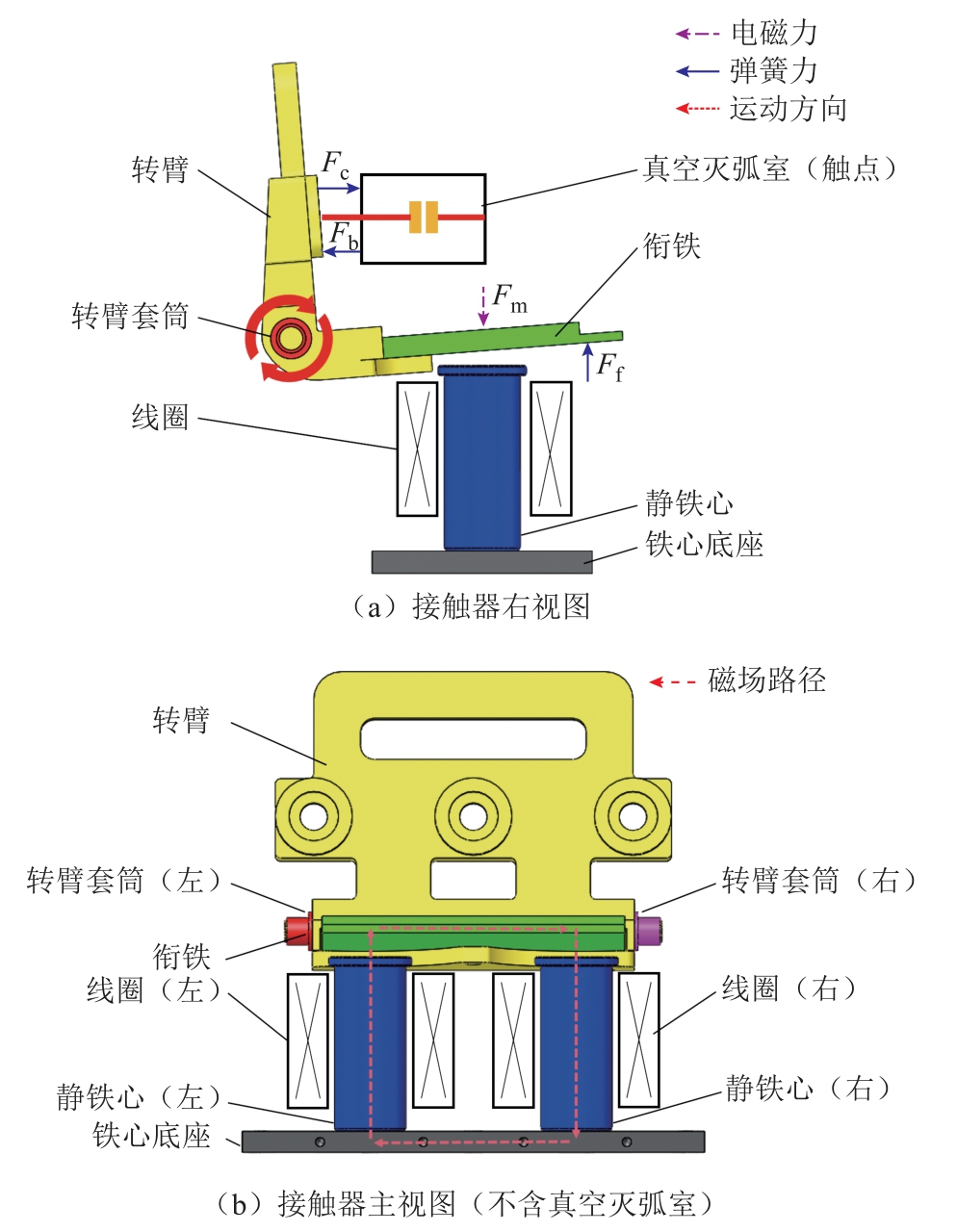
图2 接触器结构示意图
Fig.2 Structure of contactor
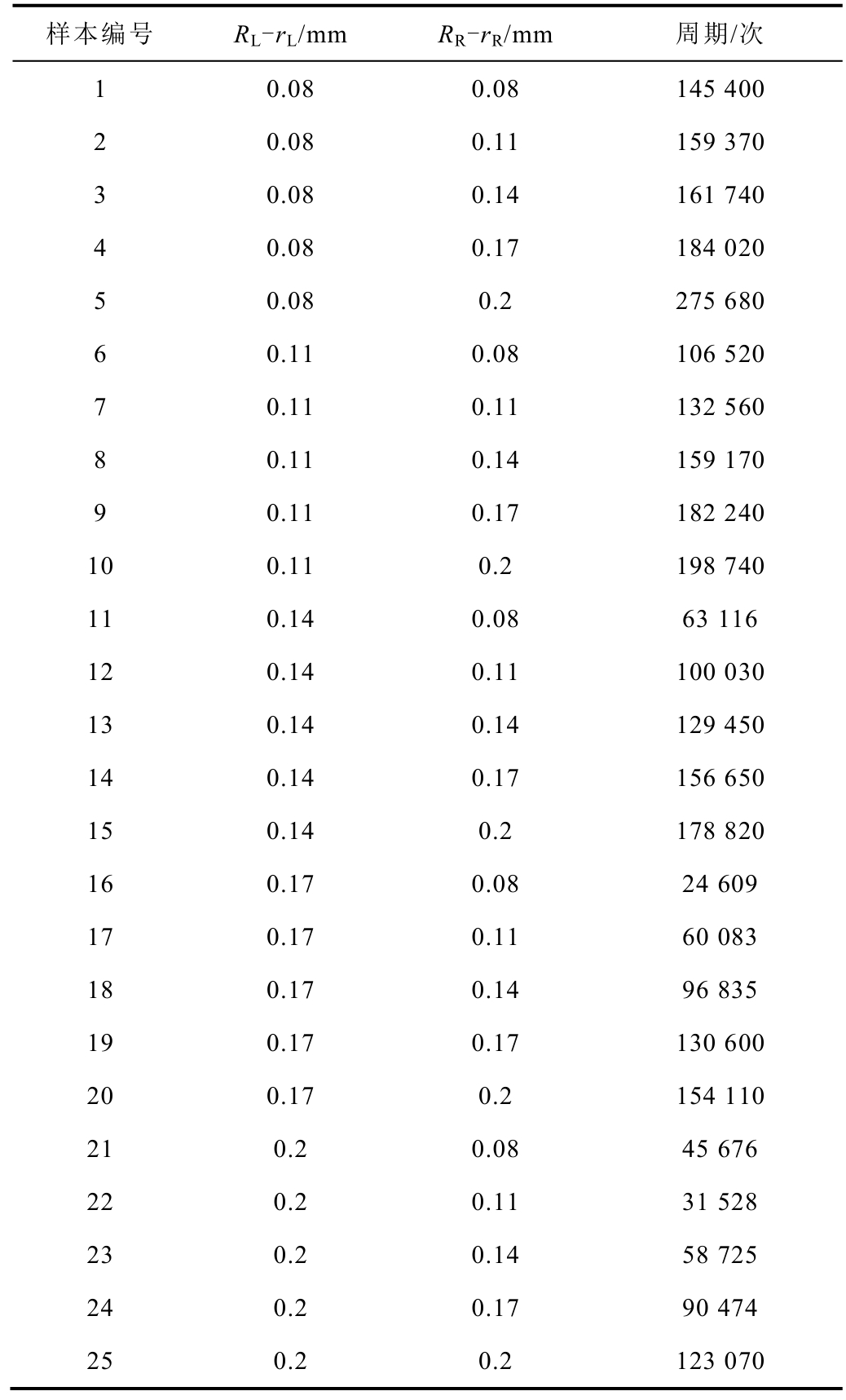
转臂与转臂套筒组成的铰链如图3 所示,OL/R为转臂两侧转轴的轴心,oL/R 为两侧转臂套筒的轴心。为实现接触器的顺畅运动,转臂的转轴外径rL/R 需小于套筒的孔径RL/R 则能满足间隙配合。假设孔与轴均不存在圆度偏差,则孔与轴的间隙xL/R=RL/R-rL/R。孔轴间隙x 使动作中的转臂与转臂套筒间接触力FL/R 偏离设计值,造成转臂的断裂周期发生波动。

图3 转臂铰链的制造参数
Fig.3 Manufacturing parameters of joint
2.2 计算模型
真空交流接触器的磁路结构为转动式,在触点闭合的过程中瞬态磁场方程为[9,14]

式中,A 为矢量磁位,并认为无穷远处矢量磁位为0;μ 为磁导率;Js和Je分别为电流密度和涡流密度;σ 为电导率;φ 为电位;B 为磁通密度;H 为磁场强度。接触器内电磁机构的相关参数见表1。
表1 接触器电磁机构参数
Tab.1 Parameters of contactor electromagnetic mechanism

在求出磁场强度后,根据磁通密度、磁场强度和磁场能量密度积分获得磁场能量,之后通过虚功法获取求解域内的电磁吸力矩Mm 为

式中,Wm 为磁场能量;V 为求解域体积;θ0 为衔铁在电磁吸力下的转动角度;根据电磁力的计算结果建立多体动力学方程对接触器中各零件运动状态进行描述为[15]
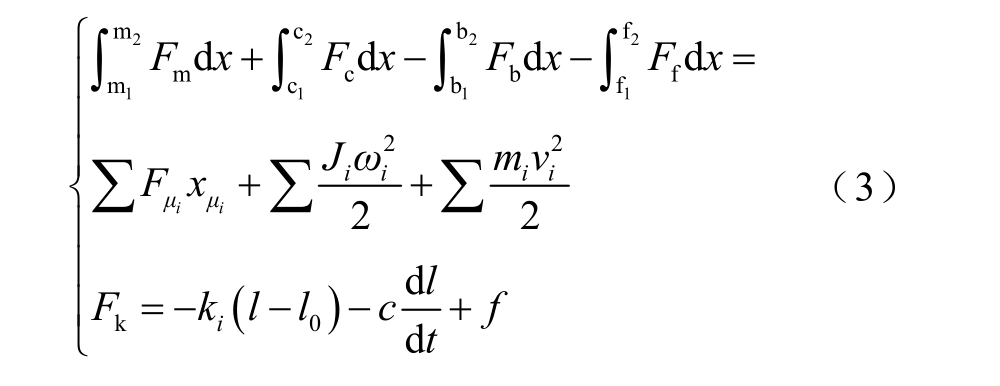
式中,Fc 为开关管的自闭力,能够辅助触点停留在分断状态;Fb 为保持力;Ff 为反力;m1、c1、b1 与f1 对应各力Fm、Fc、Fb、Ff 计算参数在接触器闭合前的状态;m2、c2、b2 与f2 对应各力Fm、Fc、Fb、Ff 计算参数在接触器闭合后的状态;F μ i为各运动构件间的摩擦力,依照接触零件材质确定;x μi为各运动构件间发生的摩擦位移;Ji 和ωi 分别为零件的转动惯量和角速度;mi 为各运动部件的归一化质量;vi 为各零件的运动速度;Fk 为各弹簧的反力;ki 为各弹簧的刚度系数;l 和l0 分别为弹簧的自由长度和初始长度;c 为弹簧阻尼系数;f 为弹簧预载荷。在进行多体动力学计算时,可以将转臂与转臂转轴间的接触力视作一个含阻尼的弹簧。对Lankarani-Nikravesh 接触模型进行改进,使其能够表现含间隙孔轴间的接触力FL/R 和摩擦力 Fμ i[16]分别为

式中,KL/R 为孔与轴间的接触刚度;x 为孔轴间隙;|x0|为孔轴间的轴心距离,在|x0|<x 时轴侵入到孔的表面产生接触力FL/R;e 为力指数;D 为碰撞过程的阻尼系数;δ 为相对碰撞速度;μL/R 为孔与轴间的摩擦系数;vL/R 为孔与轴间接触点的相对切向线速度。接触刚度KL/R 的计算过程如下。

式中,RL/R 和rL/R 分别为转臂套筒孔半径和转臂轴半径;σi+σj 为转臂套桶材质i 和转臂轴材质j 的等效弹性模量之和;σi,j、υi, j、Ei,j 分别为单一转臂套桶材质i 和转臂轴材质j 的等效弹性模量、泊松比、弹性模量。在通过多体动力学方程计算转臂的载荷状态后,可通过连续介质本构方程对该零件的应力和应变进行计算[17]。

式中,下标x、y、z 为直角坐标系的三个轴向;εx、εy、εz 为x、y、z 轴的法向应变;σx、σy、σz 为x、y、z 轴的法向应力; γ yz、γ zx、γ xy 为零件在yz、zx、xy平面上的剪切应变; τy x、τ y z、τ xy 为零件在yz、zx、xy 平面上的剪切应力;E 为杨氏模量;υ 为泊松比;G 为剪切模量;。
由于裂纹萌生占零件整个断裂过程绝大部分时间,可以使用裂纹萌生周期对零件的断裂周期进行评价。根据应力计算的结果,结合实测的材料S-N 曲线通过Gerber模型对转臂的裂纹萌生周期进行计算[18]。

式中,σa 为应力幅值;σm 为平均应力;Se 为疲劳极限;Su 为极限抗拉强度。在转臂工作一定周期N 后,若σm 超过材料 S-N 曲线中的退化极限抗拉强度 Su'Su′则认为发生断裂。接触器内转臂材质为PA66,转臂轴套材质为Q235。衔铁、静铁心和铁心底座的材质为纯铁,各材料的主要物理性能见表2。
表2 材料属性
Tab.2 Properties of materials
标准BP 神经网络的预测精度受训练样本数量限制,通过鲸鱼算法(WOA)对标准BP 神经网络的权值和阈值进行优化能够极大地提高预测精度。WOA 通过模拟鲸鱼搜索、包围、捕食的行为建立数学模型,以捕捉最优参数[19-20]。
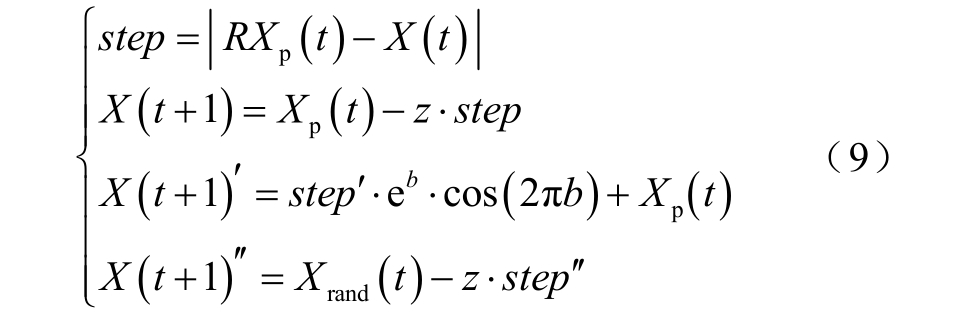
式中,step 为包围时的更新步长;Xp(t)为最优个体位置;X(t)为当前个体位置;t 为当前迭代数;R 为对目标的扰动;z 为随机变量;b 为螺旋形状的常数;step'为捕食时的更新步长;Xrand 为从种群中任意选取某一个体的位置;step″为探索时的更新步长。
2.3 预测结果
从产线中随机抽取25 台真空交流接触器作为研究样本,通过实测获得转臂套筒孔内径RL/R 的分布范围为8.1~8.25mm,转臂轴外径rL/R 的分布范围为7.85~7.95mm。根据分布范围使用式(1)~式(6)搭建虚拟样机完成电磁场和多体动力学的计算,得到转臂在工作过程中的载荷如图4 所示。

图4 转臂的载荷计算结果
Fig.4 Calculated loads of rotating lever
从图4 中载荷的变化趋势可以发现,在转臂两侧铰链中孔轴间隙改变后,衔铁和静铁心间的气隙变化使二者间的接触力产生波动。受转臂左右铰链孔轴间隙不同的影响,使一侧静铁心与衔铁间的接触力始终大于另一侧。通过式(7)和式(8)对转臂的应力分布和断裂周期进行计算,该结果如图5所示。

图5 转臂的裂纹计算结果
Fig.5 Calculation results of crack
在衔铁与两个静铁心间接触力不同的影响下,转臂上对称布置的三个固定通孔的应力情况并不相同。由于单侧固定通孔的应力大于另一侧,使裂纹产生在应力较大的固定通孔附近。在动作过程中,裂纹逐渐扩展直至贯穿到另一侧的固定通孔。图5a虚线圈内为转臂的应力峰值区域,图5b 虚线圈内为 断裂周期最小的区域。通过将仿真结果与失效样品照片图5c 作对比,可以确定仿真对应力分布和断裂位置的计算结果较为准确。对于25 台研究样本中转臂断裂周期的计算结果见表3。
表3 断裂周期计算结果
Tab.3 Fracture cycle results
使用高速摄像机拍摄接触器在工作过程中的转臂动作视频,经过图像处理后转化为转臂的运动速度,通过将实验和虚拟样机获得的转臂运动速度进行对比验证虚拟样机的准确性。图6a 为高速摄像实验示意图,高速摄像机的采样帧数设置为11 000 f/s,曝光时间设置为85μs。为避免低曝光状态下无法捕捉到转臂的运动状态,需要使用补光源对转臂区域进行补光。图6b 为高速摄像拍摄结果与虚拟样机的转臂运动速度结果对比,其中最大误差为7.3%,能够说明虚拟样机的计算值与实测值较为相符。

图6 虚拟样机计算结果的验证
Fig.6 Verification experiment of calculation results
使用表3 内的计算数据训练BP 神经网络。选择最佳的隐含层节点数为4,输入层节点数为2,输出层节点数为1。训练方法采用L-M 法,最大训练步数为1 000,学习速率为0.01,训练最小误差为0.000 1[20]。将全部样本划分为训练样本和测试样本,其中训练样本为1~15 号,测试样本为16~25 号。为提高BP 神经网络的预测精度,使用WOA 对BP神经网络中的权值和阈值参数进行优化,并以训练集的方均误差作为适应度函数。在适应度函数值越小时训练越准确,且兼顾模型的预测精度更好。WOA 优化算法中初始种群规模为30,最大进化代数为50[20]。虚拟样机预测结果和两种神经网络的预测值如图7 所示,标准BP 神经网络预测结果的平均绝对百分比误差为233.3%,WOA-BP 神经网络的平均绝对百分比误差为12.1%。相较于标准BP神经网络,WOA-BP 神经网络的预测精度更高。

图7 测试样本预测结果对比
Fig.7 Comparison of predictive results
受工艺的影响,制造参数多服从于正态分布。假设r(L/R)和R(L/R)均服从正态分布,通过蒙特卡洛法从各制造参数的范围内随机抽取,组成10 000 个虚拟的接触器样本。使用WOA-BP 模型对全部虚拟样本进行预测,共耗时43 min,这与虚拟样机的单次计算时间相同。转臂的断裂周期概率密度分布如 图8 所示,使用WOA-BP 模型预测得到的断裂周期中心值位于13.3 万次。在前期的实际调研和摸底实验中,真空交流接触器在寿命试验中的转臂断裂周期为13.5 万次,使用WOA-BP 模型预测得到的结果与实验结果较为相符。
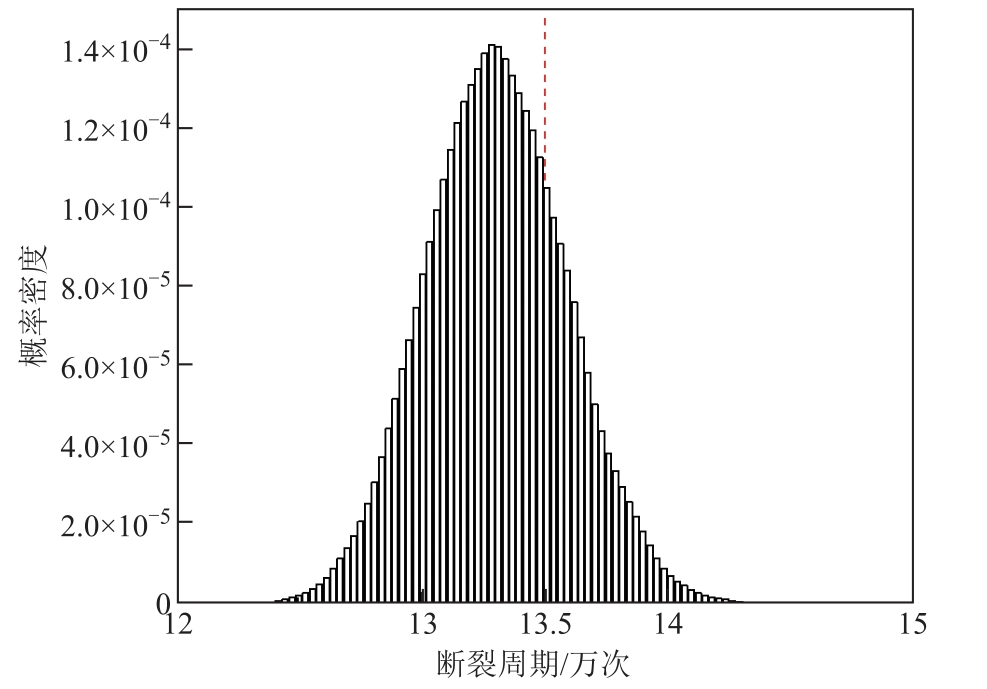
图8 预测结果
Fig.8 Predicted results
3 结论
本文建立一种根据制造参数预测真空交流接触器机械寿命的方法。首先建立考虑制造参数的虚拟样机,并根据实测获得的产品制造参数计算对应的零件断裂周期。再将样品的制造参数作为输入,虚拟样机计算的零件断裂周期作为输出训练BP 神经网络。然后使用WOA 对BP 神经网络的权值和阈值参数进行优化,训练WOA-BP 神经网络提高预测精度。最后使用WOA-BP 神经网络对蒙特卡洛法抽取的随机样本进行计算,实现根据制造参数对批量产品的机械寿命进行预测。所得的结论如下:
1)制造参数同时对真空交流接触器的电磁特性和动力学特性产生影响,通过改变磁路结构参数和传动位置参数使零件受到的载荷位置和载荷幅值同时改变,造成断裂周期发生波动。
2)使用训练后的神经网络对10 000 个虚拟接触器机械寿命进行预测,所消耗的预测时间仅与虚拟样机的单次计算时间相同。通过鲸鱼优化算法(WOA)对BP 神经网络中的权值和阈值进行优化,能够有效地提高转臂断裂周期的预测精度,使预测误差从233.3%下降至12.1%。
3)将虚拟样机的计算结果与高速摄像实验结果相对比,二者间的最大误差为7.3%。使用WOA-BP模型预测得到的断裂周期中心值与实验值较为相符,说明本方法的预测精度能够满足批量生产应用。
[1]唐西胜,邓卫,李宁宁,等.基于储能的可再生能源微网运行控制技术[J].电力自动化设备,2012,32(3): 99-103,108.Tang Xisheng,Deng Wei,Li Ningning,et al.Control technologies of micro-grid operation based on energy storage[J].Electric Power Automation Equipment,2012,32(3): 99-103,108.
[2]方朝林,许志红.基于IGBT 混联闭环控制策略的无弧智能直流接触器[J].电力自动化设备,2019,39(1):46-52.Fang Chaolin,Xu Zhihong.Arcless intelligent DC contactor based on IGBT hybrid connection closed-loop control strategy[J].Electric Power Automation Equipment,2019,39(1): 46-52.
[3]纽春萍,崔艺龄,李忠翔,等.航空接触器散热特性分析及耦合迭代热分析方法[J].高电压技术,2021,47(2): 487-494.Niu Chunping,Cui Yiling,Li Zhongxiang,et al.Thermal dissipation characteristics analysis and coupling iterative thermal analysis method of aviation contactor[J].High Voltage Engineering,2021,47(2): 487-494.
[4]刘梓权,王慧芳,管敏渊,等.隔离开关图像数据扩充方法及其在自动状态识别中的应用[J].高电压技术,2020,46(2): 441-447.Liu Ziquan,Wang Huifang,Guan Mingyuan,et al.Data augmentation method for disconnecting switch images and its application in automatic state recognition[J].High Voltage Engineering,2020,46(2): 441-447.
[5]ParkM,RheeS.A study on life evaluation and prediction of railway vehicle contactor based on accelerated life test data[J].Journal of Mechanical Science and Technology,2018,32(10):4621-4628.
[6]Ye Xuerong,Chen Hao,Sun Qisen,et al.Life-cycle reliability design optimization of high-power DC electromagnetic devices based on time-dependent non-probabilistic convex model process[J].Microelectronics Reliability,2020,114: 113795.
[7]游颖敏,王景芹,舒亮,等.基于音频特征的交流接触器电寿命预测方法[J].电工技术学报,2021,36(09): 1986-1998.You Yingmin,Wang Jingqin,Shu Liang,et al.The method of electrical life prediction considering the audio characteristics of AC contactor[J].Transactions of China Electrotechnical Society,2021,36(9): 1986-1998.
[8]赵书涛,王波,华回春,等.基于马尔科夫模型的直流断路器可靠性评估方法[J].电工技术学报,2019,34(增刊1):126-132.Zhao Shutao,Wang Bo,Hua Huichun,et al.Reliability evaluation method of DC circuit breaker based on Markov model[J].Transactions of China Electrotechnical Society,2019,34(S1): 126-132.
[9]杨文英,刘兰香,刘洋,等.考虑碰撞弹跳的接触器动力学模型建立及其弹跳特性影响因素分析[J].电工技术学报,2019,34(9): 1900-1911.Yang Wenying,Liu Lanxiang,Liu Yang,et al.Establishing of contactor dynamic model considering collision bounce and analysis of influencing factors of bounce characteristics[J].Transactions of China Electrotechnical Society,2019,34(9): 1900-1911.
[10]S H Park,K Y Ahn,B Y Lee.Dynamic analysis and structural design of links in an air circuit breaker to enhance fatigue life[J].Proceedings of the Institution of Mechanical Engineers,Part C: Journal of Mechanical Engineering Science,2005,219(1): 11-18.
[11]陈允,崔博源,黄常元,等.特高压GIL 用绝缘子材料寿命试验及预测[J].高电压技术,2020,46(12): 4106-4112.Chen Yun,Cui Boyuan,Huang Changyuan,et al.Life test and prediction of insulator materials for UHV GIL[J].High Voltage Engineering,2020,46(12): 4106-4112.
[12]刘超,赵伟涛,张强,等.真空断路器弹簧操动机构机械特性的仿真与优化[J].高压电器,2019,55(8): 65-71.Liu Chao,Zhao Weitao,Zhang Qiang,et al.Simulation and optimization for mechanical characteristics of spring operating mechanism in vacuum circuit breaker[J].High Voltage Apparatus,2019,55(8): 65-71.
[13]李奎,李晓倍,郑淑梅,等.基于BP 神经网络的交流接触器剩余电寿命预测[J].电工技术学报,2017,32(15): 120-127.Li Kui,Li Xiaobei,Zheng Shumei,et al.Residual electrical life prediction for AC contactor based on BP neural network[J].Transactions of China Electrotechnical Society,2017,32(15): 120-127.
[13]李奎,李晓倍,郑淑梅,等.基于BP 神经网络的交流接触器剩余电寿命预测[J].电工技术学报,2017,32(15): 120-127.Li Kui,Li Xiaobei,Zheng Shumei,et al.Residual electrical life prediction for AC contactor based on BP neural network[J].Transactions of China Electrotechnical Society,2017,32(15): 120-127.
[14]Fan Xingming,Zheng Yuxin,Zhang Xin.Simulation analysis of static characteristics of electromagnetic mechanism of magnetic holding relay based on ANSYS[J].Journal of Physics: Conference Series,2020,1550(4): 042067.
[15]Hu Shiwu,Guo Xinglin.A dissipative contact force model for impact analysis in multibody dynamics[J].Multibody System Dynamics,2015,35(2): 131-151.
[16]Ettore Pennestrì,Valerio Rossi,Pietro Salvini,et al.Review and comparison of dry friction force models[J].Nonlinear Dynamics,2016,83(4): 1785-1801.
[17]舒亮,吴浪,吴桂初,等.一种断路器多体动力学仿真方法[J].电工技术学报,2017,32(5): 41-48.Shu Liang,Wu Lang,Wu Guichu,et al.A new method of multibody dynamics simulation of circuit breakers[J].Transactions of China Electrotechnical Society,2017,32(5): 41-48.
[18]Park Y C,An C,Sim H B,et al.Failure analysis of fatigue cracking in the tension clamp of a rail fastening system[J].International Journal of Steel Structures,2019,19(5): 1570-1577.
[19]Mirjalili S.The whale optimization algorithm[J].Advances in Engineering Software,2016,95: 51-67.
[20]Balakrishnan N,Devasigamani A I,Anupama K R,et al.Aero-engine health monitoring with real flight data using whale optimization algorithm based artificial neural network technique[J].Optical Memory and Neural Networks,2021,30(1): 80-96.