0 引言
高压大容量电能变换器是电力系统的重要组成部分。其电压等级从数kV 到数十kV 不等,瞬时功率可达数百MW。然而,受限于当前功率器件的电压等级,传统的中点钳位(Neutral-Point Clamped,NPC)三电平拓扑难以应用到6kV 以上的高压变换器中[1]。一种有效的解决思路是采用具有更多电平的拓扑结构。目前最为广泛的多电平拓扑主要包括NPC 拓扑、飞跨电容拓扑(Flying-Capacitor,FC)和模块化多电平拓扑(Modular Moltilevel Converter,MMC)等[2-3]。但是FC 拓扑需要大量电容,难以实现高功率密度;MMC 拓扑用于电机调速时,存在电容电压低频振荡的问题。有源中点钳位五电平(Active Neutral Point Clamped five-Level,ANPC-5L)拓扑[4]因具有功率器件少、系统效率高以及可在全功率因数范围内实现电容电压平衡控制等优点,近年来成为国内外学者的研究热点。ANPC-5L 的电压矢量为53=125 个,而开关状态组合则多达到83=512个。如果在每个控制周期都对所有矢量和开关状态进行在线评估,常用的嵌入式控制器难以承担如此大的运算负荷。
为了解决五电平拓扑计算量大的问题,国内外学者提出了模型预测控制(Model Predictive Control,MPC)算法。该算法具有原理简单、多变量优化控制和鲁棒性好等优势,成为电力电子的研究热点[5-8]。文献[9]提出一种ANPC-5L 变换器永磁同步电机驱动系统的两步MPC 优化算法,通过对空间矢量图的进一步分区减少了候选电压矢量。但该算法需要进行参考矢量定位,且每个开关状态需要计算6个价值函数,因此其计算量仍然偏大。文献[10-11]为了减少计算负担,在每一个阶段中,可行的开关状态被限制到与所呈现的状态最接近的水平。然而,对可行开关状态的限制降低了转换器的输出能力,并导致较差的动态性能。文献[12]由于在整个控制周期内仅施加一个电压矢量,因此可在较宽的频率范围内产生相对较高的转矩脉动和广泛分布的电流谐波,实时性差。文献[13]针对ANPC 变换器共模电压和电容电压平衡问题,提出一种基于gh 坐标系的改进空间电压矢量调制(Space Vector Pulse Width Modulation,SVPWM)算法。所提 SVPWM 算法能够减小共模电压,但采用的是五段式开关序列设计,开关序列较多,计算复杂;文献[14]采用电压预测模型计算预测电压,经价值函数对四种电压矢量进行对比选择,输出最优开关状态,实现了三相四开关变换器离网模式操作,但是并没有解决五电平拓扑中点电压平衡问题。
本文针对ANPC-5L 拓扑的SVPWM 算法过于复杂且难以实现电容电压解耦控制[15]的问题,提出一种将前馈解耦控制与模型预测控制算法有机结合的方法,实现了电机的多目标控制,并且通过仿真及实验对比验证了所提算法的有效性。
1 有源中点钳位五电平拓扑分析与建模
1.1 拓扑结构
ANPC 拓扑是用可控功率器件代替了NPC 拓扑中的钳位二极管,目的是增加拓扑的换流路径,从而降低内外管损耗分布不均产生的影响[16]。改进型ANPC-5L 拓扑可以看作 ANPC 三电平(Active Neutral-Point Clamped three-Level,ANPC-3L)拓扑和飞跨电容两电平(Flying-Capacitor two-Level,FC-2L)拓扑组合而成的复合结构。三相ANPC-5L 拓扑电路如图1 所示,这种复合结构构造简单,控制灵活,易于向更多电平数扩展。

图1 三相ANPC-5L 拓扑电路
Fig.1 Three-phase circuit of the ANPC-5L topology
如果母线电压为4E,则支撑电容 Cu和 Cd的额定电压为2E,悬浮电容 Cfx额定电压为E。设各相中点电流为 in x,各相悬浮电容电流为 if x,输出相电流为 i x,其中x表示a、b、c 三相。
以母线中点为零电位参考点,则理想情况下单相ANPC-5L 拓扑可输出{2E,E,0,-E,-2E}共五种电平。串联器件开关频率等于基频,高频器件的开关频率等于载波频率。Fx y(t)为1 表示器件开通,为0 表示关断,y ∈ {1,2,…,12} 表示每相拓扑结构中开关管的序号。
设三相调制信号为

式中,m 为调制比;ωs为基频角频率。
根据器件的开关状态,可得ANPC-5L 变换器输出相电压为

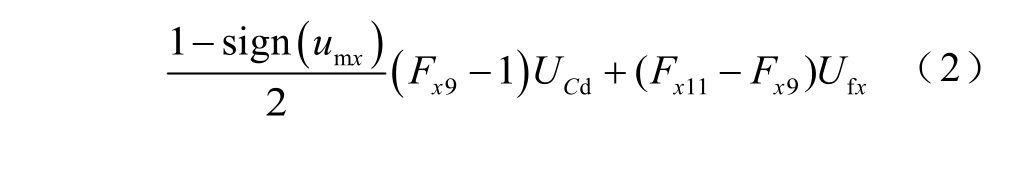
式中,U Cu、U Cd、Ufx分别为 Cu、Cd和 Cf x的电压;sign()为符号函数,其定义为

各相悬浮电容电流及中点电流为

ANPC-5L 拓扑的特点在于其具有公共直流母线,因此不需要大量的独立直流电源。此外,ANPC-5L 拓扑保留了传统NPC 三电平拓扑的优势,即在全功率因数范围内电容电压可控。使用4 500V 开关器件时,ANPC-5L 可直接接入10kV 电网而不需要前端变压器。
1.2 系统建模
电机的机械时间常数远大于其电磁时间常数,因此电流内环的动态响应速度是影响系统性能的关键因素。传统的PI 控制存在积分饱和、系统约束不好处理等问题,限制了电流环动态响应能力的进一步提升。模型预测控制算法具有动态响应快、电流跟踪性能好和控制灵活等优点,能进一步提高系统的整体性能。对于ANPC-5L 变换器永磁同步电机驱动系统,控制目标包括变换器的电容均压控制和电机的dq 轴电流跟踪控制。模型预测控制的多目标优化控制能力正好符合ANPC-5L 变换器永磁同步电机驱动系统的多目标控制需求。
永磁同步电机在转子同步坐标系下的电压方程为
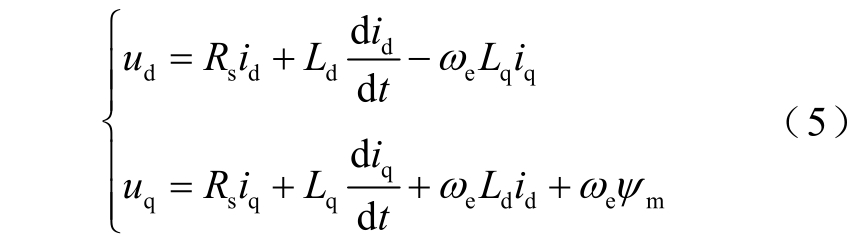
式中,ud、uq 分别为d、q 轴电压;id、iq 分别为d、q 轴电流;Ld、Lq 为直轴和交轴电感;Rs 为定子绕组电阻;ψm为永磁体磁链;ωe为电角速度。
式(5)可改写为
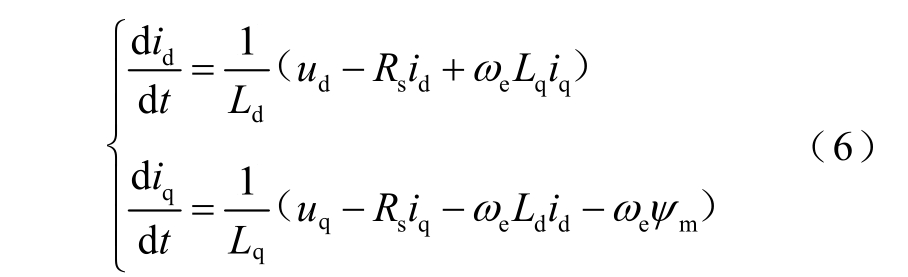
将式(6)离散化可得
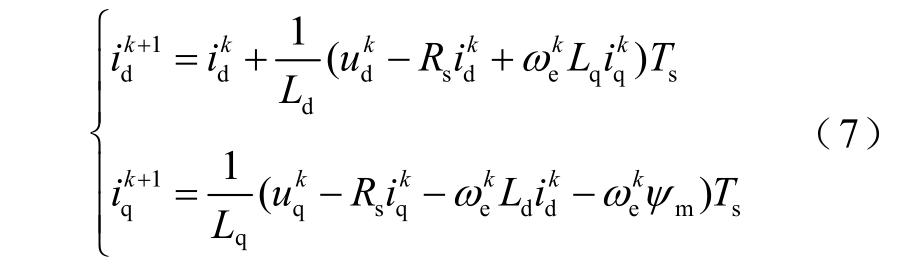
式中,k 为当前时刻;k+1 为下一时刻;Ts 为采样时间。
2 模型预测控制优化算法
模型预测控制的基本步骤为:①建立控制对象的数学模型;②预测系统变量在预定时间内的变化趋势;③根据价值函数选择最优控制变量。
为了实现对被控变量的预测,需根据控制对象数学模型建立系统变量的预测方程。通常使用前向欧拉法将控制对象模型离散化。

由文献[16]中电流预测方程可得到中点电流和悬浮电容电流的预测方程为

2.1 电压矢量与开关状态分析
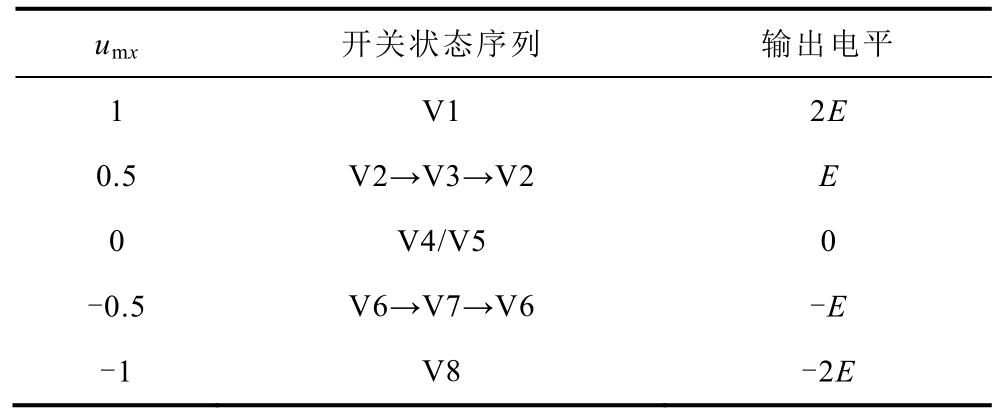
本节采用单矢量模型预测控制,由文献[16]可知,通过载波移相实现了 ANPC-5L 拓扑的等效SVPWM 算法,即两者的调制效果是相同的。当输出电压电平为2E 时,算法中的调制信号umx=1。同理,电平E 对应umx=0.5,电平0 对应umx=0,电平-E 对应umx=-0.5,电平-2E 对应umx=-1。当umx=1时,输出开关状态序列为V1;当umx=0.5 时,输出开关状态序列为V2→V3→V2,且此时V2 和V3 的占空比相等,为Ts/2;当umx=-0.5 时,输出开关状态序列为V6→V7→V6,V6 和V7 的占空比也相等;当umx=-1 时,输出开关状态序列为V8。需特别说明的是,当umx=0 时,输出开关状态为V4 或V5,此时需要根据串联器件当前状态选择开关状态。具体而言,若本周期Tx1、Tx2、Tx5 和Tx6 开通,而Tx3、Tx4、Tx7 和Tx8 关闭,则选择的开关状态为V5,反之则为V4,如此可减少串联器件的开关频率。综上所述,对于五电平空间矢量图中的任意电压矢量,都有唯一与之对应的三相离散调制信号。
调制信号与开关状态的对应关系见表1。通过选择不同的离散调制信号来表示不同的电压矢量,同时每个电压矢量输出固定的开关状态序列,降低了电压矢量和开关状态选择的复杂性,从而降低算法的在线运算量。
表1 调制信号与开关状态对应关系
Tab.1 Corresponding relationship between modulation signal and switching state
2.2 电压矢量选择优化
不同的电压矢量和开关状态对应不同的三相调制信号,且每相离散调制信号的取值集合为{1,0.5,0,-0.5,-1}。三相调制信号共125 种组合,对应五电平SVPMW 的125 个电压矢量。为了进一步减少模型预测控制的计算量,需要设计矢量选择的优化方法,剔除部分不符合约束条件的电压矢量,以减少滚动优化的次数。为此,设定变换器输出电压矢量选择的约束条件为:单相电平跳变数最大为1,即不允许跨电平跳变。因此,根据图2 可知,在每一个控制周期单相离散调制信号的最大变化值为0.5,即在每个开关周期内,每相调制信号的取值只有三种可能,那么三相共27 种组合,对应27 个矢量,有效地降低了计算量。例如,若上一周期矢量为321,则本周期候选电压矢量为图2 中标红的27 个电压矢量。

图2 矢量变化示意图
Fig.2 Schematic diagram of vector change

式中,G x取值集合为{0.5,0,-0.5},且![]() 。设表示本控制周期三相离散调制信号的一种组合,j∈{1,2,…,27},那么对应的d、q 轴电压为
。设表示本控制周期三相离散调制信号的一种组合,j∈{1,2,…,27},那么对应的d、q 轴电压为
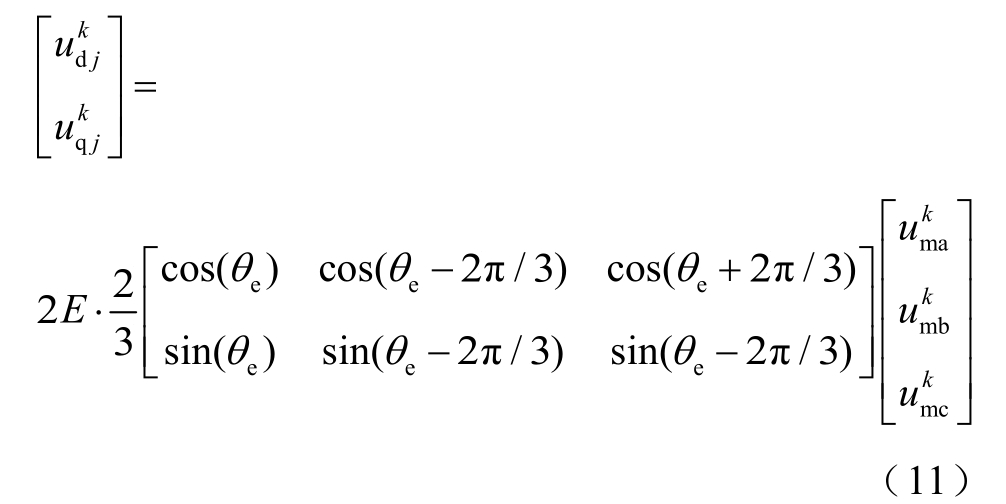
式中,θe为电机定子a 相绕组轴线与转子磁极轴线之间的电角度。
综上所述,本文提出的有限控制集预测控制算法效率优化策略具有以下特点和优势:
(1)通过调制信号的离散取值,将输出电压由连续集转换为有限集,以适用于模型预测控制。三相调制信号共125 种组合,对应五电平的125 个电压矢量。
(2)每个电压矢量输出固定的开关序列,本文所提算法不需要选择开关状态,有效地降低了算法运算量。
(3)限制单相电压电平最大跳变数为1,相应的离散调制信号的变化值为0 或0.5,从而将单个控制周期参与计算的电压矢量由125 个减少为27个,进一步降低了算法的运算量,提高了算法运行效率。
3 模型预测电压均衡控制算法
3.1 中点电流与悬浮电容电流解耦控制
文献[16]通过载波移相实现了ANPC-5L 拓扑的等效SVPWM 算法。本节在该调制算法基础上,结合第1 节的拓扑数学模型,研究电容电压解耦控制。
对于ANPC-5L 拓扑,中点电压偏移为
为了实现母线电容电压平衡控制,一个控制周期内所需的目标中点电流为

为了实现悬浮电容电压平衡控制,一个控制周期内所需的目标悬浮电容电流为
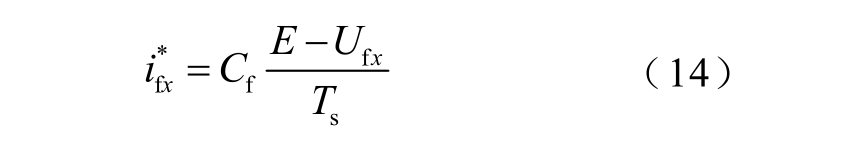
悬浮电容Cfx 额定电压为E。从式(13)和式(14)可以看出,对中点电位和悬浮电容电压的控制本质上是对中点电流和悬浮电容电流的控制。
在一个开关周期内,开关函数Fx9 的占空比dFx9与开关函数Fx11 的占空比dFx11 可表示为

由式(10)得到一个开关周期内中点电流和悬浮电容电流平均值为
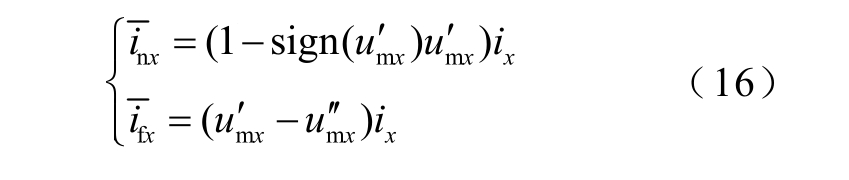
悬浮电容电流在一个开关周期内平均值为0,因此在理想情况下,不论功率因数和调制比为多少,悬浮电容电压都可保持平衡。
实际应用中如果不加以控制,悬浮电容电压会偏离其额定值。为了实现悬浮电容电流的控制,开关函数Fx9 和Fx11 的占空比应当不同,即需要采用双调制信号分别控制Fx9 和Fx11 的占空比。通过前馈补偿实现中点电流和悬浮电容电流的解耦控制。前馈解耦控制框图如图3 所示。

图3 前馈解耦控制框图
Fig.3 Feedforward decoupling control block diagram
参数Mx1 控制中点电流;参数Mx2 控制悬浮电容电流。
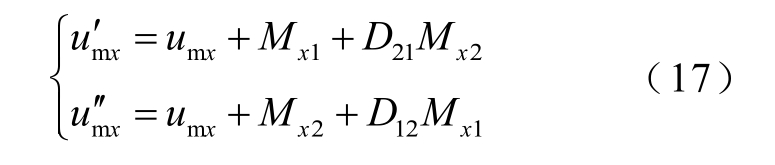
将式(17)代入式(16),一个开关周期内总中点电流和悬浮电容电流平均值为
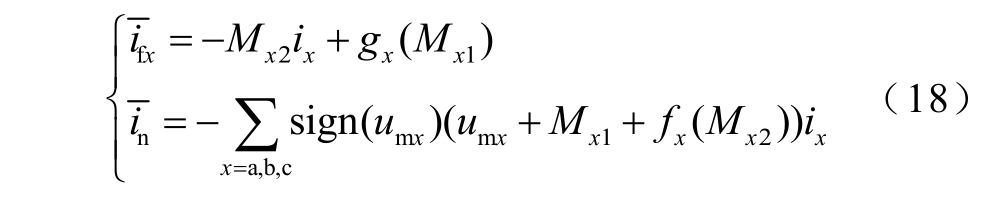
式中,sign(·)为符号函数;D21、D12 为前馈补偿器,以实现中点电流和悬浮电容电流的解耦控制。其中令fx(Mx2)=D21Mx2;gx(Mx1)=Mx1+D21Mx2-D12Mx1。如果fx(Mx2)和gx(Mx1)都等于零,那么中点电流in 只受参数Mx1 控制而与Mx2 无关,同时悬浮电容电流ifx只受参数Mx2 控制而与Mx1 无关,即实现了in 与ifx解耦,则此时D21=0,D12=1。

计算得到Mx1 和Mx2,然后将Mx1 和Mx2 用于对调制信号进行前馈补偿即可实现母线电容电压与悬浮电容电压的解耦控制。
3.2 电流预测与电压矢量寻优
模型预测控制的目标是实现ANPC-5L 变换器的电容均压控制和电机电流跟踪。在每个控制周期中,将27 种可能的离散调制信号组合代入电流预测方程,计算出下一周期的变量预测值。


图4 ANPC-5L 变换器永磁同步电机驱动系统的模型预测控制流程
Fig.4 The flow chart of ANPC-5L converter with MPC
将交直轴电流预测值、中点电流预测值与三相悬浮电容电流预测值代入价值函数,以评估当前电压矢量的控制效果。在本系统中,价值函数选取为
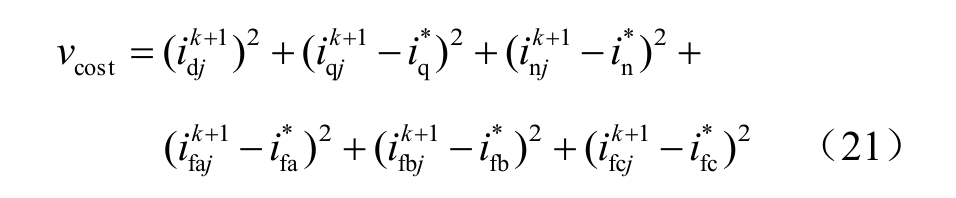
式中,前两项为“电机驱动”;后四项为“电容均压控制”,遍历所有27 种组合后,选择价值函数vcost最小的作为控制变量作用于系统。
4 仿真和实验验证
为了验证所提模型预测控制算法的有效性,将其与文献[9]所提模型预测控制算法进行仿真和实验对比。先在Matlab 环境下进行仿真验证,取得了较理想的仿真效果,并以仿真结果为基础,进行了实验平台的验证。实验中,主电路开关器件选择的是英飞凌公司的K50T60 型IGBT,控制部分由TI公司的TMS320F28335 DSP 芯片与Cyclone 公司的EP1C12Q24017 芯片组合而成。DSP 主要用于信号采集和处理,而FPGA 主要用于产生脉冲信号。直流母线电压为200V,有两个支撑电容和三个悬浮电容,支撑电容的额定电压为600V,电容值为1.3mF;三个悬浮电容额定电压为600V,电容值为1.3mF;支撑电容电阻和悬浮电容电阻都为0.1mΩ,悬浮电容电压为50V,开关频率为2kHz。本次实验负载部分使用的是永磁同步电机驱动系统,控制周期为100μs,永磁同步电机实验平台如图5 所示,实验平台电机参数见表2。

图5 永磁同步电机实验平台
Fig.5 PMSM experimental platform
表2 实验平台电机参数
Tab.2 Experimental platform parameters of PMSM
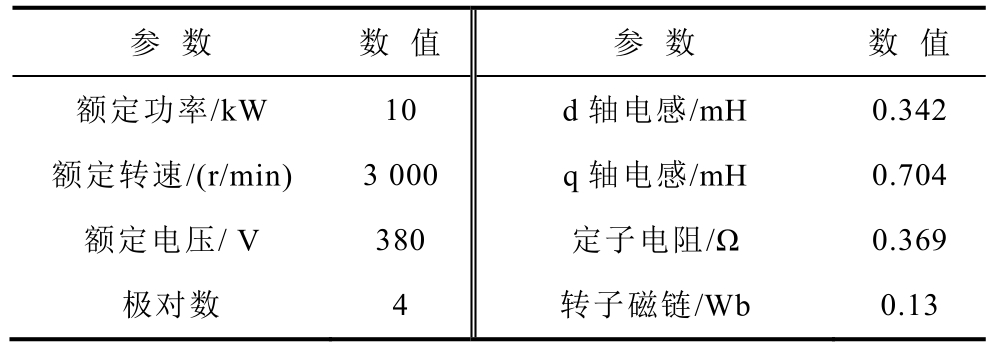
实验所用的永磁同步电机平台包括张力控制器、磁粉制动器和永磁同步电机三部分。磁粉制动器的作用是为电机提负载力矩,力矩大小由张力控制器控制。张力控制器为可控恒流源,电流调节精度为0.01A,可为磁粉制动器提供稳定的力矩控制电流。磁粉制动器输出力矩与控制电流成正比,输入2.4A 时力矩大小为100N·m。
4.1 仿真分析
本文所提算法在电机突加突卸负载工况下的仿真波形如图6 所示。起始阶段,电机以300r/min 空载运行。约在3s 时刻,为电机突加15N·m 的负载力矩,电机转速降低至280.6r/min 后迅速恢复,响应时间约为549ms。约在10s 时刻,撤去电机负载力矩,电机重新空载运行,转速上升至318.2r/min后迅速恢复,响应时间约为553ms。在整个过程中,母线电容电压与悬浮电容电压保持平衡,中点电位最大偏移度为3.86%,三相悬浮电容电压最大偏移度分别为dfa=3.43%,dfb=3.26%,dfc=3.54%。

图6 本文所提算法突加突卸负载仿真波形
Fig.6 Simulation waveforms of load step up and down of the proposed algorithm
图7 为文献[9]所提模型预测控制算法的仿真波形。电机突加负载后,电机转速降低至281.9r/min后迅速恢复,响应时间约为554ms。撤去电机负载后电机空载运行,转速上升至318.8r/min 后迅速恢复,响应时间约为556ms。在整个过程中,中点电位最大偏移度为6.35%,三相悬浮电容电压最大偏移度分别为dfa=5.47%,dfb=5.60,dfc=5.82%。

图7 文献[9]所提算法突加突卸负载仿真波形
Fig.7 Simulation waveforms of load step up and down of the algorithm proposed in Reference [9]
本文所提算法的电机正反转切换仿真波形如图8 所示。倒车前,电机负载力矩为15N·m,电机转速稳定在300r/min。约0.65s 时刻,电机给定转速由300r/min 变为-300r/min,q 轴电流由正变负而产生反向电磁转矩,使电机迅速制动,然后电机反向起动并加速至给定转速,电机反转响应时间约为941ms。在整个过程中,中点电位最大偏移度为5.32%,三相悬浮电容电压最大偏移度分别为dfa=3.99%,dfb=4.01%,dfc=4.03%。


图8 所提算法电机反转仿真波形
Fig.8 The simulation waveforms of motor reversal of the proposed algorithm
文献[9]所提模型预测控制算法的电机正反转切换仿真波形如图9 所示,其电机反转响应时间约 为942ms。在整个过程中,中点电位最大偏移度为7.45%,三相悬浮电容电压最大偏移度分别为dfa=5.76%,dfb=5.89%,dfc=6.01%。

图9 文献[9]所提MPC 算法电机反转仿真波形
Fig.9 The simulation waveforms of motor reversal of the algorithm proposed in Ref.[9]
上述仿真结果表明,将本文所提模型预测控制算法用于ANPC-5L 变换器永磁同步电机驱动系统,能够实现电机控制和电容均压控制,证明了所提算法的有效性。本文所提模型预测控制算法与文献[9]所提模型预测控制算法在电机动态控制性能上基本相当,但本文所提算法具有更好的电容均压控制效果,这主要得益于本文所提模型预测控制算法是与第2 节所提调制算法相结合,在实现多目标优化控制的同时,还能够实现电容电压解耦控制。
4.2 实验验证
本文所提算法在突加突卸负载工况下的实验波形如图10 所示。初始阶段,电机稳定运行在给定转速300r/min 左右。约在3s 时刻,控制磁粉制动器产生15N·m 的负载力矩,电机转速下降至278.2r/min后迅速恢复,响应时间约为613ms。约在10s 时刻,撤去负载力矩,电机重新空载运行,转速上升至316.6r/min 后迅速恢复,响应时间约为663ms。在整个过程中,母线电容电压与悬浮电容电压保持平衡,其中中点电位最大偏移度为5.32%,三相悬浮电容电压最大偏移度分别为 dfa=4.05%,dfb=4.72%,dfc=4.70%。

图10 本文所提算法突加突卸负载实验波形
Fig.10 Experimental waveforms of load step up and down of the algorithm proposed in this paper
文献[9]所提算法在突加突卸负载工况下的实验波形如图11 所示。突加15N·m 的负载力矩后,电机转速下降至280.6r/min 后迅速恢复,响应时间约为622ms。约在10s 时刻,撤去负载力矩,电机重新空载运行,转速上升至315.4r/min 后迅速恢复,响应时间约为654ms。在整个过程中,母线电容电压与悬浮电容电压保持平衡,其中中点电位最大偏移度为7.46%,三相悬浮电容电压最大偏移度分别为dfa=6.45%,dfb=6.72%,dfc=6.70%。

图11 文献[9]所提算法突加突卸负载实验波形
Fig.11 Experimental waveforms of load step up and down of the algorithm proposed in Ref.[9]
本文所提算法的电机正反转切换实验波形如图12 所示。倒车前,电机负载力矩为15N·m,电机转 速稳定在300r/min。约在0.65s 时刻,电机给定转速由300r/min 变为-300r/min,q 轴电流由正变负而产生反向电磁转矩,使电机迅速制动,然后电机反向起动并加速至给定转速,电机反转响应时间约为947ms。在整个过程中,中点电位最大偏移度为6.59%,三相悬浮电容电压最大偏移度分别为dfa=5.76%,dfb=5.55%,dfc=5.91%。

图12 本文所提算法电机反转实验波形
Fig.12 Experimental waveforms of motor reversal of the algorithm proposed in this paper
文献[9]所提算法的电机正反转切换仿真波形如图13 所示,其电机反转响应时间约为960ms。在整个过程中,中点电位最大偏移度为8.79%,三相悬浮电容电压最大偏移度分别为 dfa=7.62%,dfb=7.64%,dfc=7.93%。
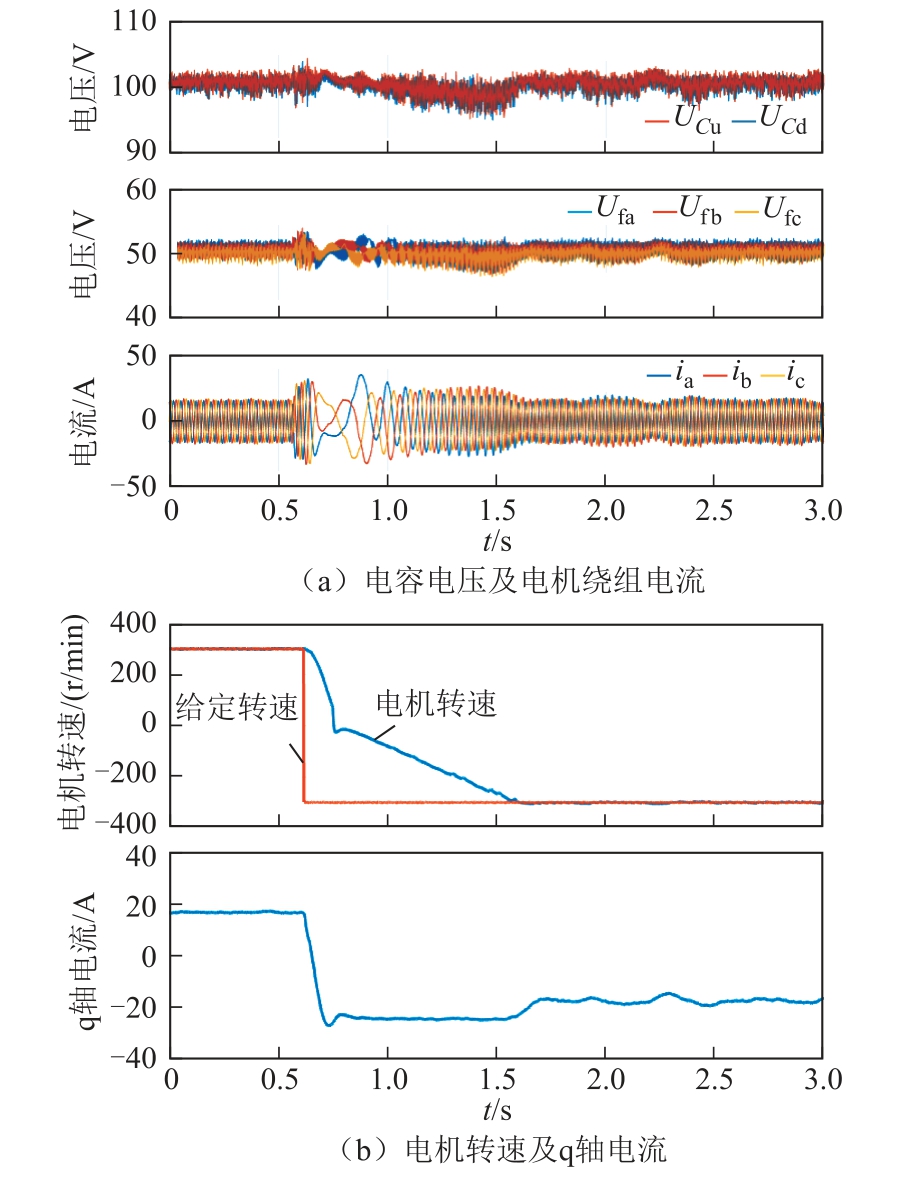
图13 文献[9]所提算法电机反转实验波形
Fig.13 Experimental waveforms of motor reversal of the algorithm proposed in Ref.[9]
上述实验结果表明,本文所提模型预测控制算法能够实现电机控制和电容均压控制,证明了算法的有效性。本文所提算法与文献[9]所提算法在电机动态控制性能上基本相当,但本文所提算法具有更好的电容均压控制效果,这与仿真结果基本相符。本文所提模型预测控制算法与文献[9]所提模型预测控制算法运行时间测量结果如图14 所示。本文所提模型预测控制算法运行时间约为32.0μs,文献[9]所提算法运行时间约为47.9μs,由此可推断出本文算法运算量降低约33.3%,有效地降低了主控芯片的在线运算负荷。
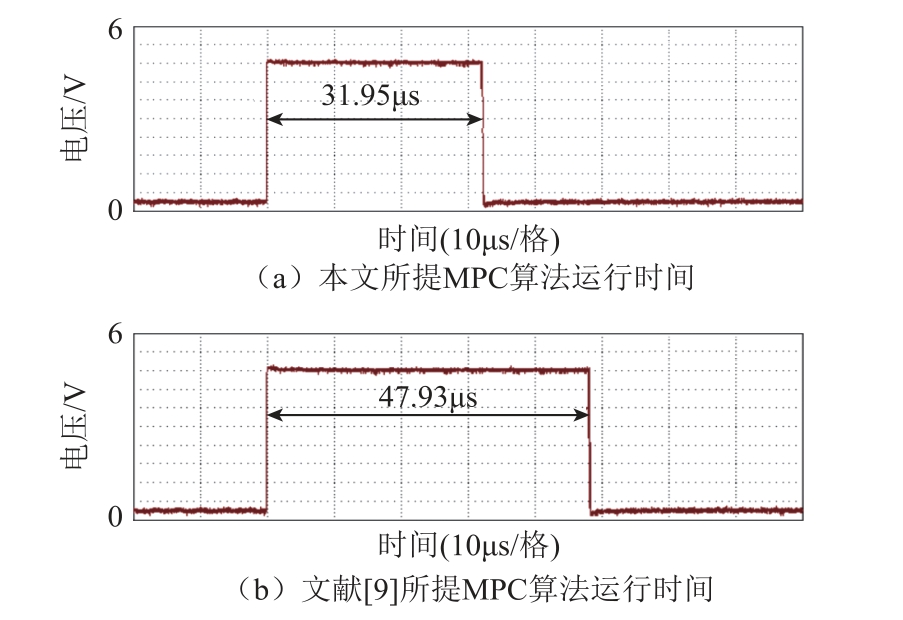
图14 两种MPC 算法运行时间对比
Fig.14 Comparison of operation time of MPC algorithm
5 结论
本文首先分析了五电平模型预测控制算法,指出该算法因电压矢量和开关状态多而存在在线运算量过大的问题;然后将前馈解耦调制方式与模型预测控制算法相结合,提出一种控制优化算法;最后通过仿真和实验证明了所提算法的有效性。具体贡献如下:
1)本文提出电压矢量和开关状态的优化选择方法,避免了复杂的开关状态选择。
2)在此基础上引入Mx1、Mx2、M21、D12 四个参数,以实现母线电容电压与悬浮电容电压的前馈补偿解耦控制。
3)将所提的前馈解耦调制方式与电流预测控制算法有机结合,通过对中点电流和悬浮电容电流的控制,实现了电机驱动和多电平电压均衡的多目标优化控制,在保证电机驱动性能的同时有效保证了电容均压。
[1]胡存刚,马大俊,王群京,等.三电平有源中点钳位逆变器损耗分布平衡控制策略[J].电工技术学报,2017,32(1): 129-138.Hu Cungang,Ma Dajun,Wang Jingqun,et al.Loss distribution balance control strategy for three-level active neutral point clamped inverter[J].Transactions of China Electrotechnical Society,2017,32(1): 129-138.
[2]Priya M,Ponnambalam P,Muralikumar K.Modular multilevel converter topologies and applications-a review[J].IET Power Electronics,2018,12(2): 170-183.
[3]Abu-Rub H,Holtz J,Rodriguez J,et al.Mediumvoltage multilevel converters-state of the art,challenges,and requirements in industrial applications[J].IEEE Transactions on Industrial Electronics,2010,57(8): 2581-2596
[4]杨国良,张玉娜,陈泰余,等.单相升降压型五电平逆变器拓扑及控制[J].电工技术学报,2019,34(14): 2922-2935.Yang Guoliang,Zhang Yuna,Chen Taiyu,et al.Topology and control of single-phase voltage rise and fall five-level inverter[J].Transactions of China Electrotechnical Society,2019,34(14): 2922-2935.
[5]郭磊磊,李国昊,金楠,等.两电平电压源逆变器双矢量调制模型预测控制: 理论分析、实验验证和推广[J].电工技术学报,2021,36(1): 39-49.Guo Leilei,Li Guohao,Jin Nan,et al.Dual vector modulation model predictive control for two-level voltage source inverter: theoretical analysis,experimental verification and popularization[J].Transactions of China Electrotechnical Society,2021,36(1): 39-49.
[6]寇佳宝,高强,滕咏哮,等.负载换流逆变器驱动电励磁同步电机无速度传感器模型预测控制方法[J].电工技术学报,2021,36(1): 68-76.Kou Jiabao,Gao Qiang,Teng Yongxiao,et al.Speed sensorless model predictive control method for electrically excited synchronous motor driven by load converter inverter[J].Transactions of China Electrotechnical Society,2021,36(1): 68-76.
[7]辛业春,王延旭,李国庆,等.T 型三电平并网逆变器有限集模型预测控制快速寻优方法[J].电工技术学报,2021,36(8): 1681-1692.Xin Yechun,Wang Yanxu,Li Guiqing,et al.Fast optimization method of finite set model predictive control for T-type three-level grid connected inverter[J].Transactions of China Electrotechnical Society,2021,36(8): 1681-1692.
[8]张建忠,胡路才,徐帅.一种零序电压注入的T 型三电平逆变器中点电位平衡控制方法[J].电工技术学报,2020,35(4): 807-816.Zhang Jianzhong,Hu Lucai,Xu Shuai.A neutral point potential balance control method for T-type threelevel inverter with zero sequence voltage injection[J].Transactions of China Electrotechnical Society,2020,35(4): 807-816.
[9]Zhou Dehong,Li Ding,Li Yunwei.Two-stage optimization-based model predictive control of 5LANPC converter-fed PMSM drives[J].IEEE Transactions on Industrial Electronics,2021,68(5): 3739-3749.
[10]Geyer T,Mastellone S Model predictive direct torque control of a five-level ANPC converter drive system[J].IEEE Transactions on Industry Applications,2012,48(5): 1565-1575.
[11]Oikonomou N,Gutscher C,Karamanakos P,et al.Model predictive pulse pattern control for the fivelevel active neutral-point-clamped inverter[J].IEEE Transactions on Industry Applications,2013,49(6): 2583-2592.
[12]Li Chushan,Shuai Wang,Guan Qingxin,et al.Hybrid modulation concept for five-level active-neutralpoint-clamped converter[J].IEEE Transactions on Power Electronics,2017,32(12): 8958-8962
[13]李俊杰,姜建国,刘云龙,等.具有共模电压减小和电容电压平衡的五电平有源中点钳位型变换器SVPWM 算法[J].电工技术学报,2018,33(13): 3109-3118.Li Junjie,Jiang Jianguo,Liu Yunlong,et al.SVPWM algorithm for five-level active neutral point clamped converter with common mode voltage reduction and capacitor voltage balance[J].Transactions of China Electrotechnical Society,2018,33(13): 3109-3118.
[14]王永辉,何帅彪,冯瑾涛,等.考虑中点电压平衡的三相四开关变换器模型预测电压控制[J].电力系统保护与控制,2019,47(12): 31-39.Wang Yonghui,He Shuaibiao,Feng Jintao,et al.Model predictive voltage control of three-phase four switch converter considering neutral point voltage balance[J].Power System Protection and Control,2019,47(12): 31-39.
[15]张宏,董海鹰,陈钊,等.基于模型预测控制的光热-光伏系统多时间尺度无功优化控制策略研究[J].电力系统保护与控制,2020,48(9): 135-142.Zhang Hong,Dong Haiying,Chen Zhao,et al.Research on multi time scale reactive power optimization control strategy of photothermal photovoltaic system based on model predictive control[J].Power System Protection and Control,2020,48(9): 135-142.
[16]Nie Ziling,Ye Weiwei,Zhu Junjie,et al.Capacitor voltage feedforward decoupling control based on third harmonic injection modulation for five-level active neutral point clamped converter[J].Journal of Power Electronics,2020,20(6): 1638-1649.