0 引言
脉冲宽度调制（Pulse Width Modulation,PWM）已广泛应用于DC-DC 变换器。它在每个固定周期中通过控制信号vc(t)与三角形载波信号vp(t)进行比较来产生占空比，从而控制变换器的功率传输。根据所用三角形载波，PWM 可以设置为前沿调制或后沿调制。基于数字控制不同调制方式下的时序图如图1 所示。
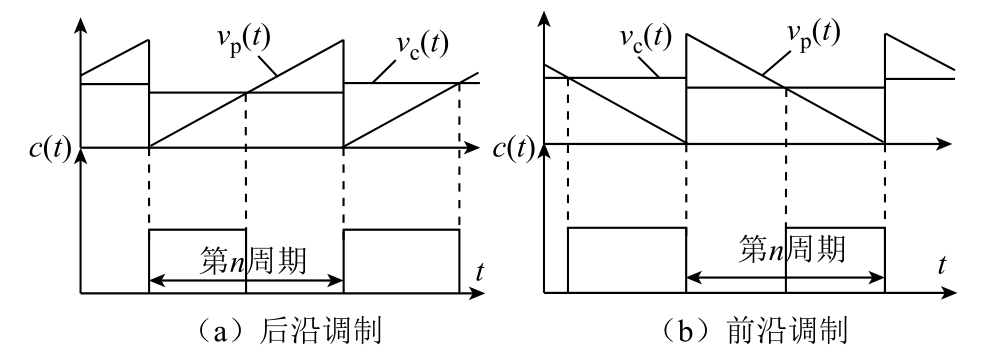
图1 基于数字控制不同调制方式下的时序图
Fig.1 Timing diagram of different modulations based on digital control
根据图1，对于前沿调制，开关管在每个周期的初始时刻断开，当控制信号与三角载波相交时开通。对于后沿调制，开关管开通和关断的顺序是相反的。前沿和后沿调制在DC-DC 变换器中有许多应用。实际上，模拟峰值电流控制的调制方法本质上是后沿调制。此外，使用前沿调制可以将模拟控制的Boost 和Flyback 型变换器转换为最小相位系统[1]。在级联变换器中，两种调制方法也通常一起应用，以减少电感电流的纹波并提高效率[2]。因此，研究不同脉冲宽度调制对变换器的影响很重要。
随着数字信号处理（Digital Signal Processing,DSP）技术的不断发展与成熟，其优越性日益突出。相比传统的模拟控制，数字控制在电路元器件老化以及环境、温度改变时的抗干扰能力更强；更重要的是，数字控制技术能够极大地简化模拟控制环路的元器件，以灵活的软件编程方式实现复杂的非线性控制策略，并且控制方案可以在微调后适配不同的功率级电路，从而使开关电源更加趋于智能和通用[3-4]。但同时，由于受到采样点位置、量化处理环节和采样保持环节，以及软件本身延迟控制特性的影响[5-6]，数字控制系统呈现出和模拟控制系统不同的非线性动力学行为[7-8]。因此必须对数字控制系统建立精确且直观的数学模型，并分析其稳定范围。
平均模型是目前应用最广泛的DC-DC 电路建模方法[9]。它关注低频扰动对于整个系统动态性能的影响[10-11]。因此，平均建模方法在忽略高频开关纹波后可以建立系统的平均等效电路，直观且便于分析。然而，平均建模方法的准确性取决于对占空比中非基波分量的抑制程度。平均建模方法忽略了高频扰动信号，而高频部分会由于采样混叠的原因影响系统的特性，所以平均模型不能对奈奎斯特频率附近的系统特性进行良好的描述[12-13]。此外，平均建模方法也不能有效地反映环路延迟，以及由电容等效串联电阻造成的Boost 和Flyback 型变换器输出电压不连续对系统特性的影响[14-15]。
对于数字控制系统，离散迭代模型逐渐成为其主要的建模方法，它对电路的描述更加切合实际特性，也更为精确[13,16-18]。离散迭代模型的建模过程不需要对状态变量进行平均，所以在各个数据采样点可以得到精确的状态变量转移特性[19-20]。文献[20-24]注重于利用离散迭代模型对DC-DC 电路的稳定性及分岔行为进行研究，其中文献[20]通过离散迭代模型分析了Boost 和Flyback 变换器在数字控制方式下的最小相位条件；文献[21]通过离散模型分析了单电感双输出降压变换器的稳定性；文献[22]通过离散模型描述了Buck 变换器的倍周期分岔现象；文献[23]使用精确离散模型分析了模拟控制Buck 变换器的分岔和混沌特性；文献[24]利用z 域模型分析了数字控制Buck 变换器发生Hopf分岔的原因。文献[25-26]更加关注不同脉冲宽度调制方法对于DC-DC 变换器的影响。文献[25]使用离散时间模型分析了V2-控制Buck 变换器在前沿调制和后沿调制下不同的动态特性；文献[26]通过采样数据模型分析了不同调制方式对模拟控制DC-DC变换器稳定性的影响。文献[12,27]根据离散模型推导出DC-DC 变换器的z 域传递函数。但是，离散迭代模型的推导过程非常复杂，涉及大量的矩阵函数和指数运算，对于模型的分析通常依赖数值计算；而且离散迭代模型没有对应的等效电路，物理意义不够明确，不利于工程应用。
到目前为止，直观且精确的等效电路模型在数字脉冲宽度调制（Digital Pulse Width Modulated,DPWM）的经典DC-DC 变换器中罕有报道。本文以运行在电流连续模式（Continuous Current Mode,CCM）的数字控制同步DC-DC 变换器为对象，利用文献[28]提出的对传统离散迭代模型进行近似的建模思想，建立数字控制DC-DC 变换器的等效电路。这种简化的建模方法已被证明在双有源桥（Dual Active Bridge,DAB）变换器上是可行的[28]。DAB 是一种电感电流为交流的PWM 调制型DC-DC 变换器，文献[28]通过改进离散迭代建模方法得到的二阶等效电路模型可用来精确描述DAB 的动态特性，并且通过忽略其电感电流动态得到了准确的一阶模型。但是，该建模方法对无法忽略电感电流动态的DC-DC 变换器的普适性尚未得到验证。本文主要利用Buck 变换器验证了这种建模思想对经典PWM 调制型DC-DC 变换器的普适性和实用性，并通过和平均模型以及传统双线性模型的对比，说明本文所得到的等效电路模型的精确性及必要性。这种方法利用离散迭代模型将一个周期中的两种开关状态简化为一种，从而得到二阶全局等效电路，克服了现有模型精确性和直观性之间的矛盾。等效电路模型精确地刻画了系统在采样点处的状态变量信息，并且有效地反映了前沿调制（Leading-Edge Modulation,LEM）和后沿调制（Trailing-Edge Modulation,TEM）对系统的影响。基于提出的模型，推导出Buck 变换器的z 域模型。接着，利用Buck变换器对模型进行充分的验证。首先，将模型计算出的Buck 变换器频率响应和实验得到的进行对比。进一步地，给出了利用z 域模型分析系统稳定性的方法，并且分析了数字控制Buck 变换器的补偿器增益，输入电压、负载电阻、电容、电感等参数的稳定边界。比较这些参数在不同模型下的稳定性边界，可以看出本文使用的全局等效电路的简单性和准确性。此外，利用等效电路模型研究了两种不同调制方式下稳定性边界随占空比变化的情况，揭示了不同调制方式对系统稳定性影响的本质。最后通过PLECS 仿真和实验平台验证了该种建模方法的正确性和有效性。
1 基于离散采样的数字控制同步DC-DC变换器的全局等效电路模型
1.1 DC-DC 变换器的状态空间描述
电压型数字控制同步DC-DC 变换器由主功率电路和数字控制电路组成。电压模式数字控制同步Buck 电路如图2 所示。主功率电路包括输入电压源Vin、主开关管S1 和整流开关管S2、电感Ls、输出电容Cs 以及负载电阻Ro。用iL(t)表示流过电感Ls 的电流，vo(t)和vC(t)分别表示输出电压和电容Cs 两端的电压，d 表示占空比。数字控制回路包括A-D 转换模块、数字补偿器和DPWM 模块。DSP 以开关频率 fs 的采样率对vo(t)进行采样并通过A-D 模块将模拟信号转换成数字信号。误差信号e[n]由输出电压vo(t)与参考电压Vref 之间的差值获得后，通过数字补偿器处理，输出控制信号u[n]。最后，u[n]通过DPWM 产生脉冲信号c(t)来控制开关S1 和S2 的通断，完成对主功率回路的控制。
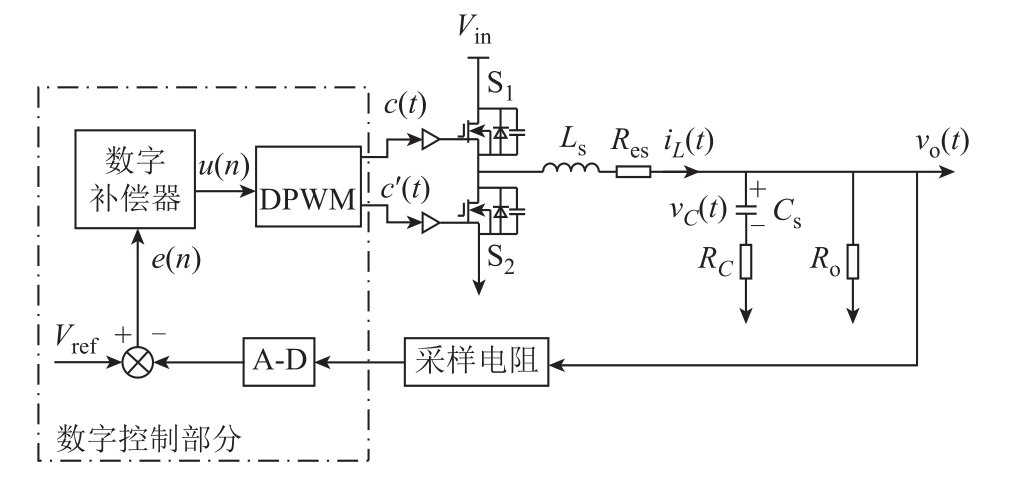
图2 电压模式数字控制同步Buck 电路
Fig.2 Digitally controlled voltage-mode synchronous Buck converter
假设同步DC-DC 变换器工作在连续导通模式。两种开关状态的电路可以分别用线性状态方程和输出方程描述为
式中，x(t)为系统的状态变量；x(t)=[iL(t) v C(t)]T；y(t)为系统的输出变量vo(t)；Aj、Bj 和Cj 分别为系统的状态矩阵、输入矩阵和输出矩阵；下标j 表示对应的第j 个开关状态。RC 和Res 分别表示电容和电感的串联等效电阻。因此，DC-DC 变换器两种开关状态的状态矩阵[A1 A2]，输入矩阵[B1 B2]和输出矩阵[C1 C2]对于Buck 变换器为
1.2 基于传统离散迭代建模方法的DC-DC 变换器模型
对于传统的离散迭代模型，采样点一般选择在一个开关周期的初始时刻，因此两个连续采样点的状态转移函数F(x[n],d,Vin,Ts)可以通过离散化和迭代式（1）中状态方程的解来获得。图3 所示为后沿调制下离散模型中的状态转移关系；xn,0 表示第n 个开关周期的状态变量采样值，记为x[n]；xn,2 表示第n+1 个开关周期状态变量采样值，记为x[n+1]；xn,1表示控制信号u[n]与载波波形相交时的状态变量采样值。所以，两个相邻采样点之间的状态转移函数FTEM(x[n],d,Vin,Ts)可以通过迭代xn,0 和xn,1 以及xn,1和xn,2 之间的状态方程得到
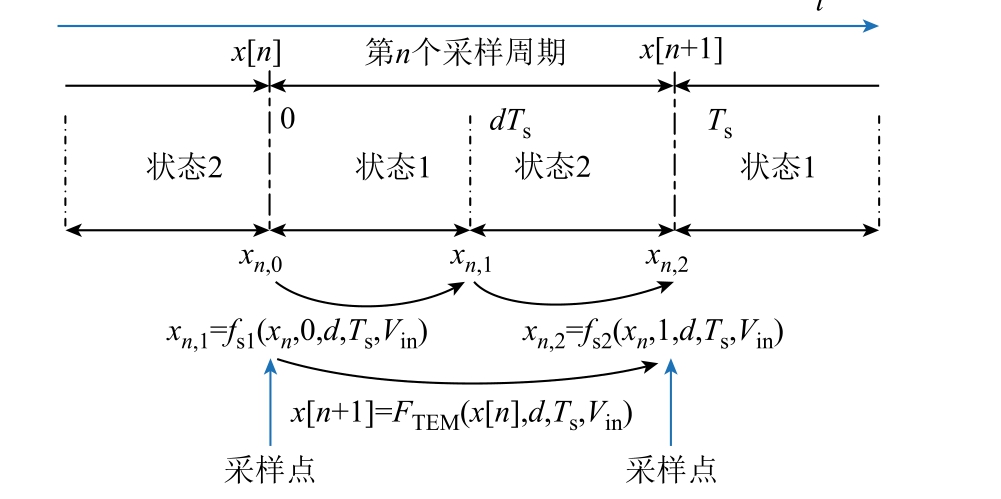
图3 后沿调制传统离散模型中状态变量的转移关系
Fig.3 Iterative relationship of the state variables with TEM for the traditional discrete model
结合输出方程，就可以得到一组描述一个周期内状态变量变化的差分方程组，即
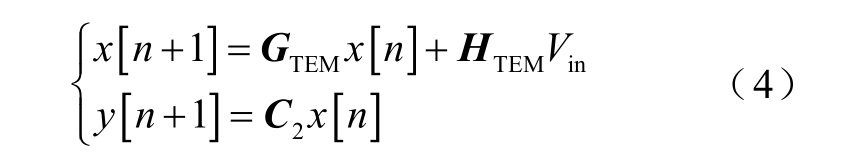
相比后沿调制，前沿调制下DC-DC 变换器在一个周期内的开关次序相反，此时输出矩阵为C1。所以前沿调制下描述系统的差分方程组为
因为Buck 变换器的输出电压是连续的，所以输出矩阵 C 在前沿调制和后沿调制方式下都是相等的，即C1=C2。而对于Boost 和Flyback 型变换器，其输出电压是不连续的。这是因为当开关S1 开通瞬间，A-D 采样到的输出电压不仅是输出电容两端的电压，还有电感电流的交流分量在RC 两端瞬间产生的一个电压阶跃。当S1 关断时，电感电流不再给电容充电，所以此时A-D 采样到的输出电压可以近似为电容两端的电压。如果采样点选择为足够靠近周期初始时刻的前一小段时间，那么此时前沿调制和后沿调制下Boost 变换器的输出矩阵应该分别选择C1 和C2。对于DC-DC 变换器，其电感电流 iL(t)的相位超前于电容电压 vC(t)，所以C2x[n]的相位也就会超前于C1x[n]。这也就意味着，对于这种采样方式的Boost 电路，其输出到控制传递函数的相位裕度在后沿调制时更大。两种调制方式在相位上的差异可以从传递函数的零点上反映出来[1,20]。
1.3 基于后沿调制的DC-DC 变换器全局等效电路
当占空比d 的扰动频率低于奈奎斯特频率时，满足香农采样定理[28]，传统的离散迭代模型能够准确地反映详细开关电路的特性。然而，传统离散模型有一定的局限性：首先，模型中存在大量指数矩阵运算，不利于工程的应用；其次，该建模方法没有直观的等效电路，所以无法有效地推导出解析的传递函数。
为了得到直观的等效电路，同时保证模型的准确性，本文提出一种DC-DC 变换器的全局等效电路。对于等效电路，状态空间可以唯一地描述为
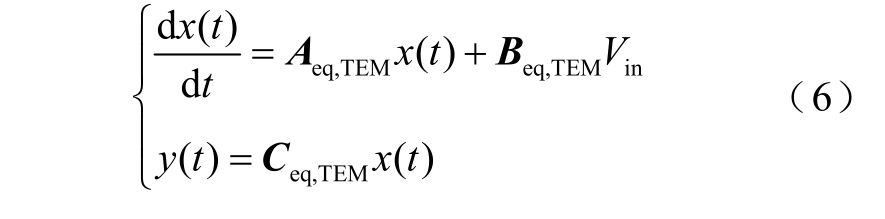
式中，Aeq,TEM、Beq,TEM 和Ceq,TEM 分别为后沿调制下等效电路的状态矩阵、输入矩阵和输出矩阵。因此，离散域中等效电路的状态变量转移关系可以简化为图4。
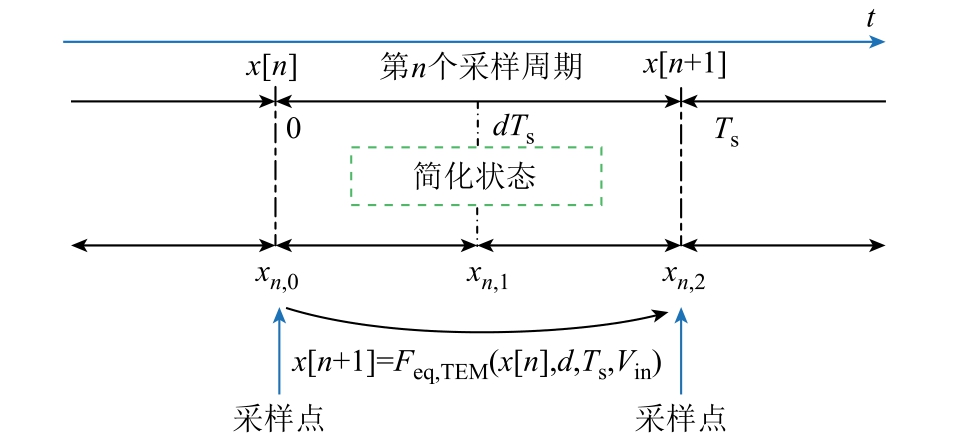
图4 后沿调制下系统简化的状态变量转移关系
Fig.4 Simplified iterative relationship of the state variable with TEM
一个开关周期内的状态转移函数不再需要对两个状态迭代。只需将式（4）中的状态方程直接离散即可，对应状态转移函数可描述为
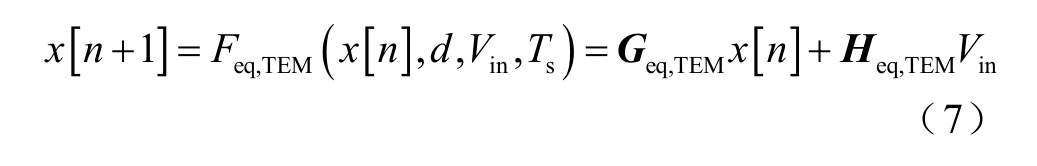
式中，Geq,TEM 和Heq,TEM 分别为等效电路的离散状态矩阵和离散输入矩阵。
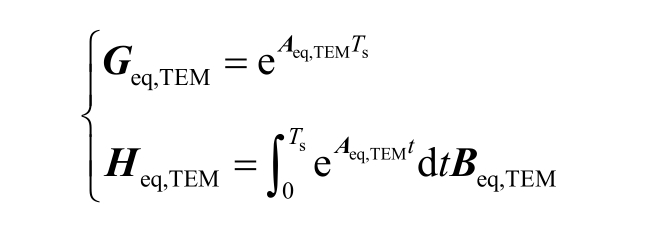
为了建立能够精确描述系统的瞬态特性以及高频幅相特性的等效电路，需要令FTEM 和Feq,TEM 充分近似。令式（3）与式（7）各项对应相等可以得到的等效电路的离散状态矩阵应该满足
通过计算式（8），可得到Aeq,TEM 和Beq,TEM 为
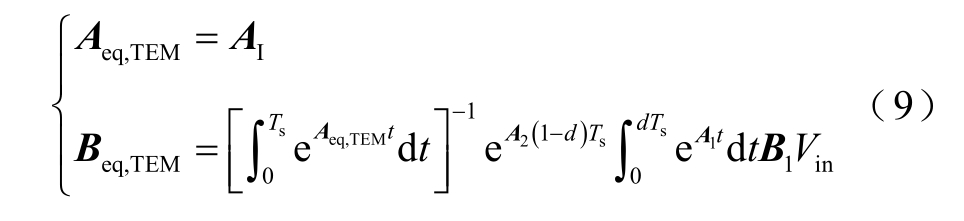
以Buck 变换器为例，对计算得到的Beq,TEM 做周期Ts的级数展开，其高次分量过小所以可以省略，保留其中最低阶的项进行近似为
所以Buck 变换器等效电路的状态空间表达为
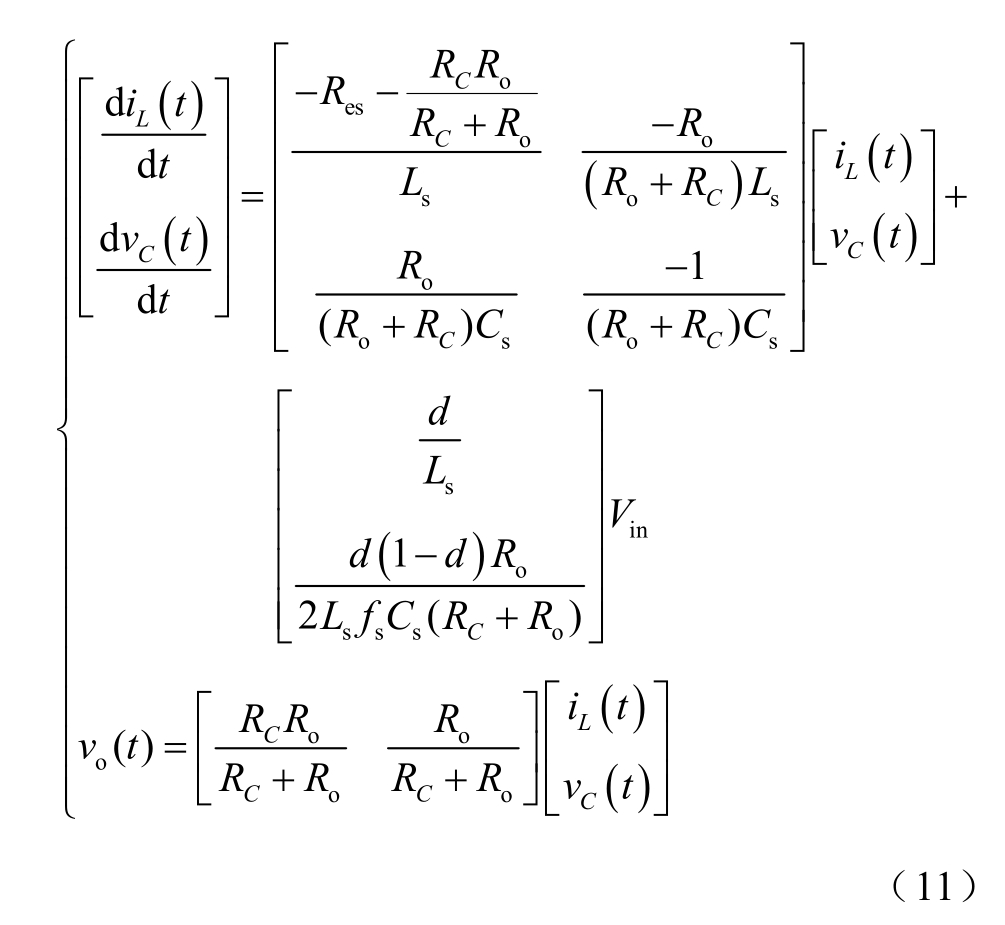
方程组（11）对应着唯一的后沿调制下Buck 变换器二阶全局等效电路，如图5 所示。
图5 后沿调制Buck 变换器二阶全局等效电路
Fig.5 The second-order global equivalent circuit of Buck converter with TEM
相比于平均模型构建的等效电路，图5 所示的基于离散迭代建模型的全局等效电路在输出端增加了一个受控电流源。为了更清楚地解释全局等效电路的物理意义，忽略RC 和Res。由图5 可以得到流过电容的电流iC(t)为
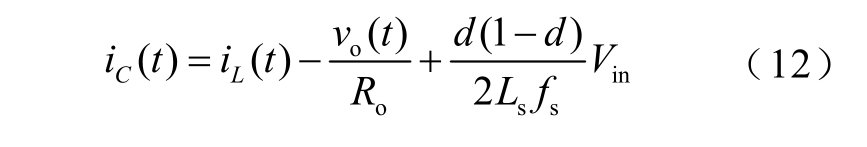
在电路稳态时，电感电流的纹波 Δ iL为
所以对于全局等效电路，电感电流 i L(t)被修正为
基于以上分析，全局等效电路相当于从输入端到输出端增加了一条额外的功率回路。这个功率回路实际上包含了平均模型中被忽略的电感电流纹波信息。因此，该模型虽然忽略了u[n]与载波波形交点处的状态变量xn,1 的信息，但准确地保留了采样点的状态变量信息。后沿调制等效电路和详细开关电路电感电流波形对比如图6 所示。等效电路的电感电流并不是详细开关电路的滑动平均值，两者的轨迹在采样点精确重合。对于后沿调制Buck 变换器，采样点是一个周期中电感电流波形的谷值，因此等效电路的电感电流波形是详细开关电路的下包络线。
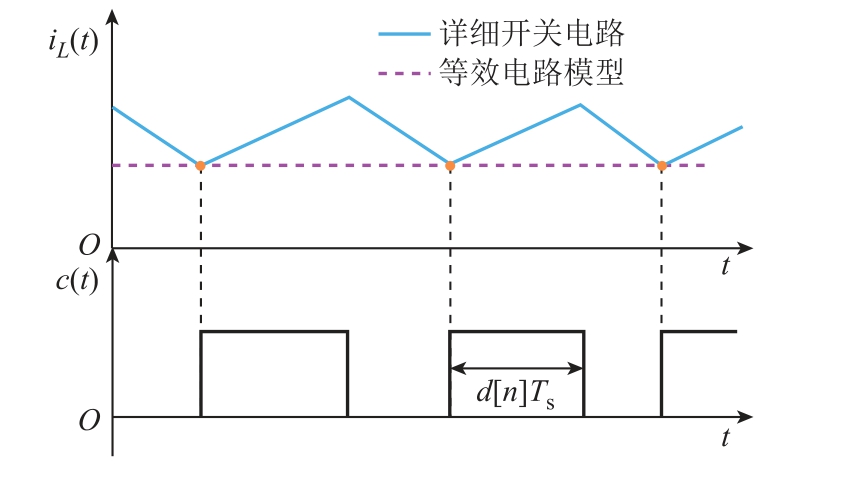
图6 后沿调制等效电路和详细开关电路电感 电流波形对比
Fig.6 Comparison of waveforms of iL(t) for equivalent circuit and detailed switching circuit with TEM
1.4 基于前沿调制的DC-DC 变换器全局等效电路
前沿调制时离散域中等效电路的状态变量转移关系如图7 所示。前沿调制的系统在一个周期Ts中开关的先后顺序与后沿调制时相反。类似地，令FLEM和Feq,LEM 充分近似，Aeq,LEM 和Beq,LEM 可表示为
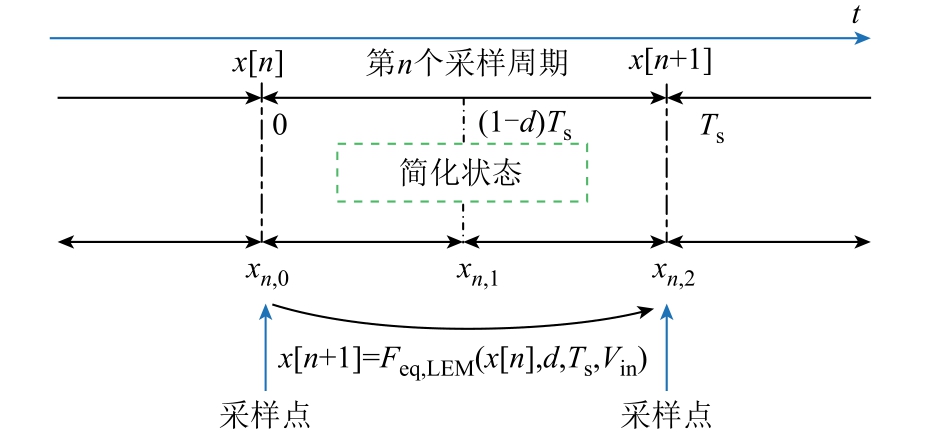
图7 前沿调制下系统简化的状态变量转移关系
Fig.7 Simplified iterative relationship of the state variable with LEM
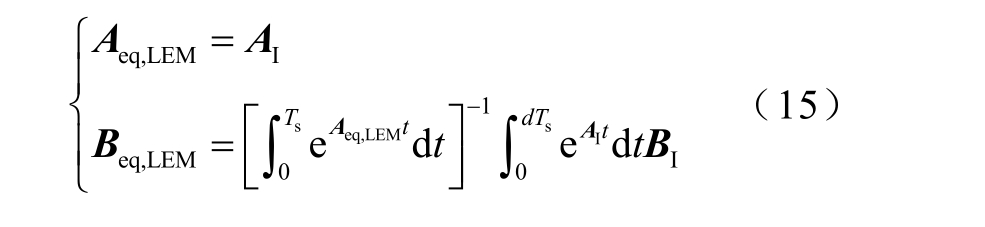
同样以Buck 变换器为例，对Beq,LEM 做周期Ts的级数展开，并且保留其中最低阶的项，即
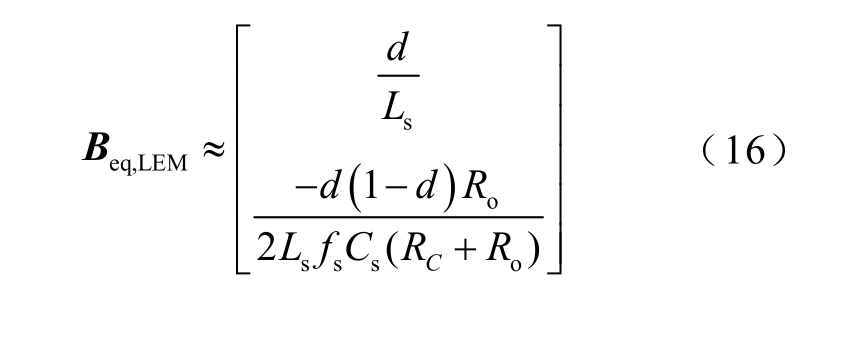
因此，前沿调制的Buck 变换器等效电路状态空间表达为
根据式（17）可以得到与之唯一对应的前沿调制Buck 等效电路模型。
前沿调制Buck 变换器二阶全局等效电路如图8 所示，与后沿调制相比，前沿调制在输出侧引入一个数值相等但方向相反的受控电流源。事实上，该受控电流源在z 域中是调制延迟的函数，前沿调制和后沿调制下的系统的主要区别也体现在该受控电流源上。经过零阶保持后，该受控电流源会对两种调制方式的动态特性和稳态特性造成不同的影响，这将在下文进行进一步的探讨。前沿调制下等效电路和详细开关电路之间电感电流的对比如图9 所示。前沿调制时Buck 变换器的电感电流是在各个峰值点进行采样的，等效电路包含了各个采样点的电流纹波信息，其电感电流波形应该是详细开关电路的上包络线。
图8 前沿调制Buck 变换器二阶全局等效电路
Fig.8 The second-order global equivalent circuit of Buck converter with LEM
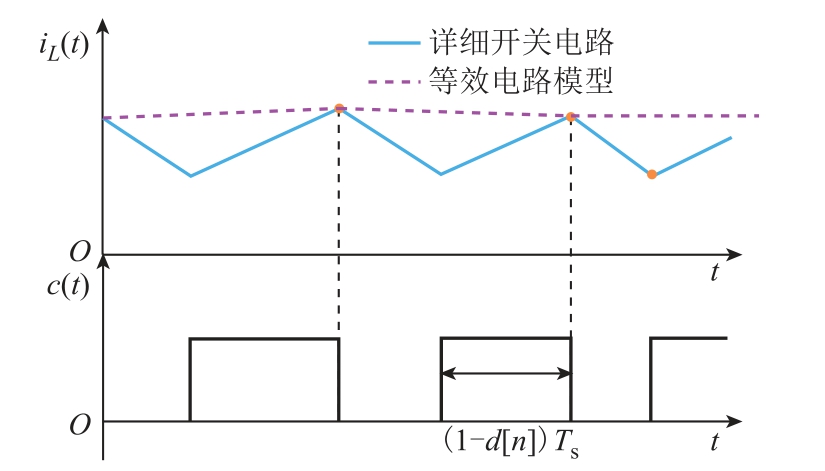
图9 前沿调制等效电路和详细开关电路电感电流 波形对比
Fig.9 Comparison of waveform of iL(t) for equivalent circuit and detailed switching circuit with LEM
2 基于全局等效电路的z 域模型
2.1 s 域传递函数
在实际工程应用中，往往要得到系统在频域上的幅相特性，以便于设计变换器的控制环路。在稳态工作点Q=(IL,Vo,D,Vin,VC)附近，对非线性状态方程引入式（18）所示的扰动并将其线性化，从而得到s 域的控制-输出的传递函数。
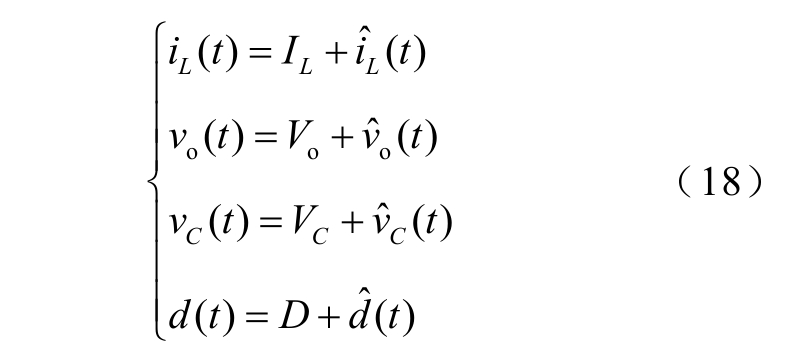
式中，D 为稳态占空比。
对状态方程式（11）和式（17）引入小信号扰动，消去稳态分量，并且忽略二阶以上的交流分量，就可以分别推导出前沿调制和后沿调制Buck 变换器在s域中的控制-输出的传递函数，对于后沿调制有
对于前沿调制有
2.2 考虑环路延迟的z 域传递函数
需要说明的是，本文不考虑DSP 中ADC 和DPWM 的量化误差。由于采样保持过程造成的延迟对系统特性有很大的影响，因此必须考虑环路总延迟td。事实上，DSP 一般采用影子寄存器模式运行，控制命令u[n]会被延迟一个周期再进行更新，这段时间记为控制延迟tcntrl。假设锯齿形调制波的振幅为1，则第n 个周期的占空比d[n]为
接着，控制信号u[n]需要通过DPWM 进行调制。载波波形和控制命令u[n]的交点到周期初始时刻的时间为调制延迟tDPWM。后沿调制和前沿调制的tDPWM 分别为d[n]Ts 和(1-d[n])Ts。因此，数字控制系统的总延迟为
然而，s 域模型没有考虑系统的零阶保持器效应和延迟效应。对于固定时间间隔采样的情况，可以将s 域模型直接离散到z 域上，以反映数字控制DC-DC 变换器中的采样和延迟特性[25]。首先，需要对数字控制回路进行建模和分析。数字控制DC-DC变换器闭环结构框图如图10 所示。其中，H(s)的增 益假设为1。数字控制闭环系统会通过采样电阻对输出电压进行采样，并通过A-D 将输出电压离散成数字量，所以A-D 模块可等效为一个周期为Ts 的采样开关。然后，将输出电压采样值送入DSP 与参考电压Vref 比较得到误差信号，该误差信号进入离散时间补偿器计算出占空比，并在下一周期初始时刻通过DPWM 模块产生数字控制信号。因此，数字控制环节可以等效于图中的补偿器Gc(s)、调制器GDPWM(s)和一拍延迟z-1 的串联，并且被采样开关采样。最后，数字控制信号通过和D-A 模块转换为模拟信号控制功率回路，整个系统具有零阶保持器效应。因此，D-A 模块可以等效为一个采样开关和一个零阶保持器环节Goh(s)的串联。也就是说c(t)此时作用于Goh(s)Geq,vd(s)。
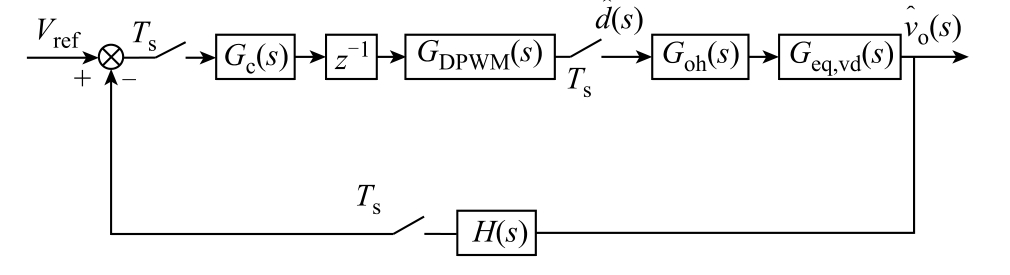
图10 数字控制Buck 变换器的结构框图
Fig.10 Block diagram of the digitally controlled Buck converter
开环z 域传递函数并不需要借助延迟算子进行复杂的变换得到，这与文献[13,20,26]中模型相比是一个关键的优势。当采样开关以周期Ts进行采样，只需要对开环传递函数Goh(s)Geq,vd(s)进行z 变换，乘以延迟环节z-1 便可以得到系统的控制到输出的z域传递函数Geq(z)，Z [⋅]表示z 变换。
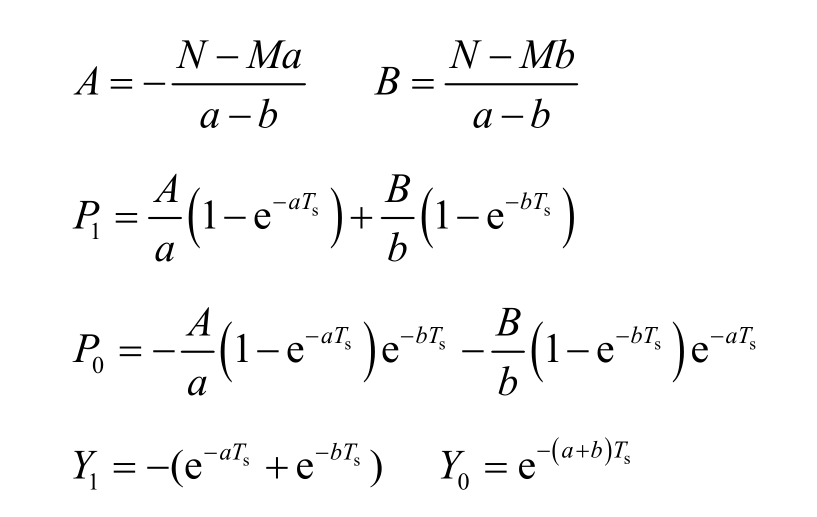
为了验证Geq(z)的准确性，以Buck 变换器为研究对象，利用Matlab 计算了不同建模方法的频率响应结果，仿真参数见表1。图11 比较了Gex(z)、Gave(s)和Geq(z)三种传递函数的幅值和相位响应。Gex(z)由传统的离散时间模型得到，其建模方法由文献[12,30]提出；Gave(s)通过延迟环节修正后的平均模型得到。
表1 Buck 变换器电路仿真参数
Tab.1 Circuit parameters of Buck converter
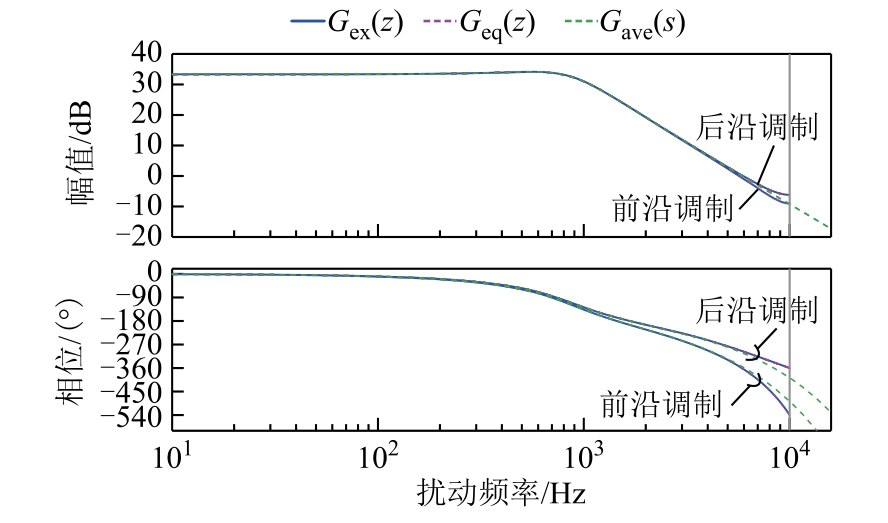
图11 控制-输出传递函数幅相特性对比
Fig.11 Magnitude and phase responses of the controloutput transfer functions obtained by different modeling methods
对于这三种模型，Gex(z)在扰动频率小于奈奎斯特频率时具有精确的频率响应，所以可作为其余两种模型的对比。从图11 可以看出开环稳态占空比D为0.25 时，前沿调制系统的相位滞后更大。因为在其他电路参数相同的情况下，采用前沿调制方式的系统具有较大的调制延迟。Geq(z)和Gex(z)的幅相特性曲线几乎重合，说明Geq(z)对系统采样和延迟特性的预测精度几乎与Gex(z)相同。然而，对于Gave(s)，由于信号混叠效应的存在，使得它无法很好地描述奈奎斯特频率附近的系统特性。对于前沿和后沿调制，电感电流纹波相对于电感电流的平均值不能被忽略，因此由于采样时的混叠效应，平均模型不能满足建模的精度要求。
同样需要说明的是，本文所提出的基于离散迭代模型推导出等效电路的建模方法对于其他DC-DC 变换器具有普遍适用性。本文提出的对DC-DC 变换器的建模方法，可以有效地反映采样点位置以及延迟对系统特性的影响。根据上文所述，Boost 和Flyback 型变换器所在的输出矩阵受到采样点位置的影响，不能简单地用平均建模的方法去处理。
3 系统稳定性分析
电路系统一般在进入闭环状态后，能够在受到外界扰动时稳定输出电压并控制传输功率。但是，闭环系统的调节能力是有一定范围的，其受到输入电压、负载和控制器增益等多方面的影响。如果超出这些参数的适用范围，那么闭环系统将会失去调节能力，系统出现明显的振荡现象，显著增大元器件的电压、电流应力，并导致损耗增加或器件损坏，严重影响电路的正常运行。本节将利用z 域模型对系统稳定性进行分析，并且研究几个重要的参数对系统稳定性的影响。
3.1 基于z 域模型的系统稳定性分析
根据图10 的框图，系统的闭环传递函数可表示为
所以闭环传递函数的特征方程D(z)为
有关参数变化对于系统稳定性的影响将以后沿调制Buck 变换器为例进行分析。前沿调制系统稳定性随参数的变化趋势与后沿调制相似。
3.2 控制器增益kp 对系统稳定性的影响
对于闭环系统来说，控制器的参数设计是非常重要的，因为其关系到系统的动态性能和稳定性。如果控制器的参数设计不合理，那么系统可能会出现振荡等不稳定现象。比例控制器的增益kp较小时，虽然系统的稳定裕度较大，但是系统调节速度慢，不符合控制器设计的标准。但是当kp 值过大，超出临界稳定增益kp,max，就会造成系统的不稳定。所以在电路参数固定后，找到最大的那个临界增益对于控制器的设计是极其重要的。
特征方程D(z)的根由一个实根和两个共轭特征根组成。对于参数见表1 的变换器系统，当kp 在[0.03,0.17]内变化时，特征方程D(z)的特征根轨迹如图12 所示。z3 表示一个实根，z1 和z2 表示一对共轭特征根。当kp 增加时，z3 的变化比z1 和z2 的变化小得多，这意味着z1 和z2 对系统稳定性的影响远大于z3。kp 变化时系统稳定性的变化见表2，共轭特征根的模随着kp 的增大而增大。当kp=0.077 时，系统的一对共轭特征根穿过单位圆。因此，kp,max 约为0.077。传统离散迭代模型可以利用雅克比矩阵判断系统的稳定性[29]，代入表1 参数得到离散迭代模型预测的kp,max 同样为0.077，说明了z 域模型对于系统稳定性预测的准确性。
图12 kp 变化时闭环特征根轨迹
Fig.12 Root loci of the characteristic roots zi (i=1,2,3) with increasing kp
表2 kp 变化时系统稳定性的变化
Tab.2 The change of system stability as kp increases
3.3 功率回路参数对系统稳定性的影响
全局等效电路不仅可以用于指导元器件选择，还可以在功率回路参数发生变化时指导控制器的设计。传统离散迭代模型、全局等效电路模型、Geq,TEM(z)和传统双线性模型预测的稳定性边界的比较如图13所示。其中，传统离散迭代模型和全局等效电路模型的稳定性是由雅可比矩阵计算得到的[1]。传统双线性模型是对传统离散模型进行一阶近似得到的[30]。但是根据文献[31-32]，对离散模型进行一阶近似后，其无法对系统稳定性进行有效预测。利用kp,max 表示功率回路参数的稳定性边界范围。传统的离散迭代模型在没有任何简化的情况下准确地反映了系统的全局稳定性，因此也用作模型比对的标准。比较图13 中所示的稳定性边界，全局等效电路模型和等效电路的传递函数Geq,TEM(z)可以准确预测参数与kp,max的关系。然而，传统的双线性模型在预测系统稳定性方面存在较大误差。这说明，本文提出的模型能够有效地反映系统的稳定性。而传统的离散模型虽然通过一阶近似可以直接得到解析模型，但是并不能准确地反映系统的稳定性，传统的离散模型还是需要借助复杂的指数矩阵计算才能得到准确的系统特性。
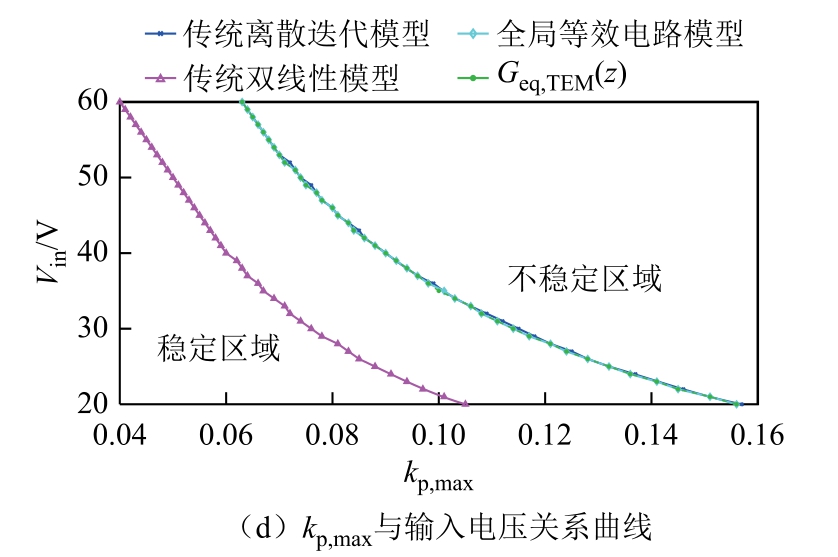
图13 参数变化时系统稳定边界的对比
Fig.13 Comparison of the stability boundary of the system when the parameters change
进一步，从特征方程式（25）和卡尔丹公式可得D(z)的特征根满足
根据图12，z3＜0 且z3 在kp 改变时几乎不变，因此，式（26）可以近似地反映共轭特征根的模二次方（即z1z2=|z1|2=|z2|2）与功率回路参数之间的关系。在式（26）中，每个kp 和Vin 都以乘积项的方式出现。所以，Vin 的增加相当于kp 的增加，导致系统稳定裕度降低。因此，在设计闭环控制器时，应基于Buck 变换器可能出现的最大输入电压进行设计。
系统的稳定边界随Ro、Ls 和Cs 的变化趋势可以通过对式（26）求导进行分析，得到
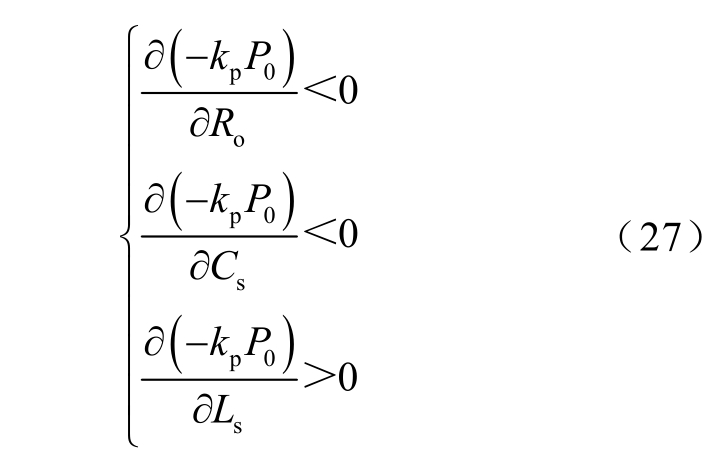
根据式（27）的结果，Ro 的增加会使共轭特征根的模增加，这意味着在较轻的负载下系统的稳定裕度会变小。因此，在设计控制参数时，要注意变换器在轻载时的稳定性，避免负载突然降低时出现振荡。
对于储能元件Cs 和Ls，根据式（27），Cs 的增大会导致系统稳定性下降，Ls 的增加使稳定边界变宽。事实上，输出电容Cs 增大会造成系统相位的进一步滞后。由电感电流与输出电压的相位关系可得
式中，ωp 为占空比扰动的频率。当Cs 增加时，输出电压相对于电感电流的相位滞后增加，导致系统鲁棒性降低。
3.4 寄生参数对系统稳定性的影响
在实际电路中，元器件的特性并不理想，在建模时需要考虑寄生参数的影响。三维图14 所示为当RC 和Res 变化时，系统稳定边界的变化趋势。为了清晰地分析RC 和Res 对系统稳定性的影响，图15a和图15b 分别给出了RC 在Res=0.04Ω 时的稳定边界，以及Res 在RC=0.004Ω 时的稳定边界。可以发现，RC和Res的存在确实可以扩大系统的稳定边界，但是过大的RC 将成为输出电压纹波的主要来源，而过大的Res 将增加电路损耗，导致系统效率降低。同 时，可以看到对于全局等效电路模型预测的稳定性边界，与传统离散迭代模型仍然准确吻合，这意味着全局等效电路模型同样也适用于分析微小寄生参数对系统的影响。
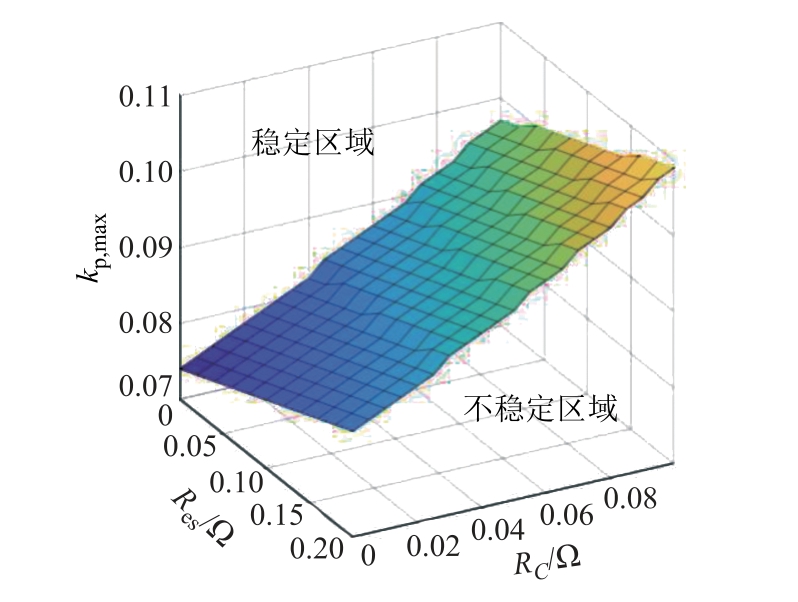
图14 RC 和Res 变化时系统稳定边界的变化趋势
Fig.14 The stability boundary of the system when RC and Res changes
图15 系统寄生参数变化时系统稳定边界的变化趋势
Fig.15 The stability boundaries of the system for different parasitic parameters
3.5 调制方式对系统稳定性的影响
前沿调制和后沿调制对系统稳定性的影响是本文的一个研究重点。根据图4 和图7 所示的二阶全局等效电路，两种调制方式之间的主要区别体现在输出侧的受控电流源，它具有相同的数值但是相反的电流流向。受控电流源的数值是关于占空比的函数，它在模型上是调制延迟tDPWM 的映射。根据等效电路模型，令前沿调制和后沿调制的受控电流源相等可解得
所以当占空比D 为50%时，两种调制方式对系统稳态和动态特性的影响完全相同。占空比变化时不同调制方式系统稳定边界的对比如图16 所示。从图16 可以得到，当系统工作在后沿调制方式时，kp,max 随着占空比D 增加而减小。对于前沿调制时的工况，则正好相反。总之，系统的稳定性会随着调制延迟tDPWM 的增加而降低。因此，当占空比D 小于50%时，应选择后沿调制。此时，采用后沿调制方式的系统延迟更小，稳定性更强。如果占空比D 大于50%，则情况正好相反。
图16 D 变化时不同调制方式系统稳定边界的对比
Fig.16 Comparison of the stability boundary of the system when D changes with different modulations
为了验证上述分析结果，在PLECS 软件平台上搭建Buck 变换器的详细开关电路和二阶等效电路，观察参考电压从6V 阶跃到12V 时系统的瞬态特性。仿真电路的基本参数见表1。需要注意的是，由于数字控制的特点，在仿真中需要加入一阶延迟环节和零阶保持器。参考电压的突然变化实际上引入了占空比D 的扰动。如图17a、图17b 所示，在参考电压阶跃后，工作在前沿调制方式下的系统从不稳定的振荡状态逐渐收敛到稳定。如图17c、图17d 所示，工作在后沿调制方式下的系统从稳定运行状态变为振荡状态。仿真现象与图16 所示的计算结果一致。当系统从稳定进入不稳定时，闭环系统失去其稳态工作点。在这种情况下，全局等效电路的波形仍然可以跟踪和表示详细的开关电路的波形，这进一步证明了所提出模型的准确性。
图17 当Vref 从6V 阶跃到12V 时，等效电路和详细开关电路仿真波形对比
Fig.17 Comparison of the stability boundary of the system when Vref steps from 6V to 12V with different modulations
4 实验结果
在本节中，建立了一个Buck 变换器的样机来验证所提出模型的准确性和理论分析结果。控制和采样过程由TI 的数字处理器TMS320F29379D 实现。样机参数见表3。
表3 Buck 变换器样机参数
Tab.3 Circuit parameters of Buck prototype
在实际应用中，变换器输出电容的设计非常重要，它关系到系统的稳定性和抑制高频电压纹波的能力。如图18 所示，计算结果和实验结果都表明，随着电容的增大，稳定边界会逐渐减小。由图13b 和3.3 节的分析可知，这主要是由于低通滤波器引起的相位滞后。如图19 所示，当Cs 为158.8μF和19.8μF 时，延迟时间分别为112μs 和14μs。但当Cs 选择为19.8μF 时，输出电压纹波较大（约0.75V），无法满足设计要求。因此，在保证电压纹波满足设计指标的前提下，应尽可能降低Cs 以提高系统的稳定性。在本实验中，Cs 由多个陶瓷电容器和一个电解电容器并联而成。通过并联多个陶瓷电容器来减小RC 是很重要的，因为过大的RC 是输出电压波纹的主要来源。但陶瓷电容器的电容随着直流偏置电压的增大而减小，因此增加了一个较大的电解电容器以稳定电容。最终，样机输出电容的 测量值为158.8μF。
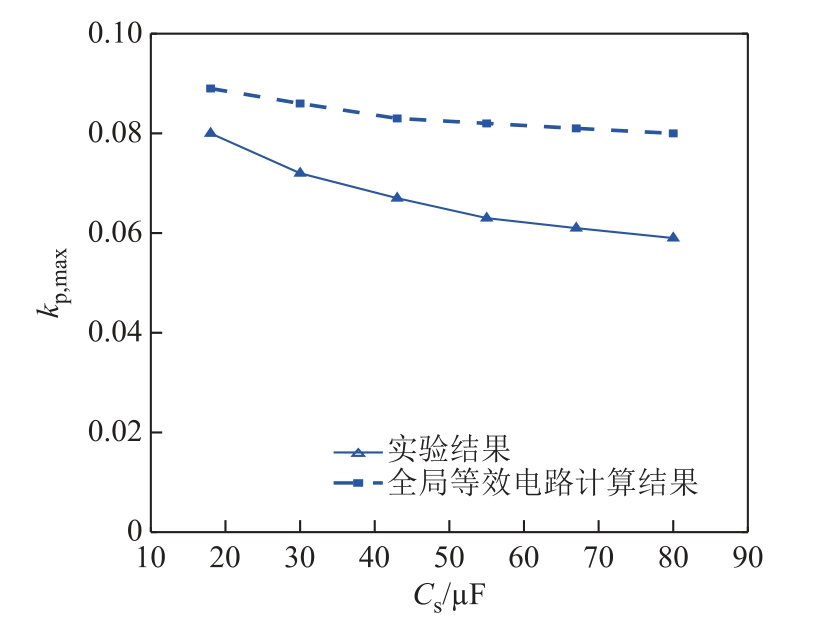
图18 当Cs 变化时，后沿调制下系统稳定边界的实验和计算结果对比
Fig.18 Comparison of system stability boundary when Cs changes
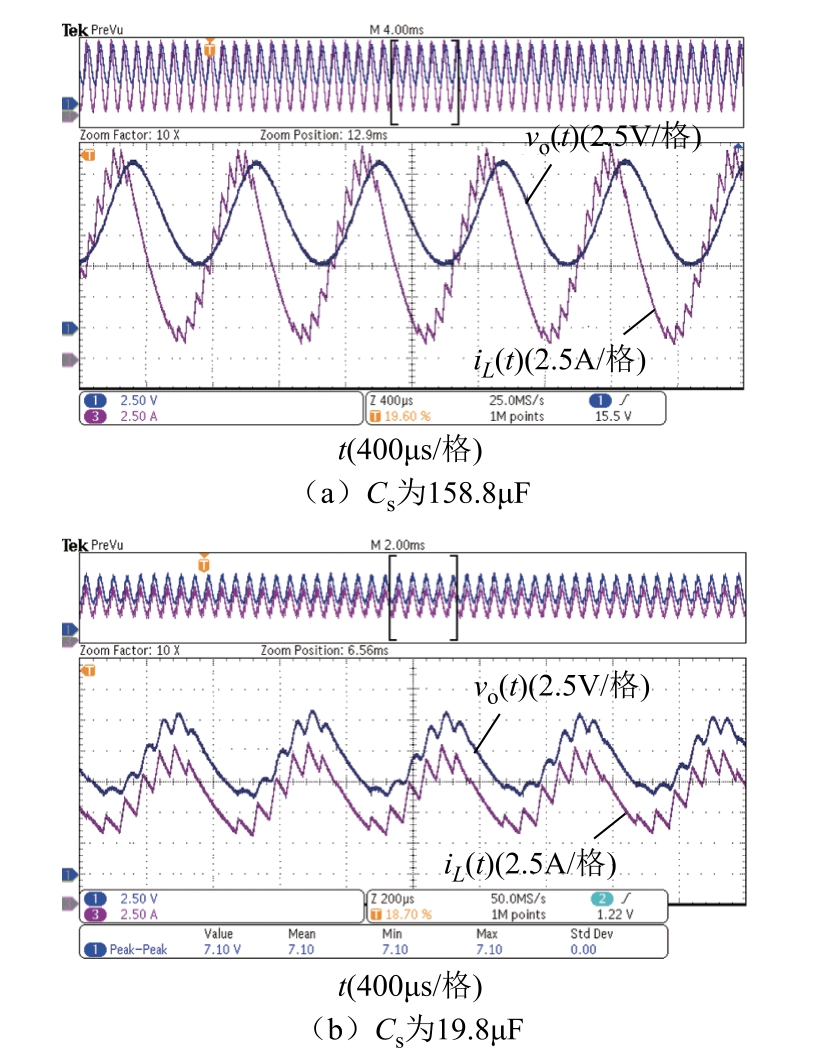
图19 选择不同输出电容Cs 的实验波形对比
Fig.19 Experimental waveform corresponding to different
图20 和图21 分别显示了变换器的调制方式为前沿调制和后沿调制时的实验波形。如图20 所示，前沿调制下的系统工作在kp=0.043 时稳定，当kp 增加到0.049 时出现不稳定振荡现象。图21 显示当kp=0.056 时，系统在后沿调制的稳定状态下运行，当kp增加到0.062 时系统发生振荡。根据理论计算，前沿调制系统和后沿调制系统的理论kp,max 分别为0.053 和0.077。相比之下，由于采样芯片的延迟以及器件和线路寄生参数的影响，kp,max 的实验结果略小于计算结果。
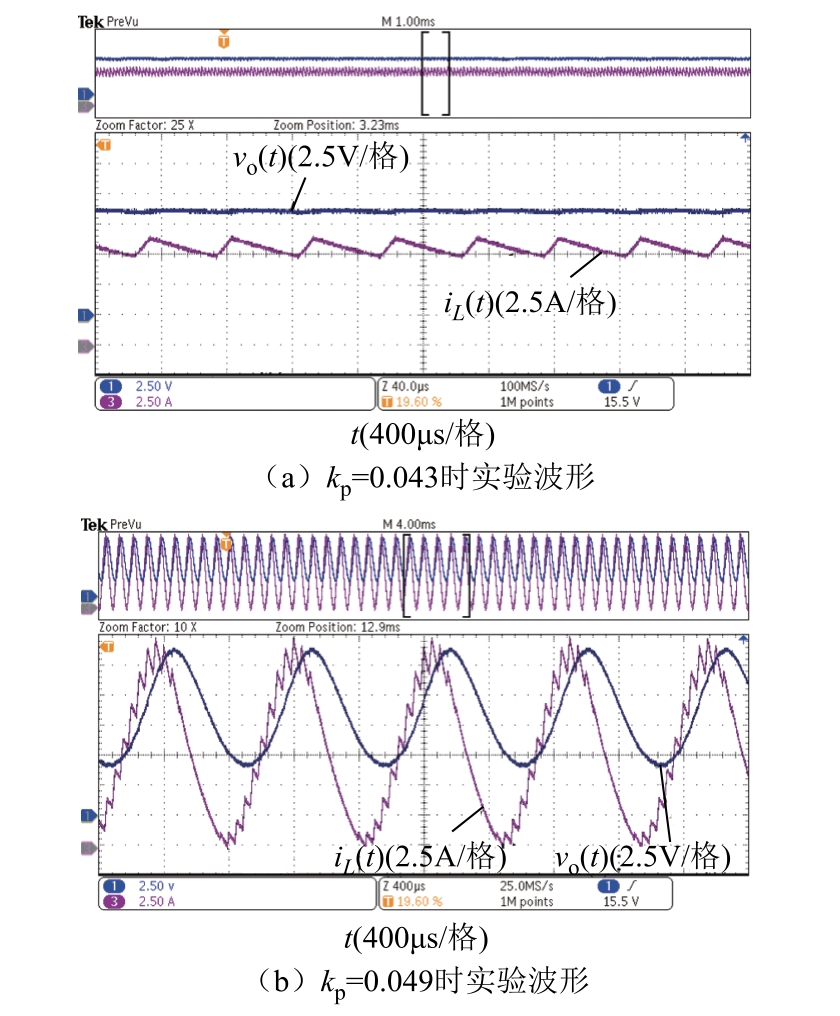
图20 前沿调制时闭环Buck 变换器的实验波形
Fig.20 Experimental waveforms of closed-loop Buck converter at LEM
图21 后沿调制时闭环Buck 变换器的实验波形
Fig.21 Experimental waveforms of closed-loop Buck converter at TEM
为了说明调制方式对系统的影响，当系统工作在两种不同调制方式时，令参考电压从6V 阶跃到12V 时进行实验。参考电压阶跃时Buck 变换器的瞬态响应如图22 所示。图22a 表明当系统工作在前沿调制方式下，参考电压阶跃扰动会使原本振荡的工作波形收敛，使系统回到稳定状态。图22b 说明后沿调制Buck 变换器在受到参考电压阶跃扰动时 会由稳定趋于不稳定状态。与图17 相比，仿真波形和实验波形的趋势和幅值在参考电压阶跃点非常接近。这表明理论分析正确地解释了前沿调制方式和后沿调制方式对系统稳定性不同的影响。
图22 当Vref 从6V 阶跃到12V 时，闭环Buck 变换器实验波形
Fig.22 Experimental waveforms of closed-loop Buck converter when Vref steps from 6V to 12V
输入输出参数值增大时系统稳定边界的比较如图23 所示。随着负载电阻和输入电压的增大，等效电路模型计算和实验得到的kp,max 有相同的减小趋势。为了进一步说明这一结果，用一组实验验证了在两种不同调制方式下，输入电压和负载电阻阶跃时系统稳定性的变化。图24 为输入电压由36V 阶跃到48V 的工作波形，图25 为负载电阻0.8Ω 阶跃到1.2Ω 的工作波形。在这两种工况下，系统由原本的稳定状态趋于不稳定的振荡。该结果与理论计算结果一致。
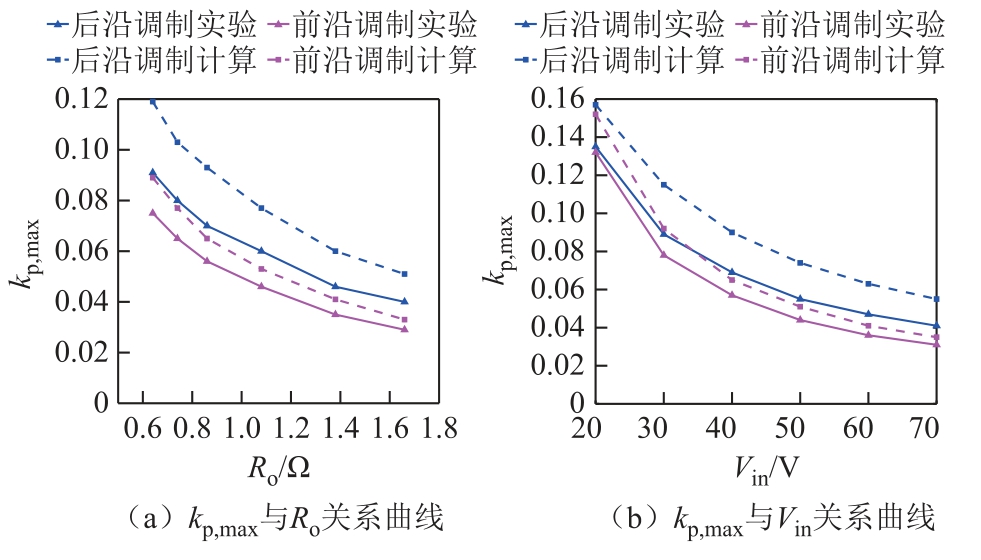
图23 实验和模型计算的系统稳定边界的对比
Fig.23 Comparison of the stability boundaries for different parameters
图24 不同调制方式下，输入电压由36V 阶跃到48V的闭环Buck 变换器实验波形
Fig.24 Experimental waveforms of closed-loop buck converter when the input voltage steps from 36V to 48V
图25 不同调制方式下，负载电阻由0.8Ω 阶跃到1.2Ω的闭环Buck 变换器实验波形
Fig.25 Experimental waveforms of closed-loop buck converter when the load steps from 0.8Ω to 1.2Ω
为了验证等效的开环控制-输出传递函数Geq(z)的精确性，对Buck 变换器样机的幅频响应进行了测试。其参数在表3 中给出。控制-输出传递函数的测量原理如图26 所示。对系统输入一个稳态工作的占空比D，并在其上叠加一个正弦小信号扰动[33]。这样，系统的输出电压vo 可以表示为稳态输出电压Vo与正弦扰动电压之和。此时，变换器的占空比为
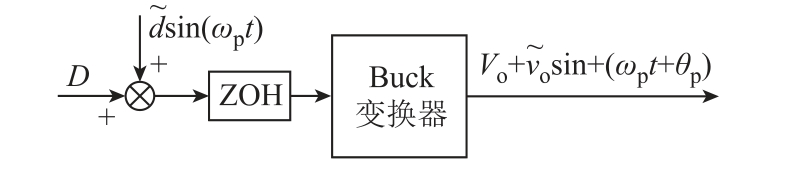
图26 控制-输出频率响应测量方法
Fig.26 Measurement principle of frequency response for control-output transfer function
变换器的输出电压为
式中，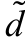
为占空比正弦小信号的幅值；ωp 为占空比正弦小信号的角频率；
为输出电压交流分量的幅值；θp为从控制端到输出端的相位差。实验中d～设为0.02，ωp 的范围为50Hz～5kHz。控制-输出的频率响应可以通过测量相应的
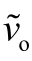和 θp来获得。如图27所示，对于不同的调制方式，在ωp=1kHz 时测量控制-输出频率响应波形。
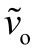可以通过测量输出电流
的交流分量的幅值乘以负载电阻来获得。在图26 中，通过用绿色脉冲标记占空比扰动的过零点，即ωpt=2kπ 时刻，并测量该时刻与相应的输出电流波形 的交流分量过零点之间的时间差，可以得到控制到输出的相位差 θp。输出电流交流分量的幅值是电流波形的峰值减去电流纹波。
图27 扰动频率为1kHz 时控制-输出频率响应波形
Fig.27 Control-output frequency response of Buck converter when the small-signal perturbation frequency is 1kHz
在实验过程中，Buck 变换器稳定运行的占空比选择为D=0.25。系统的控制-输出频率响应的实验测量结果和Geq(z)的预测结果如图28 所示。对比表明，对于两种不同的调制方式，理论结果与实验结果的幅值和相位特性均具有较好的一致性。上述对比分析也验证了模型的正确性。
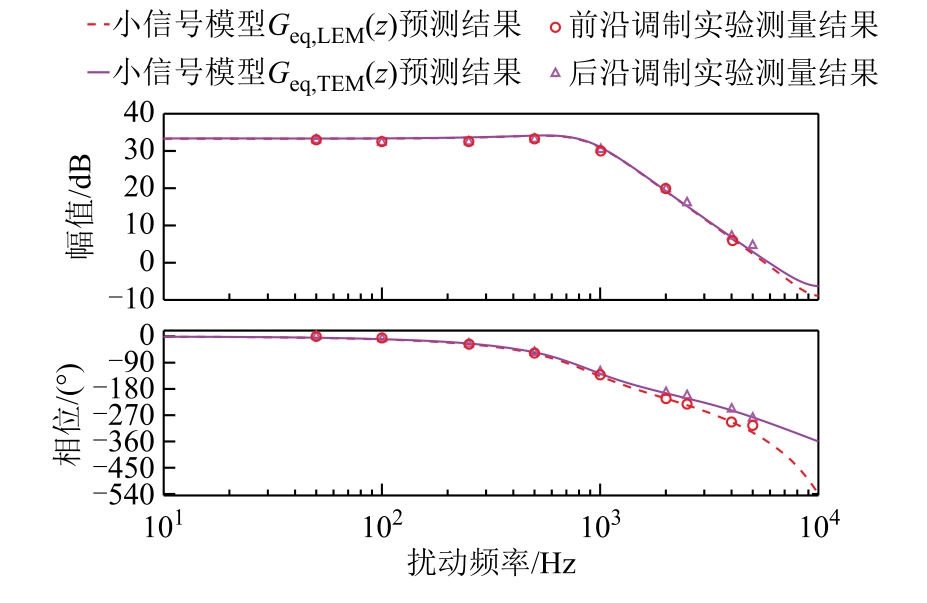
图28 Buck 变换器控制-输出频率特性对比
Fig.28 Control-output frequency characteristic comparison of Buck converter
5 结论
本文对数字控制DC-DC 变换器的离散迭代模型进行改进，分别建立了用于描述前沿调制和后沿调制方式下DC-DC 变换器的二阶全局等效电路。由于全局等效电路能够准确地保留状态变量的采样点信息，所以即使在不稳定的工作点等效电路也可以准确预测详细开关电路的工作波形。在此基础上，以Buck 变换器为例，分析了数字控制的延迟特性，推导出了基于数字控制特性的控制-输出的z 域传递函数，并和实验测量出的幅频特性进行对比，验证了模型的精确性。根据闭环传递函数特征方程的根，分析控制器增益、输入电压、负载、储能元件、寄生参数等对DC-DC 变换器稳定性的影响。同时，详细解释了不同调制方式对系统稳定性的影响。最后通过电路的PLECS 仿真和实验平台验证了理论结果的正确性和有效性。
[1]Sable D M,Cho B H,Ridley R B.Use of leading-edge modulation to transform boost and flyback converters into minimum-phase-zero systems[J].IEEE Transactions on Power Electronics,1991,6(4): 704-711.
[2]Ren Xiaoyong,Ruan Xinbo,Qian Hai,et al.Threemode dual frequency two-edge modulation scheme for four-switch buck-boost converter[J].IEEE Transactions on Power Electronics,2009,24(2): 499-509.
[3]章伟,周国华,刘啸天,等.具有快速负载瞬态响应的开关变换器数字均值电压控制方法[J].电工技术学报,2018,33(4): 856-864.Zhang Wei,Zhou Guohua,Liu Xiaotian,et al.Digital average voltage control technique for switching converter with fast load transient response[J].Transactions of China Electrotechnical Society,2018,33(4): 856-864.
[4]Buso S,Mattavelli P.Digital control in power electronics[M].US: Morgan &Claypool,2006.
[5]张森,赵剑锋,刘康礼,等.数字控制延时对电流环解耦有效性的影响[J].电工技术学报,2020,35(增刊2): 484-493.Zhang Sen,Zhao Jianfeng,Liu Kangli,et al.Research on the impacts of digital control delay on the effectiveness of current loop decoupling[J].Transactions of China Electrotechnical Society,2020,35(S2): 484-493.
[6]Peterchev A V,Sanders S R.Quantization resolution and limit cycling in digitally controlled PWM converters[J].IEEE Transactions on Power Electronics,2003,18(1): 301-308.
[7]Zou Jianlong,Ma Xikui,Du Changqing.Asymmetrical oscillations in digitally controlled power-factor-correction boost converters[J].IEEE Transactions on Circuits and Systems II: Express Briefs,2009,56(3): 230-234.
[8]Wang Jianguo,Yan Jiudun,Jiang Lin,et al.Delaydependent stability of single-loop controlled gridconnected inverters with LCL filters[J].IEEE Transactions on Power Electronics,2016,31(1): 743-757.
[9]Middlebrook R D,Cuk S.A general unified approach to modelling switching-converter power stages[C]//1976 IEEE Power Electronics Specialists Conference,Cleveland,OH,USA,1976: 18-34.
[10]Wester G W,Middlebrook R D.Low-frequency characterization of switched dc-dc converters[J].IEEE Transactions on Aerospace and Electronic Systems,1973,AES-9 (3): 376-385.
[11]Ayachit A,Kazimierczuk M K.Averaged small-signal model of PWM DC-DC converters in CCM including switching power loss[J].IEEE Transactions on Circuits and Systems II: Express Briefs,2019,66(2): 262-266.
[12]Corradini L,Maksimović D,Mattavelli P,et al.Digital control of high-frequency switched-mode power converters[M].Hoboken: John Wiley &Sons,Inc,2015.
[13]Van de Sype D M,De Gusseme K,Van den Bossche A R,et al.Small-signal z-domain analysis of digitally controlled converters[C]//2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat.No.04CH37551),Aachen,Germany,2004: 4299-4305.
[14]Shortt D J,Lee F C.Improved switching converter model using discrete and averaging techniques[J].IEEE Transactions on Aerospace and Electronic Systems,1983,AES-19(2): 190-202.
[15]皇金锋,李林鸿,谢锋,等.含有右半平面零点的开关DC-DC 变换器暂态性能分析及频域法设计[J].电工技术学报,2020,35(10): 2170-2180.Huang Jinfeng,Li Linhong,Xie Feng,et al.Transient performance analysis and frequency domain design of switched DC-DC converters with right half plane zero[J].Transactions of China Electrotechnical Society,2020,35(10): 2170-2180.
[16]高国庆,雷万钧,袁晓杰,等.双有源全桥变换器全状态离散迭代建模与输出电压纹波分析[J].电工技术学报,2021,36(2): 330-340.Gao Guoqing,Lei Wanjun,Yuan Xiaojie,et al.Fullstate discrete-time model and the output-voltageripple analysis of the dual active bridge converter[J].Transactions of China Electrotechnical Society,2021,36(2): 330-340.
[17]Verghese G C,Elbuluk M E,Kassakian J G.A general approach to sampled-data modeling for power electronic circuits[J].IEEE Transactions on Power Electronics,1986,PE-1(2): 76-89.
[18]Fang C-C,Abed E H.Sampled-data modeling and analysis of closed-loop PWM DC-DC converters[C]//1999 IEEE International Symposium on Circuits and Systems (ISCAS),Orlando,FL,USA,1999: 110-115.
[19]Packard D J.Discrete modeling and analysis of switching regulators[D].Pasadena: California Institute of Technology,1976.
[20]Yousefzadeh V,Shirazi M,Maksimovic D.Minimum phase response in digitally controlled boost and flyback converters[C]//APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition,Anaheim,CA,USA,2007: 865-870.
[21]Wang Yao,Xu Jianping,Xu Duo.Effect of circuit parameters on the stability and boundaries of peak current mode single-inductor dual-output Buck converters[J].IEEE Transactions on Industrial Electronics,2018,65(7): 5445-5455.
[22]Iu H H C,Tse C K.Bifurcation behavior in parallelconnected Buck converters[J].IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,2001,48(2): 233-240.
[23]张波,曲颖.Buck DC/DC 变换器分岔和混沌的精确离散模型及实验研究[J].中国电机工程学报,2003,23(12): 99-103.Zhang Bo,Qu Ying.Study on the experiment and the precise discrete model of bifurcation and chaos for Buck DC/DC converter [J].Proceedings of the CSEE,2003,23(12): 99-103.
[24]张笑天,马西奎,张浩.数字控制DC-DC Buck 变换器中低频振荡现象分析[J].物理学报,2008,57(10): 6174-6181.Zhang Xiaotian,Ma Xikui,Zhang Hao.Lowfrequency oscillation in digitally controlled DC-DC Buck converters[J].Acta Physica Sinica,2008,57(10): 6174-6181.
[25]Zhou Guohua,Mao Shiqin,Wang Yue,et al.Discretetime modeling and symmetrical dynamics of V²-controlled Buck converters with trailing-edge and leading-edge modulations[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2020,8(4): 3995-4008.
[26]Li Xin,Ruan Xinbo,Jin Qian,et al.Approximate discrete-time modeling of DC-DC converters with consideration of the effects of pulse width modulation[J].IEEE Transactions on Power Electronics,2018,33(8): 7071-7082.
[27]Tong Anping,Hang Lijun,Chung H S H,et al.Using sampled-data modeling method to derive equivalent circuit and linearized control method for dual-activebridge converter[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2021,9(2): 1361-1374.
[28]胡寿松.自动控制原理[M].北京: 科学出版社,2013.
[29]Shi Ling,Lei Wanjun,Li Zhuoqiang,et al.Bilinear discrete-time modeling and stability analysis of the digitally controlled dual active bridge converter[J].IEEE Transactions on Power Electronics,2017,32(11): 8787-8799.
[30]Maksimovic D,Zane R.Small-signal discrete-time modeling of digitally controlled PWM converters[J].IEEE Transactions on Power Electronics,2007,22(6): 2552-2556.
[31]Rajasekaran V,Sun Jian,Heck B S.Bilinear discretetime modeling for enhanced stability prediction and digital control design[J].IEEE Transactions on Power Electronics,2003,18(1): 381-389.
[32]Ilic M,Laeb S,Liebezeit K.Exact nonlinear analysis of switched mode power converters[C]//19th Annual IEEE Power Electronics Specialists Conference,Kyoto,Japan,1988: 977-986.
[33]Zhang Kai,Shan Zhenyu,Jatskevich J.Large-and small-signal average-value modeling of dual-activebridge DC-DC converter considering power losses[J].IEEE Transactions on Power Electronics,2017,32(3): 1964-1974.