0 引言
在国家“碳达峰、碳中和”战略目标与以新能源为主体的新型电力系统建设背景下,配电网侧面临海量分散分布的分布式可再生能源并网接入,给配电网的运行管理带来巨大的挑战[1-3]。对规模化灵活资源进行有效聚合,可从根本上解决电力系统灵活性调节能力不足的问题。但当前规模化灵活资源互动调控面临着诸多技术难题,导致大规模分布式灵活资源潜力未被充分挖掘利用。
虚拟电厂(Virtual Power Plant,VPP)作为一种聚合分布式可再生能源并实现内部资源精准管控的有效管理形式而得到广泛应用[4-7]。近年来,国内外学者针对单个VPP 在配置、计划、运行、分配四个层面的优化,开展了诸多研究。在日前计划和日内运行阶段,形成了“日前-滚动-实时”的多时间尺度优化调控架构及策略方法[8-11]。随着“双碳”“整县光伏”“新型电力系统”目标的进一步推进,多个VPP(Multiple VPPs,MVPP)共存于某一区域配电网中将是重要发展方向。VPP 间的电量资源具有时空互补特性,因此对同一个区域配电网内的MVPP 开展计及VPP 间功率互济的协同优化来实现VPP 间的利益平衡与优化,将较各VPP 独立参与电力市场获取更优的经济效益。
目前,一些文献对MVPP 协同优化调控进行了探索性研究,文献[12]以MVPP 集群运行为目标,通过独立定价以激励各VPP 参与集群优化,建立了包含日前和日内滚动在内的两阶段联合优化模型,结果表明集群联合优化可有效改善VPP 集群系统电能均衡问题,提升整体经济性。文献[13]建立了包含VPP 间双边合同签订机制在内的MVPP 日前优化模型,考虑到优化求解过程是一个典型的非凸非线性复杂问题,采用了二阶锥松弛技术对非线性部分进行替代,研究结果表明MVPP 优化模式可减小间歇性电源出力对电网造成的影响,提升整体收益。文献[14]提出了高渗透率下MVPP 日内两阶段优化调度模型,通过利润函数的风险刻画对优化过程中的不确定性进行建模,结果表明联合运行可降低决策风险。文献[15]提出基于需求响应和博弈论的MVPP 调度模式及竞价策略,各VPP 内部基于分时电价及需求响应与能源用户交互,并参与MVPP 间博弈。文献[16]建立了一主多从的优化模型,MVPP运营商从配电网层面构造 MVPP 各时段优化的上层模型,各VPP 构建内部的优化模型。
上述优化研究均为集中建模、统一求解的优化思想,未突出与MVPP 结构相匹配的多层级思想,且面向更多VPP 聚合与海量异构信息场景,采用集中建模、统一求解方法无疑增加了求解的难度。针对上述问题,文献[17]提出一种含MVPP 的主动配电网双层优化运行方法,上层以配电网运行安全及经济性为目标,下层以各VPP 利益最大化为目标,结果表明双层优化模型可有效地提高系统安全性和经济效益。文献[18]基于多代理架构,将MVPP 优化问题转换为一个双层协调优化模型,上层同样为VPP 之间的优化,而下层为VPP 内部优化问题。分层建模、单独求解的思想不仅与MVPP 调控架构相匹配,还可有效减少计算量。但上层优化与下层优化进行交互时,需将所有VPP 竞价信息进行群发,不利于各VPP 主体的隐私保护,其本质上仍为一种集中优化的思路。因此,如何在保证各VPP 隐私性的基础上,各VPP 仅能基于自身运行信息来实现多VPP 分布式协同与整体优化,是MVPP 优化的重要研究方向。
针对上述分析,本文提出一种基于“信息分离、决策协同”的MVPP 分布式优化调度方法。本文主要工作如下:①提出了MVPP 分布式协调优化互动机制;②以MVPP 协调优化调度成本最低作为目标函数,构建MVPP 多时段协调优化调度模型,并构建基于供需关系的VPP 间电量交易电价函数以提高VPP 参与内部直接交易的积极性;③基于拉格朗日对偶松弛方法对原优化问题进行解耦,形成多个VPP 优化调度子问题;④基于分布式部分可观测马尔科夫决策过程(Decentralized-Partially Observable Markov Decision Process,DEC-POMDP)构建实时优化调度模型,以最大化累积回馈值为优化目标从而考虑多时段的协同优化,并采用基于Bloch 坐标的量子遗传算法对优化问题进行求解以提高计算效率。最后,以一个包含三个VPP 的MVPP系统进行仿真分析,对本文所提方法的有效性进行验证。
1 MVPP 互动机制
本文研究的MVPP 互动机制如图1 所示。VPP运营商对内聚合可参与调节的灵活资源,对外参与VPP 间直接电量交易及电力市场电量交易,满足VPP 内部功率平衡需求及利益优化需求。各 VPP接收上级运营商下发的电价及购售电需求,对内部策略进行调整,并向上级运营商反馈竞价信息。本文所提VPP 由风电(Wind Turbine,WT)、微型燃气轮机(Micro Turbine,MT)、储能(Energy Storage System,ESS)及可控负荷(Controllable Load,CL)构成。
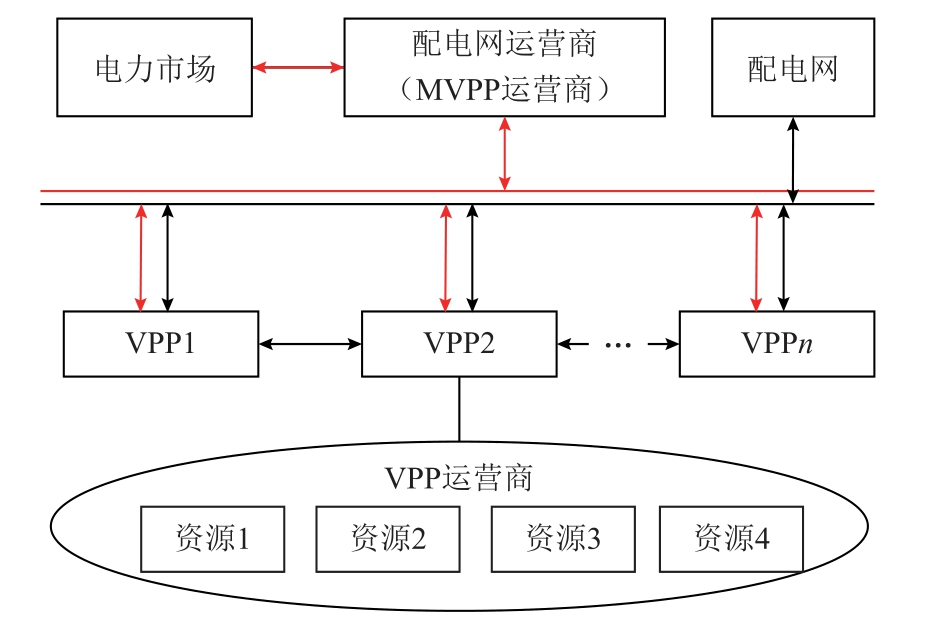
图1 MVPP 互动机制
Fig.1 MVPP interaction mechanism
配电网运营商或MVPP 运营商对VPP 进行统一管理,对下汇总各VPP 的购售电意愿并进行电价信息决策计算,将电价及其他VPP 竞价信息反馈给各VPP,各VPP 基于上述信息进行分散自主管理与协调控制;对上根据MVPP 内部功率平衡情况与电力市场进行交易,并对MVPP 最优决策进行判断,实现MVPP 整体利益最优。
2 MVPP 多时段协调优化调度模型
2.1 优化目标
对于单个VPP,其成本组成为向电网购售电收益、向其他VPP 购售电收益、切负荷补偿成本以及各类设备的运行维护成本[19]。T 时域内VPP 的成本函数为
式中,Cgrid,t、Cvpp,t、Ccl,t、Com,t 分别为向电网购售电收益、向其他VPP 购售电收益、切负荷补偿成本及设备运行成本。其具体表达式分别为

式中,kgrid,s,t、kgrid,b,t 分别为t 时刻VPP 向电网售、购电单价;kvpp,t 为t 时刻VPP 间售、购电单价;kcl为CL 单位补偿成本;kmt、kess、kwt 分别为MT、ESS、WT 单位运行成本;Pgrid,s,t、Pgrid,b,t 分别为t 时刻VPP向电网售电功率、向电网购电功率;Pvpp,s,t、Pvpp,b,t分别为向其他VPP 售电功率、购电功率;Pcl,i,t 为负荷中断功率;Pmt,i,t 为MT 发电功率;Pess,i,t 为ESS充放电功率;Pwt,i,t 为WT 发电功率;Mcl、Mmt、Mess、Mwt 分别为VPP 内CL、MT、ESS、WT 的数量。对于由N 个VPP 构成的MVPP,其协调优化目标为各VPP 运行成本之和最小,即

将式(1)代入式(3),且由于VPP 向其他VPP的售电收益等于其他VPP 向此VPP 的购电成本,故VPP 间电量交易费用可互相抵消,因此MVPP 协调优化目标函数改写为
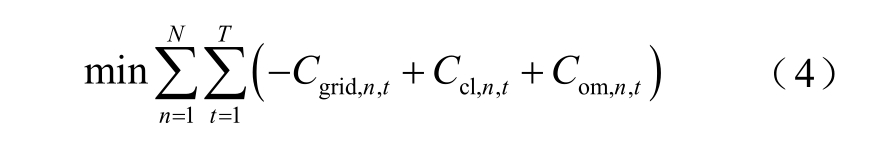
2.2 VPP 间交易电价函数
VPP 间是否有意愿直接交易取决于电价,只有在直接交易电价与电力市场定价相比具有一定优势时,才能保证VPP 间参与调度的积极性。当VPP内部交易完成后仍有电量缺额或余量时,再参与外部电力市场交易。因此,将VPP 间交易电价函数定义为
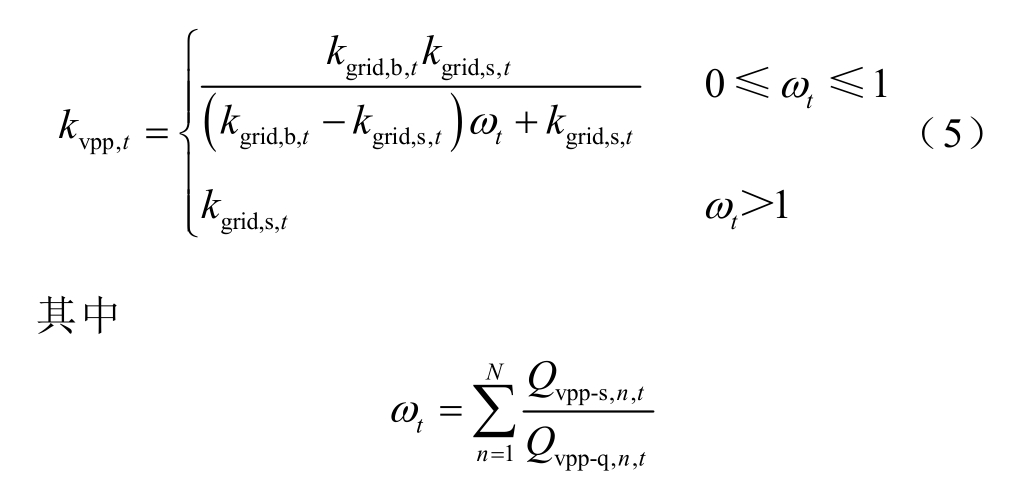
式中,Qvpp-s,n,t 与Qvpp-q,n,t 分别为VPP 的剩余电量与缺额电量。VPP 间交易电价随着供需关系变化,供需比越高则交易电价越低。VPP 剩余电量均为0 时,VPP 间交易电价与VPP 向电网购电电价一致;当剩余电量大于缺额电量时,VPP 间交易电价与VPP 向电网售电电价一致。为便于计算,本文中以WT 发电量与负荷期望用电量差值进行剩余电量与缺额电量计算。
2.3 约束条件
1)VPP 内部潮流约束
为保证电网运行的安全稳定性,对于单个VPP,其内部需满足潮流约束。本文采用线性化潮流方程[20]表示。
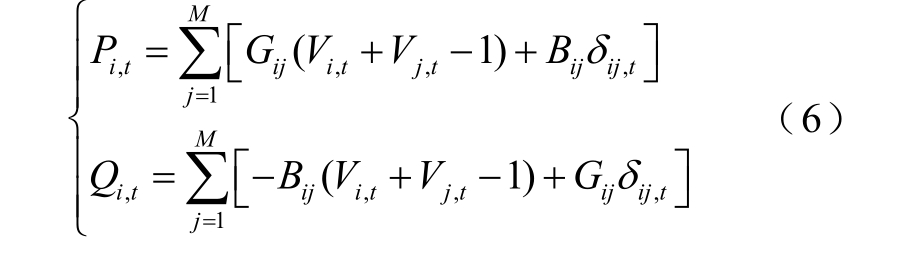
式中,M 为VPP 内节点数;Pi,t、Qi,t 分别为t 时刻节点i 注入的有功功率与无功功率;Vi,t、Vj,t 分别为节点i 与节点j 的电压;Gij、Bij 分别为节点i 与节点j 之间的电导与电纳;δij,t 为t 时刻节点i 与节点j 的相位差。
2)VPP 内部节点功率平衡约束
对于VPP 根节点o,功率平衡约束为

式中,Pload,i,t、Pess-ch,i,t、Pess-disch,i,t 分别为CL 期望用电功率、ESS 充电及放电功率;Qmt,t、Qcl,t、Qload,t 分别为MT 无功功率、负荷中断无功功率及负荷期望无功功率。
3)VPP 内部安全运行约束

4)VPP 交易约束
为避免VPP 在同一调度时段内出现低价买入、高价卖出的套利行为,设置VPP 交易约束,避免VPP 在同一时段出现双向电能交互。

式中,![]() 分别为VPP 与电网及其他VPP 最大交互功率;Ds,t、Db,t 为0-1 变量,表征VPP 售电或购电状态,1 为参与交易,0 为不参与交易。
分别为VPP 与电网及其他VPP 最大交互功率;Ds,t、Db,t 为0-1 变量,表征VPP 售电或购电状态,1 为参与交易,0 为不参与交易。
5)VPP 间交易电量平衡约束
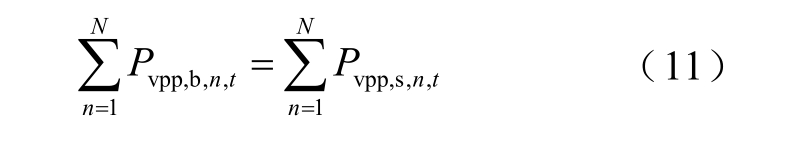
6)其他运行约束

3 基于拉格朗日松弛的MVPP 优化调度DEC-POMDP 求解
3.1 基于拉格朗日对偶松弛的MVPP 优化调度问题分解协调
第2 节所构建的MVPP 优化调度模型为集中式优化模型,求解该模型需要建立在大量信息交互的基础上。但实际上由于各VPP 分属不同利益主体,出于隐私性及安全性考虑难以实现信息完全交互。因此本文基于拉格朗日对偶松弛原理对原优化问题进行分解协调,将其转换为拉格朗日对偶优化的主子问题,降低求解难度。
首先将原MVPP 协调优化问题分解为一系列VPP 独立优化问题,则VPPn 的优化问题可改写为

其中,约束式(11)是VPP 优化子问题与外界耦合关系的体现,破坏了原问题的可分解性。因此基于拉格朗日对偶松弛理论,将式(11)松弛到目标函数中,构成拉格朗日函数。首先对式(11)进行改写,将VPPn 向其他VPP 的购售电功率移至等式左侧,将与VPPn 无关的参量移至等式右侧,并引入X、Y 两个连续变量,有

由式(10)可知,VPPn 在同一时刻仅存在一种交易行为。当 VPPn 为购电方时,Pvpp,b,n,t≥0,Pvpp,s,n,t=0,即Xn,t≥0 时,引入该约束,并将式(14)松弛到优化目标中,将VPPn 的优化目标函数改写成拉格朗日函数,有
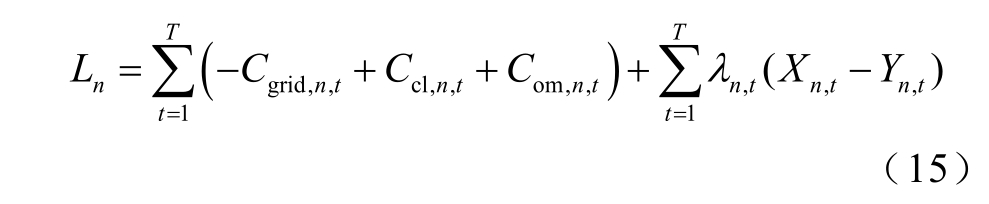
式中,λn,t 为拉格朗日乘子。
基于拉格朗日对偶松弛法分解协调后,VPP 优化调度子问题可表示为

外层优化问题可表示为
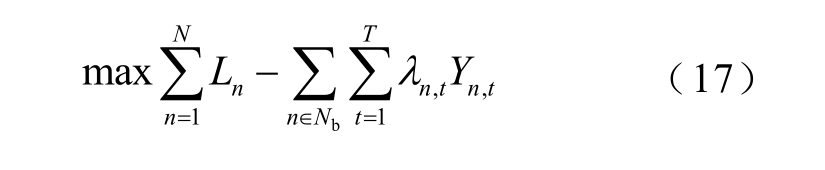
式中,Nb 为购电VPP 集合。
当VPPn 为售电方时,Xn,t<0 时,则优化问题将分解为
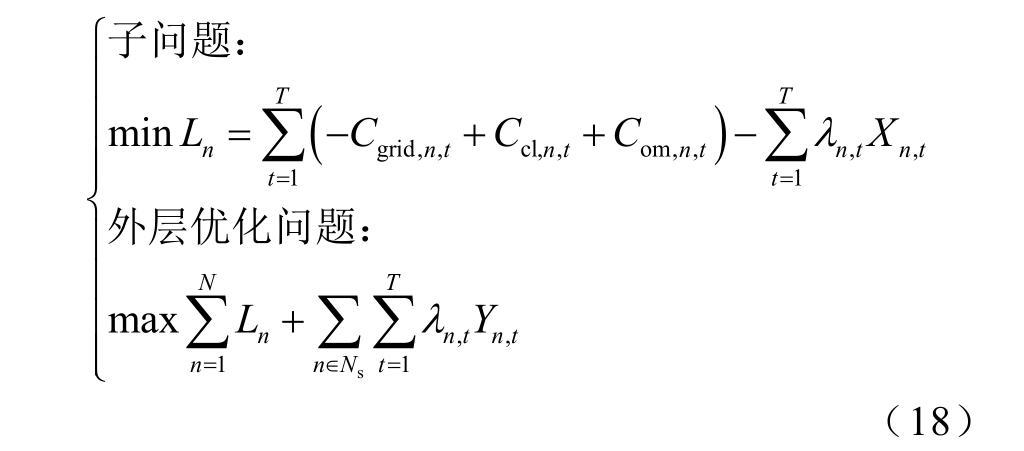
式中,Ns 为售电VPP 集合。
最终,经拉格朗日对偶松弛后,原优化问题转换为两个问题。
子问题:
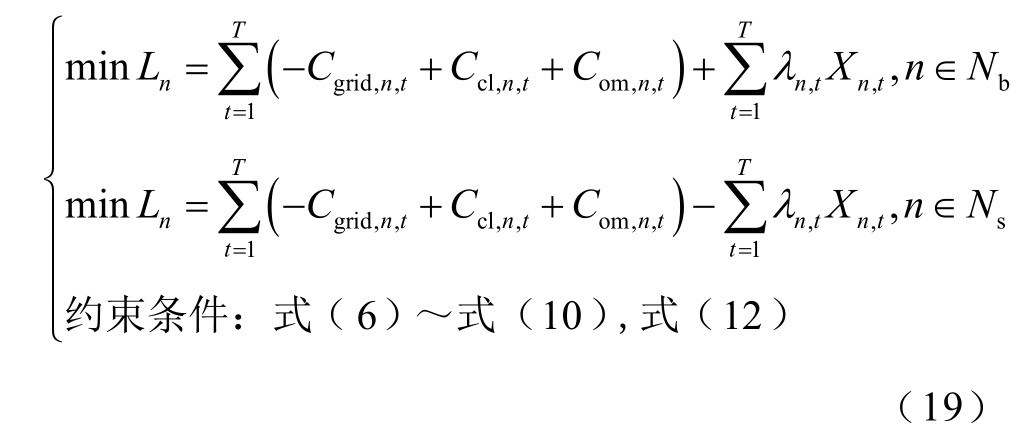
外层优化问题:
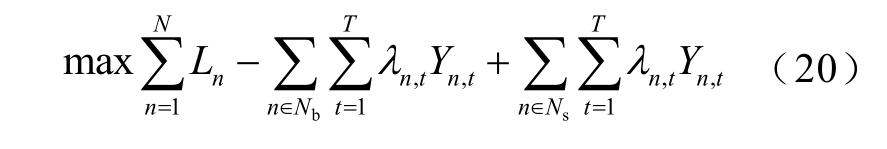
外层优化问题与VPP 优化调度子问题交替迭代,并通过更新拉格朗日乘子实现协同寻优。在协同寻优的过程中,首先对拉格朗日乘子赋任意非负初值,本文设定初值为0。外层优化将拉格朗日乘子传递给各VPP 优化调度子问题,各VPP 基于式(19)开展并行优化计算,并将优化计算结果传递给外层优化问题,采用次梯度法[21]对拉格朗日乘子进行更新,重复迭代直至收敛。本文采用判断对偶间隙的方法来判断是否收敛[21]。
3.2 基于DEC-POMDP 的MVPP 优化调度问题求解
基于拉格朗日对偶松弛,VPP 间无需交换各自的优化调度信息,各VPP 只需要知晓拉格朗日乘子的状态,即可实现最优决策。原优化问题形成了“信息分离、决策协同”的分布式优化机制,各VPP 基于拉格朗日乘子独立自主进行优化,进而实现最小化全局运行成本的目标。经上述转换后,若以各VPP运营商分别作为决策主体,MVPP 系统为环境,那么该优化问题是典型的分布式部分可观测马尔科夫决策(DEC-POMDP)问题。DEC-POMDP 是单智能体的POMDP 在多智能体协作问题上的拓展,实现分布式条件下状态非完全可观察情况下的多智能体优化决策[22]。
基于传统建模方法求解MVPP 协调优化调度问题,其求解精度往往依赖求解时段划分的精细程度与预测信息的精准程度,而采用DEC-POMDP 决策过程进行建模,则可基于实测值直接在每个调度指令下发周期内进行决策,与系统实际运行情况更加匹配的同时也大大提高了调度指令的准确性。因此,本文采用DEC-POMDP 描述MVPP 多时段协调优换调度模型,并将其转换为实时调度问题。MVPP 协调优化调度DEC-POMDP 模型主要由状态集合、行动集合、状态转移函数、观察集合、观察函数、回馈函数等部分组成,即
式中,N 为MVPP 系统中有限智能体集合;n 为各VPP 的编号,n=1,2,…,N;S 表示MVPP 系统的有限状态集合,在本文中为各VPP 内ESS 的荷电状态、WT 发电功率、负荷期望用电功率及电网电价,即S={{SOCn,t},{Pwt,n,t},{Pload,n,t},kgrid,s,t,kgrid,b,t};{An}为MVPP 的联合行动集合,An 为第n 个VPP 的有限行动集合,在本文中具体为与电网交互功率、与其他VPP 交互功率、MT 发电功率、ESS 充放电功率及 CL 的削减功率优化结果,即 An={Pgrid,n,t,Pvpp,n,t,Pmt,n,t,Pess,n,t,Pcl,n,t};T 为状态转移函数,T(s,a,s′)表示MVPP 系统由状态s 采取行动a 到状态s′的转移概率分布;{Ωn}为MVPP 系统的有限观测集合,Ωn 表征当前状态下第n 个VPP 所观测到的量,即拉格朗日乘子;O 为观察函数,(s,a,s′,o)表征MVPP 系统在状态s 采取行动a 后转移到状态s′后各VPP 联合观测到的状态o 的概率分布;R 为回馈函数,本文中具体为t 时段MVPP 协调优化的运行成本,具体表达式可参考式(20)中的外层优化目标函数。
DEC-POMDP 建模是为了获取一系列最优决策,最小化整个优化时域内MVPP 的运行成本。因此,本文引入值函数,采用累积回馈值对所选取的策略优劣进行评价,策略集π 下的值函数Vπ 实际上就是MVPP 每个时间段运行成本的总和,如式(20)所示。将其写成递归形式,有
式中,R(s,π(s))为状态s、策略π(s)下的回馈值;Vπ(s′)为状态s 转移到s′的回馈值;Tπ(s)(s,s′)为状态s 经过策略π(s)转移到状态s′的概率分布函数。通过引入值函数,本文将当前决策对未来时段的影响纳入考量。针对存在多时段耦合的变量,即ESS 荷电状态与 MT 发电功率,本文采用近似动态规划(Approximate Dynamic Programming,ADP)对值函数进行近似,获取全局最优解[23]。
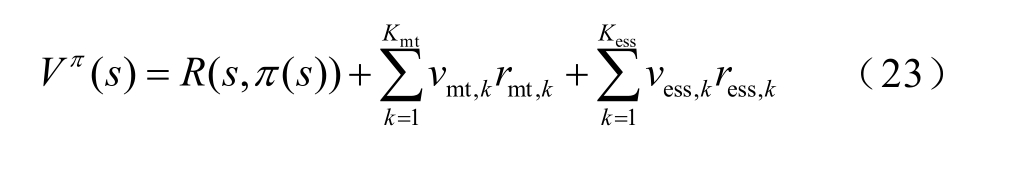
式中,K 为分段线性函数的分段数;v 为第k 个分段对应的斜率;r 为分段k 对应的横轴长度。
基于DEC-POMDP 的MVPP 协调优化 流程将MVPP 协调优化过程看作一个DEC-POMDP,在该过程的每一步,每个VPP 通过回馈方程得到回馈值并从本地观测到的整个VPP 系统运行状态,然后各VPP 控制器同时选择一个策略作为当前状态到行动的映射,经行动指令,各VPP 转换到新的状态1、2、3,组成MVPP 系统新的运行状态。整个过程最终是寻找最优策略序列使得值函数在一个优化时域内达到最优,但各VPP 每次策略的选择仅能根据由本地观测到的系统运行状态与值函数进行决策。
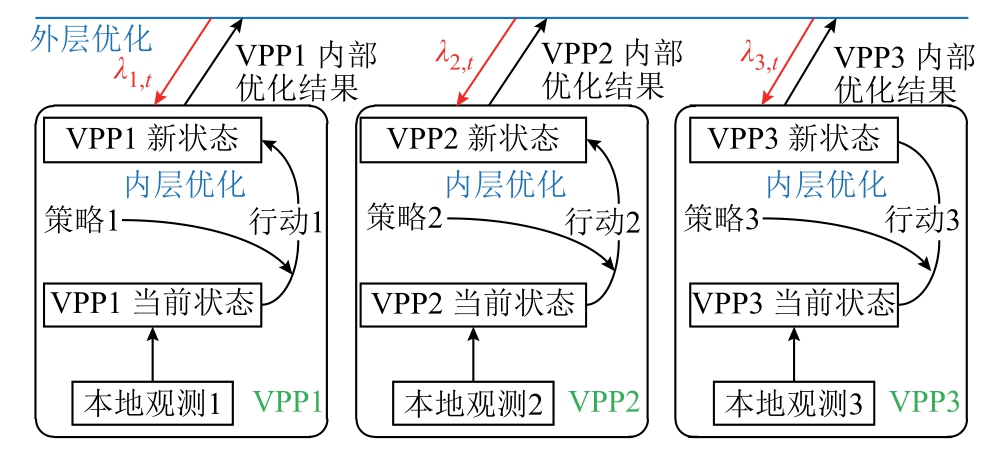
图2 基于DEC-POMDP 的MVPP 协调优化流程
Fig.2 MVPP optimal scheduling based on DEC-POMDP
3.3 基于改进量子遗传算法的DEC-POMDP 优化问题求解
3.2 节中建立的基于DEC-POMDP 的MVPP 协调优化问题中,各VPP 优化子问题相互独立,各VPP 自主决策的过程可认为是一个独立的马尔科夫决策过程(Markov Decision Process,MDP),可并行计算以提高优化效率。本文采用一种基于Bloch 球面进行量子编码的遗传算法[24-25]对VPP 优化调度子问题进行求解。首先,以VPP 优化调度子问题的可行解构成一个大小为M 的种群。种群中的个体即为VPP 优化调度子问题的一组可行解H=[h1 h2 … h5],个体中的变量即量子位h1~h5 分别对应Pgrid,t,Pvpp,t,Pmt,n,t,Pess,n,t,Pcl,n,t。
对量子位进行归一化处理并以Bloch 球面坐标进行编码,引入量子位角度参量θi、φi,编码方案为

至此,每个量子位由三个值对应,个体中的每一行都代表搜索空间中的一个优化解,有效地扩展了对搜索空间的遍历性,加速了优化进程。通过量子旋转门与量子非门对种群进行更新,以实现全局最优搜索。基于bloch 坐标的量子遗传算法基本流程如下:
1)初始化种群,并随机产生角度参量,反归一化处理各个体,得到个体及个体中的变量。
2)对个体开展适应度评估,记录适应度及对应的角度参量。
3)利用量子旋转门与量子非门更新种群。
4)记录最优个体适应度及对应的角度参量,并判断是否已达到最大迭代代数,若是,则停止运算并输出优化结果;否则,返回步骤3)。
3.4 计算流程
计算流程如图 3 所示。首先获取当前时刻MVPP 初始运行状态,并设置拉格朗日乘子初值λn,t=0。由MVPP 能量管理系统将拉格朗日乘子作为观测量发布给各VPP,各VPP 能量管理系统根据拉格朗日乘子及内部运行数据自主优化决策。各VPP能量管理系统将优化结果上传给MVPP,由MVPP能量管理系统对外层优化结果进行更新。判断是否满足收敛条件,若不满足,则更新拉格朗日乘子,重复迭代直至收敛;若满足,则各VPP 能量管理系统下发优化指令。

图3 计算流程
Fig.3 Calculation process
4 算例计算分析
4.1 算例设置
以某地区电网实际网架为基础,搭建由 3 个VPP 构成的MVPP 系统,各VPP 中WT 容量分别为500 kW、500 kW、300 kW,MT 容量均为200 kW,ESS 的容量均为100 kW/400 kW·h,CL 的最大有功功率分别为300 kW、500 kW、500 kW,并均匀分布于各节点,网架结构如图4 所示。其中,MT 最大向上、向下爬坡功率为100 kW/h;CL 的最大可削减负荷功率为当前时段期望用电负荷的10%,最大连续调节时长为6 h;ESS 充放电效率为0.9,初始荷电状态200 kW·h,荷电状态波动范围为最大容量的10%~90%。MT、CL、ESS 单位调节成本分别为0.65 元/(kW·h)、0.2 元/(kW·h)、0.1 元/(kW·h)。VPP 向电力市场购售电电价见表1。

图4 MVPP 算例结构
Fig.4 MVPP structure
表1 分时电价
Tab.1 Time-of-use power price

设置优化调度以1 h 为间隔。各VPP 内负荷及风电的日前预测值如图5 所示。为不失一般性,功率实测值为在日前预测功率的基础上叠加一符合正态分布的随机预测误差,风电、负荷的误差期望为0,均方差分别为5%、3%。


图5 MVPP 日前功率预测曲线
Fig.5 MVPP daily-ahead power prediction curve
4.2 MVPP 协调优化与独立优化对比分析
图6 为MVPP 协调优化调度结果。其中向电网售电为负,购电为正;向其他VPP 售电为负,购电为正;ESS 放电为正,充电为负。

图6 MVPP 优化调度结果
Fig.6 Results of MVPP optimal scheduling
VPP1 中,由于风电功率大于负荷功率,为多电VPP,因此VPP1 将在整个调度时域内作为售电方向少电VPP 及电网售电。0:00—2:00、5:00—10:00、14:00—15:00 与22:00—24:00 时,VPP1 向VPP2、VPP3 及电力市场售电,而由于VPP 直接交易电价优于向电网售电电价,因此VPP1 在优先满足内部VPP 购电需求的基础上以剩余电量参与电力市场。11:00—14:00 与16:00—18:00,VPP1 执行切负荷操作,这是由于切负荷补偿成本较高,因此仅在VPP向电网售电电价高于切负荷单位补偿单价时执行该操作,以最大化VPP 内部收益。11:00—21:00 期间VPP 向电网的售电电价高于MT 单位运行成本,MT 开机并在满足爬坡约束的基础上满功率运行,提高VPP 参与电力市场交易电量。ESS 则通过低储高发降低VPP 成本。
VPP2 中,风电与负荷容量较为均衡,大部分时段VPP2 能够通过内部资源的调配实现功率平衡,并以多余电量参与VPP 间交易或售至电力市场。在9:00—10:00 间,VPP2 内部调度成本高于向外部购电成本,VPP2 选择向VPP1 购电。而在10:00—24:00间,VPP2 中MT 大部分时段满功率运行,在满足内部功率需求外,余电向VPP3 售出并参与电力市场。
VPP3 中,风电功率总体小于负荷功率,当内部策略无法满足用电需求,或调度内部资源所需成本高于外部购电成本时,缺额功率优先通过向其他VPP 购入电量来补足。
图7 为VPP 间交易电价计算结果与VPP 向电网购售电电价对比情况。在0:00—9:00 与17:00— 24:00 期间,由于风电功率相对较高且负荷较轻,MVPP 内部电量严重过剩,因此VPP 内部交易电价与向电网售电电价保持一致。基于本文所提电价函数获取的内部交易电价在MVPP 系统中各VPP 存在电量互补的情况下,较电网电价具有显著优势,更能调动VPP 参与内部交易的积极性。
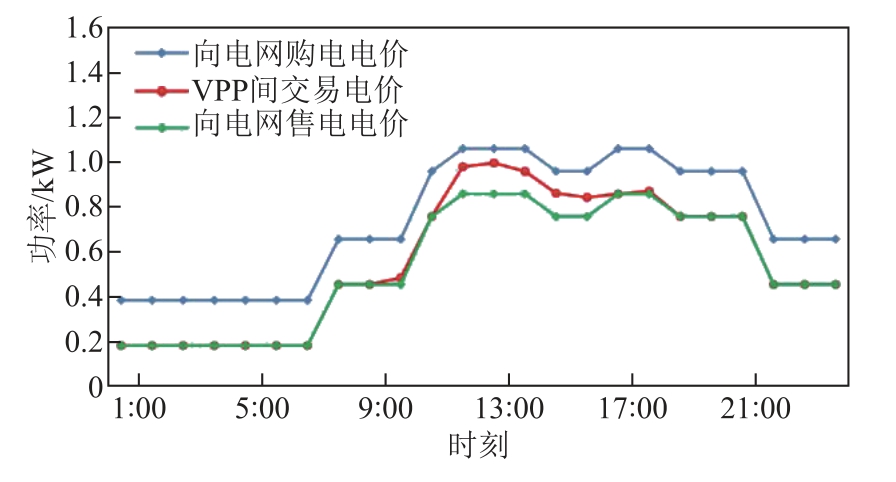
图7 VPP 间交易电价
Fig.7 Internal trading price
图8 为MVPP 协调优化和独立优化时向电网的购售电功率,0:00—9:00 期间MVPP 内部电量过剩,VPP 间交易电价与向电网售电电价保持一致,由于价格低于向电网供电电价,缺电VPP 优先选择与内部 VPP 直接进行交易,进而节约购电费用支。14:00~16:00 期间,VPP3 处于缺电状态,而由于VPP 内部交易电价优于向电网售电电价,因此VPP1与VPP2 在此时段先后向VPP3 售电。同时由表2可以看出,协调优化情况下,由于MVPP 内部存在功率互济,导致向电网的售电总量及购电总量均低于VPP 独立运行。
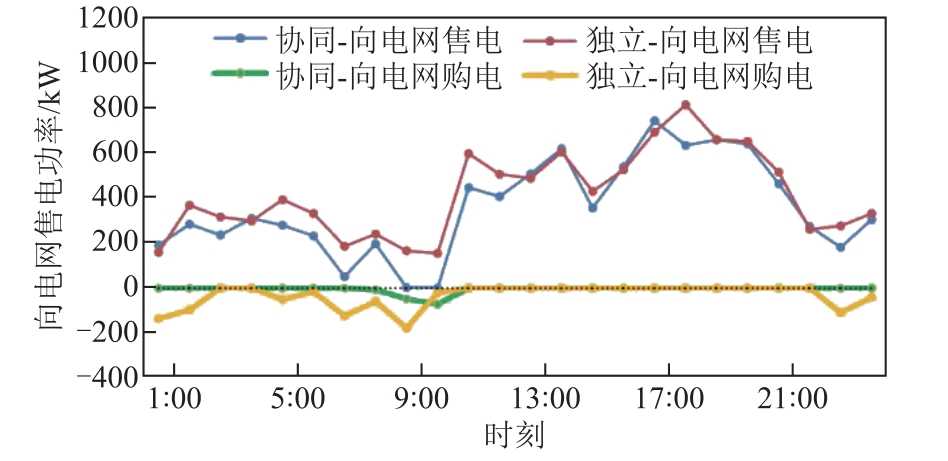
图8 MVPP 与电网交互功率
Fig.8 Exchanging power between MVPP and grid
表2 与电网交互电量
Tab.2 Exchanging electricity between MVPP and grid(单位:kW·h)
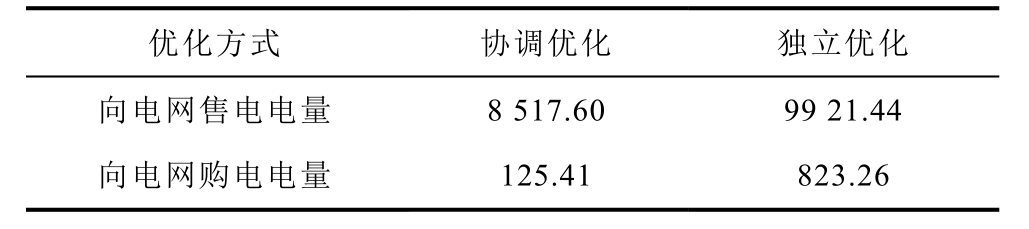
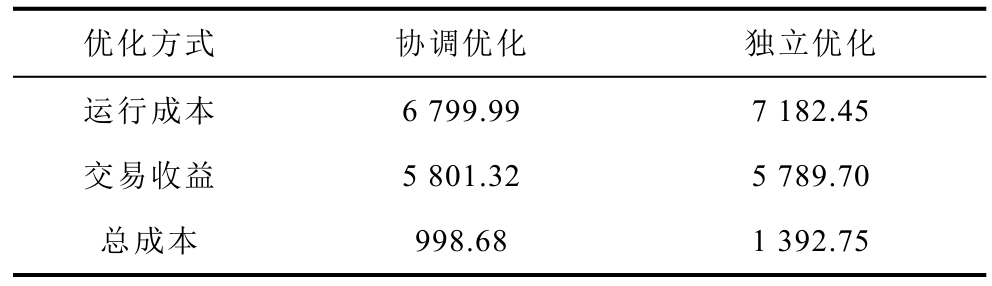
不同优化模式下成本对比见表3,可知协调优化的总成本低于独立优化总成本。这是由于独立优化模式下,各VPP 在电价高时优先调用内部资源进行功率平衡,导致VPP 内部各调控资源处于大功率运行状态,进而导致各VPP 的运行成本高于协调优化模式下的运行成本。协调优化模式下,VPP 间交易电价优于电力市场交易电价,在电价的激励下各VPP 形成功率互补优先构建交易,与电网间的交易电量则随之降低。而协调优化模式下VPP 间交易收益相互抵消,交易收益仅为向电网购售电交易收益,因此协调优化的交易收益较独立优化模式下的交易收益有所下降,但总运行成本仍低于独立优化模式。
表3 不同优化模式下成本对比
Tab.3 Cost comparison under different optimal modes(单位:元)
4.3 MVPP 分布式优化与集中式优化对比分析
以集中式和分布式优化方法分别对MVPP 协调优化调度模型进行求解,结果对比见表4。本文所提分布式优化方法与集中式优化方法计算结果基本保持一致。同时由于本文所提分布式优化方法不需建立在完全通信的基础上,仅需交互拉格朗日乘子即可,而且各子问题可并行计算提高解算效率,兼顾信息隐私及计算效率,适用范围更为广阔。迭代次数及收敛特性如图9 所示。由于本文采用拉格朗日松弛方法将问题松弛为主子问题迭代求解,且子问题可并行计算,每次迭代只消耗单个VPP 优化调度子问题的计算时间加上外层迭代时间,计算效率能够得到有效保障。并且本文采用改进的量子遗传算法进行子问题求解,相对于将优化问题转化为求解难度随变量增加而显著增加的线性或非线性规划问题,本文所提方法在求解效率上具有明显优势。
表4 集中式优化与分布式优化对比
Tab.4 Comparison of centralized and distributed optimization
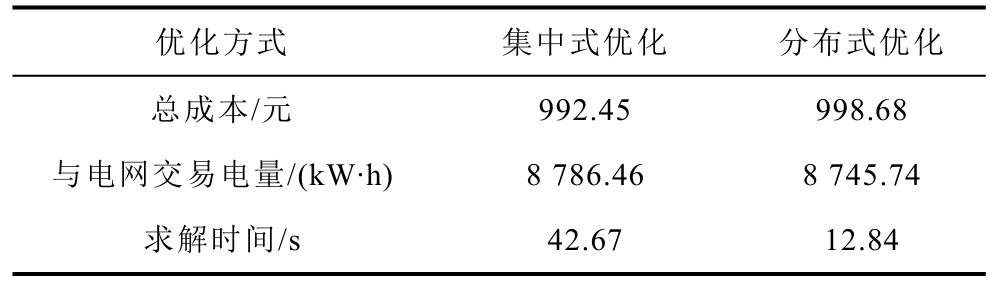

图9 迭代次数及收敛特性
Fig.9 Iteration number and convergence characteristics
4.4 基于DEC-POMDP 的MVPP 优化调度与日前优化调度对比分析
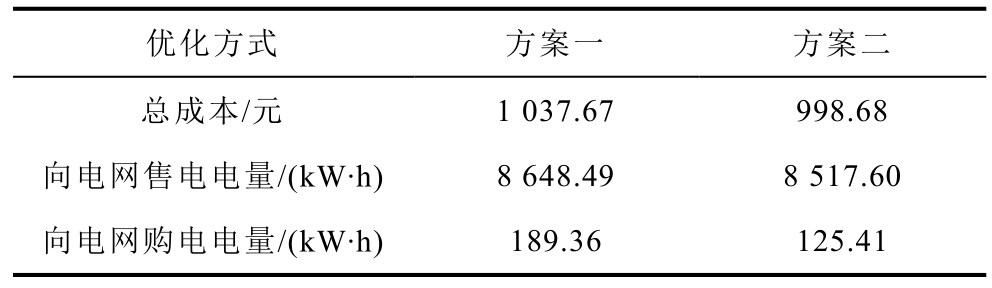
为验证本文所提基于DEC-POMDP 的MVPP 实时优化调度的优越性,进行如下对比。方案一:执行日前优化调度计划,由于风电、负荷功率波动导致的功率缺额或余量均通过电网补足或消纳;方案二:基于DEC-POMDP 开展MVPP 协调优化调度,实时调整VPP 内部资源调度指令。
基于DEC-POMDP 的实时优化调度是基于风电及负荷的实测值进行优化调度。针对风电及负荷的快速随机变化可由VPP 通过协调内部资源进行平抑或通过VPP 间功率互补消纳,避免由电网进行波动平抑而导致的成本增加或收益减少。同时该方法可以兼顾当前决策对未来时段的影响,进而实现多时段的调度最优。基于DEC-POMDP 的实时优化与日前优化调度对比见表5。由表5 可知,由于风电及负荷预测误差导致的功率缺额由VPP 内部资源出力调整进行平衡或VPP 间功率互济进行补足,使MVPP 向电网的购电量较基于日前优化的调度有所降低。
表5 基于DEC-POMDP 的实时优化与 日前优化调度对比
Tab.5 Comparison of optimal scheduling based on DECPOMDP and day-ahead optimal scheduling
5 结论
本文基于“信息分离、决策协同”的分布式控制思想,利用拉格朗日对偶松弛原理构建了一种分散架构下MVPP 分布式协同优化调度模型。主要结论如下:
1)MVPP 协调优化调度基于内部VPP 间的功率互济减少向电力市场购电电量,并构建VPP 间交易电价函数提高VPP 参与直接交易的积极性,相较各VPP 独立调度具有更高的经济性。
2)基于拉格朗日对偶松弛原理构建MVPP 分布式协调优化模型,VPP 间仅需交换少量信息即可实现全局优化,相较集中式优化更好地保障了VPP的信息隐私。
3)基于DEC-POMDP 将MVPP 多时段协调优化问题转换为实时优化调度问题,在有效应对由于预测误差造成的优化调度偏差的同时保证VPP 内可调配资源出力计划在一天内的合理分配。
[1]姜涛,张东辉,李雪,等.含分布式光伏的主动配电网电压分布式优化控制[J].电力自动化设备,2021,41(9): 102-109,125.Jiang Tao,Zhang Donghui,Li Xue,et al.Distributed optimal control of voltage in active distribution network with distributed photovoltaic[J].Electric Power Automation Equipment,2021,41(9): 102-109,125.
[2]刁涵彬,李培强,吕小秀,等.考虑多元储能差异性的区域综合能源系统储能协同优化配置[J].电工技术学报,2021,36(1): 151-165.Diao Hanbin,Li Peiqiang,Lü Xiaoxiu,et al.Coordinated optimal allocation of energy storage in regional integrated energy system considering the diversity of multi-energy storage[J].Transactions of China Electrotechnical Society,2021,36(1): 151-165.
[3]余光正,林涛,汤波,等.计及谐波裕度-均衡度的分布式电源最大准入功率计算方法[J].电工技术学报,2021,36(9): 1857-1865,1875.Yu Guangzheng,Lin Tao,Tang Bo,et al.Calculation method of distributed generator maximum access power considering balance degree of harmonic margin[J].Transactions of China Electrotechnical Society,2021,36(9): 1857-1865,1875.
[4]田立亭,程林,郭剑波,等.虚拟电厂对分布式能源的管理和互动机制研究综述[J].电网技术,2020,44(6): 2097-2108.Tian Liting,Cheng Lin,Guo Jianbo,et al.A review on the study of management and interaction mechanism for distributed energy in virtual power plants[J].Power System Technology,2020,44(6): 2097-2108.
[5]Pudjianto D,Ramsay C,Strbac G.Virtual power plant and system integration of distributed energy resources[J].IET Renewable Power Generation,2007,1(1): 10.
[6]Vasirani M,Kota R,Cavalcante R L G,et al.An agentbased approach to virtual power plants of wind power generators and electric vehicles[J].IEEE Transactions on Smart Grid,2013,4(3): 1314-1322.
[7]Mnatsakanyan A,Kennedy S W.A novel demand response model with an application for a virtual power plant[J].IEEE Transactions on Smart Grid,2015,6(1): 230-237.
[8]林毓军,苗世洪,杨炜晨,等.面向多重不确定性环境的虚拟电厂日前优化调度策略[J].电力自动化设备,2021,41(12): 143-150.Lin Yujun,Miao Shihong,Yang Weichen,et al.Dayahead optimal scheduling strategy of virtual power plant for environment with multiple uncertainties[J].Electric Power Automation Equipment,2021,41(12): 143-150.
[9]麻秀范,王戈,朱思嘉,等.计及风电消纳与发电集团利益的日前协调优化调度[J].电工技术学报,2021,36(3): 579-587.Ma Xiufan,Wang Ge,Zhu Sijia,et al.Coordinated day-ahead optimal dispatch considering wind power consumption and the benefits of power generation group[J].Transactions of China Electrotechnical Society,2021,36(3): 579-587.
[10]袁桂丽,陈少梁,刘颖,等.基于分时电价的虚拟电厂经济性优化调度[J].电网技术,2016,40(3): 826-832.Yuan Guili,Chen Shaoliang,Liu Ying,et al.Economic optimal dispatch of virtual power plant based on time-of-use power price[J].Power System Technology,2016,40(3): 826-832.
[11]张高,王旭,蒋传文.基于主从博弈的含电动汽车虚拟电厂协调调度[J].电力系统自动化,2018,42(11): 48-55.Zhang Gao,Wang Xu,Jiang Chuanwen.Stackelberg game based coordinated dispatch of virtual power plant considering electric vehicle management[J].Automation of Electric Power Systems,2018,42(11): 48-55.
[12]刘方,徐耀杰,杨秀,等.考虑电能交互共享的虚拟电厂集群多时间尺度协调运行策略[J].电网技术,2022,46(2): 642-656.Liu Fang,Xu Yaojie,Yang Xiu,et al.Multi-time scale coordinated operation strategy of virtual power plant clusters considering power interactive sharing[J].Power System Technology,2022,46(2): 642-656.
[13]陈妤,卫志农,胥峥,等.电力体制改革下的多虚拟电厂联合优化调度策略[J].电力系统自动化,2019,43(7): 42-49,165.Chen Yu,Wei Zhinong,Xu Zheng,et al.Optimal scheduling strategy of multiple virtual power plants under electricity market reform[J].Automation of Electric Power Systems,2019,43(7): 42-49,165.
[14]杨洪朝,杨迪,孟科.高比例可再生能源渗透下多虚拟电厂多时间尺度协调优化调度[J].智慧电力,2021,49(2): 60-68.Yang Hongzhao,Yang Di,Meng Ke.Multi-time scale coordination optimal scheduling of multiple virtual power plants with high-penetration renewable energy integration[J].Smart Power,2021,49(2): 60-68.
[15]Yi Zhongkai,Xu Yinliang,Zhou Jianguo,et al.Bilevel programming for optimal operation of an active distribution network with multiple virtual power plants[J].IEEE Transactions on Sustainable Energy,2020,11(4): 2855-2869.
[16]Wang Yao,Ai Xin,Tan Zhongfu,et al.Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory[J].IEEE Transactions on Smart Grid,2016,7(1): 510-519.
[17]董雷,涂淑琴,李烨,等.基于元模型优化算法的主从博弈多虚拟电厂动态定价和能量管理[J].电网技术,2020,44(3): 973-983.Dong Lei,Tu Shuqin,Li Ye,et al.A stackelberg game model for dynamic pricing and energy management of multiple virtual power plants using metamodel-based optimization method[J].Power System Technology,2020,44(3): 973-983.
[18]刘思源,艾芊,郑建平,等.多时间尺度的多虚拟电厂双层协调机制与运行策略[J].中国电机工程学报,2018,38(3): 753-761.Liu Siyuan,Ai Qian,Zheng Jianping,et al.Bi-level coordination mechanism and operation strategy of multi-time scale multiple virtual power plants[J].Proceedings of the CSEE,2018,38(3): 753-761.
[19]周博,吕林,高红均,等.多虚拟电厂日前鲁棒交易策略研究[J].电网技术,2018,42(8): 2694-2703.Zhou Bo,Lü Lin,Gao Hongjun,et al.Robust dayahead trading strategy for multiple virtual power plants[J].Power System Technology,2018,42(8): 2694-2703.
[20]向明旭,杨知方,余娟,等.配电网线性潮流模型通式及误差分析[J].中国电机工程学报,2021,41(6): 2053-2064.Xiang Mingxu,Yang Zhifang,Yu Juan,et al.Linear power flow model in distribution network: unified expression and error analysis[J].Proceedings of the CSEE,2021,41(6): 2053-2064.
[21]罗天,汪可友,李国杰,等.基于拉格朗日对偶松弛的多区域柔性直流互联电网无功优化[J].电力系统自动化,2019,43(11): 68-76.Luo Tian,Wang Keyou,Li Guojie,et al.Reactive power optimization in multi-area VSC-HVDC interconnected power grids based on Lagrangian dual relaxation[J].Automation of Electric Power Systems,2019,43(11): 68-76.
[22]Bernstein D S,Givan R,Immerman N,et al.The complexity of decentralized control of Markov decision processes[J].Mathematics of Operations Research,2002,27(4): 819-840.
[23]帅航.基于近似动态规划(ADP)的微电网日内在线优化运行方法研究[D].武汉: 华中科技大学,2019.
[24]张京钊,江涛.改进的自适应遗传算法[J].计算机工程与应用,2010,46(11): 53-55.Zhang Jingzhao,Jiang Tao.Improved adaptive genetic algorithm[J].Computer Engineering and Applications,2010,46(11): 53-55.
[25]马速良,马会萌,蒋小平,等.基于 Bloch 球面的量子遗传算法的混合储能系统容量配置[J].中国电机工程学报,2015,35(3): 592-599.Ma Suliang,Ma Huimeng,Jiang Xiaoping,et al.Capacity configuration of the hybrid energy storage system based on Bloch spherical quantum genetic algorithm[J].Proceedings of the CSEE,2015,35(3): 592-599.