0 引言
大型水轮发电机全部或部分失磁是一种较常见且严重的故障,具有凸极结构的水轮发电机相对于汽轮发电机异步功率小、调速器时滞大,在失磁后转子会更快地超速,并伴随着机组振动等现象,对机组本体及电网危害巨大[1],因此要求失磁保护更快速动作。以机端阻抗静稳边界为主判据的传统失磁保护只能通过机端测量阻抗变化的最终结果来判断是否失磁,无法反映复杂电网环境下各种扰动测量阻抗的变化,难以同时满足选择性和速动性。2018年巴西电网“3.21”大停电事故中东北部电网某大型水轮机组因受系统振荡的影响导致失磁保护误动跳闸,该机组解列加剧了系统的不稳定,以致最终崩溃[2]。随着电网结构日趋复杂以及运行环境的变化,大型水轮机失磁保护的可靠性和速动性均面临着巨大的挑战[2-3]。
鉴于现有保护的不足,国内外学者为了提高失磁保护性能进行了大量的研究工作。目前对于水轮机失磁保护的研究主要分为机理型和数据驱动型两种方法。基于机理的方法包括传统保护判据的组合改进[4-5]和基于电气量的新判据研究[6-9],前者的通用做法就是在原有判据的基础上进行组合优化,尽可能地提升保护的选择性,后者则深入剖析发电机电气量的变化规律,进而设计新的失磁判据。此类方法利用具体的规则来揭示物理现象的本质特征,在一定程度上提升了失磁保护性能,但机理模型的准确性与复杂性呈正相关[10],构建能够适应未知场景的机理型失磁保护非常困难。得益于信息技术的发展,数据驱动方法也被引入失磁保护判别[11-15],其主要利用统计分析以及人工智能(Artificial Intelligence,AI)模型判别失磁与其他异常工况,典型的算法有模糊逻辑(Fuzzy Logic)[11]、决策树(Decision Tree)[12]、人工神经网络(Artificial Neural Network,ANN)[13]、支持向量机(Support Vector Machine,SVM)[14-15]等。目前基于AI 的失磁保护原理大多采用功率、相位、转子角、阻抗等物理量进行一系列复杂的数学处理后得到时域或频域层面上的信息作为特征量,在有限的场景下进行特征提取往往会导致学习模型的泛化能力不足,模型解释能力差,但将AI 技术引入失磁保护为其提升性能提供了新途径。
传统失磁保护理论的基础是机端测量阻抗的轨迹变化规律,但其只利用了测量阻抗变化最终结果信息,忽略了动态过程。而机端测量阻抗轨迹的整个运动过程蕴含了系统大量信息,利用测量阻抗轨迹变化的动态过程能够更好地识别失磁故障。这种考虑动态过程全局的轨迹识别与预测方法在电力系统中应用较多的是暂态稳定判别[16-19]以及变压器故障识别[20-21],其中既有机理方法,也有数据驱动方法。前者的基本思想是通过选取电气量或衍生的物理量获得在二维或多维空间的可视化动态相轨迹,依据可视化表达结果深入剖析轨迹外在的几何特征,进而形成新的机理型判据,或者直接对物理时序标量轨迹进行机理分析得到判据;后者应用于暂态稳定判别时一般直接选择电气量的标量或相轨迹的时序点输入AI 模型进行预测,应用于变压器故障识别时依据固定时窗内的静态轨迹几何特征进行智能判别,此类基于AI 的数据驱动方法计算能力强,能够从数据角度挖掘关联信息,形成所涉及的相关因素与电力系统状态之间的精准映射关系[22-24],但以上特征选择中机理分析部分较薄弱或只关注静态几何特征,所提方法往往深度依赖AI 模型进行自学习从而造成“黑盒问题[25]”。随着轨迹识别在电力系统中的应用,参考较为成熟传统失磁保护的机理,利用AI 技术强大的信息关联和学习能力设计智能失磁保护是一个可行的发展方向。
借鉴轨迹识别以及AI 技术在电力系统中良好的应用效果,本文提出一种基于大型水轮发电机测量阻抗变化轨迹智能识别的失磁保护方法,分析机端测量阻抗轨迹在固定时窗内的动态时序机理特征,并引入统计学思想描述时序特征分布,通过最大相关-最小冗余算法[26](maximal Relevance Minimal Redundancy,mRMR)提取关键特征量以增强解释性,融合小样本学习的多核支持向量机[27](Multiple Kernel Learning Support Vector Machine,MKLSVM)模型判别失磁及其他异常工况。针对简单水电机组系统和近区不同类型电源接入的扩展复杂系统的仿真判别结果,证实了所提方法突破了传统失磁保护的瓶颈,解决了速动性和选择性的矛盾,具有高可靠性和优良的泛化能力,是一种具有应用前景的失磁保护方法。
1 水轮机传统失磁保护判据的不足
以图1 所示的简化三机等效水轮机送出系统为例,被研究机组机端测量阻抗实部和虚部分别为
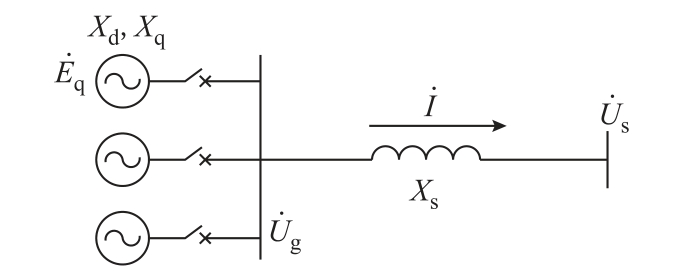
图1 简化水轮发电机送出系统
Fig.1 Simplified equivalent hydraulic generator transmission system

式中,Ug 为水轮发电机机端电压;P、Q 分别为相应的有功与无功功率。
由式(1)和式(2)可知,发电机正常运行位于阻抗平面第一或第四象限,当发电机发生失磁故障时,机端测量阻抗会进入第四象限。一般情况下,传统失磁保护定子侧主判据多采用苹果形阻抗动作特性,以逼近水滴形静稳边界曲线,辅助判据为转子低电压与无功反向判据。为了测试其保护效果,在简化水轮发电机送出系统中对失磁及其他异常工况进行仿真分析,其中苹果形阻抗动作特性按照保护厂商提供的建议和规程进行整定。
1)拒动分析
发电机系统发生失磁故障,定子侧阻抗判据需经过一定时间才可能满足,但只有最严重的开路失磁发生,阻抗判据才会及时动作,尤其对于部分失磁,动作时限最长,甚至无法动作。表1 说明了不同负载下发生部分失磁测量阻抗进入阻抗圆的时间,相应工况1~4 机端测量阻抗轨迹如图2 所示。由此可知,机理型失磁保护由于只关注失磁的最终结果,轻载工况发生较轻的部分失磁故障情况下,阻抗判据不能发挥作用。

图2 测量阻抗轨迹
Fig.2 Measurement of impedance trajectory
表1 部分失磁时阻抗判据的满足情况
Tab.1 Satisfaction of impedance criterion for partial loss of excitation fault

2)误动分析
基于机理的传统失磁保护在忽略一些影响因素的前提下,能够较好地解释失磁与其他典型异常工况测量阻抗变化的区别,但在面临运行工况及扰动的多样性与复杂性时建立精细化机理模型极其困难,准确率的提高存在瓶颈。以发电机进相工况下主变高压侧发生三相短路后造成同步振荡的工况为例,如图2 中虚线所示,机端测量阻抗轨迹在此过程中会反复进入到动作圆内,并且暂留时间最长可达0.64 s,增大了失磁阻抗判据误动作的概率。
若设置转子低电压辅助判据来防止失磁保护误动作,则上述工况相应的励磁电压变化曲线如图3所示,当阈值取0.9 (pu)时,可以看到励磁电压反复两次低于阈值,最大间隔时刻为0.52 s,也无法保证转子判据的选择性。事实上,由于转子侧电气量的获取易受干扰,误动率高[1],一般在工程应用中不会采用,所以最终只能依靠定子侧判据增加1~1.5 s 的时限躲过振荡周期,但这就使得保护的速动性受到严重影响。

图3 短路切除前后功率振荡励磁电压变化曲线
Fig.3 Variation curve of power oscillation excitation voltage before and after short circuit removal
由以上分析可知,基于机理的传统失磁保护通过设定静态阈值信息来识别失磁故障,没有有效利用故障后动态过程信息,只利用了故障后最终的静态局部信息,动作区域和延时的整定很难在保护的选择性和速动性之间找到平衡,难以适应复杂多变的运行场景,因此无法从根本上解决选择性与速动性的矛盾。
2 基于测量阻抗轨迹智能识别的失磁保护新方案
基于机理的失磁阻抗判据理论上只能体现失磁的最终结果,忽略了失磁后阻抗判据启动前的动态物理过程,而机端测量阻抗轨迹往往蕴含着丰富的系统信息,反映了失磁故障与其他异常状况。
电力系统各种典型扰动及异常工况下所对应的机端测量阻抗变化轨迹如图4 所示。对于失磁故障,机端测量阻抗轨迹由等功率阻抗圆过渡到静稳边界内,其他扰动或异常工况会使阻抗轨迹发生变化,之后或发生功角逐渐趋于稳定的同步振荡,或发生功角逐渐增大趋于失步的异步振荡。实际系统中异步振荡(包括全相和非全相)测量阻抗近似表现为圆或直线[1],考虑到系统工况的复杂性,在机端测量阻抗轨迹运动特征分析的基础上融合AI 强大的学习和信息关联能力可快速判别发电机是否发生失磁故障。

图4 简化等效系统各种扰动下的机端测量阻抗轨迹
Fig.4 Impedance trajectory of terminal measurement under various disturbance of simplified equivalent system
SVM 作为人工智能算法中常用的分类器,已经广泛应用于电力系统领域[14-15,28-29]。对于SVM 基本原理,文献[28-29]已经做了详细介绍,其核心目标就是利用核函数完成低维原始空间到高维线性空间的映射,进而寻找到低维空间中可区分不同类别的最大间隔。这里以线路距离保护为例说明SVM 的原理以及可用性。
SVM 原理示意图如图5 所示,若距离保护中采用二维阻抗平面中的方向动作特性圆,通过历史或仿真数据获得区内外短路故障时的测量阻抗样本点,若样本足够多且具有代表性,选择合适的核函数并应用样本对SVM 训练可使其分类边界逼近距离保护的动作方向圆,即在先验知识的指导下从数据的角度完成了低维动作特性的确定。事实上,SVM 通过核函数具有任意维非线性映射功能[28],能够反映复杂条件下的映射关系,此外其分类决策由少量作为支持向量的样本点所决定,这种采用结构风险最小化准则的小样本学习方法具有较强的鲁棒性和泛化能力,能够使失磁保护适用于复杂多变的电网条件。

图5 SVM 原理示意图
Fig.5 Schematic diagram of SVM
鉴于此,基于测量阻抗轨迹和SVM 分类器设计失磁保护新方案,如图6 所示,新方案包括离线和实时两部分。对于一个大型水轮发电机来说,初始离线训练样本库可来自仿真或已运行系统的历史录波数据,每次动作决策完成后,其结果经校核后均反馈到样本库可实现定期离线学习,进而可改良模型的性能。

图6 失磁保护新方案
Fig.6 Scheme of the novel loss of excitation protection
3 失磁保护新方案的实现
3.1 测量阻抗轨迹演变规律
依据测量阻抗轨迹进行判别的关键点是寻找能够准确描述轨迹变化规律的物理量,再进一步提取关键特征量。常用的轨迹运动特征包括速度、加速度、位移和转角等,通过这些特征可以揭示轨迹运动的性质[30]。速度和加速度是描述运动最基本的时序特征,测量阻抗的变化速度表明系统受各种扰动影响的大小,能够体现系统在受到扰动后从一个稳态运行点过渡到另外一个稳态运行点或者失去稳定的不同特征,而且不同故障原因也使得发电机以及系统惯性作用下的电气参数变化速率和变化规律有很大区别,这集中体现在轨迹加速度的变化规律上。设采样时间间隔Δt=25 ms,可获得固定时窗内机端测量阻抗时序点![]() ,速度vk 以及加速度ak 的计算公式为
,速度vk 以及加速度ak 的计算公式为

图7a、图7b 分别展现了失磁和振荡等各种工况下的测量阻抗轨迹速度v 以及加速度a 变化曲线。根据各种扰动及工况下测量阻抗速度与加速度变化曲线可知,各种原因造成的发电机异步振荡的速度与加速度值波动最大。这是因为异步振荡存在滑极的缘故,短路造成的同步振荡工况下由于短路的发生会使初始速度、加速度值瞬间增大,二者与其他工况有明显的区别;失磁故障的测量阻抗速度初始速度较大,随后在转为异步运行之前速度呈逐步降低的趋势,具体理论推导说明见附录。但失磁与某些非短路(超出静稳极限、甩负荷、调速器失灵等)扰动造成的同步振荡特征存在混叠现象,需要进一 步选择特征量进行区分。


图7 失磁和各种扰动振荡下的测量阻抗特征变化曲线
Fig.7 Variation curves of measured impedance characteristics under loss of excitation and various disturbance oscillation
由前文所述,考虑到失磁故障初始会从等功率圆逐步过渡到失步区域,同步振荡则从一个稳态点逐步过渡到另一个稳态点,非短路同步振荡与失磁测量阻抗轨迹变化方向存在明显不同,因此引入表征几何特征的测量阻抗幅值z 和相位θ 来区分二者,相应的计算公式为

不同扰动及工况对应的测量阻抗模值及相位变化曲线如图7c、图7d 所示。可以看到,提取相位和阻抗幅值作为特征量,物理意义十分明确,失磁故障过程中测量阻抗幅值与相位的斜率总体呈现负值,表明发电机正趋于失步,而同步振荡测量阻抗幅值与相位均呈上下波动的现象,且波动范围在缩小,表明系统正趋向于稳态点。综合前述四个时序特征量便可将失磁故障与其他扰动及异常工况区分开来。
3.2 测量阻抗特征提取
3.2.1 统计学参数计算
机端测量阻抗轨迹的速度、加速度、阻抗幅值和相位4 个时序特征可以很好地描述其轨迹整体演变规律。为了便于构建失磁保护判别模型,形成分类模型的输入特征量,可将阻抗轨迹时序特征进行统计学参数分析以描述时序特征的分布规律。
根据扰动振荡与失磁的特征序列大小水平与离散程度的明显区别可以引入均值μ、中值ε、标准差σ来描述。此外,考虑到失磁故障轨迹较短时和扰动振荡的速度大小分布具有相反的特点,引入统计学中的偏度系数γ 来描述分布偏离对称性的程度;又因失磁阻抗轨迹具有单调性,而振荡具有周期性,可利用峰度系数η来描述特征序列的分布陡峭或平滑程度。对于单个样本任意特征时间序列lk,统计学特征计算可表示为
式中,i={μ,ε,σ,γ,η}; (ΔT,Δt)表示在时窗ΔT 内序列时间间隔为Δt 时的相应统计学特征;ΔN 为相应参与计算的序列个数;STAi 表示不同的统计学参数计算公式,具体见文献[31]。m 个样本特征参数经0-1 归一化后最终形成20 维原始特征矩阵F,则F可表示为
(ΔT,Δt)表示在时窗ΔT 内序列时间间隔为Δt 时的相应统计学特征;ΔN 为相应参与计算的序列个数;STAi 表示不同的统计学参数计算公式,具体见文献[31]。m 个样本特征参数经0-1 归一化后最终形成20 维原始特征矩阵F,则F可表示为
式中, Fμ、 Fε、 Fσ、 Fγ、 Fη 分别为四种时序特征量对应的均值、中值、标准差、偏度系数、峰度系数分块矩阵。需要注意的是,新样本归一化的方式与模型训练过程相一致,若特征值越界,则取上、下限值。
3.2.2 基于信息度量的特征选择
为了减少特征数据的冗余性,防止模型过拟合,提高训练模型的泛化能力,采用Wrapper 策略[26]进行特征选择以决定特征维数,即依据所使用的AI 模型的准确率作为特征选择的最终评价指标,通过这种反馈机制能最大限度地提升学习效果。
由于信息度量标准可以衡量特征间、特征与类别之间的非线性关系,本文选择使用基于互信息[32]的mRMR 算法决定特征的选择顺序,其基本思想就是在原始特征集合中找到与最终输出结果相关性最大,但是特征之间相关性最小的一组特征,从而定义最大化目标函数为

式中,D、R 分别为特征-类相关性和特征间冗余性;I 为互信息;xi 为所有样本组成的第i 个特征行向量;Y 为标签行向量,1 表示失磁,-1 表示非失磁。
搜索算法为增量搜索法,在剩余特征集合{FFk-1}选择第k 个特征时的得分目标函数为

式中,k 为选择的特征数。
按照式(10)计算未选择的每个特征得分,按照增量入选的顺序,选取前k 个特征组成初始特征集,将不同的特征集作为模型的输入特征,以训练模型的交叉验证准确率作为最终的特征选择依据,即当准确率均值变化Δak 不再有明显提高时(本文取0.1%),选取该准确率下最少维数的特征集为最优特征集,具体特征选择的流程如图8 所示。
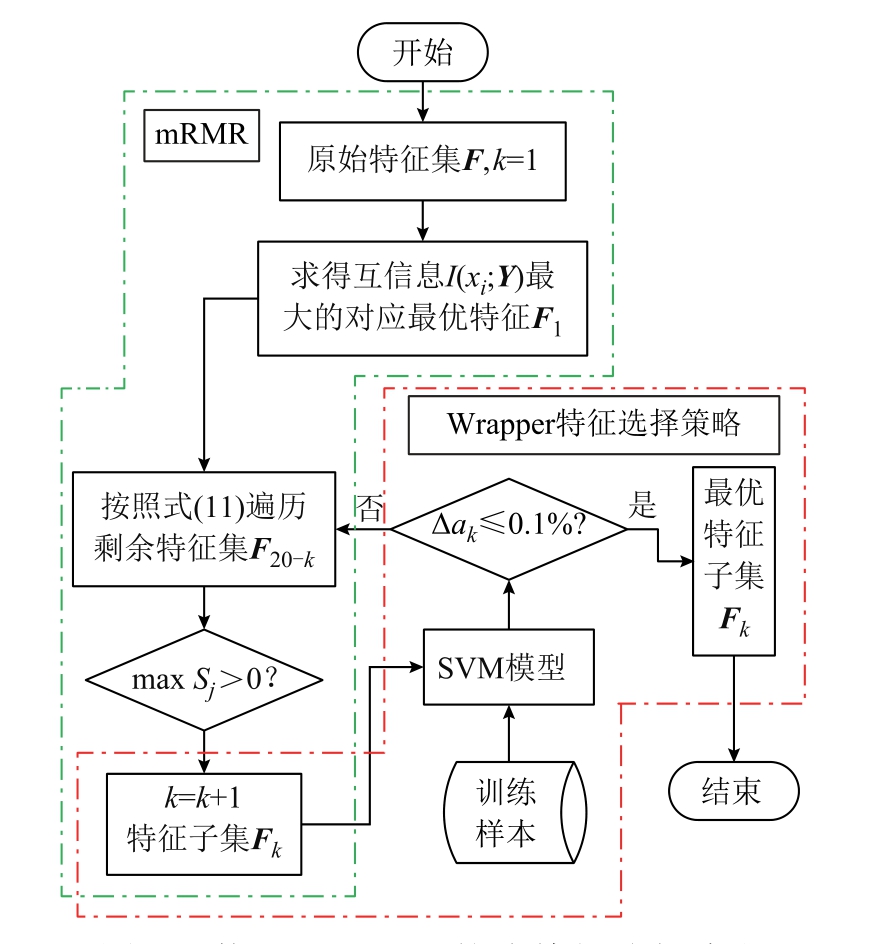
图8 使用Wrapper 策略特征选择流程
Fig.8 Feature selection process using Wrapper strategy
3.3 MKLSVM 分类模型及参数优化
依据SVM 原理,在训练前确定样本集( βi,yi),i=1,2,⋅⋅⋅,m,其中 βi 为第i 个训练样本的k 维输入特征列向量,yi∈{1,-1}表示输入样本的类别标签,1 表示失磁,-1 表示非失磁。
训练完成后在失磁保护中构造的分类判据可表示为

式中,sgn(⋅)为符号函数;ω 为法向量;λi 和b 分别为训练完成后得到的拉格朗日系数和常数;K(·)为核函数; β 为实时应用时的k 维输入特征列向量;f (β)为实时应用时的输出类别结果。
在样本确定的前提下模型的训练过程取决于满足Mercer 条件[27]的核函数以及作为λi 取值上限的惩罚系数C。核函数可分为全局核函数和局部核函数,典型的全局性多项式核函数(Polynomial kernel,Poly)与局部性径向基核函数(Radial Basis Function,RBF)分别描述为

式中,d 为正整数多项式阶数,一般取值为2 或3;δ 为RBF 核的宽度;2 δ 2表征被模型选中作为支持向量的样本的影响半径。
结合式(11)~式(13)和内积的定义可知,Poly 的作用随着两个样本点在样本空间中距离的增大而增大(夹角为正)或减小(夹角为负),但均为非零值,而RBF 则仅在两个样本点相近时,作用最明显,影响会随距离的增大而减弱。这表明局部性RBF 在训练过程中有较好的拟合效果,从而具有较强的学习能力,但在决策过程中的泛化能力弱,全局性Poly 对所有样本点都会有作用导致学习能力较弱但泛化能力强[33]。
为了进一步提高SVM 分类模型的泛化能力,兼顾全局与局部特征,利用由RBF 和Poly 核函数的线性加权组合构成核函数用来训练MKLSVM,其同样满足Mercer 条件[27],表达式为
式(14)中的α 用来调节二者权值所占的比重,取值范围为[0,1]。待确定的输入参数α、d、δ 以及C 决定MKLSVM 分类性能,其中核参数d 取值较为单一,采用经验值2,其他三个变量需要采取高效的多变量寻优算法搜索最优值。鉴于传统遗传算法采用固定的遗传算子以及赌轮选择方式会造成局部收敛及稳定性差的问题,本文采用具有精英保留规则(Elitist Preservation)的自适应遗传算法[34](Improve Genetic Algorithm,IGA),其基本思想及相应步骤为:
(1)初始化种群数量、变量区间、杂交率及变异率取值范围,设置编码方式为二进制编码。
(2)计算种群个体的适应度r 并进行排序,取位于优势位置的个体直接选择复制1/4 于下一代,新种群剩余3/4 的个体随机两两对比进行选择。
(3)将竞争选择出的3/8 种群,依次进行自适应交叉、变异操作,其中交叉率和变异率P 分别根据Sigmoid 函数导出,函数中h=9.90,具体为

(4)更新种群,重复步骤(2)和(3),直到满足终止条件。
考虑到模型需兼顾学习能力与泛化能力,目标函数设为验证集的准确率。根据训练样本可获得相应最优参数α、δ 和C 及形如式(11)的模型。在每次迭代过程中,采用固定分配比例的方式随机选择训练集与验证集对样本进行交叉验证[28],以便获得更为可靠的模型。
当训练好检测模型之后,需要对其性能进行评价,评价基础指标选取准确率ACC(accuracy)、查全率REC(Recall)和查准率PRE(Precision),进一步选取F1-score,F1-score,为兼顾REC 和PRE的加权调和平均值,其值区间为[0,1]。
3.4 基于SVM 分类函数距离的双时窗判别原理
发电机失磁故障的严重程度对测量阻抗轨迹有很大影响,严重时不足1 s 便会进入到异步状态,轻则不会过渡到异步状态,测量阻抗轨迹相差甚远。为了进一步提高失磁保护自适应能力,本文考虑不同时间窗长对分类效果的影响。一般情况下时窗越长蕴含的发电机运行信息越多,模型分类效果就越好,但是失磁故障的最终结果是异步运行,其轨迹特征和部分异步振荡相似,所以时间窗过长可能会掩盖前期的特征,尤其对于较为严重的重载失磁,这反而会导致判别模型的性能下降,选择合适的时窗是影响模型性能的一个重要因素。
由于不同电力系统的抗干扰能力不同,相同时间下轨迹变化相差极大,欲选择最佳时窗是非常困难的。结合图5 可知,边界处的样本点对是训练模型的关键,直观地看,可以通过增加一定规模应用系统的样本来提高模型的可靠性,但样本收集和筛选较为困难,考虑到SVM 的本质是基于核空间样本距离的线性分类,于是可通过样本点到SVM 边界的核空间相对判别距离对样本点进行分情况判别,由式(11)可得核空间相对判别距离为
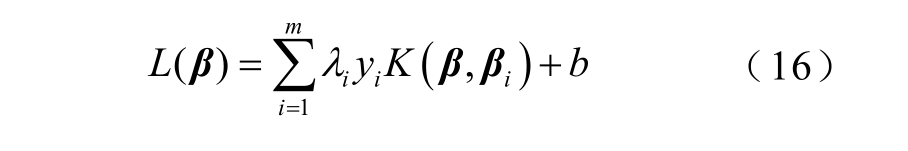
设失磁与振荡等其他扰动样本点距离中间分类面判别阈值分别为Li,min,i=1,2,当二者均取1,即表示训练得到的对称分类间隔边界,边界内为支持向量所处的临界域。当|L(β) |>Li,min 时,即当样本点位于对称分类边界外时,可通过短时窗MKLSVM直接进行决策,当|L( β)|≤Li,min 时,样本点处于临界域,这时通过截取长时窗进行第二步决策。两次决策最优特征集和辨识模型分别命名为{Fk1,MKLSVM1}与{Fk2,MKLSVM2},相应实时应用时的新样本输入特征向量为 β k1和 β k2。
通过第一步决策,可以在短时间窗内优先判别轨迹特征表现明显的严重失磁和扰动振荡,筛选出特征表现不明显的样本点进行第二步决策。这样一方面提高了判别的速度,另一方面能避免因时间窗加长导致严重失磁和扰动振荡的误分类,从而提高可靠性。综上所述,所提失磁保护方案具体实施流程如图9 所示。

图9 失磁保护方案具体实施流程
Fig.9 Specific implementation process of loss of excitation protection scheme
4 仿真算例
算例仿真样本均来自于PSCAD 时域仿真平台,仿真模型包括相互独立的简单水轮发电机输电系统与基于IEEE 39 节点考虑不同电源接入的扩展复杂电网系统,二者结构完全不同,后者模拟了未来电网的发展和变化,从而作为测试集用来评估经前者训练的失磁保护模型的泛化能力。
4.1 仿真数据采集
基于PSCAD 仿真平台搭建水轮发电机电网模型,对以三机并列经升压变压器连接到不同强弱程度的外网构成的简单电力系统进行仿真。附表2 为实验机组12 种不同的功率因数和负载运行场景,在每种负载条件下设置失磁和其他异常工况,其中,失磁主要考虑开路失磁、短路失磁与部分失磁,其他异常工况重点考虑短路以及其他扰动造成的同步振荡或异步振荡,还关注了短路切除线路和断线导致系统结构改变的场景,具体的异常工况见附表2。
在上述条件下,共计产生470 组仿真样本,包括开路失磁、经灭磁电阻短路失磁以及部分失磁各90 组共计270 组的失磁样本,涉及不同短路类型、位置、时长、过渡电阻的短路样本100 组,其他非短路扰动样本100 组。
4.2 模型训练及参数优化
在不同的时窗下,将仿真样本随机分为含300组样本的训练集,170 组样本的验证集,其中训练集用于训练分类模型,验证集用于评估模型的性能。
在进行训练之前,将原始特征集归一化后按照mRMR 对训练集进行特征选择,得分为正的特征按照选择顺序组成特征集,1 s 时窗下不同扰动多次排序均靠前的4 维特征量归一化大小如图10 所示,前3 维组成的特征空间如图11 所示。
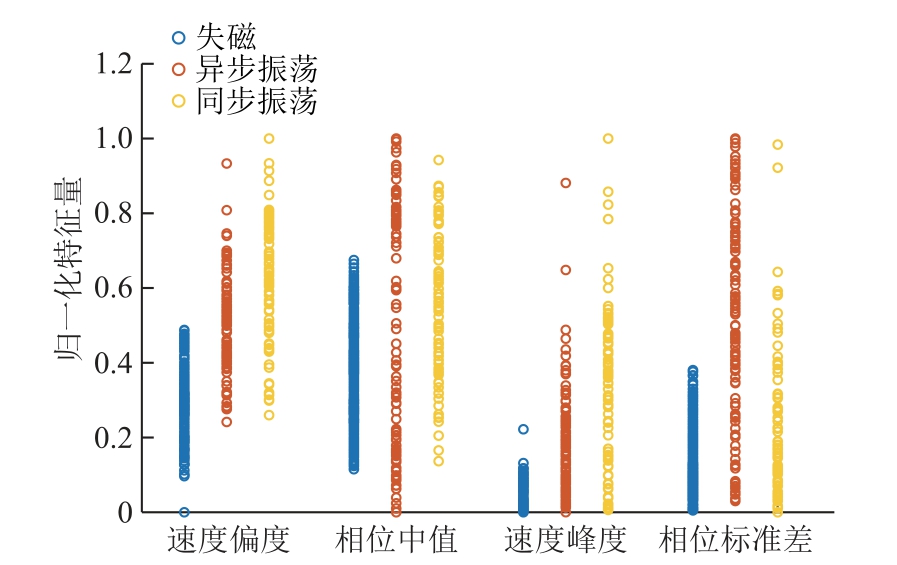
图10 不同扰动的前4 维特征归一化大小
Fig.10 Normalized size of the first four features of different disturbances

图11 前3 维归一化特征组成的特征空间
Fig.11 Feature space composed of first three-dimensional normalized features
由此可知,异步振荡的速度由于存在滑极现象,在一周期内速度具有个别极大值,所以其速度分布属于程度较大的正偏,而同步振荡则属于程度较小的正偏,又因二者存在周期性则峰度均较大;失磁故障阻抗在等功率圆的速度较大且差异很小,随着轨迹的拉长由负偏逐步过渡较小的正偏,相位中值自然也逐渐过渡为负值,另外轨迹在转为异步运行之前具有明显的单调性,所以其速度峰度很小。实际电网运行工况复杂,多发生未失稳的同步振荡,需要结合多个特征量共同判别,但由图11 可知结合前3 个特征量就已经具有很高的区分度。
为了验证具有精英保留规则的改进遗传优化算法是否具有更优良的性能,在基于1 s 时窗的最优特征集下分别采用传统遗传算法(Genetic Algorithm,GA)和粒子群算法(Particle Swarm Optimization,PSO)对参数进行优化,种群大小和最大迭代次数分别为80 和100,IGA 的杂交率范围为[0.5,0.9],变异率范围为[0.01,0.1]。三种优化方法的收敛过程如图12 所示,其他时窗下的算法收敛过程如附图2所示。由此可知,所提出的IGA 采取非线性自适应交叉变异策略能够依据种群收敛情况自行调整交叉变异概率,精英保留策略可以更好地保留每一代较优的种群。相对于GA 与PSO,IGA 一定程度上可以提高算法的寻优精度。需要注意的是,由于本文采用随机交叉验证方式训练模型,因此主要关注种群的适应度平均值。
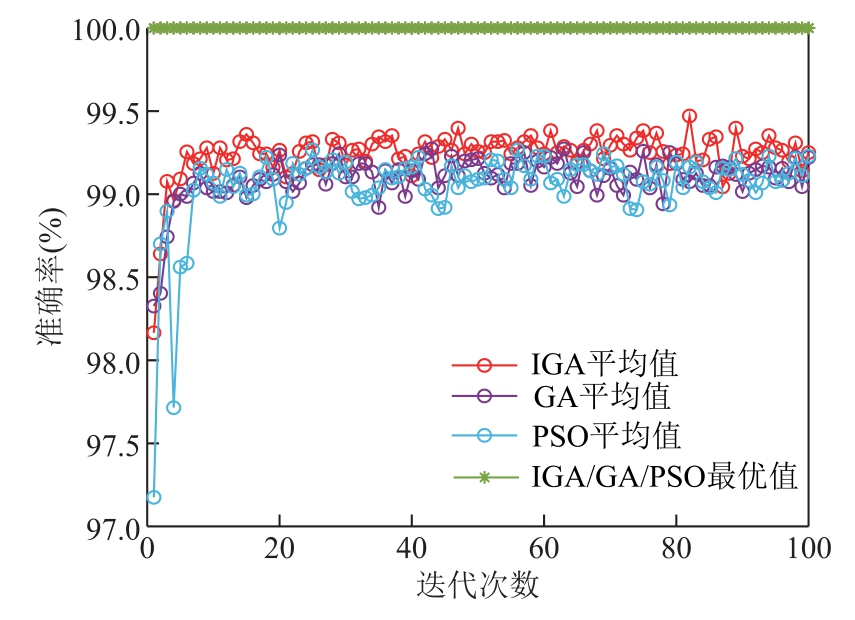
图12 不同优化算法的收敛过程
Fig.12 Convergence curves of different optimization algorithms
4.3 失磁保护测试结果
依次选择前k 个特征组成特征集Fk 输入不同时窗判别模型进行训练,同时将未进行特征选择的特征集F 也进行训练,训练最短时窗取0.3 s,其他时窗在0.5~3 s 范围内间隔0.5 s 选取。利用验证集得到的随机交叉验证和最优分类结果见附表 3 和附表4。由附表3 和附表4 可知,输入特征集为F 得到的分类准确率相对于Fk 并无太大差别,甚至会低于后者,这说明利用mRMR 特征选择算法可以去除冗余信息,提高训练效率和准确率。
单时窗下所训练模型的准确率由于轨迹差异大而达不到100%,这时可通过基于分类函数距离的双时窗失磁判别策略来提高模型的可靠性。设定临界域阈值L1,min 与L2,min 均为1,将位于临界域中包含错分样本的验证样本利用长时窗计算 Fk2 输入MKLSVM2 模型进行第二次决策。图13 展现了短时窗为0.3 s 和长时窗为1.5 s 的决策过程。可以看到,在短时窗下有7 个失磁样本和5 个扰动振荡样本位于临界域内,1 个失磁样本被漏判,也位于临界域内。将样本输入长时窗模型进行第二次决策,这时基于短时窗失磁判别模型位于临界域的所有样本全部可以脱离临界域,而唯一漏判的失磁样本也能够被修正。综上所述,经过两步决策,样本的分类准确率达到100%。

图13 验证集基于分类函数距离的双时窗决策结果
Fig.13 Two time window decision results based on classification function distance of verification set
为了更好地体现所提失磁方案的优越性,利用主判据为苹果形阻抗动作特性的传统失磁保护对验证集进行对比测试,保护采用实际广泛应用的“与”门出口逻辑,传统保护与所提保护的动作以及用时情况见表2。
表2 传统失磁保护与所提失磁保护的动作情况
Tab.2 Action of traditional and proposed loss of excitation protection

由此可见,在采用基于分类函数距离的双时窗判别策略的情况下准确率均值均能达到100%,即在1.5 s 内便可将失磁故障检测出来,对比传统失磁保护,智能失磁保护的速动性和可靠性均得到极大提升。
5 失磁保护新方案的应用分析
5.1 模型应对电网变化的泛化能力分析
为了测试模型的泛化能力,在前述系统的基础上改变仿真条件构建测试集对训练模型进行泛化能力的评估。结合IEEE 39 节点电网拓扑结构,考虑接入强弱不同的电力系统以及风光混合的新能源电力系统,在各种不同运行条件下仿真失磁故障和其他异常运行状态。系统结构如图14 所示,失磁保护方案的验证均在三台并列运行的水轮发电机之一G1 上进行,G5 为风光混合电源,在39 节点上分别设置三相和单相短路,其余仿真条件同简单电力系统。此外还考虑了附近机组增多、负荷正常波动、潮流控制、变压器分接头调整以及分布式电源侧的功率波动等工况。在上述条件下,共计产生800 组仿真测试样本,包括各类失磁样本240 组,涉及不同短路类型、位置、时长、过渡电阻的短路样本312组,其他扰动样本248 组。

图14 基于IEEE 39 节点不同电源接入的扩展电网系统
Fig.14 Extended power grid system with different power access based on IEEE 39 nodes
将仿真得到的测试集用来评估通过前述简化等效电力系统所训练的辨识模型的泛化能力,如图15所示。二者归一化方法以及输入特征相一致。

图15 辨识模型泛化能力测试示意图
Fig.15 Schematic diagram of identification model generalization ability test
不同单时窗下测试集分类结果评价指标见附表5。由此可知,单时窗下MKLSVM 均具有一定的泛化能力,基本随着时间窗长的增加准确率有所上升,分类准确率在92.81%~98.13%之间。
通过MKLSVM 采用双时窗失磁保护识别策略对测试集进行判别,设定短时窗为0.3 s,长时窗为1.5 s,得到两步决策过程如图16 所示。由图6 可知,测试集经过第二次决策,第一次决策位于临界域内的样本点一部分能脱离临界域,误判的样本点也从53 个减少到11 个,正确率大大提高。

图16 测试集基于分类函数距离的双时窗决策结果
Fig.16 Two time window decision results based on classification function distance of test set
对不同时间窗组合进行10 次交叉测试,测试结果均值见表3。由表3 可知,在采用基于分类函数距离的双窗判别策略的情况下测试集准确率均值均能达到96.95%以上,这说明在电网发生大范围变化,包括分布式能源系统接入的情况下,所提出的智能失磁识别方法仍具有优良的适用能力。
表3 测试集双时窗分类决策结果
Tab.3 The results of double time window classification decision of test set

需要说明的是,上述决策结果中误判样本主要是第一步训练未曾涉及的复杂电网工况。离线训练模型时,完全可以考虑到未来电网可能发生的变化以及相应工况,此时失磁保护的测试准确率仍可达到100%,此节仅是严格考验在未考虑电网发生大范围变化以及其他扰动情况下的适用能力。
5.2 基于MKLSVM 失磁保护判据影响因素分析
5.2.1 核函数权重
在特征选择以及模型训练优化过程中,输出核函数权重α 对验证集准确率的影响,具体如附图1所示。注意到准确率关于MKLSVM 核函数权重α 变化并不敏感,这是因为在同一仿真条件下进行模型训练和验证时,目标函数均关注训练集以及验证集分类的准确率,二者在数据分布上联系较为紧密,整个训练过程只能说明不同的核函数均具有一定的学习能力,且RBF 核函数较优于Poly 核函数,但无法充分体现模型对新样本的适应能力,所以α对模型验证集准确率影响较小。
为了对比SVM 与MKLSVM 的泛化能力效果,将权重分别设为0 和1,即多核函数退化为Poly 和RBF 单核函数,对模型进行训练和测试,测试结果见附表6 和附表7,三种模型的单时窗分类评价指标均值见表4。
表4 不同辨识模型的单时窗分类评价指标均值
Tab.4 Mean value of single time window classification evaluation indexes of different identification models

由此可知,由Poly 核函数与RBF 核函数加权组合核函数训练的MKLSVM 能够同时兼顾数据分布的局部和全局信息,泛化能力强于单核函数训练的SVM。
为了进一步说明采用多核函数训练模型融合基于分类函数距离的双时窗失磁判别策略具有优良的泛化能力的同时又具有高可靠性,短时间窗选取 0.3 s 和0.5 s,长时间窗选取1 s 和1.5 s,将单核SVM 模型采用双时窗策略分别进行4×10 次测试,测试结果取平均值。同时输出训练过程中验证集准确率均值,并与MKLSVM 模型的分类表现进行对比,结果见表5。
表5 不同辨识模型的双时窗分类评价指标均值
Tab.5 Mean value of two time window classification evaluation indexes of different identification models

由表5 可见,MKLSVM 融合双时窗判别策略可以保证失磁保护的可靠性。对于离线所训练的水轮机智能失磁保护模型来说,核函数权重α 并不是影响模型验证集准确率的关键因素,但α 会极大地影响模型的泛化能力,实际中使用混合核函数训练的模型能够保证在较强的学习能力的前提下有效增强模型的适用性。
5.2.2 时窗长短
由5.1 节可知,随着时窗的增加,验证集准确率均值并不能得到有效提升,多次交叉验证分类精度均有较小的偏差。究其原因在于不同时间段,不同类别失磁与不同类别扰动振荡的机端测量阻抗轨迹长度和特点相差甚远。
在两步决策过程中,将不同负载下失磁样本的核空间相对判别距离表示出来,长短时窗下失磁样本在核空间的相对位置如图17 所示。注意到第一步位于临界域的失磁样本往往归属于中轻载工况,满载较严重的失磁处于临界域外侧,这是因为短时窗下包含的严重失磁轨迹信息较其他失磁更多,从而更有利于重载且严重的失磁判别;若时窗过长,重载下严重的失磁会使发电机在后期步入异步运行从而掩盖前期的特征,而较轻程度的失磁却拥有更多的轨迹信息,从而更有利于其判别。这也是时窗增加但准确率却不能得到提高的原因,同时也说明失磁的严重程度与决策所需的时间窗大致成反比,恰好满足了失磁保护的速动性。

图17 长短时窗下失磁样本在核空间的相对位置
Fig.17 Relative position of loss-of-excitation samples in kernel space under long and short time windows
对于测试集而言,根据附表 5~附表 7,MKLSVM 的分类准确率随时窗的增大有所提高,而单核SVM 的分类准确率均上下波动。对于前者,时间窗越长,全局以及局部信息越丰富,与原始训练模型的已知信息匹配度越高,泛化能力也就越好;对于后者,时间窗的增长会改变数据的分布,而单核SVM 无法同时兼顾全局与局部信息,所以准确率会随数据分布的改变而有较大的波动。
综合算例的结果,可知基于水轮机机端测量阻抗轨迹变化智能识别的方法最快可在0.3 s 内将严重的失磁故障辨别出来,最慢也在1.5 s 内。实际应用时,涉及对于长短时窗选择问题,对于短时窗的选择,建议根据发电机失磁最快步入静稳边界圆时间为下限,但不能过小,以免判别程序受暂态过程影响过大,至于长时间窗,应根据系统的安全要求灵活确定。
6 结论
提出了基于水轮发电机测量阻抗轨迹变化智能识别的失磁保护新原理,与传统失磁保护相比,无需人工整定,且具有较强的适应能力,解决了速动 性和可靠性的矛盾。
1)新原理利用机理型传统失磁保护中物理含义明确的测量阻抗轨迹特征指导人工智能的框架设计,既弥补了传统失磁保护只关注局部结果的缺陷,也充分发挥了人工智能算法的全局信息挖掘能力强、计算速度快的优势。
2)采用mRMR 特征选择算法,可以最大化关键特征与类别间的相关性,同时最小化特征间的冗余性,增强了模型可解释性。利用自适应遗传算法优化兼顾全局与局部信息的MKLSVM 的同时,采用基于分类函数距离的双时窗判别策略既提升模型训练效率也增强了模型的可靠性和泛化能力。
3)提出的失磁故障判别原理与接入外电网强弱以及电网的拓扑结构无关,可以兼顾外电网附近机组动态过程对测量阻抗轨迹的影响,在电网发生大范围变化时仍具有优良的适应性。
附 录
理论推导过程如下。
以水轮发电机-无穷大系统为例,忽略发电机定子绕组的电阻及联系电抗中的电阻成分,采用标幺值进行计算,稳态下无穷大母线处通过无功功率 Qs 为
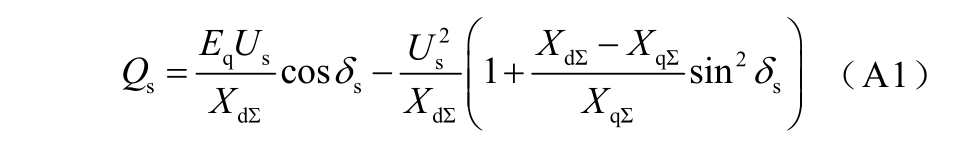
式中,XdΣ=X d + Xs,XqΣ=X q + Xs,Xd、Xq分别为凸极机直轴、交轴同步电抗,Xs为系统联系电抗;δs为发电机功角;Eq为凸极机横轴电动势;Us为系统侧电压。
在失磁初始阶段,有功功率基本保持不变,发电机的测量阻抗为[1]
式中,Ps 为无穷大母线处通过的无功功率;φ=arctan(Qs/Ps)。由式(A2)可知,测量阻抗的变化速度v 取决于φ 的变化速度,即
φ 的变化速度具体为

当对vφ 求导得

在发电机发生失磁故障后的初始阶段,定子电动势Eq的变化为[1]
式中,Eqp为部分失磁后还可提供的同步电动势,若发生全部失磁,则 Eqp为0;Eqp0为失磁前的定子电动势;Td'为定子开路时的励磁绕组时间常数,一般为0.8~1.5 s。
由式(A1)和式(A6),求得无功对时间的一阶导数为

在失磁的初始阶段,可认为 δs保持不变,于是式(A7)可简化为

在式(A8)基础上,同样假设 δs保持不变,进一步求得无功的二阶导数为
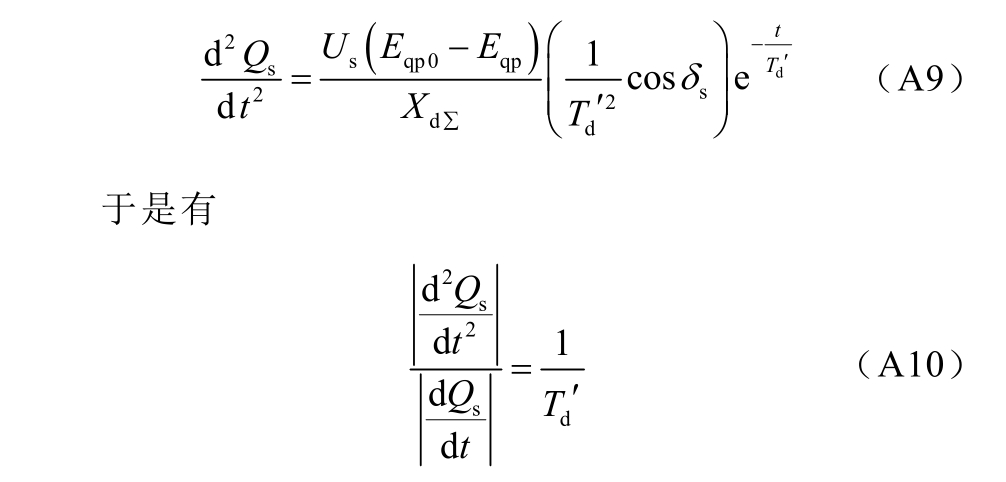
根据式(A8)~式(A10)可知,在失磁后的功角变化不大的时间内,无功的一阶导数始终为负,而二阶导数始终为正,且前者与后者的大小比值约为 Td'。由此可对式(A5)进行定性分析:当失磁导致发电机由发出无功变成吸收无功后,式(A5)始终小于零,vφ 将持续递减,即表明测量阻抗的变化速度v 将持续递减。
但以上分析忽略了次暂态过程,在失磁扰动发生的次暂态时间内,测量阻抗变化速度v 从零将会快速增大到某个值。
综合来说,失磁发生后发电机未失步前测量阻抗的变化速度可以总结为快速上升至极大值,然后持续下降。
附表1 水轮发电机出力情况
App.Tab.1 Output of hydraulic turbine
附表2 失磁与扰动场景设置
App.Tab.2 Setting of loss of excitation and disturbance scene
附表3 特征向量为Fk 时不同单时窗下的模型分类结果
App.Tab.3 Model classification results under different single time windows when feature set is Fk

附表4 特征向量为F 时不同单时窗下的模型分类结果
App.Tab.4 Model classification results under different single time windows when feature set is F
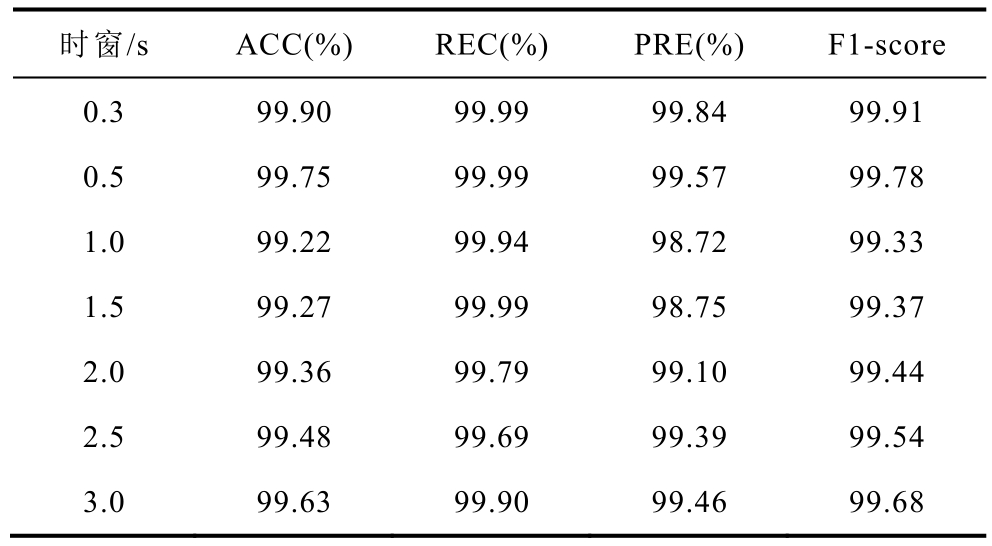
附表5 MKLSVM 不同单时窗下的分类评价结果
App.Tab.5 Classification and evaluation results of MKLSVM under different single time windows

附表6 RBF-SVM 不同单时窗下的分类评价结果
App.Tab.6 Classification and evaluation results of RBF-SVM under different single time windows

附表7 Poly-SVM 不同单时窗下的分类评价结果
App.Tab.7 Classification and evaluation results of Poly-SVM under different single time windows


附图1 验证集分类准确率随权重α 的变化
App.Fig.1 Variation curve of classification accuracy of verification set with weight α

附图2 不同时窗下不同优化算法的收敛过程
App.Fig.2 Convergence process of different optimization algorithms under different time windows
[1]姚晴林.同步发电机失磁及其保护[M].北京: 机械工业出版社,1981.
[2]常忠蛟,刘云.巴西电网“3.21”大停电中控制保护系统动作分析及启示[J].电网技术,2020,44(11): 4415-4426.Chang Zhongjiao,Liu Yun.Analysis on and inspiration of the control and protection actions during “0321/March 21” blackout in Brazilian power grid[J].Power System Technology,2020,44(11): 4415-4426.
[3]郑涛,余青蔚,詹荣荣,等.调相机接入对发电机失磁保护的影响[J].电力系统保护与控制,2018,46(4): 50-56.Zheng Tao,Yu Qingwei,Zhan Rongrong,et al.Impact of synchronous condenser access on generator loss of excitation protection[J].Power System Protection and Control,2018,46(4): 50-56.
[4]沈全荣,陈佳胜,陈俊,等.基于导纳特性的水轮发电机失磁保护新判据[J].电力自动化设备,2017,37(7): 220-223.Shen Quanrong,Chen Jiasheng,Chen Jun,et al.LOE protection criterion based on admittance characteristic for hydraulic generator[J].Electric Power Automation Equipment,2017,37(7): 220-223.
[5]李晖,鲁功强,王育学,等.大型水轮发电机失磁保护与低励限制配合问题的探讨[J].电力系统保护与控制,2014,42(5): 68-72.Li Hui,Lu Gongqiang,Wang Yuxue,et al.Discussion on coordination between loss of excitation protection and under excitation limit control for large hydrogenerator[J].Power System Protection and Control,2014,42(5): 68-72.
[6]Hasani A,Haghjoo F.Fast and secure detection technique for loss of field occurrence in synchronous generators[J].IET Electric Power Applications,2017,11(4): 567-577.
[7]Hasani A,Haghjoo F,da Silva F M F,et al.A currentbased differential technique to detect loss of field in synchronous generators[J].IEEE Transactions on Power Delivery,2020,35(2): 514-522.
[8]Noroozi N,Alinejad-Beromi Y,Yaghobi H.Fast approach to detect generator loss of excitation based on reactive power variation[J].IET Generation,Transmission &Distribution,2019,13(4): 453-460.
[9]贾德峰,王明东,傅润炜,等.抽水蓄能机组RTDS 仿真与失磁保护改进研究[J].电力系统保护与控制,2021,49(3): 158-164.Jia Defeng,Wang Mingdong,Fu Runwei,et al.RTDS simulation and improvement of excitation-loss protection for pumped storage units[J].Power System Protection and Control,2021,49(3): 158-164.
[10]李峰,王琦,胡健雄,等.数据与知识联合驱动方法研究进展及其在电力系统中应用展望[J].中国电机工程学报,2021,41(13): 4377-4389.Li Feng,Wang Qi,Hu Jianxiong,et al.Combined data-driven and knowledge-driven methodology research advances and its applied prospect in power systems[J].Proceedings of the CSEE,2021,41(13): 4377-4389.
[11]de Morais A P,Cardoso G,Mariotto L.An innovative loss-of-excitation protection based on the fuzzy inference mechanism[J].IEEE Transactions on Power Delivery,2010,25(4): 2197-2204.
[12]Amraee T.Loss-of-field detection in synchronous generators using decision tree technique[J].IET Generation,Transmission &Distribution,2013,7(9): 943-954.
[13]Ostovic V.Memory motors-a new class of controllable flux PM machines for a true wide speed operation[C]//Conference Record of the 2001 IEEE Industry Applications Conference,36th IAS Annual Meeting (Cat.No.01CH37248),Chicago,IL,USA,2001: 2577-2584.
[14]Rasoulpour M,Amraee T,Sedigh A K.Loss of field protection in synchronous generators based on data mining technique[C]//2019 Smart Grid Conference (SGC),Tehran,Iran,2019: 1-6.
[15]Rasoulpour M,Amraee T,Sedigh A K.A relay logic for total and partial loss of excitation protection in synchronous generators[J].IEEE Transactions on Power Delivery,2020,35(3): 1432-1442.
[16]吴雪莲,刘福锁,李兆伟,等.基于联络线功率轨迹特征的暂态功角稳定性分析[J].中国电机工程学报,2019,39(11): 3194-3201.Wu Xuelian,Liu Fusuo,Li Zhaowei,et al.Analysis of transient power angle stability based on the characteristics of power trajectory[J].Proceedings of the CSEE,2019,39(11): 3194-3201.
[17]王长江,姜涛,刘福锁,等.基于轨迹灵敏度的暂态过电压两阶段优化控制[J].电工技术学报,2021,36(9): 1888-1900,1913.Wang Changjiang,Jiang Tao,Liu Fusuo,et al.Twostage optimization control of transient overvoltage based on trajectory sensitivity[J].Transactions of China Electrotechnical Society,2021,36(9): 1888-1900,1913.
[18]朱存浩,马世英,郑超,等.基于实测响应轨迹的电力系统暂态不稳定判别[J].中国电机工程学报,2021,41(15): 5077-5090.Zhu Cunhao,Ma Shiying,Zheng Chao,et al.Power system transient instability identification based on real-time response trajectory[J].Proceedings of the CSEE,2021,41(15): 5077-5090.
[19]杨少波,刘道伟,安军,等.基于长短期记忆网络的电网动态轨迹趋势预测方法[J].中国电机工程学报,2020,40(9): 2854-2865.Yang Shaobo,Liu Daowei,An Jun,et al.Trend prediction method of power network dynamic trajectory based on long short term memory neural networks[J].Proceedings of the CSEE,2020,40(9): 2854-2865.
[20]戎子睿,林湘宁,金能,等.基于相空间轨迹识别和多判据融合的变压器保护新策略[J].中国电机工程学报,2020,40(6): 1924-1937.Rong Zirui,Lin Xiangning,Jin Neng,et al.A new transformer protection scheme based on the recognition of phase space trajectory and multicriteria fusion[J].Proceedings of the CSEE,2020,40(6): 1924-1937.
[21]李宗博,焦在滨,何安阳.基于等效磁化曲线智能识别的变压器保护原理[J].电工技术学报,2020,35(7): 1464-1475.Li Zongbo,Jiao Zaibin,He Anyang.Equivalent magnetization curve intelligent recognition based transformer protection[J].Transactions of China Electrotechnical Society,2020,35(7): 1464-1475.
[22]汤奕,崔晗,李峰,等.人工智能在电力系统暂态问题中的应用综述[J].中国电机工程学报,2019,39(1): 2-13,315.Tang Yi,Cui Han,Li Feng,et al.Review on artificial intelligence in power system transient stability analysis[J].Proceedings of the CSEE,2019,39(1): 2-13,315.
[23]陈宗遥,卜旭辉,郭金丽.基于神经网络的数据驱动互联电力系统负荷频率控制[J].电工技术学报,2022,37(21): 5451-5461.Chen Zongyao,Bu Xuhui,Guo Jinli.Neural network based data-driven load frequency control for interconnected power systems[J].Transactions of China Electrotechnical Society,2022,37(21): 5451-5461.
[24]吴月宝,赵晋斌,张少腾,等.基于径向基神经网络的多负载无线电能传输系统自适应阻抗匹配方法[J].电工技术学报,2021,36(19): 3969-3977.Wu Yuebao,Zhao Jinbin,Zhang Shaoteng,et al.An adaptive impedance matching method based on radial basis function neural network in multi-load wireless power transfer systems[J].Transactions of China Electrotechnical Society,2021,36(19): 3969-3977.
[25]薛禹胜,赖业宁.大能源思维与大数据思维的融合(一)大数据与电力大数据[J].电力系统自动化,2016,40(1): 1-8.Xue Yusheng,Lai Yening.Integration of macro energy thinking and big data thinking part one big data and power big data[J].Automation of Electric Power Systems,2016,40(1): 1-8.
[26]Peng Hanchuan,Long Fuhui,Ding C.Feature selection based on mutual information criteria of maxdependency,max-relevance,and Min-redundancy[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8): 1226-1238.
[27]Li Yang,Zhu Zhichuan,Hou Alin,et al.Pulmonary nodule recognition based on multiple kernel learning support vector machine-PSO[J].Computational and Mathematical Methods in Medicine,2018,2018: 1461470.
[28]黄彦浩,于之虹,史东宇,等.基于海量在线历史数据的大电网快速判稳策略[J].中国电机工程学报,2016,36(3): 596-603.Huang Yanhao,Yu Zhihong,Shi Dongyu,et al.Strategy of huge electric power system stability quick judgment based on massive historical online data[J].Proceedings of the CSEE,2016,36(3): 596-603.
[29]周艳真,吴俊勇,冀鲁豫,等.基于两阶段支持向量机的电力系统暂态稳定预测及预防控制[J].中国电机工程学报,2018,38(1): 137-147,350.Zhou Yanzhen,Wu Junyong,Ji Luyu,et al.Two-stage support vector machines for transient stability prediction and preventive control of power systems[J].Proceedings of the CSEE,2018,38(1): 137-147,350.
[30]Laube P,et al.Movement beyond the snapshot -dynamic analysis of geospatial lifelines[J].Computers,Environment and Urban Systems,2007,31(5): 481-501.
[31]王学民.应用概率统计[M].上海: 上海财经大学出版社,2005.
[32]石访,张林林,胡熊伟,等.基于多属性决策树的电网暂态稳定规则提取方法[J].电工技术学报,2019,34(11): 2364-2374.Shi Fang,Zhang Linlin,Hu Xiongwei,et al.Power system transient stability rules extraction based on multi-attribute decision tree[J].Transactions of China Electrotechnical Society,2019,34(11): 2364-2374.
[33]李阳,常佳乐,王宇阳.基于群体智能优化的MKL-SVM 算法及肺结节识别[J].工程科学学报,2021,43(9): 1157-1165.Li Yang,Chang Jiayue,Wang Yuyang.MKL-SVM algorithm for pulmonary nodule recognition based on swarm intelligence optimization[J].Chinese Journal of Engineering,2021,43(9): 1157-1165.
[34]江涛,张志安,程志,等.改进遗传算法与领航跟随法的机器人编队方法[J].计算机工程与应用,2020,56(3): 240-245.Jiang Tao,Zhang Zhian,Cheng Zhi,et al.Robot formation method with improved genetic algorithm and leader-follower[J].Computer Engineering and Applications,2020,56(3): 240-245.