0 引言
随着我国“碳达峰，碳中和”目标的提出，能源系统的低碳转型迫在眉睫。可再生能源发电具有随机性、间歇性强的特点，客观上需要一定规模的灵活调节电源与之相匹配。其中，天然气发电在与可再生能源形成互补，支持和加速可再生能源大规模发展上具有重要意义：燃气机组响应速度快、调峰能力强，是电网灵活高效的调控手段。发达国家的可再生能源发展经验表明，如果没有天然气发电支撑电力系统的调峰能力，可再生能源很难大规模使用[1]。而燃气机组装机比例的提升，势必进一步加深电力和天然气系统间异质能流的耦合关系。对于气网而言，燃气机组的快速调整是剧烈的气负荷波动，可能对气网安全运行造成不利影响。此外，燃气机组对进气口压力范围具有严格的要求，高于或低于压力范围都会威胁燃气机组的安全运行，甚至造成停运事故[2]。因此，如何应对电力-天然气互联系统中的潜在安全风险是目前学术和工业界关心的热点话题。
在电力-天然气互联系统（Electricity-Gas Interconnected System,EGIS）发生N-1 故障后，有效的校正控制措施可以消除系统安全越限，同时避免故障由耦合元件传播扩散进而引发系统间连锁故障。最优校正控制策略通过求解以故障后系统状态为基准运行点的EGIS 安全约束最优能流模型获得，但对求解效率和精度提出了更高的要求[3]。目前关于EGIS 最优能流模型的研究中，对电网普遍基于稳态潮流构建运行约束[4]。对天然气系统，其运行约束可分为三大类：基于稳态管流的运行约束[5-11]、考虑近似动态管流的运行约束[12-16]和计及精确动态管流的运行约束[17-20]。
其中，基于稳态管流的运行约束通过非凸的Weymouth 方程[21]刻画天然气系统运行情况。文献[5-7]基于气网的稳态Weymouth 方程构建了EGIS的最优能流模型，其中文献[7]针对EGIS 最优能流高维、非凸、非线性特性，提出一种多目标差分进化算法。文献[8]基于气网稳态Weymouth 方程构建了一种电-气-热综合能源系统概率最优能流模型。为了提升非凸模型的优化效率。文献[9]提出一种电-气互联系统多目标优化调度模型，并将非凸的Weymouth 方程凸松弛为二阶锥约束。文献[10]将Weymouth 分段线性化，构建EGIS 多目标优化调度模型。文献[11]基于分段线性化的Weymouth 方程，提出一种多能流混合整数规划模型。尽管EGIS 中考虑气网稳态管流对于系统中长期的规划分析具有一定参考价值，但同时必须指出，气网的动态过程与电能平衡的瞬时性相比十分缓慢，一般长达数分钟至数小时之久。求解稳态管流模型，得到的是已经运行了一段时间之后的气网状态，而忽视了其动态过渡过程。因此，对于校正控制而言，仅考虑气网稳态管流难以确保得到的控制策略不造成气网的动态管流发生安全越限。
针对稳态管流运行约束的缺陷，文献[12]将稳态Weymouth 方程与管存模型相结合，提出一种气网的近似动态管流模型，在一定程度上考虑了气网的慢动态特性。该方法在文献[13-14]中被进一步用于EGIS 的安全校正控制与日内多时段优化调度中。文献[15]针对近似动态模型中Weymouth 方程的二阶锥约束松弛间隙过大的问题，提出一种序贯锥规划算法，提高了最优能流的计算精度。但近似动态管流模型在对气网管流物理本质的精细刻画上仍显不足，且其与精确管流仿真结果的误差有待进一步分析验证。
天然气系统的动态管流过程其物理本质是管道两端压力差驱动管内气体运动，在数学上可通过一组与时间和空间相关的偏微分方程（Partial Differential Equation,PDE）精细化描述。但如果直接将PDE 作为气网的运行约束条件，则构成无限维的动态规划问题，难以直接求解。现有计及气网精确动态管流的EGIS 优化分析方法一般先通过差分法对管流PDE 进行离散化处理，将其转换为有限维的代数方程约束，然后采取相应的优化方法求解。文献[16]基于隐式有限差分法将管流PDE 转换为非线性代数方程组，然后用牛顿法求解包含该非线性方程组的EGIS 多时段暂态能流方程。文献[17]进一步基于该隐式差分管流模型，提出一种适用于预防-校正控制的EGIS 最优能流模型。但该文献同时指出，由于非线性管流约束与遍历算法的局限，该模型在求解过程中难免存在时效性降低的问题，且控制策略一般为局部最优解。文献[18]提出一种EGIS动态最优能流分析方法，基于Wendroff 格式构建了动态管流的显式差分模型，并通过算例仿真验证了该模型的精度。上述Wendroff 差分法在文献[19]中被进一步应用于EGIS 故障传播演化分析，模拟了气网中负荷波动以及输气管道泄露事故向电网的传播与扩散过程。类似地，文献[20]基于Wendroff 差分法提出一种计及电网稳态和气网动态的日内多时段规划调度模型。基于Wendroff 差分的气网管流[18]对于气网状态变量为一阶线性模型，可以通过商业求解器直接求解。但是，Wendroff 差分法对PDE 方程的拟合精度与其差分网格数量的选取关系密切：如果差分网格过于稀疏，优化结果并不能收敛到原PDE 方程的解；而如果希望获得高精度的气网管流结果，则需要设置密集的差分网格，这会大幅增加优化问题的求解规模，导致计算量上升、求解效率下降的问题。
正交配置法（Orthogonal Collocation,OC）作为求解动态规划问题的直接法，其主要思想是采用Lagrange 插值多项式对控制和状态变量同时离散[22]。与传统差分方法相比，OC 具有计算精度高、数值稳定性好等优点[23]。对基于PDE 描述的气网管流约束，采用时空正交配置法（Space-Time OC,STOC）可以将其离散化为时空配置点处的代数方程约束[24]。这为EGIS 异质能流的高效分析与优化计算提供了新的思路。目前，对基于STOC 处理EGIS 动态规划问题的工作鲜有报道。
归纳而言，当前EGIS 相关研究在电网侧建模方法相对成熟，但对于气网动态管流的处理尚存不足。尤其现有方法难以同时保证计算精度和效率，而获取最优校正控制策略需要在故障后针对系统运行状态进行在线计算，对于优化方法的精确性和高效性都具有更高的要求。为此，本文提出基于STOC构建天然气网的精确动态管流约束，并基于该约束构建以校正控制代价最小为目标的安全约束最优能流模型，以获取最优校正控制策略。最后通过算例分析验证了STOC 方法与现有方法相比在计算效率和精度上的优越性，以及所得EGIS 最优校正控制策略的有效性。
1 气网动态管流模型
1.1 动态管流的偏微分方程模型
天然气管道中的动态管流过程，其物理本质是管道两端压力差驱动管内气体运动的流体力学过程。由管道端点压力驱动的天然气流量大小取决于其成分、温度、密度、压力等物理状态。一般而言，此过程中各个变量的关系通过三个主要的方程描述：气体动量方程、物料平衡方程及状态方程。
气体动量方程描述了气体的流体力学过程，也被称为Navier-Stokes 方程，表示为[21]
式中，t 为时间；x 为管道位置；v 为气体流速；ρ 为气体密度；p 为气体压力；g 为重力加速度；α 为管道曲度；D 为管内壁直径；λ 为管壁摩擦系数。式（1）中，前三项描述了天然气的加速度、对流和静压效应；第四项与管道的高度偏差相关；第五项表示二阶偏应力张量。在忽略管道高程变化和对流效应时，第二、四项可忽略，从而Navier-Stokes 方程（1）简化为
式中，二阶偏应力张量项为非线性项，因此造成后续所构建优化模型的求解困难。文献[18]利用气体平均流速对该项进行线性化近似，并验证了该线性化近似方法能够较好地拟合原非线性偏微分方程的解。气体平均流速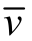
与质量流率和气体密度的关系为
式中，f 为气体质量流率；A 为输气管道的横截面积。将式（3）代入式（2）可得Navier-Stokes 方程近似表达式为
物料平衡方程描述了天然气管道中的质量守恒关系，表示为
状态方程构建了气体温度、密度和压力之间的物理关系，假设满足理想气体条件，则气体压力和密度的关系可表示为
式中，c 为气体音速；Z 为气体压缩系数；R 为普适气体常数；T 为气体热力学温度。
化简式（3）～式（6），天然气管道的动态管流模型可通过式（7）近似描述。
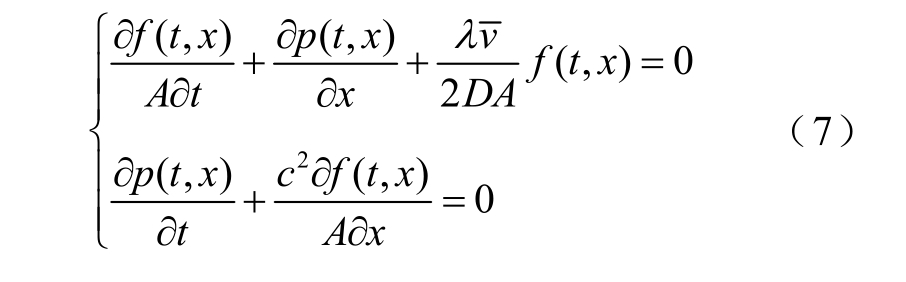
由于上述气网暂态管流偏微分方程的存在，如果直接将其作为约束条件将构成无限维的动态规划问题，难以直接求解。
1.2 基于时空正交配置法的离散动态管流模型
OC 在整个求解域上采用高阶插值多项式作为待求量的近似函数，并使微分方程在给定的配置点上精确成立。OC 不同于差分法的固定低阶速率，具有谱精度特点[23]：随着插值多项式阶次的升高，近似解将以任意阶的速率收敛于精确解，且精确解越光滑，收敛速度越快，通常可达到指数阶。因此，OC 采用较少的配置点即可达到较高的求解精度，显著降低离散问题规模，减少计算时间。此外，其形式简洁，可以方便地得到状态变量的近似解析解，同时易于求导。由于能够实现精度和效率的良好平衡，使得OC 适用于系统N-1 故障后的校正控制策略在线计算。
通常对于常微分方程，OC 通过一元Lagrange多项式对时变的状态变量在时域进行离散[22]。而对于天然气网络而言，动态管流变化不但与时间相关，还与空间位置有关。因此，本文基于STOC[24]对暂态管流模型（7）中的状态变量（即管道压力p 和质量流率f ），采用二元Lagrange 插值多项式进行时空同时离散。
设气网状态变量优化的时间域t∈[t0,tf]，空间域x∈[x0,xf]，则t 和x 可分别表示为
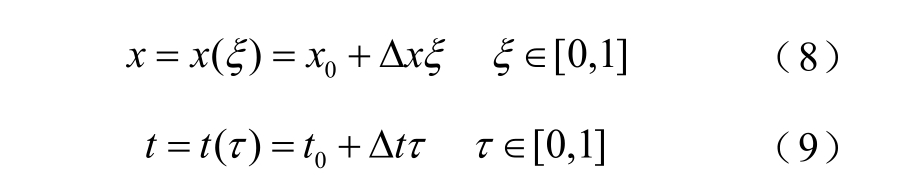
式中，ξ 为无量纲的空间坐标；τ 为无量纲的时间坐标；Δx 和Δt 分别为待优化的空间域长度（即管道长度）和时间域长度。设空间插值点个数为 Nx个，则在空间区间[x0,xf]中包括两端的x0 和xf 共有Nx+2 个空间离散点；设时间插值点个数为Nt 个，则在时间区间[t0,tf]中包括首端的t0，共有Nt+1 个时间离散点。定义Lagrange 时空插值多项式的基函数lij(ξ,τ)为
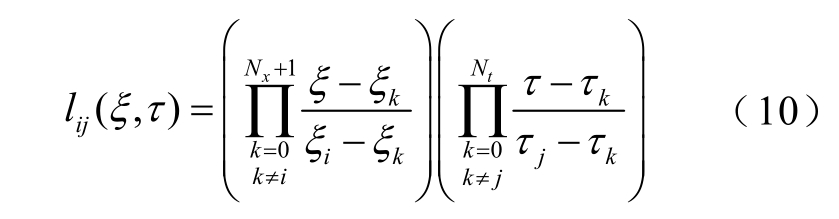
式中，变量 z i ,j为状态变量z 在时空配置点(ξi,τj)处的取值；i=0,1,…,Nx+1；j=0,1,…,Nt。
状态变量分量z 在 (xi,tj)处对于x 和t 的一阶偏导分别为
根据STOC 对气网管流偏微分方程（7）进行离散化。对于天然气管道，其质量流率和气体压力可表示为Lagrange 插值函数，即
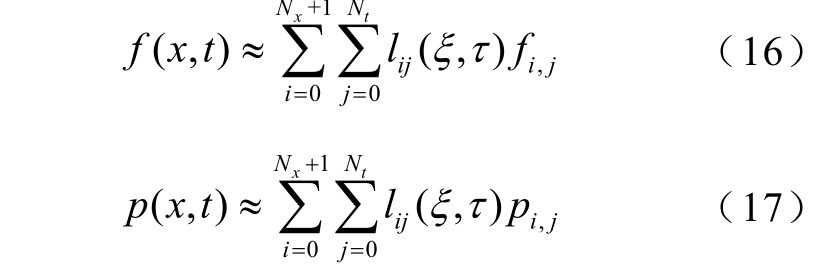
式中，fi,j 和pi,j 分别为质量流率f 和气体压力p 在时空配置点(ξi,τj)处的取值。f (x, t)和 p (x, t)的偏导可表示为
因此，无限维的偏微分方程组管流约束（7）可通过STOC 转换为在时空配置点处成立的有限维代数方程组约束。天然气管道在时空配置点(ξi,τj)处满足的约束条件为
式中，f i ,j,p i ,j为待优化决策变量。式（23）对于决策变量而言为线性化的等式约束，以其取代原PDE作为约束条件可降低优化模型的求解难度。对于单截管道而言，上述代数方程组约束共有(Nx+1)Nt 个，待优化的决策变量共有2(Nx+1)Nt 个。
1.3 时空配置点的类型与数量
采用STOC 处理气网动态管流PDE 模型（7），其精度和效率与配置点的类型与数量相关。目前常用的配置点类型有Legendre-Gauss（LG）、Legendre-Gauss-Radau（LGR）和Legendre-Gauss-Labotto（LGL）三种，其主要区别见表1[22]。
表1 三种配置点类型的区别
Tab.1 Differences between the three types of collocation point
在表1 中，LK 表示K 阶Legendre 多项式。文献[22]对基于LG、LGR 和LGL 三种类型的配置点离散后的最优控制问题的求解精度进行了详细的对比分析，验证了LG 和LGR 配置点在求解精度上略优于LGL 配置点。在文献[24]对于STOC 的验证中，状态变量在时间域采用了LGR 配置点进行离散，在空间域采用LG 配置点进行离散，所得结果验证了该方法的有效性和优越性。但文献[22,24]中算例验证考虑的均是低维的非线性控制问题，对于高维非线性的天然气网络而言，考虑到网络节点处还需满足流量平衡条件，必须将管道空间端点纳入配置点中，以便引入f(x,t)在管道端点处的状态变量参与优化。综合上述考虑，本文对气网状态变量在时间域采用LGR 配置点，在空间域采用LGL 配置点。在求解完成后，对于状态变量非配置点处的值可采用得到的Lagrange 插值多项式（16）和式（17）进行估计。
在对偏微分方程进行时空离散时，配置点数量的多少意味着Lagrange 插值多项式阶数的高低。多项式阶次越高，计算精度越高，但也会导致求解规模的增大，从而降低求解效率。因此需要对配置点数量进行合理设置。针对该问题，本文基于误差评价进行数量预估：由于STOC 离散后的约束式（23）在配置点处状态变量严格满足原偏微分方程约束式（7），而在非配置点处则可能存在一定误差，因此以配置点中间处对式（7）的违反情况作为误差评价依据，对时空配置点的数量进行预估。
2 面向校正控制的电-气互联系统安全约束最优能流模型
基于所构建的输气管道动态管流约束，本节进一步针对EGIS 中发生N-1 故障后的校正控制策略求解问题，构建以电网燃气机组和气网中的电加压站进行异质能流双向耦合的EGIS 安全约束最优能流模型。该模型以EGIS 故障前的调度策略为初始调度策略，以故障后的系统能流状态为基准运行点，以校正控制代价最小为目标函数，约束条件包含天然气系统约束、电力系统约束及电力-天然气耦合元件约束。其中，所考虑的天然气系统约束的动态管流时间窗口可根据调度系统实际情况、允许的校正控制时间和故障严重程度综合确定。对于EGIS已发生的确定N-1 故障场景所引发的安全越限，利用该优化模型可以得到控制代价最小的EGIS 协同校正控制策略，以消除越限事故，恢复系统安全运行。
2.1 天然气系统约束
安全约束最优能流模型中考虑的天然气系统约束包括动态管流约束、节点流量平衡约束、管道-节点关联约束、安全限值约束以及状态变量的边界条件约束。
设Υ 为天然气系统中节点的集合，∀m, n ∈Υ，根据所提基于STOC 的动态管流模型（23），天然气系统中的动态管流过程通过在时空配置点(ξi,τj)处满足式（24）所示约束条件。
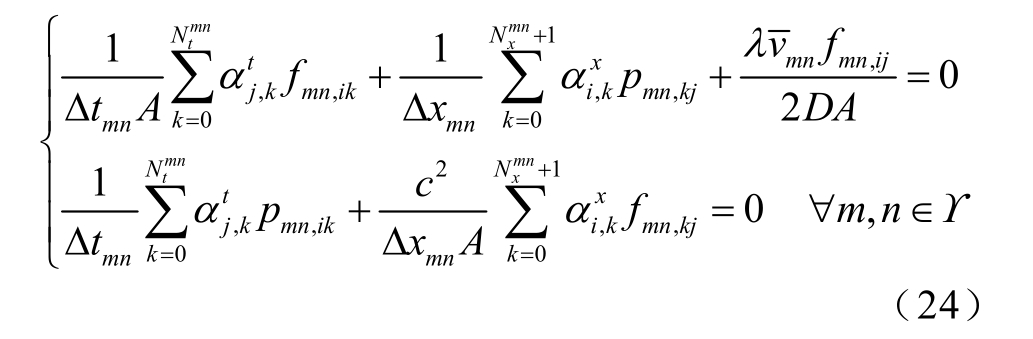
式中，fmn,ij 和pmn,ij 分别为管道mn 中管流的质量流率和气体压力在时空配置点(ξi,τj)处的取值；i=0,…,
。
在天然气系统节点处的流量平衡方程为
式中，fSm,j、fTm,j、fLm,j 分别为节点m 处气源质量流率、燃气机组进气口质量流率和其他气负荷质量流率在时间配置点τj 处的值；δin(m)和δout(m)分别为流入和流出节点m 的普通管道所连接的节点集合；
和 f mn ,0j分别为在时间配置点τj 处，气网管道nm 的出口m 处质量流率和管道mn 入口m 处的质量流率；γin (m)和 γout (m)分别为流入和流出节点m 的压缩机管道所连接的节点集合；
和 fC mn ,0j 分 别为在时间配置点τj 处，压缩机管道nm 的出口m 处质量流率和压缩机管道mn 入口处m 的质量流率。
天然气系统中的管道与节点处压力满足
式中，pm,j 为在时间配置点τj 处节点m 的压力。
天然气系统变量须满足的安全限值约束为
对于节点m， ∀m ∈Υ，需满足
2.2 电力系统约束
电力系统约束条件包括交流潮流约束和安全限值约束。为了满足在线应用对于计算效率的要求，采用基于二阶锥规划的交流潮流约束为[3,25]
式中，Λ 为电网节点的集合；PGi 和QGi 分别为节点i 常规机组有功和无功发电量；PTi 和QTi 分别为节点i 燃气机组有功和无功发电量；PLi 和QLi 分别为节点i 的有功和无功负荷功率；PCi 和PEi 分别为节点i 由电压缩机消耗的有功功率和其他电负荷有功功率；Pij 和Qij 分别为从节点i 流入j 的有功和无功功率；rij、xij、gij 和bij 分别为线路i-j 的电阻、电抗、电导和电纳；Δi 为所有与节点i 间有线路直接连接的节点集合；
分别为节点i 和j 上电压的典型值；C 为电网环路矩阵，θi 为节点i 的电压相角；二阶锥约束涉及的辅助变量定义为 Wi=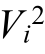
，Cij=ViVjcosθij，Sij=ViVjsinθij。
电网变量需满足的安全限值约束为
2.3 电力-天然气耦合元件约束
本文考虑的电力-天然气耦合元件包括燃气机组和加压站。其中，燃气机组对于天然气网是一种气负荷，对于电网则是一种发电设备，可以认为燃气机组的电功率与其消耗的天然气量成正比[5]。对于m ∈Υ，i ∈ Λ，假设电网节点i 的燃气发电机是天然系统节点m 的气负荷，其能量转换关系满足[13,18-19]
式中，ηTi,m 为燃气发电机的工作效率；HG 为天然气热值。
对于 m ,n ∈Υ，i ∈ Λ，假设输气管道mn 上的电加压站是电网节点 i 的电负荷，其能量转换关系满足
式中，PCi 为电网节点i 上电压缩机消耗的电功率；ηC i ,mn为管道电压缩机消耗电功率与其原动机驱动流量间的比例系数；KCmn为增压比。对于 m ,n ∈Υ，管道mn 加压站满足的安全限值和边界条件约束为
2.4 目标函数与优化模型
对气网而言，校正控制手段主要包括调整气源流量和切除气负荷。因此，气网的校正控制代价Cg定义为
对电网而言，校正控制手段主要包括发电机调整和负荷切除，其控制代价Ce 定义为有功功率校正控制量的二次函数，即
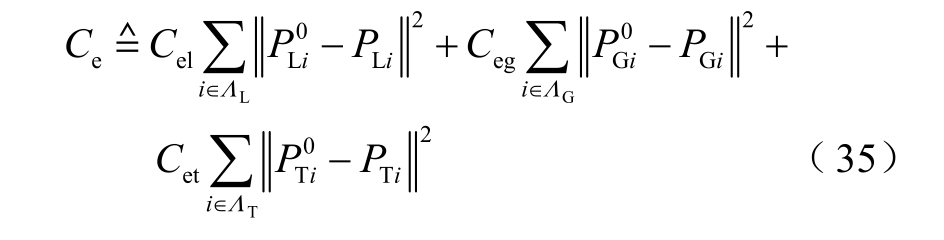
式中，ΛL、ΛG和 ΛT分别为电网中负荷、常规机组和燃气机组所在节点的集合；Cel 为切电负荷成本系数；Ceg 为常规机组调整成本系数；Cet 为燃气机组调整成本系数；
和 PL i分别为节点i 负荷在校正控制前、后的有功功率；
和 PG i分别为节点i 常规机组校正控制前、后有功功率；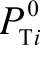
和 PT i分别为节点i 燃气机组校正控制前、后有功功率。式（35）中第一项为电网切负荷的控制代价，第二项为常规发电机调整的控制代价，第三项为燃气机组调整的控制代价。
综上所述，构建以总校正控制代价最小为目标的EGIS 安全约束最优能流模型为
式中，ugas 为天然气网相关的决策变量；uele 为电力系统相关的决策变量。
以上构建的面向校正控制的 EGIS 安全约束最优能流模型为凸优化模型，决策变量均为连续型变量，可通过CPLEX、Gurobi 等商业求解器直接求解。
3 算例验证
本节算例验证实验均在配备6 核Intel CORE i7-8850H CPU@2.60GHz、16GB 内存的计算机上进行。所有案例都在Matlab 2019b 中编码和运行，二阶锥优化模型通过CVX 调用Gurobi 9.0 求解，求解器参数设置为默认设置。
3.1 所提动态管流模型的有效性和优越性
为了验证所提基于STOC 动态管流约束的有效性，以及在求解精度和效率上的优越性，本节以单截管道为例，将STOC 法、Wendroff 显示差分法[18]与PDE 方程（7）的精确解进行对比。
假设某输气管道[18]长50km，直径为50cm。初始状况下管道入口压力为4MPa、全线质量流率为0.6Sm3/s。在仿真开始后第20min，管道出口处天然气负荷以0.001 25S·m3/(min·s)的爬坡率增大，爬坡过程持续20min，直到在40min 时管道出口气负荷达到0.625S·m 3/s。该管道、及其进出口管流变化过程示意图如图1 所示。
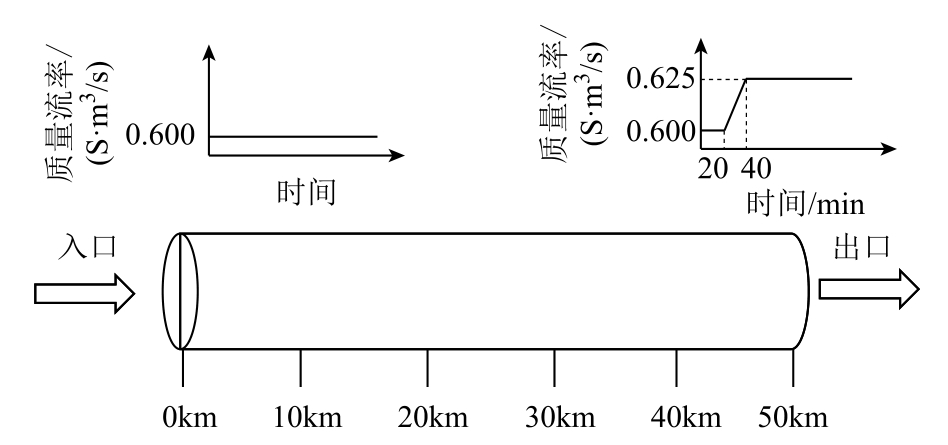
图1 单截50km 输气管道示意图
Fig.1 A single section of 50km gas pipeline
对于上述管流过程，分别以不同差分网格数量设置的Wendroff 显式差分法以及STOC 法计算管道全线的压力及质量流率，并与精确解进行对比验证。具体地：为了验证Wendroff 显示差分法求解精度以及速度与差分网格划分精细度之间的相关性，分别设置时空网格数量为Dx=14,Dt =6 作为粗糙网格划分（以下简称粗糙Wendroff 模型），Dx=52,Dt=18作为精细网格划分（以下简称精细Wendroff 模型）；在STOC 法中，时空配置点数量设置为Nx=14,Nt=6，各方法求解的时域窗口tf 均设置为7 200s。
分别基于上述方法求解，并绘制管道质量流率及气体压力随时间变化情况，如图2 所示。
图2 算例管道内流速及气体压力结果
Fig.2 Results of mass flow rate and gas pressure along the sample pipeline
将粗糙Wendroff 法（图2c 和图2d）与精确仿真结果对比，可以看出粗糙Wendroff 法的计算结果在管道流速结果接近稳态值时出现明显失真，原本管道质量流速应在接近0.625 0S·m3/s 时达到稳态峰值，而粗糙Wendroff 法的计算结果中产生了最高达0.631 5S·m3/s 的流速尖峰。在精细化差分网格后，精确Wendroff 法（图2e 和图2f）可以较为准确地刻画管流变化的实际情况，具有较高的求解精度。以上两组结果验证了Wendroff 显示差分法求解精度与差分网格划分精细度之间密切相关，差分网格越精细则求解精度越高。从图2g 和图2h 可以看出，尽管STOC 法采取了与粗糙Wendroff 法相同的时空离散网格数量，但其仿真结果与粗糙Wendroff 法相比更加稳定，尤其在对稳态峰值的刻画上没有出现明显失真。为进一步量化评估 STOC 法、粗糙Wendroff 法和精细Wendroff 法的计算精度，在管道出入口，以及距管道入口10km、20km、30km、40km共6 个空间位置分别求取流速和压力计算结果与精确解之间的误差，并将最大误差作为精度评估依据。各方法的流速和压力最大误差及计算耗时见表2。
表2 动态管流计算方法误差及计算耗时对比
Tab.2 Comparison of errors and computational times of dynamic pipe flow methods
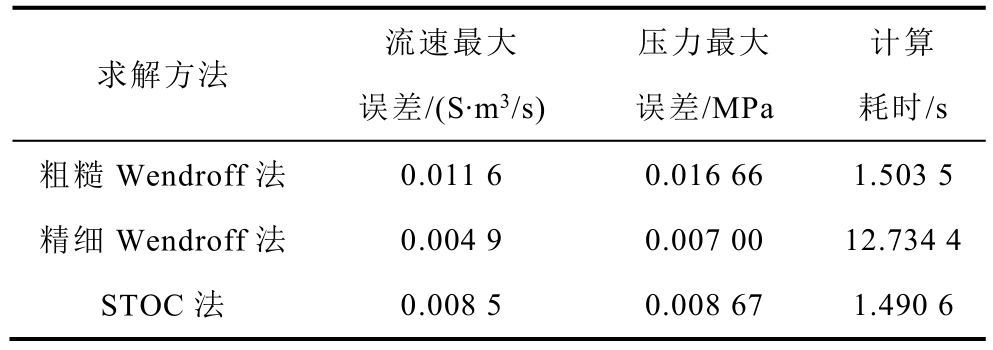
从表2 可以看出，在三种方法中，粗糙Wendroff法尽管计算耗时较低，为1.503 5s，但其流速与压力的最大误差指标为三种方法中最差，分别0.011 6S·m3/s 和0.016 66MPa。精细Wendroff 法流速和压力的最大误差为0.004 9S·m3/s 和0.007 00MPa，在三种方法中具有最好的计算精度表现。但在计算效率方面，其对单截管道的计算耗时为12.734 4s，远大于另外两种方法。这进一步说明了Wendroff 显示差分难以同时兼顾计算精度和求解效率。而STOC 法计算得到的流速和压力的最大误差分别为0.008 5Sm3/s 和0.008 67MPa，均显著优于相同离散网格设置的粗糙Wendroff 法，两个误差指标与精细Wendroff 法处于相同数量级。此外，虽然STOC 法在精度方面略差于精细 Wendroff 法，但在计算耗时上仅为精细Wendroff 法的十分之一。
上述结果验证了所提基于STOC 法计算的气网动态管流精度与已有差分方法相比，在求解精度和计算效率上的优越性。
3.2 所提EGIS 最优校正控制方法的有效性
本节以EGIS 中气网发生管道停运故障为例，应用第2 节中构建的安全约束最优能流模型求解最优校正控制策略，并验证其有效性。基于IEEE 118节点电网和比利时20 节点天然气网络构建的EGIS算例如图3 所示。
在图3 所示的EGIS 算例中，IEEE 118 bus 系统中G46、G49、G54、G66 为燃气机组发电节点，同时也是比利时20 节点天然气系统中16、10、7 和3 号节点的气负荷。算例中燃气机组的最大爬坡率均设置为30%/30min，燃气热效率为45%，常规机组爬坡率15%/30min[12]。气网故障位置位于节点1 和节点2 之间，故障导致平行管道1-2 中一段停止输送天然气，另一段继续运行。根据所提基于STOC 的气网动态管流模型对故障后的管流情况进行仿真计算。
图3 改造的EGIS 算例结构图
Fig.3 Structure diagram of the modified EGIS system
对天然气网络而言，暂态变化剧烈的管道需要较多的时空配置点以刻画其压力、质量流率对于时间和空间变量的强非线性；而对于暂态管流变化较为平缓的管道，较少的时空配置点即可实现相当精度的拟合。但是，不同管道暂态管流的波动状态在优化问题求解前难以先验确定。因此，本文中设置的时空配置点数量综合考虑了气网整体拟合精度和求解效率设置为Nx=14，Nt=6。求解得到受故障影响严重的关键管道，即继续运行的平行管道1-2，以及故障位置的下游管道2-3 处质量流率和管壁压力情况如图4 所示。
如图4a 和图4b 所示，管道1-2 故障停运后，原本应由其输送的天然气流量被迫转由其平行管道1-2 输送，导致平行管道1-2 的质量流率在短时间内由5.456 6S·m3/s 上升至10.876 4S·m3/s，并造成其入口处暂态压力大幅上升至7.167 06MPa，远远超过其安全限值6.2MPa。而从图4c 可以看出，管道2-3 进气口的质量流率由于其上游管道1-2 的故障，在短时间内出现较大幅度的下降，随着上游输气流量的转移，最终逐渐恢复到原本的进气水平；与此同时，由图4d 可见，燃气机组G66 进气口节点3 处的压力水平也由于管道2-3 流量波动发生大幅下降，压力谷值达到4.798 9MPa。在上述过程中，平行管道1-2 管壁压力的大幅越限严重威胁到EGIS 安全运行：如果管道1-2 无法承受过高的暂态压力造成气体泄漏事故，则也将退出运行；而气网节点3 暂态压力的大幅降低也威胁到燃气机组G66 的稳定供 气。如不采取应对措施可能引发连锁故障。
图4 管道1-2 故障后关键管道压力及流量变化情况
Fig.4 Variations of gas pressure and mass flow rate in critical pipelines after the outage of pipeline 1-2
针对上述故障场景，为消除由气网故障引发EGIS 连锁故障的安全隐患，通过模型（36）求解电网静态安全校正控制策略。在气网动态管流模型的时空配置点设置上，综合考虑计算精度和求解效率调整为Nx=15，Nt=8。所得EGIS 最优校正控制策略见表3，其中校正控制量按照电网基准功率100MW，气网基准质量流率1S·m3/s 标幺化，管存消耗比例定义为优化时间窗口t∈[t0,tf]内管存消耗量占气网总管存量的比值。
表3 气网管道1-2 故障后EGIS 最优校正控制策略
Tab.3 Corrective control strategies of EGIS after the failure of pipeline 1-2
从表3 的最优校正控制策略结果可以看出，针对气网管道1-2 故障，电网和气网分别通过发电机组调整和管存变化进行校正控制。为进一步分析校正控制方案中燃气机组调整对EGIS 运行状态的影响，列出燃气机组的校正控制量见表4。
表4 燃气机组校正控制量
Tab.4 Corrective control strategies of the gas-fired units
从表4 结果可以看出，为了防止气网1-2 管道停运导致其平行管道压力越限，进而引发EGIS 连锁故障，燃气机组G66 采取了主动减发0.300 0(pu)的校正控制措施，该措施实施后气网关键管道的压力及流量暂态变化过程如图5 所示。
如图5 所示，在G66 采取主动减发措施后，燃气机组进气口管道2-3 质量流率从原来的9.656 0S·m3/s下降至8.501 1S·m3/s，缓解了其上游管道1-2 故障造成的输气能力不足的压力，同时也保证了燃气机组进气口节点3 的压力水平始终位于运行安全下限5.2MPa 以上。受端气网管道1-2 压力在故障后尽管发生一定幅度波动，但始终未超过安全上限6.2MPa。上述结果表明所得最优校正控制策略可有效消除气网N-1 故障引发的EGIS 的安全越限事故，也验证了所提最优校正控制方法的有效性。
图5 校正控制后气网关键管道压力及流量变化情况
Fig.5 Variations of gas pressure and mass flow rate in critical pipelines after the corrective control
4 结论
本文面向EGIS 发生N-1 故障后的安全校正控制问题展开研究，针对现有方法对气网动态管流的处理难以兼顾计算效率和求解精度的不足，提出一种基于STOC 的EGIS 最优校正控制方法。本文的主要贡献在于：
1）基于STOC 法构建了气网动态管流约束，并探讨了时空配置点类型和数量的设置方法。与Wendroff 差分法的对比验证了STOC 法在相同离散规模下，具有更好的精度表现.
2）基于STOC 气网动态管流约束，构建了面向校正控制的EGIS 安全约束最优能流模型。算例结果验证了所得最优校正控制策略可有效消除EGIS中N-1 故障引发的安全越限事故。此外，所提方法对于在EGIS 规划、日前经济调度等其他应用场景下的动态最优能流计算也具有一定的参考价值。
本文中设置的时空配置点数量综合考虑了气网整体的拟合精度和求解效率。如何针对天然气网络中不同管道暂态管流变化情况的差异，对各个管道时空配置点数量进行更加精细化的设置，在未来值得深入研究，以便进一步提升本方法的性能。此外，考虑到电网和气网运营主体的独立性，可针对所提校正控制方法的分布式计算、更精细化的电力-天然气系统耦合设备非线性特征建模等方面展开深入研究。
[1]Craig M,Guerra O J,Brancucci C,et al.Valuing intraday coordination of electric power and natural gas system operations[J].Energy Policy,2020,141: 1-8.
[2]包铭磊,王可欣,丁一,等.考虑电、气备用协同配置的故障传播影响抑制策略[J].电力系统自动化,2022,46(5): 40-50.Bao Minglei,Wang Kexin,Ding Yi,et al.Containment strategy of failure propagation impacts considering coordinated allocation of power and natural gas reserve[J].Automation of Electric Power Systems,2022,46(5): 40-50.
[3]林涛,毕如玉,陈汝斯,等.基于二阶锥规划的计及多种快速控制手段的综合安全校正策略[J].电工技术学报,2020,35(1): 167-178.Lin Tao,Bi Ruyu,Chen Rusi,et al.Comprehensive security correction strategy based on second-order cone programming considering multiple fast control measures[J].Transactions of China Electrotechnical Society,2020,35(1): 167-178.
[4]陈泽兴,林楷东,张勇军,等.电-气互联系统建模与运行优化研究方法评述[J].电力系统自动化,2020,44(3): 11-23.Chen Zexing,Lin Kaidong,Zhang Yongjun,et al.A review of modeling and optimal operation of integrated electricity-gas system[J].Automation of Electric Power Systems,2020,44(3): 11-23.
[5]Correa-Posada C M,Sanchez-Martin P.Securityconstrained optimal power and natural-gas flow[J].IEEE Transactions on Power Systems,2014,29(4): 1780-1787.
[6]黎晨阳,张沈习,程浩忠,等.计及相关性的电-气互联区域综合能源系统概率多能流计算[J].电力系统自动化,2020,44(21): 42-49.Li Chenyang,Zhang Shenxi,Cheng Haozhong,et al.Correlation-based probabilistic multi-energy flow calculation of regional integrated energy system with combined electricity and natural gas[J].Automation of Electric Power Systems,2020,44(21): 42-49.
[7]刘明凯,王占山,邢彦丽.基于强化多目标差分进化算法的电-气互联系统最优潮流计算[J].电工技术学报,2021,36(11): 2220-2232.Liu Mingkai,Wang Zhanshan,Xing Yanli.Enhanced multi-objective differential evolutionary algorithm based optimal power flow calculation for integrated electricity and gas systems[J].Transactions of China Electrotechnical Society,2021,36(11): 2220-2232.
[8]韩佶,苗世洪,李超,等.计及相关性的电-气-热综合能源系统概率最优能量流[J].电工技术学报,2019,34(5): 1055-1067.Han Ji,Miao Shihong,Li Chao,et al.Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J].Transactions of China Electrotechnical Society,2019,34(5): 1055-1067.
[9]陈厚合,丛前,姜涛,等.多能协同的配电网供电恢复策略[J].电工技术学报,2022,37(3): 610-622.Chen Houhe,Cong Qian,Jiang Tao,et al.Distribution systems restoration with multi-energy synergy[J].Transactions of China Electrotechnical Society,2022,37(3): 610-622.
[10]徐玉琴,方楠.基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度[J].电工技术学报: 2022,37(11): 2800-2812.Xu Yuqin,Fang Nan.Multi-objective optimal scheduling of integrated electricity-gas system based on piecewise linearization and improved second order cone relaxation[J].Transactions of China Electrotechnical Society,2022,37(11): 2800-2812.
[11]Shao Chengcheng,Wang Xifan,Shahidehpour M,et al.An MILP-based optimal power flow in multicarrier energy systems[J].IEEE Transactions on Sustainable Energy,2017,8(1): 239-248.
[12]Wang Cheng,Wei Wei,Wang Jianhui,et al.Convex optimization based distributed optimal gas-power flow calculation[J].IEEE Transactions on Sustainable Energy,2018,9(3): 1145-1156.
[13]Sun Guoqiang,Chen Sheng,Wei Zhinong,et al.Corrective security-constrained optimal power and gas flow with binding contingency identification[J].IEEE Transactions on Sustainable Energy,2020,11(2): 1033-1042.
[14]Zhang Yachao,Huang Zhanghao,Zheng Feng,et al.Cooperative optimization scheduling of the electricity-gas coupled system considering wind power uncertainty via a decomposition-coordination framework[J].Energy,2020,194: 1-20.
[15]He Yubin,Yan Mingyu,Shahidehpour M,et al.Decentralized optimization of multi-area electricitynatural gas flows based on cone reformulation[J].IEEE Transactions on Power Systems,2018,33(4): 4531-4542.
[16]卫志农,梅建春,孙国强,等.电-气互联综合能源系统多时段暂态能量流仿真[J].电力自动化设备,2017,37(6): 41-47.Wei Zhinong,Mei Jianchun,Sun Guoqiang,et al.Multi-period transient energy-flow simulation of integrated power and gas energy system[J].Electric Power Automation Equipment,2017,37(6): 41-47.
[17]梅建春,卫志农,张勇,等.考虑关键故障筛选的电-气互联综合能源系统混合控制方法[J].电网技术,2019,43(1): 23-33.Mei Jianchun,Wei Zhinong,Zhang Yong,et al.Hybrid control of integrated power and gas energy systems based on significant contingency screening[J].Power System Technology,2019,43(1):23-33.
[18]Fang Jiakun,Zeng Qing,Ai Xiaomeng,et al.Dynamic optimal energy flow in the integrated natural gas and electrical power systems[J].IEEE Transactions on Sustainable Energy,2018,9(1): 188-198.
[19]Bao Zhejing,Zhang Qihong,Wu Lei,et al.Cascading failure propagation simulation in integrated electricity and natural gas systems[J].Journal of Modern Power Systems and Clean Energy,2020,8(5): 961-970.
[20]Bao Zhejing,Ye Yangli,Wu Lei.Multi-timescale coordinated schedule of interdependent electricitynatural gas systems considering electricity grid steadystate and gas network dynamics[J].International Journal of Electrical Power &Energy Systems,2020,118(105763): 1-10.
[21]Menon E S.Gas pipeline hydraulics[M].Boca Raton: CRC Press,2005.
[22]Garg D,Patterson M,Hager W W,et al.A unified framework for the numerical solution of optimal control problems using pseudospectral methods[J].Automatica,2010,46(11): 1843-1851.
[23]Trefethen L N.Spectral methods in Matlab[M].Philadelphia: Society for Industrial and Applied Mathematics,2000.
[24]Jie Hao,Yuan Meichen,Hong Weirong.A quasisequential algorithm for PDE-constrained optimization based on space-time orthogonal collocation on finite elements[J].Journal of Process Control,2021,98(1): 1-9.
[25]郑重,苗世洪,李超,等.面向微型能源互联网接入的交直流配电网协同优化调度策略[J].电工技术学报,2022,37(1): 192-207.Zheng Zhong,Miao Shihong,Li Chao,et al.Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy internet[J].Transactions of China Electrotechnical Society,2022,37(1): 192-207.