0 引言
基于电网换相换流器的高压直流(Line Commutated Converter Based High Voltage Direct Current,LCC-HVDC)输电系统在远距离大容量输电的应用场景下具有显著的优势[1-3]。为了实现“双碳”目标,需要将西部大量的清洁能源送到距离很远的东部负荷中心,而LCC-HVDC 适合于承担这样的输电任务,因此LCC-HVDC 系统在“西电东送”战略中起到重要作用[4]。随着LCC-HVDC 系统的电压等级和输送容量的不断提高,交流系统的强度相对下降[5]。已有文献研究表明LCC-HVDC 系统逆变侧连接弱交流系统会存在换相失败[6]、小干扰失稳[7-8]、送端系统暂态过电压[9-10]等问题,这些问题与控制系统息息相关。控制系统的参数对 LCCHVDC 系统稳定性和动态性能具有较大的影响,选择合适的控制参数对于系统的安全稳定运行十分重要。因此有必要研究LCC-HVDC 的控制参数优化方法,提高系统在弱交流电网下的稳定性和动态性能。
目前已有许多文献涉及HVDC 系统的控制参数优化。文献[11-14]从动态性能的角度对HVDC 系统的控制参数进行优化。文献[11]根据系统的幅值裕度和相位裕度计算控制参数可行优化区域,再利用误差时间积分(Integral of Time and Absolute Error,ITAE)指标寻找令指标取值最小的控制参数作为优化的结果;然而文献中换流器采用一阶惯性环节建模,不能精确地反映换流器的动态特性。文献[12]利用单纯形Simplex 算法,优化基于电压源换流器的高压直流输电(Voltage Source Converter based High Voltage Direct Current Transmission,VSC-HVDC)系统的控制参数,提高了VSC-HVDC 系统的动态性能。文献[13]提出一种混合单纯形-遗传算法,同时具有两类算法的优点;并利用此算法在LCC-HVDC系统准稳态模型的基础上,以ITAE 指标为目标函数优化了控制参数。文献[14]建立了较为准确的LCC-HVDC 系统的传递函数模型,采用粒子群算法,同样以ITAE 指标为优化问题的目标函数,对控制参数进行优化。此方法利用传递函数计算ITAE 指标相较于利用电磁暂态仿真计算的方法效率更高。文献[15-19]从小干扰稳定性角度提出了不同的控制参数优化方法。文献[15]推导了线性化的VSC-HVDC系统小信号模型,通过特征值分析计算系统不同类型模式的罚函数作为目标函数优化全系统的控制参数。文献[16]建立混合多端直流输电系统的小信号模型并进行特征值分析,以提高系统模态的最小阻尼比作为优化目标,用特征根对参数的灵敏度来控制参数优化的步长和方向,提高了混合多端直流输电系统在弱交流电网下的小干扰稳定性。文献[17]同样以参数灵敏度指导优化迭代过程中参数变化的方向和步长,以特征根实部为目标函数,采用回溯直线搜索算法优化三端模块化多电平换流器高压直流(Modular Multilevel Converter High Voltage Direct Current,MMC-HVDC)系统的控制参数。文献[18]根据多端混合直流输电系统的小干扰模型筛选出影响系统稳定性的主要控制参数,并得到控制参数的可行域进行可视化展示。在此基础上采用类似文献[15]的罚函数作为目标函数,利用粒子群算法实现参数优化。文献[19]建立含静止同步补偿器(Static Synchronous Compensator,STATCOM)的LCC-HVDC小干扰模型,根据特征值分析结果辨识影响系统稳定性的关键控制参数,推导了能够定量衡量系统稳定性的二次型指标作为目标函数,采用蒙特卡洛法进行参数优化,提高了系统在低短路比工况下的稳定性。综上所述,大多数文献在进行HVDC 控制参数优化时往往只关注系统的动态性能或者小信号稳定性,而不能同时兼顾。文献[20]建立将二次型指标和阻尼比相结合的目标函数,优化了LCC-MMC 混合直流输电系统的控制参数。但阻尼比只能反映系统某个模态的振荡特性,对于高阶系统而言,阻尼比指标无法反映系统整体的动态性能。因此仍有必要寻找能够同时反映系统稳定性和动态性能的指标。除此之外,很多关于LCC-HVDC 控制参数优化的研究在建模时将实际换相过程近似线性化处理导致模型不够准确,不能精确反映系统的稳定性和动态性能,限制了优化方法的效果。
针对优化目标函数不能兼顾小信号稳定性和动态性能的问题,本文引入系统能量衰减指标。在已有的文献中,能量衰减指标用于评价控制系统响应的快速性[21],能够反映系统的动态性能,但鲜有文献将其应用于控制参数优化领域。对于渐近稳定的系统,系统的能量衰减指标始终为正数;而对于振荡发散失稳的系统,能量衰减指标为负数。因此能量衰减指标类似于系统最靠近虚轴的特征值,能够反映系统的小信号稳定性。针对LCC-HVDC 建模不够精确的问题,本文参考文献[22]的建模方法,建立了考虑实际换相过程以及锁相环输出相位偏差的较为精确的LCC-HVDC 小信号模型。在此基础上,辨识了影响LCC-HVDC 在弱交流系统下稳定性的主导模态,筛选出灵敏度较高的关键控制参数作为待优化参数,利用能量衰减指标得到适用于不同运行点的可视化的待优化参数可行域,采用蒙特卡洛法,以能量衰减指标为目标函数在优化可行域内寻找近似最优的控制参数组合。最后在不同的运行点下通过根轨迹分析和电磁暂态仿真,对比了优化前后系统的稳定性和动态性能。结果表明采用优化后的控制参数时,系统在不同运行点的稳定性和动态性能均有明显提升,证明了优化方法的有效性。本文所提出的优化方法也可以为其他系统的控制参数整定问题提供参考。
1 LCC-HVDC 系统
1.1 LCC-HVDC 系统结构
本文基于某实际工程,搭建了如图1 所示的单极500 kV、额定容量1 500 MW 的双端LCC-HVDC系统。
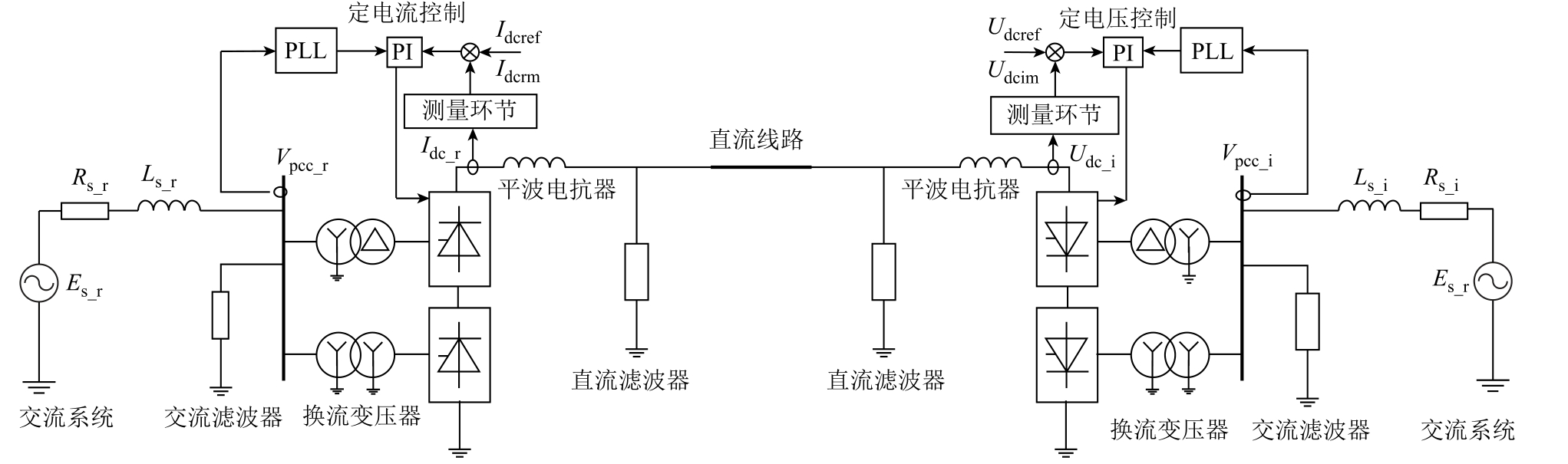
图1 LCC-HVDC 系统结构示意图
Fig.1 LCC-HVDC system structure diagram
LCC-HVDC 送电、受电端连接的交流电网以电压源Es 串联阻抗的形式进行等值。换流器经过变压器与交流系统相连,交流母线是换流变压器、交流系统、交流滤波器的公共连接点(Point of Common Coupling,PCC)。锁相环跟踪交流母线电压Vpcc 的相位,为换流器晶闸管的触发提供相位基准。整流侧的控制模式为定电流控制,逆变侧采用定电压控制模式。
LCC-HVDC 系统的电气及控制参数见附表1。
1.2 LCC-HVDC 系统的小信号模型
首先建立系统的状态空间模型,在对换流器的建模过程中,参考文献[22]考虑了实际换相过程和锁相环输出相位与交流母线电压实际相位的偏差,换流器建模的关键是计算从交流系统流入整流侧换流器的交流电流Ic_r。以交流母线A 相电压相位为基准进行Park 变换(d 轴定位Vpcc_r,q 轴滞后90°),Ic_r 的d 轴、q 轴分量为
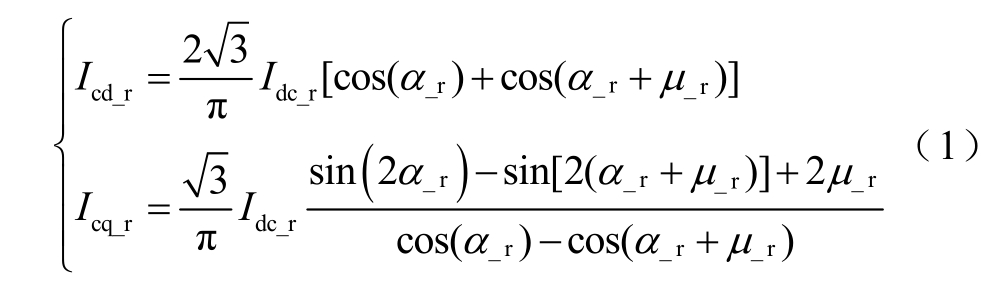
式中,Icd_r为整流侧直流电流;α_r为整流侧滞后触发角;μ_r为整流侧换相角。
同理,从逆变侧换流器流入交流系统的交流电流Ic_i 的d 轴、q 轴分量为

式中,Idc_i 为逆变侧直流电流;β_i为逆变侧超前触发角;μ_i为逆变侧换相角。
交流母线电压相位在系统受到扰动时会变化,锁相环需要经过一个动态过程才能重新跟踪母线电压相位[23]。动态过程的存在使得锁相环输出相位不能在任意时刻都与实际相位相同,由于锁相环是控制系统的相位基准,整流/逆变侧的触发角指令值与实际触发角之间会存在偏差。考虑偏差时α_r和 β_i为
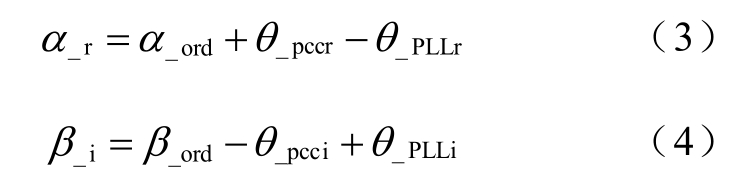
式中,θ_pccr、θ_pcci 为交 流 母线电压的 相 位;θ_PLLr、θ_PLLi为锁相环输出相位;下标r 代表整流侧,i 代表逆变侧。
改进后的模型阶跃响应的计算结果能够与电磁暂态仿真的波形吻合,相比于将换相过程近似线性化的模型可以更好地反映系统动态特性。因此,基于更精确的改进后的模型进行根轨迹分析计算的失稳临界值更接近实际的失稳临界值,失稳模态的振荡频率更接近系统的振荡频率,稳定性分析的结果更准确[22]。实际工程中输电线路很长,存在分布参数效应,直接用集总参数电路等效不够精确。已有研究表明,当线路长度小于所关心最大频率对应的波长的三十分之一时,可忽略线路的分布参数效应,此时可采用一个Π 型电路对线路进行等效[24]。对于距离很长不能忽略线路分布参数效应的线路,可以采用多个Π 型电路级联的方式得到等效电路。由于影响LCC-HVDC 系统稳定性的主要模态的频率在200Hz 以下,将所关心的最大频率设为200 Hz,对应波长的三十分之一即50 km。本文基于的实际工程中直流线路长度为1 200 km,故采用图2 所示的24 个Π 型电路等效。
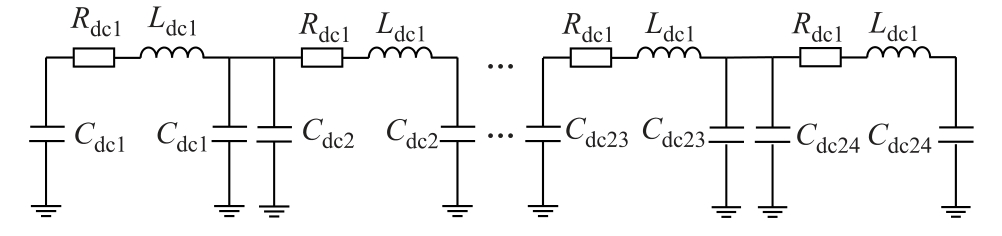
图2 直流线路等效模型
Fig.2 DC line equivalent model
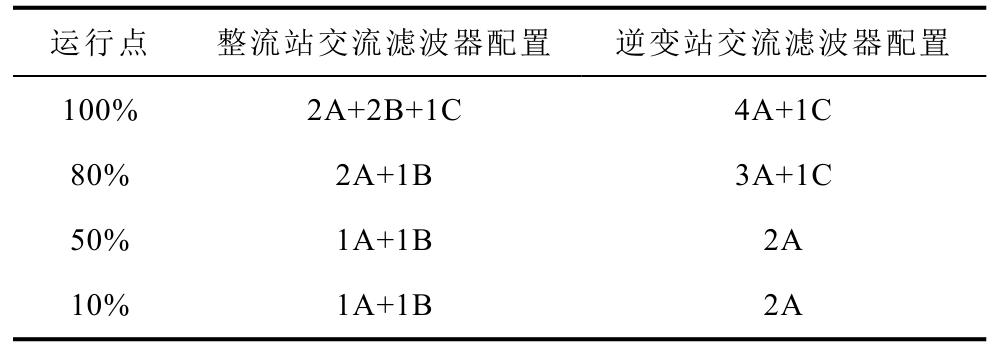
滤波器组合的结构如附图1 所示,整流侧交流滤波器有三类:A 型双调谐滤波器,滤除11、13 次谐波;B 型三调谐滤波器滤除3、24、36 次谐波;C 型单调谐滤波器,滤除48 次谐波。逆变侧交流滤波器有两类:A 型双调谐滤波器,滤除12、24 次谐波;C型单调谐滤波器,滤除36 次谐波。额定功率运行时整流侧滤波器投切策略为2A+1B+1C,逆变侧为4A+1C。建模时考虑不同功率传输水平对应的滤波器投切方式不同,不同运行点交流滤波器的配置见表1。
表1 不同运行点交流滤波器的配置
Tab.1 Configuration of AC filters at different operating points
LCC-HVDC 控制系统的详细模型可参考文献[14]。
综上所述可以得到形式如式(5)所示的状态空间方程,具体方程见文献[14,22]。本文重点研究控制参数的优化方法,故不详细描述具体模型。
在额定运行点处将状态空间方程线性化得到系统的小信号模型,表达式为
模型为115 阶,输入变量u=[Idcref,Udcref]。
通过阶跃响应对比验证小信号模型的正确性。分别令整流侧直流电流参考值和逆变侧直流电压参考值发生阶跃,将小信号模型计算的阶跃响应结果与PSCAD 中电磁暂态仿真的波形进行对比。小信号模型验证如图3 所示,模型计算结果与电磁暂态仿真基本一致,证明了小信号模型的准确性。
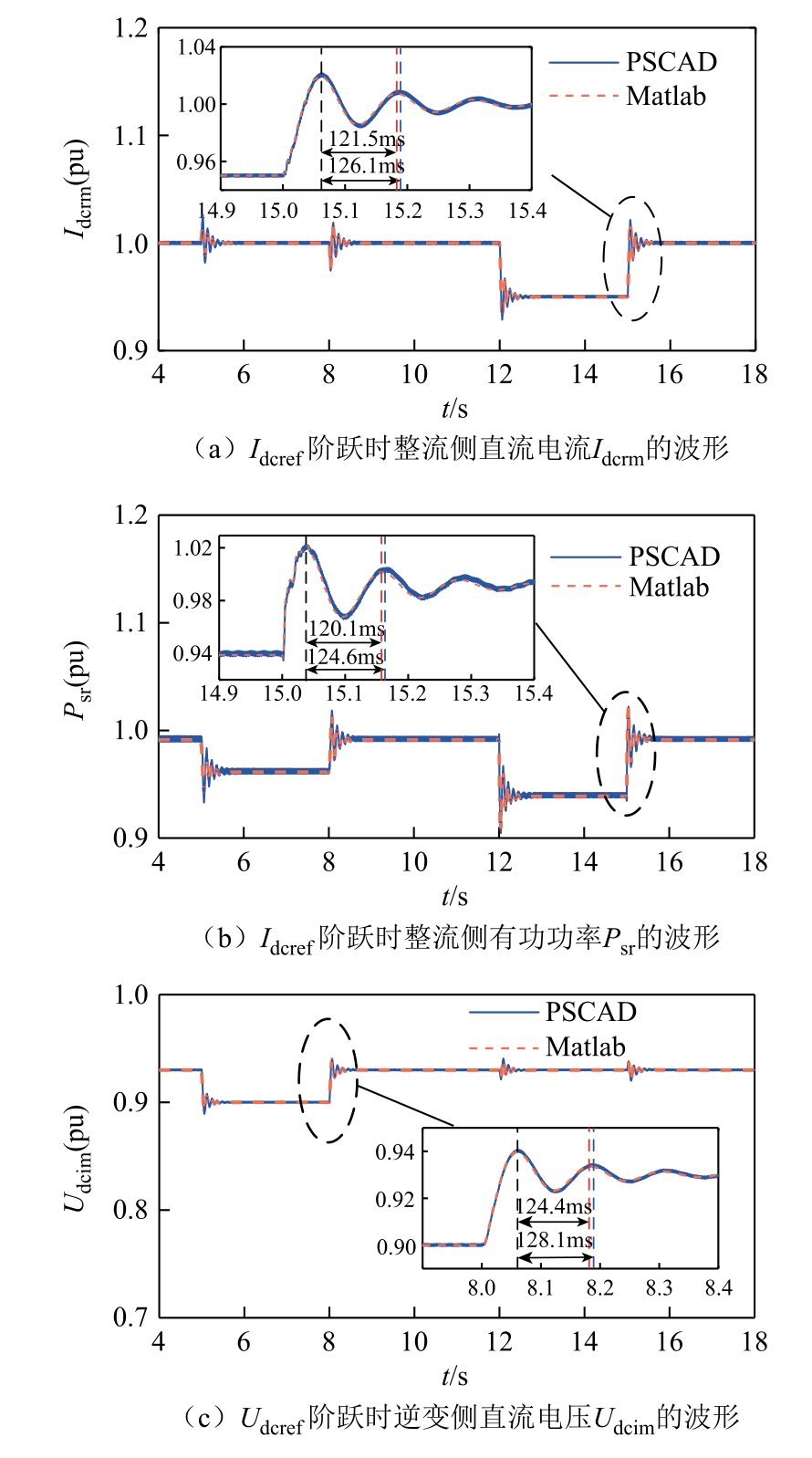
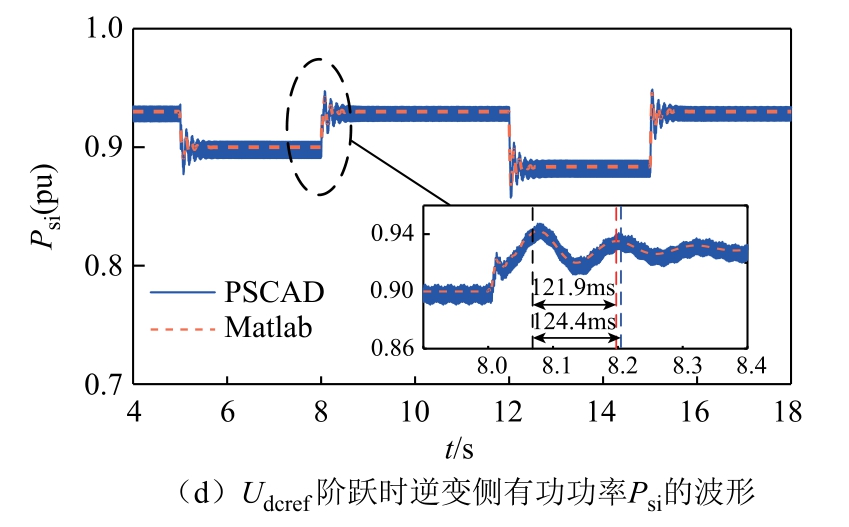
图3 小信号模型验证
Fig.3 Validation of small signal model
2 弱交流系统下LCC-HVDC 系统的小信号稳定性及动态性能
2.1 弱交流系统下LCC-HVDC 的小信号失稳及动态性能恶化现象
交流系统可能在一条线路断线等特殊情况下出现短路比下降的问题。现有文献结论表明,当LCC-HVDC 逆变侧连接短路比较小的弱交流系统时会出现小信号失稳现象[7-8]。因此,在进行参数优化前,需要对LCC-HVDC 系统进行根轨迹分析,确定逆变侧短路比下降时引起系统小信号失稳的主导模态。
系统在初始控制参数下从初始运行点(SCRr=2.5,SCRi=2.5,Idcref=1.0(pu),Udcref=0.93(pu))减小逆变侧短路比SCRi 到1.0,系统的根轨迹如图4 所示。从图4 可以看出当SCRi 降低到1.46 时,系统出现特征根实部由负变正穿越虚轴的模态,系统发生小信号失稳。为了直观验证上述结果,在PSCAD 中逐渐降低逆变侧交流系统的短路比,仿真结果如图5 所示。从图5 可以看出,SCRi 降低到1.46 时,逆变侧直流电压Udcim 出现振荡发散的波形,系统失稳频率为7.93 Hz(10/1.26 s)。小信号模型根轨迹分析计算的失稳频率为8.03 Hz,与PSCAD仿真结果接近,验证了根轨迹分析的正确性。
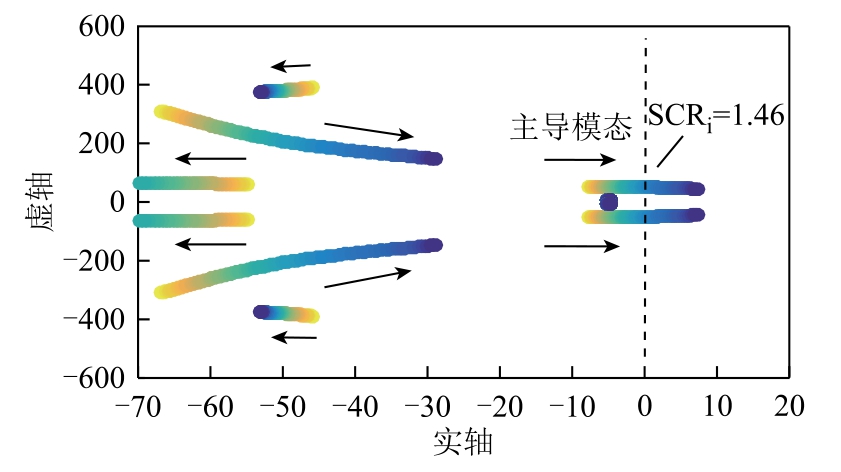
图4 初始控制参数下SCRi 下降时系统的根轨迹
Fig.4 Root locus diagram of the system when SCRi drops under initial control parameters
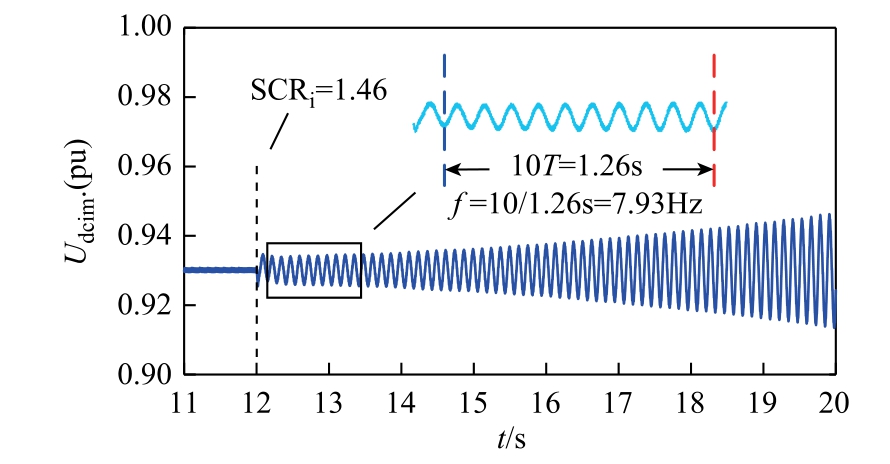
图5 初始控制参数下Udcim 仿真波形
Fig.5 Udcim simulation waveform under initial control parameters
LCC-HVDC 逆变侧连接弱交流系统不仅会导致小信号失稳,还会导致系统动态响应性能显著恶化。分别在初始运行点和逆变侧低短路比运行点(SCRi=1.6)令逆变侧直流电压参考值 Udcref 从0.93(pu)阶跃至0.90(pu),两种运行点下逆变侧直流电压的阶跃响应对比结果如图6 所示。从图6 可以看出,在初始运行点时,系统的动态响应性能较好;当逆变侧短路比降低至1.6 时,逆变侧直流电压阶跃响应的超调量和调节时间明显增加,系统的动态响应性能有较为显著的恶化。由此可见,逆变侧连接弱交流系统会导致LCC-HVDC 系统动态响应性能变差,在进行控制参数优化时不仅要考虑如何提高系统的小信号稳定性,还要关注系统的动态性能。
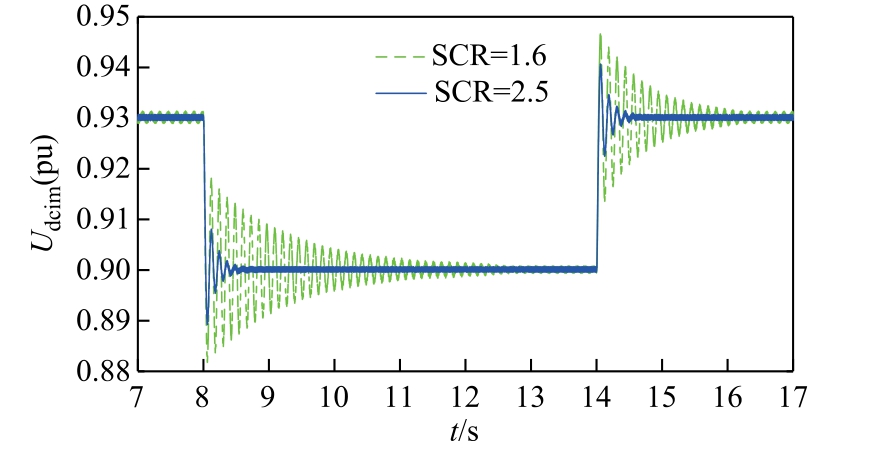
图6 不同SCRi 下系统的阶跃响应波形对比
Fig.6 Comparison of step response waveforms of systems under different SCRi
2.2 弱交流系统下影响LCC-HVDC 系统稳定性的关键控制参数
根据图4 所示的根轨迹,系统在SCRi 降低到1.46 时出现特征根实部由负变正穿越虚轴的模态,系统失稳。将穿越虚轴的模态作为主导模态,在逆变侧短路比为1.6 的弱交流系统下对主导模态进行灵敏度分析,根据主导模态对控制参数的灵敏度选出关键控制参数。灵敏度分析的结果反映了参数变化时特征根移动的方向与速度,一般将特征值对控制参数的偏导数的实部视为灵敏度[25]。灵敏度代表控制参数变化时相应模态沿着实轴移动的速度和方向,因此当主导模态对某个控制参数变化的灵敏度绝对值较大时,该参数变化会引起主导模态沿着实轴快速移动,进而较大程度地影响系统的稳定性[16]。由此可见,灵敏度绝对值较大的控制参数对系统稳定性影响较大,有必要对这些参数进行优化。主导模态对控制参数变化的灵敏度如图7 所示,主导模态对整流/逆变侧锁相环比例系数参数KpPLLr/KpPLLi、定电流/定电压控制器比例系数Kpr/Kpi 变化比较灵敏,因此选择KpPLLr、KpPLLi、Kpr、Kpi 作为待优化参数。
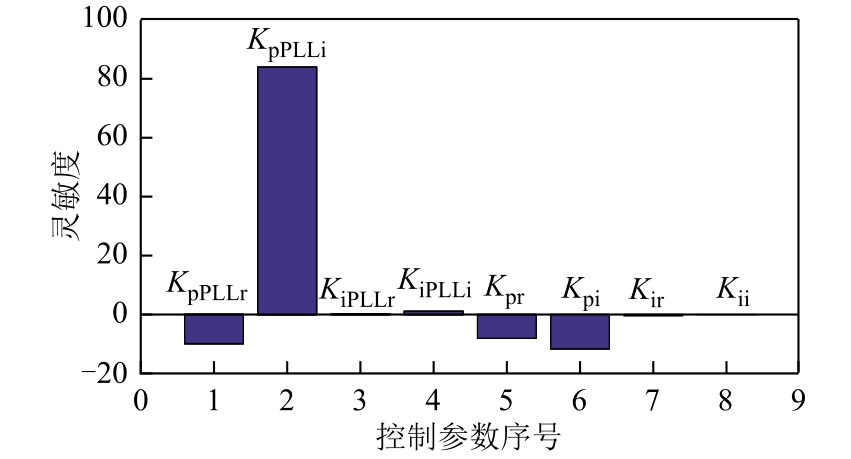
图7 主导模态对控制参数变化的灵敏度
Fig.7 Sensitivity of dominant mode to changes of control parameters
3 反映LCC-HVDC 系统稳定性和动态性能的指标
在研究系统稳定性时,李雅普诺夫函数V(x)用来表征系统的能量,并根据V(x)对时间的导数判断系统稳定性。V(x)可以看作是状态x 到平衡点距离的度量,V(x)随时间的衰减速度越快,系统恢复到平衡状态的速度越快[21]。在文献[21]中通过引入指标η 来表征系统能量的衰减速度,η 定义为
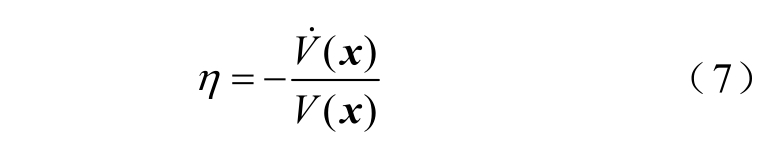
对式(7)两侧做0~t 积分可得
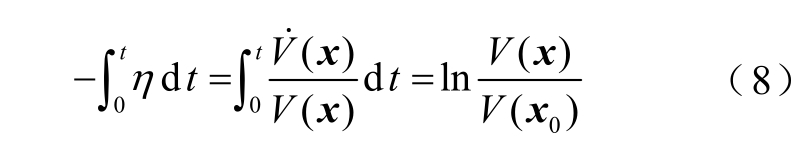
由式(8)可知
对于渐近稳定的系统而言,η 始终为正,系统能量随时间不断变小。若η 为负数,系统能量会随时间不断变大,系统失去稳定,出现发散的波形。因此,η 在一定程度上反映了系统的稳定性,可以用η 的正负来区分系统稳定/失稳。由式(9)还可以看出η 越大,系统能量衰减越快,系统受到扰动后向平衡点收敛的速度越快,系统动态性能越好。因此可以用η 来反映系统的动态性能。考虑到对于不同的状态x,η 的值会有所不同,取η 在状态空间中的最小值ηmin 作为系统的能量衰减指标。
3.1 LCC-HVDC 系统的能量衰减指标
本节介绍LCC-HVDC 系统能量衰减指标ηmin计算方法。
首先构造V(x)为二次型函数,即

式中,A 为小信号模型的状态空间矩阵;Q 为任意正定对称矩阵。按照式(7)中η 的定义,有
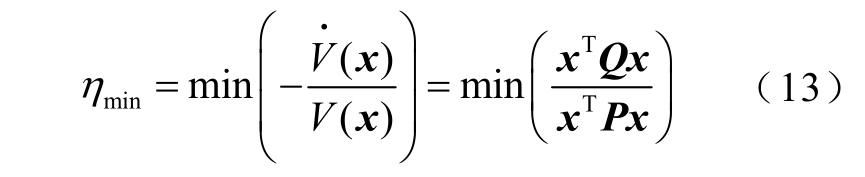
假设能量函数值为1,在 x T Px=1的条件下求η的条件极值。此时式(13)变为
令η 取极小值的状态xmin 可由拉格朗日乘子法求出。令μ 为拉格朗日乘子,构造拉格朗日函数L 为
当x 为条件极值点时,L 对x 的求导在该点处为0,可以得到
令η 取极小值的状态xmin 满足
当xmin≠0 时,Q 和P 之间的关系为
由于Q 为任意给定正定实对称矩阵,设Q 为单位阵I,则μ 对应P-1 的特征值。将式(17)代入式(13)可得
从式(19)可以看出,ηmin 为矩阵P-1 的最小特征值。将 x T Px=1条件下的结论推广到 x TPx 为任意常数的情况,无论V(x)取何值,式(17)~式(19)都成立。由此可见,η 在V(x)为定值下的条件极值与V(x)的取值无关,都为矩阵P-1 的特征值;η 在整个状态空间中的最小值ηmin 也就是所有条件极值中的最小值,即P-1 的最小特征值。
通过上述方法可以定量计算LCC-HVDC 系统的能量衰减指标ηmin,ηmin 的物理意义是状态空间中系统能量的最小衰减率。结合式(7)~式(9)可以看出,ηmin 越大系统的稳定性和动态性能越好。因此可以将ηmin 作为控制参数优化的目标函数,优化目标为寻找能够令ηmin 取最大值的控制参数组合。
3.2 利用能量衰减指标计算待优化参数可行域
在进行参数优化前除了确定目标函数,还需要确定优化问题的约束条件即待优化控制参数的可行域。本文以能量衰减指标的最大值作为目标函数,为了避免出现待优化参数取值范围过大导致优化程序的计算效率低的问题,可以选取令能量衰减指标取较大值的控制参数范围作为优化可行域,优化可行域内的点能够满足系统对稳定性和动态性能的基本要求。用此方法能够得到可视化的参数可行域,具有直观、准确的优势。
以下是优化可行域的具体计算过程。2.2 节通过灵敏度分析发现主导模态对整流/逆变侧锁相环比例系数参数KpPLLr/KpPLLi、定电流/定电压控制器比例系数Kpr/Kpi 变化比较灵敏,因此选择KpPLLi、KpPLLr、Kpi、Kpr 作为待优化参数。在SCRi=1.6 的弱交流系统运行点下,分别计算整流侧待优化参数KpPLLr、Kpr 和逆变侧待优化参数KpPLLi、Kpi 的优化可行域。以整流侧为例,具体步骤如下:①首先根据经验给出每个待优化控制参数的优化区间,无需精确计算;②保持逆变侧控制参数不变,在这个优化区间内对整流侧待优化控制参数按一定步长均匀取点,得到控制参数的组合;③分别计算每个组合下能量衰减指标的值,寻找令指标取最大值的控制参数组合,选择指标值较大的控制参数组合保留在可行域内。本文中,能量衰减指标的阈值设置为3.6×10-6。由于系统在实际运行时存在不同功率传输水平的工况,需要保证优化后的参数不仅适用于额定功率运行点,还能适用于其他工况。因此,需要得到适用于不同工况的优化可行域。分别在传输功率为额定功率100%、80%、50%、10%的运行点下重复上述过程,得到不同运行点下的可行域,取交集即可得到整流侧最终的优化可行域。按照同样的方法可以得到逆变侧的优化可行域,系统所有待优化控制参数的优化可行域如图8 所示。

图8 适用于不同工况的控制参数可行域
Fig.8 Feasible range of control parameters applicable to different working conditions
4 基于能量衰减指标和蒙特卡洛算法的LCC-HVDC 控制参数优化方法
第2 节通过灵敏度分析找到对系统稳定性影响较大的控制参数;第3 节推导了能够定量反映系统小信号稳定性和动态性能的系统能量衰减指标,并利用能量衰减指标得到适用于不同工况的优化可行域。在此基础上,可以通过在参数的优化可行域内寻找100%额定功率工况下令能量衰减指标值最大的控制参数组合作为优化的结果。蒙特卡洛法是一种基于概率统计理论、使用随机数的数值计算方法,也称随机抽样技术[26]。蒙特卡洛法的基本思想是利用抽样计算出来的数据来描述整体系统,适合于解决不能得到解析表达式的问题[27]。由于控制参数对主导模态的影响非常复杂,主导模态与控制参数的关系难以写出解析表达式,因此在可行域内寻找使能量衰减指标取最大值的控制参数组合的问题适合于采用蒙特卡洛法解决。利用蒙特卡洛法在可行域内生成随机数作为控制参数组合,当生成的随机数组合数量很大,抽样的样本数足够多,可以将所有随机数组合中令指标取最大值的组合作为优化问题的近似解。
本节介绍了控制参数优化方法的具体过程,并通过比较优化前后系统在不同运行点的稳定性和动态性能来验证优化的效果以及优化后参数在不同运行点的适用性。
4.1 LCC-HVDC 控制参数优化方法的具体过程
在100%额定功率工况下(SCRr=2.5,SCRi=1.6,Idcref=1.0(pu),Udcref=0.93(pu)),以均匀分布的方式生成随机数组合作为KpPLLr、KpPLLi、Kpr、Kpi 的样本,判断生成的随机数组合是否在图8 所示的参数可行域内,若随机数组合在可行域内,将随机数组合作为待优化控制参数的数值,计算此控制参数组合下系统的能量衰减指标值;如果随机数组合不在可行域内,重新生成随机数组合。不断迭代,直到在可行域内的随机数组合数量达到设定值10 000。在此过程中记录在可行域内令能量衰减指标取最大值的随机数组合作为优化后的控制参数并记录这组参数下系统的能量衰减指标值。参数优化的流程如图9所示。
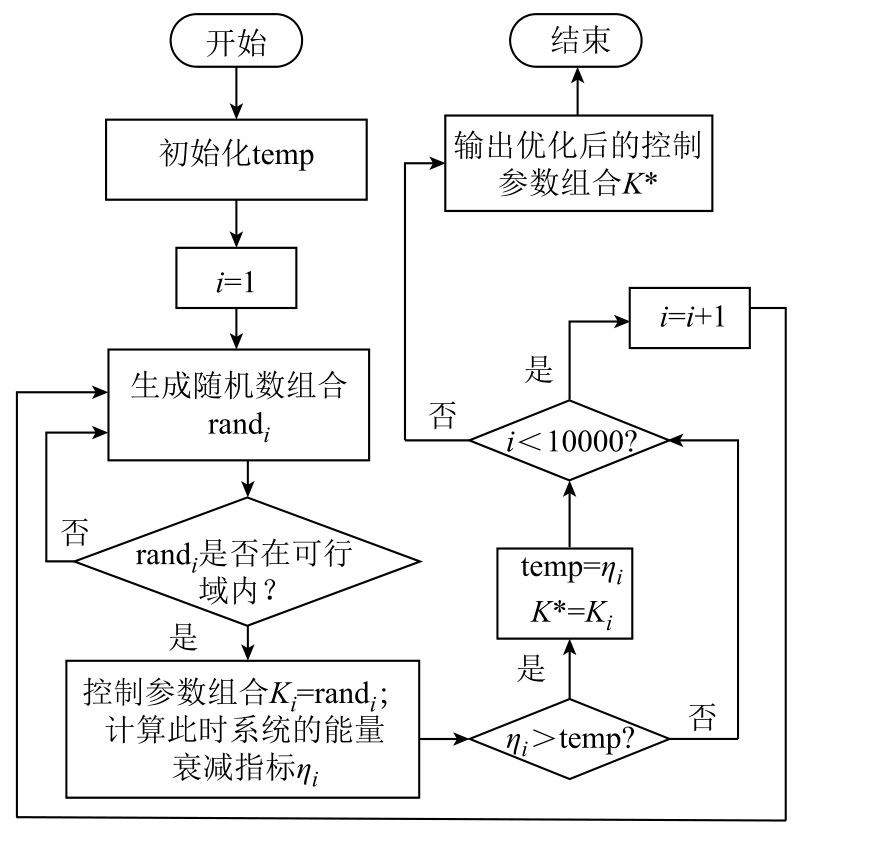
图9 控制参数优化的流程
Fig.9 Specific process of control parameter optimization
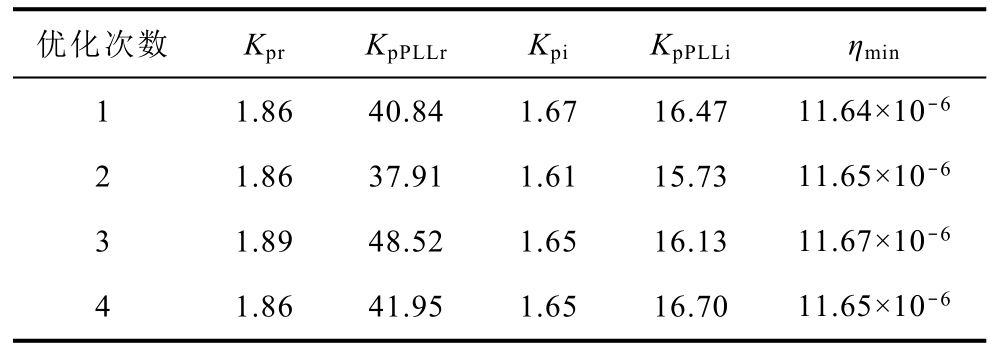
按照图9 所示的优化过程进行优化,连续10 次优化的结果见表2。从表2 可以看出,指标值ηmin在10 次测试中都非常接近,说明本文所提出的优化方法是收敛的。
表2 连续多次优化结果
Tab.2 Multiple optimization results
(续)
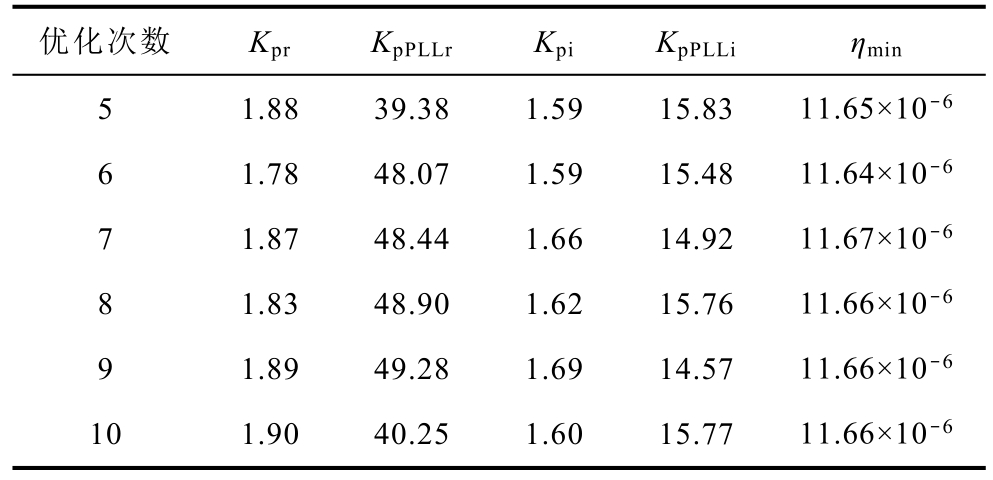
选择指标ηmin 取值最大的第3 组控制参数作为优化的结果进行有效性验证,优化前后控制参数的数值以及系统在初始参数和优化后参数下的能量衰减指标值见表3。
表3 控制参数优化前后对比
Tab.3 Comparison of control parameters before and after optimization

4.2 LCC-HVDC 控制参数优化方法的有效性验证
分别在不同的工况下对比系统采用初始控制参数和优化后控制参数时的小信号稳定性和动态响应性能,验证上述优化方法的有效性。此外,通过对比优化前后系统发生交流故障时的响应波形,证明优化后的控制参数下,系统发生换相失败后的恢复能力有一定改善。
4.2.1 100%额定功率工况
在额定工况下,保持整流侧直流电压为额定电压,整流侧直流电流参考值为1.0(pu),此时逆变侧直流电压参考值为0.93(pu)。通过比较优化前后系统的特征根随SCRi 下降而变化的轨迹可以看出优化前后系统稳定性的变化。令SCRi 从2 下降到1,优化前后系统的根轨迹如图10 所示。从图10 可以看出,在优化后的控制参数下系统在SCRi 下降的过 程中没有出现穿越虚轴的模态,所有特征根实部始终为负,系统始终保持稳定。而采用初始控制参数时,系统在SCRi=1.46 时出现穿越虚轴的模态,系统失稳。将穿越虚轴的模态视为主导模态,比较优化前后SCRi=1.6 的工况下主导模态阻尼比的变化。优化前主导模态阻尼比为0.030 3,优化后主导模态阻尼比增大到0.658 0,说明采用优化后的控制参数能够提高额定工况时系统在弱交流电网下的小信号稳定性。
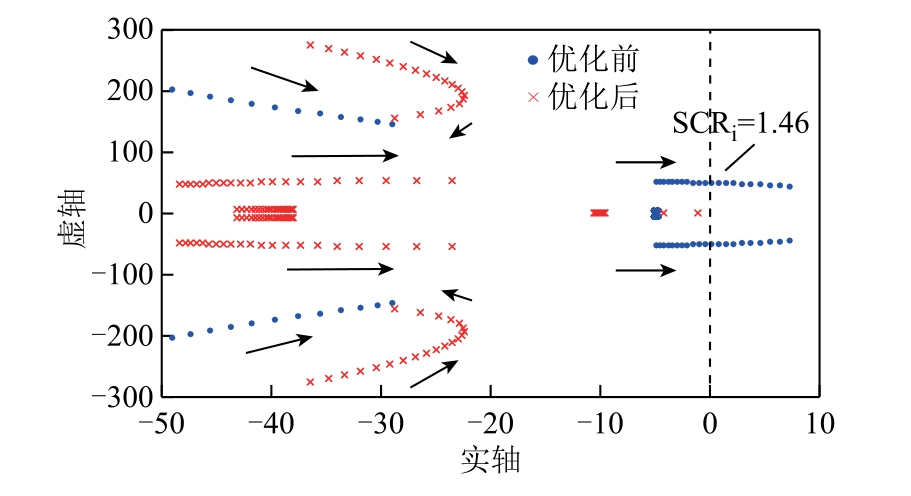
图10 100%工况下优化前后系统的根轨迹对比图
Fig.10 Comparison diagram of root locus of system before and after optimization under 100% working condition
比较优化前后系统在弱交流电网工况下的动态性能。在SCRi=1.6 的弱交流系统下,对比LCCHVDC 采用初始参数和优化后参数时的阶跃响应结果。在两组控制参数下分别令Idcref 从0.95(pu)阶跃到1.0(pu)、Udcref 从0.90(pu)阶跃到0.93(pu),整流侧直流电流Idcrm 和逆变侧直流电压Udcim 的阶跃响应波形如图11 所示。根据高压直流输电系统对阶跃响应的要求,认为超调量不超过整定值变化量的30%的系统具有良好的动态响应性能[28]。100%工况下的动态性能对比见表4。由表4 可以看出,采用优化后的控制参数Idcrm、Udcim 的超调量降低,且超调量小于30%,调节时间(定义为进入并保持在以新的稳态值为中心,偏差为阶跃变化量的10%范围内的最短时间)缩短,优化效果非常明显。
表4 100%工况下的动态性能对比
Tab.4 Comparison of dynamic performance under 100% working condition
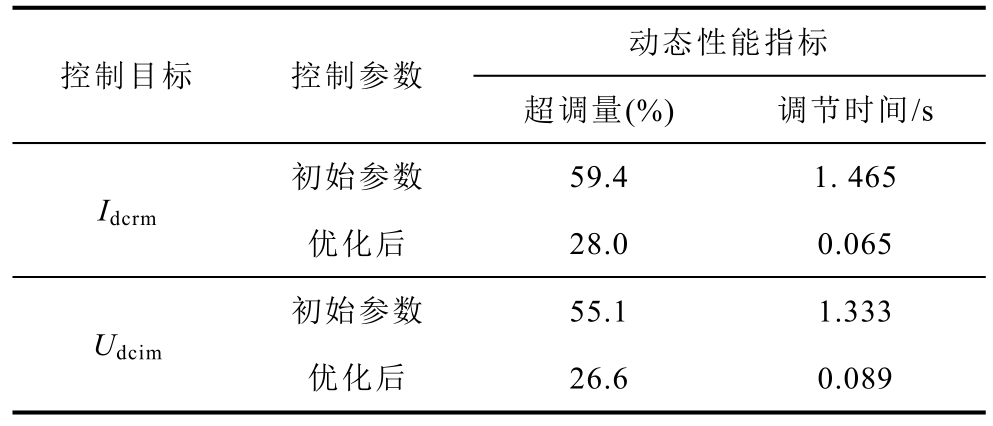
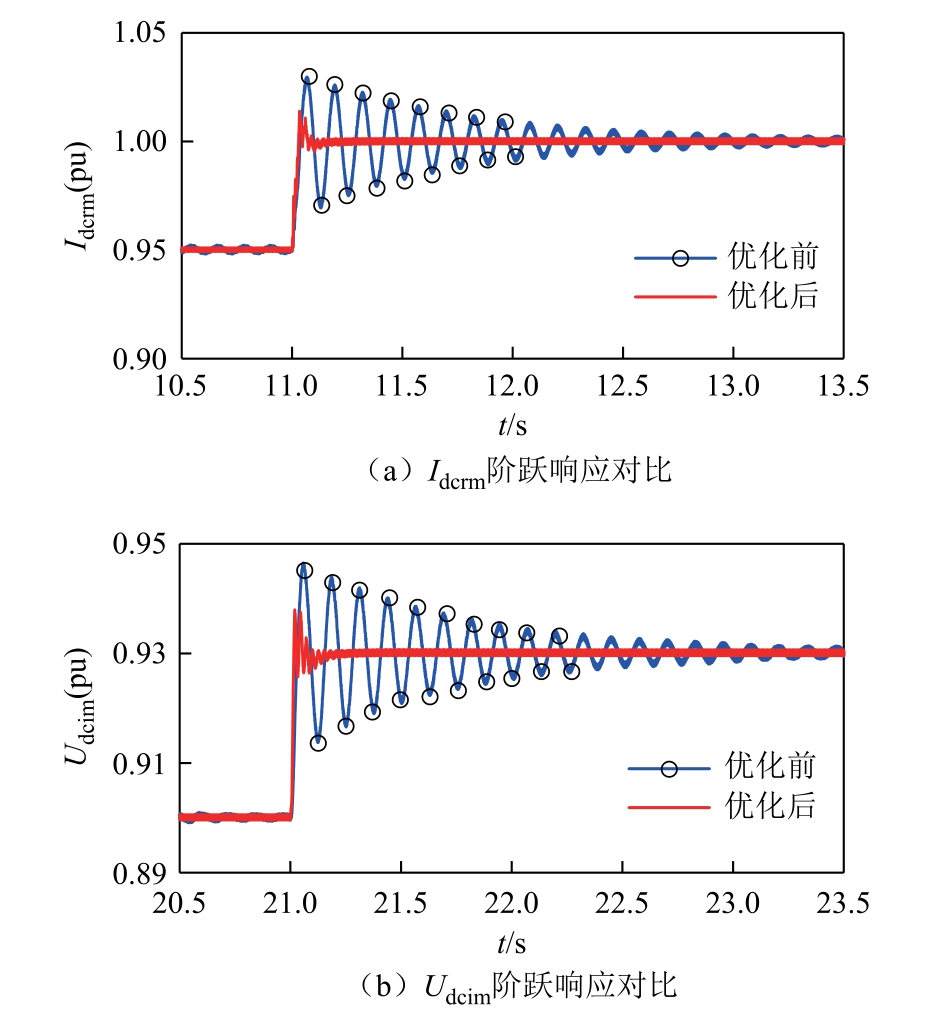
图11 100%工况下优化前后阶跃响应对比图
Fig.11 Comparison diagram of step response before and after optimization under 100% working condition
4.2.2 80%额定功率工况
在80%额定功率工况下,保持整流侧直流电压为额定电压,整流侧直流电流参考值为0.8(pu),此时逆变侧直流电压参考值为0.95(pu)。令SCRi 从2下降到1.1,从图12 可以看出,在优化后的控制参数下系统始终保持稳定,而采用初始控制参数时系统在SCRi=1.35 时失稳。定量比较优化前后主导模态在SCRi=1.6 时的阻尼比,优化前主导模态阻尼比为0.049 9,优化后主导模态阻尼比增大到0.643 7,说明采用优化后的控制参数能够提高80%额定功率工况时系统在弱交流电网下的小信号稳定性。
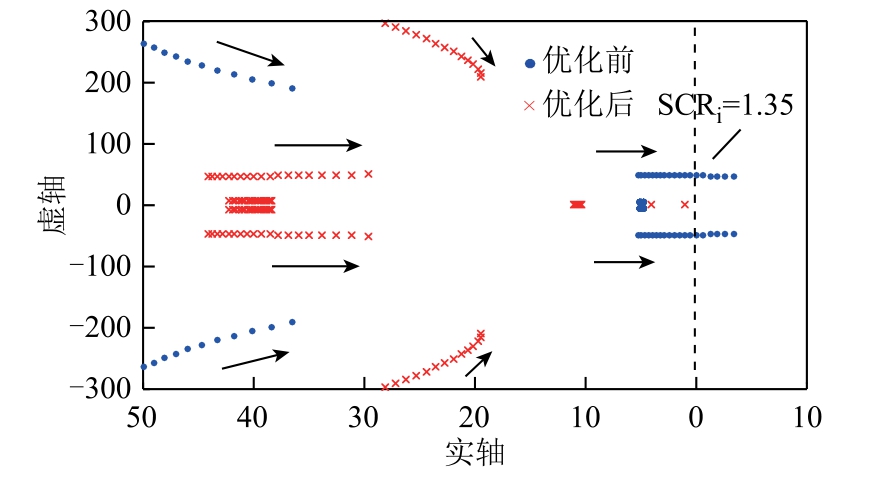
图12 80%工况下优化前后系统的根轨迹对比图 Fig.12 Comparison diagram of root locus of system before and after optimization under 80% working condition
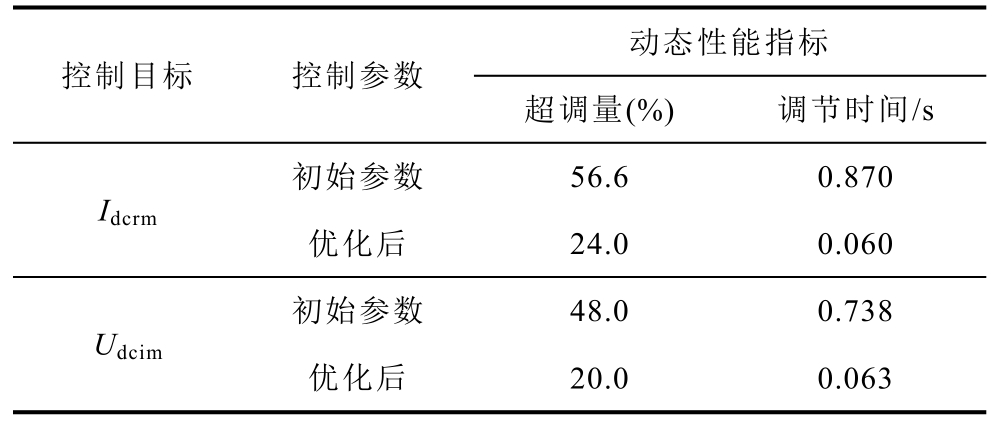
在SCRi=1.6 的弱交流系统下,分别令Idcref 从0.75(pu)阶跃到0.80(pu)、Udcref 从0.92(pu)阶跃到0.95(pu),整流侧直流电流Idcrm 和逆变侧直流电压Udcim 的阶跃响应波形如图13 所示。80%工况下的动态性能对比见表5。由表5 可以看出,优化后的Idcrm、Udcim 的超调量小于30%,调节时间明显减小,系统动态性能提升。
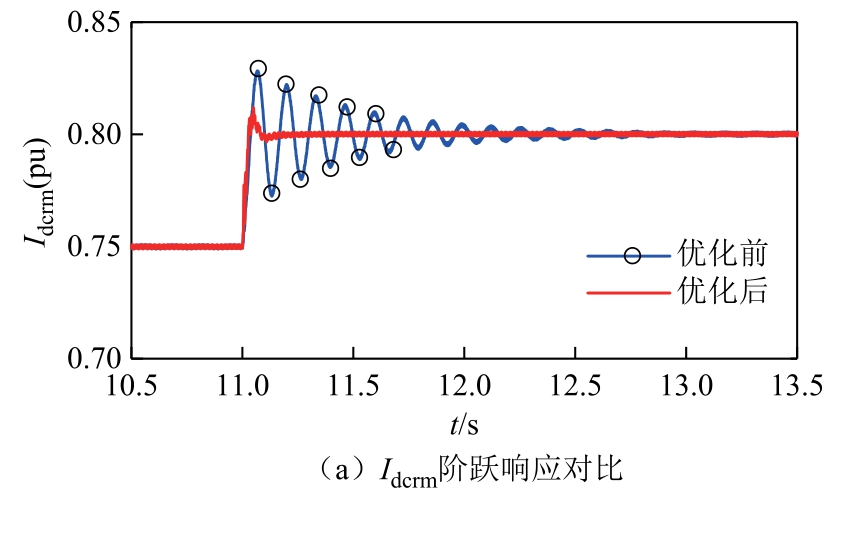
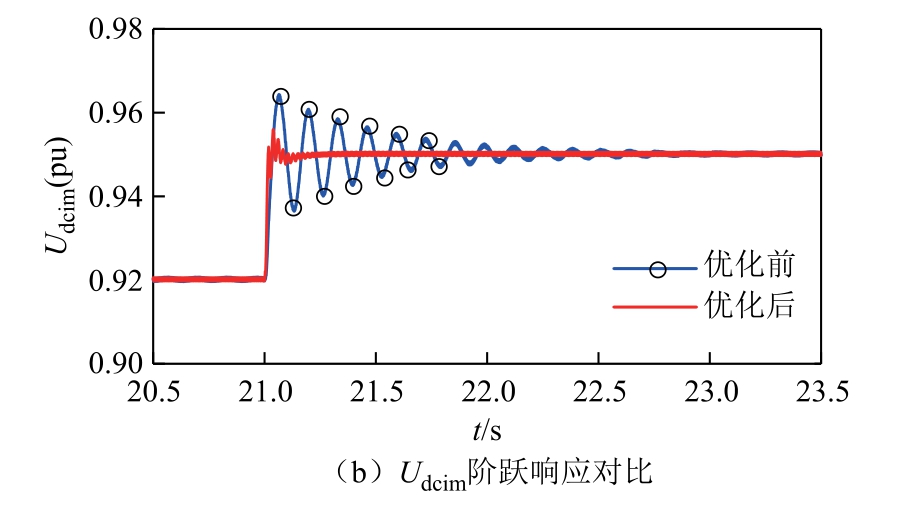
图13 80%工况下优化前后阶跃响应对比图
Fig.13 Comparison diagram of step response before and after optimization under 80% working condition
表5 80%工况下的动态性能对比
Tab.5 Comparison of dynamic performance under 80% working condition
4.2.3 50%额定功率工况
在50%额定功率工况下,保持整流侧直流电压为额定电压,整流侧直流电流参考值为0.5(pu),此时逆变侧直流电压参考值为0.99(pu)。在50%额定功率运行点,控制参数优化前后系统在SCRi 降低到1 时都不会失稳,因此通过比较优化前后系统的动态性能来验证优化有效性。
在SCRi=1.6 的弱交流系统工况下,分别令Idcref从0.45(pu)阶跃到0.50(pu)、Udcref 从0.94(pu)阶跃到0.97(pu),整流侧直流电流Idcrm 和逆变侧直流电压Udcim 的阶跃响应波形如图14 所示。50%工况下的动态性能对比见表6。由表6 可以看出,在优化后的参数下Idcrm、Udcim 的超调量小于30%,调节时间明显变小,系统在50%工况下的阶跃响应性能有所改善。
表6 50%工况下的动态性能对比
Tab.6 Comparison of dynamic performance under 50% working condition

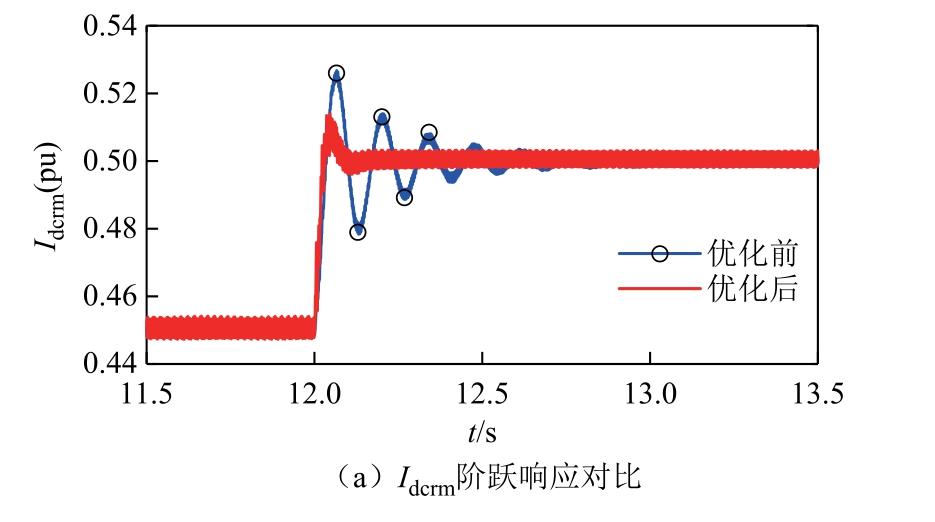
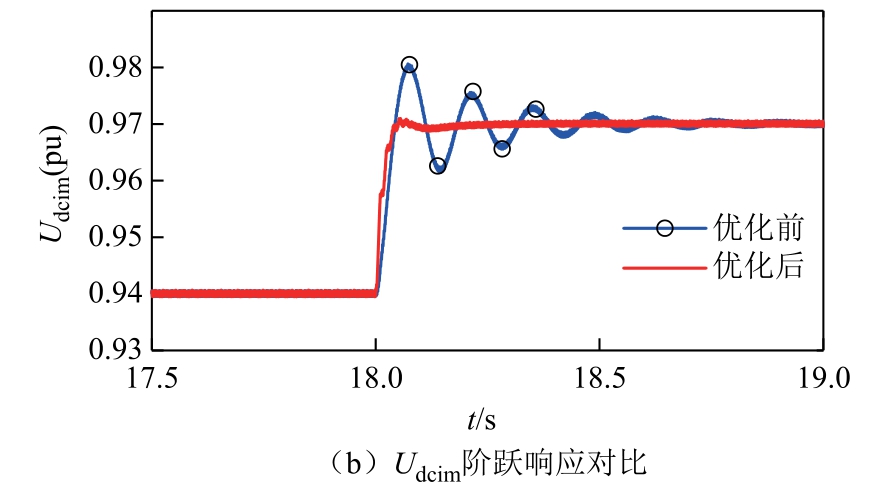
图14 50%工况下优化前后阶跃响应对比图
Fig.14 Comparison diagram of step response before and after optimization under 50% working condition
4.2.4 10%额定功率工况
在10%额定功率工况下,保持整流侧直流电压为额定电压,整流侧直流电流参考值为0.1(pu),此时逆变侧直流电压参考值为0.99(pu)。在10%额定功率运行点,控制参数优化前后系统在SCRi 降低到1 时都不会失稳,因此通过比较优化前后系统的动态性能来验证优化有效性。
在SCRi=1.6 的弱交流系统工况下,对比系统采用初始参数和优化后参数时的阶跃响应结果。在两组控制参数下分别令 Idcref 从 0.15(pu)阶跃到0.10(pu)、Udcref 从0.96(pu)阶跃到0.99(pu),整流侧直流电流Idcrm 和逆变侧直流电压Udcim 的阶跃响应波形如图15 所示。10%工况下的动态性能对比见表7。由表7 可以看出,通过优化控制参数可以令Idcrm、Udcim 的动态性能指标明显改善,超调量小于30%满足阶跃相应要求,提升了系统10%工况的动态性能。
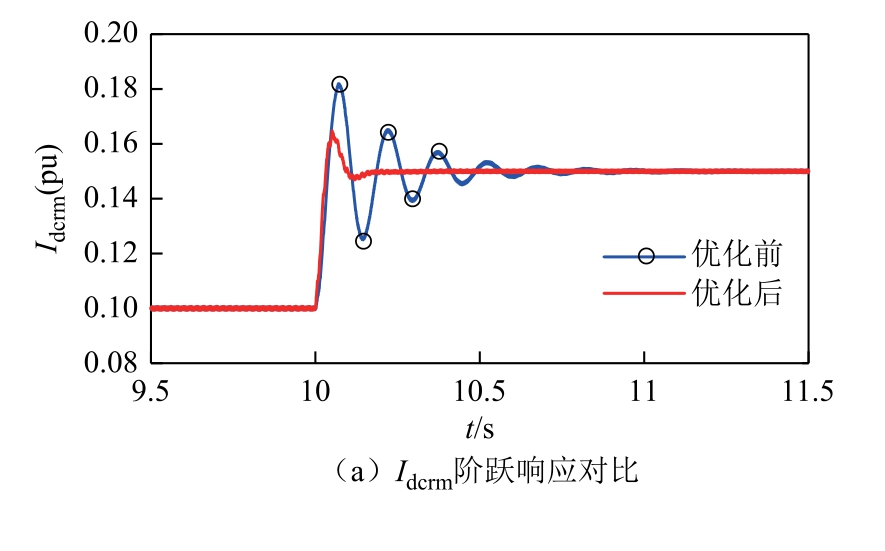
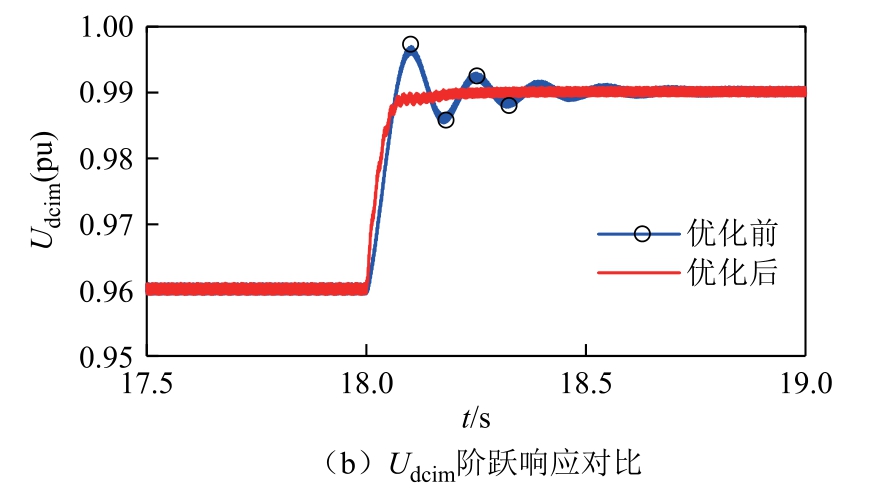
图15 10%工况下优化前后阶跃响应对比图
Fig.15 Comparison diagram of step response before and after optimization under 10% working condition
表7 10%工况下的动态性能对比
Tab.7 Comparison of dynamic performance under 10% working condition
4.2.5 交流故障恢复性能验证
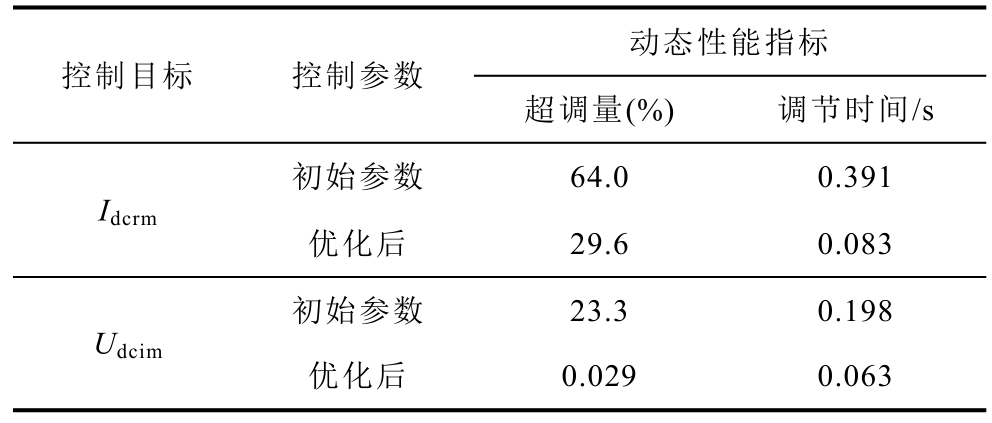
在初始短路比(SCRr=2.5,SCRi=2.5)额定工况下对比初始控制参数和优化后参数下系统的交流故障响应情况,设置逆变侧交流母线A 相在3s 时经0.5H 电感接地的短路故障,故障持续时间为0.1s,随后故障清除。上述过程中控制参数优化前后系统的故障响应情况如图16 所示,从图16a 可以看出,优化前后逆变侧关断角γ 在发生交流故障后都减小到0,系统都发生换相失败。从图16b、图16c 可以看出,优化前系统发生换相失败后不能恢复,优化后系统在故障发生0.34s 后恢复稳定运行,说明在初始短路比下采用优化后的控制参数时系统发生换相失败后的恢复能力有一定改善。
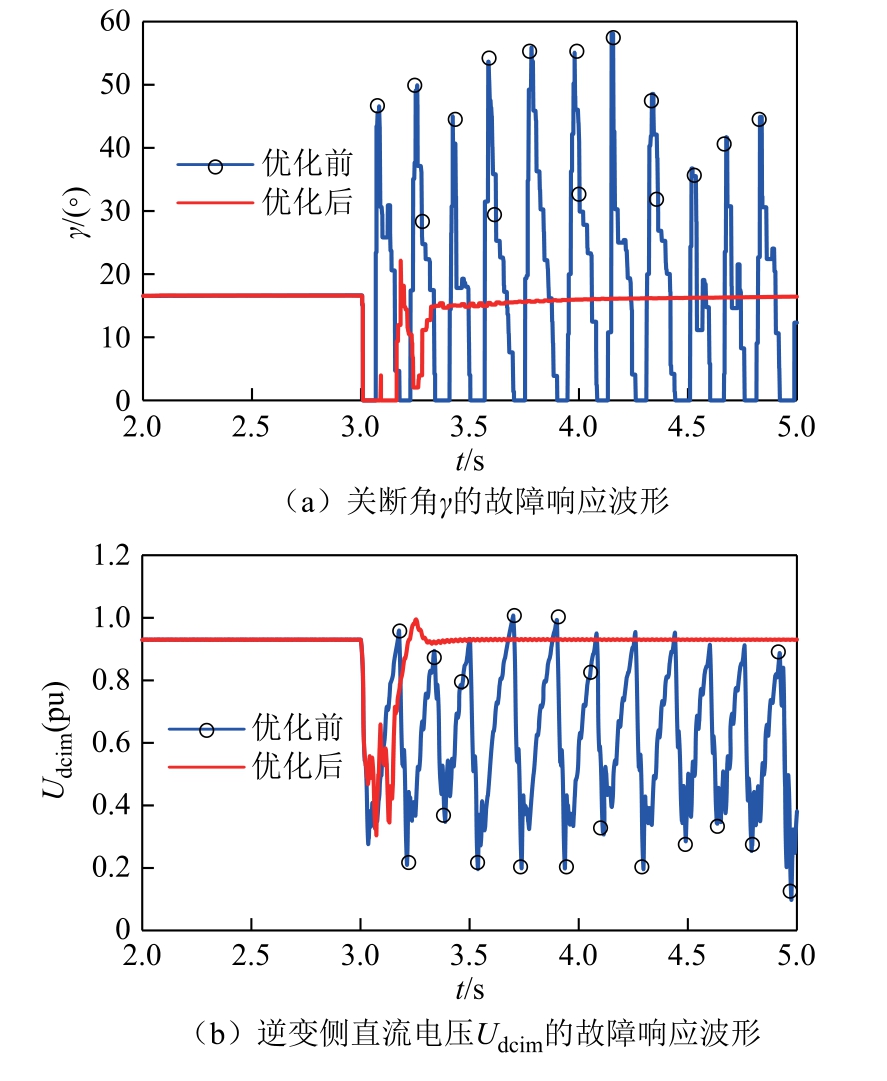
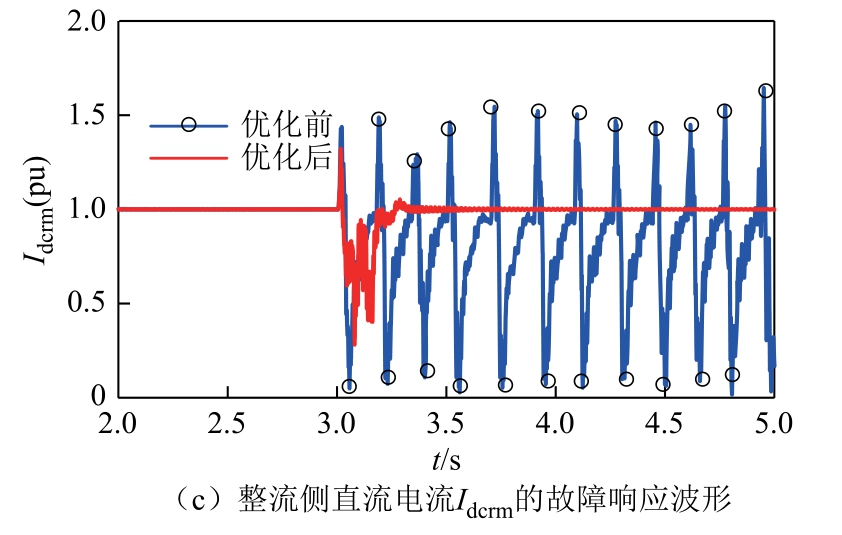
图16 交流故障响应特性对比
Fig.16 Comparison of AC fault response characteristics
5 结论
为了提高弱交流系统下LCC-HVDC 小信号的稳定性和动态性能,本文利用能量衰减指标和蒙特卡洛算法优化了对系统稳定性影响较大的关键控制参数,并在不同功率运行点下验证优化的有效性,得到如下结论:
1)LCC-HVDC 系统在逆变侧连接弱交流系统时易出现小信号失稳和动态性能恶化的问题。初始控制参数下,系统在交流系统短路比较高的时候动态性能较好,而在交流系统短路比降低后动态性能明显变差。说明在进行参数优化时有必要同时关注系统的稳定性和动态性能。
2)对引起系统失稳的主导模态进行灵敏度分析,发现主导模态对整流/逆变侧锁相环比例系数参数 KpPLLr/KpPLLi、定电流/定电压控制器比例系数Kpr/Kpi 变化比较灵敏,上述参数对LCC-HVDC 在弱交流系统下的稳定性影响较大。
3)以能量衰减指标为目标函数,可以得到适用于不同工况的优化可行域。采用蒙特卡洛法在可行域内寻找令目标函数取最大值的控制参数组合,通过在不同工况下对比测试结果,证明采用优化后的控制参数能够显著提升LCC-HVDC 在弱交流系统下的小信号稳定性和动态性能,优化结果适用于不同传输功率的工况。通过对比优化前后系统的交流故障响应结果,发现采用优化后的控制参数系统的换相失败恢复能力有一定改善,证明了本文所提出优化方法的有效性。
附 录
附表1 LCC-HVDC 系统电气/控制参数
App.Tab.1 Electrical/control parameters of LCC-HVDC system

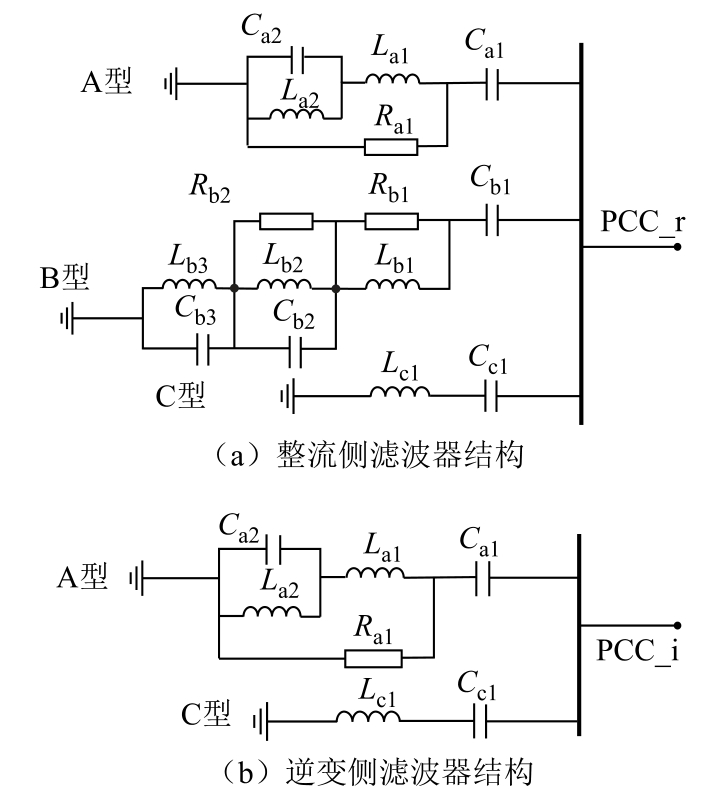
附图1 整流/逆变侧滤波器组合结构示意图
App.Fig.1 Structure diagram of rectifier/ inverter side filter combination
[1]赵畹君.高压直流输电工程技术[M].2 版.北京: 中国电力出版社,2011.
[2]许汉平,杨炜晨,张东寅,等.考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J].电工技术学报,2020,35(8): 1776-1786.Xu Hanping,Yang Weichen,Zhang Dongyin,et al.Commutation failure judgment method for multiinfeed HVDC systems considering the interaction of commutation failures[J].Transactions of China Electrotechnical Society,2020,35(8): 1776-1786.
[3]贺永杰,向往,周家培,等.LCC-MMC 串联型混合直流输电系统小信号建模[J].电工技术学报,2021,36(7): 1492-1506.He Yongjie,Xiang Wang,Zhou Jiapei,et al.Smallsignal modelling of LCC-MMC series hybrid HVDC transmission system[J].Transactions of China Electrotechnical Society,2021,36(7): 1492-1506.
[4]曾南超.高压直流输电在我国电网发展中的作用[J].高电压技术,2004,30(11): 11-12.Zeng Nanchao.Role of HVDC transmission in the power system development in China[J].High Voltage Engineering,2004,30(11): 11-12.
[5]郭春义,宁琳如,王虹富,等.基于开关函数的LCC-HVDC 换流站动态模型及小干扰稳定性[J].电网技术,2017,41(12): 3862-3868.Guo Chunyi,Ning Linru,Wang Hongfu,et al.Switching-function based dynamic model of LCCHVDC station and small signal stability analysis[J].Power System Technology,2017,41(12): 3862-3868.
[6]Rahimi E,Gole A M,Davies J B,et al.Commutation failure analysis in multi-infeed HVDC systems[J].IEEE Transactions on Power Delivery,2011,26(1): 378-384.
[7]Guo Chunyi,Zhao Chengyong,Iravani R,et al.Impact of phase-locked loop on small-signal dynamics of the line commutated converter-based high-voltage directcurrent station[J].IET Generation,Transmission &Distribution,2017,11(5): 1311-1318.
[8]郭春义,蒋雯,郑安然,等.弱交流系统下STATCOM 对LCC-HVDC 小干扰稳定裕度的影响研究[J].中国电机工程学报,2018,38(19): 5679-5686,5925.Guo Chunyi,Jiang Wen,Zheng Anran,et al.Impact of STATCOM on the small-signal stability margin of LCC-HVDC under weak AC grid conditions[J].Proceedings of the CSEE,2018,38(19): 5679-5686,5925.
[9]王长江,姜涛,刘福锁,等.基于轨迹灵敏度的暂态过电压两阶段优化控制[J].电工技术学报,2021,36(9): 1888-1900,1913.Wang Changjiang,Jiang Tao,Liu Fusuo,et al.Twostage optimization control of transient overvoltage based on trajectory sensitivity[J].Transactions of China Electrotechnical Society,2021,36(9): 1888-1900,1913.
[10]高本锋,王刚,刘毅,等.LCC-HVDC 送端电网等值方案研究[J].电工技术学报,2021,36(15): 3250-3263,3271.Gao Benfeng,Wang Gang,Liu Yi,et al.Study on equivalence method of AC system in sending-end of LCC-HVDC[J].Transactions of China Electrotechnical Society,2021,36(15): 3250-3263,3271.
[11]杨汾艳,徐政,张静.直流输电比例-积分控制器的参数优化[J].电网技术,2006,30(11): 15-20.Yang Fenyan,Xu Zheng,Zhang Jing.Study on parameter optimization of HVDC PI controllers[J].Power System Technology,2006,30(11): 15-20.
[12]郭春义,赵成勇,李广凯,等.基于Simplex 算法的VSC-HVDC 控制参数优化[J].电力自动化设备,2010,30(9): 13-17.Guo Chunyi,Zhao Chengyong,Li Guangkai,et al.Control parameter optimization based on Simplex algorithm for VSC-HVDC[J].Electric Power Automation Equipment,2010,30(9): 13-17.
[13]喻锋,王西田,杨煜,等.一种混合遗传算法在HVDC 定电流控制器参数优化中的应用[J].电力系统保护与控制,2014,42(9): 126-131.Yu Feng,Wang Xitian,Yang Yu,et al.An application of hybrid genetic algorithm in the parameters optimization of HVDC constant current controller[J].Power System Protection and Control,2014,42(9): 126-131.
[14]叶运铭,汪娟娟,陈威,等.基于小干扰动态模型的LCC-HVDC 系统控制器参数优化方法[J].南方电网技术,2021,15(4): 1-9.Ye Yunming,Wang Juanjuan,Chen Wei,et al.Controller parameters optimization method for LCCHVDC system based on small-interference dynamic model[J].Southern Power System Technology,2021,15(4): 1-9.
[15]杨佳艺,赵成勇,苑宾,等.基于粒子群优化算法的VSC-HVDC 系统的控制参数优化策略[J].电力自动化设备,2017,37(12): 178-183.Yang Jiayi,Zhao Chengyong,Yuan Bin,et al.Parameter optimization of VSC-HVDC control system based on particle swarm optimization algorithm[J].Electric Power Automation Equipment,2017,37(12): 178-183.
[16]郑安然,郭春义,殷子寒,等.提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法[J].电工技术学报,2020,35(6): 1336-1345.Zheng Anran,Guo Chunyi,Yin Zihan,et al.Optimal adjustment method of control parameters for improving small-signal stability of hybrid multiterminal HVDC system under weak AC condition[J].Transactions of China Electrotechnical Society,2020,35(6): 1336-1345.
[17]刘宛菘,秦博宇,张若微,等.模块化多电平换流器型多端高压直流输电控制参数优化方法[J].电机与控制学报,2021,25(2): 10-18,27.Liu Wansong,Qin Boyu,Zhang Ruowei,et al.Optimal design method of control parameters for MMC-MTDC[J].Electric Machines and Control,2021,25(2): 10-18,27.
[18]黄伟煌,李明,郭铸,等.基于小干扰稳定性的多端混合高压直流输电系统控制参数分析与优化方法[J].电网技术,2020,44(8): 2941-2949.Huang Weihuang,Li Ming,Guo Zhu,et al.Control parameter analysis and optimization method of multiterminal hybrid HVDC transmission system based on small signal stability[J].Power System Technology,2020,44(8): 2941-2949.
[19]崔鹏,郭春义,蒋雯,等.基于二次型指标和蒙特卡洛方法的含STATCOM 的LCC-HVDC 系统的控制参数优化[J].中国电机工程学报,2020,40(12): 3858-3866.Cui Peng,Guo Chunyi,Jiang Wen,et al.Optimization of control parameters of LCC-HVDC system with STATCOM based on Lyapunov stability and Monte Carlo algorithm[J].Proceedings of the CSEE,2020,40(12): 3858-3866.
[20]Guo Chunyi,Cui Peng,Zhao Chengyong.Optimization and configuration of control parameters to enhance small-signal stability of hybrid LCC-MMC HVDC system[J].Journal of Modern Power Systems and Clean Energy,2021,10(1): 213-221.
[21]张嗣瀛,高立群.现代控制理论[M].2 版.北京: 清华大学出版社,2017.
[22]贺永杰,向往,赵静波,等.一种用于 LCC-HVDC系统小干扰稳定性分析的改进动态相量模型[J].电网技术,2021,45(4): 1417-1428.He Yongjie,Xiang Wang,Zhao Jingbo,et al.Modified dynamic phasor model for small-signal stability analysis of LCC-HVDC system[J].Power System Technology,2021,45(4): 1417-1428.
[23]江克证,朱建行,胡家兵,等.计及开关过程的LCC-HVDC 小信号建模及其对电力系统电磁尺度稳定性分析[J].清华大学学报(自然科学版),2021,61(5): 395-402.Jiang Kezheng,Zhu Jianhang,Hu Jiabing,et al.Smallsignal modeling of LCC-HVDC systems with switching for electromagnetic timescale stability analyses of power systems[J].Journal of Tsinghua University(Science and Technology),2021,61(5): 395-402.
[24]崔翔.无损耗传输线物理模拟的集总电路级联数目确定方法[J].中国电机工程学报,2017,37(9): 2561-2570.Cui Xiang.Chained number of lumped-circuits for physical analogy of the lossless transmission lines[J].Proceedings of the CSEE,2017,37(9): 2561-2570.
[25]蒋雯.含STATCOM 的LCC-HVDC 系统小信号稳定性研究[D].北京: 华北电力大学(北京),2019.
[26]金畅.蒙特卡洛方法中随机数发生器和随机抽样方法的研究[D].大连: 大连理工大学,2006.
[27]朱陆陆.蒙特卡洛方法及应用[D].武汉: 华中师范大学,2014.
[28]傅闯,叶运铭,汪娟娟,等.基于D 分割法的LCCHVDC 系统控制器参数整定方法[J/OL].电力系统自动化,1-17[2022-02-26].http://kns.cnki.net/kcms/ detail/32.1180.TP.20220114.1056.002.html.Fu Chuang,Ye Yunming,Wang Juanjuan,et al.Dpartition method based controller parameter setting method for LCC-HVDC system[J/OL].Automation of Electric Power Systems,1-17[2022-02-26].http://kns.cnki.net/kcms/detail/32.1180.TP.20220114.1056.002.html.