0 引言
随着“双碳”目标的设定及柔性直流输电、电力电子变压器等技术的快速发展，直流配电网凭借其无需交直流转换、线路损耗小、更适于分布式电源接入等优势被纳入未来发展的蓝图[1-3]。然而，分布式电源的接入在一定程度上降低了系统阻尼[4-5]，与配电网中的恒功率负载发生交互作用[6-7]，可能会引起宽频振荡、谐振等问题，给系统的安全运行带来潜在的威胁[8-11]。
为避免上述情况的发生，有效的分析方法尤为重要，直流配电网的谐振分析通常采用阻抗分析法[12-14]和模态分析法（Resonance Modal Analysis,RMA）[15-17]。阻抗分析法中，节点导纳/阻抗矩阵因物理意义清晰、表征交互作用较为直观，成为谐振分析的常用工具[18-20]。文献[18]提出基于节点阻抗矩阵的直流配电网谐振特性分析方法，该方法能够有效辨识端口和系统谐振频率，分析换流器间的谐波交互作用关系。文献[19]利用导纳矩阵消除了负载节点及支路对辨识支路串联谐振的影响，提出了基于端口等效法的多端口支路、回路谐振辨识方法。文献[20]根据扰动源支路有无阻抗、支路为串联或并联支路进行分类，提出了考虑扰动源支路类型的节点导纳矩阵建立方法。此外，文献[4,21-23]还将节点导纳/阻抗矩阵用于实现换流器输入阻抗与系统其他节点的解耦，提出换流器输出端源测与负载侧之间、子系统间的谐振分析方法。然而，节点导纳/阻抗矩阵对系统谐振特性的描述并不全面，扰动源的谐振特性无法在该矩阵中得到体现。对于电源经换流器并入电网的场景，节点注入电流为等效电流源，而对应的输入侧扰动源可能为电压源或其他类型受控源。上述研究忽略了换流器内部参数及控制回路对扰动源输出特性的影响，使分析结果存在偏差，甚至造成谐振点遗漏[12,18]。因此，有必要对计及扰动源输出特性的直流配电网谐振分析方法展开研究。
与阻抗分析法相比，模态分析法通过矩阵特征值求解分析系统谐振峰分布，具有步骤简单、分析结果更为直观的优势。其中，模态灵敏度（Sensitivity Analysis,SA）能够量化参数的影响程度，可用于指导谐振抑制，在机械和电气领域得到了广泛的应用[24]。文献[24]首次将谐振模态关于参数的偏微分定义为该参数的模态灵敏度，并给出了线路参数的模态灵敏度计算方法。针对大规模系统互联的多参数波动场景，文献[25]提出了多参数摄动2 阶模态灵敏度计算方法，用于揭示系统中的复杂交互作用。然而，上述方法的应用场景均为传统交流系统，未讨论换流器及其控制参数的模态灵敏度计算方法。为了解决这一问题，文献[26-27]提出了控制参数的模态灵敏度计算方法，通过直接计算控制参数改变前后的模态偏移量分析参数对谐振的敏感性。上述方法在永磁同步发电机、虚拟同步机等不同场景下得到了应用，分析参数的谐振参与、影响、放大程度[28-31]。然而，此类方法仅能计算灵敏度的模值，无法区分参数改变对谐振模态的抑制/放大作用。此外，上述研究均未考虑换流器的扰动源输出特性对谐振模态的影响，并且，当系统内换流器数量较多时，对所有参数进行灵敏度计算非常繁琐。
为此，本文提出一种计及扰动源输出特性的直流配电网谐振分析模型和换流器参数模态灵敏度计算方法。首先，以输入侧扰动源为自变量，建立换流器等值阻抗模型并修正了系统阻抗矩阵，从系统尺度分析扰动源输出特性对系统谐振特性的影响机理，提出计及扰动源传递函数的系统阻抗修正模型；然后，基于该模型，从元器件参数尺度分析换流器的谐振敏感性，拓展模态灵敏度的应用场景至含换流器的直流配电网，提出计及扰动源传递函数的换流器参数模态灵敏度计算方法；最后，在PSCAD 中搭建IEEE 14 节点直流配电网仿真模型，分析扰动源传递函数的谐振特性，量化换流器参数对系统谐振特性的影响，对所提方法进行验证和应用。
1 计及扰动源传递函数的谐振分析方法
扰动源传递函数是换流器输入侧扰动源与输出侧等效电源之间的对应关系，在换流器的输入-输出特性方程中体现。阻抗模型是直流配电网谐振分析的基础，通过对状态方程进行拉普拉斯变换，可以得到其以传递函数形式体现的换流器输入-输出特性方程。对于负载侧换流器，输出特性可用等值阻抗表示；对于源侧换流器，还需考虑等效电源的输出特性，等效源通常被视为理想源[12]。然而，对于扰动经换流器注入电网的场景，受换流器内部电路及控制方式的影响，理想源不能准确地描述扰动源的谐振特性。为了分析扰动源传递函数对谐振特性的影响，表1 以电压源换流器（Voltage Source Converter,VSC）、分布式电源、恒功率负载等典型换流器为例，列出了以输入侧扰动源为自变量的等值阻抗模型，建模过程及变量含义详见附录。
表1 关键元件等效电路
Tab.1 Equivalent circuit of key components
由表1 可见，等效电流源可表示为所有输入侧扰动源与其对应扰动源传递函数的乘积和，该传递函数与换流器内部的电路及控制参数有关。为了分析扰动源传递函数对谐振特性的影响，将直流配电网节点电压与注入电流的关系用节点电压方程描述为
式中，Z 为系统阻抗矩阵；
为节点电压；
为等效电流源。
将表1 中等效电流源表达式代入式（1），则以换流器输入侧扰动源为自变量的节点电压方程为
式中，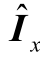
为输入侧扰动源列向量；n 为同一节点最大扰动源个数；扰动源传递函数矩阵Gx 为对角阵。式（2）对于可用表1 中等效电路表示的其他类型电源或非恒功率负载均成立。其中，ZGx 为计及了扰动源输出特性的修正系统阻抗矩阵，令
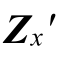′=ZGx，修正系统导纳矩阵Yx′变为
式中，Y 为原系统导纳矩阵。式（2）中，当x=1 时，若节点 m 含等效电流源，G1(m,m)为体现扰动源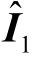
(m)输出特性的扰动源传递函数。例如，对于表1中的分布式电源有
若节点m 无扰动源或扰动源不受换流器影响，Z′(m,j)=Z(m,j)（j=1,2,…,N，N 为矩阵维数），即G1(m,m)=1。
当同一节点具有多个扰动源时（x＞1），若节点m 含扰动源，Gx(m,m)为
(m)对应的扰动源传递函数；否则，Gx(m,m)=0。以表1 中VSC 换流器为例，有
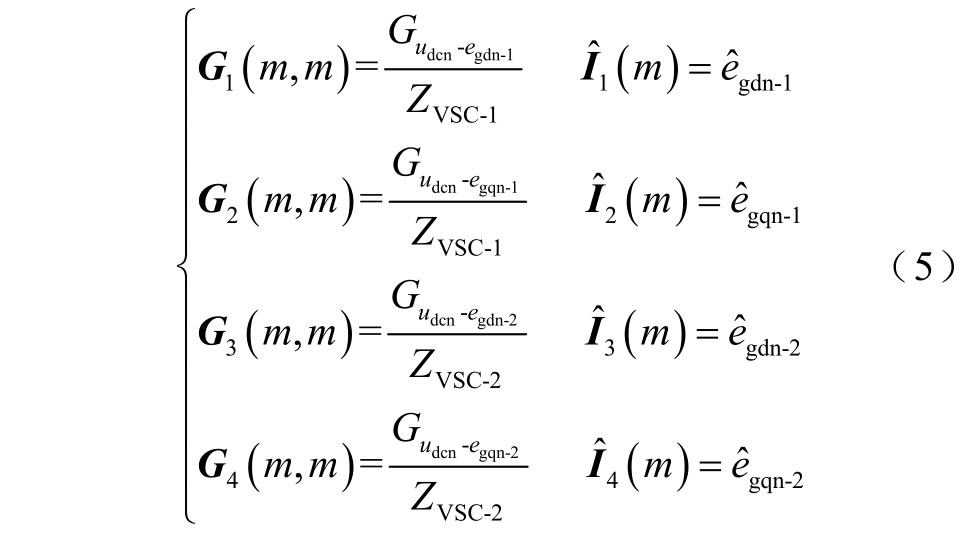
由式（2）～式（5）可知，扰动源传递函数Gx作用于Zx′相应节点的列向量，该扰动源与所有节点电压之间的输入-输出特性均受其影响；当Gx 存在谐振点时，所有节点电压将存在相应的谐振风险。传统方法仅分析系统阻抗矩阵Z 的谐振特性，对换流器输入侧扰动注入的分析结果存在偏差，甚至可能造成谐振点遗漏，给系统的安全运行带来隐患。因此，有必要计及扰动源传递函数的影响，对修正矩阵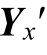
的谐振特性展开研究。
2 计及扰动源传递函数的换流器模态灵敏度计算方法
计及扰动源传递函数后，系统导纳矩阵的表达形式发生了改变，对于源侧换流器并网节点i，导纳矩阵行向量为
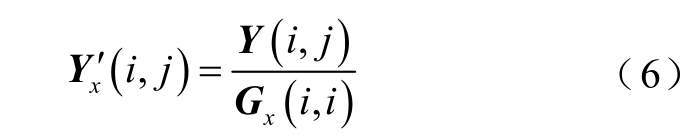
式中，i =j 时，自导纳
，ysh 为换流器的等值导纳，ysh-x 为其他并联元件在该节点的导纳，互导纳Y(i,j)（j≠i）不含换流器参数。通过改变换流器的等值导纳ysh 和扰动源传递函数Gx(i,i)，换流器内部参数作用于所在节点的自导纳Y(i,i)和相应的Yx′行向量，从而影响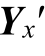
′的谐振特性。以表1 中分布式电源为例，其等值导纳ysh=1/Zpv，扰动源传递函数Gx(i,i)=Ypvs/Zpv，ysh 和Gx(i,i)均为关于分布式电源内部电路和控制参数的函数（附录中式（A5）～式（A7））。由此可知，扰动源传递函数与换流器等值阻抗（1/ysh）具有同源性，即换流器对系统谐振的作用途径不唯一。因此，系统级谐振分析难以阐述换流器的谐振作用机理和影响程度，需要开展参数尺度的研究。
影响因素分析作为一种参数尺度的谐振分析方法，其分析结果能够揭示谐振变化规律、指导参数整定和谐振抑制。其中，模态灵敏度通过计算谐振模态关于参数的偏微分，能够有效量化模态阻抗对参数的敏感程度。然而，现有方法对于换流器内部参数的应用仍具有局限性。下文结合扰动源输出特性，提出了换流器扰动源传递函数、等值导纳及其内部参数的模态灵敏度计算方法。
2.1 扰动源传递函数模态灵敏度
灵敏度的大小和正负分别起到量化谐振对参数的敏感程度和反映振荡幅度变化方向的作用[24]。灵敏度为正时，增大参量能够有效降低谐振阻抗，对谐振起到抑制作用，反之则放大谐振。然而，由于特征值λk 和扰动源传递函数Gx(i,i)均为复数，即∂λk/∂Gx(i,i)的计算结果为复数，无法直接根据该结果对 Gx(i,i) 的灵敏度进行评估，其模值
则无法区分谐振的抑制/放大效果。因此，根据模态灵敏度定义，换流器的灵敏度表达式应为
。
在式（9）的基础上，令∂λk/∂Gx(i,i)=a+jb，∂Gx(i,i)/ ∂|Gx(i,i)|=xi+jyi，则
式中，λr、λi 分别为λk 的实部和虚部。因此，可推导出扰动源传递函数Gx(i,i)的灵敏度为
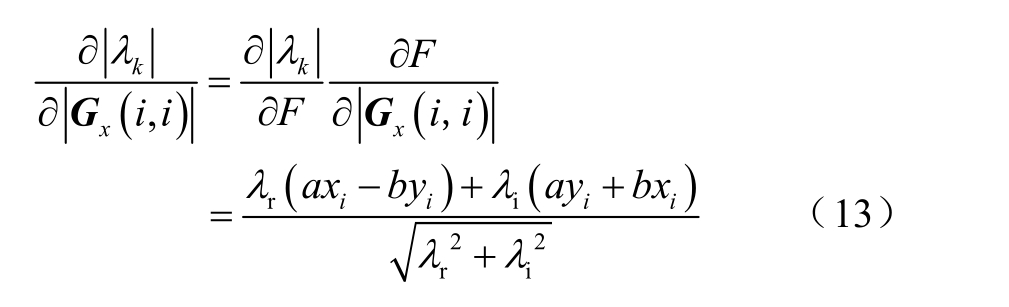
2.2 换流器等值导纳模态灵敏度
换流器等值导纳ysh位于Yx′的主对角线元素中，根据是否位于扰动源所在节点，灵敏度的表达形式存在差异。对于扰动源所在节点，根据式（6）有
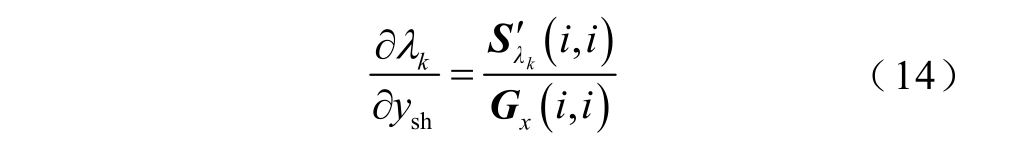
令式（14）实部为SG,r、虚部为SG,i，分别用其代替式（13）中a、b，可得出扰动源所在节点的换流器等值导纳灵敏度为
对于非扰动源所在节点，ysh=ysh,r+jysh,i，ysh,r、ysh,i 分别为等值导纳的实部和虚部。
2.3 换流器内部参数灵敏度
内部参数的灵敏度也分为换流器输入侧是否含有扰动源两种情况，对于不含扰动源的换流器，令ysh 对参数α 的偏微分为
推导步骤与式（13）类似，用Sr、Si、x、y 替代a、b、xi、yi，可推导出不含扰动源的换流器内部参数模态灵敏度为
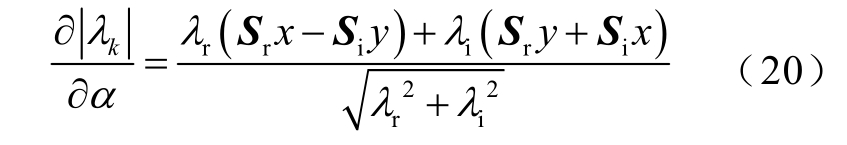
对于含有扰动源的换流器，其内部参数变化同时影响等值导纳和扰动源传递函数，特征值λk 对参数α 的偏微分为
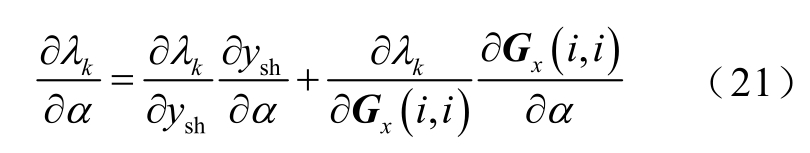
将式（9）、式（14）、式（19）代入式（21），参照式（10）～式（13）对所得结果进行处理即可获得扰动源所在换流器的内部参数灵敏度，此处不再赘述。与传统方法相比，式（21）同时计及了参数改变等值导纳和扰动源传递函数对灵敏度产生的影响，分析结果更为准确。当对不同参数的灵敏度进行比较时，需对其进行归一化处理[13]。
换流器等值导纳灵敏度是其所有内部参数的集中体现。内部参数仅能通过改变换流器的等值导纳影响谐振分布，因此，换流器等值导纳与内部参数的灵敏度具有正相关性。在实际应用中，当系统接入换流器较多时，为了减少计算量，可仅对高灵敏度换流器的内部参数进行灵敏度分析，从而缩小分析范围。
本文提出的计算方法在有效区分参数谐振抑制/放大作用的同时，能够将模态灵敏度应用于扰动源传递函数、换流器等值导纳及其内部参数（包括控制及状态参数等），拓展了传统方法的应用场景，使直流配电网的全局元器件模态灵敏度分析得以实现。参数级谐振特性分析能够高效量化谐振对参数的敏感性，评估换流器对系统的谐振作用机理和影响程度，对于确定频率下的系统优化和谐振抑制具有较强的指导作用。
3 谐振分析及灵敏度应用
为了分析扰动源传递函数对谐振的影响，验证所提修正系统阻抗模型和换流器参数灵敏度计算方法，通过PSCAD/EMTDC 搭建了IEEE 14 节点直流配电网仿真模型，从系统和元器件参数尺度分别对扰动源传递函数进行谐振机理及影响程度分析。其中，电源及负载主要由表1 中的VSC、分布式电源及恒功率负载组成，如图1 所示，换流器及滤波参 数见表2，PS1-2、PL1-5 分别对应分布式电源及负载的额定功率。鉴于可观性，图1 中未逐一标注线路及滤波器元件，仅在表2 中对其进行体现，数字编号为元件所在节点位置，如L7-8 为节点7、8 之间的串联电感，C8 为并联在节点8 的滤波电容。
图1 IEEE 14 节点直流配电网络结构
Fig.1 IEEE 14 node DC distribution network structure diagram
表2 IEEE 14 节点直流配电网滤波及换流器参数
Tab.2 The filter and converter parameters in IEEE 14 node DC distribution network
3.1 计及扰动源传递函数的系统谐振特性分析
根据提出的修正系统阻抗模型，以输入侧扰动源
为扰动量的修正后节点电压方程如式（2）所示。受换流器输入-输出特性影响，扰动源传递函数可能具有谐振点，如图2 所示，其中G1(1,1)、G2(1,1)、G3(1,1)、G4(1,1)分别对应节点1 的扰动源
。由图可见，节点11、14 的扰动源传递函数(G1(11,11)、G1(14,14))存在频率为1 726 rad/s 和1 565 rad/s的谐振点。
图2 扰动源传递函数Bode 图
Fig.2 Bode diagram of disturbance source transfer function
考虑扰动源传递函数前后阻抗矩阵Z、Z′的谐振分布见表3。考虑扰动源传递函数后，系统中存在1 565 rad/s、1 726 rad/s 和2 653 rad/s 三个谐振频率。通过仿真在0.5 s 分别注入上述频率，幅值为1 A 的扰动电流，电压波形如图3 所示。
表3 考虑扰动源传递函数前后IEEE 14 节点阻抗 谐振分布
Tab.3 Resonance frequency and amplitude of IEEE 14 node DC distribution network
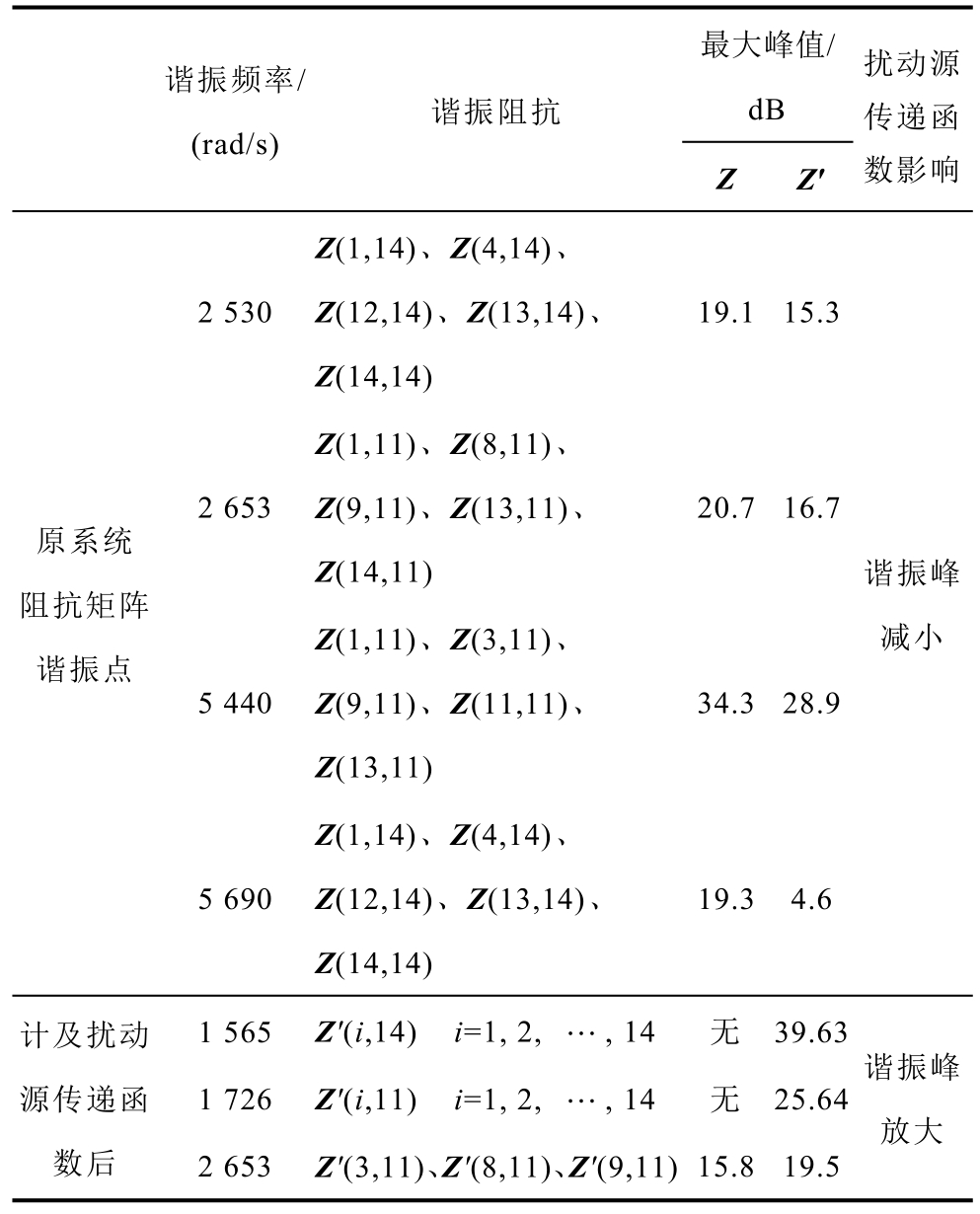
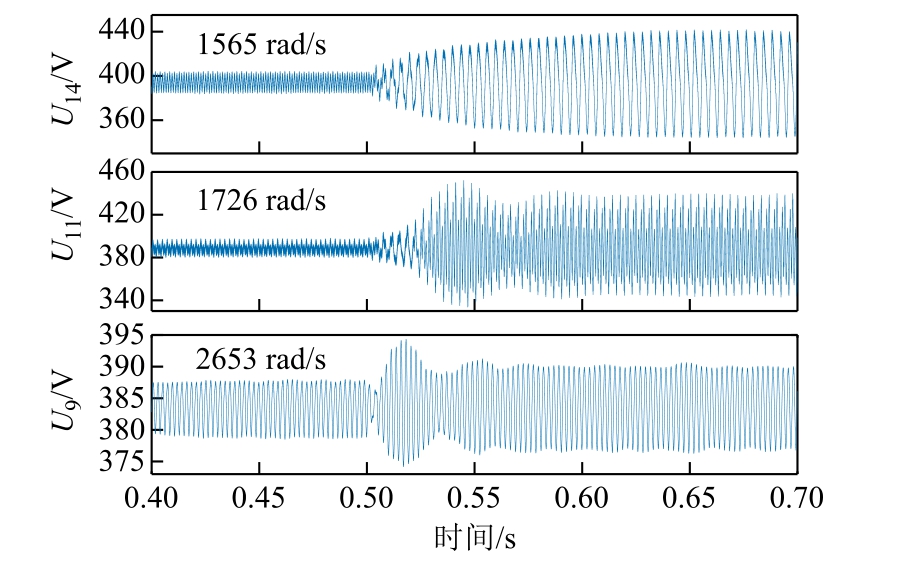
图3 扰动源传递函数引入谐振点谐波放大波形
Fig.3 Waveform on the resonance point caused by source transfer function
由表3 可知，考虑扰动源传递函数后，系统原有谐振点除2 653 rad/s 外均被不同程度抑制，并出现了新谐振点1 565 rad/s、1 726 rad/s。上述新谐振 点在Z′的第14、11 列所有元素中均有体现，并在图3 中引起了较为显著的谐波放大，而原阻抗矩阵Z中未有体现。由此可知，仅关注原系统阻抗矩阵Z的谐振特性会造成谐振点遗漏，考虑扰动源传递函数是必要的。
3.2 灵敏度及影响因素分析
根据前文提出的模态灵敏度计算方法，本节基于修正后系统导纳矩阵Y′，对图1 系统进行了包括换流器参数在内的全局元器件灵敏度分析。为便于对比，下文依次对扰动源传递函数引入谐振点和原系统阻抗矩阵谐振点进行分析。
1）扰动源传递函数引入谐振点
由3.1 节分析可知，节点11、14 的扰动源传递函数(G1(11,11)、G1(14,14))分别为系统引入了1 726 rad/s和1 565 rad/s 谐振点。根据所提换流器参数灵敏度计算方法，两谐振点的换流器等值导纳及扰动源传递函数灵敏度如图4 所示。对于1 565 rad/s 谐振点，节点14 分布式电源的等值导纳YS1 和扰动源传递函数G1(14,14)具有较高的灵敏度；对于1 726 rad/s 谐振点，节点11 分布式电源的等值导纳YS2 和扰动源传递函数G1(11,11)具有较高的灵敏度，增大或减小上述参数能起到较好的谐振抑制效果。
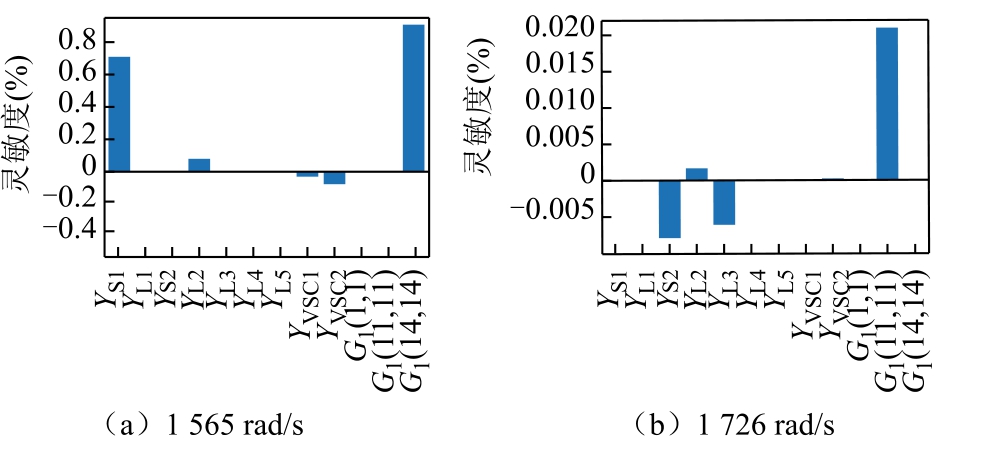
图4 换流器等值导纳及扰动源传递函数灵敏度计算
Fig.4 Sensitivity calculation of the equivalent admittance and the disturbance source transfer function
因此，进一步对分布式电源1、2 的内部参数、系统线路及滤波器参数的灵敏度进行计算，结果如图5 所示，其中橙色（浅色）部分为分布式电源内部参数。可以看到，对于1 565 rad/s 谐振点，分布式电源1 内部参数Lp1、Cp1 具有更高的灵敏度，其灵敏度均为正，增大该参数能够有效抑制谐振；对于1 726 rad/s 谐振点，分布式电源2 内部参数Cp1和滤波电容C9 灵敏度较高，增大Cp1 能够有效抑制谐振，增大C9 将导致谐振放大。
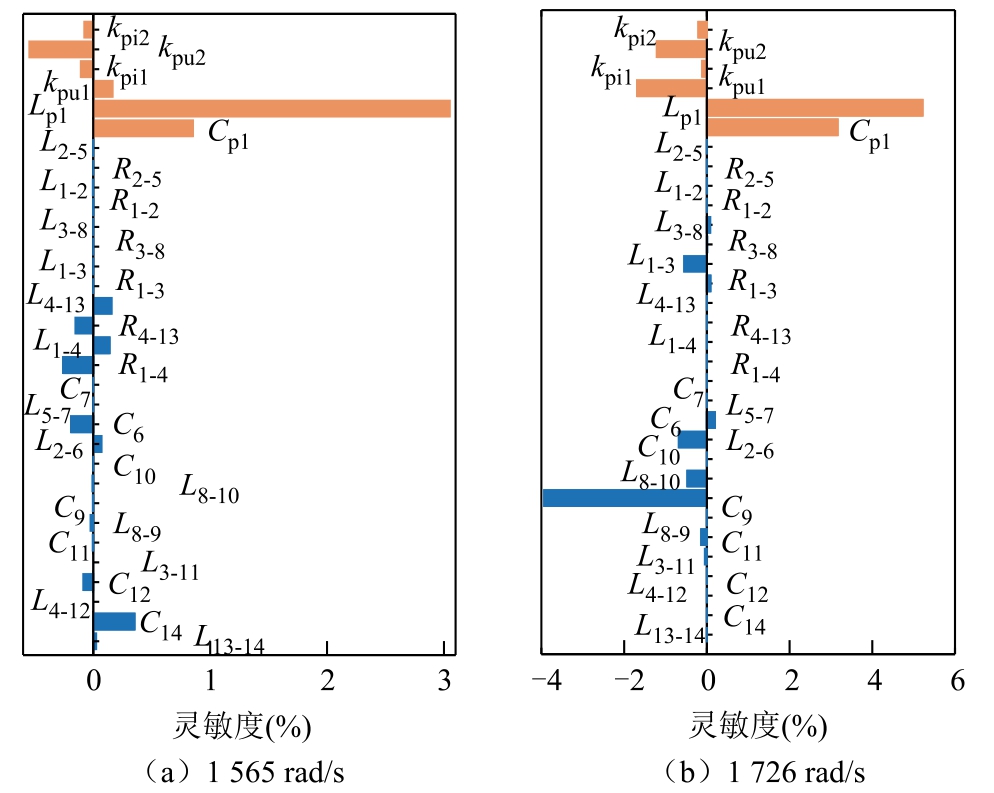
图5 线路参数及换流器内部参数灵敏度计算
Fig.5 Modal sensitivity of converters,power line and filter parameters
为了验证上述分析，在0.5 s 经分布式电源1、3 分别注入频率为1 565 rad/（s249.1 Hz）、1 726 rad/s（274.7 Hz），幅值为1 A 的谐波电流。由于上文分析中分布式电源1 内部参数Lp1 和Cp1、分布式电源2 内部参数Cp1 和滤波电容C9 分别对于谐振点1 565 rad/s 和1 726 rad/s 具有较高的灵敏度，在0.7 s分别令上述参数增大 20%，观察谐波抑制/放大情况，第14、11 节点电压仿真波形如图6 所示。
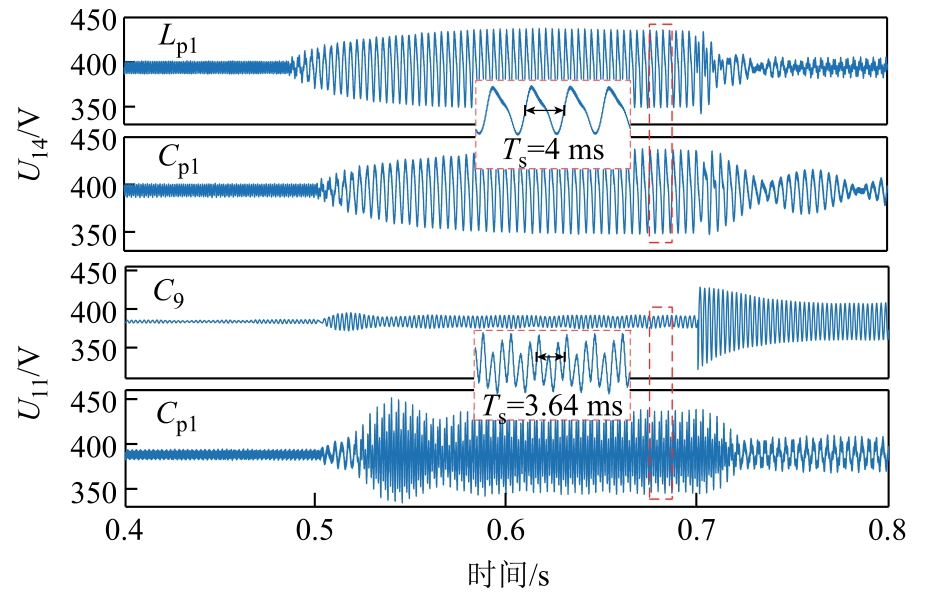
图6 扰动源传递函数引入谐振点谐波放大及抑制情况
Fig.6 Resonance amplification and suppression on the resonance point caused by the disturbance source transfer function
经过验证，改变上述参数后电压波形发生了显著变化。Lp1、Cp1（分布式电源1）、Cp1（分布式电源2）对应波形谐振得到有效抑制，C9 对应波形谐振进一步放大，与灵敏度分析结果一致。由此可见，灵敏度分析能够有效地体现参数对谐振的影响程度，为参数整定和谐振抑制提供参考。
灵敏度分析虽能高效量化参数对谐振阻抗的影响，但对伴随参数整定产生的谐振峰及频率转移体现程度有限，因此，此处进一步分析了上述敏感参数的谐振峰分布情况。图7 绘制了相应谐振频率下Lp1、Cp1（分布式电源1）、C9、Cp1（分布式电源2）以1%的步长，在取值的1±10%之间变化时，节点14、11 自阻抗的谐振峰分布。
图7 影响因素对系统阻抗的影响
Fig.7 The influence of different factors to system impedance
图7 中，波峰为不同参数取值时节点14 的自阻抗，沿箭头方向参数从小到大，波峰顶部为曲线的谐振峰。对于图7a、图7b，随参数增大，谐振峰值减小，且谐振频率发生了转移，Lp1 的谐振频率降低、Cp1谐振频率增加，与灵敏度分析和仿真结果（图5a、图6）一致。
对于影响因素曲线无法直接观测阻抗变化的情况，灵敏度分析依然具有较高的准确性。对于图7c，谐振峰值及频率的变化不规则，无法得出一致性规律，故图7c 右上角将谐振峰位置进行了放大，标注了C9 分别取实际值的1-1%、1、1+1%时波峰位置，对应i-1、i、i+1 三个点，可以看到，在i 点谐振幅值随C9增大而增大，与图5b 灵敏度计算结果一致。此外，灵敏度分析具有不受谐振频率转移干扰的优势，能够有效地体现谐振阻抗的变化。对于图7d，增加Cp1 使谐振频率减小并放大了谐振峰值，通过在1 730 rad/s 做参数-阻抗曲线可知（图7d 右上角），阻抗在该处呈抛物线分布，Cp1 的增加还有效减小了谐波电压，与该点灵敏度计算结果一致。
2）原系统阻抗矩阵谐振点
根据表3 可知，2 653 rad/s 为系统阻抗矩阵Z的原有谐振点，在Z′(3,11)、Z′(8,11)、Z′(9,11)中出现，其中以Z′(9,11)的谐振程度最高。图8a 为各换流器的灵敏度计算结果，与前两个谐振点不同，分布式电源1 等值导纳的灵敏度相对较高，扰动源传递函数的灵敏度均未明显高于其他参数，因此图8b 计算了分布式电源1 的内部参数（橙色部分）及线路和滤波器参数的灵敏度。
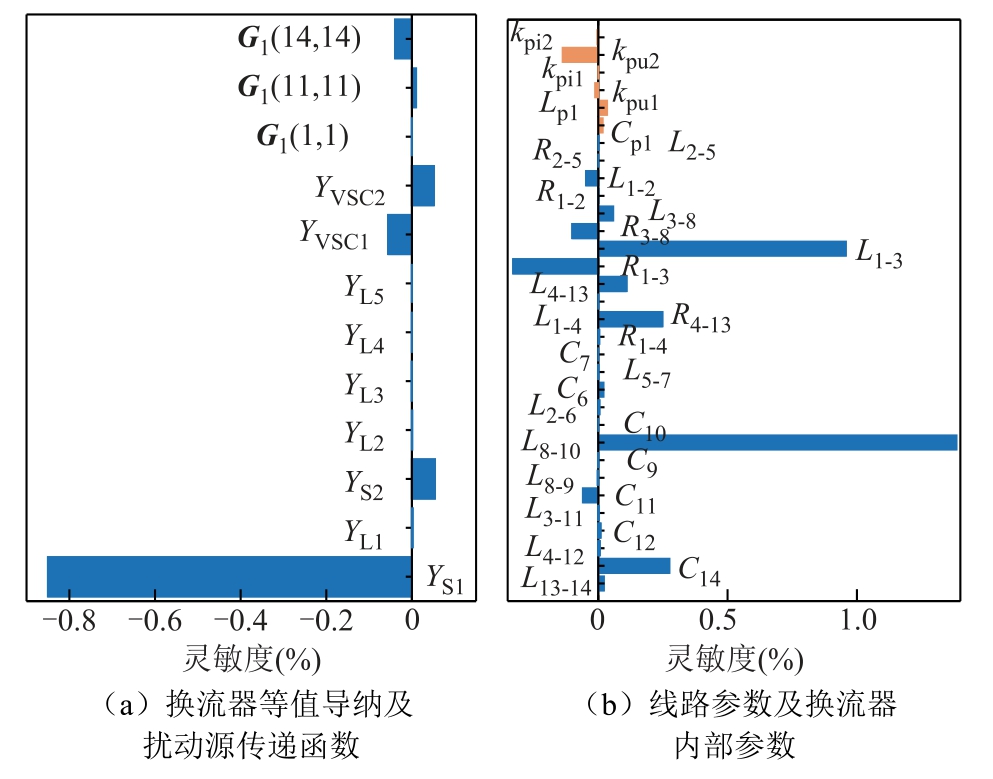
图8 换流器及线路参数灵敏度计算
Fig.8 Modal sensitivity of converters,circuit and filter parameters
与前两个谐振点相比，图8b 整体参数灵敏度较低，且线路及滤波器参数的灵敏度高于分布式电源内部参数。对于其中灵敏度较高的参数（L8-10、L1-3、C14、R1-3），除R1-3 之外，灵敏度均为正，增大此类参数能起到谐振抑制作用，但与扰动源传递函数引入的谐振点相比，该谐振点涉及节点数少，谐振程度低。
为了验证上述结论，在0.5 s 经分布式电源2 注入频率为2 653 rad/s（422.24 Hz），幅值为1 A 的谐波电流，并在0.7 s 将图8b 中灵敏度较高参数L8-10、L1-3、C14、R1-3 分别增加20%，相应电压波形曲线如图9 所示。
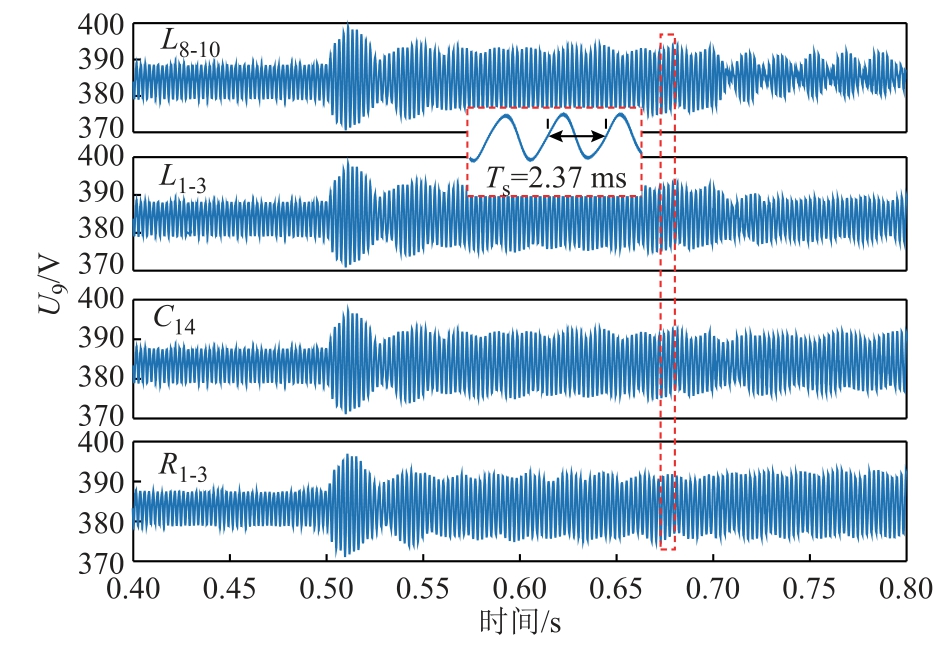
图9 原系统阻抗矩阵谐振点谐波放大及抑制情况
Fig.9 Resonance amplification and suppression on the resonance point caused by the traditional system admittance matrix
可以看到，扰动注入后电压波形出现了谐波放大，但与前两个频率相比放大程度较小。0.7 s 后，L8-10、L1-3、C14 对应波形的谐振均有小幅度减小，R1-3 对应波形的谐振幅度增大，与灵敏度分析结果一致。
图10 是L8-10、L1-3、C14、R1-3 以1%的步长，在取值的1±10%范围内变化时的系统阻抗Z′(9,11)。可以看到，随L8-10 和L1-3 增大，谐振频率降低，幅值减小；增大C14、减小R1-3 能够有效抑制谐振峰，但影响程度较小。
图10 影响因素对系统阻抗的影响
Fig.10 The influence of different factors to node impedance
综上所述，影响因素曲线与灵敏度计算分别从频率-阻抗和参数-阻抗角度对谐振特性进行分析。灵敏度计算结果不受参数变化尺度影响，能够准确观察谐振阻抗对参数微观变化的响应，影响因素曲线能够体现参数对谐振峰及谐振频率的影响，结合应用可实现谐振分析准确性与全局性的互补。
4 结论
针对忽略扰动源输出特性造成的谐振分析偏差和谐振点遗漏问题，本文首先从系统尺度，提出一种计及扰动源传递函数的系统阻抗修正模型，揭示了换流器输入侧扰动对系统谐振特性的影响机理：扰动源传递函数作用于所在节点的阻抗矩阵列向量，可能给系统引入新的谐振点，并对谐振峰计算的准确度造成影响。为了进一步分析扰动源传递函数的影响程度，基于修正后的系统阻抗矩阵，本文拓展了传统灵敏度分析应用场景，从元器件参数尺度提出了换流器、扰动源传递函数等值导纳和换流器内部参数的模态灵敏度计算方法。所提方法不受参数变化尺度影响，计算效率高，能够量化全局影响因素的谐振影响程度，为确定频率扰动下的系统谐振抑制提供依据。
附录 主要元件等值模型
1.VSC 换流站数学模型
VSC 是直流配电网系统的核心组成部分，其基本电路结构如附图1 所示。其中us、is 为交流系统出口电压和电流，Rgn 和Lgn 为连接电抗器电阻与电感，udc 和idcn 为VSC 直流侧输出电压和电流，Cdc 为直流测电容，idc 为直流线路电流。
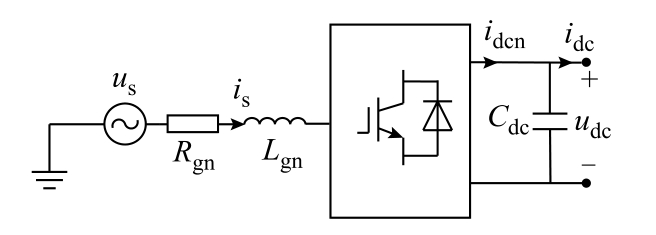
附图1 换流站子系统基本结构
App.Fig.1 Basic structure of converter substation system
在dq 同步旋转坐标系下，以交流侧电压us 为d 轴基准，小扰动下的状态方程可表示为
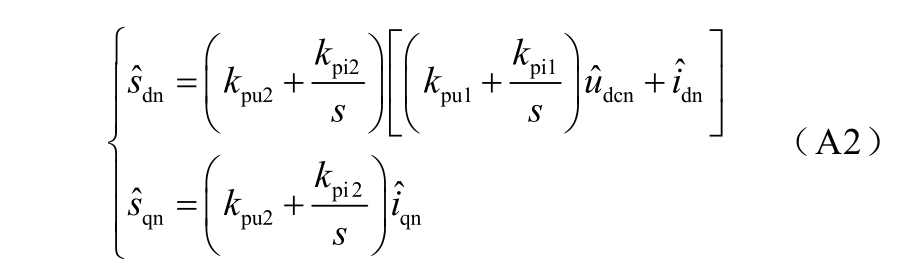
式中，kpu1、kpi1、kpu2、kpi2 分别为主站电压外环、电流内环PI 控制器的比例积分系数。式中电压电流均采用标幺值。从站控制器在小扰动下的数学模型为
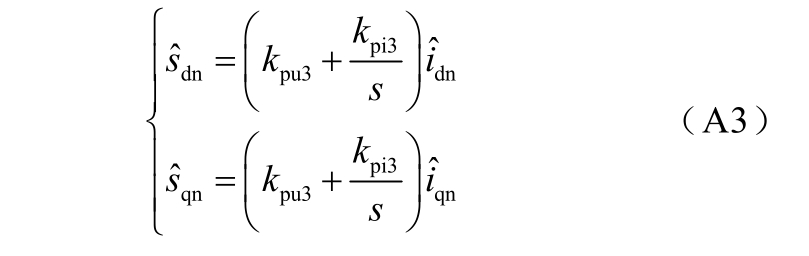
式中，kpu3、kpi3 分别为从站PI 控制器的比例积分系数。主从换流器的输出特性表达式为
式中，
分别为主站和从站的dq 轴扰动源传递函数，下标1 为主站，下标2为从站；ZVSC-1、ZVSC-2 分别为主站和从站的VSC 等值阻抗。
2.分布式电源数学模型
分布式电源为光伏电池经Boost 换流器接入直流配电网，控制策略采用基于最大功率跟踪（Maximum Power Point Tracking,MPPT）的双环控制，分布式电源基本结构附图2 所示[26]。其中upv、ipv 分别为Boost 换流器输出电压、电流，upvs、ipvs 分别为光伏电池输出电压、电流，Cp1 为输入侧电容，Cp2 为输出侧电容，Lp1 为Boost 换流器滤波电感。
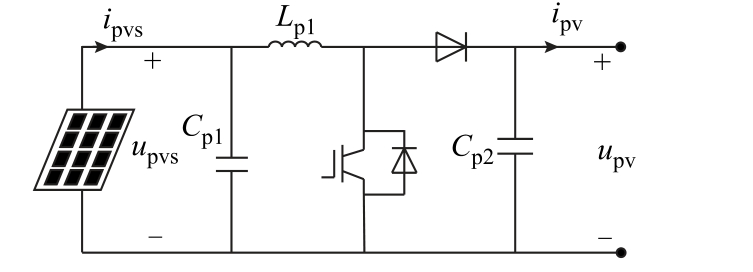
附图2 分布式电源基本结构
App.Fig.2 Basic structure of distributed power supply
小扰动下的状态空间方程为
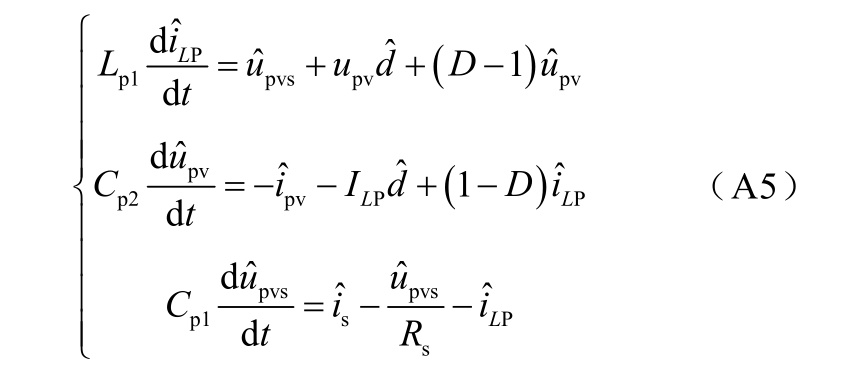
式中，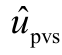
为Boost 换流器输入侧电压扰动量；
、
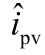分别为Boost 换流器输出侧电压、电流扰动量；D 和
分别为占空比稳态量和扰动量；ILP 和 
分别为电感电流稳态量和扰动量；
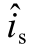和Rs 分别为光伏电池电源电流扰动量和等效阻抗。控制器的小扰动数学模型为
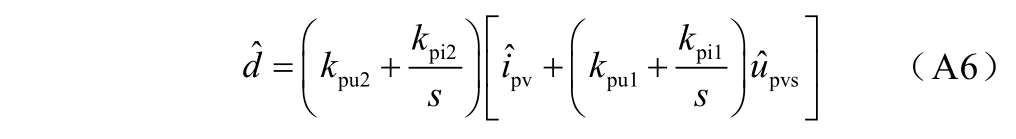
其中，输出电压
的传递函数表达式为
式中，Zpv 为输出端等效阻抗；Ypvs 为输出端电压与输入端电流之间的传递函数。将该换流器输出端等效为电流源并联阻抗时，输出端的等效电流源为
。
3.恒功率负载数学模型
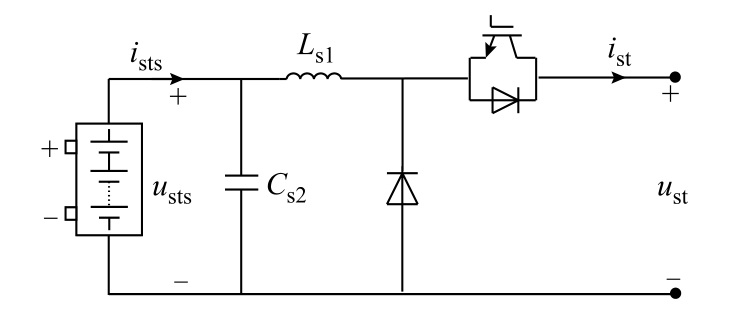
恒功率负载以储能设备和电动汽车充电桩为代表。储能电池控制单元结构如附图3 所示。
附图3 储能电池基本结构
App.Fig.3 Basic structure of energy storage battery
采用Buck 电路，控制方式为恒流控制。其中ust、ist分别为Buck 换流器输入侧电压、电流，usts、ists 分别为Buck 换流器输出侧电压、电流，Cs2 为Buck 换流器输出侧稳压电容，LS1 为滤波电感，状态方程为
式中，kp、ki 分别为PI 控制比例积分系数。电压电流的传递函数表达式为
式中，Zst 为储能换流器等效阻抗；Ysts 为电压波动等效传递函数。在后续处理中，由于在时间尺度内电压波动量较小，令
≈ 0。
采用单移相控制的双有源桥（Dual Active Bridge,DAB）电路的电动汽车充电装置控制单元结构如附图4所示。
附图4 电动汽车充电装置控制单元结构
App.Fig.4 Structure of control unit of electric vehicle device
附图4 中Le1 为变压器漏感，Ce1、Ce2 分别为直流母线侧、电动汽车侧稳压电容，uDAB、iDAB 为输入侧电压、电流，uev、iev 为输出侧电压、电流。状态方程为
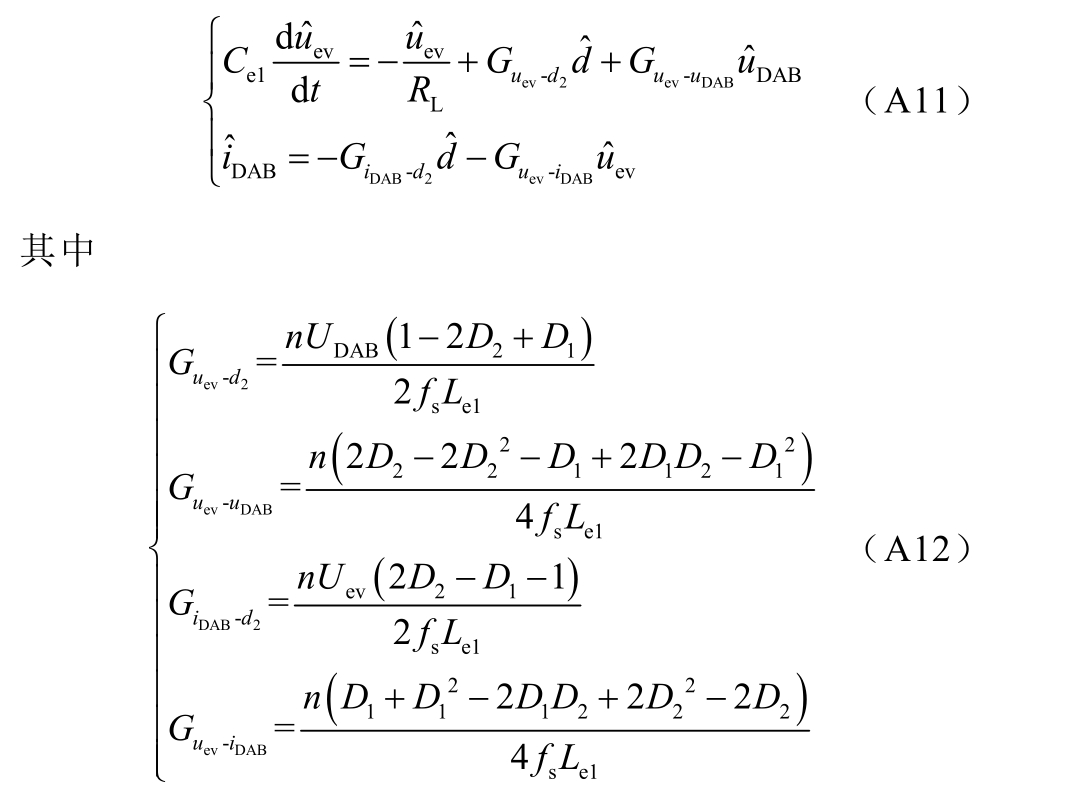
式中，Uev、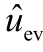
、UDAB、
DAB分别为DAB 换流器输出、输入侧电压的稳态量和扰动量；D1、D2 分别为一、二次侧移相比；RL 为负载等效阻抗；fs 为开关频率；n 为变压器一、二次电压比。控制器的小扰动数学模型为
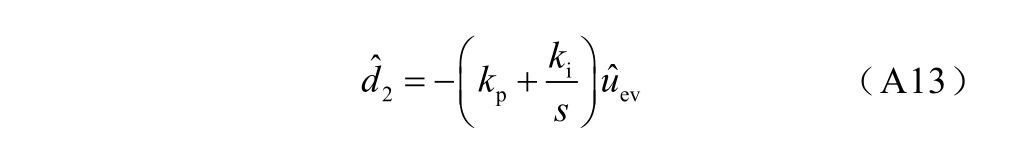
电压电流的传递函数表达式可化简为
式中，ZDAB 为DAB 换流器输入侧等效阻抗；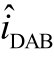
为输入电流扰动量。
[1]李海波,赵宇明,刘国伟,等.基于时序仿真的商业楼宇交流与直流配电系统能效对比[J].电工技术学报,2020,35(19): 4194-4206.Li Haibo,Zhao Yuming,Liu Guowei,et al.The time sequential simulation based energy efficiency comparison of AC and DC distribution power system in commercial buildings[J].Transactions of China Electrotechnical Society,2020,35(19): 4194-4206.
[2]郑重,苗世洪,李超,等.面向微型能源互联网接入的交直流配电网协同优化调度策略[J].电工技术学报,2022,37(1): 192-207.Zheng Zhong,Miao Shihong,Li Chao,et al.Coordinated optimal dispatching strategy of AC/DC distribution network for the integration of micro energy Internet[J].Transactions of China Electrotechnical Society,2022,37(1): 192-207.
[3]马钰,韦钢,李扬,等.考虑孤岛源-荷不确定性的直流配电网可靠性评估[J].电工技术学报,2021,36(22): 4726-4738.Ma Yu,Wei Gang,Li Yang,et al.Reliability evaluation of DC distribution network considering islanding source-load uncertainty[J].Transactions of China Electrotechnical Society,2021,36(22): 4726-4738.
[4]郑凯元,杜文娟,王海风.动态单元间交互作用对直流微电网稳定性影响的分析[J].中国电机工程学报,2021,41(23): 7963-7979.Zheng Kaiyuan,Du Wenjuan,Wang Haifeng.Analysis on the stability of DC microgrid affected by interactions among dynamic components[J].Proceedings of the CSEE,2021,41(23): 7963-7979.
[5]程林,万宇翔,齐宁,等.含多种分布式资源的配用电系统运行可靠性研究评述及展望[J].电力系统自动化,2021,45(22): 191-207.Cheng Lin,Wan Yuxiang,Qi Ning,et al.Review and prospect of research on operation reliability of power distribution and consumption system considering various distributed energy resources[J].Automation of Electric Power Systems,2021,45(22): 191-207.
[6]Mohamad A M I,Mohamed Y A R I.Investigation and enhancement of stability in grid-connected active DC distribution systems with high penetration level of dynamic loads[J].IEEE Transactions on Power Electronics,2019,34(9): 9170-9190.
[7]游逍遥,刘和平,苗轶如,等.带恒功率负载的双极性直流系统稳定性分析及其有源阻尼方法[J].电工技术学报,2022,37(4): 918-930.You Xiaoyao,Liu Heping,Miao Yiru,et al.Stability analysis and active damping method of the bipolar DC system with constant power loads[J].Transactions of China Electrotechnical Society,2022,37(4): 918-930.
[8]张美清,袁小明,胡家兵.基于自稳/致稳性的路径级数展开方法及其在含多样化电力电子装备电力系统稳定性分析中的应用[J].中国电机工程学报,2021,41(5): 1637-1654.Zhang Meiqing,Yuan Xiaoming,Hu Jiabing.Path series expansion method based on self-/ en-stabilizing properties and its application in the stability analysis of power systems with diversified power electronic devices[J].Proceedings of the CSEE,2021,41(5): 1637-1654.
[9]谢小荣,贺静波,毛航银,等.“双高”电力系统稳定性的新问题及分类探讨[J].中国电机工程学报,2021,41(2): 461-474.Xie Xiaorong,He Jingbo,Mao Hangyin,et al.New issues and classification of power system stability with high shares of renewables and power electronics[J].Proceedings of the CSEE,2021,41(2): 461-474.
[10]姜涛,李雪,李国庆,等.含多端柔性直流的交直流电力系统静态电压稳定域构建方法[J].电工技术学报,2022,37(7): 1746-1759.Jiang Tao,Li Xue,Li Guoqing,et al.A predictorcorrector algorithm for forming voltage stability region of hybrid AC/DC power grid with inclusion of VSC-MTDC[J].Transactions of China Electrotechnical Society,2022,37(7): 1746-1759.
[11]蒋海玮,徐永海,何志轩,等.考虑系统参数不确定性的谐波谐振监测点优化配置方法[J].电力系统自动化,2021,45(23): 141-151.Jiang Haiwei,Xu Yonghai,He Zhixuan,et al.Optimal placement method for harmonic resonance monitoring points considering uncertainties of system parameters[J].Automation of Electric Power Systems,2021,45(23): 141-151.
[12]黄旭程,何志兴,刘亚丽,等.考虑光伏发电单元孤岛检测影响的直流电网稳定性分析与阻尼控制[J].中国电机工程学报,2021,41(1): 109-122.Huang Xucheng,He Zhixing,Liu Yali,et al.Stability analysis and damping control of DC grid considering PV generators with island detection[J].Proceedings of the CSEE,2021,41(1): 109-122.
[13]秦垚,王晗,庄圣伦,等.海上风电场集电网的高频谐振分析[J].中国电机工程学报,2022,42(14): 5169-5181.Qin Yao,Wang Han,Zhuang Shenglun,et al.Analysis on high frequency resonance of collector network in offshore wind farm[J].Proceedings of the CSEE,2022,42(14): 5169-5181.
[14]曾志杰,肖华锋,高博,等.结合阻抗比与振荡阻尼特征的并网系统谐波谐振稳定性分析方法[J].中国电机工程学报,2020,40(22): 7201-7211.Zeng Zhijie,Xiao Huafeng,Gao Bo,et al.Stability analysis method of harmonic resonance of gridconnected generation system based on impedance ratios and oscillation damping[J].Proceedings of the CSEE,2020,40(22): 7201-7211.
[15]Markovic U,Stanojev O,Aristidou P,et al.Understanding small-signal stability of low-inertia systems[J].IEEE Transactions on Power Systems,2021,36(5): 3997-4017.
[16]陈鹏伟,姜文伟,阮新波,等.直流配电系统有源阻尼控制的阻抗释义与谐振点灵敏度参数调节方法[J].中国电机工程学报,2021,41(19): 6616-6629.Chen Pengwei,Jiang Wenwei,Ruan Xinbo,et al.Impedance explanation and resonance point sensitivity-based parameter design method of active damping applied to DC distribution system[J].Proceedings of the CSEE,2021,41(19): 6616-6629.
[17]Xu W,Huang Zhenyu,Cui Yu,et al.Harmonic resonance mode analysis[J].IEEE Transactions on Power Delivery,2005,20(2): 1182-1190.
[18]钟庆,冯俊杰,王钢,等.基于节点阻抗矩阵的直流配电网谐振特性分析[J].中国电机工程学报,2019,39(5): 1323-1334.Zhong Qing,Feng Junjie,Wang Gang,et al.Analysis of resonance characteristics of DC distribution network based on node impedance matrix[J].Proceedings of the CSEE,2019,39(5): 1323-1334.
[19]Liu Qunfeng,Ai Yongle,Li Shuai.Recognition of branch series resonance based on port equivalent method[J].CPSS Transactions on Power Electronics and Applications,2019,4(3): 197-203.
[20]唐力,胡海涛,李朝阳,等.考虑谐波源支路类型的谐波谐振分析方法[J].电力系统自动化,2019,43(16): 132-147.Tang Li,Hu Haitao,Li Zhaoyang,et al.Harmonic resonance analysis method considering branch type of harmonic source[J].Automation of Electric Power Systems,2019,43(16): 132-147.
[21]李云丰,汤广福,吴亚楠,等.直流电网建模分析与阻尼控制研究[J].中国电机工程学报,2017,37(12): 3372-3382,3664.Li Yunfeng,Tang Guangfu,Wu Yanan,et al.Modeling,analysis and damping control of DC grid[J].Proceedings of the CSEE,2017,37(12): 3372-3382,3664.
[22]陈新,张旸,王赟程.基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响[J].中国电机工程学报,2014,34(27): 4559-4567.Chen Xin,Zhang Yang,Wang Yuncheng.A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J].Proceedings of the CSEE,2014,34(27): 4559-4567.
[23]林刚,李勇,王姿雅,等.低压直流配电系统谐振机理分析与有源抑制方法[J].电网技术,2017,41(10): 3358-3364.Lin Gang,Li Yong,Wang Ziya,et al.Resonance mechanism analysis and its active damping suppression of LVDC distribution system[J].Power System Technology,2017,41(10): 3358-3364.
[24]Huang Zhenyu,Cui Yu,Xu W.Application of modal sensitivity for power system harmonic resonance analysis[J].IEEE Transactions on Power Systems,2007,22(1): 222-231.
[25]王彤,马静,王增平,等.采用多参数2 阶摄动灵敏度的电力系统低频振荡模态分析方法[J].中国电机工程学报,2013,33(34): 205-213,30.Wang Tong,Ma Jing,Wang Zengping,et al.Multiple parameter modal analysis of power system lowfrequency oscillation based on the 2nd order sensitivity matrix[J].Proceedings of the CSEE,2013,33(34): 205-213,30.
[26]杨洁,刘开培,王东旭,等.向无源网络供电的双端柔性直流输电系统小信号稳定性分析[J].中国电机工程学报,2015,35(10): 2400-2408.Yang Jie,Liu Kaipei,Wang Dongxu,et al.Small signal stability analysis of VSC-HVSC applied to passive network[J].Proceedings of the CSEE,2015,35(10): 2400-2408.
[27]Luo Jianqiang,Bu Siqi,Zhu Jiebei,et al.Modal shift evaluation and optimization for resonance mechanism investigation and mitigation of power systems integrated with FCWG[J].IEEE Transactions on Power Systems,2020,35: 4046-4055.
[28]Gao Fei,Zheng Xiancheng,Bozhko S,et al.Modal analysis of a PMSG-based DC electrical power system in the more electric aircraft using eigenvalues sensitivity[J].IEEE Transactions on Transportation Electrification,2015,1(1): 65-76.
[29]刘洋,帅智康,李杨,等.多逆变器并网系统谐波谐振模态分析[J].中国电机工程学报,2017,37(14): 4156-4164,4295.Liu Yang,Shuai Zhikang,Li Yang,et al.Harmonic resonance modal analysis of multi-inverter gridconnected systems[J].Proceedings of the CSEE,2017,37(14): 4156-4164,4295.
[30]秦本双,徐永海.多虚拟同步机并网系统功频振荡模态分析[J].中国电机工程学报,2021,41(19): 6570-6580.Qin Benshuang,Xu Yonghai.Modal analysis of multivirtual synchronous machine grid-connected powerfrequency oscillation[J].Proceedings of the CSEE,2021,41(19): 6570-6580.
[31]Li Zebiao,Hu Haitao,Tang Li,et al.Quantitative severity assessment and sensitivity analysis under uncertainty for harmonic resonance amplification in power systems[J].IEEE Transactions on Power Delivery,2020,35: 809-818.