0 引言
锂离子电池具有高能量/功率密度、低自放电率和长循环寿命等优点，在电动汽车上得到广泛应用[1]。但锂离子电池在长期服役过程中出现的电池内阻增加和容量下降等老化现象会降低电池输出能力[2]，增加电池维护成本。电池最大可用容量作为锂离子电池关键参数，直接影响电动汽车续航里程。在线电池容量准确估算作为电池管理系统（Battery Management System,BMS）的核心功能之一，其关键算法的研究成为更加有效地进行电池管理的重点和核心技术[3]。
除通过安时积分法直接测量电池最大可用容量外，电池容量估算方法可分为模型法和数据驱动法[4]。模型法基于实时测量的电池信息，通过电化学模型或等效电路模型，利用自适应控制算法实现电池容量在线估算。如Xiong Rui 等[5]利用有限元和数值计算方法简化求解电化学模型的偏微分方程，利用遗传算法进行参数辨识，并从模型参数中提取五个特征参数进行电池容量映射估算。考虑到电池退化的物理现象，J.Li 等[6]提出低阶单粒子模型，以固体电解质膜的生长量化实现容量退化和内阻增加的估算。但求解电化学模型中复杂偏微分方程对车载BMS 的微处理器提出很高的算力要求。相对于电化学模型，电池等效电路模型具有结构简单、计算量低等优点，得到更广泛的应用。基于Thevenin 模型，Lü Zhiqiang 等[7]提出简化的电池线性老化模型，以卡尔曼滤波方法实现电池容量在线估算，但忽略电池老化的非线性因素，不可避免地会带来估算误差。Chen Cheng 等[8]提出一种多尺度双H∞滤波方法同时估算电池荷电状态（State of Charge,SOC）和容量，得到较卡尔曼滤波更鲁棒和准确的结果。为了消除等效电路模型的不确定性噪声，基于优化辨识的模型参数，H.Afshari 等[9]提出基于平滑变结构滤波方法实现电池容量的在线估算。基于模型的电池容量估计易于在线实施，但电池模型的准确性和鲁棒性直接影响电池容量估算的精度。近年来，随着人工智能技术研究的深入，数据驱动法作为一类无模型方法，得到广泛关注，并逐渐应用于电池容量估算[10]。如G.W.You 等[11]提出一种基于长短时记忆机制的递归神经网络，使用实时测量的电池电压、电流、温度等数据估算电池容量。但大规模实时电池动态数据处理给电池容量估计带来沉重的计算负担。Lü Zhiqiang 等[12]以电池Thevenin 模型参数作为老化特征，以BOX-COX 变换和高斯过程回归实现电池容量在线估算。但是BOX-COX 变换的阈值给电池容量估算引入新的不确定性。基于电池内阻增量，Chen Lin 等[13]提出一种融合灰色预测模型的新陈代谢超限学习机实现电池容量估算，但误差补偿的滞后效应还有待改善。戴海峰等[14]提取对电池容量敏感的充电曲线特征，以相关向量机（Relevance Vector Machine,RVM）估算电池容量。基于数据驱动方法，电池老化特征提取是建立容量特征映射的关键技术。已有的电池老化特征如直接测量的电池信息[11]、模型参数[12-13]、充电曲线特征[14]分别从不同的角度表征电池老化。此外，不同的映射建立方式会影响电池容量估算精度。因此，基于数据驱动方法进行电池容量估计时，电池老化数据集的数量及质量、老化特征提取、数据驱动方法的计算精度和复杂度都直接影响电池容量估算精度[15]。
由于电化学模型和等效电路模型更多偏向于描述短时电池充放电特性，对于长时间尺度的电池老化状态缺乏有效描述。在暂无通用电池老化模型情况下，数据驱动法成为电池容量估算的主要技术手段。为解决数据驱动法估算电池容量中受敏感老化特征和方法的精度和复杂度影响的问题，具有训练样本少、泛化能力强、提供概率结果等优点的贝叶斯框架下的RVM 给数据驱动的电池容量估算带来不同的研究路线。但是，现有研究更多集中在标准的RVM 或核函数的优化，对RVM 的多核学习和权值及核参数同时优化改进还有待进一步挖掘。
针对以上问题，基于团队现有研究工作[16]，本文提出一种基于灰狼优化（Grey Wolf Optimizer,GWO）智能算法的多核相关向量机（Multi-Kernel Relevance Vector Machine,MKRVM）优化模型以实现电池容量在线估算。首先，针对车载电池复杂工作环境，基于免受不同放电工况和复杂多变外部环境影响的电池部分充电数据，利用非参数回归的局部加权散点平滑法（Locally Weighted Scatterplot Smoothing,LOWESS）平滑去噪容量增量曲线，以提取表征电池退化的老化特征；然后，针对MKRVM的权值和参数优化问题，利用 GWO 同时优化MKRVM 核函数权值和核参数以提高MKRVM 的学习和泛化能力；最后，针对电池容量估算方法的在线实施，利用Matlab 和LabVIEW 联合仿真建立基于MKRVM 的模拟电池在环管理系统，结合基于在线提取的电池老化特征，验证提出的容量估算方法的准确性和鲁棒性，同时与未优化的MKRVM 和单核 RVM 及常见的支持向量机（Support Vector Machine,SVM）和BP（back prpagatin）神经网络进行对比分析。
1 锂离子电池老化实验数据
为建立可靠的电池容量退化模型，首先建立锂离子电池在不同放电循环下的老化数据库，分别采用马里兰大学先进寿命周期工程研究中心（Center for Advanced Life Cycle Engineering,CALCE）发布的四个额定容量为1.10A·h 的方形电池单体老化数据集（编号CS35、CS36、CS37 和CS38）和四组在大连理工大学自主实验的电池组老化数据集。CALCE数据集将电池在 25 ℃循环进行恒流（Constant Current,CC）、恒压（Constant Voltage,CV）充电后恒流放电。四个电池单体采用相同的老化工况，详细实验流程见文献[17]。自有数据集包括4 组电池组（编号Dalian University of Technology 1-4，缩写为DUT1、DUT2、DUT3 和DUT4），通过将6 个额定容量为2.60A·h 的三星18650-26F 圆柱三元锂离子电池[18]单体自行并联焊接，定义额定容量为15.60A·h，额定电压为3.70V。搭建图1 所示的电池测试平台来模拟电池组车载工作条件。其中，新威BTS4000 电池充放电设备对四个电池组同时进行相同工况的充放电测试，恒温箱模拟电池工作时的温度条件，上位机负责完成工况设定和数据采集。参考文献[14]，在电池老化试验中控制变量为电池放电工况以及电池工作温度，设计的实验流程主要包括电池容量测试、模拟工况测试和加速老化三部分，如图2 所示。容量测试用于获取电池在不同老化状态下的动态特性参数；模拟工况测试对电池动 态放电以模拟电池在电动汽车上的实际运行工况；加速老化则将电池在低温和高温下进行多次充放电，以加速电池的老化进程。在整个电池老化实验中，依据电池规格书，电池全部以0.5C 倍率大小电流充电后进行对应放电实验。老化实验循环进行，直至25℃下的电池测试平均容量低于80%的额定容量。
图1 电池测试平台
Fig.1 The testing platform of batteries
图2 电池老化实验流程
Fig.2 Battery aging test procedure
2 电池充电特征提取
容量增量分析法将时域充电数据的电池一阶相变的电压转换为容量增量峰，对充电数据进行处理求出dQ/dV，即
式中，Q 为充电电量，通过对电流I 积分获得；V为电池实测端电压；t 为采样时间。
通常锂离子电池的充电电压范围在3.70～4.20V是识别电池容量退化的一个重要电压区间。4.20V作为恒流和恒压充电阶段转折点，由于测量噪声的存在，两个充电阶段很难区分。本文采用恒流充电阶段3.70～4.10V 范围的电压充电数据，此电压范围对应SOC 是常用充电SOC(25%～95%)[16]区间的子区间。由于采样噪声的存在，由式（1）得到的容量增量曲线的特征难以与电池容量关联[14]。本文利用非参数回归方法LOWESS，结合最小二乘回归的简单性和非线性回归的灵活性，将简单模型拟合到局部数据子集上，使用滑动窗口逐点建立一个描述数据变化的函数，函数的建立过程如下：
（1）计算第i 个滑动窗口每个数据点的权系数ω。
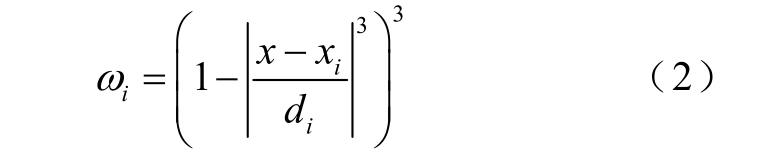
式中，x 为与当前中心点 x i相关联的跨度内的相邻点； d i为跨度内到最远的相邻点沿横坐标的距离。
（2）以加权线性最小二乘回归分析进行回归平滑，得到式（2）中 x i对应的预测值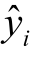
。
式中，a、b、c 为回归系数。
（3）滑动窗口至下一中心点 xi+1，重复步骤（1）～（3）直至完成全部数据的计算。
以CALCE 的CS35 电池单体为例，首先对电池老化数据进行清洗，然后取任意一次充电数据进行容量增量曲线平滑，平滑结果如图3a 所示。基于LOWESS 的平滑结果与高斯滤波平滑法（Gaussian）和移动平均平滑法（Movmean）相比[19-20]，容量增量分析法的平滑曲线更容易清晰地识别容量增量峰，容量增量曲线与X 轴围成的区域边缘也具有更平滑界线，并且能够提供比原始容量增量曲线更好的收敛性能。利用LOWESS 方法处理全生命周期内的容量增量曲线，得到图3b 所示的容量增量曲线。与此同时，对电池DUT1 实验数据进行LOWESS 平滑，得到图3c 所示全生命周期内的容量增量数据曲线。但是由于存在容量增生现象，部分电池的容量增量曲线存在微小波动。从图3b 和图3c 可以看出，随着电池循环次数的增加，容量增量峰整体呈下降趋势，导致容量增量曲线与X 轴围成区域面积逐渐减小。因此，基于容量增量分析法，通过分析转换后的容量增量峰和电池老化过程，得到电池电化学特性变化的关键信息，进而利用得到的关键信息可以建立电池外电路特性和内部电化学特性的对应关系。
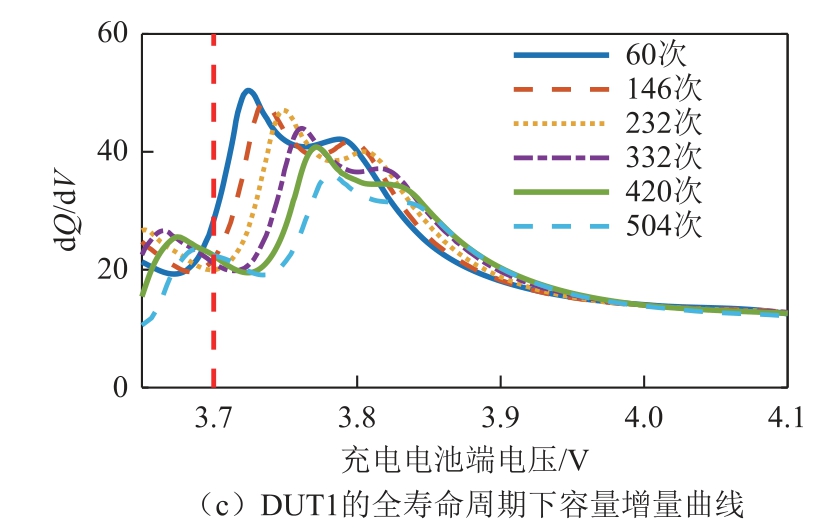
图3 电池容量增量分析曲线
Fig.3 The incremental capacity curves
由文献[21-23]的电池老化机理分析可知，电池容量增量曲线峰值下降与电池电极活性物质损失有关。随着老化周期增加，损失的活性材料已经不能用于游离锂离子的脱嵌，这些内部老化对容量增量峰产生显著的影响。容量增量曲线与X 轴围成的区域表示恒压差下电池的充电容量。对于恒压差充电容量而言，其退化趋势与电池内阻密切相关。随着电池容量下降，内阻的增加被定义为常见老化特征之一，在相同充电电流下内阻的增加会消耗更多的充电能量，降低恒压差充电容量。
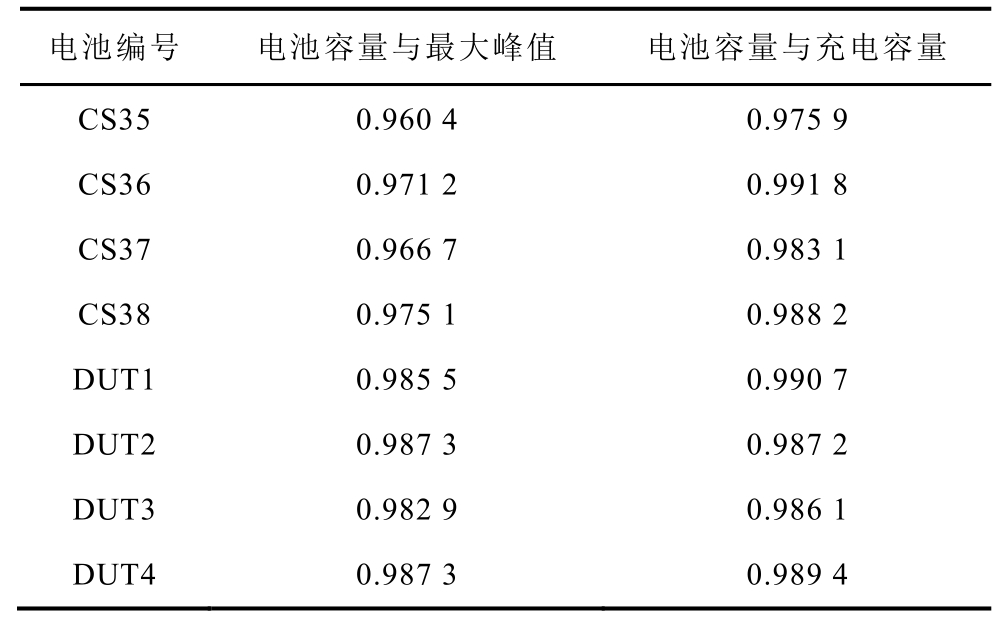
结合电池容量增量分析曲线和上述老化机理分析可知：容量增量峰与恒压差充电容量和电池性能衰退之间存在一定的电化学关联。因此，本文定义容量增量曲线的增量峰最大的峰值（见图3a）和恒压差充电容量（如图3a“面积”所示）作为表征容量退化的老化特征。以式（4）中的皮尔逊关联分析法[3]讨论电池容量和基于容量增量曲线提取的老化特征的关系，关联分析的计算结果见表1。
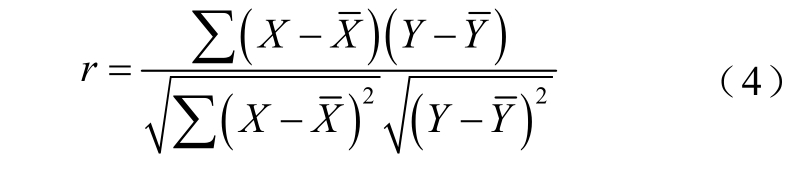
式中，r 为计算的皮尔逊关联系数； X 与Y 分别表示两个变量序列；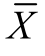
与
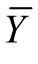表示其平均值。
从表1 可以看出：不同电池和不同老化工况下，皮尔逊关联系数均大于0.96，表明容量增量曲线增量峰峰值和恒压差充电电量与电池容量存在强相关关系，可有效表征电池容量衰减。
表1 老化特征关联分析
Tab.1 Correlation analysis of aging features
3 电池容量在线估计
3.1 多核相关向量机优化模型
式中，K (x , x n)为RVM 核函数；ω n为核函数权值；ω0 为RVM 模型偏差。更加详细的RVM 原理可参考文献[14]。
基于RVM 的多核学习将不同特性核函数进行组合，从而获得多种核函数的优点，在应对复杂数据时能兼具全局核函数和局部核函数的特性，以提高RVM 学习和泛化能力。基于RVM 的多核学习构造多核核函数为
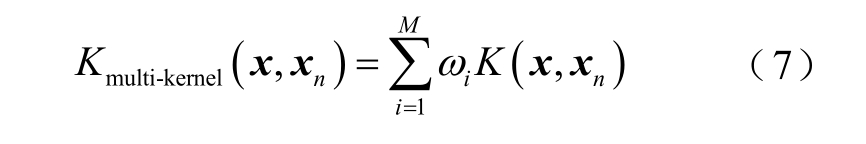
式中，Kmulti-kernel为构造的多核核函数；M 为核函数个数；ω i为第i 个核函数权值。
根据文献[17]，本文选择高斯核函数 KGaussian、线性核函数 KLinear 和Sigmoid 核函数 KSigmiod描述电池容量退化的全局与局部趋势，即
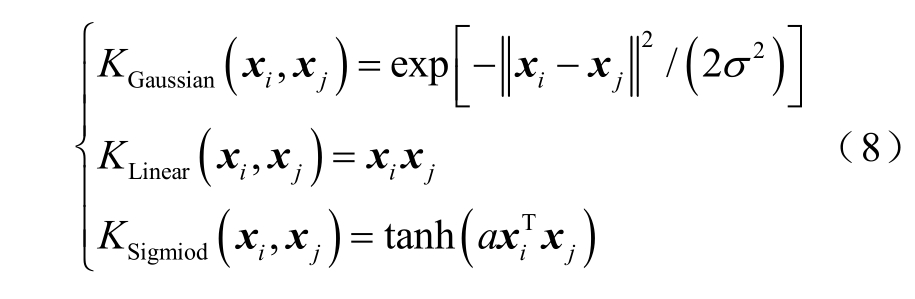
式中，σ、a 为待优化核函数的核宽度。
因此，得到MKRVM 回归模型的多核核函数表达式为
式中，ω 1、ω 2、ω3分别为待优化核函数的核权值。
目前对于式（9）中核函数的多核权值和核参数的设定还没有形成一个合理通用的准则。常基于经验选择、实验对比、大范围的搜索或通过交叉验证法进行确定。为此，本文引入GWO[24-25]算法，以方均根误差（Root Mean Square Error,RMSE）最小为目标，对核参数以及核权值同时智能优化。
结合式（8）和式（9）确定MKRVM 优化模型的适应度函数为
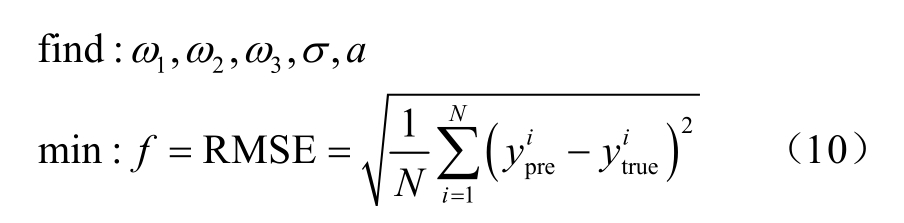
式中，N 为训练集的数据列长度；ypre和 ytrue分别为训练集的预测输出和真实输出。
在GWO 中，α 作为头狼，具有最高的领导地位，代表最优解；β 和δ 作为第二和第三领导层，代表次优解。ω 作为普通狼，服从更高等级狼的领导，代表候选解。当狼群发现猎物时，分别执行包围、狩猎和攻击等捕食策略。其数学模型为
式中，X 和 Xp分别为狼群和猎物的位置；t 为迭代次数； A 和C 为系数矩阵，通过式（12）计算。
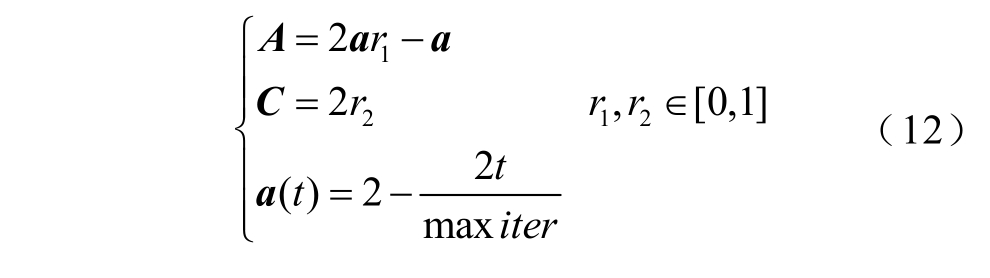
式中，maxiter 为最大迭代次数。
通过式（13）更新狼群位置。
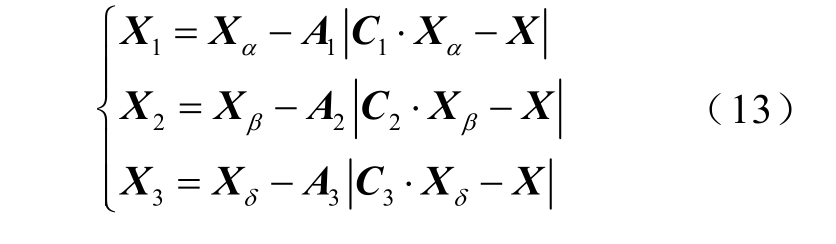
式中，Xα、Xβ、Xδ 分别为迭代更新后α、β、δ 狼群位置；Xi 分别为迭代更新后α、β、δ 狼群位置，i=1,2,3。
最终得到猎物的位置为
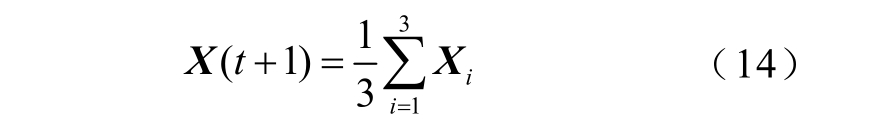
因此，利用式（11）～式（14）的不断迭代即可确定适应度函数式（10）中MKRVM 的待定参数，完成MKRVM 的核函数权值及核参数确定。
3.2 电池容量估算框架
建立基于 MKRVM 优化模型的电池容量在线估算框架如图4 所示。
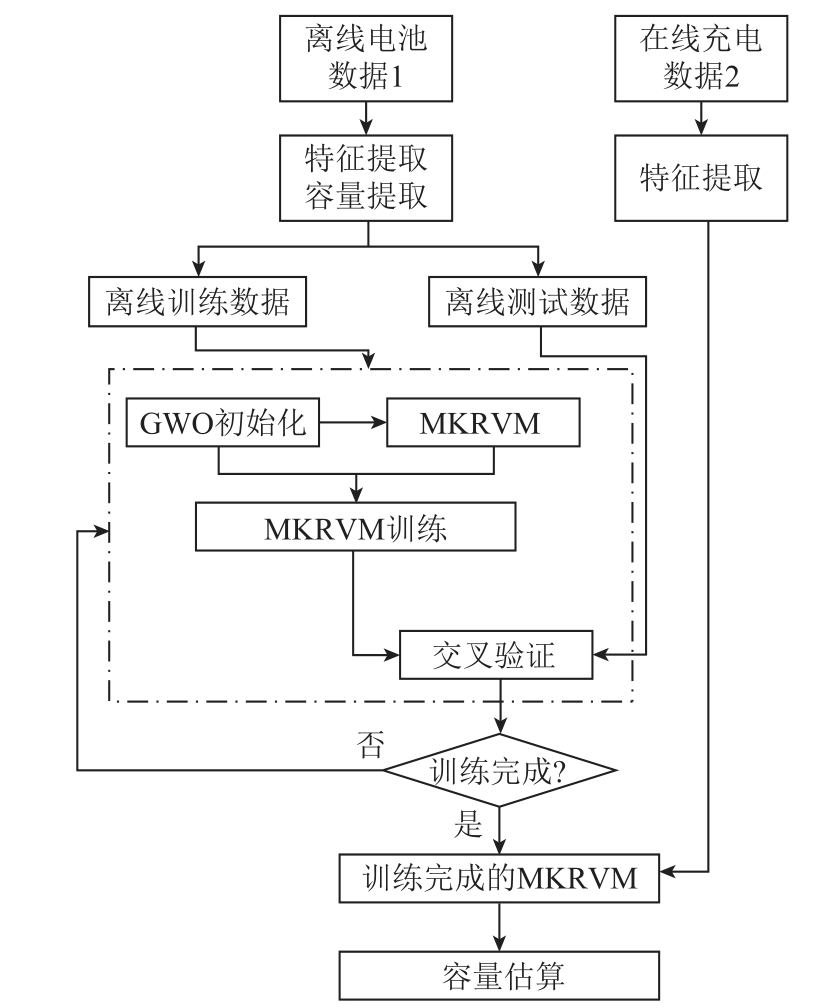
图4 容量在线估算框架
Fig.4 The framework of capacity estimation
整个容量估算框架分为三个步骤：
（1）离线电池老化数据处理。由电池老化实验获取电池全生命周期老化数据；分别提取电池老化数据中基于充电数据的老化特征和容量测试中的容量数据作为离线数据；利用5-折交叉验证将离线数据集分为离线训练数据和离线测试数据。
（2）MKRVM 优化模型训练。利用GWO 同时优化RVM 多核函数权值和核参数，并利用离线测试数据对训练完成的MKRVM 进行交叉验证。基于多次训练的最优参数，以全部数据集重新训练模型。若精度不小于原有最优精度，则完成训练；否则返回继续优化训练。
（3）容量在线估算。从在线充电数据中提取电池老化特征，输入训练完成的MKRVM 中，得到估算容量。
3.3 电池在环管理系统
为实现电池容量在线估算，利用 Matlab 和LabVIEW 联合仿真，以LabVIEW 作为人机交互界面和进行数据采集，Matlab 作为数据处理中心，嵌入MKRVM 优化模型，借助充放电设备传感器搭建的模拟电池在环管理系统如图5 所示。
图5 模拟电池在环管理系统
Fig.5 The simulated battery-in-loop BMS
从图5 可以看出，模拟电池在环管理系统主要包括三个部分。
（1）电池老化数据采集。通过电池充放电设备获取电池全生命周期内的电池老化数据。
（2）电池老化特征提取。由电池充电数据提取指定电压条件下电池部分充电数据，利用LOWESS方法平滑电池容量增量曲线，提取与电池容量具有较强关联性的恒压差充电容量和容量增量曲线峰值作为表征电池容量退化的电池老化特征。
（3）电池容量在线估计。首先，基于离线训练数据库，利用Matlab 完成灰狼优化MKRVM 构建电池老化模型；其次，基于测试数据库的电池充电数据，通过LabVIEW 软件的文件I/O 接口模拟实时电池硬件电路信号采集，每秒逐行读取电池充电数据并存储为本地Excel 文件，作为实时电池充电数据，当到达充电截止电流时，导入已保存的Excel 文件，截取充电数据提取在线老化特征；最后，将训练完成的MKRVM 优化模型嵌入LabVIEW 里，完成电池容量在线估算，将输出结果保存到本地容量估算Excel 中，并显示在BMS 交互界面上。
此外，电池充电过程的电压、电流和温度曲线，实时测量数据、电池预警和SOC 等信息也显示在交互界面上。
4 结果与验证
将不同类型电池单体和电池组老化数据集按编号分为训练数据库（奇数号电池）和测试数据库（偶数号电池）。具体地，分别以CS35 和CS37、DUT1和DUT3 确定MKRVM 优化模型参数估算CS36 和CS38、DUT2 和DUT4 的电池容量。由于不同来源电池数据集之间差别较大，分别对两类数据集单独进行验证。依据图4 和图5 所示的框架进行电池容量在线估算，并基于式（15）根据容量方差给出估算结果的95%置信区间 CI95%，结果如图6 所示。
式中，
分别为通过BMS 估计容量的平均值和实际值；cov 为协方差。
从图 6a～图 6d 容量曲线可以看出：使用MKRVM 优化模型得到的估算容量和真实容量曲线具有较高重合度。图6a～图6d 还给出了两类电池容量估算的绝对误差，其中，CALCE 电池单体数据集，最大估算误差为0.024 8A·h，百分比误差为2.25%；DUT 电池组数据的最大估算误差为0.339 1A·h，百分比误差为2.17%。对于两类不同电池，给出的95% 置信区间也基本覆盖全部真实容量波动范围。容量估算结果表明，本文提出的MKRVM 优化模型对电池容量具有较高的估算精度。需要注意的是，CALCE 单体估算误差略大于DUT 电池组，可能的原因是CALCE 电池之间一致性较差，且实验过程中存在较多容量增生现象。
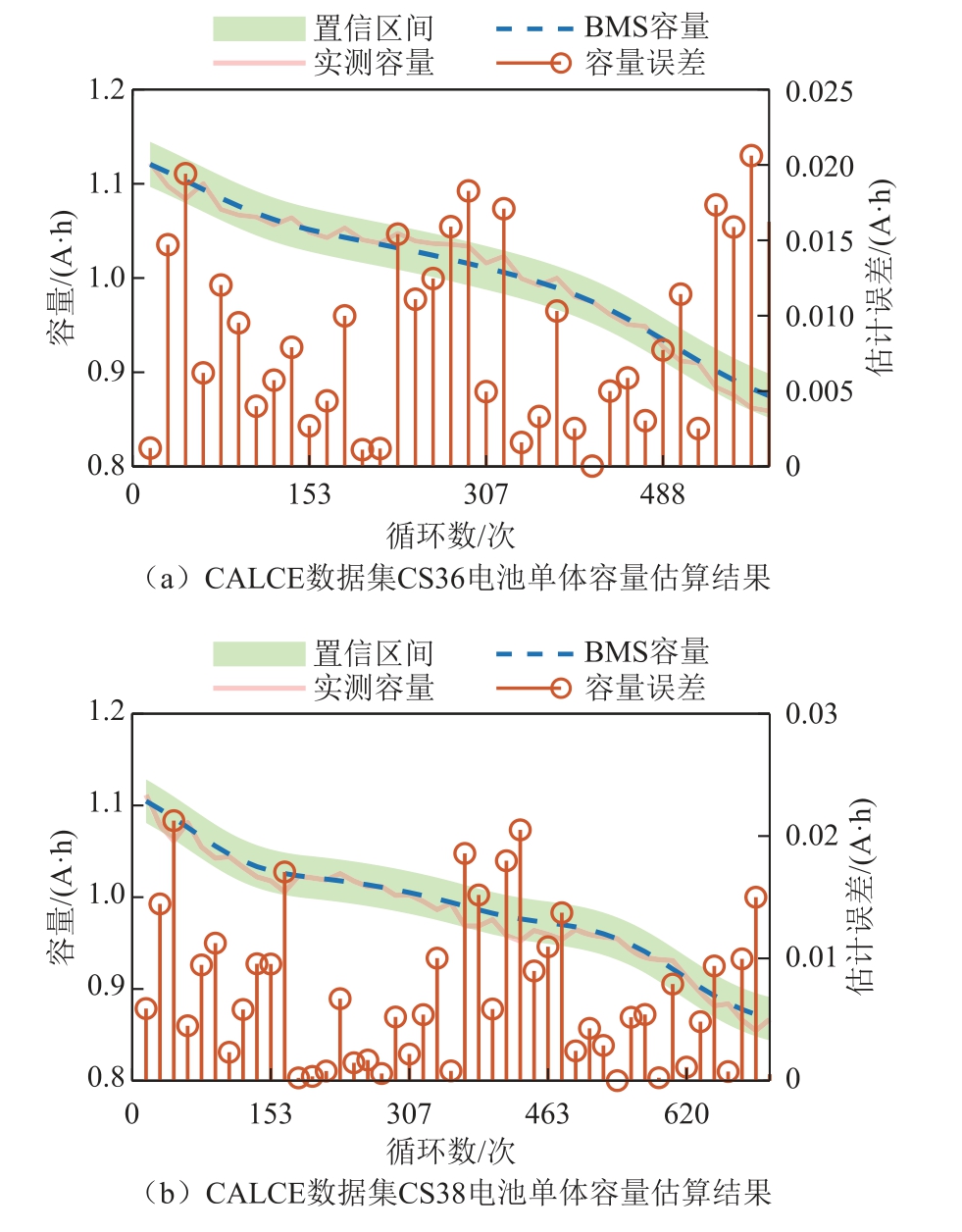
图6 不同数据集的电池容量估算结果
Fig.6 The estimation results of different battery datasets
与此同时，基于相同的电池老化数据集，通过Matlab 离线仿真对比无优化参数的MKRVM（权值参数均为1，核参数采用默认常用参数）、单核RVM、SVM、BP 神经网络等常见数据驱动方法电池容量估算精度，并计算估算结果的RMSE 和统计完成运算时间，结果见表2。
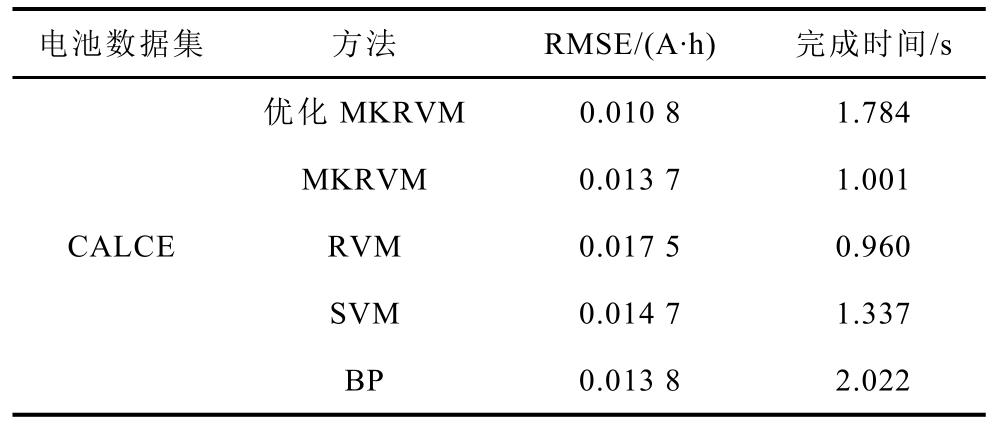
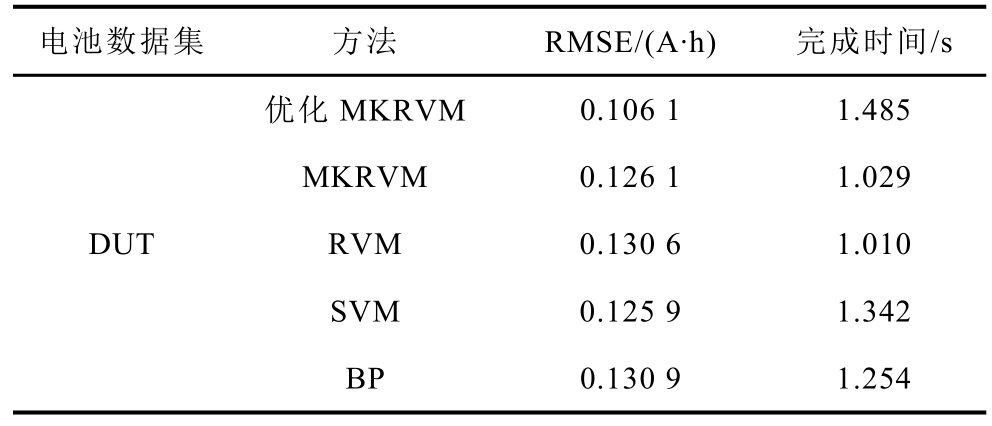
从表2 可以看出：优化的MKRVM 方法估算CALCE 电池单体容量RMSE 为0.010 8A·h，估算DUT 电池组容量RMSE 为0.106 1A·h，两者均低于其他四种方法的估算误差，表明本文所提的优化MKRVM 具有较高的估算精度。相对于其他方法的运算时间维持在约 1s，优化权值及核函数的MKRVM 由于优化过程的存在，不可避免地耗费更 多的计算时间，约0.5～0.8s。但多出的时间主要在离线训练阶段，计算过程时间耗费不足1ms。多种方法的精度和运算时间对比结果表明，多核学习和智能优化算法的结合能在略微牺牲训练时间的基础上有效提高RVM 学习和泛化能力。
表2 不同方法的电池容量估算结果对比
Tab.2 Comparison of different methods for capacity estimation
（续）
综上所述，通过不同电池老化数据验证提出的MKRVM 优化模型，结果表明该方法能提供准确的电池容量估计，并给出合理的置信区间。通过模拟在环的电池管理系统对提出方法进行在线实现，为电池管理系统开发提供理论基础。
5 结论
基于电池充电过程容量增量曲线，提取表征电池容量退化的电池老化特征，结合提出的智能优化MKRVM 模型进行电池容量在线估算，得出如下结论：
1）利用LOWESS 对电池容量增量曲线去噪，并提取基于部分容量增量曲线的老化特征（恒压差充电容量和增量峰峰值）。关联分析结果表明，提取的两个电池老化特征和容量具有较高的关联性。
2）通过灰狼优化算法同时优化RVM 的多核函数权值和核参数，建立基于MKRVM 优化模型的电池容量估算框架。
3）借助电池充放电系统传感器测量的数据，通过LabVIEW 和Matlab 联合仿真，建立基于MKRVM优化模型的在环电池管理系统。通过CALCE 电池单体老化数据集和自有DUT 电池组老化数据集验证提出的容量估算框架的有效性。
4）通过与无优化的MKRVM、单核RVM、SVM、BP 神经网络等常见数据驱动方法的对比，结果表明提出的MKRVM 优化模型具有更高的容量估算精度，不同电池和电池组估算误差不超过2.3%。
本文建立的MKRVM 优化模型是利用相同老化的电池单体和电池组数据进行容量估算，后续将尝试将电池单体MKRVM 训练模型推广到同类型电池组上，并开发无线数据采集传输和嵌入式硬件在环电池管理系统，实现所提方法在充电过程中的云端验证。
[1]朱晓庆,王震坡,Hsin Wang,等.锂离子动力电池热失控与安全管理研究综述[J].机械工程学报,2020,56(14): 91-118.Zhu Xiaoqing,Wang Zhenpo,Wang H,et al.Review of thermal runaway and safety management for lithium-ion traction batteries in electric vehicles[J].Journal of Mechanical Engineering,2020,56(14): 91-118.
[2]韩乔妮,姜帆,程泽.变温度下IHF-IGPR 框架的锂离子电池健康状态预测方法[J].电工技术学报,2021,36(17): 3705-3720.Han Qiaoni,Jiang Fan,Cheng Ze.State of health estimation for lithium-ion batteries based on the framework of IHF-IGPR under variable temperature[J].Transactions of China Electrotechnical Society,2021,36(17): 3705-3720.
[3]Lü Zhiqiang,Gao Renjing,Chen Lin.Li-ion battery state of health estimation and remaining useful life prediction through a model-data-fusion method[J].IEEE Transactions on Power Electronics,2021,36(6): 6228-6240.
[4]杨胜杰,罗冰洋,王菁,等.基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J].电工技术学报,2021,36(11): 2277-2287.Yang Shengjie,Luo Bingyang,Wang Jing,et al.State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J].Transactions of China Electrotechnical Society,2021,36(11): 2277-2287.
[5]Xiong Rui,Li Linlin,Li Zhirun,et al.An electrochemical model based degradation state identification method of lithium-ion battery for allclimate electric vehicles application[J].Applied Energy,2018,219: 264-275.
[6]Li J,Adewuyi K,Lotfi N,et al.A single particle model with chemical/mechanical degradation physics for lithium ion battery state of health (SOH) estimation[J].Applied Energy,2018,212: 1178-1190.
[7]Lü Zhiqiang,Gao Renjing.A model-based and datadriven joint method for state-of-health estimation of lithium -ion battery in electric vehicles[J].International Journal of Energy Research,2019,43: 7956-7969.
[8]Chen Cheng,Xiong Rui,Shen Weixiang.A lithiumion battery-in-the-loop approach to test and validate multiscale dual h infinity filters for state-of-charge and capacity estimation[J].IEEE Transactions on Power Electronics,2018,33(1): 332-342.
[9]Afshari H,Attari M,Ahmed R,et al.Reliable state of charge and state of health estimation using the smooth variable structure filter[J].Control Engineering Practice,2018,77: 1-14.
[10]李超然,肖飞,樊亚翔,等.基于卷积神经网络的锂离子电池 SOH 估算[J].电工技术学报,2020,35(19): 4106-4119.Li Chaoran,Xiao Fei,Fan Yaxiang,et al.An approach to lithium-ion battery SOH estimation based on convolutional neural network[J].Transactions of China Electrotechnical Society,2020,35(19): 4106-4119.
[11]You G W,Park S,Oh D.Diagnosis of electric vehicle batteries using recurrent neural networks[J].IEEE Transactions on Industrial Electronics,2017,64(6): 4885-4893.
[12]Lü Zhiqiang,Gao Renjing.Li-ion battery state of health estimation through gaussian process regression with Thevenin model[J].International Journal of Energy Research,2020,44(13): 10262-10281.
[13]Chen Lin,Wang Huimin,Liu Bohao,et al.Battery state-of-health estimation based on a metabolic extreme learning machine combining degradation state model and error compensation[J].Energy,2021,215: 119078.
[14]戴海峰,姜波,魏学哲,等.基于充电曲线特征的锂离子电池容量估计[J].机械工程学报,2019,55(20): 52-59.Dai Haifeng,Jiang Bo,Wei Xuezhe,et al.Capacity estimation of lithium-ion batteries based on charging curve features[J].Journal of Mechanical Engineering,2019,55(20): 52-59.
[15]来鑫,秦超,郑岳久,等.基于恒流充电曲线电压特征点的锂离子电池自适应容量估计方法[J].汽车工程,2019,41(1): 1-6,20.Lai Xin,Qin Chao,Zheng Yuejiu,et al.An adaptive capacity estimation scheme for lithium-ion battery based on voltage characteristic points in constantcurrent charging curve[J].Automotive Engineering,2019,41(1): 1-6,20.
[16]Lü Zhiqiang,Gao Renjing,Li Xiaoyu.A partial charging curve-based data-fusion-model method for capacity estimation of Li-ion battery[J].Journal of Power Sources,2021,483: 229131.
[17]刘月峰,赵光权,彭喜元.多核相关向量机优化模型的锂电池剩余寿命预测方法[J].电子学报,2019,47(6): 1285-1292.Liu Yuefeng,Zhao Guangquan,Peng Xiyuan.A lithium-ion battery remaining using life prediction method based on multi-kernel relevance vector machine optimized model[J].Acta Electronica Sinica,2019,47(6): 1285-1292.
[18]韦海燕,陈静,王惠民,等.新陈代谢灰色粒子滤波实现电池剩余寿命预测[J].电工技术学报,2020,35(6): 1181-1188.Wei Haiyan,Chen Jing,Wang Huimin,et al.Remaining useful life prediction of battery using metabolic grey particle filter[J].Transactions of China Electrotechnical Society,2020,35(6): 1181-1188.
[19]Li Xiaoyu,Yuan Changgui,Li Xiaohui,et al.State of health estimation for Li-ion battery using incremental capacity analysis and gaussian process regression[J].Energy,2020,190: 116467.
[20]Li Xiaoyu,Wang Zhenpo,Zhang Lei,et al.State-ofhealth estimation for Li-ion batteries by combing the incremental capacity analysis method with grey relational analysis[J].Journal of Power Sources,2019,410-411: 106-114.
[21]Birkl C,Roberts M,Mcturk E,et al.Degradation diagnostics for lithium ion cells[J].Journal of Power Sources,2017,341: 373-386.
[22]Han Xuebing,Lu Languang,Zheng Yuejiu,et al.A review on the key issues of the lithium ion battery degradation among the whole life cycle[J].eTransportation,2019,1: 100005.
[23]Schuster S,Brand M,Campestrini C,et al.Correlation between capacity and impedance of lithium-ion cells during calendar and cycle life[J].Journal of Power Sources,2016,305: 191-199.
[24]Lyu Zhiqiang,Wang Geng,Gao Renjing.Li-ion battery prognostic and health management through an indirect hybrid model[J].Journal of Energy Storage,2021,42: 102990.
[25]Mirjalili S,Mirjalili S,Lewis A.Grey wolf optimizer[J].Advances in Engineering Software,2014,69: 46-61.