0 引言
取向电工钢作为一种电磁性能优良的软磁材料，广泛用于制造各类变压器铁心[1]。在实际运行过程中，由于变压器内部的弯曲效应、硅钢片的叠压等，铁心会受到一定的挤压或拉伸应力的作用[2]，承受不同应力的硅钢片表现出来的磁特性会有很大的不同[3]。虽然拉应力引起磁特性的变化不大，但即使很小的压应力也导致磁滞回线严重变形，磁滞损耗增加[4]。因此，确定取向硅钢片的应力类型并评估其大小，对于提高变压器的运行效率是至关重要的。
目前，国内外常用的铁磁材料应力无损检测方法主要有X 射线衍射法、中子衍射法、超声波法和巴克豪森效应法等。X 射线衍射法[5]是利用应力会导致晶面间距发生改变，布拉格衍射峰也会因此发生偏移，根据移动距离来确定应力。但X 射线的探测深度只在μm 级，而硅钢片的厚度在mm 级。中子衍射法[6]的测量原理与X 射线衍射法类似，探测深度在cm 级，但由于中子激发设备价格高昂，对实验环境要求严格，测量成本昂贵，目前该方法还不能应用于民用设备。超声波法[7]基于声弹性理论，利用超声波在介质中传播的速度来评估应力，但该方法检测灵敏度低。巴克豪森效应法[8]是利用巴克豪森噪声信号对应力敏感的特性，通过提取相应的信号特征值，进行应力的评估。但巴克豪森噪声信号的测量易受传感器材料、结构、磁心与样品的间距等因素的影响[9]，而且该噪声信号具有随机性、波动性和不可复现性[10]，因此用巴克豪森信号来量化应力的大小也存在一定的困难。
文献[11-12]提出，外加应力可以看作是通过磁弹性耦合作用的等效场，该等效场与应力以及磁致伸缩应变λ 随磁化强度M 的变化率成正比。该磁力学效应理论被用于描述随时间变化的外加应力对磁化强度的影响[13-14]，以及恒定外加应力对无滞后磁化曲线影响[15-16]。P.Garikepati 等利用考虑磁力学效应的无滞后磁化曲线方程推导出无滞后初始微分磁化率 χa＇n 与应力的关系方程[16]，但无滞后磁化曲线只能通过求解方程得到，不能通过实验准确测量。L.Mierczak 等在此基础上简单认为矫顽点微分磁化率 χH＇c与无滞后初始微分磁化率 χa＇n 相等，从而得到矫顽点微分磁化率 χH＇c与应力的关系式[17]，但忽略了应力对钉扎点的影响，把钉扎系数k 当成一个不随应力变化的常数，未能准确反映出矫顽点微分磁化率与应力的关系。2002 年C.C.H.Lo 等对考虑磁力学效应的磁滞模型进行了扩展，考虑了应力对畴壁钉扎的影响，提出了扩展的磁力学磁滞模型[18]。
本文基于扩展的磁力学磁滞模型提出了一种定量检测取向电工钢片应力的新方法。首先利用扩展的考虑磁力学效应的磁滞模型，同时考虑到软磁材料钉扎系数k 近似等于矫顽场
，推导出矫顽点微分磁化率的倒数 1/
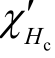与应力的线性关系表达式，得到一条线性校准曲线，可以根据测得的磁滞回线求出矫顽点的微分磁化率，进而评估出硅钢片的应力大小。然后通过实验证明了这种应力检测方法的准确性与适用性。本文给出了一条线性校准曲线，只需要测量硅钢片的磁滞回线，就可以在校准曲线上找出其对应的应力，与其他应力检测方法相比，该方法具有检测成本低、检测效率高、准确性高等优点。
1 矫顽点微分磁化率与应力的关系
1.1 扩展的磁力学磁滞模型
在外加磁场H 的作用下，无滞后磁化曲线可用Langevin 函数表示为[11]
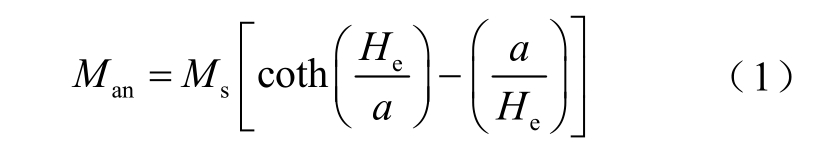
式中，Man为无滞后磁化强度；Ms 为饱和磁化强度；a 为取决于材料微观结构的常数；He为等效磁场强度，He=H+αM，M 为磁化强度，α为磁畴耦合系数。
外加应力σ 通过磁弹性耦合来改变材料的各向异性能。当施加一个恒定的应力σ 时，铁磁体的各向异性能变化量为[19]
式中，λ为铁磁体在外加磁场H 方向的磁致伸缩应变；φ为外加应力σ 和磁场H 的夹角；ν 为泊松比。这个磁弹性能可以用一个磁场强度Hσ来等效反映。
所以考虑外加应力的作用时，无滞后磁化强度曲线变为
无滞后磁化曲线只适用于描述理想或完美磁性材料，在这种情况下，磁化强度的变化没有阻碍。然而，实际铁磁体的结构并不完美，它包含各种形式的缺陷：位错、空洞和非磁性夹杂物等，这些缺陷统称为钉扎点。在外加磁场的作用下，磁畴壁运动会受到钉扎点的阻碍作用，克服钉扎点产生的能量损耗密度可表示为[20]
式中，k(σ )为钉扎系数，与钉扎点密度和钉扎能有关，应力σ 会改变畴壁两侧的钉扎能，从而改变钉扎系数[18]。钉扎系数可以表示为
式中，k0 为应力为零时的钉扎系数；n0 为钉扎点密度；
表示取平均值；λs 为饱和磁致伸缩应变；m 为磁畴磁化强度；θ为磁畴磁化强度和应力之间的夹角。
单位体积的铁磁材料实际获得的磁化能量为理想磁化能量与损耗之差，即
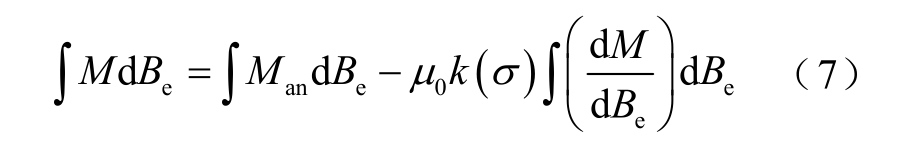
式中，Be 为磁感应强度有效值。
式（7）的等号两边分别对Be 求导得
为保证钉扎点总是阻碍磁化强度变化，引入方向系数δ，取值为
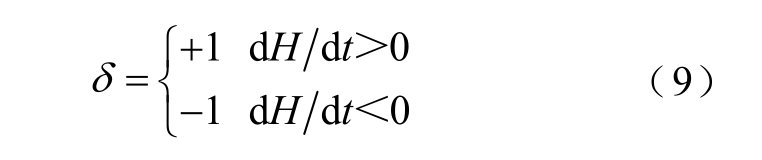
当外加磁场与应力同轴时，即φ=0°，式（8）可以转化为更简单的形式，即
在数学上，通过对式（10）进行积分来计算磁化强度M，从而模拟出不同应力下的磁滞回线。
1.2 矫顽点微分磁化率与应力的关系表达式
磁致伸缩应变λ随着磁化强度M 的变化曲线是对称的，当磁化强度M 接近于0 时，磁致伸缩应变λ可近似表示为[21-22]
式中，系数b 通过磁致伸缩测量实验确定。
在矫顽点磁化强度M(Hc)=0，由式（10）可知该点的微分磁化率可表示为
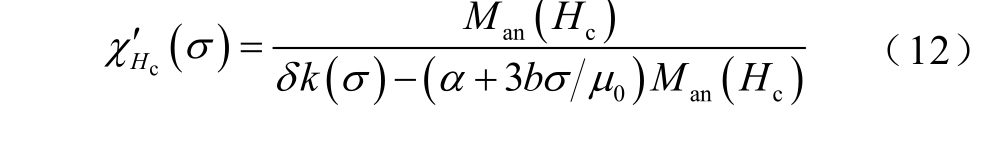
考虑dH/ dt＞0过程，此时δ=1，式（12）转化为
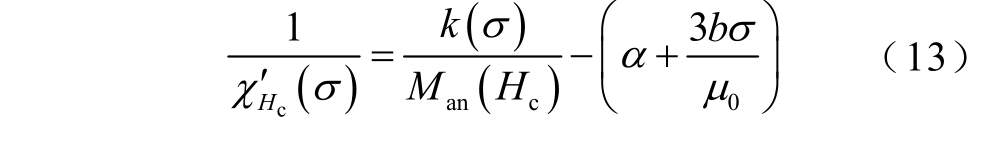
在软磁材料中钉扎系数 k(σ )近似等于矫顽场Hc，则由式（13）可得
将式（4）无滞后磁化曲线在矫顽点处线性化，可得
整理可得
将式（16）代入式（14），得到
由式（17）可知矫顽点微分磁化率的倒数 
。式（17）还可以转化为
若系数b 和σ=0 时的矫顽点微分磁化率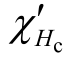
(0)已知，可根据测得的磁滞回线求出硅钢片的应力σ。
2 实验系统及样品参数
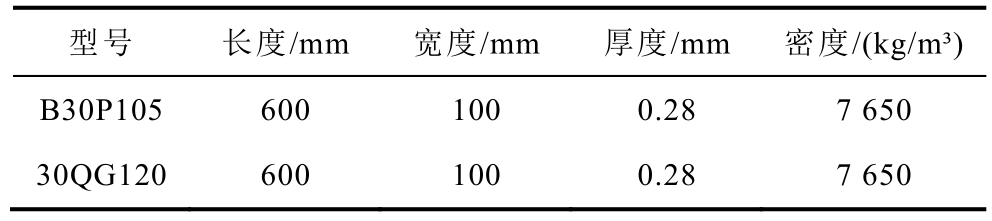
实验采用BROCKHAUS-MPG200 软磁材料测试系统测量不同应力下硅钢片的磁滞回线和磁致伸缩曲线。测试系统主要由电源系统、磁路测量装置和激光发射接收器三部分组成。为了使测量结果不受环境振动等因素的影响，实验过程中磁路测量装置和激光发射接收装置均悬浮于气垫上。磁路测量装置由励磁线圈、测量线圈和构成磁路的磁轭组成。实验过程中通过调节应力施加装置的应力旋钮，调节施加在硅钢片上的拉应力或压应力。本次实验施加的应力与磁场同轴，励磁侧施加50 Hz 的正弦波激励信号。BROCKHAUS-MPG200 软磁材料测量系统如图1 所示，两种型号的硅钢片样品参数见表1，为消除样品中残余应力的影响提前对样品进行了退火处理。
图1 BROCKHAUS-MPG200 软磁材料测量系统
Fig.1 BROCKHAUS-MPG200 soft magnetic material measurement system
表1 两种型号的硅钢片样品参数
Tab.1 Sample parameters of two types of silicon steel sheet
硅钢片中的磁场强度H 和磁感应强度B 分别为
式中，N1、N2 分别为一、二次侧线圈匝数；I1、U2分别为一次电流和二次电压；lm 为磁通路径长度；S 为硅钢片有效截面积。
3 结果与讨论
实验测得最大磁通密度Bm=1.6 T时不同应力下B30P105 硅钢片的磁致伸缩曲线如图2 所示（拉应力取正值，压应力取负值），横轴表示磁感应强度M。在拉应力的作用下磁致伸缩应变为负值，即在外加磁场的作用下磁畴收缩，随着拉应力的增大，最大磁致伸缩应变略微减小。当压应力不超过2.83 MPa时，磁致伸缩仍然为负，并且最大磁致伸缩应变的变化趋势与拉应力相同。但是当压应力超过4.25 MPa时，磁致伸缩应变为正值，即在外加磁场的作用下磁畴增大，而且最大磁致伸缩应变的值远大于拉应力下的值，变化趋势也与拉应力或压应力较小时相反，可能是压应力持续增大，硅钢片虽未发生宏观塑性形变，但发生了微观塑性形变[23]，材料的微观结构发生了改变。本文只考虑引起弹性形变的应力范围，如图2 中过原点的红色抛物线所示，通过拟合M=0附近，应力在-2.83～7.08 MPa范围内B30P105硅钢片的磁致伸缩曲线，可得式（11）中系数b1=-2.60×10-19 (A/m)-2。不同应力下30QG120 硅钢片的磁致伸缩曲线如图 3 所示，变化规律与B30P105 硅钢片相同。如图3 中过原点的红色抛物线所示，通过拟合M=0附近，应力在-1.77～10.63 MPa 范围内30QG120 硅钢片的磁致伸缩曲线，可得式（11）中系数b2=-2.36×10-19(A/m)-2。
图2 最大磁通密度Bm=1.6 T 时不同应力下B30P105硅钢片的磁致伸缩曲线
Fig.2 Magnetostrictive curves of B30P105 silicon steel sheets under different stresses at Bm=1.6 T
图3 最大磁通密度Bm=1.6 T 时不同应力下30QG120硅钢片的磁致伸缩曲线
Fig.3 Magnetostrictive curves of 30QG120 silicon steel sheets under different stresses at Bm=1.6 T
B30P105 硅钢片在-2.83～7.08 MPa 应力范围内的磁滞回线如图4 所示。图5 为图4 中灰色阴影部分的放大图，可以看出应力从负到正的过程中，矫顽点微分磁导率（dB/dH）逐渐减小。30QG120 硅钢片在-1.77～10.63 MPa应力范围内的磁滞回线如图6 所示。图7 为图6 中灰色阴影部分的放大图，从图7 可以看出30QG120 硅钢片的矫顽点微分磁导率随应力的变化规律与B30P105 硅钢片相同。
图4 B30P105 硅钢片在-2.83～7.08 MPa 应力范围内的磁滞回线
Fig.4 Hysteresis loops of B30P105 silicon steel sheets in the range of -2.83～7.08 MPa stress
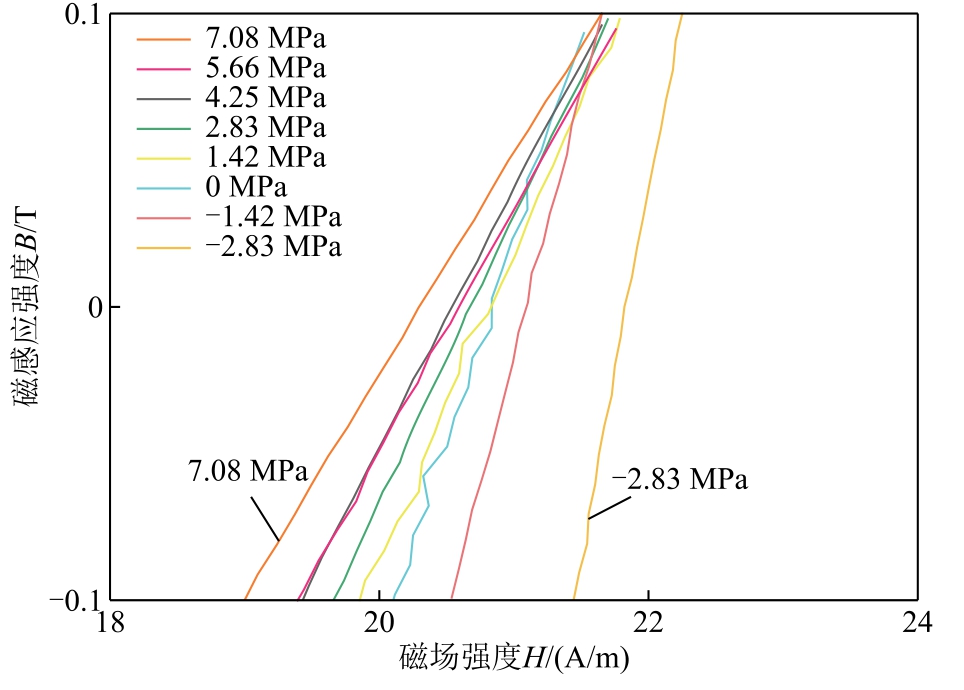
图5 B30P105 硅钢片磁滞回线局部放大图
Fig.5 Local magnification of hysteresis loops of B30P105 silicon steel sheets
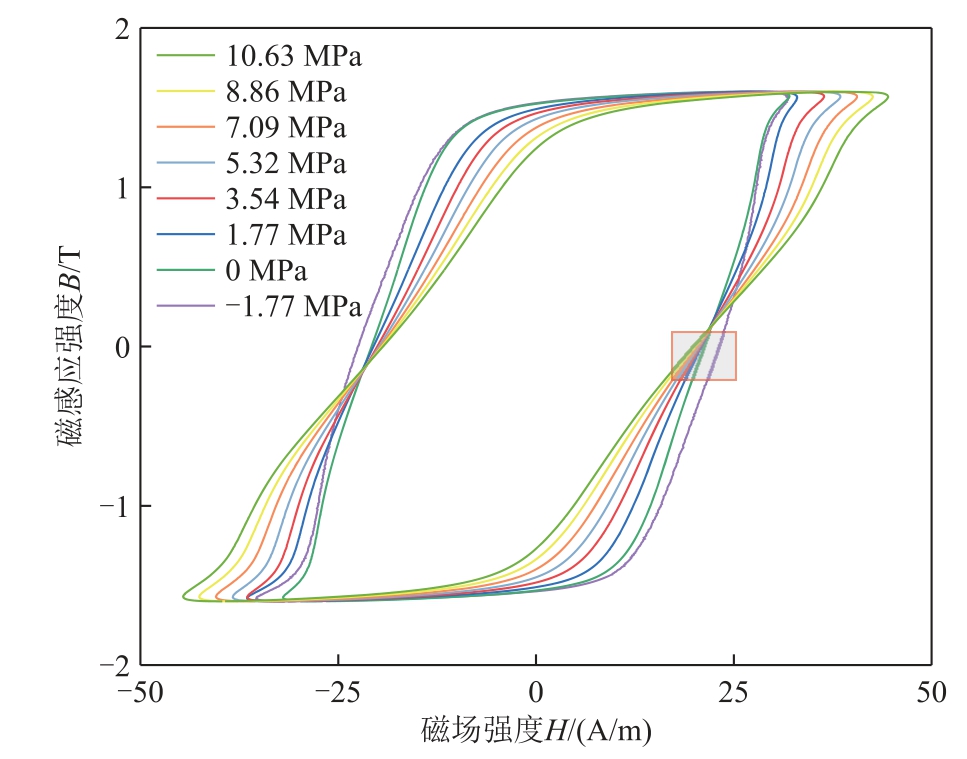
图6 30QG120 硅钢片在-1.77～10.63 MPa 应力范围内的磁滞回线
Fig.6 Hysteresis loops of 30QG120 silicon steel sheets in the range of -1.77～10.63 MPa stress
图7 30QG120 硅钢片磁滞回线局部放大图
Fig.7 Local magnification of hysteresis loops of 30QG120 silicon steel sheets
在软磁材料中磁化强度M 远大于磁场强度H，微分磁化率和相对磁导率近似相等，即
所以矫顽点微分磁化率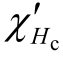
可表示为
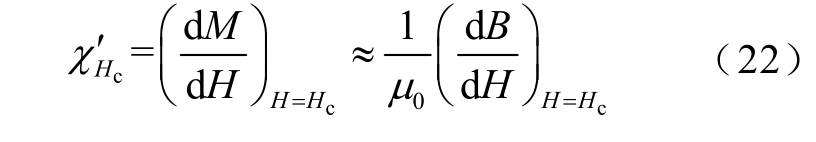
根据实验测量的磁滞回线以及式（22）可得，B30P105 和30QG120 硅钢片的矫顽点微分磁化率与应力的对应关系如图8 所示。这两种硅钢片的矫顽点磁化率随应力的变化趋势相同，表现出随压应力的增大而增大，随拉应力的增大而减小，而且压应力对矫顽点磁化率的作用要大于拉应力。
图8 B30P105 和30QG120 硅钢片的矫顽点微分磁化率与应力的对应关系
Fig.8 Relationship between differential susceptibility and stress of B30P105 and 30QG120silicon steel sheets at the coercive point
由实验数据可知，B30P105 硅钢片应力为零时矫顽点微分磁化率
（0）=1.10×105，将其与b1 同时代入式（18）可得，B30P105 硅钢片应力与矫顽点微分磁化率的关系表达式为
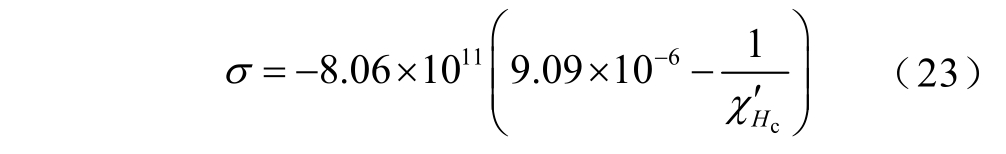
30QG120 硅钢片应力为零时矫顽点微分磁化率
（0）=0.95×105，同理可得，30QG120 硅钢片应力与矫顽点微分磁化率的关系表达式为
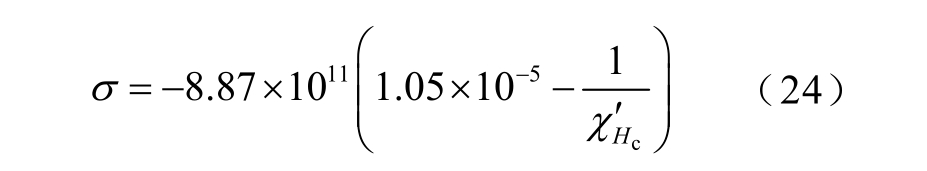
式中，应力σ 的单位为Pa。
B30P105 和30QG120 硅钢片矫顽点微分磁化率的倒数与应力的理论关系曲线如图9 所示。从图9 中 可以看出，两种硅钢片理论曲线的斜率有所不同，主要是因为两种不同型号的硅钢片磁致伸缩曲线不同，拟合曲线式（11）中的系数b 就会不相等。但两种硅钢片理论曲线和实验值之间都有很好的一致性，证明了理论推导的正确性与普适性。
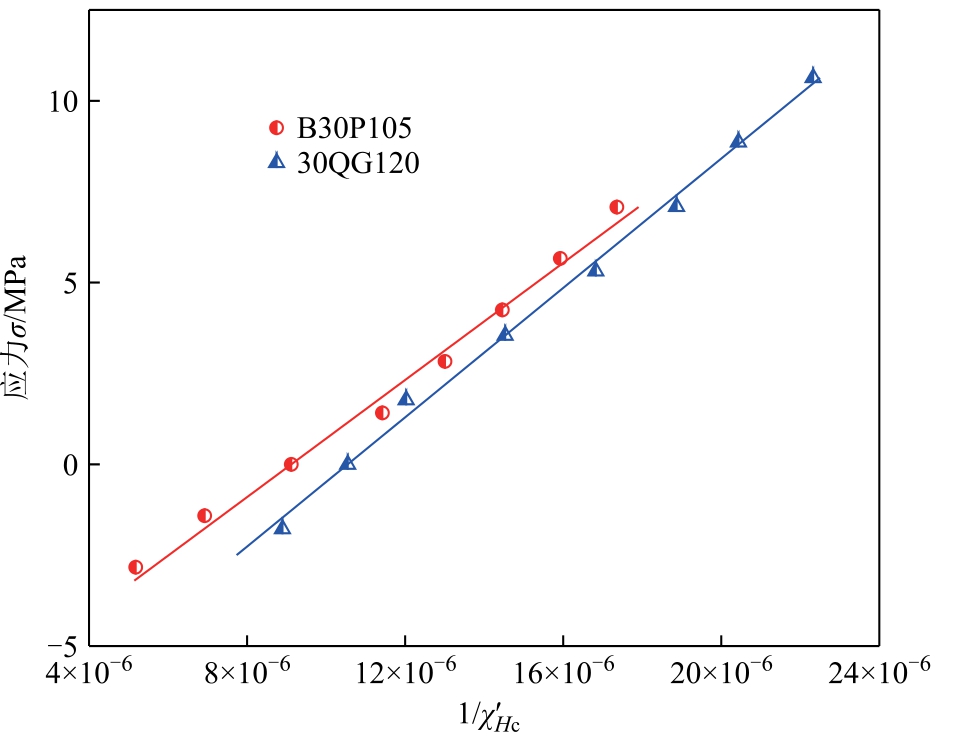
图9 B30P105 和30QG120 硅钢片矫顽点微分磁化率的倒数与应力的理论关系曲线
Fig.9 Theoretical relation curves between the reciprocal of differential susceptibility and stress of B30P105 and 30QG120 silicon steel sheets at the coercive point
4 结论
基于扩展的磁力学磁滞模型，本文提出一种定量评估硅钢片机械应力的新方法。矫顽点微分磁化率的倒数随应力线性变化，测出硅钢片的磁滞回线就可以求出硅钢片的应力大小，为检测应力提供了一条线性校准曲线。
不同型号、批次及生产厂商的硅钢片，磁致伸缩特性都会有所差别，换句话说校准曲线的斜率也会有所不同，但在实际工程应用中，只要测出应力为零和其他任意两种应力下的矫顽点微分磁化率 χH＇c，就可以较为准确地画出相应的校准曲线。这为硅钢片应力的定量评估提供了一种便捷的方法，也为其他铁磁材料的应力检测提供了一条新思路。
[1]杨庆新,李永建.先进电工磁性材料特性与应用发展研究综述[J].电工技术学报,2016,31(20): 1-12.Yang Qingxin,Li Yongjian.Characteristics and developments of advanced magnetic materials in electrical engineering: a review[J].Transactions of China Electrotechnical Society,2016,31(20): 1-12.
[2]Singh D,Rasilo P,Martin F,et al.Effect of mechanical stress on excess loss of electrical steel sheets[J].IEEE Transactions on Magnetics,2015,51(11): 1-4.
[3]Kai Y,Tsuchida Y,Todaka T,et al.Influence of stress on vector magnetic property under alternating magnetic flux conditions[J].IEEE Transactions on Magnetics,2011,47(10): 4344-4347.
[4]Augustyniak B,Piotrowski L,Jasnoch P,et al.Impact of tensile and compressive stress on classical and acoustic barkhausen effects in grain-oriented electrical steel[J].IEEE Transactions on Magnetics,2014,50(4): 1-4.
[5]Anon.Measuring casting residual stress with X-ray diffraction[J].Modern Casting,2005,95(9): 48-49.
[6]李向东,涂春磊,伍昊,等.材料内应力的检测方法[J].理化检验(物理分册),2020,56(6): 15-20.Li Xiangdong,Tu Chunlei,Wu Hao,et al.Testing method for internal stress of materials[J].Physical Testing and Chemical Analysis (Part A (Physical Testing)),2020,56(6): 15-20.
[7]张闯,李雪霏,刘素贞,等.单向载荷下铝板电磁超声兰姆波的波速响应特性[J].电工技术学报,2021,36(8): 1579-1586.Zhang Chuang,Li Xuefei,Liu Suzhen,et al.Wave velocity response characteristics of electromagnetic ultrasonic lamb wave of aluminum plate under unidirectional load[J].Transactions of China Electrotechnical Society,2021,36(8): 1579-1586.
[8]Yamazaki T,Furuya Y,Hata S,et al.Stress-driven magnetic barkhausen noise generation in FeCo magnetostrictive alloy[J].IEEE Transactions on Magnetics,2022,58(1): 1-8.
[9]Prabhu Gaunkar N.Magnetic hysteresis and barkhausen noise emission analysis of magnetic materials and composites[D].Ames,IA,USA: Iowa State University,2014.
[10]Fagan P,Ducharne B,Daniel L,et al.Multiscale modelling of the magnetic Barkhausen noise energy cycles[J].Journal of Magnetism and Magnetic Materials,2021,517: 167395.
[11]Sablik M J,Jiles D C.Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J].IEEE Transactions on Magnetics,1993,29(4): 2113-2123.
[12]Jiles D C,Kiarie W.An integrated model of magnetic hysteresis,the magnetomechanical effect,and the barkhausen effect[J].IEEE Transactions on Magnetics,2021,57(2): 1-11.
[13]Jiles D C.Theory of the magnetomechanical effect[J].Journal of Physics D: Applied Physics,1995,28(8): 1537-1546.
[14]Sablik M J,Langman R A.Approach to the anhysteretic surface[J].Journal of Applied Physics,1996,79(8): 6134-6136.
[15]Sablik M J.A model for the Barkhausen noise power as a function of applied magnetic field and stress[J].Journal of Applied Physics,1993,74(9): 5898-5900.
[16]Garikepati P,Chang T T,Jiles D C.Theory of ferromagnetic hysteresis: evaluation of stress from hysteresis curves[J].IEEE Transactions on Magnetics,1988,24(6): 2922-2924.
[17]Mierczak L,Jiles D C,Fantoni G.A new method for evaluation of mechanical stress using the reciprocal amplitude of magnetic barkhausen noise[J].IEEE Transactions on Magnetics,2011,47(2): 459-465.
[18]Lo C C H,Lee S J,Li L,et al.Modeling stress effects on magnetic hysteresis and Barkhausen emission using a hysteretic-stochastic model[J].IEEE Transactions on Magnetics,2002,38(5): 2418-2420.
[19]Jiles D C.Dynamics of domain magnetization and the Barkhausen effect[J].Czechoslovak Journal of Physics,2000,50(8): 893-924.
[20]Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis (invited)[J].Journal of Applied Physics,1984,55(6): 2115-2120.
[21]Zhu Lihua,Li Jingjing,Yang Qingxin,et al.An improved magnetostriction model for electrical steel sheet based on Jiles-Atherton model[J].IEEE Transactions on Magnetics,2020,56(3): 1-4.
[22]祝丽花,李晶晶,朱建国.服役条件下取向硅钢磁致伸缩模型的研究[J].电工技术学报,2020,35(19): 4131-4138.Zhu Lihua,Li Jingjing,Zhu Jianguo.Research on magnetostrictive model for oriented silicon steel under service conditions[J].Transactions of China Electrotechnical Society,2020,35(19): 4131-4138.
[23]Liu T,Kikuchi H,Ara K,et al.Magnetomechanical effect of low carbon steel studied by two kinds of magnetic minor hysteresis loops[J].NDT &E International,2006,39(5): 408-413.