0 引言
目前,我国电力工业已进入全国联网的新阶段,高压直流输电系统在“西电东送”和“南北互供”的战略中发挥着越来越重要的作用[1]。而换流阀是高压直流输电系统的核心设备,在运换流站中的换流阀通流能力高达5.5 kA[2]以上。工程上采用水冷却系统对换流阀内的关键器件进行散热,从而保证了换流阀的稳定安全运行。尽管冷却系统中去离子水的电导率被严格控制在0.5 μS/cm[3]以下,采用并联水路冷却结构,在特定位置安装有均压电极,从而把泄漏电流的大小控制在了极低的范围内,但是经过长期运行后水冷却系统中仍然存在电化学腐蚀与沉积问题,特别是均压电极表面会有结垢现象,从而引发内冷却水路堵塞、漏水、散热失灵等一系列问题,严重时会导致整个输电系统闭锁停运。
目前,针对换流阀水冷却系统内部的腐蚀与沉积问题,国内外学者通过试验和数值计算方法研究了换流阀水冷却系统内部的腐蚀与机理问题。P.O.Jackson 等和国内学者王远游等对运行多年的换流阀进行拆卸后,均发现均压电极表面结垢严重,分析表明垢的主要成分为含铝化合物,且一致认为垢层上的铝元素完全来源于铝制散热器的腐蚀[4-5];西门子公司经过研究后表明离子交换树脂粉末进入到去离子水中造成了水冷却系统内部呈弱碱性环境,进而引发了铝制散热器的腐蚀,使含铝元素离子进入到去离子水中并且在均压电极表面发生了沉积,使均压电极表面形成了致密的垢层[6];G.G.Karady等通过试验和仿真研究了换流阀内冷却系统水路中的泄漏电流的分布,认为泄漏电流的存在是导致铝制散热器腐蚀和均压电极结垢的主导因素[7]。
对于均压电极表面结垢机理的数值计算研究,目前主要通过建立换流阀内水冷却系统的等效电路模型计算泄漏电流的大小及分布,然后基于法拉第定律研究均压电极的结垢规律。华北电力大学卢斌先等提出了一种适用于换流阀冷却水路电极反应的等效电路,虽然确定了均压电极上腐蚀电流与泄漏电流的比例关系,但忽略了均压电极动态沉积的影响[8];贺婷婷、程一杰等通过有限元法建立了电极垢层动态沉积的二维仿真模型,考虑了电场、流体场、传质场的影响,对沉积特性进行了深入的分析,但是二维模型的建立对实际结构进行了很大程度的简化,与实际运行条件有很大偏差,导致计算结果与现场测量数据的最大偏差达到了12.2%,而且不能全方位反映均压电极表面的垢层分布[9]。
现有研究多数忽略了内冷却系统中成垢离子湍流场、传质场以及垢层动态沉积的影响,均压电极表面垢层的动态沉积不仅会影响冷却介质边界、电极反应动力学,而且整个沉积反应涉及欧姆极化、浓度极化和电化学极化过程。本文基于现有研究成果,建立了同时耦合电场、流体场、传质场的与实际结构保持一致的单个阀段内冷却系统三维仿真模型,引入了垢层动态膜阻模型,并采用加权方法与实际换流站垢层厚度统计数据相拟合,确定了等效电导率,与实际换流站的垢层统计数据偏差0.85%,较现有研究[9]的误差降低了11.35%,不仅全方位探究了换流站内均压电极垢层的生长机理,而且对垢层的生长进行了可靠预测以及公式拟合,为换流阀均压电极的检修除垢工作提供了可靠依据。
1 阀段冷却系统结构与腐蚀原理
1.1 模型结构
并联型冷却水路系统是工程中应用最为广泛的阀段冷却系统结构之一,在500 kV 换流阀中每个阀段冷却系统中含有进汇流管、出汇流管、14 个分水支流管和14 个铝制散热器,为了保证阀塔各个阀段分压均匀,在汇流管两侧安装了均压电极,并与阀段两侧散热器电气连接。为了准确模拟成垢离子在冷却水管中的运动轨迹以及在均压电极表面的沉积过程,本文根据单个阀段内各个结构的实际尺寸和相对位置,构建了单个阀段并联型水路的三维模型,如图1 所示。

图1 单个阀段并联型水路模型结构
Fig.1 A parallel waterway model structure of single valve segment
1.2 电化学腐蚀与沉积机理
对换流阀内均压电极垢层检测表明,其主要金属元素为铝(83.20%~97.72%),其次为铁(0.92%~10.76%)、铜(0.22%~1.54%)。垢层晶型主要为β三羟基铝石(96%~98%),其次为α 三水铝石(2%~3%)。铝制散热器材质为AA6063 铝合金,铝元素含量达到98.8%以上,铝散热器表面氧化膜具备很好的耐腐蚀性,但表面氧化膜被破坏后,其耐腐蚀性能会大大减弱。经过研究表明氧化膜的破坏主要是以下因素造成的:
1)水冷却系统中去离子树脂粉末的泄露,会造成局部碱性坏境,OH-会与Al2O3 发生反应。
2)冷却水中含有微量Cl-离子,Cl-离子不仅极易破坏氧化膜,而且Cl-离子与Al3+离子结合不利于Al2O3 的形成,从而加剧了铝散热器的腐蚀。
3)单个散热器中冷却水的流量约为4.5 L/min,由此产生的冲蚀作用对钝化层有一定的破坏作用。
铝散热器表面腐蚀表现为点蚀形态[10]。由于冷却水中溶解氧的存在,氧化膜作为阴极发生吸氧腐蚀形成大量的OH-,加快了氧化膜溶解,暴露的铝作为阳极发生溶解;在孔内随着Al3+水解酸性增强,会伴随析氢反应发生,产生的Al3+脱离孔隙,与阴极反应产生的OH-结合形成沉淀物,沉淀物聚集在点蚀孔周围,形成相对封闭的点蚀环境,而且有着很强的自催化特性,这种具有大阴极和小阳极的腐蚀电池加剧铝散热器的腐蚀。
铝散热器的腐蚀最终会在冷却水中生成[Al(OH)4]-(四羟基铝酸根离子)[9],而[Al(OH)4]-离子在电场、湍流场、扩散的共同作用下运动至电位相对较高的均压电极表面,进而发生电沉积反应形成垢层,具体反应[11-12]为
此外,电位相对较低的阴极均压电极表面会发生水电解反应,具体反应为
2 物理场控制方程
2.1 电场
由于垢层的动态沉积以及绝缘特性,导致电极附近电解质的电位实时变化,所以水冷却系统中的电位分布,满足电流连续方程和微分欧姆定律[13]。水冷却系统中的水管为PVDF 材料,其电导率较低,所以对于水管边界满足绝缘边界条件[9]。
在±500 kV 换流站中晶闸管在关断状态下,相邻铝制散热器会承受幅值3.2 kV 左右的交直流复合电压。现有研究表明直流电压对水冷却系统内部的电化学腐蚀和沉积的影响远大于交流电压的影响[8],因此本文忽略了交流电压分量的影响,对均压电极以及铝制散热器施加恒定电位,其边界条件[14]为

式中,n 为从左至右铝制散热器序号;U0 为相邻铝制散热器的电位差,汇流管两侧的均压电极的电位分别与两侧的散热器保持一致。
2.2 电极动态沉积反应及垢层模型
电极表面的垢层是多孔隙的,垢层的参数包括厚度、覆盖率、孔隙率、电导率,并且随时间变化。实际垢层动态沉积行为数学描述复杂,为了深入研究电极表面垢层的动态生长对沉积反应的影响,做出以下假设:
(1)垢层中不含有钙质沉积物等其他产物,全部由Al(OH)3 组成,且坚固、质密、绝缘,一旦沉积在电极表面将不会发生脱落和溶解。
(2)沉积反应优先发生在未被沉积物覆盖的电极表面。
(3)介质中的离子浓度较低,属于稀溶液。
(4)垢层具有恒定的摩尔质量、密度和电导率以及孔隙率。
将垢层上的电位差Δ φs,film 引入电极动力学方程中,对Butler-Volmer 方程进行修正,以考虑垢层的动态沉积对沉积反应的影响,其方程为
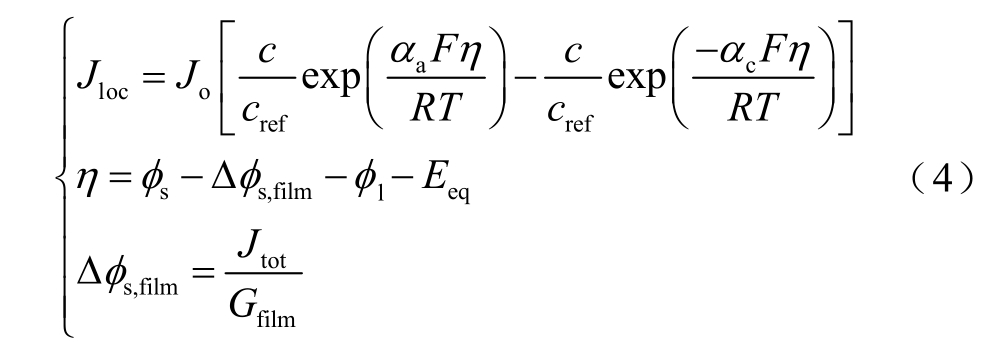
式中,Jloc 为局部电流密度(A/m2);Jo 为交换电流密度(A/m2);c 为离子浓度(mol/m3);cref 为离子参考浓度,cref=0.02 mol/m3;αa 为阳极传递系数;αc为阴极传递系数;T 为去离子水温度(K);F 为法拉第常数,F=96 485 C/mol;R 为气体常数,R=8.314 J/(mol·K);η 为过电动势(V);φs 为外施电位(V);φl为电解质电位(V);Eeq 为平衡电位(V);Δφs,film为垢层电位差(V);Gfilm 为垢层单位面积等效电导(S/m2);Jtot 为通过垢层的总电流密度(A/m2)。
垢层单位面积等效电导Gfilm 的计算公式为
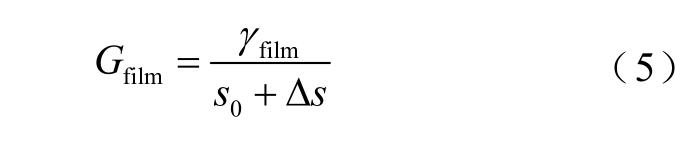
式中,s0 为垢层的初始厚度(m);Δs 为垢层厚度增量(m);γfilm为垢层的等效电导率(S/m)。垢层厚度增量Δs 计算公式为
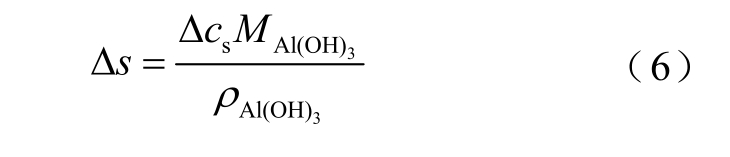
式中,cs 为表面浓度(mol/m2),Δcs 为单位面积反应离子的消耗量(mol/m2);MAl(OH)3 为垢层Al(OH)3的摩尔质量(0.078 kg/mol);ρAl(OH)3 为垢层Al(OH)3的密度(2 420 kg/m3)。垢层厚度的生长速率vdep,top 为
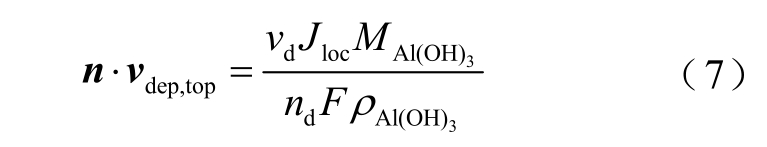
式中,vd 为化学当量系数;nd 为参与反应的电子数。
表面浓度cs 满足常微分方程
垢层总厚度stot 计算公式为

均压电极阳极沉积和阴极水解模型采用方程式(1)和方程式(2)进行描述,具体参数与现有研究[15]保持一致。
2.3 传质场
冷却系统去离子水介质中的离子浓度分布满足Nernst-Plank 方程[16],进汇流水管的入口设置为第一类浓度约束边界条件,即
式中,co,c 为离子浓度(1×10-5 mol/m3),去离子水中离子浓度一般在10-5 数量级。出汇流水管的出口设置为无通量边界条件,即
水管的其他边界设置为无通量条件,即
2.4 流体场
水冷却系统内冷却水的流动为高雷诺数的湍流、不可压缩流动。对于湍流问题的求解需要使用足够精细的网格,不仅需要足够大的计算内存,而且收敛性较差,计算缓慢。为了提高计算速度,本文认为水冷却系统内部冷却水的速度场分布只与水管的结构和流量有关,所以采取以下耦合方案:首先在湍流场中进行稳态计算,然后在计算结果中提取速度场分布计算结果,将速度场分布耦合进传质场,最后传质场和电场进行耦合瞬态计算,研究其垢层随时间的变化。所以本文采用k-ε 湍流稳态模型,其方程[17]为
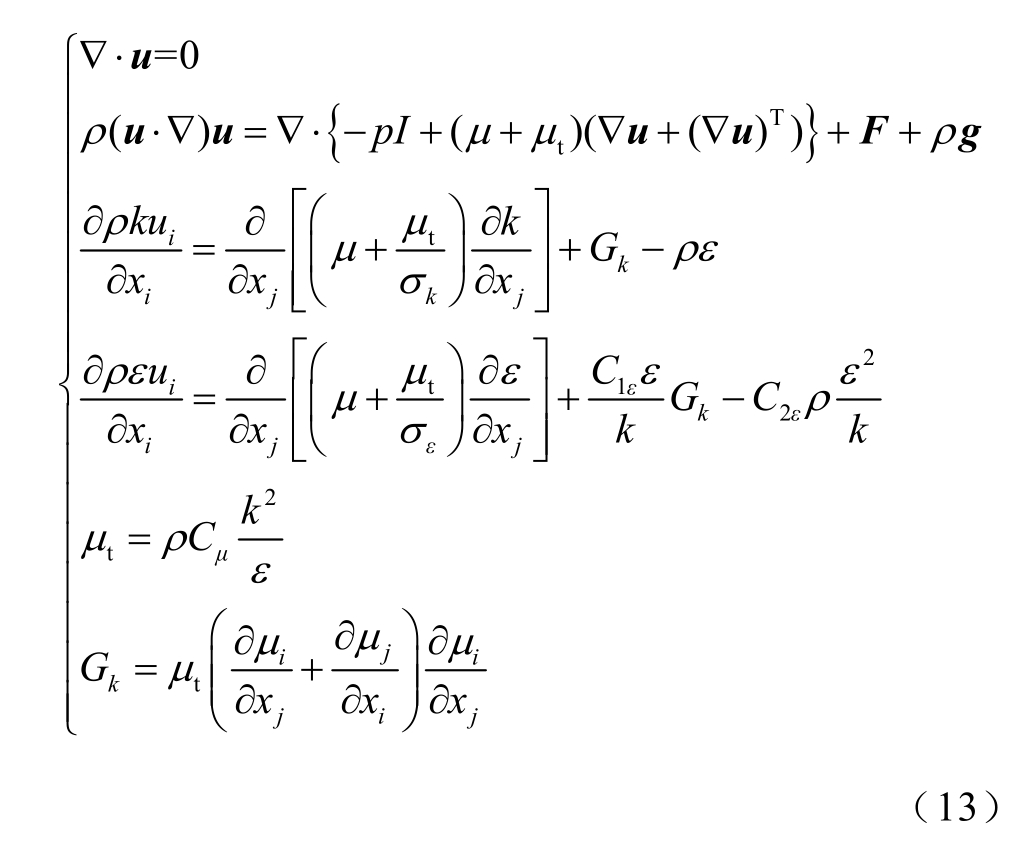
式中,u 为水流速度;p 为压强(Pa);g 为重力加速度(m/s2);F 为体积力;μt 为湍流动力粘度;μ 为动力粘度(N·s/m2);Gk 为由于平均速度梯度引起的湍动能k 的产生项;下标i,j =1,2,3,分别对应坐标方向x、y、z;C1ε 和C2ε 为相关经验常数;σk 和σε分别为与湍动能k 和耗散率ε 对应的Prandtl 数。其中C1ε=1.44,C2ε=1.92,Cμ=1.92,σk=1.0,σε=1.3。
在湍流场中,进汇流管入水口为入口边界,设置边界条件为质量流63 L/min;汇流管出水口为出口边界,设置边界条件参考压力为0;水管壁设置为无滑移边界;为了保证计算的准确性,在网格剖分中对水管边界以及电极表面边界均施加了5 层边界层条件。
3 计算结果与分析
3.1 电极电流和离子浓度分布
为了全方位表征电极表面垢层的动态沉积规律,以电极上的正弧和侧弧为研究对象,如图2a 所示,研究垢层厚度的分布变化规律。沿汇流管轴向作正截面,此时获得的阳极最外侧弧称为正弧(蓝色);在阳极中心沿垂直于正截面方向作侧截面,此时获得的阳极最外侧弧称为侧弧(红色)。
电极电流分布如图2b 所示,阳极电流集中分布在电极尖端靠近阴极侧部分,最大值达到了6.82 A/m2,阴极电流同样集中分布在电极尖端靠近阳极侧,最 大值达到了5.38 A/m2。

图2 电极模型和电极电流分布示意
Fig.2 Schematic diagram for the grading electrode model andelectrode current distribution
取进汇流管截面上[Al(OH)4]-离子的浓度分布如图3 所示,[Al(OH)4]-离子以1×10-5 mol/m3 的浓度从汇流管口流入,在阳极左侧浓度分布均匀且浓度保持在1×10-5 mol/m3;在阳极右侧离子浓度呈现分层现象,下层浓度大于上层浓度,最后趋于一致;在阳极正截面上阳极尖端靠右侧发生了集聚现象,最大浓度达到了0.23 mol/m3;在阳极侧截面上电极表面离子浓度近似均匀分布。与文献[9]相比,电极表面最大电流密度和最大离子浓度均变小,这主要是由于本文采用了更贴近实际的三维仿真模型,而文献[9]采用了近似的二维仿真模型的原因。

图3 [Al(OH)4]-离子浓度分布
Fig.3 The local concentration distribution of [Al(OH)4]-
3.2 垢层膜阻模型
图4 为国内宝鸡换流站运行3.5 年后替换下来的均压电极结垢示意图,此电极原直径为1.98 mm,长度23.8 mm。可以看出尖端的垢层厚度要大于两侧,而且经过统计表明:运行3.5 年后,阳极均压电极最大垢层厚度的平均值达到了0.71 mm,垢层中Al(OH)3 的含量达到了96%~98%。为了能够准确模拟此换流站阳极侧均压电极结垢规律,本文综合实际换流站的均压电极垢层统计数据对计算结果进行分析与验证。

图4 均压电极结垢示意
Fig.4 Schematic diagram for the deposition on grading electrode
假设垢层全部由Al(OH)3 组成且无孔隙,此时等效电导率为5×10-6 S/m,分别计算了是否考虑垢层膜阻影响时电极表面沉积质量反应速率和反应电流随时间的变化,如图5 所示。可以看出在不考虑垢层膜阻影响时质量反应速率和反应电流均为恒定值;考虑垢层膜阻影响时质量反应速率和反应电流随时间的增长而降低,并且降低速率越来越慢。
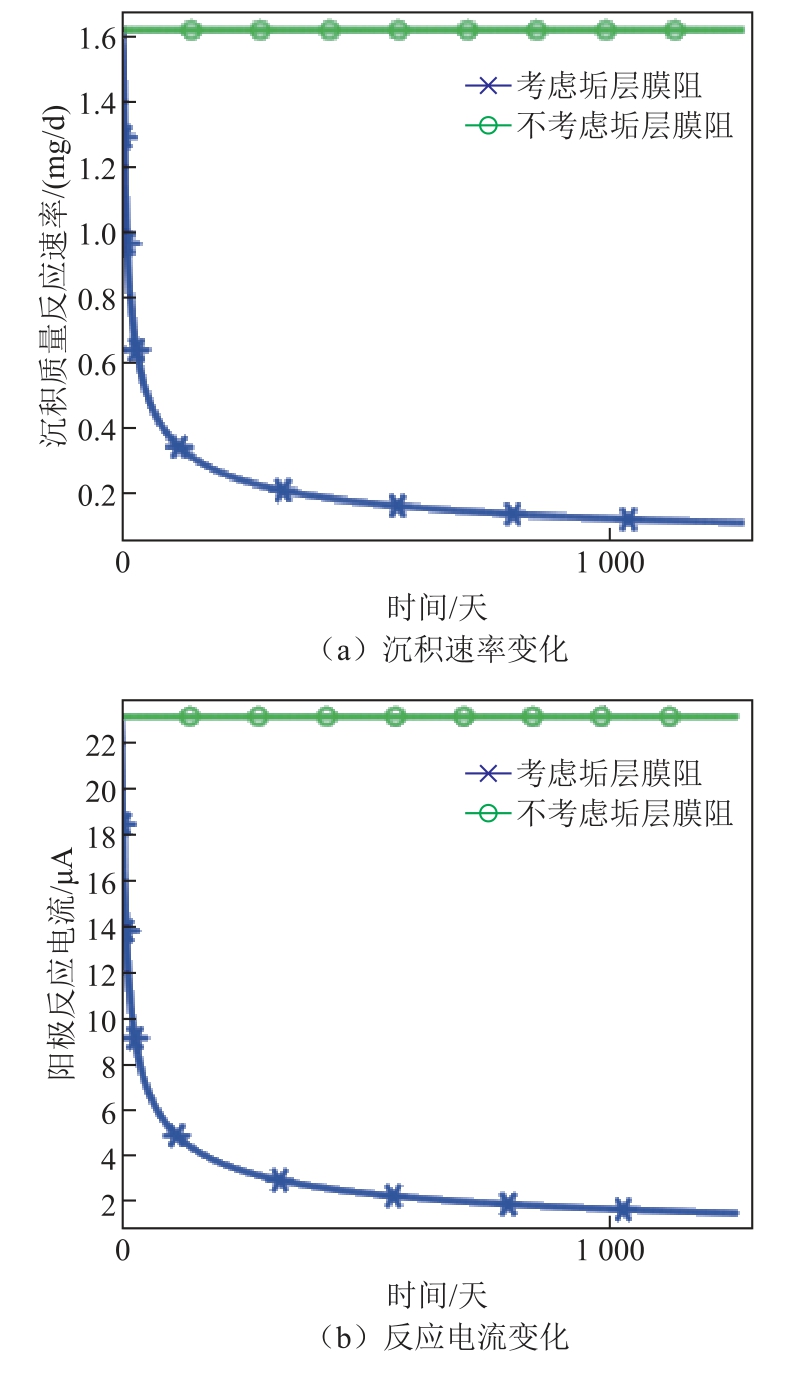
图5 垢层膜阻对沉积速率和反应电流变化影响
Fig.5 The effect of the film resistance on the change of deposition rate and reaction current
图6 为是否考虑垢层膜阻影响时3.5 年后垢层厚度分布,可以看出在不考虑垢层膜阻影响时垢层的厚度是远大于考虑垢层膜阻影响时的垢层厚度的;考虑垢层膜阻影响时垢层厚度的分布较平滑,而且垢层分布计算结果与现实换流站检修测量结果更为接近;不管是否考虑垢层膜阻的影响,电极垢层的分布特征接近一致,均是电极尖端的垢层生长速度最快,正弧右侧垢层的生长速度快于左侧,而对于侧弧垢层厚度的分布关于电极尖端对称。所以垢层膜阻的建立非常重要,但要想更为准确地模拟垢层的生长机理,则要更准确地确定垢层的等效电导率。

图6 是否考虑垢层膜阻影响时垢层厚度分布
Fig.6 The thickness distribution of sediment deposition with and without considering the influence of the film resistance
3.3 垢层膜阻等效电导率的确定及垢层厚度分布分析
垢层电导率对于垢层的生长机理有较大影响。Al(OH)3 的电导率为0.5×10-5 S/m,去离子水的电导率为 1.0×10-5 S/m,垢层的等效电导率应取值在0.5×10-5~1.0×10-5 S/m 较为合适,所以本文采用Al(OH)3 和去离子水的电导率加权[18]的方法获取垢层的等效电导率。定义垢层的等效电导率为
式中,![]() 为Al(OH)3 的电导率;γwater 为去离子水的电导率;a 和b 为加权系数,其满足关系a+b=1。
为Al(OH)3 的电导率;γwater 为去离子水的电导率;a 和b 为加权系数,其满足关系a+b=1。
本文计算了垢层电导率取值在0.5×10-5~1.0× 10-5 S/m 之间的5 组运行3.5 年后在正弧上垢层厚度的分布,如图7 所示。可以看出垢层厚度随着垢层电导率的增大而增大,等效电导率取值最大时对应的最大厚度与等效电导率取值最小时对应的最大厚度差值在0.26 mm 左右。
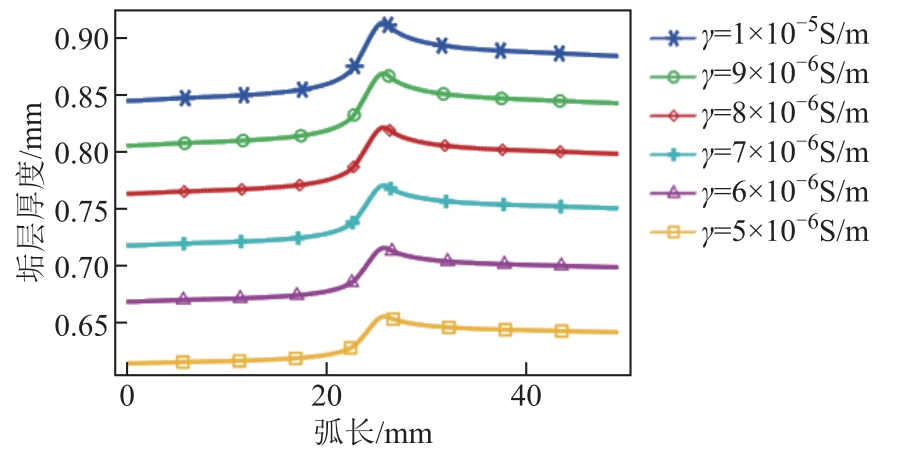
图7 运行3.5 年后垢层厚度分布
Fig.7 The thickness distribution of sediment deposition after running 3.5 years
从图7 中可以看出,电导率为6.0×10-6 S/m 时最大沉积厚度与实际运行电极沉积厚度接近。在电导率 6.0×10-6 S/m 附近搜索分析,发现电导率为5.8×10-6 S/m 时仿真沉积最大厚度与实际最相符。图8 为给出垢层等效电导率为5.8×10-6 S/m,a=0.84,b=0.16 时,且运行时间3.5 年后的均压电极垢层厚度分布。此时电极尖端的最大厚度为0.716 mm,与实际换流站的垢层统计数据偏差0.85%,所以此垢层等效电导率的取值较为合适。较现有研究[9]的误差降低了11.35%。这主要是由于本文不仅在电场和传质场采用了更贴近实际的三维仿真模型,而且流体场也采用了三维仿真模型,而文献[9]电场、传质场和流体场均采用近似的二维仿真模型。从图8 中可以进一步看出,在均压电极侧弧上垢层厚度对称分布,在正弧上右侧的垢层厚度大于左侧垢层厚度,而且在尖端垢层厚度均是最大的。

图8 运行3.5 年后垢层厚度分布
Fig.8 The thickness distribution of sediment deposition after running 3.5 years
基于已经确定的垢层等效电导率,计算了5 年内的电极表面沉积质量和沉积速率的变化,如图9所示。可以看出,在0~4 个月内电极沉积反应速率急剧下降,从最初的1.5 mg/d 下降到了0.3 mg/d,后续沉积速率缓慢降低且趋于稳定的趋势,5 年后沉积物质量达到了305 mg。

图9 5 年内阳极沉积质量与质量反应速率变化
Fig.9 The change of the anode deposition mass and the mass reaction rate within 5 years
计算了5 年内的电极表面垢层厚度分布,如图10 所示。可以看出垢层厚度越来越大,但是增长速率逐渐降低,说明了垢层的生长抑制了电极沉积反应速率;到5 年后正弧与侧弧上垢层的最大厚度分别达到了0.87 mm 和0.85 mm,平均厚度达到了0.83 mm,此时电极的最大直径达到了3.74 mm,由于电极与电极座之间的间隙富裕度非常有限,这将不利于检修除垢工作的开展。
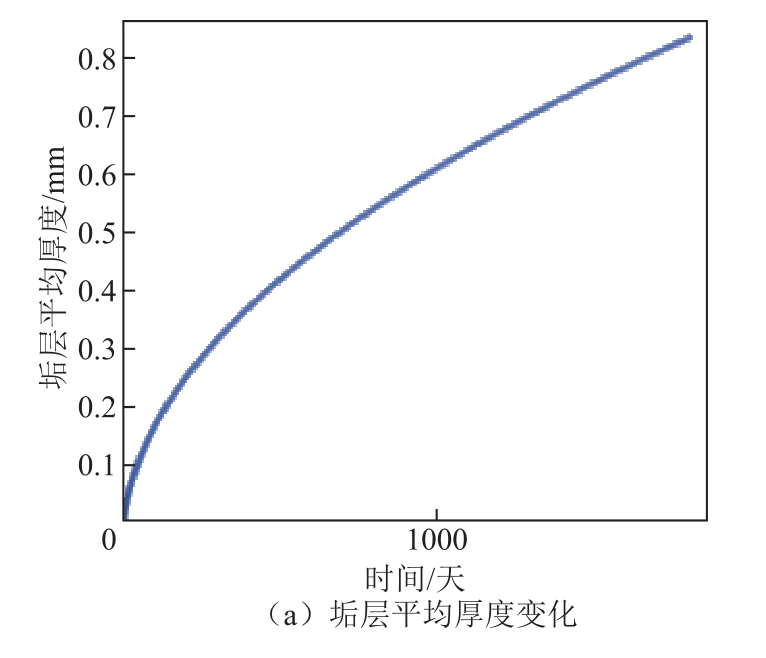

图10 5 年内垢层厚度变化
Fig.10 The change of the thickness distribution of sediment deposition within 5 years
3.4 公式拟合
从图9a 和图10a 中可以看出,沉积质量和垢层平均厚度都遵循一定的指数规律随时间增加,所以对其进行拟合,得到拟合公式为
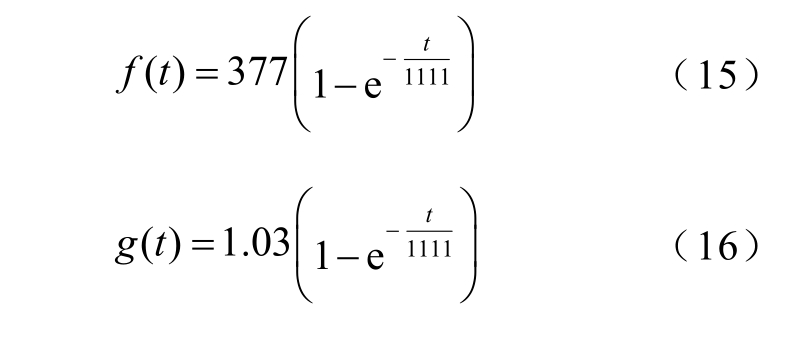
式中,f(t)为沉积质量拟合公式(mg);g(t)为垢层平均厚度拟合公式(mm);t 为运行时间(天)。拟合公式的相关性系数分别达到了 R1=0.976 8 和R2=0.985 8,说明拟合公式能够有效表征电极表面沉积质量和垢层平均厚度的变化规律。
可以看出电极表面质量沉积和垢层平均厚度的变化规律近似与一阶RC 电路的零状态响应一致,且两式呈线性关系,并具有相同的时间常数,其时间常数τ =1 111 天,当时间达到3~5 τ 时,电极上沉积的垢质质量和垢层平均厚度近似达到稳态,电极表面的沉积反应几乎停止,极限沉积质量为377 mg,极限垢层平均厚度为1.03 mm,与有限元计算结果偏差小于3.14%。
对电极表面垢质的沉积速率进行拟合,其公式为

式中,h(t)为沉积速率拟合公式(mg/d)。此拟合公式相关性系数达到了R3=0.962 0,说明此拟合公式能够有效表征电极表面沉积速率的变化规律,表明沉积速率变化呈分段单指数规律下降,在0~150 天内的衰减时间常数τ =36 天,150 天后的衰减时间常数τ =406 天,证明在初始阶段沉积速率下降迅速,150 天后沉积速率下降缓慢并趋于稳定。
3.5 电极表面垢层沉积的影响
为了研究垢层厚度的增加对均压电极均压作用的影响,计算了不同时刻时电极表面电解质电位分布和14 个支流管内总泄漏电流随垢层厚度的变化如图11 所示。可以看出随着时间和垢层厚度的增长,电极表面电解质电位在降低,5 年后电极尖端处电解质电位由原来的41.6 kV 下降到40.57 kV,下降了2.5%;随着垢层厚度的增大,支流管内总泄漏电流大小在增大,与均压电极无垢层时相比,当垢层厚度达到2 mm 时泄漏电流总量仅仅增加了1.02 μA,增加了1.53%。所以垢层的生长会不断改变冷却水中电位的分布,但总体电位变化不大,而且14 个支流管内的泄漏电流总量变化微弱,说明电极表面垢层厚度的增加对均压电极的均压效果影响微弱。
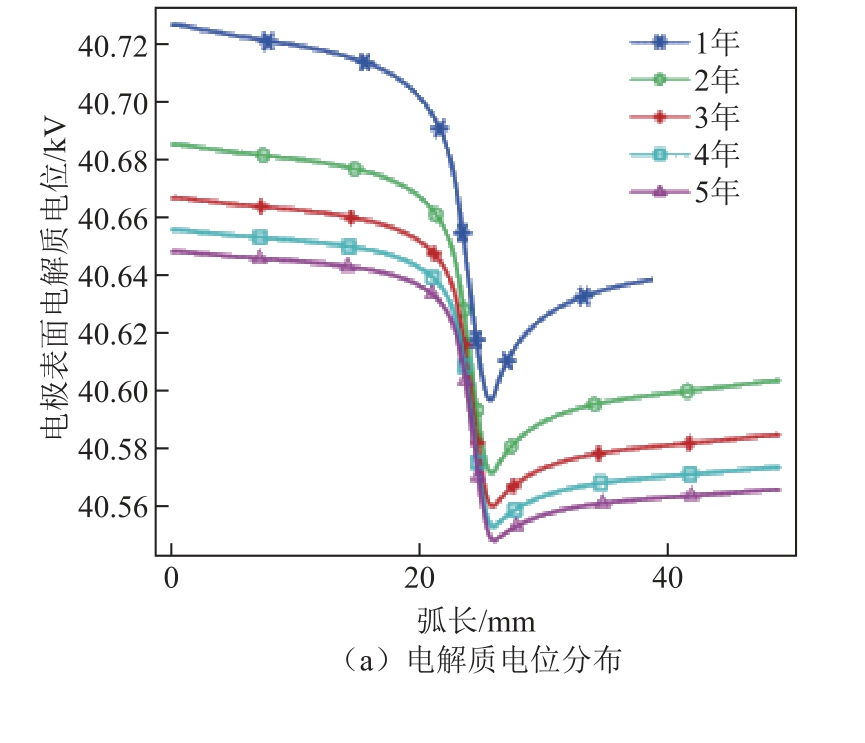

图11 电极表面电解质电位分布和支流管 总泄漏电流变化
Fig.11 Electrolyte potential distribution on the surface of electrode and the change of leakage current in the branch pipes
4 结论
建立了阀段冷却系统的三维电-流-传质场耦合模型,引入垢层动态膜阻以及等效电导率,与实际换流站的均压电极垢层统计数据进行对比,确定了等效电导率,验证了方法的准确性;研究和预测了换流站内垢层的动态生长规律以及垢层的沉积对冷却系统的影响,得到了以下结论:
1)引入垢层动态膜阻模型,结合三维场分析、现场统计数据和加权拟合方法确定了垢层的等效电导率,电导率为5.8×10-6 S/m,仿真垢层厚度与实际的统计数据偏差0.85%,有效地模拟了换流站内阳极垢层的生长规律。
2)均压电极侧弧上垢层厚度分布关于尖端对称,在正弧上右侧的垢层厚度大于左侧垢层厚度,5 年时右侧垢层厚度比左侧大0.04 mm,在两种情况下尖端垢层厚度均是最大的。
3)垢层质量和垢层平均厚度的变化规律近似与一阶RC 电路的零状态响应一致,两式呈线性关系,具有相同的时间常数,其时间常数τ=1 111 天,当时间达到3~5 τ 时,电极表面的沉积反应近乎停止,极限沉积质量为377 mg,极限垢层平均厚度为1.03 mm。沉积速率变化呈分段单指数下降规律,在0~150 天内时间常数为τ =36 天,150 天后时间常数τ=406天,沉积速率趋于0.000 2 mg/d 并达到稳定。
4)当垢层厚度达到2 mm 时,支流管泄漏电流总量增大了1.53%,支流管泄漏电流的增加意味着铝制散热器腐蚀增加。
质量沉积时间常数与去离子水浓度等参数的关系、是否可以建立质量沉积等效电路等需要将来进一步研究。
[1]刘振亚,舒印彪,张文亮,等.直流输电系统电压等级序列研究[J].中国电机工程学报,2008,28(10): 1-8.Liu Zhenya,Shu Yinbiao,Zhang Wenliang,et al.Study on voltage class series for HVDC transmission system[J].Proceedings of the CSEE,2008,28(10): 1-8.
[2]刘国友,黄建伟,舒丽辉,等.6 英寸晶闸管的研究开发与特性控制[J].变流技术与电力牵引,2007(6): 32-35.Liu Guoyou,Huang Jianwei,Shu Lihui,et al.R &D and characteristic control of 6-inch thyristors[J].Converter Technology &Electric Traction,2007(6): 32-35.
[3]赵畹君.高压直流输电工程技术[M].2 版.北京: 中国电力出版社,2011.
[4]Jackson P O,Abrahamsson B,Gustavsson D,et al.Corrosion in HVDC valve cooling systems[J].IEEE Transactions on Power Delivery,1997,12(2): 1049-1052.
[5]王远游,郝志杰,林睿.天广直流工程换流阀冷却系统腐蚀与沉积[J].高电压技术,2006,32(9): 80-83.Wang Yuanyou,Hao Zhijie,Lin Rui.Primary analysis on corrosion and deposit in valve cooling system of Tian-Guang HVDC project[J].High Voltage Engineering,2006,32(9): 80-83.
[6]Siemens.Valve cooling system maintenance manual[M].Power Transmission and Distribution,1999.
[7]Karady G G,Amarh F.Signature analysis for leakage current waveforms of polluted insulators[C]// 1999 IEEE Transmission and Distribution Conference (Cat.No.99CH36333),New Orleans,LA,USA,1999: 806-811.
[8]卢斌先,葛东阳,周建辉,等.换流阀水路冷却系统电极反应的等效电路建模[J].高电压技术,2016,42(7): 2199-2206.Lu Binxian,Ge Dongyang,Zhou Jianhui,et al.Equivalent electric circuit modeling for electrode reaction in valve cooling water system[J].High Voltage Engineering,2016,42(7): 2199-2206.
[9]贺婷婷,高兵,杨帆,等.电-流-传质场作用下的换流阀冷却系统均压电极垢层动态沉积特性研究[J].电工技术学报,2019,34(14): 2863-2873.He Tingting,Gao Bing,Yang Fan,et al.The dynamic deposition behavior of grading electrode in converter valve cooling system considering electro-velocitymass transfer field[J].Transactions of China Electrotechnical Society,2019,34(14): 2863-2873.
[10]Tian Yingfu,Li Huixi,Wang Shengping,et al.Erosion-corrosion behavior of aluminum in a 50 ℃ ethylene glycol aqueous solution simulating cooling water in HVDC transmission[J].Materials and Corrosion,2021,72(12): 1899-1907.
[11]李道豫,邱志远,李学武,等.铝在高压直流输电系统中高电压高温下的腐蚀行为研究[J].化工进展,2016,35(增刊2): 92-98.Li Daoyu,Qiu Zhiyuan,Li Xuewu,et al.Corrosion behavior of aluminum at high potential and high temperature in HVDC systems[J].Chemical Industry and Engineering Progress,2016,35(S2): 92-98.
[12]段涛,杨斌,李贤庆,等.±500 kV 换流站阀水冷系统隐患分析治理[J].电力系统保护与控制,2014,42(18): 132-138.Duan Tao,Yang Bin,Li Xianqing,et al.Analysis of potential dangers in ±500 kV converter station valve water cooling system[J].Power System Protection and Control,2014,42(18): 132-138.
[13]葛东阳.换流阀冷却系统腐蚀与沉积分析模型与影响因素研究[D].北京: 华北电力大学,2016.
[14]张望平,郑丰,郝良收,等.基于恒电位法的阀冷却系统铝散热器腐蚀特性研究[J].高压电器,2019,55(5): 175-181.Zhang Wangping,Zheng Feng,Hao Liangshou,et al.Corrosion characteristics of aluminum radiator for valve cooling system based on constant potential method[J].High Voltage Apparatus,2019,55(5): 175-181.
[15]Zahraei M,Saidi M S,Sani M.Numerical simulation of electro-deposition process influenced by force convection and migration of ions[J].Journal of Electroanalytical Chemistry,2016,782: 117-124.
[16]Weber I,Mallick B,Schild M,et al.Behavior of highly diluted electrolytes in strong electric fieldsprevention of alumina deposition on grading electrodes in HVDC transmission modules by CO2-induced pH-control[J].Chemistry (Weinheim an Der Bergstrasse,Germany),2014,20(38): 12091-12103.
[17]Yin Litao,Jin Y,Leygraf C,et al.A FEM model for investigation of micro-galvanic corrosion of Al alloys and effects of deposition of corrosion products[J].Electrochimica Acta,2016,192: 310-318.
[18]Sun Wen,Liu Guicheng,Wang Lida.A mathematical model for modeling the formation of calcareous deposits on cathodically protected steel in seawater[J].Electrochimica Acta,2012,78: 597-608.