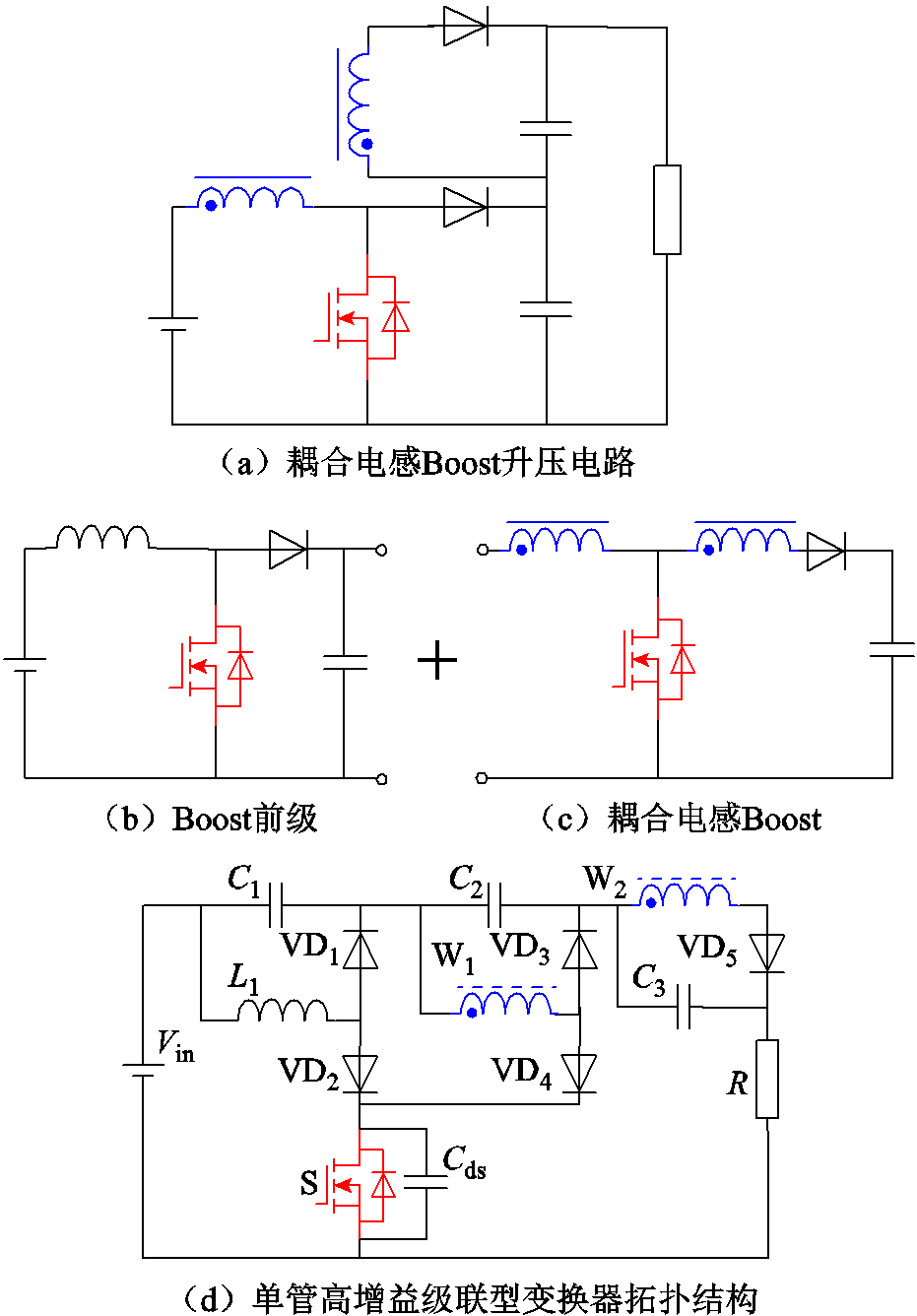
图1 变换器的演化
Fig.1 Derivation of the converter
摘要 为实现更高的电压增益,提出一种耦合电感倍压解耦磁集成高电压增益变换器。该变换器通过设计耦合电感匝数比和调节占空比来实现高电压增益,采用磁集成磁件设计方案,减少了变换器磁件的体积和数量。该文首先分析变换器器件的应力,给出变换器电压增益与占空比之间的变化关系;然后,利用磁路-电路对偶分析法推导得到耦合电感与输入电感解耦集成磁件的磁路模型,获得了输入电感与耦合电感之间的解耦磁集成设计准则;最后,搭建一台额定功率为300W的实验样机,对所提出的变换器和解耦集成磁件设计理论进行实验验证,验证了理论的正确性。变换器的效率达到93%以上,在光伏发电系统中具有一定的实用性。
关键词:高增益 耦合电感 磁集成 解耦条件
为实现2060年碳中和目标,我国能源行业不断调整能源结构,新能源发电接入电网比例不断增加。在此趋势下,如何将光伏发电系统储能电池输出的低压直流电压(12~48V)高效地转换成较高输出电压(200~400V),实现逆变并网,并网逆变前级升压这一关键技术成为研究的热点[1-4]。此外,高增益变换器广泛用于新能源汽车、燃料电池、航空电源等领域。高效、高增益、高功率密度DC-DC变换器已成为近年国内外重要研究方向之一[5-8]。
文献[9-10]提出含有开关电容网络的变换器,该变换器可以提高输出电压,但电压增益的提升能力有限。文献[11-12]将交错并联与开关电容结合,虽然可以增大变换器的功率,降低输入电流纹波,但增益提升仍然有限,无法满足高电压增益转换的场合。文献[13]将有源开关电感结构和基本耦合电感Sepic变换器结合,保留Sepic变换器特性的同时,提升了电压增益。文献[14]利用升压电路和倍压单元的N级二极管-电容-电感单元组合实现高电压增益。文献[15]提出一簇低电压应力单管高增益的变换器,给出该类变换器基本拓扑演化拓展的方法。文献[16]给出了一种两个电感之间的解耦设计方案,并将这种方法应用在双频DC-DC变换器中,减少了变换器的磁件体积。文献[17]实现磁集成与二次型开关电感的结合,提出一种新型变换器,但该变换器提高电压增益的能力有限。
本文在文献[18]的基础上,通过Boost变换器和耦合电感变换器结合,提出一种单管级联型高电压增益变换器,对该变换器的基本结构进行集成磁件设计。对变换器的模态、电压增益和功率器件的电压与电流应力进行分析,推导出耦合电感和输入电感解耦集成的基本条件,并基于该设计准则对本文所提变换器结构拓扑进行磁集成设计,实现基本变换器对于输入电感和耦合电感之间的解耦,验证该设计准则的可行性。本文的变换器有如下的优点:①仅有一个开关管,开关损耗较低,效率较高;②开关管和二级管的电压应力较低,可以降低变换器的总体成本;③具有更宽和更灵活的电压增益调节能力,通过对耦合电感匝数比和占空比调节,实现对电压增益的调节;④磁集成技术减少了磁件数量,同时利用解耦磁集成减小变换器的空间体积,提升变换器功率密度;⑤可以进行级联拓展,使该类变换器能够满足不同电压等级的需求。
本文提出的变换器的演化如图1所示。图1a所示是将Boost和耦合电感电路结合,演化出的一种基本级联型耦合电感Boost电路。在图1a拓扑基础上,通过对Boost电路输入前级结构与耦合电感Boost升压电路进行组合简化,提出一种基于耦合电感的高电压增益基本变换器拓扑,所提的拓扑结构如图1d所示。图中Vin为输入电源,C1、C2、C3为电容,VD1、VD2、VD3、VD4、VD5为二极管,S为开关管,Cds为开关管寄生电容,L1为输入电感,W1、W2为耦合电感一、二次绕组,R为负载电阻。

图1 变换器的演化
Fig.1 Derivation of the converter
本文所提出变换器的前级结构可以简化为C-D-L-D单元。该简化单元可以进行级联以实现变换器前级结构的堆叠,堆叠后的变换器可以实现电压增益的进一步提升,使该类变换器的应用场景大大拓展。级联堆叠构造的变换器原理如图2所示。
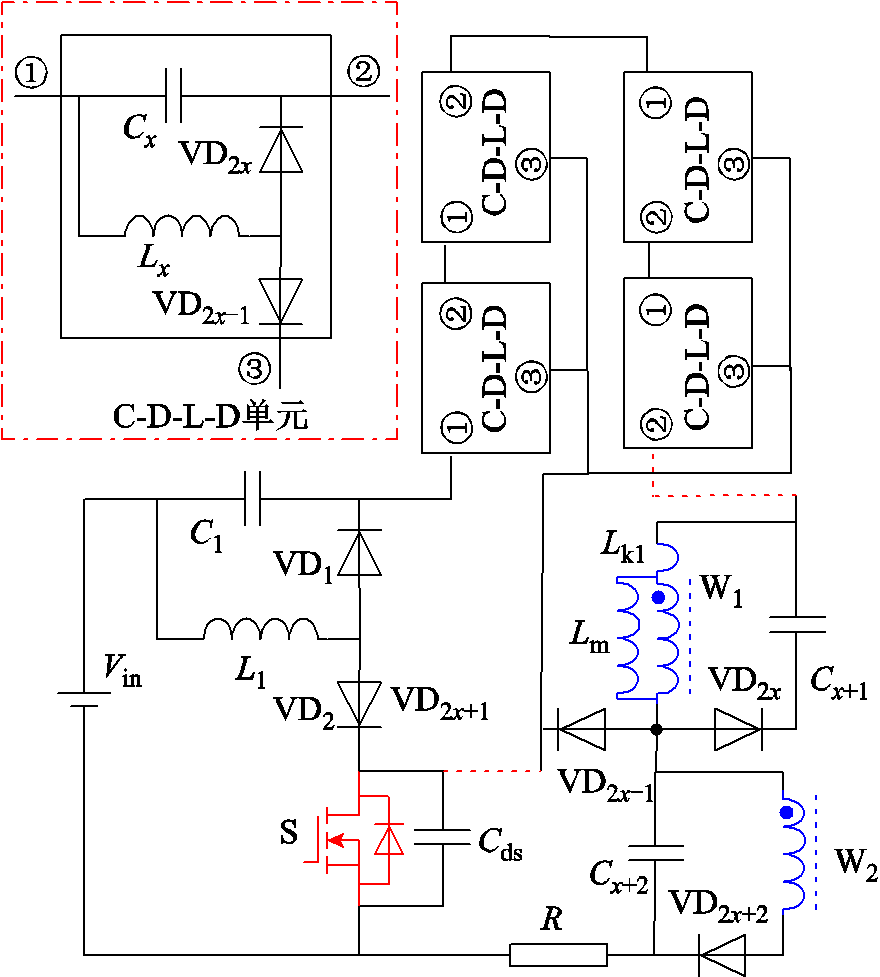
图2 变换器拓扑结构的拓展
Fig.2 Extended of converter topology
本文的变换器模态分析基于以下的前提:①除开关管S外,所有器件的寄生电容和内部电阻被忽略;②变换器的电容足够大,可以实现电感释放能量的存储;③开关周期为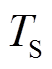 ,导通时间为
,导通时间为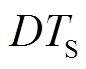 ,关断时间为(1-D)
,关断时间为(1-D)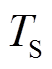 ,D为变换器的占空比;④耦合电感的励磁电感Lm远远大于耦合电感的漏感Lk。在一个周期内,变换器的主要工作波形如图3所示。
,D为变换器的占空比;④耦合电感的励磁电感Lm远远大于耦合电感的漏感Lk。在一个周期内,变换器的主要工作波形如图3所示。
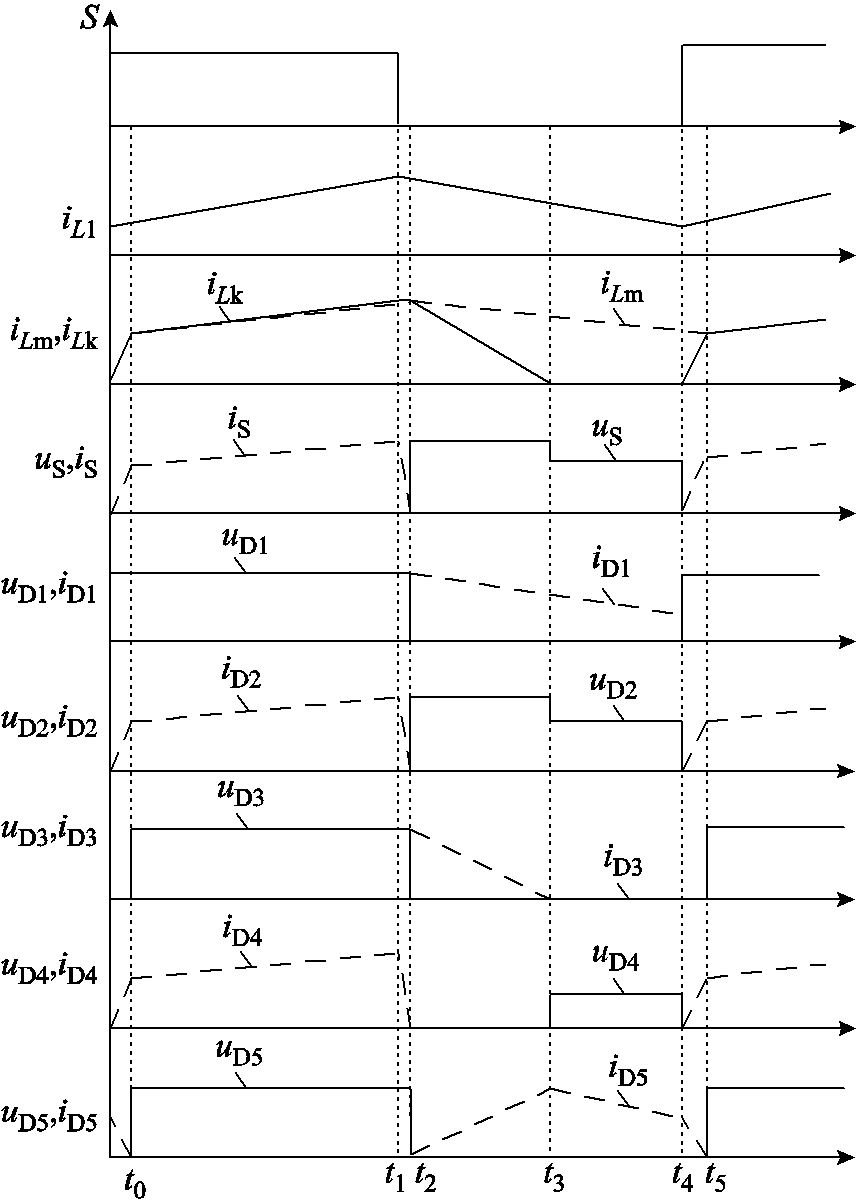
图3 变换器工作波形
Fig.3 The working waveforms of the converter
图3中ux表示各器件的电压波形,ix表示各器件的电流波形。变换器工作模态电路如图4所示。
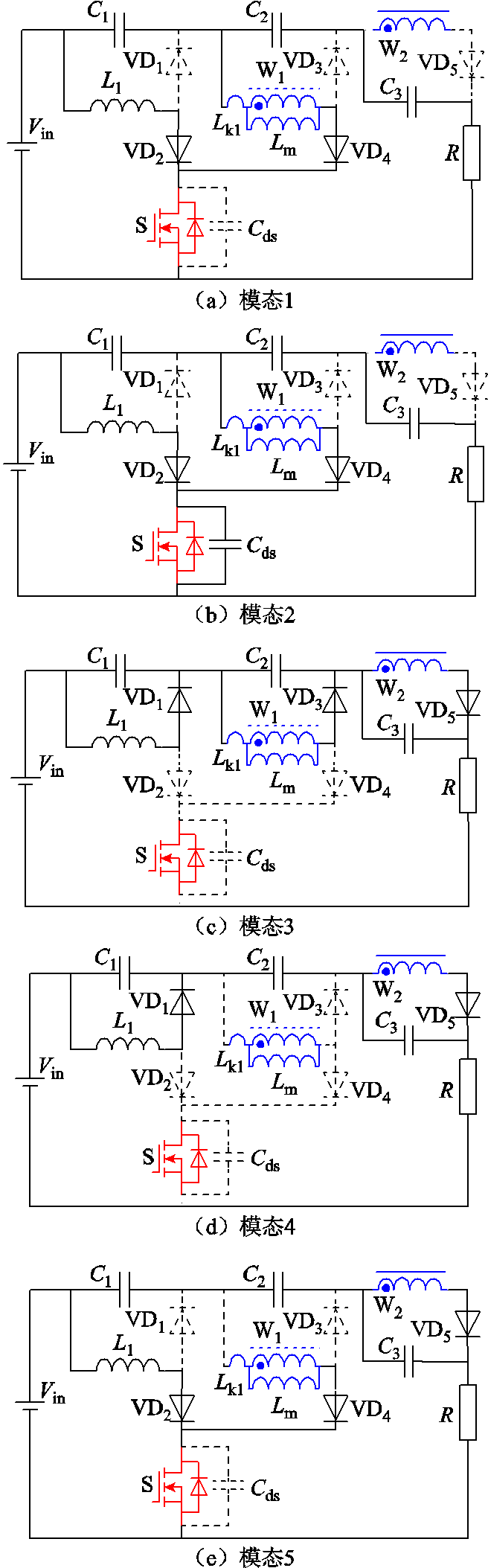
图4 变换器的工作模态电路
Fig.4 Working modal of the converter
模态1[t0, t1):在t0时刻,开关管S导通,VD2、VD4导通,VD1、VD3、VD5截止,输入电流给L1充电。电容C1储存的能量释放给W1的励磁电感和漏感。电源、C1、C2、C3给负载供电。开关管S关断,变换器进入下一个模态。
模态2[t1, t2):在t1时刻,开关管S关断,VD2、VD4导通,VD1、VD3、VD5截止。电感L1、W1的励磁电感和漏感电压反向,对寄生电容Cds进行充电,当寄生电容两端电压达到Vin+VC1+VC2时,变换器进入下一个模态。
模态3[t2, t3):在t2时刻,VD2、VD4截止,VD1、VD3、VD5导通。电感L1通过二极管给C1充电,W1的励磁电感和漏感通过VD3给C1、C2充电,W2通过VD5给电容VD3充电,一次电流iLk1降低,当一次电流iLk1降低到0时,该模态结束。
模态4[t3, t4):在t3时刻,VD2、VD3、VD4截止,VD1、VD5导通。电感L1通过VD1和VD4给C1和寄生电容Cds充电,二次电感通过VD5给C3充电,当开关管S再次导通时,该模态结束。
模态5[t4, t5):在t4时刻,开关管S导通,二极管VD2、VD4、VD5导通,VD1、VD3截止,漏感电流ilL1开始上升。
根据模态分析可知,变换器输出电压为电容C1、C2、C3电压的累积,即
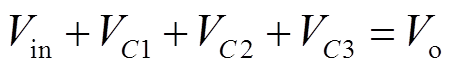 (1)
(1)
式中,Vin为输入电压;VC1为电容C1两端电压;VC2为电容C2两端电压;VC3为电容C3两端电压;Vo为输出电压。
通过输入电感两端电压的伏秒平衡计算出电容C1两端电压VC1为
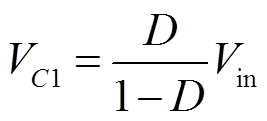 (2)
(2)
对于电压VC2通过伏秒平衡原理,结合式(2)可以推导出VC2两端电压为
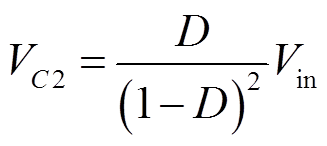 (3)
(3)
由式(3)应用伏秒平衡推导出VC3两端电压为
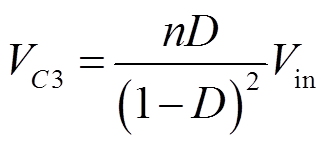 (4)
(4)
电容C1、C2的电压应力和输出电压之比VvpsC/Vo与占空比D之间的关系如图5所示。电容C1和C2两端的电压应力与占空比D成正比。
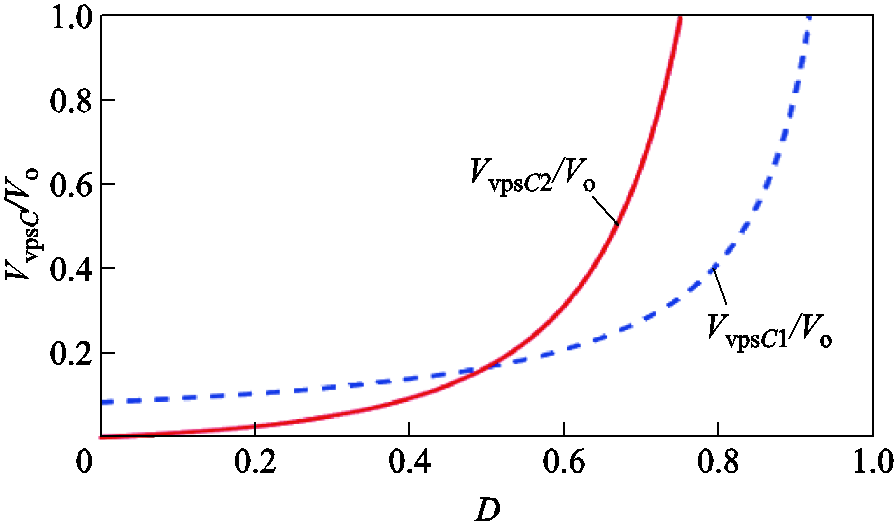
图5 电容C1、C2电压应力
Fig.5 Voltage stress curves of capacitor C1 and C2
电容C3的电压应力和输出电压之比VvpsC3/Vo与匝数比n和占空比D之间的关系如图6所示。电容C3两端的电压应力与占空比D和耦合电感匝数比n成正相关。
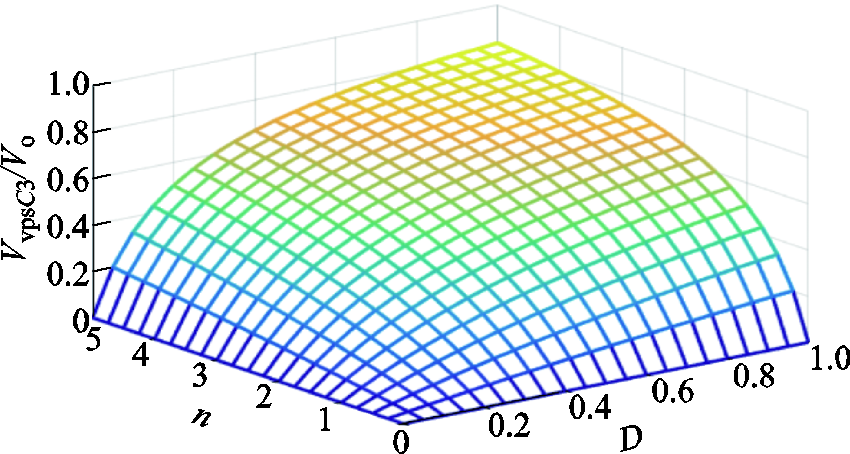
图6 电容C3的电压应力
Fig.6 Voltage stress curve of capacitor C3
将式(2)~式(4)代入式(1)推导出变换器的电压增益G为
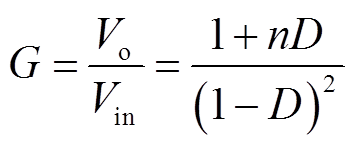 (5)
(5)
电压增益与占空比D和耦合电感匝数比n之间关系如图7所示。电压增益G与占空比D和耦合电感匝数比n成正相关。
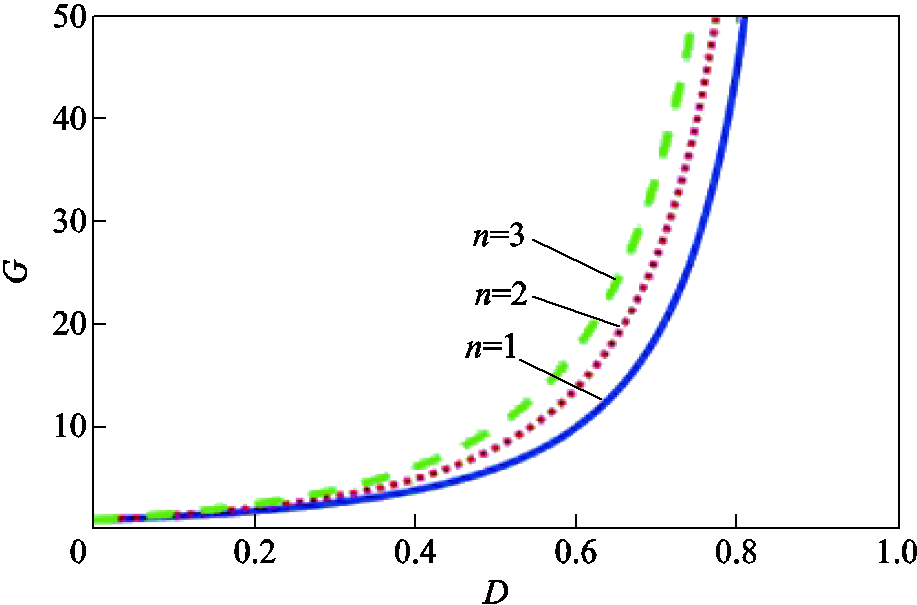
图7 电压增益与匝比n和占空比D的关系
Fig.7 Voltage gain and turn ratio n and duty cycle D relation curves
当开关管关断时,开关管两端电压应力VSvps为输入电压Vin、VC1、VC2之和,即
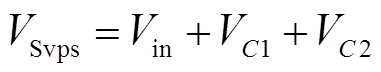 (6)
(6)
将式(2)和式(3)代入式(6)中得
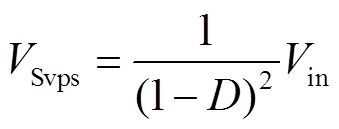 (7)
(7)
二极管VD1、VD2、VD3、VD4、VD5两端的电压应力分别为
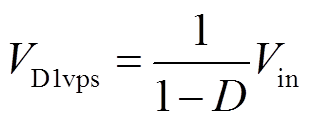 (8)
(8)
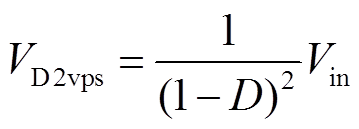 (9)
(9)
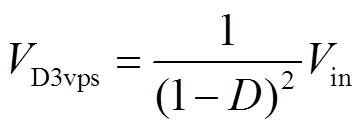 (10)
(10)
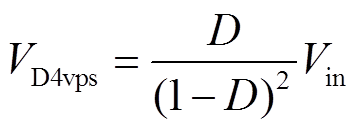 (11)
(11)
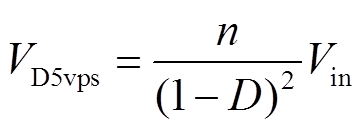 (12)
(12)
当开关管处于导通状态时,电容C3向负载放电,放电电流为Io。当开关管S关闭时,耦合电感二次侧向电容C3充电,充电电流为二极管VD5的电流ID5与输出电流之差。对电容C3应用安秒平衡可以得到二极管VD5的电流为
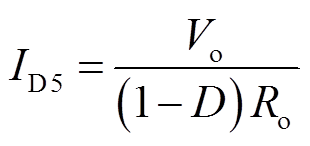 (13)
(13)
式中,ID5为耦合电感二次电流;Ro为输出电阻。
耦合电感一次励磁电流为
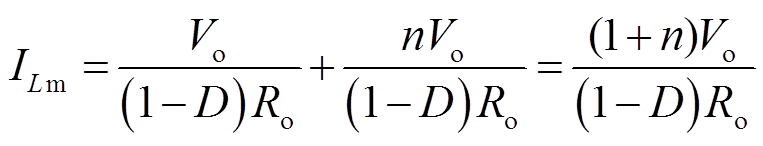 (14)
(14)
式中,ILm为励磁电感电流。
对C1应用安秒平衡得到二极管VD2的电流为
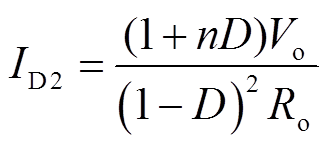 (15)
(15)
开关管S的电流应力为开通时输入电感和励磁电感电流之和,即
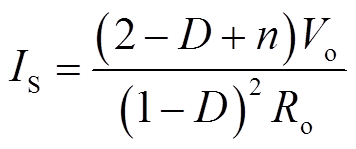 (16)
(16)
耦合电感实现稳态时的最小励磁电流为
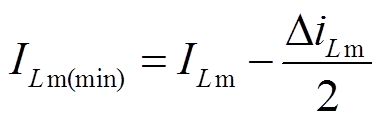 (17)
(17)
式中,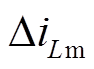 为动态励磁电流,ΔiLm为
为动态励磁电流,ΔiLm为
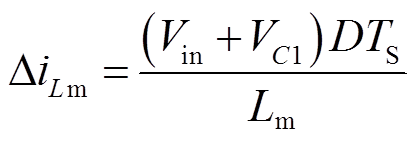 (18)
(18)
由式(2)、式(5)、式(17)、式(18)可以得出保证电流连续的最小励磁电感Lm(min)为
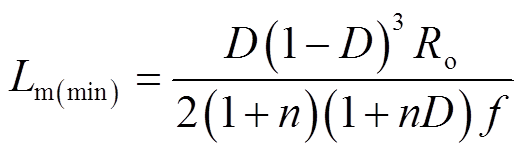 (19)
(19)
式中,f为开关频率。
所以耦合电感绕组的最小匝数为
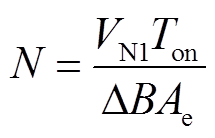 (20)
(20)
式中,VN1为耦合电感一次电压;Ton为电压作用于耦合电感一次侧的时间;ΔB为磁通密度增量;Ae为磁心的截面积。
如果变换器输入电感L1处于断续状态,无论Lm工作于连续还是断续状态,电容C2和C3的电压应力都会升高,二极管和开关管的电压应力也会升高。因此,对输入电感的设计,要使其工作在连续状态,输入电感的最小输入电流为
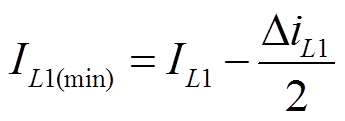 (21)
(21)
输入的动态电流为
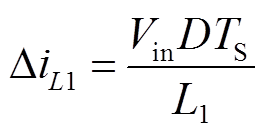 (22)
(22)
令输入电感电流IL1为零,由式(15)、式(21)、式(22)得
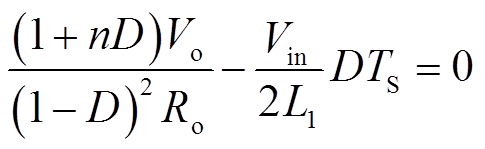 (23)
(23)
利用式(5)推导出L1工作在临界模式下的电感值为
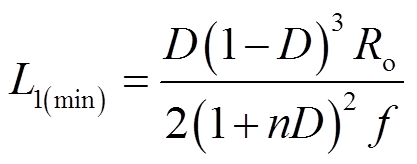 (24)
(24)
输入电感绕组的最小匝数为
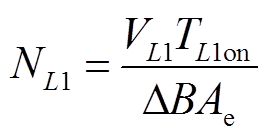 (25)
(25)
式中,VL1为耦合电感一次电压;TL1on为电压作用于电感L1的时间。
根据上述分析,开关管S的损耗为
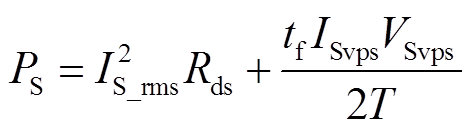 (26)
(26)
式中,IS_rms为开关管的方均根电流;Rds为开关管导通电阻;PS为开关管损耗;tf为开关管导通或关断时间。
二级管的损耗为
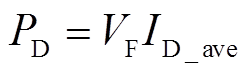 (27)
(27)
式中,PD为二级管损耗;VF为二极管正向压降;ID_ave为二极管的平均电流。
电容的损耗为
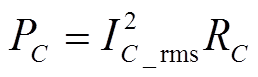 (28)
(28)
式中,PC为电容的损耗,RC为电容的电阻值,IC_rms为电容的方均根电流。
磁性元件的损耗为
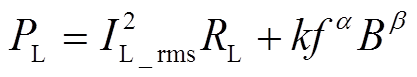 (29)
(29)
式中,PL为磁性元件的总损耗;IL_rms为磁性元件的方均根电流;RL为磁件绕线的电阻;B为磁性元件的磁通密度;k、α、β为磁心的材料参数。
变换器总损耗为
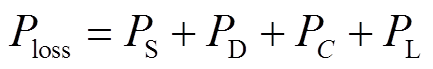 (30)
(30)
变换器的效率为
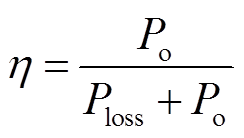 (31)
(31)
式中,η为变换器的效率;Po为变换器的输出功率。
根据上述分析,将所提出的高增益变换器与其他文献的高增益变换器进行对比分析,详细对比参数见表1。当耦合电感匝数比n=1时,本文所提的高增益变换器与其他文献中所提的高增益变换器的增益对比如图8所示。从图8中可以看出,当D>0.5时,本文所提的变换器电压增益较其他的变换器电压增益提升显著。
表1 本文变换器与其他变换器的对比
Tab.1 The comparison of the proposed converter and the others

变换器开关管数量二极管数量开关管电压应力电压增益 参考文献[19]12Vin/(1-D)2D/(1-D) 参考文献[20]23Vin/(1-D)(1+3D)/(1-D) 参考文献[21]22Vin/(1-D)(2+n)/(1-D) 本文所提变换器15Vin/(1-D)2(1+nD)/(1-D)2
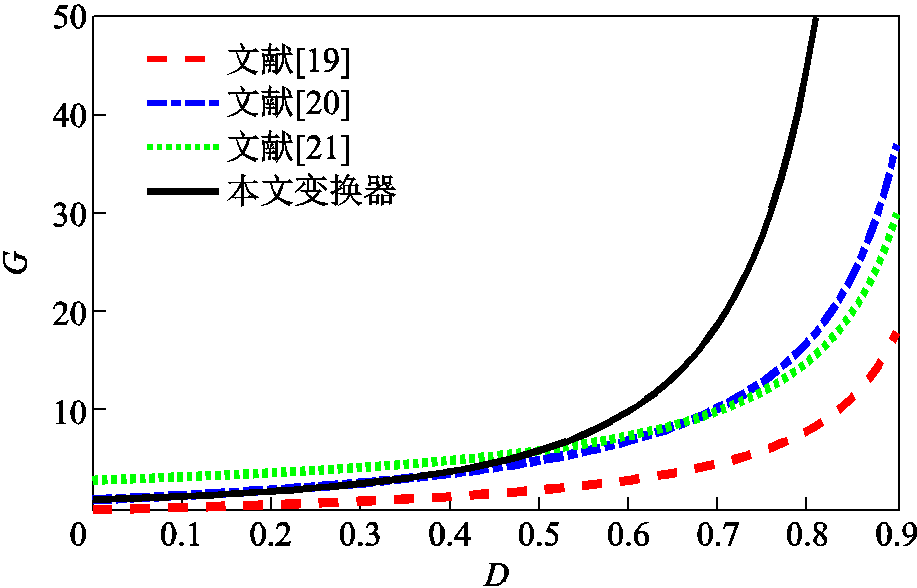
图8 匝数比n=1时变换器的电压增益对比
Fig.8 The comparison of the voltage gain under n=1
集成磁件选用EE型磁心,耦合电感一次绕组和二次绕组绕制在磁心的中柱上,输入电感L1拆分成两部分W11、W12绕组分别绕制在两侧的边柱上,实现对于输入电感和耦合电感的解耦集成。集成磁件的磁通分布如图9a所示,磁件的各段磁路尺寸如图9b所示,a、b、c、d、e、h分别为磁件的各段尺寸,g为磁件的气隙长度。
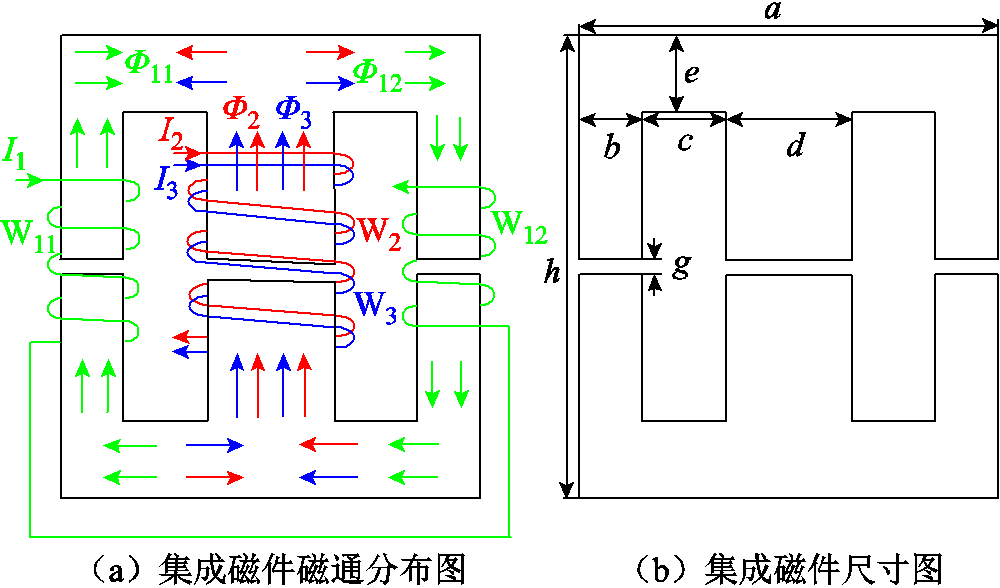
图9 集成磁件的磁通分布和磁路结构
Fig.9 The magnetic flux distribution and magnetic circuit structure of integrated magnetic components
磁件在左、右、中三路均开气隙。输入电流I1经输入电感L1在左侧产生的磁通为Φ11,在右侧产生的磁通为Φ12。耦合电感一次侧和二次侧输入电流I2和I3在绕组W2和绕组W3产生的磁通分别为Φ2、Φ3。耦合电感磁通Φ2、Φ3正向加强,输入电感L1在左侧产生的磁通为Φ11反向减弱,输入电感L1在右侧产生的磁通为Φ12正向加强,输入电感磁通Φ11、Φ12在磁件中柱上的磁通反向减弱,磁通Φ11、Φ12通过磁件的侧柱形成回路。
对集成磁件进行分析,建立磁路的等效模型,如图10a所示。图10a中N11i0、N12i0、N1i1、N2i2为各个绕组的磁动势,N11、N12、N2、N3分别为电感L1、L2、L3在磁心上缠绕的匝数,R11、R21、R31为各段磁路的磁阻,Rg为气隙的磁阻。为了便于分析,对磁路模型进行等效化简,得到化简的磁路模型如图10b所示。
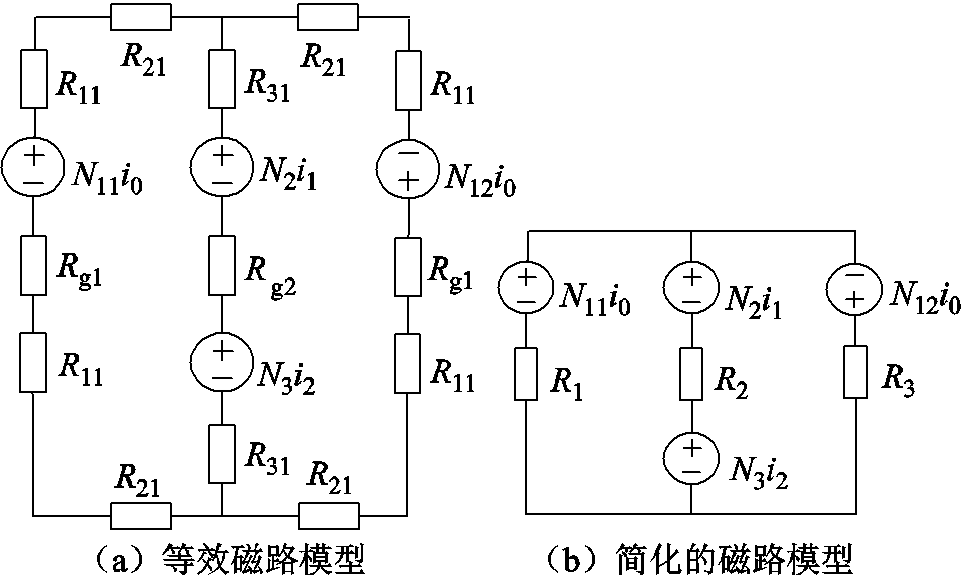
图10 集成磁件磁路-电路对偶模型
Fig.10 Magnetic circuit - circuit duality model of integrated magnetic components
根据磁阻的定义导出磁阻计算公式为
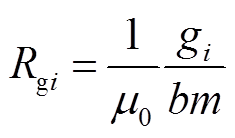 (32)
(32)
每段磁心的磁阻计算公式为
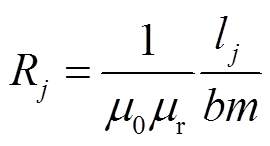 (33)
(33)
式中,μ0为空气的磁导率;μr为磁心的相对磁导率;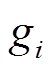 为第i段气隙的长度;b为磁心的宽度;m为磁心的厚度,lj为第j段磁心的长度。
为第i段气隙的长度;b为磁心的宽度;m为磁心的厚度,lj为第j段磁心的长度。
图10中磁阻R1、R2、R3分别为
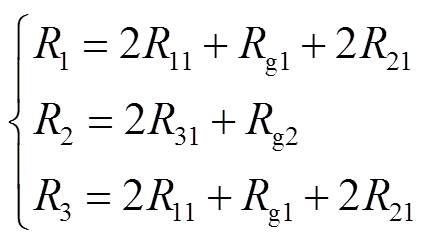 (34)
(34)
式中,R11为边柱的磁阻;Rg1为边柱的气隙磁阻;Rg2为中柱的气隙磁阻;R21为上下边柱的磁阻;R31为中柱磁阻。
输入电感L1在中柱耦合电感一次绕组W2上产生的磁通Φ12为
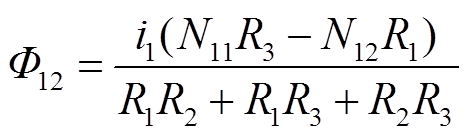 (35)
(35)
输入电感L1在中柱耦合电感二次绕组W3上产生的磁通Φ13为
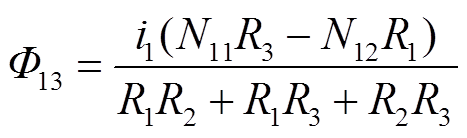 (36)
(36)
耦合电感一次绕组W2在输入电感L1上产生的磁通Φ21为
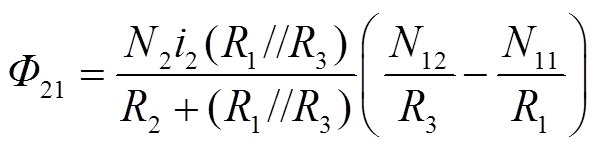 (37)
(37)
耦合电感二次绕组W3在输入电感L1上产生的磁通Φ31为
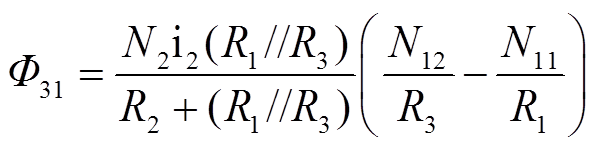 (38)
(38)
为实现完全解耦,则磁通Φ12、Φ13、Φ31、Φ21的值为0,所以要满足
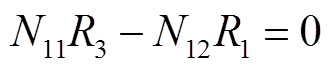 (39)
(39)
即
![]() (40)
(40)
由式(40)可知,要实现耦合电感与输入电感的完全解耦,需满足侧柱磁阻与绕组的比例关系。
为了解耦效果更好,本文采用对称的磁心结构进行解耦设计。磁心两侧的气隙长度相同,故磁件侧边的磁阻相同,所以输入电感L1缠绕在两边柱的匝数也相同。满足解耦条件时,磁件的中柱磁通密度B2为
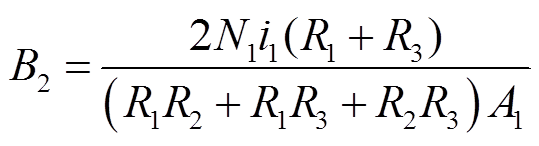 (41)
(41)
磁件的左侧柱的磁通密度B11为
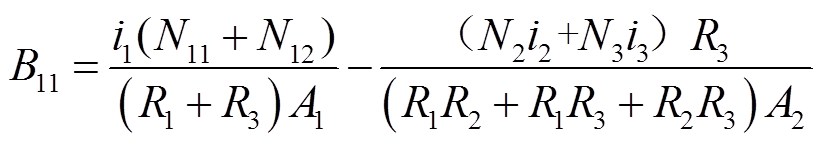 (42)
(42)
磁件的左侧柱的磁通密度B12为
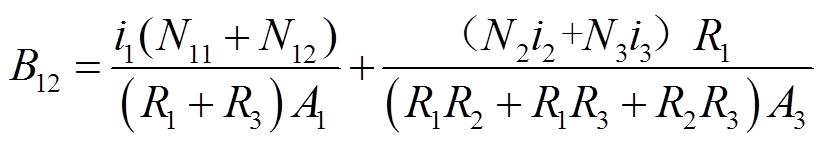 (43)
(43)
式中,A1、A2、A3分别为磁心左侧柱、中柱、右侧柱的截面积。
选用集成磁件的磁心材料为PC40,型号为E42/21/15,磁心的有效截面积为178mm2,磁心侧柱的有效面积为89mm2。由式(20)可以得到耦合电感绕制的最少匝数约为10匝,磁心的中柱磁阻为77.343 7mH-1。为了防止磁心饱和,在磁心中加入为一张纸厚度的70μm气隙。磁心加入气隙后,磁心中柱的磁阻约为437mH-1,耦合电感的绕组匝数应扩大为2.5倍。根据式(25)可以得到输入电感一侧的匝数约为11匝。表2为磁件的各绕组匝数设计参数。
表2 集成磁件绕组参数设计
Tab.2 Winding design of integrated magnetic

绕组W11W2W3W12 匝数11252511
对所设计的集成磁件进行暂态场仿真分析,如图11所示。在输入电感分立缠在EE型磁心的两侧边柱,耦合电感双线并绕在磁心的中柱,磁心的中柱和侧柱分别开70μm的气隙,保证磁心在最大电流流过的工作状态下,磁心不饱和。磁通的矢量场分布如图11所示。从图中可以看出,本设计的集成磁件最大磁通密度为0.134 8T,小于磁心材料的饱和磁通0.3T。

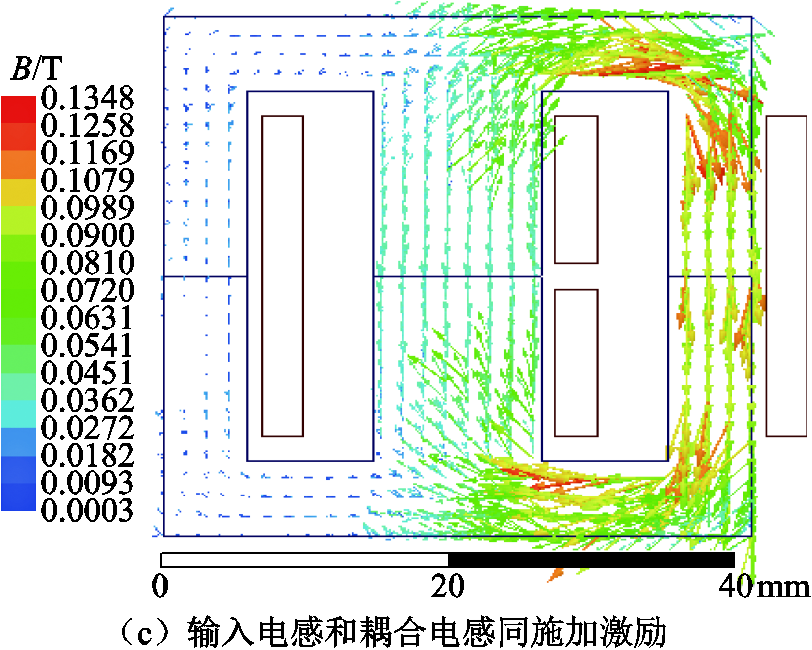
图11 集成磁件的磁通密度矢量场图
Fig.11 The flux density vector field of the integrated magnetic element
根据设计参数,采用E42/21/15磁心进行集成磁件绕制,绕制后的磁件与采用T型磁环绕制的分立磁件进行空间体积的计算对比,计算的体积见表3,集成磁件与分立磁件的实物对比如图12所示。从表3中的计算结果可以看出,集成磁件的体积较分立磁件的体积减少约24%。通过磁集成技术可以减少磁件的数量和体积。
表3 不同磁心的体积
Tab.3 Volume of cores

磁心EE42磁心T38磁环T28磁环 体积/cm326.4624.949.85

图12 集成磁件与分立磁件对比
Fig.12 Comparison of integrated and discrete magnetic components
实验样机如图13所示,样机的设计参数见表4。输入和输出的电压输出波形如图14所示。输出电压在234V左右,输入电压为24V。当占空比为0.6,耦合电感匝数比为1时,实验条件下的电压增益基本为10,结果与理论分析基本一致。
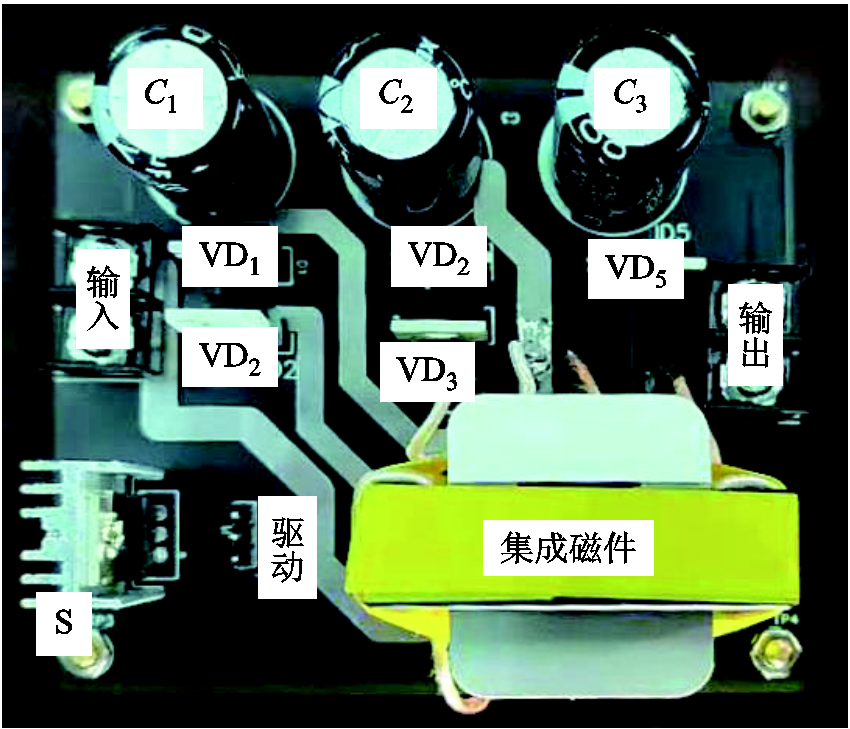
图13 实验样机
Fig.13 Experimental prototype
表4 变换器设计参数
Tab.4 Converter design parameters

参数数值(型号)参数数值(型号) 输入电压Vin/V24电容C1/μF100 输出电压Vo/V240电容C2/μF100 额定功率PN/W300电容C3/μF100 漏感Lk/μH1.2开关管SIRF640N 励磁电感Lm/μH118.7二极管VD1MRB20100CT 匝比n1二极管VD2MRB20100CT 输入电感L1/μH153.3二极管VD3MRB10200CT 开关频率ƒ/kHz50二极管VD4MRB10200CT 负载电阻R0/Ω200二极管VD5MRB10200CT 占空比D0.6磁心型号E42/21/15
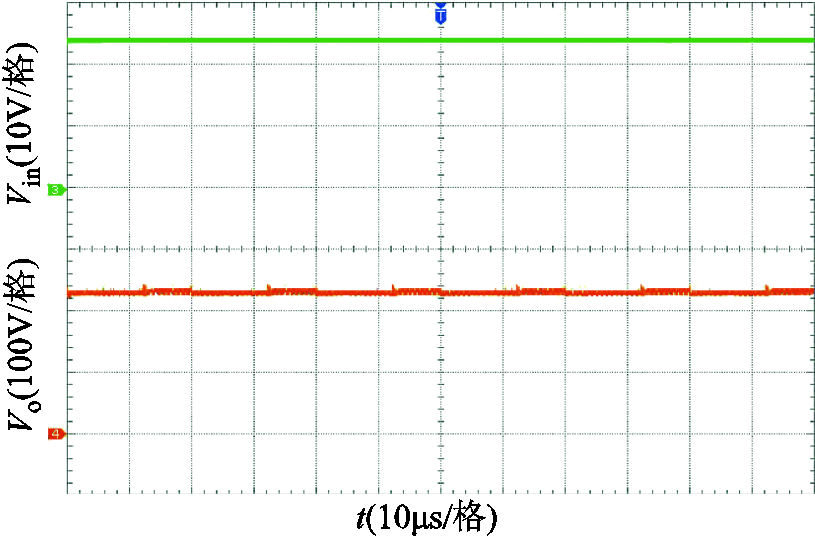
图14 输入输出电压波形
Fig.14 Input and output voltage waveforms
图15a为采用分立磁件情况下测得的耦合电感漏感电流和输入电感的电流波形,图15b为采用解耦集成设计磁件测得的耦合电感漏感电流和输入电感的电流波形。通过对比发现集成磁件和分立磁件的工作波形基本一致。
变换器功率器件的电流和电压应力波形如图16所示,从图中可以看出实验结果与理论分析基本一致。
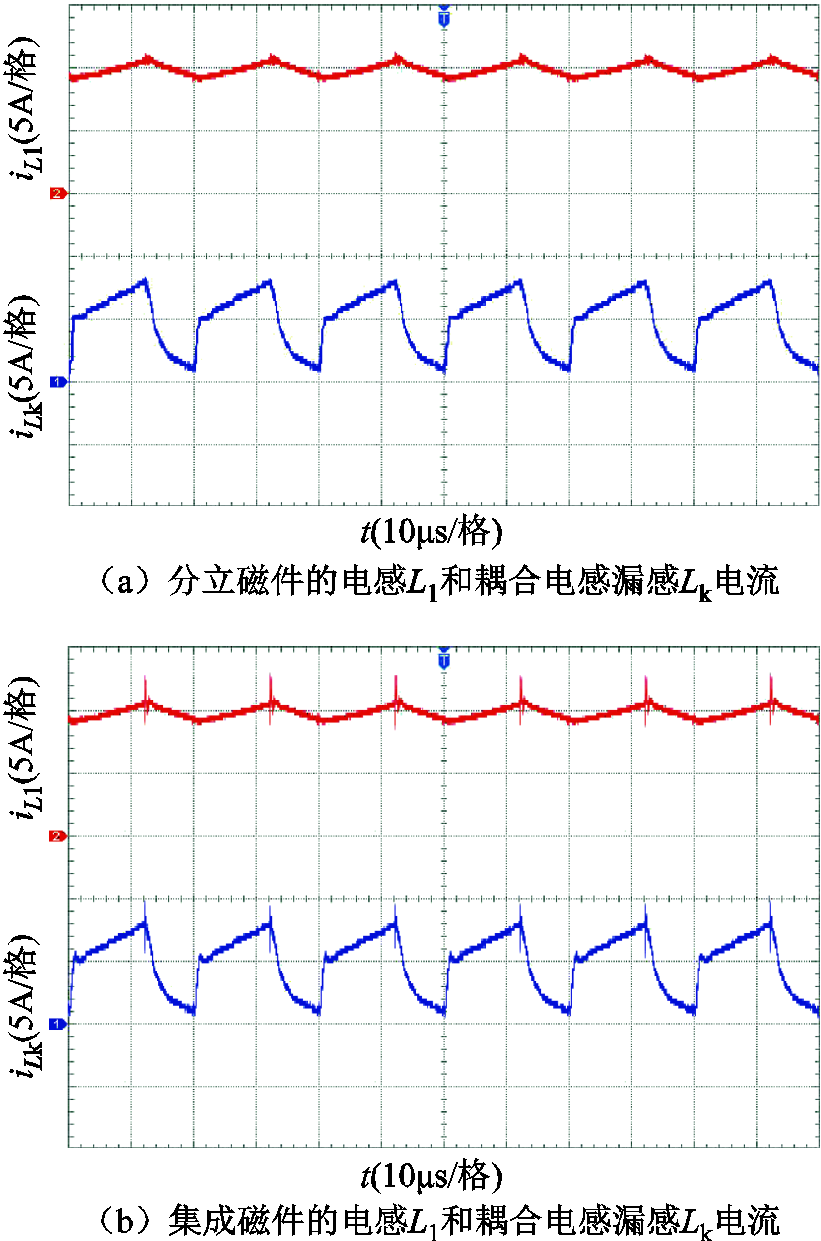
图15 分立磁件与集成磁件电流波形对比
Fig.15 Comparison diagram of current waveform between discrete and integrated magnetic components
根据实验结果和前文的损耗分析,计算出额定功率下的损耗分布如图17所示。从图中可以看出,变换器的主要损耗来源为开关管和二极管。
变换器理论分析的效率曲线与实际测量下的效率曲线如图18所示。从图18可以看出,在实验条件下,输出功率为240W时效率最高,理论最高效率为93.8%,实际测量的效率为93.2%。
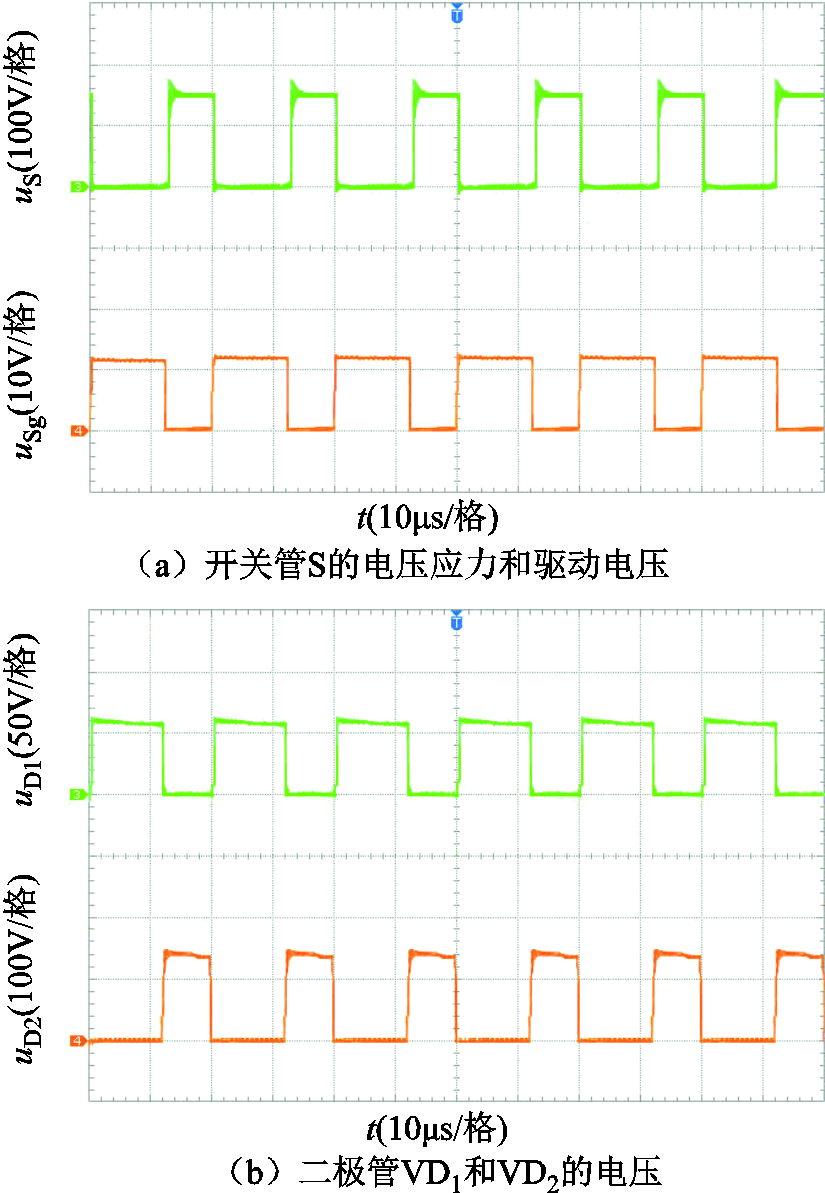
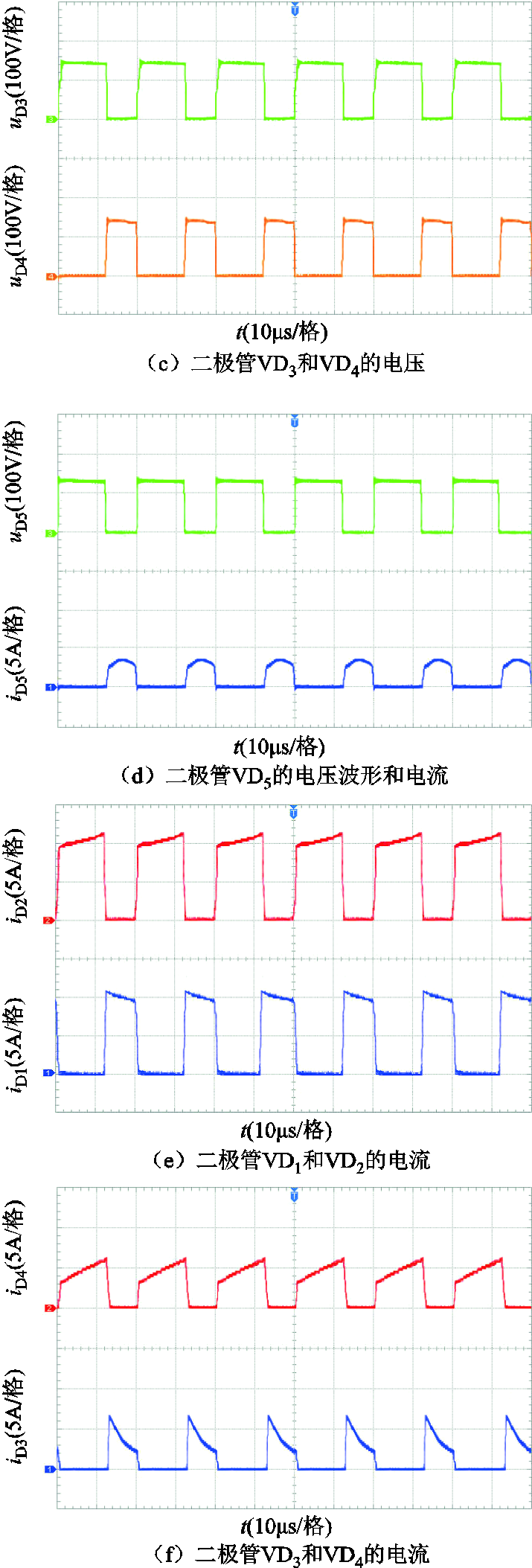
图16 变换器功率器件电流和电压应力波形
Fig.16 Current and voltage stress waveforms of the power components of the converter
针对新能源发电逆变器的前级升压单元,提出一种耦合电感倍压解耦磁集成高电压增益变换器。通过变换器模态分析和集成磁件磁路分析,获得了耦合电感和输入电感解耦集成条件,仿真分析与样机测试验证了理论分析的正确性。变换器拓扑具有以下特点:
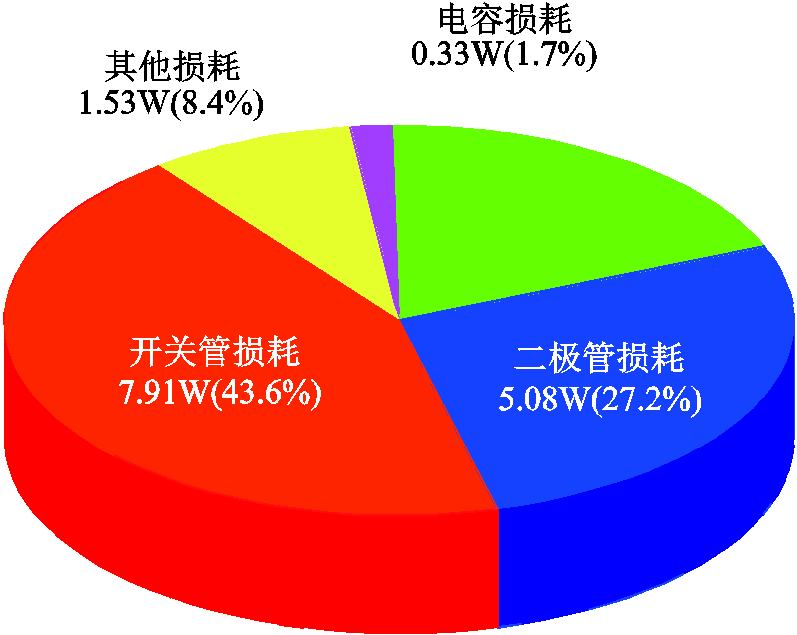
图17 器件损耗分布
Fig.17 Pie chart of device loss
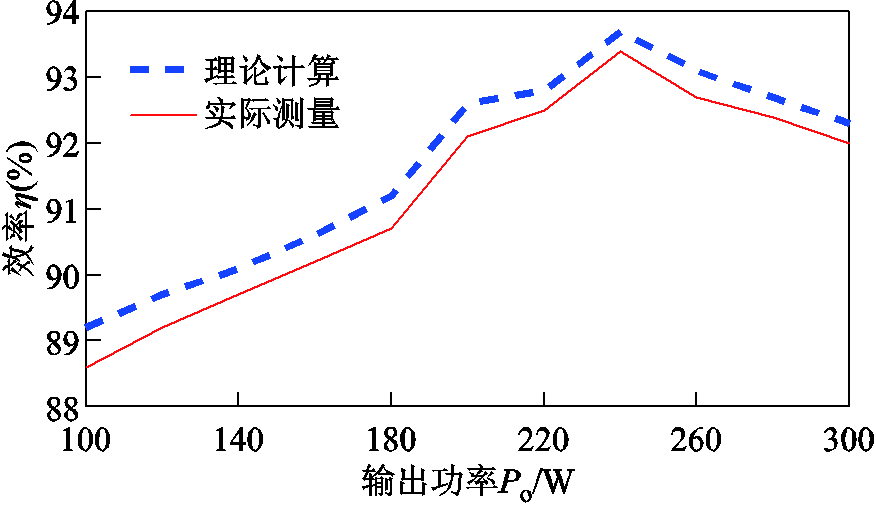
图18 变换器效率曲线
Fig.18 Curves of converter efficiency
1)变换器的电压增益与耦合电感的匝数比有关,当匝数比为2、占空比0.6时,电压增益达到13倍以上。
2)在保证变换器性能不变的情况下,采用解耦磁集成减少了磁件的数量;磁心中柱绕制耦合电感,减小了漏感。
3)变换器可以进行级联拓展,应用于多种工作场合。
参考文献
[1] 李鹏, 王瑞, 冀浩然,等. 低碳化智能配电网规划研究与展望[J]. 电力系统自动化, 2021, 45(24): 10-20.
Li Peng, Wang Rui, Ji Haoran, et al. Research and prospect of planning for low-carbon smart distribution network[J]. Automation of Electric Power Systems, 2021, 45(24): 10-20.
[2] Zhu Xiaonan, Wang Hongliang, Zhang Wenyuan, et al. A novel single-phase five-level transformer-less photovoltaic (PV) inverter[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 329-338.
[3] Fang Xupeng, Wang Xiaoli, Zhou Shixiang. An improved Y-source inverter with the capability of absorbing bus voltage spike[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2): 118-123.
[4] 张显, 史连军. 中国电力市场未来研究方向及关键技术[J]. 电力系统自动化, 2020, 44(16): 1-11.
Zhang Xian, Shi Lianjun. Future research areas and key technologies of electricity market in China[J]. Automation of Electric Power Systems, 2020, 44(16): 1-11.
[5] 王忠杰, 王议锋, 陈庆, 等. 基于 GaN 的高频 Boost 变换器优化设计[J]. 电工技术学报, 2021, 36(12): 2496-2504.
Wang Zhongjie, Wang Yifeng, Chen Qing, et al. Optimal design of high frequency Boost converter based on GaN[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2496-2504.
[6] Ebrahimi R, Madadi H, Kojabadi L. Coupled-inductor-based high step-up DC-DC converter[J]. IET Power Electronics, 2019, 12(12): 3093-3104.
[7] 佟明昊, 程明, 许芷源, 等. 电动汽车用车载集成式充电系统若干关键技术问题及解决方案[J]. 电工技术学报, 2021, 36(24): 5126-5142.
Tong Minghao, Cheng Ming, Xu Zhiyuan, et al. Key issues and solutions of integrated on-board chargers for electric vehicles[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5126-2142.
[8] Ye Yuanmao, Cheng Zhi. A family of single-stage switched-capacitor–inductor PWM converters[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5196-5205.
[9] Yao Na, Wang Yi. A switched-capacitor-based active-network converter with high voltage gain[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2959-2968.
[10] 王挺, 汤雨. 基于开关电感的有源网络升压变换器的研究[J]. 电工技术学报, 2014, 29(12): 73-79.
Wang Ting, Tang Yu. Study of active network DC-DC Boost converter based on switched inductor[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 73-79.
[11] Zhou Luowei, Zhu Binxin, Luo Quanming, et al. Interleaved non-isolated high step-up DC/DC converter based on the diode-capacitor multiplier[J]. IET Power Electronics, 2014, 7(2): 390-397.
[12] 雷浩东, 郝瑞祥, 游小杰, 等. 基于开关电容和三绕组耦合电感的高电压增益 DC-DC 变换器[J]. 电工技术学报, 2020, 35(17): 3667-3677.
Lei Haodong, Hao Ruixiang, You Xiaojie, et al. High voltage gain DC-DC converter with switched-capacitor and three-winding coupled inductor[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3667-3677.
[13] Ardi H, Ajami A. Study on a high voltage gain SEPIC-based DC-DC converter with continuous input current for sustainable energy applications[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10403-10409.
[14] Nouri T, Hosseini S. Analysis of voltage and current stresses of a generalized step-up DC-DC converter[J]. IET Power Electronics, 2014, 7(6): 1347-1361.
[15] 周磊, 张宇妍, 秦岭, 等. 低电应力无变压器单管高增益Boost变换器族[J]. 中国电机工程学报, 2020, 40(21): 7036-7046.
Zhou Lei, Zhang Yuyang, Qin Ling, et al. Low voltage stress transformer-free single-tube high-gain boost converter family[J]. Proceedings of the CSEE, 2020, 40(21): 7036-7046.
[16] 高圣伟, 王浩, 刘晓明. 新型磁集成双频DC/DC变换器[J]. 中国电机工程学报, 2020, 40(24): 8131-8144.
Gao Shengwei, Wang Hao, Liu Xiaoming. A novel double frequency DC/DC converter with magnetic integration[J]. Proceedings of the CSEE, 2020, 40(24): 8131-8144.
[17] 荣德生, 孙瑄瑨. 一种新型磁集成二次型开关电感单元[J]. 电机与控制学报, 2020, 24(4): 131-140.
Rong Desheng, Sun Xuanjin. A novel magnetic integrated secondary switched inductor unit[J]. Electric Machines and Control, 2020, 24(4): 131-140.
[18] 姚子睿, 曾君. 基于耦合电感的高增益低电压应力 Boost 变换器[J]. 中国电机工程学报, 2019, 39(12): 3659-3666.
Yao Zirui, Zeng Jun. High gain low voltage stress boost converter based on coupling inductor[J]. Proceedings of the CSEE, 2019,39(12): 3659-3666.
[19] Zhu Binxin, Hu Shishi, Liu Guanghui. Low-voltage stress buck-boost converter with a high voltage conversion gain[J]. IEEE Access, 2020, 8(12): 95188-95196.
[20] Zhao Jiawei, Chen Daolian, Jiang Jiahui. A novel transformerless high step-up DC-DC converter with active switched-inductor and quasi-Z-source network[J]. IET Power Electronics, 2021, 14(9): 1592-1605.
[21] Zheng Yifei, Xie Wenhao, Li Shouxiang. High step-up DC–DC converter with zero voltage switching and low input current ripple[J]. IEEE Transactions on Power Electronics, 2020, 35(9): 9416-9429.
Abstract In the past 10 years, considerable attention has been paid to the use of green energy. The use of renewable energy gradually increases the demand for converters. The classic boost converter is unable to provide a high voltage gain. At the same time, it increases the voltage stress of converters’ components, and the conversion efficiency is dropped. Academic and industry circles have conducted more relevant studies on high-gain converters to satisfy high voltage gain with converter performance. The converters have various voltage boost techniques such as voltage multiplier, switched-capacitor, coupled inductor, etc. Different technologies have advantages and disadvantages.
Firstly, the high gain converter is proposed based on the combination of Boost converter and coupling inductor. Then, by combining and simplifying the input side of the Boost converter and the basic stacked coupled inductor boost circuit, a high voltage gain converter topology based on the coupled inductor structure is proposed. The operation mode, voltage gain, voltage stress, current stress and other aspects of the proposed converter are analyzed, and the calculation method of the proposed converter efficiency is given, and the pie chart of quantitative calculation of the loss is given in the experimental measurement. The decoupling magnetic integration design of the proposed converter is given, and a design method to realize the decoupling magnetic integration of the coupled inductor and the independent inductor is presented. The equivalent circuit model of the integrated magnetic component designed is proposed by using the circuit-magnetic circuit analysis method. The simulation analysis of the proposed scheme verifies the rationality of the design method. Through the magnetic component design method proposed, the volume of the integrated magnetic component can be reduced by about 24% compared with that of the discrete magnetic components. Finally, the experimental prototype designed, and the waveform results of the relevant experiments are given. The effect of the current on the magnetic components of the converter before and after the decoupling magnetic integration design scheme is compared, and the efficiency curve of the prototype is given.
The input of the designed converter is connected with 24V power supply. After the lifting of the proposed converter the 240V voltage is obtained on the output side at a switching frequency of 50kHz. Adjusting the load to implementation different output power, when the output power is 100W, 120W, 120W, 140W, 160W, 180W, 200W, 220W, 240W, 260W, 280W, the corresponding efficiency is 88.4%, 89.2%, 89.7%, 90.1%, 90.8%, 91.4%, 92.1%, 93.4%, 92.5%, 92%. The experimental efficiency in the 240W load condition reaches 93.4%.
A coupling inductor voltage doubling decoupling magnetic integrated high voltage gain converter is proposed for the front stage unit of new energy power generation inverter. Through the analysis of the converter mode and the magnetic circuit of the integrated magnetic component, the decoupling integration conditions of the coupling inductance and the input inductance are obtained. A prototype is realized to confirm the validity of the theoretical analysis and the operation of the proposed converter. The converter topology has the following characteristics: (1) The voltage gain of the converter is related to the turn ratio of the coupling inductor. When the turn ratio is 2 and the duty cycle is 0.6, the voltage gain reaches more than 13 times. (2) Under the condition that the converter performance is unchanged, the decoupled magnetic integration is used to reduce the number of magnetic components, and the coupling inductance is made by winding the column in the magnetic core to reduce the leakage inductance. (3) The converter can be cascaded and expanded, so that the converter can be applied to a variety of working situations.
keywords:High gain, coupled inductor, magnetic integration, decoupling condition
DOI: 10.19595/j.cnki.1000-6753.tces.211743
中图分类号:TM46
辽宁省科学技术基金项目(2019-MS-159)、辽宁省教育厅科学技术研究项目(重点攻关)(LJ2021ZD06)和辽宁省高校创新团队项目(LT2019007)资助。
收稿日期 2021-10-30
改稿日期 2022-02-11
李洪珠 男,1974年生,博士,教授,研究方向为电力电子及其磁集成技术。E-mail:lhz_98@163.com
程利弘 男,1997年生,硕士研究生,研究方向为电力电子及其磁集成技术。E-mail:2632689062@qq.com(通信作者)
(编辑 赫 蕾)