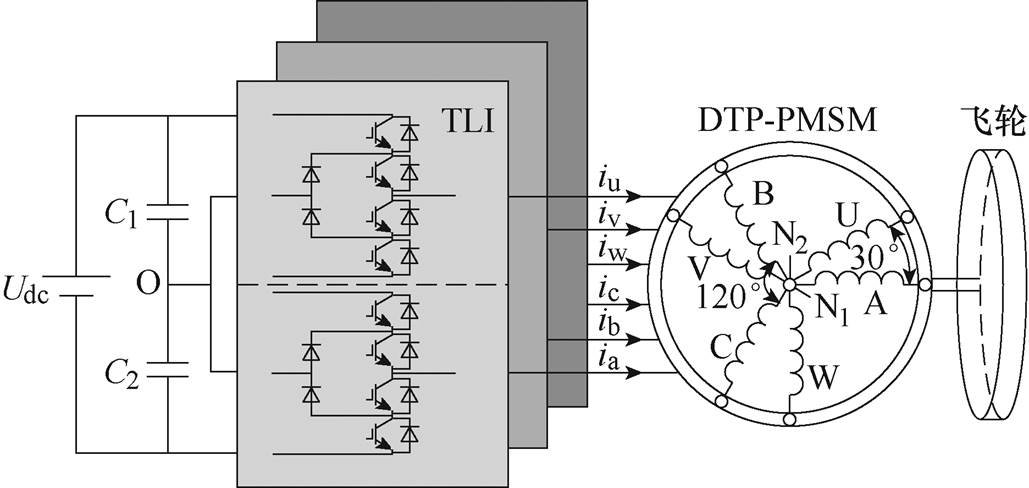
图1 飞轮储能系统拓扑
Fig.1 Topology of FESS
摘要 飞轮储能系统的工作模式要求在最短的时间内对飞轮进行可靠地充电。该文在分析传统充电控制策略的基础上，结合飞轮储能系统的工作特性，提出了一种基于非线性扰动观测器的优化充电控制策略。外环采用转速控制和能量控制相结合的方式，转速环实现恒转矩控制，能量环实现恒功率控制；引入过渡控制环节实现恒转矩控制和恒功率控制的切换；利用非线性扰动观测器估计电机损耗功率和负载功率并进行前馈补偿；基于控制系统稳态、动态和抗扰动性能的要求，给出一种控制器参数设计方法。与传统控制策略相比，所提充电控制策略恒功率控制灵活，恒转矩控制至恒功率控制切换平滑，且有效抑制了电机损耗功率和负载功率的影响，满足了飞轮储能系统的工作特性要求。最后，仿真和实验结果验证了所提策略的可行性和实用性。
关键词：飞轮储能系统 优化充电控制 能量控制 过渡控制 非线性扰动观测器
飞轮储能系统（Flywheel Energy Storage System, FESS）具有瞬时功率大、储能密度高、寿命长、效率高、环境友好等优点[1-2]，广泛应用于城轨交通制动能量回收、电力系统调峰、航空航天、电磁弹射等领域[3-5]。
FESS的充电控制通常采用基于矢量控制的双闭环级联结构，其中外环可以是转速环或者电压环。文献[6]基于转速外环电流内环的控制方案，通过恒定的q轴电流控制转速线性增加，控制简单，但充电效率低。文献[7]提出了一种多电压阈值的单飞轮储能系统控制策略，将母线电压作为外环控制量，通过比例积分（Proportional Integral, PI）调节器维持母线电压的稳定，但母线电压环具有非线性特性，该方法动态性能较差。文献[8-9]将母线电压的二次方作为反馈量对系统进行线性化处理，从能量的角度控制飞轮电机，提高了母线电压的动态响应速度，但是忽略了充电过程中飞轮电机的转速控制。在永磁同步电机调速系统中，文献[10]提出了一种以转子动能为外环控制量的双闭环矢量控制策略，与传统的双闭环矢量控制策略相比动态响应性能更优，因此，考虑到FESS的能量交换关系，可以将该策略与FESS的工作模式相结合，在实现飞轮电机能量控制的同时间接控制转速，维持转速的稳定。
针对FESS的工作模式，文献[11]采用单一的恒转矩控制，未能充分利用系统富余的能量，不满足充电过程中的工作特性要求。文献[12]提出一种利用牵引负荷功率来控制飞轮充放电的能量管理策略，实现了飞轮电机的恒功率控制，可以在短时间内吸收/释放最多的能量，但恒功率控制方式不够灵活。文献[13]通过q轴电流限幅恒转矩控制飞轮电机起动到工作转速，再以恒功率运行，然而恒转矩控制阶段始终保持较大电流，会增加系统的损耗。文献[14]结合FESS的工作模式，提出一种改进复合控制的充电控制策略，在不同工作阶段实现恒转矩、恒功率和小功率维持控制方式的快速切换，然而恒转矩控制切换至恒功率控制时电磁转矩会出现跳变，影响系统的稳定运行。
另外，FESS中的机械或电磁参数变化、负载扰动等非匹配扰动，会对飞轮电机损耗功率和负载功率造成不确定性影响[15-17]，进而影响系统的动态响应性能和鲁棒性，并造成充电功率下降。文献[8]采用非线性扰动观测器（Nonlinear Disturbance Observer, NDOB）对电机与变流器损耗功率、负载功率等总损耗功率进行统一观测并进行前馈补偿控制，但主要是基于母线电压二次方动态方程的放电控制。
针对上述问题，本文以多相多电平飞轮储能系统为研究对象，在分析传统充电控制策略的基础上，提出一种基于非线性扰动观测器的优化充电控制策略。外环采用转速控制和能量控制相结合的方式，转速环实现恒转矩控制，能量环采用飞轮动能作为控制量实现恒功率控制；引入过渡控制环节实现恒转矩控制至恒功率控制的平滑切换，设计了恒转矩区-过渡区-恒功率区-保持区的工作模式；利用NDOB估计电机损耗功率和负载功率并进行前馈补偿。然后，推导了考虑NDOB的“能量和电流”双闭环系统的传递函数，基于控制系统稳态、动态和抗扰动性能的要求，给出了一种控制器参数设计方法。最后，通过仿真和实验验证了所提策略的可行性和实用性。
本文所研究的飞轮储能系统的拓扑如图1所示，包括直流母线、三电平逆变器（There-Level Inverter, TLI）、双三相永磁同步电机（Dual Three- Phase Permanent Magnet Synchronous Motor, DTP- PMSM）、飞轮等。其中，DTP-PMSM为表贴式电机，其定子由两套星形联结的三相绕组ABC和UVW组成，两套绕组在空间上相差30 °电角度，且中性点N1和N2彼此隔离。Udc、C1、C2、O分别为直流侧电压、上电容、下电容、中点，ia、ib、ic、iu、iv、iw为DTP-PMSM的六相电流。
图1 飞轮储能系统拓扑
Fig.1 Topology of FESS
双dq坐标变换和矢量空间解耦坐标变换是DTP- PMSM常用的建模方法，其中双dq坐标变换可以对DTP-PMSM的每套三相绕组分别进行建模，不需要复杂的解耦运算[18]，在工业应用中更为实用[19]。
基于双dq坐标变换的DTP-PMSM数学模型为
（1）电压方程
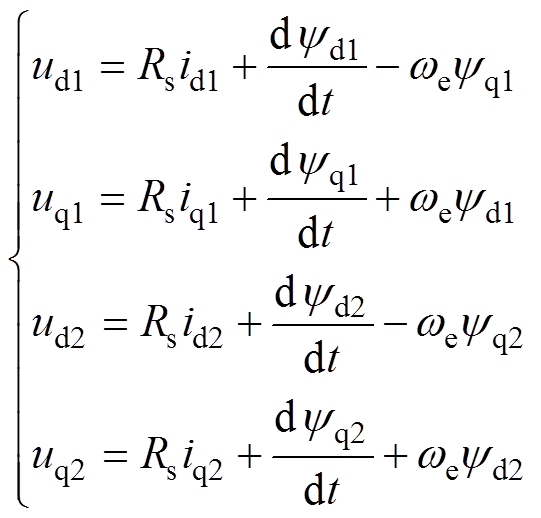（1）
式中，ud1、uq1、ud2、uq2为定子电压；id1、iq1、id2、iq2为定子电流；ψd1、ψq1、ψd2、ψq2为定子磁链；Rs为定子电阻；we为电角速度。
（2）磁链方程
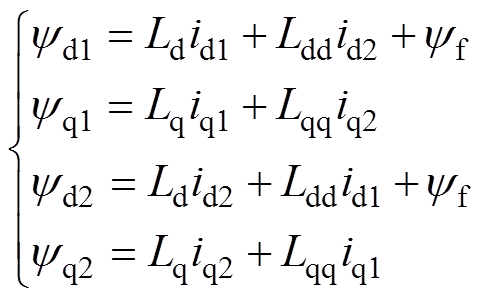（2）
式中，Ld、Lq为定子电感；Ldd、Lqq为定子互感；ψf为永磁体磁链。
（3）转矩方程
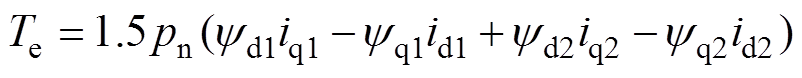（3）
式中，Te为电磁转矩；pn为极对数。
（4）机械运动方程
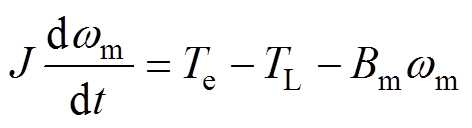（4）
式中，J、wm、TL、Bm分别为转动惯量、机械角速度、负载转矩、阻尼系数。
飞轮与DTP-PMSM的转子同轴连接，通过加减速实现电能转化为机械能存储或机械能转化为电能释放。理想状况下FESS在充放电过程中储存或释放的能量为
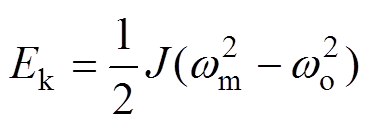（5）
式中，Ek为飞轮动能；wo为初始角速度。
传统的FESS充电控制框图如图2所示，采用id=0的矢量控制策略，其中，逆变器多为两电平结构，较少为三电平结构[20]；电机通常采用三相永磁同步电机。传统的充电控制算法一般采用基于PI调节器的“转速和电流”或“电压和电流”双闭环级联方式。图中，上标*号表示给定值，n为电机转速，q 为电机角度，Sa、Sb、Sc为三相开关信号。
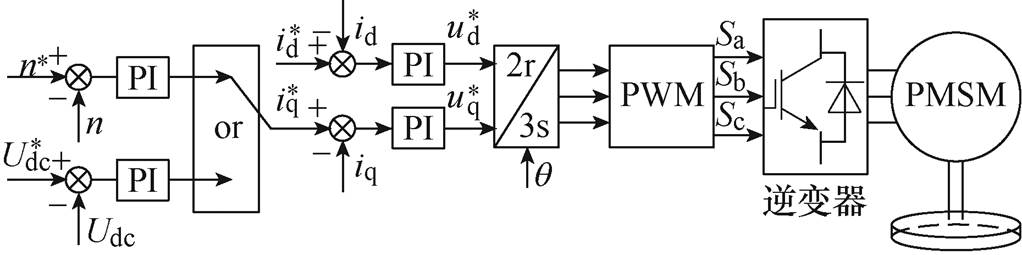
图2 传统的FESS充电控制框图
Fig.2 Block diagram of FESS traditional charging control
结合式（4）和图2，若忽略电机的负载和阻尼，电磁转矩和机械角速度变化率呈线性特性，因此，通过限制转速变化率dn/dt，可以实现电机的恒转矩控制。然而，当采用“电压和电流”双闭环级联方式时，由于母线电压环的非线性特性，恒转矩控制只能通过设置q轴电流限幅值来实现。另外，由于FESS工作模式和电机结构的限制，恒转矩控制不能满足全转速范围下系统的工作特性要求，而通过转矩查表等方式实现的电机的恒功率控制则可以发挥FESS的最大储能能力。
传统的充电控制策略过程如下：设置最小转速nmin和最大转速nmax，0～nmin之间恒转矩控制电机起动；nmin～nmax之间恒功率控制电机加速；达到nmax后，电机小功率维持。图3所示为在传统充电控制策略下电机的电磁转矩、转速和功率曲线，其中，Pe为电磁功率。
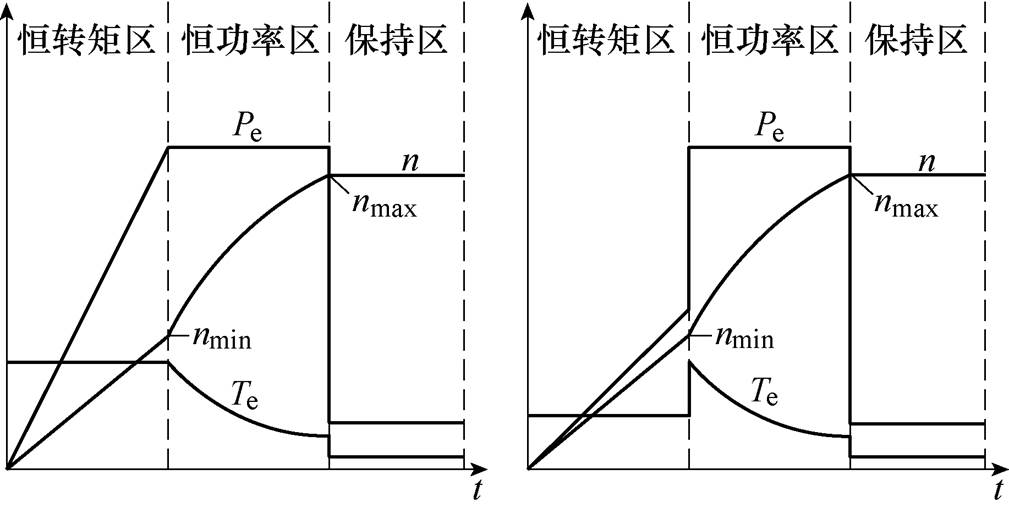
（a）传统充电控制策略 （b）改进的传统充电控制策略
图3 传统充电控制策略下的工作特性曲线
Fig.3 Operating characteristic curves of traditional charging control
图3a所示传统充电控制策略可以在较短时间内起动电机至恒功率运行，但是恒转矩控制阶段的充电电流较大，会增加电机损耗；图3b所示传统充电控制策略在图3a的基础上进行了改进，恒转矩控制更加灵活，避免了长时间的大电流，但是在恒转矩控制切换至恒功率控制时电磁转矩会出现较大的跳变，影响系统的稳定性。因此，为避免上述问题的出现，有必要对传统充电控制策略进行优化。
现有研究较少提及恒功率控制的具体实现方式，为此，本文以飞轮动能作为外环，采用“能量控制”实现DTP-PMSM的恒功率控制。
联立式（1）～式（3），DTP-PMSM的有功功率的交换关系为
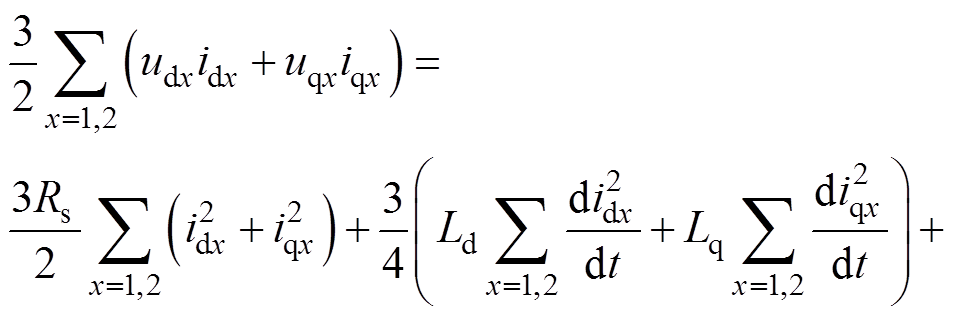
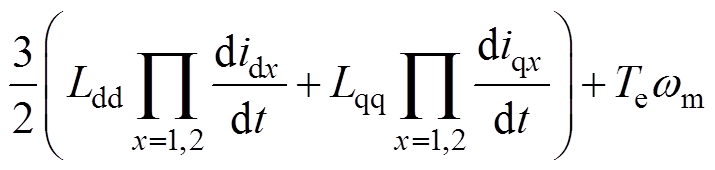（6）
同时，式（4）乘wm，可得
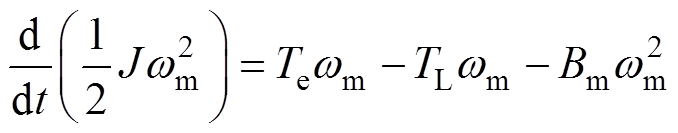（7）
式（6）和式（7）表明了FESS充电时电能转化为机械能的过程。其中，式（6）等号左边为电机的输入功率，右边第一项为电阻消耗的功率，右边第二项为电感消耗的功率，第三项为互感消耗的功率，第四项为电磁功率；式（7）中，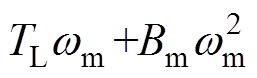
为负载与阻尼消耗的功率，
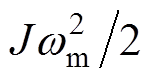为飞轮动能。
DTP-PMSM的两套绕组完全对称，若采用相同的控制参数，可以认为id1=id2，iq1=iq2。结合式（6）和式（7），并将d轴电流控制为0，可得
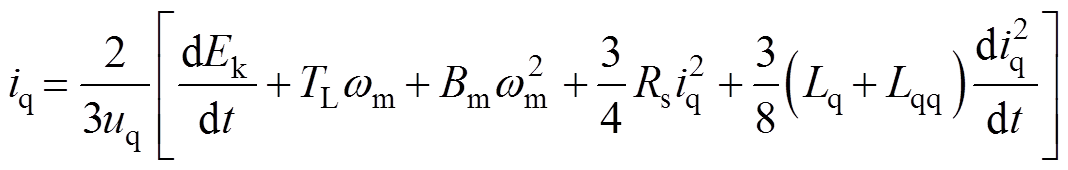（8）
其中
iq=iq1+iq2 uq=uq1=uq2
由式（8）可得FESS的能量控制框图，如图4所示。若忽略电机损耗功率和负载功率，飞轮动能给定值和反馈值的差值经过PI调节器后输出功率给定值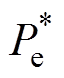
，进一步得到q轴电流给定值；若考虑电机损耗功率和负载功率，可将其进行前馈补偿，从而提高系统的抗干扰能力。
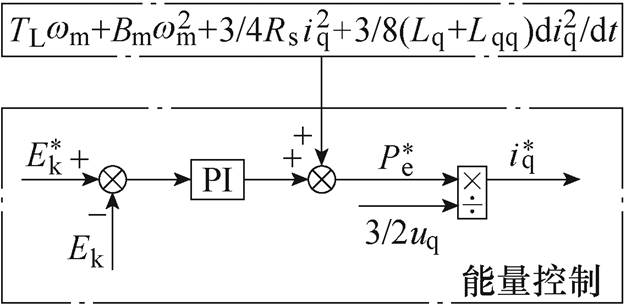
图4 能量控制框图
Fig.4 Block diagram of energy control
基于上述分析，根据FESS充电过程的工作特性要求，即转矩和时间限制，提出一种优化充电控制策略，如图5所示。图中，ai、Pi为电机角加速度和充电功率的理想值或期望值，两者经过给定环节得到转速和能量给定值，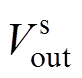
、
、
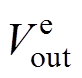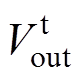分别为恒转矩控制环节、恒功率控制环节、过渡控制环节的输出量，nmid为中间转速。外环采用转速环和能量环相结合的方式，转速环实现恒转矩控制，能量环实现恒功率控制；引入过渡控制环节实现恒转矩控制和恒功率控制的平滑切换。进一步地，将充电过程分为恒转矩区、过渡区、恒功率区、保持区四个阶段。首先，采用恒转矩控制将电机起动到最小转速；其次，综合切换的快速性和稳定性，在过渡区实现转速环至能量环的平滑切换；然后，恒功率控制飞轮达到最大储能；最后，以小功率维持飞轮运行。本文采用一种加权平均的切换方法实现过渡控制，有
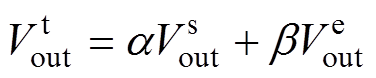（9）
其中
a=1-b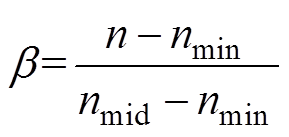 
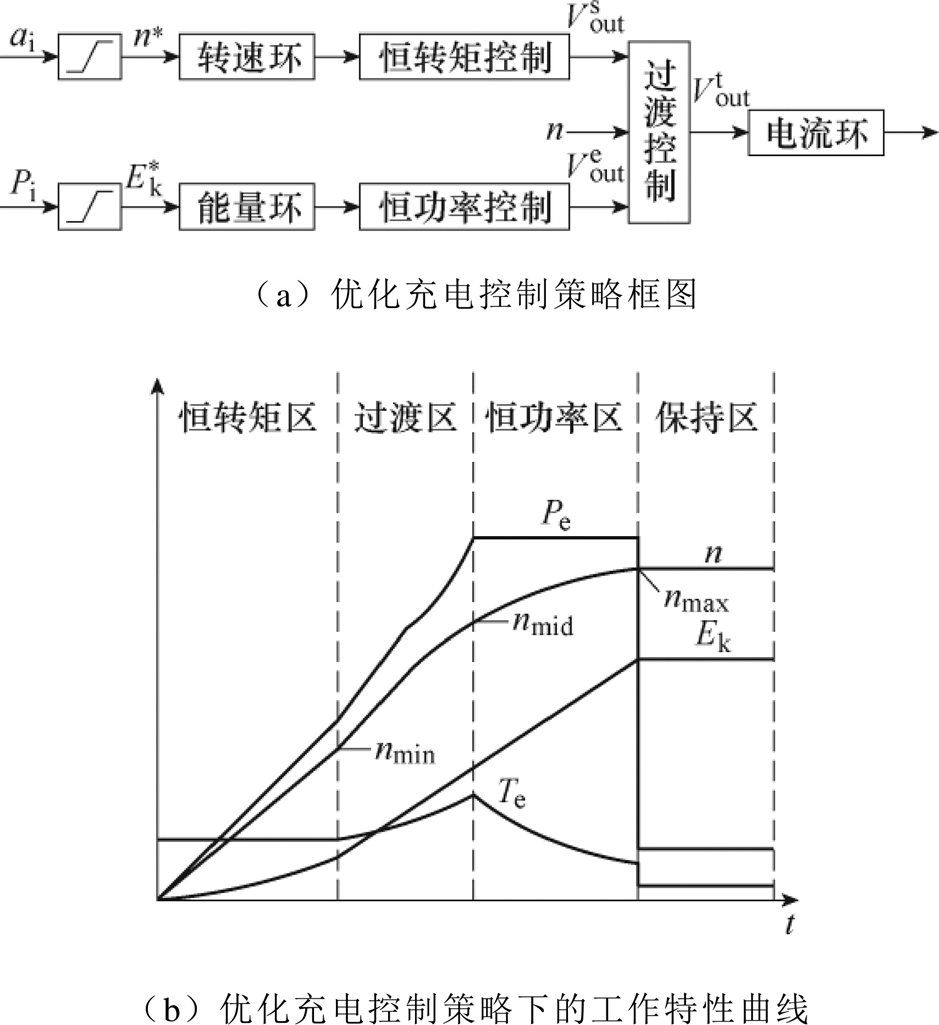
图5 优化充电控制策略及其性能分析
Fig.5 Optimized charging control strategy and its performance analysis
在优化充电控制策略下电机的电磁转矩、转速、功率和能量曲线如图5b所示，过渡区转矩曲线平滑，避免出现过大的转矩跳变。
为抑制DTP-PMSM的损耗功率和负载功率对恒功率控制阶段的影响，设计NDOB对其进行观测。定义充电过程中电机的损耗功率和负载功率为总损耗功率Ploss，可得
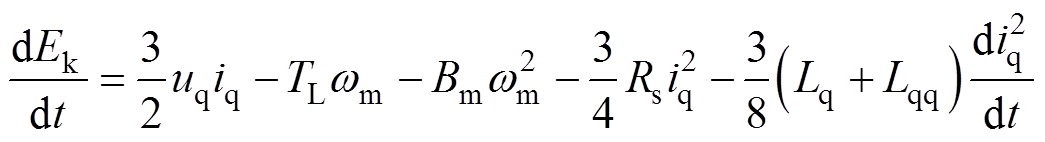
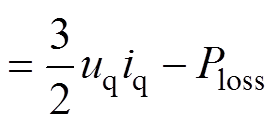（10）
设计总损耗功率观测器为
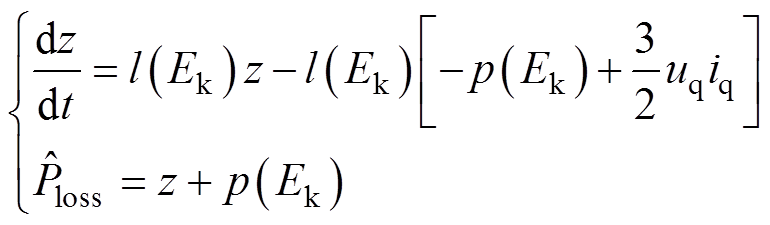（11）
式中，z、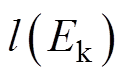
、
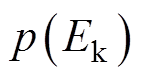分别为NDOB的状态变量、增益、待设计函数，且=
；
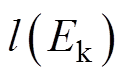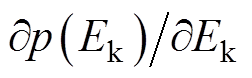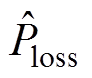为总损耗功率估计值。
实际上，在FESS充电过程中，Ploss有界且其导数随时间趋于0。为了让估计误差快速收敛，选择l(Ek)=-de（de为增益常数，de＞0），估计误差ep满足
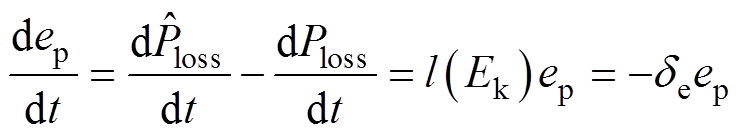（12）
其中
ep=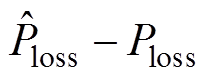
可知，NDOB能够在有限时间内跟踪总损耗功率扰动。
结合式（11）和式（12），通过拉普拉斯变换得到NDOB的传递函数为
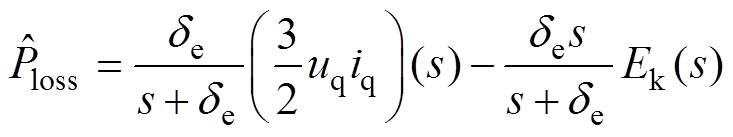（13）
NDOB结构简单且便于工程实现，可以对电机损耗功率（包括机械损耗功率和电磁损耗功率）以及负载功率进行统一观测，避免了复杂的计算。
同样地，结合式（4）可以在恒转矩控制阶段设计NDOB估计电机总损失转矩Tloss=TL+Bmwm，可得
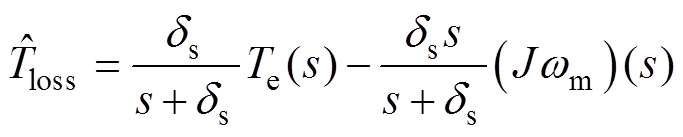（14）
式中，ds为转速环NDOB的增益常数。
本文所提出的基于NDOB的优化充电控制策略框图如图6所示，图中，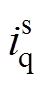
、
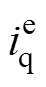分别为恒转矩控制环节、恒功率控制环节的输出量。通过将NDOB估计的电机总损失转矩和电机总损耗功率进行前馈补偿，在实现扰动抑制的同时，可以减少由过渡控制环节引入而增加的充电时间。
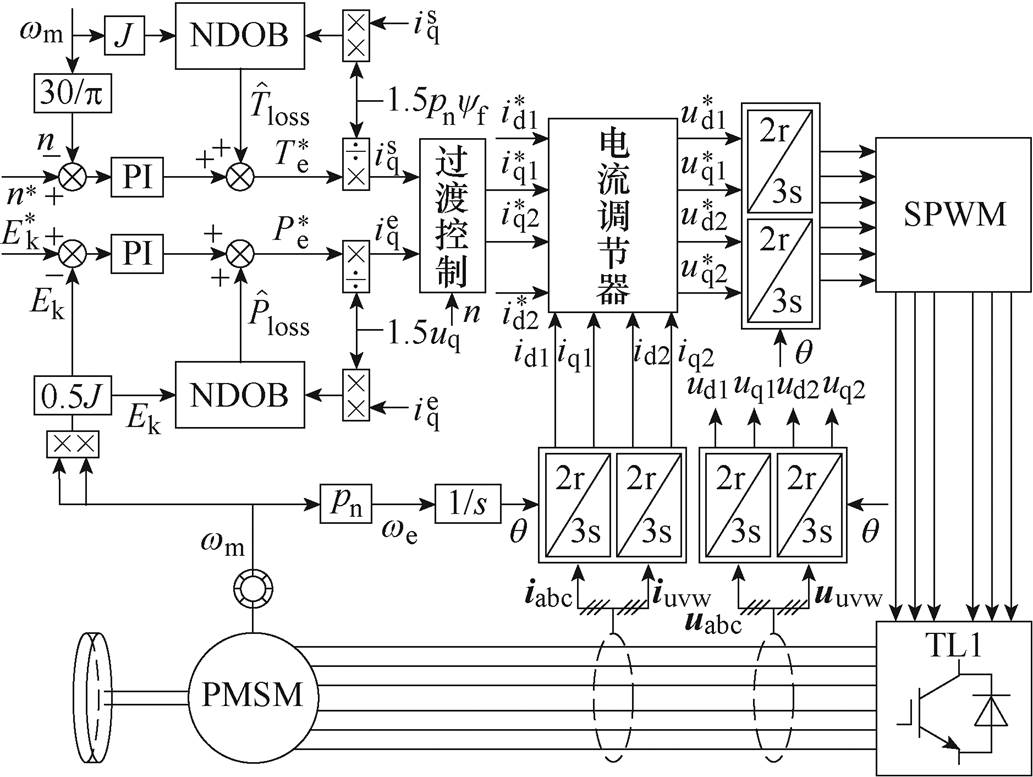
图6 本文所提出的充电控制策略框图
Fig.6 Block diagram of proposed charging control strategy for FESS
下面推导考虑电流内环和NDOB影响的闭环系统的传递函数，基于控制系统稳态、动态和抗扰动性能的要求，给出一种控制器参数设计方法。
电流内环的参数设计应在保证电流准确跟踪的同时提高快速响应能力[21-23]。DTP-PMSM不仅同套绕组存在交直轴耦合，两套绕组之间也存在交叉耦合，严重影响了电流调节器的动态性能。
因此，本文借鉴复矢量解耦的思想[24-25]，设计了DTP-PMSM的解耦策略，图7所示为电流调节器原理。图中，Kp、Ki、Kc分别为电流内环的比例、积分和解耦系数，idq1、idq2、udq1、udq2分别为复矢量形式的dq轴电流、电压。
通过对两套三相绕组的d轴或q轴的交叉耦合进行补偿，可以将DTP-PMSM等效为两个三相永磁同步电机进行复矢量解耦控制。根据零极点对消原理[26]，当Kp、Ki满足Ki/Kp=Rs/Lq时，被控对象的动态特性近似为一阶惯性环节，即
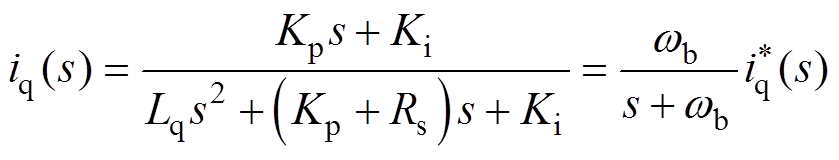（15）
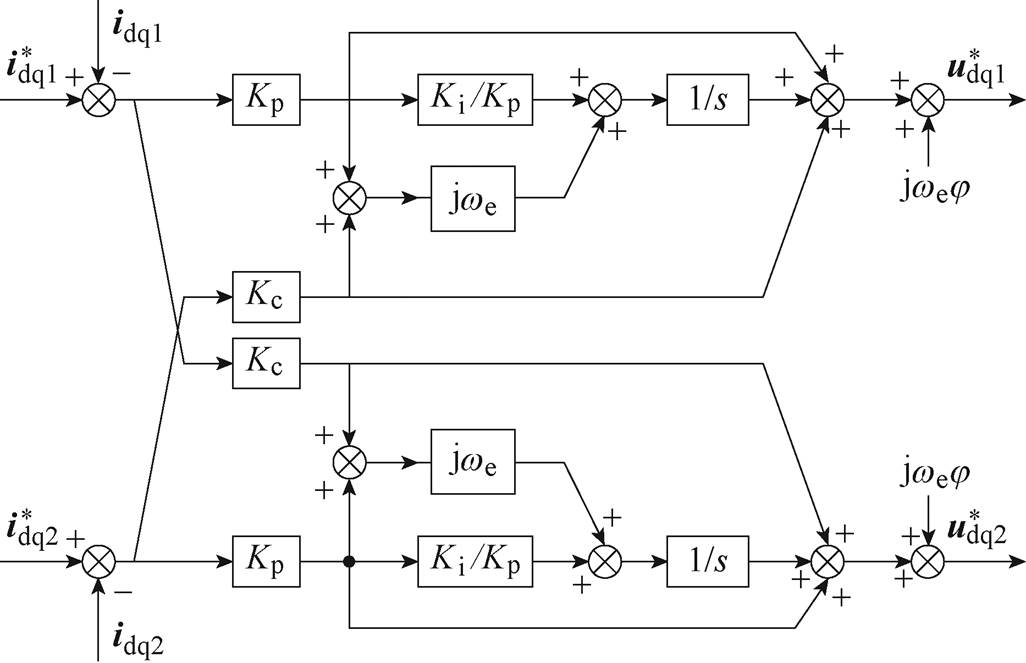
图7 电流调节器原理
Fig.7 Diagram of the current regulator
其中
Kp=wbLq Ki=wbRs
式中，wb为该一阶惯性环节的带宽频率，即闭环幅频特性下降到-3dB时对应的频率。
对式（10）进行拉普拉斯变换并结合图6可得
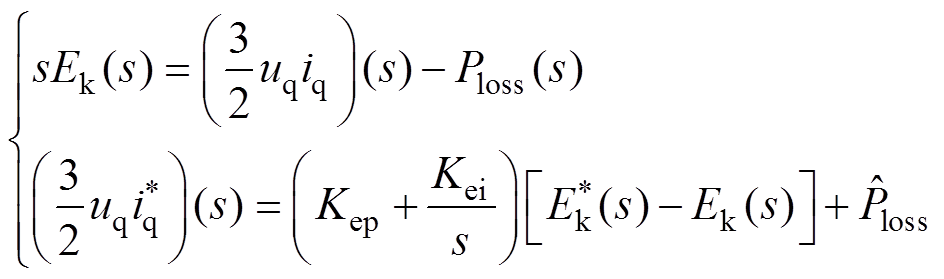（16）
式中，Kep、Kei分别为能量外环的比例和积分系数。
结合式（13）、式（15）和式（16），进一步可得
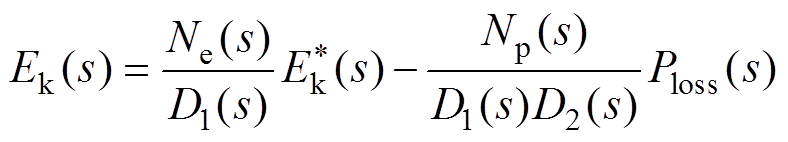（17）
其中
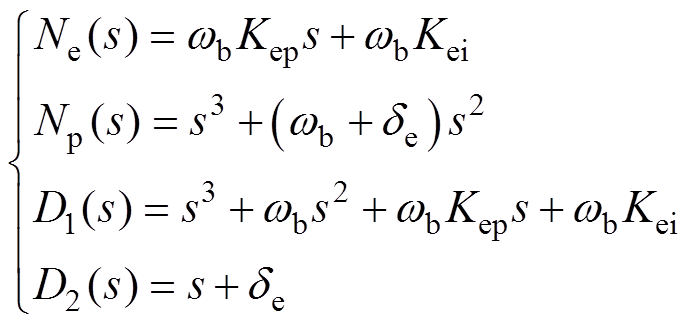（18）
式（18）表明，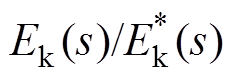
是一个三阶的系统，显然，当Kei=0时，系统降阶为2阶系统。此时特征方程D1(s)=0的特征根均为负实根或者实部为负的复数根，系统的极点均在s平面的左半部分，系统是稳定的。此外，wb＜4Kep时，系统处于欠阻尼状态，wb/Kep越大超调量越小；wb越大调整时间越小，响应速度越快。当wb≥4Kep时，系统不存在超调，且同样是wb越大响应速度越快。不过wb不宜过大，否则会放大电流噪声。一般可取wb=100Hz。
图8给出wb=100Hz时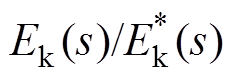的单位阶跃响应曲线和单位斜坡响应曲线。由单位阶跃响应曲线可知，当Kep≤25时，系统无超调，且Kep越大响应速度越快。由单位斜坡响应曲线可知，Kep增大至某一值后，系统对输入的跟踪误差和速度提升有限。
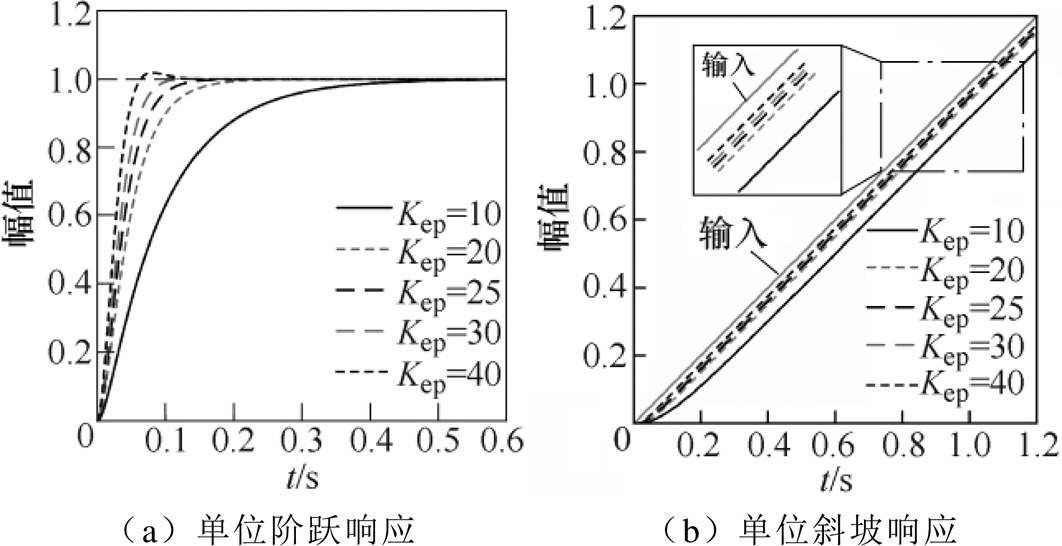
图8 单位阶跃响应和单位斜坡响应曲线
Fig.8 Curves of unit step response and unit ramp response
图9a和图9b给出Kep、de取不同值时Ek(s)/Ploss(s)的幅频特性曲线。可知，Kep、de的取值越大，系统对于电机损耗功率扰动的抑制能力越强。不过过大的Kep、de对扰动抑制能力的提升作用有限，且会放大系统噪声，降低系统可靠性。另外，图9a和图9b表明，在中高频段，系统对扰动已有较强的抑制能力，Kep、de的增大不能进一步提升扰动抑制能力，甚至会起到反面效果。图9c给出低频段Ek(s)/Ploss(s)的幅值随Kep、de取值变化的关系，可以看出，系统对低频扰动具有很强的抑制能力。综合考虑系统的稳态性能、动态性能和抗干扰能力，可选取Kep=20，de=0.01。
同样地，在恒转矩控制阶段进行参数设计，可得转速外环参数：Ksp=1, ds=0.1。
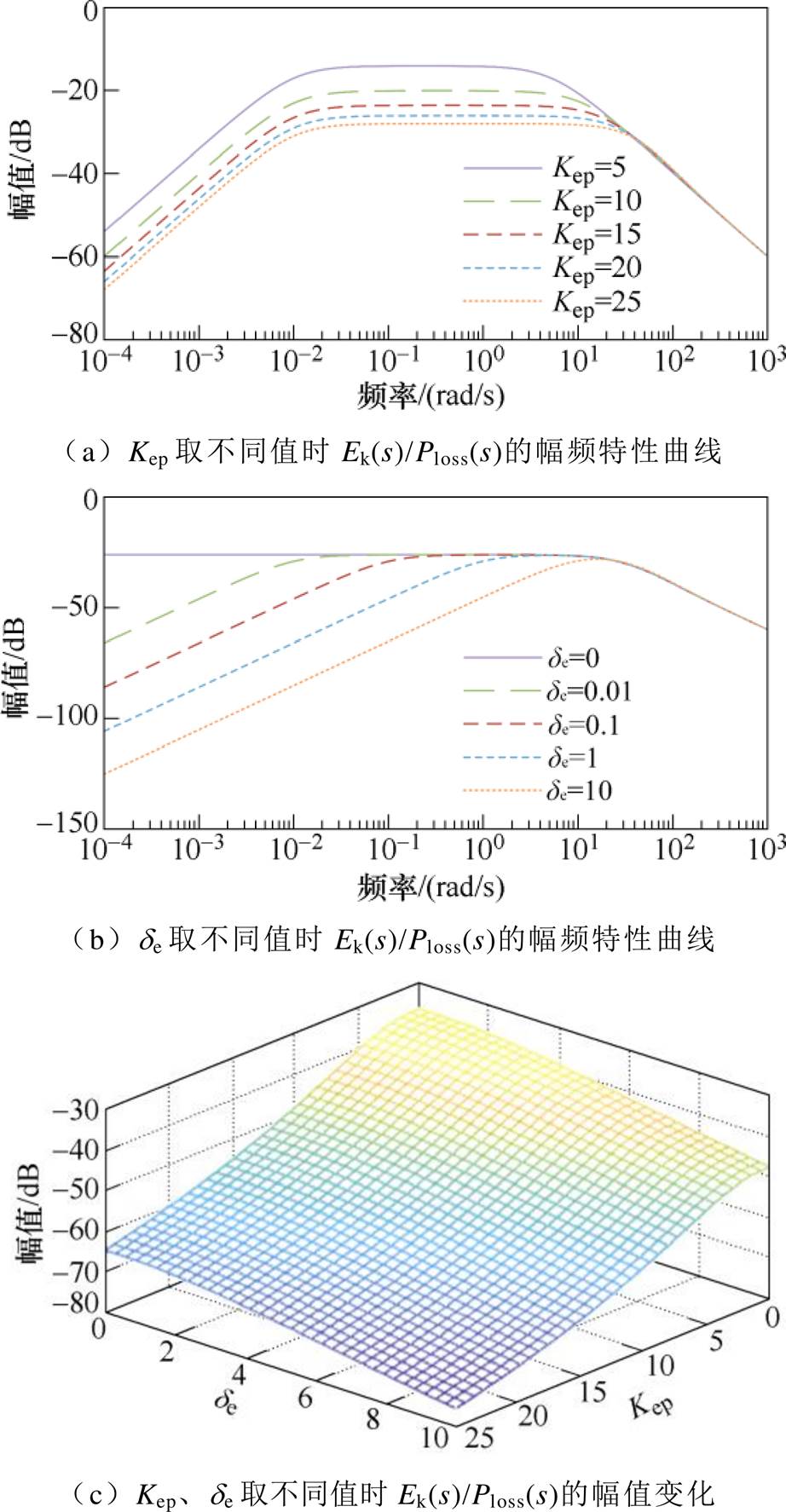
图9 Ek(s)/Ploss(s)的幅值与Kep、de的关系
Fig.9 Amplitude of Ek(s)/Ploss(s) with Kep and de
本文在Matlab/Simulink中搭建了多相多电平飞轮储能系统仿真模型，仿真参数见表1。
表1 飞轮储能系统仿真参数
Tab.1 FESS parameters
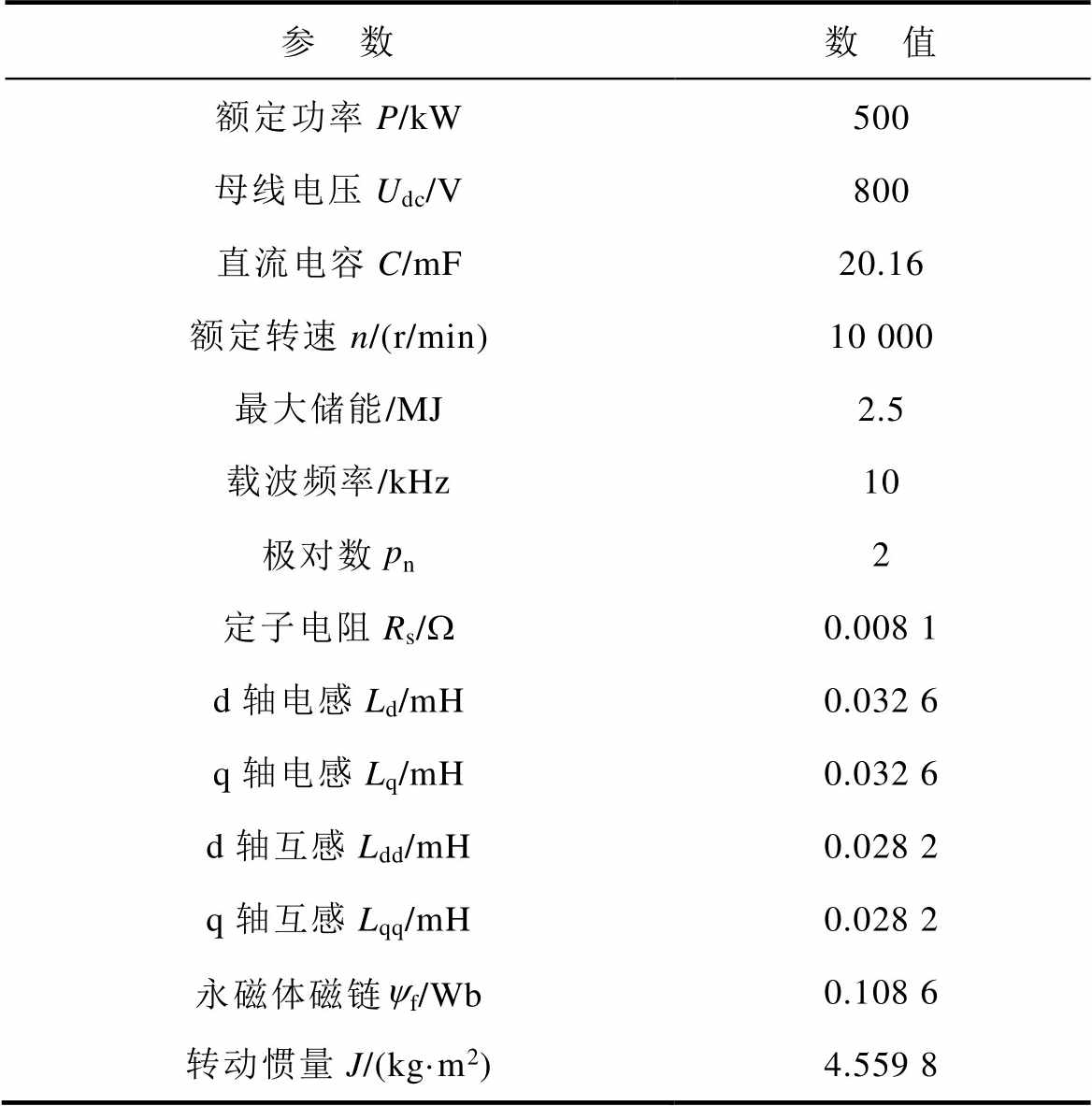
参 数数 值 额定功率P/kW500 母线电压Udc/V800 直流电容C/mF20.16 额定转速n/(r/min)10 000 最大储能/MJ2.5 载波频率/kHz10 极对数pn2 定子电阻Rs/W0.008 1 d轴电感Ld/mH0.032 6 q轴电感Lq/mH0.032 6 d轴互感Ldd/mH0.028 2 q轴互感Lqq/mH0.028 2 永磁体磁链yf/Wb0.108 6 转动惯量J/(kg·m2)4.559 8
设置充电过程中的nmax、nmid、nmin、Pi分别为10 000 r/min、6 000 r/min、4 000 r/min、100 kW。另外，为了减少仿真时间，将DTP-PMSM的转动惯量设置为实际系统的1/10，最大储能为0.25MJ。分别采用传统充电控制策略（Traditional Charging Control Strategy, TCCS）、改进的传统充电控制策或简称改进充电控制策略（Improved Charge Control Strategy, ICCS），以及优化充电控制策略（Optimized Charging Control Strategy, OCCS）进行了仿真验证。其中，恒转矩控制基于“转速和电流”双闭环，通过限制转速变化率dn/dt来实现；恒功率控制基于“能量和电流”双闭环，通过限制动能变化率dEk/dt来实现。
图10给出传统充电控制策略下的转速、动能、转矩和功率仿真波形。其中，TCCS1仅采用恒转矩控制，角加速度为209.4 rad/s2；TCCS2限制角加速度为523.6 rad/s2恒转矩起动，在转速达到4 000 r/min后恒功率运行。TCCS1和TCCS2从4 000 r/min充电至10 000 r/min的时间分别为3.03 s和2.11 s。可见，在充电过程中，TCCS1转矩小，充电时间长，功率小，储能效率低；TCCS2虽然充电时间短，储能效率高，但是恒转矩控制不够灵活，转矩过大，相应的充电电流大。
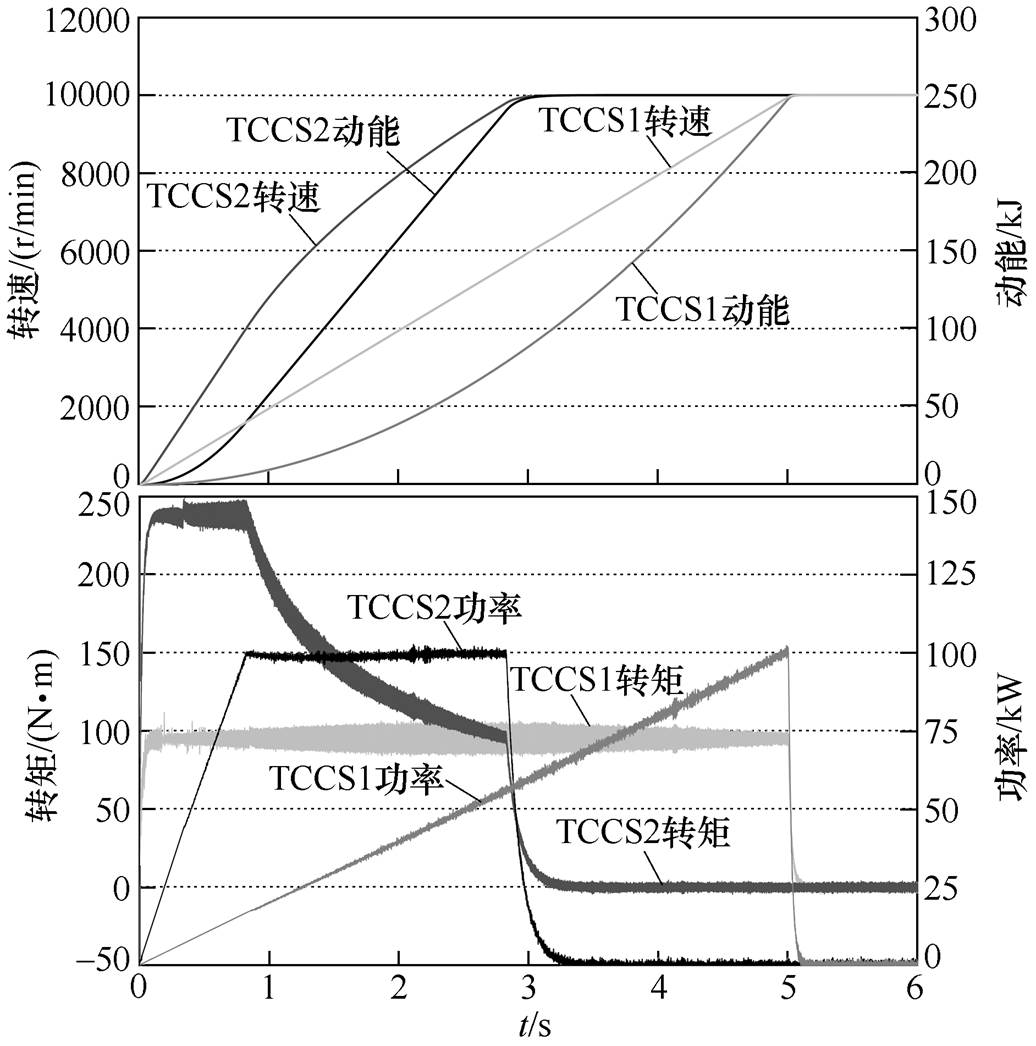
图10 传统充电控制策略下的仿真波形
Fig.10 Simulation waveforms under the traditional charging control strategy
图11给出改进充电控制策略下的转速、动能、转矩和功率仿真波形。图中，ICCS1和ICCS2在恒转矩区限制角加速度为209.4 rad/s2，并且分别在转速达到4 000 r/min和6 000 r/min时进行恒转矩控制至恒功率控制的切换。ICCS1和ICCS2从4 000 r/min充电至10 000 r/min的时间分别为2.17 s和2.71 s。可以看出，相比TCCS2，ICCS1和ICCS2在充电过程中的转矩更小，因此避免了过大的充电电流，恒转矩和恒功率控制更加灵活。然而，ICCS1和ICCS2的切换过程不够平滑，转矩存在较大的跳变。虽然相比ICCS1，ICCS2的转矩跳变较小，但是其充电时间更长。
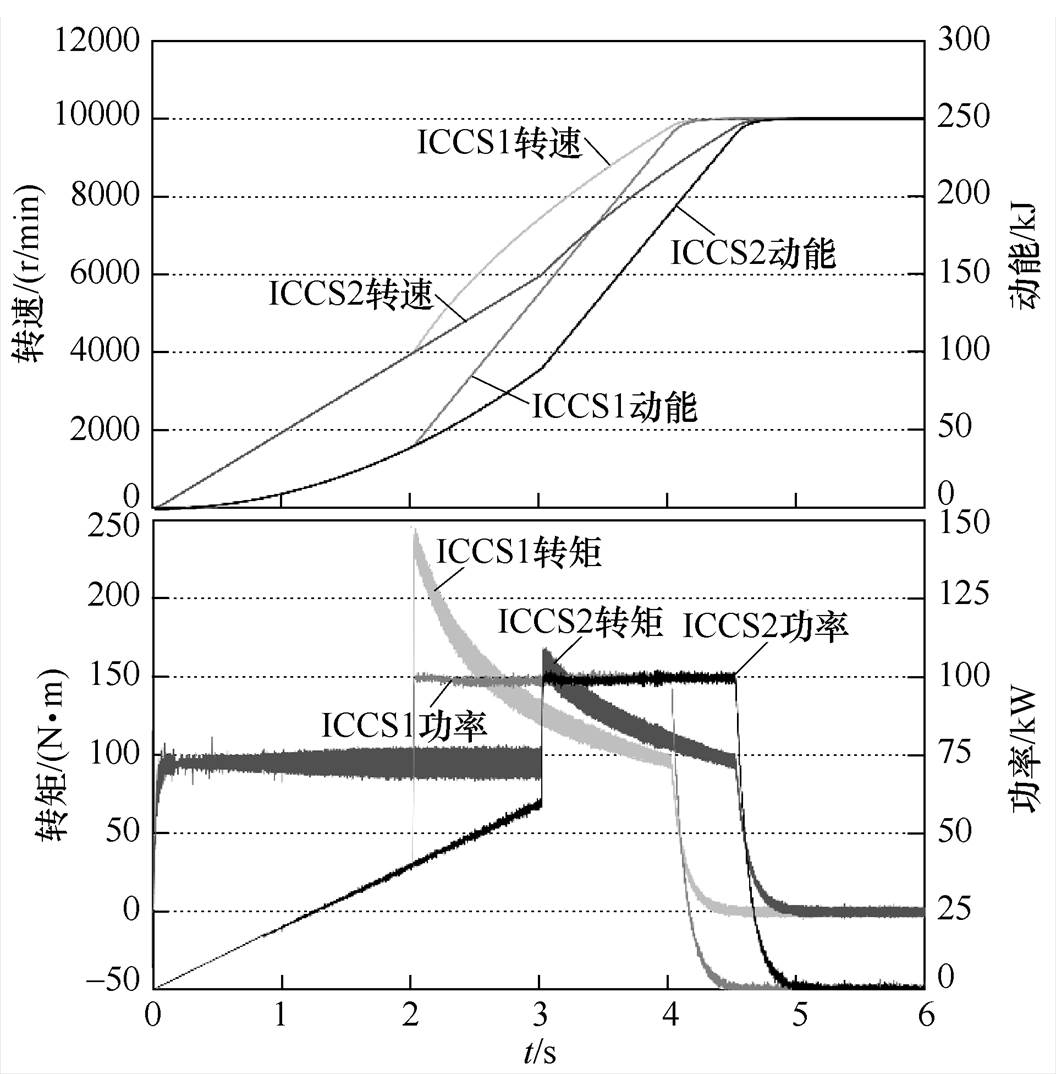
图11 改进充电控制策略下的仿真波形
Fig.11 Simulation waveforms under the improved charging control strategy
图12给出所提充电控制策略下转速、动能、转矩和功率仿真波形。其中，OCCS和OCCS+NDOB从4 000 r/min充电至10 000 r/min的时间分别为2.62 s和2.19 s。OCCS在充电过程中设置转速范围4 000～6 000 r/min为过渡区，从而使恒转矩控制至恒功率控制平滑切换，转矩不再出现跳变；OCCS+ NDOB进一步通过估计电机总损耗功率，并进行前馈补偿，降低了充电时间，提高了储能效率。
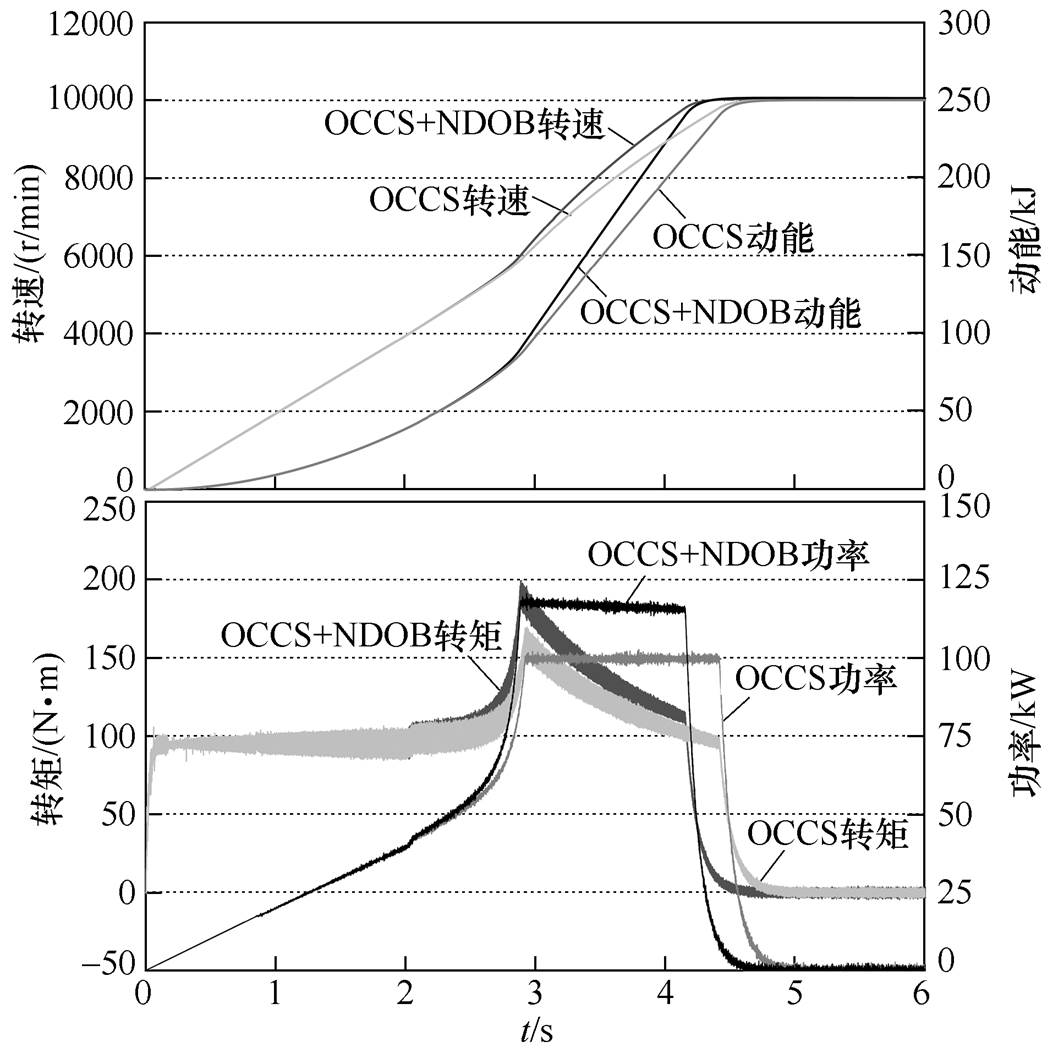
图12 所提充电控制策略下的仿真波形
Fig.12 Simulation waveforms under the proposed charging control strategy
图13为不同充电控制策略下DTP-PMSM的相电流波形对比。OCCS和OCCS+NDOB相比TCCS2，在恒转矩区的相电流更小；相比ICCS1和ICCS2，在切换过程中相电流不存在跳变。可见，相比其他充电控制策略，所提充电控制策略的充电工作特性更佳。
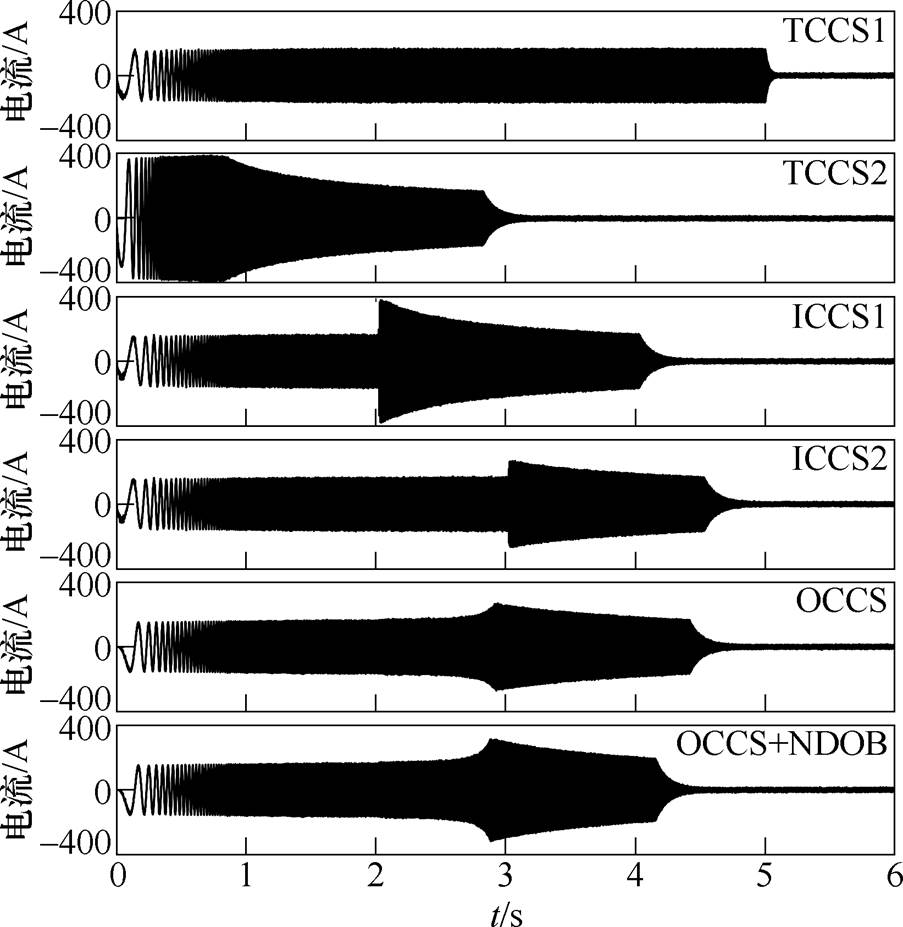
图13 不同充电控制策略下的相电流仿真波形
Fig.13 Simulation waveforms of phase current under different charging control strategies
图14为所提充电控制策略下电机总损耗功率的估计值波形。可以看出，NDOB能够在有限时间内观测跟踪总损耗功率。
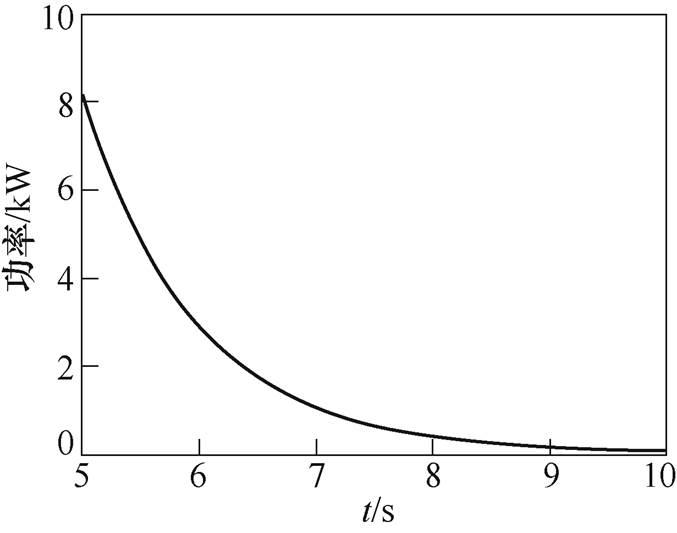
图14 电机总损耗功率观测波形
Fig.14 Total power loss observation of DTP-PMSM
为了验证所提充电控制策略的可行性和实用性，搭建了如图15所示的多相多电平飞轮储能系统实验平台，进行了充电控制实验研究。实验平台中的控制单元采用TMS320F28346（DSP）作为主控芯片，EP3C80F484I7（FPGA）作为逻辑驱动单元，实验参数见表1。
图16为采用不同充电控制策略时，DTP-PMSM的六相电流实验波形。图16a所示TCCS1限制角加速度为20.9 rad/s2，恒转矩控制充电至10 000 r/min，充电过程中的相电流峰峰值为304 A，转矩小导致充电时间长。图16b所示TCCS2在恒转矩区限制角加速度为52.4 rad/s2，在转速达到4 000 r/min后恒功率运行，相电流峰峰值最大为744A。图16c和图16d所示ICCS1和ICCS2在恒转矩区限制角加速度为20.9 rad/s2，分别在转速达到4 000 r/min和6 000 r/min后恒功率运行。图16c虽然在图16b的基础上进行了改进，避免了长时间的大电流，但是在恒转矩控制至恒功率控制切换时存在电流突变，相电流峰峰值最大为720A；图16d虽然相电流峰峰值最大仅为496A，但是充电时间明显增加。图16e在4 000 r/min和6 000 r/min之间加入过渡区，避免了相电流的突变，相电流峰峰值最大为480A，恒转矩控制至恒功率控制的切换更加平滑，但还是牺牲了充电时间。图16f在图16e的基础上加入NDOB估计电机总损耗功率并进行前馈补偿，减少了充电时间，响应速度更快。
图15 实验平台
Fig.15 Experiment platform
图16 不同充电控制策略下相电流的实验波形
Fig.16 Experimental waveforms of phase current under different charging control strategies
不同充电控制策略下电磁转矩的实验波形如图17所示。通过转矩波形对比可知，所提充电控制策略在恒转矩控制至恒功率控制的切换过程中转矩不存在跳变，切换过程更加平滑。OCCS+NDOB转矩最大值为188.5N·m，相比ICCS1的231.3N·m，降低了18.5 %；且充电时间没有明显增加。另外，相比ICCS2和OCCS，OCCS+NDOB的充电时间明显更短，充电效率更高。
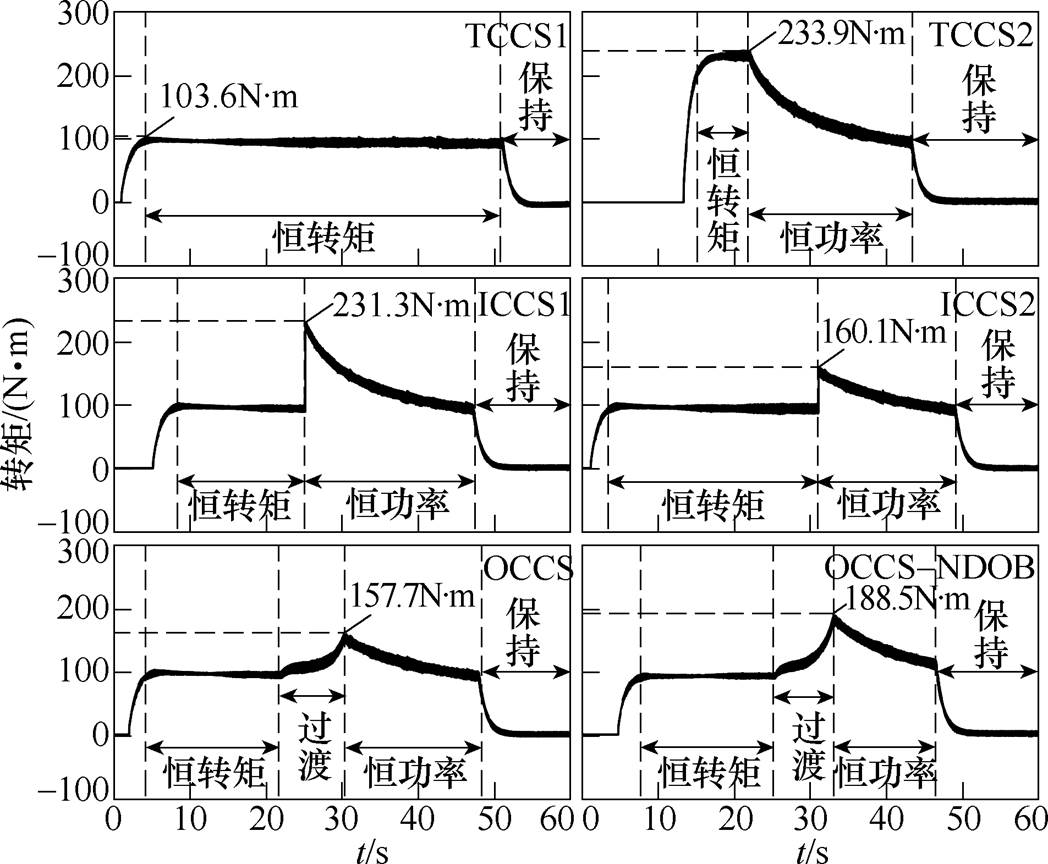
图17 不同充电控制策略下电磁转矩的实验波形
Fig.17 Experimental waveforms of torque under different charging control strategies
不同充电控制策略下转速的实验波形如图18所示。OCCS+NDOB和ICCS1从4 000 r/min充电至10 000 r/min的时间约为21.13 s，而ICCS2和OCCS分别为26.01 s和24.36 s。相比OCCS，OCCS+NDOB的充电时间降低了13.3 %，基本与ICCS1的充电时间一致。因此，虽然过渡区的引入增加了充电时间，但是可以通过NDOB提高充电效率。
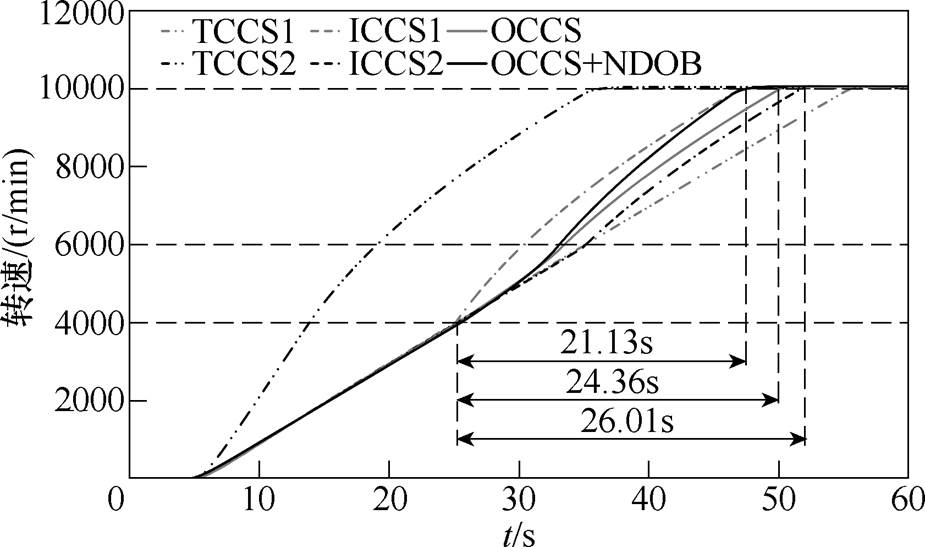
图18 不同充电控制策略下转速的实验波形
Fig.18 Experimental waveforms of speed under different charging control strategies
不同充电控制策略下功率和动能的实验波形如图19所示。由图19a可知，由于电机损耗功率和负载功率的存在，若不采用NDOB进行前馈补偿，恒功率控制阶段的实际功率并没有达到100 kW。实验中NDOB实际观测的总损耗功率为2.15 kW。
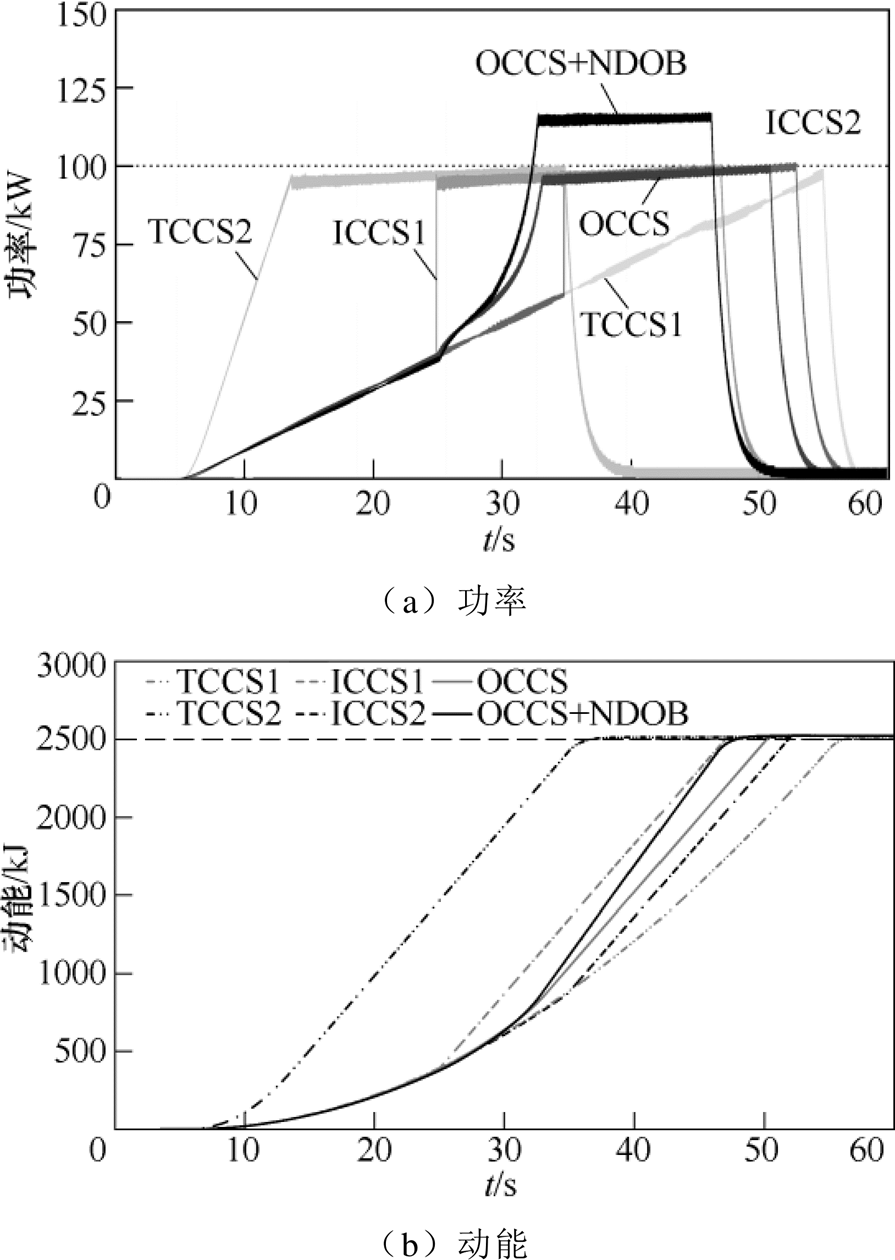
图19 不同充电控制策略下功率、动能的实验波形
Fig.19 Experimental waveforms of power and kinetic energy under different charging control strategies
不同充电控制策略的性能对比见表2，对比指标包括充电电流的峰峰值、最大转矩、充电时间、有无转矩跳变、实际功率是否达到100 kW以及储能效率。对比可知，所提充电控制策略充电电流较小、最大转矩较小、充电时间短、无转矩跳变、实际功率可达到100 kW、储能效率高，具有明显的性能优势。
表2 不同充电控制策略性能对比
Tab.2 Performance comparison of different charging control strategies
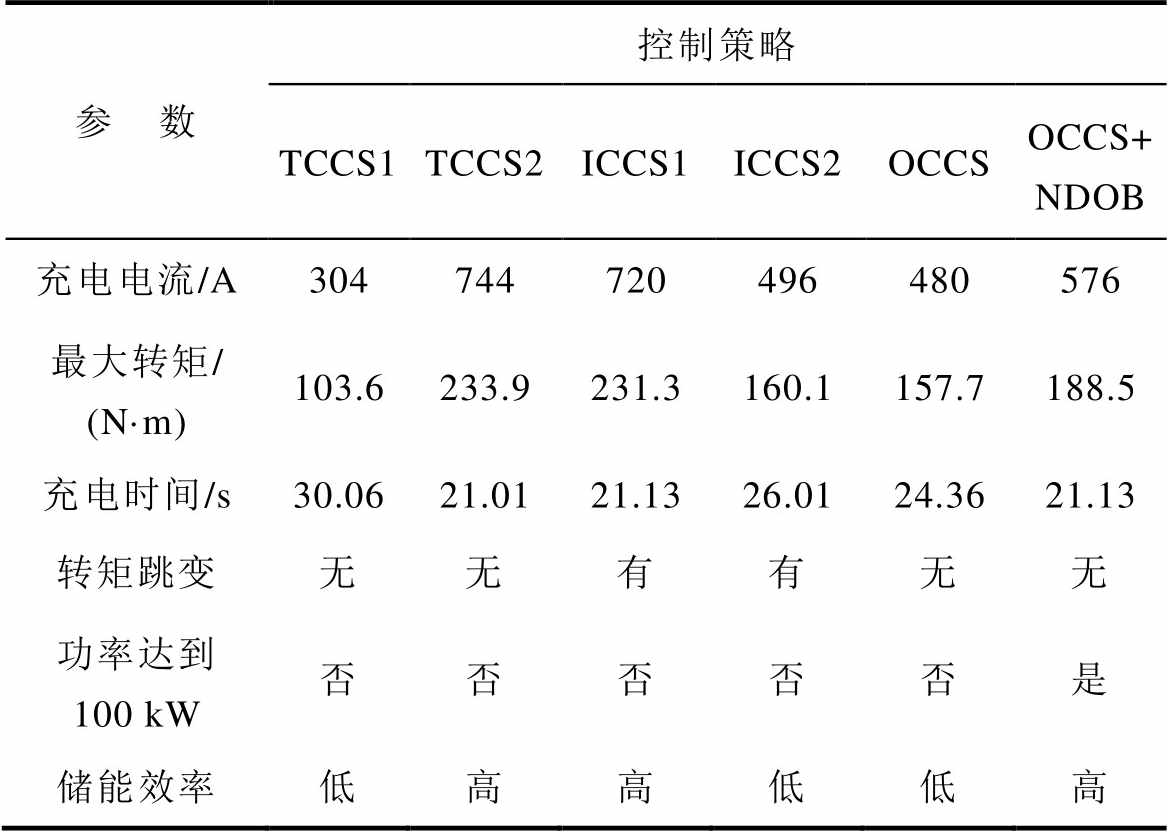
参 数控制策略 TCCS1TCCS2ICCS1ICCS2OCCSOCCS+ NDOB 充电电流/A304744720496480576 最大转矩/ (N·m)103.6233.9231.3160.1157.7188.5 充电时间/s30.0621.0121.1326.0124.3621.13 转矩跳变无无有有无无 功率达到100 kW否否否否否是 储能效率低高高低低高
本文研究和探讨了飞轮储能系统的充电控制问题，以多相多电平飞轮储能系统为研究对象，分析传统充电控制策略的不足，提出了一种基于非线性扰动观测器的优化充电控制策略，基于控制系统稳态、动态和抗扰动性能的要求，给出了一种控制器参数设计方法，并通过仿真和实验对所提策略和方法进行验证，得到如下结论：
1）验证了飞轮储能系统外环采用转速控制和能量控制相结合的方式的可行性，转速环实现恒转矩控制，能量环实现恒功率控制。
2）引入过渡控制环节实现恒转矩控制至恒功率控制的平滑切换，相比传统充电控制策略，设计的恒转矩区-过渡区-恒功率区-保持区的工作模式避免了转矩的跳变。
3）利用NDOB估计电机损耗功率和负载功率并进行前馈补偿控制，提高了系统的抗干扰能力和动态性能，并进一步降低了充电时间。
参考文献
[1] Mousavi G S M, Faraji F, Majazi A, et al. A com- prehensive review of flywheel energy storage system technology[J]. Renewable and Sustainable Energy Reviews, 2017, 67: 477-490.
[2] 张维煜, 朱熀秋. 飞轮储能关键技术及其发展现状[J]. 电工技术学报, 2011, 26(7): 141-146.
Zhang Weiyu, Zhu Huangqiu. Key technologies and development status of flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 141-146.
[3] Tziovani L, Hadjidemetriou L, Charalampous C, et al. Energy management and control of a flywheel storage system for peak shaving applications[J]. IEEE Transa- ctions on Smart Grid, 2021, 12(5): 4195-4207.
[4] 纪锋, 付立军, 王公宝, 等. 舰船综合电力系统飞轮储能控制器设计[J]. 中国电机工程学报, 2015, 35(12): 2952-2959.
Ji Feng, Fu Lijun, Wang Gongbao, et al. Controller design of flywheel energy storage for vessel integrated power systems[J]. Proceedings of the CSEE, 2015, 35(12): 2952-2959.
[5] 隋云任, 梁双印, 黄登超, 等. 飞轮储能辅助燃煤机组调频动态过程仿真研究[J]. 中国电机工程学报, 2020, 40(8): 2597-2606.
Sui Yunren, Liang Shuangyin, Huang Dengchao, et al. Simulation study on frequency modulation process of coal burning plants with auxiliary of flywheel energy storage[J]. Proceedings of the CSEE, 2020, 40(8): 2597-2606.
[6] 李树胜, 付永领, 刘平, 等. 磁悬浮飞轮储能UPS系统集成应用及充放电控制方法研究[J]. 中国电机工程学报, 2017, 37(增刊1): 170-176.
Li Shusheng, Fu Yongling, Liu Ping, et al. Research on integrated application and charging-discharging control method for the magnetically suspended flywheel storage-based UPS system[J]. Proceedings of the CSEE, 2017, 37(S1): 170-176.
[7] 李进, 张钢, 刘志刚, 等. 城轨交通用飞轮储能阵列控制策略[J]. 电工技术学报, 2021, 36(23): 4885- 4895.
Li Jin, Zhang Gang, Liu Zhigang, et al. Control strategy of flywheel energy storage array for urban rail transit[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4885-4895.
[8] 陈云龙, 杨家强, 张翔. 一种计及总损耗功率估计与转速前馈补偿的飞轮储能系统放电控制策略[J]. 中国电机工程学报, 2020, 40(7): 2358-2368, 2414.
Chen Yunlong, Yang Jiaqiang, Zhang Xiang. A discharge strategy for flywheel energy storage systems based on feedforward compensation of observed total dissipative power and rotational speed[J]. Proceedings of the CSEE, 2020, 40(7): 2358-2368, 2414.
[9] Zhang Xiang, Yang Jiaqiang. A robust flywheel energy storage system discharge strategy for wide speed range operation[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 7862-7873.
[10] 王安邦, 姜卫东, 王群京, 等. 转子动能为外环控制量的永磁同步电动机双闭环矢量控制策略[J]. 电工技术学报, 2015, 30(18): 112-120.
Wang Anbang, Jiang Weidong, Wang Qunjing, et al. Dual closed loop vector control strategy for PMSM using rotor kinetic energy as the outer loop controlling parameter[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 112-120.
[11] 刘文军, 周龙, 唐西胜, 等. 基于改进型滑模观测器的飞轮储能系统控制方法[J]. 中国电机工程学报, 2014, 34(1): 71-78.
Liu Wenjun, Zhou Long, Tang Xisheng, et al. Research on FESS control based on the improved sliding-mode observer[J]. Proceedings of the CSEE, 2014, 34(1): 71-78.
[12] 李群湛, 王喜军, 黄小红, 等. 电气化铁路飞轮储能技术研究[J]. 中国电机工程学报, 2019, 39(7): 2025-2033.
Li Qunzhan, Wang Xijun, Huang Xiaohong, et al. Research on flywheel energy storage technology for electrified railway[J]. Proceedings of the CSEE, 2019, 39(7): 2025-2033.
[13] 戴兴建, 姜新建, 王秋楠, 等. 1MW/60MJ飞轮储能系统设计与实验研究[J]. 电工技术学报, 2017, 32(21): 169-175.
Dai Xingjian, Jiang Xinjian, Wang Qiunan, et al. The design and testing of a 1MW/60MJ flywheel energy storage power system[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 169-175.
[14] 刘学, 姜新建, 张超平, 等. 大容量飞轮储能系统优化控制策略[J]. 电工技术学报, 2014, 29(3): 75-82.
Liu Xue, Jiang Xinjian, Zhang Chaoping, et al. Optimization control strategies of large capacity flywheel energy storage system[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 75-82.
[15] Ghanaatian M, Lotfifard S. Control of flywheel energy storage systems in the presence of uncer- tainties[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 36-45.
[16] Chen Wenhua, Yang Jun, Guo Lei, et al. Disturbance- observer-based control and related methods-an over- view[J]. IEEE Transactions on Industrial Electronics, 2015, 63(2): 1083-1095.
[17] 朱进权, 葛琼璇, 王晓新, 等. 基于自抗扰和负载功率前馈的高速磁悬浮系统PWM整流器控制策略[J]. 电工技术学报, 2021, 36(2): 320-329.
Zhu Jinquan, Ge Qiongxuan, Wang Xiaoxin, et al. Control strategy for PWM rectifier of high-speed maglev based on active disturbance rejection control and load power feed-forward[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 320-329.
[18] Hu Yashan, Zhu Zhiqiang, Odavic M. Comparison of two-individual current control and vector space decomposition control for dual three-phase PMSM[J]. IEEE Transactions on Industry Applications, 2017, 53(5): 4483-4492.
[19] 杨金波, 杨贵杰, 李铁才. 双三相永磁同步电机的建模与矢量控制[J]. 电机与控制学报, 2010, 14(6): 1-7.
Yang Jinbo, Yang Guijie, Li Tiecai. Modeling and vector control for dual three-phase PMSM[J]. Electric Machines and Control, 2010, 14(6): 1-7.
[20] 王鹿军, 张书烨, 赵思锋, 等. 基于NPC型三电平变换器的高速磁悬浮飞轮同步载波驱动技术[J/OL]. 电机与控制学报: 1-12[2023-01-06]. http://kns.cnki. net/kcms/detail/23.1408.TM.20220228.0907.002.html.
Wang Lujun, Zhang Shuye, Zhao Sifeng, et al. Synchronous carrier drive technology of high speed magnetic suspension flywheel based on NPC three level converter[J/OL]. Electric Machines and Control: 1-12[2023-01-06]. http://kns.cnki.net/kcms/detail/23. 1408.TM.20220228.0907.002.html.
[21] 曹文远, 韩民晓, 谢文强, 等. 基于扰动观测器的电压源型逆变器负载电流前馈控制及参数设计方法[J]. 电工技术学报, 2020, 35(4): 862-873.
Cao Wenyuan, Han Minxiao, Xie Wenqiang, et al. A disturbance-observer-based load current feedforward control and parameter design method for voltage- sourced inverter[J]. Transactions of China Electro- technical Society, 2020, 35(4): 862-873.
[22] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[23] 鲍旭聪, 王晓琳, 顾聪, 等. 超高速永磁电机驱动系统电流环稳定性分析与改进设计[J]. 电工技术学报, 2022, 37(10): 2469-2480.
Bao Xucong, Wang Xiaolin, Gu Cong, et al. Stability analysis and improvement design of current loop of ultra-high-speed permanent magnet motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2469-2480.
[24] Briz F, Degner M W, Lorenz R D. Analysis and design of current regulators using complex vectors[J]. IEEE Transactions on Industry Applications, 2000, 36(3): 817-825.
[25] 余晨辉, 汪凤翔, 林贵应. 基于在线扰动补偿的三电平PWM整流器级联式无差拍控制策略[J]. 电工技术学报, 2022, 37(4): 954-963.
Yu Chenhui, Wang Fengxiang, Lin Guiying. Cas- caded deadbeat control strategy with online dis- turbance compensation for three-level PWM recti- fier[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 954-963.
[26] 吴为, 丁信忠, 严彩忠. 基于复矢量的电流环解耦控制方法研究[J]. 中国电机工程学报, 2017, 37(14): 4184-4191, 4298.
Wu Wei, Ding Xinzhong, Yan Caizhong. Research on control method of current loop decoupling based on complex vector[J]. Proceedings of the CSEE, 2017, 37(14): 4184-4191, 4298.
Abstract The operating mode of the flywheel energy storage system (FESS) requires the flywheel to be charged reliably in the shortest time. The traditional charging control strategy adopts vector control with the speed loop or voltage loop as the outer loop, which has low charging efficiency and poor dynamic performance. Moreover, it is separate from the operating mode of FESS, which cannot realize the energy control and speed stability of the flywheel motor at the same time. The traditional implementation of the operating mode of FESS needs to be more flexible, and the electromagnetic torque will jump, which affects the system’s stability. Besides, the power loss and load power of the flywheel motor can cause the charging power to drop and affect the system’s robustness. Therefore, this paper proposes an optimized charging control strategy (OCCS) based on a nonlinear disturbance observer (NDOB).
Firstly, the outer loop adopts the combination of speed control and energy control, the speed loop realizes constant torque control, and the energy loop uses flywheel kinetic energy as a control variable to realize constant power control. Secondly, the transition control unit is proposed to realize the smooth switching between constant torque control and constant power control. Thirdly, the NDOB estimates motor power loss and load power to perform feedforward compensation. Moreover, the transfer function of the energy-current double closed-loop system considering NDOB is derived. Finally, based on the steady-state, dynamic, and anti-disturbance performance requirements of the control system, a controller parameter design method is given.
The experimental results show that in the charging process, the maximum peak-to-peak value of phase currents of OCCS is 480 A. The sudden change of the phase currents is avoided, but the charging time is still sacrificed. OCCS+NDOB applies the NDOB to estimate motor power loss and load power, reducing the charging time. The proposed charging control strategy has no torque jump in the switching process from constant torque control to constant power control, and the switching process is smooth. The maximum torque of OCCS+NDOB is 188.5 N·m, which is 18.5 % lower than 231.3 N·m of the improved charge control strategy 1 (ICCS1). In addition, compared with the improved charge control strategy 2 (ICCS2) and OCCS, OCCS+NDOB has significantly shorter charging time and higher charging efficiency. The charging time of OCCS+NDOB from 4 000 r/min to 10 000 r/min is about 21.13 s, which is consistent with ICCS1, while the charging times of ICCS2 and OCCS are 26.01 s and 24.36 s, respectively. Compared with OCCS, the charging time of OCCS+NDOB is reduced by 13.3 %. Therefore, although introducing a transition control unit increases the charging time, the charging efficiency can be improved by NDOB. In the constant power control unit, the actual power of OCCS+NDOB can reach 100 kW, while other strategies cannot reach 100 kW due to the motor power loss and load power. The total power loss observed by NDOB in the experiment is 2.15 kW.
The conclusions can be drawn as follows: (1) the feasibility of combining speed control and energy control in the outer loop of FESS is verified. The speed loop realizes constant torque control, and the energy loop realizes constant power control. (2) The transition control unit is introduced to realize the smooth switching from constant torque control to constant power control, and the jump of electromagnetic torque is avoided. (3) The NDOB is used to estimate the motor power loss and load power, and the feedforward compensation control is carried out, which improves the anti-disturbance ability and dynamic performance of the system, further reducing the charging time.
keywords：Flywheel energy storage system, optimized charging control, energy control, transition control, nonlinear disturbance observer
DOI: 10.19595/j.cnki.1000-6753.tces.221360
中图分类号：TM464
国家自然科学基金资助项目（52077219, 51807199）。
收稿日期 2022-07-16
改稿日期 2022-09-08
李忠瑞 男，1997年生，博士研究生，研究方向为多电平逆变器和多相电机控制技术。E-mail: lzrui@zju.edu.cn
艾 胜 男，1985年生，副研究员，研究方向为电力电子与电力传动。E-mail: ai__sheng@163.com（通信作者）
（编辑 崔文静）