 (1)
(1)
摘要 针对城市轨道交通高转矩永磁同步牵引电机因参数摄动和未知扰动等不确定因素造成控制性能下降的现象,提出一种基于扩展非奇异终端滑模扰动观测器的转速环新型无模型非奇异快速终端滑模控制方法。首先,依据永磁同步牵引电机在参数摄动和未知扰动下的数学模型,使用转速环的输入输出建立新型超局部模型。其次,基于新型超局部模型设计转速环的无模型非奇异快速终端滑模控制器;同时结合高阶滑模和非奇异终端滑模设计观测器来实时精准估计新型超局部模型的未知部分,通过对控制器进行前馈补偿,增强了系统的鲁棒性,提高了转速的控制精度,并减少了系统抖振。最后,通过与PI控制、无模型滑模控制进行仿真和实验综合比较,验证了所提出的控制算法对电机参数摄动和未知扰动具有较强的容错性和抗干扰性,能降低对电机精准数学模型的依赖。
关键词:高转矩永磁同步牵引电机 新型超局部模型 无模型非奇异快速终端滑模控制 扩展非奇异终端滑模扰动观测器
永磁同步牵引系统因功率密度高、过载能力强、动态转矩快等优势,已广泛应用在高速列车、城市轨道交通、矿用机车等相关领域[1-3]。与磁阻电机相比,牵引系统中的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)拥有更低的转矩脉动和噪声。经典磁场定向控制使用转速外环-电流内环的双PI闭环控制,在永磁同步牵引系统获得较好的控制效果。然而,PMSM在复杂牵引工况下容易受到未知扰动、参数摄动(如定子电阻变化、定子电感变化、永磁体失磁、转动惯量变化、黏滞摩擦系数变化)等不确定因素影响,采用传统PI控制难以抑制扰动,电机整体控制性能下降,在高性能应用场合无法达到令人满意的控制效果[4]。
针对PMSM在高性能应用场合的控制要求,许多先进控制方法被广泛应用,如预测控制[5-7]、反演控制[8]、鲁棒控制[9]、状态反馈控制[10]、自适应控制[11]、滑模控制(Sliding Mode Control, SMC)[12-13]。其中,SMC因为算法简单、对外部干扰的强鲁棒性而备受关注。传统SMC采用切换控制律改变驱动系统的动态特性,对系统参数变化不敏感,能保持快速动态响应。相比传统线性滑模渐进收敛的特点,终端滑模(Terminal Sliding Mode, TSM)可以实现有限时间收敛,但存在奇异现象[14];积分滑模方法能加快收敛速度,但系统抖振较大,而非奇异快速终端滑模(Non-singular Fast Terminal Sliding Mode, NFTSM)不仅消除了TSM存在的奇异现象,还实现了受控系统在有限时间内快速收敛[15]。文献[16]提出一种将自适应算法和NFTSM结合的控制策略,采用自适应律来降低未知扰动对系统的影响,加快了系统收敛速度,但设计策略过于复杂,难以在工程中实现。文献[17]提出一种基于干扰观测器的NFTSM控制方法,在保证系统跟踪精度的同时,也提升了系统抗干扰能力,但观测器的高增益会导致系统出现振荡和超调。虽然文献[16-17]提出的滑模控制方法对内外扰动具有一定的鲁棒性,但对电机数学模型有强依赖性,而实际运行过程中会不可避免地发生参数摄动和未知干扰[18]。
与基于模型的SMC方法相比,M. Fliess等提出的无模型控制(Model-Free Control, MFC)方法根据系统输入和输出建立超局部模型,降低了对系统具体数学模型的依赖,避免了参数不确定性、未知扰动和未建模动态对电机控制性能的影响[19]。A. Safaei等在传统超局部模型基础上,提出了一种新型超局部模型,分离出了系统已知部分,使无模型控制器的设计得到进一步简化[20]。文献[21]将MFC和非奇异终端滑模(Non-singular Terminal Sliding Mode, NTSM)结合,提出了一种新型无模型滑模控制方法,实现了PMSM在失磁故障下容错控制,但未考虑电机其他参数变化对系统的影响。文献[22]提出一种有限集无模型容错预测控制算法,有效抑制了电机参数摄动和失磁故障情况下的系统扰动,但系统跟踪精度需要提高。
国内外学者为提高MFC算法的动态控制性能,采用滑模观测器(Sliding Mode Observer, SMO)估计超局部模型的未知部分[23-25]。SMO是一种具有强鲁棒性、易于工程实现的非线性观测器,能在一定程度上抑制未知扰动和参数摄动造成的影响。文献[23]采用传统滑模观测器估计超局部模型的未知部分,通过前馈补偿有效抑制了参数摄动,但无法避免传统滑模观测器因高增益造成的抖振。文献[24]基于有限集预测控制设计了一种积分滑模观测器来估计超局部模型的未知部分,有效提升了控制系统的抗干扰能力,但无法避免相位延迟。文献[25]采用扩展滑模扰动观测器估计超局部模型的未知部分,有效抑制参数摄动下的电流脉动,提升了控制系统的鲁棒性。
为了提升城市轨道交通高转矩永磁同步牵引电机在参数摄动和未知扰动情况下的抗干扰能力和鲁棒性,本文提出一种基于扩展非奇异终端滑模扰动观测器(Extended Nonsingular Terminal Sliding Mode Disturbance Observer, ENTSMDO)的新型无模型非奇异快速终端滑模控制(Model-Free Non- singular Fast Terminal Sliding Mode Control, MFNFTSMC)方法。该方法基于PMSM转速环的新型超局部模型,将MFC和NFTSM结合设计无模型非奇异快速终端滑模控制器;同时结合高阶滑模和NTSM的优点设计ENTSMDO实时精准估计新型超局部模型的未知部分,通过对控制器进行前馈补偿,有效提高了电机控制系统的鲁棒性和抗干扰能力,降低了对电机精准数学模型依赖,实现了PMSM在参数摄动和未知扰动下的容错控制。最后,通过仿真和半实物实验,与PI控制和无模型滑模控制(Model-Free Sliding Mode Control, MFSMC)算法进行综合对比,验证了所提控制算法的有效性和优越性。
假设忽略铁心损耗,不计永磁体的磁滞和涡流损耗,不考虑参数摄动时,同步旋转dq轴坐标系下PMSM的定子电压方程为
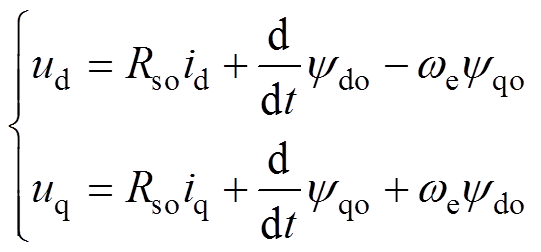 (1)
(1)
其中,定子磁链方程为
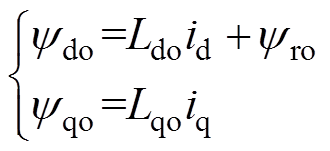 (2)
(2)
式中, 、
、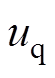 分别为定子d、q轴电压分量;
分别为定子d、q轴电压分量;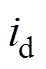 、
、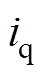 分别为定子d、q轴电流分量;
分别为定子d、q轴电流分量;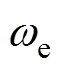 为电角速度;
为电角速度;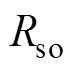 为相绕组电阻的标称值;
为相绕组电阻的标称值;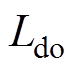 、
、 分别为定子绕组d、q轴电感的标称值;
分别为定子绕组d、q轴电感的标称值; 为转子磁链的标称值;
为转子磁链的标称值;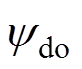 、
、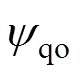 分别为定子在标称参数下的d、q轴定子磁链分量。
分别为定子在标称参数下的d、q轴定子磁链分量。
PMSM在复杂牵引工况中,受高温、机械应力等因素的影响,电磁参数(电阻、电感)和机械参数(转动惯量、黏滞摩擦系数)等内部参数会出现摄动。考虑电磁参数摄动影响,可得PMSM的数学模型为
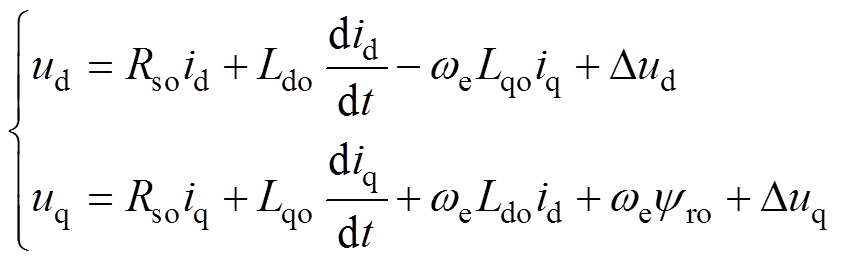 (3)
(3)
式中,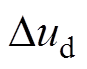 、
、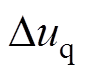 分别为电机电阻、电感参数摄动变化引起的d、q轴电压扰动量。
分别为电机电阻、电感参数摄动变化引起的d、q轴电压扰动量。
当发生电磁参数摄动时,PMSM电磁转矩方程为
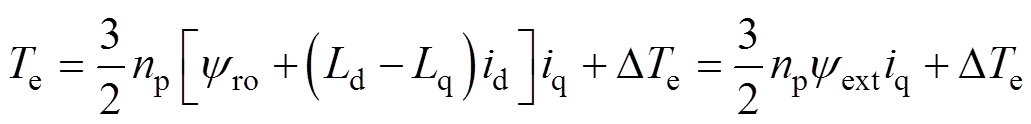 (4)
(4)
其中
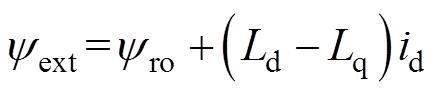
式中,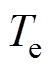 为PMSM输出的电磁转矩;
为PMSM输出的电磁转矩;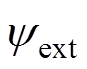 为有效磁链[26];
为有效磁链[26];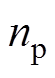 为极对数;
为极对数; 为电磁转矩的摄动量。
为电磁转矩的摄动量。
PMSM的机械运动方程为
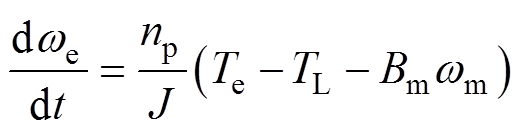 (5)
(5)
式中,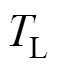 为负载转矩;
为负载转矩;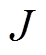 为转动惯量;
为转动惯量;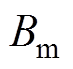 为黏滞摩擦系数;
为黏滞摩擦系数;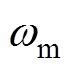 为机械角速度。
为机械角速度。
当考虑机械参数摄动时,PMSM机械运动方程为
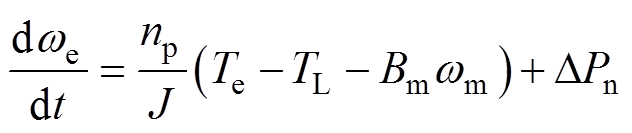 (6)
(6)
式中,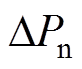 为转动惯量和黏滞摩擦系数变化引起的扰动量。
为转动惯量和黏滞摩擦系数变化引起的扰动量。
当考虑电磁参数、机械参数摄动和未知扰动时,由式(4)和式(6)可得PMSM的转速环状态方程为
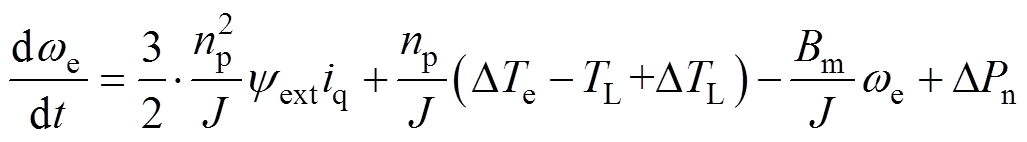 (7)
(7)
式中,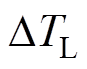 为负载转矩的未知扰动。
为负载转矩的未知扰动。
为实现永磁同步牵引电机在参数摄动和未知扰动下的高性能控制,本节将MFC和NFTSM结合,提出一种MFNFTSMC策略,并应用于转速环控制器的设计。其中,无模型控制减少对电机精准数学模型的依赖,非奇异快速终端滑模降低传统滑模固有抖振和实现系统有限时间收敛。
在单输入单输出的控制系统中,建立一阶非线性超局部模型为
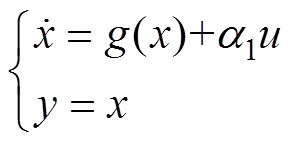 (8)
(8)
式中,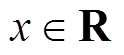 为控制系统的状态变量;y、u分别为系统输出和控制输入;
为控制系统的状态变量;y、u分别为系统输出和控制输入;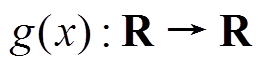 为未知非线性有界函数,满足Lipschitz有界,且只取决于x;
为未知非线性有界函数,满足Lipschitz有界,且只取决于x;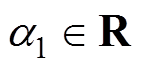 为一个待确定的非物理常数增益。
为一个待确定的非物理常数增益。
基于PMSM转速环状态方程式(7)和超局部模型式(8),可建立转速环传统超局部模型为
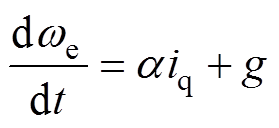 (9)
(9)
式中,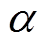 为待设计参数;g为系统已知部分和未知扰动部分,满足Lipschitz有界条件。
为待设计参数;g为系统已知部分和未知扰动部分,满足Lipschitz有界条件。
依据新型超局部模型,将式(8)中的g(x)进一步表示[20]为
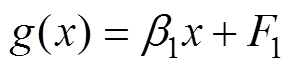 (10)
(10)
式中,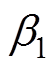 为控制系统状态增益;F1为未知非线性部分,满足Lebesgue可测量性和Lipschitz有界性。由式(10)可知,g(x)被分解成非线性未知扰动部分和线性系统状态部分。
为控制系统状态增益;F1为未知非线性部分,满足Lebesgue可测量性和Lipschitz有界性。由式(10)可知,g(x)被分解成非线性未知扰动部分和线性系统状态部分。
把式(10)代入式(8),可得新型超局部模型为
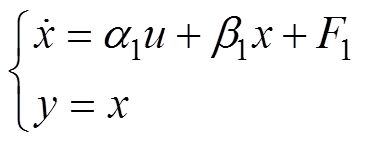 (11)
(11)
根据PMSM转速环状态方程式(7)和新型超局部模型式(11),并将新型超局部模型中的未知非线性部分扩展成状态变量,可设计转速环扩展新型超局部模型为
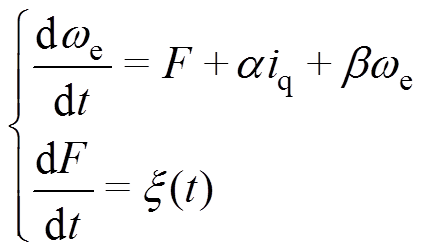 (12)
(12)
式中,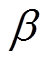 为待设计参数;F为系统已知部分和未知扰动部分,满足Lipschitz有界条件;
为待设计参数;F为系统已知部分和未知扰动部分,满足Lipschitz有界条件;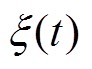 为F的变化率。
为F的变化率。
结合无模型控制和滑模控制理论,基于式(12)的转速环新型超局部模型,设计转速环无模型滑模控制器为
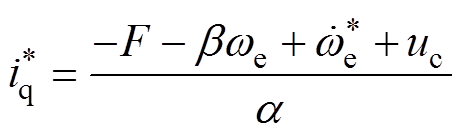 (13)
(13)
式中,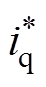 为给定的q轴电流分量;
为给定的q轴电流分量;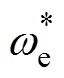 为系统给定转速;
为系统给定转速;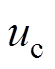 为反馈控制器控制输出。
为反馈控制器控制输出。
定义转速给定值和实际值误差为
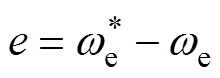 (14)
(14)
联合式(12)~式(14)可得
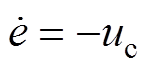 (15)
(15)
引入状态量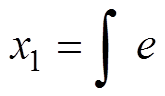 ,
,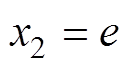 ,可得状态方程
,可得状态方程
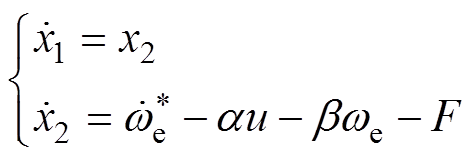 (16)
(16)
针对状态方程式(16),为了有效减小稳态误差,选用二阶的非奇异快速终端滑模面[15]为
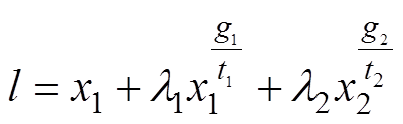 (17)
(17)
式中,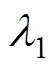 、
、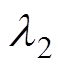 均为大于零的待设计常数;
均为大于零的待设计常数;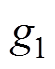 、
、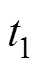 、
、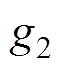 、
、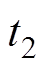 均为待设计的奇常数,其中
均为待设计的奇常数,其中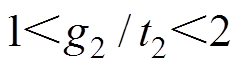 ,
,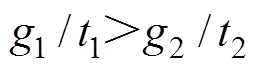 。
。
对式(17)求导,有
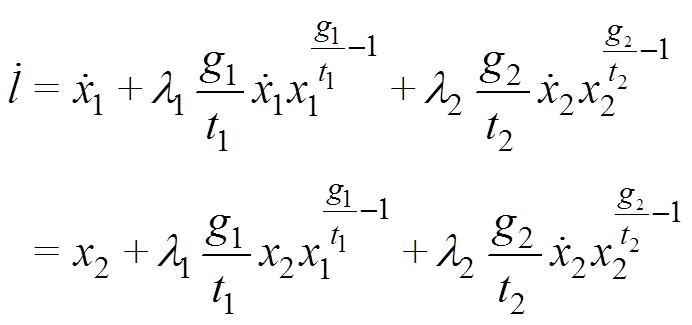 (18)
(18)
在选取式(17)的NFTSM面后,为确保状态变量保持在滑模面 上,由
上,由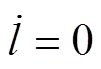 可得等效控制律
可得等效控制律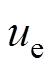 为
为
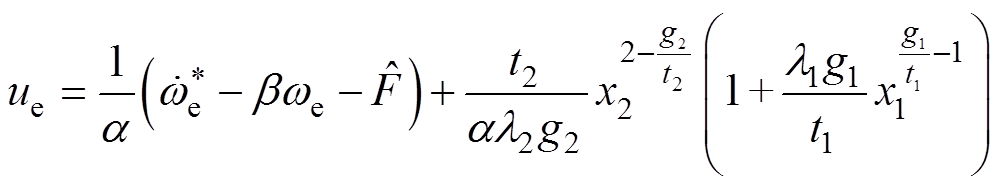 (19)
(19)
为使状态变量快速达到NFTSM面上,设计切换控制律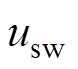 为
为
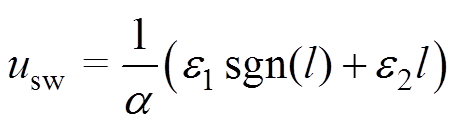 (20)
(20)
式中,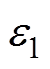 和
和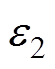 均为待设计的正常数。
均为待设计的正常数。
定理1:对于状态方程式(16),选取等效控制律式(19)和切换控制律式(20),设计转速环新型无模型滑模控制律为
 (21)
(21)
则状态误差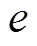 将有限时间收敛。
将有限时间收敛。
证明:选取如下Lyapunov函数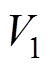 为
为
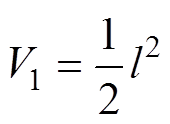 (22)
(22)
对式(22)求导,联合式(18)和式(21),得
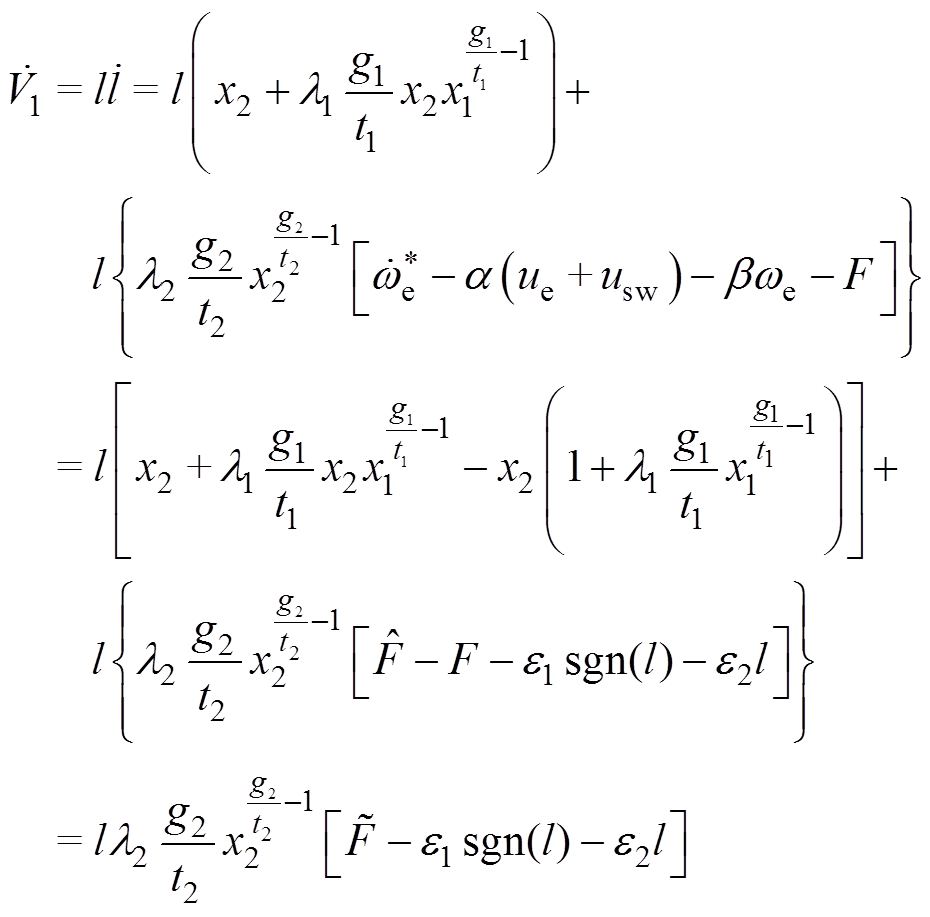
 (23)
(23)
式中,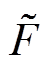 为扰动观测误差,
为扰动观测误差, ,且为有界量。其中,
,且为有界量。其中,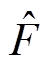 为
为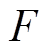 观测值,如果未知扰动的观测足够准确,
观测值,如果未知扰动的观测足够准确, 。
。
由于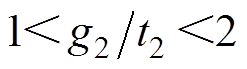 ,则
,则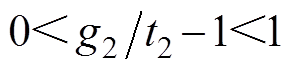 ;由于
;由于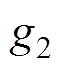 ,
, 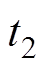 (
(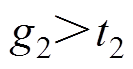 )为正奇数,则
)为正奇数,则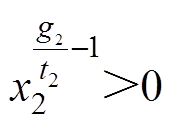 。当取
。当取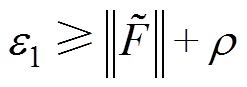
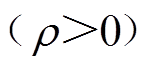 时,可得
时,可得
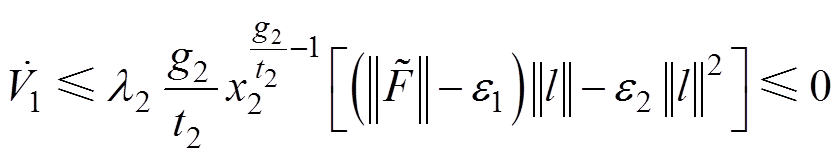 (24)
(24)
根据Lyapunov稳定性判别定理和LaSalle不变性原理,可知状态变量将会沿着滑模面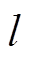 在有限时间内收敛到零,所设计的控制器达到稳定条件。
在有限时间内收敛到零,所设计的控制器达到稳定条件。
基于ENTSMDO的MFNFTSMC算法框图如图1所示。
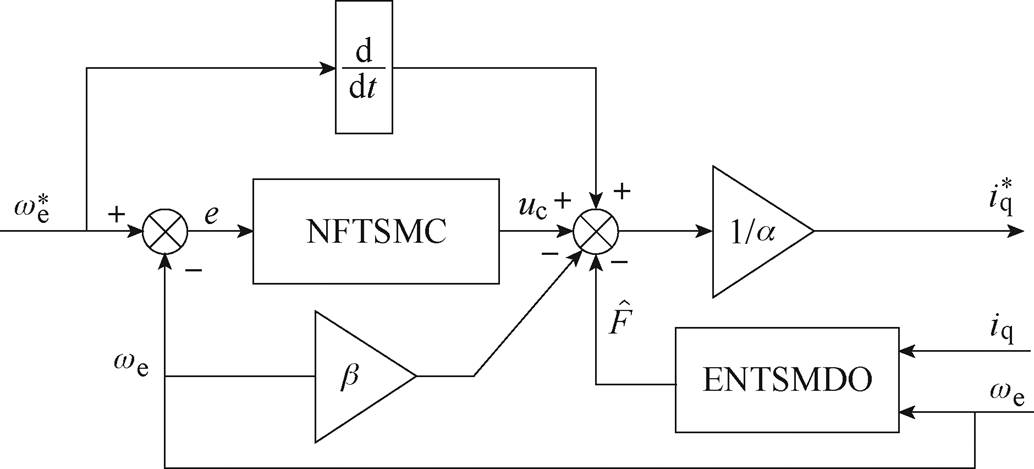
图1 基于ENTSMDO的MFNFTSMC算法框图
Fig.1 Block diagram of the ENTSMDO-based MFNFTSMC algorithm
本节结合高阶滑模和非奇异终端滑模的优点设计ENTSMDO实时精准估计新型超局部模型的未知部分,并通过对控制器进行前馈补偿,提高了系统的鲁棒性和抗干扰能力。
对式(12)描述的扩展新型超局部模型构造如下观测器
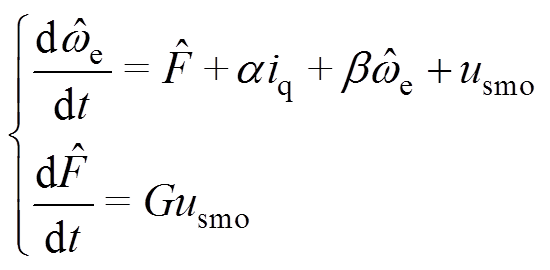 (25)
(25)
式中,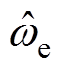 为转速
为转速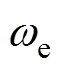 观测值;
观测值;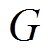 为滑模系数;
为滑模系数;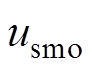 为滑模控制律。
为滑模控制律。
联合式(12)和式(25),可得观测器的误差动态方程为
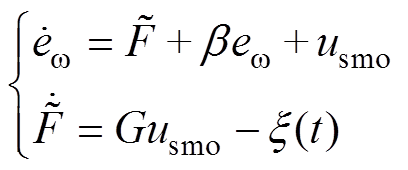 (26)
(26)
其中
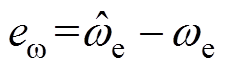
式中,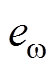 为转速观测误差。
为转速观测误差。
选取转速观测误差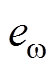 为状态变量,选取非奇异终端面[27]为
为状态变量,选取非奇异终端面[27]为
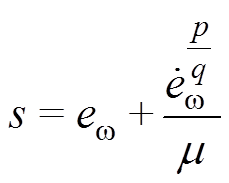 (27)
(27)
式中,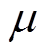 为大于零的常数;
为大于零的常数;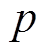 、
、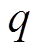 均为奇数,且
均为奇数,且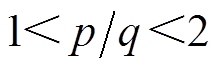 。
。
对式(27)求导,可得
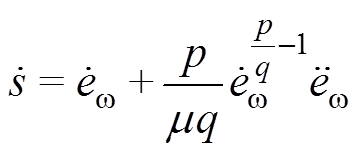 (28)
(28)
为有效抑制抖振并减少收敛时间,选取双幂次趋近律[28-29]为
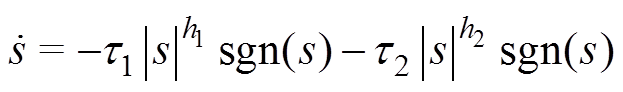 (29)
(29)
式中,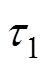 和
和 均为待设计的正常数;
均为待设计的正常数;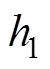 和
和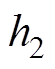 为满足
为满足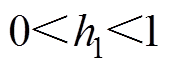 和
和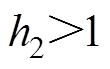 条件的待设计的正常数。
条件的待设计的正常数。
定理2:对于式(26)的误差动态方程,选取非奇异终端滑模面式(27)和双幂次趋近律式(29),为ENTSMDO设计控制律[30]为
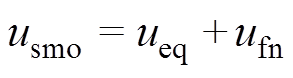 (30)
(30)
其中
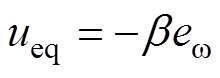
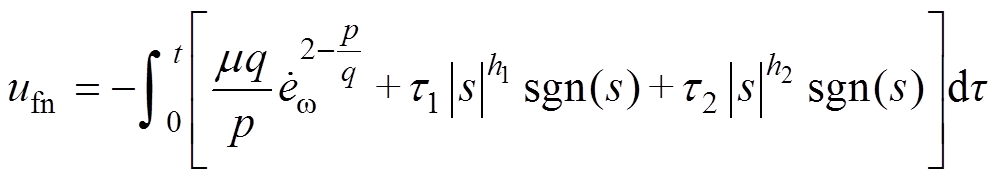
则系统误差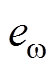 在有限时间内收敛到零。
在有限时间内收敛到零。
证明:选取如下Lyapunov函数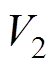 为
为
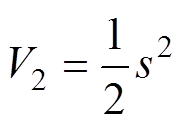 (31)
(31)
对式(31)求导,并将式(28)代入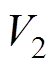 ,有
,有
 (32)
(32)
将ENTDSMO控制律式(30)代入状态误差方程式(26)可得
 (33)
(33)
对式(33)求导可得
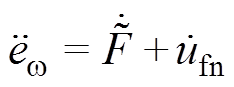 (34)
(34)
联合式(30)、式(32)、式(34),可得
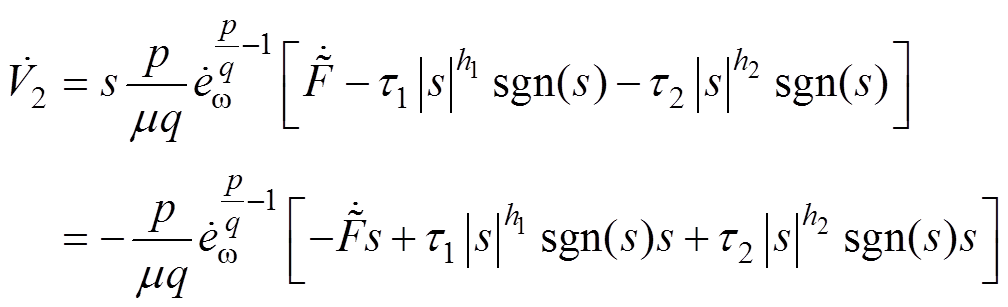
 (35)
(35)
因为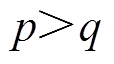 ,所以
,所以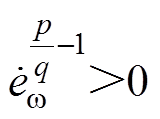 ,可以将式(35)转化为两个形式
,可以将式(35)转化为两个形式
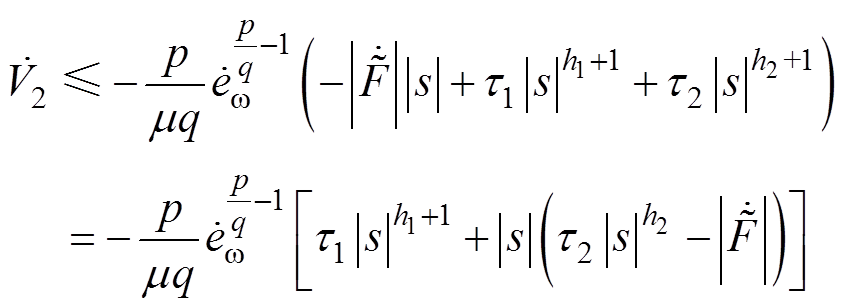 (36)
(36)
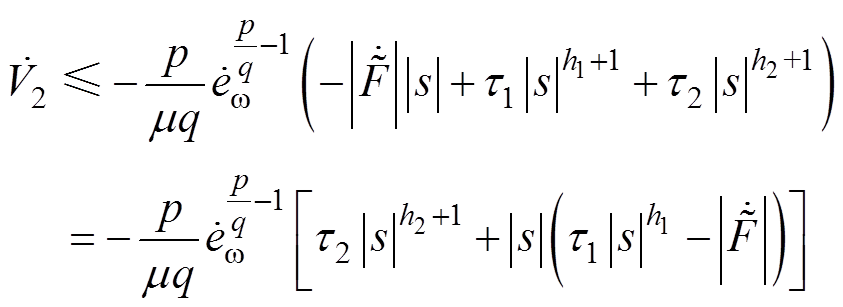 (37)
(37)
假设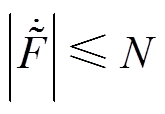 ,
,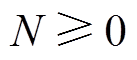 ,当
,当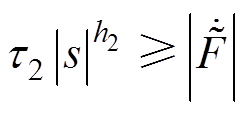 时,可得
时,可得
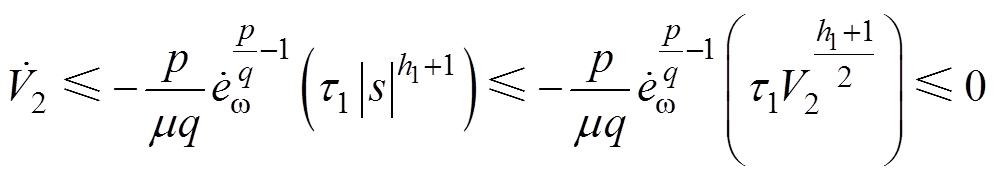 (38)
(38)
当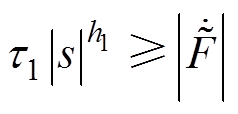 时,可得
时,可得
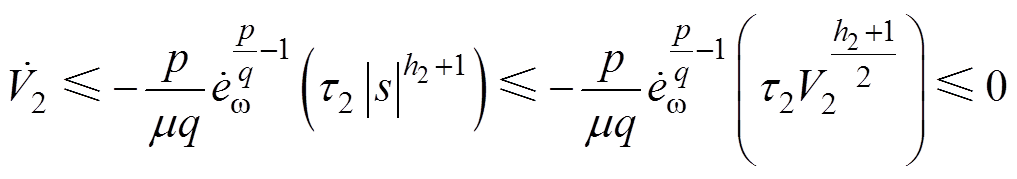 (39)
(39)
根据Lyapunov稳定性定理和比较引理[31],可知系统将满足滑模可达条件,并将在有限的时间内收敛并保持在NTSM面上,从而使系统误差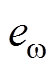 在有限时间内收敛到零。
在有限时间内收敛到零。
由式(36)可得
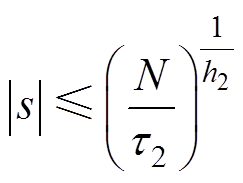 (40)
(40)
同理,由式(37)可得
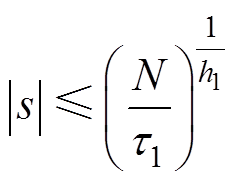 (41)
(41)
由式(40)和式(41)可得滑模面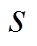 的收敛区域为
的收敛区域为
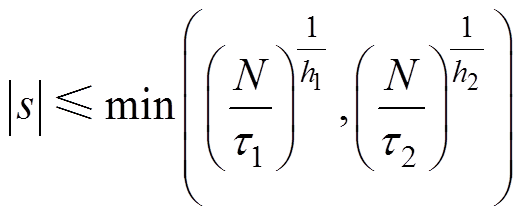 (42)
(42)
根据式(29)可得
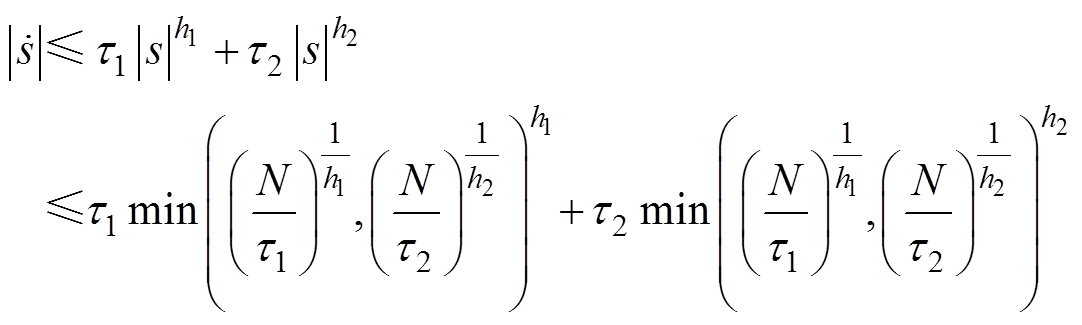
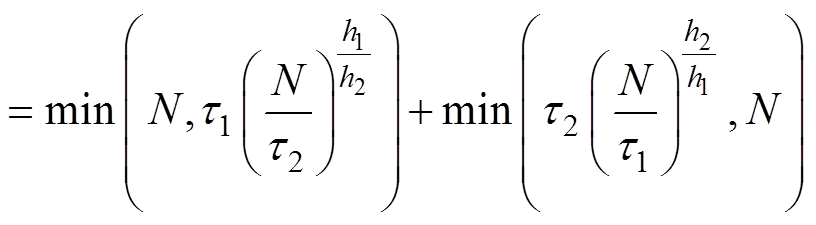 (43)
(43)
假设 为滑模面
为滑模面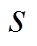 从初始值到滑模面
从初始值到滑模面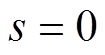 的收敛时间,经
的收敛时间,经 后系统进入终端滑模面,并且在
后系统进入终端滑模面,并且在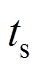 之后收敛到0,总收敛时间[27]为
之后收敛到0,总收敛时间[27]为
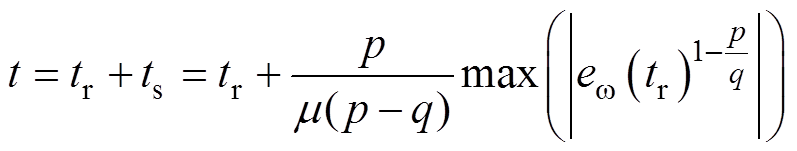 (44)
(44)
为了有效降低滑模抖振,采用饱和函数 替代符号函数,
替代符号函数, 函数为
函数为
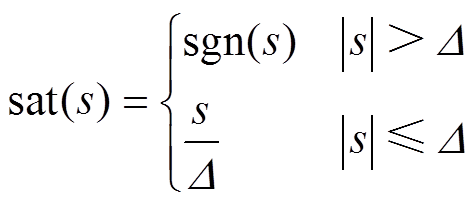 (45)
(45)
式中,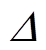 为边界层值。
为边界层值。
本文设计的基于ENTSMDO的MFNFTSMC系统框图如图2所示。控制流程如下:首先依据新型超局部模型式(11)设计转速环无模型非奇异快速终端滑模控制器;同时结合非奇异终端滑模和高阶滑模设计ENTSMDO实时精准估计新型超局部模型的未知部分,并通过对控制器的前馈补偿来实现PMSM在参数摄动和未知扰动下的容错控制。

图2 基于ENTSMDO的MFNFTSMC系统框图
Fig.2 Block diagram of the MFNFTSMC based on ENTSMD system
为了验证算法的有效性和可行性,在Matlab/ Simulink(2021b)平台搭建文中提出的基于ENTSMDO的MFNFTSMC算法,并与PI控制和无模型滑模控制[23]进行比较。电机选用长沙地铁1号线的永磁同步牵引电机,采用最大转矩电流比(Maximum Torque Per Ampere, MTPA)控制策略。标称参数见表1,直流侧电压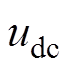 =1 500 V,采样时间为10ms。表2为三种控制方法的控制参数。
=1 500 V,采样时间为10ms。表2为三种控制方法的控制参数。
MFSMC算法中控制器选择滑模面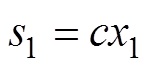 和指数趋近律
和指数趋近律 ,其中,
,其中,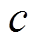 、
、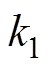 和
和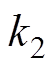 均为大于零的待设计常数;滑模观测器系数为
均为大于零的待设计常数;滑模观测器系数为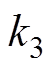 ;
;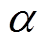 、
、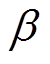 通过
通过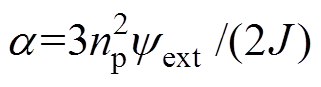 和
和 整定;PI参数整定:电流环PI参数先按Ⅰ型系统整定,再将电流环等效成转速环中的环节,最后转速环PI参数按Ⅱ型系统进行校正微调。
整定;PI参数整定:电流环PI参数先按Ⅰ型系统整定,再将电流环等效成转速环中的环节,最后转速环PI参数按Ⅱ型系统进行校正微调。
表1 PMSM标称参数
Tab.1 Nominal parameters of PMSM
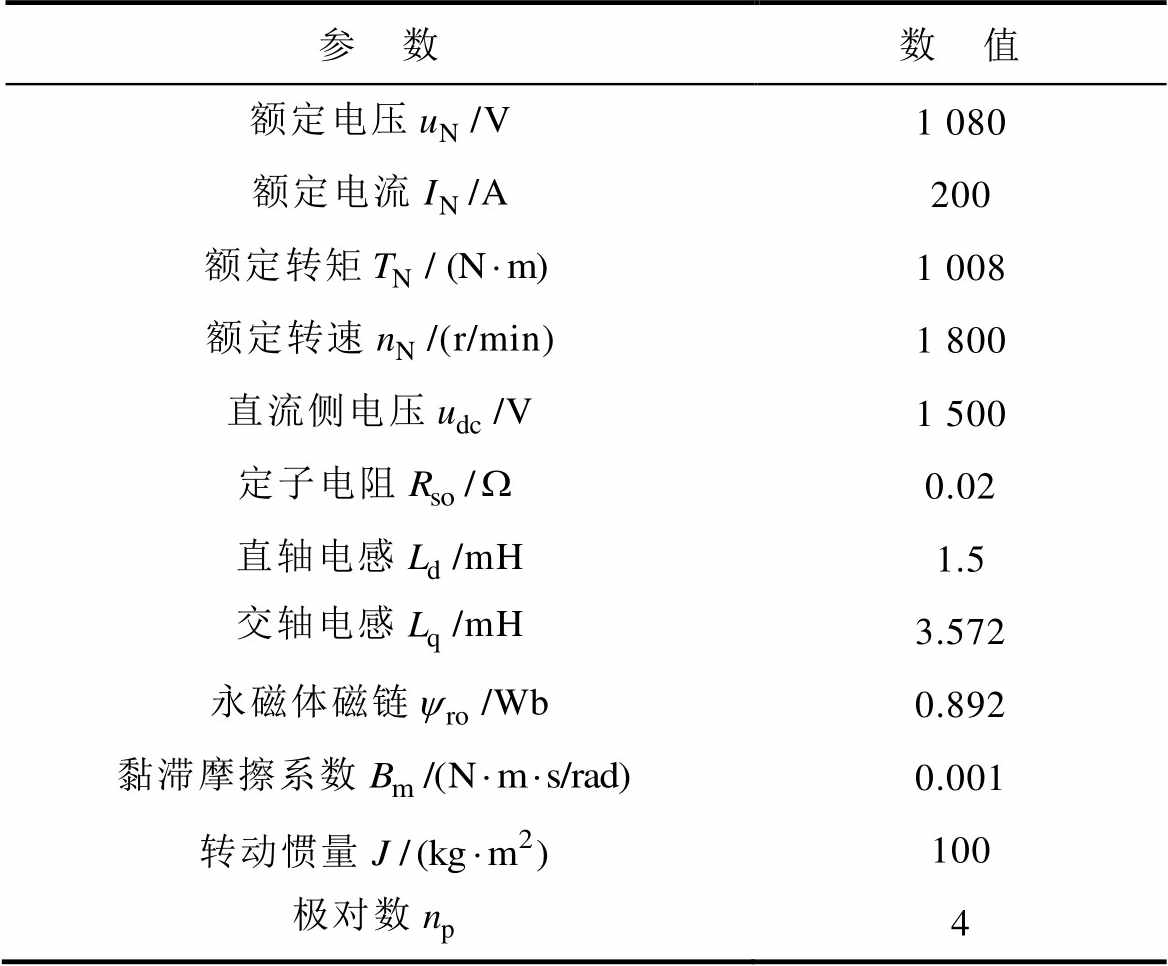
参 数数 值 额定电压/V1 080 额定电流/A200 额定转矩/1 008 额定转速/(r/min)1 800 直流侧电压/V1 500 定子电阻0.02 直轴电感/mH1.5 交轴电感/mH3.572 永磁体磁链/Wb0.892 黏滞摩擦系数0.001 转动惯量100 极对数4
表2 控制系统参数
Tab.2 Parameters of control system

PIMFSMCMFNFTSMC+ENTSMDO P=800 I=40 — — —— —— —— —— —— —— —— —— ——
为了验证不同控制算法在参数摄动和未知扰动下的整体控制性能,设置电机转动惯量 在0.5 s时由标称值增至1.6倍,即160
在0.5 s时由标称值增至1.6倍,即160 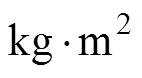 ;电阻
;电阻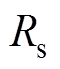 在1.5 s时增至标称值的1.4倍,即为0.028
在1.5 s时增至标称值的1.4倍,即为0.028 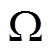 ;
;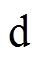 轴电感Ld在2 s由标称值增大至1.2倍,即1.8 mH;
轴电感Ld在2 s由标称值增大至1.2倍,即1.8 mH;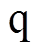 轴电感Lq在2.5 s时由标称值减小至0.6倍,即2.143 2mH;黏滞摩擦系数
轴电感Lq在2.5 s时由标称值减小至0.6倍,即2.143 2mH;黏滞摩擦系数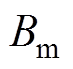 在3 s时增至到标称值的3倍,即为0.003
在3 s时增至到标称值的3倍,即为0.003 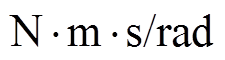 。设置转速为100
。设置转速为100  ,0.6 s时加到200
,0.6 s时加到200  ;负载转矩为300
;负载转矩为300 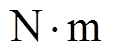 ,在1 s时加到1 000
,在1 s时加到1 000 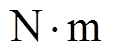 。
。
图3和图4为PI、MFSMC和MFNFTSMC三种算法的仿真对比。其中,图3a、图3b和图4a、图4b分别为直交轴电流响应曲线;图3c和图4c为输出转矩曲线;图3d和图4d为转速响应曲线。图5为定子A相电流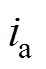 在参数摄动下的谐波频谱分析,图5a、图5b和图5c分别为PI、MFMFC和MFNFTSMC控制时A相电流
在参数摄动下的谐波频谱分析,图5a、图5b和图5c分别为PI、MFMFC和MFNFTSMC控制时A相电流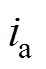 ,图5d、图5e和图5f为三种方法控制下的A相电流
,图5d、图5e和图5f为三种方法控制下的A相电流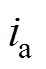 总谐波畸变率(Total Harmonics Distortion, THD)。
总谐波畸变率(Total Harmonics Distortion, THD)。
从图3a、图3b和图4a、图4b比较可知,当电机转动惯量变化后,所提出的MFNFTSMC算法控制的直交轴电流与PI控制和MFSMC算法相比,电流动态响应速度更快;在负载转矩1 s变化时,虽然MFNFTSMC算法控制下的电流有轻微超调,但能在极短时间内恢复平稳运行,有效抑制了电磁参数摄动时的电流脉动。


图3 PI和MFNFTSMC仿真对比
Fig.3 Simulation compare of PI and MFNFTSMC

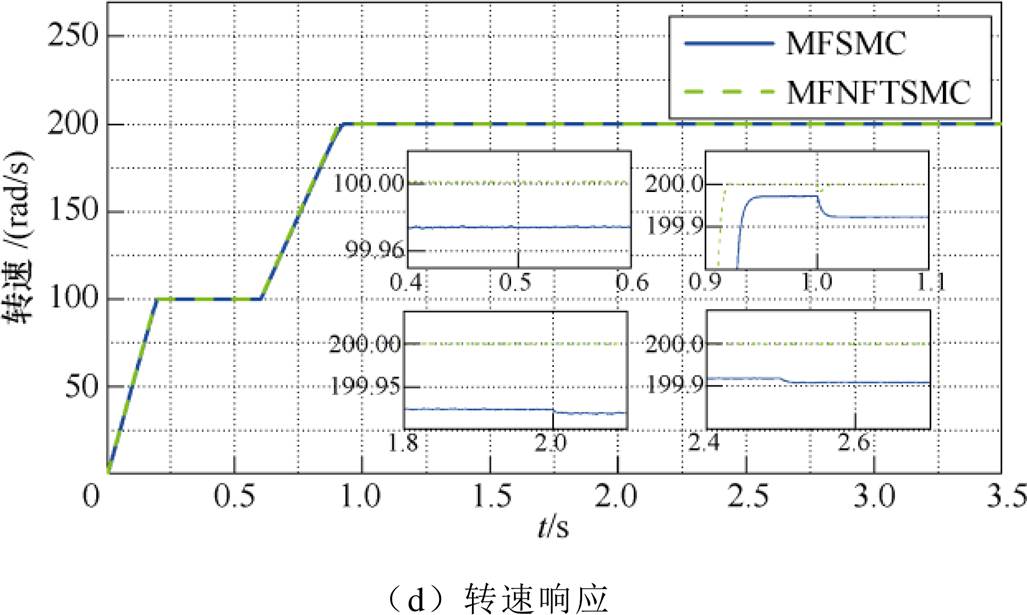
图4 MFSMC和MFNFTSMC仿真对比
Fig.4 Simulation compare of MFSMC and MFNFTSMC
从图3c和图4c比较可知,相比PI控制和MFSMC算法,MFNFTSMC算法控制的转矩变化迅速,在动态和稳态都具有更佳的控制性能,脉动 最小。
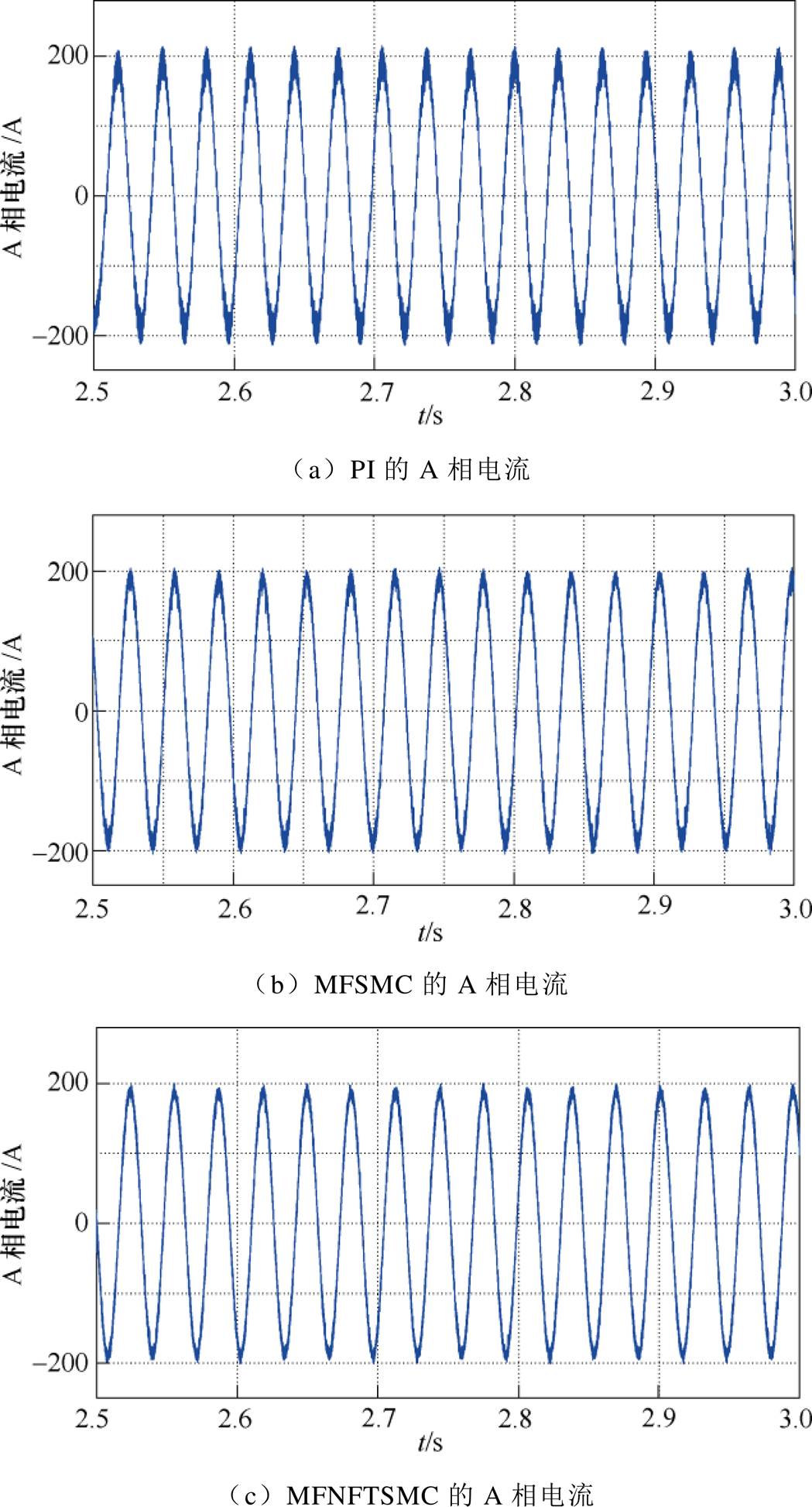

图5 A相定子电流THD分析
Fig.5 THD analysis of A phase stator current
从图3d和图4d比较可知,转动惯量变化对于电机转速暂态过程影响较大,而黏滞摩擦系数影响很小,可以忽略不计。相比PI控制和MFSMC算法,MFNFTSMC算法控制的转速受到转动惯量变化影响最小;同时在负载转矩变化、电阻和电感参数摄动时,PI控制和MFSMC算法的转速均无法恢复到给定转速,且PI控制有明显波动和超调,而MFNFTSMC算法控制的转速能在极短时间内准确跟踪到给定转速。
从图5中A相电流 电流的THD分析可知,PI控制、MFSMC算法和MFNFTSMC算法的THD分别为9.31 %、7.35 %和4.15 %。可以看出,相比较PI控制和MFSMC算法,所提出的MFNFTSMC算法能在参数摄动情况下有效抑制电流谐波。
电流的THD分析可知,PI控制、MFSMC算法和MFNFTSMC算法的THD分别为9.31 %、7.35 %和4.15 %。可以看出,相比较PI控制和MFSMC算法,所提出的MFNFTSMC算法能在参数摄动情况下有效抑制电流谐波。
通过仿真分析可知,在参数摄动和未知扰动情况下,本文提出的基于ENTSMDO的MFNFTSMC算法比PI控制和MFSMC算法具有速度响应快、鲁棒性好、抗干扰能力强和控制精度高等优点,能有效抑制电流谐波、电流和转矩脉动;同时,转速、定子电流和电磁转矩均能快速响应并达到给定值,而PI控制和MFSMC算法的暂稳态性能均受到参数摄动和未知扰动的影响,整体控制性能不佳。
当发生参数摄动和未知扰动时,采用ENTSMDO和传统SMO分别对转速环超局部模型中未知部分进行观测,图6为两者的转速跟踪误差曲线,图7为未知部分的观测曲线。
从图6可以看出,ENTSMDO具有更好的跟踪性能,而SMO在转动惯量变化后的暂态过程中有一定超调,整体跟踪误差难以达到预期效果。另外,因SMO需要采用高增益来维持控制系统的鲁棒性,所以观测器会存在一定抖振;由图7可以看出,ENTSMDO观测的未知部分波形更平滑,系统响应更快,且几乎无抖振。
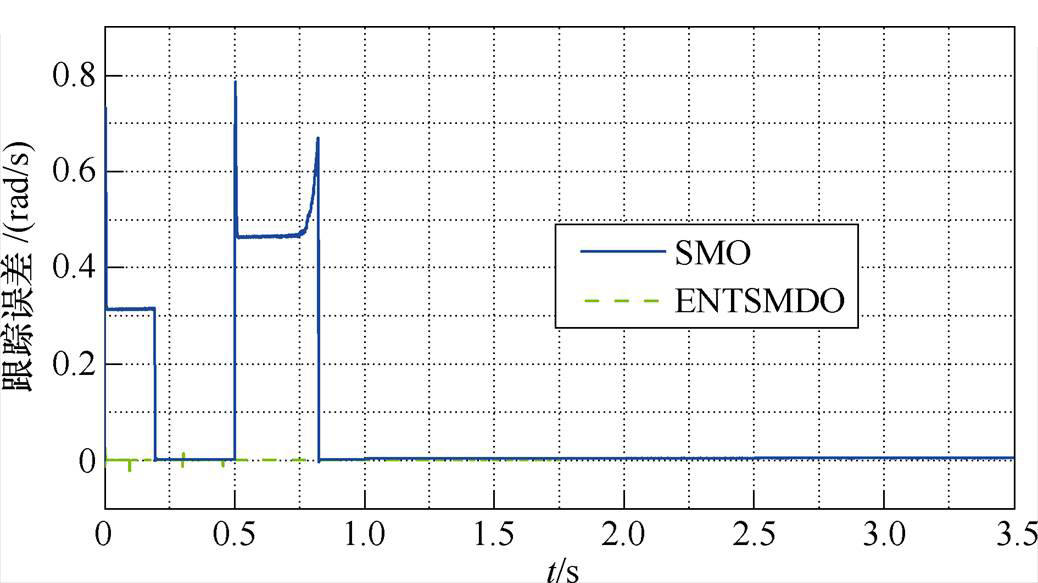
图6 转速跟踪误差
Fig.6 Speed tracking error
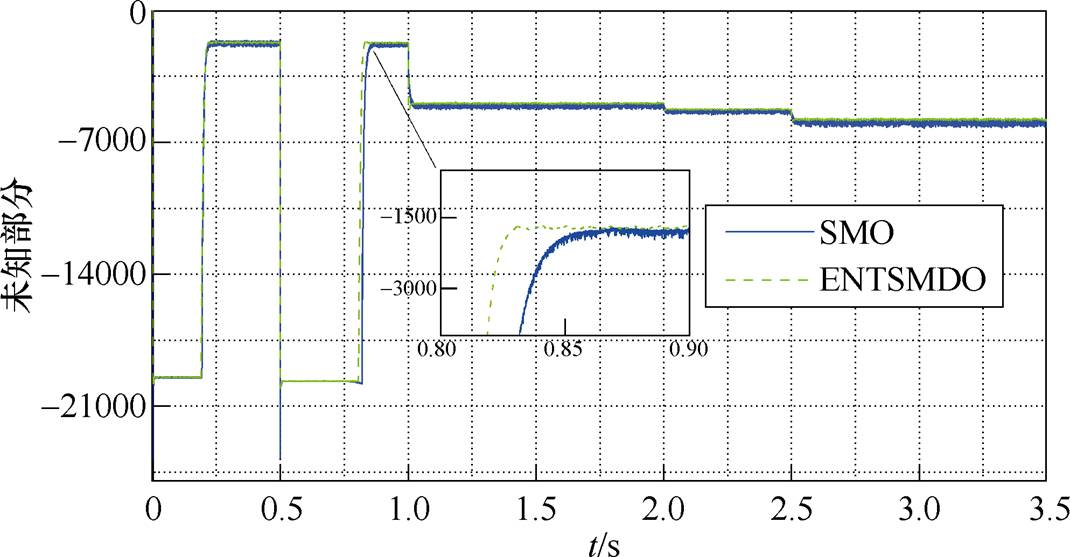
图7 未知部分观测值
Fig.7 Observed value of unknown part
因电机电磁参数和机械参数的摄动在实际电机难以模拟,本文采用RT-Lab实现PMSM驱动系统的硬件在环仿真(Hardware-In-the-Loop Simulation, HILS)实验。图8和图9分别为本文使用的RT-Lab实验台和硬件在环系统配置。DSP控制器采用TMS320F2812,电机驱动系统由RT-Lab模拟。图10为PI控制、MFSMC算法和MFNFTSMC算法的全工况实验,实验参数和仿真参数一致。

图8 RT-Lab平台
Fig.8 RT-Lab platform
从图10可知,当电机发生参数摄动和未知扰动时,PI控制和MFSMC算法整体控制性能受到影响,具体体现在转速、电流和转矩响应时间变长,电流和转矩脉动较大。此外,PI控制和MFSMC算法控制的电流和转矩波形出现了畸变,而所提出的MFNFTSMC算法波形变化平稳,能有效抑制电流和转矩脉动,这归因于ENTSMDO能精准观测超局部模型中的未知部分并进行前馈补偿,使电流和转矩变化迅速,抖动明显减小。
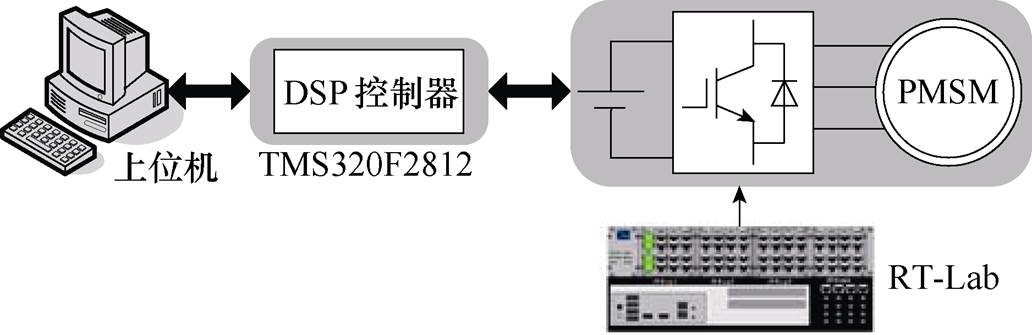
图9 RT-Lab硬件在环系统配置
Fig.9 Configuration of the RT-Lab HILS system

图10 全工况实验
Fig.10 Full working condition experimental chart
综上所述,在参数摄动和未知扰动情况下,MFNFTSMC算法具有响应速度快、鲁棒性好、抗干扰能力强等优点,有效抑制了电流和转矩脉动。
表3为PI、MFSMC和MFNFTSMC控制方法的综合控制性能比较。表中,转速静差为转速在电阻、d轴电感和q轴电感摄动时变化的幅值,转矩响应为转矩突变后重新恢复到稳态所用的时间。PI控制、MFSMC控制方法的转速在电阻、d轴电感和q轴电感发生摄动后无法恢复到给定值,而基于ENTSMDO的MFNFTSMC算法可以快速恢复到给定值。
表3 PI、MFSMC、MFNFTSMC控制方法比较
Tab.3 Comparison of PI, MFSMC, MFNFTSMC
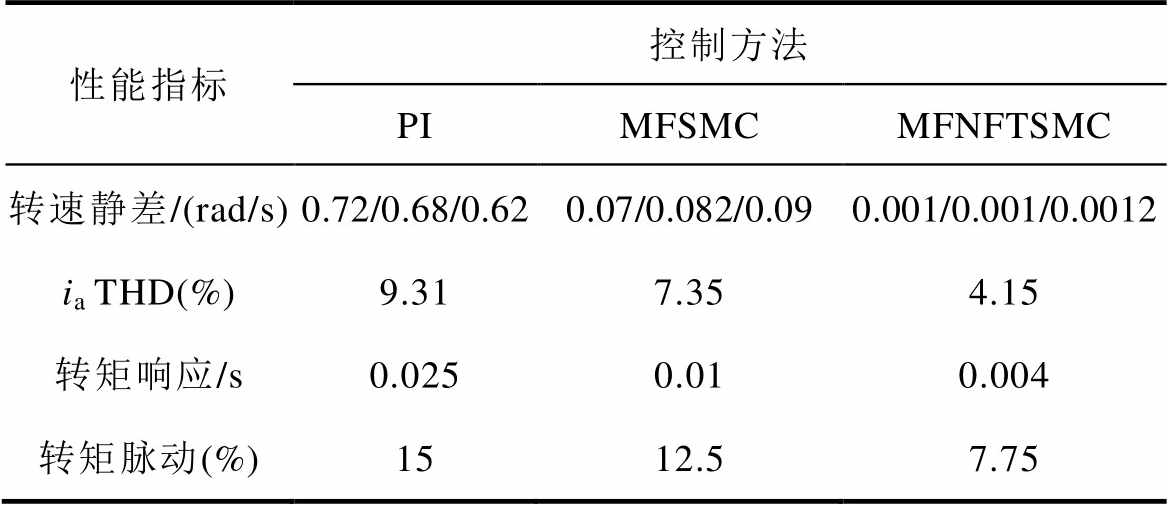
性能指标控制方法 PIMFSMCMFNFTSMC 转速静差/(rad/s)0.72/0.68/0.620.07/0.082/0.090.001/0.001/0.0012 ia THD(%)9.317.354.15 转矩响应/s0.0250.010.004 转矩脉动(%)1512.57.75
针对城市轨道交通高转矩永磁同步牵引电机在参数摄动和未知扰动情况下整体控制性能下降的现象,本文提出一种基于ENTSMDO的MFNFTSMC算法。通过与PI控制、MFSMC算法进行仿真和实验比较,得出下述结论:
1)将MFC算法和NFTSM结合设计无模型非奇异快速终端滑模控制器,在参数摄动和未知扰动下,电机的转速、电流、转矩能在极短时间内恢复到给定值,系统的动态响应速度和鲁棒性均得到提升。
2)结合高阶滑模和非奇异终端滑模设计的ENTSMDO能实时精准观测新型超局部模型的未知部分,并通过对控制器前馈补偿,有效抑制了电流和转矩脉动,保证了电机的高性能控制。
3)通过与PI、MFSMC算法综合对比,验证了基于ENTSMDO的MFNFTSMC算法在电机参数摄动和外部扰动下暂稳态性能更佳,抗干扰能力更强,实现了电机在参数摄动下的容错控制。
参考文献
[1] 姚钢, 杨浩猛, 周荔丹, 等. 大容量海上风电机组发展现状及关键技术[J]. 电力系统自动化, 2021, 45(21): 33-47.
Yao Gang, Yang Haomeng, Zhou Lidan, et al. Deve- lopment status and key technologies of large-capacity offshore wind turbines[J]. Automation of Electric Power Systems, 2021, 45(21): 33-47.
[2] 刘寅迪, 曾翔君, 骆一萍, 等. 基于MPPMSG的混合高压直流风电系统故障穿越技术[J]. 电力系统自动化, 2020, 44(8): 133-140.
Liu Yindi, Zeng Xiangjun, Luo Yiping, et al. Fault ride-through technology of hybrid HVDC wind power system based on multi-phase permanent magnet synchronous generator[J]. Automation of Electric Power Systems, 2020, 44(8): 133-140.
[3] 高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(4): 787-800.
[4] Zhao Kaihui, Zhou Ruirui, She Jinhua, et al. Demagnetization-fault reconstruction and tolerant- control for PMSM using improved SMO-based equivalent-input-disturbance approach[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(2): 701- 712.
[5] 鲍旭聪, 王晓琳, 顾聪, 等. 超高速永磁电机驱动系统电流环稳定性分析与改进设计[J]. 电工技术学报, 2022, 37(10): 2469-2480.
Bao Xucong, Wang Xiaolin, Gu Cong, et al. Stability analysis and improvement design of current loop of ultra-high-speed permanent magnet motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2469-2480.
[6] Niu Feng, Chen Xi, Huang Shaopo, et al. Model predictive current control with adaptive-adjusting timescales for PMSMs[J]. CES Transactions on Elec- trical Machines and Systems, 2021, 5(2): 108-117.
[7] 张晓光, 闫康, 张文涵. 开绕组永磁同步电机混合双矢量模型预测控制[J]. 电工技术学报, 2021, 36(1): 96-106.
Zhang Xiaoguang, Yan Kang, Zhang Wenhan. Hybrid double vector model predictive control for open- winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Elec- trotechnical Society, 2021, 36(1): 96-106.
[8] Shao Yanzhen, Yu Yanjun, Chai Feng, et al. A two-degree-of-freedom structure-based backstepping observer for DC error suppression in sensorless PMSM drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 10846-10858.
[9] 肖飞, 许观达, 连传强, 等. 永磁同步电机单电流传感器系统的三相电流重构策略[J]. 电工技术学报, 2022, 37(7): 1609-1617.
Xiao Fei, Xu Guanda, Lian Chuanqiang, et al. Three- phase current reconstruction strategy of permanent magnet synchronous machine drives using a single current sensor[J]. Transactions of China Electro- technical Society, 2022, 37(7): 1609-1617.
[10] Guo Fei, Chu Qiu, Li Chunyan, et al. Research on influence of motor parameters on the negative-salient permanent magnet synchronous motor[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(1): 77-86.
[11] 魏惠芳, 王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报, 2022, 37(4): 861-869.
Wei Huifang, Wang Limei. Adaptive fuzzy neural network time-varying sliding mode control for per- manent magnet linear synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(4): 861-869.
[12] Hou Qiankang, Ding Shihong, Yu Xinghuo. Com- posite super-twisting sliding mode control design for PMSM speed regulation problem based on a novel disturbance observer[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 2591-2599.
[13] Xu Wei, Junejo A K, Liu Yi, et al. An efficient antidisturbance sliding-mode speed control method for PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6879-6891.
[14] Yang Liang, Yang Jianying. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J]. International Journal of Robust and Nonlinear Control, 2011, 21(16): 1865-1879.
[15] 李升波, 李克强, 王建强, 等. 非奇异快速的终端滑模控制方法及其跟车控制应用[J]. 控制理论与应用, 2010, 27(5): 543-550.
Li Shengbo, Li Keqiang, Wang Jianqiang, et al. Nonsingular fast terminal-sliding-mode control method and its application on vehicular following system[J]. Control Theory & Applications, 2010, 27(5): 543-550.
[16] Liu Wei, Chen Siyi, Huang Huixian. Adaptive nonsingular fast terminal sliding mode control for permanent magnet synchronous motor based on dis- turbance observer[J]. IEEE Access, 2019, 7: 153791- 153798.
[17] Xu Bo, Zhang Lei, Ji Wei. Improved non-singular fast terminal sliding mode control with disturbance observer for PMSM drives[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2753-2762.
[18] Zhao Kaihui, Liu Wenchang, Yin Tonghuan, et al. Model-free sliding mode control for PMSM drive system based on ultra-local model[J]. Energy Engin- eering, 2022, 119(2): 767-780.
[19] Fliess M, Join C. Model-free control[J]. International Journal of Control, 2013, 86(12): 2228-2252.
[20] Safaei A, Mahyuddin M N. Adaptive model-free control based on an ultra-local model with model-free parameter estimations for a generic SISO system[J]. IEEE Access, 2018, 6: 4266-4275.
[21] Zhao Kaihui, Yin Tonghuan, Zhang Changfan, et al. Robust model-free nonsingular terminal sliding mode control for PMSM demagnetization fault[J]. IEEE Access, 2019, 7: 15737-15748.
[22] 赵凯辉, 周瑞睿, 冷傲杰, 等. 一种永磁同步电机的有限集无模型容错预测控制算法[J]. 电工技术学报, 2021, 36(1): 27-38.
Zhao Kaihui, Zhou Ruirui, Leng Aojie, et al. Finite control set model-free fault-tolerant predictive control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 27-38.
[23] 赵凯辉, 殷童欢, 张昌凡, 等. 永磁同步电机无模型滑模控制方法研究[J]. 电子测量与仪器学报, 2018, 32(4): 172-180.
Zhao Kaihui, Yin Tonghuan, Zhang Changfan, et al. Research on model-free sliding mode control of permanent magnet synchronous motor[J]. Journal of Electronic Measurement and Instrumentation, 2018, 32(4): 172-180.
[24] Mousavi M S, Davari S A, Nekoukar V, et al. Integral sliding mode observer-based ultralocal model for finite-set model predictive current control of induction motor[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2912-2922.
[25] 赵凯辉, 戴旺坷, 周瑞睿, 等. 基于扩展滑模扰动观测器的永磁同步电机新型无模型滑模控制[J]. 中国电机工程学报, 2022, 42(6): 2375-2386.
Zhao Kaihui, Dai Wangke, Zhou Ruirui, et al. Novel model-free sliding mode control of permanent magnet synchronous motor based on extended sliding mode disturbance observer[J]. Proceedings of the CSEE, 2022, 42(6): 2375-2386.
[26] Banerjee R, Sensarma P. Improved analytical method to determine flux-linkage characteristics of a switched reluctance machine[J]. IEEE Transactions on Industry Applications, 2020, 56(6): 6314-6323.
[27] 冯勇, 鲍晟, 余星火. 非奇异终端滑模控制系统的设计方法[J]. 控制与决策, 2002, 17(2): 194-198.
Feng Yong, Bao Sheng, Yu Xinghuo. Design method of non-singular terminal sliding mode control systems[J]. Control and Decision, 2002, 17(2): 194- 198.
[28] Fallaha C J, Saad M, Kanaan H Y, et al. Sliding-mode robot control with exponential reaching law[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 600-610.
[29] 李慧洁, 蔡远利. 基于双幂次趋近律的滑模控制方法[J]. 控制与决策, 2016, 31(3): 498-502.
Li Huijie, Cai Yuanli. Sliding mode control with double power reaching law[J]. Control and Decision, 2016, 31(3): 498-502.
[30] Lu En, Li Wei, Yang Xuefeng, et al. Anti-disturbance speed control of low-speed high-torque PMSM based on second-order non-singular terminal sliding mode load observer[J]. ISA Transactions, 2019, 88: 142- 152.
[31] Khalil H K. Nonlinear systems[M]. 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2002.
Abstract Permanent magnet synchronous traction systems have been widely used in high-speed trains and urban rail because of the advantages of high power density, high overload capacity, and fast dynamic torque. PI control technology has become the mainstream control method for motors owing to the advantages of the simple method and easy engineering implementation. However, PMSM is susceptible to unknown disturbances, parameter perturbation, and other uncertainties under complex traction conditions, and it is difficult to suppress the disturbances using traditional PI control. The overall control performance of the motor decreases, and satisfactory control results cannot be achieved in high-performance applications. The control performance of high torque permanent magnet traction synchronous motor in urban rail transit is degraded by uncertainties. Therefore, this paper proposes a novel model-free non-singular fast terminal sliding mode control strategy for the speed loop based on an extended non-singular terminal sliding mode disturbance observer.
Firstly, a novel ultra-model is established based on the mathematical model of the permanent magnet synchronous traction motor under parametric perturbation and unknown perturbations using the input and output of the speed loop. Secondly, the model-free non-singular fast terminal sliding mode controller is designed based on the novel ultra-model. Then, combined with the higher-order sliding and non-singular terminal sliding modes, a real-time observer is designed for estimating the unknown part of the novel ultra-model. Consequently, the system’s robustness is improved by the feedforward compensation of the controller, the control accuracy of the speed is improved, and the system jitter is reduced. Finally, a comprehensive comparison with PI control and model-free sliding mode control (MFSMC) by simulation and experiment is carried out. It is shown that the proposed control method has strong fault tolerance and anti-disturbance to motor perturbation and unknown disturbances. In addition, the dependence on the accurate mathematical model of the motor can be reduced.
Simulation and experimental results show that compared with the PT control and MFSMC method, the speed controlled by the MFNFTSMC method is the least affected by the change of rotational inertia. The speed controlled by the PI control and MFSMC method cannot recover to the given speed when the load torque changes and the resistance and inductance parameters are perturbation. In contrast, the speed controlled by the MFNFTSMC method can accurately track the given speed quickly. Meanwhile, the A-phase current total harmonics distortions (THD) of PI control and MFSMC method under parameter perturbation are 9.31 % and 7.35 %, while the MFNFTSMC method is reduced to 4.15 %. Thus, the MFNFTSMC method has an effective suppression of current harmonics. Similarly, compared with the PI control and MFSMC method, the proposed MFNFTSMC method achieves lower torque pulsation: the torque errors of the PI control and MFSMC method are about 16 % and 12.5 %, while the proposed MFNFTSMC method is only about 7.75 %. As a result, the MFNFTSMC method effectively suppresses the current pulsation problem under parameter perturbation.
The following conclusions can be drawn from the simulation and experimental analysis:(1)Combining the MFC method and NFTSM to design the model-free nonsingular fast terminal sliding mode controller, the speed, current, and torque of the motor are recovered to the given value in a short time under the parameter and unknown perturbations, and the dynamic response speed and robustness of the system are improved. (2)The designed ENTSMDO can accurately observe the unknown part of the ultra-local model in real-time and effectively suppress the current and torque ripple through the feedforward compensation of the controller, ensuring high-performance control of the motor. (3)Compared with PT control and the MFSMC method, the ENTSMDO-based MFNFTSMC method has better transient and steady-state performance and more robust anti-interference capability under motor parameter perturbation and external disturbance. It achieves fault- tolerant control of the motor under parameter perturbation.
keywords:High torque traction permanent magnet synchronous motor, novel ultra-local model, model-free non-singular fast terminal sliding mode control, extended nonsingular terminal sliding mode disturbance observer
DOI: 10.19595/j.cnki.1000-6753.tces.220615
中图分类号:TM351
国家自然科学基金项目(52172403, 62173137)、湖南省自然科学基金项目(2021JJ50052, 2020JJ6067)、湖南省教学改革研究项目(HNJG-2022-0847)、湖南省教育厅科学研究项目(21A0354, 21C0446)和湖南工业大学研究生科研创新项目(CX2204)资助。
收稿日期 2022-04-18
改稿日期 2022-06-16
赵凯辉 男,1973年生,博士,教授,硕士生导师,研究方向为永磁牵引驱动系统故障诊断及容错控制。E-mail: zhaokaihui@hut.edu.cn
黄 刚 男,1979年生,博士,副教授,硕士生导师,研究方向为永磁电机智能控制。E-mail: 12120@hut.edu.cn(通信作者)
(编辑 崔文静)