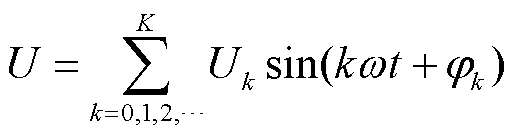 (1)
(1)
摘要 饱和电抗器作为特高压直流换流阀的核心装备,运行中产生的振动声音包含大量的信息,其状态评估对换流阀的安全运行具有重要意义。该文提出一种基于优化S变换和改进深度残差收缩网络的饱和电抗器铁心松动程度声纹识别模型。首先开展了高频脉冲激励下的饱和电抗器振动试验,并测量了不同铁心松动程度下的声纹信号;其次在声信号频谱主值区间内,根据能量聚集性优化高斯窗参数来提高声纹图谱的时频分辨率;然后对松动后的声纹特性进行分析,发现高低频比和低频分量主频占比两个特征指标仅能对松动程度较高的状态做出预警;最后采用五个不同方位测点的铁心松动数据代入基于自适应参数修正线性单元的改进深度残差收缩网络中进行训练,来消除声纹图中的冗余信息,并对不同松动程度下的特征进行独立映射,从而增强共同特征的学习能力。研究结果表明,该文模型对电抗器不同铁心松动程度的平均识别准确率达到95.93%,优于传统深度学习算法,可为饱和电抗器在线监测提供重要依据。
关键词:饱和电抗器声纹 优化S变换 铁心松动试验 特征提取 改进深度残差收缩网络
特高压直流输电技术具有输送距离长、运行方式灵活、经济高效等诸多优点,已成为新能源外送的重要手段,其中高压直流换流阀的状态直接影响到电网安全和能源送出消纳能力[1-3]。饱和电抗器作为换流阀的核心部件,起到了抑制电流变化率、高频电压冲击下分摊硅堆电压及保证晶闸管正常开断的作用[4]。但由于阀厅中设备种类繁多,导致饱和电抗器工况较为复杂。尤其在换流阀开通和关断时,饱和电抗器承受高频脉冲电压,铁心在磁不饱和与磁饱和状态之间的转换一般在数ms到数十ms的时间内完成,加剧了宽频机械振动[5]。在机械应力的长期循环疲劳持续作用下,易产生内部微小缺陷,进而出现机械结构松动、水管振动磨损和加速老化失效等问题。因此,有必要研究饱和电抗器铁心的振动特性及故障识别方法,为设备状态评估及换流阀高效运维管理提供重要依据。
目前,针对饱和电抗器振动特性的研究较少,文献[6]测量了一对铁心在不同单频点激励下的振动噪声,并采用加装阻尼弹性体的方法进行降噪。文献[7]对饱和电抗器进行电磁场及谐响应仿真分析,计算了电磁力和振动位移。上述研究主要集中于振动幅值对比及降噪处理,且所加激励与饱和电抗器实际电压波形存在差异,并未对振动特征进行深入分析。在饱和电抗器机械结构状态评估方面,目前还处于半盲状态,只能进行停电检修,难以实现早期故障识别和预测。饱和电抗器运行中产生的振动和声音信号包含大量的信息,可反映其运行状态。振动信号的采集多为接触式测量,多对铁心上均需安装振动传感器,成本较高,且多层阀塔的饱和电抗器对地电压等级不同导致绝缘块厚度不同、布点偏移等因素都会对测量结果产生影响。而声音信号监测是非接触式测量方法,测量范围广。在满足最高电压等级的安全净距前提下,多层阀塔间饱和电抗器与声传感器的测量间距可以实现统一化,实现对阀厅内多台饱和电抗器的在线监测要求。
目前,在电力设备声纹监测领域,已有一定研究,主要集中于变压器故障声信号诊断方面。文献[8]提取了变压器铁心松动噪声信号的梅尔频率倒谱系数(Mel Frequency Cestrum Coefficient, MFCC)特征向量,并采用矢量量化(Vector Quantization, VQ)算法获得了较好的铁心松动故障识别效果。随着深度学习在语音识别[9-10]、图像识别[11-12]等方面的快速发展,已有学者将其应用于变压器声信号识别中。文献[13]对变压器铁心振动声纹数据进行Mel时频谱降维,并代入到卷积神经网络中训练,来判断变压器的运行工况。文献[14]利用盲源分离、幅值相位波动性法去除掉变压器本体信号中的干扰成分,并提取50 Hz倍频倒谱系数,引入门控循环单元(Gate Recurrent Unit, GRU)网络,建立变压器直流偏磁声纹识别模型。综上所述,已有方法基于声音信号对变压器的状态识别取得了一定成果,但若将其应用于饱和电抗器中还存在一些问题:①变压器激励源多为正弦电压或含少量谐波,振动频谱分布在0~2 kHz之间,而脉冲激励下的饱和电抗器振动声信号频谱分布较广,可听声范围内均有体现,复杂程度更高;②声纹信号特征提取方法多以短时傅里叶变换为基础,难以同时体现高频及低频的特征[15-16];③不同方位麦克风收集到的铁心振动声纹分量存在差异,缺少多方位声信号的共性识别方法。
本文中,首先进行饱和电抗器铁心松动试验,模拟晶闸管开通、关断过程中产生的高频脉冲电压,并采集电信号及振动声纹信号;其次,采用基于能量聚集性公式的优化S变换(Optimized S-Transform, OST)提取声纹特征;然后,研究不同电压等级及铁心松动程度下的声纹频谱分布,构建五个特征指标对松动后的声纹特性进行分析;最后,将自适应参数修正线性单元引入深度残差收缩网络,对五个测点声信号的特征进行独立映射,建立饱和电抗器铁心松动程度多方位识别模型,并依据试验构建的数据集验证本文模型的有效性。
饱和电抗器正常运行状态下,铁心扎带具有较高的紧固力矩,加以制造工艺和铁心叠压方式的改进,硅钢片接缝处和叠片间漏磁产生的电磁力引起的振动较小,因此可认为铁心振动主要是由磁致伸缩效应所引起的。下面分析磁致伸缩与所加激励间的关系。饱和电抗器承受的高频脉冲电压可等效为多个正弦电压之和,即
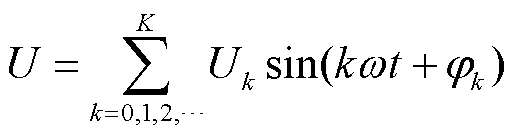 (1)
(1)
式中,Uk、jk分别为k次谐波的电压幅值和相位;ω为50Hz电压角频率;K为总谐波次数。
外加磁场下,由磁致伸缩导致硅钢片产生的微小形变[17]满足
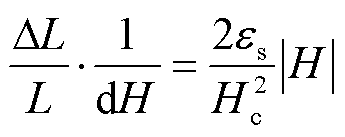 (2)
(2)
式中,DL为硅钢片形变伸缩量;L为硅钢片原始长度;es为硅钢片饱和磁致伸缩率;Hc为矫顽力;H为铁心中的磁场强度。
对式(2)进行积分求出硅钢片形变伸缩量DL,可得到饱和电抗器铁心由硅钢片磁致伸缩引起的振动为
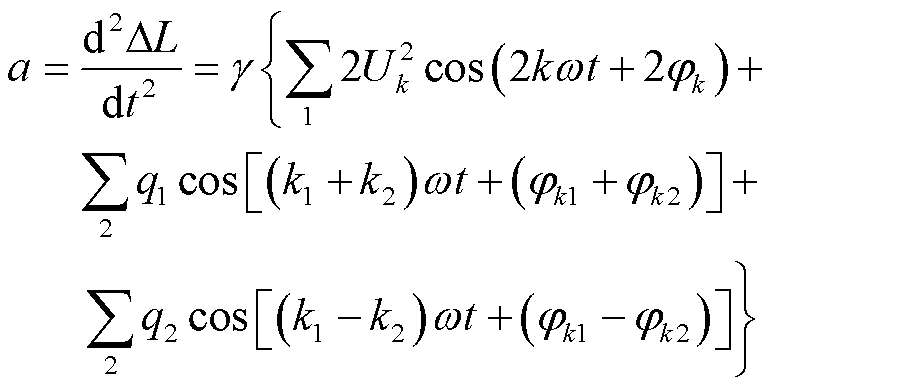
其中
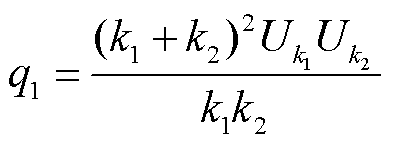 (4)
(4)
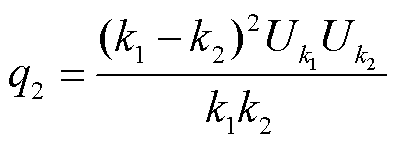 (5)
(5)
式中,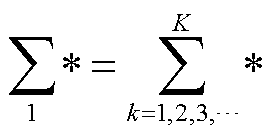 ,
,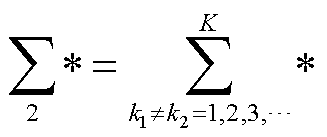 ;g 与铁心饱和磁感应强度Bs、绕组匝数Ns、硅钢片饱和磁致伸缩率es、铁心横截面积S和硅钢片原始尺寸L等参数有关。
;g 与铁心饱和磁感应强度Bs、绕组匝数Ns、硅钢片饱和磁致伸缩率es、铁心横截面积S和硅钢片原始尺寸L等参数有关。
由式(3)可知,饱和电抗器正常运行时,承受的电压中含有大量高次谐波,致使饱和电抗器铁心振动频率在50 Hz的奇、偶次倍频上均存在分量。此外,铁心的非线性特征、固有频率接近激励频率发生共振等影响因素,都会加剧铁心振动的复杂程度。
构建声纹时频谱图是提取饱和电抗器铁心振动声音信号特征的重要方法,特征提取效果会直接影响到之后铁心松动程度识别的结果。大功率晶闸管μs级导通关断过程中产生的高次电压、电流谐波使铁心振动声纹频谱变得复杂。本节利用能量聚集性公式优化高斯窗参数,对声信号进行频域加窗,来获取更高的时频分辨率。
传统S变换采用可变宽度的高斯窗函数,实现了多分辨率分析和相位更正,是短时傅里叶变换和小波变换的改进。对于时域信号x(t),其S变换定义[18]为
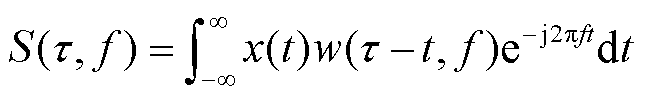 (6)
(6)
式中,f为频率;t 为调节高斯窗时域位置的参数;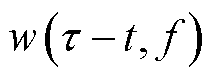 为高斯窗函数,表达式为
为高斯窗函数,表达式为
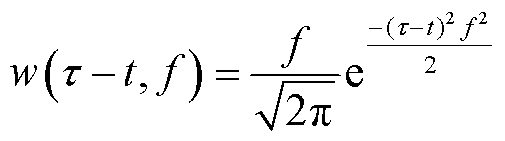 (7)
(7)
宽度因子σ定义为
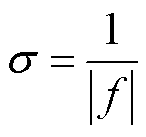 (8)
(8)
由式(8)可知,传统高斯窗函数的时域窗宽与频率成反比,即低频段的频率分辨率较高,在高频段的频率分辨率降低。饱和电抗器铁心振动声音频段分布较广,若采用传统S变换构建声纹时频谱,随着计算频率的升高,窗函数宽度迅速下降。在提取高频特征时可能会出现频带混叠、频谱泄露等问题,难以保证整个频带内都具有较高的时频分辨率。
为了改善时频分辨率,文献[19]提出了广义S变换,通过引入参数g和λ分别调节高斯窗的幅度以及随频率变化的速度,广义S变换的宽度因子变为
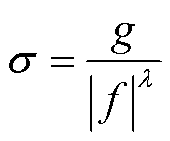 (9)
(9)
由式(9)可知,当g>1或0<λ<1时,窗宽比正常情况下变宽,频率分辨率提高。然而采用固定g值和λ值实现较好的时频分辨率是比较困难的,需要对其进行调整。同时在时域中,调节因子变化区间难以确定。
根据卷积定理,可推导出快速S变换的方程,将时域信号的傅里叶变换与高斯频域窗函数相乘,并进行快速傅里叶反变换,得到S变换的结果为
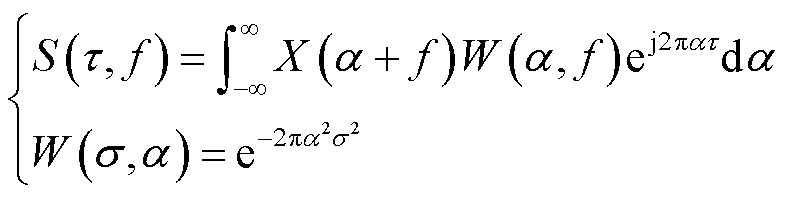 (10)
(10)
式中,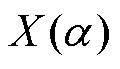 为信号x(t)的傅里叶变换;W(s,a)为高斯频域窗。快速S变换将高斯窗函数表达式由时域转换到频域,便于依据铁心振动声信号的频谱特性确定频域窗的宽度。文献[20]指出,在计算任意频点fn的S变换时,对应最优时频分辨率的sn的取值范围为
为信号x(t)的傅里叶变换;W(s,a)为高斯频域窗。快速S变换将高斯窗函数表达式由时域转换到频域,便于依据铁心振动声信号的频谱特性确定频域窗的宽度。文献[20]指出,在计算任意频点fn的S变换时,对应最优时频分辨率的sn的取值范围为
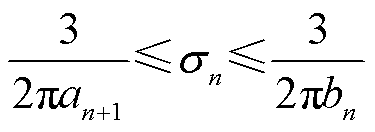 (11)
(11)
式中,an+1为相邻频点fn+1主值区间的最小值;bn为频点fn主值区间的最大值。
为了在主值区间内选出较优的sn值,本文提出了一种基于能量聚集性动态调整高斯窗宽度的优化S变换,通过改善各频率处的时频聚集性能,实现时频分辨率的整体提升。在实际应用中,离散S变换的能量聚集性计算公式为
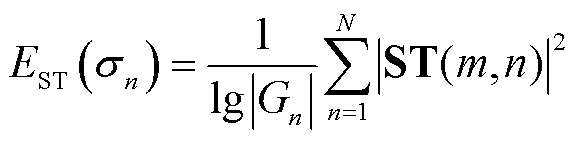 (12)
(12)
式中,ST(m,n)为离散信号的S变换矩阵,矩阵的行和列分别代表信号的频率分布与时间分布;N为时域采样点总数;Gn为频点fn所加频域窗包含的能量,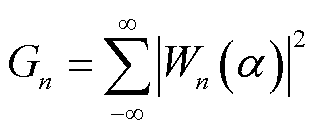 ,Wn(a)为窗函数。
,Wn(a)为窗函数。
由于受到海森堡测不准原理制约,频率分辨率与时间分辨率不能同时提高。饱和电抗器铁心振动的周期较平稳,在提取声信号时频特征的过程中,可适当降低时间分辨率来获取更高的频率分辨率。因此优化问题的目标设为能量聚集值EST(sn)最小化。
在没有引进窗函数能量Gn时,求解时存在取到范围的边界的情况,使时-频优化问题失去意义。窗函数能量Gn与原函数变化趋势相同,但存在变化率过高的问题。因此在能量聚集性计算公式中除以窗函数的对数,使sn在约束范围内部取到最优值,时、频分辨率达到较好的平衡,便于获取更加精确的声纹时频谱图。
基于优化S变换的声纹时频谱图绘制主要包括离散傅里叶变换、频点逐移加窗、傅里叶反变换等步骤。时域声信号转换为时频谱图的过程如图1所示。
图1中原始数据为时长为1 s的饱和电抗器铁心振动声音信号。不同于短时傅里叶变换,处理声信号时需要人为设定帧长、帧移等参数,优化S变换可根据信号频谱特性自适应加窗,具体流程如下:
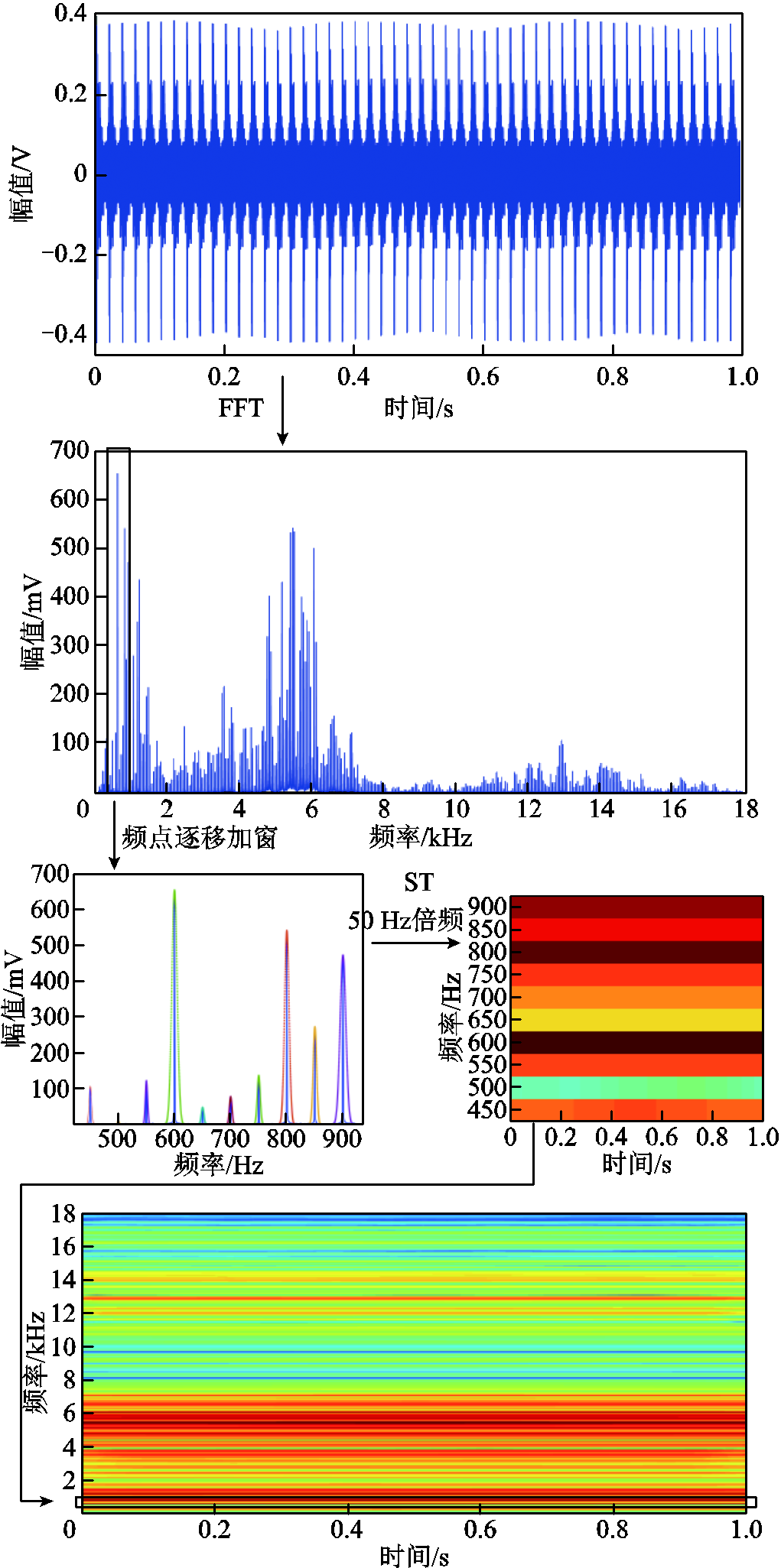
图1 时域声信号转换为时频谱图过程
Fig.1 Transition process of time domain acoustic signal to time spectrum map
1)对采集到的振动声音信号进行傅里叶变换,将时域信号转换到频域当中。
2)针对每个频点fn,根据式(11)计算与其对应的sn的取值范围。
3)根据式(10)、式(12)计算频点fn的ST矩阵和能量聚集值EST,采用内点法在步骤2)得到的范围内进行寻优,找出EST取最小值时的sn值及对应的ST矩阵,重复计算所有频率得到整个时频矩阵为
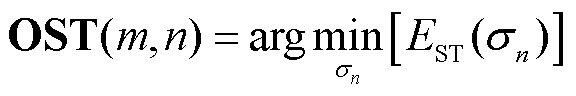 (13)
(13)
4)计算二维复数矩阵的模值|ST(m,n)|来表征不同时刻的频率含量。
根据实测声音信号频谱可知,饱和电抗器铁心振动声音主要频带范围为0~18 kHz,且频率分布在50 Hz及其倍频分量上。因此只计算50 Hz及其倍频分量的OST矩阵,减少了计算时间,并去除了50 Hz倍频外的干扰噪声分量。现场应用中,采样设备增益和摆放位置的不同导致所得到声纹时频特征矩阵的幅值存在差异。为了统一提取、分析多个测点的声纹特征,采用计算OST矩阵中不同时刻的频率占比的方法消除量纲,即
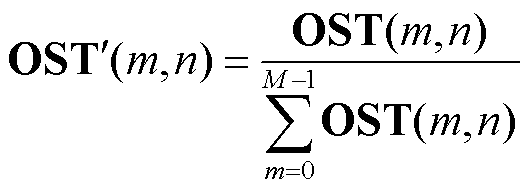 (14)
(14)
式中,M为频域采样点总数。
为了模拟饱和电抗器运行时承受的宽频电压、电流波形,在全球能源互联网研究院大功率电力电子实验室进行饱和电抗器铁心振动试验,采集了电压、电流和振动声音信号,并对不同电压等级及铁心松动程度下的振动声纹特征进行分析。
饱和电抗器振动试验平台如图2所示。试验平台的电压源为高压直流充电电源DC,电容柜Cs通过断路器K1连接试验电压源,电容柜低压端通过接地电阻Rcs和断路器Ks接地(Ks需要远程操控,当平台运行时,Ks为断开状态;当平台停止运行,电容Cs进行放电时,Ks为闭合状态)。试验平台供能电源为220 V交流电,在对应的设备柜中布置有隔离变压器和串联电抗器,对H桥中的IGBT组件进行供能。接入电压经H桥整流后为饱和电抗器提供电压激励,通过接入等效杂散电容以调节饱和电抗器上的电压峰值,用于模拟逆变侧饱和电抗器持续运行工况。所加激励能够模拟开通和关断瞬间产生
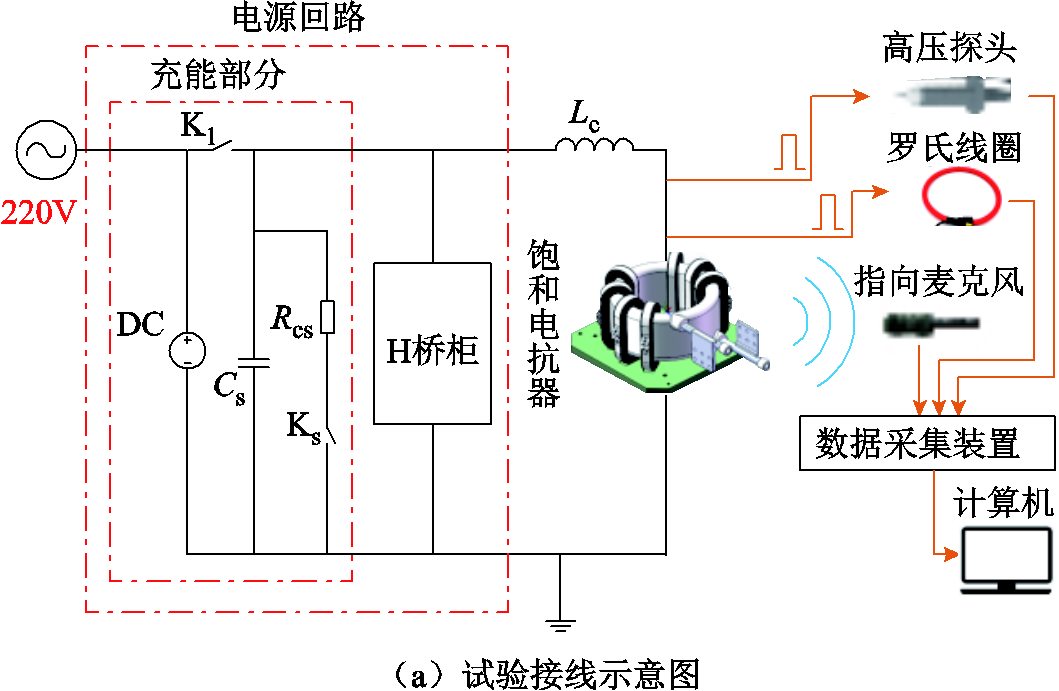

图2 饱和电抗器铁心振动试验平台
Fig.2 Saturable reactor core vibration test platform
的两个脉冲电压,且饱和电抗器上的电流近似为梯形,都与实际情况相符,能够较好地模拟饱和电抗器的振动特性。此类饱和电抗器已在哈郑、锦苏特高压直流工程中应用,其铁心及固定螺栓螺杆均取绕组中点电位,外露金属零件通过短接线连接,且外部套有绝缘护套,基本参数见表1。
表1 饱和电抗器参数
Tab.1 Parameters of saturable reactor

参数数值(型号) 饱和电抗器ARS-350/700-84 持续运行工况时的电流峰值/kA2 持续运行工况时的电流有效值/A700 电压时间面积/(mV·s)84×(1±10%) 线圈一次绕组直流电阻/mΩ≤1 额定电感/mH350×(1±10%) 铁心个数7 冷却方式水冷
试验采用的声、电信号测量系统主要由驻极电容式枪型指向麦克风、录机、高压探头、罗氏线圈、光纤隔离数据采集装置组成。麦克风具有较强的指向性,受其他噪声源干扰较小。为了对比松动铁心正面和侧面收集到的声纹特征,本试验共布置五个麦克风传感器,测点分布如图2b所示,测点1~测点5分别距饱和电抗器约0.4、0.6、0.5、0.5、0.5 m,距离地面高度约0.8 m。在模拟松动故障时,对测点2正方向的铁心进行了松动。录机采样频率为48 kHz,音质分辨率为24 bit。饱和电抗器安装在高压平台上,端子对地最高电压不超过3 kV,测量装置与饱和电抗器水平距离不低于绝缘净距。高压探头、罗氏线圈连接到光纤前端且相互隔离,光纤前端使用电池供电,距离地面高度约1.1 m,满足与地电位间10 kV工频电压的绝缘要求。光纤前端连接到数据采集系统的接收设备,采样频率为1 MHz。接收设备连接至计算机实现数据存储。
本试验所加电压波形含两个脉冲,分别模拟饱和电抗器实际运行中单阀的开通与关断过程。在这两个过程中,电压幅值和电压变化率最大,使饱和电抗器铁心充分磁化,产生的磁致伸缩效应最强,能够较好地反映铁心实际振动特性。调整前端充电电压从500 V升高到2 500 V,每次升压间隔为100 V,测量饱和电抗器电气量及铁心振动声纹信号。不同充电电压等级下饱和电抗器电压、电流波形对比如图3所示。
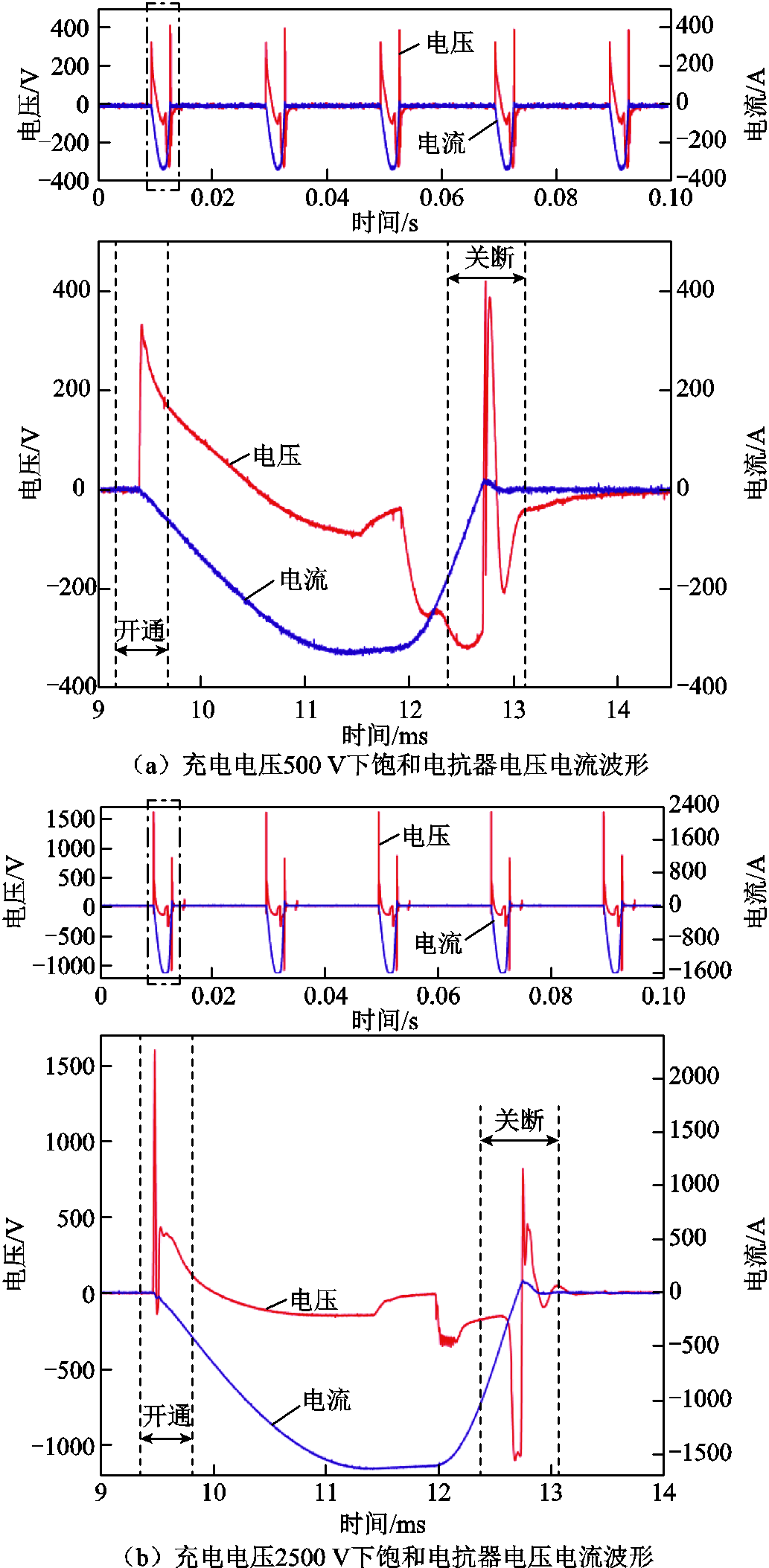
图3 饱和电抗器电压、电流波形对比
Fig.3 Comparison of saturable reactor voltage and current waveforms
由图3可知,当晶闸管开通时,饱和电抗器分担较高电压,抑制电流过快变化,铁心磁通密度也逐渐增加达到饱和状态;当晶闸管完全开通后,电抗器分压迅速下降,因此电压呈现出一个近似尖峰的波形。充电电压为500 V时,铁心电压在24 ms内从0 V上升至最高幅值333 V,但之后电压波形并未出现陡降。随着电压幅值的升高,铁心饱和速度加快。当充电电压升高至2 500 V时,铁心电压在15 ms内从0 V达到最高幅值1 593 V,分压迅速降低,产生更强的振动,与实际工作的波形更为相似。两种电压等级下饱和电抗器电流都近似为梯形,最大幅值分别为-335 A和-1 639 A,电流变化率升高了近4倍。
通过傅里叶变换,得到不同充电电压下饱和电抗器电压谐波分布如图4所示。饱和电抗器电压中含有大量谐波分量,奇次谐波和偶次谐波占比相当,且受电压幅值变化影响较小。以每2 kHz为一频段对0~20 kHz的频谱进行划分,共分为10段,分别计算不同频段的占比。随着电压幅值的不断升高,0~4 kHz所占比例逐渐降低。在充电电压达到2 500 V时比例为34.5%,下降比例约为18%,但仍为谐波主要成分;4~20 kHz占比存在波动,总体呈升高趋势。其中,充电电压500 V与600 V的谐波分量变化最为明显。进一步分析电压波形发现,充电电压为600 V时电压波形已出现突降;继续升压,电压谐波分量变化趋势减缓。
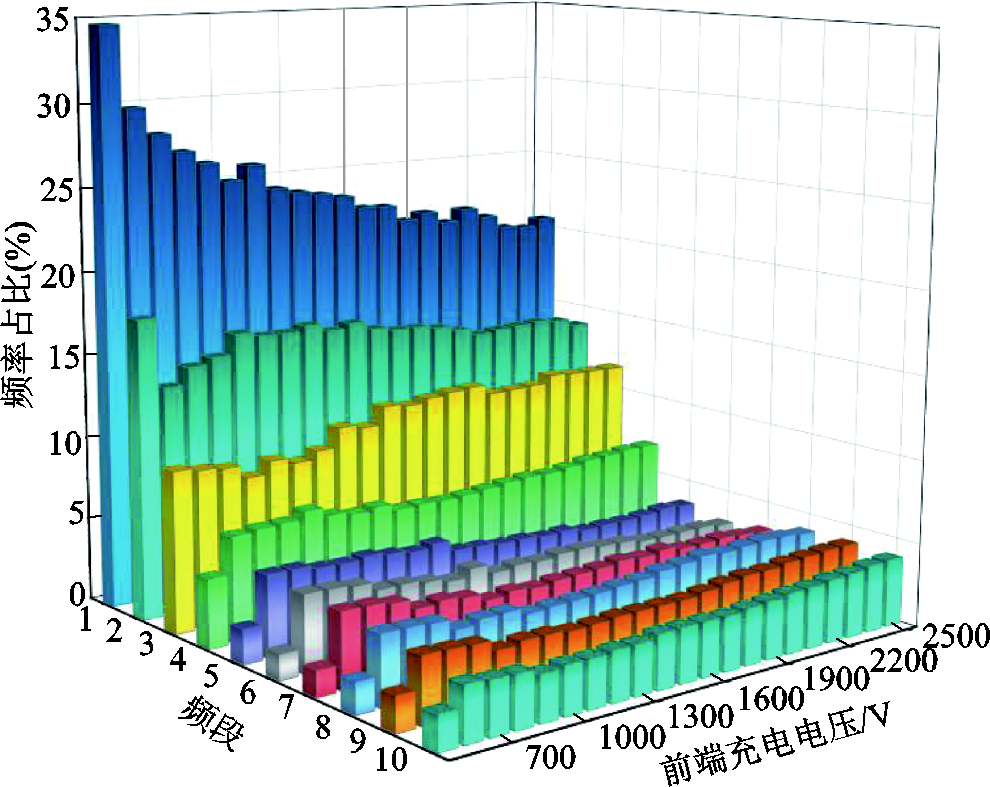
图4 不同充电电压下饱和电抗器电压谐波分布
Fig.4 Voltage harmonic distribution of saturable reactor at different charging voltages
为了研究饱和电抗器铁心振动声音随电压升高产生的变化,将五个测点的时域声信号幅值绘制成如图5所示的箱线图,上下边缘为1.5倍的数据标准差。不同测点的声音变化趋势大致相同,在电压为380 V时,所有测点的幅值在0.218 V以下,此时铁心已处于饱和状态,产生较大的振动噪声。随着电压升高,铁心磁不饱和与磁饱和状态转换加快,产生的高频分量使振动噪声显著增加,其中测点5受电压增长影响较大,声信号幅值变化超过了3倍。但饱和电抗器铁心振动与电压幅值二次方呈非线性关系,当电压幅值达到1 160 V后,声信号幅值增长速度下降,逐渐趋于平缓。
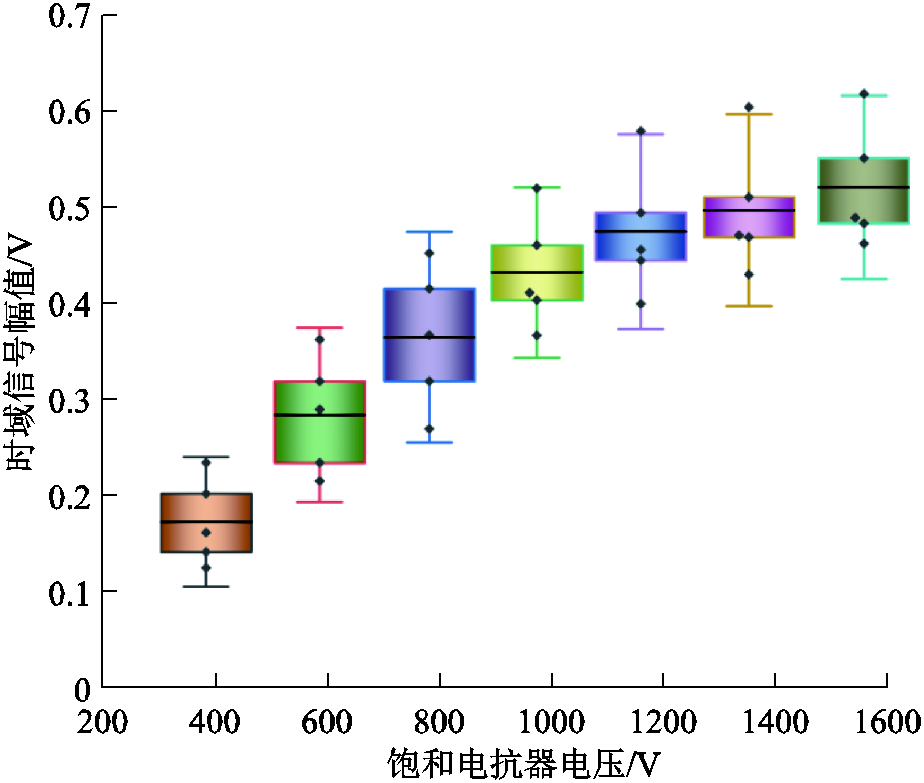
图5 饱和电抗器铁心振动声信号幅值变化箱线图
Fig.5 Box diagram of vibration and sound variation of saturable reactor core
在完成不同电压等级下饱和电抗器振动声纹试验后,进一步分析测点1~5的数据,发现各测点下的电抗器振动声纹频谱整体较为相似。因此本文仅选取饱和电抗器正面测点2的数据分析结果进行展示。声纹信号频率在50 Hz~18 kHz范围内的50 Hz倍频上均有体现,主要集中在50 Hz~8 kHz,后续进行频谱分析时均按此范围采用第2.3节的占比时频矩阵进行计算。
饱和电抗器电压中含有大量的奇、偶次谐波,使铁心的磁化过程更快、饱和程度更高。产生的振动频率也不仅是电压谐波的偶数倍,同时也包含了大量的奇数次谐波,且频带更宽,这也与理论分析的结果一致。升压试验中不同电压等级下振动声纹频率占比瀑布图如图6所示,图中只呈现了0~8 kHz的频谱分布。从图6中可以看出,电压等级较低时,频率主要集中在2 kHz以下的范围内;随着电压升高,低频分量逐渐降低,高频分量不断增加,主频段朝着高频方向偏移。当电压幅值达到973 V时,5~7 kHz范围内的频率占比已超过0~2 kHz的情况,继续升高电压,各频段的变化趋势放缓。
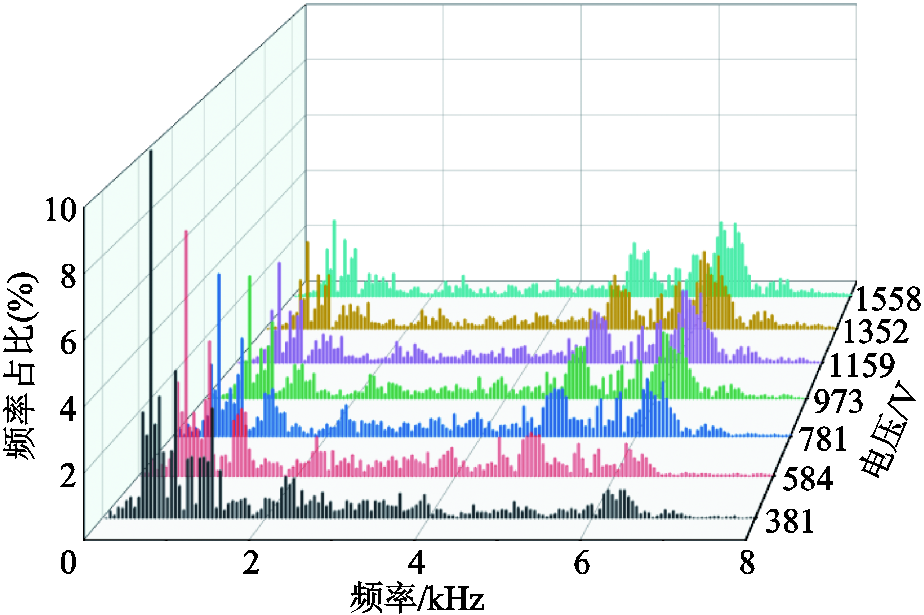
图6 不同电压等级下铁心振动声纹频率占比瀑布图
Fig.6 The proportion waterfall diagram of core vibration voiceprint frequency at different voltage levels
为了探究不同压紧力(松动程度)下的铁心振动声纹特性,本文进行了饱和电抗器铁心松动试验。其中电源电压为2 000 V(对应饱和电抗器电压 1 280 V),经上文分析,此时铁心已达到较高的饱和程度,与实际运行工况相近。铁心松动程度设置为螺钉脱落、螺钉完全松动、夹件紧固力矩为5~11 Nm(正常压紧力)共九种情况。铁心松动故障实物如图7所示。

图7 铁心松动故障实物
Fig.7 Physical image of core loosening fault
以测点2为例,饱和电抗器铁心处于正常压紧力和螺钉脱落时的声纹时域和频域信号如图8所示。
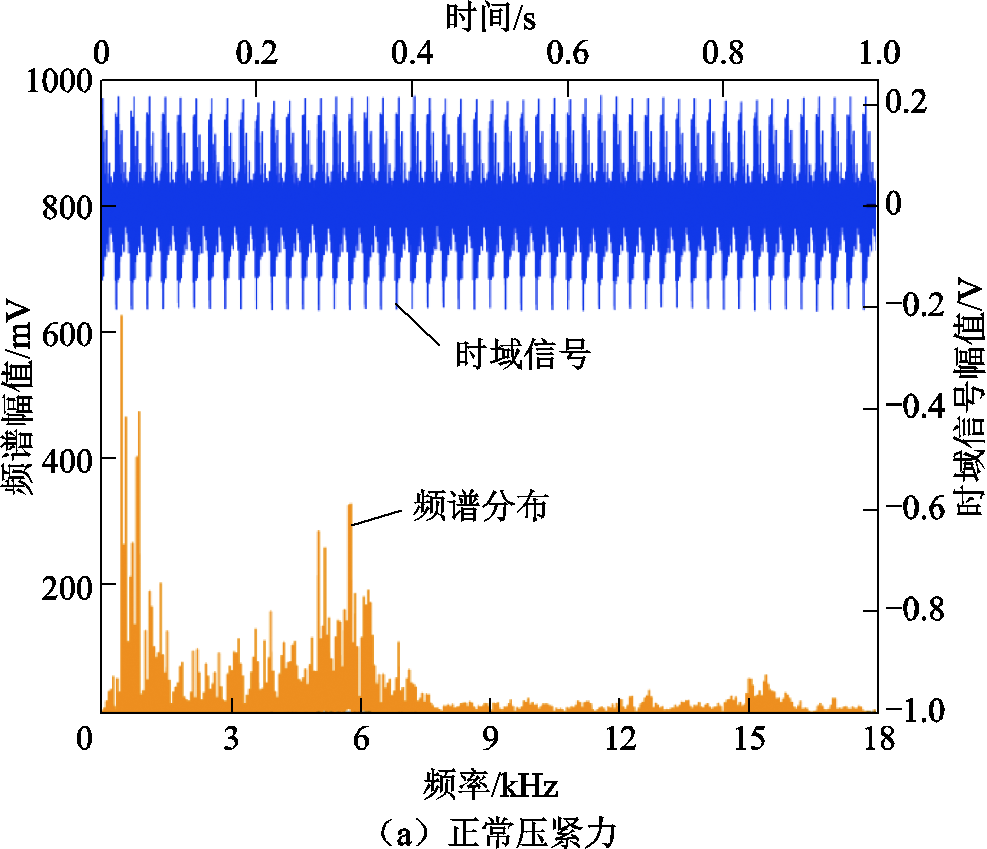
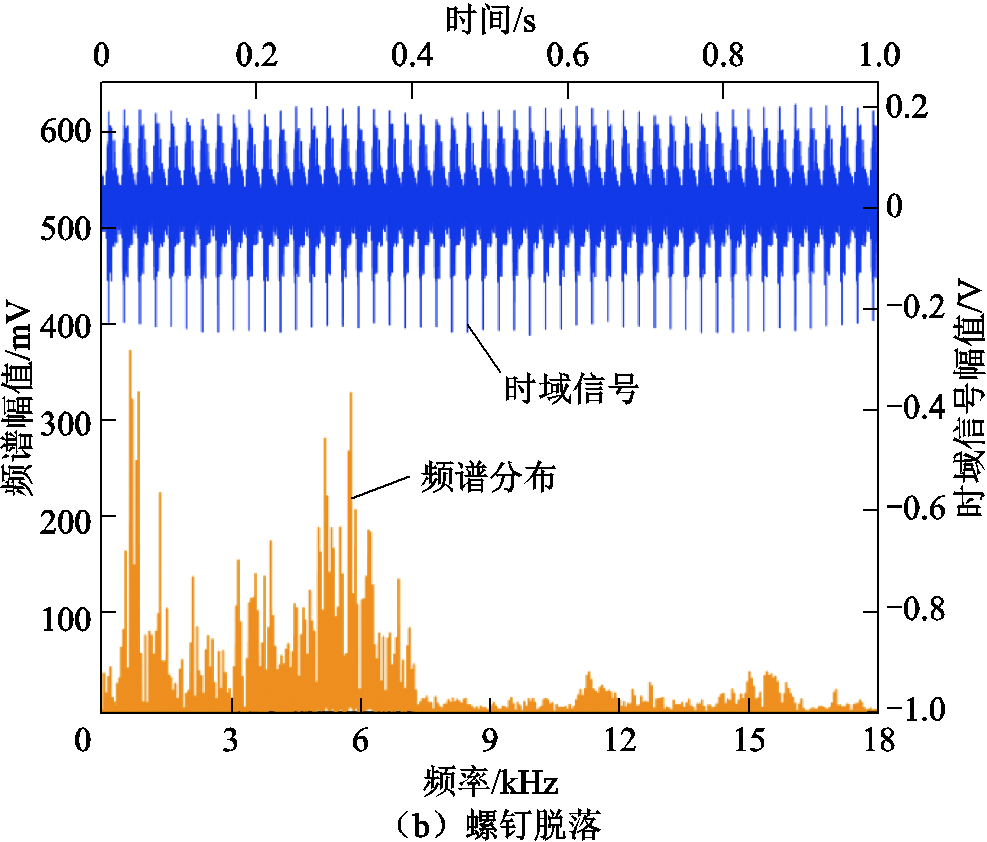
图8 铁心正常与松动时声纹的时域信号与频域分布
Fig.8 Time domain signal and spectrum distribution diagram of voiceprint for core at normal and loose
对比发现,铁心振动周期与电信号相同,均为0.02 s。松动后,时、频信号都存在一定程度的改变,其中频域信号变化较为明显,50~1 200 Hz低频分量降低,1 250~18 000 Hz高频分量升高,11 kHz后的微弱分量也得到了增强。因此本文通过对比不同的频域特征值来分析铁心松动后的振动声纹特性。
基于反映变压器机械结构的频域特征值[21]和饱和电抗器铁心振动声纹频谱特性,本文选择频谱复杂度d1、主频频率d2、奇偶次谐波比d3、低频分量主频比重d4、高低频比d5共五个特征指标,并采用五个测点的数据进行了分析和验证。以各频率分量占比R为基础(见式(15)),五个特征指标分别如式(16)~式(20)所示。
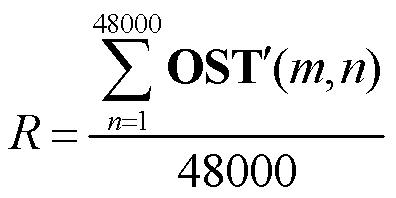 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
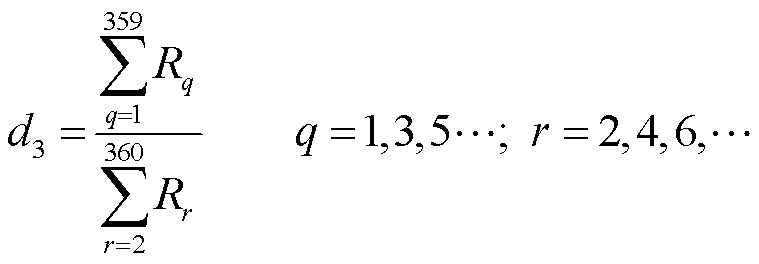 (18)
(18)
![]() (19)
(19)
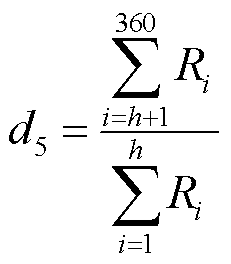 (20)
(20)
式中,Ri为50 Hz倍频的比重;i为50 Hz倍频次数;h为高低频分界频率所对应的谐波次数,本文在计算时选取1 200 Hz为分界线,即h=24。
不同松动程度下的铁心振动声纹频域特征值变化如图9所示。可以看出,不同特征值对铁心松动的灵敏度存在差异,且单个特征值在测点间的变化趋势也不尽相同。下面依次对五个特征值反映频谱变化的规律进行分析。
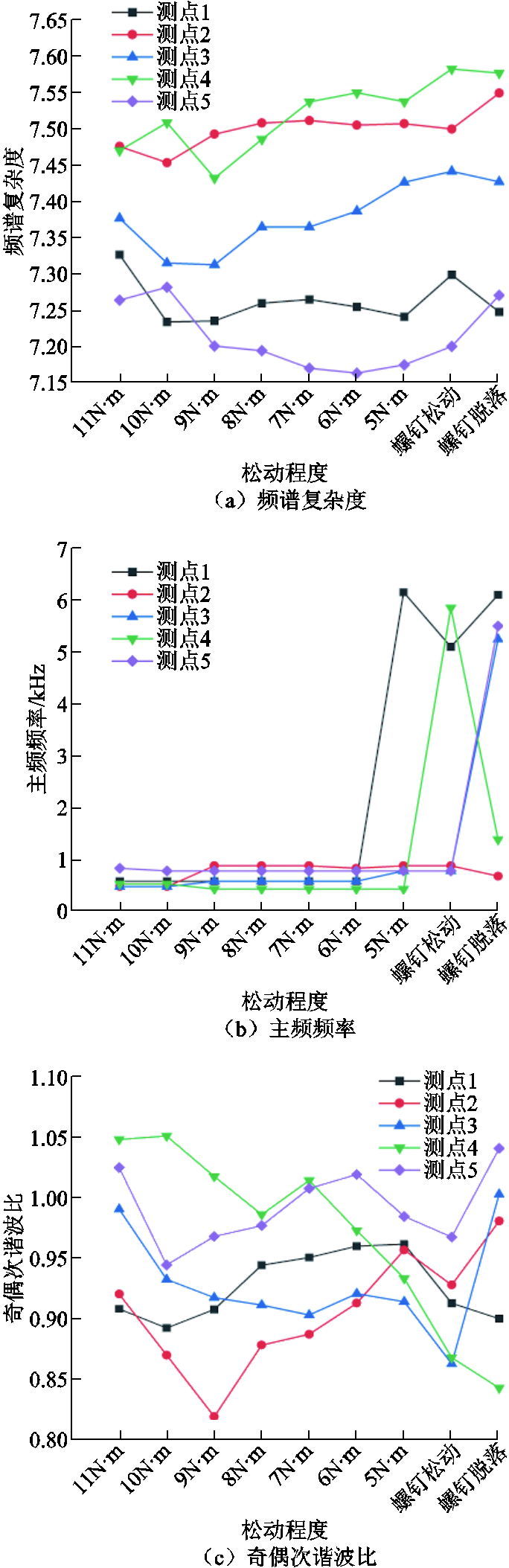
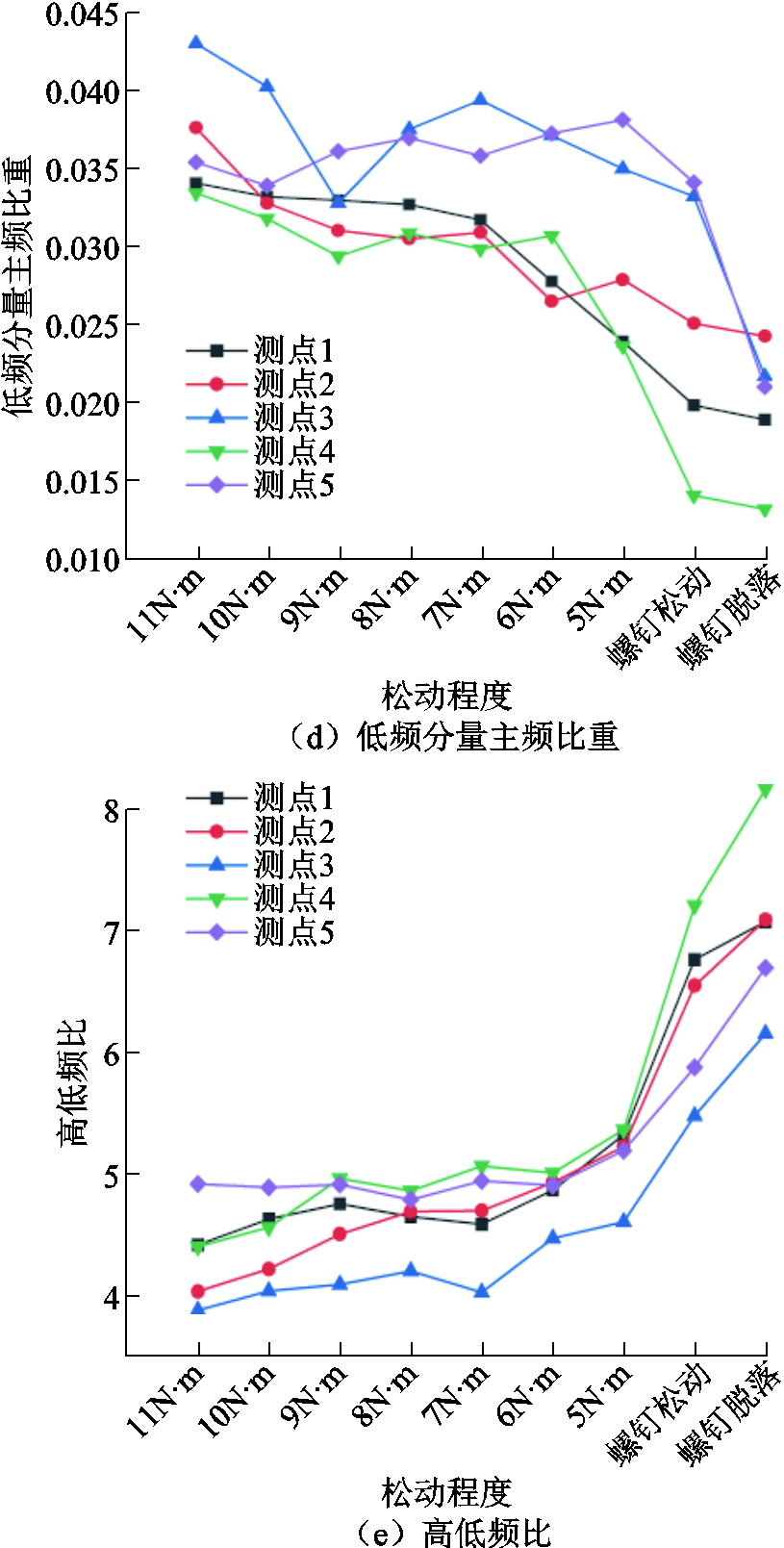
图9 不同松动程度下的铁心振动声纹频域特征值变化
Fig.9 Variation of frequency domain eigenvalues of core vibration voiceprint at different looseness conditions
1)频谱复杂度。频谱复杂度与铁心松动程度的相关性较弱,总体在7.15~7.6之间波动,且无明显的单调变化趋势。由于饱和电抗器铁心振动声纹的频带较宽,正常压紧力下,频率主要集中在8 kHz以内;铁心松动后,频率也主要在此范围内进行增减,8~20 kHz范围内的新增分量相对较少,因此频谱复杂度变化不明显。
2)主频频率。铁心松动程度较低时,主频频率均在1 kHz以内;随着松动程度增加,当压紧力达到5 Nm或螺钉完全松动后,主频频率发生突变,偏移到5 kHz以上,其中测点2的主频依旧未超过1 kHz。不同测点主频突变的临界点存在差异,且仅能反映铁心松动程度较高的情况,灵敏度较差。造成这种现象的主要原因为:铁心松动过程中,虽然低频占比降低,高频占比升高,但小幅度松动引起的高低频分量变化的差值还不足以使主频发生偏移。
3)奇偶次谐波比。铁心发生松动时,奇偶次谐波比并无明显变化规律,在0.8~1.05区间内无规则波动,且主要分布在1以下,表明偶次谐波含量略高于奇次谐波含量。
4)低频分量主频比重。正面测点1、2、4的低频分量主频比重总体呈下降趋势,在铁心松动前期变化较缓,中后期出现陡降。侧面测点3、5的曲线整体位于正面测点之上,松动前期在小范围内发生变化,螺钉松动后迅速下降。这也是由于侧面测点处于离松动铁心较远的位置,收集到有效的声音分量较小所导致的。结合不同测点的特性,设定低频分量主频比重阈值为0.033,可在一定程度下反映铁心的松动情况。
5)高低频比。随着铁心夹件压紧力的减小,高低频比在11 Nm到5 Nm范围内逐步上升,期间存在微小幅度波动;当螺钉完全松动时,由于5 Nm压紧力与螺钉完全松动之间相差的力矩较大,曲线出现陡增现象,且正面测点的增幅高于侧面测点,其中测点4在螺钉脱落状态下的高低频比值约为正常情况下的2倍。不同测点的变化趋势大致相同,可以表明铁心松动会导致高频分量占比升高,但在数值上存在差异,仅通过设置固定阈值点,并不能很好地利用高低频比这一特性来反映饱和电抗器铁心松动情况。
综上所述,当铁心发生松动时,频谱复杂度和奇偶次谐波比的变化可信度较低;主频频率在松动程度较高时产生剧烈变化,但不能在松动初期进行预警;饱和电抗器正面测点的低频分量主频比重和高低频比可以较敏感地反映出铁心的不同松动状态。但不同测点麦克风接收到的松动铁心振动声音分量存在差异,最优高低频分界线难以人为确定,这些因素都会对阈值设定产生影响。因此,采用设定特征阈值的方法只能反映松动程度较高时的状态,为达到精确判断饱和电抗器铁心松动程度的目标,需要进一步联合分析不同测点的铁心正常与松动情况下的振动声纹特征。
针对饱和电抗器铁心振动声纹的复杂特性,本节提出一种端到端的模式识别方法。搭建基于自适应参数修正线性单元(Adaptively Parametric Rectifier Linear units, APReLu)[22]的改进深度残差收缩网络(Improved Deep Residual Shrinkage Networks, IDRSN),对不同测点的声纹时频谱图进行去噪,即消除冗余信息;并对不同铁心松动程度下的声纹特征进行独立映射,提高测点间共同特征的学习能力;最后采用铁心松动数据集验证了该方法在深度特征提取方面的改进性能。
深度残差收缩网络[23](Deep Residual Shrinkage Network, DRSN)是He Kaiming等提出的,是从一种深度残差网络[24]发展而来,最先应用于机械故障的识别。本文提出一种改进深度残差收缩网络用于饱和电抗器铁心松动程度识别,网络主要由输入层、卷积层、改进残差收缩单元(Improved Residual Shrinkage Building Unit, IRSBU)、批标准化层、自适应参数修正线性单元、全局平均池化(Global Average Pooling, GAP)层和全连接(Full Connection, FC)层构成。
麦克风布置方位的变化会导致测量到的声纹信号包含不同程度的松动分量。传统残差收缩网络通常采用ReLu激活函数对全部输入信号进行固定的非线性变换。这就可能导致将同一松动状态差异较大的信号投影到不同区域,或将不同松动状态差异较小的信号投影到同一区域,对模型的训练产生消极影响。为了提高类内相同特征、类间差异特征的学习能力,本文将APReLu嵌入到深度残差收缩网络中,通过深度学习自适应获取合适的权值,改善同类信号原始特征投影后的聚类效果。自适应参数修正线性子网络如图10所示,其本质是对每个输入信号进行不同的非线性变换,即激活函数中的斜率是动态变化的。
特征图输入子网络后,经过ReLu和min(x,0)函数的输出分别反映正、负特征,融合了全局信息;采用GAP层计算图像平均值可提高特征提取的抗干扰性。对生成的两个一维向量进行级联,采用BN层加速权值学习过程。ReLu函数和Sigmoid函数可对特征进行两次非线性变换,提高差异化程度且输出数值在0~1之间,使权值系数不会过于敏感,避免对特征映射产生负面影响。最后采用PReLu函数进行计算,得到特征映射结果。
残差收缩单元采用软阈值函数去噪,根据通道间阈值是否共享,分为阈值独立型和阈值共享型两种结构。本文以抑制噪声效果更优的阈值独立型结构[23]为基础单元框架,采用APReLu激活函数代替ReLu激活函数,建立改进残差收缩单元,如图11所示。其中W、H、C分别为特征图的宽度、高度和通道数,K和M分别为卷积核个数和全连接层神经元个数。
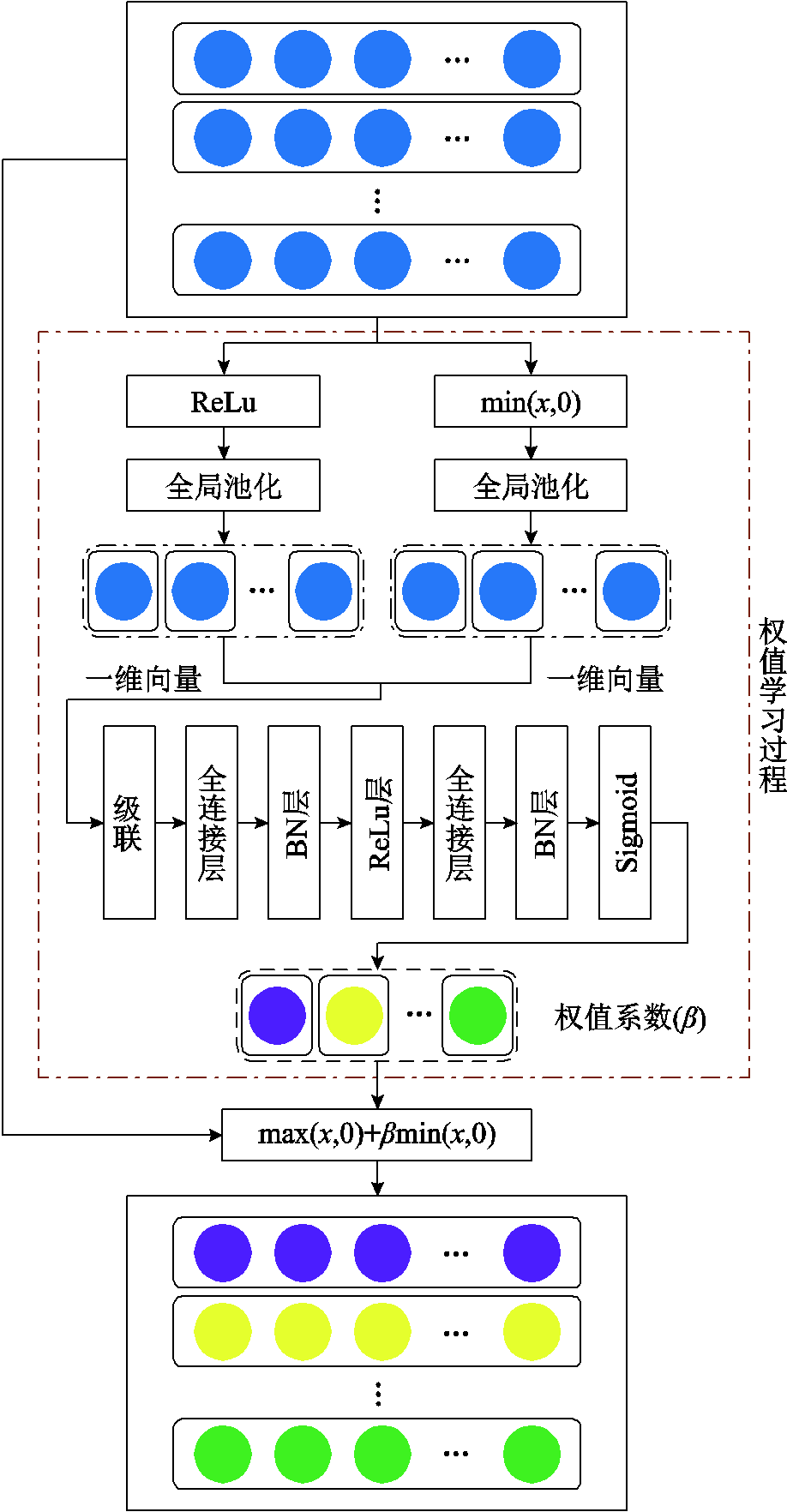
图10 自适应参数修正线性子网络
Fig.10 Adaptively parametric rectifier linear subnet
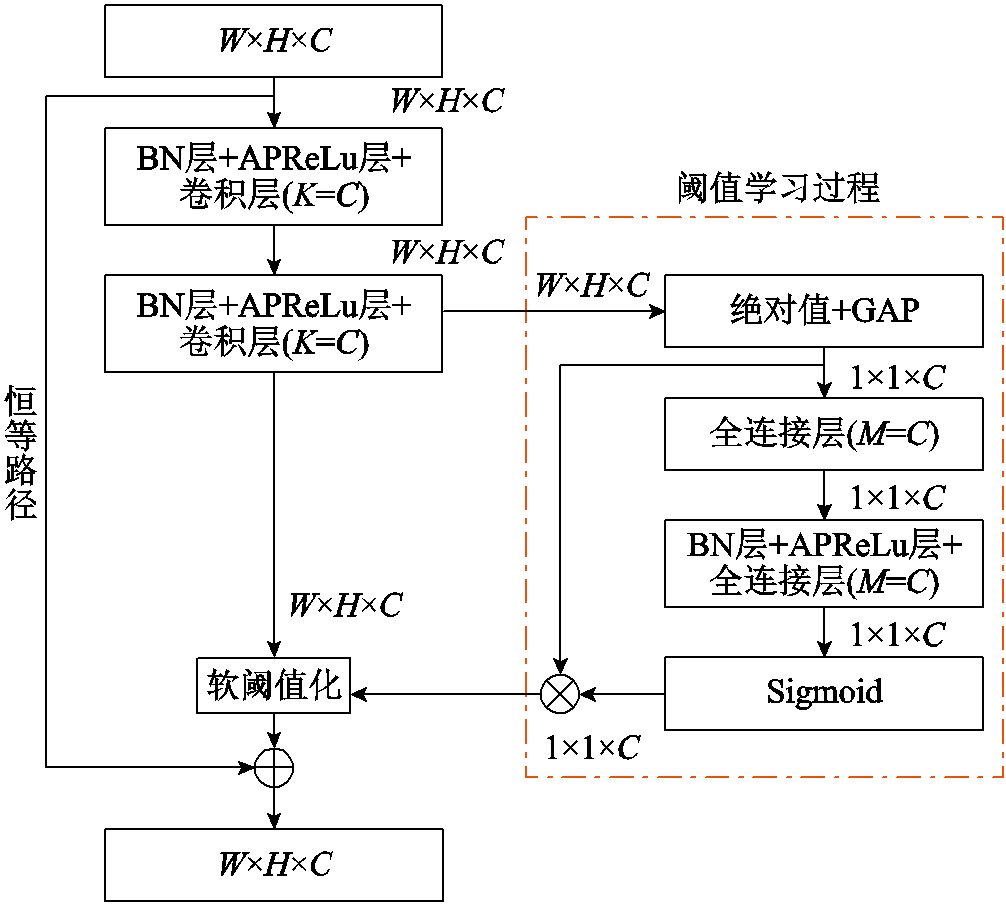
图11 基于APReLu的改进残差收缩单元
Fig.11 Improved residual shrinkage building unit based on APReLu
特征图输入子网络后,各通道均进行软阈值化。以通道c为例,其独立缩放参数及软阈值表达式分别为
![]() (21)
(21)
式中,zc为第2个全连接层第c层输出的特征;![]() 为特征图的三维矩阵,其中i、j、c分别为特征图的宽度、高度和通道。阈值确定后,对通道c的特征矩阵进行软阈值化,与残差项相加后输出结果,其他通道类似。采用上述网络计算出的阈值不会过大而过滤掉有用的特征信息,从而达到较好的去除冗余信息的效果。
为特征图的三维矩阵,其中i、j、c分别为特征图的宽度、高度和通道。阈值确定后,对通道c的特征矩阵进行软阈值化,与残差项相加后输出结果,其他通道类似。采用上述网络计算出的阈值不会过大而过滤掉有用的特征信息,从而达到较好的去除冗余信息的效果。
铁心的振动声音可以反映铁心的机械模态。为了验证改进深度残差收缩网络的有效性,本文根据铁心松动程度对五个测点的声纹数据进行了分类,共分为正常情况(11 N·m)、轻微松动(8~10 N·m)、严重松动(5~7 N·m)、完全松动和螺钉脱落五类,并随机打乱其排列顺序,防止产生过拟合现象。数据集样本分布见表2。
表2 数据集样本分布
Tab.2 Sample distribution of data sets
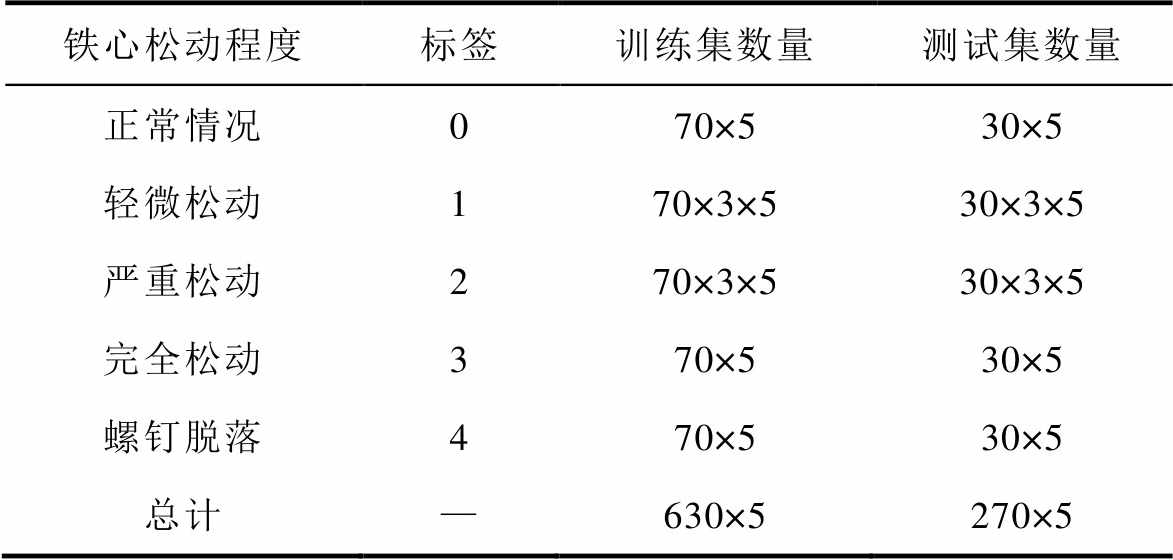
铁心松动程度标签训练集数量测试集数量 正常情况070×530×5 轻微松动170×3×530×3×5 严重松动270×3×530×3×5 完全松动370×530×5 螺钉脱落470×530×5 总计—630×5270×5
为了减少输入网络的数据量,采用第2.3节中的计算方法获取铁心振动声纹时频谱图,并将其等比缩放至128×128×3(宽度×高度×通道数)维,作为神经网络的输入。本文设计的网络结构由1个卷积层(Conv1)、4个IRSBU单元(IRSBU1~4)、1个BN层、1个APReLu层、1个GAP层和1个FC层组成。训练目标为多分类交叉熵损失函数,卷积层中padding设置的值为SAME,批处理batch_size大小为32,迭代次数为100次,IDRSN模型的具体参数设置见表3。其中,参数“3,3,2,8”表示IRSBU单元中卷积核大小为3×3,步长为2,通道数为8,依此类推。FC层使用softmax函数及L2正则化标准,正则化系数为0.000 1。
神经网络输入特征众多且结构复杂,所包含的子网络中存在多个自适应参数学习过程。不同的优化算法可能训练出不同的阈值参数,导致特征提取情况存在差异,对网络的准确率和训练速度产生影响,因此需选择合适的优化器来进行参数的学习。针对本文构建的声纹数据集和网络结构,选用SGD、Adam与AdaGrad优化器对模型进行训练,测试集的准确率与损失误差如图12所示,其他超参数保持一致。
表3 IDRSN模型的参数设置
Tab.3 Parameter settings of IDRSN model
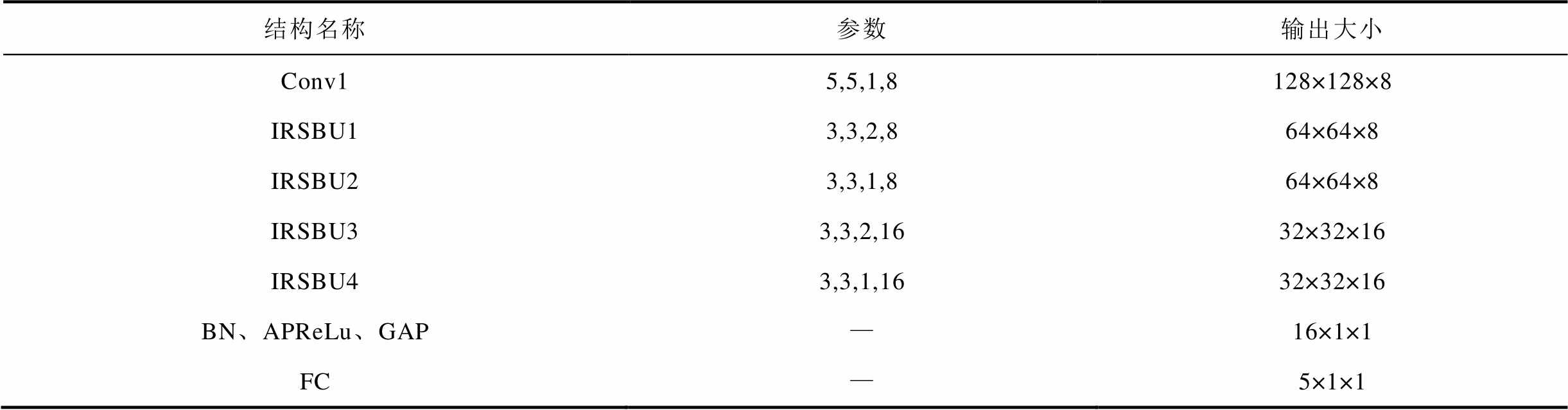
结构名称参数输出大小 Conv15,5,1,8128×128×8 IRSBU13,3,2,864×64×8 IRSBU23,3,1,864×64×8 IRSBU33,3,2,1632×32×16 IRSBU43,3,1,1632×32×16 BN、APReLu、GAP—16×1×1 FC—5×1×1
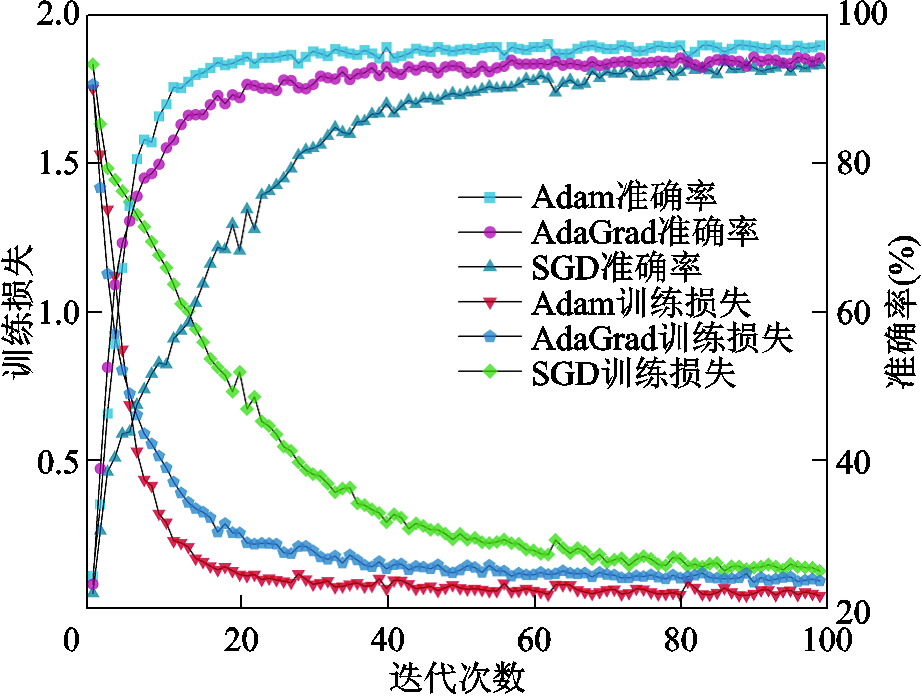
图12 不同优化器的训练误差和测试集准确率对比
Fig.12 Comparison of training error and test set accuracy of different optimizers
如图12所示,Adam优化器在迭代20次左右已经收敛,最终对五类松动程度下的饱和电抗器铁心振动声纹信号识别准确率达到了95.93%,其收敛速度、准确率、稳定度均高于AdaGrad和SGD优化器,因此本文选择Adam作为优化器进行训练。为清晰展示改进深度残差收缩网络的特征提取能力,采用t-分布式随机邻域嵌入(t-distributed Stochastic Neighbor Embedding, t-SNE)算法对最终全连接层的输出向量进行降维可视化处理,二维空间特征聚类结果如图13所示。
根据聚类结果可以看出,不同松动程度下的铁心振动声纹特征各自成群,且各种群间的距离较远,整体分界明显。但轻微松动和严重松动间存在少许混杂,其他松动程度间的区分度较高,相较于正常压紧力情况,没有出现漏判。采用多方位测点的数据进行测试,针对不同阶段的松动故障均可做出预警,证明了算法具有较强的识别能力。
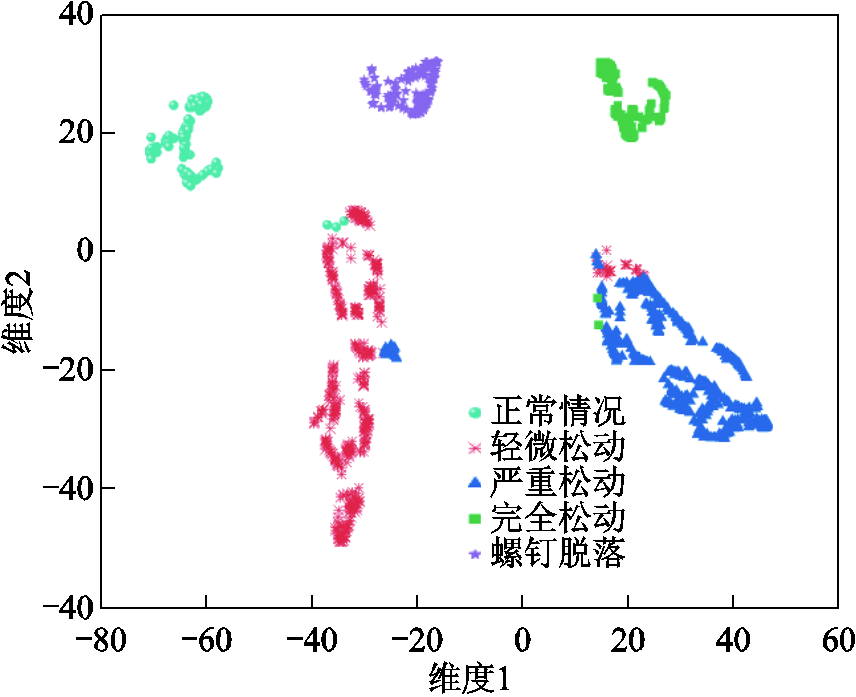
图13 本文方法所提取特征的聚类结果
Fig.13 Clustering results of the learned features by proposed method
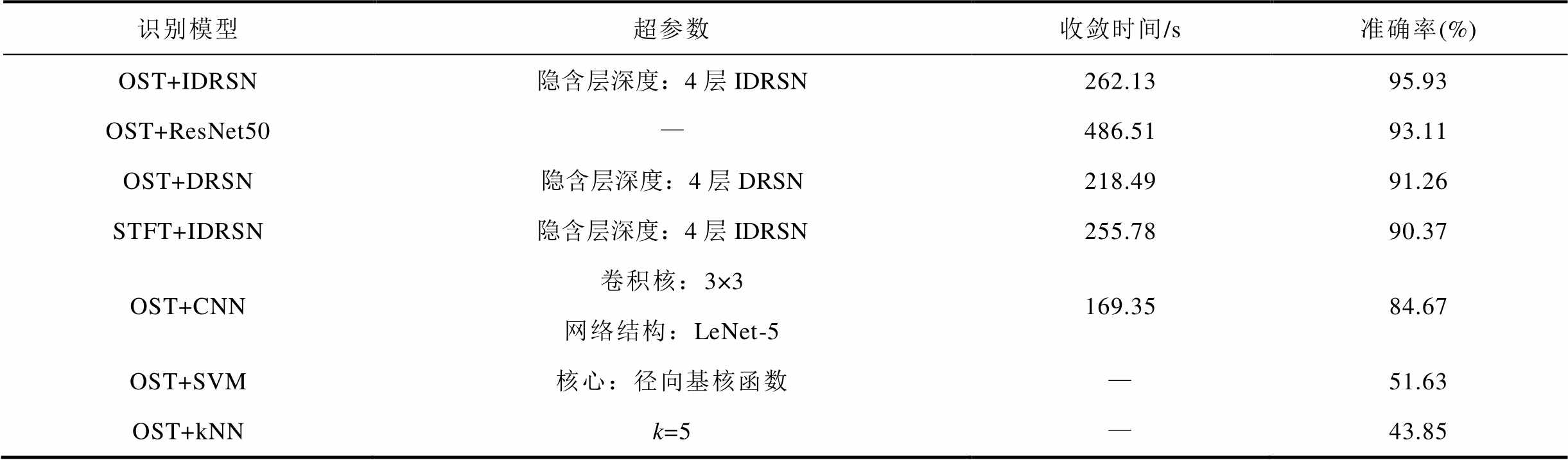
为了比较不同组合模型对铁心松动程度的识别能力,将本文模型与ResNet50、卷积神经网络(Convolutional Neural Network, CNN)等经典图像分类网络及支持向量机(Support Vector Machine, SVM)、K近邻(k-Nearest Neighbor, kNN)等传统机器学习算法进行对比。输入层图像维度、批处理大小等超参数与4.2节设置相同。在特征提取方面,基于IDRSN模型,对比优化S变换与短时傅里叶变换(Short-Time Fourier Transform, STFT)的时频特征提取效果,短时傅里叶变换的帧长为0.1 s,帧移为0.02 s。采用4.2节所构建的数据集进行训练,结果见表4。
表4 不同模型超参数设置及识别效果对比
Tab.4 Comparison of hyperparameter settings and recognition effects of different models
识别模型超参数收敛时间/s准确率(%) OST+IDRSN隐含层深度:4层IDRSN262.1395.93 OST+ResNet50—486.5193.11 OST+DRSN隐含层深度:4层DRSN218.4991.26 STFT+IDRSN隐含层深度:4层IDRSN255.7890.37 OST+CNN卷积核:3×3网络结构:LeNet-5169.3584.67 OST+SVM核心:径向基核函数—51.63 OST+kNNk=5—43.85
由表4可以看出,SVM与kNN算法对高维特征的学习能力较差,准确率在50%左右,其判断结果对五分类松动故障问题没有参考价值。CNN网络结构简单,计算速度较快,但准确率有待提高。采用时频特征提取结合深层次神经网络的方法准确率均达到了90 %以上,相较于短时傅里叶变换,优化S变换模型的准确率提高了5.56%,特征提取能力更强。为进一步展示分类情况,列举四种模型测试集的混淆矩阵如图14所示。

图14 松动程度识别混淆矩阵
Fig.14 Degree of looseness identification confusion matrix
由图14可以看出,误分类主要集中在轻微松动和严重松动之间,OST+IDRSN模型准确率最高,在松动前期的混淆度低于其他三种模型。若转换为二分类问题,即只考虑正常和松动情况,其余三种模型均存在少量的误判或漏判情况。相较于特征值诊断方法,本文模型对不同阶段的松动故障均可做出预警,对轻微松动(8~10 N·m)状态的识别准确率为91.8 %,对严重松动(5~7 N·m)状态的识别准确率为97.3 %,能够较早发现铁心松动故障,避免故障的进一步发展。对比结果表明,本文模型在饱和电抗器铁心松动程度识别中具有良好的应用效果。
为提高饱和电抗器铁心松动程度识别的准确性,本文首先通过开展饱和电抗器铁心松动试验来构建声纹数据集,再将其代入优化S变换结合改进深度残差收缩网络的模型进行训练,得到主要结论如下:
1)在高频脉冲激励下,饱和电抗器铁心在极短时间内达到饱和,振动声纹频谱中含有大量高次谐波,且50 Hz奇、偶倍频占比相当。铁心夹件松动后,50~1 200 Hz分量占比降低,1 250~18 000 Hz分量占比升高。
2)提出了采用优化S变换绘制声纹时频谱图的方法。通过利用能量聚集性公式调节频域窗参数,解决了频带混叠、频谱泄露等问题,获取了更高的时频分辨率。与短时傅里叶变换时频谱作为输入层的方法进行对比,该方法准确率提高了5.56%。
3)搭建了基于自适应参数修正线性单元的改进深度残差收缩网络。通过特征独立映射实现对不同方位收集的声纹信号的统一识别,松动程度识别准确率达到了95.93%,相比于其他传统模型拥有更高的识别精度。本文方法主要针对于饱和电抗器铁心松动故障的诊断,实际运行中还会存在铁心绝缘漆老化导致发热增大、母排螺钉松动等其他故障,其振动声纹特性有待后续进行试验研究。
参考文献
[1] 辛保安, 郭铭群, 王绍武, 等. 适应大规模新能源友好送出的直流输电技术与工程实践[J]. 电力系统自动化, 2021, 45(22): 1-8. Xin Baoan, Guo Mingqun, Wang Shaowu, et al. Friendly HVDC transmission technologies for large-scale renewable energy and their engineering practice[J]. Automation of Electric Power Systems, 2021, 45(22): 1-8.
[2] 许汉平, 杨炜晨, 张东寅, 等. 考虑换相失败相互影响的多馈入高压直流系统换相失败判断方法[J]. 电工技术学报, 2020, 35(8): 1776-1786. Xu Hanping, Yang Weichen, Zhang Dongyin, et al. Commutation failure judgment method for multi-infeed HVDC systems considering the interaction of commutation failures[J]. Transactions of China Electrotechnical Society, 2020, 35(8): 1776-1786.
[3] 孟沛彧, 王志冰, 迟永宁, 等. 适应多能源基地远距离输送电能的混合四端直流输电系统控制策略研究[J]. 电工技术学报, 2020, 35(增刊2): 523-534. Meng Peiyu, Wang Zhibing, Chi Yongning, et al. Control strategy of hybrid four-terminal HVDC transmission system dedicated for long-distance power delivery from multiple energy bases[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 523-534.
[4] 赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2004.
[5] 纪锋, 曹均正, 陈鹏, 等. 高压直流输电系统逆变侧阀饱和电抗器电气应力研究[J]. 高电压技术, 2014, 40(8): 2579-2585. Ji Feng, Cao Junzheng, Chen Peng, et al. Research of electrical stress on saturable reactor in inverter valve of high voltage direct current transmission system[J]. High Voltage Engineering, 2014, 40(8): 2579-2585.
[6] 张鹏宁, 李琳, 纪锋, 等. HVDC阳极饱和电抗器阻尼弹性体降振降噪试验研究[J]. 电网技术, 2017, 41(12): 3839-3845. Zhang Pengning, Li Lin, Ji Feng, et al. Test study on reduction of vibration and noise to damping elastomer in HVDC anode saturable reactor[J]. Power System Technology, 2017, 41(12): 3839-3845.
[7] 陶敏, 姚舒, 董妍波, 等. 特高压换流阀用饱和电抗器的振动研究与优化方案[J]. 高压电器, 2019, 55(12): 200-204. Tao Min, Yao Shu, Dong Yanbo, et al. Vibration research and optimization on UHVDC converter valve saturable reactor[J]. High Voltage Apparatus, 2019, 55(12): 200-204.
[8] 王丰华, 王邵菁, 陈颂, 等. 基于改进MFCC和VQ的变压器声纹识别模型[J]. 中国电机工程学报, 2017, 37(5): 1535-1543. Wang Fenghua, Wang Shaojing, Chen Song, et al. Voiceprint recognition model of power transformers based on improved MFCC and VQ[J]. Proceedings of the CSEE, 2017, 37(5): 1535-1543.
[9] Yi Lu, Mak M W. Adversarial data augmentation network for speech emotion recognition[C]//2019 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, 2019: 529-534.
[10] Qian Yanmin, He Tianxing, Deng Wei, et al. Automatic model redundancy reduction for fast back-propagation for deep neural networks in speech recognition[C]//2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 2015: 1-6.
[11] 王卓, 王玉静, 王庆岩, 等. 基于协同深度学习的二阶段绝缘子故障检测方法[J]. 电工技术学报, 2021, 36(17): 3594-3604. Wang Zhuo, Wang Yujing, Wang Qingyan, et al. Two stage insulator fault detection method based on collaborative deep learning[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3594-3604.
[12] 谢庆, 杨天驰, 裴少通, 等. 基于多尺度协作模型的电气设备红外图像超分辨率故障辨识方法[J]. 电工技术学报, 2021, 36(21): 4608-4616. Xie Qing, Yang Tianchi, Pei Shaotong, et al. Super-resolution identification method of electrical equipment fault based on multi-scale cooperation model[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4608-4616.
[13] 张重远, 罗世豪, 岳浩天, 等. 基于Mel时频谱-卷积神经网络的变压器铁芯声纹模式识别方法[J]. 高电压技术, 2020, 46(2): 413-423. Zhang Zhongyuan, Luo Shihao, Yue Haotian, et al. Pattern recognition of acoustic signals of transformer core based on Mel-spectrum and CNN[J]. High Voltage Engineering, 2020, 46(2): 413-423.
[14] 刘云鹏, 王博闻, 岳浩天, 等. 基于50Hz倍频倒谱系数与门控循环单元的变压器偏磁声纹识别[J]. 中国电机工程学报, 2020, 40(14): 4681-4694, 4746. Liu Yunpeng, Wang Bowen, Yue Haotian, et al. Identification of transformer bias voiceprint based on 50Hz frequency multiplication cepstrum coefficients and gated recurrent unit[J]. Proceedings of the CSEE, 2020, 40(14): 4681-4694, 4746.
[15] 黄南天, 徐殿国, 刘晓胜. 基于S变换与SVM的电能质量复合扰动识别[J]. 电工技术学报, 2011, 26(10): 23-30. Huang Nantian, Xu Dianguo, Liu Xiaosheng. Identification of power quality complex disturbances based on S-transform and SVM[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 23-30.
[16] Tang Qiu, Qiu Wei, Zhou Yicong. Classification of complex power quality disturbances using optimized S-transform and kernel SVM[J]. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9715-9723.
[17] 朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究[J]. 西安交通大学学报, 2015, 49(6): 115-125. Zhu Yeye, Ji Shengchang, Zhang Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 115-125.
[18] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.
[19] 刘宇舜, 周文俊, 李鹏飞, 等. 基于广义S变换模时频矩阵的局部放电特高频信号去噪方法[J]. 电工技术学报, 2017, 32(9): 211-220. Liu Yushun, Zhou Wenjun, Li Pengfei, et al. Partial discharge ultrahigh frequency signal denoising method based on generalized S-transform modular time-frequency matrix[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 211-220.
[20] 李盼, 娄钊瑜, 马康, 等. 一种自适应S变换在电能质量特征提取中的应用[J]. 中国电机工程学报, 2021, 41(22): 7660-7668. Li Pan, Lou Zhaoyu, Ma Kang, et al. Application of adaptive S-transform in power quality feature extraction[J]. Proceedings of the CSEE, 2021, 41(22): 7660-7668.
[21] 刘云鹏, 王博闻, 周旭东, 等. 基于162台超、特高压变压器的声纹特征预警阈值划定研究[J]. 华北电力大学学报(自然科学版), 2021, 48(5): 45-53. Liu Yunpeng, Wang Bowen, Zhou Xudong, et al. Threshold delineation research for early warning of voiceprint eigenvalues based on 162 sets of EHV and UHV transformers[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(5): 45-53.
[22] Zhao Minghang, Zhong Shisheng, Fu Xuyun, et al. Deep residual networks with adaptively parametric rectifier linear units for fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2021, 68(3): 2587-2597.
[23] Zhao Minghang, Zhong Shisheng, Fu Xuyun, et al. Deep residual shrinkage networks for fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2020, 16(7): 4681-4690.
[24] He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 2016: 770-778.
Abstract As the key equipment in converter valves, the saturable reactor is used to protect the normal opening and closing of the thyristor. However, in the process of microsecond conduction of the thyristor, the high harmonics will produce high frequency mechanical vibration and thermal shock vibration on the saturable reactor, increasing the probability of the fault of the saturable reactor. Therefore, it is of great significance to evaluate its status. Recently, some methods were proposed to monitor the state of the saturable reactor, but most of them can only monitor the abnormal temperature rise of the core, and cannot identify the mechanical failure of the core. This paper presents a voiceprint identification model of saturable reactor core looseness based on optimized S-transform (OST) and improved deep residual shrinkage network (IDRSN). The saturable reactor vibration sound is used to identify the core looseness accurately.
Firstly, the vibration test of saturable reactor at high frequency pulse excitation was carried out, and the voiceprint signals in different core looseness were measured. Secondly, in the principal value range of acoustic signal spectrum, the Gaussian window parameters were optimized by using the energy concentration formula to improve the time-frequency resolution of voiceprint spectrum. Thirdly, the voiceprint characteristics after loosening were analyzed, it was found that two characteristic indexes of high-low frequency ratio and dominant frequency ratio in low-frequency component can only give early warning to the state with high degree of loosening. Finally, the core loosening data of five different azimuth measuring points were brought into improved deep residual shrinkage network based on adaptively parametric rectifier linear unit for training, to eliminate the redundant information in the voiceprint spectrum and map the features in different degrees of looseness independently, so as to enhance the learning ability of common features.
The results of saturable reactor vibration voiceprint test show that the vibration period of saturable reactor under high-frequency pulse excitation is the same as the electrical signal, which is 0.02 s. After the core is loosened, the frequency spectrum complexity and odd even subharmonic ratio do not change significantly, and the basic frequency changes greatly when the looseness is high, but it cannot give early warning in case of slight looseness. The proportion of dominant frequency of low frequency component and the ratio of high frequency to low frequency can sensitively reflect different loose states of iron core, but the threshold is difficult to set. The basic frequency proportion of low frequency component and the ratio of high frequency to low frequency can reflect different core loosening degrees sensitively, but the threshold is difficult to set. The recognition results of test data show that the convergence time of the proposed model is 262.13 s, and the average recognition accuracy of core looseness is 95.93 %, realizing the unified recognition of five different measuring points. Compared with short time Fourier transform (STFT), the accuracy of OST is improved by 5.56 %. The comparison between IDRSN and other neural networks such as residual network50 and deep residual shrink network shows that the calculation accuracy of IDRSN is improved by 2.82 % and 4.67 % respectively, and there is no false or missing judgment.
The results show that: (1) Saturable reactor vibration voiceprint spectrum contains a large number of high order harmonics, and the ratio of 50 Hz odd and even frequency multiplication is equal. After the core clamp is loosened, the proportion of 50~1 200 Hz component decreases, and the proportion of 1 250~18 000 Hz component increases. (2) The optimized S-transform method is proposed, which solves the problems of frequency band aliasing and spectrum leakage by adjusting the frequency domain window parameters with energy concentration. Compared with STFT, it has higher time-frequency resolution. (3) An improved deep residual shrinkage network based on adaptive parameter modified linear unit is built. The uniform recognition of voiceprint signals collected in different directions is realized by independent feature mapping, which has higher recognition accuracy compared with other traditional models.
keywords:Saturable reactor voiceprint, optimized S-transform, core loosening test, feature extraction, improved deep residual shrinkage network
先进输电技术国家重点实验室开放基金(GEIRI-SKL-2020-003)和北京市自然科学基金(3212039)资助项目。
收稿日期 2021-12-21
改稿日期 2022-02-21
DOI:10.19595/j.cnki.1000-6753.tces.212059
中图分类号:TM474
刘云鹏 男,1976年生,教授,博士生导师,研究方向为电气设备在线监测及故障诊断。E-mail:liuyunpeng@ncepu.edu.cn
来庭煜 男,1998年生,硕士研究生,研究方向为电气设备在线监测及故障诊断。E-mail:laitingyu@ncepu.edu.cn(通信作者)
(编辑 李冰)