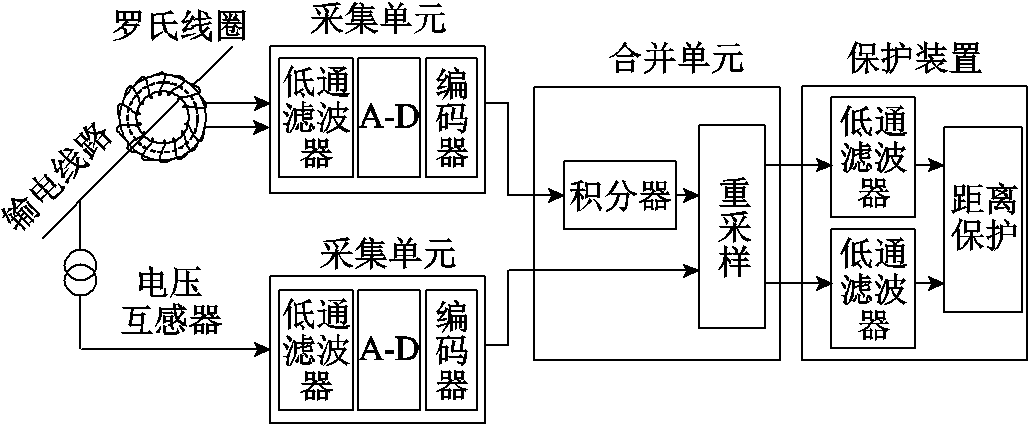
图1 传统距离保护数据传变环节
Fig.1 Data transfer in conventional distance relay
摘要 罗氏线圈电流互感器中的积分器会放大暂态传变误差,可能导致保护误动作。该文提出直接采用罗氏线圈微分信号输出进行保护计算的改进思路,并以距离保护为例,提出一种基于罗氏线圈电流互感器的等传变距离保护方法。该方法中,保护电流直接采用罗氏线圈输出的电流微分信号,消除积分器引入的暂态传变误差,并通过虚拟数字传变解决电压与电流微分信号传变不一致问题。仿真和试验结果表明,所提出的等传变距离保护方法动作速度快,受系统中高频暂态信号影响较小,性能优于现有距离保护方法。
关键词:罗氏线圈 积分器 距离保护 虚拟罗氏线圈 等传变
罗氏线圈型电流互感器由于其具有动态测量范围大、无磁饱和现象、频带响应范围宽、绝缘结构简单等诸多优点,已在电力系统中得到了广泛的工程应用[1-12]。由于罗氏线圈输出信号与被测电流的微分成正比,罗氏线圈电流互感器通常配置积分器,以恢复被测的电流信号[13-15]。
工程应用情况表明,积分器会放大罗氏线圈的暂态传变误差和模数转换误差,可能造成电流传变严重失真,导致继电保护不正确动作。文献[16]阐述了罗氏线圈电流互感器异常输出导致继电保护误动的案例。在断路器合闸时,罗氏线圈输出信号中出现了一个采样点的异常数据,该异常数据经积分器处理后,输出了峰值达5倍额定电流,持续时间长达70ms的异常数据,导致保护误动作。文献[17]分析了断路器合闸操作时罗氏线圈电流互感器异常输出的机理。系统运行操作会伴随产生高频暂态分量,在罗氏线圈微分传变特性的作用下,高频暂态分量被进一步放大,罗氏线圈在高频信号激励下会产生附加衰减直流分量,频率混叠也可能产生附加直流分量,附加的直流分量经积分器处理后,将在输出信号中叠加持续时间较长的动态附加分量,可能导致电流传变严重失真。
研究者提出了多种罗氏线圈电流互感器异常输出的优化和检测方法,但在故障暂态过程中均受到限制,并不能完全解决保护误动的问题。文献[18]指出电子式电流互感器存在一定程度的频率混叠,并提出了优化抗混叠滤波器和提高采样率的改进方法,但受罗氏线圈自身传变特性影响产生的衰减直流分量无法被消除[19],仍可能造成传变严重失真。文献[20]提出了基于直流负反馈原理的改进数字积分算法优化直流响应的方法,但该方法计算量大,且反馈环节会造成输出延时增加,影响保护动作速度。文献[21]提出利用电流同源数据特征比对的异常数据识别方法,该方法无法解决罗氏线圈自身传变特性造成的异常输出问题。文献[22]提出通过罗氏线圈和测量线圈输出信号对比判别采样数据异常的方法,但由于测量线圈无法正常传变故障电流,所以该方法应用也受到限制。
本文提出了直接采用罗氏线圈微分信号输出进行保护计算的改进思路,并以距离保护为例,提出基于罗氏线圈微分信号输出的等传变距离保护方法,为其他类型线路保护的研究提供了借鉴。
距离保护新方法直接采用罗氏线圈输出的电流微分信号,但电流微分信号无法直接与电压信号进行保护计算。根据输电线路等传变理论[23-25],线路沿线电压和电流经过相同的线性传变后,其相互关系仍满足原输电线路分布参数模型。因此,通过构造虚拟罗氏线圈数字传变环节,对电压信号进行与罗氏线圈传变特性相同的数字传变处理,使得距离保护所使用的电压、电流信号经过相同的传变环节,采用R-L模型解微分方程算法计算故障位置,判别保护是否动作。
传统距离保护的数据传变环节如图1所示,罗氏线圈输出微分信号的积分处理环节配置在合并单元中[17]。

图1 传统距离保护数据传变环节
Fig.1 Data transfer in conventional distance relay
新方法数据传变环节如图2所示,取消合并单元中的积分环节,在保护装置中电压的传变环节增加虚拟数字罗氏线圈。
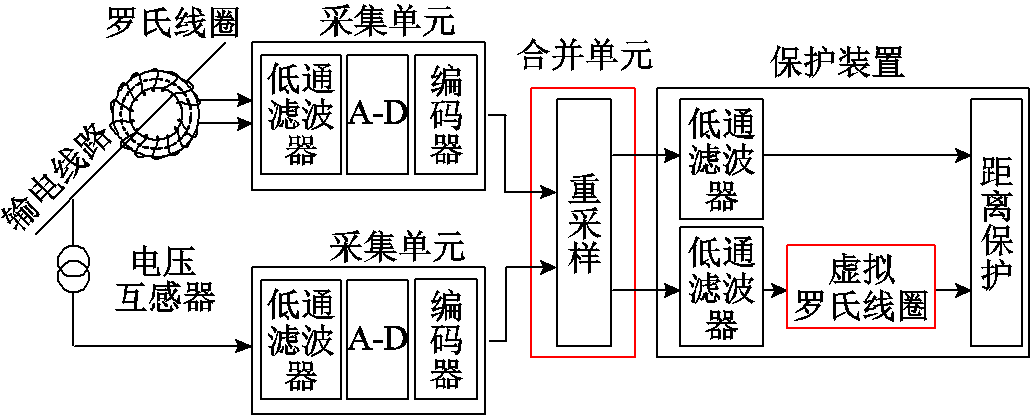
图2 新方法数据传变环节
Fig.2 Data transfer in improved distance relay
基于罗氏线圈电流互感器的等传变距离保护原理主要包括虚拟罗氏线圈数字传变方法、R-L模型解微分方程算法应用、故障点电压重构和保护动作判据。
罗氏线圈等效电路如图3所示,M为罗氏线圈互感,i(t)为一次电流,e(t)为线圈的感应电动势,RS为线圈内阻,L为线圈自感,C0为线圈匝间电容,Ra为负载电阻,u(t)为电压输出信号。
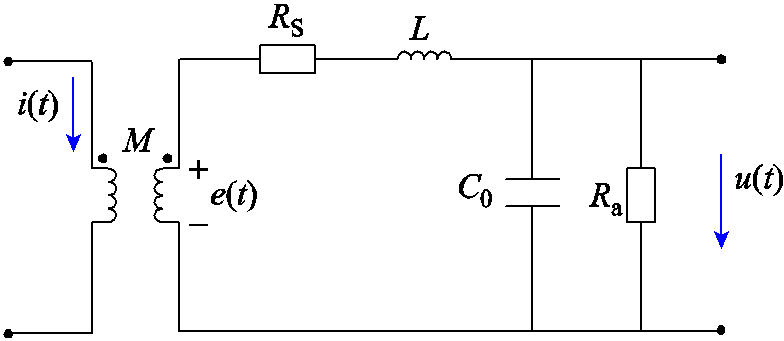
图3 罗氏线圈等效电路
Fig.3 Equivalent circuit of Rogowski coil CT
根据电感、电容元件的暂态等效电路[23],可进一步得到罗氏线圈的暂态等效电路,如图4所示。图4中,u1(t),u2(t),u3(t)分别为暂态等效电路中的三个节点电压。iL(t-Δt),iC0(t-Δt)分别为线圈自感和匝间电容的等效电流源,RL=2L/Δt,RC0=Δt/2C0。
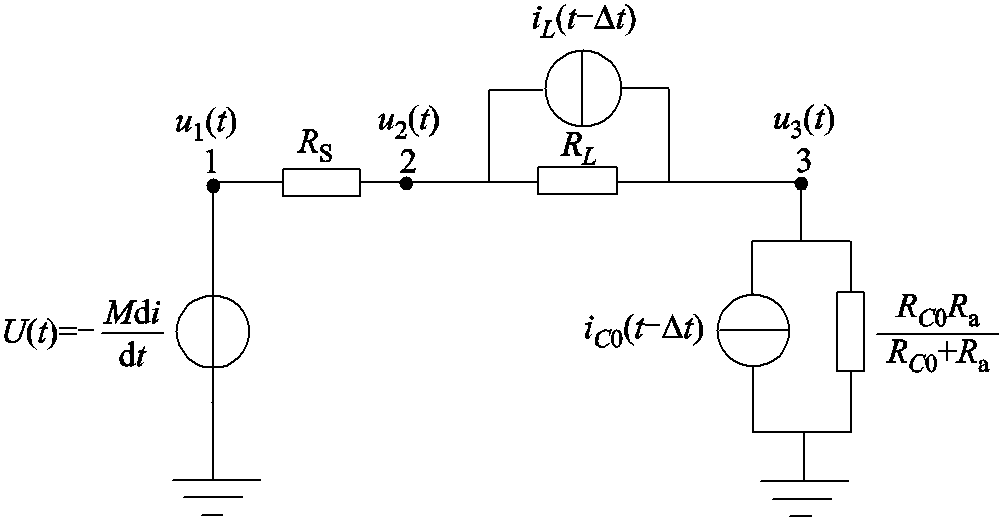
图4 罗氏线圈暂态等效电路
Fig.4 Transient equivalent circuit of Rogowski coil
根据节点电压方程,可得
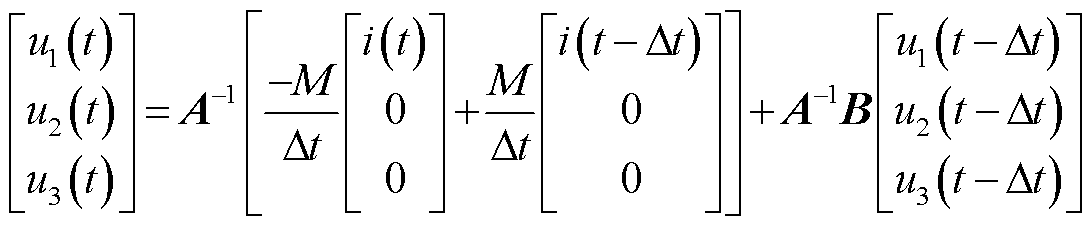 (1)
(1)
其中
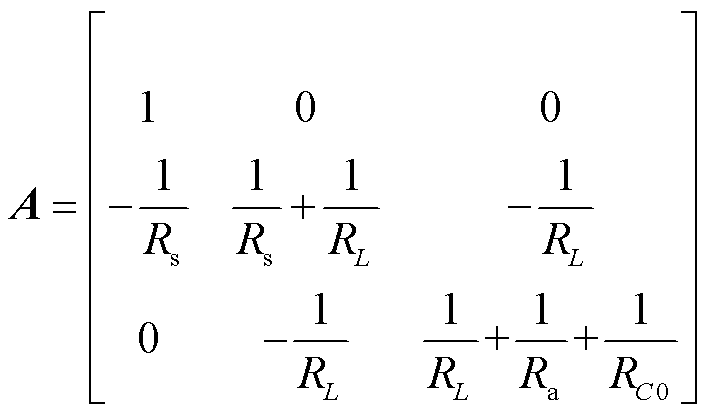 (2)
(2)
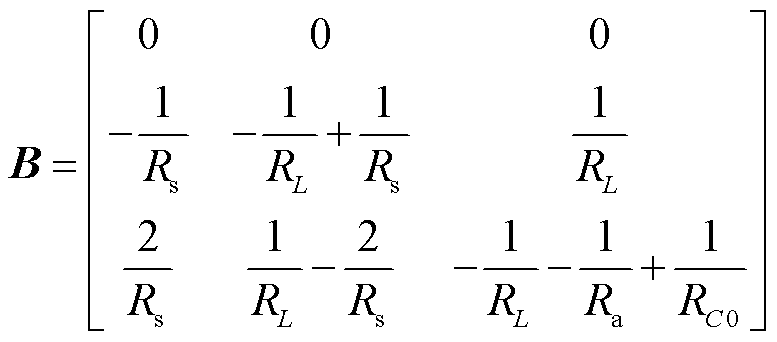 (3)
(3)
式中,u3(t)为罗氏线圈输入电流i(t)的输出信号。因此虚拟罗氏线圈数字传变方法为
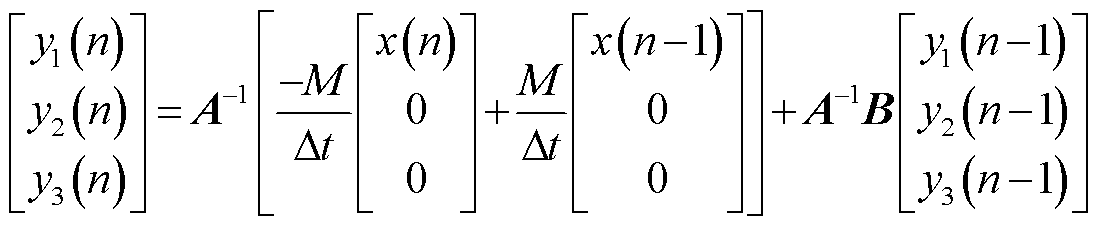 (4)
(4)
式中,x(n)为输入数据的第n个采样点的值;y1(n-1)为输出数据第n-1个采样点的计算值。
当输电线路发生故障时,故障信号中高频分量主要由线路对地分布电容引起,通过设置合适的数字低通滤波器,滤除高频分量,可降低线路分布电容的影响。不考虑分布电容影响的输电线路模型可以等效为R-L模型,以线路发生单相故障为例,说明采用R-L模型解微分方程计算故障位置的方法。
对于单相接地故障,保护安装处的测量电压和测量电流满足
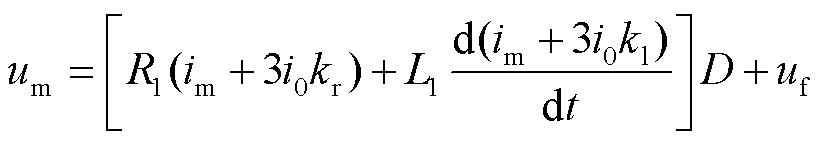 (5)
(5)
式中,kr=(R0-R1)/(3R1);kl=(L0-L1)/(3L1);um和im分别为保护安装处故障相电压和电流;3i0为保护安装处的零序电流;uf为故障点电压;R1、R0、L1、L0分别为单位长度线路的正序电阻、零序电阻、正序电感、零序电感;D为故障距保护安装处的距离。
式(5)中保护电流、保护安装处电压、故障点电压经过相同的传变环节后,方程仍成立,有
 (6)
(6)
式中,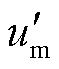 为经虚拟罗氏线圈传变环节补偿后的电压量;
为经虚拟罗氏线圈传变环节补偿后的电压量;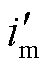 为罗氏线圈输出的电流量;
为罗氏线圈输出的电流量;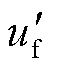 为经虚拟罗氏线圈数字传变处理后的故障点电压。
为经虚拟罗氏线圈数字传变处理后的故障点电压。
在故障发生初期,经虚拟罗氏线圈数字传变处理的保护安装处电压会存在短时暂态传变过程,如故障点电压忽略此暂态传变过程,将会产生一定的误差。因此对故障点电压进行重构,并进行虚拟数字传变处理,使其与保护安装处电压保持相同的暂态传变过程,减小故障初期计算故障,加快故障计算收敛至稳定的速度。采用与文献[26]类似的办法,对故障点电压进行重构处理。故障点电压可表示为
 (7)
(7)
式中,uf为故障点电压,由uf1和uf2两部分组成。故障前,uf1和uf2可以表示为
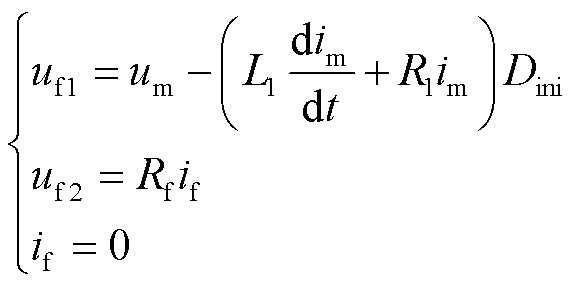 (8)
(8)
故障后,uf1和uf2可以表示为
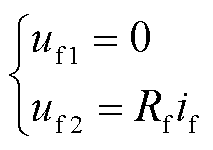 (9)
(9)
式中,L1和R1分别为单位长度的正序电感和正序电阻;Dini为故障位置到保护安装处的距离初始值;Rf为过渡电阻;if在故障发生前为零,故障发生后为故障电流。工程应用中,故障点电流通常采用保护安装处的零序电流替代[26]。
式(6)中,经虚拟罗氏线圈进行传变环节补偿后的故障点电压可表示为
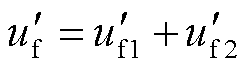 (10)
(10)
正常运行时,输电线路沿线电压降落较小,由于故障位置未知,为求解式(6),可使用沿线某一点电压来代替u'f1。为进一步减小距离保护的测距误差,采用故障点位置迭代逼近的方法。由式(6)和式(10)可知,D和Rf为未知量,取故障后一个时间段(例如5ms)的多个采样时刻数据,建立方程组,通过最小二乘法即可求解故障点到保护安装处的距离D。
故障位置计算的主要步骤如下:
(1)假设故障点位于被保护线路的中点。
(2)保护电压经虚拟罗氏线圈,补偿传变差异。
(3)根据故障点的位置对故障点电压进行重构。
(4)求解式(6)所示的微分方程,计算并更新故障点位置。
(5)控制迭代次数,达到次数则结束;否则跳转到步骤(3)。
计算分析表明,迭代三次后,新方法的故障计算结果较为稳定。
根据上述故障位置计算方法,故障后的每个采样点均可计算出对应的故障位置结果,为了衡量计算结果的稳定性,通过计算模型误差进行判别。模型误差W(n)表达式为
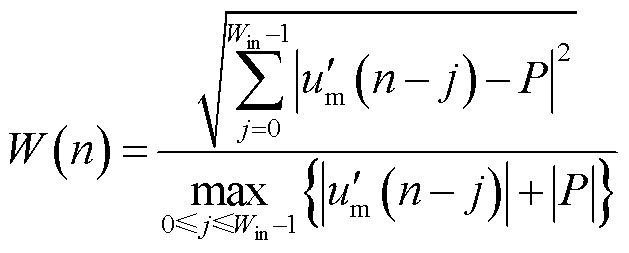 (11)
(11)
其中
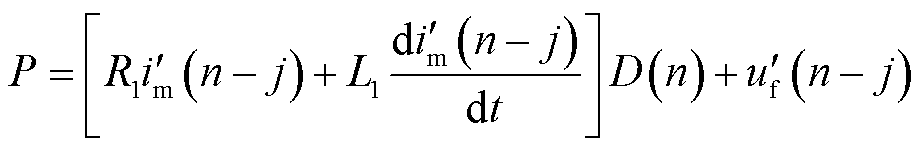 (12)
(12)
式中,Win为最小二乘法所使用的采样数据窗;n为当前最新采样点。
距离保护动作判据为
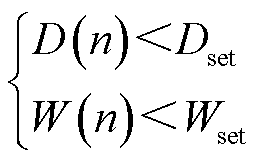 (13)
(13)
式中,D(n)为当前采样点n对应的故障位置结果;Dset为保护范围整定值;W(n)为采样点n对应的模型误差;Wset为模型误差限值,本文中取0.25。当故障位置计算结果小于定值,且模型误差小于限值,距离保护动作。
利用PSCAD软件建立了220kV输电线路模型,如图5所示,图中u(t)和i(t)分别为保护安装处电压和电流,LMN为线路长度,如未特殊说明,LMN=100km。保护安装于M侧,电流采用罗氏线圈测量。
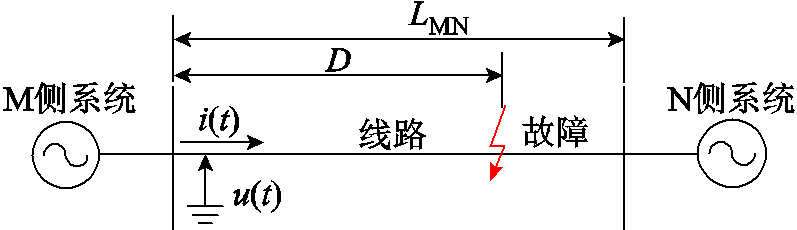
图5 220kV输电线路系统模型
Fig.5 System model of 220kV transmission line
输电线路参数为:r1=0.037 219Ω/km, x1= 0.303 986Ω/km, c1=0.012 120μF/km, r0=0.315 511Ω/km, x0=1.081 049Ω/km, c0=0.007 758μF/km。
M侧系统采用大、小两种方式,大方式下参数为:ZM1max=10Ω∠86°,ZM0max=10Ω∠83°;小方式下参数为:ZM1min=20Ω∠86°,ZM0min=20Ω∠83°。N侧系统参数为:ZN1=10Ω∠76°,ZN0=10Ω∠73°。
采用某公司生产的罗氏线圈实际参数,图3中线圈内阻Rs=288Ω,电感L=58.5mH,负载电阻Ra=32kΩ,互感系数M=10.26μH,杂散电容C0=30nF。
算法采样率设置为4kHz,图1和图2中,保护装置中数字低通滤波器为
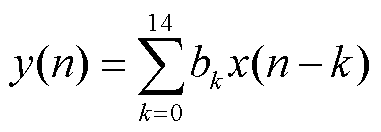 (14)
(14)
式中,滤波器系数b0~b14分别为0.010 500, 0.021 526,0.038 863, 0.059 973, 0.082 118, 0.101 736, 0.115 268, 0.120 103, 0.115 268, 0.101 736, 0.082 118, 0.059 973, 0.038 863, 0.021 526, 0.010 500。
从故障5ms后开始计算故障点位置,随采样点向后移动计算数据窗,每个采样点计算一次故障点位置和模型误差。模拟在距保护安装处0.8倍线路全长处发生不同故障电压合闸角下的单相接地和相间短路故障,新方法故障位置计算结果如图6所示,模型误差计算结果如图7所示。
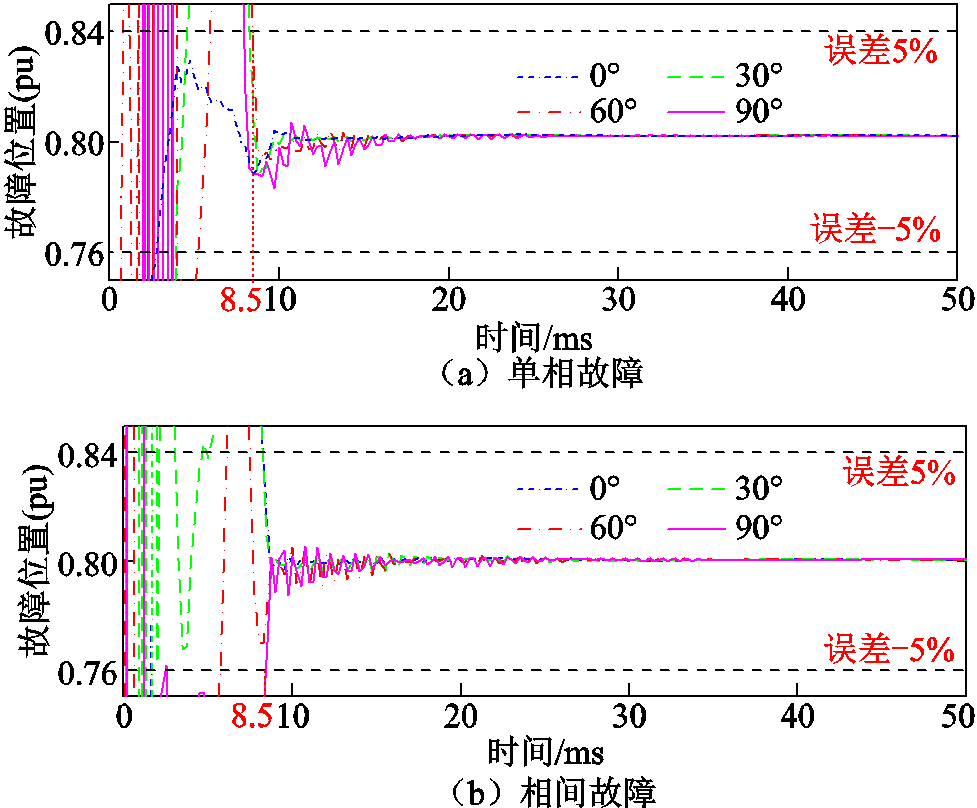
图6 故障位置计算结果
Fig.6 Fault location calculation results

图7 模型误差计算结果
Fig.7 Model error calculation results
图6中横轴为时间,以故障发生时刻为零时刻,纵轴为故障位置计算结果,数值为以线路全长为基准的标幺值。图7中纵轴为模型误差计算结果。仿真结果表明,在不同故障电压合闸角下发生故障时,新方法计算误差稳定在5%以内,且模型误差小于0.25所需的时间不大于8.75ms。
为进一步验证本文所提方法的性能,针对系统大小运行方式、不同线路长度、不同故障位置、不同故障类下算法的性能进行了仿真,并在100km和150km线路长度下对新方法的耐受过渡电阻能力进行了验证,部分结果见表1~表4,“NF”表示计算结果不在允许误差范围以内。仿真结果表明,本文所提方法不受系统运行方式、线路长度、故障位置和故障类型的影响,对于不同类型金属性故障均可在8.75ms内准确计算出故障位置,并且具有一定的耐过渡电阻能力。
表1 大方式下100km线路仿真结果 (单位:ms)
Tab.1 Simulation results for 100km line in the maximum operating mode

故障类型不同故障位置计算时间 20km50km80km100km AN8888 AN-5Ω7.757.757.758.5 AN-20Ω7.757.758.5NF AN-50Ω7.757.759NF AN-100Ω7.75814NF BC8.58.258.258 BC-1Ω8.58.58.58.25 BC-2Ω8.58.58.25NF BC-5ΩNFNFNFNF BCN8.58.258.258 ABC8.58.258.258
表2 小方式下100km线路仿真结果 (单位:ms)
Tab.2 Simulation results for 100km line in the minimum operating mode
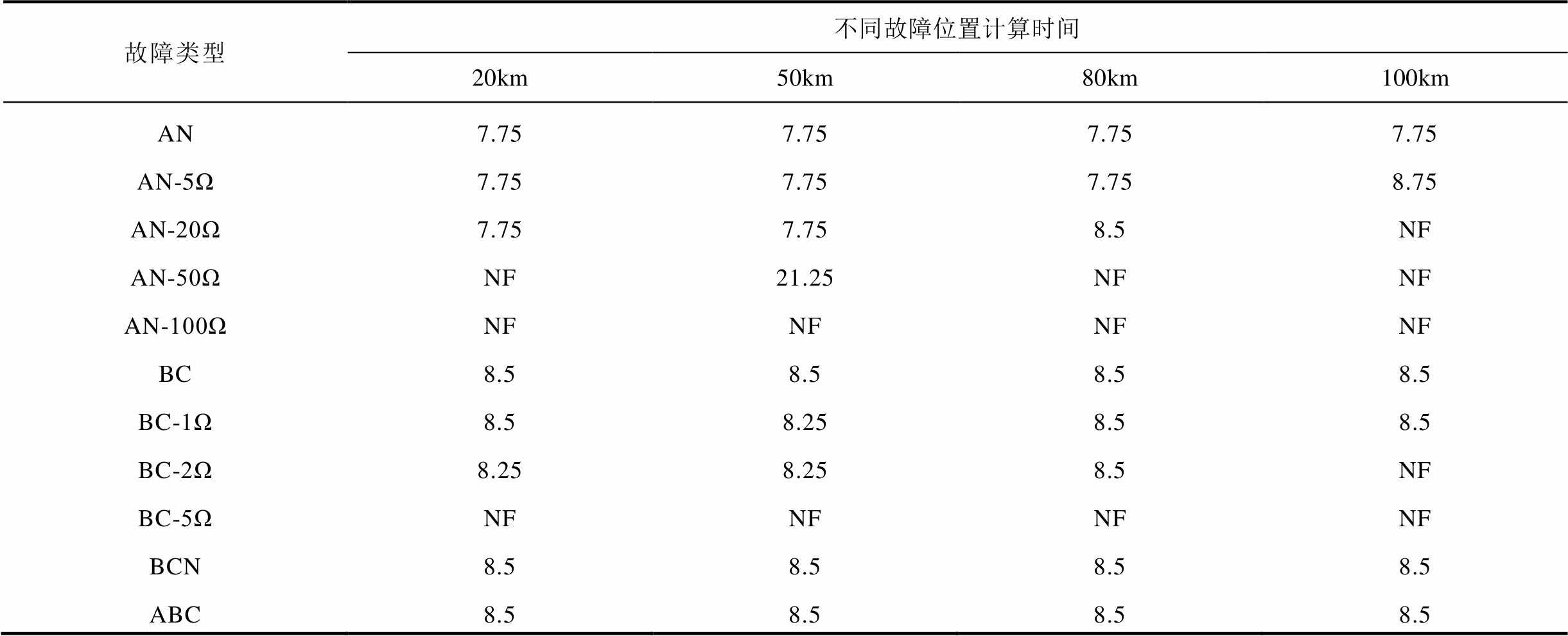
故障类型不同故障位置计算时间 20km50km80km100km AN7.757.757.757.75 AN-5Ω7.757.757.758.75 AN-20Ω7.757.758.5NF AN-50ΩNF21.25NFNF AN-100ΩNFNFNFNF BC8.58.58.58.5 BC-1Ω8.58.258.58.5 BC-2Ω8.258.258.5NF BC-5ΩNFNFNFNF BCN8.58.58.58.5 ABC8.58.58.58.5
表3 大方式下150km线路仿真结果 (单位:ms)
Tab.3 Simulation results for 150km line in the maximum operating mode

故障类型不同故障位置计算时间 30km75km120km150km AN7.757.757.758 AN-5Ω7.757.7588.5
(续)

故障类型不同故障位置计算时间 30km75km120km150km BC8.258.2588 BCN8.258.2588 ABC8.258.2588
表4 小方式下150km线路仿真结果 (单位:ms)
Tab.4 Simulation results for 150km line in the minimum operating mode

故障类型不同故障位置计算时间 30km75km120km150km AN8888 AN-5Ω8888.75 BC8.58.58.258 BCN8.58.58.258 ABC8.58.58.258
传统距离保护算法的数据传变环节如图1所示。合并单元中数字积分器的传递函数为
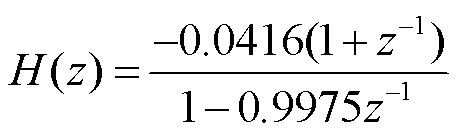 (15)
(15)
传统距离保护算法选取典型的解微分方程算法、全周傅里叶算法、半周差分算法、全周差分算法,其中,解微分方程算法表达式如式(16)所示,以5ms数据窗的数据构造微分方程组,通过最小二乘法求解。
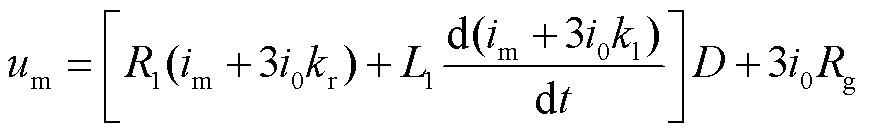 (16)
(16)
模拟系统发生故障工况和系统开关操作引起的电流数据异常工况下各算法的计算情况,对本文方法和传统距离保护算法性能进行比较。
2.3.1 系统故障工况
以图5所示仿真模型80km处发生故障为例,对不同保护算法的计算结果进行比较。发生单相经5Ω过渡电阻故障的仿真结果如图8所示。
由图8可知,本文方法的计算结果在8ms后计算误差始终稳定在5%以内,计算结果波动范围小,算法稳定性好。解微分方程、全周傅里叶、半周差分和全周差分算法的计算结果误差保持在5%以内的时间分别为30.25ms、29.5ms、15.25ms、31ms,且计算结果仍有较大波动。
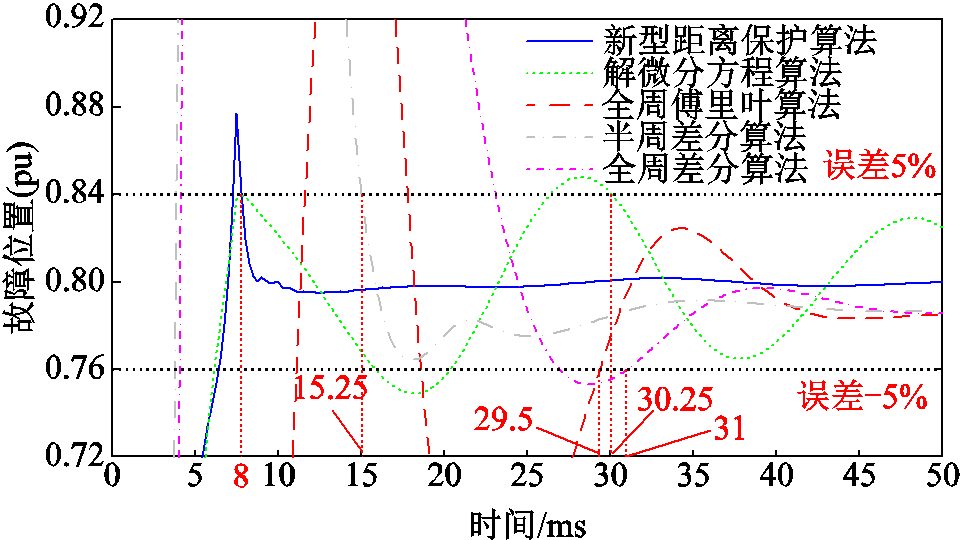
图8 不同距离保护算法故障位置计算结果
Fig.8 Calculation results of fault location for different distance relay algorithms
2.3.2 电流数据异常工况
模拟电流出现文献[16]所述的异常情况,对新方法和传统距离保护算法的动作行为进行对比。
通过在图1和图2所示的数据传变环节中罗氏线圈的输出中叠加采样异常信号,模拟系统操作开关时出现采样异常信号情况。电流叠加采样异常信号后,合并单元输出信号如图9所示,图中以采样异常信号注入的起始时刻作为0时刻。
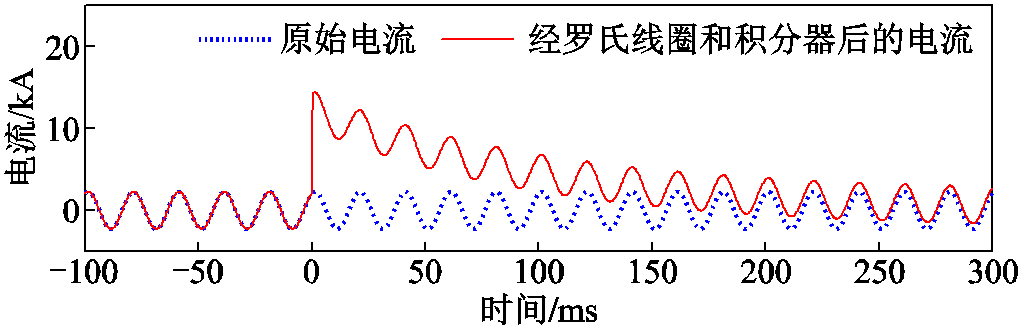
图9 叠加异常信号前电流与叠加后积分器输出电流
Fig.9 Original current and integrated current
由图9可知,在罗氏线圈的输出中有采样异常信号后,经积分器输出的信号中附加了衰减直流分量。本文方法的故障位置及模型误差计算结果分别如图10a和图10b所示,图中虚线为距离保护整定范围(80km)。由图10可知,在采样异常导致故障
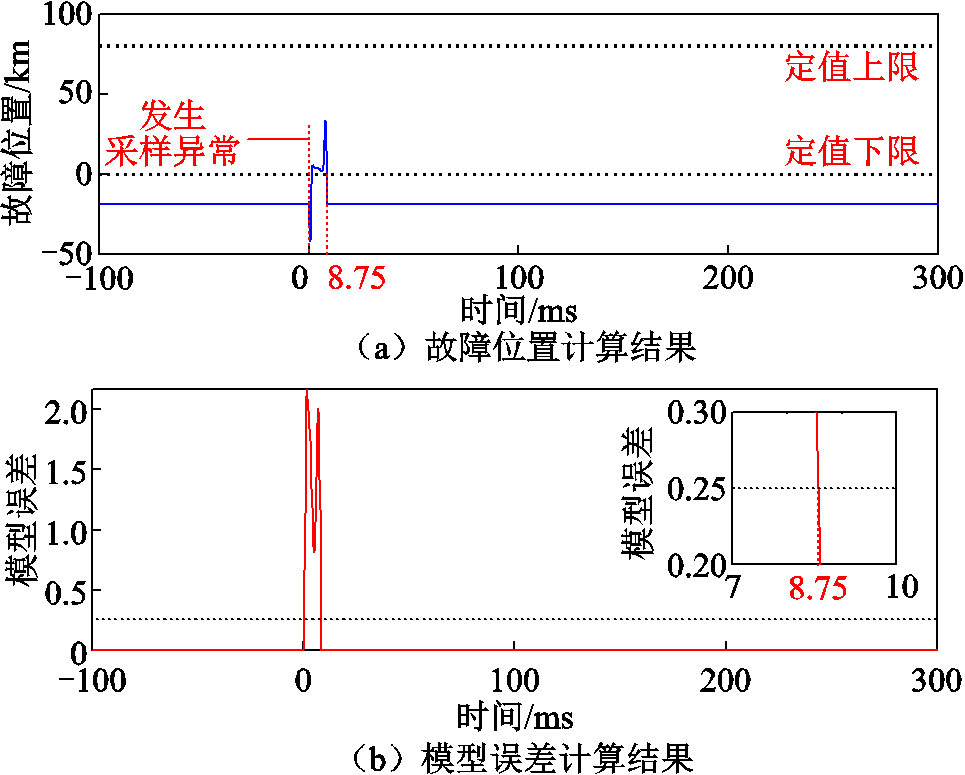
图10 等传变距离保护算法故障计算结果
Fig.10 Calculation results of the improved algorithm
位置计算结果满足动作条件时,模型误差不满足动作条件,因此采用本文方法不会出现误动作。
传统距离保护算法的计算结果如图11所示,图11a、图11b、图11c分别为解微分方程算法、全周傅氏、半周差分的计算结果,这些算法的计算结果在采样异常时会出现较长时间满足动作条件的情况。图11d为全周差分算法的计算结果,在计算数据满窗后不会误动作,但全周差分算法受采样异常信号影响的时间比新方法相对更长。
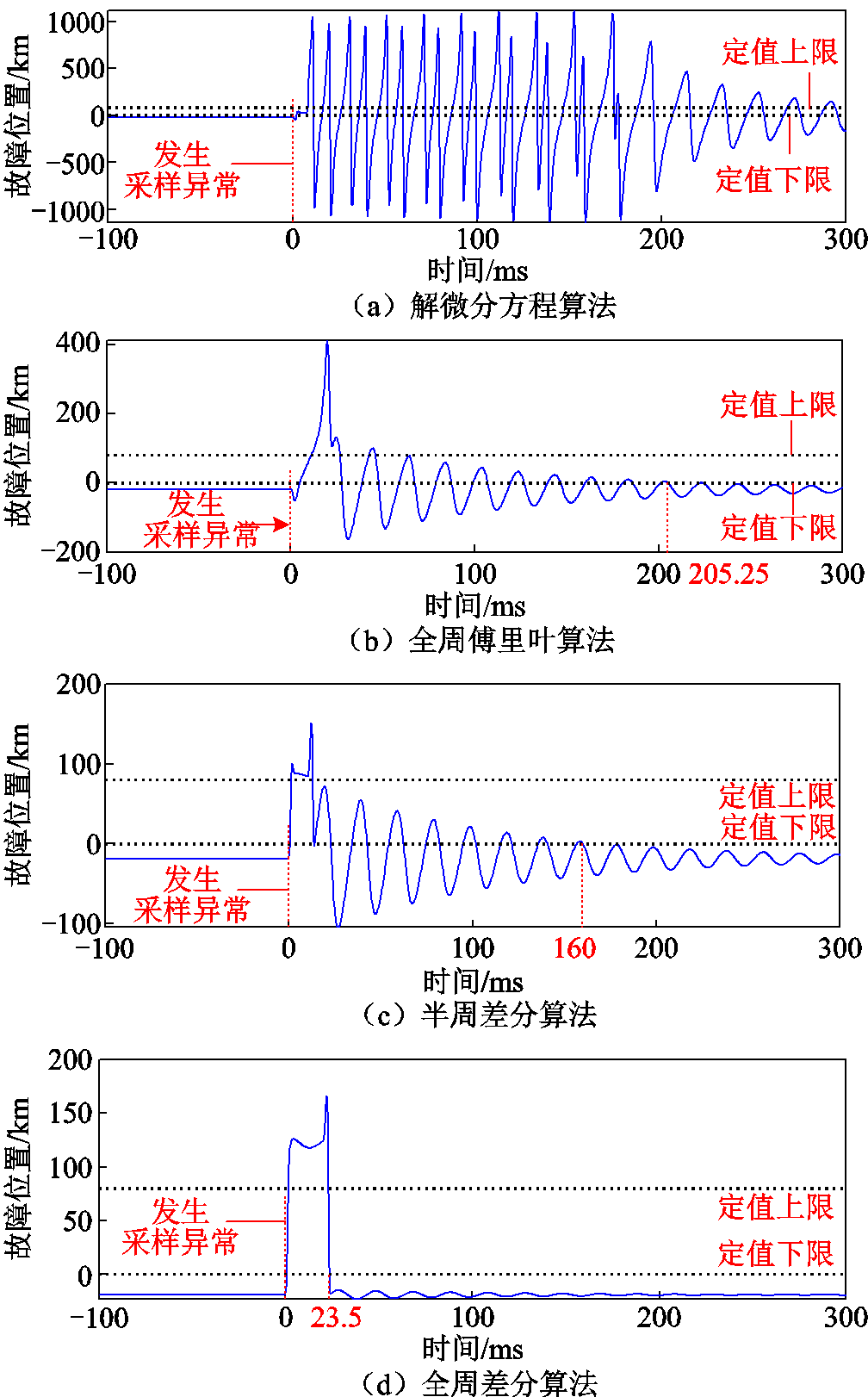
图11 传统距离保护故障位置计算结果
Fig.11 Calculation results of different distance relay algorithms
仿真测试结果表明,在系统发生故障时,本文方法相对于传统保护算法响应速度更快、计算结果稳定性更好,受采样异常影响较小。
为了验证本文提出的方法在实际保护装置中的性能,采用罗氏线圈和继电保护装置搭建如图12所示的测试环境。采用PSCAD仿真软件建立图5所示的仿真模型,对不同故障情况进行仿真,生成故障电压和电流数据。采用测试仪对故障数据进行回放,电流量通过罗氏线圈传变后输入保护装置。线路保护装置的采样频率为4kHz。

图12 等传变距离保护试验环境
Fig.12 Test environment of the improved distance relay algorithm
距离保护安装处80km发生故障时本方法的计算结果如图13所示。单相故障和相间故障的情况下新方法的计算误差稳定在5%以内的时间分别为6.5ms和9.5ms。

图13 试验结果
Fig.13 Test verification results
进一步对线路不同位置发生不同类型故障的情况进行试验,部分试验结果见表5。试验结果表明,当不同位置发生不同类型故障情况下,本文方法的计算误差稳定在5%以内所需的时间不超过10ms,与仿真验证结果一致。
表5 部分试验结果
Tab.5 Partial test results

故障类型稳定时间/ms 20km50km80km100km AN7.2556.56.75 AN-5Ω7.5777 BC109.759.59.5 BCN9.759.759.59.25 ABC9.759.759.59
为减小罗氏线圈电流互感器暂态传变误差对保护的影响,本文提出了一种等传变距离保护方法,并得出以下结论:
1)根据输电线路等传变理论,电流采用罗氏线圈输出的微分信号,电压采用经过与罗氏线圈具有相同传变环节的虚拟罗氏线圈后的信号,两者之间的关系仍然满足输电线路分布参数模型。
2)本文方法中电流直接采用罗氏线圈输出的微分信号,消除了传统罗氏线圈电流互感器的积分环节对继电保护的不利影响。
3)各种PSCAD仿真和试验结果表明,本文方法不受系统运行方式、长度线路、故障位置和故障类型的影响,在故障发生后,计算误差稳定在5%以内所需时间不大于10ms,且受采样异常信号影响较小,性能优于现有的距离保护方法。
参考文献
[1] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870. Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.
[2] 赵小军, 王瑞, 杜振斌, 等. 交直流混合激励下取向硅钢片磁滞及损耗特性模拟方法[J]. 电工技术学报, 2021, 36(13): 2791-2800. Zhao Xiaojun, Wang Rui, Du Zhenbin, et al. Hysteretic and loss modeling of grain oriented silicon steel lamination under AC-DC hybrid magnetiza-tion[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2791-2800.
[3] 杨鸣, 熊钊, 司马文霞, 等. 电磁式电压互感器“低频过电压激励-响应”逆问题求解[J]. 电工技术学报, 2021, 36(17): 3605-3613. Yang Ming, Xiong Zhao, Sima Wenxia, et al. Solution of the inverse problem of “low-frequency overvoltage excitation to response” for electromagnetic potential transformers[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3605-3613.
[4] 赵志刚, 徐曼, 胡鑫剑. 基于改进损耗分离模型的铁磁材料损耗特性研究[J]. 电工技术学报, 2021, 36(13): 2782-2790. Zhao Zhigang, Xu Man, Hu Xinjian. Research on magnetic losses characteristics of ferromagnetic materials based on improvement loss separation model[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2782-2790.
[5] 邓成林, 蔡新景, 付丁丁. 电流互感器铁心剩磁影响因素仿真分析[J]. 电气技术, 2021, 22(9): 22-26. Deng Chenglin, Cai Xinjing, Fu Dingding. Simulation analysis of factors affecting remanence of current transformer core[J]. Electrical Engineering, 2021, 22(9): 22-26.
[6] 刘毅, 赵勇, 任益佳, 等. 水中大电流脉冲放电电弧通道发展过程分析[J]. 电工技术学报, 2021, 36(16): 3525-3534. Liu Yi, Zhao Yong, Ren Yijia, et al. Analysis on the development process of arc channel for underwater high current pulsed discharge[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3525-3534.
[7] 朱梦梦, 束洪春, 何兆磊, 等. 接地极直流电流互感器宽频特性现场试验与分析[J]. 电力系统自动化, 2022, 46(6): 166-172. Zhu Mengmeng, Shu Hongchun, He Zhaolei, et al. Field test and analysis of broadband characteristics of DC current transformer on earth electrode[J]. Automation of Electric Power Systems, 2022, 46(6): 166-172.
[8] 廖文彪, 周泽昕, 詹荣荣, 等. 多类型电流互感器混联运行动模测试平台建设及对差动保护的影响[J]. 电力系统保护与控制, 2017, 45(22): 83-89. Liao Wenbiao, Zhou Zexin, Zhan Rongrong, et al. Construction of the dynamic model test platform for hybrid operation of multi type current transformer and its influence on differential protection[J]. Power System Protection and Control, 2017, 45(22): 83-89.
[9] 李振华, 沈聚慧, 李振兴, 等. 隔离开关电弧模型及对Rowgowski线圈电流互感器的传导干扰研究[J]. 电力系统保护与控制, 2020, 48(16): 131-139. Li Zhenhua, Shen Juhui, Li Zhenxing, et al. Research on an arc model of a disconnector for conduction interference of a Rogowski coil electronic transformer[J]. Power System Protection and Control, 2020, 48(16): 131-139.
[10] Li Jue, Liu Hao, Martin K E, et al. Electronic transformer performance evaluation and its impact on PMU[J]. IET Generation, Transmission & Distribution, 2019, 13(23): 5396-5403.
[11] Wang Dong, Gao Houlei, Zou Guibin, et al. Ultra-high-speed travelling wave directional protection based on electronic transformers[J]. IET Generation, Transmission & Distribution, 2017, 11(8): 2065-2074.
[12] Ghanbari T, Samet H, Jarrahi M A, et al. Implementation of Rogowski coil based differential protection on electric arc furnace transformers of mobarakeh steel company: design step[C]//2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe, Palermo, 2018: 1-5.
[13] 王宇, 孟令雯, 汤汉松, 等. ECT采集单元积分回路的暂态特性改进及其检测系统研发[J]. 电力系统保护与控制, 2021, 49(10): 98-104. Wang Yu, Meng Lingwen, Tang Hansong, et al. Improvement of transient characteristics and development of a testing system of an integration circuit in ECT acquisition unit[J]. Power System Protection and Control, 2021, 49(10): 98-104.
[14] 戴魏, 郑玉平, 白亮亮, 等. 保护用电流互感器传变特性分析[J]. 电力系统保护与控制, 2017, 45(19): 46-54. Dai Wei, Zheng Yuping, Bai Liangliang, et al. Analysis of protective current transformer transient response[J]. Power System Protection and Control, 2017, 45(19): 46-54.
[15] Habrych M, Wisniewski G, Miedziński B, et al. HDI PCB Rogowski coils for automated electrical power system applications[J]. IEEE Transactions on Power Delivery, 2018, 33(4): 1536-1544.
[16] 白世军, 郭乐, 曾林翠, 等. 变压器空载合闸对隔离断路器电子式CT干扰分析及防护[J]. 高压电器, 2018, 54(8): 81-90, 97. Bai Shijun, Guo Le, Zeng Lincui, et al. Interference analysis and protection of electronic current transformer in DCB during no-load closing of transformer[J]. High Voltage Apparatus, 2018, 54(8): 81-90, 97.
[17] Jing Shi, Huang Qi, Tang Fan, et al. Study on additional dynamic component of electronic current transducer based on Rogowski coil and its test approach[J]. IEEE Transactions on Industry Applications, 2020, 56(2): 1258-1265.
[18] 朱梦梦, 罗强, 曹敏, 等. 电子式电流互感器传变特性测试与分析[J]. 电力系统自动化, 2018, 42(24): 143-149. Zhu Mengmeng, Luo Qiang, Cao Min, et al. Test and analysis of transfer characteristics of electronic current transformer[J]. Automation of Electric Power Systems, 2018, 42(24): 143-149.
[19] Pang Fubin, Liu Yu, Ji Jianfei, et al. Transforming characteristics of the Rogowski coil current transformer with a digital integrator for high-frequency signals[J]. The Journal of Engineering, 2019, 2019(16): 3337-3340.
[20] 宋涛. Rogowski线圈电流互感器中的高精度数字积分器技术研究[J]. 高电压技术, 2015, 41(1): 237-244. Song Tao. Technical research of accurate digital integrators for Rogowski coil current transformer[J]. High Voltage Engineering, 2015, 41(1): 237-244.
[21] Jiang Xianguo, Li Zhongqing, Wang Xingguo, et al. Identification methods of SV distortion of smart substation relay protection[C]//2014 International Conference on Power System Technology, Chengdu, 2014: 1963-1968.
[22] 李仲青, 周泽昕, 黄毅, 等. 数字化变电站继电保护适应性研究[J]. 电网技术, 2011, 35(5): 210-215. Li Zhongqing, Zhou Zexin, Huang Yi, et al. Research on applicability of relay protection in digital substations[J]. Power System Technology, 2011, 35(5): 210-215.
[23] 文明浩. 基于虚拟电容式电压互感器的能量平衡保护[J]. 中国电机工程学报, 2007, 27(24): 11-16. Wen Minghao. A new protection scheme based on energy balance with virtual CVT[J]. Proceedings of the CSEE, 2007, 27(24): 11-16.
[24] 文明浩, 陈德树, 尹项根, 等. 远距离输电线路等传变瞬时值差动保护[J]. 中国电机工程学报, 2007, 27(28): 59-65. Wen Minghao, Chen Deshu, Yin Xianggen, et al. Long transmission line current differential protection by using instantaneous value after equal transfer processes[J]. Proceedings of the CSEE, 2007, 27(28): 59-65.
[25] 陈玉, 文明浩, 王祯, 等. 基于低频电气量的超高压交流线路出口故障快速保护[J]. 电工技术学报, 2020, 35(11): 2415-2426. Chen Yu, Wen Minghao, Wang Zhen, et al. A high speed protection scheme for outgoing line fault of HVAC transmission lines based on low frequency components[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2415-2426.
[26] 文明浩, 陈德树, 尹项根. 超高压线路等传变快速距离保护[J]. 中国电机工程学报, 2012, 32(4): 145-150, 6. Wen Minghao, Chen Deshu, Yin Xianggen. Fast distance protection of EHV transmission lines based on equal transfer processes[J]. Proceedings of the CSEE, 2012, 32(4): 145-150, 6.
Abstract Since the output voltage of the coil is proportional to the rate of change of the primary current, it is required to be integrated to recover the measured current, which is usually realized by electronic integrator circuits. High-frequency transient signals tend to be generated during power system operation or short-circuit faults. After being processed by the integrator, the output signal of electronic transformer may be seriously distorted, resulting in mal-operation of the relay. Many researchers have proposed a variety of detection methods for abnormal output of the Rogowski coil, but the impact of additional components caused by integrators on protection cannot be avoided. An improved method of line relay directly using the differential output of Rogowski coil is put forward. Besides, a distance relay based on Rogowski coil current transformer by using instantaneous value after equal transfer processes is proposed. In the novel scheme, the current differential signal output by Rogowski coil is directly used to eliminate the influence of transient transmission error introduced by integrator.
Firstly, according to the equal transfer process of transmission lines(ETPTL) theory, the virtual Rogowski coil digital transmission link is constructed to process the voltage signal with the same transmission characteristics as the Rogowski coil digital transmission link, so that the voltage and current signals used for distance protection pass through the same transmission link. Secondly, the R-L equations are solved by least square method to calculate the fault location, so as to improve the stability of the calculation results. Thirdly, the voltage at the fault point is reconstructed and passed through the digital transmission link of virtual Rogowski coil to make it have the same transient transmission process as the voltage at the protection installation, so as to reduce the initial calculation error of fault and accelerate the convergence of fault calculation to stability. Finally, a method of model error discrimination is proposed. According to the R-L model, the voltage of the protection installation can be calculated from the calculation results of the fault location. It is compared with the actual voltage at the protection installation site to verify the calculation results of fault location, so as to prevent the distance protection from misoperation under working conditions such as abnormal data interference.
Simulation results demonstrate that the performance of the proposed distance relay method is not affected by the system operation mode, line length, fault location and fault type. In the case of metal fault, it can accurately calculate the fault location within 8.75 ms, and has a certain ability to withstand transition resistance. Compared with the traditional algorithm, the new algorithm has faster calculation speed, smaller fluctuation range and better stability under fault conditions and it is less affected by abnormal current signal transfer. To verify the performance of the improved distance relay algorithm proposed in this paper in practical applications, an actual Rogowski coil and relay device are used to build a test environment to test different fault conditions. The experiment results show that when different faults occur at different points, the time required for the measurement error of the improved distance relay to stabilize within 5% does not exceed 10ms, which is consistent with the simulation test results.
The study comes to the following conclusions: (1) According to the ETPTL theory, the current signal directly adopts the differential output of Rogowski coil, the voltage signal adopts the output of a virtual Rogowski coil with the same transfer features, so the relationship between them still satisfy the distributed parameter model of the original transmission line. (2) The current signal of the improved distance relay is directly from the Rogowski coil transducer without the integrator. It can radically eliminate the impacts of the Rogowski coil transducer integrator on the relay. (3) Various PSCAD simulation and experiment results show that it takes no more than 10ms for the measurement error of the improved distance relay to be stabilized within 5%, which is signed prior to the present method. The novel proposal immunes to system operation mode and can be applied to different length lines.
keywords:Rogowski coil, integrator, distance relay, virtual type of Rogowski coil, equal transfer process
国家自然科学基金项目(51877090)和国家电网有限公司总部科技项目(4000-202222070A-1-1-ZN)资助。
收稿日期 2021-10-20
改稿日期 2022-04-13
DOI:10.19595/j.cnki.1000-6753.tces.211661
中图分类号:TM773
李宝伟 男,1984年生,博士研究生,高级工程师,研究方向为电力系统保护与控制。E-mail:xjtc_libaowei@126.com(通信作者)
石 欣 女,1983年生,硕士,高级工程师,研究方向为电力系统建模仿真。E-mail:xjtc_shixin@126.com
(编辑 赫蕾)