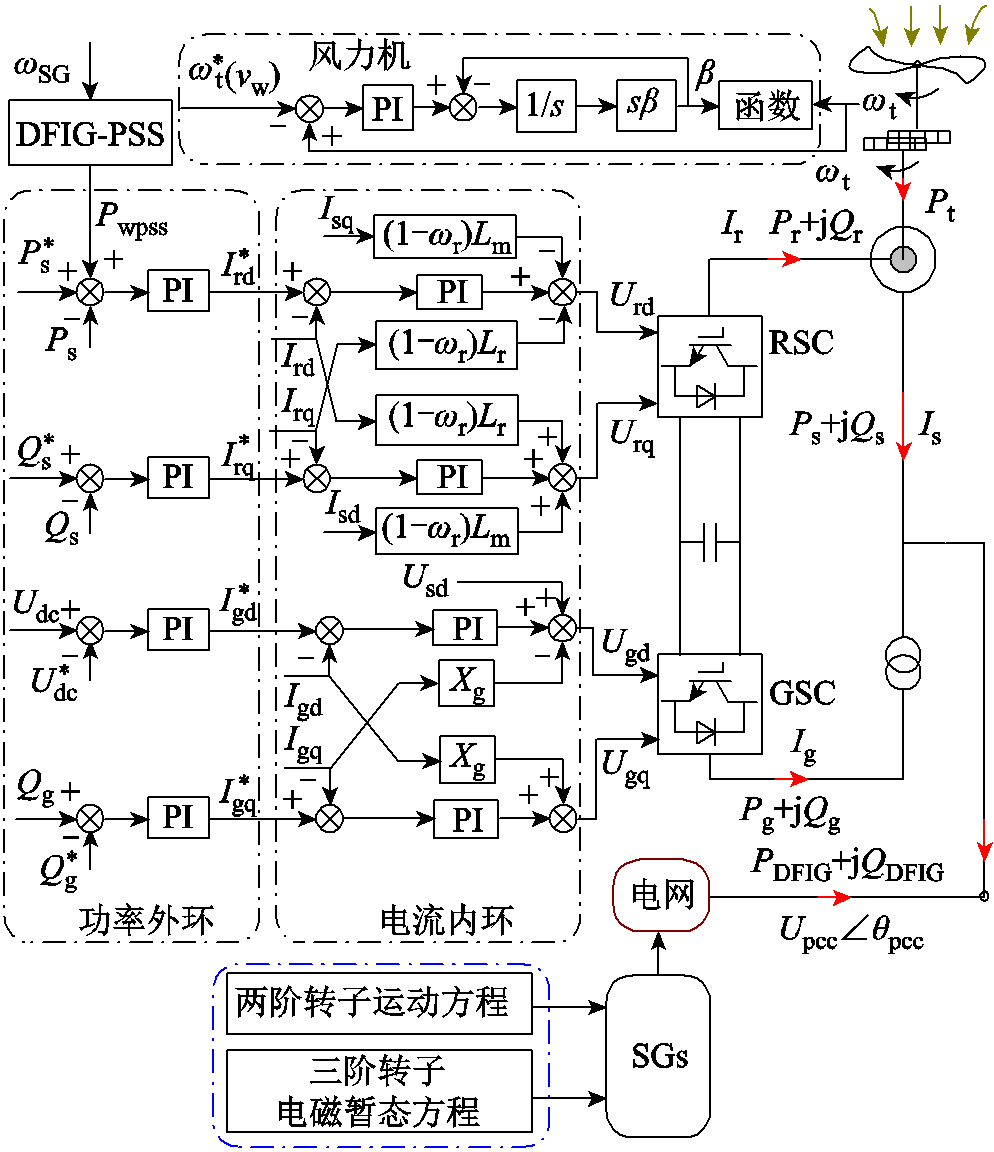
图1 并网DFIG控制策略
Fig.1 Control strategy of grid-integrated DFIG
摘要 随着大量风电并网,双馈感应发电机(DFIG)与同步发电机(SG)间的动态交互,将加剧SG功角振荡。基于特征值分析的控制参数优化,未考虑非线性元件和大扰动场景。该文从抑制功角振荡出发,以SG转速为DFIG电力系统稳定器(PSS)输入信号,建立风电并网电力系统动态模型。在微分方程中引入中间变量,以解耦状态变量轨迹灵敏度。区分状态变量与代数变量对应的雅可比矩阵,推导DFIG并网电力系统轨迹灵敏度的解析表达。设定目标函数为SG功角偏差相对值二次方对时间积分,按时间顺序累加功角对控制参数的轨迹灵敏度,得到目标函数对控制参数的梯度信息。考虑DFIG-PSS可能弱化转子侧变流器(RSC)控制效果,提出基于轨迹灵敏度的RSC和DFIG-PSS参数协调优化方法。给出4机2区域系统仿真结果,验证了所提方法对DFIG并网系统功角振荡的阻尼效果。
关键词:功角振荡 参数优化 轨迹灵敏度 双馈感应发电机 电力系统稳定器
近年来风电机组如双馈感应发电机(Doubly-Fed Induction Generator, DFIG)大量并网,改变了同步发电机(Synchronous Generator, SG)的出力和电网惯性[1-4]。DFIG与SG间的动态交互[5-6],导致SG转速变化更加明显,降低了系统阻尼振荡能力[7-8]。
为抑制振荡、提高系统稳定性,改善阻尼是常见措施[9-10]。文献[11]考虑时滞影响,优化自抗扰控制器与广域电力系统稳定器(Power System Stabilizer, PSS)参数,得到系统最佳阻尼。文献[12]在并入PSS前提下,为使系统能够承受柔性交流输电设备严重故障,增加静态同步补偿器和静态无功补偿器。通过分析对电力系统稳定性影响及其与PSS相互作用,协调优化控制器参数,增强系统阻尼。文献[13]分析DFIG阻抗特性,选择在转子侧变流器(Rotor Side Converter, RSC)或网侧变流器(Gird Side Converter, GSC)引入高频共振阻尼器,另一变换器改善电能质量。文献[14]引入功率振荡阻尼器(Power Oscillation Damper, POD)以降低DFIG并网后的低频振荡。对DFIG和系统其他部分建立开环子系统,采用平衡截断法简化传递函数以量化POD对DFIG振荡的影响,将其设为约束以优化控制器参数。文献[15-16]研究了DFIG变流器PI参数对系统稳定影响,发现PI参数与系统强耦合,修改PI参数可增强系统阻尼[17-18]。位于SG或DFIG的PSS结构简单,常用于增加阻尼[19]。为研究DFIG对系统阻尼影响,文献[20-21]基于阻尼转矩,分析DFIG对SG轴系影响,认为前者可能放大系统振荡甚至导致失稳。基于特征值分析,文献[22]提出在RSC电流控制中引入次同步谐振阻尼控制器。文献[23]提出了PSS阻尼控制的序列二次规划优化方法,解决了由于特征值函数非光滑性而无法同时保证最优性和收敛性的问题。文献[24]推导DFIG-PSS传递函数灵敏度,基于特征值灵敏度优化控制器参数。
上述方法都是基于特定断面线性化,忽略了元件的非线性,不能研究大扰动后控制效果[25]。小扰动分析只能判断振荡衰减特性,不能量化一段时间内参数偏差,而功角振荡/失稳是基于参数偏差定义。
轨迹灵敏度可定量描述运行参数或结构发生变化后系统轨迹变化和动态性能[26-27]。基于轨迹灵敏度,文献[28-30]对系统关键参数、模型参数、误差主导参数进行辨识;文献[31]分析功角对故障切除时间灵敏度与系统稳定性的关系,建立稳定评价指标;文献[32]基于轨迹灵敏度优化暂态过电压和恢复阶段电压,将非线性控制模型转换为以控制量增量为控制变量的二次规划模型。但是上述轨迹灵敏度均采用摄动法,需要反复修改扰动量、计算轨迹,过程繁琐且计算量大。文献[33]基于轨迹灵敏度,优化DFIG附加频率控制中低通滤波器参数,为风电并网系统功角振荡分析与抑制提供了新思路。
为降低DFIG并网对系统功角振荡影响,本文引入DFIG-PSS并借助轨迹灵敏度优化其控制参数以增强系统阻尼,其中难点在于:
(1)DFIG与SG的动态交互,不但改变系统阻尼,还增强系统参数耦合,需要对DFIG进行建模并与SG联立分析。
(2)微分方程中多状态变量的轨迹灵敏度相互耦合,且不能区分状态变量与代数变量的雅可比矩阵,无法借助其建立轨迹灵敏度的解析表达。
(3)在转子侧变流器有功外环引入DFIG-PSS,RSC原有控制参数控制效果可能被削弱。
针对上述问题,本文考虑SG与DFIG动态交互,选择SG转速为DFIG-PSS输入信号,建立DFIG并网系统动态模型。引入中间变量修改微分方程,将状态变量轨迹灵敏度解耦,建立DFIG并网系统轨迹灵敏度的解析表达。设定目标函数为SG功角偏差相对值对时间积分,按仿真步长累加功角对控制参数的轨迹灵敏度,得到目标函数对控制参数的梯度信息。考虑DFIG-PSS通过RSC有功外环引入,且积分系数过大会削弱比例系数的控制效果,选择RSC比例控制参数为待优化变量。最后提出基于轨迹灵敏度优化RSC和DFIG-PSS参数,以提高系统阻尼振荡能力。给出4机2区域系统仿真结果,以验证所提参数优化方法的振荡抑制效果。
风力机建模与转子侧变流器控制风电并网电力系统控制策略如图1所示[34]。SG采用模型包括两阶转子运动方程与三阶转子电磁暂态方程。DFIG风力机捕获风能,驱动感应电机发电。传动轴采用两质量块模型。变流环节由RSC、GSC和直流电容组成。RSC和GSC的功率外环与电流内环实现有功/无功解耦控制。运行参数包括电压、电流、功率等,控制参数包括DFIG出力参考值、时间常数、PI参数等。

图1 并网DFIG控制策略
Fig.1 Control strategy of grid-integrated DFIG
风力机捕获功率为
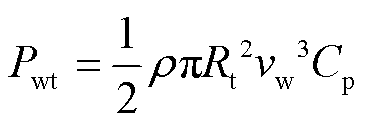 (1)
(1)
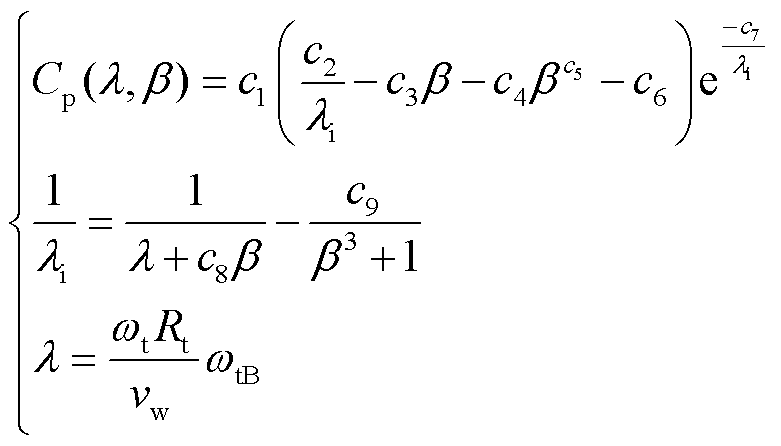 (2)
(2)
式中,ρ为空气密度;Rt为风机半径;vw为风速;Cp为风能捕捉系数,Cp通常由风机制造商给出,由叶尖速比λ和桨距角β决定;c1~c9为拟合系数;λi为中间变量;ωt和ωtB分别为风力机转速及其基准值。
将风力机与低速轴作为一质量块,齿轮箱与高速轴作为另一质量块,轴系方程为
 (3)
(3)
式中,Ht、Hr分别为风力机和电机惯性时间常数;K为刚度系数;D为阻尼系数;ωr、ωrB分别为电机转速及基准值;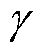 为传动轴扭转角;Te为电磁转矩。
为传动轴扭转角;Te为电磁转矩。
以下基于DFIG简化模型推导定子出力与RSC间的关系,从而得到DFIG-PSS设计思路。第2节中DFIG并网系统轨迹灵敏度解析表达和控制参数优化,均采用详细DFIG模型。DFIG出力包括定子出力和GSC出力。取定子电压定向d轴,不计定子磁链暂态和定子电阻。联立定子磁链,定子出力为
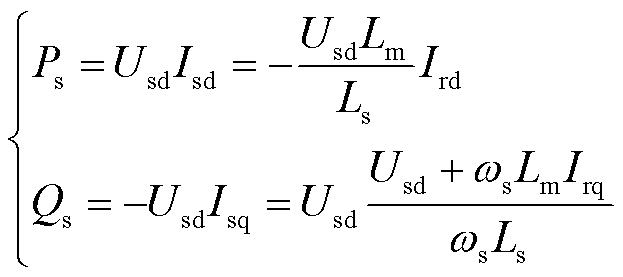 (4)
(4)
式中,P为有功功率;Q为无功功率;U为电压;I为电流;ω为转速;下标d和q分别表示d轴和q轴;下标s、r分别表示定子和转子参数;Ls为定子电感,Ls=Lsσ+Lm;Lsσ为定子漏感;Lm为励磁电感。
文献[35]表明,在RSC有功/无功控制环并入PSS,均可改善系统阻尼。但是无功调制可能恶化DFIG定子暂态,有功调制更为有效。转子电流影响DFIG定子出力,可调节转子电压以控制转子电流。直流电压较为稳定,对DFIG出力影响较小。变流器控制参数不同程度地影响系统阻尼振荡能力,增大GSC电流内环比例参数和RSC有功功率外环积分参数时系统更容易失稳[36]。
DFIG与SG动态交互逻辑如图2所示。在大扰动后,SG机械转矩与电磁转矩不平衡,转速变化,吸收或释放动能以维持稳定性。而DFIG没有功角稳定概念;采用变流器控制,导致DFIG与系统解耦,不能主动响应外部扰动。因此大规模风电接入可能导致系统阻尼降低。为此在RSC有功外环引入DFIG-PSS,增加有功调制信号Pwpss以吸收或释放DFIG转子动能[37],提高系统抑制功角振荡的能力。
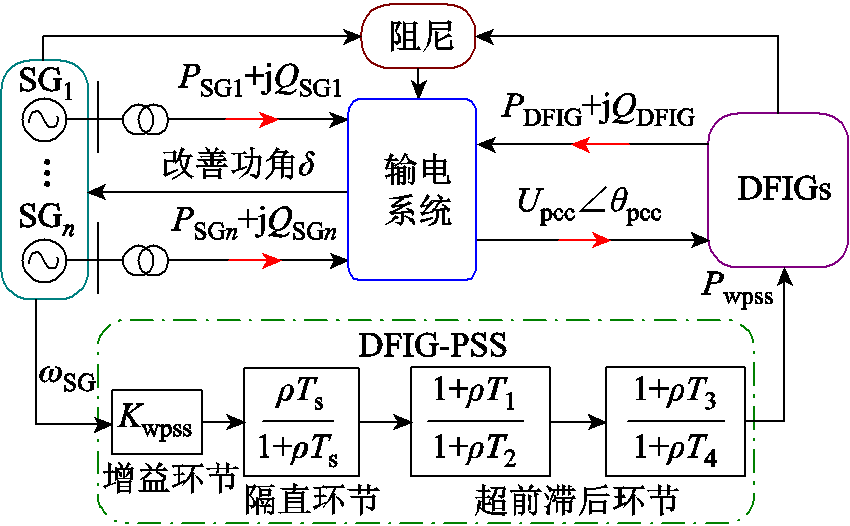
图2 DFIG与SG间动态交互逻辑
Fig.2 Dynamic interaction between DFIG and SG
参考SG-PSS,DFIG-PSS包括:增益环节,增加阻尼;隔直环节,维持信号恒定四个部分[38];两个超前滞后环节,用于相位补偿。考虑SG转速变化是功角振荡主要原因,取前者为DFIG-PSS输入,通过调节DFIG转子电流,改变有功输出以阻尼功角振荡。
含DFIG电力系统动态特性描述为
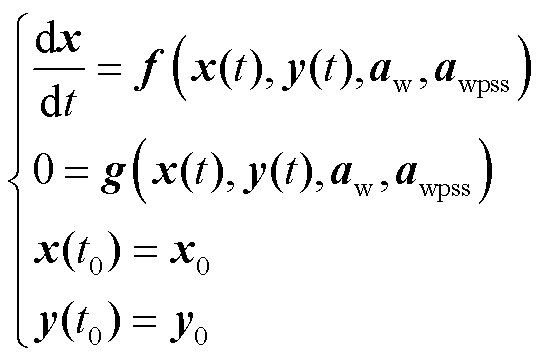 (5)
(5)
式中,f、g、x、y分别为系统微分方程、代数方程、状态变量和代数变量;aw为RSC控制参数;awpss为DFIG-PSS控制参数;t为时间;下标0表示初值。区分状态变量和代数变量,以控制参数描述系统参数轨迹F为
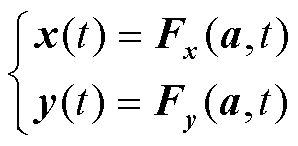 (6)
(6)
式中,a=[awawpss]。在a=a0处泰勒展开并忽略高阶项,得到
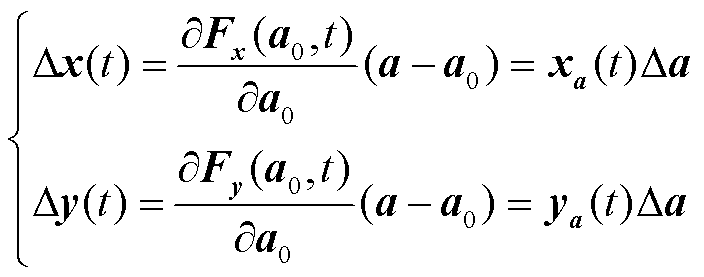 (7)
(7)
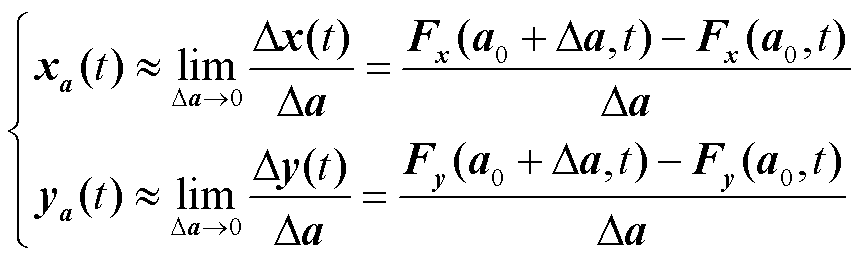 (8)
(8)
式中,xa(t)和ya(t)分别为x(t)和y(t)对a的轨迹灵敏度。当Da足够小时,式(7)近似为式(8),该轨迹灵敏度求解方法称为摄动法,其缺点是在计算多个轨迹灵敏度时,过程繁琐,计算量较大。
为此推导轨迹灵敏度的解析表达。对式(5)微分方程f进行积分,并对a求偏导得
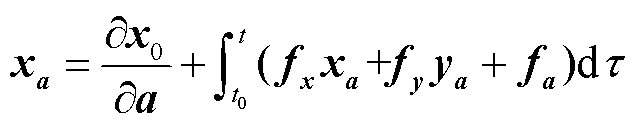 (9)
(9)
式中,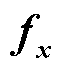 、
、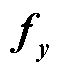 、
、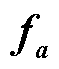 为雅可比矩阵。
为雅可比矩阵。
本文控制参数aw和awpss均不影响稳态初值,因此轨迹灵敏度初值为零。系统状态变量为a和t的连续函数,对参数与时间求导可交换顺序,可得
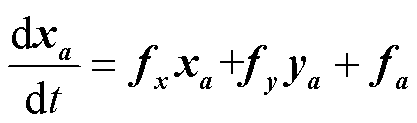 (10)
(10)
类似对代数方程进行积分、求导,最后得DFIG并网系统的轨迹灵敏度解析表达为
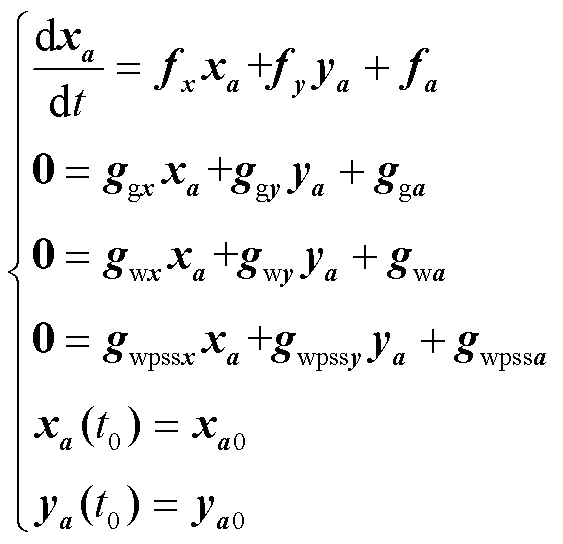 (11)
(11)
式中,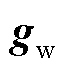 为含RSC控制参数的代数方程;gwpss为含DFIG-PSS控制参数的代数方程;gg为DFIG代数方程(不含gw和gwpss);ggx、ggy、gwx、gwy、gwpssx、gwpssy分别为gg、gw、gwpss的雅可比矩阵;xa0、ya0为轨迹灵敏度初值。
为含RSC控制参数的代数方程;gwpss为含DFIG-PSS控制参数的代数方程;gg为DFIG代数方程(不含gw和gwpss);ggx、ggy、gwx、gwy、gwpssx、gwpssy分别为gg、gw、gwpss的雅可比矩阵;xa0、ya0为轨迹灵敏度初值。
式(11)第一行左端含有多个状态变量且为非线性方程,各变量轨迹灵敏度耦合,不易直接计算。为此引入中间变量,使状态变量和状态方程解耦,以便后续建立轨迹灵敏度的解析表达。针对本文研究对象(DFIG-PSS与RSC控制参数),以下给出解耦过程。定义中间变量A1、A2、A3、A4、B1、B2、B3为
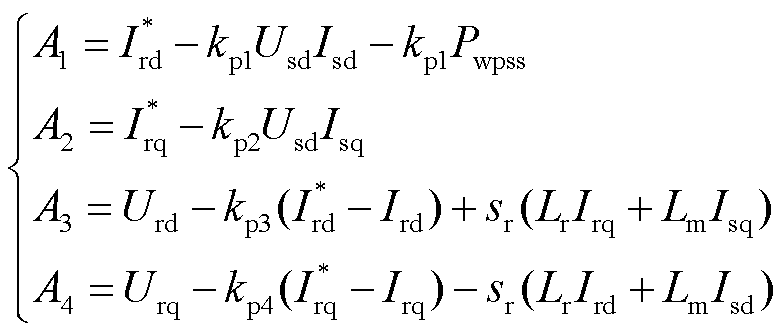 (12)
(12)
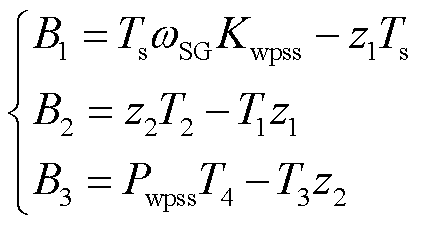 (13)
(13)
式中,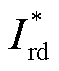 和
和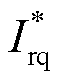 分别为转子电流Ird和Irq参考值;kp为比例系数;ki为积分系数;sr为DFIG转差率;z1和z2分别为隔直环节和超前滞后环节输出;ωSG为SG转速;Kwpss为增益倍数;Ts为隔直时间常数;T1、T3为超前时间常数;T2、T4为滞后时间常数。
分别为转子电流Ird和Irq参考值;kp为比例系数;ki为积分系数;sr为DFIG转差率;z1和z2分别为隔直环节和超前滞后环节输出;ωSG为SG转速;Kwpss为增益倍数;Ts为隔直时间常数;T1、T3为超前时间常数;T2、T4为滞后时间常数。
设e为a中任一参数,求取对e的偏导,可得出系统方程对控制参数e的偏导。以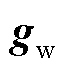 、
、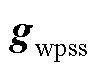 为例,给出对e的轨迹灵敏度解析表达式为
为例,给出对e的轨迹灵敏度解析表达式为
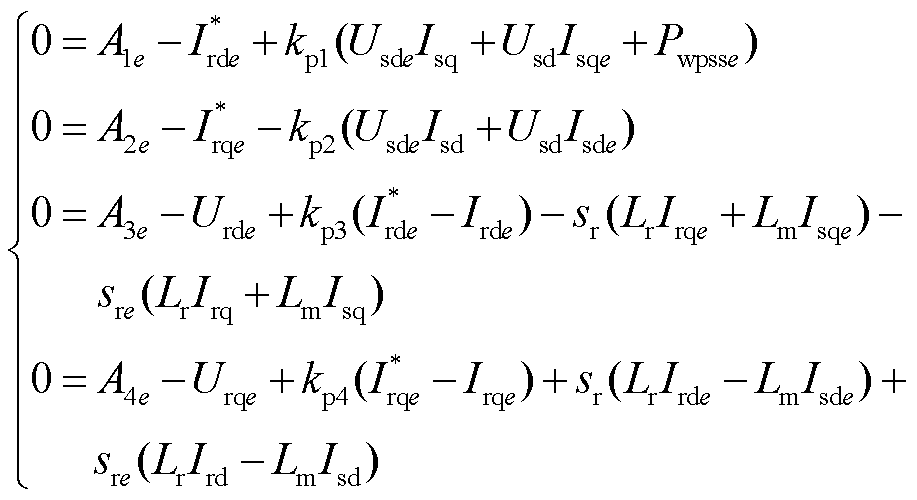 (14)
(14)
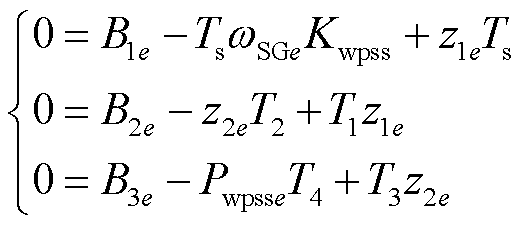 (15)
(15)
根据式(12),联立RSC功率外环和电流内环控制方程,转换微分方程中状态变量,可得
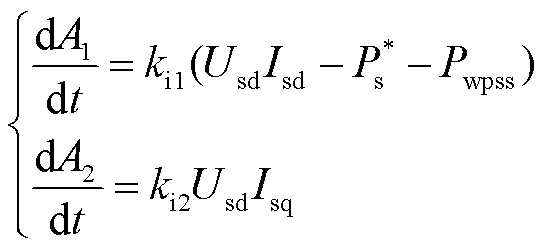 (16)
(16)
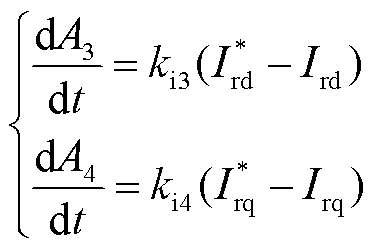 (17)
(17)
式中,Ps*和Qs*分别为定子有功功率和无功功率参考值。
根据式(13),联立DFIG-PSS方程并转换为
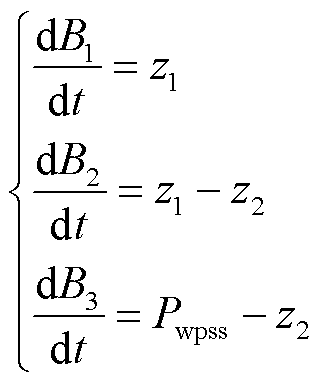 (18)
(18)
式(16)~式(18)左端仅有一个状态变量,系统所有状态变量(包括新增中间变量)在左端行成一个对角矩阵,状态变量轨迹灵敏度解耦。状态变量与代数变量的雅可比矩阵分别在矩阵上层与下层。
本文待优化控制参数仅出现在式(12)和式(13),因此fa=0,gga=0。对转换后式(11)进行差分,得到对a轨迹灵敏度为
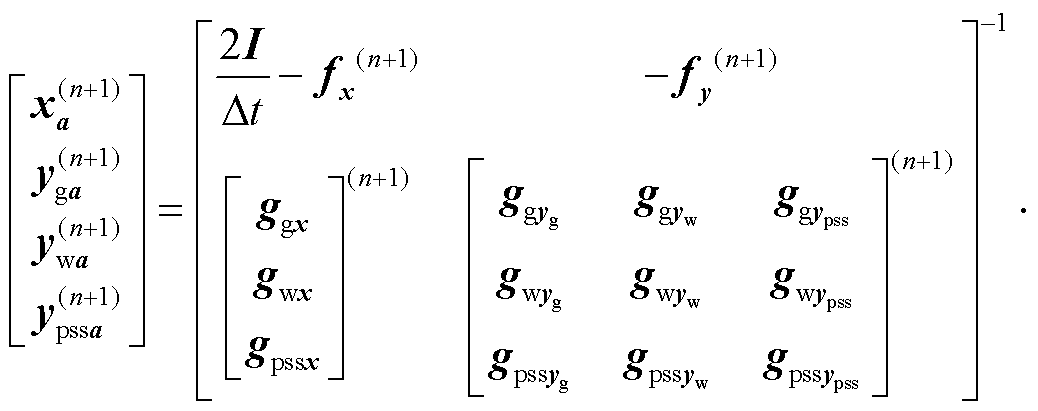
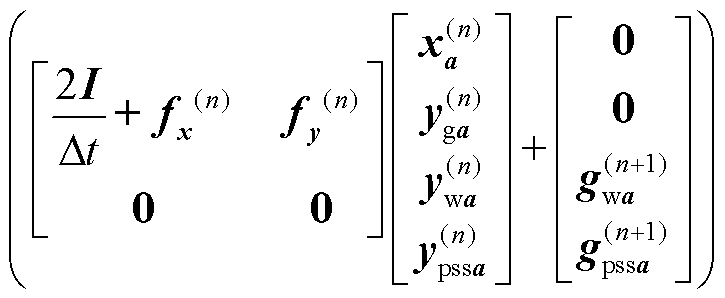 (19)
(19)
式中,Dt为时域仿真步长;I为单位矩阵;n和n+1分别表示前后时刻。
为抑制SG功角振荡,以暂态过程中SG功角差与其稳态值比值二次方的积分,作为性能指标。为消除功角初值大小影响,取功角偏差相对值,建立目标函数J为
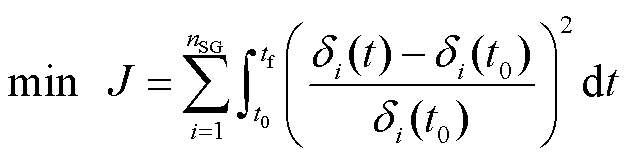 (20)
(20)
式中,δi(t)为第i台SG在t时刻的功角值;tf为时域仿真结束时刻;nSG为SG数量。
按仿真步长划分暂态过程时间段,累加各时段功角对a的轨迹灵敏度,得J对a的梯度信息为
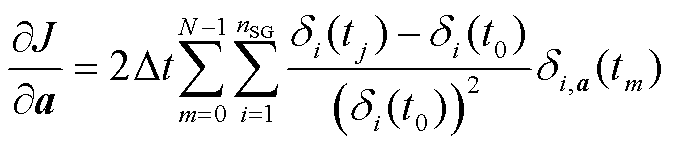 (21)
(21)
式中,N为时域仿真步长数;δi,a(tm)为第i个SG功角对控制参数a在tm时刻的轨迹灵敏度。
由图2得DFIG-PSS传递函数式为
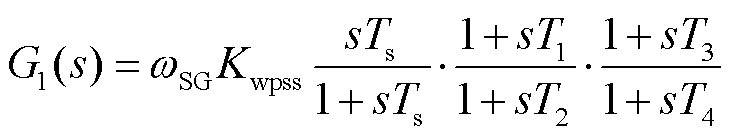 (22)
(22)
将DFIG-PSS输入比较点和d轴转子电流比较点后移,得到RSC等效有功控制如图3所示。
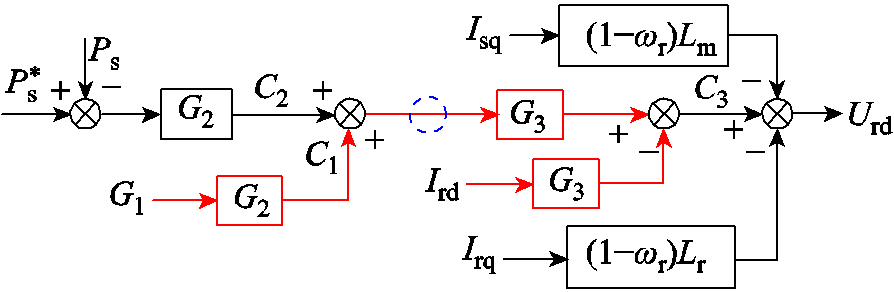
图3 RSC等效有功控制
Fig.3 Equivalenced active power control to RSC
忽略定子有功扰动,得DFIG-PSS参数与RSC有功控制间关系式为
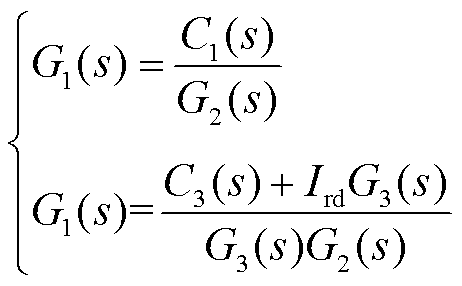 (23)
(23)
式中,G2和G3为PI环节传递函数。由此可见DFIG-PSS影响RSC控制参数,需要协调优化两者参数。
DFIG-PSS参数中,Ts、T2、T4惯性较强,对控制效果影响不大,依据经验取Ts=5s,T2=T4= 0.2s[9,25]。Kwpss、T1、T3对控制效果影响较大。DFIG-PSS输出是RSC功率外环的输入,可能降低后者控制效果,且RSC积分系数较小,否则将削弱比例系数控制效果和系统稳定性[16,36]。因此建立约束条件式为
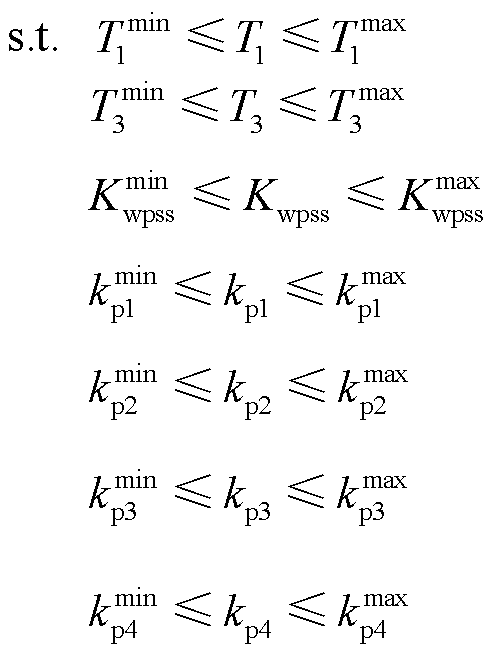 (24)
(24)
式中,上标min与max分别表示下限和上限。
考虑SG与DFIG动态交互,借助轨迹灵敏度解析表达,统一优化DFIG-PSS和RSC参数,增强系统阻尼,改善系统功角稳定,抑制DFIG振荡。基于轨迹灵敏度的DFIG-PSS和RSC参数优化流程如图4所示,其中加粗字体为重点和创新点。相比文献[35]只对风力机控制参数优化,本文关注问题不同,且协调范围更大一些。考虑目标函数非线性,采用内点法求解,后者需要目标函数和约束条件的一阶和二阶梯度。为减小计算量,采用BFGS算法得到海森矩阵。
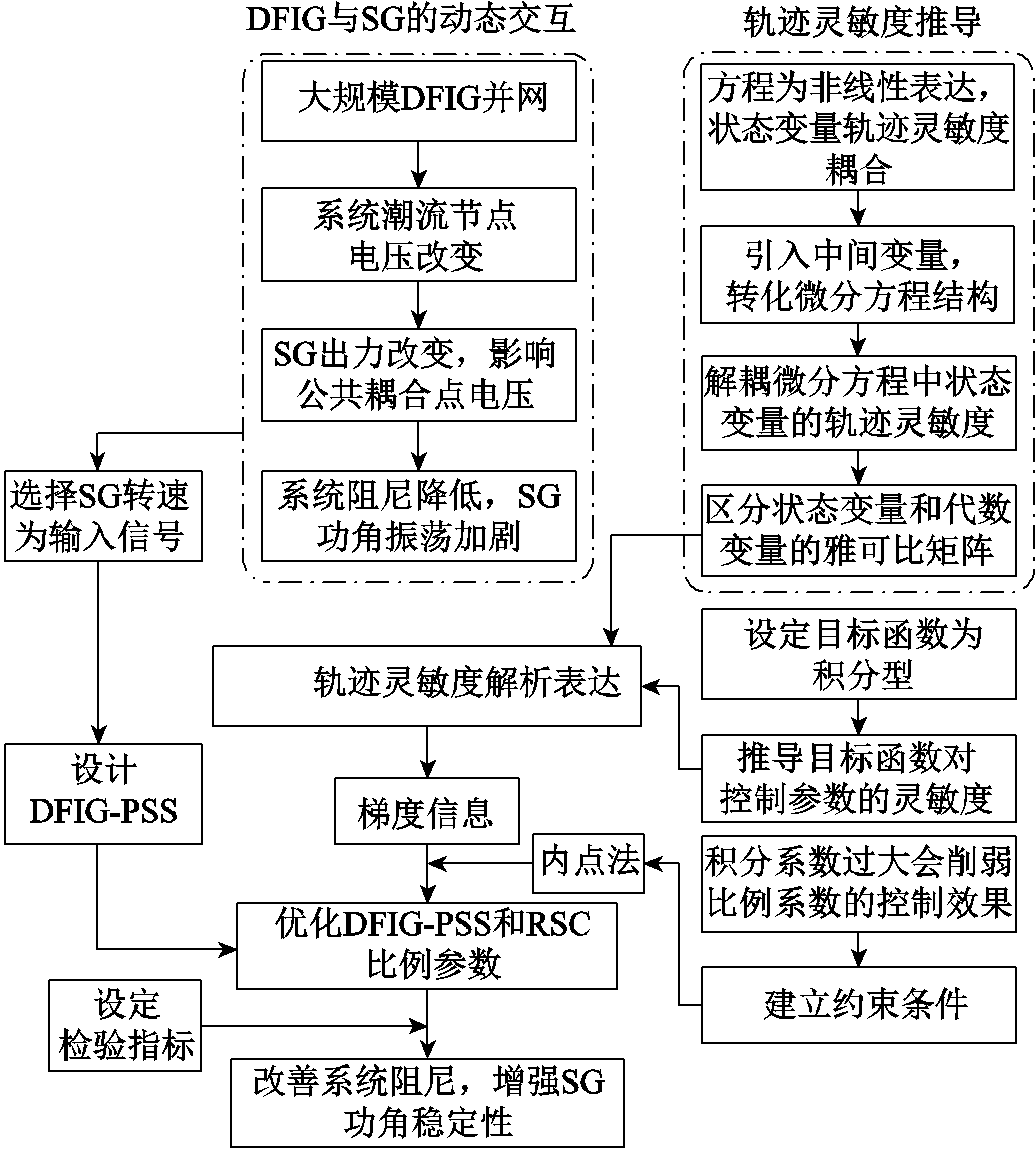
图4 基于轨迹灵敏度的DFIG-PSS和RSC参数优化
Fig.4 Parameter optimization to DFIG-PSS and RSC based on trajectory sensitivity
定义功角差振幅最大优化比例Mwa,即最大优化量Dδmax与优化前的最大振荡幅值δmax的比值,以检验参数优化效果。以功角差初值±5%为基准,定义功角差最大收敛提前比例Mcr,为优化后收敛时间tcraf与优化前收敛时间tcr的比值。定义DFIG功率振荡幅值最大优化比例Mpo,为最大功率优化量DPmax与优化前的最大功率Pmax的比值。Mwa、Mcr、Mpo表达式为
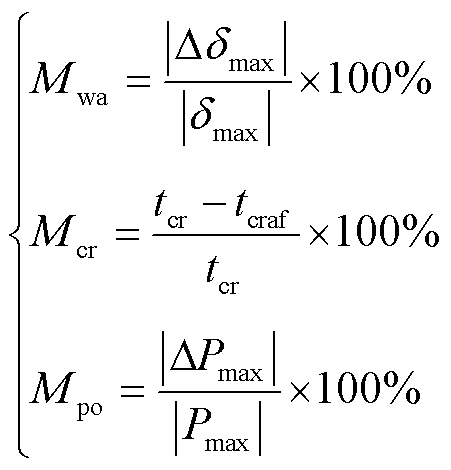 (25)
(25)
风力机捕捉风能与风速大小有关。当风速低于额定风速时,桨距角不启动,风机运行于最大功率点跟踪方式,风机转速随风速变化,得到最佳叶尖速比和最大捕获功率。当风速继续增加,风力机将处于恒转速方式(转速上限)。当风速继续增加,风力机通过增加桨距角或者降低转速,处于恒功率方式(额定功率)。当风速稍高于切入风速时,风力机处于恒转速方式(转速下限),可类似建模。上述风速和风力机运行方式变化,影响转速和桨距角取值,但是不影响本文控制参数优化算法。
实际风电场内各DFIG风速、集电线路阻抗不同,对于电网影响和贡献也存在一定差异。将风电场等效为一台DFIG[39-40],可以减小计算规模、改善收敛性,适合电场内风速变化不大、集电阻抗很小的场景。一般来说,如果研究对象只是风电场,应对每台DFIG进行建模;如果是电力系统,可以适当等值风电场。本文研究对象是风电并网后电力系统功角稳定性,风电场等值处理对系统稳定影响较为有限,因此可以等值风电场。如果需要考虑风速差异,可以将同一馈线上一串DFIG等值为一台,从而用有限几台DFIG来等效风电场。风电场或DFIG数量,不影响本文算法适用性。
本文所提基于轨迹灵敏度的风电并网系统控制优化算法,适用于不同运行场景、故障模式、电网安全问题、待优化参数。从实际运行角度考虑,控制参数设置应相对稳定。因此所设定控制参数应该对其他运行方式和故障模式具有一定适应能力。一般来说,控制优化很难界定适用范围,但是通过设置不同扰动/故障模式,可以检验算法应用效果。
针对所提算法编写Matlab程序。计算机配置:Intel(R) Core(TM)i5-3470 CPU,3.20 GHz,4GB内存。完成一次时域仿真时间约为12.64s。计算轨迹灵敏度时间21.05s。优化DFIG-PSS时间218.29s,优化RSC时间263.64s,统一优化时间为396.59s。
选择4机2区域系统进行验证,四机两区域测试系统如图5所示。SG参数见文献[33],取SG1为平衡机组,负荷采用恒阻抗模型。在节点7连接一个风电场,其由2串组成,各有25台DFIG,风速分别为9m/s和11m/s。DFIG单机参数见附表1和附表2[14]。考虑风速间的差异,将每串等值为一台,共有两台DFIG。
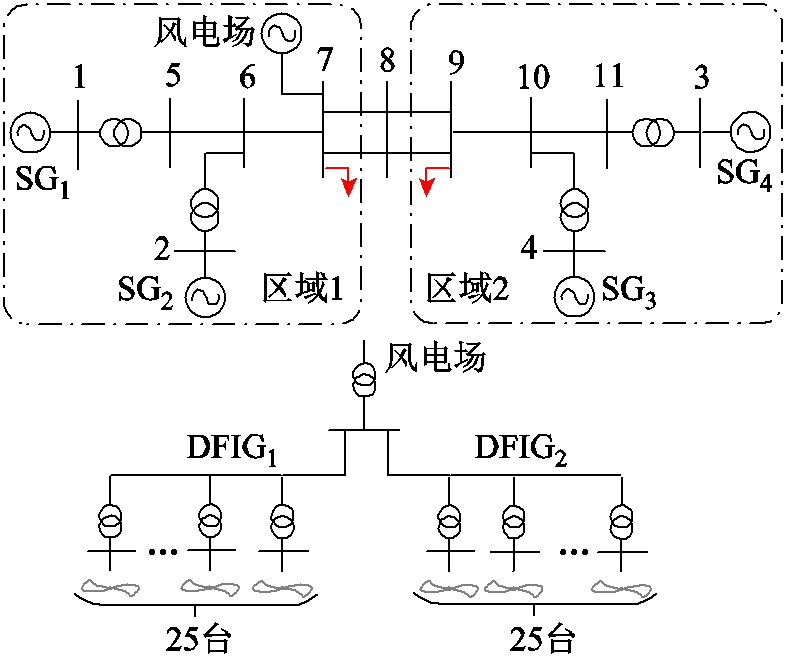
图5 四机两区域测试系统
Fig.5 4-SG 2-area test system
设9号节点0.5s时三相短路,0.1s后故障清除。有无DFIG时的SG有功功率如图6所示,DFIG并网影响系统潮流,改变节点电压和相位、SG出力,SG振荡振幅及持续时间增加。有无DFIG-PSS时的DFIG1转子电流如图7所示,其振荡幅值与持续时间明显增加。引入DFIG-PSS后,增加有功调制信号,在增加电网阻尼能力的同时,削弱了RSC控制效果。
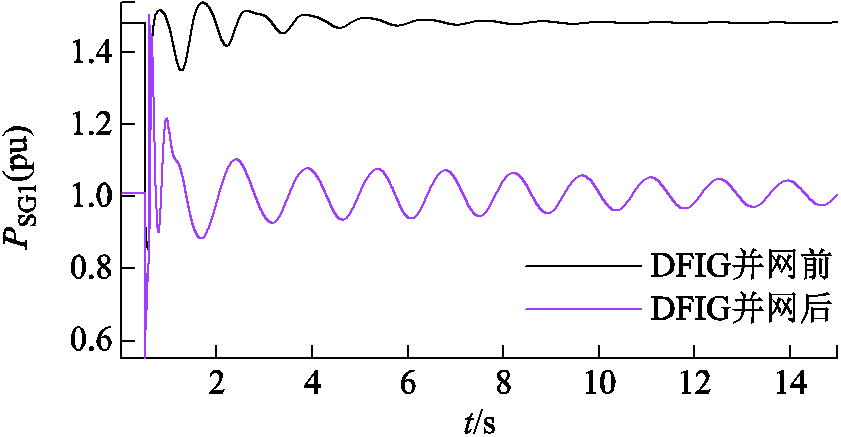
图6 有无DFIG时的SG有功功率
Fig.6 Active output of SG without/with DFIG
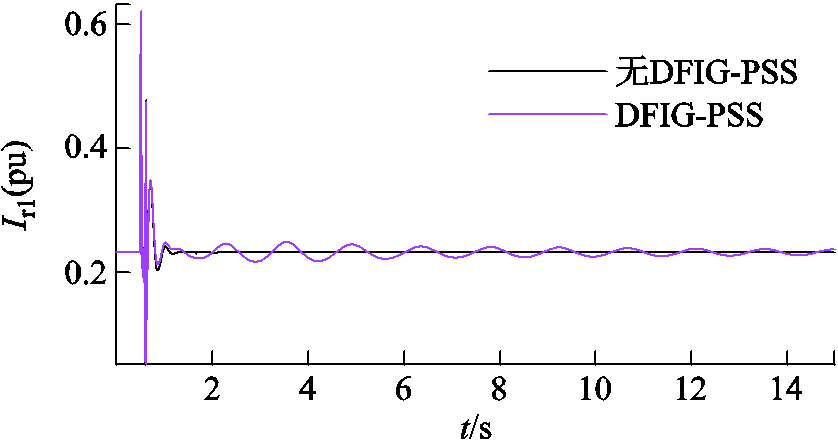
图7 有无DFIG-PSS时的DFIG1转子电流
Fig.7 Rotor current of DFIG1 without/with DFIG-PSS
取摄动值10–5(pu),采用摄动法计算轨迹灵敏度,检验本文解析表达精度。两种方式下,SG1和SG3功角对DFIG1参数T1和kp4的轨迹灵敏度基本重合,如图8所示。轨迹灵敏度解析表达的误差见表1,最大误差0.783 69 %,验证了所提解析表达的正确性。
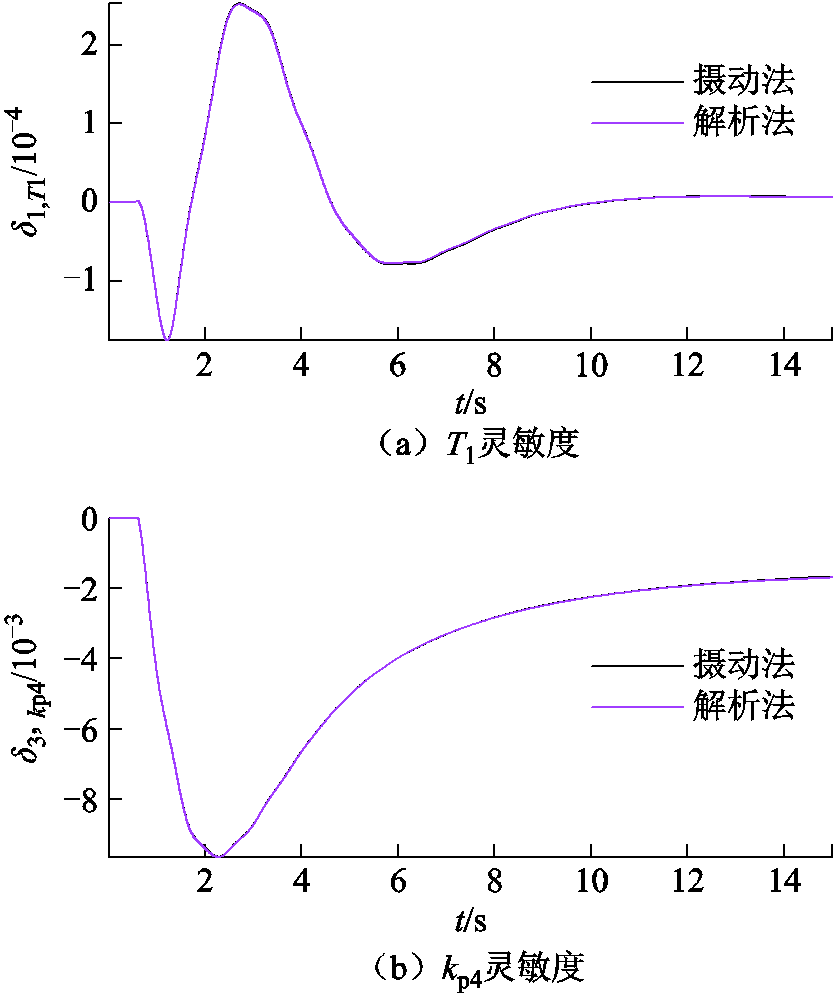
图8 SG功角对控制参数的轨迹灵敏度
Fig.8 Trajectory sensitivity of power angle of SG to control parameter
表1 轨迹灵敏度解析表达的误差
Tab.1 Error of analytical expression of trajectory sensitivity

轨迹灵敏度时间/s摄动法解析法误差(%) δ1,T13.51.941 9×10-41.934 3×10-40.391 37 7.5-4.940 0×10-5-4.910 0×10-50.607 28 11.56.380 0×10-66.330 0×10-60.783 69 14.56.830 0×10-66.780 0×10-60.732 06
(续)

轨迹灵敏度时间/s摄动法解析法误差(%) δ3,kp43.5-7.647 4×10-3-7.656 2×10-30.115 07 7.5-3.053 8×10-3-3.052 6×10-30.039 29 11.5-1.995 2×10-3-2.000 2×10-30.340 81 14.5-1.736 6×10-3-1.733 0×10-30.207 30
保持RSC比例参数不变,增加积分参数,见表2,设计a、b、c三个方案,两台SG间功角差仿真结果如图9所示。随ki增加,SG功角振荡峰值增加。当ki3和ki4取10-1数量级,系统功角失稳。
表2 RSC积分控制参数的取值
Tab.2 Values of the RSC integral control parameters

方案ki1ki2ki3ki4 a4.204×10-25.541×10-22.102×10-32.102×10-3 b2.943×10-13.879×10-12.102×10-22.102×10-2 c4.204×10-15.541×10-12.102×10-22.102×10-3
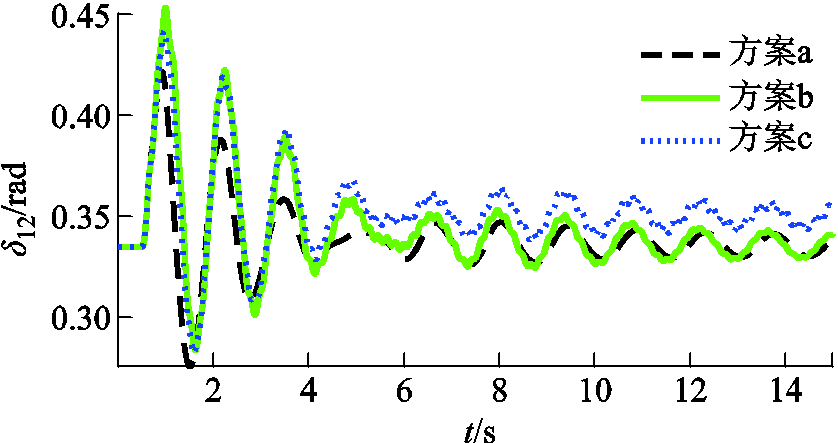
图9 RSC不同ki下SG功角差
Fig.9 SG power angle difference with different ki of RSC
保持RSC控制参数不变,DFIG-PSS1和DFIG-PSS2的控制参数Kwpss、T1、T3均分别为-1.85、0.65s、0.65s。可调范围均分别为[–2.5, 15]、[0.527s,0.85s]、[0.527s,0.85s]。取收敛精度为10–6,优化上述参数,20次迭代后收敛。最优值Kwpss1=14.95,Kwpss2=14.75,T11=T31=0.75s,T12=T32=0.723s。优化前后SG功角差如图10所示。优化前,系统对振荡阻尼能力较弱,δ23和δ23振幅较大且长时间不能平稳。优化后,系统阻尼能力增强,功角振幅降低,持续时间减小,收敛时间提前。优化后SG功角差的最大优化比例Mwa和最大收敛提前比例Mcr见表3。δ23的Mwa最大为47.88%。Mcr最大为83.23%(32.518s),δ23在6.551s时开始收敛。以上结果证明了所提DFIG-PSS参数优化方法对提高系统抑制功角振荡的能力具有积极作用。
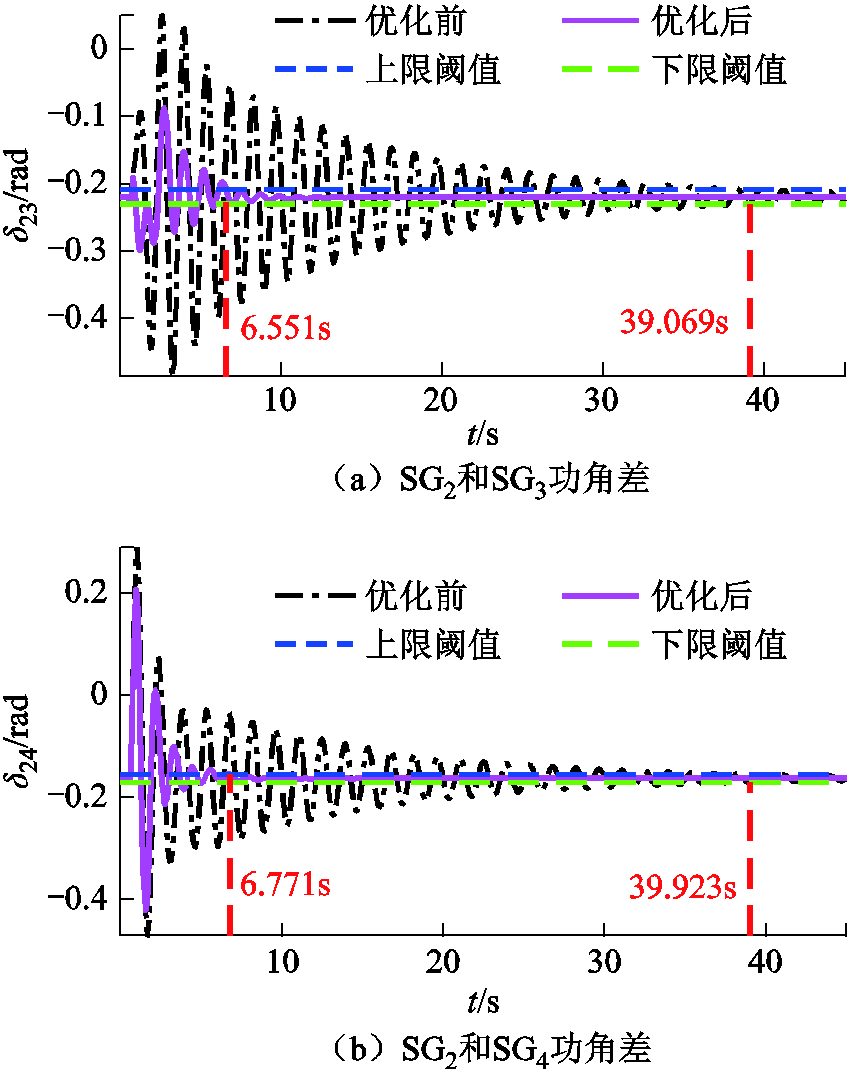
图10 优化DFIG-PSS参数前后SG功角差
Fig.10 Power angle difference between SGs before/after optimization to DFIG-PSS parameters
表3 优化DFIG-PSS后SGs功角差的Mwa和Mcr
Tab.3 Mwa and Mcr of power angle difference between SGs after optimization to DFIG-PSS

参数数值 δ23δ24 δmax/rad0.4860.472 2 Dδmax/rad0.232 70.201 3 Mwa(%)47.8842.63 tcr/s39.06939.923 tcraf/s6.5516.771 Mcr(%)83.2383.04
DFIG1和DFIG2控制参数kp1~kp4初值分别为0.57、0.65、0.02、0.047 5,可调范围[0.52,0.75]、[0.51,0.67 5]、[0.018 5,0.068 5]、[0.01,0.057]。经14次迭代后优化收敛,DFIG1最优值为0.725、0.52、0.065、0.012 5,DFIG2最优值为0.717、0.54、0.063 2、0.013 6。DFIG出力和SG功角差如图11所示。优化前,SG功角振幅大,持续时间长。优化后,SG功角振幅和持续时间减小,阻尼振荡能力加强。
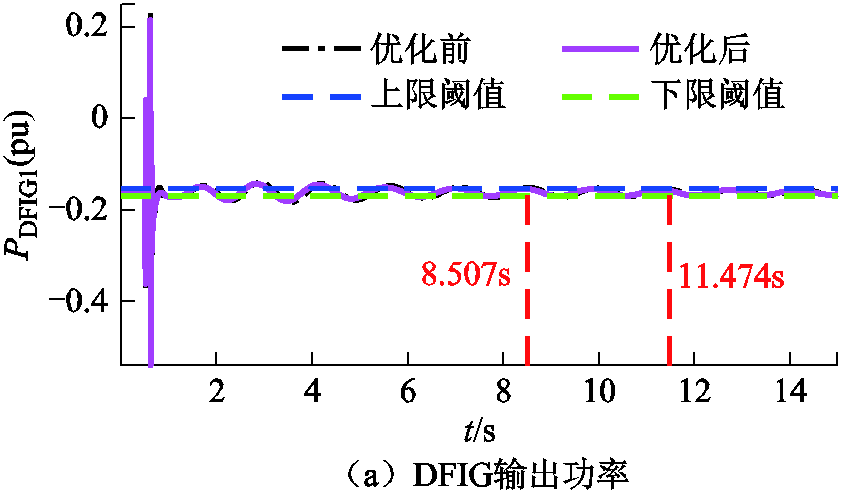
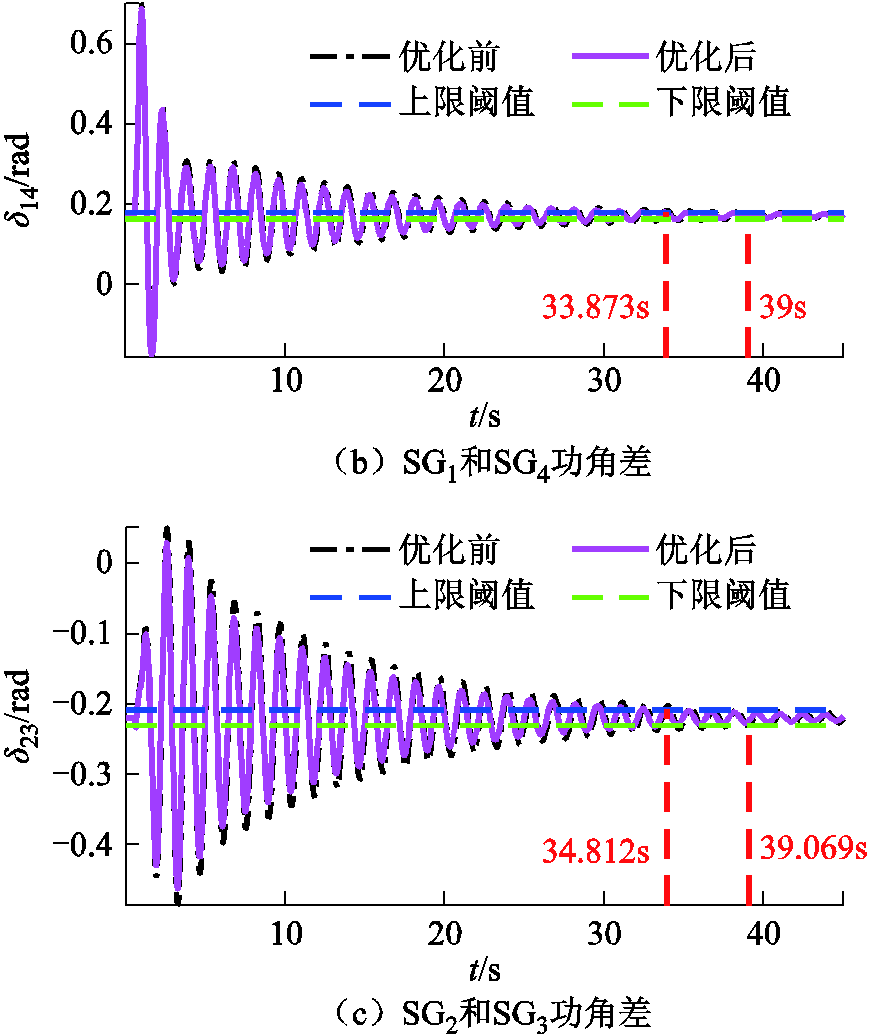
图11 优化RSC参数前后DFIG出力和SG功角差
Fig.11 DFIG output and power angle difference between SGs before/after optimization to RSC parameters
优化RSC参数后DFIG出力的Mpo和Mcr及SGs 功角差的Mwa和Mcr见表4。功率振幅最大优化比例Mpo达9.19 %,提前2.797s(24.28 %)收敛。SG功角差Mwa最大达6.67 %,δ14最大提前5.127s(13.15 %)收敛。
表4 优化RSC参数后DFIG出力的Mpo和Mcr及SGs功角差的Mwa和Mcr
Tab.4 Mpo and Mcr of the DFIG output and Mwa and Mcr of power angle difference betweensGs after optimization to RSC parameters
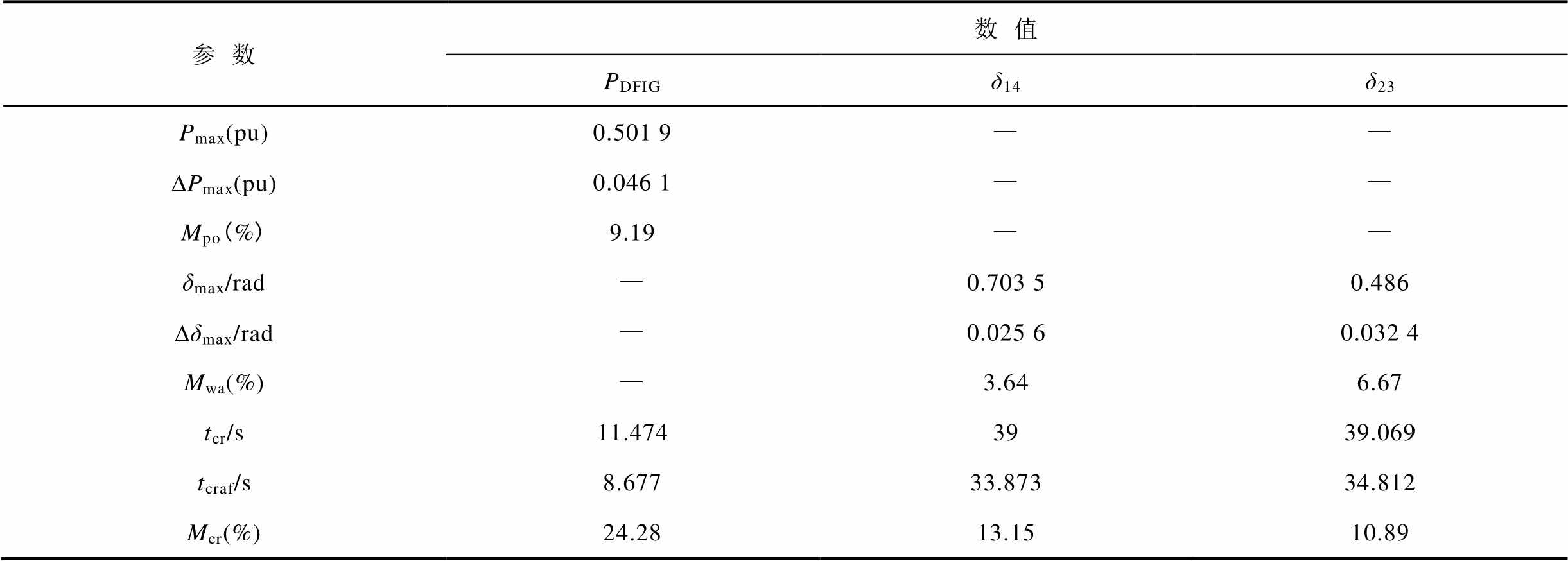
参数数值 PDFIGδ14δ23 Pmax(pu)0.501 9—— DPmax(pu)0.046 1—— Mpo(%)9.19—— δmax/rad—0.703 50.486 Dδmax/rad—0.025 60.032 4 Mwa(%)—3.646.67 tcr/s11.4743939.069 tcraf/s8.67733.87334.812 Mcr(%)24.2813.1510.89
保持DFIG-PSS和RSC参数初值和取值范围、优化收敛精度不变。同时优化两者,经过25次迭代后收敛。仅优化DFIG-PSS和同时优化两者参数的SG功角差如图12所示,其振荡幅值及持续时间均明显减小。
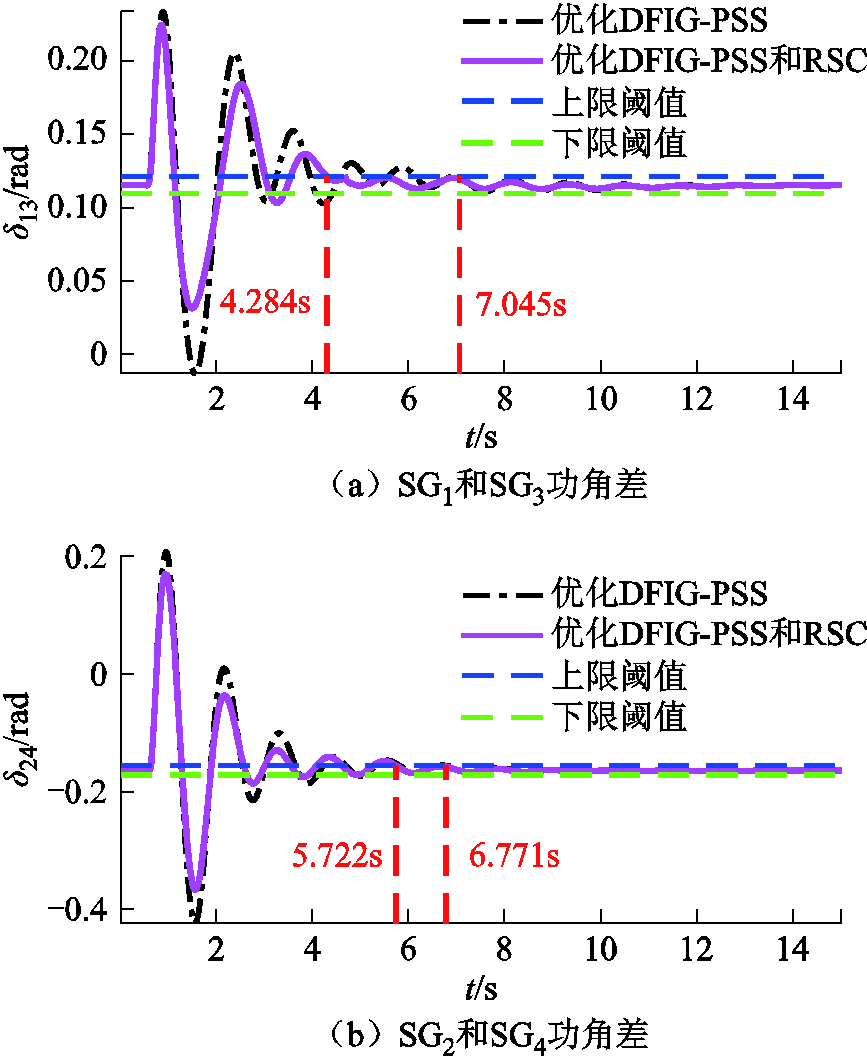
图12 优化DFIG-PSS和RSC参数后SGs功角差
Fig.12 Power angle difference between SGs after optimization to DFIG-PSS and RSC parameters
优化两参数后功角差的Mwa和Mcr见表5,振荡幅值最大优化比例为20.45%,最大提前2.761s(39.19 %)收敛。同时优化两者,进一步增强了系统阻尼振荡的能力,证明了本文所提DFIG-PSS和RSC参数优化方法对于提高系统抑制DFIG并网振荡的能力起积极作用。
表5 优化DFIG-PSS和RSC参数后功角差的Mwa和Mcr
Tab.5 Mwa and Mcr of power angle difference between SGs after optimization DFIG-PSS and RSC parameters
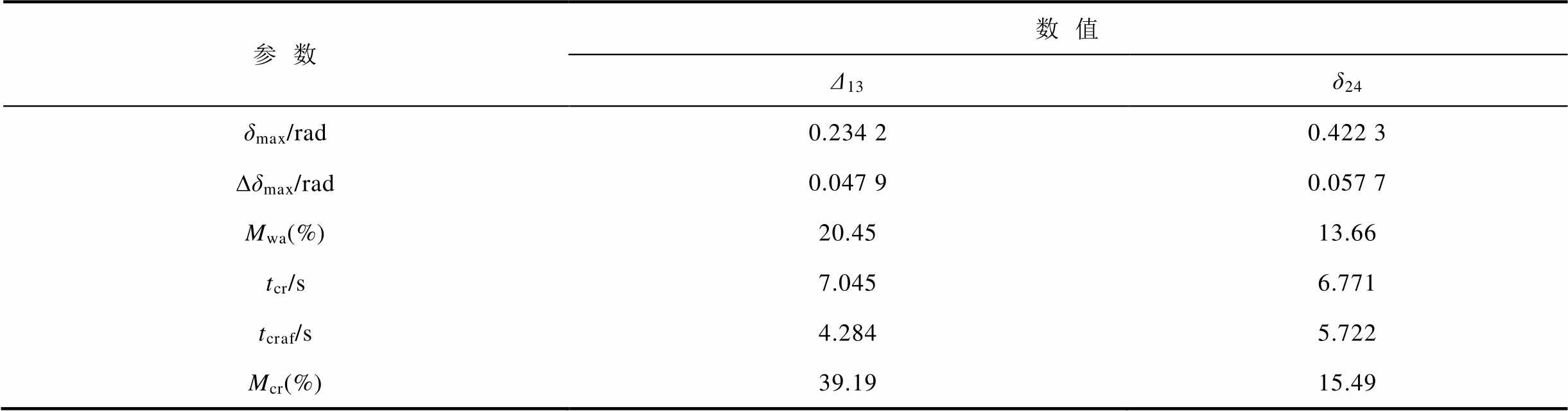
参数数值 Δ13δ24 δmax/rad0.234 20.422 3 Dδmax/rad0.047 90.057 7 Mwa(%)20.4513.66 tcr/s7.0456.771 tcraf/s4.2845.722 Mcr(%)39.1915.49
为检验所提算法适应性,新增以下仿真场景:
场景一:将三相短路地点由节点9改为节点5,0.5s时故障发生,0.1s后故障切除。
场景二:两台DFIG风速分别由9m/s和11m/s改为11m/s和13m/s,0.5s时节点9三相短路,0.1s后故障切除。
场景三:0.5s时,节点4突增100MW负荷。
附图1、附图2和附图3分别给出三个场景的仿真结果。相比优化前,优化后功角振荡幅值和持续时间明显降低。由于增益系数较大,有功负荷突増后功角振荡幅值较大,但是收敛时间显著减少,控制参数优化依然有效。
本文以SG转速为DFIG-PSS输入信号,得到DFIG并网电力系统扰动后轨迹灵敏度的解析表达。为抑制SG功角振荡,取目标函数为SG功角差相对值二次方的积分,基于轨迹灵敏度提供的梯度信息,优化DFIG控制参数。考虑DFIG-PSS可能弱化RSC控制效果,协调优化两者控制参数。仿真结果表明:
1)所建立轨迹灵敏度解析表达误差较小,可准确量化控制参数对系统功角振荡的影响。
2)相比于仅优化DFIG-PSS参数,同时优化DFIG-PSS参数与RSC比例系数,在减缓DFIG振荡的同时,可增强系统阻尼,减小SG间功角差振幅。
3)RSC功率外环比例系数增大,电流内环比例系数减小,可有效调节DFIG输出功率,降低系统振荡风险。
实际电网运行中稳定控制的设备很多。从实际应用考虑,下一步可以研究SG与DFIG控制参数的协调优化。
附 录
附表1 2 MW双馈风电机组结构参数
App.Tab.1 Configurational parameters of 2MW DFIG
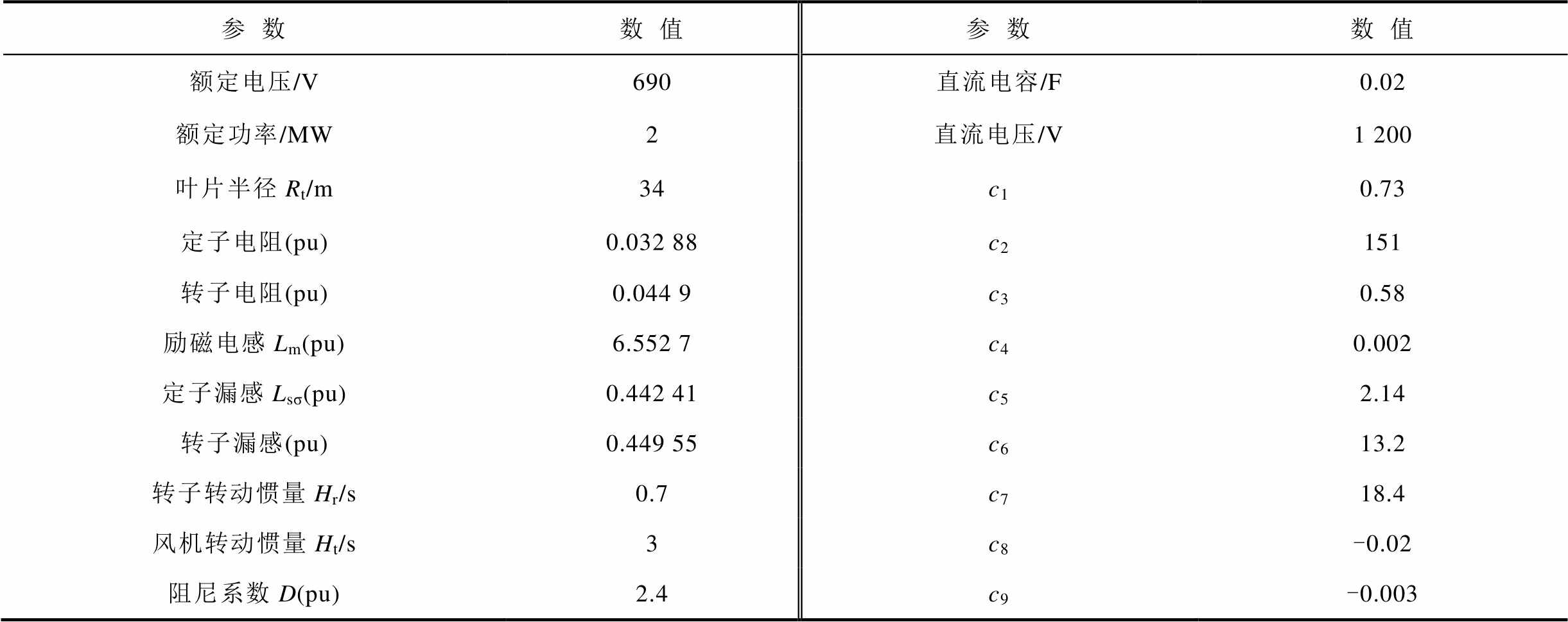
参数数值参数数值 额定电压/V690直流电容/F0.02 额定功率/MW2直流电压/V1 200 叶片半径Rt/m34c10.73 定子电阻(pu)0.032 88c2151 转子电阻(pu)0.044 9c30.58 励磁电感Lm(pu)6.552 7c40.002 定子漏感Lsσ(pu)0.442 41c52.14 转子漏感(pu)0.449 55c613.2 转子转动惯量Hr/s0.7c718.4 风机转动惯量Ht/s3c8-0.02 阻尼系数D(pu)2.4c9-0.003
附表2 DFIG PI控制参数
App.Tab.2 PI control parameters of the DFIG
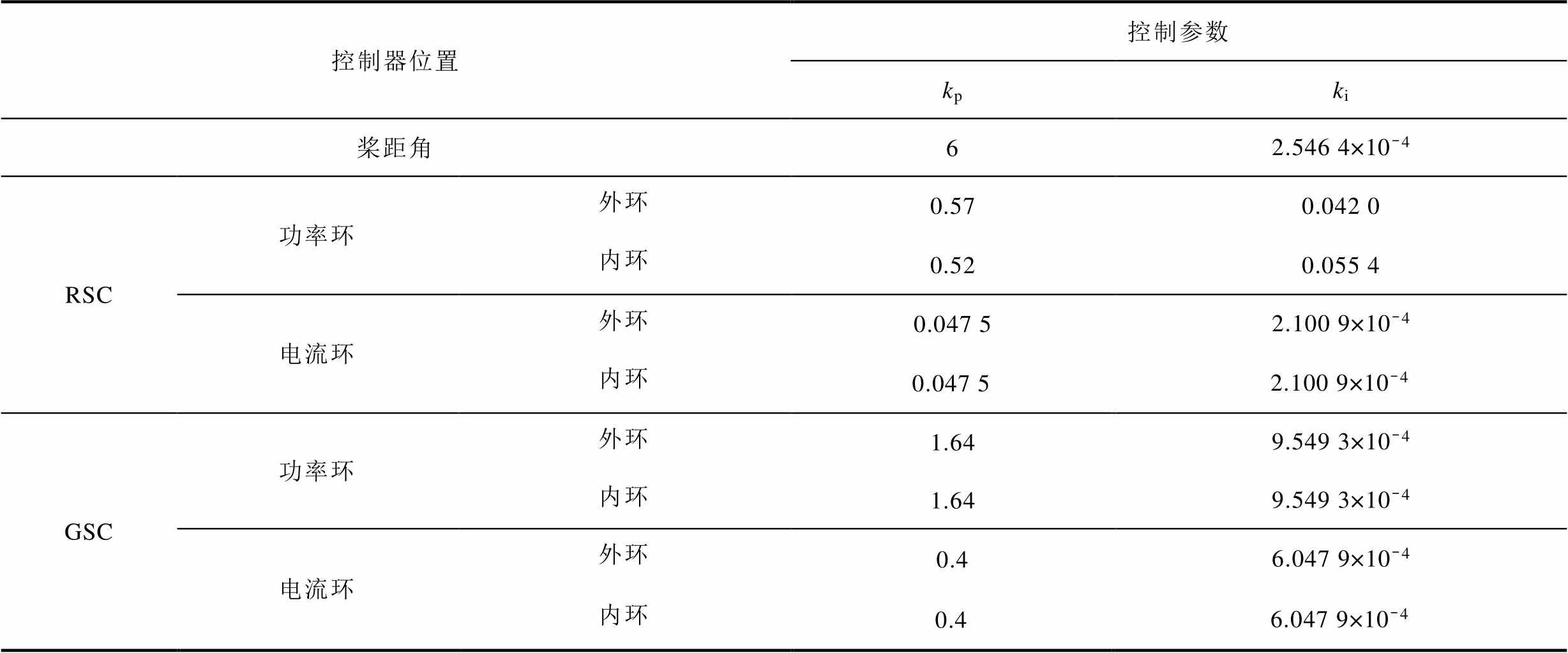
控制器位置控制参数 kpki 桨距角62.546 4×10-4 RSC功率环外环0.570.042 0 内环0.520.055 4 电流环外环0.047 52.100 9×10-4 内环0.047 52.100 9×10-4 GSC功率环外环1.649.549 3×10-4 内环1.649.549 3×10-4 电流环外环0.46.047 9×10-4 内环0.46.047 9×10-4
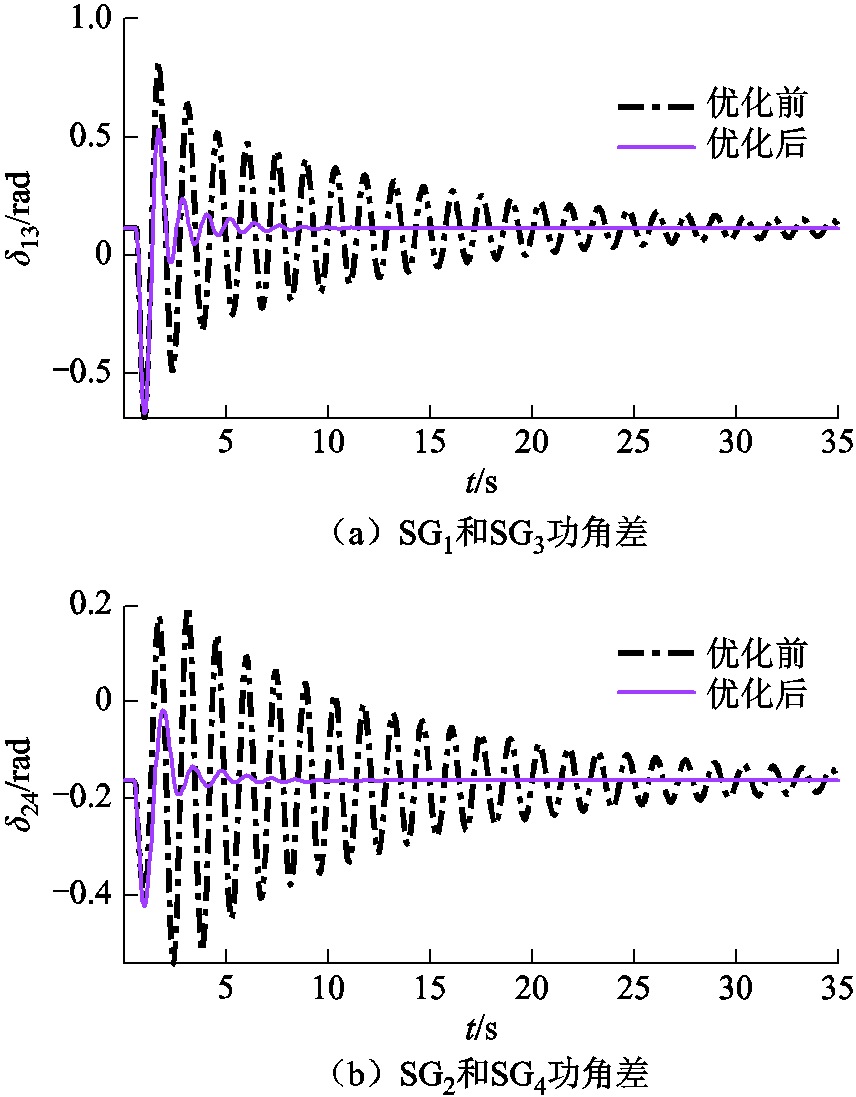
附图1 节点5三相短路后参数优化效果
App.Fig.1 Effect of parameter optimization after 3-phase fault at bus 5
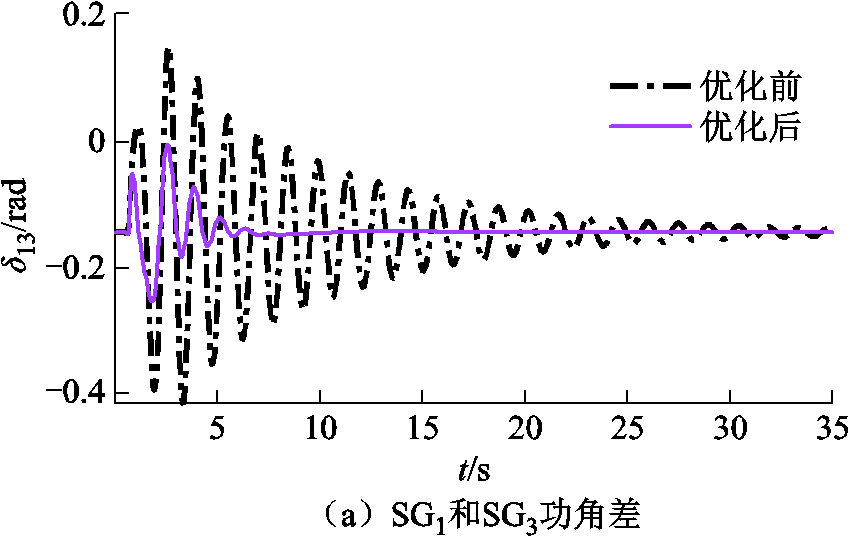
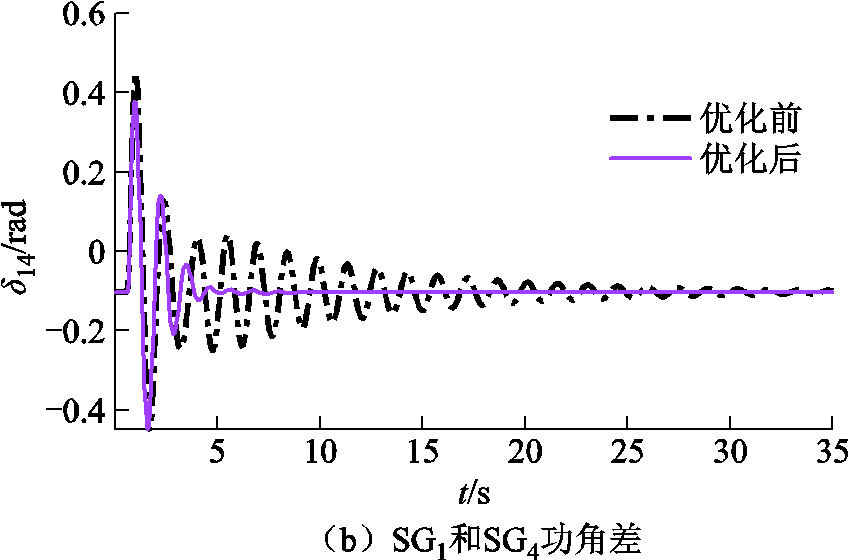
附图2 风速突变后参数优化效果
App.Fig.2 Effect of parameter optimization after sudden change of wind speed
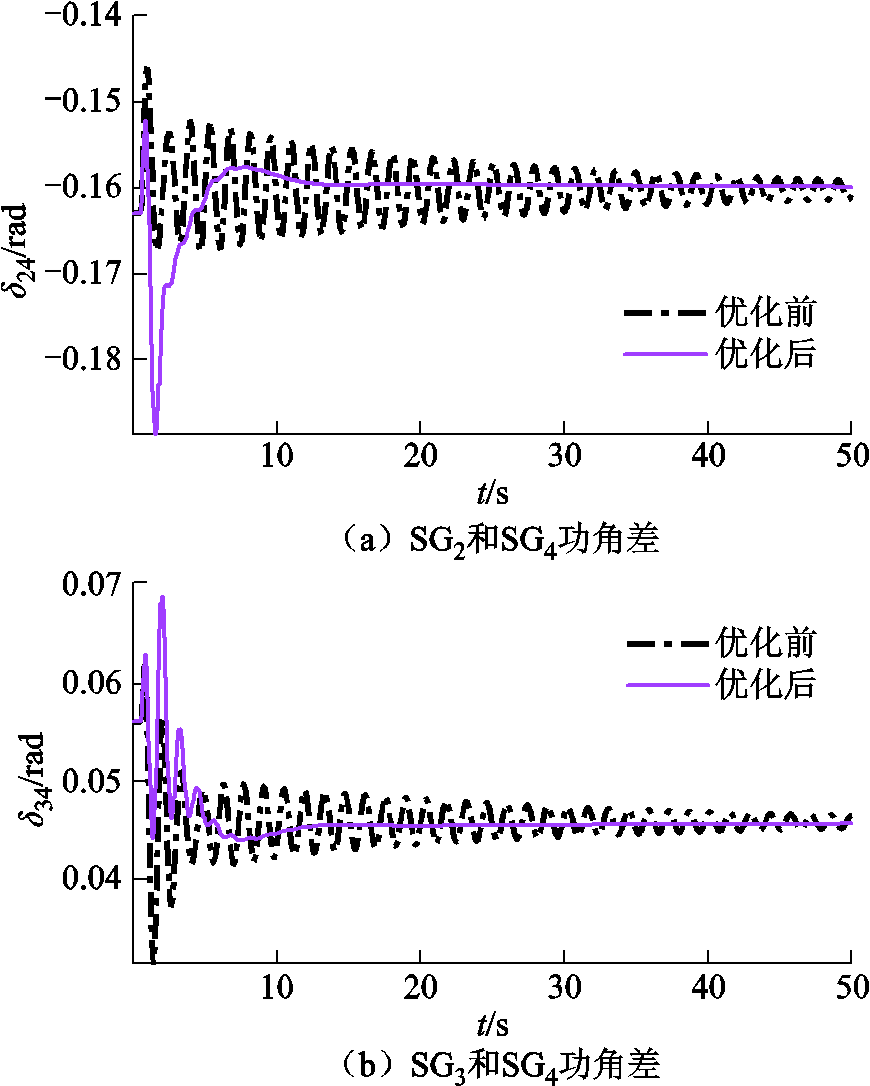
附图3 负荷突增后参数优化效果
App.Fig.3 Effect of parameter optimization after sudden change of load
参考文献
[1] Ma Jing, Shen Yaqi, Phadke A G. DFIG active damping control strategy based on remodeling of multiple energy branches[J]. IEEE Transactions on Power Electronics, 2020, 36(4): 4169-4186.
[2] Rosado L, Samanes J, Gubía E, et al. Robust active damping strategy for DFIG wind turbines[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14525-14538.
[3] Gao Chao, Liu Hui, Jiang Hao, et al. Research on the sub-synchronous oscillation in wind power connected to series compensated power system and its influencing factors[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(3): 334-340.
[4] 孙军, 蒋天龙, 王仰铭, 等. 不平衡电网下双馈感应发电机的虚拟同步机控制优化策略[J]. 电力系统自动化, 2020, 44(10): 135-144. Sun Jun, Jiang Tianlong, Wang Yangming, et al. Optimization strategy of virtual synchronous generator control for doubly-fed induction generator in unbalanced power grid[J]. Automation of Electric Power Systems, 2020, 44(10): 135-144.
[5] 刘俊磊, 曹娜, 钱峰, 等. 考虑双馈风电机组变流器控制参数的风电场内机组振荡分析[J]. 电力系统自动化, 2021, 45(10): 42-49. Liu Junlei, Cao Na, Qian Feng, et al. Analysis of unit oscillation in wind farm considering control parameters of converter for DFIG-based wind turbine[J]. Automation of Electric Power Systems, 2021, 45(10): 42-49.
[6] Du Wenjuan, Chen Xiao, Wang Haifeng. Impact of dynamic interactions introduced by the DFIGs on power system electromechanical oscillation modes[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4954-4967.
[7] 薛安成, 王清, 毕天姝. 双馈风机与同步机小扰动功角互作用机理分析[J]. 中国电机工程学报, 2016, 36(2): 417-425. Xue Anchen, Wang Qing, Bi Tianshu. Study on the mechanism of small signal dynamic interaction between doubly-fed induction generator and synchronous generator[J]. Proceedings of the CSEE, 2016, 36(2): 417-425.
[8] Morshed M J, Fekih A. A probabilistic robust coordinated approach to stabilize power oscillations in DFIG-based power systems[J]. IEEE Transactions on Industrial Informatics, 2019, 15(10): 5599-5612.
[9] Zhang Chen, Ke Deping, Sun Yuanzhang, et al. Coordinated supplementary damping control of DFIG and PSS tosuppress inter-area oscillations with optimally controlled plant dynamics[J]. IEEE Transactions on Sustainable Energy, 2018, 9(2): 780-791.
[10] 苏田宇, 杜文娟, 王海风. 多直驱永磁同步发电机并联风电场次同步阻尼控制器降阶设计方法[J].电工技术学报, 2019, 34(1): 116-127. Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for subsynchronous damping controller of multi-PMSGs parallel wind farm[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 116-127.
[11] 马燕峰, 霍亚欣, 李鑫, 等. 考虑时滞影响的双馈风电场广域附加阻尼控制器设计[J].电工技术学报, 2020, 35(1): 158-166. Ma Yanfeng, Huo Yaxin, Li Xin, et al. Design of wide area additional damping controller for doubly fed wind farms considering time delays[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 158-166.
[12] Bhukya J, Mahajan V. Optimization of controllers parameters for damping local area oscillation to enhance the stability of an interconnected system with wind farm[J]. International Journal of Electrical Power and Energy Systems, 2020, 119: 1-23.
[13] Pang Bo, Nian Heng. Collaborative control and allocation method of RSC and GSC for DFIG system to suppress high-frequency resonance and harmonics[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10509-10519.
[14] Li Shenghu, Zhang Hao, Yan Yunsong, et al. Parameter optimization to power oscillation damper(POD) considering its impact on the DFIG[J]. IEEE Transactions on Power Systems, DOI: 10.1109/ TPWRS.2021.3104816.
[15] Chen Aikang, Xie Da, Zhang Daming, et al. PI parameter tuning of converters for sub-synchronous interactions existing in grid-connected DFIG wind turbines[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6345-6355.
[16] 秦超, 曾沅, 苏寅生, 等. 基于安全域的大规模风电并网系统低频振荡稳定分析[J]. 电力自动化设备, 2017, 37(5): 100-106. Qin Chao, Zeng Yuan,su Yinsheng, et al. Low- frequency oscillatory stability analysis based on security region for power system with large-scale wind power[J]. Electric Power Automation Equipment, 2017, 37(5): 100-106.
[17] Bhukya J, Mahajan V. Optimization of damping controller for PSS and SSSC to improve stability of interconnected system with DFIG based wind farm[J]. International Journal of Electrical Power and Energy Systems, 2019, 108: 314-335.
[18] Tian Xinshou, Chi Yongning, Li Yan, et al. Coordinated damping optimization control of sub-synchronous oscillation for DFIG and SVG[J]. CSEE Journal of Power and Energy Systems, 2021, 7(1): 140-149.
[19] Prakash T, Singh V P, Mohantys R. A synchrophasor measurement based wide-area power system stabilizer design for inter-area oscillation damping considering variable time-delays[J]. International Journal of Electrical Power and Energy Systems, 2019, 105: 131-141.
[20] 王一珺, 杜文娟, 陈晨, 等. 基于改进复转矩系数法的风电场并网引发电力系统次同步振荡研究[J]. 电工技术学报, 2020, 35(15): 3258-3269. Wang Yijun, Du Wenjuan, Chen Chen, et al. Study on sub-synchronous oscillations of power systems caused by grid-connected wind farms based on the improved complex torque coefficients method[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3258-3269.
[21] 王一珺, 杜文娟, 王海风. 基于改进复转矩系数法的多风电场接入引发多机电力系统次同步振荡机理分析[J]. 中国电机工程学报, 2021, 41(7): 2383-2394. Wang Yijun, Du Wenjuan, Wang Haifeng. Analysis of subsynchronous oscillation in multi-machine power system caused by the integration of multiple wind farms based on improved complex torque coefficient method[J]. Proceedings of the CSEE, 2021, 41(7): 2383-2394.
[22] Yao Jun, Wang Xuewei, Li Jiawei, et al. Sub-synchronous resonance damping control for series-compensated DFIG-based wind farm with improved particle swarm optimization algorithm[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 849-859.
[23] 李佩杰, 黄淑晨, 李滨, 等. 基于梯度采样序列二次规划方法的PSS参数协调优化[J]. 中国电机工程学报, 2021, 41(8): 2734-2743. Li Peijie, Huang Shuchen, Li Bin, et al. Simultaneous coordination and optimization for the parameters of PSS based on sequential quadratic programming with gradient sampling[J]. Proceedings of the CSEE, 2021, 41(8): 2734-2743.
[24] 李生虎, 张浩. 风电系统振荡模式对DFIG-PSS传递函数的灵敏度分析[J]. 电力系统保护与控制, 2020, 48(16): 11-17. Lishenghu, Zhang Hao. Sensitivity analysis of the oscillation modes to the transfer function of DFIG- PSS in a wind power system[J]. Power System Protection and Control, 2020, 48(16): 11-17.
[25] 张国洲, 易建波, 滕予非, 等. 多运行方式下多机 PSS 的协调优化方法[J]. 电网技术, 2018, 42(9): 2797-2805. Zhang Guozhou, Yi Jianbo, Teng Yufei, et al. Coordinated optimization of multi-machine power system stabilizers under multiple operating conditions[J]. Power System Technology, 2018, 42(9): 2797-2805.
[26] Yuan Heling, Xu Yan. Preventive-corrective coordinated transient stability dispatch of power systems with uncertain wind power[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3616-3626.
[27] Wieler P L C, Kuiava R, Souza W. Transient stability constrained optimal power flow based on trajectory sensitivity for power dispatch of distributed synchronous generators[J]. IEEE Latin America Transactions, 2020, 18(7): 1247-1254.
[28] Wang Tong, Gao Mingyang, Mi Dengkai, et al. Dynamic equivalent method of PMSG-based wind farm for power system stability analysis[J]. IET Generation, Transmission & Distribution, 2020, 14(17): 3488-3497.
[29] 张剑, 何怡刚. 基于轨迹灵敏度分析的永磁直驱风电场等值模型参数辨识[J]. 电工技术学报, 2020, 35(15): 3304-3313. Zhang Jian, He Yigang. Parameters identification of equivalent model of permanent magnet synchronous generator wind farm based on analysis of trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3304-3313.
[30] 刘征帆, 安军, 蒋振国, 等. 基于轨迹灵敏度频域特征提取的电力系统仿真误差主导参数识别[J]. 电力自动化设备, 2021, 41(3): 144-150. Liu Zhengfan, An Jun, Jiang Zhenguo, et al. Dominant parameter identification of power system simulation error based on frequency domain characteristic extraction of trajectory sensitivity[J]. Electric Power Automation Equipment, 2021, 41(3): 144-150.
[31] 邹建林, 安军, 穆钢, 等. 基于轨迹灵敏度的电力系统暂态稳定性定量评估[J]. 电网技术, 2013, 38(3): 694-699. Zou Jianlin, An Jun, Mu Gang, et al. Quantitative assessment of the transient stability of power system based on trajectory sensitivity[J]. Power System Technology, 2013, 38(3): 694-699.
[32] 王长江, 姜涛, 刘福锁, 等. 基于轨迹灵敏度的暂态过电压两阶段优化控制[J]. 电工技术学报, 2021, 36(9): 1888-1913. Wang Changjiang, Jiang Tao, Liu Fusuo, et al. Two-stage optimization control of transient overvoltage based on trajectory sensitivity[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1888-1913.
[33] 李生虎, 李卓鹏, 张浩, 等. 基于风电并网电力系统拓展轨迹灵敏度的DFIG控制参数优化[J]. 太阳能学报, 2021, 42(6): 369-376. Li Shenghu, Li Zhuopeng, Zhang Hao, et al. Control parameter optimization to DFIG-integrated power system based on extended trajectory sensitivity[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 369-376.
[34] Karunanayake C, Ravishankar J, Dong Zhaoyang. Nonlinears SR damping controller for DFIG based wind generators interfaced to series compensated transmission systems[J]. IEEE Transactions on Power Systems, 2020, 35(2): 1156-1165.
[35] Edrah M, Zhao Xiaowei, Hung W, et al. Effects of POD control on a DFIG wind turbine structural system[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 765-774.
[36] 陈良双, 吴思奇, 喻文倩, 等. 基于转子侧附加阻尼控制的双馈风机并网次/超同步振荡抑制方法[J]. 电力系统保护与控制, 2021, 49(15): 47-58. Chen Liangshuang, Wu Siqi, Yu Wenqian, et al. A sub/super-synchronous oscillation suppression method for a DFIG-connected grid based on additional damping control on the roto rside converter[J]. Power System Protection and Control, 2021, 49(15): 47-58.
[37] 戚军, 吴仟, 陈康, 等. 考虑时变时滞影响的大型双馈风力发电系统附加阻尼控制[J]. 电网技术, 2019, 43(12): 4440-4450. Qi Jun, Wu Qian, Chen Kang, et al. Additional damping control of largescale DFIG-based wind power generation system considering time-varying delays[J]. Power System Technology, 2019, 43(12): 4440-4450.
[38] Gurung N, Bhattarai R, Kamalasadan S. Optimal oscillation damping controller design for large-scale wind integrated power grid[J]. IEEE Transactions on Industry Applications, 2020, 56(4): 4225-4235.
[39] 姚骏, 孙鹏, 刘瑞阔, 等. 弱电网不对称故障期间双馈风电系统动态稳定性分析[J]. 中国电机工程学报, 2021, 41(21): 7225-7236.Yao Jun, Sun Peng, Liu Ruikuo, et al. Dynamic stability analysis of DFIG-based wind power system during asymmetric faults of weak grid[J]. Proceedings of the CSEE, 2021, 41(21): 7225-7236.
[40] 章艳, 张萌, 高晗. 基于阻耗系数的双馈风机系统阻尼控制研究[J]. 电网技术, 2021, 45(7): 2781-2790. Zhang Yan, Zhang Meng, Gao Han. Damping control for grid connected DFIG system based on dissipated energy coefficient[J]. Power System Technology, 2021, 45(7): 2781-2790.
Abstract With the increasing wind turbine generators integrated partially or completely through the converters, the damping capability of the power system is decreased, which will intensify the dynamic interaction among the doubly-fed induction generators (DFIGs) and the synchronous generators (SGs), and yield the power angle oscillation among the SGs. The angular oscillation is usually suppressed by the power system stabilizer (PSS) installed at the SGs. It may also be suppressed by the PSS at the DFIGs, i.e. DFIG-PSS, or by adjusting the control parameters of the DFIGs. The DFIG-PSS is often installed at the outer loop of the rotor-side converter (RSC). The control effect of the RSC may be weakened by the DFIG-PSS. Hence the control parameters of the DFIG-PSS and the RSC are to be optimized together. The parameter optimization based on the eigenvalue analysis is for small disturbances. It does not consider the system nonlinearity and large disturbance, hence is incompetent to suppress the oscillation which is usually quantified by a period of dynamic process.
In this paper, a coordinated optimization model to the parameters of the DFIG-PSS and the RSC based on the trajectory sensitivity is newly proposed. The DFIG-PSS is designed to suppress the power angle oscillation by controlling the DFIGs to absorb or release the energy. The dynamic model of power system with the control strategy of the DFIG including the DFIG-PSS is derived. The intermediate variables are introduced to the differential equations to decouple the trajectory sensitivities. The Jacobian matrices of the state variables and the algebraic variables are distinguished to derive the analytical expression of the trajectory sensitivities, which is computationally efficient than deriving the trajectory sensitivities from the parameter perturbation method. Then the gradient information of the objective function with respect to the control parameters is obtained. Based on the location of the DFIG-PSS and the relation of the PI parameters, the control parameters to be optimized are decided. With the gradients, the interior-point method is applied to optimize the parameters of both the DFIG-PSS and the RSC.
Based on above algorithm, the Matlab program for the dynamic control and the angular oscillation of the power system with the DFIGs is written by the authors. The simulation results on the 4-SG 2-area test system are given to verify the control effect. It is shown that the relation between the control parameters and the power angle oscillation is quantified by the gradient derived from the analytical expression of the trajectory sensitivity with desirable accuracy. After the optimization, the gain of the outer active power loop of the RSC increases, and the gain of the inner current loop decreases, which help to regulate the output of the DFIG and reduce the risk of the angular oscillation. It is also found that the parameter optimization to both the DFIG-PSS and the RSC has better effect on reducing the amplitude of the power angle difference and accelerating the convergence than optimizing the DFIG-PSS only.
The proposed algorithm is beneficial to the wind turbine generators, e.g. the DFIGs, functioning similarly as the SGs and participating into the system stability control. With more and more SGs displaced by the wind turbine generators, the proposed algorithm may be applied to improve the angular and oscillational stability of the power systems.
keywords:Power angle oscillation, parameter optimization, trajectory sensitivity, doubly-fed induction generator, power system stabilizer
国家自然科学基金资助项目(51877061)。
收稿日期 2021-10-21
改稿日期 2022-01-21
DOI:10.19595/j.cnki.1000-6753.tces.211662
中图分类号:TM712; TM614
李生虎 男,1974年生,教授,博士生导师,研究方向风电并网电力系统分析与控制、电力系统可靠性与概率仿真、高压直流和柔性交流输电技术。E-mail:shenghuli@hfut.edu.cn(通信作者)
张亚海 男,1994年生,硕士研究生,研究方向风电并网电力系统分析与控制。E-mail:2019110363@mail.hfut.edu.cn
(编辑 赫蕾)