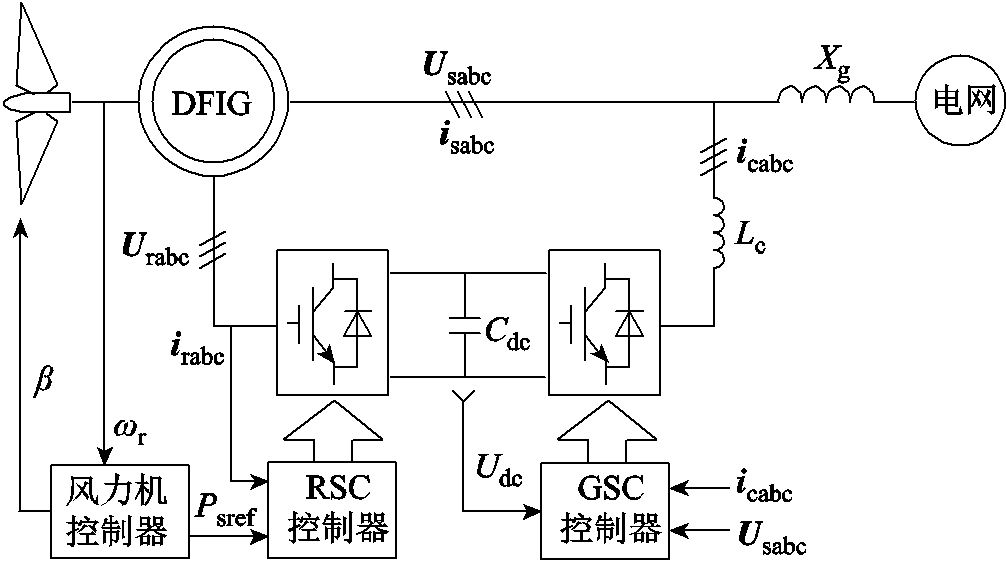
图1 电压源型双馈风电机组并网结构
Fig.1 Structure diagram of voltage-sourced DFIG integrated system
摘要 随着我国新能源装机规模日益扩大，电网对并网风电机组的性能要求逐渐从被动跟随电网转变为主动支撑电网，由此使得基于虚拟同步控制的电压源型风电机组具有广阔的应用前景。但是，目前对于此类新型风电机组的宽频动态特性的研究尚有不足，鉴于此，该文通过建立电压源型双馈机组的类Phillips-Heffron模型，从电气阻尼的角度研究其由虚拟同步控制环节主导的低频模态的振荡特性及失稳机理，并探究不同控制参数及电网条件对电压源型双馈机组电气阻尼特性的影响。研究结果表明，当系统其他动态部分引入的电气负阻尼大于虚拟同步控制环节固有的正阻尼时，电压源型双馈机组将面临低频振荡失稳的风险。最后讨论了可提高电压源型双馈机组低频段电气阻尼的应对措施，设计了类电力系统静态稳定器（PSS），可有效抑制机组低频振荡问题。该研究结果可指导实际工程中电压源型风电机组的控制器设计方案及参数整定优化。
关键词：虚拟同步控制 电压源型双馈机组 电气阻尼 低频振荡 振荡抑制
随着国家“双碳”战略目标的提出，能源电力领域正做出积极响应，体现在大力推进可再生能源替代化石能源消耗，加快构建以新能源为主体的新型电力系统[1-2]。截至2020年，我国新能源发电装机规模占比已达到28.8%，其中西北电网新能源最大出力占总发电出力高达44.4%，可见，以风电、光伏为代表的新能源发电在我国的定位正逐渐从辅助电源转变为主力电源[3]。然而，随着新能源接入比例增加，大量同步机组被替代，导致系统逐渐弱化（低惯量、低短路比），其后果就是系统的调频/调压能力被削弱，同时，“双高”电力系统的宽频带振荡问题也越发严重[4-6]。
针对以上问题，国内外学者广泛研究了新能源发电装备的电网友好型控制技术，旨在提高新能源对电网的主动支撑能力[7-10]。以风电为例，根据所表现出的外特性，电网友好型机组主要可分为电流源型和电压源型两大类[11-12]。其中电流源型机组不改变传统风电机组的基本控制方式，通过检测电网频率/电压变化，在功率外环中附加控制支路以调整有功/无功指令，从而实现对电力系统的频率/电压动态支撑，此类风电机组对电网可等效认为是P-Q节点[12-13]。由于它本质上仍为矢量控制模式，通过锁相环并网，因此与传统风电机组类似，对弱阻尼电网的适应性差，次/超同步振荡问题突出，且不具备独立组网的能力[13]。因此，此类机组必然无法适应未来新能源占比进一步提高，甚至达到100%电力电子化的应用场景。文献[13]指出基于频率/电压检测反馈的逆变电源在引入惯量和调频主动支撑功能时，虽然不会出现新的振荡模态，但会削弱原有振荡模态的阻尼，在弱阻尼电网中易发生振荡失稳；文献[14]研究了低短路比条件下，附加惯量支撑和一次调频控制环节对双馈风电锁相环主导次同步振荡模态的影响，指出频率检测延时会降低系统的稳定性。
电压源型风电机组直接控制其输出电压的幅值和相角，使机组从P-Q模式转变为V-θ模式，从而实现对电网频率和电压的主动支撑[15-16]。与电流源型机组相比，它不需要锁相环即可与电网自同步，具备主动“建立电网”的能力，在未来以新能源为主体的新型电力系统中将具有广阔的应用前景和价值[17]。与此同时，对电压源型风电机组并网稳定性的研究也显得尤为重要。文献[12]基于特征值分析，重点研究了电压源和电流源控制模式下变流器并网系统的振荡模态差异性，以及不同控制参数对模态稳定性的影响趋势；文献[18]从序阻抗的角度对比了电压源型双馈机组（Double Fed Induction Generator, DFIG）与传统双馈机组在全频段内稳定性的区别，指出电压源型双馈机组具有更宽的电流环参数适配性；文献[19]研究了电压源型双馈风电场经串补并网场景下的次同步振荡问题及主要参数对振荡的影响情况。总的来说，现有研究文献对电压源型风电机组的宽频动态特性已有较深入的认识，但仍存在一些不足：一是对风电机组振荡稳定性的研究多集中于次/超同步频段及中/高频段，缺少对虚拟同步控制环节引入的低频模态稳定性的单独分析[12,18-19]；二是研究方法多采用特征值分析或阻抗分析的方式，需要对机组全部动态环节建立详细模型，并且分析结果更偏向于风电并网系统的全局（全频段）稳定性，而难以对失稳模态机理进行解释[20-21]。
在此背景下，本文以虚拟同步控制方式下的电压源型双馈风电机组为研究对象，通过建立其类Phillips-Heffron动力学模型，重点研究虚拟同步控制环节主导的低频模态稳定性；基于该模型，可在降低建模阶数的同时借鉴传统电力系统低频振荡分析思路，从阻尼的角度揭示电压源型双馈风电机组低频失稳机理及影响因素，并提出有效提高系统电气阻尼的低频振荡抑制方法；相关分析结果均通过电磁暂态仿真进行了验证。
电压源型双馈风电机组与传统双馈风电机组相比，主要有两点不同：①转子侧变流器控制逻辑由基于定子电压/磁链定向的电流矢量控制变为基于内电势矢量调节的幅值-相位控制；②风轮机主控模块中的最大功率跟踪控制曲线变为超速-减载（一般为10%）曲线，目的是保留一定的功率为电压源型风电机组的主动支撑提供相对稳定的能量来源。其中，转子侧变流器的控制对于双馈机组小信号稳定性的影响最为关键。
典型的电压源型双馈风电并网系统结构图和转子侧功率外环-电压电流双闭环控制框图分别如图1和图2所示。在功率环中，定子有功功率指令值来自风轮机主控制器算法，与常规矢量控制不同的是，该有功指令不再直接控制转子侧电流，而是与实际定子有功功率比较后，通过虚拟同步机转子运动方程，产生双馈机组的定子电压并网同步频率和相角[18]，该角度将代替传统双馈风电中锁相环输出角度的作用，用于定子电压电流的坐标变换中；此外，再通过无功-电压调差控制生成定子电压幅值指令，该电压指令值将作为电压环的输入电压参考值，与实际定子电压经PI控制器后得到转子电流的参考值，该电流参考值在电流环中进一步与实际转子电流经PI控制器后输出转子电压的指令值，用于控制转子侧变流器的开断。在该控制过程中，功率环输出的定子电压幅值和相角共同构成了电压源型双馈机组的内电势指令。此外，图2中定子有功功率参考值除接受来自主控的指令外，还附加了频率-有功调差分量，可用于模拟风电机组对系统频率变化时的一次调频作用，这与虚拟同步控制中的惯量支撑和无功-电压调差控制中的电压支撑共同构成了电压源型双馈风电机组的电网友好型主动支撑技术。
图1 电压源型双馈风电机组并网结构
Fig.1 Structure diagram of voltage-sourced DFIG integrated system
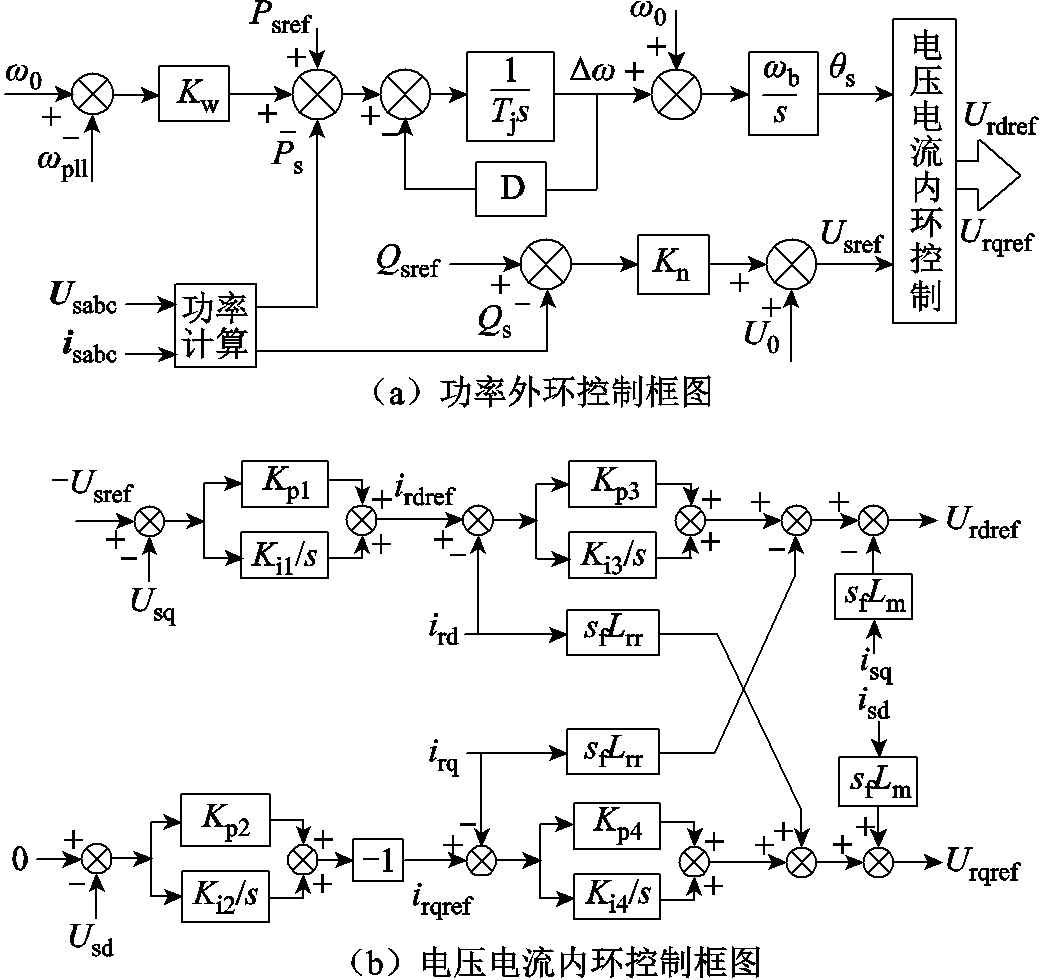
图2 电压源型双馈机组转子侧变流器控制框图
Fig.2 Rotor-side control diagram of voltage-sourced DFIG
图1和图2中各变量符号含义如下：Psref、Qsref分别为双馈机组定子有功、无功功率参考值；Ps、Qs分别为定子有功、无功的实际值；Usabc、isabc为定子电压电流信号；Urabc、irabc为转子电压电流信号；电压电流符号下标中abc变为dq后表示相关变量的dq轴分量值；ω0为额定频率标幺值，ωpll为并网点频率测量值；Usref、θs为定子电压幅值和相角指令值；Kw、Kn分别为有功和无功调差系数；Tj为虚拟惯性时间常数，D为虚拟阻尼系数；Kp1～Kp4、Ki1～Ki4分别为电压电流双闭环的PI控制参数；Xg为电网等效电抗；Lm、Lrr为异步电机电抗参数，sf为电机转差率。以上各变量均为标幺值。
电压源型双馈机组其他部分如网侧变流器控制、风力机控制等与传统双馈机组相同，此处不再赘述。已有文献指出，采用虚拟同步控制技术的风电机组或逆变电源的宽频动态特性与采用矢量控制时有较大的差异，当参数设置不当时，可能导致风电机组或逆变电源振荡失稳[12,18]。本文后续部分将针对图1中虚拟同步控制环节引入的低频振荡模态开展研究，以借鉴传统电力系统低频振荡分析思路，从阻尼的角度揭示电压源型双馈风电机组低频失稳机理及影响因素。
一般来说，在分析电压源型双馈机组虚拟同步控制环节主导的低频模态稳定性时，仅需对风电并网系统中的慢动态环节进行详细建模（如风力机控制和电压环控制），而忽略其快动态过程（如电流环控制）。此外，考虑到双馈风电机组的动态特性主要受机侧变流器影响，而网侧变流器影响较弱，本文在建模分析时假设直流母线电容足够大能维持直流电压恒定，则网侧变流器对扰动的响应可忽略[18]。
图1中，频率-有功调差环节和虚拟同步控制环节对应的二阶数学模型为
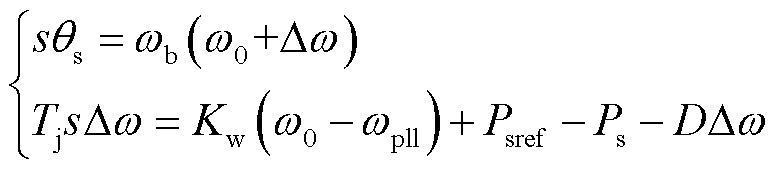（1）
式中，s为微分算子；ωb为角频率基准值；Δω为功率控制环中间变量。对式（1）进行线性化处理并消去式中Δω，即可得到该环节对应的二阶微分动态方程为
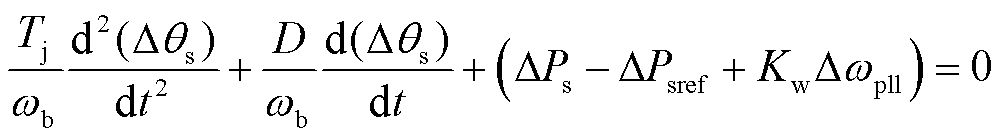（2）
为了定量分析该二阶系统的动态响应特性，首先需要建立式中ΔPs、ΔPsref、Δωpll等与自变量Δθs之间的关系。
1）ΔPs与Δθs关系
首先，异步电机定子输出功率表达式为
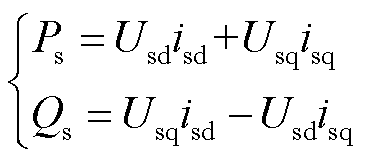（3）
式中，定子电流的方向为机端节点流向电机内部。
进一步忽略异步电机的定子电压方程中磁链动态过程，仅考虑准稳态部分，可表示为
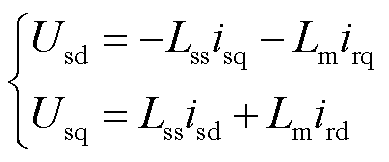（4）
式中，Lss为定子等效两相绕组自感；Lm为定转子绕组间互感。
根据本小节开始部分的假设条件，在忽略电流环的快速动态过程时，认为电压环输出的转子电流指令值即为实际转子电流值，即式（4）中转子电流ird、irq可表示为
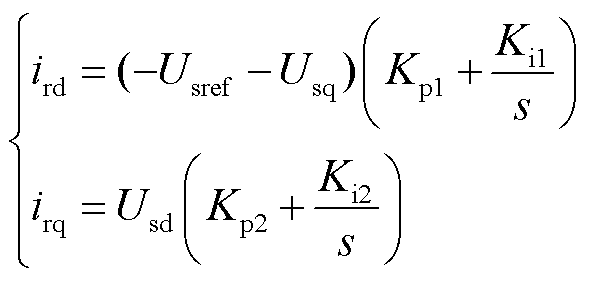（5）
进一步，式（5）中定子电压指令值可根据图1中无功-电压调差控制环节得到
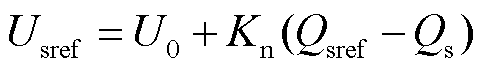（6）
式中，U0为定子额定电压标幺值，一般取1。
此外，由双馈风电机组的运行特性可知，在稳态情况下，双馈机组转子侧通过背靠背变流器向电网馈入的有功功率Pr为
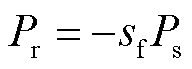（7）
因此，在不考虑网侧变流器的扰动响应时，可认为双馈机组整体向电网输出的有功功率Pg为
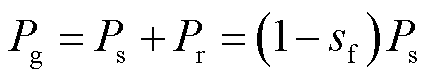（8）
式（8）表现在电流量上，即线路电流与电机定子电流间的关系为
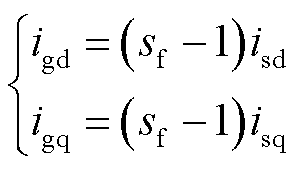（9）
式中，igd、igq分别为线路上电流的d、q轴分量。
图1中，外部电网用内电抗为Xg的电源等效，该等效电抗对应的准稳态方程为
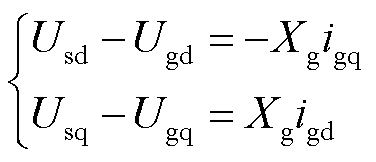（10）
式中，Ugd、Ugq分别为电网等效电压的d、q轴分量。
还需要指出的是，根据图2中电压环控制可知，电压源型双馈机组在稳态运行时，机端定子电压定向于虚拟同步控制确定的dq坐标系（dvsg、qvsg）的q轴反方向上，因此该dq坐标系与常规锁相环（定子电压定向于d轴）确定的dq坐标系（dpll、qpll）间相位相差90°。不同坐标系间的位置关系及电网电压矢量与机端电压矢量间的关系如图3所示。其中A为任意矢量，Us0、Ug0分别为机端和无穷大电源稳态电压，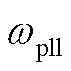
和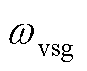
分别为锁相环和虚拟同步控制确定的角频率。
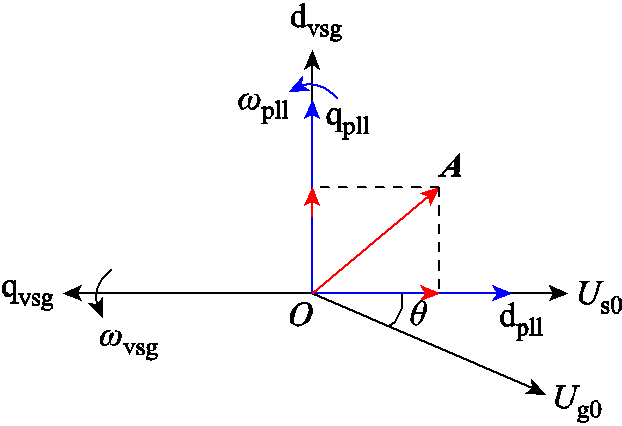
图3 不同参考坐标系间位置关系
Fig.3 Relationship between different reference coordinate
根据图3关系，可知电网电压Ug在虚拟同步控制确定的dq坐标系中的分量表达式为
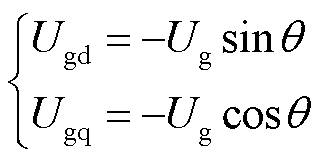（11）
式中，θ=θs-θE-π，θE为无穷大电网电压矢量角度。
将式（3）～式（11）进行线性化处理并作拉氏变换，然后联立即可得到定子有功功率的变化量ΔPs与定子电压相位变化量Δθs之间的关系为
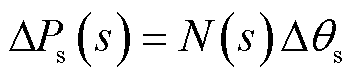（12）
式中，N(s)体现了转子侧变流器无功-电压调差控制、电压环控制以及电网侧参数等对虚拟同步控制环节低频阻尼特性的影响，其具体表达式见附录。
2）ΔPsref与Δθs关系
式（2）中定子有功指令值由风电机组主控下达，主控中主要包括超速减载运行曲线和转速控制两部分逻辑，其框图如图4所示。
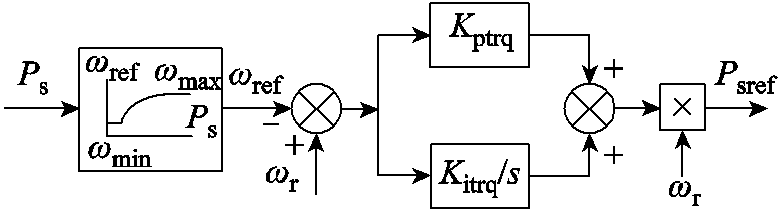
图4 双馈风电机组转速控制框图
Fig.4 Diagram of DFIG rotor speed control
根据图4，可得到定子有功指令值的表达式为
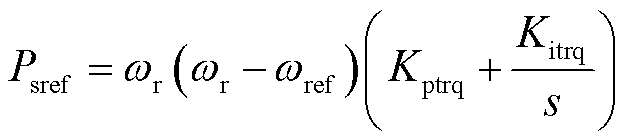（13）
式中，Kptrq、Kitrq为转速控制PI参数；ωr、ωref分别为转子转速实际值和指令值，本文中采用的超速减载拟合曲线分段表达式为
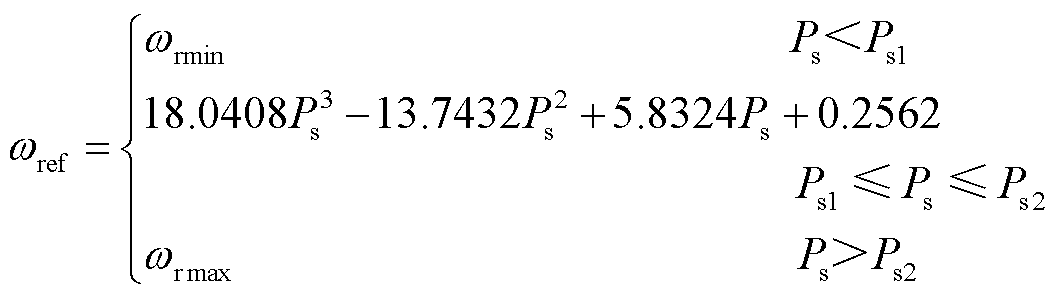（14）
式中，Ps1、Ps2取值分别为风电机组最大功率跟踪运行区的最小和最大定子有功功率的10%；ωrmin、ωrmax分别为风电机组的最小和最大运行转速。
风电机组转子按照刚体转子运动考虑，其对应方程为
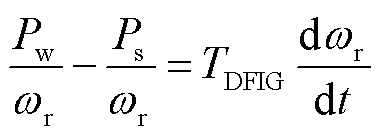（15）
式中，TDFIG为双馈机组轴系惯性时间常数；Pw为风轮机输出的机械功率，在确定机组型号和风速条件下，Pw仅与ωr一个变量相关。
联立式（13）～式（15），并将其线性化处理，即可得到定子有功指令值的变化量ΔPsref与实际定子有功功率变化量ΔPs之间的关系为
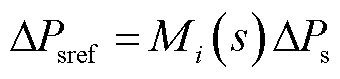（16）
式中，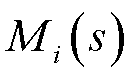
体现了主控中转速控制环节对虚拟同步控制环节低频阻尼特性的影响，其具体表达式见附录，其中i=1,2,3分别代表式（14）中三段不同的运行区间。
3）Δωpll与Δθs关系
实际风电机组中的频率检测实现方式多样，本文选择以锁相环输出的频率经过低通滤波后作为图1中的的实测频率反馈信号ωpll。锁相环测频控制框图如图5所示，图中KpPLL、KiPLL为锁相环PI参数，Tm为滤波时间常数，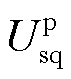
为锁相环dq坐标系下的定子电压q轴分量，θpll为锁相环输出角度。
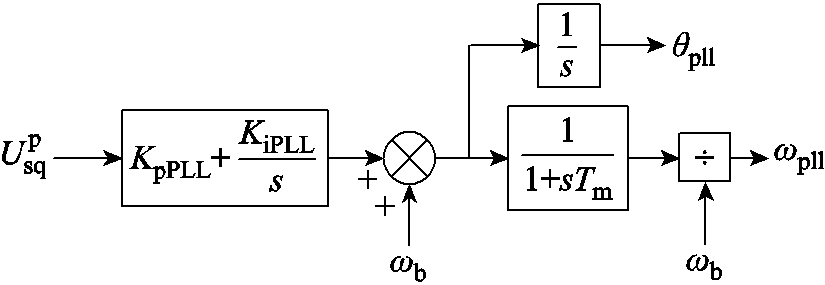
图5 锁相环频率测量框图
Fig.5 Diagram of frequency measurement using PLL
根据图5，可得到频率检测环节的方程为
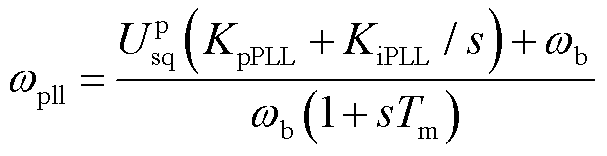（17）
锁相环输出角度对应为
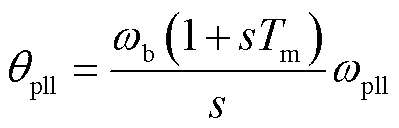（18）
此外，根据图3所示的锁相环dq坐标系与虚拟同步控制dq坐标系间的位置关系，可得到定子电压在两个坐标系中的转换关系式为
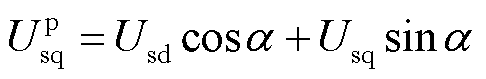（19）
式中，α=θpll-θs+π/2；有上标‘p’的变量表示锁相环坐标系中的变量，无上标的变量表示虚拟同步控制坐标系中的变量。稳态运行时，有
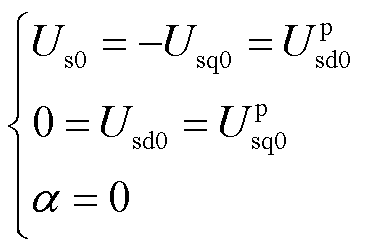（20）
联立式（17）～式（20），将其线性化处理，即可得到实际检测频率的变化量Δωpll与定子电压相位变化量Δθs之间的关系为
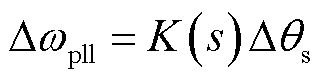（21）
式中，K(s)体现了锁相环测量电网频率的动态过程对虚拟同步控制环节低频阻尼特性的影响，其具体表达式见附录。
进一步将式（12）、式（16）、式（21）代入式（2）中，即可得到用于电压源型双馈机组低频动态分析的模型，如图6所示，可明显看到该模型与传统同步机低频振荡分析采用的Phillips-Heffron模型类似，其中包含了可能对电压源型双馈风电低频动态特性产生影响的所有慢动态环节。图中虚拟同步控制自身小扰动动态部分可类比同步机二阶转子运动方程动态，其中含有该环节的固有阻尼分量；而其他三个主要部分对虚拟同步控制环节的影响则可以类比同步机励磁控制系统对转子运动动态的影响，理论上如果能够分析出这三个部分给虚拟同步控制环节引入的附加阻尼大小，并将其与虚拟同步控制环节的固有正阻尼进行比较，则电压源型双馈机组的低频动态特性及其稳定机理即可被清晰地揭示。
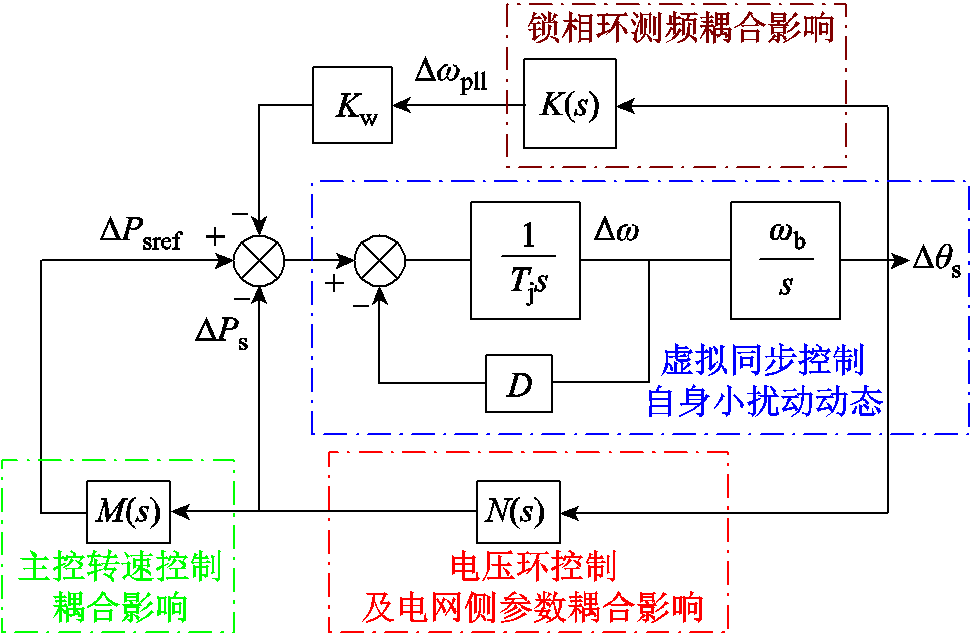
图6 电压源型双馈机组低频动态分析模型
Fig.6 The low frequency dynamic analysis model of voltage-sourced DFIG
根据图6中的模型，可得到虚拟同步控制环节完整的小扰动动态频域方程为
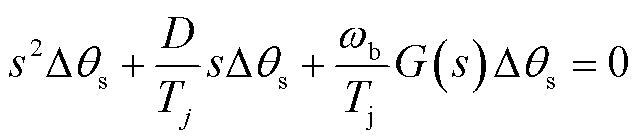（22）
式中，G(s)=N(s)-M(s)N(s)+KwK(s)，体现了图6中其他三个子部分对虚拟同步控制环节低频段阻尼的综合影响效果。式（22）对应的的特征方程为
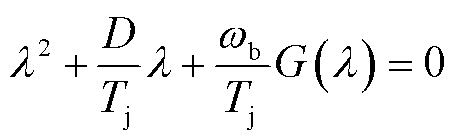（23）
理论上，该方程的解（特征根λ）即表征了虚拟同步控制环节主导的低频模态的稳定性。但是由2.1节中建模过程可知，G(λ)实际上是一个复杂多项式，因此，很难直接求解式（23）的根。
为此，本节提出一种基于特征方程中G(λ)的频率特性曲线辅助求解振荡模态频率和阻尼的方法。假设所关注的虚拟同步控制环节主导的低频振荡模式为λ=σ±jω，当该模态呈现弱阻尼特性时，可近似认为其实部接近虚轴位置，即有σ≈0，此时λ≈jω，将其代入G(λ)，则G(λ)可表示为
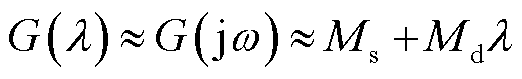（24）
式中，Ms=Real(G(λ))；Md=Imag(G(λ))/ω。
将式（24）代入式（23）中，可得到特征方程的近似表达式为
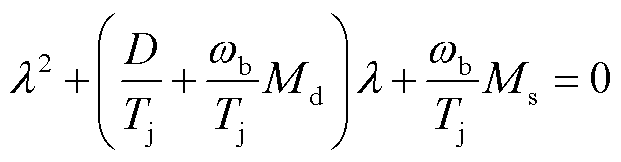（25）
当式（25）满足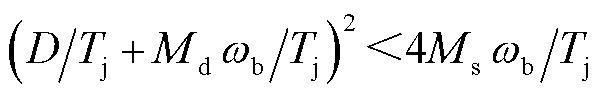
时，可得到方程特征根对应的实部（反应模态阻尼）和虚部（反应模态频率）的表达式分别为
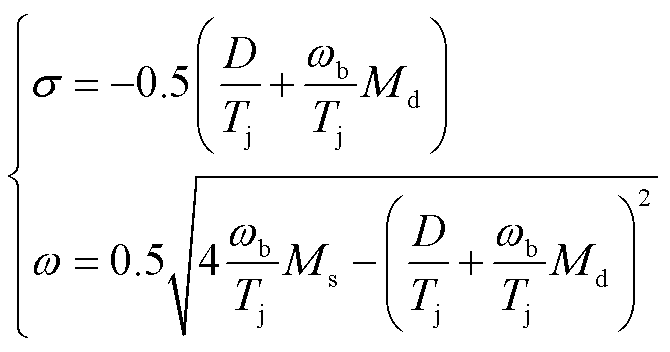（26）
由式（26）可看出，虚拟同步控制主导低频振荡模态的总阻尼可分为两部分：其中D/Tj项表示虚拟同步控制环节的固有阻尼分量，其值为正；而ωbMd/Tj项表示风电机组其他动态环节引入的附加阻尼分量，其值受模态振荡频率、风电运行状态、系统结构参数及控制参数等影响。如果计算出该附加阻尼分量值为负，并且绝对值比固有正阻尼分量更大，则风电机组整体在低频段将呈现负阻尼特性，面临振荡失稳的风险，此即为电压源型双馈风电小扰动低频稳定性的机理解释。
进一步地，由于式（26）中Ms和Md均是频率ω的函数，因此为了得到阻尼的定量值，必须首先计算出低频振荡的频率。根据式（26）的第二项可知，通过构建式（27）所示的函数F，然后利用数值计算软件得到其随频率ω的变化曲线，即可根据该频率曲线与0轴的交点估算出低频振荡的频率。
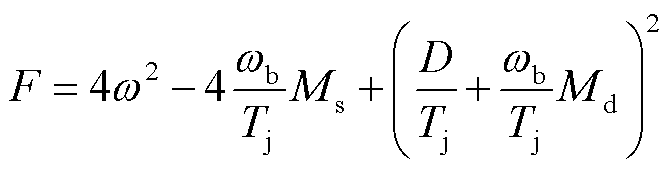（27）
同时也可以得到式（26）中阻尼σ随频率变化的曲线，然后在该曲线中找到与振荡频率对应的值，即可量化判断风电机组的低频模式总阻尼大小，从而评估电压源型双馈机组虚拟同步控制主导低频模态的失稳风险。
本节以图1所示电压源型双馈风电并网系统为例，采用第2节中提出的阻尼量化分析方法，研究电压源型双馈机组的低频稳定性，并重点探究电网条件和机组控制参数对低频段电气阻尼特性的影响。算例中双馈机组用一台100MW的等值机表示，其余主电路及控制系统参数见表1，表中两级升压变压器与无穷大电源内电抗之和即为图1中从电机机端看进电网的等效电抗，即Xg=XT1+XT2+Xs。
表1 主电路及控制系统参数
Tab.1 Parameters of circuit and control
参数数值参数数值 Kw100Tm0.01 Kn0.1Lm(pu)2.176 7 Tj6Ls(pu)0.142 5 D10Lr(pu)0.142 5 Kp1, Ki10.1, 13.42XT1(0.69kV/35kV)(pu)0.059 5 Kp2, Ki20.1, 13.42XT2(35kV/220kV)(pu)0.1 KpPLL, KiPLL50, 1 000Xs(pu)0.173 8
电网强度是影响电力电子装置并网稳定性的关键因素之一，主要通过式（10）与风电机组控制系统耦合在一起。调节等效电源内阻抗Xs的值，使得公共连接点短路比（SCR=1/Xs）在2～9之间变化，用于模拟不同强度的电网。保持表1中其他参数不变，根据式（26）和式（27）分别画出不同强度电网下用于估算振荡频率和阻尼的曲线，如图7所示。可以看到，随着电网强度增大，低频振荡频率略微减小，变化不大；但阻尼曲线明显向下移动，表示由交流电网与风电机组控制耦合作用引入的负阻尼分量变大。更具体地，当系统短路比由3增大为9时，对应振荡频率由1.46Hz降低为1.42Hz，而阻尼由2.73s-1减小为-0.39s-1，此时模态阻尼由正变负，表明电压源型双馈风电并网系统存在小扰动低频振荡失稳的风险。
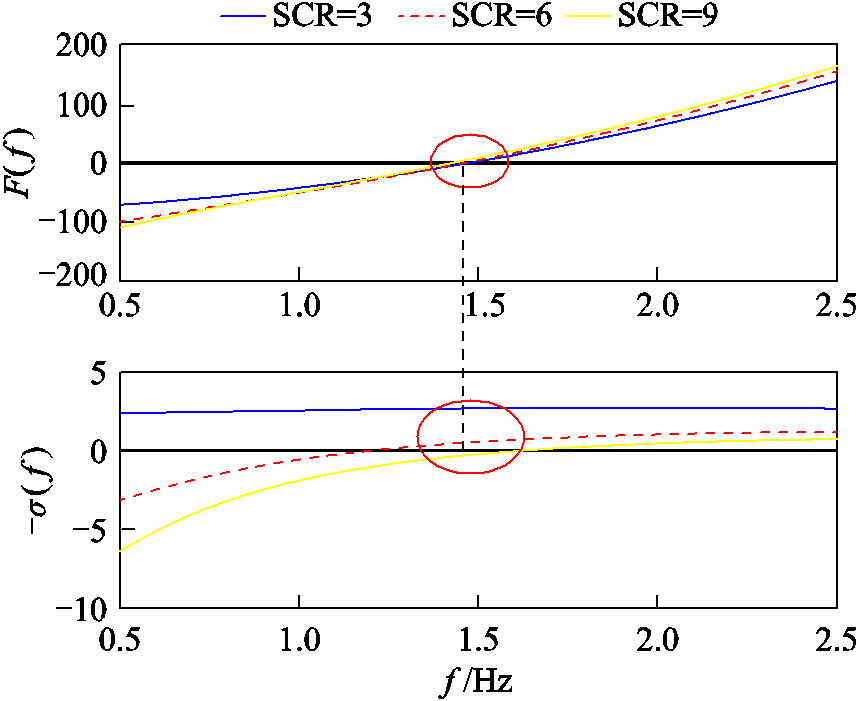
图7 低频振荡模态随电网强度变化分析
Fig.7 The analysis of low-frequency oscillation mode varying with grid strength
用于验证上述理论分析的电磁暂态仿真结果如图8所示。仿真中，保持其他参数不变且与阻尼分析中一致，仅在10s时将交流系统短路比由3调整为9。可见，当并网系统的短路比增大后，风电机组输出的有功功率波形迅速发散振荡，系统由稳定变为不稳定状态，与图7中低频模态阻尼由正变负的结论相同。该结果说明电压源型风电机组在低短路比条件下的动态特性优于在强电网下的性能，这与传统矢量控制方式下的电流源型机组恰好相反。基于此，可考虑在未来实际应用时，将同一风场内的机组按照合适的比例分别配置为电流源型和电压源型，以适应不同强度的电网条件。
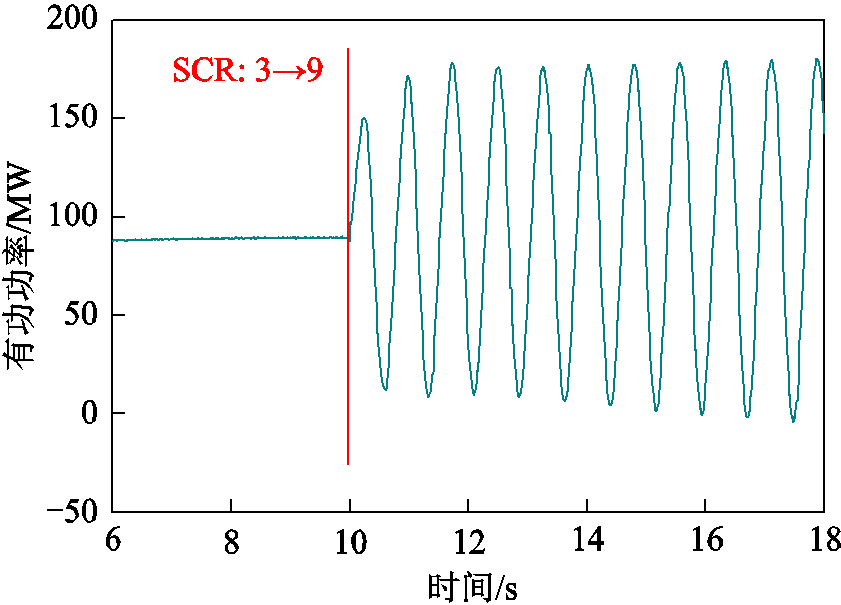
图8 短路比变化时风电机组有功功率响应
Fig.8 The active power response of wind turbine varying with SCR
3.2.1 虚拟惯性时间常数
在图2所示控制中，虚拟惯性时间常数Tj的大小反映了电压源型双馈机组对电网惯量支撑的能力，而根据式（26）可知，Tj越大，低频模态的阻尼越小。因此，在实际中进行参数设计时，需要合理整定Tj取值。
本节仅从小扰动稳定性的角度给出电压源型双馈风电低频模态频率和阻尼随Tj的变化趋势，结果如图9所示。可见，随着Tj增大，构造函数F的频率曲线向左移动，对应模态频率减小，与模态频率对应的阻尼也呈减小趋势。更具体地，当Tj由3增大为7时，对应振荡频率由2.03Hz降低为1.34Hz，而阻尼由1.24s-1减小为-0.33s-1，此时模态阻尼由正变负，表示系统存在小扰动低频振荡失稳的风险。
用于验证Tj对电压源型双馈风电并网稳定性影响的电磁暂态仿真结果如图10所示。可明显看到，随着Tj的增大，风电机组输出有功功率在系统遭受扰动后的振荡幅度更大，特别是在Tj增大至7时，有功功率波形已呈现发散振荡趋势，表明此参数下系统变为不稳定状态，与理论分析结果一致。该结果也说明在设计虚拟惯量参数时，必须协调考虑对机组的惯量需求和振荡约束。
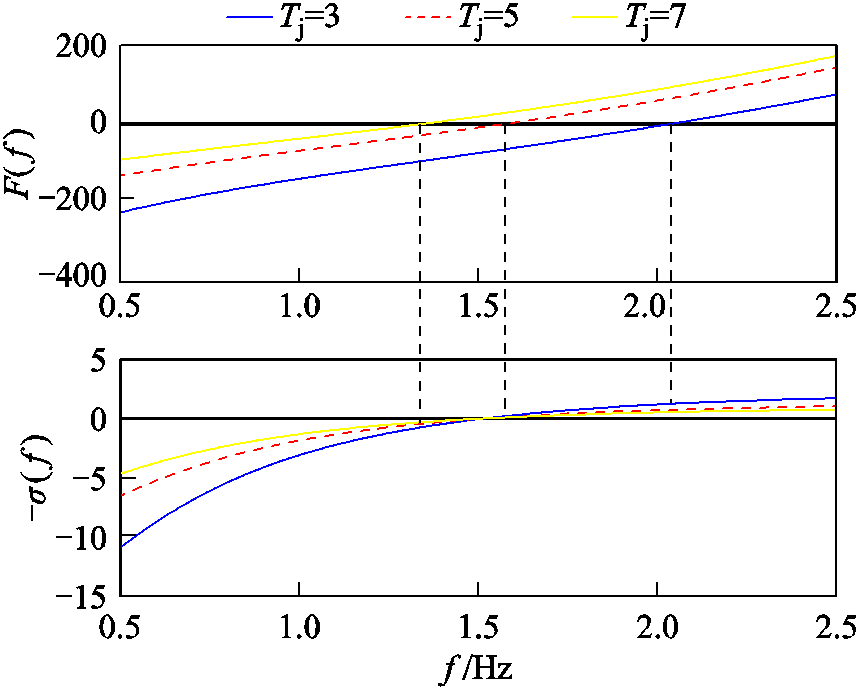
图9 低频振荡模态随虚拟惯性时间常数Tj变化分析
Fig.9 The analysis of low-frequency oscillation mode varying with virtual inertia Tj
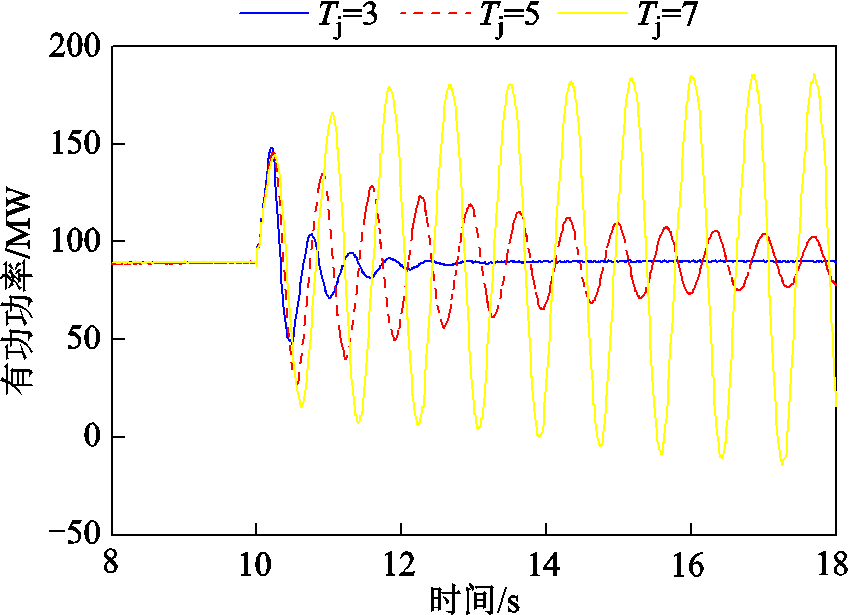
图10 Tj变化时风电机组小扰动有功功率响应
Fig.10 The active power response of wind turbine varying with Tj
3.2.2 虚拟阻尼系数
根据式（26）定性可知，增大虚拟阻尼系数D可有效提高低频振荡模态的阻尼，但是实际上在进行控制参数整定时也不能无限增大该值，因为过大的D可能导致风电机组响应速度的下降，影响机组其他方面的性能。同样仅从小扰动稳定性的角度给出D取值对低频模态的影响趋势，结果如图11所示。可见，随着D值减小，构造函数F的频率曲线保持不变，即对应模态频率基本不变，而与模态频率对应的阻尼曲线向下移动，表示负阻尼分量变大。具体地，当D由30减小为10时，对应振荡频率为1.44Hz不变，而阻尼由1.5s-1减小为-0.15s-1，此时模态阻尼由正变负，表示系统存在小扰动低频振荡失稳的风险。
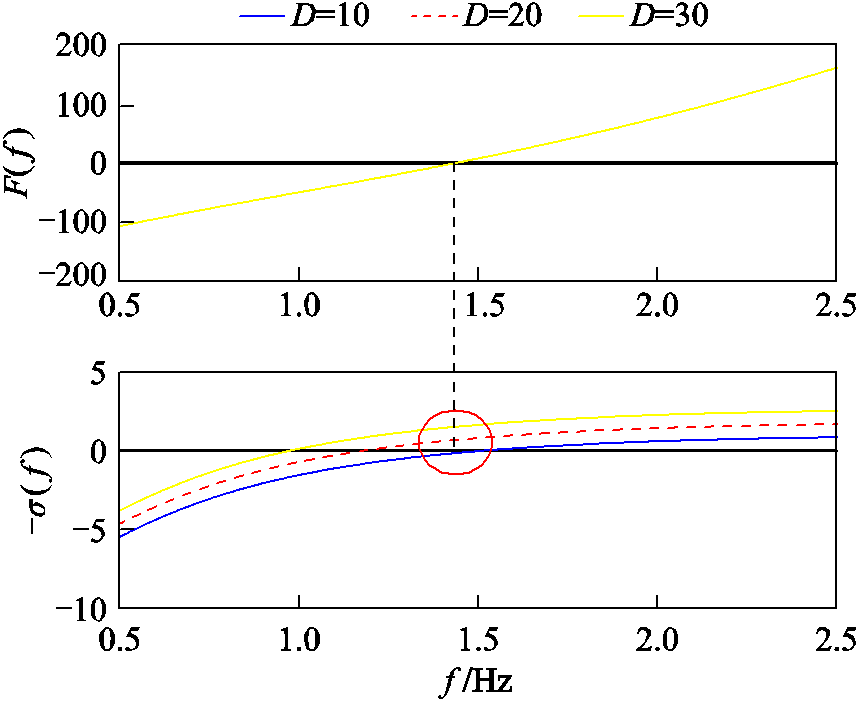
图11 低频振荡模态随虚拟阻尼系数D变化分析
Fig.11 The analysis of low-frequency oscillation mode varying with virtual damping coefficient D
D变化时风电机组小扰动有功功率响应如图12所示。可明显看到，随着D值增大，风电机组输出有功功率在系统遭受扰动后收敛速度更快，即机组的稳定性更高，与图11中阻尼增大的理论分析结果一致。该结果说明在实际应用中可通过适当增大电压源型机组的虚拟阻尼值以提升机组对电网的适应能力。
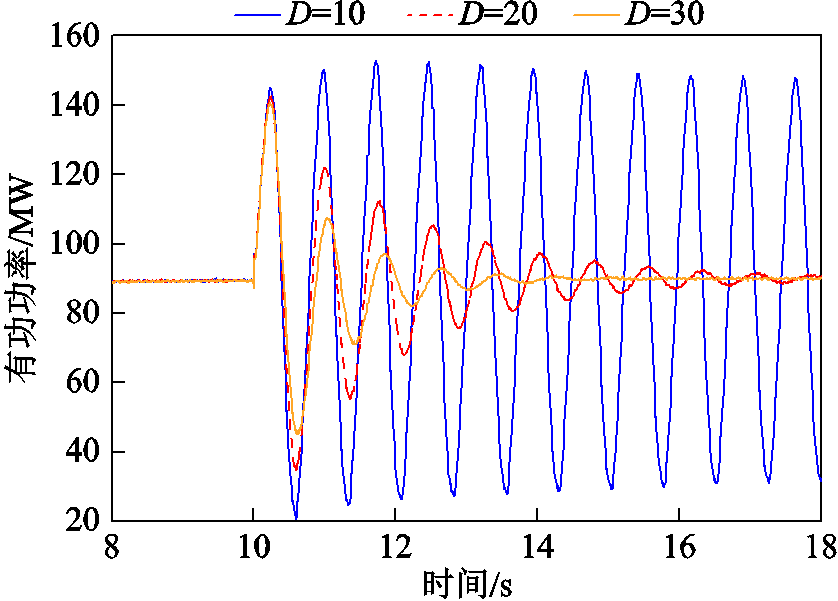
图12 D变化时风电机组小扰动有功功率响应
Fig.12 The active power response of wind turbine varying with D
3.2.3 频率-有功调差系数
图2中频率-有功调差系数Kw的大小反映了电压源型双馈机组对电网进行一次调频支撑的能力。从小扰动稳定性的角度分析Kw取值对低频模态的影响趋势，结果如图13所示。可见，随着Kw取值增大，构造函数F的频率曲线向右移动，即对应的模态频率增大，而阻尼曲线向上移动，表示负阻尼分量减小。具体地，当Kw由130减小为90时，对应振荡频率由1.57Hz减小为1.39Hz，而阻尼由0.63s-1减小为-0.45s-1，此时模态阻尼由正变负，表示系统存在小扰动低频振荡失稳的风险。
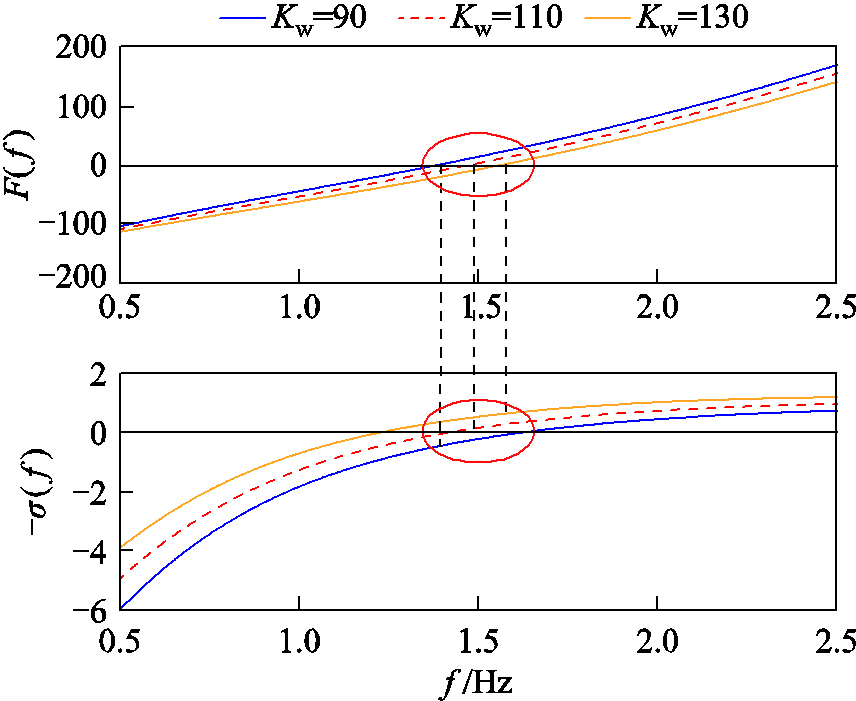
图13 低频振荡模态随Kw变化分析
Fig.13 The analysis of low-frequency oscillation mode varying with Kw
Kw变化时风电机组小扰动有功功率响应如图14所示。可明显看到，随着Kw值增大，风电机组输出有功功率在系统遭受扰动后收敛速度更快，即机组的稳定性更高，与图13中阻尼更大的理论分析结果一致。同时该结果也说明有功调差系数对机组调频功能和振荡阻尼的效果是同向的，在设计该参数时不存在相互矛盾的制约因素。
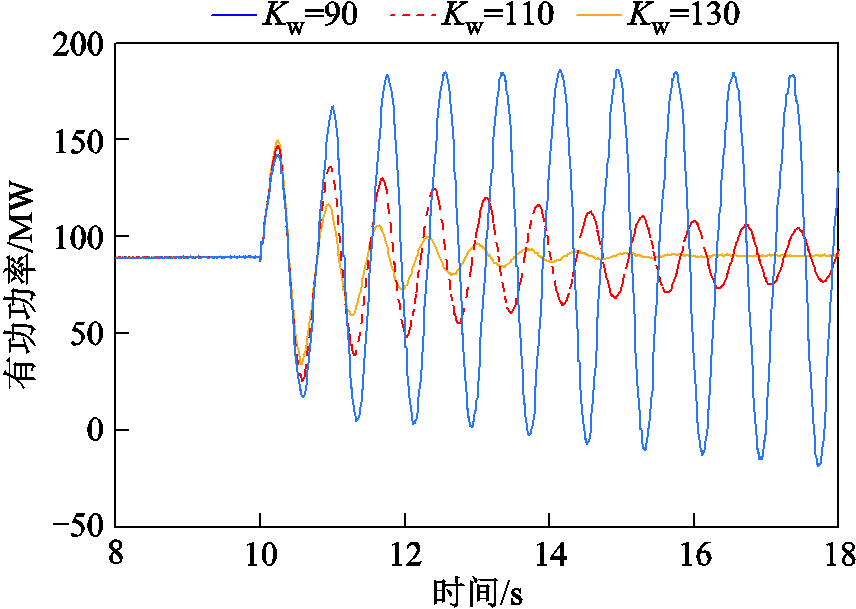
图14 Kw变化时风电机组小扰动有功功率响应
Fig.14 The active power response of wind turbine varying with Kw
3.2.4 无功-电压调差系数
图2中无功-电压调差系数Kn的大小反映了电压源型双馈机组对电网进行电压支撑的能力。从小扰动稳定性的角度分析Kn取值对低频模态的影响趋势，结果如图15所示。可见，随着Kn在一定范围内增大，构造函数F的频率曲线和阻尼曲线都基本保持不变，具体地，当Kn由0.05增大为0.15时，对应振荡频率保持1.43Hz不变，而阻尼基本保持 -0.15s-1不变，表明低频振荡模态的频率和阻尼受无功-电压调差参数的影响很小。
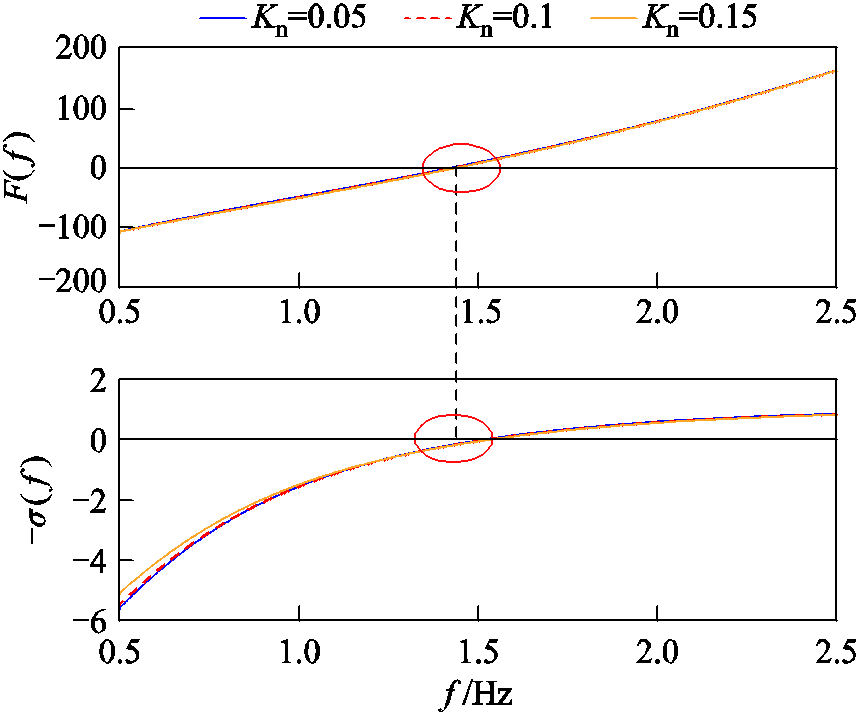
图15 低频振荡模态随Kn变化分析
Fig.15 The analysis of low-frequency oscillation mode varying with Kn
对Kn分别取0.05、0.1和0.15时风电机组小扰动有功功率响应如图16所示。可见，随着Kn取值的变化，风电机组输出有功功率在系统遭受扰动后的响应曲线几乎相同，即三种参数情况下的阻尼相差不大，机组的稳定性也基本不变，与理论分析结果一致。此外，对比前述各控制参数的分析结果可知，无功调差系数对电压源型机组稳定性的影响远低于其他参数的影响，而造成该结果的原因还有待进一步深入分析。
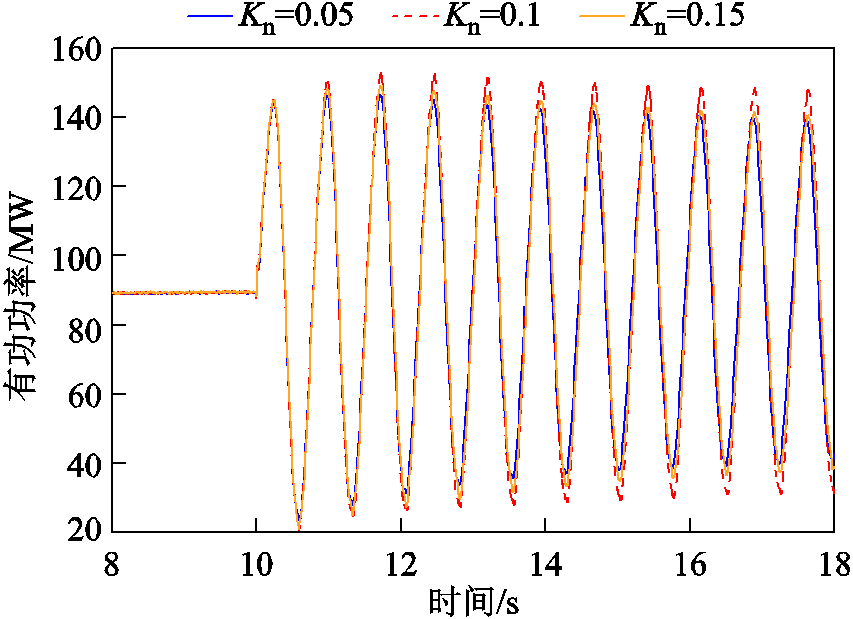
图16 Kn变化时风电机组小扰动有功功率响应
Fig.16 The active power response of wind turbine varying with Kn
3.2.5 其他参数
以上重点分析了功率外环中涉及的四个主要控制参数对电压源型双馈机组低频振荡模态稳定性的影响。采用本文所提方法，还可以进一步评估分析频率测量环节参数、电压环控制参数等对低频模态的影响。限于篇幅，此处不再对其他参数一一进行详细分析，各参数对低频振荡模态的影响趋势归纳总结见表2。
表2 各参数对低频振荡模态的影响
Tab.2 Effects of various parameters on low frequency oscillation mode
参数（增大趋势）模态频率变化模态阻尼变化 电网短路比SCR略微减小减小 虚拟惯性常数Tj减小减小 虚拟阻尼系数D不变增大 有功调差系数Kw增大增大 无功调差系数Kn不变基本不变 电压环比例增益Kp1基本不变增大 电压环积分增益Ki1增大增大 锁相环比例增益KpPLL基本不变略微减小 锁相环积分增益KiPLL基本不变基本不变 频率检测滤波常数Tm基本不变减小
根据第3节的分析结果可知，电压源型双馈风电机组在某些运行场景和参数下，由虚拟同步控制环节主导的低频振荡模态可能出现弱阻尼甚至负阻尼的情况。这一方面不利于风电机组本身的稳定运行，另一方面也可能导致与系统中其他常规机组发生低频相互作用，引发全网机组间的功率摇摆，后者将严重威胁大电网的安全稳定运行[22]。因此有必要采取相应措施，改善电压源型双馈风电机组的低频动态特性，降低低频振荡发生风险。
对风电机组的控制参数进行优化调整是最直接且有一定效果的方式。根据表2中总结的各控制参数对低频振荡模态的影响规律，优化调整参数整定值，可在一定程度上提高模态阻尼。但是这种做法有必要考虑不同参数对其他频段（如次/超同步频率）动态特性及对电网主动支撑功能的影响，不能顾此失彼。因此，如果采取该措施，需要协调考虑多参数间协调配合整定问题。
本节提出一种基于附加支路的稳定控制器。类比传统同步机系统中用于抑制低频振荡而广泛使用的电力系统静态稳定器（Power System Stabilizer, PSS），考虑在电压源型双馈风电机组的无功-电压调差控制环路中附加稳定控制支路，结构如图17所示。以双馈机组定子有功功率作为反馈信号，Kg为稳定器增益系数，G1(s)用于隔直和低通滤波，G2(s)用于补偿一定的相位，稳定控制器输出的附加信号叠加在定子电压指令值中。通过合理设计控制器参数（Kg=0.04，T1=0.01，T2=0.243 8，T3=0.053，n=1），有望提高电压源型风电机组的低频段电气阻尼。
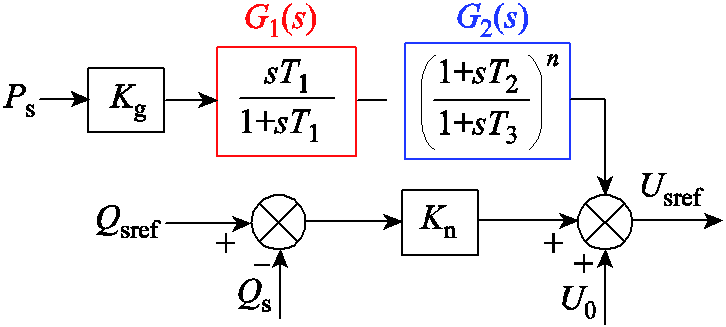
图17 用于抑制低频振荡的稳定控制器
Fig.17 Diagram of damping controller used for suppressing low frequency oscillation
为定量分析所提稳定控制器对电压源型双馈机组低频模态阻尼的提升效果，只需将第2节中低频稳定性分析模型中的式（6）改为式（28）即可。
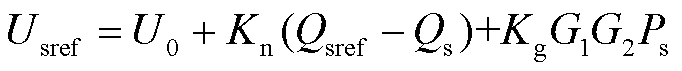（28）
增大虚拟阻尼系数和采用稳定控制器两种方式对电压源型双馈机组低频模态阻尼的影响对比结果如图18所示。可见，两种做法与不采取任何措施相比均能有效提高低频振荡模态的阻尼，降低机组发生低频振荡风险，且采用稳定控制器比仅增大虚拟阻尼系数对模态阻尼的提升效果更加明显。
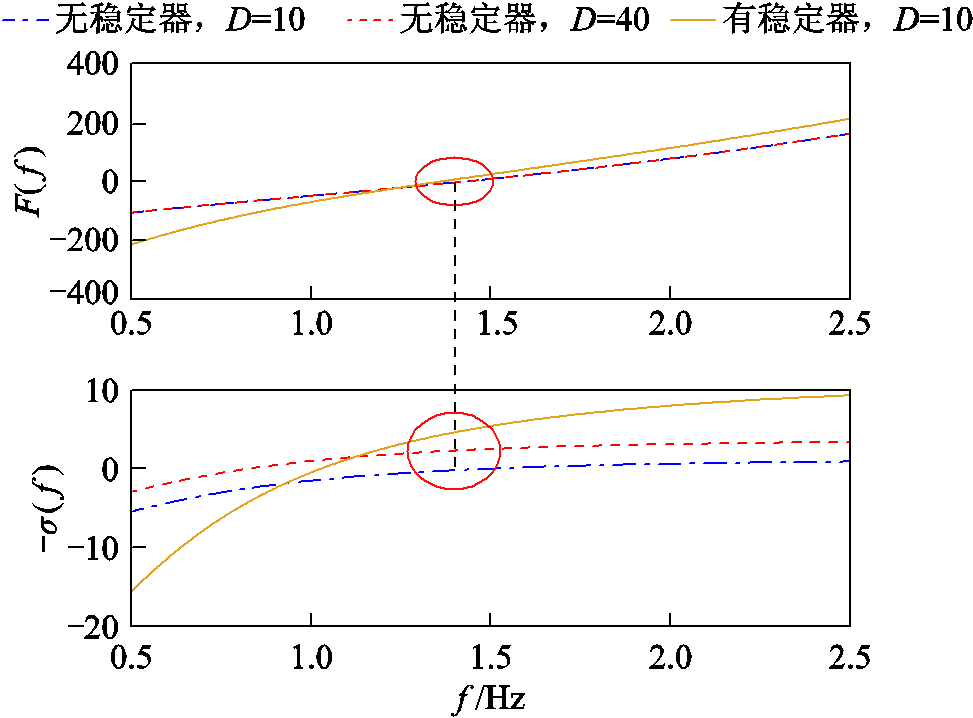
图18 不同措施对模态阻尼的提升效果比较
Fig.18 Comparison of improving effect of different measures on mode damping
不同抑制措施下风电机组小扰动有功功率响应如图19所示。可以明显看到，增大虚拟阻尼系数或投入稳定控制器后，风电机组在遭受扰动后的有功功率响应曲线均能很快收敛下来，表明机组的低频模态阻尼得到极大提升，与理论分析结果一致。
此外，值得说明的是，采用稳定控制器的做法对于抑制未来高比例新能源接入系统中的多机间低频振荡也能取得较好的效果，限于篇幅，该部分内容将不在本文中展开。
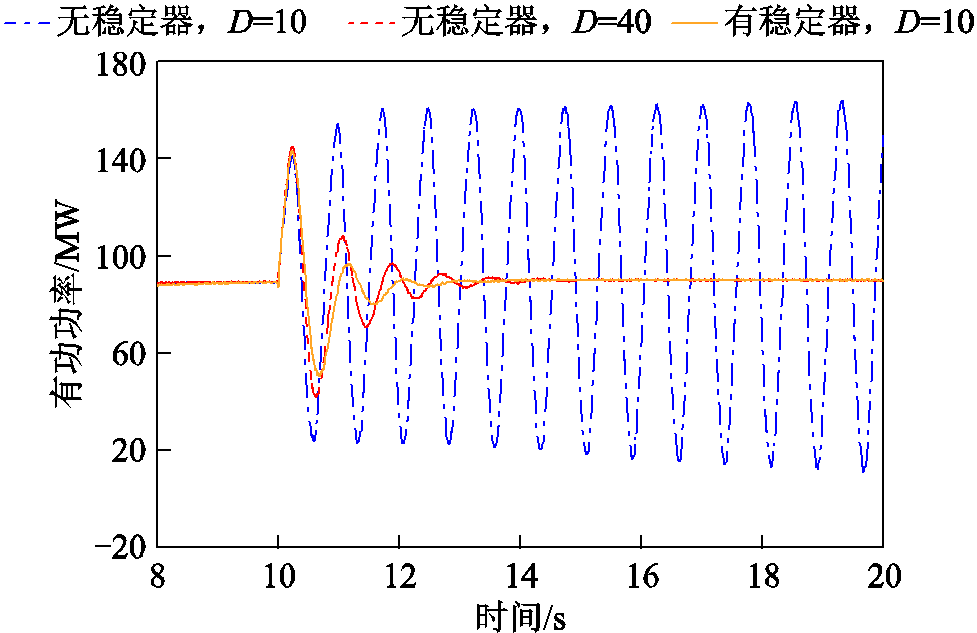
图19 不同抑制措施下风电机组小扰动有功功率响应
Fig.19 The active power response of wind turbine on different oscillation suppresion measures
本文针对采用虚拟同步控制方式的电压源型双馈机组并网系统低频稳定性问题，类比对传统同步机机电振荡问题的研究思路，首先建立了其类Phillips-Heffron低频稳定性分析模型，然后从电气阻尼的角度解释了电压源型双馈机组发生低频振荡失稳的机理，并进一步探究了不同运行控制参数对机组低频电气阻尼的影响趋势。在此基础上，设计了可有效抑制电压源型双馈机组低频振荡的稳定控制器。得到的结论具体如下：
1）本文推导建立了仅考虑电压源型双馈机组慢动态环节的类Phillips-Heffron模型，适用于量化分析虚拟同步控制环节主导低频振荡模态的阻尼特性。
2）当交流系统和机组其他控制环节耦合引入的电气阻尼分量为负，且绝对值大于虚拟同步控制环节的固有正阻尼时，风电机组整体在低频段将呈现负阻尼特性，面临低频振荡失稳的风险。
3）电压源型双馈机组在强电网下阻尼反而更弱，与基于矢量控制的并网变流器特性相反；虚拟同步控制中的有功环参数比无功环参数对机组低频模态阻尼特性的影响更显著。
4）增大虚拟阻尼系数或在无功-电压调差控制回路中投入稳定控制器均能有效提高电压源型双馈机组低频模态阻尼，抑制低频振荡。
基于本文内容，后续研究工作将重点聚焦于电压源型双馈机组在复杂多机系统中的动态特性分析，包括电压源型风电机组与传统同步机、电流源型风电机组间的相互作用及协调运行等。
附 录
1. N(s)的表达式
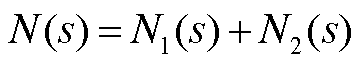
式中
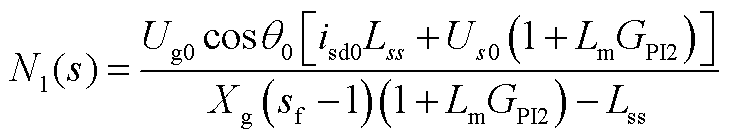
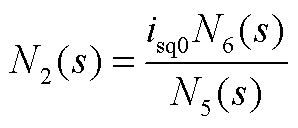
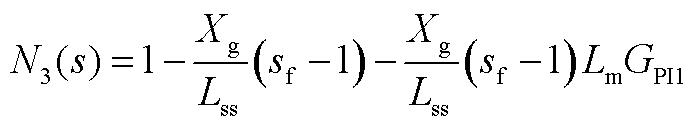
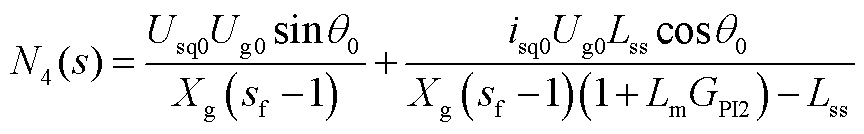
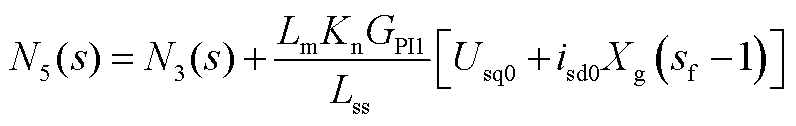
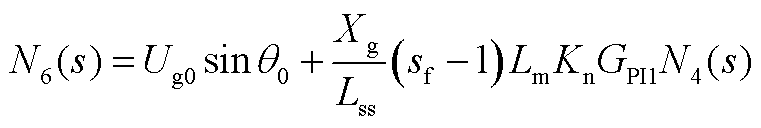
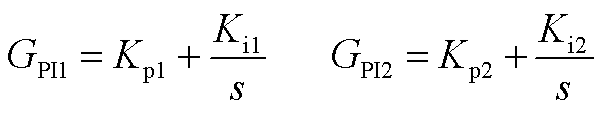
2. Mi(s)的表达式
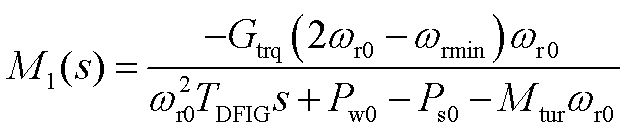
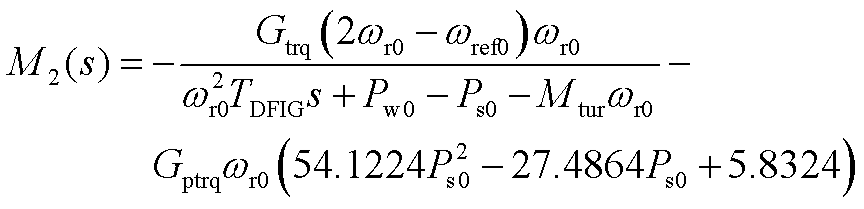
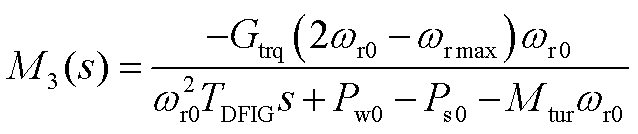
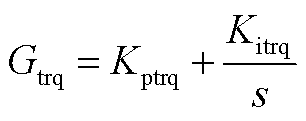
式中，Mtur为与风轮机半径、风速等相关的常数。
3. K(s)的表达式
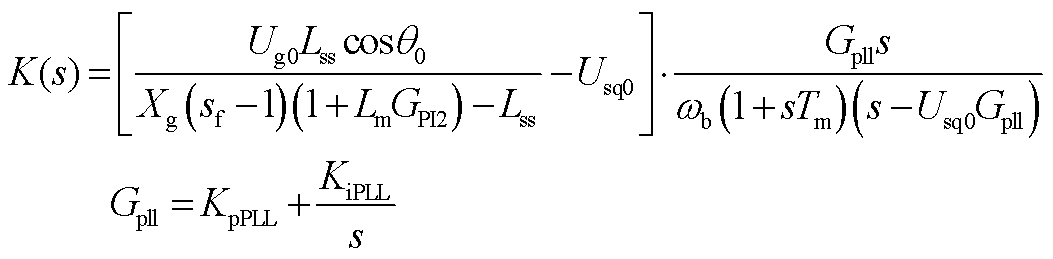
参考文献
[1] 李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259.
Li Hui, Liu Dong, Yao Danyang. Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(18): 6245-6259.
[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[3] 张柏林, 郁娇山, 黄万龙, 等. 甘肃地区高比例新能源大外送电网面临的挑战及思考[J]. 电网与清洁能源, 2020, 36(4): 81-89.
Zhang Bolin, Yu Jiaoshan, Huang Wanlong, et al. Chanllenges and reflections on the power grid of high proportion of new energy in Gansu province[J]. Power System and Clean Energy, 2020, 36(4): 81-89.
[4] 盛逸标, 林涛, 陈宝平, 等. 面向新能源外送系统次/超同步振荡的控制器参数协调优化[J]. 电工技术学报, 2019, 34(5): 983-993.
Sheng Yibiao, Lin Tao, Chen Baoping, et al. Coordination and optimization of controller parameters for subsynchronous/supersynchronous oscillation in new energy delivery systems[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 983-993.
[5] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292.
Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transa-ctions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[6] 薛安成, 王子哲, 付潇宇, 等. 基于非光滑分叉的直驱风机次同步振荡机理分析[J]. 电力系统自动化, 2020, 44(7): 87-92.
Xue Ancheng, Wang Zizhe, Fu Xiaoyu, et al. Mechanism analysis of subsynchronous oscillation in direct-driven wind turbine based on non-smooth bifurcation[J]. Automation of Electric Power Systems, 2020, 44(7): 87-92.
[7] 温春雪, 黄耀智, 胡长斌, 等. 虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制[J]. 电工技术学报, 2020, 35(2): 494-502.
Wen Chunxue, Huang Yaozhi, Hu Changbin, et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 494-502.
[8] Meng Xin, Liu Jinjun, Liu Zeng. A generalized droop control for grid-supporting inverter based on comparison between traditional droop control and virtual synchronous generator control[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5416-5438.
[9] Zhang Xueguang, Xia Danni, Fu Zhichao, et al. An improved feedforward control method considering PLL dynamics to improve weak grid stability of grid-connected inverters[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5143-5151.
[10] 年珩, 庞博, 许国东, 等. 应对并补电网下DFIG系统高频谐振的宽频阻抗重塑策略[J]. 电力系统自动化, 2018, 42(18): 48-56.
Nian Heng, Pang Bo, Xu Guodong, et al. Reshaping strategy of wide frequency impedance for DFIG system to suppress high frequency resonance under parallel compensation grid[J]. Automation of Electric Power Systems, 2018, 42(18): 48-56.
[11] Pattabiraman D, Lasseter R H, Jahns T M. Comparison of grid following and grid forming control for a high inverter penetration power system[C]//2018 IEEE Power & Energy Society General Meeting, Portland, USA, 2018: 1-5.
[12] 孙大卫, 刘辉, 赵峰, 等. 不同逆变电源主动支撑控制方式的对比研究[J]. 电网技术, 2020, 44(11): 4359-4369.
Sun Dawei, Liu Hui, Zhao Feng, et al. Comparison of inverter generators with different support control methods[J]. Power System Technology, 2020, 44(11): 4359-4369.
[13] 孙大卫, 刘辉, 高舜安, 等. 电流控制型虚拟同步发电机的小信号建模与稳定性分析[J]. 电网技术, 2018, 42(9): 2983-2993.
Sun Dawei, Liu Hui, Gao Shunan, et al. Small-signal modeling and stability analysis of current-controlled virtual synchronous generators[J]. Power System Technology, 2018, 42(9): 2983-2993.
[14] 朱廷猛, 孙海顺, 秦世耀, 等. 弱电网下双馈风机并网系统的次同步振荡研究[J]. 电网技术, 2021, 45(5): 1641-1648.
Zhu Tingmeng, Sun Haishun, Qin Shiyao, et al. Sub-synchronous oscillation in DFIG system connected to weak grid[J]. Power System Technology, 2021, 45(5): 1641-1648.
[15] Zhong Qingchang, George W. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[16] 颜湘武, 贾焦心, 王德胜, 等. 基于P/ω“导纳”的并联虚拟同步机功频响应建模与分析[J]. 电工技术学报, 2020, 35(15): 3191-3202.
Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. Modeling and analysis of active power- frequency response of parallel VSGs using a P/ω “admittance” [J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3191-3202.
[17] Ndreko M, Ruberg S, Winter W. Grid forming control scheme for power systems with up to 100% power electronic interfaced generation: a case study on Great Britain test system[J]. IET Renewable Power Generation, 2020, 14(8): 1268-1281.
[18] 谢震, 许可宝, 秦世耀, 等. 基于电压源型和电流源型双馈风电机组稳定性对比分析[J]. 电网技术, 2021, 45(5): 1724-1735.
Xie Zhen, Xu Kebao, Qin Shiyao, et al. Comparative analysis of doubly-fed wind turbine stability based on voltage source and current source[J]. Power System Technology, 2021, 45(5): 1724-1735.
[19] Gu Kanghui, Wu Feng, Zhang Xiaoping, et al. SSR analysis of DFIG-based wind farm with VSM control strategy[J]. IEEE Access, 2019(7): 118702-118711.
[20] 章艳, 高晗, 张萌. 不同虚拟同步机控制下双馈风机系统频率响应差异研究[J]. 电工技术学报, 2020, 35(13): 2889-2990.
Zhang Yan, Gao Han, Zhang Meng. Research on frequency response difference of doubly-fed induction generator system controlled by different virtual synchronous generator controls[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2889-2990.
[21] Liu Jia, Miura Y, Ise T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3600-3611.
[22] Kundur P. Power system stability and control[M]. New York: McGraw-Hill, 1994.
Abstract Almost all wind turbines currently used in practical projects use the grid-following control method, which is characterized by the risk of oscillation instability in weak grids, and therefore this control method is inevitably unable to adapt to power system scenarios with increasing penetration of renewable energy sources. To address this issue, some researchers have proposed the grid-forming control method, which can actively support the grid voltage and thus have the ability to operate stably in weak grid conditions. However, the existing work is insufficient in the investigation of oscillation characteristics of grid-forming units, especially for the low-frequency stability and instability mechanism introduced by the virtual synchronous control part. This paper presents an analysis method for this problem. By establishing the generalized Phillips-Heffron model of voltage-sourced DFIG, it can accurately assess the damping characteristics and oscillation risk of the low-frequency mode.
Firstly, a typical grid-forming control strategy applied to DFIG is introduced, including its power outer loop and voltage-current inner loop structure. Secondly, a mathematical model of the grid-forming DFIG-connected power system considering only its slow dynamic part is established, which has the same form as the Phillips-Heffron model used in the low-frequency oscillations analysis of synchronous machines, based on which, the oscillation frequency and electrical damping calculation method of the low-frequency mode dominated by the virtual synchronous control are derived. Thirdly, by applying the aforementioned damping quantification analysis method and electromagnetic transient simulation, the effects of short-circuit ratio, wind power output, and various control parameters on the low-frequency oscillation characteristics of grid-forming DFIG are analyzed. Finally, a stabilization controller attached to the reactive-voltage loop is proposed to improve the low-frequency damping characteristics of grid-forming DFIG and reduce its low-frequency oscillation risk.
The analysis results of the grid-forming DFIG integrated system show that when the grid-side short-circuit ratio increases from 3 to 9, the damping of the low-frequency oscillation mode dominated by the virtual synchronous control will decrease from 2.73s-1 to -0.39s-1, leading to the system oscillation instability. This indicates that the dynamic characteristics of the grid-forming DFIG under weak grid conditions are better than those under strong grid conditions, which is the opposite of the conventional grid-following DFIG. Besides, the analysis of other parameters shows that the damping of the low-frequency mode tends to decrease as the virtual inertia coefficient increases, the virtual damping coefficient decreases, the active power-frequency droop coefficient decreases, and the proportional and integral gains of the voltage loop control decrease, while the reactive power-voltage droop coefficient has almost no effect on the damping of low-frequency mode. The comparison results between scenarios with and without the stabilization controller show that this attached controller can effectively improve the oscillation damping under strong grid conditions, and it works better than just increasing the virtual damping coefficient. The results of the time-domain simulations are all consistent with the damping analysis results, indicating that the proposed method for analyzing the low-frequency oscillation characteristics of grid-forming DFIG is accurate and effective.
The following conclusions can be drawn from the analysis results: (1) When the electrical damping introduced by the coupling of AC system and other control links of the grid-forming DFIG is negative, and its absolute value is greater than the inherent positive damping of the virtual synchronous control, the grid-forming DFIG as a whole will show negative damping characteristics in the low-frequency band and face the risk of low-frequency oscillation instability. (2) The damping of the grid-forming DFIG is smaller under strong grid conditions, contrary to that of the grid-following converter. (3) the proposed method can accurately analyze the low-frequency oscillation characteristics of grid-forming units under small disturbances.
keywords: Virtual synchronous control, voltage-sourced wind turbine, electrical damping, low-frequency oscillation, oscillation suppression
国家重点研发计划（2018YFB0904001）和国家电网公司科技项目（SGJB0000TKJS1801242）资助。
收稿日期 2021-10-13
改稿日期 2021-11-23
DOI:10.19595/j.cnki.1000-6753.tces.211618
中图分类号：TM71
韩应生 男，1996年生，博士研究生，研究方向为新能源电力系统稳定性分析与控制。E-mail：hust_hanys@hust.edu.cn
孙海顺 男，1971年生，教授，博士生导师，研究方向为电力系统分析与仿真、FACTS、船舰电力系统等。E-mail：haishunsun@hust.edu.cn（通信作者）
（编辑 赫蕾）