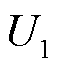 表示风电机组并入点电压;
表示风电机组并入点电压;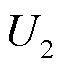 表示风电机组定子电压;
表示风电机组定子电压;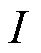 表示线路电流;
表示线路电流;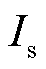 表示定子电流;
表示定子电流;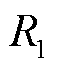 表示线路电阻;
表示线路电阻;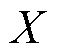 表示线路漏抗;
表示线路漏抗;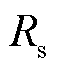 表示定子电阻;
表示定子电阻;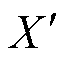 表示定子漏抗;
表示定子漏抗;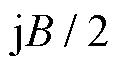 表示无功补偿的电容;
表示无功补偿的电容;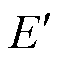 表示暂态电动势。
表示暂态电动势。摘要 随着新型电力系统的发展,强间歇性、随机性的风电点多面广地接入配电网,导致其潮流分布发生了巨大变化,给配电网安全可靠运行带来挑战。尤其在配电网运行控制过程中,数据计算、指令传输、指令响应等多环节均存在的不确定性耗时,可能会造成控制策略失灵乃至局部节点电压越限,因此,精准掌握配电网的最大可调控时延即时滞稳定裕度非常必要。为此,该文首先构建了计及时滞的含风电配电网节点电压安全分析偏导数微分超越方程的数学模型;然后提出一种Lyapunov-Krasovskii泛函构造方法,并应用Wirtinger不等式技巧处理泛函导数中的积分项,实现对所构建偏导数微分超越方程的求解,得到稳定判据,获知其时滞稳定裕度;最后借助典型案例和IEEE 33算例进行仿真验证。结果表明,该文所得稳定判据具有更低的保守性,以期为不确定时滞影响下的配电网运行控制提供理论依据。
关键词:配电网 时滞 电压安全 Lyapunov-Krasovskii泛函 Wirtinger不等式
随着“碳达峰、碳中和”国家能源政策的推进和新型电力系统的发展,强间歇性、强随机性的风电点多面广地接入配电网成为常态[1],导致配电网的潮流分布发生巨大变化,给配电网运行控制带来了挑战[2]。尤其是波动性风电功率的注入,会引起配电网局部节点电压越限[3],轻则使用户用能质量降低,严重时会造成电气设备损坏[4]。在配电网运行控制过程中,测量和调控数据的采集、发送、传输与处理过程常存在通信延迟现象[5];同时,拓扑分析、潮流计算等科学计算也存在不确定性延时[6]。以上时滞现象的叠加影响导致配电网电压安全运行控制的预设参数失效,系统运行工况会进一步恶化。其核心关键是以往的配电网安全运行控制分析模型较少考虑时滞或者按照固定常数的延时执行,难以满足实际需求。因此,构建含风电配电网运行控制的时滞分析模型,获知系统保持稳定状态所允许的最大时滞,即时滞稳定裕度,不仅是含风电的配电网精准调控、安全运行的基础[7],也是调度运行管理人员关注的重点,值得深入研究。
目前,针对配电网运行控制的时滞稳定性分析,国内外文献不多。参照大电网,电力系统时滞稳定性分析方法主要有频域法和时域法[8]。频域法是将理论上发展较为完善的线性系统稳定性分析理论推广到线性时滞系统,其稳定条件是系统的特征根全部位于复平面的左半平面。但是,由于时滞系统特征方程中存在超越项,在数学上有无穷多种可能的解,导致特征方程的求解特别困难。学者们广泛采用Rekasius变换[9]、Pade近似法[10]、Smith补偿技术[11]等对超越项进行变换求解,基本实现了对定常时滞和系统参数已知的时滞电力系统模型求解,但对于复杂变化的时滞项仍难以处理,从而极大地限制了频域法的适用范围。时域法是目前时滞系统进行稳定性分析最主要的方法之一[12]。它通过对Lyapunov-Krasovskii(L-K)直接法的推演得到稳定判据,避免了频域法中繁杂的计算和时滞项的处理。然而,基于L-K直接法得到的判稳条件只是系统稳定的充分非必要条件,其保守性无法避免[13]。为降低判据保守性,国内外学者从构造更优的L-K泛函和采用更优的变换技术两方面展开了研究。文献[14]构建了能够体现时滞电力系统多元信息融合的增广L-K泛函,并应用Bessel-Legendre不等式处理泛函导数中的积分项,减小了时滞电力系统的保守性。文献[15]提出一种广义的自由权矩阵方法来估计函数正向差分中的求和项,解决了原来求和项不能提供延迟变化信息的问题。文献[16]对积分不等式进行改进,并与自由权矩阵结合,降低了解析误差和判据保守性。文献[17]提出一个替代性不等式,并与Wirtinger不等式结合,得到逆凸组合不等式,降低了保守性。文献[18]推导出一种改进的逆凸组合不等式,系统的时滞上限进一步增加。为解决配电网时滞问题,文献[19]构建分布式光伏接入配电网的时滞补偿模型,解决了通信延迟和闭环控制带来的滞后性问题。综上所述,以上文献在一定程度上降低了电力系统时滞稳定裕度的保守性,但是目前在配电网节点电压安全分析研究中考虑时滞因素的相关文献,还较为缺乏。
为此,借鉴大电网时滞稳定性分析方法,考虑到配电网拓扑结构复杂、设备类型多样等特点,结合风电出力的不确定性,本文深入开展了计及时滞的含风电配电网节点电压安全分析研究。首先,分析含风电的配电网电压安全运行控制过程中时滞产生机理,得到配电网时滞系统模型的偏导数微分超越方程一般形式;然后,针对时滞系统模型中超越项难以求解的问题,提出一种增广向量和L-K泛函的构造方法,并利用Wirtinger不等式对泛函导数中的积分项进行估计处理,以降低稳定判据的保守性,实现对时滞稳定裕度的求解;最后,基于典型案例,通过与相同参数设置下不同方法的结果进行对比,证明本文方法的有效性,进一步通过IEEE 33算例证明本文方法有效地扩大了系统的稳定运行区域,且降低了稳定判据的保守性。本文所提方法可为含风电的配电网节点电压安全运行精准调控提供数值参考,也为实现配电网与用户侧可再生能源的良好互动和稳定响应奠定理论基础,以促进未来新型电力系统更好地适应高比例风/光等新能源的接入。
一般而言,待求解变量数与系统状态变量数近似呈二次方关系,导致时滞模型求解变量多且求解时间长,因此时滞系统研究大多从低阶简单系统开始,进而掌握复杂系统的规律。为探究含风电的配电系统节点电压时滞稳定性,本文以接入小规模风电机组为例[20],构建以典型IEEE 33为原型的时滞配电系统模型。其中,风电机组接入点处的戴维南等效模型如图1所示。图1中,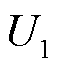 表示风电机组并入点电压;
表示风电机组并入点电压;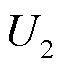 表示风电机组定子电压;
表示风电机组定子电压;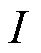 表示线路电流;
表示线路电流;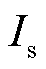 表示定子电流;
表示定子电流;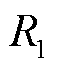 表示线路电阻;
表示线路电阻;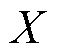 表示线路漏抗;
表示线路漏抗;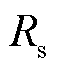 表示定子电阻;
表示定子电阻;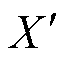 表示定子漏抗;
表示定子漏抗;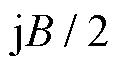 表示无功补偿的电容;
表示无功补偿的电容;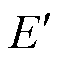 表示暂态电动势。
表示暂态电动势。
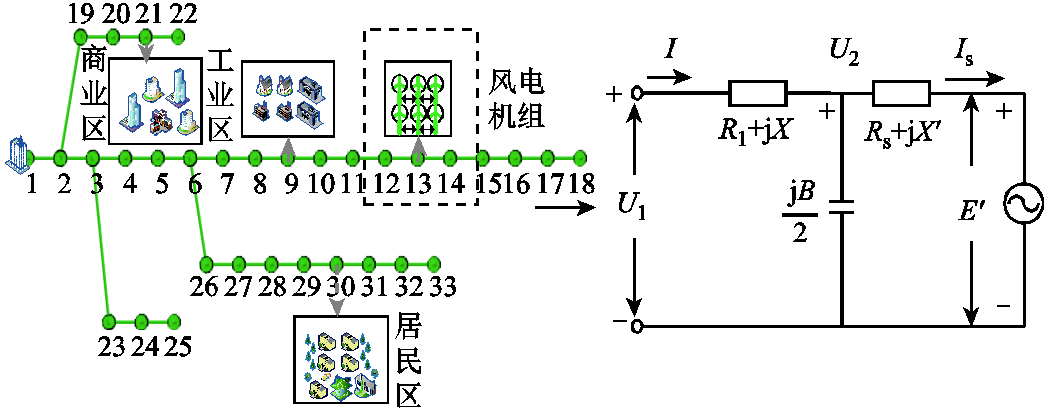
图1 风电机组接入点处戴维南等效模型
Fig.1 Thevenin equivalent model at the wind turbine access point
风电机组的定子电流方程为
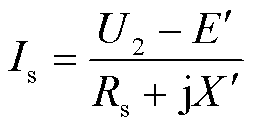 (1)
(1)
其中
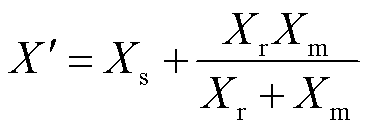 (2)
(2)
式中,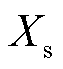 为励磁电抗;
为励磁电抗;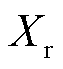 为转子漏抗;
为转子漏抗; 为定子漏抗。风电机组的电磁暂态方程为
为定子漏抗。风电机组的电磁暂态方程为
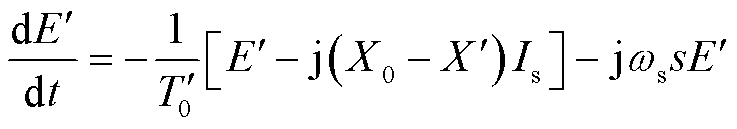 (3)
(3)
式中,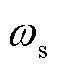 为定子电角频率;
为定子电角频率;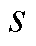 为转差率。
为转差率。
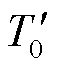 和
和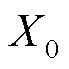 计算式为
计算式为
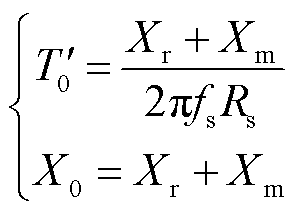 (4)
(4)
式中,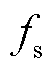 为电网频率。
为电网频率。
风电机组机电动力学方程为
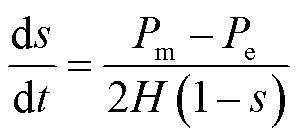 (5)
(5)
式中,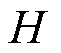 为惯性系数;
为惯性系数; 为风机机械输入功率;
为风机机械输入功率; 为机械功率,计算式为
为机械功率,计算式为
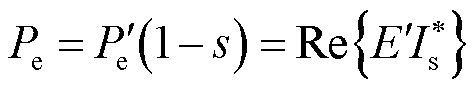 (6)
(6)
式中,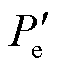 为电磁功率;Re表示实部。
为电磁功率;Re表示实部。
当风电机组稳定运行时,假设其相关初值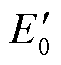 、
、 、
、 、
、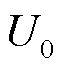 在机组出现小扰动后,在平衡点附近进行线性化处理并忽略2阶无穷小变量
在机组出现小扰动后,在平衡点附近进行线性化处理并忽略2阶无穷小变量 和
和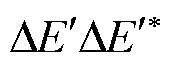 ,可以获得状态方程式(7)。
,可以获得状态方程式(7)。
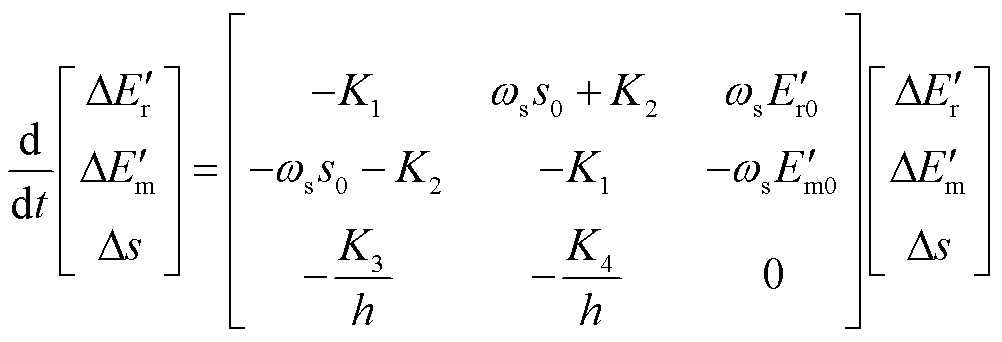 (7)
(7)
式中,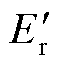 和
和 分别为
分别为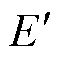 的实部和虚部;
的实部和虚部;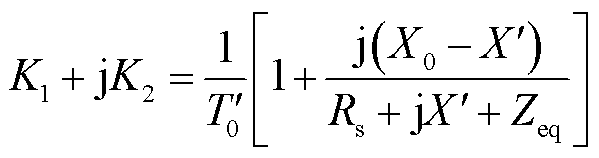 ;
;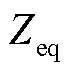 为母线等值阻抗;
为母线等值阻抗;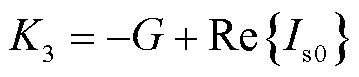 ;
;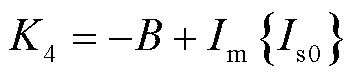 ;
;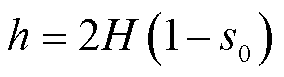 ;
;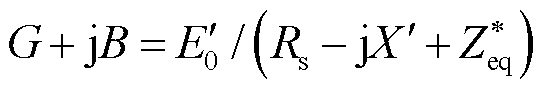 ;
;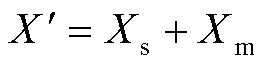 。
。
由戴维南等效电路图,得到
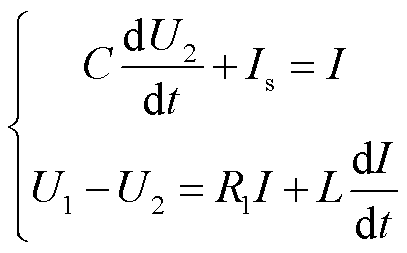 (8)
(8)
式中,C为电容。式(8)经过线性化处理后得到
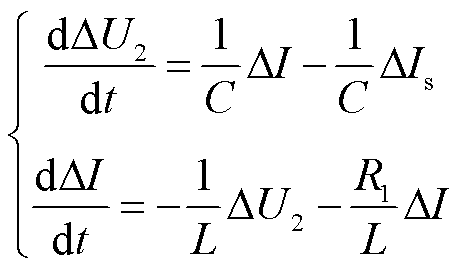 (9)
(9)
将式(1)代入式(9)得
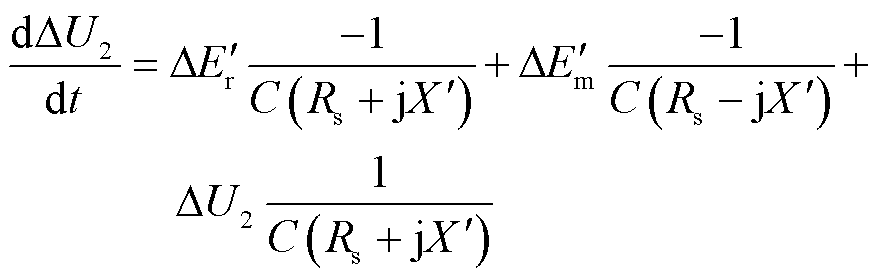
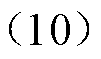
在式(7)、式(9)、式(10)的参数中考虑通信延时,即相关参数的时滞表示形式分别为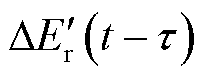 、
、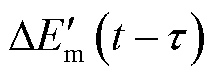 、
、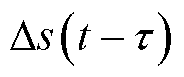 、
、 和
和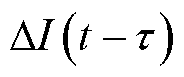 ,则式(7)、式(9)、式(10)整理后得到
,则式(7)、式(9)、式(10)整理后得到
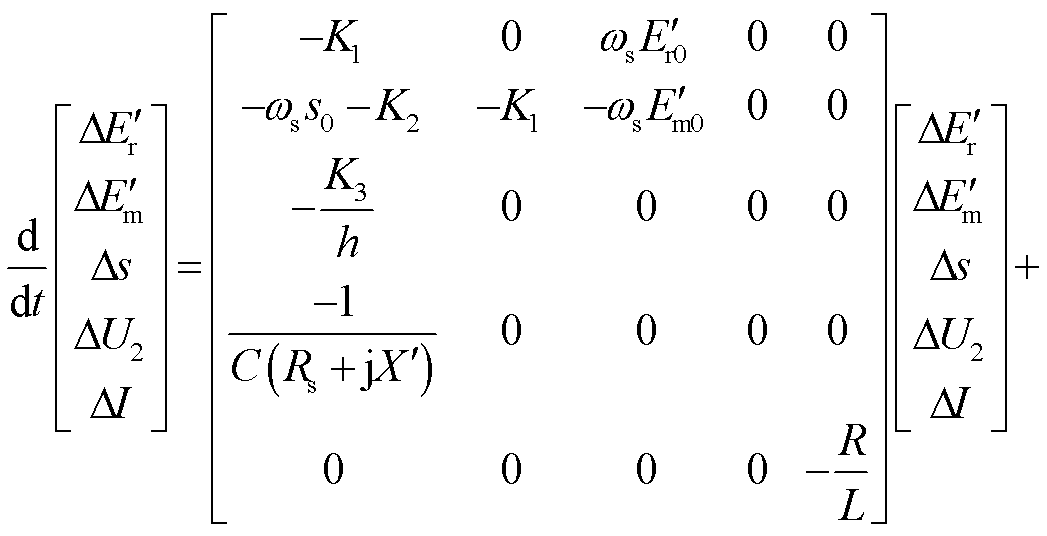
 (11)
(11)
此时,式(11)可表示为
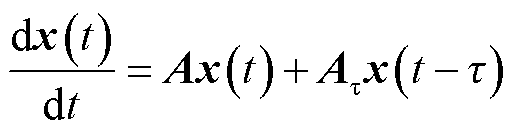 (12)
(12)
其中
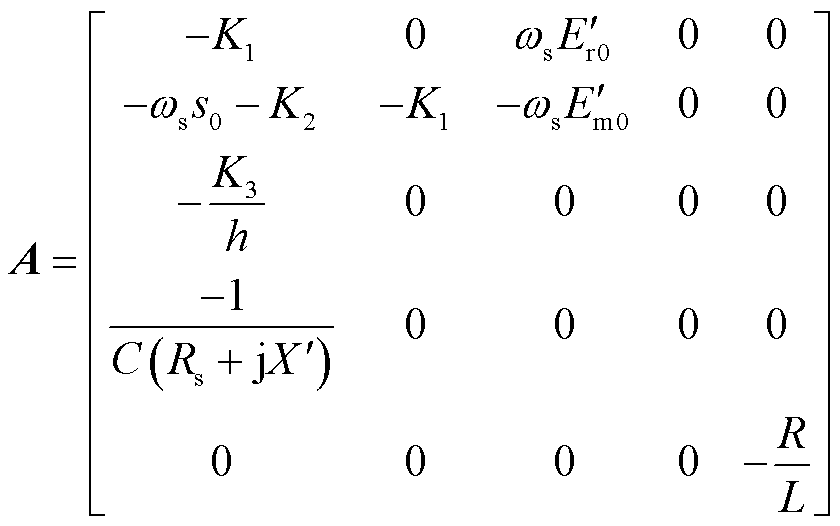
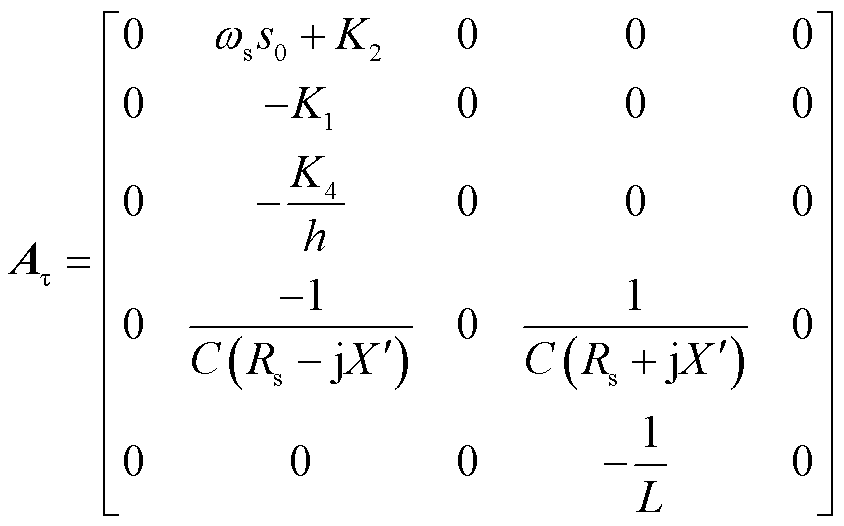
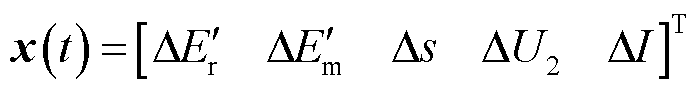
于是,得到配电网时滞系统模型的一般形式,即
 (13)
(13)
式中,x(t)为系统的状态变量,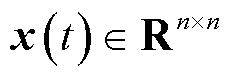 ;
;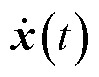 为
为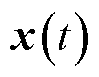 导数;A、
导数;A、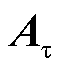 为系统矩阵;
为系统矩阵;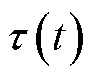 为满足
为满足 的时滞函数;
的时滞函数;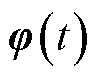 为初始值。
为初始值。
式(13)是典型的偏导数微分超越方程,直接解析求解通常十分困难。为此,本文通过构造合适的L-K泛函,再将判稳条件转换为标准线性矩阵不等式(Linear Matrix Inequality,LMI)形式,最后利用LMI求解器进行求解。
根据目前时滞系统的研究,时滞被分为两种:定常时滞和时变时滞。其中,根据时变时滞导数的信息是否已知,时变时滞又分为三种:①时滞导数具有确定的上下界;②时滞导数具有确定的上界;③时滞的导数未知,也被称为随机时滞。在实际情况中,时变时滞导数的信息一般很难得到,因此本文重点研究更加符合实际情况的随机时滞模型。本文的稳定判据适用于研究随机时滞影响下电力系统在稳定状态下所允许的最大时滞。
一般而言,判断时滞系统稳定的充分条件是泛函正定且其导数负定,因此构造更优的L-K泛函和采用更优的放缩变换技术可以简化推导过程,以达到降低判据求解难度和判据保守性的目的[21]。为求解本文时滞方程式(13),首先,充分利用时滞的上下界信息,提出一种增广向量和L-K泛函的构造方法;然后,对泛函导数进行放缩处理得到稳定判据;最后,将稳定判据转换成LMI形式并利用LMI求解器得到稳定裕度。
Schur补引理[22]:对于对称矩阵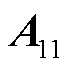 ,
,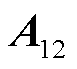 ,
,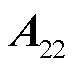 ,以下三个条件等价;①
,以下三个条件等价;①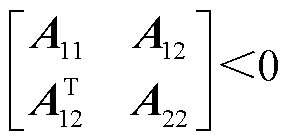 ;②
;②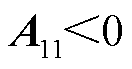 ,
,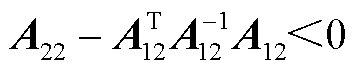 ;③
;③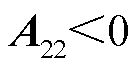 ,
,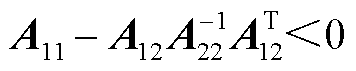 。
。
引理1[23]:令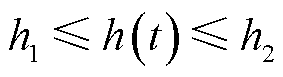 ,则对任意矩阵
,则对任意矩阵 且
且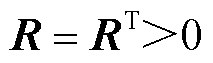 ,以及适当的维数矩阵
,以及适当的维数矩阵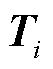 和
和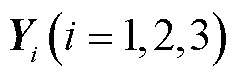 ,有不等式(14)成立。
,有不等式(14)成立。
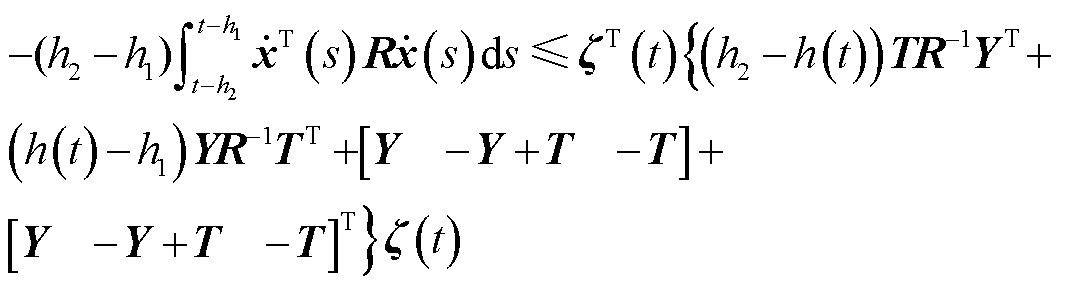
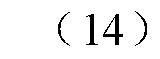
式中,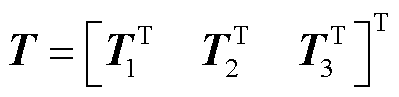 ;
;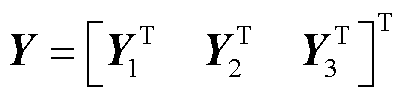 ;
;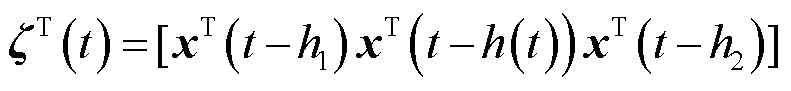 。
。
引理2[17]:对于给定的正定矩阵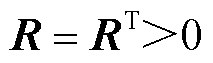 以及可微函数
以及可微函数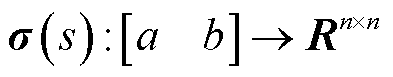 且
且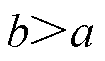 ,有不等式(15)成立。
,有不等式(15)成立。
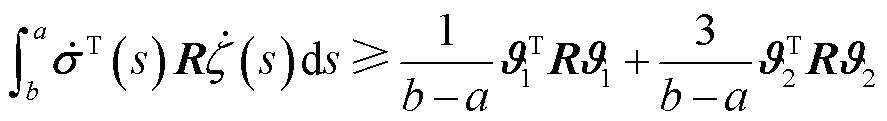 (15)
(15)
式中,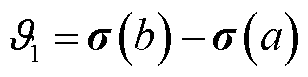 ;
; 。
。
引理3[24]:假设 为具有适当维数的矩阵,
为具有适当维数的矩阵, 为
为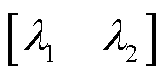 上的变函数,则使矩阵不等式
上的变函数,则使矩阵不等式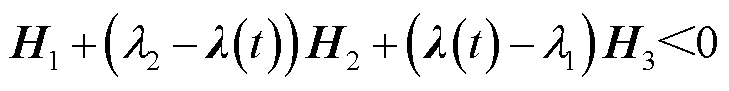 成立的充要条件是
成立的充要条件是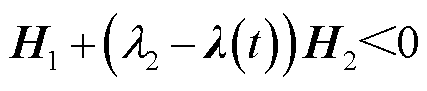 且
且 。
。
引理4[25]:对于 存在一阶连续导数,给定任意矩阵
存在一阶连续导数,给定任意矩阵 ,常数
,常数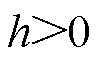 及向量函数
及向量函数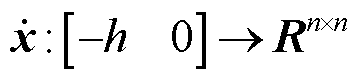 ,有不等式(16)成立。
,有不等式(16)成立。
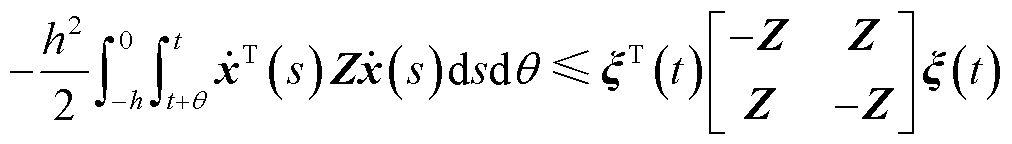 (16)
(16)
式中,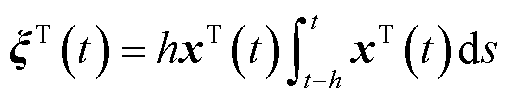 。
。
利用Lyapunov稳定性定理分析本文时滞系统稳定性的基本思路为:构造L-K泛函并采用Wirtinger积分不等式处理泛函导数中的积分项,再借助LMI工具箱求解稳定裕度。其中,LMI工具箱所能求解的线性矩阵不等式的阶次最多不超过50~60阶,因此分析高维电力系统首要考虑的问题就是模型降阶。由于时滞相关项在整个系统变量中只占少数,因此可以利用常见的Hankel算法、Schur算法等降阶方法将系统模型等价地分为时滞相关部分和时滞无关部分,从而实现系统的降维。其中,本文利用Schur补引理进行降阶。
在泛函中引入新的增广变量以及积分项,并结合文献[16],针对系统(13)构造的L-K泛函为
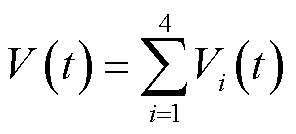 (17)
(17)
对泛函进行求导,利用相关引理对导数进行放缩变换,基于Lyapunov稳定性原理,即当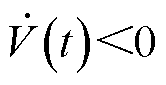 时,系统是渐近稳定的,最终得到稳定性定理1,泛函导数放缩变换及定理1推导过程见附录。
时,系统是渐近稳定的,最终得到稳定性定理1,泛函导数放缩变换及定理1推导过程见附录。
定理1:对给定常量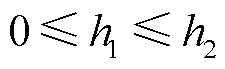 和
和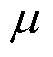 ,若存在正定矩阵P,
,若存在正定矩阵P, ,
, ,
,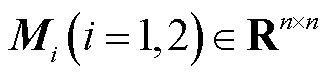 及适当维数的自由矩阵
及适当维数的自由矩阵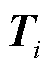 、
、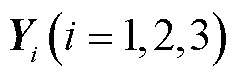 使得式(18)成立,则系统式(13)是渐近稳定的。
使得式(18)成立,则系统式(13)是渐近稳定的。
 (18)
(18)
式中
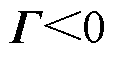
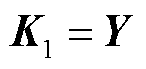
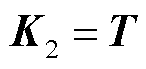

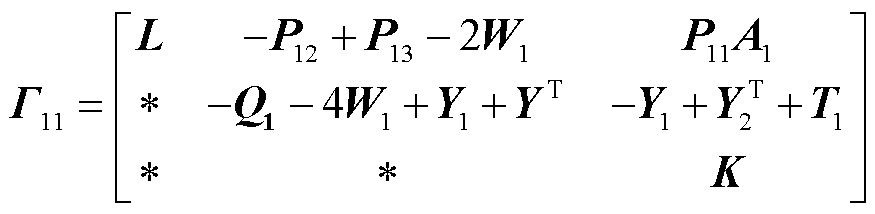

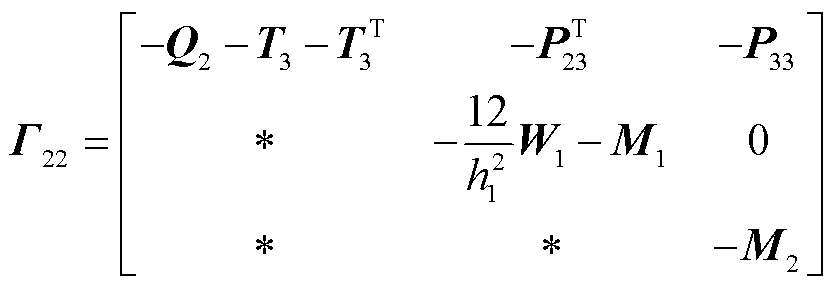
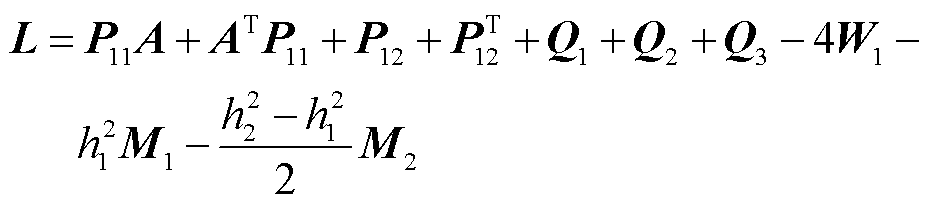
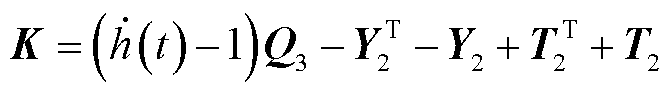
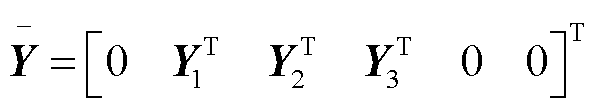
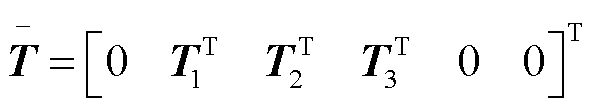
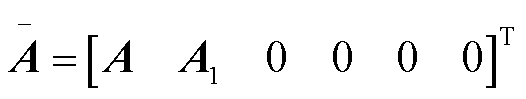

综上所述,得到本文所构建时滞配电系统的稳定判据,即定理1。由式(18)可以发现,借助LMI求解器所获知的时滞稳定裕度上界值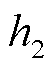 ,就是本文所构建时滞配电系统的最大时滞稳定裕度值。
,就是本文所构建时滞配电系统的最大时滞稳定裕度值。
为验证本文所提稳定裕度求解方法的有效性和优越性,分别在典型二阶系统和接入不同组风电机组的IEEE 33节点配电系统中进行仿真验证。
系统时滞上界值越大,系统安全运行区域越大,表明所得稳定判据保守性越小。因此,可以通过比较时滞上界值来衡量时滞系统稳定判据的保守性。基于典型二阶系统进行验证分析,通过与改进积分不等式的方法[26]和构造新型L-K泛函并对积分区间进行时滞分割的方法[27]进行对比,验证本文方法的保守性。
对于配电网时滞系统式(13),A、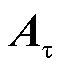 取值为
取值为
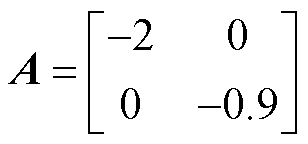
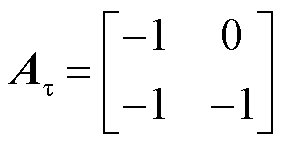
当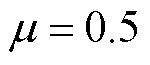 及
及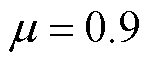 时,给定时滞下界
时,给定时滞下界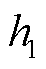 ,分别求得定理1与文献[26-27]稳定判据对应的时滞稳定裕度,结果如图2所示。
,分别求得定理1与文献[26-27]稳定判据对应的时滞稳定裕度,结果如图2所示。
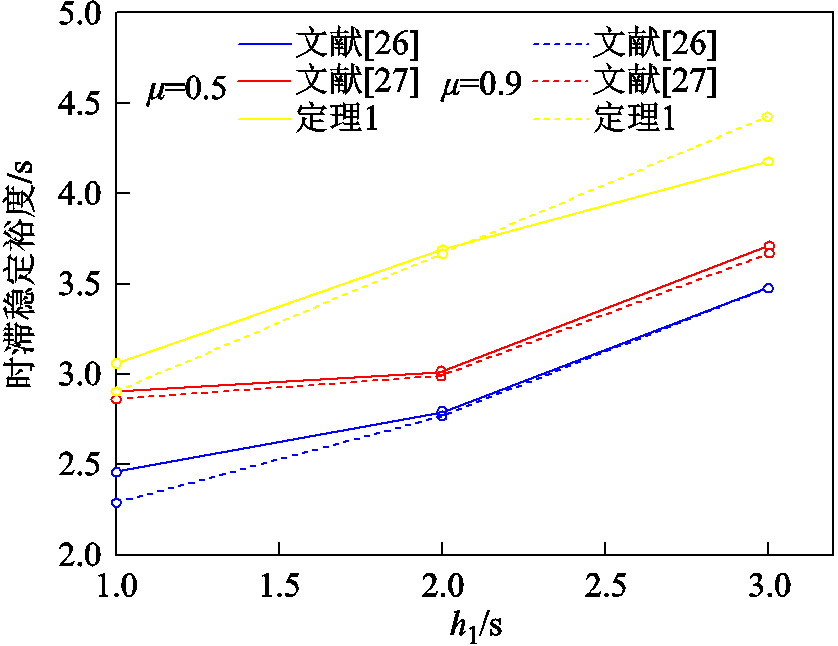
图2 给定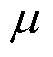 和
和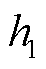 时系统最大允许时滞上界
时系统最大允许时滞上界
Fig.2 Upper bound of the maximum allowable time delay for given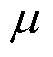 and
and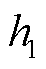
由图2观察得,在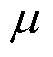 的不同取值下,时滞稳定裕度会随着
的不同取值下,时滞稳定裕度会随着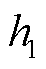 的增大而呈增加趋势。在相同参数设置下,本文系统最大允许时滞上界值高于文献[26-27]。因此,在典型二阶系统中,本文方法可显著降低稳定判据保守性。
的增大而呈增加趋势。在相同参数设置下,本文系统最大允许时滞上界值高于文献[26-27]。因此,在典型二阶系统中,本文方法可显著降低稳定判据保守性。
配电网拓扑结构如图3所示,分布式电源(Distributed Generation, DG)的接入位置参考文献[28],风电机组参数参考文献[29]。其中,配电网基准功率为10MW,基准电压为12.66kV,1号节点接变电站低压侧母线。通过仿真风电机组出力波动导致配电网部分节点电压越限的过程,观察时滞影响下节点电压的变化,证明本文方法的正确性和研究的必要性。
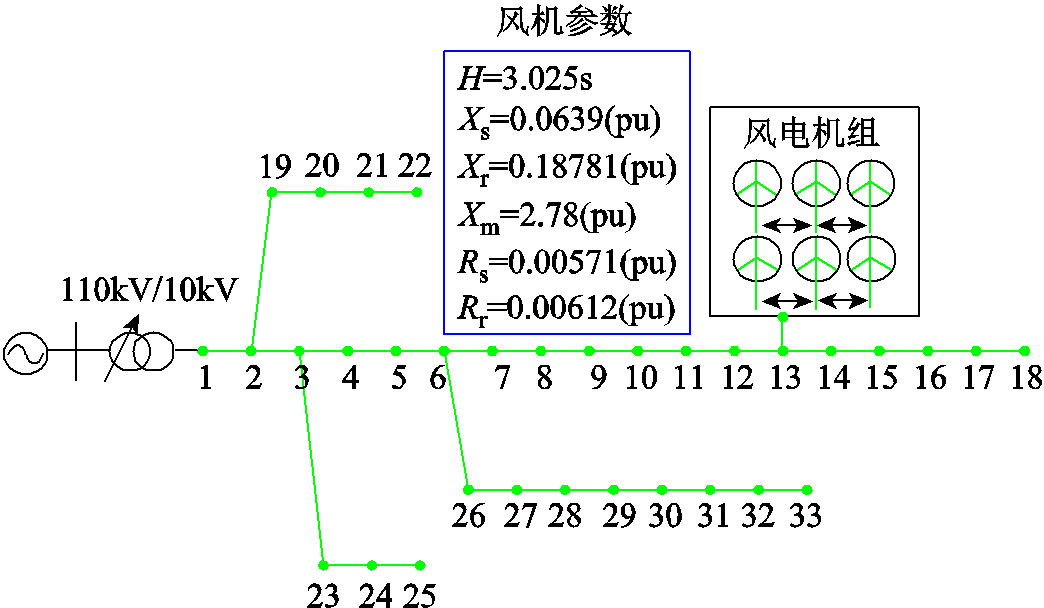
图3 含单台风电机组的IEEE 33节点配电网
Fig.3 A single wind turbine connected to IEEE 33-bus distribution network
3.2.1 基础数据
根据IEEE 33数据和风电机组参数[29],可得到状态矩阵A和At为
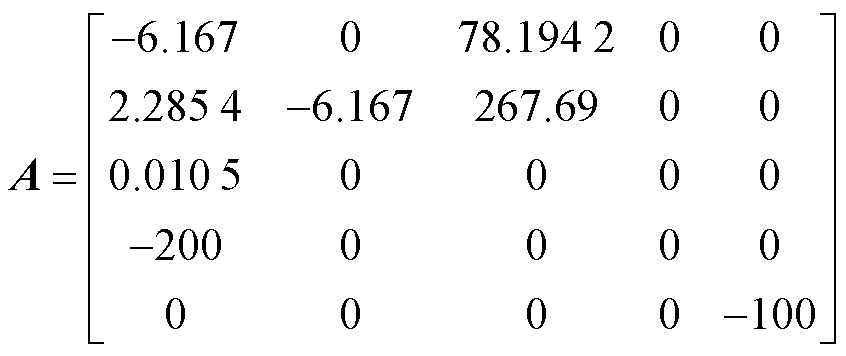
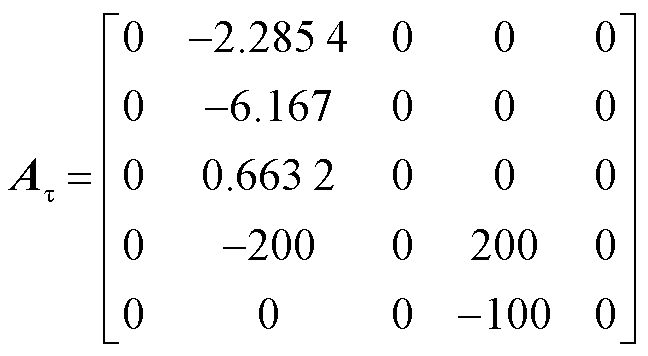
数值代入过程见附录。求解得到最大时滞上界值为5.1s。
3.2.2 仿真验证
风电机组接入后,配电网33节点电压变化如图4所示。其中,12、13、14、15、16节点电压越限。
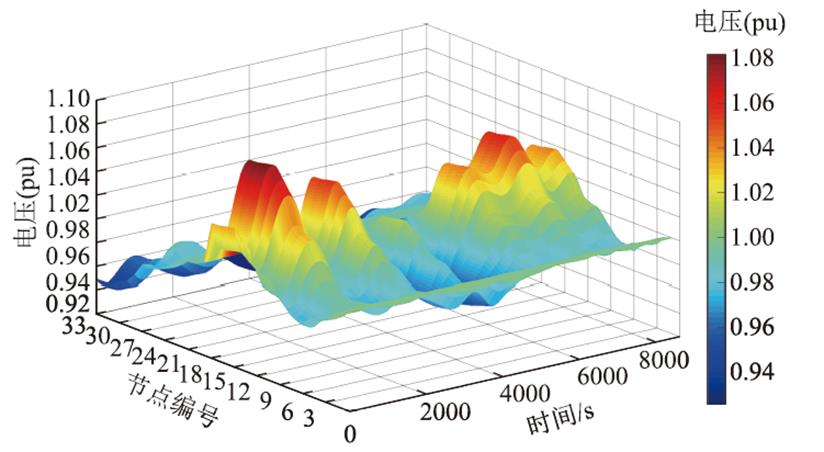
图4 调压前,含单台风电机组配电网节点电压变化
Fig.4 Voltage changes of the distribution network with a single wind turbine before voltage regulation
本文采用以电压质量为目标的无功电压优化策略[30]:利用风电无功余量进行无功优化,将节点电压和额定电压偏差的方差作为目标,达到提升系统电压水平的目的。保证系统电压偏差最小的目标函数如式(19)所示。约束条件包括功率平衡约束、节点电压约束、平衡节点约束、风机出力约束、无功补偿约束等,此处不再赘述,可参考文献[30]。
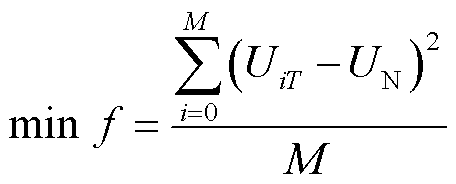 (19)
(19)
式中,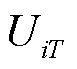 为节点
为节点 在T时刻的电压值;
在T时刻的电压值;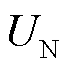 为系统的额定电压;M为系统的节点数量。
为系统的额定电压;M为系统的节点数量。
在不考虑配电网时滞情况下,调压后各节点电压变化如图5所示,未出现电压越限问题。
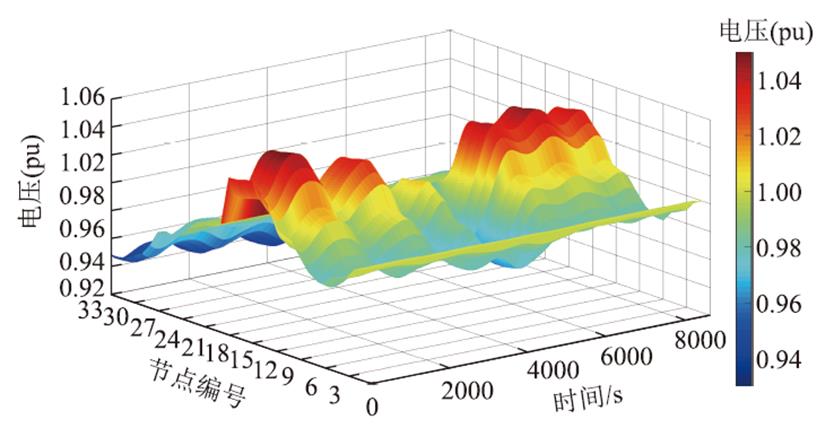
图5 调压后,含单台风电机组配电网节点电压变化
Fig.5 Voltage changes of the distribution network with a single wind turbine after voltage regulation
然而,实际情况中调控信号的时滞影响不可忽略,导致节点电压不会因调控指令而立刻变化。根据本文方法求得的最大时滞上界值为5.1s,设置调控时滞分别为0s、5.1s、5.2s,观察15节点电压的变化,仿真对比如图6所示。
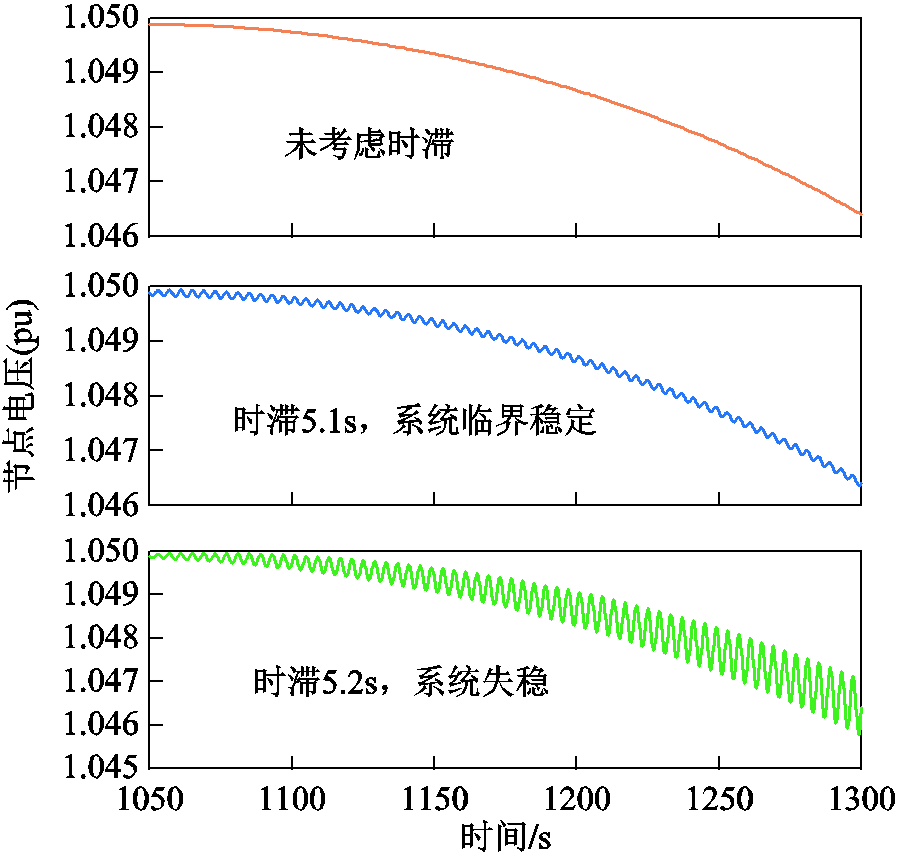
图6 含单台风电机组配电网仿真对比
Fig.6 Simulation comparison of the distribution network with a single wind turbine
通过对比仿真结果,得到以下结论:
(1)如图6所示,未考虑时滞影响调控后的系统不能适应波动性电源的运行,且无法准确地反映与风电机组之间的动态响应;未按照时滞稳定裕度调节,配电网节点电压处于失稳状态;按照时滞稳定裕度调节,配电网节点电压在安全运行范围内变化,风电机组能更好地跟踪调度运行指令,使电压可控性满足配电网的需求。
(2)时滞上界值为5.1s时,系统电压临界稳定;大于5.1s时,即超过稳定上界,配电系统逐渐振荡失去稳定,仿真结果验证了对于接入单台风电机组的配电系统,本文时滞稳定裕度求解的正确性和必要性。
为进一步验证本文方法的有效性,求解接入双台风电机组配电系统的稳定裕度。双台风电机组的接入位置参考文献[28],含双台风电机组的IEEE 33节点配电网如图7所示。

图7 含双台风电机组的IEEE 33节点配电网
Fig.7 Two wind turbines connected to IEEE 33-bus distribution network
通过仿真风电机组出力波动导致配电网部分节点电压越限的过程,观察时滞影响下节点电压的变化,证明本文判据的正确性和保守性。
3.3.1 基础数据
根据IEEE 33节点配电网数据并结合文献[29,31]中风电机组的参数,可得到状态矩阵A和At为


数值代入过程见附录。求解得到最大时滞上界值为5.9s。
3.3.2 仿真验证
风电机组接入后,配电网33节点电压变化如图8所示,13、14、15、16、17、18节点电压发生越限。
为消除电压越限问题,有必要进行配电网的电压运行控制,本文采用文献[30]的调压策略。在不考虑调控信号时滞情况下,调压后各节点电压未出现越限问题,如图9所示。

图8 调压前,含双台风电机组配电网节点电压变化
Fig.8 Voltage changes of the distribution network with two wind turbines before voltage regulation
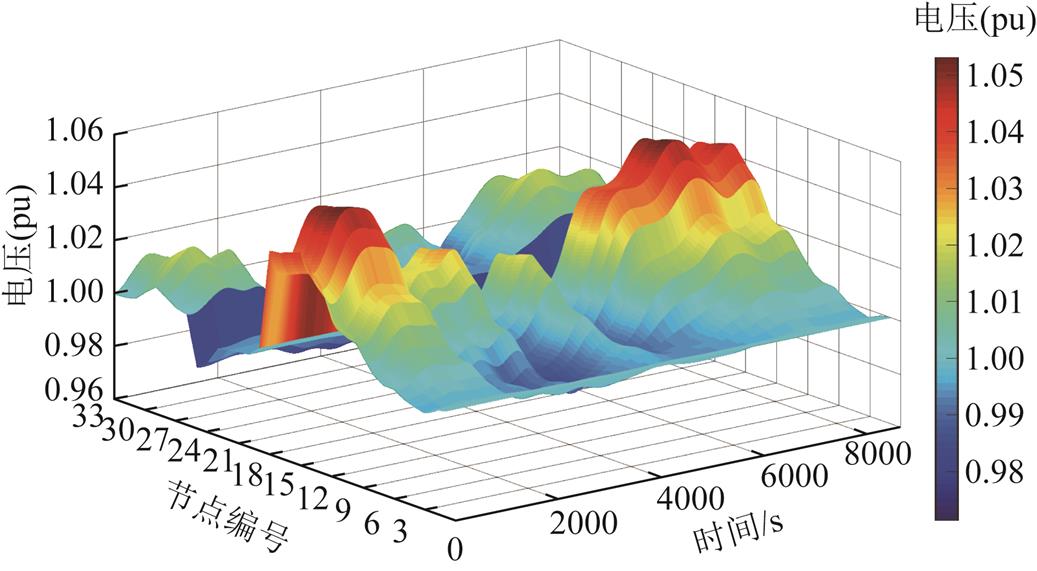
图9 调压后,含双台风电机组配电网节点电压变化
Fig.9 Voltage changes of the distribution network with two wind turbines after voltage regulation
然而,实际情况中调控信号的时滞影响不可忽略,导致节点电压不会立刻变化。根据本文方法求得的最大时滞上界值为5.9s,分别设置时滞为0s、5.9s、6.0s,观察15节点电压变化,仿真对比如图10所示。
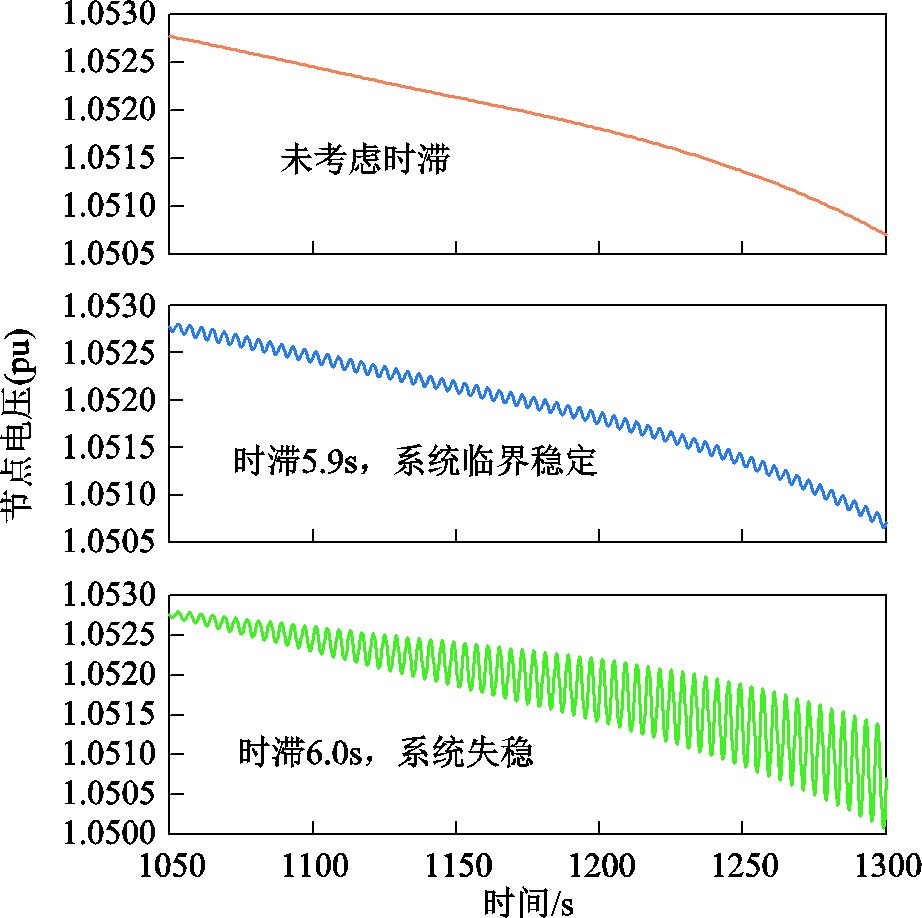
图10 含双台风电机组配电网仿真对比
Fig.10 Simulation comparison of the distribution network with two wind turbines
通过仿真对比结果,得到以下结论:
(1)与单台风电机组的情况一致,按照时滞稳定裕度调节后,配电网节点电压能够适应波动性电源的运行、准确反映与配电网系统间的动态响应,并且在安全运行范围内变化。
(2)在时滞上界值为5.9s时,系统电压临界稳定;大于5.9s时,即超过稳定上界,系统逐渐振荡失去稳定,仿真结果验证了对于接入双台风电机组的配电网系统,本文时滞稳定裕度求解的正确性和必要性。
综上所述,在配电网节点电压安全控制过程中,当调控信号的通信时延超过所得时滞稳定裕度,配电网会出现部分节点电压越限并逐步恶化。基于图6和图10的仿真对比,可以发现:随着高比例风电的接入,系统通信、数据采集、数据处理等过程会更加复杂多样,系统时滞也会逐渐增大。因此,为实现配电网系统安全动态调控并提高运行控制精度,在研究系统安全运行时,必须充分考虑调控通信延时等时滞因素,并利用保守性较小的方法求解时滞稳定裕度,为系统动态调控提供可靠的数值参考。
在相同时滞参数取值下,利用文献[26-27]方法求出单台风电机组、双台风电机组接入IEEE 33配电网时,保证系统安全运行的最大时滞上界值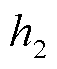 ,结果见表1。
,结果见表1。
表1 不同方法的时滞上界值(单位:s)
Tab.1 Different methods to obtain the upper bound of time delay

方法单台风电机组双台风电机组 文献[26]3.184.202 文献[27]3.424.86 本文5.15.9
由表1结果得到以下结论:
(1)在相同时滞参数取值下,无论是单台风电机组还是双台风电机组接入配电网,本文方法求得的稳定判据保守性更低,时滞稳定裕度更大,系统具有更大的稳定运行区域,证明了本文方法的优越性。
(2)随着波动性电源接入规模增大,发电机组分布松散性更强,时滞影响更加严重,而文献[26-27]在接入更多台风电机组情况下求得的时滞上界值会更保守,因此不能为配电网电压调控和安全运行提供精准的数据参考,将直接影响配电网调控的高效性与准确性。
针对科学计算耗时、通信延时等时滞现象造成含风电配电网电压越限的问题,本文建立了含风电的配电网节点电压运行分析的时滞模型,基于Lyapunov稳定性理论,构建了新的L-K增广型泛函,并在处理泛函导数积分项时引入Wirtinger积分不等式,最终得到了以线性矩阵不等式表示的稳定判据,获知了系统时滞稳定裕度,并通过案例分析得到以下结论:
1)时滞现象对系统动态响应效果具有显著影响,间歇性风电带来的多重时滞环节需要在配电网系统模型中加以考虑。
2)本文方法可用于分析随机时滞影响下系统安全运行的时滞上界值。当调控通信时间小于时滞上界值时,系统能够保持稳定;而当调控通信时间超过时滞上界值时,系统电压会逐渐失去稳定。在相同时滞参数取值下,本文得到的系统稳定裕度更大,说明本文有效降低了判据保守性。
本文所得时滞上界值可解决时滞影响下调度中心无法实现对风电机组等波动性电源精准调控这一难题,能够在既定电源结构下充分挖掘机组的控制灵活性,保证配电系统的安全运行并提高风电机组可控性,实现精细化、精准化调控。为顺应双碳目标下新型电力系统的变革,时滞电力系统与人工智能、云计算以及大数据等新兴技术关系密切,研究时滞电力系统与信息技术多元融合下的稳定裕度将成为未来的热门方向,以期为我国打造具有精准评估、快速应变能力的坚强智能电网提供关键技术并成为能源系统与信息系统交互耦合的桥梁。
与此同时,本研究中仍存在一些问题亟须考虑:
1)在接入高比例可再生能源的电力系统中,需要考虑各发电机组之间、各场群之间的协调,以避免造成发电机组各自调节后电网电压并不理想甚至恶化的结果。
2)需要考虑电力系统过高维度带来的高计算量问题。高维度电力系统的计算复杂度会随着系统维度的增加呈指数倍增长。因此,如何降低高维度时滞电力系统的计算复杂度也已经成为亟须解决的问题。
附 录
1. 式(17)到式(18)的推导
从泛函构建到泛函求导,再根据稳定性定理对泛函导数进行放缩,最终得到稳定判据——定理1的过程。
本文构造的Lyapunov-Krasovskii泛函[16]为
 (A1)
(A1)
其中
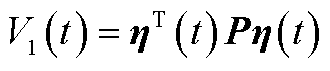

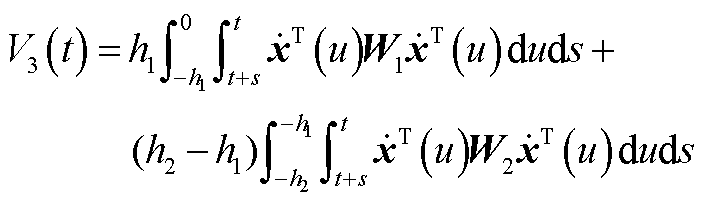

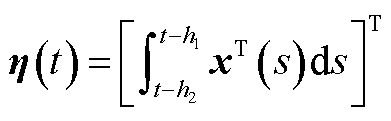
式中,P、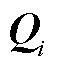
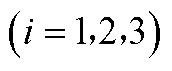 、
、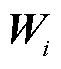
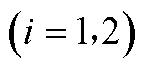 、
、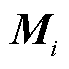
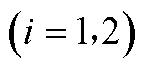 为正定矩阵。
为正定矩阵。
构造适当的L-K泛函后,对泛函进行求导,利用相关引理对泛函导数进行放缩变换。
结合引理3对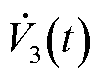 中的
中的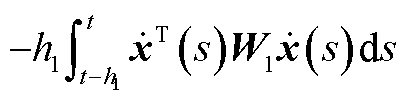 进行估计得
进行估计得

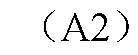
结合引理4对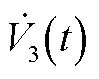 中的
中的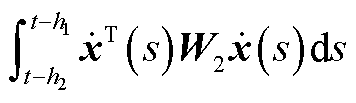 进行估计得
进行估计得
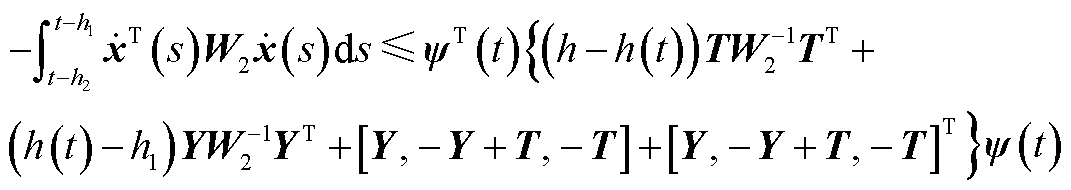 (A3)
(A3)
式中
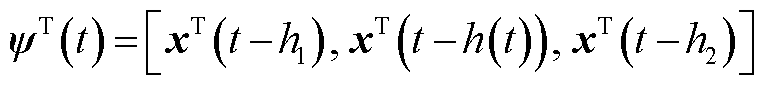
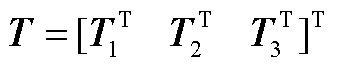
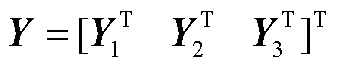
基于Lyapunov稳定性原理,当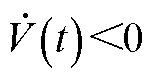 时,系统是渐近稳定的,可得
时,系统是渐近稳定的,可得
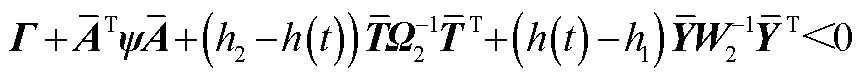 (A4)
(A4)
式中,上标“-”表示共轭。
利用引理2对式(A4)进一步处理,可得
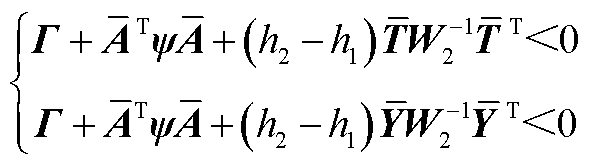 (A5)
(A5)
对式(A5)进一步运用Schur补引理得到保证系统渐近稳定的结论,即定理1。
定理1:对于给定常量 和
和 ,若存在正定矩阵P,
,若存在正定矩阵P,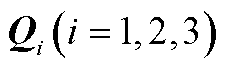 ,
,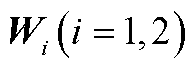 ,
,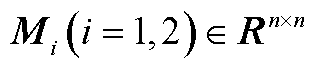 及适当维数的自由矩阵
及适当维数的自由矩阵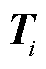 、
、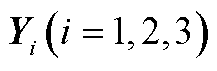 使得式(A6)成立,则系统(13)是渐近稳定的。
使得式(A6)成立,则系统(13)是渐近稳定的。
 (A6)
(A6)
2. 系数矩阵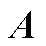 和
和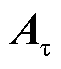 的推导
的推导
经式(1)~式(10)的推导,最终得到如式(12)所示的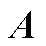 和
和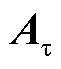 。
。
对于单组风电机组有[29]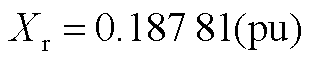 ;
;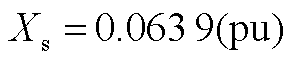 ;
;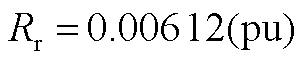 ;
;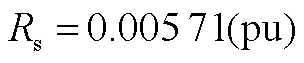 ;
;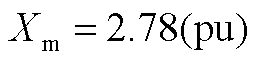 ;
;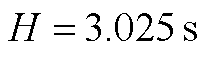 ;
;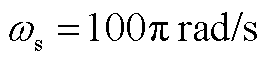 ;
;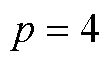 ;
;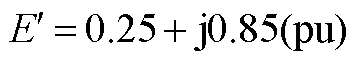 ;
;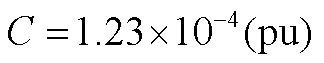 ;
;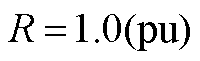 ;
;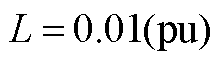 。
。
代入对应数值,得到
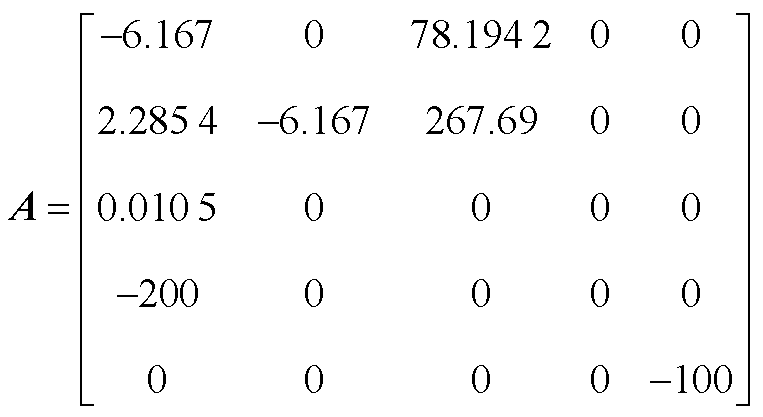 (A7)
(A7)
 (A8)
(A8)
对于双组风电机组有[29,31]: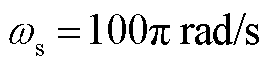 ;
;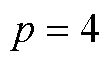 ;
;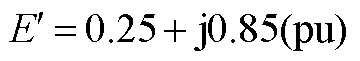 ;
;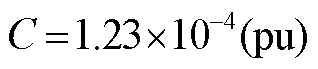 ;
;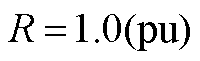 ;
;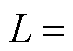
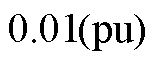 ;
;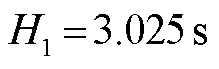 ;
;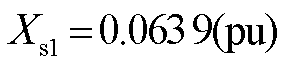 ;
;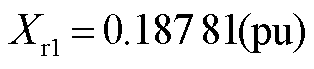 ;
;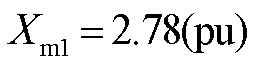 ;
;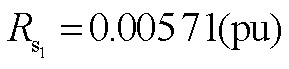 ;
;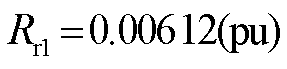 ;
;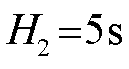 ;
;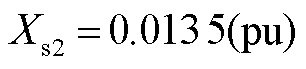 ;
;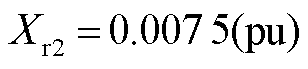 ;
;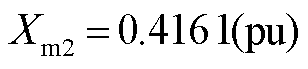 ;
;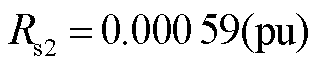 ;
;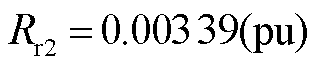
代入对应数值,得到
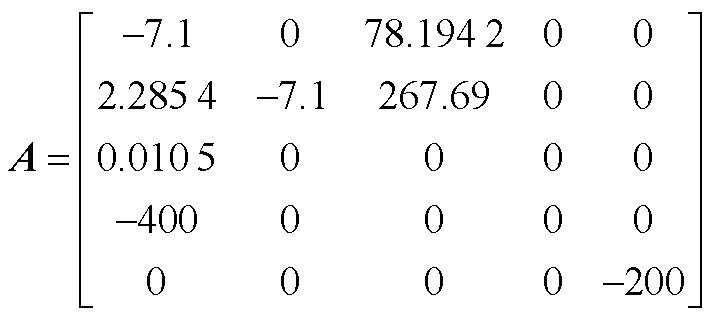 (A9)
(A9)
 (A10)
(A10)
参考文献
[1] 曾博, 徐富强, 刘一贤, 等. 综合考虑经济-环境-社会因素的多能耦合系统高维多目标规划[J]. 电工技术学报, 2021, 36(7): 1434-1445. Zeng Bo, Xu Fuqiang, Liu Yixian, et al. High-dimensional multiobjective optimization for multi-energy coupled system planning with consideration of economic, environmental and social factors[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1434-1445.
[2] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467. Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[3] 朱泽安, 周修宁, 王旭, 等. 基于稳暂态联合仿真模拟的区域多可再生能源系统评估决策[J]. 电工技术学报, 2020, 35(13): 2780-2791. Zhu Zean, Zhou Xiuning, Wang Xu, et al. Evaluation and decision-making of regional multi-renewable energy system based on steady-transient integrated simulation[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2780-2791.
[4] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[5] 李保杰, 李进波, 李洪杰, 等. 土耳其“3.31”大停电事故的分析及对我国电网安全运行的启示[J]. 中国电机工程学报, 2016, 36(21): 5788-5795, 6021. Li Baojie, Li Jinbo, Li Hongjie, et al. Analysis of Turkish blackout on March 31, 2015 and lessons on China power grid[J]. Proceedings of the CSEE, 2016, 36(21): 5788-5795, 6021.
[6] 张沛, 田佳鑫, 谢桦. 计及多个风场预测误差的电力系统风险快速计算方法[J]. 电工技术学报, 2021, 36(9): 1876-1887. Zhang Pei, Tian Jiaxin, Xie Hua. A fast risk assessment method with consideration of forecasting errors of multiple wind farms[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1876-1887.
[7] Dong Chaoyu, Jia Hongjie, Xu Qianwen, et al. Time-delay stability analysis for hybrid energy storage system with hierarchical control in DC microgrids[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 6633-6645.
[8] 乐健, 赵联港, 廖小兵, 等. 考虑控制时滞和参数不确定的虚拟同步电机并网系统稳定性分析[J]. 中国电机工程学报, 2021, 41(12): 4275-4286. Le Jian, Zhao Liangang, Liao Xiaobing, et al. Stability analysis of grid-connected inverter system containing virtual synchronous generator under time delay and parameter uncertainty[J]. Proceedings of the CSEE, 2021, 41(12): 4275-4286.
[9] Cao Yulei, Li Chongtao, He Tingyi, et al. A novel rekasius substitution based exact method for delay margin analysis of multi-area load frequency control systems[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5222-5234.
[10] 郭春义, 彭意, 徐李清, 等. 考虑延时影响的MMC-HVDC系统高频振荡机理分析[J]. 电力系统自动化, 2020, 44(22): 119-126. Guo Chunyi, Peng Yi, Xu Liqing, et al. Analysis on high-frequency oscillation mechanism for MMC-HVDC system considering influence of time delay[J]. Automation of Electric Power Systems, 2020, 44(22): 119-126.
[11] 马燕峰, 霍亚欣, 李鑫, 等. 考虑时滞影响的双馈风电场广域附加阻尼控制器设计[J]. 电工技术学报, 2020, 35(1): 158-166. Ma Yanfeng, Huo Yaxin, Li Xin, et al. Design of wide area additional damping controller for doubly fed wind farms considering time delays[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 158-166.
[12] 古丽扎提·海拉提, 王杰. 多时滞广域测量电力系统稳定分析与协调控制器设计[J]. 电工技术学报, 2014, 29(2): 279-289. Gulizhati Hailati, Wang Jie. Multiple time delays analysis and coordinated stability control for power system wide area measurement[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 279-289.
[13] Zhang Chuanke, He Yong, Jiang Lin, et al. Notes on stability of time-delay systems: bounding inequalities and augmented Lyapunov-Krasovskii functionals[J]. IEEE Transactions on Automatic Control, 2017, 62(10): 5331-5336.
[14] 肖伸平, 张天, 唐军, 等. 基于PI控制的时滞电力系统稳定性分析[J]. 电网技术, 2020, 44(10): 3949-3954. Xiao Shenping, Zhang Tian, Tang Jun, et al. Stability analysis for power systems with time-delay based on PI control[J]. Power System Technology, 2020, 44(10): 3949-3954.
[15] Zhang Chuanke, He Yong, Jiang L, et al. Delay-variation-dependent stability of delayed discrete-time systems[J]. IEEE Transactions on Automatic Control, 2016, 61(9): 2663-2669.
[16] 钱伟, 王晨晨, 费树岷. 区间变时滞广域电力系统稳定性分析与控制器设计[J]. 电工技术学报, 2019, 34(17): 3640-3650. Qian Wei, Wang Chenchen, Fei Shumin. Stability analysis and controller design of wide-area power system with interval time-varying delay[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3640-3650.
[17] Seuret A, Gouaisbaut F. Wirtinger-based integral inequality: application to time-delay systems[J]. Automatica, 2013, 49(9): 2860-2866.
[18] Zhang Xianming, Han Qinglong, Seuret A, et al. An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay[J]. Automatica, 2017, 84: 221-226.
[19] 窦晓波, 葛浦东, 全相军, 等. 计及不确定时滞的有源配电网无功电压鲁棒控制[J]. 中国电机工程学报, 2019, 39(5): 1290-1301. Dou Xiaobo, Ge Pudong, Quan Xiangjun, et al. Reactive power and voltage robust control for active distribution network considering uncertain delay[J]. Proceedings of the CSEE, 2019, 39(5): 1290-1301.
[20] 周明, 元博, 张小平, 等. 基于SDE的含风电电力系统随机小干扰稳定分析[J]. 中国电机工程学报, 2014, 34(10): 1575-1582. Zhou Ming, Yuan Bo, Zhang Xiaoping, et al. Stochastic small signal stability analysis of wind power integrated power systems based on stochastic differential equations[J]. Proceedings of the CSEE, 2014, 34(10): 1575-1582.
[21] Lee T H, Park J H. Improved stability conditions of time-varying delay systems based on new Lyapunov functionals[J]. Journal of the Franklin Institute, 2018, 355(3): 1176-1191.
[22] 钱伟, 蒋鹏冲. 时滞电力系统带记忆反馈控制方法[J]. 电网技术, 2017, 41(11): 3605-3611. Qian Wei, Jiang Pengchong. A method of memory feedback control for power system with time-delay[J]. Power System Technology, 2017, 41(11): 3605-3611.
[23] Sun Jian, Liu G P, Chen Jie, et al. Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J]. Automatica, 2010, 46(2): 466-470.
[24] Wu Min, Peng Chen, Zhang Jin, et al. Further results on delay-dependent stability criteria of discrete systems with an interval time-varying delay[J]. Journal of the Franklin Institute, 2017, 354(12): 4955-4965.
[25] Zhang Xianming, Han Qinglong. New Lyapunov-Krasovskii functionals for global asymptotic stability of delayed neural networks[J]. IEEE Transactions on Neural Networks, 2009, 20(3): 533-539.
[26] 李宁, 孙永辉, 卫志农, 等. 基于Wirtinger不等式的电力系统延时依赖稳定判据[J]. 电力系统自动化, 2017, 41(2): 108-113. Li Ning, Sun Yonghui, Wei Zhinong, et al. Delay-dependent stability criteria for power system based on Wirtinger integral inequality[J]. Automation of Electric Power Systems, 2017, 41(2): 108-113.
[27] 汪豪, 钱伟, 郭建峰, 等. 变时滞影响下广域电力系统的H∞控制[J]. 电力系统保护与控制, 2021, 49(18): 70-80. Wang Hao, Qian Wei, Guo Jianfeng, et al. H∞ control for a wide-area power system with time-varying delay[J]. Power System Protection and Control, 2021, 49(18): 70-80.
[28] 孟庭如, 邹贵彬, 许春华, 等. 一种分区协调控制的有源配电网调压方法[J]. 中国电机工程学报, 2017, 37(10): 2852-2860. Meng Tingru, Zou Guibin, Xu Chunhua, et al. A voltage regulation method based on district-dividing coordinated control for active distribution network[J]. Proceedings of the CSEE, 2017, 37(10): 2852-2860.
[29] Pidre J C, Carrillo C J, Lorenzo A E F. Probabilistic model for mechanical power fluctuations in asynchronous wind parks[J]. IEEE Transactions on Power Systems, 2003, 18(2): 761-768.
[30] 刘华志, 李永刚, 王优胤, 等. 无功电压优化对新能源消纳的影响[J]. 电工技术学报, 2019, 34(增刊2): 646-653. Liu Huazhi, Li Yonggang, Wang Youyin, et al. Influence about reactive power voltage optimization on the dissipation of new energy[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 646-653.
[31] 张子泳, 胡志坚, 刘宇凯. 计及广域信号时变时滞影响的大型双馈风力发电系统附加鲁棒阻尼控制[J]. 电工技术学报, 2014, 29(4): 246-255. Zhang Ziyong, Hu Zhijian, Liu Yukai. Additional robust damping control of large scale DFIG-based wind power generation system with wide-area signals' time-varying delay influence[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 246-255.
Abstract The superposition effect of time-delay phenomenon leads to the failure of preset parameters for the safe operation control of distribution network voltage, and the system operation condition is further deteriorated. However, the previous analysis models of distribution network security operation control seldom consider the time-delay or execute according to the time-delay of a fixed constant, which is difficult to meet the actual demand. At the same time, there is still a lack of relevant literature that considers the time-delay factor in the node voltage security analysis of distribution network. In order to address these issues, this paper has carried out in-depth research on node voltage security analysis of wind power distribution network with time-delay. By solving the time-delay stability margin, a numerical reference is provided for the accurate regulation of the safe operation of the node voltage of the distribution network with wind power.
Firstly, construct a mathematical model of partial derivative differential transcendental equation for node voltage safety analysis of time-delay distribution networks with wind power. Then, propose a Lyapunov-Krasovskii generalized function construction method, and apply Wirtinger's inequality technique to deal with the integral term in the generalized derivative to solve the constructed partial derivative differential transcendental equation and obtain the stability criterion to know its time-delay stability margin. Finally, the simulation is verified with the help of the typical case and IEEE 33 examples.
Simulation results of typical second-order systems show that the proposed method can significantly reduce the conservatism of stability criteria. Simulation results of distribution network with a single wind turbine generator unit show that when the upper limit of time-delay is 5.1 s, the system voltage is critical stable; when it is greater than 5.1 s, that is, it exceeds the upper limit of stability, and the distribution system gradually loses stability. Simulation results of distribution network with two wind turbine generators show that the system voltage is critical stable when the upper limit of time-delay is 5.9s; when it is greater than 5.9s, that is, it exceeds the upper limit of stability, and the system gradually loses stability. The regulated system without considering the effect of time-delay can not adapt to the operation of fluctuating power supply, and can not accurately reflect the dynamic response with wind turbines. After adjusting according to the time-delay stability margin, the node voltage of the distribution network can adapt to the operation of fluctuating power sources, accurately reflect the dynamic response with the distribution network system, and change within the safe operation range.
The following conclusions can be drawn from the simulation analysis: (1) Time-delay has a significant impact on the dynamic response of the system, and multiple time-delay links caused by intermittent wind power need to be considered in the distribution network system model. (2) The method presented in this paper can be used to analyze the upper bound of time-delay for safe operation of systems under the influence of random time delays. When the control communication time is less than the upper bound of the delay, the system can maintain stability. When the control communication time exceeds the upper limit of time-delay, the system voltage will gradually lose stability. Under the same delay parameter value, the system stability margin obtained in this paper is larger, which shows that this paper effectively reduces the conservatism of the criterion.
keywords:Distribution network, time-delay, voltage safety, Lyapunov-Krasovskii function, Wirtinger inequality
国家电网有限公司总部科技项目(5100-202155018A-0-0-00)、国家自然科学基金项目(51807134)和电力系统大型发电设备安全控制与仿真国家重点实验室开放基金课题(N0.SKLD21KM10)资助。
收稿日期 2021-12-24
改稿日期 2022-03-23
DOI:10.19595/j.cnki.1000-6753.tces.212097
中图分类号:TM712
崔庆雪 女,1999年生,硕士研究生,研究方向为配电网时滞不确定性分析。E-mail:a1023480040@163.com
葛磊蛟 男,1984年生,副教授,硕士生导师,研究方向为智能配电网态势感知、新能源并网优化控制和智能配用电大数据云计算技术等。E-mail:legendglj99@tju.edu.cn(通信作者)
(编辑 赫蕾)